MP034
Para começar
Avaliação diagnóstica
Olá! Vamos fazer estas atividades e descobrir o que você já sabe?
- Vanessa, Marcos, Roberto e Beatriz fizeram uma pesquisa entre seus amigos para saber qual é o esporte favorito deles. Cada amigo só poderia votar em um esporte. Eles juntaram todos os dados e produziram um gráfico.

Fonte: Pesquisa feita por Vanessa, Roberto, Marcos e Beatriz (mar. 2023).
- Quem entrevistou mais amigos? Quantos foram entrevistados no total?
_____
PROFESSOR
Resposta: Cada um entrevistou 10 amigos, isto é, a mesma quantidade. No total, 40 entrevistados (4 × 10 = 10 + 10 + 10 + 10).
- Qual foi o esporte menos votado no total? Quantos votos obteve?
_____
PROFESSOR
Resposta: Vôlei, com 8 votos.
- Para Vanessa, o esporte mais votado no total foi o futebol, e para Marcos foi o basquete. Quem está correto? Explique.
_____
PROFESSOR
Resposta: Ambos. Futebol (6 + 4 + 1 + 5 = 16) e basquete (2 + 4 + 8 + 2 = 16).
- Marcos fez uma pesquisa sobre basquete. Leia e responda às questões.
Oscar Schmidt é o maior pontuador brasileiro de basquete, em sua carreira fez 49.737 pontos, sendo 7.693 nas 326 partidas vestindo a camisa da Seleção Brasileira de Basquete.
Fonte: http://fdnc.io/eUj. Acesso em: 21 jun. 2021.
Jogadores mais famosos do basquete
Tabela: equivalente textual a seguir.
|
Jogador |
Kobe Bryant |
Michael Jordan |
Magic Johnson |
Oscar Schmidt |
Kevin Durant |
LeBron James |
Yao Ming |
Shaquille O’Neal |
|---|---|---|---|---|---|---|---|---|
|
Altura (em metro) |
1,98 |
1,98 |
2,06 |
2,05 |
2,08 |
2,06 |
2,29 |
2,16 |
Fonte: Pesquisa de Marcos (mar. 2023).
MANUAL DO PROFESSOR
As atividades propõem uma avaliação diagnóstica, sob a perspectiva da avaliação formativa. Faça a leitura com os estudantes, orientando-os a mobilizarem os conhecimentos que dominam.
São contempladas as Unidades Temáticas Números, Geometria, Álgebra, Grandezas e medidas e Probabilidade e estatística. Pretende-se verificar se os estudantes: reconhecem números com 5 ordens, sua composição e decomposição, comparação entre o maior e o menor, ordenação e arredondamento até uma centena de milhar completa, além de procedimentos de cálculo mental, uso e aplicação das propriedades das operações e resolução de problemas do campo aditivo e multiplicativo; identificam sequência recursiva; reconhecem ângulos retos, paralelismo e simetria de reflexão em figuras poligonais; medem intervalos de tempo; medem perímetros; identificam eventos com maior ou menor chance de acontecer; fazem análise de dados em tabela de dupla entrada; entre outros conhecimentos.
Comente que o objetivo é auxiliá-los a expressarem o que já sabem e destacar os conhecimentos que terão a oportunidade de aprender e de ampliar. As atividades podem ser lidas em grupo, porém cada estudante deve registrar sua resposta individualmente, da melhor maneira possível, auxiliando o professor a planejar e a rever seu trabalho para o ano letivo. Caso eles respondam oralmente, convém tomar nota das respostas.
Atividade 1
Inicialmente, os estudantes devem fazer a leitura e compreender os dados do gráfico, incluindo as legendas. Os dados podem ser lidos separadamente, com base na pesquisa de cada estudante, ou na totalidade, considerando os votos recebidos em cada esporte.
Logo, os estudantes mobilizarão o pensamento algébrico sobre o significado de equivalente do sinal de igualdade, ao resolver propostas que evidenciam as propriedades da igualdade.
No item a, eles devem fazer a leitura individual do número de participantes da pesquisa de cada jovem. A percepção da equivalência na quantidade pode facilitar a resposta da segunda parte da questão, pois poderão multiplicar 4 × 10, sem necessariamente fazer nova contagem.
No item b, os estudantes precisam fazer uso da legenda. É esperado que percebam que o azul, correspondente ao vôlei, teve a menor quantidade de votos (2 + 2 + 1 + 3).
BNCC em foco na dupla de páginas:
EF05MA01, EF05MA02, EF05MA05, EF05MA07, EF05MA08, EF05MA10, EF05MA11, EF05MA12, EF05MA17, EF05MA19, EF05MA24
MP035
- Qual figura geométrica plana a quadra de basquete lembra? Quantos ângulos ela tem e de que tipo são? Ela tem lados paralelos?
_____

PROFESSOR
Resposta: A quadra lembra um retângulo; ela tem 4 ângulos retos; tem lados paralelos dois a dois.- Qual é a medida do perímetro da quadra de basquete? Registre como pensou.
_____
PROFESSOR
Resposta: A medida do perímetro é 86 m.PROFESSOR
Exemplos de respostas: 28 + 28 + 15 + 15 = 2 × 28 + 2 × 15 = 56 + 30 = 86
- Qual é a medida da área dessa quadra? Registre como pensou.
_____
PROFESSOR
Resposta: A medida da área é 420 m².PROFESSOR
Exemplos de respostas: 28 × 15 = 20 × 15 + 8 × 15 = 300 + 120 = 420
- Uma miniquadra retangular de basquete, cujas medidas sejam a metade das medidas dessa quadra, tem o perímetro igual à metade do perímetro dela? Tem a área igual à metade da área dela?
_____
PROFESSOR
Resposta: Sim, 2 × 14 + 2 × 7,5 = 43 = 86 ÷ 2. Não, a área da miniquadra é um quarto da área da quadra, 14 × 7,5 = 105 = 420 ÷ 4.
- Quantos pontos
Oscar
Schmidt fez fora da Seleção Brasileira de Basquete? Indique o antecessor e o sucessor desse número.
_____
PROFESSOR
Resposta: 42.044 pontos (49.737 − 7.693 = 42.044). Antecessor: 42.043; sucessor: 42.045.
- Indique na reta numérica a localização da medida da altura de cada um dos jogadores da lista de Marcos.
PROFESSOR
Sugestão de resposta: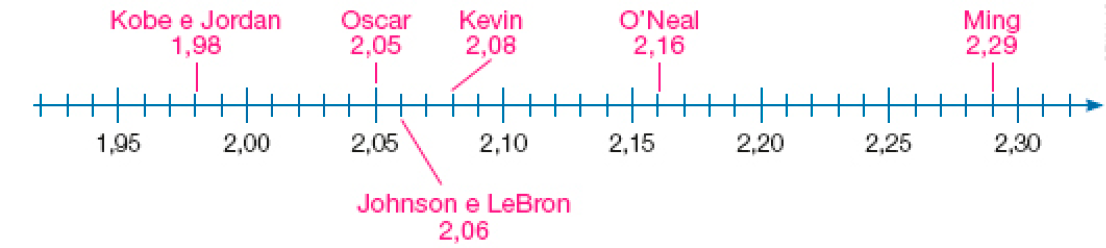
MANUAL DO PROFESSOR
No item c, devem escolher e justificar quem está correto. Para isso, terão de fazer a contagem de votos da cor verde e da vermelha, de acordo com a legenda. As parcelas são diferentes, mas as somas resultam em equivalência de votos. É importante observar a justificativa, pois ela dará indícios do quanto os estudantes estão mobilizando o pensamento algébrico e a argumentação matemática.
Atividade 2
Os estudantes devem observar a representação da quadra e dos elementos que a compõem. Terão de ler e compreender a tabela, além de ler as informações que envolvem números naturais com até 5 ordens.
No item a, os estudantes devem associar a imagem da quadra ao retângulo, que tem entre suas propriedades o fato de possuir lados dois a dois paralelos e 4 ângulos retos.
No item b, eles devem calcular a medida do perímetro da quadra obtido pela adição 28 + 28 + 15 + 15 ou pela adição e multiplicação associadas 2 × 28 + 2 × 15. Verifique se não foram desconsiderados os dois lados paralelos aos indicados pelas medidas 28 m e 15 m.
No item c, ao calcularem a medida da área da quadra, o registro pode ser feito de algumas maneiras, resultando no mesmo valor.
No item d, devem calcular o perímetro da miniquadra e comparar com o resultado do item b. Espera-se que observem que a medida do perímetro de um retângulo é proporcional às medidas de seus lados. Também devem calcular a medida da área da miniquadra, comparar com a resposta do item c e concluir que ela é um quarto da medida da área da quadra. Espera-se que observem que a medida da área de um retângulo não é proporcional às medidas de seus lados.
No item e, os estudantes devem encontrar o termo que torna a igualdade verdadeira (49.737 = 7.693 + ?), chegando ao resultado 42.044.
No item f, serão mobilizados conhecimentos sobre os números racionais, a comparação de quantidades e sua localização na reta numérica. Os estudantes devem evidenciar o quanto compreendem as regras do sistema de numeração decimal que envolvem os números racionais.