MP036

Comentários para o professor:

Introdução da Unidade 1

A grandeza e a natureza do rio Amazonas, no seu encontro com o rio Negro, são apresentadas na abertura da Unidade em exemplos diversificados de números naturais que podem ser explorados: na ordem de unidade de milhar (6.962 km de extensão), na ordem de centena de milhar (216.342 m³, a vazão a cada segundo), unidade de milhão (5.846.100 km², a bacia Amazônica).

Conforme a BNCC, o 5º ano representa a última etapa dos Anos Iniciais do Ensino Fundamental, prevista para a formação dos estudantes. Em relação à Unidade Temática Números, o documento aponta para a necessidade de que, ao final dessa fase, os estudantes tenham se apropriado de conhecimentos acerca das características do sistema de numeração decimal, na perspectiva do desenvolvimento de habilidades relativas a leitura, escrita e ordenação de números naturais e racionais. Por isso, as atividades propostas nesta Unidade buscam a retomada, a ampliação e o aprofundamento de conhecimentos já construídos em anos anteriores, sobretudo no 4º ano.

Assim, a leitura, a escrita e a ordenação de números naturais até a ordem de dezenas de milhar passam, neste ano, para as centenas de milhar, de forma a acentuar a compreensão das principais características do sistema de numeração decimal. Esses conhecimentos são necessários para que, no 6º ano, os estudantes comparem, ordenem, leiam e escrevam tanto os números naturais quanto os racionais em sua representação decimal, fazendo uso da reta numérica. A respeito disso, vale destacar as diferentes atividades propostas, cujo objetivo é a ordenação de números naturais na reta numérica.

Além disso, mantém-se a característica desta coleção em relação às conexões entre as diferentes Unidades Temáticas. São propostas atividades relativas à Probabilidade e estatística com o intuito de favorecer a construção de conhecimentos abordados nesta Unidade, bem como de outros, particularmente a interpretação de dados estatísticos apresentados em textos, tabelas e gráficos. Os conhecimentos sobre esse tema desenvolvidos até o 4º ano tratavam da análise de dados apresentados em tabelas e gráficos. No 6º ano, além da interpretação, tratarão da resolução de situações envolvendo dados de pesquisas trabalhados em tabelas e em diferentes tipos de gráficos, por meio da redação de textos, com o objetivo de sintetizar conclusões.

Ainda em relação à Probabilidade e estatística, há atividades que envolvem resultados possíveis de experimentos aleatórios, com estimativa de serem igualmente prováveis ou não. Envolvem, também, a probabilidade de ocorrência de um resultado nesses eventos, particularmente quando todos os resultados possíveis têm a mesma chance de ocorrer.

Esses conhecimentos e outros a serem abordados nas próximas Unidades, como os números racionais, devem possibilitar aos estudantes, ainda neste volume e no 6º ano, calcularem a probabilidade de um evento aleatório, expressando-a por meio de uma fração, de um número na forma decimal ou de percentual, comparando esse número com a probabilidade obtida por meio de sucessivos experimentos.

Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletiva. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.

Competências gerais favorecidas

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Competências específicas favorecidas

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

MP037

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

Sugestão de roteiro de aula

Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.

Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item Números com até 9 algarismos desta Unidade.

Roteiro de aula – Números com até 9 algarismos

1 ª parte – Preparação – Tempo sugerido: 10 minutos

Recorde rapidamente a trajetória do aprendizado sobre os números naturais vivenciada, perguntando aos estudantes se lembram de quando conheceram os dez algarismos ou dígitos, a ideia de número posicional, o significado do zero, as primeiras ordens.

Pergunte a eles se lembram qual é o significado de dígito. Caso não lembrem, recorde que dígito é sinônimo de dedo, e que, em nossa anatomia, temos dez dedos, daí a possível ideia de agrupamentos de 10 em 10: 10 unidades = 1 centena; 10 centenas = 1 unidade de milhar etc.

Pergunte que outras ordens eles conhecem. Estimule-os a lembrarem da dezena de milhar, da centena de milhar e da recente unidade de milhão.

Agora, é um bom momento para retomar a abertura da Unidade com os dados sobre o rio Amazonas. Extensão do rio: 6.982 km, vazão da água: 216.342 m³ a cada segundo, bacia Amazônica: 5.846 100 km². Faça-os perceber o quanto ampliamos a ordem de grandeza da numeração para chegar ao que conhecemos e o quanto ainda podemos ampliar. Essa ampliação trouxe alguma dificuldade para leitura, comparação e registro. Por isso, surgiu a necessidade de juntar os agrupamentos, ou seja, de agrupar as ordens, originando então a ideia de classe, de 3 em 3 ordens.

2 ª parte – Leitura e atividades – Tempo sugerido: 50 minutos

Solicite aos estudantes que leiam a atividade 1 e que respondam às questões propostas. Verifique se há dificuldade de transferir o aprendizado sobre composição/decomposição, leitura e registro para as novas e ampliadas ordens de grandeza. Valide coletivamente a resolução dessa atividade.

A seguir, peça que leiam com atenção e que resolvam as atividades 2, 3 e 4. Após o tempo que julgar suficiente, valide as respostas dadas.

Para finalizar, solicite que, em duplas, leiam e resolvam o Desafio, que pode ser feito com o auxílio de uma calculadora. Em uma roda de conversa, promova e encaminhe uma discussão sobre o desperdício de água potável. Alerte-os que, embora os dados da abertura sobre o volume/vazão do rio Amazonas deem a impressão de que esse recurso natural seja infinito, na verdade, a porcentagem de água potável na natureza é ínfima. De cada 100 litros de água existentes na Terra, cerca de 97 litros estão no mar (água salgada) e cerca de 3 litros apenas são de água doce. Desses 3 litros, somente 1 litro é acessível. No item b, é necessário fazer arredondamento.

MP038

UNIDADE 1. Números naturais

Imagem: Ilustração. Vanessa, Marcos, Roberto e Beatriz estão com colete salva-vidas e dentro de um barco. Ao lado deles, um homem com colete os observa e outro homem com colete está segurando e observando um bloco de notas. Ao lado, destaque para as anotações: Rio Amazonas; Extensão do rio: 6.982 km. Vazão da água: 216.342 metros cúbicos a cada segundo. Bacia amazônica: 5.846.100 kilometros quadrados. O barco está sobre um rio com água escura e abaixo do barco há uma mancha marrom. Ao fundo, vegetação. Fim da imagem.

LEGENDA: Encontro das águas entre o rio Negro e o rio Amazonas, próximo a Manaus, Amazonas, em 2019. FIM DA LEGENDA.

MANUAL DO PROFESSOR

Objetivos da Unidade

Ler, escrever, comparar e ordenar números naturais até a classe dos milhões com compreensão das principais características do sistema de numeração decimal.
Compor e decompor números naturais por meio de adições e multiplicações.
Decompor números que indicam medidas de tempo, em anos, recorrendo a outras unidades de medida de tempo: anos, décadas, séculos e milênios.
Localizar e representar números naturais na reta numérica.
Realizar arredondamentos de números naturais.
Explorar e completar sequências numéricas.
Ler e interpretar textos com dados numéricos.
Interpretar dados estatísticos apresentados em textos, tabelas e gráficos.
Determinar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não.
Identificar eventos em um experimento aleatório e determinar a probabilidade de ocorrência desses eventos.
Esta Unidade aborda o sistema de numeração decimal, abrangendo: o reconhecimento do valor posicional dos algarismos nos números, a leitura e a exploração de números das classes dos milhões, comparações entre números dessas grandezas, arredondamentos que facilitam a realização de estimativas e de cálculo mental e a análise dos resultados que se obtêm por algoritmos e com a calculadora.

BNCC em foco:

EF05MA01, EF05MA19, EF05MA22, EF05MA24, EF05MA25

MP039

Boxe complementar

Para refletir...

Os quatro amigos estão passeando no encontro das águas dos rios Negro e Amazonas.

Observe as informações da placa e escreva por extenso o número que representa a medida do comprimento do Rio Amazonas.

PROFESSOR

Resposta: Seis mil, novecentos e oitenta e dois quilômetros.

Quantos litros de água cabem na caixa-d'água da casa onde você mora?

PROFESSOR

Resposta pessoal.

Sabendo que cada 1 m³ é igual a 1.000 litros, escreva com algarismos quantas caixas-d'água de 1.000 litros o Rio Amazonas enche em cada segundo.

PROFESSOR

Resposta: 216.342 caixas-d'água em cada segundo.

Fim do complemento

MANUAL DO PROFESSOR

A situação retratada na abertura possibilita que os estudantes retomem o que aprenderam sobre números nos anos anteriores. É um bom momento para observar o que eles sabem a respeito da leitura e da escrita dos números com até 6 algarismos.

Antes da realização das atividades, incentive os estudantes a localizarem as personagens e a observarem os dados que aparecem na ampliação do folheto.

Para refletir...

Na primeira questão, estabeleça comparações com a realidade próxima dos estudantes, como a distância entre duas cidades conhecidas, por exemplo.

Solicite aos estudantes que observem o número que corresponde à vazão do rio. Se necessário, explique o significado desse termo. Explique também como se lê m³ (metro cúbico) e o que significa, sem se aprofundar. Observe se eles identificam a ordem de grandeza desse número.

A comparação com a capacidade das caixas-d’água domésticas pode levar à impressão de que a água disponível é infinita, o que não é verdade. Se julgar conveniente, proponha uma pesquisa ou apresente dados sobre as proporções de água salgada e doce no planeta e sobre a potabilidade dessa água. Esse pode ser um bom momento para discutir as possíveis fontes de poluição da água, como esgoto, lixo, agrotóxicos etc.

MP040

Sequência numérica

Observe a sequência de números.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, ...

Os números que formam essa sequência são chamados de números naturais.

Qual é o primeiro número dessa sequência? _____

PROFESSOR
Resposta: Zero.

Veja como Lucas e Rebeca descreveram a sequência dos números naturais.

Imagem: Ilustração. Lucas, menino com cabelo encaracolado e camiseta branca está com o dedo indicador direito levantado, olhando para cima e sorrindo. Ele fala: O zero é o primeiro número natural, e cada número a partir do número 1 é o anterior mais 1. Ao lado, Rebeca, menina loira com cabelo preso, óculos e camiseta branca está com a mão esquerda atrás das costas e a direita virada para cima. Ela diz: Cada número é o anterior menos 1. Fim da imagem.

Quem descreveu a sequência dos números naturais de forma correta?
_____

PROFESSOR
Resposta: Lucas.

Responda às questões.
1. Qual é o maior número natural de quatro dígitos que pode ser formado com os algarismos 1, 0, 4 e 5, sem repeti-los? E o menor?
  _____
  
  PROFESSOR
  Resposta: Maior: 5.410; menor: 1.045.
1. Qual é o maior número natural de cinco dígitos que pode ser formado com os algarismos 2, 0, 9, 3 e 7, sem repeti-los? _____
  
  PROFESSOR
  Resposta: 97.320
1. Qual é o menor número natural de cinco dígitos que pode ser formado com os algarismos 2, 3, 1, 9 e 4, sem repeti-los? _____
  
  PROFESSOR
  Resposta: 12.349
1. Rita quer escrever números naturais maiores que 1.000. Quantos números ela pode escrever? _____
  
  PROFESSOR
  Atenção professor: Espera-se que os estudantes percebam que Rita pode escrever quantos números ela quiser. Fim da observação.

MANUAL DO PROFESSOR

Objetivo

Ler, escrever e ordenar números naturais com compreensão das principais características do sistema de numeração decimal.
Estas páginas apresentam o conceito de número natural por meio da sequência desses números, na qual se acrescenta 1 unidade a um dado número para a obtenção do seguinte. Ao observar esse processo, que permite criar indefinidamente números naturais, os estudantes são incentivados a perceberem que a sequência dos números naturais é infinita. O reconhecimento da sequência dos números naturais é importante na identificação de características como: o maior e o menor número formado por certa quantidade de algarismos, a determinação do sucessor e do antecessor de um número natural e o estabelecimento de sequências numéricas segundo um padrão de formação.

Atividade 1

Esta atividade envolve o entendimento do conceito de número natural por meio da lei de formação da sequência desses números.

Complemente a atividade perguntando: “Existe um número natural que pode ser considerado o maior de todos?”. Discuta as respostas e esclareça eventuais dúvidas. Incentive os estudantes a compreenderem que todo número natural tem um sucessor e, por isso, não podemos afirmar que existe um número natural maior de todos. Explique aos estudantes que os números naturais estão associados a uma contagem e pergunte se conhecem algum número que não seja natural e em que contextos ele aparece; é possível que mencionem números na forma de fração e na forma decimal, já estudados no ano anterior, como: $\frac{1}{2}$ ; $\frac{3}{4}$ ; 0,5; 1,8 etc.

Atividade 2

Nesta atividade, o objetivo é determinar o maior ou o menor número natural que atenda a certas condições. Relembre aos estudantes que algarismo e dígito são sinônimos.

BNCC em foco:

EF05MA01; competência geral 2

MP041

Observe a ilustração e responda às questões.

Imagem: Ilustração. Um homem está sentado e segurando um papel com o número 354. Ele olha para o papel e pensa: Ufa! Chegou a minha vez. Na frente dele há duas pessoas sentadas atrás de balcões e sobre elas há um painel com as informações: SENHA 354 – DIRIJA-SE AO CAIXA 02. Fim da imagem.

Qual era o número da senha de quem foi chamado antes desse homem?
_____

PROFESSOR
Resposta: 353

Qual será o número da senha de quem for chamado logo depois dele?
_____

PROFESSOR
Resposta: 355

Se, em um banco, os números das senhas têm no máximo quatro algarismos, qual é o maior número possível de senha? _____

PROFESSOR
Resposta: 9.999

Leia as falas de Jairo e Elaine e, em seguida, complete o quadro.

Tabela: equivalente textual a seguir.

Antecessor	Número	Sucessor
_____	725	_____
_____	999	_____
14.998	_____	15.000
_____	50.000	_____
_____	56.790	_____

PROFESSOR

Resposta: 724, 726.
998, 1.000.
14.999.
49.999, 50.001
56.789, 56.791.

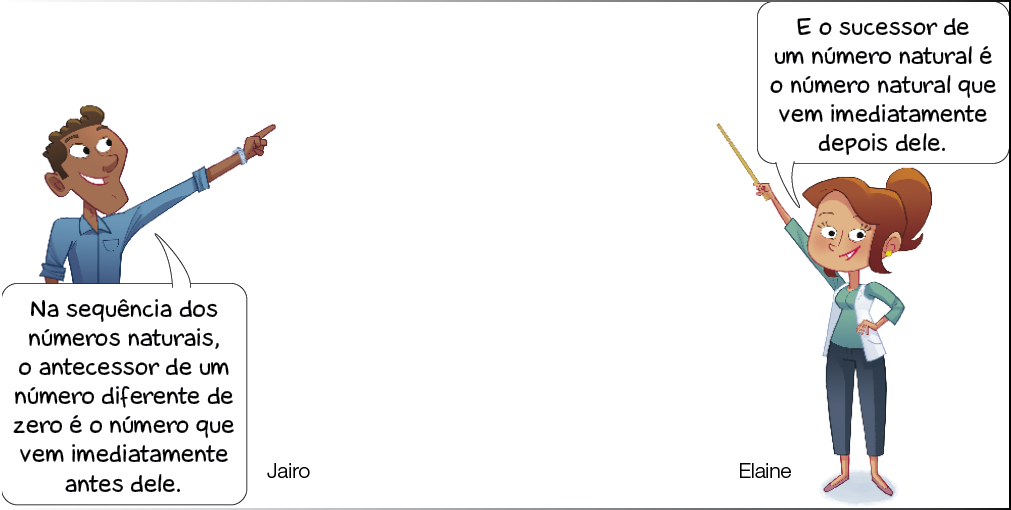
Imagem: Ilustração. Jairo, homem com cabelo encaracolado e camisa azul está apontado para a informação ANTECESSOR. Ele fala: Na sequência dos números naturais, o antecessor de um número diferente de zero é o número que vem imediatamente antes dele. Ao lado, Elaine, mulher com cabelo castanho e preso, colete branco está segurando um objeto comprido e apontando para a palavra SUCESSOR. Ela fala: E o sucessor de um número natural é o número natural que vem imediatamente depois dele. Fim da imagem.

Leia as falas de Nicole e de Enzo e, em seguida, responda às questões.

Imagem: Ilustração. Nicole, menina ruiva com camiseta branca está sentada e segurando um livro. Ela olha para o lado e fala: O sucessor do sucessor do número que eu escrevi é 218. Ao seu lado, Enzo, menino com cabelo preto e curto e camiseta branca está sentado e segurando um livro. Ele sorri e diz: O antecessor do antecessor do número que eu escrevi é 415. Atrás deles há livros em estantes e computadores. Fim da imagem.

Que número Nicole escreveu? _____

PROFESSOR
Resposta: 216

Que número Enzo escreveu? _____

PROFESSOR
Resposta: 417

MANUAL DO PROFESSOR

Atividades 3, 4 e 5

Estas atividades trabalham as ideias de sucessor e de antecessor de um número natural.

Na atividade 4, dê especial atenção ao preenchimento dos antecessores de números terminados em zero, pois talvez os estudantes não usem a subtração para obtê-los, e sim o conhecimento que têm da estrutura do sistema de numeração decimal, já que o número zero é o primeiro número natural e não tem antecessor. Porém, 50.000, por exemplo, é o número quarenta e nove mil, novecentos e noventa e nove (escrito como 49.999) mais 1.

A atividade 5 exige a compreensão do significado de sucessor do sucessor de um número e de antecessor do antecessor de um número.

O sucessor de um número natural é o número natural que vem imediatamente depois dele, ou seja, o número que é obtido adicionando-se 1 unidade a ele; o sucessor do sucessor de um número natural é o número natural que vem imediatamente depois do sucessor desse número, ou seja, o número que é obtido adicionando-se 2 unidades ao número considerado. De modo similar, o antecessor do antecessor de um número natural é 2 unidades menor que esse número.

BNCC em foco:

EF05MA01; competência geral 2

MP042

Representação dos números naturais

Leia as falas de Lucas e de Nicole e, depois, responda às questões.

Imagem: Ilustração. Lucas com a mão direita atrás das costas e a esquerda virada para cima fala: Qualquer número natural do sistema de numeração decimal pode ser representado por 10 símbolos, chamados dígitos ou algarismos. Ao lado, Nicole com o cotovelo direito apoiado na mão esquerda e o dedo indicador direito levantado, sorri e fala: No sistema de numeração decimal, agrupamos de 10 em 10 para fazer a contagem. Fim da imagem.

Quais são os 10 símbolos do sistema de numeração decimal?
_____

PROFESSOR
Resposta: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.

Observe os agrupamentos, complete as lacunas e responda: quantas bolinhas há no total?

Imagem: Ilustração. Um cubo transparente com mil bolinhas coloridas dentro 1 milhar Fim da imagem.

_____ unidades

PROFESSOR

Resposta: 1.000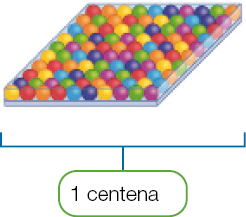

Imagem: Ilustração. Uma placa transparente com cem bolinhas coloridas dentro 1 centena Fim da imagem.

_____ unidades

PROFESSOR

Resposta: 100

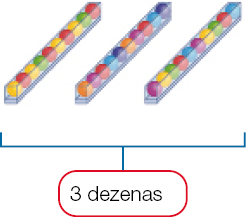
Imagem: Ilustração. Três barras transparentes com dez bolinhas coloridas dentro de cada uma 3 dezenas Fim da imagem.

_____ unidades

PROFESSOR

Resposta: 30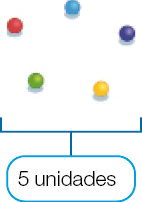

Imagem: Ilustração. Cinco bolinhas coloridas 5 unidades. Fim da imagem.

No total, há _____ bolinhas.

PROFESSOR

Resposta: 1.135

MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais até a ordem das dezenas de milhar com compreensão das principais características do sistema de numeração decimal.
Compor e decompor números naturais.
Decompor números que indicam medidas de tempo, em ano, recorrendo a outras unidades de medida de tempo: ano, década, século e milênio.
O estudo do sistema de numeração decimal merece destaque em todos os anos do Ensino Fundamental, uma vez que o tema exige revisões e ampliações constantes para que os estudantes compreendam suas características e empreguem os números de diferentes ordens em situações diversas.

Nas atividades destas páginas, os agrupamentos e as trocas realizadas no sistema de numeração decimal são o foco. É importante que as várias resoluções sejam consideradas, socializadas e comparadas.

Verifique se os estudantes compreendem que o sistema de numeração decimal se apoia em agrupamentos de 10 em 10 e no valor posicional dos algarismos (assunto da dupla de páginas seguinte). É importante possibilitar a reflexão sobre as regras de composição dos números do sistema de numeração decimal e salientar que, sem essas regras de agrupamento, seria muito difícil operar com números de diferentes ordens.

Atividade 1

Caso ainda apresentem dificuldade na visualização dos agrupamentos de 10 em 10, use o Material Dourado, que possibilita a representação de unidades de milhar, centenas, dezenas e unidades.

BNCC em foco:

EF05MA01

Sugestão de atividade

Fazendo agrupamentos para contar
Você já fez alguma contagem cujo resultado fosse um número maior que 10?
E maior que 100?
E maior que 1.000?
Descreva o que você contou e como você se organizou para não errar na contagem.

Além de responder às questões, os estudantes devem refletir sobre as estratégias de contagem, além de socializá-las. Espera-se que os estudantes que já fizeram as contagens dos questionamentos tenham percebido que, quanto maior o resultado da contagem, maior é a necessidade de realizar agrupamentos para organizá-la.

MP043

Uma fábrica embala miçangas em potes com, exatamente, 10, 100 ou 1.000 unidades.
1. No total, quantas miçangas há nos potes representados abaixo?

Imagem: Ilustração. À esquerda, um pote gigante com 1.000 miçangas dentro. No centro, seis potes grandes com 100 miçangas dentro de cada um. À direita, cinco potes pequenos com 10 miçangas dentro de cada um. Fim da imagem.

No total, há _____ miçangas.

PROFESSOR

Resposta: 1.650

Qual é o menor número de potes com 10, 100 ou 1.000 unidades necessários para embalar 6.230 miçangas?
_____

PROFESSOR
Resposta: 6 potes com 1.000 unidades, 2 potes com 100 unidades e 3 potes com 10 unidades.

Há 4.230 parafusos para serem distribuídos em embalagens com 10, 100 ou 1.000 unidades.

Imagem: Fotografia. Vários parafusos espalhados. Fim da imagem.

Quantas embalagens haverá de cada tipo? Dê duas respostas possíveis.

_____

PROFESSOR

Exemplos de resposta: 4 embalagens de 1.000,

PROFESSOR

2 embalagens de 100 e 3 embalagens de 10;

PROFESSOR

42 embalagens de 100 e 3 embalagens de 10.

Complete o quadro fazendo a decomposição do período em cada caso.

Quadro: equivalente textual a seguir.

Período	Milênios	Séculos	Décadas	Anos
2.357 anos	2	3	5	7
4.589 anos	_____	_____	_____	_____
10.592 anos	_____	_____	_____	_____

PROFESSOR

Exemplo de resposta: 4, 5, 8, 9.

PROFESSOR

10, 5, 9, 2.

MANUAL DO PROFESSOR

Atividade 2

Os estudantes devem atentar-se à informação de que, em cada pote, há exatamente a quantidade indicada de miçangas: 10, 100 ou 1 000. Assim, em um pote com capacidade para 100 miçangas não haverá quantidade menor nem maior que 100 unidades, e assim por diante. Incentive-os a perceberem que a menor quantidade de potes necessários é obtida quando se usa a maior quantidade de potes possível com maior capacidade, ou seja, primeiro utilizam-se todos os potes possíveis com capacidade para 1.000 miçangas (potes grandes), depois os com 100 miçangas (potes médios), por fim, os com 10 (potes pequenos).

Pergunte: “É possível embalar qualquer quantidade de miçangas com as condições e os tipos de potes do problema?” Espera-se que eles percebam que, com a condição de ter exatamente 10, 100 ou 1.000 miçangas nos potes, só é possível embalar quantidades expressas por números múltiplos de 10.

Atividade 3

Chame a atenção para o fato de que, diferentemente da situação da atividade anterior, este problema não exige a menor quantidade de embalagens, por isso há mais de uma possibilidade de resposta – o que pode ser confirmado pela comparação com as respostas dos colegas.

Atividade 4

Lembre os estudantes de que:

1 década corresponde a 10 anos;
1 século corresponde a 10 décadas ou 100 anos;
1 milênio corresponde a10 séculos ou 1.000 anos.
Comente que é possível fazer outras decomposições dos números que indicam esses períodos de tempo. Por exemplo:
2 357 anos é igual a 23 séculos, 5 décadas e 7 anos, ou 2 milênios e 357 anos;
10 592 anos é igual a 105 séculos, 9 décadas e 2 anos, ou 10 milênios e 592 anos.
BNCC em foco:

EF05MA01, EF05MA19; competência geral 2

Sugestão de atividade

Nova organização de miçangas

Proponha uma discussão sobre como embalar 9 035 miçangas utilizando as mesmas premissas expostas na atividade 2. É importante que os estudantes percebam que não haverá pote médio e que 5 miçangas ficarão soltas (unidades), pois não completam a quantidade necessária para o pote pequeno. Incentive os estudantes a analisarem outras quantidades de miçangas, de modo a aumentarem o repertório de agrupamentos e trocas no sistema de numeração decimal.

MP044

Valor posicional

Observe o preço da televisão abaixo e a representação da quantia que Fernanda possui.

Imagem: Ilustração. Fernanda segura uma bolsa e acima dela há um balão de pensamento com a imagem de quatro cédulas de duzentos reais, quatro cédulas de cem reais e quatro moedas de um real. Na frente dela há uma televisão sobre uma caixa e uma placa com a informação: PROMOÇÃO R$ 1240,00. Fim da imagem.

Quantos reais Fernanda possui? _____

PROFESSOR
Resposta: 1.204 reais.

Qual é o valor da televisão? _____

PROFESSOR
Resposta: 1.240 reais.

Observe o valor de cada algarismo do número que expressa a quantia que Fernanda possui e do número que expressa o preço da televisão.

1.204

4 - 4 unidades

0 - 0 dezena

2 - 2 centenas

1 - 1 unidade de milhar

1.240

0 - 0 unidade

4 - 4 dezenas

2 - 2 centenas

1 - 1 unidade de milhar

Os dois números são formados com os mesmos algarismos, mas os algarismos 0 e _____ não têm o mesmo valor posicional nos dois números.

PROFESSOR

Resposta: 4

O valor de um algarismo em um número depende da posição que ele ocupa nesse número.

MANUAL DO PROFESSOR

Objetivo

Compor e decompor números naturais, considerando o valor posicional dos algarismos.
A invenção de um sistema numérico com valor posicional foi um dos maiores avanços para tornar mais prático o registro dos números e a criação de algoritmos para cálculos.

O objetivo das atividades destas páginas é desafiar os estudantes a observarem, reconhecerem e fazerem uso dessa característica fundamental do sistema de numeração decimal: cada símbolo (chamado de algarismo ou dígito) tem seu valor determinado pela posição que ocupa no número.

Se os estudantes ainda apresentarem dificuldade na compreensão dessa característica, proponha a realização de atividades com o uso do ábaco, pois ele possibilita representar a posição dos algarismos de um número em suas ordens.

Atividade 1

Oferece aos estudantes a oportunidade de perceberem o que muda quando se altera a ordem dos algarismos de um número. Leia a situação proposta com eles e pergunte: “A quantia que Fernanda possui é suficiente para ela comprar a televisão?”. Espera-se que os estudantes percebam que não, pois 1.204 < 1.240.

Comente que o sistema de numeração decimal (também denominado sistema de numeração indo-arábico) não é o único em que está presente a ideia de valor posicional. Por volta de 2.000 a.C., os babilônios já dispunham de um sistema de numeração em que a posição do símbolo era importante, no entanto eles trabalhavam com agrupamentos de 60 em 60 (sistema sexagesimal). Os maias, povo que habitou a América Central a partir do século IV d.C., usavam um sistema de numeração com valor posicional em que os agrupamentos eram formados de 20 em 20 (sistema vigesimal).

BNCC em foco:

EF05MA01, EF05MA19; competência geral 2

MP045

Em cada caso, escreva o valor posicional de cada algarismo do número.

3.579

9 - _____ unidades

PROFESSOR

Resposta: 9

7 - _____ dezenas ou _____ unidades

PROFESSOR

Resposta: 7, 70

5 - _____ centenas ou _____ unidades

PROFESSOR

Resposta: 5, 500

3 - _____ unidades de milhar ou _____ unidades

PROFESSOR

Resposta: 3, 3.000

1.284

4 - _____ unidades

PROFESSOR

Resposta: 4

8 - _____ dezenas ou _____ unidades

PROFESSOR

Resposta: 8, 80

2 - _____ centenas ou _____ unidades

PROFESSOR

Resposta: 2, 200

1 - _____ unidade de milhar ou _____ unidades

PROFESSOR

Resposta: 1, 1.000.

Escreva quantas unidades vale o algarismo 7 em cada número.

27 - _____

PROFESSOR
Resposta: 7

712 - _____

PROFESSOR
Resposta: 700

6.975 - _____

PROFESSOR
Resposta: 70

76.518 - _____

PROFESSOR
Resposta: 70.000

27 001 - _____

PROFESSOR
Resposta: 7.000

751.841 - _____

PROFESSOR
Resposta: 700.000

Agora, responda: em qual desses números o algarismo 7 tem valor posicional maior?
_____

PROFESSOR
Resposta: No número 751.841.

Descubra o número em cada caso.

Imagem: Ilustração. Vista aérea de um homem andando e segurando a mão de um menino. Na frente deles há uma rua com faixa de pedestres. Ao fundo, uma mulher está andando na calçada e entre eles há postes com as luzes acesas. Ao redor há casas e árvores. Fim da imagem.

O número de lâmpadas que foram compradas para a iluminação de ruas em um bairro tem quatro algarismos: dois deles são 1, outro vale 3.000 e outro vale 60. Que número é esse?
_____

PROFESSOR
Resposta: 3.161

O número de pessoas que cabem em um galpão é o menor número de 4 algarismos diferentes no qual aparece o algarismo 5 com o valor igual a 50 unidades. Que número é esse?
_____

PROFESSOR
Resposta: 1.052

MANUAL DO PROFESSOR

Atividade 2

Apresente aos estudantes um número com mais ordens, como 31.742, e peça que escrevam o valor posicional de cada algarismo:

31.742

2 - 2 unidades

4 - 4 dezenas ou 40 unidades

7 - 7 centenas ou 700 unidades

1 - 1 unidade de milhar ou 1.000 unidades

3 - 3 dezenas de milhar ou 30.000 unidades

Atividade 3

Amplie a atividade e peça aos estudantes que digam qual é o valor posicional de cada algarismo dos números apresentados. Depois solicite que leiam esses números em voz alta. Aproveite para verificar se estão fazendo corretamente a leitura dos números.

Atividade 4

Esta atividade oferece aos estudantes a oportunidade de:

aplicarem a característica posicional no registro de números;

solucionarem desafios que envolvam a identificação e o estabelecimento de relações entre os algarismos e o valor posicional de cada um em um número.

Depois de resolverem individualmente as questões, promova uma roda de conversa para que compartilhem suas estratégias e discutam respostas diferentes da que cada um apresentou.

BNCC em foco:

EF05MA01; competência geral 2

Sugestão de leitura para o professor

Livro

CENTURIÓN, Marília. Números e operações: conteúdo e metodologia da Matemática. São Paulo: Scipione, 1995.

Nessa obra, a autora toma por base o pressuposto de que o estudante constrói seu conhecimento a partir de ações. São abordados diversos aspectos importantes para a atuação do professor em sala de aula, como a importância da história da Matemática, o conhecimento acerca de outros sistemas de numeração, o uso de materiais manipuláveis e recursos didáticos, curiosidades e sugestões de atividades práticas.

MP046

Ordens e classes

De acordo com o Instituto Brasileiro de Geografia e Estatística (IBGE), em 2020, a população estimada do município de Santo André, no estado de São Paulo, era de 721.368.
1. Escreva esse número no quadro de ordens e classes.

Imagem: Ilustração. Enzo faz o número três com a mão direita e fala: Cada classe é formada por 3 ordens. Fim da imagem.

Tabela: equivalente textual a seguir.

2ª classe ou classe dos milhares			1ª classe ou classe das unidades simples
6ª ordem	5ª ordem	4ª ordem	3ª ordem	2ª ordem	1ª ordem
centenas de milhar (CM)	dezenas de milhar (DM)	unidades de milhar (UM)	centenas (C)	dezenas (D)	unidades (U)
7	2	_____	_____	_____	_____

PROFESSOR

Resposta: 1, 3, 6, 8

Para facilitar a leitura dos números, costumamos separá-los em classes.

Imagem: Ilustração. Enzo aponta para o lado e diz: Atenção! Para separar as classes, agrupamos as ordens do número de 3 em 3, da direita para a esquerda. Fim da imagem.

721 - 2ª classe (milhares)

368 - 1ª classe (unidades simples)

A ordem de grandeza desse número é a centena de milhar.

Lemos - _____

PROFESSOR
Resposta: Setecentos e vinte e um mil, trezentos e sessenta e oito.

Observe o número da placa e marque com um X a frase verdadeira.

( ) A ordem de grandeza desse número é a dezena de milhar.

( ) Os algarismos 6, 5 e 8 compõem a classe dos milhares.

( ) O algarismo 8 vale 800 nesse número.

PROFESSOR
Resposta correta: Os algarismos 6, 5 e 8 compõem a classe dos milhares.

MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais até a ordem das centenas de milhar com compreensão das principais características do sistema de numeração decimal.
Ler e interpretar texto com dados numéricos.
Nestas páginas, o objetivo é possibilitar aos estudantes reconhecerem que a leitura de um número está relacionada com a classe e com a ordem de cada algarismo. Por exemplo, no número 308.217, os algarismos 3, 0 e 8 estão na 2ª classe (ou classe dos milhares) e por isso devem ser lidos como “trezentos e oito mil”, enquanto os algarismos 2, 1 e 7, na 1ª classe (ou classe das unidades simples), devem ser lidos como “duzentos e dezessete”.

Atividade 1

Se os estudantes manifestarem curiosidade acerca da organização das classes em grupos de três algarismos, explique que ela está relacionada com o fato de a quantidade 3 ser facilmente reconhecível em apenas um relance. Pesquisadores do desenvolvimento do raciocínio matemático sabem que o cérebro humano é capaz de reconhecer a quantidade três em uma coleção de objetos sem realizar a contagem – o que alguns denominam “senso numérico”. Há pessoas que conseguem estender essa capacidade de percepção para quantidades como quatro ou cinco efetuadas com tanta rapidez que escapam à percepção consciente.

Atividade 2

Os estudantes devem reconhecer as classes e a ordem de grandeza de um número de 6 algarismos. Verifique se compreenderam o significado dos termos classe e ordem. Peça que corrijam as frases erradas:
A ordem de grandeza desse número é a centena de milhar.
O algarismo 8 vale 8.000 nesse número.
Comente que, quando falamos em ordem de grandeza de um número, estamos tentando transmitir a ideia do “tamanho” do número ou, ainda, de quantos algarismos esse número é composto. Por exemplo, afirmar que a ordem de grandeza do número 48 091 é a dezena de milhar permite identificar que ele tem 5 algarismos: três da classe das unidades simples e dois da classe dos milhares (unidade e dezena).

BNCC em foco:

EF05MA01

MP047

Imagem: Ícone: Calculadora. Fim da imagem.

Usando uma calculadora, faça aparecer no visor os números a seguir.
1. Um número com três algarismos, em que o algarismo 4 tenha valor igual a 400 unidades. _____
  
  PROFESSOR
  Exemplo de respostas: 423
1. Um número com seis algarismos, em que o algarismo 5 tenha valor igual a 5 dezenas de milhar. _____
  
  PROFESSOR
  Resposta: 353.002
1. Um número com cinco algarismos, em que o algarismo 2 tenha valor igual a 2.000 unidades. _____
  
  PROFESSOR
  Resposta: 42.004
1. Um número com seis algarismos, em que o algarismo 3 tenha valor igual a 3 centenas de milhar. _____
  
  PROFESSOR
  Resposta: 312.476

Leia a notícia e, depois, escreva como lemos cada um dos números que aparecem nela.

Museus mais visitados em 2017

O Instituto Brasileiro de Museus (Ibram) divulgou os três museus mais visitados em 2017. São eles: o Museu Imperial, em Petrópolis (RJ), que recebeu 400.839 visitantes; o Museu da Inconfidência, em Ouro Preto (MG), com um público de 174.382 pessoas; e o Museu Histórico Nacional, na cidade do Rio de Janeiro (RJ), que recebeu 137.479 visitantes.

Imagem: Fotografia de uma construção com dois andares, paredes brancas com detalhes marrons e uma torre com relógio no meio. Fim da imagem.

LEGENDA: Museu da Inconfidência, Ouro Preto, Minas Gerais, em 2020. FIM DA LEGENDA.

FONTE: Informações obtidas em: https://www.museus.gov.br/museus-ibram-receberam-mais-12-milhao-de-visitantes-em-2017/ . Acesso em: 15 fev. 2021.

_____

PROFESSOR

Resposta: Dois mil e dezessete; quatrocentos mil, oitocentos e trinta e nove; cento e setenta e quatro mil, trezentos e oitenta e dois; cento e trinta e sete mil, quatrocentos e setenta e nove.

Usando somente algarismos, escreva os números que a professora está ditando.

_____

PROFESSOR

Resposta: 7.249

_____

PROFESSOR

Resposta: 180.046

MANUAL DO PROFESSOR

Atividade 3

Ao usar a calculadora como meio de registro, os estudantes podem refletir sobre o valor posicional dos algarismos em cada número digitado. Eles devem digitar os números solicitados observando duas características: a quantidade de algarismos do número e o valor posicional indicado para certo algarismo desse número. Há muitas possibilidades de resposta para cada item. Por exemplo, no item a, pede-se que o algarismo 4 tenha valor de 400 unidades; assim, qualquer número de três algarismos em que o algarismo das centenas seja igual a 4 é um exemplo de resposta, podendo ser escrito qualquer algarismo na ordem das dezenas e na ordem das unidades.

Aproveite a oportunidade do uso da calculadora para que eles pensem sobre os registros numéricos e as operações aritméticas. Por exemplo, em relação ao item a, peça que efetuem uma operação de modo que, a partir do número que escreveram, cheguem ao número 100; nesse caso, eles podem fazer subtrações sucessivas para chegar até o número desejado. Pode-se pedir também que efetuem uma operação de modo que, a partir do número que escreveram, cheguem ao número 900; nesse caso, eles podem fazer adições sucessivas até chegar ao número desejado.

Atividade 4

Além da escrita por extenso dos números do texto, explore a comparação entre eles e o valor posicional de seus algarismos.

Atividade 5

Se julgar necessário, amplie a atividade ditando novos números para que os estudantes os representem com algarismos e por extenso. Depois, peça que identifiquem o maior e o menor, a quantidade de algarismos e os valores posicionais, de modo a resgatar as ideias trabalhadas.

BNCC em foco:

EF05MA01

MP048

Composição e decomposição

A família de Ana juntou as economias que fez durante um ano e conseguiu a quantia a seguir.

Imagem: Ilustração. Uma senhora, Ana, um menino e um homem estão sentados em volta de uma mesa. Acima deles há um balão de pensamento com a imagem de dez cédulas de cem reais, seis cédulas de dez reais e oito moedas de um real. Fim da imagem.

Complete o quadro com a quantidade de cédulas e moedas que a família de Ana conseguiu juntar.

Quadro: equivalente textual a seguir.


_____	_____	_____

PROFESSOR

Resposta: 10, 6, 8

Veja como Ana e seu irmão calcularam a quantia economizada e responda.

Imagem: Ilustração. Rosto de Ana. Fim da imagem.

1.000 + 60 + 8 = _____

PROFESSOR

Resposta: 1.068

Imagem: Ilustração. Rosto do irmão de Ana. Fim da imagem.

10 × 100 + 6 × 10 + 8 × 1 = _____

PROFESSOR

Resposta: 1.068

Qual é a quantia economizada pela família de Ana? _____

PROFESSOR
Resposta: 1.068 reais

Imagem: Ícone: Oral. Fim da imagem.

Se a família de Ana tivesse mais 10 cédulas de 10 reais, qual seria a quantia total economizada? Explique como você calculou . _____

PROFESSOR
Resposta: 1.168 reais;

PROFESSOR
resposta pessoal.

MANUAL DO PROFESSOR

Objetivo

Compor e decompor números naturais por meio de adições e multiplicações.
Atividade 1

Nesta atividade, os estudantes devem mobilizar os conhecimentos que têm sobre o sistema de numeração decimal, reconhecer as ordens de um número de 4 algarismos para compor o número 1 068 e responder às questões, usando o sistema monetário brasileiro como suporte. Socialize os diferentes procedimentos que aparecerem.

BNCC em foco:

EF05MA01; competência específica 3

Sugestão de atividade

Completando ideias

Peça aos estudantes que reproduzam e completem no caderno as seguintes frases:
O algarismo da ordem das unidades no resultado da adição 762 + 581 é...
(Resposta: 3)
O resultado de 1.800 – 947 é um número que está entre...
(Resposta possível: 800 e 900)
O número 12.345 pode ser decomposto como...
(Resposta esperada: 10.000 + 2.000 + 300 + 40 + 5. Esclareça que há outras decomposições possíveis.)

Verifique como os estudantes realizam as operações propostas. É um bom momento para levantar seus conhecimentos prévios. Socialize as estratégias utilizadas e, se necessário, disponibilize o Material Dourado para eles utilizarem.

MP049

Complete os _____ com o número correspondente ao resultado de cada um dos itens. Depois, escreva a ordem de grandeza do número obtido.

7 × 10.000 + 3 × 1

_____ _____ _____ _____ _____

PROFESSOR

Resposta: 7, 0, 0, 0, 3.

Ordem de grandeza - Dezena de milhar

10.000 + 6.000 + 300 + 5

_____ _____ _____ _____ _____

PROFESSOR

Resposta: 1, 6, 3, 0, 5.

Ordem de grandeza - _____

PROFESSOR

Resposta: Dezena de milhar

200.000 + 80.000 + 400

_____ _____ _____ _____ _____

PROFESSOR

Resposta: 2, 8, 0, 4, 0, 0.

Ordem de grandeza - _____

PROFESSOR

Resposta: Centena de milhar

6 × 1.000 + 3 × 100 + 3 × 10 + 6

_____ _____ _____ _____ _____

PROFESSOR

Resposta: 6, 3, 3, 6.

Ordem de grandeza - _____

PROFESSOR

Resposta: Unidade de milhar

300.000 + 20.000 + 5 .000 + 80

_____ _____ _____ _____ _____ _____

PROFESSOR

Resposta: 3, 2, 5, 0, 8, 0.

Ordem de grandeza - _____

PROFESSOR

Resposta: Centena de milhar

1 × 200.000 + 4 × 1.000 + 7 × 1

_____ _____ _____ _____ _____ _____

PROFESSOR

Resposta: 2, 0, 4, 0, 0, 7.

Ordem de grandeza - _____

PROFESSOR

Resposta: Centena de milhar

300.000 + 20.000 + 500 + 80

_____ _____ _____ _____ _____ _____

PROFESSOR

Resposta: 3, 2, 0, 5, 8, 0.

Ordem de grandeza - _____

PROFESSOR

Resposta: Centena de milhar

7 × 10 + 1 × 100 + 9 × 10.000

_____ _____ _____ _____ _____

PROFESSOR

Resposta: 9, 0, 1, 7, 0.

Ordem de grandeza - _____

PROFESSOR

Resposta: Dezena de milhar

Decomponha os números a seguir.
1. 457.890 = _____
  
  PROFESSOR
  Exemplo de resposta: 400.000 + 50.000 + 7.000 + 800 + 90
1. 555.876 = _____
  
  PROFESSOR
  Exemplo de resposta: 5 × 100.000 + 5 × 10.000 + 5 × 1.000 + 8 × 100 + 7 × 10 + 6 × 1

Identifique o erro na decomposição do número 139.570 e cerque-o com uma linha. Em seguida, escreva a decomposição correta.
139.570 = 1 × 100.000 + 3 × 30.000 + 9 × 1 000 + 5 × 100 + 7 × 10

PROFESSOR
Resposta correta: 3 × 30.000

_____

PROFESSOR
Exemplo de resposta: 1 × 100.000 + 3 × 10.000 + 9 × 1.000 + 5 × 100 + 7 × 10

MANUAL DO PROFESSOR

Atividade 2

Explore as decomposições apresentadas nos itens de a a h, peça aos estudantes que determinem o número formado em cada caso e registre-o na lousa. Depois, os estudantes podem preencher os quadrinhos.

Atividade 3

Peça aos estudantes que comparem o que fizeram com as respostas de alguns colegas, para que percebam que podem existir outras maneiras de decompor um mesmo número. Caso não surjam diferenças, apresente outros modos na lousa.

Atividade 4

Uma maneira de os estudantes perceberem o erro é pedir-lhes que escrevam a decomposição proposta do número 139.570, para que percebam que nesse tipo de decomposição os algarismos do número são multiplicados pelos grupos de 10 que são formados em cada ordem. Desse modo, no lugar de 30.000 deveríamos ter 10.000, já que teremos a multiplicação por 3.

Depois de realizarem a atividade, peça que comparem essa forma de decomposição com esta:

139.570 = 100.000 + 30.000 + 9.000 + 500 + 70

Desse modo, podem verificar em que situação o 30.000 aparece.

BNCC em foco:

EF05MA01; competência específica 3

MP050

Ordenação e comparação

O administrador de um site decidiu comparar o acesso às páginas de jogos e de notícias. Para isso, ele colocou um contador nessas páginas. Observe.

Imagem: Ilustração. À esquerda, um monitor e na tela, imagem de jogos coloridos e a informação: VISITANTES – 875.210. À direita, outro monitor e na tela, imagem de notícias e a informação: VISITANTES – 874.632. Fim da imagem.

Complete os quadros com os algarismos de cada número.

Quadro: equivalente textual a seguir.

CM	DM	UM	C	D	U
_____	_____	_____	_____	_____	_____

PROFESSOR

Resposta: 8, 7, 5, 2, 1, 0

Quadro: equivalente textual a seguir.

CM	DM	UM	C	D	U
_____	_____	_____	_____	_____	_____

PROFESSOR

Resposta: 8, 7, 4, 6, 3, 2.

Como o administrador pode comparar esses números? Complete com é maior que ou com é menor que.

875. 210

0 - 0

1 - 10

2 - 200

5 - 5.000

7 - 70.000

8 - 800.000

874. 632

2 - 2

3 - 30

6 - 600

4 - 4.000

7 - 70.000

8 - 800.000

875.210 > 874.632 → 875.210 _____ 874.632

PROFESSOR

Resposta: é maior que

Preencha os quadros com números de seis algarismos para que as desigualdades sejam verdadeiras.

786.000 < _____

PROFESSOR
Exemplo de resposta: 786.984

135.796 > _____

PROFESSOR
Resposta: 123.456

_____ > 312.945

PROFESSOR
Resposta: 451.625

_____ < 625.584

PROFESSOR
Resposta: 287.622

MANUAL DO PROFESSOR

Objetivos

Ler, escrever, comparar e ordenar números naturais até a ordem das centenas de milhar.
Organizar dados coletados por meio de uma tabela.
Oferecer situações de comparação entre números compostos de muitas ordens incentiva os estudantes a buscarem estratégias apropriadas. É fundamental garantir a liberdade deles na elaboração de estratégias.

A ação de comparar números leva à consolidação do conceito de número. As estratégias para decidir qual é o maior (ou o menor) número mobiliza diferentes conhecimentos e exige a compreensão das regras do sistema de numeração.

Atividade 1

Peça aos estudantes que façam a leitura de cada número, escrevam-nos por extenso e os decomponham segundo suas ordens (no caderno):
875.210: oitocentos e setenta e cinco mil, duzentos e dez; 8 centenas de milhar, 7 dezenas de milhar, 5 unidades de milhar, 2 centenas, 1 dezena e zero unidade;
874.632: oitocentos e setenta e quatro mil, seiscentos e trinta e dois; 8 centenas de milhar, 7 dezenas de milhar, 4 unidades de milhar, 6 centenas, 3 dezenas e 2 unidades.
O administrador deve começar comparando os algarismos da ordem das centenas de milhar: são iguais a 8. Depois, os algarismos das dezenas de milhar: são iguais a 7. Então, os algarismos da ordem das unidades de milhar: um deles é 5 e outro é 4. Logo, o número que tem o algarismo 5 na ordem das unidades de milhar é o maior.

Atividade 2

Esta atividade possibilita a busca de resposta por meio da análise de uma dada estratégia. Promova um momento para que possam compartilhar suas respostas, e assim perceber que não há uma única, mas inúmeras respostas possíveis.

BNCC em foco:

EF05MA01

MP051

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

Pinte de acordo com a legenda.
Números menores que 99;999.

Números maiores que 99.999 e menores que 499.999.

Números maiores que 499.999.

56.652

PROFESSOR

Resposta: azul

165.874

PROFESSOR

Resposta: amarelo

561.652

PROFESSOR

Resposta: vermelho

12.598

PROFESSOR

Resposta: azul

451.585

PROFESSOR

Resposta: amarelo

985.259

PROFESSOR

Resposta: vermelho

654.681

PROFESSOR

Resposta: vermelho

710.028

PROFESSOR

Resposta: vermelho

Fernando pesquisou a população estimada de algumas cidades brasileiras, divulgada pelo IBGE em 2020, e anotou em um papel, mas os dados escritos foram embaralhados. Leia as dicas e ajude Fernando a organizar esses dados.

Imagem: Ilustração. Papel com as informações: Aracaju-SE; 664.908; 156.174; Palmas-TO; 306.296; Boa Vista-RR; Vitória-ES; 419.652; Paranaguá-PR; 365.855. Fim da imagem.

Complete a tabela.

População estimada de algumas cidades brasileiras em 2020

Tabela: equivalente textual a seguir.

Cidade	População estimada
Palmas (TO)	_____
Boa Vista (RR)	_____
Aracaju (SE)	_____
Paranaguá (PR)	_____
Vitória (ES)	_____

PROFESSOR

Resposta: 306.296, 419.652, 664.908, 156.174, 365.855.

Fonte dos dados: Instituto Brasileiro de Geografia e Estatística (IBGE). Disponível em: http://fdnc.io/eU8. Acesso em: 13 fev. 2021.

Boxe complementar:

Dica

Entre essas cidades, a que tinha a menor população era Paranaguá e a que tinha a maior população era Aracaju.
O número que representa a população de Vitória possui o algarismo 8 com valor posicional de 800 unidades.
A população de Boa Vista é maior que a de Palmas.

Fim do complemento.

Ordene os números do maior para o menor.
_____

PROFESSOR
Resposta: 664.908, 419.652, 365.855, 306.296, 156.174.

MANUAL DO PROFESSOR

Atividade 3

Os estudantes podem usar a seguinte estratégia:

Para determinar os números menores que 99.999, podem observar que esse é o maior número possível de 5 algarismos, de modo que basta procurar números com 5 algarismos ou menos e pintá-los de azul.
Para determinar os números maiores que 499.999, podem observar que 499.999 é o antecessor de 500.000, de modo que basta procurar os números que sejam iguais ou maiores que 500.000 e pintá-los de vermelho.
Os números maiores que 99.999 e menores que 499.999 são aqueles que estão entre 99.999 e 499.999, ou seja, serão todos os números restantes, que deverão ser pintados de amarelo.
Atividade 4

Esta atividade possibilita a comparação e a identificação de dados populacionais de algumas cidades brasileiras expressos em números de 6 algarismos, por meio da análise de algumas dicas envolvendo características do nosso sistema de numeração.

BNCC em foco:

EF05MA01, EF05MA25; competência específica 3

MP052

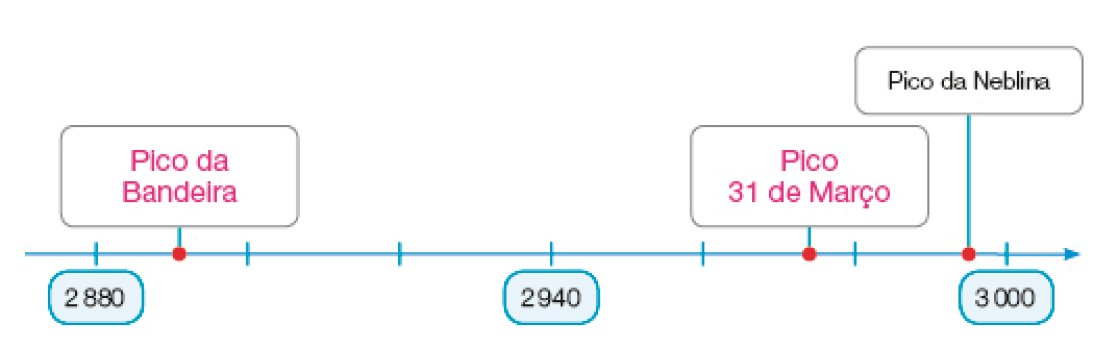
Reta numérica

De acordo com o IBGE, os três pontos mais elevados do Brasil são: Pico da Neblina, Pico 31 de Março e Pico da Bandeira. A altitude de cada um deles é, respectivamente: 2.995 m, 2.974 m e 2.891 m.

Imagem: Fotografia. Pico coberto de vegetação. Ao fundo, nuvens escuras. Fim da imagem.

LEGENDA: Pico da Neblina em Santa Isabel do Rio Negro, Amazonas, em 2017. FIM DA LEGENDA.

Imagem: Fotografia. Pico coberto de neblina. Fim da imagem.

LEGENDA: Pico 31 de Março em Santa Isabel do Rio Negro, Amazonas, em 2017. FIM DA LEGENDA.

Imagem: Fotografia. Pico cinza com vegetação. Ao fundo, o céu azul. Fim da imagem.

LEGENDA: Pico da Bandeira na divisa entre Espírito Santo e Minas Gerais, em 2017. FIM DA LEGENDA.

De acordo com as informações acima, complete ordenadamente as altitudes, da menor para a maior.

Altitude (m): _____ < _____ < _____

PROFESSOR

Resposta: 2.891 < 2.974 < 2.995

Nome do ponto: _____ < _____ < _____

PROFESSOR

Resposta: Pico da Bandeira < Pico 31 de Março < Pico da Neblina

Complete a reta numérica que indica as altitudes dos pontos mais elevados do Brasil.

Imagem: Ilustração. Reta numérica que vai de 2.880 a 3.000. Da esquerda para a direita: 2.880; 2.940; Pico da Neblina; 3.000. Resposta: Reta numérica: 2.880; Pico da Bandeira; 2.940; Pico 31 de Março; Pico da Neblina; 3.000. Fim da imagem.

Marque com os seguintes números na reta numérica:

Imagem: Ilustração. Reta numérica que vai de 200.000 a 800.000, alternando em 50.000. Da esquerda para a direita: 200.000; 800.000. Resposta: 200.000; 250.000; 375.000; 500.000; 625.000; 750.000; 800.000. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos

Comparar e ordenar números naturais.
Localizar e representar números naturais (de até 6 algarismos) na reta numérica.
As atividades destas páginas tratam da representação de números na reta numérica.

A reta numérica pode auxiliar na comparação numérica. Pela localização na reta, os estudantes podem identificar qual número é maior ou menor.

A ação de comparar é de extrema importância para a compreensão do conceito de número. As estratégias, para além da reta numérica, para decidir qual é o maior (ou menor) número entre dois ou mais números apresentados mobilizam diferentes conhecimentos dos estudantes e requerem que compreendam as regras do sistema de numeração decimal.

Atividades 1 e 2

Retome a reta numérica com os estudantes e auxilie-os a localizarem os números envolvidos em cada atividade. Reproduza retas numéricas na lousa e peça a alguns voluntários que localizem os números e expliquem como pensaram. Ao final, promova uma roda de conversa para verificar se todos compreenderam as representações feitas e retome o que for necessário.

BNCC em foco:

EF05MA01

MP053

Marque com um X o valor de A, representado na reta numérica abaixo.

Imagem: Ilustração. Reta numérica que vai de 4.500 a 8.500, alternando em 100. Da esquerda para a direita: 4.500; 5.500; A (cinco marcas antes de 8.500); 8.500. Fim da imagem.

( ) 7.950

( ) 8.000

( ) 8.100

( ) 8.200

PROFESSOR
Resposta correta: b

Em cada item, marque com os números dos quadros na reta numérica.

Imagem: Ilustração. Reta numérica que vai de 23.900 a 24.350, alternando em 50. Da esquerda para a direita: 23.900; 24.350. Resposta: 23.800; 23.900; 24.050; 24.300; 24.350. Fim da imagem.

Imagem: Ilustração. Reta numérica que vai de 169.000 a 174.000, alternando em 1.000. Da esquerda para a direita: 169.000; 174.000. Resposta: 168.000; 169.000; 171.000; 174.000; 178.000. Fim da imagem.

Imagem: Ilustração. Reta numérica que vai de 109.600 a 110.500, alternando em 100. Da esquerda para a direita: 109.600; 110.500. Resposta: 109.600; 109.900; 110.000; 110.100; 110.500. Fim da imagem.

Na reta abaixo estão representados os preços de passagens de Natal (RN) para Fortaleza (CE) oferecidas por três empresas rodoviárias. Analise a reta e as afirmações seguintes e escreva V para verdadeira ou F para falsa.

Imagem: Ilustração. Reta numérica da esquerda para a direita: Ponto A, uma marcação, ponto B, três marcações, ponto C. Fim da imagem.

( ) A empresa rodoviária que cobra o maior preço pela passagem é a empresa C.

PROFESSOR
Resposta: V

( ) O preço da passagem na empresa A é menor do que na empresa C, mas é maior do que o preço cobrado na empresa B.

PROFESSOR
Resposta: F

( ) Se o preço da passagem na empresa B é R$ 69,85 e na empresa C é R$ 77,85, então na empresa A é R$ 65,85.

PROFESSOR
Resposta: V

MANUAL DO PROFESSOR

Atividades 3 e 4

Antes de os estudantes realizarem estas atividades, peça que observem as retas numéricas e que verifiquem, em cada uma delas, quantas unidades se avança de um traço para outro. Espera-se que percebam, por exemplo, que, na atividade 3, de um traço para outro se avançam 100 unidades, enquanto no item a da atividade 4 se avançam 50 unidades.

Atividade 5

Nesta atividade, os estudantes devem avaliar cada sentença com base na reta numérica apresentada e decidir se é verdadeira ou falsa.

Para ampliar, pode-se pedir que criem outras sentenças usando as informações da reta numérica para um colega classificá-las como verdadeiras ou falsas.

Ao final, promova uma roda de conversa para socializar o que foi realizado.

BNCC em foco:

EF05MA01

MP054

Trabalhando com números

Cátia, Jonas e Simone são operadores de caixa em um supermercado. Veja quantas moedas de R$ 1,00 e cédulas de R$ 10,00 e de R$ 100,00 eles tinham no caixa no fim do dia e complete o quadro.

Quadro: equivalente textual a seguir.

Nome do operador de caixa				Quantia total
Cátia	7	0	5	_____
Jonas	8	9	0	_____
Simone	3	5	7	_____

PROFESSOR

Resposta: R$ 705,00; R$ 890,00; R$ 357,00.

Descubra a regra e complete cada sequência com os números que faltam.
1. 100, 300, 500, 700, _____, _____, _____
  
  PROFESSOR
  Exemplo de respostas: 900, 1.100, 1.300
1. 6, 60, 600, 6.000, _____, _____
  
  PROFESSOR
  Resposta: 60.000, 600.000
1. 999.999, 999.996, 999.993, _____, _____, _____
  
  PROFESSOR
  Resposta: 999.990, 999.987, 999.984
1. 870.000, 850.000, 830.000, _____, _____
  
  PROFESSOR
  Resposta: 810.000, 790.000
1. 101.101, 121.121, 141.141, _____, _____ , 201.201
  
  PROFESSOR
  Resposta: 161.161, 181.181
1. 123.56, 234.567, 345.678, _____, _____ , 679.011
  
  PROFESSOR
  Resposta: 456.789, 567.900

Escreva o número pedido em cada caso.
1. O maior número cuja ordem de grandeza é a unidade de milhar. _____
  
  PROFESSOR
  Resposta: 9.999
1. O menor número cuja ordem de grandeza é a unidade de milhar. _____
  
  PROFESSOR
  Resposta: 1.000
1. O maior número de 6 algarismos. _____
  
  PROFESSOR
  Resposta: 999.999
1. O menor número de 5 algarismos. _____
  
  PROFESSOR
  Resposta: 10.000
1. O antecessor de 100.000. _____
  
  PROFESSOR
  Resposta: 99.999
1. Coloque em ordem crescente os números escritos nos itens anteriores desta atividade.
  _____
  
  PROFESSOR
  Resposta: 1.000, 9.999, 10.000, 99.999, 999.999.

MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais.
Compor e decompor números naturais.
Representar números naturais (de até 6 algarismos) na reta numérica.
Explorar e completar sequências numéricas.
Atividade 1

Peça a um estudante que mostre na lousa como fez para calcular o total que cada operador de caixa tinha no fim do dia, discutindo os procedimentos e incentivando os colegas a apresentarem estratégias diferentes.

Atividade 2

Avalie a conveniência de os estudantes trabalharem com uma calculadora. Caso trabalhem, oriente-os previamente. Explore a regularidade de cada sequência enfatizando as ordens e as classes.

No item a, os números avançam de 200 em 200; pergunte: “A partir de qual número aparecerá mais uma ordem?” (A partir do 1.100.).

No item b, a regularidade está na permanência do algarismo 6 e no aumento de ordens.

No item c, há a diminuição de 3 em 3 unidades, e a ordem dos números é a mesma, ou seja, todos são da ordem das centenas de milhar.

No item d, há diminuição de 20.000 em 20.000 (ou 2 dezenas de milhar).

No item e, há aumento de 20.020 (ou 2 dezenas de milhar e 2 dezenas) a cada número da sequência, a partir do segundo.

Por fim, no item f, há o aumento de 111.111 unidades.

Atividade 3

Explore mais a atividade propondo alterações na formulação de alguns itens, como determinar o maior e o menor número com algarismos distintos entre si cuja ordem de grandeza seja a unidade de milhar. No primeiro caso, o maior número é 9.876; no segundo caso, a exigência de algarismos distintos leva ao número 1.023.

BNCC em foco:

EF05MA01, EF05MA24

MP055

Complete a reta numérica com os números das placas.

Imagem: Ilustração. Placas com os números: 437.874; 160.000; 554.760; 89.970; 298.965; 365.847. Fim da imagem.

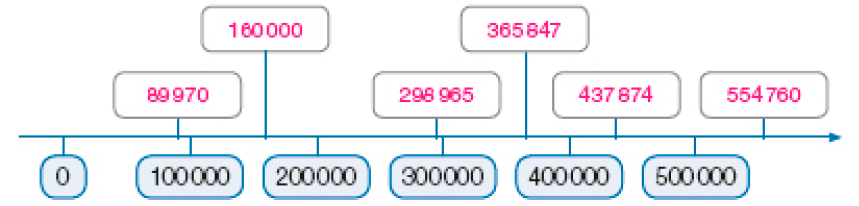
Imagem: Ilustração. Reta numérica que vai de 0 a 500.000, alternando em 100.000. Da esquerda para a direita: 0; 89.970; 100.000; 160.000; 200.000; 298.965; 300.000; 365.847; 400.000; 437.874; 500.000; 554.760. Fim da imagem.

Complete o quadro.

Quadro: equivalente textual a seguir.

Número	Leitura	Ordem de grandeza
37.076	_____	_____
965.115	_____	_____
345.670	_____	_____
2.634	_____	_____

PROFESSOR

Resposta: Leitura: Trinta e sete mil e setenta e seis; Novecentos e sessenta e cinco mil, cento e quinze; Trezentos e quarenta e cinco mil, seiscentos e setenta; Dois mil, seiscentos e trinta e quatro.

PROFESSOR

Ordem de grandeza: Dezena de milhar; Centena de milhar; Centena de milhar; Unidade de milhar.

Observe como Rebeca decompôs o número 374 523 usando o valor posicional.

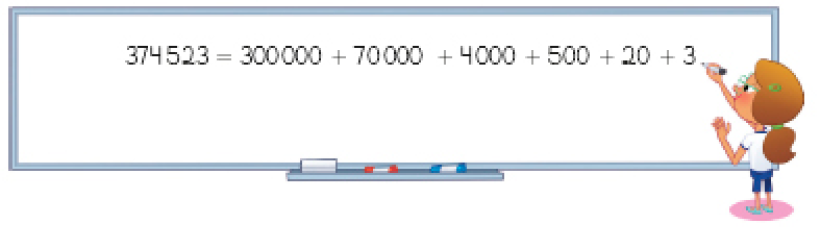
Imagem: Ilustração. Receba sorri e escreve uma conta em uma lousa: 374.523 = 300.000 + 70.000 + 4.000 + 500 + 20 + 3. Fim da imagem.

Agora, faça como Rebeca e decomponha os números abaixo.

237.128 = _____

PROFESSOR
Resposta: 200.000 + 30.000 + 7.000 + 100 + 20 + 8

495.736 = _____

PROFESSOR
Resposta: 400.000 + 90.000 + 5.000 + 700 + 30 + 6

702 120 = _____

PROFESSOR
Resposta: 700.000 + 2.000 + 100 + 20

MANUAL DO PROFESSOR

Atividade 4

Peça aos estudantes que se reúnam em duplas para esta atividade. Quando concluírem, reproduza na lousa a reta numérica e solicite a uma das duplas que indique a posição dos números e explique como os localizaram.

Atividade 5

Se necessário, ajude os estudantes a preencherem o quadro, orientando-os, primeiro, a lerem os números apresentados e, depois, a reconhecerem a ordem à qual pertencem. Por exemplo, o número 37.076 tem o primeiro algarismo (3) na ordem das dezenas de milhar, portanto o algarismo 3 representa 30.000 unidades; assim, o número deve ser lido como “trinta e sete mil e setenta e seis”.

Atividade 6

Depois de os estudantes realizarem a atividade, peça que leiam cada decomposição e, em seguida, escrevam no caderno os números por extenso, o que lhes possibilitará perceberem a relação existente entre a decomposição de um número por suas ordens e a leitura (ou escrita por extenso) desse número.

BNCC em foco:

EF05MA01

MP056

O milhão

Observe a cena.

Imagem: Ilustração. Um homem com boné aponta para um cesto de coleta vermelho e fala: Não devemos jogar o óleo usado na pia. Cada litro pode contaminar 25.000 litros de água. Em volta dele, três pessoas se aproximam segurando garrafas com óleo. Ao fundo, árvores. Fim da imagem.

Fonte dos dados: Programa de Reciclagem de Óleo de Fritura da Sabesp. Disponível em: http://fdnc.io/eUk. Acesso em: 15 fev. 2021.

Agora, complete a tabela.

Quantidade de água que pode ser contaminada

Tabela: equivalente textual a seguir.

Quantidade de óleo (em litro)	Quantidade de água (em litro)
1	25.000
2	50.000
3	_____
4	_____
10	250.000
20	_____
30	_____
40	_____

Fonte: Programa de Reciclagem de Óleo de Fritura da Sabesp. Disponível em: http://fdnc.io/eUk. Acesso em: 15 fev. 2021.

PROFESSOR

Resposta: 75.000; 100.000; 500.000; 750.000; 1.000.000.

Imagem: Ilustração. O homem com boné fala: 40 litros de óleo podem poluir um milhão de litros de água. Fim da imagem.

Veja o número um milhão no quadro de ordens e complete.

Tabela: equivalente textual a seguir.

7ª ordem	6ª ordem	5ª ordem	4ª ordem	3ª ordem	2ª ordem	1ª ordem
unidades de milhão	centenas de milhar	dezenas de milhar	unidades de milhar	centenas	dezenas	unidades
1	0	0	0	0	0	0

1 milhão = _____ centenas de milhar = _____ de unidades

PROFESSOR

Resposta: 10, 1.000.000

MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais até a ordem das unidades de milhão.
Explorar e completar sequências numéricas.
Interpretar dados apresentados em tabela.
O objetivo de trabalhar com números de ordens cada vez maiores é possibilitar a ampliação da compreensão do sistema de numeração decimal por meio de leitura, representação e estimativa de números “grandes” em situações diversas. Por isso, as atividades destas páginas exploram uma quantidade pouco usual para os estudantes dessa faixa etária: o milhão.

Atividade 1

A situação apresentada propõe a compreensão do milhão a partir do aumento proporcional dos números que devem ser completados na tabela. Se 1 litro de óleo pode contaminar 25.000 litros de água, proporcionalmente, 40 litros de óleo podem contaminar 1.000.000 de litros de água.

Converse com os estudantes sobre a importância de fazer o descarte correto do óleo usado na cozinha. Proponha que conversem sobre esse assunto com as pessoas com quem moram.

BNCC em foco:

EF05MA01, EF05MA24; competência geral 7; competência específica 4

Sugestão de trabalho interdisciplinar

Pesquisando usos do número 1 milhão

Peça aos estudantes que pesquisem em revistas, jornais, livros e na internet o uso do termo um milhão. Esta atividade pode ser trabalhada com outros componentes curriculares, como:
Geografia: pesquisa sobre populações de cidades consideradas metrópoles, como São Paulo, Rio de Janeiro, Tóquio, Cidade do México, Nova York etc.
História: pesquisa sobre as espécies ancestrais do ser humano atual há 1 milhão de anos: como eram suas características físicas etc.
Ciências: pesquisa sobre o número de organismos presentes em áreas pequenas, como em um formigueiro ou cupinzeiro, em uma nuvem de gafanhotos etc.

MP057

Complete as sequências numéricas crescentes de acordo com a regra de cada uma.

Imagem: Ilustração. Papéis com números: 500.000; 600.000; 700.000; 800.000; 900.000; 1.000.000. Fim da imagem.

Imagem: Ilustração. Papéis com números: 950.000; 960.000; 970.000; 980.000; 990.000; 1.000.000. Fim da imagem.

Imagem: Ilustração. Papéis com números: 900.000; 920.000; 940.000; 960.000; 980.000; 1.000.000. Fim da imagem.

Imagem: Ícone: Mental. Fim da imagem.

Uma construtora está vendendo vinte casas por R$ 50 000,00 cada uma.
1. A construtora já recebeu o valor pela venda de duas dessas casas.
  Qual foi o valor recebido? _____
  
  PROFESSOR
  Resposta: R$ 100.000,00 (100 mil reais).
1. Com a venda de dez casas, quanto a construtora receberá no total? E com a venda das vinte casas?
  _____
  
  PROFESSOR
  Resposta: R$ 500.000,00 (500 mil reais); R$ 1.000.000,00 (1 milhão de reais).

Responda às questões.
1. 1.000 pessoas cabem em um estádio de futebol? E 1.000.000 de pessoas? _____
  
  PROFESSOR
  Atenção professor: Espera-se que os estudantes respondam sim para a primeira pergunta e não para a segunda. Fim da observação.
1. A população do município onde você vive é maior que 1.000.000 de habitantes?
  _____
  
  PROFESSOR
  Resposta pessoal.
1. A população do estado ao qual pertence seu município é maior que 1.000.000 de habitantes?
  _____
  
  PROFESSOR
  Resposta pessoal.
1. Quantas moedas de são necessárias para formar R$ 1.000.000,00?
  _____
  
  PROFESSOR
  Resposta: 1.000.000 de moedas de 1 real.
1. Quantas cédulas de formam R$ 1.000.000,00?
  _____
  
  PROFESSOR
  Resposta: 10.000 cédulas de 100 reais.
1. A distância aérea entre Florianópolis (S C) e Campo Grande (MS) é de aproximadamente 1.000 km. Quantas viagens aéreas de Florianópolis a Campo Grande é preciso fazer para percorrer 1.000.000 de quilômetros?
  _____
  
  PROFESSOR
  Resposta: 1.000 viagens.

MANUAL DO PROFESSOR

Atividade 2

Para completar as sequências, os estudantes terão de identificar a ordem de grandeza dos números e observar uma regularidade entre eles. É importante que desenvolvam as habilidades de contar de 1 mil em 1 mil, de 10 mil em 10 mil, de 20 mil em 20 mil, de 100 mil em 100 mil etc. Peça a eles que expliquem oralmente a regra observada em cada sequência. Caso apresentem outras respostas, será necessário analisá-las e discuti-las. Para isso, solicite que justifiquem a resposta; se houver lógica, ela deverá ser aceita.

Atividade 3

Esta atividade propõe a compreensão do milhão apresentando sua composição associada ao sistema monetário brasileiro.

Propicie um momento de compartilhamento das estratégias utilizadas pelos estudantes, fazendo uma correção coletiva e validando as respostas com eles.

Atividade 4

As estimativas relacionadas às situações exemplificadas auxiliam os estudantes a construírem a noção de quantidade relativa ao milhão, como a capacidade de pessoas em um estádio de futebol.

Além disso, as diferentes decomposições do número 1.000.000 permitem aos estudantes estabelecerem a relação entre o milhão e os números de outras ordens de grandeza, como 10 mil e 100 mil. Se julgar oportuno, pergunte: “Quantas cédulas de 50 reais formam a quantia 1 milhão de reais?” (20.000 cédulas.).

BNCC em foco:

EF05MA01, EF05MA24; competência específica 3

MP058

Números com até nove algarismos

De acordo com o Instituto Brasileiro de Geografia e Estatística (IBGE), em 2020 a população brasileira era de 211.735.692 habitantes. Observe o número 211.735.692 no quadro de ordens e classes e faça o que se pede.

Tabela: equivalente textual a seguir.

3ª classe ou classe dos milhões			2ª classe ou classe dos milhares			1ª classe ou classe das unidades simples
9ª ordem	8ª ordem	7ª ordem	6ª ordem	5ª ordem	4ª ordem	3ª ordem	2ª ordem	1ª ordem
centenas de milhão	dezenas de milhão	unidades de milhão	centenas de milhar	dezenas de milhar	unidades de milhar	centenas	dezenas	unidades
2	1	1	7	3	5	6	9	2

Complete a decomposição.
211.735.692 = 200.000.000 + 10.000.000 + 1.000.000 + _____ + _____ + 5.000 + _____ + _____ + _____

PROFESSOR
Resposta: 700.000; 30.000; 600; 90; 2.

Qual é a ordem de grandeza de 211.735.692? _____

PROFESSOR
Resposta: Centena de milhão.

Como lemos esse número? _____

PROFESSOR
Resposta: Duzentos e onze milhões, setecentos e trinta e cinco mil, seiscentos e noventa e dois.

Leia o diálogo e responda às questões.

Imagem: Ilustração. Alex, homem com cavanhaque está sentado em um banco. Ele fala: Sérgio, o prêmio da loteria desta semana é de cento e dezenove milhões, cento e quarenta e dois mil, cento e quarenta e quatro reais. Ao seu lado, Sérgio, homem ruivo com cabelo encaracolado está sentado. Ele responde: Isso é muito dinheiro, Alex. Esse número que você falou é tão grande que nem sei como escrevê-lo! Fim da imagem.

Escreva, somente com algarismos, o número que Sérgio falou. _____

PROFESSOR
Resposta: 119.142.144

Em quantas classes podemos separar esse número? _____

PROFESSOR
Resposta: 3 classes.

Qual é a ordem de grandeza desse número? _____

PROFESSOR
Resposta: Centena de milhão.

MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais até a classe dos milhões.
Compor e decompor números naturais.
Ler e interpretar texto com dados numéricos.
Diferentes atividades envolvem composições e decomposições de números com até 9 algarismos.

Para que os estudantes construam uma noção mais próxima de números dessa ordem de grandeza, leve uma calculadora para a sala e questione: “Quantos ônibus de 50 lugares seriam necessários para transportar 100 milhões de pessoas? Quantos estádios de futebol com capacidade para 80 mil pessoas seriam necessários para acomodar 100 milhões de pessoas?” (Respectivamente 2.000.000 de ônibus e 1.250 estádios de futebol.). Supondo que o número 100.000.000 não caiba no visor da calculadora, pode ser decomposto: 50.000.000 + 50.000.000.

Atividade 1

Verifique se os estudantes compreendem que o número 211.735.692 tem 9 ordens e que compõem um número da grandeza das centenas de milhão em uma terceira classe numérica, a dos milhões.

Peça que deem exemplos de números com a mesma ordem de grandeza do número que representa a população brasileira estimada em 2020.

Explique que o IBGE é o órgão responsável pelo recenseamento da população brasileira, que consiste na contagem do número de habitantes, com dados socioeconômicos da população (como o número, em cada residência, de pessoas que trabalham, a renda familiar e o nível de escolaridade). Apresente dados atualizados sobre a população de alguns países ou a distribuição populacional entre os estados de nosso país. Comente o conceito de densidade demográfica, explicando que existem estados com grande área e menor número de habitantes, como o Amazonas, e estados com área menor e maior número de habitantes, como o Rio de Janeiro.

Atividade 2

Esta atividade explora a transposição para a forma numérica com algarismos da escrita por extenso. O trabalho com números da classe dos milhões traz algumas dificuldades para os estudantes quanto a estimar o “tamanho” desses números. Amplie as comparações sugeridas anteriormente, com o uso de calculadora. Desse modo, é possível desenvolver a noção do valor de quantias altas como essa.

BNCC em foco:

EF05MA01

MP059

Imagem: Ícone: mental. Fim da imagem.

Componha os números a seguir.
1. 63.000.000 + 468.000 + 600 = _____
  
  PROFESSOR
  Resposta: 63.468.600
1. 2.000.000 + 175.000 + 45 = _____
  
  PROFESSOR
  Resposta: 2.175.045
1. 535.000.000 + 247 = _____
  
  PROFESSOR
  Resposta: 535.000.247

Decomponha os números considerando o valor de cada algarismo. Depois, escreva como se lê cada um deles.
1. 7.102.359
  _____
  
  PROFESSOR
  Exemplo de respostas: 7.102.359 = 7.000.000 + 100.000 + 0 + 2.000 + 300 + 50 + 9
  
  PROFESSOR
  Sete milhões, cento e dois mil, trezentos e cinquenta e nove.
1. 103.224.500
  _____
  
  PROFESSOR
  Resposta: 103.224.500 = 100.000.000 + 0 + 3.000.000 + 200.000 + 20.000 + 4 000 + 500 + 0 + 0
  
  PROFESSOR
  Cento e três milhões, duzentos e vinte e quatro mil e quinhentos.
1. 456.000.000
  _____
  
  PROFESSOR
  Resposta: 456.000.000 = 400.000.000 + 50.000.000 + 6.000.000 + 0 + 0 + 0 + 0 + 0 + 0
  
  PROFESSOR
  Quatrocentos e cinquenta e seis milhões.

Boxe complementar:

Desafio

Observe o cartaz abaixo.

Imagem: Ilustração de um cartaz. Na parte superior, um cano com vazamento. No centro, a informação: Cuidado com vazamentos. Um furo de 4 mm no encanamento desperdiça, aproximadamente, 13.260 litros de água por mês. Na parte inferior, dois canos. Fim da imagem.

Fonte dos dados: http://fdnc.io/eUm. Acesso em: 15 fev. 2021.

CRÉDITO: SIDNEY MEIRELES

Aproximadamente, quantos litros serão desperdiçados por dia? _____

Resposta: 442 litros.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

Na reforma çdo sistema hidráulico da escola de Felipe foram reparados 10 vazamentos de 4 mm. Quantos litros de água poderiam ser desperdiçados em um ano? Pinte o quadrinho com o valor mais próximo.

1 milhão de litros de água.

1 milhão e meio de litros de água.

2 milhões de litros de água.

Resposta correta: 1 milhão e meio de litros de água.

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 3

Explora o cálculo mental de adições com números naturais da classe dos milhões. Verifique se os estudantes percebem que o cálculo com números formados por muitos zeros é bem simples; não exige algoritmos ou calculadora. O intuito é que os estudantes façam a composição do número.

Atividade 4

Explora a decomposição e a leitura (escrita por extenso) de números da classe dos milhões. Comente com os estudantes que a decomposição efetuada segue a forma como lemos, mas que há outras decomposições possíveis para esses números. Por exemplo: o número 7.102.359 poderia ser decomposto em 71 centenas de milhar, 23 centenas e 59 unidades.

Desafio

A calculadora pode ser utilizada na resolução deste desafio. Para responder ao item a, os estudantes podem considerar que 1 mês corresponde a 30 dias e, assim, calcular o resultado de 13.260 litros dividido por 30; para responder ao item b, devem considerar que 1 ano corresponde a 12 meses e calcular o resultado de 12 vezes 13.260 litros.

BNCC em foco:

EF05MA01; competências gerais 2 e 7; competências específicas 2 e 3

MP060

Arredondamentos

Em um condomínio, há 3 casas à venda, conforme as imagens a seguir.

Imagem: Ilustração 1. Uma casa térrea e ao lado há uma placa com a informação: VENDE-SE R$ 178.000,00. Fim da imagem.

Imagem: Ilustração 2. Um sobrado e ao lado há uma placa com a informação: VENDE-SE R$ 289.000,00. Fim da imagem.

Imagem: Ilustração 3. Um sobrado grande e ao lado há uma placa com a informação: VENDE-SE R$ 318.000,00. Fim da imagem.

O valor da casa 1 está mais próximo de 100 mil ou de 200 mil reais?
_____

PROFESSOR
Resposta: De 200 mil reais.

Qual é o arredondamento do número 289.000 para a centena de milhar mais próxima? _____

PROFESSOR
Resposta: 300.000

O valor da casa da imagem 3 está mais próximo de 300 mil ou de 400 mil reais?
_____

PROFESSOR
Resposta: De 300 mil reais.

Qual é o arredondamento do número 318.000 para a dezena de milhar mais próxima? _____

PROFESSOR
Resposta: 320.000

e) Localize o valor de cada uma das 3 casas na reta numérica abaixo.

Imagem: Ilustração. Reta numérica que vai de 100.000 a 300.000, alternando de 100.000. Da esquerda para a direita: 100.000; 178.000; 200.000; 289.000; 300.000; 318.000. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

Pinte com os números que são mais próximos de cem mil do que de duzentos mil.

Imagem: Ilustração. Papel com o número: 168.219. Fim da imagem.

Imagem: Ilustração. Papel com o número: 109.201. Fim da imagem.

Imagem: Ilustração. Papel com o número: 127.302. Fim da imagem.

Imagem: Ilustração. Papel com o número: 197.000. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais.
Representar números naturais na reta numérica.
Realizar arredondamentos de números naturais.
Interpretar dados estatísticos apresentados em tabela e em gráfico.
As atividades destas páginas foram elaboradas para favorecer a reflexão dos estudantes a respeito dos critérios de arredondamento.

Aqui, os estudantes precisam retomar a organização em ordens e classes do sistema de numeração decimal, que foi ampliada ao longo do estudo de números. Por isso, convém representar os números presentes nas atividades no Quadro Valor de Lugar (centenas de milhão, dezenas de milhão, unidades de milhão, centenas de milhar etc.).

Atividade 1

Nesta atividade, a reta numérica aparece como suporte, pois, por meio do recurso visual, os estudantes podem identificar com mais facilidade se o arredondamento de determinado número deve ser feito para um número maior (à direita) ou para um número menor (à esquerda). Assim, ao trabalhar com a reta numérica, eles percebem que devem optar por arredondar determinado número para aquele que fica localizado a uma menor distância dele na reta numérica.

Se necessário, ajude os estudantes a compreenderem o critério usado no arredondamento de um número para a ordem solicitada.

BNCC em foco:

EF05MA01

Atividade 2

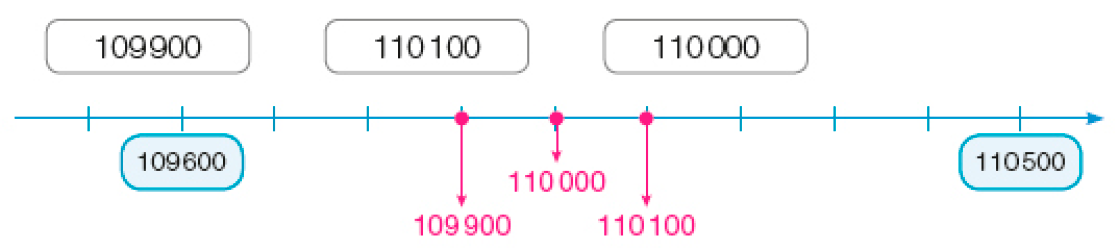
Uma sugestão que pode ser dada para os estudantes é que, inicialmente, eles escrevam os números dos quadros em ordem crescente e observem em que posição colocariam o 100 mil e o 200 mil nessa sequência. Depois, basta que comparem os números que ficaram mais próximos do 100 mil.

O arredondamento é um processo particularmente útil em contextos que apresentam quantidades “grandes” – expressas por números compostos de muitas ordens – e nos quais não há necessidade de trabalhar com valores exatos.

Para arredondar, por exemplo, o número 178.000 para a centena de milhar mais próxima, eles devem observar que “178” está mais próximo de “2 centenas” que de “1 centena”, de modo que deve ser arredondado para “2 centenas” e, assim, o número 178.000 será arredondado para 200 mil.

MP061

Complete o quadro com os arredondamentos indicados.

Quadro: equivalente textual a seguir.

Número	Arredondamento para a centena de milhar mais próxima	Arredondamento para a dezena de milhar mais próxima	Arredondamento para a unidade de milhar mais próxima
463.236	500.000	_____	_____
176.012	_____	_____	_____
632.698	_____	_____	_____

PROFESSOR

Resposta: Arredondamento para a centena de milhar mais próxima: 200.000; 600.000.

PROFESSOR

Arredondamento para a dezena de milhar mais próxima: 460.000; 180.000; 630.000.

PROFESSOR

Arredondamento para a unidade de milhar mais próxima: 463.000; 176.000; 633.000.

Paulo, Márcia, Ana e Rafael eram candidatos em uma eleição para prefeito de uma cidade, em 2022. Observe a tabela e o gráfico a seguir, que mostram a quantidade de votos que cada um recebeu, e faça o que se pede.

Eleição para prefeito

Tabela: equivalente textual a seguir.

Candidato	Votos
Paulo	570.308
Márcia	610.017
Ana	390.879
Rafael	240.920

Fonte: Responsável pela apuração dos votos (30 out. 2022).

Imagem: Gráfico em barras. Eleição para prefeito. No eixo vertical, o candidato e no eixo horizontal, os votos. coluna verde: 390.879 votos; coluna laranja: 240.920 votos; coluna vermelha:: 570.308 votos; coluna azul: 610.017 votos. Fim da imagem.

Fonte: Responsável pela apuração dos votos ( 30 out. 2022).

PROFESSOR

Resposta: Ana, Rafael, Paulo, Márcia.

A que candidato corresponde a coluna verde do gráfico? E a coluna cor de laranja? E a coluna vermelha? E a coluna azul?
_____

PROFESSOR
Resposta: Verde: Ana; Laranja: Rafael; Vermelha: Paulo; Azul: Márcia.

Complete o gráfico com o nome dos candidatos.

PROFESSOR
Resposta pessoal.

Quantos votos esses candidatos receberam juntos, aproximadamente?
_____

PROFESSOR
Exemplo de resposta: Aproximadamente 1.800.000 votos.

Reúna-se com um colega e conversem sobre como cada um pensou para resolver o item anterior.

PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR

Atividade 3

O objetivo desta atividade é levar os estudantes a perceberem que existe mais de um arredondamento possível para um mesmo número; o que vai determinar a escolha da ordem em que será feito o arredondamento é a situação a ser resolvida. Para auxiliar os estudantes no preenchimento das colunas do quadro, de modo que reconheçam as possibilidades de resultados, relembre:

as centenas de milhar que devem ser consideradas para os arredondamentos: 100 mil, 200 mil, 300 mil, 400 mil etc.;
as dezenas de milhar que devem ser consideradas para os arredondamentos: 10 mil, 20 mil, 30 mil, 40 mil etc.;
as unidades de milhar que devem ser consideradas para os arredondamentos: 1 mil, 2 mil, 3 mil, 4 mil etc.
Atividade 4

Nesta atividade, os estudantes podem observar a utilidade do arredondamento de números “grandes” em uma situação concreta; no caso, a transposição do número de votos de cada candidato da tabela (valores exatos) para o gráfico (valores arredondados). Os arredondamentos são, então, utilizados no cálculo aproximado do “total de votos”.

BNCC em foco:

EF05MA01, EF05MA24; competências específicas 2 e 3

MP062

A Matemática me ajuda a ser

... alguém que compreende as diferenças

Você sabia que existem cães que são treinados para ajudar pessoas com deficiência visual a se locomover? Esses cães são chamados de cães-guia.

Em 25 de abril, é comemorado o Dia Internacional do Cão-Guia. As primeiras notícias sobre as tentativas de treinar cães para auxiliar cegos datam de 1780, na França. No Brasil, existe um projeto desde 2015 para implantar centros de formação de treinadores de cães-guia em todas as regiões do país. Esse projeto é relevante, considerando que há cerca de 7 milhões e 300 mil brasileiros com deficiência visual, de acordo com a Pesquisa Nacional de Saúde de 2013, do IBGE.

O decreto 5.904, de 21 de setembro de 2006, regulamenta a Lei nº 11.126, de 27 de junho de 2005, que assegura “à pessoa com deficiência visual usuária de cão-guia o direito de ingressar e permanecer com o animal nos veículos e nos estabelecimentos públicos e privados de uso coletivo”. Essa lei também define que deficiência visual limita-se à “cegueira e baixa visão”.

Imagem: fotografia de um homem correndo e segurando a coleira de um cachorro grande com pelo bege. Atrás dele há mais pessoas correndo. Fim da imagem.

LEGENDA: Homem com seu cão-guia em Boston, nos Estados Unidos, em 2018. FIM DA LEGENDA.

Em 2021, uma parceria envolvendo a Secretaria Especial do Esporte, do Ministério da Cidadania, o Comitê Paralímpico Brasileiro (CP B) e o Centro de Treinamento e Formação de Cães-Guias do Instituto Federal Catarinense (IFC – Camboriú), permitiu a quatro atletas paralímpicos, com deficiência visual, receberem cães-guias para auxiliá-los nas tarefas do dia a dia.

Os cães-guias possibilitam aos deficientes visuais adquirirem um nível maior de independência. Os animais auxiliam em várias tarefas cotidianas, como atravessar a rua, parar em sinais, evitar obstáculos e encontrar as portas dos estabelecimentos.

A maioria das pessoas não sabe como se comportar ao encontrar um cão-guia. Veja algumas dicas:

Peça autorização ao dono antes de interagir com o cão-guia e evite brincar com ele para não distraí-lo.
Sempre caminhe do lado direito do deficiente visual.
Se encontrá-lo num restaurante, não dê comida ao cão-guia, pois ele tem uma dieta especial para manter sua saúde.
Se estiver com um cão, controle-o para evitar algum acidente com o cão-guia de outra pessoa.

Informações obtidas em: http://fdnc.io/eUn e http://fdnc.io/eUo. Acessos em: 15 fev. 2021.

Imagem: Ilustração. Placa quadrada com a silhueta de uma pessoa andando e segurando uma bengala. Ao redor, pisos táteis. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos

Ler e escrever números naturais.
Ler e interpretar textos com dados numéricos.
Interpretar dados estatísticos apresentados em textos.
A proposta desta dupla de páginas é levar os estudantes a refletirem sobre o que pode ser feito para ajudar pessoas com deficiência a diminuírem as dificuldades no dia a dia.

Você pode explorar a situação propondo uma pesquisa sobre as leis que vigoram em nosso país em relação aos cidadãos com algum tipo de deficiência. Os estudantes devem ser orientados a respeitar as diferenças individuais e a reconhecer que todas as pessoas têm os mesmos direitos. Se julgar conveniente, leve para a sala de aula o Estatuto da Criança e do Adolescente e comente alguns de seus artigos.

BNCC em foco:

EF05MA01, EF05MA24; competências gerais 7 e 10; competências específicas 1 e 2

Sugestão de trabalho interdisciplinar

Aproveite a situação para propor uma pesquisa sobre as principais causas de deficiências visuais, se possível com dados numéricos. Os estudantes podem obter informações sobre o percentual de pessoas com deficiência visual cujas causas sejam decorrentes de doenças (congênitas ou adquiridas) ou de acidentes. Você também pode pedir que pesquisem a respeito de atitudes que reduzam o risco de tais incidências (como prevenção de acidentes) ou, ao contrário, atitudes que agravem doenças ligadas a perdas visuais. O resultado dessas pesquisas pode ser transformado em cartazes para exposição em murais na escola, a fim de levar mais informações à comunidade.

Podem ser desenvolvidos interessantes trabalhos interdisciplinares sobre o tema.

MP063

Tome nota

Em que dia é comemorado o Dia Internacional do Cão-Guia? _____

PROFESSOR
Resposta: Em 25 de abril.

Em que ano foram divulgadas as primeiras notícias sobre as tentativas de treinar cães para auxiliar cegos? _____

PROFESSOR
Resposta: Em 1780.

Quantos cães-guia a parceria do CPB com o IFC disponibilizou para atletas paralímpicos em 2021? _____

PROFESSOR
Resposta: 4

Quantos brasileiros, aproximadamente, têm deficiência visual de acordo com a Pesquisa Nacional de Saúde de 2013? Registre essa quantidade com todos os algarismos.
_____

PROFESSOR
Resposta: Aproximadamente 7.300.000.

Reflita

Como você se sentiria se fosse impedido de entrar em um local ao qual tem o direito de ir?

Em julho de 2019, uma consumidora teve o serviço negado pelo motorista de aplicativo. O condutor alegou que não transportava cachorro e manteve a recusa mesmo diante da afirmação da consumidora de que estava amparada pela lei nº 11.126, de 2005, por se tratar de um cão-guia. A empresa foi notificada pelo Procon-SP.
Fonte dos dados: http://fdnc.io/eUq. Acesso em: 1º mar. 2021.

O que você acha da atitude do motorista de negar a entrada do cão-guia no seu carro?

PROFESSOR
Respostas pessoais.

Imagem: Ilustração. Mão de uma pessoa segurando a coleira de um cachorro grande com pelo bege. Em seguida, placa em um poste, quadrada com a silhueta de uma pessoa segurando a coleira de um cão-guia. Ao fundo, uma casa. Fim da imagem.

MANUAL DO PROFESSOR

Tome nota Atividades 1 a 4

Peça aos estudantes que busquem no texto as informações. Eles podem destacar com lápis de cor os dados que julgarem importantes.

Reflita Atividades 1 e 2

Converse com os estudantes sobre pessoas com algum tipo de deficiência. Pergunte a eles se conhecem alguns obstáculos que essas pessoas enfrentam no dia a dia. Depois, proponha uma reflexão sobre ações que o poder público poderia tomar para melhorar as condições de locomoção e acessibilidade de pessoas com deficiência, assim como atitudes que cada cidadão pode tomar para ajudar essas pessoas em situações cotidianas. Pergunte também se já tiveram de auxiliar pessoas com algum tipo de deficiência em algum momento, como foi e o que fizeram nesses casos. Discuta atitudes de respeito e de solidariedade.

Promova uma discussão com a turma sobre as respostas de cada um para as questões propostas.

BNCC em foco:

EF05MA01; competências gerais 7 e 10; competências específicas 1 e 2

Sugestão para o professor

Vídeo

Thays Martinez. Disponível em: http://fdnc.io/eUp. Acesso em: 3 ago. 2021.

Nesse vídeo, é mostrada uma entrevista com a advogada Thays Martinez, na qual ela fala sobre sua luta pelo direito de os cidadãos com deficiência visual terem acesso a qualquer local público ou privado com seus cães-guia. Deficiente visual desde os 4 anos de idade, a advogada conta alguns detalhes de sua luta e os motivos que a levaram a se graduar em Direito pela Universidade de São Paulo, entre outras coisas.

MP064

Compreender informações

Análise de resultados possíveis

Em um jogo, é a vez de Paulo girar uma roleta dividida em oito partes de mesmo tamanho. Para ganhar, ele precisa que a roleta pare no maior número.

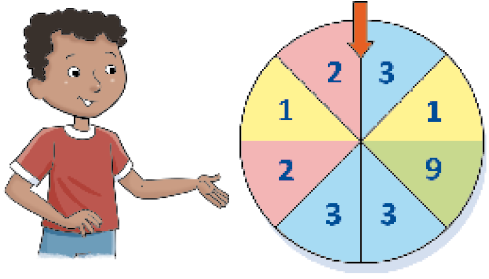
Imagem: Ilustração. Paulo, menino com cabelo encaracolado está com a mão esquerda virada para cima. Ao seu lado há uma roleta colorida com números. No sentido horário: 3 (azul), 1 (amarelo), 9 (verde), 3 (azul), 3 (azul), 2 (vermelho), 1 (amarelo), 2 (vermelho). Há uma seta entre os número 2 (vermelho) e 3 (azul). Fim da imagem.

Quais são os possíveis números em que a roleta pode parar? _____

PROFESSOR
Resposta: 1, 2, 3 e 9

Qual número Paulo deve conseguir para ganhar o jogo? _____

PROFESSOR
Resposta: 9

Todos os números da roleta têm a mesma probabilidade de sair? Por quê?
_____

PROFESSOR
Resposta: Não, porque os números aparecem em quantidades diferentes de partes.

Qual é o resultado mais provável de sair na roleta? Por quê?
_____

PROFESSOR
Resposta: O número 3, porque é o que aparece em mais partes da roleta.

Quantas vezes precisamos girar a roleta para ganhar o jogo?
_____

PROFESSOR
Resposta: Não é possível determinar essa resposta, pois a cada giro não se pode afirmar qual número sairá com certeza, embora já se conheçam todos os possíveis resultados.

Considere o seguinte experimento aleatório: lançar um dado comum (com faces numeradas de 1 a 6) e observar o número que aparece na face que fica voltada para cima. Nesse experimento, cada resultado possível tem a mesma probabilidade de ocorrer, ou seja, é igualmente provável que ocorra como os demais?
_____

PROFESSOR
Resposta: Sim, pois cada número distinto ocorre em uma face (considerando-se que o dado comum seja “honesto”).

MANUAL DO PROFESSOR

Objetivos

Determinar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não.
Identificar eventos em um experimento aleatório e determinar a probabilidade de ocorrência desses eventos.
Atividade 1

Se possível, retrate a situação na sala de aula, para que os estudantes a vivenciem, dando mais significado ao aprendizado.

No item a, espera-se que percebam que os resultados possíveis quando a roleta para são os números que aparecem nela: 1, 2, 3 e 9.

Em uma roda de conversa, discuta os itens b, c, d e e, de modo que os estudantes possam expor o que pensam e confrontem suas hipóteses com as dos colegas. No item c, espera-se que reconheçam que os números não têm a mesma probabilidade de sair, pois aparecem em quantidades diferentes, logo o número 3 é o resultado mais provável. No item e, discuta com eles a impossibilidade de saber, com certeza, o número que sairá na roleta a cada giro.

Atividade 2

Verifique se os estudantes compreenderam também que os resultados favoráveis a certo evento são aqueles entre os possíveis resultados que fazem com que o evento considerado ocorra.

O experimento de lançar um dado comum e observar a face que fica virada para cima já deve ter sido vivido pelos estudantes muitas vezes, principalmente em situações de jogo. Mesmo assim, se possível, traga dados para a sala de aula e proponha essa experimentação.

Espera-se que eles percebam que cada face tem a mesma probabilidade de ocorrer que as demais. Comente que o conjunto formado por todos os resultados possíveis de experimentos aleatórios em que isso ocorre é denominado equiprovável (cada resultado é igualmente provável de ocorrer).

BNCC em foco:

EF05MA22; competência geral 2; competências específicas 4 e 6

MP065

Em uma urna há bolas idênticas numeradas de 1 a 13. Considere o seguinte experimento aleatório: sortear uma bola e observar seu número.
1. Quais são todos os possíveis resultados desse experimento?
  _____
  
  PROFESSOR
  Resposta: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 e 13.
1. Nesse experimento, cada resultado possível tem a mesma probabilidade de ocorrer que os demais?
  _____
  
  PROFESSOR
  Resposta: Sim, pois as bolas são idênticas (exceto pelos números diferentes).
1. Quais são os resultados favoráveis ao evento “sair uma bola com número ímpar”? _____
  
  PROFESSOR
  Resposta: 1, 3, 5, 7, 9, 11 e 13.

Em um saco há 10 bolinhas do mesmo tamanho, de cores diferentes e feitas do mesmo material, conforme mostra a ilustração abaixo.
Considerando que se sorteie uma dessas bolinhas, sem olhar, responda às questões.

Imagem: Ilustração. Um saco transparente e fechado. Dentro há duas bolinhas vermelhas, três azuis e cinco verdes. Fim da imagem.

Que cores podem sair nesse sorteio?
_____

PROFESSOR
Resposta: Vermelho, azul ou verde.

Cada cor tem a mesma probabilidade de sair no sorteio? Por quê?
_____

PROFESSOR
Resposta: Não, porque as quantidades de bolinhas de cada cor são diferentes.

O que é mais provável de ocorrer: sortear uma bolinha vermelha ou uma bolinha verde? Por quê? _____

PROFESSOR
Resposta: É mais provável sortear uma bolinha verde que uma vermelha, porque há mais bolas verdes que vermelhas.

O que tem menor chance de ocorrer: sortear uma bolinha vermelha ou sortear uma bolinha azul? Por quê?
_____

PROFESSOR
Resposta: Sortear uma bolinha vermelha tem menor chance de ocorrer que sortear uma bolinha azul, porque há menos bolas vermelhas que azuis.

Qual é a probabilidade de sortear uma bolinha roxa? Por quê?
_____

PROFESSOR
Resposta: Nenhuma ou zero, ou seja, é de 0 em 10, pois não há bolinhas roxas no saco.

Escreva um evento diferente dos anteriores e peça a um colega que determine a probabilidade de ele ocorrer. _____

PROFESSOR
Resposta: Exemplo de resposta: Evento: “Sair uma bolinha azul”; probabilidade: é $3 décimos$ , ou seja, 3 bolinhas azuis em 10.

MANUAL DO PROFESSOR

Atividade 3

A primeira providência é verificar se os estudantes percebem que há 13 bolas na urna (numeradas de 1 a 13) e que o fato de elas serem idênticas garante que todas as bolas tenham a mesma probabilidade de serem sorteadas.

As questões propostas podem ser realizadas em duplas. A troca de ideias enriquece o aprendizado. Depois, peça a cada dupla que crie outros eventos desse experimento e troque com outra dupla: determina a probabilidade de ocorrência dos eventos que a outra criou. Em seguida, socialize com toda a turma.

Atividade 4

Incentive os estudantes a trocarem ideias com os colegas. Depois de eles responderem aos itens a e b, pergunte: “O conjunto de todos os possíveis resultados desse experimento é equiprovável (apresenta as mesmas probabilidades de acontecer) ou não? Por quê?”. Espera-se que eles percebam que não se trata de um conjunto equiprovável pelo fato de as quantidades de bolinhas de cada cor serem diferentes.

Deixe que discutam os demais itens e verifique quanto eles se apropriaram dos conceitos trabalhados: resultados possíveis de um experimento aleatório, evento, resultados favoráveis a um evento, probabilidade de ocorrência de um evento.

Se necessário, retome na lousa as questões que os estudantes tiveram mais dificuldades para solucionar.

Ainda na atividade 4, comente com os estudantes que sortear uma bolinha roxa é um exemplo do que chamamos de evento impossível, aquele que tem probabilidade zero de ocorrer. Se julgar oportuno, apresente a eles um exemplo de evento certo, aquele que com certeza ocorrerá. Pergunte: “Qual é a probabilidade de sair uma bolinha vermelha ou azul ou verde?”. Espera-se que os estudantes percebam que é $10 décimos$ .
BNCC em foco:

EF05MA22; competência geral 2; competências específicas 4 e 6

MP066

O que você aprendeu

Responda às questões, representando os números somente com algarismos.
1. 25 dezenas de pessoas são quantas pessoas? _____
  
  PROFESSOR
  Resposta: 250 pessoas.
1. 14 centenas de aves são quantas aves? _____
  
  PROFESSOR
  Resposta: 1.400 aves.
1. 40 dezenas de milhar de árvores são quantas árvores? _____
  
  PROFESSOR
  Resposta: 400.000 árvores.
1. 4 milhões de estrelas são quantas estrelas? _____
  
  PROFESSOR
  Resposta: 4.000.000 de estrelas.

Determine, com algarismos e por extenso, o valor do algarismo 3 em cada número.

6.931 _____

PROFESSOR
Resposta: 30; trinta

36.524 _____

PROFESSOR
Resposta: 30.000; trinta mil

26.513 _____

PROFESSOR
Resposta: 3; três

23.001 _____

PROFESSOR
Resposta: 3 000; três mil

326.524 _____

PROFESSOR
Resposta: 300.000; trezentos mil

) 600.310 _____

PROFESSOR
Resposta: 300; trezentos

Ordene os números dos vagões do menor para o maior.

Imagem: Ilustração. Trem de madeira com vagões atrás. Em cada vagão há um número: 856.003; 256.350; 990.009; 856.023; 256.200; 500; 759.000. Fim da imagem.

_____

PROFESSOR

Resposta: 500, 256.200, 256.350, 759.000, 856.003, 856.023, 990.009.

Pedro pensou em um número que:
- está entre 374.000 e 380.000;
- tem o 1 como último algarismo;
- na reta numérica está mais próximo de 374.000 que de 380.000.
  Qual dos números a seguir foi o número em que Pedro pensou?

( ) 379.621

( ) 373.999

( ) 374.261

( ) 378.621

PROFESSOR
Resposta correta: c.

Imagem: Ilustração. Pedro, menino com cabelo castanho e encaracolado está com a mão direita sob o queixo. Acima dele há um balão de pensamento com um ponto de interrogação dentro. Fim da imagem.

MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.

Atividade 1

Esta atividade explora composições diversas de números. Observe o grau de desenvoltura dos estudantes ao decodificarem a informação, o que pode mostrar quanto eles compreenderam as características do sistema de numeração decimal. Amplie a atividade fornecendo outros números por decomposições variadas.

Atividade 2

Aproveite para sugerir que escrevam outros números até a classe dos milhões e registrem o valor posicional de cada um de seus algarismos. Por exemplo, para o número 29.866.154, obtém-se:

29.866.154

4 - 4

5 - 50

1 - 100

6 - 6.000

6 - 60.000

8 - 800.000

9 - 9.000.000

2 - 20.000.000

Atividades como esta permitem retomar o estudo do valor posicional dos algarismos nas diferentes classes do sistema de numeração decimal já estudadas.

Atividade 3

Observe como procedem para comparar e montar a sequência. Promova a socialização das sequências formadas, para que eles discutam possíveis diferenças e exponham suas estratégias.

BNCC em foco:

EF05MA01

Atividade 4

Esta atividade trabalha a comparação entre números e arredondamento. Verifique se os estudantes compreendem todas as condições. Veja, por exemplo, se eles identificam que o último algarismo de um número é o da ordem das unidades.

Os estudantes podem observar que, em todas as alternativas, os números apresentados satisfazem à condição de “estar entre 374.000 e 380.000”, mas o número correspondente à alternativa b pode ser descartado, pois não tem o algarismo das unidades igual a 1, como pedido. Dentre os números restantes, o procurado deve estar mais perto de 374.000 que de 380.000 na reta numérica, ou seja, precisa ser menor que 375.000.

Observando os números disponíveis, verifica-se que o único que atende a essas condições é 374.261, correspondente à alternativa c.

MP067

Avaliação processual

Imagem: Ícone: mental. Fim da imagem.

Observe a tabela e calcule mentalmente o que se pede.

Telespectadores que assistiram ao programa Cante Bem

Tabela: equivalente textual a seguir.

Ano	Número de pessoas
2021	55.845
2022	87.125
2023	56.890

Fonte: Programa Cante Bem (7 jan. 2023).

Qual é o número aproximado de pessoas que assistiram ao programa Cante Bem nesse período de três anos?
_____

PROFESSOR
Exemplo de resposta: Aproximadamente 200.000 pessoas.

O número da senha do diário de Tainá tem seis dígitos sequenciais que não se repetem. O primeiro dígito é 3.
Determine o número dessa senha.

_____

PROFESSOR
Resposta: 345.678

Imagem: Ilustração. Tainá menina ruiva com cabelo comprido está segurando um aparelho eletrônico. Na tela, a informação: DIÁRIO e uma senha com seis dígitos escondidos. Fim da imagem.

Arredonde para a centena de milhar mais próxima de cada número.

216. 314 - _____

PROFESSOR
Resposta: 200.000

98.651 - _____

PROFESSOR
Resposta: 100.000

486.018 - _____

PROFESSOR
Resposta: 500.000

359.123 - _____

PROFESSOR
Resposta: 400.000

142.321 - _____

PROFESSOR
Resposta: 100.000

f) 873.952 - _____

PROFESSOR
Resposta: 900.000

87.265 - _____

PROFESSOR
Resposta: 100 000

h) 349.265 - _____

PROFESSOR
Resposta: 300.000

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.

Reconheço as características do sistema de numeração decimal para escrever e ler números com até 9 algarismos?
Consigo localizar números naturais em retas numéricas?

PROFESSOR
Respostas pessoais.

MANUAL DO PROFESSOR

Atividade 5

Uma possibilidade é arredondar os números apresentados antes de iniciar os cálculos para a dezena de milhar exata mais próxima:

55.845 → 60.000

87.125 → 90.000

56.890 → 60.000

Desse modo, temos:

60.000 + 90.000 + 60.000 = 210.000

Lembre os estudantes de que os arredondamentos podem ser a partir de outras ordens, o que alterará o resultado.

Atividade 6

Esta atividade pode ser feita em duplas para que os estudantes discutam o significado de “dígitos sequenciais” e exponham suas ideias.

Atividade 7

Proponha outros arredondamentos: para a dezena de milhar mais próxima e para a unidade de milhar mais próxima.

Autoavaliação

As duas questões possibilitam aos estudantes avaliarem como estão seus conhecimentos sobre números naturais.

Na primeira questão, é possível mediar o processo de autoavaliação pedindo a eles que elenquem algumas das características do sistema de numeração que auxiliam na leitura e na escrita de números naturais, por exemplo, o agrupamento de 10 em 10, o valor posicional e o reconhecimento dos 10 algarismos.

Na segunda questão, os estudantes são convidados a pensar sobre o uso de retas numéricas como apoio para ordenação ou até mesmo comparação numérica. Caso seja necessário, coloque uma reta numérica na lousa para que eles verifiquem como estão seus conhecimentos.

BNCC em foco:

EF05MA01, EF05MA24

MP068

Comentários para o professor:

Conclusão da Unidade 1

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem	Desempenho	Observação
Consegue fazer leitura, escrita e comparação de números naturais de até 9 ordens?	_____	_____
Representa e localiza números naturais na reta numérica?	_____	_____
Resolve problemas envolvendo medidas de comprimento e de capacidade?	_____	_____
Identifica eventos e analisa todos os resultados possíveis de um evento aleatório?	_____	_____
Interpreta e organiza dados apresentados em textos, tabelas e gráficos?	_____	_____
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?	_____	_____
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?	_____	_____