MP069
Introdução da Unidade 2
Um evento comum e integrante de uma proposta de educação inclusiva, participativa e de preservação da cultura de toda comunidade escolar brasileira, a festa junina, compõe a situação retratada na abertura desta Unidade, que propicia a exploração de objetos de estudo como as quatro operações.
A abordagem norteadora das atividades propostas refere-se à Unidade Temática Números. Nela, estão envolvidos conhecimentos já construídos acerca da adição e da subtração e, também, da multiplicação e da divisão. Assim, retomam-se atividades cujos conhecimentos referem-se àqueles desenvolvidos durante o 4º ano e dizem respeito à resolução e elaboração de problemas com números naturais, envolvendo as operações citadas, por meio de diferentes estratégias, entre elas o cálculo por estimativa, o cálculo mental e os algoritmos, devidamente contextualizadas. Há também atividades que abordam a resolução de problemas que envolvem variação de proporcionalidade direta entre duas ou mais grandezas.
As atividades relacionadas à Probabilidade e estatística estão presentes e ampliam os conhecimentos construídos ao longo do 4º ano sobre a análise de dados apresentados em tabelas e gráficos, conduzindo os estudantes à interpretação de dados e informações mostrados em tabelas de dupla entrada e em gráficos de colunas duplas, com o uso do termo frequência.
Além disso, espera-se que os estudantes adquiram conhecimentos envolvendo a escrita de textos que sintetizem as conclusões advindas da interpretação desses dados. Esses estudos devem favorecer a interpretação e a resolução de situações envolvendo dados de pesquisas sobre conhecimentos previstos para o 6º ano.
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
Competência específica favorecida
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
MP070
UNIDADE 2. As quatro operações

MANUAL DO PROFESSOR
Objetivos da Unidade
- Reconhecer os termos das operações: adição, subtração, multiplicação e divisão.
- Resolver e elaborar problemas de adição e subtração com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
- Resolver e elaborar problemas de multiplicação e divisão com números naturais (com divisor natural e diferente de zero), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
- Explorar sequências numéricas e determinar elementos ausentes.
- Resolver problemas que envolvam variação de proporcionalidade direta entre duas grandezas (de comprimento, de tempo e de capacidade).
- Interpretar dados estatísticos apresentados em tabelas e gráficos.
- Explorar operações aritméticas por meio de uma situação de planejamento financeiro.
- Refletir sobre consumo e planejamento financeiro.
Nesta Unidade, os estudantes voltam a ter contato com as quatro operações já estudadas em anos anteriores – adição, subtração, multiplicação e divisão –, ampliando o uso dos algoritmos usuais, o cálculo por estimativas e o cálculo mental.
Nestas páginas, são apresentadas algumas situações que mobilizam os conhecimentos anteriores dos estudantes sobre as operações de adição, subtração e multiplicação. Dê-lhes um tempo para localizarem na ilustração os dados necessários para a resolução das questões e, a seguir, decidirem que operações conduzirão às respostas.
BNCC em foco:
EF05MA07, EF05MA08, EF05MA12, EF05MA24, EF05MA25
MP071
Boxe complementar
Para refletir...
A escola organizou uma festa junina.
De manhã, foram 1.142 visitantes e à tarde, mais 427. No total, quantas pessoas foram à festa? _____
PROFESSOR
Resposta: 1.569 pessoas.Beatriz foi eleita miss caipirinha. Roberto, que foi eleito mister caipirinha, teve 620 votos a menos que ela. Quantos votos Roberto recebeu?
_____
PROFESSOR
Resposta: 920 votos.A mãe de Francisco fez 50 maçãs do amor e 100 pedaços de bolo. Quanto foi arrecadado com a venda desses doces? _____
PROFESSOR
Resposta: 550 reais.Fim do complemento
MANUAL DO PROFESSOR
Incentive os estudantes a procurarem as personagens Beatriz, Marcos, Roberto e Vanessa na cena.
Para refletir...
Para responder à primeira questão, os estudantes devem observar as informações fornecidas: de manhã, 1.142 pessoas visitaram a festa junina; à tarde, compareceram mais 427 pessoas. Desse modo, para encontrar o total de pessoas que foram à festa, basta adicionar as quantidades de pessoas informadas nos dois períodos:
1.142 + 427 = 1.569
Na segunda questão, os estudantes devem buscar na cena a quantidade de votos que Beatriz recebeu e fazer uma subtração para encontrar a resposta:
1.540 – 620 = 920
Para responder à terceira questão, os estudantes devem buscar os valores unitários de cada doce (maçã do amor e pedaço de bolo) que a mãe de Francisco fez. Como as quantidades de doces (50 e 100) não são pequenas, espera-se que os estudantes utilizem multiplicações para obter a quantia arrecadada por cada tipo de doce. E, ao final, adicionem essas duas quantias. Assim:
- maçã do amor: 50 × 3 = 150
- pedaço de bolo: 100 × 4 = 400
- 150 + 400 = 550 (550 reais)
Socialize as estratégias usadas pelos estudantes para responderem às questões. Momentos como esse contribuem para a aprendizagem, colocando-os em contato com diferentes estratégias.
MP072
Jogo: Mangos!
Material: 2 conjuntos de cartas vermelhas numeradas de 1 a 12, 2 conjuntos de cartas azuis numeradas de 1 a 12, 2 cartas curinga e 30 fichas ou grãos.

Jogadores: 2, 3 ou 4.
Regras:
- Cada jogador recebe 4 fichas que valem 100 mangos cada uma; o restante das fichas fica ao lado e será chamado de “banco”. Todas as cartas coloridas são embaralhadas, e cada jogador recebe 5 delas; o restante das cartas fica virado para baixo, no centro da mesa, formando um único monte para compras.
- Cada jogador, na sua vez, vira a primeira carta do monte para compras e escolhe uma de suas cartas para fazer uma operação. Se a carta escolhida for azul, o jogador deverá fazer uma adição. Se for vermelha, deverá subtrair o menor número do maior. Por exemplo, se virar uma carta com o número 11 (não importa a cor) e o jogador escolher uma carta azul com o número 6, o resultado será 17, pois 11 + 6 = 17. Se a carta do jogador for vermelha com o número 6, o resultado será 5, pois 11 − 6 = 5.
- O jogador que obtiver resultado 0, 12 ou 24 ganhará 100 mangos do banco. Se o resultado for 13, 16 ou 19, o jogador deverá dizer “Mangos!” e pegar 100 mangos de qualquer um de seus adversários.
- As cartas usadas devem ser deixadas de lado. O jogador pega uma nova carta do monte para si, ficando sempre com 5 cartas nas mãos, até que acabem as cartas do monte.
- O curinga substitui qualquer carta, à escolha do jogador, lembrando que os números das cartas vão de 1 a 12.
- O jogo termina quando as cartas do monte de compras acabarem.
- Vence o jogador que tiver juntado a maior quantidade de mangos no fim do jogo.
MANUAL DO PROFESSOR
Objetivo
- Resolver e elaborar problemas de adição e subtração com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
Este é um jogo dinâmico que envolve os estudantes tanto na realização de suas próprias jogadas quanto na verificação do resultado obtido pelos adversários.
À medida que vão, mentalmente, realizando os cálculos, com o objetivo de obter os números 0, 12 ou 24, ou, ainda, 13, 16 ou 19, os estudantes vão memorizando alguns resultados úteis para o cálculo mental em outras situações além do jogo.
Variações
Uma variação desse jogo seria acrescentar outras regras. Por exemplo: caso o jogador obtivesse o número 1 como resultado de uma subtração, ganharia 200 mangos; se ele obtivesse o número 5 (por adição ou subtração), ganharia 300 mangos.
BNCC em foco:
EF05MA07; competência geral 2; competência específica 3
MP073
Questões sobre o jogo
- Quais são as diferentes maneiras de
obter
o resultado 12 para que um jogador ganhe 100 mangos do banco?
_____
PROFESSOR
Exemplo de resposta: 9 + 3.
- Qual é a maior soma possível em uma jogada? E qual é o
menor
resultado possível?
_____
PROFESSOR
Resposta: A maior soma possível é 24; o menor resultado possível é zero.
- Observe a carta que foi virada nesta rodada e responda: quais cartas o jogador precisa ter para ganhar 100 mangos do banco?
_____
PROFESSOR
Resposta: Carta de número 5 na cor azul ou carta de número 7 na cor vermelha.

- Em outra jogada, a carta virada na mesa foi a de
número
6. Quais cartas o jogador precisaria ter para pegar 100 mangos de um adversário?
_____
PROFESSOR
Resposta: Carta de número 7 na cor azul ou carta de número 10 na cor azul.
- Observe as cartas de Paulo e responda às questões.

-
É possível que Paulo consiga pegar 100 mangos de algum de seus adversários? Por quê?
_____
PROFESSOR
Resposta: Não.PROFESSOR
Resposta possível: Todas as cartas de Paulo são vermelhas, logo, ele deve efetuar uma subtração cujo resultado seja menor do que 13.
-
Que carta deverá ser virada para que Paulo ganhe 100 mangos do banco?
_____
PROFESSOR
Exemplo de resposta: Paulo pode virar uma carta com o número 11.
MANUAL DO PROFESSOR
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões.
Na questão 1, os estudantes devem perceber que podem obter 12 com as adições: 11 + 1; 10 + 2; 9 + 3; 8 + 4; 7 + 5; 6 + 6.
Na questão 2, espera-se que os estudantes percebam que a maior soma possível é 24 (obtida com 12 na carta virada e com 12 em uma carta azul, ou um curinga), e que o menor resultado possível é zero (obtido com uma carta vermelha com o mesmo número da carta virada, ou um curinga).
Na questão 3, os estudantes devem observar na imagem a carta que foi virada, que tem o número 7. Como, para ganhar 100 mangos, é preciso obter resultado 0, 12 ou 24, os estudantes devem perceber que o jogador precisa de uma carta azul com o número 5 ou de uma carta vermelha com o número 7, ou um curinga.
Na questão 4, os estudantes devem compreender que, para pegar 100 mangos de um adversário, devem obter um resultado igual a 13, 16 ou 19. Como na carta virada há o número 6, o jogador precisa de uma carta azul com o número 7 ou de uma carta azul com o número 10, ou um curinga. Nenhuma carta vermelha serve.
Na questão 5, no item a, um exemplo de explicação é: “Não, porque, com essas cartas, é possível apenas fazer subtrações, e não há número algum que possa ser subtraído das cartas de 1 a 12 cujo resultado seja 13, 16 ou 19. No item b, como as cartas de Paulo são vermelhas, ele deverá fazer subtrações. Então, para ganhar 100 mangos do banco, Paulo deverá virar uma carta comum dos seguintes números: 2, 4, 5, 8 ou 11.
BNCC em foco:
EF05MA07; competência geral 2; competência específica 3
MP074
Adição
- A tabela a seguir mostra a quantidade de veículos que passaram por uma rodovia nas primeiras duas horas de um dia.
Veículos por período
Tabela: equivalente textual a seguir.
|
Período |
Quantidade de veículos |
|---|---|
|
1ª hora |
13.416 |
|
2ª hora |
15.962 |
Fonte: Administradora da rodovia (2 jan. 2023).
- Ao todo, quantos veículos passaram por essa rodovia nas duas primeiras horas desse dia?
Para obter o total de veículos que passaram por essa rodovia nas duas primeiras horas desse dia, precisamos calcular o resultado da adição de 13.416 com 15.962. Veja como Ana efetuou essa adição.
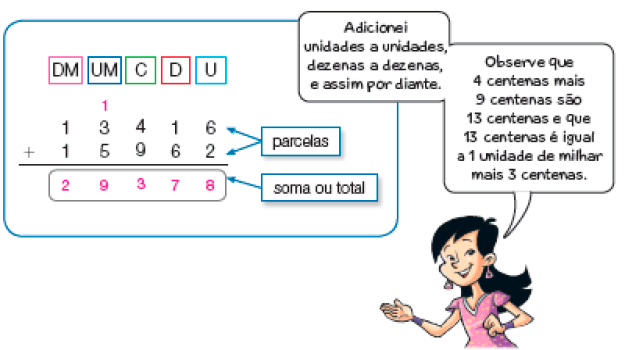
Ao todo, _____ veículos passaram por essa rodovia nas duas primeiras horas desse dia.
PROFESSOR
Resposta: 29.378- Se na 3ª hora desse dia o
número
de veículos dobrar em relação à
1ª
hora, quantos veículos terão passado pela rodovia nessas três horas?
_____
PROFESSOR
Resposta: 56.210 veículos.
PROFESSOR
Exemplos de cálculo:

MANUAL DO PROFESSOR
Objetivos
- Reconhecer os termos da operação de adição.
- Resolver problemas de adição com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
- Interpretar dados estatísticos apresentados em tabela.
As atividades destas páginas oferecem a oportunidade de identificar como os estudantes efetuam os cálculos de adição e socializam diferentes estratégias de resolução. Ao longo de todo o Ensino Fundamental, são propostos problemas que podem ser resolvidos por meio de uma ou mais adições com números naturais. Os enunciados vão se tornando mais complexos, abrangendo diferentes situações e números maiores que os usados anteriormente. Nessa etapa da escolarização, espera-se que os estudantes já tenham uma boa compreensão da estrutura do nosso sistema de numeração, pois os reagrupamentos são realizados com base nessa estrutura.
Atividade 1
Retome ou apresente, caso os estudantes ainda não conheçam, os termos que participam de uma adição e seu resultado. Utilize sempre a nomenclatura desses termos, para que aos poucos eles sejam incorporados.
Para ampliar a atividade, proponha outras adições com números da classe dos milhares, para os estudantes resolverem pelo algoritmo usual.
Por exemplo:
- 34.338 + 28.645 (62.983)
- 34.857 + 21.695 (56.552)
- 180.629 + 356.864 (537.493)
BNCC em foco:
EF05MA07, EF05MA24
Sugestão de atividade
Quadrado mágico
Proponha aos estudantes que disponham os números de 1 a 9 no quadrado ao lado, de tal modo que a soma em cada linha, em cada coluna e em cada diagonal seja sempre 15.
Apresentamos abaixo um exemplo de resposta.
Tabela: equivalente textual a seguir.
2
7
6
9
5
1
4
3
8
CRÉDITO: ADILSON SECCO
MP075



- Em uma calculadora, digite o
número
1.245. Depois, usando apenas a tecla
 e as teclas de números, obtenha o
número
4.587.
e as teclas de números, obtenha o
número
4.587. - Converse com o professor e os colegas sobre o modo como você pensou para
obter
esse número.
PROFESSOR
Resposta: +3.342.PROFESSOR
Respostas pessoais.
- Converse com o professor e os colegas sobre o modo como você pensou para
obter
esse número.

- Faça um cálculo aproximado e marque com um
X
a alternativa correta.
João tinha 1.900 reais e recebeu mais 790 reais. Com quantos reais ele ficou?
( ) Menos de 2.100 reais.
( ) Entre 2.100 e 2.500 reais.
( ) Mais de 2.600 reais.
PROFESSOR
Resposta correta: Mais de 2.600 reais.
- Descubra o algarismo que corresponde a cada símbolo e registre-os.

 =
_____
=
_____
PROFESSOR
Resposta: 9
 =
_____
=
_____
PROFESSOR
Resposta: 1
 =
_____
=
_____
PROFESSOR
Resposta: 7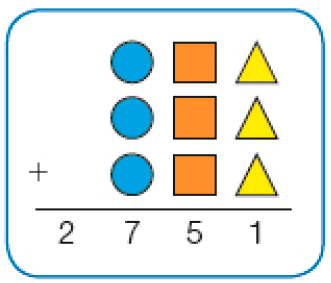
- Observe os dois cálculos e descubra qual está correto.

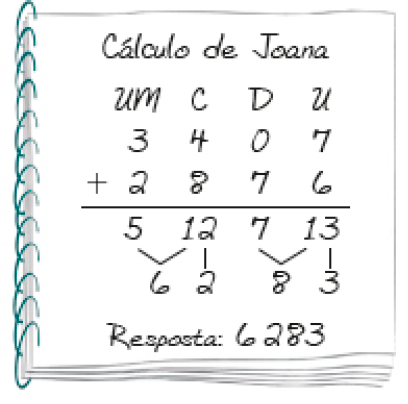
O cálculo de _____ está correto.
PROFESSOR
Resposta: Joana


- Converse com um
colega
sobre como Gilberto e Joana pensaram para fazer o cálculo.
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 2
A calculadora pode e deve ser usada em benefício do aprendizado, até mesmo em associação ao cálculo mental. Esta atividade é um desafio aritmético a ser resolvido na calculadora.
Atividade 3
Para fazer o cálculo aproximado, os estudantes podem recorrer a diferentes estratégias: observar que, para obter 2.100 reais a partir de 1.900 reais, faltam 200 reais; como João recebeu mais de 200 reais (790 reais), podem concluir que ele ficou com mais de 2.100 reais; observar que 1.900 reais é um valor que está próximo de 2.000 reais e que 790 reais está próximo de 800 reais, de modo que as duas quantias, juntas, totalizam aproximadamente 2.800 reais, valor superior a 2.600 reais.
Atividade 4
Os estudantes podem começar observando que o resultado da adição das unidades representadas pelas figuras amarelas é igual a um número cujo algarismo das unidades é igual a 1; por tentativas, ou por recorrência à memória, eles devem concluir que o triângulo corresponde ao algarismo 7, pois 7 + 7 + 7 = 21. Como as 2 dezenas de 21 são adicionadas às demais dezenas, concluem que o resultado da adição de 2 aos valores correspondentes das três figuras laranja é igual ao algarismo 5; isso só é possível se o valor correspondente à cada figura laranja for 1. A soma dos valores das três figuras azuis é 27, o que permite concluir que cada círculo corresponde ao algarismo 9, pois 9 + 9 + 9 = 27.
Ao pensar nos números que podem produzir a configuração apresentada, os estudantes exploram as regularidades do sistema de numeração decimal.
Para determinar o valor de cada figura, eles devem aplicar os conhecimentos que já têm a respeito da adição.
BNCC em foco:
EF05MA07
Atividade 5
Espera-se que os estudantes percebam que Gilberto não fez os reagrupamentos necessários. No caso do cálculo de Joana, espera-se que eles percebam que, embora ela tenha feito os registros como Gilberto, em seguida fez os reagrupamentos necessários. Assim, o cálculo correto é o de Joana.
Explicite aos estudantes os reagrupamentos feitos por Joana:
- 13 unidades correspondem a 1 dezena e 3 unidades, por isso ela reagrupou essa dezena com as 7 dezenas já determinadas, formando 8 dezenas;
- o mesmo raciocínio foi empregado para as centenas: como 12 centenas correspondem a 1 unidade de milhar e 2 centenas, ela reagrupou essa unidade de milhar com as 5 unidades de milhar já existentes, ficando com 6 unidades de milhar.
MP076
Subtração
- Adílson queria comprar um trator agrícola usado para o seu sítio, e o modelo de que gostou custava 49.468 reais. Depois de algumas pesquisas, Adílson comprou o trator em uma promoção por 46.734 reais.

- De quantos reais foi a economia de Adílson?
Vamos calcular o valor que Adílson economizou subtraindo 46.734 de 49.468. Complete o cálculo.
A economia de Adílson foi de _____ reais.
PROFESSOR
Resposta: 2.734- Se a economia de Adílson tivesse sido de 4.362 reais, qual seria o valor de compra desse trator?
_____
PROFESSOR
Resposta: 45.106 reais.
PROFESSOR
Resposta: Exemplo de cáluculo:



- Digite o
número
12.500 em uma calculadora. Depois, usando apenas as teclas de números e a tecla
 , faça aparecer no visor o
número
1.678.
, faça aparecer no visor o
número
1.678. PROFESSOR
Resposta: −10.822- Converse com o professor e os colegas sobre como você pensou para resolver esse problema.
PROFESSOR
Respostas pessoais.
- Converse com o professor e os colegas sobre como você pensou para resolver esse problema.
MANUAL DO PROFESSOR
Objetivos
- Reconhecer os termos da operação de subtração.
- Resolver problemas de subtração com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
- Interpretar dados estatísticos apresentados em gráfico de barras.
O objetivo das atividades destas páginas é retomar conceitos e procedimentos relacionados à subtração, com enunciados mais complexos e números de ordens de grandeza maiores que os trabalhados em anos anteriores. Os estudantes devem ser incentivados a fazer os cálculos por estratégias variadas.
Atividade 1
Retome ou apresente, caso os estudantes ainda não conheçam, os termos de uma subtração e seu resultado.
Antes que os estudantes realizem os cálculos pelo algoritmo usual, peça que estimem os resultados.
Lembre-os de que cada unidade de uma ordem pode ser trocada por 10 unidades da ordem imediatamente inferior. Por exemplo: 1 dezena por 10 unidades, 1 centena por 10 dezenas, 1 unidade de milhar por 10 centenas, 1 dezena de milhar por 10 unidades de milhar, e assim por diante.
Atividade 2
Esta atividade apresenta outro momento de exploração da calculadora. Sempre que possível, leve calculadoras para a sala de aula (ou peça aos estudantes que levem) para explorarem atividades desse tipo nas aulas que tratam das operações.
Exemplo de resposta: Subtraí 10.000 de 12.500 e obtive 2.500 como resto. Depois, subtraí 800, obtendo um novo resto de 1.700. Então subtraí 22, e o resto foi 1.678.
BNCC em foco:
EF05MA07
MP077

- Faça um cálculo aproximado e marque com um
X
a alternativa correta.
Sabrina é nadadora de provas de médias distâncias. Na segunda etapa de uma competição, ela nadou 2.008 metros e, assim, completou os 3.108 metros da prova.
- Qual foi a distância, em metro, da primeira etapa dessa prova?
( ) Menos de 800 metros.
( ) Entre 800 e 900 metros.
( ) Entre 1.000 e 1.200 metros.
PROFESSOR
Resposta correta: Entre 1.000 e 1.200 metros.

- Uma editora levou para uma feira 2.150 livros, dos quais 1.235 foram vendidos nas duas primeiras horas.
- Os livros vendidos nas duas primeiras horas representam mais ou menos da metade da quantidade total de livros que a editora levou para essa feira?
_____
PROFESSOR
Resposta: Mais da metade.
- Se todos os livros dessa editora foram vendidos, quantos foram vendidos após as duas primeiras horas?
_____
PROFESSOR
Resposta: 915 livros.
- Os livros vendidos nas duas primeiras horas representam mais ou menos da metade da quantidade total de livros que a editora levou para essa feira?
- Observe o gráfico abaixo, que mostra o número de internações em um hospital municipal no período de 2020 a 2022. Depois, responda às questões.
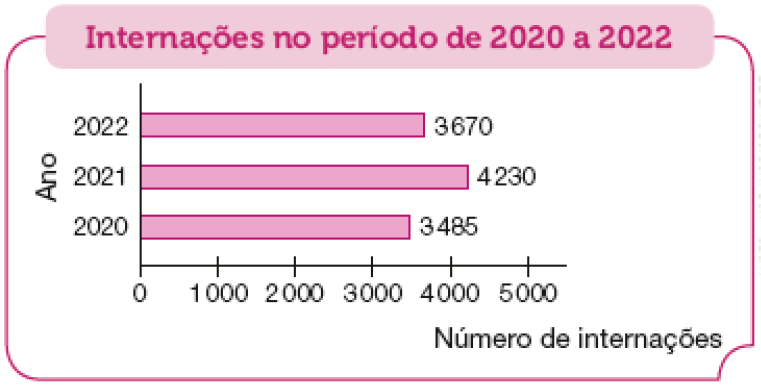
Fonte: Administração do hospital (2022).
- Em qual período houve diminuição do
número
de internações?
_____
PROFESSOR
Resposta: De 2021 para 2022.
- De quantas internações foi essa diminuição?
_____
PROFESSOR
Resposta: A diminuição foi de 560 internações.
- Qual foi o
número
total de internações nesses três anos?
_____
PROFESSOR
Resposta: 11.385 internações.
MANUAL DO PROFESSOR
Atividade 3
Para realizar a estimativa solicitada, os estudantes podem raciocinar assim:
- Se o percurso fosse de 3.008 metros, significaria que Sabrina tinha percorrido 1.000 metros na primeira etapa, pois: 1.000 + 2.008 = 3.008.
- Como o percurso foi de 3.108 metros, maior que 3.008 metros, pode-se concluir que Sabrina tinha nadado mais de 1.000 metros para completar 3.108 metros.
Atividade 4
No item a, se necessário, retome a noção de metade. Verifique que estratégias os estudantes utilizam para fazer a comparação com a metade.
- Eles podem decompor 2.150 em suas ordens para obter a metade: 2.150 = 2.000 + 100 + 50. Então, a metade dessa quantidade é: 1.000 + 50 + 25= 1.075.
- Eles podem decompor 2.150 em duas parcelas iguais: 2.150 = 1.075 + 1.075, ou seja, a metade de 2.150 é 1.075.
- Eles podem subtrair 1 235 de 2 150 para observar se obtêm um valor igual a 1.235: 150 − 1.235 = 915.
- Desse modo, podem concluir que 1.235 é mais da metade de 2.150.
Há outras maneiras. Socialize com a turma os procedimentos utilizados.
No item b, os estudantes devem verificar quantos livros ainda há para vender após as duas primeiras horas (2.150 − 1.235 =.915).
Assim, podem concluir que após as duas primeiras horas foram vendidos 915 livros (o restante do que havia sido levado).
Atividade 5
Nesta atividade, os estudantes precisam ler os dados representados em um gráfico de barras, em que cada barra representa o número de internações realizadas em cada ano em um hospital. Depois da resolução, peça que elaborem outra questão com base nos dados do gráfico, para que um colega a responda.
BNCC em foco:
EF05MA07, EF05MA24
MP078
Estratégias de cálculo
- Observe o esquema abaixo e faça o que se pede.
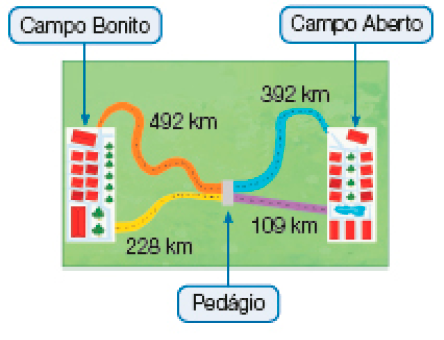

- Descubra, sem fazer cálculos, o caminho mais curto para ir de Campo Bonito a Campo Aberto. Explique como você pensou para escolher esse caminho.
PROFESSOR
Resposta: Caminho amarelo e roxo.
- Calcule, aproximadamente, a distância, em quilômetro, do caminho mais curto.
_____
PROFESSOR
Exemplo de resposta: 340 km

- Leia o diálogo e responda à questão.
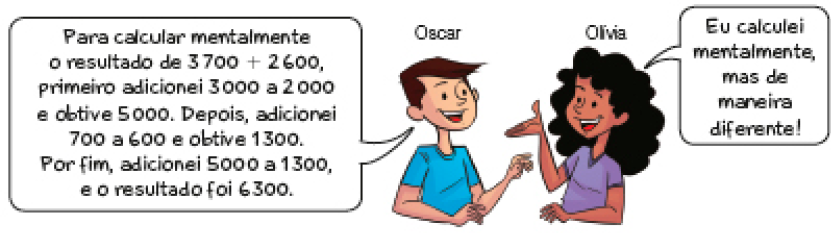
- De que maneira Olívia pode ter calculado mentalmente o resultado dessa adição?
_____
PROFESSOR
Exemplo de resposta: Primeiro ela pode ter adicionado 3.700 a 3.000, obtendo 6.700. Como adicionou 3.000 em vez de 2.600, ela deve subtrair 400 de 6.700, encontrando o resultado .300.


- Calcule mentalmente o resultado de cada operação. Depois, explique ao professor e aos colegas que estratégias você utilizou para efetuar esses cálculos.
PROFESSOR
Respostas pessoais.
- 15 + 3 + 17 =
_____
PROFESSOR
Resposta: 35
- 35 + 12 + 15 =
_____
PROFESSOR
Resposta: 62
- 180 + 420 + 15 =
_____
PROFESSOR
Resposta: 615
- 1.250 + 260 + 540 =
_____
PROFESSOR
Resposta: 2.050
MANUAL DO PROFESSOR
Objetivo
- Resolver e elaborar problemas de adição e subtração com números naturais, utilizando cálculo por estimativa e cálculo mental.
Como os procedimentos de cálculo não devem ser limitados aos cálculos escritos e exatos, o objetivo destas páginas é incentivar também a realização de cálculos mentais e estimativas, tanto em adições quanto em subtrações.
Atividade 1
Os estudantes podem observar na ilustração que os comprimentos indicados nos caminhos amarelo e roxo são menores do que os indicados nos caminhos laranja e azul e, assim, concluir que a soma dos dois comprimentos menores será menor que a soma dos comprimentos maiores.
Atividade 2
Organize os estudantes em duplas. Verifique se eles apresentam outras maneiras de calcular mentalmente o resultado de 3.700 + 2.600 e valide as estratégias de cálculo apresentadas.
Ao buscar estratégias pessoais ou analisar as estratégias de outros, os estudantes podem ampliar o repertório de estratégias de cálculo mental e de estimativas. As aproximações e os arredondamentos trabalhados em momentos anteriores também contribuem para a realização dos cálculos solicitados.
Atividade 3
Promova uma roda de conversa para os estudantes compartilharem as estratégias usadas. Uma possibilidade é formar dezenas ou centenas inteiras para calcular o resultado das operações apresentadas. Observe se eles são capazes de adicionar as parcelas em uma ordem diferente das que foram apresentadas. Por exemplo, no item a, 15 + 3 + 17, os estudantes podem adicionar 3 a 17 para obter 20 e então adicionar 15 para obter 35 (em vez de adicionar 15 a 3, obtendo 18, e adicionando a 17 para chegar a 35).
É importante insistir em que os procedimentos de cálculo mental sejam baseados nas propriedades aritméticas. Em hipótese alguma o cálculo mental deve ser entendido como “algoritmo na cabeça”.
Por isso é fundamental oferecer aos estudantes várias situações que favoreçam a busca e a escolha de estratégias pessoais, assim como oportunidades de discussão e trocas de ideias. Então, não se deve ensinar estratégias. Somente produzindo as próprias estratégias de cálculo é que os estudantes conseguem atribuir significado a esses cálculos.
BNCC em foco:
EF05MA07
MP079

- Faça cálculos aproximados e responda às questões.

- Quanto Roberto pagará, aproximadamente, se comprar o computador e a televisão?
_____
PROFESSOR
Exemplo de resposta: Aproximadamente, 2.300 reais.
- Se Ana comprar os três produtos da promoção, quanto ela pagará aproximadamente?
_____
PROFESSOR
Exemplo de resposta: Aproximadamente, 3.500 reais.
- Tatiana quer comprar dois produtos da promoção pagando o mínimo possível. Quais
devem
ser esses produtos? Quanto, aproximadamente, Tatiana pagará?
_____
PROFESSOR
Resposta: A geladeira e a televisão; Tatiana pagará, aproximadamente, 2 000 reais.


- Elabore um problema que possa ser resolvido por uma adição ou por uma subtração, usando estratégias de cálculo mental. Então, proponha a um colega que o resolva. Depois, conversem sobre a estratégia de resolução usada por seu colega e a pensada por você.
PROFESSOR
Resposta pessoal.Boxe complementar:
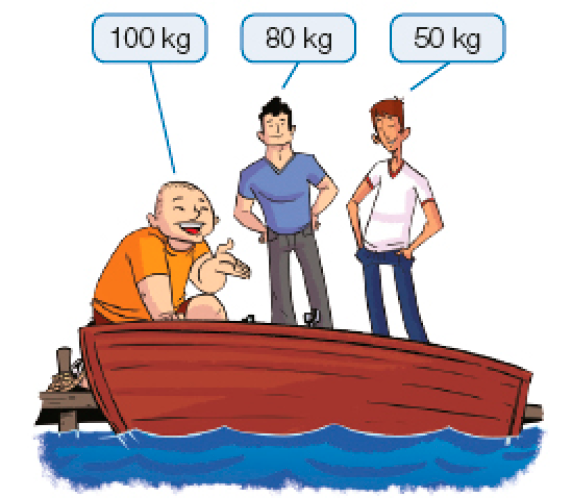
Desafio
Três amigos vão acampar. Eles precisam atravessar um rio com um barco que suporta, no máximo, 140 kg de carga. Os amigos têm 50 kg, 80 kg e 100 kg cada um. Como eles podem fazer a travessia com o menor número possível de viagens?
CRÉDITO: ILUSTRAÇÕES: RONALDO BARATA
PROFESSOR
Resposta: Fazendo 5 viagens.Fim do complemento.
Boxe complementar:
Dica
- Lembre-se de que o barco precisa de, pelo menos, 1 pessoa para levá-lo de uma margem a outra do rio.
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 4
Oriente os estudantes a observarem a ordem de grandeza dos números envolvidos para então escolherem a melhor estratégia de arredondamento.
No item b, é provável que arredondemos números para a centena mais próxima, ordem mais alta do menor número, correspondente ao preço da televisão.
Atividade 5
Depois de os estudantes trocarem e resolverem os problemas, peça a cada um que apresente na lousa a resolução e a estratégia empregada para que os demais façam a validação, sob sua orientação.
Desafio
Eis uma adaptação de um problema clássico da Matemática. Para resolvê-lo, é preciso observar quais combinações podem ser feitas, uma vez que a soma das massas não pode ultrapassar 140 kg. Muitos estudantes observarão que o homem de 100 kg deve ficar sozinho no barco, pois não poderá ser transportado com nenhum dos outros dois, que têm 50 kg e 80 kg. O desafio é, portanto, organizar as viagens para que o barco possa ir e voltar de uma margem à outra. É natural que eles tentem fazer com que o homem de 100 kg seja o primeiro a chegar ao outro lado do rio. Devem observar, no entanto, que não é uma boa opção, uma vez que, se na primeira viagem o barco atravessar o rio com apenas um homem, esse mesmo homem precisará levar o barco para os outros dois. Assim, devem perceber que a 1ª viagem será com os homens de 50 kg e 80 kg. O retorno à margem de partida pode ser com qualquer deles, desde que este fique na margem de partida e o barco retorne somente com o de 100 kg. Finalmente, o homem que, após a 1ª travessia, ficou aguardando, agora deverá voltar e buscar o amigo.
Então, a quantidade mínima de viagens necessárias será 5.
A descrição das 5 viagens (menor quantidade possível):
1ª viagem: vão os homens de 50 kg e 80 kg; 2ª viagem: volta o homem de 80 kg; 3ª viagem: vai o homem de 100 kg; 4ª viagem: volta o homem de 50 kg; 5ª viagem: vão os homens de 50 kg e 80 kg; ou, então,
1ª viagem: vão os homens de 50 kg e 80 kg; 2ª viagem: volta o homem de 50 kg; 3ª viagem: vai o homem de 100 kg; 4ª viagem: volta o homem de 80 kg; 5ª viagem: vão os homens de 50 kg e 80 kg.
BNCC em foco:
EF05MA07
MP080
Multiplicação
- Maurício trabalha como guia em um parque turístico brasileiro. Nas visitas guiadas por ele, as turmas são compostas de 14 pessoas. No último ano, ele realizou 142 visitas guiadas. Quantas pessoas foram guiadas por Maurício nesse último ano? Complete o cálculo.
- Primeiro, calculamos 4 vezes 142. 4 vezes 2 unidades são 8 unidades. 4 vezes 4 dezenas são 16 dezenas ou 1 centena e 6 dezenas. 4 vezes 1 centena são 4 centenas.
- Depois, calculamos 10 vezes 142. 10 vezes 2 unidades são 20 unidades ou 2 dezenas. 10 vezes 4 dezenas são 40 dezenas ou 4 centenas. 10 vezes 1 centena são 10 centenas ou 1 unidade de milhar.
- Finalmente, adicionamos os resultados de 4 × 142 e 10 × 142.
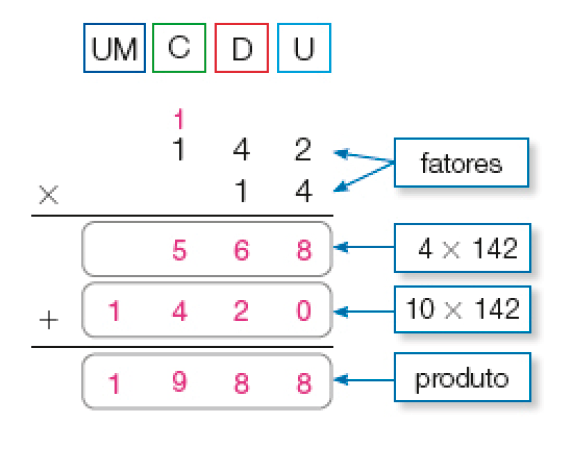
Nesse último ano, _____ pessoas foram guiadas por Maurício.
PROFESSOR
Resposta: 1.988- Calcule o resultado em cada caso.
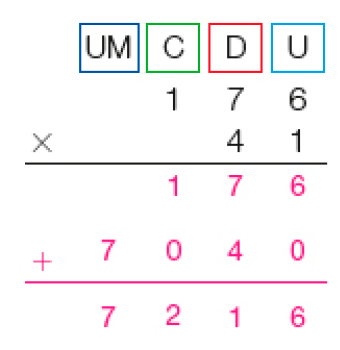
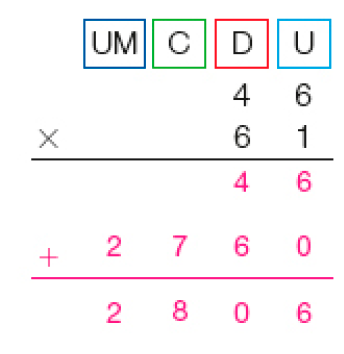
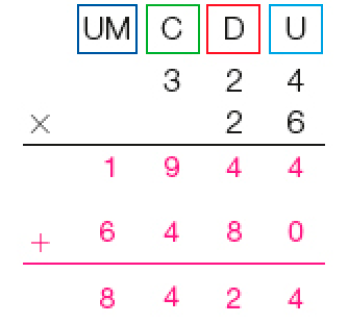
MANUAL DO PROFESSOR
Objetivos
- Reconhecer os termos da operação de multiplicação.
- Resolver e elaborar problemas de multiplicação com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
As atividades destas páginas buscam retomar e ampliar o algoritmo usual da multiplicação com números de 2 e de 3 algarismos.
Atividade 1
Apresente os termos da multiplicação e seu resultado. Sempre que possível, utilize a nomenclatura desses termos para que os estudantes possam, aos poucos, apropriar-se deles.
Reproduza na lousa todas as etapas do algoritmo usual apresentado nesta atividade, para que os estudantes possam acompanhar passo a passo.
Atividade 2
Aproveite esta atividade para observar o grau de desenvoltura dos estudantes com o algoritmo usual da multiplicação que envolva fatores de 2 ou 3 algarismos.
BNCC em foco:
EF05MA08
Sugestão de leitura para o professor
Artigo
MAGINA, Sandra; SANTOS, Aparecido dos; MERLINI, Vera. Comparação multiplicativa: a força que a expressão exerce na escolha das estratégias de resolução dos estudantes. Disponível em:
https://xiii.ciaem-redumate.org/index.php/xiii_ciaem/xiii_ciaem/paper/viewFile/448/337 . Acesso em: 29 mar. 2021.
O artigo apresenta dados de uma pesquisa realizada com estudantes de 3º e 5º anos a respeito das estratégias utilizadas em problemas do campo multiplicativo. Os autores enfatizam a importância das consignas e a influência de algumas expressões na escolha das estratégias de resolução dos estudantes. Esses estudos auxiliam a prática na formulação de novas situações-problema e na compreensão das diferentes ideias envolvidas na multiplicação e na divisão.
MP081
- Luana e Vítor querem comprar a mesa e as 4 cadeiras mostradas na ilustração abaixo.
Veja os cálculos aproximados que eles fizeram do preço total a ser pago pela mesa com as cadeiras.

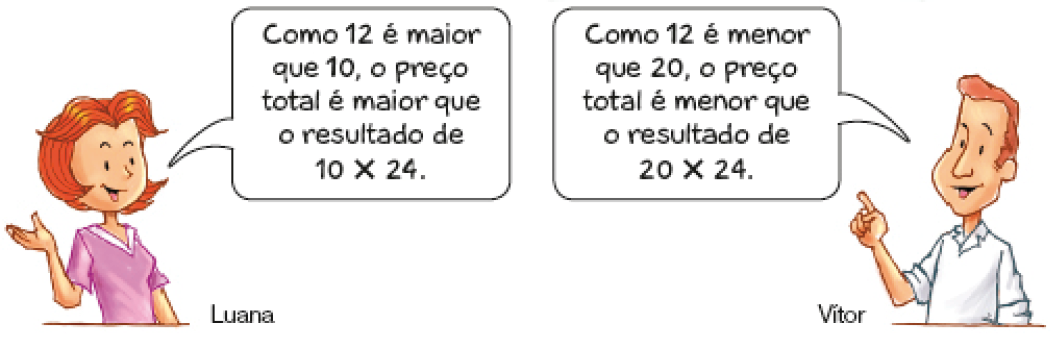

- Qual é o resultado do cálculo de Luana? E o de Vítor?
_____
PROFESSOR
Resposta: O preço é maior que R$ 240,00; o preço é menor que R$ 480,00.
- Qual desses cálculos você acha que está mais próximo do valor total a ser pago? Justifique sua resposta.
_____
PROFESSOR
Atenção professor: Espera-se que o estudante perceba que 12 está mais próximo de 10 que de 20, portanto, o cálculo de Luana estará mais próximo do valor a ser pago. Fim da observação.
- Qual é o
preço
total da mesa com as cadeiras?
_____
PROFESSOR
Resposta: R$ 288,00PROFESSOR
Exemplos de cálculo:PROFESSOR
10 × 24 = 240PROFESSOR
2 × 24 = 48PROFESSOR
240 + 48 = 288

- Giovana queria calcular o resultado da multiplicação 18 × 32, mas a tecla
 de sua calculadora estava quebrada. Veja as teclas que ela apertou para resolver o problema.
de sua calculadora estava quebrada. Veja as teclas que ela apertou para resolver o problema.

- Qual foi o resultado encontrado por Giovana? Compare esse
número
com o resultado de 18 × 32.
_____
PROFESSOR
Resposta: 576; os resultados são iguais.

- Explique a um
colega
o raciocínio que Giovana utilizou.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
No item a, os estudantes devem verificar que o cálculo de Luana resulta em 240 reais e o cálculo de Vítor resulta em 480 reais.
No item b, espera-se que os estudantes percebam que 12 está mais próximo de 10 do que de 20; portanto, o cálculo de Luana está mais próximo do valor real a ser pago do que o cálculo de Vítor.
Verifique as estratégias utilizadas pelos estudantes ao responderem o item c, socialize-as e valide-as com a turma.
Atividade 4
Antes de os estudantes realizarem o item a, pode-se propor que realizem a multiplicação 18 × 32 pelo algoritmo usual.
Explore a situação perguntando: “De que outra maneira Giovana poderia ter resolvido esse problema?”. Outra maneira possível seria fazer a multiplicação 20 × 32 e depois subtrair 32 duas vezes.
No item b, espera-se que os estudantes percebam que, ao calcular o resultado de 19 × 32, são acrescentadas 32 unidades ao resultado que seria obtido na multiplicação 18 × 32. Por isso, Giovana subtraiu 32 ao final para compensar esse acréscimo.
BNCC em foco:
EF05MA08
MP082
- Um avião tem capacidade para transportar 174 passageiros a cada voo. Quantos passageiros, no máximo, ele pode transportar em 123 voos?
PROFESSOR
Resposta: Exemplo de cálculo: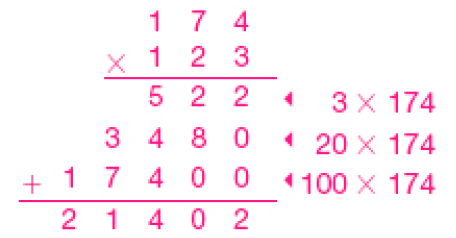
O avião pode transportar, no máximo, _____ passageiros nesses voos.
PROFESSOR
Resposta: 21.402- Complete o texto a seguir, tornando-o um problema que possa ser resolvido por meio de uma multiplicação.
PROFESSOR
Respostas pessoais.
Firmino comprou um _____ e irá pagá-lo em _____ parcelas de _____ reais.
Pergunta: _____?
Resposta: _____

- Depois, troque de livro com um colega para que ele resolva o problema que você elaborou.
- Observe o que Lucas está dizendo e faça o que se pede.

- Escreva a multiplicação em que Lucas pensou.
_____
PROFESSOR
Resposta: 2 × 10 = 20 ou 10 × 2 = 20


- Veja como Cátia resolveu mentalmente a operação 19 × 5:
19 × 5 = 50 + 45 = 95
- Troque ideias com um
colega
sobre a estratégia usada por Cátia.
PROFESSOR
Respostas pessoais.
- Troque ideias com um
colega
sobre a estratégia usada por Cátia.
MANUAL DO PROFESSOR
Atividade 5
Depois de os estudantes resolverem a atividade, peça que discutam com os colegas outro modo de calcular, expondo suas opiniões. Algumas vezes, é difícil para eles expressarem o raciocínio empregado em um cálculo. Por isso, devem ser incentivados a exporem suas ideias e a conhecerem outras possibilidades de resolução. Um cálculo possível é:
- como 174 = 100 + 70 + 4, calculamos 123 × 100 = 12.300; 123 × 70 = 8.610 e 123 × 4 = 492; depois, adicionamos esses produtos (12.300 + 8.610 + 492), obtendo 21.402.
Atividade 6
Os estudantes devem considerar uma mercadoria e um valor próximo ao preço real para determinar a quantidade de parcelas e seu valor. Ao elaborar a pergunta, eles devem considerar que a multiplicação será usada para respondê-la. Aproveite o momento para conversar sobre os diferentes problemas elaborados e as estratégias usadas na resolução.
Atividade 7
Se julgar necessário, retome os conceitos de par e ímpar. Os estudantes podem resolver por tentativas, mas incentive-os a organizarem algumas hipóteses sobre os fatores:
- Os fatores podem ser maiores que 20? Por quê? (Não, pois o produto é 20.)
- Procure duplas de números naturais que multiplicados resultem 20. (Possibilidades: 1 e 20, 2 e 10, 4 e 5.)
- Quais dessas duplas são formadas por dois números pares? (Apenas 2 e 10.)
Assim, os estudantes podem concluir que os fatores são 2 e 10 e compor: 2 × 10 = 20 ou 10 × 2 =20.
Atividade 8
Veja se os estudantes entenderam a estratégia usada. Permita que troquem ideias sobre isso e, se julgar conveniente, proponha outras multiplicações para que resolvam mentalmente.
BNCC em foco:
EF05MA08
MP083
Divisão
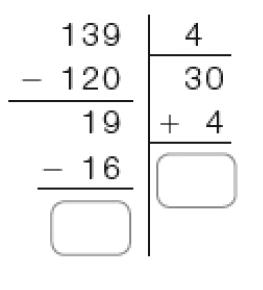
- Veja duas maneiras de calcular o resultado de 139 ÷ 4.
Cálculo por meio de estimativas

PROFESSOR
Resposta: 120; 34; 3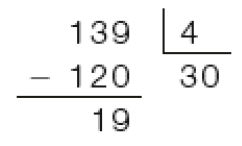
PROFESSOR
Resposta: 3; 34.Cálculo com o algoritmo usual
Como a divisão de 1 centena por 4 não resulta em centena, colocamos zero no quociente e dividimos 13 dezenas por 4.
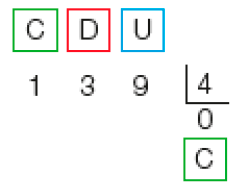
Dividindo 13 dezenas por 4, obtemos 3 dezenas, e resta 1 dezena. 1 dezena e 9 unidades formam 19 unidades.
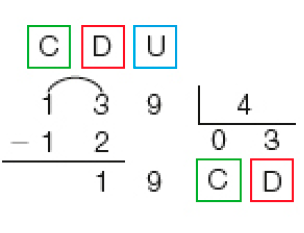
Dividimos 19 unidades por 4. Obtemos 4 unidades e restam 3 unidades.
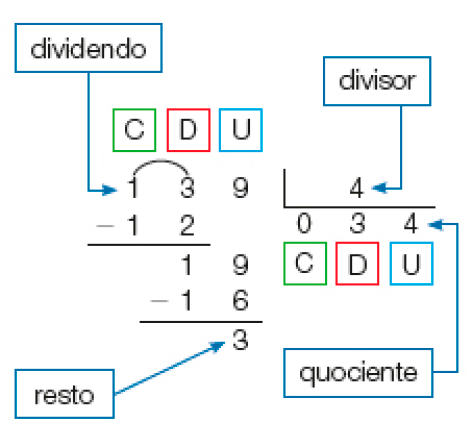
139 ÷ 4 = _____, e restam _____ unidades.
PROFESSOR
Resposta: 34; 3.MANUAL DO PROFESSOR
Objetivo
- Resolver problemas de divisão com números naturais (com divisor natural e diferente de zero), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
Fique atento à linguagem empregada em um cálculo de divisão, usando o nome das ordens envolvidas em cada etapa. Ao apresentar o algoritmo usual, explique o uso do arco sobre alguns algarismos no dividendo.
Atividade 1
Retome (ou apresente) os termos da divisão. Procure usar essa nomenclatura para que os estudantes se apropriem dela.
Na divisão de 139 por 4, por exemplo, como não podemos dividir 1 centena por 4 e obter um quociente natural, colocamos zero no quociente (pois 1 já seria muito) e continuamos a divisão, transformando essa 1 centena em 10 dezenas e adicionando-as às 3 dezenas já existentes. Por isso, na sequência, aparece um arco no 13, indicando que consideramos agora 13 dezenas para dividir por 4. Ressalte a importância de colocar no quociente a indicação da ordem a que corresponde o algarismo inserido em cada etapa. Como 13 dezenas dividido por 4 resulta 3 dezenas com resto de 1 dezena, no quociente da chave, devemos colocar 3 na casa das dezenas, de modo que os estudantes já podem concluir que o quociente é um número de 2 algarismos, pois será composto de dezenas e de unidades (nas centenas temos zero, que não será considerado). Optamos por colocar o zero à esquerda no quociente para que fique clara a necessidade da troca de 1 centena por 10 dezenas. Ao usar o zero à esquerda, fica mais fácil a compreensão do zero intercalado no quociente. Conforme os estudantes forem dominando as operações pelo algoritmo, esse zero à esquerda deixará de ser necessário.
BNCC em foco:
EF05MA08
MP084
- Calcule o resultado de cada operação.
- 319 ÷ 5
PROFESSOR
Resposta: Quociente: 63; resto: 4.
- 624 ÷ 7
PROFESSOR
Resposta: Quociente: 89; resto: 1.
- 406 ÷ 4
PROFESSOR
Resposta: Quociente: 101; resto: 2.
- 941 ÷ 8
PROFESSOR
Resposta: Quociente: 117; resto: 5.
- 319 ÷ 5

- Natália fez alguns cálculos e verificou que 40 ÷ 8 = 5.
Com base nesse resultado, calcule mentalmente o resultado de cada divisão.
- 80 ÷ 8 =
_____
PROFESSOR
Resposta: 10
- 160 ÷ 8 =
_____
PROFESSOR
Resposta: 20
- 200 ÷ 8 =
_____
PROFESSOR
Resposta: 25
- 400 ÷ 8 =
_____
PROFESSOR
Resposta: 50
- 80 ÷ 8 =
_____
- Leia o cálculo incorreto que Rodrigo fez.


- Por que o cálculo feito por Rodrigo está errado?
PROFESSOR
Resposta pessoal.
- Qual é o
número
exato de sacos de que ele precisará para embalar os 520
kg
de arroz?
_____
PROFESSOR
Resposta: 104 sacos.
PROFESSOR
Exemplo de cálculo: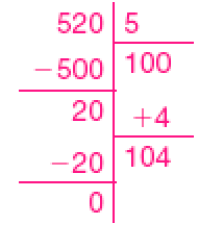
- Em um condomínio de prédios, há 1.020 apartamentos. Esse condomínio é formado por 5 prédios com o mesmo
número
de apartamentos em cada um deles. Quantos apartamentos há em cada prédio?
_____
PROFESSOR
Resposta: 204 apartamentos.
PROFESSOR
Exemplo de cálculo: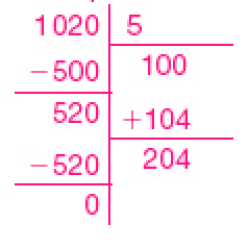
MANUAL DO PROFESSOR
Atividade 2
Esta é uma ótima oportunidade para verificar as estratégias de cálculo dos estudantes. Aproveite para verificar se eles percebem que, quando o resto for diferente de 0, só poderá ser um número menor que o divisor.
Atividade 3
Promova uma roda de conversa para os estudantes compartilharem as estratégias usadas.
Atividade 4
Para o item a, uma resposta possível é: Porque 500 dividido por 5 é igual a 100, e, como 520 é maior que 500, o número de sacos de que Rodrigo precisa será maior do que 100.
Atividade 5
Esta atividade possibilita aos estudantes reconhecerem a importância de usar as indicações das ordens correspondentes no quociente da divisão. Ao dividir 1 unidade de milhar por 5, não se obtêm unidades de milhar inteiras, então coloca-se zero no quociente. Ao dividir 10 centenas por 5, obtêm-se 2 centenas e sobra zero centena. Desse modo, temos apenas as 2 dezenas já existentes para dividir por 5, que não resulta em dezenas inteiras, por isso coloca-se zero no quociente e consideram-se 20 unidades, que, divididas por 5, resultam em 4 unidades, formando o quociente 204. Nessa etapa (2 dezenas divididas por 5) é comum que alguns estudantes nada escrevam no quociente e dividam 20 por 5 diretamente, chegando ao quociente 24, que não é correto.
BNCC em foco:
EF05MA08
MP085
Divisões com divisor de dois algarismos
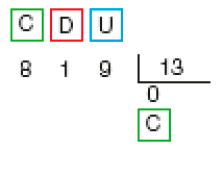
- Veja duas maneiras de calcular o resultado de 819 dividido por 13.
Cálculo por meio de tentativas

PROFESSOR
Resposta: 63; zero.Cálculo com o algoritmo usual
Como a divisão de 8 centenas por 13 não resulta em centena, colocamos zero no quociente e dividimos 81 dezenas por 13.
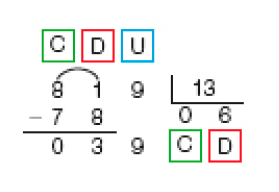
Dividindo 81 dezenas por 13, obtemos 6 dezenas e restam 3 dezenas.
3 dezenas e 9 unidades formam 39 unidades.
Rascunho
1 × 13 = 13
2 × 13 = 26
3 × 13 = 39
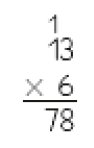
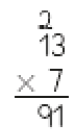
Dividimos 39 unidades por 13.
Obtemos 3 unidades e resta 0 unidade.
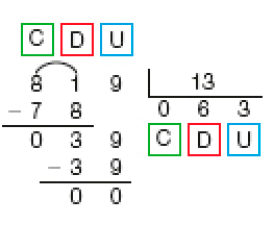
Portanto: 819 ÷ 13 = _____
PROFESSOR
Resposta: 63MANUAL DO PROFESSOR
Objetivos
- Resolver problemas de divisão com números naturais (com divisor natural e diferente de zero), utilizando estratégias diversas.
- Interpretar dados estatísticos apresentados em tabela.
O algoritmo usual baseia-se na compreensão do sistema decimal de numeração, em particular dos reagrupamentos feitos pelas trocas. Se houver disponibilidade, use o Material Dourado para evidenciá-las.
Atividade 1
O algoritmo usual é detalhado, para que os estudantes possam ter clareza de cada passo dele.
Nesse caso, como os quocientes parciais devem ser multiplicados por divisor com 2 algarismos. É fundamental que os estudantes realizem essas multiplicações mentalmente ou as registrem no papel. Por exemplo, em 819 ÷ 13, a divisão de 81 dezenas por 13 exige que se determine o número que deve multiplicar 13 de modo que se aproxime mais de 81, sem ultrapassá-lo. Isso exige algumas tentativas (mentais ou escritas) até que se verifique que 6 é o quociente procurado, pois 6 × 13 = 78 e 7 × 13 = 91.
Aproveite as etapas do algoritmo usual para estabelecer relação com a divisão por estimativas, mostrando que, por exemplo, o primeiro algarismo diferente de zero obtido no quociente, 6 (dezenas), indica a melhor estimativa com dezenas inteiras para essa divisão.
Quando se faz um arco sobre o 81 no número 819, não se está modificando esse número, ou reduzindo-o a 81, mas apenas considerando uma parte desse número. Isso ocorre por não ser possível dividir 8 centenas por 13 e obter centenas inteiras. Coloca-se, então, zero no quociente e dividem-se 81 dezenas.
BNCC em foco:
EF05MA08
MP086
- Calcule o quociente e o resto de cada operação.
- 853 ÷ 24 =
_____
PROFESSOR
Resposta: 35Resto: _____
PROFESSOR
Resposta: 13
PROFESSOR
Exemplo de cálculos: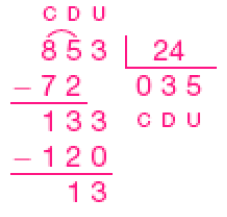
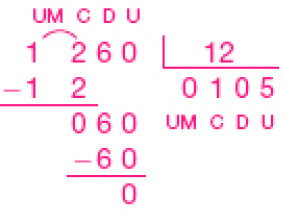
- 1.260 ÷ 12 =
_____
PROFESSOR
Resposta: 105Resto: _____
PROFESSOR
Resposta: 0
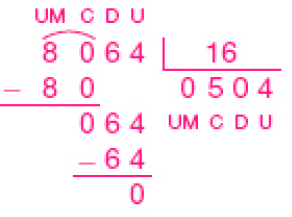
- 8.064 ÷ 16 =
_____
PROFESSOR
Resposta: 504Resto: _____
PROFESSOR
Resposta: 0
- 1.576 ÷ 25 =
_____
PROFESSOR
Resposta: 63Resto: _____
PROFESSOR
Resposta: 1
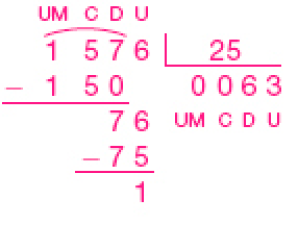
- Débora tem uma banca de frutas na feira. Ela quer vender 1.116 laranjas em dúzias.
- Quantas dúzias serão formadas?
_____
PROFESSOR
Resposta: 93 dúzias.
- Se cada dúzia de laranjas for vendida a R$ 8,00, quantos reais Débora obterá?
_____
PROFESSOR
Resposta: 744 reais.
- Quantas dúzias serão formadas?
PROFESSOR
Exemplos de cálculo:PROFESSOR
a) 1.116 ÷ 12 = 93PROFESSOR
b) 93 × 8 = 744- Joaquim colocará 1.044 pêssegos em 18 caixas com a mesma quantidade em cada uma.
- Quantos pêssegos ele colocará em cada caixa?
_____
PROFESSOR
Resposta: 58 pêssegos.PROFESSOR
Exemplo de cálculo:
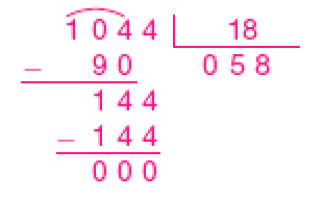
- Quantos pêssegos ele colocará em cada caixa?
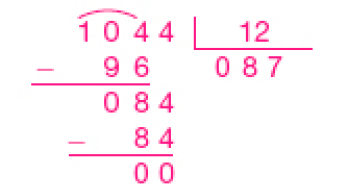
- Quantos pêssegos ele teria que colocar a mais em cada caixa para diminuir o
número
de caixas para 12?
_____
PROFESSOR
Resposta: 29 pêssegos.PROFESSOR
Exemplo de cálculo:
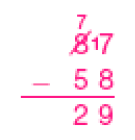
MANUAL DO PROFESSOR
Atividade 2
Incentive os estudantes a realizarem as divisões desta atividade por dois métodos: por estimativas e pelo algoritmo usual. Por exemplo, a divisão de 853 por 24 pode ser feita assim:
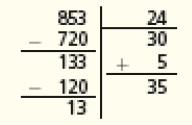
Os estudantes devem verificar que os resultados são os mesmos que os obtidos com o algoritmo usual. No item d, caso encontrem dificuldades, explique que, como não conseguimos dividir 1 unidade de milhar por 25 e obter unidades de milhar inteiras, colocamos zero na casa das unidades de milhar no quociente e tentamos dividir 15 centenas; como também não conseguimos dividir 15 centenas por 25 e obter centenas inteiras, colocamos outro zero na casa das centenas no quociente e consideramos 150 dezenas, que com as 7 dezenas já existentes formam 157 dezenas. Um arco é colocado em 157 para indicar isso.
Atividade 3
Incentive os estudantes a usarem mais de uma estratégia em seus cálculos e a socializarem-nas com os colegas, sob sua orientação.
Atividade 4
No item b, espera-se que os estudantes compreendam que, se a quantidade de caixas (divisor) vai ser diminuída para 12, a quantidade de pêssegos em cada caixa (quociente) aumentará. Assim, uma maneira de resolver a questão é calcular o novo quociente (para 12 caixas) e encontrar a diferença em relação ao quociente já obtido (para 18 caixas).
Dividindo 1.044 por 12, obtém-se quociente 87, que indica o total de pêssegos de cada caixa. Logo, foram colocados 29 pêssegos a mais (87 − 58).
BNCC em foco:
EF05MA08
MP087
- Um grupo de 540 torcedores quer ir de ônibus assistir a uma partida de futebol em outra cidade. Quantos ônibus, no mínimo, serão necessários para levar todos os torcedores? _____
PROFESSOR
Resposta: Serão necessários, no mínimo, 13 ônibus.PROFESSOR
Exemplo de cálculo: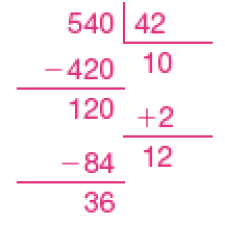

- Observe, na tabela abaixo, a quantidade de estudantes que frequentavam o período da manhã e o período da tarde da Escola Aprender, em 2022.
Quantidade de estudantes por período
Tabela: equivalente textual a seguir.
|
Período |
Quantidade de estudantes |
|---|---|
|
Manhã |
240 |
|
Tarde |
300 |
Fonte: Secretaria da Escola Aprender (dez. 2022).
- Quantas turmas com 30 estudantes é possível formar no período da manhã? E no período da tarde?
_____
PROFESSOR
Resposta: Período da manhã: 8 turmas; Período da tarde: 10 turmas.
- Luís usou exatamente 6 metros de fita adesiva para cobrir todas as arestas de um modelo de cubo.
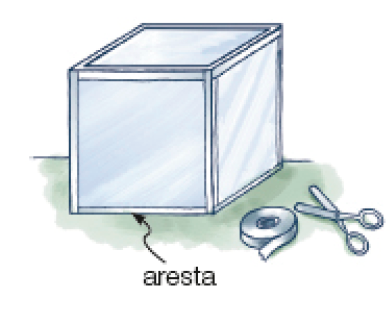
- Qual é a medida do comprimento total de fita adesiva que Luís usou, em centímetro?
_____
PROFESSOR
Resposta: 600 centímetros.
- Se em todas as arestas Luís usou pedaços de fita de mesmo tamanho, qual é a medida do comprimento, em centímetro, de cada aresta desse
modelo
de cubo?
_____
PROFESSOR
Resposta: 50 centímetros.PROFESSOR
Exemplo de cálculo: 600 ÷ 12 = 50

- Augusto quer dividir 650 por 50 com uma calculadora, mas ela está com a tecla
 quebrada. Registre em seu
caderno
como ele pode resolver esse problema.
quebrada. Registre em seu
caderno
como ele pode resolver esse problema. PROFESSOR
Resposta variável.
MANUAL DO PROFESSOR
Atividade 5
Espera-se que os estudantes percebam que, embora a divisão de 540 por 42 dê quociente 12 (total de ônibus com lotação máxima), a quantidade mínima de ônibus deve ser 13, para levar os 36 torcedores que sobraram (resto da divisão).
Atividade 6
Esta atividade mobiliza outros tipos de conhecimento dos estudantes além de cálculos de divisão, como a leitura de dados organizados em tabela.
Atividade 7
Esta atividade trabalha divisão, além de outros conhecimentos como noções de geometria (cubo/aresta) e medidas de comprimento (centímetro).
Atividade 8
Uma possível resposta para essa atividade é: Augusto pode subtrair 50 de 650 seguidamente, até o resultado ser igual a zero, ou até quando não for mais possível realizar a subtração. O resultado será o número de vezes que ele subtrair 50, ou seja, 13 vezes.
Outra maneira de obter esse quociente é fazer aproximações por meio de multiplicações do resultado 650. Os estudantes podem multiplicar, por exemplo, 6 × 50, obtendo 300; então, podem tentar 10 × 50, obtendo 500, e assim por diante, fazendo novas tentativas até chegar a 13 × 50, que resulta em 650. Peça que comparem suas estratégias e discutam os resultados observados.
BNCC em foco:
EF05MA08, EF05MA24
MP088
Mais estratégias de cálculo
- Lucas deseja calcular mentalmente o resultado de 5 × 23. Veja o raciocínio de Lucas.


- Faça como Lucas e calcule o resultado em cada caso.
- 5 × 18 =
_____
PROFESSOR
Resposta: 90
- 4 × 45 =
_____
PROFESSOR
Resposta: 180
- 6 × 72 =
_____
PROFESSOR
Resposta: 432
- 7 × 53 =
_____
PROFESSOR
Resposta: 371
- 3 × 48 =
_____
PROFESSOR
Resposta: 144
- 8 × 205 =
_____
PROFESSOR
Resposta: 1.640



- Agora, pense em uma estratégia para calcular mentalmente estas multiplicações. Depois, explique aos colegas e ao professor a sua estratégia.
- 50 × 18 =
_____
PROFESSOR
Resposta: 900
- 40 × 45 =
_____
PROFESSOR
Resposta: 1.800
- 50 × 24 =
_____
PROFESSOR
Resposta: 1.200
- 200 × 45 =
_____
PROFESSOR
Resposta: 9.000
- 800 × 35 =
_____
PROFESSOR
Resposta: 28.000
- 300 × 62 =
_____
PROFESSOR
Resposta: 18.600PROFESSOR
Respostas pessoais.
- Janete deseja calcular o resultado aproximado de 324 ÷ 39. Veja o raciocínio de Janete.

- Agora, faça como Janete e calcule o resultado aproximado das divisões a seguir.
- 413 ÷ 48 =
_____
PROFESSOR
Exemplo de resposta: 8.
- 513 ÷ 53 =
_____
PROFESSOR
Exemplo de resposta: 10.
- 272 ÷ 67 =
_____
PROFESSOR
Exemplo de resposta: 4.
- 570 ÷ 71 =
_____
PROFESSOR
Exemplo de resposta: 8.
- 625 ÷ 89 =
_____
PROFESSOR
Exemplo de resposta: 7.
- 718 ÷ 77 =
_____
PROFESSOR
Exemplo de resposta: 9.
MANUAL DO PROFESSOR
Objetivos
- Resolver problemas de multiplicação e divisão com números naturais (com divisor natural e diferente de zero), utilizando cálculo por estimativa e cálculo mental.
- Resolver problemas que envolvam variação de proporcionalidade direta entre duas grandezas (de comprimento, de tempo e de capacidade).
- Resolver problemas de adição e subtração com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
Para desenvolver procedimentos de cálculo, é necessário conhecer propriedades, tanto do nosso sistema de numeração quanto das operações. Por vezes, estudantes dessa idade têm dificuldade em comunicar o raciocínio, por isso devem ser incentivados a exporem com clareza suas ideias e a conhecerem outras possibilidades de resolução.
Atividade 1
Os estudantes devem usar o recurso da decomposição de um dos fatores para calcular o produto. É também apropriado levá-los a calcularem mentalmente com números múltiplos de 10, 100, 1.000 etc.
Atividade 2
A estratégia é trabalhar a multiplicação, operação inversa da divisão. Para esta atividade, é necessário que os estudantes já tenham bastante familiaridade com as listas de multiplicação de 1 a 10, pois, após o arredondamento dos números envolvidos na divisão, devem procurar nas listas de multiplicação a quantidade mais apropriada para a situação.
BNCC em foco:
EF05MA08
MP089
- Cláudia comprou um fogão por 476 reais e vai pagá-lo em 4 prestações mensais e iguais. Veja de que maneira ela calculou o valor aproximado de cada prestação.


- Faça outro cálculo do valor aproximado de cada prestação.
PROFESSOR
Resposta pessoal.
- Agora, calcule o valor exato de cada prestação e compare com o valor
obtido
no item anterior. Eles ficaram próximos?
_____
PROFESSOR
Resposta pessoal.
PROFESSOR
Resposta: Exemplo de cálculo:
- O carro de Geraldo consome 1 litro de etanol para percorrer 9 quilômetros. Em 6 minutos, o carro
percorre
9 quilômetros. Agora, faça o que se pede.
- Complete o quadro.
Quadro: equivalente textual a seguir.
|
Distância percorrida |
Tempo |
Litros de etanol |
|---|---|---|
|
9 km |
6 min |
1 litro |
|
27 km |
_____ min |
_____ litros |
|
_____ km |
_____ min |
7 litros |
|
_____ km |
60 min |
_____ litros |
PROFESSOR
Resposta: 18, 3.PROFESSOR
63, 42.PROFESSOR
90, 10.- Quantos minutos e quantos litros de etanol Geraldo vai gastar para percorrer 27 quilômetros?
_____
PROFESSOR
Resposta: 18 minutos e 3 litros de etanol.
- Quantos quilômetros o carro de Geraldo
percorre
com 7 litros de etanol? E quanto tempo ele leva para fazer esse percurso?
_____
PROFESSOR
Resposta: 63 quilômetros; 42 minutos.
- De quantos litros de etanol o carro de Geraldo precisa para se deslocar por uma hora? Quantos quilômetros ele consegue percorrer nesse período?
_____
PROFESSOR
Resposta: 10 litros de etanol; 90 quilômetros.
MANUAL DO PROFESSOR
Atividade 3
Para o item a desta atividade, uma possível resposta é: 400 ÷ 4 = 100 e 480 ÷ 4 = 120. Então, 476 ÷ 4 tem quociente entre 100 e 120. Isso significa que o valor da prestação está entre 100 reais e 120 reais.
Para o item b, os estudantes podem efetuar a divisão 476 ÷ 4 = 119 ou, ainda, fazer outras multiplicações até obterem 476, observando as divisões feitas nas estimativas (119 × 4 = 476).
Atividade 4
Os estudantes devem perceber qual é a relação estabelecida entre os quilômetros para repetir proporcionalmente o aumento do tempo e a quantidade consumida de litros de etanol. Na exploração dos dados, é possível perceber que os 9 quilômetros são multiplicados por 3 para a obtenção dos 27 quilômetros. Desse modo, os 6 minutos e 1 litro de etanol também devem ser multiplicados por 3. Depois, observando o tempo já registrado, pode-se perceber que os 6 minutos são multiplicados por 10 para a obtenção dos 60 minutos. Assim, deve-se fazer o mesmo com os quilômetros e litros correspondentes. Por fim, observando as quantidades de litros já conhecidas, pode-se perceber que 1 litro é multiplicado por 7 para a obtenção dos 7 litros. E, assim, fazemos o mesmo com os quilômetros e os minutos correspondentes.
BNCC em foco:
EF05MA08, EF05MA12
MP090
- Tomás e Gisele estão brincando. Tomás entregou a ela uma cartela com um número em destaque e quatro algarismos embaixo desse número.

18
1, 2, 6, 1
Os cálculos devem seguir estas regras:
- Só podem ser usados dois dos quatro algarismos localizados embaixo do número em destaque.
- Cada algarismo só pode ser usado uma vez.
- O último cálculo deve ser realizado com os resultados dos dois cálculos anteriores.
- Podem ser utilizadas apenas as quatro operações básicas.
Veja abaixo a solução apresentada por Gisele.
18
1, 2, 6, 1
1 + 2 = 3
6 × 1 = 6
6 + 3 = 9
Aplique as regras do jogo criado por Tomás e Gisele e complete as cartelas considerando que o resultado seja:
- a metade dos números em destaque.
24
2, 3, 4, 8
PROFESSOR
Resposta: 3 × 2 = 6PROFESSOR
8 ÷ 4 = 2PROFESSOR
6 × 2 = 1236
5, 2, 6, 1
PROFESSOR
Resposta: 2 × 6 = 12PROFESSOR
5 + 1 = 6PROFESSOR
12 + 6 = 18- o dobro dos números em destaque.
20
2, 5, 6, 8
PROFESSOR
Resposta: 5 × 6 = 30PROFESSOR
8 + 2 = 10PROFESSOR
30 + 10 = 4015
3, 7, 6, 4
PROFESSOR
Resposta: 4 × 7 = 28PROFESSOR
6 ÷ 3 = 2PROFESSOR
28 + 2 = 30MANUAL DO PROFESSOR
Atividade 5
Nesta atividade, os estudantes precisarão utilizar estratégias de cálculo usando as quatro operações para responder ao comando. Para encontrar os resultados, é necessário relembrar o conceito de dobro e de metade. A proposta pode ser adaptada com diferentes comandos, como triplo, terça parte, a operação que gere o número que está em destaque etc.
Sugestão de atividade
Divisão enigmática
Na divisão “enigmática” abaixo, cada símbolo representa um algarismo diferente. Descubra o algarismo correspondente a cada símbolo.
 ÷ 6 = 76, com resto igual a 0.
÷ 6 = 76, com resto igual a 0.
Resposta:
 = 4
= 4
 = 5
= 5
 = 6
= 6
Espera-se que os estudantes percebam que o dividendo é um número de 3 algarismos. Eles devem perceber que, se o quociente é 76 e o divisor é 6 (com resto zero), é porque 76 × 6 resulta no dividendo desconhecido. Assim, podem concluir que basta efetuar essa multiplicação para obter o dividendo e, daí, obter o valor de cada símbolo.
Então, como 76 × 6 = 456, obtém-se que a figura triangular vale 4, a figura quadrada vale 5 e a figura circular, 6.
Se julgar necessário, peça aos estudantes que montem o esquema da chave para que percebam a relação da multiplicação envolvida. Pode-se propor outros números para a realização da atividade.
BNCC em foco:
EF05MA07, EF05MA08
MP091
Sequências numéricas
- Complete cada sequência numérica de acordo com a regra indicada.
- Sempre adicionar 5.
1, 6, 11, 16, 21, _____, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 26, 31, 36, 41, 46, 51
- Sempre subtrair 2.
100, 98, 96, 94, 92, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 90, 88, 86, 84, 82
- Sempre adicionar 11.
33, 44, 55, 66, 77, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 88, 99, 110, 121, 132
- Sempre subtrair 10.
1.130, 1.120, 1.110, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 1.100, 1.090, 1.080, 1.070, 1.060.
- Sempre adicionar 5.
- Juliano
escreveu
uma sequência numérica que começava no
número
20. Para
obter
o próximo número, ele adicionou 10 e subtraiu 4. Seguindo essa regra, Juliano obteve a sequência de números abaixo.
20, 26, 32, 38, 44, 50, 56, 62, 68 74
Clarice escreveu a sequência numérica abaixo, que também começa no número 20. Para obter o próximo número, ela sempre adicionou 6.
20, 26, 32, 38, 44, 50, 56, 62, 68, 74

- Apesar de
terem
seguido regras diferentes, por que Juliano e Clarice obtiveram sequências numéricas iguais?
PROFESSOR
Resposta pessoal.
- Agora é sua vez. Crie duas regras diferentes que formem sequências numéricas iguais.
_____
PROFESSOR
Resposta variável.
- Apesar de
terem
seguido regras diferentes, por que Juliano e Clarice obtiveram sequências numéricas iguais?
MANUAL DO PROFESSOR
Objetivos
- Resolver e elaborar problemas de adição e subtração com números naturais, utilizando estratégias diversas.
- Resolver e elaborar problemas de multiplicação e divisão com números naturais (com divisor natural e diferente de zero), utilizando estratégias diversas.
- Explorar sequências numéricas e determinar elementos ausentes.
Atividade 1
Verifique se os estudantes identificam e compreendem o padrão de formação indicado para cada sequência. Observe os procedimentos que eles usam ao buscar os elementos desconhecidos. Se necessário, reproduza cada sequência na lousa com os estudantes.
Atividade 2
No item a, espera-se que os estudantes compreendam que adicionar 10 a um número e logo em seguida subtrair 4 do total obtido é o mesmo que adicionar 6 a esse número; por isso, as sequências numéricas são iguais.
No item b, é provável que os estudantes usem adição e subtração. Incentive-os a utilizarem também multiplicações e divisões. Socialize as sequências criadas.
BNCC em foco:
EF05MA07
MP092
- Considere que os três números abaixo representam os três primeiros termos de uma sequência numérica.
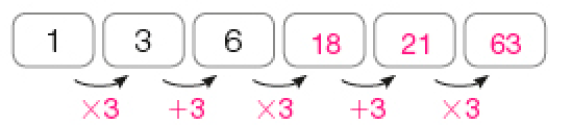
- Crie uma regra de formação para essa sequência numérica e escreva os próximos três termos da sequência.
_____
PROFESSOR
Exemplo de resposta: O próximo número é formado pelo triplo do número anterior, e o número seguinte a esse, pela adição de 3 unidades ao número anterior.

- Compare sua sequência numérica com as dos colegas. Depois,
conversem
sobre as diferentes sequências e regras que foram criadas.
PROFESSOR
Resposta pessoal.
- Thaís e Eduardo foram andar de kart. O kart de Thaís completava uma volta na pista em 2 minutos, e o de Eduardo completava uma volta em 3 minutos. Esses karts partiram do início da pista juntos e mantiveram sempre os mesmos tempos em cada volta.

- Complete os quadros com os instantes em que os karts de Thaís e Eduardo passaram pelo início da pista.
Quadro: equivalente textual a seguir.
|
Thaís |
0 |
2 |
4 |
_____ |
_____ |
_____ |
_____ |
_____ |
|---|---|---|---|---|---|---|---|---|
|
Eduardo |
0 |
3 |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
PROFESSOR
Resposta: Thais: 6, 8, 10, 12, 14.PROFESSOR
Eduardo: 6, 9, 12, 15, 18, 21- Após a partida, depois de quantos minutos os karts de Thaís e Eduardo passaram juntos pela primeira vez pelo início da pista?
_____
PROFESSOR
Resposta: 6 minutos.
- Eles passarão juntos novamente, no início da pista, aos 24 minutos? Explique como você pensou para responder a essa questão.
_____
PROFESSOR
Resposta: Sim.PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Verifique se os padrões criados pelos estudantes fazem sentido. Por exemplo, alguns deles podem pensar nesta sequência: 1, 3, 6, 1, 3, 6, 1, 3, 6, ... No entanto, para desafiá-los, caso já não tenha surgido, proponha que descubram um padrão envolvendo adições. Espera-se que observem na sequência 1, 3, 6, ... o seguinte padrão:
1º termo: 1
2º termo: 3 = 1 + 2
3º termo: 6 = 3 + 3
Desse modo, os três próximos termos serão:
4º termo: 6 + 4 = 10
5º termo: 10 + 5 = 15
6º termo: 15 + 6 = 21
Assim, formarão a sequência: 1, 3, 6, 10, 15, 21, ...
Atividade 4
Comente com os estudantes que kart é uma modalidade de automobilismo que envolve veículos de quatro rodas, com um único assento. Ao observarem o tempo, em minuto, em que cada kart passa pelo início da pista, no item a, os estudantes poderão concluir os momentos em que os karts de Thaís e Eduardo se encontram. Assim, devem observar que depois de 6 minutos da partida eles se encontraram pela primeira vez no início da pista (item b).
No item c, espera-se que os estudantes respondam sim, pois eles se encontram depois de: 6 minutos, 12 minutos, 18 minutos, 24 minutos, e assim por diante. Como explicação, alguns poderão dizer que escreveram os próximos termos das sequências até concluírem que 24 pertence às duas sequências. Caso algum estudante justifique sua resposta por meio da observação das regularidades das sequências, peça que compartilhe-a com os demais colegas.
BNCC em foco na dupla de páginas:
EF05MA07, EF05MA08
Sugestão de atividade
“Mágica” na calculadora
Com uma calculadora em mãos, os estudantes devem digitar as teclas:

CRÉDITO: ADILSON SECCO
Eles devem observar os números que vão aparecendo no visor. Explique que a tecla de igualdade é denominada tecla inteligente, porque “guarda” a última operação e a repete.
MP093
- A professora Kátia pediu aos estudantes que escrevessem uma sequência numérica de acordo com as dicas abaixo.
Boxe complementar:
Dica
- O primeiro número da sequência numérica é 568.
- Na sequência numérica, há sete números.
- Adicionamos 12 ao primeiro número para obter o segundo número. Essa regra é repetida para encontrar os demais números dessa sequência.
Fim do complemento.

- Analise as sequências numéricas que Joana e Sofia criaram seguindo as dicas que a professora Kátia determinou e identifique a sequência correta.
PROFESSOR
Resposta: A sequência correta é a de Sofia.
- Uma abelha pousou nas flores de alguns vasos.

Imagine que essa abelha continuará pousando em um vaso a cada três vasos que ela percorrer.
- Sabendo que os vasos são numerados com uma sequência crescente, qual será o
número
do próximo vaso em que ela pousará após ter pousado no vaso 12?
_____
PROFESSOR
Resposta: 15
- Em qual
destes
três vasos a abelha pousará: no de
número
36, 37 ou 38?
_____
PROFESSOR
Resposta: 36
- Outra abelha
percorre
esses mesmos vasos. Ela pousa em um vaso a cada quatro vasos que ela percorre. O
1º
vaso em que ela pousou foi o de
número
0. Qual será o
número
do 10º vaso em que ela pousará?
_____
PROFESSOR
Resposta: 36
MANUAL DO PROFESSOR
Portanto, os números que vão aparecendo no visor representam a sequência dos números naturais a partir do 2.
Proponha outras teclas de modo que surjam sequências diferentes para que os estudantes identifiquem seus termos, por exemplo:

CRÉDITO: ADILSON SECCO
Nesse caso, a operação que está sendo “guardada” é + 2 e, portanto, os números que vão aparecendo no visor representam a sequência dos números naturais pares a partir do 2.
Atividade 5
Peça aos estudantes que compartilhem e justifiquem suas respostas. Em seguida, oriente-os a descreverem qual foi o erro cometido por Joana ao construir a sequência. Espera-se que percebam que Joana alternou o número adicionado, ora 10, ora 12.
Atividade 6
Esta atividade trabalha com as ideias de divisão exata e divisão não exata.
Pode-se pedir a alguns dos estudantes que exponham modos de resolução do item b. Vejamos algumas possibilidades:
- Fazer os desenhos dos vasos até o vaso de número 38 e, seguindo o percurso da abelha, que pousa sempre de três em três vasos, chegar até o vaso de número 36.
- Observar uma regularidade nos números correspondentes aos vasos em que a abelha pousa: são todos números resultantes de multiplicações do tipo “vezes 3”. Apenas o número 36 tem essa mesma característica.
- Observar que os números 0, 3, 6, 9 e 12 podem ser divididos por 3 sem deixar resto. Isso ocorre porque 3 cabe um
número
exato de vezes em cada um deles. Testando os números 36, 37 e 38, notamos que apenas 36 também pode ser dividido por 3 sem deixar resto.
Se julgar oportuno, explique que números desse tipo são chamados de múltiplos de 3.
MP094
Compreender problemas
Para resolver
Problema 1
Enzo brincou uma vez na barraca de argolas da festa junina de sua escola. Nessa brincadeira, há duas cores de argola: as amarelas, que valem 2 pontos, e as azuis, que valem 3 pontos.
PROFESSOR
Resposta: Exemplo de cálculos:PROFESSOR
6 × 2 = 12PROFESSOR
24 − 12 = 12PROFESSOR
12 ÷ 3 = 4
- Enzo fez 24 pontos no total. Sabendo que ele acertou argolas das duas cores e que 6 delas eram amarelas, descubra quantas argolas azuis ele acertou para fazer os 24 pontos.
_____
PROFESSOR
Resposta: 4 argolas azuis.
Problema 2
Viviane e Lara são primas. Nenhuma delas tem mais de 6 irmãos. Leia o diálogo delas com atenção e descubra quantos irmãos tem cada uma delas.

Viviane tem _____ irmãos, e Lara, _____ irmãos.
PROFESSOR
Resposta: 3, 4MANUAL DO PROFESSOR
Objetivo
- Resolver problemas envolvendo as quatro operações, utilizando estratégias diversas.
Os problemas podem ser resolvidos por tentativas e análise de erros, fundamental para que não se use uma estratégia totalmente aleatória, em que o acerto aconteça por sorte.
Problema 1
Sabendo que Enzo fez 24 pontos e acertou 6 argolas amarelas, temos:
6 × 2 pontos = 12 pontos
Como Enzo fez ao todo 24 pontos e acertou argolas amarelas (12 pontos) e argolas azuis, fazendo 24 − 12 = 12, obtemos a quantidade de pontos que ele fez com as argolas azuis: 12 pontos. Como cada argola azul vale 3 pontos, fazemos 12 ÷ 3 = 4. Assim, Enzo acertou 4 argolas azuis.
Problema 2
Com a informação de que nem Viviane nem Lara tem mais de 6 irmãos, começamos as tentativas. Com base na fala de Viviane, sabemos que ela tem 1 irmão a menos que Lara:
Tabela: equivalente textual a seguir.
Número de irmãos de Lara
6
Número de irmãos de Viviane
5
Número de irmãos de Lara se tivesse mais 2 irmãos
8
Conclusão: 8 não é o dobro de 5. Então, essa não é a solução.
Continuamos as tentativas, diminuindo o valor até testar o valor 4:
Tabela: equivalente textual a seguir.
Número de irmãos de Lara
4
Número de irmãos de Viviane
3
Número de irmãos de Lara se ela tivesse mais 2 irmãos
6
Como 6 é o dobro de 3, essa é a solução.
BNCC em foco na dupla de páginas:
EF05MA07, EF05MA08
MP095
Para refletir
- Observe os cálculos que Pedro e Bianca fizeram para resolver o Problema 1.
Cálculos de Pedro

PROFESSOR
Resposta: 3 argolas azuis: 3 × 3 pontos = 9 pontos.PROFESSOR
4 argolas azuis: 4 × 3 pontos = 12 pontos.PROFESSOR
Enzo jogou 4 argolas azuis.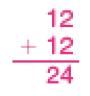
Cálculos de Bianca

PROFESSOR
Resposta: como 1 argola azul vale 3 pontos, basta dividir 12 por 3:PROFESSOR
12 ÷ 3 = 4.PROFESSOR
Enzo jogou 4 argolas azuis.- Agora, descubra a estratégia de cada um para resolver o problema. Depois, termine os cálculos até chegar ao número de argolas azuis.
PROFESSOR
Exemplos de respostas nos cálculos.- Sobre o Problema 2, marque com um
X
a única frase correta.
- ( ) Juntas, Viviane e Lara têm 10 irmãos.
- ( ) Viviane tem 1 irmão a menos que Lara.
- ( ) Lara tem o dobro da quantidade de irmãos de Vivane.
- ( ) Lara tem 5 irmãos.
PROFESSOR
Resposta correta: b

- Augusto e Laís deram respostas erradas para o Problema 2. Explique por que cada uma das respostas está errada.

PROFESSOR
Exemplo de respostas:PROFESSOR
Nenhuma das duas tem mais que 6 irmãos.PROFESSOR
A diferença entre as duas quantidades é de 1 irmão.MANUAL DO PROFESSOR
Para refletir Atividades 1, 2 e 3
Em uma roda de conversa, analise com os estudantes os cálculos de Pedro e Bianca, na atividade 1, e as frases da atividade 2.
O aspecto mais interessante da atividade 3 é levar os estudantes a perceberem quais são as limitações do problema 2 que justificam a impossibilidade das respostas apresentadas como erradas. Vale notar que os estudantes só compreendem de fato um problema depois desse tipo de análise. Então, um caminho é analisar respostas impossíveis antes de encontrar soluções corretas, porque essa análise gera informações que conduzem à resposta correta.
Os estudantes devem perceber que a resposta da estudante é errada porque nenhuma das duas meninas tem mais de 6 irmãos; e a resposta do estudante está errada porque a diferença entre as duas quantidades de irmãos é de 1 unidade.
Aproveitando os problemas apresentados, peça aos estudantes que, em duplas, modifiquem o problema 1 de modo que a resposta seja “6 argolas azuis”, e o problema 2 para que a resposta seja “Viviane tem 4 irmãos e Lara tem 6 irmãos”.
Exemplo de respostas:
- Problema 1: Enzo fez 30 pontos no total.
- Problema 2: Nenhuma menina tem mais de 6 irmãos.
Viviane: “Se eu tivesse mais 2 irmãos, passaria a ter a mesma quantidade de irmãos que Lara tem.”
Lara: “Se eu tivesse menos 4 irmãos, teria a metade da quantidade de irmãos que Viviane tem.”
MP096
Compreender informações
Organizar dados em tabelas e em gráficos
- Para comprar livros para a biblioteca, a diretora de uma escola fez uma pesquisa com todos os estudantes de 5º ano sobre o tipo preferido de leitura. Cada um deles votou em apenas um tipo.
- Complete a tabela com os resultados anotados pela diretora.
Tipo de leitura favorito
Tabela: equivalente textual a seguir.
|
Tipo de leitura |
Votação (cada traço vale 10 votos) |
Quantidade de votos - Frequência (quantidade de vezes que cada informação aparece) |
|---|---|---|
|
Quadrinhos |
|
_____ |
|
Fantasia |
|
_____ |
|
Aventura |
|
_____ |
|
Ficção |
|
20 |
Fonte: Diretora da escola (dez. 2022).
PROFESSOR
Resposta: 140, 60, 80- A diretora fez um gráfico pictórico de acordo com os dados da tabela. Ajude-a e complete o gráfico.

Fonte: Diretora da escola (dez. 2022).
PROFESSOR
Resposta: 20- Quantos votos vale o símbolo
 ?
_____
?
_____
PROFESSOR
Resposta: 20 votos.
- Qual é a frequência de cada tipo de leitura citado?
_____
PROFESSOR
Resposta: Quadrinhos: 140; mistério: 60; aventura: 80; ficção: 20.
- Que tipo de leitura é o preferido pelos estudantes de 5º ano?
_____
PROFESSOR
Resposta: Quadrinhos.
- Quantos estudantes de 5º ano há
nessa
escola?
_____
PROFESSOR
Resposta: 300 estudantes.
MANUAL DO PROFESSOR
Objetivos
- Organizar dados coletados por meio de tabelas e gráfico pictórico.
- Interpretar dados apresentados em gráfico de colunas duplas.
- Apresentar texto escrito sobre a síntese dos resultados de uma pesquisa.
Atividade 1
Para preencher a tabela do item a, os estudantes devem atentar para o fato de cada traço indicar 10 votos. Se julgar necessário, explore com eles os dados que a tabela apresenta. Ressalte que a quantidade de votos corresponde à frequência de cada tipo de leitura citado.
No gráfico pictórico do item b, espera-se que os estudantes percebam que cada livro corresponde a 20 votos. Verifique se eles fazem relação com os dados da tabela. Peça que exponham como pensaram para completar o gráfico. Explore com os estudantes as frequências de cada tipo de leitura.
Discuta as demais questões em uma roda de conversa, incentivando a exposição das ideias, a fim de que justifiquem as respostas e as estratégias de cálculo mental, e também comparem as soluções para ampliar o repertório.
Pode-se propor essa mesma pesquisa na classe, pedindo a um estudante que registre na lousa o resultado da votação. Depois de finalizada a atividade, peça aos estudantes que organizem os dados da pesquisa feita em classe em um gráfico pictórico. Socialize e discuta com eles cada gráfico. Peça a eles que comparem os resultados da pesquisa com os do livro.
BNCC em foco:
EF05MA25
MP097
- Após o encerramento do
1º
trimestre do ano letivo, a professora Paula
promoveu
um debate com os estudantes da turma em que ela leciona sobre a importância da presença nas aulas.
Paula apresentou aos estudantes o gráfico abaixo, que mostra como eles se comportaram quanto às faltas nesse trimestre. Esse tipo de gráfico é denominado gráfico de colunas duplas.


- Observe o gráfico e converse com um
colega
sobre os elementos que aparecem nele. Na opinião de vocês, o que as cores indicam?
PROFESSOR
Atenção professor: Espera-se que os estudantes reconheçam que as colunas amarelas referem-se às meninas e que as colunas verdes referem-se aos meninos. Fim da observação.
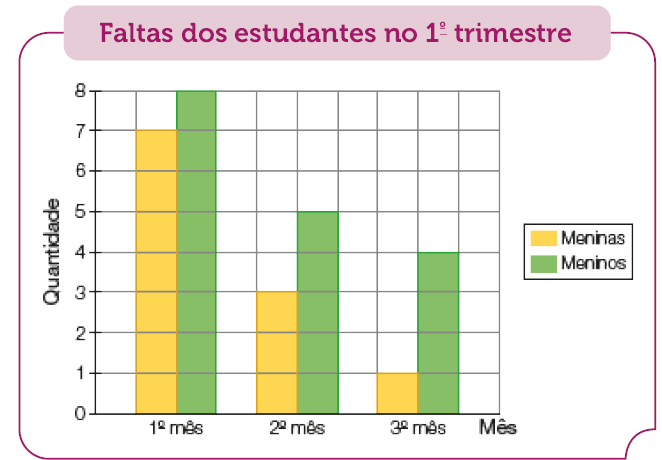
Fonte: Turma da professora Paula (maio 2023).
- Complete a tabela de dupla entrada abaixo com os dados do gráfico.
Faltas dos estudantes no 1º trimestre
Tabela: equivalente textual a seguir.
|
Mês Estudantes |
1º mês |
2º mês |
3º mês |
|---|---|---|---|
|
Meninos |
_____ |
_____ |
_____ |
|
Meninas |
_____ |
_____ |
_____ |
Fonte: Turma da professora Paula (maio 2023).
PROFESSOR
Resposta: Meninos: 8 faltas, 5 faltas, 4 faltas.PROFESSOR
Meninas: 7 faltas, 3 faltas, 1 falta.- Escreva uma frase para descrever o que mudou do
1º
para o 3º mês em relação ao
número
de faltas dos meninos.
_____
PROFESSOR
Exemplo de resposta: No 1º mês, houve 8 faltas entre os meninos; já no 3º mês, esse número diminuiu para 4 faltas.
- O que os dados do gráfico mostram em relação ao
número
de faltas dos que estudam com a professora Paula?
_____
PROFESSOR
Exemplo de resposta: O número de faltas foi diminuindo ao longo do trimestre entre os meninos e entre as meninas. Em todos os meses, as meninas tiveram menos faltas do que os meninos.

- Entre os que estudam com Paula, quem mais diminuiu o
número
de faltas: os meninos ou as meninas? Explique para um
colega
como você descobriu isso.
PROFESSOR
Resposta: As meninas, pois foram de 7 faltas para 1 falta, enquanto os meninos foram de 8 para 4 faltas.
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, é apresentado um gráfico de colunas duplas com dados sobre as faltas dos estudantes no primeiro trimestre de um ano, mostrando quantas faltas são dos meninos e quantas são das meninas em cada mês. Os estudantes devem observar e discutir com os colegas acerca dos elementos do gráfico (item a). Eles podem reconhecer o título “Faltas dos estudantes no 1 º trimestre”, que indica do que se trata o gráfico, a fonte dos dados “Turma da professora Paula (maio 2023)” e as informações das colunas, que correspondem aos primeiros 3 meses do ano, e suas alturas, às quantidades de faltas. Espera-se que os estudantes reconheçam que as colunas amarelas referem-se às faltas das meninas e que as colunas verdes referem-se às faltas dos meninos dessa turma.
Outro aspecto desta atividade é exigir a correta interpretação dos dados apresentados no gráfico para sua transcrição em uma tabela de dupla entrada (item b). Nesse exercício de transposição, os estudantes já obtêm subsídios para resolver as questões subsequentes (itens de c até e), fazer diferentes comparações e tirar conclusões.
No item e, espera-se que os estudantes identifiquem que foram as meninas quem mais diminuíram o número de faltas nesse período, pois foram de 7 faltas para 1 falta, enquanto os meninos foram de 8 para 4 faltas.
BNCC em foco:
EF05MA24, EF05MA25
Os gráficos de colunas já são conhecidos pelos estudantes como forma de organizar e representar dados numéricos. Esta atividade envolve gráficos de colunas duplas, em que cada coluna é identificada por uma cor e pela respectiva legenda. Esse recurso oferece a possibilidade de comparar duas categorias em um mesmo gráfico. Os estudantes devem perceber que a observação de cada eixo (horizontal e vertical), bem como da legenda, é fundamental para a compreensão desses gráficos.
Aproveite o momento da atividade 2 e converse com os estudantes sobre as faltas deles. Peça que listem alguns motivos importantes para não faltarem sem necessidade. Exemplo de resposta: perder a explicação do conteúdo; não participar das atividades com os colegas etc.
MP098
O que você aprendeu
Avaliação processual


- Observe a ilustração e faça o que se pede.
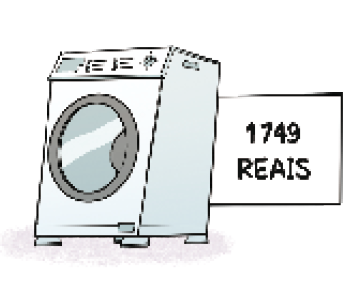
Suzana e Carlos querem comprar esta máquina de lavar roupas. Suzana tem 1.323 reais, e Carlos tem 591 reais. Aproximadamente, juntos, eles têm a quantia suficiente para comprar a máquina de lavar roupas? Explique sua resposta.
_____
PROFESSOR
Resposta: Sim.PROFESSOR
Resposta pessoal.- Veja o que Rafael está dizendo. Depois, responda às questões.

- Qual é o salário total de Rafael, em real?
_____
PROFESSOR
Resposta: 3.315 reais.
- Se Rafael pagar 1.684 reais de aluguel e as despesas com a alimentação da família, quantos reais sobrarão para outras despesas?
_____
PROFESSOR
Resposta: 1.631 reais.
PROFESSOR
Exemplos de cálculo:PROFESSOR
a) 2 .030 + 1.285 = 3.315PROFESSOR
b) 3.315 − 1.684 = 1.631- Para completar a tabela abaixo, referente ao número de habitantes de um município, responda à questão do item a. Depois, responda às demais questões.
Habitantes de um município
Tabela: equivalente textual a seguir.
|
Gênero Idade |
Masculino |
Feminino |
|---|---|---|
|
Até 18 anos |
1.724 |
_____ |
|
Maiores de 18 anos |
_____ |
1.539 |
Fonte: Prefeitura do município (28 fev. 2023).
PROFESSOR
Resposta: 1.836; 2.465.- Sabendo que o total de habitantes de até 18 anos é de 3.560 e que o total de maiores de 18 é de 4.004, quantos habitantes há, ao todo, nesse município?
_____
PROFESSOR
Resposta: 7.564 habitantes.
- Há quantos habitantes do gênero masculino a mais que do gênero feminino nesse município?
_____
PROFESSOR
Resposta: 814
- Nesse município, quantos habitantes do gênero feminino maiores de 18 anos há a menos que habitantes do gênero masculino maiores de 18 anos?
_____
PROFESSOR
Resposta: 926
PROFESSOR
Exemplos de cálculo:PROFESSOR
a) 3.560 + 4.004 = 7.564PROFESSOR
b) 4.189 − 3.375 = 814PROFESSOR
c) 2.465 − 1.539 = 926MANUAL DO PROFESSOR
Objetivo
- Retomar os conceitos estudados.
A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Espera-se que os estudantes respondam, por um cálculo aproximado, que sim. Fazendo uma estimava do total que os dois têm juntos já é possível responder à questão: 1.300 + 590 = 1.890. Juntos eles têm uma quantia maior que o valor dessa máquina de lavar roupas.
Atividade 2
Explore a atividade perguntando aos estudantes: “Considerando que Rafael usou apenas um dos salários (2.030 reais) para o pagamento do aluguel e despesas de alimentação (1.684 reais), quanto resta desse salário?” (346 reais.) “E quanto resta no total?” (1.631 reais.)
Atividade 3
A leitura de tabelas é uma habilidade importante para o desenvolvimento geral do raciocínio matemático. Os estudantes devem ler e completar uma tabela de dupla entrada e observar que ela apresenta as informações relacionadas à idade dos habitantes de um município em duas faixas etárias. Além disso, há uma classificação com relação ao gênero: “masculino” ou “feminino”. As questões devem ser resolvidas por meio de cálculos de adição e de subtração.
Abordar as diversas ideias do campo aditivo nas atividades possibilita que os estudantes desenvolvam de maneira integrada as habilidades relacionadas a essas operações, que deixam de ser vistas como operações isoladas.
É importante estimular que eles selecionem o caminho mais adequado para a resolução, explorando diferentes estratégias de cálculo. Pode-se aproveitar essa série de atividades para avaliar como os estudantes avançaram nos procedimentos de cálculo e em que pontos ainda apresentam alguma dificuldade.
BNCC em foco:
EF05MA07, EF05MA24
MP099
- Para um show de música, foram vendidos 2.563 ingressos. Se cada ingresso custou 24 reais, qual foi a quantia arrecadada com a venda dos ingressos?
_____
PROFESSOR
Resposta: 61.512 reais.
PROFESSOR
Exemplo de cálculo:PROFESSOR
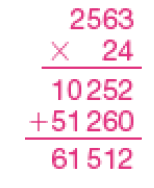

- Graziela digitou o
número
916 na calculadora e quer
obter
o
número
76 usando apenas as teclas
 ,
,  e as teclas de números. Como Graziela pode resolver esse problema?
e as teclas de números. Como Graziela pode resolver esse problema? _____
PROFESSOR
Exemplo de resposta: Graziela pode subtrair 900 de 916 e depois adicionar 60 ao resultado.
- Mônica pagou uma televisão em 15 prestações iguais. O total pago foi 1 275 reais. Qual era o valor de cada prestação?
_____
PROFESSOR
Resposta: 85 reais.
PROFESSOR
Exemplo de cálculo:PROFESSOR

- Para cada sequência numérica, determine uma possível regra de formação e, de acordo com essa regra, escreva os números seguintes.
- 14, 19, 24, 29,
_____,
_____,
_____,
_____,
_____
PROFESSOR
Exemplo de resposta: 34, 39, 44, 49, 54.
- 15, 18, 20, 23, 25, 28,
_____,
_____,
_____
PROFESSOR
Exemplo de resposta: 30, 33, 35
- 14, 19, 24, 29,
_____,
_____,
_____,
_____,
_____
Autoavaliação

- Consigo realizar cálculos de adição, subtração, multiplicação e divisão por meio de estratégias pessoais? E usando o algoritmo usual?

- Identifico as regularidades em sequências numéricas?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 4
Esta atividade explora a multiplicação envolvendo um fator de 4 algarismos e outro de 2 algarismos. Deixe que os estudantes escolham a estratégia que quiserem para realizarem o cálculo. Socialize e valide as diferentes estratégias utilizadas. Apresente o algoritmo usual na lousa como mais uma estratégia possível, verificando e sanando possíveis dúvidas que os estudantes ainda apresentem.
Atividade 5
Explore as diferentes resoluções da atividade, pedindo a alguns estudantes que escrevam na lousa como pensaram, de modo que os demais possam validar as estratégias utilizadas.
Atividade 6
Esta atividade explora uma divisão em que o dividendo tem 4 algarismos e o divisor é um número de 2 algarismos. Os estudantes podem realizar o cálculo com a estratégia que preferirem. Espera-se, porém, que o algoritmo usual seja utilizado por algum dos estudantes. Se ele não aparecer, apresente-o na lousa, verificando e sanando possíveis dúvidas. Ao final, peça que refaçam a divisão usando um procedimento diferente daquele já utilizado por eles.
Atividade 7
Em uma roda de conversa, peça aos estudantes que exponham suas ideias e as sequências que montaram. A cada sequência apresentada, os demais estudantes devem descobrir o padrão de formação antes de o estudante que a criou dar sua explicação.
BNCC em foco:
EF05MA07, EF05MA08
Autoavaliação
Na primeira questão, os estudantes poderão observar algumas atividades em que os algoritmos tenham sido utilizados para verificar se compreendem as regras de funcionamento. Enfatize que há outras formas de realizar os cálculos, mas o objetivo agora é avaliar como estão os procedimentos no tipo de algoritmo utilizado na unidade.
Na segunda questão, os estudantes poderão verificar seus conhecimentos iniciais algébricos, analisando quanto conseguem identificar padrões e regularidades em sequências com diferentes tipos de intervalos.
MP100
Comentários para o professor:
Conclusão da Unidade 2
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue resolver e elaborar problemas de adição e subtração com números naturais, utilizando cálculo mental, por estimativa e algoritmos? |
_____ |
_____ |
|
Consegue resolver e elaborar problemas de multiplicação e divisão com números naturais, utilizando cálculo mental, por estimativa e algoritmos? |
_____ |
_____ |
|
Resolve problemas que envolvam a proporcionalidade direta entre duas grandezas? |
_____ |
_____ |
|
Interpreta dados apresentados em tabelas e gráficos de colunas duplas? |
_____ |
_____ |
|
Organiza dados coletados em tabelas e gráficos pictóricos? |
_____ |
_____ |
|
Apresenta texto sobre os resultados de uma pesquisa? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opinião e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP101
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |