MP102
Comentários para o professor:
Introdução da Unidade 3
Assim como em Unidades anteriores, a abertura cumpre a função de despertar a atenção dos estudantes, artística e prazerosamente, para os conceitos a serem abordados. Constitui-se, assim, em um amplo campo a ser explorado em abordagens diversas, além das questões propostas na seção Para refletir ...
Os conhecimentos desenvolvidos ao longo do 4º ano acerca das relações entre figuras geométricas planas e figuras geométricas não planas serão, nesse momento, retomados, ampliados e aprofundados na perspectiva de que, além de prismas e pirâmides, os estudantes associem cilindros e cones a suas planificações, analisando, nomeando e comparando seus atributos. Esses conhecimentos constituem aportes necessários a fim de que, durante o 6º ano, os estudantes quantifiquem e relacionem o número de vértices, faces e arestas de prismas e pirâmides ao polígono que compõe suas bases, e que também os associem – nesses e em outros poliedros convexos – por meio da Relação de Euler ( V – A + F = 2).
As atividades propostas nesta Unidade envolvendo polígonos têm como objetivo promover o reconhecimento, a nomeação e a comparação dessas figuras a partir da observação de seus lados, vértices e ângulos, desenhando-os com material de desenho ou por meio de tecnologias digitais. Além disso, em relação aos ângulos de figuras poligonais, as atividades visam ao reconhecimento da congruência entre eles, assim como da proporcionalidade entre seus lados correspondentes. Para isso, são utilizadas situações de ampliação e redução em malhas quadriculadas e, também, as tecnologias digitais. Algumas atividades, ainda, retomam conhecimentos desenvolvidos durante o 4º ano, como o reconhecimento de ângulos retos em figuras poligonais com o uso de esquadros e softwares de Geometria, além das classificações de ângulos representantes de um quarto de volta (com aplicação na construção de retas perpendiculares e em trajetos feitos em malhas quadriculares), meia-volta e volta completa.
Cabe observar que os conhecimentos ora abordados constituem a base para os estudos a serem desenvolvidos ao longo do 6º ano relativos ao reconhecimento, à nomeação e à comparação de polígonos acerca de lados, vértices e ângulos, além da classificação em regulares e não regulares, tanto em suas representações planas quanto em faces de poliedros.
A abordagem de atividades relativas à Probabilidade e estatística amplia os conhecimentos construídos no 4º ano sobre a análise de dados apresentados em gráficos de colunas. Desse modo, as atividades têm como objetivo principal a leitura e interpretação de dados apresentados em gráficos de linhas, na perspectiva de que, no 6º ano, os estudantes tenham conhecimentos necessários para interpretarem e resolverem situações que envolvam dados de pesquisas sobre diferentes contextos, sintetizando suas conclusões por meio da redação de textos.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletiva. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.
Competências específicas favorecidas
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
MP103
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item Ampliação e redução de figuras desta Unidade.
Roteiro de aula – Ampliação e redução de figuras
1 ª parte – Introdução – Tempo sugerido: 15 minutos
Organize as carteiras de modo que os estudantes possam trabalhar em duplas. Para a composição dos grupos, sugira escolhas livres, porém fique atento e auxilie aqueles que estiverem com dificuldade em encontrar colegas para realizar a atividade.
Para cada dupla, distribua duas folhas de papel sulfite A4.
Peça que façam o seguinte procedimento:
1. Preserve uma das folhas e identifique-a com (III).
2. Juntando os dois lados menores, dobre a outra folha exatamente ao meio, vinque e corte na dobra.
3. Repita o item 2 com uma das metades obtidas. Identifique uma das novas metades com (II). Esta é a metade da metade da folha original A4.
4. Com a outra metade obtida no item 3, repita o item 2. E, com uma das novas metades, repita novamente o item 2, identificando uma das novas metades com (I). Esta é a metade da metade da metade da folha original A4.
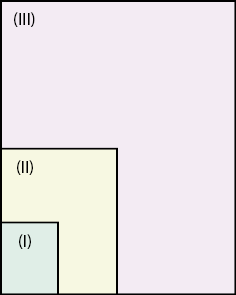
A seguir, peça que coloquem os papéis (I), (II) e (III) um sobre o outro, nessa ordem, de modo que um dos cantos fiquem juntos, assim como os lados maiores também devem ficar juntos.
Comente com os estudantes que as figuras (I), (II) e (III) têm a mesma forma, que os lados de (III) têm o dobro das medidas de (II) e que os lados deste têm o dobro das medidas de (I). Além disso, todos os ângulos de (I), (II) e (III) têm a mesma medida. Logo:
• (III) é uma ampliação de (II) e de (I).
• (II) é uma ampliação de (I).
• (I) é uma redução de (II) e de (III).
• (II) é uma redução de (III).
2 ª parte – Cálculo mental – Tempo sugerido: 35 minutos
Faça a leitura com a turma da atividade 1 e, por cerca de 10 minutos (sugestão), deixe que a completem no livro. Porém, antes de seguir adiante, valide o resultado obtido. É importante que, para a continuidade, não haja dúvidas.
Anuncie o tempo de 5 minutos (sugestão) para a resolução da atividade 2.
Leia, com a turma, a atividade 3 e proponha que a completem no livro. Após 15 minutos (sugestão), peça argumentações voluntárias de 2 ou 3 estudantes para validar a resposta.
Finalmente, peça que resolvam as atividades 4 e 5 (sugestão: 10 minutos) e valide as respostas com a turma.
MP104
UNIDADE 3. Geometria

MANUAL DO PROFESSOR
Objetivos da Unidade
- Analisar, nomear e comparar os atributos de figuras geométricas não planas.
- Classificar figuras geométricas não planas.
- Associar figuras geométricas não planas a suas planificações.
- Identificar vértices, faces e arestas em poliedros.
- Identificar giros e ângulos e suas medidas.
- Identificar ângulo reto.
- Medir ângulos usando um transferidor e reconhecer o grau como unidade de medida de ângulo.
- Interpretar a movimentação de pessoas ou de objetos no plano.
- Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos.
- Classificar triângulos e quadriláteros.
- Analisar os ângulos internos de triângulos.
- Desenhar polígonos utilizando material de desenho e tecnologias digitais.
- Reconhecer a congruência dos ângulos e a proporcionalidade entre os lados correspondentes de figuras poligonais em situações de ampliação e de redução em malhas quadriculadas.
- Explorar figuras que provocam ilusão de óptica.
- Perceber ilusões visuais em representações geométricas.
- Ler e interpretar dados apresentados em gráficos de linhas.
- Organizar dados coletados por meio de gráfico.
- Produzir textos para sintetizar conclusões dos resultados de uma pesquisa.
BNCC em foco:
EF05MA14, EF05MA16, EF05MA17, EF05MA18, EF05MA24
MP105
Boxe Complementar
Para refletir...

Beatriz, Marcos, Roberto e Vanessa estão passando o dia em um parque.
Que objetos desta cena se parecem com figuras geométricas não planas?
PROFESSOR
Exemplo de resposta: A construção lembra uma pirâmide; as peças de sinalização lembram cones; a latinha de suco no carrinho lembra um cilindro; o bebedouro e alguns bancos lembram um paralelepípedo.Os visitantes do teatro recebem a planificação de um modelo desse teatro, que tem a forma de uma pirâmide de base quadrada. Quais figuras planas compõem essa planificação?
PROFESSOR
Resposta: Triângulos e quadrado.Fim do complemento
MANUAL DO PROFESSOR
Incentive os estudantes a procurarem as personagens Beatriz, Marcos, Roberto e Vanessa no parque e a esclarecerem o enigma: por que a menina que está comendo maçã do amor está assustada? A menina está assustada porque uma abelha está rondando sua maçã do amor.
Para refletir...
Dê um tempo aos estudantes para que observem a cena de abertura com atenção. Depois, peça que respondam às questões propostas. Aproveite para explorar o nome correto das figuras mencionadas. Por exemplo, ao reconhecerem a latinha que está no carrinho de sucos e sorvetes, diga que ela se parece com a figura geométrica não plana cilindro.
Depois que os estudantes reconhecerem os objetos e as figuras geométricas não planas, sugira que classifiquem os objetos de acordo com um critério de sua escolha. Um critério possível é classificar os objetos em arredondados (latinha de suco, cones de sinalização, rodas) dos não arredondados (bebedouro, observatório, bancos). Eles devem esboçar a planificação da superfície do modelo do teatro e identificar nela um quadrado e 4 triângulos.
Depois que os estudantes responderem às questões, peça que digam como descobriram quais eram as figuras geométricas planas.
MP106
Poliedros e corpos redondos
- Rodrigo tem alguns modelos de figuras geométricas planas feitos de cartolina e alguns modelos de figuras geométricas não planas feitos de acrílico.
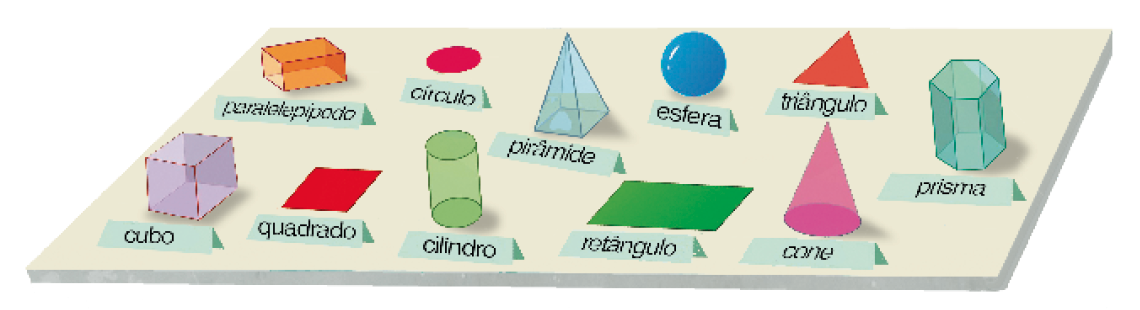
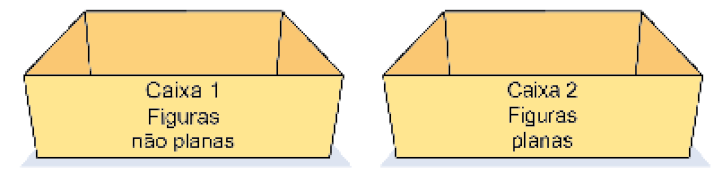
- Para ajudar Rodrigo a colocar os modelos na caixa certa, marque com um
X
os modelos que
devem
ir para a Caixa 1 e cerque com uma linha os modelos que
devem
ir para a Caixa 2.
PROFESSOR
Resposta: caixa 1: paralelepípedo; pirâmide; esfera; prisma; cubo; cilindro; cone.PROFESSOR
Caixa 2: círculo; triângulo; quadrado; retângulo.

- Rodrigo quer separar os modelos da Caixa 1 em dois grupos para organizá-los melhor. Como você acha que ele deveria separar esses modelos? Converse com seus colegas sobre isso.
PROFESSOR
Exemplos de resposta: Modelos de figuras arredondadas em uma caixa e de figuras não arredondadas em outra; ou figuras com pelo menos um “bico” em uma caixa e sem “bico” na outra.

- Qual é a figura “intrometida” em cada caso? Marque-a com um X .
a)

PROFESSOR
Resposta correta: prismab)
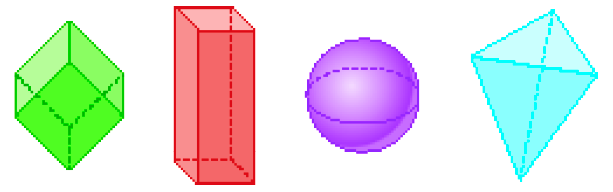
PROFESSOR
Resposta correta: esfera


- Agora, reúna-se com um colega e conversem sobre o que o levou a escolher essas figuras.
PROFESSOR
Exemplo de respostas: a) É a única figura não arredondada.PROFESSOR
b) É a única figura arredondada.MANUAL DO PROFESSOR
Objetivos
- Analisar, nomear e comparar os atributos de figuras geométricas não planas.
- Classificar figuras geométricas não planas em poliedros ou corpos redondos.
Atividade 1
Ao identificar similaridades e diferenças entre figuras geométricas, os estudantes adquirem subsídios para o entendimento dos critérios de classificação mais razoáveis para agrupar essas figuras. A proposta desta atividade é conduzir os estudantes a compreenderem os critérios que permitem organizar as figuras geométricas em dois grupos: o das figuras planas e o das figuras não planas. No item b, que solicita uma subclassificação das figuras não planas em dois grupos, é importante observar as explicações dos estudantes para o critério por eles adotado. Verifique se a separação de figuras que propõem atende a uma lógica. Caso o critério deles seja inadequado, questione-os e ofereça dicas para outras classificações, até chegar aos dois grupos desejados.
Atividade 2
Observe se os estudantes entenderam que “figura intrometida” é aquela que não apresenta características comuns às demais figuras.
Ao distinguir visualmente corpos redondos de alguns poliedros, os estudantes têm a oportunidade de aplicar o que foi concluído na atividade anterior a respeito da distinção entre corpos arredondados e corpos não arredondados, ao mesmo tempo em que se preparam para uma primeira sistematização dos conceitos que definem poliedros e corpos redondos, apresentada na atividade seguinte.
Explore a situação pedindo a eles que justifiquem sua escolha e que analisem coletivamente se o argumento faz sentido no contexto da atividade.
BNCC em foco:
EF05MA16
Sugestão para o professor
Vídeo
Mão na forma: diálogo geométrico . Disponível em: http://fdnc.io/eUr. Acesso em: 26 jul. 2021.
Nesse vídeo, são apresentadas diversas figuras geométricas presentes no cotidiano, na natureza e na Matemática, explorando a história da Geometria e as propriedades dessas figuras. Há sugestões de atividades práticas de construção de modelos de figuras não planas, utilizando moldes, como o tetraedro e o cubo, que são vistos da mesma maneira, independentemente da posição de observação.
MP107

- Observe as figuras e leia o texto. Depois, responda às questões.

Cubo
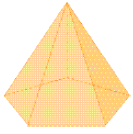
Pirâmide de base pentagonal

Paralelepípedo

Prisma de base triangular

Esfera

Cone

Cilindro
Observação:
Algumas dessas figuras são arredondadas. É o caso da esfera, do cone e do cilindro, que são exemplos de figuras chamadas corpos redondos.
Outras figuras são não arredondadas. É o caso do cubo, da pirâmide de base pentagonal, do paralelepípedo e do prisma de base triangular, que são exemplos de figuras chamadas poliedros, que significa “muitas faces”.
Fim da observação.
- O que há de parecido nos poliedros? E de diferente?
PROFESSOR
Exemplo de resposta: O que há de parecido: os poliedros têm arestas e suas faces são planas; o que há de diferente: eles podem ter número diferente de faces.
- O que há de parecido nos corpos redondos? E de diferente?
PROFESSOR
Exemplo de resposta: O que há de parecido: eles são arredondados; o que há de diferente: o cone tem um “bico”, e o cilindro e a esfera não têm; o cone e o cilindro têm parte plana, e a esfera não tem.

- Nos quadros abaixo, desenhe ou escreva o nome de objetos que lembram a figura geométrica indicada.
PROFESSOR
Respostas variáveis.
- Corpos redondos
Tabela: equivalente textual a seguir.
|
Esfera |
Cone |
Cilindro |
|---|---|---|
|
_____ |
_____ |
_____ |
- Poliedros
Tabela: equivalente textual a seguir.
|
Paralelepípedo |
Prisma de base hexagonal |
Pirâmide |
|---|---|---|
|
_____ |
_____ |
_____ |
MANUAL DO PROFESSOR
Atividade 3
Os estudantes provavelmente usarão uma linguagem não formal para responder às perguntas.
Depois da resolução, verifique se eles compreenderam que os poliedros têm faces em forma de polígonos (triângulo, quadrado, retângulo, pentágono, hexágono etc.) e que o mesmo não ocorre em relação aos corpos redondos desta atividade. Comente que o elemento vértice não é exclusivo dos poliedros, pois o corpo redondo cone também possui vértice.
Atividade 4
Espera-se que os estudantes citem objetos do cotidiano. No caso de corpos redondos, por exemplo: bola (esfera), casquinha de sorvete (cone) e lata de suco (cilindro); e no caso dos poliedros: caixa de creme dental (paralelepípedo), caixa de presente (prisma de base hexagonal) e enfeites (pirâmide).
BNCC em foco:
EF05MA16
Sugestão de leitura para o professor
Artigo
PAIS, Luiz Carlos. Uma análise do significado da utilização de recursos didáticos no ensino da Geometria. Disponível em: http://fdnc.io/eUs. Acesso em: 30 mar. 2021.
Esse artigo descreve uma pesquisa que aborda o problema da utilização de recursos didáticos no ensino da Geometria na Educação Fundamental. A ideia do artigo é aprimorar o uso desses recursos, uma vez que se constata que a manipulação de objetos concretos pode, por vezes, restringir-se a uma atividade puramente empírica, negando os valores formativos mais amplos do conteúdo geométrico.
MP108
Planificação de superfícies
- Osvaldo é carpinteiro e quer organizar de acordo com o tamanho os
pregos
que
usa
em seus trabalhos. Para isso, ele vai guardar os
pregos
em várias caixinhas cúbicas iguais, que serão encaixadas em sua maleta de materiais.
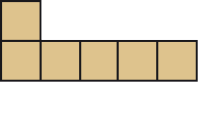
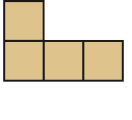
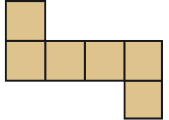
Observe as planificações abaixo e descubra qual delas Osvaldo deve escolher como molde para fazer as caixinhas cúbicas.
a)
b)
c)
d)
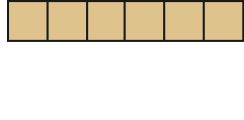
PROFESSOR
Resposta correta: imagem c.

- Converse com o professor e os colegas sobre os moldes que não
devem
ser escolhidos por Osvaldo. Por que esses moldes não formam uma caixa cúbica?
PROFESSOR
Resposta pessoal.
- Observe a representação da planificação abaixo e da figura geométrica não plana obtida a partir dela.
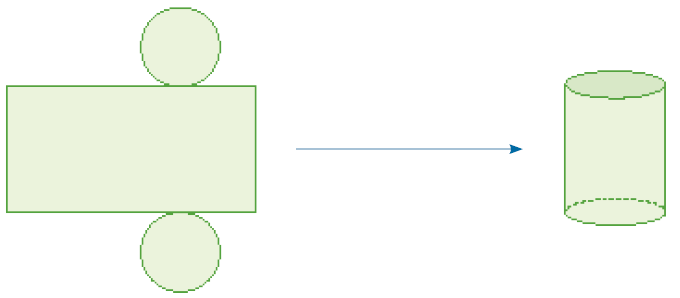
- Agora, escreva o nome das figuras geométricas não planas que podemos obter com cada planificação representada a seguir.
a)
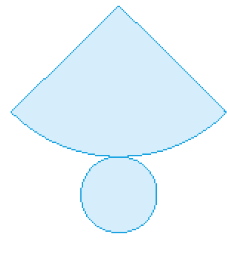
_____
PROFESSOR
Resposta: Cone.b)
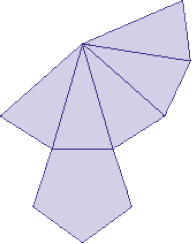
_____
PROFESSOR
Resposta: Pirâmide de base pentagonal.c)
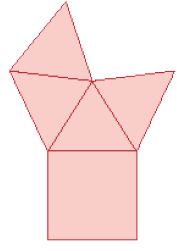
_____
PROFESSOR
Resposta: Pirâmide de base quadrada.MANUAL DO PROFESSOR
Objetivos
- Analisar, nomear e comparar os atributos de figuras geométricas não planas.
- Associar figuras geométricas não planas (prismas, pirâmides, cilindros e cones) a suas planificações.
Antes das atividades deste tópico, proponha aos estudantes que levem para a sala de aula embalagens de papelão variadas, que sejam facilmente desmontáveis. Eles poderão desmontá-las e recortar as abas de colagem para obter as planificações. Peça que observem as partes recortadas e as desenhem no caderno ou que representem a figura geométrica que a embalagem lembra.
Atividade 1
Se possível, providencie moldes como os da atividade para que, em duplas ou em grupos, os estudantes analisem, montem as figuras e discutam com o colega ou com o grupo para descobrirem qual figura pode formar a caixa cúbica.
Em seguida, peça que recortem e dobrem cada modelo e verifiquem se as previsões iniciais estavam corretas.
Esta atividade favorece a construção de um vocabulário geométrico para a comunicação entre os colegas no momento da discussão das possibilidades de montagem, o desenvolvimento da visualização espacial e a observação de diferentes soluções para um mesmo problema.
Atividade 2
O estudo da planificação de modelos de figuras não planas permite aos estudantes associarem faces de figuras não planas com figuras planas. A compreensão dessas ideias é facilitada pela manipulação de objetos concretos.
BNCC em foco:
EF05MA16; competência específica 6
Sugestão de atividade
Manuseando figuras geométricas
Distribua à turma moldes para montarem modelos de algumas figuras não planas: cone, cilindro, paralelepípedo, pirâmide de base quadrada e prisma de base triangular, por exemplo.
Os estudantes devem manusear os modelos das figuras geométricas e analisá-los, percebendo as diferenças quanto à forma e distinguindo os polígonos que representam cada uma de suas faces (no caso dos poliedros). Sugira que anotem no caderno os dados que obtiverem da análise e depois os comparem com os de um colega.
MP109
- Rubens vai montar 4 modelos de poliedros utilizando recortes de papelão e fita adesiva. Circule os recortes que Rubens deverá utilizar para montar cada modelo.
Tabela: equivalente textual a seguir.
|
Poliedro |
A |
B |
C |
D |
E |
F |
G |
H |
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PROFESSOR
Resposta: Poliedro: paralelepípedo - A, B, E, F, G, H.PROFESSOR
Poliedro: cubo - A, B, C, E, G, H.PROFESSOR
Poliedro: pirâmide - A, B, C, F, H.PROFESSOR
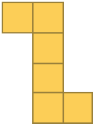
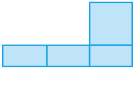
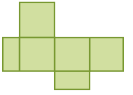
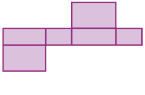
Poliedro: prisma - A, B, C, D, E, F, G, H.- Observe as planificações a seguir.
a)
b)
c)
d)
PROFESSOR
Resposta: A figura em a corresponde à planificação de um cubo e a em d, à de um paralelepípedo.PROFESSOR
Na figura em b, teria de ser acrescentado um retângulo igual aos desenhados e, no seu prolongamento, um quadrado igual ao desenhado, mas no lado oposto. Na figura em c, basta mudar a posição do retângulo não alinhado aos três quadrados, justapondo-o ao retângulo alinhado, e acrescentar um quadrado no lugar do retângulo removido.- Reproduza essas representações de planificações, em tamanho maior, em uma folha de papel mais firme, como cartolina. Recorte-as e tente montar modelos de poliedros. Se não conseguir, indique as alterações que devem ser feitas nas representações das planificações de modo que seja possível montar algum modelo. Marque com um X as planificações acima que possibilitam a montagem dos modelos.
PROFESSOR
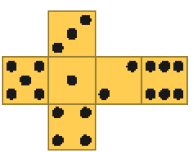
Resposta correta: a e d.- Abaixo, foi representado um dado em três posições diferentes.
- Qual destas figuras representa a planificação da superfície desse dado?

a)
b)
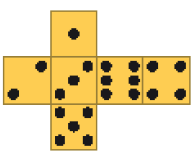
c)
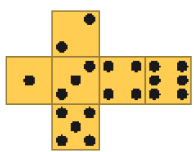
d)
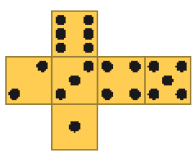
PROFESSOR
Resposta correta: a.MANUAL DO PROFESSOR
Atividade 3
Para a resolução desta atividade, os estudantes devem considerar a disposição das partes da planificação que lembram figuras planas, ou seja, compreender que, para uma planificação ser correta, não basta justapor as partes em qualquer posição.
Espera-se que os estudantes percebam que, para a construção de modelos de figuras não planas, as partes da planificação não podem se sobrepor e o modelo tem de fechar completamente.
Atividade 4
Para auxiliar na resolução desta atividade, leve para a sala de aula embalagens que lembrem um paralelepípedo, um cubo e um prisma de base quadrada. Permita que os estudantes manipulem as caixas, pois isso favorece a visualização de figuras não planas e suas planificações. No caso de remontarem as embalagens, acrescentando ou não outras faces, podem unir as partes usando fita adesiva.
Atividade 5
Caso julgue oportuno, proponha aos estudantes que decalquem as planificações em uma cartolina e as recortem. Depois, eles devem desenhar as faces do dado de acordo com cada uma das quatro planificações.
BNCC em foco:
EF05MA16
MP110
Mais poliedros
- Analise os poliedros e, depois, complete o quadro com as informações correspondentes.
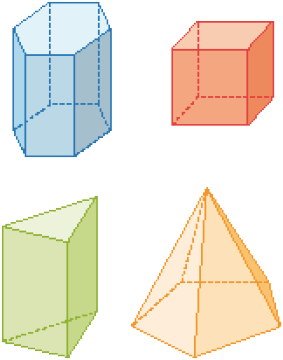
Tabela: equivalente textual a seguir.
|
Poliedro |
Quantidade de vértices |
Quantidade de faces |
Quantidade de arestas |
|---|---|---|---|
|
Prisma de base hexagonal |
_____ |
_____ |
_____ |
|
Cubo |
_____ |
_____ |
_____ |
|
Prisma de base triangular |
_____ |
_____ |
_____ |
|
Pirâmide de base pentagonal |
_____ |
_____ |
_____ |
PROFESSOR
Resposta: Prisma de base hexagonal. Quantidade de vértices: 12. Quantidade de faces: 8. Quantidade de arestas: 18.PROFESSOR
Cubo. Quantidade de vértices: 8. Quantidade de faces: 6. Quantidade de arestas: 12.PROFESSOR
Prisma de base triangular. Quantidade de vértices: 6. Quantidade de faces: 5. Quantidade de arestas: 9.PROFESSOR
Prisma de base pentagonal. Quantidade de vértices: 6. Quantidade de faces: 6. Quantidade de arestas: 10.- Durante a aula de Geometria, Júlia aprendeu uma regularidade presente nos poliedros.

- Agora que você também já sabe essa regularidade, descubra o número de arestas de cada figura a seguir.
- Poliedro com 8 vértices e 8 faces -
_____
PROFESSOR
Resposta: 14 arestas.
- Poliedro com 8 vértices e 6 faces -
_____
PROFESSOR
Resposta: 12 arestas.
- Poliedro com 14 vértices e 9 faces -
_____
PROFESSOR
Resposta: 21 arestas.

- Considere uma pirâmide com 10 arestas. Indique o polígono da base dessa pirâmide, o
número
de vértices e o
número
de faces. Depois, represente-a no espaço ao lado.
Polígono da base - _____
PROFESSOR
Resposta: Pentágono.Número de vértices - _____
PROFESSOR
Resposta: 6Número de faces - _____
PROFESSOR
Resposta: 6
PROFESSOR
Exemplo de desenho: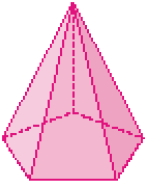
MANUAL DO PROFESSOR
Objetivos
- Analisar, nomear e comparar os atributos de figuras geométricas não planas.
- Identificar vértices, faces e arestas em poliedros.
Atividade 1
Nesta atividade, os estudantes devem contar os vértices, as arestas e as faces de cada poliedro e preencher o quadro.
Se possível, traga modelos dessas figuras geométricas para os estudantes manusearem e validarem suas respostas.
Atividade 2
Explore com os estudantes a relação descrita por Júlia. Explique que qualquer poliedro segue esta relação: o número de vértices ( V ) mais o números de faces ( F) é igual ao número de arestas (A) mais 2, ou seja: V + F = A + 2.
Desse modo, espera-se que os estudantes adicionem o número de vértices com o número de faces e, depois, subtraiam 2 da soma obtida.
- 8 + 8 − 2 = 14
- 8 + 6 − 2 = 12
- 14 + 9 − 2 = 21
Atividade 3
Os estudantes podem iniciar desenhando a base pentagonal e as outras arestas e, depois, contar a quantidade de vértices e faces.
Caso não seja fácil visualizar, por meio do desenho, a quantidade de faces da pirâmide, os estudantes podem usar a relação que aprenderam na atividade anterior.
BNCC em foco:
EF05MA16; competência específica 3
MP111
Medida de ângulo
- Observe a abertura de cada um dos ângulos representados.
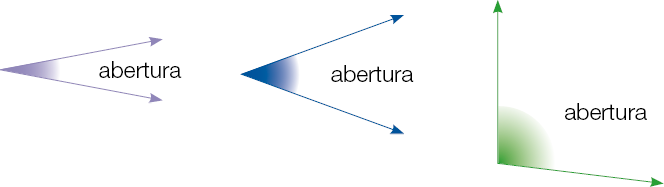
Esses ângulos têm aberturas diferentes. Quanto maior a abertura de um ângulo, maior é sua medida.
O ângulo destacado na cor _____ é o de maior medida.
PROFESSOR
Resposta: verdePara medir um ângulo, é preciso medir sua abertura.
Cada abertura está associada a uma medida em grau.
- Veja como Adriana determinou a medida do ângulo em destaque.
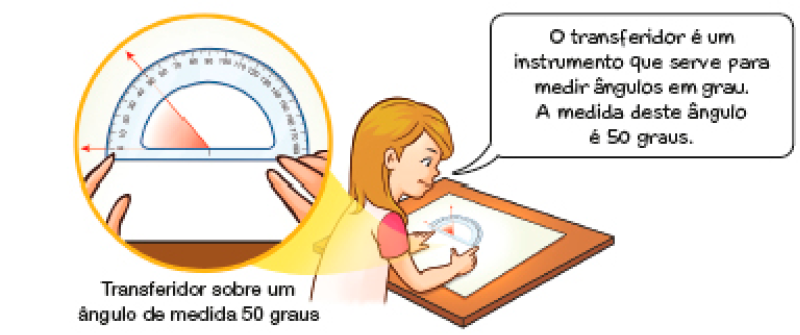
Qual é a medida de cada um destes ângulos em destaque?
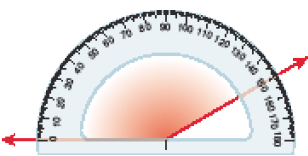
A medida deste ângulo é _____ graus.
PROFESSOR
Resposta: 150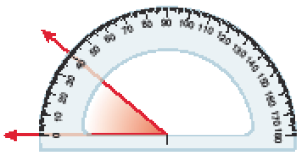
A medida deste ângulo é _____ graus.
PROFESSOR
Resposta: 40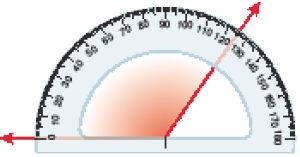
A medida deste ângulo é _____ graus.
PROFESSOR
Resposta: 125MANUAL DO PROFESSOR
Objetivos
- Identificar giros e ângulos e suas medidas.
- Medir ângulos usando um transferidor.
- Reconhecer o grau como unidade de medida de ângulo.
- Identificar ângulo reto.
- Interpretar a movimentação de pessoas ou de objetos no plano.
Atividade 1
Esta atividade e as da página seguinte ampliam os conhecimentos dos estudantes referentes aos ângulos, explorando a unidade de medida grau por meio da utilização de instrumentos como o transferidor.
Se possível, peça aos estudantes que levem um transferidor para a aula e explore com eles cada elemento, desde o formato do instrumento, que permite a medição das aberturas formadas por semirretas (ou segmentos de reta no caso de ângulos de polígonos), até os números registrados em graus. Explore também a situação ilustrada para que os estudantes aprendam a utilizar o instrumento, posicionando o zero em uma das semirretas. Depois, peça a eles que meçam alguns ângulos em espaços da sala de aula.
BNCC em foco:
EF05MA17
Ângulos na história
Proponha aos estudantes uma conversa para resgatar os conhecimentos sobre a unidade de medida grau. É possível que a associem à temperatura, grau Celsius, que não é uma associação correta. Explique que a unidade de medida de ângulo grau é um resquício de práticas comuns há milhares de anos, quando os babilônios (povo que habitava a região conhecida atualmente como Iraque) empregavam a divisão do ano em 360 dias e a cada dia do ano associavam uma posição (grau) na circunferência que representava 1 ano completo. Após um ciclo de 360 dias, o ano reiniciava, com as mesmas estações.
MP112
- Observe a figura abaixo e complete o quadro.

Quadro: equivalente textual a seguir.
|
Giro |
Medida do ângulo em grau |
|---|---|
|
Volta completa |
_____ |
|
Meia-volta |
_____ |
|
Um quarto de volta |
_____ |
PROFESSOR
Resposta: 360; 180; 90.- Observe os ângulos destacados no retângulo.
Cada um dos ângulos destacados no retângulo é chamado de ângulo reto.

Observe o transferidor e responda: Qual é a medida do ângulo reto?
_____
PROFESSOR
Resposta: 90 graus.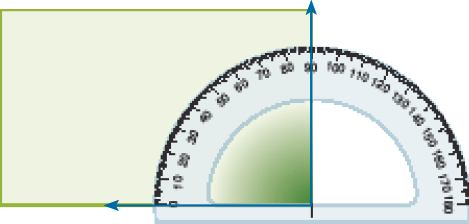

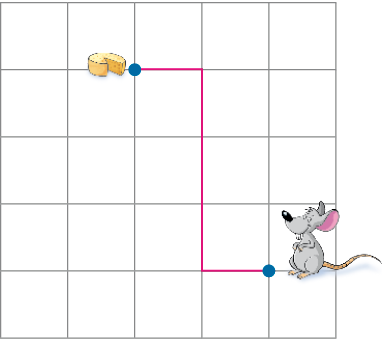
- De acordo com as orientações a seguir, desenhe o caminho que o ratinho seguiu sobre as linhas da malha até encontrar o queijo.
Caminho seguido pelo ratinho:
- Andou 1 lado de quadradinho à frente.
- Girou 90 graus para a direita e andou 3 lados de quadradinho à frente.
- Girou 90 graus para a esquerda e andou 1 lado de quadradinho à frente, encontrando o queijo.
MANUAL DO PROFESSOR
Atividade 2
Os estudantes podem estimar as medidas dos três ângulos tomando como referência o ângulo de um quarto de volta, que mede 90 graus. Após a resolução, sugira que verifiquem suas estimativas medindo as aberturas dos três ângulos com o transferidor.
Atividade 3
Esta atividade explora a classificação dos ângulos, tomando como referência o ângulo de medida 90 graus. Esse conhecimento facilita a compreensão de algumas propriedades dos polígonos; por exemplo, a de o retângulo ser um quadrilátero com quatro ângulos internos de 90 graus, ou seja, quatro ângulos retos, daí o nome retângulo. Peça aos estudantes que deem exemplos de onde é possível observar ângulos retos. Eles podem dar como resposta o ângulo formado entre duas paredes ou os ângulos dos cantos de um livro ou de uma folha de papel de formato retangular. O ângulo reto é usado como referência para classificar ângulos de medidas maiores que 90 graus e menores que 180 graus (ângulos obtusos) e ângulos de medidas menores que 90 graus (ângulos agudos). Destaque também que o ângulo raso (180 graus) pode ser a composição de dois ângulos retos (90 graus).
Atividade 4
Explique aos estudantes que o ratinho anda sobre as linhas da malha.
Destaque a similaridade entre a leitura do trajeto feito pelo ratinho na malha quadriculada e as indicações de caminhos que precisamos fazer em muitas situações cotidianas.
BNCC em foco:
EF05MA14, EF05MA17; competência específica 6
MP113
Polígonos
- Leia o diálogo e faça o que se pede.


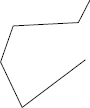
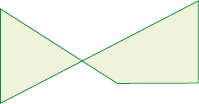
- Indique com a letra P as figuras que são polígonos. Justifique sua resposta.


PROFESSOR
Exemplo de justificativa: As figuras I e IV não são polígonos; a figura I, porque é aberta, e a figura IV, porque as linhas do contorno se cruzam.

- Agora, em uma folha de papel, faça uma composição com diferentes desenhos de polígonos.
PROFESSOR
Resposta variável.- Vinícius comprou um brinquedo de encaixar peças para sua filha.
No brinquedo, há uma base na qual a criança deve encaixar 5 pecinhas. Veja os desenhos das peças desse brinquedo e, depois, responda às questões.

- Em qual das bases é possível encaixar todas as 5 peças?
_____
PROFESSOR
Resposta: Base 2.

Base 1

Base 2

Base 3
- Quais dessas peças têm um encaixe que lembra o
contorno
de um polígono? Quais são esses polígonos?
_____
PROFESSOR
Resposta: Peças 2 e 4; Triângulo e pentágono.
MANUAL DO PROFESSOR
Objetivo
- Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos.
Os estudantes já tiveram contato com alguns tipos de polígono em anos anteriores; portanto, são capazes de reconhecer a nomenclatura a eles associada e algumas de suas características.
Atividade 1
Esta atividade possibilita consolidar o conceito de polígono e aplicá-lo na identificação de contraexemplos, de figuras que não são polígonos.
Certamente os estudantes não usarão uma linguagem formal. Espera-se, no entanto, que percebam que os polígonos são figuras planas fechadas cujo contorno pode ser traçado com uma régua e os trechos desse contorno não se cruzam. Caso tenham dificuldade em identificar figuras fechadas, apresente mais exemplos de figuras abertas, como:
CRÉDITO: ADILSON SECCO
Atividade 2
Antes de iniciar a atividade, desenhe na lousa algumas figuras planas e peça aos estudantes que respondam oralmente se o desenho representa ou não um polígono. Em caso afirmativo, peça-lhes que identifiquem o polígono formado.
Os estudantes devem se lembrar de que polígonos são figuras planas fechadas cujo contorno pode ser traçado com uma régua.
Para a resolução desta atividade, pode-se solicitar aos estudantes que desenhem o encaixe de cada peça ao lado das pecinhas. Depois, eles devem relacionar essas figuras com as bases do item a.
BNCC em foco:
EF05MA17
Sugestão de trabalho interdisciplinar
Ao final das atividades sobre polígonos, realize um trabalho interligado com História e Arte. Sugira aos estudantes que, utilizando papel celofane e color set, confeccionem um vitral que apresente diversas representações de figuras geométricas planas.
Conte a eles que os vitrais, presentes principalmente nas imensas janelas de igrejas datadas da Idade Média, são elementos decorativos que apresentam desenhos. Mostre algumas imagens que ilustrem esses vitrais e também o contexto histórico.
Após terminarem de criar seus vitrais, sugira uma exposição de todos os trabalhos na sala de aula.
MP114
- Observe a representação de um polígono e algumas de suas partes destacadas. Depois, preencha o quadro com as informações correspondentes.
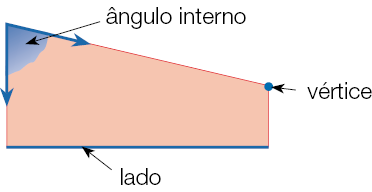
Quadro: equivalente textual a seguir.
|
Polígono |
Quantidade de lados |
Quantidade de vértices |
Quantidade de ângulos internos |
|---|---|---|---|
|
|
3 |
3 |
_____ |
|
|
_____ |
_____ |
_____ |
|
|
_____ |
_____ |
_____ |
|
|
_____ |
_____ |
_____ |
|
|
_____ |
_____ |
_____ |
PROFESSOR
Resposta: Triângulo: 3.PROFESSOR
Polígono amarelo: 4, 4, 4.PROFESSOR
Polígono azul: 5, 5, 5.PROFESSOR
Hexágono: 6, 6, 6.PROFESSOR
Octógono: 7, 7, 7.- Que regularidade podemos observar entre as quantidades nesse quadro?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que as quantidades nesse quadro sugerem que nos polígonos a quantidade de lados é igual à quantidade de vértices e à quantidade de ângulos internos. Fim da observação.4. Leia o que Renato está dizendo.


- Agora, indique qual das figuras a seguir representa um polígono regular.
a)

b)

c)

d)

PROFESSOR
Resposta correta: d.MANUAL DO PROFESSOR
Atividade 3
Ao completar o quadro com a quantidade de lados, vértices e ângulos internos de alguns polígonos, os estudantes têm a oportunidade de verificar que há regularidade desses elementos em cada tipo de polígono. Chame a atenção para a denominação dos polígonos segundo o número de lados. É comum, por exemplo, se referirem ao polígono de 4 lados como “quadrado”, não como “quadrilátero”; mostre então outros exemplos, diferentes do quadrado, de polígonos com quatro lados.
Atividade 4
Incentive os estudantes a usarem a régua para comparar as medidas dos lados. Para comparar as medidas dos ângulos, eles podem decalcá-los em folha de papel de seda e sobrepô-los aos ângulos dos polígonos desenhados.
Caso julgue oportuno, peça aos estudantes que tragam um transferidor para a sala de aula e oriente-os a realizarem a medição dos ângulos utilizando esse instrumento.
BNCC em foco:
EF05MA17; competência específica 6
MP115
Triângulos
- Otávio e João brincavam de representar triângulos com palitos. Observe os ângulos destacados e complete.
Estes triângulos têm _____ ângulo reto. Eles são chamados de triângulos retângulos.
PROFESSOR
Resposta: um.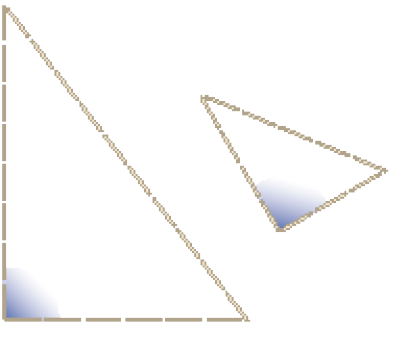
Estes triângulos não têm nenhum ângulo reto. Eles não são triângulos _____.
PROFESSOR
Resposta: retângulos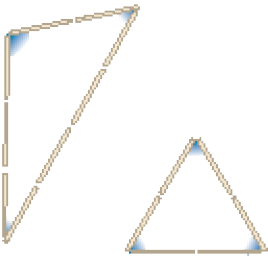
- Larissa, Michele e Míriam viram os meninos com os palitos e também entraram na brincadeira. Agora, observe os lados dos triângulos e complete.
Estes triângulos têm _____ lados com a mesma medida. Eles são chamados de triângulos equiláteros.
PROFESSOR
Resposta: todos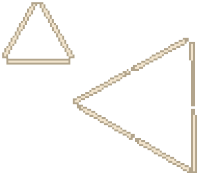
Estes triângulos têm _____ lados com a mesma medida. Eles são chamados de triângulos isósceles .
PROFESSOR
Resposta: 2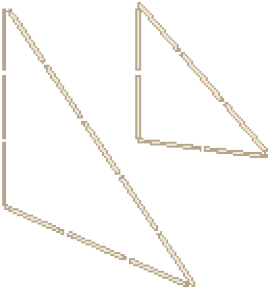
Estes triângulos têm todos os lados com _____ diferentes. Eles são chamados de triângulos escalenos.
PROFESSOR
Resposta: medidas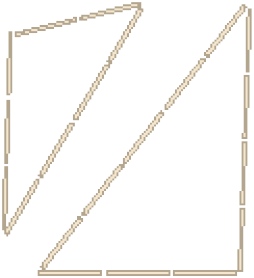
MANUAL DO PROFESSOR
Objetivos
- Reconhecer, nomear e comparar triângulos.
- Classificar triângulos quanto às medidas dos lados.
- Analisar os ângulos internos de triângulos.
Atividades 1 e 2
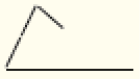
Nestas atividades, os estudantes poderão explorar a classificação de triângulos quanto às medidas dos lados – em equilátero, isósceles ou escaleno –, assim como a classificação particular de triângulo retângulo pelo reconhecimento da presença (ou não) de um ângulo reto. Vale notar que o triângulo retângulo tem especial importância na Matemática: suas propriedades possibilitam a determinação de inúmeras medidas de comprimento, além das deduções das relações trigonométricas, que serão estudadas nos anos seguintes. Comente que não é possível um triângulo ter mais de um ângulo reto. Para justificar, desenhe na lousa dois lados de um triângulo perpendiculares entre si, como mostra a Figura 1. Depois, desenhe um terceiro lado perpendicular a um dos lados anteriores, como na Figura 2.
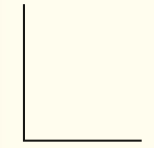
LEGENDA: Figura 1. FIM DA LEGENDA.
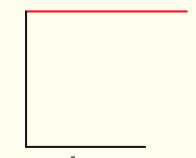
LEGENDA: Figura 2. FIM DA LEGENDA.
CRÉDITO: ADILSON SECCO
Os estudantes poderão observar que, ao acrescentarmos um segundo ângulo reto, não é possível “fechar” o triângulo, o que permite concluir que um triângulo não pode ter dois ângulos internos retos.
BNCC em foco:
EF05MA17
Sugestão de atividade
Representando triângulos com palitos
Peça aos estudantes que, usando palitos de sorvete com mesma medida de comprimento, representem triângulos que tenham lados com as seguintes medidas:
- 2, 2 e 2
palitos
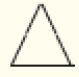
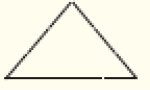
- 2, 3 e 5
palitos
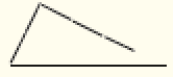
- 3, 3 e 4
palitos
- 1, 2 e 4
palitos
CRÉDITO: ADILSON SECCO
Espera-se que percebam que, com a quantidade de palitos indicada nos itens b e d, não é possível construir o triângulo pedido.
MP116
- Meça os lados dos triângulos representados e classifique cada um deles em equilátero, isósceles ou escaleno.
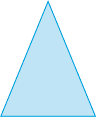
_____
PROFESSOR
Resposta: Isósceles.
_____
PROFESSOR
Resposta: Equilátero.
_____
PROFESSOR
Resposta: Escaleno.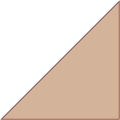
_____
PROFESSOR
Resposta: Isósceles.- Agora, faça o que se pede.
- Qual triângulo tem um ângulo reto? Descubra sobrepondo o canto de uma
folha
de papel sulfite a cada um dos ângulos internos.
_____
PROFESSOR
Resposta: O triângulo marrom.
- Você acha que um triângulo retângulo pode ter dois ângulos retos?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que não é possível. Fim da observação.
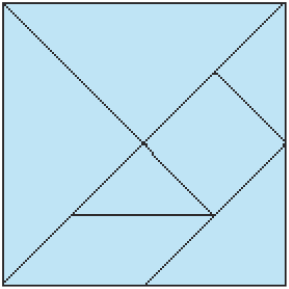
- Observe as 7 peças de um Tangram e responda.
- Quantas peças triangulares há nesse quebra-cabeça?
_____
PROFESSOR
Resposta: 5 peças.
- Há triângulos retângulos representados no Tangram? Se há, quantos são?
_____
PROFESSOR
Resposta: Sim; cinco.
- Os triângulos representados no Tangram são equiláteros,
isósceles
ou escalenos? Use uma régua para ajudá-lo.
_____
PROFESSOR
Resposta: Isósceles.
- Quantas peças triangulares há nesse quebra-cabeça?
_____
Boxe complementar:
Desafio
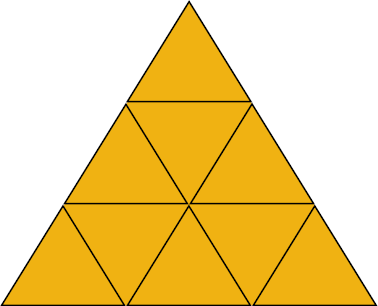
Quantos triângulos equiláteros estão representados na figura abaixo?
_____
PROFESSOR
Resposta: 13
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 3
Amplie a atividade e peça aos estudantes que desenhem e recortem representações de alguns triângulos equiláteros, isósceles e escalenos. Depois, incentive-os a descobrirem se é possível dobrá-los de modo que a linha da dobra possa ser associada a um eixo de simetria. Os triângulos equiláteros têm três eixos de simetria (linhas de dobra), enquanto os isósceles têm apenas um eixo de simetria e os escalenos não têm nenhum, como mostram as figuras.
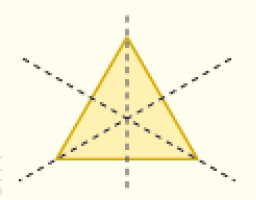
Equilátero
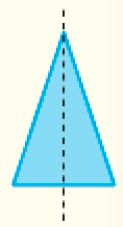
Isóceles
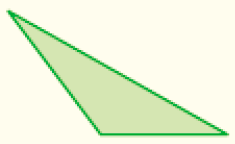
CRÉDITO: ADILSON SECCO
Escaleno
Atividade 4
Nesta atividade, os estudantes são motivados a reconhecerem diferentes triângulos entre as peças do Tangram, devendo então classificá-los quanto à medida dos lados. Uma ampliação da questão pode ser feita pedindo também a classificação pelo critério angular; eles devem concluir que são triângulos retângulos. Proponha que expliquem como realizaram as classificações.
Desafio
Há 13 triângulos, sendo:
- 9 triângulos pequenos;
- 1 triângulo grande, formado pelos 9 triângulos pequenos;
- 3 triângulos médios, formados cada um por 4 triângulos pequenos, como se vê a seguir.
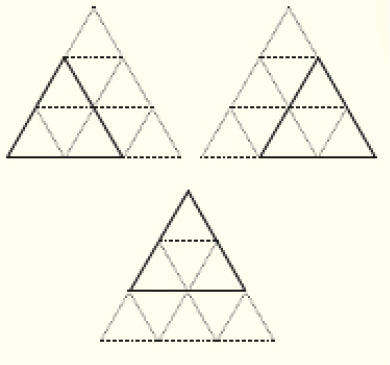
CRÉDITO: ADILSON SECCO
BNCC em foco:
EF05MA17; competência geral 2; competência específica 6
MP117
Quadriláteros
- Com o auxílio de uma régua e o canto de uma folha retangular, identifique algumas características comuns dos quadriláteros representados abaixo e forme dois ou mais grupos de acordo com essas características.
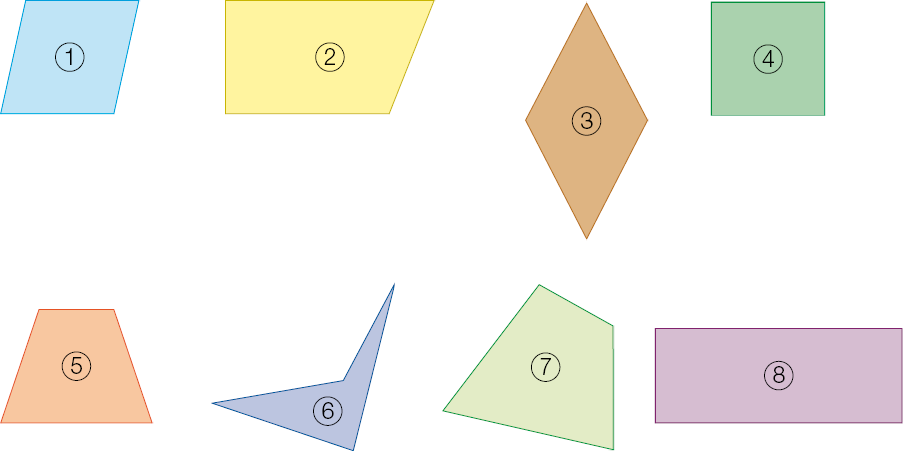
PROFESSOR
Exemplo de resposta: Grupo A: 4 e 8 (têm dois pares de lados paralelos e quatro ângulos retos). Grupo B: 2, 6 e 7 (têm os quatro lados de medidas diferentes).PROFESSOR
Grupo C: 1 e 3 (têm dois pares de lados paralelos e não têm ângulos retos). Grupo D: 5 (tem apenas dois lados de mesma medida).


- Qual foi o critério utilizado para formar os grupos? Converse com o professor e os colegas.
PROFESSOR
Resposta pessoal.
- Veja como Sandra separou quadriláteros semelhantes aos da atividade 1 em três grupos e responda às questões.
Grupo A
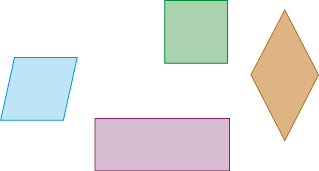
Grupo B

Grupo C
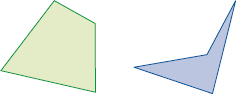
- Em que grupo cada quadrilátero tem dois pares de lados paralelos?
_____
PROFESSOR
Resposta: Grupo A.
- Em que grupo cada quadrilátero tem apenas um par de lados paralelos?
_____
PROFESSOR
Resposta: Grupo B.
- No Grupo C, cada polígono tem quantos pares de lados paralelos?
_____
PROFESSOR
Resposta: Nenhum.
MANUAL DO PROFESSOR
Objetivos
- Reconhecer, nomear e comparar quadriláteros, considerando lados, vértices e ângulos.
- Classificar quadriláteros.
- Classificar paralelogramos.
- Desenhar quadriláteros.
Estas atividades conduzem os estudantes ao conceito de quadrilátero como um polígono de 4 lados. A exploração dos quadriláteros é feita com base na identificação de características comuns e de diferenças entre várias dessas figuras.
Atividade 1
Para a distinção de tipos de quadrilátero e de suas propriedades, esta atividade sugere algumas classificações, possibilitando comparar o paralelismo entre os lados de alguns polígonos e a observação de ângulos retos em algumas figuras.
Atividade 2
Incentive os estudantes a apontarem os pares de lados paralelos em cada caso para verificar se de fato os reconhecem. Aproveite para perguntar: “Se tivessem de separar as figuras do grupo A de acordo com semelhanças entre elas, como fariam esses novos agrupamentos?”. É possível que reconheçam que o retângulo e o quadrado podem ser agrupados como paralelogramos que têm 4 ângulos retos, ou que o quadrado e o losango podem ser agrupados como paralelogramos que têm os 4 lados de mesma medida.
Peça aos estudantes que indiquem os pares de lados paralelos dos quadriláteros dos grupos A e B.
BNCC em foco:
EF05MA17
MP118
- Leia as explicações de Marisa e Leandro.

- Agora, observe novamente os grupos de figuras da atividade 2 que Sandra separou e identifique o grupo dos trapézios e o grupo dos paralelogramos.
_____
PROFESSOR
Resposta: Paralelogramos: Grupo A. Trapézios: Grupo B.
- Desenhe os seguintes quadriláteros na malha quadriculada a seguir.
- Um trapézio.
- Um paralelogramo.
- Um paralelogramo com 4 ângulos retos.
- Um quadrilátero que não tenha nenhum par de lados paralelos.
PROFESSOR
Exemplo de desenhos: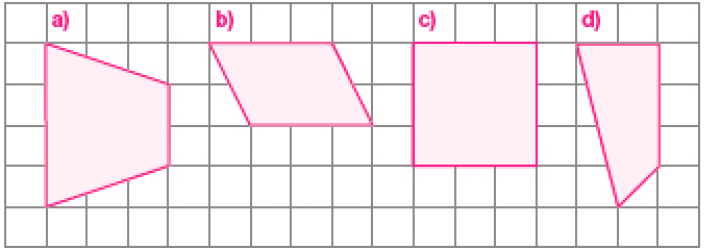
- Observe os paralelogramos representados a seguir e responda às questões.

- O que eles têm em comum em relação aos ângulos?
_____
PROFESSOR
Resposta: Ambos têm 4 ângulos retos.
- Qual é a diferença entre esses paralelogramos?
_____
PROFESSOR
Exemplo de resposta: O paralelogramo azul tem todos os lados com a mesma medida de comprimento, e o paralelogramo laranja não tem.
MANUAL DO PROFESSOR
Atividades 3 e 4
A ideia de paralelismo é usada como critério de subclassificação dos quadriláteros em grupos com: dois pares de lados paralelos (paralelogramos), um único par de lados paralelos (trapézios) ou nenhum par de lados paralelos.
Na atividade 3, as definições apresentadas possibilitam a compreensão de que trapézios e paralelogramos são figuras distintas pelo critério de quantidade de pares de lados paralelos: o trapézio, com apenas um par, e o paralelogramo, com dois pares.
Chamamos a atenção para o fato de haver divergência em relação a essas definições. Alguns autores preferem definir o trapézio como um quadrilátero que tem pelo menos um par de lados paralelos, ou seja, os paralelogramos também seriam trapézios.
Embora as duas definições sejam aceitas, é preciso, nessa fase do aprendizado, optar por uma delas para não confundir os estudantes. Recomendamos, portanto, que sejam mantidas as definições apresentadas no livro. Nos Anos Finais do Ensino Fundamental, os estudantes terão oportunidades de retomar e discutir as implicações de cada definição.
O uso de malha quadriculada na atividade 4 tem o objetivo de facilitar a obtenção dos pares de lados paralelos no desenho das figuras.
Atividade 5
Pergunte: “Qual dessas figuras é um quadrado?”. Espera-se que reconheçam o retângulo azul como um quadrado.
BNCC em foco:
EF05MA17
Sugestão de atividades
Explorando paralelogramos
Distribua aos estudantes representações de alguns paralelogramos reproduzidos em folhas de papel sulfite e peça-lhes que os recortem.
Em seguida, oriente-os a fazer um corte em cada paralelogramo obtendo um ou mais trapézios. Veja um exemplo na figura abaixo.
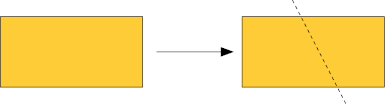
CRÉDITO: ADILSON SECCO
MP119
- Representações de paralelogramos são frequentes em objetos e construções do nosso dia a dia.

LEGENDA: Janelas retangulares em casas no município de São João del-Rei, Minas Gerais, em 2017. FIM DA LEGENDA.
Nestas casas, identificamos janelas que lembram um retângulo.

LEGENDA: Composição com quadriláteros, 2017. FIM DA LEGENDA.
Neste mosaico, as figuras laranja são losangos.

LEGENDA: Placa de travessia escolar em São Bernardo do Campo, São Paulo, em 2021. FIM DA LEGENDA.
Na placa de área escolar, identificamos um quadrado.


- Reúna-se com um
colega
e
conversem
sobre como vocês poderiam descrever esses paralelogramos para uma pessoa que não os conheça. Dica: observem os lados e os ângulos dessas figuras.
PROFESSOR
Resposta pessoal.
- Observe na malha quadriculada abaixo o esquema que representa o caminho feito pelo cachorro de Edu em seu quintal.
O cachorro partiu do ponto A, em vermelho. Depois, seguiu o trajeto indicado pelas setas.
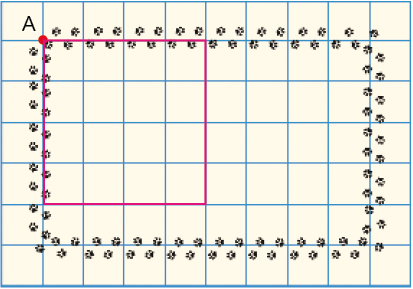
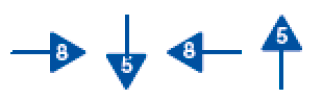
- O caminho que o cachorro de Edu fez tem o
contorno
de qual figura geométrica?
_____
PROFESSOR
Resposta: De um retângulo.
- Modifique o trajeto do cachorro de Edu para que ele tenha o
contorno
de um quadrado. Trace esse trajeto na malha e registre-o com setas.
PROFESSOR
Exemplo de resposta:

MANUAL DO PROFESSOR
Atividade 6
Esta atividade possibilita aos estudantes verificarem como os quadriláteros estão representados em muitas situações à nossa volta, destacando os paralelogramos que podem ser identificados na arquitetura, na arte e em placas de trânsito, por exemplo. Certamente os estudantes usarão uma linguagem não formal. Por exemplo: “Os quadrados têm os quatro lados iguais, os losangos parecem balões, e os retângulos têm a forma de uma lousa”. É importante que percebam características comuns e diferenças entre essas figuras.
Atividade 7
Explique aos estudantes que o número em cada seta indica a quantidade de lados dos quadrinhos do pátio que devem ser percorridos. Sugira que criem outras instruções, usando setas numeradas, para um colega desenhar em papel quadriculado o trajeto pensado, ou então que façam o inverso: desenhem um trajeto no papel quadriculado para um colega escrever as instruções correspondentes por meio de setas numeradas.
BNCC em foco:
EF05MA17; competência específica 2
MP120
- Leia as explicações.

- Que tipos de paralelogramo têm os quatro ângulos retos?
_____
PROFESSOR
Resposta: O retângulo e o quadrado.
- Que tipos de paralelogramo têm os quatro lados de mesma medida?
_____
PROFESSOR
Resposta: O losango e o quadrado.
- Leia o que Margarida está dizendo e responda às questões.

- A figura que Margarida desenhou é um quadrilátero?
_____
PROFESSOR
Resposta: Sim.
- Essa figura pode ser um retângulo? Justifique.
_____
PROFESSOR
Resposta: Não, pois os retângulos têm 4 ângulos retos.
- Essa figura pode ser um quadrado? Por quê?
_____
PROFESSOR
Resposta: Não, pois, apesar de ter os 4 lados de mesma medida, a figura não tem 4 ângulos retos.
- Que figura Margarida desenhou?
_____
PROFESSOR
Resposta: Um losango.
MANUAL DO PROFESSOR
Atividade 8
Ao desenvolver um trabalho de classificação de quadriláteros, é importante esclarecer aos estudantes os critérios empregados, para que possam comparar as características comuns e as diferenças entre os vários tipos de quadriláteros.
Levando em conta as medidas dos ângulos internos, os quadriláteros podem ser classificados de outras maneiras. Por exemplo, um quadrilátero com dois pares de lados paralelos é um paralelogramo; se esse paralelogramo tiver quatro lados de mesma medida, será um losango; e se esse losango tiver os quatro ângulos internos de mesma medida, será um quadrado. Portanto, o quadrado é um caso particular de losango, que, por sua vez, é um caso particular de paralelogramo.
Veja a seguir uma representação em diagrama da classificação de quadriláteros.
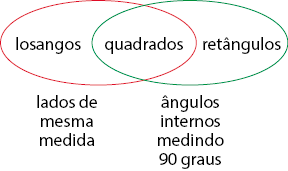
Atividade 9
Esta atividade contribui para a sistematização das principais características dos quadriláteros.
Peça aos estudantes que também justifiquem a resposta dada nos itens a e d.
Uma possibilidade de justificativa seria:
- A figura que Margarida desenhou é um quadrilátero, pois sua primeira afirmação é de que a figura é um paralelogramo, e todo paralelogramo é um quadrilátero.
- Margarida desenhou um losango, que é um paralelogramo com lados de mesma medida e sem ângulos retos.
BNCC em foco:
EF05MA17; competência específica 3
MP121
Desenhando polígonos
- Veja como Joaquim iniciou o desenho de um quadrado em uma malha quadriculada com o auxílio de uma régua.
Primeiro, eu desenhei um segmento de reta de medida igual à soma das medidas dos lados de três quadradinhos.
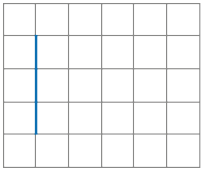
Depois, desenhei outro segmento, de mesma medida. Para formar o ângulo reto, considerei o ângulo interno de um quadradinho da malha.
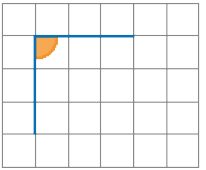

- Desenhe na malha quadriculada a seguir um quadrado como o de Joaquim.
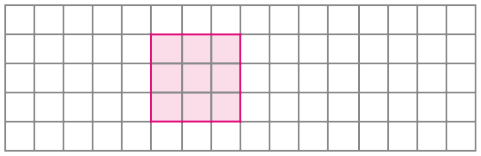

- Na malha quadriculada a seguir, represente um retângulo, um trapézio, um triângulo escaleno e um pentágono.
PROFESSOR
Exemplo de desenhos:
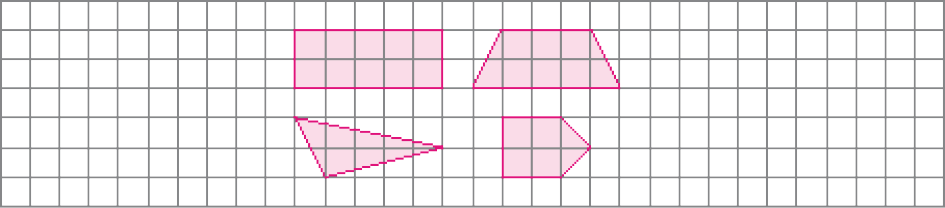
- Entre os polígonos que você desenhou, quais têm lados paralelos?
_____
PROFESSOR
Exemplo de respostas de acordo com o exemplo de desenhos: Retângulo, trapézio e pentágono.

- Como os lados dos quadradinhos da malha quadriculada auxiliam na construção dos lados paralelos desses polígonos? Converse com o professor e os colegas.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivos
- Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos.
- Desenhar polígonos utilizando material de desenho e tecnologias digitais.
Atividade 1
Espera-se que os estudantes utilizem a malha quadriculada para auxiliar nos desenhos dos polígonos. Como a malha quadriculada é formada por quadradinhos, os estudantes podem se apropriar desse fato para construir o quadrado corretamente (4 lados de mesmo comprimento e com ângulos de 90 graus).
Atividade 2
Caso julgue necessário, se alguns estudantes apresentarem dificuldade para relembrar a característica de cada polígono, faça uma revisão sobre a nomenclatura e algumas das características desses polígonos.
Espera-se que os estudantes concluam que, como a malha é quadriculada e os lados dos quadrados são paralelos, as linhas horizontais são paralelas, assim como as linhas verticais, e esse fato auxilia na construção dos lados paralelos desses polígonos. A régua tem a parte numerada chanfrada e pode fazer o esquadro escorregar sobre ela. Caso haja dificuldade, oriente os estudantes a encostarem o esquadro no outro lado da régua.
BNCC em foco:
EF05MA17; competência específica 5
MP122
- Fernanda representou duas retas perpendiculares usando régua e esquadro. Veja como ela fez.
Primeiro, eu tracei uma reta r.
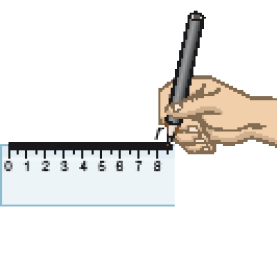
Depois, coloquei um dos lados do ângulo reto do esquadro apoiado na régua e tracei uma reta s, pelo outro lado.

As retas r e s formam quatro ângulos retos. O ponto de encontro entre elas é o vértice desses ângulos.
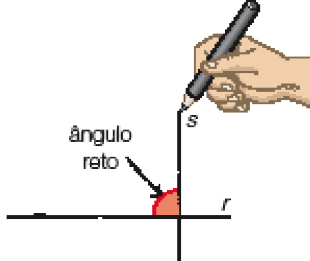

- No caderno, trace uma reta r e, depois, construa uma reta s perpendicular a ela com o auxílio de esquadro e régua.
Depois de traçar as retas perpendiculares, Fernanda construiu um triângulo retângulo.
Marquei 5 cm na reta r e tracei um segmento.
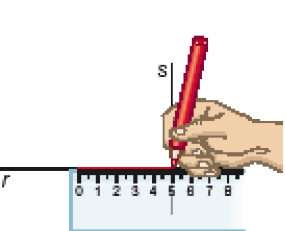
Depois, sobre a reta s, tracei um segmento de 3 cm.
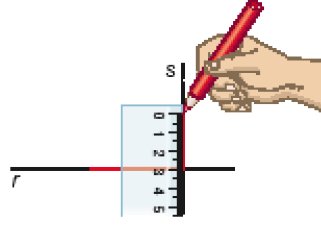
Por fim, tracei o terceiro lado do meu triângulo.
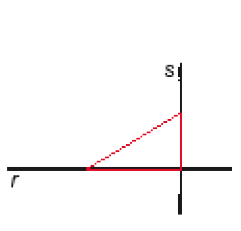

- No caderno, trace um triângulo retângulo de lados medindo 4
cm
e 6 cm.

- Após traçar as retas r e s, perpendiculares, explique como você faria para construir um quadrado com lados apoiados nessas retas. Converse com o professor e os colegas e registre sua explicação a seguir.
_____
PROFESSOR
Atenção professor: Espera-se que considerem o traçado de outras retas perpendiculares, para garantir a construção dos ângulos retos, e, também, que essas perpendiculares formem dois pares de retas paralelas, cuja distância seja a mesma, para formar os lados dos quadrados. Fim da observação.
MANUAL DO PROFESSOR
Atividade 3
Esta atividade propicia aos estudantes verificarem o passo a passo para representar, com régua e esquadro, retas perpendiculares que permitem a construção de um triângulo retângulo.
Durante a realização da atividade, verifique se os estudantes manuseiam os instrumentos corretamente e auxilie-os, caso seja necessário.
No item c, espera-se que expliquem, com as próprias palavras, como farão para construir o quadrado. Espera-se que considerem o traçado de outras retas perpendiculares para garantir a construção dos quatro ângulos retos e, também, que essas perpendiculares formem dois pares de retas paralelas, cuja distância seja a mesma, para formar os lados dos quadrados. Futuramente, usando um compasso, o estudante poderá lançar mão de outra estratégia para traçar o quadrado pedido.
BNCC em foco:
EF05MA17; competência específica 5
MP123
- A professora de Lúcia propôs a seguinte atividade à classe.

Para representar os triângulos na malha quadriculada, Lúcia utilizou os quadradinhos da malha como referência para as medidas dos lados e dos ângulos.
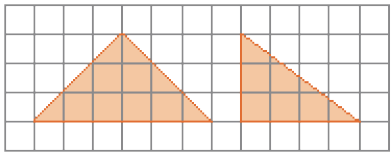
PROFESSOR
Atenção professor: Espera-se que os estudantes concluam que, como a malha é quadriculada e os ângulos internos dos quadradinhos são retos e os lados têm mesma medida, esse fato auxilia a construção do ângulo reto e dos lados de mesma medida. Fim da observação.

- Os triângulos que Lúcia representou estão de acordo com o pedido da professora? Justifique sua resposta.
No software , Lúcia utilizou ferramentas para traçar segmentos e para traçar retas perpendiculares, além da ferramenta de régua.
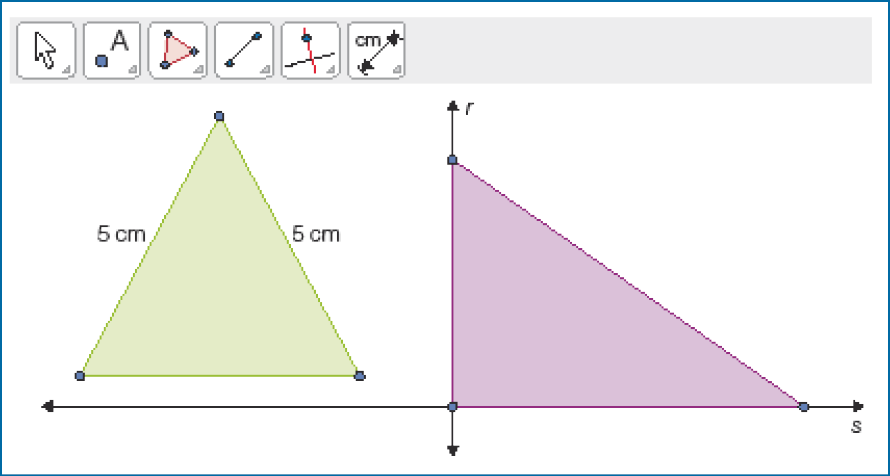


- Na sua opinião, por que Lúcia utilizou essas ferramentas para representar os triângulos? Converse com o professor e os colegas.
PROFESSOR
Resposta pessoal.PROFESSOR
Atenção professor: Espera-se que os estudantes concluam que, ao traçar as retas perpendiculares, Lúcia construiu o ângulo reto do triângulo retângulo e que a ferramenta de régua permite obter segmentos de mesma medida para construir o triângulo isósceles. Fim da observação.MANUAL DO PROFESSOR
Atividade 4
Se possível, proponha aos estudantes que representem os polígonos na malha quadriculada e no computador, utilizando um software de geometria dinâmica. Amplie a atividade pedindo a construção de um triângulo isósceles e retângulo.
Sugestão de aplicativo
Caso os computadores da escola tenham acesso à internet, sugerimos o uso de aplicativo de geometria dinâmica on-line. Disponível em: http://fdnc.io/a7G. Acesso em: 30 mar. 2021.
BNCC em foco:
EF05MA17; competência específica 5
MP124
- Sérgio deve construir um paralelogramo e um trapézio utilizando um software de geometria dinâmica. Para essa construção, Sérgio poderá utilizar as seguintes ferramentas:
 → permite traçar segmentos de reta
→ permite traçar segmentos de reta
 → permite determinar a medida de um segmento de reta
→ permite determinar a medida de um segmento de reta
 → permite traçar retas paralelas
→ permite traçar retas paralelas
 → permite traçar retas perpendiculares
→ permite traçar retas perpendiculares
- Para construir um paralelogramo, que ferramentas você utilizaria?
_____
PROFESSOR
Atenção professor: Os estudantes devem explicar, com suas próprias palavras, como fariam para construir o paralelogramo. O importante é perceberem que a figura obtida deve ter dois pares de lados paralelos. Fim da observação.
- E para construir um trapézio, que ferramentas você utilizaria?
_____
PROFESSOR
Atenção professor: Nesse caso, é importante perceberem que a figura obtida deve ter um par de lados paralelos. Fim da observação.

- Se a ferramenta que permite traçar retas paralelas não estivesse habilitada, Sérgio conseguiria construir algum paralelogramo? Converse com o professor e os colegas.
PROFESSOR
Atenção professor: Espera-se que os estudantes concluam que seria possível traçar um retângulo ou um quadrado, por meio da construção de retas perpendiculares. Fim da observação.
- No espaço a seguir, construa a representação de um paralelogramo e a de um trapézio, indicando as ferramentas que você utilizaria se
fosse
construí-los no
software
de geometria dinâmica.
_____
PROFESSOR
Exemplo de resposta: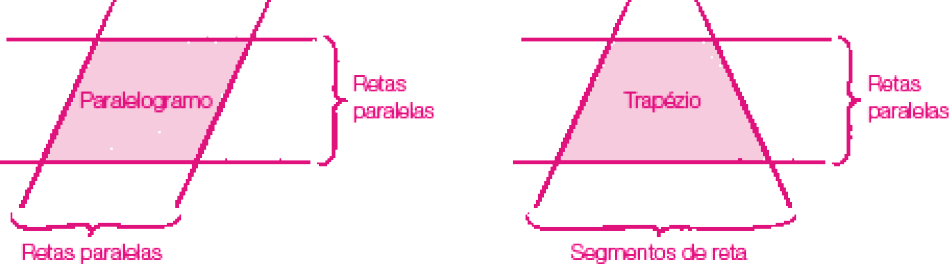
MANUAL DO PROFESSOR
Atividade 5
Se possível, proponha aos estudantes que representem esses polígonos utilizando um software de geometria dinâmica.
No item d, verifique se os estudantes percebem que a régua e o esquadro são os instrumentos que poderiam ser usados para a construção do paralelogramo e do trapézio.
BNCC em foco:
EF05MA17; competência específica 5
MP125
Ampliação e redução de figuras
- Observe as figuras que Fábio pintou na malha quadriculada.
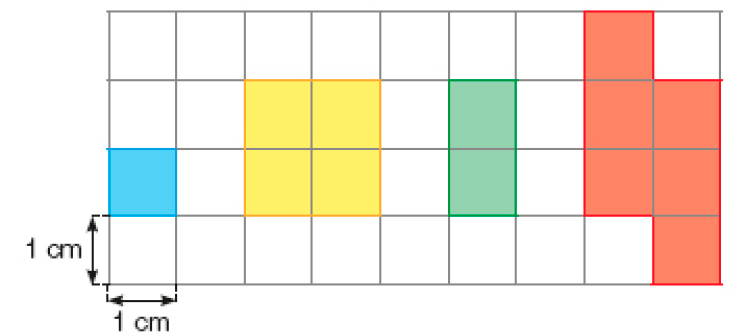

- Agora, responda às questões.
- O que há de parecido entre as figuras azul e amarela?
_____
PROFESSOR
Exemplo de resposta: Ambas as figuras são representações de quadrados.
- Ao comparar as figuras azul e verde, que diferenças você observa? E nas figuras azul e vermelha?
_____
PROFESSOR
Exemplo de resposta: A figura azul é a representação de um quadrado, e a figura verde não; a figura azul é a representação de um quadrado, e a figura vermelha não.
- Escreva o que é necessário para que uma figura seja uma ampliação de outra figura. Depois, converse com seus colegas e o professor sobre isso.
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que, para uma figura ser a ampliação de outra, ela deve ter a mesma forma que a figura da qual ela é uma ampliação. Além disso, se, por exemplo, a medida de um lado for dobrada, as medidas de todos os outros lados também deverão ser dobradas. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
- Desenhar polígonos utilizando material de desenho ou tecnologias digitais.
- Reconhecer a congruência dos ângulos e a proporcionalidade entre os lados correspondentes de figuras poligonais em situações de ampliação e de redução em malhas quadriculadas.
Atividade 1
Esta atividade (assim como as seguintes) trabalha a ampliação e a redução de figuras com o auxílio de malha quadriculada.
Depois da resolução desta atividade, converse com os estudantes sobre o que é ampliar ou reduzir uma figura e como, nesses processos, devemos garantir a proporcionalidade. Reforce a compreensão de que a ampliação aumenta (proporcionalmente) o tamanho da figura original mantendo sua forma, enquanto a redução o diminui, também mantendo sua forma (proporcionalmente).
O desenvolvimento do tema ampliação e redução de figuras em sala de aula é importante por dois motivos. Primeiro, por sua presença e aplicação em situações reais, como nos mapas em diferentes escalas ou nas cópias xerográficas. Segundo, esse trabalho contribui para o desenvolvimento geral da percepção geométrica ao possibilitar a observação das características da figura original que se alteram e daquelas que não se alteram nos processos de ampliação ou de redução. Poderíamos destacar, como característica variante, o tamanho (medidas de segmentos, área) e, como característica invariante, a forma da figura (posição dos lados, medidas dos ângulos, quantidade de lados).
BNCC em foco:
EF05MA18
MP126
- Compare as medidas dos lados da figura laranja e da figura verde.
A figura verde é uma ampliação ou uma redução da figura laranja? Justifique.
_____
PROFESSOR
Resposta: A figura verde é uma redução da figura laranja, pois a medida de cada lado foi reduzida pela metade.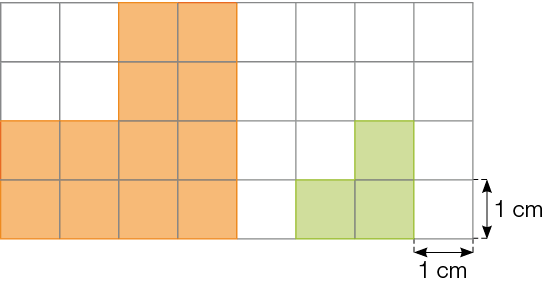
- Observe a figura e faça o que se pede na malha quadriculada abaixo.
PROFESSOR
Exemplos de desenho: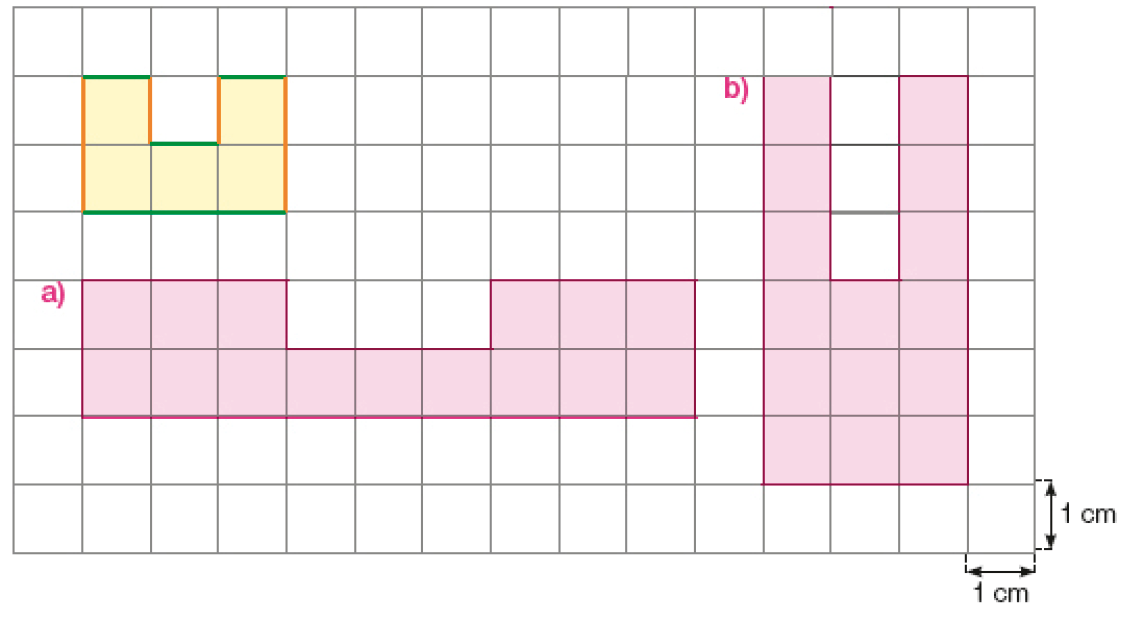

- Desenhe uma figura triplicando apenas as medidas das linhas verdes. A figura que você obteve é uma ampliação da figura pintada de amarelo? Por quê?
_____
PROFESSOR
Resposta: Não. Exemplo de justificativa: A figura ficou com a forma diferente; ela ficou “mais larga”.
- Desenhe outra figura triplicando apenas as medidas das linhas laranja. A figura que você obteve é uma ampliação da figura pintada de amarelo? Por quê?
_____
PROFESSOR
Resposta: Não. Exemplo de justificativa: A figura ficou com a forma diferente; ela ficou “mais alta”.
- Triplicando todas as medidas da figura inicial, teremos uma figura com largura medindo quantos centímetros? E com altura medindo quantos centímetros?
_____
PROFESSOR
Resposta: 9 cm; 6 cm.
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, os estudantes podem aplicar as ideias discutidas na atividade anterior. Para reforçar o fato de que a figura verde representa uma redução da figura laranja (a figura verde tem a mesma forma da laranja, mas os lados da figura verde têm a metade da medida dos lados correspondentes na figura laranja), peça à turma que observe que cada lado do quadrinho da malha tem 1 centímetro e pergunte: “Qual é o perímetro da figura laranja? E o perímetro da figura verde?”(16 cm; 8 cm).
Atividade 3
Discuta com os estudantes: “Em cada caso, como ficou a nova figura? O que há de parecido entre ela e a figura original? E o que há de diferente?”. Espera-se que percebam que houve uma distorção da figura original, alterando-se sua forma, apesar de as figuras continuarem sendo polígonos com o mesmo número de lados da figura original.
Comente a importância da ampliação de imagens em instrumentos como microscópios ou mesmo em uma simples lupa, observando que diversos profissionais trabalham com esses instrumentos, como biólogos, técnicos de laboratório, relojoeiros, ourives, entre outros.
BNCC em foco:
EF05MA18; competência específica 5
MP127

- Desenhe uma ampliação da figura azul, conforme as orientações de Cristina.
PROFESSOR
Exemplo de desenho: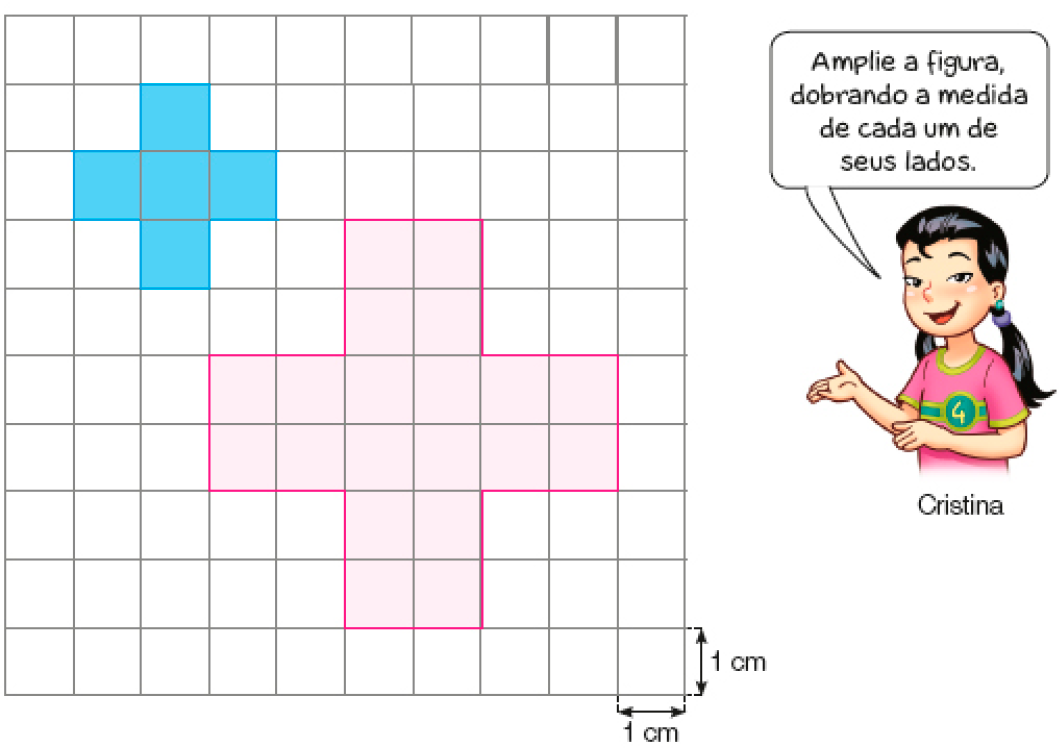

- Desenhe na malha quadriculada a seguir um paralelepípedo cujas arestas tenham seis vezes a medida da aresta correspondente do paralelepípedo laranja.
PROFESSOR
Exemplo de desenho: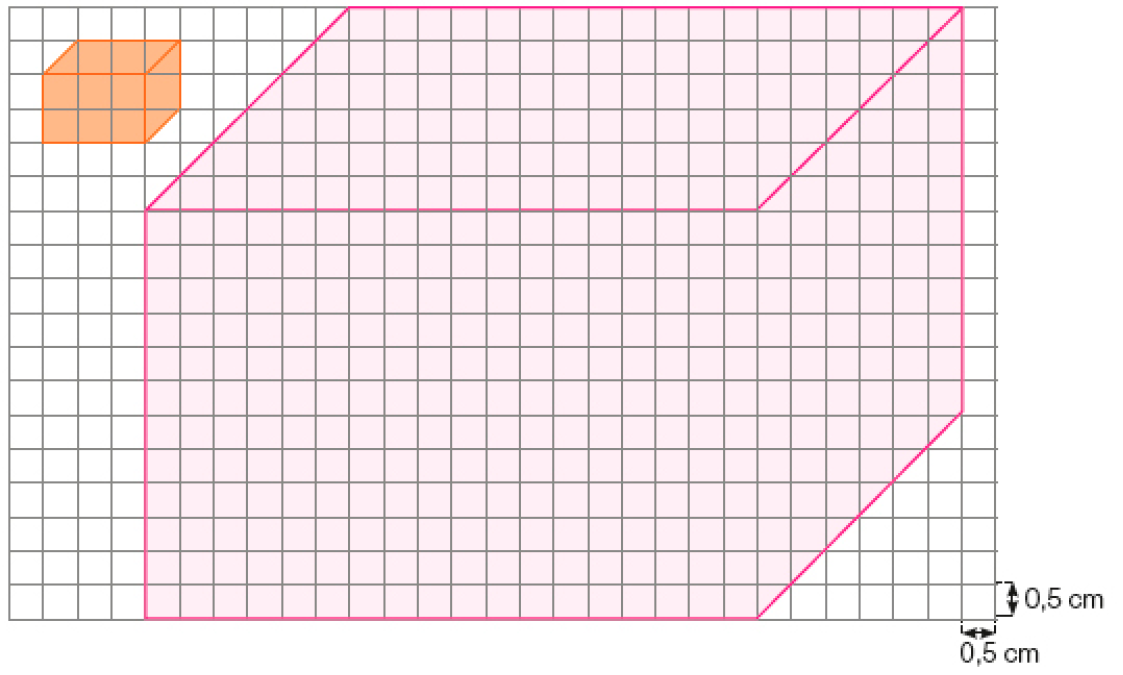
MANUAL DO PROFESSOR
Atividade 4
Nesta atividade, os estudantes devem considerar as orientações de Cristina para fazer a ampliação da figura azul. É importante observarem que, nesse caso, a forma da figura não se altera.
Se necessário, explique aos estudantes que são correspondentes entre si, por exemplo, as arestas verticais, assim como as arestas horizontais e também as arestas inclinadas.
Atividade 5
Ao propor aos estudantes a ampliação de uma figura não plana (o paralelepípedo), esta atividade oferece uma interessante extensão do que foi trabalhado até agora com figuras planas. Os estudantes têm a oportunidade de observar que os procedimentos do processo de ampliação (e, consequentemente, do processo de redução) se mantêm no caso de figuras com três dimensões.
Eles podem ter dificuldades em representar figuras geométricas não planas na malha quadriculada, uma vez que essa habilidade envolve a noção de perspectiva. Nessas representações, alguns elementos da figura podem parecer não corresponder visualmente ao objeto real, tornando-se um dificultador à compreensão. Na representação de um cubo na malha quadriculada, por exemplo, a face lateral, que é um quadrado, parece um losango por estar em perspectiva. Para ajudar os estudantes a fazerem esse tipo de representação e minimizar alguns equívocos – como pensarem que algumas faces do cubo não são quadradas –, sugerimos fazê-la também em uma malha pontilhada.
Os pontos da malha pontilhada favorecem a visualização de algumas figuras geométricas não planas, como o cubo.
BNCC em foco:
EF05MA18
Sugestão de atividade
Para ampliar a atividade 5, distribua malhas pontilhadas para os estudantes e peça que representem ampliações e reduções de cubos nessa malha, como na figura abaixo.
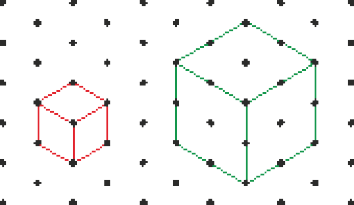
CRÉDITO: ADILSON SECCO
MP128
- Maiara estava desenhando polígonos em um software de geometria dinâmica em seu computador. Ela desenhou um quadrilátero e quer desenhar outro que represente uma ampliação do primeiro quadrilátero.

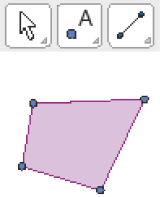
Ela reproduziu outro quadrilátero como esse usando o recurso de copiar e colar do programa. Assim, obteve dois quadriláteros de mesmas medidas de lados e de ângulos internos. Veja a figura abaixo.
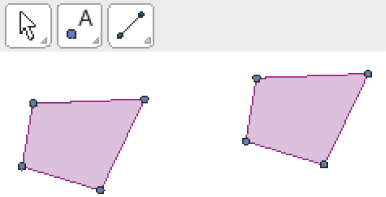
Com o objetivo de obter uma ampliação, Maiara “esticou” os lados do segundo quadrilátero. Veja a seguir os quadriláteros que ela obteve.
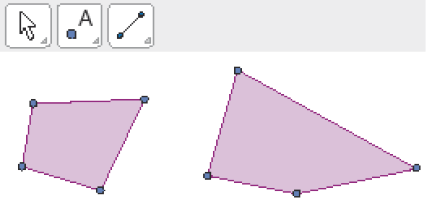
- O que aconteceu com os ângulos internos do segundo quadrilátero quando Maiara “esticou” seus lados?
_____
PROFESSOR
Resposta: Suas medidas foram alteradas.
- O segundo quadrilátero representa uma ampliação do primeiro quadrilátero? Justifique sua resposta.
_____
PROFESSOR
Atenção professor: Espera-se que o estudante perceba que, se as medidas dos ângulos foram alteradas, os quadriláteros não têm a mesma forma, logo, um deles não é ampliação do outro. Fim da observação.
- Converse com o professor e os colegas sobre o modo como Maiara construiu essa ampliação.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 6
Esta atividade possibilita aos estudantes reconhecerem, em uma situação de ampliação, se uma figura foi ou não ampliada na mesma proporção.
Para o item b, espera-se que os estudantes afirmem que o segundo quadrilátero não representa uma ampliação do primeiro, pois os lados não foram ampliados na mesma proporção. Não é esperado que, nesse momento, a justificativa seja completa, considerando as medidas dos ângulos internos desse quadrilátero.
Aproveite para dizer aos estudantes que, em uma ampliação ou redução, as medidas dos ângulos se mantêm e as medidas dos lados aumentam ou diminuem proporcionalmente, mantendo a forma da figura original.
BNCC em foco:
EF05MA18; competência específica 5
MP129
- Após construir o quadrilátero, Maiara descobriu outra função do software que estava utilizando.

Permite construir um polígono regular qualquer. Para isso, basta construir um segmento de reta, que será um dos lados do polígono, e indicar a quantidade de lados que tal polígono terá.
Maiara quer construir o desenho de um pentágono regular e vai usar a função descrita acima. Assim, ela construiu um segmento de reta de 3 cm e indicou que o polígono deveria ter 5 lados. Veja, abaixo, o pentágono que ela obteve.
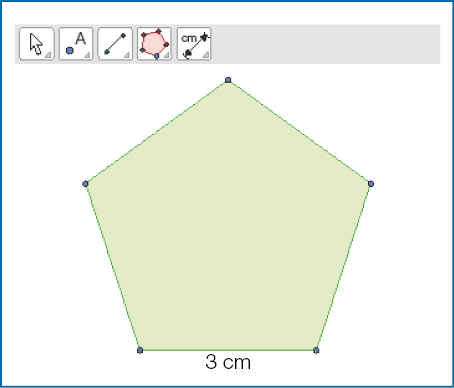
Ela descobriu que, ao mexer no comprimento do primeiro segmento construído, as medidas dos ângulos internos do pentágono não mudam. Além disso, ela descobriu que, se dobrasse a medida desse segmento, as medidas dos outros lados também dobrariam.


- Com essa ferramenta, Maiara conseguiria
obter
uma ampliação ou uma redução desse pentágono? Converse com o professor e com os colegas.
PROFESSOR
Resposta: Sim; resposta pessoal.
- Se ela quiser que as medidas dos lados desse pentágono sejam reduzidas pela metade, qual deverá ser a medida do primeiro segmento construído?
_____
PROFESSOR
Resposta: 1,5 cm
- Indique o que Maiara
deve
fazer para obter:
- um hexágono de 3
cm
de lado e outro hexágono que tenha os lados medindo o dobro de 3 cm;
_____
PROFESSOR
Exemplo de resposta: Maiara pode usar a ferramenta para construir um segmento de reta de 3 cm e indicar que o polígono deve ter 6 lados. Depois, ela pode dobrar a medida do segmento de reta e obter o outro hexágono. - um octógono de 2
cm
de lado e outro que tenha os lados medindo a metade de 2 cm.
_____
PROFESSOR
Exemplo de resposta: Maiara pode usar a ferramenta para construir um segmento de reta de 2 cm e indicar que o polígono deve ter 8 lados. Depois, ela pode dividir a medida do segmento de reta pela metade e obter o outro octógono.
- um hexágono de 3
cm
de lado e outro hexágono que tenha os lados medindo o dobro de 3 cm;
MANUAL DO PROFESSOR
Atividade 7
Espera-se que os estudantes percebam que o software que Maiara estava usando pode ser utilizado para obter uma ampliação ou redução de polígonos regulares, visto que, quando ela mexeu no comprimento de um dos segmentos os outros lados também mudaram proporcionalmente.
Sugestão de atividade
Ampliações, reduções e deformações
Antecipadamente, prepare o seguinte material:
I. três fotografias iguais, mas de tamanhos diferentes (ampliações ou reduções);
II. uma mesma figura plana em três tamanhos (ampliações ou reduções);
III. um mesmo texto de jornal em três tamanhos (ampliações ou reduções);
IV. um mesmo gráfico em três tamanhos (ampliações ou reduções);
outras imagens que apareçam na forma original e deformadas.
O material descrito de I a IV pode ser obtido com uma máquina copiadora, por meio da função de reduzir e/ou ampliar, ou imprimindo-se imagens de computador em tamanhos diferentes.
As imagens distorcidas (descritas em V) podem ser obtidas em programas de desenho para computadores.
Em sala de aula, essas imagens devem ser recortadas e embaralhadas. A ideia é que, coletivamente, os estudantes construam um painel com as figuras e as respectivas ampliações e reduções. No mesmo painel, devem ser colocados os exemplos de distorções.
BNCC em foco:
EF05MA18; competência específica 5
MP130
Matemática em textos
Leia
Ilusões visuais e representações geométricas
As figuras a seguir provocam ilu sões visuais, que podem ser de vários tipos. Na figura A, é possível perceber pelo menos duas ideias diferentes; na figura B, há ideia de movimentação, os pontos parecem piscar nos vértices dos pequenos quadrados representados; por fim, na figura C, é possível se confundir em relação ao comprimento dos traços horizontais.
Figura A

Figura B

Figura C
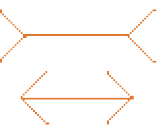
Normalmente, usa-se o termo “ilusão de óptica” quando nos referimos a essas confusões que acontecem com nossas percepções visuais. Entretanto, as ilusões visuais podem ter vários motivos para além da questão óptica, envolver outros sentidos e até mesmo os conhecimentos que temos sobre o tipo de imagem que nos é apresentado. As ilusões visuais que envolvem relações de espaço podem ser chamadas de ilusões geométricas.
Muitos artistas utilizam conhecimentos sobre as ilusões visuais em suas construções artísticas para produzir ilusões intencionalmente. Entretanto, em muitas situações, não há a intenção de provocar ilusões, mas algumas confusões podem acontecer por meio dos conhecimentos dos observadores. Veja.
Figura D
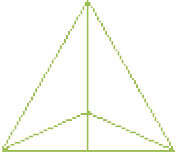
Com base na representação geométrica (figura D) e nos conhecimentos sobre poliedros, podemos dizer que se trata da representação de um tetraedro. No entanto, se utilizarmos nossos conhecimentos sobre polígonos, podemos dizer que a figura representa triângulos que formam outros. Assim, além da ilusão de óptica, que causa confusão propositalmente, podemos destacar as percepções confusas em representações geométricas que exploramos em nossas aulas.
MANUAL DO PROFESSOR
Objetivos
- Analisar, nomear e comparar os atributos de figuras geométricas não planas.
- Reconhecer, nomear e comparar polígonos e desenhá-los.
- Explorar figuras que provocam ilusão de óptica.
- Perceber ilusões visuais em representações geométricas.
Pergunte aos estudantes se conhecem outras ilustrações ou obras artísticas que explorem ilusões de óptica para ampliar as discussões sobre o tema. Se possível, leve mais alguns exemplos para a aula. O trabalho com ilusões de óptica ou outros tipos de imagens que podem gerar confusões pode auxiliar no desenvolvimento das percepções visuais. Após a exploração do texto, verifique se os estudantes compreendem que as ilusões podem ser derivadas de vários fatores, para além da questão óptica. Cite, por exemplo, as ilusões que podem ocorrer a partir de representações geométricas, que dependem também dos conhecimentos que os observadores possuem sobre as figuras.
Aproveite o tema para conversar sobre a importância das representações geométricas e das escolhas que podem ser feitas para evitar percepções dúbias. Comente que qualquer representação não será capaz de apresentar todas as características de um objeto ou de uma figura geométrica, pois trata-se de uma representação e não do objeto em si. Dê ênfase às perdas de características maiores quando as representações são de dimensões diferentes do objeto ou figura; por exemplo, para representar uma embalagem de creme dental (tridimensional) em um desenho bidimensional, serão utilizadas técnicas que permitam ao observador identificar uma tridimensionalidade que não existe no papel.
BNCC em foco:
EF05MA16, EF05MA17; competência geral 3; competência específica 6
MP131
Responda


Observe novamente as figuras A, B e C no texto e converse com seus colegas sobre as questões abaixo.
- Quais desenhos podem ser visualizados na figura A?
- O que acontece se você inclinar a cabeça para um dos lados ao olhar para a figura B?
- Qual traço é maior na figura C?
PROFESSOR
Respostas pessoais.
Analise
- Observe os segmentos de reta perpendiculares que foram representados ao lado. Qual deles tem maior medida de comprimento: o
vertical
ou o horizontal?
_____
PROFESSOR
Resposta: Os dois têm a mesma medida de comprimento.
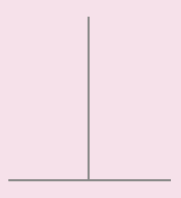

- Qual figura geométrica a imagem abaixo pode representar? Compare sua resposta com a de um
colega
e justifique a sua.
_____
PROFESSOR
Resposta: É possível visualizar a representação de um hexágono composto de triângulos, a vista superior de uma pirâmide de base hexagonal ou, ainda, a representação de um cubo.PROFESSOR
Resposta pessoal.
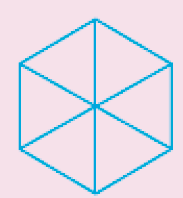
Aplique


- Escolha um poliedro ou um polígono e represente-o abaixo por meio de desenho. Depois, peça a um
colega
que descubra a figura representada.
_____
PROFESSOR
Desenho pessoal.

- Com base nas atividades apresentadas, elabore com seus colegas dicas que possam ajudar na representação de figuras geométricas planas ou figuras geométricas não planas.
PROFESSOR
Resposta variável.MANUAL DO PROFESSOR
Responda
Espera-se que os estudantes percebam, na figura A, tanto o vaso branco como o rosto de perfil de duas pessoas. Já na figura B, ao inclinarem a cabeça, espera-se que a “movimentação” dos pontos diminua. Por fim, na figura C, os estudantes devem perceber que os traços horizontais têm o mesmo comprimento. Se necessário, peça que os meçam com régua.
Analise Atividade 1
Solicite aos estudantes que respondam à pergunta sem medir os segmentos de reta. Depois, utilizando a régua, poderão comprovar que os segmentos são de mesmo comprimento.
Atividade 2
Enfatize que as três figuras podem ser visualizadas na mesma representação. Caso seja necessário, utilize linhas tracejadas para destacar cada uma delas.

CRÉDITO: ADILSON SECCO
Se os estudantes apresentarem outras percepções, peça que as justifiquem e socializem com a turma.
Aplique
Atividades 1 e 2
Na atividade 1, socialize os diferentes desenhos.
Na atividade 2, para o levantamento de dicas, os estudantes poderão apontar o uso de legendas que indiquem se a representação é de uma figura plana ou tridimensional, ou apontar técnicas de representação tridimensional (ou perspectiva) ou ainda o uso de cores, linhas tracejadas e sombras para facilitar as visualizações. Valorize todas as dicas apresentadas, desde que sejam acompanhadas de justificativas coerentes.
BNCC em foco:
EF05MA16, EF05MA17; competência geral 3; competência específica 6
MP132
Compreender informações
Ler e interpretar gráfico de linha
- Clóvis é dono de uma loja que vende modelos de poliedros para escolas. Veja o gráfico de linha que ele construiu para mostrar a quantidade de modelos vendidos a cada mês de 2022.
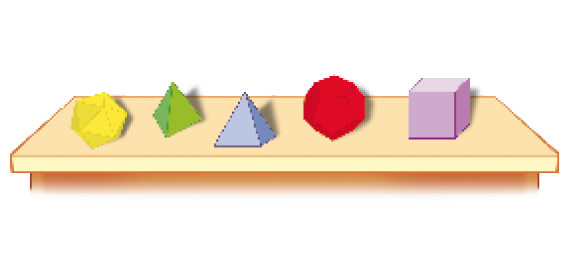
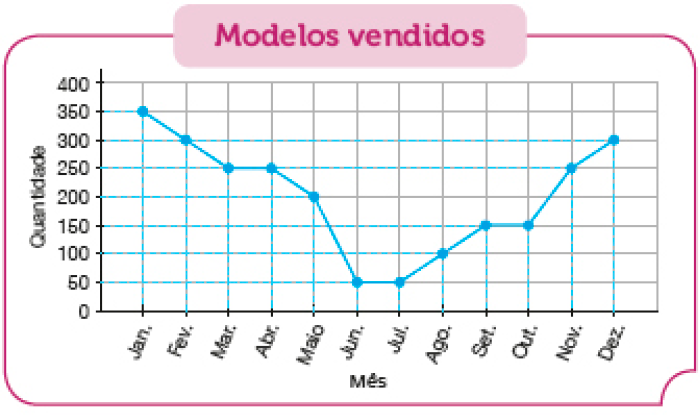
Fonte: Administração da loja de Clóvis (jan. 2023).
- Em qual mês Clóvis vendeu mais modelos?
_____
PROFESSOR
Resposta: Janeiro.
- E em quais meses ele vendeu menos?
_____
PROFESSOR
Resposta: Junho e julho.
- A partir de qual mês as vendas mensais começaram a aumentar?
_____
PROFESSOR
Resposta: Julho.d) Complete os quadros com os dados do gráfico.
Vendas no 1º trimestre
Janeiro: 350
Fevereiro: _____
PROFESSOR
Resposta: 300Março: + 250
Total: _____
PROFESSOR
Resposta: 900Vendas no 2º trimestre
Abril: _____
PROFESSOR
Resposta: 250Maio: _____
PROFESSOR
Resposta: 200Junho: + 50
Total: _____
PROFESSOR
Resposta: 500- Sabendo que, no
1º
trimestre, Clóvis vendeu apenas modelos de cubos e, no 2º trimestre, apenas modelos de pirâmides, quantos modelos de cubos e de pirâmides foram vendidos no
1º
semestre?
_____
PROFESSOR
Resposta: 900 cubos e 500 pirâmides.
- Quantos modelos foram vendidos no
1º
semestre?
_____
PROFESSOR
Resposta: 1.400 modelos.
MANUAL DO PROFESSOR
Objetivos
- Ler e interpretar dados apresentados em gráficos de linhas.
- Organizar dados coletados por meio de gráfico.
- Produzir textos para sintetizar conclusões dos resultados de uma pesquisa.
Atividade 1
Se julgar conveniente, apresente o nome dos poliedros: amarelo (icosaedro), vermelho (dodecaedro). Espera-se que os estudantes reconheçam o cubo (roxo) e as pirâmides (verde e azul).
Os estudantes devem observar os dados apresentados no gráfico para fazer o que se pede nos itens a a f.
BNCC em foco:
EF05MA24; competências específicas 1, 3, 4 e 6
MP133
- José fez um gráfico para mostrar a movimentação na primeira semana de fevereiro de 2023, em seu lava-rápido. Veja abaixo.
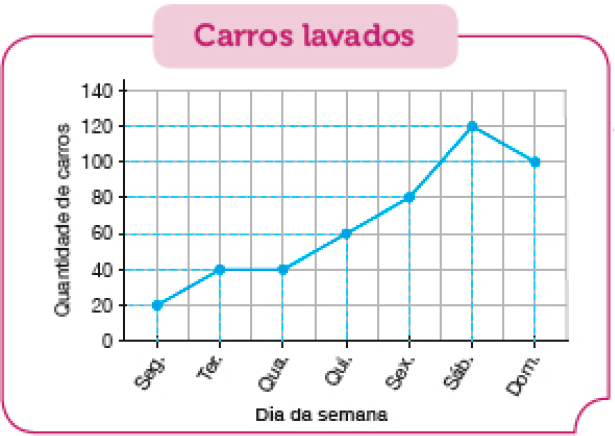
Fonte: Lava-rápido de José (fev. 2023).
Ele deseja fazer uma promoção para ter 20 lavagens a mais por dia nas segundas, terças e quartas-feiras. Nesses dias, José cobrará apenas 8 reais por lavagem.
- Faça, no caderno, dois quadros: um que mostre o ganho diário atual (com
preço
de 10 reais cada lavagem) nesses três dias; e outro que mostre o ganho diário previsto com a promoção de 8 reais cada lavagem.
PROFESSOR
Resposta: Preço de 10 reais: segunda-feira = 200 reais, terça-feira = 400 reais e quarta-feira = 400 reais; Preço de 8 reais: segunda-feira = 320 reais, terça-feira = 480 reais e quarta-feira = 480 reais.
- Com a promoção, qual é o aumento, em real, esperado nos ganhos de segunda a quarta-feira?
_____
PROFESSOR
Resposta: É esperado um aumento de 280 reais de segunda a quarta-feira a cada semana.
- Se José
fizesse
a promoção apenas no fim de semana, qual seria o ganho diário previsto nos fins de semana?
_____
PROFESSOR
Resposta: Sábado: 1 120 reais; domingo: 960 reais (total: 2 080 reais).
- Reúna-se com um
colega
para descobrir o que é mais vantajoso para José: fazer a promoção de segunda a quarta-feira ou no fim de semana? Depois, no caderno, escrevam um texto com a conclusão a que chegaram.
PROFESSOR
Resposta pessoal.
- Laís fez 4 avaliações de Geometria, cada uma com 10 questões. Veja no quadro abaixo o total de acertos de Laís em cada uma dessas avaliações.
Quadro: equivalente textual a seguir.
|
1ª avaliação |
2ª avaliação |
3ª avaliação |
4ª avaliação |
|---|---|---|---|
|
sobre poliedros e corpos redondos |
sobre giros e ângulos |
sobre polígonos e seus elementos |
sobre ampliação e redução de figuras |
|
5 acertos |
5 acertos |
8 acertos |
10 acertos |
- Faça, em papel quadriculado, um gráfico que mostre o desempenho de Laís.
PROFESSOR
Resposta pessoal.
- Converse com um
colega
sobre esse gráfico e, no caderno, escreva uma conclusão sobre o desempenho de Laís: ela melhorou ou piorou seus conhecimentos de Geometria? Em qual tema ela teve melhor desempenho?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 2
No item c, ressalte que o ganho diário atual (sem promoção) nos fins de semana é: para sábado, 1 200 reais; para domingo, 1 000 reais; comum total de 2 200 reais. Peça a eles que comparem as duas situações no fim de semana.
No item d, sugira aos estudantes que calculem o ganho de José de segunda-feira até domingo com a promoção de segunda a quarta-feira, e depois calculem o ganho de José de segunda-feira até domingo com a promoção no fim de semana. Espera-se que os estudantes utilizem as conclusões dos itens anteriores e percebam que, para José, é mais vantajoso fazer a promoção de segunda a quarta-feira, pois, se fosse feita no fim de semana, José deixaria de ganhar 120 reais.
Atividade 3
No item a, espera-se que os estudantes façam um gráfico de linhas. Eles podem também apresentar outro tipo de gráfico, como de colunas ou de barras.
Exemplo de gráfico de linhas:
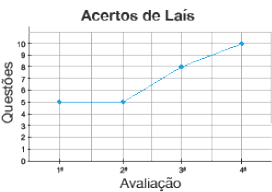
Fonte: Boletim de Laís (maio 2023).
CRÉDITO: FERNANDO JOSÉ FERREIRA
No item b, espera-se que os estudantes percebam que Laís melhorou a partir da 3ª avaliação e que seu melhor desempenho foi em ampliação e redução de figuras.
BNCC em foco:
EF05MA24; competências específicas 1, 3, 4 e 6
MP134
O que você aprendeu
- Assinale apenas as frases certas.
( ) Todas as faces dos poliedros são polígonos.
( ) Figuras geométricas arredondadas são poliedros.
( ) O cone e o cilindro são poliedros.
( ) Os prismas e as pirâmides são poliedros.
PROFESSOR
Respostas corretas: Todas as faces dos poliedros são polígonos.PROFESSOR
Os prismas e as pirâmides são poliedros.
- Observe a figura abaixo e responda à questão.
Marque com X a figura a seguir que representa uma redução dessa figura.

( )
( )
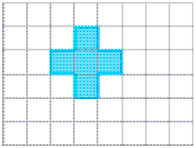
( )
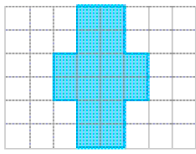
PROFESSOR
Resposta correta: figura 2.- Leia o texto e responda à questão.
Mariana e duas amigas estavam brincando com pedaços de corda. Depois, outras crianças chegaram para brincar também.
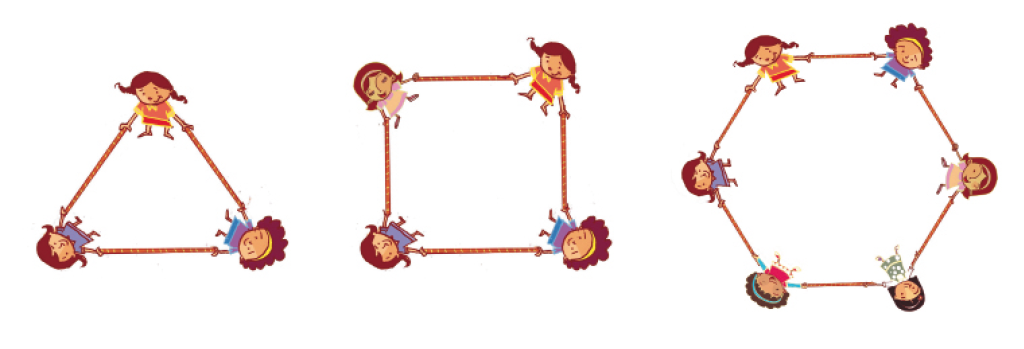
- As figuras formadas com as crianças e os pedaços de
corda
lembram o
contorno
de polígonos. Quais são esses polígonos
_____
PROFESSOR
Resposta: Triângulo, quadrado e hexágono.
- A medida dos ângulos formados nessas figuras com a chegada de mais crianças aumentou ou diminuiu?
_____
PROFESSOR
Resposta: Aumentou.
MANUAL DO PROFESSOR
Objetivo
- Retomar os conceitos estudados.
A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Peça aos estudantes que corrijam as frases erradas.
Exemplos de correção para os itens incorretos:
- Figuras geométricas arredondadas não são poliedros.
- O cone e o cilindro são corpos redondos.
Atividade 2
Para resolver a questão, os estudantes devem observar cada figura e descobrir qual tem todas as medidas reduzidas na mesma proporção em relação à figura original. Outra opção é observar em qual delas não houve distorção da aparência da figura original. Em ambas as resoluções, os estudantes devem concluir que a segunda figura, da esquerda para a direita, é a redução da figura original.
Atividade 3
Pode-se reproduzir essa brincadeira com os estudantes, na quadra da escola, utilizando uma corda amarrada pelas pontas. Eles reproduzirão figuras parecidas com os contornos dos polígonos mostrados na ilustração (triângulo, quadrado, hexágono etc.) até perceberem que, quanto mais estudantes, mais vértices e lados terá o polígono resultante.
BNCC em foco:
EF05MA16, EF05MA17, EF05MA18
MP135
Avaliação processual
- Na ordem em que aparecem representados, da esquerda para a direita, os triângulos abaixo são:
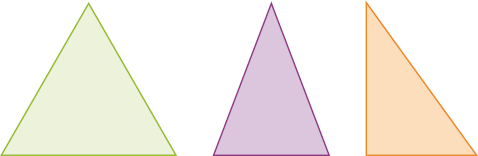
- ( ) equilátero, escaleno e isósceles.
- ( ) isósceles, equilátero e retângulo.
- ( ) equilátero, isósceles e retângulo.
- ( ) isósceles, equilátero e escaleno.
PROFESSOR
Resposta correta: c.

- Desenhe três trapézios como o representado abaixo.

Em cada trapézio, trace uma reta de modo que ela forme as duas figuras indicadas em cada caso.
- 2 trapézios.
_____
PROFESSOR
Exemplo de respostas: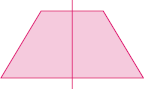
- 2 triângulos.
_____
PROFESSOR
Exemplo de respostas: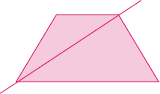
- 1 trapézio e 1 triângulo.
_____
PROFESSOR
Exemplo de respostas: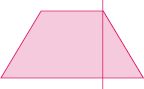
Autoavaliação

- Consigo classificar quadriláteros com base em suas características?

- Realizo ampliações e reduções de figuras sem deformá-las?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 4
Incentive os estudantes a usarem a régua para comparar as medidas dos lados. Para comparar as medidas dos ângulos, eles podem decalcá-los em folha de papel de seda e sobrepô-los aos ângulos dos polígonos desenhados.
Atividade 5
Nesta atividade, os estudantes devem decompor figuras planas em duas outras, traçando retas. Caso tenham dificuldade de visualizar mentalmente os cortes que devem ser feitos para obter as figuras, sugira que, com uma régua, simulem a reta a ser traçada, observando diretamente as duas partes formadas. Proponha que apresentem as respostas e as discutam, pois pode haver mais de uma solução em cada caso. Esta atividade pode ser ampliada se solicitar a eles que obtenham um paralelogramo e um triângulo. Outros exemplos de respostas:
- para o item a:

- para o item b:

- para o item c:
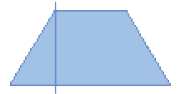
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
BNCC em foco:
EF05MA17, EF05MA18
Autoavaliação
Na primeira questão, os estudantes avaliarão seus conhecimentos sobre quadriláteros. Espera-se que percebam que alguns quadriláteros podem ter mais de uma classificação de acordo com as características, por exemplo, um quadrado é também um retângulo, pois possui 4 ângulos retos.
Na segunda questão, ampliações e reduções devem ser consideradas de modo a manter as proporções das figuras iniciais. Assim, os estudantes poderão avaliar se conseguem perceber quais medidas devem ser alteradas para manter as proporções e os ângulos da figura transformada.
MP136
Comentários para o professor:
Conclusão da Unidade 3
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Representa e localiza objetos no plano? |
_____ |
_____ |
|
Classifica figuras não planas em poliedros ou corpos redondos? |
_____ |
_____ |
|
Associa figuras não planas às suas planificações? |
_____ |
_____ |
|
Identifica vértices, faces e arestas em poliedros? |
_____ |
_____ |
|
Classifica triângulos e quadriláteros? |
_____ |
_____ |
|
Identifica ângulo reto, agudo e obtuso? |
_____ |
_____ |
|
Reconhece a congruência de ângulos? |
_____ |
_____ |
|
Amplia e reduz figuras poligonais em malha quadriculada? |
_____ |
_____ |
|
Interpreta e organiza dados coletados em tabelas e em gráficos de colunas e de linhas? |
_____ |
_____ |
|
Produz texto sobre os resultados de uma pesquisa? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |