MP137

Introdução da Unidade 4

A abertura desta Unidade traz um contexto no qual as quatro operações com números naturais são aplicadas na prática de comércio popular. Nela encontram-se várias maneiras de explorar os conceitos a serem tratados ao longo da Unidade, além das questões da seção Para refletir ...

Nesta Unidade, serão aprofundados os estudos relativos a Números. Retomam-se estudos das quatro operações com números naturais e ampliam-se estudos com resolução e elaboração de problemas de contagem, compreendendo o princípio multiplicativo com o uso de diagramas de árvore ou tabelas. Esses conhecimentos têm sido construídos ao longo dos anos Iniciais do Ensino Fundamental, notadamente no 4º ano, por meio de atividades cujas propostas eram resolução e elaboração de problemas aplicando essas operações com diferentes estratégias; resolução e elaboração de problemas com diferentes significados da multiplicação e, também, no caso da divisão, com os significados de repartição equitativa e medida. Destaca-se ainda sua relevância na construção de conhecimentos previstos para o 6º ano, com problemas que utilizam cálculos com números naturais, por meio de diferentes estratégias, compreendendo os processos envolvidos.

A Unidade Temática Álgebra está presente com atividades que abordam a construção de conhecimentos relativos à resolução de problemas com a variação de proporcionalidade direta entre duas grandezas. Há também atividades cujo objetivo é promover a construção da ideia de equivalência, possibilitando que os estudantes concluam que uma igualdade não se altera ao adicionar ou subtrair um mesmo número a seus dois membros ou ao multiplicar ou dividir seus dois membros por um mesmo número. Outras atividades envolvem conhecimentos acerca da resolução e elaboração de problemas com a conversão em sentença matemática por meio de uma igualdade e com uma operação na qual um dos termos é desconhecido. Por fim, conhecimentos relativos à partilha de uma quantidade em duas partes desiguais são abordados na perspectiva de que os estudantes compreendam a ideia de razão entre as partes e destas com o todo.

Os conhecimentos de Álgebra destacados acima favorecem o uso da noção de igualdade matemática para determinar valores desconhecidos na resolução de problemas. Promovem também resolução e elaboração de problemas envolvendo a partilha de uma quantidade em duas partes desiguais, por meio de relações aditivas e multiplicativas, assim como da razão entre as partes e entre uma das partes e o todo, conhecimentos a serem construídos no 6º ano.

A leitura e a interpretação de dados apresentados em gráficos de setores ou em gráficos de colunas duplas estão nas atividades que abordam o tema Probabilidade e estatística. Tais conhecimentos representam a ampliação daqueles abordados no 4º ano. Eles serão necessários na resolução de situações que envolvam dados de pesquisas sobre diferentes contextos apresentados em tabelas e gráficos, além da redação de textos sintetizando conclusões, conhecimentos a serem tratados no 6º ano.

As habilidades e os objetivos de aprendizagem que se pretende desenvolver requerem variáveis dinâmicas em sala de aula e podem demandar uma organização individual, em duplas, em grupos ou coletiva.

Competências gerais favorecidas

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

Competências específicas favorecidas

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

MP138

UNIDADE 4. Mais operações

Imagem: Ilustração. Marcos, Beatriz, Roberto, Vanessa, uma senhora, dois homens e uma mulher estão andando em uma rua e ao lado deles há uma feira com barracas, frutas, legumes e verduras. Resposta: Marcos, Beatriz, Roberto e Vanessa estão aqui. Nas barracas, placas com as informações: PROMOÇÃO - PIMENTÃO 8 REAIS A BANDEJA; PEPINO 5 REAIS O QUILOGRAMA; TOMATE 9 REAIS A BANDEJA; BATATA 3 REAIS O QUILOGRAMA; ALFACE 3 REAIS A UNIDADE. Atrás das barracas há homens e ao fundo, casas e carros. Fim da imagem.
MANUAL DO PROFESSOR

Objetivos da Unidade

  • Resolver situações que envolvam expressões numéricas com as quatro operações fundamentais.
  • Resolver e elaborar problemas de adição, subtração, multiplicação e divisão com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
  • Resolver problemas que envolvam a noção de proporcionalidade entre duas grandezas.
  • Resolver problemas envolvendo a partilha de uma quantidade em partes desiguais e a ideia de razão entre as partes e delas com o todo.
  • Identificar e representar frações, associando-as à ideia de parte de um todo.
  • Resolver problemas simples de contagem envolvendo o princípio multiplicativo, por meio de diagramas de árvore ou por tabelas.
  • Explorar as propriedades de uma igualdade, para construir a noção de equivalência.
  • Resolver problemas envolvendo medidas de massa.
  • Resolver e elaborar problemas envolvendo sentenças matemáticas expressas por uma igualdade em que um dos termos é desconhecido.
  • Realizar pesquisa e organizar dados coletados por meio de gráficos.
  • Ler e interpretar dados apresentados em tabelas, gráficos de setores e de colunas duplas.

    BNCC em foco:

    EF05MA03, EF05MA07, EF05MA08, EF05MA09, EF05MA10, EF05MA11, EF05MA12, EF05MA13, EF05MA19, EF05MA24, EF05MA25

MP139

Boxe complementar

Para refletir...

As crianças foram à feira com dona Maria, a avó de Roberto.

• Dona Maria comprou 3 kg de batata e pagou 15 reais. Quanto ela pagaria se tivesse comprado 6 kg de batata?

PROFESSOR Resposta: 30 reais.

• Maria também comprou duas bandejas de pimentão e dois quilogramas de pepino. Uma expressão que permite calcular quantos reais Maria pagará por essa compra é:

8 × 2 + 5

2 × (8 + 5)

8 + 2 + 5 + 2

PROFESSOR Resposta correta: 2 × (8 + 5)

Fim do complemento

MANUAL DO PROFESSOR

Explore a cena com os estudantes. Incentive-os a procurarem as personagens Marcos, Vanessa, Roberto e Beatriz.

Nos dias de feira, é comum pessoas jogarem cascas de frutas e restos de outos alimentos na rua. Comente com os estudantes que o lixo jogado nas ruas entope os bueiros, e, quando chove, a água da chuva não tem para onde escoar, o que causa alagamentos.

Os alagamentos, além de causar prejuízos emocionais e financeiros, facilitam a transmissão de doenças, como a leptospirose.

Se julgar oportuno, realize um trabalho com Ciências da Natureza e peça aos estudantes que pesquisem sobre os efeitos nocivos do descarte incorreto de resíduos. Sugira que pesquisem como deve ser feito o descarte correto de materiais, como pilhas e baterias, que contêm metais pesados em seu interior.

Para refletir...

Dê um tempo para os estudantes observarem a ilustração com calma e buscarem as informações necessárias para os cálculos que respondem à questão proposta. Espera-se que eles percebam a ideia de dobro entre 3 e 6. Se por 3 kg, ela paga 15 reais, por 6 kg ela vai pagar o dobro, ou seja, 30 reais.

É possível que sintam dificuldade em associar a expressão 2 × (8 + 5) com as operações 2 × 8, 2 × 5 e 2 × 8 + 2 × 5. Promova uma roda de conversa para que os estudantes discutam as estratégias que utilizaram. Peça a alguns deles que expliquem oralmente como raciocinaram para chegar aos resultados, aproveitando para esclarecer eventuais dúvidas. Uma das possibilidades é eles resolverem todas as expressões dadas para compararem os resultados.

MP140

Expressões numéricas

  1. O preço de uma corrida de táxi é igual à bandeirada (quantia fixa) mais os quilômetros percorridos multiplicadoçs pelo custo de cada quilômetro. Onde Mário reside, a bandeirada custa R$ 5,00, e cada quilômetro rodado, R$ 3,00.
    1. Quanto Mário pagará por uma corrida de 13 quilômetros?
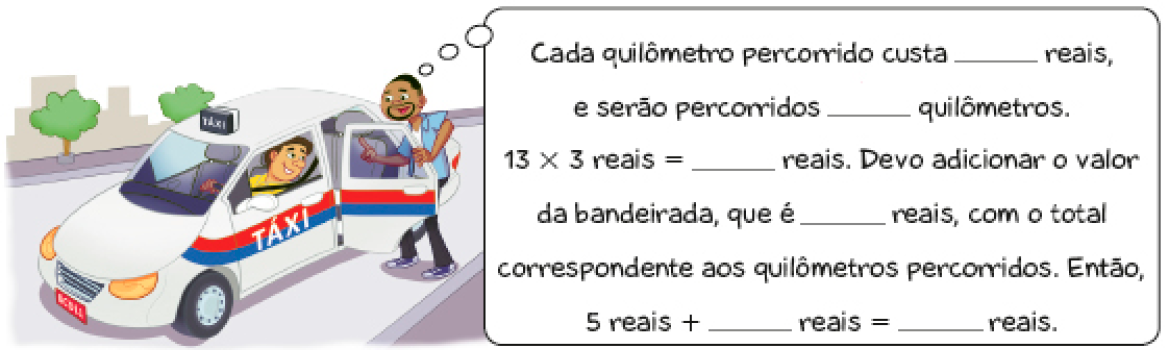
Imagem: Ilustração. Um homem entra em um táxi e pensa: Cada quilômetro percorrido custa espaço para resposta reais, e serão percorridos espaço para resposta quilômetros. 13 x 3 reais = espaço para resposta. Devo adicionar o valor da bandeirada, que é espaço para resposta reais, com o total correspondente aos quilômetros percorridos. Então, 5 reais + espaço para resposta reais = espaço para resposta reais Fim da imagem.
PROFESSOR Resposta: 3; 13; 39; 5; 39; 44.

Observe que os cálculos feitos por Mário podem ser representados por meio de uma expressão numérica:

Mário pagará _____ reais pela corrida.

PROFESSOR Resposta: 44

5 + 13 × 3

  1. Qual é o resultado da expressão 5 + 13 × 3 quando fazemos primeiro a adição? E quando fazemos primeiro a multiplicação?

Fazendo primeiro a adição:

5 + 13 × 3 = _____ × 3 = _____

PROFESSOR Resposta: 18; 54

Fazendo primeiro a multiplicação:

5 + 13 × 3 = 5 + _____ = _____

PROFESSOR Resposta: 39; 44
  1. Os resultados obtidos são iguais? Qual deles corresponde ao valor pago por Mário?

    _____

    PROFESSOR Resposta: Não; 44 reais.

    Essa situação indica que, em uma expressão numérica, a ordem em que as operações são efetuadas deve obedecer a algumas regras, pois não podemos ter uma expressão numérica com mais de um resultado.

1ª regra: As multiplicações e as divisões devem ser efetuadas primeiro, na ordem em que aparecem. Depois, devem ser efetuadas as adições e as subtrações, na ordem em que aparecem.

2ª regra: Se as expressões apresentarem parênteses, as operações que estiverem dentro deles deverão ser feitas primeiro, seguindo a ordem vista na 1ª regra.

MANUAL DO PROFESSOR

Objetivo

  • Resolver situações que envolvam expressões numéricas com as quatro operações fundamentais.

    Atividade 1

    Acompanhe a leitura da turma sobre a situação apresentada nesta atividade e esclareça eventuais dúvidas. Explique que, para ser compreendida por todos, a linguagem matemática segue algumas regras, de modo que não surjam respostas ambíguas ou equivocadas. Assim, as regras que envolvem as expressões numéricas precisam ser usadas corretamente para que cada sequência de cálculos tenha uma única resposta. O uso de parênteses e outros recursos têm por objetivo organizar a ordem de realização dos cálculos.

    Após a resolução das questões, pergunte: “Se o preço da bandeirada fosse 10 reais e cada quilômetro rodado custasse 2 reais, quanto Mário deveria pagar no total?”. Espera-se que façam: 10 + (13 × 2) = 10 + 26 = 36.

    Assim, Mário deveria pagar 36 reais.

    BNCC em foco:

    EF05MA07, EF05MA08

MP141

  1. Observe o cálculo da expressão numérica (3 + 4 × 5) − 13 feito por Ana e responda à questão.

(3 + 4 × 5) − 13 = ?

Como há parênteses, devemos fazer primeiro 4 × 5, que é igual a 20. Depois, calculamos 3 + 20, que é igual a 23. Finalmente, fazemos 23 − 13, que é igual a 10.

  1. Por que Ana calculou primeiro o resultado de 4 × 5, e não de 3 + 4?

    _____

    PROFESSOR Resposta: Porque devemos fazer primeiro a multiplicação.
  1. Se os parênteses estivessem da seguinte maneira: (3 + 4) × 5 − 13, o resultado obtido por Ana seria diferente? Justifique sua resposta.

    _____

    PROFESSOR Resposta: Sim, pois: (3 + 4) × 5 − 13 = 7 × 5 − 13 = 35 − 13 = 22.
  1. Escreva uma expressão numérica correspondente à quantia total em cada caso. Depois, calcule o valor dessas expressões.
PROFESSOR Resposta: Exemplo de cálculos:
Imagem: Fotografia. Duas cédulas de dez reais, duas cédulas de cinco reais e uma moeda de um real. Fim da imagem.
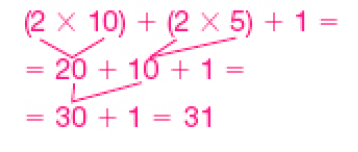
PROFESSOR Resposta: Esquema. (2 x 10) + (2 x 5) + 1 = 2 x 10 = 20 2 x 5 = 10 = 20 + 10 + 1 20 + 10 = 30 30 + 1 = 31
Imagem: Fotografia. Três cédulas de cinquenta reais e duas cédulas de vinte reais. Fim da imagem.
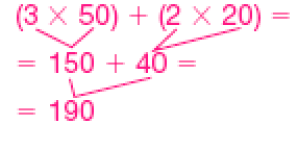
PROFESSOR Resposta: Esquema. (3 x 50) + (2 x 20) = 3 x 50 = 150 2 x 20 = 40 150 + 40 = 190
Imagem: Fotografia. Uma cédula de duzentos reais, três cédulas de dez reais e uma moeda de um real. Fim da imagem.
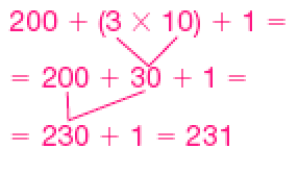
PROFESSOR Resposta: Esquema. 200 + (3 x 10) + 1 = 200 + 30 + 1 200 + 30 = 230 + 1 = 231
  1. Use somente os números 2, 3 e 4 uma única vez para criar uma expressão numérica cujo resultado seja:
  1. 20

    _____

PROFESSOR Exemplo de respostas: (2 + 3) × 4
  1. 24

    _____

PROFESSOR Resposta: 2 × 3 × 4
  1. 14

    _____

PROFESSOR Resposta: 2 × (3 + 4)
  1. 6

    _____

PROFESSOR Resposta: 4 × 3 ÷ 2
MANUAL DO PROFESSOR

Atividade 2

Espera-se que percebam que, embora haja parênteses, dentro deles há duas operações; portanto, a multiplicação deve ser efetuada primeiro. Caso haja ainda dúvida sobre a prioridade da multiplicação em relação à adição, explique que o número que está multiplicando o 5 na expressão 3 + 4 x 5 é o 4 e não o (3 + 4). A multiplicação pode ser escrita na forma de adição: 3 + 5 + 5+ 5+ 5 = 23.

Atividade 3

Verifique se os estudantes percebem que podem representar as quantias considerando a quantidade de cada tipo de cédula. Por exemplo, no item a, há 2 cédulas de 10 reais, portanto, 2 × 10; 2 cédulas de 5 reais, ou seja, 2 × 5, e apenas 1 moeda de 1 real, compondo a expressão: (2 × 10) + (2 × 5) + 1.

Atividade 4

Os estudantes devem elaborar uma expressão numérica cujo resultado seja o valor dado e contenha os números indicados. Esclareça que poderão combinar operações em uma mesma expressão.

Sugestão de atividade

Resolvendo um problema

Preencha cada quadrinho da expressão a seguir com o sinal de adição (+) ou o de multiplicação (×), de modo que o resultado obtido seja o maior possível, e depois o menor possível.

3 Ilustração. Quadrinho preto.4 Ilustração. Quadrinho preto.0 Ilustração. Quadrinho preto.1

Após os estudantes tentarem resolver, discutam as possíveis soluções:

  • Entre 3 e 4, inserir o sinal de multiplicação, pois 3 + 4 = 7, enquanto 3 × 4 = 12.
  • Entre 4 e zero, colocar o sinal de adição, pois 12 + 0 = 12, enquanto 12 × 0 = 0.
  • Entre 0 e 1, colocar o sinal de adição, pois 12 + 1 = 13, enquanto 12 × 1 = 12.

    Maior resultado possível: 3 × 4 + 0 + 1 = 13.

    Menor resultado possível: 3 × 4 × 0 × 1 = 0.

    BNCC em foco:

    EF05MA07, EF05MA08

MP142

  1. Complete as lacunas com os números abaixo, sem repeti-los, para que as igualdades sejam verdadeiras.
Imagem: Ilustração. Flores coloridas com números dentro de cada uma: flor rosa (1), flor laranja (2), flor verde (3), flor vermelha (4), flor roxa (5), flor lilás (6). Fim da imagem.
  1. _____ − ( _____ + _____) = 1
    PROFESSOR Exemplo de resposta: 6 − (3 + 2) = 1
  1. ( _____ − _____ ) × _____ = 10
    PROFESSOR Exemplo de resposta: (4 − 2) × 5 = 10
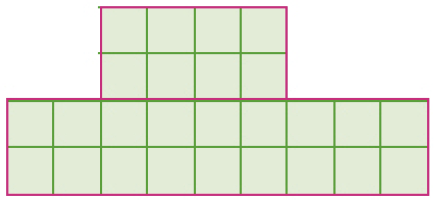
  1. Calcule a quantidade de quadrinhos em cada caso por meio de uma expressão numérica.
Imagem: Ilustração. Duas fileiras com quatro quadradinhos verdes cada. Abaixo há duas fileiras com nove quadradinhos verdes cada. Resposta: Há uma linha em volta das fileiras, dividindo-as em dois grupos. Fim da imagem.
PROFESSOR Exemplo de respostas: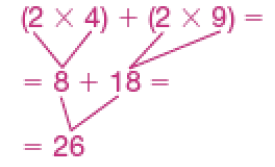
Imagem: Esquema. (2 x 4) + (2 x 9) 2 x 4 = 8 2 x 9 = 18 8 + 18 = 26 Fim da imagem.
Imagem: Ilustração. À esquerda, três colunas com quatro quadradinhos laranja cada. Ao lado, quatro colunas com dois quadradinhos laranja cada. À direita, duas colunas com quatro quadradinhos laranja cada. Resposta: Há uma linha em volta das colunas, dividindo-as em três grupos. Fim da imagem.
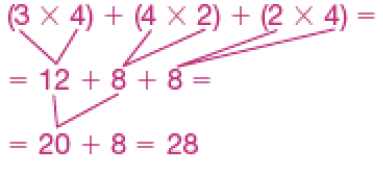
Imagem: Esquema. (3 x 4) + (4 x 2) + (2 x 4) 3 x 4 = 12 4 x 2 = 8 2 x 4 = 8 12 + 8 + 8 12 + 8 = 20 20 + 8 = 28. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Veja, abaixo, como Amanda calculou o resultado de 9 × 23. Depois, pinte abaixo a expressão numérica que corresponde aos cálculos de Amanda.
Imagem: Ilustração. Amanda, mulher com cabelo encaracolado e preso fala: 9 é igual a 10 menos 1. Primeiro, eu fiz 10 vezes 23, que é igual a 230. Depois, multipliquei 1 por 23, que é igual a 23. Por último, subtraí esse resultado do primeiro: 230 menos 23 = 207. O resultado obtido foi 207. Fim da imagem.

(10 × 23) − (1 + 23)

(10 × 23) − (1 × 23)

10 × (23 − 1) + 23

PROFESSOR Resposta correta: (10 × 23) − (1 × 23)
MANUAL DO PROFESSOR

Atividade 5

No item a, os estudantes podem procurar, entre os números dados, dois cuja diferença seja igual a 1. Dentre esses pares, o menor deve ser o resultado da operação dentro dos parênteses. Precisam, então, verificar quais podem ser expressos por uma adição de dois dos números dados.

Espera-se que observem que o resultado da operação dentro dos parênteses, no item b, deve ser um dos fatores de uma multiplicação cujo produto é 10. Assim, eles podem verificar que, de 1 a 6, apenas 2 × 5 = 10 (ou 5 × 2 = 10), ou seja, um dos fatores deve ser 2 e o outro, 5.

Atividade 6

A figura pode ser decomposta de vários modos para que seja representada por meio de expressões numéricas, quando o formato não corresponde a uma organização retangular, em que bastaria multiplicar linha por coluna.

No item a, uma opção é repartir a figura em dois retângulos, um composto de 2 linhas e 4 colunas (2 × 4), e o outro composto de 2 linhas e 9 colunas (2 × 9). Assim, (2 × 4) + (2 × 9) = 26.

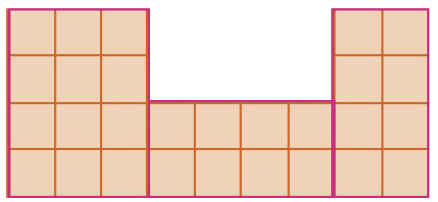
Já a figura do item b pode ser repartida em três retângulos: um retângulo de 3 colunas e 4 linhas, outro com 4 colunas e 2 linhas, e, por fim, um com 2 colunas e 4 linhas. Desse modo, (3 × 4) + (4 × 2) + (2 × 4) = 28.

Atividade 7

Amanda aplicou uma propriedade que pode ser muito útil em situações de cálculo mental.

Ela procurou simplificar a multiplicação usando o que já conhece para efetuar multiplicações do tipo 10 vezes. O que ela fez mentalmente pode ser explicado assim: “Como formei 10 grupos de 23, mas só teria de formar 9, então tirei 1 grupo de 23”.

BNCC em foco:

EF05MA07, EF05MA08; competências específicas 3 e 6

MP143

  1. Escreva a expressão numérica correspondente a cada situação e resolva-a.
    1. Bruno tinha 48 figurinhas e ganhou outras 12. Depois, dividiu igualmente suas figurinhas com seu irmão Laerte. Com quantas figurinhas cada um ficou?
PROFESSOR Resposta: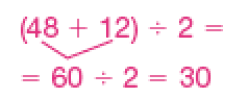 Esquema. (48 + 12) dividido por 2 = 48 + 12 = 60 dividido por 2 = 30

_____

PROFESSOR Resposta: Cada um ficou com 30 figurinhas.
  1. Um livro tem 250 páginas. Célia leu 50 páginas na segunda-feira e pretende terminar a leitura nos próximos 5 dias, lendo a mesma quantidade de páginas por dia. Quantas páginas ela deverá ler no sábado?
PROFESSOR Resposta: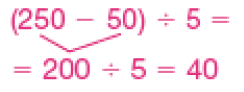 Esquema. (250 menos 50) dividido por 5 = 2000 dividido por 5 = 40

_____

PROFESSOR Resposta: Célia deverá ler 40 páginas no sábado.
  1. Complete as igualdades com os símbolos +, −, × ou ÷.
  1. 3 _____ 4 _____ 2 = 10
    PROFESSOR Resposta: ×; −
  1. 3 _____ 4 _____ 2 = 6
    PROFESSOR Resposta: ×; ÷
  1. 3 _____ 4 _____ 2 = 9
    PROFESSOR Resposta: +; +
  1. 3 _____ 4 _____ 2 = 5
    PROFESSOR Resposta: +; −

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Leia o texto e responda às perguntas.

Míriam apertou as teclas Ilustração. Teclas: 2; x; 3; +; 5; =. de sua

calculadora para calcular o resultado da expressão numérica 2 × (3 + 5).

  1. Qual foi o resultado encontrado por Míriam? E qual é o resultado certo?

    _____

    PROFESSOR Resposta: 11; 16.
  1. Qual foi o erro cometido por ela?

    _____

    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 8

Nesta atividade, os estudantes são incentivados a representarem uma situação na forma de uma expressão numérica. As habilidades relacionadas com a comunicação de ideias matemáticas são muito importantes e podem ser complementadas com atividades similares a essa.

Atividade 9

Observe as estratégias usadas pelos estudantes e socialize-as com toda a turma, validando-as com eles.

Atividade 10

Aproveite a atividade para apresentar aos estudantes as teclas de memória da calculadora. É importante perceberem que, em calculadoras, que não respeitam a ordem das operações, o uso dessas teclas possibilita garantir manualmente a ordem das operações ao armazenar na memória resultados parciais (que estariam entre parênteses).

A tecla Ilustração. Tecla: M+. serve para armazenar resultados de operações ou números que precisarão ser usados posteriormente. Uma vez que o número que se deseja armazenar esteja no visor da calculadora, deve-se apertar a tecla Ilustração. Tecla: M+. , desde que a memória da calculadora esteja vazia. Quando se deseja usar esse número armazenado, basta teclar Ilustração. Tecla: MRC. e o número armazenado aparece novamente no visor (em algumas calculadoras, a tecla Ilustração. Tecla: MRC. aparece como Ilustração. Tecla: MR. ).

CRÉDITO: ADILSON SECCO

BNCC em foco:

EF05MA07, EF05MA08; competências específicas 3 e 6

Sugestão de atividade

Jogo dos 4 quatros

Coloque os sinais das operações de adição (+), subtração (–), multiplicação (×) e divisão (÷) para que as igualdades sejam verdadeiras.

Respostas possíveis:

4 ÷ 4 − 4 ÷ 4 = 0; 4 ÷ 4 × 4 ÷ 4 = 1; 4 ÷ 4 + 4 ÷ 4 = 2

MP144

Jogo: Achei!

Material: Tabuleiro com 49 casas, como mostra o modelo abaixo, 5 conjuntos de 9 fichas numeradas de 1 a 9, 4 fichas com o número 0 e 50 cartas numeradas de 1 a 50. Todo o material deve ser confeccionado pelos jogadores.

Imagem: Ilustração. Tabuleiro com sete colunas e sete fileiras. Fim da imagem.

LEGENDA: Modelo de tabuleiro FIM DA LEGENDA.

Imagem: Ícone: Grupo. Fim da imagem.

Jogadores: 2, 3 ou 4

Regras:

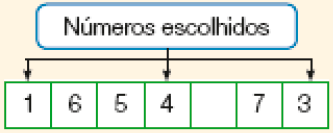
Imagem: Esquema. Números escolhidos. 1, 6, 5, 4, vazio, 7, 3. Há uma seta para 1, 4 e 3. Fim da imagem.

Cálculos possíveis:

1 × 4 + 3 = 7 ou 1 × 4 − 3 = 1

3 × 4 + 1 = 13 ou 3 × 4 − 1 = 11

MANUAL DO PROFESSOR

Objetivos

  • Resolver situações que envolvam expressões numéricas.
  • Resolver problemas de adição, subtração e multiplicação com números naturais.

    Oriente os estudantes para que, na confecção do tabuleiro, as casas sejam maiores que as fichas, que devem ser quadrangulares. As cartas devem ser retangulares e também de tamanho maior que as fichas, para que não se misturem. Pode-se pedir que pintem as cartas e as fichas com cores diferentes.

    Nesse jogo dinâmico, o desafio recomeça a cada carta retirada do monte de compras, pois os estudantes realizam muitas tentativas, ou seja, muitos cálculos mentais além do que é o certo. Como o jogo explora a combinação de diferentes operações na realização do cálculo mental, ele pode ser jogado no decorrer de todo o ano. Jogá-lo uma única vez tem pouca contribuição para o objetivo de desenvolver procedimentos de cálculo mental. Desse modo, a sugestão é retomá-lo em vários momentos ao longo do ano.

    BNCC em foco:

    EF05MA07, EF05MA08; competência geral 9; competência específica 7

MP145

Questões sobre o jogo

  1. Um jogador retirou uma carta com o número 48, observou as fichas com os números 6, 7 e 6 em uma mesma linha do tabuleiro e falou em voz alta “Achei!”. Como ele conseguiu obter o resultado 48?

    _____

    PROFESSOR Resposta: Calculando 6 × 7 + 6.
  1. Observe uma parte de um tabuleiro.
Imagem: Ilustração. Uma menina com cabelo comprido está sentada e de costas. Na frente dela há um tabuleiro sobre uma mesa. No tabuleiro há três colunas e três fileiras com números. Fileira 1: 2, 9, 4. Fileira 2: 8, 7, 3. Fileira 3: 0, 5, 1. Fim da imagem.
  1. com os números das fichas que estão na horizontal e usando somente a adição com o 3º número?

    _____

    PROFESSOR Resposta: 22 (2 × 9 + 4); 59 (8 × 7 + 3); 1 (0 × 5 + 1); 38 (4 × 9 + 2); 29 (3 × 7 + 8); 5 (1 × 5 + 0).
  1. com os números das fichas que estão na vertical e usando somente a subtração com o 3º número? _____
    PROFESSOR Resposta: 16 (2 × 8 − 0); 58 (9 × 7 − 5); 11 (4 × 3 − 1); 26 (5 × 7 − 9).
  1. com os números das fichas da diagonal e usando somente a adição com o 3º número? _____
    PROFESSOR Resposta: 15 (2 × 7 + 1); 9 (1 × 7 + 2); 28 (4 × 7 + 0); 4 (0 × 7 + 4).
  1. Se uma ficha com o número 0 (zero) for usada na multiplicação, qual será o maior resultado que se poderá obter? Justifique sua resposta.

    _____

    PROFESSOR Resposta: O maior resultado será 9, pois zero vezes qualquer número é igual a zero, e adicionando qualquer número com zero o resultado será sempre esse número, que pode ser, no máximo, 9.
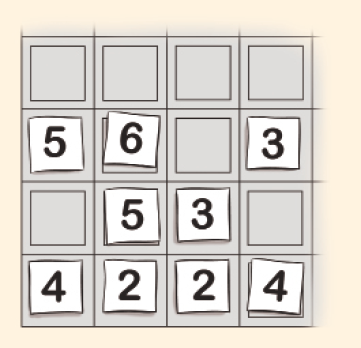
  1. Um jogador tirou a carta de número 27, e dois jogadores falaram ao mesmo tempo “ Achei! ”. Observando a parte do tabuleiro onde estavam os números das fichas que eles usaram, que operações eles podem ter feito para obter o resultado 27?
Imagem: Ilustração. Tabuleiro com quatro colunas e quatro fileiras com números. Fileira 1: vazio, vazio, vazio, vazio. Fileira 2: 5, 6, vazio, 3. Fileira 3: vazio, 5, 3, vazio. Fileira 4: 4, 2, 2, 4. Fim da imagem.

_____

PROFESSOR Resposta: 5 × 6 − 3 na linha horizontal e 5 × 5 + 2 na linha diagonal.
MANUAL DO PROFESSOR

Questões sobre o jogo

Nestas questões, os estudantes devem observar e analisar situações do jogo, verificando resultados que podem ocorrer e registrando como obtê-los.

Na questão 2, item b, os estudantes devem perceber que os resultados das expressões 0 × 8 − 2 e 1 × 3 − 4 não correspondem a nenhum dos números das cartas (0 − 2 e 3 − 4 são subtrações que, nesse momento, os estudantes não farão, pois não resultam em números naturais).

Variações

Pode-se ampliar o tabuleiro com números maiores ou ainda acrescentar a operação de divisão como alternativa, além da multiplicação.

Também é possível deixar que os estudantes decidam quando o jogo acaba: por exemplo, após um número predeterminado de jogadas ou quando não houver mais 3 fichas em uma mesma linha do tabuleiro.

BNCC em foco:

EF05MA07, EF05MA08; competência geral 9; competência específica 7

MP146

Problemas com mais de uma operação

  1. Veja como Liliane resolveu o problema a seguir e complete.

    Para a estreia de um espetáculo circense, foram colocadas à venda 1 500 entradas. Pela manhã, foram vendidas 389 entradas, e à tarde, 450. Quantas entradas ainda estão à venda?

Imagem: Ilustração. Liliane, mulher com cabelo comprido e tiara fala: Primeiro, identifiquei os dados e a pergunta do problema. Depois, analisei o que devia ser feito e resolvi o problema. Fim da imagem.

Pergunta: Quantas entradas ainda estão à venda?

Dados: Foram colocadas à venda 1 500 entradas. Pela manhã, foram vendidas 389 entradas, e à tarde, 450.

Primeiro, ela calculou quantas entradas foram vendidas ao todo.

389 + 450 = _____

PROFESSOR Resposta: 839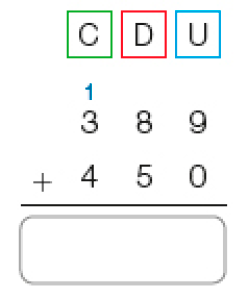
Imagem: Conta de adição na vertical. Acima, as siglas: C, D, U. Em seguida, o número 389 (acima do número 3 há um número 1 pequeno). Em seguida, sinal de adição e o número 450. Abaixo, traço horizontal e o resultado: espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 839

Depois, ela calculou quantas entradas ainda não foram vendidas, subtraindo o total de entradas vendidas das que foram colocadas à venda.

1 500 − _____ = _____

PROFESSOR Resposta: 839; 661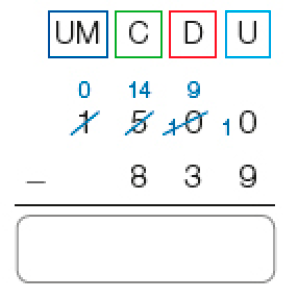
Imagem: Conta de subtração na vertical. Acima, as siglas: UM, C, D, U. Em seguida, o número 1.500 (o número 1 está cortado com o número 0 pequeno em cima. O número 5 está cortado com o número 14 pequeno em cima. O número 0 está cortado com o número 1 pequeno ao lado e o número 9 pequeno em cima. O outro número 0 está com o número 1 pequeno ao lado). Em seguida, sinal de subtração e o número 839. Abaixo, traço horizontal e o resultado: espaço apra resposta. Fim da imagem.
PROFESSOR Resposta: 661

Ainda estão à venda _____ entradas.

PROFESSOR Resposta: 661
MANUAL DO PROFESSOR

Objetivo

  • Resolver e elaborar problemas de adição, subtração, multiplicação e divisão com números naturais, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

    Atividade 1

    Leia a situação com os estudantes. Discuta com eles a explicação de Liliane, que mostra os passos da estratégia que ela usou para resolver o problema.

    Peça aos estudantes que identifiquem os dados descritos na situação, que são as informações conhecidas e, em seguida, solicite que algum estudante faça esse registro na lousa. Depois, com os demais colegas, peça que identifiquem a pergunta do problema, que também será registrada na lousa.

    Antes de apresentar a resolução feita por Liliane, solicite aos estudantes que troquem ideias e resolvam coletivamente. Escolha outro estudante para fazer os registros na lousa.

    Depois, peça que acompanhem no livro a resolução feita e completem o que for necessário.

    BNCC em foco:

    EF05MA07

    Sugestão de atividade

    Cálculo do total de quadrinhos coloridos

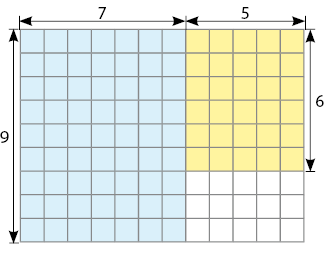
    Registre os quadrinhos da parte azul e os da parte amarela da figura ao lado por meio de uma expressão numérica. Depois, determine essa quantidade de quadrinhos.

    Podemos calcular os quadrinhos de cada parte colorida e, depois, adicioná-los, obtendo a expressão numérica: 7 × 9 + 5 × 6.

    Imagem: Ilustração. À esquerda, sete colunas e nove fileiras de quadradinhos azuis. À direita, cinco colunas e seis fileiras e quadradinhos amarelos. Abaixo, cinco colunas e três fileiras de quadradinhos amarelo-claro. Fim da imagem.

    CRÉDITO: ADILSON SECCO

MP147

  1. Há 5 dias, Tomás começou a ler um livro de histórias sobre o espaço. Nos últimos 5 dias, ele leu 28 páginas por dia. Para terminar o livro, ainda faltam 52 páginas. Quantas páginas tem esse livro?
    1. Qual é a pergunta desse problema?

      _____

      PROFESSOR Resposta: Quantas páginas tem esse livro?
Imagem: Ilustração. Tomás, jovem ruivo está sentado e lendo um livro. Fim da imagem.
  1. Quais são os dados do problema?

    _____

    PROFESSOR Resposta: Tomás leu, em 5 dias, 28 páginas por dia.
    PROFESSOR Faltam 52 páginas para terminar o livro.
  1. Explique como você pode resolver esse problema.
    PROFESSOR Exemplo de cálculo:
    PROFESSOR 5 × 28 = 140
    PROFESSOR 140 + 52 = 192

O livro de Tomás tem _____ páginas.

PROFESSOR Resposta: 192
  1. Resolva os problemas.
    1. Vânia faz bombons para vender em embalagens com 12 unidades sortidas. Em um fim de semana, ela fez 150 bombons de morango, 120 de coco e 140 de cereja. Quantas embalagens ela conseguirá montar com esses bombons?
      PROFESSOR Resposta: 120 + 140 + 150 = 410
      PROFESSOR 410 ÷ 12 = 34, com resto 2

_____

PROFESSOR Resposta: Ela montará 34 embalagens e sobrarão 2 bombons.
  1. Bruno comprou 12 cadernos para seus filhos ao preço de 11 reais cada um. Se ele pagou essa compra com uma cédula de 200 reais, quanto ele recebeu de troco?
    PROFESSOR Resposta: 12 × 11 = 132
    PROFESSOR 200 − 132 = 68

_____

PROFESSOR Resposta: Bruno recebeu 68 reais de troco.
MANUAL DO PROFESSOR

Atividade 2

A resolução deste problema exige que os estudantes façam primeiro uma multiplicação e, em seguida, uma adição.

Para o item c, uma possível resposta é: primeiro determino a quantidade de páginas que Tomás já leu multiplicando 28 por 5 e, depois, adiciono 52 ao produto encontrado para determinar o total de páginas do livro.

Atividade 3

No item a, pergunte: “Quantos bombons, no mínimo, Vânia ainda precisará fazer para embalar todos os bombons sem que haja sobras?”. Espera-se que os estudantes respondam que ela precisará fazer mais 10 bombons (e usará 35 embalagens nas quais caibam 12 unidades).

No item b, se necessário, retome a ideia de troco. Para ampliar, pode-se pedir que representem esse problema por meio de uma expressão numérica. Espera-se que os estudantes identifiquem a expressão 200 − 12 × 11, que resulta em 68.

BNCC em foco:

EF05MA07, EF05MA08

Podemos também calcular o total de quadrinhos do retângulo maior e, depois, subtrair os quadrinhos brancos, obtendo a expressão numérica: 9 × 12 − 5 × 3.

Em qualquer dos procedimentos, o total de quadrinhos coloridos é 93.

Desse modo, os estudantes são levados a reconhecer a equivalência entre as expressões, que representam maneiras diferentes de calcular o mesmo resultado. Trabalhar com distintas expressões contribui para evidenciar estratégias e procedimentos de cálculo mental. A expressão numérica representa uma sistematização do registro de cálculo mental.

Nas atividades desta página (e nas duas próximas páginas) exploramos o cálculo de um valor desconhecido com base nas propriedades de uma igualdade.

MP148

  1. Considere as informações a seguir.
    1. Um modelo de máquina de lavar roupas está sendo vendido por 12 parcelas de 191 reais.
    1. II) No pagamento à vista, há um desconto de 100 reais.
Imagem: Ilustração. Uma máquina de lavar roupas. Acima, placa com a informação: OFERTA – 12 VEZES DE R$ 191,00. Fim da imagem.
  1. Elabore um problema utilizando as informações indicadas acima. A pergunta desse problema deve permitir que sua resolução seja obtida por meio de duas operações: uma multiplicação e uma subtração.

    _____

    PROFESSOR Exemplo de problema: Márcio comprou uma máquina de lavar roupas que estava em oferta por 12 parcelas de 191 reais. Ao pagar à vista, ele teve um desconto de 100 reais. Quanto Márcio pagou por essa máquina de lavar roupas?
  1. Agora, resolva o problema que você criou.
PROFESSOR Exemplo de resposta:
PROFESSOR 191 × 12 = 2.292
PROFESSOR 2.292 − 100 = 2.192
PROFESSOR Márcio pagou 2 192 reais por essa máquina de lavar roupas.
  1. Veja a seguir o enunciado de um problema com algumas informações incompletas e faça o que se pede.

Valéria comprou um _____ pelo valor de _____ reais.

Ela também comprou uma _____ por _____ reais. Se ela dividiu, no cartão, o valor total da compra desses dois itens em _____ parcelas iguais, qual foi o valor de cada parcela?

PROFESSOR Exemplo de resposta: sapato; 120; blusa; 80; 4.
  1. Complete o enunciado desse problema com informações adequadas.
  1. Agora, resolva o enunciado do problema que você completou.
PROFESSOR Exemplo de resposta:
PROFESSOR 120 + 80 = 200
PROFESSOR 200 ÷ 4 = 50
PROFESSOR O valor de cada parcela foi 50 reais.
MANUAL DO PROFESSOR

Atividade 4

Leia as informações com os estudantes e ajude-os a analisá-las.

Um cálculo possível para o exemplo apresentado é: Como 191 é igual a 200 menos 9, calculamos 12 × 200 = 2 .400 e 12 × 9 = 108. Depois, subtraímos 108 de 2 .400, obtendo 2 .292. Como Márcio teve um desconto de 100 reais, basta subtrair 100 de 2. 292 para obter o valor que ele pagou pela máquina de lavar roupas. Logo, pagou 2 .192 reais.

Atividade 5

Incentive os estudantes a analisarem as informações que devem considerar para completar o problema.

Sugira que troquem com um colega os problemas completados, a fim de resolvê-los. Em seguida, devem conversar sobre as diferenças e semelhanças entre os problemas.

Depois de os estudantes resolverem o problema do colega, peça que discutam outro modo de calcular, expondo suas estratégias. Algumas vezes, é difícil para os estudantes expressarem o raciocínio empregado na realização de um cálculo. Por esse motivo, eles devem ser incentivados a exporem suas ideias e a conhecerem outras possibilidades de resolução.

BNCC em foco:

EF05MA07, EF05MA08

MP149

Proporcionalidade

  1. Veja quais são os ingredientes para uma receita de biscoitinhos de goiaba.

Ingredientes

2 xícaras (chá) de farinha de trigo

150 gramas de manteiga

1 xícara (chá) de açúcar

3 colheres (sopa) de água

150 gramas de goiabada firme cortada em tiras finas

Imagem: Fotografia. Biscoitos com goiabada em cima sobre uma bandeja. Fim da imagem.
  1. Sabendo que essa receita rende 36 biscoitinhos, quantos gramas de goiabada seriam necessários para fazer 18 biscoitinhos? E 72? Explique suas respostas.

    _____

    PROFESSOR Resposta: Como 18 é a metade de 36, para fazer 18 biscoitinhos são necessários 75 gramas de goiabada; como 72 é o dobro de 36, são necessários 300 gramas de goiabada.
  1. Maria quer fazer 360 desses biscoitinhos para vender. Quanto ela precisará de cada ingrediente para fazer esses biscoitinhos? Complete a lista a seguir com as quantidades correspondentes.

    _____ xícaras (chá) de farinha de trigo

    PROFESSOR Resposta: 20

    _____ gramas de manteiga

    PROFESSOR Resposta: 1.500

    _____ xícaras (chá) de açúcar

    PROFESSOR Resposta: 10

    _____ colheres (sopa) de água

    PROFESSOR Resposta: 30

    _____ gramas de goiabada firme cortada em tiras finas

    PROFESSOR Resposta: 1.500
  1. Pesquise na internet ou com seus familiares os ingredientes para fazer uma receita de brigadeiros. Descubra a quantidade de porções que é possível preparar com essa receita.

    Copie essas informações em seu caderno. Depois, reescreva a receita considerando a quantidade de cada ingrediente para que ela seja suficiente para servir uma porção a cada colega de sua classe. Considere que poderão sobrar porções, mas não poderão faltar.

    PROFESSOR Resposta variável.
MANUAL DO PROFESSOR

Objetivo

  • Resolver problemas que envolvam a noção de proporcionalidade entre duas grandezas.

    Atividade 1

    No item b, espera-se que os estudantes percebam que 360 é 10 × 36. Sendo assim, devem multiplicar por 10 todos os ingredientes da receita.

    Atividade 2

    Peça aos estudantes que façam a pesquisa antecipadamente e socializem as diferentes receitas que trouxerem. Embora a atividade solicite apenas os ingredientes, se julgar oportuno, peça que tragam também o modo de fazer. Se possível, escolha uma receita fácil e prepare com a turma. Alerte os estudantes de que eles não devem mexer com fogo nem com utensílios cortantes; devem sempre contar com o auxílio de um adulto para isso.

    A seguir, apresentamos uma sugestão para trabalhar com ingredientes de uma receita.

    Bolo da Denise

    Ingredientes:

    2 ovos

    2 xícaras (chá) de açúcar

    2 colheres (sopa) de margarina

    3 xícaras (chá) de farinha de trigo

    1 xícara (chá) de leite

    1 colher (sopa) de fermento em pó

    Supondo que essa receita renda 16 pedaços e que uma classe tenha 30 estudantes, pergunte: “O que deve ser feito para preparar essa receita para essa classe?”. Espera-se que os estudantes percebam que é necessário dobrar a quantidade dos ingredientes (ou fazer duas receitas dessa) assim o bolo renderá o dobro de pedaços (em geral), ou seja, 32 pedaços, que serão suficientes para os 30 estudantes e para o professor.

    BNCC em foco:

    EF05MA08, EF05MA12; competência geral 5; competência específica 5

MP150

Boxe complementar:

Desafio

Jair vende bombons em caixas de 6, 8 e 12 unidades. Ele paga 3 reais em cada caixa e a caixa com 8 bombons tem o custo de 19 reais. Nesse valor ele já incluiu a quantia gasta com a caixa.

Imagem: Ilustração. Caixa redonda e azul (BOMBONS 8 UNIDADES). Em seguida, caixa com formato de coração vermelho (BOMBONS 6 UNIDADES). Ao lado, caixa quadrada e amarela (BOMBONS 12 UNIDADES). Fim da imagem.

CRÉDITO: ANDRÉ VALLE

Sabendo que o preço de cada bombom é sempre o mesmo, determine o custo das caixas com 6 e 12 bombons.

_____

Resposta: 6 unidades: 15 reais; 12 unidades: 27 reais.

Fim do complemento.

  1. Veja a planta que Mariano fez de sua residência.
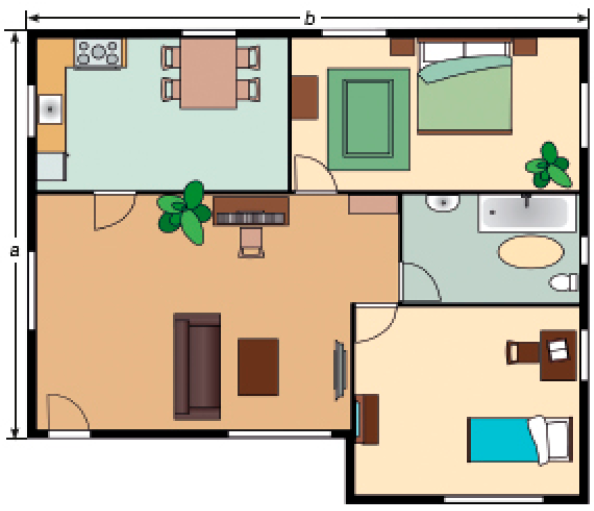
Imagem: Ilustração. Planta de uma casa, medindo a de comprimento e b de largura. Na parte superior há uma cozinha e um quarto de casal. Abaixo há uma sala, um banheiro e um quarto de solteiro. Fim da imagem.

Para fazer essa representação, Mariano considerou que cada centímetro, na planta, corresponde a 1 metro na realidade.

MANUAL DO PROFESSOR

Desafio

Incentive os estudantes a socializarem a estratégia que utilizaram, expondo aos colegas como pensaram.

Uma resolução possível é:

  • Como cada embalagem custa 3 reais, o valor relativo aos 8 bombons será (19 − 3) reais, ou seja, 16 reais. Assim, uma embalagem com 4 unidades (metade de 8) deve ter um valor relativo aos bombons de 8 reais (metade de 16).
  • Como 6 unidades correspondem a (4 + 2) unidades, verificamos que 6 unidades correspondem a “4 unidades mais metade de 4 unidades”, ou seja, o valor relativo a 6 bombons será “8 reais mais metade de 8 reais”, isto é, (8 + 4) reais ou 12 reais. Acrescentando o custo de 3 reais da embalagem, o valor de venda da embalagem com 6 bombons é 15 reais.
  • Como 12 unidades é o dobro de 6 unidades, o valor relativo aos 12 bombons é o dobro do valor relativo aos 6 bombons, ou seja, é o dobro de 12 reais ou, ainda, é 24 reais. Acrescentando o custo de 3 reais da embalagem, o valor de venda da embalagem com 12 bombons é 27 reais.

    Atividade 3

    Nesta atividade, os estudantes devem medir os lados indicados com uma régua, expressando as medidas obtidas em centímetro, e usar a correspondência feita por Mariano: cada centímetro no desenho corresponde a 1 metro na realidade. Espera-se que os estudantes obtenham na planta desenhada 8 cm em a e 11 cm em b. Assim, podem concluir que a = 8 metros e b = 11 metros.

    BNCC em foco:

    EF05MA07, EF05MA08, EF05MA12

MP151

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. O quarto de Luísa tem formato retangular de lados medindo 3 m e 2 m. Desenhe no espaço a seguir a representação do quarto de Luísa, sendo que cada 3 cm da sua representação deve corresponder a 1 m na realidade.

    _____

PROFESSOR Exemplo de desenho:
PROFESSOR Imagem: Ilustração. Retângulo medindo 9 cm de largura e 6 cm de comprimento. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Diego iniciou a construção de um gráfico de colunas para indicar o valor das vendas de sua loja de calçados nos 4 primeiros meses de 2023.

Valor das vendas (em real)

Jan. - 50.000 reais

Fev. - 20.000 reais

Mar. - 30.000 reais

Abr. - 40.000 reais

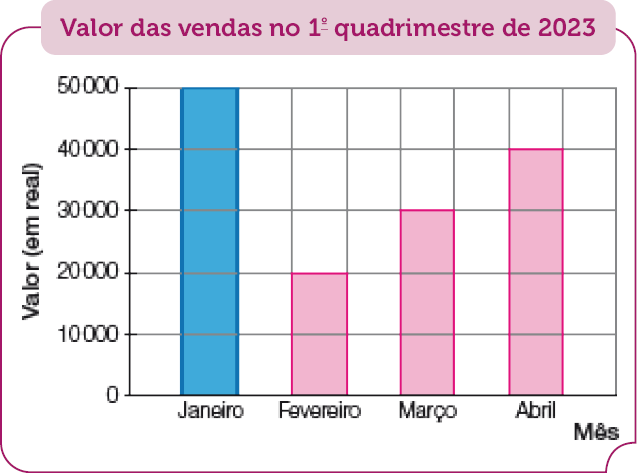
Imagem: Gráfico de colunas. Valor das vendas no 1º quadrimestre de 2023. No eixo vertical, o valor (em real) e no eixo horizontal, o mês. Janeiro: 50.000 reais. Fevereiro: 20.000 reais. Março: 30.000 reais. Abril: 40.000 reais. Fim da imagem.

Fonte: Dados obtidos por Diego (maio 2023).

  1. Qual foi o valor das vendas referentes ao mês de janeiro? _____
    PROFESSOR Resposta: 50.000 reais.
  1. Com o auxílio de uma régua, meça, no gráfico, a coluna correspondente ao mês de janeiro. Qual é a altura, em centímetro, dessa coluna? _____
    PROFESSOR Resposta: 5 cm.
  1. Para fazer o gráfico, Diego considerou que cada 1 cm de altura das colunas corresponde a quantos reais em vendas? _____
    PROFESSOR Resposta: 10.000 reais.

    d) Desenhe, no gráfico, as colunas correspondentes aos outros três meses.

MANUAL DO PROFESSOR

Atividade 4

Como cada 3 cm no desenho correspondem a 1 m na realidade, espera-se que os estudantes percebam que 3 m devem ser representados no desenho por um lado de 9 cm e que 2 m correspondem, no desenho, a um lado de 6 cm. Assim, eles devem desenhar um retângulo de lados 9 cm e 6 cm.

Para ilustrar essa planta, eles podem desenhar a vista de cima dos móveis do quarto de Luísa.

Atividade 5

Explore o gráfico com os estudantes. Espera-se que eles percebam que cada quadrinho que compõe as colunas equivale a 10.000 reais.

Com o auxílio de uma régua, os estudantes verificarão que o lado do quadrinho da malha mede 1 cm; assim, a coluna de janeiro tem 5 cm de altura, a coluna de fevereiro, 1 cm, a coluna de março, 3 cm e a coluna de abril tem 4 cm.

BNCC em foco:

EF05MA08, EF05MA12, EF05MA25

Sugestão de leitura para o professor

Artigo

MONTEIRO, Carlos Eduardo Ferreira. Interpretação de gráficos: atividade social e conteúdo de ensino. Disponível em: http://fdnc.io/eUt. Acesso em: 31 mar. 2021.

O artigo oferece um pouco da história da representação de dados em gráficos, dos diferentes contextos em que são empregados na mídia e de seu uso como conteúdo de ensino. Destaca que os gráficos, muitas vezes, não têm caráter descritivo, mas podem induzir interpretações, fornecer base para argumentações etc. Apresenta a fundamentação teórica em que se baseiam algumas considerações a respeito de gráficos como mediadores sociais, assim como uma discussão sobre os gráficos como campo de investigação.

MP152

Repartir em partes iguais e em partes desiguais

  1. Fábio ajudou sua professora a arrumar em uma estante os 100 livros doados. Os livros foram distribuídos em cinco prateleiras. Em uma delas, foram colocados livros de fábulas e nas outras quatro prateleiras foram colocados livros de histórias infantis.

    Sabendo que em todas as prateleiras foi colocada a mesma quantidade de livros, responda às questões.

    1. Quantos livros doados são de histórias infantis?

      _____

      PROFESSOR Resposta: 80 livros.
    1. E quantos são de fábulas?

      _____

      PROFESSOR Resposta: 20 livros.
Imagem: Ilustração. Fábio, jovem com cabelo encaracolado está com uma mochila nas costas e colocando um livro em uma estante. Fim da imagem.

• Agora, marque com um X as sentenças verdadeiras.

  1. Os livros de fábulas representam:

    ( ) metade de todos os livros doados.

    ( ) um terço de todos os livros doados.

    ( ) um quarto de todos os livros doados.

    ( ) um quinto de todos os livros doados.

    PROFESSOR Resposta correta: um quinto de todos os livros doados.
  1. Comparando a quantidade de livros de fábulas e de histórias infantis, podemos dizer que:

    ( ) os livros de fábulas correspondem a um quarto dos livros de histórias infantis.

    ( ) os livros de fábulas correspondem a um terço dos livros de histórias infantis.

    ( ) os livros de fábulas correspondem à metade dos livros de histórias infantis.

    ( ) os livros de fábulas correspondem a um quinto dos livros de histórias infantis.

    PROFESSOR Resposta correta: os livros de fábulas correspondem a um quarto dos livros de histórias infantis.
MANUAL DO PROFESSOR

Objetivos

  • Resolver e elaborar problemas de multiplicação e divisão com números naturais.
  • Resolver problemas envolvendo a partilha de uma quantidade em partes iguais e partes desiguais e a ideia de razão entre as partes e delas com o todo.
  • Identificar e representar frações, associando-as à ideia de parte de um todo.

    Atividade 1

    Leia o enunciado e analise com os estudantes as informações contidas nele:

  • 100 livros para arrumar;
  • livros distribuídos nas 5 prateleiras da estante;
  • em uma prateleira foram colocados os livros de fábulas;
  • nas quatro prateleiras restantes foram colocados os livros de histórias infantis;
  • em todas as prateleiras há a mesma quantidade de livros.

    Desse modo, os estudantes terão de obter a quantidade de livros de cada prateleira (100 ÷ 5 = 20), que são 20 livros para, então, determinar quantos são de histórias infantis – em 4 prateleiras: 80 livros – e quantos livros são de fábulas – em 1 prateleira: 20 livros.

    As comparações feitas nas demais questões, em relação ao todo e entre as partes, desenvolvem a ideia de divisão e a noção de fração, que serão estudadas mais adiante (na Unidade 5), além da noção de razão (assunto estudado no Ensino Fundamental II).

    Os estudantes podem verificar essas comparações observando as quantidades (20 em relação a 100, no item c, e 20 em relação a 80, no item d), ou observando a estante e as prateleiras (como suas partes).

    BNCC em foco:

    EF05MA03, EF05MA08, EF05MA13; competências específicas 3 e 6

MP153

  1. Zélia e seu pai fizeram um bolo de laranja. Depois de pronto, eles o dividiram em duas partes de mesmo tamanho. Uma dessas partes, eles dividiram em 16 pedaços iguais e a outra metade foi dividida em 4 pedaços iguais.
Imagem: Fotografia. Um homem está atrás de uma menina e eles estão segurando uma tigela e um batedor. Na frente deles há vários ingredientes sobre uma mesa. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Represente, na malha quadriculada a seguir, como o bolo de Zélia ficou após dividi-lo totalmente.
    PROFESSOR Exemplo de desenho:
Imagem: Ilustração. Malha quadriculada. À esquerda, um quadrado grande, composto por quatro quadrados médios. Ao lado, um quadrado grande, composto por quatro quadrados médios e cada um é composto por quatro quadrados pequenos. Fim da imagem.
  1. Cada um dos 4 pedaços iguais que eles obtiveram a partir de uma metade corresponde à:

    ( ) oitava parte do bolo inteiro.

    ( ) quarta parte do bolo inteiro.

    ( ) metade do bolo inteiro.

    PROFESSOR Resposta correta: oitava parte do bolo inteiro.
  1. É possível repartir um dos 4 pedaços iguais para obter um pedaço como um dos 16 pedaços menores? Explique.

    _____

    PROFESSOR Resposta: Sim; dividindo um dos 4 pedaços iguais em 4 partes iguais.
  1. Se todo o bolo fosse dividido em pedaços iguais aos menores, quantos pedaços de bolo seriam obtidos?

    _____

    PROFESSOR Resposta: 32 pedaços.
MANUAL DO PROFESSOR

Atividade 2

Esta atividade também explora as mesmas ideias da atividade anterior, no entanto o inteiro considerado é um bolo (inteiro contínuo) e não unidades de livros (inteiro discreto). Nesse caso, a representação geométrica é fundamental, e a malha quadriculada é um facilitador para essa representação.

Se julgar conveniente, sugira aos estudantes que considerem o bolo no formato retangular, para facilitar as repartições. Após a realização do item a, socialize os diferentes desenhos que podem aparecer:

Imagem: Ilustração. À esquerda, um quadrado grande, composto por quatro quadrados médios. À direita, um quadrado grande, composto por quatro quadrados médios e cada um é composto por quatro quadrados pequenos. No centro, um quadrado grande, composto por quatro quadrados médios e cada um é composto por quatro quadrados pequenos. À direita, um quadrado grande, composto por quatro quadrados médios. Abaixo. Na parte superior há quatro quadrados médios compostos por quatro quadrados pequenos cada um. Na parte inferior há quatro quadrados médios. Fim da imagem.

CRÉDITO: ADILSON SECCO

No item b, a comparação é parte/todo: um dos 4 pedaços (de uma metade) é comparado ao bolo todo. Se necessário, peça aos estudantes que destaquem na outra metade os 4 pedaços (maiores) para que percebam que no bolo todo cabem 8 desses pedaços e, assim, cada pedaço (dos 4 maiores) corresponde à oitava parte do bolo (inteiro).

No item c, a comparação é parte/parte: espera-se que os estudantes percebam que cada um dos 16 pedaços menores corresponde à quarta parte de um dos 4 pedaços maiores. Logo, para obter um dos pedaços menores deve-se repartir um dos pedaços maiores em 4 partes iguais.

No item d, observando a conclusão do item c, os estudantes podem verificar que cada um dos 4 pedaços maiores dá origem a 4 dos pedaços menores, em cada metade do bolo há 16 pedaços menores, ou seja, o bolo todo contém 32 desses pedaços menores.

BNCC em foco:

EF05MA03, EF05MA13; competências específicas 3 e 6

MP154

  1. Jurandir pretende construir uma casa ocupando metade de um terreno. Em um terço desse terreno, ele construirá a lavanderia e a garagem. No restante do terreno, fará um pomar.
Imagem: Ilustração. Jurandir, homem com boné e macacão está agachado e plantando mudas em um terreno. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Represente, na malha quadriculada a seguir, a divisão desse terreno.
PROFESSOR Exemplo de desenho:
Imagem: Ilustração. Malha quadriculada. Quadrado composto por trinta e seis quadradinhos. Na parte superior, a casa composta por dezoito quadradinhos. Em seguida, a lavanderia e garagem, compostos por doze quadradinhos e abaixo, o pomar, composto por seis quadradinhos. Fim da imagem.
  1. Marque com um X as alternativas corretas.

    Podemos dizer que a parte destinada ao pomar equivale:

    ( ) à metade da parte ocupada pela casa.

    ( ) à metade da parte ocupada pela lavanderia e garagem.

    ( ) a um terço da parte ocupada pela casa.

    ( ) a um terço da parte ocupada pela lavanderia e garagem.

    ( ) a um quinto de todo o terreno.

    ( ) a um sexto de todo o terreno.

    PROFESSOR Respostas corretas:
    PROFESSOR à metade da parte ocupada pela lavanderia e garagem.
    PROFESSOR a um terço da parte ocupada pela casa.
    PROFESSOR a um sexto de todo o terreno.
  1. Escreva uma situação em que determinada quantidade foi dividida em duas partes desiguais. Uma dessas partes deve corresponder a um quinto do total.

    _____

    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 3

Vamos considerar o quadrado, cujo lado é formado por 6 lados de quadrinho da malha quadriculada, como sendo o terreno (observe exemplo de resposta apresentado na malha).

Fixando a frente do terreno, pode-se concluir que:

  • a profundidade do terreno corresponde a 6 lados de quadrinho;
  • a casa tem a metade dessa profundidade, ou seja, 3 lados de quadrinho;
  • a região com a lavanderia e a garagem tem a terça parte da profundidade do terreno, ou seja, 2 lados de quadrinho;
  • a região restante, do pomar, tem 1 lado de quadrinho na profundidade.

    Desse modo, pode-se comparar cada parte com o todo e alguma parte com outra, concluindo que a parte destinada ao pomar cabe:

  • 6 vezes no terreno;
  • 3 vezes na parte destinada à casa;
  • e 2 vezes na parte com a lavanderia e a garagem.

    Ou seja, a parte destinada ao pomar equivale à:

  • sexta parte do terreno;
  • terça parte da casa;
  • metade da parte destinada à lavanderia e à garagem.

    Peça aos estudantes que observem a quantidade de quadrinhos que determina cada lado do terreno que desenharam. Desse modo, eles poderão marcar e identificar as partes mais facilmente. É possível que os estudantes desenhem o terreno retangular (a malha quadriculada sugere isso). Pergunte: “E se o terreno fosse circular, seria mais fácil ou mais difícil fazer essa repartição?”. Se julgar conveniente, distribua dois círculos de papel para cada estudante e peça que pintem, em um deles, uma metade, no outro, uma terça parte.

    BNCC em foco:

    EF05MA03, EF05MA13; competências específicas 3 e 6

    Atividade 4

    Nesta atividade, espera-se que os estudantes compreendam que devem tomar um inteiro, reparti-lo em 5 partes iguais, tomar uma dessas partes para corresponder à quinta parte do todo e juntar o restante para ser a segunda parte (maior que a primeira).

MP155

Possibilidades

  1. Márcia comprará uma calça e uma blusa para seu aniversário.

    Como na loja há 2 possibilidades de cor de calça e 2 possibilidades de cor de blusa, ela está em dúvida sobre a combinação que vai escolher.

Imagem: Ilustração. Márcia, mulher loira está sorrindo e olhando uma vitrine com roupas. Ao lado, placa com a informação: MODA PRIMAVERA/VERÃO. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Pinte na tabela as possíveis combinações que Márcia tem para escolher uma calça e uma blusa nessa loja.
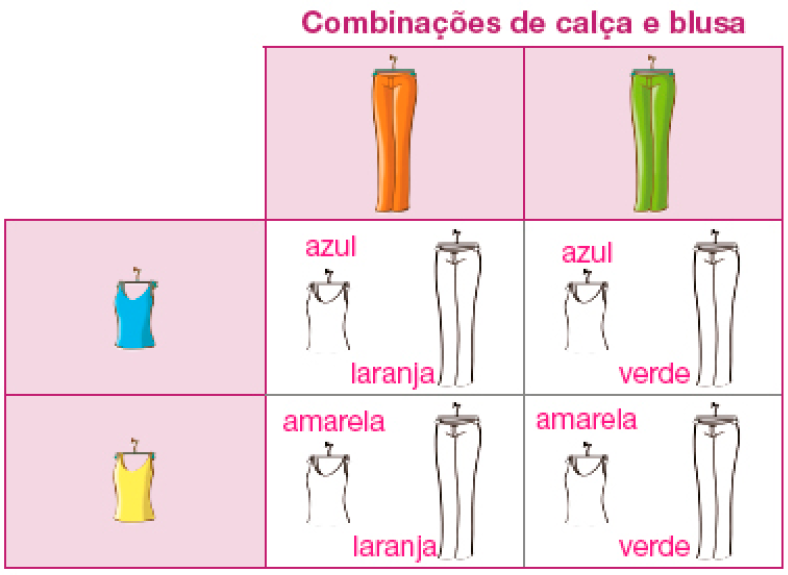
Imagem: Tabela. Combinação de calça e blusa. Ilustração. Calça laranja. Calça verde. Blusa azul. Blusa amarela. Resposta: Blusa azul e calça laranja. Blusa azul e calça verde. Blusa amarela e calça laranja. Blusa amarela e calça verde. Fim da imagem.

Fonte: Anotações de Márcia (maio 2023).

  1. Quantas são as combinações possíveis que Márcia tem para escolher a roupa que quer comprar? _____
    PROFESSOR Resposta: 4

    Essa quantidade pode ser representada por uma multiplicação.

    _____ (Número de possibilidades de calça) × _____ (Número de possibilidades de blusa) = _____ (Número de combinações possíveis de uma calça e uma blusa)

    PROFESSOR Resposta: 2 × 2 = 4
  1. Se tivesse mais uma possibilidade de cor de blusa, o que aconteceria com a quantidade de combinações possíveis para Márcia? Justifique sua resposta por meio de uma multiplicação.

    _____

    PROFESSOR Resposta: Aumentaria para 6 possibilidades, pois 2 × 3 = 6.
MANUAL DO PROFESSOR

Objetivo

  • Resolver problemas simples de contagem envolvendo o princípio multiplicativo por meio de tabelas e diagramas de árvore.

    Atividade 1

    Os estudantes reconhecem a combinação de possibilidades como uma das ideias da multiplicação, ou seja, que o cálculo do número de combinações pode ser obtido por uma multiplicação. Comente que, em algumas situações, a informação de quantas possibilidades há para uma combinação de dois ou mais eventos não é suficiente, pois é preciso saber quais são essas possibilidades. Nesses casos, a organização das possibilidades em uma tabela de dupla entrada facilita a contagem e a determinação de cada combinação possível. Se necessário, relembre a característica principal das tabelas de dupla entrada: o preenchimento de cada célula da tabela deve ser feito levando-se em consideração o cruzamento da informação da linha (fileira horizontal) com a informação da coluna (fileira vertical). Explore a ideia multiplicativa relacionada com o cálculo do número de possibilidades fazendo perguntas do tipo: “Quantas combinações de uma calça com uma blusa haveria se a quantidade de calças fosse 3? E se a quantidade de blusas também fosse 3?”. Espera-se que respondam 6 e 9, respectivamente.

    BNCC em foco:

    EF05MA09

MP156

  1. Márcio foi comprar um aquário e um peixe para seu filho.
Imagem: Ilustração. Márcio, homem com cabelo castanho fala: Quero comprar um peixinho e um aquário. Ao seu lado, um menino observa. Na frente deles, um homem com cabelo preto está atrás de um balcão com aquários. Ele sorri e responde: Temos peixes azuis e laranja, e aquários arredondados e retangulares. Fim da imagem.
  1. Complete o esquema abaixo, chamado de árvore de possibilidades, com as possibilidades de compra que Márcio tem.
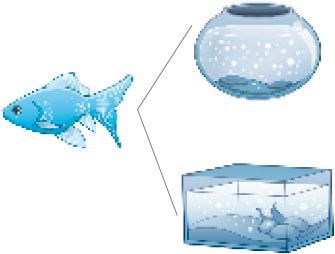
Imagem: Ilustração. Peixe azul. Ao lado, Aquário arredondado. Aquário retangular. Fim da imagem.

peixe azul e _____

PROFESSOR Resposta: aquário arredondado

_____ e aquário retangular

PROFESSOR Resposta: peixe azul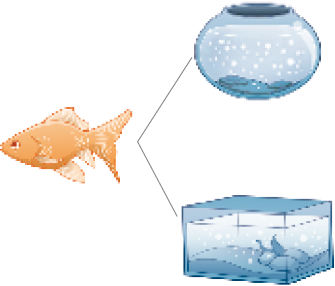
Imagem: Ilustração. Peixe laranja. Ao lado, Aquário arredondado. Aquário retangular. Fim da imagem.

peixe laranja e _____

PROFESSOR Resposta: aquário arredondado

_____ e _____

PROFESSOR Resposta: peixe laranja e aquário retangular
  1. Quantas são as possibilidades de compra? _____
    PROFESSOR Resposta: 4
  1. Represente essa quantidade por uma multiplicação. _____
    PROFESSOR Resposta: 2 × 2 = 4
  1. Se fossem 5 espécies de peixes e 3 tipos de aquário, quantas possibilidades de compra Márcio teria? Explique como você calculou essa quantidade.

    _____

    PROFESSOR Resposta: 15 possibilidades.
    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 2

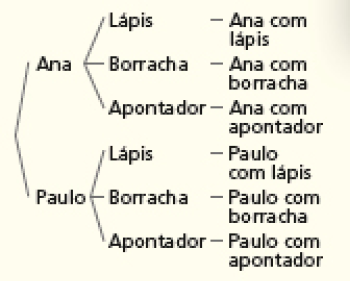
Antes de iniciar esta atividade, apresente uma situação similar. Peça a dois estudantes que se levantem e coloque diante deles três objetos quaisquer, como lápis, borracha e apontador. Em seguida, os colegas devem contar todas as combinações de um estudante com um objeto cada. Peça a um terceiro estudante que registre na lousa, da maneira que quiser, as combinações feitas. É possível que esse estudante registre os resultados sem uma organização que facilite a observação da turma. Então, faça na lousa uma tabela de dupla entrada com os possíveis resultados. Digamos que os estudantes sejam Ana e Paulo.

Tabela: equivalente textual a seguir.

Material/Estudante

Lápis

Borracha

Apontador

Distribuição de materiais

Ana

Ana com lápis

Ana com borracha

Ana com apontador

Paulo

Paulo com lápis

Paulo com borracha

Paulo com apontador

Fonte: Estudantes considerados (maio 2023).

Apresentar a tabela de dupla entrada facilita a observação da quantidade de combinações: há 2 estudantes e 3 objetos. São 6 possibilidades (2 × 3 = 6).

Ainda antes de iniciar a atividade 2, depois da elaboração (na lousa) da tabela de dupla entrada sugerida, mostre o mesmo resultado fazendo um diagrama de árvore de possibilidades, para que os estudantes relacionem ambas as representações da situação:

Imagem: Esquema. Ana - Lápis, borracha, apontador. Ana com lápis, Ana com borracha, Ana com apontador. Paulo - Lápis, borracha, apontador. Paulo com lápis, Paulo com borracha, Paulo com apontador. Fim da imagem.

BNCC em foco na dupla de páginas:

EF05MA09

Voltando à situação proposta na atividade, pergunte: “Quantas possibilidades de compra de um peixinho e de um aquário Márcio teria se, além do peixinho azul e do laranja, a loja também vendesse peixinhos amarelos?”. Peça que representem a nova situação em uma árvore de possibilidades.

MP157

  1. Carlos inventou um código com letra e número para emplacar os carrinhos de sua coleção. O código tem uma letra (A ou B) e um número (1, 2 ou 3). Veja os exemplos.

    A1; B3

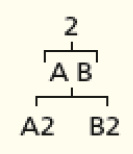
  1. Complete a árvore de possibilidades com as possibilidades que Carlos tem de formar uma placa.
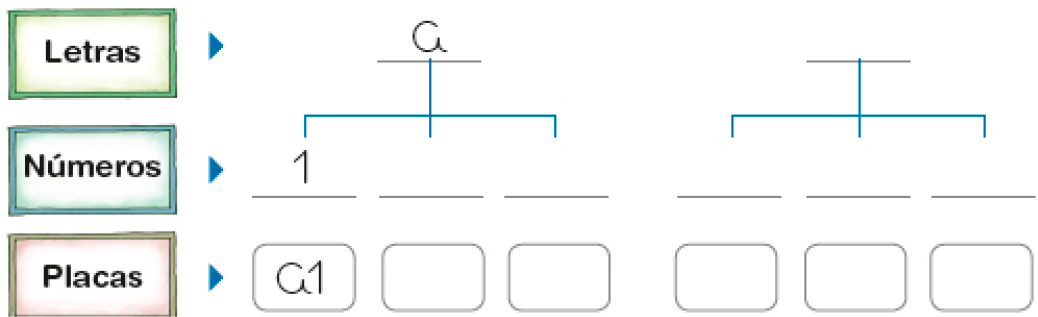
Imagem: Ilustração. Árvore de possibilidades. À esquerda, na parte superior, a letra A. Abaixo, os números: 1, espaço para resposta, espaço para resposta. Em seguida, as placas: A1, espaço para resposta, espaço para resposta, À direita, na parte superior, a letra espaço para resposta. Abaixo, os números: espaço para resposta, espaço para resposta, espaço para resposta. Em seguida, as placas: espaço para resposta, espaço para resposta, espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 2; 3.
PROFESSOR A2; A3.
PROFESSOR B
PROFESSOR 1; 2; 3
PROFESSOR B1; B2; B3
  1. Quantas são as possibilidades de formar uma placa? _____
    PROFESSOR Resposta: 6
  1. O que Carlos poderia fazer para dobrar o número de possibilidades?

    _____

    PROFESSOR Exemplo de resposta: Carlos poderia usar 4 letras e 3 números ou 2 letras e 6 números.
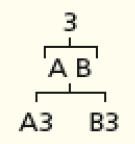
  1. Ricardo faz esculturas de três formatos diferentes (de cão, de gato e de urso). Há duas possibilidades de cor (cinza e marrom) para cada formato.

    a) Complete com as diferentes possibilidades de esculturas.

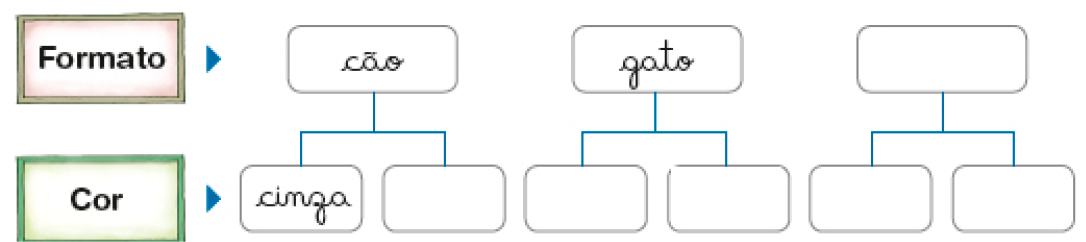
Imagem: Ilustração. Árvore de possibilidades. À esquerda, na parte superior, o formato: Cão. Abaixo, a cor: cinza, espaço para resposta. No centro, na parte superior, o formato: Gato. Abaixo, a cor: espaço para resposta. espaço para resposta. À direita, na parte superior, o formato: espaço para resposta. Abaixo, a cor: espaço para resposta. espaço para resposta. Fim da imagem.
PROFESSOR Resposta: cão: marrom.
PROFESSOR gato: cinza; marrom.
PROFESSOR urso: cinza; marrom.
  1. Escreva uma multiplicação para representar a quantidade de tipos de escultura que Ricardo faz. ____
    PROFESSOR Exemplos de resposta: 3 × 2 = 6 ou 2 × 3 = 6

    Imagem: Ícone: mental. Fim da imagem.

  1. Se, além das cores cinza e marrom, também tivesse a cor laranja, quantos seriam os tipos de escultura que ele faz? _____
    PROFESSOR Resposta: 9 tipos.

    Imagem: Ícone: mental. Fim da imagem.

  1. Se, além das três cores e dos três formatos, tivesse as opções de tamanhos grande e pequeno, quantos seriam os tipos de escultura? _____
    PROFESSOR Resposta: 18 tipos.
MANUAL DO PROFESSOR

Atividade 3

Pergunte aos estudantes em que outras situações aparecem códigos como o da atividade. Talvez citem as placas de automóveis, nas quais se combinam grupos de 3 letras do alfabeto com grupos de 4 algarismos. As novas placas combinam 4 algarismos e 3 números, na seguinte sequência: AAA1A11.

Explore a atividade fazendo perguntas, como: “E se fosse acrescentada mais uma letra ao sistema de códigos de Carlos, quantas placas poderiam ser formadas ao todo? E se fosse acrescentado um algarismo ao sistema de Carlos, quantas placas poderiam ser criadas?”. Espera-se que os estudantes verifiquem que, no primeiro caso, seriam formadas 9 placas (3 × 3 = 9), enquanto no segundo caso poderiam ser formadas 8 placas (2 × 4 = 8).

É interessante discutir com a turma o motivo de os resultados obtidos não serem iguais. Se necessário, explique que, no primeiro caso, ao acrescentar uma nova letra, esta se combinaria com cada um dos 3 algarismos, gerando 3 novas placas em relação às 6 que poderiam ser obtidas inicialmente. Já no segundo caso, o novo algarismo acrescentado se combinaria com cada uma das 2 letras disponíveis, gerando 2 novas placas. Logo, acrescentar uma letra ao código forneceu uma placa a mais que ao acrescentar um novo algarismo.

Atividade 4

Os estudantes devem representar o total de possibilidades por meio de uma escrita multiplicativa. Talvez percebam que podem multiplicar a quantidade de formatos das esculturas pela quantidade de cores, podendo representar por 2 × 3 ou 3 × 2.

No item c, ao propor uma nova cor, os estudantes precisarão rever a quantidade de possibilidades.

No item d, sugira a eles que construam a árvore de possibilidades incluindo, além da nova cor e dos formatos, os tamanhos de escultura. Peça que escrevam uma multiplicação para representar essa nova situação (3 × 3 × 2).

A cada situação, é importante que os estudantes socializem a estratégia utilizada, se preferiram utilizar a escrita multiplicativa, a árvore de possibilidades ou outra. Proponha que registrem no caderno a estratégia empregada por eles e pelos colegas para a construção de repertório.

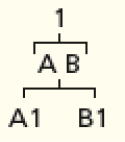
Para ampliar as reflexões da atividade 3, proponha aos estudantes que montem a árvore começando pelos números e, depois, peça que observem as diferenças na organização e a igualdade do resultado.

Imagem: Esquema. À esquerda, na parte superior, o número 1. Abaixo, as letras A, B. Em seguida, as combinações: A1, B1. Fim da imagem.

Imagem: Esquema, na parte superior, o número 2. Abaixo, as letras A, B. Em seguida, as combinações: A2, B2. Fim da imagem.

Imagem: Esquema, na parte superior, o número 3. Abaixo, as letras A, B. Em seguida, as combinações: A3, B3. Fim da imagem.

MP158

Propriedades da igualdade

  1. Veja a balança de dois pratos a seguir.
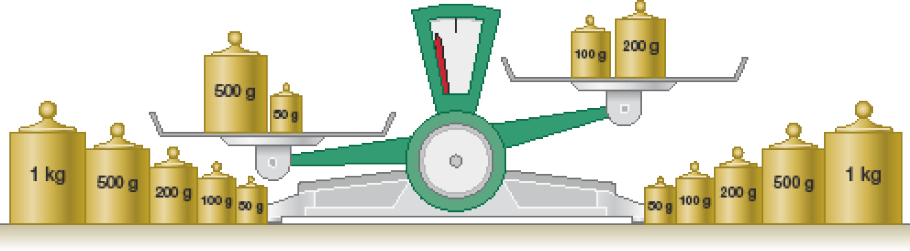
Imagem: Ilustração. Balança de pratos inclinada para à esquerda. No prato à esquerda há dois pesos: 500 g e 50 g. No prato à direita há dois pesos: 100 g e 200 g. À esquerda e à direita da balança, os pesos: 1 kg, 500 g, 200 g, 100 g e 50 g. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

  1. Observe a balança de dois pratos que está em equilíbrio e nivelada.
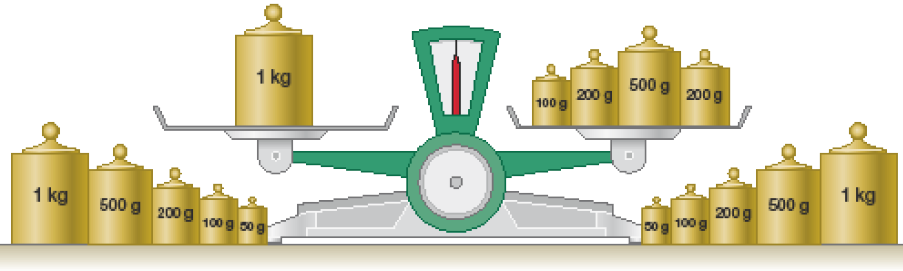
Imagem: Ilustração. Balança de pratos em equilíbrio. No prato à esquerda há um peso: 1 kg. No prato à direita há quatro pesos: 100 g, 200 g, 500 g e 200 g. À esquerda e à direita da balança, os pesos: 1 kg, 500 g, 200 g, 100 g e 50 g. Fim da imagem.
  1. Entre as sentenças a seguir, marque com um X qual representa a relação entre as medidas das massas dos pratos da balança acima.

1.000 g = 100 g + 200 g + 500 g + 200 g

1.000 g > 100 g + 200 g + 500 g + 200 g

1.000 g < 100 g + 200 g + 500 g + 200 g

PROFESSOR Resposta correta: 1.000 g = 100 g + 200 g + 500 g + 200 g
  1. O que acontecerá com a balança se colocarmos um peso de 500 g em cada um dos pratos? _____
    PROFESSOR Resposta: Continuará em equilíbrio e nivelada.
  1. Represente essa nova situação por meio de uma sentença.

    _____

    PROFESSOR Resposta: 500 g + 1.000 g = 100 g + 200 g + 500 g + 200 g + 500 g
MANUAL DO PROFESSOR

Objetivos

  • Resolver e elaborar problemas de adição, subtração, multiplicação e divisão com números naturais.
  • Explorar as propriedades de uma igualdade, para construir a noção de equivalência.
  • Resolver problemas envolvendo medidas de massa.

    Atividade 1

    Espera-se que os estudantes percebam que, para a balança entrar em equilíbrio, as massas dos dois pratos deverão ser iguais. Explore com eles modos de igualar as massas nessas balanças com os pesos disponíveis. Veja alguns exemplos.

    Tabela: equivalente textual a seguir.

    No prato da esquerda

    No prato da direita

    Ilustração. Dois pesos: 500 g e 50 g.

    Ilustração. Quatro pesos: 100 g, 200 g, 200 g e 50 g.

    Ilustração. Um peso: 1 kg.

    Ilustração. Dois pesos de 500 g cada.

    Ilustração. Quatro pesos de 50 g cada.

    Ilustração. Um peso de 200 g.

    CRÉDITO: ADILSON SECCO

    Atividade 2

    No item b, espera-se que os estudantes compreendam que, se for colocada a mesma massa em cada um dos pratos da balança que já está em equilíbrio, isso não altera o equilíbrio (os dois pratos permanecerão na mesma altura).

    No item c, os estudantes devem escrever a mesma sentença que pintaram no item a, acrescentando 500 g em cada membro da igualdade, isto é:

    1.000 g = 100 g + 200 g + 500 g + 200 g

    1.000 g + 500 g = 100 g + 200 g + 500 g + 200 g + 500 g.

    BNCC em foco:

    EF05MA07, EF05MA10, EF05MA19; competências específicas 3 e 6

MP159

  1. A balança a seguir está em equilíbrio e nivelada.
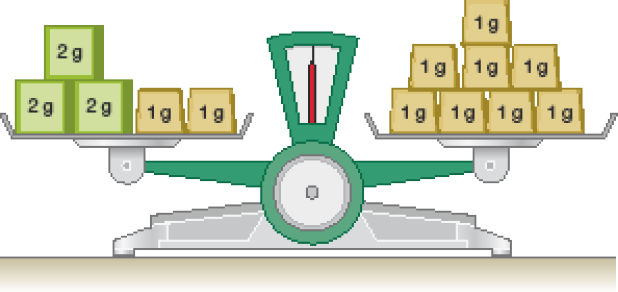
Imagem: Ilustração. Balança de pratos em equilíbrio. No prato à esquerda há cinco pesos: três de 2 g e dois de 1 g. No prato à direita há oito pesos de 1 g cada. Fim da imagem.

Podemos representar essa situação pela sentença:

2 g + 2 g + 2 g + 1 g + 1 g = 1 g + 1 g + 1 g + 1 g + 1 g + 1 g + 1 g + 1 g

  1. Quantos gramas há em cada prato da balança? _____
    PROFESSOR Resposta: 8 g.
  1. Se tirarmos metade do que há em cada prato, o que acontecerá com a balança? Explique sua resposta.

    _____

    PROFESSOR Resposta: Ela permanecerá em equilíbrio e nivelada, pois 8 ÷ 2 = 8 ÷ 2.
  1. E o que acontecerá com a balança se deixarmos, em cada prato, o dobro do que ele tem? Como podemos representar essa situação por meio de uma sentença? _____
    PROFESSOR Resposta: A balança permanecerá em equilíbrio e nivelada.
    PROFESSOR Exemplo de resposta: 2 × 8 = 2 × 8.
  1. Considere a igualdade a seguir.

500 + 600 = 300 + 800

1º membro: 500 + 600

2º membro: 300 + 800

  1. Adicione um mesmo número a ambos os membros dessa igualdade. O que aconteceu?
    PROFESSOR Resposta: A igualdade se manteve.
  1. Agora, subtraia um mesmo número de ambos os membros dessa igualdade. O que aconteceu?
    PROFESSOR Resposta: A igualdade se manteve.
  1. Converse com o professor e os colegas sobre o que observaram nos itens a e b. Depois, escreva uma conclusão.
    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 3

Se julgar oportuno, formalize mais estas propriedades da igualdade:

  • multiplicando os dois membros de uma igualdade por um mesmo número natural, continuaremos a ter uma igualdade;
  • dividindo de maneira exata cada membro de uma igualdade por um mesmo número natural não nulo, continuaremos a ter uma igualdade.

    Atividade 4

    No item c, solicite aos estudantes que digam o número que adicionaram ou subtraíram em ambos os membros da igualdade. Depois, aproveite esse momento para formalizar que, ao adicionar ou subtrair um mesmo valor em ambos os membros de uma igualdade, ela não se altera.

    BNCC em foco:

    EF05MA07, EF05MA08, EF05MA10, EF05MA19; competências específicas 3 e 6

MP160

  1. Rodrigo e Sandra começaram a colecionar figurinhas de álbum de super-heróis. As figurinhas são vendidas em pacotes com 4 unidades. Na semana passada, Sandra comprou 5 pacotes e ganhou outros 3 pacotes de sua prima. Rodrigo comprou 6 pacotes e ganhou mais 8 figurinhas de um colega.
Imagem: Ilustração. Álbum de figurinhas aberto. Ao lado há três figurinhas. Fim da imagem.
  1. Quantas figurinhas tem cada um? _____
    PROFESSOR Resposta: 32 figurinhas.
  1. Marque com um X a sentença que relaciona a quantidade de figurinhas de Rodrigo com a quantidade de Sandra.

    5 × 4 + 3 × 4 > 6 × 4 + 8

    5 × 4 + 3 × 4 = 6 × 4 + 8

    5 × 4 + 3 × 4 < 6 × 4 + 8

    PROFESSOR Resposta correta: 5 × 4 + 3 × 4 = 6 × 4 + 8
  1. Nesta semana, cada um ganhou o triplo de figurinhas do que tinha na semana passada. Quantas figurinhas cada um ganhou?

    _____

    PROFESSOR Resposta: 96 figurinhas.
  1. Escreva uma sentença que relacione a quantidade de figurinhas ganhas por Rodrigo e por Sandra nesta semana.

    _____

    PROFESSOR Exemplo de resposta: 3 × (5 × 4 + 3 × 4) = 3 × (6 × 4 + 8)
  1. Em cada caso, elabore uma situação que possa ser representada pela igualdade.

    (7 + 3 + 4) = (11 + 3)

    (7 + 3 + 4) ÷ 2 = (11 + 3) ÷ 2

PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 5

Para ampliar a atividade, explore a igualdade, mostrando os passos que trabalham a ideia da propriedade distributiva da multiplicação em relação à adição:

5 × 4 + 3 × 4 = 6 × 4 + 8

5 × 4 + 3 × 4 = 24 + 8

5 × 4 + 3 × 4 = 32

(5 + 3) × 4 = 32

8 × 4 = 32

Assim:

5 × 4 + 3 × 4 =

= (5 + 3) × 4

Atividade 6

Exemplo de situação: Clarice leu um livro em 3 dias: no primeiro dia ela leu 7 páginas, no segundo dia, 3 páginas e no terceiro, 4 páginas. Pedro leu em 2 dias o mesmo livro de Clarice, mas leu 11 páginas no primeiro dia e 3 no segundo.

  1. Escreva uma sentença matemática que relacione a quantidade total de páginas lidas por Clarice e por Pedro.

    Clarice leu: (7 + 3 + 4) páginas;

    Pedro leu: (11 + 3) páginas.

    Como eles leram a mesma quantidade de páginas (14), a sentença que relaciona essas quantidades é uma igualdade: (7 + 3 + 4) = (11 + 3).

  2. Se Clarice e Pedro lessem no primeiro dia a metade da quantidade de páginas que leram ao todo, quantas páginas cada um teria lido no primeiro dia?

    Clarice: (7 + 3 + 4) ÷ 2 = 14 ÷ 2 = 7;

    Pedro: (11 + 3) ÷ 2 = 14 ÷ 2 = 7.

    Nesse caso, cada um deles teria lido 7 páginas no primeiro dia.

  3. Escreva uma sentença matemática que relacione a quantidade de páginas que cada um leu no primeiro dia na situação descrita no item b.

    Então, a sentença que relaciona essas duas quantidades é outra igualdade:

    (7 + 3 + 4) ÷ 2 = (11 + 3) ÷ 2

    BNCC em foco:

    EF05MA07, EF05MA08, EF05MA10; competências específicas 3 e 6

MP161

Valor desconhecido

  1. Ana quer descobrir a medida da massa de uma das caixinhas verdes que estão na balança. A balança está em equilíbrio e nivelada.
Imagem: Ilustração. Balança de pratos em equilíbrio. No prato à esquerda há cinco caixinhas: quatro com X g e uma com 5 g. No prato à direita há seis caixinhas: três com X g e três com 5 g. Abaixo, balança de pratos em equilíbrio. No prato à esquerda há uma caixinha com X g. No prato à direita há duas caixinhas com 5 g. À esquerda e à direita desta balança há três pesos com X g e um peso com 5 g. 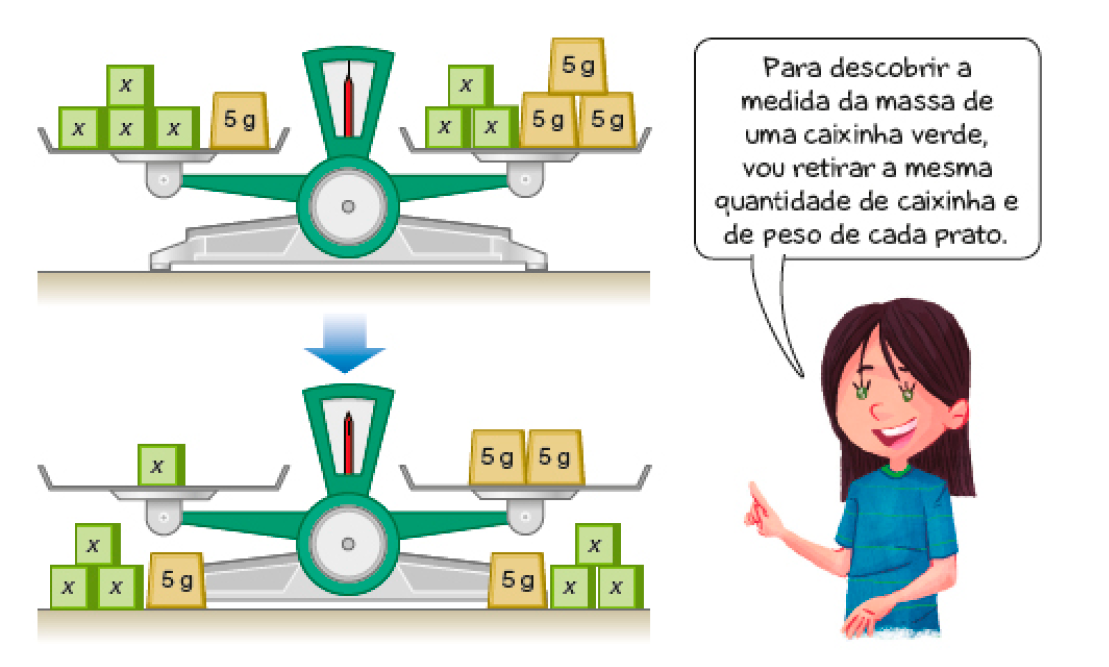Ao lado, Ana, jovem com cabelo preto e comprido fala: Para descobrir a medida da massa de uma caixinha verde, vou retirar a mesma quantidade de caixinha e de peso de cada prato. Fim da imagem.
  1. Na balança a seguir, todas as laranjas têm mesma massa.
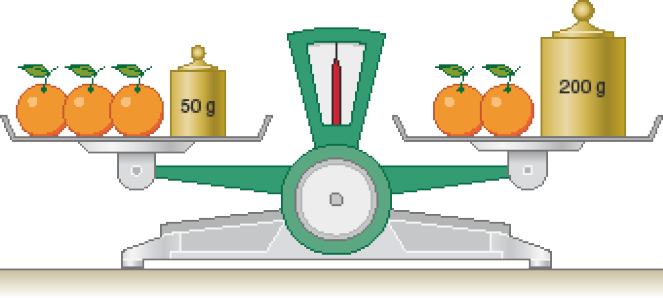
Imagem: Ilustração. Balança de pratos em equilíbrio. No prato à esquerda há três laranjas e um peso de 50 g. No prato à direita há duas laranjas e um peso de 200 g. Fim da imagem.
MANUAL DO PROFESSOR

Objetivos

  • Resolver problemas de adição, subtração, multiplicação e divisão com números naturais.
  • Resolver e elaborar problemas envolvendo sentenças matemáticas expressas por uma igualdade em que um dos termos é desconhecido.
  • Resolver problemas envolvendo medidas de massa.

    Atividade 1

    Espera-se que os estudantes compreendam que, ao ser retirada a mesma massa de cada prato, o equilíbrio é mantido. Assim, foram retiradas 3 caixas verdes e 5 gramas de cada prato, restando 1 caixa verde no prato da esquerda e dois pesos de 5 gramas (10 gramas) no prato da direita.

    Como a balança permanece em equilíbrio, as massas contidas em cada prato são iguais e, assim, a massa da caixa verde é 10 gramas. É importante discutir o que deve ser retirado de cada prato e por quê. A finalidade é deixar em um dos pratos da balança apenas o objeto cuja massa se deseja descobrir e no outro prato, apenas objetos com massas conhecidas, mantendo sempre o equilíbrio da balança.

    Atividade 2

    Espera-se que os estudantes percebam que devem retirar de cada prato da balança duas laranjas. Como a balança continuará em equilíbrio, juntos, a laranja e o peso de 50 g têm a mesma massa do peso de 200 g. Assim, é possível descobrir que a laranja possui 150 g.

    BNCC em foco:

    EF05MA11, EF05MA19

MP162

  1. Escreva, em cada quadrinho, o número que falta para tornar cada igualdade verdadeira.
  1. _____ + 25 = 36
    PROFESSOR Resposta: 11
  1. _____ − 12 = 26
    PROFESSOR Resposta: 38
  1. 2 × _____ = 100
    PROFESSOR Resposta: 50
  1. _____ ÷ 7 = 9
    PROFESSOR Resposta: 63
  1. 5 + 10 = 9 + _____
    PROFESSOR Resposta: 6
  1. 4 × 10 = _____ × 2
    PROFESSOR Resposta: 20

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

  1. A professora de Virgínia propôs um desafio à turma. Veja.
Imagem: Ilustração. Lousa com o texto: Maristela já leu 65 páginas de um livro, Afonso leu 82 páginas desse mesmo livro, mas ainda faltam 22 páginas para terminá-lo. Quantas páginas faltam para Maristela terminar de ler esse livro? Fim da imagem.

Virgínia resolveu esse problema da seguinte maneira:

Imagem: Ilustração. Caderno aberto com o texto: Como os livros são iguais, posso escrever: 65 + quadrado azul = 82 + 22; Determino a quantidade de páginas que tem o livro, calculando: 82 + 22 = 104; Assim, posso escrever: 65 + quadrado azul = 104; Se eu subtrair 65 de ambos os membros da igualdade, eu obtenho o número de páginas que faltam para Maristela terminar de ler o livro: 65 + quadrado azul - 65 = 104 – 65; quadrado azul = 39; Faltam 39 páginas. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 3

Após a resolução da atividade, proponha uma roda de conversa para que os estudantes exponham como pensaram.

Atividade 4

Leia o problema com os estudantes. Peça que destaquem as informações e a pergunta:

  • Maristela já leu 65 páginas de um livro.
  • Afonso leu 82 páginas desse mesmo livro.
  • Faltam 22 páginas para Afonso terminar o livro.
  • Quantas páginas faltam para Maristela terminar o livro?

    Os estudantes devem perceber que, se o livro é o mesmo, a quantidade total de páginas é a mesma também.

    Dê um tempo para pensarem em uma estratégia de resolução, antes de apresentar o procedimento de Virgínia.

    Reproduza os passos da resolução de Virgínia na lousa. Verifique se os estudantes compreenderam todos os passos.

    Em uma roda de conversa, discuta com a turma a resolução de Virgínia e peça aos estudantes que exponham a resolução deles.

    BNCC em foco:

    EF05MA07, EF05MA08, EF05MA11

MP163

  1. Paulo tinha uma quantia de dinheiro, e Davi tinha 7 286 reais. Se Davi tinha 1 817 reais a menos que Paulo, quantos reais tinha Paulo?
PROFESSOR Exemplo de cálculo:
PROFESSOR Ilustração. Quadrinho rosa.= 7.286 + 1.817
PROFESSOR Ilustração. Quadrinho rosa.= 9.103

Paulo tinha _____ reais.

PROFESSOR Resposta: 9.103
  1. Durante uma campanha foram arrecadados 260 quilogramas de material reciclável, entre plásticos, metais e papéis. Sabe-se que metade da massa de material reciclável arrecadado refere-se a plásticos e que um quinto do total são metais. Quantos quilogramas de papel foram arrecadados?
Imagem: Ilustração. Três cestos de lixo recicláveis: um vermelho, um amarelo e um azul. Fim da imagem.
PROFESSOR Exemplos de cálculo:
PROFESSOR 260 ÷ 2 = 130
PROFESSOR 260 ÷ 5 = 52
PROFESSOR 260 = 130 + 52 + Ilustração. Quadrinho branco.
PROFESSOR 260 = 182 + Ilustração. Quadrinho rosa.
PROFESSOR 260 − 182 = 182 + Ilustração. Quadrinho rosa.− 182
PROFESSOR 78 = Ilustração. Quadrinho rosa.

Foram arrecadados _____ quilogramas de papel.

PROFESSOR Resposta: 78
  1. Danilo foi ao cinema com 4 amigos, e todos pagaram o mesmo valor pelo ingresso. Além disso, cada um comprou uma pipoca de 5 reais para comer enquanto assistiam ao filme. Sabendo que no total eles gastaram 90 reais, qual foi o preço de cada ingresso?
PROFESSOR Exemplo de cálculo:
PROFESSOR 90 = 5 × 5 + 5 × Ilustração. Quadrinho branco.
PROFESSOR 90 = 25 + 5 × Ilustração. Quadrinho branco.
PROFESSOR 90 − 25 = 25 + 5 × − 25
PROFESSOR 65 = 5 × Ilustração. Quadrinho branco.
PROFESSOR 13 = Ilustração. Quadrinho branco.

O preço de cada ingresso foi _____ reais.

PROFESSOR Resposta: 13
  1. Elabore um problema que possa ser resolvido pela determinação de um valor desconhecido representado pelo quadrinho da igualdade a seguir:

    5 + Ilustração. Quadrinho azul.= 2 × 10

    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Para realizar as atividade 5, 6 e 7, leia o enunciado de cada problema com os estudantes, incentivando-os a registrarem resumidamente as informações contidas nos enunciados e a destacarem a pergunta.

Reúna-os em duplas para resolverem cada problema, o que enriquecerá o aprendizado e aumentará o repertório de estratégias de cada um deles. Socialize as diferentes estratégias, validando-as com a turma.

Atividade 5

Se Davi tinha 1 .817 reais a menos que Paulo, é necessário adicionar essa quantia ao dinheiro de Davi para obter o que Paulo tinha:

7 .286 + 1 .817 = 9 103

Atividade 6

Exemplo de solução:

  • Se, dos 260 quilogramas arrecadados, metade era de plástico, então 130 quilogramas eram referentes à massa de plástico.
  • Se, da massa total arrecadada, a quinta parte era composta de metais, dividindo 260 quilogramas por 5, obtemos 52 quilogramas de metais.
  • Conhecendo a massa total arrecadada (260) e as massas correspondentes ao plástico e aos metais (182), determinamos a massa referente ao papel (260 − 182): 78 quilogramas.

    Atividade 7

    Os estudantes podem pensar no seguinte esquema:

    (valor dos 5 ingressos) + (valor das 5 pipocas) = total gasto

    Desse modo, do total gasto devem tirar o que foi pago pelas pipocas, obtendo o preço dos 5 ingressos.

    Em seguida, devem dividir o resto obtido por 5, determinando o preço de cada ingresso.

    Preço do ingresso: (90 − 5 × 5) ÷ 5 = 13

    BNCC em foco:

    EF05MA07, EF05MA08, EF05MA11

    Atividade 8

    Exemplo de problema: Clóvis comprou um livro cujo preço é o dobro de 10 reais. Ele deu 5 reais de entrada e pagou o restante no mês seguinte. Qual é o valor desse restante?

    A entrada de 5 reais adicionada ao valor restante equivale ao preço do livro, que é o dobro de 10 reais:

    5 + 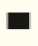Ilustração. Quadrinho preto.= 2 × 10

    O valor desconhecido representa o restante a ser pago no mês seguinte, ou seja, o restante é 15 reais.

MP164

Matemática em textos

Leia

Número nas tirinhas

A Matemática ajuda a compreender muitos tipos de texto, como as tirinhas. Normalmente, uma tirinha combina texto escrito e desenho em uma sequência de quadrinhos. Como o principal objetivo de muitas tirinhas é divertir o leitor, elas apresentam uma situação comum do dia a dia, fazendo uso do humor.

Veja abaixo algumas dessas tirinhas.

Imagem: Tirinha composta por três quadros. Apresenta Cebolinha, menino com cinco fios de cabelo, camiseta verde, bermuda preta e sapatos marrons, que troca o R pelo L. E Marcelinho, menino com cabelo preto e penteado para cima, camiseta preta, bermuda azul e tênis vermelho. As falas estão dentro de balões. Quadro um: Marcelinho com o dedo indicador esquerdo levantado fala: SE DORMIRMOS EM MÉDIA 8 HORAS POR DIA, AOS 40 ANOS TEREMOS DORMIDO O EQUIVALENTE A 13 ANOS... Quadro dois: Cebolinha com a mão esquerda na cintura e a direita virada para cima responde: SE BLINCALMOS EM MÉDIA 8 HOLAS POR DIA, AOS 40 TELEMOS UM ADULTO FELIZ... Na frente dele, Marcelinho segura um livro com a mão direita e escuta com os olhos arregalados e a boca virada para baixo. Ao fundo, casa e plantas. Quadro três: Marcelinho e Cebolinha sorriem e brincam com uma bola. Ao lado, o livro sobre o gramado. Na capa, o título: CADERNO DE MATEMÁTICA. Ao fundo, o sol, casas e árvores. Fim da imagem.
Imagem: Tirinha composta por quatro quadros. Apresenta Charlie Brown, menino com pouco cabelo e camiseta amarela com linhas pretas. E Sally Brown, menina loira com cabelo encaracolado no topo da cabeça e roupa azul. As falas estão dentro de balões. Quadro um: Charlie e Sally estão sentados atrás de uma mesa e virados um de frente para o outro. Charlie segura um lápis e um papel e pergunta: BEM, QUANTO É 5 vezes 10? Sally responde: COMO VOU SABER? Quadro dois: Charlie olha para o papel e pergunta: QUANTO DÁ 6 vezes 20? Sally com a cabeça apoiada na mão direita, olha para frente e responde: SEI LÁ. Quadro três: Charlie segura o papel e pergunta: E 2 vezes 11? Sally olha para o menino e responde: TÁ BRINCANDO? Quadro quatro: Charlie coloca o papel na mesa, olha para o lado e pergunta: PREFERE QUE EU FAÇA PERGUNTAS MAIS SIMPLES? Sally com a cabeça apoiada na mão esquerda, olha para o menino e responde: POR QUÊ? PAREÇO ESTAR DESANIMADA? Fim da imagem.
Imagem: Tirinha composta por cinco quadros. Apresenta Níquel, ratinho azul-claro. E Gatinha, ratinha azul-escuro. As falas estão dentro de balões. Quadro um: Níquel sentado de costas e com as patas levantadas, olha para o céu escuro com estrelas e fala: PENSE NUM NÚMERO DE UM A DEZ! Ao seu lado, Gatinha está sentada de costas e responde: ÃN. Quadro dois: Níquel olha para o lado e fala: AGORA MULTIPLIQUE POR TRÊS E SOME CINCO! A Gatinha responde: ÃN. Quadro três: Níquel levanta as patas, sorri e diz: DIVIDA POR DOIS E SOME QUATRO! A Gatinha responde: ÃN. Quadro quatro: Níquel pergunta: POSSO ADIVINHAR? A Gatinha responde: PODE! Quadro cinco: Níquel olha para o lado e fala: VOCÊ NEM SEQUER PENSOU NO PRIMEIRO NÚMERO! A Gatinha olha para o lado, sorri e responde: FANTÁSTICO! Fim da imagem.
MANUAL DO PROFESSOR

Objetivo

  • Resolver e elaborar problemas de multiplicação e divisão com números naturais.

    A proposta destas páginas é promover uma reflexão a respeito do papel da Matemática na compreensão de textos com características mais informais, como as tirinhas. De modo geral, a presença da Matemática nesse tipo de texto relaciona-se à visão que muitas pessoas têm dessa disciplina: difícil de entender. Como contraponto, algumas tirinhas retratam personagens que realizam cálculos com muita facilidade, surpreendendo os demais. Aproveite para discutir isso com os estudantes, considerando que:

  • A dificuldade que muitas pessoas sentem em compreender a Matemática não faz com que ela seja um assunto compreensível apenas para pessoas com capacidades especiais; ressalte que é natural as pessoas terem graus diferenciados de habilidades em quaisquer atividades: música, atividades esportivas, artesanato etc., e que isso não deve inibir ninguém em suas tentativas de desenvolvimento.
  • As habilidades de cálculo são parte importante do rol de habilidades matemáticas que a escola procura desenvolver, mas não a única: as habilidades geométricas, de raciocínio lógico, de orientação espacial e outras também são trabalhadas durante a escolarização, sendo naturais as diferenças de desempenho de indivíduo para indivíduo, em conformidade com suas habilidades pessoais.

    BNCC em foco:

    EF05MA08; competência geral 4; competências específicas 1 e 3

MP165

Responda

  1. Veja a tirinha do Marcelinho e responda.
    1. De acordo com Marcelinho, dormir 8 horas por dia por 40 anos é equivalente a dormir por quanto tempo? _____
      PROFESSOR Resposta: 13 anos.
    1. Se dormirmos 8 horas por dia, quantas horas teremos dormido em um ano?

      _____

      PROFESSOR Resposta: 2.920 horas.
      PROFESSOR Exemplo de cálculo: 8 × 365 = 2.920
  1. Observe a segunda tirinha e faça o que se pede.
    1. Que tipo de operação Charlie Brown e Sally estão estudando? _____
      PROFESSOR Resposta: Multiplicação.

      Imagem: Ícone: mental. Fim da imagem.

    1. Faça as multiplicações que estão na tirinha.

      5 × 10 = _____

      PROFESSOR Resposta: 50

      6 × 20 = _____

      PROFESSOR Resposta: 120

      2 × 11 = _____

      PROFESSOR Resposta: 22

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Escolha um número de 1 a 10. Usando uma calculadora, siga as instruções de Níquel Náusea. Que resultado você encontrou?
PROFESSOR • 4 (número escolhido)
PROFESSOR • 4 × 3 = 12 e 12 + 5 = 17
PROFESSOR • 17 ÷ 2 = 8,5 e 8,5 + 4 = 12,5

Analise

Aplique

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Responda

Na atividade 2, incentive os estudantes a fazerem o cálculo mentalmente.

Analise

Explore as respostas dadas pelos estudantes e peça a eles que digam o que acham da fala do Cebolinha.

Aplique

Para auxiliar os estudantes, peça que recordem situações já vividas em que a Matemática ajudou ou dificultou em alguma resolução de conflito.

Depois de criarem as tirinhas, proponha que as duplas façam uma exposição na sala para que todos possam ver as produções dos colegas.

BNCC em foco:

EF05MA08; competência geral 4; competências específicas 1 e 3

MP166

Compreender informações

Interpretar dados organizados em gráficos

  1. Em um Centro Esportivo Municipal, foi feita uma pesquisa para saber que esporte seus frequentadores preferem. O resultado foi apresentado por meio de um gráfico de setores em 19 de fevereiro, Dia do Esportista.
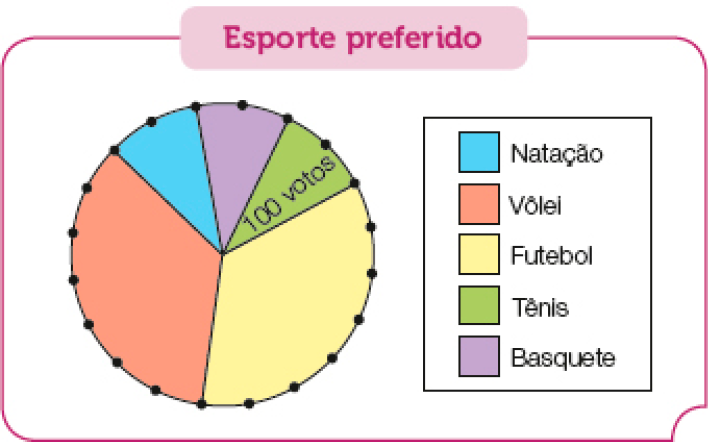
Imagem: Gráfico em setores. Esporte preferido. Gráfico circular dividido em esportes. Há duas partes grandes (Vôlei e Futebol) e três partes pequenas com 100 votos (Natação, Basquete e Tênis). Fim da imagem.

Fonte: Administração do Centro Esportivo Municipal. (jan. 2023)

  1. Identifique a quantidade de votos (frequência) correspondente a cada esporte e complete a tabela a seguir.

Esporte preferido

Tabela: equivalente textual a seguir.

Esporte

Quantidade de votos

Natação

_____

Vôlei

_____

Futebol

_____

Tênis

_____

Basquete

_____

Fonte: Administração do Centro Esportivo Municipal (jan. 2023).

PROFESSOR Resposta: 100; 350; 350; 100; 100.
  1. Que esporte foi o mais votado? Como você pensou? _____
    PROFESSOR Resposta: Houve empate entre vôlei e futebol, que foram os esportes mais votados.

    Imagem: Ícone: Grupo. Fim da imagem.

  1. Em grupo, com a ajuda de seu professor, organizem uma pesquisa para saber a preferência dos estudantes de sua turma em relação aos esportes mencionados nesse gráfico. Em seguida, apresentem o resultado da pesquisa em um gráfico.
    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Objetivos

  • Ler e interpretar dados apresentados em tabelas, gráficos de setores e de colunas duplas.
  • Realizar pesquisa e organizar os dados coletados por meio de gráficos.
  • Produzir texto para sintetizar conclusões dos resultados de uma pesquisa.

    Atividade 1

    No item a, espera-se que os estudantes verifiquem que no círculo há 20 partes iguais (separadas pelos pontos no contorno) e que duas delas correspondem a 100 votos, ou seja, cada parte equivale a 50 votos. Assim, podem concluir que as cores verde, azul e roxa correspondem a 100 votos cada uma; e a amarela e a vermelha, a 350 votos cada.

    No item b, os estudantes devem perceber que houve empate entre vôlei e futebol, por ambos serem os esportes mais votados.

    No item c, auxilie os estudantes na coleta de dados, organizando a pesquisa e marcando as preferências na lousa. Em seguida, organize os estudantes em grupos para a produção do gráfico. Avalie a possibilidade de os estudantes elaborarem um gráfico de setores. Cada arco unidade deverá medir 360° dividido por n, em que 3 é o número de estudantes participantes da pesquisa. Caso haja dificuldade, uma opção pode ser a construção de um gráfico de colunas.

    BNCC em foco:

    EF05MA24, EF05MA25; competências gerais 2 e 4; competências específicas 3 e 4

MP167

  1. Em uma agência bancária existem três caixas eletrônicos: A, B e C. Depois de esvaziados, cada um deles foi abastecido apenas com cédulas de 100 reais e 10 reais.

    O gráfico abaixo apresenta a quantidade de cédulas que cada um desses caixas recebeu.

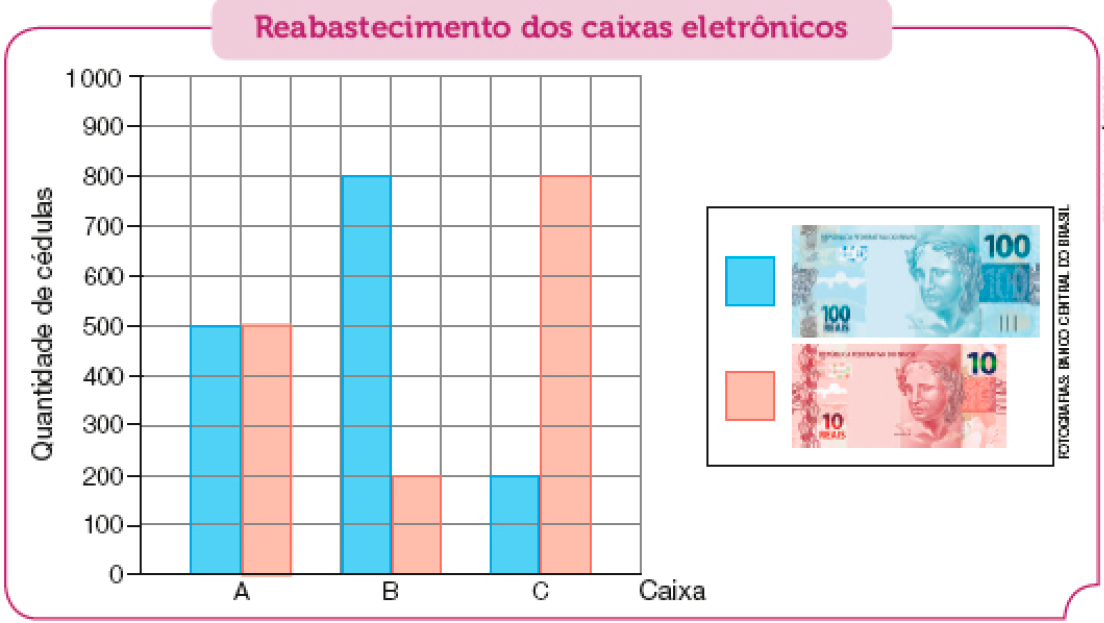
Imagem: Gráfico de colunas. Reabastecimento dos caixas eletrônicos. No eixo vertical, a quantidade de cédulas e no eixo horizontal, o caixa. Caixa A: Cédulas de 100 reais: 500; Cédulas de 10 reais: 500. Caixa B: Cédulas de 100 reais: 800; Cédulas de 10 reais: 200. Caixa C: Cédulas de 100 reais: 200; Cédulas de 10 reais: 800. Ao lado, a legenda com a foto de uma cédula de cem reais e uma cédula de dez reais. Fim da imagem.

Fonte: Gerência da agência bancária considerada (jun. 2023).

  1. Que caixa eletrônico recebeu mais cédulas de 100 reais? _____
    PROFESSOR Resposta: O caixa B.
  1. Que caixa eletrônico recebeu mais cédulas de 10 reais? _____
    PROFESSOR Resposta: O caixa C.
  1. O caixa que recebeu a maior quantia é aquele que tem a maior quantidade de cédulas? Escreva um texto para explicar sua resposta. _____
    PROFESSOR Resposta: Não.
    PROFESSOR Exemplo de explicação: O caixa B recebeu a maior quantia, mas não a maior quantidade de cédulas, já que todos os caixas receberam 1.000 cédulas cada um.
  1. É possível retirar 3.000 reais em cédulas de 10 reais de qualquer um desses caixas? Por quê? _____
    PROFESSOR Resposta: Não, porque o caixa B só tem 2.000 reais em cédulas de 10 reais.
  1. Descreva, se existir, uma maneira de retirar 3.000 reais de cada um desses caixas, independentemente do tipo de cédulas retiradas.

    _____

    PROFESSOR Resposta: Exemplo de resposta: A → 30 cédulas de 100 reais
    PROFESSOR B → 10 cédulas de 100 reais e 200 de 10 reais
    PROFESSOR C → 15 cédulas de 100 reais e 150 de 10 reais
MANUAL DO PROFESSOR

Atividade 2

Em uma roda de conversa, explore o gráfico com os estudantes, os elementos e as informações que podem ser obtidos nele. É importante verificar se eles compreendem que o gráfico informa a quantidade de cédulas que cada caixa recebeu e que o tipo de cédula está associado à cor da coluna e é indicado pela legenda.

Espera-se que os estudantes possam verificar, observando a altura das colunas azuis, que o caixa B recebeu mais cédulas de 100 reais, e, observando a altura das colunas vermelhas, que o caixa C recebeu mais cédulas de 10 reais.

No item d, espera-se que os estudantes concluam que não, porque o caixa B só tem 2.000 reais em cédulas de 10 reais.

BNCC em foco:

EF05MA24; competências gerais 2 e 4; competências específicas 3 e 4

MP168

O que você aprendeu

Avaliação processual

  1. Francisco tinha 3 cédulas de 100 reais e 4 cédulas de 20 reais. Ele gastou 50 reais. Qual expressão melhor representa o dinheiro que Francisco ainda tem?

    ( ) (3 × 100 + 4 × 20) − 50

    ( ) (3 × 100 + 4 × 20) − (50 + 1)

    ( ) 3 + 100 + 4 + 20 − (50 + 1)

    ( ) 3 × (100 + 20) − 50

    PROFESSOR Resposta: Resposta correta: (3 × 100 + 4 × 20) − 50
  1. Alguns estudantes de uma escola foram visitar uma área de proteção a tartarugas marinhas. Para fazer a visita com o guia, formaram-se grupos de 6 estudantes. Havia 3 guias, e cada um orientou a visita de 5 grupos.

    No total, quantos estudantes foram a essa visita?

Imagem: Ilustração. Um homem com boné e uniforme azul está segurando o desenho de uma tartaruga. Na frente dele, seis jovens o observam. Atrás deles há uma placa com a imagem de uma tartaruga e ao lado, o mar. Fim da imagem.
PROFESSOR Exemplos de cálculo:
PROFESSOR 5 × 6 = 30
PROFESSOR 3 × 30 = 90

_____ estudantes foram a essa visita.

PROFESSOR Resposta: 90
  1. Em uma fábrica de tijolos, duas máquinas produzem 352 tijolos por hora. Em 6 horas, quantos tijolos serão produzidos por quatro máquinas iguais a essas?
Imagem: Ilustração. Um homem com luvas e macacão está com as mãos em uma máquina. Na frente há tijolos empilhados sobre um suporte. Fim da imagem.
PROFESSOR Exemplos de cálculo:
PROFESSOR 352 × 6 = 2.112
PROFESSOR 2.112 × 2 = 4.224

Serão produzidos _____ tijolos.

PROFESSOR Resposta: 4.224

Imagem: Ícone: Dupla. Fim da imagem.

  1. Reúna-se com um colega e escreva em seu caderno o nome de 4 frutas de que você gosta e de 3 sucos de que ele gosta. Depois, escrevam no caderno todas as combinações possíveis de uma refeição formada por 1 fruta e 1 suco.
    PROFESSOR Resposta: 12 combinações.
    PROFESSOR Resposta variável.
MANUAL DO PROFESSOR

Objetivo

  • Retomar os conceitos estudados.

    A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.

    Atividade 1

    Observe as estratégias utilizadas pelos estudantes, socialize e valide-as com a turma.

    Atividade 2

    Havia grupos de 6 estudantes. Como são 3 guias e cada um orientou 5 grupos, uma expressão que traduz essa situação é:

    3 × 5 × 6 = 3 × 30 = 90

    Atividade 3

    Oriente os estudantes a organizarem as informações:

  • 2 máquinas produzem 352 tijolos por hora.
  • Em 6 horas, quantos tijolos 4 dessas máquinas produzem?

    Como há variação na quantidade de horas e de máquinas, sugira aos estudantes que façam os cálculos por etapas.

    Cálculo de quantos tijolos 2 dessas máquinas produzem em 6 horas:

  • Em 1 hora: 352 tijolos;
  • em 2 horas: (2 × 352) tijolos;
  • em 3 horas: (3 × 352) tijolos;
  • em 6 horas: (6 × 352) tijolos, ou seja, 2.112 tijolos.

    Cálculo de quantos tijolos 4 dessas máquinas produzem em 6 horas:

  • Se 2 máquinas produzem 2.112 tijolos nesse tempo, concluímos que, dobrando a quantidade de máquinas, a produção também dobra;
  • sendo assim, 4 máquinas produzem (2 × 2.112) tijolos em 6 horas, ou seja, 4.224 tijolos.

    Atividade 4

    Incentive os estudantes a organizarem as combinações por meio de uma tabela de dupla entrada e da árvore de possibilidades.

    BNCC em foco:

    EF05MA07, EF05MA08, EF05MA09, EF05MA12

MP169

  1. Sabendo que a balança mostrada a seguir está em equilíbrio e nivelada, determine a medida da massa, em grama, do livro.
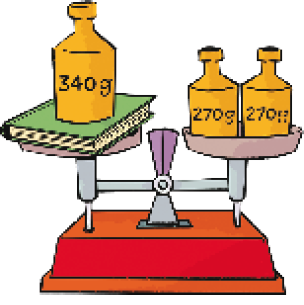
Imagem: Ilustração. Balança de pratos em equilíbrio. No prato à esquerda há um livro e um peso de 340 g. No prato à direita há dois pesos com 270 g. Fim da imagem.
PROFESSOR Exemplo de cálculo:
PROFESSOR 340 + Ilustração. Quadrinho rosa.= 270 + 270
PROFESSOR 340 + Ilustração. Quadrinho rosa.= 540
PROFESSOR 340 − 340 + Ilustração. Quadrinho rosa.= 540 − 340
PROFESSOR Ilustração. Quadrinho rosa.= 200

A medida da massa do livro é igual a _____ gramas.

PROFESSOR Resposta: 200
  1. Uma empresa utilizou o espaço de um galpão para estabelecer a produção, o depósito e o escritório. Metade desse espaço será ocupada pela produção, a outra metade será destinada ao depósito e ao escritório. O escritório ocupará um quarto dessa metade.

    Agora, marque com um X a sentença verdadeira em cada caso.

    1. Qual é a relação entre o espaço ocupado pelo escritório e todo o galpão?

      ( ) O escritório ocupará metade do galpão.

      ( ) O escritório ocupará um quarto do galpão.

      ( ) O escritório ocupará um oitavo do galpão.

      PROFESSOR Resposta correta: O escritório ocupará um oitavo do galpão.
    1. Qual é a relação entre o espaço ocupado pelo depósito e todo o galpão?

      ( ) O depósito ocupará metade do galpão.

      ( ) O depósito ocupará três oitavos do galpão.

      ( ) O depósito ocupará um quinto do galpão.

      PROFESSOR Resposta correta: O depósito ocupará três oitavos do galpão.

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 5

Espera-se que os estudantes observem que a massa do livro é determinada pela expressão: 2 × 270 − 340.

Valorize as estratégias utilizadas, socialize e valide-as com os estudantes, incentivando-os a desenharem como fica a balança para descobrir a massa do livro, mantendo o equilíbrio.

Atividade 6

Leia o enunciado com os estudantes e verifique se eles compreenderam cada informação. Incentive-os a representarem a situação com um desenho, já que o todo considerado é a área do galpão. Nesse caso, eles devem relacionar as partes com o todo.

Um possível desenho é:

Imagem: Ilustração. Um retângulo dividido em dois quadrados. À esquerda, Produção. À direita, o quadrado está dividido em duas partes, acima, parte menor (Escritório) e abaixo, parte maior (Depósito). Fim da imagem.

CRÉDITO: FERNANDO JOSÉ FERREIRA

BNCC em foco:

EF05MA07, EF05MA08, EF05MA11, EF05MA13

Autoavaliação

Nesta Unidade, os estudantes se aproximam ainda mais dos conhecimentos algébricos. Na primeira questão, poderão verificar o quanto conseguem utilizar a linguagem matemática para representar situações; neste caso, especialmente por meio de expressões numéricas. É possível ampliar a pergunta de modo que eles também avaliem se conseguem resolver as expressões utilizando as regras aprendidas.

Na segunda questão, os estudantes poderão avaliar seus conhecimentos de combinação. É interessante pedir que avaliem o quanto a árvore de possibilidades ajuda no cálculo de possibilidades de combinações; a questão pode ser ampliada possibilitando que os estudantes verifiquem se também utilizam outros meios para analisar as possibilidades de combinações.

MP170

Comentários para o professor:

Conclusão da Unidade 4

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem

Desempenho

Observação

Resolve problemas de adição e subtração com números naturais?

_____

_____

Resolve problemas de multiplicação e divisão com números naturais?

_____

_____

Resolve problemas de contagem por meio de diagramas de árvore ou por tabelas?

_____

_____

Compreende e sabe explorar as propriedades da igualdade?

_____

Resolve e elabora problemas em que um dos termos da sentença matemática seja desconhecido?

_____

_____

Resolve problemas que envolvam a proporcionalidade direta entre duas grandezas?

_____

_____

Resolve problemas envolvendo a partilha de uma quantidade em partes iguais e em partes desiguais?

_____

_____

Resolve problemas envolvendo medidas de massa?

_____

_____

Interpreta e organiza dados apresentados em gráficos de setores e de colunas?

_____

_____

Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?

_____

_____

Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?

_____

_____

MP171

Sugestão de ficha de autoavaliação do estudante

O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.

Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.

Tabela: equivalente textual a seguir.

Autoavaliação

Nome:

Marque um X em sua resposta para cada pergunta.

Sim

Mais ou menos

Não

1. Presto atenção nas aulas?

_____

_____

_____

2. Pergunto ao professor quando não entendo?

_____

_____

_____

3. Sou participativo?

_____

_____

_____

4. Respeito meus colegas e procuro ajudá-los?

_____

_____

_____

5. Sou educado?

_____

_____

_____

6. Faço todas as atividades com capricho?

_____

_____

_____

7. Trago o material escolar necessário e cuido bem dele?

_____

_____

_____

8. Cuido dos materiais e do espaço físico da escola?

_____

_____

_____

9. Gosto de trabalhar em grupo?

_____

_____

_____

10. Respeito todos os meus colegas de turma, professores e funcionários?

_____

_____

_____