MP172
Comentários para o professor:
Introdução da Unidade 5
A abertura desta Unidade reproduz uma situação vivenciada em casa por muitos estudantes: a aplicação de uma receita culinária – no caso, um bolo – e sua lista de ingredientes, com as respectivas quantidades, algumas das quais representadas por frações, referentes a certa porção. Nem sempre essa porção representa as necessidades de quem vai implementá-la, daí ser preciso determinar novas quantidades proporcionais à nova porção desejada. Assim, a abertura cumpre a função de proporcionar um contexto com dados de problemas a serem resolvidos e dando oportunidade de exploração de conceitos tratados ao longo da Unidade.
Nesta Unidade, destacam-se os estudos sobre frações. São propostas atividades a fim de que os estudantes construam conhecimentos relativos à ideia de fração e às operações com esses números. Entre esses conhecimentos, evidenciam-se: a identificação e a representação de frações, associando-as ao resultado de uma divisão ou à ideia de parte de um todo, com recurso à reta numérica; a identificação de frações equivalentes; a comparação e a ordenação de frações, relacionando-as a pontos na reta numérica; a resolução e a elaboração de problemas de adição, subtração, multiplicação e divisão com frações.
As frações foram objeto de estudo durante o 4º ano, e sua abordagem possibilitou aos estudantes o reconhecimento das frações unitárias mais usuais como unidades de medida menores que uma unidade. Esses conhecimentos serão, neste momento, ampliados e aprofundados para as frações impróprias e para os números mistos.
Além disso, a apropriação desses novos conhecimentos favorecerá a compreensão, a comparação e a ordenação de frações associadas às ideias de partes de inteiros e de resultados de divisão, assim como a resolução e a elaboração de problemas envolvendo adição e subtração com números racionais positivos na representação fracionária, conforme previsto nos estudos a serem desenvolvidos ao longo do 6º ano.
Ainda em relação a Números, as atividades propostas relacionam porcentagens às representações fracionárias. Assim, pretende-se que os estudantes associem representações, como 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro, para o cálculo de porcentagens. São conhecimentos necessários para que, no 6º ano, os estudantes resolvam e elaborem problemas envolvendo porcentagens a partir da ideia de proporcionalidade, utilizando, para isso, estratégias pessoais, cálculo mental e calculadora.
Retomam-se também nesta Unidade os estudos sobre Probabilidade e estatística com o objetivo de que os estudantes calculem probabilidades de resultados de um experimento aleatório. Com essa abordagem, pretende-se que, no 6º ano, os estudantes mobilizem esses conhecimentos a fim de calcularem a probabilidade de um evento aleatório, expressando-a por meio de uma fração, de um número na forma decimal ou percentual, comparando esse número com a probabilidade obtida por meio de sucessivos experimentos. Para isso, consideram-se também os conhecimentos a serem construídos ainda neste ano e que dizem respeito aos números racionais.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletiva. Além disso, requerem boas estratégias de gestão de tempo, de espaço e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.
Competências específicas favorecidas
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
MP173
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item Adição e subtração desta Unidade.
Sugestão de roteiro de aula – Adição e subtração – 1 ª parte – Introdução – Tempo sugerido: 15 minutos
As primeiras operações com números na forma de fração apresentam uma complexidade considerável para o estudante de 5º ano. Por isso, devem ser acompanhadas de uma linguagem ilustrativa ou material manipulável que dê suporte e faça com que o resultado tenha significado e que o procedimento seja compreendido pelo estudante.
Providencie para cada estudante tiras de papel, sem marcação alguma, de mesmo comprimento e largura. Sugerimos, para facilitar que tenham o comprimento igual à largura de uma folha A4.
Anuncie que a aula tem início com o cálculo de uma adição com frações.
Escreva na lousa a expressão + = ?
Pergunte como poderiam representar, com uma das tiras, a fração . Considere as propostas da turma e, caso não tenha a que será sugerida em seguida, proponha que sigam as etapas:
1) Dobrar a tira ao meio. Desdobrar, reforçar com lápis as marcas de dobra e observar que cada parte representa .
2) Com a tira dobrada, dobrar novamente ao meio. Desdobrar, reforçar com lápis as marcas de dobra, observar que cada parte representa , e que da tira corresponde a + ou a .
3) Dobrar novamente ao meio a tira dobrada. Desdobrar, reforçar as marcas de dobra, observar que cada parte representa , e que da tira corresponde a + + + ou a .
Pergunte aos estudantes se eles perceberam que estão fazendo adições com frações.
Registre na lousa o que eles já fizeram:
+ = e + + + = .
Para ver se compreenderam, peça que identifiquem, na tira dividida em 8 partes iguais, seguido de e que pintem com cores diferentes as partes referentes a cada uma dessas frações. Então escrevam no caderno o resultado de + . Registre na lousa: + = .
2 ª parte – Atividade 1 do item Adição e subtração – Tempo sugerido: 15 minutos
Leia com os estudantes a introdução e o item a da atividade 1 da página 156. Acompanhe as respostas. Caso os estudantes apresentem dificuldade, oriente-os a usarem outra tira dobrada em 8 partes iguais e, nela, identificarem a fração seguida da fração para obter .
A seguir, oriente-os a utilizarem nova tira dividida em 8 partes iguais para resolverem o item b da atividade 1. Eles devem pintar 7 partes das 8 partes que é o inteiro (a tira inteira), ou seja, pintar e responder quantas partes falta pintar. Devem concluir que falta 1 parte ou .
MP174
UNIDADE 5. Frações

MANUAL DO PROFESSOR
Objetivos da Unidade
- Ler, identificar e representar frações (menores ou maiores que a unidade), associando-as ao resultado de uma divisão ou ao significado de parte de um todo.
- Identificar e representar frações aparentes.
- Comparar e ordenar números racionais positivos na forma fracionária.
- Identificar e representar frações equivalentes.
- Reconhecer e interpretar números mistos.
- Resolver problemas de adição e subtração envolvendo números racionais.
- Localizar e representar números racionais na forma fracionária na reta numérica.
- Efetuar adição e subtração com números na forma fracionária.
- Resolver problemas de multiplicação envolvendo números racionais.
- Efetuar multiplicação de um número natural por um número na forma fracionária.
- Desenvolver a noção de porcentagem e sua relação com a fração centesimal.
- Associar as representações 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens.
- Resolver problemas que envolvam a noção de proporcionalidade entre duas grandezas.
- Interpretar dados apresentados em tabela e texto.
- Determinar a probabilidade de ocorrência de um evento em um experimento aleatório em que cada resultado possível tem a mesma chance de ocorrer (espaço amostral equiprovável).
BNCC em foco:
EF05MA03, EF05MA04, EF05MA05, EF05MA06, EF05MA07, EF05MA08, EF05MA12, EF05MA23, EF05MA24
MP175
Boxe Complementar
Para refletir...
As crianças estão participando de uma aula de culinária.
Para obter o rendimento de 40 porções do bolo de cenoura, qual será a quantidade necessária de óleo?
_____
PROFESSOR
Resposta: 1 xícara (chá) de óleo.

Na lista dos ingredientes para o bolo de cenoura, há o número 2 . O que você entende por essa representação?
PROFESSOR
Resposta pessoal.Fim do complemento
MANUAL DO PROFESSOR
A abertura apresenta aos estudantes uma situação que pode ser bastante familiar: a descrição de quantidades de ingredientes em uma receita culinária. Além da exploração da receita, peça aos estudantes que descrevam outros elementos da cena e, se possível, que relatem outras situações vivenciadas em laboratórios ou cozinhas nas quais tenha sido necessário o uso de números na forma de fração. Antes das atividades propostas, incentive os estudantes a procurarem as personagens Marcos, Beatriz, Roberto e Vanessa.
Para refletir...
Na primeira questão, os estudantes devem observar que os ingredientes da receita do bolo de cenoura são para 20 porções. Como se desejam 40 porções, espera-se que percebam que devem dobrar a quantidade de todos os ingredientes. Verifique as estratégias que eles utilizam para o cálculo do dobro de xícara (chá) de óleo. Os estudantes precisam reconhecer, na receita, a indicação como metade ou “meio”da unidade de medida (xícara de chá). Sugira que escrevam por extenso a quantidade indicada (meio ou metade), facilitando que descubram que o dobro de “meia xícara” é “1 xícara”. Eles devem deduzir que duas metades formam 1 unidade, ou que 1 unidade pode ser repartida em duas metades, de modo que, com 1 xícara de óleo, é possível fazer duas receitas de bolo de cenoura.
Na segunda questão, os estudantes precisam lidar com o número misto 2 , relativo à quantidade de farinha de trigo solicitada na receita. Explique que esse número – no caso, lido como “duas xícaras e meia” (ou dois e meio) – representa 2 xícaras (de chá) inteiras de farinha de trigo mais xícara. Espera-se que eles entendam que 2 é um número que tem uma parte inteira e uma parte fracionária.
MP176
Leitura de frações
- Para completar o acabamento do piso, Vladimir vai usar apenas parte de uma lajota de cerâmica.

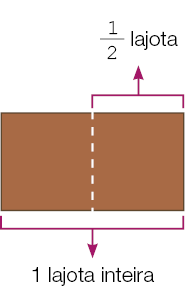
- Que fração representa metade da lajota?
_____
PROFESSOR
Resposta:
- Se Vladimir dividisse a lajota em três partes de mesmo tamanho e usasse uma delas, que fração da lajota ele usaria?
_____
PROFESSOR
Resposta: Ele usaria um terço (ou ) da lajota.- Rute precisava de um quarto de litro de leite para fazer um doce.
Ela dividiu 1 litro de leite em quatro porções iguais, ou seja, com a mesma quantidade, e separou apenas uma delas para fazer o doce.
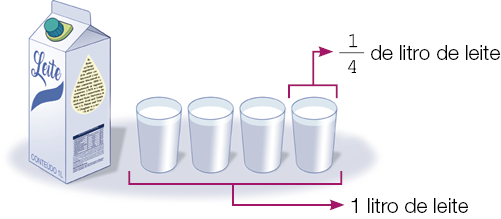

- Se Rute precisasse de (um quinto) de um litro de leite, como ela poderia fazer para obter essa porção?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que, nesse caso, Rute deveria dividir o litro de leite em 5 porções iguais e usar 1 dessas porções. Fim da observação.MANUAL DO PROFESSOR
Objetivo
- Ler, identificar e representar frações (menores ou maiores que a unidade), associando-as ao resultado de uma divisão ou ao significado de parte de um todo.
As atividades destas páginas apresentam situações que possibilitam o trabalho com fração com o significado de “parte do todo” e exploram a representação de quantidades por meio da fração (numerador e denominador), assim como a leitura de frações. O principal significado a ser trabalhado com os estudantes é o de que, nessa representação, as partes em que o todo é dividido são iguais e a fração representa uma única quantidade, um único número.
Atividade 1
Na situação apresentada, chame a atenção para o fato de que não basta dividir a lajota em 2 partes para que uma delas corresponda a da lajota. Essas partes devem ser de mesmo tamanho, isto é, devem ter a mesma área. Se Vladimir dividisse a lajota deste modo, por exemplo:
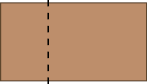
CRÉDITO: ADILSON SECCO
cada uma das partes não corresponderia a da lajota. Note que a resposta esperada para o item b é “um terço” da lajota, mas qualquer outra fração equivalente a essa, por exemplo , também estaria correta. Essa consideração é válida para várias das atividades desta Unidade, dado que, mais adiante, o conceito de frações equivalentes será tratado em tópico específico.
BNCC em foco:
EF05MA03
Atividade 2
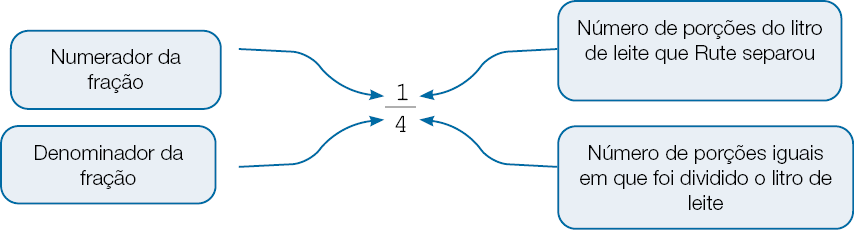
Esta atividade possibilita verificar se os estudantes compreenderam o que representa o numerador e o denominador de uma fração em uma situação-problema como a apresentada, ou seja, em que o numerador mostra quantas porções do litro de leite foram separadas, e o denominador revela em quantas porções iguais foi dividido o litro de leite.
MP177
- Você sabia que, para ler uma fração, é preciso conhecer seu denominador? Observe.
Tabela: equivalente textual a seguir.
|
F rações que têm denominador de 2 a 9 |
|||
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
Tabela: equivalente textual a seguir.
|
Frações que têm denominador 10, 100 ou 1.000 |
||
|---|---|---|
|
|
|
|

Tabela: equivalente textual a seguir.
|
|
|
|
- Agora, leia as frases abaixo e escreva como lemos a fração que aparece em cada uma delas.
- Meu carro tem do tanque com combustível.
_____
PROFESSOR
Resposta: Três quartos.
- Em de um cartaz, há um texto. No restante dele, há uma ilustração.
_____
PROFESSOR
Resposta: Nove décimos.
- Foi feita uma pesquisa no Clube Verde e verificou-se que das pessoas não frequentam o clube no período noturno.
_____
PROFESSOR
Resposta: Onze centésimos.
- Um funcionário teve o direito de receber do seu salário quando foi demitido.
_____
PROFESSOR
Resposta: Cinco doze avos.

- Reúna-se com um
colega
e
conversem
sobre o que significa cada fração nas frases.
PROFESSOR
Resposta pessoal.
- Reúna-se com um
colega
e
conversem
sobre o que significa cada fração nas frases.
MANUAL DO PROFESSOR
Atividade 3
É importante os estudantes reconhecerem que a maioria das frações não tem um nome específico como as frações com denominador de 2 a 9 (meios, terços, quartos, quintos etc.) e as frações com denominador 10, 100 ou 1.000 (décimos, centésimos, milésimos). Assim, na maioria dos casos, ao fazer a leitura da fração, é necessário acrescer a palavra avos.
Sugira a cada estudante que componha outras frações para que um colega escreva, no caderno, como são lidas. A ênfase deve ser em frações mais usuais, mas os estudantes dessa faixa etária podem demonstrar curiosidade por saber como são lidas outras frações.
Se julgar oportuno, faça algumas perguntas com o objetivo de verificar se compreenderam o significado das frações nas frases. Por exemplo:
- No item b, em que fração do cartaz há uma ilustração? (Em do cartaz.)
- No item d, o funcionário teve direito de receber mais que a metade ou menos que a metade do salário? (Menos que a metade.)
BNCC em foco:
EF05MA03
Um pouco de história
Há milhares de anos, os povos antigos já usavam frações, criadas provavelmente pela necessidade de medir quantidades não inteiras e representar essas medidas. As representações eram bastante diferentes das atuais.
Os egípcios usavam com frequência frações com numerador 1, ou seja, as que representavama divisão do número 1 por um número natural não nulo, como , e .
Os babilônios, por sua vez, usavam frações com denominador 60, 60 × 60 etc.
MP178
Fração de uma quantidade
- Antônio convidou 50 pessoas para comemorar seu aniversário em sua casa.
Conferindo a lista de convidados, percebeu que dessas pessoas eram homens e eram mulheres.
- Quantos homens foram convidados?
Para saber a quantidade de homens, calculamos de 50.
- Quantos homens foram convidados?

PROFESSOR
Resposta: 10Portanto, _____ homens foram convidados para a festa de Antônio.
PROFESSOR
Resposta: 20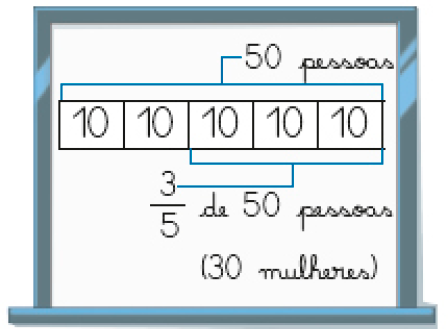
- Quantas mulheres foram convidadas?
Para saber a quantidade de mulheres, calculamos de 50.
Sabemos que de 50 é igual a _____ .
PROFESSOR
Resposta: 10Então, de 50 = 3 × _____ = _____ .
PROFESSOR
Resposta: 10, 30Portanto, _____ mulheres foram convidadas para a festa de Antônio.
PROFESSOR
Resposta: 30
- Amélia usou das 24 rosas do canteiro para fazer um lindo buquê. Quantas rosas ela usou para fazer esse buquê?
_____
PROFESSOR
Resposta: 18 rosas.
MANUAL DO PROFESSOR
Objetivo
- Identificar e representar frações (menores ou maiores que a unidade), associando-as ao resultado de uma divisão ou ao significado de parte de um todo.
Atividade 1
Na situação apresentada, inicialmente aplicamos o conceito de fração em um todo discreto (como uma quantidade de ovos, de bolinhas, de pessoas etc.). Para isso, formamos grupos com os elementos desse todo, de modo que os grupos tenham a mesma quantidade de elementos, e então escolhemos alguns desses grupos.
Incentive os estudantes a representarem diversas situações por meio de esquemas para facilitar o entendimento de cada situação. Isso vale especialmente nos casos em que é dada a parte e se pede o todo, que são questões mais difíceis do que calcular a fração de uma quantidade.
Aproveite o exemplo da situação para formular outra questão: “Em uma festa, dos convidados correspondem a 20 convidados. Quantas pessoas foram convidadas, ao todo, para essa festa?”. Para responder a essa questão, os estudantes podem fazer o esquema a seguir.
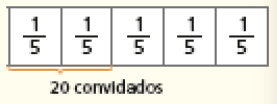
Como 20 corresponde a 2 partes iguais de um total de 5 partes, conclui-se que cada parte corresponde a 10 convidados (20 ÷ 2 = 10). Como há 5 partes, e cada parte corresponde a 10 convidados, ao todo há 50 convidados (5 × 10 = 50).
Atividade 2
Espera-se que os estudantes percebam que de 24 rosas correspondem a 3 grupos de 6 rosas, ou seja, 18 rosas. Outra possibilidade de resolução é calcular de 24, o que corresponde a dividir 24 por 4, obtendo 6, e depois subtrair 6 de 24 (total de rosas), resultando em 18 (24 − 6). Ao subtrair 6 de 24, retirou-se do total, sobrando do total, que correspondem a 18.
BNCC em foco:
EF05MA03
MP179
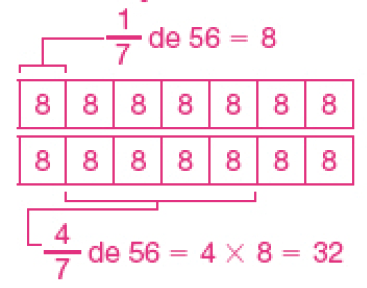
- Na escola de Valéria, 56 crianças se inscreveram para ir a uma excursão. No dia da excursão, dessas crianças não pôde comparecer.
Agora, responda.
- Quantas crianças não foram à excursão?
_____
PROFESSOR
Resposta: 8 crianças.
- Se das crianças inscritas eram meninas, quantas meninas se inscreveram para ir à excursão?
_____
PROFESSOR
Resposta: 32 meninas.
- Quantas crianças não foram à excursão?
PROFESSOR
Exemplo de estratégia de resolução:PROFESSOR

- Responda às questões.
-
de
 corresponde a quantas laranjas?
_____
corresponde a quantas laranjas?
_____
PROFESSOR
Resposta: 16 laranjas.
-
de
 corresponde a quantos envelopes?
_____
corresponde a quantos envelopes?
_____
PROFESSOR
Resposta: 20 envelopes.
-
de
 correspondem a quantos envelopes?
_____
correspondem a quantos envelopes?
_____
PROFESSOR
Resposta: 20 envelopes.
- Que fração de 80 envelopes corresponde a uma quantidade maior de envelopes: ou ?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que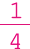 de 80 envelopes e
de 80 envelopes e 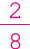 de 80 envelopes correspondem à mesma quantidade de envelopes: 20. Fim da observação.
de 80 envelopes correspondem à mesma quantidade de envelopes: 20. Fim da observação.
-
de
- Um livro tem 40 páginas, e Felipe leu delas.
- A quantidade de páginas que falta para Felipe ler corresponde a que fração do total de páginas desse livro?
_____
PROFESSOR
Resposta:
- Faltam quantas páginas para Felipe terminar de ler esse livro?
_____
PROFESSOR
Resposta: 10 páginas.
- A quantidade de páginas que falta para Felipe ler corresponde a que fração do total de páginas desse livro?
_____

MANUAL DO PROFESSOR
Atividade 3
Após a realização desta atividade, pergunte: “Quantos são os meninos inscritos?” (24 meninos inscritos: 56 − 32 = 24.).
Atividade 4
Os cálculos relativos aos itens b e c podem conduzir os estudantes à percepção de que frações escritas de maneiras diferentes podem representar uma mesma parte de um todo. Mais adiante, nesta Unidade, eles vão aprender que essas frações são chamadas de equivalentes.
No item d, espera-se que os estudantes percebam que de 80 envelopes e de 80 envelopes correspondem à mesma quantidade: 20 envelopes.
Atividade 5
- Explore a atividade com algumas questões adicionais. Por exemplo:
- Quantas páginas do livro Felipe já leu? (30 páginas.)
- Felipe leu mais ou menos da metade do livro? (De 4 partes do livro, Felipe já leu 3 partes, então ele leu mais da metade do livro.)
- Se Felipe ler o restante do livro em 2 dias, lendo a mesma quantidade de páginas em cada um dos dias, quantas páginas ele lerá por dia? (5 páginas por dia.)
BNCC em foco:
EF05MA03; competência específica 6
MP180
Fração que representa um número natural
- Observe o que aconteceu na casa de Bernardo e Kauã. Em seguida, faça o que se pede.
Antes

Depois

- Bernardo comeu a
torta
inteira?
_____
PROFESSOR
Resposta: Sim.
-
da
torta
são o mesmo que
_____
torta
inteira.
PROFESSOR
Resposta: 1
-
representam 1 inteiro (ou 1 unidade) - =
_____
PROFESSOR
Resposta: 1
- Observe como representamos com uma fração a quantidade de figuras pintadas e complete.
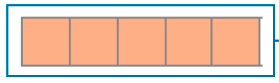 → representam 1 inteiro (ou 1 unidade) → =
_____
→ representam 1 inteiro (ou 1 unidade) → =
_____
PROFESSOR
Resposta: 1
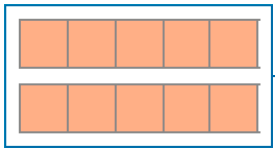 → representam 2 inteiros (ou 2 unidades) → =
_____
→ representam 2 inteiros (ou 2 unidades) → =
_____
PROFESSOR
Resposta: 2Frações que representam números naturais são chamadas de frações aparentes.
- Escreva uma fração aparente para representar a quantidade de figuras pintadas em cada caso.
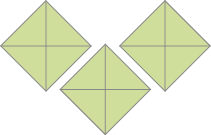
PROFESSOR
Resposta: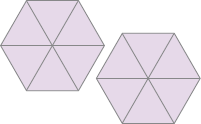
PROFESSOR
Resposta: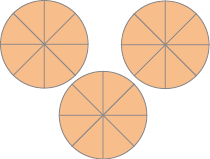
PROFESSOR
Resposta:MANUAL DO PROFESSOR
Objetivos
- Identificar e representar frações aparentes, associando-as ao resultado de uma divisão.
- Identificar frações equivalentes.
As atividades destas páginas exploram a representação em fração de quantidades inteiras, ou seja, de números naturais. Trabalham, assim, as frações aparentes e orientam o cálculo de quantidades desse tipo de fração por meio da divisão do numerador pelo denominador.
Atividades 1 e 2
Observe se, recorrendo às tabelas de multiplicações, os estudantes percebem que, sempre que o numerador da fração é o resultado de uma multiplicação em que um dos fatores é o denominador (numerador múltiplo do denominador), essa fração corresponde a um número natural. Por exemplo, considerando a fração de denominador 5 (atividade 2), os estudantes podem observar que, a cada grupo de cinco quintos, forma-se uma nova unidade: cinco quintos (1 inteiro), dez quintos (2 inteiros), quinze quintos (3 inteiros), vinte quintos (4 inteiros), e assim por diante.
Atividade 3
Aproveite para perguntar: “Se, em vez de 4 partes, cada figura do item a fosse dividida em 3 partes iguais, que fração corresponderia a 3 unidades?”. Os estudantes devem observar que, se 3 terços formam 1 unidade, é preciso triplicar 3 terços para obter 3 unidades, chegando-se, então, a nove terços
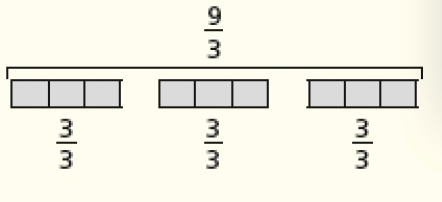
CRÉDITO: ADILSON SECCO
BNCC em foco:
EF05MA03; competência específica 6
MP181
- Em cada fração aparente, divida o numerador pelo denominador e descubra o número natural que ela representa.
- = 12 ÷ 4 = 3
-
=
_____
=
_____
PROFESSOR
Resposta: 21 ÷ 3; 7
-
=
_____
=
_____
PROFESSOR
Resposta: 10 ÷ 2; 5
-
=
_____
=
_____
PROFESSOR
Resposta: 20 ÷ 5; 4
-
=
_____
=
_____
PROFESSOR
Resposta: 24 ÷ 6; 4
-
=
_____
=
_____
PROFESSOR
Resposta: 36 ÷ 4; 9
- Escreva duas frações aparentes para representar cada número.
- 1
PROFESSOR
Exemplo de resposta:PROFESSOR
ou
- 2
PROFESSOR
Resposta: ou
- 3
PROFESSOR
Resposta: ou
- 4
PROFESSOR
Resposta: ou
- Leia o diálogo entre Cida e Tânia e responda às questões.


- Tânia interpretou corretamente o que Cida falou? Justifique.
PROFESSOR
Resposta: Não, pois 6 metades de queijo correspondem a 3 queijos inteiros, não a 4.
- Represente por uma fração aparente as 6 metades de queijo.
_____
PROFESSOR
Resposta:

- Desenhe no caderno figuras para representar cada fração aparente.
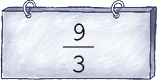
PROFESSOR
Exemplo de desenhos:
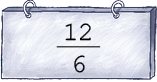
PROFESSOR
Resposta:
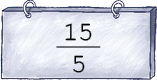
PROFESSOR
Resposta:
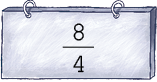
PROFESSOR
Resposta:
MANUAL DO PROFESSOR
Atividade 4
Esta atividade incentiva os estudantes a observarem regularidades nos resultados de escritas de frações aparentes e a compararem com os resultados obtidos por meio de divisões. Por exemplo, podem ser pensados como 4 grupos de seis sextos; como seis sextos correspondem a 1 unidade, 4 desses grupos formam 4 unidades.
O resultado de 24 ÷ 6 fornece 4 unidades, o que indica uma equivalência entre os dois procedimentos. A fração como resultado (ou quociente) de uma divisão será estudada de forma mais detalhada nas páginas seguintes.
Atividade 5
Os estudantes devem observar que qualquer número natural pode ser representado na forma de fração, o que lhes facilitará o futuro estudo das operações que envolvem frações. Reconhecendo representações diferentes de uma mesma quantidade, eles terão condições de estabelecer relações entre elas e poderão escolher a forma mais conveniente a cada situação. Além disso, as frações aparentes ajudam os estudantes a se familiarizarem com a ideia de frações impróprias, pois passam a considerar a possibilidade de frações que correspondem a quantidades superiores a 1 unidade.
Atividade 6
Pergunte aos estudantes: “Quantas metades de queijo formam 4 queijos?”. Eles devem responder 8 metades. Depois, peça que representem com uma fração aparente as 8 metades de queijo .
Atividade 7
Após a realização desta atividade, peça aos estudantes que compartilhem com os colegas as figuras que fizeram. Assim, eles perceberão que, apesar de as frações serem as mesmas, elas podem ser representadas por inteiros de formatos e tamanhos diferentes.
BNCC em foco:
EF05MA03, EF05MA04; competência específica 6
MP182
Frações equivalentes
- Hélio, Lúcia e Sandra desenharam figuras iguais. Observe como cada um as dividiu em partes iguais e pintou uma ou mais partes de azul e complete.
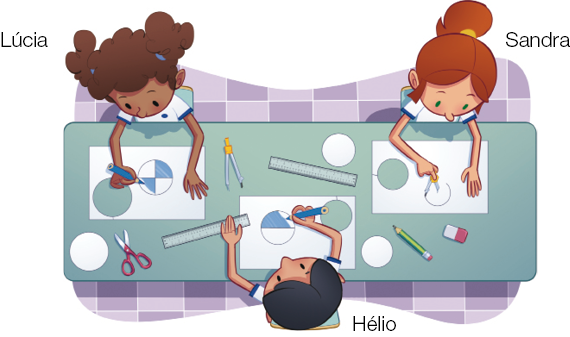
Desenho de Hélio
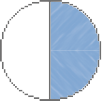
Hélio dividiu sua figura em 2 partes iguais e pintou 1 parte.
Hélio pintou da figura.
Desenho de Lúcia
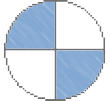
Lúcia dividiu sua figura em 4 partes iguais e pintou 2 partes.
Lúcia pintou _____ da figura.
PROFESSOR
Resposta:Desenho de Sandra
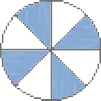
Sandra dividiu sua figura em 8 partes iguais e pintou 4 partes.
Sandra pintou _____ da figura.
PROFESSOR
Resposta:da figura, da figura e da figura representam a mesma parte da figura,
ou seja, a metade dela.
As frações que representam uma mesma parte de um mesmo todo são chamadas de frações equivalentes.
Então, podemos dizer que , e são frações equivalentes.
Indicamos desta forma: = ou = ou = ou = =
MANUAL DO PROFESSOR
Objetivos
- Identificar e representar frações (menores ou maiores que a unidade), associando-as ao resultado de uma divisão ou ao significado de parte de um todo.
- Identificar e representar frações equivalentes.
- Comparar números racionais positivos (representação fracionária).
Atividade 1
O trabalho com frações equivalentes é desenvolvido de modo que, observando esquemas gráficos e regularidades nas escritas numéricas, os estudantes possam identificar e produzir frações que mantêm essa relação. Um modo simples de apresentar o conceito é explorando a linguagem proporcional: “uma parte em duas”, ou “uma de duas partes”, ou, ainda, “uma em duas” para a fração . A compreensão dessa linguagem é notavelmente facilitada por esquemas gráficos. Para demonstrar que existem diversas frações equivalentes à fração , por exemplo, reproduza, na lousa, o esquema a seguir.
 2 de 3 partes ou
2 de 3 partes ou
 4 de 6 partes ou
4 de 6 partes ou
 6 de 9 partes ou
6 de 9 partes ou
CRÉDITO: ADILSON SECCO
Por verificação visual, os estudantes compreendem que a parte pintada em cada figura tem a mesma área que a das outras duas figuras. E, por isso, a expressão “duas de três partes” equivale às expressões “quatro de seis partes” ou “seis de nove partes”, equivalência que pode ser expressa, em linguagem matemática, pela igualdade: . Portanto, essas frações representam a mesma parte do todo, ou seja, são frações equivalentes.
BNCC em foco:
EF05MA03, EF05MA04; competência específica 6
MP183
- Recorte as tiras da página 263 e faça o que se pede.
- Quantos pedaços de da tira são necessários para sobrepor, sem falta e sem sobra, um dos pedaços de da tira?
_____
PROFESSOR
Resposta: 2 pedaços.
- Quantos pedaços de da tira são necessários para sobrepor, sem falta e sem sobra, um dos pedaços de da tira?
_____
PROFESSOR
Resposta: 2 pedaços.
- Pinte com
 as fichas com as frases verdadeiras.
as fichas com as frases verdadeiras.
- Quantos pedaços de da tira são necessários para sobrepor, sem falta e sem sobra, um dos pedaços de da tira?
_____
da tira correspondem a da tira.
PROFESSOR
Resposta: amareloda tira correspondem a da tira.
da tira correspondem a da tira.
PROFESSOR
Resposta: amareloda tira correspondem a da tira.
PROFESSOR
Resposta: amarelo- Crie uma pergunta para ser respondida usando as tiras de fração.
_____
PROFESSOR
Exemplo de pergunta: Quantos pedaços de são necessários para sobrepor, sem falta e sem sobra, um dos pedaços de da tira? (3 pedaços.)

- Pinte a parte da figura que corresponde a cada fração.
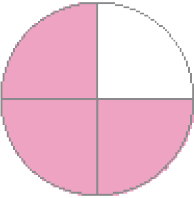
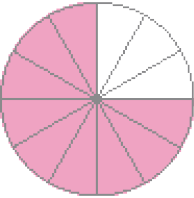
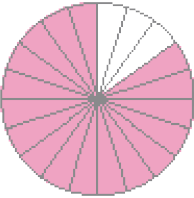
- Quais dessas frações são equivalentes?
_____
PROFESSOR
Resposta: As frações e são equivalentes.
- Escreva uma fração equivalente à fração .
_____
PROFESSOR
Exemplo de resposta:
MANUAL DO PROFESSOR
Atividade 2
Esta atividade induz os estudantes à compreensão de que existem diferentes formas de representar as mesmas quantidades por meio de frações.
A proposta de trabalhar com tiras de papel facilita o estudo de frações equivalentes, uma vez que desafia os estudantes a observarem e a compararem diferentes frações de um mesmo todo (nesse caso, a tira completa), para então concluírem quais dessas frações são equivalentes. A vivência concreta favorece a atribuição de significado ao conceito em estudo.
Incentive os estudantes a usarem as tiras de papel para inventar novas perguntas, relacionando as frações equivalentes, e a trocá-las depois com um colega para que sejam respondidas por ele.
No item c, peça aos estudantes que corrijam a frase errada. Exemplo de correção: da tira correspondem a da tira.
Atividade 3
Ao reconhecerem representações diferentes de um mesmo número, os estudantes estabelecerão relações entre elas e poderão escolher a forma mais adequada ou conveniente para cada situação. No decorrer do Ensino Fundamental II, terão a oportunidade de rever e ampliar essas representações. Em estudos mais avançados entenderão o conceito classe de equivalência.
Aproveite a atividade para pedir aos estudantes que escrevam as frações que representam a parte não pintada de cada figura, ou seja, as que têm a cor de fundo igual à cor de fundo da página, e as comparem. Espera-se que obtenham , e respectivamente, e percebam que e são frações equivalentes.
BNCC em foco:
EF05MA03, EF05MA04, EF05MA05
MP184
- Veja como Lucas obteve outras frações equivalentes.

PROFESSOR
Resposta: 3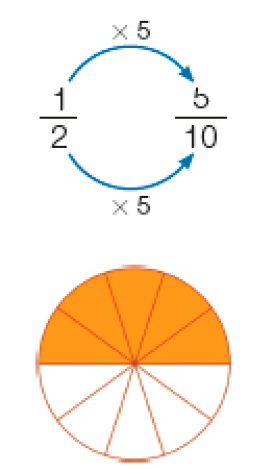
e são frações equivalentes.
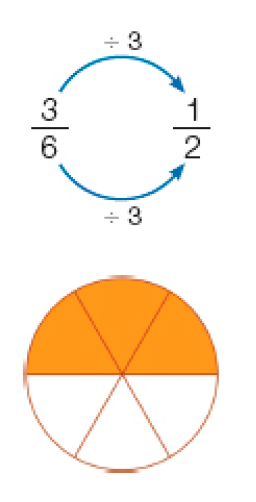
e são frações equivalentes.
Ao multiplicar ou dividir o numerador e o denominador de uma fração por um mesmo número diferente de zero, obtemos uma fração equivalente.
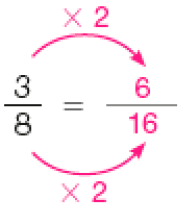
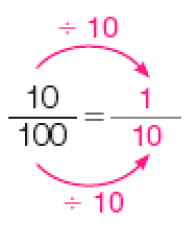
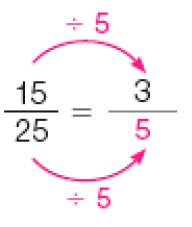
- Complete para obter frações equivalentes.
PROFESSOR
Resposta: Há outras respostas para os itens e e fa)
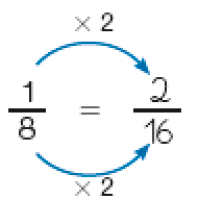
b)
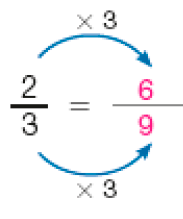
c)
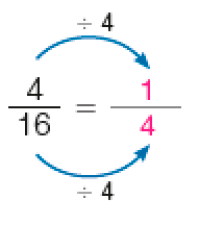
d)
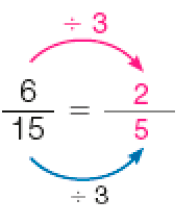
e)
f)
g)
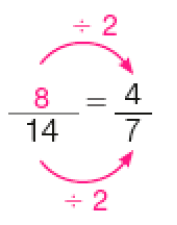
MANUAL DO PROFESSOR
Atividade 4
O principal objetivo da situação apresentada é incentivar os estudantes a observarem que as frações equivalentes envolvem proporcionalidade entre os respectivos numeradores e entre os respectivos denominadores. Por exemplo, a fração é equivalente à fração , pois 5 é o quíntuplo de 1, e 10 é o quíntuplo de 2. O esquema a seguir pode ajudar a compreender as multiplicações de Lucas.


CRÉDITO: ADILSON SECCO
Eles podem observar que a quantidade de partes iguais em que o todo está dividido passou de 2 para 10 (foi multiplicada por 5) e que a quantidade de partes pintadas da figura passou de 1 para 5 (também foi multiplicada por 5), mantendo inalterada a relação entre as partes pintadas e o todo.
É importante que não pensem, equivocadamente, que, se for adicionado um mesmo número ao numerador e ao denominador de uma fração, a fração resultante será equivalente à fração dada.
Além da manipulação de tiras de papel, proposta na atividade 4, é possível usar o material que ficou conhecido como barras ou escala de Cuisenaire – um recurso pedagógico criado pelo professor belga Émile Georges Cuisenaire Hottelet (1891-1980), que, diante das dificuldades matemáticas manifestadas pelos estudantes, decidiu criar um material concreto de apoio a suas aulas.
BNCC em foco:
EF05MA04
Sugestão de atividade
Distribua tiras de papel de mesmo tamanho para que os estudantes as dividam e pintem algumas de suas partes de modo que obtenham frações equivalentes. Poderão assim verificar a validade nos casos em que as partes pintadas e o total de partes da figura dobraram, triplicaram, quadruplicaram etc.
MP185
- Escreva uma fração para representar a parte colorida de cada figura.
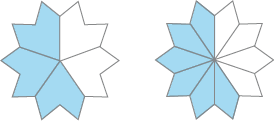
PROFESSOR
Resposta:-
b)

PROFESSOR
Resposta:
-
b)
- Observando essas figuras, que frações equivalentes você identifica?
_____ = _____
PROFESSOR
Resposta: =_____ = _____
PROFESSOR
Resposta: =
- Observe as tiras coloridas e responda à questão.
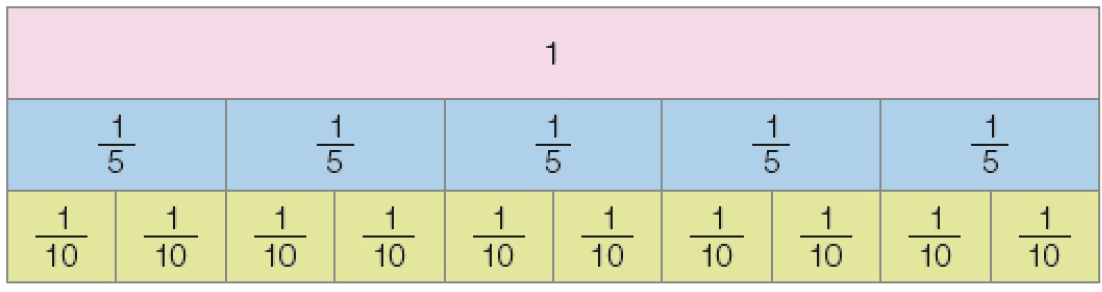
- Qual é a fração equivalente a que tem denominador igual a 10?
_____
PROFESSOR
Resposta:
- Ivo e Noely estão resolvendo os mesmos problemas de Matemática.

- Quantos problemas cada um resolveu? Justifique sua resposta.
_____
PROFESSOR
Resposta: Tanto Ivo como Noely resolveram 2 problemas.PROFESSOR
Exemplo de justificativa: Pela fala de Noely, sabe-se que há 8 problemas e que ela resolveu 2; de 8 problemas são 2 problemas (8 ÷ 4 = 2).
MANUAL DO PROFESSOR
Atividade 5
Esta atividade incentiva os estudantes a observarem regularidades em figuras e em frações, e a compararem as frações observando se elas representam ou não a mesma parte de um inteiro considerado. Por exemplo, eles podem observar que os termos da fração são, respectivamente,o dobro dos termos da fração e, por isso, elas são equivalentes.
Atividade 6
Nesta atividade, os estudantes devem obter uma fração equivalente à fração dada que atenda a uma condição específica. A fração equivalente a ser determinada deve ter denominador igual a 10, o que indica que o denominador da fração inicial (5) foi multiplicado por 2, portanto o numerador da fração equivalente também deve ser multiplicado por 2, levando à fração .
Atividade 7
Peça aos estudantes que criem diálogos semelhantes ao apresentado nesta atividade para que os colegas descubram as quantidades envolvidas. Eles devem estar atentos às quantidades e às frações escolhidas, para que as divisões sejam convenientes.
BNCC em foco:
EF05MA03, EF05MA04, EF05MA05; competência específica 3
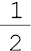 - um meio ou meio
- um meio ou meio 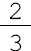 - dois terços
- dois terços 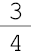 - três quartos
- três quartos 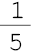 - um quinto
- um quinto 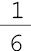 - um
sexto
- um
sexto
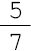 - cinco sétimos
- cinco sétimos 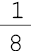 - um oitavo
- um oitavo 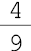 - quatro nonos
- quatro nonos 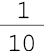 - um
décimo
- um
décimo
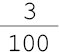 - três centésimos
- três centésimos 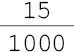 - quinze milésimos
- quinze milésimos 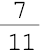 -
sete
onze avos
-
sete
onze avos 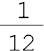 - um doze avos
- um doze avos 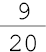 - nove vinte avos
- nove vinte avos