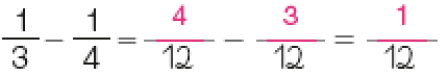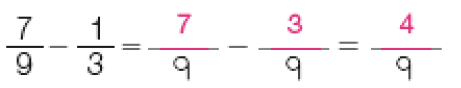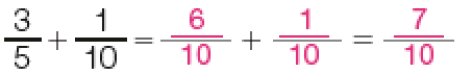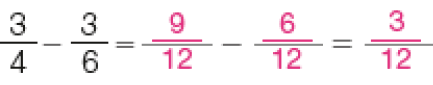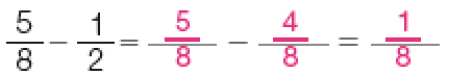MP186
- Responda às questões.
- Que fração é equivalente a e tem denominador 20?
_____
PROFESSOR
Resposta:
- Que fração é equivalente a e tem denominador 8?
_____
PROFESSOR
Resposta:
- Que fração é equivalente a e tem denominador 2?
_____
PROFESSOR
Resposta:
- Que fração é equivalente a e tem denominador 20?
_____
- Escreva uma fração equivalente em cada caso.
-
=
_____
PROFESSOR
Exemplo de respostas:
-
=
_____
PROFESSOR
Resposta:
-
=
_____
PROFESSOR
Resposta:
-
=
_____
- Complete as frases.
- As frações
_____
e
_____
são frações equivalentes a .
PROFESSOR
Exemplo de respostas: e
- As frações
_____
e
_____
são frações equivalentes a .
PROFESSOR
Resposta: e
- As frações
_____
e
_____
são frações equivalentes a .
- Ivan, Juarez e Denílson estudam na mesma sala. Dois deles estão dizendo a mesma coisa sobre a quantidade de meninas da turma, só que de formas diferentes. Quem são os dois? Justifique sua resposta usando frações.

_____
PROFESSOR
Resposta: Juarez e Denílson.PROFESSOR
Exemplo de justificativa: =MANUAL DO PROFESSOR
Atividade 8
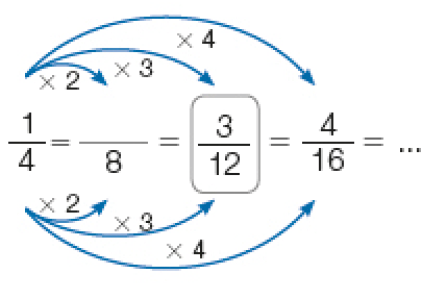
Nesta atividade, os estudantes devem obter uma fração equivalente à fração dada que atenda a uma condição específica. Por exemplo, no item a, a fração equivalente deve ter denominador igual a 20, o que indica que o denominador da fração inicial (10) foi multiplicado por 2, portanto o numerador da fração equivalente também deve ser multiplicado por 2, levando à fração . No item c, o denominador 12 e o numerador 6 devem ser divididos por 6, levando à fração .
O uso de figuras para os estudantes verificarem as frações equivalentes é indicado em atividades desse tipo. Por isso, peça aos estudantes que façam desenhos para representá-las.
Atividade 9
Os estudantes devem perceber que, para obter uma fração equivalente, basta multiplicar ou dividir o numerador e o denominador por um mesmo número natural não nulo.
Atividade 10
Para explorar mais esta atividade, depois das resoluções, peça aos estudantes que criem uma condição para que um colega obtenha a fração equivalente sob essa condição.
Atividade 11
Nesta atividade, os estudantes devem comparar as frações associadas a cada fala dos meninos. Observando as frações , e eles percebem que e são equivalentes. Pergunte: “Como poderia ser a frase de Denílson se ele e Ivan estivessem dizendo a mesma coisa de maneiras diferentes?”. Uma possibilidade seria: “De cada 3 estudantes, 2 são meninas. A justificativa para essa resposta pode ser: = ”.
BNCC em foco:
EF05MA03, EF05MA04, EF05MA05
MP187
Fração como representação de quociente
- Tia Olinda dividiu igualmente 2 barras de chocolate entre seus 3 sobrinhos. Que fração corresponde à parte da barra de chocolate que cada sobrinho recebeu?
Primeiro, ela dividiu cada barra de chocolate em _____ pedaços iguais.
PROFESSOR
Resposta: 3
Cada pedaço corresponde a _____ de 1 barra de chocolate.
PROFESSOR
Resposta:Depois, como havia 6 pedaços e 3 sobrinhos, cada um recebeu _____ pedaços.
PROFESSOR
Resposta: 2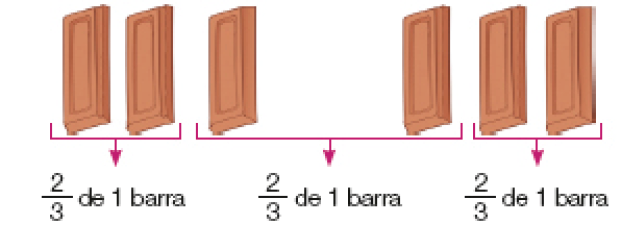
A fração é o quociente de _____.
PROFESSOR
Resposta: 2 ÷ 3Os 2 pedaços de barra de chocolate que cada sobrinho recebeu correspondem a _____ de 1 barra.
PROFESSOR
Resposta:- Lúcia vai dividir 1 maçã igualmente entre 2 pessoas. Escreva uma fração para representar a parte da maçã que cada pessoa receberá.
_____
PROFESSOR
Resposta:

- Um feirante dividiu 1 melancia em 4 partes de mesmo tamanho e vendeu uma parte para cada cliente.

- Que fração representa a parte da melancia que cada um dos clientes comprou?
_____
PROFESSOR
Resposta:
- A fração que você
escreveu
é resultado de qual divisão: 1 ÷ 4 ou 4 ÷ 1?
_____
PROFESSOR
Resposta: 1 ÷ 4
- Que fração representa a parte da melancia que cada um dos clientes comprou?
_____
MANUAL DO PROFESSOR
Objetivo
- Identificar e representar frações, associando-as ao resultado de uma divisão.
Atividades 1, 2 e 3
O objetivo destas atividades é associar a representação na forma de fração ao resultado (quociente) de uma divisão, ou seja, levar os estudantes à compreensão de que o quociente da divisão de um número natural (numerador como dividendo) por outro número natural não nulo (denominador como divisor) pode ser representado por uma fração.
Na atividade 1, acompanhe com os estudantes a divisão das barras de chocolate, observando se compreenderam que o resultado da divisão (2 pedaços de uma barra) corresponde ao resultado da divisão de 2 unidades (as duas barras) por 3 (os três sobrinhos). Se necessário, proponha que reproduzam essa e outras divisões com folhas de papel divididas em partes iguais, para representar as frações envolvidas.
Aproveite para perguntar: “Se as 2 barras de chocolate fossem repartidas igualmente entre 5 colegas, que fração da barra de chocolate cada um receberia?”.
Oriente os estudantes a representarem as barras com duas tiras de papel de mesmo tamanho. Em seguida, peça que façam a divisão de cada uma das tiras em 5 pedaços de mesmo tamanho, para depois distribuírem os pedaços entre 5 colegas e perceberem que cada um receberia de 1 barra.
BNCC em foco:
EF05MA03
MP188
- Magda tem 4
folhas
de cartolina para dividir igualmente entre 6 estudantes, e não pode haver sobra.
Para isso, ela dividiu cada folha em 6 partes iguais.
PROFESSOR
Exemplo de pintura:


- Usando 6 cores diferentes, pinte as partes de cartolina que cada estudante recebeu.
- Escreva uma fração que represente a quantidade de
folha
que cada estudante recebeu.
_____
PROFESSOR
Resposta:
- Rafaela usa uma forma retangular para fazer as tortas de frango que ela vende. A torta é vendida inteira ou cortada, de acordo com o pedido do cliente. Veja a representação de dois tipos de divisão que ela costuma fazer.
LEGENDA: Tipo 1. FIM DA LEGENDA.

LEGENDA: Tipo 2. FIM DA LEGENDA.
- Que fração da
torta
representa cada pedaço do Tipo 1?
_____
PROFESSOR
Resposta: da torta.
- Que fração da
torta
representa cada pedaço do Tipo 2?
_____
PROFESSOR
Resposta: da torta.
- Considere a quantia de 1 real.
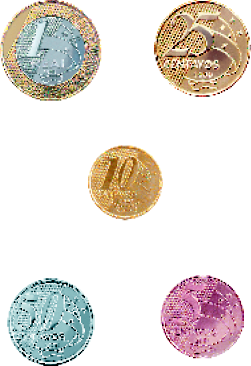
Que fração de 1 real vale:
- uma moeda de 5 centavos?
_____
PROFESSOR
Resposta: de 1 real.
- uma moeda de 10 centavos?
_____
PROFESSOR
Resposta: de 1 real.
- uma moeda de 25 centavos?
_____
PROFESSOR
Resposta: de 1 real.
- uma moeda de 50 centavos?
_____
PROFESSOR
Resposta: de 1 real.
MANUAL DO PROFESSOR
Atividade 4
Outra resposta possível no item b é a fração . Para que os estudantes consigam visualizá-la, peça que considerem cada 2 partes (de um total de 6) como uma única parte maior, como mostra a figura abaixo.
CRÉDITO: ADILSON SECCO
Assim, cada criança recebeu 2 de 3 dessas partes maiores. Então, podemos dizer que cada um recebeu de uma cartolina.
Atividade 5
Sugira aos estudantes que escrevam por extenso o valor que cada fração representa:
- Um doze avos.
- Um sexto.
Atividade 6
Para esta atividade, espera-se que os estudantes associem que 1 real é o inteiro considerado e que 1 real equivale a 100 centavos.
É interessante mostrar a eles que uma maneira de obter as frações do real correspondentes às moedas do sistema monetário brasileiro é montando frações que traduzam essa comparação e determinando a fração equivalente às frações montadas.
No item a, por exemplo, no caso da moeda de 5 centavos:
= = =
Logo, 5 centavos correspondem a de 1 real.
BNCC em foco:
EF05MA03, competência específica 3
MP189
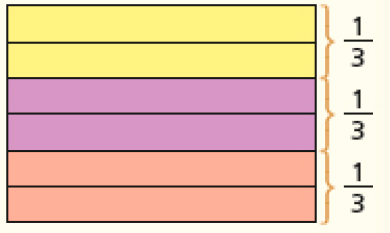
Número misto
- Fabíola dividiu igualmente 4 pizzas do tipo brotinho entre seus 3 filhos e não houve sobra. Quanto de pizza cada filho recebeu?

Primeiro, Fabíola deu 1 pizza para cada filho.
Sobrou _____ pizza.
PROFESSOR
Resposta: 1
Depois, Fabíola deu mais da pizza para cada um.
Cada filho recebeu _____ pizza inteira mais _____ de pizza.
PROFESSOR
Resposta: 1,1 pizza mais de pizza pode ser representado por
1 + ou 1 de pizza.
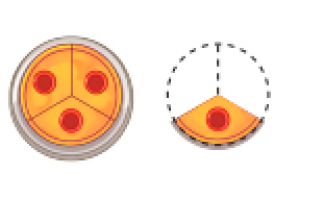
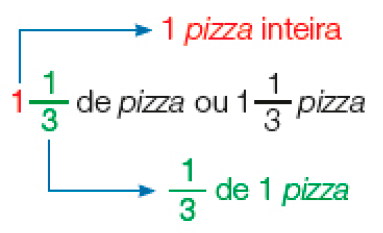
Lemos →1 pizza e de pizza
1 é um número misto, ou seja, ele é formado por um número natural (parte inteira) e uma fração da unidade.
Veja como um número misto pode ser representado por uma fração.
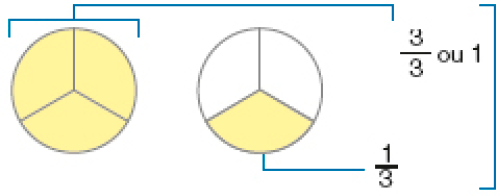
1 = 1 + = + =
Então, cada filho recebeu _____ de pizza ou _____ de pizza.
PROFESSOR
Resposta: 1 ;MANUAL DO PROFESSOR
Objetivos
- Reconhecer e interpretar números mistos.
- Resolver problemas de adição envolvendo números racionais.
O objetivo deste tópico é mobilizar o reconhecimento e a interpretação de números mistos, isto é, de números formados por uma parte inteira (um número natural não nulo) e por uma parte em forma de fração.
Assim como as frações aparentes, os números mistos podem facilitar os futuros cálculos com operações. É importante os estudantes reconhecerem os usos sociais dessa representação.
Atividade 1
Se julgar oportuno, comente que toda fração que representa uma quantidade superior a 1 unidade (como a fração ) é denominada fração imprópria, enquanto as frações que representam quantidades menores que a unidade são chamadas de frações próprias. Nas frações impróprias, o numerador é maior que ou igual ao denominador. Nas frações próprias, o numerador é menor que o denominador.
BNCC em foco:
EF05MA03, EF05MA07
MP190
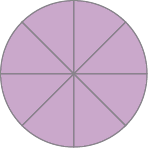
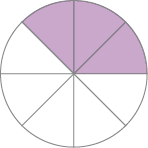
- Marque com um
X
a figura que representa 2 chocolates, sabendo que
 corresponde a 1 chocolate.
corresponde a 1 chocolate.

( )

( )

( )
PROFESSOR
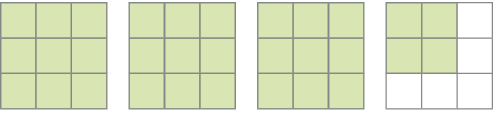
Resposta correta: a- Represente com um número misto a parte pintada em cada caso.
a)
_____
PROFESSOR
Resposta: 1b)
_____
PROFESSOR
Resposta: 3- Sabendo que Nílson repartiu igualmente 3
folhas
entre 2 pessoas, responda.
- Quanto de
folha
cada uma recebeu?
_____
PROFESSOR
Resposta: 1 de folha.
- A quantidade que cada uma recebeu é maior ou
menor
que 1 de folha? Justifique.
_____
PROFESSOR
Resposta: Maior, pois 1 de folha é uma folha mais um quarto de folha, e cada pessoa recebeu 1 de folha, ou seja, uma folha e meia.
- Quanto de
folha
cada uma recebeu?
_____
- Ana usou 2 xícaras de açúcar para fazer um bolo. De quantas xícaras de açúcar ela precisaria para fazer dois desses bolos?
_____
PROFESSOR
Resposta: De 5 xícaras.
- Veja a seguir como Isabel representou um número misto com uma fração.
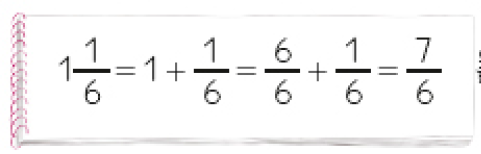
- Represente com uma fração cada número misto da mesma forma que Isabel.
- 1 =
_____
PROFESSOR
Resposta: 1 + = + =
- 2 =
_____
PROFESSOR
Resposta: 2 + = + =
- 3 =
_____
PROFESSOR
Resposta: 3 + = + =
- 4 =
_____
PROFESSOR
Resposta: 4 + = + =
MANUAL DO PROFESSOR
Atividade 2
Alguns estudantes podem conhecer uma “regra prática” para obter a fração correspondente a um número misto; para 3 por exemplo, a regra tem estas etapas:
- multiplica-se o denominador (7) pela parte inteira (3):
3 × 7 = 21;
- ao resultado
obtido
(21), adiciona-se o numerador (4):
21 + 4 = 25;
- o numerador da fração imprópria será o resultado anterior (25), mantendo o denominador inicial (7); portanto, correspondem a 3 .
Sugerimos que, aceitando essa regra, ela seja justificada: mostre que, nesse caso, a parte inteira (3) pode ser representada pela fração (3 × 7 = 21), que, adicionada a , totaliza .
Atividade 3
Convém esclarecer que entendemos a parte pintada como aquela com a cor diferente da cor de fundo da página. Proponha aos estudantes que, no caderno, desenhem e pintem outras figuras para que um colega escreva os números mistos e as frações que representam as partes pintadas.
Atividade 4
No item b, os estudantes devem perceber que a quantidade de inteiros é a mesma (1) e que metade é maior que um quarto.
Atividade 5
Para fazer 2 bolos, Ana deve usar o dobro da quantidade de xícaras:
2 × 2 = 2 × (2 + ) =
= (2 × 2) + (2 × ) = 4 + 1 = 5
Verifique a estratégia usada pelos estudantes. Por exemplo, eles podem fazer uma adição:
(2 + ) + (2 + ) =
= 2 + + 2 + =
= 2 + 2 + 1 = 5
BNCC em foco:
EF05MA03, EF05MA07; competência específica 6
Atividade 6
Os estudantes devem perceber que números mistos podem ser representados na forma de fração usando como recurso adições de frações equivalentes.
MP191
Reta numérica
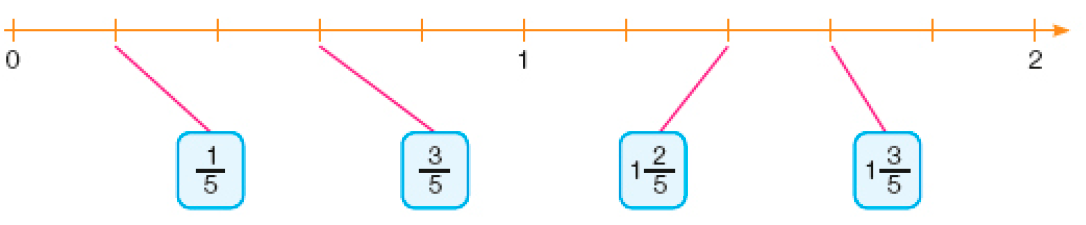
- Ligue cada fração à posição exata ou aproximada que ocupa na reta numérica.
a)
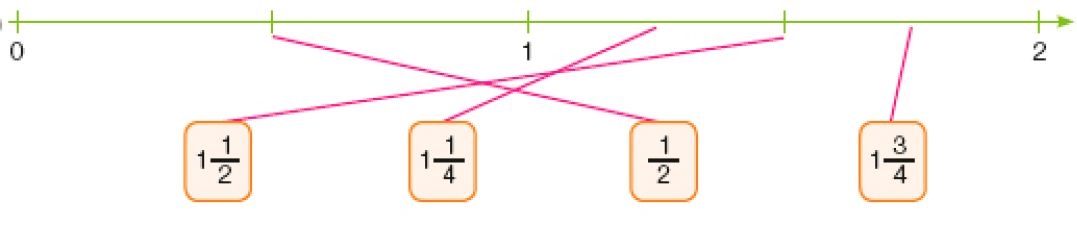
b)
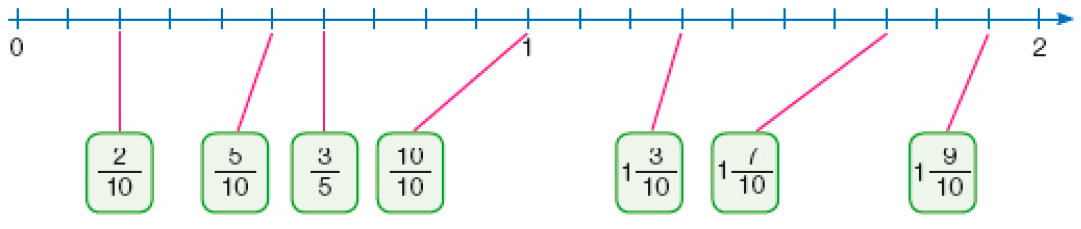
c)
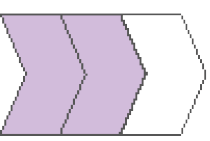
- Observe as partes pintadas de cada figura e escreva uma fração correspondente. Em seguida, marque com um ponto vermelho o local que a fração ocupa na reta numérica.
_____
PROFESSOR
Resposta: →
_____
PROFESSOR
Resposta: →
c)
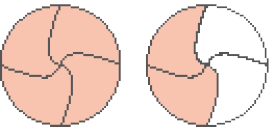
_____
PROFESSOR
Resposta: →
MANUAL DO PROFESSOR
Objetivo
- Localizar e representar números racionais na forma fracionária na reta numérica.
Atividade 1
A reta do item a mostra os intervalos entre 0 e 1 e entre 1 e 2, divididos em 5 partes iguais. Cada parte equivale a e, da esquerda para a direita, cada marca à direita do zero corresponde, respectivamente, aos números , , , , (ou 1), 1 , 1 , 1 , 1 e 1 (ou 2).
No item b, para localizar na reta o ponto que representa a fração , os estudantes podem observar que o intervalo de 0 a 1 foi dividido em 2 partes iguais e que a marca que representa essa divisão indica a metade desse intervalo, ou seja, . Como o intervalo entre 1 e 2 também foi dividido em 2 partes iguais, a marca central desse intervalo corresponde a 1 . Para localizar aproximadamente o número 1 , a estratégia é reconhecer que esse número equivale a 1 + , ou seja, é a mais que 1 e deve estar posicionado à direita de 1, imaginando o intervalo de 1 a 2 dividido em 4 partes iguais (cada parte equivale a ), e associar a primeira marca à direita de 1 (que deve estar no ponto médio do intervalo entre 1 e 1 ).
Atividade 2
Espera-se que os estudantes repitam o raciocínio da atividade 1. Como os intervalos de 0 a 1 e de 0 a 2 estão repartidos em partes iguais, basta localizarem a posição correspondente a cada fração.
BNCC em foco:
EF05MA03, EF05MA05; competência específica 6
MP192
Comparação de frações
- Em uma aula de Educação Física, os estudantes realizaram um treino de corrida. Nesse treino, Elias chegou até o meio da pista, Grazielle correu dessa pista e Kleiton alcançou da pista. Observe o esquema e faça o que se pede.
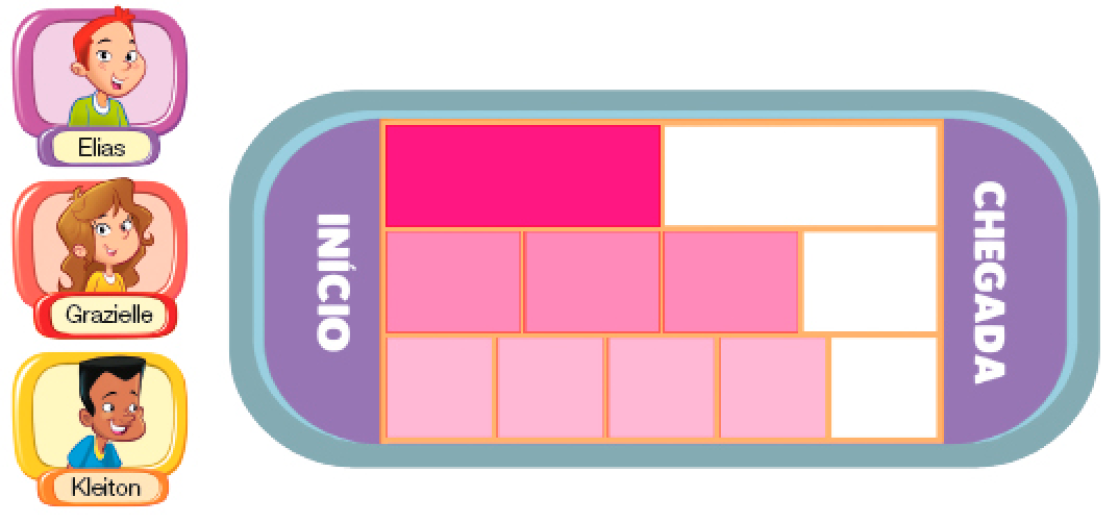

- Pinte a parte do caminho que cada estudante percorreu.
- Quem percorreu a maior distância?
_____
PROFESSOR
Resposta: Kleiton.
- Quem percorreu a
menor
distância?
_____
PROFESSOR
Resposta: Elias.Ao comparar duas ou mais frações com o mesmo denominador, a maior fração será aquela com o maior numerador. Se compararmos as frações e , veremos que < , porque 1 < 3, ou > , porque _____ > _____.
PROFESSOR
Resposta: 3; 1.Ao comparar duas ou mais frações com denominadores diferentes, precisamos obter frações de mesmo denominador e que sejam equivalentes àquelas que queremos comparar. Depois, comparamos os novos numeradores.
Para comparar as frações e , vamos formar frações equivalentes a elas que tenham o mesmo denominador.
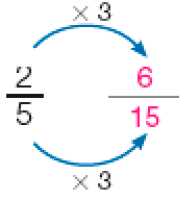
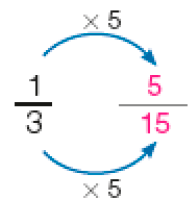
Como, > , concluímos que _____ .
PROFESSOR
Resposta: >MANUAL DO PROFESSOR
Objetivos
- Identificar frações equivalentes.
- Comparar e ordenar números racionais positivos na forma fracionária.
Nestas páginas, os estudantes verão estratégias para comparar frações. Para ampliar os conhecimentos, é importante conseguirem identificar quais números são maiores, menores ou equivalentes. Uma estratégia que facilita a compreensão é o uso de esquemas e desenhos.
Atividade 1
A situação apresentada tem como suporte visual a pista de corrida já dividida em partes, permitindo visualizar melhor quem percorreu a maior e quem percorreu a menor distância. Entretanto, é preciso desenvolver outras estratégias para quando não for possível utilizar esquemas visuais.
Nesta atividade, a outra estratégia apresentada é a comparação de numeradores quando os denominadores são iguais. No caso de denominadores diferentes, uma possibilidade é encontrar frações equivalentes para realizar a comparação e, assim, obter frações de mesmo denominador. Outras regularidades podem ser percebidas para essas comparações. Assim, proponha que os estudantes também apresentem estratégias diferentes, sempre verificando a validade delas.
BNCC em foco:
EF05MA04, EF05MA05
MP193
- Observe as figuras e escreva uma fração para cada uma. Em seguida, compare cada par de frações e complete com <, > ou =.
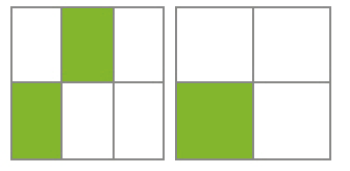
_____ _____ _____
PROFESSOR
Resposta: >
_____ _____ _____
PROFESSOR
Resposta: =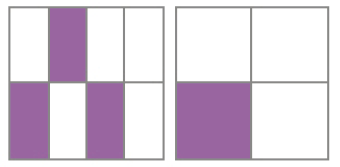
_____ _____ _____
PROFESSOR
Resposta: >- Compare os pares de frações e complete com <, > ou =.
-
_____
PROFESSOR
Resposta: <
-
_____
PROFESSOR
Resposta: =
-
_____
PROFESSOR
Resposta: <
-
_____
PROFESSOR
Resposta: >
-
_____
- Analise as informações a seguir e responda.
Tabela: equivalente textual a seguir.
|
Atividade de lazer de Otávio |
Quantidade de horas |
|---|---|
|
Futebol
|
|
|
Leitura
|
|
|
Pipa
|
|
- Em qual atividade Otávio permaneceu por mais tempo?
_____
PROFESSOR
Resposta: Futebol.
- Analise as frações de hora em que Otávio participou das atividades acima e escreva-as em ordem crescente.
_____
PROFESSOR
Resposta: , e
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, os estudantes têm o apoio de desenhos; entretanto, nem todos facilitam a comparação devido à maneira como estão pintados. Sugira que encontrem as frações equivalentes para a confirmação das respostas.
Atividade 3
Nesta atividade, os estudantes não contam com o apoio de esquemas ou desenhos para comparar as frações. Logo, eles precisarão desenvolver outras estratégias. Nesse caso, podem encontrar frações equivalentes com denominadores iguais e, assim, realizar a comparação.
Atividade 4
Peça aos estudantes que socializem as estratégias para a comparação das representações fracionárias. É possível que utilizem frações equivalentes diferentes ou desenhem esquemas para que possam compará-las.
BNCC em foco:
EF05MA04, EF05MA05; competência específica 6
MP194
Adição e subtração
- Bento vai pintar um lote de 8 vasos ornamentais para o seu jardim. De manhã, ele vai pintar 5 desses vasos e à tarde vai pintar mais 2 deles.

- Que fração do lote ele pintará nesse dia?
De manhã, Bento pintará _____ vasos do lote; à tarde, pintará mais _____ vasos.
PROFESSOR
Resposta: 5; 2.Ao todo, ele pintará _____ vasos do lote.
PROFESSOR
Resposta: 7Os 5 vasos que ele pintará de manhã correspondem a do lote, e os 2 vasos que pintará à tarde correspondem a _____ do lote.
PROFESSOR
Resposta:+ = _____
PROFESSOR
Resposta:Ao todo, Bento pintará _____ do lote de vasos nesse dia.
PROFESSOR
Resposta:
- Quanto ainda faltará pintar?
Se Bento pintar hoje 7 dos 8 vasos, então sobrará _____ vaso do lote.
PROFESSOR
Resposta: 1O lote inteiro pode ser representado pela fração .
− = _____
PROFESSOR
Resposta:Faltará pintar _____ do lote de vasos.
PROFESSOR
Resposta:
MANUAL DO PROFESSOR
Objetivos
- Identificar e representar frações (menores ou maiores que a unidade), associando-as ao resultado de uma divisão ou ao significado de parte de um todo.
- Identificar frações equivalentes.
- Efetuar adição e subtração com números na forma fracionária.
- Resolver problemas de adição e subtração envolvendo números racionais.
Os estudantes poderão observar que, quando efetuamos adições ou subtrações com frações de denominadores iguais, basta adicionar ou subtrair os numeradores e manter o denominador. A explicação para essa regularidade é que, quando adicionamos (ou subtraímos) metades com metades, terços com terços, e assim por diante, as partes adicionadas (ou subtraídas) são de mesmo “tamanho” (correspondem à mesma parte de um todo). Entretanto, se os denominadores são diferentes, por exemplo, metades e quintos, não é possível adicioná-los diretamente e continuar referindo-se a eles como metades ou quintos.
Atividade 1
Esta atividade propicia observar a compreensão do processo de adição e subtração com frações de mesmo denominador. Verifique se os estudantes fazem o cálculo de maneira mecânica e sem a compreensão do processo ou se entendem que, na situação apresentada no item a, basta adicionar os numeradores (5 + 2) e manter o denominador (8).
BNCC em foco:
EF05MA07
MP195
- Priscila plantou árvores frutíferas em seu terreno. Em do terreno, ela plantou laranjeiras e em do mesmo terreno plantou goiabeiras.

- Que fração do terreno representa a parte onde foram plantadas as laranjeiras e goiabeiras?
Veja como Rebeca fez para calcular o resultado da adição + .
Frações equivalentes a
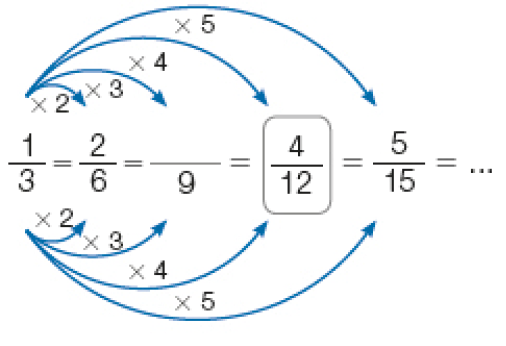
PROFESSOR
Resposta: 3Frações equivalentes a
PROFESSOR
Resposta: 2
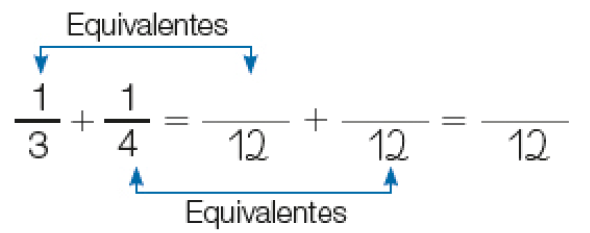
PROFESSOR
Respostas: 4; 3; 7.Então, a plantação de laranjeiras e de goiabeiras representa _____ do terreno.
PROFESSOR
Resposta:- O restante do terreno ainda não possui árvores plantadas. Que fração representa essa parte sem plantação?
O terreno inteiro pode ser representado pela fração
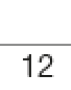 .
. PROFESSOR
Resposta: 12A parte com árvores plantadas representa _____ do terreno.
PROFESSOR
Resposta: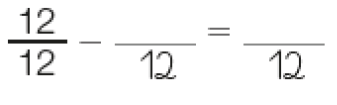
PROFESSOR
Resposta: 7; 5A parte sem árvores plantadas é igual a _____ do terreno.
PROFESSOR
Resposta:
MANUAL DO PROFESSOR
Atividade 2
Considerando o trabalho inicial feito com adições e subtrações de números na forma de fração, esta atividade proporciona aos estudantes perceberem, com base na observação de regularidades, como podem usar as frações equivalentes para efetuar essas operações quando seus denominadores são diferentes.
O objetivo é levar a turma a realizar essas operações nos casos mais simples e sem o uso de regras ou de definições formais. O recurso de esquemas e desenhos auxilia na visualização da operação realizada.
Na situação apresentada, é preciso estar atento aos comentários dos estudantes para saber se compreendem a lógica do raciocínio proposto ou se apenas seguem os passos sem compreendê-los. Represente a resolução de Rebeca em um esquema como este:
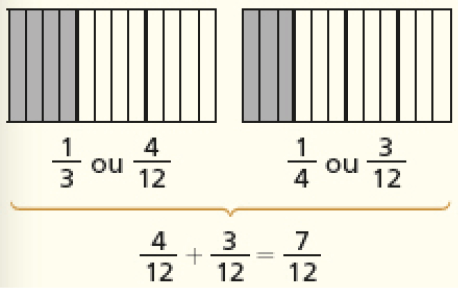
CRÉDITO: ADILSON SECCO
BNCC em foco:
EF05MA04, EF05MA07; competência específica 6
MP196
- Bruna pintou a parte verde, e Gustavo pintou a parte laranja de algumas figuras. Escreva uma adição para representar as partes pintadas de cada figura.
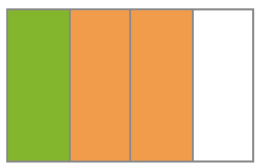
_____ + = _____
PROFESSOR
Resposta: ;
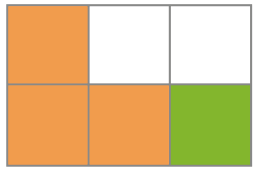
_____ + _____ = _____
PROFESSOR
Resposta: + =
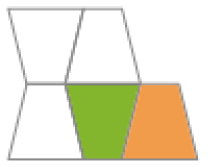
_____ + _____ = _____
PROFESSOR
Resposta: + =- Calcule a medida da massa de cada saco e complete.
a)

 =
_____
kg
=
_____
kg
PROFESSOR
Resposta:b)
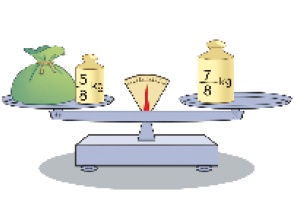
 =
_____
kg
=
_____
kg
PROFESSOR
Resposta:c)

 =
_____
kg
=
_____
kg
PROFESSOR
Resposta:- Rafaela vai a uma excursão que durará 9 horas. Ela sabe que, dessas 9 horas, 2 horas serão usadas para visitar uma cachoeira e 3 horas levarão para conhecer o centro histórico de uma cidade.
- Que fração do total de horas será gasta, ao todo, na visita à cachoeira e ao centro histórico da cidade?
_____
PROFESSOR
Resposta:PROFESSOR
+ =
- Que fração do tempo total da excursão sobrará para outras atividades?
_____
PROFESSOR
Resposta:PROFESSOR
+ =
- Que fração do total de horas será gasta, ao todo, na visita à cachoeira e ao centro histórico da cidade?
_____

- Marque com um
X
as operações cujo resultado seja 1.
- + ( )
- + ( )
- + ( )
- − ( )
- − 1 ( )
-
− 0 ( )
PROFESSOR
Respostas corretas: a; b; f.
MANUAL DO PROFESSOR
Atividade 3
Aproveite para perguntar que fração da figura ficou sem pintar em cada item. Espera-se que respondam: , e respectivamente.
Atividade 4
Espera-se que os estudantes mobilizem seus conhecimentos sobre balança de dois pratos em equilíbrio. Utilize essa oportunidade para observar se eles compreendem a lógica do raciocínio que permite calcular a massa de alguns sacos.
Atividade 5
Você pode perguntar: “Se o tempo gasto com a visita à cachoeira fosse de 5 horas e o tempo gasto para conhecer o centro histórico fosse de 3 horas, que fração do tempo total da excursão sobraria para as outras atividades?” ( ).
Atividade 6
Estimule os estudantes a utilizarem o cálculo mental, visto que as frações apresentam o mesmo denominador.
No item e, os estudantes podem expressar 1 como a fração e, assim, concluir que o resultado é zero.
No caso do item f, espera-se que os estudantes percebam que, ao subtrair zero de qualquer número, o resultado é o próprio número.
BNCC em foco:
EF05MA03, EF05MA07; competências específicas 3 e 6
MP197
- Observe as figuras e encontre o resultado da adição e da subtração das frações.
-
+ =
_____
PROFESSOR
Resposta possível:PROFESSOR
ou ou 1

-
− =
_____
PROFESSOR
Resposta possível:PROFESSOR
ou ou
- Calcule o resultado de cada adição e subtração.
-
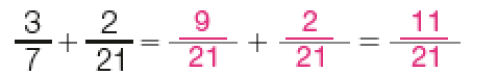
PROFESSOR
Atenção professor: Há outras respostas para os itens c, d, e e f. Fim da observação.
-
- Arthur comprou um pacote com 8 biscoitos.
De manhã, ele comeu dos biscoitos, à tarde, comeu mais desses biscoitos.
- Que fração dos biscoitos Arthur não comeu?
_____
PROFESSOR
Resposta:PROFESSOR
Exemplo de cálculos:PROFESSOR
+ = + =PROFESSOR
− =
- Quantos biscoitos ele não comeu?
_____
PROFESSOR
Resposta: 3 biscoitos.
- Que fração dos biscoitos Arthur não comeu?
_____


- Virgínia tomará do suco da jarra desenhada ao lado, e César tomará do suco dessa jarra.
- Que fração do total de suco restará na jarra?
_____
PROFESSOR
Resposta: ouPROFESSOR
Exemplo de cálculos:PROFESSOR
+ = + =PROFESSOR
− =
- Essa fração corresponde a mais ou a menos que a metade do suco que há na jarra?
_____
PROFESSOR
Resposta: Exatamente à metade do suco.PROFESSOR
=
- Que fração do total de suco restará na jarra?
_____
MANUAL DO PROFESSOR
Atividade 7
Peça a alguns estudantes que expliquem na lousa como chegaram aos resultados da adição e da subtração. Um exemplo de resolução:
- + = + =
-
− = − =
Você também pode explorar as diversas formas de expressar o resultado, uma vez que podem ser empregadas frações equivalentes.
Atividade 8
Nesta atividade, os estudantes devem realizar a operação entre as frações sem o auxílio de uma representação gráfica. Incentive-os a buscarem mais de uma resposta nos itens c, d, e e f.
Atividade 9
Pergunte: “Quantos biscoitos Arthur comeu de manhã? E à tarde?”. Espera-se que os estudantes respondam, respectivamente, 3 e 2 biscoitos.
Atividade 10
Aproveitando a situação, determine um valor numérico que indique a quantidade de suco na jarra, para que os estudantes calculem frações dessa quantidade e verifiquem que, juntos, Virgínia e César tomaram a metade do suco.
Por exemplo, se havia 600 mL na jarra, a quantidade consumida seria a seguinte:
Virgínia: de 600 mL
600 mL ÷ 5 = 120 mL
1 × 120 mL = 120 mL
César: de 600 mL
3 × 60 mL = 180 mL
Portanto, juntos, Virgínia e César teriam consumido 120 mL + 180 mL = 300 mL (metade de 600 mL).
BNCC em foco:
EF05MA04, EF05MA07
MP198
Multiplicação com fração
- Um melão foi dividido em 8 fatias de mesmo tamanho. Três amigos, Emily, Hudson e Nícolas, comeram 2 fatias do melão cada um. Que fração do melão eles comeram?
Cada amigo comeu do melão.
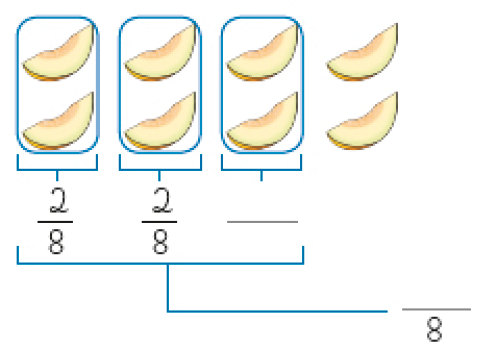
PROFESSOR
Resposta: , 6Os 3 amigos juntos comeram 3 vezes do melão.
3 × = + 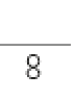 +
+ 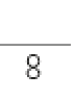 =
= 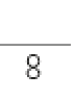
PROFESSOR
Resposta: 2; 2; 6Emily, Hudson e Nícolas comeram, juntos, _____ do melão.
PROFESSOR
Resposta:- Igor tem 3 tábuas de mesmo comprimento. Ele vai separar a metade delas para fazer uma estante. Que fração de tábua Igor usará para fazer a estante?
Vamos calcular de 3, ou seja, × 3.
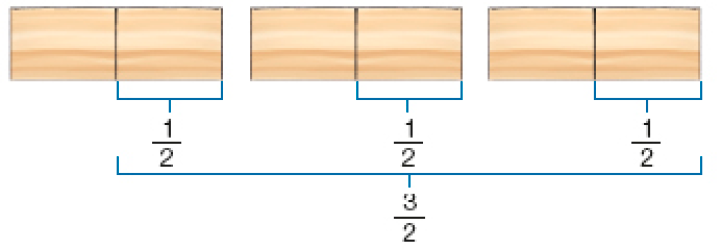
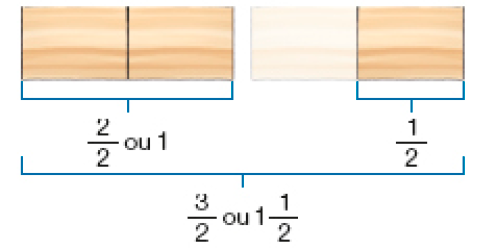
Então, de 3 é o mesmo que × 3 = _____ ou 1 .
PROFESSOR
Resposta:Igor usará _____ ou _____ de tábua para fazer a estante.
PROFESSOR
Resposta: ; 1MANUAL DO PROFESSOR
Objetivos
- Efetuar multiplicação de um número natural por um número na forma fracionária.
- Resolver problemas de multiplicação envolvendo números racionais.
Atividades 1 e 2
É possível que os estudantes utilizem seus conhecimentos sobre as operações com números naturais para realizar os cálculos com números racionais. Assim, toda vez que uma operação é apresentada, é importante relembrá-los de que se trata de outro conjunto numérico e que, portanto, algumas características e técnicas de cálculo podem ser diferentes. Nestas atividades, as multiplicações envolvem os dois tipos de número.
Na situação da atividade 1, um número natural vezes uma fração; na da atividade 2, a ordem é invertida. Deve ficar claro para os estudantes que, nas duas situações, a fração pode ser repetida a quantidade de vezes indicada pelo número natural para a obtenção dos resultados. O desafio será, em alguns problemas, identificar qual representação fracionária atende à situação. O uso de desenhos e esquemas pode ajudar na compreensão desses dois tipos de multiplicação.
BNCC em foco:
EF05MA08
MP199
- Complete.
- 5 × = + + + + =
-
 × = + + + =
× = + + + =

- Pinte e complete.
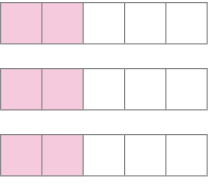
-
de 3 =
PROFESSOR
Exemplo de pintura.
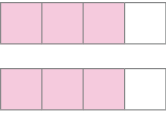
-
de 2 =
_____
PROFESSOR
Resposta:PROFESSOR
Exemplo de pintura.
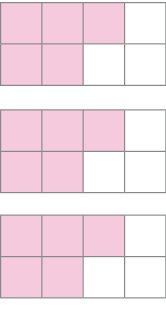
-
de 3 =
_____
PROFESSOR
Exemplo de pintura.
- Emerson fez um
bolo
gelado e, após cortá-lo em 16 pedaços iguais, guardou-o na geladeira. Cada vez que ia à cozinha, ele comia 2 pedaços desse bolo.
- Que fração do
bolo
Emerson comeu, se ele foi 3 vezes à cozinha?
PROFESSOR
Exemplo de cálculo:PROFESSOR
3 × =
- Que fração do
bolo
Emerson comeu, se ele foi 3 vezes à cozinha?
Emerson comeu _____ do bolo.
PROFESSOR
Resposta:- Calcule.
- 4 × =
_____
PROFESSOR
Resposta:
- 2 × =
_____
PROFESSOR
Resposta:
-
de 3 =
_____
× 3 =
_____
PROFESSOR
Resposta: ; 3
-
de 6 =
_____
×
_____
=
_____
PROFESSOR
Resposta: ; 6;
-
de =
_____
×
_____
=
_____
PROFESSOR
Resposta: ; ;
-
de =
_____
×
_____
=
_____
PROFESSOR
Resposta: ; ;
- 4 × =
_____
MANUAL DO PROFESSOR
Atividade 3
O objetivo desta atividade é que os estudantes desenvolvam outras estratégias para resolverem a multiplicação de um número natural por uma fração quando não for possível utilizar um esquema visual.
Atividade 4
As ilustrações desta atividade propiciam aos estudantes fortalecerem a compreensão da multiplicação de números na forma fracionária por números naturais.
Atividade 5
Antes da resolução desta atividade, proponha aos estudantes que destaquem as informações fornecidas para facilitar a resolução.
Atividade 6
A atividade explora multiplicações envolvendo números naturais e números racionais na forma de fração. Comente que é comum expressar o resultado pela fração equivalente mais simples (o que chamamos de simplificação de frações).
BNCC em foco:
EF05MA08

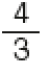 de hora
de hora 
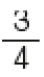 de hora
de hora 
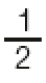 de hora
de hora