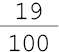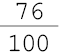MP200
Porcentagem
- Bruno trabalha em uma fábrica de chocolates. A figura ao lado representa a fôrma na qual Bruno despejou o chocolate derretido para resfriá-lo. Que fração da fôrma foi preenchida por chocolate?
40 partes de uma fôrma com 100 partes iguais podem ser representadas pela fração _____ ou por 40%.
PROFESSOR
Resposta:
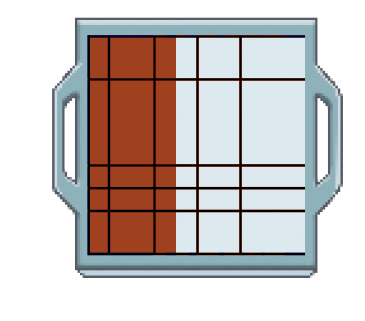

Podemos, então, dizer que ou 40% da fôrma está preenchida com chocolate.
- Agora, responda: que porcentagem da fôrma não ficou preenchida com chocolate?
_____
PROFESSOR
Resposta: 60% da fôrma.
- Reescreva as frases usando porcentagem.
- 5 em cada 100 cães - 5% dos cães.
- 18 em cada 100 crianças -
_____
PROFESSOR
Resposta: 18% das crianças.
-
das flores do jardim -
_____
PROFESSOR
Resposta: 25% das flores do jardim.
MANUAL DO PROFESSOR
Objetivos
- Resolver problemas de multiplicação envolvendo números racionais.
Desenvolver a noção de porcentagem e sua relação com a fração centesimal.
- Associar as representações 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens.
Atividade 1
Peça aos estudantes que deem exemplos de outras situações em que aparece o símbolo de porcentagem (%). Explore a situação apresentada perguntando: “Se Bruno tivesse despejado chocolate em da fôrma, que porcentagem dela seria preenchida com chocolate?”. Espera-se que os estudantes percebam que 70% da fôrma seria preenchida com chocolate.
Atividade 2
Esta atividade explora a escrita de diferentes quantidades percentuais. Aproveite para trabalhar o raciocínio multiplicativo, perguntando: “Em um total de 200 cães, 5 em cada 100 cães correspondem a quantos cães? E em relação a um total de 300 cães?”. Espera-se que os estudantes respondam 10 e 15 cães, respectivamente.
BNCC em foco:
EF05MA06, EF05MA08; competências específicas 2 e 6
MP201
- Havia 100 correspondências para
serem
distribuídas por um entregador. Apenas 5 delas não foram entregues, porque as pessoas não estavam em casa. Que porcentagem das correspondências não foi entregue?
_____
PROFESSOR
Resposta: 5% das correspondências.

- Adriana ganhou um prêmio de 300 reais por ter sido a melhor vendedora do mês na loja em que trabalha. Ela decidiu dar 10% do prêmio a seu filho, Gabriel. Adriana vai dar 10% de 300 reais, ou seja, 10 reais de cada 100 reais que ela ganhou, como mostrado no esquema a seguir.


- Agora, responda: se Adriana desse 20% do prêmio para seu filho, quantos reais ele ganharia?
_____
PROFESSOR
Resposta: 60 reais.
- Leia o que o vendedor Ricardo disse. Depois, responda às questões.

- De quantos reais é esse desconto?
_____
PROFESSOR
Resposta: De 300 reais.
- Calcule o
preço
dessa TV se ela for paga à vista.
_____
PROFESSOR
Resposta: 900 reais.

- Agora, conte aos colegas e ao professor como você pensou para responder aos itens anteriores.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Os estudantes devem entender que a porcentagem de um todo corresponde a uma fração desse todo, com denominador 100. Por exemplo, calcular 25% de 200 reais (ou de de 200 reais) significa que se deseja saber quantos reais se obtêm tomando 25 reais em cada 100 reais. Como “25 em 100” equivale a “1 em 4”, pode-se calcular de 200, ou seja: 200 ÷ 4 = 50. Portanto, 25% de 200 = 50.
Atividade 4
Nesta atividade, é mostrado o raciocínio empregado no cálculo de porcentagens de uma quantia (300 reais). Nesta situação, 10% significam 10 reais em cada 100 reais; por isso, há uma cédula de 10 reais em correspondência a cada 100 reais, de modo que, para 300 reais, haverá três cédulas de 10 reais, ou seja, 30 reais.
Para calcular 20% do prêmio, os estudantes podem raciocinar de forma similar, ou seja, 20 reais em cada 100 reais; como temos 300 reais, basta calcular 20 reais mais 20 reais mais 20 reais, obtendo o total de 60 reais.
Podemos usar o mesmo raciocínio do enunciado da atividade para o cálculo da fração de uma quantidade. No caso, para calcular de 300, dividem-se 300 em 100 partes iguais: 300 ÷ 100 = 3; depois, efetua-se a multiplicação 10 × 3 = 30.
Atividade 5
Os estudantes devem perceber que 25% é a metade de 50%. Então, se 50% de um valor corresponde à metade desse valor, 25% corresponde à metade da metade, ou seja, do valor. Peça, então, que respondam às mesmas questões propostas, mas considerando o valor de 1.200 reais para a mercadoria. Nesse caso, o desconto seria de 300 reais, e o preço à vista, 900 reais.
BNCC em foco:
EF05MA06, EF05MA08; competências específicas 2, 3 e 6
MP202

- Calcule o valor do desconto em cada situação e represente-o, pintando a barra. Depois, responda às questões.

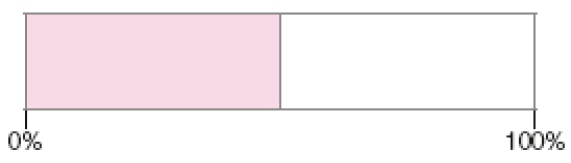
- Bruna comprou a impressora à vista.
De quantos reais foi o desconto? _____
PROFESSOR
Resposta: R$ 250,00 - Qual foi o valor pago pela impressora?
_____
PROFESSOR
Resposta: R$ 250,00


- Filomena comprou a máquina de lavar com desconto.
De quantos reais foi o desconto? _____
PROFESSOR
Resposta: R$ 700,00 - Quanto ela pagou pela máquina de lavar?
_____
PROFESSOR
Resposta: R$ 2.100,00c)

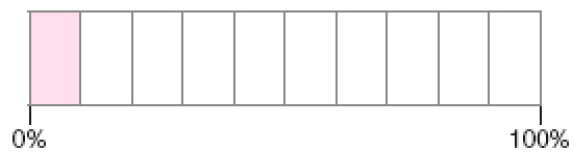
- Penélope comprou a blusa com desconto.
De quantos reais foi o desconto? _____
PROFESSOR
Resposta: R$ 6,00 - Quanto ela pagou pela blusa?
_____
PROFESSOR
Resposta: R$ 54,00
MANUAL DO PROFESSOR
Atividade 6
Nesta atividade, os estudantes poderão utilizar as barras, já divididas em cada situação, como apoio para calcular os descontos e os valores pagos em cada produto. É importante eles perceberem que a barra completa representa 100% (o valor total de cada produto) e que a quantidade de partes em que a barra foi dividida está de acordo com a porcentagem de desconto.
No item a, o desconto é de 50%; portanto, a barra foi dividida em duas partes iguais (50% + 50% = 100%), sabendo que o valor total é de 500 reais, basta calcular a metade (50%) para descobrir o desconto (parte pintada da barra: 250 reais) e o valor pago (parte em branco da barra: 250 reais).
Já no item b, a porcentagem de desconto é de 25%; portanto, a barra está dividida em quatro partes iguais (25% + 25% + 25% + 25% = 100%). O mesmo procedimento pode ser feito: utilizar o valor total e dividi-lo em quatro partes para identificar o valor do desconto (uma parte pintada) e o valor pago (as demais 3 partes em branco). No caso dos 25%, os estudantes ainda poderão estabelecer a relação de metade da metade do valor para calcular o desconto, já que 50 é metade de 100, e 25 é metade de 50.
E no item c, temos um desconto de 10%; motivo pelo qual a barra foi dividida em 10 partes iguais (10% + 10% + 10% + 10% + 10% + 10% + 10% + 10% + 10% + 10% = 100%). Nesse caso, o valor total pode ser dividido por 10 para descobrir o valor do desconto (uma parte pintada) e o valor pago (as outras 9 partes em branco).
BNCC em foco:
EF05MA06, EF05MA08; competências específicas 2, 3 e 6
MP203


- Murilo recebe mesada de seus pais. Da quantia recebida, ele gasta 60% na cantina da escola, 15% com a assinatura de um jogo on-line, 15% com despesas diversas e o restante, 10 reais, ele guarda em um cofrinho.

- Agora, em dupla, responda às questões.
- Qual é a porcentagem da mesada que Murilo guarda no cofrinho?
_____
PROFESSOR
Resposta: 10%
- Que quantia Murilo recebe de seus pais mensalmente?
_____
PROFESSOR
Resposta: 100 reais.
- Quantos reais Murilo
usa
na cantina da escola?
_____
PROFESSOR
Resposta: 60 reais.

- Em um teste com 20 questões, Eduarda respondeu corretamente do total.
- Que porcentagem representa essa fração? Escreva ou desenhe como você pensou.
_____
PROFESSOR
Resposta: 75%
- Que porcentagem representa essa fração? Escreva ou desenhe como você pensou.
_____
PROFESSOR
Exemplo de resposta: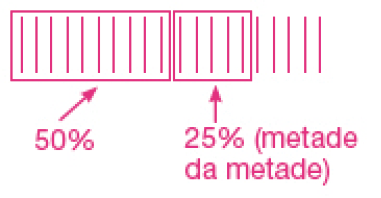
Boxe complementar:
Desafio
Dalva quer calcular 25% de 1120 com sua calculadora, mas as teclas  ,
,  e
e  estão quebradas.
estão quebradas.
CRÉDITO: ADILSON SECCO

Desenhe as teclas que você apertaria para saber o resultado desse cálculo.
PROFESSOR
Exemplos de desenho: ou
ou 
Qual é o resultado do cálculo? _____
PROFESSOR
Resposta: 280Fim do complemento.
MANUAL DO PROFESSOR
Atividade 7
Verifique as estratégias utilizadas pelos estudantes para calcularem o valor da mesada e dos demais itens. Este problema pode trazer alguma dificuldade, já que o valor total não é dado, como na maioria das situações anteriores. Uma possibilidade é calcular todas as porcentagens apresentadas (60% + 15% + 15% = 90%) e verificar qual é a porcentagem restante (10%) que corresponde aos 10 reais, facilitando o cálculo do valor total (100 reais) e do valor utilizado na cantina da escola.
Atividade 8
Observe as estratégias utilizadas pelos estudantes na resolução. Depois, peça que as compartilhem com os colegas.
Desafio
Deixe os estudantes pensarem sobre esse desafio e compartilharem as estratégias. Depois, verifique se perceberam que 25% de uma quantidade equivale a dela, ou seja, basta dividir a quantidade por para determinar 25% dela.
BNCC em foco:
EF05MA06, EF05MA08; competência geral 2; competências específicas 2, 3 e 6
MP204
Compreender problemas
Para resolver
Problema 1
Heloísa adora fazer tortas. Ela sempre faz as tortas em forma circular, com um palito que marca seu centro. Para dividi-las em pedaços, que não precisam ser do mesmo tamanho, Heloísa sempre faz cortes em linha reta passando pelo centro da torta.

- Quantos cortes, passando pelo centro, Heloísa precisa fazer em uma
torta
para
obter
12 pedaços?
_____
PROFESSOR
Resposta: 6 cortes.
Problema 2
Observe a sequência de figuras abaixo.
Figura 1
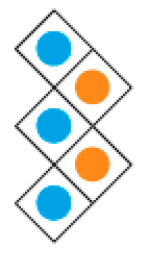
Figura 2

Figura 3
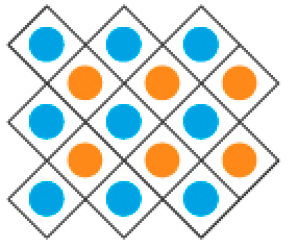
Figura 4
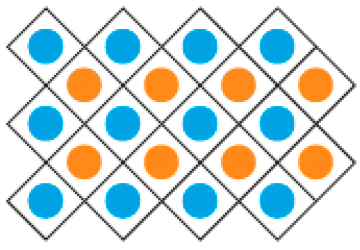
- Qual é o padrão (figura que se repete) dessa sequência?
PROFESSOR
Exemplos de resposta:PROFESSOR

PROFESSOR
• azulPROFESSOR
• laranja ou figura 1.
- Seguindo esse padrão, quantas
bolinhas
laranja haveria na figura que tivesse 18
bolinhas
azuis?
_____
PROFESSOR
Resposta: 12 bolinhas laranja.
- E quantas
bolinhas
azuis haveria na figura que tivesse 16
bolinhas
laranja?
_____
PROFESSOR
Resposta: 24 bolinhas azuis.
MANUAL DO PROFESSOR
Objetivos
• Resolver problemas de multiplicação envolvendo números racionais.
• Resolver problemas que envolvam a noção de proporcionalidade entre duas grandezas.
• Interpretar dados apresentados em tabela.
Os problemas apresentados nestas páginas exploram as regularidades e os padrões em sequências de figuras, ajudando a estruturar uma parte essencial do pensamento matemático: a habilidade em descobrir, em uma dada sequência, o padrão (o modelo) que se repete e que possibilita reconhecer outros elementos na sequência.
Para resolver Problema 1
Considerando as três primeiras situações de corte da torta, os estudantes podem inferir que o padrão deve ser o acréscimo de 2 novos pedaços a cada corte efetuado. A condição de cada corte ter de passar pelo centro da torta facilita, para essa faixa etária, o reconhecimento do padrão encontrado na situação.
Problema 2
Para resolver as questões propostas neste problema, é interessante os estudantes conversarem e trocarem ideias que permitam a descoberta do padrão envolvido na sequência de figuras. Nesse caso, um quadro como o mostrado a seguir ajuda a perceber as regularidades numéricas.
Tabela: equivalente textual a seguir.
|
Número da figura |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Número de bolinhas azuis |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
|
Número de bolinhas laranja |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
BNCC em foco:
EF05MA08, EF05MA12; competência geral 2; competências específicas 2, 3 e 6
MP205
Para refletir


- Compare sua solução do Problema 1 com a de um colega. Algum de vocês usou desenhos para resolvê-lo?
PROFESSOR
Resposta pessoal.
- Luciano usou um quadro para buscar uma regularidade e chegar à solução do Problema 1.
Tabela: equivalente textual a seguir.
|
Número de cortes |
Número de pedaços |
|---|---|
|
1 |
2 |
|
2 |
4 |
|
3 |
6 |
|
4 |
8 |
|
5 |
10 |
PROFESSOR
Exemplos de resposta: “Sim; o número de pedaços obtidos é igual ao dobro do número de cortes feitos na torta.”. Ou: “Sim; a cada corte a mais que se faz, o número de pedaços aumenta em dois.”.

- Na sua opinião, esse quadro ajuda a resolver o problema? Você percebe alguma regularidade que permita resolvê-lo?
- Veja como Karine pretende resolver o item b do Problema 2.

Figura 1
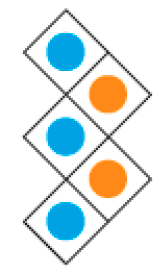
- Na sua opinião, que operação Karine
deve
fazer para chegar ao
número
de
bolinhas
laranja?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes respondam: 6 × 2 = 12 ou 2 + 2 + 2 + 2 + 2 + 2 = 12. Fim da observação.
MANUAL DO PROFESSOR
Para refletir
Atividade 1
Espera-se que, ao trocar ideias sobre diferentes possibilidades de resolução, os estudantes observem que o desenho pode ser um bom recurso para resolver esse tipo de problema. Entretanto, se há a necessidade de fazer muitos desenhos, é interessante buscar outra estratégia para a resolução, como encontrar uma regularidade.
Atividade 2
Ao apresentar um quadro que organiza os números envolvidos na sequência de cortes da torta, esta atividade dá aos estudantes a oportunidade de perceberem a utilidade desse recurso para a resolução do problema. Se preciso, ajude-os na leitura do quadro, para que identifiquem a regularidade necessária para a descoberta do padrão da sequência de figuras. Oriente-os a observarem como ocorre a variação dos números em cada coluna do quadro. Espera-se que eles notem que, enquanto na coluna da esquerda o número de cortes aumenta em 1 unidade, o número correspondente de pedaços de torta, na coluna da direita, aumenta em 2 unidades. Eles devem deduzir que o número de pedaços de torta é igual ao dobro do número de cortes realizados passando pelo centro da torta.
Esse padrão permite determinar o número de pedaços de torta para números maiores de cortes sem a necessidade de desenhar as figuras subsequentes e contar os pedaços resultantes. Assim, para saber quantos pedaços serão obtidos por 11 cortes que passam pelo centro da torta, basta calcular: 2 × 11 = 22; ou seja, serão obtidos 22 pedaços de torta. Aplicando o raciocínio inverso, determinamos quantos cortes serão necessários para obter, por exemplo, 18 pedaços de torta: 18 ÷ 2 = 9; ou seja, serão necessários 9 cortes que passem pelo centro da torta para obter 18 pedaços.
BNCC em foco:
EF05MA08, EF05MA12; competência geral 2; competências específicas 2, 3 e 6
Atividade 3
Verifique se os estudantes compreendem o raciocínio de Karine. Depois de validar as respostas, registre na lousa as operações sugeridas para que Karine obtivesse o total de bolinhas laranja.
MP206
A matemática me ajuda a ser
...uma pessoa consciente sobre a extinção das espécies
Há cerca de 8,7 milhões de espécies na Terra, entre animais, plantas e outros seres vivos. As espécies ameaçadas de extinção sofrem com os problemas ambientais e com a ação predatória do ser humano.
Espécie ameaçada
É uma população que está desaparecendo a ponto de entrar em extinção. A União Internacional para a Conservação da Natureza e dos Recursos Naturais (IUCN) divulgou um documento, chamado Lista Vermelha, que mostra a situação de milhares de espécies. Até 2019, a lista englobava mais de 105 mil tipos de seres vivos.
Disponível em: http://fdnc.io/eUu. Acesso em: 5 mar. 2021.

Fonte dos dados: Lista das espécies da fauna brasileira ameaçadas de extinção. Disponível em: http://fdnc.io/3TQ. Acesso em: 16 mar. 2021.
LEGENDA: Lista brasileira ‒ A lista das espécies da fauna brasileira ameaçadas de extinção mais recente é de 2014 e tem 1.173 espécies de animais. FIM DA LEGENDA.
MANUAL DO PROFESSOR
Objetivos
- Desenvolver a noção de porcentagem e sua relação com a fração centesimal.
- Associar as representações 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens.
- Interpretar dados apresentados em texto.
Explore a leitura do infográfico, destacando que não há uma sequência rígida de leitura, uma vez que as informações são apresentadas em cartas, que podem ser lidas na ordem desejada.
Os quatro animais apresentados correm risco de serem extintos, mas estão categorizados. Para isso, chame a atenção dos estudantes para o ícone aplicado no canto superior esquerdo de cada carta e a “legenda” destacada na carta “Riscos de extinção”.
Explore a leitura de cada mapa, indicando a região onde cada animal pode ser encontrado.
No site do ICMBio, Instituto Chico Mendes de Conservação da Biodiversidade (disponível em: http://fdnc.io/3TQ. Acesso em: 1º abr.
2021.), está publicada a lista de espécies da fauna brasileira ameaçadas de extinção, atualizada em 2014.
É possível realizar uma busca por espécie, e para cada espécie há informações sobre a classificação taxonômica, categoria do risco de extinção, critérios, referências bibliográficas e resumo das justificativas que indicaram o risco de extinção, além de outras informações pertinentes.
BNCC em foco:
EF05MA24; competências gerais 1, 7 e 10; competências específicas 2, 3 e 8
MP207
Tome nota
- Qual é a população estimada de pandas-vermelhos na Índia?
_____
PROFESSOR
Resposta: 5.000 pandas-vermelhos.
- Escreva por extenso o
número
que representa o total de espécies na Terra.
_____
PROFESSOR
Resposta: Oito milhões e setecentos mil.
Reflita
- Reescreva a frase usando porcentagem.
Quase das espécies catalogadas na lista sofre algum tipo de ameaça de extinção.
_____
PROFESSOR
Resposta: Quase 25% das espécies catalogadas na lista sofrem algum tipo de ameaça de extinção.

- Discuta com seus colegas o significado desse número.
PROFESSOR
Resposta pessoal.
- Pesquise dados sobre outro animal que sofre risco de extinção. Faça uma lista e, depois, conte para os colegas e o professor.
PROFESSOR
Resposta pessoal.
- Discuta com seus colegas o significado desse número.
MANUAL DO PROFESSOR
Tome nota
Atividade 1
Para calcular de 20 mil pandas-vermelhos, os estudantes podem dividir o total de pandas-vermelhos livres na natureza por 4, obtendo 5.000 pandas-vermelhos, localizados na Índia.
Amplie a atividade e proponha uma reflexão sobre a importância e o significado de alguns animais viverem em cativeiro.
Atividade 2
Sugira aos estudantes que releiam o texto e encontrem a informação sobre a quantidade total de espécies na Terra.
Reflita Atividade 1
Espera-se que os estudantes percebam que, das espécies catalogadas na lista, quase 25% sofrem algum tipo de ameaça de extinção.
Atividade 2
Leve para a sala de aula outros textos sobre animais que também estejam em extinção ou uma lista dos principais animais brasileiros que estão em extinção.
BNCC em foco:
EF05MA03, EF05MA06, EF05MA24; competências gerais 1, 7 e 10; competências específicas 2, 3 e 8
Sugestão de trabalho interdisciplinar
Aproveite a atividade 1 do Reflita para fazer um trabalho em conjunto com Ciências. Promova uma discussão com os estudantes a respeito do aumento de espécies de animais em extinção no mundo, decorrente de muitos problemas ambientais bem como da interferência do ser humano na natureza. Pergunte: “O que nós podemos fazer para evitar que mais animais entrem em extinção?”.
MP208
Compreender informações
Cálculo da probabilidade de um evento ocorrer
- Bárbara está brincando com um jogo de trilha e faltam poucas casas para ela atingir o FIM e vencer. Para andar com seu pino, ela lança um dado comum em forma de cubo e anda tantas casas quanto for o
número
que aparece na face que fica voltada para cima.
- Quais afirmações são corretas?
_____
PROFESSOR
Resposta: As duas afirmações são corretas.
- Quais afirmações são corretas?

A probabilidade de sair o número 3 na face que fica para cima no dado é , porque existe 1 possibilidade de sair o número 3 dentre as 6 possibilidades que existem ao todo.
A probabilidade de sair um número par na face que fica para cima no dado é , porque existem 3 possibilidades de sair um número par dentre as 6 possibilidades que existem ao todo.
- Bárbara também pode usar um dado com todas as faces triangulares iguais (numeradas de 1 a 4). Nesse caso, ela anda com seu pino o
número
da face que fica voltada para baixo. Em qual desses dois dados a probabilidade de sair o
número
3 é maior? E de sair
número
par?
_____
PROFESSOR
Resposta: A probabilidade de sair número 3 é maior no dado com faces triangulares, já que nele temos 1 chance em 4. Já a probabilidade de sair número par é a mesma nos dois dados: 1 em 2, pois no dado cúbico temos 3 em 6 e no dado piramidal temos 2 em 4 (ou seja, os dois casos correspondem à metade).
- Veja no tabuleiro abaixo a posição do pino vermelho, de Bárbara. Quantas casas ela precisa andar com seu pino para vencer essa rodada?
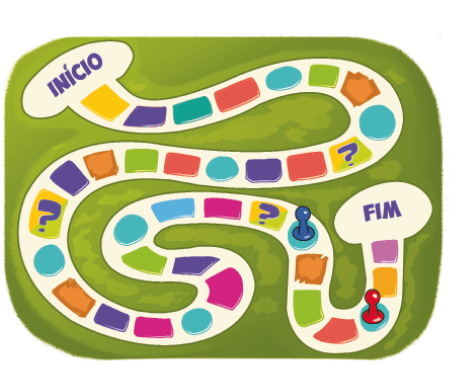
____
PROFESSOR
Resposta: Ela precisa andar 3 casas.
- Qual dado ela
deve
escolher para
obter
3
nessa
rodada? Por quê?
_____
PROFESSOR
Atenção professor: Espera-se que o estudante perceba que ela deve escolher o dado piramidal, já que nele a probabilidade de sair 3 é maior. Fim da observação.
MANUAL DO PROFESSOR
Objetivo
- Determinar a probabilidade de ocorrência de um evento em um experimento aleatório em que cada resultado possível tem a mesma chance de ocorrer (espaço amostral equiprovável).
Nestas páginas, buscamos dar significado à ideia de probabilidade e incentivar os estudantes a avaliarem e expressarem matematicamente a probabilidade de ocorrência de determinado evento.
Atividade 1
Se possível, providencie dados para que os estudantes possam manuseá-los e verificar o número de faces de cada um e os possíveis resultados no lançamento de cada um deles.
No item a, ressalte que, no lançamento de qualquer um dos dados, cada um dos resultados possíveis tem a mesma chance de ocorrer (no dado cúbico é de 1 em 6; no dado piramidal, de 1 em 4). Comente que, nesse caso, a medida da chance de ocorrência de um evento A é dada pela probabilidade de o evento A ocorrer, P (A), e que corresponde a uma fração cujo numerador é o número de resultados favoráveis ao evento A, e o denominador é o número de resultados possíveis.
Mostre aos estudantes que, por exemplo, se o evento A for “sair número par” no lançamento com o dado cúbico, o número de casos favoráveis será 3 (ou seja, as faces pares: 2, 4 e 6), e o número de resultados possíveis será 6 (pois são 6 faces ao todo). Daí:
P (A) = = = 50%
No item b, esclareça que, apesar de a probabilidade de sair o número 3 ser maior no dado piramidal, isso não significa que o número 3 sairá de fato.
Pesquisas na área da Educação Matemática indicam que o estudo de probabilidade pode ser desenvolvido com estudantes do Ensino Fundamental, desde que realizado em contextos apropriados à faixa etária e sem o uso de fórmulas.
É importante considerar que o cálculo da probabilidade (ou da medida de chance) de ocorrência de um evento não é uma noção intuitiva para os estudantes e que mesmo a realização de experimentos pode levar a falsas concepções.
Pergunte: “Em qual dado a probabilidade de obter o número 6 é maior?”. Espera-se que respondam que é no dado cúbico, pois não há face 6 no outro dado.
No item c, é possível verificar que faltam 3 casas para o pino de Bárbara atingir a casa FIM. Portanto, com o dado piramidal é maior a probabilidade de sair o 3.
BNCC em foco na dupla de páginas:
EF05MA23; competência geral 2; competências específicas 3, 4 e 6
MP209
- Dez crianças estão concorrendo ao sorteio de um livro. Entre elas há meninos e meninas com idades variadas. O nome de cada criança está escrito em um papel, colocado em uma urna da qual será sorteado um nome.
Observe as tabelas e responda.
Crianças concorrendo
Tabela: equivalente textual a seguir.
|
Meninos |
Meninas |
|---|---|
|
6 |
4 |
Fonte: Organizador do sorteio (5 abr. 2023).
Crianças concorrendo
Tabela: equivalente textual a seguir.
|
Até 8 anos |
Mais de 8 anos |
|---|---|
|
7 |
3 |
Fonte: Organizador do sorteio (5 abr. 2023).
- Qual destas frases está errada? Marque com um X .
6 das 10 crianças são meninos.
7 em 10 crianças têm até 8 anos.
3 das 7 crianças têm mais de 8 anos.
PROFESSOR
Resposta correta: 3 das 7 crianças têm mais de 8 anos.- Para fazer um gráfico de setores, a figura abaixo foi repartida em 10 partes iguais. Cada uma dessas partes representa uma das crianças que concorrem ao livro. Complete a legenda.
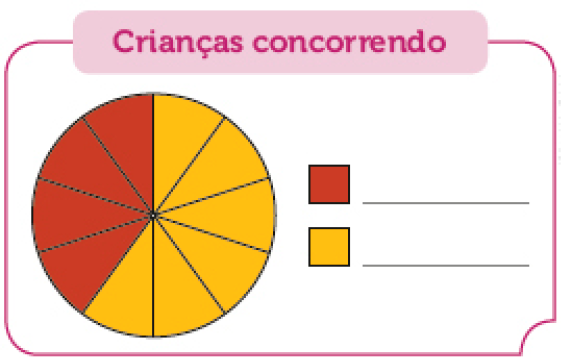
Fonte: Organizador do sorteio (5 abr. 2023).
PROFESSOR
Resposta: vermelho - MeninasPROFESSOR
amarelo - Meninos- Há maior chance de ser sorteado um menino ou uma menina? Justifique sua resposta.
_____
PROFESSOR
Resposta: Um menino, pois há mais meninos do que meninas.
- Qual é a probabilidade de ser sorteado um menino? E de ser sorteada uma menina?
_____
PROFESSOR
Resposta: menino: ; menina:
- Qual é a probabilidade de ser sorteada uma criança com mais de 8 anos?
_____
PROFESSOR
Resposta:- Você usou o gráfico de setores acima para responder a essa questão? Por quê?
PROFESSOR
Atenção professor: Espera-se que o estudante perceba que, com o gráfico dado, não é possível responder a essa questão, pois não há informações sobre a idade das crianças. Ele precisa usar a segunda tabela dada acima. Fim da observação.

- Como
deve
ser o gráfico de setores relativo ao
número
de crianças que concorrem ao livro de acordo com a idade delas? Converse com um
colega
sobre esse gráfico e
elabore
uma legenda para ele.
PROFESSOR
Resposta: O gráfico deve ser um círculo repartido em 10 partes iguais, com 7 dessas partes pintadas de uma mesma cor (por exemplo, azul) e as outras 3 partes pintadas de outra cor (por exemplo, verde). Desse modo, uma possível legenda é dada a seguir. Azul: crianças com até 8 anos; Verde: crianças com mais de 8 anos.PROFESSOR
Respostas variáveis.
- Você usou o gráfico de setores acima para responder a essa questão? Por quê?
MANUAL DO PROFESSOR
Atividade 2
Os estudantes precisam observar que, para calcular a probabilidade de um menino ser sorteado, é preciso saber a quantidade de meninos (6) e o total de crianças (10) e representar a relação entre essas quantidades (“6 em 10”) na forma de fração , ou na forma de porcentagem (60%). Mais adiante, eles verão a forma decimal (0,6). Aplicando o mesmo raciocínio, descobrirão a probabilidade de ser sorteada:
- uma menina;
- uma criança com até 8 anos de idade;
- uma criança com mais de 8 anos de idade.
Explore a atividade perguntando: “Se chegasse mais uma menina com menos de 8 anos de idade, o que aconteceria com as probabilidades dos itens d e e ?”. Espera-se que percebam que a probabilidade de um menino ser sorteado passaria a ser de e que a probabilidade de uma menina ser sorteada seria de , enquanto a probabilidade de ser sorteada uma criança com mais de 8 anos de idade seria de .
Nessa atividade, não há uma percepção natural de que, se o número de meninos é maior que o de meninas, a probabilidade de um menino ser sorteado é maior. Se, ao realizar o experimento, obtiverem resultados iguais, muitos estudantes podem acreditar que a quantidade de meninos e meninas não interfere no resultado, pois ainda cultivam a falsa concepção de que a probabilidade depende da sorte.
MP210
O que você aprendeu
- Escreva uma fração para representar a parte pintada de cada figura.
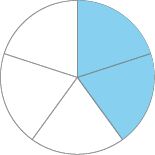
_____
PROFESSOR
Resposta:
_____
PROFESSOR
Resposta: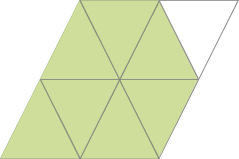
_____
PROFESSOR
Resposta: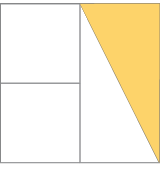
_____
PROFESSOR
Resposta:- Escreva dois números naturais entre os quais está cada fração.
-
_____
< <
_____
PROFESSOR
Exemplo de respostas: 1, 2.
-
_____
< <
_____
PROFESSOR
Exemplo de respostas: 3, 4.
-
_____
< <
_____
PROFESSOR
Exemplo de respostas: 2, 3.
-
_____
< <
_____
PROFESSOR
Exemplo de respostas: 5, 6.
-
_____
< <
_____
- Théo precisa comprar 1 quilograma de carne moída para fazer quibes. Em cada bandeja à venda no supermercado, há quilograma de carne. Quantas dessas bandejas Théo terá de comprar para fazer os quibes?
_____
PROFESSOR
Resposta: 3 bandejas.

- Complete.
Tabela: equivalente textual a seguir.
|
Porcentagem |
19% |
38% |
_____ |
_____ |
|---|---|---|---|---|
|
Leitura |
_____ |
38 por cento |
76 por cento |
_____ |
|
Fração |
|
_____ |
|
_____ |
|
Significado |
19 em cada 100 |
_____ |
_____ |
5 em cada 100 |
PROFESSOR
Resposta: 76%; 5%; 19 por cento; 5 por cento; ; ; 38 em cada 100; 76 em cada 100.MANUAL DO PROFESSOR
Objetivo
- Retomar os conceitos estudados.
A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Reforce que a parte pintada é a parte não branca.
Chame a atenção dos estudantes para a figura do item d. Para associar uma fração a uma parte destacada de uma figura, deve-se considerar a que área do todo (figura) essa parte corresponde, e não à forma como foi dividida. Nessa figura, a metade da esquerda está dividida em duas partes retangulares de mesma área, e a metade da direita, em duas partes triangulares de mesma área. Portanto, cada uma das quatro partes corresponde a da figura.
Aproveite para pedir a eles que escrevam como se lê cada uma das frações. Amplie a atividade solicitando-lhes que escrevam as frações que representam a parte não pintada das figuras.
Atividade 2
Os estudantes devem observar que é possível transformar as frações na forma mista, o que facilitará a comparação com os números naturais.
Por exemplo, no item a, temos:
= 1 + = 1
Então, essa fração encontra-se entre os números naturais 1 e 2.
Proponha aos estudantes o seguinte desafio: “A massa de um tijolo é igual a 1 quilograma mais a massa de metade do tijolo. Qual é a massa do tijolo inteiro?”. Espera-se que cheguem à resposta 2 quilogramas, pois, como a massa de um tijolo inteiro é igual à massa de duas metades do tijolo, podemos dizer que a massa de duas metades do tijolo é igual a 1 quilograma mais a massa de metade do tijolo. Logo, a massa de metade do tijolo é 1 quilograma, e a massa do tijolo inteiro é 2 quilogramas.
BNCC em foco:
EF05MA03, EF05MA05, EF05MA06, EF05MA08
Atividade 3
Os estudantes podem justificar a resposta por meio de esquemas, números ou palavras.
Uma justificativa possível é: “1 é o mesmo que 1 inteiro mais uma metade. Como 1 inteiro é o mesmo que duas metades, temos que 1 é o mesmo que três metades. Então, como cada bandeja tem quilograma de carne, serão necessárias três bandejas”.
Atividade 4
É interessante ampliar o quadro e deixá-lo exposto como apoio a outras atividades sobre o tema.
MP211
- Pedro quer comprar uma bola. Ele economizou em um mês o equivalente a do
preço
da bola e, no mês seguinte, a do preço. Que fração do
preço
da bola ainda falta para Pedro comprá-la?
_____
PROFESSOR
Resposta:

- Marque com um X os quadros com cálculo correto.
a) 3 × = 2
b) 10 × = 2
c) 5 × =
d) 6 × =
e) 4 × =
PROFESSOR
Respostas corretas: a, c e d.- Qual é a única frase verdadeira? Marque com um
X
.
- ( ) 1% de 400 pessoas é o mesmo que 8 pessoas.
- ( ) 3% de 500 figurinhas são 15 figurinhas.
- ( ) 10% de 200 reais são 10 reais.
- ( ) Uma camiseta que custava 100 reais teve um desconto de 15% e passou a custar 115 reais.
PROFESSOR
Resposta correta: b
- Marina comprou um armário. Ela vai pagá-lo em 5 prestações iguais. Que porcentagem do valor total representa cada prestação?
_____
PROFESSOR
Resposta: 20%
Autoavaliação

- Consigo
obter
frações equivalentes a uma fração dada?

- Compreendo a
ideia
de porcentagem?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 5
Peça aos estudantes que escrevam uma expressão que represente a situação e, depois, tentem resolvê-la utilizando o cálculo mental, já que as frações apresentam o mesmo denominador. Exemplos de expressões:
- - ou - ( + )
Atividade 6
Observe como os estudantes resolvem as multiplicações propostas e, depois de validar as respostas, compartilhe as estratégias usadas na resolução.
Atividade 7
Sugira aos estudantes a reescrita das frases para torná-las verdadeiras.
Por exemplo:
- 1% de 400 pessoas é o mesmo que 4 pessoas.
- 10% de 200 reais são 20 reais.
- Uma camiseta que custava 100 reais teve 15% de desconto, passando a custar 85 reais.
Atividade 8
Os estudantes podem resolver essa questão fazendo um desenho que represente o todo (o inteiro) repartido em 5 prestações iguais. Desse modo, eles podem perceber que cada prestação representa um quinto do valor total. Escrevendo a fração um quinto como uma fração equivalente de denominador 100, encontrarão 20%.
BNCC em foco:
EF05MA06, EF05MA07, EF05MA08
Autoavaliação
Nesta Unidade, os estudantes entraram em contato com diversos conceitos relacionados às representações fracionárias. A primeira questão foca na ideia de equivalência, importante para que possam operar com frações. Assim, peça que avaliem quanto compreenderam as relações de equivalência a partir das atividades realizadas.
A segunda questão traz a ideia de porcentagem, muito utilizada no cotidiano. Os estudantes deverão avaliar se esse conceito já está claro para que possam ampliar os conhecimentos sobre o tema ou se ainda será necessário retomá-lo.
MP212
Comentários para o professor:
Conclusão da Unidade 5
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Identifica e representa frações próprias, aparentes e impróprias associando-as ao resultado de uma divisão ou à ideia de parte de um todo? |
_____ |
_____ |
|
Compara e ordena frações localizando-as na reta numérica? |
_____ |
_____ |
|
Identifica frações equivalentes? |
_____ |
_____ |
|
Associa porcentagem à fração centesimal? |
_____ |
_____ |
|
Associa as representações 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro? |
_____ |
_____ |
|
Resolve e elabora problemas de adição e subtração com números racionais? |
_____ |
_____ |
|
Resolve e elabora problemas de multiplicação com frações? |
_____ |
|
|
Resolve problemas que envolvam a variação de proporcionalidade direta entre duas grandezas? |
_____ |
_____ |
|
Determina a probabilidade de ocorrência de eventos em um experimento aleatório? |
_____ |
_____ |
|
Interpreta e aplica dados apresentados em textos e tabelas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |