MP213

Comentários para o professor:

Introdução da Unidade 6

A Unidade Temática Grandezas e medidas ocorre em contextos o mais variados possível. Porém, pode-se dizer que uma loja de materiais de construção é um universo apropriado para tratar dessa Unidade. Assim, a abertura favorece abordagens múltiplas dos conceitos a serem vistos ao longo da Unidade, o que propicia ao professor um diagnóstico dos conhecimentos e das dificuldades dos estudantes.

Os conhecimentos abordados referem-se a Grandezas e medidas. No entanto, como será observado, as conexões com outras Unidades Temáticas, entre elas, Números e Geometria, estão presentes nas diversas atividades propostas envolvendo medidas.

Assim, os conhecimentos construídos sobre frações permitem a resolução e a elaboração de problemas envolvendo Grandezas e medidas, como comprimento, área, massa, tempo, temperatura, com recurso a transformações entre unidades de medida mais usuais. Já as conexões entre Grandezas e medidas e Geometria se dão por meio de atividades que promovem o reconhecimento do volume como grandeza associada a figuras geométricas não planas. Além disso, conhecimentos apropriados pelos estudantes ao longo do 4º ano relativos a medidas e estimativas de comprimento, massa e capacidade, com o uso de unidades de medidas padronizadas e mais usuais, favorecem a construção de novos conhecimentos. Da mesma maneira, esses novos conhecimentos serão alicerces para outros a serem construídos durante o 6º ano, relativos a resolução e elaboração de problemas envolvendo as mesmas grandezas, além de capacidade e volume, sem uso de fórmulas, inseridos em contextos originários de situações reais relacionadas, também, às outras áreas do conhecimento.

Em relação aos conhecimentos relacionados a medidas de área, destacam-se atividades envolvendo relações entre perímetros e áreas de figuras geométricas, possibilitando aos estudantes concluírem, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e vice-versa.

Os estudos acerca da medida, comparação e estimativa de área de figuras planas em malha quadriculada, com o reconhecimento de que duas figuras com formas diferentes podem ter a mesma medida de área, desenvolvidos no 4º ano, são aportes para a compreensão das relações entre área e perímetro. Além disso, tal compreensão permitirá aos estudantes analisarem e descreverem mudanças que ocorrem no perímetro e na área de um quadrado ao ampliar ou reduzir igualmente as medidas de seus lados, buscando o entendimento de que o perímetro é proporcional à medida do lado, o que, entretanto, não ocorre com a área, conhecimento a ser desenvolvido no 6º ano.

Nesta Unidade também estão presentes atividades envolvendo Probabilidade e estatística, que se caracterizam pela possibilidade de ampliação dos conhecimentos desenvolvidos ao longo do 4º ano. Nesse sentido, pretende-se superar os conhecimentos acerca da análise de dados apresentados em tabelas e gráficos, passando para a interpretação desses mesmos dados, neste momento, apresentados por meio de gráficos de linhas e de setores. Esses conhecimentos devem favorecer a interpretação e a resolução de situações envolvendo dados de pesquisas sobre contextos distintos e a redação de textos para sintetizar conclusões, previstos para o 6º ano.

Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletiva. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.

Competências específicas favorecidas

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

MP214

UNIDADE 6. Grandezas e medidas

Imagem: Ilustração. À esquerda, Roberto e Beatriz estão sorrindo na frente de um balcão e ao lado deles há uma mulher com cabelo preso. (Resposta: Roberto e Beatriz estão aqui). No balcão há cordas, fitas e caixas. Acima do balcão há uma caixa de vidro e uma etiqueta com as medidas: (60 x 30 x 30) cm. Atrás do balcão há pisos quadrados e uma estante com vários produtos de construção. Acima, um relógio com o ponteiro pequeno entre os números quatro e cinco e o ponteiro grande no número nove. (Resposta: O relógio está marcando 16:45). No centro há latas de tinta empilhadas e ao lado, pisos expostos com uma placa e a informação: PROMOÇÃO DE PISOS. Ao lado, Vanessa e um senhor observam os pisos. (Reposta: Vanessa está aqui). Atrás deles, Marcos e um homem entram na loja. (Resposta: Marcos está aqui). Em seguida, um caminhão com sacas empilhadas está parado na frente da loja e ao lado há um relógio digital de rua com a informação: MATERIAL DE CONSTRUÇÃO É AQUI - 26 ºC. Ao fundo, casas e prédios. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos da Unidade

Resolver problemas que envolvam a noção de proporcionalidade entre duas grandezas.
Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade.
Desenvolver a noção de perímetro, medindo o contorno de figuras.
Concluir, por meio de investigações, que figuras de medidas de perímetro iguais podem ter medidas de área diferentes, assim como figuras que têm a mesma medida de área podem ter medidas de perímetro diferentes.
Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos.
Refletir sobre os cuidados com a audição.
Interpretar dados apresentados em textos, tabelas e gráficos.
Organizar dados coletados por meio de gráficos de setores e de linhas.
Produzir texto escrito para síntese dos resultados de uma pesquisa.
Explore os elementos que aparecem na imagem e incentive os estudantes a procurarem na cena as personagens Marcos, Beatriz, Vanessa e Roberto.

BNCC em foco:

EF05MA08, EF05MA12, EF05MA19, EF05MA20, EF05MA21, EF05MA24, EF05MA25

MP215

Boxe complementar

Para refletir...

Qual é a medida da largura, da altura e do comprimento, em centímetro, do aquário para o qual as personagens estão olhando?

_____

PROFESSOR

Resposta: 30 cm, 30 cm e 60 cm.

Qual é a medida da capacidade, em litro, de cada lata de tinta para parede?

_____

PROFESSOR

Resposta: 20 L

Imagem: Ícone: Oral. Fim da imagem.

Como você faria para descobrir quantos sacos de cimento há no caminhão, sem contá-los um a um?

PROFESSOR

Resposta pessoal.

Fim do complemento

MANUAL DO PROFESSOR

Para refletir...

Promova uma roda de conversa com os estudantes e peça que discutam as questões propostas. Espera-se que reconheçam a altura com facilidade. Se necessário, para que identifiquem o comprimento e a largura, traga um modelo do aquário para que os estudantes o observem de variadas posições.

Em seguida, pergunte se alguém pode explicar o que é capacidade de um recipiente (quantidade máxima que o recipiente pode conter de água, de areia etc.). Verifique também se reconhecem o símbolo da unidade litro (L).

Para a terceira questão, organize os estudantes em duplas. Se julgar necessário, distribua cubinhos do Material Dourado a cada dupla e peça que façam vários empilhamentos, contando a quantidade de cubinhos utilizados em cada um desses empilhamentos.

Durante a resolução, identifique as estratégias pessoais desenvolvidas pelos estudantes. É possível que façam a contagem dos cubinhos um a um, ou utilizem a multiplicação como recurso para o cálculo, ou ainda que façam estimativas por comparações entre empilhamentos já feitos. Peça que busquem uma maneira de obter essa quantidade sem contar os cubinhos um a um.

Espera-se que os estudantes multipliquem a quantidade de sacos da largura pela quantidade do comprimento e pela quantidade da altura (4 × 6 × 7) e reconheçam que há 168 sacos no caminhão.

Peça a cada dupla que explique como chegou à resposta, discutindo as diferentes estratégias empregadas.

Para explorar a imagem, pergunte: “A loja fecha às 18 horas. Por quantos minutos ela ainda ficará aberta?” (75 minutos.).

MP216

Medidas de comprimento

Metro e centímetro

Leia o que Renata está dizendo.

Imagem: Ilustração. Renata, mulher loira com cabelo preso. Ela segura um tecido amarelo e fala: Vou costurar estas duas partes de tecido de 50 centímetros de comprimento cada uma para formar uma tira de 1 metro de comprimento. Na frente dela há uma máquina de costurar e um tecido roxo. Fim da imagem.

Quantos centímetros são necessários para formar 1 metro? _____

PROFESSOR
Resposta: 100 centímetros.

Para fazer uma faixa de 4 metros, Renata usou 5 peças de tecido de mesma medida de comprimento, e não houve sobras. Qual era o comprimento, em centímetro, de cada uma dessas peças? _____

PROFESSOR
Resposta: 80 centímetros.

Renata queria conferir se uma peça de tecido tinha 1 metro de comprimento. Para isso, usou uma régua graduada de 30 centímetros. Explique como ela pode ter feito essa medição.

PROFESSOR
Resposta pessoal.

Indicamos:

1 metro por 1 m
1 centímetro por 1 cm
1 m = 100 cm

Observe uma borracha, um caderno e um lápis como os representados abaixo. Depois, estime as medidas deles. Use a unidade de medida que julgar mais adequada.
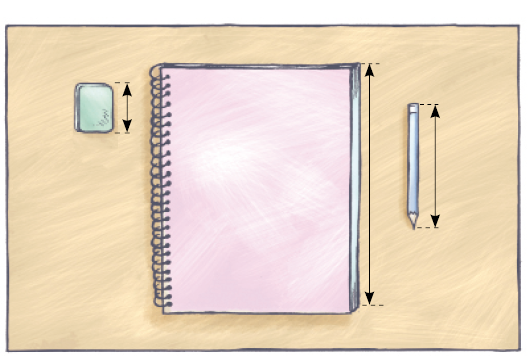
1. Borracha: _____
  
  PROFESSOR
  Exemplo de estimativas: 5 cm
1. Caderno: _____
  
  PROFESSOR
  Resposta: 5 cm
1. Lápis: _____
  
  PROFESSOR
  Resposta: 5 cm

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

Agora, com uma régua, meça os objetos que você observou e compare as medidas obtidas com as suas estimativas.

PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR

Objetivo

Resolver problemas envolvendo as medidas de comprimento: metro e centímetro.
Atividade 1

Se possível, leve para a sala de aula algumas fitas métricas e pedaços de barbante com 50 cm e 100 cm (1 m) de comprimento cada um, para que, em grupos, os estudantes reproduzam a situação da atividade usando barbante no lugar de tecido.

Mais uma vez, é possível explorar o significado dos termos envolvidos na relação entre metro e centímetro, lembrando aos estudantes que o prefixo centi indica “centésimo”, de modo que 1 cm corresponde a 1 centésimo de metro; portanto, em 1 m há 100 cm.

Exemplo de resposta para o item c: Renata pode ter feito medidas de 30 cm ao longo do tecido, seguindo a linha lateral até completar 1 m.

Atividade 2

Situações de estimativa de medidas de comprimento, como a apresentada nesta atividade, são fundamentais para a consolidação das noções de medida e distância. Os estudantes devem, primeiro, avaliar que a unidade de medida centímetro é a mais adequada às medições solicitadas e, depois, estimar os resultados de cada medição, confirmando-os por meio de medições com régua. Peça que, antes das medições com régua, comparem as estimativas feitas para cada objeto. Assim, terão a oportunidade de discutir o que é possível ou impossível, muito provável ou pouco provável.

BNCC em foco:

EF05MA19

MP217

Centímetro e milímetro

Observe a borracha de João no início e no fim de um ano escolar.

Início do ano

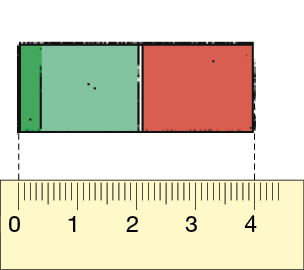
Imagem: Ilustração. Uma borracha deitada e abaixo há uma régua. A ponta esquerda da borracha está sobre o número zero e a ponta direita sobre o número quatro. Fim da imagem.

Fim do ano

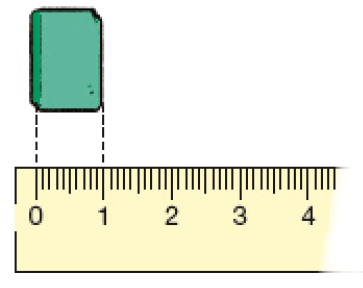
Imagem: Ilustração. Uma borracha em pé sobre uma régua. A lateral esquerda da borracha está sobre o número zero e a lateral direita sobre o número um. Fim da imagem.

Qual era o comprimento da borracha, em centímetro, no início do ano? E no fim do ano? _____

PROFESSOR
Resposta: 4 centímetros; 1 centímetro.

A borracha diminuiu _____ milímetros do início para o fim do ano.

PROFESSOR
Resposta: 30

Indicamos: 1 milímetro por 1 mm

1 cm = 10 mm

Adriana e Júlio mediram com uma régua a largura, o comprimento e a espessura de uma mesma revista. Veja as anotações que eles fizeram.

Adriana

Largura: 20 centímetros

Comprimento: 30 centímetros

Espessura: 1 centímetro

Júlio

Largura: 20 centímetros

Comprimento: 30 centímetros

Espessura: 10 milímetros

Imagem: Ícone: Oral. Fim da imagem.

Adriana e Júlio obtiveram medidas diferentes? Explique.

Em dupla, escolham um objeto. Em seguida, cada um deve medir esse objeto com uma régua. Depois, comparem as medidas obtidas.

PROFESSOR

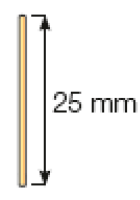
Respostas pessoais.

Marcelo precisa fazer um trabalho usando 8 pedaços de palitos de bambu iguais ao da ilustração abaixo. Quantos centímetros desses palitos ele usará ao todo?

PROFESSOR
Resposta: 20 cm.

Imagem: Ilustração. Um palito medindo 25 mm de comprimento. Fim da imagem.

MANUAL DO PROFESSOR

Objetivo

• Resolver problemas envolvendo as medidas de comprimento: centímetro e milímetro.

Atividade 1

Pergunte aos estudantes: “Em que situações podemos usar a unidade de medida de comprimento centímetro? E a unidade de medida de comprimento milímetro?”.

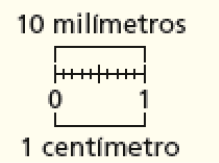
A régua é um instrumento de medida de comprimento familiar aos estudantes. Por apresentar de forma explícita a divisão do centímetro em milímetro, é um ótimo recurso concreto para a compreensão da relação entre essas unidades, como 10 milímetros equivalem a 1 centímetro.

Atividade 2

Ao comparar dois registros de uma mesma medição, os estudantes podem confirmar a relação 1 cm = 10 mm e também exercitar medições com régua que incluam as duas unidades de medida.

Observe como eles realizam medições em milímetro; devem compreender que a medida expressa em milímetro corresponde ao número de unidades (espaços entre duas marcas de milímetros consecutivas da régua), não ao número de marcas contadas do início ao fim (11 marcas em 1 centímetro):

Imagem: Ilustração. À esquerda, o número zero e à direita, o número um. Entre eles há nove riscos. Acima, a informação: dez milímetros e abaixo, um centímetro. Fim da imagem.

CRÉDITO: ADILSON SECCO

No item a, a única diferença foi a unidade de medida usada na espessura. As medidas foram as mesmas, pois 1 cm é igual a 10 mm.

Atividade 3

Esta atividade propõe o cálculo com medidas expressas em milímetro para a posterior conversão em centímetro (8 × 25 mm = 200 mm = 20 cm).

Ampliamos o trabalho com a grandeza comprimento, observando a adequação do milímetro às medidas de comprimento menores que o centímetro, e a relação entre essas duas unidades de medida (1 centímetro equivale a 10 milímetros). Da mesma maneira que nos demais tópicos dedicados à comparação de unidades de medida, o objetivo não é que os estudantes façam transformações entre essas unidades de maneira descontextualizada, mas que explorem essas relações para desenvolverem habilidades de estimar medidas. Essas relações serão mais bem compreendidas se eles tiverem a oportunidade de observar e usar uma régua milimetrada.

BNCC em foco:

EF05MA19

MP218

Quilômetro e metro

Leia a conversa entre Artur e Leila. Depois, responda às questões.

Imagem: Ilustração. Artur, homem com cabelo curto sorri e fala: Para ir da minha casa ao trabalho, eu caminho 500 metros. Ao lado, Leila, mulher com cabelo comprido responde: Isso não é nada! Para ir da minha casa ao trabalho, eu caminho o dobro dessa distância. Caminho 1 quilômetro. Fim da imagem.

Quantos metros Leila caminha da sua casa até o trabalho? _____

PROFESSOR
Resposta: 1.000 metros.

Em quais outras situações costumamos usar a unidade de medida quilômetro?
_____

PROFESSOR
Exemplos de resposta: Para indicar a distância entre cidades, o percurso de uma maratona, a extensão de um rio.

Indicamos: 1 quilômetro por 1 km

1 km = 1.000 m

Imagem: Ícone: Oral. Fim da imagem.

Augusto pegou um ônibus para visitar sua avó, que mora a 10 km de distância da casa dele. O ônibus já percorreu 6 000 m do caminho. Ele percorreu mais ou menos da metade desse caminho?

PROFESSOR
Resposta: O ônibus percorreu mais da metade do caminho.

Imagem: Ícone: mental. Fim da imagem.

Três dias por semana, Marta treina em uma pista de corrida que tem 800 metros de comprimento. Em cada dia de treino, ela dá 5 voltas completas nessa pista.

Imagem: Fotografia. Uma mulher está correndo em uma pista. Ao fundo, árvores. Fim da imagem.

Quantos quilômetros Marta percorre em um dia de treino? E em uma semana de treino? _____

PROFESSOR
Resposta: 4 quilômetros; 12 quilômetros.

Se Marta correr 1 quilômetro a mais por dia de treino, quantos quilômetros ela percorrerá em uma semana de treino?
_____

PROFESSOR
Resposta: 15 quilômetros.

MANUAL DO PROFESSOR

Objetivo

Resolver problemas envolvendo as medidas de comprimento: quilômetro e metro.
Atividade 1

Antes de propor esta atividade, questione os estudantes se conhecem outras unidades de medida de comprimento além de metro, centímetro e milímetro. Por exemplo: “Vocês já ouviram falar de outras unidades de medida de comprimento? Para medir distâncias muito grandes, é prático usar o centímetro? Se não, que unidade de medida podemos usar?”. Conforme as atividades forem discutidas e resolvidas, será possível retomar essas ideias iniciais e compará-las com os conceitos sistematizados nesta página.

Atividade 2

Pergunte aos estudantes: “Quantos metros o ônibus tinha percorrido quando chegou exatamente à metade do caminho?” (5.000 m).

Atividade 3

No item a, espera-se que os estudantes utilizem os valores em metro para resolver a situação e, depois, façam a conversão para quilômetro.

Possíveis cálculos:
Em um dia (5 voltas):
5 × 800 m = 4.000 m = 4 km
Em uma semana (treino 3 vezes por semana):
3 × 4 km = 12 km

BNCC em foco:

EF05MA19

MP219

Perímetro

Lígia pintou um quadro retangular, como mostra a imagem ao lado, e agora colocará uma moldura nele. Para isso, ela precisa calcular a medida do comprimento do contorno desse quadro.
Qual é a medida do comprimento do contorno desse quadro?

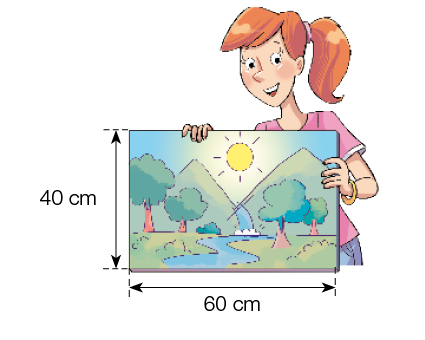
Imagem: Ilustração. Lígia, mulher ruiva com cabelo preso está sorrindo e segurando um quadro com a imagem de um rio, árvores, montanhas e o sol. O quadro tem 40 cm de comprimento e 60 cm de largura. Fim da imagem.

60 cm + _____ cm + _____ cm + _____ cm = _____ cm

PROFESSOR

Resposta: 40; 60; 40; 200.

A medida do contorno do quadro tem _____ metros de comprimento.

PROFESSOR

Resposta: 2

O comprimento do contorno de uma figura é seu perímetro.

Imagem: Ícone: mental. Fim da imagem.

Sabendo que todos os lados de cada figura abaixo têm a mesma medida, calcule a medida do perímetro de cada uma delas, em centímetro.

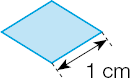
Imagem: Ilustração. Um quadrado com 1 cm. Fim da imagem.

Medida do perímetro = _____ cm

PROFESSOR

Resposta: 4

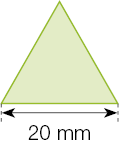
Imagem: Ilustração. Um triângulo com base de 20 mm. Fim da imagem.

Medida do perímetro = _____ cm

PROFESSOR

Resposta: 6

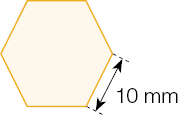
Imagem: Ilustração. Um hexágono com 10 mm. Fim da imagem.

Medida do perímetro = _____ cm

PROFESSOR

Resposta: 6

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

Pinte três representações retangulares diferentes que tenham, cada uma, a medida do perímetro igual a 14 cm.

PROFESSOR

Exemplos de pintura: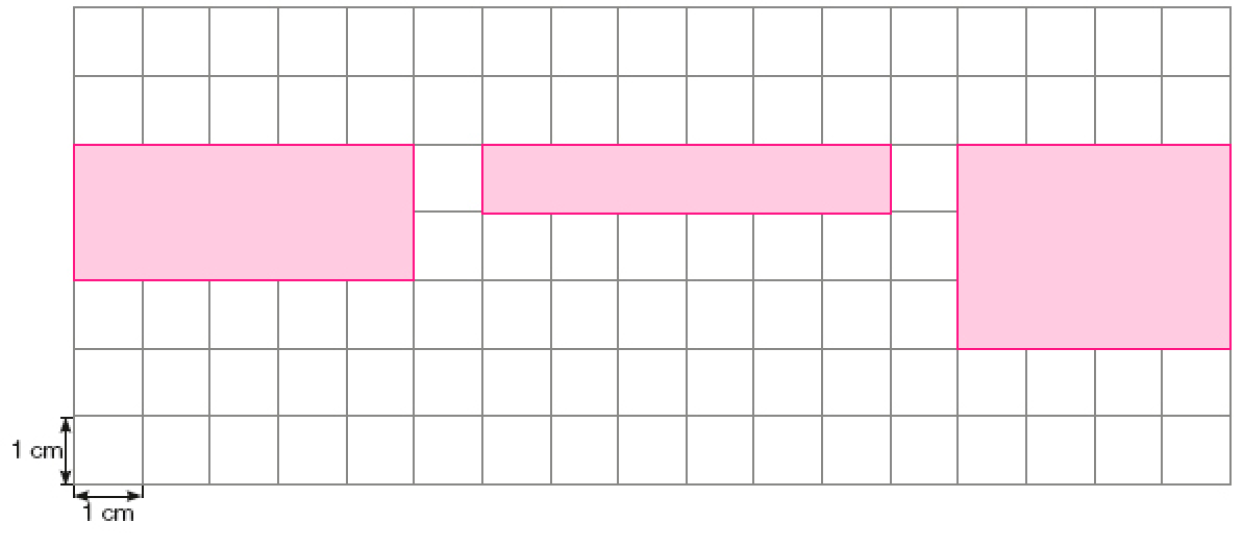

Imagem: Ilustração. Malha quadriculada. Cada quadradinho mede 1 cm de comprimento e 1 cm de largura. Há um retângulo ocupando dez quadradinhos. Em seguida, uma faixa ocupando seis quadradinhos. À direita, um retângulo ocupando doze quadradinhos. Fim da imagem.

MANUAL DO PROFESSOR

Objetivo

Desenvolver a noção de perímetro, medindo o contorno de figuras.
Atividade 1

Incentive os estudantes a desenvolverem estratégias pessoais para calcular o comprimento do contorno do quadro de Lígia. Depois, pergunte como chegaram às medidas dos outros lados do quadro retangular.

Para apresentar a resposta em metro, eles deverão fazer a conversão de 100 centímetros em 1 metro (100 cm = 1 m).

Aproveite a situação apresentada e pergunte: “Em que outras situações do dia a dia é necessário saber calcular a medida do perímetro?”. É possível que os estudantes mencionem o cálculo da medida do comprimento de arame a ser comprado para cercar um terreno ou da metragem de renda a ser usada para contornar a borda de uma toalha etc.

Atividade 2

Verifique se os estudantes percebem que, no caso de figuras poligonais, o cálculo da medida do perímetro é dado pela soma das medidas dos lados do polígono. É importante observarem que as medidas dos lados das figuras apresentadas são iguais.

Atividade 3

Peça aos estudantes que socializem os desenhos com os colegas e discutam semelhanças e diferenças.

BNCC em foco:

EF05MA19

MP220

Há um projeto para a construção de uma pista quadrangular de atletismo que contornará um parque. No entanto, ainda não se sabe se a medida de cada lado será 1.200 metros ou 1.400 metros.
1. Qual será a maior medida, em metro, que essa pista poderá ter?
  _____
  
  PROFESSOR
  Resposta: 5.600 metros.
  
  PROFESSOR
  Exemplo de cálculo:
  
  PROFESSOR
  1.400 + 1.400 + 1.400 + 1.400 = 5.600
1. E qual será a menor medida, em metro, que essa pista poderá ter?
  _____
  
  PROFESSOR
  Resposta: 4.800 metros.
  
  PROFESSOR
  Exemplo de cálculo:
  
  PROFESSOR
  1.200 + 1.200 + 1.200 + 1.200 = 4.800

A medida do contorno do terreno retangular de Gérson é igual a 60 metros. A frente desse terreno mede 10 metros de comprimento.

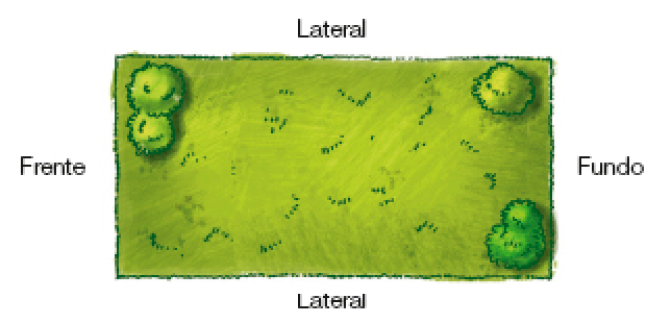
Imagem: Ilustração. Vista de cima de um terreno com grama e árvores. Acima e abaixo, a informação: Lateral. À esquerda, Frente e à direita, Fundo. Fim da imagem.

Elabore uma pergunta para a situação descrita e, em seguida, responda a ela.

PROFESSOR
Resposta variável.

Boxe complementar:

Desafio

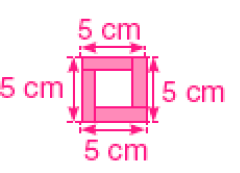
O quadrado mostrado abaixo foi dividido em 4 retângulos iguais.

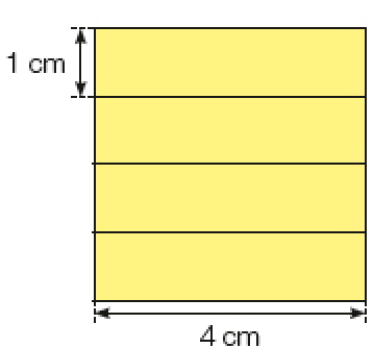
Imagem: Ilustração. Quadrado dividido em quatro retângulos com 1 cm de comprimento cada. O quadrado mede 4 cm de largura. Fim da imagem.

Depois, os 4 retângulos foram reagrupados formando uma nova figura, como mostrado abaixo.

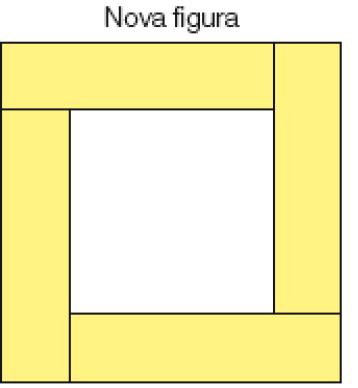
Imagem: Ilustração. Nova figura. Dois retângulos na vertical e dois na horizontal sobrepostos, formando um quadrado vazado. Fim da imagem.

CRÉDITO: FERNANDO JOSÉ FERREIRA

Qual é a medida do contorno dessa nova figura?

_____

Resposta: 20 cm

Imagem: Ilustração. Dois retângulos na vertical e dois na horizontal sobrepostos, formando um quadrado vazado. Cada retângulo mede 5 cm de comprimento. Fim da imagem.

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 4

Espera-se que os estudantes associem a ideia de que a pista quadrangular de atletismo tem lados de comprimentos iguais.

No item a, para calcular o maior perímetro possível da pista, os estudantes devem considerar o lado com a maior medida: 1.400 metros.

No item b, a menor medida da pista, que equivale ao menor perímetro possível, é obtida quando a pista tem lado igual a 1.200 metros.

Para ampliar a atividade, proponha que calculem a medida do perímetro, se a pista for um retângulo com medidas de lado 1.400 m e 1.200 m (5.200 m).

Atividade 5

Sugestões de perguntas:

Quantos metros tem o fundo do terreno? (10 m)
Quanto mede cada lateral do terreno? (20 m)
Se Gérson decidir construir um muro que contorne apenas as laterais e o fundo do terreno, qual será o comprimento, em metro, desse muro? (50 m)
Depois, sugira aos estudantes que troquem de pergunta com um colega.

BNCC em foco:

EF05MA19

Desafio

O quadrado foi dividido em 4 retângulos iguais. De acordo com a figura inicial, descobrimos que cada lado do quadrado mede 4 cm, pois são todos iguais. Assim, cada lado da nova figura mede 5 cm, e a medida do contorno é obtida fazendo 4 vezes 5 cm, que é igual a 20 cm.

Pergunte: “Qual é a medida do contorno da parte branca formada no interior dessa figura?” (12 cm).

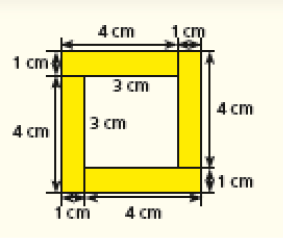
CRÉDITO: ADILSON SECCO

MP221

Medidas de tempo

Hora, meia hora e um quarto de hora

O time Pavão Cinza está jogando contra o Galo Branco. O jogo deveria ter começado às 19 horas, mas o início atrasou 30 minutos. Veja a narração de um momento do jogo e, em seguida, responda às questões.

Imagem: Ilustração. Um homem com fones de ouvidos e terno está segurando um microfone. Ele fala: Goooool! Edinho do Galo Branco faz o 1 gol da partida aos 30 minutos do primeiro tempo do jogo. Na frente dele, vista de cima de jogadores em um campo de futebol. Fim da imagem.

Boxe complementar:

Dica

Uma partida de futebol é dividida em dois tempos de 45 minutos cada um, com um intervalo de 15 minutos entre eles.

Fim do complemento.

O tempo de atraso desse jogo corresponde a que fração de uma hora?
_____

PROFESSOR
Resposta: Corresponde a meia hora (ou $\frac{1}{2}$ hora).

A que horas Edinho marcou o primeiro gol da partida?
_____

PROFESSOR
Resposta: Às 20 horas.

Marcos sai do trabalho às 19 horas e demora uma hora e meia para chegar em casa. Ele chegará em tempo de assistir a todo o segundo tempo da partida em casa? Explique como você pensou.

PROFESSOR
Resposta: Sim.

PROFESSOR
Resposta pessoal.

Cada intervalo de tempo de 30 minutos corresponde a meia hora (ou $\frac{1}{2}$ hora).

30 min = $\frac{1}{2}$ h

Imagem: Ícone: mental. Fim da imagem.

Camila estuda de manhã, e o portão de sua escola fecha às 7 horas. Sabendo que ela demora 30 minutos para se arrumar e tomar café e 15 minutos para chegar à escola, a que horas ela deve acordar para não chegar atrasada?
_____

PROFESSOR
Resposta: Ela deve acordar às 6 horas e 15 minutos ou antes desse horário.

MANUAL DO PROFESSOR

Objetivo

Resolver e elaborar problemas envolvendo medidas de tempo.
Atividade 1

Incentive os estudantes a observarem um relógio de ponteiros, para estabelecerem mais facilmente as relações entre as frações de hora e os minutos correspondentes.

No item c, espera-se que os estudantes respondam que sim, pois ele chegará em casa às 20 horas e 30 minutos e, se o jogo não tiver acréscimos no 1º tempo, o 2º tempo do jogo terá início nesse horário.

Atividade 2

O cálculo requerido nesta atividade não é simples, pois envolve uma estimativa de tempo pensada “ao inverso” (A que horas devo sair para não chegar atrasado?). Dê o tempo necessário para a resolução e, depois, explore a situação pedindo aos estudantes que observem em seu dia a dia quais atividades eles precisam realizar antes de ir à escola e quanto tempo gastam em cada uma delas. Depois, peça que calculem o horário em que precisariam acordar para chegar à aula com 10 minutos de antecedência (se estudam no período da manhã) ou o horário em que teriam de almoçar para chegar à aula 10 minutos antes (se estudam no período da tarde).

Ao observar o movimento do ponteiro grande (o dos minutos), é possível perceber que:

quando esse ponteiro está apontando para o número 3, já se passou $\frac{1}{4}$ de hora (ou 15 minutos) em relação à hora “cheia”;

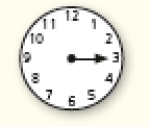
CRÉDITO: ADILSON SECCO

ao apontar para o número 6, já se passaram $2 quartos$ de hora, ou seja, $\frac{1}{2}$ hora (ou 30 minutos);

quando o ponteiro indica o número 9, significa que já se passaram $3 quartos$ de hora (ou 45 minutos) em relação à hora “cheia”.

BNCC em foco:

EF05MA19

MP222

Imagem: Ícone: mental. Fim da imagem.

Márcio treina natação três vezes por semana. Em cada dia, seu treino é dividido em 4 partes. Em cada parte do treino ele nada um estilo.

1ª parte

15 minutos de nado livre

2ª parte

15 minutos de nado costas

3ª parte

15 minutos de nado peito

4ª parte

15 minutos de nado borboleta

Um dia, o treino de Márcio começou às 10 horas. A que horas terminou esse treino, sabendo que não há intervalo entre as partes? _____

PROFESSOR
Resposta: Às 11 horas.

O tempo dedicado a cada estilo corresponde a que fração de uma hora?
_____

PROFESSOR
Resposta: Corresponde a um quarto de hora (ou $\frac{1}{4}$ hora).

Cada intervalo de tempo de 15 minutos corresponde a um quarto de hora (ou $\frac{1}{4}$ hora).

15 min = $\frac{1}{4}$ h

Carolina foi com sua mãe à feira. Elas saíram de casa às 9 horas e, quando voltaram, faltava um quarto de hora para as 10 horas.

Imagem: Ilustração. Uma mulher está segurando uma sacola com a mão direita e com a mão esquerda nas costas de uma menina, que sorri. Fim da imagem.

Quanto tempo elas ficaram fora de casa?
_____

PROFESSOR
Resposta: 45 minutos.

O tempo que elas ficaram fora de casa corresponde a quantos quartos de hora?
_____

PROFESSOR
Resposta: Corresponde a três quartos de hora (ou $3 quartos$ hora).

Veja o que Lúcia está dizendo. Em seguida, para cada item, escreva a hora correspondente, assim como Lúcia fez.

Imagem: Ilustração. Lúcia, menina ruiva com laço na cabeça fala: Se 1/4 é o mesmo que 15 minutos, 8 horas mais 1/4 de hora são 8 horas e 15 minutos. Fim da imagem.

7 horas mais $3 quartos$ de hora: _____

PROFESSOR
Resposta: 7 horas e 45 minutos.

Falta $\frac{1}{4}$ de hora para as 9 horas: _____

PROFESSOR
Resposta: 8 horas e 45 minutos.

Falta $\frac{1}{2}$ hora para as 15 horas: _____

PROFESSOR
Resposta: 14 horas e 30 minutos.

MANUAL DO PROFESSOR

Atividade 3

O foco desta atividade é o reconhecimento de que 15 minutos correspondem a $\frac{1}{4}$ de hora. Explore a associação de um relógio de ponteiros ao círculo.

No período de 1 hora, o ponteiro grande dá um giro completo no mostrador do relógio. Esse giro pode ser associado a um círculo.

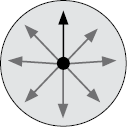
Imagem: Ilustração. Um relógio com o ponteiro no número doze. Em volta há ponteiros claros girando. Fim da imagem.

No período de 15 minutos, o ponteiro grande dá um giro correspondente a $\frac{1}{4}$ do círculo (parte pintada de azul).

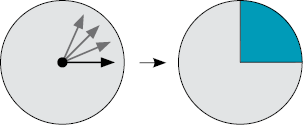
Imagem: Ilustração. À esquerda, um relógio com o ponteiro no número três. Acima há três ponteiros claros. Em seguida, uma seta para a direita, apontando para um círculo com uma parte pintada de azul. Fim da imagem.

CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO

Pode-se perguntar aos estudantes: “Quantas horas Márcio treina por semana?” (3 h).

Atividade 4

Explore a situação perguntando: “A que horas Carolina e sua mãe chegaram à casa?”. Os estudantes podem responder 9 h e 45 min ou 15 minutos para as 10 horas.

Exemplo de cálculo para o item a:

$\frac{1}{4}$ de hora = $\frac{1}{4}$ de 60 minutos = = 15 minutos

Atividade 5

Esta atividade propicia aos estudantes reconhecerem as principais partes de hora e como fazer leituras de horários envolvendo tais partes.

15 minutos = $\frac{1}{4}$ de hora

30 minutos = $\frac{1}{2}$ de hora

45 minutos = $3 quartos$ de hora

BNCC em foco:

EF05MA19

MP223

Medidas de massa

Tonelada, quilograma e grama

Rita tem um restaurante que vende comida por quilograma.

Imagem: Ilustração. Dois homens estão sentados em volta de uma mesa e comendo. Na frente deles há pratos com comida e ao lado, dois papéis com as informações: 400 g e 600 g. Um deles fala: Nossas refeições juntas mediram 1 quilograma de massa. Ao lado, Rita, mulher com cabelo castanho e curto está com a mão direita sob o queixo e olhando para cima. Ela pensa: Neste mês, vendemos 900 quilogramas de comida. Faltaram 100 quilogramas para completar 1 tonelada. Fim da imagem.

Quantos gramas formam 1 quilograma? _____

PROFESSOR
Resposta: 1.000 gramas.

Quantos quilogramas formam 1 tonelada? _____

PROFESSOR
Resposta: 1.000 quilogramas.

Se Rita cobra R$ 4,00 por 100 gramas de comida, quanto ela deve receber pela venda dessas duas refeições? _____

PROFESSOR
Resposta: R$ 40,00.

Indicamos:

1 miligrama por 1 mg
1 grama por 1 g
1 quilograma por 1 kg
1 tonelada por 1 t

1 g = 1.000 mg

1 kg = 1.000 g

1 t = 1.000 kg

Imagem: Ícone: mental. Fim da imagem.

Faça estimativas e responda às questões.
1. João foi ao açougue e comprou 1 kg e 400 g de linguiça, 2 kg e 900 g de costela e 1,5 kg de acém. Quantos quilogramas de carne, aproximadamente, ele comprou? _____
  
  PROFESSOR
  Exemplo de estimativa: 6 kg
1. Para uma obra, foram comprados 0,5 t de cimento, 1 t e 800 kg de areia e 2,5 t de pedra. Quantas toneladas de materiais, aproximadamente, foram compradas? _____
  
  PROFESSOR
  Exemplo de estimativa: 5 t

MANUAL DO PROFESSOR

Objetivo

Resolver problemas envolvendo unidades de medida de massa: tonelada, quilograma e grama.
Atividade 1

Esta atividade explora as relações entre as unidades grama e quilograma e entre as unidades quilograma e tonelada.

Peça aos estudantes que deem exemplos de situações em que é mais adequado expressar a massa em grama, quilograma ou tonelada e, depois, discuta os exemplos apresentados.

Atividade 2

As situações compreendem três das principais unidades de medida de massa: tonelada, quilograma e grama.

As relações entre essas unidades são desenvolvidas com base em comparações e conversões usuais entre elas. Por isso, não são solicitadas, por exemplo, transformações de 2 000 toneladas para a unidade grama, o que seria improvável em situações do dia a dia.

Sugira aos estudantes que, após a resolução, calculem os valores exatos das medidas de massa estimadas e comparem os resultados.

BNCC em foco:

EF05MA19

MP224

Jéssica foi ao mercado para comprar 1 2 kg de queijo e 500.000 mg de café.
1. Cada quilograma de queijo custa 32 reais. Jéssica estimou que 15 reais seriam suficientes para pagar o queijo. Ela está correta? Justifique.
  
  PROFESSOR
  Resposta pessoal.
1. Quantos pacotes de $\frac{1}{4}$ de kg de café ela deve comprar para ter o que precisa?
  _____
  
  PROFESSOR
  Resposta: 2 pacotes.

Imagem: Ilustração. Uma embalagem de queijo fatiado com 500 g e um pacote de café com 250 g. Fim da imagem.

Meio quilograma é o mesmo que 500 gramas.

Indicamos: meio quilograma por $\frac{1}{2}$ kg

$\frac{1}{2}$ kg = 500 g

Um quarto de quilograma é o mesmo que 250 gramas.

Indicamos: um quarto de quilograma por $\frac{1}{4}$ kg

$\frac{1}{4}$ kg = 250 g

Imagem: Ícone: mental. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

Observe os quadros em cada caso. Descubra qual deles indica a maior massa e pinte-o.
1. 1 t ou 1 kg
  
  PROFESSOR
  Resposta correta: 1 t
1. 300.000 mg ou 2 kg
  
  PROFESSOR
  Resposta correta: 2 kg
1. 56 kg ou 59.000 g
  
  PROFESSOR
  Resposta correta: 59.000 g
1. 60 t ou 9.700 g
  
  PROFESSOR
  Resposta correta: 60 t

Imagem: Ícone: mental. Fim da imagem.

Paulo foi ao mercado Boas Compras e comprou os produtos abaixo. Ele distribuiu os produtos em sacolas que suportam até 2 kg. Qual é o menor número de sacolas que Paulo pode ter usado? _____

PROFESSOR
Resposta: 6 sacolas.

Imagem: Ilustração. À esquerda, três pacotes de arroz com 2 kg e um pacote com um quarto kg. No centro, quatro pacotes de café com meio kg e três com 250 g. À direita, duas embalagens de frios com 500 g e duas com 250 g. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 3

Nesta atividade, os estudantes trabalham com as frações mais comuns do quilograma, associando meio quilograma a 500 gramas e um quarto de quilograma a 250 gramas.

Chame a atenção deles para a correta concordância de grama e quilograma. O correto é dizer, por exemplo, “quinhentos gramas”, e não “quinhentas gramas”.

No item a, uma justificativa é: como 1 quilograma de queijo custa 32 reais, deduz-se que meio quilograma de queijo custará metade desse valor, ou seja, 16 reais; então, Jéssica não pode comprar meio quilograma de queijo com apenas 15 reais.

No item b, comente que, embora 15 reais sejam insuficientes, a estimativa procede, pois, arredondando o preço do quilograma para a dezena mais próxima (30 reais),15 reais seriam suficientes.

Atividade 4

Os estudantes devem perceber que, para comparar massas, é necessário que elas estejam na mesma unidade de medida. Enfatize que não se comparam apenas os números, é necessário considerar as unidades de medida. Por isso, deve-se primeiro converter as medidas para uma mesma unidade de medida, depois comparar as massas.

É possível expressar as massas usando qualquer unidade de massa estudada, porém é mais fácil fazer a conversão para a menor unidade de medida que aparece. Por exemplo, no item a, convém expressar todas as massas em quilograma, pois: 1 t = 1.000 kg enquanto 1 kg = 0,001 t.

Relembre-os que o prefixo quilo indica 1.000; portanto, 1 quilograma corresponde a 1.000 gramas. Com isso, eles devem perceber que meio quilograma pode ser obtido por 1.000 g ÷ 2 = 500 g, e um quarto de quilograma pode ser obtido por 1.000 g ÷ 4 = 250 g.

BNCC em foco:

EF05MA19

Atividade 5

Um modo de resolver a questão proposta é agrupar os produtos formando 2 kg em cada grupo, o que corresponde à massa máxima que cada sacola suporta:

três sacolas: uma para cada saco de 2 kg de arroz;
uma sacola para os quatro pacotes de $\frac{1}{2}$ kg de café;
uma sacola para as duas bandejas de 500 g de frios, duas bandejas de 250 g de frios e dois pacotes de café de 250 g;
uma sacola para os itens restantes: um pacote de café de 250 g e um saco de arroz de $\frac{1}{4}$ kg.

MP225

Medidas de capacidade

Litro e mililitro

Ana foi ao mercado comprar suco. Se ela comprar 4 garrafas de suco da promoção, quantos litros ela levará a mais do que pagou?
Em cada garrafa da promoção, há 1.250 mililitros, dos quais _____ mililitros são grátis.

4 × _____ mililitros = _____ mililitros

PROFESSOR
Resposta: 250; 250; 1.000.

Imagem: Ilustração. Ana, mulher com cabelo castanho e comprido está com as mãos na cintura e de costas. Na frente dela há garrafas em uma prateleira e acima há uma placa com a informação: SUCOS EM PROMOÇÃO! PAGUE 1L E LEVE GARRAFAS COM 1L MAIS 250 ML. Fim da imagem.

Ana levará _____ litro de suco a mais do que pagou.

PROFESSOR

Resposta: 1

Indicamos: 1 litro por 1 L

1 L = 1.000 mL

A torneira de um filtro enche um copo com 200 mL de água em 8 segundos, aproximadamente.
1. Quantos segundos, aproximadamente, ela levará para encher com água uma garrafa de 1 L? _____
  
  PROFESSOR
  Resposta: 40 segundos.
  
  PROFESSOR
  Exemplo de cálculo: 1 L = 5 × 200 mL
  
  PROFESSOR
  5 × 8 s = 40 s
1. Se a torneira ficar aberta por 1 minuto e 20 segundos, quantos litros de água serão escoados nesse intervalo de tempo? _____
  
  PROFESSOR
  Resposta: 2 litros.
  
  PROFESSOR
  Exemplo de cálculo: 80 s ÷ 8 s = 10
  
  PROFESSOR
  10 × 200 mL = 2.000 mL
1. Com os 20 L de água desse galão, podemos encher, no máximo, quantas garrafas com 500 mL de capacidade? _____
  
  PROFESSOR
  Resposta: 40 garrafas.
  
  PROFESSOR
  Exemplo de cálculo: 20.000 mL ÷ 500 mL = 40

Imagem: Ilustração. Um galão de água com 20 L sobre um suporte. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

Lia encheu uma jarra com 2,5 L de leite. Agora, responda.
1. Se Lia tomar 500 mL de leite dessa jarra, quantos litros sobrarão?
  _____
  
  PROFESSOR
  Resposta: 2 litros.
1. Se a família de Lia tomar metade do leite da jarra com 2,5 L de leite, quantos mililitros de leite sobrarão? _____
  
  PROFESSOR
  Resposta: 1.250 mililitros.

MANUAL DO PROFESSOR

Objetivos

Resolver problemas envolvendo unidades de medida de capacidade: litro e mililitro.

Interpretar dados apresentados em gráfico de colunas.

Atividade 1

Dê um tempo para os estudantes analisarem a imagem com atenção. Se possível, leve para a sala de aula uma garrafa com 1 litro de água e um recipiente, graduado em mililitro, para que verifiquem a equivalência entre as unidades de medida estudadas.

Explore a atividade perguntando: “Em quais situações costumamos usar a unidade litro? E a unidade mililitro?”. Eles podem mencionar a unidade litro em medições de quantidade de água ou de sucos para consumo ou da quantidade de água para encher um filtro, um tanque, uma piscina ou uma caixa-d’água, por exemplo.

No cotidiano, a unidade mililitro aparece em medidas de frações do litro de alguns produtos, como óleo e refrigerantes, ou em dosagens de medicamentos.

Discuta os exemplos apresentados salientando que é importante saber trabalhar com essas unidades, pois o litro e o mililitro são as unidades de medida de capacidade mais usuais.

Atividade 2

O aspecto mais interessante desta atividade é relacionar medidas de capacidade (litro e mililitro) com medidas de tempo (minuto e segundo).

Apresente à turma um quadro como o mostrado a seguir, para que os estudantes o completem coletivamente.

Tabela: equivalente textual a seguir.

Capacidade (em mL)	Tempo (em segundo)
200	8
400	16
600	24
800	32
1000	40

Atividade 3

Espera-se que os estudantes percebam que 2 litros e meio equivalem a 2.500 mililitros e, assim, resolvam as questões propostas com facilidade.

Para ampliar o item b, pergunte: “E quantos mililitros de leite a família de Lia terá tomado?” (1.250 mL).

BNCC em foco:

EF05MA19

MP226

Paulo repartiu igualmente o conteúdo de uma garrafa de 1 litro de água entre 4 amigos.

Imagem: Ilustração. À esquerda, André, jovem loiro com camiseta azul. Em seguida, Bruno, jovem com cabelo encaracolado e curto e camiseta branca. No centro, Carlos, jovem loiro com óculos e camiseta rosa. E à direita, Diogo, jovem com cabelo castanho e camiseta verde. Na frente de cada um há um copo de 250 mL sobre uma mesa. Fim da imagem.

Imagem: Ilustração. André e Bruno estão bebendo água do copo. Ao lado, Carlos segura o copo e fala: Não quero água; pode beber a água do meu copo. Ao seu lado, Diogo responde: Eu não consigo beber meio litro de água. Na frente dele, o copo sobre a mesa. Fim da imagem.

Quantos litros de água cada amigo recebeu? Escreva sua resposta na forma de fração. _____

PROFESSOR
Resposta: $\frac{1}{4}$ de litro de água.

Quantos mililitros de água Diogo disse que não consegue beber? _____

PROFESSOR
Resposta: 500 mililitros.

Indicamos: um quarto de litro por $\frac{1}{4}$ L

$\frac{1}{4}$ L = 250 mL

Indicamos: meio litro por $\frac{1}{2}$ L

$\frac{1}{2}$ L = 500 mL

Se todas as jarras e canecas estão cheias de água, quantos litros de água há em cada caso?

Imagem: Ilustração. Uma jarra com meio litro e duas canecas com um quarto de litro cada uma. Fim da imagem.

_____

PROFESSOR

Resposta: 1 L

Imagem: Ilustração. Duas jarras com meio litro cada uma e duas canecas com um quarto de litro cada uma. Fim da imagem.

_____

PROFESSOR

Resposta: 1,5 L

Imagem: Ilustração. Duas jarras com meio litro cada uma e quatro canecas com um quarto de litro cada uma. Fim da imagem.

_____

PROFESSOR

Resposta: 2 L

Imagem: Ícone: Dupla. Fim da imagem.

Com um colega, elaborem um problema que possa ser respondido com as informações contidas no gráfico abaixo.

PROFESSOR
Resposta variável.

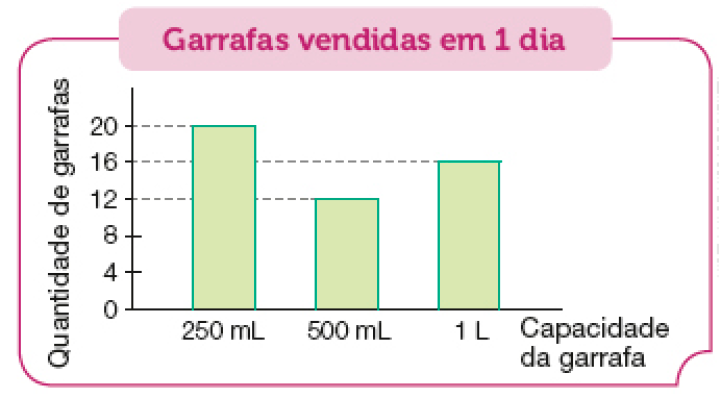
Imagem: Gráfico de colunas. Garrafas vendidas em 1 dia. No eixo vertical, a quantidade de garrafas e no eixo horizontal, a capacidade da garrafa. Capacidade: 250 mL; Quantidade: 20 garrafas. Capacidade: 500 mL; Quantidade: 12 garrafas. Capacidade: 1 L; Quantidade: 16 garrafas. Fim da imagem.

Fonte: Dados fornecidos por um supermercado (maio 2023).

MANUAL DO PROFESSOR

Atividade 4

No item b, verifique se os estudantes transformam meio litro em 500 mililitros com facilidade. Se julgar necessário, escreva na lousa que 1 litro equivale a 1.000 mililitros.

Atividade 5

Nesta atividade, os estudantes têm a oportunidade de aplicar os conhecimentos sobre frações para obter a medida da capacidade em cada caso ou para realizar a transformação de cada fração de litro em mililitro.

No item a, por exemplo, sabendo que $\frac{1}{2}$ L = 500 mL e que $\frac{1}{4}$ L = 250 mL, temos que $\frac{1}{2}$ L mais $\frac{1}{4}$ L mais $\frac{1}{4}$ L equivalem a 500 mL mais 250 mL mais 250 mL, que é igual a 1 000 mL, que é o mesmo que 1 L. De modo similar, é possível obter a capacidade nos itens b e c.

Atividade 6

Exemplo de problema com os dados do gráfico: “Foram vendidos mais litros de suco em embalagens de 250 mL ou em embalagens de 1 L?”. Espera-se que percebam que há 5 L distribuídos em garrafas de 250 mL e 16 L distribuídos em garrafas de 1 L.

BNCC em foco:

EF05MA19, EF05MA24

MP227

Medidas de temperatura

Responda às questões e faça o que se pede.
1. Ontem estava mais quente ou mais frio que hoje? _____
  
  PROFESSOR
  Resposta pessoal.
1. Qual unidade de medida de temperatura você conhece? _____
  
  PROFESSOR
  Exemplo de resposta: Grau Celsius.
1. Estime a medida da temperatura de hoje. _____
  
  PROFESSOR
  Resposta pessoal.

Célia e Fernando viajaram nas férias. Certo dia, Célia aproveitou para correr no calçadão à beira-mar, e Fernando ficou de cama.

Imagem: Ilustração. Célia, mulher ruiva com cabelo preso está correndo e segurando uma garrafa. Ao seu lado, um relógio de rua indicando 31 ºC. Ao fundo, a praia. Ao lado, Fernando, homem com cabelo castanho está sentado na cama e segurando um termômetro, que indica 38.0 ºC. Fim da imagem.

A medida da temperatura na praia é _____ graus Celsius e a medida da temperatura do corpo de Fernando é _____ graus Celsius.

PROFESSOR
Resposta: 31; 38

Em sua opinião, Fernando está doente ou não?

PROFESSOR
Resposta pessoal.

O aparelho usado para medir a temperatura é o termômetro.

O grau Celsius é uma unidade de medida de temperatura.

Indicamos: 1 grau Celsius por 1 °C.

Pesquise em um jornal ou site e registre a previsão do tempo para amanhã em sua cidade.
Data: _____

Local: _____

Medida da temperatura máxima prevista: _____

Medida da temperatura mínima prevista: _____

PROFESSOR
Respostas variáveis.

MANUAL DO PROFESSOR

Objetivos

Resolver problemas envolvendo medidas de temperatura.
Interpretar dados apresentados em gráfico de colunas.
Atividade 1

Antes de começar a discutir o tema, pergunte aos estudantes: “Como está o tempo hoje: frio, quente ou agradável?”. Com base nas respostas, comece a elaborar a ideia de medida da temperatura, que permite associar um valor a uma medida que, de outro modo, estaria apenas sujeita à avaliação sensorial de cada pessoa.

A criança desenvolve cedo as primeiras noções de medida de temperatura ao reconhecer o que é quente, frio, morno, gelado etc.

Oriente os estudantes quanto à linguagem adequada: embora, no dia a dia, falemos apenas “graus” quando nos referimos a medidas de temperatura, nas situações matemáticas ou científicas é importante especificar a unidade de medida como “grau Celsius”. Isso porque existem outras escalas de medida de temperatura, como a Fahrenheit. No Brasil, a mais usual é a Celsius.

Atividade 2

Pergunte: “Em quais situações precisamos medir a temperatura?”. Os estudantes podem responder que medimos a temperatura corporal para saber se estamos com febre, ou a temperatura ambiente para saber se está frio ou quente, ou a temperatura local para saber se, por exemplo, o freezer de uma geladeira está em temperatura adequada para a conservação dos alimentos.

Atividade 3

Esta atividade promove a pesquisa para a obtenção de previsão de temperaturas do local onde os estudantes moram.

Caso não haja previsão de tempo para essa localidade específica, proponha aos estudantes que indiquem a previsão do tempo de um município próximo ou da capital do estado.

BNCC em foco:

EF05MA19

MP228

Imagem: Ícone: mental. Fim da imagem.

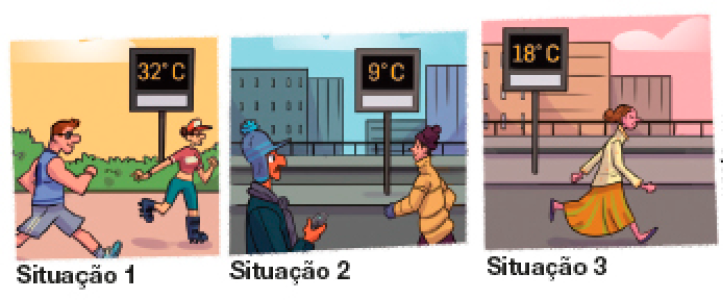
Em qual situação nas cenas abaixo o termômetro indica a menor medida de temperatura? E a maior? Qual é a diferença entre essas duas medidas?
_____

PROFESSOR
Resposta: Menor temperatura: situação 2; maior temperatura: situação 1; diferença entre as medidas: 23 °C.

Imagem: Ilustração. Situação 1. Um homem com regata e bermuda está correndo e uma pessoa com camiseta e calça está andando de patins. Atrás deles, um relógio de rua indicando 32 ºC. Situação 2. Um homem e uma mulher com gorro, casaco e luvas estão andando. Atrás deles, um relógio de rua indicando 9 ºC. Situação 3. Uma mulher com blusa, saia e sapatos está andando. Atrás dela, um relógio de rua indicando 18 ºC. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

Observe o quadro abaixo com a previsão das temperaturas máxima e mínima de algumas cidades brasileiras em certo dia de 2023.

Tabela: equivalente textual a seguir.

Cidade	Mínima prevista (ºC)	Máxima prevista (ºC)
Aracaju – SE	24	29
Maceió – AL	24	31
Goiânia – GO	21	31
Cuiabá – MT	23	33
Campo Grande – MS	21	29
Brasília – DF	19	28
São Paulo – SP	18	31
Belo Horizonte – MG	17	29
Vitória – ES	21	33
Rio de Janeiro – RJ	19	34
Porto Alegre – RS	22	28
Florianópolis – SC	21	28
Curitiba – PR	17	25

Para qual das cidades apresentadas foi prevista a menor medida da temperatura máxima para esse dia?
_____

PROFESSOR
Resposta: Curitiba.

Para qual dessas cidades foi prevista a maior diferença entre as medidas das temperaturas máxima e mínima para esse dia? De quantos graus Celsius foi essa diferença?
_____

PROFESSOR
Resposta: Rio de Janeiro. A diferença foi de 15 ºC.

Observe, abaixo, o gráfico de Roberta, que mostra as medidas das temperaturas (máxima e mínima) previstas para um dia do mês de maio em duas capitais brasileiras. Em seguida, responda às questões.

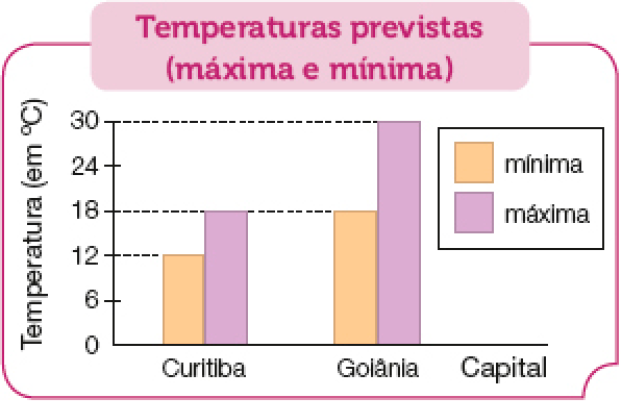
Imagem: Gráfico de colunas. Temperaturas previstas (máxima e mínima). No eixo vertical, a temperatura (em ºC) e no eixo horizontal, a capital. Curitiba: Mínima: 12 ºC; Máxima: 18 ºC. Goiânia: Mínima: 18 ºC; Máxima: 30 ºC. Fim da imagem.

Fonte: Pesquisa de Roberta (maio 2023).

Qual foi a menor medida da temperatura mínima prevista? E a maior medida da temperatura máxima prevista?
_____

PROFESSOR
Resposta: Menor temperatura mínima: 12 º C; maior temperatura máxima: 30 º C.

Qual é a diferença entre as medidas das temperaturas máxima e mínima previstas para Curitiba? E para Goiânia? _____

PROFESSOR
Resposta: Curitiba: 6 °C; Goiânia: 12 °C.

MANUAL DO PROFESSOR

Atividade 4

Aproveite o contexto para comentar com os estudantes que, para medir a temperatura corporal, atualmente apenas o termômetro digital pode ser comercializado. Explique que foi proibida a produção e a venda do termômetro de mercúrio para evitar danos à saúde e ao ambiente.

São exemplos desse instrumento: os termômetros clínicos, usados em consultórios médicos e em casa para medir a temperatura corporal; os termômetros instalados nas ruas de algumas cidades, usados para medir a temperatura ambiente; os termômetros de parede, com os quais também se mede a temperatura ambiente; os termômetros culinários, com os quais se mede a temperatura de alimentos e preparações.

Atividade 5

Antes de iniciar esta atividade, explore o quadro perguntando: “Qual cidade teve a maior medida de temperatura máxima? E qual teve a menor medida de temperatura mínima?”. Rio de Janeiro (34 ° C) e Curitiba e Belo Horizonte (17 ° C), respectivamente.

Para o item a, os estudantes devem primeiro olhar, no quadro, na coluna “Máxima” e, depois, procurar a menor medida de temperatura nessa coluna.

Se julgar oportuno, para o item b, sugira aos estudantes que criem uma coluna extra no quadro, representando a diferença entre as medidas de temperaturas máxima e mínima de cada cidade.

Atividade 6

Explore a atividade perguntando: “Qual é a diferença entre as medidas de temperatura máxima previstas para Curitiba e para Goiânia? E entre as medidas de temperatura mínima previstas para Curitiba e para Goiânia?”. Espera-se que respondam 12 °C e 6 °C, respectivamente.

BNCC em foco:

EF05MA19, EF05MA24

MP229

Medidas de área

Centímetro quadrado

Renata machucou o rosto com um espinho e foi ao médico para tratar do machucado. Veja a cena a seguir.

Imagem: Ilustração. Um médico segura um curativo pequeno e quadrado com a mão direita e com a mão esquerda no ombro de Renata fala: Não se preocupe. O curativo tem só 1 centímetro quadrado de área. Na frente dele, a jovem com cabelo comprido está sentada em uma maca e pensa: Mas que medida é essa? Fim da imagem.

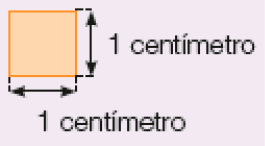
O centímetro quadrado é uma unidade de medida de superfície correspondente à área de um quadrado cujos lados medem 1 centímetro.

Indicamos: 1 centímetro quadrado por 1 cm²

Imagem: Ilustração. Quadrado com um centímetro de comprimento e um centímetro de largura. Fim da imagem.

Escreva a área, em centímetro quadrado, de cada figura.

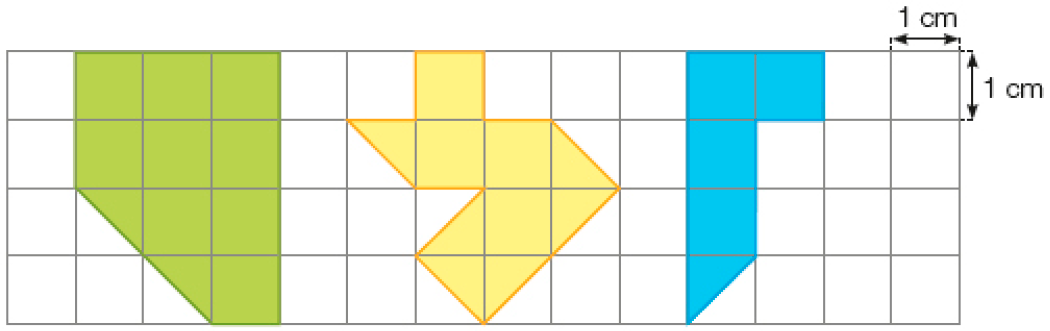
Imagem: Ilustração. Malha quadriculada. Cada quadradinho mede 1 cm de comprimento e 1 cm de largura. À esquerda, figura ocupando dez quadradinhos. No centro, figura ocupando sete quadradinhos. À direita, figura ocupando quatro quadradinhos e meio. Fim da imagem.

_____ cm²

PROFESSOR

Resposta: 10

_____ cm²

PROFESSOR

Resposta: 7

_____ cm²

PROFESSOR

Resposta: 4,5

MANUAL DO PROFESSOR

Objetivo

Resolver problemas envolvendo centímetro quadrado como unidade de medida de área.
Atividade 1

No ano anterior, os estudantes já tiveram contato com situações que envolvem medidas de superfície (área), trabalhando com malhas quadriculadas, com unidades de medida não padronizadas e com a unidade padronizada centímetro quadrado (cm²).

Nas atividades desta página e da próxima, eles vão calcular áreas em centímetro quadrado, contando quadrinhos com lados de medida 1 centímetro, o que possibilitará a visualização do centímetro quadrado.

Comente com os estudantes que essa é uma unidade adequada para expressar medidas de pequenas superfícies. Pergunte: “Que outras superfícies podem ter suas medidas expressas em centímetro quadrado?”. Eles podem mencionar a superfície de uma folha ou a de um caderno, por exemplo.

Proponha aos estudantes que desenhem outras figuras em malha quadriculada e troquem com um colega para que ele determine a área de cada figura, considerando o como unidade de medida. Chame a atenção para o fato de que, ao juntar com obtemos .

BNCC em foco:

EF05MA19, EF05MA24

MP230

Cristina está colando, em um papel retangular, papéis coloridos quadrangulares cujos lados medem 1 centímetro. Quantos centímetros quadrados ainda faltam ser preenchidos com os papéis quadrangulares?
_____

PROFESSOR
Resposta: 18 centímetros quadrados.

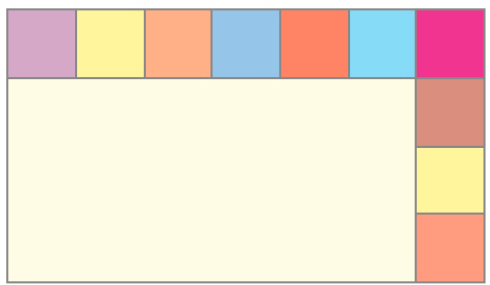
Imagem: Ilustração. Retângulo rosa-claro. Na parte superior há sete quadradinhos coloridos e à direita há quatro quadradinhos coloridos. No centro há um espaço vazio. Fim da imagem.

Descubra qual é a medida da área da figura verde abaixo, mas sem completar o quadriculado.

Imagem: Ilustração. retângulo com quadradinhos medindo 1 cm de comprimento e 1 cm de largura, ocupando sete colunas e cinco fileiras. Fim da imagem.

Imagem: Ilustração. Uma menina está sentada com o dedo indicador levantado. Ela fala: A figura verde tem espaço apra resposta cm2 de área. Fim da imagem.

PROFESSOR

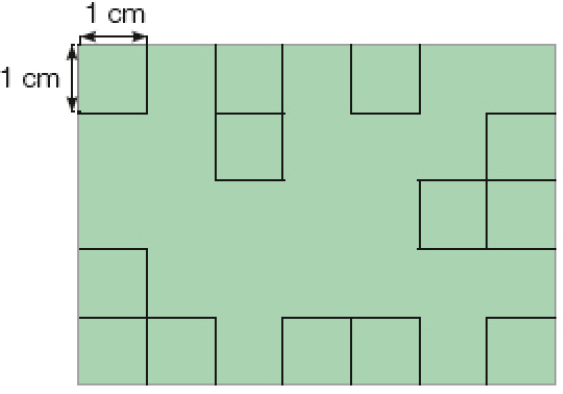
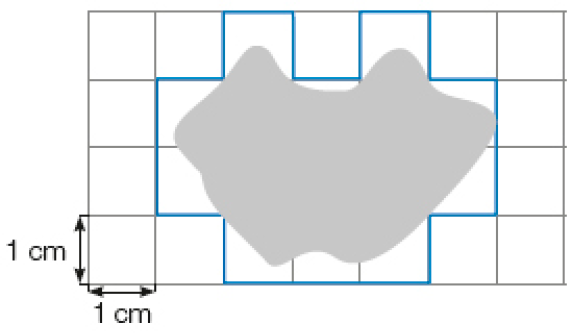
Resposta: 35

Observe como Luís estimou a medida da área de uma mancha na malha.

Imagem: Ilustração. Malha quadriculada. Cada quadradinho mede 1 cm de comprimento e 1 cm de largura. No centro há uma mancha ocupando quinze quadradinhos. Em volta da mancha, os quadradinhos estão destacados. Fim da imagem.

Imagem: Ilustração. Luís, jovem com cabelo encaracolado está apontando para a figura. Ele fala: Primeiro, fiz um contorno por fora dela, passando pelas linhas da malha. A medida da área da figura formada por esse contorno é, aproximadamente, espaço para resposta cm2. Fim da imagem.

PROFESSOR

Resposta: 15

Imagem: Ilustração. Luís com o dedo indicador levantado diz: Depois, fiz um contorno por dentro da mancha, passando pelas linhas da malha. A medida da área da figura formada por esse outro contorno espaço para resposta cm2. Vi, então, que a área da mancha era menor que a área da primeira figura e maior que a área da segunda figura. Fim da imagem.

PROFESSOR

Resposta: 5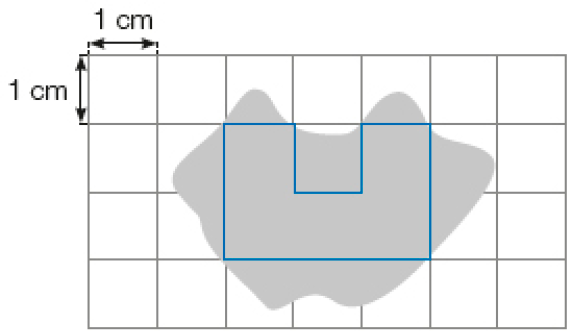

Luís obteve uma estimativa para a medida da área da mancha entre _____ cm² e _____ cm².

PROFESSOR
Resposta: 5, 15

MANUAL DO PROFESSOR

Atividade 2

Nesta atividade, os estudantes podem abandonar a ideia de contagem um a um dos quadrinhos e perceber que o cálculo da medida da área do retângulo pode ser obtido pela multiplicação dos valores que indicam suas dimensões.

Atividade 3

Observando a ilustração, os estudantes podem perceber que é possível encontrar o total de quadrinhos da figura, já que ela é composta de 5 fileiras horizontais e 7 verticais, o que resulta no total de 35 quadrinhos (5 × 7 = 35).

Como cada quadrinho tem área de 1 cm², a área da figura completa é igual a 35 cm².

Atividade 4

Esta atividade explora o cálculo da medida de área de uma figura não regular por meio de estimativa de contagem de quadrinhos.

Após a resolução, sugira aos estudantes que façam, em uma folha de papel quadriculado, outro desenho de forma irregular e o troquem com um colega, para a estimativa da medida de área do desenho utilizando a mesma estratégia empregada por Luís.

BNCC em foco:

EF05MA19

MP231

Metro quadrado

Reúna-se com seus colegas e façam o que se pede.
1. Construam uma superfície que meça 1 metro quadrado usando como material folhas de jornal, fita adesiva, fita métrica, tesoura com pontas arredondadas etc.
1. Usando a superfície construída, encontrem a medida aproximada, em metro quadrado, da área da lousa de sua classe e registrem a medida encontrada.
  _____
  
  PROFESSOR
  Resposta variável.
1. É adequado medir a superfície de seus cadernos com o metro quadrado?
  
  PROFESSOR
  Atenção professor: Espera-se que os estudantes percebam que não é adequado; o melhor seria usar a unidade de medida centímetro quadrado para medir a superfície de seus cadernos. Fim da observação.
1. Na opinião de vocês, em quais situações podemos usar a unidade de medida metro quadrado?
  
  PROFESSOR
  Exemplos de respostas: Para obter a medida da área de um imóvel, de uma lona, de um telhado.

Indicamos: 1 metro quadrado por 1 m²

A medida da área de uma superfície quadrada com lados que medem 1 metro de comprimento é igual a 1 metro quadrado.

Imagem: Ícone: mental. Fim da imagem.

Jair está numa loja de carpetes. Ele precisa forrar o piso retangular de um escritório cujas medidas são 4 metros de comprimento por 3 metros de largura, conforme o esquema a seguir.

Imagem: Ilustração. Jair, homem calvo com terno está com a mão direita sob o queixo. Na frente dele há uma placa com a informação: CARPETE DE MADEIRA R$ 50,00 O METRO QUADRADO. Ao lado, uma mulher com cabelo azul e curto está ajoelhada sobre um quadrado de madeira, que mede 1 metro de comprimento e 1 metro de largura. Atrás dela, uma faixa com a informação: VEJA 1 METRO QUADRADO DE CARPETE. Fim da imagem.

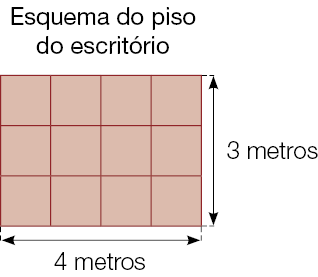
Imagem: Ilustração. Esquema do piso do escritório. Retângulo com 3 metros de comprimento e 4 metros de largura. Fim da imagem.

De quantos metros quadrados de carpete de madeira Jair precisará para forrar o piso do escritório? _____

PROFESSOR
Resposta: De 12 metros quadrados.

Quanto ele gastará se comprar o carpete de madeira dessa loja? _____

PROFESSOR
Resposta: 600 reais.

Um terreno mede 12 metros de largura por 25 metros de comprimento. Ele tem um muro em sua volta, exceto pelos dois portões de acesso: um portão com 1 metro de largura e o outro, com 2 metros.
1. Qual é a medida da área do terreno? _____
  
  PROFESSOR
  Resposta: 300 m²
1. Quantos metros de comprimento tem o muro? _____
  
  PROFESSOR
  Resposta: 71 m

MANUAL DO PROFESSOR

Objetivo

Resolver problemas envolvendo metro quadrado como unidade de medida de área.
Atividade 1

No item a, oriente os estudantes na montagem do metro quadrado. Eles devem juntar folhas de jornal e colá-las com fita adesiva. Esse tipo de atividade contribui para o desenvolvimento da capacidade de estimativa de medidas de área que envolvam o metro quadrado, assim como o reconhecimento de áreas que são medidas com essa unidade.

Ao responder ao item c, eles percebem que, para medir a superfície de um caderno, o centímetro quadrado é uma unidade mais adequada do que o metro quadrado.

Outros exemplos de resposta ao item d podem ser: na medição de uma quadra de basquete, do terreno de uma casa, da superfície de uma parede etc.

Atividade 2

Explore a situação pedindo à turma que pesquise a medida da área, em metro quadrado, de alguns locais de sua cidade, como campos de futebol ou praças públicas.

No item b, diga aos estudantes que geralmente se compra um pouco mais que a medida exata da superfície que se quer forrar, pois devem ser consideradas eventuais perdas.

Atividade 3

Peça aos estudantes que desenhem em um papel o terreno descrito, incluindo os portões, e utilizem uma régua para representar as medidas em centímetro. A representação em desenhos facilita a visualização e o raciocínio matemático dos estudantes.

No item b, sugere-se que utilizem o desenho para elaborar a estratégia de resolução. Espera-se que eles percebam que devem calcular a medida do perímetro do terreno e, do valor obtido, retirar a medida do comprimento dos portões para calcular a metragem de muro.

Espera-se que eles associem o cálculo da medida da área do terreno com o produto entre os valores das dimensões do terreno. Enfatize a importância de utilizarem a unidade de medida mais adequada para representar áreas (no caso, m²).

BNCC em foco:

EF05MA19

MP232

Quilômetro quadrado

Joaquim visitou uma reserva ecológica que tem medida da área total de 8 quilômetros quadrados.

Imagem: Ilustração. Joaquim, homem com boné e mochila grande nas costas está andando sobre uma estrada de terra. Ele sorri e pensa: Eu sei que 1 quilômetro corresponde a 1.000 metros. Mas o que é 1 quilômetro quadrado? Ao fundo, árvores, plantas e morros. Fim da imagem.

Na reserva, há lagos que ocupam uma área total de medida 3 quilômetros quadrados. O restante da reserva é ocupado por mata.

Considerando que cada Ilustração. quadradinho verde. representa 1 quilômetro quadrado, descubra qual dos desenhos abaixo tem a área equivalente à área da mata dessa reserva.

Imagem: Ilustração. Fileira de seis quadrados verdes. Fim da imagem.

( )

Imagem: Ilustração. Quatro quadrados verdes intercalados. Fim da imagem.

( )

Imagem: Ilustração. Fileira com três quadrados verdes e abaixo há dois quadrados verdes. Fim da imagem.

( )

PROFESSOR

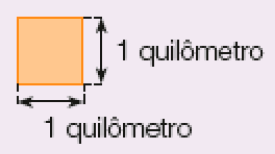
Resposta correta: figura 3.

O quilômetro quadrado é uma unidade de medida de superfície correspondente à área de um quadrado cujos lados medem 1 quilômetro.

Indicamos: 1 quilômetro quadrado por 1 km²

Imagem: Ilustração. Quadrado laranja com 1 quilômetro de comprimento e 1 quilômetro de largura. Fim da imagem.

Imagem: Ícone: Calculadora. Fim da imagem.

Observe o quadro e responda à questão.

Tabela: equivalente textual a seguir.

País	Medida da área aproximada (em km²)
Brasil	8.514.876
Uruguai	176.215

Aproximadamente quantas superfícies iguais à do Uruguai seriam necessárias para cobrir toda a superfície do Brasil?
_____

PROFESSOR
Exemplo de resposta: aproximadamente 48 superfícies.

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

Faça uma estimativa para responder à questão.
A superfície em que está localizada sua escola tem medida da área maior ou menor que 1 km²?

PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR

Objetivo

Resolver problemas envolvendo quilômetro quadrado como unidade de medida de área.
Atividade 1

Pergunte aos estudantes:
Que unidade de medida usariam para medir grandes superfícies, como a de uma cidade: centímetro quadrado, metro quadrado ou quilômetro quadrado? Espera-se que eles percebam que, para medir grandes superfícies, é necessário empregar uma unidade de medida maior que o centímetro quadrado ou o metro quadrado; costuma-se usar o quilômetro quadrado.
Em quais situações pode-se usar a unidade de medida de superfície quilômetro quadrado? Exemplo de resposta: O quilômetro quadrado pode ser usado para medir a superfície de países, estados, cidades etc.
Atividade 2

Peça aos estudantes que pesquisem a área, em quilômetro quadrado, de seu município, de seu estado e de outros países, para que possam comparar as medidas e desenvolver estimativas de áreas.

Atividade 3

Explore esta atividade dizendo que, frequentemente, os quarteirões das cidades brasileiras têm 100 m de comprimento e de largura, ou seja, uma área de 10.000 m². Logo, seriam necessários 100 quarteirões para compor uma área de 1 km².

Após introduzir esse referencial para a medida de 1 km², pergunte: “A superfície de nossa escola tem área maior ou menor que 1 km²?”.

Como nos limites da escola não é possível construir um quilômetro quadrado, ofereça aos estudantes oportunidades de relacionar essa unidade ao que já sabem sobre o metro quadrado e o centímetro quadrado, de modo que compreendam que o quilômetro quadrado corresponde à medida de superfície de um quadrado cujos lados medem 1 quilômetro de comprimento.

BNCC em foco:

EF05MA19, EF05MA24

MP233

Área e perímetro

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

Desenhe na malha quadriculada dois retângulos diferentes com medida de área igual a 10 cm².

PROFESSOR

Exemplos de desenho: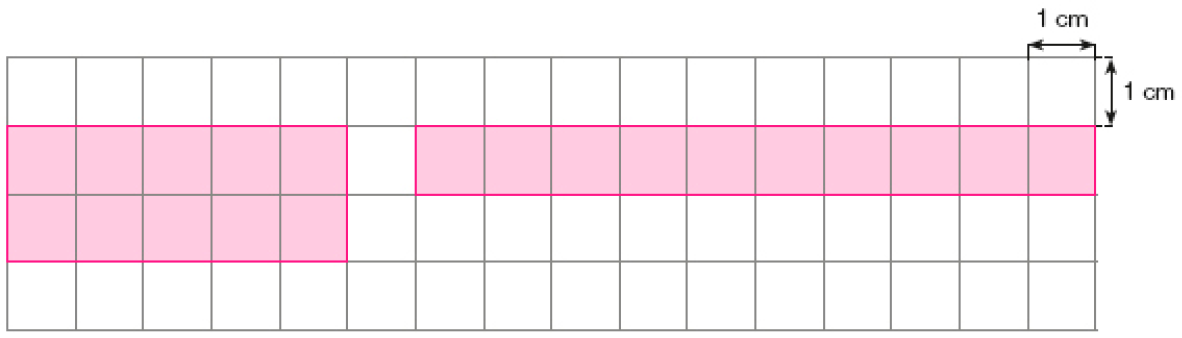

Imagem: Ilustração. Malha quadriculada. Cada quadradinho mede 1 cm de comprimento e 1 cm de largura. À esquerda, duas fileiras de cinco quadradinhos pintados de rosa, um em cima do outro. À direita, fileira com dez quadradinhos pintados de rosa. Fim da imagem.

Agora, responda à questão e faça o que se pede.

Qual é a medida do perímetro de cada retângulo que você desenhou? Elas são iguais? _____

PROFESSOR
Exemplos de resposta: 14 cm; 22 cm; não.

Converse com os colegas e o professor sobre a afirmação: figuras com mesma área podem ter perímetros diferentes.

PROFESSOR
Respostas pessoais.

No escritório de Luísa, há duas salas de reunião, como mostram os esquemas abaixo.

Sala de reunião A

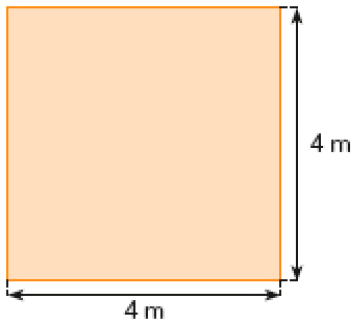
Imagem: Ilustração. Quadrado com 4 m de comprimento e 4 m de largura. Fim da imagem.

Sala de reunião B

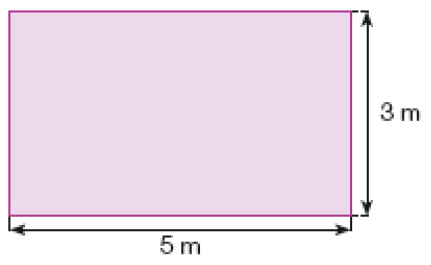
Imagem: Ilustração. Retângulo com 3 m de comprimento e 5 m de largura. Fim da imagem.

Luísa quer colocar carpete nas duas salas. De quantos metros quadrados de carpete Luísa precisará para cobrir o piso de cada uma das salas?
_____

PROFESSOR
Resposta: Sala A: 16 m²; sala B: 15 m²

Qual é a medida do perímetro de cada sala?
_____

PROFESSOR
Resposta: Sala A: 16 m; sala B: 16 m

Converse com os colegas e o professor sobre a afirmação: figuras com medidas de perímetro iguais podem ter medidas de área diferentes.

PROFESSOR
Respostas pessoais.

MANUAL DO PROFESSOR

Objetivo

Concluir, por meio de investigações, que figuras com medidas de perímetro iguais podem ter áreas diferentes, assim como figuras que têm a mesma medida de área podem ter medidas de perímetro diferentes.
Atividade 1

Peça aos estudantes que desenhem outros retângulos cujas medidas de área sejam: 12 cm², 13 cm², 16 cm² etc. Considerando só números naturais, um retângulo de medida de área igual a 13 cm² só pode ser representado de um único modo com lados iguais a 1 cm e 13 cm. Treze é um número primo, tem apenas dois divisores: 1 e ele mesmo. Quando o número correspondente à medida da área de um retângulo não é um número primo, o retângulo pode ser representado de mais de uma maneira.

Atividade 2

Pergunte: “Qual é a medida do perímetro de cada uma das salas de reunião?”. Espera-se que calculem:
medida do perímetro da sala A:
4 m + 4m + 4 m + 4m = 16 m
medida do perímetro da sala B:
3 m + 5m + 3 m + 5m = 16 m

Os estudantes devem perceber que, apesar de terem o mesmo perímetro, as medidas das áreas das duas salas são diferentes, ou seja, duas figuras de mesma medida de perímetro não têm, necessariamente, a mesma medida de área. Peça que obtenham outros retângulos de medida de perímetro igual a 16 m e depois calculem a medida da área de cada um e as comparem. Veja alguns exemplos:

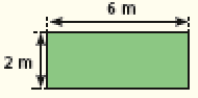
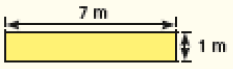
CRÉDITO: ADILSON SECCO

Calculando a medida da área de cada figura, obtemos, para o retângulo verde, o valor 12 m² (2 × 6 = 12); para o retângulo amarelo, 7 m² (7 × 1 = 7).

BNCC em foco:

EF05MA20

MP234

Ideia de volume

Na loja de materiais de construção, Jonas empilhou 18 tijolos.
Podemos dizer que a medida do volume desse empilhamento, relativa ao espaço ocupado por ele, corresponde a 18 tijolos.

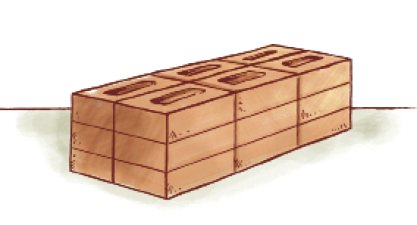
Imagem: Ilustração. Dezoito tijolos divididos em duas fileiras com três tijolos cada. Fim da imagem.

Nesse caso, o tijolo é a unidade de medida do volume relativo ao espaço ocupado pelo empilhamento.

Se os 18 tijolos fossem de tamanhos diferentes uns dos outros, seria possível concluir que a medida do volume do empilhamento corresponde a 18 tijolos? Por quê?
_____

PROFESSOR
Resposta: É importante esclarecer aos estudantes que essa conclusão não seria correta, pois assim o tijolo não seria uma unidade de medida, isto é, não poderia servir como termo de comparação.

Calcule a medida do volume de cada empilhamento usando 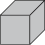como unidade de medida e registre-a.

Imagem: Ilustração. Figura composta por dezoito cubos verdes. Fim da imagem.

_____ Ilustração. Um cubo cinza.

PROFESSOR

Resposta: 18

Imagem: Ilustração. Figura composta por doze cubos vermelhos. Fim da imagem.

_____ Ilustração. Um cubo cinza.

PROFESSOR

Resposta: 12

Imagem: Ilustração. Figura composta por dezesseis cubos amarelos. Fim da imagem.

_____ Ilustração. Um cubo cinza.

PROFESSOR

Resposta: 16

Imagem: Ilustração. Figura composta por trinta e seis cubos azuis. Fim da imagem.

_____ Ilustração. Um cubo cinza.

PROFESSOR

Resposta: 36

Agora, calcule novamente a medida do volume desses empilhamentos usando como unidade de medida e registre-a.

_____

PROFESSOR
Resposta: 9

_____

PROFESSOR
Resposta: 6

_____

PROFESSOR
Resposta: 8

_____

PROFESSOR
Resposta: 18

MANUAL DO PROFESSOR

Objetivos

Reconhecer volume como grandeza associada a sólidos geométricos.
Medir volumes por meio de empilhamento de cubos.
O tópico tratado nestas páginas introduz as primeiras noções sobre volume (medida do espaço ocupado por algo), apresentando situações-problema nas quais estão presentes unidades de medida não padronizadas para o cálculo de volume – como tijolos e cubinhos.

Atividade 1

É importante que os estudantes compreendam que, se os tijolos fossem de tamanhos diferentes, não seria possível obter o volume do empilhamento tendo o tijolo como unidade de medida, uma vez que, para medir qualquer grandeza, deve haver uniformidade de tamanho dos objetos que compõem o conjunto medido, no caso, os tijolos que formam a pilha. Caso permaneça dúvida, explique aos estudantes que, por exemplo, não existem dois tipos de segundo (um maior e outro menor) como unidade de medida da grandeza tempo; não existem dois “tamanhos” de metro na grandeza comprimento.

Atividade 2

Para a resolução das questões desta atividade, espera-se que os estudantes percebam que, ao aumentar a unidade de medida do espaço ocupado pelos cubos, o número que expressa a medida do volume diminui.

No caso, quando dobramos a unidade de medida (de um cubinho para dois cubinhos), o número que expressa a medida do volume passa a ser metade do número que a expressava com a unidade de medida menor.

BNCC em foco:

EF05MA21

MP235

Observe os empilhamentos de cubos dentro das caixas transparentes e faça o que se pede.

Empilhamento A

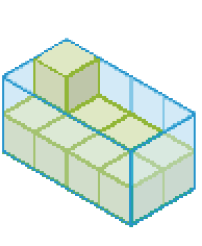
Imagem: Ilustração. Paralelepípedo transparente e dentro há nove cubos verdes com espaço para mais sete cubos. Fim da imagem.

Empilhamento B

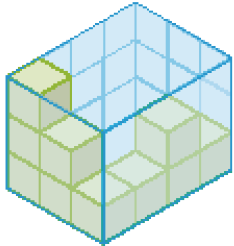
Imagem: Ilustração. Paralelepípedo transparente e dentro há dez cubos verdes com espaço para mais vinte e seis cubos. Fim da imagem.

Considerando unidade de medida, calcule a medida do volume dos empilhamentos, caso as caixas transparentes estivessem totalmente preenchidas com cubos.

Empilhamento A - _____ Ilustração. Cubo verde.

PROFESSOR

Resposta: 16

Empilhamento - _____ Ilustração. Cubo verde.

PROFESSOR

Resposta: 36

Imagine que cada seja oco e que caibam 2 litros de água em cada um. Quantos litros de água caberiam em cada caixa transparente?
_____

PROFESSOR
Resposta: Caixa do empilhamento A: 32 litros de água; caixa do empilhamento B: 72 litros de água.

Imagem: Ilustração. Um menino com cabelo castanho segura uma jarra e despeja água dentro de um cubo transparente. Fim da imagem.

Imagem: Ilustração. Uma mulher com cabelo ondulado e comprido fala: A quantidade de litros de água que você calculou corresponde à capacidade em litro dessas caixas transparentes. É comum associarmos a capacidade de um recipiente ao volume do seu interior. Fim da imagem.

Observe o cubo e responda às questões.

Imagem: Ilustração. Um cubo composto por vinte e sete cubinhos coloridos. Fim da imagem.

Considerando cada cubinho unidade de medida, qual é a medida do volume total do cubo?
_____

PROFESSOR
Resposta: 27 cubinhos.

Quanto é, em cubinho, $\frac{1}{3}$ da medida do volume total do cubo?
_____

PROFESSOR
Resposta: 9 cubinhos.

MANUAL DO PROFESSOR

Atividade 3

Os estudantes devem calcular o volume de um empilhamento indicando sua medida por meio de uma unidade não padronizada, no caso, o cubinho.

Além disso, como o problema apresenta uma relação entre os cubinhos e a quantidade de litros de água que neles caberiam se fossem ocos, os estudantes têm a oportunidade de associar volume com capacidade. Simplificadamente, podemos dizer que volume é a medida do espaço que um corpo ocupa e que capacidade é quanto (de água ou de ar, por exemplo) cabe dentro de um corpo oco. É fundamental os estudantes reconhecerem a diferença entre essas duas grandezas, associando cada uma à unidade de medida correspondente.

Atividade 4

Os estudantes devem associar o volume do cubo a uma unidade não padronizada, os cubinhos. Porém, ao contrário da atividade anterior, espera-se que eles utilizem a multiplicação para calcular a medida do volume do cubo, apesar de ser possível fazer esse cálculo contando os cubinhos um a um.

Incentive-os a enxergarem que o cubo pode ser repartido em 3 camadas de 9 cubinhos.

Assim, podem fazer 3 × 9 cubinhos = 27 cubinhos para obter o volume.

BNCC em foco:

EF05MA21

MP236

Compreender problemas

Para resolver

Problema 1

Marta precisa empilhar certa quantidade de cubinhos idênticos seguindo algumas dicas.

Leia as dicas, observe os arranjos de cubinhos a seguir e descubra qual deles corresponde ao que foi feito por Marta e quantos cubinhos ela usou.

_____

PROFESSOR

Resposta: Marta fez o arranjo 1 e usou 5 cubinhos.

Boxe complementar:

Dicas

Os cubinhos devem estar sobre uma malha quadriculada de 5 quadradinhos por 5 quadradinhos.

Usar apenas duas camadas de empilhamento.

O arranjo deve conter uma quantidade ímpar de cubinhos.

Imagem: Ilustração. Um homem loiro com cabelo comprido está com a mão esquerda sob o queixo e com uma sobrancelha levantada. Fim da imagem.

CRÉDITO: SERGIO NG E GEORGE TUTUMI

Fim do complemento.

Imagem: Ilustração. Placa com quatro fileiras e quatro colunas de quadradinhos. Há dois cubos azuis empilhados sobre um quadradinho e ao lado, três cubinhos azuis sobre outros quadradinhos. Fim da imagem.

Arranjo 1

Imagem: Ilustração. Placa com cinco fileiras e cinco colunas de quadradinhos. Há uma fileira com cinco cubos azuis em cima de quadradinhos e acima há mais três cubinhos azuis. Fim da imagem.

Arranjo 2

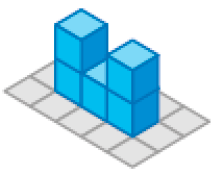
Imagem: Ilustração. Placa com três fileiras e cinco colunas de quadradinhos. Há uma fileira com três cubos azuis em cima de quadradinhos e acima há mais dois cubinhos azuis. Fim da imagem.

Arranjo 3

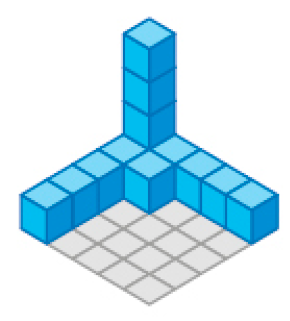
Imagem: Ilustração. Placa com cinco fileiras e cinco colunas de quadradinhos. Há duas fileiras com cinco cubos azuis em cima de quadradinhos e acima há mais três cubinhos azuis empilhados. Ao lado, um cubinho azul. Fim da imagem.

Arranjo 4

Problema 2

Dois azulejos idênticos têm, juntos, 15 cm² de medida de área. Quantos centímetros quadrados têm 6 desses azulejos? E 10 desses azulejos? _____

PROFESSOR

Resposta: 45 cm²; 75 cm².

Problema 3

Leia as informações a seguir e descubra a qual triângulo representado na malha elas se referem. _____

PROFESSOR

Resposta: Triângulo amarelo.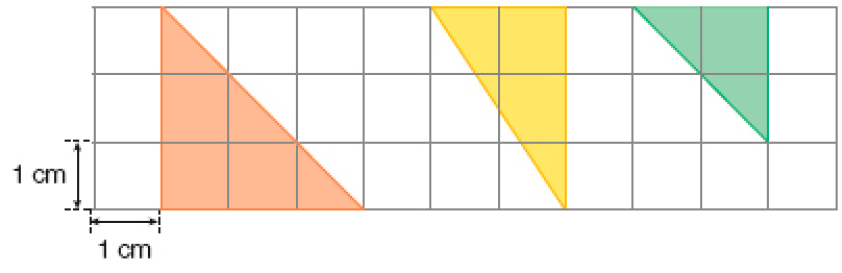

Imagem: Ilustração. Malha quadriculada. Cada quadradinho mede 1 cm de comprimento e 1 cm de largura. À esquerda há um triângulo vermelho ocupando quatro quadradinhos e meio. No centro, um triângulo amarelo ocupando três quadradinhos. À direita, um triângulo verde ocupando dois quadradinhos. Fim da imagem.

PROFESSOR

Resposta: 4,5 cm²; 3 cm²; 2 cm².

O triângulo representado tem:

medida de área maior que 2 cm²;
todos os lados de medidas diferentes;
a medida do menor lado é dada por um número par.

MANUAL DO PROFESSOR

Objetivos

Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos.
Resolver e elaborar problemas envolvendo medidas das grandezas área e volume.
Nestas páginas, também é trabalhado o conceito de proporcionalidade (noção de raciocínio algébrico), que pode ser resolvido por meio da organização dos dados.

Deixe os estudantes criarem estratégias próprias para resolverem os problemas propostos.

No Problema 2, eles precisam pensar em agrupamentos de 2: quantos 2 cabem em 6?; quantos 2 cabem em 10?. Desse modo, poderão verificar que, se 2 azulejos têm área de 15 cm², então 6 azulejos, que são 3 × 2 azulejos, terão 3 × 15 cm² de área, ou seja, 45 cm². Usando esse mesmo raciocínio, 10 azulejos, que são 5 × 2 azulejos, terão 5 × 15 cm² de área, ou seja, 75 cm².

BNCC em foco na dupla de páginas:

EF05MA12, EF05MA19; competências específicas 3 e 6

MP237

Para refletir

Em dupla, conversem para descobrir a partir de qual dica do Problema 1 cada criança tirou sua conclusão.

PROFESSOR
Resposta: Rogério usou a primeira dica; Ana usou a segunda dica; e Daniela deve ter usado todas as dicas para tirar sua conclusão.

Imagem: Ilustração. À esquerda, Rogério, jovem com boné azul fala: Marta não fez o arranjo 3. No centro, Ana, jovem com cabelo castanho e preso diz: Ela não pode ter feito o arranjo 4. À direita, Daniela, jovem loira com tiara sorri e fala: A medida do volume do arranjo de Marta é 5 cubinhos. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

Por que o Problema 2 pode ser resolvido com o esquema abaixo?
_____

PROFESSOR
Exemplo de explicação: Cada quadrinho apresenta a medida de área de 2 azulejos. Assim, 3 quadrinhos correspondem à medida de área de 6 azulejos (45 cm²) e 5 quadrinhos correspondem à medida de área de 10 azulejos (75 cm²).

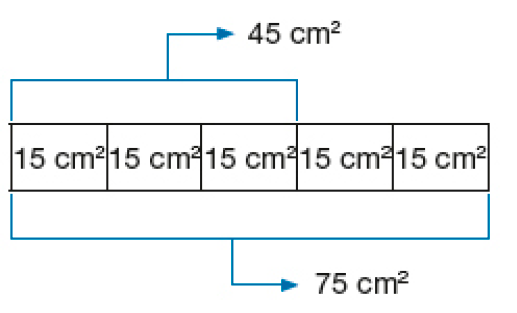
Imagem: Ilustração. Cinco retângulos lado a lado e cada um mede 15 cm2. Acima de três, a informação: 45 cm2. E abaixo de todos, a informação: 75 cm2. Fim da imagem.

A afirmação abaixo, referente ao Problema 3, é verdadeira ou falsa? Justifique.

O triângulo verde não pode ser o triângulo do qual se fala.

_____

PROFESSOR

Resposta: A afirmação é verdadeira. Exemplo de explicação: O triângulo tem dois lados de mesma medida.

Modifique o Problema 3 para que a resposta seja o triângulo laranja.
_____

PROFESSOR
Exemplo de resposta: Esse triângulo tem medida de área maior que 2 cm² e dois lados de medidas iguais.

MANUAL DO PROFESSOR

Para refletir

Atividade 1

Sugira aos estudantes que releiam os problemas para que verifiquem as informações necessárias e discutam com um colega sobre elas.

Rogério usou a dica “Os cubinhos devem estar sobre uma malha quadriculada de 5 por 5 quadradinhos”. O arranjo 3 está sobre uma malha 5 por 3. Ana usou a dica “Usar apenas duas camadas de empilhamento”. No arranjo 4 o empilhamento foi feito até a 4ª camada.

A conclusão de Daniela não foi tirada diretamente de nenhuma dica; mas ela deve ter usado todas as dicas para descobrir o arranjo de Marta.

BNCC em foco na dupla de páginas:

EF05MA12, EF05MA19; competências específicas 3 e 6

MP238

Matemática em textos

Leia

O cuidado com a audição

A Organização Mundial da Saúde (OMS) publicou em 3 de março de 2017, no Dia Mundial da Audição, que problemas de audição provocados por causas diversas já afetam 360 milhões de pessoas, dos quais 32 são crianças.

As causas para a deficiência auditiva podem ser congênitas (como infecções durante a gravidez, falta de oxigênio na hora do parto ou problema de saúde que pode danificar o nervo auditivo em recém-nascidos, por exemplo) ou adquiridas.

Essa última categoria inclui a exposição a quantidades excessivas de ruído, como escutar músicas em fones de ouvido por tempo prolongado e a volumes muito altos.

A OMS recomenda a “escuta segura”, ou seja, práticas que protegem as orelhas de ruídos muito altos em atividades ocupacionais ou de lazer, que dependem da intensidade, duração e frequência dos estímulos sonoros.

Imagem: Ilustração. À esquerda, uma menina com cabelo preto e curto está com a mão esquerda ao lado do ouvido. Em volta dela há notas e instrumentos musicais, entre eles: uma guitarra, dois sinos, um xilofone, um pandeiro, chocalhos e fones de ouvidos. Fim da imagem.

Responda

Em que dia é comemorado o Dia Mundial da Audição?
_____

PROFESSOR
Resposta: No dia 3 de março.

Quais podem ser as causas para a deficiência auditiva?
_____

PROFESSOR
Resposta: Podem ser congênitas (como infecções durante a gravidez, falta de oxigênio na hora do parto ou problema de saúde que pode danificar o nervo auditivo em recém-nascidos, por exemplo) ou adquiridas (como a exposição a quantidades excessivas de ruído, como escutar músicas em fones de ouvido por tempo prolongado e a volumes muito altos).

MANUAL DO PROFESSOR

Objetivo

Refletir sobre os cuidados com a audição.
O tema escolhido para as páginas desta seção é bastante atual, uma vez que, com a crescente urbanização mundial e com o desenvolvimento acelerado de novas tecnologias sonoras, as pessoas – sobretudo jovens e crianças – estão cada vez mais expostas aos riscos provenientes de sons intoleráveis à orelha humana, seja pela intensidade, seja pelo tempo de exposição.

Responda

Peça aos estudantes que releiam o texto em duplas e encontrem nele as respostas. Explore mais perguntando se, assim como recomenda o texto, eles limpam os fones de ouvido. Esclareça que decibel é a unidade utilizada na medida da intensidade do som, correspondente à décima parte do bel. [símb.: dB].

BNCC em foco:

EF05MA08; competências específicas 2 e 4

MP239

O limiar de segurança é de sons com volume de 85 decibéis, que podem ser ouvidos por um máximo de oito horas. Conforme o volume aumenta, o tempo seguro de exposição cai dramaticamente.

Por exemplo, o som produzido pelo trem do metrô — estimado em 100 decibéis — pode ser escutado sem danos à saúde por apenas 15 minutos por dia.

Para cuidar bem das orelhas, procure usar os fones em ambientes menos barulhentos, assim você não precisa aumentar o volume em excesso; mantenha os fones de ouvido sempre limpos, afinal eles estarão em contato com as orelhas; e não se esqueça de estabelecer alguns períodos de descanso às orelhas.

Informações obtidas em: http://fdnc.io/eUv. Acesso em: 4 ago. 2021.

Analise

Qual é o limite de sons, em decibel, que podem ser ouvidos por um máximo de 8 horas?
_____

PROFESSOR
Resposta: 85 decibéis.

Qual é o som estimado, em decibel, produzido por um trem do metrô?
_____

PROFESSOR
Resposta: 100 decibéis.

Aplique

Imagem: Ícone: Dupla. Fim da imagem.

Você se preocupa com sua audição? Reúna-se com um colega e discutam o que pode ser feito para preservá-la. Depois, façam um cartaz mostrando os cuidados que precisamos ter com nossa audição.

PROFESSOR

Resposta pessoal.

MANUAL DO PROFESSOR

Analise

O conhecimento sobre o limite das intensidades de som suportáveis e sobre o período máximo de exposição a elas contribui para maior conscientização acerca do cuidado com a saúde auditiva. É importante discutir com a turma essas informações, geralmente desprezadas pela maioria das pessoas, pois os efeitos danosos da exposição excessiva a sons agressivos à audição só aparecem ao longo dos anos.

Atividade 1

Aproveite e pergunte: “Vocês escutam música usando fones? Se sim, aproximadamente quanto tempo por dia?”. Comente com os estudantes que a medida da intensidade do som é chamada de decibel.

Atividade 2

Amplie perguntando: “Qual é a diferença entre o som produzido pelo trem do metrô e o limiar de segurança de sons? Vocês consideram essa diferença grande ou pequena?”.

Aplique

Aproveite para discutir com a turma o que é e o que não é saudável para a audição humana. Peça que pesquisem informações sobre os danos causados às orelhas pelo excesso de exposição a sons de intensidade superior a 85 decibéis e comente que existe um projeto de lei para proibir a venda de aparelhos sonoros que reproduzam sons acima de 90 decibéis.

BNCC em foco:

EF05MA24; competências específicas 2 e 4

MP240

Compreender informações

Completar e interpretar gráficos

Sueli é dona de uma imobiliária que negocia terrenos. No início de cada mês, ela registra os resultados do total de dinheiro recebido com as vendas do mês anterior. Neste mês, ao fazer suas anotações, Sueli esqueceu de anotar uma das porcentagens recebida. Veja e escreva essa porcentagem:

A venda de terrenos com menos de 200 m² representou 40% do total recebido.
A venda de terrenos de 200 a 300 m² representou 35% do total recebido.
A venda de terrenos de 301 a 400 m² representou 15% do total recebido.
A venda de terrenos com mais de 400 m² representou _____ % do total recebido.

PROFESSOR
Resposta: 10

Sueli começou a elaborar um gráfico de setores para mostrar os resultados da venda do mês anterior.
Ajude Sueli a completar o gráfico. Faça uma legenda e identifique cada setor colorido com a porcentagem correspondente do total recebido.

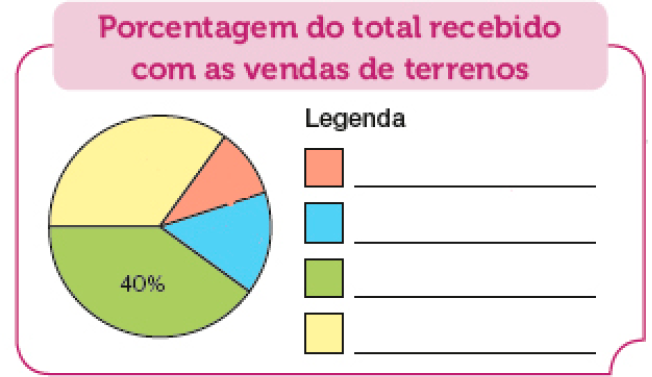
Imagem: Gráfico em setores. Porcentagem do total recebido com as vendas de terrenos. Gráfico circular dividido em quatro partes coloridas. Ao lado, a legenda: Vermelho: espaço para resposta. Azul: espaço para resposta. Verde: espaço para resposta. Amarelo: espaço para resposta No gráfico, grande parte verde (40%); parte amarela média espaço para resposta; parte azul pequena espaço para resposta; e parte vermelha menor espaço para resposta. Fim da imagem.

Fonte: Imobiliária da Sueli (jun. 2023).

PROFESSOR

Resposta: 10% - Terrenos com mais de 400 m²

PROFESSOR

15% - Terrenos entre 301 e 400 m²

PROFESSOR

40% - Terrenos com menos de 200 m²

PROFESSOR

35% - Terrenos de 200 a 300 m²

Que porcentagem representa o total recebido com as vendas?
_____

PROFESSOR
Resposta: 100% (correspondente ao círculo inteiro).

Que porcentagem do total recebido Sueli esqueceu de anotar? Essa porcentagem corresponde a que setor colorido no gráfico? _____

PROFESSOR
Resposta: 10%; setor vermelho.

Que porcentagem do total recebido corresponde à venda de terrenos de 300 m² ou menos? Que parte do gráfico essa porcentagem representa?
_____

PROFESSOR
Resposta: 75%; partes verde e amarela juntas.

Que porcentagem do total recebido representam os setores vermelho e azul juntos nesse gráfico? Essa porcentagem refere-se à venda de que tipo de terreno? _____

PROFESSOR
Resposta: 25%; refere-se à venda de terrenos com mais de 300 m².

Que tipo de terreno Sueli vendeu menos no mês anterior?
_____

PROFESSOR
Resposta: Terrenos com 400 m² ou mais.

MANUAL DO PROFESSOR

Objetivos

Interpretar dados apresentados em tabela e gráficos.
Organizar dados coletados por meio de gráficos de setores e de linhas.
Produzir texto escrito para síntese dos resultados de uma pesquisa.
Atividade 1

No item a, os estudantes devem compreender que a porcentagem que falta nas anotações de Sueli é aquela que completa 100% ao adicionarmos todas as porcentagens. Assim:

40% + 35% + 15% = 90%

100% − 90% = 10%

Logo, a venda de terrenos com mais de 400 m² equivale a 10% do total recebido.

Depois, os estudantes devem observar o gráfico de setores e completar as porcentagens de acordo com o tamanho de cada região colorida (setor). Assim, devem verificar que o menor setor é o vermelho (10%); o segundo menor é o azul (15%); o maior é o verde (40%) e o que sobrou é o amarelo (35%).

No item b, espera-se que os estudantes percebam que a soma de todas as porcentagens deve ser 100%, correspondente ao círculo inteiro.

BNCC em foco:

EF05MA24, EF05MA25; competências específicas 3 e 6

MP241

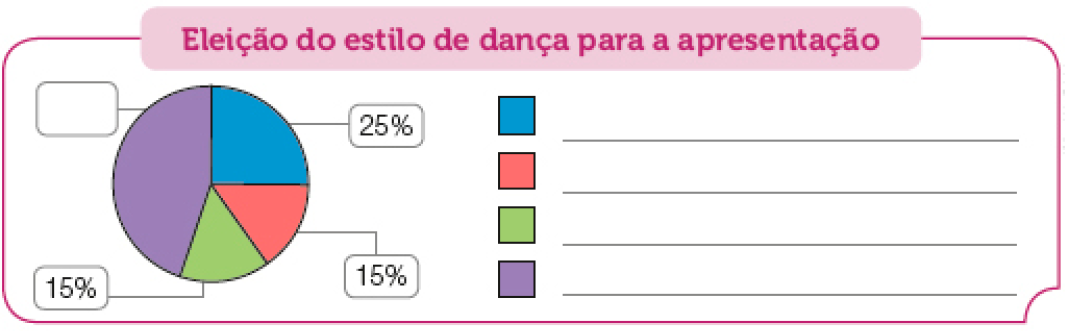
Em uma escola, 4 estilos de dança de salão foram selecionados para uma apresentação e 100 estudantes votaram, escolhendo apenas um desses estilos:
- Samba de gafieira recebeu 25 votos.
- Bolero e salsa receberam a mesma quantidade de votos.
- Forró ficou com 45 votos.
  a) Complete o gráfico com base nas informações dadas acima.

Imagem: Gráfico em setores. Eleição do estilo de dança para a apresentação. Gráfico circular dividido em quatro partes coloridas. Ao lado, a legenda: Azul: espaço para resposta. Vermelho: espaço para resposta. Verde: espaço para resposta:. Roxo: espaço para resposta. No gráfico, grande parte roxa espaço para resposta, parte azul média (25%); parte verde pequena (15%); e parte vermelha pequena (15%). Fim da imagem.

Fonte: Escola considerada (jun. 2023).

PROFESSOR

Exemplo de resposta: 25% - Samba de gafieira

PROFESSOR

Exemplo de resposta: 15% - Salsa

PROFESSOR

Exemplo de resposta: 15% - Bolero

PROFESSOR

Exemplo de resposta: 45% - Forró

Qual foi a quantidade de votos dados para o bolero? E para a salsa?
_____

PROFESSOR
Resposta: Bolero: 15 votos; salsa: 15 votos.

Algum dos estilos recebeu mais da metade dos votos? Por quê?
_____

PROFESSOR
Resposta: Não, porque no máximo um estilo recebeu 45%, não atingindo os 50% (metade).

A tabela a seguir mostra a variação da medida da temperatura em uma cidade nas 12 primeiras horas do dia.
a) Complete o gráfico de linhas com os dados da tabela.

Temperatura na cidade

Tabela: equivalente textual a seguir.

Horário	Temperatura (em grau Celsius)
0 h	16
3 h	12
6 h	16
9 h	24
12 h	28

Fonte: Sistema de meteorologia da cidade (14 jan. 2023).

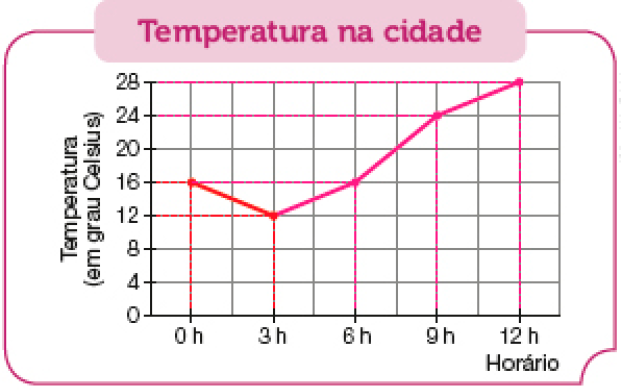
Imagem: Gráfico em linhas. Temperatura na cidade. No eixo vertical, a temperatura (em grau Celsius) e no eixo horizontal, o horário. 0 h: 16 ºC; 3 h: 12 ºC; 6 h: 16 ºC; 9 h: 24 ºC; 12 h: 28 ºC. Fim da imagem.

Fonte: Sistema de meteorologia da cidade (14 jan. 2023).

Explique como as medidas de temperatura variaram nesse período.
_____

PROFESSOR
Atenção professor: Espera-se que os estudantes observem as temperaturas correspondentes a cada horário e identifiquem que a temperatura diminuiu de 0 h a 3 h e, a partir daí, só aumentou. Fim da observação.

MANUAL DO PROFESSOR

Atividade 2

Como o todo compreende 100 elementos, facilmente os estudantes obterão as porcentagens:

Samba de gafieira: 25 votos em 100 → 25%
Forró: 45 votos em 100 → 45%
Bolero e salsa: mesma quantidade de votos
Como já temos 70 votos (25 + 45) para samba e forró juntos, faltam 30 votos para 100. Assim, bolero e salsa receberam 15 votos cada um, ou seja, 15% (15 em 100).
Observando o tamanho de cada região colorida (setor) do gráfico, os estudantes devem verificar que: setor roxo (maior) corresponde a 45%; setor azul, a 25%; setor verde e setor laranja, a 15% cada um.

Atividade 3

No item a, observando a tabela, os estudantes poderão completar o gráfico.

No item b, espera-se que os estudantes observem as temperaturas correspondentes a cada horário e identifiquem que a temperatura diminuiu de 0 h a 3 h e, a partir daí, ela só aumentou.

Para ampliar, peça que criem perguntas, com base nos dados da tabela e do gráfico, e troquem com os colegas para responderem a elas.

BNCC em foco:

EF05MA24, EF05MA25; competências específicas 3 e 6

MP242

O que você aprendeu

Avaliação processual

Responda às questões.
1. Em uma garrafa de refrigerante cabem 2 L, e em uma lata desse refrigerante cabem 355 mL. Com essa garrafa, é possível encher completamente quantas dessas latas?
  _____
  
  PROFESSOR
  Resposta: 5 latas.
1. Ao ver o preço dos dois produtos, Rodrigo disse que sai mais barato comprar refrigerante em garrafa. Por que Rodrigo fez essa afirmação?
  
  PROFESSOR
  Resposta pessoal.

Imagem: Ilustração. Uma garrafa e uma etiqueta com o valor: R$ 3,50. Ao lado, uma latinha e o valor: R$ 1,00. Fim da imagem.

Complete o quadro.
O conteúdo de cada garrafa será distribuído igualmente entre copos iguais.

Quadro: equivalente textual a seguir.

Capacidade, em litro, da garrafa	Capacidade, em mililitro, do copo	Quantidade de copos
1,5 L	500 mL	_____
_____	100 mL	15
2,0 L	_____	8

PROFESSOR

Resposta: 3; 1,5 L; 250 mL.

Imagem: Ícone: mental. Fim da imagem.

Douglas caminha diariamente 350 m da sua casa até o ponto de ônibus. Ao descer do ônibus, ele caminha mais 650 m até chegar ao seu local de trabalho. À noite, Douglas volta para casa pelo mesmo caminho.
1. Quantos quilômetros ele caminha por dia, ao todo, para ir ao trabalho e voltar para casa? _____
  
  PROFESSOR
  Resposta: 2 quilômetros.
1. Sabendo que Douglas trabalha 5 dias por semana, quantos quilômetros ele caminha em uma semana para ir ao trabalho e voltar para casa?
  _____
  
  PROFESSOR
  Resposta: 10 quilômetros.

Se 1 2 quilograma de linguiça custa R$ 8,00, quanto será pago por:
1. $\frac{1}{4}$ de quilograma de linguiça? _____
  
  PROFESSOR
  Resposta: R$ 4,00
1. 1 quilograma de linguiça? _____
  
  PROFESSOR
  Resposta: R$ 16,00
1. 2 500 gramas de linguiça? _____
  
  PROFESSOR
  Resposta: R$ 40,00

Imagem: Ilustração. Um homem com chapéu e avental brancos está sorrindo e segurando uma linguiça sobre uma balança. Na tela, o peso: 500 g. Fim da imagem.

MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.

A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.

Atividade 1

No item b, espera-se que os estudantes percebam que garrafa de 2 litros custa R$ 3,50 e seria preciso mais de 5 latinhas para completar 2 litros; como 5 latinhas custam R$ 5,00, comprar uma garrafa sai mais barato que comprar a mesma quantidade de refrigerante em lata.

Atividade 2

Após a construção e o preenchimento do quadro, peça aos estudantes que acrescentem outras linhas e as preencham. Por exemplo:

Quadro: equivalente textual a seguir.

Capacidade, em litro, de água em cada garrafa	Capacidade, em mililitro, do copo	Quantidade de copos
2,0 L	200 mL	10
2,0 L	125 mL	16
1,5 L	250 mL	6

Atividade 3

Possíveis cálculos:

no item a:
2 × (350 + 650) = 2 × 1 000 = 2 000

2 000 m = 2 km
no item b:
5 × 2 km = 10 km

Atividade 4

Os estudantes podem resolver esta atividade trabalhando diretamente com a ideia de fração ou transformando a fração de quilograma em grama:
Se $\frac{1}{2}$ kg corresponde a 2 peças de $\frac{1}{4}$ kg, conclui-se que $\frac{1}{4}$ de kg custará 8 reais divididos por 2, ou seja, 4 reais.
Como 1 kg é igual a 2 peças de $\frac{1}{2}$ kg, 1 kg custa 2 vezes 8 reais, ou seja, 16 reais.
2.500 g = 1 kg + 1 kg + $\frac{1}{2}$ kg
Logo, o preço correspondente é: 16 reais +16 reais + 8 reais = 40 reais.

BNCC em foco:

EF05MA08, EF05MA12, EF05MA19

MP243

Bruna mediu a temperatura por sete dias seguidos, durante o mês de janeiro, sempre ao meio-dia, e depois elaborou o gráfico de linha abaixo.

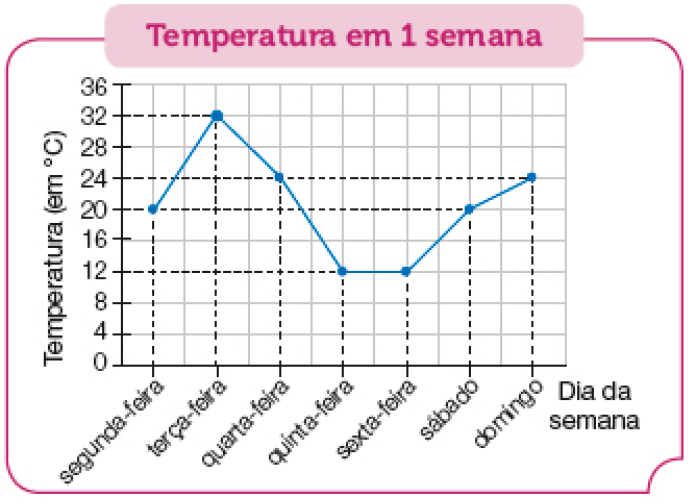
Imagem: Gráfico em linhas. Temperatura em 1 semana. No eixo vertical. A temperatura (em ºC) e no eixo horizontal, o dia da semana. segunda-feira: 20 ºC; terça-feira: 32 ºC; quarta-feira: 24 ºC; quinta-feira: 12 ºC; sexta-feira: 12 ºC; sábado: 20 ºC; domingo: 24 ºC. Fim da imagem.

Fonte: Anotações de Bruna (jan. 2023).

Entre quais dias seguidos a medida da temperatura permaneceu a mesma ao meio-dia? _____

PROFESSOR
Resposta: Entre quinta-feira e sexta-feira.

Qual é a diferença das medidas de temperatura entre terça-feira e quinta-feira ao meio-dia? _____

PROFESSOR
Resposta: 20 °C

Entre quais dias seguidos da semana houve a maior queda na medida de temperatura ao meio-dia? De quantos graus Celsius foi essa queda?
_____

PROFESSOR
Resposta: Entre quarta-feira e quinta-feira; a queda foi de 12 °C.

Calcule as medidas da área e do perímetro das figuras abaixo.

Imagem: Ilustração. Três quadrados verdes lado a lado. Cada quadrado mede 1 cm de comprimento e 1 cm de largura. Fim da imagem.

_____

PROFESSOR

Resposta: 3 cm² ; 8 cm

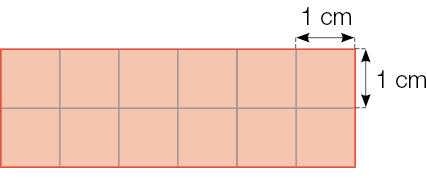
Imagem: Ilustração. Duas fileiras com seis quadrados vermelhos. Cada quadrado mede 1 cm de comprimento e 1 cm de largura. Fim da imagem.

_____

PROFESSOR

Resposta: 12 cm² ; 16 cm

Podemos preencher toda a caixa de acrílico com cubos idênticos. Quantos cubos faltam, em cada caixa, para que ela fique completa?

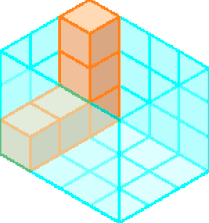
Imagem: Ilustração. Caixa transparente e dentro há cinco cubos laranja. Ao lado, espaço para mais trinta e um cubos. Fim da imagem.

_____

PROFESSOR

Resposta: 31 cubos.

Imagem: Ilustração. Caixa transparente e dentro há seis cubos laranja. Ao lado, espaço para mais doze cubos. Fim da imagem.

_____

PROFESSOR

Resposta: 12 cubos.

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.

Compreendo o uso das unidades de medida centímetro quadrado e metro quadrado para o cálculo da medida de áreas?

PROFESSOR
Respostas pessoais.
Compreendo a ideia de medida de volume?

MANUAL DO PROFESSOR

Atividade 5

Pergunte “Como ficaria o gráfico da semana anterior se, em todos os dias da semana ao meio-dia, a medida da temperatura registrada fosse 1 °C a menos que a medida apresentada no gráfico?”. Espera-se que respondam que o gráfico seria similar ao da atividade, mas com as seguintes medidas de temperatura: 19 °C, 31 °C, 23 °C, 11 °C, 11 °C, 19 °C e 23 °C, de segunda-feira a domingo, respectivamente.

Atividade 6

Explore mais esta atividade pedindo aos estudantes que resolvam os itens a e b de dois modos distintos. Espera-se que utilizem a multiplicação para calcular a medida da área de figuras retangulares, porém se lembrem que também é possível calcular a medida da área da figura adicionando-se as medidas das áreas menores dos quadrinhos que a compõem.

Verifique se, no cálculo da medida do perímetro, o estudante adicionou as quatro medidas ou se calculou o produto da soma das duas medidas diferentes dos lados por 2.

Atividade 7

Peça aos estudantes que expliquem, oralmente, como obtiveram a quantidade de cubos necessária para completar a caixa.

Autoavaliação

Embora os estudantes ainda não utilizem fórmulas matemáticas, nesta Unidade entraram em contato com a ideia de medidas de área e de volume. Desse modo, as duas questões finalizam a Unidade propondo uma autoavaliação desses conceitos.

A primeira questão diz respeito às unidades convencionais, enquanto a segunda questão é mais geral, pedindo aos estudantes que analisem como construíram conhecimentos sobre o tema.

BNCC em foco:

EF05MA19, EF05MA21, EF05MA24

MP244

Comentários para o professor:

Conclusão da Unidade 6

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem	Desempenho	Observação
Resolve e elabora problemas de multiplicação e de divisão com números naturais e racionais?	_____	_____
Resolve problemas que envolvam variação de proporcionalidade direta entre duas grandezas?	_____	_____
Resolve problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade?	_____	_____
Consegue calcular a medida do contorno de figuras planas?	_____	_____
Analisa figuras que possuem mesmo perímetro e áreas diferentes e mesma área e perímetros diferentes?	_____	_____
Reconhece volume como grandeza associada a sólidos geométricos e sabe medir volumes por meio de empilhamento de cubos?	_____	_____
Interpreta dados apresentados em tabelas e gráficos de colunas e produz texto sobre os resultados de uma pesquisa?	_____	_____
Organiza dados coletados em gráficos de setores e de linhas?	_____	_____
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?	_____	_____
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?	_____	_____

MP245

Sugestão de ficha de autoavaliação do estudante

O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.

Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.

Tabela: equivalente textual a seguir.

Autoavaliação
Nome:
Marque um X em sua resposta para cada pergunta.	Sim	Mais ou menos	Não
1. Presto atenção nas aulas?	_____	_____	_____
2. Pergunto ao professor quando não entendo?	_____	_____	_____
3. Sou participativo?	_____	_____	_____
4. Respeito meus colegas e procuro ajudá-los?	_____	_____	_____
5. Sou educado?	_____	_____	_____
6. Faço todas as atividades com capricho?	_____	_____	_____
7. Trago o material escolar necessário e cuido bem dele?	_____	_____	_____
8. Cuido dos materiais e do espaço físico da escola?	_____	_____	_____
9. Gosto de trabalhar em grupo?	_____	_____	_____
10. Respeito todos os meus colegas de turma, professores e funcionários?	_____	_____	_____