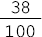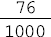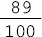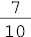MP246
Comentários para o professor:
Introdução da Unidade 7
A abertura desta Unidade apresenta uma competição esportiva e dá a “braçada inicial” para os estudos sobre os números na forma decimal, propondo questões sobre os tempos obtidos na prova de natação.
Nesta Unidade, os estudos sobre os números racionais apresentam-se nas atividades acerca da Unidade Temática Números. Conhecimentos construídos durante o 4º ano e, também, em Unidades que antecederam esta são retomados e ampliados na perspectiva da construção de novos conhecimentos. Por exemplo, os estudos sobre o sistema de numeração decimal desenvolvidos, particularmente no 4º ano, que diziam respeito ao reconhecimento de que as regras desse sistema se estendem, também, para a representação decimal de números racionais serão ampliados e aprofundados nesta Unidade. Assim, as atividades abordam conhecimentos relativos a leitura, escrita e ordenação de números racionais na forma decimal, bem como a comparação e ordenação de números racionais positivos e sua relação com pontos na reta numérica. Esses conhecimentos são necessários para que, no 6º ano, os estudantes reconheçam que os números racionais positivos podem ser expressos por frações e na forma decimal e estabeleçam relações entre essas representações.
Além desses, outros conhecimentos serão objetos de estudo nesta Unidade, entre eles, a resolução e a elaboração de problemas que envolvem as quatro operações com números racionais com representação decimal finita. Tais conhecimentos pautam-se naqueles construídos ao longo do 4º ano acerca da resolução e elaboração de problemas com números naturais envolvendo as referidas operações, por meio de distintas estratégias, por exemplo, cálculo por estimativa, cálculo mental e algoritmos.
Esses conhecimentos ora construídos são bases necessárias para a resolução e a elaboração de problemas com ampliação à potenciação, conhecimentos a serem construídos ao longo do 6º ano.
Os estudos relativos a porcentagens também estão presentes por meio de atividades cujo propósito é conduzir os estudantes à associação entre essas representações e as frações, aportes necessários para que, no 6º ano, os estudantes resolvam e elaborem problemas envolvendo porcentagens, fundamentados na ideia de proporcionalidade.
Por fim, são propostas atividades que abordam Probabilidade e estatística na perspectiva de que os estudantes se apropriem de conhecimentos relativos à organização de dados em gráficos de linhas, pautados naqueles construídos ao longo do 4º ano, cujo objetivo era a análise de dados apresentados em tabelas e gráficos de colunas. Ainda, são suportes para futuros conhecimentos, em particular a interpretação e resolução de situações envolvendo dados de pesquisas a partir de contextos diversos, com redação de textos para a síntese de conclusões, conhecimentos relativos ao 6º ano.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletiva. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências específicas favorecidas
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
MP247
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item Jogo desta Unidade.
Roteiro de aula – Jogo dos decimais
1 ª parte – Preparação – Tempo sugerido: 30 minutos
Solicite previamente aos estudantes o recorte (1 conjunto por grupo) do tabuleiro e dos dados nas páginas citadas do Material complementar. Além disso, cada grupo deve providenciar um saquinho não transparente e elaborar, em papel resistente, os 68 marcadores descritos no enunciado do jogo. Combine o tamanho dos algarismos para que eles sejam visíveis.
Para a composição dos grupos (2 a 4 estudantes), sugira escolhas livres, porém fique atento e auxilie aqueles que estiverem com dificuldade em encontrar colegas para realizar a atividade.
Organize as carteiras de modo que eles possam trabalhar nos grupos.
Faça a leitura coletiva das regras do jogo e verifique se elas foram compreendidas por todos. Avalie a necessidade de simular um início de procedimento que sirva como exemplo e elimine possíveis dúvidas. Esta orientação é válida para os jogos em geral, portanto pode ser adaptada a outras atividades semelhantes.
2 ª parte – Jogo– Tempo sugerido: 30 minutos
O tempo de cada rodada depende da dinâmica do grupo e, de certa forma, do acaso do jogo. É provável que esses tempos sejam diferentes para as equipes. Por isso, convém estabelecer de antemão um limite de tempo que julgar adequado dentro da disponibilidade e programação. Porém, é importante que o tempo fixado seja suficiente para que todos os grupos experimentem várias rodadas. Deixe-os jogar livremente, mas acompanhe as ações dos grupos para administrar impasses, caso considere necessário. Se julgar conveniente, repita essa atividade em outras aulas.
3 ª parte – Questões sobre o jogo– Tempo sugerido: 20 minutos
A seguir, peça aos estudantes que retomem o livro, respondam individualmente às questões propostas e depois troquem os livros entre os elementos do grupo para socializarem as respostas. Por fim, dialogue com a turma sobre as questões resolvidas e valide com os estudantes as respostas dadas.
MP248
UNIDADE 7. Números na forma decimal

MANUAL DO PROFESSOR
Objetivos da Unidade
- Ler, escrever, ordenar e comparar números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal, utilizando como recurso a reta numérica.
- Identificar a forma fracionária e a forma decimal de números racionais positivos.
- Compreender o valor posicional dos algarismos em números na forma decimal.
- Resolver problemas que envolvam medidas de comprimento e de massa, recorrendo a transformações entre unidades de medida.
- Resolver e elaborar problemas de adição e subtração com números racionais cuja representação decimal seja finita.
- Resolver e elaborar problemas de multiplicação com números racionais cuja representação decimal seja finita.
- Efetuar multiplicações de números racionais por 10, 100 e 1.000.
- Resolver problemas de divisão com números racionais cuja representação decimal seja finita (com divisor natural e diferente de zero).
- Efetuar divisões de números racionais por 10, 100 e 1.000.
- Associar as representações 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens, utilizando estratégias pessoais, cálculo mental e calculadora.
- Interpretar dados apresentados em textos, gráficos de colunas, de linhas e de setores.
- Organizar dados coletados por meio de gráficos de linhas.
BNCC em foco:
EF05MA02, EF05MA05, EF05MA06, EF05MA07, EF05MA08, EF05MA19, EF05MA24, EF05MA25
MP249
Boxe complementar
Para refletir...
Qual atleta chegou em terceiro lugar? Qual chegou em penúltimo lugar?
_____
PROFESSOR
Resposta: Pedro Henrique; Marcelo.Qual é a diferença entre o tempo do atleta que chegou em primeiro lugar e do que chegou em último?
_____
PROFESSOR
Resposta: 3,1 segundos.Fim do complemento
MANUAL DO PROFESSOR
Nas práticas sociais, os números na forma decimal estão muito mais presentes que os números na forma de fração. A compreensão das frações, no entanto, é imprescindível, por permitir estabelecer uma relação recíproca entre as duas representações, a da forma de fração e a da forma decimal, ampliando os significados atribuídos a esses números.
Aproveite para perguntar: “Em quais situações vocês encontram números na forma decimal?”. Os estudantes podem mencionar, por exemplo, o registro de preços de mercadorias ou o registro de medidas.
Depois explore a cena perguntando sobre a presença dos números na forma decimal. Incentive os estudantes a procurarem as personagens na cena e a esclarecerem o enigma: Por que o atleta da raia 7 está cumprimentando o atleta da raia 6? Porque ele é o vencedor.
Para refletir...
Peça aos estudantes que classifiquem desde o 1º colocado até o último.
Para responder à questão proposta, os estudantes devem observar que a diferença se encontra na parte dos segundos e dos centésimos de segundos, já que todos fizeram um tempo entre 1 minuto e 2 minutos. Se julgar necessário, proponha que comparem a parte inteira dos segundos e, depois, a parte dos centésimos de segundos (parte decimal cujo registro vem depois da vírgula). Outro fato que os estudantes devem perceber é que o primeiro colocado é aquele que concluiu a prova em menos tempo, e assim por diante.
Nesse caso, espera-se que percebam que tal comparação é feita por meio de uma subtração: o tempo do último colocado menos o tempo daquele que ficou em primeiro lugar. Verifique as estratégias que os estudantes utilizam para efetuar essa operação. Socialize e valide o resultado com os estudantes.
MP250
Décimos, centésimos e milésimos
- Conte quantas pessoas há na cena abaixo e complete as frases.

- Há _____ pessoas na cena.
- Cada pessoa corresponde a _____ décimo do total de pessoas.
-
_____
décimo
pode ser representado de duas formas:
PROFESSOR
Resposta: 10; 1; 1
- representação de 1 décimo com uma fração.
0,1 - representação de 1 décimo na forma decimal.
- Há _____ crianças na cena. Elas correspondem a _____ décimos do total de pessoas.
-
_____
décimos
podem ser representados com a fração: ou na forma decimal:
_____.
PROFESSOR
Resposta: 5; 5; 5; ; 0,5.
- Um aparelho de som tem um mostrador da intensidade de volume que varia de 0 a 1. Quanto mais alto o som, mais partes vermelhas ficam visíveis no mostrador.
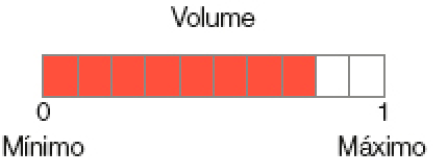
- A que fração do mostrador do aparelho de som corresponde cada parte em que ele está dividido?
_____
PROFESSOR
Resposta: 1 décimo ou 0,1 ou do mostrador.
- Qual é a intensidade do volume registrado no mostrador desse aparelho?
_____
PROFESSOR
Resposta: 8 décimos ou 0,8 ou da intensidade máxima.
MANUAL DO PROFESSOR
Objetivos
- Ler e escrever números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal.
- Identificar frações decimais e a forma decimal correspondente.
- Resolver problemas que envolvam medidas de comprimento e de massa, recorrendo a transformações entre unidades de medida.
Atividade 1
Nesta atividade, os estudantes devem associar os números racionais na forma de fração e com a representação decimal de cada um: 0,1 e 0,5. É importante que eles compreendam que os números racionais podem ser representados na forma de fração e na forma decimal.
Atividade 2
Após a resolução da atividade, peça aos estudantes que formulem outras questões para a mesma situação, como: “Que fração do mostrador falta para que a intensidade de volume atinja o máximo?” (0,2, ou seja, 2 décimos.).
BNCC em foco:
EF05MA02, EF05MA05
MP251
- Um painel luminoso é formado por uma placa com 100 lâmpadas coloridas, como mostra a figura abaixo. As lâmpadas vermelhas correspondem a que fração do total de lâmpadas?

As _____ lâmpadas vermelhas correspondem a _____ centésimos do total de lâmpadas. Podemos representar 66 centésimos de duas formas:
PROFESSOR
Resposta: 66; 66.- representação de 66 centésimos com uma fração.
0,66 - representação de 66 centésimos na forma decimal.
- Agora, escreva a representação, na forma decimal, da parte das lâmpadas que são verdes.
_____
PROFESSOR
Resposta: 0,34
- Complete o quadro abaixo.
Tabela: equivalente textual a seguir.
|
Animal |
Medida da altura em centímetro |
Medida da altura em metro |
|---|---|---|
|
Gato doméstico |
30 cm |
0,30 m |
|
Capivara |
50 cm |
_____ |
|
Leão |
_____ |
0,95 m |
|
Galinha |
35 cm |
_____ |
PROFESSOR
Resposta: 0,50 m; 95 cm; 0,35 m.

- Hugo quer comprar uma
paçoca
que custa R$ 0,35.
- Que combinação de moedas ele pode usar para pagar a
paçoca
sem que haja troco?
_____
PROFESSOR
Exemplos de resposta: uma moeda de R$ 0,10 e uma moeda de R$ 0,25; três moedas de R$ 0,10 e uma moeda de R$ 0,05.
- Se Hugo pagar com uma moeda de 1 real, quanto ele receberá de troco?
_____
PROFESSOR
Resposta: R$ 0,65
- Se Hugo quiser comprar 10 paçocas para dividir com seus amigos, quantos reais ele gastará ao todo?
_____
PROFESSOR
Resposta: R$ 3,50
- Que combinação de moedas ele pode usar para pagar a
paçoca
sem que haja troco?
MANUAL DO PROFESSOR
Atividade 3
Aproveite a figura com as 100 lâmpadas e destaque as 10 fileiras de 10 lâmpadas cada uma, para que os estudantes observem a relação entre décimos e centésimos. Pergunte: “1 fileira de lâmpadas corresponde a que fração do total de lâmpadas, considerando a quantidade de fileiras? E que fração, considerando o total de lâmpadas?” ( e .).
Desse modo, os estudantes podem perceber a igualdade entre essas representações, como frações equivalentes.
Aproveite e relacione as frações obtidas às representações decimais 0,1 e 0,10, para que os estudantes possam identificar a igualdade entre essas duas representações: 0,1 = 0,10.
Atividade 4
Tomando como ponto de partida números racionais na forma de fração, este tópico incentiva os estudantes a representarem esses mesmos números na forma decimal.
Esta atividade possibilita a exploração das representações de centésimos e o entendimento do conceito de centésimo e de sua relação com os décimos, além de ampliar a relação entre o centímetro e o metro: 1 m = 100 cm e 1 cm = 0,01 m.
Atividade 5
Após a resolução da atividade, peça aos estudantes que, em duplas, expliquem aos colegas o raciocínio que usaram para chegar às respostas.
As situações que trabalham comunidades do sistema monetário brasileiro favorecem a compreensão de números na forma decimal, já que os valores são representados por uma parte inteira (reais) e por uma parte decimal (centavos). Incentive os estudantes a realizarem cálculos mentais para resolver situações que envolvam moedas, pois é uma estratégia de cálculo de quantias muito prática de ser usada no cotidiano.
BNCC em foco:
EF05MA02, EF05MA05, EF05MA19
MP252
- Observe abaixo a quantidade de carne que Renata comprou.
Lembre-se de que 1 quilograma é o mesmo que 1.000 gramas (1 kg = 1.000 g).

- Que fração de 1
kg
de carne Renata comprou?
_____
PROFESSOR
Resposta: kg
- Quantos gramas de carne faltaram para Renata fazer essa torta?
______
PROFESSOR
Resposta: 650 gramas.
- Veja como essa medida de massa pode ser representada de duas maneiras.

650 gramas correspondem a 650 milésimos de 1 quilograma.
- representação de 650 milésimos com uma fração.
0,650 - representação de 650 milésimos na forma decimal.
- Qual é a representação na forma decimal da fração de 1
kg
de carne que Renata comprou?
_____
PROFESSOR
Resposta: 0,350 kg
- Represente com uma fração e na forma decimal a parte pintada de verde das figuras abaixo.
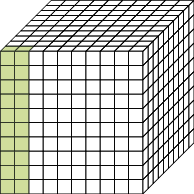
_____
PROFESSOR
Resposta:PROFESSOR

PROFESSOR
0,020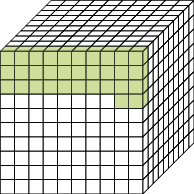
_____
PROFESSOR
Resposta:PROFESSOR

PROFESSOR
0,032

- Com uma calculadora, faça os cálculos indicados e registre as respostas obtidas.

PROFESSOR
Resposta: 0,001
PROFESSOR
Resposta: 0,002

- Desenhe as teclas que você apertaria para obter no visor da calculadora, por meio de uma divisão por 1.000, o número 0,005 e o número 0,724.
PROFESSOR
Exemplo de resposta:PROFESSOR
 ;
; 
MANUAL DO PROFESSOR
Atividade 6
Discuta com os estudantes a representação de medidas de massa em balanças digitais, nas quais a massa é, geralmente, expressa em quilograma. Pergunte: “Quais seriam as respostas se a balança indicasse que havia 430 g de carne sobre ela?”. As respostas seriam:
kg
570 g
0,430 kg ou 0,43 kg
Esta atividade, além de introduzir os milésimos e apresentar a relação entre a forma de fração e a forma decimal, permite ampliar a relação entre o grama e o quilograma: 1 kg = 1.000 g e 1 g = 0,001 kg.
Atividade 7
Após o trabalho com décimos e centésimos, esta atividade explora geometricamente a ideia de milésimo como “uma parte em 1.000”.
Atividade 8
Lembre aos estudantes que, na maioria das calculadoras, a tecla  indica a vírgula.
indica a vírgula.
Peça aos estudantes que realizem os seguintes cálculos com auxílio da calculadora:
10 ÷ 1.000 e 100 ÷ 1.000.
CRÉDITO: ADILSON SECCO
Depois, pergunte: “Por que as respostas no visor não aparecem como 0,010 e 0,100, respectivamente?”. Espera-se que observem que a calculadora “desconsidera” o algarismo zero à direita, pois a resposta esperada, por exemplo, para o cálculo 10 ÷ 1.000 (0,010 ou 10 milésimos) é igual a 0,01 ou 1 centésimo.
BNCC em foco:
EF05MA02, EF05MA05, EF05MA19
Sugestão de leitura para o professor
Artigo
CUNHA, Micheline Rizcallah Kanaan da; MAGINA, Maria Pinto. A medida e o número decimal: um estudo sobre a elaboração de conceito em crianças do nível fundamental. Disponível em: http://www.sbem.com.br/files/viii/pdf/07/1CC75464039872.pdf . Acesso em: 3 abr. 2021.
As autoras desse artigo pesquisaram a relação entre a construção do conceito de números na forma decimal no contexto das medidas. De acordo com o estudo, a incompreensão do significado de número na forma decimal não impede os estudantes de operarem com eles, mas traz consequências negativas ao longo da vida escolar, nos momentos em que será necessário elaborar relações entre esses números e outros conceitos, da Matemática ou de outras áreas.
MP253
Valor posicional
Em 2020, o piloto britânico Lewis Hamilton largou na 3ª posição na corrida do Grande Prêmio de Abu Dhabi, nos Emirados Árabes Unidos. O tempo da volta que lhe garantiu essa posição na largada foi de 95,332 segundos. Vamos escrever o valor de cada algarismo desse número.

LEGENDA: Grande Prêmio de Abu Dhabi, nos Emirados Árabes Unidos, em 2020. FIM DA LEGENDA.
Tabela: equivalente textual a seguir.
|
Parte inteira |
Parte decimal |
|||
|---|---|---|---|---|
|
D |
U |
d |
c |
m |
|
9 |
5, |
3 |
3 |
2 |
2: 2 milésimos
3: 3 centésimos
3: 3 décimos
5: 5 unidades
9: 9 dezenas
- Agora, observe o tempo das melhores voltas dos pilotos Max Verstappen e Valtteri Bottas na mesma corrida.
Tabela: equivalente textual a seguir.
|
Max Verstappen |
95,246 segundos |
|---|---|
|
Valtteri Bottas |
95,271 segundos |
- Registre o valor de cada algarismo desses números.
PROFESSOR
Resposta: 95,246PROFESSOR
6:6 milésimosPROFESSOR
4: 4 centésimosPROFESSOR
2: 2 décimosPROFESSOR
5: 5 unidadesPROFESSOR
9: 9 dezenasPROFESSOR
Resposta: 95,271PROFESSOR
1:1 milésimoPROFESSOR
7: 7 centésimosPROFESSOR
2: 2 décimosPROFESSOR
5: 5 unidadesPROFESSOR
9: 9 dezenas- Qual desses dois pilotos obteve o melhor tempo?
_____
PROFESSOR
Resposta: Max Verstappen.
MANUAL DO PROFESSOR
Objetivo
- Compreender o valor posicional dos algarismos em números na forma decimal.
Esta atividade permite aos estudantes reconhecerem o valor posicional em representações decimais, com distinção entre a parte inteira e a parte decimal. Na situação apresentada, a medida de tempo é expressa por um número maior que 1 unidade em sua forma decimal. Trata-se da medida de tempo 95,332 segundos, que pode ser lida: “noventa e cinco segundos e trezentos e trinta e dois milésimos de segundo”. Comente que a forma decimal é geralmente utilizada em situações que exigem medidas muito precisas de intervalos de tempo, com detalhamento de décimos, centésimos e milésimos de segundo, como nas corridas de Fórmula 1, em que a posição de largada é definida de acordo com o tempo da melhor volta dos pilotos em um treino classificatório ou mesmo na própria corrida.
Sugestão de trabalho interdisciplinar
Em conjunto com o professor de Educação Física, proponha aos estudantes uma pesquisa sobre outros esportes que exigem a marcação do tempo com precisão, incluindo milésimos de segundo.
Aproveite para promover uma corrida com a turma e marcar os tempos obtidos pelos estudantes, de modo que eles registrem, com algarismos e por extenso, os tempos cronometrados.
BNCC em foco:
EF05MA02
MP254
Leitura de números na forma decimal
- Os números na forma decimal aparecem com frequência nos esportes.
Atletismo do Brasil nas Paralimpíadas 2016
O atleta brasileiro Petrúcio Ferreira dos Santos ganhou a medalha de ouro nos 100 metros rasos, categoria T47 do atletismo, além de bater o recorde mundial da prova, com 10,57 segundos.

LEGENDA: Prova final da Paralimpíada no Estádio Olímpico, Rio de Janeiro, em 2016. FIM DA LEGENDA.
Verônica Hipólito foi prata nos 100 metros da categoria T38. Apesar de ter se tornado a nova recordista nas semifinais, ela acabou ficando em 2º lugar na final, cronometrando 12,88 segundos.

LEGENDA: Pódio da cerimônia de premiação da Paralimpíada, no Estádio Olímpico, Rio de Janeiro, em 2016. FIM DA LEGENDA.
Para ler um número na forma decimal, observamos primeiro a parte inteira e depois a parte decimal. Veja como lemos o número que representa o tempo do atleta Petrúcio Ferreira dos Santos.
10,57
10 - parte inteira
57 - parte decimal
Lemos - dez inteiros e cinquenta e sete centésimos.
- Agora, escreva como se lê o
número
que representa o tempo de Verônica Hipólito.
_____
PROFESSOR
Resposta: Doze inteiros e oitenta e oito centésimos.
- Escreva como lemos a medida indicada em cada caso.

_____
PROFESSOR
Exemplo de resposta: Um quilograma e duzentos e trinta e quatro milésimos de um quilograma.
_____
PROFESSOR
Exemplo de resposta: Três metros e quarenta e oito centésimos de um metro.MANUAL DO PROFESSOR
Objetivo
• Ler e escrever números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal.
Atividade 1
Na escrita por extenso dos números 10,57 e 12,88, deve ficar claro para os estudantes que a parte inteira se refere a segundos e a parte decimal, a centésimos de segundo.
Vale salientar que, nas situações cotidianas em que aparecem números na forma decimal, é comum a simplificação da leitura, conforme os exemplos:
• 10,57: dez vírgula cinquenta e sete;
• 12,88: doze vírgula oitenta e oito.
Comente que, na linguagem não formal, a leitura simplificada é aceitável, mas que, com ela, não ficam explícitas as ordens de décimos, centésimos ou milésimos. Acrescente que é necessário ficar atento às representações de medidas de tempo na forma decimal, pois a relação entre hora, minuto e segundo se dá por agrupamentos de 60, não por agrupamentos de 10, como ocorre com os algarismos do sistema de numeração decimal. Por exemplo: 2,5 minutos não correspondem a 2 minutos e 50 segundos, mas a 2 minutos mais 0,5 (meio) minuto, ou seja, a 2 minutos e 30 segundos. Por isso, não usamos a notação 2,5 e sim 2 min 30 s ou para indicar hora, 2 h 30 min. Nos relógios digitais, as unidades de medida são separadas por “:“, ou seja, 2:30.
Pergunte aos estudantes: “Como lemos 23,16 s? E 16,133 s?”. Exemplo de resposta: Vinte e três segundos e dezesseis centésimos de segundo; dezesseis segundos e cento e trinta e três milésimos de segundo.
Peça que escrevam, por extenso, o número 57,79 de dois modos diferentes. Resposta: cinquenta e sete inteiros, sete décimos e nove centésimos ou cinquenta e sete inteiros, setenta e nove centésimos ou cinquenta e sete inteiros vírgula setenta e nove.
Atividade 2
Explore as ilustrações perguntando: “O que indica a parte decimal de cada número?”. Espera-se que os estudantes respondam que as partes decimais indicam: no item a (1,234 kg), 234 gramas; no item b (3,48 m), 48 centímetros.
BNCC em foco:
EF05MA02
MP255
- Complete o quadro.
PROFESSOR
Resposta: Exemplo de respostas:Tabela: equivalente textual a seguir.
|
Número |
Como lemos |
|---|---|
|
0,4 |
_____ |
|
_____ |
catorze inteiros e trezentos e noventa e um milésimos |
|
0,084 |
_____ |
|
_____ |
um inteiro e duzentos e sete milésimos |
PROFESSOR
Resposta: Exemplo de respostas: quatro décimos; 14,391; oitenta e quatro milésimos; 1,207.- Represente com um
número
na forma decimal a parte pintada de cada uma das figuras. Em seguida, escreva como lemos esses números.
PROFESSOR
Exemplo de respostas:
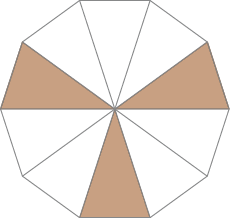
_____
PROFESSOR
Resposta: 0,3_____
PROFESSOR
Resposta: três décimosb)

_____
PROFESSOR
Resposta: 0,60_____
PROFESSOR
Resposta: sessenta centésimosc)
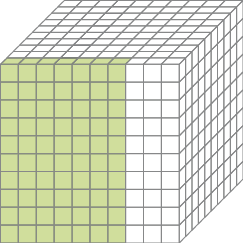
_____
PROFESSOR
Resposta: 0,070_____
PROFESSOR
Resposta: setenta milésimos- Escreva por extenso a medida do comprimento do objeto em cada imagem.
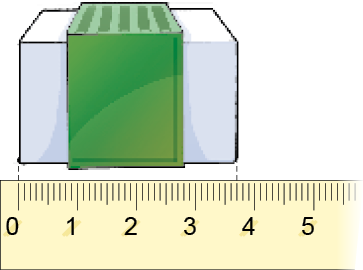
_____
PROFESSOR
Resposta: Três centímetros e sete milímetros, ou trinta e sete milímetros, ou três vírgula sete centímetros.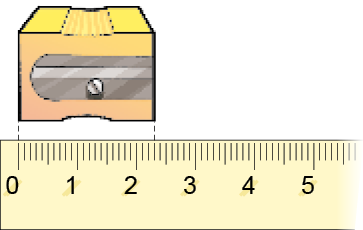
_____
PROFESSOR
Resposta: Dois centímetros e três milímetros, ou vinte e três milímetros, ou dois vírgula três centímetros.MANUAL DO PROFESSOR
Atividade 3
Promova um ditado com números na forma decimal para que os estudantes registrem, no caderno, com algarismos. Depois, faça uma correção coletiva, pedindo a voluntários que registrem na lousa os números ditados.
Atividade 4
Convém esclarecer que entendemos a parte colorida ou pintada como aquela com cor diferente da cor de fundo da página.
Aproveite a oportunidade para explicar para os estudantes as igualdades: 0,60 = 0,6 e 0,070 = 0,07.
Atividade 5
Verifique se os estudantes utilizarão a escrita simplificada, se considerarão apenas a medida total em milímetro ou se farão registro com centímetro e milímetro, separando a parte inteira e a parte decimal.
Para enriquecer o repertório, peça que socializem as respostas e valorize os modos de escrita.
BNCC em foco:
EF05MA02
MP256
Frações e números na forma decimal
- Observe que a metade de cada disco de cartolina representado abaixo está pintada de verde.

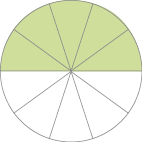
- O disco de cima foi dividido em 2 partes iguais. A parte verde pode ser representada por qual fração?
_____
PROFESSOR
Resposta:
- O disco debaixo foi dividido em 10 partes iguais. A parte verde pode ser representada por qual fração com denominador igual a 10? E por qual
número
na forma decimal?
_____
PROFESSOR
Resposta: ; 0,5
- Observe as três figuras de mesmo tamanho e faça o que se pede.
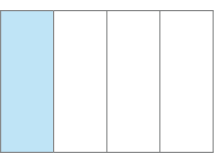
Figura I
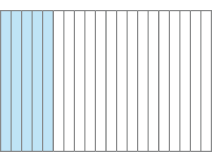
Figura II
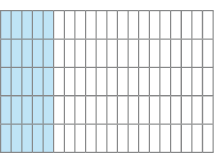
Figura III
- Em qual figura a parte pintada de azul é maior?
_____
PROFESSOR
Resposta: Em nenhuma, pois todas as partes pintadas de azul representam a mesma parte da figura.
- Escreva a fração que corresponde à parte pintada de azul em cada figura.
Figura I - _____
PROFESSOR
Resposta:Figura II - _____
PROFESSOR
Resposta:Figura III - _____
PROFESSOR
Resposta:
- Qual
número
na forma decimal corresponde à fração da parte pintada de azul da Figura
III?
_____
PROFESSOR
Resposta: 0,25

- Pinte da mesma cor os números que representam a mesma parte de um todo.
; 0,7; ; 0,07; ; 0,007.
PROFESSOR
Resposta: Cor 1 - ; ; 0,07; 0,007.PROFESSOR
Cor 2 - 0,7;
MANUAL DO PROFESSOR
Objetivos
- Ler, escrever e ordenar números racionais na forma decimal com compreensão das principais características do sistema de numeração decimal.
- Identificar a forma fracionária e a forma decimal de números racionais positivos.
Atividade 1
É importante retomar a ideia de frações equivalentes e também verificar como obtê-las.
No caso das frações apresentadas, os estudantes devem perceber que a fração é equivalente à fração , pois “1 em 2” equivale a “5 em 10” (metade do todo em cada caso).
Sugira que usem a calculadora para verificar a representação decimal de uma fração, dividindo o numerador pelo denominador em cada caso. Por exemplo, podem fazer na calculadora 1 ÷ 2 e observar o resultado no visor: 0,5.
Pergunte se conseguem obter outras frações equivalentes ao número na forma decimal 0,5. Espera-se que apresentem frações cujo numerador seja metade do denominador, como , , etc. Depois, peça que desenhem essas frações como partes de um círculo.
Atividade 2
Esta atividade possibilita aos estudantes reconhecerem a fração equivalente associada a uma quantidade (representada por figuras), o que propicia sua leitura e a rápida identificação da forma decimal correspondente. Situações desse tipo auxiliam na consolidação do conceito de números na forma decimal.
Atividade 3
Explore mais esta atividade pedindo aos estudantes que utilizem a calculadora para obter os números na forma decimal que correspondem às frações:
, e
BNCC em foco:
EF05MA02, EF05MA05
Sugestão de leitura para o professor
Dissertação
QUARESMA, Marisa Alexandra Ferreria. Ordenação e comparação de números racionais em diferentes representações: uma experiência de ensino. Disponível em: http://fdnc.io/eUw. Acesso em: 3 abr. 2021.
Além da discussão teórica e conceitual sobre os números racionais e suas representações, a dissertação defende a importância do trabalho em sala de aula com as diferentes representações desses números.
MP257

- Pinte as partes de cada figura conforme solicitado.
- da figura de rosa
PROFESSOR
Resposta: Exemplos de pintura:
- da figura de verde
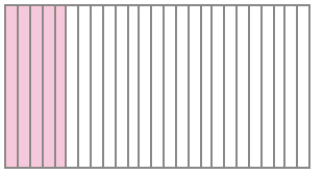
- 0,20 da figura de azul
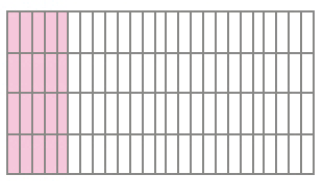

- Raquel, Elaine e Osvaldo pintaram uma tela. Quantas partes dessa tela cada um deles pintou? Para descobrir, pinte você também na representação dessa tela abaixo.

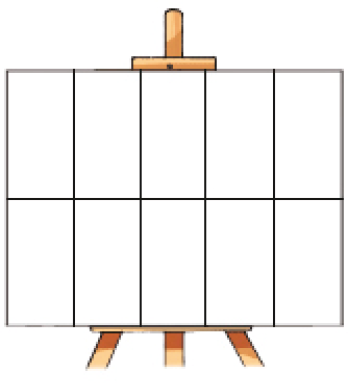
PROFESSOR
Resposta: Exemplo de pintura:PROFESSOR
vd: verdePROFESSOR
am: amareloPROFESSOR
lj: laranjaPROFESSOR
vd; vd; am; am; amPROFESSOR
lj; lj; lj; am; amRaquel pintou _____ partes da tela, Elaine pintou _____ partes, e Osvaldo
pintou _____ partes.
PROFESSOR
Resposta: 2; 5; 3.- A balança indica a medida da massa em quilograma. Complete o visor da balança com o número, na forma decimal, que
deve
aparecer nele.

PROFESSOR
Exemplo de respostas: 0,500 kg
PROFESSOR
Resposta: 0,250 kg- Escreva a fração correspondente a cada número na forma decimal.
- 0,5 =
_____
PROFESSOR
Exemplo de respostas:
- 0,36 =
_____
PROFESSOR
Resposta:
- 0,024 =
_____
PROFESSOR
Resposta:
- 0,564 =
_____
PROFESSOR
Resposta:
MANUAL DO PROFESSOR
Atividade 4
Pergunte aos estudantes se as partes que eles pintaram das figuras têm o mesmo tamanho. Espera-se que eles respondam que sim. Pergunte, então, como fizeram para descobrir.
Atividade 5
Para resolver esta atividade, os estudantes podem transformar os diferentes números em um mesmo tipo de representação: fração ou números na forma decimal. Por exemplo, podem expressar a fração da tela pintada por Raquel como 0,2 (2 décimos) e adicionar a 0,5 (5 décimos) da tela pintada por Elaine, obtendo 0,7 (7 décimos) da tela. Portanto, pode-se concluir que Osvaldo pintou 3 das 10 partes da tela, ou seja, 0,3 da tela.
Peça aos estudantes que comparem suas pinturas com as de um colega. Eles devem perceber que, embora possam ter pintado de modos diferentes, a quantidade de partes de cada cor deve ser a mesma.
Atividade 6
Se julgar oportuno, comente com os estudantes que, no visor das balanças digitais, assim como nas calculadoras, o ponto representa a vírgula. Como nesta atividade eles irão preencher o que aparece no visor da balança, oriente-os a utilizarem a vírgula para que não haja confusão.
Atividade 7
Para ampliar esta atividade, sugira aos estudantes que busquem mais de uma fração equivalente para cada número na forma decimal.
Para isso, eles podem utilizar dois principais raciocínios: acrescentar um zero no numerador e um zero no denominador; multiplicar ambos por um número que não seja múltiplo de 10.
Por exemplo, no item a:
0,5 = = =
BNCC em foco:
EF05MA02, EF05MA05
Sugestão de atividade
Reproduza o quadro abaixo para que os estudantes o completem.
Quadro: equivalente textual a seguir.
|
Fração |
Número na forma decimal |
Como lemos |
|
|
0,38 |
Trinta e oito centésimos |
|
|
0,076 |
Setenta e seis milésimos |
|
|
0,89 |
Oitenta e nove centésimos |
|
|
0,7 |
Sete décimos |
MP258
Comparação e ordenação de números na forma decimal
- Rebeca quer representar na reta numérica alguns números na forma decimal. Para isso, primeiro ela vai localizar a parte inteira e, depois, a parte decimal, dividindo em partes iguais o segmento que corresponde à unidade. Essa divisão depende da quantidade de casas decimais.
Para representar 2,3 na reta numérica, dividimos em 10 partes iguais o segmento localizado entre 2 e 3. Então, localizamos o número decimal.


- Para representar 2,34 na reta numérica, dividimos em 10 partes iguais o segmento localizado entre 2,3 e 2,4. Então, localizamos o número decimal. O segmento entre 2 e 3 ficará dividido em 100 partes iguais.

PROFESSOR
Resposta: 2,34- Para representar 2,345 na reta numérica, dividimos em 10 partes iguais o segmento localizado entre 2,34 e 2,35. Então, localizamos o número decimal. O segmento entre 2 e 3 ficará dividido em 1 000 partes iguais.

PROFESSOR
Resposta: 2,345- Quanto mais para a direita o
número
estiver na reta numérica, maior será esse número. Podemos compará-los utilizando os sinais < (menor que) ou > (maior que).
2,3 _____ 2,34 _____ 2,345
PROFESSOR
Resposta: <; <2,345 _____ 2,34 _____ 2,3
PROFESSOR
Resposta: >; >
- Localize na reta numérica os números: 4,583 e 4,587.

PROFESSOR
Resposta: 4,583, 4,587MANUAL DO PROFESSOR
Objetivo
- Comparar e ordenar números racionais na forma decimal utilizando como recurso a reta numérica.
Atividade 1
Desenhe na lousa as retas numéricas da atividade e observe se os estudantes compreendem que entre os números 2 e 3, por exemplo, a diferença é de 1 unidade, a qual pode ser subdividida em 10 décimos; por isso a reta numérica apresenta 10 intervalos entre 2 e 3, cada qual correspondendo a 1 décimo.
Aproveite o desenho feito na lousa para perguntar (enquanto aponta para posições na reta numérica entre 2 e 3) quais são os números na forma decimal correspondentes a cada um deles. Por exemplo, ao apontar para a posição imediatamente à direita de 2,3, espera-se que respondam 2,4. Comente que, quanto mais à direita o número se localizar na reta numérica, maior ele será.
Enfatize para os estudantes a importância de sempre perguntarem e sanarem suas dúvidas. Fazer perguntas é a base do conhecimento e o questionamento está associado à criatividade.
Aproveite para ampliar a discussão propondo comparações de números diferentes. Por exemplo, 1,5 e 1,43. Os estudantes devem perceber que, apesar de 1,43 ter mais casas decimais, 1,5 é maior (pois não se pode comparar 5 e 43 como se fossem inteiros). Eles devem verificar que 5 décimos é maior que 4 décimos. Também é possível considerar que 1,5 é o mesmo que 1,50 (5 décimos é igual a 50 centésimos) para facilitar a visualização, comparando 43 centésimos com 50 centésimos.
BNCC em foco:
EF05MA02
Atividade 2
Para ampliar a atividade, peça aos estudantes que localizem outros números na reta numérica representada, como 4,590 e 4,585.
MP259
- Ligue cada
número
decimal com sua representação na reta numérica.
Coluna 1
0,45
0,49
0,47
0,42
Coluna 2




PROFESSOR
Resposta: 0,45 - figura 4; 0,49 - figura 1; 0,47 - figura 3; 0,42 - figura 2.

- Usando a calculadora, aperte as teclas indicadas em cada caso e registre o número que aparecer no visor.

PROFESSOR
Resposta: 0,1
PROFESSOR
Resposta: 0,1
PROFESSOR
Resposta: 0,1


- Converse com um colega sobre o que esses resultados sugerem.
PROFESSOR
Resposta pessoal.- Veja como Márcia comparou os números 1,2 e 1,135.

- Agora, compare os números utilizando os sinais < (menor que) ou > (maior que).
- 15,43
_____
15,45
PROFESSOR
Resposta: <
- 0,05
_____
0,005
PROFESSOR
Resposta: >
- 1,111
_____
1,12
PROFESSOR
Resposta: <
- 96,1
_____
96,01
PROFESSOR
Resposta: >
- Escreva os números abaixo na ordem decrescente.

_____ > _____ > _____ > _____ > _____
PROFESSOR
Resposta: 9,23; 5,85; 5,8; 2,67; 1,671MANUAL DO PROFESSOR
Atividade 3
Amplie esta atividade apresentando outras retas numéricas na lousa para propor uma brincadeira de adivinhação de um número escolhido entre os que estão na reta numérica. Você escolhe um número qualquer do intervalo considerado, e cada estudante faz uma pergunta a seu respeito que só possa ser respondida com “sim” ou “não”. Por exemplo: “O número é maior que 3,40? Está à direita de 3,60?”. De acordo com as respostas dadas, os estudantes vão gradativamente reduzindo o intervalo em que se encontra o número escolhido; a rodada termina quando um ou mais estudantes descobrem o número.
Atividade 4
Pergunte aos estudantes: “O que esses resultados sugerem? Como se lê cada número digitado na calculadora?”. Incentive-os a observarem a atividade com atenção e a proporem novos questionamentos, por exemplo: “Se digitarmos um número natural na calculadora, ocorrerá o mesmo?”. Espera-se que eles percebam que o valor do número na forma decimal não se altera quando acrescentamos ou retiramos zeros à direita dele (0,1 = 0,10 = 0,100). Observe que isso não ocorre com números naturais.
Atividade 5
Para comparar números com quantidades diferentes de ordens decimais, os estudantes podem preencher com zeros à direita o número que apresenta menos ordens até que ambos tenham a mesma quantidade de ordens decimais. Por exemplo, para comparar 1,111 com 1,12 podem escrever 1,12 como 1,120 e observar que o número 1,111 tem 1 inteiro e 111 milésimos, enquanto 1,120 tem 1 inteiro e 120 milésimos; portanto, 1,12 é maior que 1,111.
BNCC em foco:
EF05MA02
Atividade 6
Os estudantes podem iniciar a comparação dos números preenchendo com zeros à direita para que eles tenham a mesma quantidade de casas decimais. Depois, eles devem atentar-se ao sinal de “>”, pois nesta atividade os maiores números ficam à esquerda em vez de à direita, uma vez que devem escrevê-los em ordem decrescente (do maior para o menor).
MP260
Adição e subtração com números na forma decimal
- Isabella vai comprar o micro-ondas e o fogão mostrados abaixo. Observe a imagem e responda às questões.
- Quantos reais Isabella gastará
nessa
compra?
Para descobrir, fazendo uma adição, adicionamos centésimos com centésimos e décimos com décimos. Depois, colocamos a vírgula do resultado debaixo das demais vírgulas.
- Quantos reais Isabella gastará
nessa
compra?

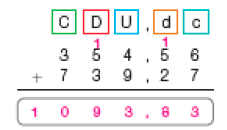
Isabella gastará nessa compra R$ _____ .
PROFESSOR
Resposta: 1.093,83- Isabella pagará à vista e, por isso, terá um desconto de R$ 55,91. Nesse caso, quantos reais ela gastará?
Podemos descobrir fazendo uma subtração.
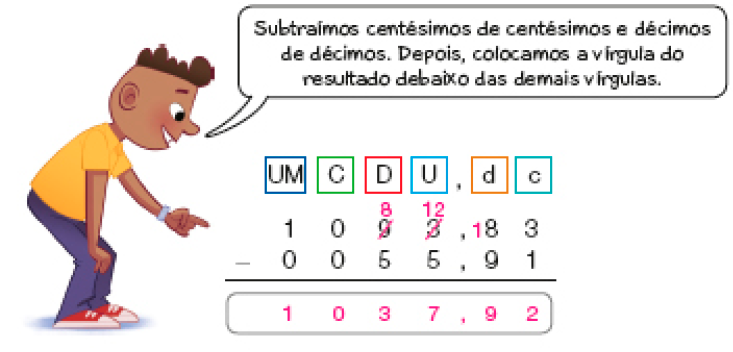
Nesse caso, Isabella gastará R$ _____ .
PROFESSOR
Resposta: 1.037,92MANUAL DO PROFESSOR
Objetivo
- Resolver e elaborar problemas de adição e subtração com números racionais cuja representação decimal seja finita.
No decorrer das atividades, apresentam-se os algoritmos usuais para a adição e a subtração com números na forma decimal, mobilizando os conhecimentos já adquiridos em relação a esses mesmos algoritmos com números naturais.
O conhecimento dos algoritmos usuais amplia o repertório de estratégias de cálculo. Contudo, isso não significa que as estratégias pessoais, como o cálculo mental, devam ser desprezadas. É fundamental, portanto, manter a linguagem adequada, garantindo a compreensão de que, tanto na parte inteira dos números envolvidos quanto em sua parte decimal, a operação seja feita ordem com ordem: milésimos adicionados a milésimos, centésimos adicionados a centésimos e décimos adicionados a décimos.
Atividade 1
Explique aos estudantes que a diferença entre os algoritmos com números naturais e os algoritmos com números na forma decimal é a incorporação das ordens dos décimos, dos centésimos e dos milésimos e a realização das respectivas trocas entre essas ordens:
- 10 milésimos formam 1 centésimo;
- 10 centésimos formam 1 décimo;
- 10
décimos
formam 1 unidade.
BNCC em foco:
EF05MA07
MP261
- Diana quer fazer a adição de 4,5 com 2,78. Veja como ela escreveu essa adição e responda às questões.


- Diana está fazendo uma afirmação correta? Justifique.
PROFESSOR
Resposta: Sim.PROFESSOR
Exemplo de justificativa: Ao acrescentar um zero à direita, na parte decimal de 4,5 (quatro inteiros e 5 décimos), representamos 4,50 (4 inteiros e 50 centésimos). Mas 5 décimos e 50 centésimos representam a mesma parte da unidade. Então:PROFESSOR
= ou 0,5 = 0,50.
- Qual é o resultado dessa adição?
_____
PROFESSOR
Resposta: 7,28PROFESSOR
Exemplo de cálculo:PROFESSOR

- Analise as falas sobre as medidas das massas corporais e complete o quadro.

Quadro: equivalente textual a seguir.
|
Nome |
Medida de massa (kg) |
|
Diego |
_____ |
|
Giovana |
_____ |
|
Nara |
_____ |
|
Oscar |
_____ |
PROFESSOR
Resposta: 47,13; 46,54; 45,85; 48,3PROFESSOR
Exemplo de cálculo:PROFESSOR

PROFESSOR

PROFESSOR


- Com a ajuda de um colega,
elabore
um problema com base no esquema abaixo. Depois, troque com outra dupla para que ela o resolva.
PROFESSOR
Respostas pessoais.
Observação: Os elementos nesta página não estão apresentados em escala de tamanho. Fim da observação.
MANUAL DO PROFESSOR
Atividade 2
Amplie a atividade e peça aos estudantes que descrevam outra estratégia para adicionar 4,5 a 2,78. Um exemplo é adicionar a parte decimal de cada número (0,5 + 0,78 = 1,28) e em seguida adicionar a parte inteira dos números (4 + 2 = 6); logo, a soma é igual a 7,28.
Atividade 3
Nesta atividade, os números na forma decimal aparecem associados a medidas de massa, que fazem parte do cotidiano dos estudantes. Peça que socializem suas estratégias de cálculo com base nas dicas das personagens. É importante valorizar também as estratégias de cálculo mental.
Atividade 4
Explore com os estudantes a ilustração e as informações nela contidas e verifique se eles as compreenderam.
Peça aos estudantes que, depois de elaborarem o problema, façam a resolução, a fim de conferir se a questão está adequada e se é possível que seja solucionada.
Caso a dupla que deve resolver esteja com dificuldades, questione: “O problema pode ser resolvido com os dados apresentados? O enunciado da questão é claro e fácil de ser compreendido?”.
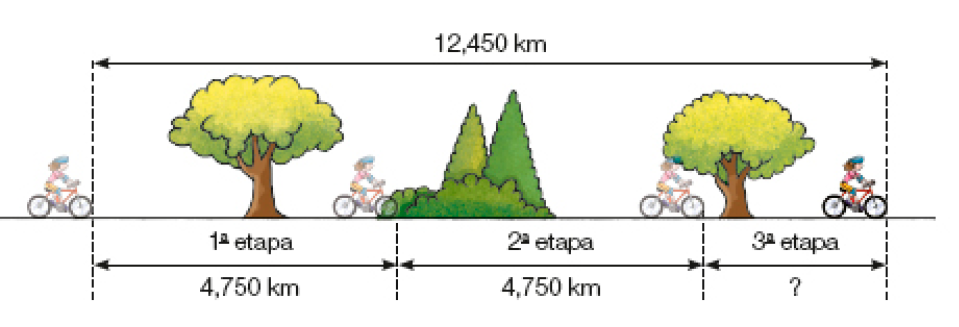
Exemplo de problema: Joana percorreu de bicicleta uma distância de 12,450 km em três etapas. Na 1ª etapa e na 2ª etapa, ela percorreu 4,750 km em cada uma. Qual foi a distância percorrida por Joana na 3ª etapa? (2,950 km).
BNCC em foco:
EF05MA07; competência específica 6
MP262
Jogo: Jogo dos decimais
Material: Tabuleiro como modelo abaixo, 68 marcadores da página 259, dados da página 261 e um saco não transparente.
Jogadores: 2 a 4
Regras:
- Os marcadores devem ser colocados no saquinho.
- Cada jogador deve sortear 16 marcadores e organizá-los em uma das cartelas no tabuleiro, colocando cada marcador em uma casa, com os números virados para cima.
- Os jogadores decidem quem começará o jogo lançando um dos dados. O primeiro é aquele que tirar o maior número no dado.
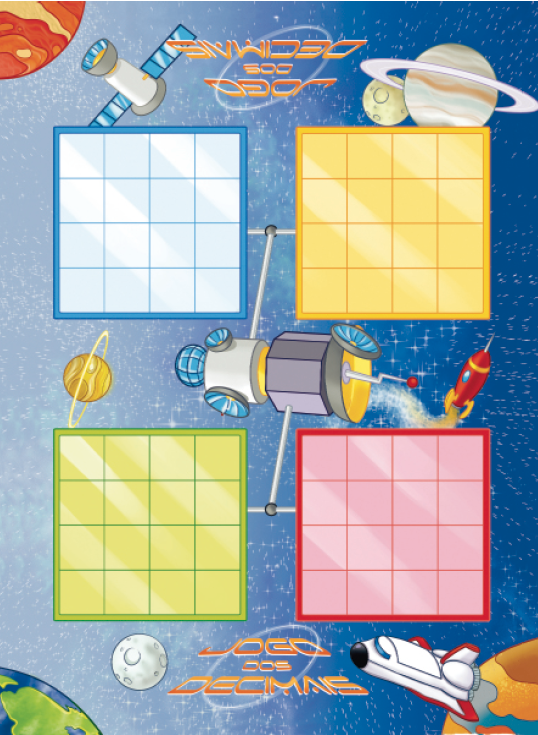
- Cada jogador, na sua vez, lança os 3 dados. Todos os jogadores que tiverem um marcador com o valor da soma dos números obtidos nos dados devem virá-lo para baixo.
- Atenção: se um jogador tiver dois marcadores com o valor da soma dos números obtidos nos dados, deverá virar para baixo apenas um marcador.
- Ganha quem virar primeiro os 4 marcadores de uma mesma fileira horizontal, vertical ou diagonal.

MANUAL DO PROFESSOR
Objetivo
- Resolver problemas de adição e subtração com números racionais cuja representação decimal seja finita.
Este jogo aborda a adição de números na forma decimal por meio de uma dinâmica que mistura sorte com habilidades de cálculo. A cada rodada, os estudantes são incentivados a calcular o resultado de uma adição de três parcelas e a localizar esse resultado em suas cartas. Um aspecto interessante dessa característica do jogo é a possibilidade de reconhecerem um erro de cálculo, pois todos os jogadores buscam a mesma resposta e, na busca pela vitória, são incentivados a verificarem os cálculos uns dos outros. Para explorar este conteúdo, relembre o trabalho realizado com números na forma decimal e os conhecimentos sobre adição com números naturais. É importante explorar as adições antes de jogarem, para que relembrem procedimentos.
Uma maneira de resgatar o trabalho com adição de decimais é recorrer ao sistema monetário, com a adição de centavos, como a adição de 10 centavos mais 25 centavos, que pode ser representada por R$ 0,10 + R$ 0,25 = R$ 0,35.
BNCC em foco:
EF05MA07
MP263
Questões sobre o jogo
- Responda.
- Qual é o
menor
valor que podemos
obter
com a adição dos dados?
_____
PROFESSOR
Resposta: 0,03
- E qual é o maior valor?
_____
PROFESSOR
Resposta: 1,50
- Qual é o
menor
valor que podemos
obter
com a adição dos dados?
_____
- Escreva os valores nas faces dos dados em branco de forma que completem o valor de cada marcador.

PROFESSOR
Resposta: 0,25; 0,25
PROFESSOR
Resposta: 0,25; 0,50
PROFESSOR
Resposta: 0,50; 0,01
PROFESSOR
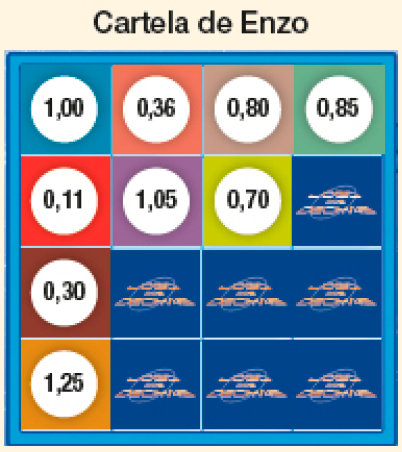
Resposta: 0,50; 0,50; 0,10- Nicole e Enzo estão jogando. Observe como estão as cartelas deles.

- Para Nicole vencer o jogo, qual valor ela
deve
tirar em cada dado?
_____
PROFESSOR
Exemplo de respostas: 0,01; 0,05 e 0,50
- E quais valores Enzo pode tirar nos dados para vencer?
_____
PROFESSOR
Exemplo de respostas: 0,10; 0,10 e 0,10 ou 0,50; 0,50 e 0,25 ou 0,50; 0,25 e 0,10
- Suponha que Nicole tenha jogado os dois primeiros dados e
obtido
0,50 e 0,50.
Quanto ela deve tirar no terceiro dado para virar um de seus marcadores, de forma que Enzo não vire nenhum dos seus? _____
PROFESSOR
Resposta: 0,50
MANUAL DO PROFESSOR
Questões sobre o jogo
Para responder à questão 1, oriente os estudantes a identificarem os números de cada face. Depois, faça perguntas como: “Quais são os números menores? E os maiores?”, para que estabeleçam relações e encontrem as possibilidades de resultados.
Na questão 2, incentive os estudantes a compartilharem suas respostas e a explicarem como pensaram. Ao compararem o que fizeram, eles poderão perceber que há várias respostas possíveis.
A questão 3 simula uma situação de jogo. Portanto, é importante socializarem as possibilidades de sorteio dos dados. Aproveite para discutir se os estudantes também estão verificando o cálculo realizado pelos adversários.
Variações
É possível que, depois de algum tempo, os estudantes queiram modificar as regras para ampliar os desafios. Sugira estas mudanças: alterar os números das cartas e/ou jogar com apenas dois dados para facilitar a realização dos cálculos e agilizar as partidas.
BNCC em foco:
EF05MA07
MP264
Multiplicação com números na forma decimal

- Sueli comprou 4 canetas coloridas.
- Quanto ela pagou pelas canetas no total?
_____
PROFESSOR
Resposta: R$ 5,00
- De quanto foi o troco, se ela pagou com uma cédula de R$ 20,00?
_____
PROFESSOR
Resposta: R$ 15,00
- Quanto ela pagou pelas canetas no total?
_____
- Sônia e Marília estão bordando juntas uma grande toalha e precisarão comprar 3 fitas coloridas, cada uma com 2,45 metros de comprimento. Quantos metros de fita elas precisarão comprar ao todo?
Vamos fazer uma adição para descobrir.

2,45 + 2,45 + 2,45 = 2,00 + 2,00 + 2,00 + 0,45 + 0,45 + 0,45 =
2,00 + 2,00 + 2,00: partes inteiras dos números
2,00 + 2,00 + 2,00: 6,00
0,45 + 0,45 + 0,45: partes decimais dos números
0,45 + 0,45 + 0,45: 1,35
6,00 + 1,35 = 7,35
Outra maneira de calcular é fazer a multiplicação 3 × 2,45.
Cálculo com o algoritmo usual
- Primeiro, calculamos 3 vezes 5 centésimos, obtendo 15 centésimos.
- Trocamos 10 centésimos por 1 décimo.
- Depois, fazemos 3 vezes 4 décimos, obtendo 12 décimos.
- 12 décimos mais 1 décimo são 13 décimos.
- Trocamos 10 décimos por 1 unidade.
- 3 vezes 2 unidades são 6 unidades.
- Acrescentando 1 unidade a 6 unidades, obtemos 7 unidades.
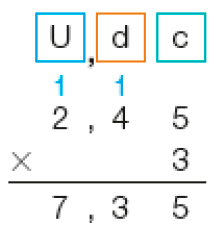
Portanto, Sônia e Marília precisarão comprar _____ metros de fita.
PROFESSOR
Resposta: 7,35- Ao todo, quantos metros de fita elas teriam de comprar se precisassem de 4 fitas de 3,15 metros de comprimento cada uma?
_____
PROFESSOR
Resposta: 12,60 metros de fita.
MANUAL DO PROFESSOR
Objetivos
- Resolver e elaborar problemas de multiplicação com números racionais cuja representação decimal seja finita.
- Efetuar multiplicações de números racionais por 10, 100 e 1.000.
Atividade 1
Explore a situação perguntando à turma: “Se Sueli comprasse 9 canetas coloridas, quanto ela gastaria? Se ela pagasse as 9 canetas com uma cédula de 50 reais, quanto sobraria?” (Sueli gastaria R$ 11,25 e sobrariam R$ 38,75.).
Atividade 2
A respeito dos cálculos efetuados por meio de uma adição, em que foram adicionadas 3 parcelas iguais da parte inteira (2,00) e 3 parcelas iguais da parte fracionária (0,45), esclareça que esses cálculos podem ser resolvidos por meio da multiplicação de cada uma dessas partes por 3, como mostrado no algoritmo usual.
Incentive os estudantes a observarem as trocas realizadas no algoritmo usual. Caso ainda tenham dúvidas, faça outras multiplicações na lousa, salientando as trocas realizadas, para que eles entendam todos os passos do procedimento.
BNCC em foco:
EF05MA08
MP265
- Na escada abaixo, a medida da altura de cada degrau é 17,8 centímetros.

- Qual é a medida, em metro, da altura dessa escada de 4 degraus?
_____
PROFESSOR
Resposta: 0,712 m
- Se essa escada tivesse 7 degraus, qual seria a medida da sua altura, em metro?
_____
PROFESSOR
Resposta: 1,246 m

- Calcule e registre suas respostas.
- 1,257 × 10 =
_____
PROFESSOR
Resposta: 12,57
- 1,257 × 100 =
_____
PROFESSOR
Resposta: 125,7
- 1,257 × 1.000 =
_____
PROFESSOR
Resposta: 1.257
- 2,45 × 10 =
_____
PROFESSOR
Resposta: 24,5
- 2,45 × 100 =
_____
PROFESSOR
Resposta: 245
- 2,45 × 1.000 =
_____
PROFESSOR
Resposta: 2.450


- Faça outras multiplicações como essas (com um dos fatores na forma decimal e o outro fator sendo 10, 100 ou 1.000). Troque ideias com seus colegas sobre o que esses resultados sugerem.
PROFESSOR
Resposta pessoal.

- Calcule mentalmente e registre suas respostas.
- Cléber tem a quantia indicada abaixo. Dez vezes essa quantia corresponde a quantos reais?
_____
PROFESSOR
Resposta: R$ 25,30

- Quantos reais Ricardo gastará para abastecer seu caminhão com 100 litros de diesel?
_____
PROFESSOR
Resposta: R$ 310,00

- Elabore um problema de multiplicação com base na ilustração. Em seguida, resolva-o.
_____
PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR
Atividade 3
Incentive os estudantes a resolverem esta situação por meio de multiplicações, embora também possam usar adições. Eles devem perceber que, se cada degrau mede 17,8 cm, 4 degraus têm 4 vezes essa medida, ou seja, 71,2 cm. Como o resultado é pedido em metro, é preciso lembrar que 1 metro tem 100 cm. Portanto, a resposta é 0,712 m. Para calcular a medida da escada com 7 degraus, segue-se o mesmo raciocínio. Para facilitar o entendimento da ordem de grandeza, sugira aos estudantes que façam estimativas antes de realizarem os cálculos.
Atividade 4
Retome com os estudantes a regularidade em multiplicações entre dois números naturais quando um deles é igual a 10, 100 ou 1.000.
As regularidades nas multiplicações do tipo “vezes 10”, “vezes 100” e “vezes 1.000”, com um número na forma decimal, precisam ser exploradas para que eles ampliem o repertório de cálculos mentais, estimativas e cálculos escritos.
Para ampliar a atividade, apresente também o procedimento da decomposição, já utilizado com números naturais. Por exemplo, a multiplicação de 13 por 87,50 pode ser feita da seguinte maneira:
- Fazendo multiplicações parciais: 10 × 87,50 = 875,00; 3 × 80,00 = 240,00; 3 × 7,00 = 21,00; 3 × 0,50 = 1,50.
- Adicionando esses resultados, obtém-se o produto procurado: 875,00 + 240,00 + 21,00 + 1,50 = 1.137,50.
Atividade 5
As situações-problema propostas incentivam a utilização do cálculo mental para atividades diárias, inclusive para estimativas.
Atividade 6
Exemplos de questões que podem ser criadas:
- Quanto vai pagar pela bicicleta quem comprá-la em 10 prestações? (R$ 159,00)
- É mais barato comprar a bicicleta à vista ou a prazo? (À vista.)
- Qual é a diferença de valor entre o pagamento à vista e a prazo? (R$ 19,00)
Incentive os estudantes a utilizarem o cálculo mental.
BNCC em foco:
EF05MA08; competência específica 6
MP266
Quociente decimal
- Joana quer dividir igualmente entre 4 crianças a quantia abaixo.

- Quanto cada criança receberá?
_____
PROFESSOR
Resposta: R$ 5,50

- Explique a um
colega
como você fez esse cálculo.
PROFESSOR
Resposta pessoal.

- Veja como Aline dividiu 81 por 2.

- Agora, calcule o resultado em cada caso.
- 17 ÷ 2 =
_____
PROFESSOR
Resposta: 8,50
- 43 ÷ 2 =
_____
PROFESSOR
Resposta: 21,5
- 21 ÷ 4 =
_____
PROFESSOR
Resposta: 5,25
- Regina dividirá um barbante de 13 centímetros em 5 partes iguais.

- Cada parte terá mais de 2 centímetros de comprimento?
_____
PROFESSOR
Resposta: Sim.
- Cada parte terá mais de 3 centímetros de comprimento?
_____
PROFESSOR
Resposta: Não.

- Lembrando que 1 centímetro é o mesmo que 10 milímetros, como você pode
obter
o resultado dessa divisão? Converse com seus colegas a esse respeito.
PROFESSOR
Resposta pessoal.
- Com seu esqueite, Tainá deu 4 voltas em torno da praça perto de sua casa e percorreu 215 metros. Qual é a medida do perímetro dessa praça?
_____
PROFESSOR
Resposta: 53,75 metros.
MANUAL DO PROFESSOR
Objetivo
- Resolver problemas de divisão com números racionais cuja representação decimal seja finita (com divisor natural e diferente de zero).
Os estudantes devem perceber que a lógica do algoritmo da divisão é a mesma já estudada, somente havendo mudança no reconhecimento das partes decimais do quociente. Em outras palavras, devem proceder do mesmo modo que com o algoritmo usual já visto para a divisão, completando a parte decimal do quociente (décimos, centésimos e milésimos). O que geralmente confunde os estudantes é a inclusão do zero para dar continuidade à divisão. Para esclarecer a razão desse procedimento, é importante insistir no significado dos reagrupamentos entre as ordens.
Atividade 1
Se necessário, esclareça que, para ser dividido entre as 4 crianças, o dinheiro deve antes ser trocado. Pergunte, então, de que maneira precisamos trocar a quantia correspondente à cédula e às moedas ilustradas para que seja possível dividi-la igualmente entre as 4 crianças.
Exemplo de explicação no item b: Dividi 20 reais em 4 quantias iguais, obtendo 5 reais. Os 2 reais restantes valem o mesmo que 200 centavos, que divididos em 4 quantias iguais resultam em 50 centavos para cada um. Então, fiz a adição: 5 reais mais 50 centavos, que é igual a 5 reais e 50 centavos (R$ 5,50).
Atividade 2
Incentive os estudantes a utilizarem a mesma técnica apresentada na fala de Aline.
Espera-se que eles efetuem a divisão das dezenas e das unidades separadamente, depois adicionem os resultados obtidos.
Esta atividade amplia o cálculo mental e a agilidade para resolver divisões com números maiores sem a utilização de uma ferramenta como a calculadora.
BNCC em foco:
EF05MA08
Atividade 3
Exemplo de resposta no item c: Divido 10 centímetros em 5 partes, obtendo 2 centímetros para cada parte. Os 3 centímetros restantes são o mesmo que 30 milímetros, que dividido por 5 é igual a 6 milímetros. Então, faço a adição dos quocientes obtidos: 2 centímetros + 6 milímetros.
Discuta com a turma maneiras de registrar o resultado dessa adição: 2 centímetros e 6 milímetros; 2,6 centímetros (pois 1 mm é 1 décimo do centímetro); 26 milímetros (pois 2 centímetros equivalem a 20 milímetros).
MP267
- Para fazer 4 varais na lavanderia de uma casa, será preciso dividir um rolo de varal de 11 metros de comprimento em 4 pedaços de mesmo comprimento.
Vamos dividir 11 por 4 para saber quantos metros terá cada varal.
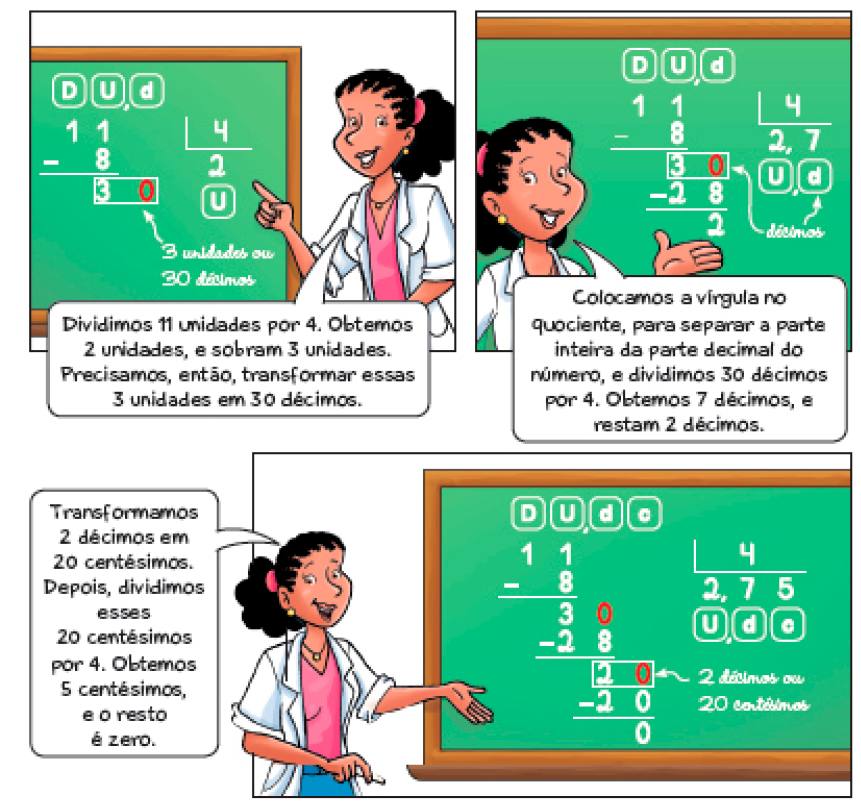
- Cada varal terá mais ou menos que 3 metros?
_____
PROFESSOR
Resposta: Menos.
- Cada varal terá
_____
metros e
_____
centímetros.
PROFESSOR
Resposta: 2; 75
- Calcule o resultado em cada caso.
- 45 ÷ 4
PROFESSOR
Resposta: 11,25
- 16 ÷ 5
PROFESSOR
Resposta: 3,2
- 21 ÷ 6
PROFESSOR
Resposta: 3,5
- 17 ÷ 8
PROFESSOR
Resposta: 2,125
- 9 ÷ 4
PROFESSOR
Resposta: 2,25
- 89 ÷ 8
PROFESSOR
Resposta: 11,125
- 39 ÷ 6
PROFESSOR
Resposta: 6,5
- 19 ÷ 8
PROFESSOR
Resposta: 2,375
- 45 ÷ 4
MANUAL DO PROFESSOR
Atividade 4
Os estudantes podem efetuar a divisão de 200 por 4 (obtendo 50) e de 15 por 4 (obtendo 3,75), separadamente. Depois, basta adicionar esses resultados para obter o quociente final, que indica a medida total: 53,75 metros.
Atividade 5
A primeira etapa do algoritmo apresenta a divisão não exata com números naturais, que os estudantes já conhecem. Justifique com eles a etapa em que as 3 unidades do resto (que é menor que o divisor 4 e, portanto, não pode ser dividido de modo que origine um quociente inteiro) são trocadas por 30 décimos, pois cada unidade equivale a 10 décimos.
Pergunte aos estudantes: “Como podemos verificar se a divisão está correta?”. Espera-se que respondam que a verificação pode ser feita pela multiplicação 4 × 2,75 = 11.
Nesta atividade, é fundamental os estudantes compreenderem que, como agora o número 30 corresponde a décimos, o resultado será expresso em décimos e, para isso, é necessário acrescentar no quociente a vírgula, separando a parte inteira da parte decimal.
Como 30 décimos dividido por 4 é igual a 7 décimos, com resto igual a 2 décimos, é preciso trocar esses 2 décimos por centésimos; como cada décimo equivale a 10 centésimos, 2 décimos serão trocados por 20 centésimos.
E, finalmente, a divisão de 20 centésimos por 4 é igual a 5 centésimos.
Depois, podem comparar as estimativas com os resultados obtidos pelo algoritmo usual.
BNCC em foco:
EF05MA08
Atividade 6
Antes de os estudantes calcularem o resultado de cada divisão, peça que escrevam, para cada item, um intervalo que indique entre quais números naturais estimam que estará o quociente. Isso contribui tanto para as estimativas de cálculos mentais quanto para a comparação entre números na forma decimal, além de ajudá-los a perceberem possíveis equívocos ao realizarem a divisão pelo algoritmo usual.
Os estudantes podem estimar que o quociente de 45 ÷ 4 está entre 11 e 12, pois: 11 × 4 = 44 e 12 × 4 = 48.
MP268
Divisão com números na forma decimal

- Fernando decidiu comprar um computador em 6 prestações de mesmo valor.
- Faça uma estimativa sobre qual será, aproximadamente, o valor de cada prestação.
_____
PROFESSOR
Exemplo de resposta: Aproximadamente R$ 300,00.

- Conte para um
colega
como você pensou para fazer a estimativa.
PROFESSOR
Resposta pessoal.
- Faça uma estimativa sobre qual será, aproximadamente, o valor de cada prestação.

- Cristiano foi com R$ 15,00 à padaria. Chegando lá, ele comprou 3 doces de mesmo
preço
e recebeu R$ 1,50 de troco.
- Quanto Cristiano pagou pelos 3 doces?
_____
PROFESSOR
Resposta: R$ 13,50
- Qual foi o
preço
de cada doce?
_____
PROFESSOR
Resposta: R$ 4,50
- Explique a um
colega
como você resolveu esse problema.
PROFESSOR
Resposta pessoal.
- Quanto Cristiano pagou pelos 3 doces?
_____

- Viviane e 3 amigos foram a uma lanchonete e gastaram R$ 36,40. Na hora de pagar a conta, eles dividiram igualmente a despesa. Quantos reais cada um pagou?
Veja como Viviane fez a divisão de R$ 36,40 por 4.
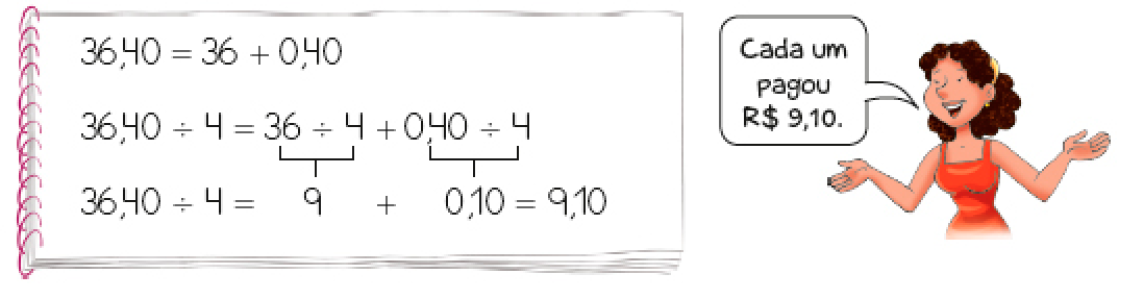
- Quanto cada um pagaria se a despesa tivesse sido de R$ 44,80?
_____
PROFESSOR
Resposta: R$ 11,20
- E se a despesa tivesse sido de R$ 49,60?
_____
PROFESSOR
Resposta: R$ 12,40
- Ana e 4 amigas compraram um pacote com 5
cadernos
por R$ 24,90. Em uma papelaria do bairro, um
caderno
igual a esses custaria R$ 7,70.
- Quantos reais cada uma pagou pelo caderno, se elas dividiram igualmente o valor do pacote com 5 unidades?
_____
PROFESSOR
Resposta: R$ 4,98

- A compra foi vantajosa? Troque ideias com um
colega
sobre isso.
PROFESSOR
Resposta pessoal.
- Quantos reais cada uma pagou pelo caderno, se elas dividiram igualmente o valor do pacote com 5 unidades?
_____
MANUAL DO PROFESSOR
Objetivos
- Resolver e elaborar problemas de divisão com números racionais cuja representação decimal seja finita (com divisor natural e diferente de zero).
- Efetuar divisões de números racionais por 10, 100 e 1.000.
- Interpretar dados apresentados em gráfico de colunas.
Atividade 1
Espera-se que, para obter um quociente aproximado, arredondem o valor antes de efetuar a divisão.
Depois, peça a voluntários que venham à frente da sala e compartilhem as estratégias utilizadas.
Atividade 2
Verifique se eles percebem que é preciso subtrair de R$ 15,00 o valor do troco (R$ 1,50), para depois dividir o resultado (R$ 13,50) por 3. Exemplo de explicação para o item c: Para o preço dos 3 doces, subtraí 1,50 de 15,00, obtendo 13,50. Para o valor de cada doce, dividi 12,00 por 3, obtendo 4,00, e dividi 1,50 por 3, obtendo 0,50. Depois, adicionei esses dois quocientes, obtendo 4,50. Logo, o preço de cada doce foi R$ 4,50.
Atividade 3
No item b, os estudantes devem fazer decomposições e composições do número 49,60.
49,60 = 48 + 1 + 0,60
49,60 = 48 + 1,60, então:
49,60 ÷ 4 = 48 ÷ 4 + 1,60 ÷ 4
48 ÷ 4 - 12
1,60 ÷ 4 = 0,40
49,60 ÷ 4 = 12 + 0,40 = 12,40
Atividade 4
No item b, espera-se que os estudantes respondam que sim e que percebam as vantagens de buscar melhores preços. A compra em conjunto permitiu uma economia de R$ 2,72 por caderno.
BNCC em foco:
EF05MA08
MP269
- Roberto aproveitou uma liquidação para comprar bermudas e camisetas para dar de presente a seus sobrinhos. O valor total da compra foi de R$ 84,52. O pagamento será realizado em 4 prestações iguais sem acréscimo. Qual será o valor de cada prestação?
Cálculo com o algoritmo usual
1º
Dividimos 8 dezenas por 4, obtendo 2 dezenas. Depois, dividimos 4 unidades por 4. Obtemos 1 unidade, e não sobra resto.
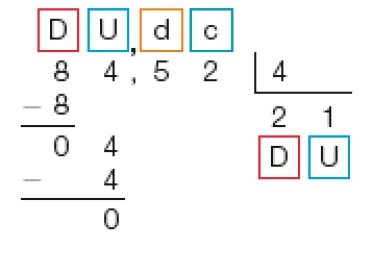
2°
Em seguida, dividimos 5 décimos por 4. Obtemos 1 décimo, e resta 1 décimo, que é o mesmo que 10 centésimos.
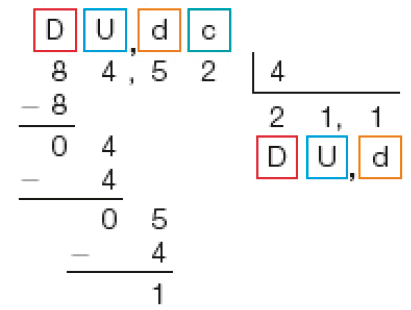
3°
Então, dividimos 12 centésimos por 4. Obtemos 3 centésimos, e o resto é zero.
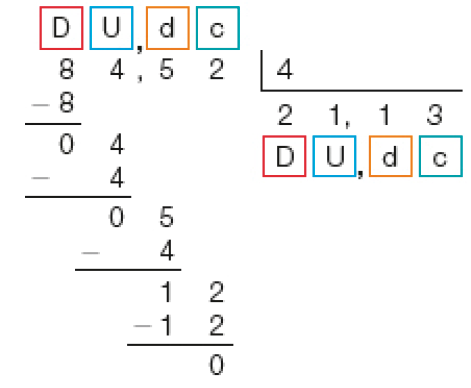

- Agora, calcule o resultado em cada caso.
- 36,60 ÷ 6
PROFESSOR
Resposta: 6,10
- 65,15 ÷ 5
PROFESSOR
Resposta: 13,03
- 72,56 ÷ 8
PROFESSOR
Resposta: 9,07
- 95,34 ÷ 3
PROFESSOR
Resposta: 31,78
- 77,76 ÷ 4
PROFESSOR
Resposta: 19,44
- 89,76 ÷ 3
PROFESSOR
Resposta: 29,92
MANUAL DO PROFESSOR
Atividade 5
Sugira aos estudantes que dividam 84,52 por 4 por meio de decomposição: 84,52 = 84 + 0,52.
Efetuamos 84 ÷ 4 = 21 e 0,52 ÷ 4 = 0,13 e adicionamos os resultados obtidos: 21 + 0,13 = 21,13.
Oriente os estudantes para a correta leitura de R$ 21,13: “vinte e um reais e treze centavos”. Pergunte: “Como podemos verificar se o resultado dessa divisão está correto?”. Espera-se que respondam que a verificação pode ser feita pela multiplicação 21,13 × 4 = 84,52.
Voltamos a salientar que a garantia da compreensão do algoritmo usual da divisão é a manutenção da ordem dos números (dezenas, unidades, décimos, centésimos) e o reconhecimento de que a vírgula continua separando a parte inteira da parte decimal.
É possível que alguns estudantes tenham aprendido outra maneira de realizar o cálculo de uma divisão em que o dividendo é um número na forma decimal: “igualando o número de casas à direita da vírgula”.
Por exemplo, no item a desta atividade, a divisão 36,60 ÷ 6 seria feita do seguinte modo: há 2 casas decimais no número 36,60, e nenhuma casa decimal no número 6; então, multiplicamos 36,60 e 6 por 100, transformando-os em 3.660 e 600, respectivamente, obtendo a operação: 3.660 ÷ 600. Esse modo de calcular pode ser justificado considerando-se que, ao multiplicarmos dividendo e divisor por um mesmo número não nulo, a divisão resultante terá o mesmo quociente da divisão original.
Lembre aos estudantes que a vírgula é colocada no quociente para separar a parte inteira da parte decimal do número.
BNCC em foco:
EF05MA08
MP270
- Reginaldo queria dividir 4 unidades em 10 partes iguais, em 100 partes iguais e em 1.000 partes iguais. Complete os quadros que ele fez e, em seguida, responda.
Quadro 1
Tabela: equivalente textual a seguir.
|
Número de unidades |
Número de décimos |
|---|---|
|
1 |
10 |
|
2 |
_____ |
|
3 |
_____ |
|
4 |
_____ |
PROFESSOR
Resposta: 20; 30; 40Quadro 2
Tabela: equivalente textual a seguir.
|
Número de unidades |
Número de centésimos |
|---|---|
|
1 |
100 |
|
2 |
_____ |
|
3 |
_____ |
|
4 |
_____ |
PROFESSOR
Resposta: 200; 300; 400Quadro 3
Tabela: equivalente textual a seguir.
|
Número de unidades |
Número de milésimos |
|---|---|
|
1 |
1.000 |
|
2 |
_____ |
|
3 |
_____ |
|
4 |
_____ |
PROFESSOR
Resposta: 2.000; 3.000; 4.000- Quatro unidades é o mesmo que quantos décimos? E quantos centésimos? E quantos milésimos?
_____
PROFESSOR
Resposta: 40 décimos; 400 centésimos; 4.000 milésimos.
- Quais das afirmações abaixo são corretas?
_____
PROFESSOR
Resposta: Todas.
Dividir 4 unidades por 10 é equivalente a dividir 40 décimos por 10.
Dividir 4 unidades por 100 é equivalente a dividir 400 centésimos por 100.
Dividir 4 unidades por 1.000 é equivalente a dividir 4.000 milésimos por 1.000.
- De acordo com o item b, qual é o resultado de 4 ÷ 10? E de 4 ÷ 100? E de 4 ÷ 1.000? Escreva os resultados por extenso e na forma decimal.
_____
PROFESSOR
Resposta: Quatro décimos ou 0,4; quatro centésimos ou 0,04; quatro milésimos ou 0,004.

- Faça os cálculos com a ajuda de uma calculadora e registre os resultados.
- 6 ÷ 10 =
_____
PROFESSOR
Resposta: 0,6
- 6 ÷ 100 =
_____
PROFESSOR
Resposta: 0,06
- 6 ÷ 1.000 =
_____
PROFESSOR
Resposta: 0,006
- 3,5 ÷ 10 =
_____
PROFESSOR
Resposta: 0,35
- 12,8 ÷ 100 =
_____
PROFESSOR
Resposta: 0,128
- 345 ÷ 1.000 =
_____
PROFESSOR
Resposta: 0,345

- Ainda com a calculadora, faça várias outras divisões por 10, por 100 e por 1 000. Depois, converse com um
colega
sobre o que vocês observaram nos quocientes obtidos.
PROFESSOR
Resposta pessoal.
- Ainda com a calculadora, faça várias outras divisões por 10, por 100 e por 1 000. Depois, converse com um
colega
sobre o que vocês observaram nos quocientes obtidos.
- 6 ÷ 10 =
_____
MANUAL DO PROFESSOR
As atividades destas páginas foram elaboradas com o intuito de possibilitar aos estudantes, pela observação de regularidades, a construção de estratégias de cálculo mental que dinamizem os cálculos de divisões desse tipo.
Atividade 6
Ao retomar a relação entre inteiros, décimos, centésimos e milésimos, os estudantes são levados a compreender que, para dividir 4 por 10, por exemplo, podemos trocar 4 inteiros por 40 décimos e depois dividi-los por 10, obtendo 4 décimos como quociente. Raciocínio semelhante pode ser aplicado às divisões por 100 e por 1.000.
Atividade 7
Espera-se que os estudantes percebam que os quocientes obtidos sugerem que:
- ao dividir um número por 10, o resultado é igual a esse número com a vírgula deslocada uma casa para a esquerda;
- ao dividir um número por 100, o resultado é igual a esse número com a vírgula deslocada duas casas para a esquerda;
- ao dividir por 1 000, o resultado tem a vírgula deslocada três casas para a esquerda.
Caso seja necessário, lembre os estudantes de que: 6 = 6,0 e 345 = 345,0.
BNCC em foco:
EF05MA08
MP271

- Em uma campanha de arrecadação de alimentos feita em um município, foram arrecadados 350 quilogramas de arroz e 650 quilogramas de feijão para
serem
divididos igualmente entre 100 famílias de um município vizinho.
Quantos quilogramas de arroz cada família receberá? E de feijão?
_____
PROFESSOR
Resposta: 3,5 quilogramas de arroz; 6,5 quilogramas de feijão.
- Calcule o resultado da divisão da medida de massa da melancia, em cada caso.

- Divisão em 10 partes iguais.
_____
PROFESSOR
Resposta: 0,8 kg
- Divisão em 100 partes iguais.
_____
PROFESSOR
Resposta: 0,08 kg
- Divisão em 10 partes iguais.
_____
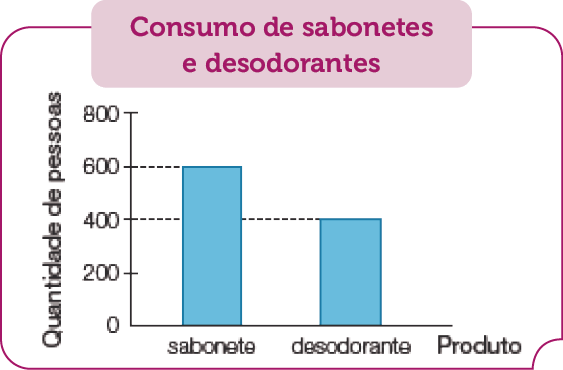
- O diretor de uma empresa que fabrica sabonetes e desodorantes encomendou duas pesquisas com consumidores de seus produtos. O gráfico a seguir mostra a quantidade de consumidores entrevistados em cada pesquisa.
Fonte: Pesquisa da professora Ana (5 fev. 2023).
- Quantos consumidores foram entrevistados ao todo?
_____
PROFESSOR
Resposta: 1 000 consumidores.
- Se dos entrevistados da pesquisa sobre o sabonete são mulheres, quantas mulheres participaram dessa pesquisa?
_____
PROFESSOR
Resposta: 400 mulheres.

- Com um colega, elaborem um problema com base na ilustração abaixo que envolva a divisão. Depois, troquem-no com outra dupla para que ela o resolva.
PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR
Atividade 8
Incentive os estudantes a utilizarem o cálculo mental para a resolução desta atividade.
Atividade 9
Nesta atividade, é interessante observar que os resultados obtidos têm a parte inteira igual a zero. Para que os estudantes compreendam a razão disso, eles devem observar que 8 quilogramas não podem ser divididos por 10 de modo que se obtenha quociente pelo menos igual a 1, pois 8 é menor que 10.
Assim, 8 quilogramas devem ser trocados por 8 000 gramas, que, divididos por 10, resultam em quociente igual a 800 gramas ou 0,8 kg. No item b, 8 000 gramas divididos por 100 resultam em quociente igual a 80 gramas ou 0,08 kg.
Atividade 10
No item a, espera-se que os estudantes interpretem o gráfico de colunas entendendo que o total de pessoas entrevistadas é o resultado de 600 + 400.
Para calcular o item b, é preciso atentar que a fração refere-se apenas às consumidoras de sabonete e, portanto, é preciso calcular de 600 pessoas.
Atividade 11
Exemplo de problema: Uma pessoa comprou os dois produtos aproveitando a promoção indicada pela ilustração (pagar em 10 vezes sem acréscimo). Qual é o valor de cada prestação?
Exemplo de resolução:
139 + 157 = 296
296 ÷ 10 = 29,6
Logo, o valor de cada prestação será de R$ 29,60.
BNCC em foco:
EF05MA08, EF05MA24; competência específica 6
Sugestão de leitura para o estudante
Livro
RAMOS, Luzia Faraco. Aventura decimal. São Paulo: Ática, 2019. (Coleção A Descoberta da Matemática.)
Nesse livro, as personagens Paulo e Glória vivenciam incríveis aventuras na Terra do Povo Pequeno, onde não há nada que não possa ser curado ou resolvido. Assim, Paulo é ajudado por três minúsculos habitantes desse lugar que têm grandes poderes: Sara, Wiujam e Ogirep. Por outro lado, Glória e Paulo mobilizam seus conhecimentos sobre números decimais para ajudar Sara a desvendar o segredo dos cubos esculpidos. O livro ainda traz um minialmanaque com informações sobre o assunto em estudo, além de jogos e desafios para os leitores testarem seus conhecimentos.
MP272
Porcentagem
- Para saber quanto é 25% de 400 doces, Sílvia montou o quadro abaixo.
- Complete-o.

- Como você faria para calcular 10% de 400 com base no quadro de Sílvia?
PROFESSOR
Exemplos de resposta: Dividiria o resultado de 100% (400) por 10, obtendo 40; ou dividiria o resultado de 50% (200) por 5, obtendo 40.
- Complete-o.
Quadro: equivalente textual a seguir.
|
Taxa percentual de 400 |
Quantidade de doces |
|---|---|
|
100% ou 100 em cada 100 |
400 |
|
50% ou 50 em cada 100 |
_____ |
|
25% ou 25 em cada 100 |
_____ |
PROFESSOR
Resposta: 200; 100- Observe a situação.

- Agora, responda às questões.
- Qual é o valor do desconto na compra à vista?
_____
PROFESSOR
Resposta: R$ 6,00
- Quanto custarão à vista os brinquedos mencionados?
_____
PROFESSOR
Resposta: R$ 54,00
- Um site de viagens realizou uma pesquisa com 600 turistas sobre a preferência entre os três restaurantes de uma cidade. O gráfico seguinte mostra o resultado.
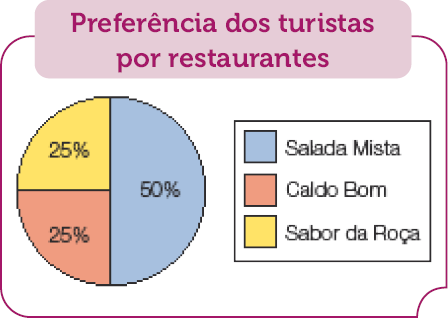
Fonte: Site de viagens (17 mar. 2023).
- Quantos turistas entrevistados disseram preferir o restaurante Salada Mista?
_____
PROFESSOR
Resposta: 300 turistas.
- Quantas pessoas preferem o restaurante Caldo Bom? E o Sabor da Roça?
_____
PROFESSOR
Resposta: 150 pessoas; 150 pessoas.
MANUAL DO PROFESSOR
Objetivos
- Associar as representações 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens, utilizando estratégias pessoais, cálculo mental e calculadora.
- Interpretar dados apresentados em gráfico de setores.
Atividade 1
Os estudantes devem entender que a porcentagem de um todo corresponde a uma fração com denominador 100. Por exemplo, calcular 25% de 200 ( ou de 200 reais) significa que se deseja saber quantos reais são obtidos tomando 25 reais em cada 100 reais. Como “25 em 100” equivale a “1 em 4”, podemos também calcular de 200, ou seja: 200 ÷ 4 = 50. Portanto: 25% de 200 = 50.
Cada estudante deve desenvolver estratégias e recursos próprios para realizar cálculos que envolvem porcentagens. A escolha da estratégia mais adequada dependerá da situação a ser resolvida, dos recursos disponíveis e também da experiência dos estudantes.
Atividade 2
Uma possibilidade de cálculo para determinar diretamente o valor a ser pago com desconto, sem ter de calcular o valor do desconto, é pensar que, se do total (100%) será dado um desconto de 10%, a garota terá de pagar 90% (100% − 10% = 90%) do valor total. Para calcular 90% de 60, podemos calcular 10% (ou 1 décimo) de 60 dividindo 60 por 10 e obtendo o quociente 6; depois, multiplicar esse valor por 9, obtendo 54, ou seja, 54 reais.
BNCC em foco:
EF05MA06, EF05MA24
Atividade 3
Aproveite o contexto para retomar com os estudantes o uso do gráfico de setores, indicado para representar os dados de modo que facilite a comparação das diferentes categorias indicadas, entre si e em relação ao todo.
MP273
- O salário de Ana é composto de uma parte fixa de R$ 1 900,00 e uma parte variável de 3% do valor total de mercadorias que ela vende no mês.

1% de 8 000 é igual a de 8.000
8.000 ÷ 100 = 80
1% de 8.000 é igual a 80.
Então, 3% de R$ 8.000,00 é igual a 3 vezes R$ 80,00, ou seja, R$ 240,00.
Salário - R$ 1.900,00 mais R$ 240,00, ou seja: R$ 2.140,00
Para calcular 3% de 8.000, o gerente de Ana usou uma calculadora.
Sabendo que 3% = = 0,03, ele calculou essa porcentagem de duas maneiras.
Cálculo com o uso da tecla %

Cálculo sem o uso da tecla %

- Agora, calcule e registre no caderno a estratégia que você utilizou.
- 5% de 500
PROFESSOR
Resposta: 25
- 15% de 200
PROFESSOR
Resposta: 30
- 20% de 600
PROFESSOR
Resposta: 120
- 80% de 150
PROFESSOR
Resposta: 120
Boxe complementar:
Desafio
Na festa junina de uma escola, estavam presentes algumas pessoas, das quais 30 eram estudantes. As outras eram funcionários ou familiares de estudantes. Observe o gráfico e descubra quantas pessoas estavam presentes nessa festa junina.
_____
PROFESSOR
Resposta: 60 pessoas.
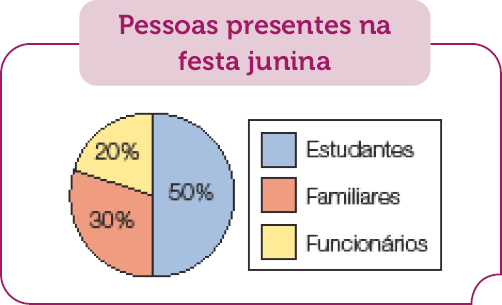
Fonte: Organizadora da festa junina (6 jun. 2023).
CRÉDITO: ADILSON SECCO
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 4
Antes de os estudantes calcularem as porcentagens solicitadas, peça que calculem 3% de 8 000, pensando em quantos grupos de 100 há em 8 000. Eles devem compreender que a divisão 8.000 ÷ 100 mostra que há 80 grupos de 100.
Se Ana recebeu 3 reais a cada 100 reais vendidos, ela recebeu ao todo 80 vezes 3 reais, ou seja, 240 reais de comissão.
Os números envolvidos nos cálculos de porcentagem dos itens a, b e c são formados por centenas inteiras, para que o foco do estudo não sejam os cálculos em si, mas o raciocínio empregado para a obtenção dos resultados.
Alerte os estudantes que há calculadoras que pedem a tecla “5” no final da primeira sequência.
Desafio
Na observação do gráfico de setores fica claro que metade das pessoas presentes na festa junina eram estudantes (pois 50% eram estudantes).
Se estavam presentes 30 estudantes, então pode-se concluir que o total de pessoas presentes era igual ao dobro de 30, ou seja, 60 pessoas.
BNCC em foco:
EF05MA06, EF05MA24
MP274
A Matemática me ajuda a ser
…uma criança que não pratica bullying
Bullying é um termo em inglês que significa intimidar. Ocorre quando alguém ou um grupo maltrata repetidamente uma pessoa para que ela se sinta humilhada, desrespeitada e com medo.
O Instituto Brasileiro de Geografia e Estatística (IBGE) fez em 2015 uma pesquisa no Brasil sobre bullying com estudantes do 9º ano.
Porcentagem aproximada de estudantes, segundo a frequência com que se sentiram humilhados, no Brasil (em 2015)
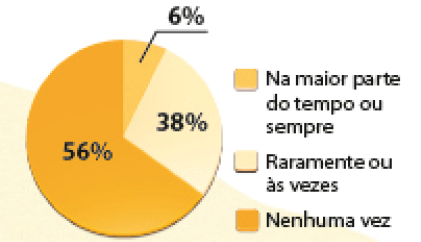
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/9oF. Acesso em: 13 mar. 2021.

Aproximadamente 20 em cada 100 estudantes entrevistados, ou seja, aproximadamente 20% deles, contaram ter esculachado, zoado, caçoado, mangado ou intimidado um colega a ponto de o magoar.
Veja como o problema do bullying em escolas atinge porcentagens próximas em todas as regiões do Brasil.
Porcentagem aproximada de estudantes que se sentiram humilhados por colegas por causa da cor ou da etnia, por região (em 2015)
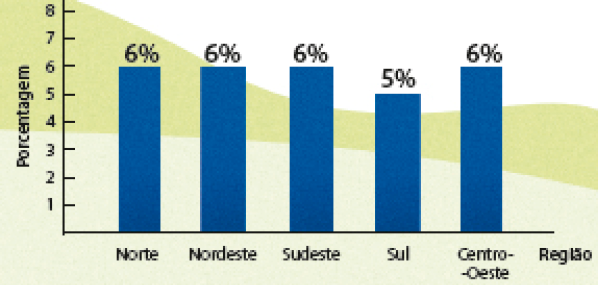
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/9oF. Acesso em: 17 maio 2021.


MANUAL DO PROFESSOR
Objetivos
- Associar as representações 10%, 25%, 50%, 75% e 100%, respectivamente, a décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens.
- Interpretar dados apresentados em texto e gráficos de colunas e de setores.
A proposta desta dupla de páginas é levar os estudantes a refletirem sobre o que é e como agir em caso de bullying . A representação escolhida para despertar a atenção para essas questões foi o infográfico, pois a combinação entre desenho e texto permite que a informação seja explicada de maneira mais dinâmica.
Comente com os estudantes que nem sempre uma briga com um amigo, uma discussão ou até mesmo um insulto entre colegas que não estão de acordo com alguma coisa são considerados bullying .
Explique que o bullying é caracterizado pela intenção de magoar e ameaçar o colega agredido, e que essa situação ocorre frequentemente sem motivo.
Comente sobre o cyberbullying, que é a prática do bullying quando se usa como meio de propagação as tecnologias de comunicação e pode ser feito em qualquer hora, de qualquer lugar e compartilhado por muitas pessoas ao mesmo tempo, de maneira anônima.
Incentive os estudantes a se manifestarem quando forem vítimas ou testemunhas de qualquer tipo de bullying e deixe claro a todos que o bullying tem consequências.
Tome nota Atividade 1
De acordo com o gráfico de setores apresentado no texto, 38% dos estudantes entrevistados se sentiram humilhados raramente ou às vezes.
Então, em cada 100 estudantes entrevistados, 38 estudantes se sentiram humilhados raramente ou às vezes.
BNCC em foco:
EF05MA06, EF05MA24
Atividade 2
A resposta vai depender da região do Brasil em que o estudante mora. Para responder a esta questão, os estudantes devem identificar no gráfico de colunas a porcentagem relativa à região onde moram.
Aproveite para discutir com a turma que a porcentagem de estudantes que se sentiram humilhados por colegas por causa da cor ou da raça em 2015 foi, aproximadamente, a mesma em todas as regiões do Brasil (5% ou 6%).
MP275
Nessa pesquisa realizada pelo IBGE, as causas das humilhações eram referentes a cor ou etnia, religião, aparência do rosto, aparência do corpo, orientação sexual, região de origem, entre outros motivos.

Porcentagem aproximada de estudantes que se sentiram humilhados por provocações devido à aparência do corpo, no Brasil (em 2015).
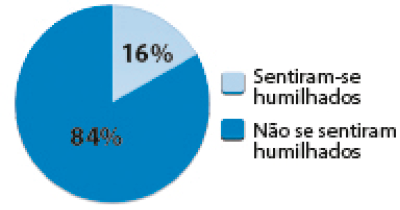
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/eUx. Acesso em 17 maio 2021.
Na pesquisa de 2015, também se perguntou se os estudantes estavam sendo legais uns com os outros.
Porcentagem aproximada de estudantes segundo a frequência com que os colegas os trataram bem e/ou foram prestativos, no Brasil (em 2015)
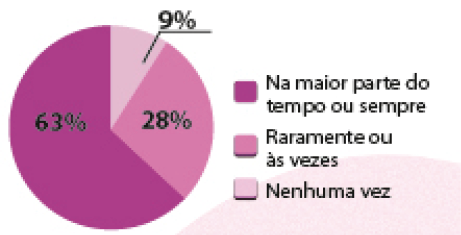
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/eUx. Acesso em 17 maio 2021.

FONTE: Informações obtidas em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/9oF. Acesso em: 26 fev. 2021.
Tome nota
- Em cada 100 estudantes entrevistados em 2015, aproximadamente quantos se sentiram humilhados raramente ou às vezes?
_____
PROFESSOR
Resposta: 38 estudantes.
- Na região do Brasil em que você mora, qual foi a porcentagem aproximada de estudantes que se sentiram humilhados por causa da cor ou da
etnia
em 2015?
_____
PROFESSOR
Resposta pessoal.
- Qual é a porcentagem aproximada de estudantes que se sentiram humilhados por provocações por causa da aparência do corpo segundo a pesquisa de 2015?
_____
PROFESSOR
Resposta: 16%
- Segundo a pesquisa de 2015, aproximadamente quantos estudantes em cada 100 entrevistados declararam que os colegas os trataram bem
e/ou
foram prestativos na maior parte do tempo ou sempre?
_____
PROFESSOR
Resposta: 63 estudantes.
Reflita


Converse com os colegas e o professor sobre as medidas que podem ser tomadas para combater o bullying na escola.
PROFESSOR
Resposta pessoal.MANUAL DO PROFESSOR
Atividade 3
Pergunte: “A quantidade de estudantes que se sentiram humilhados por provocações por causa da aparência do corpo corresponde a mais ou a menos da metade dos estudantes entrevistados? Justifique a resposta.”. Espera-se que respondam que corresponde a menos da metade, pois 16% < 50%.
Atividade 4
Uma estratégia de resolução pode ser considerar que 63% correspondem a 63 vezes 1%. Assim, sabendo que 1% de 100 corresponde a 1, a atividade pode ser resolvida multiplicando 63 por 1, ou seja, 63 estudantes.
Alerte os estudantes de que há calculadoras que pedem a tecla “=” no final da primeira sequência.
Reflita
Pergunte aos estudantes se eles sofreram ou conhecem alguém que já sofreu algum tipo de bullying e o que eles fariam se fossem vítimas ou vissem alguém sofrendo algum tipo de bullying .
Os estudantes podem responder que falariam com os pais, com um professor, com outros colegas, que não falariam para ninguém ou ainda que revidariam. Seja como for, é preciso deixar claro que sempre se deve falar com um adulto de confiança e não responder ao bullying da mesma maneira, pois violência gera violência.
Sugira aos estudantes a criação de cartazes com desenhos e colagens expressando atitudes e medidas que podem ser tomadas para combater o bullying na escola. Depois, se possível, proponha que os apresentem para a escola em uma exposição ou nos corredores, para que todos os estudantes tenham acesso.
BNCC em foco:
EF05MA06, EF05MA24; competência específica 7
MP276
Compreender informações
Organizar dados coletados em gráficos de linha
- A rodoviária da cidade de Amarópolis registra todas as viagens que seus ônibus fazem. Observe na tabela a seguir quantas viagens foram feitas por mês no 1º semestre de 2023.
Quantidade de viagens feitas por mês
Tabela: equivalente textual a seguir.
|
Mês |
Quantidade de viagens |
|---|---|
|
Janeiro |
30 |
|
Fevereiro |
25 |
|
Março |
15 |
|
Abril |
20 |
|
Maio |
10 |
|
Junho |
5 |
Fonte: Rodoviária de Amarópolis (9 jul. 2023).

Esses dados podem ser apresentados em um gráfico de linha, no qual representamos por pontos a quantidade de viagens feitas em cada mês. Depois, para visualizar melhor a variação a cada mês, os pontos correspondentes a meses seguidos são ligados por uma linha reta.
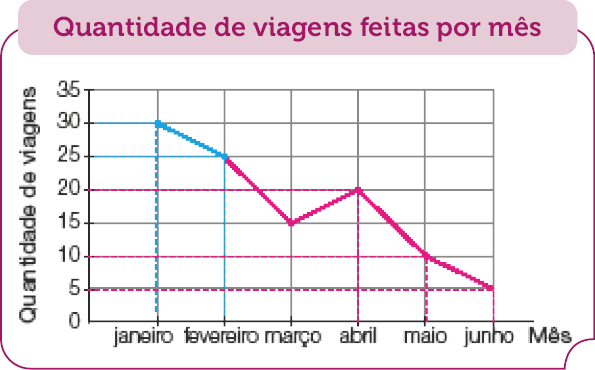
Fonte: Rodoviária de Amarópolis (9 jul. 2023).
- Complete o gráfico de linha acima com as viagens que faltam de acordo com a tabela.
- Em qual mês foram feitas mais viagens? E menos viagens?
_____
PROFESSOR
Resposta: Mais viagens: janeiro; menos viagens: junho.
- Nesse período, a quantidade de viagens só diminuiu? Justifique.
_____
PROFESSOR
Resposta: Não, de março para abril aumentou.
- Você considera mais fácil visualizar a variação entre os dados observando a tabela ou o gráfico de linha? Justifique.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivos
- Interpretar dados estatísticos apresentados em tabelas e gráficos de linhas.
- Organizar dados coletados por meio de gráficos de linhas.
Atividade 1
Oriente os estudantes na transposição dos dados da tabela para o gráfico de linhas. Inicialmente, acompanhe a marcação dos pontos, para que, em seguida, tracem uma linha para uni-los.
No item b, um exemplo de resposta é: janeiro, em que foram feitas 30 viagens, e fevereiro, quando foram feitas 25 viagens.
No item d, é provável que os estudantes digam que é mais fácil visualizar a variação dos dados pelo gráfico do que pela tabela.
BNCC em foco:
EF05MA24, EF05MA25; competência específica 3
MP277
- Daniela registrou em sua agenda o
número
de horas de estudo em cada dia da semana passada.
- Complete o gráfico de linha a seguir de acordo com essas anotações.

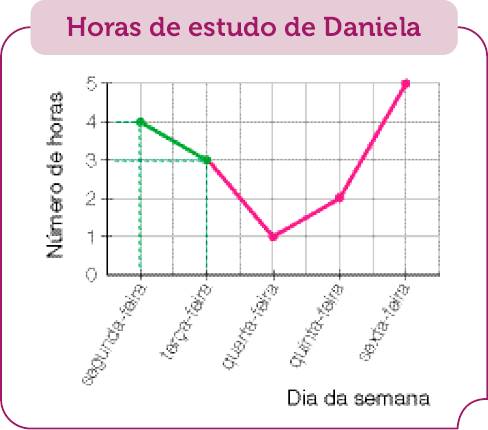
Fonte: Anotações de Daniela (11 ago. 2023).
- De segunda-feira para terça-feira, aumentou ou diminuiu a quantidade de horas de estudo? Quantas horas?
_____
PROFESSOR
Resposta: Diminuiu; 1 hora de estudo.
- Ao longo dessa semana, qual foi o dia em que Daniela estudou menos tempo?
_____
PROFESSOR
Resposta: Quarta-feira.
- O gráfico abaixo mostra o valor obtido pelas exportações de brinquedos de uma indústria no período de 5 anos.
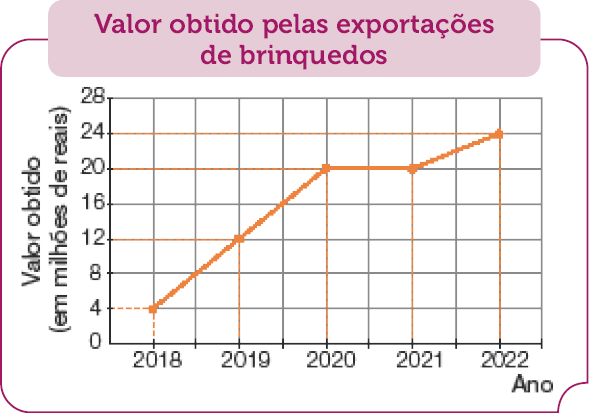
Fonte: Indústria de brinquedos (jan. 2023).
- De 2018 a 2022, o valor
obtido
sempre aumentou? Justifique.
_____
PROFESSOR
Resposta: Não, pois de 2020 para 2021 o valor obtido permaneceu o mesmo, não aumentou nem diminuiu.
- Crie duas perguntas com base nos dados do gráfico e troque com um
colega
para respondê-las.
PROFESSOR
Respostas variáveis.
MANUAL DO PROFESSOR
Atividade 2
Amplie o item b, perguntando: “E de quarta-feira para sexta-feira: houve aumento ou diminuição nas horas de estudo de Daniela?” (Houve aumento de 4 horas de estudo.).
Peça aos estudantes que construam um gráfico de linhas colocando em cada linha as horas da última semana que dedicaram aos estudos.
Atividade 3
No item a, espera-se que os estudantes reconheçam que o valor obtido nas exportações aumentou até 2020 e permaneceu constante (não aumentou nem diminuiu) de 2020 para 2021, voltando a aumentar novamente de 2021 para 2022.
No item b, exemplos de questões que podem ser feitas:
- De quanto foi o aumento do valor obtido no período de 2018 para 2019? (O aumento foi de 8 milhões de reais.)
- Houve algum outro período entre anos seguidos em que houve esse mesmo aumento? (Sim, de 2019 para 2020 o aumento também foi de 8 milhões de reais.)
- No período considerado no gráfico (de 2018 a 2022), de quanto foi o aumento do valor obtido? (O aumento foi de 20 milhões de reais.)
- Houve algum período em que o valor
obtido
diminuiu? (Não.)
BNCC em foco:
EF05MA24, EF05MA25; competência específica 3
MP278
O que você aprendeu
Avaliação processual
- Bruna competiu em um campeonato juvenil de ginástica artística feminina. A pontuação obtida por ela em cada prova é mostrada no quadro a seguir.
Quadro: equivalente textual a seguir.
|
Prova |
Pontuação |
|---|---|
|
Salto sobre o cavalo |
12,435 |
|
Barras paralelas |
10,455 |
|
Trave |
12,250 |
|
Solo |
11,850 |
- Em qual
prova
Bruna obteve a maior pontuação? E a menor?
_____
PROFESSOR
Resposta: Maior pontuação: salto sobre o cavalo; menor pontuação: barras paralelas.
- Qual é a diferença entre a maior e a
menor
pontuação
obtida
por ela?
_____
PROFESSOR
Resposta: 1,980
- Quantos pontos Bruna obteve no total?
_____
PROFESSOR
Resposta: 46,990 pontos.
- O esquema representa os municípios de Trovoadas e de Calmaria. Nesse esquema, cada centímetro corresponde a 5,4 quilômetros.
- Com uma régua, obtenha a medida da distância, em centímetros, que separa em linha reta esses dois municípios no esquema.
_____
PROFESSOR
Resposta: 5 centímetros.
- Qual é a medida da distância entre esses dois municípios em quilômetros?
_____
PROFESSOR
Resposta: 27 quilômetros.
- Escreva os números que completam os espaços indicados na reta numérica.

PROFESSOR
Resposta: 3,05; 3,22; 3,33; 3,48; 3,62; 3,77; 3,85

- Um
modelo
de pirâmide de base quadrada tem todas as arestas com comprimento de mesma medida. Se o perímetro de sua base
mede
38 centímetros, qual é a medida em centímetro do comprimento de cada aresta desse
modelo
de pirâmide?
_____
PROFESSOR
Resposta: 9,5 cm
MANUAL DO PROFESSOR
Objetivo
- Retomar os conceitos estudados.
A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Incentive os estudantes a estimarem os resultados, por exemplo, colocando-os em um intervalo. Eles podem fazer as estimativas do quadro a baixo.
Quadro: equivalente textual a seguir.
Prova
Pontuação
Limite inferior
Limite superior
Salto sobre o cavalo
12,435
12
13
Barras paralelas
10,455
10
11
Trave
12,250
12
13
Solo
11,850
11
12
Total
45
49
Portanto, o total de pontos obtidos por Bruna está entre 45 e 49 pontos.
Atividade 2
Comente que é comum o uso de medida em centímetro para representar quilômetro em um mapa. Se possível, leve à sala de aula algum mapa, dando ênfase à escala.
Atividade 3
Sugira a eles que desenhem retas numéricas e troquem com um colega: cada um encontra os números sugeridos pelo outro nas retas numéricas.
Esse tipo de atividade estimula a reflexão sobre os conteúdos necessários para representar uma reta numérica e localizar números nela.
Atividade 4
Espera-se que os estudantes observem que devem dividir o perímetro (38 cm) pelo número de arestas da base (4), já que a pirâmide tem uma base quadrada.
BNCC em foco:
EF05MA02, EF05MA05, EF05MA08, EF05MA19
MP279

- Eduardo fez a divisão mostrada abaixo. Ele usou o algoritmo usual, mas cometeu um erro.

- Qual foi o
erro
de Eduardo?
PROFESSOR
Resposta: O posicionamento da vírgula.
- Qual é o resultado correto dessa divisão?
_____
PROFESSOR
Resposta: 1,15
- Como você pode conferir se esse resultado está correto sem usar uma calculadora?
_____
PROFESSOR
Exemplo de resposta: Multiplicando 1,15 por 5, obtém-se o resultado 5,75, que corresponde ao dividendo.
- Ivan esqueceu-se de pagar uma conta no valor de R$ 230,00 até a data de vencimento. Por isso, ele teve de pagar 2% de multa sobre esse valor.
- Quanto Ivan teve de pagar de multa?
_____
PROFESSOR
Resposta: R$ 4,60
- Qual passou a ser o valor da conta?
_____
PROFESSOR
Resposta: R$ 234,60
- Quanto Ivan teve de pagar de multa?
_____
- Ricardo foi a uma loja para comprar uma televisão que custa R$ 900,00, mas ele está indeciso sobre qual das duas formas de pagamento deve escolher.

- Se Ricardo pagar à vista, quanto custará a televisão?
_____
PROFESSOR
Resposta: R$ 810,00
- Se escolher a outra forma de pagamento, quanto ele pagará, no total, pela televisão?
_____
PROFESSOR
Resposta: R$ 915,00
- De quantos reais é a diferença entre os preços das duas formas de pagamento?
_____
PROFESSOR
Resposta: R$ 105,00
Autoavaliação

- Consigo representar um
número
com uma fração e na forma decimal?

- Consigo operar com números na forma decimal?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 5
Espera-se que os estudantes observem que, como 5 ÷ 5 = 1 e 10 ÷ 5 = 2, o resultado da divisão 5,75 ÷ 5 deve estar entre 1 e 2, logo o cálculo de Eduardo está errado (o quociente não pode ser 11,5). O erro cometido foi realizar 7 dividido por 5 como se fossem 7 unidades divididas por 5, e não 7 décimos divididos por 5, que é o correto.
Analisar erros cometidos na aplicação de algoritmos possibilita aos estudantes a reflexão sobre as etapas do algoritmo e a ampliação de seu repertório de cálculos.
Exemplo de resposta para o item a: ao dividir 7 décimos por 5, o resultado é 1 décimo (não 1 unidade, como Eduardo indicou), que deveria estar separado da parte inteira (1) por uma vírgula.
Atividade 6
Comente que é aconselhável pagar as contas até a data do vencimento, para evitar multas.
No item b, os estudantes devem calcular o valor total da conta, incluindo a multa. Ou seja, 230 mais 2% de 230 é igual a R$ 234,60.
Atividade 7
As situações de comparação entre formas de pagamento de um produto são muito comuns no dia a dia e envolvem decisões com base no que é possível pagar no momento da compra.
No caso do pagamento à vista (item a), o valor de 900 reais terá um desconto de 90 reais (pois 10% de 900 é igual a 90), ou seja, o valor pago será de R$ 810,00.
No pagamento a prazo (item b), 10% do valor deverão ser pagos como entrada, ou seja, R$ 90,00. O restante será pago em 3 parcelas iguais de R$ 275,00, que é igual a R$ 825,00, totalizando R$ 915,00.
BNCC em foco:
EF05MA06, EF05MA07, EF05MA08
Autoavaliação
Na primeira questão, os estudantes poderão avaliar se conseguem estabelecer relações entre as representações fracionárias e decimais, verificando se conseguem escrever um número que está representado como fração e na forma decimal e vice-versa.
Na segunda questão, poderão avaliar se são capazes de operar com números na forma decimal e, consequentemente, se estão respeitando os valores posicionais para a realização dos cálculos.
MP280
Comentários para o professor:
Conclusão da Unidade 7
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Sabe ler, escrever, comparar e ordenar números racionais na forma decimal? |
_____ |
_____ |
|
Localiza números na forma decimal na reta numérica? |
_____ |
_____ |
|
Efetua cálculos com porcentagem e os relaciona à representação fracionária? |
_____ |
_____ |
|
Resolve problemas de adição e subtração com números racionais? |
_____ |
_____ |
|
Resolve problemas de multiplicação e divisão com números racionais? |
_____ |
_____ |
|
Resolve problemas envolvendo transformações entre as unidades de medida mais usuais de comprimento e de massa? |
_____ |
_____ |
|
Interpreta e organiza dados apresentados em tabelas e gráficos? |
_____ |
_____ |
|
Produz textos sobre os resultados de uma pesquisa? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |