Revisão dos conteúdos de anos anteriores
Faça as atividades no caderno.
Para o capítulo 1: Números naturais e sistemas de numeração
Sistema de numeração indo-arábico
O sistema de numeração indo-arábico faz agrupamentos de 10 em 10. Além disso, são utilizados dez símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, denominados algarismos.
É um sistema posicional, ou seja, os algarismos assumem valores diferentes conforme a posição que ocupam no número.
Observe alguns modos de representar o número .1524.
|
Unidades de milhar |
Centenas |
Dezenas |
Unidades |
|---|---|---|---|
|
1 |
5 |
2 |
4 |
Quadro de ordens
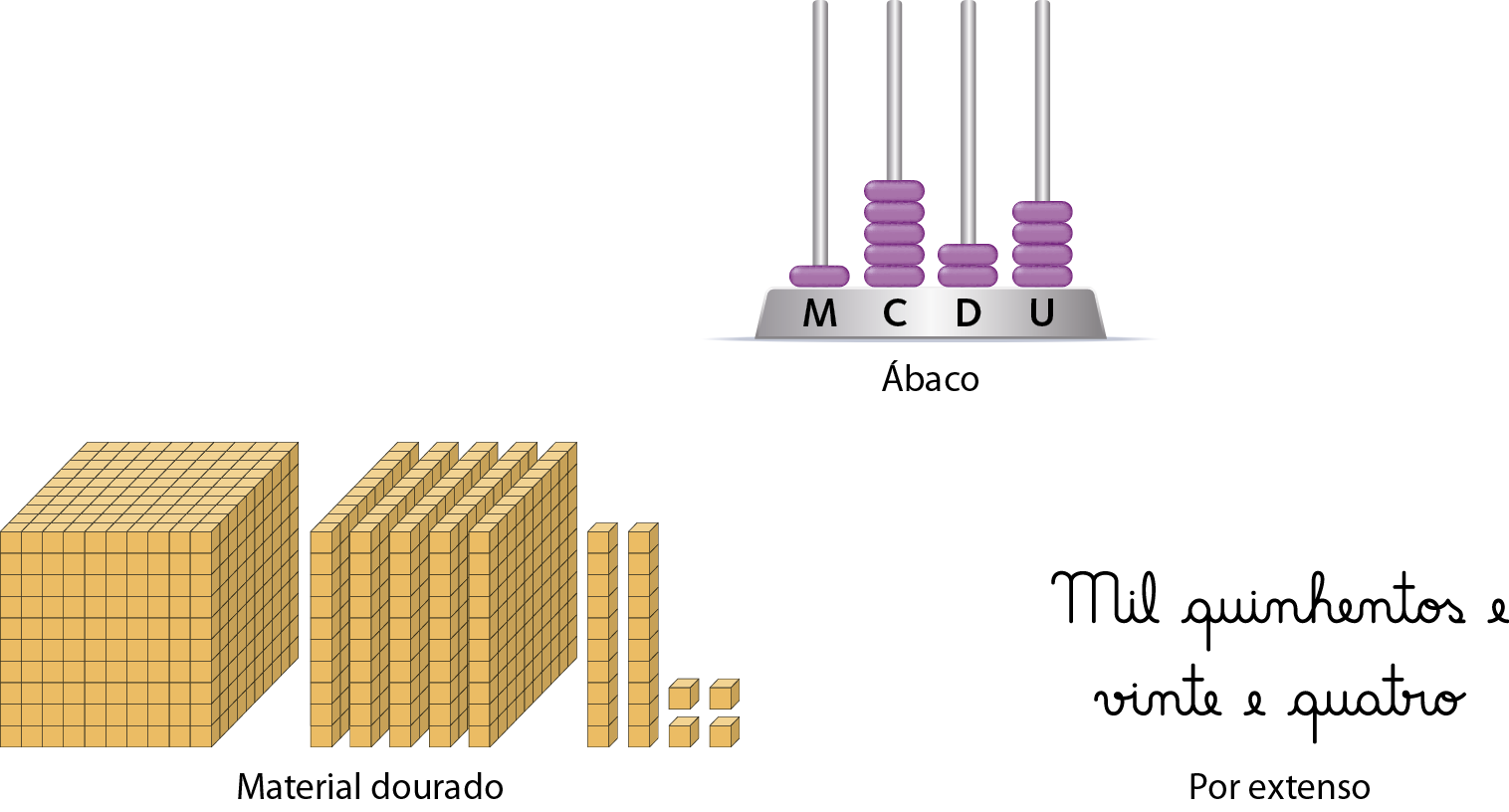
Ordens e classes
Para facilitar a leitura de um número, nós o separamos em classes, agrupando os algarismos de três em três, da direita para a esquerda. Cada classe é formada por três ordens.
|
Classe dos bilhões |
Classe dos milhões |
Classe dos milhares |
Classe das unidades simples |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
12ª ordem |
11ª ordem |
10ª ordem |
9ª ordem |
8ª ordem |
7ª ordem |
6ª ordem |
5ª ordem |
4ª ordem |
3ª ordem |
2ª ordem |
1ª ordem |
|
Centena de bilhão |
Dezena de bilhão |
Unidade de bilhão |
Centena de milhão |
Dezena de milhão |
Unidade de milhão |
Centena de milhar |
Dezena de milhar |
Unidade de milhar |
Centena simples |
Dezena simples |
Unidade simples |
1. Escreva o número formado por:
a) cinco dezenas de milhar mais oito dezenas;
b) duas dezenas de milhar mais sete centenas mais nove unidades;
c) uma unidade de milhão mais seis dezenas mais três unidades;
d) três centenas de milhão mais oito dezenas de milhar mais três centenas;
2. Dado o número .15896.7042, responda.
a) Qual é o algarismo de maior valor posicional?
b) Qual é o algarismo da 8ª ordem?
c) Qual é o nome dado à 5ª ordem?
3. Observe o número a seguir.

a) Escreva no caderno como se lê esse número.
b) Quais algarismos formam a classe dos milhões desse número?
4. Qual o valor posicional do algarismo destacado em azul em cada número?
a) 9.10017
b) .851256
c) ..6892310
d) 73..0489012
e) 1...38320420973
Versão adaptada acessível
4. Qual o valor posicional do algarismo destacado em cada número?
a) 9 1 0 0 1 7 algarismo destacado 9
b) 8 5 1 2 5 6 algarismo destacado 2
c) 6 8 9 2 3 1 0 algarismo destacado 6
d) 7 3 0 4 8 9 0 1 2 algarismo destacado 3
e) 1 3 8 3 2 0 4 2 0 9 7 3 algarismo destacado 1
Os números naturais
Iniciando pelo 0 e adicionando sempre 1 ao número anterior, obtemos a sequência dos números naturais.
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, reticências)
Antecessor de um número natural
Na sequência dos números naturais, o antecessor de um número diferente de zero é o número que vem imediatamente antes dele.
O antecessor de 11 é 10, pois: 11 ‒ 1 = 10
Sucessor de um número natural
O sucessor de um número natural é o número que vem imediatamente depois dele.
O sucessor de 10 é 11, pois: 10 + 1 = 11
5. Determine o que se pede em cada caso.
a) O sucessor de 71.
b) O antecessor de 251.
c) O antecessor do sucessor de .100000.
6. Reproduza o quadro em seu caderno e complete-o.

|
Antecessor |
Número natural |
Sucessor |
|---|---|---|
|
385 |
||
|
999 |
||
|
2.898 |
||
|
1.000.000 |
7. Faça o que se pede.
a) Começando pelo 100, escreva os 10 primeiros termos da sequência dos números naturais pares.
b) Começando pelo 301, escreva a sequência dos 10 primeiros números naturais ímpares.
Reta numérica
Os números naturais podem ser representados em uma reta, na qual cada ponto está associado a um número. Em uma reta numérica, a distância entre dois pontos correspondentes a dois números naturais consecutivos é sempre a mesma.
Com o auxílio da reta numérica, podemos comparar números naturais. O número da direita é sempre maior que o da esquerda e, portanto, o número da esquerda é menor que o da direita.

Observe alguns exemplos de comparações.
a) 0 < 1
b) 1 < 2
c) 6 > 2
d) 2 < 4
8. Escreva o número natural correspondente aos pontos a, B e C na reta numérica a seguir.

9. Desenhe no caderno uma reta numérica e represente pontos correspondentes aos números 12, 8, 10, 6 e 14. Depois, escreva-os em ordem crescente.
Para o capítulo 2: Operacões com números naturais
Adição com números naturais
Algoritmo da decomposição
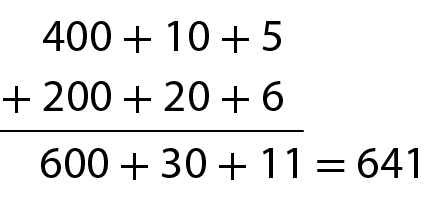
Algoritmo usual
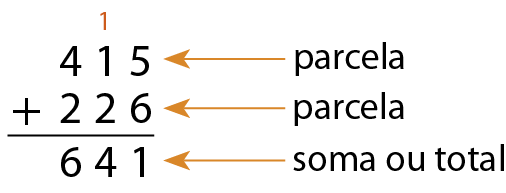
10. Calcule o resultado de cada uma das operações no caderno.
a) .2581 + .4383
b) .1150 + 563 + .3429
c) .12525 + 938 + .2627
11. Maria comprou um aparelho de televisão em duas prestações. A primeira de R$ 750,00setecentos e cinquenta reais e a segunda de R$ 635,00seiscentos e trinta e cinco reais. Quantos reais Maria pagou pelo aparelho de televisão?
12. Em um jôgo de videogame, Luísa fez 283 pontos na primeira fase e 487 na segunda fase do jôgo. Quantos pontos ela fez até agora?
Algumas propriedades da adição
Propriedade comutativa: a ordem das parcelas não altera a soma.
15 + 21 = 21 + 15
Propriedade associativa: em uma adição de três ou mais números naturais, podemos associar as parcelas de diferentes modos sem alterar a soma.
(12 + 28) + 10 = 40 + 10 = 50
12 + (28 + 10) = 12 + 38 = 50
Elemento neutro: ao adicionar zero a um número, a soma é igual ao próprio número.
35 + 0 = 35
41 + 0 = 41
13. Copie as sentenças em seu caderno e complete-as.
a) 263 +

= 527 + 263
b) .2318 + 0 = 0 +

c) .9287 + .1622 =

+ .9287
d) .10258 + .8102 =

+ .10258
14.

Calcule mentalmente o resultado de cada adição.
a) 250 + 120 + 50 + 80
b) 300 + 64 + 36 + 120
c) 450 + 0 + 275 + 25
d) 180 + 75 + 120 + 25
Subtração com números naturais
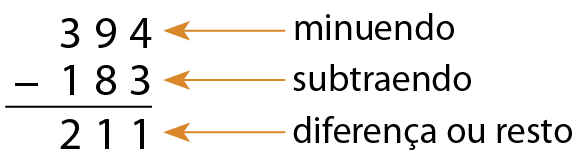
15. Calcule o resultado de cada uma das operações no caderno.
a) .8265 ‒ .3421
b) .9151 ‒ .7237
c) .11950 ‒ .2358
d) .25902 ‒ .13453
16. Em uma subtração, o minuendo é 528 e o resto é 129. Qual é o valor do subtraendo?
17. Em uma subtração, o resto é 385 e o subtraendo é 291. Qual é o valor do minuendo?
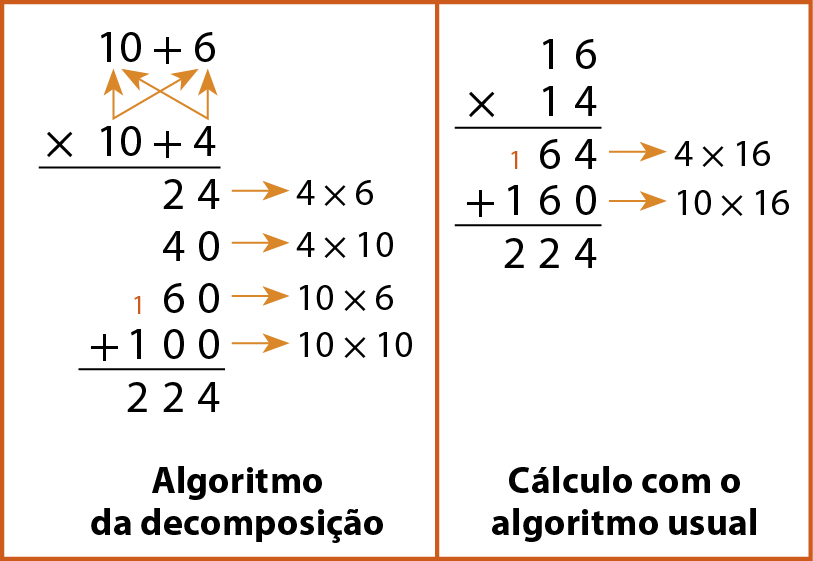
Multiplicação com números naturais
Em uma multiplicação, os números que se multiplicam são chamados de fatores e o resultado de produto.
Analise como calcular 14 × 16 de dois modos diferentes.
18. Calcule o resultado de cada uma das operações.
a) 42 × 12
b) 213 × 15
c) 310 × 18
d) 521 × 32
19. Vanessa comprou um aparelho de televisão em 12 prestações de R$ 252,00duzentos e cinquenta e dois reais. Qual foi o total gasto nessa compra?
20. O produto de dois números é 336. Um dos fatores é 12. Qual é o outro fator?
Algumas propriedades da multiplicação
Propriedade comutativa: a ordem dos fatores não altera o produto.
12 × 28 = 28 × 12
Propriedade associativa: em uma multiplicação com mais de dois números naturais, podemos associar os fatores de modos diferentes sem alterar o produto.
(10 × 18) × 5 = 10 × (18 × 5)
Propriedade distributiva da multiplicação em relação à adição: em uma multiplicação de um número natural por uma adição de duas ou mais parcelas, adicionamos os produtos de cada parcela pelo número natural.
5 × (12 + 6) = 5 × 12 + 5 × 6 = 60 + 30 = 90
A propriedade distributiva também é válida para a subtração:
4 × (15 ‒ 7) = 4 × 15 ‒ 4 × 7 = 60 ‒ 28 = 32
21. Copie as sentenças em seu caderno e complete-as.
a) 112 × 15 =

× 112
b) 219 × 156 =

× 219
c) 11 × (15 × 9) = (11 ×

) × 9
d) 25 × (18 × 7) = (25 ×

) × 7
e) 315 ×

= 102 × 315
f) .1010 ×

= 55 × .1010
22. No caderno, calcule o valor das expressões de duas maneiras.
a) 6 × (12 + 7)
b) 9 × (21 ‒ 13)
c) 10 × (15 + 8)
Divisão com números naturais

Quando o resto da divisão é zero, dizemos que a divisão é exata; quando é diferente de zero, a divisão é não exata.
23. Calcule o quociente e o resto de cada divisão no caderno.
a) 280 ÷ 12
b) 327 ÷ 9
c) 980 ÷ 10
d) .1000 ÷ 100
e) .2824 ÷ 16
f) .1025 ÷ 10
24. Mateus comprou uma motocicleta que custa R$ 12.600,00doze mil seiscentos reais. Ele vai pagar essa compra em 24 prestações iguais. Qual será o valor de cada prestação?
Para o capítulo 3: Figuras geométricas espaciais
Sólidos geométricos
Sólido é uma figura geométrica espacial e não oca, ou seja, maciça.
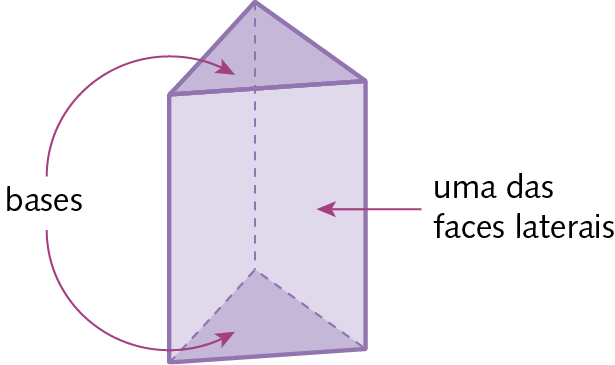
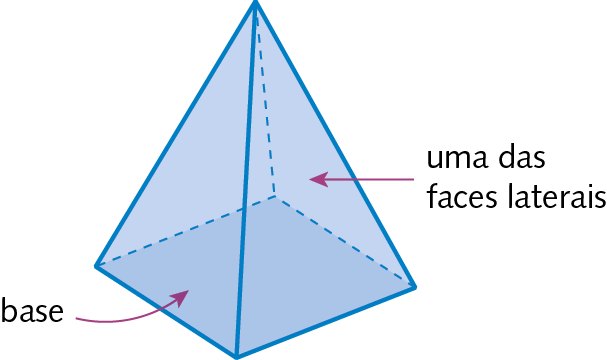
Poliedros
São sólidos geométricos que têm a superfície formada somente por partes não arredondadas, ou seja, “achatadas”.
Os prismas e as pirâmides são exemplos de poliedros.
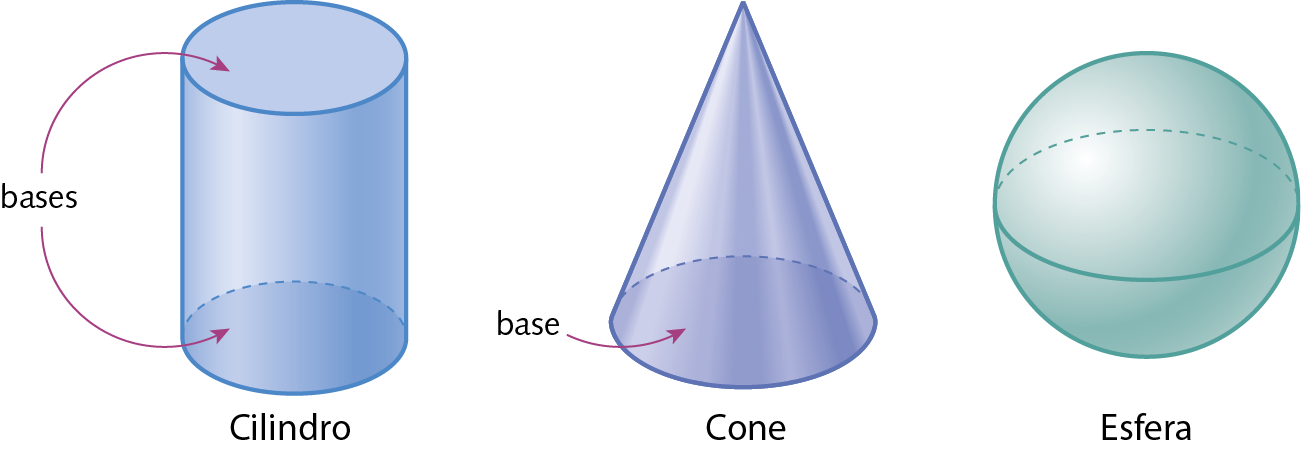
Corpos redondos
São sólidos geométricos que têm pelo menos uma parte com formato arredondado.
Os cilindros, os cones e as esferas são exemplos de corpos redondos.
25. Observe os poliedros e faça o que se pede.
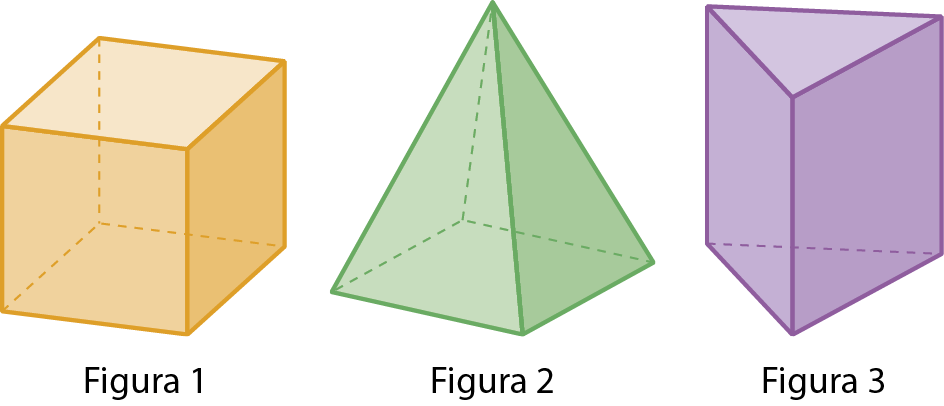
a) Reproduza o quadro no caderno e complete-o.

|
Número de faces |
Número de arestas |
Número de vértices |
|
|---|---|---|---|
|
Figura 1 |
|||
|
Figura 2 |
|||
|
Figura 3 |
b) Qual é o formato da base de cada poliedro?
c) Escreva no caderno o nome dos poliedros.
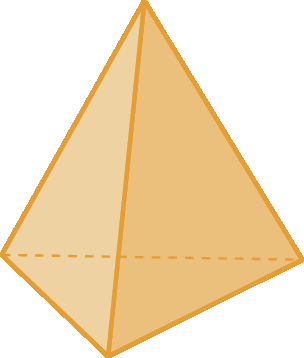
26. Qual o nome dos sólidos geométricos a seguir?
a)
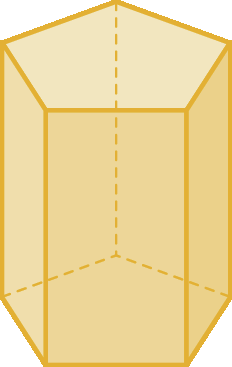
b)

c)
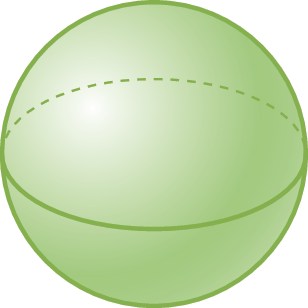
d)
Planificação da superfície de sólidos geométricos
A representação da superfície de um sólido geométrico é chamada de planificação.
Observe a planificação da superfície de alguns sólidos geométricos.
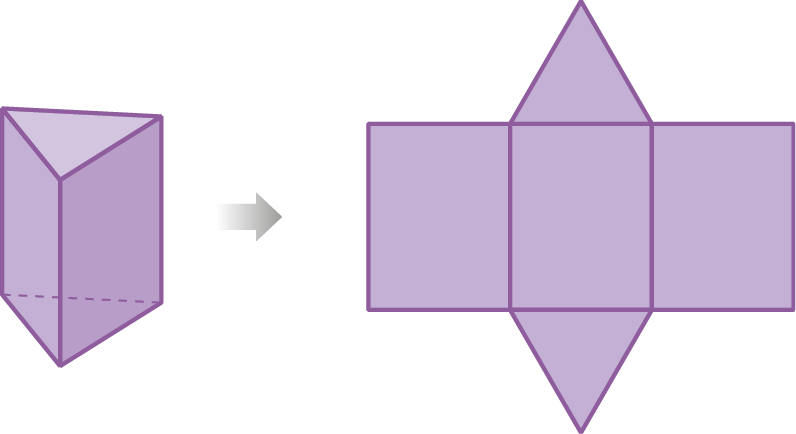
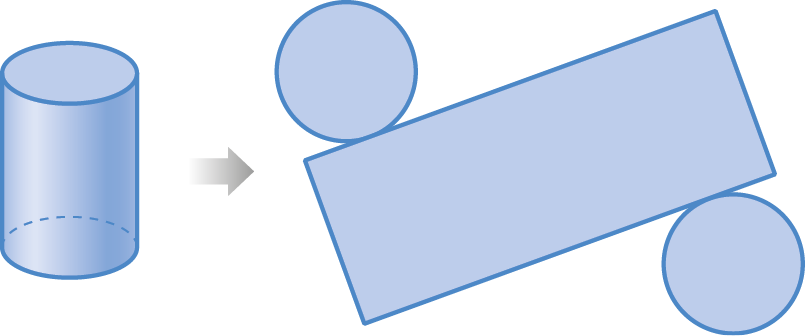
27. Qual o nome da figura cuja planificação da superfície está representada a seguir?

28. A qual sólido geométrico corresponde cada uma das planificações a seguir?
a)

b)
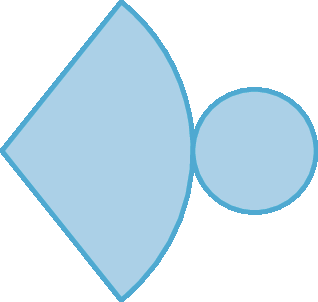
c)
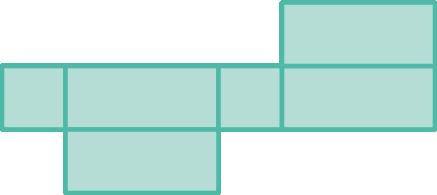
d)
Para o capítulo 4: Igualdades e desigualdades
Igualdades
Toda igualdade continuará sendo válida se:
• adicionarmos ou subtrairmos o mesmo número de seus membros;
• multiplicarmos seus membros por um mesmo número ou dividirmos seus membros por um mesmo número diferente de zero.
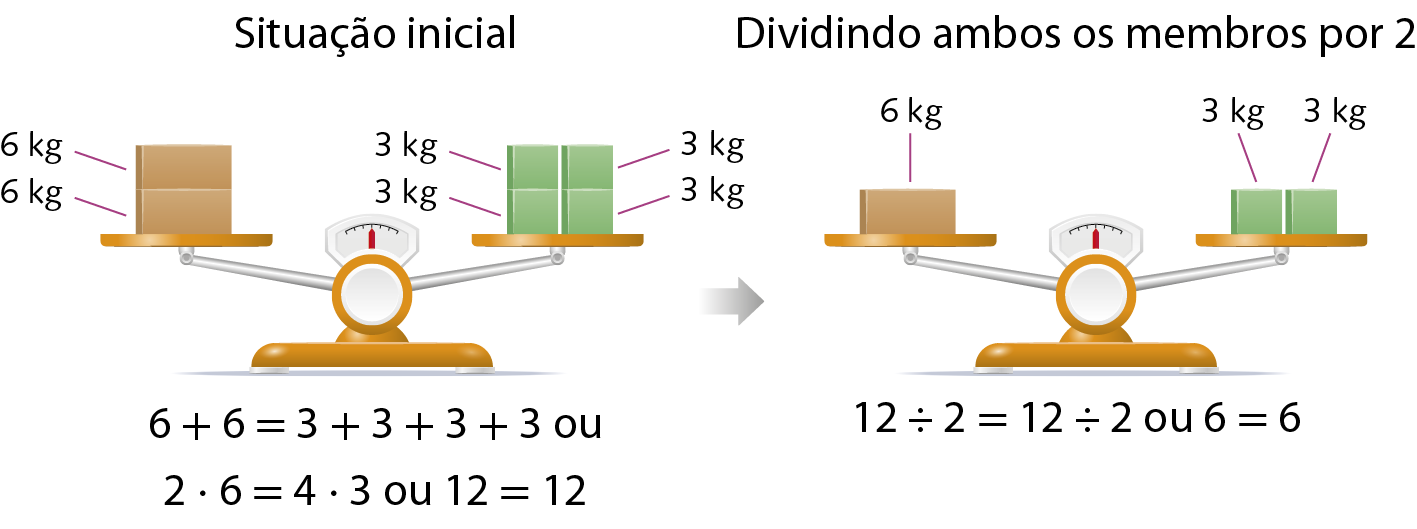
29. Em cada item, faça o que se pede e determine a igualdade correspondente.
a) Adicione 12 aos dois membros da igualdade: 25 + 32 = 12 + 45
b) Subtraia 8 dos dois membros da igualdade: 29 ‒ 7 = 15 + 7
c) Multiplique por 8 os dois membros da igualdade: 15 + 4 = 25 ‒ 6
d) Divida por 5 os dois membros da igualdade: 25 + 15 = 50 ‒ 10
30. Copie no caderno as sentenças e complete-as.
a) (120 + 300)

= 420 ÷ 2
b) 258

= 228 + 30 ‒ 150
c) .1000

= (400 + 600) × 5
d) .1200 ÷ 3 = (800 + 400)

e) 238

= 100 + 138 + 100
f) (.1600 ‒ 200)

= .1400 × 10
Para o capítulo 5: Múltiplos e divisores
Múltiplo de um número natural é o produto desse número por um número natural qualquer.
|
× |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Múltiplo de 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
... |
|
Múltiplo de 2 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
... |
|
Múltiplo de 7 |
0 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
... |
|
Múltiplo de 9 |
0 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
... |
31. Reproduza o quadro no caderno e complete-o.

|
× |
2 |
5 |
7 |
9 |
12 |
15 |
|---|---|---|---|---|---|---|
|
1 |
||||||
|
3 |
||||||
|
5 |
||||||
|
7 |
||||||
|
10 |
||||||
|
12 |
32. Escreva no caderno:
a) 10 números múltiplos de 4.
b) os múltiplos de 9 situados entre 50 e 100.
c) os cinco primeiros múltiplos de 6, a partir do próprio 6.
33. Escreva os múltiplos de 15 situados entre 100 e 200.
34. Reproduza o quadro no caderno e marque um X nos espaços correspondentes a divisões exatas. Lembre-se de que a divisão é exata quando o resto é zero.

|
Divisor |
||||||
|---|---|---|---|---|---|---|
|
Número |
2 |
3 |
5 |
6 |
9 |
10 |
|
258 |
||||||
|
356 |
||||||
|
400 |
||||||
|
525 |
||||||
|
886 |
||||||
|
990 |
||||||
|
1.000 |
||||||
|
1.050 |
||||||
|
2.256 |
||||||
|
8.250 |
||||||
Para o capítulo 6: Frações
Em uma fração, o denominador é o número que indica a quantidade de partes iguais em que o todo foi dividido. O numerador indica a quantidade de partes consideradas do todo.

Leitura de frações
a)
fração 2 sobre 3→ Lemos: “dois terços”.
b)
fração 7 sobre 100→ Lemos: “sete centésimos”.
c)
fração 13 sobre 22→ Lemos: “treze vinte dois avos”.
35. No caderno, escreva como se lê cada fração.
a)
fração 1 sobre 8
b)
fração 4 sobre 15
c)
fração 17 sobre 100
d)
fração 27 sobre 20036. Em seu caderno, escreva a fração correspondente às partes pintadas das figuras em cada caso.
a)

b)
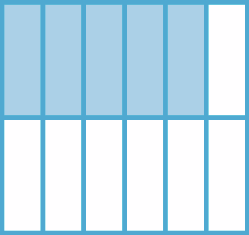
c)

d)

Número misto
A representação de um número misto é composta de uma parte inteira e de uma parte fracionária.
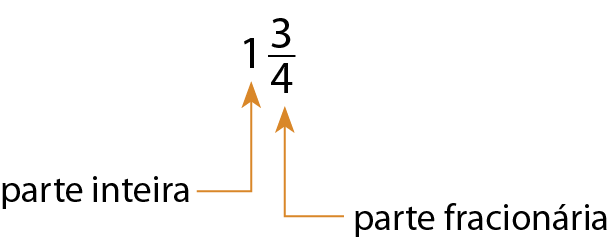
37. No caderno, represente com figuras os números mistos a seguir.
a)
Número misto 2 inteiros e 1 terço.b)
Número misto 1 inteiro e 2 terços.c)
Número misto 2 inteiros e 3 oitavos.d)
Número misto 1 inteiro e 7 nonos.38. No caderno, represente com frações os seguintes números mistos.
a)
Número misto 1 inteiro e 2 quintos.
b)
Número misto 3 inteiros e 4 nonos.
c)
Número misto 5 inteiros e 1 quarto.
d)
Número misto 8 inteiros e 3 quintos.Frações equivalentes
Frações que representam a mesma parte do inteiro são chamadas frações equivalentes.

As frações
2 terços, 4 sextos e 6 nonossão equivalentes.
39. No caderno, escreva uma fração equivalente a cada fração dada.
a)
8 sobre 16b)
25 sobre 100c)
150 sobre 450d)
75 sobre 9540. Copie as sentenças em seu caderno e complete com o número que falta para que as frações sejam equivalentes.
a)
3 sobre 8 é igual a 27 sobre quadradinho cinzab)
5 sobre 7 é igual a quadradinho cinza sobre 21c)
4 sobre 25 é igual a 20 sobre quadradinho cinzad)
quadradinho cinza sobre 7 é igual a 30 sobre 70Comparação de frações de um mesmo inteiro
Quando duas ou mais frações têm o mesmo denominador, a maior delas é a que tem maior numerador.
Quando duas ou mais frações têm o mesmo numerador, a maior delas é a que tem menor denominador.
Quando duas ou mais frações têm numeradores e denominadores diferentes, devemos obter frações equivalentes às frações iniciais que tenham o mesmo denominador ou numerador para, em seguida, compará-las.
41. Escreva as frações em ordem crescente.
a)
1 terço, 1 quarto e 1 meio.
b)
2 quintos, 3 quartos e 2 nonos.
c)
um quarto, 3 oitavos e 15 meios
d)
5 oitavos, dez 12 avos, 3 nonos42. Escreva as frações em ordem decrescente.
a)
2 quintos, 9 quintos e 1 quinto
b)
doze 18 avos, cinco 18 avos e vinte e cinco 18 avos
c)
10 sobre 35, 1 sobre 35 e 18 sobre 35
d)
51 sobre 58, 12 sobre 58 e 23 sobre 5843. Determine a maior fração de cada item.
a)
1 nono, 7 nonos e 6 nonos
b)
2 quartos, 3 oitavos e 3 quartos
c)
1 quarto, 1 nono e 1 terço
d)
4 quintos, dez 12 avos e 7 sextosAdição e subtração com frações
Mesmo denominador
Para calcular a soma ou a diferença de duas frações com denominadores iguais, adicionamos ou subtraímos os numeradores, conforme a operação desejada, e conservamos os denominadores.
a)
1 quarto mais 2 quartos é igual a 3 quartos
b)
7 nonos menos 3 nonos é igual a 4 nonosDenominadores diferentes
Para calcular a soma ou a diferença de duas frações com denominadores diferentes, encontramos frações equivalentes às iniciais, com um mesmo denominador, e então efetuamos a operação desejada.
44. Calcule o resultado das operações no caderno.
a)
1 terço mais 5 terçosb)
9 sobre 15 mais 11 sobre 15c)
7 oitavos menos 3 oitavosd)
11 sobre 20 menos 7 sobre 20e)
número misto um inteiro, dois terços mais um terçof)
3 sétimos mais 2 sobre 14g)
1 quarto mais 3 terçosh)
3 meios menos 7 oitavosi)
4 quintos menos 5 sobre 12j)
um terço mais um quarto mais um meiok)
10 sobre 15 menos 3 oitavosl)
2 terços mais 4 quintos mais um meio45. Marcos gastou
3 sétimosdo salário com despesas fixas e
2 oitavoscom outras despesas. Que fração corresponde à parte do salário que Marcos gastou?
46. Joana leu
um quartode um livro em um dia e
um terçodesse livro no segundo dia. Que fração do livro falta para Joana ler?
Multiplicação de um número natural por uma fração
Multiplicar uma fração por um número natural é o mesmo que adicioná-la tantas vezes quanto o número natural considerado.
47. Calcule o resultado de cada uma das multiplicações no caderno.
a)
6 vezes 3 sétimosb)
5 vezes 3 quartosc)
2 vezes um terçod)
9 vezes 4 sétimose)
12 vezes 3 quintosf)
15 vezes um sexto48. Na receita de um pão são utilizados
2 quintosde um tablete de fermento. Para fazer 5 receitas, quantos tabletes de fermento são necessários?
Divisão de uma fração por um número natural
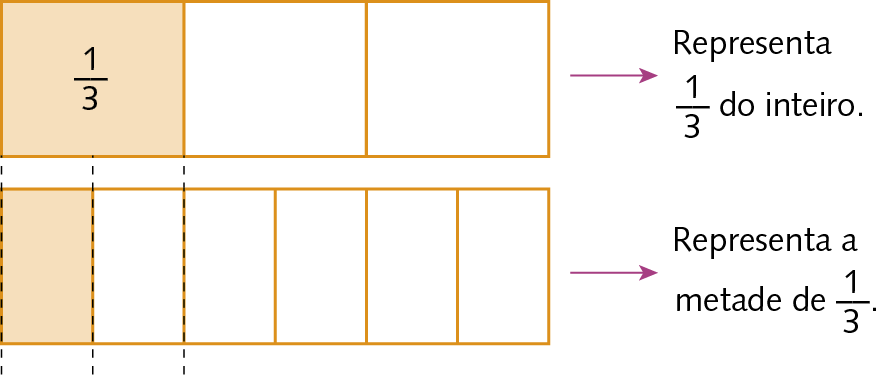
A metade de
um terçocabe seis vezes na figura inicial.
49. Calcule o resultado de cada uma das divisões no caderno.
a)
3 oitavos dividido por 2b)
um terço dividido por 2c)
3 quartos dividido por 5d)
3 quintos dividido por 550. Jorge vai dividir
3 quintosd e uma torta de maçã igualmente entre 4 pessoas. Qual fração da torta de maçã cada pessoa vai receber?
Para o capítulo 7: Números decimais
Décimos, centésimos e milésimos
Observe o valor de cada algarismo do número 8,671.
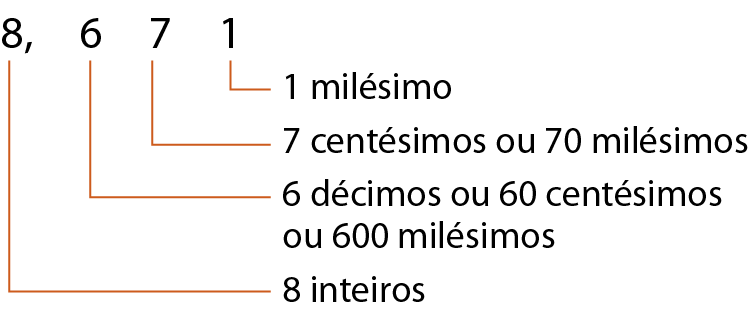
Leitura de números decimais
Para ler um número na fórma decimal, lemos primeiro a parte inteira e, depois, a parte decimal. Observe os exemplos.
a) 3,2

Podemos ler: “três inteiros e dois décimos”.
b) 0,85

Podemos ler: “oitenta e cinco centésimos”.
c) 1,632

Podemos ler: “um inteiro e seiscentos e trinta e dois milésimos”.
51. No caderno, escreva como se leem os seguintes números decimais.
a) 0,9
b) 0,215
c) 5,68
d) 0,18
e) 8,041
f) 0,005
52. Em seu caderno, escreva com algarismos os seguintes números decimais.
a) Nove inteiros e oito décimos.
b) Cento e quarenta e oito milésimos.
c) Noventa e três centésimos.
d) Setecentos e noventa e um milésimos.
e) Dois inteiros e quarenta e nove milésimos.
Comparação de números decimais
Quando as partes inteiras são diferentes
Qual número é maior: 5,3 ou 3,45?
Como 5 inteiros é maior que 3 inteiros, então 5,3 > 3,45.
Quando as partes inteiras são iguais
Qual número é maior: 5,35 ou 5,25?
Como as partes inteiras são iguais, devemos comparar as partes decimais.
35 centésimos é maior que 25 centésimos, então 5,35 > 5,25.
53. Copie os itens no caderno substituindo os

pelos sinais < ou >.
a) 1,2

1,02
b) 8,4

8,14
c) 10,15

10,51
d) 11,9

15,0
e) 2,3

0,23
f) 15,0

15,1
54. Escreva no caderno os números decimais de cada item em ordem crescente.
a) 0,31; 0,57; 0,38; 0,94
b) 3,55; 3,98; 3,07; 3,09
c) 11,12; 10,01; 0,99; 8,92
d) 5,105; 5,095; 5,555; 5,807
55. Desenhe uma reta numérica e represente pontos correspondentes aos números: 1,1; 1,5; 1,6; 1,9 e 2,1.
Adição e subtração com números decimais
Para adicionar ou subtrair números decimais, primeiro colocamos vírgula embaixo de vírgula. Depois, alinhamos os milésimos, os centésimos, os décimos, as unidades, e assim por diante. Por fim, adicionamos milésimos com milésimos, centésimos com centésimos, décimos com décimos, unidades com unidades etcétera fazendo as trocas necessárias.
a) 35,4 + 0,75
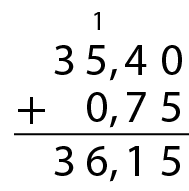
b) 60,35 ‒ 57,9

56. Calcule o resultado das operações no caderno.
a) 0,7 + 4,2
b) 18,3 + 3,05
c) 0,67 + 12,3
d) 0,8 + 1 + 10,02
e) 11,6 + 2 + 25,2
f) 3 ‒ 0,92
g) 42,7 ‒ 25,08
h) 3,005 ‒ 2,15
i) 7,82 ‒ 7,81
j) 0,018 ‒ 0,010
57. Raquel mede 1,62 métro de altura e sua irmã, Jéssica, mede 1,74 métro. Qual é a diferença entre as medidas das duas alturas?
Multiplicação com números decimais
Para multiplicar números decimais, podemos usar o algoritmo da decomposição ou o algoritmo usual.
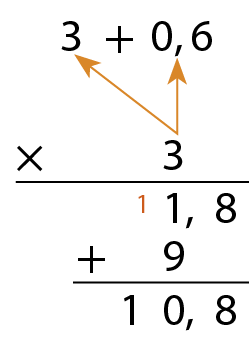
Algoritmo da decomposição
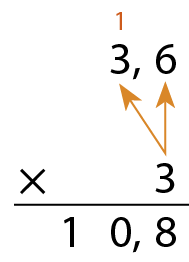
Algoritmo usual
58. Calcule o resultado das multiplicações no caderno.
a) 4,2 × 2
b) 3,45 × 4
c) 3 × 8,7
d) 8 × 1,27
e) 1,05 × 3
f) 4 × 5,25
g) 12,4 × 2
h) 10,05 × 5
59.

Calcule mentalmente o resultado de cada multiplicação.
a) 4,75 × 10
b) 8,32 × 100
c) 6,21 × .1000
d) 0,82 × 10
e) 11,5 × 100
f) 1,921 × .1000
Divisão com números decimais
Para dividir números decimais, podemos utilizar o algoritmo usual.
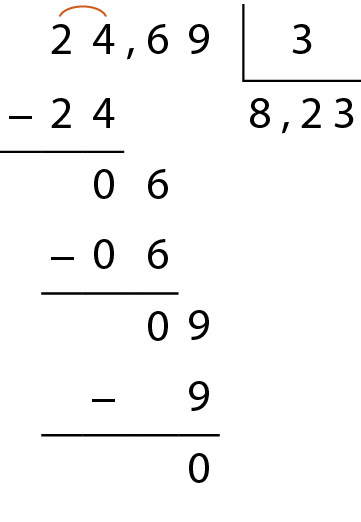
60. Calcule o resultado de cada uma das divisões no caderno.
a) 19 ÷ 2
b) 45 ÷ 4
c) 35 ÷ 4
d) 83 ÷ 5
e) 76 ÷ 8
f) 112 ÷ 5
61. Calcule o resultado de cada uma das divisões no caderno.
a) 32,4 ÷ 2
b) 12,5 ÷ 4
c) 8,16 ÷ 8
d) 15,4 ÷ 5
e) 250,3 ÷ 2
f) 12 ÷ 10
g) 12 ÷ 100
h) 12 ÷ .1000
i) 56 ÷ 100
j) 12,56 ÷ 100
Para o capítulo 8: Porcentagem
Podemos representar uma porcentagem na fórma de fração ou na fórma decimal. Observe.
Para calcular 10% de 100, podemos fazer:
62. Represente as porcentagens nas fórmas fracionária e decimal.
a) 15%
b) 32%
c) 55%
d) 4%
e) 80%
f) 99%
63. Calcule.
a) 5% de 10
b) 10% de 10
c) 50% de 100
d) 60% de 100
e) 42% de 100
f) 8% de 200
64. Mariana comprou uma calça que custa R$ 100,00cem reais. Como estava na promoção, Mariana recebeu um desconto de 25%. Quantos reais ela pagou pela calça?
Para o capítulo 9: Figuras geométricas planas
Segmento de reta, reta e semirreta
O menor caminho de um ponto a outro é chamado de segmento de reta.

Indicamos
segmento de reta MNou
segmento de reta NM.
Os pontos M e N são as extremidades do segmento
segmento de reta MN.
Se prolongarmos o segmento
segmento de reta MNsem parar nos dois lados, teremos uma reta.

Indicamos
reta MNou
reta NMou ainda reta r.
Semirreta é uma parte da reta que apresenta ponto de origem e é ilimitada em um único sentido.

Indicamos
semirreta CDO ponto C é a origem da semirreta
CD.
65. Identifique as semirretas representadas nas figuras.
a)

b)

66. Quais figuras a seguir representam um segmento de reta?
a)
b)

67. Identifique os segmentos de reta representados nas figuras.
a)
b)
Ângulos
Ângulo é a união de duas semirretas de mesma origem em um plano com uma das regiões determinadas por elas.
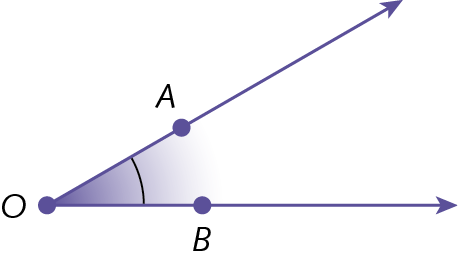
O: vértice do ângulo
lados do ângulo
Ângulo reto, ângulo agudo e ângulo obtuso
• Um ângulo é reto quando sua abertura mede 90graus.
• Um ângulo é agudo quando sua abertura mede mais que 0grau e menos que 90graus.
• Um ângulo é obtuso quando sua abertura mede mais que 90graus e menos que 180graus.
68. Classifique os ângulos a seguir em reto, agudo ou obtuso.
a)

b)
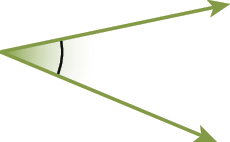
c)
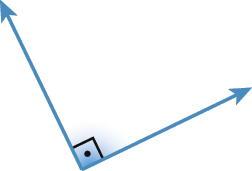
d)

69. Observe os ângulos representados a seguir e, no caderno, escreva a medida da abertura de cada um.
a)
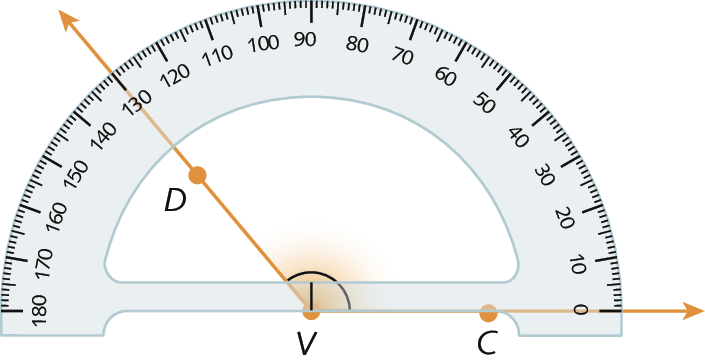
b)
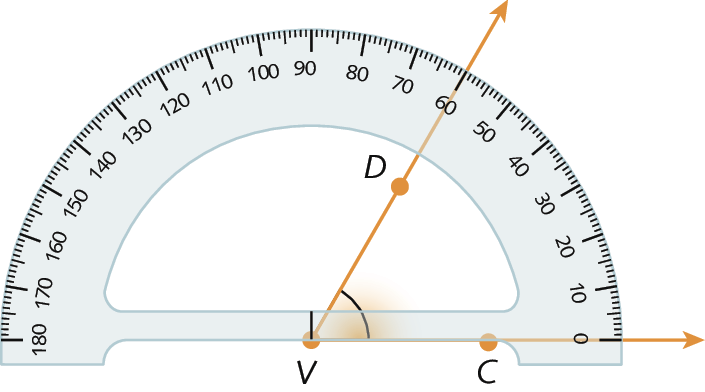
Retas paralelas e retas perpendiculares
Duas retas são paralelas quando não têm nenhum ponto em comum.

Duas retas são concorrentes quando têm apenas um ponto em comum. Quando duas retas concorrentes formam quatro ângulos retos, dizemos que são retas perpendiculares.
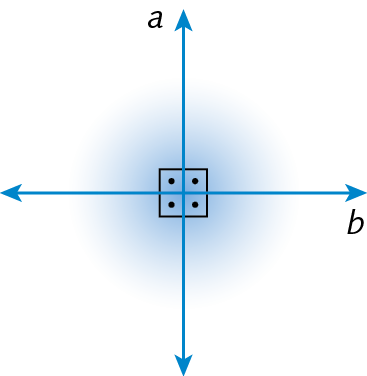
70. Observe esta figura, copie as frases no caderno e complete-as com as palavras: paralelas ou concorrentes.
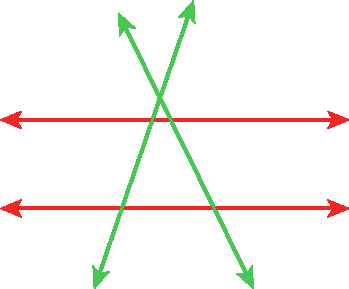
a) As retas verdes são

.
b) As retas vermelhas são

.
c) Uma reta verde e uma reta vermelha são

.
71. No caderno, usando uma régua, trace linhas para representar duas retas perpendiculares.
Polígonos
Polígono é toda figura plana formada por uma região interna contornada por segmentos de retas que não se cruzam.
Triângulos
São polígonos com três lados.

Quadriláteros
São polígonos com quatro lados.

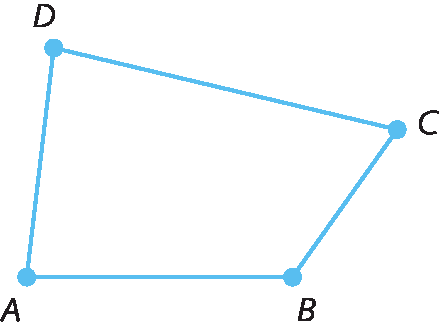
72. Classifique as figuras em triângulos ou quadriláteros.
a)

b)

c)
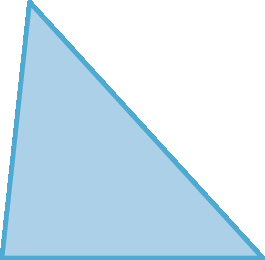
d)

Para o capítulo 10: Ampliação e redução de figuras
• Quando ampliamos proporcionalmente uma figura, as medidas das aberturas dos ângulos correspondentes não são alteradas e as medidas de comprimento dos segmentos correspondentes são proporcionais, ou seja, se dobrarmos uma das medidas de comprimento, todas deverão ser dobradas; se triplicarmos uma medida de comprimento, todas deverão ser triplicadas; e assim por diante.
• Quando reduzimos proporcionalmente uma figura, as medidas das aberturas dos ângulos correspondentes não são alteradas e as medidas de comprimento dos segmentos correspondentes são proporcionais, ou seja, se dividirmos uma das medidas de comprimento por 2, todas deverão ser divididas por 2; se dividirmos uma medida de comprimento por 3, todas deverão ser divididas por 3; e assim por diante.
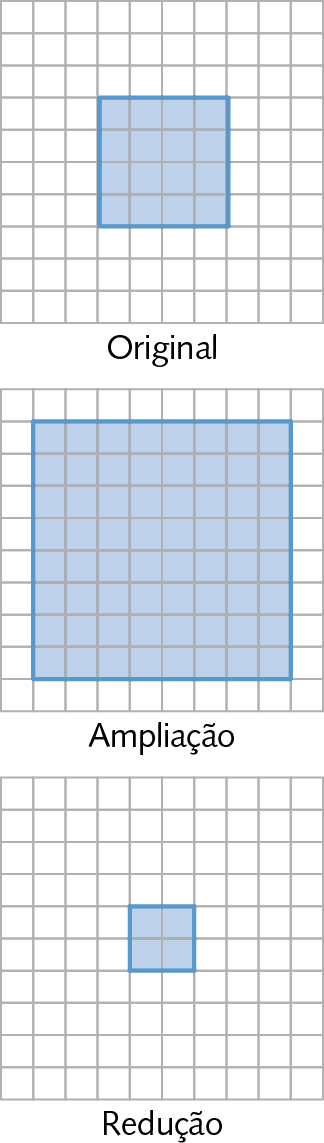
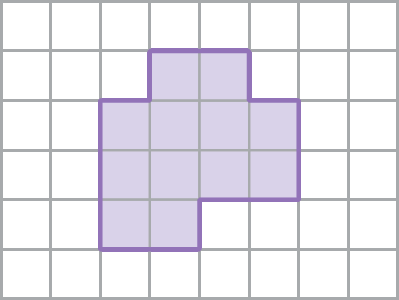
73. Em uma malha quadriculada, desenhe uma redução desta figura geométrica representada.
Para o capítulo 11: Grandezas e medidas
Medidas de comprimento
O quilômetro (cá ême), o metro (ême), o decímetro (dê ême), o centímetro (cê ême) e o milímetro (ême ême) são algumas unidades de medida padronizadas de comprimento.
1 quilômetro equivale a .1000 metros
1 quilômetro = .1000 métros
1 metro equivale a 100 centímetros
1 métro = 100 centímetros
1 metro equivale a 10 decímetros
1 métro = 10 decímetros
1 metro equivale a .1000 milímetros
1 métro = .1000 milímetros
74. Efetue no caderno as transformações a seguir.
a) 2,50 métros =

centímetros
b) 1,45 métro =

centímetros
c) 150 decímetros =

métros
d) 1,5 quilômetro =

métros
e) 1 quilômetro =

decímetros
f) 100 centímetros =

milímetros
g) .1000 milímetros =

centímetros
75. Rodrigo mede 1,65 métro de altura. Qual é a medida da altura de Rodrigo em milímetro?
Perímetro
O comprimento do contôrno de uma figura chama-se perímetro.
76. Calcule a medida do perímetro deste quadrilátero.
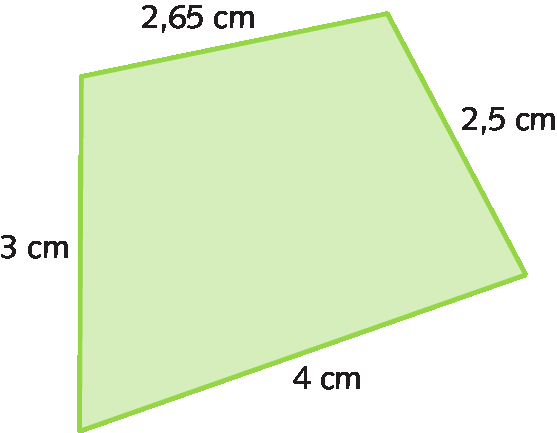
Medidas de área
O centímetro quadrado (cê ême 2 sobrescrito), o metro quadrado (ême 2 sobrescrito) e o quilômetro quadrado (cá ême 2 sobrescrito) são algumas unidades de medida padronizadas de área. Eles correspondem à medida da área de um quadrado cujos lados medem 1 centímetro, 1 metro e 1 quilômetro de comprimento, respectivamente.
77. Considere que cada quadradinho tem 1 centímetro quadrado de medida de área e calcule a medida da área de cada figura.
a)
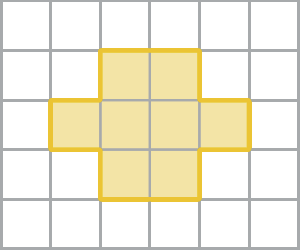
b)
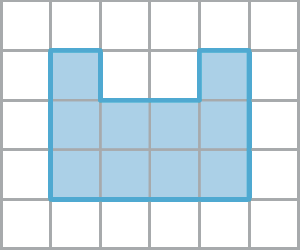
Medidas de volume
O centímetro cúbico (cê ême 3 sobrescrito) e o metro cúbico (ême 3 sobrescrito) são algumas unidades de medida padronizadas de volume. Eles correspondem à medida de volume de um cubo cujas arestas medem 1 centímetro e 1 metro de comprimento, respectivamente.
78. Considere que a medida do volume de cada cubinho é igual a 1 centímetro cúbico e calcule a medida do volume dos empilhamentos em cada caso.
a)

b)

Medidas de tempo
1 dia tem 24 horas
uma hora equivale a 60 minutos
uma hora = 60 minutos
uma minuto equivale a 60 segundos
1 minuto = 60 segundos
79. Responda às questões.
a) Quantas horas há em 3 dias?
b) Quantos minutos há em 15 horas?
c) Quantos minutos há em 1 dia?
d) Quantos segundos há em uma hora?
Medidas de massa
1 quilograma equivale a .1000 gramas
1 quilograma = .1000 gramas
uma tonelada equivale a .1000 quilogramas
uma tonelada = .1000 quilogramas
1 grama equivale a .1000 miligramas
1 grama = .1000 miligramas
80. Responda às questões.
a) Quantos gramas equivalem a 5 quilogramas?
b) Quantos quilogramas equivalem a 10 toneladas?
c) Quantos miligramas equivalem a 10 gramas?
d) Quantos gramas equivalem a uma tonelada?
Medidas de capacidade
1 litro equivale a .1000 mililitros
1 litro = .1000 mililitros
81. Responda às questões.
a) Quantos mililitros equivalem a 2 litros?
b) Quantos mililitros equivalem a 10 litros?
c) Quantos litros equivalem a .5000 mililitros?
d) Quantos litros equivalem a .1500 mililitros?
Medidas de temperatura
No Brasil, a unidade de medida de temperatura utilizada é o grau Celsius (grau cê).
82. Em um município, a medida de temperatura máxima registrada em um dia foi de 27 graus Célsius e a mínima, de 15 graus Célsius. Qual foi a diferença entre a medida da temperatura máxima e a medida da temperatura mínima registradas nesse município?
Para o capítulo 12: Probabilidade e estatística
Cálculo do número de possibilidades
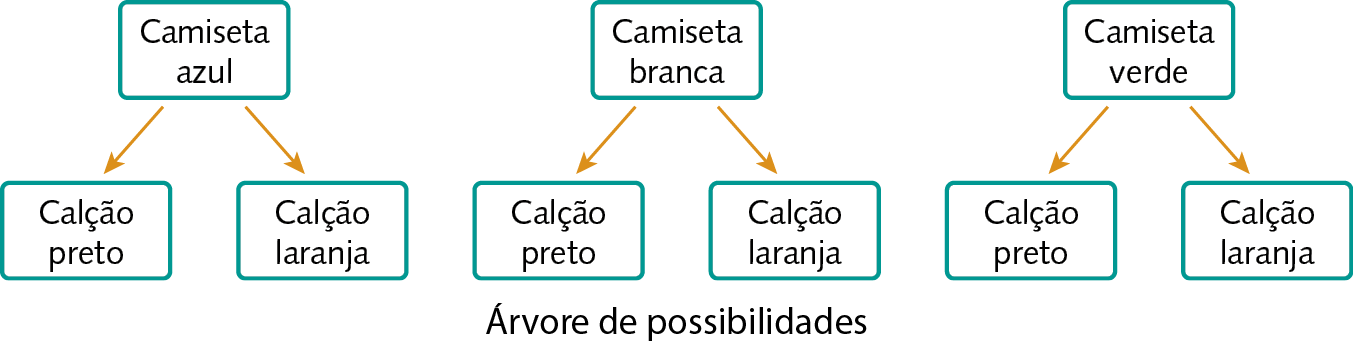
Observe como podemos determinar o número de combinações com uma camiseta e um calção em que temos 3 cores de camiseta (azul, branca e verde) e duas cores de calção (preto e laranja).
|
Camiseta |
|||
|---|---|---|---|
|
Calção |
azul |
branca |
verde |
|
laranja |
laranja e azul |
laranja e branca |
laranja e verde |
|
preto |
preto e azul |
preto e branca |
preto e verde |
Quadro de possibilidades
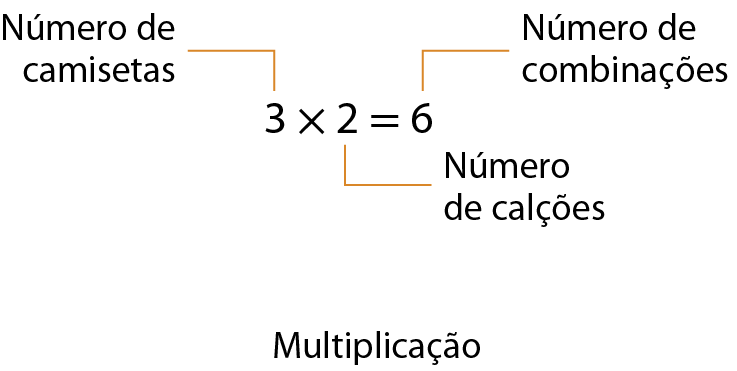
83. Um time de futebol tem 3 cores de camisas e 3 cores de calção. Entre as camisas, há uma azul, uma amarela e uma preta e, entre os calções, há um branco, um amarelo e um preto. Faça uma árvore de possibilidades com todas as combinações de camisas e calções que podem ser usadas por esse time.
84. No cardápio de uma lanchonete, há 4 opções de sanduíche, 4 opções de suco natural e duas opções de sobremesa. Indique o número de combinações possíveis de fazer com:
a) um sanduíche e um suco natural.
b) um sanduíche e uma sobremesa.
c) um sanduíche, um suco natural e uma sobremesa.