Unidade 1
Capítulo 1 Números naturais e sistemas de numeração
Capítulo 2 Operações com números naturais
Capítulo 3 Figuras geométricas espaciais

Capítulo 1 Números naturais e sistemas de numeração
Trocando ideias
Nas várias situações do dia a dia em que os números estão presentes, eles podem indicar contagem, ordem, código ou medida.
No Campeonato Mundial de Halterofilismo de 2021, em Tbilisi, na Geórgia, a brasileira Lara Lima conquistou o 1º lugar ao levantar 87 quilogramas distribuídos em 8 anilhas (sem considerar a medida da massa da barra).


▸ Com base no texto e na imagem anterior, responda: o que indicam os números 8, 1º, 87 e 7?
Neste capítulo, vamos estudar as aplicações e as fórmas de escrita e leitura dos números naturais. Além disso, vamos conhecer alguns dos sistemas de numeração utilizados por diferentes povos e aprender a usar o nosso sistema de numeração.

1 Sistemas de numeração
A ideia de contar objetos e de utilizar uma fórma de registrar essa contagem é muito antiga.
O estudo de locais onde antigas civilizações viveram levou à descoberta de objetos que provavelmente eram utilizados para marcar quantidades. O que se sabe é que os marcadores surgiram muito antes da escrita.
Nós, seres humanos, somos seres tecnológicos, pois sempre utilizamos alguma técnica para alterar a natureza e nos beneficiar. Assim, as práticas de coleta de frutos e raízes, a criação de animais e o cultivo de plantas comestíveis, iniciadas na Pré-história, podem ter dado origem à necessidade de contróle e de registro de quantidades, por meio, por exemplo, da correspondência 1 a 1: cada animal de um rebanho era contabilizado por meio da colocação de uma pedra em determinado local.
Com o tempo, esses registros foram sendo alterados e, posteriormente, deram origem a sistemas de contagem mais precisos e à utilização de símbolos.
Ao conjunto de símbolos e regras usados para representar números dá-se o nome de sistema de numeração. Diversas civilizações da Antiguidade, como a egípcia e a romana, criaram um sistema de numeração próprio.
Sistema de numeração egípcio
A civilização egípcia teve início por volta de 3200 antes de Cristo, no nordeste da África, às margens do rio Nilo. Os egípcios registravam quantidades utilizando sete símbolos. Verifique a seguir quais são esses símbolos e o valor correspondente a cada um.

No sistema de numeração egípcio:
• não havia símbolo que representasse a ausência de quantidade (o número zero);
• cada símbolo podia ser repetido até nove vezes;

• O valor de cada símbolo é sempre o mesmo, independentemente de sua posição.
• Os símbolos eram enfileirados e seus valores adicionados, não importando a ordem em que estavam escritos.

Sistema de numeração romano
Os romanos também criaram um sistema próprio, baseado em letras do alfabeto. Ainda hoje, os números romanos são usados em algumas situações. Observe as imagens a seguir.



No sistema de numeração romano, há sete símbolos, que correspondem a letras maiúsculas do alfabeto latino. Observe.

Nesse sistema de numeração:
• não existe símbolo que represente a ausência de quantidade (o número zero);
• os símbolos ih, xis, cê e ême podem ser repetidos seguidamente até três vezes, e seus valores são adicionados. Observe os exemplos a seguir.
í í = 2
í í í = 3
Xis xis = 20
xis xis xis = 30
cê cê = 200
Cê cê cê = 300
ême ême = .2000
ême ême ême = .3000
• os símbolos ih, xis ou cê escritos à esquerda de outro de maior valor indicam uma subtração quando:
a) ih aparece antes de vê ou xis;
b) xis aparece antes de éle ou cê;
c) cê aparece antes de dê ou ême.
Observe alguns exemplos.
í vê = 5 menos 1 = 4
í xis = 10 menos 1 = 9
xis éle = 50 menos 10 = 40
xis cê = 100 menos 10 = 90
cedê = 500 menos 100 = 400
cê ême = .1000 menos 100 = 900
• um símbolo colocado à direita de outro de valor igual ou maior indica uma adição de valores;
vê í í = 5 + 2 = 7
xis xis vê í í í = 20 + 5 + 3 = 28
cê éle xis xis vê í = 100 + 50 + 20 + 5 + 1= 176
ême ême éle xis vê = .2000 + 50 + 10 + 5 = .2065
ême ême ême dê cê cê éle = .3000 + 500 + 200 + 50 = .3750
• um traço horizontal colocado sobre um símbolo indica que o seu valor deve ser multiplicado por mil.
•
Símbolo. Traço horizontal sobre a letra V maiúscula.= 5 × .1000 = .5000
•
Símbolo. Traço horizontal sobre as letras L e X maiúsculas.= 60 × .1000 = .60000
Atividades
Faça as atividades no caderno.
1. Os números têm quatro importantes funções:
• contar;
• ordenar;
• medir;
• codificar.
Leia o texto a seguir.
Em uma partida que durou 111 minutos, a britânica Emma Raducanu venceu a canadense Leylah Fernandez, conquistou o título do US Open e se tornou a 1ª britânica, desde 1977, a erguer o troféu de campeã de um Grand Slamglossário . Após 10 vitórias no campeonato e o título, a tenista foi eleita revelação do ano pela dábliu tê á (Associação das Tenistas Profissionais).

Agora, escreva o que indicam os números dos itens a seguir.
a) 111
b) 1ª
c) 10
2. Escreva três situações do dia a dia em que você utiliza números.
3. Escreva com símbolos egípcios:
a) o ano em que você nasceu;
b) o número de estudantes da sua turma;
c) o ano atual.
4. Responda às questões.
a) Quais eram os símbolos usados pelos romanos para escrever os números?
b) Quais são os símbolos que podem ser repetidos seguidamente no sistema de numeração romano?
c) O número quarenta tem o mesmo valor que sessenta?
d) O que acontece com o valor do número sete quando colocamos um traço horizontal sobre ele?
5. Leia o texto a seguir e escreva os números que aparecem nele utilizando o sistema de numeração romano.
O forte mais antigo do Brasil foi erguido em Bertioga, no litoral sul do estado de São Paulo, em 1532. Destruído em uma guerra com os tupinambás, o forte foi reconstruído e reaberto em 1699. A partir de 1765, passou a ser chamado de Forte São João. Atualmente, é protegido pelo Instituto do Patrimônio Histórico e Artístico Nacional (Iphan).

6.


Diga a um colega um número maior que 500 e menor que .2000 e peça a ele que escreva esse número no sistema de numeração romano. Em seguida, verifique se ele acertou.
7. Represente os números 130 e 310 nos sistemas de numeração egípcio e romano. Depois, responda: quais são as características comuns e as diferenças entre os sistemas de numeração egípcio e romano?

2 Nosso sistema de numeração
O sistema de numeração mais utilizado atualmente é o indo-arábico. As regras desse sistema foram inventadas pelos hindus, mas foram os árabes que, ao invadir a Europa, levaram-no para lá no século treze; daí o nome “indo-arábico”.
ORIGEM E DIFUSÃO DO SISTEMA DE NUMERAÇÃO INDO-ARÁBICO
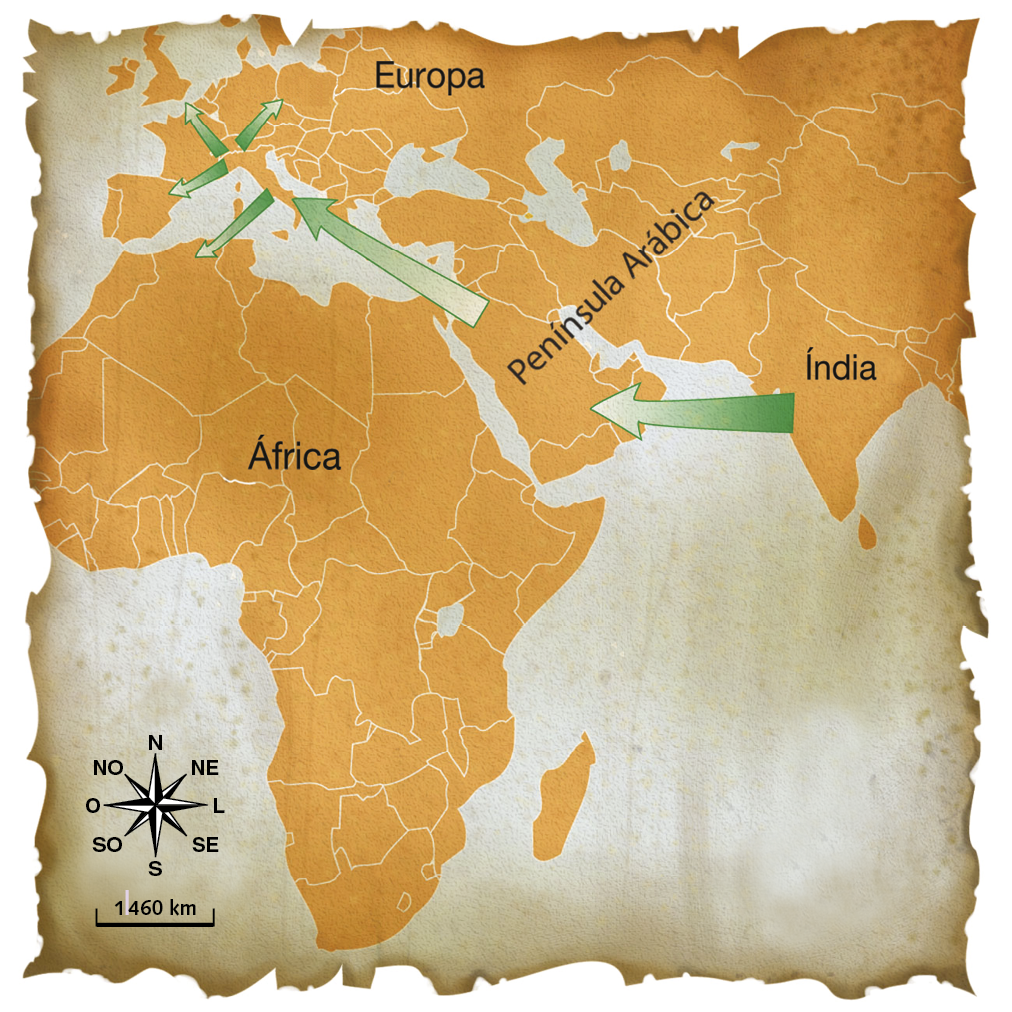
Elaborado com base em: í bê gê É. Atlas geográfico escolar. oitava edição Rio de Janeiro: í bê gê É, 2018. página 32.
Nesse sistema são utilizados dez símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, denominados algarismos. O sistema de numeração indo-arábico é um sistema de numeração decimal, pois contamos quantidades formando grupos de 10.
Esse sistema é posicional, pois o valor de cada algarismo depende de sua posição na representação do número. Por exemplo, no número 26, o algarismo 6 vale 6 unidades e, no número 63, o algarismo 6 vale 6 dezenas.
Outra característica importante do sistema de numeração indo-arábico é a existência de um símbolo para representar o zero. Nesse sistema, o símbolo zero representa a ausência de quantidade, indicando que não há agrupamento de 10 naquela posição.
A facilidade de registrar os números e de efetuar cálculos foi um dos motivos que fizeram esse sistema prevalecer.
Podemos representar alguns números do sistema de numeração indo-arábico utilizando o ábaco e o material dourado. Observe a representação do número .1325.
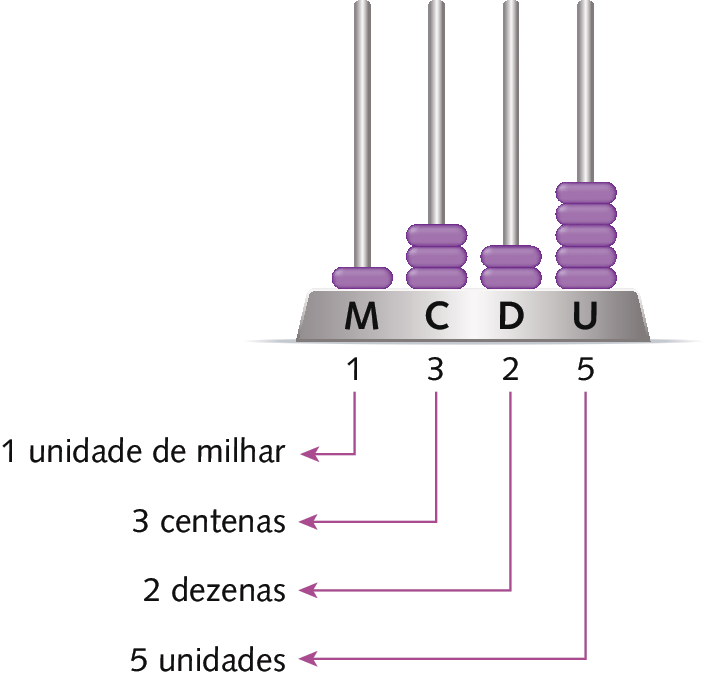
1 × .1000 + 3 × 100 + 2 × 10 + 5 = .1325
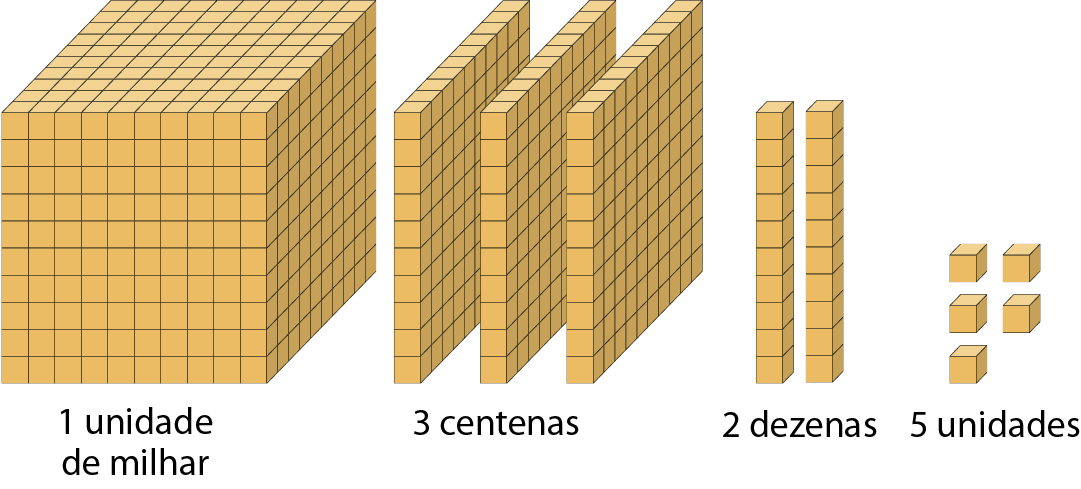
Ao escrever um número no sistema de numeração indo-arábico, cada algarismo ocupa uma ordem. Além disso, para facilitar, as ordens podem ser agrupadas de três em três abre parêntesesda direita para a esquerdafecha parênteses e estes agrupamentos são chamados de classes.
Observe, por exemplo, a representação do número ..8561243 em um quadro de ordens e classes.
|
Classe dos milhões |
Classe dos milhares |
Classe das unidades simples |
||||||
|---|---|---|---|---|---|---|---|---|
|
9ª ordem |
8ª ordem |
7ª ordem |
6ª ordem |
5ª ordem |
4ª ordem |
3ª ordem |
2ª ordem |
1ª ordem |
|
Centenas de milhão |
Dezenas de milhão |
Unidades de milhão |
Centenas de milhar |
Dezenas de milhar |
Unidades de milhar |
Centenas |
Dezenas |
Unidades |
|
8 |
5 |
6 |
1 |
2 |
4 |
3 |
||
À esquerda da classe dos milhões, são representadas a dos bilhões, a dos trilhões, a dos quatrilhões, a dos quintilhões, a dos sextilhões e assim por diante.
Observando o quadro anterior, verificamos o valor posicional do número da seguinte fórma:
..8561243 = 8 × ..1000000 + 5 × .100000 + 6 × .10000 + 1 × .1000 + 2 × 100 + 4 × 10 + 3
ou
..8561243 = ..8000000 + .500000 + .60000 + .1000 + 200 + 40 + 3
Observação
Observe o número 235 representado no quadro de ordens e classes.
|
Classe dos milhares |
Classe das unidades simples |
||
|---|---|---|---|
|
4ª ordem |
3ª ordem |
2ª ordem |
1ª ordem |
|
Unidades de milhar |
Centenas |
Dezenas |
Unidades |
|
0 |
2 |
3 |
5 |
Nesse caso, o valor que indica a maior ordem é o 2, que representa duas centenas.
Caso o zero esteja no quadro de ordens e não exista outro valor abre parêntesesdiferente de zerofecha parênteses à sua esquerda, ele deve ser desconsiderado. Então, não consideramos o zero à esquerda do 2 para determinar a ordem desse número.
Agora, tomando como exemplo o número .2350, temos:
|
Classe dos milhares |
Classe das unidades simples |
||
|---|---|---|---|
|
4ª ordem |
3ª ordem |
2ª ordem |
1ª ordem |
|
Unidades de milhar |
Centenas |
Dezenas |
Unidades |
|
2 |
3 |
5 |
0 |
Nesse caso, o valor que indica maior ordem é o 2, que representa duas unidades de milhar, ou seja, consideramos o zero, pois há outros valores à sua esquerda: 5, 3 e 2.
Atividades
Faça as atividades no caderno.
8. Escreva, utilizando algarismos, os números representados nos ábacos.
a)

b)

c)

d)

9. Escreva o número formado por:
a) sete centenas mais cinco dezenas mais três unidades;
b) oito unidades de milhar mais cinco centenas mais seis dezenas;
c) uma dezena de milhar mais sete dezenas;
d) duas unidades de milhão mais seis centenas de milhar mais nove dezenas mais oito unidades.
10. Usando os algarismos 2, 6 e 8, sem repeti-los, escreva seis diferentes números de três algarismos.
11. As décadas são contadas em agrupamentos de 10 anos. Assim, 36 anos correspondem a três décadas e seis anos.
Escreva no caderno, de fórma semelhante, os agrupamentos correspondentes a:
a) 22 anos;
b) 50 anos;
c) 69 anos.
12. Observe o número a seguir e responda às questões.

a) Quantas ordens tem esse número?
b) Qual é o algarismo da quarta ordem?
c) Qual é o algarismo que representa a ordem das centenas?
d) Qual é o algarismo que representa a maior ordem?
e) Quantas classes tem esse número?
13. Determine o número formado por:
a) (5 × 100) + (7 × 10) + 8
b) (7 × .1000) + (8 × 100) + (9 × 10) + 5
c) (2 × .10000) + (5 × .1000) + (4 × 100) + (3 × 10) + 8
d) (5 × .100000) + (8 × .1000) + (5 × 100) + 3
14.

Em uma calculadora, digite as teclas 3, 5, 3 e 8, nessa ordem.
a) Que número aparece no visor?
b) Qual o valor posicional de cada um dos algarismos 3 nesse número?
c) Se você teclar 2 após teclar 8, qual será o novo valor posicional do algarismo 3?
15.

Em um campeonato de lançamento de dardos, Pedro lançou 15 dardos, atingindo o disco conforme mostra a figura a seguir.

Quantos pontos Pedro obteve?
16. Carla contou os limões que havia levado à feira para vender. Para cada grupo de 10 limões, ela fez um traço, conforme mostra a ilustração. Terminada a contagem, sobraram seis limões em cima da mesa.
Quantos limões ela levou para a feira?

Leitura e escrita de um número no sistema indo-arábico
Saber ler e escrever números pode ser muito útil em situações do cotidiano, como reconhecer e distinguir valores.
Para ler um número:
1º) separamos o número em classes;
2º) lemos, da esquerda para a direita, o número formado em cada classe, seguido do nome da classe.
A seguir podemos observar dois exemplos de como é feita essa leitura.
a)
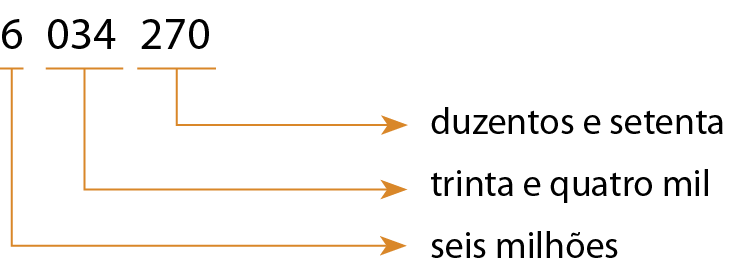
Lemos: seis milhões, trinta e quatro mil, duzentos e setenta.
b)
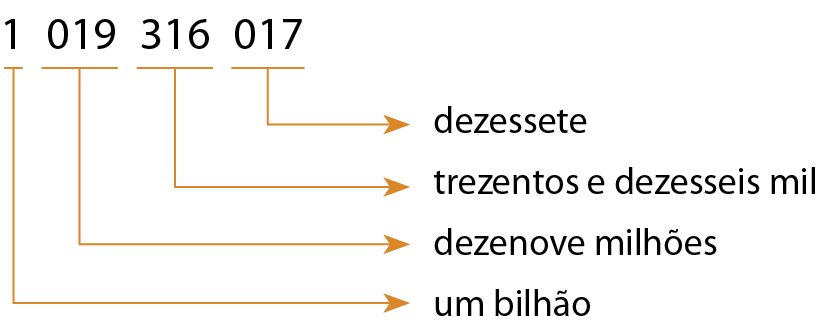
Lemos: um bilhão, dezenove milhões, trezentos e dezesseis mil e dezessete.
Observação
Quando todas as ordens de uma classe são formadas por zero, não lemos essa classe.
Confira um exemplo:
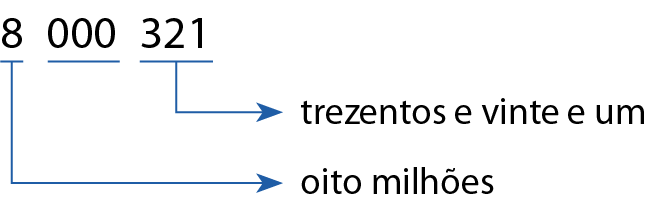
Lemos: oito milhões, trezentos e vinte e um.
De modo inverso, se conhecemos a leitura de um número, podemos escrevê-lo apenas com algarismos. Observe os exemplos:
a) setenta e três mil, seiscentos e oitenta e dois
|
Milhares |
Unidades simples |
||||
|---|---|---|---|---|---|
|
7 |
3 |
6 |
8 |
2 |
→ 73.682 |
b) dois bilhões, treze milhões, quinhentos e seis
|
Bilhões |
Milhões |
Milhares |
Unidades simples |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
2 |
0 |
1 |
3 |
0 |
0 |
0 |
5 |
0 |
6 |
→ 2.013.000.506 |
Observações
1. Para facilitar a leitura de números naturais grandes, a mídiaglossário costuma apresentá-los na fórma mista, ou seja, parte com algarismos e parte por extenso, conforme o exemplo:
Segundo a ó ême ésse, em novembro de 2021 o número de mortes por Covid-19 passava dos 5 milhões.
5 milhões correspondem a ..5000000.
2. Em alguns textos, a palavra milhão é substituída por mi, e a palavra bilhão, por bi. E pode ser usada uma vírgula para separar a maior classe das demais. Observe:
A população brasileira deve chegar a 233 mi de pessoas em 2050, segundo projeções da ONU.
233 mi correspondem a duzentos e trinta e três milhões ou ..233000000.
De acordo com estimativasglossário da ônu, na Terra haverá 9,8 bi de pessoas em 2050.
9,8 bi correspondem a nove bilhões e oitocentos milhões ou ...9800000000.
Atividades
Faça as atividades no caderno.
17. Escreva como se lê cada número.
a) 345
b) .1679
c) .8950
d) .815200
e) ..18540035
f) ..95013600
18. Escreva os números a seguir usando algarismos indo-arábicos.
a) Doze mil, cento e seis.
b) Novecentos e doze mil e trezentos.
c) Um milhão, dez mil e treze.
d) Noventa milhões, dezesseis mil e oito.
e) Dois bilhões, doze milhões e cem mil.
19. Lucas digitou as teclas 7, 6, 5, 4, 3, 2 e 1, nessa ordem, em sua calculadora. Escreva como se lê o número que Lucas obteve no visor da calculadora.
20. Luciana efetuou, em um caixa eletrônico, o pagamento das contas de água, energia, telefone, aluguel e condomínio. O valor da conta de água era igual a quarenta e cinco reais. Analise o valor das demais contas e escreva como se leem essas quantias.

21. O tiranossauro rex viveu há ..145000000 de anos, e o tricerátops, há ..67000000 de anos. Escreva como se leem esses números.
22. Escreva os números destacados nas frases a seguir usando mi para milhões, bi para bilhões ou tri para trilhões.
a) Segundo o í bê gê É, a população do estado da Paraíba em 7 de março de 2022 era de aproximadamente ..4000000 de habitantes.
b) De acordo com o í bê gê É, o pê i bê do Brasil em 2021 foi de ....8700000000000.

3 Os números naturais
Os números são usados em diferentes situações. Observe como eles aparecem na notícia a seguir.

Os números 0, 3, 6 e .2022 presentes no texto são exemplos de números naturais.
A sequência dos números naturais é: (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, reticências). O primeiro termo dessa sequência é o zero; para determinar um termo seguinte qualquer, basta adicionar 1 ao termo imediatamente anterior. A sequência dos números naturais é infinita, porque sempre haverá o próximo termo. Esse fato é indicado por reticências (reticências).
Os números naturais dessa sequência formam um conjunto numérico denominado conjunto dos números naturais, que pode ser assim representado:

= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, reticências}
Observando a sequência dos números naturais, verificamos que todo número natural tem um sucessor, também natural e único, e é obtido pelo acréscimo de uma unidade a ele, conforme os dois exemplos a seguir.
a) O sucessor de 0 é 1, pois: 0 + 1 = 1
b) O sucessor de 99 é 100, pois: 99 + 1 = 100
Todo número natural tem um sucessor.
O número natural zero não é sucessor de nenhum outro número natural. Assim, todo número natural, com exceção do zero, tem um antecessor. Para obter o antecessor de um número natural, subtraímos dele uma unidade, conforme os dois exemplos a seguir.
a) O antecessor de 10 é 9, pois: 10 menos 1 = 9
b) O antecessor de 50 é 49, pois: 50 menos 1 = 49
Observações
1. As palavras sucessivo e consecutivo têm o mesmo significado que “sucessor”. Assim:
a) o sucessivo de 89 é 90;
b) o sucessivo de 1 é 2, e o de 2 é 3;
c) o consecutivo de .1175 é .1176;
d) os números 35, 36 e 37 são consecutivos.
2. As palavras precedente e antecedente têm o mesmo significado que “antecessor”. Assim:
a) o precedente de 32 é 31;
b) o antecedente de 101 é 100.
Números pares e números ímpares
A professora Carla escreveu no quadro a sequência dos números naturais pares e a dos números naturais ímpares.

Ao observar as sequências escritas pela professora, os estudantes notaram que:
• os números pares são números naturais que terminam em 0, 2, 4, 6 ou 8;
• os números ímpares são números naturais que terminam em 1, 3, 5, 7 ou 9.

Veja que interessante
Faça as atividades no caderno.
Código de barras
O código de barras é uma representação gráfica de dados numéricos ou alfanuméricos. A decodificação, ou seja, a leitura dos dados, é realizada por um tipo de scanner, o leitor de código de barras. Os dados capturados nessa leitura óptica são convertidos em letras ou números, como você deve ter observado quando acompanha um adulto nas compras.
O código de barras evoluiu muito e ganhou uma segunda dimensão.
O código de barras bidimensional, conhecido como código QR code (quê érre é sigla da expressão em inglês Quick Response – “Resposta rápida”), pode ser facilmente escaneado com celulares equipados com câmera.



Atividades
a) Utilize um celular e descubra a frase que está escrita no QR code mostrado anteriormente.
b) O número presente nessa frase é par ou ímpar?
Número e numeral
Número é a ideia de quantidade que nos vem à mente quando contamos, ordenamos ou medimos. Numeral é toda representação escrita, falada ou digitada de um número. Para representar um número, podemos utilizar diferentes numerais.
O número de rodas do jipe-robô Curiosity, por exemplo, pode ser representado de várias maneiras.

a) Por meio de palavras denominadas numerais, como seis (numeral da língua portuguesa) ou six (numeral da língua inglesa).
b) Por meio de símbolos, também chamados de numerais, como 6 (numeral indo-arábico) ou vê í (numeral romano).
Observação
Não confunda número, numeral e algarismo. Observe os exemplos:
a) O numeral .4567 representa uma quantidade (número) e é escrito com os algarismos 4, 5, 6 e 7.
b) Minha senhaglossário bancária é formada por quatro algarismos, e não por quatro números.
Atividades
Faça as atividades no caderno.
23. Responda às questões.
a) Qual é o menor número natural?
b) Qual é o sucessor do zero?
c) Todo número natural tem sucessor?
24. Escreva o sucessor e o antecessor dos números naturais a seguir.
a) 600
b) .1001
c) .8020
d) .50000
25. Escreva três números naturais consecutivos sabendo que o maior deles é:
a) 16
b) 100
c) 699
d) .1121
26. Escreva três números naturais ímpares consecutivos, entre os quais o menor é 999.
27. Responda às questões.
a) Qual é o antecessor do maior número natural par de três algarismos?
b) Qual é o sucessor do menor número natural ímpar de cinco algarismos?
c) Qual é o sucessor ímpar de 79? E o precedente par de 100?
28. Observe a sequência a seguir:
1, 2, 4, 7, 11, 16, 22, reticências
Agora, responda: qual é o próximo número dessa sequência?

Lendo e aprendendo



Países assinam acordo para zerar desmatamento
Meta envolve mais de cem nações e deve ser atingida até 2030
Líderes de mais de cem países deram um importante passo nas discussões sobre o futuro da Terra. Durante a Conferência das Nações Unidas sobre as Mudanças Climáticas (cópi vinte e seis), na Escócia, eles se comprometeram a acabar com o desmatamento até 2030.
A participação do Brasil no acordo, chamado Forest Deal, foi muito bem recebida, pois grande parte do país é coberta pela Amazônia, maior floresta tropical do mundo. Segundo o Instituto Nacional de Pesquisas Espaciais (inpi), entre 2019 e 2020, o desmatamento na região atingiu 9,2 mil quilômetros quadrados, área seis vezes maior que a cidade de São Paulo.
Lendo e aprendendo
A previsão é de que os projetos para proteção das florestas custem cêrca de US$glossário 19 bilhões (equivalentes a R$ 105 bilhõescento e cinco reais). Desse total, US$ 12 bilhões serão financiados pelos países mais ricos do grupo, entre eles Estados Unidos, Canadá, França e Alemanha. Os US$ 7 bilhões restantes serão doados por empresas e organizações não governamentais (ônguis).
A temperatura da Terra tem aumentado rapidamente, sobretudo por causa da ação do homem. E as plantas têm um papel fundamental para amenizar esse processo: durante a fotossíntese, elas absorvem dióxido de carbono (cê ó₂), um dos gases que vêm causando o desequilíbrio no clima [reticências]
Outro gás que tem “bagunçado” a temperatura terrestre, o metano também foi motivo de acôrdo entre os países. Nesse caso, a meta é reduzir as emissões em 30% até 2030.
O Brasil é o quinto maior produtor de metano do mundo. O gás é emitido de diferentes fórmas na natureza (por exemplo, nas atividades vulcânicas), mas passou a preocupar em função do crescimento da pecuária. Isso porque bois e vacas eliminam essa substância na digestão do alimento, por meio do pum e do arroto.
PEIXOTO, F. Países assinam acôrdo para zerar desmatamento. Qualé, São Paulo, edição 39, página 12, 15 a 29 de novembro de 2021.
Faça as atividades no caderno.
Atividades
1. Responda às questões no caderno.
a) Em que mês e ano foi publicado o texto anterior?
b) Qual é o tema principal do texto?
c) O que é a cópi vinte e seis?
d) Por que a participação do Brasil na cópi vinte e seis foi considerada importante?
e) Quais são os dois gases que têm “bagunçado” a medida da temperatura terrestre?
2. No texto, alguns números naturais foram escritos de fórma abreviada. Em seu caderno, escreva estes números com todos os algarismos.
3. Copie a tabela a seguir em seu caderno e complete-a com base nas informações do texto.

|
Doadores |
Doações |
|---|---|
|
Países mais ricos |
|
|
ONGs |
Dados obtidos em: PEIXOTO, F. Países assinam acôrdo para zerar desmatamento. Qualé, São Paulo, edição 39, página 12, 15 a 29 de novembro de 2021.
4.


O que você e as pessoas ao seu redor podem fazer para preservar o meio ambiente e limitar as mudanças climáticas? Em seu caderno, responda escrevendo um pequeno texto. Depois, converse com os colegas.
Comparação de números naturais
Os jogos olímpicos são realizados com o objetivo de incentivar a integração entre os povos por meio de diferentes modalidades esportivas. Os primeiros jogos olímpicos modernos ocorreram em 1896, em Atenas, na Grécia. Os Jogos Olímpicos de Tóquio 2020 ocorreram em 2021 sem a presença de público devido à pandemia de côvid dezenóve.


O quadro a seguir apresenta os cinco países que mais conquistaram medalhas nos Jogos Olímpicos de Tóquio.
|
País |
Ouro |
Prata |
Bronze |
Total |
|---|---|---|---|---|
|
Estados Unidos |
39 |
41 |
33 |
113 |
|
China |
38 |
32 |
18 |
88 |
|
Japão |
27 |
14 |
17 |
58 |
|
Reino Unido |
22 |
21 |
22 |
65 |
|
ROC* |
20 |
28 |
23 |
71** |
* Como a Rússia estava suspensa dos jogos, os atletas russos participaram como Comitê Olímpico Russo (em inglês, Russian Olympic Committee, com sigla ROC).
** O ROC ganhou mais medalhas que o Reino Unido e o Japão, mas ficou em 5º lugar porque o primeiro critério para classificação é o número de medalhas de ouro.
Dados obtidos em: https://oeds.link/PtRZqu. Acesso em: 14 abril 2022.
Com base nos dados do quadro, podemos afirmar que:
• O número de medalhas de bronze conquistadas pelo ROC é maior que o número de medalhas de bronze conquistadas pelo Japão. Escrevemos: 23 > 17.
• O número de medalhas de prata conquistadas pelo Reino Unido é menor que o número de medalhas de ouro que esse país conquistou. Escrevemos: 21 < 22.
• O número de medalhas de prata conquistadas pelos Estados Unidos é diferente do número de medalhas de prata conquistadas pela China. Escrevemos: 41 ≠ 32.
• O número de medalhas de ouro conquistadas pelo Reino Unido é igual ao número de medalhas de bronze que esse país conquistou. Escrevemos: 22 = 22.
Atividades
Faça as atividades no caderno.
29. Escreva seis números diferentes utilizando os algarismos 4, 5 e 8 sem repeti-los. Qual é o maior deles? E o menor?
30. Escreva a sequência de números indicada em cada caso.
a) Números naturais menores que 8.
b) Números naturais maiores ou iguais a 10.
c) Números naturais entre 12 e 17.
d) Números naturais de 12 a 17.
e) Números naturais maiores que 15 e menores que 22.
31. Marina, Paula e Carla são jogadoras de vôlei. Carla é mais alta que Marina, e Paula é mais baixa que Marina. Qual delas é a mais baixa?
A reta numérica e os números naturais
Os números naturais podem ser representados em uma reta numérica, na qual cada ponto está associado a um número. Observe:
• Traçamos uma reta e marcamos o ponto O (origem).

• À direita de O, marcamos pontos consecutivos com a mesma medida da distância entre eles, determinando os pontos a, B, C, D, reticências

• Aos pontos O, a, B, C, D, reticências, fazemos corresponder os números naturais 0, 1, 2, 3, 4, reticências, respectivamente.

Assim, estabelecemos uma correspondência entre os números naturais e os pontos marcados na reta.
Com o auxílio da reta numérica, podemos comparar números naturais e afirmar se um é maior ou menor que outro. Assim, podemos refletir sobre os seguintes exemplos:
a) Como 5 está representado à direita de 2 na reta numérica, então 5 é maior que 2, ou seja: 5 > 2
b) Como 1 está representado à esquerda de 6 na reta numérica, então 1 é menor que 6, ou seja: 1 < 6
Atividades
Faça as atividades no caderno.
32. Desenhe, no caderno, uma reta numérica e registre os números 0, 3, 5 e 7.
33. Observe a reta numérica.

Agora, responda: qual é o número natural que corresponde ao ponto:
a) R?
b) S ?
c) T ?
34. Dada a reta numérica, faça o que se pede.

No caderno, escreva que ponto representa:
a) o número 9;
b) o número 12;
c) o número 4;
d) o número 15.
35. Observe a reta numérica em que a, b e c representam números naturais correspondentes aos pontos a, B e C.

Quais das sentenças a seguir são verdadeiras?
a) a > 6
b) b > 6
c) 6 < c
d) c > b
e) c < a
f) b > a
36. De acôrdo com as retas numéricas, escreva, no caderno, os números naturais correspondentes às letras C, D, F e I.
a)
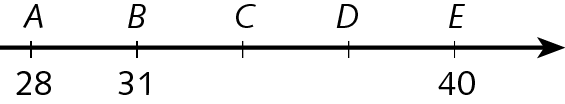
b)
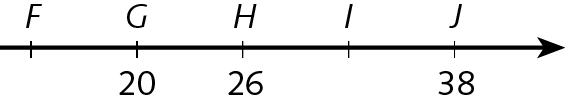
37. Reproduza a reta numérica a seguir em seu caderno.

Em seguida, indique os pontos P, Q e R na reta de acôrdo com as informações a seguir.
um Os números correspondentes aos pontos P e R são pares e maiores que zero.
dois O número correspondente ao ponto P é menor do que 3.
três Os números correspondentes aos pontos Q e R são maiores do que 4.
quatro O número correspondente ao ponto R é menor do que 7 e o número correspondente ao ponto Q é menor do que 6.
38. Paulo vai trabalhar em um novo projeto em sua empresa. Para se dedicar a esse novo trabalho, ele passou a fazer duas horas extras por dia.
Sabendo que Paulo não trabalha nos fins de semana e que o projeto durou 3 semanas, quantas horas extras Paulo trabalhou nesse projeto?
39. Fazendo uma pesquisa na internet sobre aquecimento global, Luís encontrou uma reportagem completa sobre o assunto, com mais de duzentas páginas.
Depois de ler a pesquisa, ele imprimiu da página 35 até a 178. Quantas páginas foram impressas?
40. Responda às questões.
a) Quantos números naturais existem de 25 até 50?
b) Quantos números naturais existem entre 30 e 48?
c) Para numerar de 5 até 50, quantos números naturais e quantos algarismos escrevemos?
41.


Junte-se a um colega e peça a ele que trace uma reta numérica no caderno. Em seguida, solicite que indique na reta três números escolhidos por você. Depois, verifique se ele indicou os números nos locais apropriados.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Sistemas de numeração
Sistema de numeração egípcio
• Eram utilizados sete símbolos.
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|
|
1 |
10 |
100 |
1.000 |
10.000 |
100.000 |
1.000.000 |
• Não havia símbolo para representar o número zero.
• Cada símbolo podia ser repetido até nove vezes.
• O valor de cada símbolo é sempre o mesmo, independentemente de sua posição.
• Os símbolos eram enfileirados e seus valores adicionados, não importando a ordem em que estavam escritos.
Sistema de numeração romano
• Eram utilizados sete símbolos que correspondiam às letras maiúsculas do alfabeto latino.
|
I |
V |
X |
L |
C |
D |
M |
|---|---|---|---|---|---|---|
|
1 |
5 |
10 |
50 |
100 |
500 |
1.000 |
• Não havia símbolo para representar o número zero.
• Os símbolos ih, xis, cê e ême podem ser repetidos seguidamente até três vezes, e seus valores são adicionados.
• Os símbolos ih, xis ou cê escritos à esquerda de outro de maior valor indicam uma subtração quando:
a) ih aparece antes de vê ou xis;
b) xis aparece antes de éle ou cê;
c) cê aparece antes de dê ou ême.
• Um símbolo colocado à direita de outro de valor igual ou maior indica uma adição de valores.
• Um traço horizontal colocado sobre um número indica que o seu valor deve ser multiplicado por mil.
1. Represente com números indo-arábicos.
a)

b)
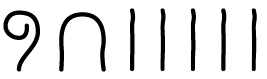
c)
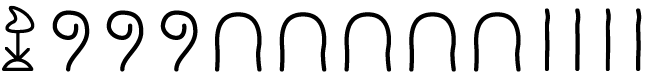
2. Represente com números romanos.
a) 39
b) 64
c) 721
d) 985
e) .1354
f) .1429
Nosso sistema de numeração
No nosso sistema de numeração (também conhecido como indo-arábico):
• podemos representar qualquer número utilizando os símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9;
• os agrupamentos são feitos de 10 em 10;
• o valor de cada algarismo depende de sua posição;
• o zero (0) representa a ausência de quantidade.
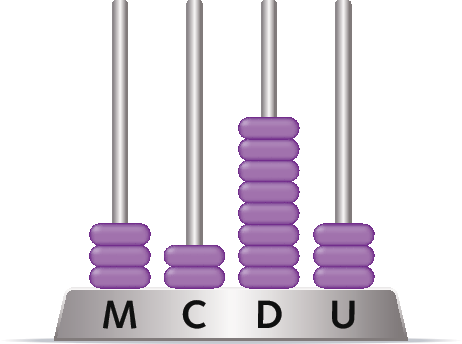
3. Observe cada ábaco e registre com algarismos os números representados.
a)
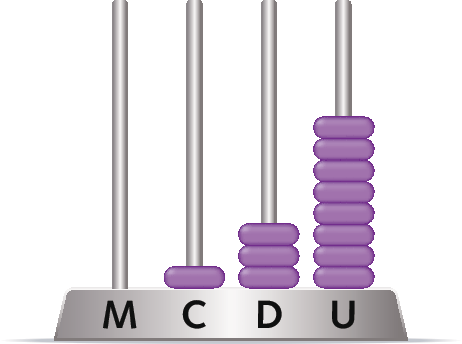
b)
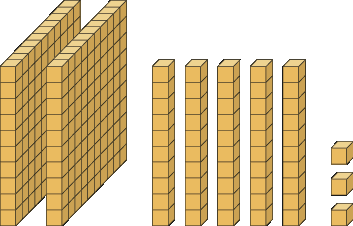
4. Registre com algarismos os números representados com as peças do material dourado em cada item.
a)
b)
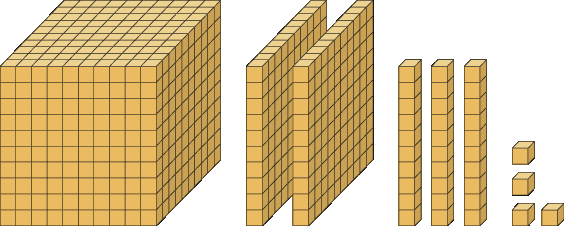
5. Escreva o número correspondente a cada decomposição.
a) 5 × .1000 + 3 × 10 + 7
b) 6 × .1000 + 4 × 100 + 9 × 10 + 1
c) 9 × .10000 + 2 × 100 + 3 × 10
d) 2 × .100000 + 4 × .1000 + 8 × 10 + 6
6. Observe o número a seguir e responda às questões.

a) Quantas ordens tem esse número?
b) Qual é o algarismo da terceira ordem?
c) Qual é o algarismo que representa a ordem dos milhares?
d) Quantas classes tem esse número?
e) Qual é o algarismo que representa a menor ordem?
7. Escreva, no caderno, como se leem os números a seguir.
a) 425
b) .1379
c) .220402
Os números naturais
O conjunto dos números naturais é representado por:

= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, reticências}
• Todo número natural tem um sucessor.
• Todo número natural, com exceção do zero, tem um antecessor.
Números pares e números ímpares
• Os números pares são números naturais que terminam em 0, 2, 4, 6 ou 8.
• Os números ímpares são números naturais que terminam em 1, 3, 5, 7 ou 9.
Comparação de números naturais
• Os números da sequência dos naturais vão aumentando à medida que acrescentamos 1 ao número anterior.
• Podemos utilizar os símbolos < (menor que), > (maior que), ≠ (diferente) e = (igual) para relacionar dois números. Observe os exemplos:
a) 123 < 231
b) .1252 >.1225
c) .3402 ≠ .2043
d) .7861 = .7861
A reta numérica e os números naturais
Os números naturais podem ser representados em uma reta numérica, na qual cada ponto está associado a um número.

8. Reproduza o quadro no caderno e complete-o.

|
Antecessor |
Número natural |
Sucessor |
|---|---|---|
|
358 |
||
|
899 |
||
|
2.561 |
||
|
11.981 |
||
|
2.351.299 |
||
|
4.000.000 |
||
|
12.981.999 |
9. Faça o que se pede.
a) Começando pelo 10, escreva no caderno a sequência dos números naturais pares com 10 números.
b) Começando pelo 13, escreva no caderno a sequência dos números naturais ímpares com 10 números.
10. Copie as sentenças verdadeiras em seu caderno.
a) 54 < 45
b) 105 = 501
c) 471 ≠ 174
d) 214 > 211
e) .1002 = .1002
f) .22022 > .22220
11. Com os algarismos 1, 3, 4, 6 e 2 e sem repetir nenhum deles, escreva:
a) o maior número possível;
b) o menor número possível;
c) o maior número que tenha o algarismo 1 na ordem das centenas;
d) um número maior que .43200 que tenha 6 como algarismo das unidades.
12. Desenhe no caderno uma reta numérica e indique nela os oito primeiros números ímpares.
13. Desenhe no caderno uma reta numérica e represente pontos correspondentes aos números 5, 8, 9, 12 e 15.
Glossário
- Grand Slam
- : Nome usado para indicar os quatro eventos mais importantes de tênis do ano: o Australian Open (Austrália), o Torneio de Roland‑Garros (França), o Torneio de Wimbledon (Inglaterra) e o US Open (Estados Unidos da América).
- Voltar para o texto
- Mídia
- : Conjunto dos meios de comunicação de massa.
- Voltar para o texto
- Estimativa
- : Cálculo para obter um resultado aproximado.
- Voltar para o texto
- Senha
- : Cadeia de caracteres que autoriza o acesso a um conjunto de operações em um sistema de computadores ou em equipamentos computadorizados, como caixas eletrônicos de bancos.
- Voltar para o texto
- US$
- : Símbolo utilizado para representar o dólar americano, isto é, a moeda oficial dos Estados Unidos da América (Estados Unidos da América).
- Voltar para o texto