Capítulo 2 Operações com números naturais
Trocando ideias

No início de 2022, o Ministério da Saúde anunciou a inclusão de crianças da faixa etária de 5 a 11 anos no Plano Nacional de Operacionalização da Vacinação contra a côvid dezenóve (PNO). Estima-se que esse público era de 20 milhões de crianças.
▸

Até o dia 07/02/2022, 3.setecentas.000 crianças haviam sido imunizadas. A partir dessa data, quantas crianças, aproximadamente, ainda precisavam tomar a vacina?
▸


Na sua opinião, qual a importância de tomar vacinas? Converse com os colegas.
Neste capítulo, vamos ampliar nossos conhecimentos sobre operações com números naturais.

1 Adição com números naturais
Observe o total de pontos conquistados pelos cinco pilotos de motovelocidade mais bem colocados no Superbike Brasil 2021.
|
Posição |
Piloto |
Pontos |
|---|---|---|
|
1ª |
Pedro Sampaio |
177 |
|
2ª |
Mauriti Junior |
129 |
|
3ª |
Léo Tamburro |
123 |
|
4ª |
Júlio Fortunado |
121 |
|
5ª |
Danilo Lewis |
77 |
Dados obtidos em: https://oeds.link/PABJXP. Acesso em: 17 abril 2022.
Qual foi o total de pontos alcançado pelos pilotos que conquistaram as três primeiras posições?
Para obter essa resposta, devemos juntar, unir ou reunir quantidades, ou seja, efetuar a operação denominada adição.
Acompanhe como podemos obter esse total:
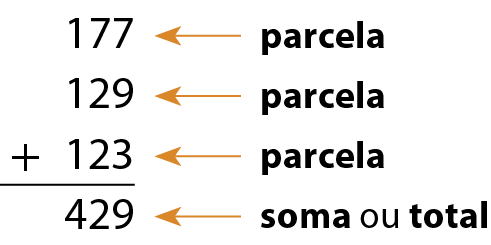
Nessa adição, os números 177, 129 e 123 são as parcelas, e 429 é a soma (ou total).
Outra ideia da adição é a de acrescentar uma quantidade à outra.
Caso houvesse mais uma corrida no campeonato citado anteriormente e o piloto Pedro Sampaio ganhasse mais 25 pontos, chegando em 1º lugar, deveríamos acrescentar esses 25 pontos aos 177:
177 + 25 = 202
Portanto, o piloto terminaria o campeonato com 202 pontos.

LEMBRE-SE: Escreva no caderno.
Algumas propriedades da adição
Vamos estudar algumas propriedades da adição.
Propriedade comutativa
▸

Adicione mentalmente:

a) Que resultados você obteve?
b) O que você percebeu?
▸ Escolha outros dois números naturais e, em seu caderno, escreva uma adição cujas parcelas são somente esses números. Depois, escreva outra adição trocando a ordem das parcelas. Finalmente, calcule o resultado das duas adições. O que você observou?
Em uma adição de números naturais, a ordem das parcelas não altera a soma.
Propriedade associativa
Vamos efetuar 8 + 12 + 10 associando as parcelas de dois modos.

▸ Escolha três números naturais. Adicione, em seu caderno, a soma dos dois primeiros números com o terceiro. Em seguida, adicione o primeiro número com a soma dos dois últimos. O que você observou?
Em uma adição de três ou mais números naturais, podemos associar as parcelas de diferentes modos sem alterar a soma.
Elemento neutro
▸

Adicione mentalmente:

a) Que resultados você obteve?
b) O que você percebeu?
O zero, quando adicionado a outro número natural qualquer, resulta sempre nesse outro número. Ou seja, o zero como parcela da adição não altera o valor da soma. Por isso, ele é chamado de elemento neutro da adição.
Observação
Nas três situações anteriores, realizamos adições em que as parcelas são números naturais. Note que as somas também são números naturais.
Atividades
Faça as atividades no caderno.
1. Considere os números a seguir.

Agora, determine os totais obtidos ao:
a) adicionar os dois maiores números;
b) adicionar os dois menores números;
c) adicionar o menor número com o maior número.
2. Observe o quadro de pontos de uma gincana e responda às questões.
|
Etapa |
|||
|---|---|---|---|
|
Nome |
1ª |
2ª |
3ª |
|
Júlio |
3.650 |
5.995 |
7.036 |
|
Marcelo |
3.543 |
2.786 |
9.999 |
|
Antônio |
4.119 |
3.830 |
8.678 |
a) Quantos pontos Júlio obteve nas três etapas?
b) Algum deles conquistou mais de 17 mil pontos nessa gincana?
c) Quem obteve mais pontos nessa gincana?
3. Com base nas medidas aproximadas do quadro a seguir, calcule a medida da área total, em quilômetro quadrado cá ême elevado a 2, da Região Sul do Brasil.
|
Estado |
Medida da área (quilômetro quadrado) |
|---|---|
|
Paraná |
199.299 |
|
Santa Catarina |
95.731 |
|
Rio Grande do Sul |
281.707 |
Dados obtidos em: https://oeds.link/G5Om6I. Acessos em: 17 abril 2022.
4. Observe a tabela com o número de habitantes das seis cidades mais populosas do Brasil em 2020.
|
Cidade |
População |
|---|---|
|
São Paulo |
12.325.232 |
|
Rio de Janeiro |
6.747.815 |
|
Brasília |
3.055.149 |
|
Salvador |
2.886.698 |
|
Fortaleza |
2.686.612 |
|
Belo Horizonte |
2.521.564 |
Dados obtidos em: https://oeds.link/6Jtiyn. Acesso em: 17 abril 2022.

Calcule a população das cidades:
a) do Sudeste listadas no quadro;
b) do Nordeste listadas no quadro.
5. Quando Laerte nasceu, o pai dele tinha 28 anos. Atualmente, Laerte tem 18 anos. Determine a soma das idades de Laerte e de seu pai hoje.
6. Determine a soma de todos os números de três algarismos diferentes que podem ser formados com os algarismos 3, 4 e 5.
7.

Ana vai usar a calculadora para determinar a soma de três números consecutivos, sabendo que o menor deles é 549. Quando foi realizar os cálculos, Ana percebeu que as teclas 0 e 9 da sua calculadora estavam com defeito. Como Ana poderá fazer esse cálculo? Qual será o resultado?
8.

Reúna-se com um colega para responder à questão: quais são os quatro números ímpares que adicionados resultam em 29?
9. Calcule.
a) 16 + 35 + 14 + 15
b) (16 + 14) + (35 + 15)
• Você achou mais fácil determinar a soma do item a ou a do item b? Explique.
10. Utilizando as propriedades comutativa e associativa, adicione os números da maneira que julgar mais simples.
a) 26 + 30 + 4 + 20
b) 33 + 12 + 7 + 0 + 8
11. Sabendo que 577 + 323 = 900, escreva o resultado de 323 + 577 sem efetuar a adição. Justifique sua resposta.
12. Por que o zero é o elemento neutro da adição?
13.

Considere a adição:
702 + 299
a) Podemos afirmar que o resultado desta adição é aproximadamente igual a .1000? Por quê?
b) Efetue mentalmente a adição anterior. Depois, explique como você fez.
14.

Reúna-se com um colega para resolver o problema a seguir.
Breno foi a uma loja de brinquedos e comprou seis miniaturas. No quadro a seguir, está a lista dessas miniaturas e o preço de cada uma.
|
Casa |
R$ 11,00 |
|
Avião |
R$ 18,00 |
|
Carro |
R$ 16,00 |
|
Navio |
R$ 24,00 |
|
Soldado |
R$ 7,00 |
|
Trem |
R$ 19,00 |
Utilizando as propriedades da adição, cada um de vocês deverá sugerir um modo de obter o total dessa compra. Depois, determinem um modo comum de resolução que considerem ser o mais simples e apresentem-no aos demais colegas da classe.

2 Subtração com números naturais
As imagens a seguir são dos dois prédios mais altos do mundo segundo o Guinness World Records.


Podemos obter a diferença entre as medidas das alturas dos prédios através da operação chamada subtração.
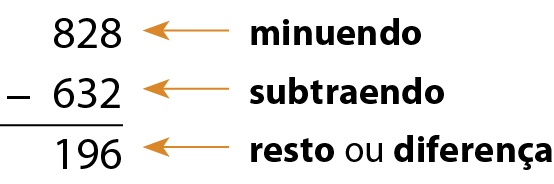
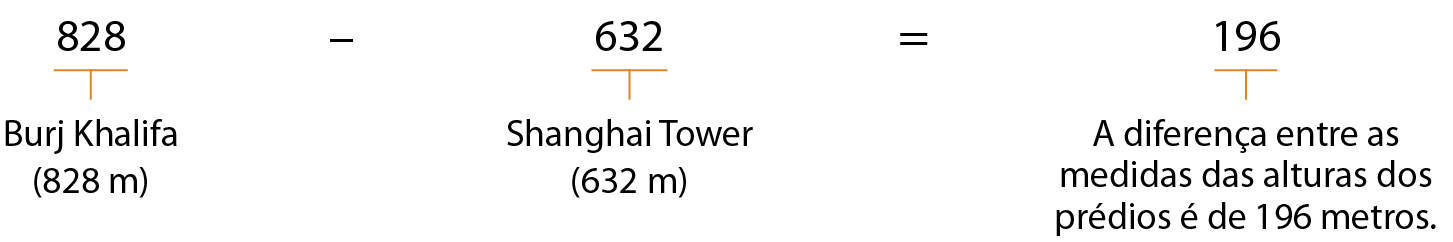
Além da ideia de comparação, a subtração também pode estar relacionada à ideia de completar e de tirar unidades. Acompanhe as situações.
Situação 1 abre parêntesesideia de completarfecha parênteses
Luís tem cinquenta e duas figurinhas. Quantas figurinhas faltam para ele completar uma centena?
Para responder a essa pergunta, devemos calcular 100 menos 52:
100 menos 52 = 48
Portanto, faltam 48 figurinhas para Luís completar uma centena.
Situação 2 abre parêntesesideia de tirarfecha parênteses
Ana tinha 5 blusas e doou 3 delas. Com quantas blusas ela ficou?
Para responder a essa pergunta, devemos calcular 5 menos 3:
5 menos 3 = 2
Portanto, Ana ficou com duas blusas.
Atividades
Faça as atividades no caderno.
15. Calcule, quando possível, o resultado das subtrações. Nem sempre é possível efetuar uma subtração entre dois números naturais.
a) 189 menos 86
b) 856 menos 799
c) 654 menos 830
d) .1050 menos 867
e) .2160 menos .3000
f) .5555 menos .5555
• Quando é possível efetuar uma subtração entre dois números naturais?
16. Responda, no caderno, às questões.
a) Qual é a diferença entre dois números iguais?
b) Qual é a diferença entre dois números pares e consecutivos?
c) Podemos afirmar que a propriedade comutativa é válida para a subtração?
17. Pedro nasceu em julho de 1993. Que idade ele terá em agosto de 2025?
18. Quantos anos você completará no ano 2030?
19. Luís utilizou R$ 700,00setecentos reais para pagar um telefone celular. Calcule o preço desse aparelho, sabendo que Luís recebeu R$ 25,00vinte e cinco reais de troco.
20.


Copie o enunciado do problema a seguir em seu caderno e complete com os dados que quiser. Depois, troque com um colega e resolva o problema dele.
Adalto comprou uma mesa por R$

e pagou com

cédulas de R$

. Quanto ele recebeu de troco?
21. Efetue as subtrações.
a) .67056 menos .9453
b) .136917 menos .85862
c) .235000 menos .196417
d) .76432 menos .65321
22.

Calcule mentalmente o resultado das subtrações.
a) 189 menos 29
b) 768 menos 59
c) 974 menos 101
d) .2358 menos 202
23. Criptografia é a arte de escrever utilizando caracteres secretos ou palavras de uma escrita que não é compreendida por todos. Decifre o criptograma a seguir e registre o valor de cada letra, sabendo que cada uma delas indica um algarismo, que letras iguais representam algarismos iguais e que letras diferentes representam algarismos diferentes.
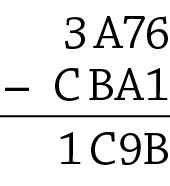
Relação fundamental da subtração
Observe a cena.

Podemos conferir o troco de duas maneiras:
• por meio de uma subtração:
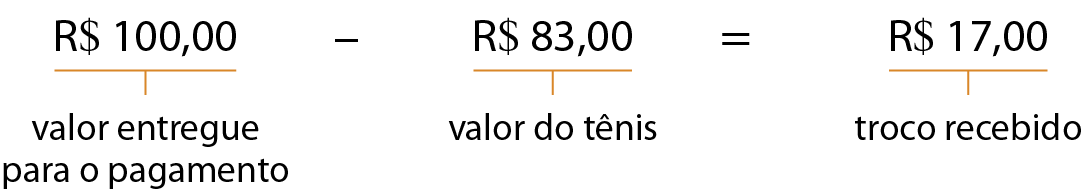

• por meio de uma adição:
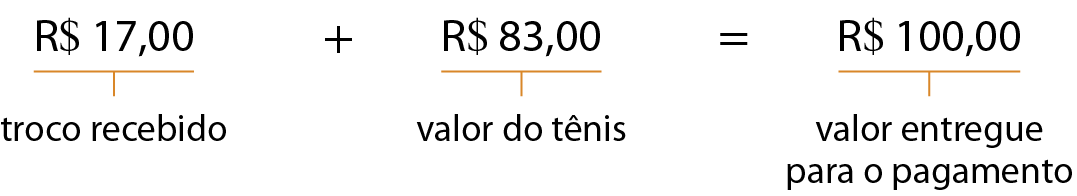

Podemos conferir o resultado de uma subtração por meio de uma adição, pois o resultado da adição do subtraendo com o resto é sempre igual ao minuendo.
Assim, podemos escrever a relação fundamental da subtração da seguinte maneira:
Se o minuendo menos o subtraendo é igual ao resto, então o subtraendo mais o resto é igual ao minuendo.
Por isso, dizemos que a adição e a subtração são operações inversas.
Atividades
Faça as atividades no caderno.
24. O piloto espanhol Alex Palou conquistou o Campeonato de Fórmula Indy em 2021 com 549 pontos, 391 a mais que o piloto brasileiro Hélio Castroneves, que concluiu a temporada em 22º lugar. Qual foi o total de pontos obtidos pelo brasileiro na Fórmula Indy em 2021?
Dados obtidos em: https://oeds.link/qpwCyrs. Acesso em: 18 janeiro 2022.

25. Resolva os problemas.
a) Em uma subtração, o subtraendo é .4738 e o resto é 149. Determine o minuendo.
b) Em uma subtração, o minuendo é .1001 e o resto é 956. Determine o subtraendo.
26. Se, em uma subtração, aumentarmos o minuendo em 20 unidades e diminuirmos o subtraendo em 15 unidades, em quanto aumentará a diferença?
27. Descubra, em cada item, o valor dos algarismos representados por

e

.
a)

b)

28. Copie os itens a seguir no caderno, substituindo cada

pelo número adequado.
a) .1860 menos

= 357
b)

menos .3545 = .1283
29. A soma de três números é .8470. O primeiro é .4319 e o segundo é .1843. Determine o terceiro número.
30.


Kátia utilizou uma calculadora e fez o seguinte cálculo:

Elabore um problema que possa ser resolvido utilizando a operação inversa da adição que Kátia efetuou.
Expressões numéricas com adições e subtrações
Na casa de Júlia havia 4 bananas; ela foi à feira e comprou mais uma dúzia; na volta para casa, acabou comendo duas. Com quantas bananas ela ficou em sua casa?

Para resolver este problema, devemos calcular o valor da expressão numérica 4 + (12 ‒ 2).

Portanto, Júlia ficou com 14 bananas em sua casa.
Observações
Nas expressões numéricas em que não há parênteses, as operações de adição e de subtração devem ser feitas na ordem em que aparecem.
• Nas expressões numéricas em que há parênteses, eles indicam as operações que devem ser feitas primeiro.
• Em uma expressão numérica na qual uma das operações é a subtração, a mudança dos parênteses pode levar a resultados diferentes. Observe os exemplos a seguir:
a)

b)
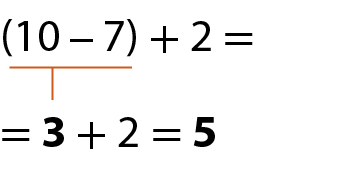
c)
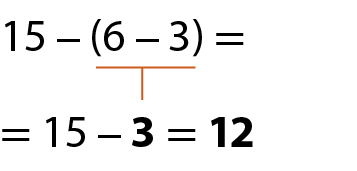
d)
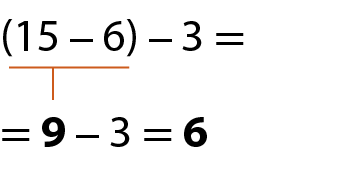
Atividades
Faça as atividades no caderno.
31. Calcule o valor de cada expressão numérica.
a) (18 menos 15 + 3) + 2
b) 30 + (50 menos 12) menos 15
c) 13 menos 8 + 7 menos 4 menos 2
d) (60 menos 12) menos (10 + 20) menos 14
e) (100 menos 35 + 15) + (200 + 135 menos 98)
f) 200 menos (40 + 50) menos 90 menos 10
32. Copie as expressões numéricas no caderno, colocando parênteses quando necessário, para determinar o resultado indicado.
a) 8 menos 3 + 4 menos 5 menos 1 = 5
b) 15 menos 8 + 7 + 8 = 8
c) 35 + 15 menos 20 + 18 = 12
d) 19 menos 8 + 5 menos 4 menos 3 = 5
e) 200 menos 120 + 80 + 70 menos 20 + 50 = 0
33. Sérgio pensou em um número. Em seguida, adicionou-lhe 10. Depois, subtraiu 13 do resultado anterior, obtendo 12. Em que número Sérgio pensou?
34. Leia as frases a seguir e escreva uma expressão numérica que corresponda a cada uma delas. Em seguida, calcule seu valor.
a) Subtraia da soma de 180 com 45 a diferença entre 210 e 107.
b) Adicione 72 à diferença entre 315 e 285.
35.

Na maioria das calculadoras modernas, encontramos estas teclas:
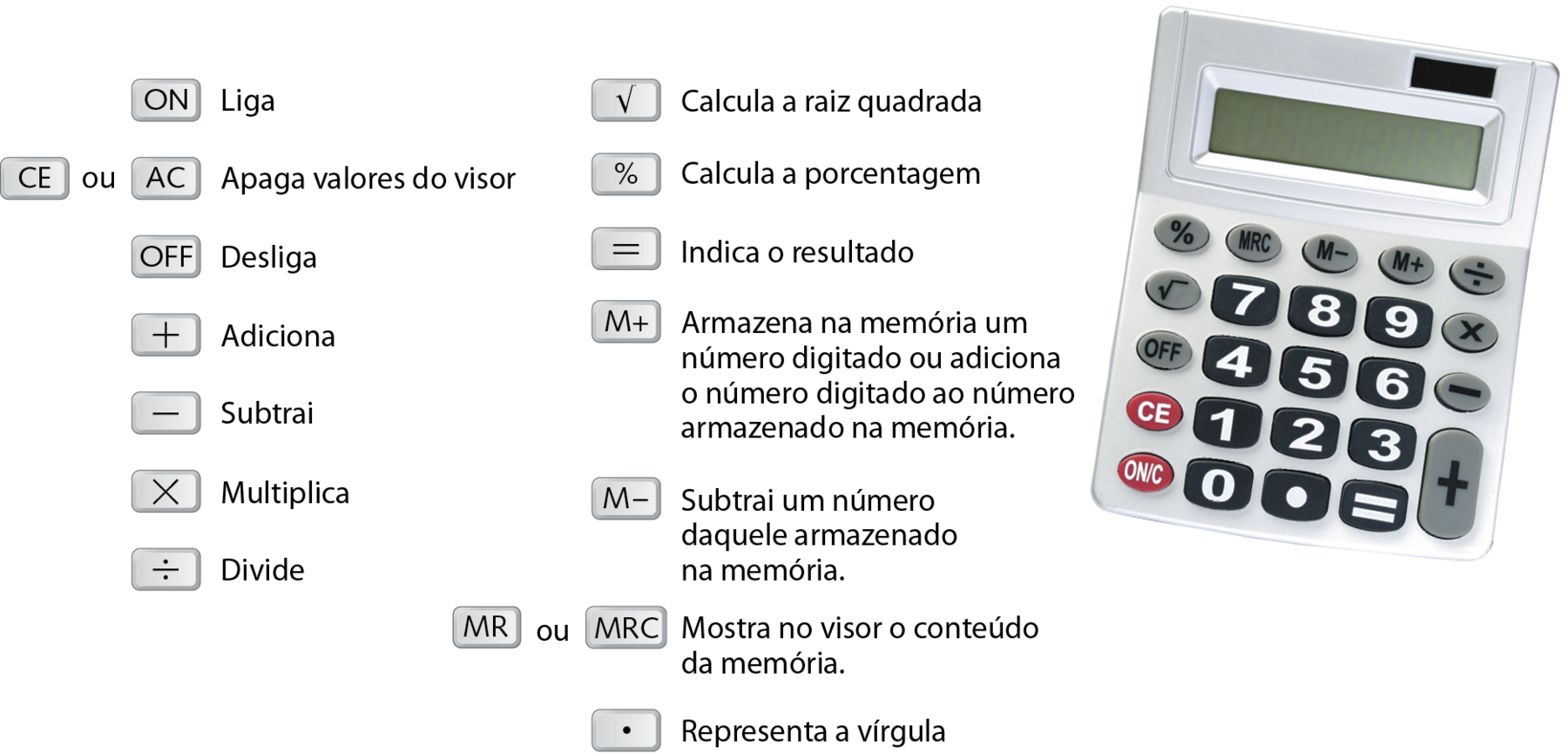
Para efetuar cálculos com a calculadora, podemos usar as funções de memória. Digite as sequências a seguir e confirme o resultado no visor.

Escreva em seu caderno a expressão numérica que corresponde ao cálculo efetuado em cada exemplo apresentado.

3 Multiplicação com números naturais
Acompanhe as situações a seguir.
Situação 1
Pedro é professor de dança de salão e está preparando uma apresentação de gafieira. Todos os alunos vão participar, formando 8 casais. Quantos alunos vão participar dessa apresentação?

O total de alunos pode ser determinado por uma adição de parcelas iguais:
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 16
Logo, 16 alunos vão participar dessa apresentação.
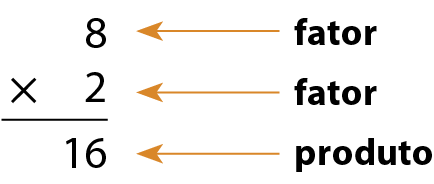
Para simplificar o registro dessa operação, fazemos:

A operação 8 × 2 = 16 é um exemplo de multiplicação. Os números 8 e 2 são os fatores, e 16, o produto.
Observações
1. Para indicar uma multiplicação, podemos utilizar um ponto (⋅) ou o sinal de vezes (×). Assim:
a) 8 × 2 = 8 ⋅ 2 = 16
b) 4 × 12 = 4 ⋅ 12 = 48
2. Utilizamos nomes especiais para indicar algumas multiplicações.
• O dôbro de 5 é o mesmo que 2 ⋅ 5.
• O triplo de 8 é o mesmo que 3 ⋅ 8.
• O quádruplo de 10 é o mesmo que 4 ⋅ 10.
• O quíntuplo de 12 é o mesmo que 5 ⋅ 12.
Situação 2
Sandra coleciona figurinhas de animais da fauna brasileira ameaçados de extinção.
Observe como são as páginas do álbum de Sandra.

Quantas figurinhas cabem em cada página?
Em cada uma das fileiras cabe a mesma quantidade de figurinhas. Esse tipo de organização é conhecido como disposição retangular.
Podemos considerar que há 4 fileiras e cabem 3 figurinhas em cada uma.
4 ⋅ 3 = 12
Ou podemos considerar que há 3 fileiras e cabem 4 figurinhas em cada uma.
3 ⋅ 4 = 12
Logo, cabem 12 figurinhas em cada página do álbum.
Situação 3
Para fazer aulas de tênis, Carlos tem 2 calções e 5 camisetas.

De quantas maneiras diferentes Carlos pode se vestir para praticar tênis?
Para encontrar a resposta, é necessário determinar todas as possibilidades que existem. Observe o esquema a seguir.

Como há 2 calções e, para cada um, há 5 camisetas, o total de possibilidades é dado por:
2 ⋅ 5 = 10
Podemos pensar, ainda, em 5 camisetas e, para cada uma, 2 calções, ou seja, 5 ⋅ 2 = 10.
Logo, Carlos pode se vestir de 10 maneiras diferentes.
Situação 4
Com R$ 28,00vinte e oito reais, compro 3 miniaturas de carro. Quanto vou pagar por 15 dessas miniaturas?
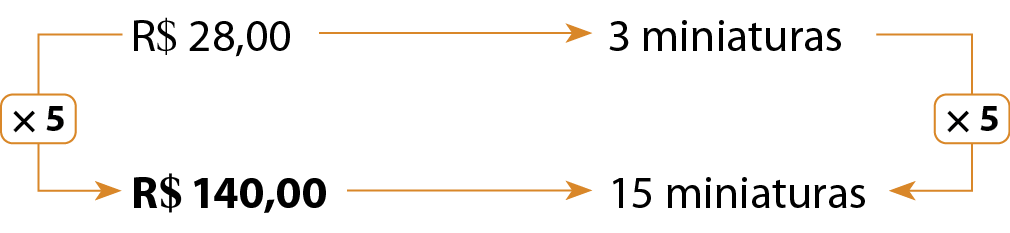
Logo, vou pagar R$ 140,00cento e quarenta reais por 15 miniaturas.
Atividades
Faça as atividades no caderno.
36. Represente cada uma das adições com uma multiplicação.
a) 8 + 8 + 8 + 8
b) 1 + 1 + 1
c) 9 + 9 + 9 + 9 + 9 + 9
d) a + a + a + a
e) 0 + 0 + 0 + 0 + 0
37. Em uma loja de materiais esportivos, há 36 caixas com 12 bolas em cada uma. Podemos calcular o total de bolas nessa loja fazendo apenas uma operação.
a) Que operação é essa?
b) Qual é o resultado dessa operação?
38.

Calcule mentalmente cada multiplicação e registre os resultados no caderno.
a) 17 ⋅ 10
b) 85 ⋅ 100
c) 19 ⋅ 0
d) 174 ⋅ .1000
e) 9 ⋅ 8 ⋅ 0
f) 59 ⋅ .1000
g) .1043 ⋅ 10
h) 75 ⋅ .10000
• O que podemos observar nas multiplicações realizadas?
39.

Calcule mentalmente o resultado de cada multiplicação. Em seguida, registre os resultados.
a) dôbro de duas centenas.
b) Triplo de meio milhar.
c) Quádruplo de uma dúzia.
d) Quíntuplo de 17.
40. Calcule.
546 + 546 + 546 + 546 + 546 + 546 + 546 + 546 + 546
41. Segundo cálculos de uma empresa de distribuição de água, uma torneira gotejando representa 46 litros de água desperdiçada por dia. Quantos litros de água são desperdiçados em 90 dias?
42. Um automóvel percorre, em média, 8 quilômetros com 1 litro de combustível e vem equipado com um tanque com capacidade de 40 litros. Supondo que o tanque de combustível esteja cheio, qual é a medida da distância máxima que esse veículo pode percorrer sem reabastecer?
43. Observe o Setor a do estacionamento de uma indústria automobilística.

a) Qual é o total de vagas do setor?
b) Quantos automóveis estão estacionados?
44. Efetue as multiplicações no caderno, observando o que elas apresentam de curioso.
a) 37 ⋅ 15
b) 37 ⋅ 18
c) 37 ⋅ 21
d) 37 ⋅ 24
•

Agora, um desafio para você: calcule 37 ⋅ .2700 mentalmente.
45. Um motor bombeia .3700 litros de água por minuto para uma cisterna. Quantos litros de água esse motor bombeará em 30 minutos?
46. De quantas maneiras diferentes é possível pintar as três faixas de uma figura como a mostrada a seguir, usando, sem repetir, as cores vermelha, verde e azul? Desenhe todas as possibilidades no caderno.

47. Bruno foi a uma loja de roupas e sapatos e comprou os seguintes itens:
• uma bermuda branca, uma azul e uma vermelha;
• uma camiseta amarela, uma lilás, uma verde e uma cinza;
• um par de tênis branco e um preto.
De quantas maneiras diferentes ele pode combinar as roupas com os tênis?
48. Em uma fábrica de eletrodomésticos, são produzidas duzentas e vinte lavadoras por dia. Em 25 dias, quantas lavadoras são fabricadas?
49.

Elabore um problema que possa ser resolvido calculando 14 × .1255.
50.


Copie o enunciado do problema a seguir em seu caderno e complete com os dados que quiser. Depois, troque com um colega e resolva o problema dele.
Manoela corre de segunda a sábado e percorre

quilômetro por dia. Quantos quilômetros ela percorre, ao todo, por semana? quilômetro por dia. Quantos quilômetros ela percorre, ao todo, por semana?
Algumas propriedades da multiplicação
Vamos conhecer algumas propriedades da multiplicação.
LEMBRE-SE: Escreva no caderno.
Propriedade comutativa
▸

Calcule mentalmente:

a) Que resultados você obteve?
b) O que você percebeu?
▸ Escolha outros dois números naturais e, em seu caderno, multiplique um pelo outro. Em seguida, multiplique os mesmos números trocando a ordem dos fatores. O que você observou?
Em uma multiplicação de números naturais, a ordem dos fatores não altera o produto.
Propriedade associativa
▸

Calcule mentalmente:

a) Que resultados você obteve?
b) O que você percebeu?
▸ Escreva, em seu caderno, três outros números naturais e multiplique o produto dos dois primeiros pelo terceiro. Em seguida, multiplique o primeiro número pelo produto dos dois últimos. O que você observou?
Em uma multiplicação com mais de dois números naturais, podemos associar os fatores de modos diferentes sem alterar o produto.
LEMBRE-SE: Escreva no caderno.
Elemento neutro
▸

Calcule mentalmente:

a) Que resultados você obteve?
b) O que você percebeu?
▸ Escreva em seu caderno alguns números naturais. Em seguida, multiplique cada um desses números por 1. O que você observou?
O número 1, quando multiplicado por outro número natural qualquer, resulta sempre nesse outro número. Ou seja, o 1 como fator da multiplicação não altera o valor do produto. Por isso, ele é chamado elemento neutro da multiplicação.
Propriedade distributiva
O painel a seguir é composto de quadradinhos azuis e amarelos.
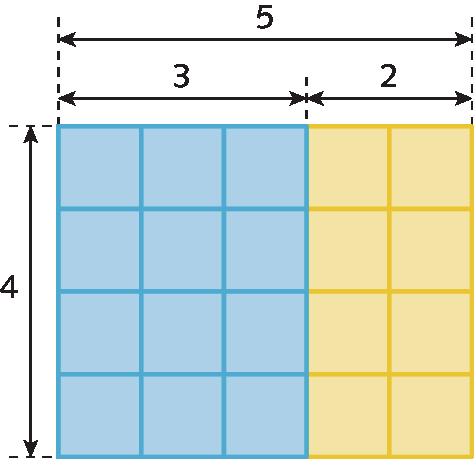
O número de quadradinhos azuis pode ser obtido multiplicando 4 por 3, e o número de quadradinhos amarelos, multiplicando 4 por 2.
Como o número total de quadradinhos do painel é igual ao número de quadradinhos azuis mais o número de quadradinhos amarelos, temos:
4 ⋅ 5 = 4 ⋅ (3 + 2) = 4 ⋅ 3 + 4 ⋅ 2
Podemos observar que, para multiplicar um número natural por uma adição de duas parcelas, adicionamos os produtos de cada parcela pelo número natural. Nesse caso, foi aplicada a propriedade distributiva da multiplicação em relação à adição.
Observação
A propriedade distributiva também pode ser aplicada de fórma análoga para a subtração. Observe os exemplos a seguir.
a) 8 ⋅ abre parênteses5 menos 3fecha parênteses = 8 ⋅ 5 menos 8 ⋅ 3 = 40 menos 24 = 16
b) 15 ⋅ abre parênteses7 menos 4fecha parênteses = 15 ⋅ 7 menos 15 ⋅ 4 = 105 menos 60 = 45
Para multiplicar um número natural por uma adição abre parêntesesou subtraçãofecha parênteses com dois ou mais termos, podemos multiplicar esse número por cada um dos termos da adição abre parêntesesou da subtraçãofecha parênteses e adicionar abre parêntesesou subtrairfecha parênteses os resultados obtidos.
Atividades
Faça as atividades no caderno.
51. Sabendo que a ê b são números naturais e a ⋅ b = 60, responda.
a) Qual é o valor de b ⋅ a?
b) Qual é o valor de 1 ⋅ a ⋅ b?
c) Qual é o valor de a ⋅ abre parêntesesb ⋅ 5fecha parênteses?
• Quais são as propriedades utilizadas para justificar as respostas de cada item?
52. Luís considerou mais fácil calcular 2 ⋅ 37 ⋅ 50 e 30 ⋅ 17 da seguinte maneira: 2 ⋅ 50 ⋅ 37 e 30 ⋅ (10 + 7). Você concorda com Luís? Justifique.
53.

Calcule mentalmente.
a) 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5
b) 100 ⋅ 375 ⋅ 2
c) 50 ⋅ 26 ⋅ 2
d) 25 ⋅ 37 ⋅ 4
54. Sabendo que a é um número natural, observe a igualdade 307 ⋅ a = 307 e responda às questões.
a) Qual é o valor de a?
b) Qual é a propriedade da multiplicação que se aplica a essa situação?
55. Em cada item, aplique a propriedade distributiva da multiplicação.
a) 5 ⋅ abre parênteses8 + 2fecha parênteses
b) 9 ⋅ abre parênteses8 menos 3fecha parênteses
c) abre parênteses2 + 8fecha parênteses ⋅ 15
d) abre parênteses8 menos 3fecha parênteses ⋅ 4
e) 10 ⋅ abre parênteses20 + 30fecha parênteses
f) 12 ⋅ abre parênteses15 menos 6fecha parênteses
56. Determine o número de quadradinhos da figura.
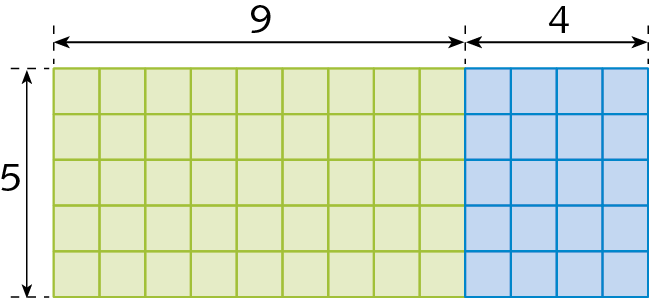

4 Divisão com números naturais
Divisão exata
Observe a situação a seguir.
Reinaldo distribuiu, em quantidades iguais, 45 bombons em cinco embalagens. Quantos bombons ele colocou em cada embalagem?

Para determinar a quantidade de bombons que Reinaldo colocou em cada embalagem, devemos dividir 45 por 5.
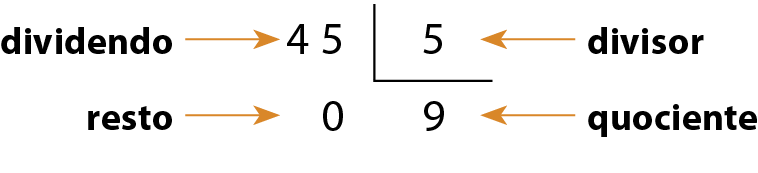

Logo, Reinaldo colocou 9 bombons em cada embalagem.
Chamamos essa operação de divisão.
Nesse caso, usamos a divisão para repartir uma quantidade em partes iguais.
Quando o resto da divisão é zero, dizemos que a divisão é exata.
Dividindo mentalmente
A professora de Ana Clara e Maurício pediu a eles que dividissem .1024 por 4 o mais rápido que conseguissem. Ambos fizeram um cálculo mental e obtiveram o resultado quase ao mesmo tempo: 256. Então, a professora pediu a eles que explicassem como haviam pensado para chegar ao resultado.
• Resposta de Ana Clara: Primeiro, dividi .1024 por 2, que resultou em 512, e, em seguida, dividi 512 por 2 novamente, resultando em 256. Como 2 vezes 2 é igual a 4, achei que fazendo assim ia dar certo.
.1024 dividido por 2 = 512
512 dividido por 2 = 256
• Resposta de Maurício: Fiz a decomposição de .1024 da seguinte maneira .1000 + 20 + 4. Então, primeiro, dividi .1000 por 4, que resultou em 250; depois, dividi 20 por 4, resultando em 5; por fim, dividi 4 por 4, tendo como resposta 1. Então, calculei 250 + 5 + 1, que resultou em 256.
.1024 = .1000 + 20 + 4
.1000 dividido por 4 = 250
20 dividido por 4 = 5
4 dividido por 4 = 1
250 + 5 + 1 = 256
Depois de ouvir as duas resoluções, a professora comentou que tanto Ana Clara quanto Maurício haviam calculado de maneira correta, mas, em comparação com a fórma utilizada por Maurício, a resolução de Ana Clara era mais simples e prática, porque apresentava menos etapas de cálculo.
Atividades
Faça as atividades no caderno.
57. Resolva os problemas.
a) Artur dividiu, igualmente, os 216 peixes do seu tanque em 12 aquários. Quantos peixes Artur colocou em cada um desses aquários?
b) Tia Lúcia repartiu R$ 480,00quatrocentos e oitenta reais igualmente entre os seus 8 sobrinhos. Quantos reais ela deu a cada um?
58. Efetue a divisão de 120 por 5 e responda.
a) Qual é o quociente dessa divisão?
b) Qual é o resto dessa divisão?
59. Efetue no caderno.
a) 156 dividido por 12
b) 320 dividido por 64
c) 900 dividido por 25
d) .10032 dividido por 8
60.

Calcule mentalmente e escreva o resultado.
a) 50 dividido por 10
b) 500 dividido por 10
c) 500 dividido por 100
d) 50 dividido por 5
61. Um caminhão transporta 24.quatrocentas e trinta e duas garrafas de suco em caixas que contêm duas dúzias de garrafas cada uma. Quantas caixas há nesse caminhão?
62.

Reúna-se com um colega e resolvam o seguinte problema.
A luz emitida pelo Sol viaja no vácuo a .300000 quilômetros por segundo. Sabendo que o Sol está a aproximadamente ..150000000 quilômetros da Terra, calculem a quantidade de segundos que a luz do Sol demora para chegar à Terra.
Expressões numéricas com as quatro operações
No cálculo de uma expressão numérica, as operações indicadas devem ser efetuadas na seguinte ordem:
1º) multiplicações e divisões, na ordem em que aparecem;
2º) adições e subtrações, na ordem em que aparecem.
Observe os exemplos a seguir.
a)
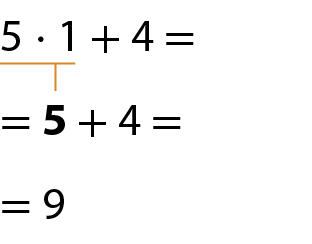
b)

c)
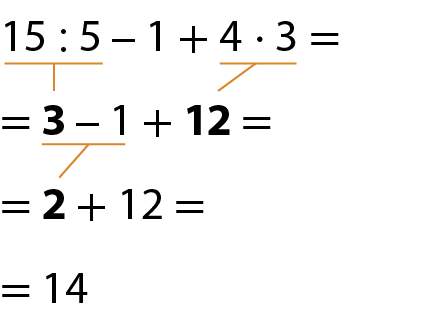
Há expressões em que aparecem sinais de associação. Nesse caso, devemos resolver as operações nesta ordem:
1º) as que estiverem entre parênteses abre parênteses fecha parênteses;
2º) as que estiverem entre colchetes abre colchete fecha colchete;
3º) as que estiverem entre chaves abre chave fecha chave.
Observe os três exemplos a seguir.
a)
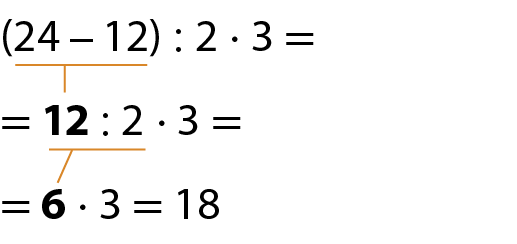
b)
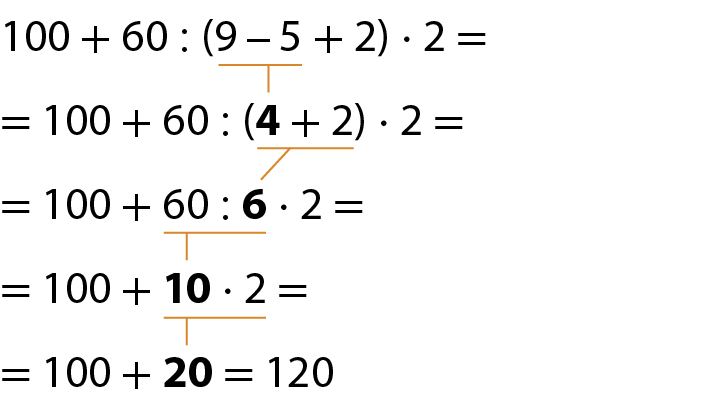
c)
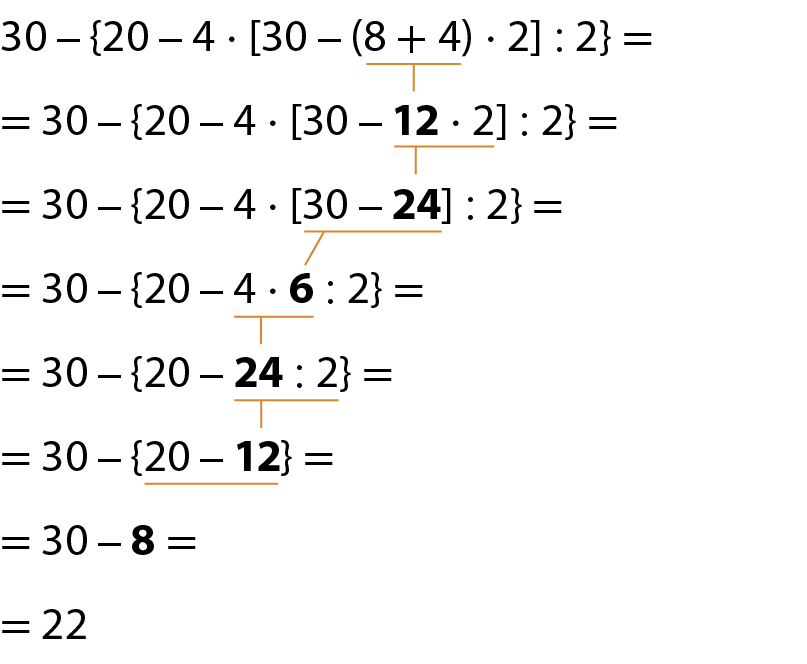
Sugestão de leitura
THOMSON, Michael. O mistério dos números perdidos. Tradução Adazir Almeida Carvalho. São Paulo: Melhoramentos, 2011.
Esse livro traz aventura, desafios e problemas numéricos interessantes para o leitor resolver, superando cada etapa até chegar ao final dessa envolvente história.
Atividades
Faça as atividades no caderno.
63. Calcule o valor das expressões numéricas.
a) 5 + 6 ⋅ 4
b) abre parênteses5 + 6fecha parênteses ⋅ 4
c) 10 + 8 ⋅ 4 menos 15
d) 200 menos 3 ⋅ 60 + 8
e) abre parênteses18 menos 15 dividido por 5 + 3fecha parênteses ⋅ 4
f) abre colcheteabre parênteses21 dividido por 7fecha parênteses ⋅ abre parênteses3 dividido por 1fecha parênteses + 6fecha colchete menos abre colcheteabre parênteses7 ⋅ 6fecha parênteses dividido por abre parênteses5 menos 2fecha parêntesesfecha colchete
g) abre chaveabre colchete13 menos abre parênteses3 ⋅ 2 + 1fecha parêntesesfecha colchete + 3 + abre parênteses5 ⋅ 2 menos 4 : 2fecha parêntesesfecha chave
64.


No caderno, elabore um problema que possa ser resolvido por meio da expressão numérica a seguir.

Depois, troque de caderno com um colega e resolva o problema criado por ele.
O colega resolveu corretamente o seu problema? Qual é a solução do problema?
Divisão não exata
Vamos dividir 38 por 7.
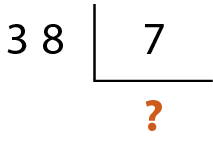
Observe que não existe nenhum número natural que, ao ser multiplicado por 7, dê como resultado 38. O número natural que, ao ser multiplicado por 7, origina o produto mais próximo e menor que 38 é 5.
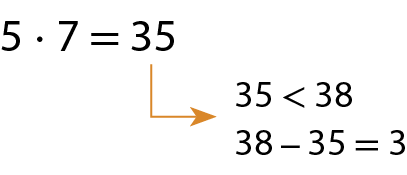
Assim, 38 : 7 é uma divisão com quociente igual a 5 e resto igual a 3. Observe:
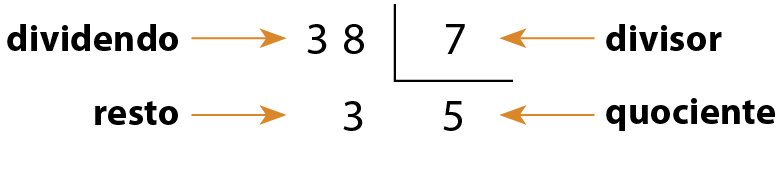
Quando o resto da divisão é diferente de zero, dizemos que a divisão é não exata.
Relação fundamental da divisão
Na divisão de 38 por 7, observamos que: 38 = 5 ⋅ 7 + 3
Em qualquer divisão, o dividendo é igual ao quociente multiplicado pelo divisor mais o resto. Essa relação é chamada de relação fundamental da divisão:
dividendo = quociente ⋅ divisor + resto
Observações
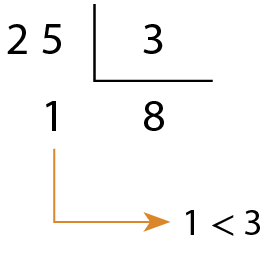
1. O resto de uma divisão entre dois números naturais é sempre menor que o divisor. Observe alguns exemplos a seguir.
a)
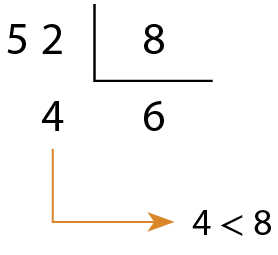
b)
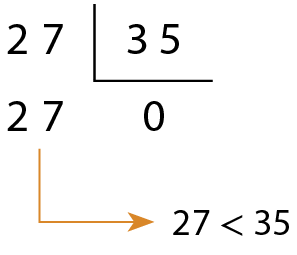
c)
2. A divisão exata é a operação inversa da multiplicação. Observe os exemplos:
a) 4 ⋅ 5 = 20
20 dividido por 5 = 4
b) 7 ⋅ 6 = 42
42 dividido por 6 = 7
3. A divisão de zero por qualquer número natural diferente de zero é sempre zero.
a) 0 dividido por 3 = 0
b) 0 dividido por 25 = 0
c) 0 dividido por .1587 = 0
4. O quociente de 6 : 0 deveria ser o número que, multiplicado por zero, resultasse em 6. Não há número que multiplicado por zero resulte em 6; logo, é impossível efetuar 6 dividido por 0.Esse raciocínio é válido para qualquer outra divisão por zero. Podemos dizer que é impossível dividir por zero, ou seja, o zero nunca pode ser divisor.
Atividades
Faça as atividades no caderno.
65. Determine o quociente e o resto de cada uma das divisões a seguir.
a) 37 dividido por 15
b) 108 dividido por 32
c) 2 332 dividido por 41
d) 5 600 dividido por 95
e) 17 890 dividido por 100
f) 1 847 dividido por 28
66. Copie as divisões no caderno, substituindo cada

pelo número que falta.
a)

b)
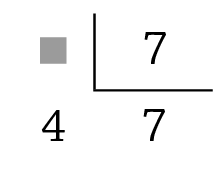
c)
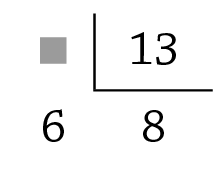
d)

e)
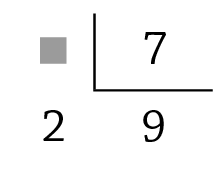
f)

67.


Junte-se a um colega e resolvam o seguinte problema.
Luísa quer dividir 528 por 132 utilizando a calculadora, mas há um problema: das teclas das operações, só funciona a da subtração. Como Luísa deverá fazer o cálculo para obter o resultado da divisão?
68. Na divisão de .60000 por .1800, quais são o quociente e o resto?
69. Em um colégio, há 540 estudantes, que serão divididos em grupos de 37 para participar de um desfile.
a) Quantos grupos completos serão formados?
b) Quantos estudantes seriam necessários para completar mais um grupo?
70. Responda às questões.
a) Qual é o quociente da divisão de zero por 10?
b) Qual é o quociente da divisão de 10 por zero?
71.

Utilizando uma calculadora, efetue a divisão de 8 por 0. O que apareceu no visor da calculadora?
72.

Junte-se a um colega e resolvam o seguinte problema.
A carga máxima permitida em um elevador é 500 quilogramas. Qual é o número mínimo de viagens necessárias para que uma pessoa com 75 quilogramas possa transportar 45 caixas de 30 quilogramas cada uma?
73.

Maria utilizou uma calculadora e fez os seguintes cálculos:

Elabore um problema que possa ser resolvido utilizando a operação inversa da multiplicação que Maria efetuou.

5 Potenciação com números naturais
Para representar uma multiplicação em que todos os fatores são iguais, podemos usar a potenciação.
Podemos representar, por exemplo, a multiplicação 4 ⋅ 4 ⋅ 4 ⋅ 4 assim: 4elevado a 4 (lemos: “quatro elevado à quarta potência” ou “quatro à quarta”). Observe:

De modo geral, na potenciação com números naturais, a base é o fator que se repete na multiplicação, o expoente indica a quantidade de vezes que o fator se repete e a potência é o resultado da operação.
Com isso, para o exemplo anterior, temos:
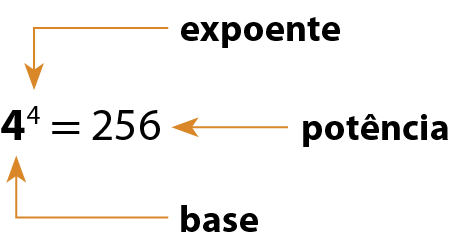
Outros exemplos podem ser:
a) 3elevado a 5 = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243
b) 0elevado a 6 = 0 ⋅ 0 ⋅ 0 ⋅ 0 ⋅ 0 ⋅ 0 = 0
c) 1elevado a 8 = 1 ⋅ 1 ⋅ 1 ⋅ 1 . 1 ⋅ 1 ⋅ 1 ⋅ 1 = 1
d) 10elevado a 3 = 10 ⋅ 10 ⋅ 10 = .1000
Observação
Quando o expoente é igual a 1, a potência é igual à base. E, quando o expoente é igual a zero, com a base diferente de zero, a potência é igual a 1. Por exemplo:
a) 5elevado a 1 = 5
b) 31elevado a 1 = 31
c) 60elevado a 0 = 1
d) 759elevado a 0 = 1
Leitura de potências
Observe como lemos algumas potências.
a) 3elevado a 2: “três elevado à segunda potência”
b) 6elevado a 7: “seis elevado à sétima potência”
c) 2elevado a 3: “dois elevado à terceira potência”
d) 4elevado a 9: “quatro elevado à nona potência”
As potências com expoentes 2 e 3 podem ser lidas de outra maneira. Vamos estudá-las.
Potência de expoente 2 ou quadrado de um número
Por causa de sua representação geométrica, as potências de expoente 2 têm nomes especiais. Acompanhe os exemplos.
a)

b)
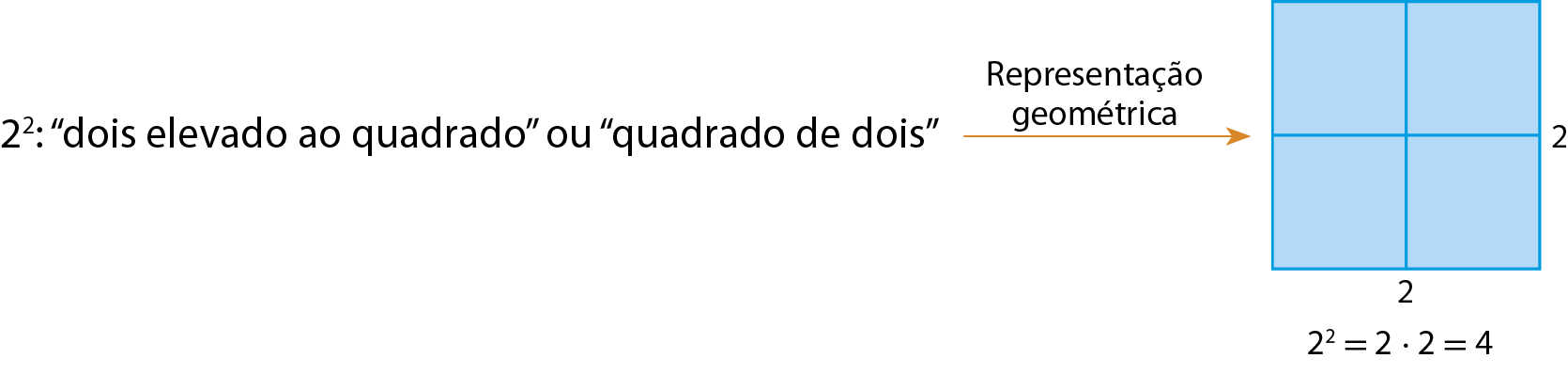
Observação
Um número natural é considerado um quadrado perfeito quando é o produto de dois números naturais iguais.
a) 1 ⋅ 1 = 1
b) 2 ⋅ 2 = 4
c) 3 ⋅ 3 = 9
d) 4 ⋅ 4 = 16
e) 5 ⋅ 5 = 25
Os números 1, 4, 9, 16 e 25 são exemplos de quadrados perfeitos.
Potência de expoente 3 ou cubo de um número
Da mesma fórma que as potências de expoente 2, as potências de expoente 3 também recebem nomes especiais. Acompanhe os exemplos.
a)

b)
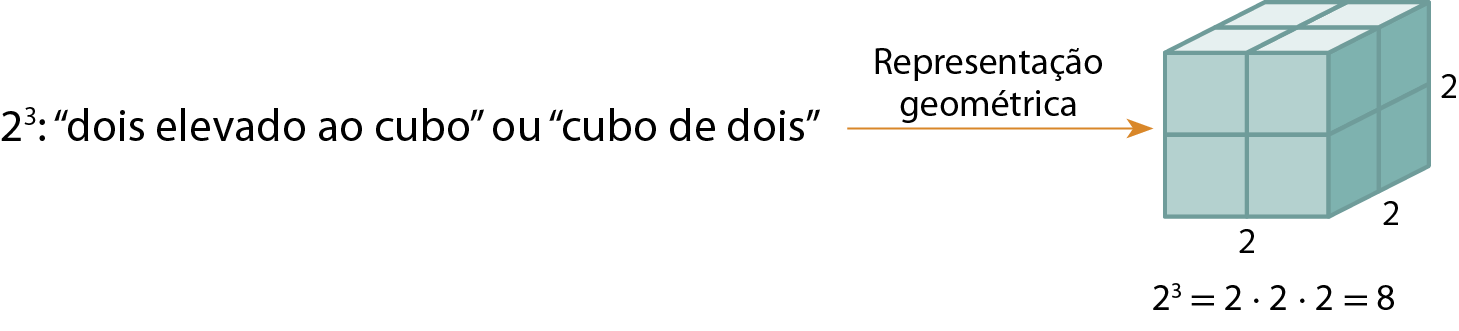
Potências de base 10
Observe as seguintes potências de base 10:
a) 10elevado a 1 = 10
b) 10elevado a 3 = 10 ⋅ 10 ⋅ 10 = .1000
c) 10elevado a 5 = 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 1.00000
Nesses exemplos, percebe-se que as potências de base 10, com expoentes naturais, são iguais a um número formado pelo algarismo 1 seguido de tantos zeros quantas forem as unidades do expoente.
Decomposição de um número usando potências de base 10
Considere, por exemplo, os números 54, 857 e .56948. Decompondo-os e aplicando potências de 10, podemos escrever:
a) 54 = 50 + 4 = 5 ⋅ 10elevado a 1 + 4 ⋅ 10elevado a 0
b) 857 = 800 + 50 + 7 = 8 ⋅ 100 + 5 ⋅ 10 + 7 = 8 ⋅ 10elevado a 2 + 5 ⋅ 10elevado a 1 + 7 ⋅ 10elevado a 0
c) .56948 = .50000 + .6000 + 900 + 40 + 8 = 5 ⋅ 10elevado a 4 + 6 ⋅ 10elevado a 3 + 9 ⋅ 10elevado a 2 + 4 ⋅ 10elevado a 1 + 8 ⋅ 10elevado a 0

Veja que interessante
Faça a atividade no caderno.
É comum, principalmente em Física, escrever números com muitos algarismos usando potência de base 10.
Tomando como exemplo a velocidade da luz, que é, aproximadamente, trezentos milhões de metros por segundo, temos:
..300000000 de metros por segundo ou 3 ⋅ ..100000000 metros por segundo ou 3 ⋅ 10elevado a 8 metros por segundo
Atividade
Escreva os números .700000 e ..2560000 utilizando potências de base 10.
Atividades
Faça as atividades no caderno.
74. Calcule o valor das potências.
a) 3elevado a 5
b) 4elevado a 3
c) 14elevado a 2
d) 2elevado a 5
e) 10elevado a 3
f) 1elevado a 6
g) 11elevado a 2
h) 15elevado a 0
i) 17elevado a 1
j) 0elevado a 5
k) 50elevado a 1
l) 20elevado a 2
75. Escreva como se leem as potências a seguir.
a) 7elevado a 2
b) 9elevado a 3
c) 10elevado a 4
d) 13elevado a 5
76. Calcule:
a) o quadrado de 13;
b) o cubo de 7;
c) três elevado à sexta potência.
77. Calcule o valor de 2elevado a 5 menos 5elevado a 2.
78. Escreva no caderno os números a seguir usando potências de base 10.
a) .600000
b) ..4500000
c) ...8000000000
d) .8700
79. O professor Daniel escreveu na lousa duas sequências com potências dos números 2 e 3.

Que números deveriam ser colocados nos quadrinhos?
80. Expresse, em potência de base 10, o número de cubinhos que formam o cubo maior da figura.

81. Determine em cada caso a potência de maior valor.
a) 100elevado a 1 ou 1elevado a 100
b) 80elevado a 0 ou 0elevado a 80
82.

Calcule mentalmente as potências.
a) 10elevado a 5
b) 10elevado a 2
c) 8 ⋅ 10elevado a 2
d) 52 ⋅ 10elevado a 3
83. Decomponha os números usando potências de 10.
a) 938
b) .4078
c) .7952
d) .60000
84. Determine o valor de 5elevado a 4 e 5elevado a 6, sabendo que 5elevado a 5 é igual a .3125. Em cada um dos casos, faça apenas um cálculo.
85. Em uma caixa como a da figura a seguir, Pedro distribuiu bolinhas de gude. Na primeira casa, ele colocou uma bolinha e, em cada uma das casas seguintes, o dôbro do número de bolinhas da anterior.
Quantas bolinhas Pedro colocou na oitava casa?

Expressões numéricas com potenciações
Agora, vamos estudar expressões numéricas envolvendo as operações com os números naturais que vimos até aqui.
Para calcular o valor de qualquer expressão numérica que contenha as operações de adição, subtração, multiplicação, divisão e potenciação, a seguinte ordem deve ser obedecida:
1º) potenciações;
2º) multiplicações e divisões abre parêntesesna ordem em que aparecemfecha parênteses;
3º) adições e subtrações abre parêntesesna ordem em que aparecemfecha parênteses.
Vale lembrar que, em expressões com sinais de associação, estes devem ser eliminados na seguinte ordem: parênteses, colchetes e chaves.
Observe os exemplos a seguir.
a)
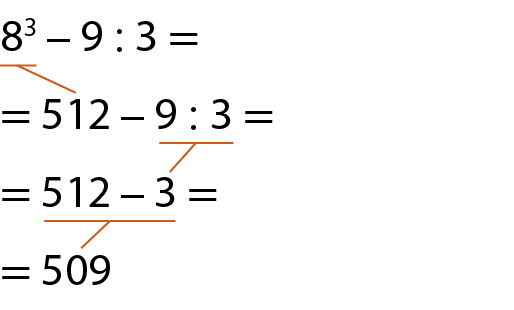
b)
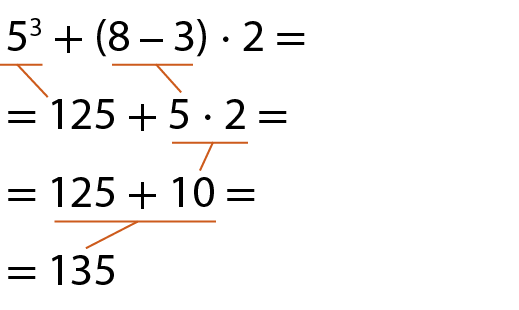
c)
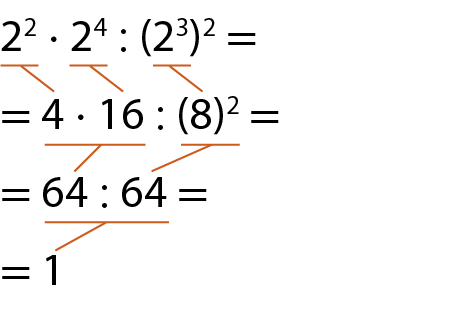
d)
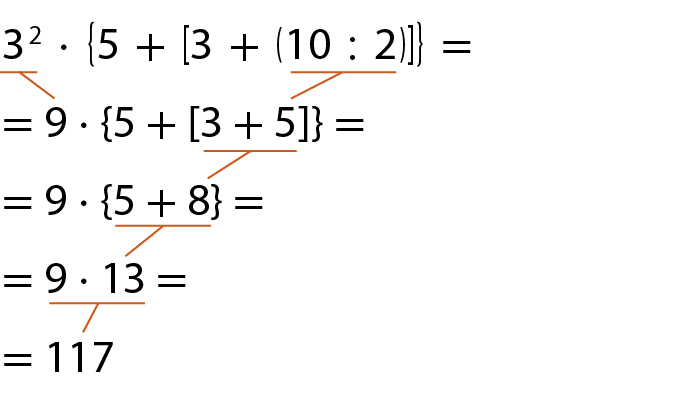
Atividades
Faça as atividades no caderno.
86. Calcule o valor das expressões numéricas.
a) 20 menos abre parênteses1elevado a 4 ⋅ 6 + 2elevado a 3fecha parênteses
b) abre parênteses2elevado a 4 menos 3 ⋅ 4fecha parênteses dividido por 2 + 5elevado a 2 dividido por 5
c) 10elevado a 2 dividido por 5elevado a 2 + 5elevado a 0 ⋅ 2elevado a 2 menos 2elevado a 3
d) abre chave6elevado a 2 + 2 ⋅ abre colchete2elevado a 3 + 2 ⋅ abre parênteses3elevado a 2 ⋅ 1elevado a 3fecha parêntesesfecha colchete menos 2elevado a 5fecha chave ⋅ 5elevado a 0
e) 55 menos abre parênteses3 ⋅ 2 + 1fecha parênteseselevado a 2 + abre parênteses4elevado a 2 + 3elevado a 2fecha parênteses dividido por 5elevado a 2 menos 1elevado a 6
87. Calcule o valor de A + B sabendo que:
a = abre parênteses3 ⋅ 2 menos 1fecha parênteseselevado a 2 e
B = abre parênteses2elevado a 2 + 1fecha parênteses ⋅ abre parênteses5 + 2elevado a 3fecha parênteses
88. Calcule a diferença entre o dôbro do cubo de 8 e o triplo do quadrado de 17.
89.


Elabore um problema que possa ser resolvido por meio de uma expressão numérica com potenciações. Depois troque seu problema com um colega e resolva o problema proposto por ele.
90.

Reúna-se com um colega, resolvam o problema a seguir e justifiquem a resposta.
Pensem em um número diferente de zero. Multipliquem-no por 3 e acrescentem 1 ao resultado. Multipliquem o novo resultado por 3 e adicionem o produto com o número em que vocês pensaram. O resultado terminará em 3. Eliminem o 3.


6 Arredondamentos e estimativas
Em muitas situações, não é necessário saber o valor exato de uma operação. Acompanhe o exemplo a seguir.
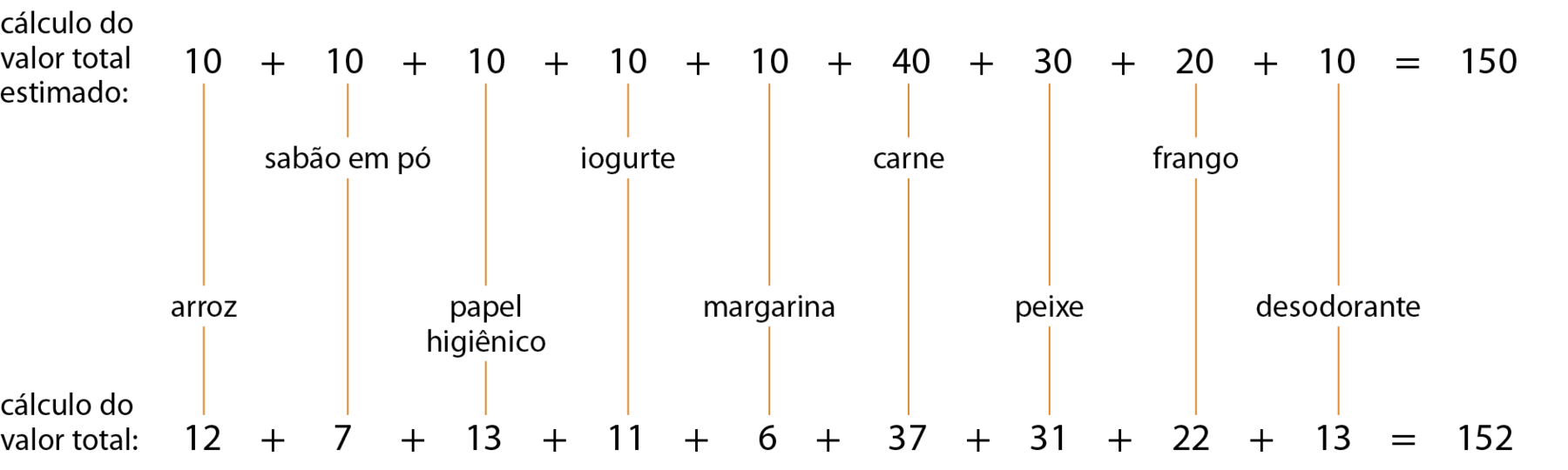
Paulo foi ao supermercado com uma cédula de 200 reais. Antes de passar no caixa, ele verificou se teria dinheiro suficiente para pagar a compra. Analise o que ele fez.

Ao fazer os cálculos, Paulo utilizou o arredondamento dos preços dos produtos para fazer a estimativa do valor total gasto na compra.
Para arredondar um número para determinada ordem decimal, temos que observar o primeiro algarismo à direita da ordem escolhida:
• se for 0, 1, 2, 3 ou 4, mantém-se o algarismo da ordem (arredondando o número “para baixo”);
• se for 5, 6, 7, 8 ou 9, arredonda-se “para cima”, ou seja, adiciona-se 1 ao algarismo da ordem.
Depois, devem-se substituir por zeros os algarismos à direita do algarismo da ordem.
A seguir temos dois exemplos de arredondamento.
a) Arredondar o número 178 para a ordem das dezenas mais próxima:

b) Arredondar o número ..29428742 para a ordem de centena de milhar mais próxima:

Atividades
Faça as atividades no caderno.
91. Faça os arredondamentos conforme indicado em cada item.
a) 369, para a centena mais próxima.
b) .357896, para a dezena de milhar mais próxima.
c) 111, para a centena mais próxima.
d) 111, para a dezena mais próxima.
92. Calcule o valor aproximado da expressão numérica

93.

Responda às questões no caderno.
a) Cite exemplos de situações em que utilizamos arredondamentos e estimativas.
b)


Elabore um problema e resolva-o usando estimativa. Peça a um colega que resolva o problema elaborado por você usando também estimativa. Agora, compare as resoluções.
94.

Maria precisa comprar uma geladeira e um fogão com um orçamento de R$ 1.850,00mil oitocentos e cinquenta reais. Ela pesquisou os preços dos produtos em duas lojas. Observe os preços, faça os cálculos mentalmente e, depois, responda às questões.

a) Se Maria tivesse que comprar os eletrodomésticos na mesma loja, em qual loja ela conseguiria realizar a compra?
b) Se Maria comprasse os eletrodomésticos em lojas diferentes, qual seria a melhor combinação e o valor total estimado da compra?

Resolvendo em equipe
Faça a atividade no caderno.
(ó bê mépi) Vovô Eduardo comemorou todos os seus aniversários a partir dos 40 anos colocando, no bolo, velinhas em fórma de algarismos de 0 a 9 para indicar sua idade. Primeiro, ele comprou as velinhas de números 0 e 4. Ele sempre guardou as velinhas para usar nos próximos aniversários, comprando uma nova somente quando não era possível indicar sua idade com as guardadas. Hoje vovô Eduardo tem 85 anos. Quantas velinhas ele comprou até hoje?

a) 10
b) 11
c) 13
d) 14
e) 16
|
Interpretação e identificação dos dados |
• Analise as informações do enunciado e anote aquelas que julgar relevantes para a resolução do problema. |
|---|---|
|
Plano de resolução |
• Calcule a quantidade de velinhas compradas para as dez primeiras comemorações de aniversário e para as comemorações de 50 a 59 anos. |
|
Resolução |
• Forme um grupo com três colegas. |
|
Verificação |
• O grupo deve reler o problema e verificar se todas as condições do enunciado foram satisfeitas. |
|
Apresentação |
• O professor vai escolher um dos grupos para apresentar o plano desenvolvido e a solução obtida. Durante a exposição, os outros grupos devem observar suas resoluções e verificar se os resultados obtidos estão de acordo com o que foi apresentado. |
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Adição com números naturais
A adição pode ser empregada com a ideia de juntar quantidades ou de acrescentar uma quantidade a outra.

Algumas propriedades da adição
Comutativa: em uma adição de números naturais, a ordem das parcelas não altera a soma.
Associativa: Em uma adição de três ou mais números naturais, podemos associar as parcelas de diferentes modos sem alterar a soma.
Elemento neutro: O zero, quando adicionado a outro número natural qualquer, resulta sempre nesse outro número. Ou seja, o zero como parcela da adição não altera o valor da soma. Por isso, ele é chamado de elemento neutro da adição.
1. Determine o resultado das adições.
a) .1231 + .3420
b) .4231 + 335 + .1320
c) .21230 + .1210 + 589
d) .112250 + .217817
e) .420789 + .1118 + .2981
2. Copie as sentenças em seu caderno e complete-as.
a) 87 + 91 = 91 +

b) .1250 + 0 = 0 +

c) .11388 + .2188 = .2188 +

d) .25257 + .9235 =

+ .22257
3. Em três meses Luana conseguiu juntar dinheiro para comprar uma bicicleta. No primeiro mês, juntou R$ 225,00duzentos e vinte e cinco reais; no segundo mês, R$ 218,00duzentos e dezoito reais; e no terceiro, R$ 175,00cento e setenta e cinco reais. Sabendo que ela gastou todo esse valor na compra, qual foi o preço da bicicleta?
Subtração com números naturais
A subtração pode ser empregada com a ideia de tirar uma quantidade de outra, de completar uma quantidade ou, ainda, de comparar duas quantidades.
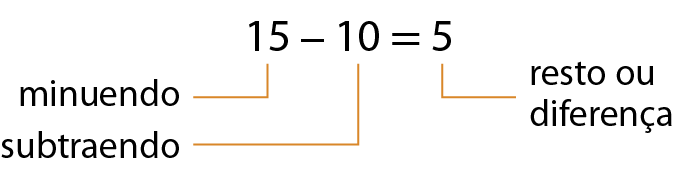
Relação fundamental da subtração
Se o minuendo menos o subtraendo é igual ao resto, então o subtraendo mais o resto é igual ao minuendo.
4. Determine o resultado das subtrações.
a) .7110 menos .1899
b) .8890 menos .6380
c) .12777 menos .11756
d) .38210 menos .15791
5. Copie as sentenças em seu caderno e complete-as.
a) 571 menos

= 289
b) .1315 menos

= 872
c)

menos .1901 = 912
d)

menos 512 = .1003
6. Em uma subtração, o resto é 439 e o subtraendo é 212. Qual é o valor do minuendo?
Expressões numéricas com adições e subtrações
• Nas expressões numéricas em que não há parênteses, as operações de adição e de subtração devem ser feitas na ordem em que aparecem.
• Nas expressões numéricas em que há parênteses, eles indicam as operações que devem ser feitas primeiro.
7. Calcule o valor de cada expressão numérica.
a) abre parênteses25 menos 18 + 13fecha parênteses + 11
b) 45 + abre parênteses70 menos 36fecha parênteses + 12
c) abre parênteses115 menos 82fecha parênteses menos abre parênteses15 + 18fecha parênteses + 9
8. Joana comprou uma geladeira que custa R$ 1.825,00mil oitocentos e vinte e cinco reais. Ela vai pagar em duas prestações. Se ela pagou R$ 1.075,00mil setenta e cinco reais na primeira prestação, qual será o valor da segunda?
9. No estoque de uma loja, havia uma.duzentas e cinquenta unidades de determinado produto. No mês de janeiro foram vendidas trezentas e sessenta e oito unidades, no mês de fevereiro, quatrocentas e vinte e cinco unidades. Para repor o estoque, no início de março, foram adicionadas quinhentas e sessenta unidades desse produto ao estoque. Quantas unidades desse produto há agora no estoque da loja?
Multiplicação com números naturais
A multiplicação pode ser empregada com a ideia de adição de parcelas iguais, a de proporcionalidade, a de disposição retangular ou a de combinação.
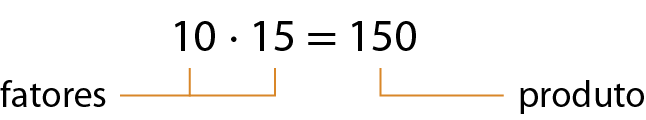
Algumas propriedades da multiplicação
Comutativa: Em uma multiplicação de números naturais, a ordem dos fatores não altera o produto.
Associativa: Em uma multiplicação com mais de dois números naturais, podemos associar os fatores de modos diferentes sem alterar o produto.
Elemento neutro: O número 1, quando multiplicado por outro número natural qualquer, resulta sempre nesse outro número. Ou seja, o 1 como fator da multiplicação não altera o valor do produto. Por isso, ele é chamado elemento neutro da multiplicação.
Distributiva: Para multiplicar um número natural por uma adição (ou subtração) com dois ou mais termos, podemos multiplicar esse número por cada um dos termos da adição (ou da subtração) e adicionar (ou subtrair) os resultados obtidos.
10. Efetue.
a) 45 ⋅ 12
b) 18 ⋅ 25
c) 320 ⋅ 8
d) 368 ⋅ 10
e) 815 ⋅ 18
f) .1236 ⋅ 50
11.

Calcule mentalmente o resultado de cada multiplicação e registre no caderno.
a) 18 ⋅ 10
b) 92 ⋅ 100
c) 112 ⋅ 10
d) 310 ⋅ 100
e) 15 ⋅ .1000
f) .1020 ⋅ 10
12. Leandro comprou uma motocicleta e vai pagar em 36 prestações iguais de R$ 585,00quinhentos e oitenta e cinco reais. Quantos reais Leandro vai pagar por essa motocicleta?
13. Uma torneira com vazamento desperdiça 300 mililitros de água por hora. Quantos mililitros de água serão desperdiçados em 1 dia?
14. Copie as sentenças em seu caderno e complete-as usando as propriedades da multiplicação.
a) 28 ⋅ 17 =

⋅ 28
b) 22 ⋅ abre parênteses10 ⋅ 13fecha parênteses = abre parênteses22 ⋅

fecha parênteses ⋅ 13
c) 115 ⋅ abre parênteses

⋅ 18fecha parênteses = abre parênteses

⋅ 100fecha parênteses ⋅

d) 54 ⋅ abre parênteses21 ⋅ 12fecha parênteses = abre parênteses54 ⋅

fecha parênteses ⋅

e) 890 ⋅ 77 =

⋅ 890
f) .5801 ⋅

= 99 ⋅ .5801
15. Calcule o valor das expressões de duas maneiras.
a) 9 ⋅ abre parênteses15 + 11fecha parênteses
b) 12 ⋅ abre parênteses18 menos 5fecha parênteses
c) 15 ⋅ abre parênteses10 + 12fecha parênteses
d) 10 ⋅ abre parênteses27 menos 12fecha parênteses
Divisão com números naturais
A divisão pode ser empregada com a ideia de repartir em partes iguais ou para descobrir quantas vezes uma quantidade cabe em outra.
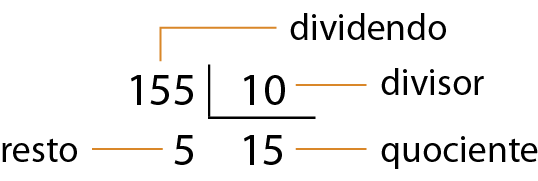
Quando o resto da divisão é zero, dizemos que a divisão é exata; quando é diferente de zero, a divisão é não exata.
Relação fundamental da divisão
dividendo = quociente ⋅ divisor + resto
16. Calcule o quociente e o resto de cada divisão.
a) 155 dividido por 10
b) 212 dividido por 6
c) 550 dividido por 15
d) 198 dividido por 9
e) .1213 dividido por 10
f) .2120 dividido por 5
17. Copie no caderno cada uma das divisões, substituindo cada

pelo número desconhecido.
a)
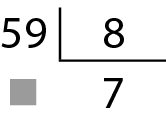
b)
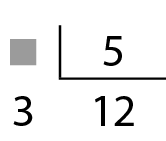
c)
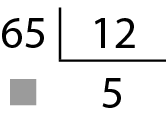
d)
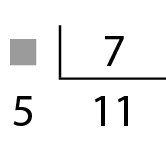
18. Mariana comprou um pacote de viagens para as férias de final de ano. Ela vai pagar esse pacote em 12 prestações iguais. Se o pacote de viagens custou R$ 10.800,00dez mil oitocentos reais, quanto Mariana vai pagar em cada prestação?
Expressões numéricas com as quatro operações
Expressões numéricas podem envolver as operações aritméticas de adição, subtração, multiplicação e divisão. Quando essas operações estão na mesma expressão, seguimos uma ordem para resolvê-las:
1º) a multiplicação ou a divisão, na ordem em que aparecem na expressão;
2º) a adição e a subtração, também na ordem em que aparecem.
Além dos parênteses, podem aparecer outros sinais de associação na expressão numérica, que determinam a ordem de realização dos cálculos. Assim, calculamos:
1º) o que está dentro dos parênteses – abre parênteses fecha parênteses;
2º) o que está dentro dos colchetes – abre colchete fecha colchete;
3º) o que está dentro das chaves – abre chave fecha chave.
19. Calcule o valor de cada expressão numérica.
a) 12 + 11 ⋅ 5
b) 15 ⋅ abre parênteses12 + 9fecha parênteses menos 7
c) abre parênteses98 menos 9 ⋅ 7fecha parênteses + abre parênteses12 + 18 dividido por 3fecha parênteses
Potenciação com números naturais
Para representar uma multiplicação em que todos os fatores são iguais, podemos usar a potenciação.
De modo geral, na potenciação com números naturais, a base é o fator que se repete na multiplicação, e o expoente indica a quantidade de vezes que esse fator se repete. Isso não vale para potências com expoente zero ou 1.
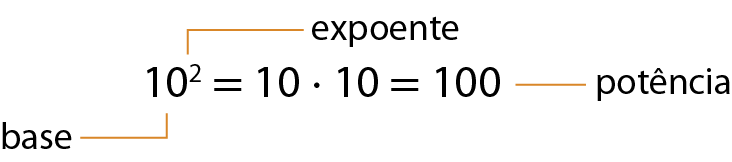
20. Calcule o valor das potências.
a) 3elevado a 2
b) 2elevado a 3
c) 9elevado a 3
d) 10elevado a 2
e) 60elevado a 0
f) 100elevado a 1
g) 30elevado a 2
h) 8elevado a 3
21. Escreva como se leem as potências a seguir.
a) 9elevado a 2
b) 10elevado a 5
c) 12elevado a 3
d) 5elevado a 4
22. Escreva no caderno os números a seguir usando potências de base 10.
a) 700
b) .380000
c) .45000
23. Um número quadrado perfeito pode ser representado geometricamente por um quadrado formado por quadradinhos menores.
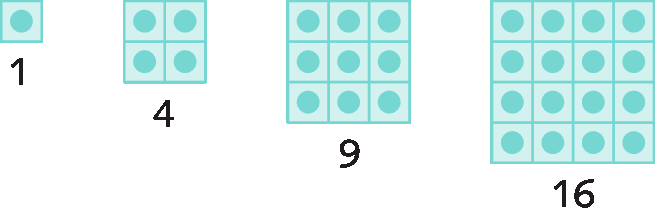
a) Considerando a sequência 1, 4, 9 e 16, quais são os dois números quadrados perfeitos seguintes?
b) Quais são os números quadrados perfeitos situados entre 150 e 250?
24. Se 2elevado a 10 = .1024, qual é o valor de 2elevado a 9? E de 2elevado a 11?
Expressões numéricas com potenciações
As operações devem ser efetuadas na seguinte ordem:
1º) potenciações;
2º) multiplicações e divisões (na ordem em que aparecem);
3º) adições e subtrações (na ordem em que aparecem).
Vale lembrar que, em expressões com sinais de associação, estes devem ser eliminados na seguinte ordem: parênteses, colchetes e chaves.
25. Calcule o valor das expressões.
a) 115 menos abre parênteses5elevado a 2 ⋅ 2 + 2elevado a 3fecha parênteses
b) abre chave148 menos 3 ⋅ abre colchete3elevado a 3 + 18 dividido por abre parênteses3elevado a 2 + 9fecha parêntesesfecha colchetefecha chave ⋅ 2elevado a 3
Arredondamento e estimativas
Para arredondar um número para determinada ordem decimal, devemos observar o primeiro algarismo à direita da ordem escolhida:
• se for 0, 1, 2, 3 ou 4, mantém-se o algarismo da ordem;
• se for 5, 6, 7, 8 ou 9, arredonda-se “para cima”, ou seja, adiciona-se 1 ao algarismo da ordem.
Depois, devem-se substituir por zeros os algarismos à direita do algarismo da ordem.
26. Faça arredondamentos conforme indicado em cada item.
a) 598, para a centena mais próxima.
b) 891, para a centena mais próxima.
c) 891, para a dezena mais próxima.