Capítulo 3 Figuras geométricas espaciais
Trocando ideias
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
No nosso dia a dia, podemos observar elementos da natureza, objetos e construções de diferentes formatos. Algumas frutas, como a laranja, se parecem com uma esfera; uma árvore conífera, como o próprio nome sugere, se parece com um cone; as colunas de alguns edifícios são parecidas com cilindros.

▸

Com quais figuras geométricas espaciais se parecem as construções e esculturas a seguir?

▸

Reúna-se com um colega e pesquisem imagens que contenham elementos que se parecem com figuras geométricas espaciais.
Neste capítulo vamos estudar algumas figuras geométricas espaciais.

1 Sólidos geométricos
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
As indústrias utilizam diferentes tipos de embalagem para acondicionar alimentos, bebidas, produtos químicos, entre outros. Muitas dessas embalagens se parecem com sólidos geométricos, como podemos observar a seguir.

Em Geometria, sólido é uma figura geométrica espacial e maciça, ou seja, não oca. Já a superfícieglossário é toda a parte visível de um sólido geométrico.
Podemos classificar os sólidos separando-os nos grupos a seguir.
Poliedros
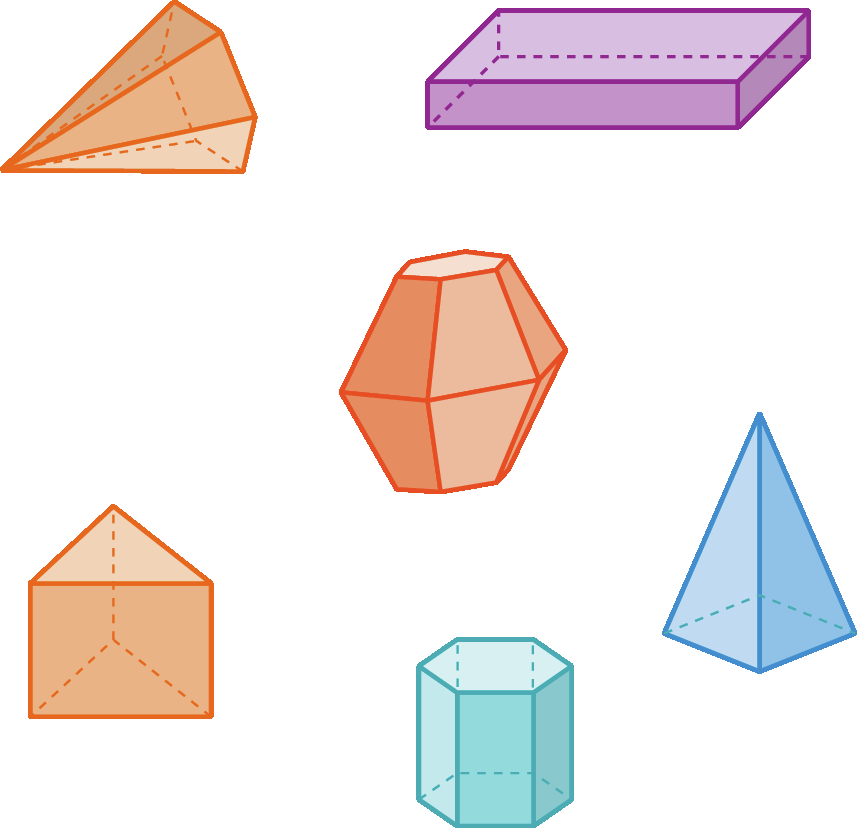
Corpos redondos
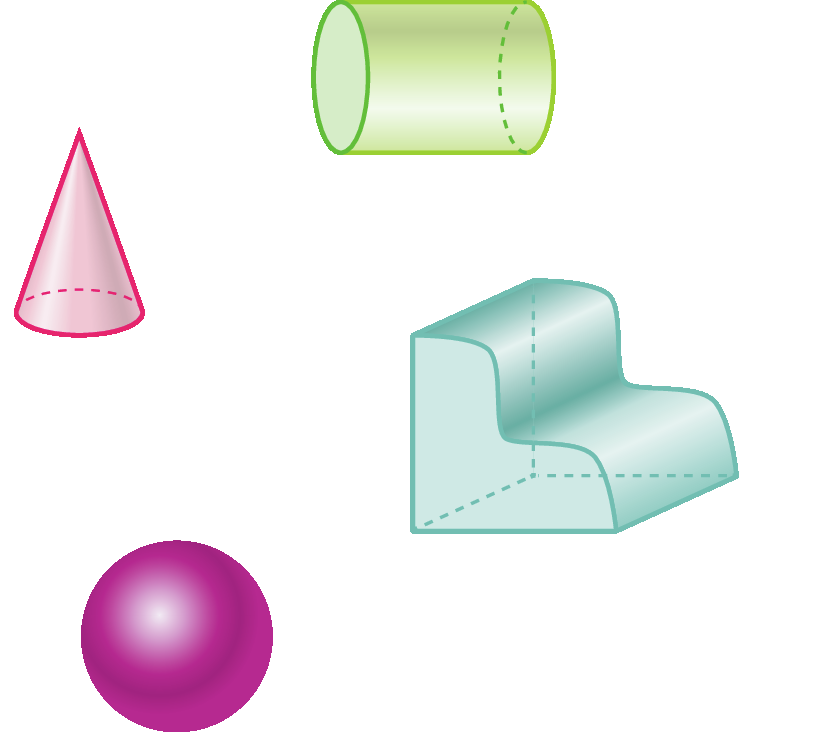
A superfície dos poliedros é formada apenas por partes planas (chamadas de face). Já a superfície dos corpos redondos apresenta pelo menos uma parte arredondada, ou seja, não plana.

2 Poliedros
Em qualquer poliedro, devemos encontrar vértices, arestas e faces. Confira:
Cada região que fórma a superfície de um poliedro é chamada face. O segmento comum a duas faces é chamado aresta, e os pontos de encontro das arestas são chamados vértices.
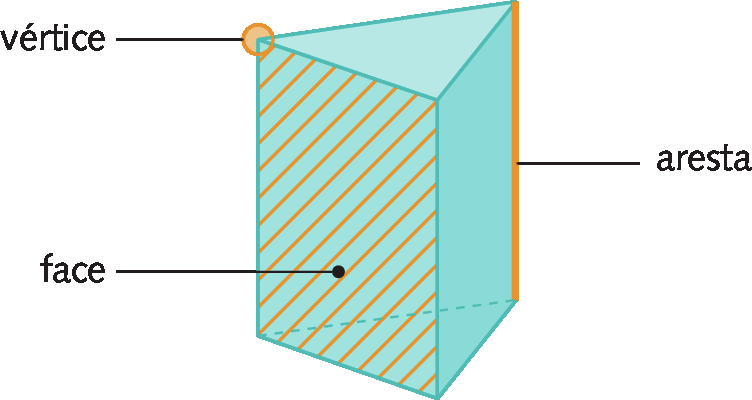
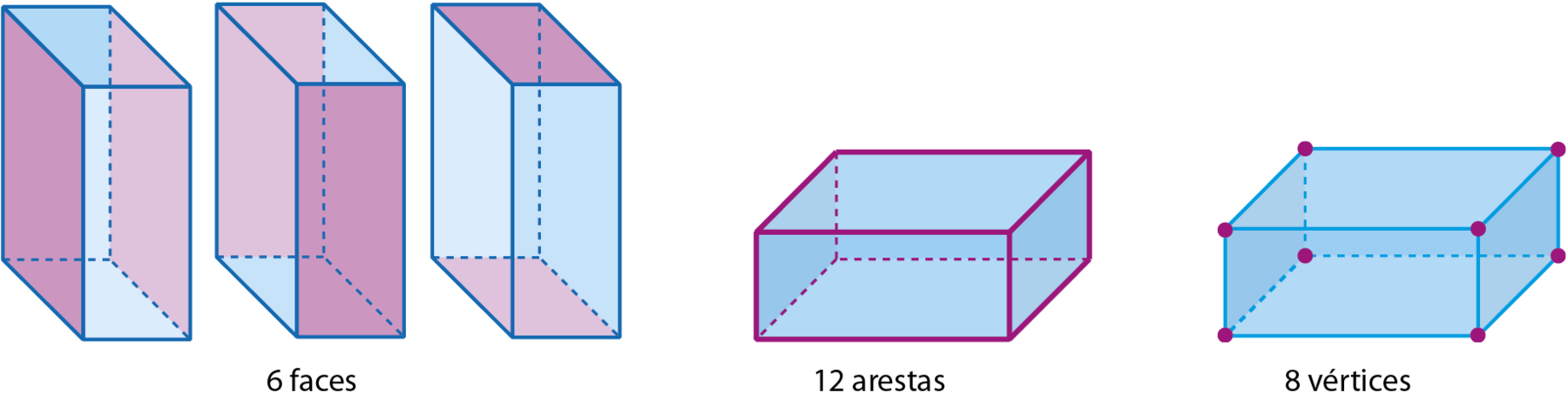
O poliedro a seguir recebe o nome de bloco retangular ou paralelepípedo reto-retângulo.
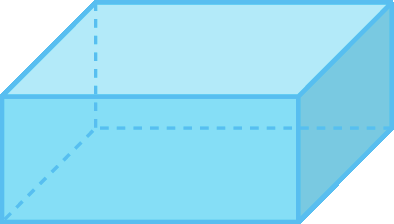
Ele tem 6 faces, 12 arestas e 8 vértices, conforme mostram as figuras a seguir.
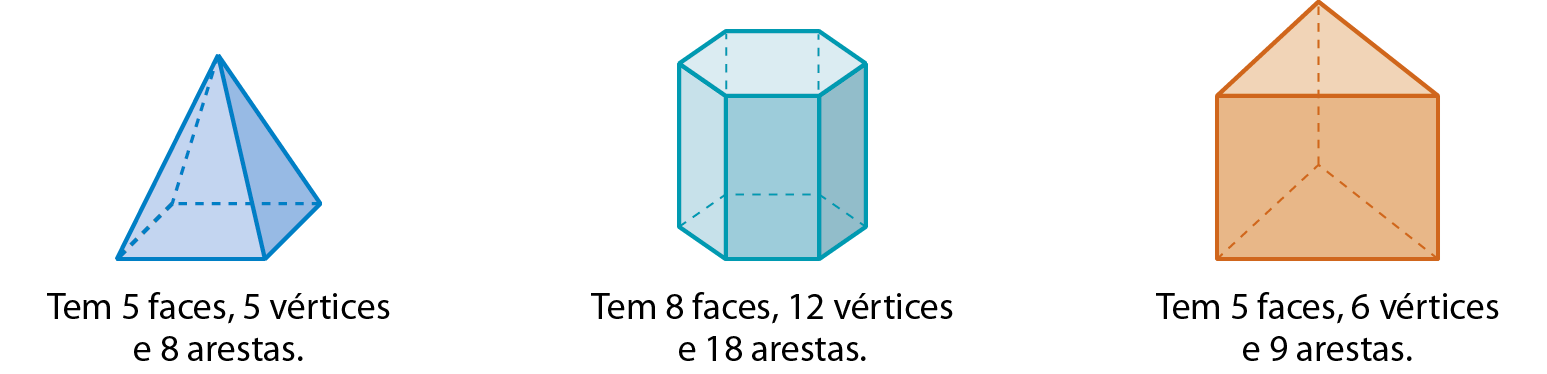
Observe, a seguir, a quantidade de faces, de vértices e de arestas de mais alguns poliedros.
▸ Organize em um quadro o número de faces, arestas e vértices dos sólidos anteriores.
▸ Para cada sólido, adicione o número de vértices (V ) ao número de faces (F ); depois, adicione 2 ao número de arestas (A). Que regularidade você observou em relação a V, F e A nos sólidos analisados?
▸ Verifique se a regularidade que você observou também é válida para outros sólidos.
Essa regularidade que relaciona o número de vértice, o número de faces e o número de arestas de um sólido geométrico é chamada de relação de Euler.
Prismas e pirâmides
Prismas
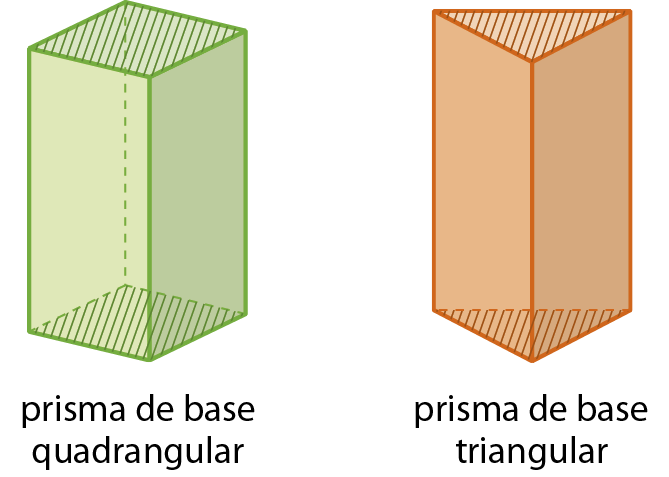
Estes sólidos geométricos são exemplos de prismas. As faces hachuradas em cada prisma são chamadas bases, e as demais, faces laterais.
Todo prisma tem duas bases paralelas e idênticas e tem faces laterais retangulares.
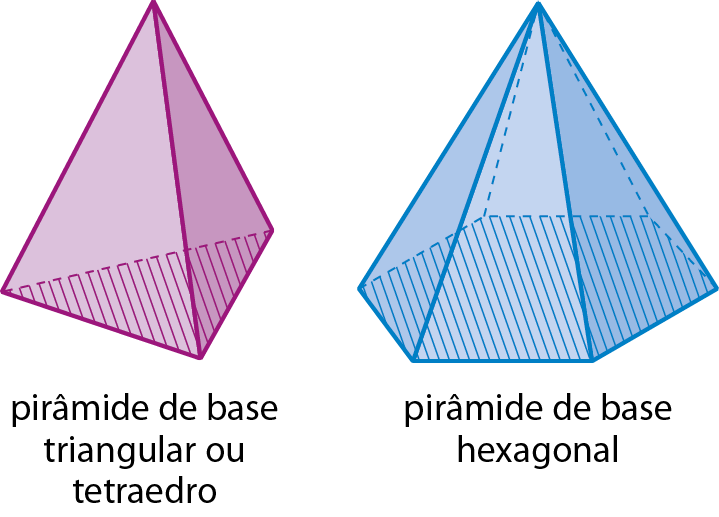
Pirâmides
Estes sólidos geométricos são exemplos de pirâmides. A face hachurada em cada pirâmide é chamada base, e as demais, faces laterais.
Nas pirâmides, todas as faces laterais são triangulares. Já a base pode ter formato triangular, quadrangular, pentagonal etcétera.
Poliedros de Platão e poliedros regulares
Para um poliedro ser de Platão, ele precisa que:
• todas as suas faces tenham o mesmo número de arestas;
• todos os vértices sejam formados pelo encontro do mesmo número de arestas.
A seguir temos o exemplo de um poliedro de Platão que não é regular.

Gire o seu dispositivo para a posição vertical
Para um poliedro ser regular, ele precisa que:
• todas as suas faces tenham o mesmo número de arestas com medidas de comprimento iguais;
• todos os vértices sejam formados pelo encontro do mesmo número de arestas.
Dessa fórma, concluímos que os poliedros regulares são casos particulares dos poliedros de Platão e existem apenas cinco:


Veja que interessante
Faça as atividades no caderno.
O Alamo
O cubo é um caso particular de bloco retangular, em que as medidas de comprimento de todas as arestas são iguais.
O Alamo, também conhecido como Astor Place Cube, é uma escultura ao ar livre que se parece com um cubo cujas arestas medem 2,4 métros de comprimento. Projetada e construída por Bernard Rosenthal, a escultura gira manualmente em tôrno de um poste escondido em seu centro.

Atividade

Por que podemos afirmar que o cubo é um poliedro regular?

3 Corpos redondos
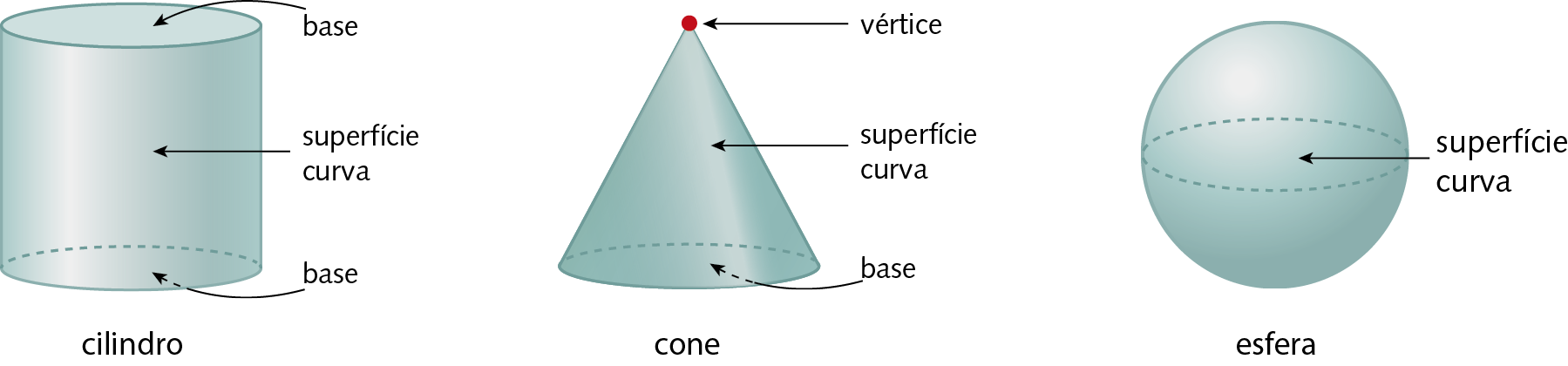
Corpos redondos são sólidos geométricos cuja superfície apresenta alguma parte não plana, arredondada. Observe os exemplos a seguir.

Analise alguns elementos do cilindro, do cone e da esfera.
Atividades
Faça as atividades no caderno.
1. Observe as fotos e escreva o nome do sólido geométrico que você associaria a cada objeto.
a)

b)

c)

d)

e)

f)

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
2. Escreva no caderno uma característica comum e uma diferença entre:
a) um prisma e um cilindro;

b) uma pirâmide e um cone.
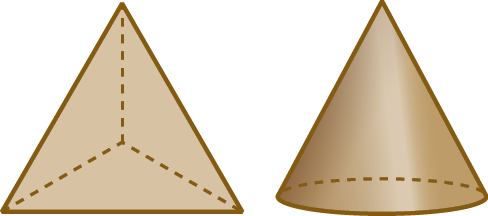
3. Determine o número de faces, de arestas e de vértices de cada figura a seguir.
a)
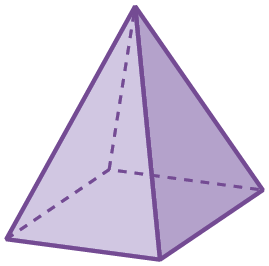
b)
4. Imagine que Paula vá friccionar uma palma da mão na outra, fazendo girar o pirulito. O movimento do pirulito remete à imagem de um sólido geométrico. Qual é esse sólido?

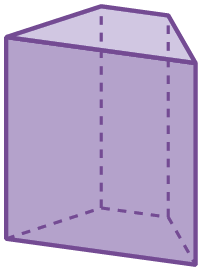
5. Observe a figura a seguir, que representa um prisma, e responda às questões.
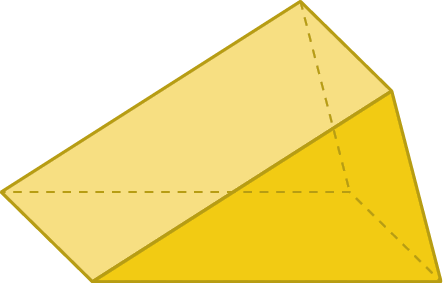
a) Na figura, há:
• quantas faces?
• quantas arestas?
• quantos vértices?
b) Qual é a figura que representa a base desse prisma?
6.

Reúna-se com um colega para resolver esta atividade.
a) Copiem o quadro a seguir no caderno e completem-no.

|
Poliedro regular |
Número de vértices |
Número de faces |
Número de arestas |
|---|---|---|---|
|
Tetraedro |
|||
|
Hexaedro |
|||
|
Octaedro |
|||
|
Dodecaedro |
|||
|
Icosaedro |
b) Para cada poliedro do quadro, verifique se a relação de Euler é válida.
7. Analise esta escultura e, depois, responda à questão.

A escultura se parece com um cubo formado por várias peças similares a paralelepípedos reto-retângulos. Quantas peças parecidas com um paralelepípedo reto‑retângulo foram utilizadas na construção dessa escultura?
Versão adaptada acessível
3. Separe embalagens ou objetos de diferentes formatos, por exemplo, caixa de pasta de dentes, caixas de presente, embalagens de alimentos etc. Manipule essas embalagens de modo a identificar suas partes, como bicos, faces e contornos laterais. Com o auxílio do professor, identifique o que poderia ser associado a vértices faces e arestas. Depois, conte o número de vértices, de faces e de arestas de todos eles e anote em seu caderno.

4 Planificação da superfície de sólidos geométricos
Mateus comprou um panetone para o lanche da tarde. Ele percebeu que a embalagem do panetone se parece com um sólido geométrico.
Mateus cortou a embalagem cuidadosamente pelas arestas e obteve sua planificação. Analise como ela ficou.

A representação da superfície da embalagem totalmente aberta é chamada de planificação.
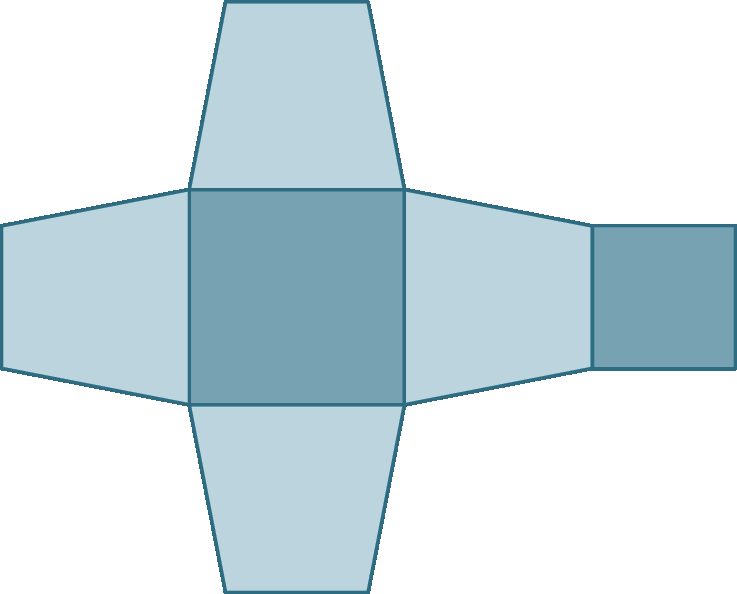
Ao fazer a planificação da superfície de um poliedro, representamos todas as suas faces. Observe os exemplos.
a) Planificação da superfície do prisma de base triangular
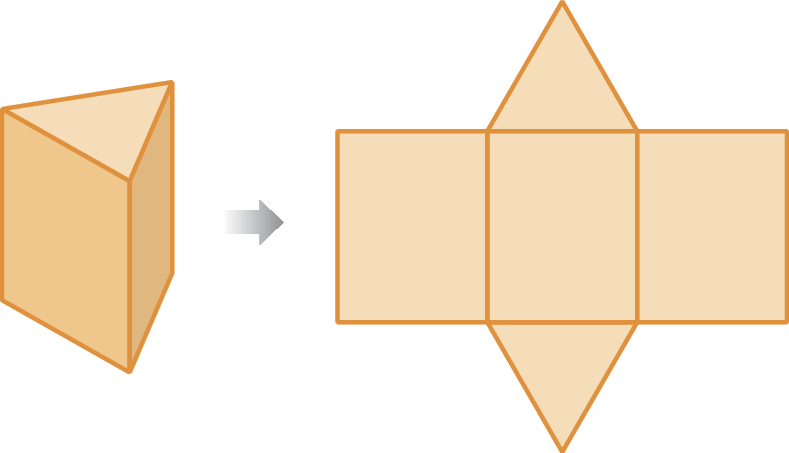
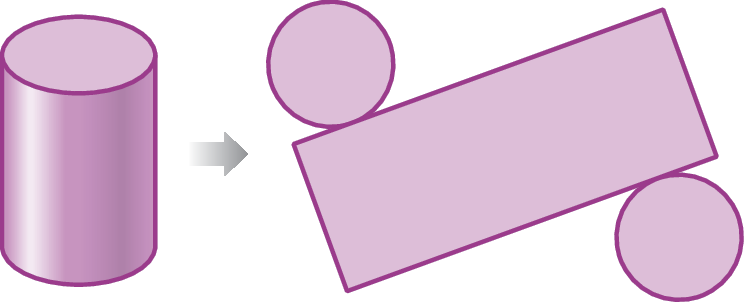
b) Planificação da superfície do cilindro
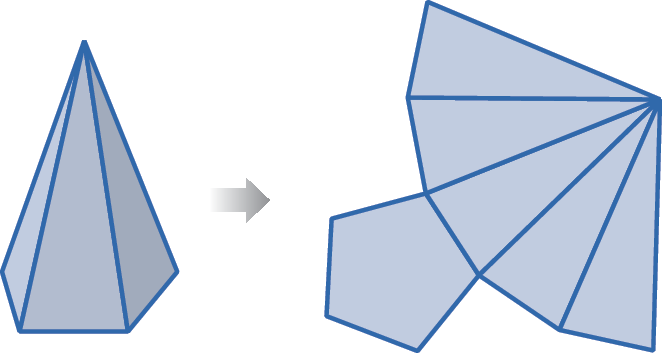
c) Planificação da superfície da pirâmide de base pentagonal
d) Planificação da superfície do cone

Atividades
Faça as atividades no caderno.
8. Em seu caderno, represente a planificação da superfície de uma embalagem que se parece com um bloco retangular. Há só uma planificação possível de se representar? Em seguida, na planificação, pinte com a mesma côr duas faces opostas do bloco, isto é, que não tenham aresta comum.
9. Caio montou um modelo de cubo por meio da planificação da sua superfície.

Identifique o modelo montado por Caio.
a)

b)

c)

d)

10. Quais figuras a seguir são planificações da superfície de um cubo?
a)
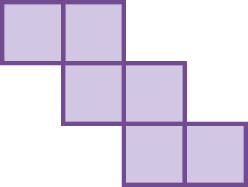
b)
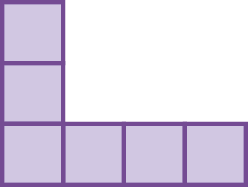
c)

d)

e)

f)

• Agora, em seu caderno, represente a planificação da superfície de um cubo diferente das que você identificou nas figuras anteriores.
11.

Na figura 1, a seguir, temos o molde de um cubo. Dobrando o molde de maneira adequada (figura 2), obtemos uma caixa cúbica (figura 3).
Observe que a face de cima e a face em contato com o plano são opostas e estão indicadas com a mesma letra.
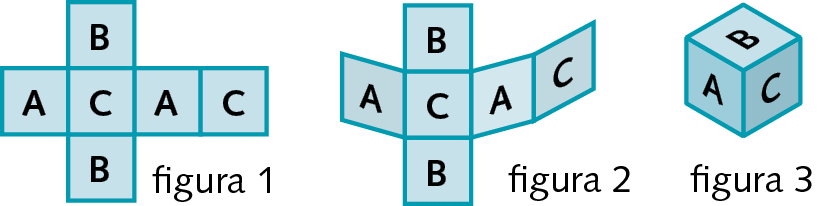
Reúna-se com um colega, copiem as figuras a seguir em uma malha quadriculada e identifiquem as faces opostas em cada uma das planificações.
a)
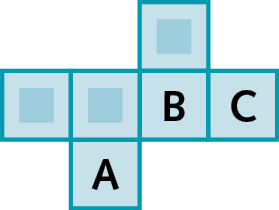
b)
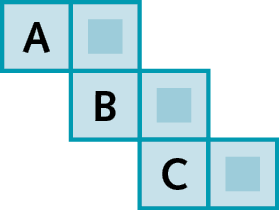
c)
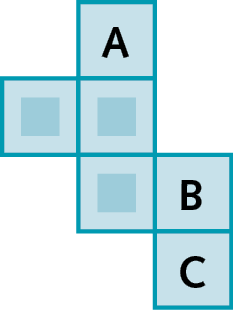
12. Uma pirâmide pentagonal cujas arestas da base têm a mesma medida de comprimento é um poliedro regular? Justifique sua resposta.
13.


Observe os poliedros a seguir e faça o que se pede.
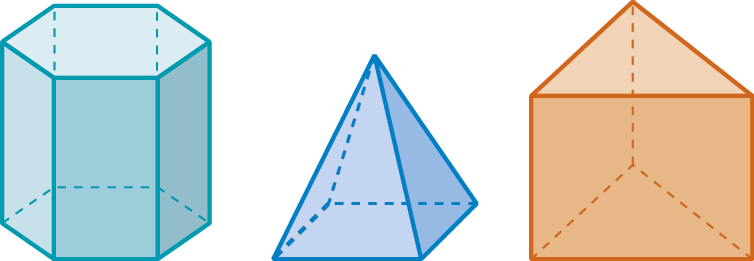
1º) No caderno, elabore três questões que podem ser respondidas observando os poliedros.
2º) Troque de caderno com um colega e responda às questões elaboradas por ele.
3º) Analise as respostas do colega e dê um retôrno a ele, dizendo o que ele respondeu corretamente e em que se equivocou.

Resolvendo em equipe
Faça a atividade no caderno.
(enêm) Conforme regulamento da Agência Nacional de Aviação Civil (anáqui), o passageiro que embarcar em voo doméstico poderá transportar bagagem de mão, contudo a soma das dimensões da bagagem (altura + comprimento + largura) não pode ser superior a 115 centímetros.
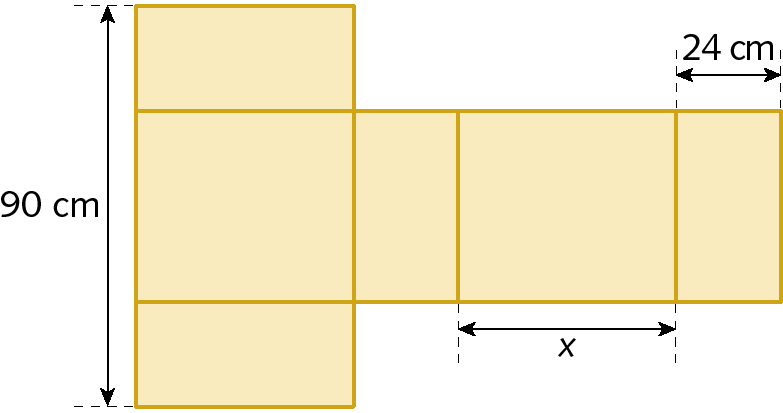
A figura mostra a planificação de uma caixa que tem a fórma de um paralelepípedo retângulo.
O maior valor possível para x, em centímetros, para que a caixa permaneça dentro dos padrões permitidos pela anáqui é:
a) 25
b) 33
c) 42
d) 45
e) 49
|
Interpretação e |
• Leia o enunciado da questão e anote os dados que você julgar relevantes para a resolução do problema. |
|---|---|
|
Plano de resolução |
• Calcule a medida da dimensão indicada de forma indireta na figura. |
|
Resolução |
• Reúna-se com um colega. Avaliem o plano de resolução de cada um e representem uma das resoluções. |
|
Verificação |
• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas. |
|
Apresentação |
• A Agência Nacional de Aviação Civil (Anac) disponibiliza em seu site uma cartilha com orientações aos passageiros sobre suas bagagens: |
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Poliedros
A superfície dos poliedros é formada apenas por partes planas (chamadas de face).
Prismas
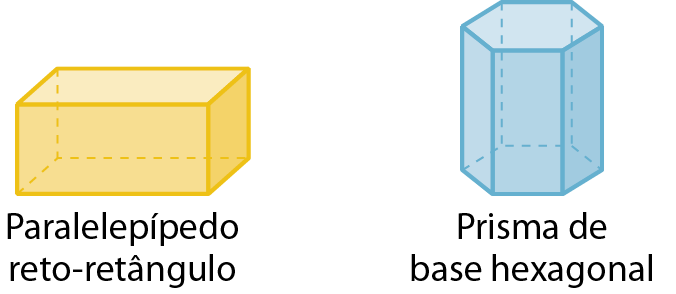
Pirâmides

Corpos redondos
A superfície dos corpos redondos apresenta pelo menos uma parte arredondada, ou seja, não plana.

1. Qual das figuras a seguir não representa um poliedro?
a)

b)
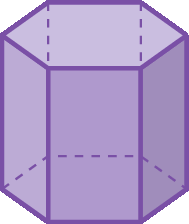
c)
d)
2. Observe os poliedros e faça o que se pede.

a) Copie o quadro no caderno e complete-o.

|
Número de faces |
Número de arestas |
Número de vértices |
|
|---|---|---|---|
|
Figura 1 |
|||
|
Figura 2 |
|||
|
Figura 3 |
b) Qual é o formato das bases de cada poliedro?
Planificação da superfície de sólidos geométricos
Os poliedros e alguns corpos redondos podem ter suas superfícies planificadas. Ao fazer a planificação da superfície de um poliedro, por exemplo, representamos todas as suas faces.
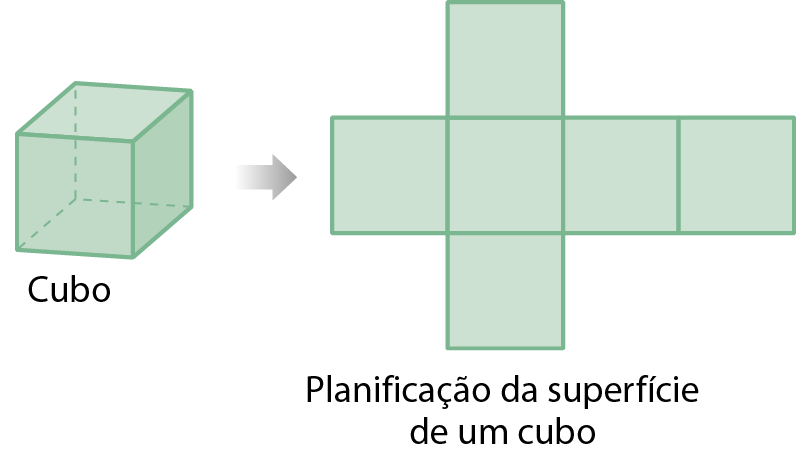
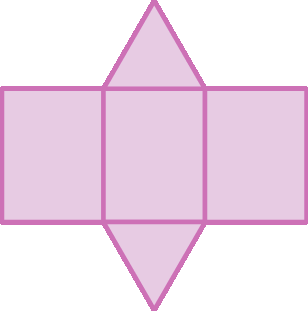
3. A qual sólido geométrico corresponde cada uma das planificações de superfície a seguir?
a)
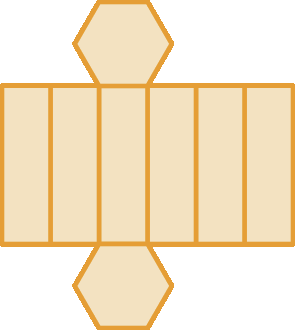
b)

c)
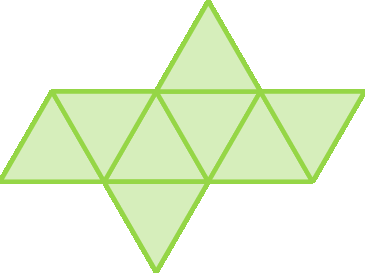
d)
É hora de extrapolar
Faça as atividades no caderno.

Você já viu quê érre côde em embalagens de produtos?
Além de poderem ser usados no lugar dos códigos de barras em produtos, os QR codes podem ter outras finalidades nas diversas situações em que aparecem: em folhetos de museus e de outras instituições, para fornecer dados; nas passagens aéreas, a fim de liberar o acesso dos passageiros; em ingressos de chôus e de cinema, para liberar a entrada, entre outras situações. Atualmente, os QR codes são bastante usados como estratégia de marketing em embalagens de diversos produtos, trazendo informações extras, promoções e até jogos.
Objetivos: Pesquisar sobre o QR code e suas aplicações, construir a embalagem de um produto e utilizar essa tecnologia para oferecer mais informações sobre o produto.

Etapa 1: Pesquisa sobre o QR code e suas aplicações.
1. Reúna-se em grupo com alguns colegas, leiam a tirinha e, depois, respondam às questões.

a) Qual é o título da tirinha?
b) Há quantos personagens na tirinha?
c) Sobre que tipo de código eles estão falando?
d) O código que aparece no primeiro quadro da tirinha representa qual frase?
2.

Pesquisem o que é QR code, como ele surgiu e quais são as suas principais aplicações.
3. Qual é a diferença entre os QR codes e os códigos de barras? Façam uma pesquisa e respondam.
4.

Existem vários aplicativos para celular e sáites que oferecem programas de leitura e criação de QR codes que podem ser baixados gratuitamente. Utilizando algum deles, descubram o que está escrito na tirinha a seguir.

▸ Qual foi o número pensado e descoberto?
5.


Criem dois QR codes: um que represente o enunciado de um problema que possa ser resolvido com a operação de divisão, e outro que contenha a solução do problema.
6.

Troquem os quê érre codes criados no item anterior com outro grupo e resolvam o problema proposto.

Etapa 2: Escolha do produto e da embalagem.
7. Retomem o estudo das planificações da superfície dos sólidos e confeccionem uma embalagem que se pareça com algum sólido geométrico.
8. Algumas questões importantes que devem ser debatidas pelo grupo:
a) Para que serve o produto?
b) Qual é o público-alvo (faixa etária, grupo social etcétera. que pode se interessar pelo produto)?
c) Que formato de embalagem vai acondicionar o produto com segurança e eficiência?
d) Que informações sobre o produto (nome, quantidade etcétera) devem aparecer na embalagem?
e) Que tipo de informação (promoção, charada, jôgo etcétera) pode estar representado por um quê érre côde na embalagem para despertar ou aumentar o interesse do público-alvo?
9.

Depois de selecionar o produto e confeccionar a embalagem, criem um QR code que represente a informação escolhida para aumentar o interesse do público-alvo. Não se esqueçam de inserir o QR code na embalagem do produto.

Etapa 3: Apresentação e análise da embalagem.
10.

Disponibilizem a embalagem criada pelo grupo para que os outros grupos conheçam o produto escolhido, leiam as principais informações e descubram o que está representado pelo QR code.
11. Anotem as dúvidas, as opiniões e as sugestões dos colegas.

Etapa 4: Síntese do trabalho realizado.
12. Questões que devem ser discutidas:
a) A embalagem confeccionada pelo grupo atingiu os objetivos propostos?
b) Os colegas conseguiram identificar o produto e suas principais informações?
c) A mensagem representada pelo QR code foi decifrada?
d) Vocês modificariam algo no processo, na embalagem e na mensagem em quê érre côde?
13. Redijam um texto que descreva o processo realizado pelo grupo na etapa 2 e que considere o resultado da etapa 3, levando em conta as reações e as sugestões dos colegas.

Glossário
- Superfície
- : Imagine a superfície de um sólido geométrico como se fosse uma casca muito fina que o envolvesse.
- Voltar para o texto