Unidade 2
Capítulo 4 Igualdades e desigualdades
Capítulo 5 Múltiplos e divisores
Capítulo 6 Frações
Capítulo 7 Números decimais

Em 2021, de setecentas e setenta cidades avaliadas em todo o país, a cidade de Morungaba, no estado de São Paulo, era a 1ª colocada no ranking do Índice de Desenvolvimento Sustentável das Cidades – Brasil (IDSC-BR). A cidade atingiu cêrca de
três quartosda medida da distância para o desempenho ótimo nos Objetivos de Desenvolvimento Sustentável (ó dê ésse).
O que são os ó dê ésse? Qual é o significado do número
três quartosnesse contexto? Ao final do estudo da Unidade, você responderá a essas e outras questões.
Capítulo 4 Igualdades e desigualdades
Trocando ideias

A pesquisa de preços é uma boa prática e póde nos ajudar a economizar na compra de determinado produto ou na aquisição de um serviço.
Vera precisava comprar um vestido e um chapéu, mas antes pesquisou o preço desses itens em duas lojas. Analise as cenas.

Se ela optar por comprar o vestido na Loja do Shopping, vai economizar R$ 15,00quinze reais, pois:
80 menos 65 = 15
A sentença matemática 80 menos 65 = 15 é uma igualdade.
▸

Em qual loja é mais vantajoso comprar o chapéu? Qual igualdade representa o valor que Vera consegue economizar ao comprar o chapéu nessa loja?
▸


Você costuma pesquisar preços antes de comprar algo? Como você faz? Converse com os colegas.
Neste capítulo, você vai estudar sentenças matemáticas expressas por igualdades e por desigualdades.

1 Sentenças matemáticas
No “Trocando ideias”, você leu e escreveu algumas sentenças que chamamos de sentenças matemáticas.
Sentença matemática é aquela escrita com símbolos matemáticos (números, sinais etcétera); ela póde ser expressa por relações de igualdade, de desigualdade, entre outras.
As sentenças matemáticas podem ser verdadeiras ou falsas. Analise os exemplos:
a)

b)

c)

d)
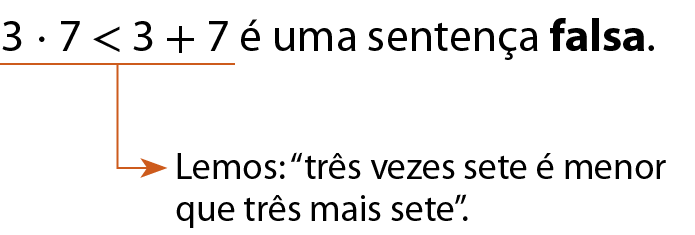
Observação
Note que, se mudarmos o sinal de uma sentença matemática, sem alterar os números, ela póde se tornar verdadeira ou falsa. Por exemplo, 13 = 11 + 2 é uma sentença verdadeira, enquanto 13 > 11 + 2 é uma sentença falsa.
Atividades
Faça as atividades no caderno.
1. Escreva em seu caderno como se leem as sentenças matemáticas a seguir.
a) 8 + 3 = 11
b) 32 > 20 dividido por 10
c) 23 ⩾ 12 + 8
d) 3 ⋅ 4 ⩽ 3 ⋅ 5
2. Quais das sentenças a seguir são verdadeiras?
a) 5 < 9
b) 7 ⋅ 2 ⩽ 7 ⋅ 3
c) 6 + 3 ≠ 9
d) 22 menos 10 > 12
3. Copie as sentenças em seu caderno substituindo o

por um símbolo que as torne verdadeiras. Use um dos símbolos: <, ⩽, =, > ou ⩾.
a) 10 + 2

6 + 3 + 2 + 1
b) 4 ⋅ 5 ⋅ 6

6 + 7 + 8
c) 3elevado a 2 ⋅ 2elevado a 2

3elevado a 2 + 2elevado a 2
d) 2elevado a 3 menos 2elevado a 2

5

2 Igualdades
Toda sentença matemática que apresenta o sinal de igual (=) é chamada de igualdade. Em uma igualdade, chamamos a expressão à esquerda do sinal de igual de 1º membro e a expressão à direita desse sinal, de 2º membro. Observe os exemplos:
a)

b)
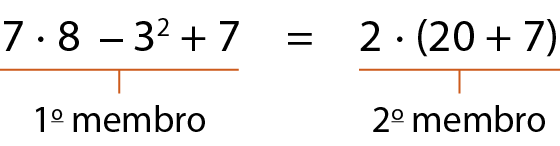
Toda igualdade é reflexiva, simétrica e transitiva. Acompanhe os exemplos:
a) Reflexiva
6 = 6 ou, ainda: 2 + 4 = 2 + 4
b) Simétrica
Se 2 + 4 = 6, então: 6 = 2 + 4
c) Transitiva
Se 7 ⋅ 7 menos 7 = 6 ⋅ 7 e 6 ⋅ 7 = 42, então: 7 ⋅ 7 menos 7 = 42
Propriedade da igualdade
A relação de igualdade não se altera quando:
• adicionamos ou subtraímos um mesmo número de seus membros;
• multiplicamos seus membros por um mesmo número ou dividimos seus membros por um mesmo número diferente de zero.
Acompanhe os exemplos.
a)
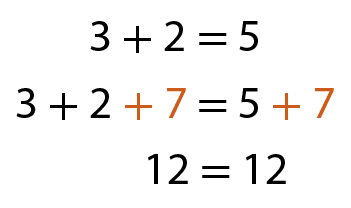
b)
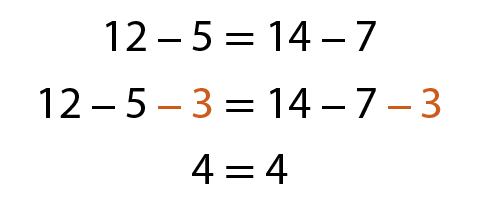
c)
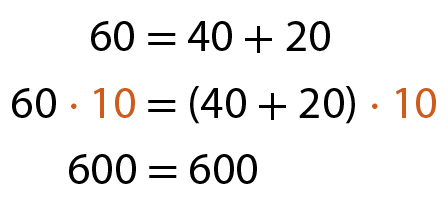
d)
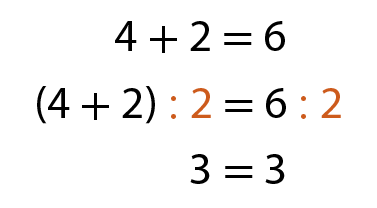
Atividades
Faça as atividades no caderno.
4. Avalie as afirmações a seguir e copie as verdadeiras em seu caderno.
a) Se adicionarmos 1 ao 2º membro de uma igualdade, ela continuará sendo uma sentença matemática verdadeira.
b) Se subtrairmos um mesmo número dos dois membros de uma igualdade, ela se manterá verdadeira.
c) Se adicionarmos 2 ao 1º membro de uma igualdade e 3 ao 2º membro da mesma igualdade, ela se manterá verdadeira.
5. Efetue em seu caderno as operações indicadas para cada sentença matemática e determine o valor de cada membro.
a) Adicione 5 aos dois membros da sentença 2 + 3 = 10 menos 5.
b) Subtraia 2 dos dois membros da sentença 14 menos 5 = 3 + 3 + 3.
c) Adicione 3 a ambos os membros da sentença 21 menos 10 = 22 menos 11.
d) Subtraia 3 de ambos os membros da sentença 13 + 2 = 6 + 6 + 3.
6. Efetue em seu caderno as operações indicadas para cada sentença matemática e determine o valor de cada membro.
a) Multiplique os dois membros da sentença 1 + 2 + 3 = 3 + 3 por 4.
b) Divida os dois membros da sentença 10 + 20 = 30 por 10.
c) Multiplique os dois membros da sentença 12 menos 6 = 2 ∙ 3 por 2.
d) Divida os dois membros da sentença 3 + 3 + 3 = 18 menos 9 por 3.
7. Mariele tinha 3 jogos de ação, 2 de corrida e 2 de futebol, totalizando 7 jogos. No seu aniversário, a quantidade de cada tipo de jôgo dobrou. Represente com uma sentença matemática expressa por uma igualdade as quantidades de jogos que ela tinha antes e depois do aniversário.
Resolvendo problemas com igualdades
Vimos até aqui que os valores do 1º membro e do 2º membro são iguais em uma sentença matemática expressa por uma igualdade. Além disso, é possível adicionar, subtrair, multiplicar ou dividir os membros por um mesmo número diferente de zero sem que a relação de igualdade se altere.
Agora, vamos resolver problemas usando essas ideias.
Problema 1
Marta vende temperos na feira. Ela usa uma balança de pratos e pequenos pesos metálicos para medir a massa de temperos para os clientes. Analise a situação a seguir.
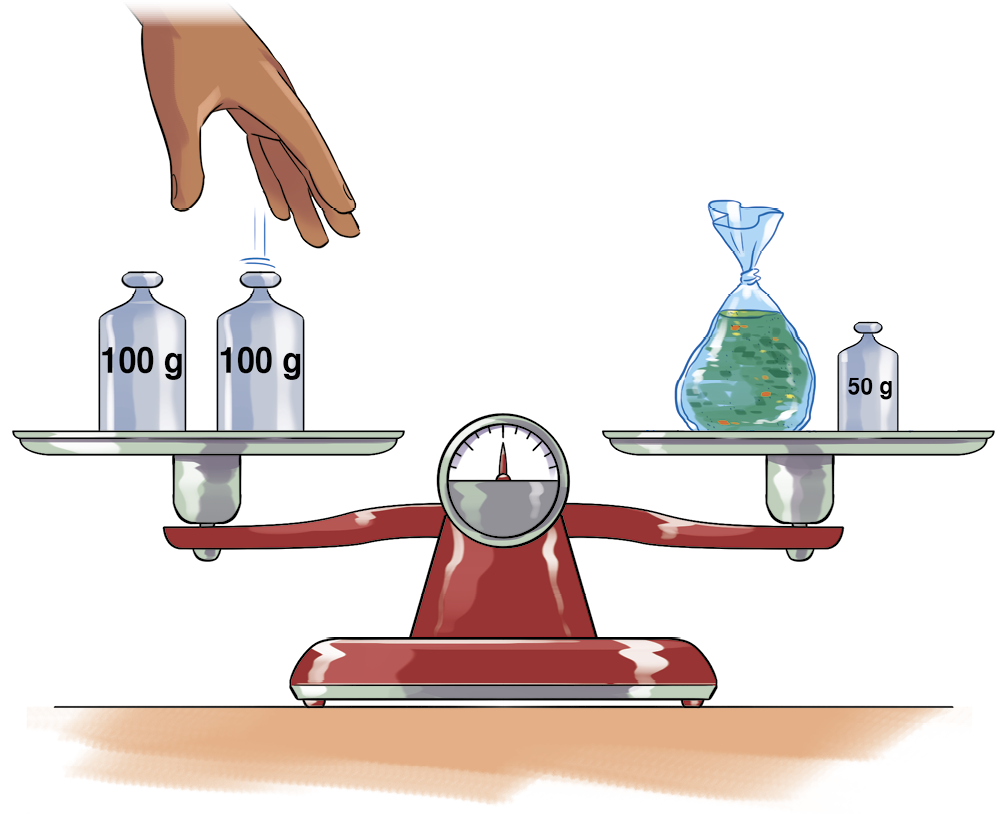
Como a balança está equilibrada, podemos representar a relação entre a medida da massa, em grama, do tempero e as medidas da massa, em grama, dos pesos com uma igualdade. Mas, como não conhecemos a medida da massa do tempero, usaremos um

para representá-la.
100 + 100 =

+ 50
Sabemos que, quando um mesmo número é subtraído dos dois membros de uma igualdade, ela se mantém verdadeira. Vamos subtrair 50 dos dois membros da igualdade.
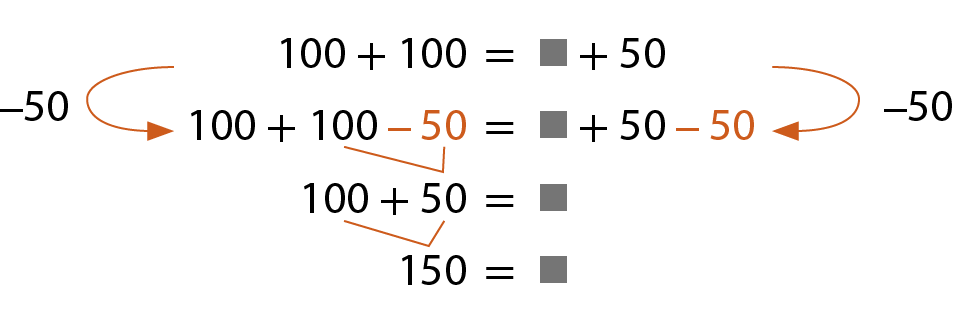
Portanto, a medida da massa do tempero é 150 gramas.
Problema 2
Paulo e Daniela estão brincando de adivinhar números.

Como o resultado das operações realizadas por Paulo é 25, Daniela resolveu representar a situação utilizando uma sentença matemática expressa por uma igualdade. Considere a representação feita por ela na lousa.

A ideia de Daniela era representar o número desconhecido por um □ e fazer operações deixando apenas o □ no primeiro membro. Acompanhe os cálculos feitos por Daniela.

Como Daniela fez operações idênticas nos dois membros da igualdade, a relação de igualdade se manteve. Assim, ela escreveu uma igualdade e usou um □ para representar o número desconhecido, descobrindo que é o 5.
Acompanhe outros exemplos.
a) O dôbro de um número mais 4 é igual a 10.
Que número é esse?
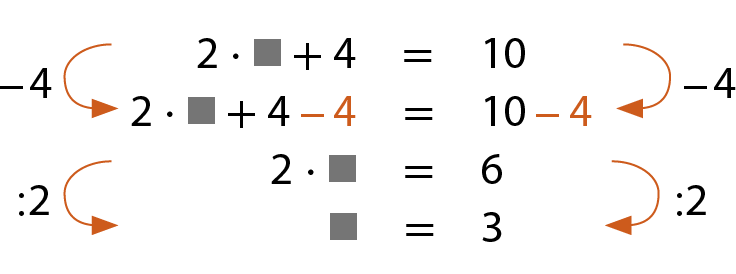
É o número 3.
b) Havia algumas maçãs em uma caixa. Comemos 3 e sobraram 8.
Quantas maçãs havia na caixa?
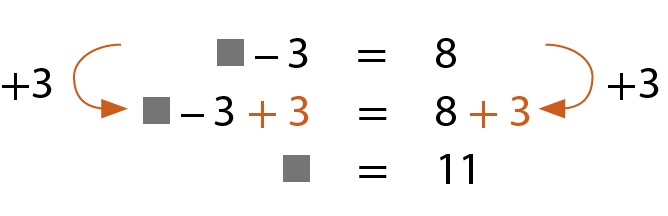
Havia 11 maçãs na caixa.

Atividades
Faça as atividades no caderno.
8. Uma balança de pratos está em equilíbrio. Em um prato, há um pacote de farinha e um pêso metálico de 200 gramas; no outro, dois pesos metálicos de 300 gramas. Faça o que se pede.
a) No caderno, represente a situação por meio de um desenho e, depois, usando uma sentença matemática.
b) Qual é a medida de massa do pacote de farinha, em grama?
9. Represente as situações usando uma sentença matemática expressa por igualdade e resolva-as em seu caderno.
a) Luiz ganhou um saquinho com bolinhas de gude. Se ele deu 10 bolinhas para Pedro e ainda ficou com 25, quantas bolinhas havia no saquinho?
b) O triplo de um número mais 1 é igual a 7. Que número é esse?
10. Descubra o número desconhecido nas sentenças matemáticas a seguir.
a)

+ 10 = 15
b) 10 menos 2 =

menos 2
c) 2 ⋅

+ 3 = 10 + 5
d) 14 menos 2 = 10 +

e) 31 = 3 ⋅

menos 8
f) 3 ⋅ (9 menos 2) = 3 ⋅

11. Em um jôgo de videogame, Paula e Vítor têm, juntos, 300 pontos. Se Paula tem o dôbro dos pontos de Vítor, qual é a pontuação de cada um?
12.


Elabore um problema no qual uma pessoa precisa comprar um agasalho e tem duas opções de marca (a e B), sendo que a marca a é mais cara. Depois, peça a um colega que o resolva.
13.

Elabore uma situação em que um garoto leva para a escola uma caixa com alguns caquis, colhidos do pé em sua casa, a fim de dividi-los com sua turma. Depois da distribuição entre os colegas, porém, ainda sobram algumas frutas na caixa. A situação deve buscar o número de caquis que o garoto levou para a escola, ou seja, esse é o número desconhecido.

3 Desigualdades
As desigualdades são sentenças matemáticas em que aparecem um dos sinais a seguir.
> (maior que)
< (menor que)
⩽ (menor ou igual a)
⩾ (maior ou igual a)
≠ (diferente)
Considere os exemplos.
a) 3 > 2
b) 8 < 9
c) 10 ⩾ 7
d) 11 ⩽ 13
e) 15 ≠ 51
Assim como nas igualdades, chamamos de 1º membro a expressão que está à esquerda do sinal de desigualdade e de 2º membro a expressão que está à direita do sinal de desigualdade. Considere o exemplo.
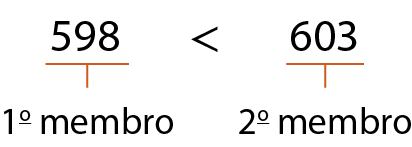
Adicionando e subtraindo números naturais aos membros de uma desigualdade
Quando adicionamos ou subtraímos um mesmo número natural dos membros de uma desigualdade, ela se mantém verdadeira.
Acompanhe os exemplos.
a)
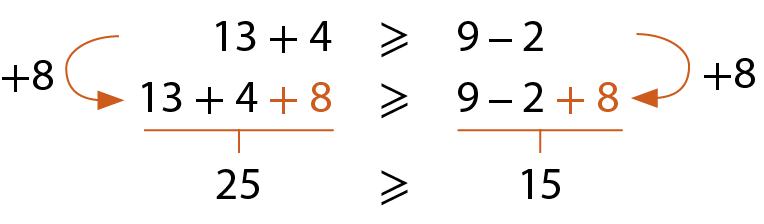
b)
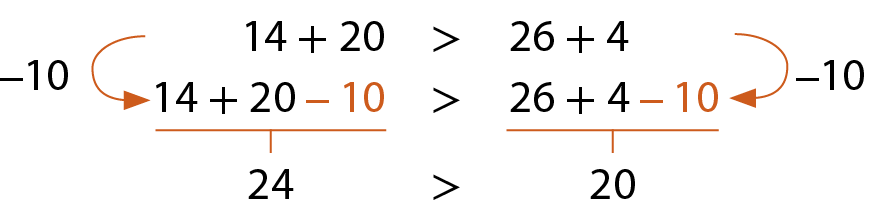

Multiplicando e dividindo os membros de uma desigualdade por números naturais
Quando multiplicamos ou dividimos os membros de uma desigualdade por um mesmo número natural, diferente de zero, a desigualdade se mantém verdadeira.
Analise os exemplos.
a)
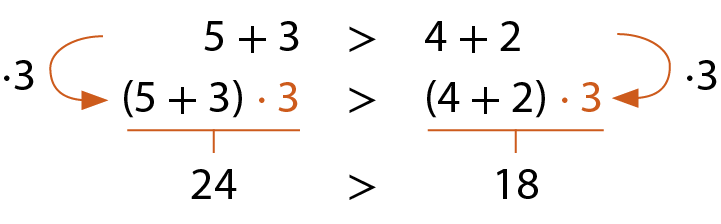
b)
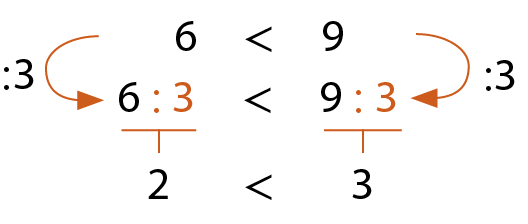

Atividades
Faça as atividades no caderno.
14. Faça as operações indicadas em cada uma das desigualdades, calculando o valor de ambos os membros.
a) Adicione 4 a ambos os membros da desigualdade 10 menos 3 > 4.
b) Subtraia 11 de ambos os membros da desigualdade 24 dividido por 2 ⩾ 6 + 6.
c) Adicione 13 a ambos os membros da desigualdade 1 + 2 + 3 ⩽ 1 ⋅ 2 ⋅ 3.
d) Subtraia 7 de ambos os membros da desigualdade 3 + 3 + 3 > (21 menos 7) dividido por 2.
15. Rodrigo tem 15 brinquedos e Mara tem 20 a mais do que ele. Fábio deu 10 brinquedos para cada um dos dois. Represente a quantidade de brinquedos de Mara e Rodrigo usando uma desigualdade em dois momentos: antes de Fábio dar os brinquedos para os dois e depois que ele deu 10 brinquedos para cada um.
16. Calcule o valor do primeiro e o do segundo membro das desigualdades e descubra quais são verdadeiras.
a) 2 ⋅ abre parênteses3 + 4fecha parênteses ⩾ 2 ⋅ abre parênteses1 + 2fecha parênteses
b) 3 ⋅ 4 < abre parênteses1 + 2fecha parênteses ⋅ abre parênteses2 + 2fecha parênteses
c) 28 dividido por 14 ⩾ 14 dividido por 7
d) 35 dividido por 7 < 49 dividido por 7
17. Efetue as operações indicadas e calcule o valor de ambos os membros das desigualdades a seguir.
a) Multiplique os dois membros da desigualdade 4 + 1 ≠ 6 por 4.
b) Divida os dois membros da desigualdade 28 > 14 por 14.
c) Multiplique os dois membros da desigualdade 19 menos 10 ⩽ 3 ⋅ 3 por 5.
d) Divida os dois membros da desigualdade 9 + 6 + 3 > 1 + 2 + 3 por 3.
18. Os irmãos Marcos e Taís têm as quantias apresentadas a seguir.
Considerando que os pais deram R$ 20,00vinte reais para eles dividirem igualmente, represente as situações antes e depois de Marcos e Taís receberem essa quantia.

19. A balança de pratos a seguir está em desequilíbrio e adicionamos um pêso metálico ao prato da direita para equilibrar a balança.
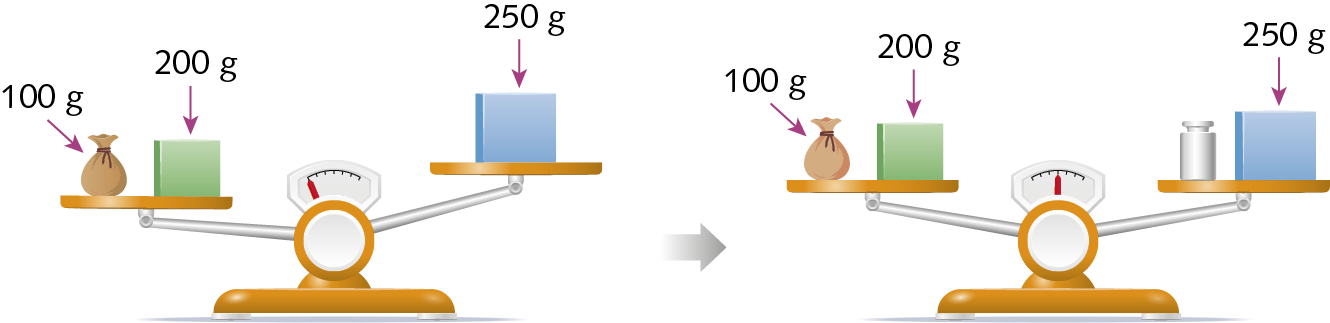
a) Qual é a medida da massa do pêso metálico adicionado?
b) Usando sentenças matemáticas, represente as situações antes e depois de adicionar esse pêso metálico.
c) Se adicionarmos um pêso metálico com a mesma medida da massa ao prato da esquerda, o que vai acontecer com a balança? Represente essa situação usando uma sentença matemática.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Sentenças matemáticas
Sentenças matemáticas são aquelas escritas com símbolos matemáticos. Elas podem ser:
verdadeiras
18 + 12 = 30
35 ⩽ 25 + 15
falsas
25 ≠ 18 + 7
12 ⋅ 5 > 60
1. Quais das sentenças matemáticas a seguir são verdadeiras?
a) 12 > 3 + 15
b) 7 ⋅ 12 = 12 ⋅ 7
c) 15 menos 5 ≠ 105 menos 95
d) 127 ⩽ 150 menos 16
2. Copie as sentenças no caderno substituindo o

por um símbolo que as torne verdadeiras. Use os símbolos: <, ⩽, =, > ou ⩾.
a) 25 + 5

12 + 5 + 15
b) 7 ⋅ 10

140 : 2
c) 12 ⋅ 5 + 50

150 menos 200 : 2 + 50
Igualdades
Igualdade é toda sentença matemática que apresenta o sinal de igual (=).
A relação de igualdade não se altera quando:
• adicionamos a seus membros ou subtraímos deles um mesmo número;
• multiplicamos ou dividimos seus membros por um mesmo número diferente de zero.
3. Efetue em seu caderno as operações indicadas para cada sentença matemática e encontre o valor de cada membro.
a) Adicione 25 aos dois membros da igualdade: 12 menos 10 = 45 menos 43
b) Subtraia 12 dos dois membros da igualdade: 30 + 11 = 56 menos 15
c) Multiplique por 9 os dois membros da igualdade: 19 + 3 = 38 menos 16
d) Divida por 6 os dois membros da igualdade: 36 menos 18 = 12 + 6
4. Represente cada situação usando uma igualdade e, em seguida, resolva-as.
a) Juliano deu 18 figurinhas repetidas para seu primo e ficou com 46 figurinhas. Quantas figurinhas Juliano tinha?
b) O dôbro de um número mais 12 é igual 58. Qual é esse número?
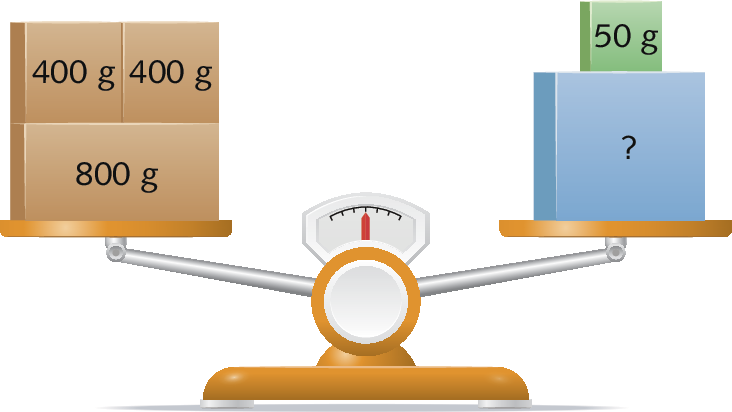
5. Nesta balança em equilíbrio, qual é a medida da massa da caixa azul em grama?
6. Descubra o número desconhecido nas sentenças matemáticas a seguir.
a)

+ 16 = 112
b) 4 ⋅ 10 +

= 52
c) 15 : 3 + 28 = 14 + 19 ⋅

7. Os irmãos Jorge e Felipe ganharam de um tio R$ 270,00duzentos e setenta reais no total. Se Jorge recebeu o dôbro do valor recebido pelo irmão, quantos reais cada um recebeu?
Desigualdades
Desigualdade é toda sentença matemática em que aparece um dos sinais a seguir.

A desigualdade se mantém verdadeira quando:
• adicionamos a seus membros ou subtraímos deles um mesmo número natural;
• multiplicamos ou dividimos um mesmo número natural, diferente de zero, de ambos os membros.
8. Calcule o valor de cada membro das desigualdades e determine se elas são verdadeiras ou falsas.
a) 10 ⋅ abre parênteses3 + 5fecha parênteses ⩾ 12 ⋅ abre parênteses2 + 3fecha parênteses
b) 10 + 2 ⋅ 5 ⩽ abre parênteses2 + 10fecha parênteses : 3
c) 36 : 2 menos 12 ≠ 6elevado a 2 menos 4elevado a 2 + 4
9. Mário tem 125 figurinhas e Luana tem cento e trinta e duas. Cada um deles recebeu 25 figurinhas de um colega. Escreva uma desigualdade para representar as situações antes e depois de Mário e Luana ganharem as figurinhas.