Capítulo 5 Múltiplos e divisores
Trocando ideias
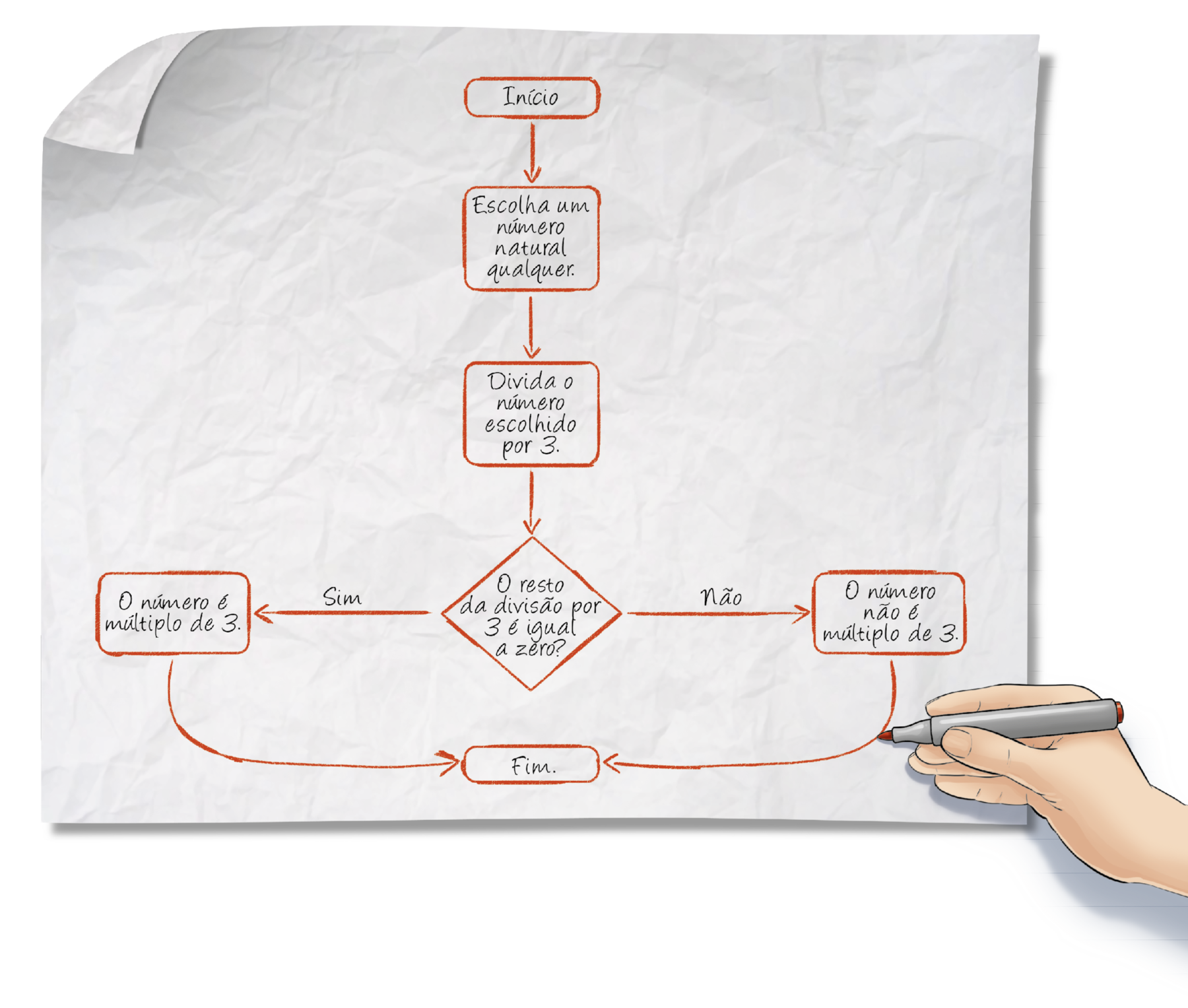
Observe o esquema a seguir.
▸


Para que serve esse esquema?
▸

Utilize o esquema anterior e verifique quais dos números a seguir são múltiplos de 3.

Os números que você identificou são exemplos de múltiplos de 3. Também podemos dizer que 3 é divisor de cada um desses números.
Neste capítulo, vamos estudar os múltiplos e os divisores de números naturais, além de reconhecer números primos e números compostos.

1 Múltiplos de um número natural
Observe, no quadro a seguir, alguns números da tabuada do 7.
|
× |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
7 |
0 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
... |
Os números 0, 7, 14, 21, 28, reticências, da tabuada do 7, são múltiplos de 7, pois podem ser obtidos multiplicando-se o 7 por um número natural qualquer: 7 ⋅ 0 = 0, 7 ⋅ 1 = 7, 7 ⋅ 2 = 14, 7 ⋅ 3 = 21, 7 ⋅ 4 = 28, reticências
Dizemos que um número natural é múltiplo de outro quando o primeiro é obtido multiplicando o segundo por um número natural qualquer.
A sequência (0, 7, 14, 21, 28, reticências) é a sequência dos múltiplos naturais de 7. Note que essa sequência começa pelo número zero, e que o padrãoglossário é sempre adicionar 7 ao termo anterior. Portanto, essa sequência é infinita.
Do mesmo modo, podemos obter a sequência dos múltiplos de qualquer número natural.
Analise outros exemplos:
a) (0, 11, 22, 33, 44, reticências) é a sequência dos múltiplos naturais de 11.
b) (0, 19, 38, 57, 76, reticências) é a sequência dos múltiplos naturais de 19.
Observações
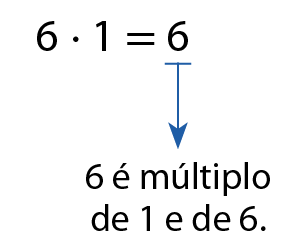
1. Todo número natural é múltiplo de 1 e dele mesmo. Verifique:
a)
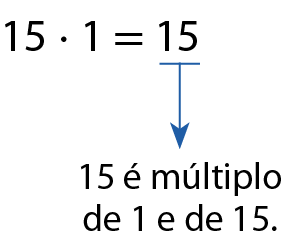
b)
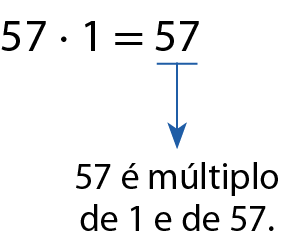
c)
2. Não existe o maior múltiplo de um número natural não nulo. A sequência dos múltiplos de um número natural, diferente de zero, é infinita.
É possível verificar se um número é múltiplo de outro. Confira os exemplos a seguir.
a) O número 72 é múltiplo de 6?
Para responder a essa pergunta, devemos verificar se 72 é igual a 6 vezes algum número natural. Para isso, vamos dividir 72 por 6. Observe.

Note que o resto da divisão de 72 por 6 é 0. Como a divisão é exata, concluímos que 72 é divisível por 6 e podemos escrever 6 ⋅ 12 = 72. Portanto, 72 é múltiplo de 6.
b) O número 270 é múltiplo de 16?
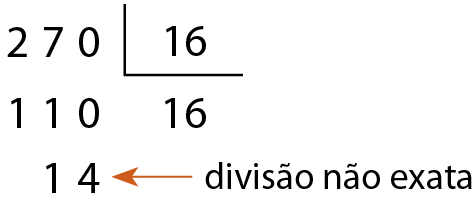
Como a divisão não é exata, concluímos que 270 não é divisível e não é múltiplo de 16.
Observações
1. O zero só tem um múltiplo: o próprio zero. Observe os exemplos a seguir.
a) 0 ⋅ 0 = 0
b) 0 ⋅ 1 = 0
c) 0 ⋅ 2 = 0
2. O zero, porém, é múltiplo de todos os números naturais. Verifique:
a)
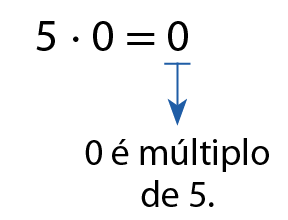
b)
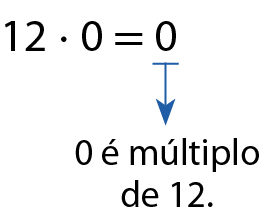
c)
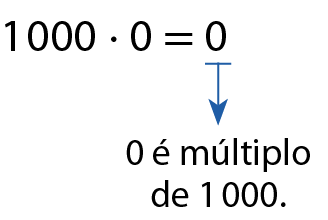
3. Podemos falar em múltiplo de zero porque existem multiplicações por zero. Porém, não podemos falar que um número é divisível por zero, uma vez que não existe divisão por zero.
Para verificar se um número é múltiplo de 2, por exemplo, podemos elaborar um esquema conforme o apresentado a seguir.
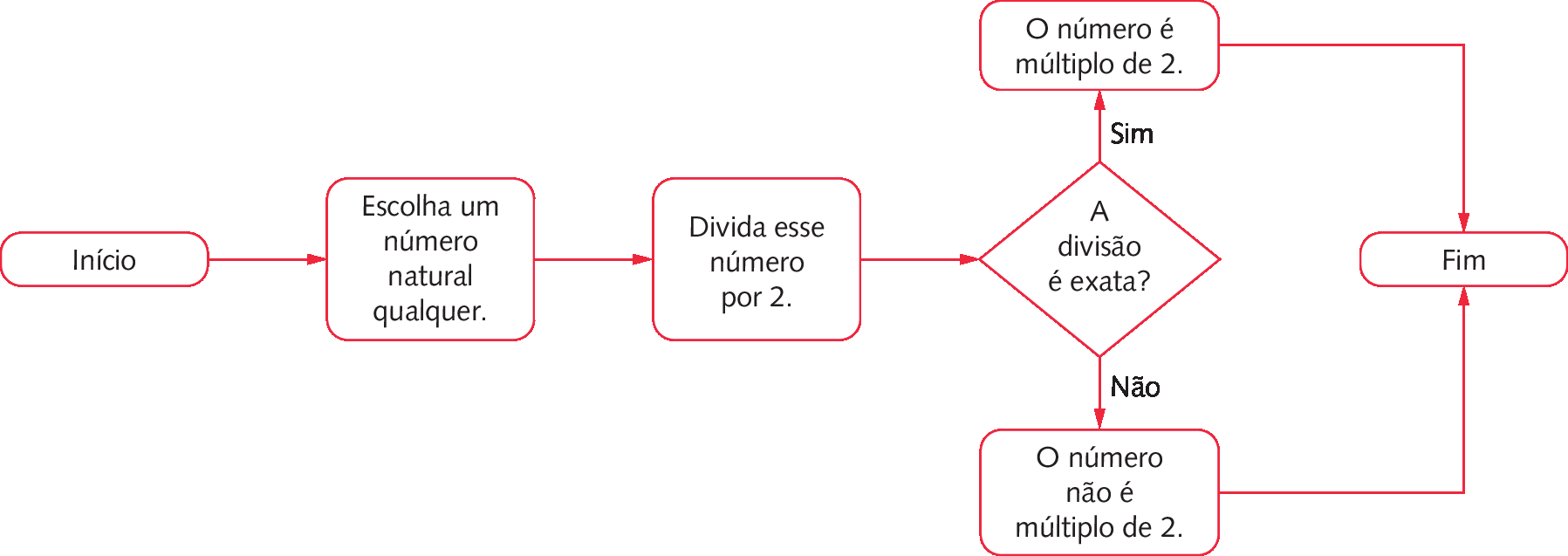
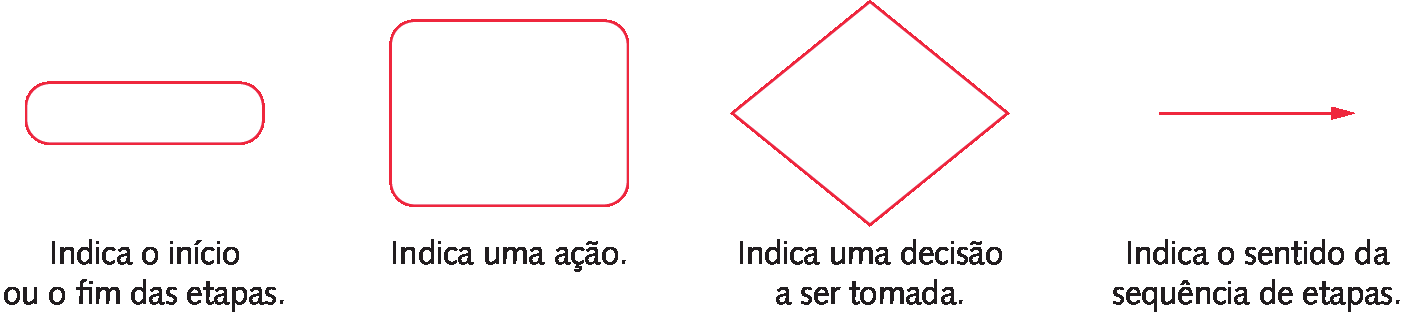
Esse esquema é um exemplo de fluxograma, um tipo de diagrama que póde ser utilizado para representar, de maneira resumida, a sequência de etapas de um procedimento. Observe o significado das figuras no fluxograma anterior.
Atividades
Faça as atividades no caderno.
1. Quais são os cinco menores múltiplos de 17?
2.

Digite, na calculadora, as teclas

. Você vai visualizar o número 23. Em seguida, digite sucessivamente a tecla

.
a) Quais foram os quatro primeiros números que apareceram no visor depois que você começou a digitar a tecla

?
b) Qual é a particularidade desses números?
3. Determine:
a) os múltiplos de 7 maiores que 50 e menores que 80;
b) os múltiplos de 16 compreendidos entre 151 e 201.
4.

Utilize o fluxograma da página anterior e verifique se alguns números naturais são ou não múltiplos de 2.
5.


Elabore, em seu caderno, um fluxograma para que um colega verifique se um número natural qualquer é ou não múltiplo de algum outro número natural.
6.
Responda às questões a seguir.
a) O número 345 é múltiplo de 7?
b) O número .1445 é múltiplo de 17?
c) Dos números 147, 385, 504 e .7401, quais são múltiplos de 21?
d) Qual é o menor número natural que devemos adicionar a 68 para obter um múltiplo de 13?
7. O número .3192 é múltiplo de 7? Depois de .3192, qual é o próximo número natural divisível por 7?
8. Determine os múltiplos de 13, 17 e 19 entre 300 e 320. Aproxime cada um deles para o múltiplo de 10 mais próximo.
9. Leia as afirmações a seguir e indique no caderno se são verdadeiras ou falsas.
a) .1856 é múltiplo de 2.
b) 91 é múltiplo de 7.
c) 169 é múltiplo de 3.
d) 100 é múltiplo de 2 e de 3.
e) 210 é múltiplo de 2, 3, 5 e 7.
f) .123456 é múltiplo de 3.
g) .123456 é múltiplo de 64.
h) .123456 é múltiplo de 5.
10.

Reúna-se com um colega e façam o que se pede.
a) Escolha um número e, em seguida, peça a seu colega que determine cinco múltiplos desse número.
b) Verifique se os múltiplos que ele determinou estão corretos.

2 Divisores de um número natural
Marcos vai montar a vitrine de sua loja de jogos eletrônicos com seis jogos que acabaram de ser lançados. Para isso, ele pensou em algumas possibilidades de como dispor os jogos em suportes.
Possibilidade 1

Possibilidade 2

Possibilidade 3

Possibilidade 4

Dizemos que os números 1, 2, 3 e 6 são os divisores naturais ou fatores naturais de 6, pois, ao dividir 6 por qualquer um desses números, obtemos uma divisão exata. Também dizemos que 6 é divisível por 1, 2, 3 e 6.
Agora, se Marcos usasse quatro suportes, conseguiria distribuir os seis jogos igualmente nesses suportes?
Como a divisão de 6 por 4 não é exata, 4 não é divisor de 6. Concluímos, portanto, que Marcos não conseguiria distribuir os seis jogos igualmente em quatro suportes.
Dizemos que um número natural é divisor ou fator de outro caso a divisão do segundo pelo primeiro seja exata.
Analise outros exemplos.
a)
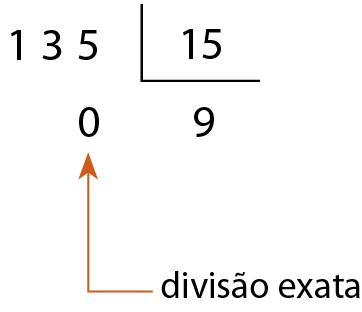
15 é divisor de 135.
b)
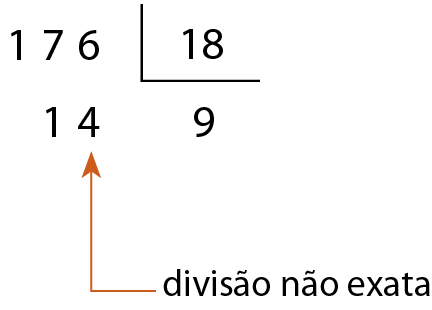
18 não é divisor de 176.
c)
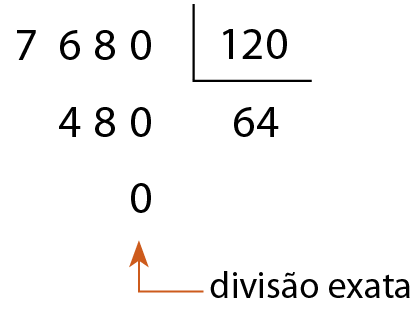
120 é divisor de .7680.
d)

23 é divisor de 322.
e)
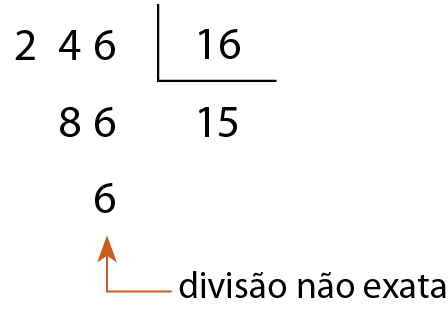
16 não é divisor de 246.
f)
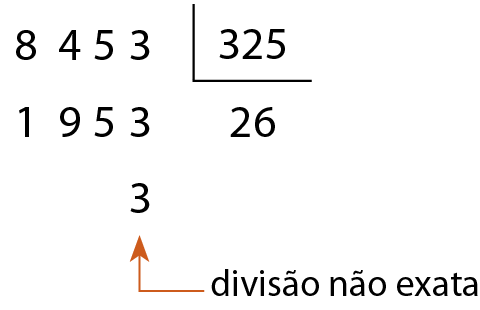
325 não é divisor de .8453.
Observações
1. O zero não é divisor de nenhum número natural.
Por exemplo: 5 dividido por 0 = ?
Note que não existe nenhum número que, multiplicado por zero, dê 5 como resultado.
2. Todo número natural diferente de zero tem como divisor ele mesmo.
a) 6 dividido por 6 = 1
6 é divisor de 6.
b) 8 dividido por 8 = 1
8 é divisor de 8.
c) 15 dividido por 15 = 1
15 é divisor de 15.
3. O número 1 é divisor de todos os números naturais.
a) 8 dividido por 1 = 8
1 é divisor de 8.
b) 12 dividido por 1 = 12
1 é divisor de 12.
c) 0 dividido por 1 = 0
1 é divisor de 0.
Atividades
Faça as atividades no caderno.
11. Efetue divisões para verificar se o número 600 é divisível por:
a) 12;
b) 15;
c) 18;
d) 24;
e) 36;
f) 90.
12. Escreva no caderno:
a) todos os fatores naturais de 30;
b) os fatores de 72 compreendidos entre 10 e 30;
c) os divisores ímpares de 40;
d) os divisores pares de 40.
13. Responda no caderno às questões a seguir.
a) Qual é o maior divisor de qualquer número não nulo?
b) Qual é o menor divisor de qualquer número?
c) O número zero é divisível por todos os outros números naturais?
d) Quais são os números que, divididos por 2, deixam resto 1?
e) Quais são os números que, divididos por 2, deixam resto zero?
14. Determine:
a) o maior número de três algarismos divisível por 2;
b) os três maiores divisores de 32;
c) o maior número de três algarismos divisível por 23.
15. Qual é o menor número que devemos adicionar a .1657 para torná‑lo um múltiplo de 100?
16. Leia as afirmações a seguir e indique, no caderno, se são verdadeiras ou falsas.
a) 2 é divisor de .1154.
b) 7 é fator de 185.
c) 3, 5, 9 e 10 são divisores de 810.
d) 2, 3, 9 e 100 são fatores de 117.
e) 8 é divisor de 84.
f) 16 é divisor de 500.
g) 32 é fator de 288.
h) 14 é divisor de 196.
17.

Junte-se a um colega, leiam a questão e a resolvam.
A professora escreveu em um quadro os divisores de 12 e os divisores de 36 em ordem crescente. Em seguida, uniu alguns desses divisores. Observem:

Que conclusões sugerem os registros da professora?
18. Copie a figura a seguir no caderno, substituindo o

pelos divisores de 36, de modo que cada número seja divisor daquele que vem depois da seta. Mas atenção: não póde haver repetição dos números!
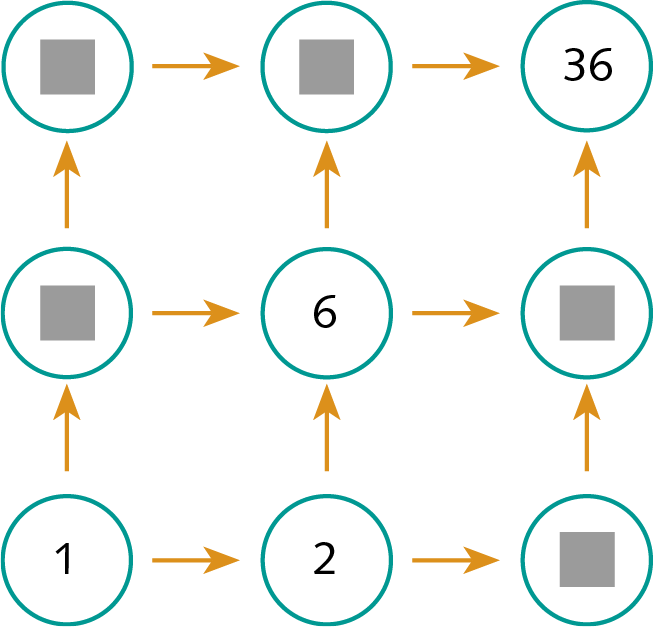
19.

Junte-se a um colega e resolvam o problema a seguir.
Adriano tem estas opções de peças de pisos cerâmicos quadrados para cobrir o chão de uma sala retangular de 300 centímetros de medida de comprimento por 240 centímetros de medida de largura.

Desconsiderando o rejunte, responda:
a) Qual é o menor número de peças amarelas necessárias para revestir o chão?
b) É possível revestir o chão com peças azuis sem recortá-las?
c) Adriano quer usar o menor número possível de peças e não quer recortar nenhuma. Qual deve ser a côr do piso dessa sala?
20.

Os gregos chamavam de número perfeito o número natural que fosse igual à soma de seus divisores própriosglossário .
Analise alguns exemplos:
|
Número perfeito |
Divisores próprios |
Cálculo da soma dos divisores próprios |
|---|---|---|
|
6 |
1, 2 e 3 |
1 + 2 + 3 = 6 |
|
28 |
1, 2, 4, 7 e 14 |
1 + 2 + 4 + 7 + 14 = 28 |
Com o auxílio de uma calculadora, verifique se o número 496 é um número perfeito.

3 Critérios de divisibilidade
Aprendemos que, para verificar se um número é divisível por outro, devemos efetuar uma divisão entre eles e analisar o resto da divisão. Quando o resto é igual a zero, o número é divisível pelo outro.
Agora, vamos estudar alguns critérios de divisibilidade que nos permitem verificar se um número é divisível por outro sem efetuar a divisão.
Critério de divisibilidade por 2
Observe estas divisões:
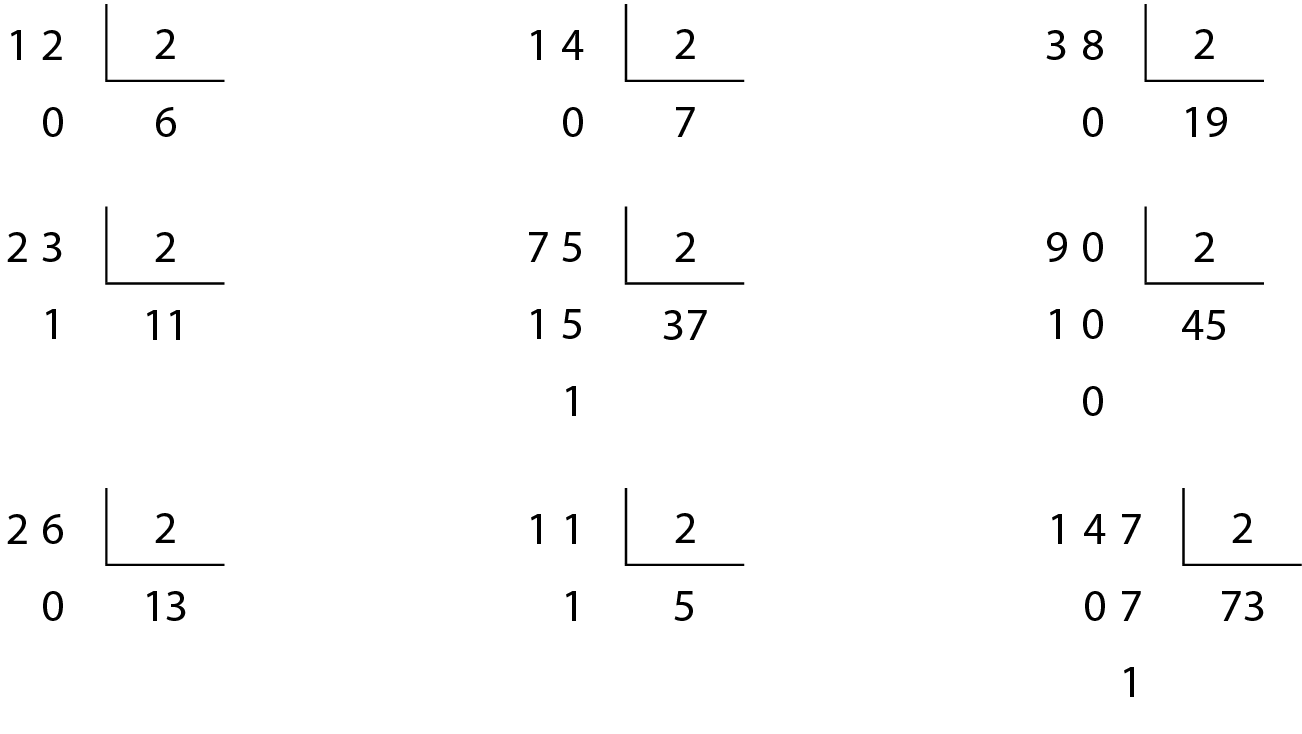
▸ Em seu caderno, divida outros números naturais por 2 e observe o resto dessas divisões.
Você deve ter percebido que, quando dividimos números pares por 2, obtemos resto zero e, quando dividimos números ímpares por 2, obtemos resto 1.
Um número natural é divisível por 2 quando é par, ou seja, quando termina em 0, 2, 4, 6 ou 8.
Podemos representar o critério de divisibilidade por 2 por meio de um fluxograma.
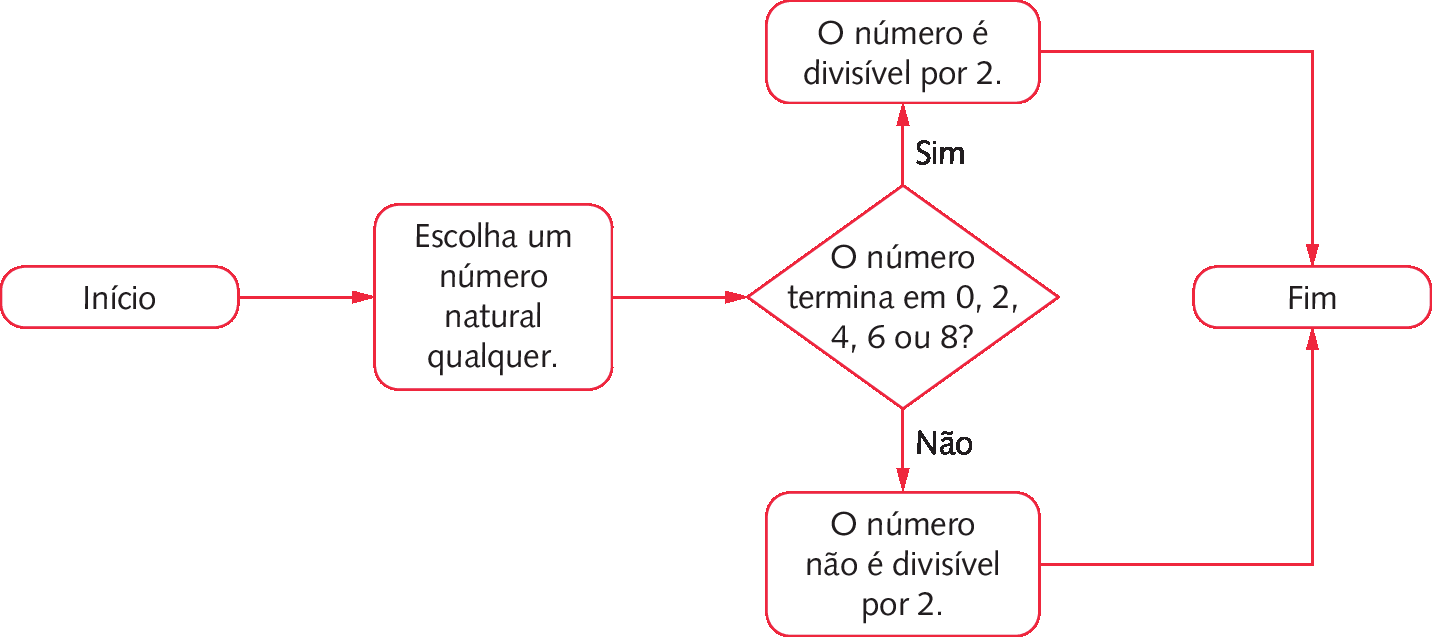
LEMBRE-SE: Escreva no caderno.
Critério de divisibilidade por 3
Observe estas divisões:
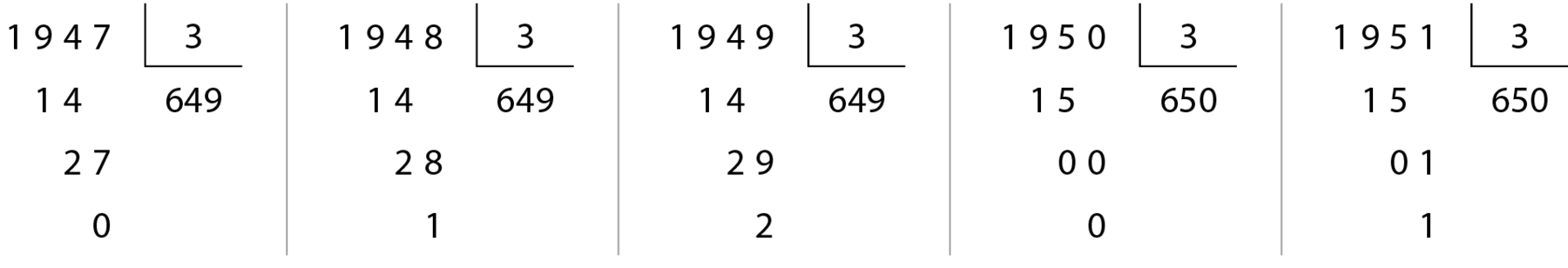
• O número .1947 é divisível por 3, pois 1 + 9 + 4 + 7 = 21 e 21 é divisível por 3.
• O número .1948 não é divisível por 3, pois 1 + 9 + 4 + 8 = 22 e 22 não é divisível por 3.
• O número .1949 não é divisível por 3, pois 1 + 9 + 4 + 9 = 23 e 23 não é divisível por 3.
• O número .1950 é divisível por 3, pois 1 + 9 + 5 + 0 = 15 e 15 é divisível por 3.
• O número .1951 não é divisível por 3, pois 1 + 9 + 5 + 1 = 16 e 16 não é divisível por 3.
▸ Sem efetuar a divisão, pense: qual é o resto da divisão de .1952 por 3? E de .1953 por 3?
▸

Calcule mentalmente 1 + 9 + 5 + 2 e 1 + 9 + 5 + 3.
▸ Agora, responda: .1952 é divisível por 3? E .1953, é divisível por 3?
Um número natural é divisível por 3 quando a soma dos seus algarismos é divisível por 3.
Podemos representar o critério de divisibilidade por 3 por meio de um fluxograma.
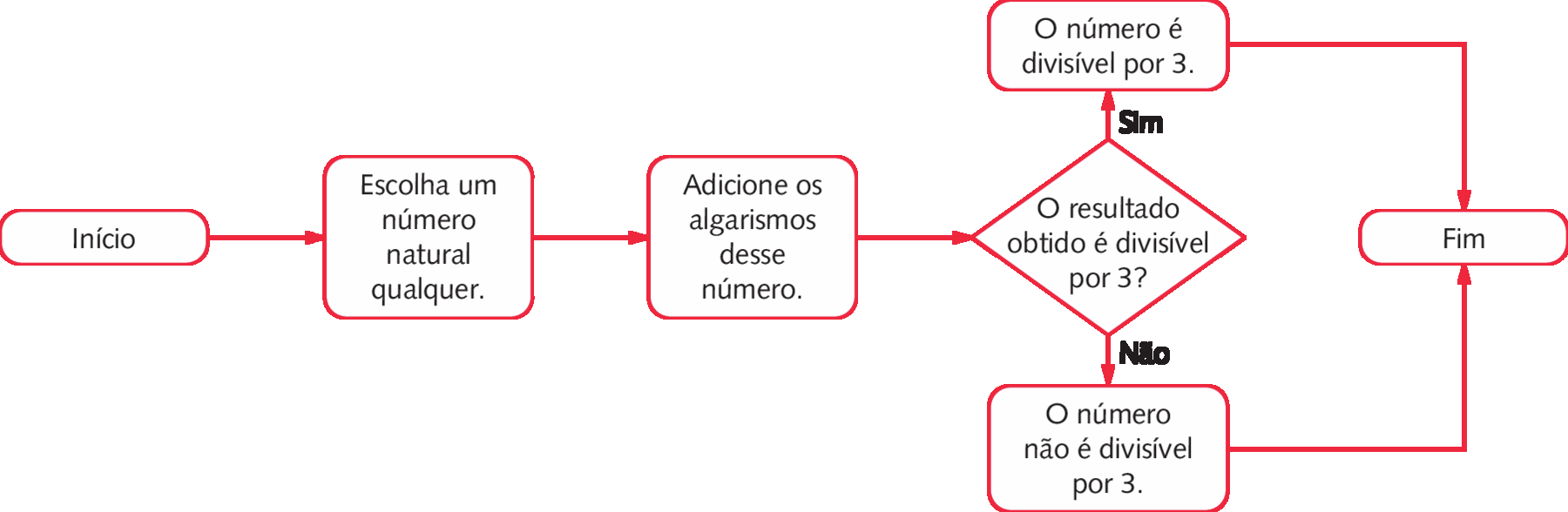
Critério de divisibilidade por 4
▸



Com uma calculadora, descubra alguns números naturais maiores ou iguais a 100 que sejam divisíveis por 4 e observe os dois últimos algarismos desses números. O que as investigações feitas por você sugerem? Converse com os colegas.
É possível verificar se um número maior ou igual a 100 é divisível por 4 analisando apenas os seus dois últimos algarismos.
Sabemos que 100 é divisível por 4, pois 100 = 4 × 25. Consequentemente, são também divisíveis por 4 todos os múltiplos de 100, como 200, 300, 700, .1100, .2300. Confira:
200 = 2 ⋅ 100 = 2 ⋅ 4 ⋅ 25
300 = 3 ⋅ 100 = 3 ⋅ 4 ⋅ 25
700 = 7 ⋅ 100 = 7 ⋅ 4 ⋅ 25
.1100 = 11 ⋅ 100 = 11 ⋅ 4 ⋅ 25
.2300 = 23 ⋅ 100 = 23 ⋅ 4 ⋅ 25
Note que 200, 300, 700, .1100 e .2300 terminam em 00.
Agora, observe estas divisões:
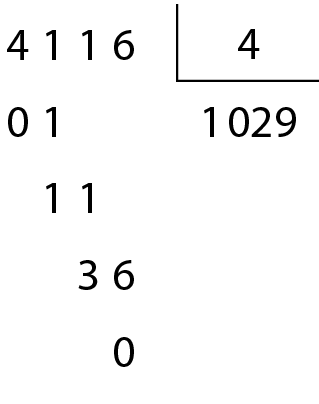
O número .4116 é divisível por 4.
Observe que:
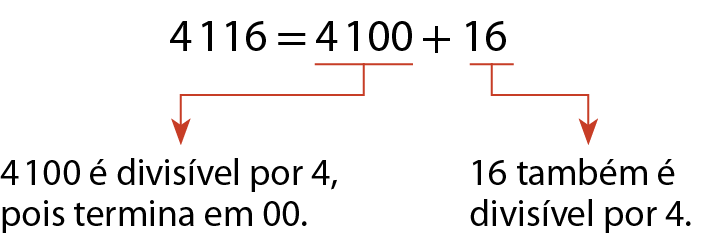
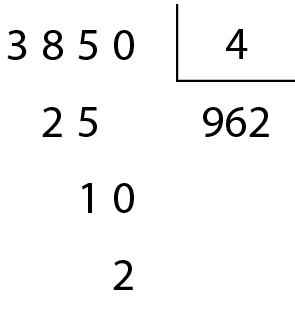
O número .3850 não é divisível por 4.
Observe que:
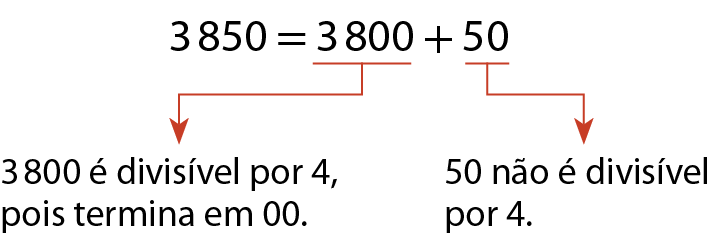
Um número natural, maior ou igual a 100, é divisível por 4 quando termina em 00 ou quando o número formado pelos seus dois últimos algarismos é divisível por 4.
Podemos representar o critério de divisibilidade por 4 por meio de um fluxograma.
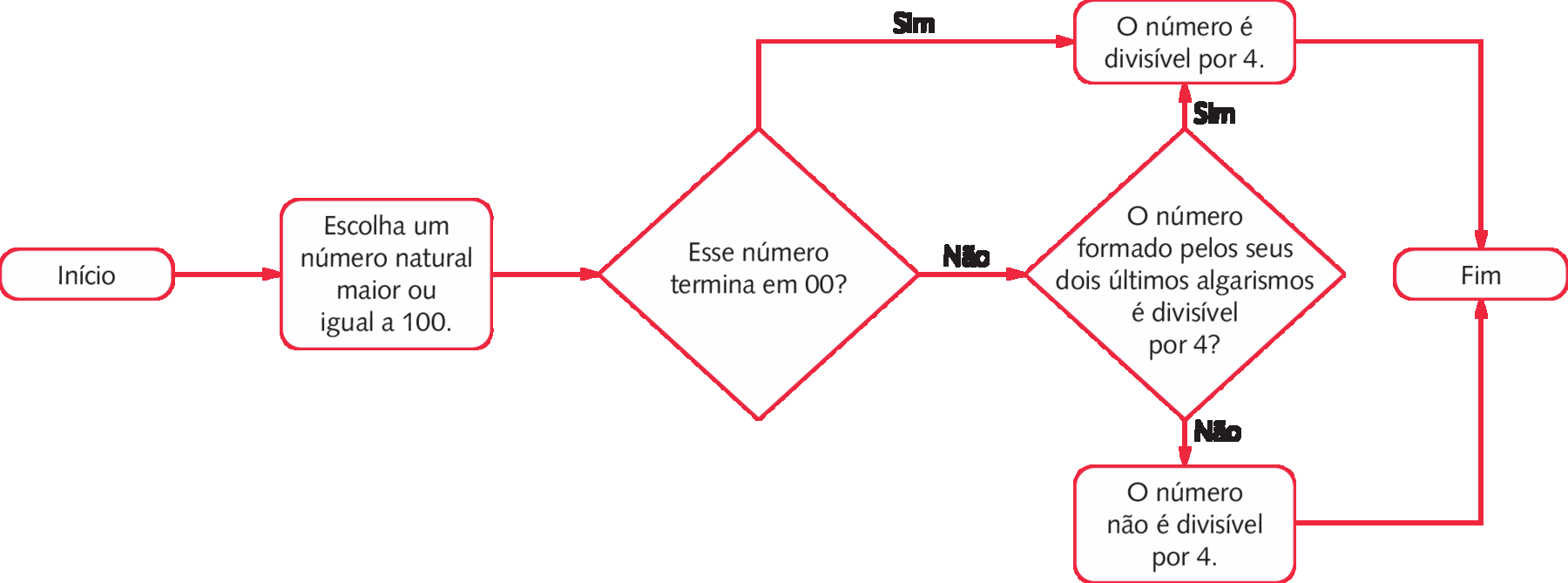
Critério de divisibilidade por 5
Observe estas divisões:
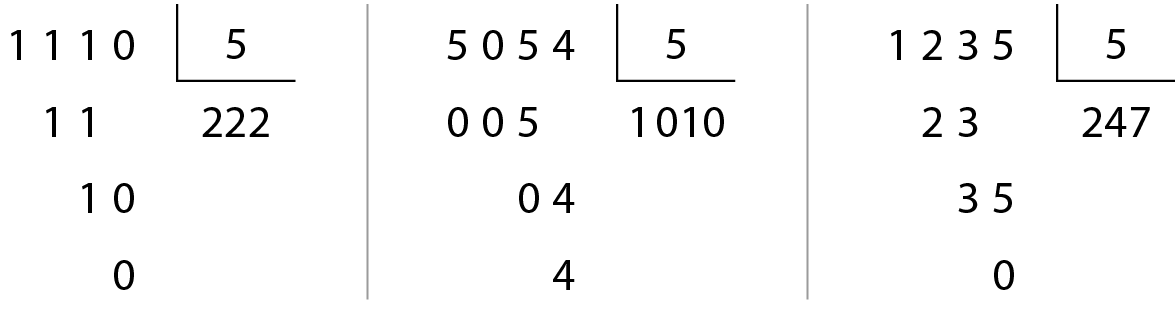

• O número .1110 é divisível por 5, pois termina em 0.
• O número .5054 não é divisível por 5, pois não termina em 0 nem em 5.
• O número .1235 é divisível por 5, pois termina em 5.
Um número natural é divisível por 5 quando termina em 0 ou em 5.
Podemos representar o critério de divisibilidade por 5 por meio de um fluxograma.
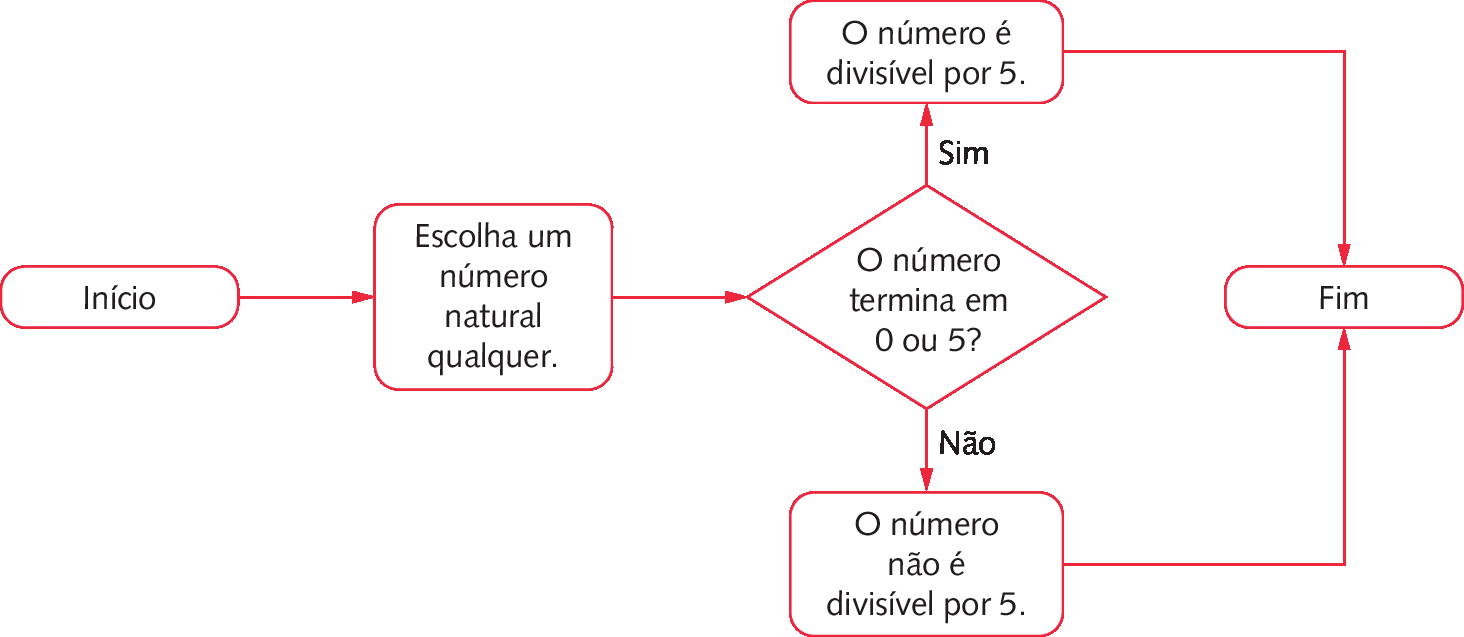
Critério de divisibilidade por 6
▸

Com uma calculadora, descubra alguns números naturais que sejam divisíveis por 6. Esses números são divisíveis por 2? E por 3?
▸


O que as investigações feitas por você sugerem? Converse com os colegas.
Observe estas divisões:

• O número 312 é divisível por 6.
O número 312 é divisível por 2, pois é par, e por 3, pois 3 + 1 + 2 = 6 e 6 é divisível por 3.
• O número 609 não é divisível por 6.
O número 609 é divisível por 3, pois 6 + 0 + 9 = 15 e 15 é divisível por 3, mas 609 não é divisível por 2, porque é ímpar.
• O número 716 não é divisível por 6.
O número 716 é divisível por 2, pois é par, mas 716 não é divisível por 3, pois 7 + 1 + 6 = 14 e 14 não é divisível por 3.
• O número .6612 é divisível por 6.
O número .6612 é divisível por 2, pois é par, e por 3, pois 6 + 6 + 1 + 2 = 15 e 15 é divisível por 3.
Um número natural é divisível por 6 quando é divisível por 2 e também por 3.
Podemos representar o critério de divisibilidade por 6 por meio de um fluxograma.
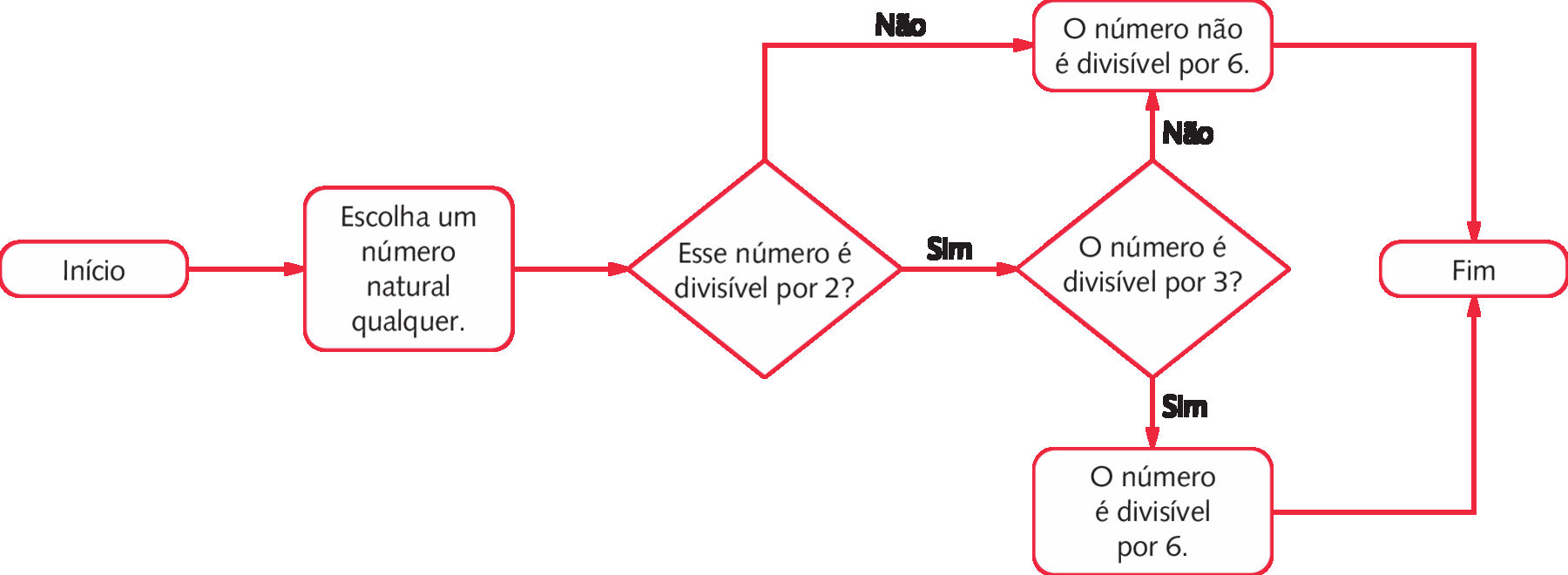
Critério de divisibilidade por 8
▸



Com uma calculadora, descubra alguns números naturais maiores ou iguais a .1000 que sejam divisíveis por 8 e observe os três últimos algarismos desses números. O que as investigações feitas por você sugerem? Converse com os colegas.
É possível verificar se um número maior ou igual a .1000 é divisível por 8 analisando apenas os seus três últimos algarismos.
Sabemos que .1000 é divisível por 8, pois .1000 = 8 ⋅ 125. Consequentemente, são também divisíveis por 8 todos os múltiplos de .1000, como .2000, .3000, .7000, .12000, .15000.
Note que .2000, .3000, .7000, .12000 e .15000 terminam em 000.
Agora, observe estas divisões:

• O número .5000 é divisível por 8, pois termina em 000.
• O número .3300 não é divisível por 8, pois o número formado por seus três últimos algarismos não é divisível por 8.
• O número .13336 é divisível por 8, pois o número formado por seus três últimos algarismos é divisível por 8.
• O número .10180 não é divisível por 8, pois o número formado por seus três últimos algarismos não é divisível por 8.
Um número natural, maior ou igual a .1000, é divisível por 8 quando termina em 000 ou quando o número formado pelos seus três últimos algarismos é divisível por 8.
Podemos representar o critério de divisibilidade por 8 por meio de um fluxograma.
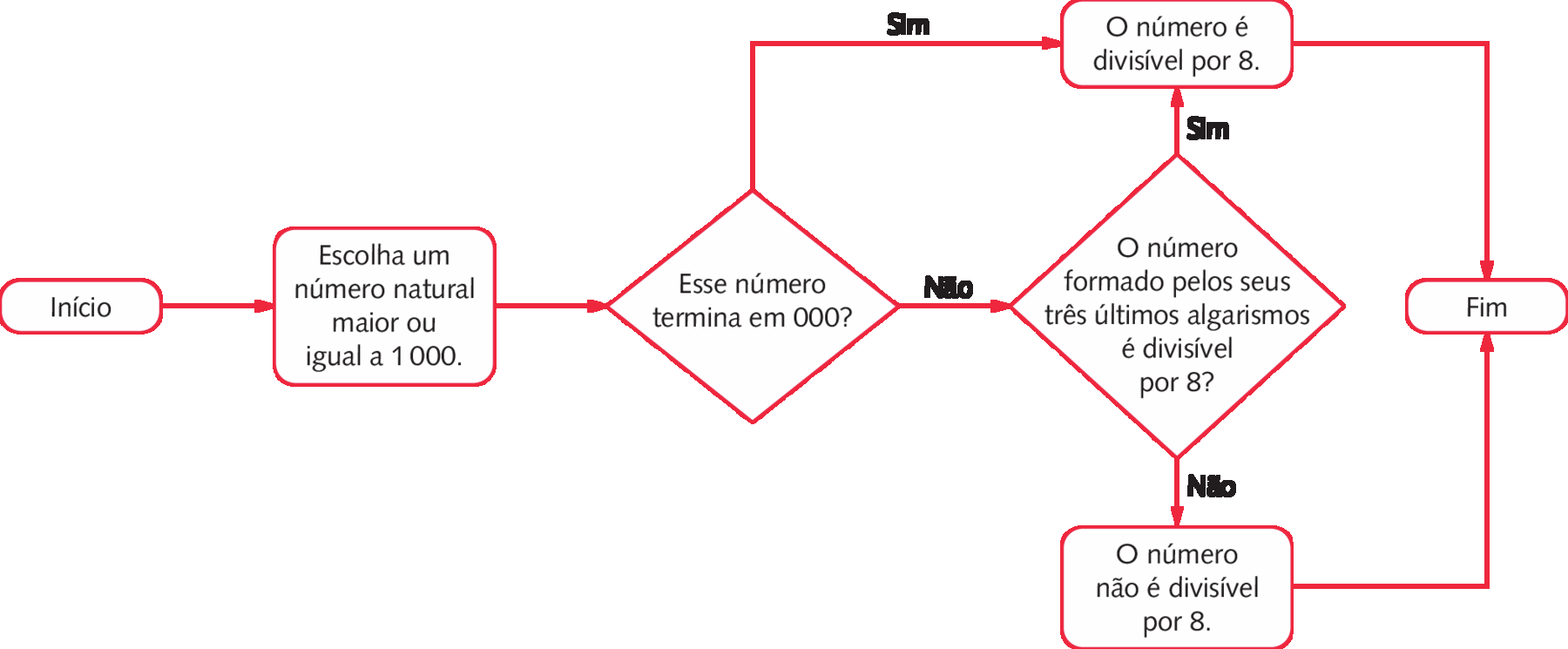
Critério de divisibilidade por 9
▸



Com uma calculadora, descubra alguns números naturais divisíveis por 9 e adicione seus algarismos. O que as investigações feitas por você sugerem? Converse com os colegas.
Observe estas divisões:
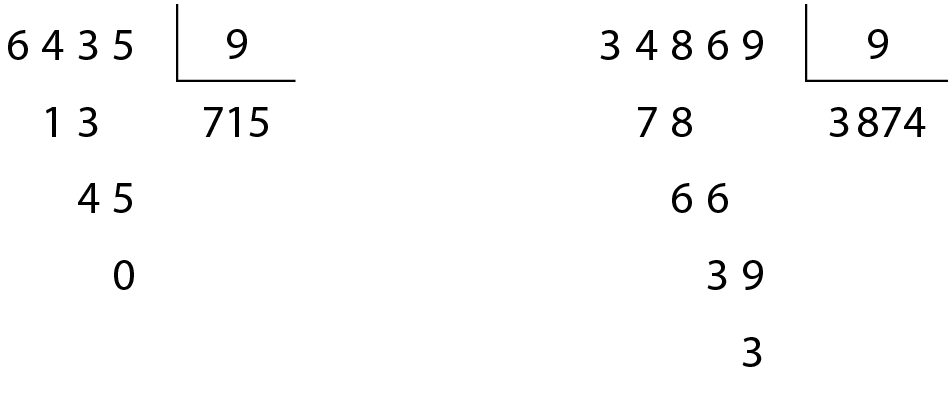
• O número .6435 é divisível por 9, pois 6 + 4 + 3 + 5 = 18 e 18 é divisível por 9.
• O número .34869 não é divisível por 9, pois 3 + 4 + 8 + 6 + 9 = 30 e 30 não é divisível por 9.
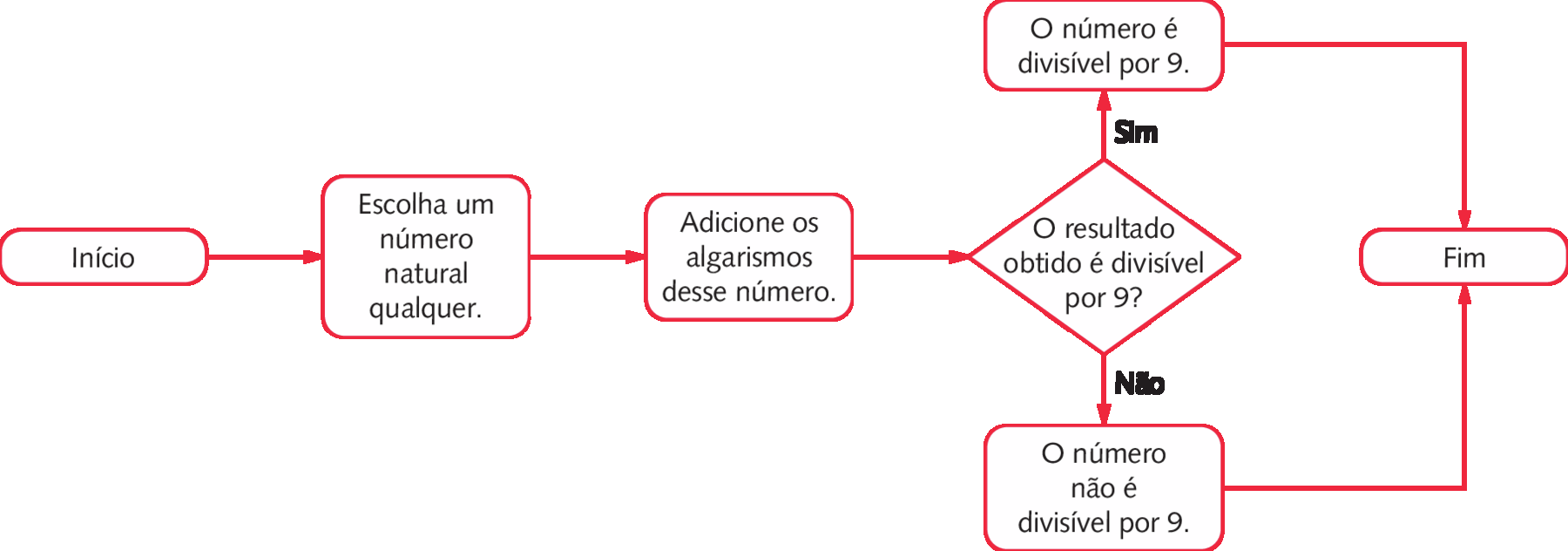
Um número natural é divisível por 9 quando a soma dos seus algarismos é divisível por 9.
Podemos representar o critério de divisibilidade por 9 por meio de um fluxograma.
Critérios de divisibilidade por 10, 100 e .1000
Observe o quadro a seguir.
|
Números divisíveis por 10 |
10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, ... |
|---|---|
|
Números divisíveis por 100 |
100, 200, 300, 400, 500, 600, 700, 800, 900, 1.000, 1.100, ... |
|
Números divisíveis por 1.000 |
1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000, 8.000, 9.000, 10.000, 11.000, ... |
▸

Que padrão você observa nos números divisíveis por 10 mostrados anteriormente? E nos números divisíveis por 100? E nos divisíveis por .1000?
▸ O padrão que você observou anteriormente sugere os critérios de divisibilidade por 10, 100 e .1000. Escreva esses critérios em seu caderno.
Atividades
Faça as atividades no caderno.
21. Copie no caderno o quadro a seguir e marque com X os divisores de cada número.

|
Divisores |
|||||
|---|---|---|---|---|---|
|
Números |
2 |
3 |
4 |
5 |
6 |
|
216 |
|||||
|
678 |
|||||
|
745 |
|||||
|
1.224 |
|||||
|
3.206 |
|||||
22. Escreva no caderno o menor número de três algarismos divisível por:
a) 2;
b) 3;
c) 4;
d) 5;
e) 6
23. Identifique os números que são divisíveis, ao mesmo tempo, por 2 e por 5.
a) 805
b) 160
c) 420
d) 222
e) .5000
f) 803
24. Em seu caderno, copie as afirmações verdadeiras.
a) Todo número divisível por 6 é também divisível por 2.
b) Todo número par é divisível por 5.
c) Nenhum número ímpar é divisível por 2.
d) Todo número divisível por 4 é também divisível por 2.
25.

Em seu caderno, represente por meio de um fluxograma os critérios de divisibilidade por 10, 100 e .1000.
26. Existe algum algarismo que póde ser colocado no lugar de

de modo que o número

seja divisível por 2? Explique seu pensamento.
27. Dado o número de três algarismos:

, pergunta‑se:
a) Esse número é divisível por 5?
b) Por quais algarismos devemos substituir

para obter um número divisível por 3?
28. Determine:
a) o maior número de três algarismos divisível por 5;
b) o menor número de três algarismos divisível, ao mesmo tempo, por 2, por 3 e por 5;
c) o maior número de três algarismos divisível, ao mesmo tempo, por 3 e por 4.
29. Registre no caderno qual dos anos apresentados a seguir é bissextoglossário .

30. Um número de quatro algarismos é representado por

.
Determine os algarismos que ao serem colocados no lugar de

tornam o número divisível por:
a) 2;
b) 3;
c) 4;
d) 5;
e) 6
31. Escreva no caderno o menor número que devemos adicionar a 763 para obtermos um número divisível por:
a) 3;
b) 5;
c) 2 e 3 ao mesmo tempo.
32. Determine o maior número de quatro algarismos diferentes que seja:
a) divisível por 2 e por 3;
b) divisível por 2, mas não por 3;
c) divisível por 3, mas não por 2;
d) não divisível por 2 nem por 3.
33. Qual é o maior número de seis algarismos divisível por 10?
34. Qual é o menor número divisível por 9 formado apenas pelo algarismo 4?
35. Considere os números 450, 660, 768, 860 e 960.
a) Quais deles são divisíveis por 3 e por 4 ao mesmo tempo? Podemos dizer que os números divisíveis por 3 e por 4 também são divisíveis por 12?
b) Quais deles são divisíveis por 3 e por 5 ao mesmo tempo? Podemos dizer que os números divisíveis por 3 e por 5 também são divisíveis por 15?
36.

Com um colega, explique por que todos os números de três algarismos iguais são divisíveis por 3.
37. Como todo número par é divisível por 2, podemos verificar se um número natural qualquer é par observando o resto de sua divisão por 2.
a) Copie as frases a seguir no caderno e, depois, complete as lacunas.
Etapa 1: Escolha um número natural e o divida por 2.
Etapa 2: O

da divisão por 2 é igual a zero?
Etapa 3: Se sim, então o número é

.
Etapa 4: Se não, o número é

.
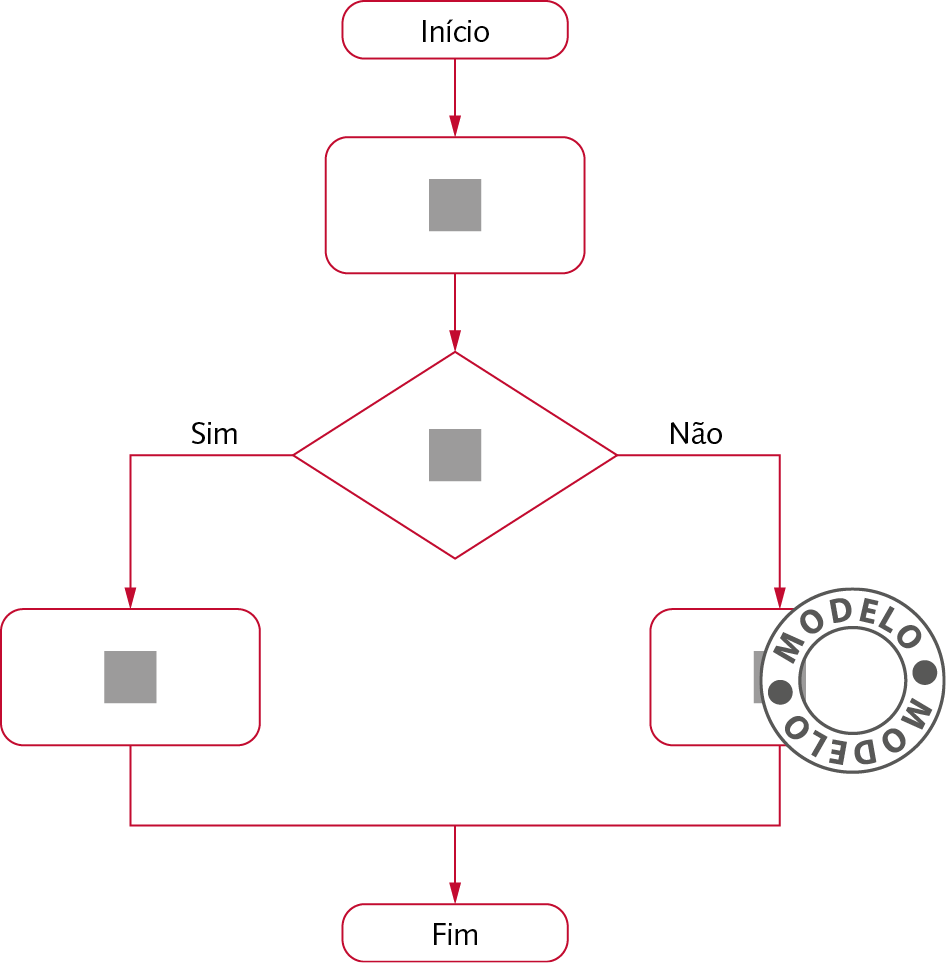
b)


Agora, em dupla, copiem o fluxograma a seguir no caderno e completem-no com as etapas do item a.

4 Números primos e números compostos
Vamos considerar o conjunto dos números naturais

= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, reticências}.
Podemos verificar que:
• 0 é divisível por qualquer número diferente de zero;
• 1 é divisível apenas por 1;
• 2 é divisível por 1 e 2;
• 3 é divisível por 1 e 3;
• 4 é divisível por 1, 2 e 4;
• 5 é divisível por 1 e 5;
• 6 é divisível por 1, 2, 3 e 6;
• 7 é divisível por 1 e 7;
• 8 é divisível por 1, 2, 4 e 8;
• 9 é divisível por 1, 3 e 9.
Podemos observar que:
• 1 é divisor de qualquer número, ou seja, qualquer número é divisível por 1;
• alguns números, como 2, 3, 5 e 7, têm exatamente dois divisores naturais: o número 1 e o próprio número; eles são chamados de números primos.
Um número é primo quando tem somente dois divisores naturais distintos: o número 1 e o próprio número.
Existem números, como 4, 6, 8 e 9, que têm mais de dois divisores naturais distintos; eles são chamados de números compostos.
Um número, diferente de zero, é composto quando tem mais de dois divisores distintos.
Os números compostos podem ser escritos como um produto de números primos. Confira os exemplos.
a) 8 = 2 ⋅ 2 ⋅ 2
b) 9 = 3 ⋅ 3
c) 12 = 2 ⋅ 2 ⋅ 3
d) 105 = 3 ⋅ 5 ⋅ 7
Observações
1. O número 1 não é primo nem composto, pois tem apenas um divisor natural (o próprio 1) e não póde ser escrito como produto de números primos.
2. O número 0 não é primo nem composto, pois tem infinitos divisores e não póde ser escrito como produto de números primos.
3. O único número natural primo que é par é o 2.
4. A palavra “primo” significa “primeiro”. Os números primos são “os primeiros”, pois outros números podem ser escritos a partir deles por meio de multiplicações. Analise alguns exemplos:
a) 16 = 2 ⋅ 2 ⋅ 2 ⋅ 2
b) 45 = 3 ⋅ 3 ⋅ 5
c) 84 = 2 ⋅ 2 ⋅ 3 ⋅ 7
Verificando se um número é primo
Para verificar se um número é primo ou composto, devemos primeiro dividir o número dado pelos números primos menores do que ele, até obtermos um quociente menor ou igual ao divisor. Depois, devemos analisar:
• se nenhuma das divisões efetuadas for exata, o número será primo;
• se qualquer uma das divisões for exata, o número será composto.
Podemos representar esse procedimento por meio de um fluxograma.
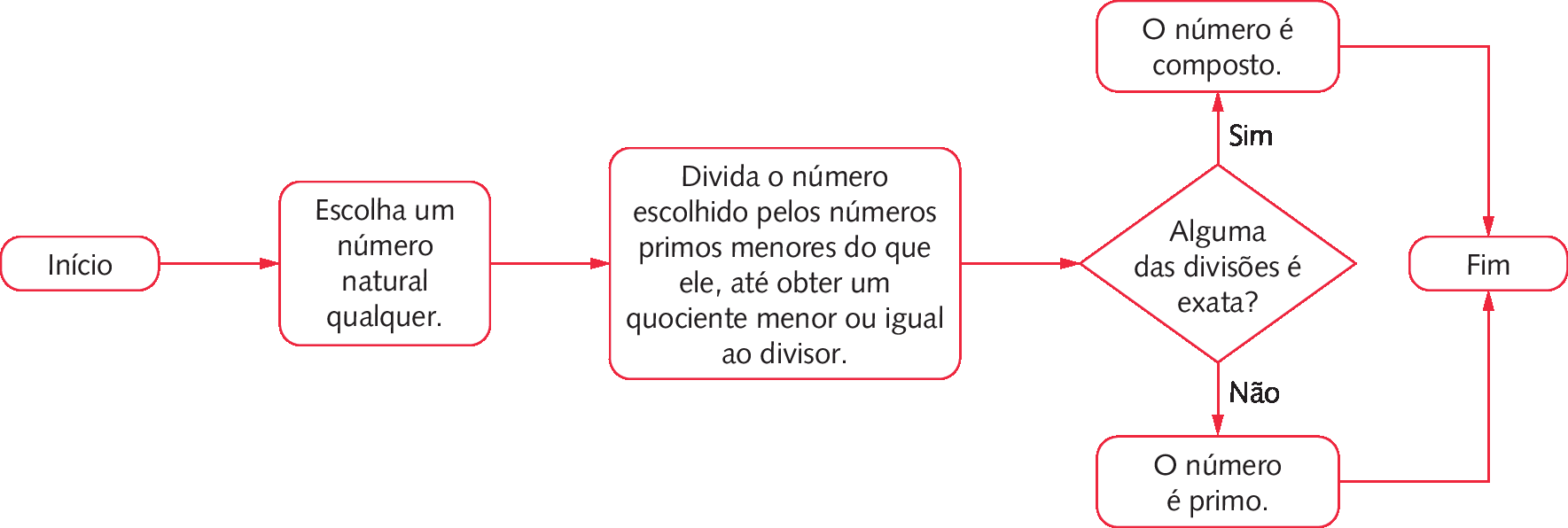
Convém utilizar o procedimento anterior quando os números são pequenos. Acompanhe os exemplos.
a) Vamos verificar se o número 71 é primo.
Observe as divisões de 71 por alguns números primos menores do que ele.
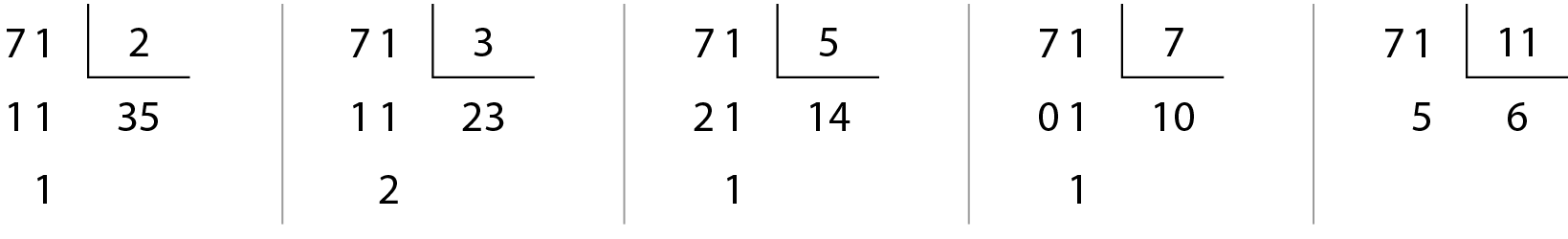
Percebemos que, na divisão por 11, o quociente 6 é menor que o divisor e a divisão não é exata. Podemos, então, afirmar que o número 71 é primo.
b) Vamos verificar se o número 667 é primo.
Pelos critérios de divisibilidade, 667 não é divisível por 2, nem por 3, nem por 5. Vamos dividir o número 667 pelos próximos números primos menores do que ele. Verifique:

Como a divisão por 23 é exata, podemos parar de dividir 667 por números primos e afirmar que o número 667 não é primo.
Foi Eratóstenes, um matemático grego nascido em 276 antes de Cristo, quem desenvolveu um método para encontrar os primeiros números primos a partir da sequência dos números naturais. Essa operação recebeu o nome de Crivo de Eratóstenes. O método consiste na disposição ordenada dos números naturais em linhas e em colunas. Com base nisso, ele eliminou os números compostos e, utilizando uma estratégia, identificou os números primos. Analise a seguir.
Vamos obter os números primos compreendidos entre 1 e 50 pelo Crivo de Eratóstenes:
1º) Eliminamos o número 1, pois já sabemos que ele não é primo.
2º) Circulamos o 2 e riscamos seus múltiplos, que são números compostos.
3º) Circulamos o 3 e riscamos seus múltiplos.
4º) Continuamos esse processo com os números que ainda não foram riscados até que não haja mais números a serem riscados ou circulados.
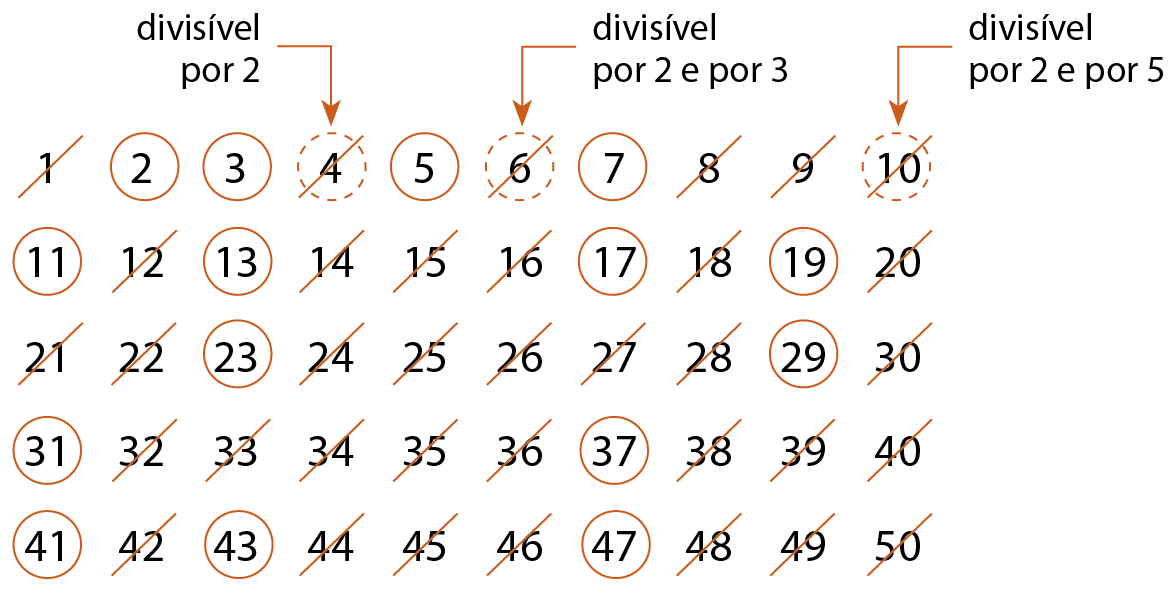
Os números 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e 47 são números primos.

Um pouco de história
Faça as atividades no caderno.
Números primos e compostos
[reticências] Os gregos antigos excluíam o 1 (unidade, a mônada) do conjunto dos primos porque não o consideravam sequer número; consideravam-no o princípio dos números, a origem ou o gerador dos números. Euclides e Aristósteles aceitavam o 2 como primo, mas isso não ocorria com os pitagóricos mais antigos. Para eles, o 2, a díade, não era de modo algum um número, mas apenas o princípio dos “pares”.


Hoje em dia, a habitual exclusão do 1 do conjunto dos números primos permite maior simplicidade no enunciado de teoremas e de fórmulas concernentes a números primos.
Euclides deu uma das primeiras contribuições significativas à teoria dos números primos ao provar que o conjunto destes números é infinito. [reticências]
FEY, James. Números primos e compostos: tópicos de história da Matemática. In: GUNDLACH, Bernard H. Números e numerais. São Paulo: Atual, 1992. página 49.
Atividade

Em seu caderno, escreva três números primos maiores do que 100. Depois, compartilhe os números que escreveu com os colegas.
Atividades
Faça as atividades no caderno.
38. Quais dos números a seguir são primos?
a) 81
b) 227
c) 463
d) 101
e) 559
f) 977
g) 808
h) 585
i) 161
39. Escreva, no caderno, todos os números primos menores que 30.
40. Escreva cada número a seguir como um produto de números primos.
a) 14
b) 35
c) 70
d) 42
e) 50
f) 100
41. O número 323 é primo? Justifique sua resposta.
42. A senha do cartão de crédito de Adriano é o produto do maior número primo de dois algarismos pelo menor número primo de três algarismos. Qual é a senha do cartão de crédito de Adriano?

43. Quais são os números primos maiores que 100 e menores que 200 nos quais o algarismo das dezenas é par e maior que o algarismo das unidades?
Decomposição em fatores primos
Todo número natural composto póde ser representado por meio de uma multiplicação de dois ou mais fatores. Verifique:
60 = 2 ⋅ 30 60 = 2 ⋅ 2 ⋅ 15 60 = 2 ⋅ 2 ⋅ 3 ⋅ 5
Temos anteriormente três fatorações do número 60.
Note que, em 60 = 2 ⋅ 2 ⋅ 3 ⋅ 5, todos os fatores são primos. Essa igualdade póde ser escrita também como 60 = 2elevado a 2 ⋅ 3 ⋅ 5. Realizamos, assim, a fatoração completa ou decomposição em fatores primos do número 60.
Analise, agora, duas maneiras diferentes de obter a fatoração completa do número 420.
Utilizando o processo das fatorações sucessivas
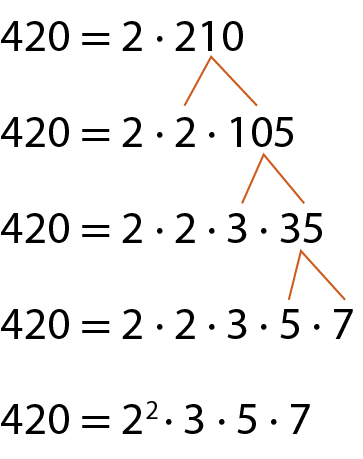

Fazendo divisões sucessivas

Clique no play e acompanhe as informações do vídeo.
420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7
420 = 2elevado a 2 ⋅ 3 ⋅ 5 ⋅ 7
Terminamos esse processo quando obtemos o quociente 1. A coluna da direita apresenta os fatores primos de 420.
Observe que utilizamos os números primos em ordem crescente por opção, mas poderíamos dispô-los em qualquer ordem.
Atividades
Faça as atividades no caderno.
44. Qual é a fatoração completa dos números a seguir?
a) 96
b) 324
c) .1024
d) .1260
e) .2870
f) .3575
45. Dado o número na fórma fatorada 2elevado a 3 ⋅ 5elevado a 2 ⋅ 7, pergunta‑se:
a) Qual é esse número?
b) Qual é o maior divisor primo desse número?
46. Escreva no caderno o número cuja fórma fatorada é igual a:
a) 2elevado a 2 ⋅ 3 ⋅ 7
b) 2elevado a 3 ⋅ 3elevado a 2 ⋅ 5
c) 2elevado a 4 ⋅ 7
d) 2 ⋅ 7elevado a 2 ⋅ 11
47. Quais são os fatores primos comuns a 30 e 140?
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Múltiplos de um número natural
Um número natural é múltiplo de outro quando o primeiro é obtido multiplicando o segundo por um número natural qualquer.
1. Escreva, no caderno, os cinco menores múltiplos de 15.
2. Determine os múltiplos de 18 compreendidos entre 160 e 240.
Divisores de um número natural
Um número natural é divisor ou fator de outro quando a divisão do segundo pelo primeiro é exata; nesse caso, o segundo número é divisível pelo primeiro.
3. Verifique se o número 256 é divisível por:
a) 2;
b) 8;
c) 12;
d) 15;
e) 16;
f) 18
4. Determine o maior número de três algarismos divisível por 4.
5. Leia as afirmações e indique se elas são verdadeiras ou falsas.
a) 4 é divisor de 240.
b) 2, 3 e 6 são divisores de 624.
c) 15 é fator de .1450.
Critérios de divisibilidade
Um número natural é divisível por:
• 2 quando ele é par;
• 3 quando a soma de seus algarismos é divisível por 3;
• 4 quando termina em 00 ou seus dois últimos algarismos formam um número divisível por 4 (para números maiores ou iguais a 100);
• 5 quando termina em 0 ou em 5;
• 6 quando é divisível por 2 e por 3;
• 8 quando termina em 000 ou seus três últimos algarismos formam um número divisível por 8 (para números maiores ou iguais a .1000);
• 9 quando a soma de seus algarismos é divisível por 9;
• 10 quando termina em 0;
• 100 quando termina em 00;
• .1000 quando termina em 000.
6. Copie o quadro a seguir no caderno e marque um xis nos espaços correspondentes aos divisores de cada número.

|
Divisor |
||||||
|---|---|---|---|---|---|---|
|
Número |
2 |
3 |
5 |
6 |
8 |
9 |
|
312 |
||||||
|
645 |
||||||
|
1.236 |
||||||
|
2.169 |
||||||
7. Identifique os números que são divisíveis por 9.
a) 909
b) .1071
c) .2304
d) .3356
Números primos e números compostos
• Um número é primo quando tem somente dois divisores naturais distintos: o número 1 e o próprio número.
• Um número, diferente de zero, é composto quando tem mais de dois divisores distintos.
Decomposição em fatores primos
Todo número natural composto pode ser representado por uma multiplicação de dois ou mais fatores primos.
756 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 7 = 2elevado a 2 ⋅ 3elevado a 3 ⋅ 7
.2925 = 3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 13 = 3elevado a 2 ⋅ 5elevado a 2 ⋅ 13
8. Quais dos números a seguir são primos?
a) 99
b) 109
c) 167
d) 281
e) 562
f) 1 021
9. Escreva, no caderno, a decomposição dos números a seguir em fatores primos.
a) 576
b) .2048
c) .1323
d) .1944
e) .2058
f) .5096
Glossário
- Padrão
- : Característica que se repete ou modelo que é seguido.
- Voltar para o texto
- Divisor próprio
- : Valor que divide um número resultando em uma divisão exata, mas que não seja o próprio número.
- Voltar para o texto
- Ano bissexto
- : Ano ao qual é acrescentado um dia, ficando com 366 dias. Anos bissextos são divisíveis por 4 e não terminam em 00. Se terminar em 00, para que seja bissexto, ele deve ser divisível por 400.
- Voltar para o texto