Parte 1
Capítulo 6 Frações
Trocando ideias

A arara-azul (Anadoríncus lassãntínus) é considerada a maior espécie de arara em todo o mundo, podendo atingir cêrca de 98 centímetros de medida de comprimento e 1,3 quilograma de medida de massa. Essa ave está atualmente ameaçada de extinção devido à caça, ao comércio clandestino e à degradação em seu abitá natural por conta do desmatamento.

No Pantanal, cêrca de
Sentença matemática: fração nove décimos.dos ninhos das araras-azuis são feitos em uma única espécie de árvore: o manduvi (Sterculia apetala).
▸

O número
Sentença matemática: fração nove décimos.é um exemplo de fração. Em quais situações do cotidiano as frações estão presentes?
▸

O que significa dizer que
Sentença matemática: fração nove décimos.dos ninhos das araras-azuis são feitos nos manduvis?
▸


Em sua opinião, o que precisa ser feito para a preservação das araras-azuis? Converse com os colegas.
Neste capítulo, vamos estudar as frações e algumas operações com frações.

1 A ideia de número fracionário
Observe a torta de legumes a seguir.
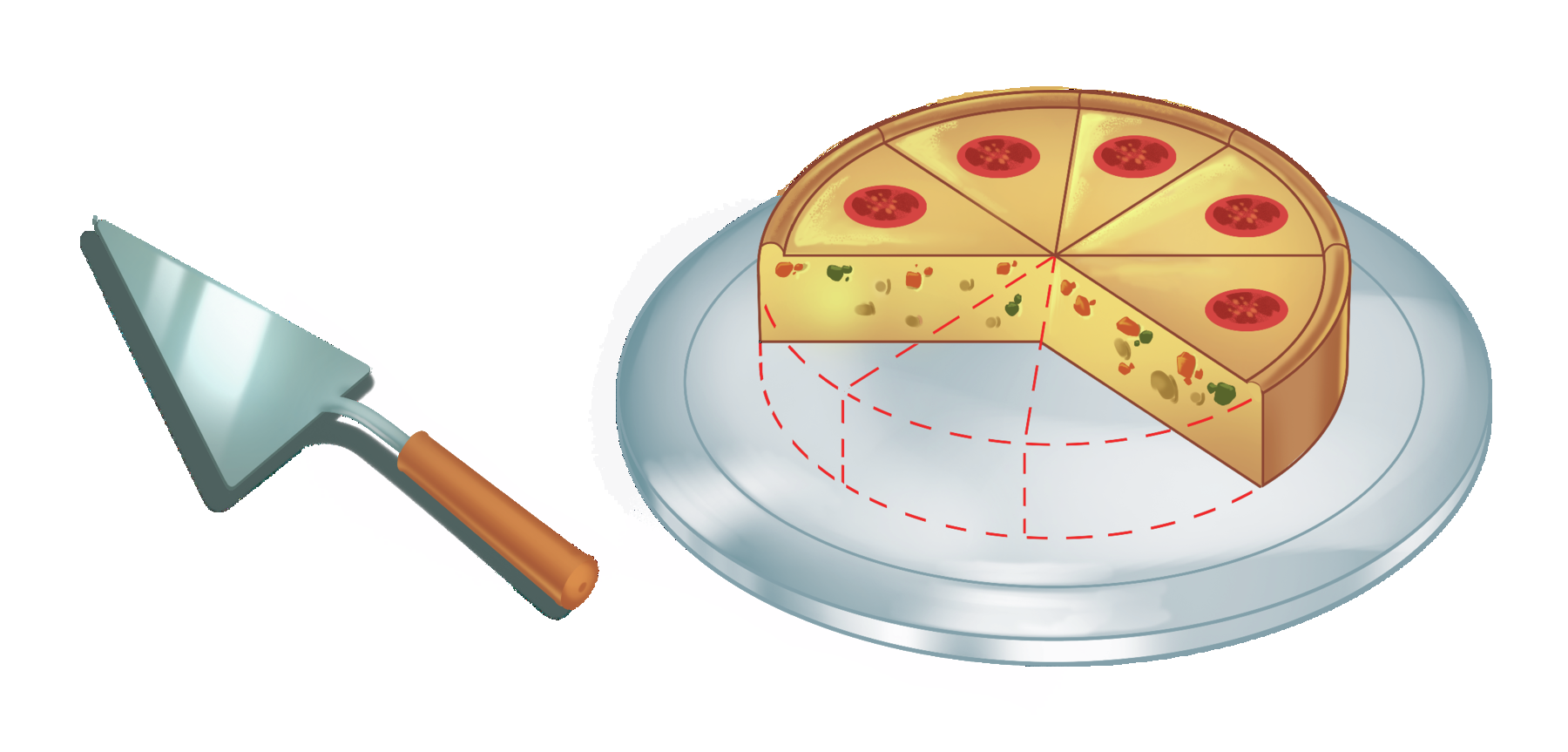
Considerando que a torta representa o todo ou o inteiro, podemos dizer que cada pedaço corresponde a
Sentença matemática: fração um sobre oito.(lemos: “um oitavo”) da torta. A parte da torta que sobrou corresponde a
Sentença matemática: fração cinco oitavos.(lemos: “cinco oitavos”) do inteiro. Os números
Sentença matemática: fração um oitavo.e
Sentença matemática: fração cinco oitavos.são exemplos de números fracionários ou frações.
Em uma fração, o denominador é o número abaixo do traço e representa a quantidade de partes iguais em que o todo foi dividido. Já o número acima do traço, o numerador, indica a quantidade de partes consideradas do todo.
Observe.
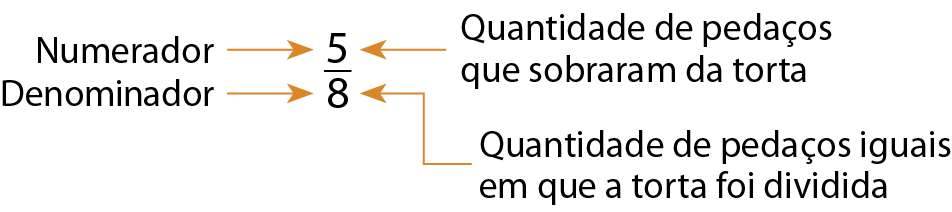
Acompanhe uma situação em que utilizamos frações.
Em um posto de saúde, 3 das 9 crianças que estavam na fila eram bebês de colo.
Três crianças correspondem a
Sentença matemática: fração três nonos.ou
fração 1 terçodo total de crianças que havia na fila (9).


▸


Quais vacinas você já tomou? Qual é a importância das vacinas? Converse com os colegas.
Observe outros exemplos.
a) A figura representa um inteiro, que foi dividido em seis partes iguais, sendo que cinco delas foram coloridas de azul.

Representamos a parte azul por
Sentença matemática: fração cinco sextos.(lemos: “cinco sextos”).
b) A figura representa um inteiro dividido em oito partes iguais, sendo que três delas foram coloridas de verde.

Representamos a parte verde por
Sentença matemática: fração três sobre oito.(lemos: “três oitavos”).
Além da ideia de parte de um inteiro, como visto nos exemplos anteriores, as frações podem transmitir a ideia de resultado de uma divisão (quociente). Por exemplo, para dividirmos 3 goiabas entre 4 pessoas, podemos cortar cada uma das goiabas em 4 partes, em que cada parte representa
Sentença matemática: fraçãoum quarto.de goiaba.
Distribuindo a cada pessoa 3 partes, cada uma receberá
Sentença matemática: fração três quartos.de goiaba.

Acompanhe outro exemplo.
Joaquim fez 5 rocamboles iguais, que foram divididos igualmente entre duas padarias. Quanto de rocambole cada uma das duas padarias recebeu?
Vamos esquematizar a divisão dos rocamboles.
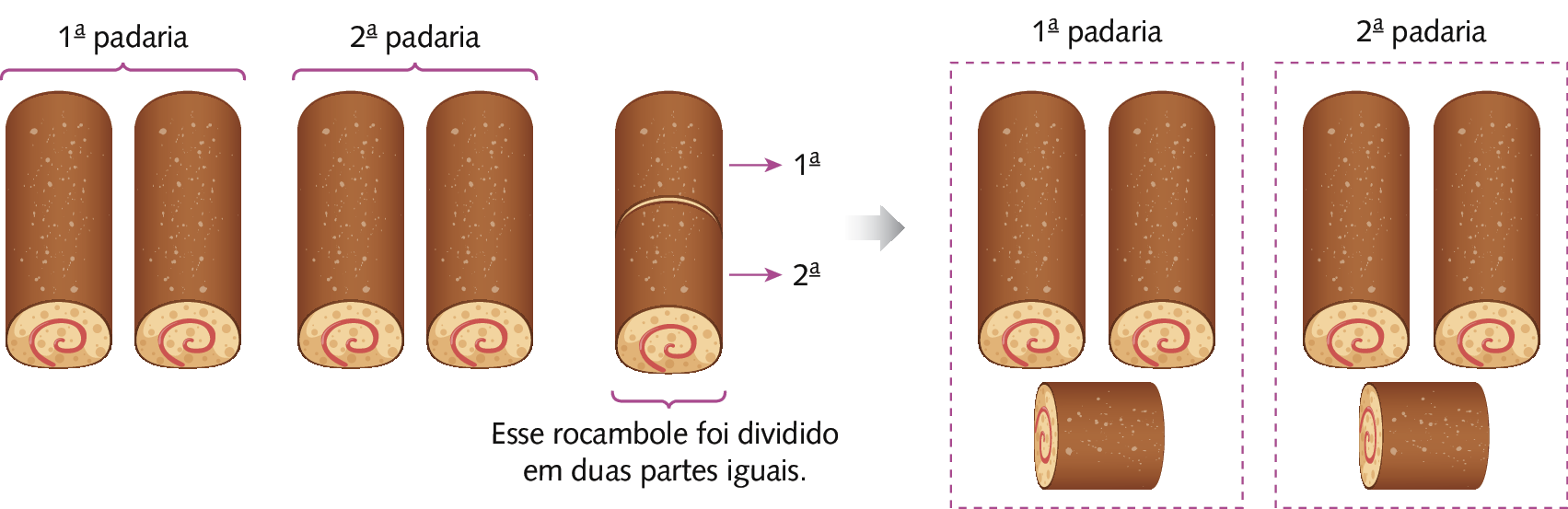
Logo, cada uma das duas padarias recebeu 2 rocamboles inteiros mais
meio.de rocambole, ou
Sentença matemática: fração cinco meios.de rocambole.

Um pouco de história
Faça as atividades no caderno.
Os egípcios e as frações
Na Antiguidade, os egípcios utilizavam frações unitárias, isto é, frações obtidas tomando somente uma parte de um inteiro dividido em partes iguais. A fração
Sentença matemática: fração dois terços.é a única exceção.
Observe estas representações empregadas pelos egípcios:

Para representar o numerador 1, os egípcios utilizavam o desenho de uma boca aberta:

As frações com numeradores diferentes de 1 eram expressas como a soma de duas ou mais frações com numeradores iguais a 1. Analise o exemplo.

Outros povos da Antiguidade utilizaram representações de frações para indicar partes de um inteiro. Os babilônicos, por exemplo, adotavam frações com denominador 60, pois essa era a base de seu sistema de numeração; já os romanos utilizavam frações com denominador 12. Essas variações são registradas em várias civilizações.
A partir do século dezesseis, surgem as frações com numeradores maiores que 1, principalmente pela influência dos hindus, com o sistema decimal, e dos árabes, que adotaram a barra para separar numerador e denominador – fórma que usamos até hoje.
BOYER, Carl; MERZBACH, Uta C. História da Matemática. São Paulo: Blucher, 2012.
Atividade
Em seu caderno, escreva a fração correspondente a cada representação:
a)
b)
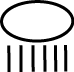
c)
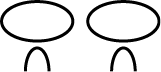
Atividades
Faça as atividades no caderno.
1. Qual é a fração que representa a parte laranja de cada uma das figuras a seguir?
a)

b)

c)

2. Represente por meio de figuras as frações a seguir.
a)
Sentença matemática: fração três sobre sete.b)
Sentença matemática: fração oito oitavos.c)
Sentença matemática: fração dois terços.d)
Sentença matemática: fração quatro quintos.3. Responda às questões a seguir.
a) Que fração do dia representa sete horas? E 12 horas?
b) Que fração da semana representa cinco dias? E sete dias?
c) Que fração do ano representa um bimestre? E um semestre?
4. Foram retiradas quatro peças de um cubo formado por diversos cubinhos iguais. Observe.
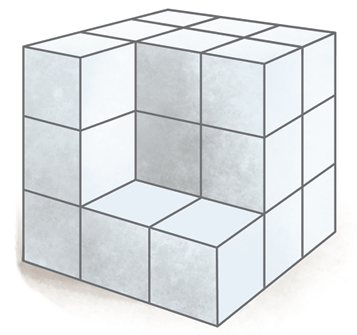
Que fração do cubo foi retirada? Que fração do cubo sobrou?
Leitura de frações
Na leitura de uma fração, lemos inicialmente o numerador e, em seguida, o denominador, que recebe nomes especiais. Observe:
Frações com denominador de 2 a 9
|
Denominador |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|---|---|---|---|---|---|---|---|---|
|
Leitura |
meio |
terço |
quarto |
quinto |
sexto |
sétimo |
oitavo |
nono |
Observe os exemplos.
a)
Sentença matemática: fração um meio.
Lemos: “dois terços”.
b)
Sentença matemática: fração um sexto.
Lemos: “um sexto”.
c)
Sentença matemática: fração três meios.
Lemos: “três meios”.
Frações cujo denominador é uma potência de base 10
|
Denominador |
10 |
100 |
1.000 |
10.000 |
... |
|---|---|---|---|---|---|
|
Leitura |
décimo |
centésimo |
milésimo |
décimo de milésimo |
... |
Observe os exemplos.
a)
Sentença matemática: fração sete décimos.
Lemos: “sete décimos”.
b)
Sentença matemática: fração catorze milésimos.
Lemos: “quatorze milésimos”.
As frações cujos denominadores são potências de base 10 são chamadas frações decimais.
Frações com outros denominadores
Lemos o numerador e, depois, o denominador seguido da palavra “avos”.
Observe os exemplos.
a)
Sentença matemática: fração treze trinta avos.Lemos: “treze trinta avos”.
b)
Sentença matemática: fração nove duzentos avos.Lemos: “nove duzentos avos”.
Atividades
Faça as atividades no caderno.
5. Escreva como se leem as frações a seguir.
a)
Sentença matemática: fração três sétimos.b)
Sentença matemática: fração um sobre seis.c)
Sentença matemática: fração nove sobre dois.d)
Sentença matemática: fração cinco sobre nove.e)
Sentença matemática: fração dezenove sobre dez mil.f)
Sentença matemática: fração três sobre dezessete.g)
Sentença matemática: fração cinco sobre cem.h)
Sentença matemática: fração sete sobre seiscentos.i)
Sentença matemática: fração quinze sobre mil.6.


Escreva por extenso três frações com denominadores de 2 a 9, três frações com denominadores que são potência de base 10 e três frações com denominadores diferentes dos casos anteriores. Em seguida, troque as frações que você escreveu com as de um colega para que cada um reescreva, com algarismos, as frações do outro.

2 Número misto
Acompanhe a situação a seguir.
Jairo ganhou da amiga duas barras de chocolate meio amargo. Cada barra é dividida em quatro partes iguais.

Nessa situação, uma barra de chocolate representa um inteiro. A fração correspondente à parte que Jairo comeu é
Sentença matemática: fração sete quartos.ou seja, uma barra inteira mais
Sentença matemática: fração três quartos.da outra barra.
Observe o esquema que representa a situação.
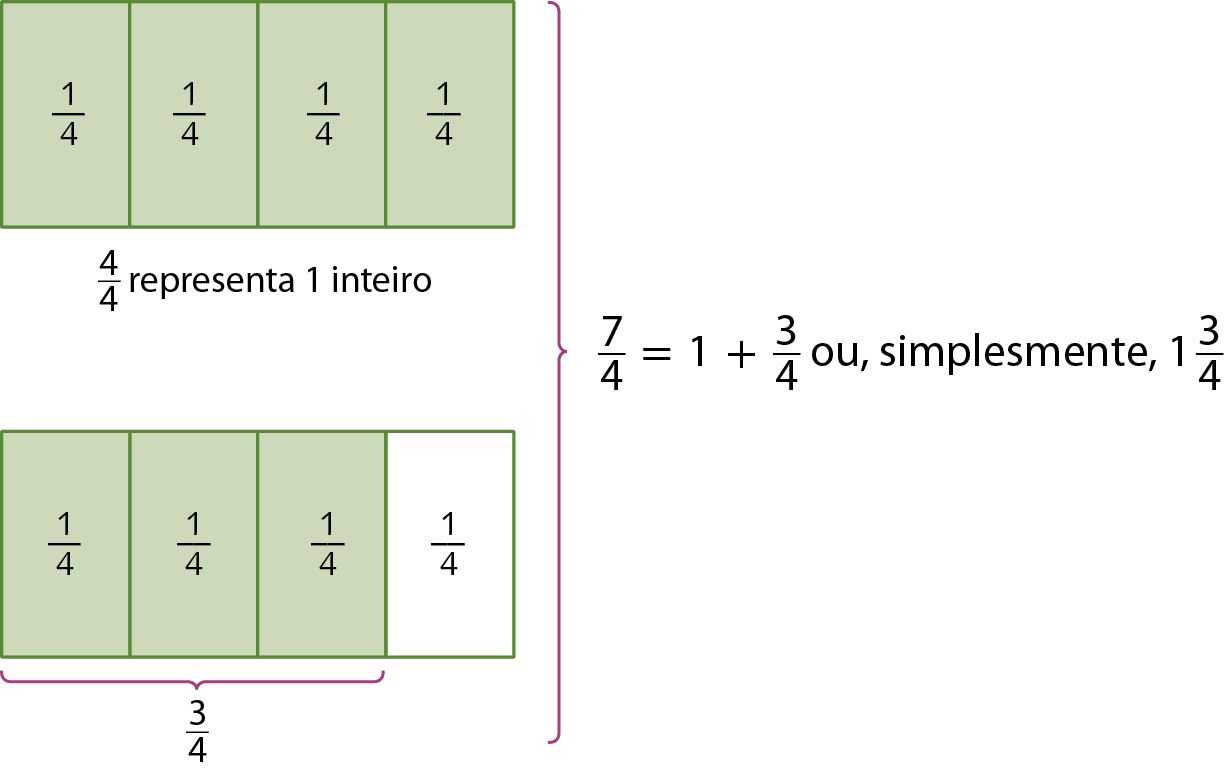
A representação
Sentença matemática: número misto: um inteiro e três quartos.é composta de uma parte inteira e de uma parte fracionária e, por isso, é denominada número misto.
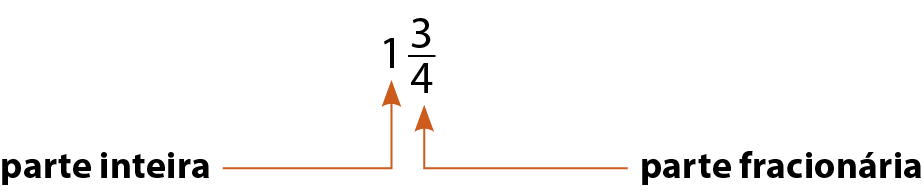
Lemos a fração
Sentença matemática: número misto: um inteiro e três quartos.como “um inteiro e três quartos”.
Considere outro exemplo.
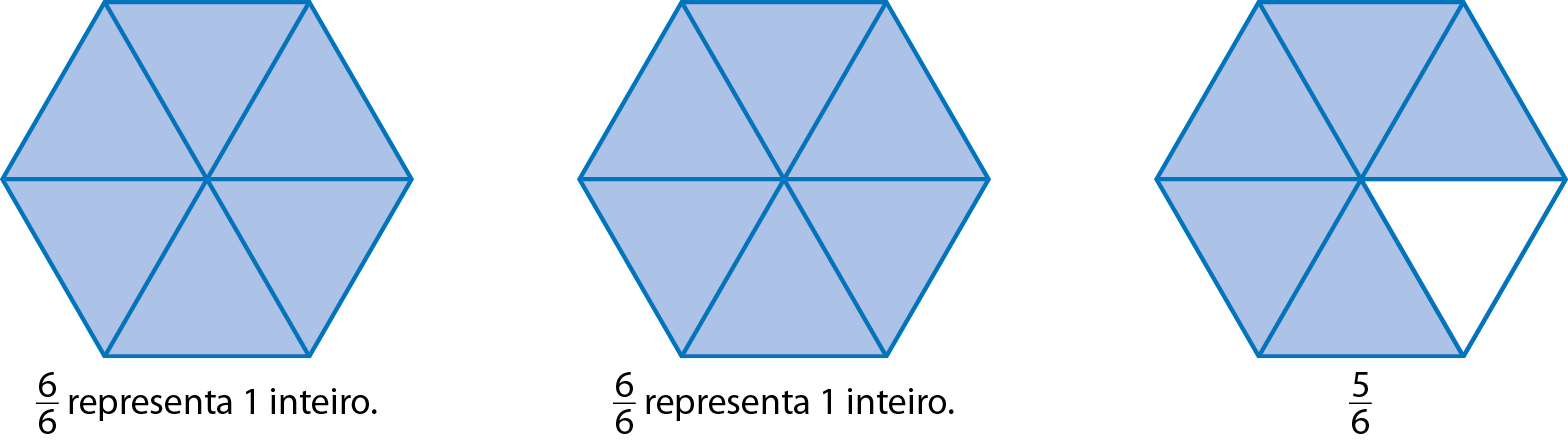
A parte colorida em azul póde ser representada por
Sentença matemática: fração dezessete sextos.ou
Sentença matemática: dois inteiros e fração cinco sobre seis.(lemos: “dois inteiros e cinco sextos”).

Atividades
Faça as atividades no caderno.
7. Escreva no caderno o número misto que representa a parte verde das figuras a seguir.
a)
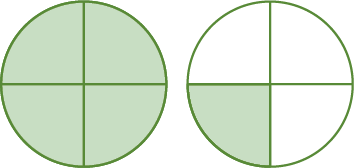
b)
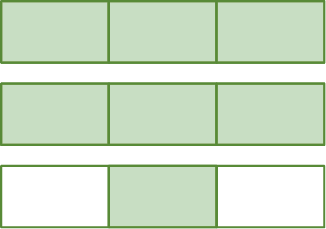
c)
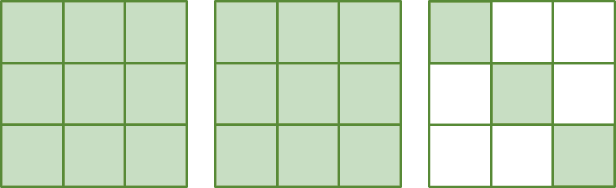
8. Represente no caderno cada fração por meio de figuras e escreva o número misto correspondente.
a)
Sentença matemática: fração sete meios.b)
Sentença matemática: fração oito quintos.c)
Sentença matemática: fração treze quartos.9. Patrícia é engenheira civil e responsável por determinar a medida da área de cada construção. Para o próximo trabalho, ela precisa definir a medida da área de três construções. Sabendo que são 5 lotes de terra e que deverão ser divididos igualmente entre as três construções, que fração representa a medida da área de cada construção?
10. Escreva, no caderno, o número de meses correspondente a:
a)
Sentença matemática: número misto: um inteiro e três quartos.de ano;
b)
Sentença matemática: número misto: dois inteiros e um sexto.de ano;
c)
Sentença matemática: número misto: cinco inteiros e um meio.de ano.
11. Quantas horas equivalem a:
a)
Sentença matemática: número misto: um inteiro e um meio.dia?
b)
Sentença matemática: número misto: um inteiro e um quarto.dia?

3 Frações equivalentes
Observe a fração que corresponde à parte pintada de lilás de cada uma das figuras.

As frações
Sentença matemática: frações dois terços, vírgula, fração quatro sextos, vírgula, fração seis nonos e fração oito doze avos.representam a mesma parte do todo.
Por esse motivo, dizemos que essas frações são equivalentes, ou seja,
Sentença matemática: frações dois terços, igual a fração quatro sextos, igual a fração seis nonos, igual a fração oito doze avos.Frações que representam a mesma parte de um inteiro são chamadas de frações equivalentes.
Propriedade das frações equivalentes
Multiplicando ou dividindo o numerador e o denominador de uma fração qualquer por um mesmo número natural diferente de zero, obtemos uma fração equivalente à fração inicial.
Vamos multiplicar e dividir, por exemplo, o numerador e o denominador da fração
Sentença matemática: fração seis oitavos.por 2.
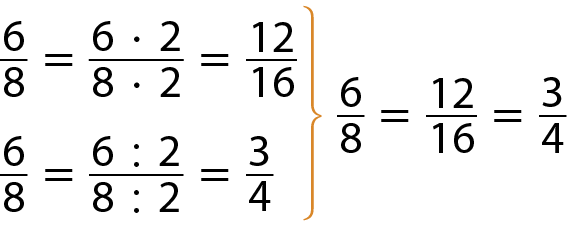

As figuras a seguir representam frações equivalentes.
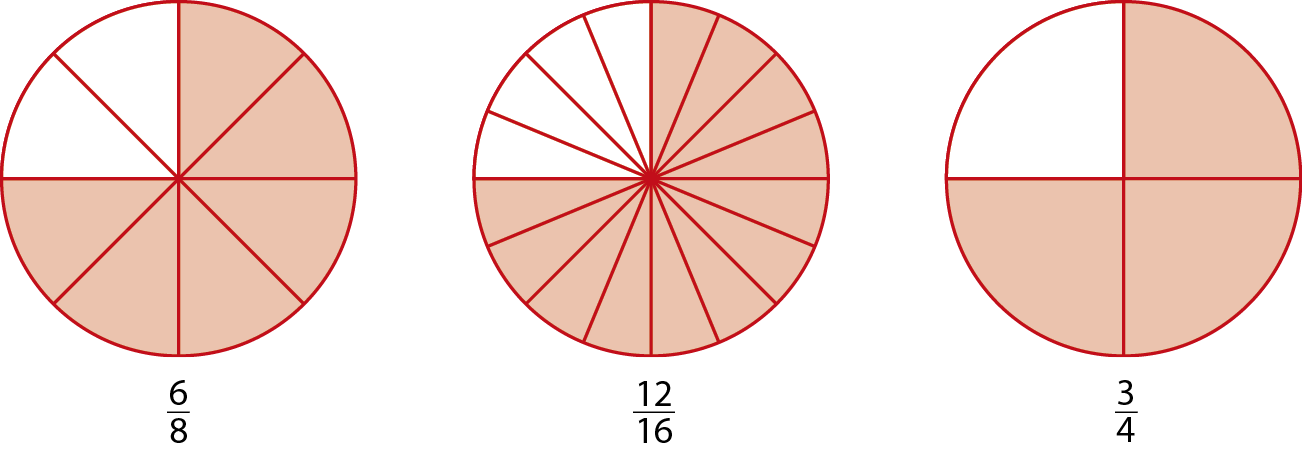
Podemos indicar:
Sentença matemática: seis oitavos igual a doze dezesseis avos igual a três quartos.
Frações e porcentagem
Economizar água é um hábito necessário. Atualmente, a falta de água é uma das grandes preocupações da humanidade. Se não modificarmos nossos hábitos, a escassez de água para consumo vai nos afetar seriamente.



Em uma pesquisa sobre consumo de água residencial, verificou-se que, de cada 100 litros gastos por dia, 50 litros são utilizados na higiene pessoal.
A relação de 50 litros em cada 100 litros póde ser representada por uma fração com denominador 100, ou seja,
Sentença matemática: fração cinquenta centésimos.Podemos também representar a fração
Sentença matemática: fração cinquenta centésimos.na fórma de porcentagem, utilizando o símbolo porcentagem: 50% (lemos: “cinquenta por cento”).
Outros exemplos:
a) 15% significa que consideramos 15 partes de um total de 100 partes iguais.
Lemos: “quinze por cento”.
b) 98% significa que consideramos 98 partes de um total de 100 partes iguais.
Lemos: “noventa e oito por cento”.
Podemos escrever algumas frações na fórma de porcentagem. Acompanhe a situação a seguir.
Andressa é dona de uma imobiliária. Neste mês, há 25 casas para alugar. Desse total, 9 são sobrados, ou seja,
Sentença matemática: fração nove sobre vinte e cinco.dessas casas são sobrados. Qual é a porcentagem de sobrados?
Multiplicando o numerador e o denominador da fração
Sentença matemática: fração nove sobre vinte e cinco.por 4, obtemos:
Sentença matemática: fração nove vinte e cinco avos igual nove vinte e cinco avos multiplicado por quatro quartos igual a trinta e seis centésimos.
A fração
Sentença matemática: fração trinta e seis centésimos.que tem denominador 100, é uma fração equivalente a
Sentença matemática: fração nove sobre vinte e cinco.Portanto, 36% das casas que estão para alugar na imobiliária de Andressa são sobrados.
Atividades
Faça as atividades no caderno.
12. Represente graficamente as frações
Sentença matemática: fração quatro quintos.e
Sentença matemática: fração doze quinze avos., mostrando que são equivalentes.
13. Escreva no caderno uma fração equivalente a:
a)
Sentença matemática: fração três quartos.cujo numerador seja 15;
b)
Sentença matemática: fração oito quarenta e oito avos.cujo numerador seja 2;
c)
Sentença matemática: fração dois terços.cujo denominador seja 27.
14. No caderno, substitua o

a fim de obter frações equivalentes em cada um dos itens.
a)
Sentença matemática: dois terços igual a figura geométrica quadrado cinza sobre trinta.b)
Sentença matemática: trinta e seis quarenta avos igual a figura geométrica quadrado cinza sobre vinte.c)
Sentença matemática: vinte sobre vinte e cinco igual a quatro sobre figura geométrica quadrado cinza.d)
Sentença matemática: sete nonos igual a trinta e cinco sobre figura geométrica quadrado cinza.e)
Sentença matemática: figura geométrica quadrado cinza sobre cinco igual a nove quarenta e cinco avos.f)
Sentença matemática: três sobre figura geométrica quadrado cinza igual a setenta e cinco centésimos.15. Determine uma fração equivalente a:
a)
Sentença matemática: fração sete sextos.de denominador 48;
b)
Sentença matemática: fração três quintos.cujo numerador seja 18.
16. Determine a fração equivalente a
Sentença matemática: fração cinco sétimos.cuja soma do numerador com o denominador é 60.
17. O indicador do nível de bateria de um smartphone marca 75% da carga total. Que fração corresponde a essa porcentagem de carga?

18. Carla tem duas laranjas para dividir com 2 amigos. Uma das laranjas está dividida ao meio e a outra, em três partes. Como Carla póde dividir as laranjas para que ela e os amigos recebam a mesma quantidade de pedaços?
Simplificação de frações
Considere a fração
Sentença matemática: fração dez sobre vinte.Se dividirmos o numerador e o denominador por 2, determinamos a fração
Sentença matemática: fração cinco décimos.equivalente a
Sentença matemática: fração dez sobre vinte.Obtivemos uma fração equivalente com numerador e denominador menores.
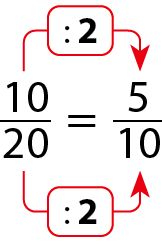
Quando dividimos o numerador e o denominador de uma fração por um mesmo número natural, diferente de 1, estamos simplificando a fração.
Simplificar uma fração significa obter uma fração equivalente com o numerador e o denominador menores que os da primeira fração.
Observe que a fração
Sentença matemática: fração cinco décimos.ainda póde ser simplificada:

Porém, a fração
meio.já não póde ser simplificada, pois não existe um número natural (diferente de 1) que seja divisor de 1 e 2 ao mesmo tempo. Dizemos que
Meioé uma fração irredutível.
O mesmo acontece com as frações
Sentença matemática: fração cinco sobre seis.,
fração oito nonose
Sentença matemática: fração cinco doze avos., que são exemplos de frações irredutíveis.