Página 127

Parte 2

Vamos, agora, simplificar a fração

\frac{36}{54}

até obtermos uma fração irredutível.

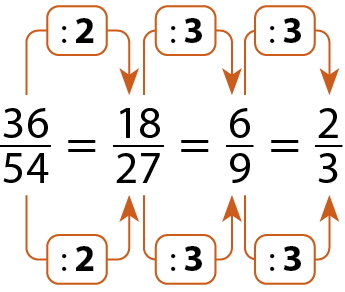
Esquema: fração trinta e seis sobre cinquenta e quatro igual a dezoito sobre vinte e sete igual a seis nonos igual a dois terços. Acima da fração trinta e seis sobre cinquenta e quatro uma seta alaranjada que chega a fração dezoito sobre vinte e sete. No meio dessa seta a indicação divisão por 2. Abaixo da fração trinta e seis sobre cinquenta e quatro uma seta alaranjada que chega a fração dezoito sobre vinte e sete. No meio dessa seta a indicação divisão por 2. Acima da fração dezoito sobre vinte e sete uma seta alaranjada que chega a fração seis nonos. No meio dessa seta a indicação divisão por 3. Abaixo da fração dezoito sobre vinte e sete uma seta alaranjada que chega a fração seis nonos. No meio dessa seta a indicação divisão por 3. Acima da fração seis nonos uma seta alaranjada que chega a fração dois terços. No meio dessa seta a indicação divisão por 3. Abaixo da fração seis nonos uma seta alaranjada que chega a fração dois terços. No meio dessa seta a indicação divisão por 3.

Podemos também simplificar essa fração dividindo o numerador e o denominador por 18.

Perceba que, com apenas uma simplificação, determinamos a fração irredutível, pois 18 é o maior divisor comum de 36 e 54.

Esquema: fração trinta e seis sobre cinquenta e quatro igual a dois terços. Acima da fração trinta e seis sobre cinquenta e quatro uma seta alaranjada que chega a fração dois terços. No meio dessa seta a indicação divisão por 18. Abaixo da fração trinta e seis sobre cinquenta e quatro uma seta alaranjada que chega a fração dois terços. No meio dessa seta a indicação divisão por 18.

Atividades

Faça as atividades no caderno.

19. Simplifique as frações até obter frações irredutíveis.

\frac{8}{24}

\frac{20}{100}

\frac{32}{80}

\frac{18}{60}

\frac{20}{80}

\frac{90}{100}

20. Identifique, no caderno, a fração que, simplificada, corresponde à fração irredutível

\frac{3}{5} .

\frac{25}{20}

\frac{24}{300}

\frac{80}{48}

\frac{60}{100}

21. O resultado de uma pesquisa feita com estudantes do 6º ano demonstrou que 80 dos 200 estudantes preferem consultar os livros da biblioteca para realizar as pesquisas escolares e que 120 preferem utilizar sites da internet. Luís afirmou que

\frac{40}{100}

dos estudantes preferem a biblioteca, e Mônica afirmou que

\frac{3}{5}

dos estudantes preferem realizar as pesquisas em sites da internet. Escreva em seu caderno a afirmativa correta.

a) A afirmação de Luís está errada.

b) As afirmações de Luís e de Mônica estão corretas.

c) A afirmação de Mônica está errada.

d) As afirmações de Luís e de Mônica estão erradas.

Página 128

4 Comparação de frações de um mesmo inteiro

Observe as situações a seguir.

Situação 1

Maurício convidou alguns amigos para passar a tarde em sua casa. O pai de Maurício fez, para o lanche da tarde, dois bolos — um de cenoura e outro de chocolate — usando a mesma fôrma retangular.

Ilustração: Cinco crianças ao redor de uma mesa circular onde há dois bolos e pratos brancos. Entre eles está em pé o pai de um dos meninos, homem de cabelo claro, óculos e camisa listrada. Os bolos estão cortados em doze pedaços. Ele segura retira um pedaço de bolo com uma espátula e diz: 'Cortei cada bolo em doze pedaços de mesma medida. Que bolo vocês querem: de cenoura ou de chocolate?' Um menino branco de cabelo castanho e camiseta verde fala: 'Eu quero um pedaço do bolo de cenoura!' Outro menino branco de camiseta branca diz: 'Eu também!'

Depois que todos comeram, sobraram

\frac{8}{12}

do bolo de chocolate e

\frac{6}{12}

do bolo de cenoura. De qual dos dois bolos sobraram mais pedaços?

Para responder a essa pergunta, é necessário comparar as frações

\frac{8}{12}

\frac{6}{12}

e verificar qual delas é a maior.

Observe a representação de cada fração. Cada figura representa um bolo, e as partes pintadas representam o que sobrou dos bolos.

Esquema. Retângulo dividido em doze partes iguais. Há 4 partes brancas e oito partes marrom. À direita da figura a fração oito doze avos.

Bolo de chocolate

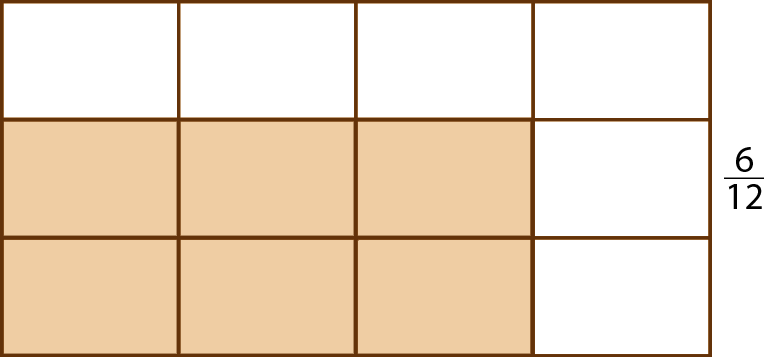
A segunda figura também é um retângulo dividido em oito partes iguais. Há 6 partes alaranjadas e seis brancas. Abaixo da figura a indicação 'bolo de cenoura' e à direita da figura a fração seis doze avos.

Bolo de cenoura

É possível comparar diretamente as frações porque os bolos foram cortados em pedaços de mesma medida. Então, observando as figuras, verificamos que:

\frac{8}{12} > \frac{6}{12}

, pois 8 > 6

Portanto, sobraram mais pedaços do bolo de chocolate.

Se duas frações têm o mesmo denominador, a maior fração é aquela que tem o maior numerador.

Página 129

Situação 2

Ilustração de três meninas, uma negra e duas brancas. Cada uma com um celular nas mãos.

Márcia, Talita e Ana brincam com o mesmo jôgo no celular. No entanto, elas avançam de fórma diferente ao longo da partida. Márcia, por exemplo, já finalizou

\frac{3}{4}

do jôgo, Talita finalizou

\frac{2}{3}

e Ana,

\frac{1}{2}

. Qual delas avançou menos no jôgo?

Para responder a essa pergunta, é necessário comparar as frações

\frac{3}{4}

\frac{2}{3}

\frac{1}{2}

e verificar qual delas é a menor.

Na representação a seguir, as figuras que correspondem ao avanço de cada jogadora.

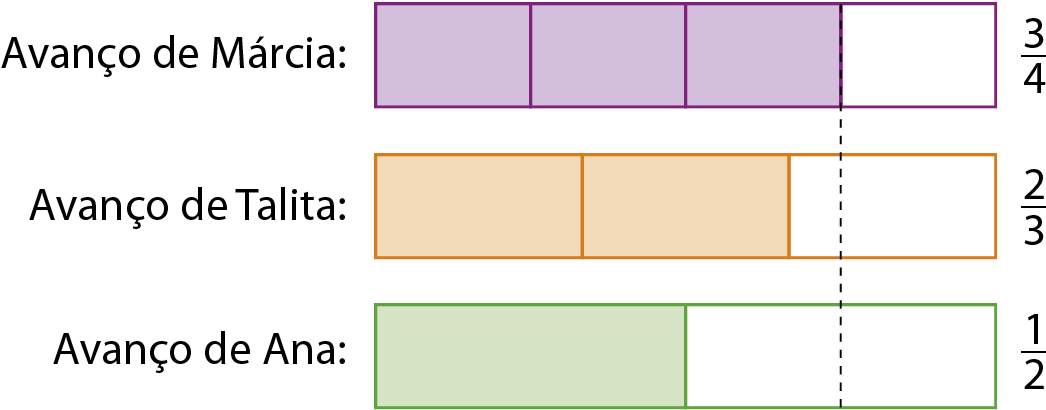
Esquema: De cima para baixo, a primeira figura é um retângulo dividido em 4 partes iguais. As 3 primeiras partes da esquerda para direita são lilás, a última parte branca. À esquerda do retângulo a indicação 'avanço de Márcia', à direita do retângulo a fração três quartos. A segunda figura é um retângulo dividido em 3 partes iguais. As 2 primeiras partes da esquerda para direita são alaranjadas, a última parte branca. À esquerda do retângulo a indicação 'avanço de Talita', à direita do retângulo a fração dois terços. A terceira figura é um retângulo dividido em 2 partes iguais. A primeira parte da esquerda para direita é verde, a última parte branca. À esquerda do retângulo a indicação 'avanço de Ana', à direita do retângulo a fração um meio.

Observando as figuras, podemos notar que Márcia obteve o maior avanço no jôgo, seguida por Talita e, depois, por Ana.

Podemos também determinar frações equivalentes de mesmo denominador para as frações iniciais e, depois, compará-las.

Esquema: De cima para baixo, primeiro a indicação Avanço de Márcia: três quartos igual a três multiplicado por 3 sobre quatro multiplicado por 3 igual a nove doze avos. Em Segundo a indicação Avanço de Talita: dois terços igual a dois multiplicado por quatro sobre três multiplicado por quatro igual a oito doze avos. Em Terceiro a indicação Avanço de Ana: um meio igual a um multiplicado por 6 sobre dois multiplicado por 6 igual a seis doze avos. À direita das indicações uma chave alaranjada. À direita da chave a indicação: "escolhemos o 12 como o denominador das frações equivalentes, pois é divisível por 2, 3 e 4 ao mesmo tempo".

Representando as frações equivalentes

\frac{9}{12}

\frac{8}{12}

\frac{6}{12}

, temos:

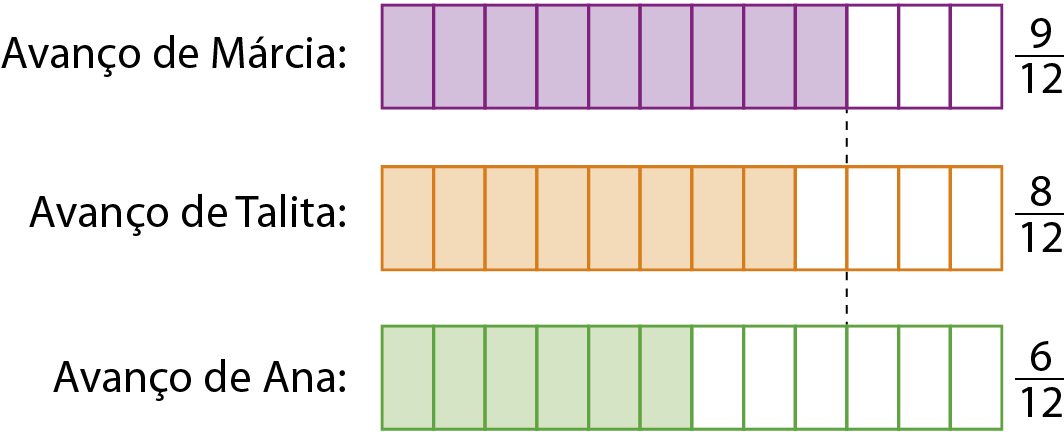
Esquema: De cima para baixo, a primeira figura é um retângulo dividido em doze partes iguais. As nove primeiras partes da esquerda para a direita são roxas, as três últimas brancas. À esquerda da figura a indicação 'Avanço de Márcia'. À direita da figura lado a fração nove doze avos. A segunda figura também é um retângulo dividido em doze partes iguais. As oito primeiras partes da esquerda para a direita são alaranjadas, as quatro últimas brancas. À esquerda da figura a indicação 'Avanço de Talita'. À direita da figura lado a fração oito doze avos. A terceira figura também é um retângulo dividido em doze partes iguais. As seis primeiras partes da esquerda para a direita são verdes, as seis últimas brancas. À esquerda da figura a indicação 'Avanço de Ana'. À direita da figura lado a fração seis doze avos.

Como 6 < 8 < 9, temos:

\frac{6}{12} < \frac{8}{12} < \frac{9}{12}

\frac{1}{2} < \frac{2}{3} < \frac{3}{4}

Portanto, Ana avançou menos no jôgo.

Página 130

Atividades

Faça as atividades no caderno.

22. Copie os itens em seu caderno substituindo cada

pelo símbolo >, < ou =.

\frac{2}{5} ▪ \frac{5}{7}

5 \frac{2}{5} ▪ \frac{27}{5}

\frac{16}{3} ▪ \frac{14}{2}

\frac{16}{35} ▪ \frac{1}{2}

23. Determine a maior fração de cada item.

\frac{3}{4}, \frac{17}{4}, \frac{9}{4}

\frac{1}{3}, \frac{7}{3}, \frac{5}{3}

\frac{1}{3}, \frac{1}{2}, \frac{1}{8}

\frac{1}{2}, \frac{5}{12}, \frac{4}{3}, \frac{1}{6}

24. Disponha as frações em ordem crescente, utilizando o símbolo < entre elas.

\frac{7}{8}, \frac{7}{3}, \frac{7}{5}, \frac{7}{10}

\frac{1}{8}, \frac{11}{12}, \frac{2}{15}, \frac{7}{20}

25.

Escreva quatro frações de mesmo numerador. Troque-as com as de um colega para que cada um reescreva as frações do outro em ordem crescente, sem reduzi-las ao mesmo denominador. Discutam e escrevam o procedimento usado.

26. Luís e Maria recebem, por mês, a mesma quantia. Luís gasta

\frac{3}{4}

do seu salário, e Maria,

\frac{2}{3}

. Quem gasta mais?

27. Na última eleição para síndico de condomínio, os candidatos Paulo, Alice e José obtiveram, respectivamente,

\frac{1}{5}

\frac{2}{8}

\frac{2}{9}

do total dos votos. Qual dos três candidatos foi o mais votado?

Ilustração: À direita, homem branco de cabelo castanho claro, camisa azul clara e calça azul. Ele está em frente de uma urna eletrônica sobre uma mesa. À frente da mesa, fila com três pessoas.

5 Fração de uma quantidade

Para estudar o cálculo da fração de uma quantidade, vamos considerar as situações a seguir.

Situação 1

Ilustração: Menino branco de cabelo preto está em um banheiro debaixo do chuveiro se ensaboando. Ele passa a bucha pelo corpo, que tem marcas de espuma.

Segundo um estudo feito pela Companhia de Saneamento do Estado de São Paulo (Sabesp), uma ducha de pressão, com o registro meio aberto, consome 135 litros de água em 15 minutos. O chuveiro elétrico, durante o mesmo tempo e com a mesma abertura do registro, consome

\frac{1}{3}

dessa quantidade. Quantos litros de água são economizados em um banho de chuveiro elétrico de 15 minutos em relação a um banho de ducha nas mesmas condições?

Vamos representar o enunciado por meio de um esquema.

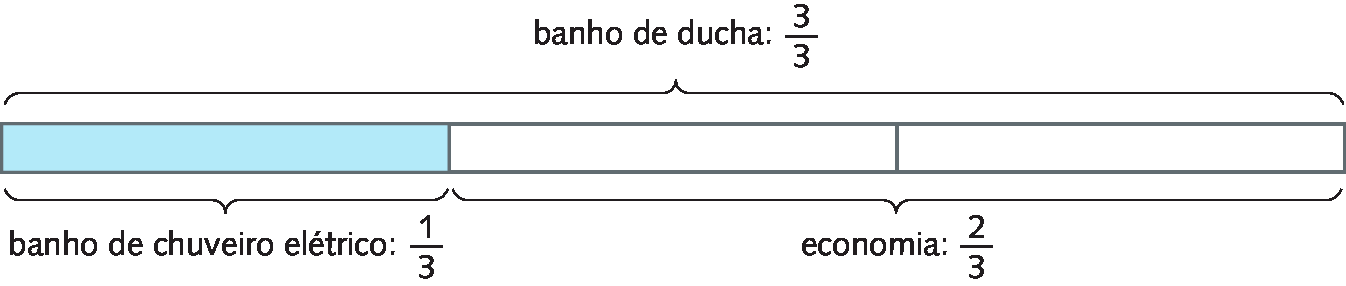
Esquema: Retângulo dividido em três partes iguais: a primeira parte, da esquerda para a direita é azul e as outras brancas. Acima do retângulo uma chave. Acima da chave a indicação 'banho de ducha: três terços'. Abaixo da parte azul do retângulo uma chave. Abaixo da chave a indicação 'banho de chuveiro elétrico: um terço'. Abaixo das partes brancas do retângulo, uma chave. Abaixo da chave a indicação 'economia: dois terços'.

Página 131

Os 135 litros de água gastos em um banho de ducha correspondem a

\frac{3}{3} .

Para obter

\frac{1}{3}

de 135 litros, calculamos: 135 litros dividido por 3 = 45 litros

A economia corresponde a

\frac{2}{3}

de 135 litros. Como

\frac{1}{3}

corresponde a 45 litros, e

\frac{2}{3}

é duas vezes essa quantidade, temos: 2 ⋅ 45 litros = 90 litros

Portanto, no banho de chuveiro elétrico são economizados 90 litros de água em relação a um banho de ducha de pressão nas mesmas condições.

Situação 2

Ilustração: Mulher branca de cabelo loiro, capacete vermelho com uma listra amarela, blusa amarela, bermuda azul com um detalhe vermelho e botas laranjas está segurando cordas e escalando uma montanha.

Uma alpinista escalou

\frac{3}{4}

de uma montanha, o que corresponde a .1200 métros. Qual é a medida da distância total a ser escalada?

Considerando que a fração

\frac{3}{4}

corresponde a .1200 métros, considere o esquema a seguir.

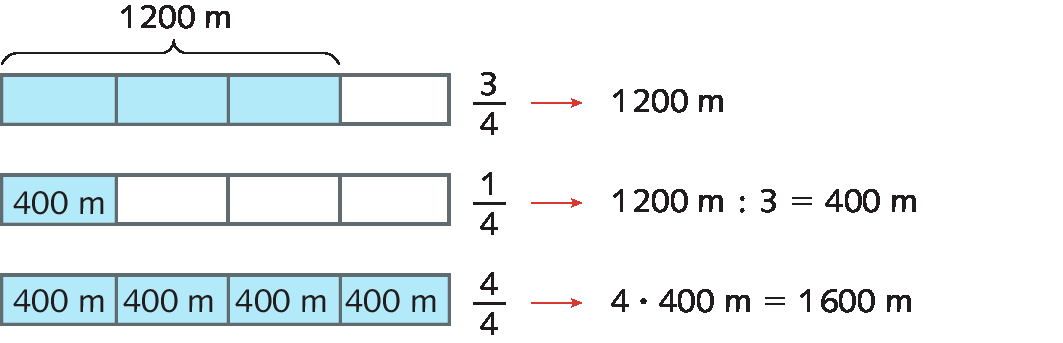
Esquema: De cima para baixo, a primeira figura é um retângulo dividido em quatro partes iguais. As três primeiras partes da esquerda para direita são azuis e a última branca. Acima das 3 partes azuis uma chave. Acima da chave a indicação 1200 metros. À direita do retângulo a fração três quartos. À direita da fração uma seta alaranjada. À direita da seta a indicação 1200 metros. A segunda figura também é um retângulo dividido em quatro partes iguais. A primeira parte da esquerda para a direita é azul, e dentro uma indicação de 400 metros. As outras três partes são brancas. À direita do retângulo a fração um quarto. À direita da fração a seta alaranjada. À direita da seta a sentença matemática 1200 metros dividido por 3 igual a 400 metros. A terceira figura também é um retângulo dividido em quatro partes iguais e azuis. Dentro de cada uma das partes a indicação de 400 metros. À direita do retângulo, a fração quatro quartos. À direita da fração uma seta alaranjada. À direita da seta a sentença matemática 4 multiplicado por 400 metros igual a 1600 metros.

Logo, a medida da distância total a ser escalada é de .1600 métros.

Situação 3

Juntam-se em um recipiente dois líquidos que não se misturam. O líquido a ocupa

\frac{2}{7}

da medida do volume total, e o líquido B corresponde a 50 mililitros. Quantos mililitros dessa mistura há no recipiente?

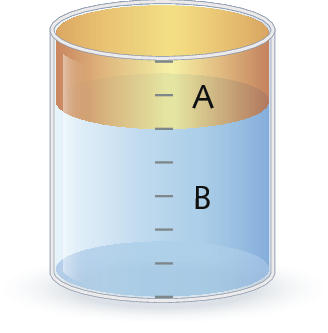
Ilustração: Recipiente em forma de sólido geométrico com duas superfícies circulares e uma arredondada com sete riscos indicando quantidade. A letra A está no sexto risco de baixo para cima e a letra B está no quarto risco de baixo para cima. Líquido azul vai até o quinto risco de cima para baixo e o líquido laranja dessa parte até o topo. Abaixo: O líquido A ocupa 2 sétimos da medida do volume total.

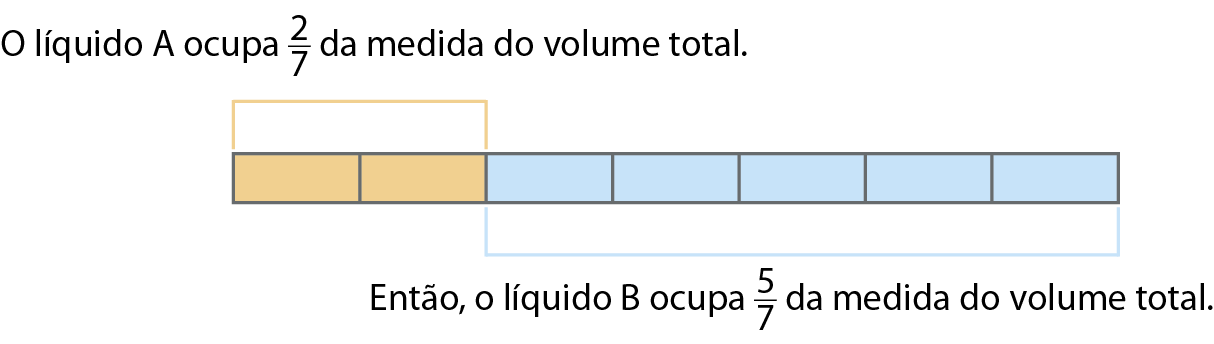
Esquema: Retângulo dividido em 7 partes iguais. As duas primeiras partes da esquerda para a direita são alaranjadas e as outras partes azuis. Acima das partes alaranjadas um retângulo branco com contorno alaranjado. Abaixo das partes azuis um retângulo branco com contorno azul. Abaixo do retângulo branco com contorno azul a indicação 'Então, o líquido B ocupa cinco sétimos da medida do volume total'.

Assim:

\frac{5}{7}

50 mililitros

\frac{1}{7}

50 mililitros dividido por 5 = 10 mililitros

\frac{7}{7}

7 ⋅ 10 mililitros = 70 mililitros

Logo, há 70 mililitros dessa mistura no recipiente.

Usando uma calculadora

Também podemos calcular a fração de uma quantidade usando uma calculadora.

Acompanhe o cálculo de

\frac{2}{5}

de 115 vacinas.

Ilustração: Teclas de uma calculadora indicando a operação: 115 dividido por 5 multiplicado por 2 é igual a 46.

Portanto,

\frac{2}{5}

de 115 vacinas é igual a 46 vacinas.

Página 132

Atividades

Faça as atividades no caderno.

28. Observe o indicador de combustível de um carro cuja medida da capacidade é 52 litros.

Esquema. Antes da viagem: Retângulo dividido em quatro partes iguais. Há três partes amarelas e uma branca. Depois da viagem: Mesmo retângulo anterior dividido em quatro partes iguais. Há uma parte amarela e três brancas.

a) Com quantos litros de combustível o carro ficou após a viagem?

b) Quantos litros de combustível tinha o carro ao iniciar a viagem?

29. A 61ª Olimpíada Internacional de Matemática foi realizada na Federação Russa em 2020, em São Petersburgo. A competição envolveu 105 países e havia 56 mulheres entre os participantes. Se as 56 mulheres correspondiam a

\frac{1}{10}

dos homens, quantos homens participaram da Olimpíada?

30. Para encher

\frac{2}{5}

de uma piscina são necessários .60000 litros de água. Qual é a medida da capacidade dessa piscina?

31. André comprou

\frac{5}{9}

de uma coleção de livros. Ele ainda precisa adquirir 12 volumes para completá-la. Quantos volumes há nessa coleção?

32. Uma betoneira transporta .5000 quilogramas de concreto. Em sua primeira entrega, ela despeja

\frac{7}{20}

da carga total.

a) A quantos quilogramas de concreto corresponde essa primeira remessa?

Se você pudesse utilizar uma calculadora para auxiliar na resolução do item a, que sequência de teclas usaria?

33.

Use uma calculadora e determine:

a) a metade de .22514 quilômetros;

b) dois terços de .28233 quilogramas;

c) quatro quintos de .61455 litros.

34. A atleta chinesa Gong Lijiao conquistou a medalha de ouro dos Jogos Olímpicos de Tóquio ao vencer a final do arremêssu de pêso. Determine a medida aproximada da distância a qual o pêso foi arremessado, sabendo que

\frac{2}{5}

dessa medida correspondem a aproximadamente 8 métros.

Fotografia. Atleta chinesa com cabelo preto e regata vermelha segura um peso próximo à cabeça em um campo de competição. — Gong Lijiao. Tóquio, Japão. Foto de 2021.

35.

Elabore um problema no qual duas pessoas investem valores diferentes na abertura de uma loja. Depois de certo tempo, a loja tem lucro, e esse lucro deve ser repartido proporcionalmente entre os sócios. Troque seu problema com o de um amigo e resolva o dele usando uma calculadora.

6 Adição e subtração de frações

Podemos adicionar e subtrair frações, assim como adicionamos e subtraímos números naturais. Vamos estudar agora como adicionar e subtrair frações com denominadores iguais e com denominadores diferentes.

Frações com denominadores iguais

Para explicar como era seu terreno a um amigo, Gustavo resolveu fazer um esquema em um papel quadriculado.

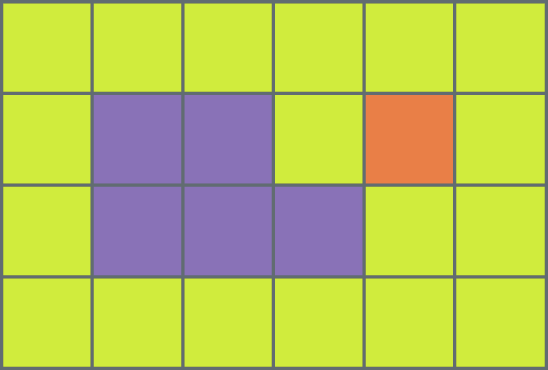
Figura geométrica: Retângulo dividido em 24 quadrados de tamanhos iguais. Cinco estão pintados de roxo, um de laranja e dezoito de verde.

A parte roxa representa a casa, a parte laranja representa a horta e a parte verde representa o quintal. Que fração do terreno de Gustavo representa a casa e a horta juntas? Que fração do terreno representa o quintal?

Página 133

Como o terreno foi dividido em 24 quadradinhos, cada quadradinho corresponde a

\frac{1}{24}

do terreno. Logo:

Fração que representa o terreno:

\frac{24}{24}

Fração que representa a casa:

\frac{5}{24}

Fração que representa a horta:

\frac{1}{24}

• A casa e a horta juntas correspondem a 6 quadradinhos abre parênteses5 + 1 = 6fecha parênteses.

A fração que representa a casa e a horta juntas é

\frac{6}{24}

, pois:

\frac{5}{24} + \frac{1}{24} = \frac{6}{24}

• O quintal corresponde a 18 quadradinhos (24 menos 6 = 18).

A fração que representa o quintal é

\frac{18}{24}

, pois:

\frac{24}{24} ‒ \frac{6}{24} = \frac{18}{24}

Em uma adição abre parêntesesou subtraçãofecha parênteses de frações cujos denominadores são iguais, adicionamos abre parêntesesou subtraímosfecha parênteses os numeradores e conservamos os denominadores.

Frações com denominadores diferentes

Os incêndios florestais destroem a mata nativa e o solo, poluem o ar, os rios e os cursos de água e causam a morte de inúmeros animais. Muitos incêndios poderiam ser evitados se as pessoas fossem mais cuidadosas quando trafegam pelas rodovias ou acampam em regiões de mata. Observe o gráfico que Alfredo elaborou com base nos dados de uma pesquisa sobre as causas dos incêndios ocorridos no verão de 2022 em uma floresta.

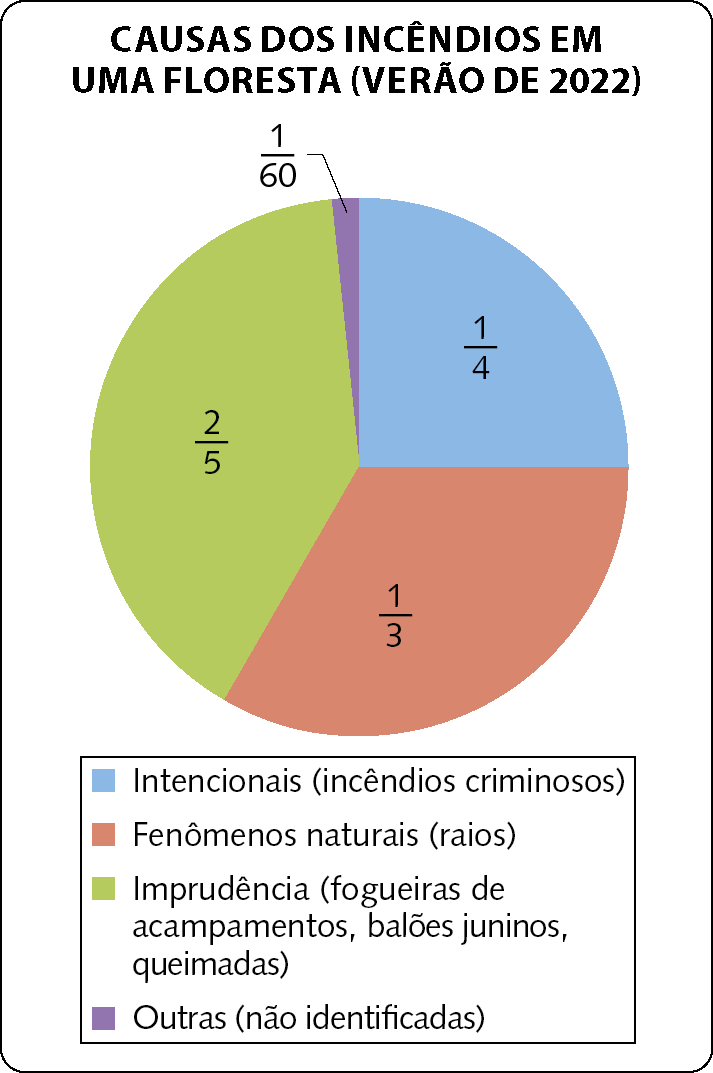
Gráfico: Gráfico de setores. Título do gráfico: Causas dos incêndios em uma floresta (verão de 2022). O gráfico possui uma legenda, e os dados contidos nele são: Intencionais (incêndios criminosos) representa um quarto do total. Fenômenos naturais (raios) representa um terço do total. Imprudência (fogueiras de acampamentos, balões juninos, queimadas) representa dois quintos do total. Outras (não identificadas) representa um sessenta avos do total. — Dados obtidos por Alfredo no verão de 2022.

• Que fração dos incêndios nessa floresta ocorreu pela ação humana, isto é, por imprudência ou por intenção no verão de 2022?

Para responder a essa pergunta, devemos calcular:

\frac{2}{5} + \frac{1}{4}

Como as frações têm denominadores diferentes, precisamos encontrar, inicialmente, frações equivalentes a

\frac{2}{5} e a \frac{1}{4}

cujos denominadores sejam iguais.

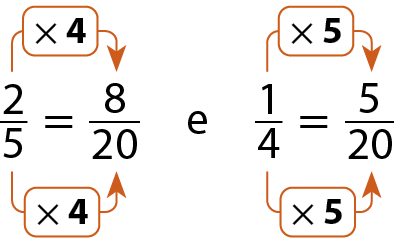
Esquema: A esquerda dois quintos igual a oito vinte avos. Acima da fração dois quintos uma seta alaranjada que chega a fração oito vinte avos. No meio dessa seta a indicação multiplicação por 4. Abaixo da fração dois quintos uma seta alaranjada que chega a fração oito vinte avos. No meio dessa seta a indicação multiplicação por 4. A direita um quarto igual a cinco vinte avos. Acima da fração um quarto uma seta alaranjada que chega a fração cinco vinte avos. No meio dessa seta a indicação multiplicação por 5. Abaixo da fração um quarto uma seta alaranjada que chega a fração cinco vinte avos. No meio dessa seta a indicação multiplicação por 5.

Assim:

\frac{2}{5} + \frac{1}{4} = \frac{8}{20} + \frac{5}{20} = \frac{13}{20}

Portanto,

\frac{13}{20}

dos incêndios foram causados pela ação humana.

Página 134

• Que fração dos incêndios representa a diferença entre os causados por fenômenos naturais e os intencionais?

Para responder a essa pergunta, calculamos:

\frac{1}{3} ‒ \frac{1}{4}

Como as frações têm denominadores diferentes, precisamos encontrar, inicialmente, frações equivalentes a

\frac{1}{3}

e a

\frac{1}{4}

cujos denominadores sejam iguais.

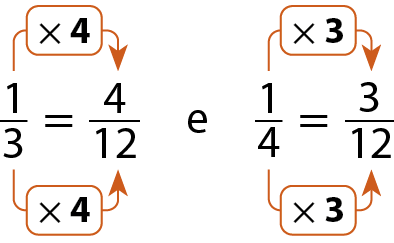
Esquema: A esquerda um terço igual quatro doze avos. Acima da fração um terço uma seta alaranjada que chega a fração quatro doze avos. No meio dessa seta a indicação multiplicação por 4. Abaixo da fração um terço uma seta alaranjada que chega a fração quatro doze avos. No meio dessa seta a indicação multiplicação por 4. A direita um quarto igual a três doze avos. Acima da fração um quarto uma seta alaranjada que chega a fração três doze avos. No meio dessa seta a indicação multiplicação por 3. Abaixo da fração um quarto uma seta alaranjada que chega a fração três doze avos. No meio dessa seta a indicação multiplicação por 3.

Assim:

\frac{1}{3} ‒ \frac{1}{4} = \frac{4}{12} ‒ \frac{3}{12} = \frac{1}{12}

Portanto,

\frac{1}{12}

dos incêndios representa a diferença entre os incêndios causados por fenômenos naturais e os intencionais.

Em uma adição (ou subtração) de frações cujos denominadores são diferentes, determinamos frações equivalentes às iniciais com um mesmo denominador, e em seguida adicionamos (ou subtraímos) os numeradores (conservando o denominador).

Observe outros exemplos.

\frac{1}{3} + \frac{2}{15} + \frac{1}{6} = \frac{10}{30} + \frac{4}{30} + \frac{5}{30} = \frac{19}{30}

3 ‒ \frac{5}{6} = \frac{3}{1} ‒ \frac{5}{6} = \frac{18}{6} ‒ \frac{5}{6} = \frac{13}{6}

\frac{2}{3} + \frac{1}{6} ‒ \frac{3}{4} = \frac{8}{12} + \frac{2}{12} ‒ \frac{9}{12} = \frac{1}{12}

2 \frac{1}{5} + \frac{2}{3} = \frac{11}{5} + \frac{2}{3} = \frac{33}{15} + \frac{10}{15} = \frac{43}{15}

Atividades

Faça as atividades no caderno.

36. Calcule o resultado das operações e simplifique quando for possível.

\frac{2}{9} + \frac{5}{9}

\frac{5}{6} ‒ \frac{2}{6}

\frac{3}{4} + \frac{1}{5}

\frac{7}{8} ‒ \frac{4}{9}

\frac{1}{7} + \frac{3}{5} + \frac{9}{14}

3 ‒ \frac{14}{5}

1 \frac{2}{11} + \frac{7}{10}

2 \frac{1}{5} ‒ 1 \frac{1}{6}

7 + \frac{2}{9}

\frac{3}{4} ‒ \frac{1}{6}

\frac{1}{5} + 2 + \frac{7}{8}

3 \frac{2}{5} ‒ \frac{1}{7}

37. Sendo A = 3, B =

3 \frac{5}{7}

e C =

2 \frac{1}{5},

determine A + B menos C.

38. Se derramarmos, em um mesmo recipiente de 2 litros de medida de capacidade, o conteúdo dos três recipientes a seguir, que quantidade de líquido obteremos?

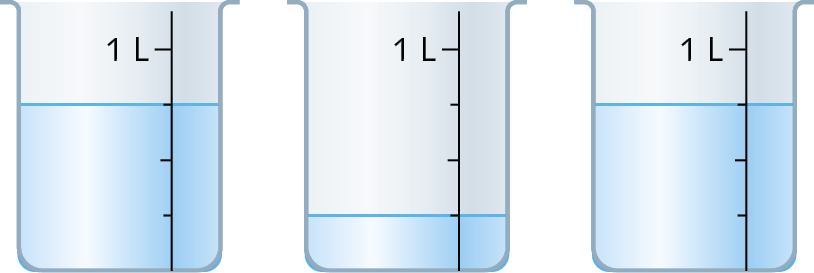
Ilustração. Três recipientes com quatro traços separados pela mesma distância. No quarto traço de baixo para cima está a indicação de 1 litro. O primeiro recipiente é preenchido com água até o terceiro traço. O segundo recipiente é preenchido com água até o primeiro traço. O terceiro recipiente é preenchido com água até o terceiro traço.

Página 135

39. Analise estas igualdades envolvendo números mistos.

•

4 + \frac{3}{5} = 4 \frac{3}{5}

•

2 \frac{3}{8} + \frac{5}{8} = 2 + (\frac{3}{8} + \frac{5}{8}) =

= 2 + \frac{8}{8} = 2 + 1 = 3

•

3 \frac{1}{2} + 2 \frac{1}{2} = (3 + 2) + (\frac{1}{2} + \frac{1}{2}) =

= 5 + 1 = 6

Agora, efetue no caderno.

5 \frac{1}{2} + 3 \frac{1}{2}

3 \frac{4}{5} + 7 \frac{1}{5}

40. Gastei

\frac{1}{7}

do meu salário com alimentação e

\frac{2}{5}

com as demais despesas. Que fração do meu salário corresponde ao que gastei?

41. Lino é entregador de revistas. Pela manhã, ele entregou

\frac{1}{5}

das revistas a serem distribuídas hoje. À tarde, entregou mais

\frac{1}{3}

do total. Restam, ainda, 14 revistas para entregar à noite. Qual é o total de revistas que Lino deve entregar hoje?

42. Determine a fração aproximada da medida da área total do retângulo que o desenho ocupa.

Ilustração. Retângulo dividido em nove partes iguais. Um pássaro laranja sobre um galho com vegetação ao redor ocupa duas partes inteiras e oito partes pela metade.

43. O líquido contido em uma vasilha ocupa

\frac{5}{8}

da sua medida de capacidade. Se forem acrescentados 21 litros à vasilha, ela ficará cheia. Qual é a medida da capacidade da vasilha?

44.

A medida da distância de uma cidade a outra é de 360 quilômetros. Paulo vai fazer o percurso entre as duas cidades com seu carro. Elabore um problema tomando por base a ideia de que Paulo percorre uma fração do caminho e retorna outra fração, depois de pegar uma entrada errada. Seu problema deve conter os seguintes itens:

a) Qual é a medida da distância total percorrida por Paulo na ida e na volta?

b) Se Paulo não errasse o caminho, quanto faltaria para ele chegar à cidade?

Troque sua questão com a de um colega e resolva a dele. Quando receber a sua de volta, confira o resultado usando uma calculadora.

7 Multiplicação de frações

Multiplicação de um número natural por uma fração

Acompanhe a situação a seguir.

Ilustração. Um senhor branco, calvo de óculos, camisa branca e calça verde está sentado em uma cadeira com as mãos nos joelhos. À frente dele, em pé, uma mulher negra de cabelo escuro, blusa laranja, calça azul e jaleco branco gesticulando com a mão direita.

Uma médica atende o mesmo número de pacientes a cada dia de trabalho. Ela trabalha de segunda a sexta-feira, atendendo, a cada dia,

\frac{1}{5}

do total de pacientes da semana. Em certa semana com feriados na quinta e na sexta-feira, que fração do total de pacientes da semana a médica atendeu?

Para responder a essa pergunta, podemos fazer:

\frac{1}{5} + \frac{1}{5} + \frac{1}{5} = 3 \cdot \frac{1}{5} = \frac{3 \cdot 1}{5} = \frac{3}{5}

Portanto, em três dias, a médica atendeu

\frac{3}{5}

do total de pacientes da semana.

Página 136

Multiplicação de duas ou mais frações

Acompanhe como podemos calcular

\frac{4}{5} \cdot \frac{1}{2} .

Esquema: da esquerda para direita, a primeira figura é um retângulo dividido em duas partes iguais. A primeira parte da esquerda para a direita é verde e o segundo branco.

A parte verde representa

\frac{1}{2}

da figura

Dividimos a parte verde em 5 partes iguais.

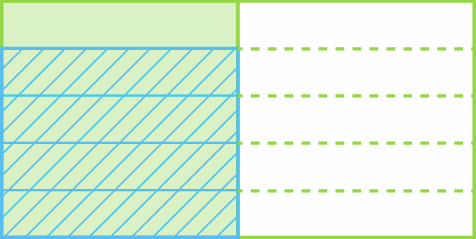
A terceira figura é um retângulo dividido em dez partes iguais. Cinco dessas partes são verdes e as outras 5 brancas. Quatro dessas partes verdes estão com listras diagonais azuis.

Considerando a parte listrada em azul, temos

\frac{4}{5}

\frac{1}{2}

, ou seja,

\frac{4}{5} \cdot \frac{1}{2},

que equivale a

\frac{4}{10}

da figura inicial.

De acôrdo com as figuras, podemos verificar que:

\frac{4}{5} \cdot \frac{1}{2} = \frac{4 \cdot 1}{5 \cdot 2} = \frac{4}{10}

O produto de duas ou mais frações é uma fração que tem como numerador o produto dos numeradores e como denominador o produto dos denominadores.

Observe outros exemplos.

\frac{5}{4} \cdot \frac{3}{11} = \frac{15}{44}

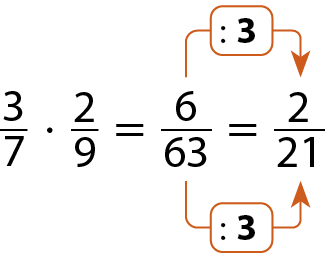
Esquema: três sétimos multiplicado por dois nonos, igual a seis sobre sessenta e três igual a dois sobre vinte e um. Acima da fração de seis sobre sessenta e três seta alaranjada que chega a fração dois sobre vinte e um. No meio dessa seta a indicação divisão por 3. Abaixo da fração de seis sobre sessenta e três seta alaranjada que chega a fração dois sobre vinte e um. No meio dessa seta a indicação divisão por 3.

\frac{1}{2} \cdot \frac{3}{5} \cdot \frac{7}{10} = \frac{21}{100}

\frac{5}{6} \cdot \frac{6}{5} = \frac{30}{30} = 1

3 \frac{1}{4} \cdot \frac{1}{3} = \frac{13}{4} \cdot \frac{1}{3} = \frac{13}{12} = 1 \frac{1}{12}

2 \frac{1}{5} \cdot \frac{5}{11} = \frac{11}{5} \cdot \frac{5}{11} = \frac{55}{55} = 1

Inverso de uma fração

Observe as multiplicações.

•

\frac{2}{3} \cdot \frac{3}{2} = \frac{6}{6} = 1

•

7 \cdot \frac{1}{7} = \frac{7}{7} = 1

•

\frac{111}{63} \cdot \frac{63}{111} = \frac{6 993}{6 993} = 1

Quando o produto de duas frações é igual a 1, dizemos que essas frações são inversas uma da outra. Assim:

•

\frac{2}{3}

é a fração inversa de

\frac{3}{2} .

•

\frac{3}{2}

é a fração inversa de

\frac{2}{3} .

• A fração inversa de

\frac{1}{7}

\frac{7}{1}

ou 7.

• A fração inversa de 7 é

\frac{1}{7} .

• A fração inversa de

\frac{63}{111}

\frac{111}{63} .

• A fração inversa de

\frac{111}{63}

\frac{63}{111} .