Parte 3
Cancelamento
O cancelamento é uma técnica utilizada para facilitar a determinação de um produto. Vamos estudar dois casos.
1º caso: quando existem fatores iguais no numerador e no denominador.
Considere alguns exemplos.
a)

b)

2º caso: quando existem múltiplos de um mesmo número no numerador e no denominador.
Analise alguns exemplos.
a)

b)

Atividades
Faça as atividades no caderno.
45. Determine os produtos, simplificando o resultado quando possível.
a)
Sentença matemática: três multiplicado por dois sétimos.b)
Sentença matemática: cinco multiplicado pelo número misto três inteiros e um quinto.c)
Sentença matemática: dois terços multiplicado por dez quartos multiplicado por nove quinze avos.d)
Sentença matemática: cinco quartos multiplicado por oito quinze avos multiplicado por um meio.e)
7 sobre 9 vezes 3 sobre 2 vezes zerof)
Sentença matemática: número misto dois inteiros e um quinto multiplicado por trinta e cinco sobre trinta e três.46. Uma loja vendeu 42 fones de ouvido. Destes,
Sentença matemática: fração dois terços.são da marca Alfa. Quantos fones de ouvido da marca Alfa foram vendidos?
47. Determine:
a) o triplo de
7 sobre 15b) o dôbro de
Sentença matemática: fração cinco oitavos.48. Um reservatório contém .2400 litros. Quantos litros cabem em
Sentença matemática: fração três quartos.desse reservatório?
49. Efetue as multiplicações utilizando o cancelamento.
a)
Sentença matemática: três quintos multiplicado por cinco sétimos.b)
Sentença matemática: um meio multiplicado por oito nonos multiplicado pelo número misto dois inteiros e um quarto.c)
Sentença matemática: trinta e seis sobre cinquenta multiplicado por trinta sobre setenta e dois multiplicado por dez sobre quarenta.d)
Sentença matemática: sete onze avos multiplicado por onze sobre vinte e oito.50. Em uma caixa há meio cento de laranjas. Se retirarmos
Sentença matemática: fração dois quintos.dessas laranjas, quantas laranjas sobrarão na caixa?
51. Joaquim quer dividir R$ 6.000,00seis mil reais entre seus três filhos desta maneira:
• o mais novo deve receber
Meiodo total;
• o do meio deve receber
fração 1 terçodo total;
• o mais velho deve receber
Sentença matemática: fração um quarto.do total.
Essa divisão é possível? Justifique sua resposta.
52.

José, Vanessa e Marcos abriram uma empresa. Cada um investiu certo valor. Em um mês, a empresa faturou R$ 33.915,00trinta e três mil novecentos e quinze reais. Na divisão dos lucros, José, Vanessa e Marcos receberam, respectivamente,
fração 1 terço,
Sentença matemática: fração dois quintos.e
Sentença matemática: fração um sétimo.do total faturado, e o restante foi usado com despesas gerais. Com o auxílio de uma calculadora, determine o valor gasto com as despesas.

8 Divisão de frações
Divisão de um número natural por uma fração
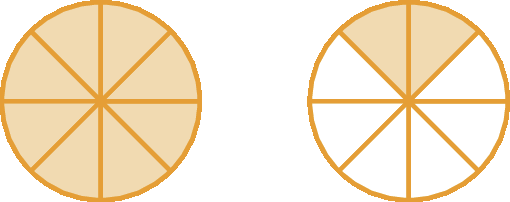
Marília comprou duas pizzas grandes para servir aos amigos. Cada pizza é dividida em 8 pedaços iguais. Marília e seus amigos comeram um pedaço de pizza cada um. Quantas pessoas comeram pizza?
Para resolver esse problema, inicialmente, dividimos cada pizza em 8 partes iguais.
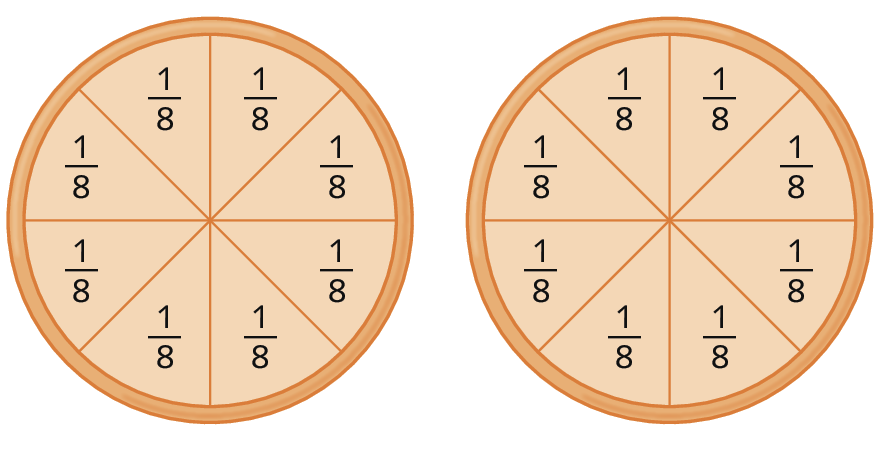
Cada uma dessas partes corresponde a
Sentença matemática: fração um oitavo.de uma pizza.
Observando a ilustração, percebemos que
Sentença matemática: fração um oitavo.de uma pizza cabe 16 vezes em duas pizzas:
cabe 16 vezes em 2, ou seja,
Sentença matemática: dois dividido por um oitavo igual dezesseis.Portanto, 16 pessoas comeram pizza.
Observe que:
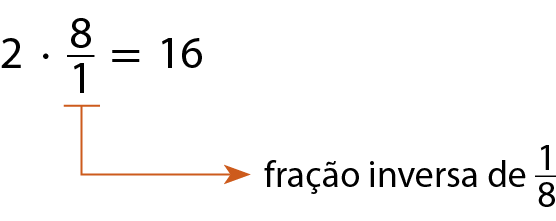
Dividir por
Sentença matemática: fração um oitavo.é o mesmo que multiplicar por
Sentença matemática: fração oito sobre um., que é a fração inversa de
Sentença matemática: fração um oitavo..
Divisão de uma fração por um número natural
Qual é a metade de
Sentença matemática: fração um terço.Para responder a essa pergunta, observe o esquema a seguir.
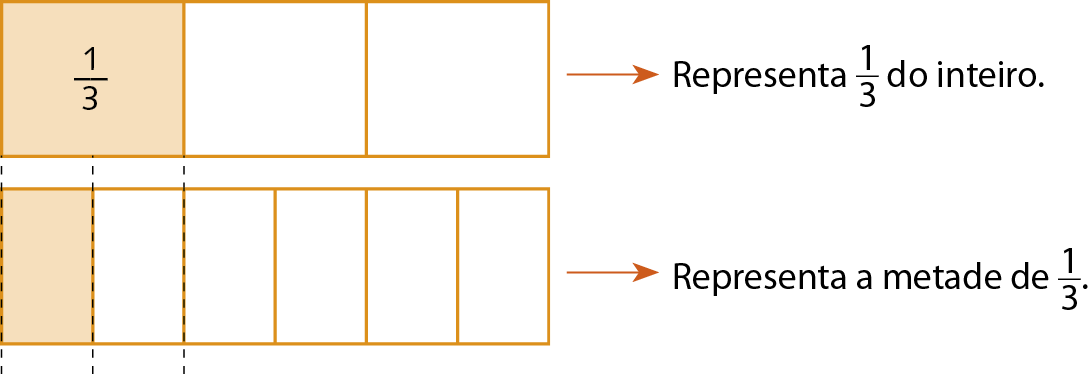
Note que a metade de
Sentença matemática: fração um terço.cabe seis vezes na figura inicial. Portanto, a fração que representa a metade de
Sentença matemática: fração um terço.é
Sentença matemática: fração um sexto.. Então:
Perceba que:
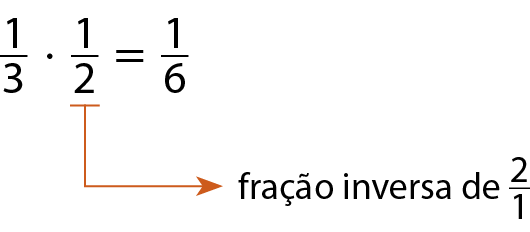
Dividir por 2 é o mesmo que multiplicar por
Sentença matemática: fração um meio., que é a fração inversa de
Sentença matemática: fração dois sobre um..
Divisão de uma fração por outra fração
Qual é o quociente da divisão de
Sentença matemática: fração três quintos.por
Sentença matemática: fração um décimo.?
A operação consiste em determinar quantas vezes
Sentença matemática: fração um décimo.cabe em
Sentença matemática: fração três quintos.. Observe o esquema.
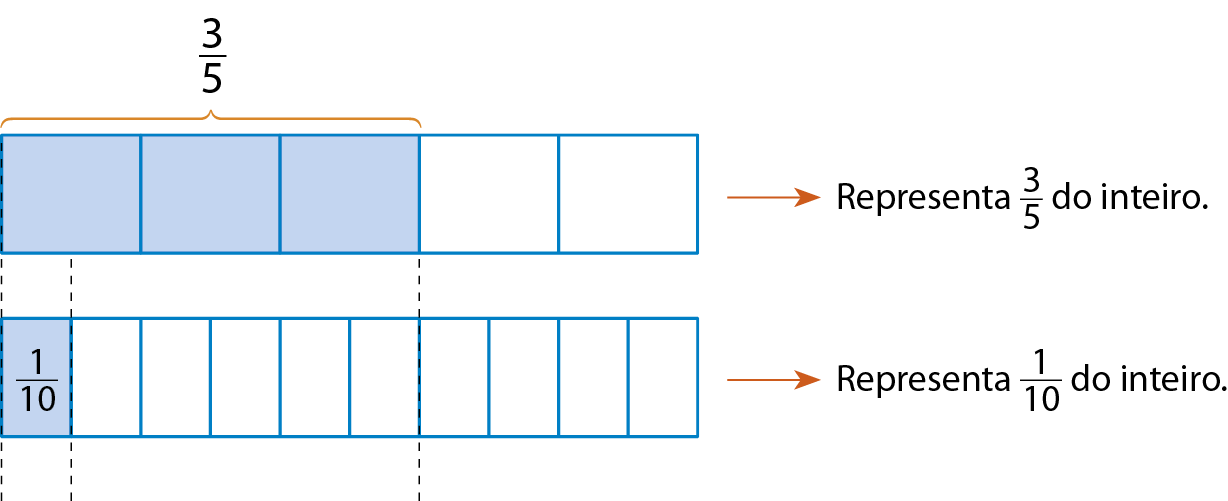
Nesse caso, apenas observando a figura, percebemos que
Sentença matemática: fração um décimo.cabe seis vezes em
Sentença matemática: fração três quintos..
Assim:
Sentença matemática: três quintos dividido por um sobre dez igual a seis.Logo, o quociente de
Sentença matemática: fração três quintos.por
Sentença matemática: fração um décimo.é 6.
Perceba que:
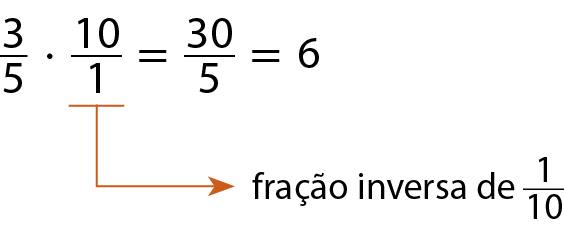
Dividir por
Sentença matemática: fração um décimo.é o mesmo que multiplicar por
Sentença matemática: fração dez sobre um., que é a fração inversa de
Sentença matemática: fração um décimo..
Na divisão de uma fração por outra, multiplicamos a primeira fração pela fração inversa da segunda.
Observe outros exemplos.
a)
Sentença matemática: três quintos dividido por sete nonos igual a três quintos multiplicado por nove sétimos, igual a vinte e sete sobre trinta e cinco.b)
Sentença matemática: dois dividido por três quintos igual a dois multiplicado por cinco terços, igual a dez terços, igual a número misto três inteiros e um terço.c)
Sentença matemática: dez dezessete avos dividido por dois igual a dez dezessete avos multiplicado por um meio, igual a cinco dezessete avos.Sugestão de leitura
TEIXEIRA, Martins R. Uma aventura na mata. São Paulo: éfe tê dê, 1997. (Coleção Matemática em mil e uma histórias).
Por meio de resoluções de problemas envolvendo frações, Neco e Teco dedicam-se a preservar a natureza e a resolver as complicações dos fenômenos naturais.
Observação
Para representar a divisão de frações, podemos usar também a notação:
Atividades
Faça as atividades no caderno.
53. Efetue as divisões, simplificando o resultado quando possível.
a)
Sentença matemática: quatro dividido por um meio.b)
Sentença matemática: sessenta dividido por três oitavos.c)
Sentença matemática: dois nonos dividido por número misto um inteiro e um terço.d)
Sentença matemática: um meio dividido por quatro.e)
Sentença matemática: dez dividido por dois quintos.f)
Sentença matemática: três oitavos dividido por cinco.54. Quantos copos com medida de capacidade de
Sentença matemática: fração um quarto.de litro podemos encher com 10 garrafas de 1 litro?
55. Calcule:
a)
Sentença matemática: dois sétimos dividido por três quintos.b)
Sentença matemática: dez dividido por dois quintos.c)
Sentença matemática: três sétimos dividido por seis décimos.56. Eneias preparou um refresco misturando
Sentença matemática: fração três quartos.de litro de suco de acerola com
Sentença matemática: fração três quartos.de litro de suco de laranja,
Sentença matemática: fração três quartos.de litro de leite condensado e
Sentença matemática: fração um quarto.de litro de suco de limão.

Em seguida, serviu doses iguais do refresco em dez taças. Que fração do litro caberá, no máximo, em cada taça?
57. Um aquecedor solar residencial tem um grande reservatório de água para uso na cozinha e em cinco banheiros. Sabendo que
fração 1 terçodessa medida de capacidade é utilizado na cozinha, que fração seria disponibilizada para cada banheiro, supondo que os cinco tenham igual consumo?


9 Potenciação de frações
Luís e Pâmela são irmãos e gostam muito de programas de tê vê. No entanto, o pai disse que eles poderiam ficar em frente à tê vê metade
Sentença matemática: fração um meio.do tempo que gostariam, enquanto a mãe indicou que o tempo deveria ser ainda menor, para que pudessem ver seus amigos nos momentos de lazer e estudar. Ela sugeriu, então, reduzir esse tempo novamente pela metade
Sentença matemática: fração um meio.. Dessa fórma, o tempo máximo que Luís e Pâmela poderiam dedicar a seus programas de tê vê seria de
Sentença matemática: fração um meio.de
Sentença matemática: fração um meio.daquele que gostariam, ou seja:
Para elevar uma fração a determinado expoente, devemos elevar o numerador e o denominador a esse expoente.
Analise alguns exemplos.
a)
Sentença matemática: abre parênteses, dois quintos, fecha parênteses, elevado a quatro, igual a dois quintos multiplicado por dois quintos, multiplicado por dois quintos, multiplicado por dois quintos, multiplicado por dois quintos, igual a dois elevado a quatro sobre cinco elevado a quatro igual a dezesseis sobre seiscentos e vinte e cinco.b)
Sentença matemática: abre parênteses, número misto um inteiro e dois quintos, fecha parênteses, elevado a três, igual a abre parênteses, sete quintos, fecha parênteses, elevado a três, igual a sete elevado a três sobre cinco elevado a três, igual a trezentos e quarenta e três, sobre cento e vinte e cinco, igual a número misto dois inteiros e noventa e três sobre cento e vinte e cinco.As definições utilizadas para os números naturais também são válidas para os números na fórma de fração. Assim:
• Toda potência de expoente 1 é igual à própria base.
a)
Sentença matemática: abre parênteses, um sétimo, fecha parênteses, elevado a um é igual a fração um sétimo.b)
Sentença matemática: abre parênteses, treze quartos, fecha parênteses, elevado a um é igual a fração treze quartos.• Toda potência de expoente zero e base diferente de zero é igual a 1.
a)
Sentença matemática: abre parênteses, três quintos, fecha parênteses, elevado a zero é igual a um.b)
Sentença matemática: abre parênteses, duzentos sobre sete, fecha parênteses, elevado a zero é igual a um.Atividade
Faça a atividade no caderno.
58. Calcule o valor das potências.
a)
Sentença matemática: abre parênteses, três quintos, fecha parênteses, elevado a dois.b)
Sentença matemática: abre parênteses, um meio, fecha parênteses, elevado a quatro.c)
Sentença matemática: abre parênteses, oito terços, fecha parênteses, elevado a um.d)
Sentença matemática: abre parênteses, dois terços, fecha parênteses, elevado a três.e)
Sentença matemática: abre parênteses, número misto três inteiro e um meio, fecha parênteses, elevado a dois.f)
Sentença matemática: abre parênteses, cento e noventa e nove sobre quinhentos, fecha parênteses, elevado a zero.Expressões numéricas
O cálculo de expressões numéricas envolvendo frações segue a mesma ordem estudada para o cálculo das expressões numéricas com números naturais:
1º) potenciações;
2º) multiplicações e divisões, na ordem em que aparecem;
3º) adições e subtrações, na ordem em que aparecem.
Quando, nas expressões, aparecem sinais de associação, estes devem ser resolvidos na seguinte ordem: parênteses ( ), colchetes [ ] e chaves { }.
Analise como calcular o valor de algumas expressões numéricas.
a)
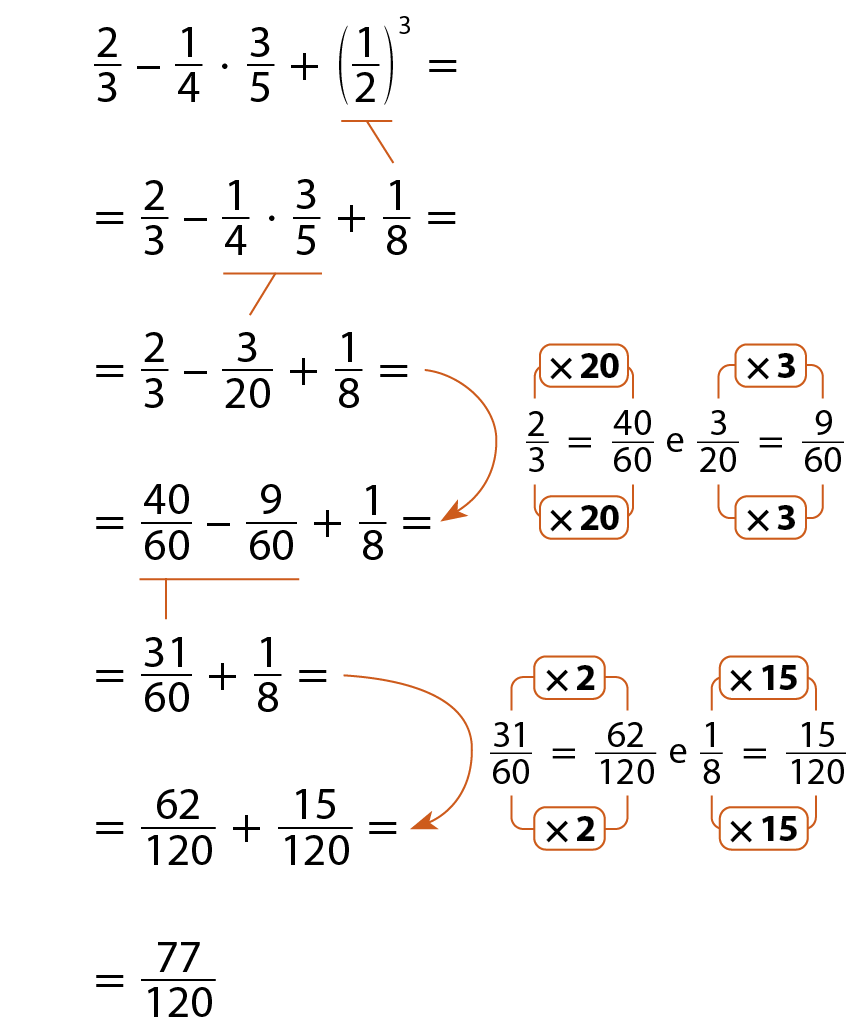
b)
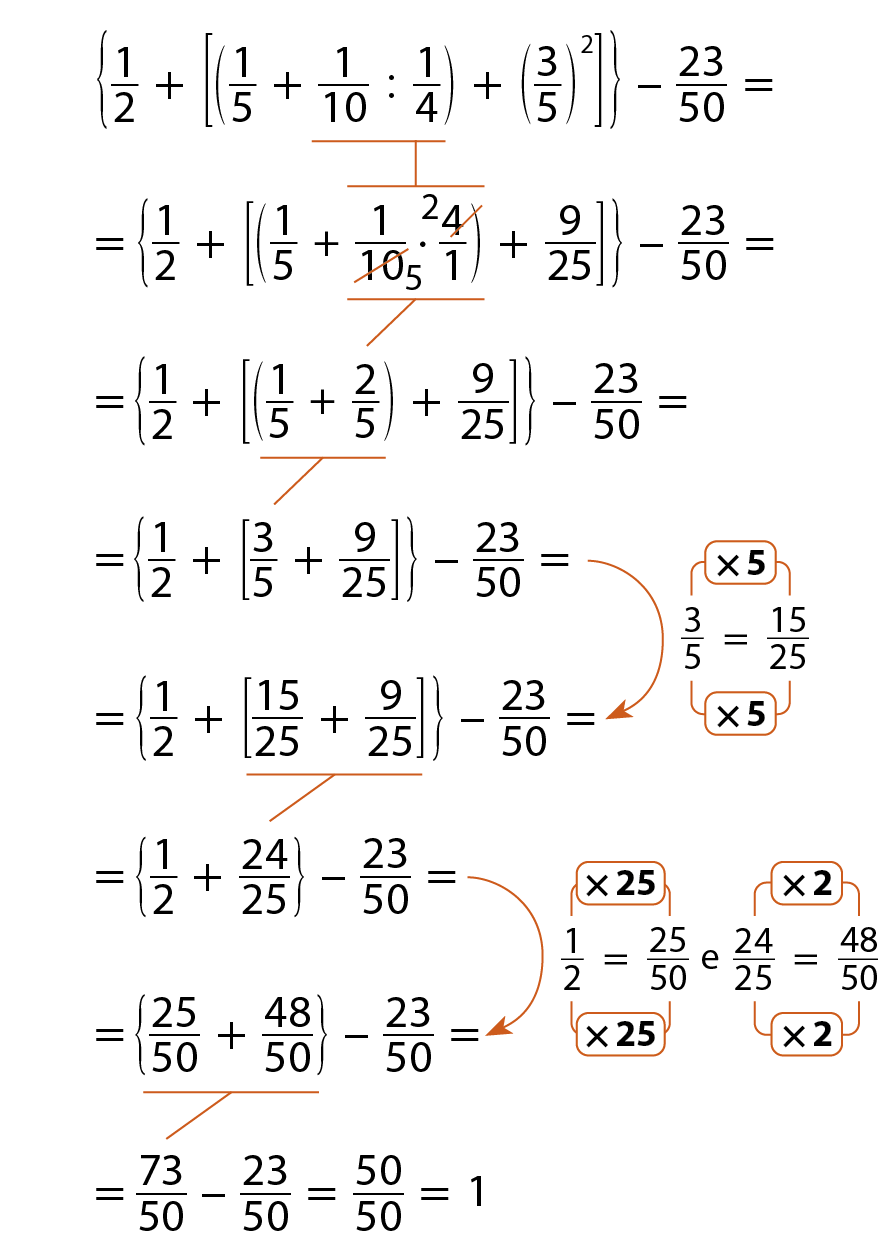
Sugestão de leitura
RAMOS, Luzia Faraco. Frações sem mistérios. São Paulo: Ática, 2008. (Coleção A descoberta da Matemática).
Enigmas, suspense e frações aguardam você nesse interessante livro.
Atividades
Faça as atividades no caderno.
59. Calcule o valor das expressões numéricas a seguir
a)
Sentença matemática: cinco sextos mais um meio multiplicado por três quartos.b)
Sentença matemática: cinco menos sete quartos multiplicado por um meio.c)
Sentença matemática: dois terços multiplicado por um quinto mais dois inteiros e um quarto.d)
Sentença matemática: três quintos mais dois nonos dividido por dois terços.e)
Sentença matemática: dois sétimos multiplicado por três quintos menos um oitavo dividido por cinco sextos.f)
Sentença matemática: três quartos mais cinco nonos dividido por um sexto.60. Calcule o valor das expressões numéricas a seguir.
a)
Sentença matemática: abre parênteses, dois terços menos um oitavo multiplicado por quatro sétimos, fecha parênteses, dividido por dois sétimos multiplicado por quatro nonos.b)
Sentença matemática: vinte sobre cem dividido, abre chaves, onze quartos menos, abre colchetes, três meios mais abre parênteses, um meio mais um quarto, fecha parênteses, fecha colchetes, fecha chaves.c)
Sentença matemática: abre parênteses, um menos um meio, fecha parênteses, elevado a dois, dividido, abre colchetes, abre parênteses, um menos três quartos, fecha parênteses, elevado a dois, multiplicado por oito mais, abre parênteses, um meio, fecha parênteses, elevado a dois, fecha colchetes.
Resolvendo em equipe
Faça a atividade no caderno.
(enêm) A música e a matemática se encontram na representação dos tempos das notas musicais, conforme a figura a seguir.

Um compasso é uma unidade musical composta de determinada quantidade de notas musicais em que a soma das durações coincide com a fração indicada como fórmula do compasso. Por exemplo, se a fórmula de compasso é
Sentença matemática: fração um meio., poderia haver um compasso ou com duas semínimas ou uma mínima ou quatro colcheias, sendo possível a combinação de diferentes figuras. Um trecho musical de oito compassos, cuja fórmula é
Sentença matemática: fração três quartos., poderia ser preenchido com
a) 24 fusas.
b) 3 semínimas.
c) 8 semínimas.
d) 24 colcheias e 12 semínimas.
e) 16 semínimas e 8 semicolcheias.
|
Interpretação e identificação dos dados |
• Identifique a definição de compasso no enunciado do problema. |
|---|---|
|
Plano de resolução |
• Releia o enunciado da questão e calcule o valor de 8 compassos de cada um. |
|
Resolução |
• Junte-se a um colega. |
|
Verificação |
• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas. |
|
Apresentação |
• Depois de resolver a questão, cada aluno da dupla deve escrever um pequeno texto explicando o processo de resolução, citando as dificuldades e como as superaram. Se cometeram algum erro durante a resolução, é importante que anotem e tentem compreender por que erraram. Em seguida, o professor vai convidar algumas duplas para ler seus textos. |
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
A ideia de número fracionário
As frações também podem aparecer quando nos referimos à parte de uma figura ou quando comparamos o número de alguns objetos com o total de objetos de um grupo.
Em uma fração, o denominador é o número abaixo do traço e representa a quantidade de partes iguais em que o todo foi dividido. Já o número acima do traço, o numerador, indica a quantidade de partes consideradas do todo. Considere o exemplo a seguir.
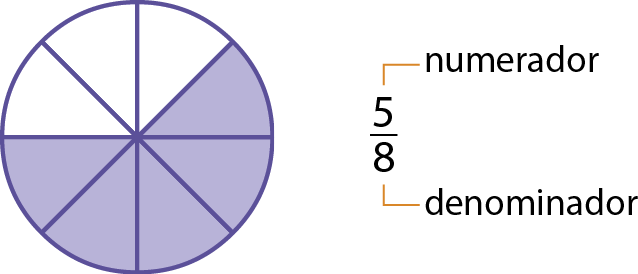
Lemos: “cinco oitavos”.
1. Qual é a fração que representa a parte verde de cada uma das figuras a seguir?
a)

b)
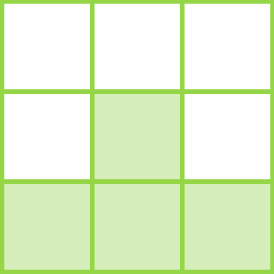
c)
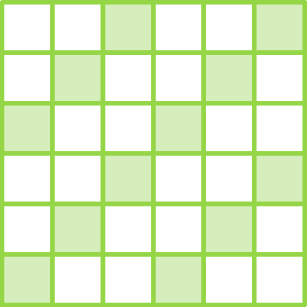
d)

2. Escreva no caderno como se lê cada uma das frações.
a)
Sentença matemática: fração quatro sobre sete.b)
Sentença matemática: fração um sobre nove.c)
Sentença matemática: fração seis sobre dez.d)
Sentença matemática: fração doze sobre cem.e)
Sentença matemática: fração quatro sobre mil.f)
Sentença matemática: fração doze sobre vinte e três.Número misto
É um número composto de uma parte inteira e uma parte fracionária.
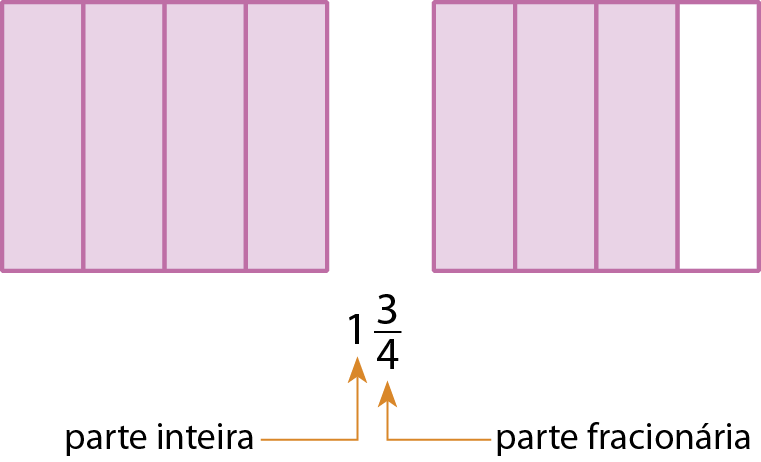
3. Escreva no caderno o número misto que representa a parte colorida das figuras.
a)

b)
4. Transforme os números mistos em frações.
a)
Sentença matemática: número misto: um inteiro e três quartos.b)
Sentença matemática: número misto: dois inteiros e nove onze avosc)
Sentença matemática: número misto: quatro inteiros e sete nonos.d)
Sentença matemática: número misto: sete inteiros e dois sétimos.Frações equivalentes
Frações que representam a mesma parte de um inteiro são chamadas de frações equivalentes.
5. No caderno, substitua o

a fim de obter frações equivalentes em cada um dos itens.
a)
Sentença matemática. Doze sobre quinze igual vinte e quatro sobre retângulo cinza.b)
Sentença matemática. Seis sobre vinte igual a retângulo cinza sobre sessenta.c)
Sentença matemática. Vinte e cinco sobre cem igual a cinco sobre figura retângulo cinza.d)
Sentença matemática. Retângulo cinza sobre dezesseis igual trinta e cinco sobre oitenta.6. Simplifique as frações a seguir até torná-las irredutíveis.
a)
Sentença matemática: fração dez sobre vinte e cinco.b)
Sentença matemática: fração dezoito sobre cento e cinquenta.c)
Sentença matemática: fração doze sobre sessenta.d)
Sentença matemática: fração noventa e seis sobre cento e doze.Comparação de frações de um mesmo inteiro
Frações com mesmo denominador
Quando duas ou mais frações têm o mesmo denominador, a maior delas é a que tem o maior numerador.
pois: 8 > 6
Frações com denominadores diferentes
Para comparar frações que têm numeradores e denominadores diferentes, devemos obter frações equivalentes às frações iniciais que tenham o mesmo denominador para, em seguida, compará-las.
pois:
dois terços é igual a oito doze avos,
um quarto igual a três doze avose
oito doze avos é maior que três doze avos7. Copie os itens no caderno substituindo cada

pelo símbolo >, < ou =.
a)
Sentença matemática: cinco onze avos, quadrado cinza sete onze avos.b)
Sentença matemática: dois sétimos, quadrado cinza quatro quintos.c)
Sentença matemática: nove meios, quadrado cinza, quinze quartos.d)
Sentença matemática: quinze sobre trinta e nove, quadrado cinza cinco treze avos.8. Determine a maior fração de cada item.
a)
Sentença matemática: fração nove sobre oito.,
Sentença matemática: fração três oitavos.e
Sentença matemática: fração sete sobre oito..
b)
Sentença matemática: fração um quinto.,
Sentença matemática: fração quatro terços.e
Fração 2 sextos.
c)
Sentença matemática: fração dois terços.,
Sentença matemática: fração um quarto.e
Sentença matemática: fração três quintos..
d)
Sentença matemática: fração quatro sobre dez.,
Sentença matemática: fração cinco sobre doze.e
Sentença matemática: fração quinze sobre vinte e cinco..
9. Escreva as frações em ordem crescente.
a)
Sentença matemática: fração um quarto.,
Sentença matemática: fração dois terços.e
Sentença matemática: fração quatro quintos..
b)
Sentença matemática: fração dois quintos.,
Sentença matemática: fração três oitavos.e
Sentença matemática: fração nove sobre quinze..
c)
Sentença matemática: fração três quartos.,
Sentença matemática: fração dois sextos.e
Sentença matemática: fração dois terços..
d)
Sentença matemática: fração quatro nonos.,
fração 1 terçoe
Sentença matemática: fração dois sétimos..
Fração de uma quantidade
Para calcular
Sentença matemática: fração um quinto.de 150, podemos fazer:
150 : 5 = 30
Logo,
Sentença matemática: fração um quinto.de 150 é igual a 30.
10. Lucas gastou
fração 1 terçodo salário para pagar as despesas do mês. Sabendo que o salário de Lucas é de R$ 4.500,00quatro mil quinhentos reais, qual foi o valor dessas despesas?
11. Maria está participando de uma corrida. Ela já percorreu
Sentença matemática: fração três quartos.do trajeto, o que corresponde a .3375 metros. Qual é a distância total a ser percorrida nessa prova?
12. Marcos e Jorge são irmãos. Eles compraram um jôgo de videogame. Marcos pagou
Sentença matemática: fração três quintos.do jôgo e Jorge pagou R$ 46,00quarenta e seis reais. Quanto custou esse jôgo?
13. Rogério, Cristiane e Patrícia compraram um pacote de amoras por R$ 12,00doze reais. Rogério pagou
fração 1 terçodo pacote, Cristiane pagou metade do valor pago por Rogério e Patrícia pagou o restante. Qual é o valor que Patrícia pagou pelas amoras?
14. Um atacadista possuía duas.seiscentas sacas de arroz. Ele vendeu
Sentença matemática: fração quatro treze avos.dessas sacas ao primeiro freguês. Do que sobrou, vendeu
fração 1 terçoao segundo freguês. Então, novamente do que sobrou, vendeu
Sentença matemática: fração três décimos.ao terceiro freguês. Quantas sacas restaram?
Adição e subtração de frações
Frações com denominadores iguais
Adicionamos (ou subtraímos) os numeradores e conservamos os denominadores.
Frações com denominadores diferentes
Determinamos frações equivalentes às iniciais, com um mesmo denominador, e depois adicionamos (ou subtraímos) os numeradores (conservando o denominador).
a)
Sentença matemática: três oitavos mais quatro oitavos igual a sete oitavos.b)
Sentença matemática: cinco sextos menos dois terços igual a cinco sextos menos quatro sextos igual a um sexto.15. Calcule o resultado das operações.
a)
Sentença matemática: quatro nonos mais nove quintos.b)
Sentença matemática: doze sobre vinte e um mais dez sobre vinte e um.c)
Sentença matemática: doze sobre quinze menos cinco sobre quinze.d)
Sentença matemática: três sétimos menos um sétimo.e)
Sentença matemática: dois inteiros e quatro quintos mais três quintos.f)
Sentença matemática. Um sexto mais cinco nonos.g)
Sentença matemática. Dois terços menos quatro sétimos.h)
Sentença matemática. Cinco oitavos menos oito quinze avos.i)
Sentença matemática. Fração 1 quarto mais 1 terço mais 1 quintoj)
Sentença matemática. Oito nonos menos sete décimos.16. Um aquário está com
Sentença matemática: fração quatro quintos.de sua medida de capacidade. Acrescentando 12 litros de água, o aquário ficará completamente cheio. Qual é a medida da capacidade desse aquário?
17. Efetue as operações a seguir, simplificando quando possível.
a)
Sentença matemática: dois inteiros e um terço mais um inteiro e três quartos.b)
Sentença matemática: um meio mais um quinto menos três sextos.c)
Sentença matemática: oito menos sete meios.d)
Sentença matemática: sete meios menos um inteiro e um oitavo.Multiplicação de frações
O produto de duas frações é um número na fórma de fração que tem como numerador o produto dos numeradores e como denominador o produto dos denominadores.
18. Calcule o resultado de cada uma das multiplicações.
a)
Sentença matemática. 8 vezes 7 nonos.b)
Sentença matemática: dois quintos multiplicado por 12.c)
Sentença matemática: um quarto multiplicado por três nonos.d)
Sentença matemática: nove quinze avos multiplicado por cinco terços.e)
Sentença matemática: três oitavos multiplicado por quatro quintos.f)
Sentença matemática: cinco nonos vezes quatro décimos.19. Beto vendeu 100 números de uma rifa a familiares e colegas. Destes,
Sentença matemática: fração dois quintos.dos números foram vendidos a familiares dele. Quantos números foram vendidos a colegas de Beto?
20. Que fração do triângulo maior o triângulo menor representa?
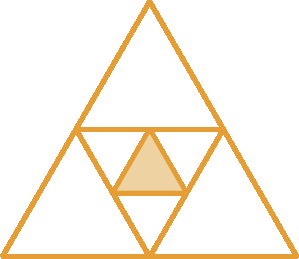
Divisão de frações
Na divisão de uma fração por outra, multiplicamos a primeira fração pela fração inversa da segunda.
21. Calcule o resultado de cada uma das divisões.
a)
Sentença matemática: quatro nonos dividido por 3.b)
Sentença matemática: quarenta dividido por dois terços.c)
Sentença matemática: quatro sétimos dividido por um meio.d)
Sentença matemática: três quinze avos dividido por dois terços.e)
Sentença matemática: dois sétimos dividido por quatro nonos.f)
Sentença matemática. fração 9 15 avos dividido por fração 5 nonos22. Calcule no caderno.
a)
Sentença matemática: um meio dividido por três oitavos.b)
Sentença matemática: seis dividido por um quarto.23. Da quantia que recebo mensalmente, aplico
Sentença matemática: fração três sétimos.em caderneta de poupança, o que corresponde a R$ 540,00quinhentos e quarenta reais. Qual é a quantia total que recebo mensalmente?
Potenciação de frações
Para elevar uma fração a determinado expoente, devemos elevar o numerador e o denominador a esse expoente.
24. Calcule o valor das potências.
a)
Sentença matemática: dois terços elevado a dois.b)
Sentença matemática: quatro terços elevado a três.c)
Sentença matemática: fração um centésimo elevado a zero.d)
Sentença matemática: fração noventa e nove centésimos elevado a um.e)
Sentença matemática: abre parênteses, três inteiros e um meio, fecha parênteses, elevado a dois.f)
Sentença matemática: fração três quintos elevado a três.Expressões numéricas
O cálculo de expressões numéricas envolvendo frações segue a mesma ordem estudada para o cálculo das expressões numéricas com números naturais:
1º) potenciações;
2º) multiplicações e divisões, na ordem em que aparecem;
3º) adições e subtrações, na ordem em que aparecem.
Quando, nas expressões, aparecem sinais de associação, estes devem ser resolvidos na seguinte ordem: parênteses ( ), colchetes [ ] e chaves { }.
25. Calcule o valor da expressão numérica a seguir.
26. Calcule o valor das expressões a seguir.
a)
Sentença matemática: três meios ao quadrado mais, abre colchetes, três inteiros e um terço menos três inteiros e um quarto mais um meio elevado ao cubo, fecha colchetes.b)
Sentença matemática: abre colchetes, abre parênteses, dois terços dividido por um doze avos mais dois, fecha parênteses dividido por um décimo ao quadrado menos dez elevado ao cubo, fecha colchetes.