Página 174

Unidade 3

Capítulo 8 Porcentagem

Capítulo 9 Figuras geométricas planas

Capítulo 10 Ampliação e redução de figuras

Foto. Fachada de um prédio com foto de Mario Quintana e grafite de Eduardo Cobra. Mario Quintana, senhor de cabelos grisalhos, está vestido com paletó. O grafite é colorido, pintado sobre a foto e toda a fachada, formado por quadriláteros de lados iguais, quadriláteros de lados opostos de mesma medida e triângulos. Há também no grafite um beija-flor azul, formado por figuras geométricas. Este toca seu bico na cabeça de Mario Quintana. O dia está ensolarado e com nuvens. — Mario Quintana, obra do artista Eduardo Kobra, localizada na fachada de um dos prédios do Colégio Farroupilha, em Porto Alegre (Rio Grande do Sul). Foto de 2022. Você conhece a arte do grafite? Quais figuras geométricas planas é possível identificar na obra apresentada? Depois que planejou o desenho, como o artista fez para reproduzi-lo na fachada do prédio? Ao final do estudo desta Unidade, você responderá a essas e outras questões.

Página 175

Capítulo 8 Porcentagem

Trocando ideias

Observe as porcentagens presentes no infográfico a seguir.

Infógráfico.
Gráfico de setores. Embalagens longa vida: 42,7%. Ilustração. 3 garrafas longa vida de tamanhos diferentes e uma lixeira de papel azul.
Gráfico de setores. Embalagens de plástico: 23,1%. Ilustração. Embalagens de plástico de produtos de limpeza, pets e potes com formato de blocos retangulares de plástico e uma lixeira de plástico vermelha.

Gráfico de setores. Latas de aço: 47,1%. Ilustração. Latas de metal cilíndricas e com formato de blocos retangulares e uma lixeira de metal amarela.

Gráfico de setores. Latas de alumínio: 98,7%. Ilustração. Latas de refrigerantes e sucos e uma lixeira de metal amarela.

Gráfico de setores. Papel: 66,9%. Ilustração. Uma pilha de papel e papéis amassados encima e ao lado da pilha e uma lixeira de papel azul.

Dados obtidos em: https://oeds.link/1PQDnk. Acesso em: 17 maio 2022.

▸

Que números aparecem na fórma de porcentagem nesse infográfico? Em que situações cotidianas números como esses são utilizados?

▸

A quantidade de toneladas de latas de alumínio comercializadas no Brasil em 2021 é maior ou menor do que quatrocentas e nove mil toneladas? Por quê?

▸

Qual é a importância da reciclagem para o meio ambiente?

Neste capítulo, vamos estudar porcentagens e algumas de suas aplicações.

Página 176

1 Porcentagem

O símbolo porcentagem (lemos: por cento) é usado junto a um número para indicar uma porcentagem.

Observe a manchete deste jornal de 2018.

Ilustração. Jornal com a manchete "Apenas 22% dos municípios brasileiros têm coleta seletiva de resíduos". Abaixo da manchete 4 latas de coleta seletiva na sequencia: azul, vermelha, amarela e verde.

Nela, podemos ver que 22% (lemos: vinte e dois por cento) dos municípios brasileiros tinham coleta seletiva de resíduos em 2018, isto é, 22 em cada 100 municípios brasileiros tinham coleta seletiva de resíduos em 2018.

22 em cada 100 pode ser representado pela fração

\frac{22}{100}

. Assim:

22 % = \frac{22}{100}

Porcentagem de um valor

Acompanhe a situação a seguir.

Em uma escola de natação, há 50 alunos. As turmas são divididas de acôrdo com o nível de aprendizado de cada aluno. 50% dos alunos da escola fazem parte da turma de Daniela e André. Analise como cada um pensou para calcular quantos alunos havia na turma deles.

Outra maneira de calcular 50% de 50 é utilizando uma calculadora. Observe a sequência de teclas usadas:

Ilustração. Representação de uma sentença matemática utilizando teclas de calculadora. Tecla cinco, tecla zero, tecla com símbolo de multiplicação, tecla cinco, tecla zero e tecla com símbolo de porcentagem.

Página 177

Porcentagem de figuras

Dividindo uma figura em partes iguais e selecionando algumas dessas partes, conseguimos determinar a porcentagem correspondente às partes selecionadas. Observe os exemplos a seguir.

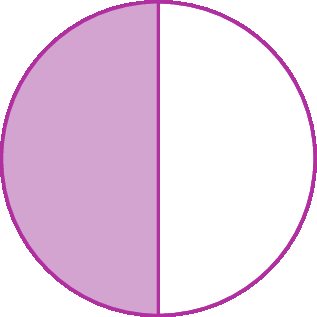
a) Dividindo a figura em duas partes iguais e pintando uma, dizemos que 50% dela foi pintada.

Esquema. À esquerda temos que 50 porcento é igual a fração 50 sobre cem que é igual a fração um meio. À direita, uma parte pintada, seta saindo da frase e chegando no numerador 1. Parte iguais em que a figura foi dividida, seta saindo da frase e chegando no denominador 2.

Figura geométrica. Círculo dividido em duas partes iguais com uma parte pintada de rosa.

b) Dividindo a figura em quatro partes iguais e pintando uma, dizemos que 25% dela foi pintada.

Esquema. À esquerda, 25 porcento é igual a fração 25 sobre 100 que é igual a fração um quarto. À direita, uma parte pintada, seta saindo da frase e chegando no numerador 1. Partes iguais em que a figura foi dividida, seta saindo da frase e chegando no denominador 4.

Figura geométrica. Quadrado dividido em quatro partes iguais com uma parte pintada de azul.

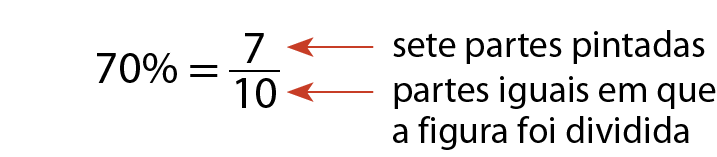
c) Dividindo a figura em dez partes iguais e pintando sete, dizemos que 70% dela foi pintada.

Esquema. À esquerda, 70 porcento é igual a fração 70 sobre 10 que é igual a fração um sétimo. À direita, uma parte pintada, seta saindo da frase e chegando no numerador 7. Partes iguais em que a figura foi dividida, seta saindo da frase e chegando no denominador 10.

Retângulo dividido em 10 partes quadradas iguais: 7 são laranjas e 3 são brancas.

Agora, acompanhe a seguinte situação.

Anderson era proprietário de um terreno e resolveu lotearglossário sua propriedade em 10 partes (lotes) iguais, como mostra a representação a seguir.

Figura geométrica. Retângulo dividido em dez partes iguais.

Uma empresa apresentou uma proposta para comprar quatro desses lotes. Para saber que porcentagem do terreno a empresa queria comprar, Anderson elaborou o esquema a seguir.

Primeiro, para descobrir a porcentagem de cada lote, ele fez:

Do lado esquerdo. esquema, Na primeira linha: à esquerda, 100%. À direita, 10 lotes. Entre eles uma linha reta. Na segunda linha: à esquerda, 10%. À direita, 1 lote. Entre eles uma linha reta. Saindo da primeira linha uma seta para a segunda linha, indicando divisão por 10. Do lado lado direito, retângulo dividido em 10 partes quadradas iguais. Em cada uma delas está escrito 10 por cento. Um destas partes é verde e as outras 9 são brancas.

Assim, percebeu que cada lote equivalia a 10% do terreno.

Em seguida, ele obteve a porcentagem do terreno correspondente a 4 lotes:

Do lado esquerdo. esquema, Na primeira linha: à esquerda, 10%. À direita, 1 lote. Entre eles uma linha reta. Na segunda linha: à esquerda, 40%. À direita, 4 lotes. Entre eles uma linha reta. Saindo da primeira linha uma seta para a segunda linha, indicando multiplicação por 4. Do lado lado direito, retângulo dividido em 10 partes quadradas iguais. Em cada uma delas está escrito 10 por cento. 4 destas partes são verdes e as outras 6 são brancas.

Com isso, Anderson constatou que a empresa queria comprar 40% do terreno.

Página 178

Atividades

Faça as atividades no caderno.

1. Calcule as porcentagens a seguir.

a) 30% de 240

b) 25% de 10

c) 1% de .1000

d) 12,5% de 550

e) 90% de 180

f) 230% de 70

André resolveu utilizar a calculadora para transformar frações em porcentagens. Analise como ele pensou.

1º) Para transformar a fração

\frac{1}{8}

em porcentagem, divido 1 por 8, ou seja, faço 1 dividido por 8 na calculadora. O resultado é 0,125.

2º) Multiplico o resultado obtido por 100, já que quero transformar o número em porcentagem, ou seja, faço 0,125 × 100. O resultado é 12,5.

3º) Então, a fração

\frac{1}{8}

equivale a 12,5%.

Faça como André e, com o auxílio de uma calculadora, transforme as seguintes frações em porcentagem:

\frac{3}{16}

\frac{7}{5}

\frac{37}{40}

\frac{135}{80}

3. Reproduza os esquemas no caderno e complete-os com os valores correspondentes a cada quadradinho.

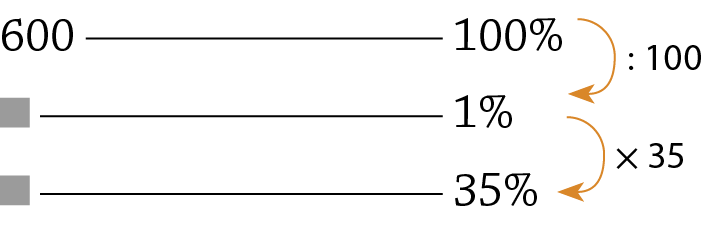
Esquema. Na primeira linha: à esquerda, 600. À direita, 100%. Entre eles uma linha reta. Na segunda linha: à esquerda, quadradinho cinza. À direita, 1%. Entre eles uma linha reta. Na terceira linha: à esquerda, quadradinho cinza. À direita 35%. Entre eles uma linha reta. Saindo da primeira linha uma seta para a segunda linha, indicando divisão por 100. Saindo da segunda linha e chegando na terceira linha, seta indicando multiplicação por 35.

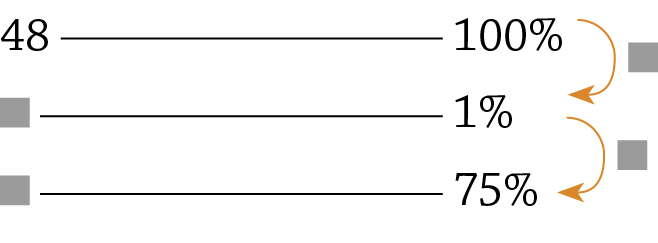
Esquema. Na primeira linha: à esquerda, 48. À direita, 100%. Entre eles uma linha reta. Na segunda linha: à esquerda, quadradinho cinza. À direita, 1%. Entre eles uma linha reta. Na terceira linha: à esquerda, quadradinho cinza. À direita 75%. Entre eles uma linha reta. Saindo da primeira linha uma seta para a segunda linha, indicando quadradinho cinza. Saindo da segunda linha e chegando na terceira linha, uma seta indicando quadradinho cinza.

Esquema. Na primeira linha: à esquerda, 64. À direita, 80%. Entre eles uma linha reta. Na segunda linha: à esquerda, quadradinho cinza. À direita, 10%. Entre eles uma linha reta. Na terceira linha: à esquerda, 48. À direita quadradinho cinza. Entre eles uma linha reta. Saindo da primeira linha uma seta para a segunda linha, indicando divisão por 8. Saindo da segunda linha e chegando na terceira linha, seta indicando quadradinho cinza.

4. No caderno, relacione as palavras em destaque no quadro a com as porcentagens correspondentes no quadro B.

Quadro. Quadro A Um quarto de pizza. A metade de um terreno. O dobro de batatas fritas. A décima parte do caminho. Um quinto do meu salário.
Quadro. Quadro B vinte porcento duzentos porcento dez porcento vinte e cinco porcento cinquenta porcento

Mariana quer comprar um jôgo que custa R$ 60,00sessenta reais. Ela conseguiu juntar 10% desse valor. Calcule mentalmente quantos reais Mariana já tem.

Analise como Daniela calculou mentalmente 25% de 280.

Ilustração. Menina indígena de cabelo comprido preto, vestindo uma camiseta laranja com detalhes azuis na gola. Ela gesticula com as mãos enquanto fala: Sei que 25 porcento equivale a um quarto. Dividindo 280 por 4, obtenho 70.

a) Faça como Daniela e calcule 25% de .1200.

b) Seguindo o raciocínio dela, como você faria para calcular 75% de 150?

7. O número 20 corresponde a quanto por cento de 80? E de 100?

Se 12 bolas equivalem a 50% do total de bolas, que quantidade equivale a 75% das bolas? Explique a um colega como você fez para determinar o valor.

Página 179

9. Em um ponto de reciclagem, a coleta de um dia arrecadou 400 quilogramas de resíduos, dos quais 10% eram de latas de alumínio e 60% de papelão. O restante era de outros materiais.

Foto. 4 cestos para coleta de lixo recicláveis, um ao lado do outro. Da esquerda para a direita: azul, verde, laranja e amarelo.

Quantos quilogramas de outros materiais foram coletados? Explique a um colega como você fez para determinar esse valor.

b) Quantos quilogramas correspondem às latas de alumínio e ao papelão juntos?

Com os dados do enunciado, elabore uma pergunta e troque-a com a de um colega. Em seguida, verifiquem como cada um respondeu à pergunta recebida.

10. No curso de Educação Física, os estudantes escolhem a modalidade esportiva em que pretendem se especializar. Dos 200 estudantes inscritos no curso, sabe-se que:

• 20% escolheram tênis;

• 30% escolheram vôlei;

• 25% escolheram basquete;

• 25% escolheram futebol.

Com base nessas informações, reproduza o quadro a seguir no caderno e complete-o.

Esporte	Quantidade de estudantes
Tênis
Vôlei
Basquete
Futebol

11.

No caderno, faça uma lista com 10 porcentagens e troque-a com a de um colega para transformar as porcentagens em frações e em números decimais. Enquanto seu colega transforma as porcentagens da sua lista, você faz o mesmo com a lista de porcentagens dele. Depois, reúnam-se para verificar se todas as transformações foram realizadas corretamente.

12.

Escolha uma figura geométrica e desenhe-a no caderno. Divida-a em partes iguais e pinte algumas delas para que um colega indique a porcentagem das partes pintadas. Faça o mesmo com a figura elaborada por ele. Em seguida, analise a resposta do seu colega e dê-lhe um retôrno, dizendo se ele realizou a tarefa corretamente ou se equivocou na resolução.

Porcentagem escrita na fórma decimal

Observe alguns exemplos de como podemos escrever uma porcentagem na fórma de um número decimal.

27 % = \frac{27}{100} = 0, 27

42 % = \frac{42}{100} = 0, 42

6,25 % = \frac{6, 25}{100} = 0, 0625

10 % = \frac{10}{100} = 0, 1

1 % = \frac{1}{100} = 0, 01

130 % = \frac{130}{100} = 1, 30 = 1, 3

Também podemos calcular a porcentagem de um valor utilizando os números decimais. Para isso, transformamos a porcentagem em um número na fórma decimal e fazemos a multiplicação. Observe os exemplos.

a) 30% de 150

0,3 ⋅ 150 = 45

b) 12,5% de 420

0,125 ⋅ 420 = 52,5

Página 180

Atividades

Faça as atividades no caderno.

13. Expresse as porcentagens a seguir utilizando números decimais.

a) 9%

b) 16%

c) 87%

d) 170%

14. Dividindo dois números naturais, é possível obter um número decimal. Escolha um exemplo em que isso aconteça e expresse esse número em porcentagem.

15. Juliana e Carlos discutiam sobre como expressar frações e números decimais na fórma de porcentagem. Observe o diálogo deles.

Ilustração. Carlos disse: — Se uma fração tiver denominador 100, então sua representação na forma de porcentagem é o numerador acompanhado do símbolo %. Por exemplo, a fração 17 centésimos igual a 17 por cento. Juliana respondeu: — Muito interessante a sua observação, Carlos! 0,17 também equivale a 17%, porque essa é a forma decimal da fração 17 centésimos.

Dê um exemplo semelhante ao utilizado por Carlos e Juliana.

2 Problemas envolvendo porcentagem

Vamos estudar alguns tipos de problema que envolvem porcentagem.

Determinação de uma porcentagem

João fez uma pesquisa na rua em que mora e constatou que 74 das 185 casas separam lixo para coleta seletiva. Podemos representar essa quantidade em relação ao todo da seguinte maneira:

\frac{74}{185} = 0, 4 = \frac{4}{10} = \frac{40}{100} = 40 %

Observe, nas igualdades anteriores, que 40% = 0,4.

Assim, 74 casas representam 40% de 185 casas.

Atividades

Faça as atividades no caderno.

16. Um jogador de futebol, durante um campeonato, cobrou 20 pênaltis. Dessas cobranças, 70% dos chutes foram convertidos em gol. Quantos gols de pênalti esse jogador fez?

Ilustração. Garoto de cabelo preto e enrolado, vestindo camiseta amarela com uma faixa vermelha, bermuda azul com faixa amarela na lateral, meião e chuteira. Ele está dominando uma bola de futebol no gramado em direção a uma trave com um goleiro.

17. O salário de Roberval era R$ 1.420,00mil quatrocentos e vinte reais. Ele teve aumento de 30%. De quanto foi o aumento em reais? Qual é o novo salário de Roberval?

Página 181

18. O valor do condomínio do edifício onde André mora é R$ 480,00quatrocentos e oitenta reais. Quem paga até o dia 10 de cada mês recebe desconto de 12%.

Agora, responda.

a) Qual é o valor a ser pago com esse desconto?

b) Por que as pessoas que moram em apartamento pagam, mensalmente, um valor pelo condomínio? Essas pessoas podem fazer algo para reduzir esse valor?

19. Em certo mês, Brenda teve um lucro de R$ 4.800,00quatro mil oitocentos reais em sua banca de jornal. Ele destinou 25% desse valor para a compra de um toldo.

Agora, responda.

a) Quanto Brenda gastou com a compra do toldo?

b) O que é lucro? Como podemos calculá-lo?

20.

Acompanhe quatro diferentes modos de obter 25% de 160 com uma calculadora.

Ilustração. Teclas de calculadora. Primeira linha, 160 vezes 25 dividido por 100 é igual. Na segunda linha, visor indicando 40. Terceira linha, 25 dividido por 100, vezes 160 é igual. Na quarta linha, visor indicando 40. Quinta linha, 160 vezes 25 porcento é igual. Na sexta linha, visor indicando 40.

De qualquer um desses modos, obtemos 40 como resultado.

Agora é a sua vez! Escolha um modo e determine:

a) 85% de .12000;

b) 5,7% de 590.

21. Segundo estimativa do Instituto Brasileiro de Geografia e Estatística (í bê gê É), em 1º de julho de 2021, a população brasileira chegou a 213,3 milhões de habitantes. O município de São Paulo continuou sendo o mais populoso do país, com 12,4 milhões de habitantes.

a) Escreva o número de habitantes do Brasil e do município de São Paulo em 1º de julho de 2021, utilizando apenas algarismos.

b) Qual porcentagem aproximada da população do Brasil representava a população do município de São Paulo?

Reúna-se com um colega e pesquisem a população do estado e da cidade onde vocês moram. Depois, respondam: qual é a porcentagem aproximada da população do estado que representa a população da cidade em que vocês moram?

Determinação do total com base em uma taxa percentual

Rubens saiu de sua casa para ir ao supermercado. Andou inicialmente 300 métros, que correspondem a 15% da medida da distância total. Qual é a medida da distância da casa de Rubens ao supermercado?

Clique no play e acompanhe a reprodução do Áudio.

Transcrição do áudio

Educação financeira

Duração: 4:09min. Página: 181.

>> [Locutor] Educação financeira

Som de algo não identificado.

>> [Cauã] [Ao fundo, chamando] Tauane, anda logo!

>> [Tauane] [Tom mais alto] Já estou indo, Cauã!

Som de passos rápidos.

>> [Cauã] [Tom de contrariado] Por que você demorou tanto?

>> [Tauane] Ora, eu estava conferindo o troco.

>> [Cauã] Ué, eu pensei que você tivesse trazido o dinheiro contado para comprar duas caixas de leite.

>> [Tauane] Sim, eu trouxe o dinheiro já separado, mas teve um descontinho.

>> [Cauã] [Tom de questionamento] Tinha alguma promoção no mercadinho?

>> [Tauane] Sim. Comprando duas caixas de leite, a segunda sai pela metade do preço.

>> [Cauã] [Tom animado] Parece bom! [Tom de questionamento] Mas o que você fez para conferir o troco?

>> [Tauane] [Tom explicativo] Bem, cada caixa de leite custa R$ 4,00. Levando duas, a segunda caixa terá um desconto de 50%, que equivale à metade do preço, ou seja, R$ 2,00. A outra caixa sai pelo valor normal: R$ 4,00. Portanto, nessa promoção, as duas caixas custaram R$ 6,00. Eu estava com R$ 8,00, então, fazendo 8 – 6, temos 2. O troco foi, portanto, de R$ 2,00.

>> [Cauã] Hum... [Tom de questionamento] O que temos de fazer para saber qual é a porcentagem total do desconto?

>> [Tauane] [Tom explicativo] Como o desconto de 50% foi aplicado sobre o valor de apenas uma caixa, esse valor representa ¼ do preço de duas caixas, ou seja, 25% do preço total. Portanto, [tom enfático] economizei 25% do dinheiro que havia trazido!

>> [Cauã] [Tom de questionamento] E se você tivesse comprado quatro caixas de leite, a porcentagem seria maior ou a promoção seria a mesma?

>> [Tauane] Seria a mesma. Pensa comigo: considerando quatro caixas, duas sairiam pelo preço normal e duas pela metade do preço. Então, o desconto seria de 25%.

>> [Cauã] [Tom enfático] Entendi! Então, comprar quatro caixas de leite nessa promoção equivale a pagar apenas três delas. Eles podiam ter colocado o anúncio: “Compre 3 caixas de leite e leve [tom enfático] 1 grátis!”.

>> [Tauane] Sim! Ou, então, “Pague 3, leve 4!”.

>> [Cauã e Tauane] HAHAHAHA! [Risos]

>> [Cauã] Muito legal! Mas... [Tom de questionamento] Por que você não usou o dinheiro que sobrou para comprar outra coisa? As pessoas economizam em uma coisa para gastar em outra, certo?

>> [Tauane] Cauã, nem sempre as pessoas economizam para um gasto planejado. É importante ter uma reserva, pois ninguém sabe como será o futuro: necessidades básicas, problemas de saúde ou [tom enfático] até mesmo uma viagem inesperada podem ocorrer! Já pensou, se você não estiver preparado, vai ter que depender de empréstimos... E, se puder evitar isso, vai ser [tom enfático] muito melhor!

>> [Cauã] É verdade! Quando alguém faz um empréstimo, depois precisa devolver um valor maior do que pegou! E, assim, além de gastar muito mais, corre o risco de ficar endividado.

>> [Tauane] [Tom empolgado de confirmação] Exatamente!

>> [Cauã] [Tom de questionamento] O que você vai fazer com o dinheiro que economizou?

>> [Tauane] Estou guardando os trocos das compras já há alguns meses. Vou juntar tudo e colocar em uma aplicação financeira que rende 1% ao mês.

>> [Cauã] [Tom de questionamento] E o que isso significa?

>> [Tauane] [Tom explicativo] Significa que, se eu aplicar, por exemplo, R$ 1.000,00mil reais e o rendimento for 1% ao mês, então, depois de 1 mês, eu terei R$ 10,00 a mais na conta. Porque 1% de R$ 1.000,00mil reais é R$ 10,00.

>> [Cauã] [Tom de questionamento] Mas esse valor é fixo? Todo mês vai aumentar R$ 10,00?

>> [Tauane] [Tom explicativo] Não, o rendimento é com base no montante de dinheiro que você tiver na conta. Então, usando meu exemplo, no final do primeiro mês, eu teria R$ 1.010,00mil dez reais, e o 1% que vai render no próximo mês será sobre esse novo valor total.

>> [Cauã] [Tom animado] Gostei da ideia! Só que eu estava pensando em investir meu dinheiro em outro negócio...

>> [Tauane] [Tom de interesse] E qual seria esse negócio, Cauã?

>> [Cauã] [Tom brincalhão] Um videogame! HAHAHAHA! [Risos]

>> [Tauane] Olha só! Investir suas economias pode te ajudar a chegar no valor do videogame mais rapidamente!

>> [Cauã] [Tom empolgado] Verdade! [Tom de questionamento] Você me ajuda com isso?

>> [Tauane] [Tom enfático] Claro!

Créditos

Todos os áudios inseridos neste conteúdo são da Free Sound.

15 % = \frac{15}{100}

300 métros

1 % = \frac{1}{100}

300 métros : 15 = 20 métros

100 % = \frac{100}{100}

100 ⋅ 20 métros = .2000 métros

Logo, a medida da distância da casa de Rubens ao supermercado é de .2000 métros.

Página 182

Devemos ter atenção especial para algumas situações, como a que segue.

Larissa recebia um salário de R$ 1.500,00mil quinhentos reais na empresa onde trabalhava. Ela mudou de emprêgo e passou a receber R$ 4.500,00quatro mil quinhentos reais. Como o salário foi triplicado, poderíamos pensar que o aumento foi de 300%, mas não foi.

Analise os cálculos realizados a seguir.

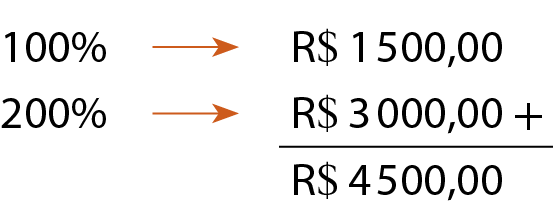
Esquema. Na primeira linha, à esquerda 100 porcento e à direita, 1500 reais. Entre eles uma seta da esquerda para a direita. Na segunda linha, à esquerda 200 porcento e à direita, 3000 reais. Entre eles uma seta da esquerda para à direita.
Os números escritos à direita, formam um algoritmo usual da adição. Na primeira linha 1500 reais, e na segunda linha 3000 reais com o sinal da adição. Abaixo, um traço horizontal. Abaixo o número 4500 reais.

Logo, o aumento foi de 200% (300% ‒ 100% = 200%).

Atividades

Faça as atividades no caderno.

22. Segundo uma pesquisa feita em dezembro de 2023, uma.seiscentas pessoas preferem ler o jornal a, o que corresponde a 32% dos entrevistados. Quantos foram os entrevistados?

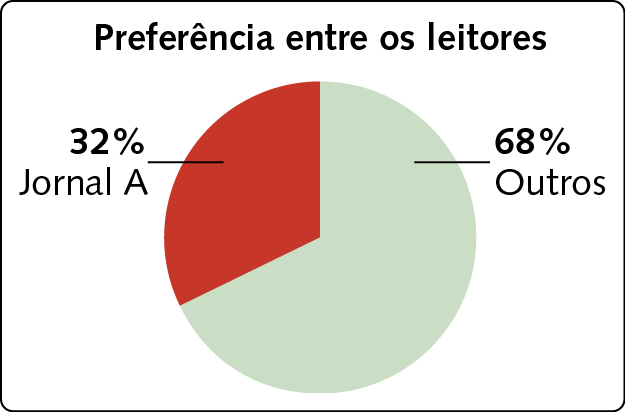
Gráfico de setores. PREFERÊNCIA ENTRE OS LEITORES.
Jornal A, em vermelho, 32%. Outros, em verde, 68%.

Dados obtidos pelos pesquisadores em dezembro de 2023.

23. Por ter tirado notas baixas, Gisele perdeu R$ 18,00dezoito reais de sua mesada, o que corresponde a 20% do que recebia. Qual era o valor da mesada de Gisele?

24. Em uma eleição, o candidato a obteve 640 mil votos, o que correspondeu a 32% dos eleitores. Quantos eram os eleitores?

25. Sabe-se que 32,5% de uma quantia corresponde a R$ 130,00cento e trinta reais. Qual é essa quantia?

26. O tenista sérvio Novak Djokovic sagrou-se campeão do Aberto da Austrália de 2021, vencendo o tenista russo Daniil Medvedev por 3 sets a 0. dicovitch venceu 19 dos games disputados, e Medvedev, 9.

Foto. Homem branco de cabelos castanhos, vestido com uma blusa verde e branca, beijando uma taça de prata, entre as mãos. A foto foi tirada à noite. — Novak Djokovic comemorando o título do Aberto da Austrália. Foto de 2021.

a) Qual é a porcentagem dos sets vencidos por dicovitch nessa partida?

b) Podemos afirmar que dicovitch venceu mais de 70% dos games disputados?

27. Em uma turma, 80% dos estudantes foram aprovados, 15%, reprovados, e os seis estudantes restantes desistiram do curso. Quantos estudantes havia nessa turma?

Página 183

Lendo e aprendendo

À esquerda, ícone do tema pluralidade cultural e à direita, ícone do tema formação cidadã.

Foto. Aglomeração de pessoas ao pé de um morro de pedra, com vegetação verde. Há pessoas, subindo o morro, pessoas descendo o morro e pessoas paradas no pé do morro. Há uma placa com o escrito: "LIMITE VENEZUELA-BRASIL. O dia está ensolarado e sem nuvens. — Refugiados venezuelanos na fronteira do Brasil com a Venezuela. Foto de 2019.

Perguntas e respostas para entender a questão dos refugiados

Saiba de onde vem a maioria dos refugiados que estão no Brasil em busca de novas oportunidades

[reticências]

Qual é a diferença entre os termos “refugiado” e “migrante”?

São consideradas refugiadas as pessoas que saem de seu país de origem para escapar de situações perigosas, como conflitos armados e perseguições. Ao se mudar para novas nações, esses indivíduos buscam segurança e garantia de direitos básicos, como saúde e educação.

Já os migrantes escolhem se deslocar, ou seja, realizam a mudança por livre e espontânea vontade, sem ser pressionados por fatores externos (como guerras). Essas pessoas se mudam para novos países para buscar novas oportunidades, como um trabalho melhor ou a possibilidade de aprender um novo idioma.

De onde vieram os refugiados que moram no Brasil?

A maior parte dos refugiados que chegam ao Brasil vieram da Venezuela. De acôrdo com o áquinur (Agência da Organização das Nações Unidas Para Refugiados), em 2019, cêrca de 65% dos refugiados que vieram para o país eram venezuelanos. Isso porque a Venezuela vive uma intensa crise política, social, humanitária e econômica (faltam alimentos, remédios e itens de higiene), o que leva os cidadãos a buscar ajuda em outros territórios. Ao todo, há cêrca de 45 mil refugiados venezuelanos vivendo no Brasil.

Depois da Venezuela, o país com a segunda maior população de refugiados no Brasil é a Síria. Estima-se que aproximadamente .3800 sírios tenham se mudado para cá em virtude da guerra e de condições precárias de vida, enfrentadas pelos habitantes de lá há dez anos [reticências].

Em seguida na classificação de locais de origem está o Congo, com .1209 refugiados vivendo no Brasil. Há anos, o território africano sofre com confrontos armados e atos de violência contra a população [reticências].

Página 184

Lendo e aprendendo

O Brasil recebe muitos refugiados?

De acôrdo com o instituto Ipsos, empresa de pesquisa e inteligência de mercado, o Brasil é o terceiro país mais aberto a receber refugiados do mundo. O estudo, divulgado em 16 de junho, revela que 78% dos brasileiros (ou seja, quase oito a cada dez) apoiam a recepção de refugiados. O país fica atrás apenas da Argentina e da Itália, em que as taxas de aceitação são de 79%.

Só na cidade de São Paulo, por exemplo, cêrca de 20 mil pessoas estão tentando regularizar seus documentos (para ter acesso a direito como o de trabalhar no Brasil). O dado é da Associação Brasileira de Especialistas em Migração e Mobilidade Internacional (Abemmi), que ajuda estrangeiros a se regularizar no Brasil.

[reticências]

Fontes: áquinur, Comitê Internacional da Cruz Vermelha, Folha de São Paulo e Instituto Ipsos. Perguntas e respostas para entender a questão dos refugiados. Jornal Joca, 17 junho 2021. Disponível em: https://oeds.link/Yobwk8. Acesso em: 28 abril 2022.

Conheça mais

O Museu da Imigração do Estado de São Paulo tem eventos e exposições (presenciais e virtuais pelo site do museu) para preservar a história dos imigrantes do passado e para mostrar que a migração é um fenômeno sempre atual.

Atividades

1. Responda às questões no caderno.

a) Quando esse texto foi publicado?

b) Os dados presentes no texto foram obtidos de quais fontes?

c) Quem são os refugiados?

d) De que país vieram a maior parte dos refugiados que viviam no Brasil em 2019?

e) Quais eram os dois países mais abertos a receber refugiados no mundo em 2021?

2. Copie as tabelas seguir em seu caderno e complete-as com base nas informações do texto.

Apoio dos brasileiros aos refugiados
Condição	Porcentagem
Apoiam
Não apoiam

Dados obtidos pelo Instituto Ipsos em junho de 2021.

Apoio de argentinos e italianos aos refugiados
Condição	Porcentagem
Apoiam
Não apoiam

Dados obtidos pelo Instituto Ipsos em junho de 2021.

3. Identifique a alternativa correta.

a) Migrante são as pessoas que decidem sair de seu país de origem para escapar de problemas político-econômicos.

b) O número de refugiados sírios no Brasil era duas vezes maior que o do Congo.

c) Argentina e Itália são os únicos países do mundo que acolhem os refugiados.

d) cêrca de 35% dos refugiados que vieram para o Brasil em 2019 não eram venezuelanos.

Em seu caderno, escreva um texto sobre a questão dos refugiados. Depois, leia o seu texto em voz alta para a turma.

Página 185

Resolvendo em equipe

Faça a atividade no caderno.

(enêm) O LIRAa, Levantamento Rápido do Índice de Infestação por aédis aêgipiti, consiste num mapeamento da infestação do mosquito aédis aêgipiti. O LIRAa é dado pelo percentual do número de imóveis com focos do mosquito, entre os escolhidos de uma região em avaliação. O serviço de vigilância sanitária de um município, no mês de outubro do ano corrente, analisou o LIRAa de cinco bairros que apresentaram o maior índice de infestação no ano anterior. Os dados obtidos para cada bairro foram:

um. 14 imóveis com focos de mosquito em 400 imóveis no bairro;

dois. 6 imóveis com focos de mosquito em 500 imóveis no bairro;

três. 13 imóveis com focos de mosquito em 520 imóveis no bairro;

quatro. 9 imóveis com focos de mosquito em 360 imóveis no bairro;

cinco. 15 imóveis com focos de mosquito em 500 imóveis no bairro.

O setor de dedetização do município definiu que o direcionamento das ações de contrôle iniciará pelo bairro que apresentou o maior índice do LIRAa.

Disponível em: https://oeds.link/0Srzw4. Acesso em: 28 outubro 2015.

As ações de contrôle iniciarão pelo bairro

a. um

b. dois

c. três

d. quatro

e. cinco

Interpretação e identificação dos dados	• Na leitura do enunciado, compreenda o significado do índice apresentado. • Observe a relação entre a quantidade de imóveis com foco e a quantidade de imóveis no bairro.
Plano de resolução	• Trace uma linha de raciocínio para determinar a proporção entre a quantidade de imóveis com foco e a quantidade de imóveis no bairro, de forma que seja possível a comparação entre elas.
Resolução	• Apresente seu plano de resolução a um colega. • Discutam as diferenças e as semelhanças entre os planos e verifiquem as melhores estratégias. • Em conjunto, resolvam o problema, fazendo as anotações individuais no caderno.
Verificação	• Considerando a resposta encontrada, verifique se ela satisfaz às condições determinadas no enunciado.
Apresentação	• Complemente a questão simulando essa situação para uma cidade fictícia.

Página 186

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Porcentagem

Toda fração com denominador 100 representa uma porcentagem. Analise os exemplos.

\frac{15}{100} = 15 %

\frac{21}{100} = 21 %

Porcentagem de um valor

Para calcular 15% de 200, podemos fazer:

15% de 200

\frac{15}{100} \cdot 200 = \frac{3 000}{100} = 30

Porcentagem de figuras

Figura geométrica. Círculo dividido em 4 partes iguais, com uma parte pintada de vermelho.

A parte vermelha corresponde a

\frac{1}{4}

da figura, ou seja, 25%.

Figura geométrica. Retângulo dividido em 10 partes iguais, com 4 partes pintadas de verde.

A parte verde corresponde a

\frac{4}{10}

da figura, ou seja, 40%.

Porcentagem escrita na fórma decimal

Uma porcentagem pode ser escrita na fórma de um número decimal. Para isso, transformamos a porcentagem em uma fração com denominador 100 e efetuamos a divisão do numerador pelo denominador.

45 % = \frac{45}{100} = 0,45

5 % = \frac{5}{100} = 0, 05

1. Calcule as porcentagens a seguir.

a) 10% de 150

b) 1% de 220

c) 0,5% de 350

d) 15% de .1850

2. Analise esta figura, formada por quadrados de mesma medida de comprimento dos lados.

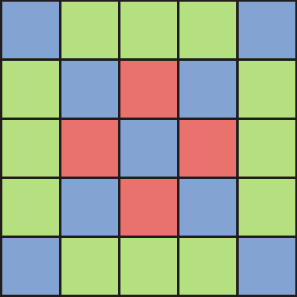
Figura geométrica. Quadrado dividido com 5 linhas e 5 colunas, totalizando 25 quadradinhos de mesma medida. Na primeira linha, temos a seguinte sequência de cores, da esquerda para a direita: 1 azul, 3 verdes e 1 azul. Na segunda linha, da esquerda para a direita: 1 verde, 1 azul, 1 vermelho, 1 azul e 1 verde. Na terceira linha, da esquerda para a direita: 1 verde, 1 vermelho, 1 azul, 1 vermelho e 1 verde. Na quarta linha, da esquerda para a direita: 1 verde, 1 azul, 1 vermelho, 1 azul e 1 verde. Na quinta linha, da esquerda para a direita: 1 azul, 3 verdes e 1 azul.

Escreva no caderno a porcentagem da figura colorida de:

a) verde;

b) azul;

c) vermelho.

3. Jonas está economizando dinheiro para comprar uma mochila que custa R$ 120,00cento e vinte reais. Ele já conseguiu guardar 40% do valor total. Quantos reais Jonas já economizou?

4. Expresse as porcentagens a seguir utilizando números decimais.

a) 12%

b) 78%

c) 7%

d) 99%

5. Reproduza o quadro a seguir no caderno e complete-o.

Número decimal	Fração	Porcentagem
	$1 sobre 2$
	$1 sobre 20$
	$25 sobre 10$

6. Juliano comprou um aparelho de televisão e obteve um desconto de 8% no valor do produto. Sabendo que esse aparelho de televisão custa R$ 1.850,00mil oitocentos e cinquenta reais, responda às questões.

a) Qual foi o valor do desconto recebido por Juliano?

b) Quantos reais ele pagou pelo aparelho de televisão?

7. Mariana acertou 75% das questões de uma prova de vestibular. Sabendo que havia 80 questões nessa avaliação, quantas questões Mariana acertou?

8. Jorge utiliza transporte público para ir ao trabalho. Ele pega um ônibus para ir e um ônibus para voltar, cinco vezes por semana, e cada passagem custa R$ 4,40quatro reais e quarenta centavos. Após um reajuste de 5% no valor da passagem, quantos reais Jorge vai gastar por semana?

9. Em uma prova de atletismo, um atleta já percorreu 45% do percurso total, o que corresponde a .2250 métros. Qual é a medida da distância, em metro, do percurso dessa prova?

10. Rose comprou um carro e pagou de entrada R$ 10.200,00dez mil duzentos reais, o que corresponde a 30% do valor total do veículo. Quantos reais ainda faltam para Rose pagar esse carro?

Glossário

Lotear: : Dividir um terreno ou imóvel.; Voltar para o texto