Capítulo 9 Figuras geométricas planas
Trocando ideias

As diferentes obras visuais indígenas são caracterizadas pelos grafismos, que são desenhos que representam figuras geométricas ou imagens de pessoas e de animais. Os grafismos estão presentes, por exemplo, na pintura corporal e no artesanato.


Nos grafismos presentes nas fotos anteriores, é possível encontrar a representação de diferentes figuras geométricas planas.
▸

Quais figuras geométricas planas você consegue identificar na pintura corporal dos indígenas e na peneira?
▸


Reúna-se com três colegas e pesquisem mais sobre a arte indígena. Depois, compartilhem com a turma o que pesquisaram.
Neste capítulo, vamos estudar algumas figuras geométricas planas.

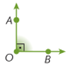
1 Representação de ponto, reta e plano
Observe este poliedro.
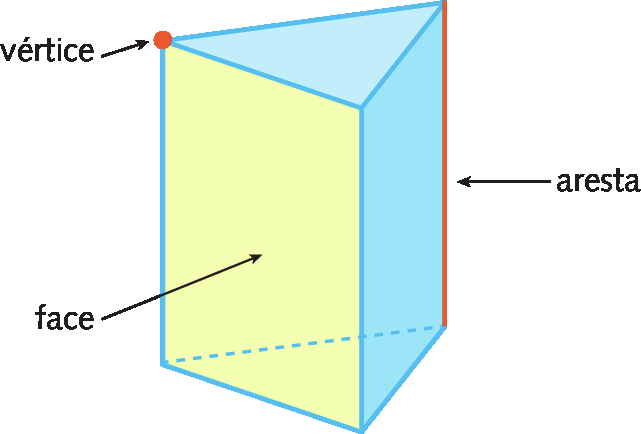
Nele, podemos identificar vértices, arestas e faces.
Confira que, no encontro de três arestas, temos um vértice, que é um ponto.
Para nomear os pontos, usamos letras maiúsculas do alfabeto; por exemplo: A, B, C etcétera.
O prolongamento de uma aresta do poliedro nos dá a ideia de uma reta. As retas não têm largura ou comprimento, têm apenas direção e são representadas por letras minúsculas do alfabeto; por exemplo: r, s, t etcétera.
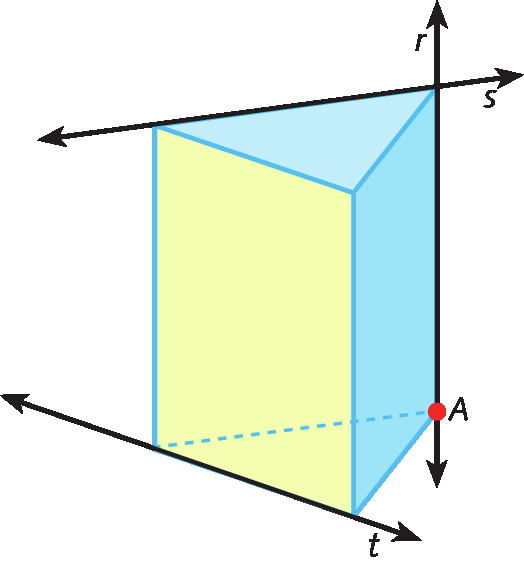
Ao representar uma reta, desenhamos apenas parte dela; as setas em suas extremidades indicam que elas continuam nos dois sentidos.
Nesta representação, dizemos que o ponto a pertence à reta r, mas não pertence às retas s e t. Também podemos dizer que a reta r passa pelo ponto a.
Também podemos prolongar a face amarela do poliedro, dando a ideia de plano. As faces do poliedro estão contidas em planos.
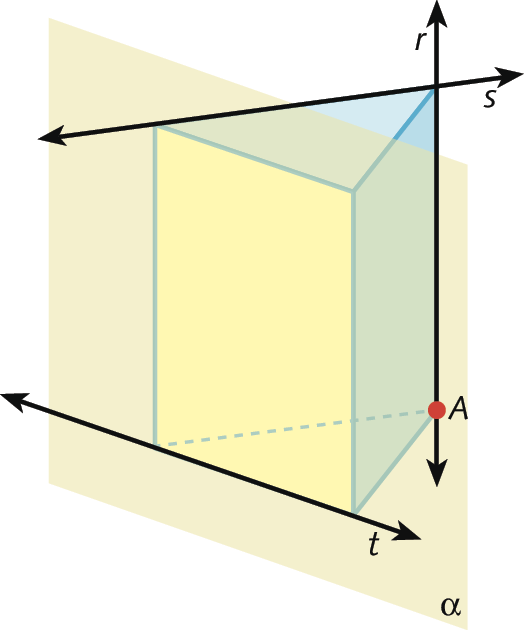
Nesta representação, dizemos que o ponto a não pertence ao plano alfa (alfa), que a reta t está contida no plano alfa e que as retas r e s não estão contidas no plano alfa. Também podemos dizer que o plano alfa contém a reta t, mas que esse plano não contém as retas r e s.
Os planos são representados por letras minúsculas do alfabeto grego; por exemplo: alfa (alfa), beta (beta), γ (gama) etcétera

O plano não tem fronteiras, ou seja, é ilimitado. Ao representar um plano, desenhamos apenas parte dele.
Atividades
Faça as atividades no caderno.
1. Marque no caderno dois pontos, a e B, e desenhe uma reta passando por eles. Tente traçar outra reta que também passe pelos pontos a e B. Essa segunda reta é diferente da anterior?
2. Que ideia (ponto, reta ou plano) sugere:
a) um fio esticado?
b) o piso de uma sala?
c) a ponta de uma caneta?
d) uma lousa?
e) o encontro de duas paredes?
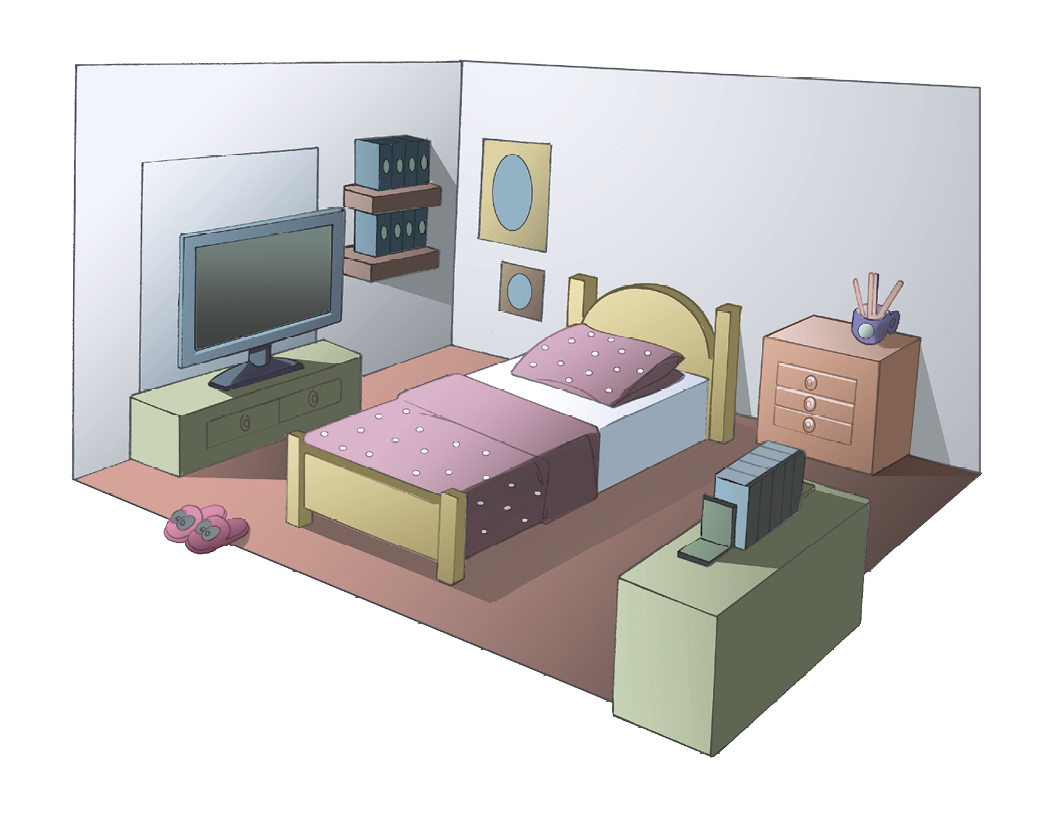
3. Observe a figura e identifique os elementos que se parecem com pontos, retas e planos.
4. Marque no caderno um ponto a e trace uma reta passando por ele. Você pode traçar dez retas passando por esse ponto? Quantas retas você pode traçar passando por esse ponto?
5. Copie a figura no caderno e represente:
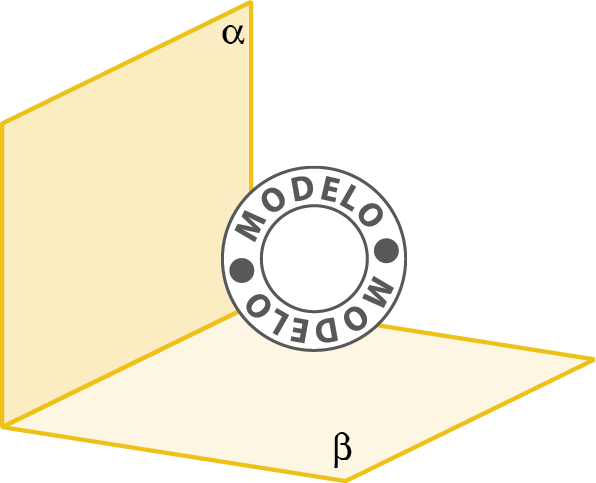
a) uma reta r contida no plano alfa;
b) uma reta s contida no plano beta;
c) um ponto ê pertencente ao plano alfa;
d) um ponto F pertencente ao plano beta;
e) um ponto G pertencente aos planos alfa e beta.
6. Observe a representação dos pontos a, B, C e D a seguir.

Quantas retas distintas podemos traçar de modo que cada uma passe por dois desses pontos?

2 Semirreta e segmento de reta
Semirreta
Observe a reta r contida no plano α e os pontos a, O e B, distintos, pertencentes a ela.
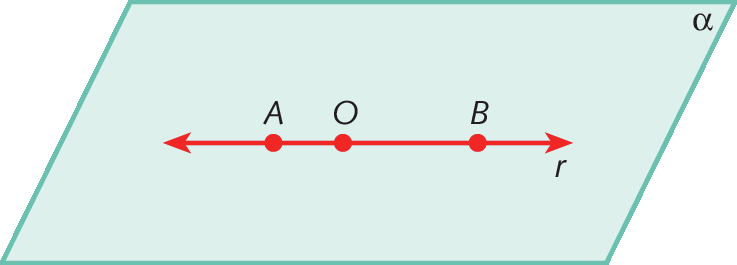
O ponto O determina duas semirretas em r:

O ponto O é chamado de origem das semirretas. A semirreta de origem em O que passa pelo ponto a e a semirreta de origem em O que passa pelo ponto B podem ser representadas, respectivamente, por
Símbolo. Segmento de reta OB.e
Símbolo. Letras maiúsculas O e B com um traço com ponta de seta do lado direito sobre elas..
Segmento de reta
Observe agora a reta r contida no plano α e os pontos a e B, distintos, pertencentes a ela. A parte da reta compreendida entre esses dois pontos, incluindo‑os, é denominada segmento de reta.
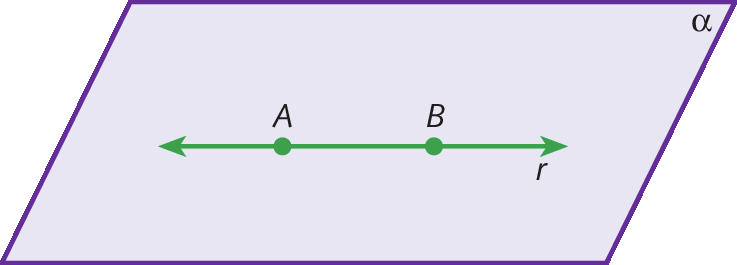
O segmento de reta limitado por a e B pode ser representado por
Segmento de reta AB.ou
Símbolo. Letras maiúsculas B e A com um traço sobre elas..

a e B são chamadas de extremidades desse segmento de reta.
Medida do comprimento de um segmento de reta
Considere os segmentos de reta
Segmento de reta AB.e
Símbolo. Segmento de reta CD.. Usaremos o segmento de reta
Símbolo. Segmento de reta CD.como unidade de medida de comprimento.

Com o auxílio de um compasso, podemos verificar quantas vezes a medida relativa ao comprimento do segmento de reta
Símbolo. Segmento de reta CD.“cabe” no segmento de reta
AB.
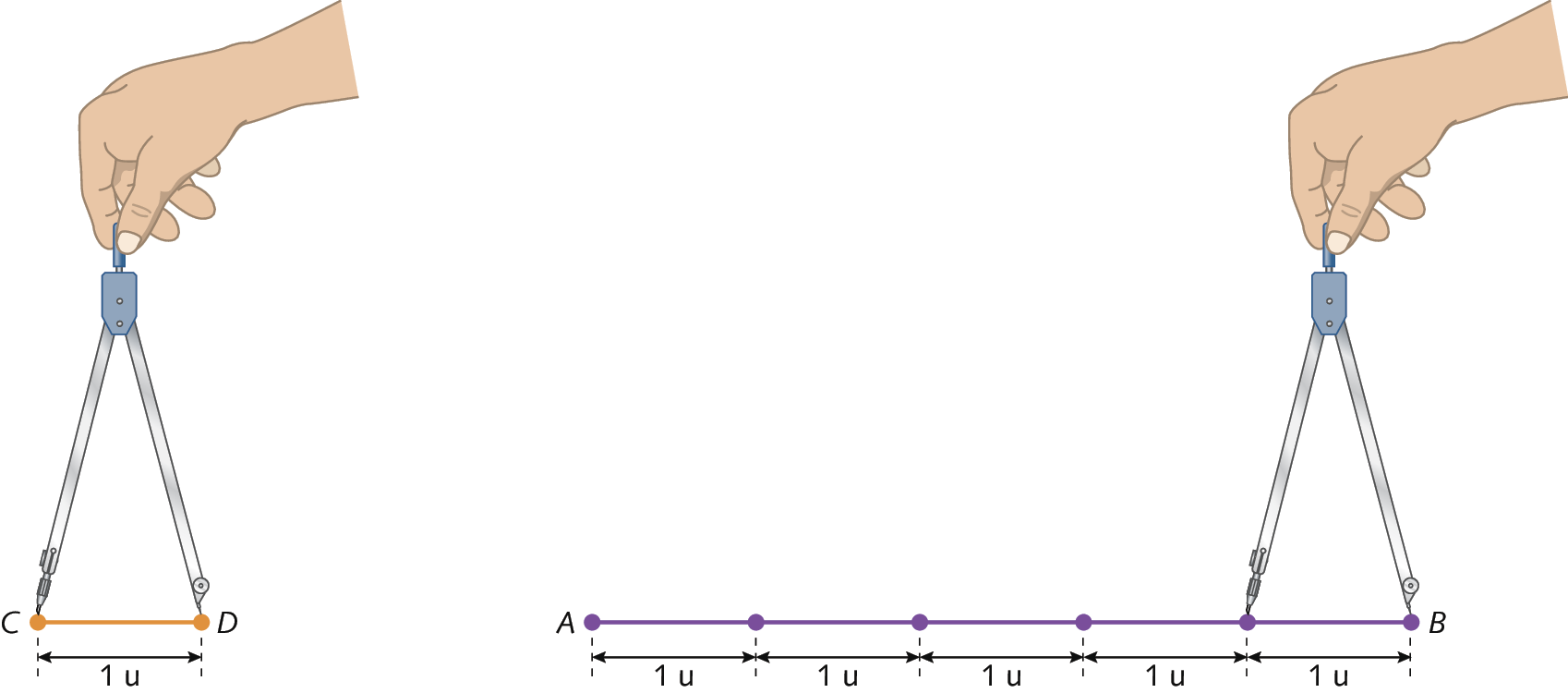
Assim, concluímos que a medida de comprimento do segmento de reta
Segmento de reta AB.é igual a cinco unidades de medida e indicamos por medida de
Segmento de reta AB.= 5 unidades ou A bê = 5 unidades.
Medir o comprimento de um segmento de reta significa compará-lo com a medida de comprimento de outro segmento de reta, utilizando-o como unidade de medida.
Segmentos de reta congruentes
Consideremos os segmentos de reta
Segmento de reta AB.e
Símbolo. Segmento de reta CD.e o segmento

, tomado como unidade de medida de comprimento.
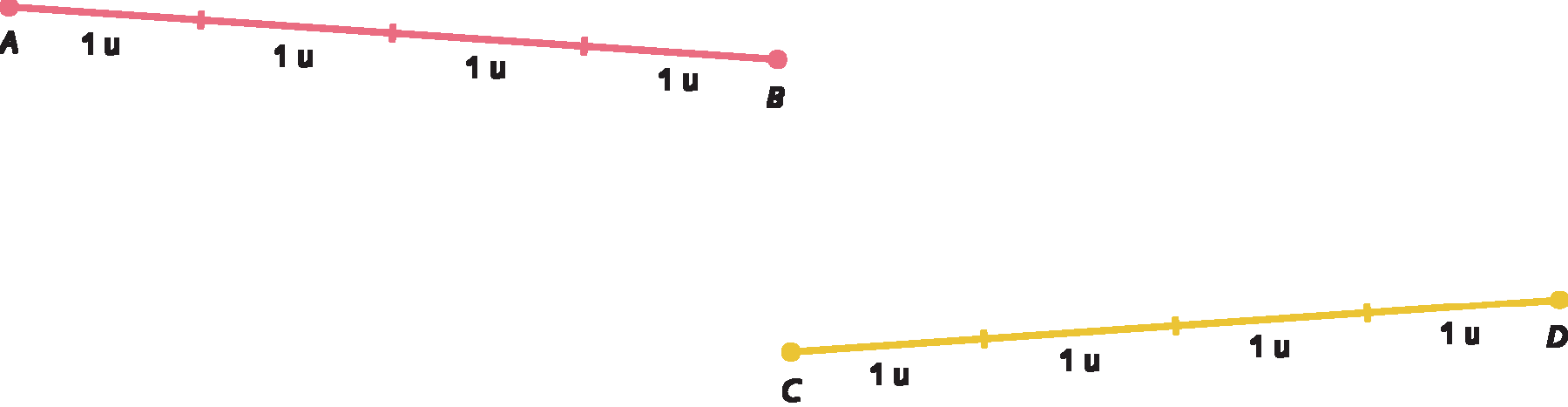
Observe que os segmentos de reta
Segmento de reta AB.e
Símbolo. Segmento de reta CD.têm medidas de comprimento iguais a 4 unidades; por isso, são chamados de segmentos de reta congruentes. Indicamos
Sentença matemática. Segmento de reta AB, símbolo de igualdade com o til sobre ele, segmento de reta CD..
Dois segmentos de reta são congruentes quando têm medidas de comprimento iguais.
Atividades
Faça as atividades no caderno.
Cuidado! Evite acidentes ao usar o compasso nas atividades 11 e 14.
7. No caderno, identifique as semirretas representadas nas figuras.
a)

b)
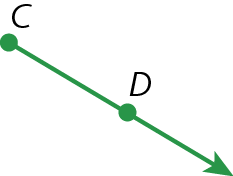
c)
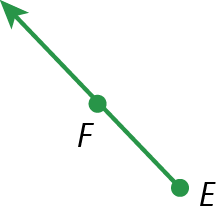
d)

8. Observe a figura a seguir e identifique:

a) as semirretas de origem no ponto O;
b) o ponto comum das semirretas
O B
e
O A.
9. Identifique os segmentos de reta representados nas figuras.
a)
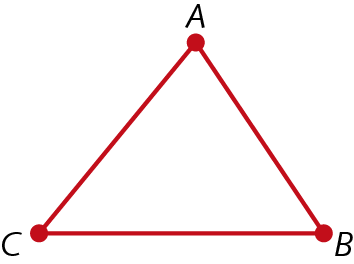
b)
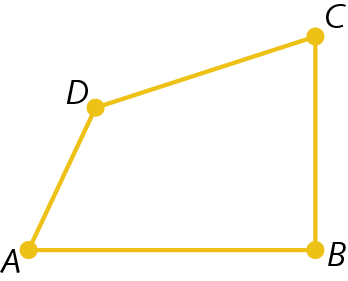
10. Marque, no caderno, quatro pontos, a, B, C e D, de modo que quaisquer três deles não estejam na mesma reta.
a) Trace todos os segmentos de reta com extremidades em dois desses pontos. Quantos segmentos de reta você pôde traçar?
b) Trace todas as semirretas que têm origem em um desses pontos e que passam por outro deles. Quantas semirretas você pôde traçar?
11. Com o auxílio de um compasso, determine a medida de comprimento dos segmentos de reta a seguir, tomando como unidade de medida de comprimento o segmento de reta

.
a)

b)

c)

d)

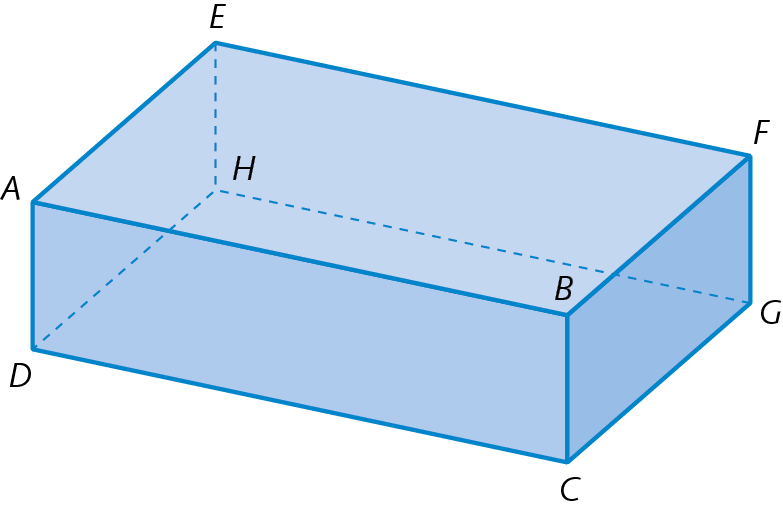
12. No bloco retangular representado a seguir, os segmentos de reta
Símbolo. Segmento de reta AD.,
B C,
F G
e
Símbolo. Segmento de reta EH.são congruentes. Identifique outros segmentos de reta congruentes e anote no caderno.
13. Identifique os segmentos de reta congruentes, tomando como unidade o segmento de reta

, e anote no caderno.
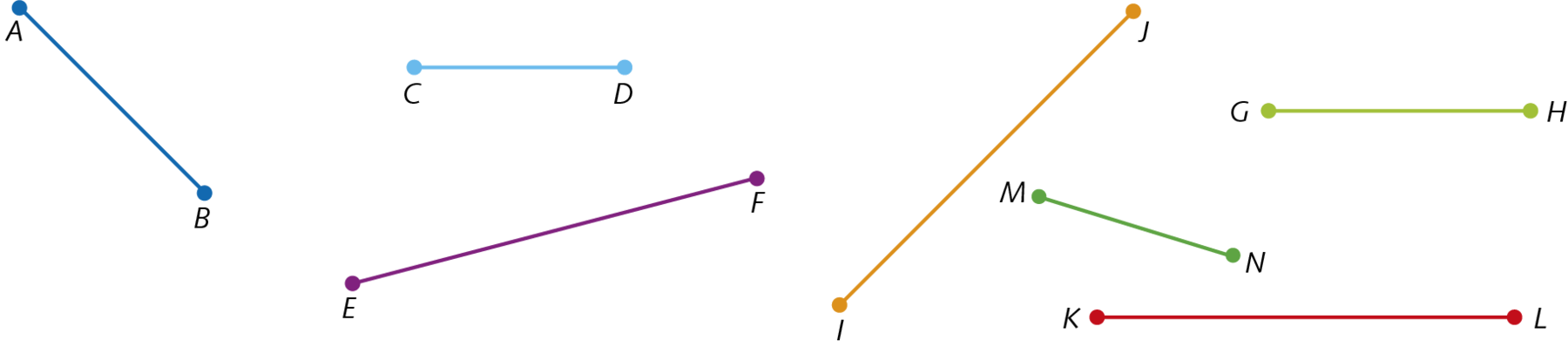
14. Observe esta figura.
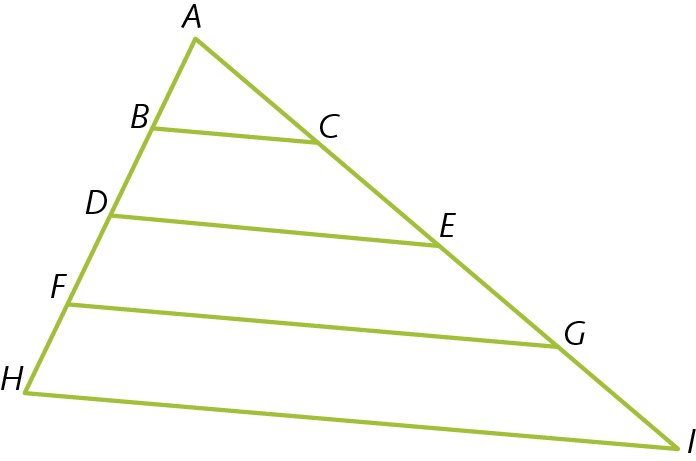
Com um compasso, verifique as seguintes medidas, respectivamente, nas unidades A bê = 1 xis, á cê = 1 ípsilon e BC = 1 z:
a) á dê, A Ê e dê ê;
b) á éfe, á gê e FG;
c) á agá, á í e agá í.
15. Quantos segmentos de reta distintos podemos determinar na figura?


3 Ângulos
O conceito de ângulo está presente em várias situações do cotidiano.
Duas semirretas de mesma origem determinam, no plano que as contém, duas regiões. Nesta representação, temos uma região verde e uma região roxa.
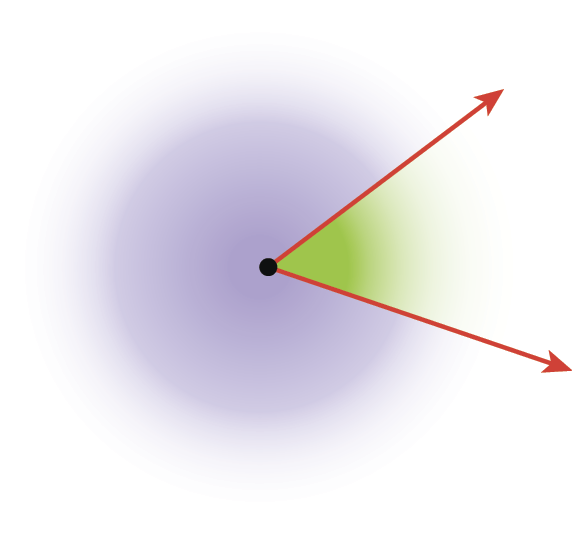
As semirretas reunidas com cada uma dessas regiões determinam dois ângulos. Identificamos o ângulo com o qual vamos trabalhar com um pequeno arco.

• Os dois ângulos podem ser indicados por
Símbolo. AOB em letras maiúsculas com sinal acima da letra O que se parece com o acento circunflexo.(lemos: “ângulo á ó bê” ),
Símbolo. BOA em letras maiúsculas com sinal acima da letra O que se parece com o acento circunflexo.ou
Símbolo. O em letra maiúscula com sinal sobre ele que se parece com o acento circunflexo.. O pequeno arco no desenho indica o ângulo a que estamos nos referindo.
• A origem O é o vértice do ângulo.
• As semirretas
Símbolo. Semirreta OA.e
Símbolo. Letras maiúsculas O e B com um traço com ponta de seta do lado direito sobre elas.são os lados do ângulo.
Ângulo é a união de duas semirretas que têm a mesma origem com uma das regiões do plano limitada por elas.
O ângulo também pode ser associado à ideia de giro. Alguns radares, comumente utilizados por controladores de voo, apresentam um segmento de reta que gira em tôrno do centro do visor, descrevendo um ângulo como um giro.
Medida da abertura de um ângulo
A grandeza associada a um ângulo é a abertura considerada entre seus lados.

Para medir essa grandeza, dividimos uma volta completa em 360 partes iguais e usamos uma dessas partes como unidade de medida da abertura de um ângulo. Essa unidade de medida é conhecida como grau e seu símbolo é graus.
Assim, a medida da abertura do ângulo que corresponde a uma volta completa é 360graus.

A medida da abertura do ângulo de meia-volta é 180graus, que é denominado ângulo raso.

Podemos medir a abertura de um ângulo utilizando um instrumento de medida chamado transferidor.

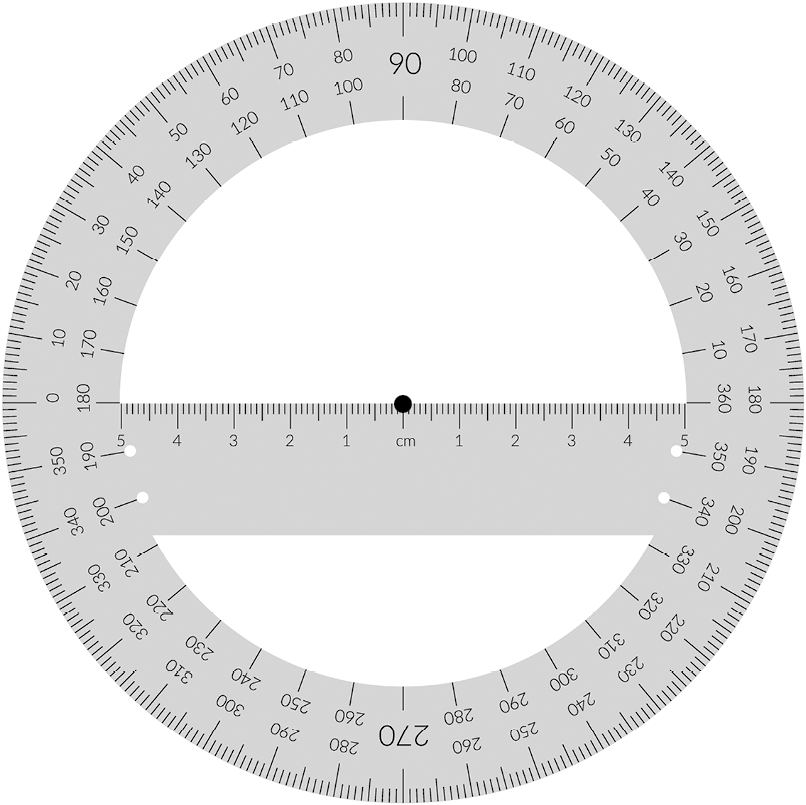
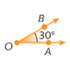
Observe o ângulo
Símbolo. Ângulo AOB.a seguir.
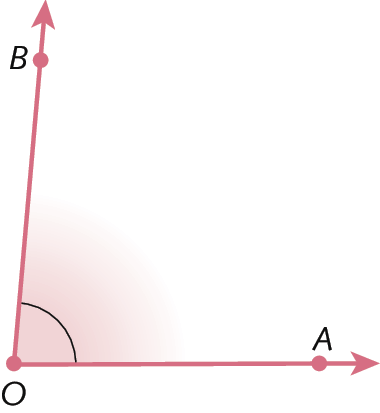
Utilizando um transferidor, vamos medir a abertura do ângulo
Símbolo. Ângulo AOB.. Acompanhe o procedimento a seguir:
1º) Devemos fazer o vértice do ângulo coincidir com o centro do transferidor.
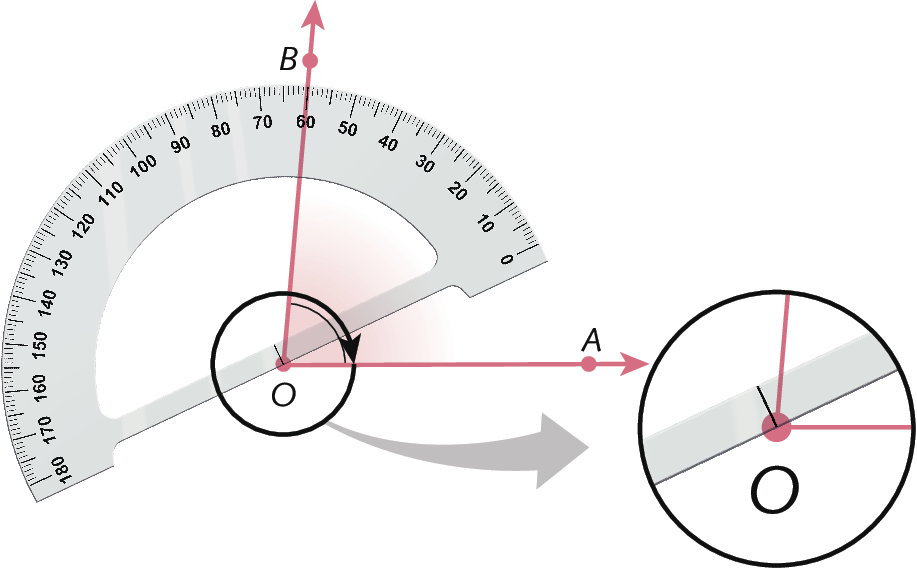
2º) Alinhamos um dos lados do ângulo com a linha do transferidor, chamada linha de terra, que indica zero grau.
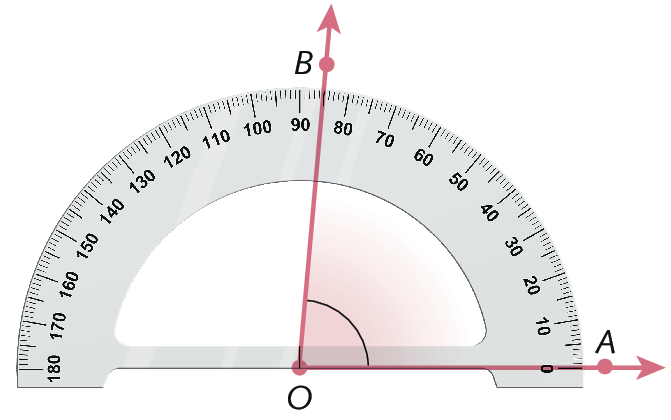
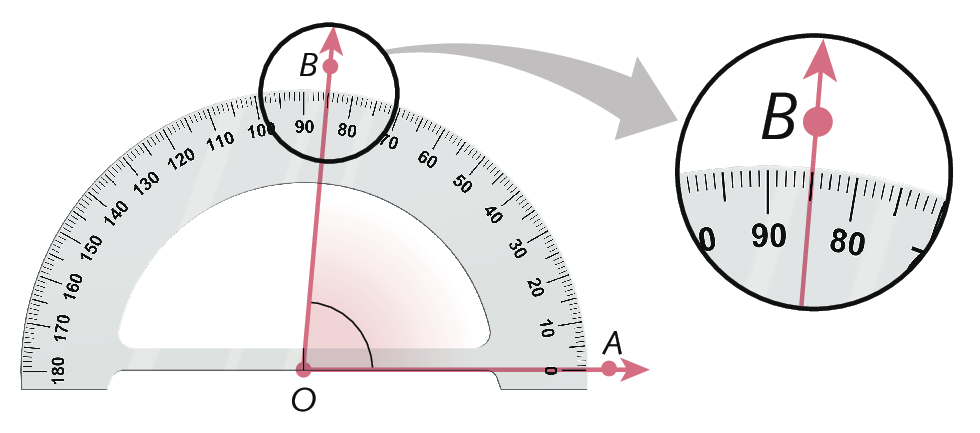
3º) Verificamos a medida da abertura do ângulo, que é o valor indicado no transferidor pelo alinhamento com o outro lado do ângulo. Nesse exemplo, a abertura do ângulo mede 85graus. Indicamos por medida de
entre parênteses ângulo A O B= 85graus.
Ângulo reto, ângulo agudo e ângulo obtuso
• Um ângulo é reto quando sua medida de abertura é igual a 90graus. Um ângulo de
Sentença matemática. Fração um sobre quatro.de volta é um ângulo reto.

• Um ângulo é agudo quando sua medida de abertura é maior que 0grau e menor que 90graus.
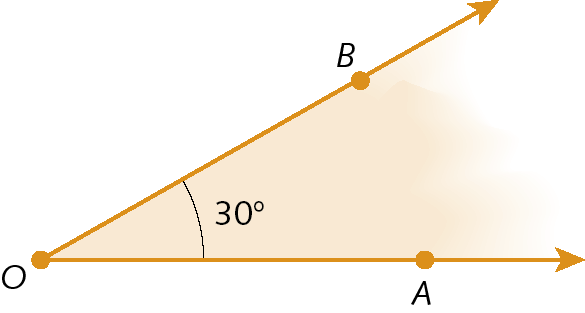
• Um ângulo é obtuso quando sua medida de abertura é maior que 90graus e menor que 180graus.
Construção de um ângulo com o transferidor
Vamos construir um ângulo cuja abertura mede 50graus utilizando um transferidor.
1º) Traçamos uma semirreta
Símbolo. Semirreta OA..

2º) Centramos o transferidor em O e posicionamos a linha que indica zero grau com a semirreta
Símbolo. Semirreta OA.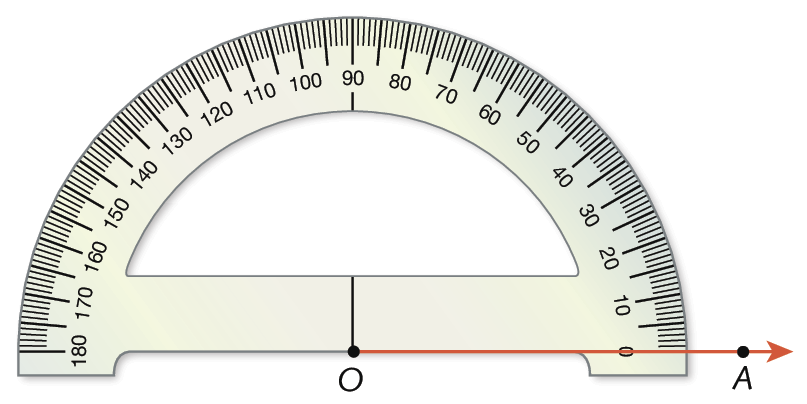
3º) Marcamos o ponto B em 50graus junto à escala do transferidor.
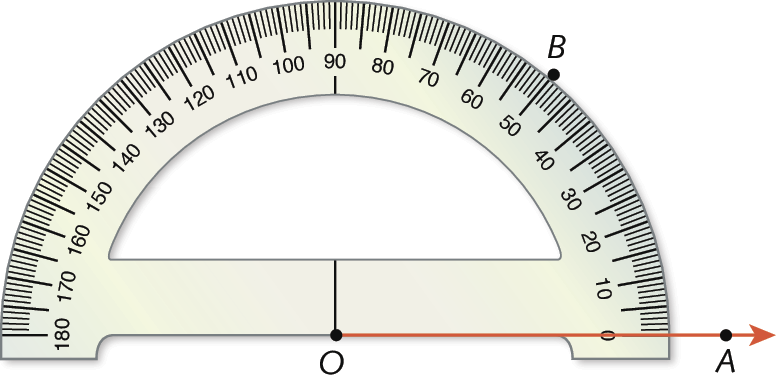
4º) Retiramos o transferidor e traçamos a semirreta
Símbolo. Letras maiúsculas O e B com um traço com ponta de seta do lado direito sobre elas.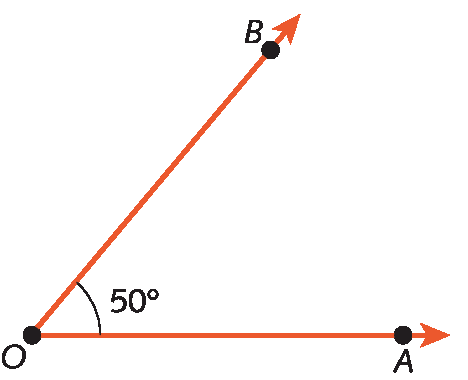
Atividades
Faça as atividades no caderno.
16. Utilizando um transferidor, desenhe no caderno dois ângulos: um de medida de abertura igual a 40graus e outro de medida de abertura igual a 110graus.
17. No caderno, classifique cada um dos ângulos a seguir em agudo, obtuso, reto ou raso.
a)
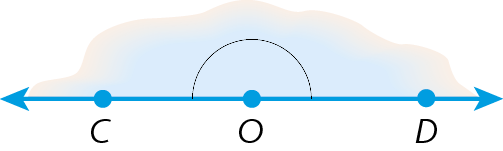
b)
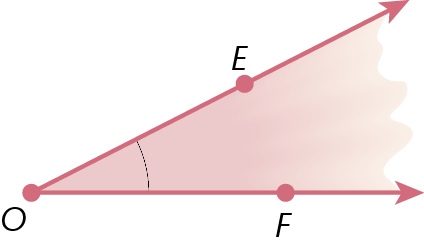
c)
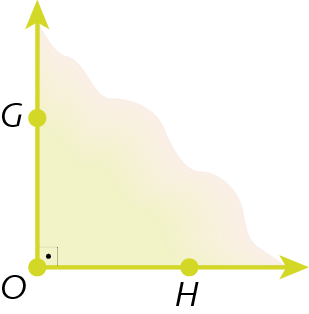
d)
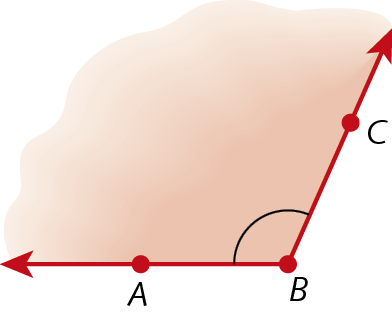
Versão adaptada acessível
17. Represente ângulos retos, agudos, obtusos e rasos com palitos de fósforo usados ou outro material similar que seu professor irá disponibilizar.
18. Observe a figura e indique, no caderno:

a) o ângulo;
b) o vértice do ângulo;
c) as semirretas que formam o ângulo.
19. Lucas e Caio desenharam dois ângulos. Usando um transferidor, responda: Qual deles desenhou o ângulo de maior medida de abertura? Justifique sua resposta.

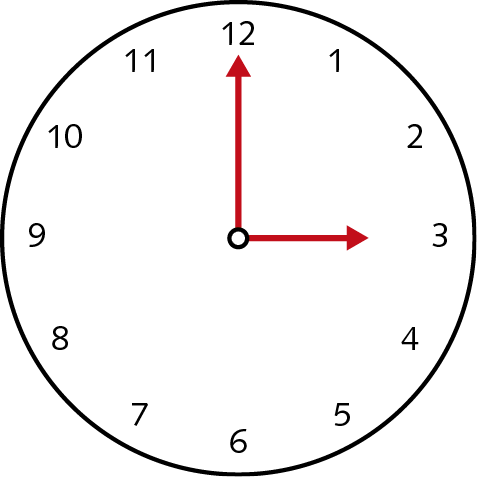
20. O relógio a seguir marca 3 horas. Quais são as medidas de abertura dos dois ângulos formados pelos ponteiros do relógio?
21. Usando um transferidor, determine a medida de abertura de três ângulos diferentes em cada figura.
a)
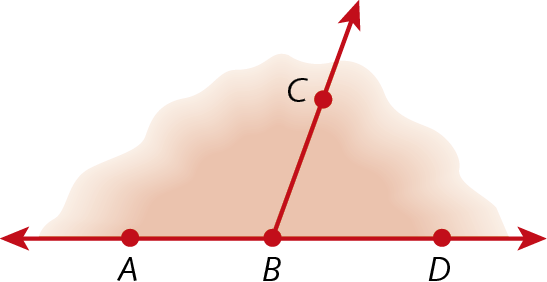
b)
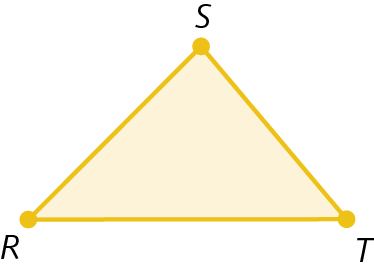
22. Na figura a seguir, há dois ângulos retos, um agudo e um obtuso. Com o auxílio de um transferidor, identifique-os e registre-os no caderno.

23. Determine, com um transferidor, as medidas de abertura dos ângulos dos esquadros.
a)

b)

24. Tainara está fazendo algumas manobras em seu skate. Se ela der um giro de
Sentença matemática. Fração 3 sobre 4.de volta, quanto medirá a abertura do ângulo desse giro?
25. Observe a ilustração de uma sala de projeção.
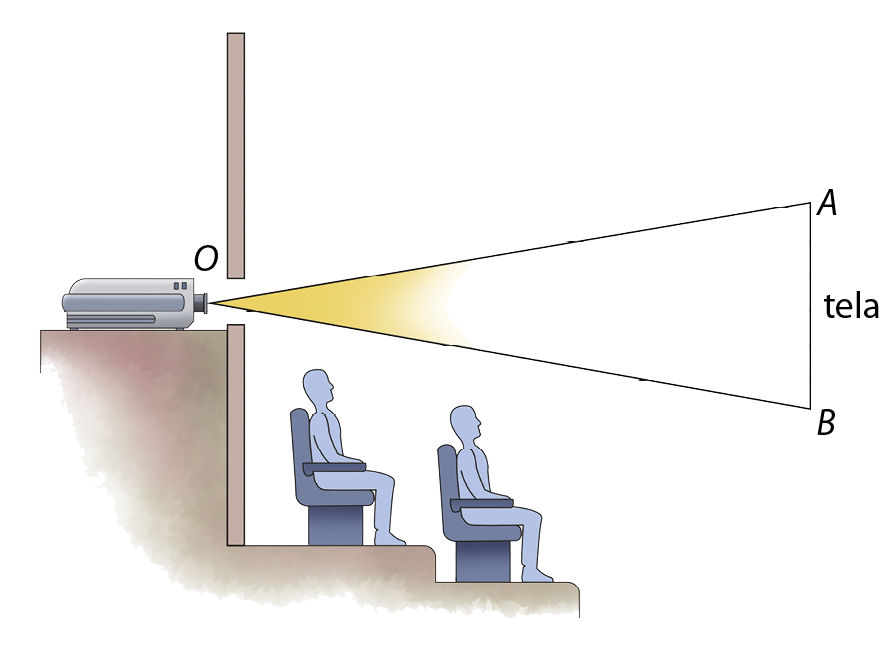
Com um transferidor, indique, no caderno, as medidas de abertura dos ângulos
Símbolo. Ângulo AOB.e
Símbolo. Ângulo OAB..

4 Retas paralelas e retas perpendiculares
Dizemos que duas retas que estão em um mesmo plano são paralelas quando elas não possuem nenhum ponto em comum. Quando duas retas se cruzam, nós as chamamos de retas concorrentes; além disso, quando esse cruzamento fórma um ângulo reto (ângulo cuja medida de abertura é de 90graus), afirmamos que as retas são perpendiculares.
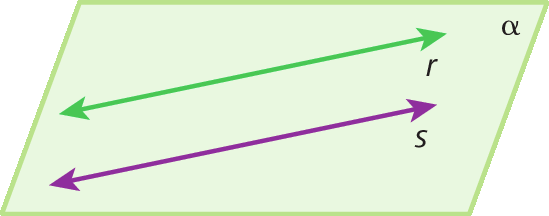
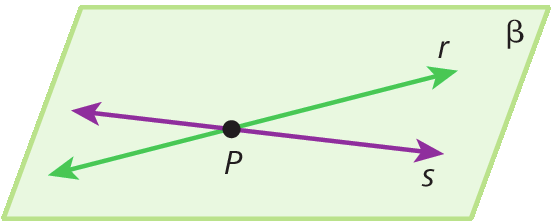
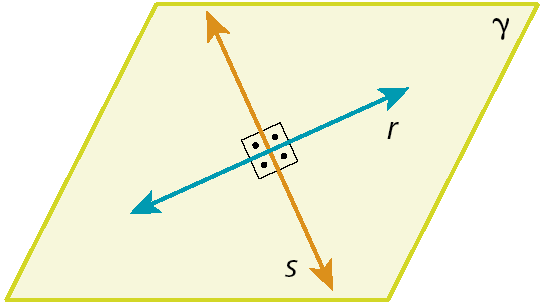
Palmas, capital do estado de Tocantins, é uma cidade planejadaglossário . A avenida JK é paralela às avenidas LO-03 e LO-05 (elas não se cruzam) e é concorrente à avenida NS 2.
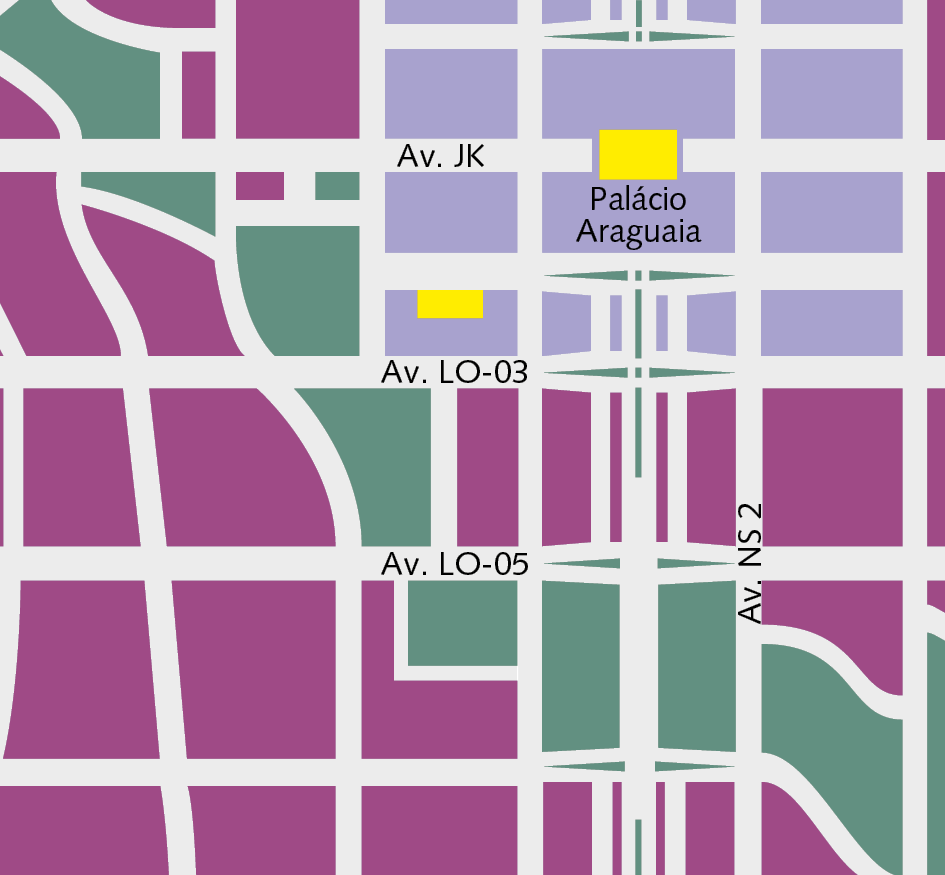

As ruas representadas nesse mapa podem ser associadas a retas. Analise como podemos fazer essa associação:
Construção geométrica de retas paralelas com régua e esquadro
Com os esquadros, podemos traçar alguns ângulos, por exemplo, de medidas de abertura iguais a 30graus, 45graus e 60graus, além de retas paralelas e retas perpendiculares.


Contornando um esquadro de 30graus, podemos traçar ângulos de medidas de abertura iguais a 30graus, 60graus e 90graus. Enquanto que, contornando um esquadro de 45graus, podemos traçar ângulos de medidas de abertura iguais a 45graus e 90graus.
Utilizando uma régua e um esquadro qualquer, vamos traçar uma reta s paralela à reta r.
1º) Alinhamos o esquadro com a reta r e encostamos a régua na lateral do esquadro, mantendo‑a fixa, como mostra a figura.
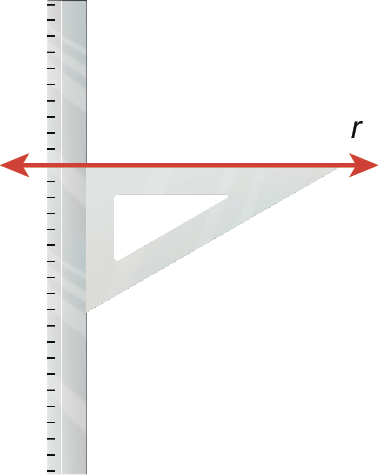
2º) Deslizamos o esquadro mantendo a régua como apôio e traçamos uma reta paralela à reta r.
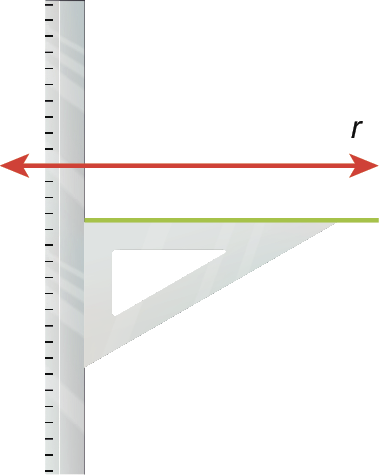
3º) Podemos completar a figura colocando pontas de setas nas extremidades, para indicar que a reta continua nos dois sentidos, e nomeá-la com a letra s. Obtemos, assim, s⫽r.

Construção geométrica de retas perpendiculares com régua e esquadro
Agora, vamos usar uma régua e um esquadro qualquer para traçar uma reta t perpendicular à reta r.
1º) Alinhamos a régua com a reta r.

2º) Apoiamos o esquadro sobre a régua e determinamos um ângulo reto.
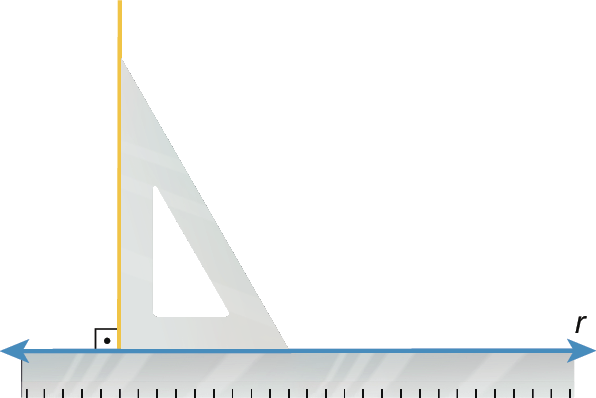
3º) Completamos a figura, prolongando e nomeando a reta t. Obtemos, assim, t ⊥ r.
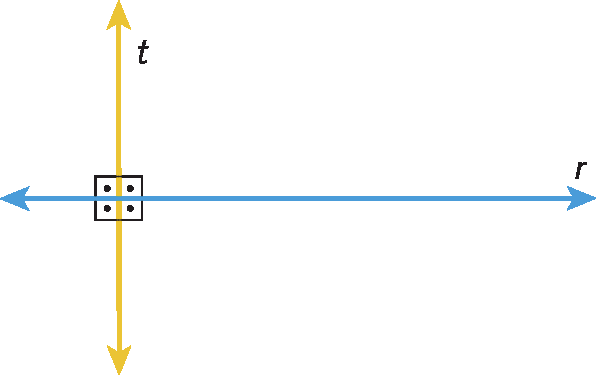

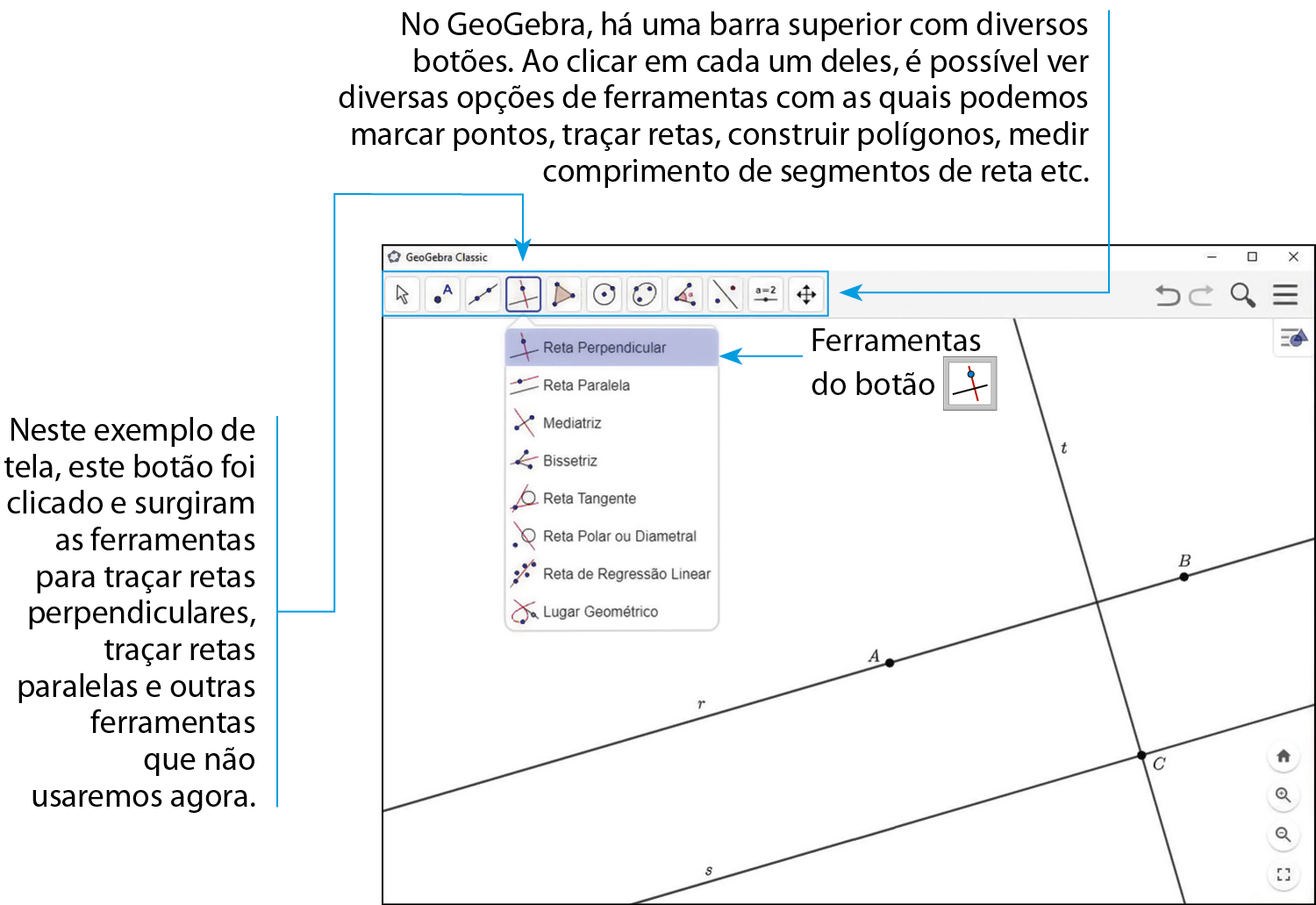
Tecnologias digitais em foco
Retas, semirretas, segmentos de reta e ângulos
Nesta seção, utilizaremos o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar para construir pontos, retas paralelas, retas perpendiculares, semirretas, segmentos de reta e ângulos.
Construa
Siga os passos a seguir para representar os pontos (a, B e C), as retas paralelas (r e s) e as retas perpendiculares (t e s).
1º) Usando a ferramenta

, marque três pontos não alinhados: a, B e C.
2º) Usando a ferramenta
, trace a reta r, que passa pelos pontos a e B.
3º) Usando a ferramenta

, trace a reta s, paralela a r, que passa pelo ponto C.
4º) Usando a ferramenta
, trace a reta t, perpendicular a s, que passa pelo ponto C.
Agora, faremos a construção da semirreta
Símbolo. Semirreta EA.e dos segmentos de reta
entre parênteses segmento de reta E A e segmento de reta C D.
5º) Marque o ponto D no ponto de intersecção entre as retas r e t.
6º) Marque um ponto ê qualquer sobre a reta s e use a ferramenta
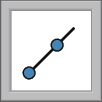
para traçar a semirreta com origem em E que passa pelo ponto a.
7º) Usando a ferramenta

, trace o segmento de reta com extremidades nos pontos C e D.
8º) Trace o segmento de reta com extremidades nos pontos a e ê.
Tecnologias digitais em foco
Explore
Faça o que se pede nas questões a seguir utilizando as ferramentas do GeoGebra e sua construção inicial.
a) Utilize a ferramenta
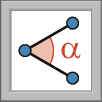
para medir a abertura do ângulo
Símbolo. Ângulo CEA.e a do ângulo
DCE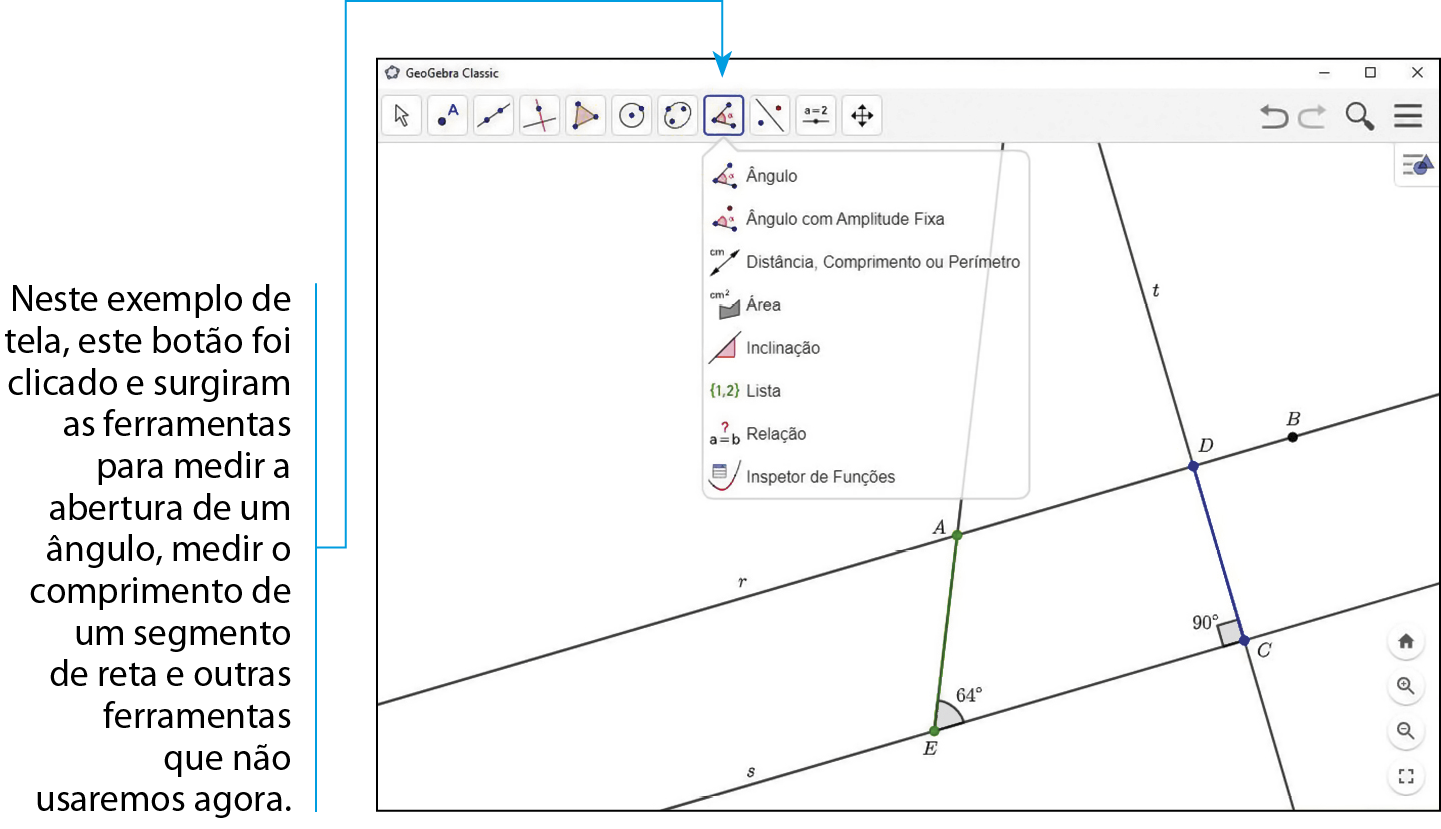
b) Utilize a ferramenta

e meça o comprimento dos segmentos de reta
Símbolo. Segmento de reta AE.e
Símbolo. Segmento CD..
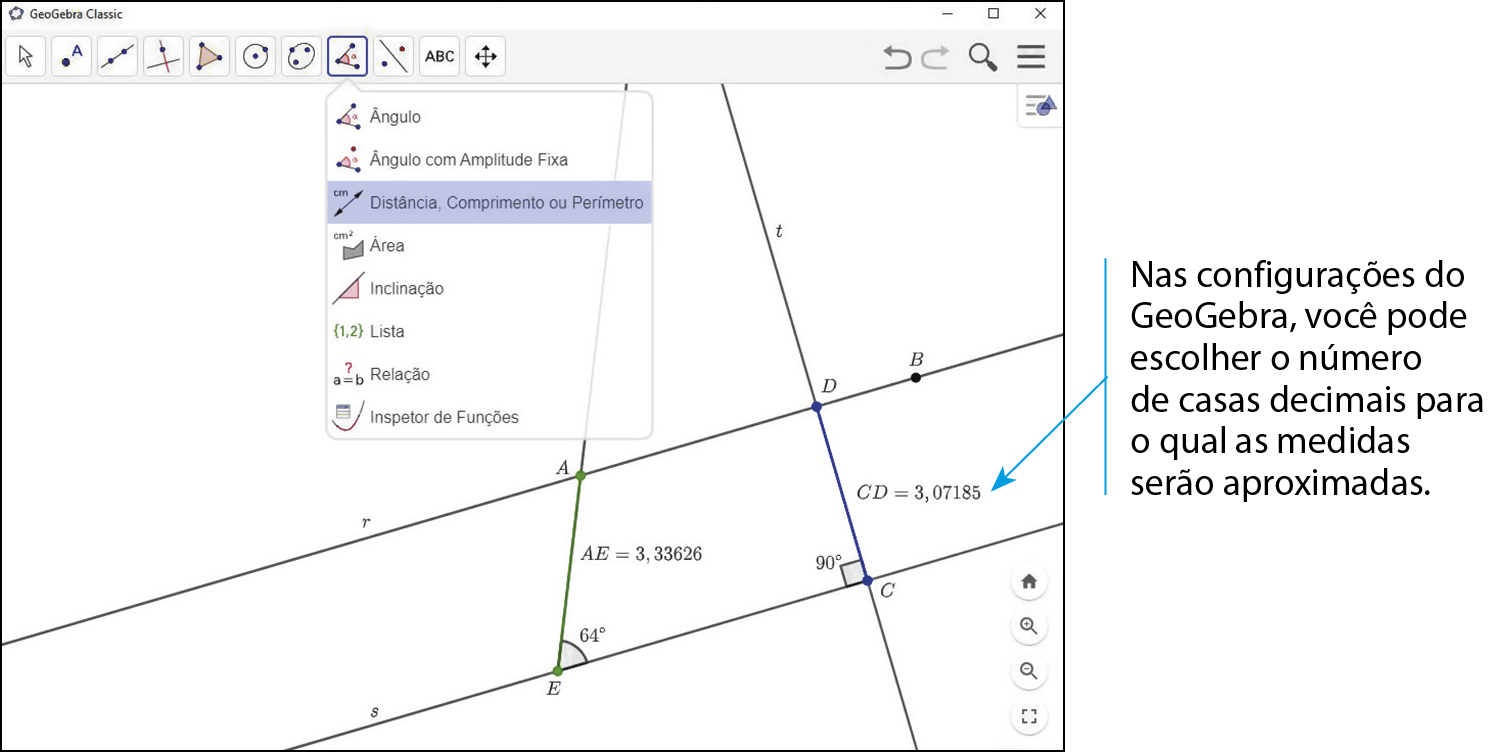
c) Agora, arraste o ponto ê sobre a reta s e compare as medidas de comprimentos dos segmentos
Símbolo. Segmento de reta AE.e
Símbolo. Segmento CD.. Para que as medidas dos comprimentos destes segmentos sejam iguais, qual deve ser a medida de abertura do ângulo
Símbolo. Ângulo CEA.?
d) Continue arrastando o ponto ê sobre a reta s e verifique se é possível obter um segmento de reta com medida de comprimento menor que a medida de comprimento do segmento de reta
Símbolo. Segmento CD.e) O que a investigação sugere a respeito da medida de comprimento de um segmento com extremidades em duas retas paralelas? Quando essa medida é mínima?
Atividades
Faça as atividades no caderno.
26. Reescreva, no caderno, as afirmativas verdadeiras.
a) Se duas retas, que estão no mesmo plano, não apresentam nenhum ponto em comum, essas retas são paralelas.
b) Retas perpendiculares não se cruzam.
c) Duas retas paralelas apresentam apenas um ponto em comum.
d) Duas retas são perpendiculares quando formam um ângulo cuja abertura mede 90graus.
27. Utilizando régua e esquadro, desenhe, no caderno, duas retas paralelas e duas retas perpendiculares às duas retas paralelas traçadas.
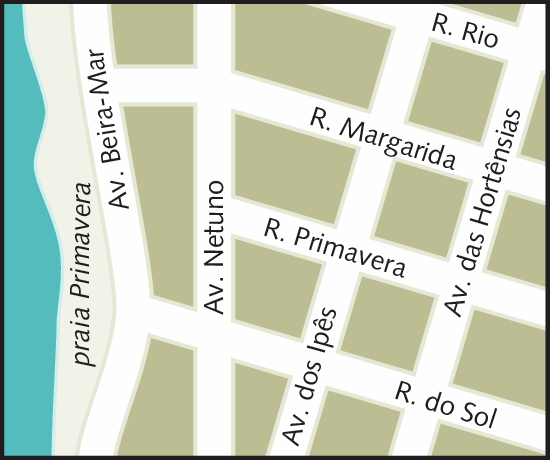
28. Observe o mapa fictício e identifique:
a) dois pares de ruas ou avenidas paralelas;
b) dois pares de ruas ou avenidas perpendiculares.
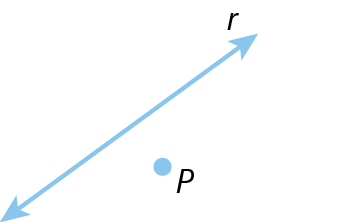
29. Copie em seu caderno as retas r e s e os pontos P e Q. Em seguida, utilizando régua e esquadro, trace uma reta paralela a r pelo ponto P e uma reta perpendicular a s pelo ponto Q.
a)
b)
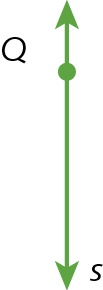
30. Usando mais de um esquadro, podemos traçar alguns ângulos contornando a composição dos esquadros. Por exemplo, com um esquadro de 30graus e um esquadro de 45graus, podemos representar um ângulo de medida de abertura igual a 75graus.

Utilizando um esquadro de 30graus e um esquadro de 45graus, represente ângulos de medida de abertura igual a:
a) 105graus
b) 120graus
c) 135graus
d) 150graus

5 Polígonos
Observe o recorte de um mosaico.

Podemos identificar nesse mosaico algumas figuras geométricas.
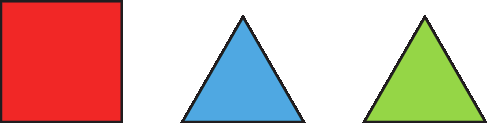
O contôrno de cada uma dessas figuras geométricas é formado apenas por segmentos de reta. Eles formam uma linha poligonal.
Observe, agora, este outro mosaico.
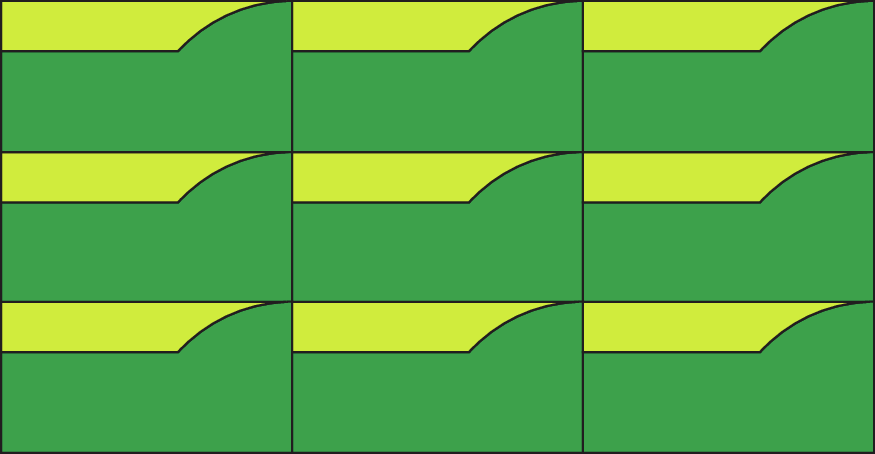
Os contornos das figuras presentes nesse mosaico não são formados apenas por segmentos de reta. Eles formam uma linha não poligonal.

As linhas poligonais podem ser assim classificadas:
|
Não simples (linhas se cruzam) |
Simples (linhas não se cruzam) |
|
|---|---|---|
|
Abertas |
|
|
|
Fechadas |
|
|
Uma linha poligonal fechada simples com sua região interna fórma uma figura geométrica plana chamada de polígonoglossário .

Polígonos convexos e polígonos não convexos
Os polígonos podem ser classificados em convexos ou não convexos.
Para distinguir cada um desses tipos, podemos tomar dois pontos quaisquer (a e B, por exemplo) no interior de um polígono. Se o segmento de reta
Símbolo. Segmento de reta AB.sempre estiver contido em sua região interna, trata‑se de um polígono convexo; caso contrário, trata-se de um polígono não convexo.
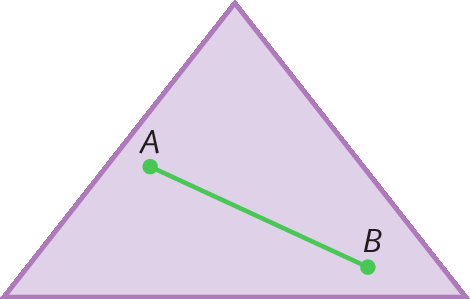
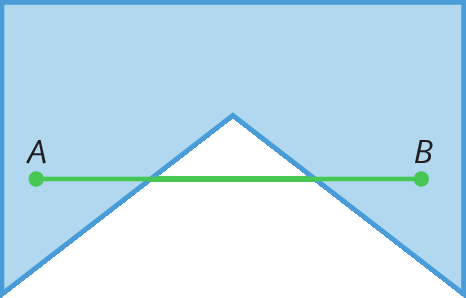
Analise alguns outros exemplos.
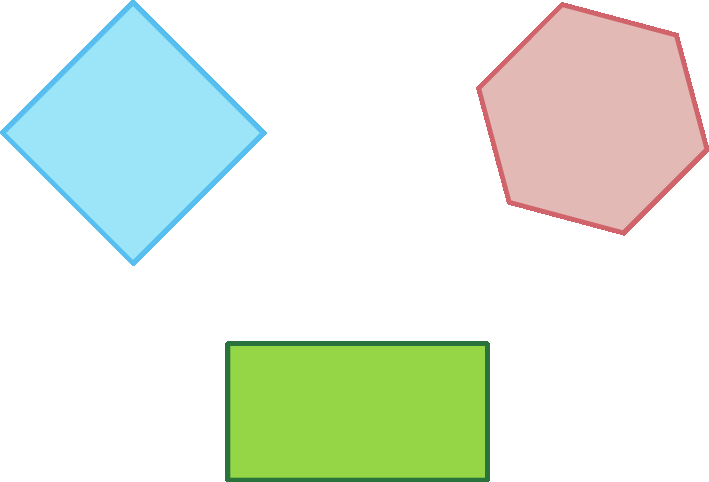

A partir de agora, vamos trabalhar com os polígonos convexos, chamando-os apenas de polígonos.
Elementos de um polígono
A figura a seguir representa um polígono; nele temos:
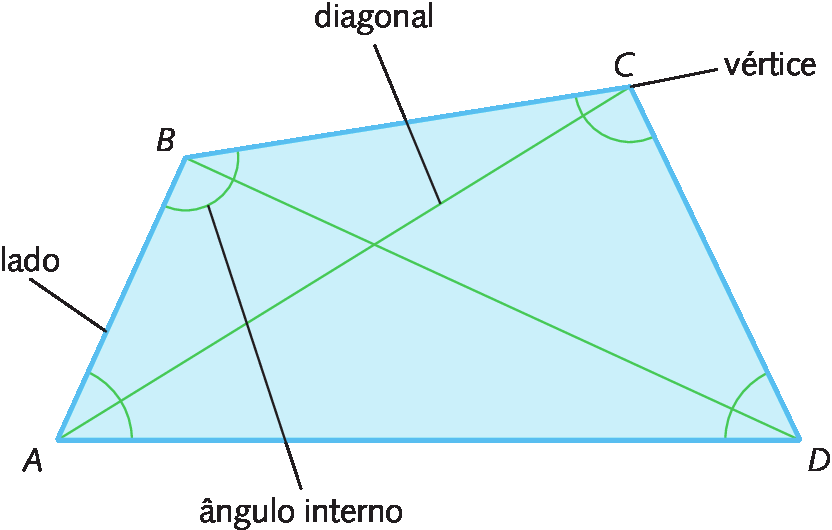
• os segmentos de reta
Símbolo. Segmento de reta AB.,
Símbolo. Segmento de reta BC.,
Símbolo. Segmento de reta CD.e
Símbolo. Segmento de reta DA. formam o contôrno do polígono e são chamados de lados do polígono.
• os pontos a, B, C e D são o encontro de dois lados consecutivos e são chamados de vértices do polígono.
• os ângulos
Símbolo. Ângulo DAB.,
Símbolo. Ângulo ABC.,
Símbolo. Ângulo BCD.e
Símbolo. Ângulo CDA.são formados por dois lados consecutivos e são chamados de ângulos internos do polígono.
• os segmentos de reta
Segmento de reta AC.e
Símbolo. Segmento de reta BD.unem dois vértices não consecutivos e são chamados de diagonais do polígono.
Classificação dos polígonos
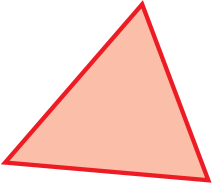
Os polígonos recebem o nome de acôrdo com o número de lados ou ângulos internos. Por exemplo, o polígono de 5 lados é chamado de pentágono, do grego penta (cinco) + gonos (ângulos). Confira mais exemplos.
|
Número de lados |
Nome |
Representação geométrica |
|---|---|---|
|
3 |
triângulo |
|
|
4 |
quadrilátero |
|
|
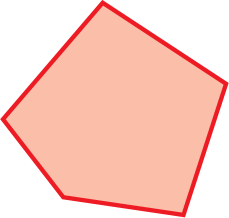
5 |
pentágono |
|
|
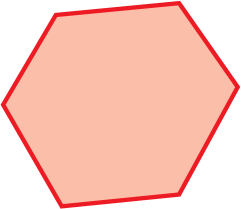
6 |
hexágono |
|
|
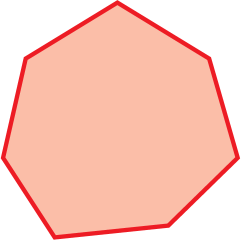
7 |
heptágono |
|
|
8 |
octógono |
|
|
Número de lados |
Nome |
Representação geométrica |
|---|---|---|
|
9 |
eneágono |
|
|
10 |
decágono |
|
|
11 |
undecágono |
|
|
12 |
dodecágono |
|
|
15 |
pentadecágono |
|
|
20 |
icoságono |
|
Os polígonos em que todos os ângulos internos têm a mesma medida de abertura e todos os lados têm a mesma medida de comprimento são chamados de polígonos regulares.
Atividades
Faça as atividades no caderno.
31. Classifique cada uma das linhas poligonais a seguir em aberta simples, aberta não simples, fechada simples ou fechada não simples.
a)

b)

c)

d)

32. Classifique cada um dos polígonos em convexo ou não convexo.
a)

b)

c)

d)

33. No caderno, copie as afirmativas verdadeiras.
a) Podemos construir um polígono de dois lados.
b) Em todo polígono, o número de lados é igual ao número de vértices.
c) O polígono com 20 vértices chama‑se icoságono.
34. Entre as figuras a seguir, identifique o polígono.
a)

b)

c)

d)

35. Em cada figura a seguir, dê o nome do polígono e indique seus lados, vértices, ângulos internos e diagonais.
a)

b)

36. Com o auxílio de uma régua, construa em seu caderno os polígonos a seguir.
a) Pentágono ABCDE.
b) Octógono ABCDEFGH.
c) Quadrilátero ABCD.

6 Triângulos
Na tela reproduzida a seguir, o artista húngaro Vítor Vasarely (1908-1997) dispôs diversos triângulos a fim de criar a ilusão de um objeto não plano.

Os triângulos podem ser classificados quanto às medidas de comprimento de seus lados e quanto às medidas de abertura de seus ângulos internos.
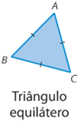
De acôrdo com a medida de comprimento de seus lados, os triângulos podem ser classificados em equilátero, escaleno ou isósceles.
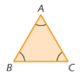
• Triângulo equilátero
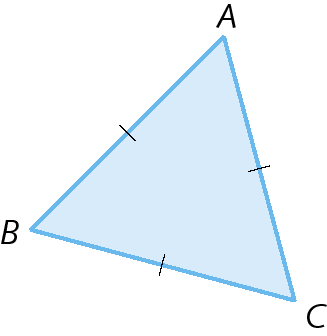
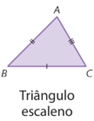
• Triângulo escaleno
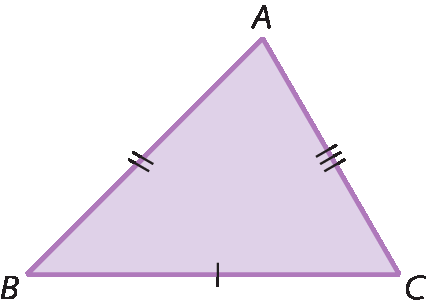
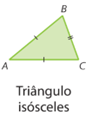
• Triângulo isósceles
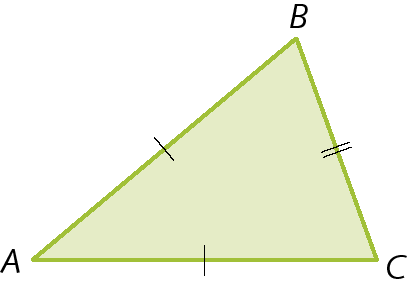
De acôrdo com a medida de abertura de seus ângulos internos, os triângulos podem ser classificados em acutângulo, obtusângulo ou retângulo.
• Triângulo acutângulo
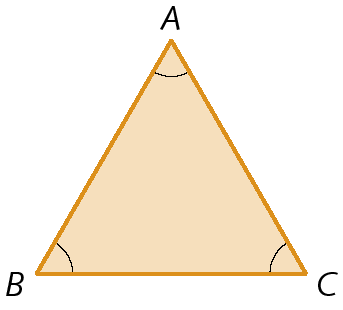
• Triângulo obtusângulo
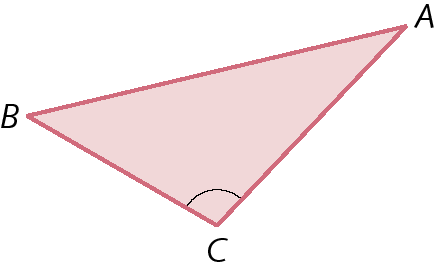
• Triângulo retângulo
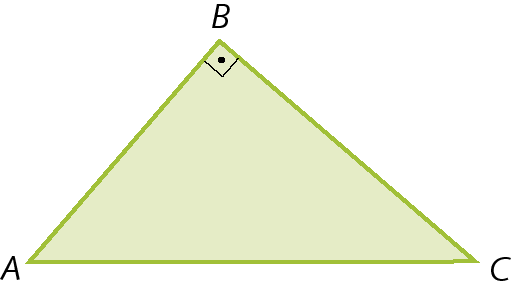
Atividades
Faça as atividades no caderno.
37. Utilizando uma régua, meça o comprimento dos lados dos triângulos e classifique cada um deles em equilátero, escaleno ou isósceles.
a)

b)

c)

d)

e)

f)

38. Classifique cada triângulo a seguir em acutângulo, obtusângulo ou retângulo.
a)
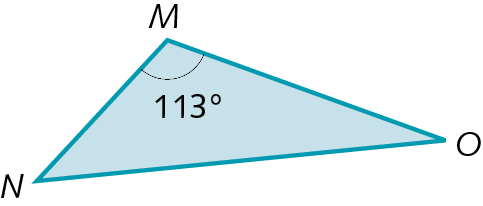
b)
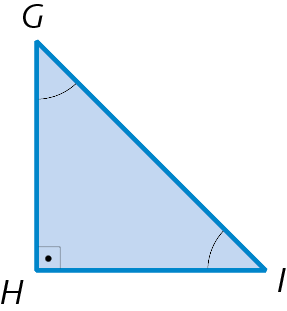
c)
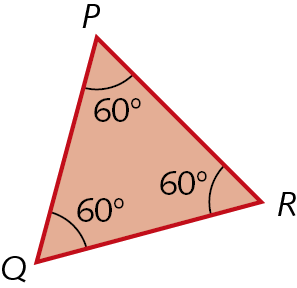
d)
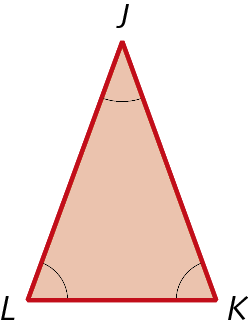
39.

Desenhe, em uma folha avulsa, três triângulos. Troque seus triângulos com um colega e peça-lhe que meça a abertura dos ângulos internos dos três triângulos. Em seguida, cada um deve calcular a soma das medidas de abertura dos ângulos internos de cada triângulo. Compare os resultados que obteve com os do colega. O que vocês observaram?
40. Quantos triângulos há em cada figura? No caderno, identifique todos os triângulos.
a)
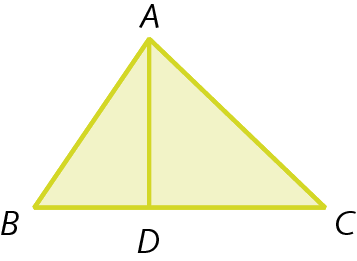
b)
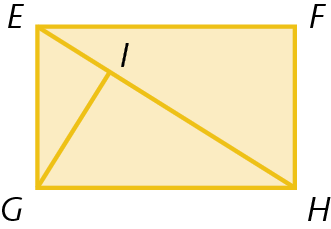
c)
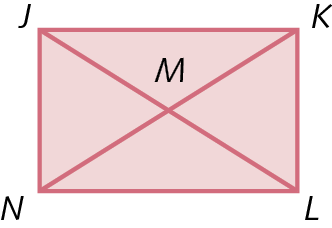
41. Copie, no caderno, as afirmativas verdadeiras.
a) Todo triângulo equilátero é também isósceles.
b) Um triângulo obtusângulo tem dois ângulos internos agudos.
c) O triângulo equilátero tem ângulos internos com a mesma medida de abertura.
d) É possível traçar um triângulo obtusângulo equilátero.
e) O triângulo equilátero tem lados com a mesma medida de comprimento.

7 Quadriláteros
Na tela reproduzida a seguir, o artista brasileiro Luiz Sacilotto (1924-2003) dispôs quadriláteros em diferentes posições para criar a ilusão de linhas curvas. Observe:

Quadrilátero é um polígono com quatro lados. Analise o quadrilátero a bê cê dê a seguir.
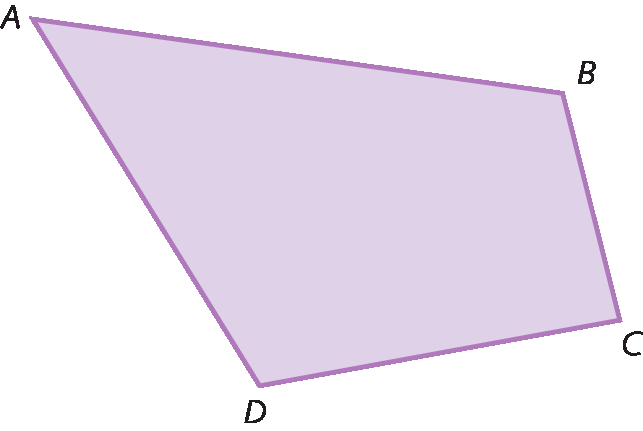
Note, a seguir, como os quadriláteros podem ser classificados.
Paralelogramos
Paralelogramos são quadriláteros que têm dois pares de lados paralelos.

⫽
Símbolo. Segmento de reta CD.e
Símbolo. Segmento de reta AD.⫽
Símbolo. Segmento de reta BC.Em um paralelogramo, lados opostos têm a mesma medida de comprimento. Assim, no paralelogramo anterior, temos:
A bê = DC e á dê = BC
Destacando três importantes paralelogramos, temos: o retângulo, o losango e o quadrado.
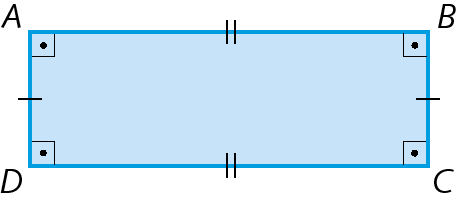
Retângulo
Retângulo é o paralelogramo que tem os quatro ângulos retos.
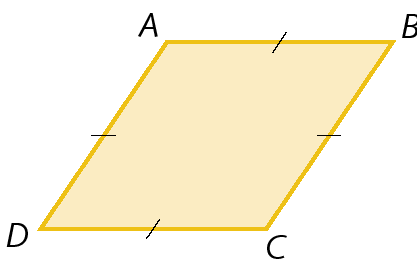
Losango
Losango é o paralelogramo cujos lados têm a mesma medida de comprimento, ou seja, são congruentes.
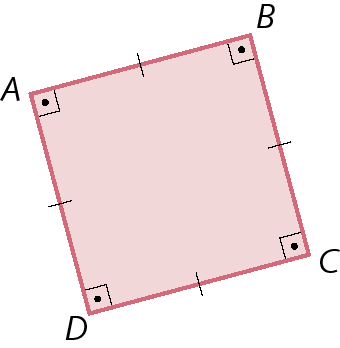
Quadrado
Quadrado é o paralelogramo cujos lados têm a mesma medida de comprimento e os quatro ângulos são retos.
Vamos estudar algumas relações entre retângulo, losango e quadrado:
▸ Um quadrado é um retângulo? Justifique sua resposta.
▸ Todo retângulo é um quadrado? Justifique sua resposta.
▸ Todo retângulo é um losango? Justifique sua resposta.
▸ Todo losango é um quadrado? Justifique sua resposta.
▸ Todo quadrado é um losango? Justifique sua resposta.
Trapézios
Trapézio é o quadrilátero que tem apenas um par de lados paralelos.

⫽
Símbolo. Segmento de reta CD.Observe a seguir os trapézios retângulo, isósceles e escaleno e suas características.
Trapézio retângulo
É aquele que tem dois ângulos retos.

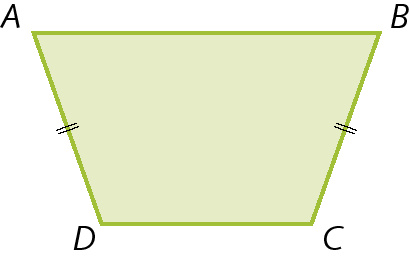
Trapézio isósceles
É aquele que tem os lados não paralelos congruentes.
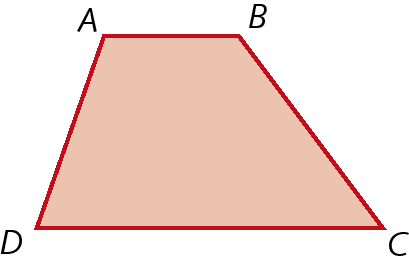
Trapézio escaleno
É aquele que tem as medidas dos comprimentos dos lados não paralelos diferentes.
Observação
Há quadriláteros que não são paralelogramos nem trapézios.

Atividades
42. Classifique cada um dos quadriláteros a seguir em paralelogramo ou trapézio.
a)

b)

43. Com o auxílio de uma régua e de um transferidor, classifique, no caderno, os paralelogramos a seguir.
a)

b)

c)

d)

44. Classifique cada afirmação a seguir em verdadeira ou falsa, corrigindo as falsas.
a) Todo quadrado é um retângulo.
b) Todo trapézio é um paralelogramo.
c) Um trapézio pode ser um retângulo.
d) Todo quadrado é também um losango.
e) Um losango pode ser um retângulo.
f) Existem retângulos que não são paralelogramos.
g) Todo paralelogramo é um losango.
h) Existem retângulos que são losangos.
45. Desenhe no caderno:
a) um quadrilátero que não tenha lados paralelos;
b) um quadrilátero que tenha dois pares de lados paralelos;
c) um quadrilátero que tenha apenas um par de lados paralelos.
• Qual desses itens representa um trapézio?
46. Responda às questões no caderno.
a) Qual é o quadrilátero que tem quatro ângulos retos e quatro lados congruentes?
b) Qual é o quadrilátero que tem os lados opostos paralelos?
47.

Desenhe três quadriláteros quaisquer. Troque-os com um colega para que cada um de vocês meça a abertura dos ângulos internos dos três quadriláteros do outro. Em seguida, calculem a soma das medidas de abertura dos ângulos internos de cada quadrilátero. Comparem os seus resultados. O que vocês observaram?
48. O pintor suíço Paul Klee (1879‑1940) foi um mestre da arte abstrata. Observe o quadro reproduzido na imagem a seguir.

Em seu caderno, indique algumas das figuras geométricas do quadro que lembram polígonos.
49. Com régua e esquadro, construa no caderno:
a) um quadrado a bê cê dê cuja medida de comprimento do lado seja 2 centímetros;
b) um trapézio ê éfe gê agá, tal que
medida de
Símbolo. Ângulo E.= medida de
Símbolo. Ângulo F.= 90graus
medida de
Símbolo. Segmento EH.= 1,5 centímetro e
medida de
Símbolo. Segmento FG.= 3 centímetros.

Tecnologias digitais em foco
Quadriláteros
Nesta seção, utilizaremos o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar para construir quadriláteros e investigar uma das propriedades do paralelogramo.
Construa
Para construir um quadrilátero qualquer, selecione a ferramenta
e clique em 4 pontos quaisquer da tela. A construção deve ser finalizada clicando novamente no ponto em que a construção foi iniciada.
Essa ferramenta possibilita também construir quadriláteros a partir de 4 pontos já marcados na tela.
Você pode transformar o quadrilátero construído em convexo ou não convexo, arrastando um de seus 4 vértices.
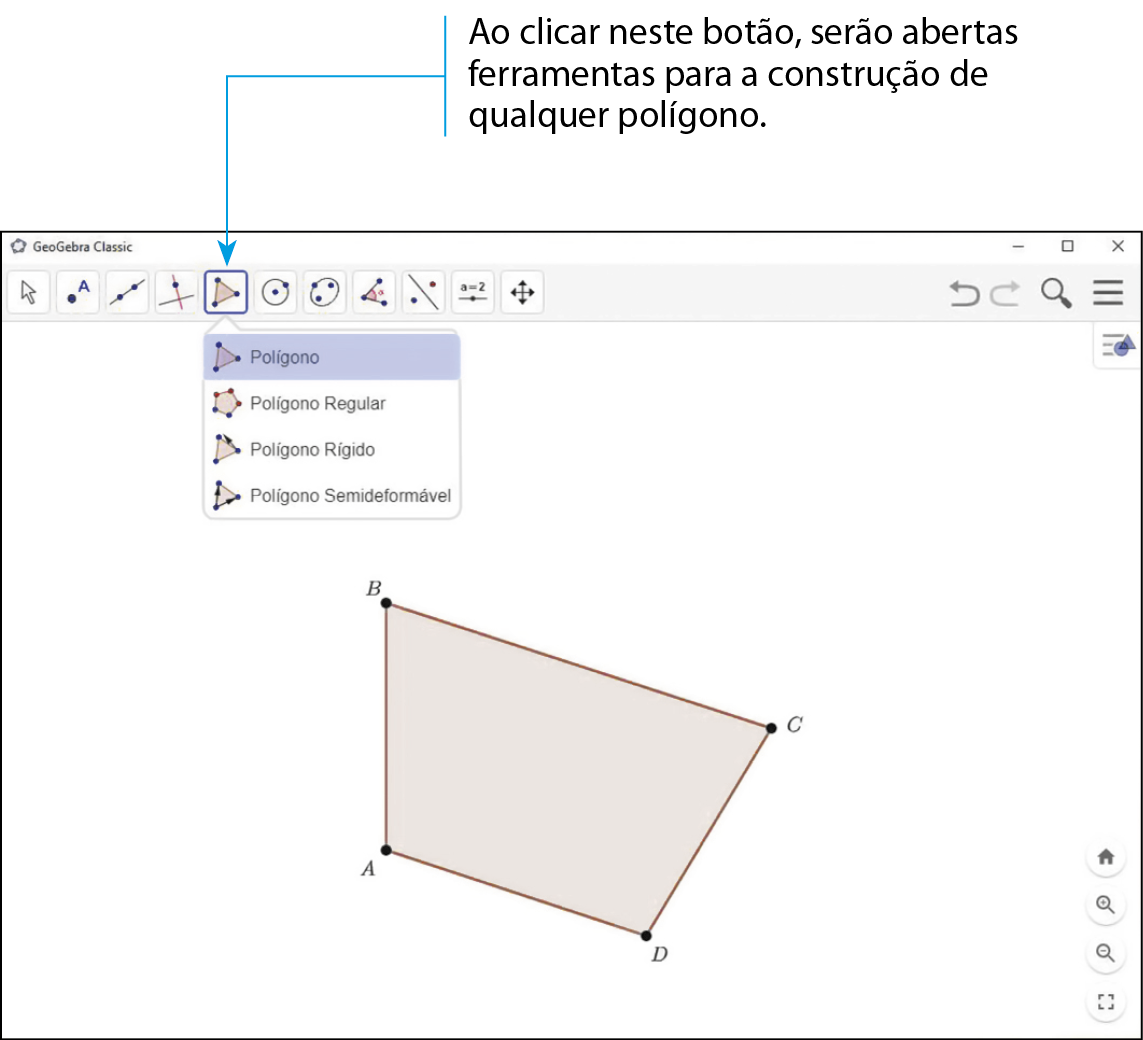
Agora, siga os passos a seguir para construir um paralelogramo.
1º) Marque 3 pontos não colineares a, B e C.
2º) Trace a reta r que passa por a e B e a reta s que passa por B e C.
3º) Trace uma reta p, paralela à reta r, passando por C.
4º) Trace uma reta q, paralela à reta s, passando por a.
5º) Marque o ponto D, intersecção das retas p e q.
6º) Utilize a ferramenta

e construa o quadrilátero ABCD, que será um paralelogramo.
Tecnologias digitais em foco
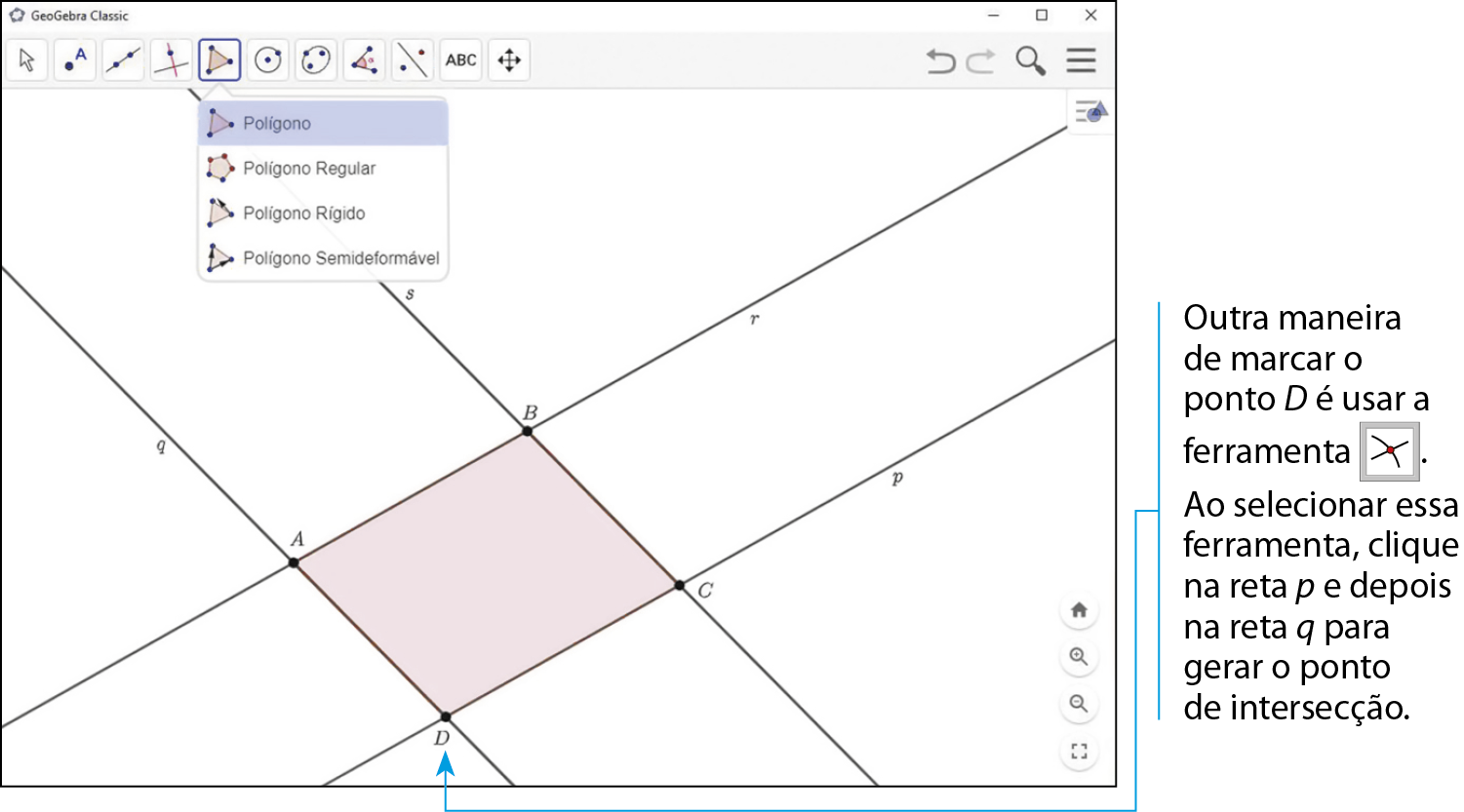
Você pode verificar que qualquer reta perpendicular ao lado
Símbolo. Segmento de reta AB.também é perpendicular ao lado
Símbolo. Segmento de reta CD.e que qualquer reta perpendicular ao lado
Símbolo. Segmento de reta BC.também é perpendicular ao lado
Símbolo. Segmento de reta DA.Agora, siga os passos a seguir para construir um trapézio.
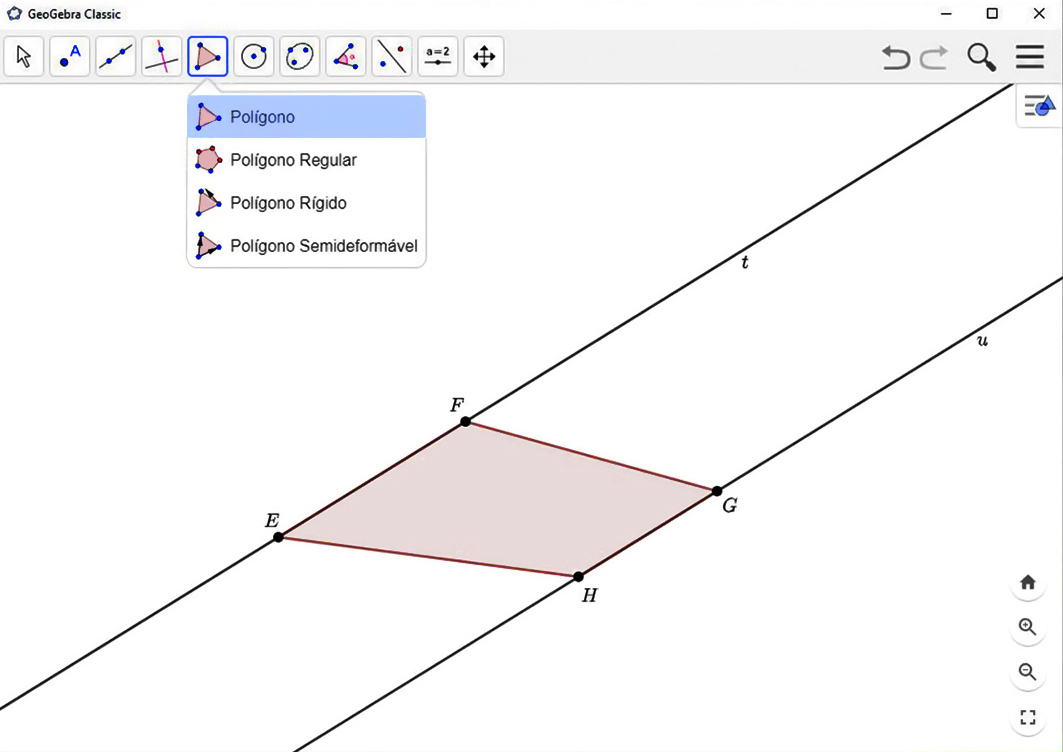
1º) Marque 3 pontos não colineares ê, F e G.
2º) Trace a reta t, que passa por ê e F.
3º) Trace uma reta u, paralela à reta t, passando por G.
4º) Marque um ponto H qualquer na reta u de modo que o segmento
Símbolo. Segmento EH.não cruze o segmento
Símbolo. Segmento FG.e que FG não seja igual a EH.
5º) Utilize a ferramenta
e construa o quadrilátero EFGH, que será um trapézio.
Explore
a)

Por que o quadrilátero a bê cê dê, construído anteriormente, é um paralelogramo?
b) Meça os lados do paralelogramo que você criou e mova os pontos dessa figura. O que acontece com as medidas dos lados do paralelogramo?
c) Por que o quadrilátero ê éfe gê agá construído anteriormente é um trapézio?
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Representação de ponto, reta e plano
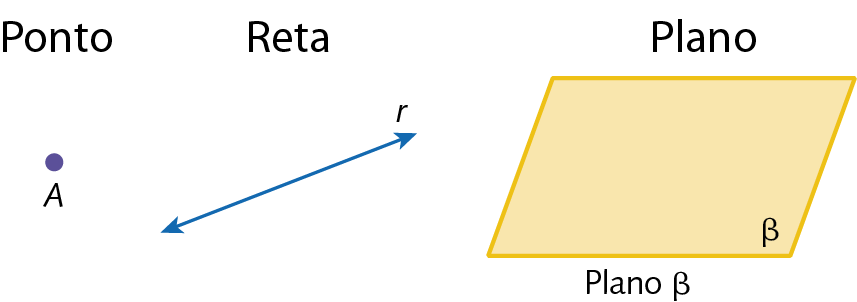
1. Observe a figura a seguir.
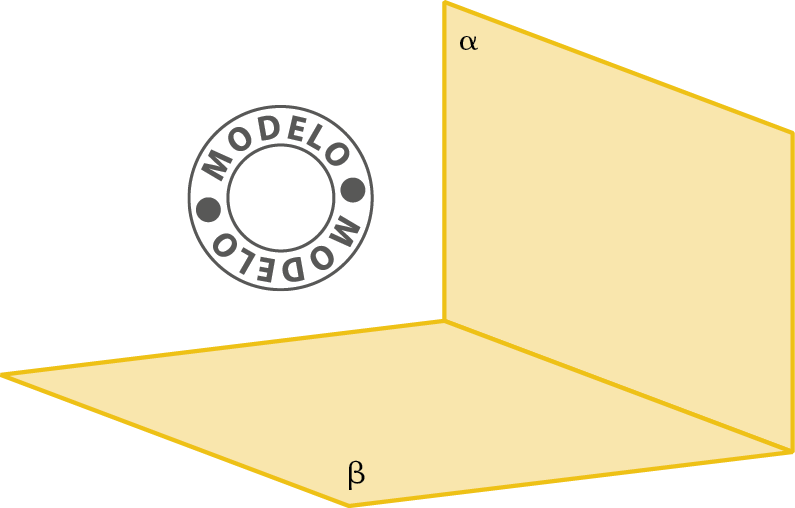
Copie a figura no caderno e represente:
a) uma reta r contida no plano alfa;
b) uma reta s contida no plano beta;
c) um ponto a que pertence ao plano alfa;
d) um ponto B que pertence ao plano beta;
e) um ponto C que pertence aos planos alfa e beta.
Semirreta e segmento de reta
Semirreta

Segmento de reta

2. Identifique as semirretas representadas nas figuras.
a)
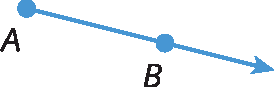
b)
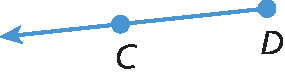
3. Quais figuras a seguir representam um segmento de reta?
a)

b)

c)

d)

4. Identifique os segmentos de reta representados nas figuras.
a)
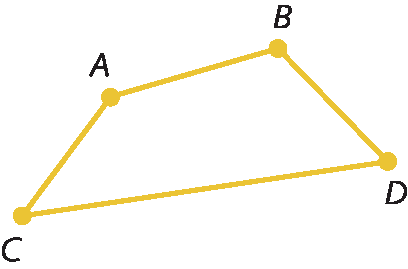
b)
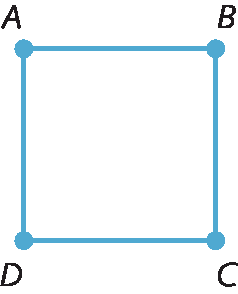
Ângulos
Ângulo é a união de duas semirretas, que têm a mesma origem, com uma das regiões do plano limitada por elas.
|
Classificação de ângulos |
||
|---|---|---|
|
|
|
|
5. Utilizando um transferidor, desenhe no caderno dois ângulos: um de medida de abertura igual a 60graus e outro de medida de abertura igual a 130graus.
6. Classifique os ângulos de cada item em reto, agudo ou obtuso.
a)
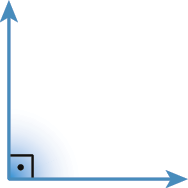
b)
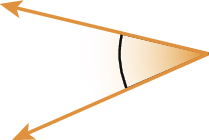
c)
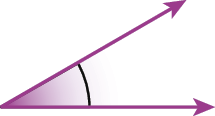
d)

Retas paralelas e retas perpendiculares
Retas concorrentes
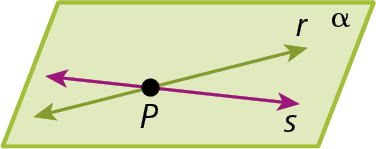
Retas paralelas
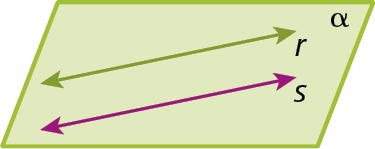
Retas perpendiculares
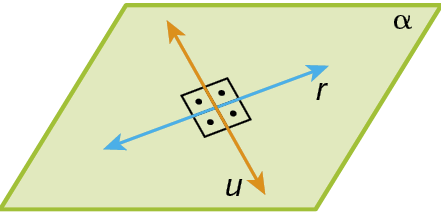
7. No caderno, utilizando régua e esquadro, represente um par de retas paralelas e um par de retas perpendiculares.
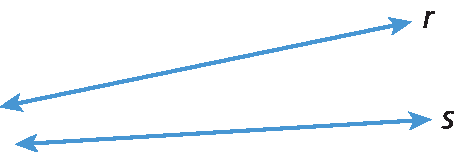
8. Observe a representação de um par de retas e, em seguida, responda: Essas retas são concorrentes? Justifique sua resposta.
Polígonos
Uma linha poligonal fechada simples com sua região interna fórma uma figura geométrica plana chamada de polígono.

Os polígonos recebem o nome de acôrdo com o número de lados ou de ângulos internos.
9. Quais das figuras são polígonos?
a)

b)

c)

d)

10. No caderno, construa os polígonos a seguir.
a) Quadrilátero a bê cê dê.
b) Hexágono á bê cê dê é éfe.
Triângulos
Triângulo é um polígono com três lados.
|
Classificação de acordo com as medidas dos comprimentos dos lados |
||
|---|---|---|
|
|
|
|
|
Classificação de acordo com as medidas de abertura dos ângulos |
||
|---|---|---|
|
|
|
|
11. Utilizando uma régua, meça o comprimento dos lados dos triângulos e classifique cada um deles em equilátero, escaleno ou isósceles.
a)
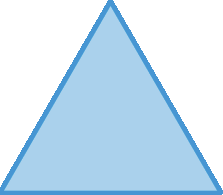
b)

c)
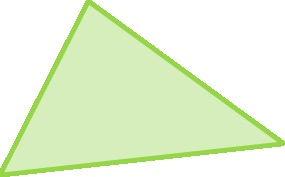
d)

12. Desenhe, no caderno, um triângulo acutângulo, um triângulo obtusângulo e um triângulo retângulo.
Quadriláteros
Quadrilátero é um polígono com quatro lados.
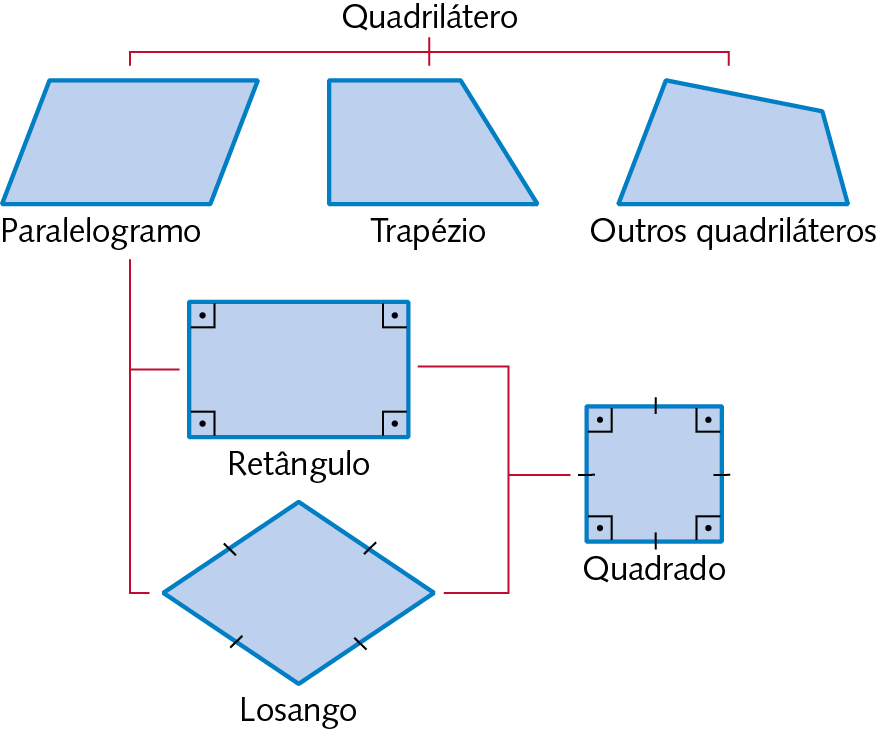
13. No caderno, desenhe um paralelogramo, um trapézio, um quadrado, um retângulo e um losango.
Glossário
- Cidade planejada
- : cidade projetada detalhadamente, desde seu início, com o objetivo de minimizar problemas comuns ao processo de urbanização.
- Voltar para o texto
- Polígono
- : palavra de origem grega: poli: muitos; gonos: ângulos.
- Voltar para o texto