Página 217

Capítulo 10 Ampliação e redução de figuras

Trocando ideias

O alfaiate digital é o profissional que, com o auxílio da tecnologia, trabalha para obter medidas precisas e garantir que as peças de roupa sirvam perfeitamente no corpo do cliente. Essa profissão é considerada uma das “profissões do futuro”.

Observe o esbôço feito por um alfaiate digital.

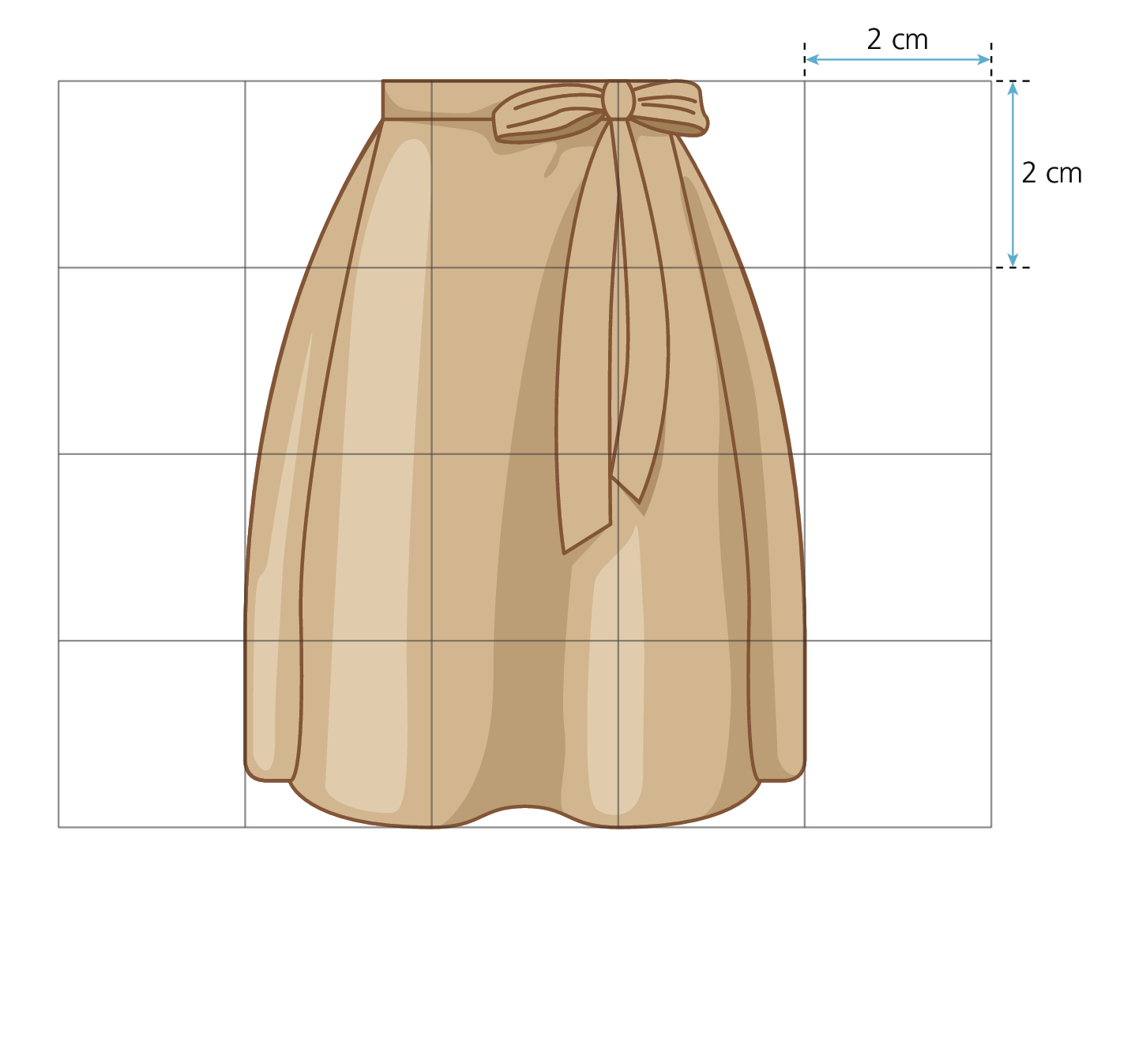
Ilustração. Saia bege representada em uma malha quadriculada composta de 20 quadrados com lados medindo 2 centímetros de comprimento cada um. São quatro fileiras e cinco colunas. A saia ocupa 3 colunas de quadrados.

▸

Qual dos esboços a seguir é uma redução do esbôço feito pelo alfaiate digital?

esbôço um

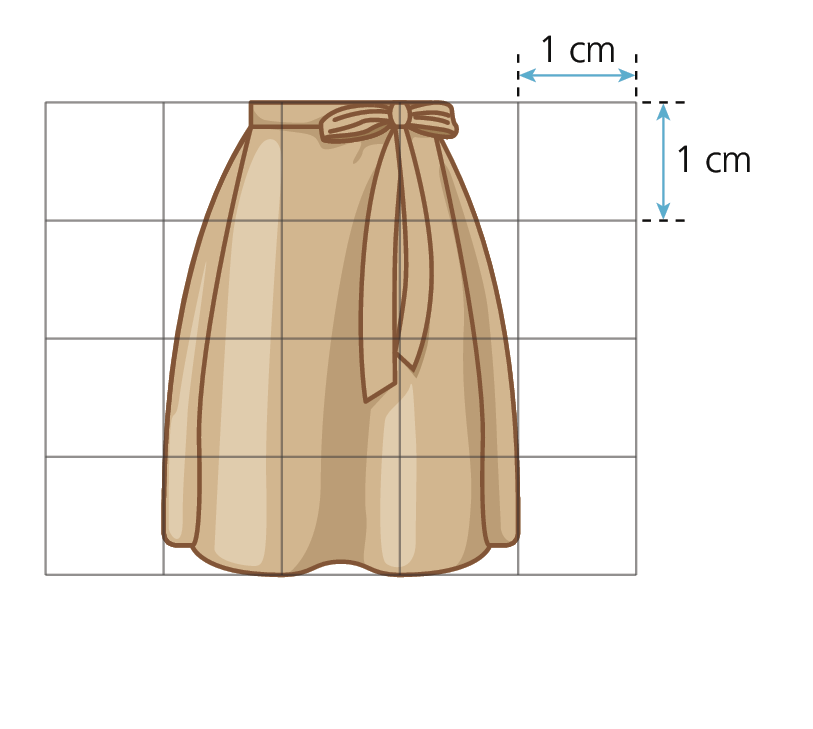
Ilustração. Saia bege representada em uma malha quadriculada composta de 20 quadrados com lados medindo 1 centímetros de comprimento cada um. São quatro fileiras e cinco colunas. A saia ocupa 3 colunas de quadrados. Ela possui o mesmo formato da saia da imagem anterior.

esbôço dois

▸

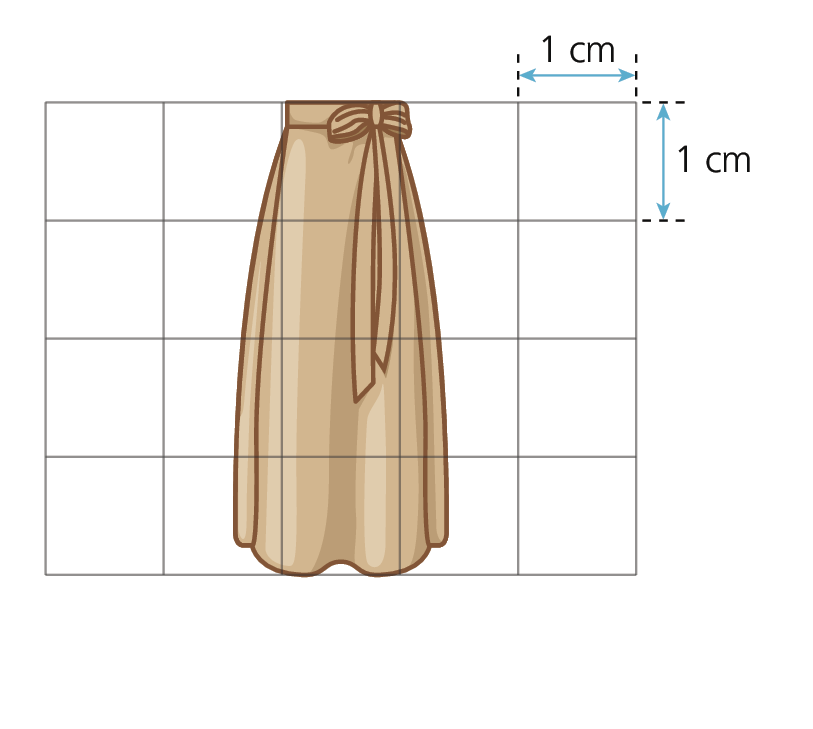
Como você faria para obter uma ampliação do esbôço feito pelo alfaiate digital? ampliação do esbôço feito pelo alfaiate digital?

▸

Você conhece alguma outra profissão que deve surgir ou crescer em breve? Se sim, qual? Converse com os colegas.

Neste capítulo, vamos estudar o plano cartesiano e também a ampliação e redução de figuras.

Página 218

1 Representação de um polígono no plano cartesiano

Para representar um ponto, podemos utilizar o plano cartesiano e indicar a localização desse ponto por meio de um par ordenado.

Plano cartesiano

O plano cartesiano é composto de duas retas numéricas perpendiculares, chamadas eixos, que, em geral, indicamos por x (eixo horizontal) e y (eixo vertical). O eixo horizontal é chamado de eixo das abscissas e o eixo vertical é chamado de eixo das ordenadas.

O ponto de intersecção dos dois eixos é denominado origem e é representado pela letra O.

Plano cartesiano. Retas numéricas perpendiculares que se intersectam no ponto O que corresponde ao número zero. Na reta numérica horizontal estão representados os números 0, 1, 2, 3 e 4 e ela está identificada com a letra x. Há uma seta para ela com a indicação: Eixo das abscissas. Na reta numérica vertical estão representados os números 0, 1, 2, 3 e 4 e ela está identificada com a letra y. Há uma seta para ela com a identificação: Eixo das ordenadas.

Par ordenado

Um par ordenado (x, y) é dado pelas coordenadas x e y, sendo x a abscissa e y a ordenada.

No plano cartesiano a seguir, para indicar a posição do ponto P, usamos o par ordenado (4, 2).

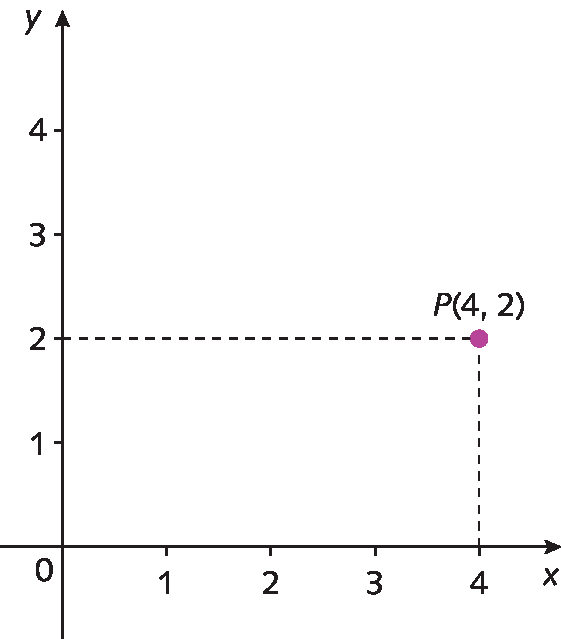
Plano cartesiano. Mesma figura anterior mas sem as identificações de Eixo das abscissas e eixo das ordenadas. No plano cartesiano, está representado o ponto P que corresponde ao par ordenado (4, 2). Do número 4 representado no eixo das abscissas, parte uma linha vertical tracejada. Do número 2 representado no eixo das ordenadas parte uma linha horizontal tracejada. As duas linhas tracejadas se encontram no ponto P.

Os números 4 e 2 são chamados coordenadas cartesianas do ponto P. A primeira coordenada é a abscissa do ponto, e a segunda é a ordenada do ponto. Observe que a abscissa do ponto é um número do eixo x e a ordenada do ponto é um número do eixo y.

Página 219

Um pouco de história

Faça a atividade no caderno.

René Decárte

René Decárte (1596-1650), matemático, físico e filósofo francês, escreveu, em 1637, O discurso do método, obra que explica o raciocínio científico. Nessa obra, Decárte estabeleceu um sistema de referência para localizar pontos no plano cartesiano. Em seu trabalho, Decárte buscou associar a Geometria à Álgebra, o que contribuiu muito para o desenvolvimento da Matemática.

Ilustração: caricatura de homem de cabelos compridos, sobrancelhas compridas e bigode fino. — Caricatura de René Decárte.

Atividade

Reúna-se com 3 colegas e pesquisem algumas aplicações do plano cartesiano. Depois, compartilhem o que pesquisaram com a turma.

Representação de um polígono

Para representar um polígono no plano cartesiano, podemos associar seus vértices a pares ordenados, unir esses pontos com segmentos de reta e, por fim, pintar o interior da figura.

Observe a representação do polígono ABCD com vértices a(2, 2), B(5, 5), C (5, 3) e D (4, 1) no plano cartesiano.

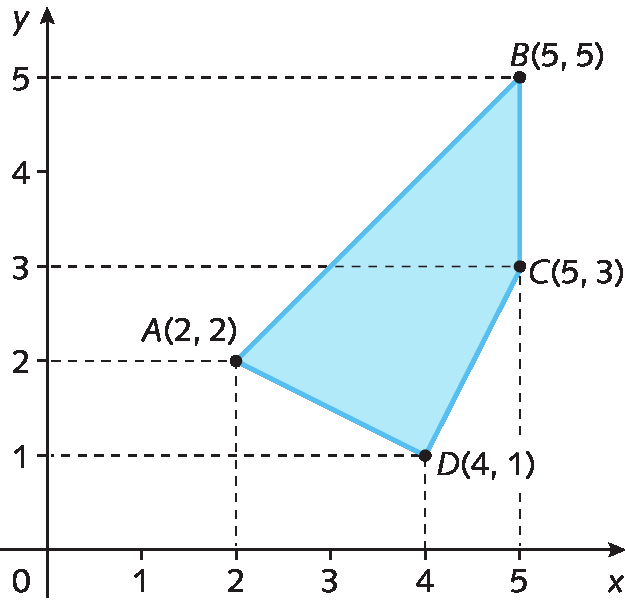
Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4 e 5 e eixo y com as representações dos números 0, 1, 2, 3, 4 e 5. No plano está representado um quadrilátero azul com vértices nos pontos A de abscissa 2 e ordenada 2, B de abscissa 5 e ordenada 5, C de abscissa 5 e ordenada 3 e D de abscissa 4 e ordenada 1.

Atividades

Faça as atividades no caderno.

1. Em seu caderno, construa um plano cartesiano e represente nele os pontos a(2, 2), B (3, 1), C (5, 0), D (0,2), ê (0, 0) e F (3, 4).

2. Determine as coordenadas de cada ponto marcado no plano cartesiano a seguir.

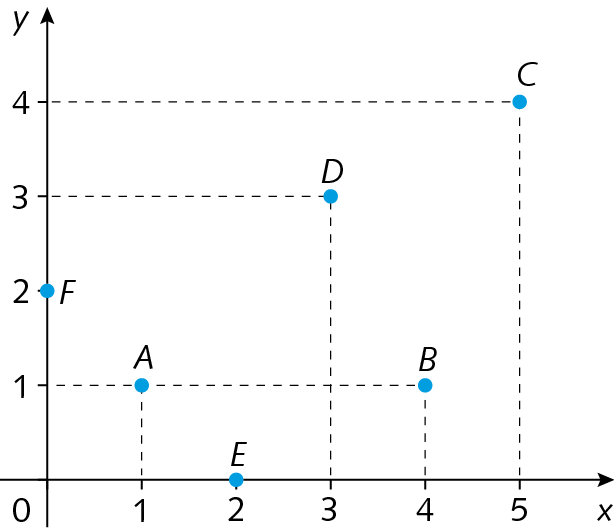
Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4 e 5 e eixo y com as representações dos números 0, 1, 2, 3 e 4. No plano estão representados os pontos A de abscissa 1 e ordenada 1, B de abscissa 4 e ordenada 3, C de abscissa 5 e ordenada 4, D de abscissa 3 e ordenada 3, E de abscissa 2 e ordenada 0 e F de abscissa 0 e ordenada 2.

3. No caderno, construa um quadrilátero com os vértices nos pontos a(2, 1), B (3, 3), C (4, 3) e D (4, 1). Esse quadrilátero é um paralelogramo ou um trapézio?

4. Conhecendo as coordenadas a(1, 2), B (3, 4) e C (5, 2), que correspondem aos vértices de um quadrado, construa, no plano cartesiano, o quadrado ABCD.

Página 220

2 Figuras semelhantes

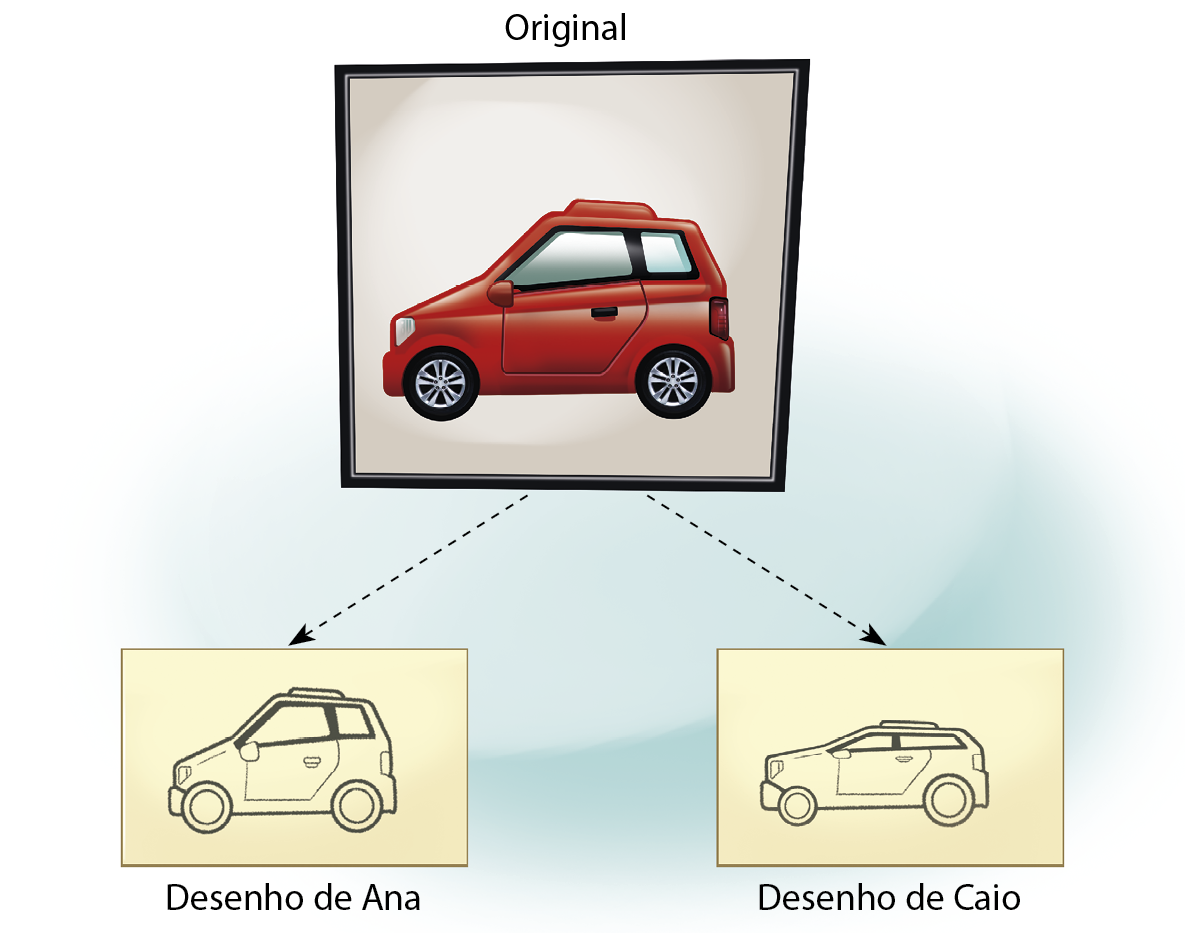
Quando ampliamos ou reduzimos proporcionalmente uma figura sem deformá-la, produzimos uma figura semelhante. Observe a seguir os desenhos que Ana e Caio fizeram ao tentar copiar a imagem do quadro pendurado na parede. Ana parece ter feito uma figura semelhante, mas Caio, não. No desenho de Caio, as medidas não parecem proporcionais à figura original.

Ilustração: Um quadro com fundo bege com a lateral esquerda de um carro vermelho desenhado. Duas setas tracejadas de cima para baixo. Na seta que vai para a esquerda um outro desenho idêntico do carro, sem estar pintado, numa folha bege. Abaixo a legenda Desenho de Ana. Na seta que vai para a direita um desenho de um carro diferente do outro, em uma folha bege. Abaixo a legenda Desenho de Caio.

Ampliação e redução de figuras planas na malha quadriculada

Podemos usar uma malha quadriculada para ampliar ou reduzir figuras planas.

Na ampliação, mantemos as medidas de abertura dos ângulos e multiplicamos todas as medidas de comprimento dos segmentos de reta por um mesmo número maior que 1.

Na redução, também mantemos as medidas de abertura dos ângulos, mas dividimos todas as medidas de comprimento dos segmentos de reta por um mesmo número maior que 1.

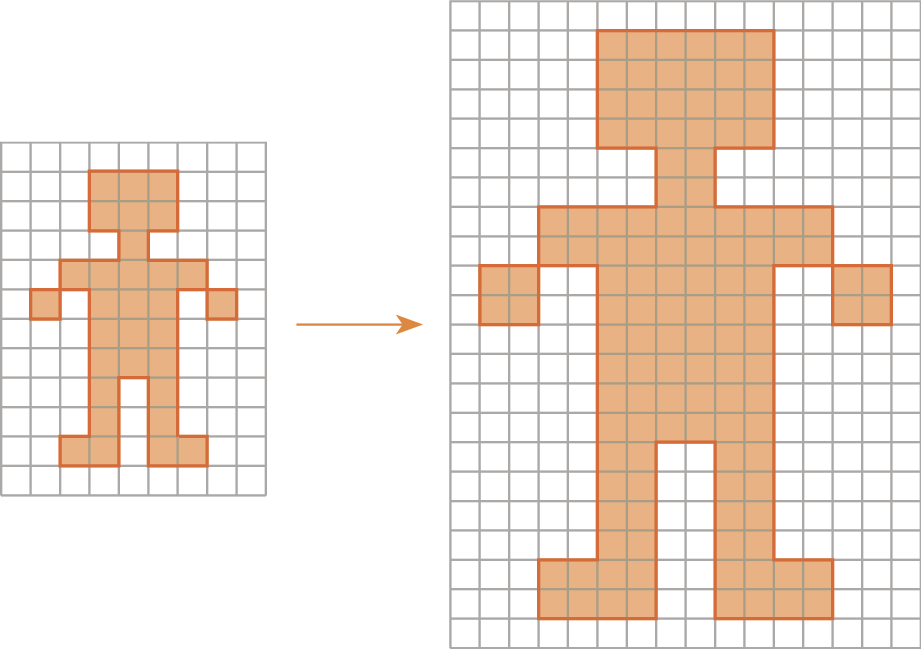
Ilustração. Do lado esquerdo, figura que se parece com um robô representado em uma malha quadriculada. A malha é composta de 12 linhas com 9 quadradinhos cada. O robô ocupa 31 quadradinhos.
A cabeça do robô tem formato retangular e é composta de 2 fileiras com 3 quadradinhos cada.
O pescoço do robô tem um quadradinho.
O tronco tem formato retangular e é composto de 4 fileiras com 3 quadradinhos cada.
Os braços ocupam dois quadradinhos cada.
As pernas ocupam 2 fileiras com um quadradinho.
E os pés ocupam 2 quadradinhos. Seta para a direita.
Do lado direito, figura que se parece com um robô representado em uma malha quadriculada. A malha é composta de 22 linhas com 16 quadradinhos cada. O robô ocupa 124 quadradinhos.
A cabeça do robô tem formato retangular e é composta de 4 fileiras com 6 quadradinhos cada.
O pescoço do robô tem formato de quadrado e é composto de 2 fileiras com 2 quadradinhos cada.
O tronco tem formato retangular e é composto de 8 fileiras com 6 quadradinhos cada.
Os braços ocupam 8 quadradinhos.
As pernas ocupam 3 fileiras com 2 quadradinhos cada.
Os pés ocupam 2 fileiras com 4 quadradinhos cada.
A figura representada na malha do lado direito é uma ampliação da figura representada na malha do lado esquerdo.

▸ Na ampliação da figura anterior, por quanto multiplicamos cada medida de comprimento?

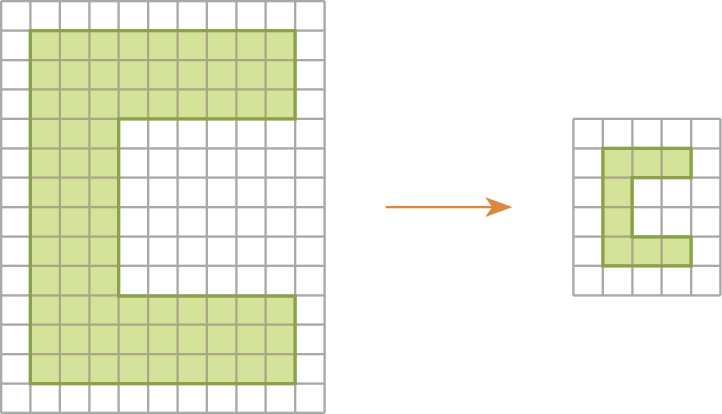
Ilustração. Do lado esquerdo, figura que se parece com a letra C representada em uma malha quadriculada. A malha é composta de 14 linhas com 11 quadradinhos cada. A figura ocupa 72 desses quadradinhos. Seta para a direita.
Do lado direito, figura que se parece com a letra C representada em uma malha quadriculada. A malha é composta de 6 linhas com 5 quadradinhos cada. A figura ocupa 8 desses quadradinhos.
A figura representada na malha do lado direito é uma redução da figura representada na malha do lado esquerdo.

▸ Na redução da figura anterior, por quanto dividimos cada medida de comprimento?

Página 221

Ampliação e redução de figuras planas no plano cartesiano

Como vimos, para representar polígonos no plano cartesiano, associamos seus vértices a pares ordenados. Dessa fórma, podemos representar o triângulo ABC de vértices a(1, 1), B(2, 3) e C(3, 2) como indicado a seguir.

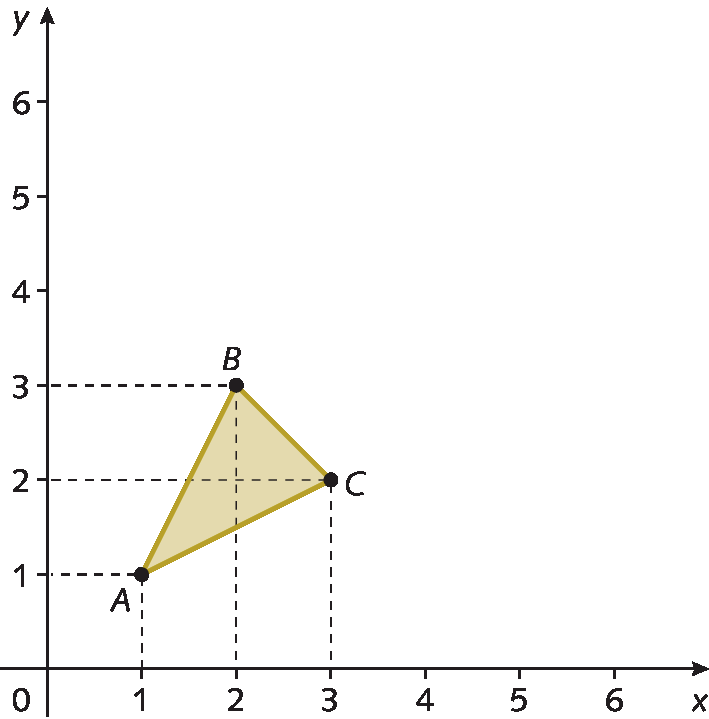
Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4, 5 e 6 e eixo y com as representações dos números 0, 1, 2, 3, 4, 5 e 6. No plano está representado um triângulo marrom com vértices nos pontos A de abscissa 1 e ordenada 1, B de abscissa 2 e ordenada 3 e C de abscissa 3 e ordenada 2.

Para reduzir o triângulo ABC anterior, podemos dividir as coordenadas de cada vértice pelo mesmo número e, para ampliá-lo, podemos multiplicar as coordenadas de cada vértice pelo mesmo número. Esse número, em ambos os casos, deve ser maior que 1.

Observe uma redução e uma ampliação do triângulo ABC.

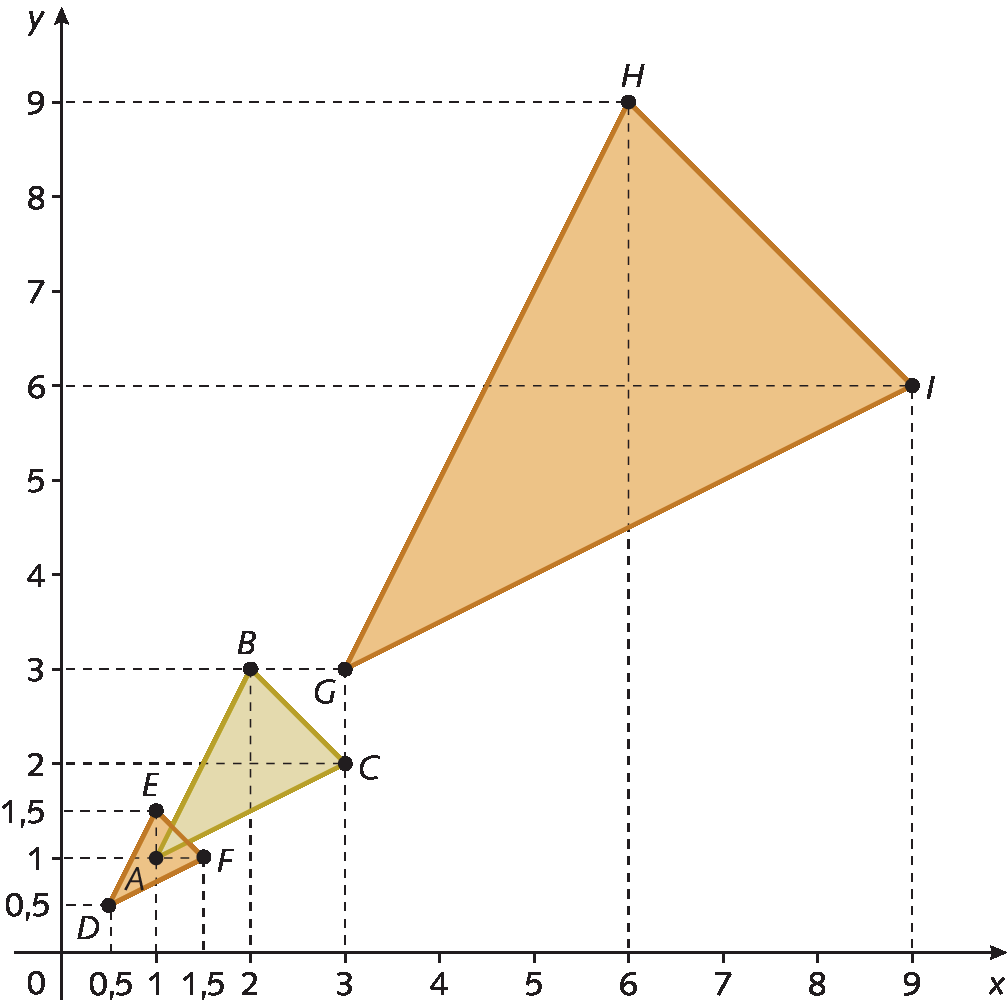
Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 e eixo y com as representações dos números 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. No plano estão representados três triângulos, um marrom e dois alaranjados. O triângulo alaranjado maior tem vértices nos pontos G de abscissa 3 e ordenada 3, H de abscissa 6 e ordenada 9 e I de abscissa 9 e ordenada 6. O triângulo marrom, tem vértices nos pontos A de abscissa 1 e ordenada 1, B de abscissa 2 e ordenada 3 e C de abscissa 3 e ordenada 2. O triângulo alaranjado menor tem vértices nos pontos D de abscissa 0,5 e ordenada 0,5, E de abscissa 1 e ordenada 1,5 e F de abscissa 1,5 e ordenada 1.

O triângulo DEF é uma redução do triângulo ABC. Para construí-lo, dividimos as coordenadas dos vértices do triângulo ABC por 2, obtendo os vértices D(0,5; 0,5), E(1; 1,5) e F(1,5; 1).

O triângulo GHI é uma ampliação do triângulo ABC. Para construí-lo, multiplicamos as coordenadas dos vértices do triângulo ABC por 3, obtendo os vértices G(3, 3), H(6, 9) e I(9, 6).

Página 222

Tecnologias digitais em foco

Ampliação e redução de figuras

Nesta seção utilizamos a ferramenta TucaProg ou outro recurso que seu professor pode indicar para criar um polígono no plano cartesiano e obter sua ampliação e redução.

Para resolver alguns problemas com o auxílio de um computador, é necessário utilizarmos algoritmos. Algoritmo é uma sequência finita e bem-definida de passos que resolve um problema ou determina a ordem de realização de uma tarefa.

À esquerda da interface do TucaProg, há um menu com as opções disponíveis, “Desenho”, “Movimento”, “Repetição” e “Números”. Ao completar as instruções, você clica no botão play, disponível nos comandos, e Tuca (o pássaro) desenhará no plano cartesiano de acôrdo com o passo a passo descrito.

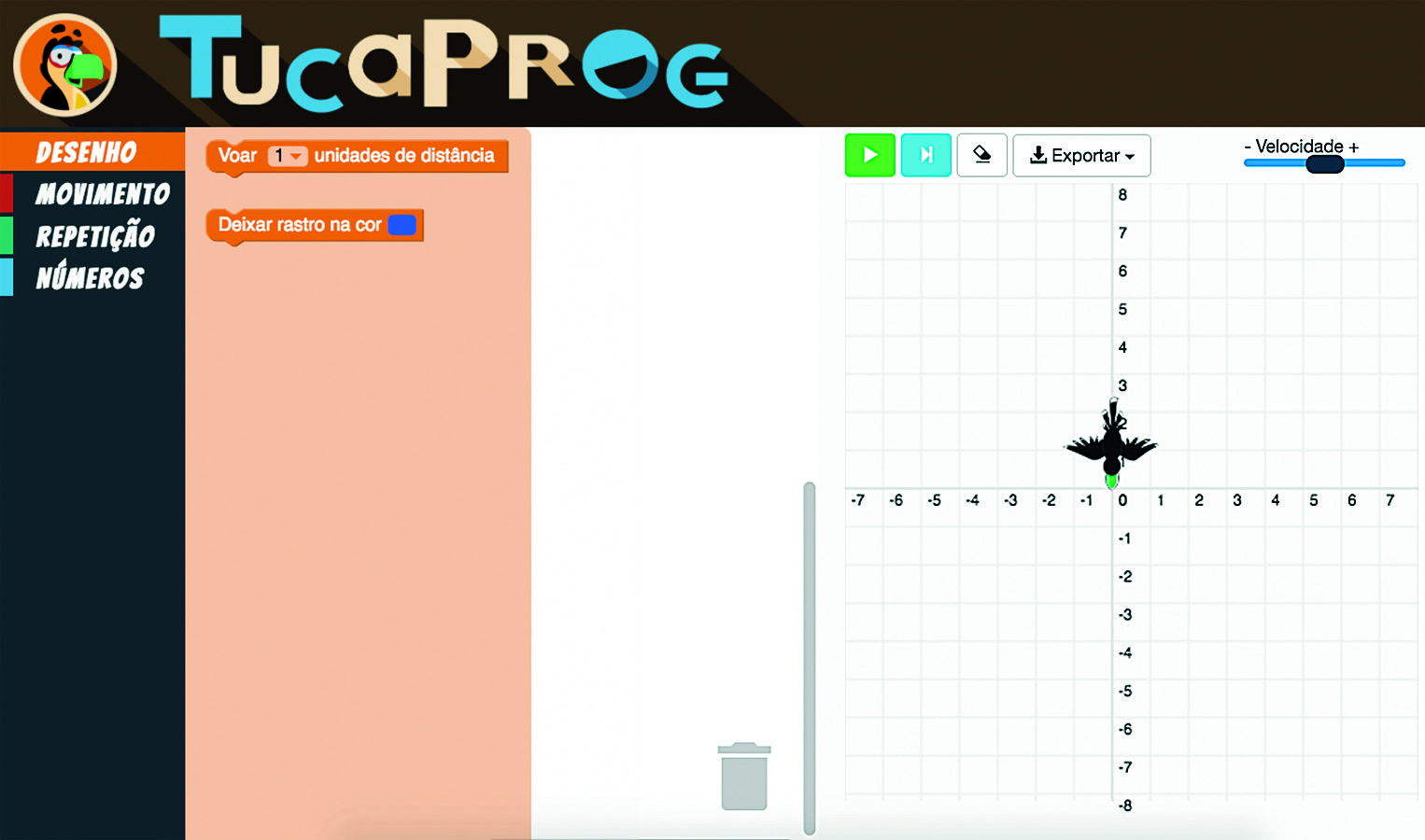
Captura de tela da ferramenta TucaProg. Na parte superior esquerda está o logotipo da ferramenta: símbolo de um tucano com bico verde e corpo laranja e preto. Do lado direito do logotipo o nome Tucaprog. Na lateral esquerda, de cima para baixo, há um menu com as ferramentas Desenho, Movimento, Repetição e Números. A ferramenta Desenho está selecionada. À direita das ferramentas, há uma faixa com dois comandos indicados: Na parte superior: voar 1 unidade de distância. Na parte inferior: Deixar rastro na cor azul. À direita da faixa, há a representação de um plano cartesiano com um tucano voando de cima para baixo, com bico encostado na origem e corpo paralelo ao eixo y. No eixo x, estão representados os números menos 7, menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5, 6 e 7. No eixo y, estão representados os números menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5 e 6. No canto inferior esquerdo deste plano há a representação de uma lixeira. Na parte superior do plano, há alguns botões e uma barra para aumentar e diminuir a medida da velocidade.

Construa

Vamos construir o contôrno de um quadrado, montando um bloco de instruções na área de programação, de acôrdo com a sequência a seguir.

1º) Informamos o par ordenado que indica o local onde o Tuca iniciará o desenho.

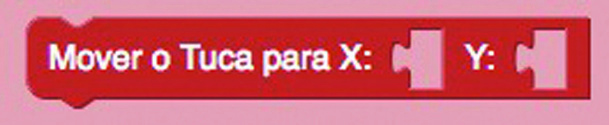
Captura de tela da ferramenta Tucaprog. Comando Mover Tuca para X, espaço para completar, Y, espaço para completar.

Página 223

Tecnologias digitais em foco

2º) Bloco de repetições: dentro desse bloco, informamos quais instruções serão repetidas e quantas vezes.

Captura de tela da ferramenta Tucaprog. Na linha de cima comando Repita, espaço para completar, vezes. Na linha de baixo, comando passos.

3º) Então, indicamos o sentido no qual desejamos que o Tuca gire para começar a desenhar.

Captura de tela da ferramenta Tucaprog. Comando Virar o sentido anti-horário 90°.

4º) Por fim, indicamos a medida da distância que o Tuca deve percorrer voando.

Captura de tela da ferramenta Tucaprog. Comando Voar 1 unidades de distância.

5º) Essas instruções, complementadas com as informações numéricas (coordenadas, quantidades e medidas em grau), produzem o contôrno de um quadrado.

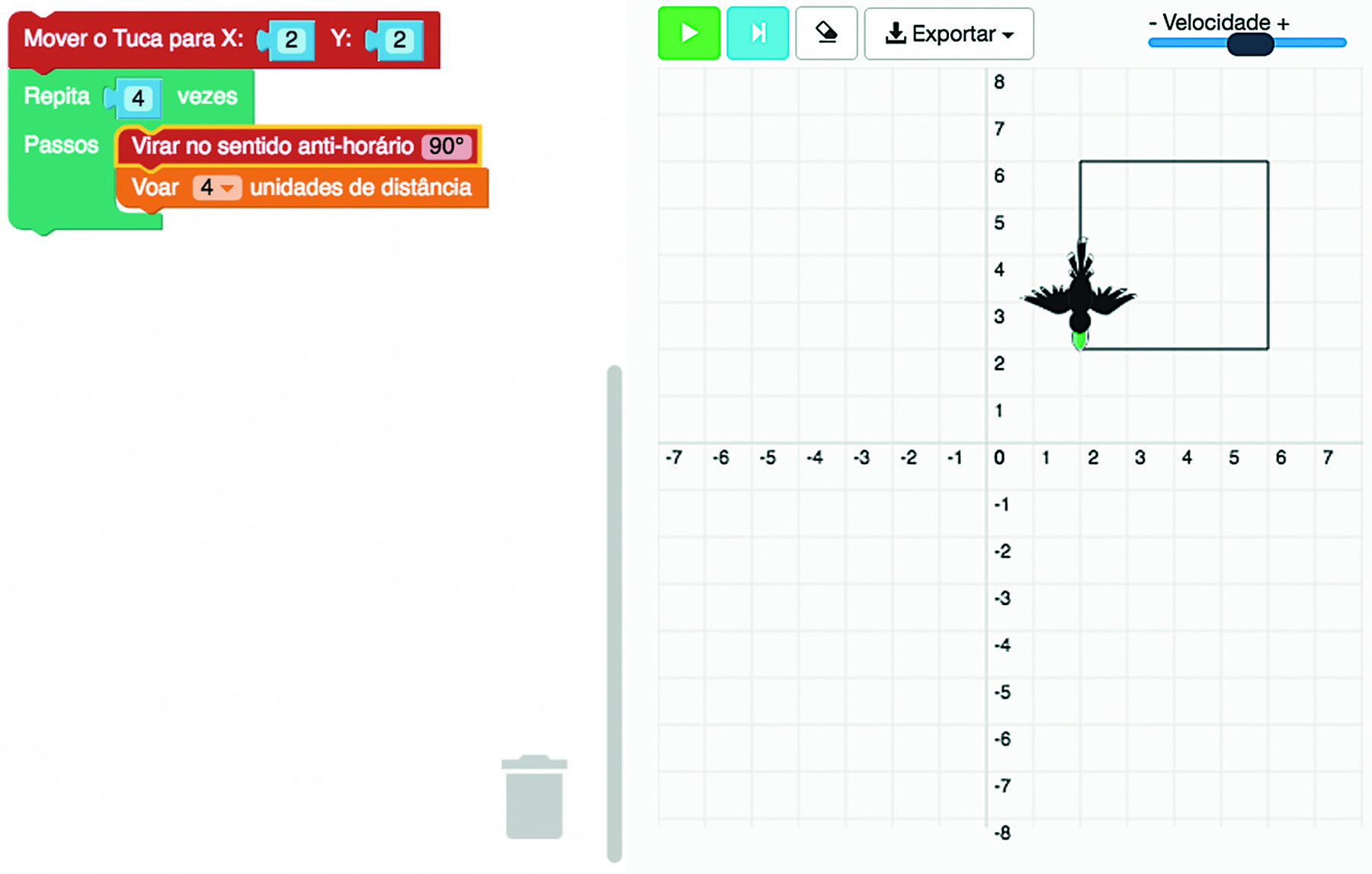
Captura de tela da ferramenta Tucaprog. De cima para baixo, na primeira linha comando Mover Tuca para X, 2 e Y, 2.
Na segunda linha, o comando Repita 4 vezes.
Na terceira linha, o comando Passos, virar
no sentido anti-horário 90°.
Na quarta linha, o comando Voar 4 unidades de distância.
Print da ferramenta TucaProg. Há a representação de um plano cartesiano com um tucano voando de cima para baixo, com bico encostado no ponto de abscissa 2 e ordenada 2. No eixo x, estão representados os números menos 7, menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5, 6 e 7. No eixo y, estão representados os números menos 8, menos 7, menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5, 6, 7 e 8.
No canto inferior esquerdo deste plano há a representação de uma lixeira.
Na parte superior do plano, há alguns botões e uma barra para aumentar e diminuir a medida da velocidade.
Há a representação de um quadrado com contorno preto com vértices nos pontos de abscissa 6 e ordenada 2, abscissa 6 e ordenada 6, abscissa 2 e ordenada 2 e abscissa 2 e ordenada 6.

Explore

Continue a montagem do bloco de instruções, de modo a construir uma redução e uma ampliação do contôrno de quadrado obtido.

Página 224

Atividades

Faça as atividades no caderno.

5. A figura B é uma redução da figura a? Justifique sua resposta.

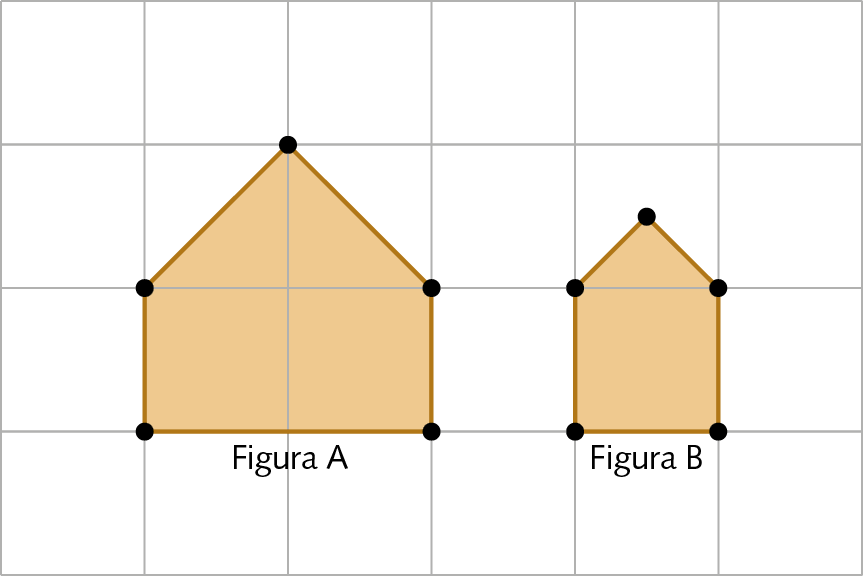
Esquema. Em uma malha quadriculada, à esquerda está representado um polígono de 5 lados alaranjado. Em cada um dos seus vértices há um ponto preto. Abaixo da figura, a indicação 'Figura A'. A Figura A ocupa dois quadrados inteiros e dois pela metade da malha. À direita está representado um polígono de 5 lados alaranjado. Em cada um dos seus vértices há um ponto preto. Abaixo da figura, a indicação 'Figura B'. A Figura B ocupa um quadrado inteiro e um quarto de um quadrado da malha.

6. Utilize uma folha de papel quadriculado para ampliar a figura a seguir. Multiplique a medida de comprimento de todos os segmentos de reta por 3.

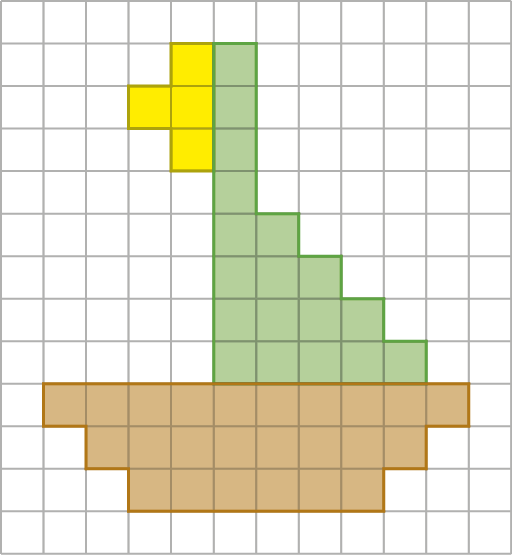
Ilustração. Figura que se parece com um barco representada em uma malha quadriculada. A malha é composta de 13 linhas com 12 quadradinhos cada. O barco ocupa 46 quadradinhos.
A vela do barco, que é verde, ocupa 18 quadradinhos e tem uma bandeira amarela que ocupa 4 quadradinhos no seu topo.
O casco do barco é marrom e ocupa 24 quadradinhos.

7. Em uma folha de papel quadriculado, reduza a figura a seguir. Divida a medida de comprimento de todos os segmentos de reta por 2.

Ilustração. Figura que se parece com um emoji amarelo representada em uma malha quadriculada. O emoji lembra a figura de um círculo e possui boca, olhos e sobrancelhas pretas. A malha é composta de 30 linhas com 32 quadradinhos cada.

8. No plano cartesiano, faça uma ampliação do pentágono ABCDE de vértices a(1, 1), B (2, 2), C (3, 2), D (3, 1) e ê (2, 0), de fórma que a medida de comprimento de seus lados tenha o dobro das medidas de comprimento dos lados originais.

9. Os pares ordenados (1, 1), (3, 1) e (3, 2) correspondem aos vértices de uma redução do polígono cujos vértices correspondem aos pares ordenados (2, 2), (6, 2) e (6, 4)? Justifique sua resposta.

Página 225

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Representação de um polígono no plano cartesiano

A localização de pontos em um plano é feita com o auxílio de duas retas numéricas perpendiculares, chamadas eixos, que, em geral, indicamos por x (eixo horizontal) e y (eixo vertical). Esses eixos determinam o plano cartesiano. O ponto de intersecção dos dois eixos é denominado origem e é representado pela letra O.

Cada ponto desse plano pode ser representado por dois números entre parênteses, que chamamos par ordenado.

Representação de um polígono

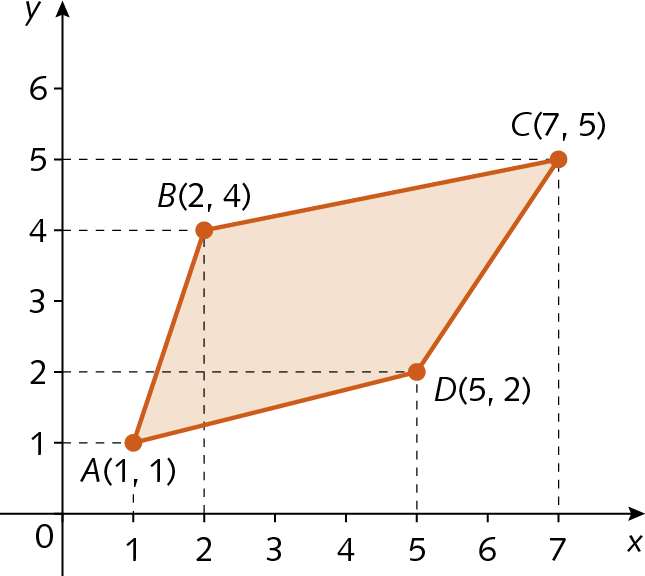
Observe, a seguir, a representação do polígono ABCD com vértices a(1, 1), B(2, 4), C(7, 5) e D(5, 2) no plano cartesiano.

Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4, 5, 6 e 7 e eixo y com as representações dos números 0, 1, 2, 3, 4, 5 e 6. No plano está representado um quadrilátero alaranjado com vértices nos pontos A de abscissa 1 e ordenada 1, B de abscissa 2 e ordenada 4, C de abscissa 7 e ordenada 5 e D de abscissa 5 e ordenada 2.

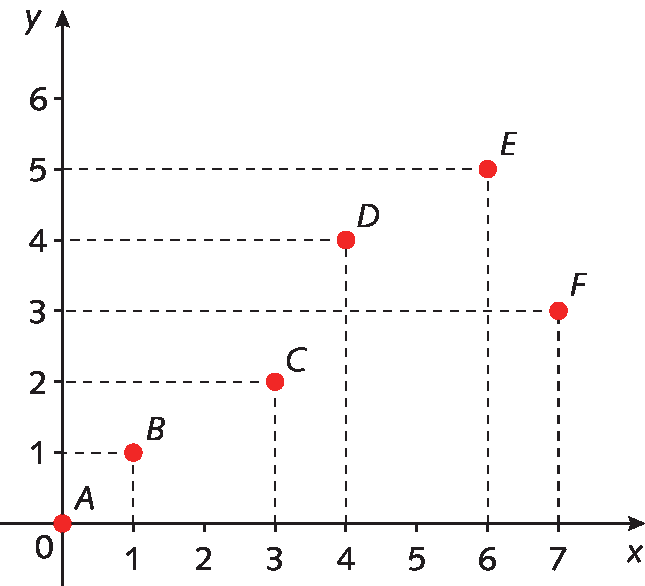
1. Escreva as coordenadas de cada ponto marcado no plano cartesiano a seguir.

Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4, 5, 6 e 7 e eixo y com as representações dos números 0, 1, 2, 3, 4, 5 e 6. No plano estão representados os pontos A de abscissa 0 e ordenada 0, B de abscissa 1 e ordenada 1, C de abscissa 3 e ordenada 2, D de abscissa 4 e ordenada 4, E de abscissa 6 e ordenada 5 e F de abscissa 7 e ordenada 3.

2. Em seu caderno, represente em um plano cartesiano os pontos a(2, 3), B(4, 4), C(3, 6), D(5, 2) e ê(6, 1).

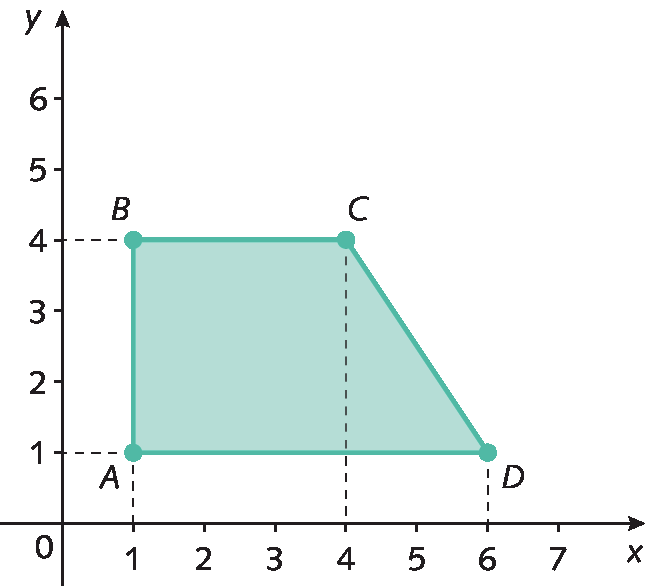
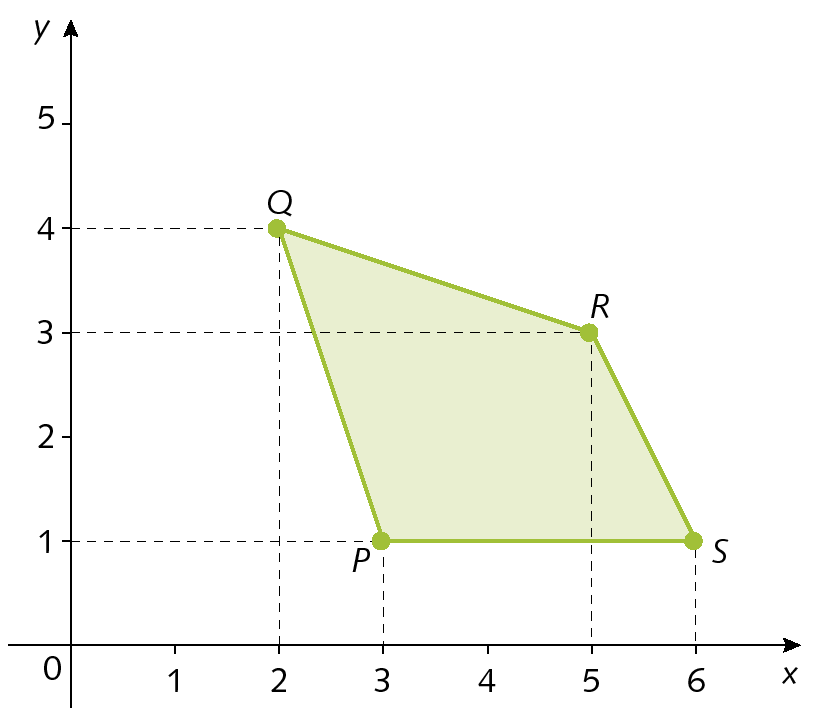
3. Determine os pares ordenados correspondentes aos vértices do trapézio representado no plano cartesiano a seguir.

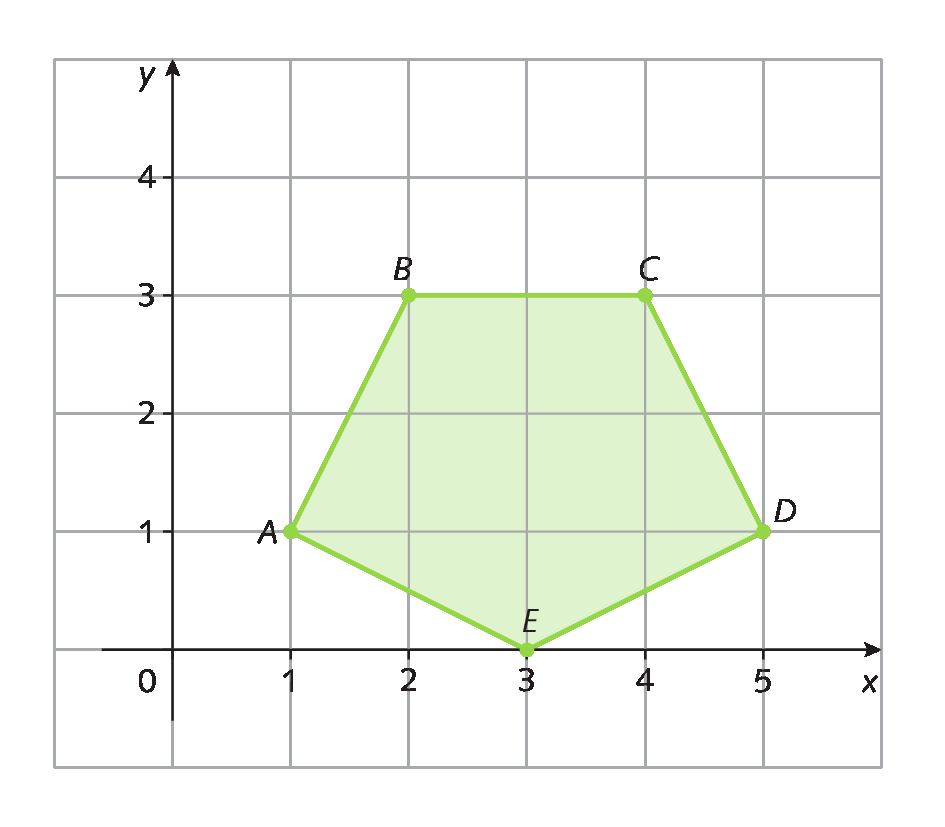
4. Quais são as coordenadas dos vértices a, B, C, D e ê do pentágono a seguir?

Plano cartesiano representado em uma malha quadriculada. Eixo x com as representações dos números 0, 1, 2, 3, 4 e 5 e eixo y com as representações dos números 0, 1, 2, 3 e 4. No plano está representado um polígono de 5 lados com vértices nos pontos A de abscissa 1 e ordenada 1, B de abscissa 2 e ordenada 3, C de abscissa 4 e ordenada 3, D de abscissa 5 e ordenada 1 e E de abscissa 3 e ordenada 0.

5. Os pares ordenados a(1, 1), B(1, 4), C(4, 4) e D(4, 1) correspondem aos vértices de qual polígono?

6. Construa em um plano cartesiano um triângulo retângulo com um ângulo reto em (2, 0), um vértice em (2, 3) e a base no eixo x com duas unidades a mais de medida de comprimento do que a medida referente à altura.

7. Um triângulo isósceles é construído em um plano cartesiano com a base no eixo x medindo duas unidades de comprimento e com o vértice oposto à base associado ao par ordenado (2, 3). Quais são as coordenadas dos vértices da base?

8. Em seu caderno, construa um plano cartesiano e represente o paralelogramo com vértices nos pontos a(0, 0), B(1, 4), C(6, 5) e D(5, 1).

Página 226

Figuras semelhantes

Ampliação e redução de figuras planas em malha quadriculada

Podemos usar uma malha quadriculada para ampliar ou reduzir figuras planas.

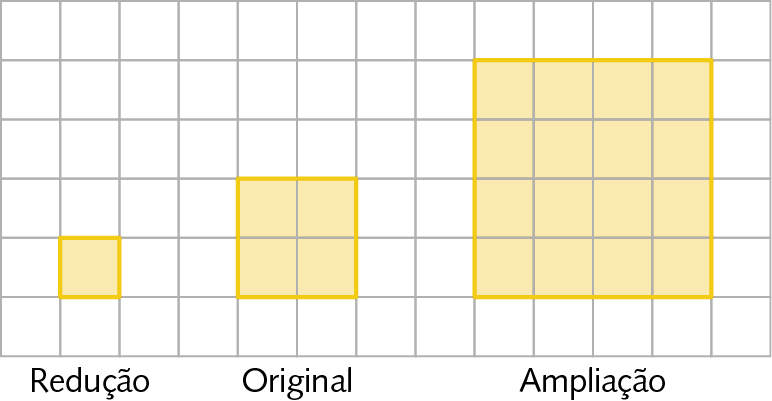
Esquema. Em uma malha quadriculada, de 6 linhas com 13 quadradinhos cada, da esquerda para a direita: a primeira figura é um quadrado alaranjado que ocupa 1 quadradinho. Abaixo do quadrado a indicação 'Redução'. A segunda figura é um quadrado alaranjado que ocupa 4 quadradinhos. Abaixo do quadrado a indicação 'Original'. A terceira figura é um quadrado alaranjado que ocupa 16 quadradinhos. Abaixo do quadrado a indicação 'Ampliação'.

Na ampliação, mantemos as medidas de abertura dos ângulos e multiplicamos todas as medidas de comprimento dos segmentos de reta por um mesmo número maior que 1.

Na redução, também mantemos as medidas de abertura dos ângulos, mas dividimos as medidas de comprimento dos segmentos de reta por um mesmo número maior que 1.

Ampliação e redução de figuras planas no plano cartesiano

O triângulo GHI é uma ampliação do triângulo ABC e o triângulo DEF é uma redução do triângulo ABC.

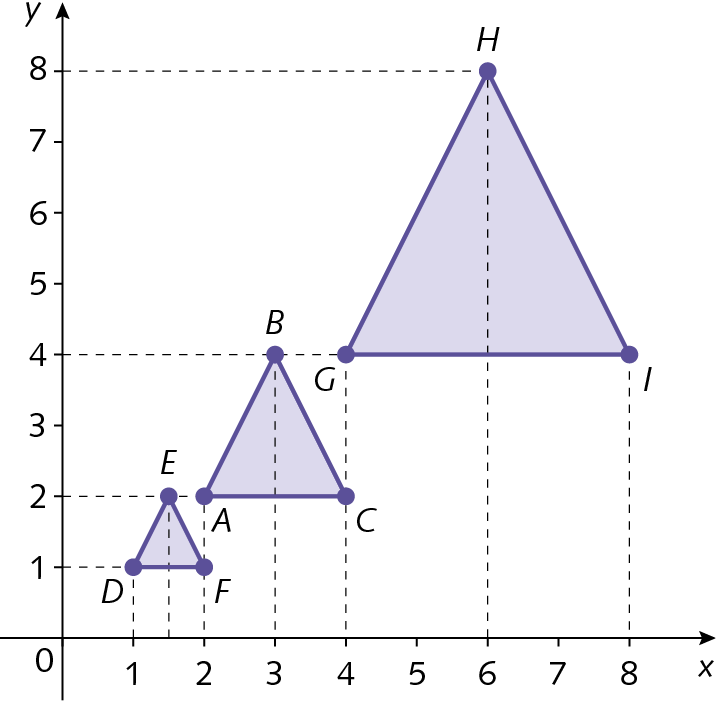
Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4, 5, 6, 7 e 8 e eixo y com as representações dos números 0, 1, 2, 3, 4, 5, 6, 7 e 8. No plano estão representados três triângulos roxos. O triângulo maior tem vértices nos pontos G de abscissa 4 e ordenada 4, H de abscissa 6 e ordenada 8 e I de abscissa 8 e ordenada 4. O triângulo médio, tem vértices nos pontos A de abscissa 2 e ordenada 2, B de abscissa 3 e ordenada 4 e C de abscissa 4 e ordenada 3. O triângulo menor tem vértices nos pontos D de abscissa 1 e ordenada 1, E de abscissa 1,5 e ordenada 2 e F de abscissa 2 e ordenada 1.

Para reduzir o triângulo ABC anterior, podemos dividir as coordenadas de cada vértice pelo mesmo número e, para ampliá-lo, podemos multiplicar as coordenadas de cada vértice por um mesmo número. Esse número, em ambos os casos, deve ser maior que 1.

9. A figura B é uma ampliação da figura a? Justifique sua resposta.

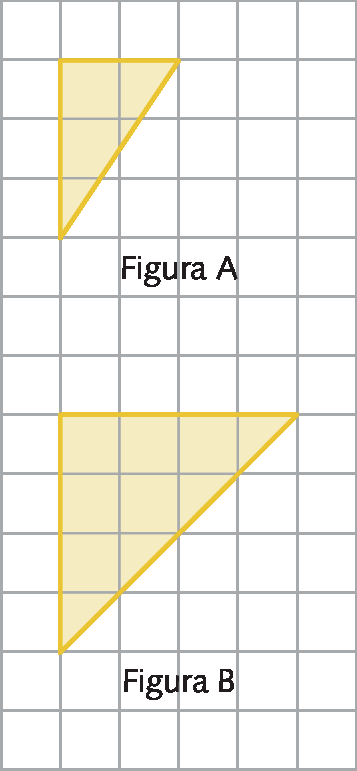
Ilustração. Em uma malha quadriculada, de 13 linhas com 6 quadradinhos cada, de cima para baixo: a primeira figura é um triângulo alaranjado que ocupa aproximadamente 3 quadradinhos. Abaixo do triângulo a indicação ‘Figura A’. A segunda figura é um triângulo alaranjado que ocupa aproximadamente 8 quadradinhos. Abaixo do triângulo a indicação ‘Figura B’.

10. Em uma folha de papel quadriculado, amplie a figura a seguir. Multiplique a medida de comprimento de todos os segmentos de reta por 2.

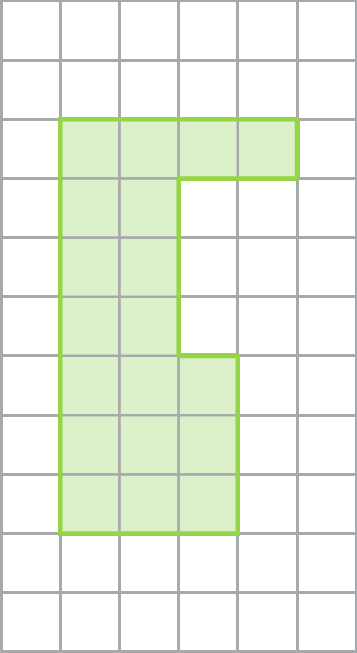
Ilustração. Malha quadriculada, de 11 linhas com 6 quadradinhos cada com a representação de uma figura verde. De cima para baixo, na terceira linha, da esquerda para a direita, a partir do segundo, há 4 quadrados verdes. Nas quarta, quinta e sexta linhas, da esquerda para a direita, a partir do segundo, há dois quadrados verdes em cada. Nas sétima, oitava e nona linhas, da esquerda para a direita, a partir do segundo quadradinho, há 3 quadradinhos verdes.

11. O polígono representado a seguir é uma redução do polígono com os vértices associados aos pontos a(6, 2), B(4, 8), C(10, 6) e D(12, 2)?

Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4, 5 e 6 e eixo y com as representações dos números 0, 1, 2, 3, 4 e 5. No plano está representado um quadrilátero verde com vértices nos pontos P de abscissa 3 e ordenada 1, Q de abscissa 2 e ordenada 4, R de abscissa 5 e ordenada 3 e S de abscissa 6 e ordenada 1.

Página 227

É hora de extrapolar

Faça as atividades no caderno.

Você já pensou em como os murais são feitos?

A arte do grafite, diretamente conectada ao movimento hip-hop, tornou-se popular na década de 1970 nos bairros de Nova iórque como um tipo de manifestação, por meio de desenhos e mensagens, para expressar a realidade dos menos favorecidos e refletir sobre ela. Ao mesmo tempo, artistas brasileiros desenvolveram as próprias técnicas, alguns com um toque de brasilidade, e se tornaram conhecidos mundialmente. Hoje em dia, os grafites estão cada vez mais presentes nos espaços públicos: tornando a arte acessível à população, propiciando a reflexão e a crítica a problemas sociais e contribuindo para a revitalização urbana, como o mural Etnias, do artista brasileiro Eduardo Kobra.

Conheça mais

Você pode conhecer telas e projetos de Eduardo Kobra acessando a página oficial do artista na internet.

Objetivos: Pesquisar a arte do grafite e a técnica de ampliação de desenhos para a realização de obras de arte, que serão expostas na sala de aula e na escola.

Etapa 1: Análise do mural Etnias.

Fotografia: Um enorme mural pintado em uma parede. No centro uma imagem de um menino indígena, com cocar e rosto pintado com traçados amarelos, azuis, vermelhos, laranjas e verdes. No lado direito do painel, está a imagem de uma mulher negra com cabelos longos e encaracolados. Próximo a essa imagem duas mulheres andam pela calçada. O dia está ensolarado sem nuvens no céu. — Em 2016, Eduardo Kobra e sua equipe realizaram o maior grafite do planeta, o mural Etnias, com 3 mil metros quadrados, na zona portuária da cidade do Rio de Janeiro. O mural traz os representantes de cinco povos, um de cada continente: os Mursi (África), os Kayin (Ásia), os Tapajós (Américas), os Supi (Europa) e os Huli (Oceania).

Reúna-se em grupo com os colegas, analisem o mural da foto e respondam às questões.

a) Quais povos foram representados no mural?

b) Em entrevista, Kobra disse que o mural procura passar a mensagem de paz e união dos povos. Vocês acham que, de fato, a obra transmite essa mensagem? Justifiquem.

c) Como vocês acham que foi feita essa obra de arte? Que materiais e técnicas foram usados?

d) Quais figuras geométricas planas é possível identificar na obra apresentada?

Leiam o texto sobre a quantidade de tinta e o tempo de elaboração do mural.

“Na confecção da obra, foram usadas 3 mil latas de spray, 700 litros de tinta colorida e .1800 litros de tinta branca para o fundo. Para que ficasse pronta antes da Rio-2016, Eduardo Kobra e sua equipe encararam uma maratona de 12 horas de trabalhos diários durante dois meses. E essa não foi a única parte complicada: ele estima ter levado três meses para chegar ao resultado final do desenho, fruto de uma pesquisa profunda sobre povos nativos ao redor do globo.”

Disponível em: https://oeds.link/YgMwrj. Acesso em: 2 maio 2022.

a) Qual foi o total de tinta, em litro, usado no mural? Que porcentagem representa a quantidade de tinta colorida? E de tinta branca?

b) Quantos meses foram necessários para finalizar o mural, considerando todas as etapas? Que porcentagem representa o tempo gasto apenas para chegar ao resultado final do desenho, antes de iniciar o trabalho na parede?

Página 228

Etapa 2: Pesquisa sobre a arte do grafite e o uso da técnica de ampliação de desenhos.

3. Pesquisem em jornais, revistas e na internet:

• o significado da expressão “grafite”;

• técnicas usadas por grafiteiros;

• mulheres grafiteiras e suas obras.

4. Para a realização de suas obras, Kobra, assim como muitos artistas, desenha primeiro no papel. Em seguida, usa uma malha quadriculada com referências de localização, como no jôgo “batalha-naval”, numerando as linhas e as colunas. Assim, depois de preparar e quadricular o muro, com quadrados maiores, usando as mesmas referências do papel, é necessário reproduzir no muro o que foi feito no papel.

Fotografia: um homem branco, com camiseta branca, chapéu marrom, está grafitando uma parede. Na sua mão esquerda ele segura a lata de spray de tinta. Na mão direita ele segura uma folha sobre uma madeira com o desenho que ele está reproduzindo na parede. Do desenho que ele está segurando, sai um círculo destacando o desenho em um tamanho maior onde é possível identificar uma pessoa negra com pinturas verdes, vermelhas e amarelas no rosto. A pessoa tem um adereço na cabeça que tem enfeites ao lado do rosto — Técnica utilizada por Eduardo Kobra para a confecção de suas obras de arte.

a) Em uma malha quadriculada, numerem as linhas e as colunas e desenhem figuras geométricas planas (retângulos, triângulos, pentágonos etcétera).

b) Em uma cartolina, tracem uma malha quadriculada, com quadrados maiores, e reproduzam as figuras geométricas feitas anteriormente, respeitando as referências de localização de cada quadrado.

Etapa 3: Elaboração de obras de arte com a técnica de ampliação.

5. Escolham um tema ou uma mensagem que julguem importante e que possa ser representado(a) com um desenho: meio ambiente, diversidade cultural, cidadania etcétera.

6. Façam em uma malha quadriculada um desenho que expresse a mensagem escolhida pelo grupo.

7. Reproduzam o desenho em uma cartolina, mas em tamanho maior, usando a técnica estudada.

8. Agora, façam um desenho em um malha quadriculada e peçam a outro grupo que faça a ampliação do desenho em uma cartolina.

Etapa 4: Exposição e análise das obras de arte.

9. Disponibilizem as obras criadas pelo grupo para que os outros analisem e opinem sobre o significado e a mensagem representada em cada obra.

10. Anotem as dúvidas, as opiniões e as sugestões dos colegas.

11. Se possível, escolham uma ou mais obras para serem reproduzidas em paredes da escola.

Etapa 5: Síntese do trabalho realizado.

12. Algumas questões que devem ser discutidas:

a) As obras de arte atenderam aos objetivos propostos?

b) Vocês acreditam que a arte pode levar à reflexão de problemas sociais?

13. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.