Unidade 4
Capítulo 11 Grandezas e medidas
Capítulo 12 Probabilidade e estatística
Capítulo 11 Grandezas e medidas
Trocando ideias

A sinalização de trânsito informa e orienta os usuários das vias. Respeitar a sinalização garante um trânsito mais organizado e seguro para os condutores e pedestres. Observe alguns exemplos de sinalização nas cenas a seguir.
CENA um

CENA dois

▸

Que grandeza e que unidade de medida estão relacionadas a cada cena anterior?
▸


Qual é o significado das placas a seguir? Converse com os colegas.



Neste capítulo, vamos estudar as grandezas e as medidas que estão presentes em diferentes situações do nosso cotidiano.

1 Grandeza comprimento
Unidades de medida de comprimento
A primeira grandeza que vamos estudar será o comprimento. O Sistema Internacional de Unidadesglossário (ésse Í) adota o metro (símbolo: ême) como unidade‑padrão para medir o comprimento.
Observe algumas situações que envolvem medidas de comprimento em metro.


A palavra “metro” vem do grego métron e significa “o que mede”.

Um pouco de história
Faça a atividade no caderno.
O sistema métrico decimal
Na Antiguidade, cada povo utilizava uma unidade de medida, o que dificultava as trocas de produtos entre pessoas de sociedades diferentes. Com o desenvolvimento do comércio, tornou-se cada vez mais difícil a troca de informações e as negociações.
Por causa dessa dificuldade, em 1789, a Academia de Ciências da França unificou o sistema de medidas no país com base em padrões precisos, científicos e simples. Dessa fórma, foi criado o sistema métrico decimal, instituído oficialmente em junho de 1799. Ele recebeu esse nome porque, com base em uma unidade-padrão, as demais unidades são obtidas por meio da multiplicação ou da divisão dessa unidade por 10, por 100, por .1000 etcétera.
O Sistema Internacinal de Unidades, aprovado em 1960 e utilizado hoje em quase todos os países, é a versão atualizada do sistema métrico decimal.
Atividade
Você conhece outra unidade de medida que faz parte do Sistema Internacinal de Unidades? Qual?
O metro é a unidade de medida de comprimento adequada para todas as situações? Que unidade devemos usar para medir, por exemplo, a distância entre dois bairros? E para medir o comprimento de um inseto? Para casos como esses, foram criados os múltiplos e os submúltiplos do metro.
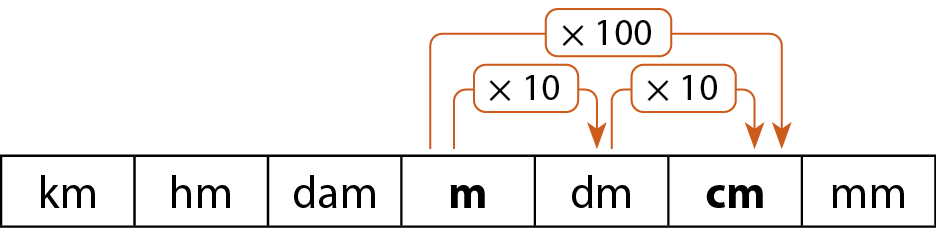
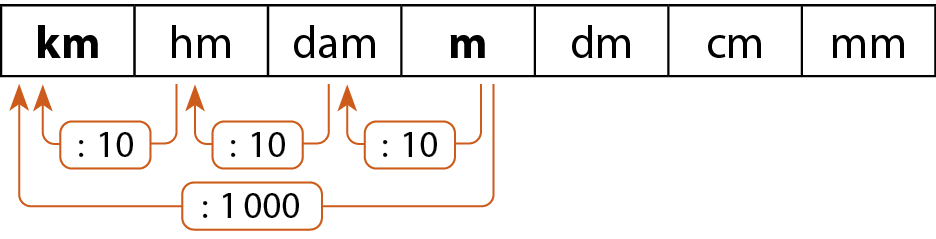
Observe o quadro a seguir, que apresenta os múltiplos (unidades maiores que o metro) e os submúltiplos (unidades menores que o metro) do metro que fazem parte do Sistema Internacinal de Unidades.
|
Múltiplos |
Unidade-padrão |
Submúltiplos |
|||||
|---|---|---|---|---|---|---|---|
|
Unidade |
quilômetro |
hectômetro |
decâmetro |
metro |
decímetro |
centímetro |
milímetro |
|
Símbolo |
km |
hm |
dam |
m |
dm |
cm |
mm |
|
Relação com o metro |
1.000 m |
100 m |
10 m |
1 m |
0,1 m |
0,01 m |
0,001 m |
Para medidas extremamente pequenas, como as de seres microscópicos, em que se exige grande precisão, utilizamos submúltiplos menores que o milímetro, como o micrômetroglossário (micrométro).
1 micrômetro = 1 micrométro = 0,000001 métro
Para medir distâncias extremamente grandes, como a distância entre estrelas e planetas, utilizamos a unidade astronômica (U A), que equivale a aproximadamente 150 bilhões de metros. Essa é a medida aproximada da distância entre a Terra e o Sol.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
Instrumentos de medida de comprimento
Podemos utilizar diferentes instrumentos para medir comprimentos. Veja alguns.
• Instrumentos do dia a dia




• Instrumentos de precisão


• Instrumentos que utilizam ondas


▸ Você conhece outros instrumentos de medida de comprimento? Se sim, quais? Responda no caderno.
Transformações envolvendo unidades de medida de comprimento
Utilizando o quadro de unidades, podemos converter uma unidade de medida de comprimento em outra. Considere os exemplos a seguir.
a) 4 metros em centímetros
1 métro = 100 centímetros
4 métros = 4 ⋅ 100 centímetros = 400 centímetros
Portanto, 4 metros é igual a 400 centímetros.
b) 4 metros em quilômetros
1 métro =
Fração um milésimoquilômetro = 0,001 quilômetro
4 métros = 4 ⋅ 0,001 quilômetro = 0,004 quilômetro
Portanto, 4 metros é igual a 0,004 quilômetro.

Veja que interessante
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
O pé, a polegada, a jarda e a milha
O pé, a polegada, a jarda e a milha não fazem parte do sistema métrico decimal e são medidas de comprimento usadas em países de língua inglesa.
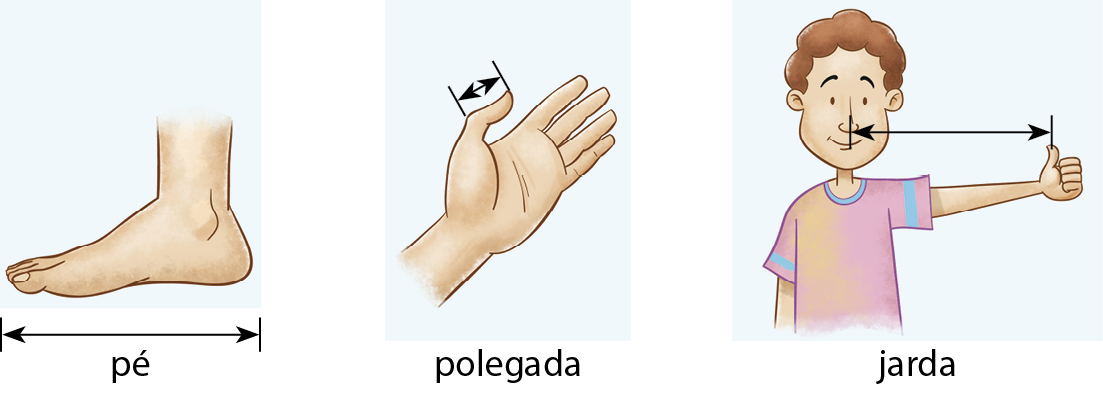
Observe as relações dessas unidades de medida com o metro:
• 1 pé equivale a 30,48 centímetros;
• uma polegada equivale a 2,54 centímetros;
• uma jarda equivale a 91,44 centímetros;
• uma milha terrestre equivale a .1609 metros;
• uma milha marítima equivale a .1852 metros.
Verifique que:
• 1 pé equivale a 12 polegadas;
• uma jarda equivale a 3 pés.
As fotos a seguir mostram exemplos de uso das unidades de medida jarda e pé.


Atividade


Você conhece alguma situação cotidiana em que utilizamos a unidade de medida polegada? Se sim, qual? Converse com os colegas.
Atividades
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
1. Para medir uma grandeza, podemos usar unidades padronizadas de medida (centímetro, metro etcétera) ou unidades não padronizadas de medida (palmo, passo etcétera).

a) Utilize seu palmo e responda: Qual é a medida da altura de sua cadeira em palmos?
b) Utilize seu passo e responda: Qual é a medida da largura da sala de aula em passos?
c)

Compare as medidas obtidas nos itens a e bê com as de um colega. Elas são iguais ou diferentes? Justifique a resposta.
2. Qual é a necessidade de usar o Sistema Internacinal de Unidades?
3. Qual é a unidade mais adequada para medir:
a) o comprimento de um móvel?
b) a distância entre duas cidades?
c) o comprimento de uma caneta?
d) a espessura de uma folha de papel?
4. Qual é o instrumento de medida mais adequado para medir:
a) a largura da página de um livro?
b) a espessura de uma folha de papel?
5. Paula mediu, com uma régua graduada em centímetro, o comprimento da tampa da sua caneta. Sabendo que cada um desses centímetros está dividido em dez partes (milímetros), responda às questões.

a) Qual é a medida do comprimento da tampa da caneta em centímetro?
b) Qual é a medida do comprimento da tampa da caneta em milímetro?
6. Faça o que se pede.
a) Com uma régua, meça o comprimento e a largura da sua borracha e escreva essas medidas em centímetro e milímetro.
b) Meça a largura do livro usando o comprimento da sua borracha como unidade de medida.
c) Sem usar a régua, determine a medida da largura do livro em centímetro e milímetro.
7. Em um prédio, foram utilizados tubos de aço de 4 polegadas para a tubulação de incêndio. A quantos centímetros correspondem 4 polegadas? (uma polegada = 2,54 centímetros)
8. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a) 8 métros =

centímetros
b) 12 métros =

milímetros
c) 70 métros =

decâmetros
d) 95 métros =

hectômetros
9. Responda às questões no caderno.
a) 15 quilômetros equivalem a quantos metros?
b) 3,8 metros equivalem a quantos milímetros?
c) 0,65 metro equivale a quantos centímetros?
d) .5000 metros equivalem a quantos quilômetros?
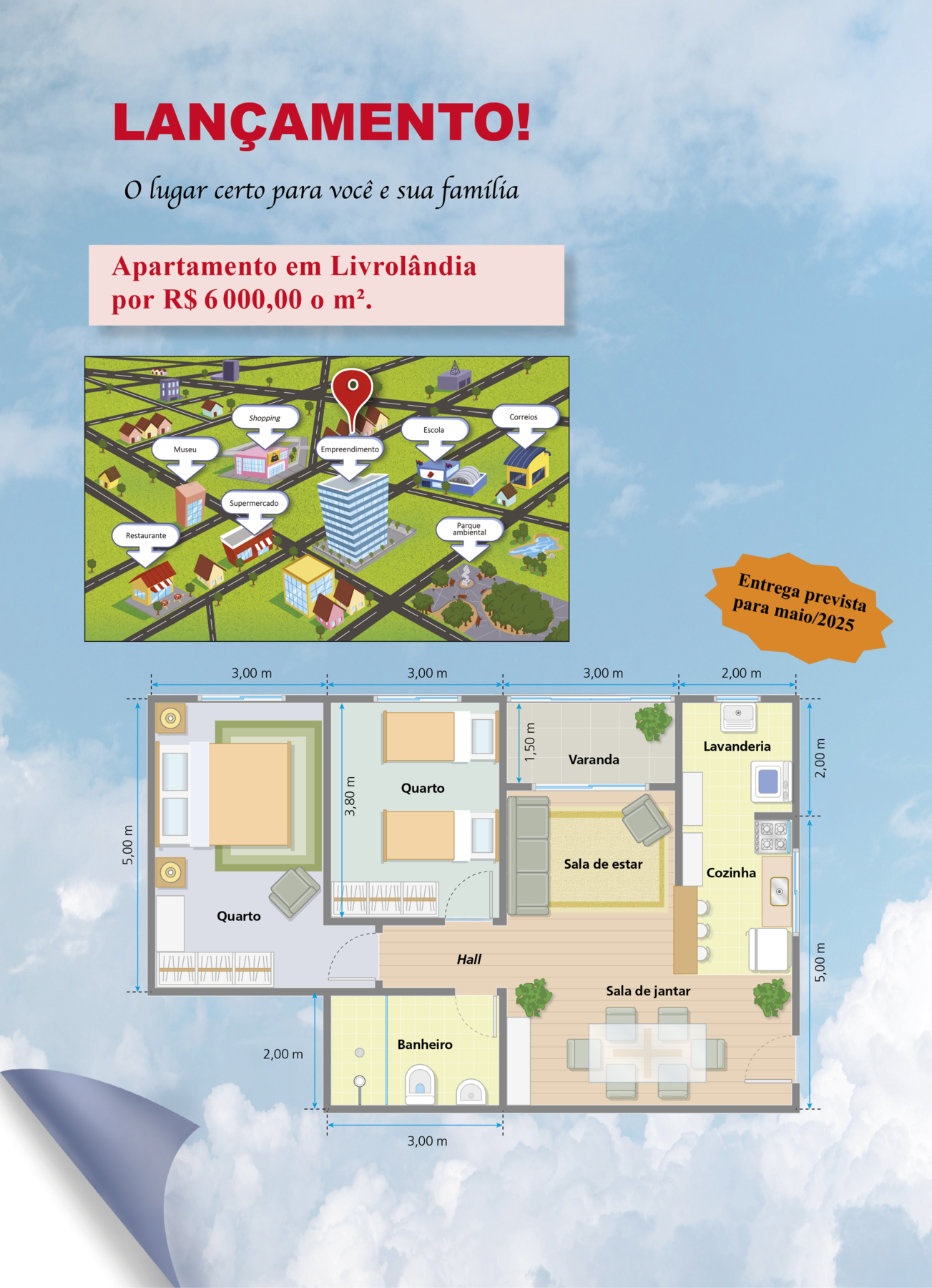
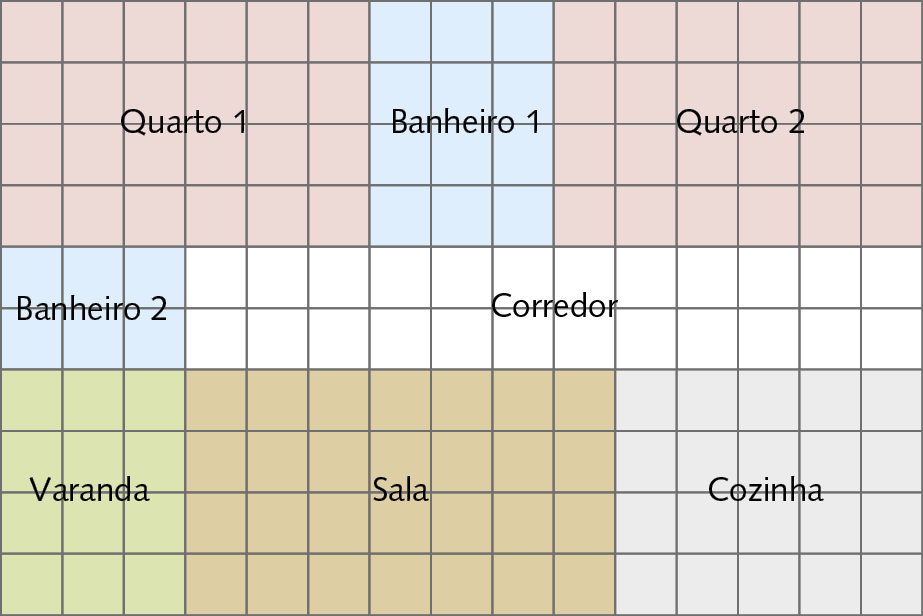
10. Observe a planta baixa de um apartamento. Nela, cada centímetro equivale a 100 centímetros da medida do comprimento real do apartamento.
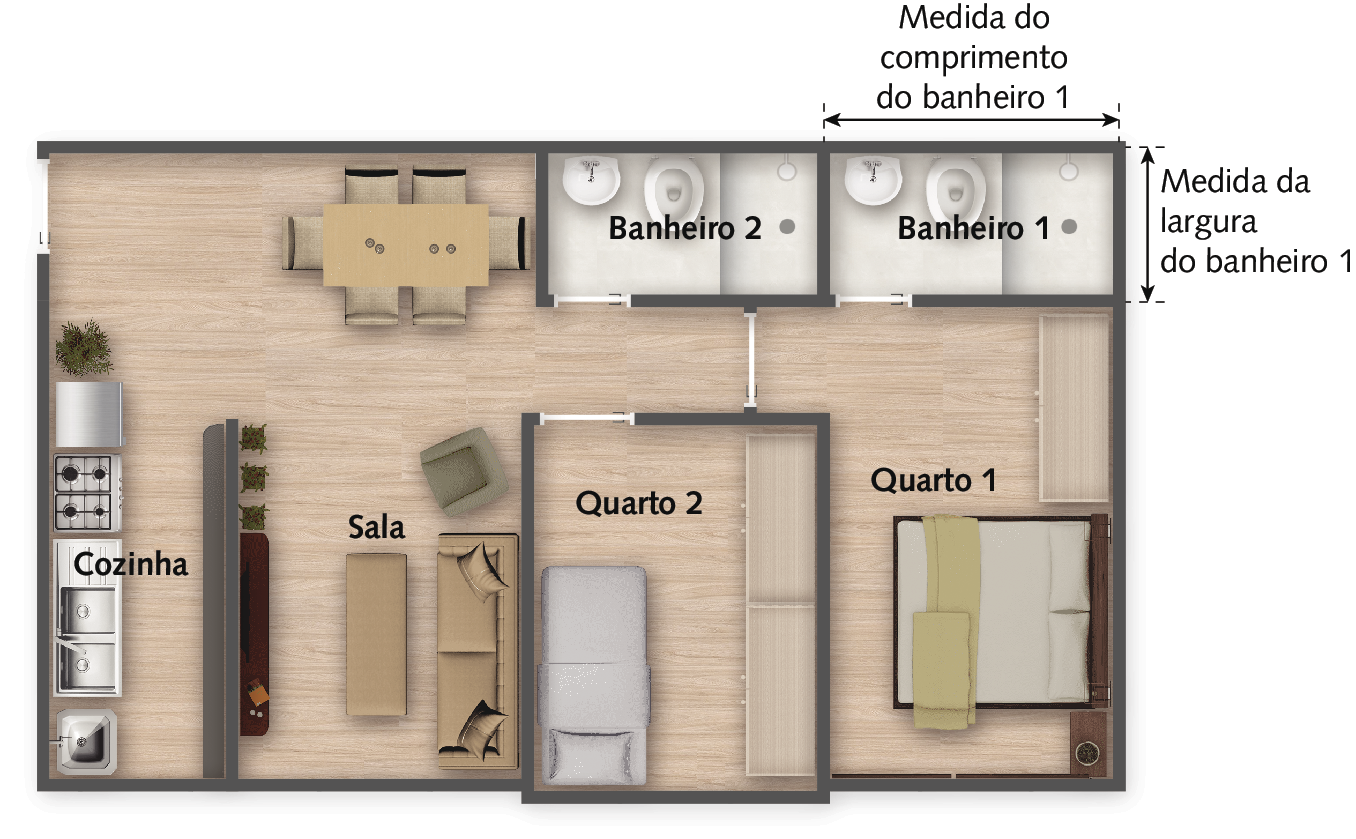
a) Com uma régua, meça o comprimento do banheiro 1.
b) Qual é a medida do comprimento real do banheiro 1 em centímetro?
c) Qual é a medida da largura real do banheiro 1 em metro?
d)


Elabore um problema com base nessa planta baixa. Depois, troque seu problema com um colega e resolva o problema proposto por ele.
11. A corrida das quinhentas milhas de Indianápolis é uma das mais tradicionais do automobilismo. O circuito oval da pista tem, aproximadamente, duas vírgula cinco milhas de medida de comprimento. Considerando que uma milha equivale a 1,61 quilômetro, responda às questões a seguir.
a) Qual é a medida do comprimento da pista (circuito oval) em quilômetro?
b) Quantos quilômetros são percorridos nessa corrida?
12. O atleta brasileiro Thiago Braz atingiu a marca de 5,95 metros em um torneio de salto com vara na Sérvia. A quantos centímetros corresponde esse salto?
Medida de perímetro
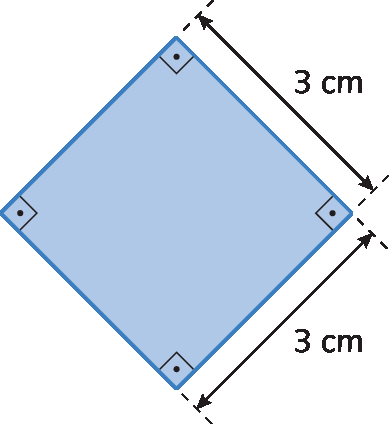
O comprimento do contôrno de uma figura geométrica plana é chamado de perímetro dessa figura.

Para determinar a medida do perímetro deste retângulo, adicionamos as medidas de comprimento de todos os lados da figura:
5 centímetros + 5 centímetros + 2,4 centímetros + 2,4 centímetros = 14,8 centímetros
A medida do perímetro de uma figura geométrica plana é a medida do comprimento do contôrno dessa figura.
Veja mais alguns exemplos.
a)
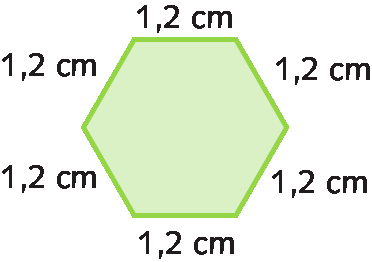
Medida do perímetro:
1,2 centímetro + 1,2 centímetro + 1,2 centímetro + 1,2 centímetro + 1,2 centímetro + 1,2 centímetro = 7,2 centímetros
b)
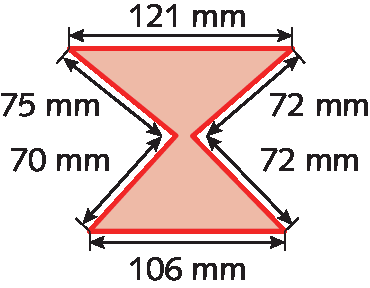
Medida do perímetro:
121 milímetros + 72 milímetros + 72 milímetros + 106 milímetros + 70 milímetros + 75 milímetros = 516 milímetros
Sugestão de leitura
BURNS, Marilyn. Espaguete e almôndegas para todos!
Uma história matemática. Ilustrações de Debbie Tilley. Tradução Gilda de Aquino. São Paulo: Brinque-Book, 2007.
Com as divertidas confusões da família Costa, você vai conhecer mais noções de perímetro.
Atividades
Faça as atividades no caderno.
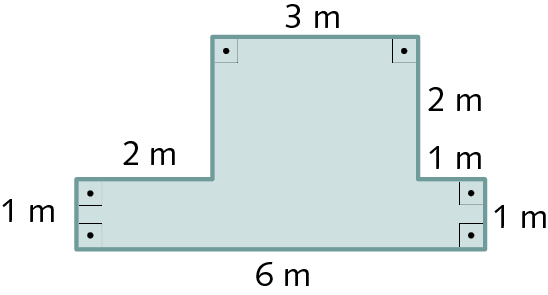
13. Meça o comprimento dos lados e determine, em milímetro, a medida do perímetro de cada polígono a seguir.
a)

b)

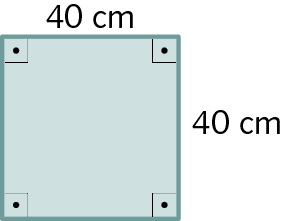
14. Calcule a medida do perímetro de um quadrado cujo lado mede 13 centímetros de comprimento.
15. Determine, em milímetro, a medida do perímetro de um hexágono regular cujo comprimento do lado meça 5,6 centímetros.
16. A medida do perímetro de um quadrado é 2 decâmetros. Calcule a medida de comprimento do lado em metro.
17. Em uma malha quadriculada, construa três polígonos diferentes que tenham 8 centímetros de medida de perímetro.
18. Um terreno retangular tem 36,8 métros de medida de comprimento e com sua largura mede
Três quartosdo comprimento. Calcule a medida do perímetro do terreno.
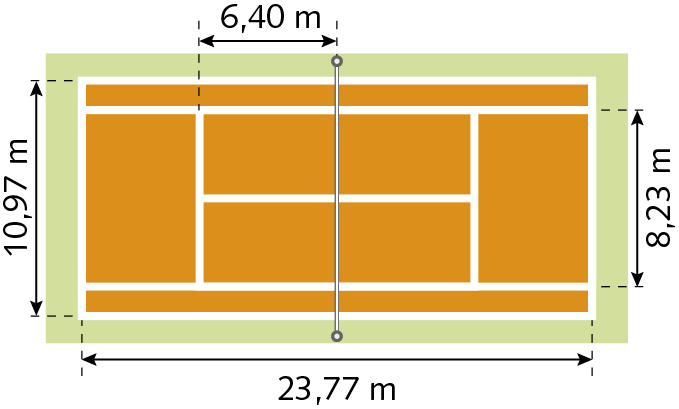
19. Quantos metros de fita branca são necessários, aproximadamente, para marcar todas as linhas‑limite de uma quadra de tênis oficial (conforme medidas indicadas na figura)?
20. Observe a planta baixa de uma residência. A escala dessa planta (no canto inferior esquerdo) indica que cada centímetro na planta equivale a 100 centímetros de medida de comprimento real.
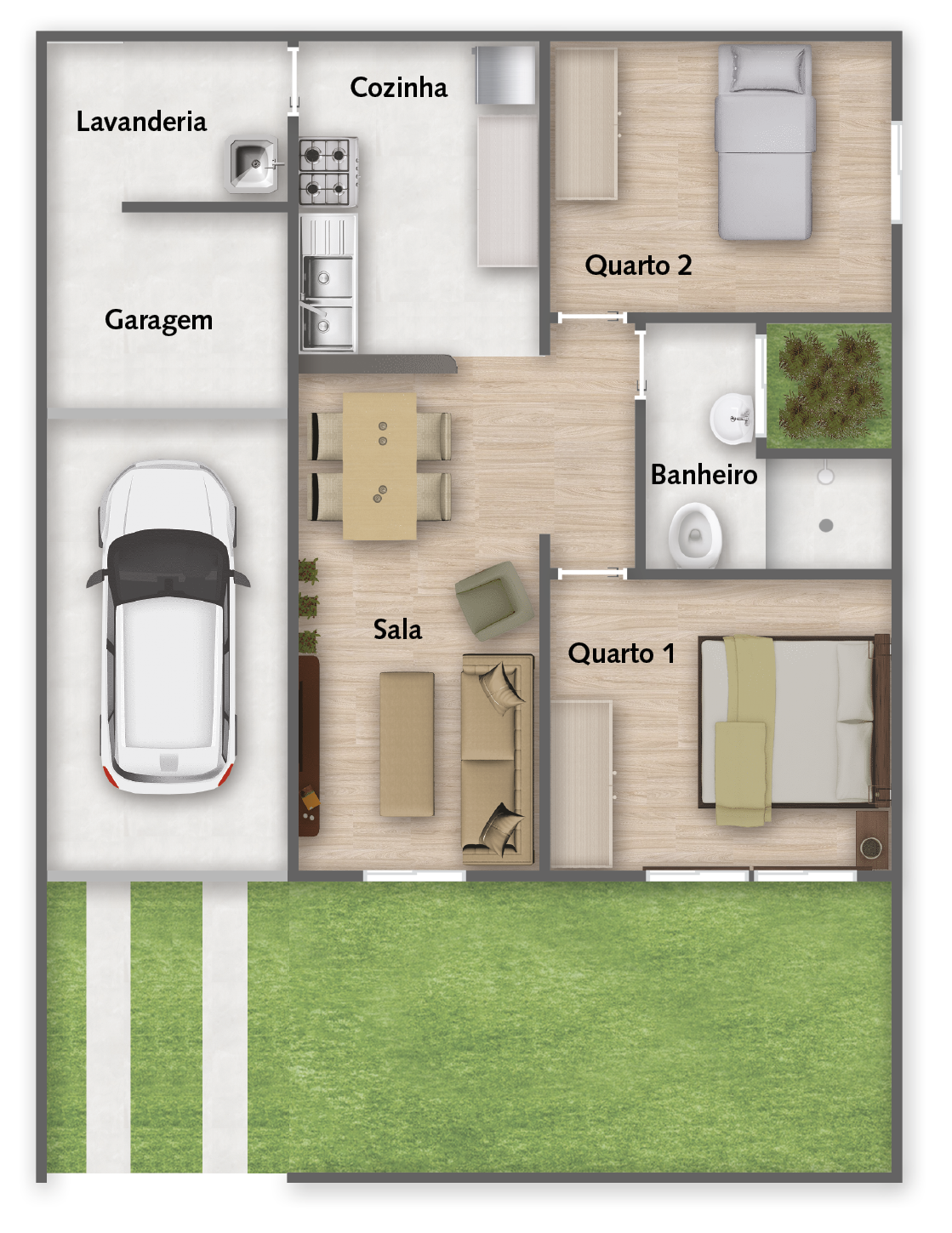
a) Com o auxílio de uma régua, determine a medida do perímetro real do quarto 2 em metro.
b) Com o auxílio de uma régua, determine a medida do perímetro real da cozinha em metro.
c) Com o auxílio de uma régua, determine a medida do perímetro real do banheiro em metro.
d) Com o auxílio de uma régua, determine a medida do perímetro real do terreno em metro.
e) Se for feita uma reforma no quarto 1 que aumente, na planta baixa, 1 centímetro da medida do comprimento e 2 centímetros da largura, quanto aumentará, em metro, a medida do perímetro real desse cômodo?
f)


Elabore um problema envolvendo a medida do perímetro de um ou mais cômodos da residência representada por esta planta baixa. Depois, troque seu problema com um colega e resolva o problema proposto por ele.

2 Grandeza tempo
Unidades de medida de tempo
Três amigos foram ao cinema. A sessão teve início às 10 horas da manhã, e a duração do filme foi de duas horas e meia.

Na situação apresentada, as medidas de tempo são utilizadas para indicar o horário de início da sessão e a duração do filme.
Como um dia tem 24 horas, cada hora tem 60 minutos e cada minuto tem 60 segundos, podemos escrever:

Para medir o tempo, podemos utilizar o relógio, que marca horas, minutos e segundos.
Observe os exemplos de um relógio digital e de um relógio de ponteiros.


Alguns relógios digitais podem apresentar as 24 horas do dia de fórmas diferentes, por exemplo:
a) 3 horas 15 minutos (antes do meio-dia) ou 15 horas 15 minutos (após o meio-dia)
b) 8 horas 25 minutos 4 segundos (antes do meio-dia) ou 20 horas 25 minutos 4 segundos (depois do meio-dia)
Os relógios de ponteiros representam o dia em dois grupos de 12 horas, antes e após o meio-dia, sem distinção na marcação dos ponteiros.
Observação
Não é correto escrever, por exemplo, 2,40 horas para representar duas horas 40 minutos, pois o sistema de medidas de tempo não é decimal. Observe:


Veja que interessante

O relógio de sol
A observação de fenômenos periódicos começou há milhares de anos. As civilizações antigas já observavam o movimento dos astros no céu e organizavam sua rotina com base em alguns padrões. O relógio de sol, instrumento que mede o tempo de acôrdo com o movimento da projeção da sombra do sol, é um exemplo da prática dessas observações.
Em 2017, foi inaugurado em Curitiba, capital do estado do Paraná, um observatório solar que é uma réplica de monumentos encontrados em sítios arqueológicos que estudam antigos povos indígenas. A observação da natureza sempre fez parte da cultura indígena; por isso, esses povos perceberam, por exemplo, que há um ciclo lunar que se repete, que há períodos de chuvas e de secas intensas, de frio e de calor intensos também e que o sol nasce no leste e se põe no oeste. A construção de relógios de sol servia para esses povos se orientarem geograficamente e estabelecerem os melhores períodos para caçar, pescar, plantar e colhêr.

Atividade

Reúna-se com três colegas e pesquisem como funciona um relógio de sol. Depois, compartilhem com a turma o que encontraram.
Atividades
Faça as atividades no caderno.
21. Escreva, em seu caderno, o horário indicado em cada relógio.
a)

b)

c)

d)

22. Quantos segundos há em:
a) uma hora?
b) 1 dia?
23. Quantos minutos há em:
a)
Meiahora?
b)
Um quarto dehora?
c)
três quartos de
hora?
24. Desenhe no caderno quatro relógios de ponteiros marcando os seguintes horários:
a)

b)

c)

d)

25. Faça uma lista de suas atividades diárias começando pela hora em que você acorda e terminando pela hora em que você dorme.
a) Escreva a hora em que começa e a duração de cada tarefa.
b)

Compare a sua lista com a de um colega. Quais são as semelhanças e as diferenças entre elas?
26. Luciana começou a estudar às 8 horas 20 minutos e terminou às 12 horas 50 minutos. Durante quanto tempo Luciana estudou?
27. Anita chegou ao consultório do dentista 15 minutos antes do horário marcado. Se o relógio da recepção marcava 9 horas 35 minutos, qual era o horário da consulta de Anita?
28. Um relógio marca 11 horas 30 minutos, mas está parado por três quartos de hora. Que horas são?
29. Responda no caderno.
a) Durante uma hora, o ponteiro dos minutos dá quantas voltas completas no relógio?
b) Durante um minuto, o ponteiro dos segundos dá quantas voltas completas no relógio?
30. No Grande Prêmio de Fórmula 1 de abú dábi de 2021, o vencedor foi Max Verstappen, com a medida de tempo de uma hora 30 minutos 17,345 segundos. O segundo colocado, Lewis Hamilton, recebeu a bandeirada 2,256 segundos após o vencedor. Qual foi a medida de tempo da prova de Lewis Hamilton?
31. Observe a data de fabricação e validade de alguns produtos que Paulo comprou no dia 3/1/2024.

Agora, faça o que se pede.
a) Qual dos produtos que ele comprou tem a data de validade mais próxima?
b) Qual dos produtos ele pode consumir em até 6 meses?
c)


Elabore um problema envolvendo as datas de fabricação e validade dos produtos que Paulo comprou. Depois, troque-os com um colega e resolva o problema proposto por ele.
32. Uma mangueira despeja 0,2 litro de combustível por segundo no tanque de um automóvel. Quanto tempo leva, em minuto, para encher um tanque de 60 litros?

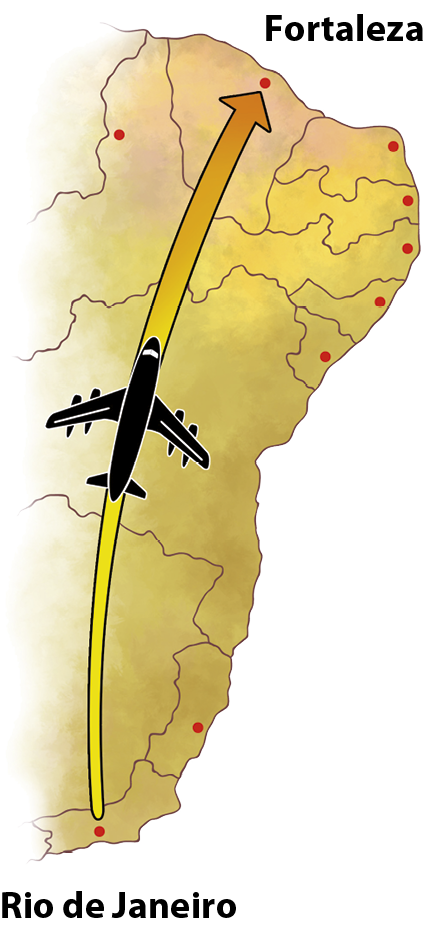
33. Um avião partiu do Rio de Janeiro (Rio de Janeiro) para Fortaleza (Ceará), sem escalas, às 17 horas 15 minutos de determinado dia.
Sabendo que a duração do voo é duas horas 50 minutos, qual é o horário previsto para o avião chegar a Fortaleza?

3 Grandeza área
Unidades de medida de área
O estado do Rio Grande do Sul, cuja capital é Porto Alegre, é um dos 10 maiores estados do Brasil. A medida da área desse estado é de, aproximadamente, .281738 quilômetros quadrados. O quilômetro quadrado corresponde à medida da área de um quadrado cujos lados medem 1 quilômetro de comprimento.
ESTADO DO RIO GRANDE DO SUL
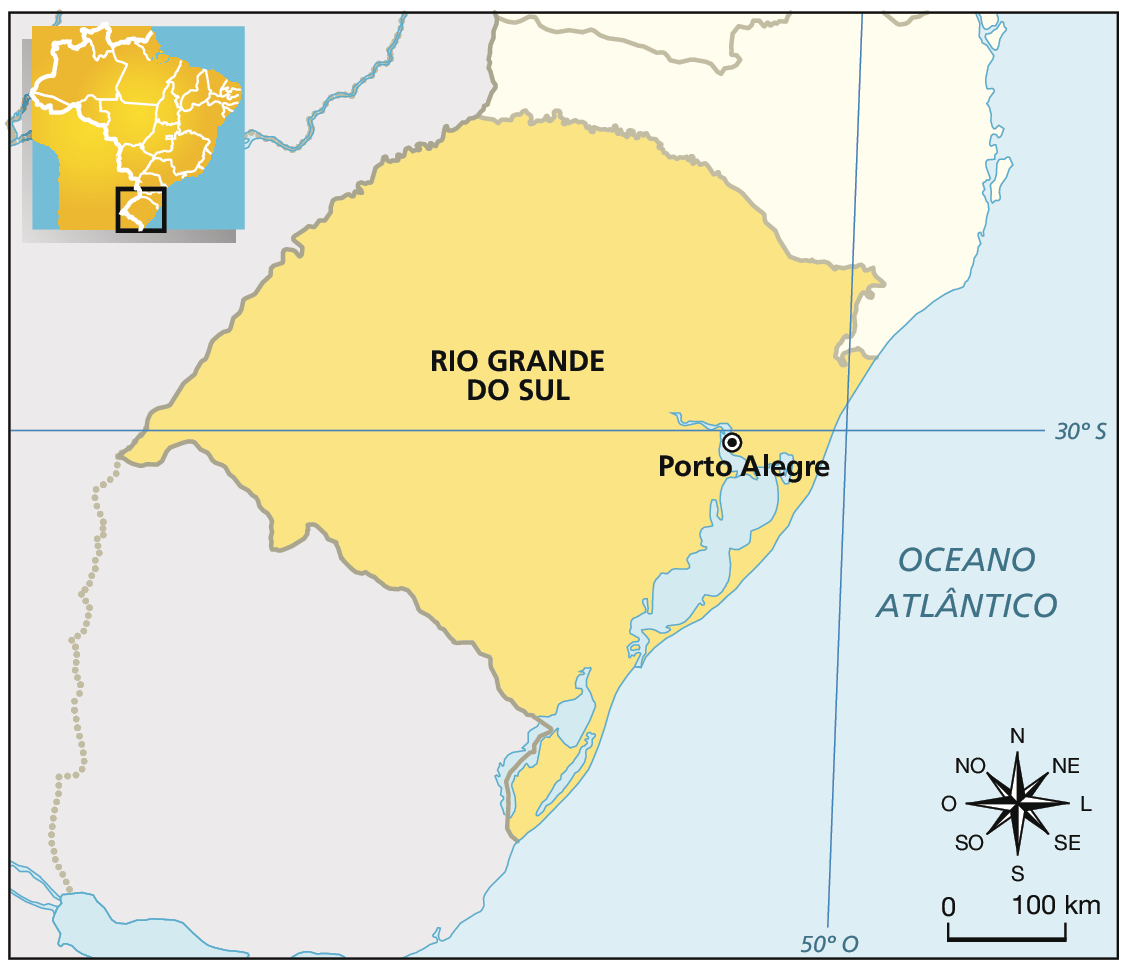
Elaborado com base em: Instituto Brasileiro de Geografia e Estatística. Atlas geográfico escolar. oitava edição Rio de Janeiro: Instituto Brasileiro de Geografia e Estatística, 2018. página 94.
Utilizando como unidade de medida de área o

, podemos afirmar que a medida da área da figura a seguir é igual a 6

, ou seja, sua medida de área é 6

.
Utilizando a mesma figura, mas agora tomando como unidade de medida de área o

, podemos afirmar que a medida da área da figura a seguir é 12

.

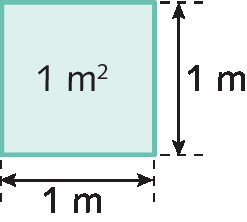
No Sistema Internacional de Unidades (ésse Í), a unidade-padrão de medida de área é o metro quadrado (ême 2 sobrescrito). O metro quadrado corresponde à medida da área de um quadrado de lados medindo 1 metro de comprimento.
Além do metro quadrado, há seus múltiplos, como o quilômetro quadrado (cá ême 2 sobrescrito), e seus submúltiplos, como o centímetro quadrado (cê ême 2 sobrescrito).
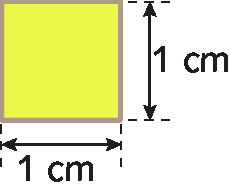
A medida da área da figura a seguir é 8 centímetros quadrados.

A unidade de medida de área utilizada foi o centímetro quadrado (cê ême 2 sobrescrito). O centímetro quadrado corresponde à medida da área de um quadrado de lados medindo 1 centímetro de comprimento.
Observe, no quadro a seguir, os múltiplos e submúltiplos do metro quadrado que fazem parte do Sistema Internacinal de Unidades.
|
Múltiplos |
Unidade-padrão |
Submúltiplos |
|||||
|---|---|---|---|---|---|---|---|
|
Unidade |
quilômetro quadrado |
hectômetro quadrado |
decâmetro quadrado |
metro quadrado |
decímetro quadrado |
centímetro quadrado |
milímetro quadrado |
|
Símbolo |
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|
Relação com o metro quadrado |
1.000.000 m² |
10.000 m² |
100 m² |
1 m² |
0,01 m² |
0,0001 m² |
0,000001 m² |
O decâmetro quadrado, o hectômetro quadrado e o quilômetro quadrado são utilizados para medir a área de grandes superfícies; o decímetro quadrado, o centímetro quadrado e o milímetro quadrado são usados na medição da área de pequenas superfícies.

Veja que interessante
A lagoa Rodrigo de Freitas
Com 2,4 quilômetros quadrados de medida de área, a lagoa Rodrigo de Freitas é cercada por vários bairros cariocas (Lagoa, Ipanema, Leblon, Gávea e Jardim Botânico), emoldurada por montanhas e com vista para o Cristo Redentor.
Em seu entôrno, há um estádio de remo (Estádio de Remo da Lagoa), uma ciclovia pavimentada, medindo 7,5 quilômetros de extensão, diversos equipamentos de lazer e quiosques de alimentação, que oferecem itens da gastronomia regional e internacional. Com uma área que mede .204000 métros quadrados, o entôrno da lagoa é o maior centro gastronômico ao ar livre da América Latina. Por tudo o que oferece – incluindo um magnífico pôr do sol –, a lagoa Rodrigo de Freitas é sempre muito procurada por moradores da cidade e turistas.

Atividade


Que local da cidade onde mora você considera bonito e interessante para visitar? Conte para os colegas.
Transformações envolvendo as unidades de medida de área
Observe os quadrados de mesma medida de área ilustrados a seguir.
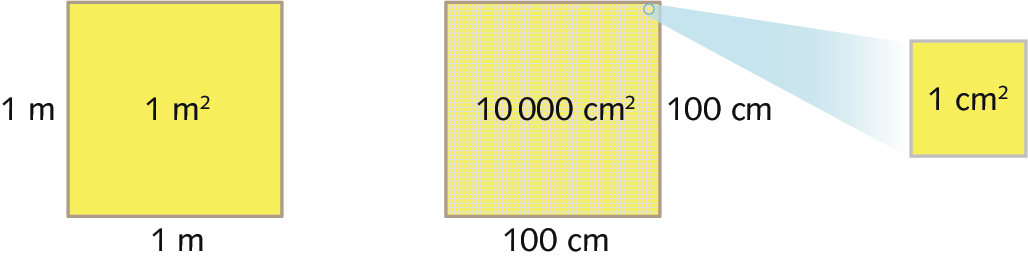
Como 1 metro equivale a 100 centímetros, podemos dividir um quadrado cujos lados medem 1 metro de comprimento em .10000 quadradinhos de 1 centímetro quadrado de medida de área. Então: 1 métro quadrado = .10000 centímetros quadrados
Assim, para converter uma medida de área expressa em metro quadrado para centímetro quadrado, multiplicamos essa medida por .10000; para converter uma medida de área expressa em centímetro quadrado para metro quadrado, dividimos essa medida por .10000.
Observe que cada unidade de medida de área equivale a 100 vezes a unidade imediatamente inferior.

Confira os exemplos.
a) Transformar 18,124 decâmetros quadrados em metro quadrado.

Para transformar decâmetro quadrado em metro quadrado (uma posição à direita), devemos multiplicar por 100.
18,124 decâmetros quadrados ⋅ 100 = .1812,4 métros quadrados
Ou seja: 18,124 decâmetros quadrados = .1812,4 métros quadrados
b) Transformar 793,2 decâmetros quadrados em quilômetro quadrado.
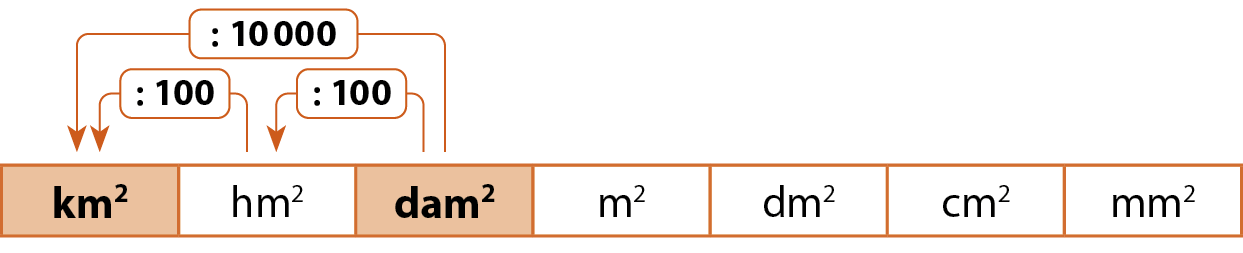
Para transformar decâmetro quadrado em quilômetro quadrado (duas posições à esquerda), devemos dividir por .10000.
793,2 decâmetros quadrados dividido por .10000 = 0,07932 quilômetro quadrado
Ou seja: 793,2 decâmetros quadrados = 0,07932 quilômetro quadrado

Lendo e aprendendo

Área de favelas dobra em 35 anos
Estudo mostra ainda impacto da expansão urbana sobre vegetação nativa
Aos 25 anos e sem ter onde morar, Yara Lima juntou-se a outras pessoas que haviam ocupado um terreno na zona leste de São Paulo. O local estava coberto por mato, sem água encanada e eletricidade. Mesmo assim, o número de barracos cresceu e, aos poucos, as primeiras casas foram surgindo, formando a comunidade Jardim Glória.
Exemplos como esse tornaram-se comuns no Brasil. Um estudo divulgado pelo Mapbiomas, instituto que pesquisa assuntos relacionados ao meio ambiente, mostra que a área de favelas no País cresceu 105% nos últimos 35 anos abre parêntesesou seja, dobrou de tamanhofecha parênteses.
A ocupação desordenada é hoje um dos principais problemas das grandes cidades. Sem dinheiro para moradia adequada, muitas pessoas se instalam em locais onde não há serviços básicos, como água, energia, esgôto, transporte público e escolas.
[reticências]
Outro fator que preocupa é o impacto sobre o meio ambiente. Segundo o estudo, de 1985 a 2020, o Brasil perdeu o equivalente a 388 mil campos de futebol de vegetação nativa. O impacto é resultado tanto de obras formais abre parêntesesrodovias, prédios, indústrias etcéterafecha parênteses como informais.
No estado do Amazonas, por exemplo, de toda a nova área urbana que surgiu no período, metade é composta de favelas.
PEIXOTO, F. Área de favelas dobra em 35 anos. Qualé, São Paulo, edição 39, página 4, 15 a 29 de novembro de 2021.
Atividades
1. Qual das alternativas a seguir corresponde ao tema principal do texto?
a) História de vida de Yara Lima.
b) Formação da comunidade Jardim Glória.
c) Aumento da medida da área urbana.
d) Aumento da medida da área ocupada por favelas.
2. Qual é a intenção da autora do texto ao contar a história de Yara Lima?
3. Segundo estudo feito pelo Mapbiomas, em 1985, a medida da área ocupada por comunidades no Brasil era de 89 mil hectares e essa medida passou para 185 mil hectares em 2021. Sabendo que 1 hectare equivale a .10000 metros quadrados, calcule quanto cresceu a medida da área ocupada por comunidades no Brasil entre 1985 e 2020.
4.

O surgimento das comunidades está associado, entre outras coisas, à desigualdade social e à falta de planejamento urbano. Além disso, boa parte das pessoas que vivem em favelas não dispõe de condições mínimas de infraestrutura como saneamento básico. Se você fosse o prefeito da cidade, o que faria para frear o crescimento das comunidades? E para melhorar as condições de vida das pessoas que lá vivem? Responda às questões escrevendo um pequeno texto. Depois, compartilhe o que escreveu com os colegas.
Atividades
Faça as atividades no caderno.
34. No caderno, determine a medida da área de cada figura considerando o

e o

as unidades de medida de área.

35. Se a medida da área de 1

é 1 centímetro quadrado, determine, no caderno, a medida da área das figuras a seguir.
a)

b)

36. Observe a planta de um apartamento. Sabendo que a área de um

mede 1 métro quadrado, determine no caderno a medida da área de cada ambiente.
37. Determine a unidade de medida mais adequada para expressar:
a) a medida da área da cidade onde você mora;
b) a medida da área da capa de um livro.
38. No caderno, substitua cada

pelo número adequado.
a) 5 métros quadrados =

centímetros quadrados
b) 8,76 quilômetros quadrados =

decâmetros quadrados
c) .3000 centímetros quadrados =

métros quadrados
d) .15400 milímetros quadrados =

decímetros quadrados
e) 0,35 decâmetro quadrado =

decímetros quadrados
f) .50000 métros quadrados =

hectômetros quadrados
39. Um operário está pintando uma parede de 12,5 métros quadrados. Sabendo que ele já pintou .34500 centímetros quadrados, expresse, em metro quadrado, a medida da área que falta pintar.
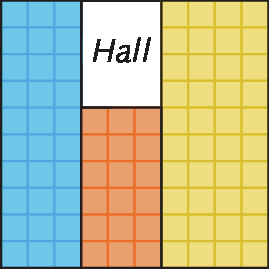
40. Um galpão é formado por um hall e três depósitos, como mostra esta figura.
Determine a medida da área de cada quadradinho da figura, em metro quadrado, sabendo que a área do hall mede 12 métros quadrados. Determine a medida da área de cada um dos depósitos, em metro quadrado.
41. A área de um terreno mede 100 hectares. Uma plantação de café ocupa
dois quintosda medida da área do terreno. Quantos metros quadrados correspondem à plantação?
42. O preço de um imóvel é determinado, entre outros fatores, pelo valor do metro quadrado. No ano passado, Josué decidiu vender seu apartamento. Para ter uma base de preço, ele acompanhou, no último quadrimestre do ano, o valor do metro quadrado dos imóveis do bairro onde mora. Em setembro, o valor do metro quadrado era R$ 5.800,00cinco mil oitocentos reais; em outubro, R$ 5.800,00cinco mil oitocentos reais; em novembro, R$ 5.740,00cinco mil setecentos e quarenta reais e, em dezembro, R$ 5.860,00cinco mil oitocentos e sessenta reais.
a) Em qual mês desse quadrimestre o valor do metro quadrado foi mais baixo?
b) Josué vendeu seu apartamento de 70 métros quadrados no mês de dezembro. Quanto ele recebeu, em reais, pela venda do apartamento?
Medida da área de um retângulo
Considere um retângulo cuja base mede 4 centímetros de comprimento e a altura mede 3 centímetros de comprimento.
Vamos considerar um quadrado de 1 centímetro quadrado como unidade de medida de área. Veja, na figura a seguir, que esse quadrado “cabe” exatamente 12 vezes no retângulo.
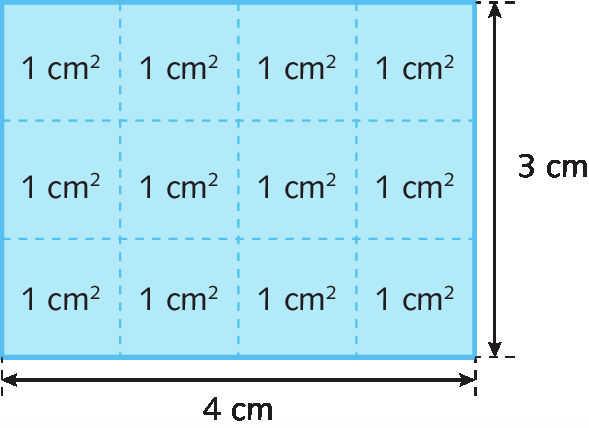
Assim, verificamos que a medida da área do retângulo é 12 centímetros quadrados.
A medida dessa área também pode ser obtida assim:

A medida da área de um retângulo é o produto das medidas de comprimento da base e da altura.
Observação
Podemos calcular a medida da área de qualquer retângulo (com lados de medidas de comprimento inteiras ou não inteiras) multiplicando a medida do comprimento da base pela medida de comprimento da altura. Esse procedimento não será demonstrado nesta coleção, mas é verdadeiro.
Analise os exemplos.
a) A medida da área deste retângulo é dada por:
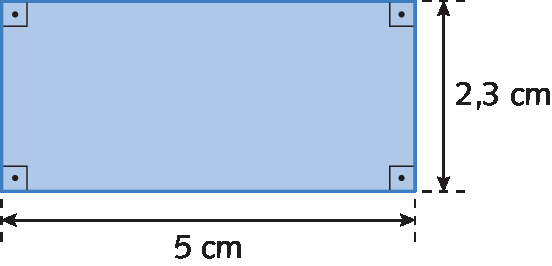
Aretângulo = 5 centímetros ⋅ 2,3 centímetros = 11,5 centímetros quadrados
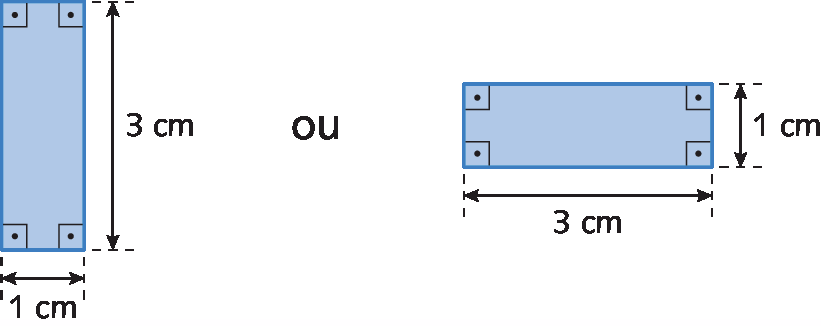
b) Vamos desenhar um retângulo sabendo que sua medida de área é igual a 3 centímetros quadrados e que um de seus lados mede 3 centímetros de comprimento.
Para desenhar o retângulo, precisamos conhecer as medidas de comprimento dos dois lados não paralelos, mas só sabemos a medida de comprimento de um. Como a medida da área do retângulo é obtida multiplicando as medidas de comprimento da base e da altura, devemos descobrir qual é a outra medida que, ao ser multiplicada por 3 centímetros, resulta em 3 centímetros quadrados. Há duas possibilidades: 1 centímetro ⋅ 3 centímetros = 3 centímetros quadrados ou 3 centímetros ⋅ 1 centímetro = 3 centímetros quadrados
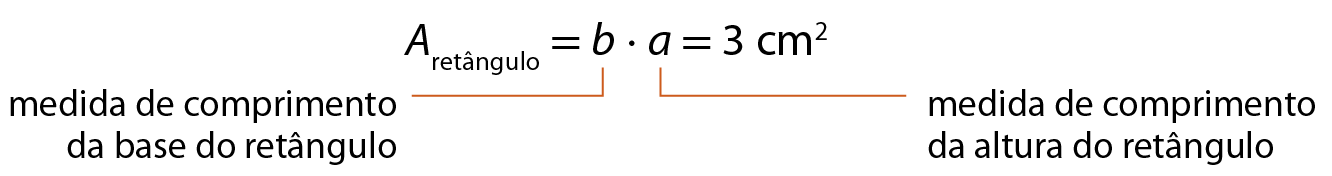
Se a base do retângulo mede 3 centímetros de comprimento, a altura mede 1 centímetro de comprimento. Agora, se a base mede 1 centímetro de comprimento, então a altura mede 3 centímetros de comprimento.
Portanto, um retângulo cuja área mede 3 centímetros quadrados e o comprimento de um de seus lados mede 3 centímetros pode ser desenhado como mostram estas figuras.
Observação
Ao calcular a medida da área de um retângulo, devemos verificar se as medidas de comprimento da base e da altura estão na mesma unidade de medida.
Medida da área de um quadrado
O quadrado é um caso particular de retângulo cujos lados têm a mesma medida de comprimento. Portanto, calculamos a medida da área de um quadrado da mesma maneira que calculamos a medida da área de um retângulo.
Observe os exemplos.
a) Determine a medida da área de um quadrado cuja medida do lado é 2,4 centímetros de comprimento.
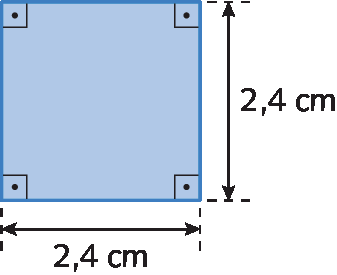
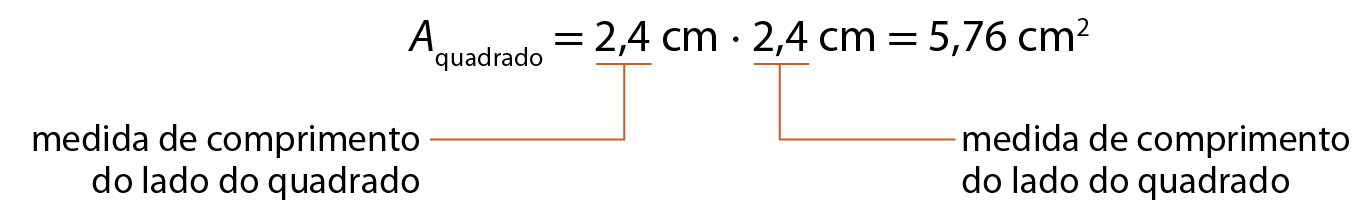
b) Vamos desenhar um quadrado de medida de área igual a 9 centímetros quadrados.
Nesse caso, a medida do lado do quadrado é 3 centímetros de comprimento, pois: 3 centímetros ⋅ 3 centímetros = 9 centímetros quadrados
Atividades
Faça as atividades no caderno.
43. Calcule a medida da área das figuras.
a)
b)

c)
44. No caderno, calcule a medida da área de um retângulo de 20 centímetros de medida do comprimento por 8 centímetros de medida da largura.
45. Calcule a medida da área de um azulejo quadrado com 20 centímetros de medida de comprimento do lado.
46. Lúcia comprou um terreno retangular que tem 24 metros de medida de frente e 15 metros de medida de lateral. Qual é a medida da área do terreno que Lúcia comprou?
47. De acôrdo com o Instituto Nacional de Metrologia, Qualidade e Tecnologia (Inmetro), as medidas das dimensões oficiais de uma trave de futebol são as indicadas no esquema a seguir.

Qual é a medida da área aproximada delimitada pela trave e pelo solo?
48. Um pedreiro construiu um muro de 30 métros de medida do comprimento por 1,6 métro de medida da altura. Sabendo que, em média, são utilizados 25 tijolos por metro quadrado, responda: Quantos tijolos, no mínimo, ele utilizou nessa construção?
49. O piso de um quarto de 4 métros de medida do comprimento e 3 métros de medida da largura vai ser revestido com peças de cerâmica de fórma quadrada com 20 centímetros de medida de comprimento do lado.
a) Qual é a medida da área, em metro quadrado, do piso do quarto?
b) Qual é a medida da área, em centímetro quadrado, de cada peça de cerâmica?
c) Quantas peças de cerâmica, no mínimo, serão necessárias para revestir o piso desse quarto?
50. Em cada andar de um prédio de 12 andares, há três janelas de vidro fumê. Sabendo que cada janela tem 350 centímetros de medida do comprimento por 120 centímetros de medida da largura, responda: Quantos metros quadrados de vidro fumê foram utilizados nesse prédio?
51. Meça com a régua o comprimento dos lados dos retângulos a seguir e calcule a medida da área e a medida do perímetro de cada um.
a)

b)

• Qual retângulo tem maior medida de área? Qual tem maior medida de perímetro?
52. Observe estes quadrados.
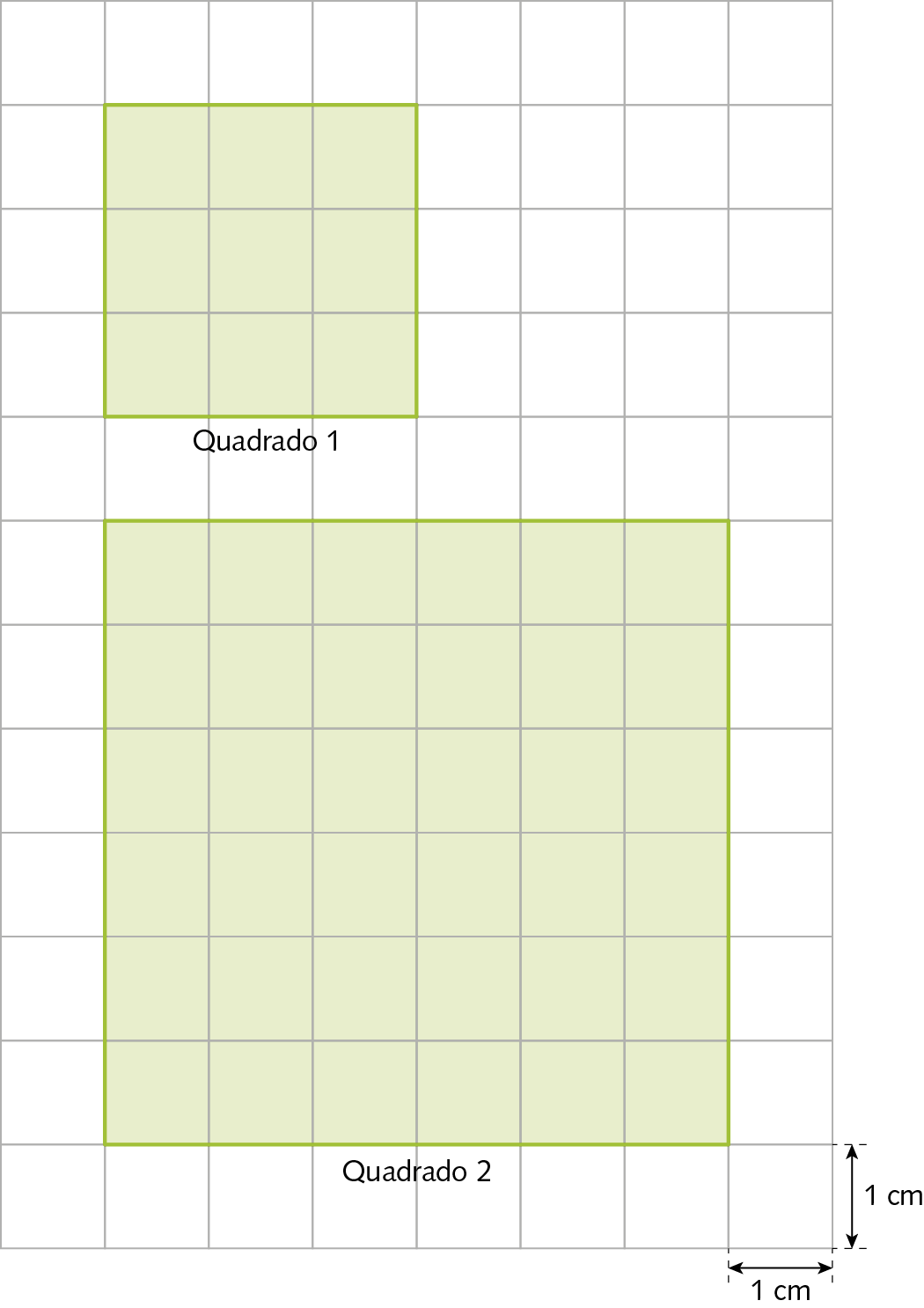
Agora, faça o que se pede.
a) Calcule a medida do perímetro e a medida da área do quadrado 1.
b) Calcule a medida do perímetro e a medida da área do quadrado 2.
c) Comparando o quadrado 1 com o 2, o que aconteceu com a medida do perímetro? E com a medida da área?
d) Em uma folha de papel quadriculado, construa um quadrado, cuja medida de comprimento do lado seja um terço da medida de comprimento do lado do quadrado 2. Em seguida, calcule a medida do perímetro e a medida da área desse quadrado.
e) O que você pode afirmar sobre a medida do perímetro e a medida da área do quadrado que você construiu comparando com a medida do perímetro e a medida da área do quadrado 2?
53. Desenhe em seu caderno:
a) um quadrado de medida de área igual a 16 centímetros quadrados;
b) um retângulo de medida de área igual a 12 centímetros quadrados e que tenha um lado medindo 4 centímetros de comprimento.
54.

Em uma malha, Fábio desenhou um quadrado cujo comprimento do lado mede 1 centímetro; depois, desenhou outro quadrado cujo comprimento do lado mede 2 centímetros; em seguida, desenhou outro quadrado cujo comprimento do lado mede 3 centímetros, e assim por diante, até o quadrado cujo comprimento do lado mede 10 centímetros.
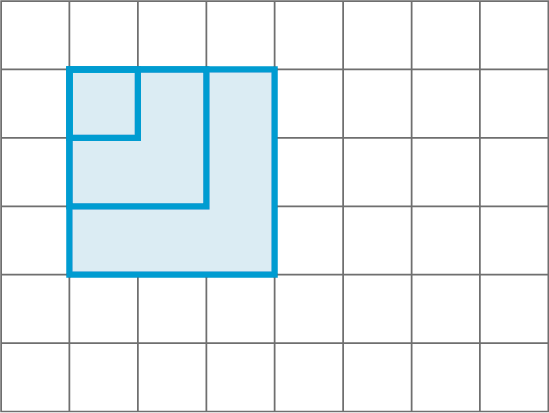
a) Escrevam no caderno a sequência das medidas de comprimento dos lados dos quadrados.
b) Escrevam no caderno a sequência das medidas dos perímetros dos quadrados.
c) Quando dobramos a medida de comprimento do lado do quadrado, o que acontece com a medida do perímetro?
d) Quando triplicamos a medida de comprimento do lado do quadrado, o que acontece com a medida do perímetro?
e) Observem que o quadrado de medida de perímetro de 4 centímetros tem lado medindo 1 centímetro de comprimento, o quadrado de medida de perímetro de 8 centímetros tem lado medindo 2 centímetros de comprimento, o quadrado de medida de perímetro de 12 centímetros tem lado medindo 3 centímetros de comprimento. Como podemos obter a medida do perímetro de um quadrado a partir da medida de comprimento do lado? Expliquem sua resposta.
f) Qual é a medida do perímetro do quadrado cujo lado mede 36,2 centímetros de comprimento?
g) Escrevam a sequência das medidas da área dos quadrados.
h) Quando dobramos a medida de comprimento do lado do quadrado, a medida da área também dobra? E quando triplicamos a medida de comprimento do lado do quadrado, a medida da área também triplica?
i) Quando aumentamos (ou diminuímos) a medida de comprimento do lado de um quadrado, as medidas do perímetro e da área do novo quadrado também aumentam (ou diminuem). Essas transformações são proporcionais?
55. Observe a planta baixa de um estúdio de pilates.
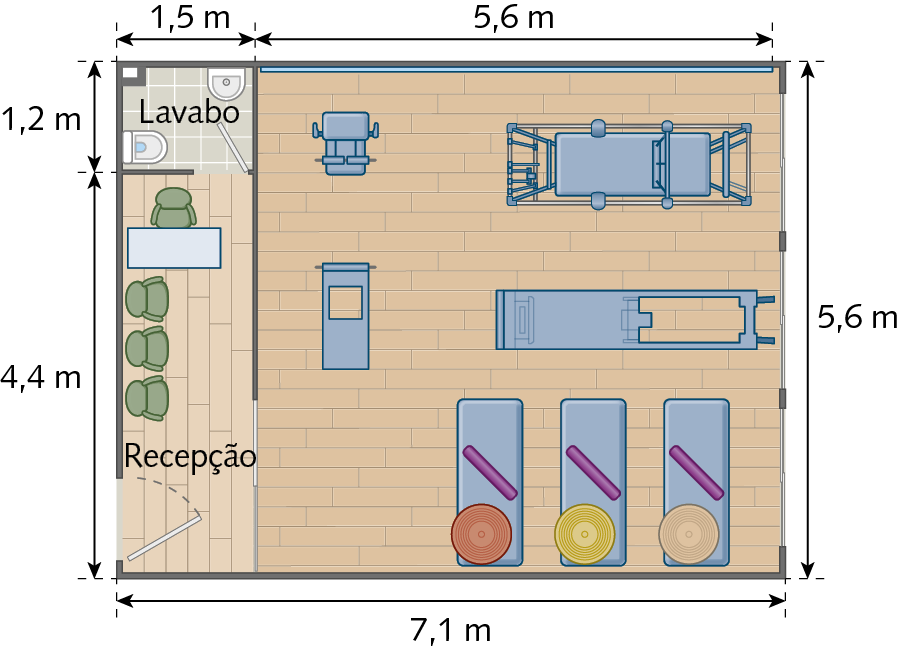
a) Quantos cômodos estão representados na planta baixa?
b) Qual é a medida da área e a medida do perímetro do cômodo quadrado em que estão os aparelhos usados no pilates?
c) Qual é a medida da área da recepção? E a do lavabo?
56. Desenhe em seu caderno a planta baixa de sua sala de aula. Não esqueça de representar os móveis e indicar as medidas das paredes.
57. O Auditório Ibirapuera foi concebido por Oscar Niemáier para apresentações musicais e está localizado dentro do Parque Ibirapuera, em São Paulo.

Fernanda, estudante de arquitetura, fez um esbôço da vista aérea do trecho do Parque Ibirapuera em que é possível ver o auditório. Considere o esquema a seguir.
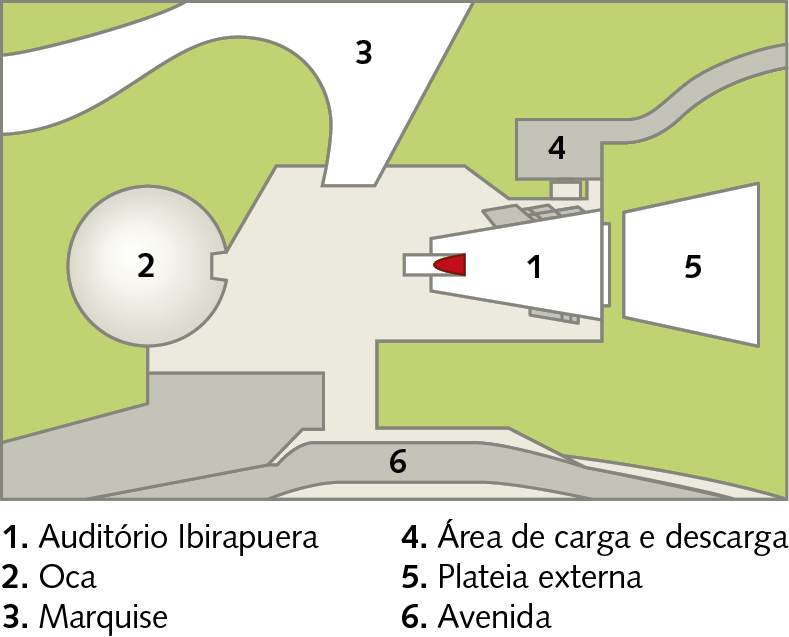
a) O Auditório Ibirapuera está identificado no esquema por qual número? A representação do auditório se parece com qual figura geométrica?
b) A representação de qual edifício se parece com um círculo?
c) Você conhece outras obras de Niemáier? Se sim, quais? Onde elas estão localizadas?
58.

Em uma folha de papel quadriculado, em duplas, desenhem a vista aérea da escola onde estudam. Não se esqueçam de indicar todos os elementos que fazem parte dela: salas de aula, pátio, quadra poliesportiva, estacionamento etcétera.

Veja que interessante
Faça a atividade no caderno.
A arquitetura escolar e seu papel no aprendizado
Como a arquitetura e a organização física de uma escola podem influenciar o aprendizado dos estudantes? Segundo Doris Kowaltowski, professora da Faculdade de Engenharia Civil, Arquitetura e Urbanismo da unicâmpi, o ambiente escolar funciona como o “terceiro professor”. O espaço físico influencia a fórma como as pessoas convivem nele e também estimula e facilita o ensino. Para Doris, o projeto arquitetônico deve dialogar com a pedagogia da escola e a construção deve ser feita em parceria com a comunidade escolar.
Dados obtidos em: https://oeds.link/dt24LZ. Acesso em: 26 julho 2022.

Atividade
Você acha que a arquitetura e a organização física da escola podem interferir no seu aprendizado? Justifique sua resposta.
Medida da área de um triângulo retângulo
Para calcular a medida da área de um triângulo retângulo cuja base mede 6 centímetros de comprimento e a altura mede 2 centímetros de comprimento, Solange usou uma malha de papel quadriculado.

Observe que sempre é possível, a partir de um triângulo retângulo, construir um retângulo com as mesmas medidas de comprimento da base e da altura e cuja medida da área é o dôbro da medida da área do triângulo.
A medida da área de um triângulo retângulo é a metade do produto das medidas de comprimento da base e da altura.
Atividades
Faça as atividades no caderno.
59. Observe as figuras geométricas desenhadas na malha quadriculada.
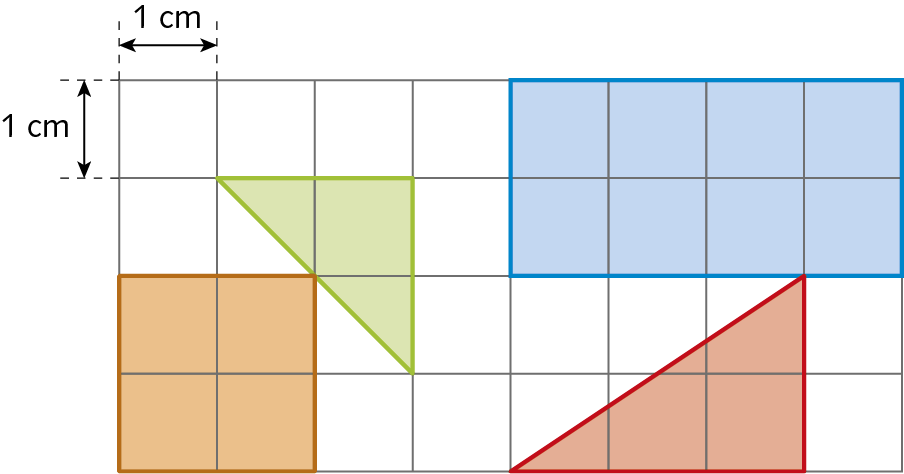
a) Quantos triângulos verdes cabem no quadrado laranja? E no retângulo azul?
b) Qual é a razão entre a medida da área do triângulo verde e a medida da área do quadrado laranja? E entre a medida da área do triângulo verde e a medida da área do retângulo azul?
c) Qual é a medida da área do retângulo azul? E a medida da área do triângulo vermelho?
d) Qual é a razão entre a medida da área do triângulo vermelho e a medida da área do retângulo azul?
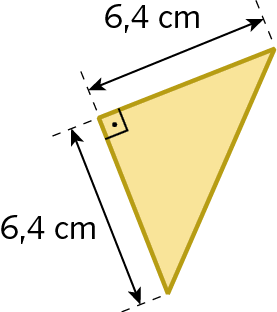
60. Calcule a medida da área de cada triângulo retângulo a seguir.
a)
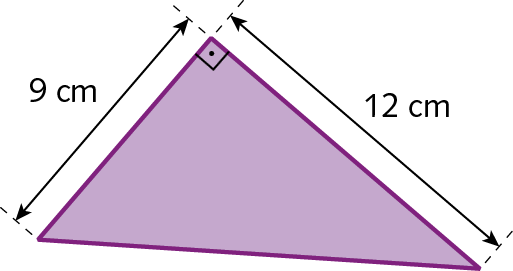
b)

4 Grandeza volume
Unidade de medida de volume
Durante a aula de Matemática, a professora pediu aos estudantes que observassem dois blocos.
A esses dois blocos ou aos sólidos geométricos correspondentes, podemos associar a grandeza volume.
Veja como calcular a medida do volume desses dois blocos.
Para calcular a medida do volume, devemos considerar uma unidade de medida de volume e contar quantas vezes essa unidade cabe em seu interior. Assim, tomando como unidade de medida de volume o

, podemos calcular a medida do volume dos dois blocos.


A medida do volume desse bloco é 20

.

unidade de medida de volume
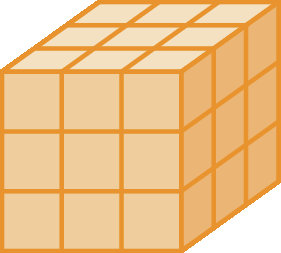
A medida do volume desse bloco é 27

.
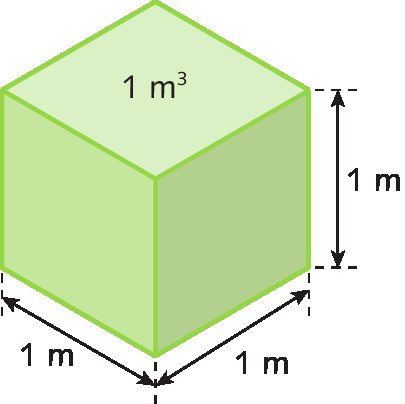
Podemos utilizar outras unidades de medida de volume. No Sistema Internacinal de Unidades, a unidade-padrão de medida de volume é o metro cúbico (ême 3 sobrescrito), que corresponde ao espaço ocupado por um cubo cujas arestas medem 1 metro de comprimento.
Há também outras unidades de medida de volume que derivam do metro cúbico: os múltiplos e os submúltiplos.
Observe, no quadro a seguir, os múltiplos e submúltiplos do metro cúbico que fazem parte do Sistema Internacinal de Unidades.
|
Múltiplos |
Unidade-padrão |
Submúltiplos |
|||||
|---|---|---|---|---|---|---|---|
|
Unidade |
quilômetro cúbico |
hectômetro cúbico |
decâmetro cúbico |
metro cúbico |
decímetro cúbico |
centímetro cúbico |
milímetro cúbico |
|
Símbolo |
km³ |
hm³ |
dam³ |
m³ |
dm³ |
cm³ |
mm³ |
|
Relação com o metro cúbico |
1.000.000.000 m³ |
1.000.000 m³ |
1.000 m³ |
1 m³ |
0,001 m³ |
0,000001 m³ |
0,000000001 m³ |

Veja que interessante
Faça a atividade no caderno.
Canal do Panamá
O Canal do Panamá é um canal marítimo com 82 quilômetros de medida da extensão que liga o Oceano Atlântico ao Oceano Pacífico, no Panamá. O canal é considerado um ponto importante para o comércio internacional em razão da grande redução do percurso feito pelos navios, e seus principais usuários são os Estados Unidos e a China.
O canal contém três eclusas para os navios atravessarem. Nelas, a água funciona como um elevador. Por exemplo, quando o navio chega ao canal pelo Oceano Atlântico, entra na comporta com a água no mesmo nível do oceano. Os portões são fechados e as válvulas de enchimento são abertas, elevando o navio 26 métros, até o nível do Lago de Gatun. Depois, as válvulas são fechadas e os portões superiores são abertos. Assim, o navio sai da comporta para o lago e segue para as outras comportas, nas quais acontece o processo inverso de descida até o nível do Oceano Pacífico.
Em junho de 2016, foi inaugurada a ampliação do Canal do Panamá, com a construção de uma hidrovia que permite a passagem de navios muito maiores. As novas comportas têm, aproximadamente, .430000 métros cúbicos de medida de volume.
Dados obtidos em: https://oeds.link/Z6FOIq e https://oeds.link/BQBgI4. Acessos em: 5 maio 2022.

Atividade
Qual é a medida aproximada do volume das comportas construídas no Canal do Panamá em centímetros cúbicos?
Transformações envolvendo as unidades de medida de volume
Observe os cubos de mesma medida de volume ilustrados a seguir.
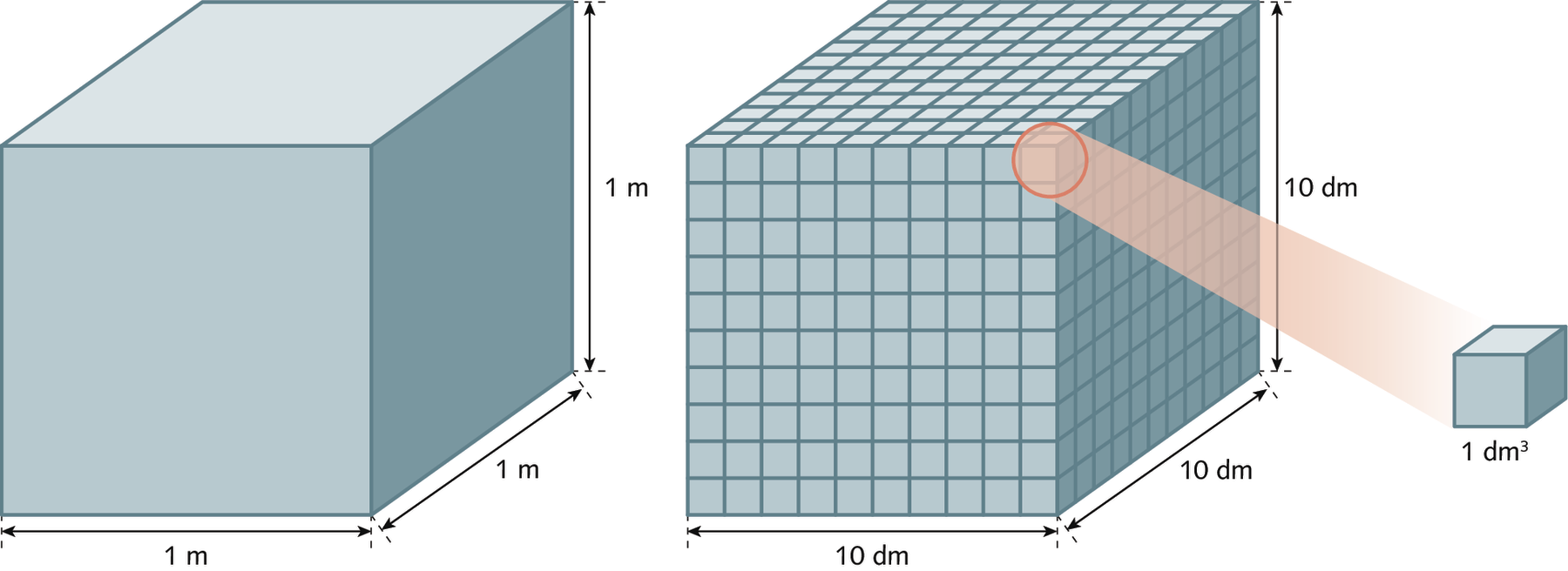
Como 1 metro equivale a 10 decímetros, podemos dividir um cubo cujo comprimento das arestas mede 1 metro em .1000 cubinhos de 1 decímetro cúbico de medida de volume. Então: 1 métro cúbico = .1000 decímetros cúbicos
Assim, para converter uma medida expressa em metro cúbico para decímetro cúbico, multiplicamos essa medida por .1000; para converter uma medida expressa em decímetro cúbico para metro cúbico, dividimos essa medida por .1000.
Observe que cada unidade de medida de volume equivale a .1000 vezes a unidade imediatamente inferior.

Observe os exemplos.
a) Transformar 3,27 métros cúbicos em decímetro cúbico.

Para transformar metro cúbico em decímetro cúbico (uma posição à direita), devemos multiplicar por .1000.
3,27 métros cúbicos ⋅ 1 000 = .3270 decímetros cúbicos
Ou seja: 3,27 métros cúbicos = .3270 decímetros cúbicos
b) Transformar .4568,7 centímetros cúbicos em metro cúbico.
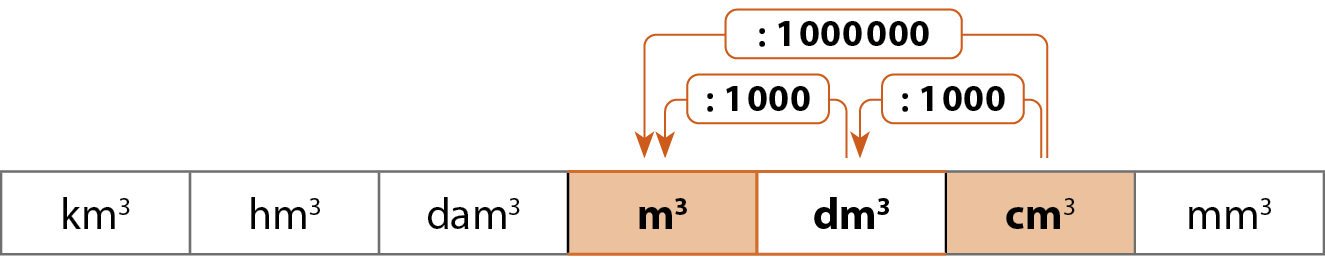
Para transformar centímetro cúbico em metro cúbico abre parêntesesduas posições à esquerdafecha parênteses, devemos dividir por ..1000000.
.4568,7 centímetros cúbicos dividido por ..1000000 centímetros cúbicos = 0,0045687 métro cúbico
Ou seja: .4568,7 centímetros cúbicos = 0,0045687 métro cúbico
Atividades
Faça as atividades no caderno.
61. Utilizando esta unidade de medida de volume, calcule e registre a medida do volume dos blocos a seguir.

unidade de medida de volume
a)

b)

c)

d)

62. Qual destes blocos tem a maior medida de volume?
a)
b)

c)
d)

63. Os dois blocos a seguir têm a mesma medida de volume, mas fórmas diferentes.
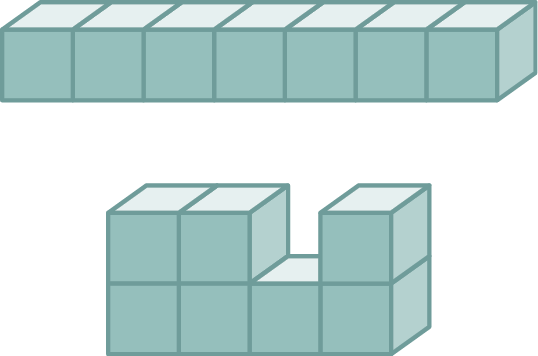
No caderno, explique por que isso ocorre e, depois, desenhe um terceiro bloco com outro formato e mesma medida de volume dos anteriores.
64. Quantas vezes 100 decímetros cúbicos cabem em 10 métros cúbicos?
65. Copie no caderno os itens a seguir substituindo cada

pelo número adequado.
a) 18 métros cúbicos =

decímetros cúbicos
b) .6500 quilômetros cúbicos =

hectômetros cúbicos
c) 750 decímetros cúbicos =

métros cúbicos
d) 0,84 centímetro cúbico =

milímetros cúbicos
e) 3,15 decâmetros cúbicos =

métros cúbicos
f) 0,0084372 métro cúbico =

centímetros cúbicos
66. Um caminhão transporta dois blocos de pedra: um com 400 decímetros cúbicos de medida de volume e outro com 0,38 métro cúbico de medida de volume. Qual é a diferença de medida de volume dos dois blocos, em metro cúbico?
Medida do volume de um paralelepípedo reto-retângulo
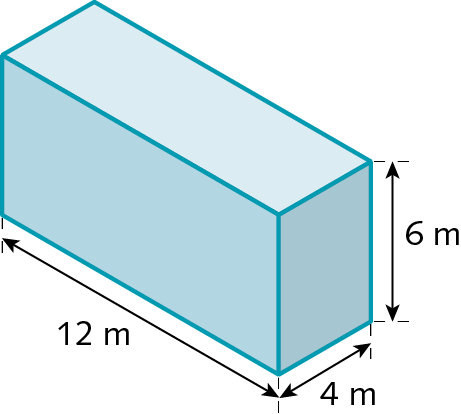
O paralelepípedo reto-retângulo a seguir tem 3 centímetros de medida de comprimento, 2 centímetros de medida de largura e 3 centímetros de medida de altura.
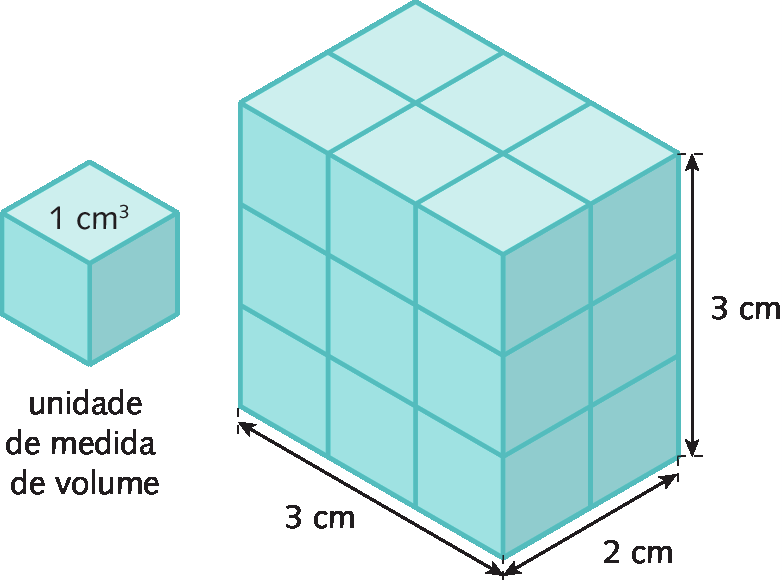
Para determinar a medida do volume desse paralelepípedo, utilizamos como unidade de medida de volume um cubo com arestas que medem 1 centímetro de comprimento, cujo volume mede 1 centímetro cúbico.
O cubo “cabe” exatamente 18 vezes no paralelepípedo. Observe a figura.
Assim, verificamos que a medida do volume desse paralelepípedo reto-retângulo é 18 centímetros cúbicos. A medida desse volume também pode ser obtida pela multiplicação das medidas do comprimento, da largura e da altura do paralelepípedo:

A medida do volume de um paralelepípedo reto-retângulo é igual ao produto das medidas do comprimento, da largura e da altura.
Observação
Podemos calcular a medida do volume de qualquer paralelepípedo abre parêntesescom lados de medidas de comprimento inteiras ou não inteirasfecha parênteses multiplicando as medidas do comprimento, da largura e da altura. Esse procedimento não será demonstrado nesta coleção, mas é verdadeiro.
Observe os exemplos.
a) A medida do volume do paralelepípedo reto-retângulo que tem 6 métros de medida de comprimento, 2 métros de medida de largura e 3 métros de medida de altura é dada por:
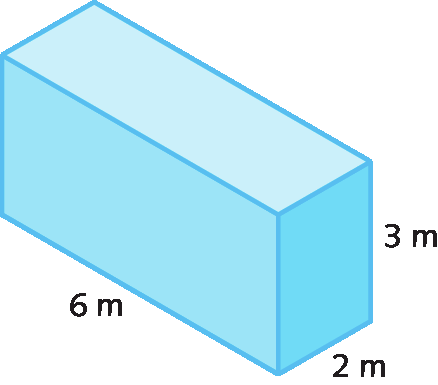
Vparalelepípedo = abre parênteses6 ⋅ 2 ⋅ 3fecha parênteses métros cúbicos = 36 métros cúbicos
b) Vamos desenhar um paralelepípedo reto-retângulo sabendo que a medida do volume é igual a 27 centímetros cúbicos e que o comprimento e a largura medem 3 centímetros.
Para desenhar esse paralelepípedo, precisamos descobrir a medida da altura. Como a medida do volume de um paralelepípedo é obtida multiplicando as medidas do comprimento, da largura e da altura, temos que descobrir qual é o número que, ao ser multiplicado por 9 abre parênteses3 ⋅ 3fecha parênteses, resulta em 27.
Vparalelepípedo = abre parênteses3 ⋅ 3 ⋅ símbolo de ponto de interrogaçãofecha parênteses centímetros cúbicos = 27 centímetros cúbicos
A medida da altura é 3 centímetros, pois: 3 centímetros ⋅ 3 centímetros ⋅ 3 centímetros = 27 centímetros cúbicos
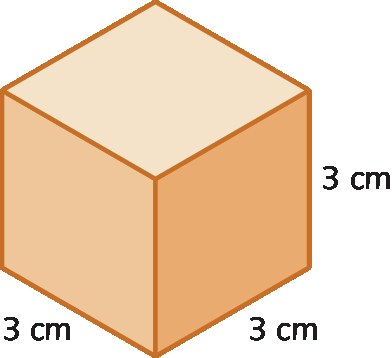
Observe que o paralelepípedo desenhado é um cubo, pois todas as suas arestas têm a mesma medida de comprimento abre parênteses3 centímetrosfecha parênteses.
Atividades
Faça as atividades no caderno.
67. Determine a medida do volume de um cubo com arestas que medem 6 métros de comprimento.
68. Quantos decímetros cúbicos há em uma caixa‑d’água cúbica com arestas que medem 0,4 métro de comprimento?
69. Quantos cubinhos com aresta medindo 2 centímetros de comprimento “cabem” em um cubo cuja aresta mede 20 centímetros de comprimento?
70.

Usando uma calculadora, determine, no caderno, a medida do volume deste sólido geométrico.

71. Determine a medida do volume de um bloco retangular cujo comprimento mede 10 métros, a largura mede 8,5 métros e a altura mede 2,4 métros.
72. Determine, no caderno, a medida do volume de cada bloco retangular a seguir.
a)
b)

c)

d)
73. Determine a medida do volume de uma caixa retangular cujo comprimento mede 5 centímetros, a largura mede 3,5 centímetros e a altura mede 1,6 centímetro.
74. Qual é a medida do volume, em metro cúbico, desta lata de tinta?

75. Um tanque com formato de paralelepípedo reto-retângulo tem 828 métros cúbicos de medida de volume, 8 métros de medida de largura e 11,5 métros de medida de altura. Qual é a medida do comprimento do tanque?
76. Lucas comprou esta bola para presentear o sobrinho. Que medida de volume deve ter a menor caixa de presente, de formato cúbico, para embalar a bola?


5 Grandeza capacidade
Unidades de medida de capacidade
Considerando que o objeto tridimensional é um recipiente (objeto com espaço interno disponível), surge o conceito de capacidade, que corresponde ao volume da parte interna do recipiente.
A medida da capacidade dos recipientes de alguns produtos que utilizamos no dia a dia é indicada nos rótulos. Observe estas embalagens de água:

A unidade-padrão de medida de capacidade no Sistema Internacinal de Unidades é o litro. A medida da capacidade de um cubo cujas arestas medem 1 decímetro (dê ême) de comprimento corresponde a 1 litro.
Assim:
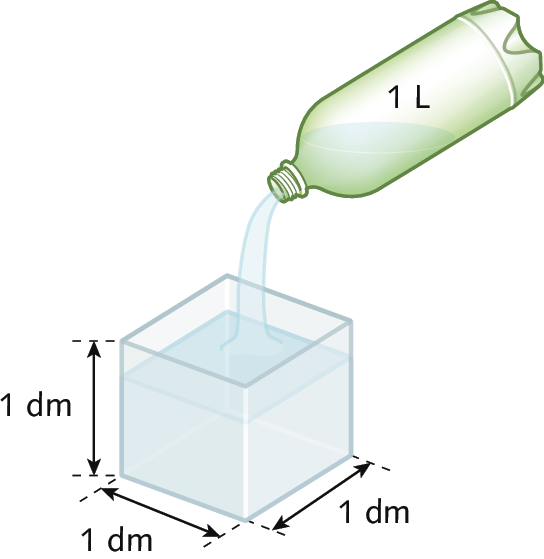
1 litro = 1 decímetro cúbico
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
O símbolo do litro pode ser
ou éle.
Além da unidade-padrão de medida de capacidade, temos seus múltiplos e submúltiplos.
Entre os submúltiplos do litro, uma unidade de medida de capacidade muito utilizada é o mililitro (mL). O mililitro corresponde à milésima parte do litro.
1 litro = .1000 mililitros

Observe, no quadro a seguir, os múltiplos e submúltiplos do litro que fazem parte do Sistema Internacinal de Unidades.
|
Múltiplos |
Unidade-padrão |
Submúltiplos |
|||||
|---|---|---|---|---|---|---|---|
|
Unidade |
quilolitro |
hectolitro |
decalitro |
litro |
decilitro |
centilitro |
mililitro |
|
Símbolo |
kL |
hL |
daL |
L |
dL |
cL |
mL |
|
Relação com o litro |
1.000 L |
100 L |
10 L |
1 L |
0,1 L |
0,01 L |
0,001 L |

Veja que interessante

Aprenda a controlar o consumo de água
O hidrômetro é o aparelho utilizado para medir o consumo de água.

Você já observou como funciona o hidrômetro? Se você mora em uma casa, localize o aparelho e comece a registrar a leitura regularmente. Dessa fórma, você poderá conferir sua conta, controlar a água consumida e descobrir possíveis vazamentos. Uma torneira gotejando, por exemplo, desperdiça 40 litros por dia. Já com um filete de água correndo, o desperdício é de 130 litros por dia.
Como economizar água no dia a dia
Mantenha a torneira fechada enquanto escova os dentes.

Tome banhos de no máximo 5 minutos, mantendo o registro fechado ao se ensaboar.

Mantenha a torneira fechada ao ensaboar a louça. Faça isso também quando desfolhar verduras e hortaliças, descascar frutas e legumes, cortar aves, carnes, peixes etcétera.

Use a vassoura para varrer a calçada, pois, ao usar a mangueira, o desperdício chega a 279 litros a cada 15 minutos de uso.

Regue as plantas com um regador ou mangueira com esguicho-revólver, pela manhã ou à noite, para evitar a evaporação.

Ao lavar roupas no tanque, mantenha a torneira fechada enquanto ensaboa e esfrega a roupa, pois a cada 15 minutos aberta o gasto de água é de 270 litros (o dôbro de água gasta em um ciclo completo de lavagem em uma máquina com capacidade de 5 quilogramas).

Dados obtidos em: https://oeds.link/Btljpv. Acesso em: 26 julho 2022.
Clique no play e acompanhe a reprodução do Áudio.
Atividade

Que atitudes podem ser tomadas no dia a dia para ajudar a reduzir o consumo de água? Converse sobre isso com os colegas.
Transcrição do áudio
Consumo de água em uma cidade grande
Duração: 10:01min. Página: 259.
>> [LOCUTOR] Consumo de água em uma cidade grande
>> [Locutor] Como funciona o abastecimento de água em uma cidade grande? De onde vem a água que a gente consome em casa? Para onde ela vai depois que a utilizamos?
>> [Locutor] Conversamos com o engenheiro sanitarista Paulo Ferreira a respeito dos sistemas de abastecimento de água nas metrópoles brasileiras, sobretudo no que diz respeito aos volumes de produção e consumo desse recurso nas nossas grandes cidades.
>> [Paulo Ferreira] Bem, uma cidade grande, em primeiro lugar, nós precisamos definir o que é cidade grande, né? No caso do Brasil, nós definimos cidade grande acima de 1 milhão de habitantes. O Brasil tem 5 mil municípios, né? E 80% desses 5 mil municípios são de pequeno porte; quer dizer, menor que 50 mil habitantes. A diferença são cidades médias e grandes.
>> [Paulo Ferreira] Então, imaginamos uma cidade grande, de 1 milhão de habitantes, de 1 milhão para cima, a complexidade fica muito maior em termos de abastecimento de água.
>> [Paulo Ferreira] Em primeiro lugar, tendo definida a população, você vai estabelecer qual é o valor de [sic] cada habitante que teria direito, vamos dizer assim... Qual é a cota que cada habitante teria direito à água. >> [Paulo Ferreira] De uma maneira geral, nos projetos o cálculo é um pouco mais sofisticado, a gente adota 200 litros por habitante por dia; quer dizer, seria a quantidade necessária para uma pessoa viver confortavelmente, em termos de abastecimento de água, para todas as necessidades que ela tem em cada dia. Então 200 litros por habitante por dia. Se você multiplicar isso aí pelo número de habitantes, você vai ter então a quantidade de água necessária para abastecer aquela cidade.
>> [Paulo Ferreira] Outros parâmetros existem, outros parâmetros existem para você calcular não só a quantidade de água necessária, mas também calcular como essa água ela [sic] é utilizada durante o dia — que nós chamamos, então, coeficiente de consumo. Normalmente no saneamento você usa coeficiente de consumo do dia de maior consumo e coeficiente da hora de maior consumo. Por exemplo, você tem, no verão, você tem os dias de verão, você tem um consumo maior. E, dentro do dia de verão, tem umas horas [em] que você tem um consumo maior. Então, é dessa forma que é calculada a quantidade de água necessária para uma cidade grande.
>> [Paulo Ferreira] Definido [sic] então a quantidade de água necessária, você vai procurar aonde você vai encontrar esse recurso hídrico de maneira mais econômica. Para isso, você vai levar em conta diversos fatores. Por exemplo, a distância que tá esse recurso hídrico que você possa retirar da... daquele rio, daquele recurso hídrico, né?, aquela quantidade necessária para a cidade. Às vezes se você tem uma cidade que tem mais de um recurso hídrico, o que favorece. Então, você estabelece, dentro dessa lógica, quais são os recursos que você pode utilizar ou qual é o recurso hídrico que você vai utilizar.
>> [Paulo Ferreira] Normalmente, numa cidade grande você não tem só um sistema, ou seja, você não tira a água só de um recurso hídrico; você tira de outras... outros rios também, perfazendo então alguns sistemas de abastecimento de água para aquela cidade, né?
>> [Paulo Ferreira] E aí você tem o percurso natural da água. Definido [sic] então a quantidade de água [de] que você precisa, definido o recurso hídrico do qual você vai retirar essa quantidade de água, você tem aí o encaminhamento normal, né? Você tem que tirar essa água do recurso hídrico, normalmente você tira através de uma elevatória, porque os recursos hídricos sempre estão normalmente em pontos baixos, né? Há algumas exceções no mundo, mas normalmente eles estão sempre em pontos baixos.
>> [Paulo Ferreira] Então se retira essa água através de uma elevatória, essa elevatória encaminha essa água para uma estação de tratamento de água. Normalmente é um tratamento convencional, né? Tratamento convencional, ele tem algumas fases: coagulação, floculação, decantação, filtração e reservação.
>> [Paulo Ferreira] Então, essa água passa por esse processo; quanto menos produto químico ela exigir para ser uma água considerada uma água potável, uma água de boa qualidade, uma água que você possa transmitir, transferir para a população, quanto menos produtos químicos utilizados, melhor — não só por causa do custo, mas como [sic] também por precaução e em termos de saúde pública.
>> [Paulo Ferreira] Essa água então, tendo sido tratada, passa no reservatório. Esse reservatório, através de um conjunto de adutoras, ele encaminha para outros reservatórios. Desses reservatórios que ficam, vamos dizer assim, nos bairros da cidade, saem linhas que a gente chama de rede — aí, sim, seria a rede de distribuição —, e a rede de distribuição, então, percorrendo todas as ruas da cidade, tem as ligações domiciliares; a água chega no [sic] cidadão. Ele ocupa essa água, se ele estiver dentro daquela regra nossa lá de 200 litros por habitante por dia, ele ocupa esses 200 litros a que, vamos dizer assim, ele teria direito, e boa parte... 80% desse recurso hídrico que ele ocupa, volta para o sistema; 80%. Então de 200 litros que ele ocuparia por dia, 160 volta para o sistema. Que são o quê? Água de lavagem de roupa, sua higiene pessoal. Essa água volta para uma outra rede, que seria aí a rede de esgoto, que vai sofrer o processo inverso. Ela caminha, vai para uma estação de tratamento de esgoto, essa estação de tratamento de esgoto depura essa água e aí volta para o recurso hídrico normalmente. Esse é o caminho numa cidade grande. Uma cidade pequena não difere muito disso não, só a escala que muda.
>> [Locutor] Qual o volume de água de que uma cidade precisa diariamente e anualmente em média?
>> [Paulo Ferreira] Mais ou menos eu expliquei aí como é que calcula, né?... usando 200 litros por habitante por dia, multiplica pelo número de habitantes, né? E aí você vai fazer esse [sic], vai calcular a quantidade de água necessária.
>> [Paulo Ferreira] Mas a forma de você calcular é essa: você imagina a cota per cápita, quer dizer, quanto é a quantidade disponível para cada habitante. Normalmente, a gente usa em torno de 200. Normalmente o que eu digo é o seguinte: esse número, ele é um pouco mais trabalhado, né? Só para você ter uma ideia, por exemplo, um americano médio consome 450 litros por habitante por dia, né? A região do Nordeste do Brasil, por exemplo, você pode dimensionar para 120 litros por habitante por dia. Então, você vê que é uma discrepância muito grande. Depende muito assim do nível de desenvolvimento.
>> [Paulo Ferreira] Numa cidade grande, como você... é o tema aí que a gente está discutindo, acho que normalmente 200 litros por habitante por dia tá num bom tamanho. São Paulo tem lugares [em] que você usa 300 litros por habitante por dia... né?
>> [Paulo Ferreira] É, é o consumo de água, não é? Então, para você calcular aí a cidade precisaria fazer essa continha aí.
>> [Locutor] Quais são os desafios para equilibrar a produção de água à quantidade necessária para o consumo?
>> [Paulo Ferreira] Bom, esse desafio realmente é enorme, né? [Riso.] Realmente é enorme. Porque você... A água está ficando cada vez mais escassa e está ficando cada vez mais distante para você buscar essa água para abastecer a população.
>> [Paulo Ferreira] Então, o primeiro desafio que nós temos é saber que a água é um recurso universal, mas é um recurso finito, é um recurso que acaba.
>> [Paulo Ferreira] Então, nós precisamos tomar muito cuidado com isso. Quais são os cuidados que nós devemos tomar? Em primeiro lugar, preservando ao máximo a água que a gente tem, de maneira que a gente não utilize a água de maneira predatória. Por exemplo, varrer calçada com água potável, água tratada, não é uma forma racional de usar água. É melhor você armazenar água de chuva e você limpar a calçada com essa água de chuva.
>> [Paulo Ferreira] Então você tem que economizar água. No seu uso diário, por exemplo, no banho você deve economizar água; na hora [em] que você vai escovar os dentes, você deve economizar água; na hora [em] que você vai fazer a barba, deve economizar água; você tá lavando louça, deve economizar água. Como que você economiza água? Você fechando [sic] a torneira. Então, quando você tá tomando banho, você toma banho com a mesma qualidade, mas num tempo menor. Quando você tá escovando dente, você fecha a torneira. Quando você tá lavando alguma louça, alguma coisa na cozinha, enquanto você tá ensaboando, você fecha a torneira. Essas são formas simples de você economizar água, né? Alguns até utilizam a descarga — é um grande consumidor de água, a descarga de banheiro —, alguns utilizam a água do banho, eles armazenam a água do banho e depois usam essa água para descarga. É uma forma muito inteligente de você economizar água e também [de] baratear a sua conta de água no final do mês.
Vinheta
Créditos Studio Núcleo de Criação
Transformações envolvendo as unidades de medida de capacidade
Observe no quadro de unidades de medida de capacidade, visto anteriormente, que cada unidade de medida de capacidade equivale a 10 vezes a unidade imediatamente inferior.
Confira os exemplos.
a) 1 decalitro = 10 litros
b) 1 litro = 10 decilitros
Sabemos que 1 litro corresponde a .1000 mililitros. Assim, para converter uma medida expressa em litros para mililitros, multiplicamos essa medida por .1000; para converter uma medida expressa em mililitros para litros, dividimos essa medida por .1000.
Observe os exemplos.
a) Transforme 3,5 litros em mililitros.
3,5 litros = .3500 mililitros abre parênteses3,5 litros ⋅ .1000 = .3500 mililitrosfecha parênteses
b) Transforme 600 mililitros em litro.
600 mililitros = 0,60 litro abre parênteses600 litros : .1000 = 0,60 mL)
Atividades
Faça as atividades no caderno.
77. Com uma garrafa de 1 litro de água, quantos copos de 200 mililitros podemos encher?

78. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a) 1 litro =

mililitros
b) 1,5 litro =

mililitros
c.
Meiolitro =

mililitros
d.
um quartolitro =

mililitros
79. Qual é a medida da capacidade, em litro, de um recipiente cúbico cujo comprimento da aresta mede 2 decímetros?
80. Uma torneira com defeito desperdiça 250 mililitros por hora. Quantos litros de água essa torneira desperdiça em uma semana?
81. Uma caixa-d’água de 600 litros está cheia. Em um fim de semana foram gastos
sete 12 avosdesse volume. Quantos litros de água sobraram na caixa-d’água?
82. Emília distribuiu o conteúdo de 8 embalagens de 750 mililitros de suco de caju em copos de 200 mililitros. Quantos copos foram utilizados por Emília?
83. Quantos litros há em 500 decímetros cúbicos?
84. A parte interna de um freezer horizontal mede 1,6 métro de comprimento, 60 centímetros de largura e
meiométro de altura. Qual é a medida da capacidade do freezer em litro?

85. Em uma vasilha, cuja capacidade mede 20 litros, há 17,5 litros de água. Foi colocada uma pedra nessa vasilha, o que a fez encher até a borda. Calcule a medida do volume dessa pedra em decímetro cúbico.
86.

Reúna-se com um colega para resolver a situação a seguir.
Raquel viu que o hidrômetro de sua casa, no mês de março, marcava 468 métros cúbicos.
No mês seguinte, ela verificou de novo o hidrômetro, que dessa vez marcava 494 métros cúbicos.
a) Qual foi o consumo de água, em metro cúbico, na casa de Raquel?
b) Sabendo que 1 decímetro cúbico corresponde a 1 litro, quantos litros de água Raquel consumiu?
c) Pesquisem na cidade em que vocês moram a tarifa cobrada pela água e verifiquem quanto Raquel pagaria se morasse na mesma cidade que vocês.

6 Grandeza massa
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
Unidades de medida de massa
Observe as situações a seguir.


A balança é o instrumento utilizado para medir a massa de um corpo.
Veja alguns tipos de balança.


Massa é a quantidade de matéria de um corpo.
O grama (gê) e o quilograma (cá gê) são as unidades mais usadas para medir a massa de um corpo.
A unidade-padrão de medida de massa no Sistema Internacinal de Unidades é o quilograma (cá gê). Na prática, porém, usamos o grama como unidade de referência para obter seus múltiplos e submúltiplos.


Observação
A palavra “grama”, empregada no sentido de “unidade de medida de massa de um corpo”, é um substantivo masculino. Por isso, ao escrever e pronunciar essa unidade, seus múltiplos e submúltiplos, devemos fazer a concordância corretamente. Veja os exemplos a seguir.
a) 2 quilogramas

Lemos: “dois quilogramas”.
b) 500 miligramas

Lemos: “quinhentos miligramas”.
c) 801 gramas

Lemos: “oitocentos e um gramas”.
Observe o quadro a seguir, que apresenta os múltiplos e submúltiplos do grama que fazem parte do Sistema Internacinal de Unidades.
|
Múltiplos |
Unidade de referência |
Submúltiplos |
|||||
|---|---|---|---|---|---|---|---|
|
Unidade |
quilograma |
hectograma |
decagrama |
grama |
decigrama |
centigrama |
miligrama |
|
Símbolo |
kg |
hg |
dag |
g |
dg |
cg |
mg |
|
Relação com o grama |
1.000 g |
100 g |
10 g |
1 g |
0,1 g |
0,01 g |
0,001 g |
Uma unidade de medida muito utilizada para corpos maiores, mas que não faz parte do Sistema Internacinal de Unidades, é a tonelada (tê). Uma tonelada equivale a .1000 quilogramas, ou seja, uma tonelada = .1000 quilogramas.
Transformações envolvendo as unidades de medida de massa
Observe no quadro anterior que cada unidade de medida de massa equivale a 10 vezes a unidade imediatamente inferior.
Observe os exemplos.
a) 1 decagrama = 10 gramas
b) 1 grama = 10 decigramas
Sabemos que 1 quilograma corresponde a .1000 gramas. Assim, para converter em grama uma medida expressa em quilograma, multiplicamos essa medida por .1000; para converter em quilograma uma medida expressa em grama, dividimos essa medida por .1000.
Observe os exemplos.
a) Transforme 8,5 quilogramas em grama.
8,5 quilogramas = .8500 gramas (8,5 quilogramas ⋅ .1000 = .8500 quilogramas)
b) Transforme 750 gramas em quilograma.
750 gramas = 0,75 quilograma (750 gramas : .1000 = 0,75 quilograma)
Atividades
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
87. Observe as embalagens e registre, no caderno, a medida da massa, em quilograma, de cada produto.

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
88. Escreva, no caderno, a melhor unidade para expressar a medida da massa de:
a)

b)

c)

89. Há várias maneiras de medir a quantidade de ingredientes necessária para preparar bolos e outros alimentos. Observe os ingredientes de uma receita de pão.

Algumas quantidades são determinadas por unidades de medida não padronizadas, como colhér ou xícara; outras, por unidades de medida padronizadas.
a) Que ingredientes da receita estão indicados com uma unidade de medida padronizada?
b) Qual é a unidade de medida padronizada mais adequada para medir a quantidade de farinha de trigo da receita?
c) Compare as quantidades de leite de coco e óleo de girassol da receita. Qual é a maior? Explique.
90. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a) 104 gramas =

quilogramas
b) 8,5 gramas =

miligramas
c) 11,4 quilogramas =

gramas
d) 8,6 toneladas =

quilogramas
91. Uma caminhonete tem medida de massa igual a 800 quilogramas. Após ser carregada com quatro caixas iguais, passa a ter medida de massa igual a uma tonelada. Qual é a medida de massa de cada uma dessas caixas?

92. Mariana foi à feira e comprou 4 quilogramas de maçã a R$ 1,60um reais e sessenta centavos o quilograma e 3,5 quilogramas de laranja a R$ 0,80zero reais e oitenta centavos o quilograma. Quanto ela gastou?
93. Oscar dividiu um queijo de 1 quilograma em oito partes iguais. Qual é a medida de massa, em grama, de cada uma dessas partes?
94. Para fazer um bolo, são necessários duzentas e oitenta gramas de farinha de trigo. Quantos quilogramas de farinha de trigo são necessários para fazer cinco bolos?

95. Um petroleiro transporta .60000 toneladas. Quantos barris de 120 quilogramas podem ser enchidos com o petróleo transportado por esse petroleiro?

96. Um pacote de aveia traz as informações nutricionais mostradas no quadro a seguir.
|
Quantidade por porção |
|
|---|---|
|
Valor energético |
105 kcal |
|
Carboidratos |
16 g |
|
Proteínas |
4,6 g |
|
Gorduras totais |
2,3 g |
|
Fibra alimentar |
3,4 g |
a) Quantos gramas de fibra uma pessoa ingere ao consumir uma colhér de sopa de aveia?
b) Aproximadamente, quantos gramas de carboidratos 1 quilograma de aveia contém?

7 Grandeza temperatura
No Brasil, a unidade de medida de temperatura utilizada é o grau Celsius (grau cê). O termômetro é o instrumento usado para medir a temperatura.
Observe as situações a seguir.



Atividades
Faça as atividades no caderno.
97. Liste em seu caderno três situações do dia a dia em que você se preocupa com a medida da temperatura.
98. Observe as medidas da temperatura registradas em alguns termômetros.



a) Quais são as medidas de temperatura registradas nos termômetros? Escreva, no caderno, essas medidas em ordem crescente.
b) Qual é a diferença entre a maior e a menor medida de temperatura registrada?
99. O termo “amplitude térmica” é utilizado para representar a variação da medida de temperatura em uma cidade, determinando a diferença entre as medidas de temperatura máxima e mínima registradas.
a) Em uma cidade, a medida de temperatura máxima registrada foi de 18 graus Célsius e a mínima, de 9 graus Célsius, em um mesmo dia. Qual foi a amplitude térmica?
b) Pesquise quais foram as medidas de temperatura máxima e mínima registradas em sua cidade no mês de janeiro e determine a amplitude térmica desse mês.
100.


Observe as medidas de temperatura máxima de algumas cidades do Brasil registradas pelo Instituto Nacional de Meteorologia em 17 de dezembro de 2021.
|
Cidade |
Medida de temperatura (em graus Celsius) |
|---|---|
|
Palmas (TO) |
32,4 |
|
Ibotirama (BA) |
35,3 |
|
Picos (PI) |
37,0 |
|
João Pessoa (PB) |
30,9 |
Dados obtidos em: https://oeds.link/r0bPRG. Acesso em: 5 maio 2022.
No caderno, elabore três problemas que possam ser resolvidos usando os dados da tabela. Depois, troque de caderno com um colega e responda às questões elaboradas por ele.

Resolvendo em equipe
Faça a atividade no caderno.
(enêm) Uma lata de tinta, com a fórma de um paralelepípedo retangular reto, tem as dimensões, em centímetro, mostradas na figura.

Será produzida uma nova lata, com os mesmos formato e volume, de tal modo que as dimensões de sua base sejam 25% maiores que as da lata atual.
Para obter a altura da nova lata, a altura da lata atual deve ser reduzida em
a) 14,4%
b) 20,0%
c) 32,0%
d) 36,0%
e) 64,0%
|
Interpretação e identificação dos dados |
• Analise o enunciado e responda: A lata de tinta tem o formato de qual sólido geométrico? |
|---|---|
|
Plano de resolução |
• Calcule a medida do volume da lata de tinta da figura. |
|
Resolução |
• Reúna-se com um colega. |
|
Verificação |
• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas. |
|
Análise da situação |
• Calculem a medida da área total da superfície da lata de tinta original e da nova lata. Em seguida, indiquem a lata que gera maior gasto de material para ser confeccionada. |
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Grandeza comprimento
Quadro de unidades de medida de comprimento
|
Múltiplos |
Unidade-padrão |
||
|---|---|---|---|
|
quilômetro |
hectômetro |
decâmetro |
metro |
|
km |
hm |
dam |
m |
|
1.000 m |
100 m |
10 m |
1 m |
|
Unidade-padrão |
Submúltiplos |
||
|---|---|---|---|
|
metro |
decímetro |
centímetro |
milímetro |
|
m |
dm |
cm |
mm |
|
1 m |
0,1 m |
0,01 m |
0,001 m |
Medida de perímetro
A medida do perímetro de uma figura geométrica plana é a medida do comprimento do contôrno dessa figura.
1. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a) 4,50 métros =

centímetros
b) 0,35 métro =

milímetros
c) 32 métros =

decâmetros
d) 126 métros =

hectômetros
e) .10000 métros =

quilômetros
f) 90 quilômetros =

métros
g) 0,01 quilômetro =

milímetros
h) 8 quilômetros =

decâmetros
i) 4,8 quilômetros =

hectômetros
j) 0,12 quilômetro =

decímetros
2. Responda às questões no caderno.
a) 25 quilômetros equivalem a quantos metros?
b) 4,6 metros equivalem a quantos milímetros?
c) 0,89 metro equivale a quantos centímetros?
d) .12000 metros equivalem a quantos quilômetros?
3. Calcule a medida do perímetro de um quadrado com lados medindo 12,5 centímetros de comprimento.
4. Um terreno retangular mede 18,6 métros de largura, e a medida do comprimento é o dóbro da medida da largura. Qual é a medida do perímetro desse terreno?
Grandeza tempo
1 dia = 24 horas
uma hora = 60 minutos
uma minuto = 60 segundos
5. Quantos segundos há em 1 dia?
6. Quantos minutos há em:
a)
Meiahora?
b)
Um quinto dehora?
c)
Uma inteira e meiahora?
d)
Três quartos dehora?
7. A aula de natação de Lucas começou às 7 horas 30 minutos e terminou às 8 horas 42 minutos. Quanto tempo durou a aula de natação de Lucas?
8. Helena chegou ao escritório 25 minutos antes do horário marcado para uma reunião. Se o relógio dela marcava 8 horas 40 minutos, qual era o horário da reunião?
9. Uma torneira tem vazão de 0,2 litro de água por segundo. Quanto tempo leva, em minuto, para encher um recipiente cuja medida de capacidade é 60 litros?
10. Um ônibus faz o percurso da cidade a até a cidade B em duas horas 36 minutos. Se o ônibus partiu da cidade a às 13 horas 15 minutos, qual é o horário previsto para chegar à cidade B?
Grandeza área
|
Múltiplos |
Unidade-padrão |
||
|---|---|---|---|
|
quilômetro quadrado |
hectômetro quadrado |
decâmetro quadrado |
metro quadrado |
|
km2 |
hm2 |
dam2 |
m2 |
|
1.000.000 m2 |
10.000 m2 |
100 m2 |
1 m2 |
|
Unidade-padrão |
Submúltiplos |
||
|---|---|---|---|
|
metro quadrado |
decímetro quadrado |
centímetro quadrado |
milímetro quadrado |
|
m2 |
dm2 |
cm2 |
mm2 |
|
1 m2 |
0,01 m2 |
0,0001 m2 |
0,000001 m2 |
Medida da área de um retângulo
A medida da área de um retângulo é o produto das medidas de comprimento da base e da altura.
Medida da área de um triângulo retângulo
A medida da área de um triângulo retângulo é a metade do produto das medidas de comprimento da base e da altura.
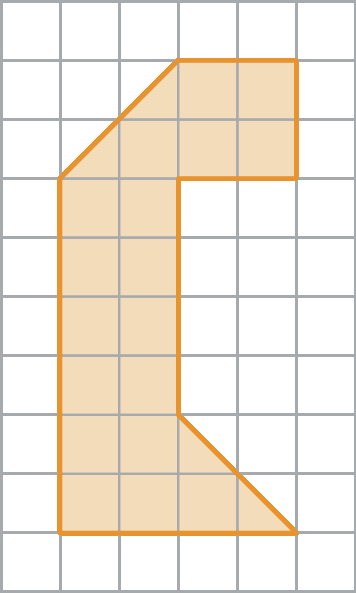
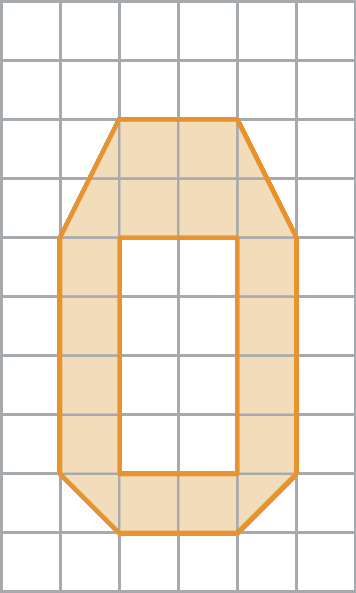
11. Se a medida da área de 1

é 1 centímetro quadrado, determine, no caderno, a medida da área das figuras a seguir.
a)
b)
12. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a) 8 métros quadrados =

centímetros quadrados
b) 9,82 quilômetros quadrados =

decâmetros quadrados
c) .5000 centímetros quadrados =

métros quadrados
d) .12000 milímetros quadrados =

decímetros quadrados
e) 0,85 decâmetro quadrado =

decímetros quadrados
f) .60000 métros quadrados =

hectômetros quadrados
g) 1 quilômetro quadrado =

decâmetros quadrados
h) 0,55 quilômetro quadrado =

hectômetros quadrados
13. Calcule a medida de área de um terreno retangular cuja medida do comprimento é 25,8 métros e a medida da largura é 12,6 métros.
14. Jonas vai revestir o piso de uma garagem com porcelanato e vai usar peças com formato quadrado medindo 0,4 métro de comprimento do lado. Se a garagem tem formato retangular medindo 6 métros de comprimento e 4 métros de largura, quantas peças de porcelanato, no mínimo, serão necessárias?
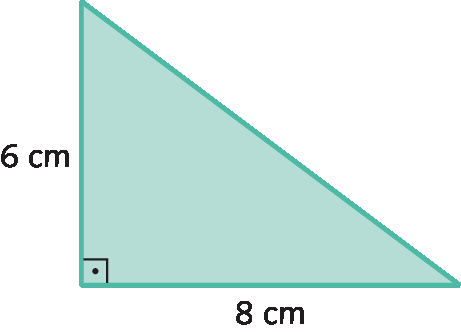
15. Calcule a medida de área de cada triângulo retângulo a seguir.
a)
b)
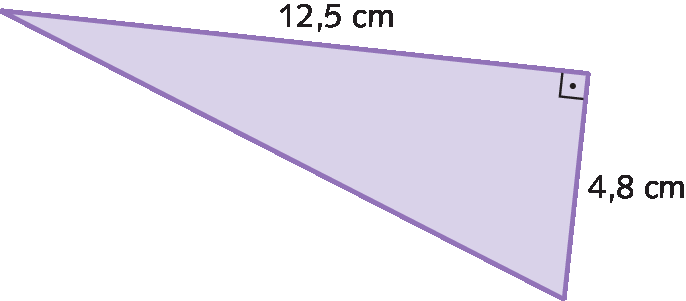
Grandeza volume
|
Múltiplos |
Unidade-padrão |
||
|---|---|---|---|
|
quilômetro cúbico |
hectômetro cúbico |
decâmetro cúbico |
metro cúbico |
|
km3 |
hm3 |
dam3 |
m3 |
|
1.000.000.000 m3 |
1.000.000 m3 |
1.000 m3 |
1 m3 |
|
Unidade-padrão |
Submúltiplos |
||
|---|---|---|---|
|
metro cúbico |
decímetro cúbico |
centímetro cúbico |
milímetro cúbico |
|
m3 |
dm3 |
cm3 |
mm3 |
|
1 m3 |
0,001 m3 |
0,000001 m3 |
0,000000001 m3 |
Medida do volume de um paralelepípedo reto-retângulo
A medida do volume de um paralelepípedo reto‑retângulo é igual ao produto das medidas do comprimento, da largura e da altura.
16. Calcule a medida do volume dos empilhamentos em cada caso, sabendo que a medida do volume de cada cubinho é igual a 1 centímetro cúbico.
a)

b)

17. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a) 15 métros cúbicos =

decímetros cúbicos
b) .8200 quilômetros cúbicos =

hectômetros cúbicos
c) 550 decímetros cúbicos =

métros cúbicos
d) 0,98 centímetro cúbico =

milímetros cúbicos
e) 8,17 decâmetros cúbicos =

métros cúbicos
f) 0,092 métro cúbico =

centímetros cúbicos
g) 6,78 centímetros cúbicos =

milímetros cúbicos
h) 600 quilômetros cúbicos =

hectômetros cúbicos
18. Determine a medida de volume de um cubo cujo comprimento da aresta mede 8 centímetros.
19. Determine a medida de volume de um bloco retangular que mede 8,5 métros de comprimento, 12 métros de largura e 4,2 métros de altura.
Grandeza capacidade
|
Múltiplos |
Unidade-padrão |
||
|---|---|---|---|
|
quilolitro |
hectolitro |
decalitro |
litro |
|
kL |
hL |
daL |
L |
|
1.000 L |
100 L |
10 L |
1 L |
|
Unidade-padrão |
Submúltiplos |
||
|---|---|---|---|
|
litro |
decilitro |
centilitro |
mililitro |
|
L |
dL |
cL |
mL |
|
1 L |
0,1 L |
0,01 L |
0,001 L |
20. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a)
um quartolitro =

mililitros
b) 1,45 litro =

mililitros
c)
meiolitro =

mililitros
d) 12,5 litros =

mililitros
21. Uma torneira com defeito desperdiça 150 mililitros de água por hora. Quantos litros de água essa torneira desperdiça em 1 dia?
22. Qual é a medida de capacidade, em litro, de um aquário com formato de cubo cujo comprimento da aresta mede 5 decímetros?
Grandeza massa
|
Múltiplos |
Unidade-de referência |
||
|---|---|---|---|
|
quilograma |
hectograma |
decagrama |
grama |
|
kg |
hg |
dag |
g |
|
1.000 g |
100 g |
10 g |
1 g |
|
Unidade-de referência |
Submúltiplos |
||
|---|---|---|---|
|
grama |
decigrama |
centigrama |
miligrama |
|
g |
dg |
cg |
mg |
|
1 g |
0,1 g |
0,01 g |
0,001 g |
23. Copie, no caderno, os itens a seguir substituindo cada

pelo número adequado.
a) 208 gramas =

quilogramas
b) 10,2 gramas =

miligramas
c) 25,2 quilogramas =

gramas
d) 12 centigramas =

quilogramas
e) 0,5 quilograma =

decagramas
f) 0,9 decigrama =

gramas
24. No mercado, João comprou 1,6 quilograma de batata a R$ 3,80três reais e oitenta centavos o quilograma e 2,5 quilogramas de carne bovina a R$ 48,50quarenta e oito reais e cinquenta centavos o quilograma. Quanto ele gastou?
Grandeza temperatura
No Brasil, a unidade de medida de temperatura utilizada é o grau Celsius abre parêntesesgrau cêfecha parênteses.
25. Em um município, a medida de temperatura máxima registrada em um dia foi de 34,5 graus Célsius e a mínima, 28,6 graus Célsius. Qual foi a diferença entre as medidas de temperatura máxima e mínima registradas nesse dia?
Glossário
- Sistema Internacional de Unidades
- : sistema utilizado para padronizar unidades de medida em todo o mundo.
- Voltar para o texto
- Micrômetro
- : milionésima parte de um metro.
- Voltar para o texto