Página 270

Capítulo 12 Probabilidade e estatística

Trocando ideias

A energia eólica é a energia gerada a partir dos ventos. Considerada uma fonte de energia limpa e renovável, ela ganhou relevância na composição da matriz elétrica, ocupando hoje o terceiro lugar em geração, ficando atrás da hidrelétrica e da térmica. Observe os gráficos a seguir.

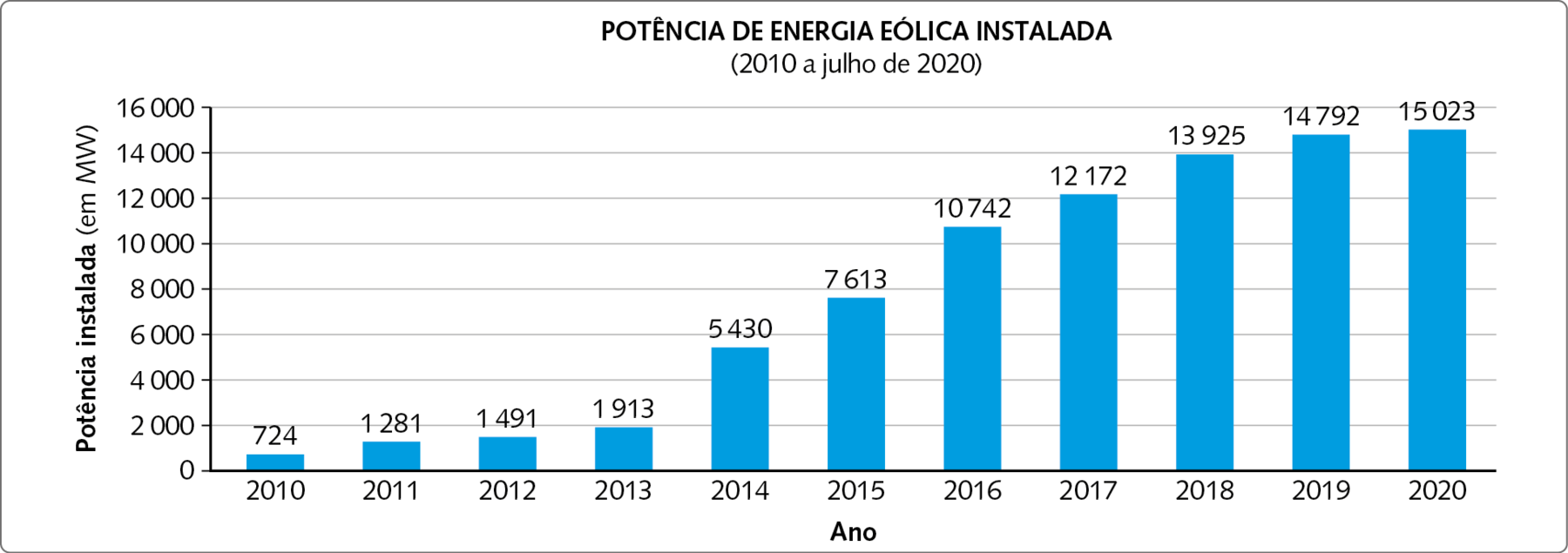
Gráfico. Gráfico de barras simples verticais. Gráfico representando a potência de energia eólica instalada de 2mil 10 a julho de 2mil 20. No eixo vertical, estão indicadas as potências instaladas em megawatts. De baixo para acima: 0, 2 mil, 4 mil, 6 mil, 8 mil, 10 mil, 12 mil, 14 mil e 16 mil. No eixo horizontal, estão indicados os anos: 2 mil 10, 2 mil 11, 2 mil 12, 2 mil 13, 2 mil 14, 2 mil 15, 2 mil 16, 2 mil 17, 2 mil 18, 2 mil 19, 2 mil 20. As potências instaladas em cada ano foram: 2 mil 10: 724; 2 mil 11: mil 281; 2 mil 12: mil 491; 2 mil 13: mil 913; 2 mil 14: 5 mil 430; 2 mil 15: 7 mil 613; 2 mil 16: 10 mil 742; 2 mil 17: 12 mil 172; 2 mil 18: 13 mil 925; 2 mil 19: 14 mil 792; 2 mil 20: 15 mil 23.

MWglossário

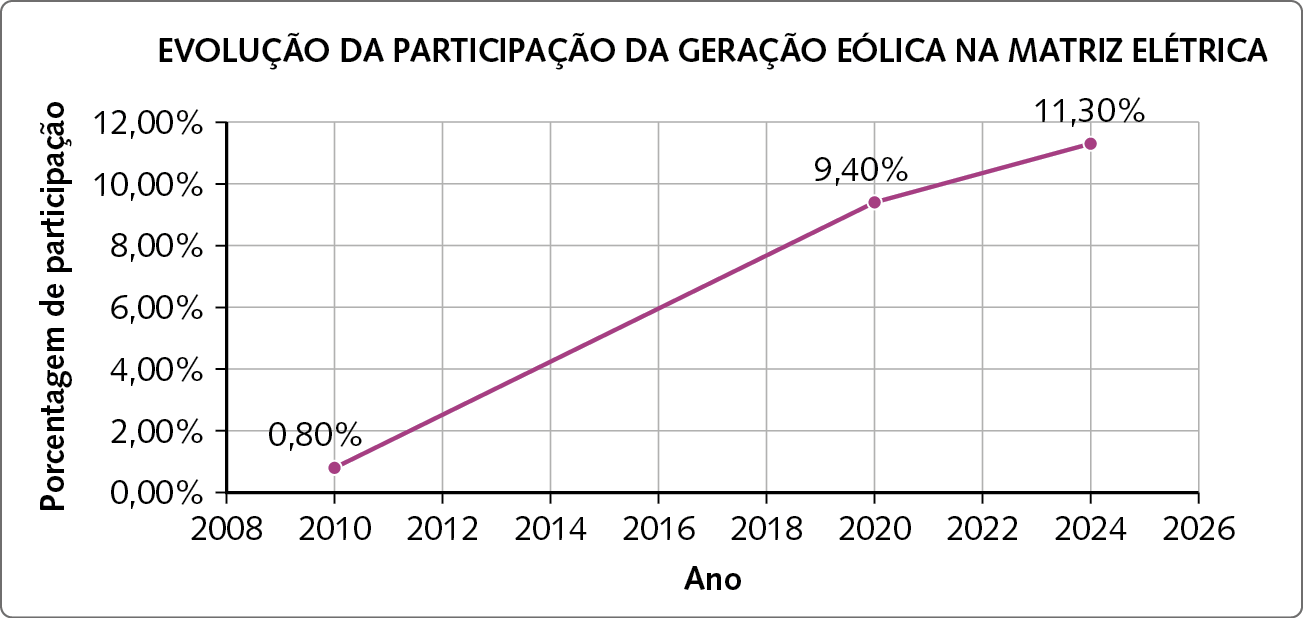
Gráfico. Gráfico de segmentos. Gráfico que mostra a evolução da participação da geração eólica na matriz elétrica. No eixo vertical, estão indicadas as porcentagens de participação: 0 vírgula 00 por cento, 2 vírgula 00 por cento, 4 vírgula 00 por cento, 6 vírgula 00 por cento, 8 vírgula 00 por cento, 10 vírgula 00 por cento e 12 vírgula 00 por cento. No eixo horizontal, estão indicados os anos: 2 mil 8, 2 mil 10, 2 mil 12, 2 mil 14, 2 mil 16, 2 mil 18, 2 mil 20, 2 mil 22, 2 mil 24 e 2 mil 26. Em 2 mil 10, a porcentagem de participação da geração eólica foi de 0 vírgula 80 por cento, em 2 mil 20 foi de 9 vírgula 40 por cento e em 2 mil 24 foi de 11 vírgula 30 por cento.

Dados obtidos em: https://oeds.link/E5Yxf5. Acesso em: 5 maio 2022.

Ilustração. Uma ampla área com pequenos morros e um céu cheio de nuvens, com diversas torres de energia eólica no solo.

▸

Qual é a importância do uso de fontes de energia renováveis? Converse com os colegas.

▸

Em que situações, gráficos como os que aparecem nesta página são utilizados?

▸

Tire algumas conclusões com base nesses gráficos e compartilhe com os colegas.

Neste capítulo, vamos estudar diferentes tipos de gráficos estatísticos, as etapas de uma pesquisa e o conceito de probabilidade.

Página 271

1 Probabilidade

A probabilidade é a medida da chance de algo acontecer.

A seguir, vamos estudar como calcular o número de possibilidades e a probabilidade.

Cálculo do número de possibilidades

Quando queremos escolher uma roupa, um lanche, um filme ou o sabor de um sorvete, por exemplo, pode haver mais de uma possibilidade de escolha.

Acompanhe as situações a seguir.

Situação 1

Cláudio tem cartões com os algarismos 4, 5 e 6. Ele quer formar um número de três algarismos utilizando esses três cartões. Quantos números ele pode representar com esses cartões?

Ilustração. Menino negro com cabelos cacheados castanhos, usando uma blusa azul. Ele está sentado em uma mesa de estudos segurando três cartões vermelhos em suas mãos.

As possibilidades de números que Cláudio pode formar estão apresentadas a seguir.

Ilustração. Conjunto de 6 trios de cartas. Na primeira linha, da esquerda para a direita, o primeiro trio de cartas é composto pelos números 4, 5 e 6. O segundo trio é composto pelos números 5, 4 e 6, e o terceiro trio é composto pelos números 6, 4 e 5. Na segunda linha, da esquerda para a direita, o primeiro trio de cartas é composto pelos números 4, 6 e 5. O segundo trio é composto pelos números 5, 6 e 4, e o terceiro trio é composto pelos números 6, 5 e 4.

Portanto, Cláudio pode representar 6 números com os três cartões.

Situação 2

Alice tem duas caixas, cada uma com quatro bolas de cores diferentes. Ela resolveu levar uma bola de cada caixa para o colégio. Quantos pares diferentes de bolas podem ser formados por Alice?

Ilustração. Duas caixas contendo quatro bolas cada, de cores diferentes. Na caixa 1, do lado esquerdo, estão as bolas nas cores roxo, verde, amarelo, e rosa. Na caixa 2, do lado direito, estão as bolas na cores vermelho, laranja, marrom e azul.

Podemos listar todas as possibilidades de pares com a ajuda do esquema a seguir.

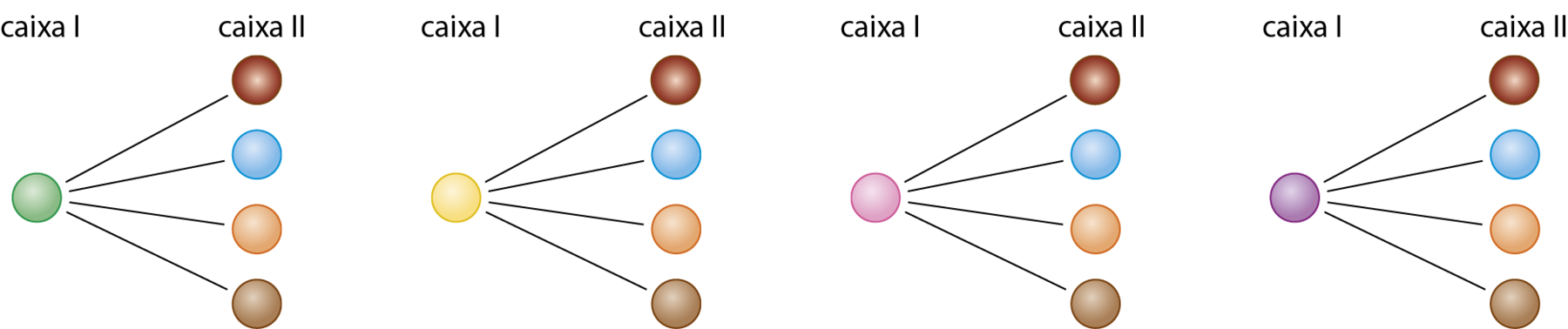
Esquema. 4 esquemas de possibilidades de pares com bolas das caixas 1 e 2, representado da esquerda para a direita. O primeiro esquema possui a bola verde da caixa 1 no centro e fio preto conectado às bolas da caixa 2, nas cores vermelho, azul, laranja e marrom, de cima para baixo. O segundo esquema possui a bola amarela da caixa 1 no centro e fio preto conectado às bolas da caixa 2, nas cores vermelho, azul, laranja e marrom, de cima para baixo. O terceiro esquema possui a bola rosa da caixa 1 no centro e fio preto conectado às bolas da caixa 2, nas cores vermelho, azul, laranja e marrom, de cima para baixo. O quarto esquema possui a bola roxa da caixa 1 no centro e fio preto conectado às bolas da caixa 2, nas cores vermelho, azul, laranja e marrom, de cima para baixo.

O esquema apresentado é um exemplo de árvore de possibilidades.

Portanto, Alice pode formar 16 pares diferentes de bolas.

Página 272

Atividades

Faça as atividades no caderno.

1. Henrique ganhou camisas e bermudas novas. Entre as camisas havia uma vermelha, uma azul e uma preta e, entre as bermudas, havia uma azul e uma branca. Faça uma árvore de possibilidades com todas as combinações entre camisas e bermudas que podem ser montadas por Henrique.

Cama com 5 peças de roupa em cima: duas bermudas nas cores branco e azul, e 3 blusas nas cores azul, preto e vermelha.

2. Desenhe 10 bandeiras. Em seguida, pinte-as com as cores azul, vermelha e amarela, colocando-as em diferentes posições. Depois, determine quantas bandeiras diferentes é possível obter usando apenas essas três cores.

Ilustração. Bandeira dividida com três faixas cinzas

3. Determine todas as adições possíveis de dois números naturais cuja soma seja 6.

4. Observe a placa e responda à questão.

Fotografia. Placa de automóvel retangular com uma tarja azul na parte superior escrita 'Brasil' e a bandeira do Brasil representada na parte superior direita. No centro, há uma sequência de letras e números, da esquerda para direita: B, R, A, 1, E, 3, 4. No canto inferior esquerdo, há a sigla 'BR'.

• Quantas placas distintas existem como anterior, alterando apenas a ordem das três primeiras letras?

5. Escreva um exemplo de situação com várias possibilidades.

6. O restaurante em que Roberto almoça vai servir hoje:

Ilustração. Papel com as indicações: 3 tipos de macarrão: espaguete, integral e talharim; 4 tipos de molho: à bolonhesa, quatro queijos, ao sugo e branco; 2 tipos de sobremesa: gelatina e salada de frutas.

Qual é o total de opções para Roberto escolher um macarrão com môlho e uma sobremesa?

Cálculo de probabilidade

Ao lançar uma “moeda honestaglossário ”, conseguimos prever se vai sair cara ou se vai sair coroa? Quando nos inscrevemos num sorteio, conseguimos saber quem será sorteado? Ao lançar um “dado honestoglossário ”, conseguimos garantir que número aparecerá na face superior?

Esses são exemplos de situações cujo resultado não conseguimos prever exatamente e, por isso, são chamadas de experimentos aleatórios. No entanto, podemos medir a chance desses resultados ocorrerem calculando o que chamamos de probabilidade.

Por exemplo, ao lançar uma “moeda honesta”, qual é a probabilidade de sair coroa?

Os resultados possíveis ao lançar uma “moeda honesta”, são cara e coroa. A chance de sair coroa, ao lançar uma “moeda honesta”, é de uma em duas possibilidades. Assim, dizemos que a probabilidade de sair coroa é de

\frac{1}{2}

ou 0,5 ou 50%.

Página 273

Agora, acompanhe as situações a seguir.

Situação 1

Cláudio escreveu todos os números de três algarismos usando apenas os algarismos 4, 5 e 6 e os colocou em um saco. Qual é a probabilidade de uma pessoa retirar, sem ver, um número par desse saco?

Há 6 números no saco: 456, 546, 645, 465, 564 e 654.

Entre os resultados possíveis existem 4 números pares: 456, 546, 564 e 654. Ou seja, há 4 resultados favoráveis em 6 resultados possíveis.

Portanto, a probabilidade de uma pessoa retirar, sem ver, um número par do saco é:

\frac{4}{6} = \frac{2}{3}

ou, aproximadamente, 0,66 ou 66%.

Situação 2

Jéferson e Cleide foram à sorveteria. Enquanto Cleide retirava os sorvetes no balcão, Jéferson procurava um lugar para eles sentarem. Mas Jéferson se esqueceu de dizer à amiga quais eram os sabores das bolas de sorvete que ele queria: uma de limão e outra de morango.

A sorveteria oferece cinco sabores: morango, creme, limão, chocolate e abacaxi. Cleide sabia apenas que Jéferson gostaria de duas bolas de sabores diferentes. Qual é a probabilidade de Cleide acertar a combinação de sabores de sorvete do amigo?

Os cinco sabores – morango, creme, limão, chocolate e abacaxi – podem ser combinados da seguinte maneira:

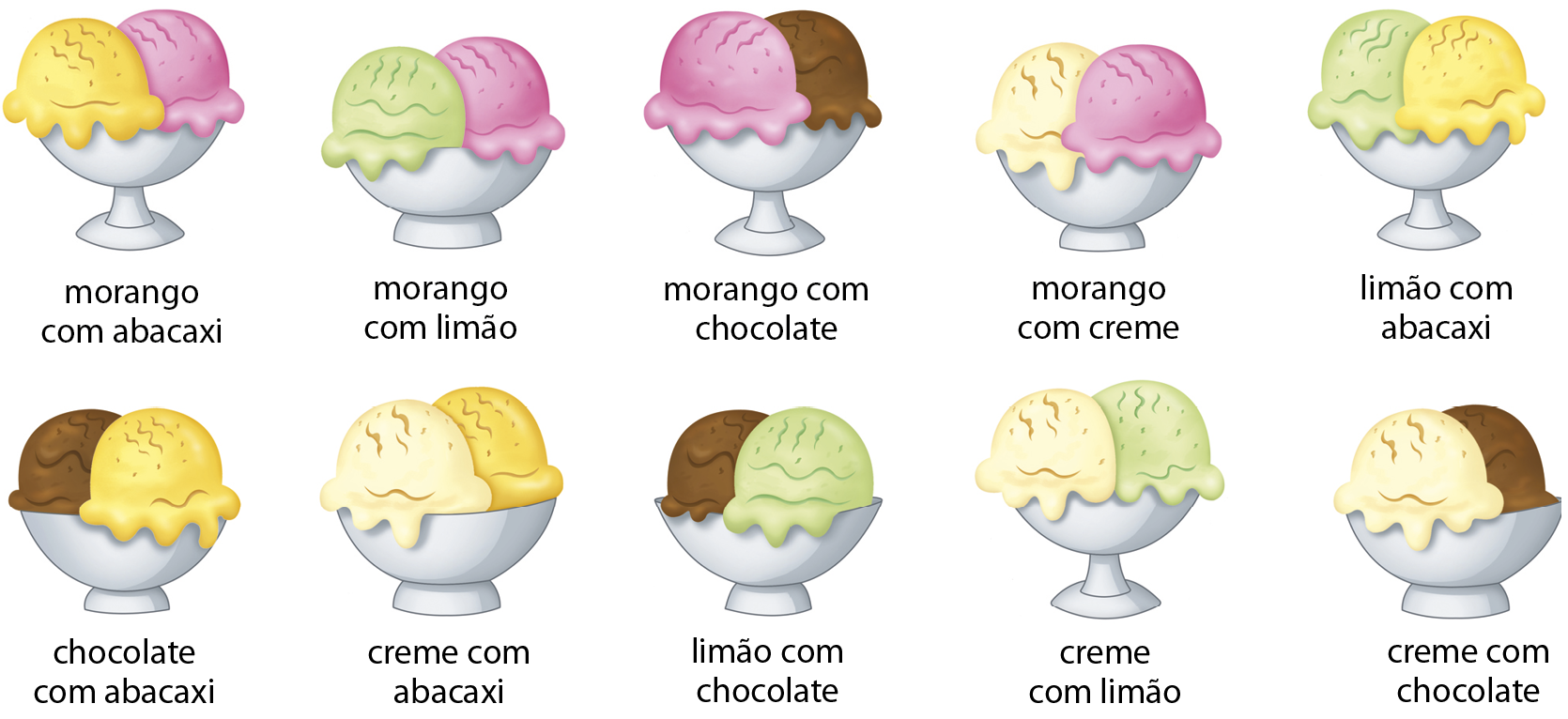
Ilustrações.10 taças de sorvete de massa com duas bolas de sabores diferentes cada. Na primeira linha, da esquerda para direita: taça de morango com abacaxi, taça de morango com limão, taça de morango com chocolate, taça de morango com creme e taça de limão com abacaxi. Na segunda linha, da esquerda para direita: taça de Chocolate com abacaxi, taça de creme com abacaxi, taça de limão com chocolate, taça de creme com limão e taça de creme com chocolate.

Portanto, existem 10 possibilidades para combinar dois sabores.

A probabilidade de Cleide acertar os sabores que Jéferson deseja é de 1 em 10, ou seja,

\frac{1}{10}

ou 0,1 ou 10%.

Observação

1. A probabilidade pode ser indicada por uma fração, por um número na fórma decimal ou por uma porcentagem.

2. A probabilidade é um número que varia de 0 a 1.

3. O cálculo da probabilidade é feito para os resultados de experimentos aleatórios.

Página 274

Atividades

Faça as atividades no caderno.

7. Ana Laura colocou 13 bolas amarelas, 10 roxas e duas verdes dentro de um saco preto. Em seguida, solicitou a um amigo que sorteasse uma bola. Qual é a probabilidade de a bola sorteada ser verde?

8. Qual é a probabilidade de ser sorteado um número ímpar no conjunto de números a seguir?

Quadro. Quadro com conjunto de números, representados da esquerda para a direita. Na primeira linha: 56, 45, 67, 876, 453, 765, 9, 87 63, 564 Na segunda linha: 3, 1, 34, 58, 97, 90, 78, 98, 91, 21. Na terceira linha: 456, 678, 875, 431, 457, 873, 971, 999, 111, 551

Reúna-se com um colega e faça o que se pede. Vocês vão precisar de uma moeda, um lápis ou uma caneta e uma folha de papel sulfite ou o caderno.

a) Reproduzam o quadro a seguir em uma folha do sulfite ou caderno. Agora, cada um deve lançar uma “moeda honesta” 10 vezes e, após cada lançamento, registrar as ocorrências no quadro: se apareceu “cara” ou “coroa”.

Quadro 1 – Lançamento da “moeda honesta” (10 lançamentos)
Resultado	Quantidade de vezes que saiu cada resultado
Cara
Coroa

Observe um exemplo de como o quadro deverá ser preenchido.

Quadro 1 – Lançamento da “moeda honesta” (10 lançamentos)
Resultado	Quantidade de vezes que saiu cada resultado
Cara	/ / / / / / /	7
Coroa	/ / /	3

b) Reproduzam este outro quadro em uma folha de sulfite ou caderno. Agora, cada um deve lançar uma “moeda honesta” 40 vezes e registrar as ocorrências no quadro.

Quadro 2 – Lançamento da “moeda honesta” (40 lançamentos)
Resultado	Quantidade de vezes que saiu cada resultado
Cara
Coroa

c) Qual foi a face da “moeda honesta” que apareceu mais vezes nos 10 lançamentos? Qual é o percentual de ocorrência dessa face com relação ao total de lançamentos?

d) Qual foi a face da “moeda honesta” que apareceu mais vezes nos 40 lançamentos? Qual é o percentual de ocorrência dessa face com relação ao total de lançamentos?

Observe as porcentagens dos itens anteriores sobre o lançamento de uma “moeda honesta”. Se lançarmos a “moeda honesta” mais uma vez, podemos afirmar com certeza que face aparecerá? Justifiquem a sua resposta.

O que aconteceria com a porcentagem de ocorrências de “caras” e “coroas” se vocês lançassem a “moeda honesta” .50000 vezes?

Página 275

10. Júlio e Carla estão brincando com um “dado honesto”. Depois de cada lançamento feito por Júlio, Carla registra, no quadro, o número que aparece na face superior do “dado honesto”. Ela já registrou o resultado de 25 lançamentos. Agora, observe a conclusão de Júlio após observar os registros feitos por Carla. Você concorda com Júlio?

Ilustração. Júlio e Carla jogando dado. Do lado esquerdo, Júlio, um menino branco com cabelo castanho enrolado e que usa óculos, blusa verde e calça azul. Ele está jogando um dado sobre a mesa e um balão ao lado dele diz: Se eu lançar o 'dado honesto' mais uma vez, vai aparecer a face 6, pois a probabilidade de sair essa face é maior. Do lado direito, Carla, menina negra que usa camiseta rosa e calça azul. Ela anota em um quadro com 6 linhas. Na primeira linha, face 1 do dado e 5 risquinhos verticais. Na segunda linha, face 2 do dado e 4 risquinhos verticais. Na terceira linha, face 3 do dado e 2 risquinhos verticais. Na quarta linha, face 4 do dado e 4 risquinhos verticais. Na quinta linha, face 5 do dado e 2 risquinhos verticais. Na sexta linha, face 6 do dado e 8 risquinhos verticais.

11. Carlos trabalha na companhia de trânsito da cidade, atuando no departamento responsável pela análise dos dados. Ele precisa entregar um estudo sobre acidentes para o mês de maio. Para isso, dispõe dos seguintes dados:

Número de acidentes causados por excesso de velocidade no 1º quadrimestre (2024)
Mês	Acidentes causados por excesso de velocidade	Total de acidentes
Janeiro	53	1.000
Fevereiro	56	1.042
Março	79	1.572
Abril	74	1.500

Dados obtidos pela companhia de trânsito da cidade de Carlos no 1º quadrimestre de 2024.

• Entre o total de acidentes esperados para o mês de maio, qual é o percentual estimado daqueles causados por excesso de velocidade?

12.

A professora Marta construiu um fluxograma para verificar se o resultado de um experimento aleatório é certo ou impossível.

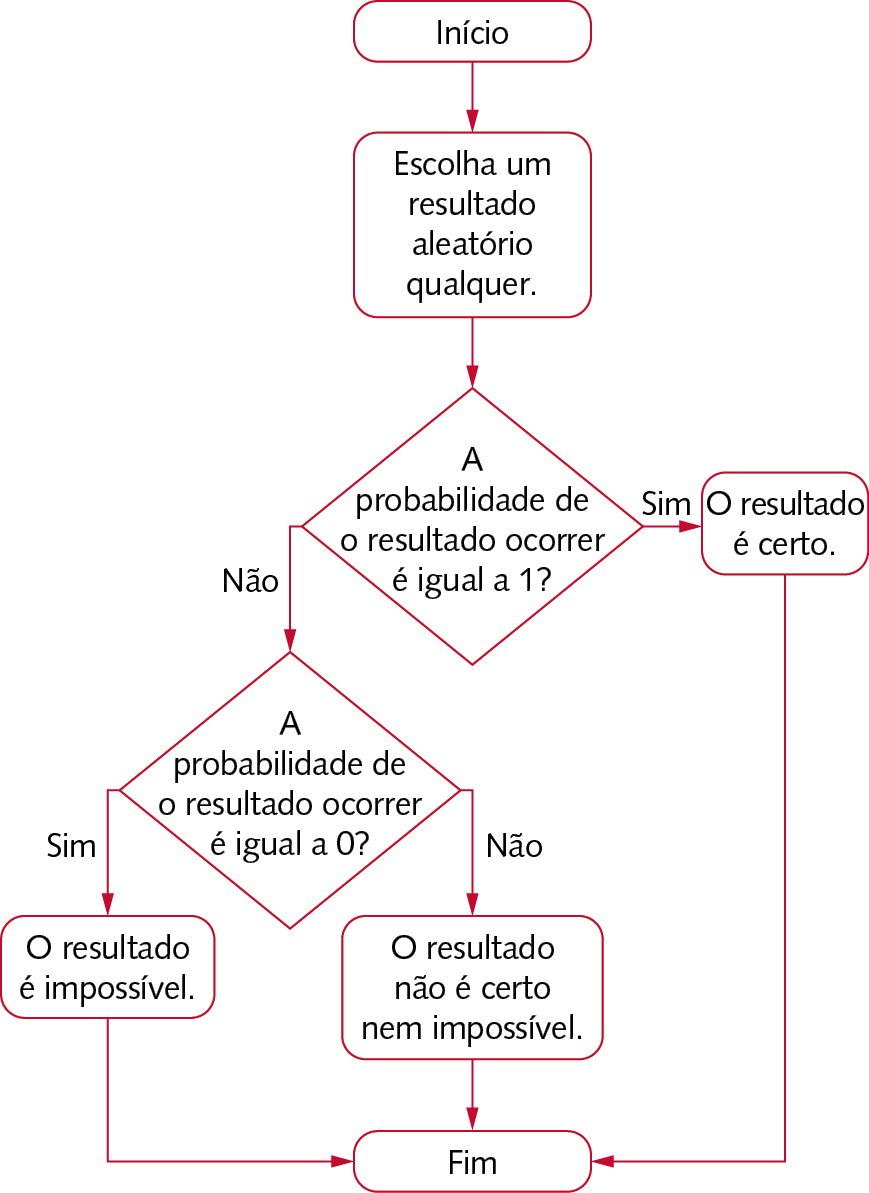
Fluxograma. Verificação do resultado de um experimento, com oito caixas e ligadas por setas, o fluxograma é representado na vertical e as setas são multidirecionais. Na parte superior, primeiro tem o Início, seta para baixo, Escolha um evento aleatório qualquer, seta para baixo para 'A probabilidade de o evento ocorrer é igual a 1?'. À direita, seta horizontal com a opção Sim para 'O resultado é certo.' e seta direta para o fim. À esquerda, seta para baixo com a opção Não para 'A probabilidade de o evento ocorrer é igual a 0?'. À esquerda, seta para baixo com a opção Sim para 'O resultado é impossível.', que se conecta ao fim. À direita, seta para baixo com a opção Não para 'O resultado não é certo nem impossível.', que se conecta ao fim.

Agora, utilize o fluxograma para classificar estes resultados dos experimentos aleatórios dados.

A: Lançar dois “dados honestos” e a soma das faces obtidas ser 15.

B: Lançar um “dado honesto” e sair um número de 1 a 6.

C: Lançar um “dado honesto” e sair um número par.

13.

Considere a figura a seguir e crie uma questão que envolva probabilidade. Peça a um colega que a resolva e, depois, corrija-a.

Ilustração. Saco com 22 bolinhas: 10 verdes e 12 vermelhas.

Clique no play e acompanhe a reprodução do Áudio.

Transcrição do áudio

Cara ou coroa?

Duração: 7:44min. Página: 275.

>> [LOCUTOR] Cara ou coroa?

>> [Locutor] Algumas situações do nosso dia a dia podem ser analisadas por meio da estatística e de cálculos de probabilidade. As chances de chover em determinado lugar, de se nascer com olhos azuis ou até mesmo de tirar cara num simples lançamento de moeda são alguns dos exemplos que envolvem o cálculo de probabilidade.

>> [Locutor] Conversamos a respeito desse tema com Cileda de Queiroz, Matemática e especialista em Educação Estatística. Vamos ouvi-la?

>> [Locutor] Você poderia dar uma breve definição de probabilidade? Em que situações do dia a dia nós lidamos com ela?

>> [Cileda de Queiroz] Bom, primeiro nós temos que pensar: O que é o acaso? Se não falar de acaso, você não pode falar de probabilidade. Hoje em dia, nós podemos considerar esse acaso como uma complexidade de causas. Isso desde o início do século XX — que se considera isso. Que que significa? Muitas e muitas causas pequenininhas, bem baralhadas, mas que, juntas, elas produzem um efeito que eu consigo observar. Por exemplo, um jogador vai marcar... vai cobrar um pênalti. Mesmo que eu conheça o jogador, conheça todas as ações dele quando ele costuma cobrar um pênalti, conheça o goleiro, têm outras causas que podem influenciar — um jeito de tocar na bola, vento, tudo pode influenciar. Então, nós não podemos ter certeza se esse gol vai ser marcado ou não, né? E aí, se nós pensarmos nisso, hoje em dia, a nossa vida tá toda permeada de situações assim; toda permeada de situações nas quais a incerteza ou esse acaso não nos permite conhecer, ter certeza do resultado final da evolução do que eu tô observando. E, assim, a gente diz que... nós dizemos que a probabilidade, ela é entendida como uma medida dessa incerteza, quando uma situação tá se desenvolvendo.

>> [Locutor] Em um jogo de futebol, o árbitro sorteia, por meio de cara ou coroa, qual dos dois times dará início à partida. Ao fim do lançamento de uma moeda, a probabilidade de sair cara ou de dar coroa é de metade para cada resultado. Podemos então concluir que os dois times terão chances iguais de ganhar a posse de bola, certo?

>> [Cileda de Queiroz] Bom, se essa moeda for equilibrada ou honesta, como a gente diz, o que eu já falo, os dois times têm chances iguais. Que que significa isso? Se o juiz joga a moeda para cima de uma forma que ela gire no ar, então a probabilidade de cada resultado é a mesma — do cara ou do coroa. Por que que isso acontece? A moeda é um objeto, que ela tem, teoricamente, o... ela é simétrica perfeitamente em relação ao centro desse objeto. Por isso é que ela tem meio para cada lado. No entanto, se alguém mexer alguma coisa, vamos supor que eu consiga adulterar essa moeda, essa simetria acaba. É nesse caso que nós vamos dizer que essa moeda é viciada. O outro caso a moeda é honesta. E, aí, com a viciada a gente não tem certeza se os resultados são iguais. Aliás, a gente tem certeza que não são.

>> [Locutor] Outra questão: uma mesma pessoa foi escalada para arbitrar uma série de quatro jogos de futebol. Utilizando sempre a mesma moeda nos quatro lançamentos que fez, esse árbitro obteve um total de quatro coroas. Podemos então desconfiar de que aquela moeda estava viciada? Se a probabilidade para cada resultado possível é metade, por que saíram quatro coroas, em vez de duas caras e duas coroas?

>> [Cileda de Queiroz] Bom, olha bem. Dá para ficar com a pulga atrás da orelha, não é? No entanto, cada jogo é completamente independente do outro. Então, cada vez que ele joga a moeda, é como se tivesse contando do zero, tá? Então, para falar de probabilidade, novamente, a gente tem que considerar a ação do acaso. Logo, isso faz com que a cada vez se renove a chance cara ou coroa como meio.

>> [Locutor] Agora, você pode falar um pouco sobre o cálculo da probabilidade, dos pontos de vista da definição clássica e da definição frequentista?

>> [Cileda de Queiroz] Novamente eu vou fixar bem nessa parte da... de observar a ação do acaso. Por que que eu vou fazer isso? Porque era muito comum, até o início do século XX, que se falasse de probabilidade sem prestar atenção se existia acaso ou não. E aí, se não tem, não é probabilidade, é como se fosse uma experiência num laboratório, que eu vou fazer uma experiência de química, por exemplo. Eu tenho certeza do que vai acontecer. Isso não é acaso.

>> [Cileda de Queiroz] A probabilidade de um evento que resulta da ação do acaso é uma razão, tá? Se você olhar, às vezes você vai encontrar como sendo... éuma fração, é um número racional, eu acho que é mais forte que isso; ela é uma razão entre o número de vezes que esse evento ocorre efetivamente e o número total de ocorrências possíveis, considerando um mesmo experimento aleatório. Para considerarmos esse enfoque, que é o da... da definição clássica, todos esses resultados possíveis, eles precisam ter exatamente a mesma probabilidade. Eles só ocorrem nesse caso, que é uma definição que a gente deve ao Laplace. E ao... Primeiro foi o Fermat, a correspondência entre o Pascal e Fermat, que gerou isso lá no século XVII, e aí o Laplace tentou formalizar. Então, todas os eventos... todos os eventos têm que ter a mesma chance, tá?

>> [Cileda de Queiroz] Já na definição frequentista, consideramos que um mesmo experimento é realizado ou observado um número muito grande de vezes. Por exemplo, ao invés de calcular a moeda equilibrada, a chance de cada lado é meio, vamos pensar o que acontece se nós lançarmos essa moeda só e ficarmos observando os resultados. Mas aí tem que prestar atenção. É um número muito, muito grande de vezes. Geralmente, mais do que mil vezes essa repetição do experimento. E, nesse caso, a frequência relativa é que vai permitir, desse grande número de vezes, estimar a probabilidade. Que que quer dizer isso? Existe uma tendência de que esse valor da frequência relativa oscile em torno do valor da probabilidade, como se fosse um fiel de balança, ok?

Vinheta

Créditos

Studio Núcleo de Criação

Página 276

2 Estatística

A Estatística é o ramo da Matemática que envolve a coleta e a organização de dados referentes a diversos fenômenos, para depois analisá-los e interpretá-los.

É por meio das pesquisas estatísticas que podemos indicar qual é a população do Brasil ou estudar os efeitos de novos medicamentos, por exemplo.

As tabelas e os gráficos que encontramos nos meios de comunicação, como jornais e revistas, resultam do processo estatístico, que, em geral, é realizado em várias etapas, como:

1. planejamento e coleta dos dados;

2. organização dos dados;

3. exposição dos dados em tabelas e/ou gráficos e conclusões.

Podemos representar as etapas do processo estatístico por meio de um fluxograma:

O processo estatístico

Acompanhe a situação a seguir, que traz um exemplo da aplicação do processo estatístico.

Joana resolveu fazer uma pesquisa sobre a quantidade de água que é gasta em um banho de chuveiro, depois de ler a seguinte notícia:

Ilustração. Papel com a notícia: De acordo com o Ministério do Meio Ambiente, cerca de 70% da superfície da Terra é coberta por água. No entanto, mesmo com tanta água, enfrentaremos uma crise de abastecimento no século XXI. Por volta de 2050, estima-se que quase 50% da população mundial não terá água suficiente para o consumo.

Acompanhe os passos seguidos por Joana.

1º passo: planejamento e coleta de dados

Antes de iniciar a coleta de dados, Joana pesquisou a quantidade de água que é gasta em um banho de chuveiro elétrico de 15 minutos e constatou que são gastos 45 litros de água.

Ela continuou a pesquisar e descobriu que o ideal é tomar banho em 5 minutos, pois o gasto se reduz a 15 litros de água. Com base nessas informações, ela entrevistou seus colegas de turma, coletando as seguintes informações: “nome“ e “medida do tempo gasto no banho (em minutos)”.

Após encerrar as entrevistas, Joana inseriu os dados coletados em uma planilha eletrônica.

Ilustração. Representação de parte de uma planilha eletrônica mostrando as linhas de 1 a 21 e as colunas A e B. Na linha 1: Nome na coluna A e, na coluna B, medida do tempo gasto no banho, abre parênteses, em minutos, fecha parênteses. Na linha 2: Abel; 10 minutos Na linha 3: Antônio, 10 minutos Na linha 4: Breno, 20 minutos Na linha 5: Cláudia, 25 minutos Na linha 6: Dionísio, 20 minutos Na linha 7: Douglas, 30 minutos Na linha 8: Edmilson, 5 minutos Na linha 9: Everaldo, 15 minutos Na linha 10: Fábio, 10 minutos Na linha 11: Guilherme, 5 minutos Na linha 12: Horácio, 10 minutos Na linha 13: Joana, 5 minutos Na linha 14: Lúcia, 10 minutos Na linha 15: Mariana, 10 minutos Na linha 16: Mônica, 10 minutos Na linha 17: Nair, 15 minutos Na linha 18: Otávio, 15 minutos Na linha 19: Pedro, 10 minutos Na linha 20: Ricardo, 15 minutos Na linha 21: Soraia, 30 minutos

Página 277

2º passo: organização dos dados

Joana organizou os dados sobre a medida do tempo gasto no banho em ordem crescente, utilizando uma função da planilha eletrônica que classifica e organiza automaticamente os dados selecionados de acôrdo com a necessidade (do maior para o menor ou do menor para o maior). E, depois, calculou o consumo de água (em litros) de cada um.

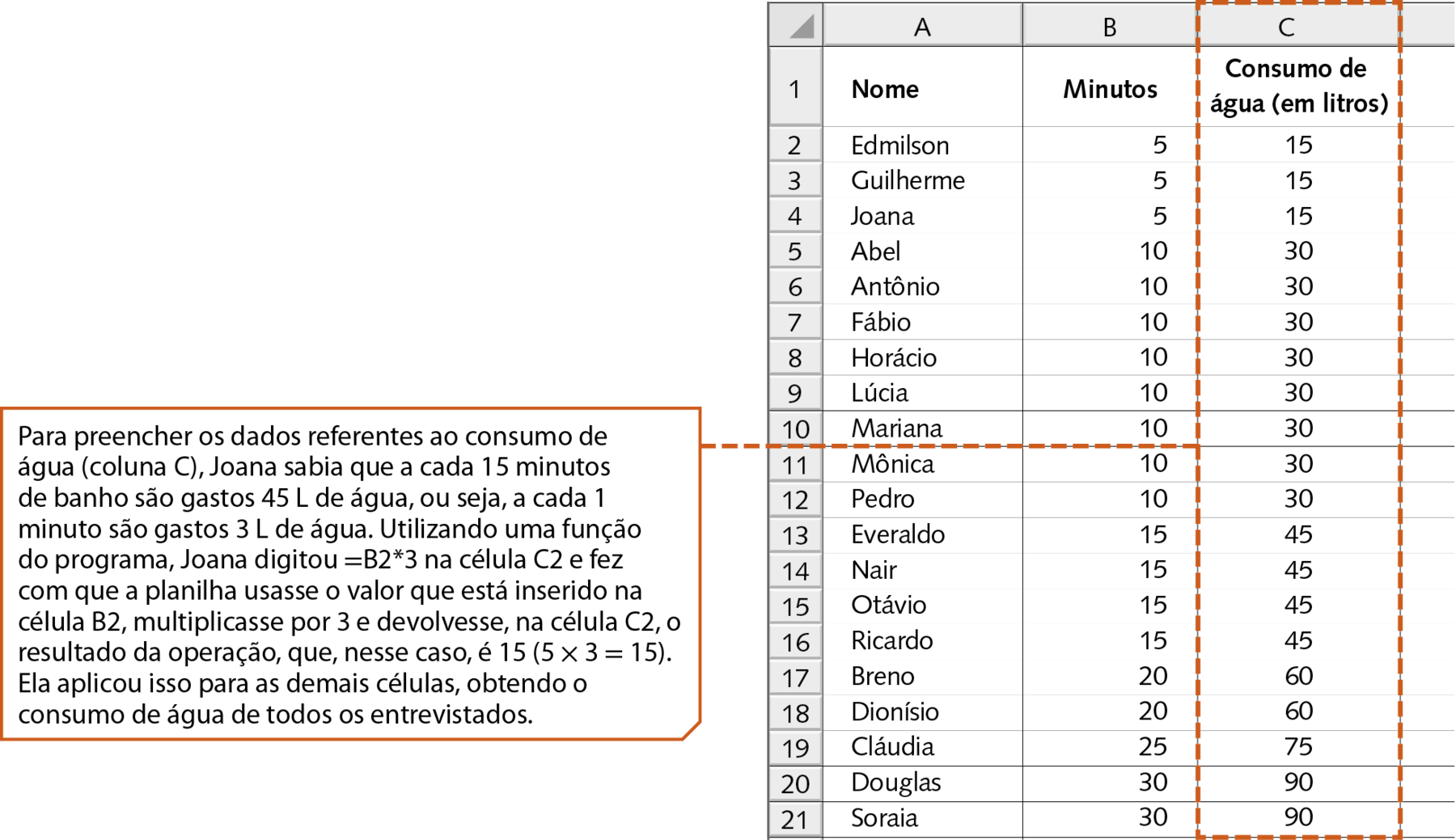
Esquema. Representação de parte de uma planilha eletrônica mostrando as linhas de 1 a 21 e as colunas A, B e C. Na linha 1, da esquerda para a direita: nome, minutos, consumo de água (em litros). Na coluna C (consumo de água), há um destaque com linha tracejada vermelha e fio conectado ao comentário: 'Para preencher os dados referentes ao consumo de água, Joana sabia que a cada 15 minutos de banho são gastos 45 litros de água, ou seja, a cada 1 minuto são gastos 3 litros de água. Utilizando uma função do programa, Joana digitou, igual B2, asteriscos, 3 na célula C2 e fez com que a planilha usasse o valor que está inserido na célula B2, multiplicasse por 3 e devolvesse, na célula C2, o resultado da operação, que, nesse caso, é 15 (5 vezes 3 igual a 15). Ela aplicou isso para as demais células, obtendo o consumo de água de todos os entrevistados.' Na linha 2: Edmilson, 5, 15. Na linha 3: Guilherme, 5, 15. Na linha 4: Joana, 5, 15. Na linha 5: Abel, 10, 30. Na linha 6: Antônio, 10, 30. Na linha 7: Fábio, 10, 30. Na linha 8: Horácio, 10, 30. Na linha 9: Lúcia, 10, 30. Na linha 10: Mariana, 10, 30. Na linha 11: Mônica, 10, 30. Na linha 12: Pedro, 10, 30. Na linha 13: Everaldo, 15, 45. Na linha 14: Nair, 15, 45. Na linha 15: Otávio, 15, 45. Na linha 16: Ricardo, 15, 45. Na linha 17: Breno, 20, 60. Na linha 18: Dionísio, 20, 60. Na linha 19: Cláudia, 25, 75. Na linha 20: Douglas, 30, 90. Na linha 21: Soraia, 30, 90.

3º passo: exposição dos dados e conclusões

Joana montou uma tabela relacionando o consumo de água (em litros) e o número de pessoas que consumiram cada uma das quantidades.

Ilustração. Representação de parte de uma planilha eletrônica mostrando as linhas de 1 a 9 e as colunas A e B. Na linha 1, título Consumo de água na hora do banho. Na linha 2: Consumo de água (em litros) na coluna A e, na coluna B, números de pessoas. Na linha 3: 15, 3. Na linha 4: 30, 8. Na linha 5: 45, 4. Na linha 6: 60, 2. Na linha 7: 75, 1. Na linha 8: 90, 2. Na linha 9: informação 'dados obtidos por Joana em janeiro de 2024'

Com base nos dados da tabela, Joana também construiu um gráfico de barras simples verticais, usando uma ferramenta da planilha eletrônica.

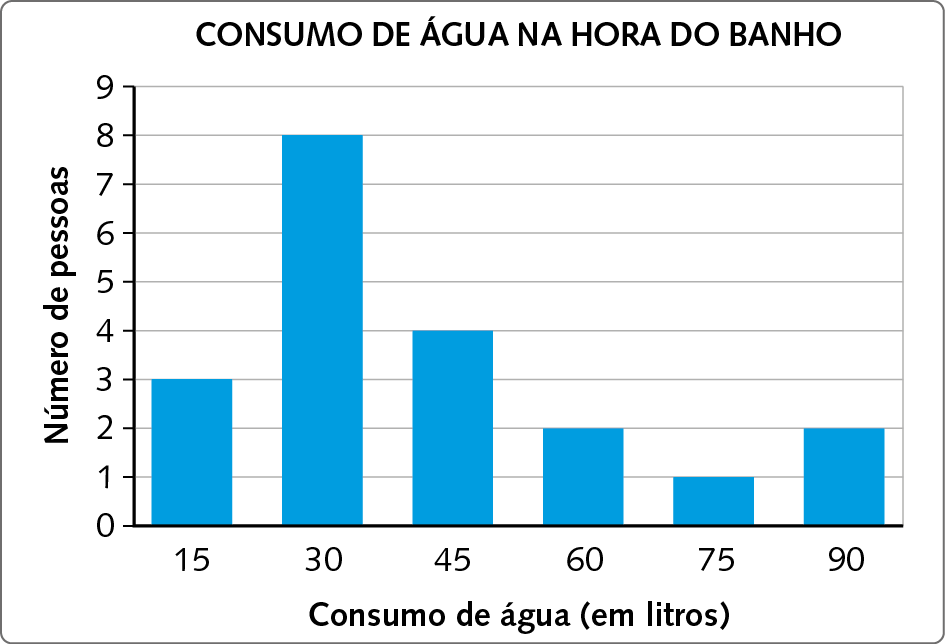
Gráfico. Gráfico em barras simples verticais. Gráfico representando o 'consumo de água na hora do banho'. No eixo vertical, estão indicados os números de pessoas. De baixo para acima: 0 pessoa, 1 pessoa, 2 pessoas, 3 pessoas, 4 pessoas, 5 pessoas, 6 pessoas, 7 pessoas, 8 pessoas, 9 pessoas. No eixo horizontal, estão indicados o consumo de água em litros. Da esquerda para a direita: 15 litros, 30 litros, 45 litros, 60 litros, 75 litros, 90 litros. O consumo de água por pessoa foram: Consumo de 15 litros de água no banho: 3 pessoas Consumo de 30 litros de água no banho: 8 pessoas Consumo de 45 litros de água no banho: 4 pessoas Consumo de 60 litros de água no banho: 2 pessoas Consumo de 75 litros de água no banho: 1 pessoas Consumo de 90 litros de água no banho: 2 pessoas

Dados obtidos por Joana em janeiro de 2024.

Página 278

Com base na tabela e no gráfico, Joana chegou a algumas conclusões:

• a maior parte dos estudantes da turma consome 30 litros de água no banho;

• o número de estudantes que consome 60 litros de água no banho é igual ao número de estudantes que consome 90 litros;

• 3 dos 20 entrevistados, ou seja, 15% deles, consomem a quantidade de água ideal (15 litros de água em um banho de 5 minutos);

• o número de estudantes que consomem 75 litros de água no banho corresponde a 25% do total de estudantes que consome 45 litros;

• se cada um dos entrevistados tomar um banho por dia, serão consumidos no total 840 litros de água por dia.

Gráficos estatísticos

Os gráficos estatísticos são utilizados para apresentar dados, tornando mais fácil e rápida a compreensão do fato em estudo. Na situação anterior, Joana construiu um gráfico estatístico denominado gráfico de barras simples verticais. A seguir, vamos estudar esse e outros tipos de gráficos estatísticos.

Gráfico de barras

Esse tipo de gráfico é utilizado principalmente para comparar informações. Os dados são representados por retângulos. As bases dos retângulos devem ter a mesma medida de largura, e as medidas das alturas são proporcionais ao valor da frequência que representam. Os retângulos podem estar apoiados tanto no eixo horizontal quanto no eixo vertical. Observe os exemplos a seguir.

Gráfico de barras simples verticais

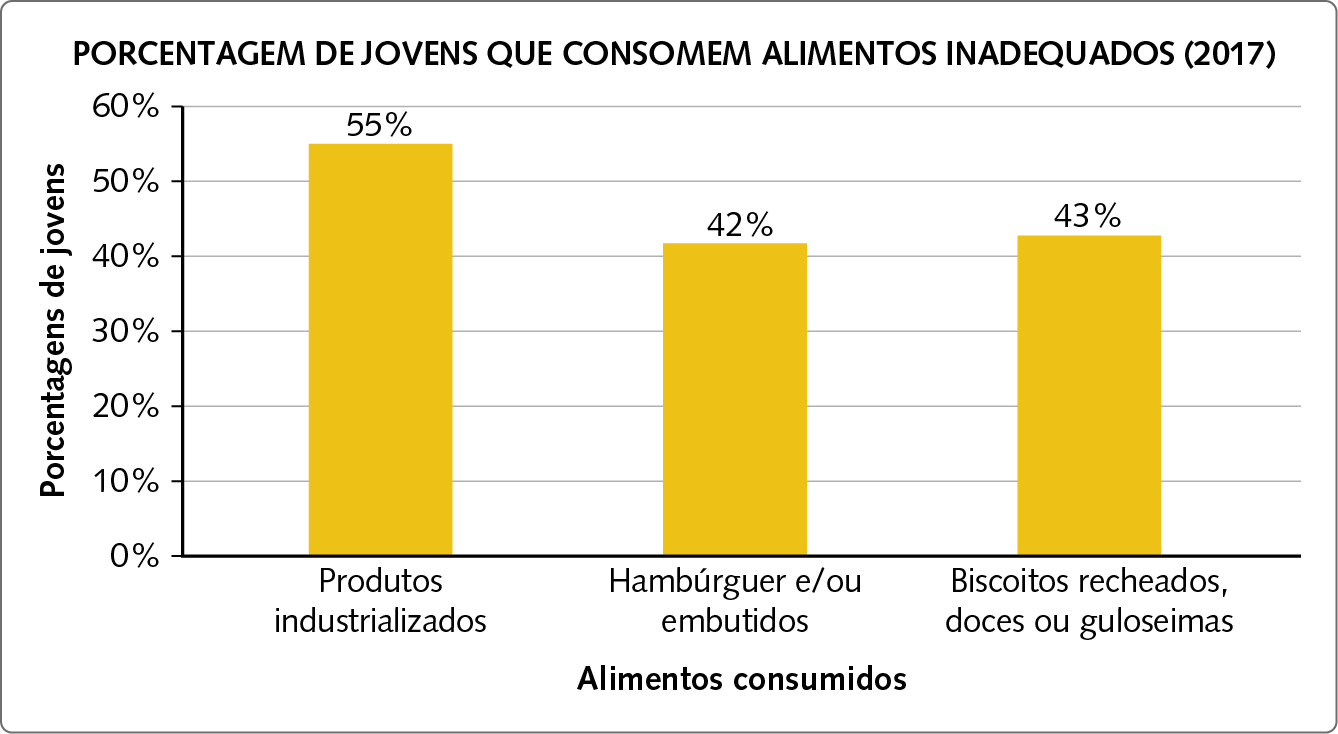
Dados obtidos em: https://oeds.link/Qlsk9l. Acesso em: 17 maio 2022.

Observe que o título e a fonte do gráfico nos informam que os dados apresentados tratam de alimentação dos jovens acompanhados pelo Sistema Único de Saúde (sús) em todo o Brasil e que foram obtidos pelo Sistema de Vigilância Alimentar e Nutricional (Sisvan).

De acôrdo com o gráfico, em 2017, 55% desses jovens consumiram produtos industrializados (macarrão instantâneo, salgadinho de pacote ou biscoito salgado). Além disso, 42% desses jovens ingeriram hambúrguer e/ou embutidos; e 43%, biscoitos recheados, doces ou guloseimas.

Página 279

Gráfico de barras simples horizontais

Podemos observar que o Brasil foi o país que ganhou mais títulos na Copa do Mundo de futebol masculino. Argentina, Uruguai e França conquistaram a mesma quantidade de títulos, ou seja, dois títulos, enquanto Alemanha e Itália conquistaram quatro títulos cada uma.

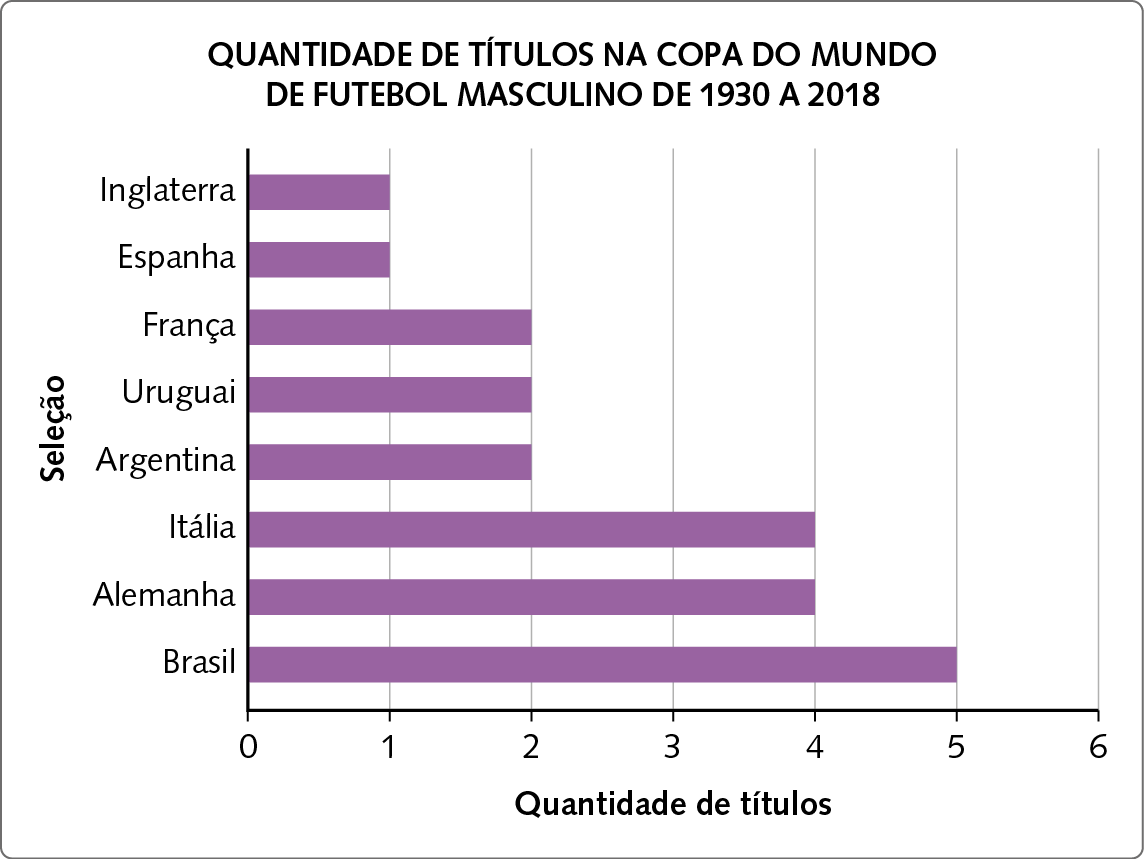
Dados obtidos em: https://oeds.link/y0FFgo. Acesso em: 5 maio 2022.

Observação

O gráfico de barras simples verticais geralmente é chamado de “gráfico de colunas”, e o gráfico de barras simples horizontais é chamado de “gráfico de barras”.

Gráfico de barras múltiplas

Esse tipo de gráfico é utilizado para comparar duas ou mais informações referentes ao tema abordado. Nesse gráfico, os dados também são representados por retângulos, apoiados no eixo horizontal ou no vertical. Observe o exemplo a seguir.

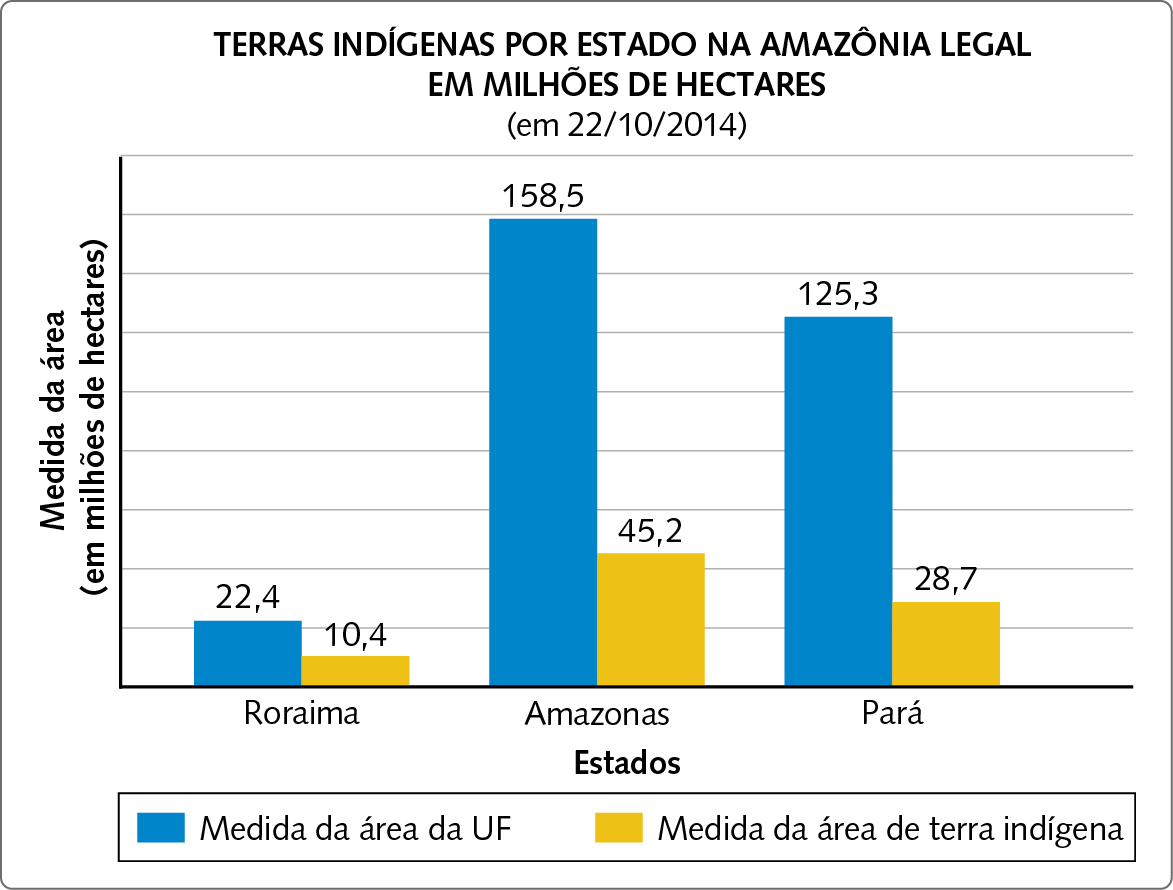
Gráfico. Gráfico de barras duplas verticais relacionado às terras indígenas na Amazônia legal em milhões de hectares em 22 de outubro de 2014. No eixo vertical, estão indicadas medidas da área (em milhões de hectares). No eixo horizontal, estão indicados os estados de Roraima. Amazonas e Pará. Na legenda, a cor azul corresponde à medida da área da Unidade Federativa e a cor amarela corresponde à medida da área de terra indígena. Roraima: medida da área da Unidade Federativa, 22 vírgula 4: medida da área de terra indígena, 10 vírgula 4. Amazonas: medida da área da Unidade Federativa, 158 vírgula 5; medida da área de terra indígena, 45 vírgula 2. Pará: medida da área da Unidade Federativa, 125 vírgula 3; medida da área de terra indígena, 28 vírgula 7.

Dados obtidos em: https://oeds.link/lSCviO. Acesso em: 5 maio 2022.

De acôrdo com o gráfico anterior, em 22/10/2014, o estado de Roraima tinha medida de área igual a aproximadamente 22,4 milhões de hectares, sendo que aproximadamente 10,4 milhões de hectares eram de terras indígenas, enquanto o estado do Amazonas tinha medida de área igual a aproximadamente 158,5 milhões de hectares, sendo que aproximadamente 45,2 milhões de hectares eram de terras indígenas.

Página 280

Gráfico de segmentos

Esse tipo de gráfico é usado quando queremos observar a variação de algum fato ao longo do tempo.

A Floresta Amazônica é a maior floresta tropical do mundo, com enorme diversidade de vida animal e vegetal. A derrubada de árvores para o comércio de madeira, na maior parte das vezes feita de fórma ilegal, a formação de pastagens para o gado, os garimpos e as atividades de mineração reduzem ano a ano a medida da área coberta pela floresta. Observe no gráfico a seguir a medida da área da floresta devastada ano a ano.

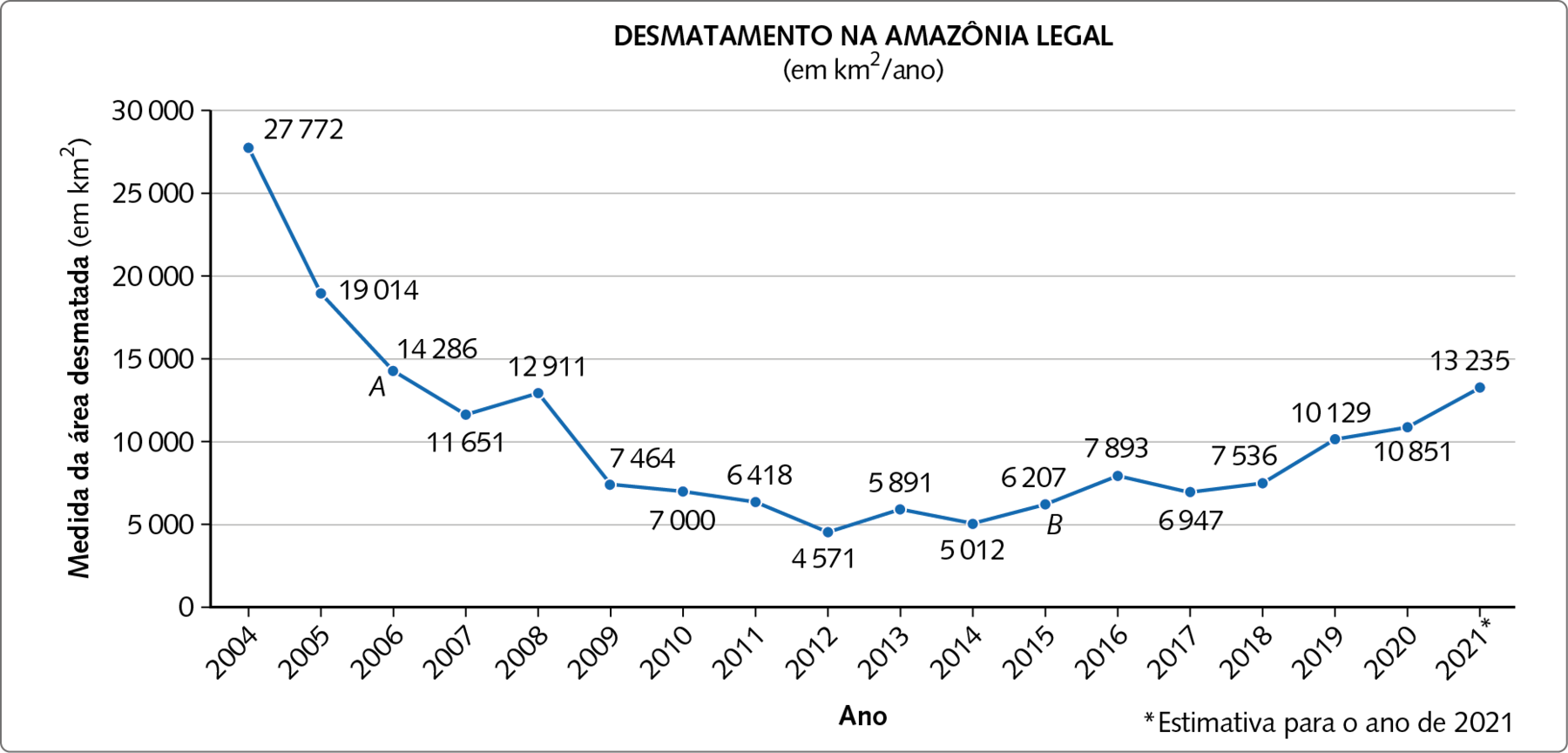
Gráfico. Gráfico de segmentos representando o 'desmatamento na Amazônia Legal (em quilômetro quadrado por ano)'. No eixo horizontal, estão indicadas anos. Da esquerda para a direita: 2mil4, 2mil5, 2mil6, 2mil7, 2mil8, 2mil9, 2mil10, 2mil11, 2mil12, 2mil13, 2mil14, 2mil15, 2mil16, 2mil17, 2mil18, 2mil19, 2mil20, 2mil21. No eixo vertical, estão indicadas medidas da área desmatada. De baixo para acima: zero, 5mil, 10mil, 15mil, 20mil, 25mil, 30mil. O desmatamento na Amazônia Legal em cada ano foi: 2mil4: 27772; 2mil5: 19014; 2mil6, ponto A: 14286; 2mil 7: 11651; 2mil8: 12911; 2mil9: 7464; 2mil10: 7000; 2mil11: 6418; 2mil12: 4571; 2mil13: 5891; 2mil14: 5012; 2mil15, ponto B: 6207; 2mil16: 7893; 2mil17: 6947; 2mil18: 7356; 2mil19: 10129; 2mil20: 10851; uma estimativa para 2mil21: 13235.

Dados disponíveis em: https://oeds.link/54BCRz. Acesso em: 5 maio 2022.

Observe que, no eixo horizontal, ficam os anos em que os dados foram coletados. No eixo vertical, fica a medida da área desmatada de cada ano.

No gráfico, representamos por pontos a medida da área, em quilômetro quadrado, desmatada na Amazônia Legal nos anos em que os dados foram coletados. Por exemplo, o ponto a indica que, em 2006, foram desmatados .14286 quilômetros quadrados da Amazônia Legal, enquanto o ponto B indica que, em 2015, o desmatamento foi de .6207 quilômetros quadrados. Finalmente, os pontos são ligados por segmentos de reta. Por isso, recebe o nome de gráfico de segmentos.

Atividades

Faça as atividades no caderno.

14.

Junte-se a um colega e observem, na tabela, o número de latas de alumínio coletadas por uma rede de lanchonetes, após a aplicação da nova política para a reciclagem do lixo na empresa a partir do ano de 2020 até 2024.

• Construam um gráfico de barras simples verticais com base nos dados da tabela. Depois, escrevam no caderno afirmações baseadas no gráfico.

Coleta de latas de alumínio para reciclagem
Ano	Número de latas (em milhões)
2020	1.400
2021	1.600
2022	2.800
2023	3.800
2024	8.000

Dados obtidos pela rede de lanchonetes entre 2020 e 2024.

Página 281

15.

Observe o gráfico e elabore questões com base nele.

Peça a um colega que as responda. Depois, corrija as respostas.

Esquema. Do lado esquerdo um gráfico de barras na horizontais. Gráfico representando o 'rendimento médio mensal da população residente, por região no ano de 2mil19'. No lado direito um mapa do Brasil com divisões das regiões. No eixo horizontal, estão indicadas o rendimento médio mensal. Da esquerda para a direita: 0 reais, 1 mil reais, 2 mil reais, 3 mil reais. No eixo vertical, estão indicado o Brasil e as regiões. De baixo para acima: Centro -Oeste, Sudeste, Sul, Norte, Nordeste, Brasil. O rendimento médio mensal do Brasil e as regiões foram: Brasil: 2mil308 reais. Nordeste: 1mil588 reais. Norte: 1mil687 reais. Sul: 2mil549 reais. Sudeste: 2mil650 reais. Centro - Oeste: 2mil506 reais. Do lado direito do gráfico há a ilustração de um mapa do Brasil divido pelas regiões: Sul na cor azul; Sudeste na cor lilás, Centro-oeste na cor amarela, Norte na cor verde e Nordeste na cor alaranjada.

Dados obtidos em: https://oeds.link/UNFS9x. Acesso em: 15 junho 2022.

16. O gráfico a seguir apresenta a população estimada de alguns estados brasileiros para os anos de 2021 e 2025.

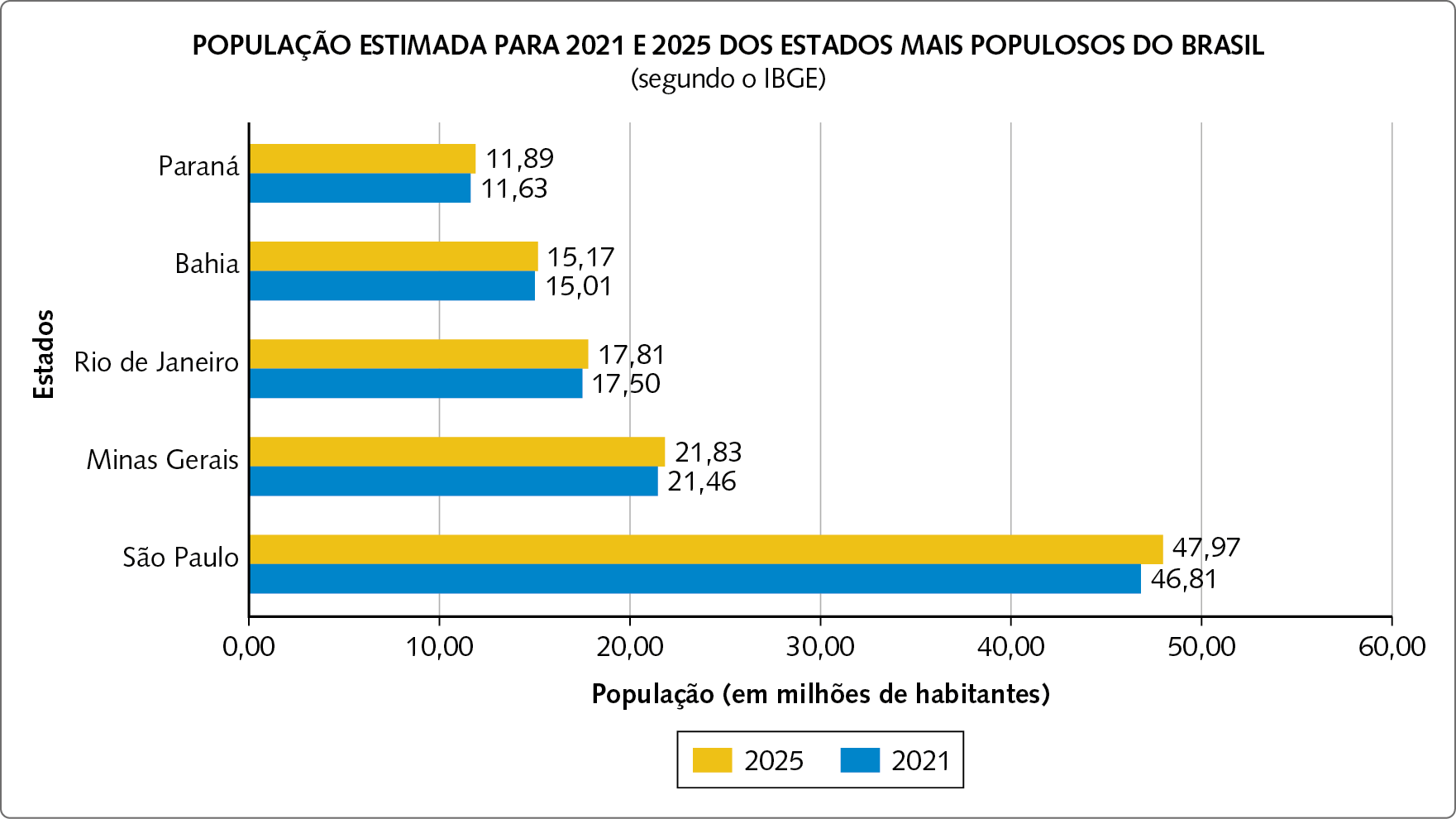
Gráfico. Gráfico de barras duplas horizontais. Apresenta a 'População estimada para 2mil21 e 2mil25 dos estados mais populosos do Brasil'. Há duas barras para cada estado: a barra amarela corresponde a 2mil25 e a barra azul corresponde a 2mil21. No eixo horizontal, está indicada a população (em milhões de habitantes). Da esquerda para a direita: zero, 10, 20, 30, 40, 50 e 60. No eixo vertical, estão indicados estados. De baixo para acima: São Paulo, Minas Gerais, Rio de Janeiro, Bahia, Paraná. São Paulo: em 2mil21: 46,81; em 2mil25: 47,97. Minas Gerais: em 2mil21: 21,46; em 2mil25: 21,83. Rio de Janeiro: em 2mil21: 17,50; em 2mil25: 17,81. Bahia: em 2mil21: 15,01; em 2025: 15,17. Paraná: em 2mil21: 11,63; em 2mil25: 11,89.

Dados obtidos em: https://oeds.link/UXJxj1. Acesso em: 5 maio 2022.

Com base no gráfico, responda.

a) Qual era a população estimada do estado do Paraná em 2021?

b) Qual estado tem a maior população estimada para 2025?

c) Com relação a 2021, podemos dizer que o crescimento da população do Estado de São Paulo será o maior entre os estados listados, segundo a estimativa feita pelo í bê gê É. Você concorda com essa afirmação? Justifique sua resposta.

Página 282

17. A tabela apresenta a produção de uma montadora de carros esportivos durante o 2º semestre de 2023.

Produção de carros esportivos no 2º semestre de 2023
Mês	Número de carros produzidos
Julho	60
Agosto	160
Setembro	210
Outubro	280
Novembro	420
Dezembro	100

Dados obtidos pela montadora de carros no 2º semestre de 2023.

Construa um gráfico de segmentos com base nos dados dessa tabela e, depois, analise as afirmações a seguir, classificando cada uma delas em verdadeira ou falsa. Corrija a(s) falsa(s).

a) A maior queda de produção da montadora de carros esportivos foi entre os meses de novembro e dezembro.

b) A montadora produziu mais carros em novembro do que nos meses de julho, agosto e setembro juntos.

18.

Reúna-se com três colegas e realizem uma pesquisa seguindo as etapas do fluxograma a seguir.

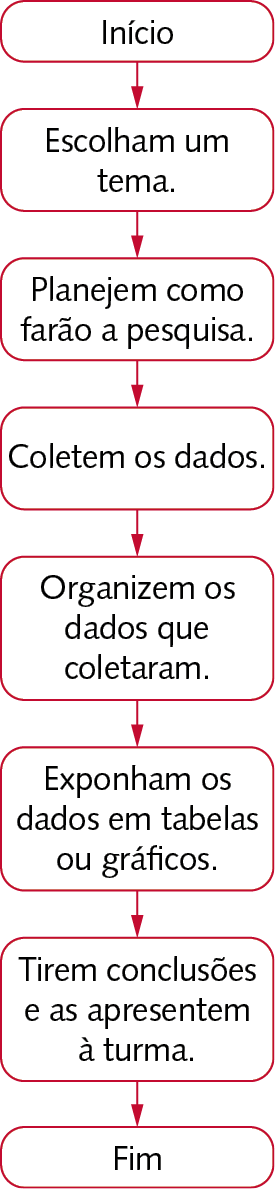
Fluxograma. Etapas para uma pesquisa organizado sequencial na vertical. 'Início', seta na vertical para baixo na etapa, 'Escolha um tema' seta na vertical para baixo na etapa, 'Planejem como farão a pesquisa.', seta na vertical para baixo na etapa, 'Coletem dados' seta na vertical para baixo na etapa, 'Organizem os dados que coletaram', seta na vertical para baixo na etapa, Exponham os dados em tabelas ou gráficos', seta na vertical para baixo na etapa, ' Tirem conclusões e as apresentem à turma' seta na vertical para baixo na etapa, 'Fim'.

19.

Faça uma pesquisa buscando informações sobre os colegas de turma. Escolha um dos temas a seguir.

Tema 1: Sua família separa os diferentes tipos de resíduo doméstico? Há coleta seletiva de lixo na região onde você mora?

Tema 2: Quantas vezes por semana você consome verduras e legumes?

Lembre-se das etapas de um processo estatístico. Usando uma planilha eletrônica, construa um gráfico e escreva um texto apresentando o que você concluiu da pesquisa.

Página 283

Resolvendo em equipe

Faça a atividade no caderno.

(enêm) A figura apresenta dois gráficos com informações sobre as reclamações diárias recebidas e resolvidas pelo Setor de Atendimento ao Cliente (sác) de uma empresa, em uma dada semana. O gráfico de linha tracejada informa o número de reclamações recebidas no dia, o de linha contínua é o número de reclamações resolvidas no dia. As reclamações podem ser resolvidas no mesmo dia ou demorar mais de um dia para serem resolvidas.

O gerente de atendimento deseja identificar os dias da semana em que o nível de eficiência pode ser considerado muito bom, ou seja, os dias em que o número de reclamações resolvidas excede o número de reclamações recebidas.

O gerente de atendimento pôde concluir, baseado no conceito de eficiência utilizado na empresa e nas informações do gráfico, que o nível de eficiência foi muito bom na

a) segunda e na terça-feira.

b) terça e na quarta-feira.

c) terça e na quinta-feira.

d) quinta-feira, no sábado e no domingo.

e) segunda, na quinta e na sexta-feira.

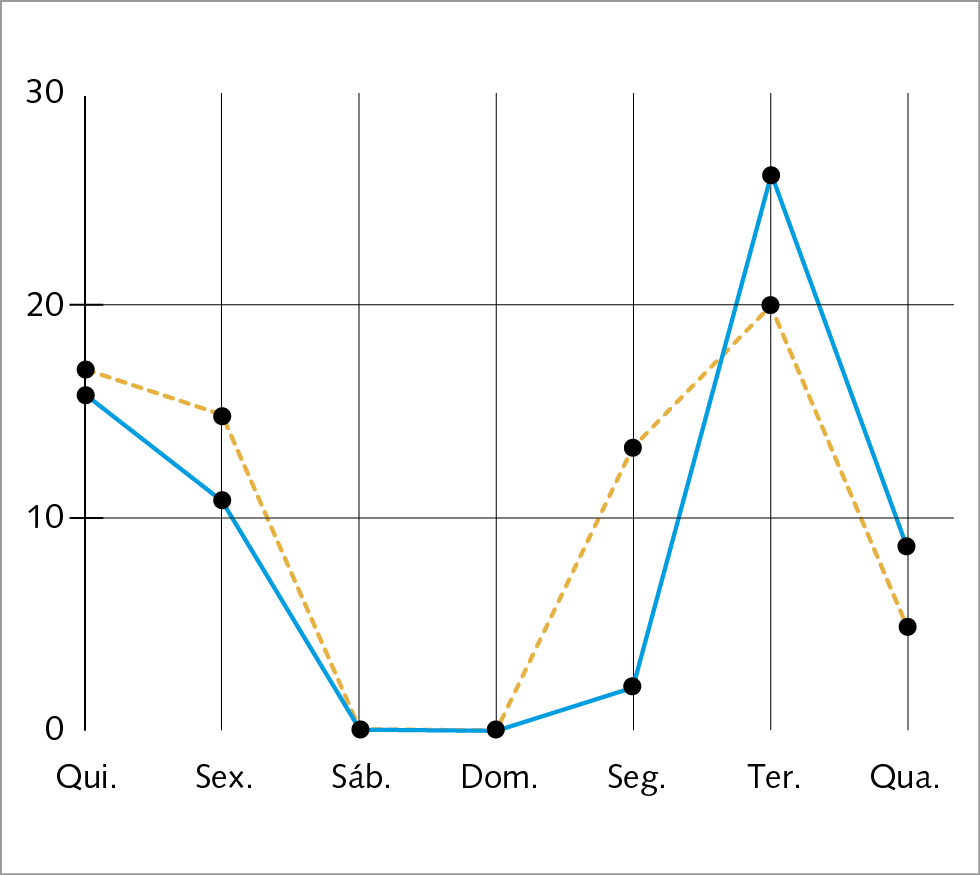
Gráfico. Gráfico de segmentos. Gráfico representação reclamações recebidas e resolvidas pelo Setor de Atendimento (SAC) de uma empresa. No eixo horizontal, estão indicados os dias da semana. Da esquerda para direita: quinta, sexta, sábado, domingo, segunda, terça e quarta. No eixo vertical, estão indicados a quantidade de reclamações. De baixo para acima: zero reclamações, 10 reclamações, 20 reclamações e 30 reclamações. Uma linha vermelha tracejada corresponde o número de reclamações recebidas e uma linha continua azul informa as reclamações resolvidas. Os valores correspondentes em cada dia da semana foram: Quinta: 16 reclamações recebidas e 15 reclamações resolvidas Sexta: 15 reclamações recebidas e 11 reclamações resolvidas Sábado: não houve reclamações Domingo: não houve reclamações Segunda: 13 reclamações recebidas e 3 reclamações resolvidas Terça: 20 reclamações recebidas e 26 reclamações resolvidas Quarta: 5 reclamações recebidas e 9 reclamações resolvidas

Interpretação e identificação dos dados	• Identifique as informações representadas nos eixos horizontal e vertical do gráfico. • O gráfico apresenta duas linhas distintas: uma tracejada e outra contínua. O que essas linhas representam?
Plano de resolução	• Na quinta-feira, o número de reclamações recebidas foi maior ou menor que o número de reclamações resolvidas? Explique. • Observando o gráfico, o que podemos concluir a respeito do sábado e do domingo? • Elabore um plano de resolução explicitando suas estratégias.
Resolução	• Junte-se a três colegas. • Cada integrante do grupo deverá apresentar seu plano de resolução aos demais. • Após a discussão sobre as estratégias, elaborem uma resolução única. Para isso, escolham um dos planos apresentados e organizem um processo de resolução. Observação Resolvam o problema de forma coletiva, mas façam o registro individual no caderno.

Página 284

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Probabilidade

Cálculo do número de possibilidades

Observe as bolas coloridas nas caixas 1 e 2.

Ilustração. Duas caixas contendo 5 bolas de cores diferentes. Na caixa 1, do lado esquerdo, há 2 bolas na cores azul e vermelha. Na caixa 2, do lado direito, há 3 bolas na cores laranja, verde e preto.

Podemos determinar o número de pares de combinações com uma bola da caixa 1 e uma bola da caixa 2, utilizando uma árvore de possibilidades.

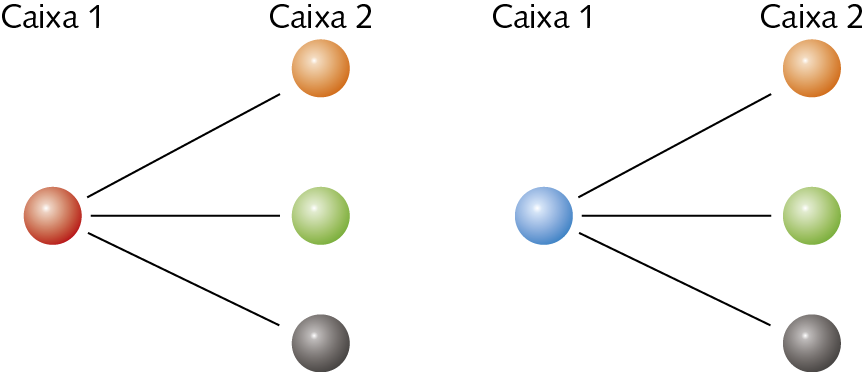
Árvore de possibilidades

Portanto, podemos fazer 6 pares diferentes.

Cálculo de probabilidade

A medida da chance de um resultado ocorrer é chamada de probabilidade. Observe os exemplos:

a) A probabilidade de obter a face cara no lançamento de uma "moeda honesta" é de 1 em 2 ou

\frac{1}{2}

ou 0,5 ou 50%.

b) A probabilidade de obter a face com número 3 no lançamento de um "dado honesto" é de 1 em 6 ou

\frac{1}{6}

c) Em uma urna há 5 bolinhas idênticas que se diferenciam apenas pela côr: 3 são azuis e duas são vermelhas. A probabilidade de retirar, sem olhar, uma bolinha vermelha é de duas em 5 ou

\frac{2}{5}

ou 0,4 ou 40%. Já a probabilidade de retirar, sem olhar, uma bolinha azul é de 3 em 5 ou

\frac{3}{5}

ou 0,6 ou 60%.

• A probabilidade pode ser indicada por uma fração, por um número na fórma decimal ou por uma porcentagem.

• A probabilidade é um número que varia de 0 a 1.

• O cálculo da probabilidade é feito para experimentos aleatórios.

1. Maria ganhou uma boneca com blusinhas e saias. Entre as blusinhas havia uma azul, uma vermelha e uma amarela e, entre as saias, havia uma branca, uma cinza e uma rosa. Faça uma árvore de possibilidades com todas as combinações entre blusinhas e saias que podem vestir a boneca.

2. Em uma sorveteria há 4 opções de sabor de sorvete de frutas: morango, uva, abacaxi e limão e 3 opções de cobertura: mel, chocolate e amendoim. Faça uma árvore de possibilidades com todas as combinações entre sabor de sorvete e cobertura que podem ser feitos.

3. Ao lançarmos um “dado honesto”, qual é a probabilidade de obter a face com o número 6?

4. Ao lançarmos uma “moeda honesta”, qual é a probabilidade de obter a face cara?

5. Em uma urna há 10 bolinhas idênticas que se diferem apenas pela côr. Sabendo que há 5 bolinhas verdes, 4 bolinhas azuis e uma bolinha laranja, qual é a probabilidade de retirar, sem olhar, uma bolinha verde dessa urna? E uma bolinha laranja?

6. Em uma urna há fichas idênticas numeradas de 0 a 9. Qual é a probabilidade de ser sorteada uma ficha com um número ímpar?

7. Ao lançarmos um dado, qual é a probabilidade de aparecer um número ímpar na face superior?

8. Sofia está participando de um sorteio em que 200 bilhetes podem ser sorteados. Ela possui 4 bilhetes, e seu amigo Caio, 2 bilhetes.

a) Quais são as probabilidades de cada um nesse sorteio?

b) Se o número de bilhetes fosse 100, a probabilidade de Sofia ser sorteada, considerando os seus 4 bilhetes, seria maior ou menor? Justifique sua resposta.

Página 285

Estatística

O processo estatístico

1º passo: planejamento e coleta de dados;

2º passo: organização dos dados;

3º passo: exposição dos dados e conclusão.

Gráficos estatísticos

• Gráfico de barras

É utilizado principalmente para comparar informações.

• Gráfico de barras múltiplas

É utilizado para comparar duas ou mais informações referentes ao tema abordado.

• Gráfico de segmentos

É usado quando queremos observar a variação de algum fato ao longo do tempo.

9. Em janeiro de 2024, Lucas coletou os dados referentes à preferência musical dos estudantes do 6º ano. Observe esses dados na tabela.

Construa um gráfico de barras simples horizontais com base na tabela.

Preferência musical dos estudantes do 6º ano
Gênero musical	Número de estudantes
Samba	18
Rock	25
Funk	22
Reggae	12
Outros	15

Dados obtidos por Lucas em janeiro de 2024.

10. Giovana é gerente de uma loja que vende automóveis. Em janeiro de 2024, ela fez uma pesquisa para saber a quantidade de automóveis vendidos no segundo semestre do ano anterior. Observe os dados que Giovana coletou na tabela a seguir.

Quantidade de automóveis vendidos no segundo semestre de 2023
Mês	Número de automóveis
Julho	250
Agosto	190
Setembro	210
Outubro	240
Novembro	260
Dezembro	300

Dados obtidos por Giovana em janeiro de 2024.

No caderno, construa um gráfico de segmentos com base nos dados da tabela. Depois, escreva algumas afirmações baseadas no gráfico.

11. Observe o gráfico de segmentos e responda às questões.

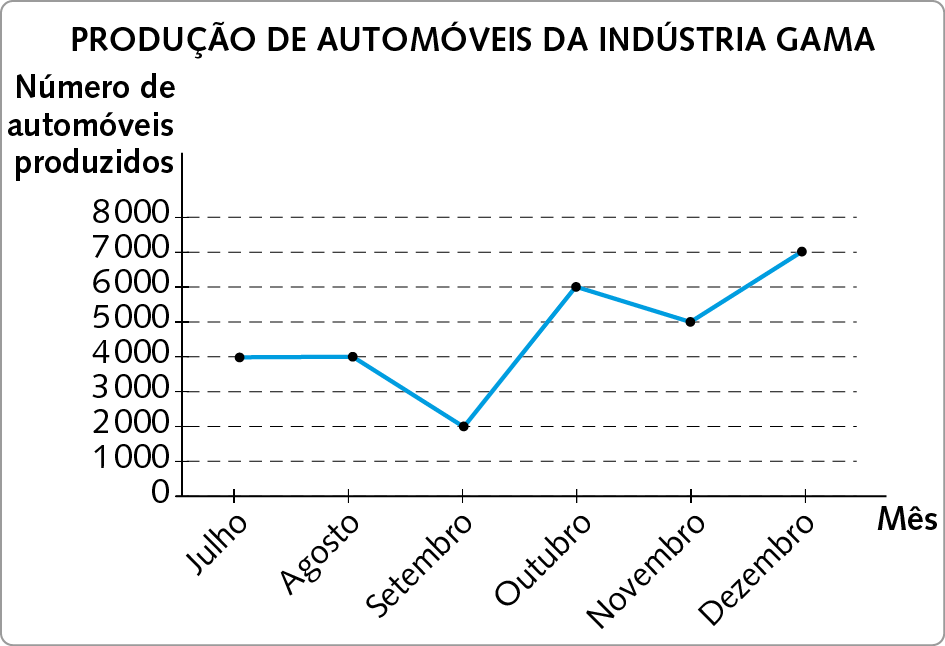
Gráfico. Gráfico de segmentos. Gráfico representando a 'produção de automóveis da indústria Gama' No eixo horizontal, estão indicados os meses. Da esquerda para direita: Julho, agosto, setembro, outubro, novembro e dezembro. No eixo vertical, estão indicados os número de automóveis produzidos. De baixo para acima: 1mil automóvel, 2mil automóveis, 3mil automóveis, 4mil automóveis, 5mil automóveis, 6mil automóveis, 7mil automóveis, 8mil automóveis. Os automóveis produzidos nos meses foram: Julho: 4mil automóveis Agosto: 4mil automóveis Setembro: tem queda para 2mil automóveis Outubro: tem alta para 6mil automóveis Novembro: tem queda para 5mil automóveis Dezembro: tem alta para 7mil automóveis

Dados obtidos pela indústria Gama no 2º semestre de 2023.

a) Qual foi o mês de menor produção de automóveis dessa indústria? E o maior?

b) De setembro a outubro a produção de automóveis aumentou ou diminuiu? E de outubro a novembro?

12. Observe o gráfico das exportaçõesglossário e importaçõesglossário de certo país durante o 1º semestre de 2023.

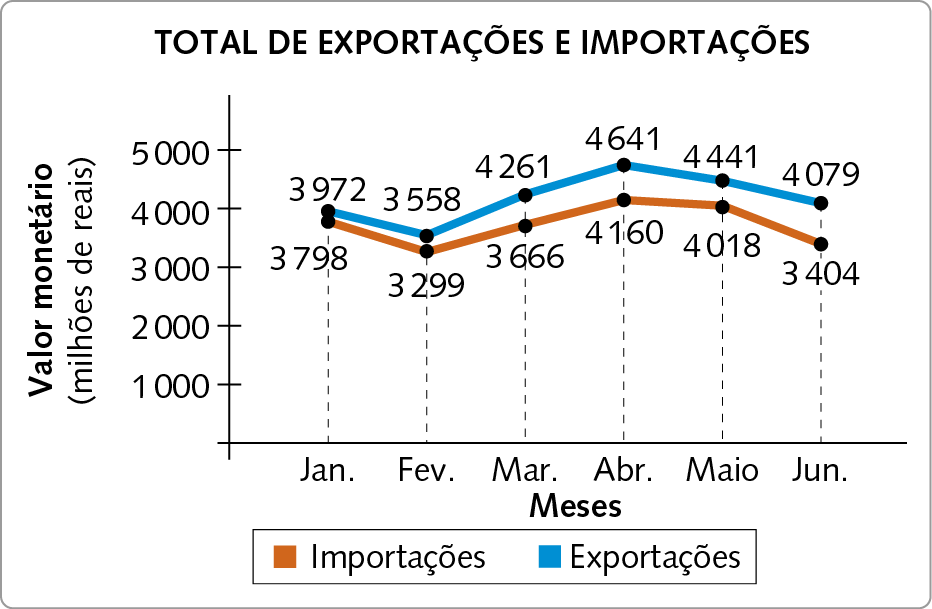
Gráfico. Gráfico de dois segmentos. Gráfico representando o 'total de exportação e importações'. As importações são representadas por uma linha laranja e as exportações são representadas por uma linha azul. No eixo horizontal, estão indicados os meses, da esquerda para a direita: janeiro, fevereiro, março, abril, maio e junho. No eixo vertical, estão indicados os valores monetários (em milhões de reais), de baixo para acima: 0, 1000, 2000, 3000, 4000, 5000. Em janeiro: importações: 3798; exportações: 3972. Em fevereiro: importações: 3299; exportações: 3558. Em março: importações: 3666; exportações: 4261. Em abril: importações: 4160; exportações: 4641. Em maio: importações: 4018; exportações: 4441. Em junho: importações: 3404; exportações: 4079.

Dados obtidos pelo govêrno do país no 1º semestre de 2023.

a) Em que mês o país atingiu o maior índice de exportações? Qual foi o valor?

b) Em que mês o país obteve o melhor saldo (diferença entre o valor da exportação e o da importação) na balança comercial? Qual foi o valor?

Página 286

É hora de extrapolar

Faça as atividades no caderno.

Se você fosse vender um imóvel, que informações colocaria no anúncio?

Um imóvel pode ser grande ou pequeno, sofisticado ou simples. Comprar ou vender um imóvel é um processo que envolve bastante dinheiro. Por isso, é importante analisar com cautela alguns itens no ato da compra ou venda. Por exemplo, no momento da compra, devemos considerar a localização, o estado de conservação e o valor do imóvel.

Objetivos: Pesquisar, comparar e analisar dados sobre o mercado imobiliário do município em que reside, construir uma planta baixa de uma residência específica e elaborar e apresentar uma revista.

Etapa 1: Pesquisa, comparação e análise de dados sobre o mercado imobiliário.

1. Reúna-se em grupo com os colegas e pesquisem, em jornais e revistas (impressos ou digitais), anúncios imobiliários de residências do seu município. Os anúncios devem apresentar a planta baixa, a localização (bairro), a metragem e o valor do imóvel.

Façam o levantamento dos dados coletados dos imóveis anunciados, organizando-os, com o auxílio de uma planilha eletrônica, em uma tabela como a mostrada a seguir.

DADOS DOS IMÓVEIS COLETADOS PELO GRUPO [inserir nome do seu grupo]
Identificação do imóvel	Localização	Medida da área (m²)	Número de dormitórios	Valor (R$)
Imóvel 1

Dados obtidos pelo Grupo [inserir nome do seu grupo].

• Agora, insiram mais uma coluna na tabela, indicando o valor do metro quadrado, de acôrdo com os valores apresentados para a metragem e o preço do imóvel.

3. Compartilhem a tabela finalizada com a turma. Com base na análise dos dados apresentados nas tabelas, respondam às questões.

a) Quais são o maior e o menor valor apresentados para o metro quadrado?

b) Qual é a região do município que apresenta o menor valor do metro quadrado? Levantem hipóteses sobre o porquê de essa região apresentar esse valor.

c) Qual é a região do município que apresenta o maior valor do metro quadrado? Levantem hipóteses sobre o porquê de essa região apresentar esse valor.

d) A medida da área varia de acôrdo com a região?

e) Com relação ao número de dormitórios, varia de acôrdo com a metragem e/ou com a região?

4. No Brasil, existem alguns indicadores que trazem a medida da área útil mínima total recomendada para uma habitação em relação ao número de dormitórios e à ocupação prevista (número de moradores), considerando dormitórios, salas, cozinha, banheiro e área de serviço.

Página 287

A seguir, temos a medida da área útil indicada pelo Instituto de Pesquisas Tecnológicas (í pê tê).

Medida da área útil mínima total recomendada para habitação (em m2), segundo o IPT
Número de dormitórios	Número de moradores	Medida da área mínima da habitação
1 dormitório	2 moradores	35 m2
2 dormitórios	4 moradores	43 m2
3 dormitórios	6 moradores	51 m2

Dados obtidos em: https://oeds.link/iT5G9B. Acesso em: 5 maio 2022.

a) Na pesquisa realizada sobre os anúncios imobiliários, há imóveis nos quais a medida da área útil é menor que a medida da área mínima recomendada, de acôrdo com o número de dormitórios apresentado na planta baixa? Converse com os colegas sobre o público ao qual esse imóvel se destina.

b) Pesquisem sobre os imóveis com medida de área útil menor que 35 métros quadrados e as soluções encontradas para a divisão e a ocupação desses espaços. Compartilhem com os demais colegas da turma.

Etapa 2: Construção da planta baixa de uma residência específica.

5. Observando os dados da etapa 1, o grupo deverá projetar a planta baixa de uma residência para 4 moradores. Mas, antes, observe novamente o anúncio da abertura desta Unidade e faça o que se pede:

a) Quais unidades de medida aparecem no anúncio? A quais grandezas elas estão relacionadas?

b) Calcule a medida da área e o valor total do apartamento do anúncio?

6. As questões a seguir devem ser discutidas pelo grupo antes da construção.

a) Qual será a localização da residência?

b) Qual será a medida da área total (em métro quadrado) útil da residência?

c) Quantos dormitórios vocês pretendem projetar? Haverá outros cômodos na residência? Se sim, quais?

d) De acôrdo com a localização e a medida da área determinadas, qual será o valor do imóvel?

7. Definidas as características da residência, observem a tabela a seguir e determinem as medidas de cada cômodo (dormitórios, salas, banheiro, cozinha e área de serviço).

Analisem o gráfico e façam o que se pede.

Dica: façam um rascunho de como será a planta baixa da residência, insiram as medidas e verifiquem se os valores estão corretos, determinando a medida da área útil total definida na atividade 6.

Medidas de comprimento mínimas dos cômodos das habitações, segundo a NBR 15575 (ABNT)*
Dependência	Medida da área mínima (em m²)	Medida do comprimento do menor lado (em m)
Copa/cozinha conjugada com a sala	14,00	2,40
Dormitório único ou principal	9,00	2,50
Demais dormitórios	7,00	2,40
Banheiro	2,20	1,10 (exceto no boxe)
Área de serviço	1,40	1,20
Corredor ou escada interna à unidade	0,8 (medida da largura mínima, em m)

*A Associação Brasileira de Normas Técnicas (á bê eni tê) é o órgão responsável pela regularização das normas técnicas no Brasil. A Ene bê érre 15575 é a norma publicada pela á bê eni tê que traz critérios e métodos sobre as edificações habitacionais.

Dados obtidos em: https://oeds.link/iT5G9B. Acesso em: 5 maio 2022.

Página 288

8. Construam a planta baixa da residência para 4 moradores com as características definidas pelo grupo.

Etapa 3: Elaboração da revista.

9. Com os colegas do grupo e com base nas características da residência definidas anteriormente, elaborem um anúncio para vender o imóvel da etapa 2.

Algumas dicas para produzir o anúncio estão apresentadas a seguir.

• Além de fotos do local, coloquem as plantas baixas, pois comunicam à pessoa interessada o formato e a organização dos cômodos.

• Façam uma descrição detalhada do imóvel: número de dormitórios e de banheiros, medida da área, vaga de garagem, valor do imóvel, detalhes da infraestrutura (se há churrasqueira, sacada etcétera), entre outras informações.

• Descrevam a localização do imóvel com detalhes, indicando as conveniências próximas (escola, hospital, como é o acesso a transporte etcétera).

• Preencham com cuidado as informações para contato.

10.

Agora, elaborem uma revista, impressa ou digital, com a turma. Cada grupo deverá compor duas páginas da revista: uma que apresente os resultados e um texto conclusivo sobre os imóveis pesquisados na etapa 1 e na qual vocês poderão inserir gráficos utilizando uma planilha eletrônica; e outra com o anúncio elaborado na atividade 9.

Etapa 4: Apresentação e análise das revistas.

11. Disponibilizem a revista para que todos os estudantes analisem as páginas criadas e opinem sobre as informações apresentadas na pesquisa e nos anúncios.

12. Anotem as dúvidas, as opiniões e as sugestões dos colegas.

13. Depois dos ajustes necessários, façam uma exposição da revista para a comunidade escolar.

Etapa 5: Síntese do trabalho realizado.

14. Ao final, algumas questões devem ser discutidas:

a) Quais foram as dificuldades encontradas em cada etapa?

b) Como a pesquisa realizada na etapa 1 ajudou a determinar as características do imóvel para a construção da planta baixa?

c) Os anúncios atenderam aos objetivos propostos? Faltou alguma informação relevante?

15. Com base na reflexão sobre as questões anteriores, observem os anúncios pesquisados para a etapa 1 e o anúncio elaborado na etapa 3 e respondam: há anúncios que não trazem as informações necessárias para o consumidor? Deem exemplos, mostrando que informações faltam e justificando o motivo pelo qual elas são importantes.

16. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.

Glossário

MW: : é uma sigla que indica Megawatt. Um Megawatt é uma unidade de medida de potência que equivale a um milhão de Watts (dáblio).; Voltar para o texto

Moeda honesta: : é aquela que, ao ser lançada, a chance de sair cara é igual a chance de sair coroa.; Voltar para o texto

Dado honesto: :é aquele que, ao ser lançado, a chance de obter qualquer uma das faces é igual.; Voltar para o texto

Exportações: :são os bens e produtos vendidos a outros países.; Voltar para o texto

Importações: : são os bens e produtos comprados de outros países.; Voltar para o texto