Página 289

Teste seus conhecimentos

1. De acôrdo com projeção feita pelo Instituto Brasileiro de Geografia e Estatística (í bê gê É), no comêço de 2022, a população brasileira era composta de mais de duzentas e quatorze milhões de pessoas. Esse número pode ser expresso como:

a) .214000

b) ..200140000

c) ..214000000

d) ...214000000000

2. Elaine escreveu todos os números naturais possíveis utilizando os algarismos 1, 2, 3 e 4 sem repeti-los. Depois, ela subtraiu o maior número escrito do menor. A diferença obtida foi:

a) 198

b) .2889

c) .2997

d) .3087

3. Leandro fez uma campanha de arrecadação de alimentos para 20 famílias que são atendidas pela prefeitura do município em que vive. Ele conseguiu arrecadar 305 quilogramas de alimento. Se ele dividir os alimentos igualmente, cada família vai receber:

a) 14 quilogramas de alimento e não sobrará nada.

b) 14 quilogramas de alimento e sobrarão 25 quilogramas.

c) 15 quilogramas de alimento e não sobrará nada.

d) 15 quilogramas de alimento e sobrarão 5 quilogramas.

4. Vitor construiu um modelo de papel do sólido geométrico apresentado a seguir.

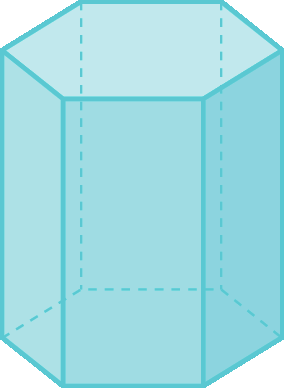
Figura geométrica. Sólido geométrico azul que tem 2 faces hexagonais idênticas e paralelas e 6 faces retangulares paralelas duas a duas.

Se Vitor recortar o modelo dele nas arestas, quantas figuras planas ele vai obter?

a) 3

b) 8

c) 12

d) 18

Versão adaptada acessível

4. Manipule o modelo de sólido geométrico que seu professor vai disponibilizar.

Se o modelo fosse recortado nas arestas, quantas figuras planas seriam obtidas?

5. Kátia pegou dois envelopes e colocou a mesma quantia em dinheiro em cada um deles. Sabendo que, em um envelope, foram colocadas duas cédulas de 10 reais, uma cédula de 20 reais e uma cédula de 50 reais, no segundo envelope foram colocadas:

a) cinco cédulas de 10 reais e duas cédulas de 20 reais.

b) duas cédulas de 10 reais e três cédulas de 20 reais.

c) seis cédulas de 10 reais e duas cédulas de 5 reais.

d) três cédulas de 10 reais e seis cédulas de 5 reais.

6. Leia o que três amigos disseram sobre números.

Bruno: “Todo número primo é divisível por 3”.

Carla: “Se um número é divisível por 5, então 5 é múltiplo desse número”.

Daniel: “Todo número divisível por 10 é divisível por 5”.

Quem disse algo verdadeiro?

a) Apenas Daniel.

b) Apenas Carla e Bruno.

c) Apenas Bruno.

d) Apenas Carla e Daniel.

7. No bairro em que Vivian mora, o carteiro passa a cada 5 dias. Sabendo que, no dia 2 de março, o carteiro passou no bairro de Vivian, quantas vezes ele passou durante o mês de março?

a) 4

b) 5

c) 6

d) 7

8. Uma competição envolvendo diferentes modalidades será realizada na mesma pista, de modo que

\frac{1}{8}

da pista será para corrida com obstáculos,

\frac{1}{4}

para ciclismo e o restante para prática de skate. A fração da pista que será reservada para a prática de skate é:

\frac{4}{8}

\frac{3}{8}

\frac{5}{8}

\frac{7}{8}

9. Rubens fez um pudim de leite que rendeu 800 gramas. Ele vai guardar

\frac{3}{4}

do pudim e dar o restante para Isabela. Quantos quilogramas de pudim Isabela vai receber?

a) 100 gramas

b) 200 gramas

c) 400 gramas

d) 600 gramas

10. Para se preparar para uma competição, Camila nada 1 quilômetro durante seu treinamento diário. Se ela nadou apenas 0,25 quilômetro, significa que Camila completou:

\frac{1}{4}

de seu treinamento diário.

\frac{2}{5}

de seu treinamento diário.

\frac{3}{4}

de seu treinamento diário.

\frac{3}{5}

de seu treinamento diário.

Página 290

Teste seus conhecimentos

11. Gustavo comprou um produto e pagou em 4 vezes de R$ 132,45cento e trinta e dois reais e quarenta e cinco centavos. Sabendo que ele não deu entrada, quanto custou esse produto?

a) R$ 33,12trinta e três reais e doze centavos

b) R$ 264,90duzentos e sessenta e quatro reais e noventa centavos

c) R$ 529,80quinhentos e vinte e nove reais e oitenta centavos

d) R$ 662,25seiscentos e sessenta e dois reais e vinte e cinco centavos

12. Luana possui uma empresa que teve lucro nos últimos meses. Após realizar o planejamento do próximo ano e para dividir esse lucro com os funcionários, ela decidiu que daria aumento para 16% deles. Como essa empresa tem 250 trabalhadores, vão receber aumento salarial:

a) 20 funcionários.

b) 40 funcionários.

c) 80 funcionários.

d) 210 funcionários.

13. Jandira foi assistir a uma peça de teatro. Após 20 minutos de apresentação, 25% da peça já havia se passado. Qual era a duração da peça?

a) 40 minutos.

b) uma hora.

c) uma hora e 10 minutos.

d) uma hora e 20 minutos.

14. Segundo pesquisa do Datafolha em 2019, a maioria das mulheres vítimas de agressão não denuncia o agressor ou não procura ajuda de familiares ou de amigos. Nessa pesquisa, realizada com duas.084 mulheres, constatou-se que 52% delas ficaram caladas. Quantas mulheres, aproximadamente, buscaram ajuda?

a) oitocentas e cinquenta

b) .1000

c) uma.quatrocentas

d) .1100

15. Jonas desenhou um hexágono regular e marcou o centro dessa figura. Depois, uniu cada vértice do hexágono ao centro. Quantos triângulos ele obteve?

a) 1

b) 2

c) 3

d) 6

16. Considere um quadrado cujo comprimento do lado mede 5 centímetros e um triângulo equilátero cujo comprimento do lado também mede 5 centímetros. Ao unir essas duas figuras fazendo coincidir o lado de uma com o lado da outra, obtém-se um:

a) triângulo.

b) quadrado.

c) pentágono.

d) hexágono.

17. Em um mesmo plano cartesiano, foram desenhados um triângulo á bê cê e um triângulo á′bit′centésimo′, ampliação do triângulo á bê cê. Considere que as coordenadas do triângulo original são a(1, 1), B(2, 3) e C(4, 4). Sabendo que á′(3, 3), as coordenadas dos outros dois pontos do triângulo ampliado são:

a) bit′(6, 9) e centésimo′(12, 12)

b) bit′(9, 6) e centésimo′(12, 12)

c) bit′(6, 9) e centésimo′(16, 16)

d) bit′(9, 6) e centésimo′(16, 16)

18. Rute desenhou um triângulo retângulo que mede 7,5 centímetros quadrados de área. Sabendo que o comprimento da altura desse triângulo mede 6 cm, quanto mede o comprimento da base dele?

a) 1,25 centímetro

b) 2,5 centímetros

c) 7,5 centímetros

d) 15 centímetros

19. Quantos litros de água cabem, no máximo, em um recipiente que tem formato de paralelepípedo reto-retângulo e as dimensões medem 4 decímetros, 6 decímetros e 2 decímetros?

a) 24 litros.

b) 48 litros.

c) .24000 litros.

d) .48000 litros.

20. Observe a quantidade de aniversariantes da sala de Túlio por trimestre.

Trimestre	Número de aniversariantes
1º trimestre	4
2º trimestre	8
3º trimestre	3
4º trimestre	10

Será realizado um sorteio na sala de aula em que o nome de cada aluno tem a mesma chance de sair. A probabilidade de sortear alguém que faz aniversário no 1º semestre é:

a) 0,16

b) 0,32

c) 0,48

d) 0,52

21. A escola em que Richard estuda fez uma campanha de arrecadação de material de plástico ou de metal reciclável em 2023 e os estudantes organizaram um gráfico com a quantidade de material, em porcentagem, que cada turma do 6º ano arrecadou.

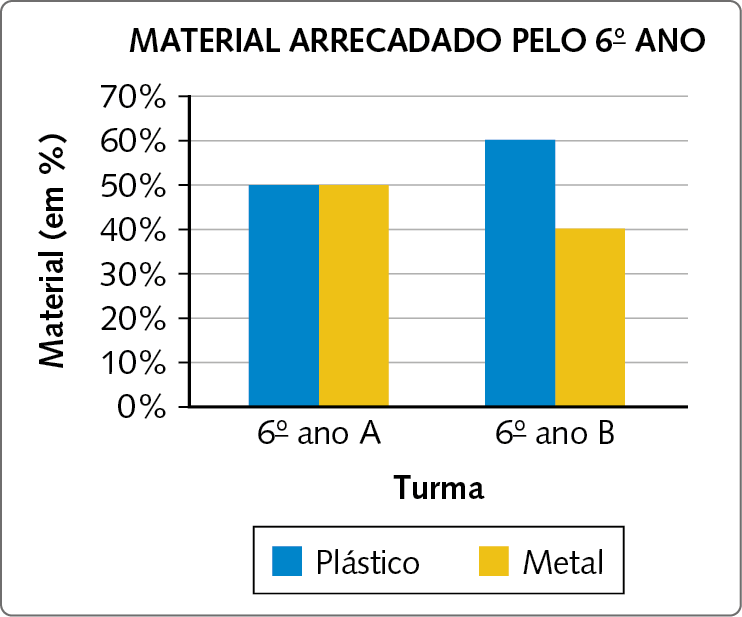
Gráfico. Gráfico de duas barras verticais. Gráfico representando o 'material arrecadado pelo sexto ano'. No eixo horizontal, estão indicadas as turmas. Da esquerda para a direita: sexto A e sexto B. No eixo vertical, estão indicadas as porcentagens de material arrecadado. De baixo da acima: zero por cento, 10 por cento, 20 por cento, 30 por cento, 40 por cento, 50 por cento, 60 por cento, 70 por cento. Uma barra azul corresponde a plástico e uma barra amarela corresponde a metal. A turma sexto ano A arrecadaram 50% de plastico e 50% de metal. A turma sexto ano B arrecadaram 60% de plastico e 40% de metal.

Dados obtidos pelos estudantes da escola de Richard em 2023.

Considerando que as turmas arrecadaram a mesma quantidade total, o material mais arrecadado foi:

a) o plástico pela turma a.

b) o plástico pela turma B.

c) o metal pela turma a.

d) o metal pela turma B.

Página 291

Respostas

Revisão dos conteúdos de anos anteriores

Para o capítulo 1: Números naturais e sistemas de numeração

Páginas 10 e 11

1. a) .5080

b) .20709

c) ..1000063

d) ..300080300

2. a) 1

b) 5

c) Dezena de milhar.

3. a) Trezentos e cinquenta e seis bilhões, quatrocentos e nove milhões, duzentos e dezessete mil e vinte e cinco.

4. a) 900 mil.

b) 200

c) 6 milhões.

d) 30 milhões.

e) 100 bilhões.

5. a) 72

b) 250

c) .100000

Antecessor	Número natural	Sucessor
384	385	386
998	999	1.000
2.898	2.899	2.900
999.999	1.000.000	1.000.001

7. a) (100, 102, 104, 106, 108, 110, 112, 114, 116, 118)

b) (301, 303, 305, 307, 309, 311, 313, 315, 317, 319)

8. ei: 42; B: 45; C: 48.

9. 6, 8, 10, 12 e 14. Construção de figura.

Para o capítulo 2: Operações com números naturais

Páginas 11 a 13

10. a) .6964

b) .5142

c) .16090

11. R$ 1.385,00mil trezentos e oitenta e cinco reais

12. 770 pontos.

13. a) 527

b) .2318

c) .1622

d) .8102

14. a) 500

b) 520

c) 750

d) 400

15. a) .4844

b) .1914

c) .9592

d) .12449

16. 399

17. 676

18. a) 504

b) .3195

c) .5580

d) .16672

19. R$ 3.024,00três mil vinte e quatro reais

20. 28

21. a) 15

b) 156

c) 15

d) 18

e) 102

f) 55

22. a) 114

b) 72

c) 230

23. a) quociente: 23; resto: 4.

b) quociente: 36; resto: 3.

c) quociente: 98; resto: 0.

d) quociente: 10; resto: 0.

e) quociente: 176; resto: 8.

f) quociente: 102; resto: 5.

24. R$ 525,00quinhentos e vinte e cinco reais

Para o capítulo 3: Figuras geométricas espaciais

Páginas 13 e 14

25. a)

	Número de faces	Número de arestas	Número de vértices
Figura 1	6	12	8
Figura 2	5	8	5
Figura 3	5	9	6

b) Quadrangular, quadrangular e triangular.

c) Prisma de base quadrangular, pirâmide de base quadrangular, prisma de base triangular.

26. a) Prisma de base pentagonal

b) Cone

c) Esfera

d) Pirâmide de base triangular

27. Cubo

28. a) Pirâmide de base quadrada

b) Cone

c) Paralelepípedo

d) Pirâmide de base triangular

Para o capítulo 4: Igualdades e desigualdades

Página 15

29. a) 69 = 69

b) 14 = 14

c) 152 = 152

d) 8 = 8

30. a) ÷ 2

b) ‒ 150

c) × 5

d) ÷ 3

e) + 100

f) × 10

Para o capítulo 5: Múltiplos e divisores

Páginas 15 e 16

31.

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180

32. a) Resposta possível: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.

b) 54, 63, 72, 81, 90 e 99.

c) 6, 12, 18, 24 e 30.

33. 105, 120, 135, 150, 165, 180 e 195.

34.

Número	2	3	5	6	9	10
	Divisor
258	X	X		X
356	X
400	X		X			X
525		X	X
886	X
990	X	X	X	X	X	X
1.000	X		X			X
1.050	X	X	X	X		X
2.256	X	X		X
8.250	X	X	X	X		X

Para o capítulo 6: Frações

Páginas 16 a 18

35. a) um oitavo

b) quatro quinze avos

c) dezessete centésimos

d) vinte e sete duzentos avos

36. a) Exemplo de resposta:

\frac{3}{6}

\frac{5}{12}

\frac{3}{4}

d) Exemplo de resposta:

\frac{16}{36}

37. Construção de figuras.

38. a)

\frac{7}{5}

\frac{31}{9}

\frac{21}{4}

\frac{43}{5}

39. a) Exemplo de resposta:

\frac{1}{2}

b) Exemplo de resposta:

\frac{1}{4}

c) Exemplo de resposta:

\frac{1}{3}

d) Exemplo de resposta:

\frac{15}{19}

40. a) 72

b) 15

c) 125

d) 3

41. a)

\frac{1}{4}

\frac{1}{3}

\frac{1}{2}

\frac{2}{9}

\frac{2}{5}

\frac{3}{4}

\frac{1}{4}

\frac{3}{8}

\frac{15}{2}

\frac{3}{9}

\frac{5}{8}

\frac{10}{12}

42. a)

\frac{9}{5}

\frac{2}{5}

\frac{1}{5}

\frac{25}{18}

\frac{12}{18}

\frac{5}{18}

\frac{18}{35}

\frac{10}{35}

\frac{1}{35}

\frac{51}{58}

\frac{23}{58}

\frac{12}{58}

43. a)

\frac{7}{9}

\frac{3}{4}

\frac{1}{3}

\frac{7}{6}

44. a)

\frac{6}{3}

\frac{20}{15}

\frac{4}{8}

\frac{4}{20}

\frac{6}{3}

\frac{8}{14}

\frac{15}{12}

\frac{5}{8}

\frac{23}{60}

\frac{13}{12}

\frac{35}{120}

\frac{59}{30}

45.

\frac{38}{56}

46.

\frac{5}{12}

Página 292

Respostas

47. a)

\frac{18}{7}

\frac{15}{4}

\frac{2}{3}

\frac{36}{7}

\frac{36}{5}

\frac{15}{6}

48. 2 tabletes de fermento.

49. a)

\frac{3}{16}

\frac{1}{6}

\frac{3}{20}

\frac{3}{25}

50.

\frac{3}{20}

Para o capítulo 7: Números decimais

Páginas 18 a 20

51. a) Exemplo de resposta: nove décimos

b) Exemplo de resposta: duzentos e quinze milésimos

c) Exemplo de resposta: cinco inteiros e sessenta e oito centésimos

d) Exemplo de resposta: dezoito centésimos

e) Exemplo de resposta: oito inteiros e quarenta e um milésimos

f) Exemplo de resposta: cinco milésimos

52. a) 9,8

b) 0,148

c) 0,93

d) 0,791

e) 2,049

53. a) >

b) >

c) <

d) <

e) >

f) <

54. a) 0,31; 0,38; 0,57; 0,94

b) 3,07; 3,09; 3,55; 3,98

c) 0,99; 8,92; 10,01; 11,12

d) 5,095; 5,105; 5,555; 5,807

55. Construção de figura.

56. a) 4,9

b) 21,35

c) 12,97

d) 11,82

e) 38,8

f) 20,8

g) 17,62

h) 0,855

i) 0,01

j) 0,008

57. 0,12 m

58. a) 8,4

b) 13,8

c) 26,1

d) 10,16

e) 3,15

f) 21

g) 24,8

h) 50,25

59. a) 47,5

b) 832

c) .6210

d) 8,2

e) .1150

f) .1921

60. a) 9,5

b) 11,25

c) 8,75

d) 16,6

e) 9,5

f) 22,4

61. a) 16,2

b) 3,125

c) 1,02

d) 3,08

e) 125,15

f) 1,2

g) 0,12

h) 0,012

i) 0,56

j) 0,1256

Para o capítulo 8: Porcentagem

Página 20

62. a)

\frac{15}{100}

; 0,15

\frac{32}{100}

; 0,32

\frac{55}{100}

; 0,55

\frac{4}{100;}

0,04

\frac{80}{100}

; 0,8

\frac{99}{100}

; 0,99

63. a) 0,5

b) 1

c) 50

d) 60

e) 42

f) 16

64. R$ 75,00setenta e cinco reais

Para o capítulo 9: Figuras geométricas planas

Páginas 20 a 22

65. a)

\vec{B A}

\vec{C D}

66. A figura do item a.

67. a)

\overline{A B}

\overline{B C}

\overline{C A}

\overline{A B}

\overline{B C}

\overline{C D}

\overline{D A}

68. a) obtuso

b) agudo

c) reto

d) obtuso

69. a) 130graus

b) 60graus

70. a) concorrentes

b) paralelas

c) concorrentes

71. Construção de figura.

72. a) Quadrilátero

b) Triângulo

c) Triângulo

d) Quadrilátero

Para o capítulo 10: Ampliação e redução de figuras

Página 22

73. Construção de figura.

Para o capítulo 11: Grandezas e medidas

Páginas 22 a 24

74. a) 250

b) 145

c) 15

d) .1500

e) .10000

f) .1000

g) 100

75. .1650 milímetros

76. 12,15 centímetros

77. a) 8 centímetros quadrados

b) 10 centímetros quadrados

78. a) 14 centímetros cúbicos

b) 15 centímetros cúbicos

79. a) setenta e duas horas.

b) 900 minutos.

c) .1440 minutos.

d) .3600 segundos.

80. a) .5000 gramas.

b) .10000 quilogramas.

c) .10000 miligramas.

d) ..1000000 gramas.

81. a) .2000 mililitros.

b) .10000 mililitros.

c) 5 litros.

d) 1,5 litros.

82. 12 graus Célsius

Para o capítulo 12: Probabilidade e estatística

Página 24

83. Construção de árvore de possibilidades.

84. a) 16 combinações.

b) 8 combinações.

c) trínta e duas combinações.

Capítulo 1

Revisão dos conteúdos deste capítulo

Páginas 43 e 44

1. a) 29

b) 115

c) .1354

2. a. XXXIX

b) LXIV

c) DCCXXI

d) CMLXXXV

e) MCCCLIV

f) MCDXXIX

3. a) 138

b) .3283

4. a) 253

b) .1234

5. a) .5037

b) .6491

c) .90230

d) .204086

6. a) quatro

b) 8

c) 6

d) duas

e) 2

7. a) quatrocentos e vinte e cinco

b) mil trezentos e setenta e nove

c) duzentos e vinte mil, quatrocentos e dois

Antecessor	Número natural	Sucessor
357	358	359
898	899	900
2.561	2.562	2.563
11.979	11.980	11.981
2.351.298	2.351.299	2.351.300
3.999.999	4.000.000	4.000.001
12.981.998	12.981.999	12.982.000

9. a) (10, 12, 14, 16, 18, 20, 22, 24, 26, 28)

b) (13, 15, 17, 19, 21, 23, 25, 27, 29, 31)

10. Sentenças dos itens c, d e ê.

11. a) .64321

b) .12346

c) .64132

d) .43216

12. Construção de figura.

13. Construção de figura.

Capítulo 2

Revisão dos conteúdos deste capítulo

Páginas 71 a 73

1. a) .4651

b) .5886

c) .23029

d) .330067

e) .424888

2. a) 87

b) .1250

c) .11388

d) .9235

3. R$ 618,00seiscentos e dezoito reais

4. a) .5211

b) .2510

c) .1021

d) .22419

5. a) 282

b) 443

c) .2813

d) .1515

6. 651

7. a) 31

b) 91

c) 9

8. R$ 750,00setecentos e cinquenta reais

9. .1017

10. a) 540

b) 450

c) .2560

d) .3680

e) .14670

f) .61800

11. a) 180

b) .9200

c) .1120

d) .31000

e) .15000

f) .10200

12. R$ 21.060,00vinte e um mil sessenta reais

13. .7200 mililitros

14. a) 28 · 17 = 17 · 28

b) 22 · (10 · 13) = (22 · 10) · 13

c) 115 · (100 · 18) = (115 · 100) · 18

d) 54 · (21 · 12) = (54 · 21) · 12

Página 293

Respostas

e) 890 · 77 = 77 · 890

f) .5801 · 99 = 99 · .5801

15. a) 234

b) 156

c) 330

d) 150

16. a) quociente: 15; resto: 5.

b) quociente: 35; resto: 2.

c) quociente: 36; resto: 10.

d) quociente: 22; resto: 0.

e) quociente: 121; resto: 3.

f) quociente: 424; resto: 0.

17. a) 3

b) 63

c) 5

d) 82

18. R$ 900,00novecentos reais

19. a) 67

b) 308

c) 53

20. a) 9

b) 8

c) 729

d) 100

e) 1

f) 100

g) 900

h) 512

21. a) nove elevado ao quadrado

b) dez elevado à quarta potência

c) doze elevado ao cubo

d) cinco elevado à quarta potência

22. a) 7 ⋅ 102

b) 38 ⋅ 104

c) 45 ⋅ 103

23. a) 25 e 36

b) 169, 196, 225

24. 512; .2048

25. a) 57

b) 512

26. a) 600

b) 900

c) 890

Capítulo 3

Revisão dos conteúdos deste capítulo

Página 83

1. alternativa d

2. a)

	Número de faces	Número de arestas	Número de vértices
Figura 1	8	18	12
Figura 2	7	12	7
Figura 3	6	12	8

b) Hexagonal, hexagonal e quadrangular.

3. a) prisma de base hexagonal

b) cilindro

c) octaedro

d) pirâmide de base triangular

Capítulo 4

Revisão dos conteúdos deste capítulo

Página 95

1. Itens b e d.

2. a) < ou ⩽

b) = ou ⩽ ou ⩾

c) > ou ⩾

3. a) 27 = 27

b) 29 = 29

c) 198 = 198

d) 3 = 3

4. a)

‒ 18 = 46; 64

b) 2 ⋅

+ 12 = 58; 23

5. .1550 gramas

6. a) 96

b) 12

c) 1

7. Jorge: R$ 180,00cento e oitenta reais; Felipe: R$ 90,00noventa reais

8. a) verdadeira

b) falsa

c) verdadeira

9. Antes: 125 < 132; depois: 125 + 25 < 132 + 25

Capítulo 5

Revisão dos conteúdos deste capítulo

Página 116

1. 0, 15, 30, 45 e 60.

2. 162, 180, 198, 216 e 234.

3. Os números dos itens a, b e ê.

4. 996

5. a) verdadeira

b) verdadeira

c) falsa

Número	2	3	5	6	8	9
	Divisor
312	X	X		X	X
645		X	X
1.236	X	X		X
2.169		X				X

7. Os números dos itens a, b e c são divisíveis.

8. Os números dos itens b, c, d e f são primos.

9. a) 26 ⋅ 32

b) 211

c) 33 ⋅ 72

d) 23 ⋅ 35

e) 2 ⋅ 3 ⋅ 73

f) 23 ⋅ 72 ⋅ 13

Capítulo 6

Revisão dos conteúdos deste capítulo

Páginas 144 a 146

1. a)

\frac{1}{8}

\frac{4}{9}

\frac{12}{36}

\frac{7}{12}

2. a) quatro sétimos

b) um nono

c) seis décimos

d) doze centésimos

e) quatro milésimos

f) doze vinte e três avos

3. a)

1 \frac{5}{9}

1 \frac{2}{8}

4. a)

\frac{7}{4}

\frac{31}{11}

\frac{43}{9}

\frac{51}{7}

5. a) 30

b) 18

c) 20

d) 7

6. a)

\frac{2}{5}

\frac{3}{25}

\frac{1}{5}

\frac{6}{7}

7. a) <

b) <

c) >

d) =

8. a)

\frac{9}{8}

\frac{4}{3}

\frac{2}{3}

\frac{15}{25}

9. a)

\frac{1}{4}, \frac{2}{3} e \frac{4}{5}

\frac{3}{8}, \frac{2}{5} e \frac{9}{15}

\frac{2}{6}, \frac{2}{3} e \frac{3}{4}

\frac{2}{7}, \frac{1}{3} e \frac{4}{9}

10. R$ 1.500,00mil quinhentos reais

11. .4500 métros

12. R$ 115,00cento e quinze reais

13. R$ 6,00seis reais

14. oitocentas e quarenta sacas

15. a)

\frac{101}{45}

\frac{22}{21}

\frac{7}{15}

\frac{2}{7}

\frac{17}{5}

\frac{13}{18}

\frac{2}{21}

\frac{11}{120}

\frac{47}{60}

\frac{17}{90}

16. 60 litros

17. a)

\frac{49}{12}

\frac{1}{5}

\frac{9}{2}

\frac{19}{8}

18. a)

\frac{56}{9}

\frac{24}{5}

\frac{3}{36} = \frac{1}{12}

\frac{45}{45} = 1

\frac{12}{40} = \frac{3}{10}

\frac{20}{90} = \frac{2}{9}

19. 60 números

20.

\frac{1}{4}

⋅

\frac{1}{4}

\frac{1}{16}

21. a)

\frac{4}{27}

b) 60

\frac{8}{7}

\frac{3}{10}

\frac{9}{14}

\frac{27}{25}

22. a)

\frac{4}{3}

b) 24

23. R$ 1.260,00mil duzentos e sessenta reais

24. a)

\frac{4}{9}

\frac{64}{27}

c) 1

\frac{99}{100}

\frac{49}{4}

\frac{27}{125}

25.

\frac{131}{20}

26. a) 0

\frac{59}{24}

Capítulo 7

Revisão dos conteúdos deste capítulo

Páginas 170 e 171

1. a) exemplo de resposta: oito décimos

b) exemplo de resposta: um inteiro e quinhentos e dez milésimos

c) exemplo de resposta: quatro inteiros e trinta e seis centésimos

d) exemplo de resposta: dois inteiros e noventa e cinco centésimos

e) exemplo de resposta: nove inteiros e cinquenta e seis milésimos

f) exemplo de resposta: sete milésimos

2. a) 10,9

b) 0,232

c) 1,037

3. a) >

b) <

c) >

d) <

e) >

f) <

4. a) 0,19; 0,48; 0,71; 0,95

b) 4,07; 4,12; 4,29; 4,5

c) 15,06; 18,15; 27,09; 27,13

d) 0,198; 1,9; 6,99; 7,08

Página 294

Respostas

5. a ‒ quatro; B ‒ dois; C ‒ três e D ‒ um

6. a) 6,9

b) 27,51

c) 12,62

d) 11,2

e) 35,1

f) 0,883

g) 4,44

h) 0,88

7. R$ 432,40quatrocentos e trinta e dois reais e quarenta centavos

8. R$ 12,50doze reais e cinquenta centavos

9. a) 16,2

b) 20,9

c) 1,18

d) 0,028

10. a) 82

b) 61,9

c) 90

d) .18100

11. R$ 1.177,50mil cento e setenta e sete reais e cinquenta centavos

12. R$ 104,40cento e quatro reais e quarenta centavos

13. a) 4,55

b) 1,9

c) 1,7

d) 221

14. a) 0,358

b) 2,68

c) 0,109

d) 0,5071

15. 12 laços

16. R$ 0,40zero reais e quarenta centavos

17. .5000 ladrilhos coloridos

18. itens: a, c e d

19. a) 3,076

b) 4,166

c) 6,533

d) 5,789

20. a) 0,111reticências; período: 1

b) 1,2333reticências; período: 3

d) 0,1212reticências; período: 12

e) 44,444reticências; período: 4

21. a) 16,38

b) 38,25

c) 10,657

d) 0

Capítulo 8

Revisão dos conteúdos deste capítulo

Página 186

1. a) 15

b) 2,2

c) 1,75

d) 277,5

2. a) 48%

b) 36%

c) 16%

3. R$ 48,00quarenta e oito reais

4. a) 0,12

b) 0,78

c) 0,07

d) 0,99

Porcentagem	Fração	Número decimal
50%	$divisão de 1 sobre 2$	0,5
5%	$divisão de 1 sobre 20$	0,05
250%	$divisão de 25 sobre 10$	2,5

6. a) R$ 148,00cento e quarenta e oito reais

b) R$ 1.702,00mil setecentos e dois reais

7. 60 questões

8. R$ 46,20quarenta e seis reais e vinte centavos

9. .5000 métros

10. R$ 23.800,00vinte e três mil oitocentos reais

Capítulo 9

Revisão dos conteúdos deste capítulo

Páginas 215 e 216

1. Construção de figura.

2. a)

\vec{A B}

\vec{D C}

3. Itens a e d.

4. a)

\overline{A B}, \overline{B D}, \overline{C D} e \overline{C A}

\overline{A B}, \overline{B C}, \overline{C D} e \overline{D A}

5. Construção de figuras.

6. a) reto

b) agudo

c) agudo

d) obtuso

7. Construção de figuras.

8. Sim, pois, ao prolongarmos a representação dessas retas, elas têm um ponto em comum.

9. Itens a e d.

10. a) Construção de figura.

b) Construção de figura.

11. a) equilátero

b) isósceles

c) escaleno

d) escaleno

12. Construção de figuras.

13. Construção de figuras.

Capítulo 10

Revisão dos conteúdos deste capítulo

Páginas 225 e 226

1. a(0, 0), B(1, 1), C(3, 2), D(4, 4), ê(6, 5) e F(7, 3)

2. Construção de figuras.

3. a(1, 1), B(1, 4), C(4, 4) e D(6, 1)

4. a(1, 1), B(2, 3), C(4, 3), D(5, 1) e ê(3, 0)

5. quadrado

6. Construção de figuras.

7. (1, 0) e (3, 0)

8. Construção de figura.

9. Não, porque elas não são figuras semelhantes (as medidas de comprimento dos lados correspondentes das figuras a e B não são proporcionais).

10. Construção de figura.

11. Sim, pois todas as coordenadas foram divididas por 2.

Capítulo 11

Revisão dos conteúdos deste capítulo

Páginas 267 a 269

1. a) 450

b) 350

c) 3,2

d) 1,26

e) 10

f) .90000

g) .1000

h) 800

i) 48

j) .1200

2. a) .25000 métros

b) .4600 milímetros

c) 89 centímetros

d) 12 quilômetros

3. 50 centímetros

4. 111,6 métros

5. .86400 segundos

6. a) 30 minutos

b) 12 minutos

c) 90 minutos

d) 45 minutos

7. uma hora 12 minutos

8. 9 horas 5 minutos

9. 5 minutos

10. 15 horas 51 minutos

11. a) 20 centímetros quadrados

b) 17 centímetros quadrados

12. a) .80000

b) .98200

c) 0,5

d) 1,2

e) .8500

f) 6

g) .10000

h) 55

13. 325,08 métros quadrados

14. 150 peças

15. a) 24 centímetros quadrados

b) 30 centímetros quadrados

16. a) 20 centímetros cúbicos

b) 32 centímetros cúbicos

17. a) .15000

b) 8,2

c) 0,55

d) 980

e) .8170

f) .92000

g) .6780

h) .600000

18. 512 centímetros

19. 428,4 métros cúbicos

20. a) 250

b) .1450

c) 500

d) .12500

21. 3,6 litros

22. 125 litros

23. a) 0,208

b) .10200

c) .25200

d) 0,00012

e) 50

f) 0,09

24. R$ 127,33cento e vinte e sete reais e trinta e três centavos

25. 5,9 graus Célsius

Capítulo 12

Revisão dos conteúdos deste capítulo

Páginas 284 e 285

1. Construção de árvore de possibilidades.

2. Construção de árvore de possibilidades.

\frac{1}{6}

4. 50%

\frac{1}{2}; \frac{1}{10}

6. 50%

7. 50%

8. a) A probabilidade de Sofia ganhar o sorteio é 2%, e a de Caio é 1%.

b) Maior, porque a probabilidade seria 4%.

9. Construção de gráfico.

10. Construção de gráfico.

11. a) setembro; dezembro

b) aumentou; diminuiu

12. a) abril; .4641 milhões de reais

b) junho; 675 milhões de reais de saldo

Teste seus conhecimentos

Páginas 267 a 269

1. alternativa c

2. alternativa d

3. alternativa d

4. alternativa b

5. alternativa a

6. alternativa a

7. alternativa c

8. alternativa c

9. alternativa b

10. alternativa a

11. alternativa c

12. alternativa b

13. alternativa d

14. alternativa b

15. alternativa d

16. alternativa c

17. alternativa a

18. alternativa b

19. alternativa b

20. alternativa c

21. alternativa b

Página 295

Referências bibliográficas comentadas

AABOE, Asger. Episódios da história antiga da Matemática. Rio de Janeiro: Sociedade Brasileira de Matemática, 1984.

Este livro, organizado em quatro capítulos, permite que o leitor tenha contato com os primórdios da Matemática por meio de episódios históricos.

BERLONQUIN, Pierre. 100 jogos geométricos. Lisboa: Gradiva, 2005.

Este livro apresenta 100 jogos geométricos ordenados criteriosamente pelo autor, do mais fácil para o mais difícil, para que, enquanto o leitor se diverte, adquira maior rapidez de raciocínio e uma notável flexibilidade intelectual.

BOLT, Brian. Actividades matemáticas. Lisboa: Gradiva, 1991.

Este livro contém atividades matemáticas destinadas a estimular o pensamento criativo e incentivar o leitor a desenvolver a compressão de números, conceitos espaciais e pensamento matemático em geral.

BOYER, Carl Benjamin. História da Matemática. tradução Elza F. Gomide. São Paulo: Edgard Blücher; êduspi, 2010.

Este livro apresenta um estudo aprofundado da história da Matemática desde o Egito antigo até as tendências mais recentes. Mostra também a fascinante relação entre o desenvolvimento dos conhecimentos sobre números, fórmas e padrões e a evolução da humanidade.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: Ministério da Educação; Secretaria de Educação Básica, 2018.

Documento de caráter normativo que define o conjunto orgânico e progressivo de aprendizagens essenciais que todos os estudantes devem desenvolver ao longo das etapas e modalidades da Educação Básica.

BROCARD, Joana; SERRAZINA, Lurdes; ROCHA, Isabel. O sentido do número: reflexões que entrecruzam teoria e prática. Lisboa: Escolar, 2008.

Neste livro, reúne-se um conjunto de textos produzidos no âmbito do projeto “Desenvolvendo o sentido do número: perspectivas e exigências curriculares”, cujo trabalho se centrou em tôrno do desenvolvimento do sentido do número para as crianças, concebeu materiais para as aulas e refletiu sobre características do currículo que favorecem o sentido do número.

CARVALHO, Dione Lucchesi de. Metodologia do ensino da Matemática. São Paulo: Cortez, 2009.

Este livro subsidia o futuro professor no domínio dos conteúdos básicos e da metodologia da Matemática e sugere uma transformação no modo de perceber e compreender o papel dessa disciplina no currículo escolar.

CENTURIÓN, Marília. Conteúdo e metodologia da Matemática: números e operações. São Paulo: Scipione, 2001.

Este livro baseia-se na ideia de que o estudante constrói seu próprio conhecimento com base em suas ações e problematizações. Aborda as principais dúvidas tanto do estudante de Pedagogia quanto do professor dos anos iniciais do Ensino Fundamental.

DANTE, Luiz Roberto. Didática da resolução de problemas de Matemática. São Paulo: Ática, 2002.

Este livro propõe a discussão dos fatores que atuam negativamente no aprendizado de Matemática, classifica os vários tipos de problema que se apresentam e mostra as etapas envolvidas na sua resolução.

EVES, Howard. Introdução à história da Matemática. Campinas: unicâmpi, 2011.

Este livro busca introduzir a história da Matemática aos estudantes de graduação dos cursos superiores dessa disciplina. Assim sendo, além da narrativa histórica, há muitos expedientes pedagógicos visando assistir, motivar e envolver o estudante.

GRANDO, Regina Célia. O jôgo e a Matemática no contexto da sala de aula. São Paulo: Paulus, 2004.

Este livro mostra a riqueza pedagógica que existe na utilização correta de jogos, para ensinar Matemática, para desenvolver o pensamento criativo e até mesmo para transformar o êrro em aprendizado.

IFRAH, Georges. História universal dos algarismos. Rio de Janeiro: Nova Fronteira, 1997.

Este livro oferece, em linguagem acessível, uma visão completa e inovadora da epopeia do cálculo entre as civilizações. Um convite para uma viagem impressionante às origens da representação simbólica dos números.

IFRAH, Georges. Os números: a história de uma grande invenção. Rio de Janeiro: Globo, 1998.

Este livro traça uma resumida, mas completa, história da Matemática, acompanhando a evolução do raciocínio de nossos ancestrais desde a Pré-História, passando por civilizações como a dos egípcios, babilônios, fenícios, gregos, romanos, hebreus, maias, chineses, hindus e árabes.

Página 296

Referências bibliográficas comentadas

IMENES, Luiz Márcio. A numeração indo-arábica. São Paulo: Scipione, 1990. (Vivendo a Matemática).

Este livro discorre sobre os sistemas de numeração, em uma proposta integrada com História, explorando a Matemática de uma maneira divertida, mas comprometida com o conteúdo.

KAMII, Constance. Reinventando a Aritmética: implicações da teoria de piagê. Campinas: Papirus, 1995.

Este livro faz uma análise crítica do ensino da Aritmética para as crianças dos primeiros anos do Ensino Fundamental. Com toda sua sensibilidade e seu conhecimento da teoria piagetiana, a autora aborda temas como importância da interação social, autonomia como finalidade da educação, numerais, adição e subtração.

KARLSON, Paul. A magia dos números. Rio de Janeiro: Globo, 1961.

Este livro usa a história da Matemática como bússola em uma jornada desde a Aritmética até o cálculo diferencial e integral. O que destaca essa obra não é apenas a linguagem informal e muitas vezes mordaz do autor, mas principalmente o grau de detalhismo que ele concedeu aos inúmeros assuntos que compõem o livro.

LIMA, Elon lages. Meu professor de Matemática e outras histórias. Rio de Janeiro: Sociedade Brasileira de Matemática, 2004.

Este livro é composto de pequenos ensaios sobre Matemática elementar. Em uma coleção de capítulos independentes, aborda tópicos de Matemática que constam dos programas escolares dos diferentes níveis de ensino.

MARANHÃO, Maria Cristina S. Matemática. São Paulo: Cortez, 1994. (Magistério).

Este livro reflete sobre a problemática do ensino da Matemática com base na experiência da autora, bem como nos estudos e nas pesquisas na área. Dessa maneira, a autora sugere o desenvolvimento de alguns temas que considera indispensáveis para preparar um estudante para o Ensino Médio.

PÓLYA, George. A arte de resolver problemas. tradução Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 2006.

Este livro aborda a resolução de problemas como um recurso para desafiar a curiosidade dos leitores. O autor destaca a importância de situações que apresentam indagações aos estudantes e contribuem para que desenvolvam o interesse pelo raciocínio independente.

ROSA NETO, Ernesto. Didática da Matemática. São Paulo: Ática, 2010.

Este livro é destinado a educadores interessados em educação matemática. Levando em consideração o interacionismo e a psicogenética, discute os principais tópicos da Matemática de Pré-escola e Ensino Fundamental, viabilizando sua aplicação em sala de aula.

SMOLE, Kátia Stocco; DINIZ, Maria Ignez. Ler, escrever e resolver problemas: habilidades básicas para aprender Matemática. Porto Alegre: Artmed, 2001.

Este livro contribui para a discussão sobre o lugar e o significado das competências e das habilidades no Ensino Fundamental, enfatizando as habilidades de ler, escrever e resolver problemas de Matemática.

TAHAN, Malba. Matemática divertida e curiosa. Rio de Janeiro: Record, 2012.

Este livro traz recreações e curiosidades da Matemática que transformam a aridez dos números e a exigência de raciocínio em brincadeira, ao mesmo tempo útil e prazerosa. O autor consegue fazer a união da ciência com o lúdico, transformando a leitura em um agradável passatempo.

TAHAN, Malba. O homem que calculava. Rio de Janeiro: Record, 2001.

O livro narra a história de Beremiz Samir, um viajante com o dom intuitivo da Matemática, manejando os números com a facilidade de um ilusionista. Problemas aparentemente sem solução tornam-se de uma transparente simplicidade quando expostos a ele.

TOLEDO, Marília; TOLEDO, Mauro. Teoria e prática de Matemática. São Paulo: FTD, 2009.

O livro constitui uma valiosa ferramenta para os professores dos anos iniciais do Ensino Fundamental. A obra trabalha o desenvolvimento das habilidades matemáticas básicas fundamentado em problemas ligados à experiência prática do estudante, em jogos e em situações que estimulam sua participação na construção de conceitos e o ajudam a compreender a relevância da Matemática como instrumento de transformação da realidade.

ZABALA, Antoni (organizador). Como trabalhar os conteúdos procedimentais em aula. tradução Ernani Rosa. 2. ed. Porto Alegre: Artmed, 1999.

Este livro, por meio de uma abordagem prática, mostra como trabalhar 42 conteúdos procedimentais que pertencem a diferentes áreas do Ensino Fundamental.

ZARO, Milton. Matemática experimental. São Paulo: Ática, 1996.

O objetivo deste livro é estimular a criatividade do professor no desenvolvimento de atividades com os estudantes, aplicando o método científico na Matemática por meio da técnica da redescoberta, exercitando a redação de textos e experimentos.

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180