Página cinquenta e dois

Resoluções e comentários das atividades

Parte 1

Unidade 1

REVISÃO DE CONTEÚDOS DE ANOS ANTERIORES

Para o capítulo 1: Números naturais e sistemas de numeração

Páginas 10 e 11

1. a) .50080

b) .20709

c) ..1000063

d) ..300080300

2. a) 1

b) 5

c) Dezena de milhar.

3. a) Trezentos e cinquenta e seis bilhões, quatrocentos e nove milhões, duzentos e dezessete mil e vinte e cinco.

b) Os algarismos 4, 0 e 9.

4. a. 900 mil.

b) 200

c) 6 milhões.

d) 30 milhões.

e) 100 bilhões.

5. a) 72

b) 250

c) .100000

Antecessor	Número natural	Sucessor
384	385	386
998	999	1.000
2.898	2.899	2.900
999.999	1.000.000	1.000.001

7. a) (100, 102, 104, 106, 108, 110, 112, 114, 116, 118)

b) (301, 303, 305, 307, 309, 311, 313, 315, 317, 319)

8. Analisando a reta, percebemos que ela cresce de 1 em 1, então a: 42; B: 45 e C: 48.

Ilustração. Reta numérica com o número 40 representado na extremidade esquerda e o ponto C na extremidade direita. O trecho entre 40 e C está dividido em 8 partes iguais por meio de pontos. Da esquerda para a direita estão os pontos 40, ponto sem descrição, A, 43, ponto sem descrição, B, ponto sem descrição, ponto sem descrição, C.

9. Uma representação possível:

Ilustração. Reta numérica com o número 6 representando a extremidade esquerda e 14 representando a extremidade direita, o trecho entre 6 e 14 está dividido em 4 partes iguais por meio de pontos, da esquerda para a direita estão os pontos 6, 8, 10, 12 e 14.

Em ordem crescente: 6, 8, 10, 12 e 14.

Para o capítulo 2: Operações com números naturais

Páginas 11 a 13

10. a) .2581 + .4383 = .6964

b) .1150 + 563 + .3429 = .5142

c) .12525 + 938 + .2627 = .16090

Cálculos:

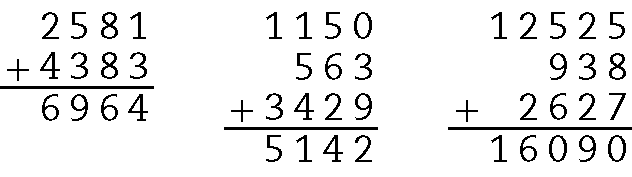
Algoritmo usual da adição. 2 mil 581 mais 4 mil 383. Na primeira linha, 2 mil 581. Abaixo, à esquerda, sinal de adição, à direita, 4 mil 383 alinhado ordem a ordem com 2 mil 581. Abaixo, traço horizontal. Abaixo, 6 mil 964, alinhado ordem a ordem com 2 mil 581 e 4 mil 383. Algoritmo usual da adição. 1 mil 150 mais 563 mais 3 mil 429. Na primeira linha, 1 mil 150. Abaixo, 563 alinhado ordem a ordem com 1 mil 150. Abaixo, à esquerda sinal de adição, à direita 3 mil 429 alinhado ordem a ordem com 1 mil 150 e 563. Abaixo, traço horizontal. Abaixo, 5 mil 142 alinhado ordem a ordem com 1 mil 150, 563 e 3 mil 429. Algoritmo usual da adição. 12 mil 525 mais 938 mais 2 mil 627. Na primeira linha, 12 mil 525. Abaixo, 938 alinhado ordem a ordem com 12 mil 525. Abaixo, à esquerda sinal de adição, à direita, 2 mil 627 alinhado ordem a ordem com 12 mil 525 e 938. Abaixo, traço horizontal. Abaixo, 16 mil 090 alinhado ordem a ordem com 12 mil 525, 938 e 2 mil 627.

11. Adicionando os valores das prestações, temos:

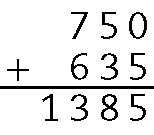
Algoritmo usual da adição. 750 mais 635. Na primeira linha, 750. Abaixo, à esquerda, sinal de adição, à direita, 635 alinhado ordem a ordem com 750. Abaixo, traço horizontal. Abaixo, 1 mil 385, alinhado ordem a ordem com 750 e 635.

Logo, Maria pagou R$ 1.385,00mil trezentos e oitenta e cinco reais pelo aparelho de televisão.

12. Adicionado os pontos das duas fases, temos:

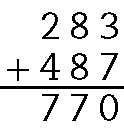
Algoritmo usual da adição. 283 mais 487. Na primeira linha, 283. Abaixo, à esquerda, sinal de adição, à direita, 487 alinhado ordem a ordem com 283. Abaixo, traço horizontal. Abaixo, 770, alinhado ordem a ordem com 283 e 487.

Luísa fez 770 pontos.

13. a) 263 + 527 = 527 + 263

b) .2318 + 0 = 0 + .2318

c) .9287 + .1622 = .1622 + .9287

d) .10258 + .8102 = .8102 + .10258

14. a) 250 + 120 + 50 + 80 = 300 + 200 = 500

b) 300 + 64 + 36 + 120 = 420 + 100 = 520

c) 450 + 0 + 275 + 25 = 450 + 300 = 750

d) 180 + 75 + 120 + 25 = 300 + 100 = 400

15. a) .8265 ‒ .3421 = .4844

b) .9151 ‒ .7237 = .1914

c) .11950 ‒ .2358 = .9592

d) .25902 ‒ .13453 = .12449

Cálculos:

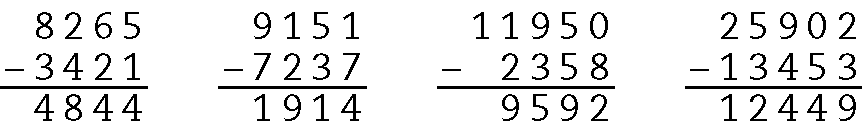
Algoritmo usual da subtração. 8 mil 265 menos 3 mil 421. Na primeira linha, 8 mil 265. Abaixo, à esquerda sinal de subtração, à direita 3 mil 421 alinhado ordem a ordem com 8 mil 265. Abaixo, traço horizontal. Abaixo, 4 mil 844 alinhado ordem a ordem com 8 mil 265 e 3 mil 421. Algoritmo usual da subtração. 9 mil 151 menos 7 mil 237. Na primeira linha, 9 mil 151. Abaixo, à esquerda sinal de subtração, à direita 7 mil 237, alinhado ordem a ordem com 9 mil 151. Abaixo, traço horizontal. Abaixo, 1 mil 914, alinhado ordem a ordem com 9 mil 151 e 7 mil 237. Algoritmo usual da subtração. 11 mil 950 menos 2 mil 358. Na primeira linha, 11 mil 950. Abaixo, à esquerda sinal de subtração, à direita, 2 mil 358 alinhado ordem a ordem com 11 mil 950. Abaixo, traço horizontal. Abaixo, 9 mil 592, alinhado ordem a ordem com 11 mil 950 e 2 mil 358. Algoritmo usual da subtração. 25 mil 902 menos 13 mil 453. Na primeira linha, 25 mil 902. Abaixo, à esquerda sinal de subtração, à direita, 13 mil 453 alinhado ordem a ordem com 25 mil 902. Abaixo, traço horizontal. Abaixo, 12 mil 449 alinhado ordem a ordem com 25 mil 902 e 13 mil 453.

16. Para calcular o subtraendo, podemos fazer

528 ‒ 129 .

Assim, temos:

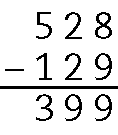
Algoritmo usual da subtração. 528 menos 129. Na primeira linha, 528. Abaixo, à esquerda, sinal de subtração, à direita, 129 alinhado ordem a ordem com 528. Abaixo, traço horizontal. Abaixo, 399 alinhado ordem a ordem com 528 e 129.

Logo, o subtraendo é 399.

17. Para calcular o minuendo, podemos fazer 385 + 291

. Assim, temos:

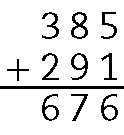
Algoritmo usual da adição. 385 menos 291. Na primeira linha, 385. Abaixo, à esquerda sinal de adição, à direita 291 alinhado ordem a ordem com 385. Abaixo, traço horizontal. Abaixo, 676 alinhado ordem a ordem com 385 e 291.

Logo, o minuendo é 676.

18. a) 42 ⋅ 12 = 504

b) 213 ⋅ 15 = .3195

c) 310 ⋅ 18 = .5580

d) 521 ⋅ 32 = .16672

Cálculos:

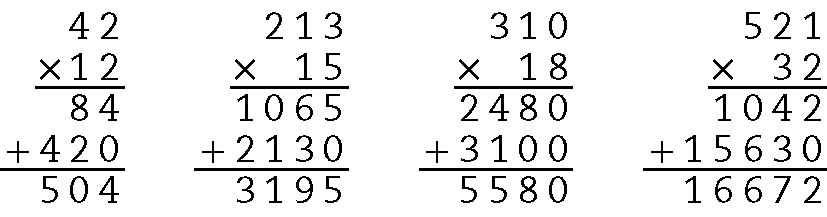
Algoritmo usual da multiplicação. 42 vezes 12. Na primeira linha, 42. Abaixo, à esquerda sinal de multiplicação, à direita 12 alinhado ordem a ordem com 42. Abaixo, traço horizontal. Abaixo, 84 alinhado ordem a ordem com 42 e 12. Abaixo, à esquerda sinal de adição, à direita 420 alinhado ordem a ordem com 42, 12 e 84. Abaixo, traço horizontal. Abaixo, 504 alinhado ordem a ordem com 42, 12, 84 e 420. Algoritmo usual da multiplicação. 213 vezes 15. Na primeira linha, 213. Abaixo, à esquerda sinal de multiplicação, à direita 15 alinhado ordem a ordem com 213. Abaixo, traço horizontal. Abaixo, 1 mil 065 alinhado ordem a ordem com 213 e 15. Abaixo, à esquerda sinal de adição, à direita 2 mil 130 alinhado ordem a ordem com 213, 15 e 1 mil 065 Abaixo, traço horizontal. Abaixo, 3 mil 195 alinhado ordem a ordem com 213, 15, 1 mil 065 e 2 mil 130. Algoritmo usual da multiplicação. 310 vezes 18. Na primeira linha, 310. Abaixo, à esquerda sinal de multiplicação, à direita 18 alinhado ordem a ordem com 310. Abaixo, traço horizontal. Abaixo, 2 mil 480 alinhado ordem a ordem com 310 e 18. Abaixo, à esquerda sinal de adição, à direita 3 mil e 100 alinhado ordem a ordem com 310, 18 e 2 mil 480. Abaixo, traço horizontal. Abaixo, 5 mil 580 alinhado ordem a ordem com 310, 18, 2 mil 480 e 3 mil e 100. Algoritmo usual da multiplicação. 521 vezes 32. Na primeira linha, 521. Abaixo, à esquerda sinal de multiplicação, à direita 32 alinhado ordem a ordem com 521. Abaixo, traço horizontal. Abaixo, 1 mil 042 alinhado ordem a ordem com 521 e 32. Abaixo, à esquerda sinal de adição, à direita 15 mil 630 alinhado ordem a ordem com 521, 32 e 1 mil 042. Abaixo, traço horizontal. Abaixo, 16 mil 672 alinhado ordem a ordem com 521, 32, 1 mil 042 e 15 mil 630.

Página cinquenta e três

19. Para calcular o total gasto nessa compra, podemos multiplicar a quantidade de prestações pelo valor delas. Assim, temos:

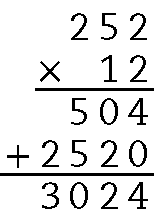
Algoritmo usual da multiplicação. 252 vezes 12. Na primeira linha, 252. Abaixo, à esquerda sinal de multiplicação, à direita 12 alinhado ordem a ordem com 252. Abaixo, traço horizontal. Abaixo, 504 alinhado ordem a ordem com 252 e 12. Abaixo, à esquerda sinal de adição, à direita 2 mil 520 alinhado ordem a ordem com 252, 12 e 504 Abaixo, traço horizontal. Abaixo, 3 mil 024 alinhado ordem a ordem com 252, 12, 504 e 2 mil 520.

Logo, o total gasto nessa compra foi R$ 3.024,00três mil vinte e quatro reais.

20. Sabendo que

⋅ 12 = 336, para descobrir o valor de

, podemos calcular 336 : 12. Assim, temos:

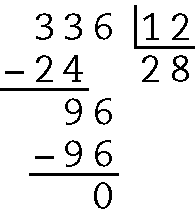
Algoritmo usual da divisão. 336 dividido por 12. Na primeira linha, 336, chave da divisão e dentro da chave 12. Abaixo, à esquerda, sinal de subtração, à direita 24, alinhado aos algoritmos da ordem das dezenas e centenas de 336, à direita abaixo da chave o quociente 28. Abaixo, traço horizontal. Abaixo, 96, alinhado ordem a ordem com 336. Abaixo, à esquerda sinal de subtração, à direita 96 alinhado ordem a ordem com 336 e 96. Abaixo, traço horizontal. Abaixo, o resto, 0.

Portanto, o outro fator é 28.

21. a) 112 ⋅ 15 = 15 ⋅ 112

b) 219 ⋅ 156 = 156 ⋅ 219

c) 11 ⋅ (15 ⋅ 9) = (11 ⋅ 15) ⋅ 9

d) 25 ⋅ (18 ⋅ 7) = (25 ⋅ 18) ⋅ 7

e) 315 ⋅ 102 = 102 ⋅ 315

f) .1010 ⋅ 55 = 55 ⋅ .1010

22. a) 6 ⋅ (12 + 7) = 6 ⋅ 12 + 6 ⋅ 7 = 72 + 42 = 114 ou 6 ⋅ (12 + 7) = 6 ⋅ 19 = 114

b) 9 ⋅ (21 ‒ 13) = 9 ⋅ 21 ‒ 9 ⋅ 13 = 189 ‒ 117 = 72 ou 9 ⋅ (21 ‒ 13) = 9 ⋅ 8 = 72

c) 10 ⋅ (15 + 8) = 10 ⋅ 15 + 10 ⋅ 8 = 150 + 80 = 230 ou 10 ⋅ (15 + 8) = 10 ⋅ 23 = 230

23. a) Quociente 23 e resto 4.

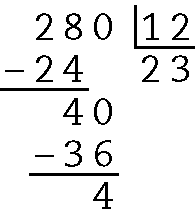
Algoritmo usual da divisão. 280 dividido por 12. Na primeira linha, o número 280, chave da divisão, dentro da chave o número 12. Abaixo, à esquerda sinal de subtração, à direita o número 24 alinhado a ordem das dezenas e da centenas do número 280, abaixo da chave o quociente 23. Abaixo, traço horizontal. Abaixo, o número 40 alinhado a ordem das unidades e das dezenas do número 280. Abaixo, à esquerda sinal de subtração, à direita, o número 36, alinhado ordem a ordem com o número 40. Abaixo, traço horizontal. Abaixo, o resto 4.

b) Quociente 36 e resto 3.

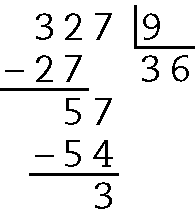
Algoritmo usual da divisão. 327 dividido por 9. Na primeira linha, o número 327, chave da divisão, dentro da chave o número 9. Abaixo, à esquerda sinal de subtração, à direita o número 27 alinhado a ordem das dezenas e da centenas do número 327, abaixo da chave o quociente 36. Abaixo, traço horizontal. Abaixo, o número 57 alinhado a ordem das unidades e das dezenas do número 327. Abaixo, à esquerda sinal de subtração, à direita, o número 54, alinhado ordem a ordem com o número 57. Abaixo, traço horizontal. Abaixo, o resto 3.

c) Quociente 98 e resto 0.

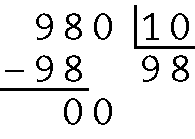
Algoritmo usual da divisão. 980 dividido por 10. Na primeira linha, o número 980, chave da divisão, dentro da chave o número 10. Abaixo, à esquerda sinal de subtração, à direita o número 98 alinhado a ordem das dezenas e da centenas do número 980, abaixo da chave o quociente 98. Abaixo, traço horizontal. Abaixo, o resto 00.

d) Quociente 10 e resto 0.

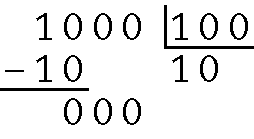
Algoritmo usual da divisão. 1000 dividido por 100. Na primeira linha, o número 1000, chave da divisão, dentro da chave o número 100. Abaixo, à esquerda sinal de subtração, à direita o número 10 alinhado a ordem das centenas e da unidade de milhar do número 1000, abaixo da chave o quociente 10. Abaixo, traço horizontal. Abaixo, o resto 000.

e) Quociente 176 e resto 8.

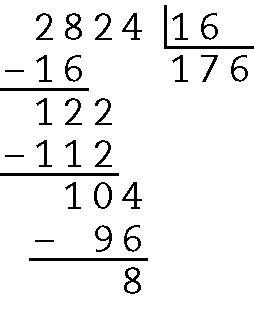
Algoritmo usual da divisão. 2 mil 824 dividido por 16. Na primeira linha, o número 2 mil 824, chave da divisão, dentro da chave o número 16. Abaixo, à esquerda sinal de subtração, à direita o número 16 alinhado a ordem das centenas e ordem da unidade de milhar do número 2 mil 824, abaixo da chave o quociente 176. Abaixo, traço horizontal. Abaixo, o número 122 alinhado a ordem das dezenas, centenas e unidade de milhar do número 2 mil 824. Abaixo, à esquerda sinal de subtração, à direita, o número 112, alinhado ordem a ordem com o número 122. Abaixo, traço horizontal. Abaixo, o número 104 alinhado a ordem das unidades, dezenas e centenas do número 2 mil 824. Abaixo, à esquerda sinal de subtração, à direita o número 96 alinhado ordem a ordem ao número 104. Abaixo, traço horizontal. Abaixo, o resto 8.

f) Quociente 102 e resto 5.

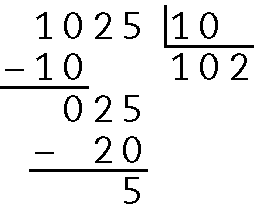
Algoritmo usual da divisão. 1 mil e 025 dividido por 10. Na primeira linha, 1 mil e 25, chave da divisão e dentro da chave 10. Abaixo, à esquerda, sinal de subtração, à direita 10, alinhado aos algoritmos da ordem das centenas e milhares de 1 mil e 25, à direita abaixo da chave o quociente 102. Abaixo, traço horizontal. Abaixo, 025, alinhado ordem a ordem com 1 mil e 25. Abaixo, à esquerda sinal de subtração, à direita 20 alinhado ordem a ordem 025. Abaixo, traço horizontal. Abaixo, o resto, 5.

24. Para descobrir qual será o valor de cada prestação, podemos dividir o preço da motocicleta pela quantidade de prestações. Assim, temos:

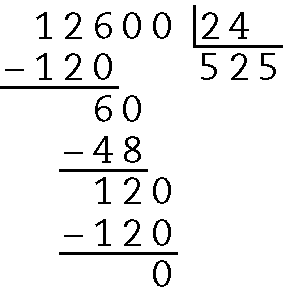
Algoritmo usual da divisão. 12 mil e 600 dividido por 24. Na primeira linha, 12 mil 600, chave da divisão e dentro da chave 24. Abaixo, à esquerda, sinal de subtração, à direita 120, alinhado aos algoritmos da ordem das centenas e milhar e dezena de milhar de 12 mil 600, à direita abaixo da chave o quociente 525. Abaixo, traço horizontal. Abaixo, 60, alinhado a ordem das unidades do número120. Abaixo, à esquerda sinal de subtração, à direita 48 alinhado ordem a ordem com 60. Abaixo, traço horizontal. Abaixo, 120, os algarismos 1 e 2 estão alinhados respectivamente a ordem das dezenas e das unidades dos números 60 e 48. Abaixo, à esquerda sinal de subtração, à direita, 120 alinhado ordem a ordem com 120. Abaixo, traço horizontal. Abaixo, o resto 0.

O valor de cada prestação será R$ 525,00quinhentos e vinte e cinco reais.

Para o capítulo 3: Figuras geométricas espaciais

Páginas 13 e 14

25. a)

	Número de faces	Número de arestas	Número de vértices
Figura 1	6	12	8
Figura 2	5	8	5
Figura 3	5	9	6

b) Figura 1: base quadrangular; figura 2: base quadrangular; figura 3: base triangular.

c) Figura 1: prisma de base quadrangular; figura 2: pirâmide de base quadrangular; figura 3: prisma de base triangular.

26. a) Prisma de base pentagonal

b) Cone

c) Esfera

d) Pirâmide de base triangular

27. Cubo

28. a) Pirâmide de base quadrada

b) Cone

c) Paralelepípedo

d) Pirâmide de base triangular

Para o capítulo 4: Igualdades e desigualdades

Página 15

29. a) 25 + 32 = 12 + 45

25 + 32 + 12 = 12 + 45 + 12

57 + 12 = 57 + 12

69 = 69

b) 29 ‒ 7 = 15 + 7

29 ‒ 7 ‒ 8 = 15 + 7 ‒ 8

22 ‒ 8 = 22 ‒ 8

14 = 14

Página cinquenta e quatro

c) 15 + 4 = 25 ‒ 6

(15 + 4) ⋅ 8 = (25 ‒ 6) ⋅ 8

15 ⋅ 8 + 4 ⋅ 8 = 25 ⋅ 8 ‒ 6 ⋅ 8

12 + 32 = 200 ‒ 48

152 = 152

d) 25 + 15 = 50 ‒ 10

(25 + 15) : 5 = (50 ‒ 10) : 5

40 : 5 = 40 : 5

8 = 8

30. a) (120 + 300) : 2 = 420 : 2

b) 258 ‒ 150 = 228 + 30 ‒ 150

c) .1000 ⋅ 5 = (400 + 600) ⋅ 5

d) .1200 : 3 = (800 + 400) : 3

e) 238 + 100 = 100 + 138 + 100

f) (.1600 ‒ 200) ⋅ 10 = 1400 ⋅ 10

Para o capítulo 5: Múltiplos e divisores

Páginas 15 e 16

31.

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180

32. a) Resposta possível: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.

b) Os múltiplos de 9 entre 50 e 100 são: 54, 63, 72, 81, 90 e 99.

c) Os cinco primeiros múltiplos de 6, a partir dele, são: 6, 12, 18, 24, 30.

33. Os múltiplos de 15 entre 100 e 200 são: 105, 120, 135, 150, 165, 180 e 195.

34.

Número	2	3	5	6	9	10
	Divisor
258	X	X		X
356	X
400	X		X			X
525		X	X
886	X
990	X	X	X	X	X	X
1.000	X		X			X
1.050	X	X	X	X		X
2.256	X	X		X
8.250	X	X	X	X		X

Para o capítulo 6: Frações

Páginas 16 a 18

35. a) um oitavo.

b) quatro quinze avos.

c) dezessete centésimos.

d) vinte e sete duzentos avos.

36. Exemplos de resposta:

\frac{3}{6}

\frac{5}{12}

\frac{3}{4}

\frac{16}{36}

37. Exemplos de resposta:

Esquema. Retângulo dividido em 3 partes iguais, todas as partes são alaranjadas. Abaixo, retângulo dividido em 3 partes iguais, todas as partes são alaranjadas. Abaixo, retângulo dividido em 3 partes iguais, da esquerda para a direita, uma parte é alaranjada.

Esquema. Retângulo dividido em 3 partes iguais, todas as partes são alaranjadas. Abaixo, retângulo dividido em 3 partes iguais, da esquerda para a direita, duas partes são alaranjadas.

Esquema. Retângulo dividido em 8 partes iguais, organizadas em 2 linhas e 4 colunas, todas as partes são alaranjadas. Abaixo, retângulo dividido em 8 partes iguais, organizadas em 2 linhas e 4 colunas, todas as partes são alaranjadas. Abaixo, retângulo dividido em 8 partes iguais, organizadas em 2 linhas e 4 colunas, da esquerda para a direita, na primeira linha, 3 partes são alaranjadas.

Esquema. Retângulo dividido em 9 partes iguais, organizadas em 3 linhas e 3 colunas, todas as partes são alaranjadas. Abaixo, retângulo dividido em 9 partes iguais, organizadas em 3 linhas e 4 colunas, da esquerda para a direita as duas primeiras colunas e a primeira parte da terceira coluna são alaranjadas, totalizando 7 partes alaranjadas.

38. a)

1 \frac{2}{5} = \frac{1 \cdot 5}{5} + \frac{2}{5} =

\frac{5}{5}

\frac{2}{5}

\frac{7}{5}

3 \frac{4}{9} = \frac{3 \cdot 9}{9} + \frac{4}{9} = \frac{27}{9} + \frac{4}{9} = \frac{31}{9}

5 \frac{1}{4} = \frac{5 \cdot 4}{4} + \frac{1}{4} =

\frac{20}{4}

\frac{1}{4}

\frac{21}{4}

d) 8

\frac{3}{5}

\frac{8 \cdot 5}{5}

\frac{3}{5}

\frac{40}{5}

\frac{3}{5}

\frac{43}{5}

39. Exemplos de respostas:

\frac{1}{2}

\frac{1}{4}

\frac{1}{3}

\frac{15}{19}

40. a)

\frac{3}{8} = \frac{3 \cdot 9}{8 \cdot 9} = \frac{27}{72}

\frac{5}{7} = \frac{5 \cdot 3}{7 \cdot 3} = \frac{15}{21}

\frac{4}{25} = \frac{4 \cdot 5}{25 \cdot 5} = \frac{20}{125}

\frac{3}{7} = \frac{3 \cdot 10}{7 \cdot 10} = \frac{30}{70}

41. Para facilitar a comparação de frações com denominadores diferentes, é possível comparar frações equivalentes a elas que tenham denominadores iguais.

a) Como:

\frac{1}{3} = \frac{4}{12}

\frac{1}{4} = \frac{3}{12}

\frac{1}{2} = \frac{6}{12}

Temos que:

\frac{3}{12}

\frac{4}{12}

\frac{6}{12}

Portanto, em ordem crescente, temos:

\frac{1}{4}, \frac{1}{3}

\frac{1}{2} .

b) Como:

\frac{2}{5} = \frac{72}{180}

\frac{3}{4} = \frac{135}{180}

\frac{2}{9} = \frac{40}{180}

Temos que:

\frac{40}{180}

\frac{72}{180}

\frac{135}{180}

Portanto, em ordem crescente, temos:

\frac{2}{9}, \frac{2}{5}

\frac{3}{4} .

Página cinquenta e cinco

c) Como:

\frac{1}{4} = \frac{2}{8}

\frac{3}{8}

\frac{15}{2} = \frac{60}{8}

Temos que:

\frac{2}{8}

\frac{3}{8}

\frac{60}{8}

Portanto, em ordem crescente, temos:

\frac{1}{4}, \frac{3}{8}

\frac{15}{2} .

d) Como:

\frac{5}{8} = \frac{45}{72}

\frac{10}{12} = \frac{60}{72}

\frac{3}{9} = \frac{24}{72}

Temos que:

\frac{24}{72}

\frac{45}{72}

\frac{60}{72}

Portanto, em ordem crescente, temos:

\frac{3}{9}, \frac{5}{8}

\frac{10}{12} .

42. Como são frações de mesmo denominador, basta comparar os numeradores.

\frac{9}{5}, \frac{2}{5} e \frac{1}{5}

\frac{25}{18}, \frac{12}{18} e \frac{5}{18}

\frac{18}{35}, \frac{10}{35} e \frac{1}{35}

\frac{51}{58}, \frac{23}{58} e \frac{12}{58}

43. a)

\frac{7}{9}

b) Considerando frações equivalentes, com denominador igual a 8, temos:

\frac{2}{4} = \frac{4}{8}

\frac{3}{4} = \frac{6}{8}

Portanto, a maior fração é

\frac{3}{4}

c) Como todas as frações têm o mesmo numerador, a maior é aquela com menor denominador. Nesse caso,

\frac{1}{3}

é a menor fração.

d) Considerando frações equivalentes, com denominador igual a 30, temos:

\frac{4}{5} = \frac{24}{30}

\frac{10}{12} = \frac{5}{6} = \frac{25}{30}

\frac{7}{6} = \frac{35}{30}

Portanto, a maior fração é

\frac{7}{6}

44. a)

\frac{1}{3} + \frac{5}{3} = \frac{6}{3}

\frac{9}{15} + \frac{11}{15} = \frac{20}{15}

\frac{7}{8} ‒ \frac{3}{8} = \frac{4}{8}

\frac{11}{20} ‒ \frac{7}{20} = \frac{4}{20}

\frac{3}{3} + \frac{2}{3} + \frac{1}{3} = \frac{6}{3}

\frac{3}{7} + \frac{2}{14} = \frac{3}{7} + \frac{1}{7} = \frac{4}{7}

\frac{1}{4} + \frac{3}{3} = \frac{3}{12} + \frac{12}{12} = \frac{15}{12}

\frac{3}{2} ‒ \frac{7}{8} = \frac{12}{8} ‒ \frac{7}{8} = \frac{5}{8}

\frac{4}{5} ‒ \frac{5}{12} = \frac{48}{60} ‒ \frac{25}{60} = \frac{23}{60}

\frac{1}{3} + \frac{1}{4} + \frac{1}{2} = \frac{4}{12} + \frac{3}{12} + \frac{6}{12} = \frac{13}{12}

\frac{10}{15} ‒ \frac{3}{8} = \frac{80}{120} ‒ \frac{45}{120} = \frac{35}{120}

\frac{2}{3} + \frac{4}{5} + \frac{1}{2} = \frac{20}{30} + \frac{24}{30} + \frac{15}{30} = \frac{59}{30}

45. Adicionado as frações correspondentes aos dois gastos, temos:

\frac{3}{7} + \frac{2}{8} = \frac{24}{56} + \frac{14}{56} = \frac{38}{56}

Marcos gastou

\frac{38}{56}

do salário.

46. Calculando a diferença entre o total de páginas do livro e a soma das frações que corresponde às páginas já lidas, temos:

1 ‒ (\frac{1}{4} + \frac{1}{3}) = 1 ‒ (\frac{3}{12} + \frac{4}{12}) = 1 ‒ \frac{7}{12} = \frac{12}{12} ‒ \frac{7}{12} = \frac{5}{12}

Falta

\frac{5}{12}

do livro para Joana ler.

47. a)

6 \cdot \frac{3}{7} = \frac{18}{7}

5 \cdot \frac{3}{4} = \frac{15}{4}

2 \cdot \frac{1}{3} = \frac{2}{3}

d) 9

\cdot \frac{4}{7} = \frac{36}{7}

e) 12

\cdot \frac{3}{5} = \frac{36}{5}

15 \cdot \frac{1}{6} = \frac{15}{6}

48.

5 \cdot \frac{2}{5} = \frac{10}{5} = 2

São necessários 2 tabletes de fermento.

49. a)

\frac{3}{8} : 2 = \frac{3}{16}

\frac{1}{3} : 2 = \frac{1}{6}

\frac{3}{4} : 5 = \frac{3}{20}

\frac{3}{5} : 5 = \frac{3}{25}

50.

\frac{3}{5} : 4 = \frac{3}{20}

Cada pessoa receberá

\frac{3}{20}

da torta.

Para o capítulo 7: Números decimais

Páginas 18 a 20

51. Exemplos de resposta:

a) nove décimos

b) duzentos e quinze milésimos

c) cinco inteiros e sessenta e oito centésimos

d) dezoito centésimos

e) oito inteiros e quarenta e um milésimos

f) cinco milésimos

52. a) 9,8

b) 0,148

c) 0,93

d) 0,791

e) 2,049

53. a) 1,2 > 1,02

b) 8,4 > 8,14

c) 10,15 < 10,51

d) 11,9 < 15,0

e) 2,3 > 0,23

f) 15,0 < 15,1

Página cinquenta e seis

54. a) 0,31; 0,38; 0,57; 0,94

b) 3,07; 3,09; 3,55; 3,98

c) 0,99; 8,92; 10,01; 11,12

d) 5,095; 5,105; 5,555; 5,807

55.

Ilustração. Reta numérica com 1 vírgula 1 representado na extremidade esquerda e 2 vírgula 1 representado na extremidade direita. Da esquerda para direita há os pontos representados por 1 vírgula 1, 1 vírgula 5, 1 vírgula 6, 1 vírgula 9 e 2 vírgula 1.

56. a)

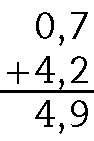
Algoritmo usual da adição. 0 vírgula 7 mais 4 vírgula 2. Na primeira linha, 0 vírgula 7. Abaixo, à esquerda sinal de adição, à direita 4 vírgula 2, alinhado ordem a ordem com 0 vírgula 7. Abaixo, traço horizontal. Abaixo, 4 vírgula 9 alinhado ordem a ordem com 0 vírgula 7 e 4 vírgula 2.

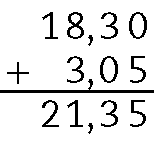
Algoritmo usual da adição. 18 vírgula 30 mais 3 vírgula 05. Na primeira linha, 18 vírgula 30. Abaixo, à esquerda sinal de adição, à direita 3 vírgula 05, alinhado ordem a ordem com 18 vírgula 30. Abaixo, traço horizontal. Abaixo, 21 vírgula 35 alinhado ordem a ordem com 18 vírgula 30 e 3 vírgula 05.

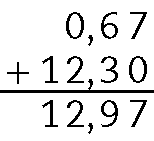
Esquema: Algoritmo usual da adição. 0 vírgula 67 mais 12 vírgula 30. Na primeira linha, 0 vírgula 67. Abaixo, à esquerda sinal de adição, à direita 12 vírgula 30, alinhado ordem a ordem com 0 vírgula 67. Abaixo, traço horizontal. Abaixo, 12 vírgula 97 alinhado ordem a ordem com 0 vírgula 67 e 12 vírgula 30.

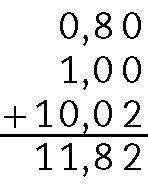
Algoritmo usual da adição. 0 vírgula 80 mais 1 vírgula 00 mais 10 vírgula 02. Na primeira linha 0 vírgula 80. Abaixo, o número 1 vírgula 00 alinhado ordem a ordem com 0 vírgula 80. Abaixo, à esquerda sinal de adição, à direita 10 vírgula 02 alinhado ordem a ordem com 0 vírgula 80 e 1 vírgula 00. Abaixo, traço horizontal. Abaixo, 11 vírgula 82 alinhado ordem a ordem com 10 vírgula 02.

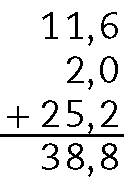
Algoritmo usual da adição. 11 vírgula 6 mais 2 vírgula 0 mais 25 vírgula 2. Na primeira linha 11 vírgula 6. Abaixo, 2 vírgula 0 alinhado ordem a ordem com 11 vírgula 6. Abaixo, à esquerda sinal de adição, à direita 25 vírgula 2 alinhado ordem a ordem com 11 vírgula 6 e 2 vírgula zero. Abaixo, traço horizontal. Abaixo, 38 vírgula 8, alinhado ordem a ordem com 25 vírgula 2.

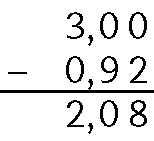
Algoritmo usual da subtração. 3 vírgula 00 menos 0 vírgula 92. Na primeira linha, 3 vírgula 00. Abaixo, à esquerda sinal de subtração, à direita 0 vírgula 92, alinhado ordem a ordem com 3 vírgula 00. Abaixo, traço horizontal. Abaixo, 2 vírgula 08 alinhado ordem a ordem com 3 vírgula 00 e 0 vírgula 92.

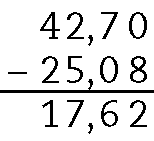
Algoritmo usual da subtração. 42 vírgula 70 menos 25 vírgula 08. Na primeira linha, 42 vírgula 70. Abaixo, à esquerda sinal de subtração, à direita 25 vírgula 08, alinhado ordem a ordem com 42 vírgula 70. Abaixo, traço horizontal. Abaixo, 17 vírgula 62 alinhado ordem a ordem com 42 vírgula 70 e 25 vírgula 08.

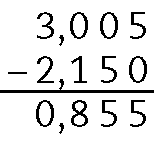
Algoritmo usual da subtração. 3 vírgula 005 menos 2 vírgula 150. Na primeira linha, 3 vírgula 005. Abaixo, à esquerda sinal de subtração, à direita 2 vírgula 150, alinhado ordem a ordem com 3 vírgula 005. Abaixo, traço horizontal. Abaixo, 0 vírgula 855 alinhado ordem a ordem com 3 vírgula 005 e 2 vírgula 150.

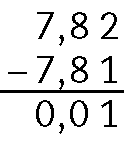
Algoritmo usual da subtração. 7 vírgula 82 menos 7 vírgula 81. Na primeira linha, 7 vírgula 82. Abaixo, à esquerda sinal de subtração, à direita 7 vírgula 81, alinhado ordem a ordem com 7 vírgula 82. Abaixo, traço horizontal. Abaixo, 0 vírgula 01 alinhado ordem a ordem com 7 vírgula 81.

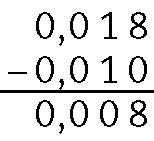
Algoritmo usual da subtração. 0 vírgula 018 menos 0 vírgula 010. Na primeira linha, 0 vírgula 018. Abaixo, à esquerda sinal de subtração, à direita 0 vírgula 010, alinhado ordem a ordem com 0 vírgula 018. Abaixo, traço horizontal. Abaixo, 0 vírgula 008 alinhado ordem a ordem com 0 vírgula 018 e 0 vírgula 010.

57. Podemos calcular:

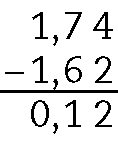
Algoritmo usual da subtração. 1 vírgula 74 menos 1 vírgula 62. Na primeira linha, 1 vírgula 74. Abaixo, à esquerda sinal de subtração, à direita 1 vírgula 62 alinhado ordem a ordem com 1 vírgula 74. Abaixo, traço horizontal. Abaixo, 0 vírgula 12, alinhado ordem a ordem com 1 vírgula 74 e 1 vírgula 62.

A diferença da medida da altura das duas é de 0,12 métro.

58. a)

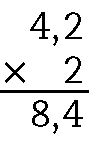
Algoritmo usual da multiplicação. 4 vírgula 2 vezes 2. Na primeira linha, 4 vírgula 2. Abaixo à esquerda sinal de multiplicação, à direita o número 2 alinhado a ordem dos décimos de 4 vírgula 2. Abaixo traço horizontal. Abaixo, 8 vírgula 4 alinhado ordem a ordem com 4 vírgula 2.

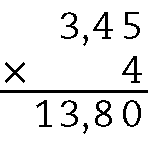
Algoritmo usual da multiplicação. 3 vírgula 45 vezes 4. Na primeira linha, 3 vírgula 45. Abaixo à esquerda sinal de multiplicação, à direita o número 4 alinhado a ordem dos centésimos de 3 vírgula 45. Abaixo traço horizontal. Abaixo, 13 vírgula 80 alinhado ordem a ordem com 3 vírgula 45.

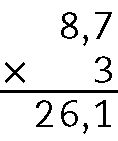
Algoritmo usual da multiplicação. 8 vírgula 7 vezes 3. Na primeira linha, 8 vírgula 7. Abaixo à esquerda sinal de multiplicação, à direita o número 3 alinhado a ordem dos décimos de 8 vírgula 7. Abaixo traço horizontal. Abaixo, 26 vírgula 1 alinhado ordem a ordem com 8 vírgula 7.

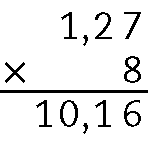
Algoritmo usual da multiplicação. 1 vírgula 27 vezes 8. Na primeira linha, 1 vírgula 27. Abaixo à esquerda sinal de multiplicação, à direita o número 8 alinhado a ordem dos centésimos de 1 vírgula 27. Abaixo traço horizontal. Abaixo, 10 vírgula 16 alinhado ordem a ordem com 1 vírgula 27.

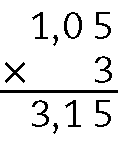
Algoritmo usual da multiplicação. 1 vírgula 05 vezes 3. Na primeira linha, 1 vírgula 05. Abaixo à esquerda sinal de multiplicação, à direita o número 3 alinhado a ordem dos centésimos de 1 vírgula 05. Abaixo traço horizontal. Abaixo, 3 vírgula 15 alinhado ordem a ordem com 1 vírgula 05.

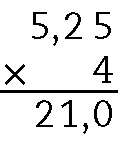
Algoritmo usual da multiplicação. 5 vírgula 25 vezes 4. Na primeira linha, 5 vírgula 25. Abaixo à esquerda sinal de multiplicação, à direita o número 4 alinhado a ordem dos centésimos de 5 vírgula 25. Abaixo traço horizontal. Abaixo, 21 vírgula 0 alinhado ordem a ordem com 5 vírgula 25.

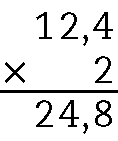
Algoritmo usual da multiplicação. 12 vírgula 4 vezes 2. Na primeira linha, 12 vírgula 4. Abaixo à esquerda sinal de multiplicação, à direita o número 2 alinhado a ordem dos décimos de 12 vírgula 4. Abaixo traço horizontal. Abaixo, 24 vírgula 8 alinhado ordem a ordem com 12 vírgula 4.

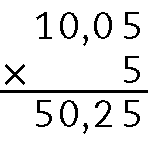
Algoritmo usual da multiplicação. 10 vírgula 05 vezes 5. Na primeira linha, 10 vírgula 05. Abaixo à esquerda sinal de multiplicação, à direita o número 5 alinhado a ordem dos centésimos de 10 vírgula 05. Abaixo traço horizontal. Abaixo, 50 vírgula 25 alinhado ordem a ordem com 10 vírgula 25.

59. a) 4,75 ⋅ 10 = 47,5

b) 8,32 ⋅ 100 = 832

c) 6,21 ⋅ .1000 = .6210

d) 0,82 ⋅ 10 = 8,2

e) 11,5 ⋅ 100 = .1150

f) 1,921 ⋅ .1000 = .1921

60. a)

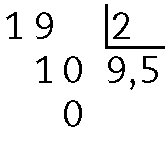
Esquema. Algoritmo da divisão de 19 por 2. Na primeira linha, à esquerda o número 19 . À direita, na chave, o número 2. Abaixo da chave, o número 9 vírgula 5. Abaixo, o número 10, alinhado com a ordem das unidades do número 19 do dividendo. Abaixo, o resto 0.

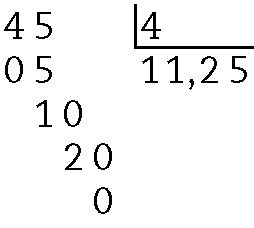
Esquema. Algoritmo da divisão de 45 por 4. Na primeira linha, à esquerda o número 45. À direita, na chave, o número 4. Abaixo da chave, o número 11 vírgula 25. Abaixo, o número 5, alinhado com a ordem das unidades do número 45 do dividendo. Abaixo, o número 10 alinhado a ordem das unidades do dividendo. Abaixo, o número 20 alinhado a ordem das unidades do número 10. Abaixo, o resto 0.

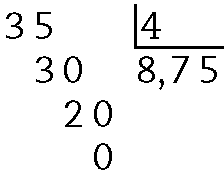
Esquema. Algoritmo da divisão de 35 por 4. Na primeira linha, à esquerda o número 35 . À direita, na chave, o número 4. Abaixo da chave, o número 8 vírgula 75. Abaixo, o número 30, alinhado com a ordem das unidades do número 35 do dividendo. Abaixo, o número 20 alinhado a ordem das unidades do número 30. Abaixo, o resto 0.

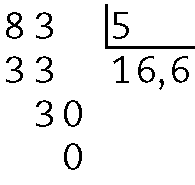
Esquema. Algoritmo da divisão de 83 por 5. Na primeira linha, à esquerda o número 83 . À direita, na chave, o número 5. Abaixo da chave, o número 16 vírgula 6. Abaixo, o número 33, alinhado ordem a ordem com o número 83 do dividendo. Abaixo, o número 30 alinhado a ordem das unidades do número 33. Abaixo, o resto 0.

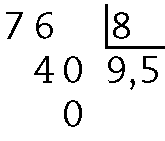
Esquema. Algoritmo da divisão de 76 por 8. Na primeira linha, à esquerda o número 76. À direita, na chave, o número 8. Abaixo da chave, o número 9 vírgula 5. Abaixo, o número 40, alinhado com a ordem das unidades do número 76 do dividendo. Abaixo, o resto 0.

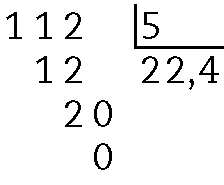
Esquema. Algoritmo da divisão de 112 por 5. Na primeira linha, à esquerda o número 112. À direita, na chave, o número 5. Abaixo da chave, o número 22 vírgula 4. Abaixo, o número 12, alinhado a ordem das unidades e das dezenas do número 112 do dividendo. Abaixo, o número 20 alinhado a ordem das unidades do número 12. Abaixo, o resto 0.

61. a)

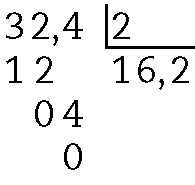
Esquema. Algoritmo da divisão de 32 vírgula 4 por 2. Na primeira linha, à esquerda o número 32 vírgula 4. À direita, na chave, o número 2. Abaixo da chave, o número 16 vírgula 2. Abaixo, o número 12, alinhado a parte inteira do número 32 vírgula 4 do dividendo. Abaixo, o número 4 alinhado a ordem dos décimos do dividendo. Abaixo, o resto 0.

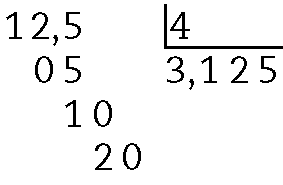
Esquema. Algoritmo da divisão de 12 vírgula 5 por 4. Na primeira linha, à esquerda o número 12 vírgula 5. À direita, na chave, o número 4. Abaixo da chave, o número 3 vírgula 125. Abaixo, o número 5, alinhado a ordem dos décimos do número 12 vírgula 5 do dividendo. Abaixo, o número 10 alinhado a ordem dos décimos do dividendo. Abaixo, o resto 20.

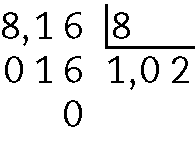
Esquema. Algoritmo da divisão de 8 vírgula 16 por 8. Na primeira linha, à esquerda o número 8 vírgula 16. À direita, na chave, o número 8. Abaixo da chave, o número 1 vírgula 02. Abaixo, o número 016, alinhado ordem a ordem com o número 8 vírgula 16 do dividendo. Abaixo, o resto 0.

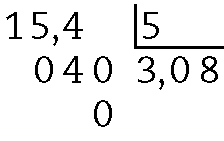
Esquema. Algoritmo da divisão de 15 vírgula 4 por 5. Na primeira linha, à esquerda o número 15 vírgula 4. À direita, na chave, o número 5. Abaixo da chave, o número 3 vírgula 08. Abaixo, o número 040, alinhado a ordem dos décimos do número 15 vírgula 4 do dividendo. Abaixo, o resto 0.

Esquema. Algoritmo da divisão de 250 vírgula 3 por 2. Na primeira linha, à esquerda o número 250 vírgula 3. À direita, na chave, o número 2. Abaixo da chave, o número 125 vírgula 15. Abaixo, o número 5, alinhado a ordem das dezenas da parte inteira do número 250 vírgula 3 do dividendo. Abaixo, o número 10 alinhado a ordem das dezenas e das unidades da parte inteira do dividendo. Abaixo, o número 3 alinhado a ordem dos décimos do dividendo. Abaixo, o número 10, com algarismo 1 alinhado a ordem dos décimos do dividendo. Abaixo, o resto 0

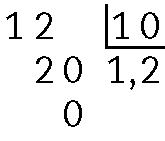
Esquema. Algoritmo da divisão de 12 por 10. Na primeira linha, à esquerda o número 12. À direita, na chave, o número 10. Abaixo da chave, o número 1 vírgula 2. Abaixo, o número 20, alinhado com a ordem das unidades do número 12 do dividendo. Abaixo, o resto 0.

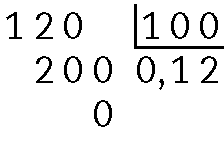
Esquema. Algoritmo da divisão de 120 por 100. Na primeira linha, à esquerda o número 120. À direita, na chave, o número 100. Abaixo da chave, o número 0 vírgula 12. Abaixo, o número 200, alinhado com a ordem das unidades e das dezenas do número 120 do dividendo. Abaixo, o resto 0.

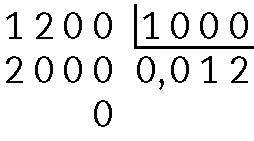
Esquema. Algoritmo da divisão de 1 mil 200 por 1 mil. Na primeira linha, à esquerda o número 1 mil e 200. À direita, na chave, o número 1 mil. Abaixo da chave, o número 0 vírgula 012. Abaixo, o número 2 mil, alinhado ordem a ordem com número 1 mil e 200 do dividendo. Abaixo, o resto 0.

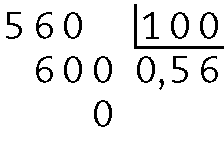
Esquema. Algoritmo da divisão de 560 por 100. Na primeira linha, à esquerda o número 560. À direita, na chave, o número 100. Abaixo da chave, o número 0 vírgula 56. Abaixo, o número 600, alinhado com a ordem das unidades e das dezenas do número 560 do dividendo. Abaixo, o resto 0.

Esquema. Algoritmo da divisão de 12 vírgula 56 por 100. Na primeira linha, à esquerda o número 12 vírgula 56. À direita, na chave, o número 100. Abaixo da chave, o número 0 vírgula 1 mil 256. Abaixo, o número 256, com os algarismos 2, 5 e 6 alinhados respectivamente com os algarismos 2, 5 e 6 do número 12 vírgula 56 do dividendo. Abaixo, o número 560 com os algarismos 5 e 6 alinhado a ordem dos centésimos e dos décimos do dividendo. Abaixo, o número 600 com os algarismos das dezenas e centenas alinhados aos algarismos das unidades e das dezenas do número 560. Abaixo, o resto 0

Para o capítulo 8: Porcentagem

Página 20

62. a)

15 % = \frac{15}{100} = 0,15

32 % = \frac{32}{100} = 0,32

55 % = \frac{55}{100} = 0,55

4 % = \frac{4}{100} = 0,04

80 % = \frac{80}{100} = 0,8

99 % = \frac{99}{100} = 0,99

63. a)

5 % d e 10 = \frac{5}{100} \cdot 10 = \frac{50}{100} = 0,5

10 % d e 10 = \frac{10}{100} \cdot 10 = \frac{100}{100} = 1

50 % d e 100 = \frac{50}{100} \cdot 100 = \frac{5 000}{100} = 50

60 % d e 100 = \frac{60}{100} \cdot 100 = 60

42 % d e 100 = \frac{42}{100} \cdot 100 = 42

8 % d e 200 = \frac{8}{100} \cdot 200 = \frac{1 600}{100} = 16

64. Como 25% de 100 é 25, então o desconto foi de R$ 25,00vinte e cinco reais e o valor final da calça foi R$ 75,00setenta e cinco reais.

Para o capítulo 9: Figuras geométricas planas

Páginas 20 a 22

65. a)

\vec{B A}

\vec{C D}

66. a) É um segmento de reta.

b) Não é segmento de reta.

67. a)

\bar{A B}, \bar{B C} e \bar{C A}

\bar{A B}, \bar{B C}, \bar{C D} e \bar{D A}

Página cinquenta e sete

68. a) ângulo obtuso.

b) ângulo agudo.

c) ângulo reto.

d) ângulo obtuso.

69. a) 130graus

b) 60graus

70. a) As retas verdes são concorrentes.

b) As retas vermelhas são paralelas.

c) Uma reta verde e uma reta vermelha são concorrentes.

71. Exemplo de resposta.

Ilustração. Duas retas perpendiculares com ângulo de 90 graus indicado em um dos quatro ângulos formados.

72. a) Quadrilátero.

b) Triângulo.

c) Triângulo.

d) Quadrilátero.

Para o capítulo 10: Ampliação e redução de figuras

Página 22

73.

Ilustração. Malha quadriculada composta por 6 linhas e 10 colunas, à esquerda, figura geométrica composta 12 unidades de área com 9 lados e 10 vértices À direita figura geométrica composta por 3 unidades de área com 9 lados e 10 vértices, com formato idêntico à figura da esquerda.

Para o capítulo 11: Grandezas e medidas

Páginas 22 a 24

74. a) 2,50 métros = 250 centímetros

b) 1,45 métros = 145 centímetros

c) 150 decímetros = 15 métros

d) 1,5 quilômetro = .1500 métros

e) 1 quilômetro = .10000 decímetros

f) 100 centímetros = .1000 milímetros

g) .1000 milímetros = 100 centímetros

75. 1,65 métro = 1 650 milímetros

76. (3 + 2,65 + 2,5 + 4) centímetros = 12,15 centímetros

77. Por contagem:

a) 8 centímetros quadrados

b) 10 centímetros quadrados

78. a) [(2 ⋅ 2 ⋅ 3) + (2 ⋅ 1 ⋅ 1)] centímetros cúbicos = [12 + 2] centímetros cúbicos = 14 centímetros cúbicos

b) [(2 ⋅ 2 ⋅ 3) + (1 ⋅ 1 ⋅ 1) + (2 ⋅ 1 ⋅ 1)] centímetros cúbicos =

= [12 + 1 + 2] centímetros cúbicos = 15 centímetros cúbicos

79. a) 3 ⋅ 24 = 72. Há setenta e duas horas em 3 dias.

b) 15 ⋅ 60 = 900. Há 900 minutos em 15 horas.

c) 24 ⋅ 60 = .1440. Há .1440 minutos em 1 dia.

d) 60 ⋅ 60 = .3600. Há .3600 segundos em uma hora.

80. a) 5 ⋅ .1000 = .5000. 5 quilogramas equivalem a .5000 gramas.

b) 10 ⋅ .1000 = .10000. 10 toneladas equivalem a .10000 quilogramas.

c) 10 ⋅ .1000 = .10000. 10 gramas equivalem a .10000 miligramas.

d) 1 ⋅ .1000 ⋅ .1000 = ..1000000. uma tonelada equivale a ..1000000 gramas.

81. a) 2 ⋅ .1000 = .2000. 2 litros equivalem a .2000 mililitros.

b) 10 ⋅ .1000 = .10000. 10 litros equivalem a .10000 mililitros.

c) .5000 : .1000 = 5. .5000 mililitros equivalem a 5 litros.

d) .1500 : .1000 ⋅ 1,5 = ..1000000. .1500 mililitros equivalem a 1,5 litro.

82. 27 ‒ 15 = 12. Logo, a diferença foi de 12 graus Célsius.

Para o capítulo 12: Probabilidade e estatística

Página 24

83. Uma possível representação:

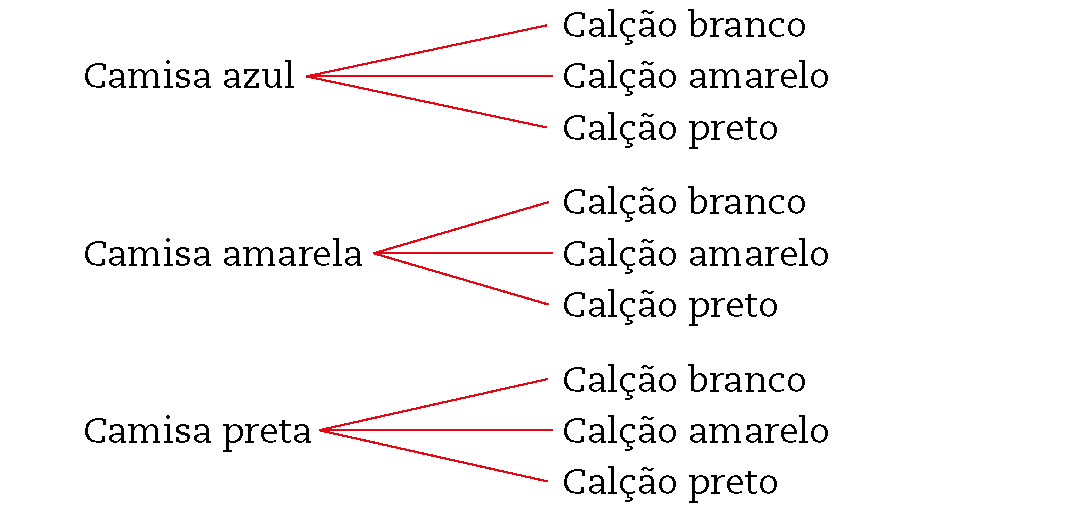
Esquema. À esquerda, camisa azul, à direita calção branco. Abaixo, calção amarelo. Abaixo, calção preto. Fio vermelho relacionando camisa azul a calção branco, fio vermelho relacionando camisa azul a calção amarelo, fio vermelho relacionando camisa azul a calção preto. Esquema. À esquerda, camisa amarela, à direita calção branco. Abaixo, calção amarelo. Abaixo, calção preto. Fio vermelho relacionando camisa amarela a calção branco, fio vermelho relacionando camisa amarela a calção amarelo, fio vermelho relacionando camisa amarela a calção preto. Esquema. À esquerda, camisa preta, à direita calção branco. Abaixo, calção amarelo. Abaixo, calção preto. Fio vermelho relacionando camisa preta a calção branco, fio vermelho relacionando camisa preta a calção amarelo, fio vermelho relacionando camisa preta a calção preto.

84. a) 16 combinações, pois 4 ⋅ 4 = 16.

b) 8 combinações, pois 4 ⋅ 2 = 8.

c) trínta e duas combinações, pois 4 ⋅ 4 ⋅ 2 = 32.

Capítulo 1 – Números naturais e sistemas de numeração

Trocando ideias – página 26

8 indica contagem (número de anilhas);

1º indica ordem (colocação da brasileira Lara Lima no Mundial de Halterofilismo);

87 indica uma medida (medida da massa das 8 anilhas juntas);

7 indica um código (número que identifica a atleta representada na imagem).

Atividades – página 29

1. a) Refere-se à medida do tempo de duração da partida, portanto indica medida.

b) Refere-se à colocação de Emma Raducanu no US Open de 2021, portanto indica ordem.

c) Refere-se ao número de vitórias de Emma Raducanu no US Open, portanto indica contagem.

2. Resposta pessoal. De modo geral, situações que envolvem dinheiro e medidas são as mais comuns.

3. As respostas do item a são variáveis; no entanto, serão próximas entre os estudantes da turma. As respostas para os itens b e c devem ser a mesma para toda a turma.

Página cinquenta e oito

4. a) Os símbolos usados pelos romanos eram I, V, X, L, C, D e M.

b) Os símbolos que podem ser repetidos seguidamente, até três vezes, são: I, X, C e M.

c) Não; XL vale 40 (50 – 10 = 40) e LX vale 60 (50 + 10 = 60).

d) Se colocarmos um traço horizontal sobre o número vê í í, seu valor é multiplicado por .1000. Como VII corresponde a 7, se colocarmos o traço passará a valer .7000.

5. .1532 = .1000 + 500 + (10 + 10 + 10) + (1 + 1) → ême dê xis xis xis í í

.1699 = .1000 + 500 + 100 + (100 – 1) + (10 – 1) →

→ ême dê cê xis cê í xis

.1765 = .1000 + 500 + (100 + 100) + 50 + 10 + 5 →

→ ême dê cê cê éle xis vê

6. Resposta pessoal. É interessante registrar o número no sistema indo-arábico para que sejam feitas a comparação e validação da representação do mesmo número no sistema de numeração romano.

7. Representações:

130 →

Símbolo. Uma linha curva, similar ao número 9 e 3 ferraduras com aberturas para baixo.

e cê xis xis xis

310 →

Símbolo. 3 linhas curvas, similares ao número 9 e uma ferradura com aberturas para baixo.

e cê cê cê xis

Exemplo de resposta: Nos dois sistemas não há um símbolo para representar o número zero; no sistema de numeração egípcio, ao contrário do sistema de numeração romano, a ordem em que os símbolos estão organizados não altera o valor representado.

Atividades – página 32

8. a) 3 ⋅ 10 + 6 ⋅ 1 = 30 + 6 = 36

b) 2 ⋅ 100 + 8 ⋅ 10 + 4 ⋅ 1 = 200 + 80 + 4 = 284

c) 3 ⋅ .1000 + 5 ⋅ 100 + 1 ⋅ 10 + 8 ⋅ 1 = .3000 + 500 + 10 + 8 = .3518

d) 7 ⋅ .1000 + 9 ⋅ 1 = .7000 + 9 = .7009

9. a) 7 ⋅ 100 + 5 ⋅ 10 + 3 = 700 + 50 + 3 = 753

b) 8 ⋅ .1000 + 5 ⋅ 100 + 6 ⋅ 10 = .8000 + 500 + 60 = .8560

c) 1 ⋅ 10 ⋅ .1000 + 7 ⋅ 10 = .10000 + 70 = .10070

d) 2 ⋅ ..1000000 + 6 ⋅ 100 ⋅ .1000 + 9 ⋅ 10 + 8 = ..2000000 + .600000 + 90 + 8 = ..2600098

10. Começam com 2: 268 e 286

Começam com 6: 628 e 682

Começam com 8: 862 e 826

Logo, os números são: 268, 286, 628, 682, 862 e 826.

11. a) 22 pode ser escrito como 2 ⋅ 10 + 2, logo corresponde a duas décadas e dois anos.

b) 50 pode ser escrito como 5 ⋅ 10, logo corresponde a cinco décadas.

c) 69 pode ser escrito como 6 ⋅ 10 + 9, logo corresponde a seis décadas e nove anos.

12. a) Quatro ordens (unidade, dezena, centena e unidade de milhar).

b) O algarismo da quarta ordem é o 9.

c) O algarismo que representa a ordem das centenas é o 6.

d) O algarismo que representa a maior ordem é o 9.

e) O número .9678 tem duas classes (das unidades simples e dos milhares).

13. a) 500 + 70 + 8 = 578

b) .7000 + 800 + 90 + 5 = .7895

c) .20000 + .5000 + 400 + 30 + 8 = .25438

d) .500000 + .8000 + 500 + 3 = .508503

14. a) .3538

b) Um deles vale .3000 e o outro vale 30.

c) Aparecerá no visor o número .35382, então o primeiro valerá .30000 e o outro valerá 300.

15. Considerando cada setor do alvo, podemos contar quantos dardos temos:

1 ponto → 6 dardos

10 pontos → 6 dardos

100 pontos → 3 dardos

Logo, o total de pontos obtidos foi:

6 ⋅ 1 + 6 ⋅ 10 + 3 ⋅ 100 = 6 + 60 + 300 = 366

Pedro obteve 366 pontos.

16. Considerando que cada traço corresponde a um grupo de 10 limões, o total de limões registrados foi:

5 ⋅ 10 + 5 ⋅ 10 + 5 ⋅ 10 + 2 ⋅ 10 = 50 + 50 + 50 + 20 = 170

Como sobraram 6 limões sobre a mesa, o total de limões levados para a feira foi 176 (170 + 6 = 176).

Atividades – página 34

17. a) trezentos e quarenta e cinco

b) mil, seiscentos e setenta e nove

c) oito mil, novecentos e cinquenta

d) oitocentos e quinze mil e duzentos

e) dezoito milhões, quinhentos e quarenta mil e trinta e cinco

f) noventa e cinco milhões, treze mil e seiscentos

18. a) .12000 + 106 = .12106

b) .900000 + .12000 + 300 = .912300

c) ..1000000 + .10000 + 13 = ..1010013

d) ..90000000 + .16000 + 8 = ..90016008

e) ...2000000000 + ..12000000 + .100000 = ...2012100000

19. 7.654.321 se lê como: sete milhões, seiscentos e cinquenta e quatro mil, trezentos e vinte e um.

20. R$ 86,00oitenta e seis reais se lê: oitenta e seis reais; R$ 127,00cento e vinte e sete reais se lê: cento e vinte e sete reais; R$ 415,00quatrocentos e quinze reais se lê: quatrocentos e quinze reais; R$ 169,00cento e sessenta e nove reais se lê: cento e sessenta e nove reais.

21. 145.000.000 se lê: cento e quarenta e cinco milhões;

67.000.000 se lê: sessenta e sete milhões.

22. a) 4.000.000 corresponde a 4 milhões, portanto 4 mi.

b) 8.700.000.000.000 corresponde a 8 trilhões e 700 bilhões, portanto 8,7 tri.

Veja que interessante – página 36

a) Aparece a frase “Matemática é 10!”.

b) O número que aparece é o 10, que é um número par.

Página cinquenta e nove

Atividades – página 37

23. a) O menor número natural é o zero.

b) O sucessor de 0 é 1 (0 + 1 = 1).

c) Sim, todo número natural tem sucessor, basta somar 1.

24. a) sucessor: 601, antecessor: 599

b) sucessor: .1002, antecessor: .1000

c) sucessor: .8021, antecessor: .8019

d) sucessor: .50001, antecessor: .49999

25. Em cada caso, como já sabemos o maior número, basta procurar os antecessores:

a) 14, 15 e 16.

b) 98, 99 e 100.

c) 697, 698 e 699.

d) .1119, .1120 e .1121.

26. Se o menor número é 999, para encontrar o próximo número ímpar, devemos somar 2; obtido o número, somamos 2 novamente:

999 + 2 = .1001 e .1001 + 2 = .1003

Portanto, os três números são 999, .1001 e .1003.

27. a) O maior número natural par de três algarismos é o 998. O antecessor de 998 é o 997.

b) O menor número natural ímpar de cinco algarismos é o .10001. O sucessor de .10001 é o .10002.

c) O sucessor ímpar de 79 é o 81 (79 + 2 = 81). O precedente par de 100 é o 98 (100 – 2 = 98).

28. Na sequência dada, podemos observar que os números vão aumentando e podemos escrever quantas unidades são acrescidas a cada elemento, conforme registrado a seguir:

Esquema. Na primeira linhas os números 1, 2, 4, 7, 11, 16, 22, reticências.
Abaixo, seta de 1 a 2 com cota mais 1, seta de 2 a 4 com cota mais 2, seta de 4 a 7 com cota mais 3, seta de 7 a 11 com cota mais 4, seta de 11 a 16 com cota mais 6, seta de 16 a 22 com cota mais 6.

Seguindo essa lógica, para encontrar o número que vem após o 22, devemos acrescentar 7, ou seja, 22 + 7 = 29. Portanto, o próximo número será 29.

Lendo e aprendendo – página 39

1. a) O texto foi publicado em novembro de 2021.

b) O tema principal é o acôrdo envolvendo mais de 100 nações para zerar o desmatamento.

c) cópi vinte e seis é a 26ª Conferência das Nações Unidas sobre as Mudanças Climáticas.

d) Porque grande parte do Brasil é coberta pela Amazônia, que é a maior floresta tropical do mundo.

e) Os dois gases são: dióxido de carbono (CO₂) e metano.

2. 9,2 mil: .9200

19 bilhões: ...19000000000

105 bilhões: ...105000000000

12 bilhões: ...12000000000

7 bilhões: ...7000000000

3. A tabela completa ficará assim:

FINANCIAMENTO DOS GASTOS PREVISTOS COM OS PROJETOS PARA PROTEÇÃO DAS FLORESTAS (COP26)
Doadores	Doações (em dólares)
Países mais ricos	12.000.000.000
ONGs	7.000.000.000

4. Resposta pessoal. Espera-se que os estudantes apontem ações como consumo consciente, usar menos plástico, reciclar sempre que possível, reduzir consumo de água e de energia, utilizar transporte público, entre tantas outras.

Atividades – página 41

29. Começa com 4: 458 e 485

Começa com 5: 548 e 584

Começa com 8: 845 e 854

Em ordem crescente, os números são: 458, 485, 548, 584, 845 e 854

Assim, o maior deles é 854 e o menor é 458.

30. a) Menores que 8: (0, 1, 2, 3, 4, 5, 6, 7).

b) Maiores ou igual a 10, significa que o 10 faz parte da sequência: (10, 11, 12, 13, reticências).

c) Entre 12 e 17 significa que nem o 12 nem o 17 fazem parte dessa sequência: (13, 14, 15, 16).

d) Nesse caso, o 12 e o 17 fazem parte da sequência. A sequência será: (12, 13, 14, 15, 16, 17).

e) Maiores que 15 e menores que 22, eles não estarão na sequência: (16, 17, 18, 19, 20, 21).

31. Se Carla é mais alta que Marina, e Paula é mais baixa que Marina, podemos concluir que nem Carla nem Marina são as mais baixas das jogadoras.

Logo, Paula é a mais baixa.

Atividades – página 42

32. Traçamos uma reta, marcamos o ponto 0 e marcamos pontos consecutivos à direita de zero, sempre à mesma distância entre eles. Em seguida, identificamos a localização na reta numérica dos números dados:

Ilustração. Reta numérica com número 0 representado na extremidade esquerda e o número 7 representado na extremidade direita. O trecho entre 0 e 7 está dividido em 7 partes iguais indicadas por pontos. Da esquerda para a direita abaixo do primeiro ponto está o número 0, abaixo do quarto ponto está o número 3, abaixo do sexto ponto está o número 5 e abaixo do oitavo ponto está o número 7.

33. Como os números 0 e 6 estão representados na reta numérica, é possível afirmar que são números consecutivos, conforme a ilustração a seguir:

Ilustração. Reta numérica com o número 0 representado na extremidade esquerda e o número 6 representado na extremidade direita. O trecho entre 0 e 6 está dividido em 6 partes iguais representadas por meio de pontos. Abaixo de cada ponto, da esquerda para a direita estão os números 0, 1, 2, 3, 4, 5 e 6. Acima do ponto 0 está a letra O, acima do ponto 2 está a letra R, acima do ponto 4 está a letra S e acima do ponto 5 está a letra T.

Portanto:

a) R = 2

b) S = 4

c) T = 5

34. Analisando a reta numérica e os pontos dados, é possível perceber que os pontos estão distantes uma unidade:

Ilustração. Reta numérica, com o número 0 representado na extremidade esquerda e o número 15 representado na extremidade direita. O trecho de 0 a 15 está dividido em 15 partes iguais representadas por meio de pontos. Abaixo de cada ponto da esquerda para a direita estão os números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Acima do ponto 0 está a letra O, acima do ponto 4 está a letra A, acima do ponto 7 está a letra B, acima do ponto 9 está a letra C, acima do ponto 12 está a letra D, acima do ponto 15 está a letra E.

Página sessenta

Portanto:

a) O número 9 corresponde ao ponto C.

b) O número 12 corresponde ao ponto D.

c) O número 4 corresponde ao ponto a.

d) O número 15 corresponde ao ponto ê.

35. Observando a reta numérica, é possível analisar cada sentença.

Ilustração. Reta numérica com a letra a minúscula representada na extremidade esquerda e a letra c minúscula representada na extremidade direita. O trecho entre a e c está dividido em 4 partes iguais por meio de pontos. Da esquerda para a direita, abaixo do primeiro ponto está a letra a minúscula e acima está a letra A maiúscula, abaixo do terceiro ponto esta o número 6, abaixo do quarto ponto está a letra b minúscula e acima está a letra B maiúscula, abaixo do quinto ponto está a letra c minúscula e acima está a letra C maiúscula.

a) Como a está representado à esquerda de 6, a é menor que 6. Falsa.

b) Como b está representado à direita de 6, b é maior que 6. Verdadeira.

c) Como 6 está representado à esquerda de c, 6 é menor que c. Verdadeira.

d) Como c está representado à direita de b, c é maior que b. Verdadeira.

e) Como c está representado à direita de a, c é maior que a. Falsa.

f) Como b está representado à direita de a, b é maior que a. Verdadeira.

Portanto, são verdadeiras as sentenças b, c, d, f.

36. Primeiro, devemos encontrar a escala utilizada entre dois pontos consecutivos e, então, determinamos os números correspondentes aos pontos indicados.

a) A distância entre a e B é igual a 3 (31 ‒ 28 = 3). Portanto, após o número 31, temos o número 34; e após o número 34 temos o número 37.

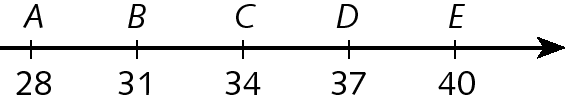
Ilustração. Reta numérica com o número 28 representado na extremidade esquerda e o número 40 representado na extremidade direita. o trecho entre 28 e 40 está dividido em 5 partes iguais por meio de traços. Abaixo de cada traço, da esquerda para a direita estão os números 28, 31, 34, 37, 40. Acima de cada traço da esquerda para a direita estão as letras A, B, C, D, E.

b) A distância entre G e H é igual a 6 (26 ‒ 20 = 6). Portanto, antes do número 20, temos o número 14 (20 ‒ 6 = 14); e após o número 26 temos o número 32 (26 + 6 = 32).

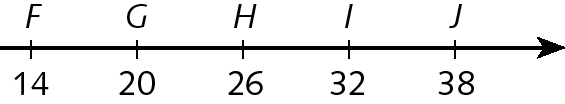
Ilustração. Reta numérica com o número 14 representado na extremidade esquerda e o número 38 representado na extremidade direita. O trecho entre 14 e 38 está dividido em 4 partes iguais representadas por meio de traços. Abaixo de cada traço, da esquerda para a direita estão os números 14, 20, 26, 32, 38. Acima de cada traço da esquerda para a direita estão as letras F, G, H, I, J.

37. Observando a reta apresentada, temos indicados os números 0 e 1, então podemos concluir que, entre dois pontos consecutivos a distância é uma unidade, ou seja, estão representados números naturais consecutivos a partir do zero.

Assim, já é possível escrever os demais números que representam os números na reta numérica:

Agora, vamos analisar as informações apresentadas em relação a cada ponto:

- O número correspondente ao ponto P:

É par.

É menor do que 3.

Os números naturais menores de 3 são 2, 1 e 0, sendo que 0 e 2 são pares, e P deve ser maior que 0. Portanto, P corresponde ao 2.

- O número correspondente ao ponto R:

É par.

É maior que 4.

É menor que 7.

Os números maiores que 4 e menores que 7 são: 5 e 6. Entre eles, apenas o 6 é par, logo o número correspondente ao ponto R é o 6.

- O número correspondente ao ponto Q:

É maior que 4.

É menor que 6.

O único número que está de acôrdo com essas condições é o 5. Portanto, Q corresponde ao 5.

Logo, a reta ficará:

Ilustração. Reta numérica com o número 0 na extremidade esquerda e a letra R representada na extremidade direita. O trecho entre 0 e R está dividida em 6 partes iguais por meio de pontos. Abaixo do segundo ponto, da esquerda para a direita está o número 1. Acima do primeiro ponto, da esquerda para a direita está o número 0, acima do terceiro ponto está a letra P, acima do sexto ponto está a letra Q e acima do sétimo ponto está a letra R.

38. Em uma semana temos 5 dias que não são finais de semana (já que Paulo não trabalha nos finais de semana). Em 3 semanas, será um total de 15 dias (3 ⋅ 5 = 15). Como ele fez duas horas extras por dia, no total serão 30 horas extras (2 ⋅ 15 = 30).

39. Para saber o total de páginas, podemos fazer:

178 ‒ 35 = 143

Mas como a página de número 35 também foi impressa, teremos mais uma página, ou seja, o total de 144 páginas impressas.

Podemos nos certificar que somar mais uma página é o procedimento correto com números menores. Por exemplo, se imprimirmos da página 1 até a página 4, sabemos que haverá a impressão de 4 páginas (página 1, página 2, página 3 e página 4). Logo, se fizermos apenas 4 ‒ 1 = 3 desconsideraremos uma página; por isso, se usarmos a subtração para encontrar a resposta de um problema similar, deveremos sempre somar mais uma página.

40. Para resolver a atividade, podemos escrever todos os números em cada item ou utilizar a mesma ideia da atividade 39.

a) De 25 até 50, significa que inclui tanto o 25 quanto o 50 e podemos fazer 50 ‒ 25 = 25 e para incluir o número 25 fazemos 25 + 1 = 26. Logo, há 26 números naturais de 25 até 50.

b) Entre 30 e 48 significa que não podemos incluir os extremos (30 e 48). Fazemos 48 ‒ 30 = 18 e para excluir o 48 fazemos 18 ‒ 1 = 17. Logo, há 17 números naturais entre 30 e 48.

c) De 5 até 50 significa que inclui os extremos e podemos fazer 50 ‒ 5 = 45 e 45 + 1 = 46. Assim, há 46 números de 5 até 50.

Para saber quantos algarismos escrevemos, podemos calcular separadamente os números de 1 algarismo e os números de 2 algarismos:

- de 5 até 9 são 5 números de 1 algarismo cada um, o que dará um total de 5 algarismos (5 ⋅ 1 = 5).

- de 10 até 50 são 41 números de 2 algarismos cada um, o que dará um total de 82 algarismos (41 ⋅ 2 = 82).

O total de algarismos será 5 + 82 = 87.

De 5 até 50 escrevemos 46 números e 87 algarismos.

41. Resposta pessoal. A resposta estará adequada se a distância entre os pontos na reta numérica estiver correta de acôrdo com os números escolhidos; lembrando que se forem escolhidos dois números próximos e um terceiro muito distante (por exemplo, os números 1, 2 e 150), não será simples criar uma escala que comporte todos eles e será apenas um esboço.

Página sessenta e um

Revisão dos conteúdos deste capítulo – páginas 43 e 44

1. a) 10 + 10 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 29

b) 100 + 10 + 1 + 1 + 1 + 1 + 1 = 115

c) .1000 + 100 + 100 + 100 + 10 + 10 + 10 + 10 + 10 +

+ 1 + 1 + 1 + 1 = .1354

2. a) 39 = (10 + 10 + 10) + (10 ‒ 1) → XXXIX

b) 64 = (50 + 10) + (5 ‒ 1) → LXIV

c) 721 = (500 + 100 + 100) + (10 + 10) + 1 → DCCXXI

d) 985 = (.1000 ‒ 100) + 50 + (10 + 10 + 10) + 5 → CMLXXXV

e) .1354 = .1000 + (100 + 100 + 100) + 50 + (5 ‒ 1) → MCCCLIV

f) .1429 = .1000 + (500 ‒ 100) + (10 + 10) + (10 ‒ 1) → MCDXXIX

3. a) 1 ⋅ 100 + 3 ⋅ 10 + 8 = 138

b) 3 ⋅ .1000 + 2 ⋅ 100 + 8 ⋅ 10 + 3 = .3283

4. a) 2 ⋅ 100 + 5 ⋅ 10 + 3 = 253

b) 1 ⋅ .1000 + 2 ⋅ 100 + 3 ⋅ 10 + 4 = .1234

5. a) .5000 + 30 + 7 = .5037

b) .6000 + 400 + 90 + 1 = .6491

c) .90000 + 200 + 30 = .90230

d) .200000 + .4000 + 80 + 6 = .204086

6. a) 4 ordens: unidade, centena, dezena e unidade de milhar.

b) O algarismo da terceira ordem (ordem das centenas) é o 8.

c) O algarismo da ordem dos milhares é o 6.

d) O número .6842 tem duas classes: classe das unidades simples e classe dos milhares.

e) A menor ordem é a das unidades e está representada pelo algarismo 2.

7. a) 425 se lê: quatrocentos e vinte e cinco.

b) 1.379 se lê: mil trezentos e setenta e nove.

c) 220 402 se lê: duzentos e vinte mil quatrocentos e dois.

8. Para completar o quadro, usamos o fato de que para obter o sucessor de um número natural, basta acrescentar uma unidade e, para encontrarmos o antecessor de um número natural diferente de zero, subtraímos dele uma unidade.

Antecessor	Número natural	Sucessor
357	358	359
898	899	900
2.561	2.562	2.563
11.979	11.980	11.981
2.351.298	2.351.299	2.351.300
3.999.999	4.000.000	4.000.001
12.981.998	12.981.999	12.982.000

9. a) A partir do 10, basta acrescentar de 2 em 2, pois são números pares: (10, 12, 14, 16, 18, 20, 22, 24, 26, 28).

b) A partir do 13, basta acrescentar de 2 em 2, pois são números ímpares: (13, 15, 17, 19, 21, 23, 25, 27, 29, 31).

10. Analisando cada sentença:

a) Falsa, pois 54 > 45.

b) Falsa, pois 105 ≠ 501.

c) Verdadeira, pois, apesar de serem formados pelos mesmos algarismos, representam números diferentes.

d) Verdadeira, pois 214 > 211.

e) Verdadeira, pois .1002 = .1002.

f) Falsa, pois .22022 < .22220.

Logo, são verdadeiras as sentenças: c, d, e.

11. Considerando os algarismos 1, 3, 4, 6 e 2, sem repetição:

a) Para escrever o maior número possível, usamos o algarismo de maior valor na maior ordem, e assim sucessivamente; o maior número é .64321.

b) Para escrever o menor número possível, usamos o algarismo de maior valor na menor ordem, e assim sucessivamente; o menor número será o .12346.

c) Se o algarismo 1 ficar na ordem das centenas, os demais devem ficar de modo que o algarismo de maior valor fique na maior ordem, e assim sucessivamente; o número será .64132.

d) Como o número deve ser maior do que .43200 e o algarismo 6 tem que está na ordem das unidades, então os algarismos da 5ª, 4ª e 3ª ordens deverão ser 4, 3 e 2, respectivamente. Dessa maneira, o número será .43216.

12. Os primeiros oito números ímpares são: 1, 3, 5, 7, 9, 11, 13 e 15; portanto, a reta que os representa será:

Ilustração. Reta numérica com o número 1 representado na extremidade esquerda e o número 15 representado na extremidade direita. O trecho entre 1 e 15 está dividido em 7 partes iguais por meio de pontos. Abaixo de cada ponto, da esquerda para a direita estão os números 1, 3, 5, 7, 9, 11, 13, 15.

13. Para começar, devemos traçar uma reta e marcar pontos igualmente distantes, depois marcamos os pontos correspondentes aos valores indicados:

Ilustração. Reta numérica com o número 5 representado na extremidade esquerda e o número 15 representado na extremidade direita. O trecho entre 5 e 15 está dividido proporcionalmente em 4 partes por meio de pontos. Abaixo de cada ponto, da esquerda para a direita estão os números 5, 8, 9, 12, 15.

Capítulo 2 – Operações com números naturais

Trocando ideias – página 45

• O público dessa faixa etária era de aproximadamente 20 milhões sendo que 3.setecentas.000 crianças havia sido imunizadas até aquele dia. Para saber aproximadamente quantas crianças ainda precisam ser imunizadas, calculamos:

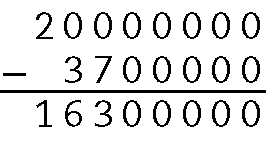
Algoritmo usual da subtração. 20 milhões menos 3 milhões e 700 mil. Na primeira linha 20 milhões. Abaixo, à esquerda, sinal de subtração, à direita, 3 milhões e 700 mil alinhado ordem a ordem com 20 milhões. Abaixo, traço horizontal. Abaixo, 16 milhões e 300 mil

Portanto, faltam 16.trezentas.000 crianças para serem vacinadas.

• Resposta pessoal. Espera-se que, ao conversar com os colegas, os estudantes indiquem aspectos como: diminuição do número de casos da doença, menos hospitalizações, menor gasto com medicações e equipamentos de saúde, diminuição do número de mortes, entre outros.

Página sessenta e dois

Algumas propriedades da adição – página 47

Propriedade comutativa

a) 12 + 28 = 40 e 28 + 12 = 40

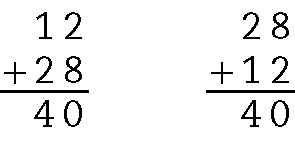
Algoritmo usual da adição. 12 mais 28. Na primeira linha o número 12. Abaixo, à esquerda, sinal da adição, à direita o número 28, alinhado ordem a ordem com o número 12. Abaixo, traço horizontal. Abaixo, 40. Algoritmo usual da adição. 28 mais 12. Na primeira linha o número 28. Abaixo, à esquerda, sinal da adição, à direita o número 12, alinhado ordem a ordem com o número 28. Abaixo, traço horizontal. Abaixo, 40.

b) Espera-se que os estudantes percebam que o resultado foi o mesmo, apesar da troca de ordem das parcelas.

Propriedade associativa

Exemplo de resposta:

Se escolhermos os números 10, 15 e 4

A soma dos dois primeiros com o terceiro:

(10 + 15) + 4 = 25 + 4 = 29

Adicionar o primeiro com a soma dos dois últimos: 10 + (15 + 4) = 10 + 19 = 29

Espera-se que os estudantes percebam que, embora tenham associado as parcelas de maneiras diferentes, o resultado permaneceu o mesmo.

Elemento neutro

a) 58 + 0 = 58 0 + 45 = 45

b) Espera-se que os estudantes percebam que, ao adicionar o zero a qualquer número, a soma será o próprio número.

Atividades – páginas 48 e 49

1. a) Os dois maiores números são .8916 e .7435.

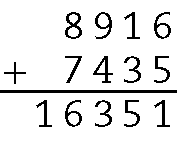
Algoritmo usual da adição. 8 mil 916 mais 7 mil 435. Na primeira linha, o número 8 mil 916. Abaixo, à esquerda sinal da adição, à direita o número 7 mil 435 alinhado ordem a ordem com 8 mil 916. Abaixo, traço horizontal. Abaixo, 16 mil 351.

Portanto, o total obtido é .16351.

b) Os dois menores números são 794 e .1576.

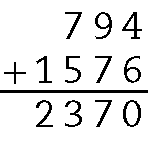
Algoritmo usual da adição. 794 mais 1 mil 576. Na primeira linha o número 794. Abaixo, à esquerda, sinal da adição, à direita, 1 mil 576 alinhado ordem a ordem com 794. Abaixo, traço horizontal. Abaixo, 2 mil 370.

Portanto, o total obtido é .2370.

c) O menor número é 794 e o maior é .8916.

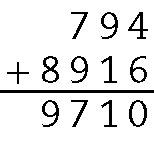
Algoritmo usual da adição. 794 mais 8 mil 916. Na primeira linha o número 794. Abaixo, à esquerda, sinal da adição, à direita, 8 mil 916 alinhado ordem a ordem com 794. Abaixo, traço horizontal. Abaixo, 9 mil 710.

Portanto, o total obtido é .9710.

2. a) Precisamos adicionar os pontos que Júlio fez em cada etapa .3650 + .5995 + .7036:

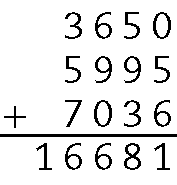
Algoritmo usual da adição. 3 mil 650 mais 5 mil 995 mais 7 mil e 36. Na primeira linha o número 3 mil 650. Abaixo, o número 5 mil 995, alinhado ordem a ordem com 3 mil 650. Abaixo, à esquerda, sinal da adição, à direita o número 7 mil e 36, alinhado ordem a ordem com 5 mil 995 e 3 mil 650. Abaixo, traço horizontal. Abaixo, 16 mil 681.

Júlio fez .16681 pontos.

b) Determinamos o total de pontos de Marcelo fazendo .3543 + .2786 + .9999:

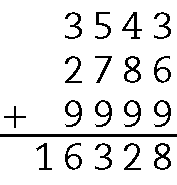
Algoritmo usual da adição. 3 mil 543 mais 2 mil 786 mais 9 mil 999. Na primeira linha o número 3 mil 543. Abaixo, o número 2 mil 786, alinhado ordem a ordem com 3 mil 543. Abaixo, à esquerda sinal de adição, à direita o número 9 mil 999, alinhado ordem a ordem com 3 mil 543 e 2 mil 786. Abaixo, traço horizontal. Abaixo, 16 mil 328.

E o total de pontos de Antônio fazendo .4119 + .3830 + .8678:

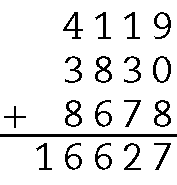
Algoritmo usual da adição. 4 mil 119 mais 3 mil 830 mais 8 mil 678. Na primeira linha o número 4 mil 119. Abaixo, o número 3 mil 830, alinhado ordem a ordem com 4 mil 119. Abaixo, à esquerda sinal de adição, à direita o número 8 mil 678, alinhado ordem a ordem com 4 mil 119 e 3 mil 830. Abaixo, traço horizontal. Abaixo, 16 mil 627.

Logo, podemos concluir que nenhum deles conquistou mais de 17 mil pontos na gincana.

c) Comparando o total de pontos de cada um, podemos concluir que Júlio foi quem fez mais pontos.

3. Para encontrar a medida aproximada da área da Região Sul do Brasil, calculamos:

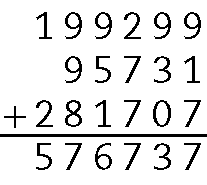
Algoritmo usual da adição. 199 mil 299 mais 95 mil 731 mais 281 mil 707. Na primeira linha o número 199 mil 299. Abaixo, o número 95 mil 731, alinhado ordem a ordem com 199 mil 299. Abaixo, à esquerda sinal de adição, à direita o número 281 mil 707, alinhado ordem a ordem com 199 mil 299 e 95 mil 731. Abaixo, traço horizontal. Abaixo, 576 mil 737.

A medida aproximada da área da Região Sul do Brasil é .576737 quilômetros quadrados.

4. a) Entre as cidades listadas na tabela, fazem parte da Região Sudeste: São Paulo, Rio de Janeiro e Belo Horizonte. Para determinar a população dessas cidades juntas, calculamos:

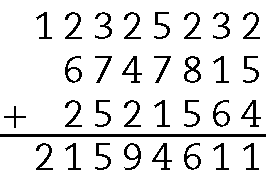
Algoritmo usual da adição. 12 milhões 325 mil 232 mais 6 milhões 747 mil 815 mais 2 milhões 521 mil 564. Na primeira linha o número 12 milhões 325 mil 232. Abaixo, o número 6 milhões 747 mil 815, alinhado ordem a ordem com 12 milhões 325 mil 232. Abaixo, à esquerda sinal de adição, à direita o número 2 milhões 521 mil 564, alinhado ordem a ordem com 12 milhões 325 mil 232 e 6 milhões 747 mil 815. Abaixo, traço horizontal. Abaixo, 215 milhões 946 mil 611.

Logo, a soma da população dessas cidades é ..21594611 habitantes.

b) Entre as cidades listadas, fazem parte da Região Nordeste: Salvador e Fortaleza. Para determinar a população dessas cidades juntas, calculamos:

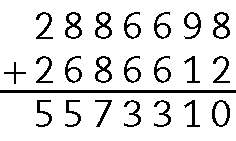
Algoritmo usual da adição. 2 milhões 866 mil 698 mais 2 milhões 686 mil 612. Na primeira linha o número 2 milhões 886 mil 698. Abaixo, à esquerda sinal de adição, à direita o número 2 milhões 686 mil 612, alinhado ordem a ordem com 2 milhões 886 mil 698. Abaixo, traço horizontal. Abaixo, 5 milhões 573 mil 310.

Logo, a soma da população dessas cidades é ..5573310 habitantes.

5. Se o pai de Laerte tinha 28 anos quando o filho nasceu e hoje Laerte tem 18 anos, a idade atual do pai de Laerte é 46 anos (28 + 18 = 46). Assim a soma das idades de Laerte e de seu pai hoje é 64 anos (46 + 18 = 64).

6. Primeiro, listamos todos os números que podem ser formados com os algarismos 3, 4 e 5 sem repeti-los:

Números começando com 3: 345 e 354.

Números começando com 4: 435 e 453.

Números começando com 5: 534 e 543.

Então, determinamos a soma desses 6 números:

Algoritmo usual da adição. 345 mais 354 mais 435 mais 453 mais 534 mais 543. Na primeira linha, o número 345. Abaixo, o número 354 alinhado ordem a ordem com 345. Abaixo, o número 435, alinhado ordem a ordem com 345 e 354. Abaixo, o número 453, alinhado ordem a ordem com 345, 345 e 435. Abaixo, o número 534 alinhado ordem a ordem com 345, 354, 435 e 453. Abaixo, à esquerda sinal da adição, à direita o número 543 alinhado ordem a ordem com 345, 354, 435, 453 e 534. Abaixo, traço horizontal. Abaixo, 2 mil 664.

A soma de todos esses números é igual a .2664.

7. Exemplo de resposta: Se o menor número é 549, os demais são 550 e 551.

É possível usar os seguintes fatos: 549 = 548 + 1 e 550 = 551 ‒ 1. Portanto, um modo de calcular 549 + 550 + 551, usando calculadora com as teclas 0 e 9 com defeito, é: 548 + 1 + 551 ‒ 1 + 551.

Portanto, faltam 16.trezentas.000 crianças para serem vacinadas.

O resultado é .1650.

Há outras maneiras de fazer esse cálculo usando a calculadora mesmo sem usar as teclas 0 e 9. Por exemplo, considerar que 549 = 554 ‒ 5 e 550 = 548 + 2. O resultado sempre será o mesmo, ou seja, .1650.

Página sessenta e três

8. É impossível determinar estes números, uma vez que, ao adicionar quatro números ímpares, o resultado será um número par. Os estudantes podem usar o método de tentativa e êrro para verificar essa resposta.

9. a) 16 + 35 + 14 + 15 = 51 + 14 + 15 = 65 + 15 = 80

b) (16 + 14) + (35 + 15) = 30 + 50 = 80

Espera-se que os estudantes percebam que a expressão do item b torna a resolução mais simples.

10. Vejamos uma das possibilidades de uso das propriedades para cada caso:

a) 26 + 30 + 4 + 20 = 26 + 4 + 30 + 20 = = (26 + 4) + (30 + 20) = 30 + 50 = 80

b) 33 + 12 + 7 + 0 + 8 = 33 + 7 + 12 + 8 = = (33 + 7) + (12 + 8) = 40 + 20 = 60

11. O resultado é 900, pois são as mesmas parcelas em ordem diferente. Utilizando a propriedade comutativa, veremos que os resultados de 577 + 323 e 323 + 577 são iguais.

12. Resposta pessoal. Espera-se que os estudantes apresentem justificativas como: acrescentar zero não altera o resultado; zero é o elemento nulo; o zero é neutro porque não altera o resultado.

13. a) Sim, pois 702 é próximo de 700 e 299 é próximo de 300; assim como 700 + 300 = .1000, temos que 702 + 299 será próximo de .1000.

b) Um modo de resolver mentalmente:

702 + 299 = (700 + 2) + (300 ‒ 1) = = (700 + 300) + (2 ‒ 1) = .1000 + 1 = .1001

14. Exemplo de resolução:

11 + 18 + 16 + 24 + 7 + 19 =

(11 + 19) + (16 + 24) + 7 + 18 =

(30 + 40) + (7 + 18) =

70 + 25 = 95

Assim, o valor total da compra é R$ 95,00noventa e cinco reais.

Atividades – páginas 50 e 51

15. a) 189 ‒ 86 = 103

b) 856 ‒ 799 = 57

c) 654 ‒ 830 não é possível calcular no conjunto dos números naturais, pois 654 é menor que 830.

d) .1050 ‒ 867 = 183

e) .2160 ‒ .3000 não é possível calcular no conjunto dos números naturais, pois .2160 é menor que .3000.

f) .5555 ‒ .5555 = 0

• Só é possível efetuar uma subtração entre dois números naturais quando o minuendo for maior ou igual ao subtraendo.

16. a) Vejamos alguns exemplos:

55 ‒ 55 = 0 129 ‒ 129 = 0 36 ‒ 36 = 0

A diferença entre dois números iguais será sempre igual a zero.

b) Vejamos alguns exemplos:

48 ‒ 46 = 2 322 ‒ 320 = 2 .1000 ‒ 998 = 2

A diferença entre dois números pares e consecutivos será sempre igual a 2.

c) A propriedade comutativa não é válida para a subtração. Os estudantes poderão dar exemplos, como 190 ‒ 50 = 140, sendo que não é possível calcular 50 ‒ 190 no conjunto dos números naturais.

17. Para saber a idade de Pedro, efetuamos .2025 ‒ .1993:

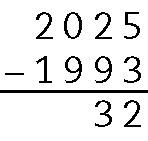
Algoritmo usual da subtração. 2 mil 025 menos 1 mil 993. Na primeira linha, o número 2 mil 025. Abaixo, à esquerda sinal de subtração, à direita, o número 1 mil 993, alinhado ordem a ordem com 2 mil 025. Abaixo, traço horizontal. Abaixo, 32.

Em agosto de 2025 Pedro já terá feito aniversário, então ele terá 32 anos.

18. Resposta pessoal. Todos os estudantes devem subtrair o ano em que nasceu de .2030. Por exemplo, quem nasceu em 2012, deve fazer .2030 ‒ 2012.

19. Se sabemos que Luís entregou R$ 700,00setecentos reais e recebeu R$ 25,00vinte e cinco reais de troco, então calculamos 700 ‒ 25 para encontrar o valor do telefone celular.

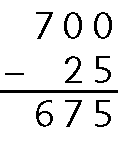
Algoritmo usual da subtração. 700 menos 25. Na primeira linha, o número 700. Abaixo, à esquerda sinal de subtração, à direita, o número 25 alinhado ordem a ordem com 700. Abaixo, traço horizontal. Abaixo, 675.

O preço do telefone celular foi R$ 675,00seiscentos e setenta e cinco reais.

20. Resposta pessoal. Mas alguns fatores importantes devem ser considerados

• o preço da mesa deve estar dentro da realidade do contexto vivido pelos estudantes. Por exemplo, valores abaixo de R$ 100,00cem reais podem estar fóra da realidade, assim como valores acima de R$ 10.000,00dez mil reais.

• o valor total entregue para pagar a mesa deve ser, necessariamente, maior ou igual ao valor da mesa.

• não é razoável usar neste tipo de situação cédulas de R$ 2,00dois reais, por exemplo. Pois não é prático e nem usual estar com duzentas e cinquenta cédulas de R$ 2,00dois reais.

Exemplo de resposta:

Adalto comprou uma mesa por R$ 850,00oitocentos e cinquenta reais e pagou com 9 cédulas de R$ 100,00cem reais. Adalto recebeu de troco R$ 50,00cinquenta reais.

21. a)

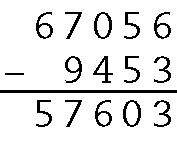
Algoritmo usual da subtração. 67 mil 056 menos 9 mil 453. Na primeira linha, o número 67 mil 056. Abaixo, à esquerda, sinal da subtração, à direita, o número 9 mil 453 alinhado ordem a ordem com 67 mil 056. Abaixo, traço horizontal. Abaixo, 57 mil 603.

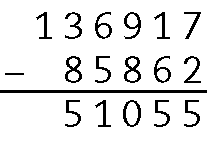
Algoritmo usual da subtração. 136 mil 917 menos 85 mil 862. Na primeira linha, o número 136 mil 917. Abaixo, à esquerda sinal da subtração, à direita 85 mil 862 alinhado ordem a ordem com 136 mil 917. Abaixo, traço horizontal. Abaixo, 51 mil 055.

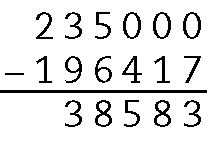
Algoritmo usual da subtração. 235 mil menos 196 mil 417. Na primeira linha, o número 235 mil. Abaixo, à esquerda sinal da subtração, à direita o número 196 mil 417 alinhado ordem a ordem com 235 mil. Abaixo, traço horizontal. Abaixo, 38 mil 583.

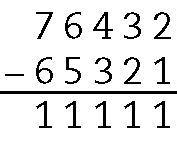
Algoritmo usual da subtração. 76 mil 432 menos 65 mil 321. Na primeira linha o número 76 mil 432. Abaixo, à esquerda sinal da subtração, à direita o número 65 mil 321 alinhado ordem a ordem com 76 mil 432. Abaixo, traço horizontal. Abaixo, 11 mil 111.

22. Exemplos de resposta:

a) 189 ‒ 29 = ( 100 + 80 + 9 ) ‒ ( 20 + 9 ) =

= 100 + ( 80 ‒ 20 ) + ( 9 ‒ 9 ) = 100 + 60 + 0 = 160

b) 768 ‒ 59 = ( 700 + 68 ) ‒ 59 =

= 700 + ( 68 ‒ 59 ) = 700 + 9 = 709

c) 974 ‒ 101 = ( 900 + 74 ) ‒ ( 100 + 1 ) =

= ( 900 ‒ 100 ) + ( 74 ‒ 1 ) = 800 + 73 = 873

d) .2358 ‒ 202 = (.2000 + 300 + 58) ‒ (200 + 2) =

= .2000 + (300 ‒ 200) + (58 ‒ 2) = .2000 + 100 + 56 =

= .2156

23. Na ordem das unidades é preciso efetuar 6 ‒ 1 = B, então B = 5.

Na ordem das dezenas é preciso efetuar 17 ‒ a = 9, então a = 8.

Página sessenta e quatro

Por fim, o valor de C pode ser obtido com a substituição dos valores encontrados (de B e de a) no algoritmo. Assim, temos C = 2.

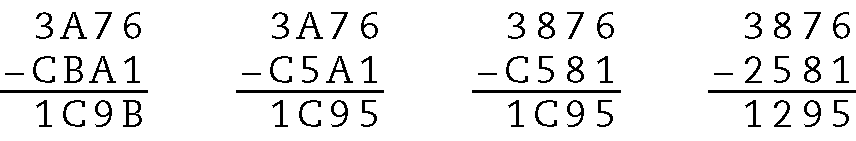
Algoritmo usual da subtração, 3 A 76 menos CBA1. Na primeira linha, 3, no lugar do algarismo das centenas, 76. Abaixo, à esquerda sinal de subtração, à direita, C, como algarismo da ordem da milhar, B como algarismo da ordem das centenas, A como algarismo da ordem das dezenas, 1 como algarismo da ordem das unidades, alinhado ordem a ordem com 3A76. Abaixo, traço horizontal. Abaixo, 1, C como algarismo da ordem das centenas, 9, B como algarismo na ordem das unidades. Algoritmo usual da subtração. 3A76 menos C5A1. Na primeira linha, 3, A como algarismo da ordem das centenas, 76. Abaixo,à esquerda sinal de subtração, à direita, C como algarismo da ordem da milhar, 5, A como algarismo da ordem das dezenas, 1, alinhado ordem a ordem com 3A76. Abaixo, traço horizontal. Abaixo, 1, C como algarismo das centenas, 95. Algoritmo usual da subtração. 3 mil 876 menos C581. Na primeira linha, o número 3 mil 876. Abaixo, à esquerda sinal da subtração, à direita C como algarismo da ordem da milhar, 581, alinhado ordem a ordem com 3 mil 876. Abaixo, traço horizontal. Abaixo, 1C95. Algoritmo usual da subtração. 3 mil 876 menos 2 mil 581. Na primeira linha, o número 3 mil 876. Abaixo, à esquerda sinal da subtração, à direita o número 2 mil 581, alinhado ordem a ordem com 3 mil 876. Abaixo, traço horizontal. Abaixo, 1 mil 295.

Atividades – página 52

24. Pontuação de Alex = 549.

Pontuação de Hélio = 549 ‒ 391 = 158

Hélio Castroneves conquistou 158 pontos na Fórmula Indy em 2021.

25. a) Utilizando a relação fundamental, teremos que o minuendo é .4887.

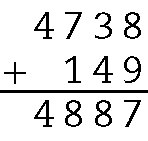
Algoritmo usual da adição. 4 mil 738 mais 149. Na primeira linha o número 4 mil 738. Abaixo, à esquerda sinal da adição, à direita o número 149, alinhado ordem a ordem com 7 mil 738. Abaixo, traço horizontal. Abaixo, 4 mil 887.

b) Utilizando a relação fundamental, teremos que o subtraendo é 45.

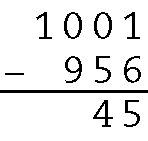
Algoritmo usual da subtração. 1 mil 001 menos 956. Na primeira linha o número 1 mil 001. Abaixo, à esquerda sinal da subtração, à direita 956, alinhado ordem a ordem com 1 mil 001. Abaixo, traço horizontal. Abaixo, 45.

26. Pelo algoritmo da subtração, temos:

Algoritmo da subtração. minuendo menos subtraendo. Na primeira linha, minuendo. Abaixo, à esquerda, sinal da subtração, à direita, subtraendo. Abaixo, traço horizontal. Abaixo, diferença.

• aumentando o minuendo em 20 unidades, a diferença aumentará em 20 unidades;

• diminuindo o subtraendo em 15 unidades, a diferença aumentará em 15 unidades.

Ao realizar as duas ações, a diferença aumentará em 20 + 15.

Logo, a diferença aumentará em 35 unidades.

27. a) Para calcular o valor de

Pela relação fundamental da subtração, verificamos que 7 + 5 = 12, então o resultado será

= 2.

Para encontrar o valor de

, podemos calcular:

.5329 ‒ .3455 = .1874. Logo,

= 8

Algoritmo usual da subtração. 5 mil 3, triângulo cinza ocultado o algarismo da ordem das dezenas,9 menos 1 mil, quadrado cinza ocultando o algarismo da ordem das centenas, 74. Na primeira linha o número 53, triângulo cinza ocultado o algarismo da ordem das dezenas,9. Abaixo, à esquerda, sinal de subtração, à direita, o número 1, quadrado cinza ocultando o algarismo da ordem das centenas, 74, alinhado ordem a ordem com 53, triângulo cinza ocultado o algarismo da ordem das dezenas 9. Abaixo, traço horizontal. Abaixo, 3 mil 455. Algoritmo usual da subtração. 5 mil 329 menos 1 mil, quadrado cinza ocultando o algarismo da ordem das centenas 74. Na primeira linha, o número 5 mil 329. Abaixo, à esquerda, sinal de subtração, à direita 1 mil, quadrado cinza ocultando o algarismo da ordem das centenas 74, alinhado ordem a ordem com 5 mil 329. Abaixo, traço horizontal. Abaixo, 3 mil 455. Algoritmo usual da subtração. 5 mil 329 menos 3 mil 455. Na primeira linha, o número 5 mil 329. Abaixo, à esquerda, sinal da subtração, à direita, o número 3 mil 455 alinhado ordem a ordem com 5 mil 329. Abaixo, traço horizontal. Abaixo, 1 mil 874.

27. b) Para calcular o valor de

, devemos nos atentar aos valores das unidades simples, pois não é possível fazer 5 ‒ 8, mas podemos fazer 15 ‒ 8. Então,

= 2.

Utilizando a relação fundamental, temos .2707 + .6728 = .9435, e assim

= 4.

Algoritmo usual da subtração. 9 mil, triângulo cinza ocultando o algarismo da ordem das centenas menos 6 mil 7, quadrado cinza ocultando o algarismo da ordem das dezenas. Na primeira linha, o número 9 mil, triângulo cinza, 35. Abaixo, à esquerda, sinal da subtração, à direita, o número 6 mil 7, quadrado cinza, 8, alinhado ordem a ordem com 9 mil, triângulo cinza, 35. Abaixo, traço horizontal. Abaixo, 2 mil 707. Algoritmo usual da subtração. 9 mil, triângulo cinza ocultando o algarismo da ordem das centenas menos 6 mil 728. Na primeira linha, o número 9 mil, triângulo cinza, 35. Abaixo, à esquerda, sinal da subtração, à direita, o número 6 mil 728 alinhado ordem a ordem com 9 mil, triângulo cinza, 35. Abaixo, traço horizontal. Abaixo, 2 mil 707. Algoritmo usual da subtração. 9 mil 435 menos 6 mil 728. Na primeira linha, o número 9 mil 435. Abaixo, à esquerda sinal de subtração, à direita o número 6 mil 728 alinhado ordem a ordem com 9 mil 435. Abaixo, traço horizontal. Abaixo, 2 mil 707.

28. a) Para determinar o valor de

, fazemos a subtração: .1860 ‒ 357 = .1503; então, a sentença completa será .1860 ‒ .1503 = 357.

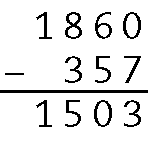
Algoritmo usual da subtração. 1 mil 870 menos 357. Na primeira linha o número 1 mil 870. Abaixo, à esquerda, sinal da subtração, à direita o número 357, alinhado ordem a ordem com 1 mil 870. Abaixo, traço horizontal. Abaixo, 1 mil 503.

b) Pela relação fundamental da subtração:

.3545 + .1283 = .4828, logo a sentença completa será .4828 ‒ .3545 = .1283.

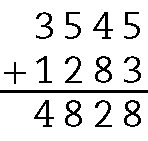
Algoritmo usual da adição. 3 mil 545 mais 1 mil 283. Na primeira linha o número 3 mil 545. Abaixo, à esquerda sinal da adição, à direita o número 1 mil 283 alinhado ordem a ordem com 3 mil 545. Abaixo, traço horizontal. Abaixo, 4 mil 828.

29. Para calcular o terceiro número, podemos fazer:

.8470 ‒ (.4319 + .1843) = .8470 ‒ .6162 = .2308.

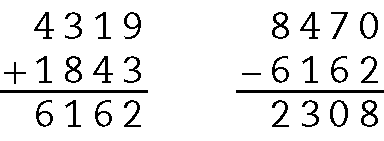
Algoritmo usual da adição. 4 mil 319 mais 1 mil 843. Na primeira linha o número 4 mil 319. Abaixo, à esquerda sinal de adição, à direita, 1 mil 843, alinhado ordem a ordem com 4 mil 319. Abaixo, traço horizontal. Abaixo, 6 mil 162. Algoritmo usual da subtração. 8 mil 470 menos 6 mil 162. Na primeira linha, o número 8 mil 470. Abaixo, à esquerda sinal da subtração, à direita o número 6 mil 162, alinhado ordem a ordem com 8 mil 470. Abaixo, traço horizontal. Abaixo, 2 mil 308.

Assim, o terceiro número é o .2308.

30. Resposta pessoal. Exemplo de problema que pode ser elaborado: Kátia quer comprar um jôgo de sofás no valor de R$ 3.099,00três mil noventa e nove reais. Ela já tem R$ 1.874,00mil oitocentos e setenta e quatro reais. Quanto Kátia deve juntar para ter todo o dinheiro? (Resposta: Kátia deve juntar R$ 1.225,00mil duzentos e vinte e cinco reais (.3099 ‒ .1874 = .1225)).

Atividades – página 53

31. a) (18 ‒ 15 + 3) + 2 = (3 + 3) + 2 = 6 + 2 = 8

b) 30 + (50 ‒ 12) ‒ 15 = 30 + 38 ‒ 15 = 68 ‒ 15 = 53

c) 13 ‒ 8 + 7 ‒ 4 ‒ 2 = 5 + 7 ‒ 4 ‒ 2 = 12 ‒ 4 ‒ 2 = 8 ‒ 2 = 6

d) (60 ‒ 12) ‒ (10 + 20) ‒ 14 = 48 ‒ 30 ‒ 14 = 18 ‒ 14 = 4

e) (100 ‒ 35 + 15) + (200 + 135 ‒ 98) = = (65 + 15) + (335 ‒ 98) = 80 + 237 = 317

f) 200 ‒ (40 + 50) ‒ 90 ‒ 10 = 200 ‒ 90 ‒ 90 ‒ 10 = = 110 ‒ 90 ‒ 10 = 20 ‒ 10 = 10

32. Com tentativas e erros, podemos encontrar:

a) 8 ‒ 3 + 4 ‒ (5 ‒ 1) = 5 + 4 ‒ 4 = 9 ‒ 4 = 5

b) 15 ‒ (8 + 7) + 8 = 15 ‒ 15 + 8 = 0 + 8 = 8

c) 35 + 15 ‒ (20 + 18) = 50 ‒ 38 = 12

d) 19 ‒ (8 + 5) ‒ (4 ‒ 3) = 19 ‒ 13 ‒ 1 = 6 ‒ 1 = 5

e) 200 ‒ (120 + 80) + 70 ‒ (20 + 50) =

= 200 ‒ 200 + 70 ‒ 70 = 0 + 70 ‒ 70 = 0

33. Podemos fazer a seguinte representação para a questão, usando

no lugar do número desconhecido:

(

+ 10) ‒ 13 = 12

Se pensarmos de trás para frente e considerarmos que

+ 10 =

, poderemos observar que:

‒ 13 = 12.Ou seja, utilizando a relação fundamental, teremos que

= 12 + 13 = 25.

Ou seja,

+ 10 = 25, o que nos levará a

= 25 ‒ 10 = 15.

Logo, o número que Sérgio pensou foi 15.

É possível conferir essa resposta: 15 + 10 ‒ 13 = 25 ‒ 13 = 12.

34. a) (180 + 45) ‒ (210 ‒ 107) = 225 ‒ 103 = 122

b) (315 ‒ 285) + 72 = 30 + 72 = 102

35. (10 + 20 + 5) ‒ 35

(40 ‒ 20 ‒ 5) + 15

Atividades – páginas 56 e 57

36. a) 8 + 8 + 8 + 8 = 4 ⋅ 8

b) 1 + 1 + 1 = 3 ⋅ 1

c) 9 + 9 + 9 + 9 + 9 + 9 = 6 ⋅ 9

Página sessenta e cinco

d) a + a + a + a = 4 ⋅ a

e) 0 + 0 + 0 + 0 + 0 = 5 ⋅ 0

37. a) Podemos fazer uma multiplicação: 36 ⋅ 12.

b) 36 ⋅ 12 = 432

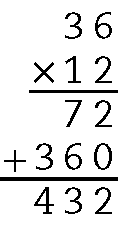
Algoritmo usual da multiplicação. 36 vezes 12. Na primeira linha, o número 36. Abaixo, à esquerda sinal da multiplicação, à direita o número 12, alinhado ordem a ordem com 36. Abaixo, traço horizontal. Abaixo, o número 72 alinhado ordem a ordem com 36 e 12. Abaixo, à esquerda, sinal da adição, à direita o número 360, alinhado ordem a ordem com 72. Abaixo, traço horizontal. Abaixo, 432.

O resultado dessa operação é 432.

38. a) 17 ⋅ 10 = 170

b) 85 ⋅ 100 = .8500

c) 19 ⋅ 0 = 0

d) 174 ⋅ .1000 = .174000

e) 9 ⋅ 8 ⋅ 0 = 0

f) 59 ⋅ .1000 = .59000

g) .1043 ⋅ 10 = .10430

h) 75 ⋅ .10000 = .750000

• Exemplo de resposta: Podemos observar que ao multiplicar um número natural por 0, o resultado será sempre igual a 0. Ou que ao multiplicar um número natural por 10, 100 ou .1000, o resultado é o número acrescentando 1, 2 ou 3 zeros, respectivamente.

39. a) 2 ⋅ 2 ⋅ 100 = 4 ⋅ 100 = 400

b) 3 ⋅ 500 = .1500

c) 4 ⋅ 12 = 48

d) 5 ⋅ 17 = 85

40. 546 + 546 + 546 + 546 + 546 + 546 + 546 + 546 + 546 = = 9 ⋅ 546 = .4914

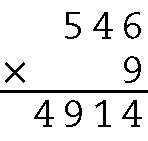
Algoritmo usual da multiplicação. 546 vezes 9. Na primeira linha, o número 546. Abaixo, à esquerda sinal da multiplicação, à direita o número 9, alinhado ordem a ordem com 546. Abaixo, traço horizontal. Abaixo, 4 mil 914.

41. Para saber devemos multiplicar 46 ⋅ 90 = .4140.

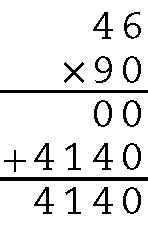
Algoritmo usual da multiplicação. 46 vezes 90. Na primeira linha o número 46. Abaixo, à esquerda sinal de multiplicação, à direita o número 90 alinhado ordem a ordem com o número 46. Abaixo, traço horizontal. Abaixo, 00. Abaixo, à esquerda sinal de adição, à direita o número 4 mil 140. Abaixo, traço horizontal. Abaixo, 4 mil 140.

São desperdiçados .4140 litros de água em 90 dias.

42. Fazemos 8 ⋅ 40 = 320.

O carro pode percorrer no máximo 320 quilômetros sem reabastecer.

43. a) Como são 4 fileiras de 9 vagas em cada uma, calculamos 4 ⋅ 9 = 36. São 36 vagas no total.

b) Considerando que há 36 vagas e 6 estão desocupadas (por contagem), calculamos 36 ‒ 6 = 30. Então, estão estacionados 30 carros.

44. a) 37 ⋅ 15 = 555

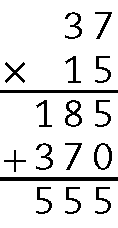
Algoritmo usual da multiplicação. 37 vezes 15. Na primeira linha, o número 37. Abaixo, à esquerda sinal de multiplicação, à direita o número 15, alinhado ordem a ordem com 37. Abaixo, traço horizontal. Abaixo, o número 185. Abaixo, à esquerda sinal de adição, à direita o número 370 alinhado ordem a ordem com 185. Abaixo, traço horizontal. Abaixo, 555.

b) 37 ⋅ 18 = 666

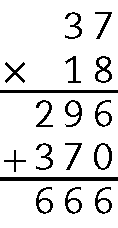
Algoritmo usual da multiplicação. 37 vezes 18. Na primeira linha, o número 37. Abaixo, à esquerda sinal de multiplicação, à direita o número 18, alinhado ordem a ordem com 37. Abaixo, traço horizontal. Abaixo, o número 296. Abaixo, à esquerda sinal de adição, à direita o número 370 alinhado ordem a ordem com 185. Abaixo, traço horizontal. Abaixo, 666.

c) 37 ⋅ 21 = 777

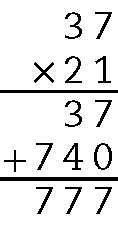
Algoritmo usual da multiplicação. 37 vezes 21. Na primeira linha, o número 37. Abaixo, à esquerda sinal de multiplicação, à direita o número 21, alinhado ordem a ordem com 37. Abaixo, traço horizontal. Abaixo, o número 37. Abaixo, à esquerda sinal de adição, à direita o número 740 alinhado ordem a ordem com 37. Abaixo, traço horizontal. Abaixo, 777.

d) 37 ⋅ 24 = 888

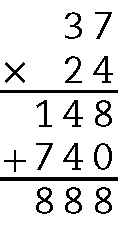
Algoritmo usual da multiplicação. 37 vezes 24. Na primeira linha, o número 37. Abaixo, à esquerda sinal de multiplicação, à direita o número 24, alinhado ordem a ordem com 37. Abaixo, traço horizontal. Abaixo, o número 148. Abaixo, à esquerda sinal de adição, à direita o número 740 alinhado ordem a ordem com 148. Abaixo, traço horizontal. Abaixo, 888.

• Se compararmos cada um dos itens, observamos que:

- um dos fatores é 37;

- os resultados são números de 3 algarismos iguais: 555, 666, 777 e 888;

- se escrevermos o outro fator, teremos a sequência: 15, 18, 21 e 24, ou seja, aumentando de 3 em 3.

Seguindo essa lógica, a próxima multiplicação seria 37 ⋅ 27 e o resultado seria 999.

Se 37 ⋅ 27 = 999, então 37 ⋅ 2700 = .99900.

45. Podemos usar o mesmo raciocínio da atividade anterior:

.3700 ⋅ 30 = 37 ⋅ 30 ⋅ 100 = .1110 ⋅ 100 = .111000

Ou calcular o produto .3700 ⋅ 30. Podemos começar por .3700 ⋅ 3:

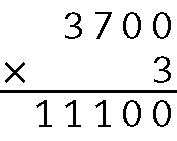
Algoritmo usual da multiplicação. 3 mil 700 vezes 3. Na primeira linha o número 3 mil 700. Abaixo, à esquerda, sinal de multiplicação, à direita, o número 3. Abaixo, traço horizontal. Abaixo, 11 mil e 100.

Como .3700 ⋅ 3 = .11100, então .3700 ⋅ 30 = = .11100 ⋅ 10 = .111000

Esse motor bombeará 111 000 litros de água em 30 minutos.

46. Utilizando as cores vermelha, verde e azul, sem repetir, temos:

3 possibilidades para a primeira parte;

duas possibilidades para a segunda parte;

uma possibilidade para a última parte.

Então: 3 ⋅ 2 ⋅ 1 = 6

Podemos fazer todas as combinações:

Vermelha	Verde	Azul
Vermelha	Azul	Verde
Verde	Vermelha	Azul
Verde	Azul	Vermelha
Azul	Vermelha	Verde
Azul	Verde	Vermelha

Total de 6 combinações.

47. Como temos 3 possibilidades de bermudas, 4 possibilidades de camisetas e duas possibilidades de tênis, podemos encontrar o total de combinações, calculando:

3 ⋅ 4 ⋅ 2 = 12 ⋅ 2 = 24

Ou seja, Bruno pode combinar essas peças de 24 maneiras diferentes.

48. Para calcular o número de lavadoras, devemos multiplicar: 220 ⋅ 25:

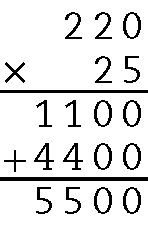
Algoritmo usual da multiplicação. 220 vezes 25. Na primeira linha, o número 220. Abaixo, à esquerda sinal de multiplicação, à direita o número 25 alinhado ordem a ordem com 220. Abaixo, traço horizontal. Abaixo, o número 1 mil 100. Abaixo, à esquerda, sinal de adição, à direita o número 4 mil 400, alinhado ordem a ordem com 1 mil 100. Abaixo, traço horizontal. Abaixo, 5 mil 500.

Logo, são fabricadas 5.quinhentas lavadoras em 25 dias.

49. Exemplo de problema que pode ser elaborado: Renata se inscreveu em um curso de línguas e realizará o pagamento em 14 parcelas de R$ 1.255,00mil duzentos e cinquenta e cinco reais cada uma. Calcule o valor total do curso (Resposta: R$ 17.570,00dezessete mil quinhentos e setenta reais).

50. Resposta pessoal. Exemplo de como o enunciado pode ser completado: Manoela corre de segunda a sábado e percorre 12 quilômetros por dia. Quantos quilômetros ela percorre, ao todo, por semana? (Resposta: Manoela corre o total de 72 quilômetros por semana (6 ⋅ 12 quilômetros = 72 quilômetros)).

Nesse caso é importante levar em consideração o contexto e a viabilidade, uma vez que se trata de uma pessoa que corre essa quilometragem todos os dias. Valores iguais ou maiores que 20 quilômetros, por exemplo, não são possíveis.

Página sessenta e seis

Algumas propriedades da multiplicação – página 57

Propriedade comutativa

a) 7 ⋅ 8 = 56 e 8 ⋅ 7 = 56

b) Espera-se que os estudantes percebam que, ao alterar a ordem dos fatores, o produto permanece o mesmo.

Propriedade associativa

a) (6 ⋅ 2) ⋅ 3 = 12 ⋅ 3 = 36 e 6 ⋅ (2 ⋅ 3) = 6 ⋅ 6 = 36

b) Espera-se que os estudantes percebam que, apesar de terem associado os fatores de maneiras diferentes, o produto permaneceu o mesmo.

Elemento neutro

a) 1 ⋅ 25 = 25 e 34 ⋅ 1 = 34

b) Espera-se que os estudantes percebam que, ao multiplicar um número por 1, o produto é o mesmo número.

Atividades – página 59

51. a) Como b ⋅ a = a ⋅ b, teremos que b ⋅ a = 60.

b) Como 1 ⋅ a ⋅ b = a ⋅ b, teremos que 1 ⋅ a ⋅ b = 60.

c) Sabendo que a ⋅ (b ⋅ 5) = (a ⋅ b) ⋅ 5 e a ⋅ b = 60, teremos que a ⋅ (b ⋅ 5) = 60 ⋅ 5 = 300.

• Comutativa, elemento neutro e associativa, respectivamente.

52. Resposta pessoal. Espera-se que os estudantes observem que, nos dois casos, o uso das propriedades pode facilitar os cálculos de acôrdo com os valores envolvidos. Vejamos cada caso:

2 ⋅ 37 ⋅ 50 = 2 ⋅ 50 ⋅ 37 = 100 ⋅ 37 = .3700

Calcular o dôbro de 50 é mais simples do que o dôbro de 37.

Para calcular uma multiplicação por 100, basta acrescentar 00 no número.

30 ⋅ 17 = 30 ⋅ (10 + 7) = 30 ⋅ 10 + 30 ⋅ 7 = 300 + 210 = 510

Decompondo o número 17, temos multiplicações menores e mais simples, sendo uma delas por 10.

De modo geral, se o estudante souber como utilizar adequadamente as propriedades, perceberá que o cálculo mental ficará mais simples.

53. Vejamos algumas possibilidades que facilitariam o cálculo mental em cada caso:

a) 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 = 2 ⋅ 3 ⋅ 4 ⋅ 5 = (2 ⋅ 5) ⋅ (3 ⋅ 4) =

= 10 ⋅ 12 = 120

• o 1 é elemento neutro da multiplicação, então podemos tirá-lo;

• usando as propriedades comutativa e associativa, buscamos um produto que resulte em 10;

• para multiplicar um número por 10, basta acrescentar um 0 à escrita desse número.

b) 100 ⋅ 375 ⋅ 2 = 100 ⋅ (2 ⋅ 375) = 100 ⋅ (375 + 375) =

= 100 ⋅ 750 = .75000

• associamos 375 com 2 para calcular o dôbro de 375 por meio da adição;

• multiplicamos 750 por 100, ou seja, basta acrescentar 00 após esse número.

c) 50 ⋅ 26 ⋅ 2 = (50 ⋅ 2) ⋅ 26 = 100 ⋅ 26 = .2600

• aplicamos a comutativa e associativa para ter resultado 100;

• multiplicamos 26 por 100, ou seja, basta acrescentar 00 após esse número.

d) 25 ⋅ 37 ⋅ 4 = (25 ⋅ 4) ⋅ 37 = 100 ⋅ 37 = .3700

• aplicamos a comutativa e associativa para ter resultado 100;

• multiplicamos 37 por 100, ou seja, basta acrescentar 00 após esse número.

54. a) Se 307 ⋅ a = 307, então a é o elemento neutro da multiplicação, ou seja, a = 1.

b) A propriedade do elemento neutro, já que o 307 foi multiplicado por um número e o resultado foi o próprio 307.

55. a) 5 ⋅ (8 + 2) = 5 ⋅ 8 + 5 ⋅ 2 = 40 + 10 = 50

b) 9 ⋅ (8 ‒ 3) = 9 ⋅ 8 ‒ 9 ⋅ 3 = 72 ‒ 27 = 45

c) (2 + 8) ⋅ 15 = 2 ⋅ 15 + 8 ⋅ 15 = 30 + 120 = 150

d) (8 ‒ 3) ⋅ 4 = 8 ⋅ 4 ‒ 3 ⋅ 4 = 32 ‒ 12 = 20

e) 10 ⋅ (20 + 30) = 10 ⋅ 20 + 10 ⋅ 30 = 200 + 300 = 500

f) 12 ⋅ (15 ‒ 6) = 12 ⋅ 15 ‒ 12 ⋅ 6 = 180 ‒ 72 = 108

56. Quadradinhos verdes: 5 ⋅ 9 = 45.

Quadradinhos azuis: 5 ⋅ 4 = 20.

Total de quadradinhos: 45 + 20 = 65.

Ou usando a expressão: 5 ⋅ ( 9 + 4 ) = 5 ⋅ 13 = 65.

Atividades – página 60

57. a) Dividindo 216 por 12:

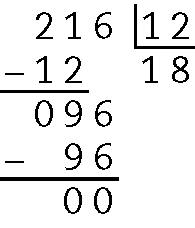
Algoritmo usual da divisão. 216 dividido por 12. Na primeira linha, à esquerda o número 216, à direita, na chave, o número 12. Abaixo, à esquerda o sinal de subtração, à direita o número 12, alinhado com os algarismos da ordem das dezenas e centenas do número 216, abaixo da chave o número 18. Abaixo, traço horizontal. Abaixo, o número 96, alinhado ordem a ordem com 216. Abaixo, à esquerda, sinal de subtração, à direita o número 96 alinhado ordem a ordem com 96. Abaixo, traço horizontal. Abaixo, 00.

Logo, Artur colocou 18 peixes em cada aquário.

b) Dividindo 480 por 8:

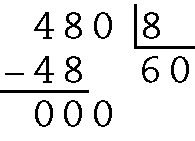
Algoritmo usual da divisão. 480 dividido por 8. Na primeira linha, à esquerda o número 480, à direita, na chave, o número 8. Abaixo, à esquerda sinal da subtração, à direita o número 48 alinhado a ordem da dezena e da centena do número 480. Abaixo da chave, o número 60. Abaixo, traço horizontal. Abaixo, 000.

Tia Lúcia deu 60 reais para cada sobrinho.

58.

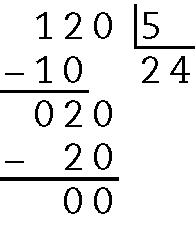
Algoritmo usual da divisão. 120 dividido por 5. Na primeira linha, à esquerda o número 120, à direita, na chave, o número 5. Abaixo, à esquerda sinal da subtração, à direita o número 10 alinhado aos algarismos das ordem das dezenas e das centenas. Abaixo da chave, o número 24. Abaixo, traço horizontal. Abaixo, o número 20 alinhado ordem a ordem com 120. Abaixo, à esquerda sinal da subtração, à direita o número 20 alinhado ordem a ordem com 20. Abaixo, traço horizontal. Abaixo, 00.

a) O quociente é 24.

b) O resto é zero.

59. a)

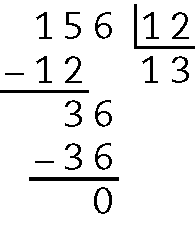
Algoritmo usual da divisão. 156 dividido por 12. Na primeira linha, à esquerda o número 156, à direita, na chave, o número 12. Abaixo, à esquerda, sinal da subtração, à direita o número 12 alinhado aos algarismos da ordem das dezenas e das centenas do número 156. Abaixo, traço horizontal. Abaixo, o número 36 alinhado ordem a ordem com 156. Abaixo, à esquerda sinal de subtração, à direita o número 36, alinhado ordem a ordem com 36. Abaixo, traço horizontal. Abaixo, 0.

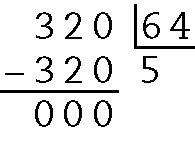
Algoritmo usual da divisão. 320 dividido por 64. Na primeira linha, à esquerda o número 320, à direita, na chave, o número 64. Abaixo, à esquerda sinal de subtração, à direita o número 320, alinhado ordem a ordem com 320. Abaixo da chave o número 5. Abaixo, traço horizontal. Abaixo, 000.

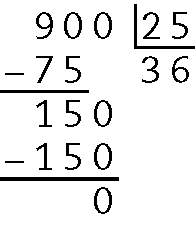
Algoritmo usual da divisão. 900 dividido por 25. Abaixo, à esquerda sinal de subtração, à direita o número 75, alinhado a ordem das dezenas e das centenas do número 900. Abaixo da chave, o número 36. Abaixo, traço horizontal. Abaixo, o número 150 alinhado ordem a ordem com o número 900. Abaixo, à esquerda, sinal de subtração, à direita o número 150, alinhado ordem a ordem com 150. Abaixo, traço horizontal. Abaixo, 0.

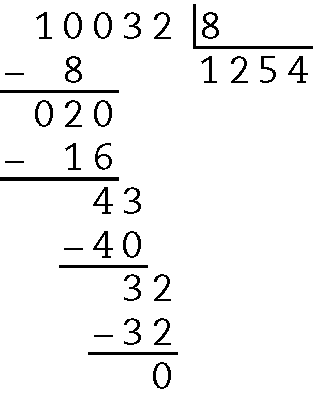
Algoritmo usual da divisão. 10 mil 032 dividido por 8. Na primeira linha, à esquerda, o número 10 mil 032, à direita, na chave, o número 8. Abaixo, à esquerda, sinal da subtração, à direita o número 8, alinhado ao algarismo da ordem da unidade da milhar. Abaixo da chave o número 1 mil 254. Abaixo, traço horizontal. Abaixo, o número 20 alinhado a ordem das centenas e da unidade de milhar do número 10 mil 032. Abaixo, à esquerda sinal da subtração, à direita o número 16, alinhado ordem a ordem com o número 20. Abaixo, traço horizontal. Abaixo, o número 43, alinhado aos algarismos da ordem das dezenas e das centenas do número 10 mil 032. Abaixo, à esquerda sinal da subtração, à direita o número 40 alinhado ordem a ordem com 43. Abaixo, traço horizontal. Abaixo, o número 32, alinhado a ordem das unidades do número 40. Abaixo, à esquerda sinal da subtração, à direita o número 32, alinhado ordem a ordem com 32. Abaixo, traço horizontal. Abaixo, 0.

Página sessenta e sete

60. a) 50 : 10 = 5

b) 500 : 10 = 50

c) 500 : 100 = 5

d) 50 : 5 = 10

61. Duas dúzias correspondem a 24 unidades (2 ⋅ 12 = 24), então devemos dividir .24432 por 24:

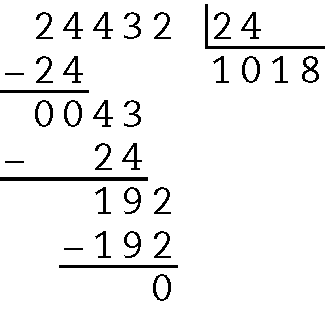
Algoritmo usual da divisão. 24 mil 432 dividido por 24. Na primeira linha, à esquerda, o número 24 mil 432, à direita na chave o número 24. Abaixo, à esquerda, sinal da subtração, à direita o número 24 alinhado aos algarismos da ordem das unidades de milhar e a ordem das dezenas de milhar do número 24 mil 432. Abaixo da chave o número 1 mil 018. Abaixo, traço horizontal. Abaixo, o número 43, alinhado aos algarismos da ordem das dezenas e das centenas do número 24 mil 432. Abaixo, à esquerda sinal de subtração, à direita o número 24 alinhado ordem a ordem com o número 43. Abaixo, traço horizontal. Abaixo, o número 192. Abaixo, à esquerda sinal de subtração, a direita o número 192 alinhado ordem a ordem com o número 192. Abaixo, traço horizontal. Abaixo, 0.

Logo, há .1018 caixas nesse caminhão.

62. Fazemos a seguinte divisão:

..150000000 : .30000 = .1500 : 3 = 500

A luz do Sol demora 500 segundos para chegar à Terra.

Atividades – página 61

63. a) 5 + 6 ⋅ 4 = 5 + 24 = 29

b) (5 + 6) ⋅ 4 = 11 ⋅ 4 = 44

c) 10 + 8 ⋅ 4 ‒ 15 = 10 + 32 ‒ 15 = 42 ‒ 15 = 27

d) 200 ‒ 3 ⋅ 60 + 8 = 200 ‒ 180 + 8 = 20 + 8 = 28

e) (18 ‒ 15 : 5 + 3) ⋅ 4 = (18 ‒ 3 + 3) ⋅ 4 = (15 + 3) ⋅ 4 =

= 18 ⋅ 4 = 72

f) [(21 : 7) ⋅ (3 : 1) + 6] ‒ [(7 ⋅ 6) : (5 ‒ 2)] =

= [3 ⋅ 3 + 6] ‒ [42 : 3] =

= [9 + 6] ‒ [14] = 15 ‒ 14 = 1

g) {[13 ‒ (3 ⋅ 2 + 1)] + 3 + (5 ⋅ 2 ‒ 4 : 2)} =

= {[13 ‒ (6 + 1)] + 3 + (10 ‒ 2)} =

= {[13 ‒ 7] + 3 + 8} =

= {6 + 3 + 8} = {9 + 8} = 17

64. Resposta pessoal. Exemplo de problema que pode ser elaborado: Um restaurante tinha no estoque 2 sacos de farinha, cada um com 20 quilogramas. Após utilizar 13 quilogramas de farinha, quantos quilogramas restaram no estoque?

Exemplo de resolução: 2 quilogramas ⋅ 20 quilogramas ‒ 13 quilogramas = 40 quilogramas ‒ 13 quilogramas = 27 quilogramas

Resposta: Restaram 27 quilogramas de farinha no estoque.

Atividades – página 63

65. a)

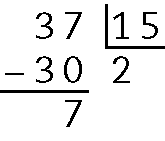
Algoritmo usual da divisão. 37 dividido por 15.
Na primeira linha, à esquerda o número 37, à direita, na chave, o número 15.
Abaixo, à esquerda sinal de subtração, à direita o número 30 alinhado ordem a ordem com 37. Abaixo da chave, o número 2.
Abaixo, traço horizontal.
Abaixo, o resto 7.

Quociente 2 e resto 7.

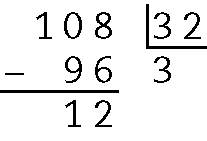
Algoritmo usual da divisão. 108 dividido por 32. Na primeira linha, à esquerda o número 108, à direita, na chave, o número 32. Abaixo, à esquerda sinal de subtração, à direita o número 96 alinhado ordem a ordem com 108. Abaixo da chave, o número 3. Abaixo, traço horizontal. Abaixo, o resto 12.

Quociente 3 e resto 12.

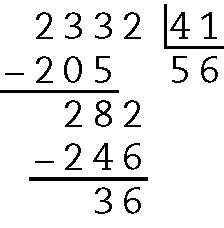
Algoritmo usual da divisão. 2 mil 332 dividido por 41. Na primeira linha, à esquerda o número 2 mil 332, à direita, na chave, o número 41. Abaixo, à esquerda sinal de subtração, à direita o número 205 alinhado aos algarismos da ordem das dezenas, centenas e unidade de milhar do número 2 mil 332. Abaixo da chave, o número 56. Abaixo, traço horizontal. Abaixo, o número 282 alinhado ordem a ordem com 2 mil 332. Abaixo, à esquerda sinal de subtração, à direita o número 246 alinhado ordem a ordem com 246. Abaixo, traço horizontal. Abaixo, o resto 36

Quociente 56 e resto 36.

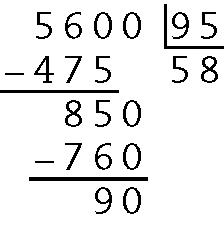
Algoritmo usual da divisão, 5 mil 600 dividido por 95. Na primeira linha, à esquerda, o número 5 mil 600, à direita, na chave o número 95. Abaixo, à esquerda sinal da subtração, à direita o número 475 alinhado aos algarismos da ordem das dezenas, das centenas e da unidade de milhar do número 5 mil 600. Abaixo da chave, o número 58. Abaixo, traço horizontal. Abaixo, o número 850 alinhado ordem a ordem com 5 mil 600. Abaixo, à esquerda sinal de subtração, à direita o número 760 alinhado ordem a ordem com 850. Abaixo, traço horizontal. Abaixo, o número 90.

Quociente 58 e resto 90.

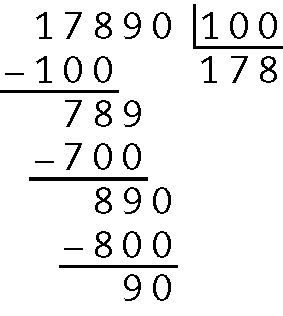
Algoritmo usual da divisão. 17 mil 890 dividido por 100. Na primeira linha, à esquerda o número 17 mil 890, à direita, na chave, o número 100. Abaixo, à esquerda sinal de subtração, à direita número 100, alinhado aos algarismos da ordem das centenas, da unidade de milhar e da dezena de milhar do número 17 mil 890. Abaixo da chave, o número 178. Abaixo, traço horizontal. Abaixo, o número 789, alinhado aos algarismos da ordem das dezenas, das centenas e da unidade de milhar do número 17 mil 890. Abaixo, à esquerda sinal de subtração, a direita o número 700 alinhado ordem a ordem com 789. Abaixo, traço horizontal. Abaixo, o número 890, alinhado ordem a ordem com 17 mil 890. Abaixo, à esquerda sinal de subtração, à direita o número 800, alinhado ordem a ordem com 789. Abaixo, traço horizontal. Abaixo, 90.

Quociente 178 e resto 90.

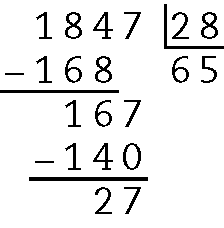
Algoritmo usual da divisão. 1 mil 847 dividido por 28. Na primeira linha, à esquerda o número 1 mil 847, à direita, na chave, o número 28. Abaixo, à esquerda sinal de subtração, à direita o número 168, alinhado aos algarismos da ordem das dezenas, centenas e unidade de milhar do número 1 mil 847. Abaixo da chave, o número 65. Abaixo, traço horizontal. Abaixo, o número 167, alinhado ordem a ordem com 1 mil 847. Abaixo, à esquerda sinal de subtração, à direita o número 140, alinhado ordem a ordem com 167. Abaixo, traço horizontal. Abaixo, 27.

Quociente 65 e resto 27.

66. Para encontrar o número que falta, utilizamos a relação fundamental da divisão:

a) 48 ‒ 9 ⋅ 5 = 48 ‒ 45 = 3

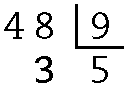
Algoritmo usual da divisão. 48 dividido por 9. Na primeira linha, à esquerda o número 48, à direita, na chave, o número 9. Abaixo, o número 3 alinhado ordem a ordem com 48. Abaixo da chave, o número 5. O número 3 está em destaque.

b) 7 ⋅ 7 + 4 = 49 + 4 = 53

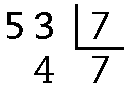
c) 13 ⋅ 8 + 6 = 104 + 6 = 110

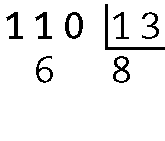
Algoritmo usual da divisão. 110 dividido por 13. Na primeira linha, à esquerda o número 110, à direita, na chave, o número 13. O número 110 está em destaque. Abaixo, o número 6 alinhado com o algarismo da ordem das dezenas com 110. Abaixo da chave, o número 8.

d) (54 ‒ 6) : 8 = 6

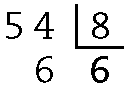
Algoritmo usual da divisão. 54 dividido por 8. Na primeira linha, à esquerda o número 54, à direita, na chave, o número 6. Abaixo, o número 6 alinhado ordem a ordem com 54. Abaixo da chave, o número 6. O número 6, abaixo da chave está em destaque.

e) 7 ⋅ 9 + 2 = 63 + 2 = 65

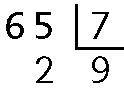
Algoritmo usual da divisão. 65 dividido por 7. Na primeira linha, à esquerda o número 65, à direita, na chave, o número 7. O número 65 está em destaque. Abaixo, o número 2 alinhado ordem a ordem com 48. Abaixo da chave, o número 9.

f) (78 ‒ 3) : 5 = 75 : 5 = 15

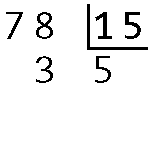
Algoritmo usual da divisão. 78 dividido por 15. Na primeira linha, à esquerda o número 78, à direita, na chave, o número 15. O número 15 está em destaque. Abaixo, o número 3 alinhado ordem a ordem com 78. Abaixo da chave, o número 5.

67. Os estudantes deverão analisar quantas vezes o 132 cabe em 528. Para isso, devem usar apenas a subtração:

528 ‒ 132 = 396

396 ‒ 132 = 264

264 ‒ 132 = 132

132 ‒ 132 = 0

Logo, o número 132 cabe exatamente 4 vezes no número 528, ou seja, 528 : 132 = 4.

Luísa deve calcular quantas vezes 132 cabe em 528; e, para isso, ir subtraindo 132. O resultado será 4 vezes.

68.

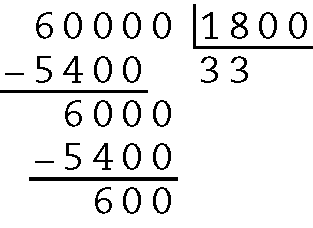
Algoritmo usual da divisão. 60 mil dividido por 1 mil 800. Na primeira linha, à direita o número 60 mil, à esquerda na chave o número 1 mil 800. Abaixo, à esquerda sinal de subtração, à direita o número 5 mil 400 alinhado aos algarismos da ordem da dezena, centena, unidade de milhar e dezena de milhar de 60 mil. Abaixo da chave o número 33. Abaixo, traço horizontal. Abaixo, o número 6 mil alinhado ordem a ordem com 60 mil. Abaixo, à esquerda sinal de subtração, à direita o número 5 mil 400 alinhado ordem a ordem com 6 mil. Abaixo, traço horizontal. Abaixo, o resto 600.

Quociente 33 e resto 600.

69. a)

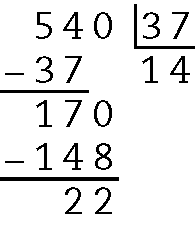
Algoritmo usual da divisão. 540 dividido por 37. Na primeira linha, à direita o número 540, à esquerda na chave, o número 37. Abaixo, à esquerda sinal de subtração, à direita o número 37 alinhado aos algarismos da dezena e da centena do número 540. Abaixo, traço horizontal. Abaixo, o número 170 alinhado ordem a ordem com 540. Abaixo, à esquerda sinal de subtração, à direita o número 148 alinhado ordem a ordem com 170. Abaixo, traço horizontal. Abaixo, o resto 22.

Serão formados 14 grupos completos.

b) Como restaram 22 estudantes sem grupo, para completar mais um grupo, seria preciso mais 15 estudantes, pois 37 ‒ 22 = 15.

70. a) 0 : 10 = 0. Ou seja, o quociente é zero.

b) 10 : 0 = ? Não existe essa divisão.

Página sessenta e oito

71. No visor da calculadora aparecerá uma mensagem de êrro, pois não é possível dividir 8 por 0. As mensagens podem variar de acôrdo com a calculadora utilizada.

72. Considerando que em todas as viagens de elevador a pessoa de 75 quilogramas também estará, a carga máxima para as caixas em cada viagem será de 425 quilogramas (500 ‒ 75 = 425).

Como cada caixa tem 30 quilogramas, para saber quantas caixas poderemos levar por viagem, calculamos:

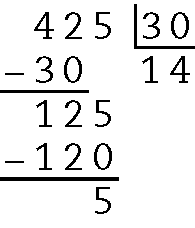
Algoritmo usual da divisão. 425 dividido por 30. Na primeira linha, à direita o número 425, à esquerda na chave o número 30. Abaixo, à esquerda o número 30, alinhado a ordem das dezenas e centenas do número 425. Abaixo da chave o número 14. Abaixo, traço horizontal. Abaixo o número 125 alinhado ordem a ordem com 425. Abaixo, à esquerda sinal de subtração a direita o número 120 alinhado ordem a ordem com 125. Abaixo, traço horizontal. Abaixo, o resto 5.

Ou seja, por viagem, é possível carregar um máximo de 14 caixas.

Como são 45 caixas, calculamos a quantidade de viagens necessárias:

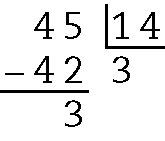
Algoritmo usual da divisão. 45 dividido por 14. Na primeira linha à esquerda o número 45, à direita na chave, o número 14. Abaixo, à esquerda sinal de subtração, à direita o número 42 alinhado ordem a ordem com 45. Abaixo da chave, o número 3. Abaixo, traço horizontal. Abaixo, o resto 3.

Como fazendo 3 viagens, sobram 3 caixas, são necessárias no mínimo 4 viagens para transportar as 45 caixas.

73. Resposta pessoal. Exemplo de problema que pode ser elaborado: Ao longo de 9 dias de viagem, Roberto percorreu um total de 729 quilômetros. Quantos quilômetros ele percorreu, em média, por dia?

(Resposta: Roberto percorreu, em média, 81 quilômetros por dia (729 : 9 = 81)).

Veja que interessante – página 65

.700000 = 7 ⋅ 105

..2560000 = 256 ⋅ 104

Atividades – página 66

74. a) 3⁵ = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 243

b) 4³ = 4 ⋅ 4 ⋅ 4 = 64

c) 14²  = 14 ⋅ 14 = 196

d) 2⁵ = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32

e) 10³ = 10 ⋅ 10 ⋅ 10 = .1000

f) 1⁶ = 1 ⋅ 1 ⋅ 1 ⋅ 1 ⋅ 1 ⋅ 1 = 1

g) 11² = 11 ⋅ 11 = 121

h) 15⁰ = 1

i) 17¹ = 17

j) 0⁵ = 0 ⋅ 0 ⋅ 0 ⋅ 0 ⋅ 0 = 0

k) 50¹ = 50

l) 20² = 20 ⋅ 20 = 400

75. a) Sete elevado ao quadrado (ou sete elevado à segunda potência).

b) Nove elevado ao cubo (ou nove elevado à terceira potência.

c) Dez elevado à quarta potência.

d) Treze elevado à quinta potência.

76. a) 13² = 13 ⋅ 13 = 169

b) 7³ = 7 ⋅ 7 ⋅ 7 = 49 ⋅ 7 = 343

c) 3⁶ = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 729

77. 2⁵ ‒ 5² = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ‒ 5 ⋅ 5 = 32 ‒ 25 = 7

78. a) .600000 = 6 ⋅ 10⁵

b) ..4500000 = 45 ⋅ 10⁵

c) ...8000000000 = 8 ⋅ 10⁹

d) .8700 = 87 ⋅ 10²

79. Os números que preenchem os quadrinhos são:

2¹ = 2 e 2⁰ = 1

3¹ = 3 e 3⁰ = 1

80. 10 ⋅ 10 ⋅ 10 = 103

81. a) 100¹ = 100 e 1¹⁰⁰ = 1, logo 100¹ é o maior valor.

b) 80⁰ = 1 e 0⁸⁰ = 0, logo 80⁰ é o maior valor.

82. a) 10⁵ = .100000

b) 10² = 100

c) 8 ⋅ 10² = 800

d) 52 ⋅ 10³ = .52000

83. a) 938 = 900 + 30 + 8 = 9 ⋅ 100 + 3 ⋅ 10 + 8 = 9 ⋅ 10² + 3 ⋅ 10¹ + 8 ⋅ 10⁰

b) .4078 = .4000 + 70 + 8 = 4 ⋅ 10³ + 7 ⋅ 10¹ + 8 ⋅ 10⁰

c) .7952 = .7000 + 900 + 50 + 2 = 7 ⋅ 10³ + 9 ⋅ 10² + 5 ⋅ 10¹+ 2 ⋅ 10⁰

d) .60000 = 6 ⋅ 10⁴

84. Sabendo que 55 = .3125, podemos fazer:

5⁴ = 5⁵ : 5 = .3125 : 5 = 625

5⁶ = 5⁵ ⋅ 5 = .3125 ⋅ 5 = .15625

85.

Casa	bolinha(s)	Potência que representa a quantidade de bolinhas
1ª casa: 2ª casa: 3ª casa: 4ª casa: 5ª casa: 6ª casa: 7ª casa: 8ª casa:	1 2 ⋅ 1 = 2 2 ⋅ 2 = 4 2 ⋅ 4 = 8 2 ⋅ 8 = 16 2 ⋅ 16 = 32 2 ⋅ 32 = 64 2 ⋅ 64 = 128	20 21 22 23 24 25 26 27

Na oitava casa Pedro colocou 128 bolinhas.

Atividades – página 67

86. a) 20 ‒ (1⁴ ⋅ 6 + 2³) = 20 ‒ (1 ⋅ 6 + 8) = 20 ‒ (6 + 8) = 20 ‒ 14 = 6

b) (2⁴ ‒ 3 ⋅ 4) : 2 + 5² : 5 = (16 ‒ 12) : 2 + 25 : 5 = 4 : 2 + 5 = 2 + 5 = 7

c) 10² : 5² + 5⁰ ⋅ 2² ‒ 2³ = 100 : 25 + 1 ⋅ 4 ‒ 8 = 4 + 4 ‒ 8 = 8 ‒ 8 = 0

d) {6² + 2 ⋅ [2³ + 2 ⋅ (3² ⋅ 1³)] ‒ 2⁵} ⋅ 5 ⁰ = {36 + 2 ⋅ [8 + 2 ⋅ (9 ⋅ 1)] ‒ 32} ⋅ 1 = {36 + 2 ⋅ [8 + 18] ‒ 32} = {36 + 2 ⋅ 26 ‒ 32} = {36 + 52 ‒ 32} = {88 ‒ 32} = 56

e) 55 ‒ (3 ⋅ 2 + 1)² + (42 + 32) : 5² ‒ 1⁶ = 55 ‒ (6 + 1)² + (16 + 9) : 25 ‒ 1 = 55 ‒ 7² + 25 : 25 ‒ 1 = 55 ‒ 49 + 1 ‒ 1 = 6 + 1 ‒ 1 = 7 ‒ 1 = 6

87. A + B = (3 ⋅ 2 ‒ 1)² + (22 + 1) ⋅ (5 + 23) = (6 ‒ 1)² + (4 + 1) ⋅ (5 + 8) = 5² + 5 ⋅ 13 = 25 + 65 = 90

88. A diferença entre o dôbro do cubo de 8 e o triplo do quadrado de 17:

2 ⋅ 8³ ‒ 3 ⋅ 17² = 2 ⋅ 512 ‒ 3 ⋅ 289 = .1024 ‒ 867 = 157

Página sessenta e nove

89. Resposta pessoal. Exemplo de problema que pode ser elaborado: Marina está pintando cubinhos para usar de material manipulável na escola. Ela pintou a seguinte quantidade de cubinhos de cada côr:

25 → vermelho

62 → amarelo

9 ⋅ (42 ‒ 2)² → azul

Escreva uma expressão numérica que represente a quantidade de cubinhos que ela pintou. (Resposta: 25 + 62 + 9 ⋅ (42 ‒ 2)²).

90. Exemplo de resposta:

Número pensado: 50

Multiplicar por 3: 50 ⋅ 3 = 150

Acrescente 1: 150 + 1 = 151

Multiplique por 3: 151 ⋅ 3 = 453

Somar com o número pensado: 453 + 50 = 503

Eliminar o 3 das unidades: 50

Chegamos ao número pensado, ou seja, 50.

Atividades – página 69

91. a) 400 b) .360000 c) 100 d) 110

92. Aproximando 323 : 111 + 32, teremos:

300 : 100 + 30 = 3 + 30 = 33.

93. a) Resposta pessoal. Exemplos de resposta: Para saber o valor aproximado de uma compra, ou para encontrar a medida aproximada sem o uso de um instrumento de medida.

b) Resposta pessoal. Exemplo de problema que pode ser elaborado:

Um caminhoneiro percorreu em 3 dias da semana 289 quilômetros e em 2 dias da semana 502 quilômetros. Quantos quilômetros ele percorreu, aproximadamente, nesses 5 dias?

(Resultado estimado: .1600 quilômetros, pois: 3 ⋅ 300 + 2 ⋅ 500 = 600 + .1000 = .1600.)

94. a) Loja A: .1250 + 580 = .1830

Loja B: .1500 + 400 = .1900

Ela conseguiria realizar a compra na Loja A.

b) A melhor combinação seria escolher os eletrodomésticos mais baratos, ou seja, geladeira da Loja A (R$ 1.254,00mil duzentos e cinquenta e quatro reais) e o fogão da loja B (R$ 399,00trezentos e noventa e nove reais), então o valor total estimado seria: R$ 1.600,00mil seiscentos reais, pois .1200 + 400 = .1600.

Resolvendo em equipe – página 70

Interpretação e identificação dos dados

um Vovô Eduardo precisou comprar as velas de números 1, 2 e 3, para os aniversários de 41, 42 e 43 anos, respectivamente.

dois Sim, precisou comprar mais uma vela de número 4 para representar 44 anos.

Plano de resolução

Para as dez primeiras comemorações, ou seja, de 40 até 49 anos: precisou comprar 11 velas, sendo uma de cada algarismo (0, 1, 2, 3, 5, 6, 7, 8 e 9) e duas do algarismo 4.

Para as comemorações de 50 até 59 anos, precisou comprar apenas mais uma do algarismo 5, para representar 55 anos.

Uma das estratégias que podem ser utilizadas pelos estudantes é a escrita dos números 40 a 85 e a contagem das velas de aniversário já usadas e das que serão compradas até o 85º aniversário.

Resolução

Continuando o raciocínio anterior, podemos encontrar a quantidade de velas necessárias, além das que já tem:

Para as comemorações de 60 até 69 anos: uma vela do 6, para representar 66.

Para as comemorações de 70 até 79 anos: uma vela do 7, para representar 77.

Para as comemorações de 80 até 85 anos: nenhuma vela nova

Assim o total de velas necessárias foi 14, pois 11 + 1 + 1 + 1 = 14. Alternativa d.

Revisão dos conteúdos deste capítulo – páginas 71 a 73

1. a)

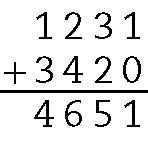
Algoritmo usual da adição. 1 mil 231 mais 3 mil 420. Na primeira linha, o número 1 mil 231. Abaixo, à esquerda sinal da adição, à direita o número 3 mil 420 alinhado ordem a ordem com 1 mil 231. Abaixo, traço horizontal. Abaixo, o número 4 mil 651.

.1231 + .3420 = .4651

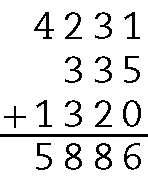
Algoritmo usual da adição. 4 mil 231 mais 335 mais 1 mil 320. Na primeira linha, o número 4 mil 231. Abaixo, o número 335 alinhado ordem a ordem com 4 mil 231. Abaixo, à esquerda sinal da adição, à direita o número 1 mil 320 alinhado ordem a ordem com 4 mil 231 e 335. Abaixo, traço horizontal. Abaixo, o número 5 mil 886.

.4231 + 335 + .1320 = .5886

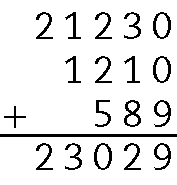
Algoritmo usual da adição. 21 mil 230 mais 1 mil 210 mais 589. Na primeira linha, o número 21 mil 230. Abaixo, o número 1 mil 210, alinhado ordem a ordem com 21 mil 230 Abaixo, à esquerda sinal da adição, à direita o número 589 alinhado ordem a ordem com 21 mil 230 e 1 mil 210. Abaixo, traço horizontal. Abaixo, o número 23 mil 029.

.21230 + .1210 + 589 = .23029

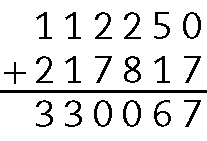
Algoritmo usual da adição. 112 mil 250 mais 217 mil 817. Na primeira linha, o número 112 mil 250. Abaixo, à esquerda sinal da adição, à direita o número 217 mil 817 alinhado ordem a ordem com 112 mil 250. Abaixo, traço horizontal. Abaixo, o número 330 mil 067.

.112250 + .217817 = .330067

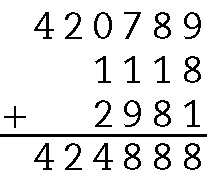
Algoritmo usual da adição. 420 mil 789 mais 1 mil 118 mais 2 mil 981. Na primeira linha, o número 420 mil 789. Abaixo, o número 1 mil 118, alinhado ordem a ordem com 420 mil 789. Abaixo, à esquerda sinal da adição, à direita o número 2 mil 981 alinhado ordem a ordem com 420 mil 789 e 1 mil 118. Abaixo, traço horizontal. Abaixo, o número 424 mil 888.

.420789 + .1118 + .2981 = .424888

2. Utilizando a propriedade comutativa da adição, podemos completar da seguinte fórma:

a) 87 + 91 = 91 + 87

b) .1250 + 0 = 0 + .1250

c) .11388 + .2188 = .2188 + .11388

d) .25257 + .9235 = .9235 + .25257

3. Para saber quanto foi o preço da bicicleta, adicionamos os três valores acumulados:

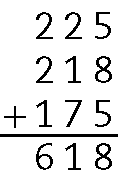
Algoritmo usual da adição. 225 mais 218 mais 175. Na primeira linha o número 225. Abaixo, o número 218 alinhado ordem a ordem com 225. Abaixo, à esquerda sinal da adição, à direita o número 175 alinhado ordem a ordem com 225 e 218. Abaixo, traço horizontal. Abaixo, o número 618.

Logo, Luana pagou pela bicicleta o valor de R$ 618,00seiscentos e dezoito reais.

4. a)

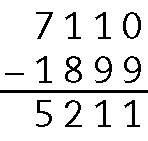
Algoritmo usual da subtração. 7 mil 110 menos 1 mil 899. Na primeira linha o número 7 mil 110. Abaixo, à esquerda sinal da subtração, à direita o número 1 mil 899 alinhado ordem a ordem com 7 mil 110. Abaixo, traço horizontal. Abaixo, o número 5 mil 211.

.7110 ‒ .1899 = .5211

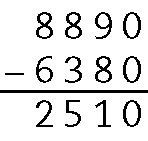
Algoritmo usual da subtração. 8 mil 890 menos 6 mil 380. Na primeira linha o número 8 mil 890. Abaixo, à esquerda sinal da subtração, à direita o número 6 mil 380 alinhado ordem a ordem com 8 mil 890. Abaixo, traço horizontal. Abaixo, o número 2 mil 510.

.8890 ‒ .6380 = .2510

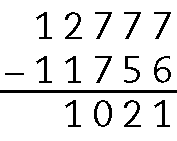
Algoritmo usual da subtração. 12 mil 777 menos 11 mil 756. Na primeira linha o número 12 mil 777. Abaixo, à esquerda sinal da subtração, à direita o número 11 mil 756 alinhado ordem a ordem com 12 mil 777. Abaixo, traço horizontal. Abaixo, o número 1 mil 021.

.12777 ‒ .11756 = .1021

Página setenta

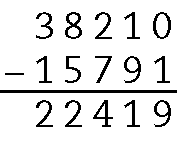
Algoritmo usual da subtração. 38 mil 210 menos 15 mil 791. Na primeira linha o número 38 mil 210. Abaixo, à esquerda sinal da subtração, à direita o número 15 mil 791 alinhado ordem a ordem com 38 mil 210. Abaixo, traço horizontal. Abaixo, o número 22 mil 419.

.38210 ‒ .15791 = .22419

5. a)

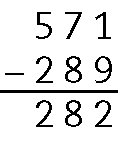
Algoritmo usual da subtração. 571 menos 289. Na primeira linha o número 571. Abaixo, à esquerda sinal da subtração, à direita o número 289 alinhado ordem a ordem com 571. Abaixo, traço horizontal. Abaixo, o número 282.

571 ‒ 282 = 289

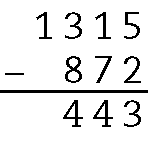
Algoritmo usual da subtração. 1 mil 315 menos 872. Na primeira linha o número 1 mil 315. Abaixo, à esquerda sinal da subtração, à direita o número 872 alinhado ordem a ordem com 1 mil 315. Abaixo, traço horizontal. Abaixo, o número 443.

.1315 ‒ 443 = 872

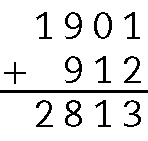
Algoritmo usual da adição. 1 mil 901 mais 912. Na primeira linha o número 1 mil 901. Abaixo, à esquerda sinal da adição, à direita o número 912 alinhado ordem a ordem com 1 mil 901. Abaixo, traço horizontal. Abaixo, o número 2 mil 813.

.2813 ‒ .1901 = 912

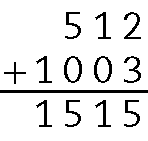
Algoritmo usual da adição. 512 mais 1 mil 003. Na primeira linha o número 512. Abaixo, à esquerda sinal da adição, à direita o número 1 mil 003 alinhado ordem a ordem com 512. Abaixo, traço horizontal. Abaixo, o número 1 mil 515.

.1515 ‒ 512 = .1003

6. Devemos descobrir o minuendo:

? ‒ 212 = 439.

Para isso fazemos a operação inversa:

Logo, o minuendo é 651.

7. a) (25 ‒ 18 + 13) + 11 = (7 + 13) + 11 = 20 + 11 = 31

b) 45 + (70 ‒ 36) + 12 = 45 + 34 + 12 = 79 + 12 = 91

c) (115 ‒ 82) ‒ (15 + 18) + 9 = 33 ‒ 33 + 9 = 0 + 9 = 9

8. Para saber quanto falta para a 2ª prestação, fazemos:

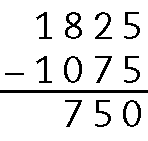
Algoritmo usual da subtração. 1 mil 825 menos 1 mil 075. Na primeira linha o número 1 mil 825. Abaixo, à esquerda sinal da subtração, à direita o número 1 mil 075 alinhado ordem a ordem com 1 mil 825. Abaixo, traço horizontal. Abaixo, o número 750.

Logo, o valor da 2ª prestação será R$ 750,00setecentos e cinquenta reais.

9. A expressão associada a essa situação é: (.1250 ‒ 368) ‒ 425 + 560

E sua resolução é:

(.1250 ‒ 368) ‒ 425 + 560 = 882 ‒ 425 + 560 = = 457 + 560 = .1017

Logo, há .1017 unidades desse produto no estoque da loja em março.

10. a)

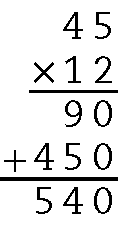
Algoritmo usual da adição. 439 mais 212. Na primeira linha o número 439. Abaixo, à esquerda sinal da adição, à direita o número 212 alinhado ordem a ordem com 439. Abaixo, traço horizontal. Abaixo, o número 651.

45 ⋅ 12 = 540

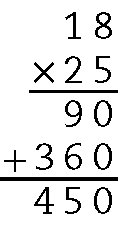
Algoritmo usual da multiplicação. 18 vezes 25. Na primeira linha o número 18. Abaixo, à esquerda, o sinal de multiplicação, à direita o numero 25, alinhado ordem a ordem ao número 18. Abaixo, traço horizontal. Abaixo, o número 90. Abaixo, à esquerda sinal da adição, à direita o número 360, alinhado ordem a ordem com 90. Abaixo, traço horizontal. Abaixo, o número 450.

18 ⋅ 25 = 450

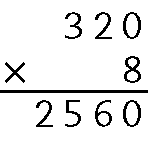
Algoritmo usual da multiplicação. 320 vezes 8. Na primeira linha o número 320. Abaixo, à esquerda, o sinal de multiplicação, à direita o numero 8, alinhado ordem a ordem ao número 320. Abaixo, traço horizontal. Abaixo, o número 2 mil 560.

320 ⋅ 8 = .2560

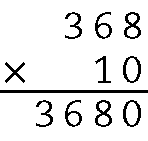
Algoritmo usual da multiplicação. 368 vezes 10. Na primeira linha o número 368. Abaixo, à esquerda, o sinal de multiplicação, à direita o numero 10, alinhado ordem a ordem ao número 368. Abaixo, traço horizontal. Abaixo, o número 3 mil 680.

368 ⋅ 10 = .3680

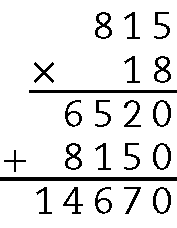
Algoritmo usual da multiplicação. 815 vezes 18. Na primeira linha o número 815. Abaixo, à esquerda, o sinal de multiplicação, à direita o numero 18, alinhado ordem a ordem ao número 815. Abaixo, traço horizontal. Abaixo, o número 6 mil 520. Abaixo, à esquerda sinal da adição, à direita o número 8 mil 150, alinhado ordem a ordem com 6 mil 520. Abaixo, traço horizontal. Abaixo, o número 14 mil 670.

815 ⋅ 18 = .14670

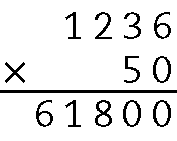
Algoritmo usual da multiplicação. 1 mil 236 vezes 50. Na primeira linha o número 1 mil 236. Abaixo, à esquerda, o sinal de multiplicação, à direita o numero 50, alinhado ordem a ordem ao número 1 mil 236. Abaixo, traço horizontal. Abaixo, o número 61 mil 800.

.1236 ⋅ 50 = .61800

11. a) 18 ⋅ 10 = 180

b) 92 ⋅ 100 = .9200

c) 112 ⋅ 10 = .1120

d) 310 ⋅ 100 = .31000

e) 15 ⋅ .1000 = .15000

f) .1020 ⋅ 10 = .10200

12.

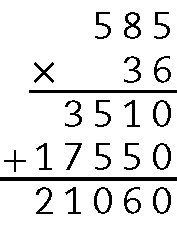
Algoritmo usual da multiplicação. 585 vezes 36. Na primeira linha o número 585. Abaixo, à esquerda, o sinal de multiplicação, à direita o numero 36, alinhado ordem a ordem ao número 585. Abaixo, traço horizontal. Abaixo, o número 3 mil 510. Abaixo, à esquerda sinal da adição, à direita o número 17 mil 550, alinhado ordem a ordem com 3 mil 510. Abaixo, traço horizontal. Abaixo, o número 21 mil 060.

Leandro vai pagar R 21.060,00vinte e um mil sessenta reais por essa motocicleta.

13. Como 1 dia tem 24 horas, calculamos 300 ⋅ 24 = .7200.

Logo, .7200 mililitros de água são desperdiçados em 1 dia.

14. a) 28 ⋅ 17 = 17 ⋅ 28

b) 22 ⋅ (10 ⋅ 13) = (22 ⋅ 10) ⋅ 13

c) 115 ⋅ (100 ⋅ 18) = (115 ⋅ 100) ⋅ 18

d) 54 ⋅ (21 ⋅ 12) = (54 ⋅ 21) ⋅ 12

e) 890 ⋅ 77 = 77 ⋅ 890

f) .5801 ⋅ 99 = 99 ⋅ .5801

15. a) 9 ⋅ (15 + 11) = 9 ⋅ 26 = 234 ou 9 ⋅ 15 + 9 ⋅ 11 = 135 + 99 = 234

b) 12 ⋅ (18 ‒ 5) = 12 ⋅ 13 = 156 ou 12 ⋅ 18 ‒ 12 ⋅ 5 = 216 ‒ 60 = 156

c) 15 ⋅ (10 + 12) = 15 ⋅ 22 = 330 ou 15 ⋅ 10 + 15 ⋅ 12 = 150 + 180 = 330

d) 10 ⋅ (27 ‒ 12) = 10 ⋅ 15 = 150 ou 10 ⋅ 27 ‒ 10 ⋅ 12 = 270 + 120 = 150

16. a)

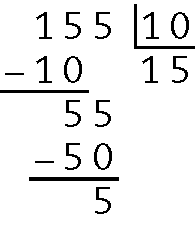
Algoritmo usual da divisão. 155 dividido por 10. na primeira linha, à esquerda, o número 155, à direita, na chave, o número 10. Abaixo, à esquerda, sinal da subtração, à direita o número 10 alinhado aos algarismos da ordem das dezenas e das centenas do número 155. Abaixo da chave, o número 15. Abaixo, traço horizontal. Abaixo, o número 55, alinhado ordem a ordem com 155. Abaixo, à esquerda sinal de subtração, à direita o número 50 alinhado ordem a ordem com 55. Abaixo, traço horizontal. Abaixo, o resto, 5.

Quociente 15 e resto 5.

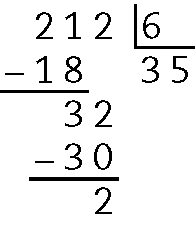
Algoritmo usual da divisão. 212 dividido por 6. na primeira linha, à esquerda, o número 212, à direita, na chave, o número 6. Abaixo, à esquerda, sinal da subtração, à direita o número 18 alinhado aos algarismos da ordem das dezenas e das centenas do número 212. Abaixo da chave, o número 35. Abaixo, traço horizontal. Abaixo, o número 32, alinhado ordem a ordem com 212. Abaixo, à esquerda sinal de subtração, à direita o número 30 alinhado ordem a ordem com 32. Abaixo, traço horizontal. Abaixo, o resto, 2.

Quociente 35 e resto 2.

Página setenta e um

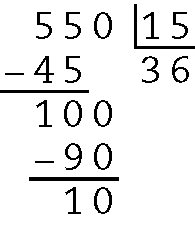
Algoritmo usual da divisão. 550 dividido por 15. na primeira linha, à esquerda, o número 550, à direita, na chave, o número 15. Abaixo, à esquerda, sinal da subtração, à direita o número 45 alinhado aos algarismos da ordem das dezenas e das centenas do número 550. Abaixo da chave, o número 36. Abaixo, traço horizontal. Abaixo, o número 100, alinhado ordem a ordem com 550. Abaixo, à esquerda sinal de subtração, à direita o número 90 alinhado ordem a ordem com 100. Abaixo, traço horizontal. Abaixo, o resto, 10.

Quociente 36 e resto 10.

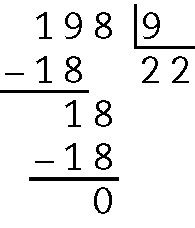
Algoritmo usual da divisão. 198 dividido por 9. Na primeira linha, à esquerda, o número 198, à direita, na chave, o número 9. Abaixo, à esquerda, sinal da subtração, à direita o número 18 alinhado aos algarismos da ordem das dezenas e das centenas do número 198. Abaixo da chave, o número 22. Abaixo, traço horizontal. Abaixo, o número 18, alinhado ordem a ordem com 198. Abaixo, à esquerda sinal de subtração, à direita o número 18 alinhado ordem a ordem com 18. Abaixo, traço horizontal. Abaixo, o resto, 0.

Quociente 22 e resto 0.

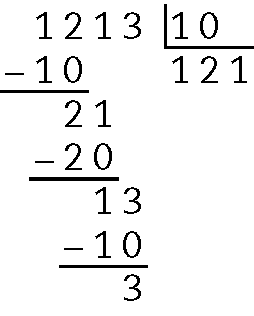
Algoritmo usual da divisão. 1 mil 213 dividido por 10. Na primeira linha, à esquerda, o número 1 mil 213, à direita, na chave, o número 10. Abaixo, à esquerda, sinal da subtração, à direita o número 10 alinhado aos algarismos da ordem das centenas e da unidade de milhar do número 1 mil 213. Abaixo da chave, o número 121. Abaixo, traço horizontal. Abaixo, o número 21, alinhado a ordem das dezenas e das centenas com 1 mil 213. Abaixo, à esquerda sinal de subtração, à direita o número 20 alinhado ordem a ordem com 21. Abaixo, traço horizontal. Abaixo, o número 13 alinhado ordem a ordem com 1 mil 213. Abaixo, à esquerda sinal de subtração, à direita o número 10, alinhado ordem a ordem com 13. Abaixo, traço horizontal Abaixo, o resto, 3.

Quociente 121 e resto 3.

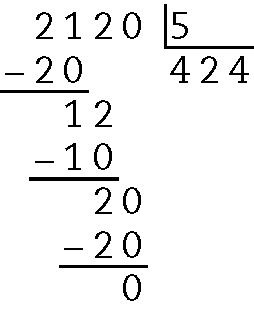
Algoritmo usual da divisão. 2 mil 120 dividido por 5. Na primeira linha, à esquerda, o número 2 mil 120, à direita, na chave, o número 5. Abaixo, à esquerda, sinal da subtração, à direita o número 20 alinhado aos algarismos da ordem das centenas e da unidade de milhar do número 2 mil 120. Abaixo da chave, o número 424. Abaixo, traço horizontal. Abaixo, o número 12, alinhado a ordem das dezenas e das centenas com 2 mil 120. Abaixo, à esquerda sinal de subtração, à direita o número 10 alinhado ordem a ordem com 12. Abaixo, traço horizontal. Abaixo, o número 20 alinhado ordem a ordem com 2 mil 120. Abaixo, à esquerda sinal de subtração, à direita o número 20, alinhado ordem a ordem com 20. Abaixo, traço horizontal Abaixo, o resto, 0.

Quociente 424 e resto 0.

17. Utilizando a relação fundamental da divisão, podemos encontrar os valores em cada caso:

a) 59 ‒ 8 ⋅ 7 = 59 ‒ 56 = 3

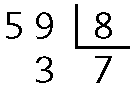
Algoritmo usual da divisão. O dividendo é 59, o divisor é 8, o quociente é 7 e o resto é 3.

b) 5 ⋅ 12 + 3 = 60 + 3 = 63

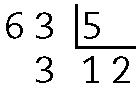
Algoritmo usual da divisão. O dividendo é 63, o divisor é 5, o quociente é 12 e o resto é 3.

c) 65 ‒ 5 ⋅ 12 = 65 ‒ 60 = 5

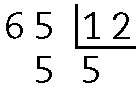
Algoritmo usual da divisão. O dividendo é 65, o divisor é 12, o quociente é 5 e o resto é 5.

d) 7 ⋅ 11 + 5 = 77 + 5 = 82

18. Fazemos .10800 : 12 para encontrar o valor de cada prestação:

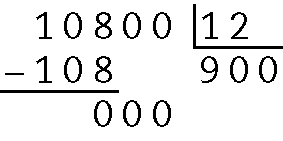
Algoritmo usual da divisão. 10 mil 800 dividido por 12. Na primeira linha, à esquerda o número 10 mil 800, à direita, na chave, o número 12. Abaixo, à esquerda sinal de subtração, à direita o número 108, alinhado aos algarismos da ordem das centenas, da unidade de milhar e da dezena de milhar do número 10 mil 800. Abaixo da chave, o número 900. Abaixo, traço horizontal. Abaixo, o resto 000.

Logo, Mariana vai pagar R$ 900,00novecentos reais em cada prestação.

19. a) 12 + 11 ⋅ 5 = 12 + 55 = 67

b) 15 ⋅ (12 + 9) ‒ 7 = 15 ⋅ 21 ‒ 7 = 315 ‒ 7 = 308

c) (98 ‒ 9 ⋅ 7) + (12 + 18 : 3) = (98 ‒ 63) + (12 + 6) =

= 35 + 18 = 53

20. a) 3² = 3 ⋅ 3 = 9

b) 2³ = 2 ⋅ 2 ⋅ 2 = 8

c) 9³ = 9 ⋅ 9 ⋅ 9 = 81 ⋅ 9 = 729

d) 10² = 10 ⋅ 10 = 100

e) 60⁰ = 1

f) 100¹ = 100

g) 30² = 30 ⋅ 30 = 900

h) 8³ = 8 ⋅ 8 ⋅ 8 = 64 ⋅ 8 = 512

21. a) Nove elevado ao quadrado ou nove elevado à segunda potência.

b) Dez elevado à quinta potência.

c) Doze elevado ao cubo ou doze elevado à terceira potência.

d) Cinco elevado à quarta potência.

22. a) 700 = 7 ⋅ 10²

b) .380000 = 38 ⋅ 10⁴

c) .45000 = 45 ⋅ 10³

23. a) 5² = 25; 6² = 36

b) 13² = 169; 14² = 196; 15² = 225

24. 2¹⁰ = .1024; 2¹⁰ : 2 = 2⁹ = 512;

2¹⁰= .1024; 2¹⁰ ⋅ 2 = 2 ¹¹ = .2048;

25. a) 115 ‒ (5² ⋅ 2 + 2³) = 115 ‒ (25 ⋅ 2 + 8) =

= 115 ‒ (50 + 8) = 115 ‒ 58 = 57

b) {148 ‒ 3 ⋅ [3³ + 18 : (3² + 9)]} ⋅ 2³ =

= {148 ‒ 3 ⋅ [27 + 18 : (9 + 9)]} ⋅ 8 = = {148 ‒ 3 ⋅ [27 + 18 : 18]} ⋅ 8 = = {148 ‒ 3 ⋅ [27 + 1]} ⋅ 8 = {148 ‒ 3 ⋅ 28} ⋅ 8 = = {148 ‒ 84} ⋅ 8 = 64 ⋅ 8 = 512

26. a) 600

b) 900

c) 890

CAPÍTULO 3 – FIGURAS GEOMÉTRICAS ESPACIAIS

Trocando ideias – página 74

• Pirâmide, prisma e esfera, respectivamente.

• Resposta pessoal. Em sites, folhetos, revistas e outras fontes, podem-se encontrar diferentes imagens que se assemelham a figuras geométricas espaciais.

Poliedros – página 76

Número de faces (F)	Número de vértices (V)	Número de arestas (A)
5	5	8
8	12	18
5	6	9

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180

×	2	5	7	9	12	15
1	2	5	7	9	12	15
3	6	15	21	27	36	45
5	10	25	35	45	60	75
7	14	35	49	63	84	105
10	20	50	70	90	120	150
12	24	60	84	108	144	180