Parte 2
|
Sólido |
V + F |
A + 2 |
|---|---|---|
|
|
5 + 5 = 10 |
8 + 2 = 10 |
|
|
8 + 12 = 20 |
18 + 2 = 20 |
|
|
5 + 6 = 11 |
9 + 2 = 11 |
• A regularidade observada é que V + F = a + 2.
• A regularidade observada é válida para todos os sólidos.
Veja que interessante – página 78
Espera-se que os estudantes respondam que sim, pois todas as suas faces têm o mesmo número de arestas regulares e todos os vértices são formados pelo encontro do mesmo número de arestas.
Atividades – página 79
1. a) Esfera.
b) Cone.
c) Cilindro.
d) Prisma.
e) Prisma.
f) Pirâmide.
2. Exemplos de resposta:
a) Ambos são sólidos geométricos e possuem duas bases paralelas congruentes; porém o prisma é um poliedro e o cilindro é um corpo redondo.
b) Ambos são sólidos geométricos e possuem uma única base; porém a pirâmide é um poliedro e o cone é um corpo redondo.
3. a) 5 faces, 8 arestas e 5 vértices.
b) 6 faces, 12 arestas e 8 vértices.
4. O movimento do pirulito remete à imagem de uma esfera.
5. a) Há 5 faces, 9 arestas e 6 vértices.
b) A base desse prisma é representada por um triângulo.
6. a)
|
Poliedro regular |
Número de vértices |
Número de faces |
Número de arestas |
|---|---|---|---|
|
Tetraedro |
4 |
4 |
6 |
|
Hexaedro |
8 |
6 |
12 |
|
Octaedro |
6 |
8 |
12 |
|
Dodecaedro |
20 |
12 |
30 |
|
Icosaedro |
12 |
20 |
30 |
b) Podemos conferir se a relação é válida, usando os dados do quadro anterior e organizando um novo quadro:
|
Poliedro regular |
V + F |
A + 2 |
|---|---|---|
|
Tetraedro |
4 + 4 = 8 |
6 + 2 = 8 |
|
Hexaedro |
8 + 6 = 14 |
12 + 2 = 14 |
|
Octaedro |
6 + 8 = 14 |
12 + 2 = 14 |
|
Dodecaedro |
20 + 12 = 32 |
30 + 2 = 32 |
|
Icosaedro |
12 + 20 = 32 |
30 + 2 = 32 |
A relação de Euler é válida para todos os poliedros do quadro, pois, em cada caso, o número de faces adicionado ao número de vértices é igual ao número de arestas mais 2 (V + F = a + 2).
7. Para encontrar o total de peças, podemos fazer 16 ⋅ 16 = 256.
Portanto, foram utilizadas duzentas e cinquenta e seis peças nessa construção.
Atividades – Página 81
8. Resposta pessoal. Espera-se que os estudantes percebam que há mais de uma maneira de representar a planificação.
9. Alternativa c.
10. As figuras dos itens a, c e d são planificações de um cubo.
Exemplo de resposta:

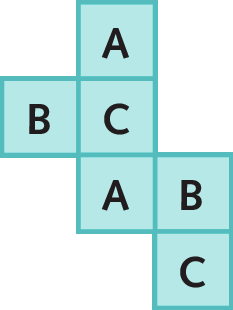
11. a)
b)
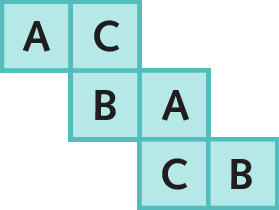
c)
12. Não, pois os poliedros regulares têm todas as faces iguais e, na pirâmide citada, a base é pentagonal (5 lados) e as faces laterais são triangulares.
13. Respostas pessoais. Espera-se que os estudantes elaborem perguntas que envolvam características dos poliedros e contagem de seus elementos.
Resolvendo em equipe – página 82
Interpretação e identificação dos dados
umApenas uma dimensão foi diretamente identificada: 24 centímetros.
doisNão todas, é possível identificar apenas mais uma dimensão, que é indicada de maneira indireta por 90 centímetros.
Plano de resolução
• Se chamarmos de a a medida da largura da caixa, teremos que: 24 + 24 + a = 90. Como 90 ‒ 24 ‒ 24 = 42, então a medida do comprimento da largura da caixa é 42 centímetros.
Resolução
Sabendo que a soma das medidas da altura, comprimento e largura pode ser, no máximo, igual a 115 centímetros e como já conhecemos duas dimensões, podemos chamar de x a medida de comprimento desconhecida, assim:
x + 42 + 24 = 115
Como 115 ‒ 42 ‒ 24 = 73 ‒ 24 = 49, concluímos que o valor máximo para x é 49 centímetros.
Alternativa e.
Revisão dos conteúdos deste capítulo – Página 83
1. Das figuras apresentadas, apenas o cilindro apresenta superfície que não é plana. Portanto, o único que não representa um poliedro.
Alternativa d.
2. a)
|
Número de faces |
Número de arestas |
Número de vértices |
|
|---|---|---|---|
|
Figura 1 |
8 |
18 |
12 |
|
Figura 2 |
7 |
12 |
7 |
|
Figura 3 |
6 |
12 |
8 |
b) Figura 1: base hexagonal; Figura 2: base hexagonal; Figura 3: base quadrangular.
3. a) Prisma de base hexagonal.
b) Cilindro.
c) Octaedro.
d) Prisma de base triangular.
É hora de extrapolar – páginas 84 e 85
1. a) O título é “Resposta rápida”.
b) Há dois personagens: o tucano e o macaco bugio.
c) Sobre o código QR code.
d) A frase apresentada é: “Isso não é um labirinto, Caco! É um QR code”.
2. Resposta pessoal. Espera-se que os estudantes realizem pesquisas em fontes confiáveis para encontrar as respostas.
Uma sugestão: https://oeds.link/hWy7AP. Acesso em: 13 junho 2022.
3. Exemplo de resposta:
O QR code consegue armazenar mais informações incluindo links, coordenadas geográficas e texto. Enquanto o código de barras armazena uma sequência numérica.
O código de barras é lido por um equipamento específico, enquanto o QR code pode ser lido pela câmera de celular.
4. Quadro 1: “Eu vou adivinhar o número que você está pensando”; “3”; “Essa eu quero ver.”
Quadro 2: “Você pensou no 3.”; “Que demais! Você é mágico?”
Quadro 3: “Não, eu usei um aplicativo para ler QR code.”; “Você acabou de perder um fã.”
• O número pensado e descoberto foi o 3.
5. Resposta pessoal. Espera-se que os estudantes elaborem um problema e, em seguida, usem um aplicativo que crie QR code com o texto do problema, e outro com a resposta.
8. Respostas pessoais. Espera-se que, durante o debate realizado pelos estudantes, eles façam pesquisas sobre a existência de produtos similares e se o produto tem relevância social.
9. Resposta pessoal.
10. Projeto pessoal. Apresentação e análise de embalagem com QR code.
11. Resposta pessoal.
12. Respostas pessoais.
13. Resposta pessoal.
UNIDADE 2
CAPÍTULO 4 – IGUALDADES E DESIGUALDADES
Trocando ideias – página 87
• É mais vantajoso comprar o chapéu na loja do bairro. A igualdade que representa a economia é 42 ‒ 30 = 12, logo Vera economizaria R$ 12,00doze reais.
• Resposta pessoal. Espera-se que os estudantes tenham a oportunidade de relatar situações em que observem a importância de pesquisar preços.
Atividades – página 88
1. a) Oito mais três é igual a onze.
b) Trinta e dois é maior que vinte dividido por dez.
c) Vinte e três é maior ou igual a doze mais oito.
d) Três vezes quatro é menor ou igual a três vezes cinco.
2. a) 5 < 9 é verdadeira
b) 7 ⋅ 2 ⩽ 7 ⋅ 3 é verdadeira, pois 14 ⩽ 21
c) 6 + 3 ≠ 9 é falsa, pois 6 + 3 = 9
d) 22 ‒ 10 > 12 é falsa, pois 22 ‒ 10 = 12
3. a) Como 10 + 2 = 12 e 6 + 3 + 2 + 1 = 12, então podemos afirmar que:
10 + 2 = 6 + 3 + 2 + 1 ou
10 + 2 ⩽ 6 + 3 + 2 + 1 ou
10 + 2 ⩾ 6 + 3 + 2 + 1
b) Como 4 ⋅ 5 ⋅ 6 = 120 e 6 + 7 + 8 = 21, então podemos afirmar que:
4 ⋅ 5 ⋅ 6 > 6 + 7 + 8 ou
4 ⋅ 5 ⋅ 6 ⩾ 6 + 7 + 8
c) Como 32 ⋅ 22 = 9 ⋅ 4 = 36 e 32 + 22 = 9 + 4 = 13, então podemos afirmar que:
32 ⋅ 22 ⩾ 32 + 22 ou
32 ⋅ 22 > 32 + 22
d) Como 2 3 ‒ 2 2 = 8 ‒ 4 = 4, então podemos afirmar que:
23 ‒ 22 ⩽ 5 ou
23 ‒ 22 < 5
Atividades – páginas 89 e 90
4. a) Afirmação falsa, pois, se adicionarmos 1 apenas ao 2º membro, vamos desequilibrar essa igualdade.
Por exemplo:
6 + 5 = 11 (partindo de uma sentença verdadeira)
6 + 5 = 11 + 1 (adicionando 1 apenas no 2º membro)
11 ≠ 12
b) Afirmação verdadeira, pois manteremos o equilíbrio ao subtrair o mesmo número dos dois membros.
Por exemplo:
6 + 5 = 11 (partindo de uma sentença verdadeira)
6 + 5 ‒ 1 = 11 ‒ 1 (subtraindo 1 de cada um dos membros)
10 = 10 (chegamos a uma sentença verdadeira)
c) Afirmação falsa, pois, se adicionarmos 2 ao 1º membro e 3 ao 2º membro, vamos desequilibrar essa igualdade.
6 + 5 = 11 (partindo de uma sentença verdadeira)
6 + 5 + 2 = 13 e 11 + 3 = 14 (adicionando 2 ao 1º membro e 3 ao 2º membro)
13 ≠ 14 (chegamos a uma sentença falsa)
5. a) 2 + 3 = 10 ‒ 5
2 + 3 + 5 = 10 ‒ 5 + 5
5 + 5 = 5 + 5
10 = 10
b) 14 ‒ 5 = 3 + 3 + 3
14 ‒ 5 ‒ 2 = 3 + 3 + 3 ‒ 2
9 ‒ 2 = 9 ‒ 2
7 = 7
c) 21 ‒ 10 = 22 ‒ 11
21 ‒ 10 + 3 = 22 ‒ 11 + 3
11 + 3 = 11 + 3
14 = 14
d) 13 + 2 = 6 + 6 + 3
13 + 2 ‒ 3 = 6 + 6 + 3 ‒ 3
15 ‒ 3 = 12 + 3 ‒ 3
12 = 15 ‒ 3
12 = 12
6. a) 1 + 2 + 3 = 3 + 3
4 ⋅ (1 + 2 + 3) = 4 ⋅ (3 + 3)
4 + 8 + 12 = 12 + 12
12 + 12 = 24
24 = 24
b) 10 + 20 = 30
(10 + 20) : 10 = 30 : 10
10 : 10 + 20 : 10 = 3
1 + 2 = 3
3 = 3
c) 12 ‒ 6 = 2 ⋅ 3
2 ⋅ (12 ‒ 6) = 2 ⋅ (2 ⋅ 3)
2 ⋅ 6 = 2 ⋅ 6
12 = 12
d) 3 + 3 + 3 = 18 ‒ 9
(3 + 3 + 3) : 3 = (18 ‒ 9) : 3
9 : 3 = 9 : 3
3 = 3
7. Exemplo de resposta:
Antes do aniversário: 3 + 2 + 2 = 7
Depois do aniversário: 2 ⋅ (3 + 2 + 2) = 2 ⋅ 7 = 14
Atividades – página 92
8. a) Desenho:
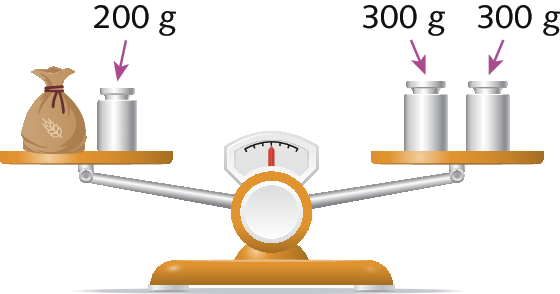
Sentença matemática:

+ 200 = 300 + 300
b) Resolvendo a sentença matemática do item anterior:

+ 200 = 300 + 300

+ 200 ‒ 200 = 300 + 300 ‒ 200

= 600 ‒ 200

= 400
Logo, a medida de massa do pacote de farinha é 400 gramas.
9. a)

‒ 10 = 25

‒ 10 + 10 = 25 + 10

= 35
Logo, havia 25 bolinhas no saquinho.
b) 3 ⋅

+ 1 = 7
3 ⋅

+ 1 ‒ 1 = 7 ‒ 1
3 ⋅

= 6
(3 ⋅

) : 3 = 6 : 3

= 2
O número é 2.
10. a)

+ 10 = 15

+ 10 ‒ 10 = 15 ‒ 10

= 5
O número desconhecido é 5.
b) 10 ‒ 2 =

‒ 2
10 ‒ 2 + 2 =

‒ 2 + 2
8 + 2 =

10 =

O número desconhecido é 10.
c) 2 ⋅

+ 3 = 10 + 5
2 ⋅

+ 3 ‒ 3 = 10 + 5 ‒ 3
2 ⋅

= 15 ‒ 3
(2 ⋅

) : 2 = (15 ‒ 3) : 2

= 12 : 2

= 6
O número desconhecido é 6.
d) 14 ‒ 2 = 10 +

14 ‒ 2 ‒ 10 = 10 +

– 10
12 ‒ 10 =

2 =

O número desconhecido é 2.
e) 31 = 3 ⋅

‒ 8
31 + 8 = 3 ⋅

‒ 8 + 8
39 = 3 ⋅

39 : 3 = (3 ⋅

) : 3
13 =

O número desconhecido é 13.
f) 3 ⋅ (9 ‒ 2) = 3 ⋅

3 ⋅ 7 = 3 ⋅

21 : 3 = ( 3 ⋅

) : 3
7 =

O número desconhecido é 7.
11. Exemplo de resolução:
Se chamarmos de

a pontuação de Vítor, a pontuação de Paula será 2 ⋅

. A sentença que expressa essa situação é:

+ 2

= 300
Resolvendo:
3

= 300
(3

) : 3 = 300 : 3

= 100
Vítor fez 100 pontos e Paula fez 200 pontos.
12. Resposta pessoal. Exemplo de problema que pode ser elaborado:
Alex pesquisou o preço de um agasalho e encontrou duas marcas: a e B. O agasalho da marca a custa R$ 150,00cento e cinquenta reais, que é R$ 12,00doze reais mais caro que o da marca B. Descubra quanto custa o agasalho da marca B.
Exemplo de resolução:
Se o preço da marca B for representado por

, temos a seguinte igualdade:
150 =

+ 12
Resolvendo:
150 ‒ 12 =

+ 12 ‒ 12
138 =

Logo, o agasalho da marca B custa R$ 138,00cento e trinta e oito reais.
13. Resposta pessoal. Exemplo de problema que pode ser elaborado:
Maurício colheu caquis e distribuiu igualmente entre seus 4 amigos. Cada amigo recebeu 10 caquis e ainda sobram 3 caquis para Maurício. Quantos caquis Maurício colheu?
Exemplo de resolução:
Se o número de caquis colhidos for representado por

, teremos a seguinte igualdade:

= 4 ⋅ 10 + 3
Resolvendo:

= 40 + 3

= 43
Logo, ele colheu 43 caquis.
Atividades – página 94
14. a) 10 ‒ 3 > 4
10 ‒ 3 + 4 > 4 + 4
7 + 4 > 8
11 > 8
b) 24 : 2 ⩾ 6 + 6
24 : 2 ‒ 11 ⩾ 6 + 6 ‒ 11
12 ‒ 11 ⩾ 12 ‒ 11
1 ⩾ 1
c) 1 + 2 + 3 ⩽ 1 ⋅ 2 ⋅ 3
1 + 2 + 3 + 13 ⩽ 1 ⋅ 2 ⋅ 3 + 13
3 + 3 + 13 ⩽ 2 ⋅ 3 + 13
6 + 13 ⩽ 6 + 13
19 ⩽ 19
d) 3 + 3 + 3 > (21 ‒ 7) : 2
3 + 3 + 3 ‒ 7 > (21 ‒ 7) : 2 ‒ 7
9 ‒ 7 > 14 : 2 ‒ 7
2 > 7 ‒ 7
2 > 0
15. Uma possibilidade de resposta:
Antes: 15 + 20 > 15
Depois: 15 + 20 + 10 > 15 + 10
16. a) 2 ⋅ (3 + 4) ⩾ 2 ⋅ (1 + 2)
2 ⋅ 12 ⩾ 2 ⋅ 3
24 ⩾ 6
Verdadeira
b) 3 ⋅ 4 < (1 + 2) ⋅ (2 + 2)
12 < 3 ⋅ 4
12 < 12
Falsa
c) 28 : 14 ⩾ 14 : 7
2 ⩾ 2
Verdadeira
d) 35 : 7 < 49 : 7
5 < 7
Verdadeira
17. a) 4 + 1 ≠ 6
4 ⋅ (4 + 1) ≠ 4 ⋅ 6
4 ⋅ 5 ≠ 24
20 ≠ 24
b) 28 > 14
28 : 14 > 14 : 14
2 > 1
c) 19 ‒ 10 ⩽ 3 ⋅ 3
5 ⋅ (19 ‒ 10) ⩽ 5 ⋅ (3 ⋅ 3)
5 ⋅ 9 ⩽ 5 ⋅ 9
45 ⩽ 45
d) 9 + 6 + 3 > 1 + 2 + 3
(9 + 6 + 3) : 3 > (1 + 2 + 3) : 3
(18) : 3 > (6) : 3
6 > 2
18. Antes: 5 + 5 + 5 + 10 < 20 + 10
Depois: 5 + 5 + 5 + 10 + (20 : 2) < 20 + 10 + (20 : 2)
19. a) Podemos observar que:
• na primeira pesagem o prato da esquerda tem medida de massa total 300 gramas (100 + 200 = 300). Portanto, a diferença entre a medida da massa dos dois pratos é 50 gramas (300 ‒ 250 = 50)
• o prato da esquerda nas duas situações tem as mesmas massas.
• Logo, o pêso metálico tem medida de massa 50 gramas.
b) Representações por sentenças:
1ª pesagem: 100 + 200 > 250
2ª pesagem: 100 + 200 = 250 + 50
c) A balança ficará desequilibrada, com maior massa no prato da esquerda.
100 + 200 + 50 > 250 + 50
Revisão dos conteúdos deste capítulo – página 95
1. a) 12 > 3 + 15 12 > 18 Sentença falsa
b) 7 ⋅ 12 = 12 ⋅ 7 84 = 84 Sentença verdadeira
c) 15 ‒ 5 ≠ 105 ‒ 95 10 = 10 Sentença falsa
d) 127 ⩽ 150 ‒ 16 127 ⩽ 134 Sentença verdadeira
Logo, as sentenças verdadeiras são dos itens b e d.
2. a) Como 25 + 5 = 30 e 12 + 5 + 15 = 32, então podemos afirmar que:
25 + 5 ⩽ 12 + 5 + 15 ou
25 + 5 < 12 + 5 + 15
b) Como 7 ⋅ 10 = 70 e 140 : 2 = 70, então podemos afirmar que:
7 ⋅ 10 = 140 : 2 ou
7 ⋅ 10 ⩽ 140 : 2 ou
7 ⋅ 10 ⩾ 140 : 2
c) Como 12 ⋅ 5 + 50 = 60 + 50 = 110 e 150 ‒ 200 : 2 + 50 = 150 ‒ 100 + 50 = 50 + 50 = 100, então podemos afirmar que:
12 ⋅ 5 + 50 ⩾ 150 ‒ 200 : 2 + 50 ou
12 ⋅ 5 + 50 > 150 ‒ 200 : 2 + 50
3. a) 12 ‒ 10 = 45 ‒ 43
12 ‒ 10 + 25 = 45 ‒ 43 + 25
2 + 25 = 2 + 25
27 = 27
b) 30 + 11 = 56 ‒ 15
30 + 11 ‒ 12 = 56 ‒ 15 ‒ 12
41 ‒ 12 = 41 ‒ 12
29 = 29
c) 19 + 3 = 38 ‒ 16
9 ⋅ (19 + 3) = 9 ⋅ (38 ‒ 16)
9 ⋅ 22 = 9 ⋅ 22
198 = 198
d) 36 ‒ 18 = 12 + 6
(36 ‒ 18) : 6 = (12 + 6) : 6
18 : 6 = 18 : 6
3 = 3
4. a) Se representarmos o número desconhecido por

, temos: temos:

‒ 18 = 46
Resolvendo:

‒ 18 + 18 = 46 + 18

= 64
Juliano tinha 64 figurinhas.
b) Se representarmos o número desconhecido por

, temos:
2 ⋅

+ 12 = 58
Resolvendo:
2 ⋅

+ 12 ‒ 12 = 58 ‒ 12
(2 ⋅

) : 2 = 46 : 2

= 23
Logo, o número é 23.
5. Representando a situação com uma sentença matemática, temos:
400 + 400 + 800 = 50 + ?
.1600 ‒ 50 = 50 + ? ‒ 50
.1550 = ?
Logo, a medida da massa da caixa azul é .1550 gramas.
6. a)

+ 16 = 112

+ 16 ‒ 16 = 112 ‒ 16

= 96
b) 4 ⋅ 10 +

= 52
40 +

‒ 40 = 52 ‒ 40

= 12
c) 15 : 3 + 28 = 14 + 19 ⋅

5 + 28 = 14 + 19 ⋅

33 = 14 + 19 ⋅

33 ‒ 14 = 14 + 19 ⋅

‒ 14
19 = 19 ⋅

19 : 19 = (19 ⋅

) : 19
1 =

7. Se chamarmos de

o valor que Felipe recebeu, o valor recebido por Jorge será 2 ⋅

. A sentença que expressa essa situação é:

+ 2

= 270.
Resolvendo:
3

= 270
(3

) : 3 = 270 : 3

= 90
Se Felipe recebeu R$ 90,00noventa reais e Jorge recebeu o dôbro disso, então Jorge recebeu R$ 180,00cento e oitenta reais.
8. a) 10 ⋅ (3 + 5) = 10 ⋅ 8 = 80 e 12 ⋅ (2 + 3) = 12 ⋅ 5 = 60
Logo, 10 ⋅ (3 + 5) ⩾ 12 ⋅ (2 + 3) é verdadeira, pois 80 ⩾ 60.
b) 10 + 2 ⋅ 5 = 10 + 10 = 20 e (2 + 10) : 3 = 12 : 3 = 4
Logo, 10 + 2 ⋅ 5 ⩽ (2 + 3) : 3 é falsa, pois 20 > 4.
c) 36 : 2 ‒ 12 = 18 ‒ 12 = 6
6 2 ‒ 4 2 + 4 = 36 ‒ 16 + 4 = 20 + 4 = 24
Logo, 36 : 2 ‒ 12 ≠ 6 2 ‒ 4 2 + 4 é verdadeira, pois 6 ≠ 24.
9. Antes: 125 < 132
Depois: 125 + 25 < 132 + 25
CAPÍTULO 5 – MÚLTIPLOS E DIVISORES
Trocando ideias – página 96
• O esquema serve para verificar se um número é ou não múltiplo de 3.
• Verificando para cada número, temos:
7 : 3 tem resto igual a 1.
9 : 3 tem resto igual a 0.
23 : 3 tem resto igual a 2.
24 : 3 tem resto igual a 0.
22 : 3 tem resto igual a 1.
15 : 3 tem resto igual a 0.
33 : 3 tem resto igual a 0.
41 : 3 tem resto igual a 2.
São múltiplos de 3, os números 9, 15, 24 e 33.
Atividades – página 99
1. Calculando os cinco menores múltiplos de 17, temos:
0 ⋅ 17 = 0; 1 ⋅ 17 = 17; 2 ⋅ 17 = 34; 3 ⋅ 17 = 51 e 4 ⋅ 17 = 68.
Portanto, os cinco menores múltiplos de 17 são: 0, 17, 34, 51 e 68.
2. a) 46, 69, 92 e 115.
b) Esses são os quatro primeiros múltiplos de 23, com exceção do zero e dele próprio.
3. a) Como 7 ⋅ 7 = 49, então vamos encontrar os múltiplos de 7, a partir de 7 ⋅ 8.
8 ⋅ 7 = 56; 9 ⋅ 7 = 63; 10 ⋅ 7 = 70; 11 ⋅ 7 = 77; 12 ⋅ 7 = 84
Portanto, os múltiplos de 7 maiores que 50 e menores que 80 são: 56, 63, 70 e 77.
b) Como 10 ⋅ 16 = 160, então vamos encontrar os múltiplos de 16, a partir de 10 ⋅ 16.
10 ⋅ 16 = 160; 11 ⋅ 16 = 176; 12 ⋅ 16 = 192; 13 ⋅ 16 = 208
Portanto, os múltiplos de 16 compreendidos entre 151 e 201 são: 160, 176 e 192.
4. Resposta pessoal. Espera-se que os estudantes escolham números pares e ímpares para testar no fluxograma, de modo a encontrar os números múltiplos de 2, e os não múltiplos de 2.
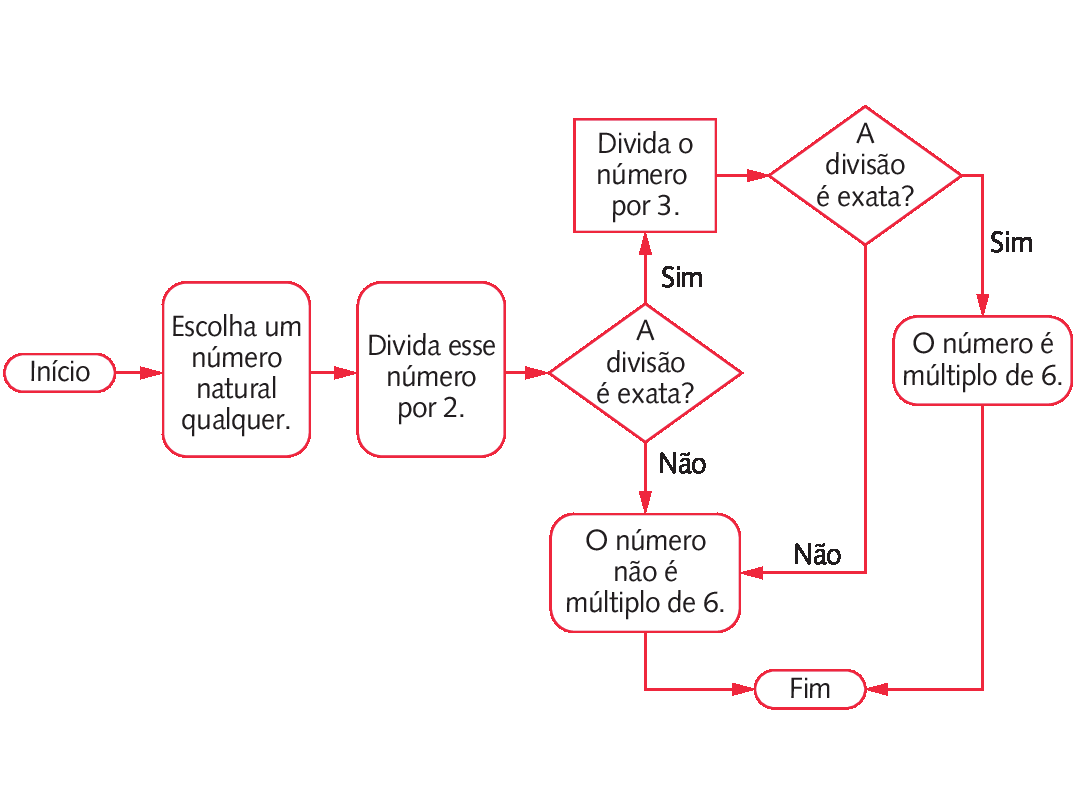
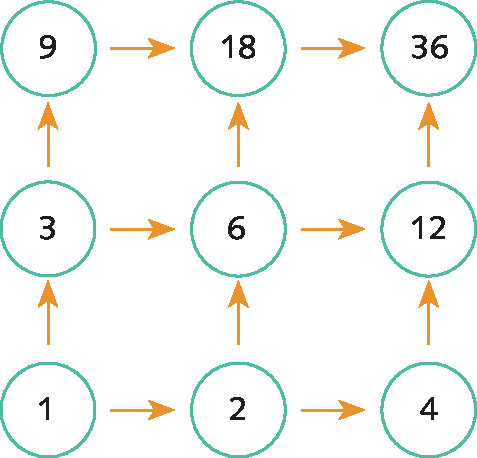
5. Resposta pessoal. Espera-se que os estudantes construam corretamente o fluxograma utilizando as figuras corretamente. Veja um exemplo para números múltiplos de 6.
6. a)
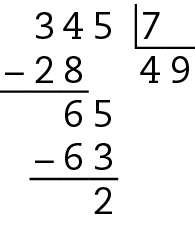
O número 45 não é múltiplo de 7, pois a divisão de 345 por 7 não é exata.
b)
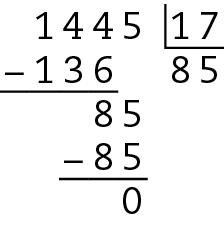
O número .1445 é múltiplo de 17, pois a divisão de .1445 por 17 é exata.
c)
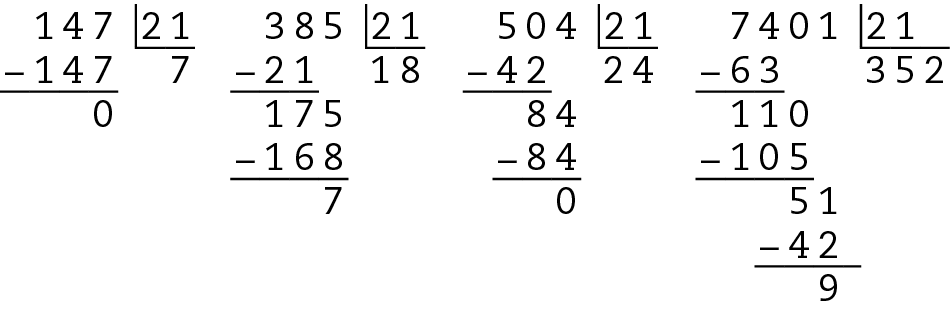
Os números 147 e 504 são múltiplos de 21, pois a divisão por 21 é exata.
d) Exemplo de resolução:
Podemos encontrar alguns múltiplos de 13 até chegar ou ultrapassar o 68:
0, 13, 26, 39, 65, 78
Então, o próximo múltiplo de 13 maior que 68 é o 78. Como 78 ‒ 68 = 10, precisamos adicionar 10 a 68 para obter um múltiplo de 13.
7. Primeiro verificamos se .3192 é múltiplo de 7.
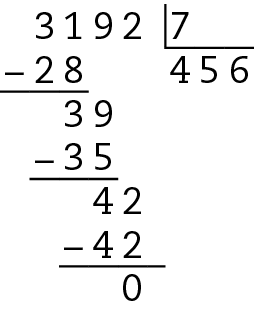
Sim, .3192 é múltiplo de 7.
Para encontrarmos o próximo múltiplo de 7, podemos calcular: .3192 + 7 = .3199.
8. Entre 300 e 320:
Múltiplo de 13: 312, pois 24 ⋅ 13 = 312
Múltiplo de 17: 306, pois 18 ⋅ 17 = 306
Múltiplo de 19: 304, pois 16 ⋅ 19 = 304
Aproximando para um múltiplo de 10, teremos, nessa ordem: 310, 310 e 300.
9. a) Verdadeira, pois .1856 = 928 ⋅ 2.
b) Verdadeira, pois 91 = 13 ⋅ 7.
c) Falsa, pois 169 : 3 tem resto igual a 1.
d) Falsa, pois 100 é múltiplo de 2 (100 = 50 ⋅ 2), mas não é múltiplo de 3 (já que 100 : 3 tem resto igual a 1).
e) Verdadeira, pois 210 = 105 ⋅ 2; 210 = 70 ⋅ 3; 210 = 42 ⋅ 5;
210 = 30 ⋅ 7.
f) Verdadeira, pois .123456 = .41152 ⋅ 3.
g) Verdadeira, pois .123456 = .1929 ⋅ 64.
h) Falsa, pois .123456 : 5 tem resto igual a 1.
10. Respostas pessoais. Exemplo de resposta:
a) Determine 5 menores múltiplos de 38 que são maiores que 100. (114, 152, 190, 228, 266).
b) Estão corretos, pois 114 = 3 ⋅ 38; 152 = 4 ⋅ 38;
190 = 5 ⋅ 38; 228 = 6 ⋅ 38 e 266 = 7 ⋅ 38.
Atividades – páginas 101 e 102
11. a.
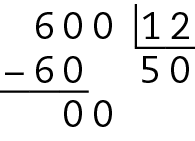
b)
c)
d)
e)
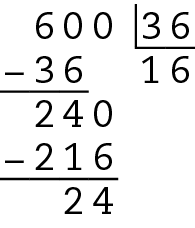
f)
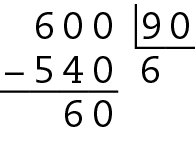
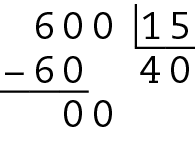
Logo, 600 é divisível pelos números dos itens a, b, d.
12. a) Vejamos diferentes maneiras de escrever 30 por meio de um produto de dois números naturais:
1 ⋅ 30
2 ⋅ 15
3 ⋅ 10
5 ⋅ 6
Portanto, os fatores naturais de 30 são: 1, 2, 3, 5, 6, 10, 15 e 30.
b) Vejamos diferentes maneiras de escrever 72 por meio de um produto de dois números naturais:
1 ⋅ 72
2 ⋅ 36
3 ⋅ 24
4 ⋅ 18
6 ⋅ 12
8 ⋅ 9
Portanto, os fatores naturais de 72 compreendidos entre 10 e 30 são: 12, 18 e 24.
c) Os divisores de 40 são: 1, 2, 4, 5, 8, 10, 20, 40.
Assim, os divisores ímpares de 40 são: 1 e 5.
d) Os divisores pares de 40 são: 2, 4, 8, 10, 20 e 40.
13. a) O maior divisor de um número é o próprio número.
b) O menor divisor é de qualquer número é o 1.
c) Sim, o zero só não divisível por ele mesmo, pois não existe divisão por zero.
d) São os números ímpares que deixam resto 1 quando divididos por 2.
e) São os números pares que deixam resto 0 quando divididos por 2.
14. a) O maior número par de 3 algarismos é o 998.
b) Os divisores de 32 são: 1, 2, 4, 8, 16 e 32. Então os três maiores são 8, 16 e 32.
c) Exemplo de resolução:
Considerando que o maior número de 3 algarismos é o 999, podemos fazer:
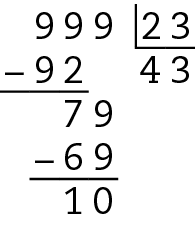
Logo, temos que 999 não é divisível por 23, mas 23 ⋅ 43 = 989 é divisível por 23 e é o maior possível número de 3 algarismos divisível por 23.
15. Uma possível resolução:
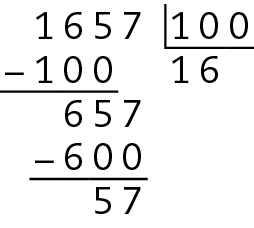
Como o resto da divisão de .1657 por 100 é 57, devemos encontrar quanto falta para completar 100, ou seja, 100 ‒ 57 = 43. Logo, o menor número a ser adicionado é 43.
16. a) Como .1154 = 2 ⋅ 577, podemos dizer que 2 é divisor de .1154.
Logo, a afirmação é verdadeira.
b)
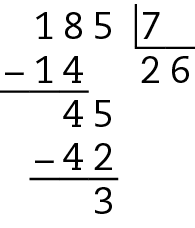
Como a divisão não é exata, a afirmação é falsa.
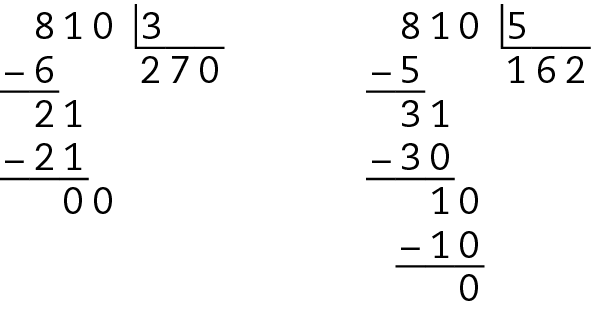
c)
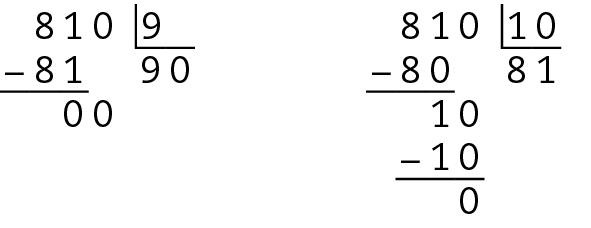
Todas essas divisões têm resto igual a zero. Portanto, a afirmação é verdadeira.
d)
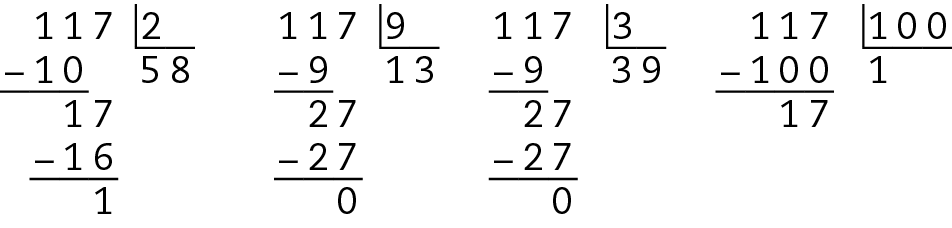
Observando os restos de cada divisão, podemos dizer que 3 e 9 são fatores de 117, mas 2 e 100 não. Portanto, a afirmação é falsa.
e)
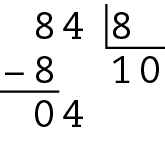
Como a divisão não é exata, 8 não é divisor de 84. Portanto, a afirmação é falsa.
f)
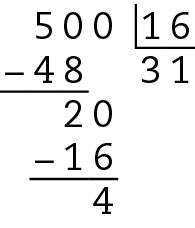
Como a divisão não é exata, 16 não é divisor de 500. Portanto, a afirmação é falsa.
g)
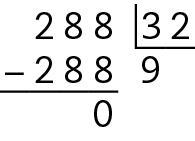
Como a divisão é exata, 32 é fator de 288. Portanto, a afirmação é verdadeira.
h)
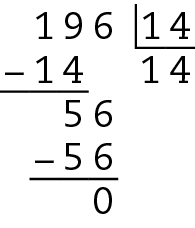
Como a divisão é exata, 14 é divisor de 196. Portanto, a afirmação é verdadeira.
17. Resposta pessoal. Exemplo de resposta:
Esses registros sugerem que, ao escrever os divisores de um número em ordem crescente, o produto dos números equidistantes resulta neste próprio número. Quando há um número ímpar de divisores, o divisor que fica bem ao centro nessa sequência, quando multiplicado por ele mesmo, resultará no número o qual está se buscando os divisores.
18.
19. a) Primeiro verificamos as seguintes divisões (considerando as dimensões do chão e do piso cerâmico):

Isso significa que para cobrir:
• o comprimento desse chão (que tem 300 centímetros) precisaremos de 4 fileiras de peças quadradas de 80 centímetros, pois apenas 3 não bastarão.
• a largura desse chão (que tem 240 centímetros) precisaremos de 3 fileiras de peças quadradas de 80 centímetros.
Assim, o total de peças quadradas de 80 centímetros será 3 ⋅ 4 = 12 peças.
b) Considerando agora que a peça quadrada tem o comprimento do lado de medida 30 centímetros:

Como as duas divisões são exatas, não será preciso recortar nenhuma peça azul para revestir o chão.
c) Vamos testar as peças que ainda não foram usadas nos itens anteriores (verde e rosa):
A cerâmica verde tem o comprimento do lado medindo 60 centímetros.

A cerâmica rosa tem o comprimento do lado medindo 45 centímetros.

Ou seja, com peças verdes é possível cobrir o chão sem cortes, mas com as peças rosa isso não é possível.
Como visto no item b, com as cerâmicas de côr azul não precisa de cortes e no item a vimos que com peças amarelas precisamos de córte.
Como cada peça verde tem maior medida de área que a peça azul, será necessário menos cerâmica verde. Portanto, o piso deverá ser verde.
20.
|
Número perfeito |
496 |
|---|---|
|
Divisores próprios |
1, 2, 4, 8, 16, 31, 62, 124 e 248 |
|
Cálculo da soma dos divisores próprios |
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496 |
496 é um número perfeito.
Critério de divisibilidade por 3 – página 104
• Como os restos de uma divisão são sempre 0, 1 e 2, e .1951 dividido por 3 tem resto 1, .1952 dividido por 3 tem resto 2. E .1953 dividido por 3, tem resto 0.
• 1 + 9 + 5 + 2 = 10 + 7 = 17; 1 + 9 + 5 + 3 = 10 + 8 = 18
• .1952 não é divisível por 3, pois 17 não é divisível por 3; .1953 é divisível por 3, pois 18 é divisível por 3.
Critério de divisibilidade por 4 – página 104
• Espera-se que os estudantes respondam que as investigações sugerem que um número natural maior ou igual a 100 é divisível por 4 quando termina em 00 ou quando o número formado pelos seus dois últimos algarismos é divisível por 4.
Critério de divisibilidade por 6 – página 106
• Espera-se que os estudantes respondam que as investigações sugerem que um número natural é divisível por 6 quando é divisível por 2 e também por 3.
Critério de divisibilidade por 8 – página 107
• Espera-se que os estudantes respondam que as investigações sugerem que um número natural, maior ou igual a .1000, é divisível por 8 quando termina em 000 ou quando o número formado pelos seus três últimos algarismos é divisível por 8.
Critério de divisibilidade por 9 – página 108
• Espera-se que os estudantes respondam que as investigações sugerem que um número natural é divisível por 9 quando a soma dos seus algarismos é divisível por 9.
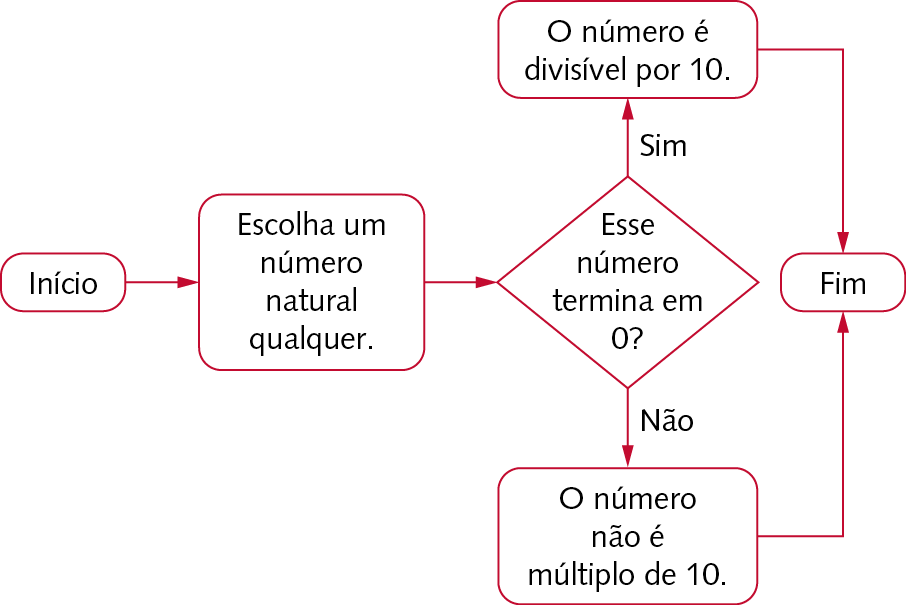
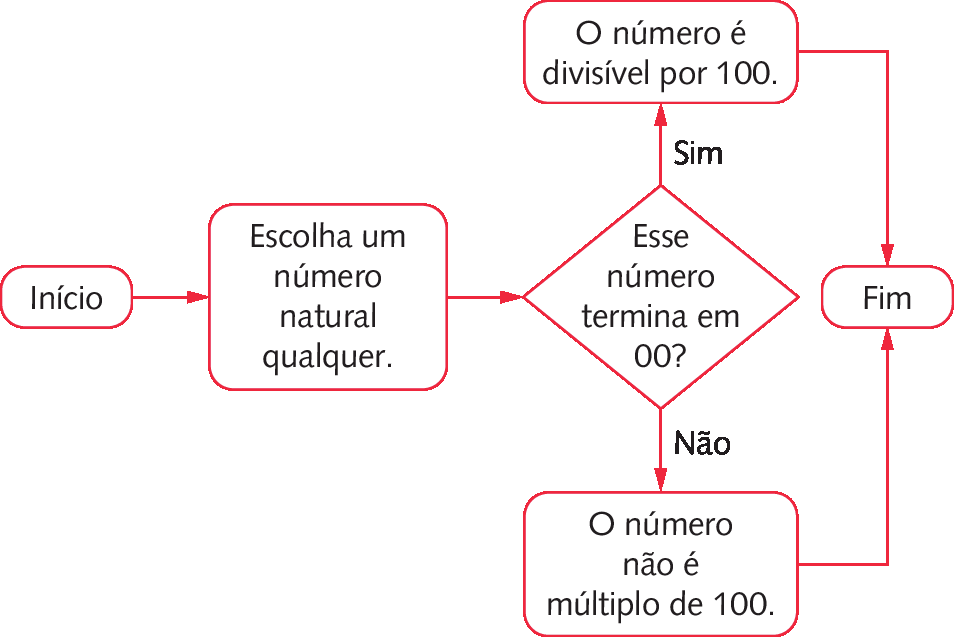
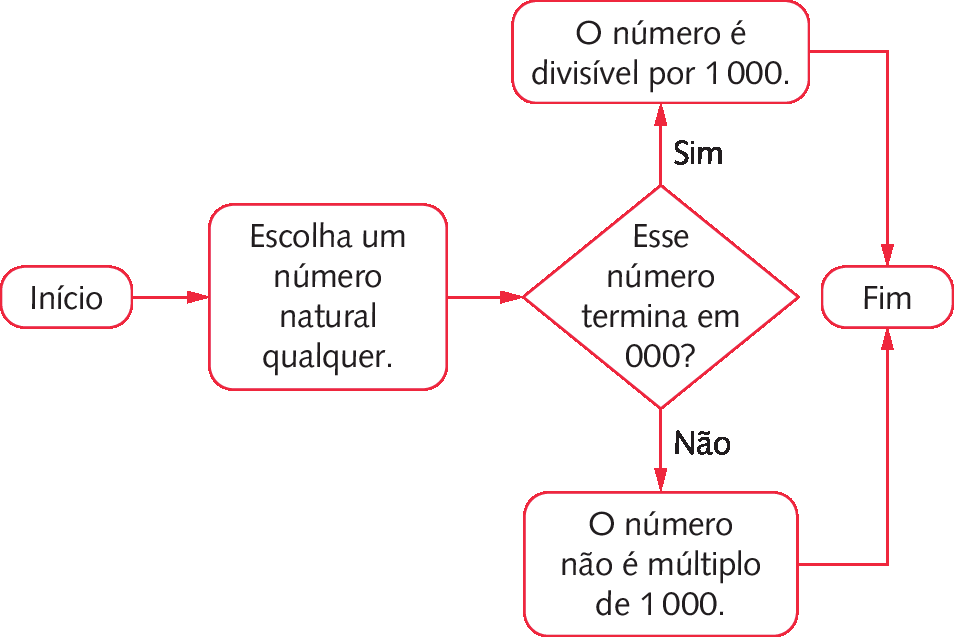
Critérios de divisibilidade por 10, 100 e .1000 – página 109
• Espera-se que os estudantes percebam que os números divisíveis por 10 terminam em 0, os números divisíveis por 100 terminam em 00 e os números divisíveis por .1000 terminam em 000.
• Um número natural é divisível por 10 se terminar em 0, é divisível por 100 se terminar em 00 e é divisível por .1000 se terminar em 000.
Atividades – páginas 109 e 110
21.
|
Divisores |
|||||
|---|---|---|---|---|---|
|
Números |
2 |
3 |
4 |
5 |
6 |
|
216 |
x |
x |
x |
x |
|
|
678 |
x |
x |
x |
||
|
745 |
x |
||||
|
1.224 |
x |
x |
x |
x |
|
|
3.206 |
x |
||||
22. Considerando que o menor número de 3 algarismos é o 100, vejamos para cada caso:
a) Para ser divisível por 2, basta ser par: 100.
b) Para ser divisível por 3, deve ter a soma dos algarismos divisível por 3, então 102 é divisível por 3, pois 1 + 0 + 2 = 3.
c) Para ser divisível por 4, deve terminar em 00, então 100 é divisível por 4.
d) Para ser divisível por 5, deve terminar em 5 ou 0, então 100 é divisível por 5.
e) Para ser divisível por 6, deve ser divisível por 2 e por 3, então 102 é par e é divisível por 3.
23. Para ser divisível por 2 e também por 5, deve terminar em 0. Então, os números 160, 420 e .5000 estão de acôrdo com essas condições. Ou seja, itens b, c, e.
24. a) Verdadeira, pois para ser divisível por 6 deve ser por 2 e também por 3.
b) Falsa, pois apenas os pares terminados em 0 são divisíveis por 5.
c) Verdadeira, pois apenas números pares são divisíveis por 2.
d) Verdadeira, pois todos os números divisíveis por 4 são pares.
Logo, são verdadeiras as afirmações: a, c, d.
25. Exemplos de resposta:
26. Espera-se que os estudantes observem que, para ser divisível por 2, basta verificarmos o último algarismo do número. Nesse caso, o último é 3, ou seja, o número é ímpar e nunca será divisível por 2, independentemente do algarismo que colocarmos no lugar de

.
27. a) Não é divisível por 5, pois termina em 6.
b) Observando o número 5

6, verificamos que a soma dos algarismos já conhecidos é igual a 11 (5 + 6 = 11). Assim, para termos um valor que seja divisível por 3, precisamos chegar aos valores: 12, 15 ou 18. E, para obter tais valores, 5 + 6 = 11). Assim, para termos um valor que seja divisível por 3, precisamos chegar aos valores: 12, 15 ou 18. E, para obter tais valores,

poderá ser: 1, 4 e 7.
Conferindo:
516 é divisível por 3: 5 + 1 + 6 = 12 e 12 é divisível por 3.
546 é divisível por 3: 5 + 4 + 6 = 15 e 15 é divisível por 3.
576 é divisível por 3: 5 + 7 + 6 = 18 e 18 é divisível por 3.
28. a) O maior número de três algarismos é o 999. Para ser divisível por 5, deve terminar em 0 ou 5. Então o número procurado é o 995.
b) O menor número de 3 algarismos é o 100. Para ser divisível por 2 e por 5, deve terminar em 0. Daí, teremos o número 1

0. Como a soma desses 3 algarismos deve ser um número divisível por 3, nessas condições o 120 é o menor número.
c) O maior número de três algarismos é o 999, ele é divisível por 3, mas não é por 4. Diminuindo e buscando o número divisível por 3 anterior a esse, teremos o 996. Como 96 é divisível por 4, 996 também é. Portanto, 996 é divisível por 3 e por 4.
29. Testando cada uma:
1500: não é bissexto, pois termina em 00 e não é divisível por 400.
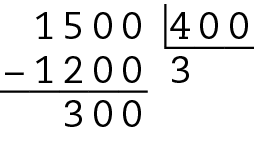
1554: não é bissexto, pois 54 não é divisível por 4, logo 1554 também não será.
1594: não é bissexto, pois 94 não é divisível por 4, logo 1594 também não será.
1764: é bissexto, pois 64 é divisível por 4.
Portanto, o único ano bissexto é 1764.
30. a) Para ser divisível por 2, tem que ser par. Então as possibilidades para

serão: 0, 2, 4, 6 e 8.
b) Como a soma dos algarismos conhecidos é 1 + 2 + 3 = 6, então para continuar sendo um número divisível por 3, as possibilidades para

serão: 0, 3, 6 e 9.
c) Para ser divisível por 4, o número 3

deverá ser divisível por 4, então as possibilidades para

serão: 2 e 6.
d) Para ser divisível por 5, deve terminar em 0 ou 5, então as possibilidades para

serão: 0 e 5.
e) Para ser divisível por 6, deve ser divisível por 2 e por 3. Usando as respostas anteriores (itens a e b), as possibilidades para

serão: 0 e 6.
31. a) Como 7 + 6 + 3 = 16, basta adicionar 2 para termos um número divisível por 3.
b) Como o número termina em 3, basta adicionar 2 para que termine em 5 e seja divisível por 5.
c) Para ser divisível por 2, podemos adicionar 1, 3, 5, 7, reticências
Para ser divisível por 3, podemos adicionar 2, 5, 8, reticências
Então o menor valor será adicionar 5.
32. O maior número de algarismos diferentes é o .9876, vamos usá-lo como ponto de partida:
a) .9876 é par, então é divisível por 2.
9 + 8 + 7 + 6 = 30 e 30 é divisível por 3, então .9876 é divisível por 3.
Logo, .9876 é divisível por 6 e é o número procurado.
b) Como não pode ser divisível por 3, mas deve ser divisível por 2, procuramos o par anterior a .9876, ou seja, .9874. (Observe que ele não é divisível por 3, já que 9 + 8 + 7 + 4 = 28 e 28 não é divisível por 3.
c) Como não deve ser divisível por 2, não pode ser par. Como deve ser divisível por 3, procuramos o número divisível por 3 anterior a .9876, que é o .9873.
d) É .9875, pois é ímpar e não divisível por 3.
33. O maior número tem o algarismo 9 em todas as casas, exceto a última que deve ser ocupada pelo zero: .999990.
34. Para ser divisível por 9, a soma dos algarismos deve ser um número divisível por 9.
Podemos testar:
44 soma 8, não divisível por 9
444 soma 12, não divisível por 9
.4444 soma 16, não divisível por 9
.44444 soma 20, não divisível por 9
.444444 soma 24, não divisível por 9
..4444444 soma 28, não divisível por 9
..44444444 soma 32, não divisível por 9
..444444444 soma 36, divisível por 9
Logo, o número é ..444444444.
35. a) 450 é divisível por 3, mas não é por 4.
660 é divisível por 3 e por 4.
768 é divisível por 3 e por 4.
860 não é divisível por 3, mas é por 4.
960 é divisível por 3 e por 4.
Logo, os números 660, 768 e 960 são divisíveis por 3 e por 4.
Esses números também são divisíveis por 12, pois:
660 = 12 ⋅ 55
768 = 12 ⋅ 64
960 = 12 ⋅ 80
Podemos dizer que números divisíveis por 3 e por 4 são também divisíveis por 12.
b) 450 é divisível por 3 e por 5.
660 é divisível por 3 e por 5.
768 é divisível por 3, mas não por 5.
860 não é divisível por 3, mas é por 5.
960 é divisível por 3 e por 5.
Logo, os números 450, 660 e 960 são divisíveis por 3 e por 5.
Esses números também são divisíveis por 15, pois:
450 = 15 ⋅ 30
660 = 15 ⋅ 44
960 = 15 ⋅ 64
Podemos dizer que números divisíveis por 3 e por 5 são também divisíveis por 15.
36. Resposta pessoal. Exemplo de resposta: Sempre que somo três números naturais iguais é o mesmo que multiplicar esse número por 3, logo obterei um múltiplo de 3 e, por consequência, um número divisível por 3.
37. a) Etapa 2: O resto da divisão por 2 é igual a zero?
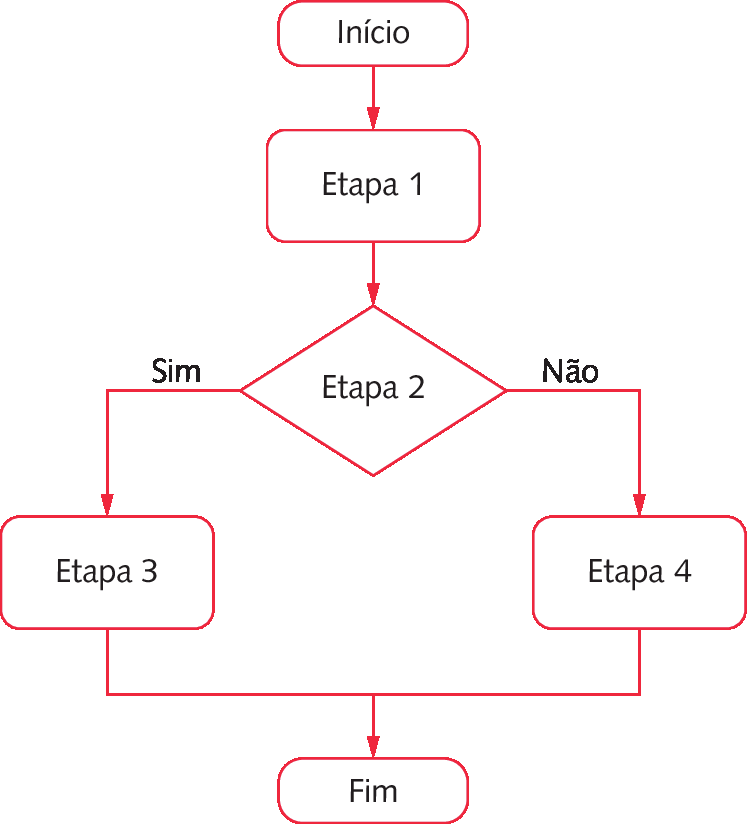
Etapa 3: Se sim, então o número é par.
Etapa 4: Se não, o número é ímpar.
b)
Um pouco de história – página 113
Resposta pessoal. Exemplos de resposta: 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197
Atividades – página 114
38. a) 81 não é primo, pois 81 = 9 ⋅ 9
b) 227 é primo.
c) 463 é primo.
d) 101 é primo.
e) 559 não é primo, pois 559 = 13 ⋅ 43.
f) 977 é primo.
g) 808 não é primo, pois 808 = 2 ⋅ 404.
h) 585 não é primo, pois 585 = 5 ⋅ 117.
i) 161 não é primo, pois 161 = 7 ⋅ 23.
39. Números primos menores que 30: 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29.
40. a) 14 = 2 ⋅ 7
b) 35 = 5 ⋅ 7
c) 70 = 2 ⋅ 5 ⋅ 7
d) 42 = 2 ⋅ 3 ⋅ 7
e) 50 = 2 ⋅ 5 ⋅ 5
f) 100 = 2 ⋅ 2 ⋅ 5 ⋅ 5
41. 323 não é um número primo, pois: 323 = 17 ⋅ 19, ou seja, além de ser divisível por 1 e por ele mesmo, também é divisível por 17 e por 19.
42. Os números primos do intervalo apresentado são: 83, 89, 97, 101, 103.
Então:
Maior número primo de dois algarismos: 97
Menor número primo de três algarismos: 101
Logo, a senha será 97 ⋅ 101 = .9797.
43. Os números primos maiores que 100 e menores que 200 são:
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
Entre eles, os números que o algarismo das dezenas é par são:
101, 103, 107, 109, 149, 163, 167, 181.
Entre esses, os únicos números em que o algarismo das dezenas é maior que o algarismo das unidades são: 163 e 181.
Decomposição em fatores primos – página 114
• Espera-se que os estudantes concluam que vão obter a mesma fatoração completa, não importando o modo como se inicia a fatoração do número.
Atividades – página 115
44. a) 96 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 = 25 ⋅ 3
b) 324 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 22 ⋅ 34
c) .1024 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 2 10
d) .1260 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 7 = 22 ⋅ 32 ⋅ 5 ⋅ 7
e) .2870 = 2 ⋅ 5 ⋅ 7 ⋅ 41
f) .3575 = 5 ⋅ 5 ⋅ 11 ⋅ 13 = 52 ⋅ 11 ⋅ 13
45. a) 23 ⋅ 52 ⋅ 7 = 8 ⋅ 25 ⋅ 7 = 200 ⋅ 7 = .1400
b) Pela decomposição, observamos que o maior divisor primo de .1400 é o 7.
46. a) 22 ⋅ 3 ⋅ 7 = 4 ⋅ 3 ⋅ 7 = 12 ⋅ 7 = 84
b) 23 ⋅ 32 ⋅ 5 = 8 ⋅ 9 ⋅ 5 = 72 ⋅ 5 = 360
c) 24 ⋅ 7 = 16 ⋅ 7 = 112
d) 2 ⋅ 72 ⋅ 11 = 2 ⋅ 49 ⋅ 11 = 98 ⋅ 11 = .1078
47. Podemos fazer a decomposição de cada um desses números em fatores primos:
30 = 2 ⋅ 3 ⋅ 5 e 140 = 22 ⋅ 5 ⋅ 7
Logo, os fatores primos comuns a eles são 2 e 5.
Revisão dos conteúdos deste capítulo – página 116
1. 0, 15, 30, 45 e 60.
2. Como 18 ⋅ 10 = 180, podemos testar 18 ⋅ 9 = 162.
Assim, temos:
18 ⋅ 9 = 162; 18 ⋅ 10 = 180; 18 ⋅ 11 = 198; 18 ⋅ 12 = 216; 18 ⋅ 13 = 234
Assim, os múltiplos procurados serão: 162, 180, 198, 216 e 234.
3. a)
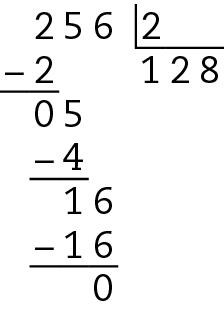
b)
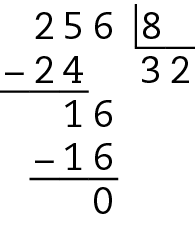
c)
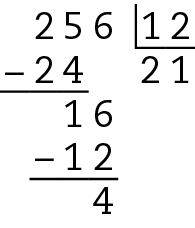
d)
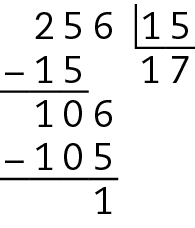
e)
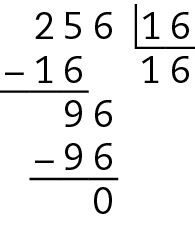
f)
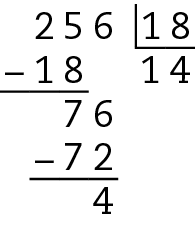
Assim, considerando apenas as divisões exatas, 256 é divisível por 2, 8 e 16 (itens a, b, ê).
4. O maior número de 3 algarismos é o 999, mas ele não é divisível por 4.
Diminuindo para encontrar um divisível por 4:
998 não é, pois 98 não é divisível por 4.
996 é, pois 96 é divisível por 4.
Logo, o número é 996.
5. a) Como 40 é divisível por 4, então 240 é divisível por 4.
Portanto, 4 é divisor de 240.
Afirmação verdadeira.
b) 624 é par, logo 2 é divisor de 624.
Como 6 + 2 + 4 = 12 e 12 é divisível por 3, então 624 é divisível por 3.
Como 624 é divisível por 2 e por 3, também é divisível por 6.
Afirmação verdadeira.
c) Fazendo os cálculos:
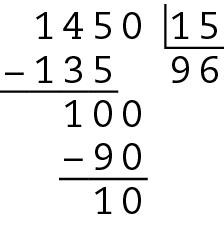
Como a divisão não é exata, .1450 não é divisível por 15.
Afirmação falsa.
6. Fazendo por divisor:
• Por 2:
São pares (logo podem ser divididos por 2): 312, .1236
• Por 3 e por 9:
Calculando a soma dos algarismos:
3 + 2 + 1 = 6 312 é divisível por 3, mas não por 9.
6 + 4 + 5 = 15 645 é divisível por 3, mas não por 9.
1 + 2 + 3 + 6 = 12 .1236 é divisível por 3, mas não por 9.
2 + 1 + 6 + 9 = 18 .2169 é divisível por 3 e por 9.
• Por 5:
Os números que terminam em 0 ou 5: 645.
• Por 8:
312 é divisível por 8, pois 312 = 8 ⋅ 39.
645 não é divisível por 8, pois é ímpar.
236 não é divisível por 8, pois o resto de 236 : 8 é igual a 4.
169 não é divisível por 8, pois é ímpar, então .2169 também não é divisível por 8.
A tabela preenchida ficará:
|
Divisor |
||||||
|---|---|---|---|---|---|---|
|
Número |
2 |
3 |
5 |
6 |
8 |
9 |
|
312 |
x |
x |
x |
x |
||
|
645 |
x |
x |
||||
|
1.236 |
x |
x |
x |
|||
|
2.169 |
x |
x |
||||
7. a) 9 + 0 + 9 = 18 Como 18 é divisível por 9, então 909 é divisível por 9.
b) 1 + 0 + 7 + 1 = 9 Como 9 é divisível por 9, então .1071 é divisível por 9.
c) 2 + 3 + 0 + 4 = 9 Como 9 é divisível por 9, então .2304 é divisível por 9.
d) 3 + 3 + 5 + 6 = 17 Como 17 não é divisível por 9, então .3356 não é divisível por 9.
8. a) 99 não é primo, pois é divisível por 3, 9 e 11.
b) 109 é primo.
c) 167 é primo.
d) 281 é primo.
e) 562 não é primo, pois é par (diferente de 2).
f) .1021 é primo.
9. a) 576 = 26 ⋅ 32
b) .2048 = 211
c) .1323 = 33 ⋅ 72
d) .1944 = 23 ⋅ 35
e) .2058 = 2 ⋅ 3 ⋅ 73
f) .5096 = 23 ⋅ 72 ⋅ 13
Cálculos:

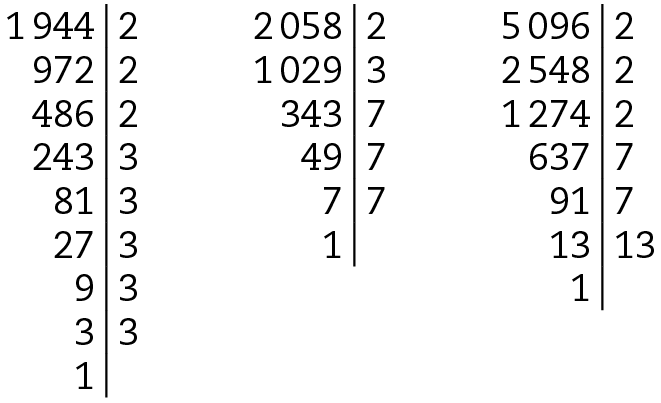
Capítulo 6 – Frações
Trocando ideias – página 117
• Resposta pessoal. Exemplos de resposta: Receitas culinárias, representação de quantidades, medidas de tempo.
• Espera-se que os estudantes respondam utilizando vocabulário próprio que significa que de cada 10 ninhos de araras-azuis 9 são feitos nos manduvis.
• Resposta pessoal. Exemplos de resposta: preservação das florestas, fiscalização para combater o tráfico de animais, criação de centros de tratamento de animais.
Um pouco de história – página 120
a)
Sentença matemática. Fração 1 sobre 5.b)
Sentença matemática. Fração 1 sobre 6c)
Sentença matemática. Fração 2 sobre 10.ou
Sentença matemática. Fração 1 sobre 5.Atividades – página 120
1. a)
Sentença matemática. Fração 5 sobre 8.b)
Sentença matemática. Fração 4 sobre 8.c)
Sentença matemática. Fração 3 sobre 5.2. Exemplos de representação gráfica:
a)

b)

c)

d)

3. a) Como um dia tem 24 horas, então as frações serão, respectivamente,
Sentença matemática. Fração 7 sobre 24e
Sentença matemática. Fração 12 sobre 24.
b) Como uma semana tem 7 dias, então as frações serão, respectivamente,
Sentença matemática. Fração 5 sobre 7e
Sentença matemática. Fração 7 sobre 7.
c) Como um ano tem 12 meses, as frações, nessa ordem, serão:
Sentença matemática. Fração 2 sobre 12e
Sentença matemática. Fração 6 sobre 12.
4. Podemos observar que o cubo maior era formado por 27 cubinhos (pois 3 ⋅ 3 ⋅ 3 = 27). Assim:
• Fração que foi retirada:
Sentença matemática. Fração 4 sobre 27• Fração que sobrou:
Sentença matemática. Fração 23 sobre 27Atividades – página 121
5. a) três sétimos
b) um sexto
c) nove meios
d) cinco nonos
e) dezenove décimos de milésimos
f) três dezessete avos
g) cinco centésimos
h) sete seiscentos avos
i) quinze milésimos
6. Resposta pessoal. Exemplos de resposta:
→ um terço
→ três quintos
→ quatro nonos
→ um décimo
→ nove décimos
→ oito décimos
→ três onze avos
→ um vinte avos
→ vinte e sete milésimos
Atividades – página 123
7. a)
Fração 1 inteiro e 1 quartob)
Fração 2 inteiros e 1 terçoc)
Fração 2 inteiros e 3 nonos8. Exemplos de representações gráficas:
a)

b)

c)

9. Podemos representar os 5 lotes:

Em seguida, dividir cada um dos lotes em 3 partes iguais:
Como os terrenos deverão ser divididos igualmente entre as 3 construções, e temos um total de 15 partes, podemos considerar que cada construção ocupará 5 destas partes.

Assim, a fração que representa a medida da área de cada construção é
Fração 1 inteiro e 2 terçosou
Sentença matemática. Fração 5 sobre 3.
10. Sabendo que 1 ano tem 12 meses, podemos fazer:
a)
Fração 1 inteiro e 3 quartos de 12 é igual a 12 mais fração 3 quartos de 12 é igual a 12 mais 9 igual a 21Logo, são 21 meses.
b)
Fração 2 inteiros e 1 sexto de 12 é igual a 2 vezes 12 mais fração 1 sexto de 12 é igual a 24 mais 2 igual a 26Logo, são 26 meses.
c)
Fração 5 inteiros e 1 meio de 12 é igual a 5 vezes 12 mais fração 1 meio de 12 é igual a 60 mais 6 igual a 66Logo, são 66 meses.
11. Sabendo que 1 dia tem 24 horas:
a)
Fração 1 inteiro e 1 meio de 24 é igual a 24 mais fração 1 meio de 24 é igual a 24 mais 12 igual a 36Logo, são 36 horas.
b)
Fração 1 inteiro e 1 quarto de 24 é igual a 24 mais fração 1 quarto de 24 é igual a 24 mais 6 igual a 30Logo, são 30 horas.
Atividades – página 126
12. Exemplo de representação:
13. a) Para que o numerador seja 15, precisamos multiplicar o numerador e o denominador por 5, obtendo a fração
Sentença matemática. Fração15 sobre 20.
b) Para que o numerador seja 2, precisamos dividir o numerador e o denominador por 4, obtendo a fração
Sentença matemática. Fração 2 sobre 12.
c) Para que o denominador seja 27, precisamos multiplicar o numerador e o denominador por 9, obtendo a fração
Sentença matemática. Fração 18 sobre 27.
14. a) Multiplicar numerador e denominador por 10:
Sentença matemática. 2 terços é igual 20 sobre 30..
b) Dividir numerador e denominador por 2:
Sentença matemática.36 sobre 40 é igual a 18 sobre 20..
c) Dividir numerador e denominador por 5:
Esquema. 20 sobre 25 é igual a 4 quintos..
d) Multiplicar numerador e denominador por 5:
Sentença matemática. 7 sobre 9 é igual a 35 sobre 45..
e) Dividir numerador e denominador por 9:
Sentença matemática. 9 sobre 45 é igual a 1 quinto..
f) Dividir numerador e denominador por 25:
Sentença matemática. 75 centésimos é igual a 3 quartos..
15. a) Para completar
7 sextos igual a quadrado preto sobre 48, precisamos multiplicar numerador e denominador por 8 e obteremos
Sentença matemática. Fração 56 sobre 48.
b) Para completar
3 quintos igual a 18 sobre quadrado preto, precisamos multiplicar numerador e denominador por 6 e obteremos
Sentença matemática. Fração 18 sobre 30.
16. Uma maneira de resolver é encontrar frações equivalentes a
Sentença matemática. Fração 5 sobre 7e calcular a soma indicada até encontrar o valor 60.
5 sétimos é igual a 10 sobre 14 é igual a 15 sobre 21 é igual a 20 sobre 28 é igual a 25 sobre 35 é igual a 30 sobre 42
Adicionando o numerador e o denominador de cada fração, nessa ordem, obtemos: 12; 24; 36; 48; 60 e 72. Assim, a fração cuja soma é 60 é
Sentença matemática. Fração 25 sobre 35.
17. Há diferentes frações que podem representar essa porcentagem:
Sentença matemática. 75 por cento é igual a 75 centésimos é igual a 18 sobre 24, é igual a 3 quartos.
18. Resposta pessoal. Exemplo de resposta:
Como a divisão deve ser feita entre 3 pessoas, podemos fazer:
• a laranja que está dividida ao meio: cada uma das metades pode ser dividida em 3 partes iguais e cada um deles recebe duas dessas partes;
• a laranja que está dividida em 3 partes, basta dar uma parte para cada pessoa.
Atividades – página 127
19. Uma possibilidade de cálculo é fazendo várias divisões, como aparece a seguir. Mas, como estudado, também é possível fazer apenas uma divisão para chegar à fração irredutível.
a)
Sentença matemática. 8 sobre 24 é igual a 4 sobre 12 é igual a 2 sextos é igual a 1 terço.b)
20 centésimos é igual a 10 sobre 50 é igual a 5 sobre 25 é igual a 1 quintoc)
Sentença matemática. 32 sobre 80 é igual a 16 sobre 40 é igual a 8 sobre 20 é igual a 4 sobre 10 é igual a 2 quintos.d)
Sentença matemática. 18 sobre 60 é igual a 9 sobre 30 é igual a 3 sobre 10.e)
Sentença matemática. 20 sobre 80 é igual a 10 sobre 40 é igual a 5 sobre 20 é igual a 1 quarto.f)
Sentença matemática. 90 centésimos é igual a 45 sobre 50 é igual a 9 sobre 10.20. Uma possibilidade é procurar a fórma irredutível de cada uma das frações:
a)
Sentença matemática. 25 sobre 20 é igual a 5 quartos.b)
Sentença matemática. 24 sobre 300 é igual a 12 sobre 150 é igual a 6 sobre 75 é igual a 2 sobre 25.c)
Sentença matemática. 80 sobre 48 é igual a 40 sobre 24 é igual a 20 sobre 12 é igual a 10 sextos é igual a 5 terços.d)
Sentença matemática. 60 centésimos é igual a 30 sobre 50 é igual a 15 sobre 25 é igual a 3 quintos.Logo, a fração procurada é a do item d:
Sentença matemática. Fração 60 sobre 100.
Vale destacar que podemos descartar a fração do item c mesmo sem fazer cálculos, pois seu numerador é maior que o denominador e sabemos que qualquer fração equivalente a
Sentença matemática. Fração 3 sobre 5não poderá ter o numerador maior que o denominador.
21. Segundo as informações, temos:
Preferem biblioteca:
Sentença matemática. Fração 80 sobre 200Preferem internet:
Sentença matemática. Fração 120 sobre 200Fazendo simplificações dessas frações, temos:
Sentença matemática. 80 sobre 200 é igual a 40 sobre 100 é igual a 20 sobre 50 é igual a 4 sobre 25.
e
Sentença matemática. 120 sobre 200 é igual a 60 sobre 100 é igual a 30 sobre 50 é igual a 15 sobre 25 é igual a 3 quintos.Analisando cada fala:
Luís:
Sentença matemática. Fração 40 sobre 100preferem biblioteca; correta, pois
Sentença matemática. Fração 40 sobre 100e
Sentença matemática. Fração 80 sobre 200são equivalentes.
Mônica:
Sentença matemática. Fração 3 sobre 5preferem internet; correta, pois
Sentença matemática. Fração 120 sobre 200e
Sentença matemática. Fração 3 sobre 5são equivalentes.
Logo, a alternativa b é a correta.
Atividades – página 130
22. a) Usando equivalência, temos que
Sentença matemática 2 quintos é igual a 14 sobre 35.e
Sentença matemática. 5 sétimos é igual a 25 sobre 35.; logo,
2 quintos é menor que 5 sétimos.
b) Sabemos que:
Sentença matemática. 5 inteiros e 2 quintos é igual a 25 quintos mais 2 quintos é igual a 27 sobre 5.; logo,
Sentença matemática. 5 inteiros e 2 quintos é igual a 27 quintos..
c) Usando equivalência, temos que
16 sobre 3 é igual a 32 sobre 6e
Sentença matemática. 14 meios é igual a 42 sobre 6.; logo,
Sentença matemática. 16 sobre 3 é menor que 14 meios..
d) Usando equivalência, temos que
Sentença matemática. 16 sobre 35 é igual a 32 sobre 70e
Sentença matemática. 1 meio é igual a 35 sobre 70.; logo,
Sentença matemática. 16 sobre 35 é menor que 1 meio..
23. a) Como todas têm o mesmo denominador, a maior fração é aquela de maior numerador, ou seja,
Sentença matemática. Fração 17 sobre 4.
b) Como todas têm o mesmo denominador, a maior fração é aquela de maior numerador, ou seja,
Sentença matemática. Fração 7 sobre 3.
c) Como todas têm o mesmo numerador, a maior fração é aquela de menor denominador, pois assim o todo será dividido em menos partes. Nesse caso, a maior fração é
Sentença matemática. Fração 1 sobre 2.
d) Como os denominadores e numeradores são diferentes, para fazer a comparação, escrevemos todas as frações equivalentes com o mesmo denominador. Nesse caso, buscaremos uma fração equivalente a cada uma delas, sempre com denominador 12. Teremos:
1 meio é igual a 6 sobre 12
Sentença matemática. 4 terços é igual a 16 sobre 12.
1 sexto é igual a 2 sobre 12
Assim, devemos comparar as frações:
Sentença matemática. Fração 6 sobre 12,
Sentença matemática. Fração 5 sobre 12,
Fração 16 sobre 12, Fração 2 sobre 12Nesse caso, a maior fração é a
Sentença matemática. Fração 16 sobre 12, ou seja, a maior fração é
Sentença matemática. Fração 4 sobre 3.
Outro modo de resolução: entre as quatro frações, apenas uma tem o numerador maior que o denominador, então ela é a maior fração:
Sentença matemática. Fração 4 sobre 3.
24. a) Como todos os numeradores são iguais, podemos escrever:
Sentença matemática. 7 décimos é menor que 7 oitavos é menor que 7 quintos é menor que 7 terços.
Quanto maior o denominador, menor é a fração.
b) Nesse caso, escrevemos todas as frações equivalentes, buscando o denominador em comum, que pode ser o 120:
Sentença matemática. 1 oitavos é igual a 15 sobre 120.
Sentença matemática. 11 sobre 12 é igual a 110 sobre 120.
Sentença matemática. 2 sobre 15 é igual a 16 sobre 120.
Sentença matemática. 7 sobre 20 é igual a 42 sobre 120.
Dessa fórma, temos que:
Sentença matemática.15 sobre 120 é menor que 16 sobre 120 é menor que 42 sobre 120 é menor que 110 sobre120.
E, portanto:
Sentença matemática. 1 oitavos é menor que 2 sobre 15 é menor que 7 sobre 20 é menor que 11 sobre 12.
25. Respostas pessoais. Espera-se que os estudantes observem que basta escrever as frações de modo que os denominadores fiquem em ordem decrescente.
26. Para comparar essas frações, podemos fazer:
Sentença matemática. 3 quartos é igual a 9 sobre 12
e
Sentença matemática. 2 terços é igual a 8 sobre 12., então podemos afirmar que
3 quartos é maior que 2 terços, logo Luís gasta mais.
27. Buscando frações equivalentes com denominador igual a 360:
Sentença matemática. 1 quinto é igual a 72 sobre 360.
Sentença matemática. 2 oitavos é igual a 90 sobre 360.
Sentença matemática. 2 nonos é igual a 80 sobre 360.
Logo, a maior fração é a
Sentença matemática. Fração 2 sobre 8que corresponde à candidata Alice.
Atividades – página 132
28. a) Se a capacidade total desse tanque é de 52 litros, então a capacidade de
Sentença matemática. Fração 1 sobre 4desse tanque será igual a 13 litros (pois
Sentença matemática. Fração 1 sobre 4de 52 = 52 : 4 = 13). Assim, o carro ficou com 13 litros de combustível após a viagem.
b) Ao iniciar a viagem, o carro estava com
Sentença matemática. Fração 3 sobre 4da capacidade do tanque. Como cada
Sentença matemática. Fração 1 sobre 4corresponde a 13 litros, havia um total de 39 litros (3 ⋅ 13 = 39).
29. Se 56 mulheres correspondem a
Sentença matemática. Fração 1 sobre 10do número de homens, o número de homens pode ser calculado fazendo 10 ⋅ 56 = 560. Logo, 560 homens participaram da 61ª Olimpíada Internacional de Matemática.
30. Se
Sentença matemática. Fração 2 sobre 5correspondem a .60000 litros, então
Sentença matemática. Fração 1 sobre 5corresponde a .30000 litros (duas partes correspondem a .60000 litros, então uma parte corresponde a .30000 litros) e
Sentença matemática. Fração 5 sobre 5corresponde a .150000 litros (.30000 ⋅ 5 = .150000).
A capacidade dessa piscina é de .150000 litros.
31. Se ele comprou
5 nonosda coleção, significa que falta comprar
Fração 4 sobre 9.. Como 12 volumes correspondem a
Fração 4 sobre 9., então 3 (12 : 4 = 3) volumes correspondem a
Sentença matemática. Fração 1 sobre 9da coleção.
Por fim, para encontrar
Sentença matemática. Fração 9 sobre 9da coleção (o que corresponde à coleção completa), calculamos 9 ⋅ 3 = 27.
Nessa coleção há 27 volumes.
32. a)
7 sobre 20de .5000 = .5000 : 20 ⋅ 7 = 250 ⋅ 7 = .1750
A primeira remessa corresponde a .1750 quilogramas.
b) Exemplo de resposta:

33. a)

.11257 quilômetros
b)

.18822 quilogramas
c)

.49164 litros.
34. Se
2 quintosdessa medida correspondem a aproximadamente 8 métros, temos que:
Sentença matemática. Fração 1 sobre 5.da medida corresponderá a aproximadamente 4 métros (8 : 2 = 4) e
Sentença matemática. Fração 5 sobre 5dessa medida corresponderá a aproximadamente 20 métros (4 ⋅ 5 = 20).
Assim, a medida da distância foi de aproximadamente 20 métros.
35. Resposta pessoal. Exemplo de problema que pode ser elaborado:
Isabela e Renata compraram bijuterias para vender. Isabela gastou R$ 300,00trezentos reais e Renata gastou R$ 600,00seiscentos reais em mercadorias. O lucro relativo à venda dessas bijuterias foi de R$ 3.000,00três mil reais.
Como repartir esses R$ 3.000,00três mil reais entre elas de modo que o valo seja proporcional ao que investiram?
Exemplo de resposta:
O total gasto com a compra das bijuterias foi R$ 900,00novecentos reais, sendo que Isabela contribuiu com
Sentença matemática. Fração 1 sobre 3e Renata com
Sentença matemática. Fração 2 sobre 3. Assim, para dividir o lucro R$ 3.000,00três mil reais, Isabela deve receber R$ 1.000,00mil reais e Renata R$ 2.000,00dois mil reais.
Atividades – páginas 134 e 135
36. a)
Expressão numérica horizontal. 2 nonos mais 5 nonos é igual a 7 nonos.b)
Expressão numérica horizontal. 5 sextos menos 2 sextos é igual a 3 sextos é igual a 1 meio.c)
Expressão numérica horizontal. 3 quartos mais 1 quinto é igual a 15 sobre 20 mais 4 sobre 20 é igual a 19 sobre 20.d)
Expressão numérica horizontal. 7 sobre 8 menos 4 sobre 9 é igual a 63 sobre 72 menos 32 sobre 72 é igual a 31 sobre 72.e)
Expressão numérica horizontal. 1 sétimo mais 3 quintos mais 9 sobre 14 é igual a 10 sobre 70 mais 42 sobre 70 mais 45 sobre 70 é igual a 97 sobre 70.f)
Expressão numérica horizontal. 3 menos 14 sobre 5 é igual a 15 sobre 5 menos 14 sobre 5 igual a 1 sobre 5.g)
1 inteiro e 2 sobre 11 mais 7 sobre 10 é igual a 13 sobre 11 mais 7 sobre 10 é igual a 130 sobre 110 mais 77 sobre 110 é igual a 207 sobre 110.h)
Expressão numérica horizontal. 2 inteiros e 1 quinto menos 1 inteiro e 1 sexto é igual 11 sobre 5 menos 7 sextos é igual a 66 sobre 30 menos 35 sobre 30 é igual a 31 sobre 30.i)
Expressão numérica horizontal. 7 mais 2 nonos é igual a 63 nonos mais 2 nonos é igual a 65 nonos.j)
Expressão numérica horizontal. 3 quartos menos 1 sexto é igual a 9 sobre 12 menos 2 sobre 12 é igual a 7 sobre 12.k)
Expressão numérica horizontal. 1 quinto mais 2 mais 7 oitavos é igual a 8 sobre 40 mais 80 sobre 40 mais 35 sobre 40 é igual a 123 sobre 40.l)
Expressão numérica horizontal. 3 inteiros e 2 quintos menos 1 sétimo é igual a 17 sobre 5 menos 1 sobre 7 é igual a 119 sobre 35 menos 5 sobre 35 é igual a 114 sobre 35.37.
Expressão numérica horizontal. A mais B menos C é igual a 3 mais 3 inteiros e 5 sétimos menos 2 inteiros e 1 quinto é igual a 3 mais 26 sétimos menos 11 quintos é igual a 105 sobre 35 mais 130 sobre 35 menos 77 sobre 35 é igual a 158 sobre 35.38. Podemos representar a fração do litro de cada recipiente, na ordem em que estão ilustrados:
3 sobre 4, 1 sobre 4e
Sentença matemática. Fração 3 sobre 4. Adicionando esses valores, temos:
Expressão numérica horizontal. 3 quartos mais 1 quarto mais 3 quartos é igual a 7 quartos é igual a 1 inteiros e 3 quartos.
Assim o total será de
Sentença matemática. Fração 7 sobre 4litros ou 1
Sentença matemática. Fração 3 sobre 4litros.
39. a)
Expressão numérica horizontal. 5 inteiros e 1 meio mais 3 inteiros e 1 meio é igual a, abre parênteses, 5 mais 3 fecha parênteses, mais abre parênteses, 1 meio mais 1 meio, fecha parênteses, é igual a 8 mais 2 sobre 2 é igual a 8 mais 1 é igual a 9.b)
Expressão numérica horizontal. 3 inteiros e 4 quintos mais 7 inteiros e 1 quinto é igual a , abre parênteses, 3 mais 7, fecha parênteses, mais, abre parênteses, 4 quintos mais 1 quinto, fecha parênteses, é igual a 10 mais 5 quintos é igual a 10 mais 1 é igual a 11.40. Adicionando os valores correspondentes ao que gastei, temos:
Expressão numérica horizontal. 1 sobre 7 mais 2 quintos é igual a 5 sobre 35 mais 14 sobre 35 é igual a 19 sobre 35.
Logo, gastei
Sentença matemática. Fração 19 sobre 35do salário.
41. Vejamos, primeiro, a fração de revistas que já foi entregue:
Expressão numérica horizontal. 1 quinto mais 1 terço é igual a 3 sobre 15 mais 5 sobre 15 é igual a 8 sobre 15.
Se já foram entregues
Sentença matemática. Fração 8 sobre 15das revistas, então faltam
Sentença matemática. Fração 7 sobre 15para serem entregues.
Como
Sentença matemática. Fração 7 sobre 15correspondem a 14 revistas, então
Sentença matemática. Fração 1 sobre 15corresponde a 2 revistas e
Sentença matemática. Fração 15 sobre 15correspondem a 30 revistas.
Logo, o total de revistas que Lino deve entregar hoje é igual a 30.
42. Analisando a figura, podemos notar que há um retângulo inteiro ocupado,
Sentença matemática. Fração 4 sobre 4de retângulo ocupado, mais duas vezes duas metades de retângulo, resultando aproximadamente
Sentença matemática. Fração 4 sobre 9da figura inteira.
43. Pelas informações apresentadas, podemos concluir que 21 litros correspondem a
Sentença matemática. Fração 3 sobre 8da capacidade. Dessa fórma:
7 litros correspondem a
Sentença matemática. Fração 1 sobre 8da capacidade da vasilha.
56 (8 ⋅ 7 = 56) litros correspondem a
Sentença matemática. Fração 8 sobre 8da capacidade da vasilha.
A medida da capacidade da vasilha é 56 litros.
44. Resposta pessoal. Exemplo de problema que pode ser elaborado:
Paulo vai fazer uma viagem entre duas cidades que distam 360 quilômetros. Na viagem de ida, tudo transcorreu bem, mas na volta, após percorrer
Sentença matemática. Fração 1 sobre 2.do total do caminho de volta, ele percebeu que errou o caminho e percorreu
Sentença matemática. Fração 1 sobre 4a mais que o esperado.
Respostas (às perguntas que já estão no livro):
a) Na ida ele percorreu 360 quilômetros. Na volta ele percorreu 450 quilômetros, pois
Sentença matemática. 360 mais fração 1 sobre 4 de 360 é igual a 360 mais 90 igual a 450. No total foram percorridos 810 quilômetros (360 + 450 = 810).
b) Se ele não errasse o caminho na volta, faltariam 180 quilômetros para chegar (pois já tinha percorrido metade dos 360 quilômetros).
Atividades – página 137
45. a)
Expressão numérica horizontal. 3 vezes 2 sétimos é igual a 6 sétimos.b)
Expressão numérica horizontal. 5 vezes 3 inteiros e 1 quinto é igual a 5 vezes 16 sobre 5 é igual a 16.c)
Expressão numérica horizontal. 2 terços vezes 10 quartos vezes 9 sobre 15 é igual a 2 terços vezes 5 meios vezes 3 quintos é igual a 1.d)
Expressão numérica horizontal. 5 quartos vezes 8 sobre 15 vezes 1 meio é igual a 1 sobre 1 vezes 2 terços vezes 1 meio é igual a 1 terço.e)
Expressão numérica horizontal. 7 nonos vezes 3 meios vezes 0 é igual a 0.f)
Expressão numérica horizontal. 2 inteiros e 1 quinto vezes 35 sobre 33 é igual a 11 sobre 5 vezes 35 sobre 33 é igual a 7 terços.46.
Expressão numérica horizontal. 2 terços de 42 é igual a 2 vezes 42 dividido por 3 é igual a 84 dividido por 3 é igual a 28.Foram vendidos 28 aparelhos da marca Alfa.
47. a)
Expressão numérica horizontal. 3 vezes 7 sobre 15 é igual a 7 sobre 5.b)
Expressão numérica horizontal. 2 vezes 5 oitavos é igual a 5 quartos.48.
Sentença matemática. 3 quartos de 2 mil e 400 é igual a 3 vezes 2 mil e 400 dividido por 4 é igual a 7 mil e 200 dividido por 4 é igual a mil e 800.Cabem .1800 litros em
Sentença matemática. Fração 3 sobre 4do reservatório.
49. a)
Expressão numérica horizontal. 3 quintos vezes 5 sétimos é igual a 3 sobre 1 vezes 1 sétimo é igual a 3 sétimos.b)
Expressão numérica horizontal. 1 meio vezes 8 nonos vezes 2 inteiros e 1 quarto é igual a 1 vezes 4 nonos vezes 9 quartos é igual a 1.c)
Expressão numérica horizontal. 36 sobre 50 vezes 30 sobre 72 vezes 10 sobre 40 é igual a 1 quinto vezes 3 meios vezes 1 quarto é igual a 3 sobre 40.d)
Expressão numérica horizontal. 7 sobre 11 vezes 11 sobre 28, é igual a 1 sobre 1 vezes 1 quarto é igual a 1 quarto.50. Há meio cento, ou seja, há 50 laranjas.
Sentença matemática. 2 quintos de 50 é igual a 2 vezes 50 dividido por 5; é igual a 100 dividido por 5 é igual a 20.
Se há 50 e retirarmos 20, sobrarão 30 laranjas.
51. Exemplo de resolução.
Podemos juntar todas as frações:
Expressão numérica horizontal. 1 meio mais 1 terço mais 1 quarto é igual a 6 sobre 12 mais 4 sobre 12 mais 3 sobre 12 é igual a 13 sobre 12.
Então, percebemos que a soma das frações é maior do que o inteiro, então essa divisão não é possível.
52. Com a calculadora, encontramos:
Sentença matemática. Um terço de 33 mil 915 é igual a 11 mil 305.
Sentença matemática. 2 quintos de 33 mil 915 é igual a 13 mil 566.
Sentença matemática. Um sétimo de 33 mil 915 é igual a 4 mil 845.
Soma dos valores recebidos por José, Vanessa e Marcos: .11305 + .13566 + .4845 = .29716
O valor gasto com as despesas foi R$ 4.199,00quatro mil cento e noventa e nove reais
(.33915 ‒ .29716 = .4199).
Atividades – página 140
53. a)
Expressão numérica horizontal. 4 dividido por 1 meio é igual a 4 vezes 2 é igual a 8.b)
Expressão numérica horizontal. 60 dividido por 3 oitavos é igual a 60 vezes 8 terços é igual a 20 vezes 8 é igual a 160.c)
Expressão numérica horizontal. 2 nonos dividido por 1 inteiro e 1 terço é igual a 2 nonos dividido por 4 terços é igual a 2 nonos vezes 3 quartos é igual a 1 terço vezes 1 meio é igual a 1 sexto.d)
Expressão numérica horizontal. 1 meio dividido por 4 é igual a 1 meio vezes 1 quarto é igual a 1 oitavo.e)
Expressão numérica horizontal. 10 dividido por 2 quintos é igual a 10 vezes 5 meios é igual a 5 vezes 5 é igual a 25.f)
Expressão numérica horizontal. 3 oitavos dividido por 5 é igual a 3 oitavos vezes 1 quinto é igual a 3 sobre 40.54. Em 10 garrafas de 1 litro temos 10 litros. Então:
Expressão numérica horizontal. 10 dividido por 1 quarto é igual a 10 vezes 4 é igual a 40.
Precisamos de 40 copos.
55. a)
Expressão numérica horizontal. 2 sobre 7 dividido por 3 quintos é igual a 2 sétimos vezes 5 terços é igual a 10 sobre 21.b)
Expressão numérica horizontal. 10 dividido por 2 quintos é igual a 10 vezes 5 meios é igual a 5 vezes 5 é igual a 25.c)
Expressão numérica horizontal. fração com numerador 3 sétimos e denominador 6 décimos é igual a 3 sétimos vezes 10 sextos é igual a 1 sétimo vezes 10 meios, é igual a 1 sétimo vezes 5 é igual a 5 sétimos.56. Para saber o total de refresco obtido, fazemos:
Expressão numérica horizontal. 3 quartos mais 3 quartos mais 3 quartos mais 1 quarto é igual a 10 quartos.
Agora, dividindo em 10 taças:
Expressão numérica horizontal. 10 quartos dividido por 10 é igual a 10 quartos vezes 1 décimo é igual a 1 quarto.
Assim, cada taça terá, no máximo,
Fração 1 sobre 4de litro.
57. Primeiro, calculamos a fração correspondente aos 5 banheiros:
Expressão numérica horizontal. 1 menos 1 terço é igual a 3 terços menos 1 terço é igual a 2 terços.
Agora, calculamos a fração correspondente à água disponibilizada para cada banheiro:
Expressão numérica horizontal. 2 terços dividido por 5 é igual a 2 terços vezes 1 quinto é igual a 2 sobre 15.
Logo, a fração disponibilizada para cada banheiro é
Sentença matemática. Fração 2 sobre 15.
Atividades – página 141
58. a)
Expressão numérica horizontal. Abre parênteses, 3 quintos, fecha parênteses, elevado a 2, é igual a 3 elevado a 2 sobre 5 elevado a 2, é igual a 9 sobre 25.b)
Expressão numérica horizontal. Abre parênteses, 1 meio, fecha parênteses, elevado a 4 é igual a 1 elevado a 4 sobre 2 elevado a 4 é igual a 1 sobre 16.c)
Expressão numérica horizontal. Abre parênteses, 8 terços, fecha parênteses, elevado a um, é igual a 8 terços.d)
Expressão numérica horizontal. Abre parênteses, 2 terços, fecha parênteses, elevado a 3 é igual a 2 elevado a 3 sobre 3 elevado a 3 é igual a 8 sobre 27.e)
Expressão numérica horizontal. Abre parênteses, 3 inteiros e 1 meio, fecha parênteses, elevado a 2, é igual a 2 elevado a 3 sobre 3 elevado a 3 é igual a 8 sobre 27.f)
Expressão numérica horizontal. Abre parênteses, 199 sobre 500, fecha parênteses, elevado a 0 é igual a 1.Atividades – página 142
59. a)
Expressão numérica horizontal. 5 sextos mais 1 meio vezes 3 quartos é igual a 5 sextos mais 3 oitavos é igual a 20 sobre 24 mais 9 sobre 24 é igual a 29 sobre 24.b)
Expressão numérica horizontal. 5 menos 7 quartos vezes 1 meio é igual a 5 menos 7 oitavos é igual a 40 oitavos menos 7 oitavos é igual a 33 sobre 8.c)
Expressão numérica horizontal. 2 terços vezes 1 quinto mais 2 inteiros e 1 quarto é igual a 2 sobre 15 mais 9 quartos é igual a é igual a 8 sobre 60 mais 135 sobre 60 mais 143 sobre 60.d)
Expressão numérica horizontal. 3 quintos mais 2 nonos dividido por 2 terços é igual a 3 quintos mais 2 nonos vezes 3 meios é igual a 3 quintos mais 1 terço é igual a 9 sobre 15 mais 5 sobre 15 é igual a 14 sobre 15.e)
Expressão numérica horizontal. 2 sétimos vezes 3 quintos menos 1 oitavo dividido por 5 sextos é igual a 6 sobre 35 menos 1 oitavo vezes 6 quintos é igual a 6 sobre 35 menos 3 sobre 20 é igual a 24 sobre 140 menos 21 sobre 140 é igual a 3 sobre 140.f)
Expressão numérica horizontal. 3 quartos mais 5 nonos dividido por 1 sexto é igual a 3 quartos mais 5 nonos vezes 6 sobre 1 é igual a 3 quartos mais 10 terços é igual a 9 sobre 12 mais 40 sobre 12 é igual a 49 sobre 12.60. a)
Sentença matemática. Abre parênteses, 2 terços menos 1 oitavo vezes 4 sétimos, fecha parênteses, dividido por 2 sétimos vezes 4 nonos é igual a, abre parênteses, 2 terços menos 1 sobre 14, fecha parênteses, dividido por 2 sétimos vezes 4 nonos é igual a 28 sobre 42 menos 3 sobre 42, fecha parênteses, dividido por 2 sétimos vezes 4 nonos, igual .Sentença matemática. igual 25 sobre 42 dividido por 2 sétimos vezes 4 nonos é igual a 25 sobre 42 vezes 7 meios vezes 4 nonos é igual a 25 sextos vezes 2 nonos, é igual a 25 terços vezes 1 nono é igual a 25 sobre 27.
b)
Sentença matemática. 27 centésimos dividido por, abre chaves 11 quartos, menos, abre colchetes, 3 meios mais, abre parênteses, 1 meio mais 1 quarto, fecha parênteses, fecha colchetes, fecha chaves, igual.Sentença matemática. Igual, 27 centésimos dividido por, abre chaves, 11 quartos menos, abre colchetes, 3 meios mais 3 quartos, fecha colchetes, fecha chaves, é igual a 27 centésimos dividido por, abre chaves 11 quartos menos, abre colchetes, 6 quartos mais 3 quartos, fecha colchetes, fecha chaves, é igual a 27 centésimos dividido por, abre chaves, 11 quartos menos 9 quartos, igual 27 centésimos dividido por 2 quartos, igual 27 centésimos vezes 4 meios igual 27 sobre 50.
c)
Sentença matemática. Abre parênteses, 1 menos 1 meio, fecha parênteses, elevado a 2, dividido por, abre colchetes, abre parênteses, 1 menos 3 quartos, fecha parênteses, elevado a 2 vezes 8 mais, abre parênteses, 1 meio, fecha parênteses, elevado a 2, fecha colchetes, é igual a, abre parênteses, 2 sobre 2 menos 1 meio, fecha parênteses, elevado a 2, dividido por, abre colchetes, abre parênteses, 4 quartos menos 3 quartos, fecha parênteses, elevado a 2 vezes 8 mais, abre parênteses, 1 meio, fecha parênteses, elevado a 2, fecha colchetes, é igual.Abaixo, abre parênteses, 1 meio, fecha parênteses, elevado a 2, dividido por, abre colchetes, abre parênteses, 1 quarto, fecha parênteses, elevado a 2, vezes 8 mais, abre parênteses, 1 meio, fecha parênteses, elevado a 2, fecha colchetes, é igual a 1 quarto dividido por, abre colchetes, 1 sobre 16 vezes 8 mais 1 quarto, fecha colchetes, é igual a 1 quarto dividido por, abre colchetes, 1 meio mais 1 quarto, fecha colchetes, igual.
Sentença matemática. igual 1 quarto dividido por 3 quartos igual 1 terço.
Resolvendo em equipe – página 143
Interpretação e identificação dos dados
• Um compasso é uma unidade musical composta de determinada quantidade de notas musicais, em que a soma das durações coincide com a fração indicada como fórmula do compasso.
Sentença matemática. Fração 1 sobre 2
=
Sentença matemática. Fração 1 sobre 4+
Sentença matemática. Fração 1 sobre 4;
Sentença matemática. Fração 1 sobre 2=
Sentença matemática. Fração 1 sobre 2;
Sentença matemática. Fração 1 sobre 2=
Sentença matemática. Fração 1 sobre 8+
Sentença matemática. Fração 1 sobre 8+
Sentença matemática. Fração 1 sobre 8+
Sentença matemática. Fração 1 sobre 8Plano de resolução
•
Esquema. Cálculo horizontal. 8 vezes 3 quartos é igual a 6.•
Esquema. Cálculo horizontal. 24 vezes 1 sobre 32 é igual a 3 quartos.Resolução
a)
Sentença matemática. 24 vezes fração 1 sobre 32 é diferente de 6b)
Sentença matemática. 3 vezes fração 1 sobre 4 é diferente de 6c)
Sentença matemática. 8 vezes fração 1 sobre 4 é diferente de 6d)
Sentença matemática. 24 vezes fração 1 sobre 8 mais 12 vezes fração 1 sobre 4 é igual a 3 mais 3 é igual a 6e)
Sentença matemática. 16 vezes fração 1 sobre 4 mais 8 vezes 1 sobre 16 é igual a 4 mais fração 1 sobre 2 é igual a fração 4 e 1 sobre 2 é igual a fração 9 sobre 2 diferente de 6Revisão dos conteúdos deste capítulo – páginas 144 a 146
1. a)
Sentença matemática. Fração 1 sobre 8b)
Sentença matemática. Fração 4 sobre 9c)
Expressão numérica horizontal. 12 sobre 36 é igual a 6 sobre 18 é igual a 3 nonos é igual a 1 terço.d)
Sentença matemática. Fração 7 sobre 122. a) Quatro sétimos.
b) Um nono.
c) Seis décimos.
d) Doze centésimos.
e) Quatro milésimos.
f) Doze vinte e três avos.
3. a)
Sentença matemática. Fração 1 e 5 sobre 9b)
Sentença matemática. Fração 1 e 2 sobre 84. a)
Expressão numérica horizontal. 1 inteiro e 3 quartos é igual a 4 mais 3 sobre 4, é igual a 7 quartos.b)
Expressão numérica horizontal. 2 inteiros e 9 sobre 11 é igual a 22 mais 9 sobre 11 é igual a 31 sobre 11.c)
Expressão numérica horizontal. 4 inteiros e 7 nonos é igual a 36 mais 7 sobre 9 é igual a 43 sobre 9.d)
Expressão numérica horizontal. 7 inteiros e 2 sétimos é igual a 49 mais 2 sobre 7 é igual a 51 sobre 7.5. a)
Sentença matemática. 12 sobre 15 é igual a 24 sobre 30.b)
Sentença matemática. 6 sobre 20 é igual a 18 sobre 60.c)
Sentença matemática. 25 centésimos é igual a 5 sobre 20.d)
Sentença matemática. 7 sobre 16 é igual a 35 sobre 80.6. a)
Sentença matemática. 10 sobre 25 é igual a 2 quintos.b)
Sentença matemática. 18 sobre 150 é igual a 9 sobre 75 é igual a 3 sobre 25.c)
Sentença matemática. 12 sobre 60 é igual a 6 sobre 30 é igual a 3 sobre 15, é igual a 1 quinto.d)
Sentença matemática. 96 sobre 112 é igual a 48 sobre 56 é igual a 24 sobre 28 é igual a 12 sobre 14 é igual a 6 sétimos.7. a)
Sentença matemática. 5 sobre 11 é menor que 7 sobre 11.b)
Sentença matemática. 2 sétimos é igual a 10 sobre 35e
Sentença matemática. 4 quintos é igual a 28 sobre 35, logo
Sentença matemática. 2 sétimos é menor que 4 quintos.c)
Sentença matemática. 9 meios é igual a 18 quartos, logo
Sentença matemática. 9 meios é maior que 15 quartos.d)
Sentença matemática. 5 sobre 13 é igual a 15 sobre 39.8. a)
Fração 9 sobre 8é a maior fração.
b) Como
Sentença matemática. um quinto igual a 6 sobre 30,
Sentença matemática. 4 terços igual a 40 sobre 30e
Sentença matemática. 2 sobre 6 igual a 10 sobre 30, então
Sentença matemática. Fração 4 sobre 3é a maior fração.
c) Como
Sentença matemática. 2 terços igual a 40 sobre 60,
Sentença matemática. um quarto igual a 15 sobre 60e
Sentença matemática. 3 quintos igual a 36 sobre 60, então
Sentença matemática. Fração 2 sobre 3é a maior fração.
d) Como
Sentença matemática. 4 décimos igual a 2 quintos igual a 24 sobre 60,
Sentença matemática. 5 sobre 12 igual a 25 sobre 60e
Sentença matemática. 15 sobre 25 igual a 3 quintos igual a 36 sobre 60, então
Sentença matemática. fração 15 sobre 25é a maior fração.
9. a) Como
Sentença matemática. fração um quarto igual a 15 sobre 60,
Sentença matemática. fração dois terços igual a 40 sobre 60e
Sentença matemática. fração quatro quintos igual a 48 sobre 60, então
Sentença matemática. 1 quarto é menor que 2 terços é menor que 4 quintos..
b) Como
Sentença matemática. fração dois quintos igual a 16 sobre 40,
Sentença matemática. Fração três oitavos igual a 15 sobre 40.e
Sentença matemática. Fração 9 sobre 15 igual a 3 quintos igual a 24 sobre 40., então
Sentença matemática. 3 oitavos é menor que 2 quintos é menor que 9 sobre 15..
c) Como
Sentença matemática. 3 quartos igual a 9 sobre 12.,
Sentença matemática. 2 sextos igual a 4 sobre 12.e
Sentença matemática. 2 terços igual a 8 sobre 12., então
Sentença matemática. 2 sextos é menor que 2 terços é menor que 3 quartos..
d) Como
Sentença matemática. 4 nonos igual a 28 sobre 63.,
Sentença matemática. 1 terço igual a 21 sobre 63.e
Sentença matemática. 2 sétimos igual a 18 sobre 63., então
Sentença matemática. 2 sétimos é menor que 1 terço é menor que 4 nonos..
10.
Sentença matemática. um terço de 4 mil e 500 igual a 4 mil e 500 dividido por 3 igual a mil e 500.O valor dessas despesas foi R$ 1.500,00mil quinhentos reais.
11. Se
Sentença matemática. Fração 3 sobre 4do trajeto correspondem a .3375 métros, então:
Sentença matemática. Fração 1 sobre 4
do trajeto corresponde a .1125 métros (.3375 : 3 = .1125)
Sentença matemática. Fração 4 sobre 4
do trajeto corresponde a .4500 métros ( .1125 ⋅ 4 = .4500 )
A distância total a ser percorrida na prova é .4500 métros.
12. Se Marcos pagou
Sentença matemática. Fração 3 sobre 5do jôgo e Jorge pagou o restante, então Jorge pagou
Sentença matemática. Fração 2 sobre 5do jôgo.
Assim, se
Sentença matemática. Fração 2 sobre 5do jôgo correspondem a R$ 46,00quarenta e seis reais, então:
Sentença matemática. Fração 1 sobre 5
do jôgo corresponde a R$ 23,00vinte e três reais (46 : 2 = 23)
Sentença matemática. Fração 5 sobre 5
do jôgo corresponde a R$ 115,00cento e quinze reais (23 ⋅ 5 = 115)
Logo, esse jôgo custou R$ 115,00cento e quinze reais.
13. Se Rogério pagou
Sentença matemática. Fração 1 sobre 3de R$ 12,00doze reais, ele pagou R$ 4,00 quatro reais
(12 : 3 = 4)
Se Cristiane pagou metade do valor pago por Rogério, ela pagou R$ 2,00dois reais (4 : 2 = 2)
Como Patrícia pagou o restante, ela pagou:
12 – (4 + 2) = 12 – 6 = 6
Patrícia pagou R$ 6,00seis reais.
14. Se o atacadista vendeu
Sentença matemática. Fração 4 sobre 13das sacas para o primeiro freguês, sobraram
Sentença matemática. Fração 9 sobre 13das sacas
Sentença matemática. Abre parênteses, 13 sobre 16 menos 4 sobre 13 é igual a 9 sobre 13, fecha parênteses..
Para o segundo freguês ele vendeu
Sentença matemática. Fração 1 sobre 3de
Sentença matemática. Fração 9 sobre 13, que é
Sentença matemática. Fração 3 sobre 13 Sentença matemática. Cálculo horizontal. Abre parênteses, 1 terço vezes 9 sobre 13 é igual a 3 sobre 13, fecha parênteses.
, então sobraram
Sentença matemática. Fração 6 sobre 13das sacas
Sentença matemática. Cálculo horizontal. Abre parênteses, 9 sobre 13 menos 3 sobre 13 é igual a 6 sobre 13, fecha parênteses..
Para o terceiro freguês ele vendeu
Sentença matemática. Fração 3 sobre 10de
Sentença matemática. Fração 6 sobre 13das sacas, que é
Sentença matemática. Fração 9 sobre 65 Sentença matemática. Abre parênteses, 3 décimos vezes 6 sobre 13 é igual a 9 sobre 65, fecha parênteses.
, então sobraram
Sentença matemática. Fração 21 sobre 65das sacas
Sentença matemática. Abre parênteses, 6 sobre 13 menos 9 sobre 65 é igual a 21 sobre 65, fecha parênteses.E
Sentença matemática. Fração 21 sobre 65de .2600 é:
Sentença matemática. 21 sobre 65 vezes 2 mil 600 é igual a 840.
Restaram oitocentas e quarenta sacas.
15. a)
Sentença matemática. 4 nonos mais 9 quintos é igual a 20 sobre 45 mais 81 sobre 45 é igual a 101 sobre 45.
b)
Sentença matemática. 12 sobre 21 mais 10 sobre 21 é igual a 22 sobre 21.c)
Sentença matemática. 12 sobre 15 menos 5 sobre 15 é igual a 7 sobre 15.d)
Sentença matemática. 3 sétimos menos 1 sétimos é igual a 2 sétimos.e)
Sentença matemática. 2 inteiros e 4 quintos mais 3 quintos é igual a 14 quintos mais 3 quintos é igual a 17 quintos é igual a 3 inteiros e 2 quintos.f)
Sentença matemática. 1 sexto mais 5 nonos é igual a 3 sobre 18 mais 10 sobre 18 é igual 13 sobre 18.g)
Sentença matemática. 2 terços menos 4 sétimos é igual a 14 sobre 21 menos 12 sobre 21 é igual a 2 sobre 21.h)
Sentença matemática. 5 oitavos menos 8 sobre 15 é igual a 75 sobre 120 menos 64 sobre 120 é igual a 11 sobre 120.i)
Sentença matemática. 1 quarto mais 1 terço mais 1 quinto é igual a 15 sobre 60 mais 20 sobre 60 mais 12 sobre 60 é igual a 47 sobre 60.j)
Sentença matemática. 8 nonos menos 7 décimos é igual a 80 sobre 90 menos 63 sobre 90 é igual a 17 sobre 90.16. Se o aquário está
Sentença matemática. Fração 4 sobre 5com água, significa que está
Sentença matemática. Fração 1 sobre 5
sem água.
Como
Sentença matemática. Fração 1 sobre 5corresponde a 12 litros, então
Sentença matemática. Fração 5 sobre 5correspondem a ( 12 ⋅ 5 ) litros = 60 litros.
Logo, o aquário tem 60 litros de medida de capacidade.
17. a)
Sentença matemática. 2 inteiros e 1 terço mais 1 inteiro e 3 quartos, igual, 6 terços mais 1 terço mais 4 quartos mais 3 quartos, igual, 7 terços mais 7 quartos, igual, 28 sobre 12 mais 21 sobre 12, igual, 49 sobre 12 é igual a 4 inteiros e 1 sobre 12.b)
Sentença matemática. 1 meio mais 1 quinto menos 3 sextos, igual, 15 mais 6 menos 15, sobre 30, igual, 6 sobre 30 é igual a 1 quinto.c)
Sentença matemática. 8 menos 7 meios é igual a fração com numerador 16 menos 7 e denominador dois é igual a 9 meios.d)
Sentença matemática. 7 meios menos 1 inteiro e 1 oitavo é igual a 7 meios menos fração com numerador 8 mais 1 e denominador 8, é igual a, fração com numerador 28 menos 9 e denominador 8, é igual a 19 oitavos.18. a)
8 vezes 7 nonos igual 56 nonos.b)
Sentença matemática. 2 quintos vezes 12 é igual a 24 quintos.
c)
Sentença matemática. 1 quarto vezes 3 nonos é igual a 3 sobre 36 é igual a 1 sobre 12.d)
Sentença matemática. 9 sobre 15 vezes 5 terços é igual a 45 sobre 45 é igual a 1.e)
Sentença matemática. 3 oitavos vezes 4 quintos é igual a 12 sobre 40 é igual a 3 décimos.f)
Sentença matemática. 5 nonos vezes 4 décimos é igual a 20 sobre 90 é igual a 2 nonos.19. Se
Sentença matemática. Fração 2 sobre 5dos números da rifa foram vendidos a familiares, então
Sentença matemática. Fração 3 sobre 5foram vendidos aos colegas.
Sentença matemática. Fração 3 sobre 5
Logo, 60 números foram vendidos aos colegas de Beto.
20. O triângulo maior foi dividido em 4 partes iguais; portanto, cada triângulo intermediário corresponde a
Sentença matemática. Fração 1 sobre 4do triângulo maior.
Por sua vez, o triângulo intermediário também foi dividido em 4 partes iguais.
Então o menor triângulo corresponde a
Sentença matemática. Fração 1 sobre 16do triângulo maior
Abre parênteses, fração 1 quarto vezes fração 1 quarto igual a fração 1 sobre 16, fecha parênteses.21. a)
Sentença matemática. 4 nonos dividido por 3 é igual a 4 nonos vezes 1 terço é igual a 4 sobre 27.b)
Sentença matemática. 40 dividido por fração 2 sobre 3 é igual a 40 vezes fração 3 sobre 2 é igual a fração 120 sobre 2 é igual a 60
c)
Sentença matemática. Fração 4 sobre 7 dividido pela fração 1 sobre 2 é igual a fração 4 sobre 7 vezes 2 é igual a fração 8 sobre 7d)
Sentença matemática. 3 sobre 15 vezes 2 terços é igual a 3 sobre 15 vezes 3 meios é igual a 9 sobre 30 é igual a 3 décimos.
e)
Sentença matemática. 2 sétimos dividido por 4 nonos é igual a 2 sétimos vezes 9 quartos é igual a 18 sobre 28 é igual a 9 sobre 14.f)
Sentença matemática. 9 sobre 15 dividido por 5 nonos é igual a 9 sobre 15 vezes 9 quintos é igual a 81 sobre 75 é igual a 27 sobre 25.22. a)
Sentença matemática. 1 meio dividido por 3 oitavos é igual a 1 meio vezes 8 terços é igual a 8 sextos é igual a 4 terços.b)
Sentença matemática. 6 dividido por 1 quarto é igual a 6 vezes 4 é igual a 24.23. Se
Sentença matemática. 3 sétimoscorrespondem a R$ 540,00quinhentos e quarenta reais, então
Sentença matemática. 1 sétimocorresponde a R$ 180,00cento e oitenta reais (540 : 3 = 180).
Se
Sentença matemática. 1 sétimocorresponde a R$ 180,00cento e oitenta reais, então
Sentença matemática. Fração 7 sobre 7correspondem a R$ 1.260,00mil duzentos e sessenta reais (180 ⋅ 7 = .1260).
Logo, a quantia mensal é de R$ 1.260,00mil duzentos e sessenta reais.
24. a)
Sentença matemática. Abre parênteses, 2 terços, fecha parêntese elevado a 2 é igual a 4 nonos.b)
Sentença matemática. Abre parênteses, 4 terços, fecha parênteses, elevado a 3 é igual a 64 sobre 27.c)
Sentença matemática. Abre parênteses, 1 centésimo, fecha parênteses, elevado a 0 é igual a 1.d)
Sentença matemática. Abre parêntese, 99 centésimos, fecha parênteses, elevado a 1 é igual a 99 centésimos.e)
Sentença matemática. Abre parênteses, 3 inteiros e 1 meio, fecha parênteses, elevado a 2 é igual a, abre parênteses, 7 meios, fecha parênteses, elevado a 2 é igual a 49 quartos.f)
Sentença matemática. Abre parênteses, 3 quintos, fecha parênteses, elevado a 3 é igual a 27 sobre 125.25.
Sentença matemática. Abre parênteses, 3 quartos menos 2 quintos, fecha parênteses, vezes 1 meio mais, abre parênteses, 5 meios, fecha parênteses, elevado a 2, mais, abre parênteses, 1 meio dividido por 4, fecha parênteses, igual, abre parênteses, 15 sobre 20 menos 8 sobre 20, fecha parênteses, vezes 1 meio mais 25 quartos, mais, abre parênteses, 1 meio vezes 1 quarto, fecha parênteses, igual.Sentença matemática. Igual 7 sobre 20 vezes 1 meio mais 25 quartos, mais 1 oitavo, igual, 7 sobre 40 mais 250 sobre 40 mais 5 sobre 40, igual, 262 sobre 40,é igual a 131 sobre 20.
26. a)
Sentença matemática. Abre colchetes, abre parênteses, 2 terços dividido por 1 sobre 12 mais 2, fecha parênteses, dividido por, abre parênteses, 1 décimo, fecha parênteses, elevado a 2, menos 10 elevado a 3, fecha colchetes, igual, abre colchetes, abre parênteses, 2 terços vezes 12 mais 2, fecha parênteses, dividido por 1 centésimo menos 1 mil, fecha colchetes, igual.Sentença matemática. Igual, abre colchetes, abre parênteses, 8 mais 2, fecha parênteses, dividido por 1 centésimo menos 1 mil, fecha colchetes, igual, abre colchetes, 10 dividido por 1 centésimo menos 1 mil, fecha colchetes, igual.
Sentença matemática. Igual, abre colchetes, 10 vezes 100 menos 1 mil, fecha colchetes, igual a 0.
b)
Sentença matemática. Abre parênteses, 3 meios, fecha parênteses, elevado a 2, mais, abre colchetes, 3 inteiros e 1 terço, menos, 3 inteiros e 1 quarto, mais, abre parênteses, 1 meio, fecha parênteses, elevado a 3, fecha colchetes, igual, 9 quartos, mais, abre colchetes, 10 terços, menos, 13 quartos mais 1 oitavo, fecha colchetes, igual.Sentença matemática. Igual 9 quartos, mais, abre colchetes, 80 sobre 24 menos 78 sobre 24 mais 3 sobre 24, fecha colchetes, igual, 9 quartos, mais 5 sobre 24, igual, 54 sobre 24 mais 5 sobre 24 é igual a 59 sobre 24.
CAPÍTULO 7 – NÚMEROS DECIMAIS
Trocando ideias – página 147
• Resposta pessoal. Exemplos de resposta: Utilizamos com os preços dos produtos no mercado, o valor a pagar no posto de combustível, ao verificar a temperatura do termômetro etcétera.
• Como 15,083 é maior que 15 e menor que 16, faltou menos de 1 ponto.
Atividades – página 152
1. a) sete décimos
b) trezentos e dezessete milésimos
c) cinco inteiros e sessenta e nove centésimos
d) vinte e oito centésimos
e) sete inteiros e trinta e oito milésimos
f) oito milésimos
2. a) 7 inteiros + 6 décimos → 7,6
b) 36 milésimos → 0,036
c) 78 centésimos → 0,78
d) 126 décimos, o algarismo 6 deve estar na 1ª ordem decimal → 12,6
e) 20 inteiros + 4 décimos → 20,4
f) 645 milésimos → 0,645
g) 79 centésimos → 0,79
3. a)
Sentença matemática. 0 vírgula 76, igual 76 centésimos, igual, 19 sobre 25.b)
Sentença matemática. 0 vírgula 025, igual, 25 sobre 1 mil, igual, 1 sobre 40.c)
Sentença matemática. 12 vírgula 7, igual, 127 décimos.d)
Sentença matemática. 17 vírgula 22, igual, 1 mil 722 centésimos, igual, 861 sobre 50.e)
Sentença matemática. 50 vírgula 06, igual, 5 mil 006 centésimos, igual, 2 mil 503 sobre 50.f)
Sentença matemática. 0 vírgula 019, igual, 19 milésimos.4. a) 2,5 = 2 inteiros + 5 décimos = 20 décimos + 5 décimos = 25 décimos
b) 5 inteiros = 50 décimos
c) 300 centésimos = 30 décimos = 3 unidades
5.
Sentença matemática. 0 vírgula 04, igual, 4 centésimos, igual, 1 sobre 25.Sentença matemática. 0 vírgula 025, igual, 25 sobre 1 mil, igual, 1 sobre 4.
Atividades – página 153
6. a) 1,2 ≠ 0,12 → 1,20 ≠ 0,12
b) 15 = 15,00 → 15,00 = 15,00
c) 2,06 ≠ 2,6 → 2,06 ≠ 2,60
d) 3,6 = 3,60 → 3,60 = 3,60
e) 0,17 = 0,17000 → 0,17000 = 0,17000
f) 16 ≠ 160 → 16 unidades ≠ 160 unidades
7. a) 7,04 < 7,40, pois 04 < 40
b) 6,200 > 6,196, pois 200 > 196
c) 9,870 > 9,799, pois 870 > 799
d) 10,1 < 11, pois 10 < 11
8. a) 0,75; 0,80; 0,07 → 0,07 < 0,75 < 0,8
b) 2,300; 2,350; 1,197 → 1,197 < 2,3 < 2,35
c) 3,1416; 3,2000; 3,1430 → 3,1416 < 3,143 < 3,2
9. a) 1,36; 0,36; 6,13 → 6,13 > 1,36 > 0,36
b) 0,38; 3,08; 3,80 → 3,8 > 3,08 > 0,38
c) 2,14; 2,00; 2,20 → 2,2 > 2,14 > 2
10. Basta organizar as alturas em ordem crescente e associar com os jogadores que já estão em ordem crescente:
1,79 métro; 1,83 métro; 2 métros; 2,04 métros e 2,13 métros
Ivo: 1,79 métro; Paulo: 1,83 métro; Jorge: 2 métros; Léo: 2,04 métros; Pedro: 2,13 métros
11. Basta organizar os valores em ordem crescente e associar com as letras em ordem alfabética:
0,25 < 1,0898 < 1,69 < 2,5
quatro < três < um < dois
a ‒ quatro; B ‒ três; C ‒ um; D ‒ dois
Atividades – página 155
12. a)
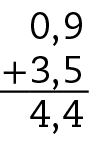
b)
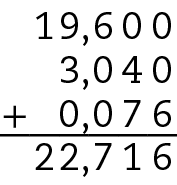
c)
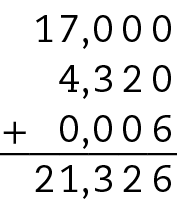
d)
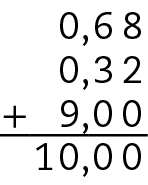
e)
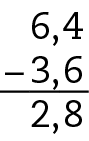
f)
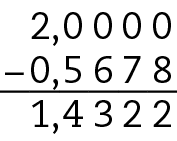
g)

h)
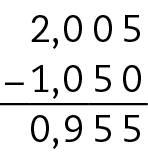
i)
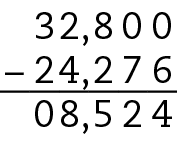
j)
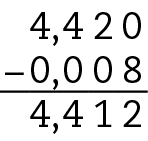
13.
Sentença matemática. 2 inteiros e 3 quartos, igual, 2 mais 0 vírgula 75, igual a 2 vírgula 75.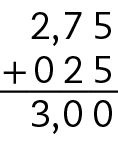
Há na jarra 3 litros.
14.
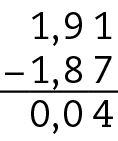
A diferença da medida da altura deles é de 0,04 metro.
15.
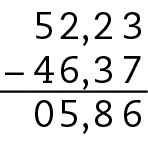
A diferença entre os dois lançamentos foi de 5,86 metros.
16. O estudante pode apresentar várias estratégias de cálculo mental. Resposta possível:
a) 15,65 + 0,9
15,65 + 1 = 16,65
16,65 ‒ 0,1 = 16,55
b) 16,05 ‒ 0,9
16,05 ‒ 1 = 15,05
15,05 + 0,1 = 15,15
c) 21,33 + 0,09
21,33 + 0,1 = 21,43
21,43 ‒ 0,01 = 21,42
d) 21,33 ‒ 0,09
21,33 ‒ 0,1 = 21,23
21,23 + 0,01 = 21,24
17. a) É menor que 5, pois 20 ‒ 18 = 2. É menor que 2, pois 18,25 é maior que 18. É maior que 1, pois 18,25 é menor que 19.
b)

O troco que Vânia recebeu foi R$ 1,75um reais e setenta e cinco centavos.
18. Resposta pessoal.
Os estudantes deverão elaborar um problema em que a estratégia de resolução seja uma subtração na qual o subtraendo é 10,6 e a diferença é 15,7, ou o subtraendo é 15,7 e a diferença é 10,6.
Atividades – páginas 157 a 159
19. a)

b)
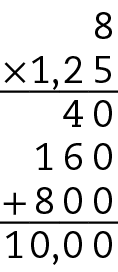
c)
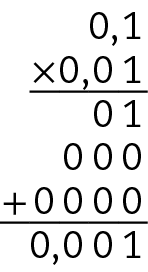
d)
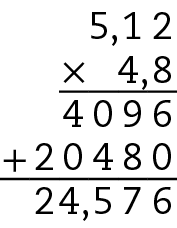
e)
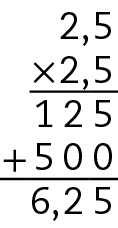
f)
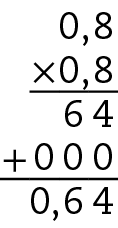
g)
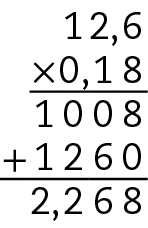
h)
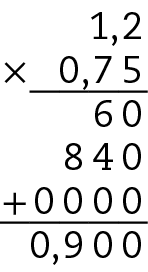
i)
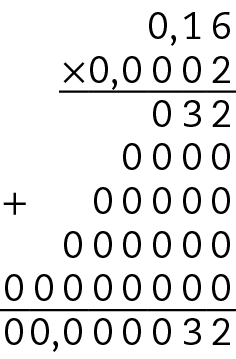
j)
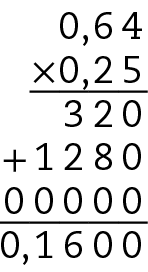
20. a) Espera-se que os estudantes observem que o resultado tem os mesmos algarismos do primeiro fator e a vírgula é deslocada para a direita tantas casas quantos forem os zeros do segundo fator.
b) Resposta pessoal. Espera-se que os estudantes cheguem ao resultado 368,9. Ao multiplicar por 100, os algarismos deslocam-se duas casas para a direita.
21. a)
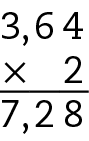
b)
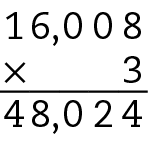
22. a = 0,5 ⋅ 0,12 = 0,060
b = 0,25 ⋅ 0,06 = 0,0150
0,060 ‒ 0,015 = 0,045
O valor de a ‒ b será 0,045.
23. a)

O resultado será 7,006652.
b)

O resultado será 0,49.
24.
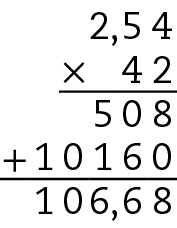
A medida corresponde a 106,68 centímetros.
25. a) Resposta pessoal. Os estudantes poderão arredondar 0,65 para 0,7 e .2200 para .2000, obtendo .1400 métros (0,7 ⋅ .2000 = .1400).
b)
Ana terá percorrido .1430 metros.
c) Resposta pessoal. Os estudantes deverão comparar os resultados e observar se a estratégia de arredondamento foi adequada, ou seja, se o resultado obtido com o arredondamento foi próximo ao valor real.
26. a) 63,2. Basta deslocar os algarismos para a ordem imediatamente superior.
b) .6702. Basta deslocar os algarismos três ordens imediatamente superiores.
c) 0,05. Basta deslocar os algarismos duas ordens imediatamente superiores.
d) 314,5. Basta deslocar os algarismos duas ordens imediatamente superiores.
e) 12; Basta deslocar os algarismos três ordens imediatamente superiores.
f) 90; Basta deslocar os algarismos duas ordens imediatamente superiores.
g) 90; Basta deslocar os algarismos três ordens imediatamente superiores.
h) .121400; Basta deslocar os algarismos quatro ordens imediatamente superiores.
27. a = 2,00 ‒ 0,35 = 1,65
b = 2 + 0,35 = 2,35
Portanto, a ⋅ b = 3,8775.
28.
Lucas gastou R$ 16,62dezesseis reais e sessenta e dois centavos.
29. a) Arredondando 0,69 para 0,70 e 108 para 110:
110 × 0,70 = 77
Portanto,
77 + 56 = 133
Júlio gastou aproximadamente R$ 133,00cento e trinta e três reais.
b)
74,52 + 56 = 130,52
Júlio gastou exatamente R$ 130,52cento e trinta reais e cinquenta e dois centavos.
c) Resposta pessoal. Os estudantes deverão comparar os resultados e observar se a estratégia de arredondamento foi adequada, ou seja, se a estimativa foi próxima ao valor exato.
30. a) 0,222222222
b) 0,444444444
c) 0,555555555
0,72, pois observando a sequência:
0,18 = 2 ⋅ 0,09
0,36 = 4 ⋅ 0,09
0,45 = 5 ⋅ 0,09
0,72 = 8 ⋅ 0,09
31.
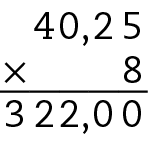
1000 ‒ 322 = 678
A área destinada ao lazer é de 678 metros quadrados.
32. 2,3 ⋅ 0,5 ⋅ 30 = 34,5
2,8 ⋅ 0,5 ⋅ 30 = 42
34,5 + 42 = 76,5
O consumo total de energia por esses dois aparelhos será 76,5 quilowatts-hora.
33. a) 5 ⋅ 1,3 = 6,5
Cinco pães têm 6,5 gramas de gordura.
b) 4,1 ⋅ 2 = 8,2
Deveria comer 2 pães.
34. 63,88 ⋅ 10 = 638,8
63,88 ⋅ 100 = 6 388
63,88 ⋅ 1000 = 63 880
Neste dia o preço de 10 sacas de arroz era R$ 638,80seiscentos e trinta e oito reais e oitenta centavos; de 100 sacas de arroz era R$ 6.388,00seis mil trezentos e oitenta e oito reais e de 1 000 sacas de arroz era R$ 63.880,00sessenta e três mil oitocentos e oitenta reais.
35.
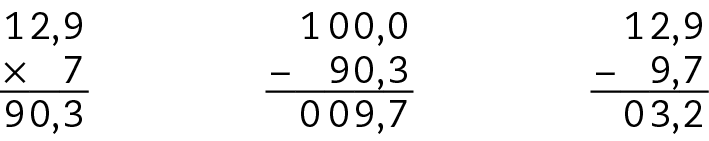
Carlos recebeu R$ 9,70nove reais e setenta centavos de troco. Para comprar 8 peças, ele deveria acrescentar R$ 3,20três reais e vinte centavos.
36. a) 1 ⋅ 22 = 22
2 ⋅ 22 = 44
O produto deve estar entre 22 e 44. Logo, é possível ser 34,1.
b) 3 ⋅ 19 = 57
4 ⋅ 19 = 76
O produto deve estar entre 57 e 76. Logo, é impossível ser 619,4.
c) 4 ⋅ 45 = 180
5 ⋅ 45 = 225
O produto deve estar entre 180 e 225. Logo, é impossível ser .18495.
d) 5 ⋅ 64 = 320
6 ⋅ 65 = 390
O produto deve estar entre 320 e 390. Logo, é possível ser 363,52.
37. a) Resposta pessoal. Os estudantes deverão completar com valores verossímeis.
b) Resposta pessoal. A resposta dependerá dos valores utilizados nas lacunas.
38. a) 0,2 ⋅ 0,2 ⋅ 0,2 = 0,008
b) 1,2 ⋅ 1,2 = 1,44
c) 1
d) 1,4 ⋅ 1,4 ⋅ 1,4 = 2,744
e) 0,7 ⋅ 0,7 = 0,49
f) 0,6 ⋅ 0,6 ⋅ 0,6 = 0,216
g) 0,3 ⋅ 0,3 ⋅ 0,3 ⋅ 0,3 = 0,0081
h) 0,1 ⋅ 0,1 ⋅ 0,1 ⋅ 0,1 ⋅ 0,1 = 0,00001
Atividades – páginas 163 e 164
39. a)
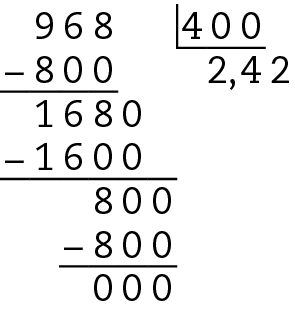
b)
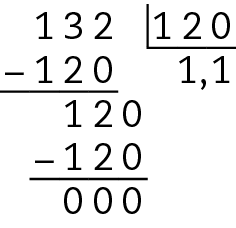
c)
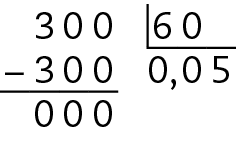
d)
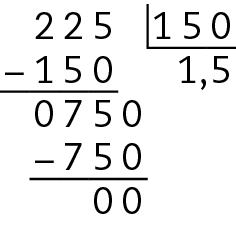
e)
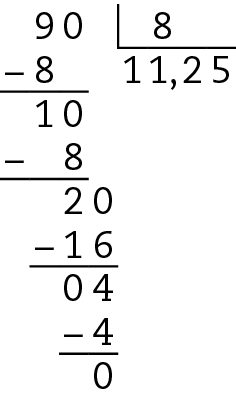
f)
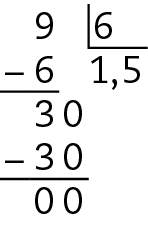
g)
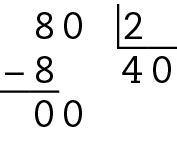
h)
i)

j)
Sim, como pode ser observado nos itens g e h.
40. a) Espera-se que os estudantes percebam que, ao dividir por 10, os algarismos deslocam uma ordem imediatamente à direita. Ao dividir por 100, os algarismos deslocam duas ordens imediatamente à direita. Ao dividir por .1000, os algarismos deslocam três ordens imediatamente à direita.