Revisão dos conteúdos de anos anteriores
Faça as atividades no caderno.
Para o capítulo 1: Números naturais e sistemas de numeração
Sistema de numeração indo-arábico
O sistema de numeração indo-arábico faz agrupamentos de 10 em 10. Além disso, são utilizados dez símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, denominados algarismos.
É um sistema posicional, ou seja, os algarismos assumem valores diferentes conforme a posição que ocupam no número.
Observe alguns modos de representar o número .1524.
|
Unidades de milhar |
Centenas |
Dezenas |
Unidades |
|---|---|---|---|
|
1 |
5 |
2 |
4 |
Quadro de ordens
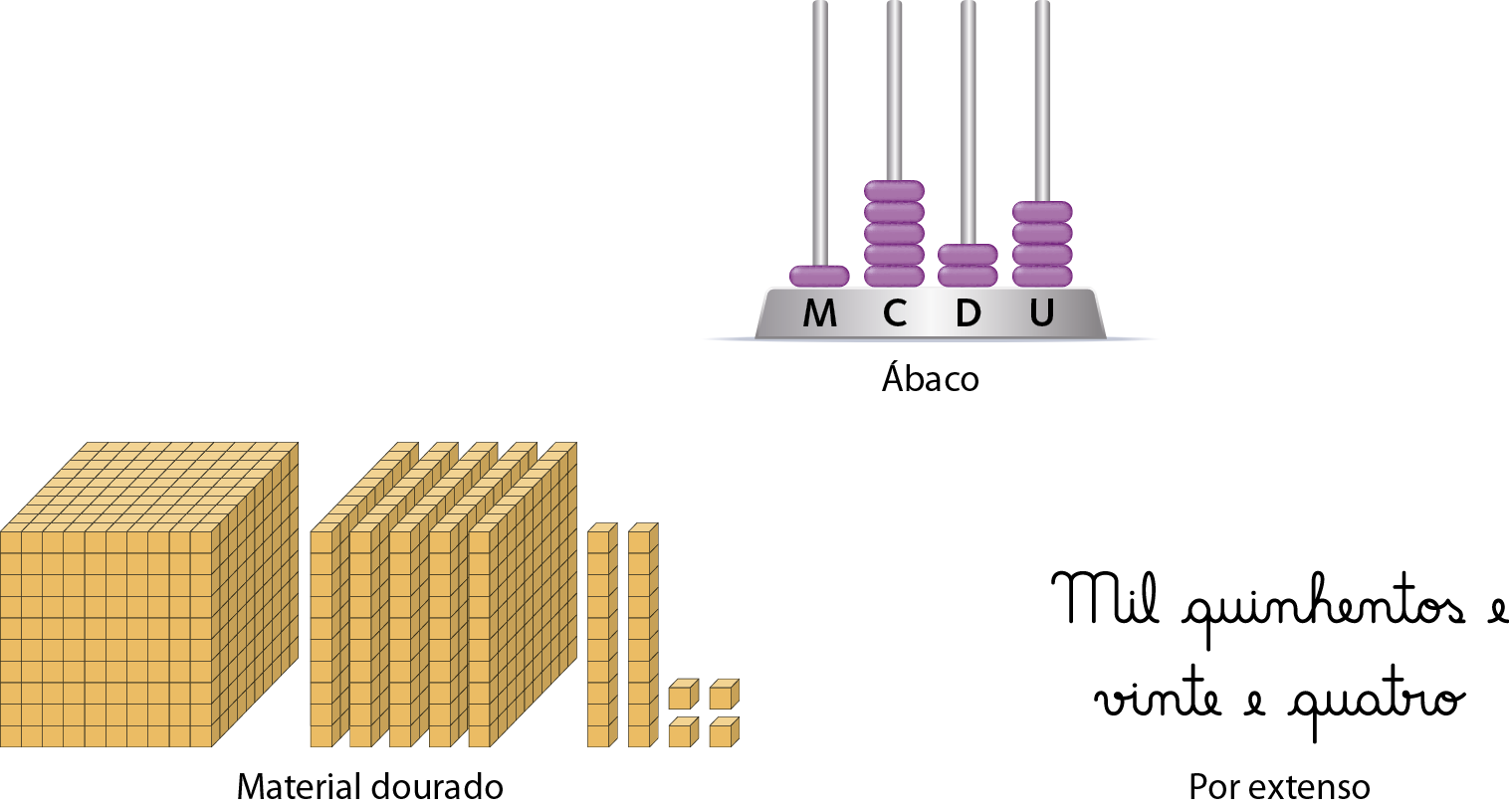
Ordens e classes
Para facilitar a leitura de um número, nós o separamos em classes, agrupando os algarismos de três em três, da direita para a esquerda. Cada classe é formada por três ordens.
|
Classe dos bilhões |
Classe dos milhões |
Classe dos milhares |
Classe das unidades simples |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
12ª ordem |
11ª ordem |
10ª ordem |
9ª ordem |
8ª ordem |
7ª ordem |
6ª ordem |
5ª ordem |
4ª ordem |
3ª ordem |
2ª ordem |
1ª ordem |
|
Centena de bilhão |
Dezena de bilhão |
Unidade de bilhão |
Centena de milhão |
Dezena de milhão |
Unidade de milhão |
Centena de milhar |
Dezena de milhar |
Unidade de milhar |
Centena simples |
Dezena simples |
Unidade simples |
1. Escreva o número formado por:
a) cinco dezenas de milhar mais oito dezenas;
b) duas dezenas de milhar mais sete centenas mais nove unidades;
c) uma unidade de milhão mais seis dezenas mais três unidades;
d) três centenas de milhão mais oito dezenas de milhar mais três centenas;
2. Dado o número .15896.7042, responda.
a) Qual é o algarismo de maior valor posicional?
b) Qual é o algarismo da 8ª ordem?
c) Qual é o nome dado à 5ª ordem?
3. Observe o número a seguir.

a) Escreva no caderno como se lê esse número.
b) Quais algarismos formam a classe dos milhões desse número?
4. Qual o valor posicional do algarismo destacado em azul em cada número?
a) 9.10017
b) .851256
c) ..6892310
d) 73..0489012
e) 1...38320420973
Versão adaptada acessível
4. Qual o valor posicional do algarismo destacado em cada número?
a) 9 1 0 0 1 7 algarismo destacado 9
b) 8 5 1 2 5 6 algarismo destacado 2
c) 6 8 9 2 3 1 0 algarismo destacado 6
d) 7 3 0 4 8 9 0 1 2 algarismo destacado 3
e) 1 3 8 3 2 0 4 2 0 9 7 3 algarismo destacado 1
Orientação para acessibilidade
Respostas
a) 900 mil
b) 200
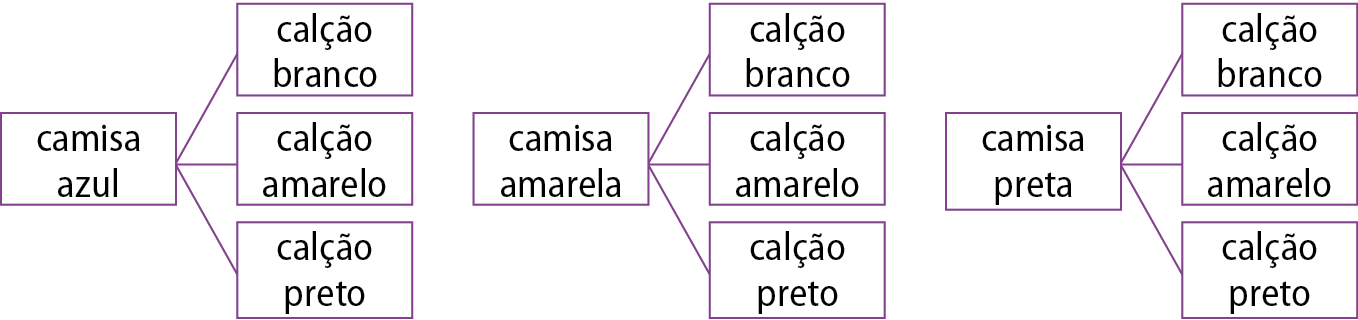
c) 6 milhões
d) 30 milhões
e) 100 bilhões
Respostas e comentários
1. a) .50080
1. b) .20709
1. c) ..1000063
1. d) ..300080300
2. a) 1
2. b) 5
2. c) Dezena de milhar.
3. a) Trezentos e cinquenta e seis bilhões, quatrocentos e nove milhões, duzentos e dezessete mil e vinte e cinco.
3. b) 4, 0 e 9.
4. a) 900 mil.
4. b) 200.
4. c) 6 milhões.
4. d) 30 milhões.
4. e) 100 bilhões.
Revisão dos conteúdos de anos anteriores
Sistema de numeração indo-arábico
• Caso os estudantes tenham dificuldades para realizar a atividade 1, incentive-os a fazê-la com o apôio do ábaco ou de peças do material dourado. Caso a escola não disponha desses materiais, você pode, junto com a turma, confeccioná-los com materiais recicláveis. Esses materiais serão úteis durante todo o ano letivo.
• Na atividade 2, antes de os estudantes iniciarem a resolução, solicite que indiquem, oralmente, o nome da ordem de todos os algarismos, partindo do 2 (unidade) e indo até o 1 (centena de milhão).
• Para a leitura de números, como na atividade 3, relembre os nomes das classes dos números.
• Para a atividade 4, é interessante verificar com os estudantes se eles conhecem a diferença entre número e algarismo. Mais à frente esses conceitos serão apresentados e detalhados, mas pode ser que o assunto venha à discussão agora. Um número é um conceito abstrato relacionado a quantidade, medição ou contagem; o numeral é a maneira (gráfica, oral) de representar essa quantidade; finalmente, o algarismo é o símbolo gráfico, atrelado a algum sistema específico, que representa o número.
O sistema de numeração indo-arábico é posicional porque a posição do algarismo no número indica sua ordem de grandeza. Isso pode ser facilmente compreendido pedindo aos estudantes o número formado pelos algarismos 4 e 7, por exemplo; e, por fim, comente que a cada três ordens se tem uma nova classe.
Os números naturais
Iniciando pelo 0 e adicionando sempre 1 ao número anterior, obtemos a sequência dos números naturais.
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, reticências)
Antecessor de um número natural
Na sequência dos números naturais, o antecessor de um número diferente de zero é o número que vem imediatamente antes dele.
O antecessor de 11 é 10, pois: 11 ‒ 1 = 10
Sucessor de um número natural
O sucessor de um número natural é o número que vem imediatamente depois dele.
O sucessor de 10 é 11, pois: 10 + 1 = 11
5. Determine o que se pede em cada caso.
a) O sucessor de 71.
b) O antecessor de 251.
c) O antecessor do sucessor de .100000.
6. Reproduza o quadro em seu caderno e complete-o.

|
Antecessor |
Número natural |
Sucessor |
|---|---|---|
|
385 |
||
|
999 |
||
|
2.898 |
||
|
1.000.000 |
7. Faça o que se pede.
a) Começando pelo 100, escreva os 10 primeiros termos da sequência dos números naturais pares.
b) Começando pelo 301, escreva a sequência dos 10 primeiros números naturais ímpares.
Reta numérica
Os números naturais podem ser representados em uma reta, na qual cada ponto está associado a um número. Em uma reta numérica, a distância entre dois pontos correspondentes a dois números naturais consecutivos é sempre a mesma.
Com o auxílio da reta numérica, podemos comparar números naturais. O número da direita é sempre maior que o da esquerda e, portanto, o número da esquerda é menor que o da direita.

Observe alguns exemplos de comparações.
a) 0 < 1
b) 1 < 2
c) 6 > 2
d) 2 < 4
8. Escreva o número natural correspondente aos pontos a, B e C na reta numérica a seguir.

9. Desenhe no caderno uma reta numérica e represente pontos correspondentes aos números 12, 8, 10, 6 e 14. Depois, escreva-os em ordem crescente.
Para o capítulo 2: Operacões com números naturais
Adição com números naturais
Algoritmo da decomposição
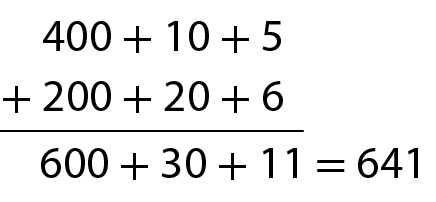
Algoritmo usual
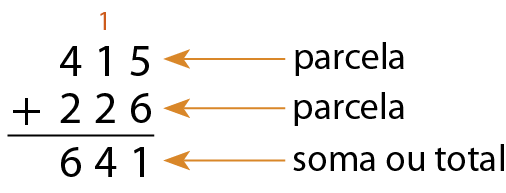
10. Calcule o resultado de cada uma das operações no caderno.
a) .2581 + .4383
b) .1150 + 563 + .3429
c) .12525 + 938 + .2627
11. Maria comprou um aparelho de televisão em duas prestações. A primeira de R$ 750,00setecentos e cinquenta reais e a segunda de R$ 635,00seiscentos e trinta e cinco reais. Quantos reais Maria pagou pelo aparelho de televisão?
12. Em um jôgo de videogame, Luísa fez 283 pontos na primeira fase e 487 na segunda fase do jôgo. Quantos pontos ela fez até agora?
Respostas e comentários
5. a) 72
5. b) 250
5. c) .100000
6. Resposta em Orientações.
7. a) (100, 102, 104, 106, 108, 110, 112, 114, 116, 118)
7. b) (301, 303, 305, 307, 309, 311, 313, 315, 317, 319)
8. A: 42; B: 45; C: 48.
9. 6, 8, 10, 12 e 14.

10. a) .6964
10. b) .5142
10. c) .16090
11. R$ 1.385,00mil trezentos e oitenta e cinco reais
12. 770 pontos.
Os números naturais
Apresente aos estudantes, de fórma oral, alguns números aleatórios (por exemplo: 2, ‒6, 3, ‒15, 5, 1, 100, ‒.5000) e solicite que respondam se são números naturais ou não.
Com os números naturais determinados por eles, peça-lhes que digam qual é o seu sucessor e o seu antecessor; caso tenham dificuldade, mostre que, para encontrar o sucessor, basta adicionar 1 e, para encontrar o antecessor, basta subtrair 1.
• Nas atividades 5 e 6, os estudantes devem determinar sucessores e antecessores dos números dados. Caso algum estudante tenha dificuldade, relembre que ele deve subtrair 1 do número proposto para encontrar o antecessor ou adicionar 1 ao número proposto para encontrar o sucessor.
Resposta da atividade 6:
|
Antecessor |
Número natural |
Sucessor |
|---|---|---|
|
384 |
385 |
386 |
|
998 |
999 |
1.000 |
|
2.898 |
2.899 |
2.900 |
|
999.999 |
1.000.000 |
1.000.001 |
• Na atividade 7, se julgar necessário, proponha aos estudantes um campeonato de par ou ímpar. Essa brincadeira auxiliará na compreensão e na fixação dos conceitos de par e ímpar importantíssimos mais à frente.
Reta numérica
Para a melhor compreensão da comparação dos números naturais, desenhe uma reta numérica na lousa com 20 tracinhos e solicite aos estudantes que digam números naturais para serem colocados abaixo dos tracinhos (essa proposta auxiliará na realização da atividade 8). Na sequência, solicite a dois estudantes que escolham números distintos e, em seguida, que informem qual é o maior entre os dois (essa proposta auxiliará na resolução da atividade 9).
Mostre também que o símbolo de maior é representado por > (maior que) e que o símbolo de menor é expresso por < (menor que).
Adição com números naturais
• Nas atividades 11 e 12, verifique as diferentes estratégias utilizadas pelos estudantes e, se julgar necessário, peça que utilizem o algoritmo da decomposição para efetuar a adição.
Algumas propriedades da adição
Propriedade comutativa: a ordem das parcelas não altera a soma.
15 + 21 = 21 + 15
Propriedade associativa: em uma adição de três ou mais números naturais, podemos associar as parcelas de diferentes modos sem alterar a soma.
(12 + 28) + 10 = 40 + 10 = 50
12 + (28 + 10) = 12 + 38 = 50
Elemento neutro: ao adicionar zero a um número, a soma é igual ao próprio número.
35 + 0 = 35
41 + 0 = 41
13. Copie as sentenças em seu caderno e complete-as.
a) 263 +

= 527 + 263
b) .2318 + 0 = 0 +

c) .9287 + .1622 =

+ .9287
d) .10258 + .8102 =

+ .10258
14.

Calcule mentalmente o resultado de cada adição.
a) 250 + 120 + 50 + 80
b) 300 + 64 + 36 + 120
c) 450 + 0 + 275 + 25
d) 180 + 75 + 120 + 25
Subtração com números naturais
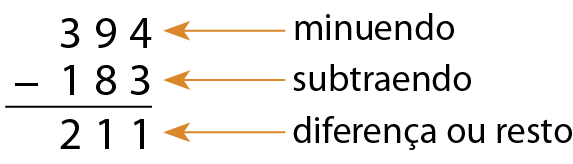
15. Calcule o resultado de cada uma das operações no caderno.
a) .8265 ‒ .3421
b) .9151 ‒ .7237
c) .11950 ‒ .2358
d) .25902 ‒ .13453
16. Em uma subtração, o minuendo é 528 e o resto é 129. Qual é o valor do subtraendo?
17. Em uma subtração, o resto é 385 e o subtraendo é 291. Qual é o valor do minuendo?
Multiplicação com números naturais
Em uma multiplicação, os números que se multiplicam são chamados de fatores e o resultado de produto.
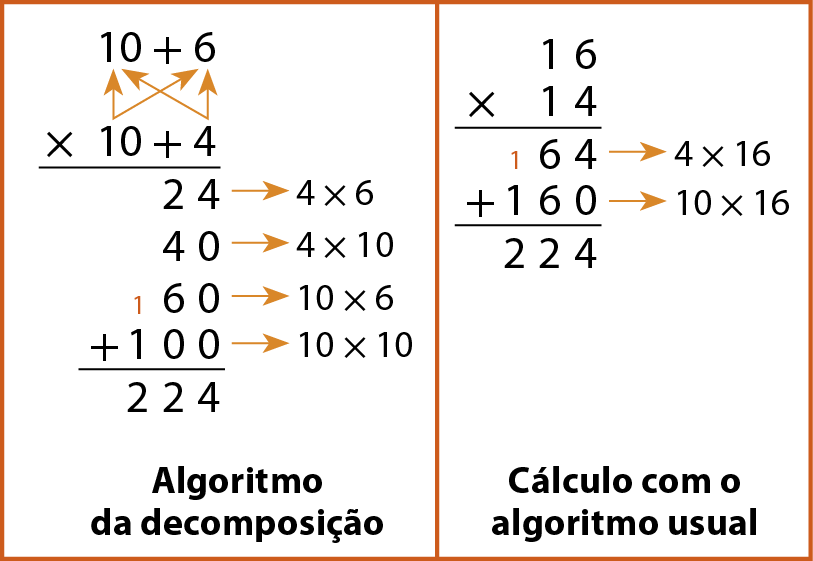
Analise como calcular 14 × 16 de dois modos diferentes.
18. Calcule o resultado de cada uma das operações.
a) 42 × 12
b) 213 × 15
c) 310 × 18
d) 521 × 32
19. Vanessa comprou um aparelho de televisão em 12 prestações de R$ 252,00duzentos e cinquenta e dois reais. Qual foi o total gasto nessa compra?
20. O produto de dois números é 336. Um dos fatores é 12. Qual é o outro fator?
Algumas propriedades da multiplicação
Propriedade comutativa: a ordem dos fatores não altera o produto.
12 × 28 = 28 × 12
Propriedade associativa: em uma multiplicação com mais de dois números naturais, podemos associar os fatores de modos diferentes sem alterar o produto.
(10 × 18) × 5 = 10 × (18 × 5)
Propriedade distributiva da multiplicação em relação à adição: em uma multiplicação de um número natural por uma adição de duas ou mais parcelas, adicionamos os produtos de cada parcela pelo número natural.
5 × (12 + 6) = 5 × 12 + 5 × 6 = 60 + 30 = 90
A propriedade distributiva também é válida para a subtração:
4 × (15 ‒ 7) = 4 × 15 ‒ 4 × 7 = 60 ‒ 28 = 32
Respostas e comentários
13. a) 527
13. b) .2318
13. c) .1622
13. d) .8102
14. a) 500
14. b) 520
14. c) 750
14. d) 400
15. a) .4844
15. b) .1914
15. c) .9592
15. d) .12449
16. 399
17. 676
18. a) 504
18. b) .3195
18. c) .5580
18. d) .16672
19. R$ 3.024,00três mil vinte e quatro reais
20. 28
Subtração com números naturais
• Na atividade 17, relembre os estudantes de que, em uma subtração, o minuendo é o primeiro elemento da operação, o subtraendo é o segundo elemento e o resto (ou diferença) é o resultado dessa operação. Se necessário, mostre que, nesse caso, vale aplicar a operação inversa da subtração, que é a adição, para achar o valor do minuendo.
Multiplicação com números naturais
Para trabalhar a multiplicação com números naturais, é possível propor uma atividade com um quadro (como o do modelo a seguir).

Nele, os estudantes calculam as multiplicações e pintam as respostas conforme esta legenda.
0 até 9: rosa
10 até 29: amarelo
30 até 50: verde
60 até 150: azul
• Na atividade 19, alguns estudantes podem ficar com dúvida sobre o significado do termo “prestação”. Explique a eles o sentido dessa palavra e exponha exemplos de uso no dia a dia para melhor entendimento do problema.
• Na atividade 20, pode-se criar uma lista de múltiplos do número 12 até chegar ao resultado 336 ou utilizar a operação inversa da multiplicação, que é a divisão.
21. Copie as sentenças em seu caderno e complete-as.
a) 112 × 15 =

× 112
b) 219 × 156 =

× 219
c) 11 × (15 × 9) = (11 ×

) × 9
d) 25 × (18 × 7) = (25 ×

) × 7
e) 315 ×

= 102 × 315
f) .1010 ×

= 55 × .1010
22. No caderno, calcule o valor das expressões de duas maneiras.
a) 6 × (12 + 7)
b) 9 × (21 ‒ 13)
c) 10 × (15 + 8)
Divisão com números naturais

Quando o resto da divisão é zero, dizemos que a divisão é exata; quando é diferente de zero, a divisão é não exata.
23. Calcule o quociente e o resto de cada divisão no caderno.
a) 280 ÷ 12
b) 327 ÷ 9
c) 980 ÷ 10
d) .1000 ÷ 100
e) .2824 ÷ 16
f) .1025 ÷ 10
24. Mateus comprou uma motocicleta que custa R$ 12.600,00doze mil seiscentos reais. Ele vai pagar essa compra em 24 prestações iguais. Qual será o valor de cada prestação?
Para o capítulo 3: Figuras geométricas espaciais
Sólidos geométricos
Sólido é uma figura geométrica espacial e não oca, ou seja, maciça.
Poliedros
São sólidos geométricos que têm a superfície formada somente por partes não arredondadas, ou seja, “achatadas”.
Os prismas e as pirâmides são exemplos de poliedros.
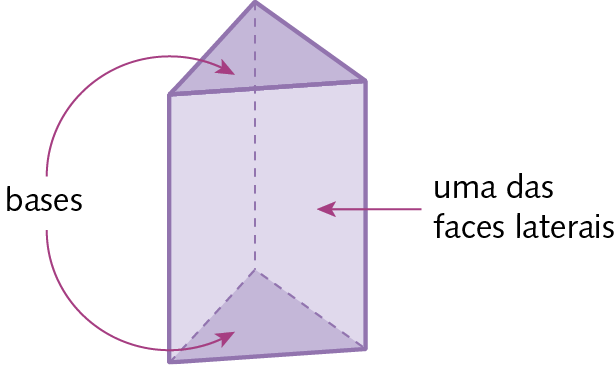
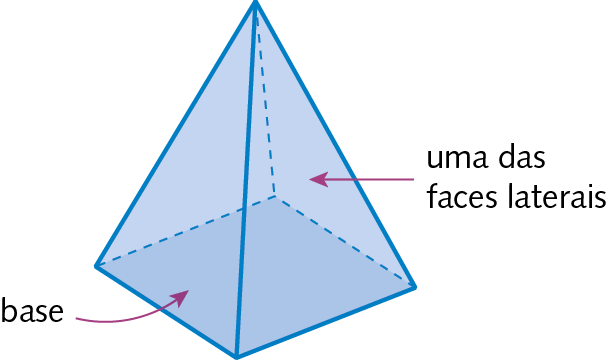
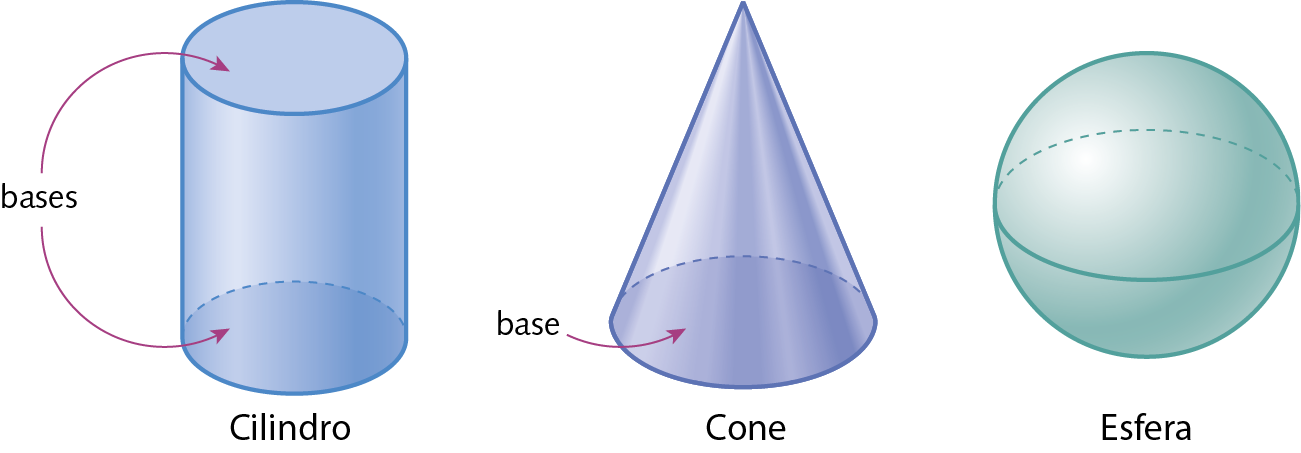
Corpos redondos
São sólidos geométricos que têm pelo menos uma parte com formato arredondado.
Os cilindros, os cones e as esferas são exemplos de corpos redondos.
Respostas e comentários
21. a) 15
21. b) 156
21. c) 15
21. d) 18
21. e) 102
21. f ) 55
22. a) 114
22. b) 72
22. c) 230
23. a) quociente: 23; resto: 4.
23. b) quociente: 36; resto: 3.
23. c) quociente: 98; resto: 0.
23. d) quociente: 10; resto: 0.
23. e) quociente: 176; resto: 8.
23. f) quociente: 102; resto: 5.
24. R$ 525,00quinhentos e vinte e cinco reais
Algumas propriedades da multiplicação
• A atividade 21 visa observar a compreensão dos estudantes em relação às propriedades comutativa e associativa.
• Na atividade 22, destaque o pedido do enunciado para calcular cada item de duas maneiras. Caso os estudantes tenham dificuldades para pensar em dois modos para efetuar as expressões, leve-os a perceber que podem calcular a operação entre parênteses e, depois, efetuar a multiplicação ou podem usar a propriedade distributiva da multiplicação.
Divisão com números naturais
Se julgar necessário, recorde com os estudantes que os elementos da divisão podem ser relacionados da seguinte fórma:
dividendo = quociente ⋅ divisor + resto
• Na atividade 23, solicite aos estudantes que verifiquem a resposta que deram a alguns itens por meio da relação anterior.
Sólidos geométricos
Para o estudo e a melhor compreensão dos sólidos geométricos, separe os estudantes em grupos e entregue a cada grupo o nome de um sólido geométrico (pirâmide, prisma, esfera, cone, cilindro). Peça à turma que cada um procure em sua casa objetos que lembrem esses sólidos geométricos. Em sala de aula, solicite aos estudantes que façam uma breve descrição de seus objetos relacionando suas partes com faces, arestas e vértices.
Caso surjam dúvidas sobre o conceito de face, aresta e vértice, dê uma breve explicação a eles. Além disso, deixe claro que os objetos que encontramos no dia a dia não são de fato os sólidos que estudamos em Geometria, eles apenas se parecem com eles.
Essa atividade auxiliará na resolução da atividade 25.
25. Observe os poliedros e faça o que se pede.
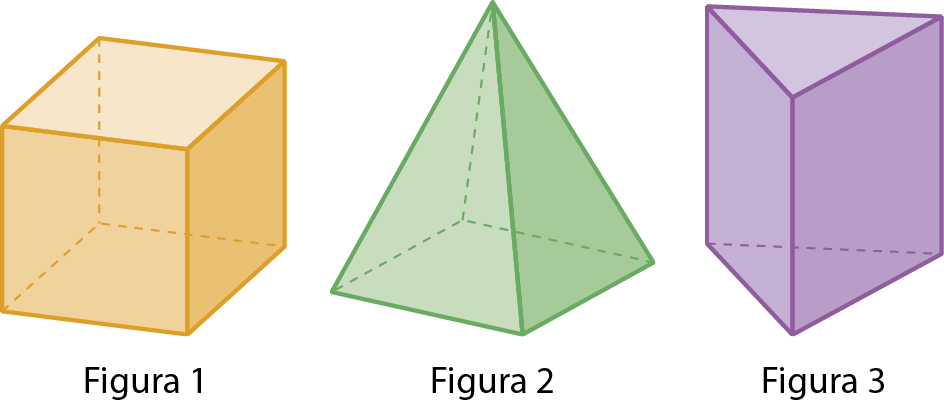
a) Reproduza o quadro no caderno e complete-o.

|
Número de faces |
Número de arestas |
Número de vértices |
|
|---|---|---|---|
|
Figura 1 |
|||
|
Figura 2 |
|||
|
Figura 3 |
b) Qual é o formato da base de cada poliedro?
c) Escreva no caderno o nome dos poliedros.
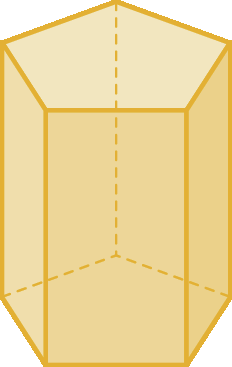
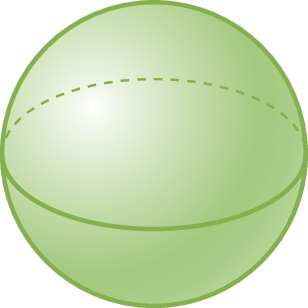
26. Qual o nome dos sólidos geométricos a seguir?
a)
b)

c)
d)
Planificação da superfície de sólidos geométricos
A representação da superfície de um sólido geométrico é chamada de planificação.
Observe a planificação da superfície de alguns sólidos geométricos.
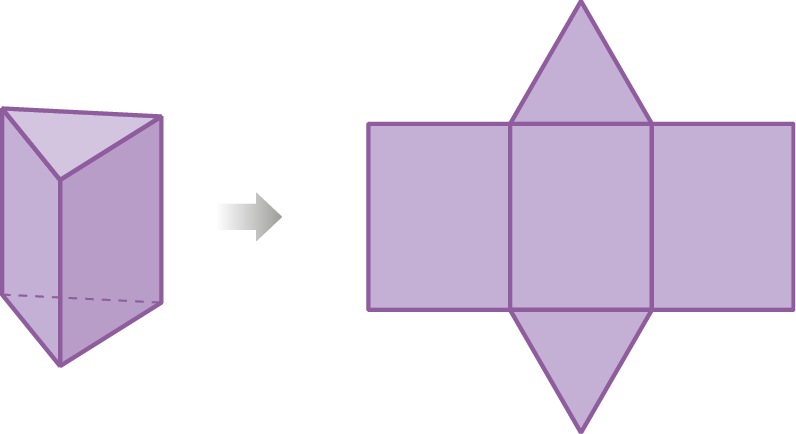
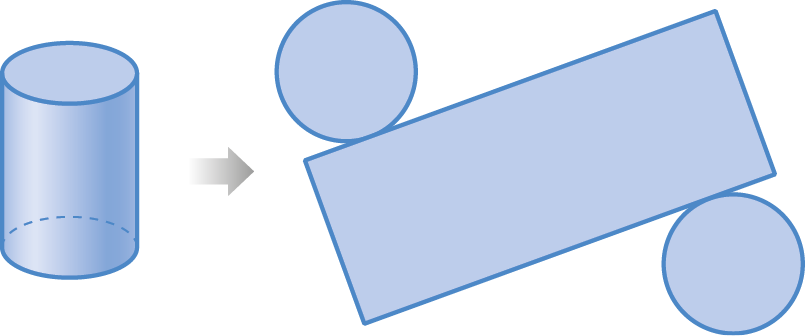
27. Qual o nome da figura cuja planificação da superfície está representada a seguir?

28. A qual sólido geométrico corresponde cada uma das planificações a seguir?
a)

b)
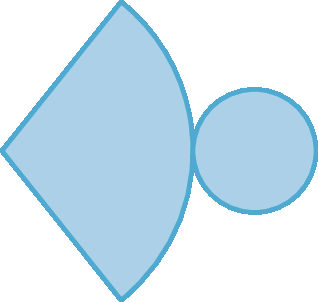
c)
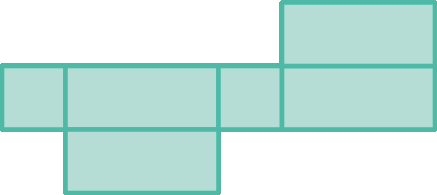
d)
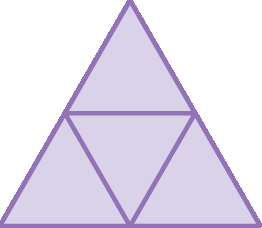
Respostas e comentários
25. a) Resposta em Orientações.
25. b) Quadrangular, quadrangular e triangular.
25. c) Prisma de base quadrangular, pirâmide de base quadrangular, prisma de base triangular.
26. a) Prisma de base pentagonal
26. b) Cone
26. c) Esfera
26. d) Pirâmide de base triangular
27. Cubo
28. a) Pirâmide de base quadrada
28. b) Cone
28. c) Paralelepípedo
28. d) Pirâmide de base triangular
Resposta do item a da atividade 25:
|
Número de faces |
Número de arestas |
Número de vértices |
|
|---|---|---|---|
|
Figura 1 |
6 |
12 |
8 |
|
Figura 2 |
5 |
8 |
5 |
|
Figura 3 |
5 |
9 |
6 |
Planificação da superfície de sólidos geométricos
Se possível, providencie antecipadamente folhas com representações da superfície de sólidos geométricos. Organize a turma em grupos e distribua as folhas entre eles. Na sequência, peça aos estudantes que construam os modelos de sólidos geométricos utilizando fita adesiva. Essa experimentação ajudará na resolução das atividades 27 e 28.
Para o capítulo 4: Igualdades e desigualdades
Igualdades
Toda igualdade continuará sendo válida se:
• adicionarmos ou subtrairmos o mesmo número de seus membros;
• multiplicarmos seus membros por um mesmo número ou dividirmos seus membros por um mesmo número diferente de zero.
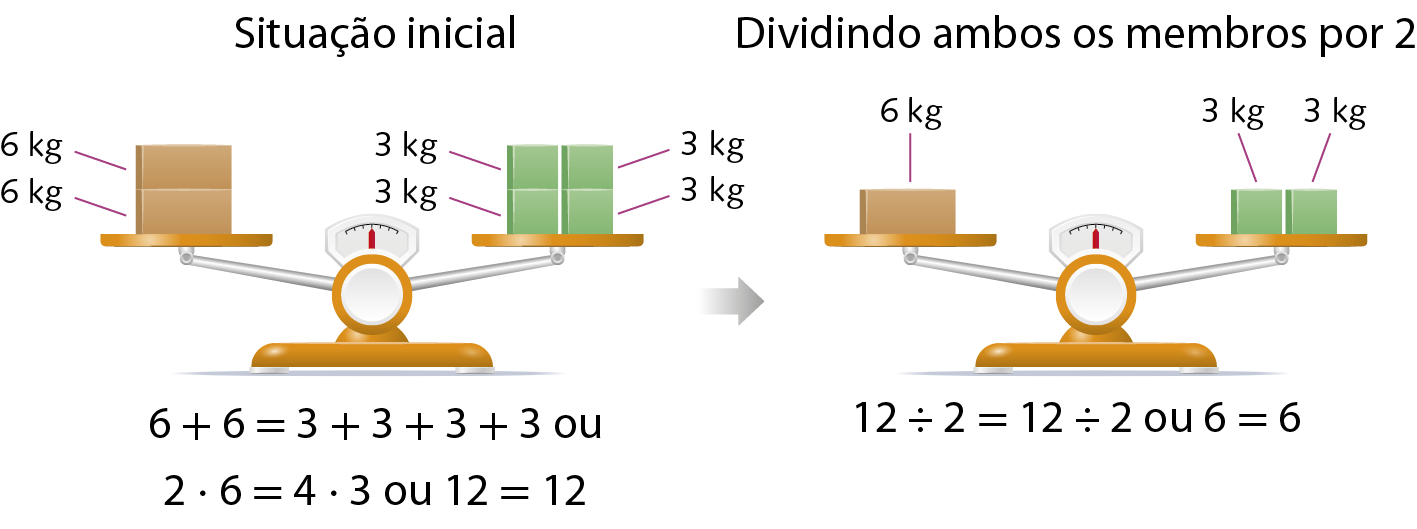
29. Em cada item, faça o que se pede e determine a igualdade correspondente.
a) Adicione 12 aos dois membros da igualdade: 25 + 32 = 12 + 45
b) Subtraia 8 dos dois membros da igualdade: 29 ‒ 7 = 15 + 7
c) Multiplique por 8 os dois membros da igualdade: 15 + 4 = 25 ‒ 6
d) Divida por 5 os dois membros da igualdade: 25 + 15 = 50 ‒ 10
30. Copie no caderno as sentenças e complete-as.
a) (120 + 300)

= 420 ÷ 2
b) 258

= 228 + 30 ‒ 150
c) .1000

= (400 + 600) × 5
d) .1200 ÷ 3 = (800 + 400)

e) 238

= 100 + 138 + 100
f) (.1600 ‒ 200)

= .1400 × 10
Para o capítulo 5: Múltiplos e divisores
Múltiplo de um número natural é o produto desse número por um número natural qualquer.
|
× |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Múltiplo de 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
... |
|
Múltiplo de 2 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
... |
|
Múltiplo de 7 |
0 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
... |
|
Múltiplo de 9 |
0 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
... |
31. Reproduza o quadro no caderno e complete-o.

|
× |
2 |
5 |
7 |
9 |
12 |
15 |
|---|---|---|---|---|---|---|
|
1 |
||||||
|
3 |
||||||
|
5 |
||||||
|
7 |
||||||
|
10 |
||||||
|
12 |
32. Escreva no caderno:
a) 10 números múltiplos de 4.
b) os múltiplos de 9 situados entre 50 e 100.
c) os cinco primeiros múltiplos de 6, a partir do próprio 6.
33. Escreva os múltiplos de 15 situados entre 100 e 200.
Respostas e comentários
29. a) 69 = 69
29. b) 14 = 14
29. c)152 = 152
29. d) 8 = 8
30. a) ÷ 2
30. b) ‒ 150
30. c) × 5
30. d) ÷ 3
30. e) + 100
30. f) × 10
31. Resposta em Orientações.
32. a) Resposta possível: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
32. b) 54, 63, 72, 81, 90 e 99.
32. c) 6, 12, 18, 24 e 30.
33. 105, 120, 135, 150, 165, 180 e 195.
Igualdades
Para o trabalho com igualdades e desigualdades, se possível, construa uma balança com os estudantes, utilizando um cabide, dois barbantes presos nas extremidades do cabide e sacos presos a esses barbantes. Coloque objetos nos sacos e mostre aos estudantes que, quando os sacos estão na mesma altura, a balança fica em equilíbrio (ou seja, existe uma igualdade entre as medidas de massa); quando um saco está mais baixo que outro, a balança fica em desequilíbrio (ou seja, há uma desigualdade entre as medidas de massa). A ideia de associar o equilíbrio da balança às condições de igualdade ou de desigualdade em uma sentença matemática favorece o desenvolvimento do raciocínio lógico-matemático por analogia.
• Na atividade 30, se necessário, relembre as propriedades da adição e da multiplicação.
Para a melhor compreensão dos múltiplos e divisores, organize a sala em grupos de até 4 estudantes e defina para cada grupo dois números naturais; para um dos números, peça aos estudantes que escrevam 10 múltiplos e, para o outro número, peça que escrevam seus divisores; por fim, cada grupo apresentará aos demais seus resultados e como chegou a eles. Visando dificultar essa proposta (caso esteja muito fácil), solicite a um grupo que determine os dois números de um outro grupo e, depois, verifique se o grupo indicou os múltiplos e divisores adequadamente. Esse procedimento auxiliará na resolução das atividades 31, 32, 33 e 34.
• Resposta da atividade 31:
|
× |
2 |
5 |
7 |
9 |
12 |
15 |
|---|---|---|---|---|---|---|
|
1 |
2 |
5 |
7 |
9 |
12 |
15 |
|
3 |
6 |
15 |
21 |
27 |
36 |
45 |
|
5 |
10 |
25 |
35 |
45 |
60 |
75 |
|
7 |
14 |
35 |
49 |
63 |
84 |
105 |
|
10 |
20 |
50 |
70 |
90 |
120 |
150 |
|
12 |
24 |
60 |
84 |
108 |
144 |
180 |
34. Reproduza o quadro no caderno e marque um X nos espaços correspondentes a divisões exatas. Lembre-se de que a divisão é exata quando o resto é zero.

|
Divisor |
||||||
|---|---|---|---|---|---|---|
|
Número |
2 |
3 |
5 |
6 |
9 |
10 |
|
258 |
||||||
|
356 |
||||||
|
400 |
||||||
|
525 |
||||||
|
886 |
||||||
|
990 |
||||||
|
1.000 |
||||||
|
1.050 |
||||||
|
2.256 |
||||||
|
8.250 |
||||||
Para o capítulo 6: Frações
Em uma fração, o denominador é o número que indica a quantidade de partes iguais em que o todo foi dividido. O numerador indica a quantidade de partes consideradas do todo.

Leitura de frações
a)
fração 2 sobre 3→ Lemos: “dois terços”.
b)
fração 7 sobre 100→ Lemos: “sete centésimos”.
c)
fração 13 sobre 22→ Lemos: “treze vinte dois avos”.
35. No caderno, escreva como se lê cada fração.
a)
fração 1 sobre 8
b)
fração 4 sobre 15
c)
fração 17 sobre 100
d)
fração 27 sobre 20036. Em seu caderno, escreva a fração correspondente às partes pintadas das figuras em cada caso.
a)

b)
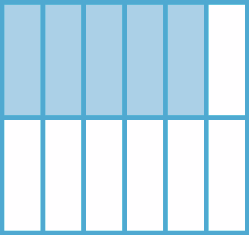
c)

d)

Número misto
A representação de um número misto é composta de uma parte inteira e de uma parte fracionária.
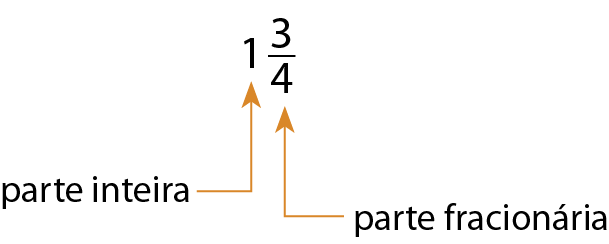
37. No caderno, represente com figuras os números mistos a seguir.
a)
Número misto 2 inteiros e 1 terço.b)
Número misto 1 inteiro e 2 terços.c)
Número misto 2 inteiros e 3 oitavos.d)
Número misto 1 inteiro e 7 nonos.38. No caderno, represente com frações os seguintes números mistos.
a)
Número misto 1 inteiro e 2 quintos.
b)
Número misto 3 inteiros e 4 nonos.
c)
Número misto 5 inteiros e 1 quarto.
d)
Número misto 8 inteiros e 3 quintos.Respostas e comentários
34. Resposta em Orientações.
35. a) um oitavo.
35. b) quatro quinze avos.
35. c) dezessete centésimos.
35. d) vinte e sete duzentos avos.
36. a) Exemplo de resposta:
3 sextos36. b)
5 doze avos36. c)
3 quartos36. d) Exemplo de resposta:
16 trinta e seis avos37. Resposta em Orientações.
38. a)
7 quintos38. b)
31 nonos38. c)
21 quartos38. d)
43 quintosResposta da atividade 34:
|
Divisor |
||||||
|
Número |
2 |
3 |
5 |
6 |
9 |
10 |
|---|---|---|---|---|---|---|
|
258 |
X |
X |
X |
|||
|
356 |
X |
|||||
|
400 |
X |
X |
X |
|||
|
525 |
X |
X |
||||
|
886 |
X |
|||||
|
990 |
X |
X |
X |
X |
X |
X |
|
1.000 |
X |
X |
X |
|||
|
1.050 |
X |
X |
X |
X |
X |
|
|
2.256 |
X |
X |
X |
|||
|
8.250 |
X |
X |
X |
X |
X |
|
Para clarificar a ideia de fração, é possível, por exemplo, levar uma barra de chocolate para a sala de aula e quebrá-la em algumas partes iguais, mostrando que a barra inteira representa o inteiro e o número de pedaços representa as partes que compõem o inteiro. Essa proposta auxilia na resolução da atividade 36.
Número misto
Se julgar necessário, desenhe na lousa, por exemplo, duas barrinhas de mesmo tamanho e mesmo número de divisões; uma barrinha deve ser completamente pintada (representará o valor inteiro) e a outra deverá ser pintada parcialmente e representará a parte fracionária. Junto com a turma, indique uma fração e um número misto correspondentes à representação. Faça quantas representações achar necessário. Essa proposta visa auxiliar na resolução das atividades 37 e 38.
• Resposta da atividade 37:
a)
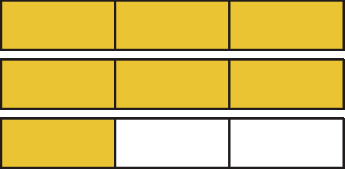
b)

c)
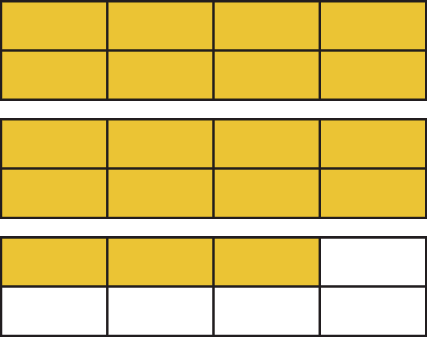
d)
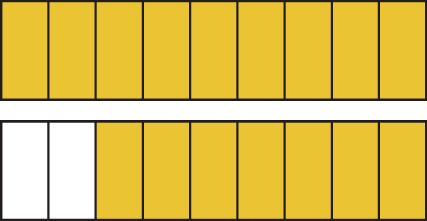
Frações equivalentes
Frações que representam a mesma parte do inteiro são chamadas frações equivalentes.

As frações
2 terços, 4 sextos e 6 nonossão equivalentes.
39. No caderno, escreva uma fração equivalente a cada fração dada.
a)
8 sobre 16b)
25 sobre 100c)
150 sobre 450d)
75 sobre 9540. Copie as sentenças em seu caderno e complete com o número que falta para que as frações sejam equivalentes.
a)
3 sobre 8 é igual a 27 sobre quadradinho cinzab)
5 sobre 7 é igual a quadradinho cinza sobre 21c)
4 sobre 25 é igual a 20 sobre quadradinho cinzad)
quadradinho cinza sobre 7 é igual a 30 sobre 70Comparação de frações de um mesmo inteiro
Quando duas ou mais frações têm o mesmo denominador, a maior delas é a que tem maior numerador.
Quando duas ou mais frações têm o mesmo numerador, a maior delas é a que tem menor denominador.
Quando duas ou mais frações têm numeradores e denominadores diferentes, devemos obter frações equivalentes às frações iniciais que tenham o mesmo denominador ou numerador para, em seguida, compará-las.
41. Escreva as frações em ordem crescente.
a)
1 terço, 1 quarto e 1 meio.
b)
2 quintos, 3 quartos e 2 nonos.
c)
um quarto, 3 oitavos e 15 meios
d)
5 oitavos, dez 12 avos, 3 nonos42. Escreva as frações em ordem decrescente.
a)
2 quintos, 9 quintos e 1 quinto
b)
doze 18 avos, cinco 18 avos e vinte e cinco 18 avos
c)
10 sobre 35, 1 sobre 35 e 18 sobre 35
d)
51 sobre 58, 12 sobre 58 e 23 sobre 5843. Determine a maior fração de cada item.
a)
1 nono, 7 nonos e 6 nonos
b)
2 quartos, 3 oitavos e 3 quartos
c)
1 quarto, 1 nono e 1 terço
d)
4 quintos, dez 12 avos e 7 sextosAdição e subtração com frações
Mesmo denominador
Para calcular a soma ou a diferença de duas frações com denominadores iguais, adicionamos ou subtraímos os numeradores, conforme a operação desejada, e conservamos os denominadores.
a)
1 quarto mais 2 quartos é igual a 3 quartos
b)
7 nonos menos 3 nonos é igual a 4 nonosDenominadores diferentes
Para calcular a soma ou a diferença de duas frações com denominadores diferentes, encontramos frações equivalentes às iniciais, com um mesmo denominador, e então efetuamos a operação desejada.
Respostas e comentários
39. a) Exemplo de resposta:
um meio39. b) Exemplo de resposta:
um quarto39. c) Exemplo de resposta:
um terço39. d) Exemplo de resposta:
15 dezenove avos40. a) 72
40. b) 15
40. c) 125
40. d) 3
41. a)
um quarto, um terço e um meio41. b)
2 nonos, 2 quintos e 3 quartos41. c)
1 quarto, 3 oitavos e 15 meios41. d)
3 nonos, 5 oitavos e dez 12 avos42. a)
9 quintos, 2 quintos e 1 quinto42. b)
25 sobre 18, 12 sobre 18 e 5 sobre 1842. c)
18 sobre 35, 10 sobre 35 e 1 sobre 3542. d)
51 sobre 58, 23 sobre 58 e 12 sobre 5843. a)
7 nonos43. b)
3 quartos43. c)
1 terço43. d)
7 sextosFrações equivalentes
Para auxiliar no desenvolvimento das atividades 39 e 40, relembre os estudantes de que, para que as frações sejam equivalentes, é preciso dividir ou multiplicar o numerador e o denominador pelo mesmo valor.
Comparação de frações de um mesmo inteiro
Para relembrar a comparação de frações, proponha um jôgo em que os estudantes são distribuídos em equipes. Cada equipe recebe várias frações escritas em papéis separados que devem estar virados de cabeça para baixo. Nessa proposta, os participantes devem, a cada rodada, virar duas frações, compará-las e descobrir qual relação há entre elas. Esse jôgo auxilia os estudantes a criar estratégias que podem ser utilizadas na resolução das atividades 41, 42 e 43.
Adição e subtração com frações
Se achar conveniente, mostre aos estudantes como adicionar ou subtrair frações com denominadores iguais utilizando figuras.
Considere, por exemplo, a figura a seguir, que foi dividida em 6 partes iguais:

A fração que corresponde à parte verde é
1 sextoe a fração que corresponde à parte amarela é
3 sextosPortanto, a parte pintada da figura é
4 sextospois:
1 sexto mais 3 sextos é igual a 4 sextosJá a parte que não foi pintada corresponde a
2 sextosda figura, pois
6 sextos menos 4 sextos é igual a 2 sextosAo trabalhar a adição e a subtração com frações de denominadores diferentes, incentive-os a recorrer ao conceito de frações equivalentes.
44. Calcule o resultado das operações no caderno.
a)
1 terço mais 5 terçosb)
9 sobre 15 mais 11 sobre 15c)
7 oitavos menos 3 oitavosd)
11 sobre 20 menos 7 sobre 20e)
número misto um inteiro, dois terços mais um terçof)
3 sétimos mais 2 sobre 14g)
1 quarto mais 3 terçosh)
3 meios menos 7 oitavosi)
4 quintos menos 5 sobre 12j)
um terço mais um quarto mais um meiok)
10 sobre 15 menos 3 oitavosl)
2 terços mais 4 quintos mais um meio45. Marcos gastou
3 sétimosdo salário com despesas fixas e
2 oitavoscom outras despesas. Que fração corresponde à parte do salário que Marcos gastou?
46. Joana leu
um quartode um livro em um dia e
um terçodesse livro no segundo dia. Que fração do livro falta para Joana ler?
Multiplicação de um número natural por uma fração
Multiplicar uma fração por um número natural é o mesmo que adicioná-la tantas vezes quanto o número natural considerado.
47. Calcule o resultado de cada uma das multiplicações no caderno.
a)
6 vezes 3 sétimosb)
5 vezes 3 quartosc)
2 vezes um terçod)
9 vezes 4 sétimose)
12 vezes 3 quintosf)
15 vezes um sexto48. Na receita de um pão são utilizados
2 quintosde um tablete de fermento. Para fazer 5 receitas, quantos tabletes de fermento são necessários?
Divisão de uma fração por um número natural
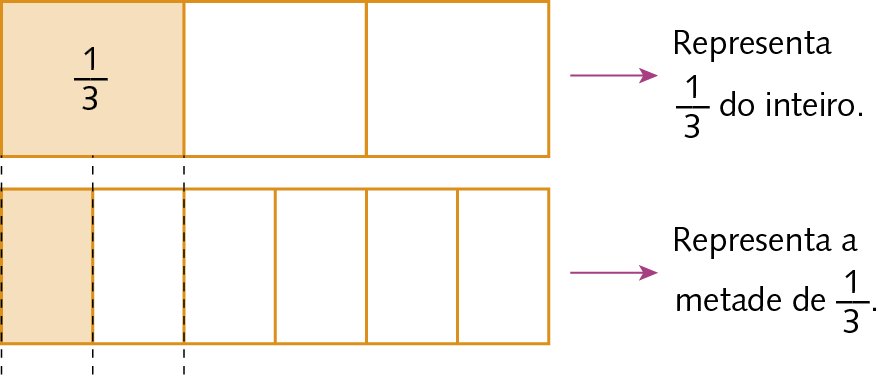
A metade de
um terçocabe seis vezes na figura inicial.
49. Calcule o resultado de cada uma das divisões no caderno.
a)
3 oitavos dividido por 2b)
um terço dividido por 2c)
3 quartos dividido por 5d)
3 quintos dividido por 550. Jorge vai dividir
3 quintosd e uma torta de maçã igualmente entre 4 pessoas. Qual fração da torta de maçã cada pessoa vai receber?
Para o capítulo 7: Números decimais
Décimos, centésimos e milésimos
Observe o valor de cada algarismo do número 8,671.
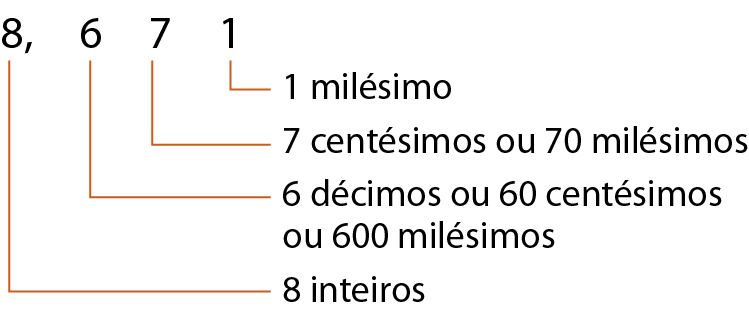
Leitura de números decimais
Para ler um número na fórma decimal, lemos primeiro a parte inteira e, depois, a parte decimal. Observe os exemplos.
a) 3,2

Podemos ler: “três inteiros e dois décimos”.
b) 0,85

Podemos ler: “oitenta e cinco centésimos”.
c) 1,632

Podemos ler: “um inteiro e seiscentos e trinta e dois milésimos”.
Respostas e comentários
44. a)
6 terços44. b)
20 sobre 1544. c)
4 oitavos44. d)
4 sobre 2044. e)
6 terços44. f)
8 sobre 1444. g)
15 sobre 1244. h)
5 oitavos44. i)
23 sobre 6044. j)
13 sobre 1244. k)
35 sobre 12044. l)
59 sobre 3045.
38 sobre 5646.
5 sobre 1247. a)
18 sétimos47. b)
15 quartos47. c)
2 terços47. d)
36 sobre 747. e)
36 sobre 547. f)
15 sextos48. 2 tabletes de fermento.
49. a)
3 sobre 1649. b)
1 sexto49. c)
3 sobre 2049. d)
3 sobre 2550.
3 sobre 20Faça a correção das atividades 44, 45 e 46 coletivamente e, sempre que possível, permita que os estudantes utilizem figuras para a realização dos cálculos ou para a compreensão do enunciado dos problemas propostos.
Multiplicação de um número natural por uma fração
Caso a operação não tenha ficado clara para os estudantes, exiba mais exemplos na lousa.
Após concluírem as atividades 47 e 48, peça que expliquem a estratégia que usaram para chegar aos resultados.
Divisão de uma fração por um número natural
Antes de explorar o cálculo
um terço÷ 2 com a turma, pergunte se o resultado será maior ou menor do que
um meio. Espera-se que os estudantes percebam que
um terçoé menor do que
um meio, e a fração está sendo dividida por um número maior do que 1; portanto, o resultado obtido ao dividi-la continuará menor que
um meio.
Nas atividades 49 e 50, antes de os estudantes efetuarem os cálculos, incentive-os a estimar o resultado que será obtido.
Décimos, centésimos e milésimos
Em um número decimal, à direita da vírgula, temos as casas decimais denominadas da seguinte fórma: para uma casa decimal, décimo; para duas casas decimais, centésimo; para três casas decimais, milésimo. Visando ao bom entendimento dos estudantes, apresente-lhes alguns números decimais e solicite que os escrevam na lousa por extenso.
Mostre para a turma que há mais de uma maneira de ler um número decimal. Por exemplo, podemos ler 3,2 como “três inteiros e vinte centésimos”, “três inteiros e duzentos centésimos” etcétera.
Se julgar interessante, faça uma atividade oral com alguns números decimais para analisar se os estudantes compreenderam os termos referentes às casas decimais. Isso os ajudará a realizar a atividade 51.
51. No caderno, escreva como se leem os seguintes números decimais.
a) 0,9
b) 0,215
c) 5,68
d) 0,18
e) 8,041
f) 0,005
52. Em seu caderno, escreva com algarismos os seguintes números decimais.
a) Nove inteiros e oito décimos.
b) Cento e quarenta e oito milésimos.
c) Noventa e três centésimos.
d) Setecentos e noventa e um milésimos.
e) Dois inteiros e quarenta e nove milésimos.
Comparação de números decimais
Quando as partes inteiras são diferentes
Qual número é maior: 5,3 ou 3,45?
Como 5 inteiros é maior que 3 inteiros, então 5,3 > 3,45.
Quando as partes inteiras são iguais
Qual número é maior: 5,35 ou 5,25?
Como as partes inteiras são iguais, devemos comparar as partes decimais.
35 centésimos é maior que 25 centésimos, então 5,35 > 5,25.
53. Copie os itens no caderno substituindo os

pelos sinais < ou >.
a) 1,2

1,02
b) 8,4

8,14
c) 10,15

10,51
d) 11,9

15,0
e) 2,3

0,23
f) 15,0

15,1
54. Escreva no caderno os números decimais de cada item em ordem crescente.
a) 0,31; 0,57; 0,38; 0,94
b) 3,55; 3,98; 3,07; 3,09
c) 11,12; 10,01; 0,99; 8,92
d) 5,105; 5,095; 5,555; 5,807
55. Desenhe uma reta numérica e represente pontos correspondentes aos números: 1,1; 1,5; 1,6; 1,9 e 2,1.
Adição e subtração com números decimais
Para adicionar ou subtrair números decimais, primeiro colocamos vírgula embaixo de vírgula. Depois, alinhamos os milésimos, os centésimos, os décimos, as unidades, e assim por diante. Por fim, adicionamos milésimos com milésimos, centésimos com centésimos, décimos com décimos, unidades com unidades etcétera fazendo as trocas necessárias.
a) 35,4 + 0,75
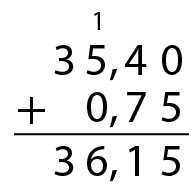
b) 60,35 ‒ 57,9

56. Calcule o resultado das operações no caderno.
a) 0,7 + 4,2
b) 18,3 + 3,05
c) 0,67 + 12,3
d) 0,8 + 1 + 10,02
e) 11,6 + 2 + 25,2
f) 3 ‒ 0,92
g) 42,7 ‒ 25,08
h) 3,005 ‒ 2,15
i) 7,82 ‒ 7,81
j) 0,018 ‒ 0,010
57. Raquel mede 1,62 métro de altura e sua irmã, Jéssica, mede 1,74 métro. Qual é a diferença entre as medidas das duas alturas?
Multiplicação com números decimais
Para multiplicar números decimais, podemos usar o algoritmo da decomposição ou o algoritmo usual.
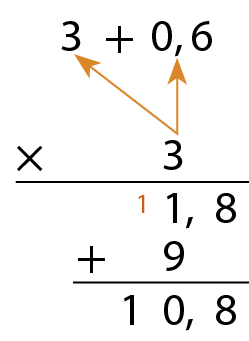
Algoritmo da decomposição
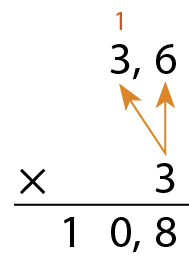
Algoritmo usual
58. Calcule o resultado das multiplicações no caderno.
a) 4,2 × 2
b) 3,45 × 4
c) 3 × 8,7
d) 8 × 1,27
e) 1,05 × 3
f) 4 × 5,25
g) 12,4 × 2
h) 10,05 × 5
Respostas e comentários
51. a) Exemplo de resposta: nove décimos
51. b) Exemplo de resposta: duzentos e quinze milésimos
51. c) Exemplo de resposta: cinco inteiros e sessenta e oito centésimos
51. d) Exemplo de resposta: dezoito centésimos
51. e) Exemplo de resposta: oito inteiros e quarenta e um milésimos
51. f ) Exemplo de resposta: cinco milésimos
52. a) 9,8
52. b) 0,148
52. c) 0,93
52. d) 0,791
52. e) 2,049
53. a) >
53. b) >
53. c) <
53. d) <
53. e) >
53. f) <
54. a) 0,31; 0,38; 0,57; 0,94
54. b) 3,07; 3,09; 3,55; 3,98
54. c) 0,99; 8,92; 10,01; 11,12
54. d) 5,095; 5,105; 5,555; 5,807
55.

56. a) 4,9
56. b) 21,35
56. c) 12,97
56. d) 11,82
56. e) 38,8
56. f) 2,08
56. g) 17,62
56. h) 0,855
56. i) 0,01
56. j) 0,008
57. 0,12 métro
58. a) 8,4
58. b) 13,8
58. c) 26,1
58. d) 10,16
58. e) 3,15
58. f) 21
58. g) 24,8
58. h) 50,25
Na atividade 52, se os estudantes tiverem dificuldade, represente um quadro de ordens na lousa para auxiliá-los na escrita dos números decimais.
Comparação de números decimais
Para mostrar aos estudantes a comparação de números decimais, escolha três estudantes cujas alturas são próximas. Tome as medidas de cada um e escreva-as na lousa, sem identificar a quem corresponde cada medida. Peça então que a turma identifique a qual estudante corresponde cada medida de altura: o estudante mais alto terá atribuída a ele a maior medida decimal, e assim por diante.
• Na atividade 53, se necessário, relembre o significado dos sinais de maior que (>) e menor que (<).
• Na atividade 54, relembre os estudantes do significado dos termos “crescente” e “decrescente” e, caso sintam dificuldade, oriente-os a começar comparando a parte inteira e, depois, a parte decimal.
Adição e subtração com números decimais
Para facilitar o cálculo com números decimais, lembre aos estudantes a maneira de fazer adição e subtração com os números naturais e, em seguida, com os decimais. Caso haja dificuldade, peça que alinhem as vírgulas e completem as casas decimais que for necessário com zero. Isso poderá ajudar na resolução da atividade 56.
Na atividade 57, leve os estudantes a perceber que encontrar a diferença entre dois números se refere ao resultado de uma subtração entre dois números. Portanto, para a resolução da atividade, peça que façam a subtração da maior medida da altura pela menor, uma vez que não podemos ter medidas de altura negativas.
Multiplicação com números decimais
A multiplicação entre um número natural e um número decimal inicialmente é feita do mesmo modo que a multiplicação entre números naturais, mas, no final, deve ser considerada a quantidade de casas decimais do produto a partir da quantidade de casas decimais dos fatores.
Na atividade 58, confira principalmente a quantidade de casas decimais em cada produto.
59.

Calcule mentalmente o resultado de cada multiplicação.
a) 4,75 × 10
b) 8,32 × 100
c) 6,21 × .1000
d) 0,82 × 10
e) 11,5 × 100
f) 1,921 × .1000
Divisão com números decimais
Para dividir números decimais, podemos utilizar o algoritmo usual.

60. Calcule o resultado de cada uma das divisões no caderno.
a) 19 ÷ 2
b) 45 ÷ 4
c) 35 ÷ 4
d) 83 ÷ 5
e) 76 ÷ 8
f) 112 ÷ 5
61. Calcule o resultado de cada uma das divisões no caderno.
a) 32,4 ÷ 2
b) 12,5 ÷ 4
c) 8,16 ÷ 8
d) 15,4 ÷ 5
e) 250,3 ÷ 2
f) 12 ÷ 10
g) 12 ÷ 100
h) 12 ÷ .1000
i) 56 ÷ 100
j) 12,56 ÷ 100
Para o capítulo 8: Porcentagem
Podemos representar uma porcentagem na fórma de fração ou na fórma decimal. Observe.
Para calcular 10% de 100, podemos fazer:
62. Represente as porcentagens nas fórmas fracionária e decimal.
a) 15%
b) 32%
c) 55%
d) 4%
e) 80%
f) 99%
63. Calcule.
a) 5% de 10
b) 10% de 10
c) 50% de 100
d) 60% de 100
e) 42% de 100
f) 8% de 200
64. Mariana comprou uma calça que custa R$ 100,00cem reais. Como estava na promoção, Mariana recebeu um desconto de 25%. Quantos reais ela pagou pela calça?
Para o capítulo 9: Figuras geométricas planas
Segmento de reta, reta e semirreta
O menor caminho de um ponto a outro é chamado de segmento de reta.

Indicamos
segmento de reta MNou
segmento de reta NM.
Os pontos M e N são as extremidades do segmento
segmento de reta MN.
Se prolongarmos o segmento
segmento de reta MNsem parar nos dois lados, teremos uma reta.

Indicamos
reta MNou
reta NMou ainda reta r.
Semirreta é uma parte da reta que apresenta ponto de origem e é ilimitada em um único sentido.

Indicamos
semirreta CDO ponto C é a origem da semirreta
CD.
65. Identifique as semirretas representadas nas figuras.
a)

b)

66. Quais figuras a seguir representam um segmento de reta?
a)
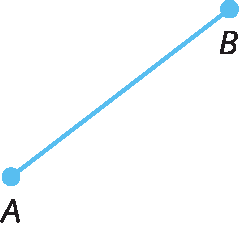
b)

Respostas e comentários
59. a) 47,5
59. b) 832
59. c) .6210
59. d) 8,2
59. e) .1150
59. f) .1921
60. a) 9,5
60. b) 11,25
60. c) 8,75
60. d) 16,6
60. e) 9,5
60. f) 22,4
61. a) 16,2
61. b) 3,125
61. c) 1,02
61. d) 3,08
61. e) 125,15
61. f) 1,2
61. g) 0,12
61. h) 0,012
61. i) 0,56
61. j) 0,1256
62. a)
15 sobre 10062. b)
32 sobre 10062. c)
55 sobre 10062. d)
4 sobre 10062. e)
80 sobre 10062. f )
99 sobre 10063. a) 0,5
63. b) 1
63. c) 50
63. d) 60
63. e) 42
63. f) 16
64. R$ 75,00setenta e cinco reais
65. a)
semirreta BA65. b)
semirreta CD66. A figura do item a.
Na atividade 59, leve os estudantes a notar que, ao multiplicar números decimais por potências de dez, a vírgula se desloca uma posição para a direita a cada fator 10.
Divisão com números decimais
Para fazer a divisão de um número decimal por um número natural há duas maneiras:
• fazer a divisão normalmente, como se fossem dois números naturais, e apenas acrescentar a vírgula após a parte do quociente correspondente à parte inteira do dividendo;
• transformar o número decimal em número natural, multiplicando-o por uma potência de dez com o número de zeros correspondentes à quantidade de casas decimais do dividendo, e multiplicar o divisor pela mesma potência de dez para que o quociente continue o mesmo.
Essa explicação pode auxiliar os estudantes na resolução da atividade 61.
Porcentagem
• Na atividade 63, oriente os estudantes a calcular em partes cada item, ou seja, primeiro transformar a porcentagem em uma fração e, depois, multiplicar pelo número desejado.
• Na atividade 64, se houver dúvidas, explique aos estudantes que o termo “desconto” significa redução de uma parte do valor total; em razão disso, chame a atenção deles para o fato de que a atividade pede o valor pago e não o valor descontado.
Segmento de reta, reta e semirreta
• Na atividade 65, oriente os estudantes a verificar o sentido das semirretas, ou seja, a identificar sua origem e para onde estão indo.
• Na atividade 66, caso o estudante não consiga identificar quais são os segmentos de reta, retome o conceito e leve-os a perceber que a figura do item b não representa o menor caminho entre os pontos C e D.
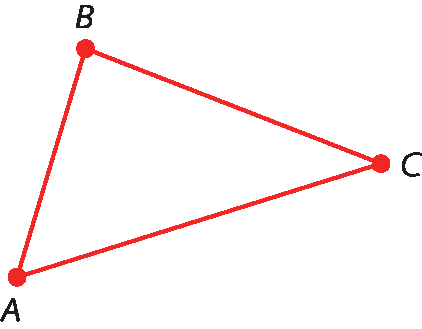
67. Identifique os segmentos de reta representados nas figuras.
a)
b)
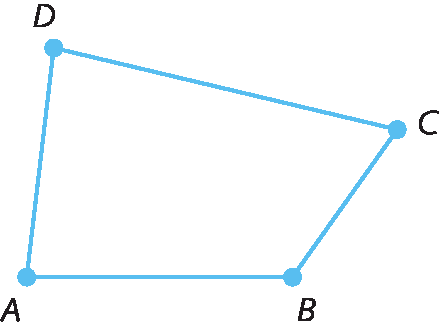
Ângulos
Ângulo é a união de duas semirretas de mesma origem em um plano com uma das regiões determinadas por elas.
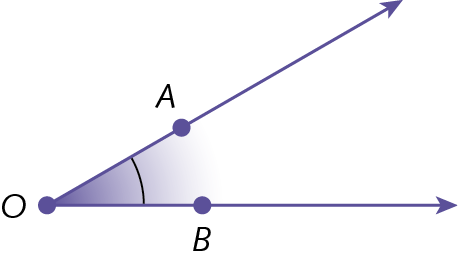
O: vértice do ângulo
lados do ângulo
Ângulo reto, ângulo agudo e ângulo obtuso
• Um ângulo é reto quando sua abertura mede 90graus.
• Um ângulo é agudo quando sua abertura mede mais que 0grau e menos que 90graus.
• Um ângulo é obtuso quando sua abertura mede mais que 90graus e menos que 180graus.
68. Classifique os ângulos a seguir em reto, agudo ou obtuso.
a)

b)
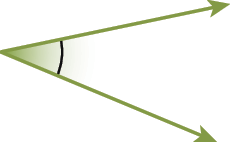
c)
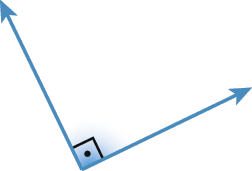
d)

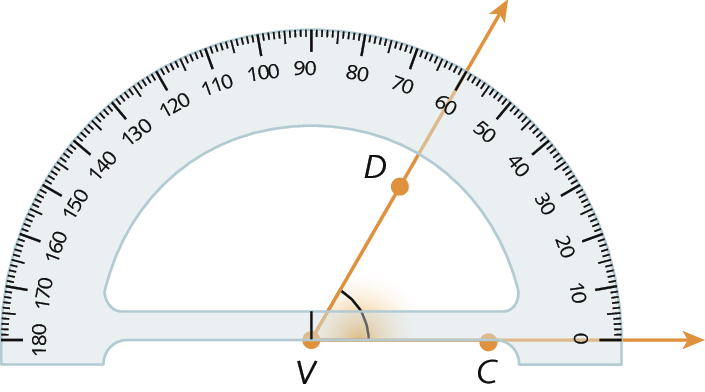
69. Observe os ângulos representados a seguir e, no caderno, escreva a medida da abertura de cada um.
a)
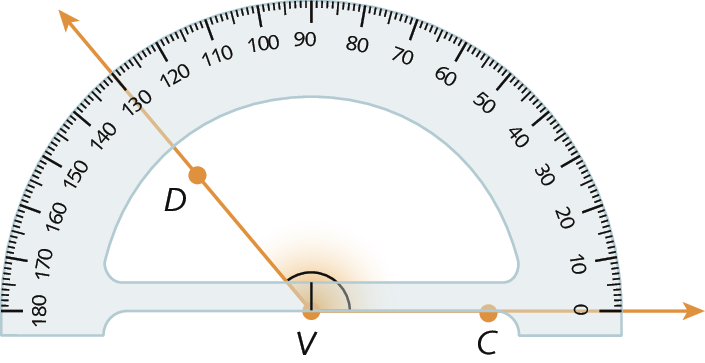
b)
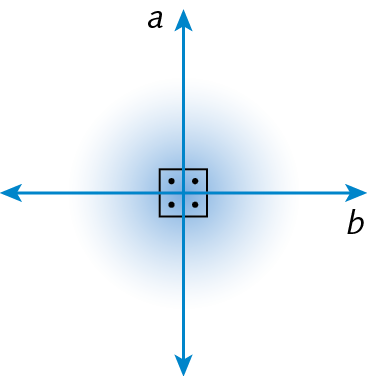
Retas paralelas e retas perpendiculares
Duas retas são paralelas quando não têm nenhum ponto em comum.

Duas retas são concorrentes quando têm apenas um ponto em comum. Quando duas retas concorrentes formam quatro ângulos retos, dizemos que são retas perpendiculares.
70. Observe esta figura, copie as frases no caderno e complete-as com as palavras: paralelas ou concorrentes.
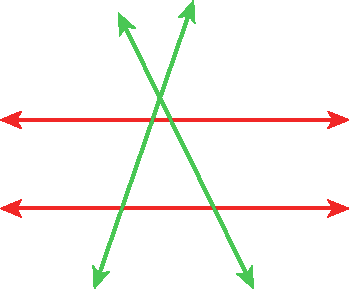
a) As retas verdes são

.
b) As retas vermelhas são

.
c) Uma reta verde e uma reta vermelha são

.
71. No caderno, usando uma régua, trace linhas para representar duas retas perpendiculares.
Respostas e comentários
67. a)
segmento de reta AB, segmento de reta BC e segmento de reta CA67. b)
segmento de reta AB, segmento de reta BC, segmento de reta CD e segmento de reta DA68. a) obtuso
68. b) agudo
68. c) reto
68. d) obtuso
69. a) 130graus
69. b) 60graus
70. a) concorrentes
70. b) paralelas
70. c) concorrentes
71. Resposta pessoal.
Na atividade 67, se necessário, destaque aos estudantes que todo segmento de reta tem duas extremidades.
Ângulos
Para trabalhar com ângulos, você pode providenciar um relógio analógico de parede e fazer alguns questionamentos, por exemplo:
• O que são ângulos?
• Como podemos representar um ângulo no relógio?
• O que são um ângulo reto, um ângulo agudo e um ângulo obtuso? Como podemos indicá-los no relógio?
Peça aos estudantes que deem exemplos de locais em que podemos observar ângulos no nosso dia a dia. Pergunte também onde podemos encontrar ângulos na sala de aula.
• Na atividade 69, relembre-os como podemos observar a medida de abertura de ângulos em um transferidor.
Retas paralelas e retas perpendiculares
Faça duas representações de retas paralelas na lousa, uma embaixo da outra. Pergunte a eles o nome dessas retas. É esperado que respondam que se trata de retas paralelas. Se necessário, informe a eles que elas nunca irão se interceptar.
Depois, faça um desenho de duas retas que pareçam paralelas, mas, dessa vez, uma deve estar levemente inclinada em relação à outra. Comente que uma característica das retas paralelas é que elas guardam sempre a mesma medida de distância, independentemente do ponto em que for tomada.
Peça a eles que, no caderno, desenhem retas paralelas, perpendiculares e concorrentes, identificando-as com legendas. Essa proposta auxiliará na resolução das atividades 70 e 71.
Polígonos
Polígono é toda figura plana formada por uma região interna contornada por segmentos de retas que não se cruzam.
Triângulos
São polígonos com três lados.

Quadriláteros
São polígonos com quatro lados.

72. Classifique as figuras em triângulos ou quadriláteros.
a)

b)

c)
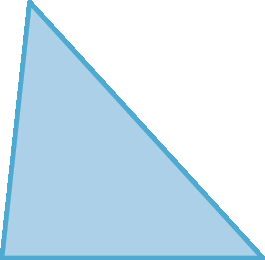
d)

Para o capítulo 10: Ampliação e redução de figuras
• Quando ampliamos proporcionalmente uma figura, as medidas das aberturas dos ângulos correspondentes não são alteradas e as medidas de comprimento dos segmentos correspondentes são proporcionais, ou seja, se dobrarmos uma das medidas de comprimento, todas deverão ser dobradas; se triplicarmos uma medida de comprimento, todas deverão ser triplicadas; e assim por diante.
• Quando reduzimos proporcionalmente uma figura, as medidas das aberturas dos ângulos correspondentes não são alteradas e as medidas de comprimento dos segmentos correspondentes são proporcionais, ou seja, se dividirmos uma das medidas de comprimento por 2, todas deverão ser divididas por 2; se dividirmos uma medida de comprimento por 3, todas deverão ser divididas por 3; e assim por diante.
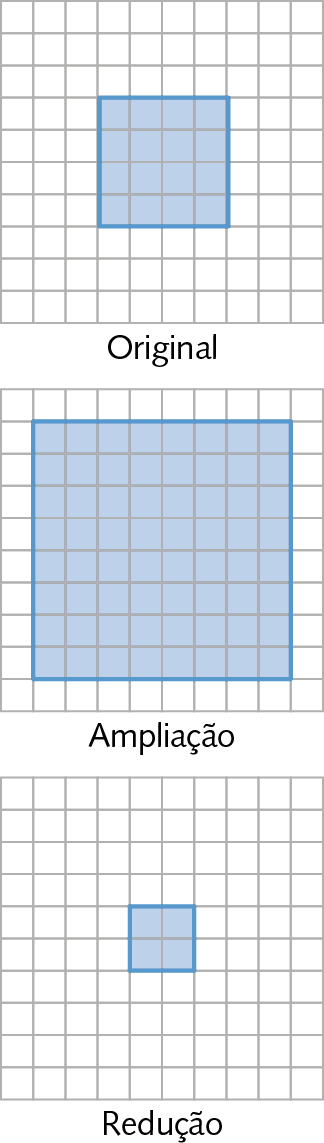
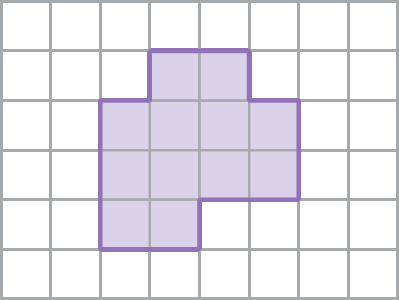
73. Em uma malha quadriculada, desenhe uma redução desta figura geométrica representada.
Para o capítulo 11: Grandezas e medidas
Medidas de comprimento
O quilômetro (cá ême), o metro (ême), o decímetro (dê ême), o centímetro (cê ême) e o milímetro (ême ême) são algumas unidades de medida padronizadas de comprimento.
1 quilômetro equivale a .1000 metros
1 quilômetro = .1000 métros
1 metro equivale a 100 centímetros
1 métro = 100 centímetros
1 metro equivale a 10 decímetros
1 métro = 10 decímetros
1 metro equivale a .1000 milímetros
1 métro = .1000 milímetros
Respostas e comentários
72. a) Quadrilátero
72. b) Triângulo
72. c) Triângulo
72. d) Quadrilátero
73. Exemplo de resposta em Orientações.
Polígonos
Pergunte aos estudantes o que eles sabem sobre polígonos, triângulos e quadriláteros. A partir das respostas, leve-os a compreender que a quantidade de lados e a de ângulos de um polígono são as mesmas, que triângulos têm 3 lados e 3 ângulos, enquanto quadriláteros têm 4 lados e 4 ângulos. Essa proposta ajudará a resolver a atividade 72.
Se possível, providencie antecipadamente folhas com malha quadriculada para que os estudantes façam algumas ampliações e reduções de figuras. Por exemplo, peça que desenhem um quadrado com 3 quadradinhos de medida de comprimento de lado e, em seguida, solicite que façam uma ampliação e uma redução dessa figura.
• Na atividade 73, peça que façam também uma ampliação da figura.
Exemplo de resposta da atividade 73:

Medidas de comprimento
Após a leitura do boxe, represente na lousa um quadro das unidades de medida de comprimento e suas conversões e pergunte aos estudantes qual é a unidade de medida adequada para expressar algumas medidas de comprimento, por exemplo, a medida da distância entre dois municípios, a medida da altura de uma pessoa ou a medida da largura de um caderno. É importante compreender que, embora essas medidas possam ser expressas em diferentes unidades de medida, umas são mais indicadas que outras. Por exemplo, cite a medida da distância em linha reta entre a cidade de São Paulo e a cidade de Salvador: .1454 quilômetros ou ..1454000 métros ou ..145400000 centímetros ou ...1454000000 milímetros. Os estudantes deverão concluir que a melhor unidade é a que demanda a menor quantidade de algarismos. Dessa maneira, é possível verificar que é mais fácil e usual expressar essa medida utilizando o quilômetro como unidade de medida. Esse é um exemplo do exercício do raciocínio inferencial.
74. Efetue no caderno as transformações a seguir.
a) 2,50 métros =

centímetros
b) 1,45 métro =

centímetros
c) 150 decímetros =

métros
d) 1,5 quilômetro =

métros
e) 1 quilômetro =

decímetros
f) 100 centímetros =

milímetros
g) .1000 milímetros =

centímetros
75. Rodrigo mede 1,65 métro de altura. Qual é a medida da altura de Rodrigo em milímetro?
Perímetro
O comprimento do contôrno de uma figura chama-se perímetro.
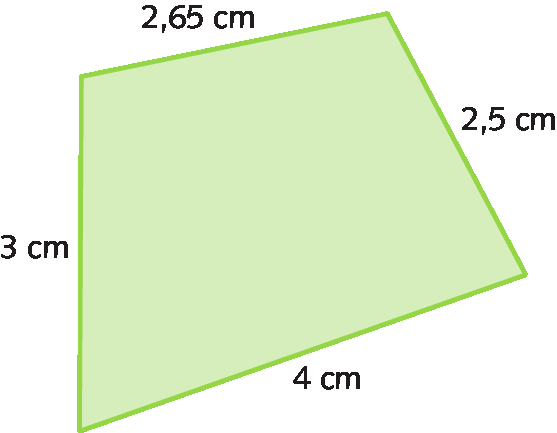
76. Calcule a medida do perímetro deste quadrilátero.
Medidas de área
O centímetro quadrado (cê ême 2 sobrescrito), o metro quadrado (ême 2 sobrescrito) e o quilômetro quadrado (cá ême 2 sobrescrito) são algumas unidades de medida padronizadas de área. Eles correspondem à medida da área de um quadrado cujos lados medem 1 centímetro, 1 metro e 1 quilômetro de comprimento, respectivamente.
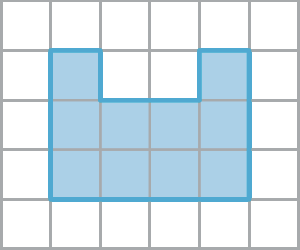
77. Considere que cada quadradinho tem 1 centímetro quadrado de medida de área e calcule a medida da área de cada figura.
a)
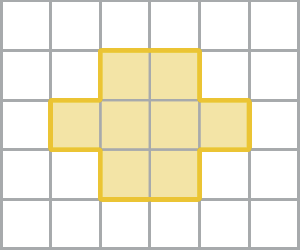
b)
Medidas de volume
O centímetro cúbico (cê ême 3 sobrescrito) e o metro cúbico (ême 3 sobrescrito) são algumas unidades de medida padronizadas de volume. Eles correspondem à medida de volume de um cubo cujas arestas medem 1 centímetro e 1 metro de comprimento, respectivamente.
78. Considere que a medida do volume de cada cubinho é igual a 1 centímetro cúbico e calcule a medida do volume dos empilhamentos em cada caso.
a)

b)

Medidas de tempo
1 dia tem 24 horas
uma hora equivale a 60 minutos
uma hora = 60 minutos
uma minuto equivale a 60 segundos
1 minuto = 60 segundos
79. Responda às questões.
a) Quantas horas há em 3 dias?
b) Quantos minutos há em 15 horas?
c) Quantos minutos há em 1 dia?
d) Quantos segundos há em uma hora?
Medidas de massa
1 quilograma equivale a .1000 gramas
1 quilograma = .1000 gramas
uma tonelada equivale a .1000 quilogramas
uma tonelada = .1000 quilogramas
1 grama equivale a .1000 miligramas
1 grama = .1000 miligramas
80. Responda às questões.
a) Quantos gramas equivalem a 5 quilogramas?
b) Quantos quilogramas equivalem a 10 toneladas?
c) Quantos miligramas equivalem a 10 gramas?
d) Quantos gramas equivalem a uma tonelada?
Respostas e comentários
74. a) 250
74. b) 145
74. c) 15
74. d) .1500
74. e) .10000
74. f) .1000
74. g) 100
75. .1650 milímetros
76. 12,15 centímetros
77. a) 8 centímetros quadrados
77. b) 10 centímetros quadrados
78. a) 14 centímetros cúbicos
78. b) 15 centímetros cúbicos
79. a) setenta e duas horas.
79. b) 900 minutos.
79. c) .1440 minutos.
79. d) .3600 segundos.
80. a) .5000 gramas.
80. b) .10000 quilogramas.
80. c) .10000 miligramas.
80. d) ..1000000 gramas.
Na atividade 75, sugira aos estudantes que utilizem o quadro de unidades de medida de comprimento para fazer a conversão de metros em milímetro. Se houver dificuldade, peça que localizem o metro no quadro e verifiquem como fazer para chegar aos milímetros, multiplicando ou dividindo.
Medidas de área
Na atividade 77, espera-se que os estudantes contem a quantidade de quadradinhos que formam cada figura e multipliquem essa quantidade pela medida de área de cada quadradinho. No entanto, permita que utilizem estratégias próprias e, ao final, oriente-os a compartilhá-las com a turma.
Medidas de volume
Explique aos estudantes que o volume é o espaço ocupado por um objeto tridimensional.
Na atividade 78, caso os estudantes tenham dificuldade para contar os cubinhos, lembre-os de que há cubinhos que estão presentes nos empilhamentos, mas que não são visíveis por estarem encobertos por outros cubinhos.
Medidas de tempo
Na atividade 79, se julgar necessário, faça um quadro na lousa com as unidades de medida de tempo e suas conversões.
Medidas de massa
Se possível, leve uma balança para a sala de aula e pese alguns objetos. Antes, peça aos estudantes que estimem a melhor unidade para essa medição – se são gramas ou quilogramas. As balanças eletrônicas fornecem a medida por meio de uma conversão digital, enquanto as balanças mecânicas, cuja medida é dada por um ponteiro que se move sobre uma escala graduada, são analógicas. Faça um novo quadro na lousa com as unidades de medida de massa e suas conversões para auxiliar na resolução da atividade 80.
Medidas de capacidade
1 litro equivale a .1000 mililitros
1 litro = .1000 mililitros
81. Responda às questões.
a) Quantos mililitros equivalem a 2 litros?
b) Quantos mililitros equivalem a 10 litros?
c) Quantos litros equivalem a .5000 mililitros?
d) Quantos litros equivalem a .1500 mililitros?
Medidas de temperatura
No Brasil, a unidade de medida de temperatura utilizada é o grau Celsius (grau cê).
82. Em um município, a medida de temperatura máxima registrada em um dia foi de 27 graus Célsius e a mínima, de 15 graus Célsius. Qual foi a diferença entre a medida da temperatura máxima e a medida da temperatura mínima registradas nesse município?
Para o capítulo 12: Probabilidade e estatística
Cálculo do número de possibilidades
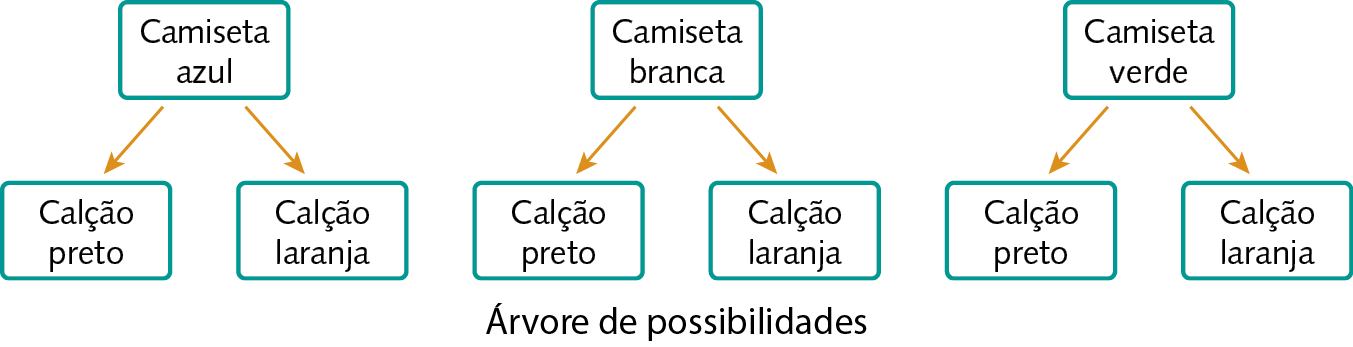
Observe como podemos determinar o número de combinações com uma camiseta e um calção em que temos 3 cores de camiseta (azul, branca e verde) e duas cores de calção (preto e laranja).
|
Camiseta |
|||
|---|---|---|---|
|
Calção |
azul |
branca |
verde |
|
laranja |
laranja e azul |
laranja e branca |
laranja e verde |
|
preto |
preto e azul |
preto e branca |
preto e verde |
Quadro de possibilidades
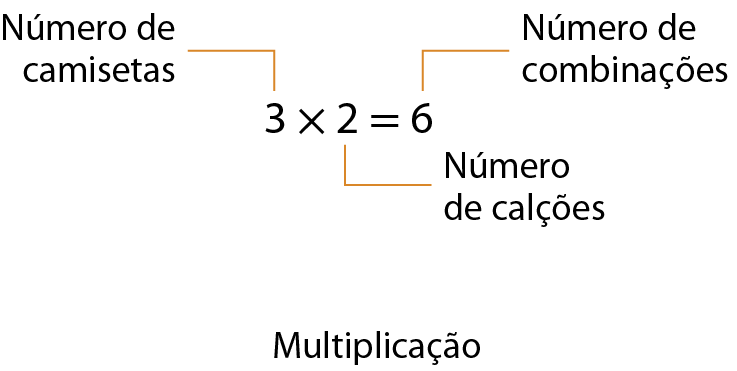
83. Um time de futebol tem 3 cores de camisas e 3 cores de calção. Entre as camisas, há uma azul, uma amarela e uma preta e, entre os calções, há um branco, um amarelo e um preto. Faça uma árvore de possibilidades com todas as combinações de camisas e calções que podem ser usadas por esse time.
84. No cardápio de uma lanchonete, há 4 opções de sanduíche, 4 opções de suco natural e duas opções de sobremesa. Indique o número de combinações possíveis de fazer com:
a) um sanduíche e um suco natural.
b) um sanduíche e uma sobremesa.
c) um sanduíche, um suco natural e uma sobremesa.
Respostas e comentários
81. a) .2000 mililitros.
81. b) .10000 mililitros.
81. c) 5 litros.
81. d) 1,5 litros.
82. 12 graus Célsius
83. Resposta em Orientações.
84. a) 16 combinações.
84. b) 8 combinações.
84. c) trínta e duas combinações.
Medidas de capacidade
Para auxiliar na resolução da atividade 81, escreva na lousa a conversão do litro para o mililitro e vice-versa.
Medidas de temperatura
A temperatura é medida atualmente em três escalas: Fahrenheit (nos Estados Unidos), Celsius (no resto do mundo) e Kelvin (no contexto científico). A temperatura é uma medida do estado de agitação das partículas que compõem um material.
Na atividade 82, caso os estudantes tenham dificuldade, oriente-os a subtrair a medida de temperatura mínima da medida de temperatura máxima e, assim, obter a diferença entre as duas medidas.
Cálculo do número de possibilidades
Para levantar alguns questionamentos sobre o cálculo do número de possibilidades, leia com os estudantes o boxe azul e proponha as questões a seguir.
• O que se entende por um dado “honesto” ou moeda “honesta”?
• Ao lançar uma “moeda honesta” para o alto, quais são os possíveis resultados? E ao lançar duas moedas ao mesmo tempo?
• Quais resultados eu poderia obter ao lançar um “dado honesto”? E ao lançar dois dados ao mesmo tempo?
Espera-se que os estudantes percebam que, ao adicionar outra moeda ou dado, a determinação do número de possibilidades depende de um número maior de etapas.
• Resposta da atividade 83: