Unidade 2
Capítulo 4 Igualdades e desigualdades
Capítulo 5 Múltiplos e divisores
Capítulo 6 Frações
Capítulo 7 Números decimais

Em 2021, de setecentas e setenta cidades avaliadas em todo o país, a cidade de Morungaba, no estado de São Paulo, era a 1ª colocada no ranking do Índice de Desenvolvimento Sustentável das Cidades – Brasil (IDSC-BR). A cidade atingiu cêrca de
três quartosda medida da distância para o desempenho ótimo nos Objetivos de Desenvolvimento Sustentável (ó dê ésse).
O que são os ó dê ésse? Qual é o significado do número
três quartosnesse contexto? Ao final do estudo da Unidade, você responderá a essas e outras questões.
Respostas e comentários
Abertura da Unidade
Bê êne cê cê:
• Competência geral 9 (a descrição está na página seis).
• Competência específica 8 (a descrição está na página sete).
• Habilidade ê éfe zero seis ême ah zero sete.
Objetivos:
• Motivar os estudantes a estudar os conteúdos da Unidade 2.
• Levantar os conhecimentos prévios dos estudantes sobre as frações.
Tema contemporâneo transversal:

Inicie o trabalho explicando aos estudantes que o Índice de Desenvolvimento Sustentável das Cidades – Brasil (IDSC-BR) mede o progresso total para o cumprimento de todos os 17 Objetivos de Desenvolvimento Sustentável (ó dê ésse) e varia de 0 a 100 pontos. Diga que a cidade de Morungaba obteve, em 2021, 73,4 pontos, ou seja, atingiu aproximadamente
três quartosda pontuação máxima. Entre outros quesitos, essa cidade destacou-se pela produção e pelo consumo sustentáveis e pela proteção à vida terrestre. Para saber mais sobre a classificação dos municípios brasileiros, acesse https://oeds.link/BBzDgV (acesso em: 30 junho 2022).
Peça aos estudantes que conversem sobre as questões propostas. Aproveite a oportunidade para verificar se sabem lidar com a ideia de parte de um todo das frações. Embora, no fim desta Unidade, a questão seja retomada na seção É hora de extrapolar, você pode aprofundar o trabalho com ela solicitando aos estudantes que façam um esquema para representar a distância mencionada no texto e que represente a parte correspondente à fração
três quartos.
Por incentivar o diálogo e a interação entre os estudantes, a proposta desta Abertura de Unidade favorece o desenvolvimento da competência geral 9 e da competência específica 8 da Bê êne cê cê.
No capítulo 4, serão estudadas as igualdades e as desigualdades. No capítulo 5, o foco serão os conceitos de múltiplo e divisor, bem como o estudo dos critérios de divisibilidade. As frações e as operações com frações serão estudadas no capítulo 6. Por fim, no capítulo 7, a ênfase será nos números decimais e nas operações que os envolvem.
Na seção É hora de extrapolar, os estudantes entrarão em contato com a Agenda 2030 da ônu e terão a oportunidade de conhecer os 17 ó dê ésse. Nessa seção, os estudantes farão um cartaz relacionado a um dos ó dê ésse.
(ê éfe zero seis ême ah zero sete) Compreender, comparar e ordenar frações associadas às ideias de partes de inteiros e resultado de divisão, identificando frações equivalentes.
Capítulo 4 Igualdades e desigualdades
Trocando ideias

A pesquisa de preços é uma boa prática e póde nos ajudar a economizar na compra de determinado produto ou na aquisição de um serviço.
Vera precisava comprar um vestido e um chapéu, mas antes pesquisou o preço desses itens em duas lojas. Analise as cenas.

Se ela optar por comprar o vestido na Loja do Shopping, vai economizar R$ 15,00quinze reais, pois:
80 menos 65 = 15
A sentença matemática 80 menos 65 = 15 é uma igualdade.
▸

Em qual loja é mais vantajoso comprar o chapéu? Qual igualdade representa o valor que Vera consegue economizar ao comprar o chapéu nessa loja?
▸


Você costuma pesquisar preços antes de comprar algo? Como você faz? Converse com os colegas.
Neste capítulo, você vai estudar sentenças matemáticas expressas por igualdades e por desigualdades.
Respostas e comentários
Trocando ideias: primeiro item: Loja do Bairro; 42 menos 30 = 12; segundo item: respostas pessoais.
CAPÍTULO 4 – IGUALDADES E DESIGUALDADES
Trocando ideias
Bê êne cê cê:
• Competência geral 9 (a descrição está na página seis).
• Competência específica 8 (a descrição está na página sete).
Objetivos:
• Levantar os conhecimentos prévios dos estudantes sobre a ideia de igualdade.
• Refletir sobre a importância de realizar pesquisa de preços.
Tema contemporâneo transversal:

Inicie a aula comentando com os estudantes que o valor de um mesmo produto ou serviço costuma variar de um estabelecimento para o outro; por esse motivo, é importante realizar uma pesquisa de preços antes de comprar um produto ou serviço. Diga que a pesquisa de valores em lojas físicas pode ser feita visitando o estabelecimento ou consultando os folhetos (com indicação de preços) que esses estabelecimentos costumam divulgar para seus clientes. Tratando-se de compras pela internet, a pesquisa pode ser feita consultando site por site ou usando ferramentas que já fazem esse tipo de pesquisa. Nessas ferramentas, o usuário digita o nome do produto, então, é feita uma busca rápida dos preços em diversos estabelecimentos para que seja feita uma comparação.
Depois dessa conversa inicial, peça aos estudantes que analisem a situação apresentada e respondam às questões. Espera-se que percebam e compreendam a ideia de desigualdade, observando que o vestido é mais barato na “Loja do shopping” e que o chapéu é mais barato na “Loja do bairro”. É possível ampliar a proposta e solicitar a eles que escrevam uma igualdade para representar o valor total economizado por Vera após realizar essa pesquisa de preços:
15 + 12 = 27
Reserve um momento da aula para que conversem sobre suas experiências com pesquisa de preços. O diálogo e a interação promovidos nesta dinâmica favorecem o desenvolvimento da competência geral 9 e da competência específica 8 da Bê êne cê cê.

1 Sentenças matemáticas
No “Trocando ideias”, você leu e escreveu algumas sentenças que chamamos de sentenças matemáticas.
Sentença matemática é aquela escrita com símbolos matemáticos (números, sinais etcétera); ela póde ser expressa por relações de igualdade, de desigualdade, entre outras.
As sentenças matemáticas podem ser verdadeiras ou falsas. Analise os exemplos:
a)

b)

c)

d)
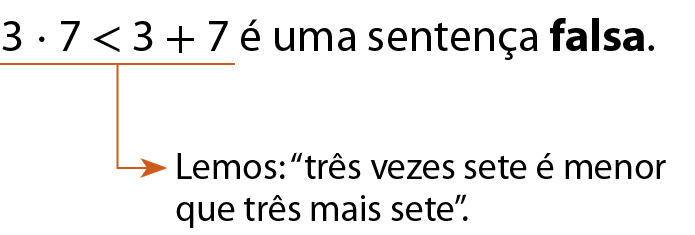
Observação
Note que, se mudarmos o sinal de uma sentença matemática, sem alterar os números, ela póde se tornar verdadeira ou falsa. Por exemplo, 13 = 11 + 2 é uma sentença verdadeira, enquanto 13 > 11 + 2 é uma sentença falsa.
Atividades
Faça as atividades no caderno.
1. Escreva em seu caderno como se leem as sentenças matemáticas a seguir.
a) 8 + 3 = 11
b) 32 > 20 dividido por 10
c) 23 ⩾ 12 + 8
d) 3 ⋅ 4 ⩽ 3 ⋅ 5
2. Quais das sentenças a seguir são verdadeiras?
a) 5 < 9
b) 7 ⋅ 2 ⩽ 7 ⋅ 3
c) 6 + 3 ≠ 9
d) 22 menos 10 > 12
3. Copie as sentenças em seu caderno substituindo o

por um símbolo que as torne verdadeiras. Use um dos símbolos: <, ⩽, =, > ou ⩾.
a) 10 + 2

6 + 3 + 2 + 1
b) 4 ⋅ 5 ⋅ 6

6 + 7 + 8
c) 3elevado a 2 ⋅ 2elevado a 2

3elevado a 2 + 2elevado a 2
d) 2elevado a 3 menos 2elevado a 2

5
Respostas e comentários
1. a) Oito mais três é igual a onze.
1. b) Trinta e dois é maior que vinte dividido por dez.
1. c) Vinte e três é maior ou igual a doze mais oito.
1. d) Três vezes quatro é menor ou igual a três vezes cinco.
2. a) verdadeira
2. b) verdadeira
2. c) falsa
2. d) falsa
3. a) =, ⩽ ou ⩾
3. b) ⩾ ou >
3. c) ⩾ ou >
3. d) < ou ⩽
Sentenças matemáticas
Objetivo:
Reconhecer sentenças matemáticas.
Justificativa
Neste capítulo, o foco é o estudo de igualdades e desigualdades que são exemplos de sentenças matemáticas. Compreender o conceito e reconhecer diferentes sentenças matemáticas é o primeiro passo para que os estudantes consigam entender as propriedades das igualdades e das desigualdades.
Mapeando conhecimentos
Pergunte aos estudantes se sabem o que é uma sentença em Língua Portuguesa abre parêntesesenunciado de sentido completofecha parênteses e, depois, em Matemática abre parêntesesaquela escrita com símbolos matemáticosfecha parênteses. Incentive alguns deles a escrever na lousa exemplos de sentenças matemáticas.
Para as aulas iniciais
Caso perceba que os estudantes já dominam o conceito de sentença matemática, considere abordar o assunto com base nas sentenças que eles escreveram na lousa. Você pode pedir a eles que avaliem quais sentenças são verdadeiras ou falsas e, depois, solicitar que façam modificações nas sentenças falsas para torná-las verdadeiras.
É importante explorar com os estudantes a conversão de sentenças matemáticas da língua materna abre parênteseslíngua portuguesafecha parênteses para a linguagem algébrica, e vice-versa. A compreensão dos conceitos em Matemática é favorecida quando os estudantes mobilizam duas ou mais representações diferentes do mesmo conceito.
• Na atividade 2, se julgar pertinente, peça aos estudantes que escrevam as sentenças verdadeiras por extenso no caderno e que corrijam as sentenças falsas.
• Na atividade 3, verifique se os estudantes dão como resposta um ou mais símbolos. Se estiverem usando apenas um dos símbolos indicados, pergunte se existe mais de uma opção, ou seja, mais de um símbolo que torne a sentença verdadeira.

2 Igualdades
Toda sentença matemática que apresenta o sinal de igual (=) é chamada de igualdade. Em uma igualdade, chamamos a expressão à esquerda do sinal de igual de 1º membro e a expressão à direita desse sinal, de 2º membro. Observe os exemplos:
a)

b)
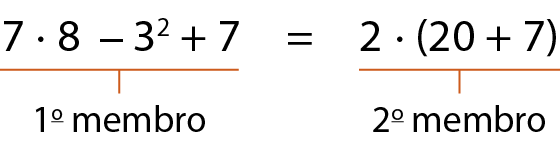
Toda igualdade é reflexiva, simétrica e transitiva. Acompanhe os exemplos:
a) Reflexiva
6 = 6 ou, ainda: 2 + 4 = 2 + 4
b) Simétrica
Se 2 + 4 = 6, então: 6 = 2 + 4
c) Transitiva
Se 7 ⋅ 7 menos 7 = 6 ⋅ 7 e 6 ⋅ 7 = 42, então: 7 ⋅ 7 menos 7 = 42
Propriedade da igualdade
A relação de igualdade não se altera quando:
• adicionamos ou subtraímos um mesmo número de seus membros;
• multiplicamos seus membros por um mesmo número ou dividimos seus membros por um mesmo número diferente de zero.
Acompanhe os exemplos.
a)
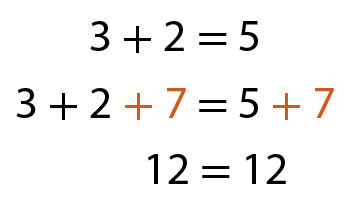
b)
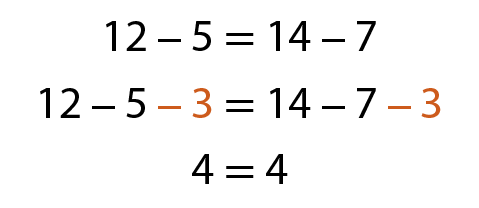
c)
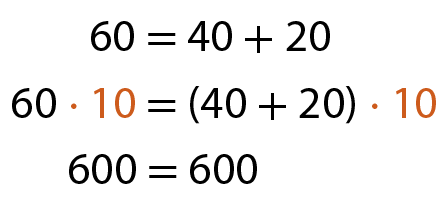
d)
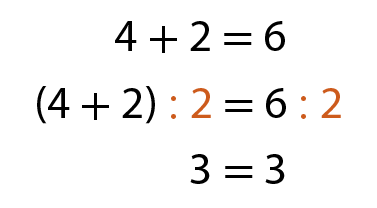
Atividades
Faça as atividades no caderno.
4. Avalie as afirmações a seguir e copie as verdadeiras em seu caderno.
a) Se adicionarmos 1 ao 2º membro de uma igualdade, ela continuará sendo uma sentença matemática verdadeira.
b) Se subtrairmos um mesmo número dos dois membros de uma igualdade, ela se manterá verdadeira.
c) Se adicionarmos 2 ao 1º membro de uma igualdade e 3 ao 2º membro da mesma igualdade, ela se manterá verdadeira.
5. Efetue em seu caderno as operações indicadas para cada sentença matemática e determine o valor de cada membro.
a) Adicione 5 aos dois membros da sentença 2 + 3 = 10 menos 5.
b) Subtraia 2 dos dois membros da sentença 14 menos 5 = 3 + 3 + 3.
c) Adicione 3 a ambos os membros da sentença 21 menos 10 = 22 menos 11.
d) Subtraia 3 de ambos os membros da sentença 13 + 2 = 6 + 6 + 3.
Respostas e comentários
4. a) falsa
4. b) verdadeira
4. c) falsa
5. a)
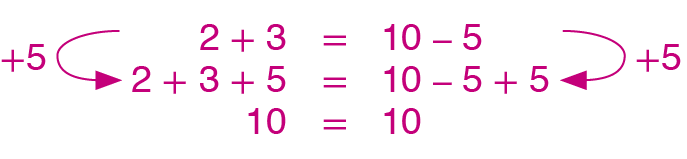
5. b)
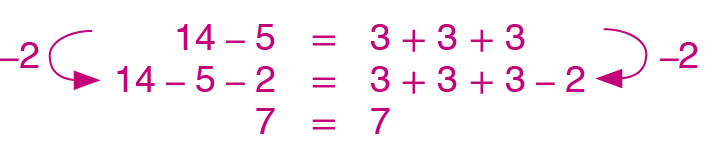
5. c)
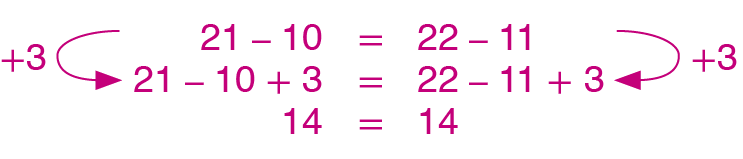
5. d)
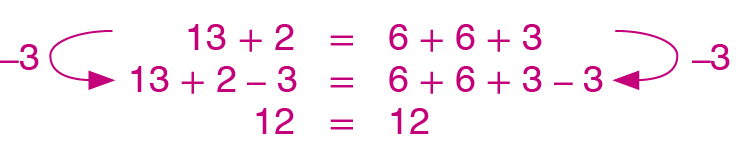
Igualdades
BNCC:
Habilidade ê éfe zero seis ême ah um quatro.
Objetivos:
• Compreender o conceito de igualdade.
• Reconhecer que a relação de igualdade matemática não se altera ao adicionar, subtrair, multiplicar ou dividir os seus dois membros por um mesmo número.
• Utilizar a relação de igualdade para determinar valores desconhecidos na resolução de problemas.
Justificativa
Os três objetivos anteriores dialogam e contribuem para o desenvolvimento da habilidade ê éfe zero seis ême ah um quatro. Além disso, saber lidar com igualdades é um passo importante para que os estudantes consigam, mais adiante, resolver alguns tipos de equação.
Mapeando conhecimentos
Reúna os estudantes em duplas e peça a cada dupla que adicione, subtraia, multiplique e divida os dois membros de algumas igualdades por um mesmo número diferente de zero. Depois, incentive-os a verbalizar o que observaram.
Para as aulas iniciais
Considere trabalhar a revisão das propriedades das igualdades presentes na seção Revisão dos conteúdos de anos anteriores. Depois, proponha aos estudantes que façam as atividades 29 e 30.
As propriedades reflexiva, simétrica e transitiva podem ser exemplificadas na lousa. Não é necessário que os estudantes identifiquem as propriedades pelos nomes nesse momento, mas é importante que compreendam essas propriedades para desenvolver as habilidades relacionadas à Álgebra no decorrer dos Anos Finais do Ensino Fundamental.
• Após a realização das atividades 4 e 5, pergunte aos estudantes se acreditam que exista algum limite no número de operações que podem ser realizadas. Por exemplo, para igualdade do item a da atividade 5, pergunte se poderíamos adicionar um mesmo número aos dois membros da igualdade infinitas vezes. Espera-se que os estudantes percebam que, se a mesma operação abre parêntesesadição ou subtraçãofecha parênteses com o mesmo número for realizada em ambos os membros da igualdade, ela se manterá verdadeira; portanto, as operações podem ser realizadas inúmeras vezes abre parêntesesnão há um limitefecha parênteses.
abre parêntesesê éfe zero seis ême ah um quatrofecha parênteses Reconhecer que a relação de igualdade matemática não se altera ao adicionar, subtrair, multiplicar ou dividir os seus dois membros por um mesmo número e utilizar essa noção para determinar valores desconhecidos na resolução de problemas.
6. Efetue em seu caderno as operações indicadas para cada sentença matemática e determine o valor de cada membro.
a) Multiplique os dois membros da sentença 1 + 2 + 3 = 3 + 3 por 4.
b) Divida os dois membros da sentença 10 + 20 = 30 por 10.
c) Multiplique os dois membros da sentença 12 menos 6 = 2 ∙ 3 por 2.
d) Divida os dois membros da sentença 3 + 3 + 3 = 18 menos 9 por 3.
7. Mariele tinha 3 jogos de ação, 2 de corrida e 2 de futebol, totalizando 7 jogos. No seu aniversário, a quantidade de cada tipo de jôgo dobrou. Represente com uma sentença matemática expressa por uma igualdade as quantidades de jogos que ela tinha antes e depois do aniversário.
Resolvendo problemas com igualdades
Vimos até aqui que os valores do 1º membro e do 2º membro são iguais em uma sentença matemática expressa por uma igualdade. Além disso, é possível adicionar, subtrair, multiplicar ou dividir os membros por um mesmo número diferente de zero sem que a relação de igualdade se altere.
Agora, vamos resolver problemas usando essas ideias.
Problema 1
Marta vende temperos na feira. Ela usa uma balança de pratos e pequenos pesos metálicos para medir a massa de temperos para os clientes. Analise a situação a seguir.
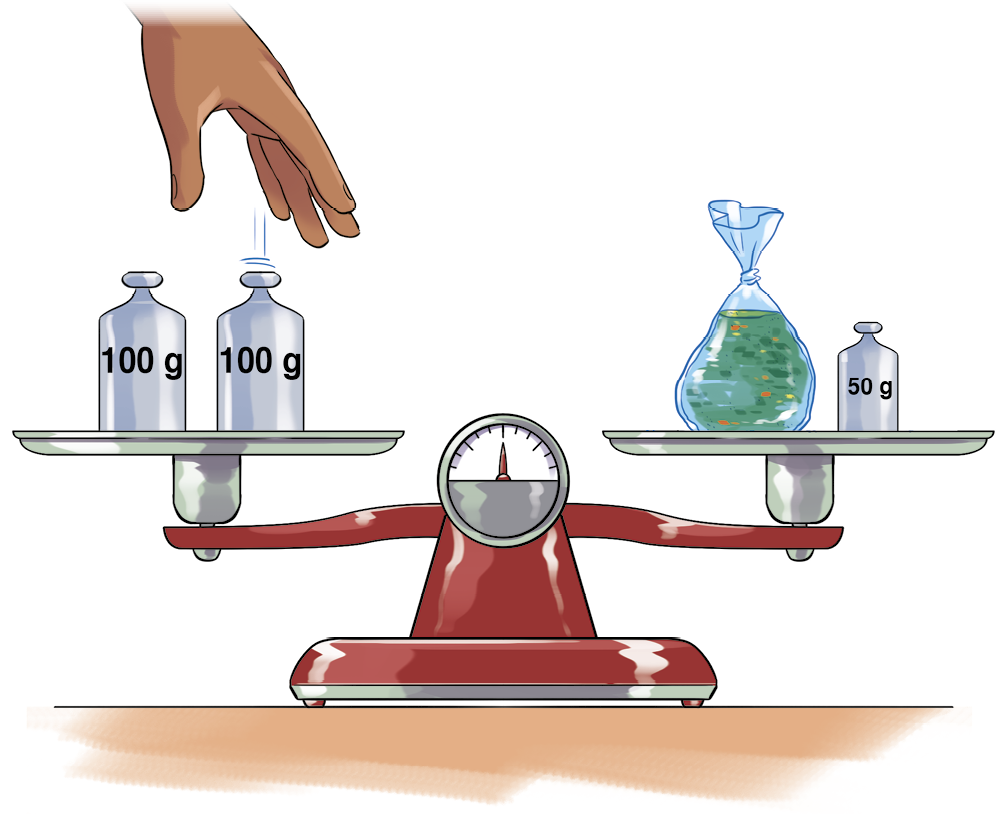
Como a balança está equilibrada, podemos representar a relação entre a medida da massa, em grama, do tempero e as medidas da massa, em grama, dos pesos com uma igualdade. Mas, como não conhecemos a medida da massa do tempero, usaremos um

para representá-la.
100 + 100 =

+ 50
Sabemos que, quando um mesmo número é subtraído dos dois membros de uma igualdade, ela se mantém verdadeira. Vamos subtrair 50 dos dois membros da igualdade.
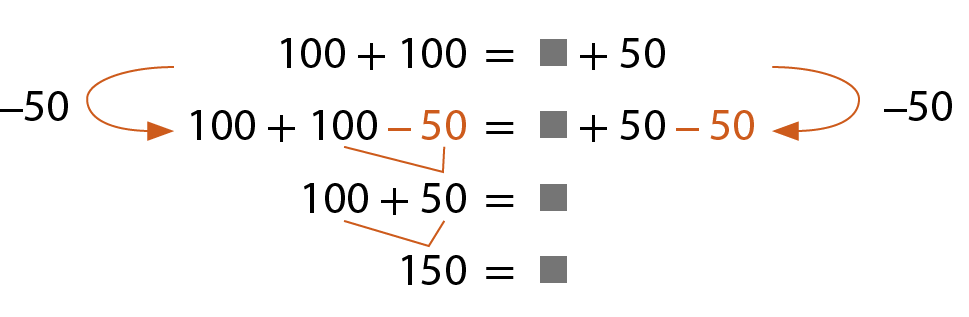
Portanto, a medida da massa do tempero é 150 gramas.
Respostas e comentários
6. a)
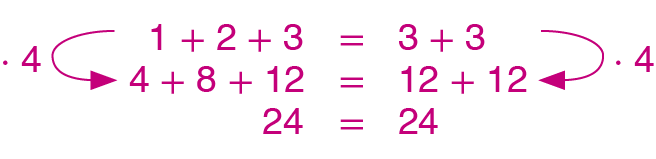
6. b)
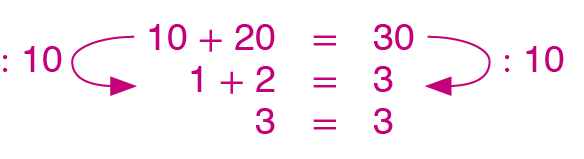
6. c)
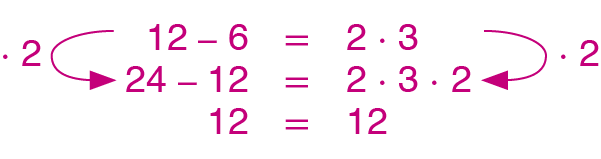
6. d)
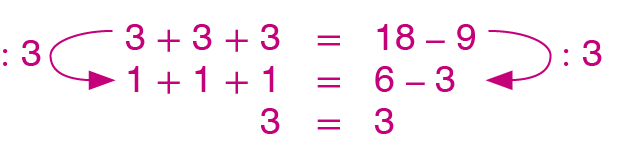
7. Exemplo de resposta:
antes: 3 + 2 + 2 = 7
depois: 6 + 4 + 4 = 14
Sugestão de atividade extra
Oriente os estudantes a se organizar em duplas. Distribua jornais e revistas para cada dupla e peça que recortem imagens de pessoas. Então, solicite que montem uma história com as personagens escolhidas. Nessa história, deve haver uma situação de igualdade abre parêntesesnão necessariamente envolvendo dinheirofecha parênteses que implique o uso de adição e de subtração, mantendo a igualdade verdadeira. No fim, solicite às duplas que apresentem a história aos colegas, explicitando na lousa os cálculos envolvidos na situação.
Resolvendo problemas com igualdades
Até esse momento, os estudantes refletiram a respeito das operações realizadas em ambos os membros de uma igualdade a fim de mantê-la verdadeira. Agora, focaremos no desenvolvimento da resolução de problemas aplicando as técnicas e as propriedades vistas, promovendo o desenvolvimento da habilidade ê éfe zero seis ême ah um quatro.
Problema 2
Paulo e Daniela estão brincando de adivinhar números.

Como o resultado das operações realizadas por Paulo é 25, Daniela resolveu representar a situação utilizando uma sentença matemática expressa por uma igualdade. Considere a representação feita por ela na lousa.

A ideia de Daniela era representar o número desconhecido por um □ e fazer operações deixando apenas o □ no primeiro membro. Acompanhe os cálculos feitos por Daniela.

Respostas e comentários
Sugestão de atividade extra
Peça a cada estudante que elabore um problema semelhante ao apresentado – a ideia é que tentem adivinhar números. Organize a turma em duplas; enquanto um estudante realiza os cálculos para descobrir o “número secreto”, o outro analisa e valida os cálculos. Realize mais de uma rodada de adivinhação, orientando-os a começar com uma situação simples e a aumentar o nível de dificuldade a cada nova rodada.
Como Daniela fez operações idênticas nos dois membros da igualdade, a relação de igualdade se manteve. Assim, ela escreveu uma igualdade e usou um □ para representar o número desconhecido, descobrindo que é o 5.
Acompanhe outros exemplos.
a) O dôbro de um número mais 4 é igual a 10.
Que número é esse?
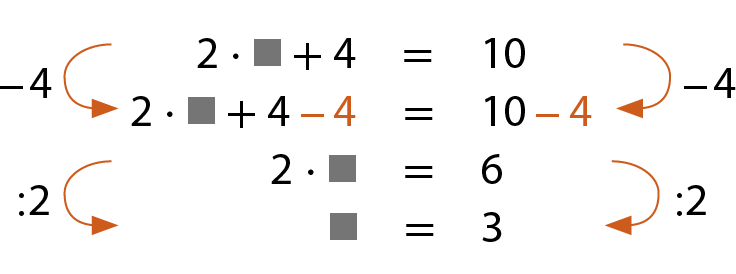
É o número 3.
b) Havia algumas maçãs em uma caixa. Comemos 3 e sobraram 8.
Quantas maçãs havia na caixa?
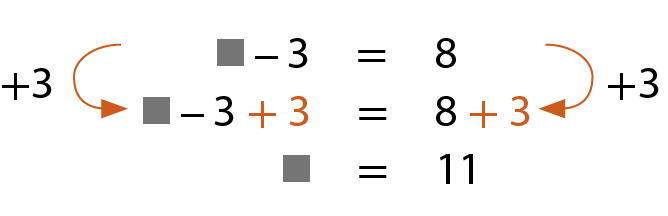
Havia 11 maçãs na caixa.

Atividades
Faça as atividades no caderno.
8. Uma balança de pratos está em equilíbrio. Em um prato, há um pacote de farinha e um pêso metálico de 200 gramas; no outro, dois pesos metálicos de 300 gramas. Faça o que se pede.
a) No caderno, represente a situação por meio de um desenho e, depois, usando uma sentença matemática.
b) Qual é a medida de massa do pacote de farinha, em grama?
9. Represente as situações usando uma sentença matemática expressa por igualdade e resolva-as em seu caderno.
a) Luiz ganhou um saquinho com bolinhas de gude. Se ele deu 10 bolinhas para Pedro e ainda ficou com 25, quantas bolinhas havia no saquinho?
b) O triplo de um número mais 1 é igual a 7. Que número é esse?
10. Descubra o número desconhecido nas sentenças matemáticas a seguir.
a)

+ 10 = 15
b) 10 menos 2 =

menos 2
c) 2 ⋅

+ 3 = 10 + 5
d) 14 menos 2 = 10 +

e) 31 = 3 ⋅

menos 8
f) 3 ⋅ (9 menos 2) = 3 ⋅

11. Em um jôgo de videogame, Paula e Vítor têm, juntos, 300 pontos. Se Paula tem o dôbro dos pontos de Vítor, qual é a pontuação de cada um?
12.


Elabore um problema no qual uma pessoa precisa comprar um agasalho e tem duas opções de marca (a e B), sendo que a marca a é mais cara. Depois, peça a um colega que o resolva.
13.

Elabore uma situação em que um garoto leva para a escola uma caixa com alguns caquis, colhidos do pé em sua casa, a fim de dividi-los com sua turma. Depois da distribuição entre os colegas, porém, ainda sobram algumas frutas na caixa. A situação deve buscar o número de caquis que o garoto levou para a escola, ou seja, esse é o número desconhecido.
Respostas e comentários
8. a) Desenho em Orientações; ■ + 200 = 300 + 300
8. b) 400 gramas
9. a) ■ menos 10 = 25; 35
9. b) 3 ⋅ ■ + 1 = 7; 2
10. a) 5
10. b) 10
10. c) 6
10. d) 2
10. e) 13
10. f) 7
11. Paula: 200 pontos; Vítor: 100 pontos
12. Resposta pessoal.
13. Resposta pessoal.
Sugestão de atividade extra
Para enriquecer o trabalho com cálculo mental e ampliar a compreensão da linguagem algébrica, peça aos estudantes que respondam às questões a seguir. Os cálculos deverão ser feitos mentalmente, e as respostas, dadas oralmente. Caso haja necessidade, oriente os estudantes e esclareça as dúvidas.
• Duas vezes um número dá 4. Que número é esse? Resposta: 2
• Três vezes um número dá 9. Que número é esse? Resposta: 3
• Três vezes um número dá 15. Que número é esse? Resposta: 5
• O resultado de duas vezes um número mais 1 dá 21. Que número é esse? Resposta: 10
Após o último item, pergunte aos estudantes o que aconteceria se omitíssemos a expressão “O resultado de”. Espera-se que percebam que a conversão para a linguagem algébrica poderia ser ambígua.
No caso, poderíamos ter tanto
2 ⋅ x + 1 = 21 quanto 2 ⋅ (x + 1) = 21, em que não determinaríamos o valor desconhecido no conjunto dos números naturais.
Se julgar necessário, para ampliar, peça que respondam também às questões a seguir.
• O resultado de três vezes um número mais 5 dá 20. Que número é esse? Resposta: 5
• Um número mais o seu dôbro dá 24. Que número é esse? Resposta: 8
• Um número dividido por 4 dá 6. Que número é esse? Resposta: 24
• O quociente de um número dividido por 2 mais 5 dá 18. Que número é esse? Resposta: 26
• Trinta menos duas vezes um número dá 12. Que número é esse? Resposta: 9
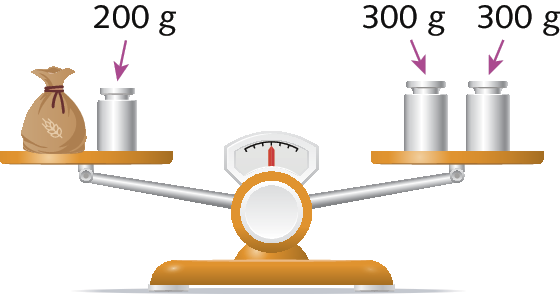
• Exemplo de desenho do item a da atividade 8:

3 Desigualdades
As desigualdades são sentenças matemáticas em que aparecem um dos sinais a seguir.
> (maior que)
< (menor que)
⩽ (menor ou igual a)
⩾ (maior ou igual a)
≠ (diferente)
Considere os exemplos.
a) 3 > 2
b) 8 < 9
c) 10 ⩾ 7
d) 11 ⩽ 13
e) 15 ≠ 51
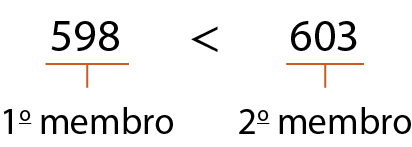
Assim como nas igualdades, chamamos de 1º membro a expressão que está à esquerda do sinal de desigualdade e de 2º membro a expressão que está à direita do sinal de desigualdade. Considere o exemplo.
Adicionando e subtraindo números naturais aos membros de uma desigualdade
Quando adicionamos ou subtraímos um mesmo número natural dos membros de uma desigualdade, ela se mantém verdadeira.
Acompanhe os exemplos.
a)
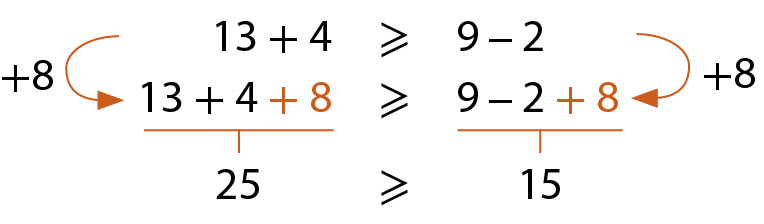
b)
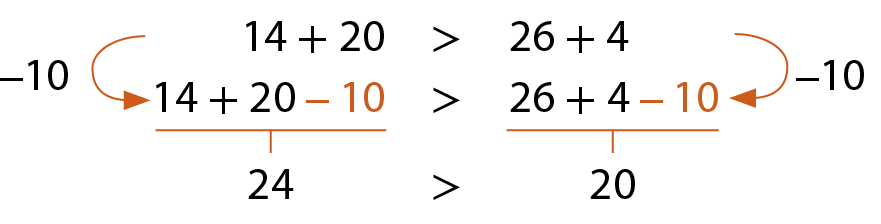

Multiplicando e dividindo os membros de uma desigualdade por números naturais
Quando multiplicamos ou dividimos os membros de uma desigualdade por um mesmo número natural, diferente de zero, a desigualdade se mantém verdadeira.
Analise os exemplos.
a)
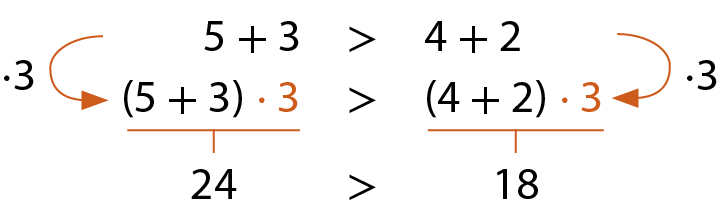
b)
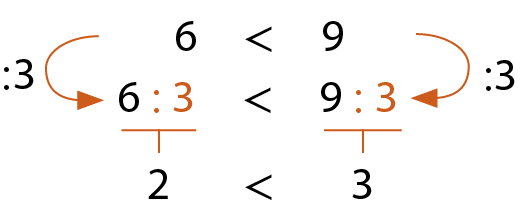

Respostas e comentários
Desigualdades
BNCC:
Competências gerais 8 e 9 (as descrições estão na página seis).
Objetivos:
• Compreender o conceito de desigualdade.
• Efetuar operações com os membros de uma desigualdade.
Justificativa
A compreensão do conceito de desigualdade e a realização de operações com os membros de uma desigualdade ampliam os conhecimentos adquiridos pelos estudantes no tópico anterior. Além disso, visa deixá-los preparados para o estudo de resoluções de inequações, que será abordado nos anos seguintes do Ensino Fundamental.
Mapeando conhecimentos
Reúna os estudantes em duplas e peça a cada dupla que adicione, subtraia, multiplique e divida os dois membros de algumas desigualdades por um mesmo número diferente de zero. Depois, incentive-os a verbalizar o que puderem observar.
Para as aulas iniciais
Se possível, leve uma balança de dois pratos para a sala de aula e deixe os estudantes à vontade para explorar algumas operações com os membros de desigualdades, colocando ou tirando “pesos” dos pratos dessa balança. Atividades como essa, que envolvem experimentação, podem auxiliá-los a superar eventuais dificuldades que tenham tido na tarefa inicial.
Adicionando e subtraindo números naturais aos membros de uma desigualdade
Reproduza na lousa os exemplos abordados na página e faça o passo a passo das passagens, esclarecendo as dúvidas dos estudantes.
Multiplicando e dividindo os membros de uma desigualdade por números naturais
Se julgar necessário, registre outras desigualdades na lousa e sugira aos estudantes que façam operações de multiplicação e divisão em ambos os membros dessas sentenças matemáticas.
Atividades
Faça as atividades no caderno.
14. Faça as operações indicadas em cada uma das desigualdades, calculando o valor de ambos os membros.
a) Adicione 4 a ambos os membros da desigualdade 10 menos 3 > 4.
b) Subtraia 11 de ambos os membros da desigualdade 24 dividido por 2 ⩾ 6 + 6.
c) Adicione 13 a ambos os membros da desigualdade 1 + 2 + 3 ⩽ 1 ⋅ 2 ⋅ 3.
d) Subtraia 7 de ambos os membros da desigualdade 3 + 3 + 3 > (21 menos 7) dividido por 2.
15. Rodrigo tem 15 brinquedos e Mara tem 20 a mais do que ele. Fábio deu 10 brinquedos para cada um dos dois. Represente a quantidade de brinquedos de Mara e Rodrigo usando uma desigualdade em dois momentos: antes de Fábio dar os brinquedos para os dois e depois que ele deu 10 brinquedos para cada um.
16. Calcule o valor do primeiro e o do segundo membro das desigualdades e descubra quais são verdadeiras.
a) 2 ⋅ abre parênteses3 + 4fecha parênteses ⩾ 2 ⋅ abre parênteses1 + 2fecha parênteses
b) 3 ⋅ 4 < abre parênteses1 + 2fecha parênteses ⋅ abre parênteses2 + 2fecha parênteses
c) 28 dividido por 14 ⩾ 14 dividido por 7
d) 35 dividido por 7 < 49 dividido por 7
17. Efetue as operações indicadas e calcule o valor de ambos os membros das desigualdades a seguir.
a) Multiplique os dois membros da desigualdade 4 + 1 ≠ 6 por 4.
b) Divida os dois membros da desigualdade 28 > 14 por 14.
c) Multiplique os dois membros da desigualdade 19 menos 10 ⩽ 3 ⋅ 3 por 5.
d) Divida os dois membros da desigualdade 9 + 6 + 3 > 1 + 2 + 3 por 3.
18. Os irmãos Marcos e Taís têm as quantias apresentadas a seguir.
Considerando que os pais deram R$ 20,00vinte reais para eles dividirem igualmente, represente as situações antes e depois de Marcos e Taís receberem essa quantia.

19. A balança de pratos a seguir está em desequilíbrio e adicionamos um pêso metálico ao prato da direita para equilibrar a balança.
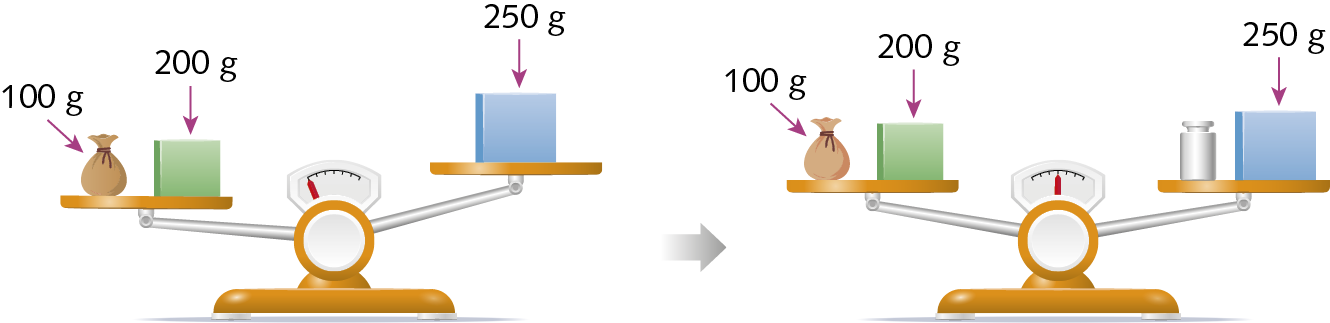
a) Qual é a medida da massa do pêso metálico adicionado?
b) Usando sentenças matemáticas, represente as situações antes e depois de adicionar esse pêso metálico.
c) Se adicionarmos um pêso metálico com a mesma medida da massa ao prato da esquerda, o que vai acontecer com a balança? Represente essa situação usando uma sentença matemática.
Respostas e comentários
14. a)
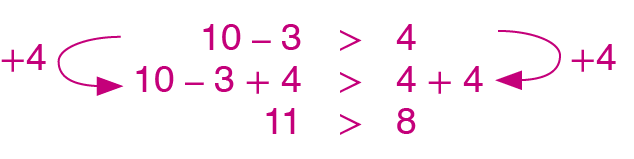
14. b)
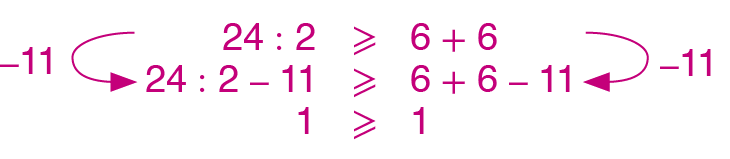
14. c)
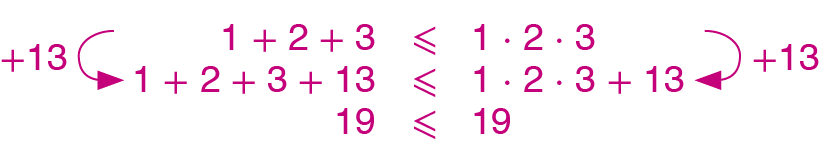
14. d)
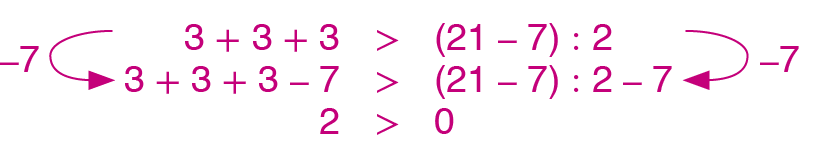
15. Antes: 15 + 20 > 15;
depois: 15 + 20 + 10 > 15 + 10
16. a) verdadeira
16. b) falsa
16. c) verdadeira
16. d) verdadeira
17. a)
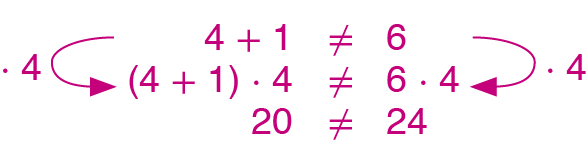
17. b)
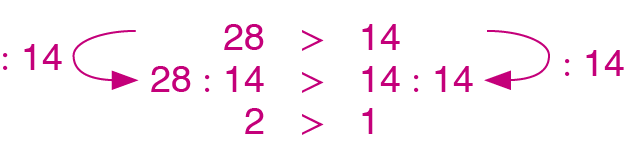
17. c)
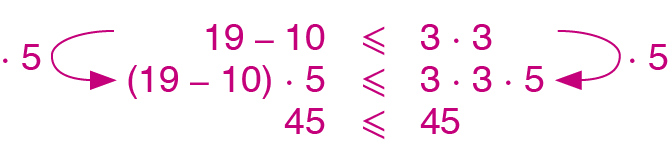
17. d)
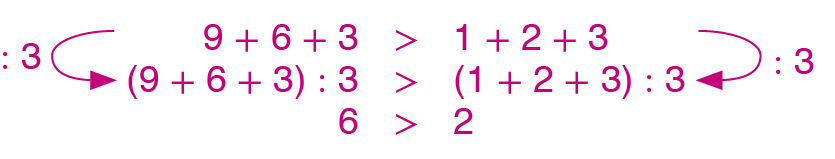
18. Antes: 5 + 5 + 5 + 10 < 20 + 10; depois: 5 + 5 + 5 + 10 + 10 < 20 + 10 + 10
19. a) 50 gramas
19. b) Antes: 100 + 200 > 250; depois: 100 + 200 = 250 + 50
19. c) Ela voltará a ficar desequilibrada para a esquerda; 100 + 200 + 50 > 250 + 50
Sugestão de trabalho interdisciplinar
Os termos igualdade e desigualdade são empregados amplamente não apenas em Matemática, mas também no dia a dia, em assuntos relacionados a Ciências Humanas, por exemplo. Sugerimos que se promova um debate acerca do tema “Igualdade e desigualdade: extrapolando a fronteira da Matemática”, com o auxílio dos professores de História, Geografia e Língua Portuguesa; colabora-se, assim, para o desenvolvimento das competências gerais 8 e 9 da Bê êne cê cê. Em um primeiro momento, redija com a turma um texto coletivo sobre as definições de igualdade e de desigualdade em Matemática. Depois, proponha o desenvolvimento do tema voltado à educação em direitos humanos. Em um segundo momento, organize a turma em grupos (de três a quatro estudantes) e peça aos integrantes de cada grupo que discutam entre si o que entenderam sobre igualdade e desigualdade fóra do contexto matemático. Por fim, com o auxílio dos demais professores, proponha aos grupos que pesquisem imagens que traduzam situações de desigualdade existentes na sociedade e deem opções de como é possível mudar essa realidade.
• Na atividade 15, espera-se que os estudantes relacionem, usando uma desigualdade, a quantidade de figurinhas de Mara e Rodrigo.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Sentenças matemáticas
Sentenças matemáticas são aquelas escritas com símbolos matemáticos. Elas podem ser:
verdadeiras
18 + 12 = 30
35 ⩽ 25 + 15
falsas
25 ≠ 18 + 7
12 ⋅ 5 > 60
1. Quais das sentenças matemáticas a seguir são verdadeiras?
a) 12 > 3 + 15
b) 7 ⋅ 12 = 12 ⋅ 7
c) 15 menos 5 ≠ 105 menos 95
d) 127 ⩽ 150 menos 16
2. Copie as sentenças no caderno substituindo o

por um símbolo que as torne verdadeiras. Use os símbolos: <, ⩽, =, > ou ⩾.
a) 25 + 5

12 + 5 + 15
b) 7 ⋅ 10

140 : 2
c) 12 ⋅ 5 + 50

150 menos 200 : 2 + 50
Igualdades
Igualdade é toda sentença matemática que apresenta o sinal de igual (=).
A relação de igualdade não se altera quando:
• adicionamos a seus membros ou subtraímos deles um mesmo número;
• multiplicamos ou dividimos seus membros por um mesmo número diferente de zero.
3. Efetue em seu caderno as operações indicadas para cada sentença matemática e encontre o valor de cada membro.
a) Adicione 25 aos dois membros da igualdade: 12 menos 10 = 45 menos 43
b) Subtraia 12 dos dois membros da igualdade: 30 + 11 = 56 menos 15
c) Multiplique por 9 os dois membros da igualdade: 19 + 3 = 38 menos 16
d) Divida por 6 os dois membros da igualdade: 36 menos 18 = 12 + 6
4. Represente cada situação usando uma igualdade e, em seguida, resolva-as.
a) Juliano deu 18 figurinhas repetidas para seu primo e ficou com 46 figurinhas. Quantas figurinhas Juliano tinha?
b) O dôbro de um número mais 12 é igual 58. Qual é esse número?
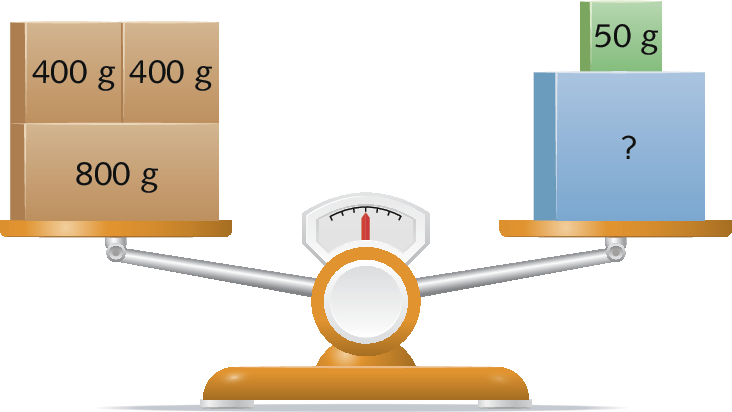
5. Nesta balança em equilíbrio, qual é a medida da massa da caixa azul em grama?
6. Descubra o número desconhecido nas sentenças matemáticas a seguir.
a)

+ 16 = 112
b) 4 ⋅ 10 +

= 52
c) 15 : 3 + 28 = 14 + 19 ⋅

7. Os irmãos Jorge e Felipe ganharam de um tio R$ 270,00duzentos e setenta reais no total. Se Jorge recebeu o dôbro do valor recebido pelo irmão, quantos reais cada um recebeu?
Desigualdades
Desigualdade é toda sentença matemática em que aparece um dos sinais a seguir.

A desigualdade se mantém verdadeira quando:
• adicionamos a seus membros ou subtraímos deles um mesmo número natural;
• multiplicamos ou dividimos um mesmo número natural, diferente de zero, de ambos os membros.
8. Calcule o valor de cada membro das desigualdades e determine se elas são verdadeiras ou falsas.
a) 10 ⋅ abre parênteses3 + 5fecha parênteses ⩾ 12 ⋅ abre parênteses2 + 3fecha parênteses
b) 10 + 2 ⋅ 5 ⩽ abre parênteses2 + 10fecha parênteses : 3
c) 36 : 2 menos 12 ≠ 6elevado a 2 menos 4elevado a 2 + 4
9. Mário tem 125 figurinhas e Luana tem cento e trinta e duas. Cada um deles recebeu 25 figurinhas de um colega. Escreva uma desigualdade para representar as situações antes e depois de Mário e Luana ganharem as figurinhas.
Respostas e comentários
1. Itens b e d.
2. a) < ou ⩽
2. b) = ou ⩽ ou ⩾
2. c) > ou ⩾
3. a) 27 = 27
3. b) 29 = 29
3. c) 198 = 198
3. d) 3 = 3
4. a) ■ menos 18 = 46; 64
4. b) 2 ⋅ ■ + 12 = 58; 23
5. .1550 gramas
6. a) 96
6. b) 12
6. c) 1
7. Jorge: R$ 180,00cento e oitenta reais; Felipe: R$ 90,00noventa reais
8. a) verdadeira
8. b) falsa
8. c) verdadeira
9. Antes: 125 < 132; depois: 125 + 25 < 132 + 25
Revisão dos conteúdos deste capítulo
Sentenças matemáticas
Ao retomar a definição de sentenças matemáticas, apresente outros exemplos na lousa e peça aos estudantes que avaliem se as sentenças escritas por você são verdadeiras ou falsas.
• Após os estudantes concluírem a atividade 1, você pode ampliar a proposta dela e solicitar que modifiquem as sentenças falsas de modo a torná-las verdadeiras. Depois, peça que compartilhem como fizeram essa modificação, pois existem diferentes maneiras de mudar estas sentenças.
• Na atividade 2, se julgar necessário, informe, em cada item, que a resposta não é única, ou seja, admite-se pelo menos dois símbolos diferentes como resposta.
Igualdades
• Na atividade 3, é necessário ter uma atenção especial com os itens c e d, pois alguns estudantes podem cometer o êrro de multiplicar ou dividir apenas um dos elementos do membro.
• Na atividade 5, você pode solicitar aos estudantes que traduzam a situação da balança por meio de uma sentença matemática. Dê especial atenção ao sinal de comparação que eles colocam: como a balança está em equilíbrio, é necessário que usem o sinal de igualdade.
• A atividade 6 pode ser resolvida por meio de cálculos mentais ou aplicando-se o fato de que a relação de igualdade não se altera quando adicionamos a seus membros ou subtraímos deles um mesmo número ou quando multiplicamos ou dividimos seus membros por um mesmo número diferente de zero. Incentive-os a desenvolver os cálculos detalhando as operações feitas em cada membro das igualdades.
Desigualdades
• Para a resolução dos itens da atividade 8, é importante que os estudantes sigam a recomendação de calcular o valor de cada membro das desigualdades. Oriente-os a fazer esses cálculos separadamente para organizarem melhor o raciocínio e evitarem equívocos.
• Caso apresentem dificuldades para realizar a atividade 9, oriente-os a fazer um esquema que ilustre a situação descrita.