Capítulo 5 Múltiplos e divisores
Trocando ideias
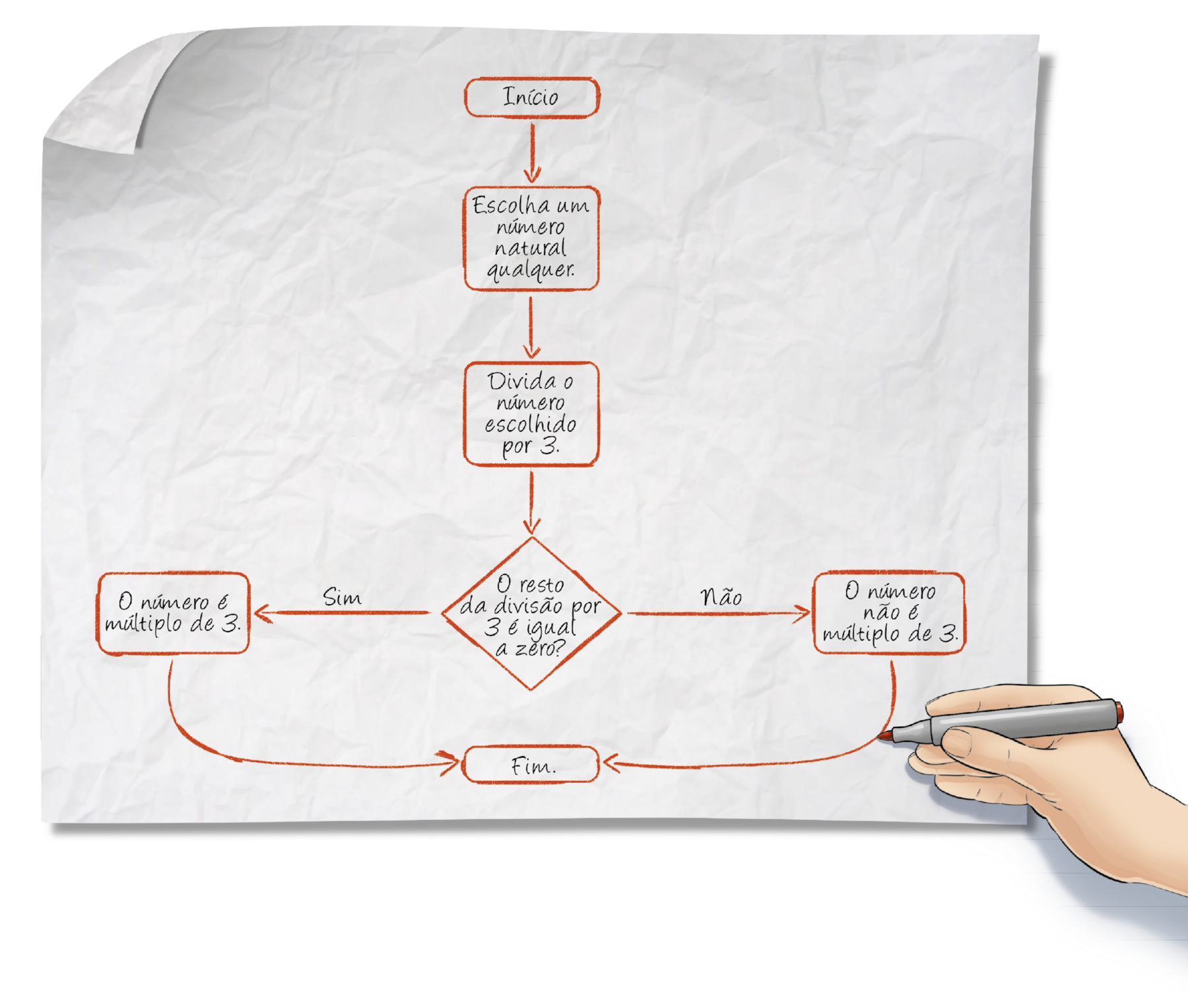
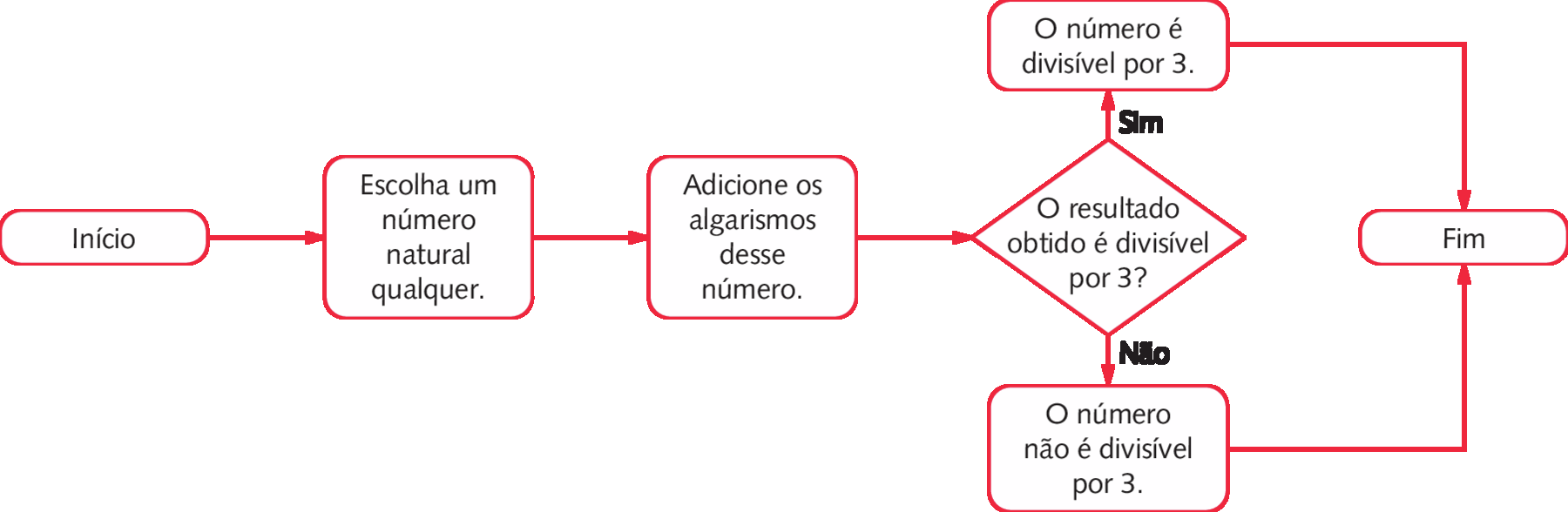
Observe o esquema a seguir.
▸


Para que serve esse esquema?
▸

Utilize o esquema anterior e verifique quais dos números a seguir são múltiplos de 3.

Os números que você identificou são exemplos de múltiplos de 3. Também podemos dizer que 3 é divisor de cada um desses números.
Neste capítulo, vamos estudar os múltiplos e os divisores de números naturais, além de reconhecer números primos e números compostos.
Respostas e comentários
Trocando ideias: primeiro item: para verificar se um número é ou não múltiplo de 3; segundo item: 9, 15, 24 e 33.
CAPÍTULO 5 – MÚLTIPLOS E DIVISORES
Trocando ideias
Bê êne cê cê:
• Competências gerais 2, 4 e 9 (as descrições estão na página seis).
• Competências específicas 2, 6 e 8 (as descrições estão na página sete).
Objetivos:
• Levantar os conhecimentos prévios dos estudantes sobre os conceitos de múltiplo e divisor.
• Ler e interpretar fluxograma.
Reproduza na lousa o esquema apresentado nesta página. Depois, dê um tempo para que os estudantes analisem e discutam entre si o que entenderam. Então, peça que respondam à primeira questão. Espera-se que eles percebam que o esquema serve para verificar se um número é ou não um múltiplo de 3. Se achar oportuno, diga que esse esquema é um exemplo de fluxograma e que eles estudarão esquemas como esse neste capítulo.
Em conjunto com a turma, verifique se alguns números são múltiplos de 3 por meio desse fluxograma e peça que realizem a atividade proposta no segundo item. Aproveite a oportunidade e verifique se os estudantes reconhecem que os números 7, 23 e 41 são primos e que o número 22 é múltiplo de 2 e de 11.
A proposta deste Trocando ideias possibilita aos estudantes lidar com diferentes linguagens (verbal e fluxograma), o que favorece o desenvolvimento da competência geral 4 e da competência específica 6 da Bê êne cê cê. Além disso, a turma é incentivada a exercitar sua curiosidade e colocar em prática o espírito de investigação, o que permite o desenvolvimento da competência geral 2 e da competência específica 2. Por fim, por promover o diálogo e a interação, a competência geral 9 e a competência específica 8 também têm o seu desenvolvimento favorecido.

1 Múltiplos de um número natural
Observe, no quadro a seguir, alguns números da tabuada do 7.
|
× |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
7 |
0 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
... |
Os números 0, 7, 14, 21, 28, reticências, da tabuada do 7, são múltiplos de 7, pois podem ser obtidos multiplicando-se o 7 por um número natural qualquer: 7 ⋅ 0 = 0, 7 ⋅ 1 = 7, 7 ⋅ 2 = 14, 7 ⋅ 3 = 21, 7 ⋅ 4 = 28, reticências
Dizemos que um número natural é múltiplo de outro quando o primeiro é obtido multiplicando o segundo por um número natural qualquer.
A sequência (0, 7, 14, 21, 28, reticências) é a sequência dos múltiplos naturais de 7. Note que essa sequência começa pelo número zero, e que o padrãoglossário é sempre adicionar 7 ao termo anterior. Portanto, essa sequência é infinita.
Do mesmo modo, podemos obter a sequência dos múltiplos de qualquer número natural.
Analise outros exemplos:
a) (0, 11, 22, 33, 44, reticências) é a sequência dos múltiplos naturais de 11.
b) (0, 19, 38, 57, 76, reticências) é a sequência dos múltiplos naturais de 19.
Observações
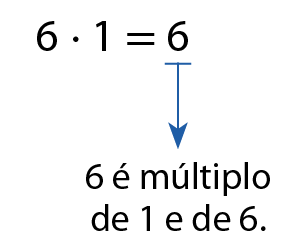
1. Todo número natural é múltiplo de 1 e dele mesmo. Verifique:
a)
b)
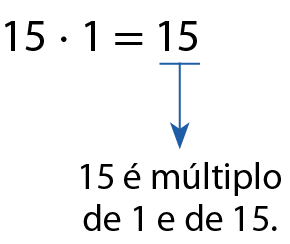
c)

2. Não existe o maior múltiplo de um número natural não nulo. A sequência dos múltiplos de um número natural, diferente de zero, é infinita.
É possível verificar se um número é múltiplo de outro. Confira os exemplos a seguir.
a) O número 72 é múltiplo de 6?
Para responder a essa pergunta, devemos verificar se 72 é igual a 6 vezes algum número natural. Para isso, vamos dividir 72 por 6. Observe.

Note que o resto da divisão de 72 por 6 é 0. Como a divisão é exata, concluímos que 72 é divisível por 6 e podemos escrever 6 ⋅ 12 = 72. Portanto, 72 é múltiplo de 6.
Respostas e comentários
Múltiplos de um número natural
Bê êne cê cê:
Habilidades ê éfe zero seis ême ah zero quatro e ê éfe zero seis ême ah zero seis.
Objetivos:
• Reconhecer e determinar múltiplos de um número natural.
• Ler, interpretar e elaborar fluxogramas.
Justificativa
Reconhecer e determinar múltiplos de um número natural é um passo importante para que os estudantes resolvam e elaborem problemas que envolvam a ideia de múltiplo e, consequentemente, desenvolvam a habilidade ê éfe zero seis ême ah zero seisponto
A habilidade ê éfe zero seis ême ah zero quatro implica construir algoritmos em linguagem natural e representá-los por fluxograma e, por isso, é de grande valia ler, interpretar e elaborar esse tipo de representação.
Mapeando conhecimentos
Na lousa, escreva algumas listas de números: uma com números múltiplos de 2, outra com números múltiplos de 3, outra com números múltiplos de 4 etcétera. Você pode escrever quantas listas achar necessário. Depois, pergunte aos estudantes o que os números de cada lista têm em comum. Por meio dessa dinâmica, você poderá diagnosticar os estudantes que conseguem e os que não conseguem reconhecer múltiplos de um número natural.
A atividade do Trocando ideias serve para mapear como os estudantes lidam com fluxogramas.
Para as aulas iniciais
Retome o conceito de múltiplo e explore o quadro com os múltiplos de 1, 2, 7 e 9 na seção Revisão dos conteúdos de anos anteriores. Depois, proponha aos estudantes que façam as atividades 31 a 33. Reserve um tempo para discutir coletivamente cada atividade e tirar as dúvidas.
Como os estudantes já viram as sequências dos números naturais, dos números pares e dos números ímpares, uma possibilidade na exploração da ideia de múltiplos de um número natural pode ser a observação e a identificação de outros padrões de sequências numéricas.
(ê éfe zero seis ême ah zero quatro) Construir algoritmo em linguagem natural e representá-lo por fluxograma que indique a resolução de um problema simples (por exemplo, se um número natural qualquer é par).
(ê éfe zero seis ême ah zero seis) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor.
b) O número 270 é múltiplo de 16?
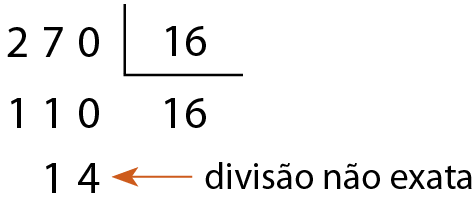
Como a divisão não é exata, concluímos que 270 não é divisível e não é múltiplo de 16.
Observações
1. O zero só tem um múltiplo: o próprio zero. Observe os exemplos a seguir.
a) 0 ⋅ 0 = 0
b) 0 ⋅ 1 = 0
c) 0 ⋅ 2 = 0
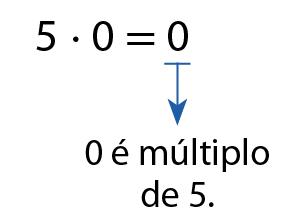
2. O zero, porém, é múltiplo de todos os números naturais. Verifique:
a)
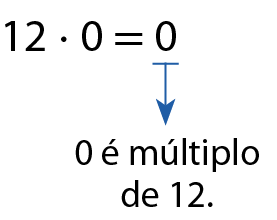
b)
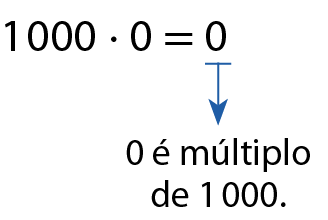
c)
3. Podemos falar em múltiplo de zero porque existem multiplicações por zero. Porém, não podemos falar que um número é divisível por zero, uma vez que não existe divisão por zero.
Para verificar se um número é múltiplo de 2, por exemplo, podemos elaborar um esquema conforme o apresentado a seguir.
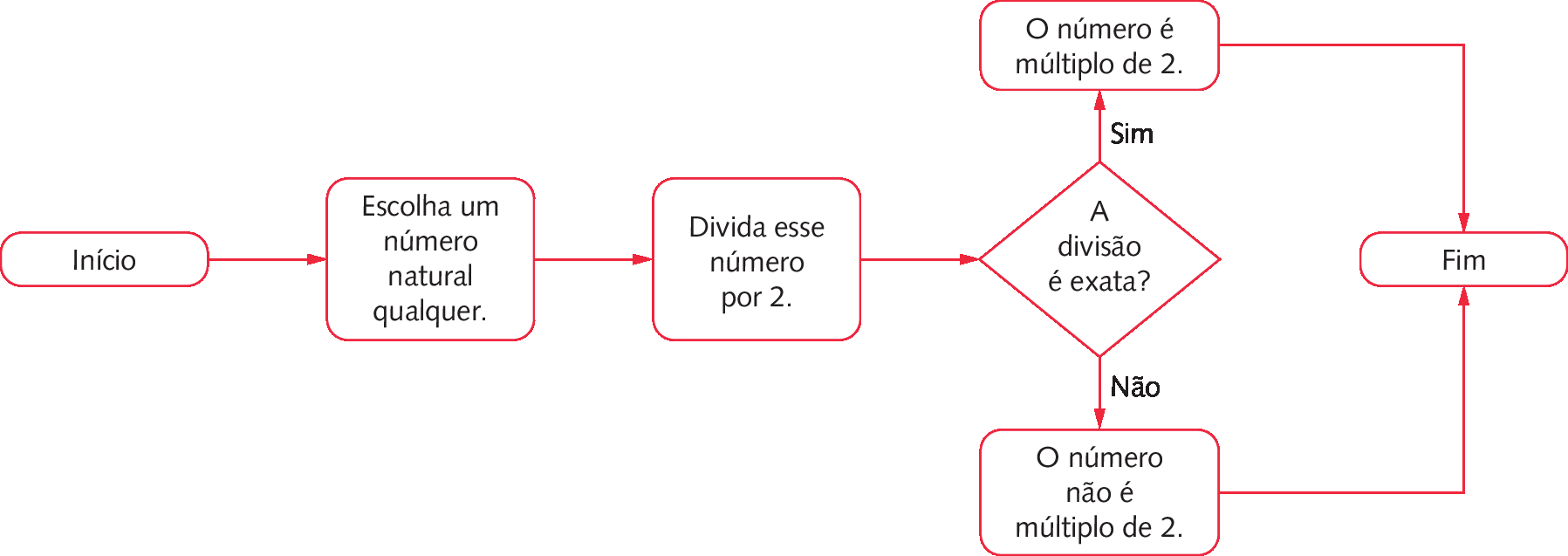
Esse esquema é um exemplo de fluxograma, um tipo de diagrama que póde ser utilizado para representar, de maneira resumida, a sequência de etapas de um procedimento. Observe o significado das figuras no fluxograma anterior.
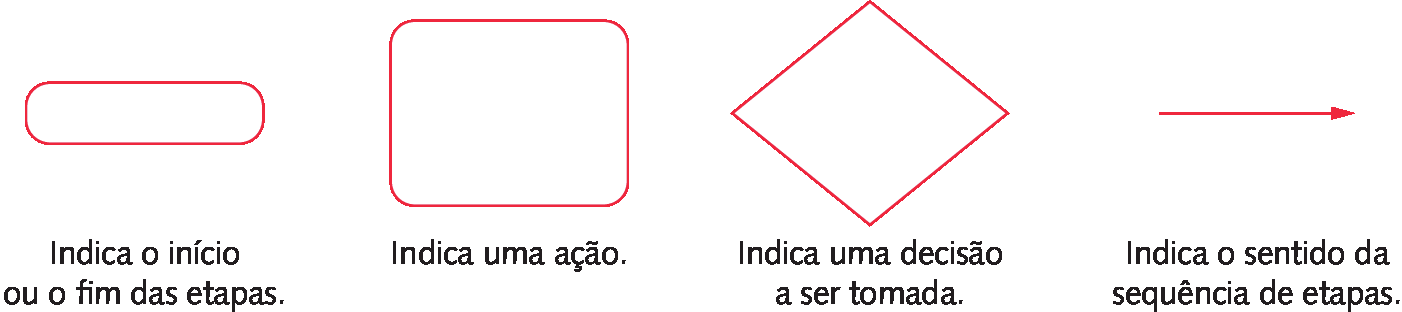
Respostas e comentários
Nesta página, aparece um fluxograma que mostra a sequência de etapas para verificar se um número é ou não múltiplo de 2. Comente com os estudantes que os fluxogramas são úteis, entre outras coisas, para representar de maneira lógica e gráfica as etapas que devemos seguir para verificar se um número é ou não múltiplo de outro número natural e são inspirados na lógica usada em linguagens de programação.
É importante que os estudantes compreendam o significado de cada figura que compõe um fluxograma. No início do uso de cada fluxograma, oriente-os a acompanhar o fluxograma apontando cada etapa e resolvendo mentalmente. Assim, eles perceberão que, ao responder à pergunta com “sim”, seguirão um caminho e, ao responder com “não”, seguirão outro caminho.
Atividades
Faça as atividades no caderno.
1. Quais são os cinco menores múltiplos de 17?
2.

Digite, na calculadora, as teclas

. Você vai visualizar o número 23. Em seguida, digite sucessivamente a tecla

.
a) Quais foram os quatro primeiros números que apareceram no visor depois que você começou a digitar a tecla

?
b) Qual é a particularidade desses números?
3. Determine:
a) os múltiplos de 7 maiores que 50 e menores que 80;
b) os múltiplos de 16 compreendidos entre 151 e 201.
4.

Utilize o fluxograma da página anterior e verifique se alguns números naturais são ou não múltiplos de 2.
5.


Elabore, em seu caderno, um fluxograma para que um colega verifique se um número natural qualquer é ou não múltiplo de algum outro número natural.
6.
Responda às questões a seguir.
a) O número 345 é múltiplo de 7?
b) O número .1445 é múltiplo de 17?
c) Dos números 147, 385, 504 e .7401, quais são múltiplos de 21?
d) Qual é o menor número natural que devemos adicionar a 68 para obter um múltiplo de 13?
7. O número .3192 é múltiplo de 7? Depois de .3192, qual é o próximo número natural divisível por 7?
8. Determine os múltiplos de 13, 17 e 19 entre 300 e 320. Aproxime cada um deles para o múltiplo de 10 mais próximo.
9. Leia as afirmações a seguir e indique no caderno se são verdadeiras ou falsas.
a) .1856 é múltiplo de 2.
b) 91 é múltiplo de 7.
c) 169 é múltiplo de 3.
d) 100 é múltiplo de 2 e de 3.
e) 210 é múltiplo de 2, 3, 5 e 7.
f) .123456 é múltiplo de 3.
g) .123456 é múltiplo de 64.
h) .123456 é múltiplo de 5.
10.

Reúna-se com um colega e façam o que se pede.
a) Escolha um número e, em seguida, peça a seu colega que determine cinco múltiplos desse número.
b) Verifique se os múltiplos que ele determinou estão corretos.
Respostas e comentários
1. 0, 17, 34, 51 e 68
2. a) 46, 69, 92 e 115
2. b) São os quatro primeiros múltiplos de 23, com exceção do zero e dele próprio.
3. a) 56, 63, 70 e 77
3. b) 160, 176 e 192
4. Resposta pessoal.
5. Resposta pessoal.
6. a) não
6. b) sim
6. c) 147 e 504
6. d) 10
7. sim; .3199
8. 13: 312 → 310; 17: 306 → 310; 19: 304 → 300
9. a) verdadeira
9. b) verdadeira
9. c) falsa
9. d) falsa
9. e) verdadeira
9. f) verdadeira
9. g) verdadeira
9. h) falsa
10. a) Resposta pessoal.
10. b) Resposta pessoal.
• A atividade 2 propõe o uso de calculadora para a formação de uma sequência numérica fazendo uso da tecla

, porém as etapas apresentadas na atividade podem variar de uma calculadora para outra. Oriente os estudantes cujas calculadoras funcionem de maneira diferente da indicada e incentive-os a buscar outras sequências de múltiplos de outros números naturais. Assim, dá-se a oportunidade aos estudantes de buscarem as próprias estratégias de resolução e de construírem seus conhecimentos matemáticos de maneira sólida.
• Para a realização da atividade 5, os estudantes são desafiados a construir um fluxograma. Caso apresentem dificuldades, oriente-os a rever o exemplo da página 98.

2 Divisores de um número natural
Marcos vai montar a vitrine de sua loja de jogos eletrônicos com seis jogos que acabaram de ser lançados. Para isso, ele pensou em algumas possibilidades de como dispor os jogos em suportes.
Possibilidade 1

Possibilidade 2

Possibilidade 3

Possibilidade 4

Dizemos que os números 1, 2, 3 e 6 são os divisores naturais ou fatores naturais de 6, pois, ao dividir 6 por qualquer um desses números, obtemos uma divisão exata. Também dizemos que 6 é divisível por 1, 2, 3 e 6.
Agora, se Marcos usasse quatro suportes, conseguiria distribuir os seis jogos igualmente nesses suportes?
Como a divisão de 6 por 4 não é exata, 4 não é divisor de 6. Concluímos, portanto, que Marcos não conseguiria distribuir os seis jogos igualmente em quatro suportes.
Dizemos que um número natural é divisor ou fator de outro caso a divisão do segundo pelo primeiro seja exata.
Respostas e comentários
Divisores de um número natural
Bê êne cê cê:
Habilidade ê éfe zero seis ême ah zero seis.
Objetivo:
Reconhecer e determinar os divisores de um número natural.
Justificativa
Reconhecer e determinar os divisores de um número natural é um passo importante para que os estudantes resolvam e elaborem problemas que envolvam a ideia de divisor e, consequentemente, desenvolvam a habilidade ê éfe zero seis ême ah zero seis.
Mapeando conhecimentos
Escreva alguns números na lousa e peça aos estudantes que determinem, utilizando suas próprias estratégias, todos os divisores desses números. Verifique se eles percebem que os fatores de determinado número são também seus divisores. Você pode organizá-los em duplas ou trios para que possam discutir suas hipóteses e compartilhar ideias.
Para as aulas iniciais
Discuta os exemplos e as estratégias apresentados pelos estudantes na dinâmica anterior. Depois, peça que façam a atividade 34 da seção Revisão dos conteúdos de anos anteriores.
Ao abordar a divisibilidade, é importante discutir com os estudantes os significados envolvidos, como “o que é ser um divisor” e “como reconhecer um divisor”. Dessa fórma, a aprendizagem dos critérios de divisibilidade passa a ser consequência dessa abordagem, sem que se torne um conjunto de regras a ser memorizado. É sempre mais interessante para eles a resolução de problemas do que a aplicação de regras preestabelecidas. Para que se apropriem do significado dos termos “ser divisor de”, “ser divisível por” e “ser múltiplo de”, proponha a divisão exata de 24 : 4 = 6 e sua operação inversa, 6 ⋅ 4 = 24. Chame a atenção dos estudantes para as seguintes observações:
• o número 4 divide 24;
• 4 é divisor de 24, ou 24 é divisível por 4;
• na operação inversa, 24 é o resultado de 4 multiplicado por 6. Portanto, 24 é múltiplo de 4 e 24 é múltiplo de 6.
Eles devem perceber que a ideia de divisor está diretamente ligada à ideia de múltiplo.
(ê éfe zero seis ême ah zero seis) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor.
Analise outros exemplos.
a)
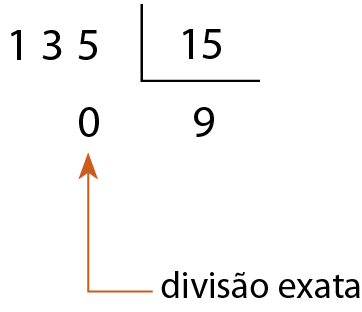
15 é divisor de 135.
b)
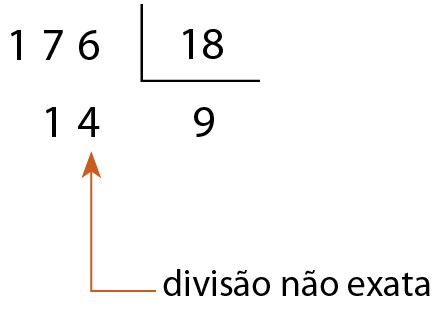
18 não é divisor de 176.
c)
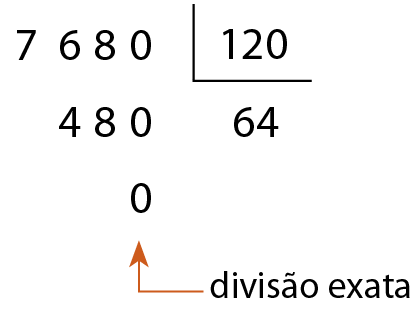
120 é divisor de .7680.
d)
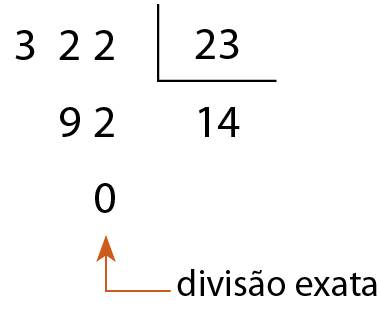
23 é divisor de 322.
e)
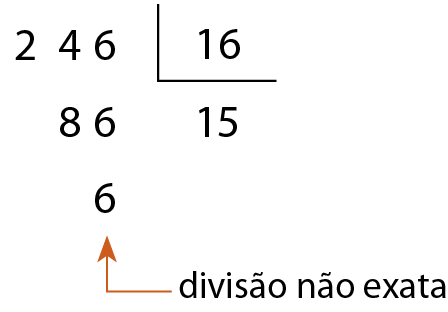
16 não é divisor de 246.
f)
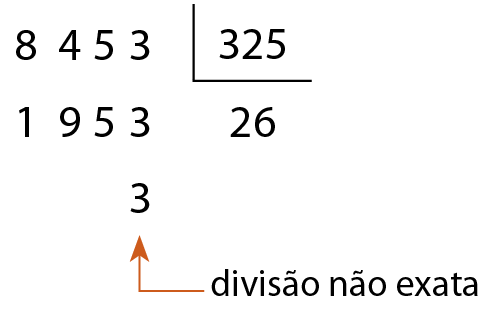
325 não é divisor de .8453.
Observações
1. O zero não é divisor de nenhum número natural.
Por exemplo: 5 dividido por 0 = ?
Note que não existe nenhum número que, multiplicado por zero, dê 5 como resultado.
2. Todo número natural diferente de zero tem como divisor ele mesmo.
a) 6 dividido por 6 = 1
6 é divisor de 6.
b) 8 dividido por 8 = 1
8 é divisor de 8.
c) 15 dividido por 15 = 1
15 é divisor de 15.
3. O número 1 é divisor de todos os números naturais.
a) 8 dividido por 1 = 8
1 é divisor de 8.
b) 12 dividido por 1 = 12
1 é divisor de 12.
c) 0 dividido por 1 = 0
1 é divisor de 0.
Atividades
Faça as atividades no caderno.
11. Efetue divisões para verificar se o número 600 é divisível por:
a) 12;
b) 15;
c) 18;
d) 24;
e) 36;
f) 90.
12. Escreva no caderno:
a) todos os fatores naturais de 30;
b) os fatores de 72 compreendidos entre 10 e 30;
c) os divisores ímpares de 40;
d) os divisores pares de 40.
13. Responda no caderno às questões a seguir.
a) Qual é o maior divisor de qualquer número não nulo?
b) Qual é o menor divisor de qualquer número?
c) O número zero é divisível por todos os outros números naturais?
d) Quais são os números que, divididos por 2, deixam resto 1?
e) Quais são os números que, divididos por 2, deixam resto zero?
14. Determine:
a) o maior número de três algarismos divisível por 2;
b) os três maiores divisores de 32;
c) o maior número de três algarismos divisível por 23.
Respostas e comentários
11. 600 é divisível pelos números dos itens a, b e d.
12. a) 1, 2, 3, 5, 6, 10, 15 e 30
12. b) 12, 18 e 24
12. c) 1 e 5
12. d) 2, 4, 8, 10, 20 e 40
13. a) ele próprio
13. b) 1
13. c) sim, com exceção do próprio zero
13. d) os números ímpares
13. e) os números pares
14. a) 998
14. b) 32, 16 e 8
14. c) 989
Sugestão de atividade extra
É possível encontrar diversos jogos envolvendo conteúdos matemáticos que, se explorados de maneira cuidadosa, crítica e planejada, também contribuem para o aprendizado dos estudantes. Um exemplo é o jôgo Achando os divisores, do site Clubes de Matemática da ó bê mépi.
Disponível em: https://oeds.link/0O8dVm. Acesso em: 30 junho 2022.
15. Qual é o menor número que devemos adicionar a .1657 para torná‑lo um múltiplo de 100?
16. Leia as afirmações a seguir e indique, no caderno, se são verdadeiras ou falsas.
a) 2 é divisor de .1154.
b) 7 é fator de 185.
c) 3, 5, 9 e 10 são divisores de 810.
d) 2, 3, 9 e 100 são fatores de 117.
e) 8 é divisor de 84.
f) 16 é divisor de 500.
g) 32 é fator de 288.
h) 14 é divisor de 196.
17.

Junte-se a um colega, leiam a questão e a resolvam.
A professora escreveu em um quadro os divisores de 12 e os divisores de 36 em ordem crescente. Em seguida, uniu alguns desses divisores. Observem:

Que conclusões sugerem os registros da professora?
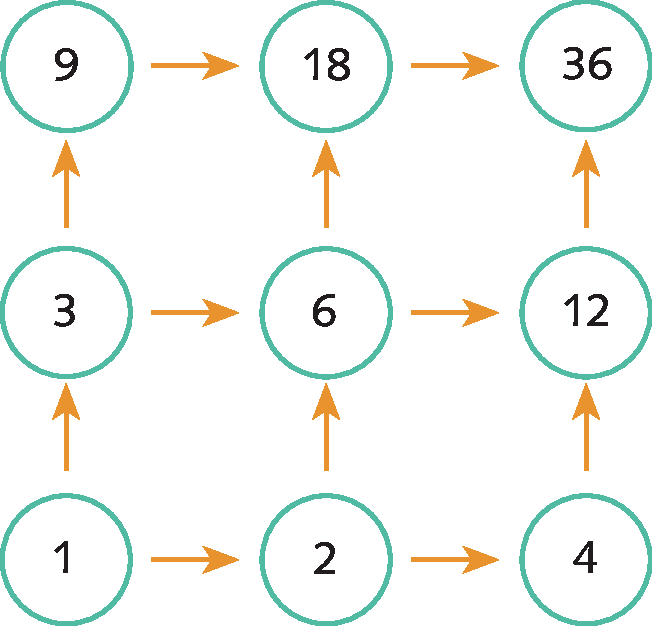
18. Copie a figura a seguir no caderno, substituindo o

pelos divisores de 36, de modo que cada número seja divisor daquele que vem depois da seta. Mas atenção: não póde haver repetição dos números!
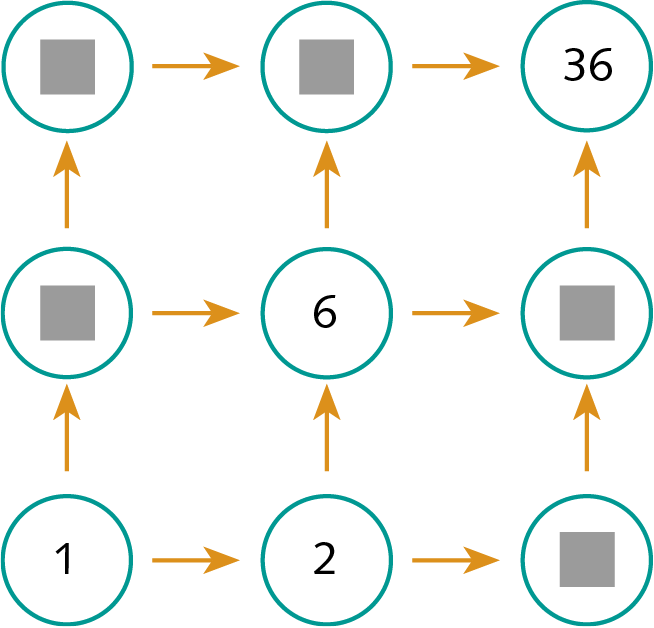
19.

Junte-se a um colega e resolvam o problema a seguir.
Adriano tem estas opções de peças de pisos cerâmicos quadrados para cobrir o chão de uma sala retangular de 300 centímetros de medida de comprimento por 240 centímetros de medida de largura.

Desconsiderando o rejunte, responda:
a) Qual é o menor número de peças amarelas necessárias para revestir o chão?
b) É possível revestir o chão com peças azuis sem recortá-las?
c) Adriano quer usar o menor número possível de peças e não quer recortar nenhuma. Qual deve ser a côr do piso dessa sala?
20.

Os gregos chamavam de número perfeito o número natural que fosse igual à soma de seus divisores própriosglossário .
Analise alguns exemplos:
|
Número perfeito |
Divisores próprios |
Cálculo da soma dos divisores próprios |
|---|---|---|
|
6 |
1, 2 e 3 |
1 + 2 + 3 = 6 |
|
28 |
1, 2, 4, 7 e 14 |
1 + 2 + 4 + 7 + 14 = 28 |
Com o auxílio de uma calculadora, verifique se o número 496 é um número perfeito.
Respostas e comentários
15. 43 16. a) verdadeira 16. b) falsa 16. c) verdadeira 16. d) falsa 16. e) falsa 16. f) falsa 16. g) verdadeira 16. h) verdadeira 17. Resposta em Orientações. 18. Resposta em Orientações. 19. a) 12 peças amarelas 19. b) sim 19. c) verde 20. 496 é um número perfeito, pois, adicionando seus divisores próprios (1, 2, 4, 8, 16, 31, 62, 124 e 248), obtemos 496.
• Na atividade 17, espera-se que os estudantes notem que o produto dos termos equidistantes de cada sequência de divisores é igual ao maior divisor obtido. Assim, para determinar os divisores de um número natural qualquer, basta encontrar todos os produtos de dois fatores que resultam nesse número. Aproveite o momento e o contexto e questione-os sobre o que é um número quadrado perfeito. Se considerar adequado, proponha uma lista de números que contenha entre eles números quadrados perfeitos e solicite que encontrem a sequência de divisores de cada um deles. Questione os estudantes sobre a quantidade de divisores de cada um deles, quais possuem números pares e quais possuem números ímpares de divisores. Comente que uma característica dos números quadrados perfeitos é o fato de serem os únicos números que possuem uma quantidade ímpar de divisores; portanto, o termo central dessa sequência multiplicado por ele mesmo será o próprio quadrado perfeito.
• Resposta da atividade 18:
• A atividade 20 traz um pequeno texto sobre o conceito de números perfeitos. Pode-se solicitar aos estudantes que pesquisem na internet sobre outros tipos de número, como números amigos: dois números são “amigos” se cada um deles é igual à soma dos divisores próprios do outro. Por exemplo, 220 e 284.
Sugestão de leitura
Para enriquecer a abordagem sobre os números quadrados perfeitos, leia o texto “Sala de estudo: quadrados perfeitos”, da Equipe COM – OBMEP.
Disponível em: https://oeds.link/Mt4Wid. Acesso em: 30 junho 2022.

3 Critérios de divisibilidade
Aprendemos que, para verificar se um número é divisível por outro, devemos efetuar uma divisão entre eles e analisar o resto da divisão. Quando o resto é igual a zero, o número é divisível pelo outro.
Agora, vamos estudar alguns critérios de divisibilidade que nos permitem verificar se um número é divisível por outro sem efetuar a divisão.
Critério de divisibilidade por 2
Observe estas divisões:
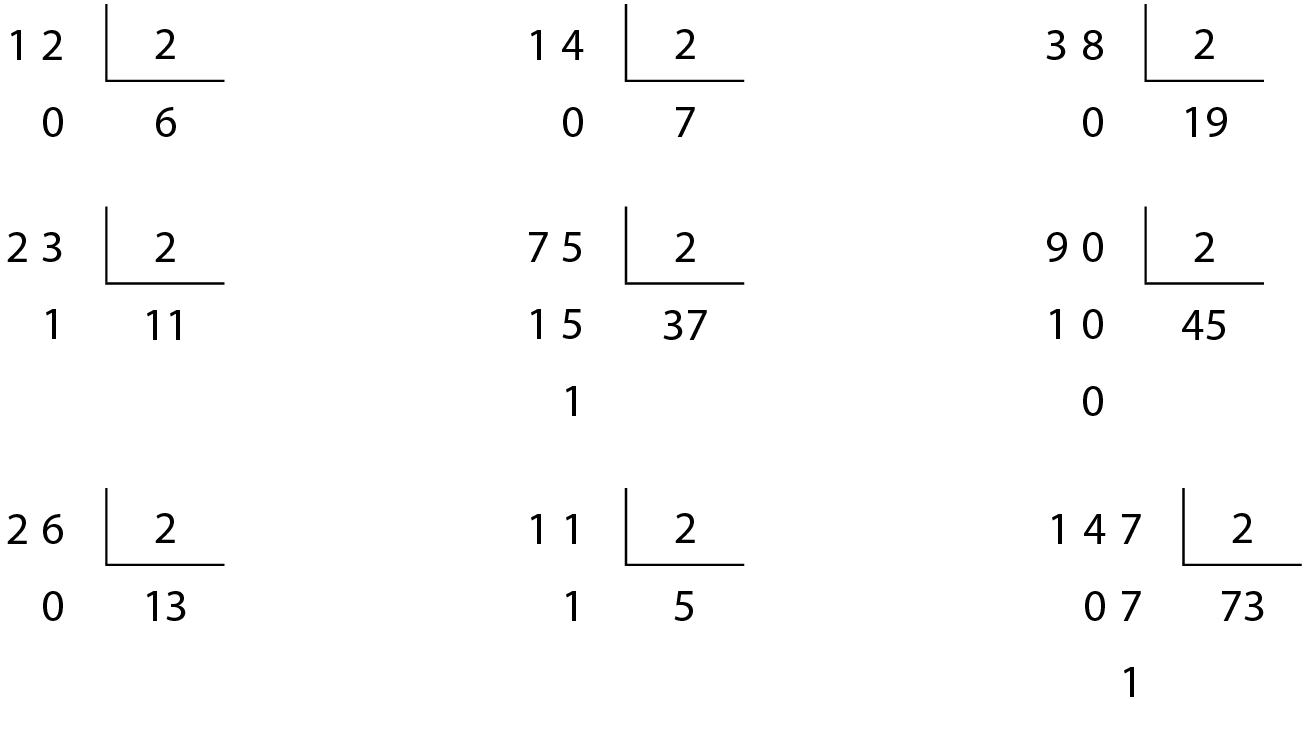
▸ Em seu caderno, divida outros números naturais por 2 e observe o resto dessas divisões.
Você deve ter percebido que, quando dividimos números pares por 2, obtemos resto zero e, quando dividimos números ímpares por 2, obtemos resto 1.
Um número natural é divisível por 2 quando é par, ou seja, quando termina em 0, 2, 4, 6 ou 8.
Podemos representar o critério de divisibilidade por 2 por meio de um fluxograma.
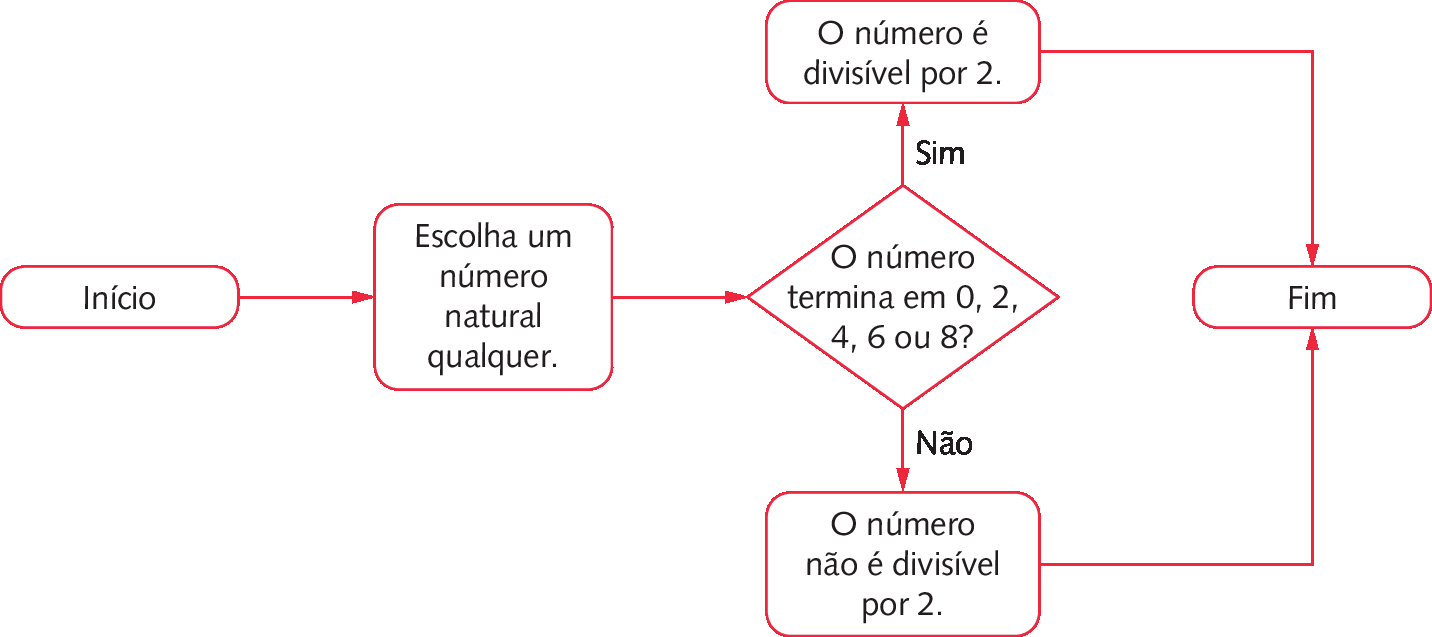
Respostas e comentários
Item: Resposta pessoal.
Critérios de divisibilidade
Bê êne cê cê:
Habilidade ê éfe zero seis ême ah zero quatro.
Objetivos:
• Compreender e aplicar os critérios de divisibilidade por: 2, 3, 4, 5, 6, 8, 9, 10, 100 e .1000.
• Ler, interpretar e elaborar fluxogramas.
Justificativa
Compreender os critérios de divisibilidade nos permite saber se um número é ou não é divisível por outro sem a necessidade de efetuar toda a divisão. Além disso, conhecer esses critérios auxiliará os estudantes a verificar, mais adiante, se um número é ou não primo.
Neste tópico, os fluxogramas serão utilizados para representar graficamente processos a serem automatizados e, por essa razão, é importante que os estudantes consigam ler, interpretar e elaborar esse tipo de representação.
Mapeando conhecimentos
Reproduza na lousa as divisões a seguir, em que o dividendo é desconhecido.
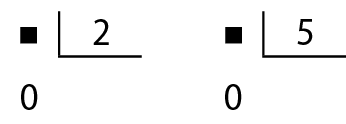
Depois, faça as seguintes questões:
• Quais números podemos colocar no lugar de

em cada caso?
• Qual é a característica comum dos números que podemos colocar no lugar de

em cada caso?
Deixe os estudantes à vontade para conversar e estabelecer conjecturas. Depois, pergunte se alguém conhece alguma regra para saber se um número é divisível por 3, 4, 6, 9, 10, 100, .1000 etcétera.
Para as aulas iniciais
Dedique as aulas iniciais para que os estudantes tenham a oportunidade de estabelecer, por meio de investigações, alguns critérios de divisibilidade que serão estudados no tópico. Oriente-os a efetuar divisões por escrito ou a fazer uso de calculadoras. Essas ações podem contribuir para que identifiquem padrões que justificam as regras práticas.
Explique que os critérios de divisibilidade nos auxiliam a determinar quais números são divisores de outro número. Essas regras permitem determinar a divisibilidade dos números sem a necessidade de efetuar longos processos de divisão, auxiliando tanto no cálculo mental como na decomposição de números naturais em fatores primos.
(ê éfe zero seis ême ah zero quatro) Construir algoritmo em linguagem natural e representá-lo por fluxograma que indique a resolução de um problema simples (por exemplo, se um número natural qualquer é par).
LEMBRE-SE: Escreva no caderno.
Critério de divisibilidade por 3
Observe estas divisões:
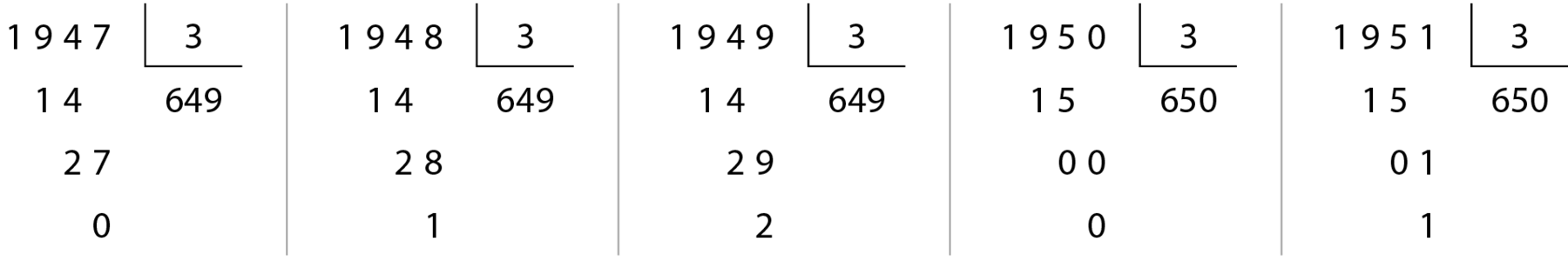
• O número .1947 é divisível por 3, pois 1 + 9 + 4 + 7 = 21 e 21 é divisível por 3.
• O número .1948 não é divisível por 3, pois 1 + 9 + 4 + 8 = 22 e 22 não é divisível por 3.
• O número .1949 não é divisível por 3, pois 1 + 9 + 4 + 9 = 23 e 23 não é divisível por 3.
• O número .1950 é divisível por 3, pois 1 + 9 + 5 + 0 = 15 e 15 é divisível por 3.
• O número .1951 não é divisível por 3, pois 1 + 9 + 5 + 1 = 16 e 16 não é divisível por 3.
▸ Sem efetuar a divisão, pense: qual é o resto da divisão de .1952 por 3? E de .1953 por 3?
▸

Calcule mentalmente 1 + 9 + 5 + 2 e 1 + 9 + 5 + 3.
▸ Agora, responda: .1952 é divisível por 3? E .1953, é divisível por 3?
Um número natural é divisível por 3 quando a soma dos seus algarismos é divisível por 3.
Podemos representar o critério de divisibilidade por 3 por meio de um fluxograma.
Critério de divisibilidade por 4
▸



Com uma calculadora, descubra alguns números naturais maiores ou iguais a 100 que sejam divisíveis por 4 e observe os dois últimos algarismos desses números. O que as investigações feitas por você sugerem? Converse com os colegas.
É possível verificar se um número maior ou igual a 100 é divisível por 4 analisando apenas os seus dois últimos algarismos.
Sabemos que 100 é divisível por 4, pois 100 = 4 × 25. Consequentemente, são também divisíveis por 4 todos os múltiplos de 100, como 200, 300, 700, .1100, .2300. Confira:
200 = 2 ⋅ 100 = 2 ⋅ 4 ⋅ 25
300 = 3 ⋅ 100 = 3 ⋅ 4 ⋅ 25
700 = 7 ⋅ 100 = 7 ⋅ 4 ⋅ 25
.1100 = 11 ⋅ 100 = 11 ⋅ 4 ⋅ 25
.2300 = 23 ⋅ 100 = 23 ⋅ 4 ⋅ 25
Note que 200, 300, 700, .1100 e .2300 terminam em 00.
Respostas e comentários
Primeiro item: 2; 0
Segundo item: 17; 18
Terceiro item: .1952 não é divisível por 3; .1953 é divisível por 3.
Quarto item: Espera-se que os estudantes respondam que as investigações sugerem que um número natural, maior ou igual a 100, é divisível por 4 quando termina em 00 ou quando o número formado pelos seus dois últimos algarismos é divisível por 4.
Mais importante que a simples memorização das regras práticas são a observação e a análise dos padrões que as justificam. A prática dessas atividades orais e escritas favorece o desenvolvimento dos diferentes tipos de raciocínio lógico-matemático (indução, dedução, abdução e raciocínio por analogia), de argumentação e de inferência.
Critérios de divisibilidade por 3
Antes de formalizar o critério de divisibilidade por 3, é importante que os estudantes tenham a oportunidade de realizar investigações. Escreva na lousa alguns números divisíveis por 3 a partir do 81. Depois, faça as seguintes questões para a turma:
• O que se pode afirmar sobre a soma dos algarismos dos números escritos na lousa?
• Os números 155 e 380 são divisíveis por 3? Calcule a soma dos algarismos de cada um desses números e verifique se essa soma é divisível por 3.
• Que padrão você observou? Esse padrão sugere qual critério para saber se um número natural é divisível por 3?
Deixe-os à vontade para conjecturar. Depois, apresente o critério e reproduza o fluxograma do livro na lousa para explorá-lo coletivamente.
Critérios de divisibilidade por 4
Antes de formalizar o critério de divisibilidade por 4, é importante realizar com os estudantes a investigação proposta com o uso da calculadora. Caso não haja quantidade suficiente de calculadoras para concretizar a atividade, você pode listar alguns números maiores que 100 e divisíveis por 4 na lousa e, depois, fazer as seguintes perguntas:
• O que se pode afirmar sobre o número formado pelos últimos dois algarismos de cada número?
• Os números que terminam em 00 são divisíveis por 4?
• Suas observações sugerem qual critério para saber se um número natural é divisível por 4?
Incentive-os a dialogar e expor o que pensam. Depois, apresente o critério adotado e reproduza o fluxograma do livro na lousa para explorá-lo coletivamente.
Agora, observe estas divisões:
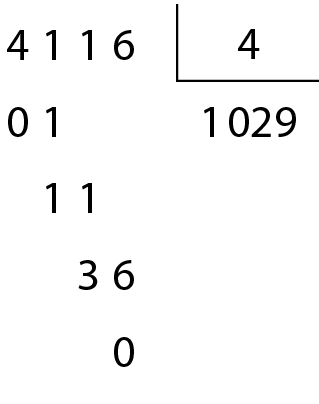
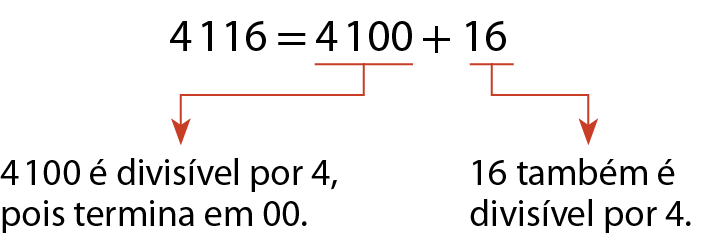
O número .4116 é divisível por 4.
Observe que:
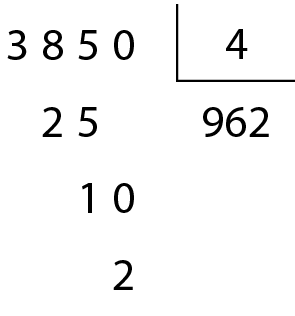
O número .3850 não é divisível por 4.
Observe que:
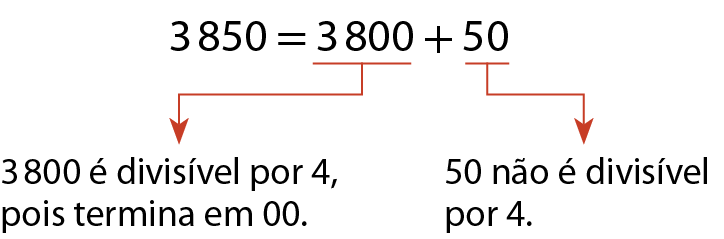
Um número natural, maior ou igual a 100, é divisível por 4 quando termina em 00 ou quando o número formado pelos seus dois últimos algarismos é divisível por 4.
Podemos representar o critério de divisibilidade por 4 por meio de um fluxograma.
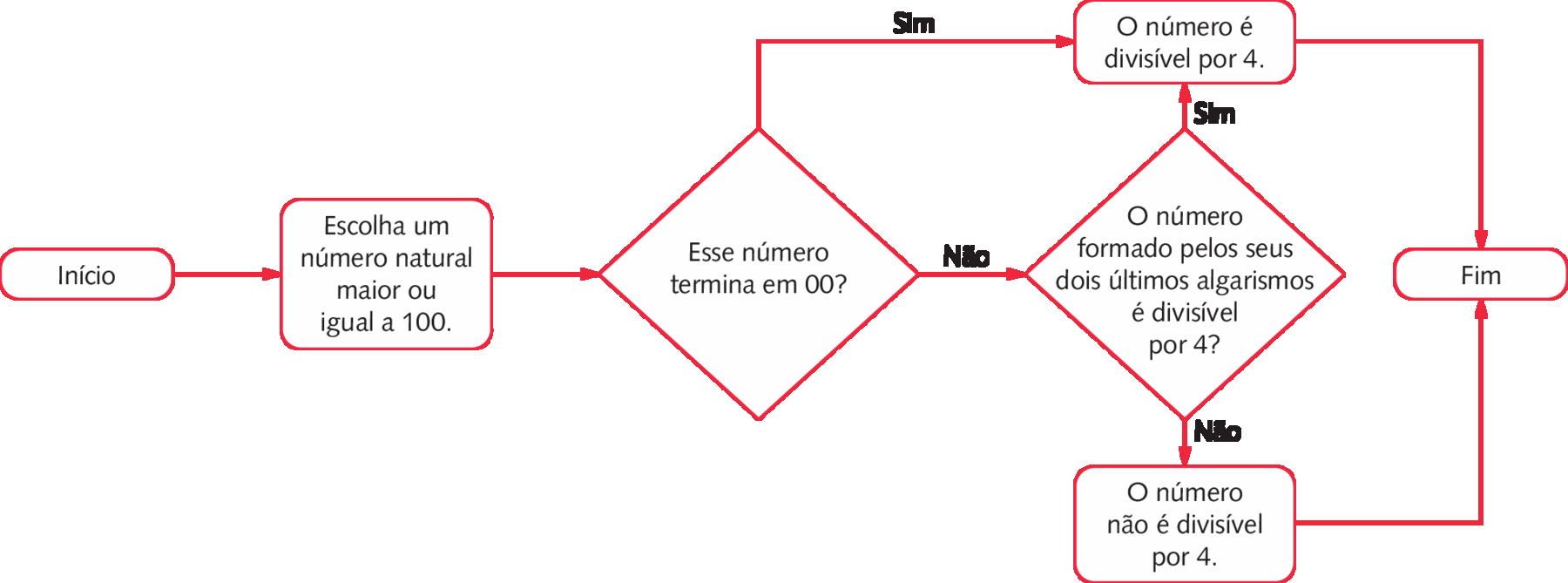
Critério de divisibilidade por 5
Observe estas divisões:
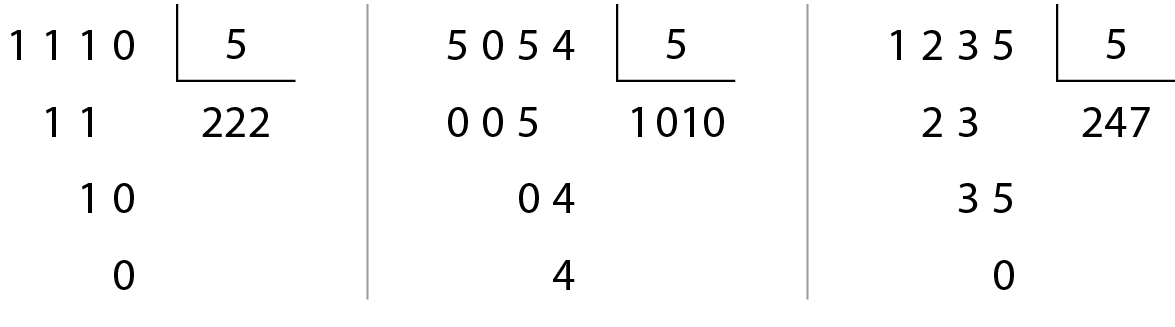

• O número .1110 é divisível por 5, pois termina em 0.
• O número .5054 não é divisível por 5, pois não termina em 0 nem em 5.
• O número .1235 é divisível por 5, pois termina em 5.
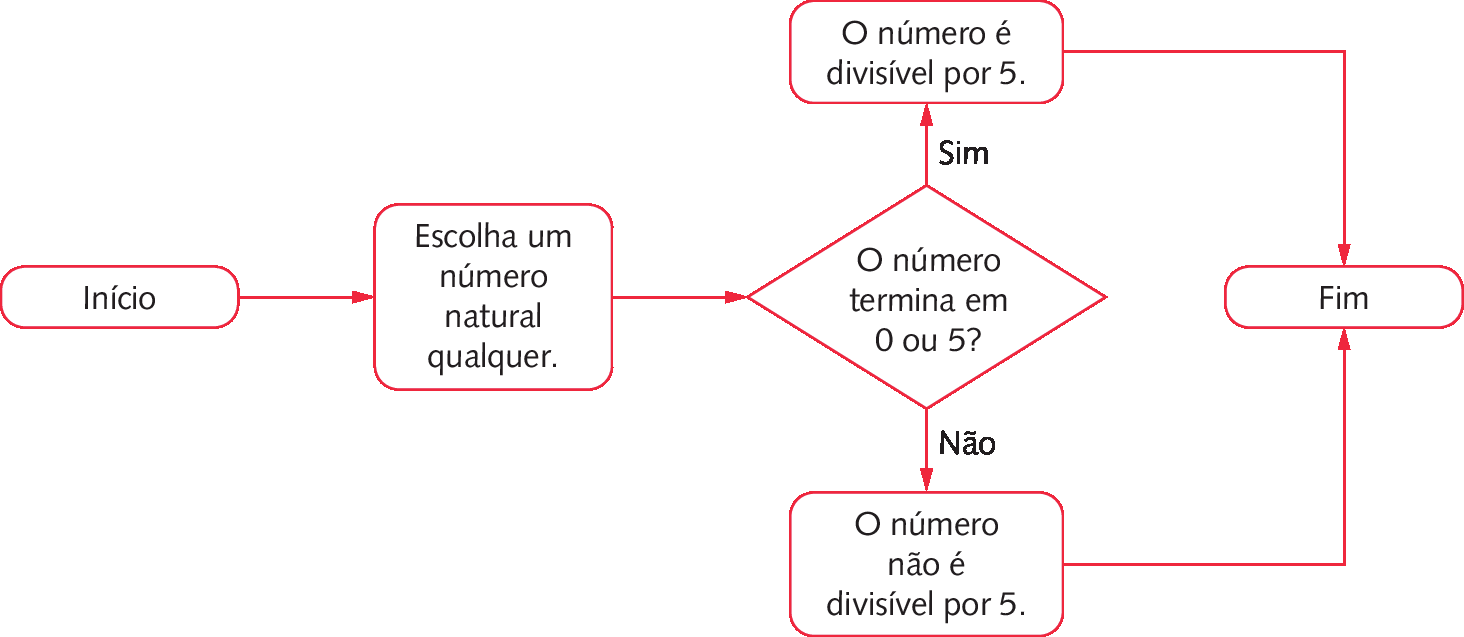
Um número natural é divisível por 5 quando termina em 0 ou em 5.
Respostas e comentários
Critérios de divisibilidade por 5
Antes de formalizar o critério de divisibilidade por 5, é importante que os estudantes tenham a oportunidade de observar com que algarismo termina alguns números divisíveis por 5. Você pode encaminhar essa investigação, fazendo as seguintes questões:
• Que padrão vocês observam no último algarismo desses números?
• Suas observações sugerem qual critério para saber se um número natural é divisível por 5?
É importante que todos tenham a oportunidade de levantar hipóteses e verbalizar o que pensam. Se achar oportuno, antes de apresentar o fluxograma, peça a eles que, dessa vez, elaborem o fluxograma que represente o critério de divisibilidade por 5.
Podemos representar o critério de divisibilidade por 5 por meio de um fluxograma.
Critério de divisibilidade por 6
▸

Com uma calculadora, descubra alguns números naturais que sejam divisíveis por 6. Esses números são divisíveis por 2? E por 3?
▸


O que as investigações feitas por você sugerem? Converse com os colegas.
Observe estas divisões:

• O número 312 é divisível por 6.
O número 312 é divisível por 2, pois é par, e por 3, pois 3 + 1 + 2 = 6 e 6 é divisível por 3.
• O número 609 não é divisível por 6.
O número 609 é divisível por 3, pois 6 + 0 + 9 = 15 e 15 é divisível por 3, mas 609 não é divisível por 2, porque é ímpar.
• O número 716 não é divisível por 6.
O número 716 é divisível por 2, pois é par, mas 716 não é divisível por 3, pois 7 + 1 + 6 = 14 e 14 não é divisível por 3.
• O número .6612 é divisível por 6.
O número .6612 é divisível por 2, pois é par, e por 3, pois 6 + 6 + 1 + 2 = 15 e 15 é divisível por 3.
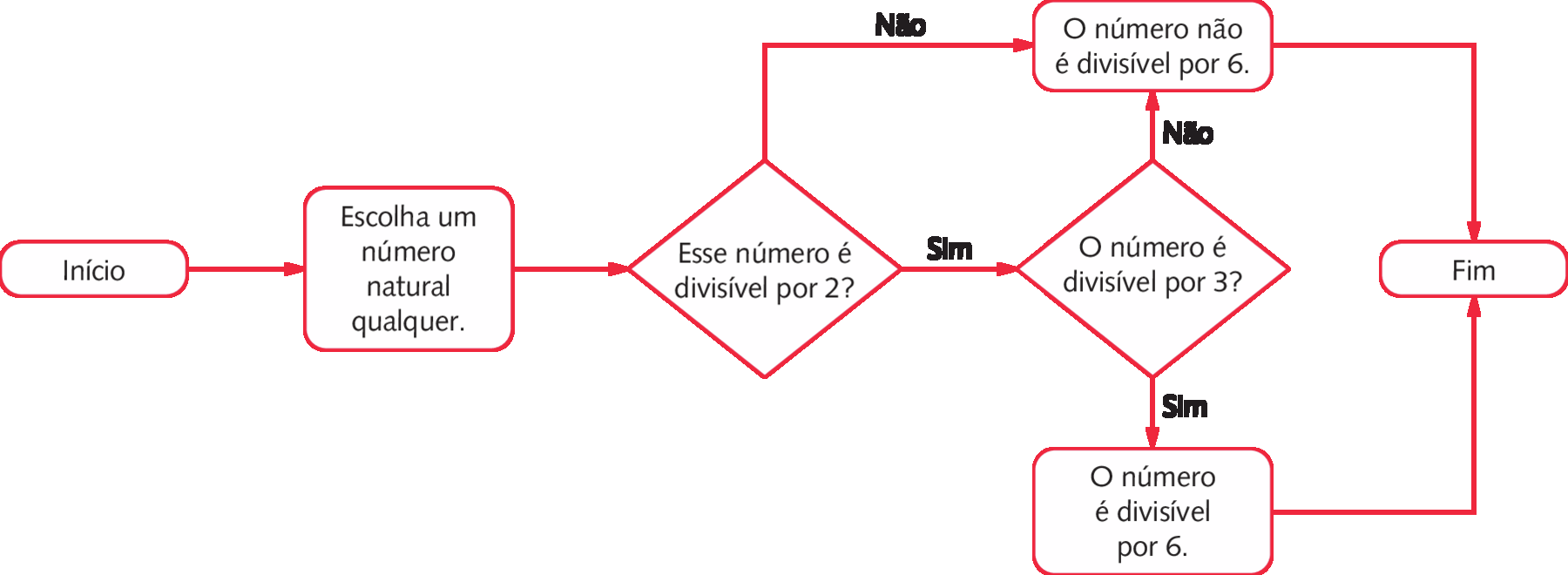
Um número natural é divisível por 6 quando é divisível por 2 e também por 3.
Respostas e comentários
Primeiro item: sim; sim.
Segundo item: Espera-se que os estudantes respondam que as investigações sugerem que um número natural é divisível por 6 quando é divisível por 2 e também por 3.
Critérios de divisibilidade por 6
Explore o critério de divisibilidade por 6 com os estudantes, pedindo que façam as atividades investigativas propostas no início do estudo. Após encontrarem o critério, peça a eles que encontrem os números que são divisíveis por 6 em um quadro com a sequência dos números de 1 ao 100.
O fluxograma que representa o critério de divisibilidade por 6 apresenta duas figuras indicativas de que uma decisão precisa ser tomada e, por esse motivo, é preciso discuti-lo coletivamente.
Podemos representar o critério de divisibilidade por 6 por meio de um fluxograma.
Critério de divisibilidade por 8
▸



Com uma calculadora, descubra alguns números naturais maiores ou iguais a .1000 que sejam divisíveis por 8 e observe os três últimos algarismos desses números. O que as investigações feitas por você sugerem? Converse com os colegas.
É possível verificar se um número maior ou igual a .1000 é divisível por 8 analisando apenas os seus três últimos algarismos.
Sabemos que .1000 é divisível por 8, pois .1000 = 8 ⋅ 125. Consequentemente, são também divisíveis por 8 todos os múltiplos de .1000, como .2000, .3000, .7000, .12000, .15000.
Note que .2000, .3000, .7000, .12000 e .15000 terminam em 000.
Agora, observe estas divisões:

• O número .5000 é divisível por 8, pois termina em 000.
• O número .3300 não é divisível por 8, pois o número formado por seus três últimos algarismos não é divisível por 8.
• O número .13336 é divisível por 8, pois o número formado por seus três últimos algarismos é divisível por 8.
• O número .10180 não é divisível por 8, pois o número formado por seus três últimos algarismos não é divisível por 8.
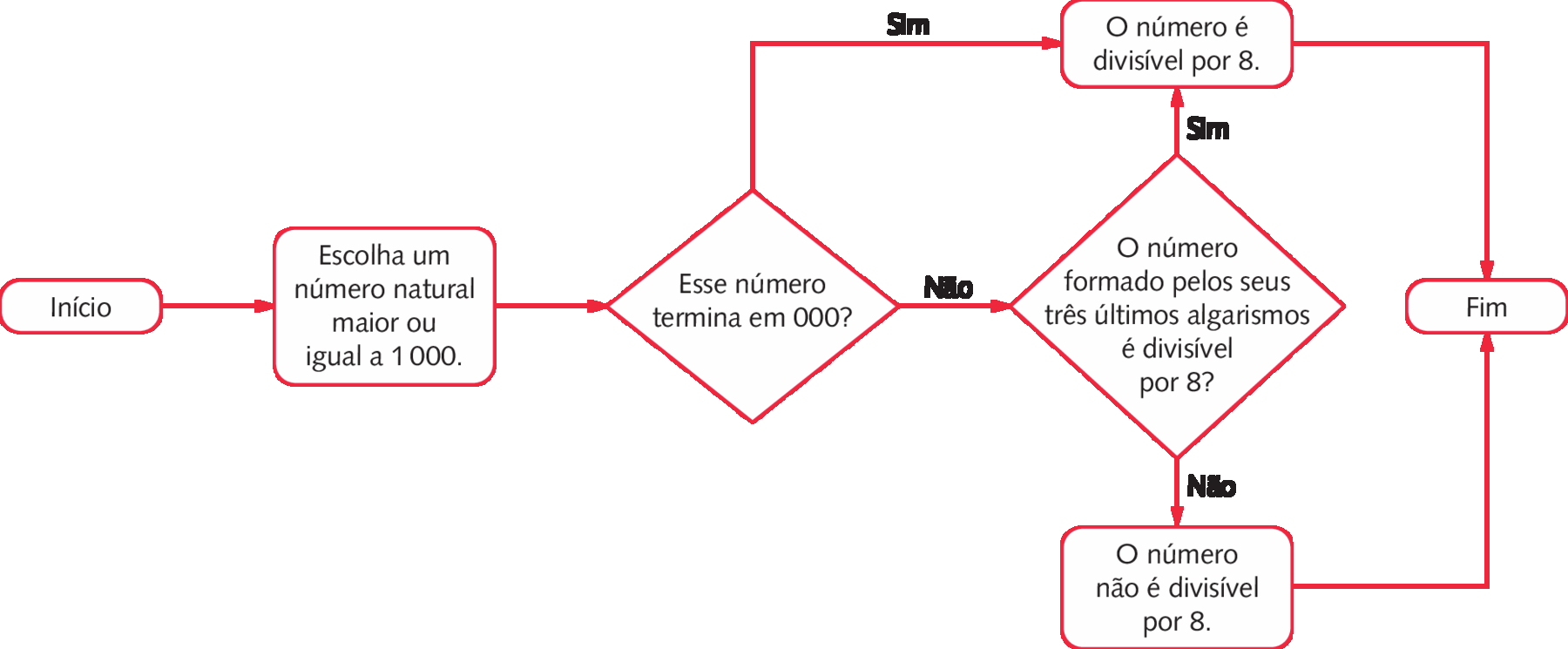
Um número natural, maior ou igual a .1000, é divisível por 8 quando termina em 000 ou quando o número formado pelos seus três últimos algarismos é divisível por 8.
Respostas e comentários
Item: Espera-se que os estudantes respondam que as investigações sugerem que um número natural, maior ou igual a .1000, é divisível por 8 quando termina em 000 ou quando o número formado pelos seus três últimos algarismos é divisível por 8.
Critérios de divisibilidade por 8
Antes de formalizar o critério de divisibilidade por 8, é importante realizar com os estudantes a investigação proposta com o uso da calculadora. Caso não haja quantidade suficiente de calculadoras para concretizar a atividade, você pode listar alguns números maiores que .1000 e divisíveis por 8 na lousa e, depois, fazer as seguintes perguntas:
• O que se pode afirmar sobre o número formado pelos últimos três algarismos de cada número?
• Os números que terminam em 000 são divisíveis por 8?
• Suas observações sugerem qual critério para saber se um número natural é divisível por 8?
Incentive-os a dialogar e expor o que pensam. Depois, apresente o critério e reproduza o fluxograma do livro na lousa para explorá-lo coletivamente.
Comente com os estudantes que esse critério não é tão prático quanto outros critérios de divisibilidade já vistos. Chame a atenção para o fato de que para determinar se um número é ou não divisível por 8 é preciso efetuar a divisão dos três últimos algarismos por 8.
Comente com os estudantes que, se o número .1683 fosse apresentado como exemplo na divisibilidade por 8, poderia ser descartado sem a análise dos três últimos algarismos, por ser ímpar.
Podemos representar o critério de divisibilidade por 8 por meio de um fluxograma.
Critério de divisibilidade por 9
▸



Com uma calculadora, descubra alguns números naturais divisíveis por 9 e adicione seus algarismos. O que as investigações feitas por você sugerem? Converse com os colegas.
Observe estas divisões:
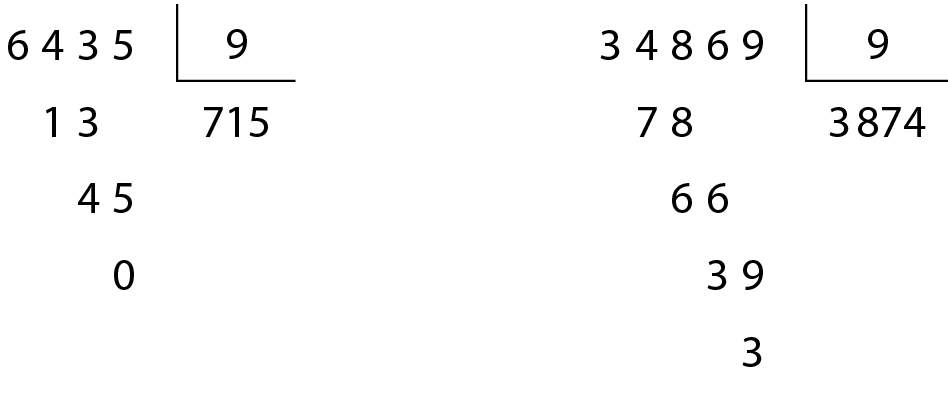
• O número .6435 é divisível por 9, pois 6 + 4 + 3 + 5 = 18 e 18 é divisível por 9.
• O número .34869 não é divisível por 9, pois 3 + 4 + 8 + 6 + 9 = 30 e 30 não é divisível por 9.
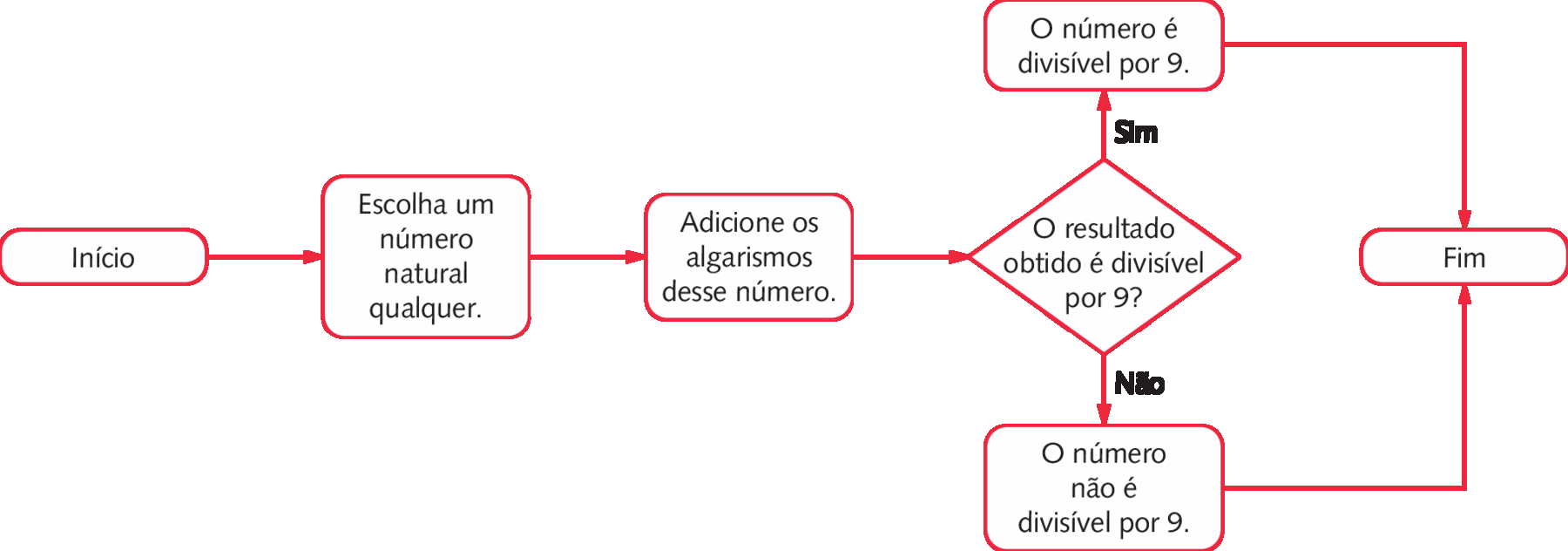
Um número natural é divisível por 9 quando a soma dos seus algarismos é divisível por 9.
Podemos representar o critério de divisibilidade por 9 por meio de um fluxograma.
Respostas e comentários
Item: Espera-se que os estudantes respondam que as investigações sugerem que um número natural é divisível por 9 quando a soma dos seus algarismos é divisível por 9.
Critérios de divisibilidade por 9
Antes de formalizar o critério de divisibilidade por 9, é importante realizar com os estudantes a investigação proposta com o uso da calculadora. Caso não haja quantidade suficiente de calculadoras para realizar a atividade, você pode listar alguns números divisíveis por 9 na lousa e, depois, fazer as seguintes questões:
• O que se pode afirmar sobre a soma dos algarismos dos números escritos na lousa?
• Suas observações sugerem qual critério para saber se um número natural é divisível por 9?
Deixe-os à vontade para estabelecer conjecturas. Peça que elaborem o fluxograma desse critério antes de apresentá-lo.
Sugestão de atividade extra
A retomada dos critérios de divisibilidade é importante para desenvolver a capacidade de avaliação sobre a divisibilidade de um número por outro. Para que isso se concretize, essa sugestão de atividade pode auxiliar o estudante nessa tarefa por meio da decomposição de um número em parcelas apropriadas, de modo que ele possa decidir mais facilmente sobre a sua divisibilidade.
Faça a seguinte pergunta: “Que outra estratégia podemos utilizar para saber se o número 258 é divisível por 6 sem efetuar a divisão e sem utilizar o critério de divisibilidade por 6?”. Para decidir se 258 é divisível por 6, pode-se decompô-lo como a soma de parcelas. A primeira parcela deve ser o número mais próximo de 258 que o estudante consiga determinar, múltiplo de 6, por exemplo, 240 (que é 6 ⋅ 40). A parcela restante deve ser analisada (nesse caso, as parcelas serão 240 e 18, já que 240 + 18 = 258).
Se for múltipla de 6, então 258 também será. Caso contrário, 258 não pode ser considerado múltiplo de 6.
Questione também se 258 é divisível por 8. É esperado que o estudante também decomponha 258 em 240 + 18 e que percebam que, embora 240 seja um múltiplo de 8, pois 8 ⋅ 30 = 240, 18 não é. Assim, conclui-se que 258 não é divisível por 8.
Os cálculos, a princípio, podem ser feitos no caderno, mas pode ser interessante, após sua apresentação, lançar um desafio de modo que os estudantes realizem os cálculos mentalmente.
Critérios de divisibilidade por 10, 100 e .1000
Observe o quadro a seguir.
|
Números divisíveis por 10 |
10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, ... |
|---|---|
|
Números divisíveis por 100 |
100, 200, 300, 400, 500, 600, 700, 800, 900, 1.000, 1.100, ... |
|
Números divisíveis por 1.000 |
1.000, 2.000, 3.000, 4.000, 5.000, 6.000, 7.000, 8.000, 9.000, 10.000, 11.000, ... |
▸

Que padrão você observa nos números divisíveis por 10 mostrados anteriormente? E nos números divisíveis por 100? E nos divisíveis por .1000?
▸ O padrão que você observou anteriormente sugere os critérios de divisibilidade por 10, 100 e .1000. Escreva esses critérios em seu caderno.
Atividades
Faça as atividades no caderno.
21. Copie no caderno o quadro a seguir e marque com X os divisores de cada número.

|
Divisores |
|||||
|---|---|---|---|---|---|
|
Números |
2 |
3 |
4 |
5 |
6 |
|
216 |
|||||
|
678 |
|||||
|
745 |
|||||
|
1.224 |
|||||
|
3.206 |
|||||
22. Escreva no caderno o menor número de três algarismos divisível por:
a) 2;
b) 3;
c) 4;
d) 5;
e) 6
23. Identifique os números que são divisíveis, ao mesmo tempo, por 2 e por 5.
a) 805
b) 160
c) 420
d) 222
e) .5000
f) 803
24. Em seu caderno, copie as afirmações verdadeiras.
a) Todo número divisível por 6 é também divisível por 2.
b) Todo número par é divisível por 5.
c) Nenhum número ímpar é divisível por 2.
d) Todo número divisível por 4 é também divisível por 2.
25.

Em seu caderno, represente por meio de um fluxograma os critérios de divisibilidade por 10, 100 e .1000.
26. Existe algum algarismo que póde ser colocado no lugar de

de modo que o número

seja divisível por 2? Explique seu pensamento.
27. Dado o número de três algarismos:

, pergunta‑se:
a) Esse número é divisível por 5?
b) Por quais algarismos devemos substituir

para obter um número divisível por 3?
28. Determine:
a) o maior número de três algarismos divisível por 5;
b) o menor número de três algarismos divisível, ao mesmo tempo, por 2, por 3 e por 5;
c) o maior número de três algarismos divisível, ao mesmo tempo, por 3 e por 4.
Respostas e comentários
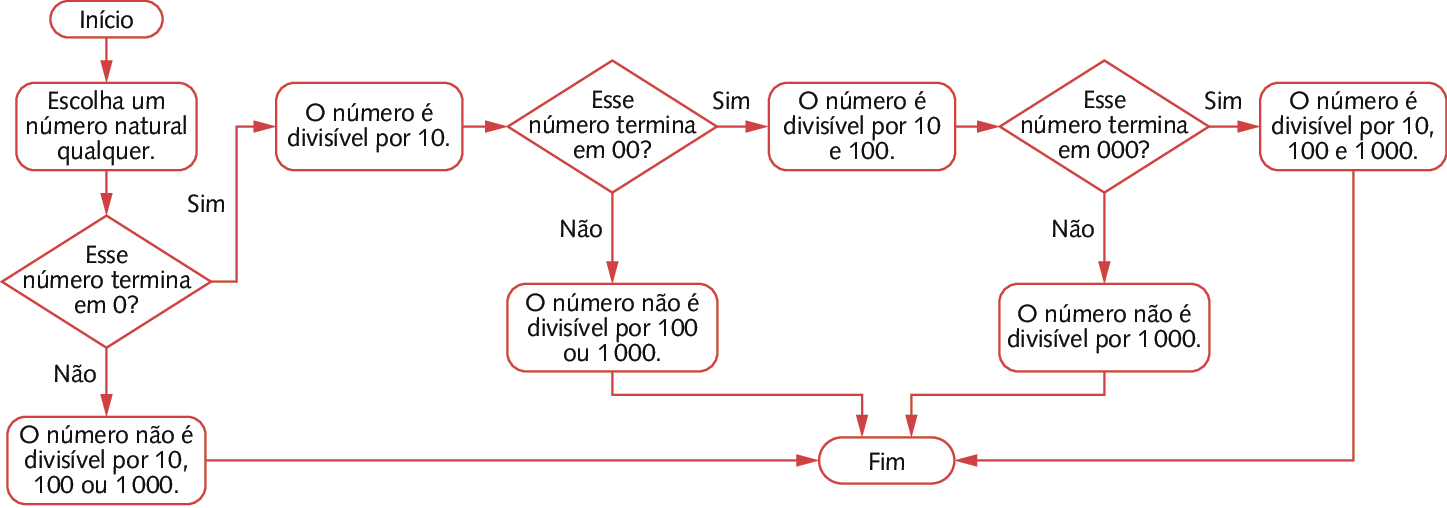
Primeiro item: Espera-se que os estudantes percebam que os números divisíveis por 10 terminam em 0, os números divisíveis por 100 terminam em 00 e os números divisíveis por .1000 terminam em 000.
Segundo item: Um número natural é divisível por 10 se terminar em 0, é divisível por 100 se terminar em 00 e é divisível por .1000 se terminar em 000.
21. Resposta em Orientações.
22. a) 100
22. b) 102
22. c) 100
22. d) 100
22. e) 102
23. números dos itens b, c, ê
24. são verdadeiras: a, c, d
25. Exemplos de resposta em Orientações.
26. Não, porque o número termina em 3 e, para ser divisível por 2, ele deve ser par, ou seja, terminar em 0, 2, 4, 6 ou 8.
27. a) não
27. b) 1, 4 ou 7
28. a) 995
28. b) 120
28. c) 996
Critérios de divisibilidade por 10, 100 e .1000
A proposta é que os estudantes estabeleçam, por meio de investigações, os critérios de divisibilidade por 10, 100 e .1000. Reúna-os em duplas ou trios, se julgar conveniente, para que possam trocar ideias. Oriente-os a listar mais números divisíveis por 10, 100 e .1000 se acharem necessário.
Antecipe a realização da atividade 25, se achar conveniente.
• Resposta da atividade 21:
|
Divisores |
|||||
|---|---|---|---|---|---|
|
Números |
2 |
3 |
4 |
5 |
6 |
|
216 |
X |
X |
X |
X |
|
|
678 |
X |
X |
X |
||
|
745 |
X |
||||
|
1.224 |
X |
X |
X |
X |
|
|
3.206 |
X |
||||
• Exemplo de resposta da atividade 25:
29. Registre no caderno qual dos anos apresentados a seguir é bissextoglossário .

30. Um número de quatro algarismos é representado por

.
Determine os algarismos que ao serem colocados no lugar de

tornam o número divisível por:
a) 2;
b) 3;
c) 4;
d) 5;
e) 6
31. Escreva no caderno o menor número que devemos adicionar a 763 para obtermos um número divisível por:
a) 3;
b) 5;
c) 2 e 3 ao mesmo tempo.
32. Determine o maior número de quatro algarismos diferentes que seja:
a) divisível por 2 e por 3;
b) divisível por 2, mas não por 3;
c) divisível por 3, mas não por 2;
d) não divisível por 2 nem por 3.
33. Qual é o maior número de seis algarismos divisível por 10?
34. Qual é o menor número divisível por 9 formado apenas pelo algarismo 4?
35. Considere os números 450, 660, 768, 860 e 960.
a) Quais deles são divisíveis por 3 e por 4 ao mesmo tempo? Podemos dizer que os números divisíveis por 3 e por 4 também são divisíveis por 12?
b) Quais deles são divisíveis por 3 e por 5 ao mesmo tempo? Podemos dizer que os números divisíveis por 3 e por 5 também são divisíveis por 15?
36.

Com um colega, explique por que todos os números de três algarismos iguais são divisíveis por 3.
37. Como todo número par é divisível por 2, podemos verificar se um número natural qualquer é par observando o resto de sua divisão por 2.
a) Copie as frases a seguir no caderno e, depois, complete as lacunas.
Etapa 1: Escolha um número natural e o divida por 2.
Etapa 2: O

da divisão por 2 é igual a zero?
Etapa 3: Se sim, então o número é

.
Etapa 4: Se não, o número é

.
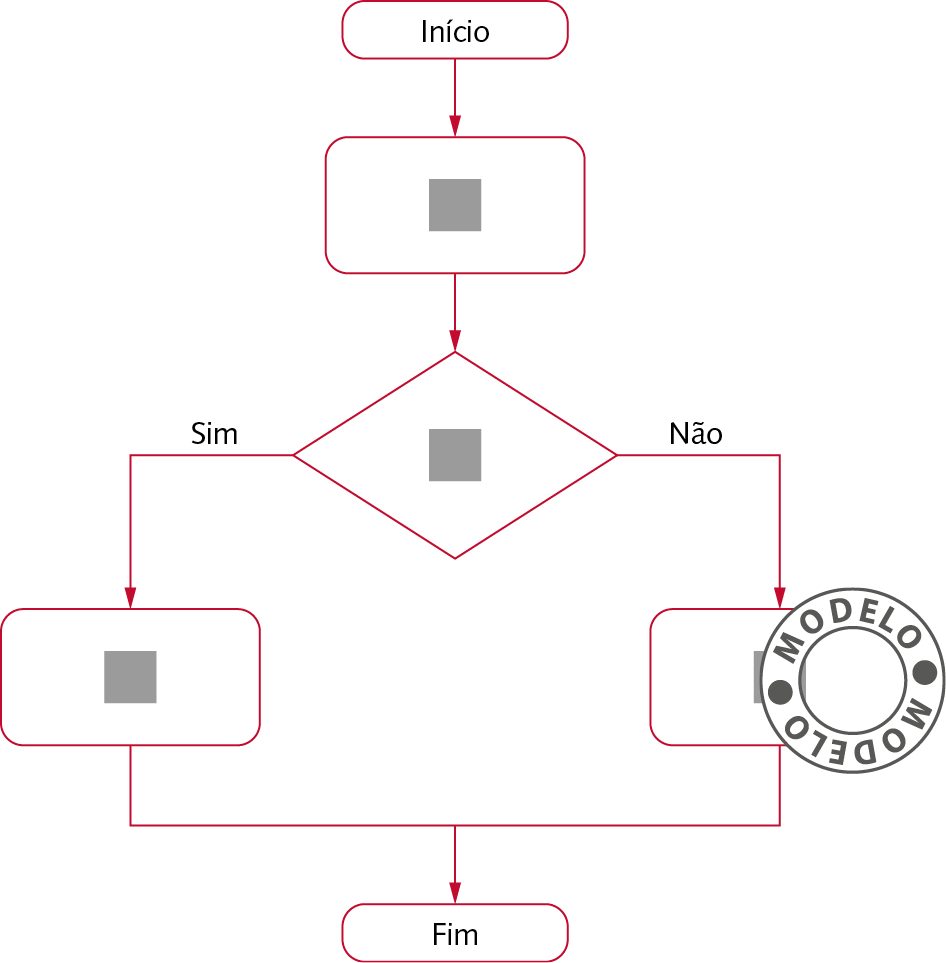
b)


Agora, em dupla, copiem o fluxograma a seguir no caderno e completem-no com as etapas do item a.
Respostas e comentários
29. .1764
30. a) 0, 2, 4, 6 e 8
30. b) 0, 3, 6 e 9
30. c) 2 e 6
30. d) 0 e 5
30. e) 0 e 6
31. a) 2
31. b) 2
31. c) 5
32. a) .9876
32. b) .9874
32. c) .9873
32. d) .9875
33. .999990
34. ..444444444
35. a) 660, 768 e 960; sim
35. b) 450, 660 e 960; sim
36. Adicionar três algarismos iguais é o mesmo que multiplicar esse algarismo por 3; logo, encontramos um múltiplo de 3.
37. a) “resto”, “par” e “ímpar”, respectivamente.
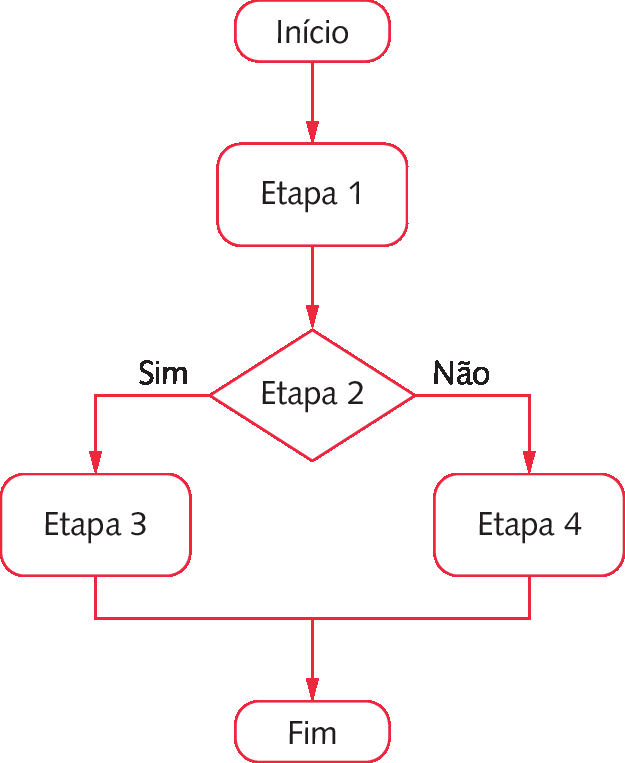
37. b) Resposta em Orientações.
• Na atividade 29, como os anos bissextos ocorrem a cada 4 anos, os estudantes podem ser induzidos a utilizar as regras de divisibilidade por 4. No entanto, comente com eles que ser divisível por 4 é apenas um dos critérios para que um ano seja bissexto.
• A atividade 37 busca desenvolver e consolidar a habilidade ê éfe zero seis ême ah zero quatro quando utiliza um esquema para explicitar situações que envolvem a divisibilidade. Como desafio, solicite aos estudantes que criem seu próprio esquema.
Etapa 1: Escolha um número natural e divida por 2.
Etapa 2: O resto da divisão por 2 é igual a zero?
Etapa 3: Se sim, então o número é par.
Etapa 4: Se não, o número é ímpar.

4 Números primos e números compostos
Vamos considerar o conjunto dos números naturais

= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, reticências}.
Podemos verificar que:
• 0 é divisível por qualquer número diferente de zero;
• 1 é divisível apenas por 1;
• 2 é divisível por 1 e 2;
• 3 é divisível por 1 e 3;
• 4 é divisível por 1, 2 e 4;
• 5 é divisível por 1 e 5;
• 6 é divisível por 1, 2, 3 e 6;
• 7 é divisível por 1 e 7;
• 8 é divisível por 1, 2, 4 e 8;
• 9 é divisível por 1, 3 e 9.
Podemos observar que:
• 1 é divisor de qualquer número, ou seja, qualquer número é divisível por 1;
• alguns números, como 2, 3, 5 e 7, têm exatamente dois divisores naturais: o número 1 e o próprio número; eles são chamados de números primos.
Um número é primo quando tem somente dois divisores naturais distintos: o número 1 e o próprio número.
Existem números, como 4, 6, 8 e 9, que têm mais de dois divisores naturais distintos; eles são chamados de números compostos.
Um número, diferente de zero, é composto quando tem mais de dois divisores distintos.
Os números compostos podem ser escritos como um produto de números primos. Confira os exemplos.
a) 8 = 2 ⋅ 2 ⋅ 2
b) 9 = 3 ⋅ 3
c) 12 = 2 ⋅ 2 ⋅ 3
d) 105 = 3 ⋅ 5 ⋅ 7
Observações
1. O número 1 não é primo nem composto, pois tem apenas um divisor natural (o próprio 1) e não póde ser escrito como produto de números primos.
2. O número 0 não é primo nem composto, pois tem infinitos divisores e não póde ser escrito como produto de números primos.
3. O único número natural primo que é par é o 2.
4. A palavra “primo” significa “primeiro”. Os números primos são “os primeiros”, pois outros números podem ser escritos a partir deles por meio de multiplicações. Analise alguns exemplos:
a) 16 = 2 ⋅ 2 ⋅ 2 ⋅ 2
b) 45 = 3 ⋅ 3 ⋅ 5
c) 84 = 2 ⋅ 2 ⋅ 3 ⋅ 7
Respostas e comentários
Números primos e números compostos
Bê êne cê cê:
• Competências gerais 1 e 6 (as descrições estão na página seis).
• Competência específica 1 (a descrição está na página sete).
• Habilidades ê éfe zero seis ême ah zero dois, ê éfe zero seis ême ah zero cinco e ê éfe zero seis ême ah zero seis.
Objetivos:
• Classificar números naturais em primos e compostos.
• Decompor um número natural em fatores primos.
Justificativa
Classificar números naturais em primos e compostos é uma parte importante da habilidade ê éfe zero seis ême ah zero cinco. O trabalho com a decomposição de números naturais em fatores primos está relacionado à parte dos objetivos propostos pela habilidade ê éfe zero seis ême ah zero dois, em que se propõe a decomposição e a composição de números naturais e também pode ajudar os estudantes a resolver e elaborar problemas que envolvam as ideias de múltiplo e divisor, o que favorece o desenvolvimento da habilidade ê éfe zero seis ême ah zero seis.
Mapeando conhecimentos
Pergunte aos estudantes se já perceberam que alguns números naturais têm apenas 2 divisores (o número 1 e o próprio número). Em seguida, peça que citem alguns exemplos. Aproveite a oportunidade para verificar se alguns deles sabem que esses números são chamados de números primos.
Para as aulas iniciais
Antecipe o trabalho com o crivo de Eratóstenes.
(ê éfe zero seis ême ah zero dois) Reconhecer o sistema de numeração decimal, como o que prevaleceu no mundo ocidental, e destacar semelhanças e diferenças com outros sistemas, de modo a sistematizar suas principais características (base, valor posicional e função do zero), utilizando, inclusive, a composição e decomposição de números naturais e números racionais em sua representação decimal.
(ê éfe zero seis ême ah zero cinco) Classificar números naturais em primos e compostos, estabelecer relações entre números, expressas pelos termos “é múltiplo de”, “é divisor de”, “é fator de”, e estabelecer, por meio de investigações, critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100 e .1000.
(ê éfe zero seis ême ah zero seis) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor.
Verificando se um número é primo
Para verificar se um número é primo ou composto, devemos primeiro dividir o número dado pelos números primos menores do que ele, até obtermos um quociente menor ou igual ao divisor. Depois, devemos analisar:
• se nenhuma das divisões efetuadas for exata, o número será primo;
• se qualquer uma das divisões for exata, o número será composto.
Podemos representar esse procedimento por meio de um fluxograma.
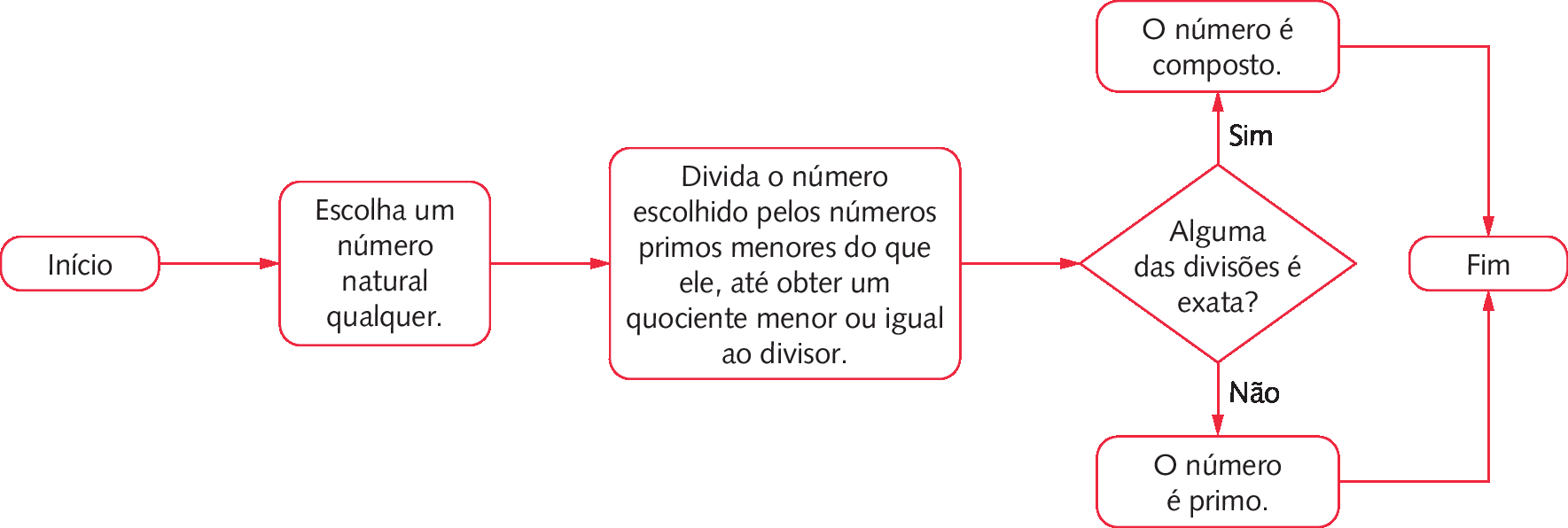
Convém utilizar o procedimento anterior quando os números são pequenos. Acompanhe os exemplos.
a) Vamos verificar se o número 71 é primo.
Observe as divisões de 71 por alguns números primos menores do que ele.
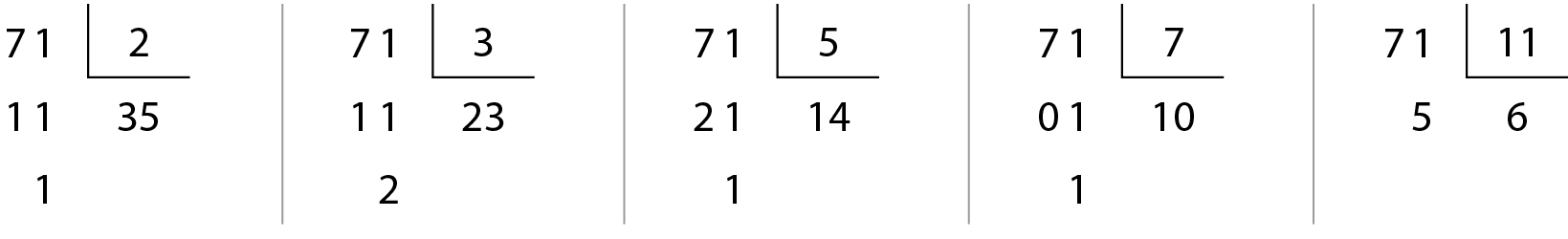
Percebemos que, na divisão por 11, o quociente 6 é menor que o divisor e a divisão não é exata. Podemos, então, afirmar que o número 71 é primo.
b) Vamos verificar se o número 667 é primo.
Pelos critérios de divisibilidade, 667 não é divisível por 2, nem por 3, nem por 5. Vamos dividir o número 667 pelos próximos números primos menores do que ele. Verifique:

Como a divisão por 23 é exata, podemos parar de dividir 667 por números primos e afirmar que o número 667 não é primo.
Respostas e comentários
Verificando se um número é primo
Para verificar se um número é primo ou composto, os estudantes devem aplicar os critérios de divisibilidade estudados.
Solicite aos estudantes que leiam o texto e acompanhem as verificações apresentadas. Depois que compreenderam o processo, peça a eles que elaborem seus próprios exemplos.
Sugestão de vídeo
O recurso Procurando Xenakis do portal ême³ Matemática Multimídia, da unicâmpi-São Paulo, traz uma introdução ao crivo de Eratóstenes e apresenta uma demonstração do teorema da infinitude dos números primos, enriquecendo o seu repertório para o conteúdo exposto.
Disponível em: https://oeds.link/3fi0xg. Acesso em: 30 junho 2022.
Foi Eratóstenes, um matemático grego nascido em 276 antes de Cristo, quem desenvolveu um método para encontrar os primeiros números primos a partir da sequência dos números naturais. Essa operação recebeu o nome de Crivo de Eratóstenes. O método consiste na disposição ordenada dos números naturais em linhas e em colunas. Com base nisso, ele eliminou os números compostos e, utilizando uma estratégia, identificou os números primos. Analise a seguir.
Vamos obter os números primos compreendidos entre 1 e 50 pelo Crivo de Eratóstenes:
1º) Eliminamos o número 1, pois já sabemos que ele não é primo.
2º) Circulamos o 2 e riscamos seus múltiplos, que são números compostos.
3º) Circulamos o 3 e riscamos seus múltiplos.
4º) Continuamos esse processo com os números que ainda não foram riscados até que não haja mais números a serem riscados ou circulados.
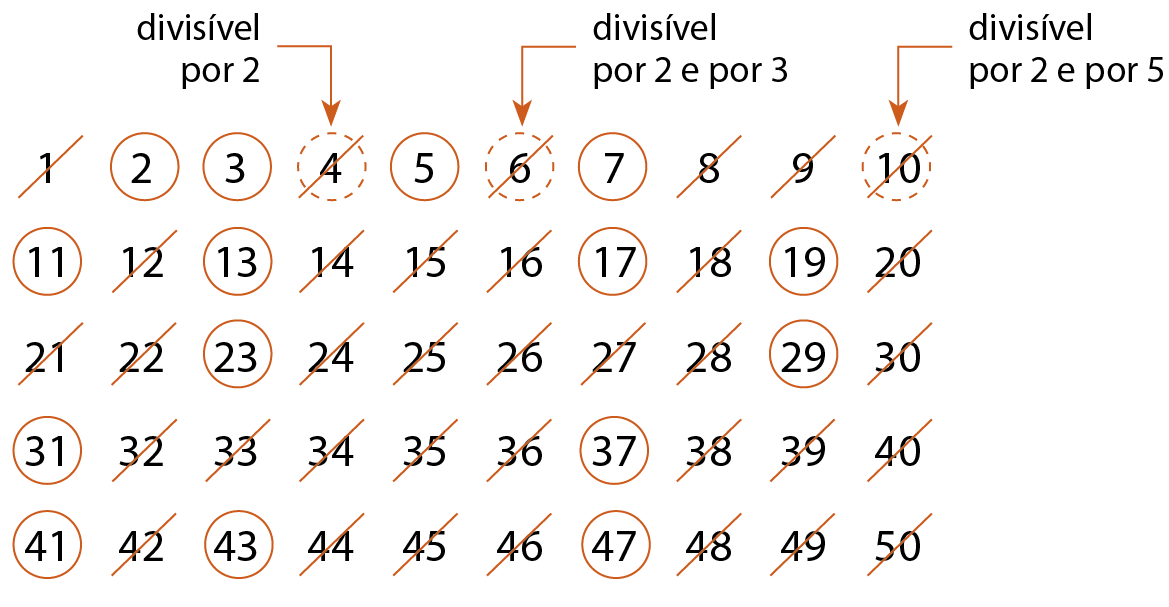
Os números 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e 47 são números primos.

Um pouco de história
Faça as atividades no caderno.
Números primos e compostos
[reticências] Os gregos antigos excluíam o 1 (unidade, a mônada) do conjunto dos primos porque não o consideravam sequer número; consideravam-no o princípio dos números, a origem ou o gerador dos números. Euclides e Aristósteles aceitavam o 2 como primo, mas isso não ocorria com os pitagóricos mais antigos. Para eles, o 2, a díade, não era de modo algum um número, mas apenas o princípio dos “pares”.


Hoje em dia, a habitual exclusão do 1 do conjunto dos números primos permite maior simplicidade no enunciado de teoremas e de fórmulas concernentes a números primos.
Euclides deu uma das primeiras contribuições significativas à teoria dos números primos ao provar que o conjunto destes números é infinito. [reticências]
FEY, James. Números primos e compostos: tópicos de história da Matemática. In: GUNDLACH, Bernard H. Números e numerais. São Paulo: Atual, 1992. página 49.
Atividade

Em seu caderno, escreva três números primos maiores do que 100. Depois, compartilhe os números que escreveu com os colegas.
Respostas e comentários
Um pouco de história: Resposta pessoal.
O boxe Um pouco de história favorece o desenvolvimento das competências gerais 1 e 6 da Bê êne cê cê e da competência específica 1 de Matemática.
Atividades
Faça as atividades no caderno.
38. Quais dos números a seguir são primos?
a) 81
b) 227
c) 463
d) 101
e) 559
f) 977
g) 808
h) 585
i) 161
39. Escreva, no caderno, todos os números primos menores que 30.
40. Escreva cada número a seguir como um produto de números primos.
a) 14
b) 35
c) 70
d) 42
e) 50
f) 100
41. O número 323 é primo? Justifique sua resposta.
42. A senha do cartão de crédito de Adriano é o produto do maior número primo de dois algarismos pelo menor número primo de três algarismos. Qual é a senha do cartão de crédito de Adriano?

43. Quais são os números primos maiores que 100 e menores que 200 nos quais o algarismo das dezenas é par e maior que o algarismo das unidades?
Decomposição em fatores primos
Todo número natural composto póde ser representado por meio de uma multiplicação de dois ou mais fatores. Verifique:
60 = 2 ⋅ 30 60 = 2 ⋅ 2 ⋅ 15 60 = 2 ⋅ 2 ⋅ 3 ⋅ 5
Temos anteriormente três fatorações do número 60.
Note que, em 60 = 2 ⋅ 2 ⋅ 3 ⋅ 5, todos os fatores são primos. Essa igualdade póde ser escrita também como 60 = 2elevado a 2 ⋅ 3 ⋅ 5. Realizamos, assim, a fatoração completa ou decomposição em fatores primos do número 60.
Analise, agora, duas maneiras diferentes de obter a fatoração completa do número 420.
Utilizando o processo das fatorações sucessivas
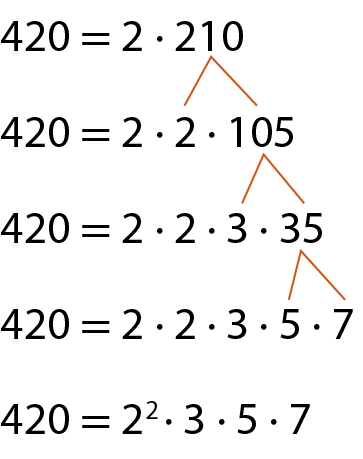

Respostas e comentários
38. números dos itens b, c, d, f
39. 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29
40. a) 14 = 2 ⋅ 7
40. b) 35 = 5 ⋅ 7
40. c) 70 = 2 ⋅ 5 ⋅ 7
40. d) 42 = 2 ⋅ 3 ⋅ 7
40. e) 50 = 2 ⋅ 5 ⋅ 5
40. f) 100 = 2 ⋅ 2 ⋅ 5 ⋅ 5
41. 323 não é um número primo, pois é divisível por 1, 17, 19 e 323.
42. .9797
43. 163 e 181
Balão de fala: Espera‑se que os estudantes concluam que vão obter a mesma fatoração completa, não importando o modo como fatoram inicialmente o número considerado.
• Para a resolução da atividade 42, os estudantes poderão determinar os números usando o método do crivo de Eratóstenes, encontrando:
• o maior número primo de dois algarismos: 97;
• o maior número primo de três algarismos: 101.
Assim: 97 ⋅ 101 = .9797
Decomposição em fatores primos
São apresentados dois métodos para decompor números naturais em fatores primos: processo das fatorações sucessivas e divisões sucessivas. Explore coletivamente o exemplo apresentado e, se achar necessário, apresente outros exemplos.
Chame a atenção dos estudantes para que percebam que a decomposição de um número em fatores primos é única, o que pode ser demonstrado.
Fazendo divisões sucessivas

Clique no play e acompanhe as informações do vídeo.
420 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7
420 = 2elevado a 2 ⋅ 3 ⋅ 5 ⋅ 7
Terminamos esse processo quando obtemos o quociente 1. A coluna da direita apresenta os fatores primos de 420.
Observe que utilizamos os números primos em ordem crescente por opção, mas poderíamos dispô-los em qualquer ordem.
Atividades
Faça as atividades no caderno.
44. Qual é a fatoração completa dos números a seguir?
a) 96
b) 324
c) .1024
d) .1260
e) .2870
f) .3575
45. Dado o número na fórma fatorada 2elevado a 3 ⋅ 5elevado a 2 ⋅ 7, pergunta‑se:
a) Qual é esse número?
b) Qual é o maior divisor primo desse número?
46. Escreva no caderno o número cuja fórma fatorada é igual a:
a) 2elevado a 2 ⋅ 3 ⋅ 7
b) 2elevado a 3 ⋅ 3elevado a 2 ⋅ 5
c) 2elevado a 4 ⋅ 7
d) 2 ⋅ 7elevado a 2 ⋅ 11
47. Quais são os fatores primos comuns a 30 e 140?
Respostas e comentários
44. a) 2elevado a 5 ⋅ 3
44. b) 2elevado a 2 ⋅ 3elevado a 4
44. c) 2elevado a 10
44. d) 2elevado a 2 ⋅ 3elevado a 2 ⋅ 5 ⋅ 7
44. e) 2 ⋅ 5 ⋅ 7 ⋅ 41
44. f) 5elevado a 2 ⋅ 11 ⋅ 13
45. a) .1400
45. b) 7
46. a) 84
46. b) 360
46. c) 112
46. d) .1078
47. 2 e 5
O estudo dos números primos é bastante importante para a construção do conhecimento matemático. A aplicação desses números é encontrada nos mais diversos problemas do dia a dia. Pode-se solicitar aos estudantes que façam uma breve pesquisa sobre o emprêgo dos números primos em situações do dia a dia, como a criptografia. Após os exercícios de familiarização, que exploram o reconhecimento e a utilização dos números primos na decomposição de um número natural, pode-se solicitar a elaboração de um problema que necessite da técnica de decomposição na resolução.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Múltiplos de um número natural
Um número natural é múltiplo de outro quando o primeiro é obtido multiplicando o segundo por um número natural qualquer.
1. Escreva, no caderno, os cinco menores múltiplos de 15.
2. Determine os múltiplos de 18 compreendidos entre 160 e 240.
Divisores de um número natural
Um número natural é divisor ou fator de outro quando a divisão do segundo pelo primeiro é exata; nesse caso, o segundo número é divisível pelo primeiro.
3. Verifique se o número 256 é divisível por:
a) 2;
b) 8;
c) 12;
d) 15;
e) 16;
f) 18
4. Determine o maior número de três algarismos divisível por 4.
5. Leia as afirmações e indique se elas são verdadeiras ou falsas.
a) 4 é divisor de 240.
b) 2, 3 e 6 são divisores de 624.
c) 15 é fator de .1450.
Critérios de divisibilidade
Um número natural é divisível por:
• 2 quando ele é par;
• 3 quando a soma de seus algarismos é divisível por 3;
• 4 quando termina em 00 ou seus dois últimos algarismos formam um número divisível por 4 (para números maiores ou iguais a 100);
• 5 quando termina em 0 ou em 5;
• 6 quando é divisível por 2 e por 3;
• 8 quando termina em 000 ou seus três últimos algarismos formam um número divisível por 8 (para números maiores ou iguais a .1000);
• 9 quando a soma de seus algarismos é divisível por 9;
• 10 quando termina em 0;
• 100 quando termina em 00;
• .1000 quando termina em 000.
6. Copie o quadro a seguir no caderno e marque um xis nos espaços correspondentes aos divisores de cada número.

|
Divisor |
||||||
|---|---|---|---|---|---|---|
|
Número |
2 |
3 |
5 |
6 |
8 |
9 |
|
312 |
||||||
|
645 |
||||||
|
1.236 |
||||||
|
2.169 |
||||||
7. Identifique os números que são divisíveis por 9.
a) 909
b) .1071
c) .2304
d) .3356
Números primos e números compostos
• Um número é primo quando tem somente dois divisores naturais distintos: o número 1 e o próprio número.
• Um número, diferente de zero, é composto quando tem mais de dois divisores distintos.
Decomposição em fatores primos
Todo número natural composto pode ser representado por uma multiplicação de dois ou mais fatores primos.
756 = 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 7 = 2elevado a 2 ⋅ 3elevado a 3 ⋅ 7
.2925 = 3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 13 = 3elevado a 2 ⋅ 5elevado a 2 ⋅ 13
8. Quais dos números a seguir são primos?
a) 99
b) 109
c) 167
d) 281
e) 562
f) 1 021
9. Escreva, no caderno, a decomposição dos números a seguir em fatores primos.
a) 576
b) .2048
c) .1323
d) .1944
e) .2058
f) .5096
Respostas e comentários
1. 0, 15, 30, 45 e 60.
2. 162, 180, 198, 216 e 234.
3. Os números dos itens a, b e ê.
4. 996
5. a) verdadeira
5. b) verdadeira
5. c) falsa
6. Resposta em Orientações.
7. Os números dos itens a, b e c são divisíveis.
8. Os números dos itens b, c, d e f são primos.
9. a) 2elevado a 6 ⋅ 3elevado a 2
9. b) 2elevado a 11
9. c) 3elevado a 3 ⋅ 7elevado a 2
9. d) 2elevado a 3 ⋅ 3elevado a 5
9. e) 2 ⋅ 3 ⋅ 7elevado a 3
9. f) 2elevado a 3 ⋅ 7elevado a 2 ⋅ 13
Revisão dos conteúdos deste capítulo
Múltiplos de um número natural
Para reforçar a diferença entre múltiplos e divisores de um número, você pode apresentar algumas multiplicações, como “3 ⋅ 5 = 15”. Tomando como base esse exemplo, sinalize que os números 3 e 5 são divisores de 15 e o 15 é múltiplo de 3 e múltiplo de 5.
• Na atividade 1, após listarem os cinco menores múltiplos de 15, peça aos estudantes que justifiquem o porquê de cada número da lista ser um múltiplo de 15. Por exemplo:
0 é múltiplo de 15, pois 15 ⋅ 0 = 0.
15 é múltiplo de 15, pois 15 ⋅ 1 = 15.
30 é múltiplo de 15, pois 15 ⋅ 2 = 30.
• Na atividade 2, é importante que os estudantes reconheçam primeiro que 160 e 240 não são múltiplos de 18. Depois, eles devem utilizar estratégias pessoais para verificar que 18 ⋅ 9 = 162. Incentive-os a compartilhar como fizeram para determinar os múltiplos de 18 entre 160 e 240.
Divisores de um número natural
• Na atividade 3, relembre aos estudantes que um número natural é divisível por outro quando a divisão é exata, ou seja, quando o resto da divisão é igual a zero.
Como dica para a resolução da atividade 4, sugira que eles primeiro verifiquem se o maior é divisível por 4, depois, oriente-os a verificar os antecessores deste número (998, 997, reticências).
• Na atividade 5, você pode solicitar aos estudantes que justifiquem os itens que classificaram como falsos.
Critérios de divisibilidade
• Para as atividades 6 e 7, solicite aos estudantes que tentem resolver primeiro mentalmente e, caso não consigam, que apliquem os critérios de divisibilidade estudados. Eles podem também efetuar os cálculos utilizando as estratégias que julgarem mais adequadas.
• Resposta da atividade 6:
|
Divisor |
||||||
|---|---|---|---|---|---|---|
|
Número |
2 |
3 |
5 |
6 |
8 |
9 |
|
312 |
X |
X |
X |
X |
||
|
645 |
X |
X |
||||
|
1.236 |
X |
X |
X |
|||
|
2.169 |
X |
X |
||||
Números primos e números compostos
• Para realizar a atividade 8, oriente os estudantes a identificar, primeiro, os números que são compostos e peça que escrevam esses números como um produto de outros dois números naturais. Por exemplo: 99 = 3 ⋅ 33 e 562 = 2 ⋅ 281.
• Se achar pertinente, peça aos estudantes que façam a atividade 9 aplicando os métodos das fatorações sucessivas e das divisões sucessivas. Dessa fórma, eles poderão se apropriar destas duas estratégias e verificar se obtém a mesma decomposição por ambos os métodos.
Glossário
- Padrão
- : Característica que se repete ou modelo que é seguido.
- Voltar para o texto
- Divisor próprio
- : Valor que divide um número resultando em uma divisão exata, mas que não seja o próprio número.
- Voltar para o texto
- Ano bissexto
- : Ano ao qual é acrescentado um dia, ficando com 366 dias. Anos bissextos são divisíveis por 4 e não terminam em 00. Se terminar em 00, para que seja bissexto, ele deve ser divisível por 400.
- Voltar para o texto