Capítulo 7 Números decimais
Trocando ideias
Em 2021, a ginasta Rebeca Andrade conquistou a medalha de ouro no salto nas Olimpíadas de Tóquio, com média de 15,083 pontos. A prata ficou com a americana MyKayla Skinner, com 14,916 pontos. A sul-coreana Yeo Seo-jeong fechou o pódio, em terceiro lugar, com 14,733 pontos.
Os números 15,083; 14,916 e 14,733 têm vírgula. Esses números são exemplos de números decimais.
▸

Em que situações do cotidiano utilizamos os números decimais?
▸


Faltou mais ou menos de 1 ponto para Rebeca Andrade ter alcançado os 16,000 pontos?
Neste capítulo, vamos estudar os números decimais e algumas operações com números decimais.
Respostas e comentários
Trocando ideias: primeiro item: resposta pessoal; segundo item: menos de 1 ponto.
CAPÍTULO 7 – NÚMEROS DECIMAIS
Trocando ideias
BNCC:
• Competência geral 9 (a descrição está na página seis).
• Competência específica 8 (a descrição está na página sete).
Objetivos:
• Levantar o conhecimento prévio dos estudantes sobre os números decimais.
• Refletir sobre as dificuldades de acesso à prática de alguns esportes por parte de crianças e adolescentes.
Inicie a aula comentando com os estudantes que a atleta Rebeca Andrade foi a primeira brasileira a conquistar duas medalhas em uma edição das olimpíadas: a medalha de prata na categoria individual geral e a medalha de ouro no salto, sendo essa última a primeira medalha na história da ginástica feminina brasileira. É possível que alguns estudantes tenham acompanhado as conquistas dessa atleta e, por esse motivo, convém reservar um momento para que compartilhem suas experiências.
Depois, explore com eles as pontuações das atletas que subiram ao pódio e chame a atenção para a presença da vírgula em cada um dos números. Aproveite a oportunidade para explorar o que estudaram sobre números decimais nos anos iniciais do Ensino Fundamental.
Conforme os estudantes forem respondendo à primeira questão, anote as respostas deles na lousa. Eles podem dizer que os números decimais estão presentes em situações de compra e venda de mercadorias, em situações que envolvem medidas etcétera. Em relação à segunda questão, incentive-os a explicar como pensaram para responder.
Você pode ampliar a proposta desse Trocando ideias verificando se sabem comparar números decimais. Para isso, proponha que comparem as pontuações obtidas pelas atletas Sunisa Li (57,433 pontos) e Angelina Melnikova (57,199 pontos) na prova do individual geral das Olimpíadas de Tóquio e concluam qual delas conquistou a medalha de ouro e qual conquistou a medalha de bronze. Deixe-os à vontade para utilizar suas estratégias pessoais.
Por promover o diálogo e a interação entre os estudantes, a proposta desse Trocando ideias favorece o desenvolvimento da competência geral 9 e da competência específica 8 da Bê êne cê cê.

1 Décimos, centésimos e milésimos
Décimos
A figura a seguir foi dividida em 10 partes iguais e três delas foram pintadas de verde.

Cada parte da figura corresponde a
1 sobre 10da figura.
A parte que está pintada de verde corresponde a
3 sobre 10da figura.
As frações
1 sobre 10e
3 sobre 10são exemplos de frações decimais.
Fração decimal é toda fração cujo denominador é uma potência de dez.
As frações decimais podem ser representadas por um número com vírgula, ou seja, por um número decimal. Observe:
• A fração
1 sobre 10pode ser representada por 0,1 (lemos: “um décimo”).
• A fração
3 sobre 10pode ser representada por 0,3 (lemos: “três décimos”).
Luís é pintor e está trabalhando nos três painéis a seguir. Ele já pintou dois painéis completos e parte do terceiro.

O que já foi pintado pode ser representado pela fração decimal
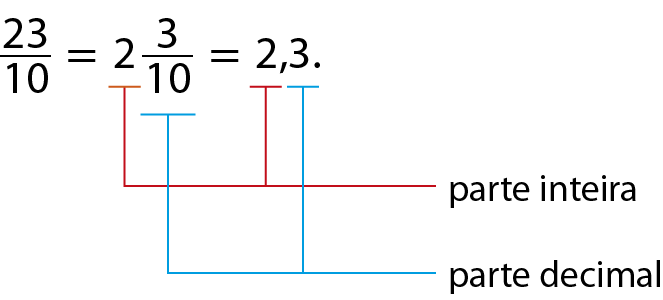
23 sobre 10, pelo número misto
2, 3 sobre 10ou pelo número decimal 2,3 (lemos: “dois inteiros e três décimos”).
Assim:
Respostas e comentários
Décimos, centésimos e milésimos
BNCC:
Habilidade ê éfe zero seis ême ah zero oito.
Objetivos:
• Compreender a ideia de décimos, centésimos e milésimos.
• Representar números decimais na reta numérica.
Justificativa
A habilidade ê éfe zero seis ême ah zero oito está relacionada a associar números na fórma de fração com denominador potência de 10 e sua representação decimal, ou seja, em perceber que
1 sobre 10 é igual a 0,1;
1 sobre 100 é igual a 0,01;
1 sobre 1000 é igual a 0,001etcétera. Dessa fórma, é importante que os estudantes compreendam a ideia de décimos, centésimos e milésimos.
Representar números decimais na reta numérica contribui, entre outras coisas, para que os estudantes percebam a relação entre décimos, centésimos e milésimos e também para que utilizem esse recurso para comparar números na forma decimal.
Mapeando conhecimentos
Reúna os estudantes em grupos e distribua peças do material dourado para eles. Depois, peça que considerem que o cubo maior representa uma unidade e faça os seguintes questionamentos:
• A qual número corresponde a placa? Como podemos representá-la na fórma de fração e na fórma decimal?
Respostas: um décimo, fração 1 sobre 10, 0,1..
• A qual número corresponde a barra? Como podemos representá-la na fórma de fração e na fórma decimal?
Respostas: um centésimo, fração 1 sobre 100, 0,01..
• A qual número corresponde o cubo menor? Como podemos representá-lo na fórma de fração e na fórma decimal?
Respostas: um milésimo, fração 1 sobre 1000, 0,001..
Por fim, peça aos grupos que representem com as peças do material dourado alguns números na fórma decimal que você vai escrever na lousa.
Para as aulas iniciais
Explore o uso de calculadora para que percebam, por exemplo, que
1 sobre 10= 1 ÷ 10 = 0,1. O foco, nesse momento, é a compreensão das diferentes representações. Se necessário, retome a ideia de fração como quociente. Depois, promova o mesmo raciocínio para
fração 1 sobre 100e
fração 1 sobre 1000.
O trabalho com décimos é feito relacionando-os a figuras e a frações. Para que haja melhor compreensão, exponha exemplos na lousa e peça aos estudantes que identifiquem o padrão existente.
Pergunte a eles qual é o número decimal que representa a parte não pintada do terceiro painel.
(ê éfe zero seis ême ah zero oito) Reconhecer que os números racionais positivos podem ser expressos nas fórmas fracionária e decimal, estabelecer relações entre essas representações, passando de uma representação para outra, e relacioná-los a pontos na reta numérica.
Centésimos
Das 100 lajotas que Ângela comprou para revestir o piso da sala de sua casa, 28 eram azuis. As lajotas de côr azul ocupam
28 sobre 100do piso dessa sala. Analise a representação a seguir.
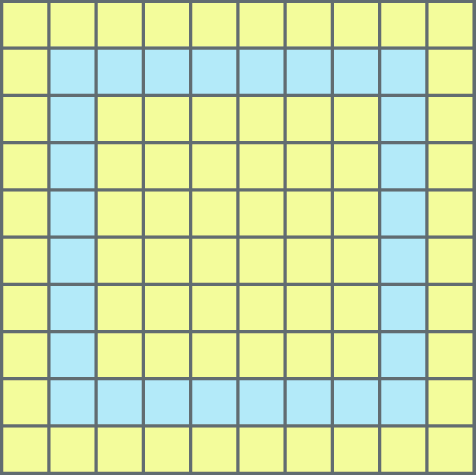
Cada lajota representa
Um centésimo.
do piso inteiro.
A parte azul do piso pode ser representada pela fração decimal
28 sobre 100ou pelo número decimal 0,28 (lemos: “vinte e oito centésimos”). Ou seja,
28 sobre 100 é igual 0,28.
Agora, tome a representação da fração
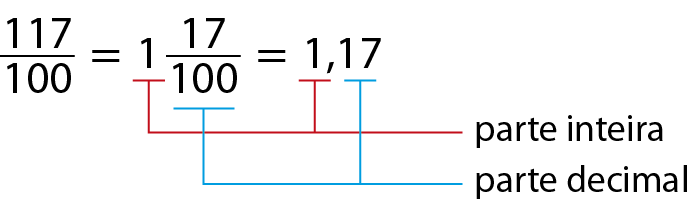
117 sobre 100:
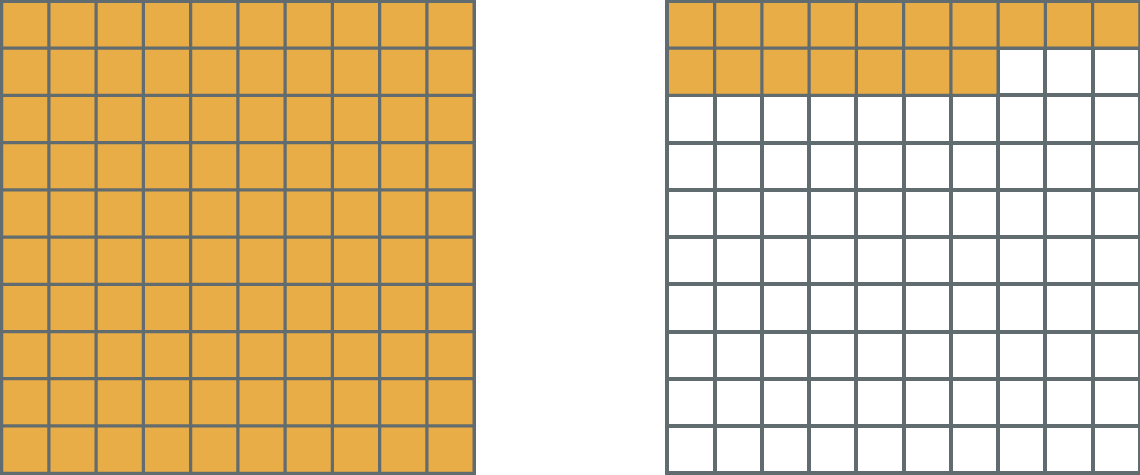
A parte pintada de laranja também pode ser representada pelo número misto
1, 17 sobre 100ou pelo número decimal 1,17 (lemos: “um inteiro e dezessete centésimos”).
Assim:
Milésimos
Observe o cubo. Considerando que todos os cubinhos pintados estão com, no mínimo, uma face visível, temos 77 cubinhos amarelos.
A parte pintada de amarelo corresponde à fração decimal
77 sobre 1000ou ao número decimal 0,077 (lemos: “setenta e sete milésimos”).
Assim:
77 sobre 1000 é igual a 0,077.
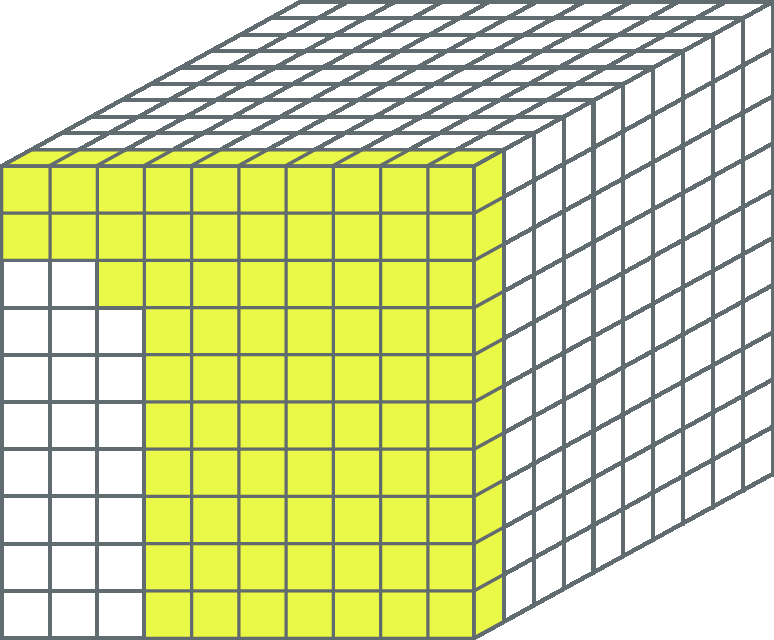
Cada cubinho representa
fração 1 sobre 1000do inteiro.
Respostas e comentários
Centésimos
Ao explorar a situação das lajotas com a turma, peça que representem a parte amarela do piso com uma fração decimal e um número decimal. Espera-se que os estudantes obtenham as seguintes representações:
72 sobre 100e 0,72. Depois, incentive-os a justificar como pensaram para chegar a essas representações.
Milésimos
Após apresentar a ideia de milésimos, solicite que representem a parte que não foi pintada de amarelo da figura com uma fração decimal e um número decimal. Espera-se que eles obtenham as seguintes representações:
923 sobre 1000e 0,923. Depois, incentive-os a justificar como pensaram para chegar a essas representações.
Sugestão de atividade extra
Solicite aos estudantes que associem frações à sua representação por meio de figuras e de números decimais. Para isso, na lousa, faça três colunas. Na primeira, escreva algumas frações; na segunda, desenhe em ordem aleatória figuras que representem as frações; na terceira coluna, escreva os números decimais correspondentes às frações. Em seguida, peça aos estudantes que informem quais são os trios (fração – representação – decimal) correspondentes. Dessa maneira, será possível diagnosticar se eles compreendem a relação entre a fração, a representação geométrica e o número decimal correspondente.
Números decimais na reta numérica
Assim como os números naturais, os números na fórma decimal ou fracionária também podem ser representados na reta numérica.
Observe como representar alguns números decimais na reta numérica.
Dividindo o intervalo de 0 a 1 em 10 partes iguais, encontramos os pontos correspondentes a
1 sobre 10,
2 sobre 10,
3 sobre 10,
4 sobre 10,
5 sobre 10,
6 sobre 10,
7 sobre 10,
8 sobre 10e
9 sobre 10.
Repetindo esse procedimento para o intervalo de 0 a
1 sobre 10, determinamos os pontos correspondentes a
Um centésimo.,
2 sobre 100,
3 sobre 100,
4 sobre 100,
5 sobre 100,
6 sobre 100,
7 sobre 100,
8 sobre 100e
9 sobre 100.
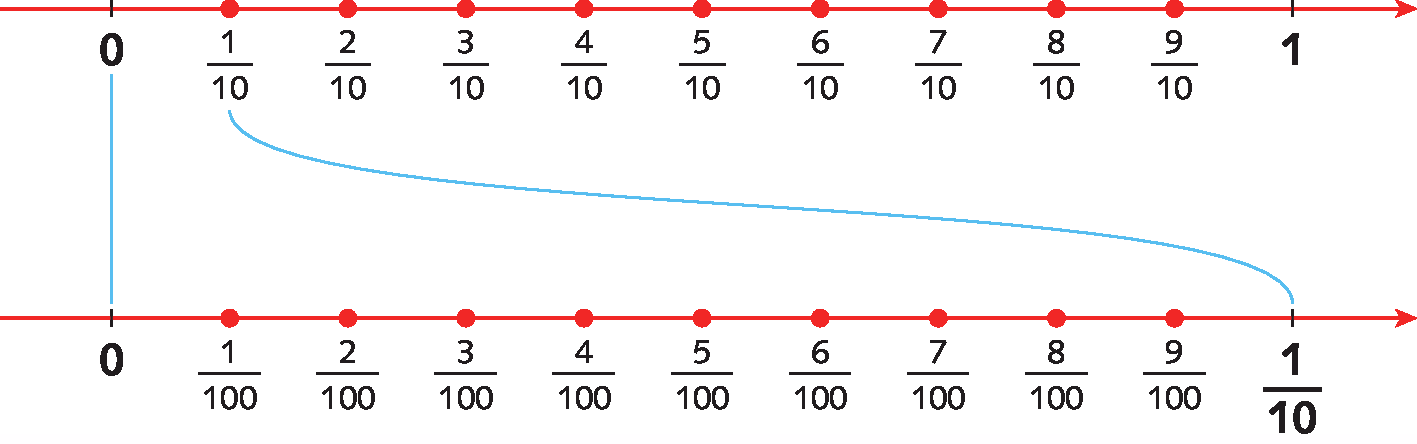
Observação
•
fração de numerador 10 e denominador 10, é igual a 1•
fração de numerador 1 décimo e denominador 10, é igual a 1 centésimo•
fração de numerador 10 e denominador 100, é igual a 1 décimoRepresentamos os números na fórma fracionária, mas também podemos representá-los nesta fórma decimal. Observe a reta numérica a seguir.

Agora, observe os pontos que correspondem aos números 0,2; 3,4 e 5,1 nesta reta numérica.


2 Leitura de números decimais
O sistema de numeração que utilizamos é posicional, isto é, o valor de um algarismo depende da posição que ele ocupa na escrita do número. Em cada ordem, o algarismo vale dez vezes o valor que teria na ordem vizinha da direita e a décima parte do valor que teria na ordem vizinha da esquerda.
Por exemplo, no número .1411, o algarismo 4 vale 400, dez vezes o que vale no número .1141, ou seja, 40. No número .1141, o algarismo 4 vale a décima parte do valor que ele tem no número .1411.
Quadro de ordens
Podemos representar números decimais em um quadro de ordens.
Analise, no quadro de ordens, a representação de 2,1; 0,79; 0,917 e 23,056.
Respostas e comentários
Números decimais na reta numérica
O uso da reta numérica é demasiadamente importante no estudo de conjuntos numéricos. Fazer uso da reta numérica auxilia, de maneira visual, na compreensão para comparar e ordenar números. Nesse tópico, relacionamos as representações fracionária e decimal a pontos da reta numérica.
Para ajudar os estudantes a compreender a divisão exemplificada na primeira reta numérica, mostre uma régua e compare as marcações feitas entre 0 e 1 com as marcações de centímetro e milímetro.
Leitura de números decimais
BNCC:
Habilidade ê éfe zero seis ême ah zero um.
Objetivo:
Ler números racionais na fórma decimal.
Justificativa
A leitura de números racionais na fórma decimal está presente em diferentes situações cotidianas: leitura de preços, leitura de números em textos publicados na mídia, leitura de medidas etcétera. Além disso, esse objetivo favorece o desenvolvimento da habilidade ê éfe zero seis ême ah zero um.
Mapeando conhecimentos
Reproduza na lousa as atividades 51 e 52 da seção Revisão dos conteúdos de anos anteriores e peça aos estudantes que as façam individualmente. Após terminarem, oriente-os a ler a revisão sobre leitura de números decimais na mesma seção.
Para as aulas iniciais
Separe alguns textos de jornais ou revistas em que apareçam números na fórma decimal. Você também pode pedir aos estudantes que providenciem esses textos com antecedência. Depois, reúna-os em duplas ou trios e solicite que escrevam como se leem os números presentes nesses textos. Considere ampliar a proposta dessa atividade discutindo com a turma o significado desses números.
(ê éfe zero seis ême ah zero um) Comparar, ordenar, ler e escrever números naturais e números racionais cuja representação decimal é finita, fazendo uso da reta numérica.
Sugestão de atividade extra
Com o objetivo de verificação do conteúdo, proponha aos estudantes que realizem as atividades do tópico “Números decimais na reta numérica”, da plataforma Khan Academy, para localizar décimos e centésimos na reta numérica. Disponível em: https://oeds.link/v84kSL e https://oeds.link/O6bjcA. Acessos em: 3 julho 2022.
|
Parte inteira |
Parte decimal |
|||||
|---|---|---|---|---|---|---|
|
Centena |
Dezena |
Unidade |
Décimo |
Centésimo |
Milésimo |
|
|
2 |
, |
1 |
||||
|
0 |
, |
7 |
9 |
|||
|
0 |
, |
9 |
1 |
7 |
||
|
2 |
3 |
, |
0 |
5 |
6 |
|
Note que a vírgula separa a parte inteira da parte decimal.
Podemos ler esses números da seguinte maneira:
• 2,1

Lemos: “dois inteiros e um décimo”.
• 0,79

Lemos: “setenta e nove centésimos”.
• 0,917

Lemos: “novecentos e dezessete milésimos”.
• 23,056

Lemos: “vinte e três inteiros e cinquenta e seis milésimos”.
É muito comum na linguagem oral e nos meios de comunicação realizar a leitura de números decimais informando apenas onde fica a vírgula.
• 2,1

Lemos: “ dois vírgula um”.
• 0,79

Lemos: “zero vírgula setenta e nove”.
• 0,917

Lemos: “zero vírgula novecentos e dezessete”.
• 23,056

Lemos “vinte e três vírgula zero cinquenta e seis”.
Note que a leitura de um número decimal é a mesma que se faz para a fração decimal correspondente.
Assim, a leitura de um número na fórma decimal nos auxilia a escrever esse número na fórma de fração decimal.
Observe os números decimais a seguir:
• 0,8

Lemos: “oito décimos”, ou seja,
8 sobre 10.
• 0,65

Lemos: “sessenta e cinco centésimos”, ou seja,
Fração 65 sobre 100..
• 5,36

Lemos: “cinco inteiros e trinta e seis centésimos”, ou seja,
5, fração 36 sobre 100..
• 0,047

Lemos: “quarenta e sete milésimos”, ou seja,
Fração 47 sobre 1000..

Podemos escrever:
•
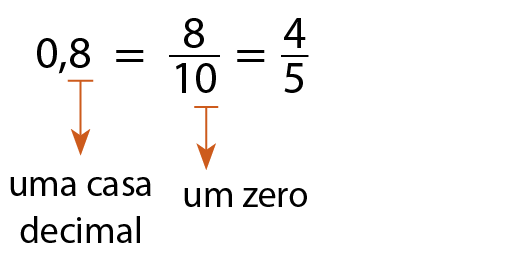
•

•

•

Respostas e comentários
Como o sistema de numeração decimal é posicional, fazer a leitura dos números decimais corretamente é de extrema importância para comunicar-se de fórma efetiva. Para ampliar o repertório dos estudantes, escreva outros exemplos de números decimais na lousa e peça a eles que os leiam em voz alta.
O uso do quadro de ordem visa auxiliar os estudantes a obter uma melhor compreensão, já que com o quadro a ordem de cada algarismo fica evidente.
Comente com os estudantes que, após transformar o número decimal em fração decimal, podemos simplificar a fração.
Sugestão de atividade extra
Proponha uma gincana aos estudantes. Para isso, será preciso providenciar duas caixas (de sapato) sem tampa, fita adesiva, números de 0 a 9 e vírgula (escritos em papel sulfite ou em cartolina e cortados, para serem colocados em cada caixa). Organize a turma em grupos. A cada rodada, apenas dois grupos vão participar. Solicite que todos se acomodem de um lado da sala. Do outro, coloque duas caixas (uma para cada grupo) contendo os números e uma vírgula.
Na lousa, escreva dois números decimais por extenso (que contenham o mesmo número de casas decimais e não tenham repetição de algarismo).
Ao seu sinal, um representante de cada grupo por vez deve correr até o lado da sala onde as caixinhas se encontram, pegar um algarismo ou a vírgula, de acôrdo com o número indicado na lousa, e fixá-lo com a fita adesiva na lousa. Depois, outro estudante do grupo faz o mesmo.
O grupo deve repetir o procedimento até que complete a representação.
Ganhará a rodada o grupo que realizar primeiro a representação correta do número.
Atividades
Faça as atividades no caderno.
1. Escreva por extenso os números decimais.
a) 0,7
b) 0,317
c) 5,69
d) 0,28
e) 7,038
f) 0,008
2. Utilize algarismos para escrever cada um dos números decimais a seguir no caderno.
a) Sete inteiros e seis décimos.
b) Trinta e seis milésimos.
c) Setenta e oito centésimos.
d) Cento e vinte e seis décimos.
e) Vinte inteiros e quatro décimos.
f) Seiscentos e quarenta e cinco milésimos.
g) Setenta e nove centésimos.
3. Converta os números decimais em frações decimais e simplifique-as quando possível.
a) 0,76
b) 0,025
c) 12,7
d) 17,22
e) 50,06
f) 0,019
4. Responda no caderno.
a) Quantos décimos há no número decimal 2,5?
b) Cinco unidades correspondem a quantos décimos?
c) Trezentos centésimos correspondem a quantas unidades?
5. Qual é a fração irredutível que representa o número decimal 0,04? E 0,25?

3 Comparação de números decimais
Comparar dois números decimais significa estabelecer uma relação de igualdade ou de desigualdade entre eles.
As figuras a seguir têm as mesmas medidas de comprimento e foram divididas em 10 e 100 partes iguais, respectivamente. Na figura da esquerda, foram pintadas quatro partes e, na da direita, 40 partes. Observe:
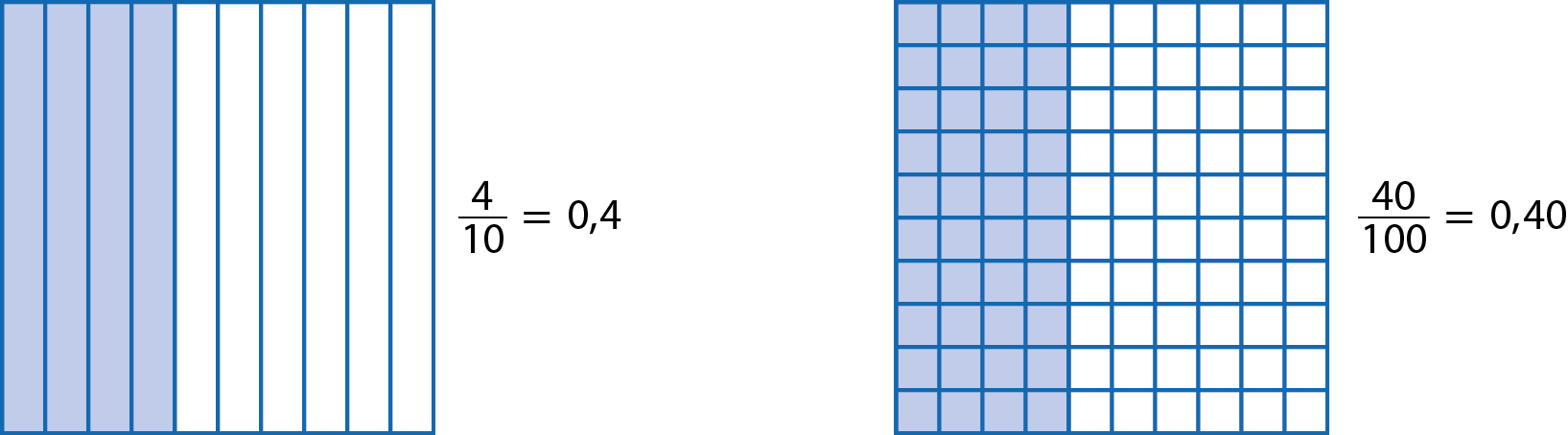
Verificamos que a parte azul representa a mesma parte do todo. Então, 0,4 e 0,40 representam uma mesma quantidade, isto é: 0,4 = 0,40.
Podemos acrescentar ou retirar zeros à direita da parte decimal de um número decimal sem alterá-lo.
Se os números decimais forem diferentes, podemos analisar dois casos:
1º caso: quando as partes inteiras são diferentes.
Nesse caso, o maior número é o que tem a maior parte inteira. Observe os exemplos.
a) 3,8 > 2,45, pois 3 > 2
b) 10,6 > 9,685, pois 10 > 9
Respostas e comentários
1. a) sete décimos
1. b) trezentos e dezessete milésimos
1. c) cinco inteiros e sessenta e nove centésimos
1. d) vinte e oito centésimos
1. e) sete inteiros e trinta e oito milésimos
1. f ) oito milésimos
2. a) 7,6
2. b) 0,036
2. c) 0,78
2. d) 12,6
2. e) 20,4
2. f) 0,645
2. g) 0,79
3. a)
Sentença matemática. 76 centésimos igual a 19 sobre 25.3. b)
Sentença matemática. 25 milésimos igual a 1 sobre 40.3. c)
Fração cento e vinte e sete sobre dez.3. d)
Sentença matemática. 1 mil 722 centésimos igual a 881 sobre 50.3. e)
Sentença matemática. 5 mil e 6 centésimos igual a 2 mil 503 sobre 50.3. f)
19 sobre 10004. a) 25 décimos
4. b) 50 décimos
4. c) 3 unidades
5.
1 sobre 25;
1 sobre 4• Para a realização da atividade 4, se julgar conveniente, proponha aos estudantes que utilizem o quadro de ordens.
Comparação de números decimais
Bê êne cê cê:
Habilidade ê éfe zero seis ême ah zero um.
Objetivo:
Comparar números racionais na fórma decimal.
Justificativa
Ao comparar quantias em reais ou em medidas, muitas vezes os estudantes comparam números racionais na fórma decimal, o que justifica a pertinência desse objetivo. Além disso, esse objetivo é de suma importância para o desenvolvimento da habilidade ê éfe zero seis ême ah zero um.
Mapeando conhecimentos
Para mapear os conhecimentos prévios dos estudantes sobre a comparação de números racionais na fórma decimal, crie um circuito de estações dentro da sala de aula. Cada uma das estações deve propor uma atividade diferente sobre números decimais. A ideia é que os estudantes, organizados em pequenos grupos de 4 ou 5 componentes, façam um rodízio pelos diversos pontos.
Cada grupo vai começar em uma estação diferente e circular a partir dela. A ideia é que os grupos cumpram as tarefas isoladamente. Se a turma estiver organizada em 4 grupos, é possível propor as seguintes estações:
Estação 1: comparar e ordenar os preços de diferentes mercadorias.
Estação 2: comparar e ordenar medidas de temperatura.
Estação 3: comparar e ordenar medidas de massa.
Estação 4: comparar e ordenar medidas de comprimento.
Para as aulas iniciais
Na seção Revisão dos conteúdos de anos anteriores, são recordados os procedimentos para comparar números na fórma decimal quando as partes inteiras são diferentes e quando as partes inteiras são iguais. Promova a leitura coletiva dessa revisão e, depois, solicite aos estudantes que façam as atividades 53, 54 e 55.
(ê éfe zero seis ême ah zero um) Comparar, ordenar, ler e escrever números naturais e números racionais cuja representação decimal é finita, fazendo uso da reta numérica.
2º caso: quando as partes inteiras são iguais.
Nesse caso, o maior número é o que tem a maior parte decimal.
É conveniente igualar, inicialmente, o número de casas decimais, acrescentando zeros, para depois comparar. Analise os exemplos.
a) 0,7 > 0,675 ou 0,700 > 0,675 (igualando as casas decimais), pois: 700 > 675
b) 8,3 > 8,03 ou 8,30 > 8,03 (igualando as casas decimais), pois: 30 > 3
Podemos encontrar os pontos correspondentes a esses números na reta numérica, que pode nos ajudar visualmente a perceber qual número é maior. Quanto mais à direita na reta numérica, maior é o número.

Atividades
Faça as atividades no caderno.
6. Copie os itens no caderno, substituindo os

pelos sinais = ou ≠.
a) 1,2

0,12
b) 15

15,00
c) 2,06

2,6
d) 3,6

3,60
e) 0,17

0,17000
f) 16

160
7. Copie os itens no caderno, substituindo os

pelos sinais < ou >.
a) 7,04

7,4
b) 6,2

6,196
c) 9,87

9,799
d) 10,1

11
8. Escreva no caderno os números decimais de cada item em ordem crescente.
a) 0,75; 0,8; 0,07
b) 2,3; 2,35; 1,197
c) 3,1416; 3,2; 3,143
9. Escreva no caderno os números decimais de cada item em ordem decrescente.
a) 1,36; 0,36; 6,13
b) 0,38; 3,08; 3,8
c) 2,14; 2; 2,2
10. Os jogadores de um time de basquete medem estas alturas: 2,04 metros; 1,83 metro; 2,13 metros; 1,79 metro e 2 metros. Observe a figura e indique a medida da altura correspondente a cada jogador.
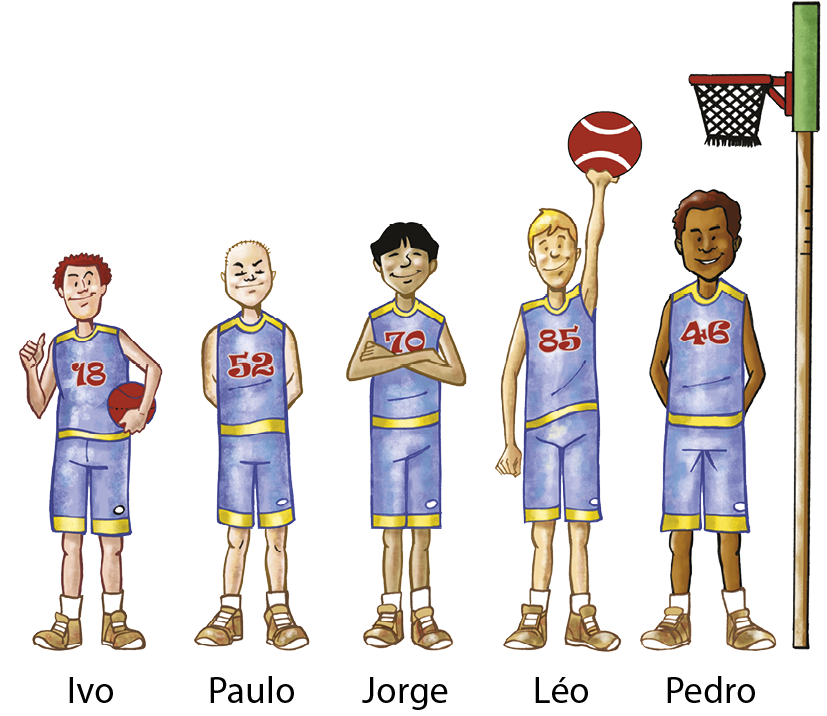
11. Observe a reta numérica a seguir e, em seguida, relacione os pontos a, B, C e D aos números decimais dados.
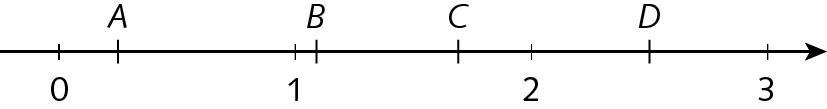
um – 1,69
dois – 2,5
três – 1,0898
quatro – 0,25
Respostas e comentários
6. a) ≠
6. b) =
6. c) ≠
6. d) =
6. e) =
6. f) ≠
7. a) <
7. b) >
7. c) >
7. d) <
8. a) 0,07 < 0,75 < 0,8
8. b) 1,197 < 2,3 < 2,35
8. c) 3,1416 < 3,143 < 3,2
9. a) 6,13 > 1,36 > 0,36
9. b) 3,8 > 3,08 > 0,38
9. c) 2,2 > 2,14 > 2
10. Ivo: 1,79 metro; Paulo: 1,83 metro; Jorge: 2 metros; Léo: 2,04 metros; Pedro: 2,13 metros
11. a ‒ quatro; bê ‒ três; cê ‒ um; dê ‒ dois
Sugestão de vídeos
Para auxiliar na compreensão e verificação do conteúdo, o vídeo disponível no tópico “Comparação entre números decimais”, na plataforma Khan Academy, explora estratégias para comparar os números decimais, considerando o valor posicional de cada algarismo e sua representação fracionária. Disponível em: https://oeds.link/m3Rkrd. Acesso em: 3 julho 2022.
• Caso os estudantes apresentem dificuldades na comparação solicitada na atividade 10, oriente-os a fazer o uso da reta numérica, facilitando, assim, o processo de comparação.
• Se achar oportuno, para a resolução da atividade 11, sugira aos estudantes que ordenem os itens um, dois, três e quatro. Dessa fórma, aplicá-los na reta numérica será intuitivo.

4 Adição e subtração com números decimais
Enrico foi a uma loja de brinquedos e comprou um robô de contrôle remoto e um jôgo de tabuleiro para sua filha. Quanto Enrico gastou?

Para resolver esse problema, podemos adicionar os preços dos dois brinquedos, efetuando 57,90 + 60,35. Analise os cálculos realizados a seguir.
Sentença matemática. 57 vírgula 90 mais 60 vírgula 35 é igual a 5 790 centésimos mais 6 035 centésimos, igual a 11 825 centésimos, igual a 118 vírgula 25.
, ou seja: R$ 118,25cento e dezoito reais e vinte e cinco centavos
Podemos também efetuar uma adição envolvendo números decimais escrevendo vírgula embaixo de vírgula e cada algarismo exatamente abaixo do algarismo de mesma ordem. Em seguida, adicionamos milésimos com milésimos, centésimos com centésimos, décimos com décimos, unidades com unidades e assim por diante. Observe a adição que calcula o gasto de Enrico.
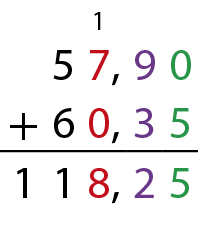
Portanto, Enrico gastou R$ 118,25cento e dezoito reais e vinte e cinco centavos para comprar os dois brinquedos.
Em algumas adições, os números não têm a mesma quantidade de casas decimais. Observe uma maneira de efetuá-las:
a) 35,4 + 0,75
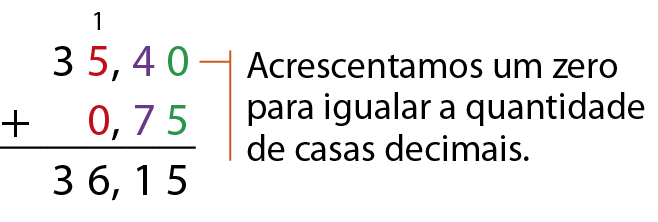
b) 6,14 + 0,007 + 1,8

Na situação anterior, quantos reais o jôgo de tabuleiro custou a mais que o robô?
Para resolver esse problema, podemos calcular a diferença entre os preços dos dois brinquedos, efetuando 60,35 ‒ 57,90. Analise os cálculos realizados a seguir.
Sentença matemática. 60 vírgula 35 menos 57 vírgula 90 igual a 6 035 centésimos menos 5 790 centésimos, igual a 245 centésimos, igual a 2 vírgula 45
, ou seja: R$ 2,45dois reais e quarenta e cinco centavos
Podemos também efetuar uma subtração envolvendo números decimais colocando vírgula embaixo de vírgula e cada algarismo exatamente abaixo do algarismo de mesma ordem. Em seguida, subtraímos milésimos de milésimos, centésimos de centésimos, décimos de décimos, unidades de unidades e assim por diante. Observe:
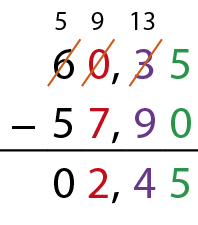
Portanto, o jôgo de tabuleiro custou R$ 2,45dois reais e quarenta e cinco centavos a mais que o robô de contrôle remoto.
Respostas e comentários
Adição e subtração com números decimais
BNCC:
Habilidade ê éfe zero seis ême ah um um.
Objetivo:
Adicionar e subtrair números racionais na fórma decimal.
Justificativa
Diferentes situações cotidianas demandam a adição e a subtração de números racionais na fórma decimal. Além disso, para elaborar e resolver problemas envolvendo esses números, conforme preconiza a habilidade ê éfe zero seis ême ah um um, é importante que os estudantes desenvolvam um repertório de estratégias de cálculo.
Mapeando conhecimentos
Apresente para a turma um problema de compra e venda de mercadorias que, para ser resolvido, exija uma adição e uma subtração com números na fórma decimal. Incentive os estudantes a dialogar e a conjecturar. Depois, peça a alguns deles que apresentem como pensaram para resolvê-lo. Esse é o momento oportuno para verificar as estratégias que empregam para adicionar e subtrair números na fórma decimal.
Para as aulas iniciais
O cálculo de adições e subtrações com o uso do algoritmo usual é relembrado na seção Revisão dos conteúdos de anos anteriores. Peça aos estudantes que leiam essa revisão e os exemplos. Se julgar necessário, apresente outros exemplos na lousa. Em seguida, proponha que façam as atividades 56 e 57.
(ê éfe zero seis ême ah um um) Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e a potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem uso de calculadora.
Em algumas subtrações, os números não têm a mesma quantidade de casas decimais. Observe uma maneira de efetuá-las:
a) 17,2 menos 5,146

b) 9 menos 0,987

Atividades
Faça as atividades no caderno.
12. Efetue as operações.
a) 0,9 + 3,5
b) 19,6 + 3,04 + 0,076
c) 17 + 4,32 + 0,006
d) 0,68 + 0,32 + 9
e) 6,4 menos 3,6
f) 2 menos 0,5678
g) 17,6 menos 17,594
h) 2,005 menos 1,05
i) 32,8 menos 24,276
j) 4,42 menos 0,008
13. Uma jarra continha
2 inteiros e 3 quartoslitros de um líquido. Foi adicionado 0,250 litro. Quantos litros há na jarra?
14. Francisco mede 1,87 metro de altura, e Marcos, 1,91 metro. Qual é a diferença entre as medidas das alturas deles?
15. O lançamento do martelo é uma modalidade olímpica de atletismo. Em uma prova, Paulo conseguiu atingir 46,37 metros, e Ricardo alcançou 52,23 metros. Qual é a diferença, em metro, entre os dois lançamentos?
16.

Hugo calculou mentalmente 3,7 + 0,9. Analise a seguir a representação de como ele pensou.
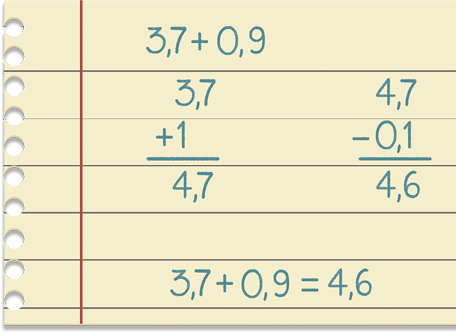
Agora, calcule mentalmente como Hugo.
a) 15,65 + 0,9
b) 16,05 menos 0,9
c) 21,33 + 0,09
d) 21,33 menos 0,09
17. Vânia foi ao pet shop e comprou 1 pacote de ração para seu gato por R$ 18,25dezoito reais e vinte e cinco centavos. Ela pagou sua compra com uma cédula de R$ 20,00vinte reais.
a)

Por estimativa, responda: O troco que Vânia recebeu é maior ou menor do que R$ 5,00cinco reais? E do que R$ 2,00dois reais? E do que R$ 1,00um reais?
b)

Utilize uma calculadora e calcule o valor do troco que Vânia recebeu.
18.


Benito utilizou uma calculadora e fez o seguinte cálculo:

Elabore um problema que possa ser resolvido utilizando a operação inversa da adição que Benito efetuou.
Respostas e comentários
12. a) 4,4
12. b) 22,716
12. c) 21,326
12. d) 10
12. e) 2,8
12. f) 1,4322
12. g) 0,006
12. h) 0,955
12. i) 8,524
12. j) 4,412
13. 3,0 litros
14. 0,04 metro
15. 5,86 metros
16. a) 16,55
16. b) 15,15
16. c) 21,42
16. d) 21,24
17. a) Menor; menor; maior.
17. b) R$ 1,75um reais e setenta e cinco centavos.
18. Resposta pessoal.
• Pode-se pedir aos estudantes que resolvam na lousa os itens da atividade 12 e expliquem a estratégia utilizada na resolução.
• Para complementar a atividade 14, pergunte aos estudantes se sabem a medida de altura deles. Caso não saibam, leve uma fita métrica para a sala de aula, escolha alguns estudantes e meça a altura de cada um deles. Mesmo que comprimento e unidade de medida de comprimento sejam objetos de estudo do capítulo 11, essa é uma boa oportunidade para sondagem do conhecimento prévio dos estudantes. Em seguida, peça a cada um deles que determine a diferença entre o estudante de maior e o de menor estatura selecionados.

5 Multiplicação com números decimais
Acompanhe as situações a seguir.
Situação 1
Quanto Marcos vai pagar pela tela de arame que quer comprar?

Para resolver esse problema, devemos calcular 2,5 ⋅ 13,48:
2,5 vezes 13,48 igual à fração 25 sobre 10, fim da fração, vezes fração 1348 sobre 100, fim da fração, é igual à fração 33700 sobre 1000, fim da fração, que é igual a 33,700.
Portanto, Marcos vai pagar R$ 33,70trinta e três reais e setenta centavos pela tela de arame.
Note que, ao multiplicar os números decimais como se eles não tivessem vírgula, temos:
25 ⋅ .1348 = .33700
Como
Um décimo vezes um centésimo é igual a um milésimo., o produto será da ordem dos milésimos, ou seja, terá 3 casas decimais.
Assim:

Para multiplicar um número decimal por outro número decimal, devemos:
• multiplicar os números como se fossem números naturais;
• colocar a vírgula no resultado, de modo que a quantidade de casas decimais seja igual à soma da quantidade de casas decimais dos fatores.
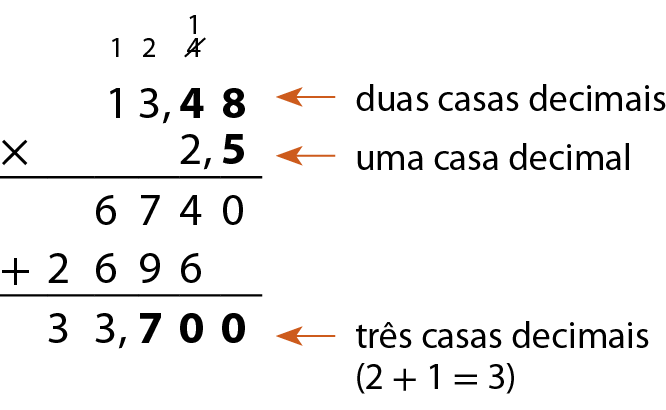
Analise mais alguns exemplos.
a) 1,842 ⋅ 0,013
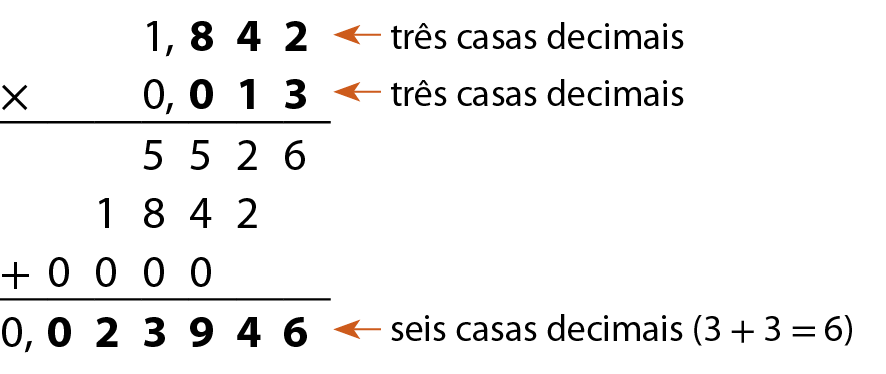
b) 8,056 ⋅ 3,0
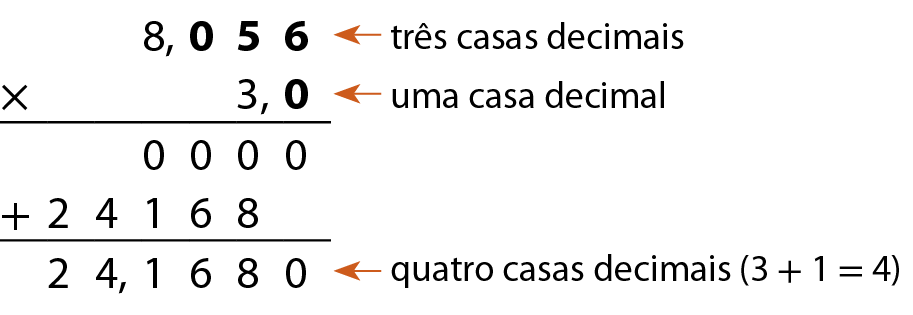
Respostas e comentários
Multiplicação com números decimais
BNCC:
Habilidade ê éfe zero seis ême ah um um.
Objetivo:
Multiplicar números racionais na fórma decimal.
Justificativa
A habilidade ê éfe zero seis ême ah um um implica, entre outras coisas, resolver e elaborar problemas envolvendo multiplicação com números na fórma decimal. Além disso, multiplicar um número na fórma decimal por outro é uma ação presente em diferentes situações cotidianas, o que justifica a pertinência do objetivo indicado.
Mapeando conhecimentos
Proponha os seguintes problemas para a turma:
1. Um quilograma de batata custa R$ 6,68seis reais e sessenta e oito centavos. Quanto vou pagar por 3 quilogramas?
2. Um metro de um fio de cobre tem medida de massa igual a 1,8 quilograma. Quantos quilogramas terão 3,5 metros desse fio?
Espera-se que os estudantes percebam que, para resolver o problema 1, precisam calcular 3 ⋅ 6,68 e, para resolver o problema 2, devem calcular 1,8 ⋅ 3,5. Depois, observe as estratégias que empregam em cada caso.
Para as aulas iniciais
Na seção Revisão dos conteúdos de anos anteriores, recorda-se como multiplicar um número natural por um número na fórma decimal por decomposição e utilizando o algoritmo usual. Reproduza os exemplos na lousa e, se achar necessário, apresente outros. Depois, peça aos estudantes que façam as atividades 58 e 59.
Peça-lhes então que, com o auxílio de uma calculadora, multipliquem números na fórma decimal. Depois, solicite que desconsiderem as vírgulas desses números e multipliquem um pelo outro. Por fim, incentive-os a comparar os resultados obtidos e conversar sobre eles.
abre parêntesesê éfe zero seis ême ah um umfecha parênteses Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e a potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem uso de calculadora.
Situação 2
Gabriela foi a uma loja de material de construção e comprou algumas caixas de revestimento para piso, a fim de terminar a reforma de sua casa.

Gabriela arredondou o valor de cada caixa e calculou quanto, aproximadamente, deveria pagar e constatou que o vendedor havia feito a conta errada. Ao refazer o cálculo, ele verificou que o valor da compra era R$ 408,45quatrocentos e oito reais e quarenta e cinco centavos.
Observação
Vale lembrar que a potenciação é uma multiplicação de fatores iguais. Observe:
2elevado a 5 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32
Com números decimais trabalhamos da mesma fórma. Observe:
abre parênteses1,2fecha parênteseselevado a 3 = 1,2 ⋅ 1,2 ⋅ 1,2 = 1,728
Analise mais alguns exemplos:
a) abre parênteses3,5fecha parênteseselevado a 2 = 3,5 ⋅ 3,5 = 12,25
b) abre parênteses0,4fecha parênteseselevado a 3 = 0,4 ⋅ 0,4 ⋅ 0,4 = 0,064
c) abre parênteses0,64fecha parênteseselevado a 1 = 0,64
d) abre parênteses0,18fecha parênteseselevado a 0 = 1
Atividades
Faça as atividades no caderno.
19. Efetue as multiplicações.
a) 2,4 ⋅ 3,5
b) 8 ⋅ 1,25
c) 0,1 ⋅ 0,01
d) 5,12 ⋅ 4,8
e) 2,5 ⋅ 2,5
f) 0,8 ⋅ 0,8
g) 12,6 ⋅ 0,18
h) 1,2 ⋅ 0,75
i) 0,16 ⋅ 0,0002
j) 0,64 ⋅ 0,25
20.

Com uma calculadora, efetue as operações a seguir.
5,248 ⋅ 10 5,248 ⋅ 100 5,248 ⋅ .1000
Agora, responda no caderno:
a) O que você observou nos resultados obtidos?
b) Você saberia calcular mentalmente 3,689 ⋅ 100? Justifique sua resposta.
Respostas e comentários
19. a) 8,4
19. b) 10
19. c) 0,001
19. d) 24,576
19. e) 6,25
19. f) 0,64
19. g) 2,268
19. h) 0,9
19. i) 0,000032
19. j) 0,16
20. a) Espera-se que os estudantes observem que o produto tem os mesmos algarismos do primeiro fator e a vírgula é deslocada para a direita tantas casas quantos forem os zeros do segundo fator.
20. b) 368,9. Ao multiplicar por 100, a vírgula é deslocada duas casas para a direita.
Depois de apresentar a situação 2, peça aos estudantes que estimem o valor da compra se Gabriela tivesse levado 41 caixas em vez de 21. Em seguida, peça que calculem o valor dessa compra. Espera‑se que eles realizem a operação 41 ⋅ 19,45 para obter a resposta para o valor da compra de 41 caixas, R$ 797,45setecentos e noventa e sete reais e quarenta e cinco centavos. Comente que o êrro cometido pelo vendedor pode ter ocorrido por um simples equívoco na execução da digitação.
• Caso os estudantes apresentem alguma dificuldade para responder ao item a da atividade 20, apresente outros exemplos. Incentive-os a investigar os padrões e enunciar uma regra prática que relacione a potência de 10 com o “deslocamento” da vírgula.
Esse tipo de atividade estimula o desenvolvimento dos diferentes tipos de raciocínio lógico-matemático abre parêntesesindução, dedução, abdução e raciocínio por analogiafecha parênteses, assim como de argumentação e de inferência.
21. Determine no caderno:
a) o dôbro de 3,64;
b) o triplo de 16,008.
22. Determine, no caderno, a menos b, sendo a = 0,5 ⋅ 0,12 e b = 0,25 ⋅ 0,06.
23.

Usando uma calculadora, determine o resultado das multiplicações e registre-o no caderno.
a) 1,234 ⋅ 5,678
b) 98 ⋅ 0,005
24. Ana comprou uma tê vê de quarenta e duas polegadas. A quantos centímetros corresponde essa medida de comprimento?
(uma polegada = 2,54 centímetrosfecha parênteses
25. O comprimento do passo de Ana mede 0,65 metro. Quantos metros ela terá percorrido depois de dar .2200 passos?
a) Arredonde 0,65 e .2200 para facilitar o cálculo e resolva o problema.
b) Resolva o problema com os números exatos.
c) Comparando as respostas dos itens anteriores, a aproximação feita no item a foi boa? Justifique.
26.

Calcule mentalmente o resultado de cada multiplicação e registre-o no caderno.
a) 6,32 ⋅ 10
b) 6,702 ⋅ .1000
c) 0,0005 ⋅ 100
d) 3,145 ⋅ 100
e) 0,012 ⋅ .1000
f) 0,9 ⋅ 100
g) 0,09 ⋅ .1000
h) 12,14 ⋅ .10000
27. Determine a ⋅ b, sendo a = 2 menos 0,35 e b = 2 + 0,35.
28. Para construir uma pista para seu trenzinho elétrico, Lucas comprou 13,85 metros de fio a R$ 1,20um reais e vinte centavos o metro. Quanto ele gastou na compra desse fio?
29. Júlio alugou um carro por um dia com estas condições: pagamento de R$ 56,00cinquenta e seis reais no recebimento das chaves mais R$ 0,69zero reais e sessenta e nove centavos por quilômetro rodado. Ao devolver o carro, ele verificou que havia rodado 108 quilômetros. Quanto ele gastou com o aluguel do veículo?
a) Arredonde 0,69 e 108 para facilitar o cálculo e resolva o problema.
b) Resolva o problema com os números exatos.
c) Comparando as respostas dos itens anteriores, a aproximação feita no item a foi boa? Justifique.
30.

Usando uma calculadora, determine o resultado destas multiplicações:
a) 1,2345679 ⋅ 0,18
b) 1,2345679 ⋅ 0,36
c) 1,2345679 ⋅ 0,45
• Agora, descubra o valor de

em:
1,2345679 ⋅

= 0,888888888
31. Em um terreno de .1000 metros quadrados foram construídas 8 salas de aula, com 40,25 metros quadrados cada uma. A área restante foi utilizada para lazer. Determine a medida da área da região destinada ao lazer.
32. Na casa de André, o ferro elétrico tem 2,3 quilowatts de potência, e o chuveiro, 2,8 quilowatts. Ao fim de 30 dias, qual será o consumo total de energia dos dois aparelhos, em quilouóts‑hora, sabendo que eles funcionam diariamente durante meia hora? abre parêntesesLembre que o consumo é igual à medida da potência multiplicada pela medida do tempo em hora.fecha parênteses

Respostas e comentários
21. a) 7,28
21. b) 48,024
22. 0,045
23. a) 7,006652
23. b) 0,49
24. 106,68 centímetros
25. a) Resposta pessoal. Exemplo de resposta: Arredondando para 0,7 e .2000, obtém-se a resposta .1400 metros.
25. b) .1430 metros
25. c) Respostas pessoais.
26. a) 63,2
26. b) .6702
26. c) 0,05
26. d) 314,5
26. e) 12
26. f) 90
26. g) 90
26. h) .121400
27. 3,8775
28. R$ 16,62dezesseis reais e sessenta e dois centavos
29. a) Resposta pessoal. Exemplo de resposta: Arredondando para 0,7 e 110, obtém-se a resposta R$ 133,00cento e trinta e três reais.
29. b) R$ 130,52cento e trinta reais e cinquenta e dois centavos
29. c) Respostas pessoais.
30. a) 0,222222222
30. b) 0,444444444
30. c) 0,555555555
30. 0,72
31. 678 metros quadrados
32. 76,5 quilowatts‑hora
• Como ampliação da atividade 23, peça aos estudantes que, em duplas, mudem a posição da vírgula de um dos fatores da multiplicação, efetuem-na novamente, usando uma calculadora, e verifiquem o que ocorreu.
• Após realizarem a atividade 26, pergunte aos estudantes se observaram algum padrão com relação à multiplicação de um decimal por 10, 100, .1000 ou .10000.
Espera-se que a maioria deles já tenha assimilado e aplicado as regras práticas que enunciaram na atividade 20.
33. Renata preparou alguns pães franceses integrais, com 50 gramas cada um.

|
Proteína |
Gordura |
Carboidrato |
|---|---|---|
|
4,1 gramas |
1,3 grama |
23,5 gramas |
Com base no quadro, responda.
a) Quantos gramas de gordura têm 5 pães feitos por Renata?
b) Para ingerir 8,2 gramas de proteína, uma pessoa deveria comer quantos pães iguais aos que Renata preparou?
34.

Segundo o Centro de Estudos Avançados em Economia Aplicada abre parêntesesCepeafecha parênteses, em 27 de janeiro de 2022, o preço médio da saca de arroz de 50 quilogramas no Brasil era de R$ 63,88sessenta e três reais e oitenta e oito centavos.
Nesse dia, qual era o preço de 10 sacas de arroz no Brasil? E de 100 sacas? E de .1000 sacas?
35. Um artesão vende cada peça de barro por R$ 12,90doze reais e noventa centavos. Carlos comprou sete dessas peças e pagou com uma cédula de R$ 100,00cem reais. Qual foi o valor total da compra? Quanto ele recebeu de troco? Para comprar oito peças, quanto Carlos deveria acrescentar à quantia de R$ 100,00cem reais?

36.

Observe como Emike fez para verificar que o resultado de 2,73 ⋅ 34 não é igual a .9282.

Faça como Emike e verifique o resultado dos cálculos a seguir.
a) 1,55 ⋅ 22 = 34,1
b) 3,26 ⋅ 19 = 619,4
c) 4,11 ⋅ 45 = .18495
d) 5,68 ⋅ 64 = 363,52
37. Faça o que se pede.
a)

Complete o enunciado do problema.

b)

Troque seu problema com um colega e resolva o problema proposto por ele.
38. Calcule no caderno.
a) abre parênteses0,2fecha parênteseselevado a 3
b) abre parênteses1,2fecha parênteseselevado a 2
c) abre parênteses0,17fecha parênteseselevado a 0
d) abre parênteses1,4fecha parênteseselevado a 3
e) abre parênteses0,7fecha parênteseselevado a 2
f) abre parênteses0,6fecha parênteseselevado a 3
g) abre parênteses0,3fecha parênteseselevado a 4
h) abre parênteses0,1fecha parênteseselevado a 5
Respostas e comentários
33. a) 6,5 gramas
33. b) 2 pães
34. R$ 638,80seiscentos e trinta e oito reais e oitenta centavos; R$ 6.388,00seis mil trezentos e oitenta e oito reais; R$ 63.880,00sessenta e três mil oitocentos e oitenta reais
35. R$ 90,30noventa reais e trinta centavos; R$ 9,70nove reais e setenta centavos; R$ 3,20três reais e vinte centavos
36. a) Correto
36. b) Incorreto
36. c) Incorreto
36. d) Correto
37. Respostas pessoais.
38. a) 0,008
38. b) 1,44
38. c) 1
38. d) 2,744
38. e) 0,49
38. f) 0,216
38. g) 0,0081
38. h) 0,00001
• Na atividade 34, incentive os estudantes a compartilhar como calcularam.
• Na atividade 36, solicite que refaçam os cálculos incorretos utilizando a estratégia que julgarem conveniente.

6 Divisão com números decimais
Divisão por um número natural diferente de zero
Luana comprou seis livros com preços iguais para seus sobrinhos, pagando, ao todo, R$ 135,00cento e trinta e cinco reais.

Quanto custou cada livro?
Para resolver esse problema, devemos calcular 135 dividido por 6.
Observe como este cálculo pode ser feito com o algoritmo da divisão.
Dividimos 135 unidades por 6 e obtemos vinte e duas unidades, sobrando 3 unidades, que é o mesmo que 30 décimos.
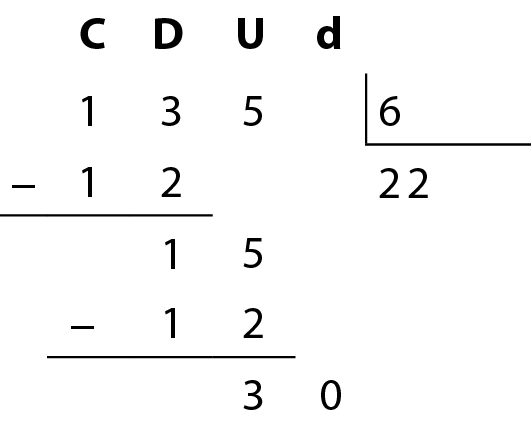
Em seguida, dividimos 30 décimos por 6. Obtemos 5 décimos e não sobra resto.

O número decimal 22,5 obtido no quociente está na fórma decimal exata, pois o resto dessa divisão é zero.
Logo, cada livro custou R$ 22,50vinte e dois reais e cinquenta centavos.
Respostas e comentários
Divisão com números decimais
BNCC:
Habilidade ê éfe zero seis ême ah um um.
Objetivo:
Dividir números racionais na fórma decimal.
Justificativa
A habilidade ê éfe zero seis ême ah um um trata da resolução e elaboração de problemas com números na fórma decimal envolvendo as quatro operações; por essa razão, dividir números na fórma decimal é um objetivo importante para que o desenvolvimento dessa habilidade se concretize. Assim como as demais operações, a divisão com números na fórma decimal também se faz presente em diversas situações cotidianas.
Mapeando conhecimentos
É importante mapear os conhecimentos dos estudantes no que tange à divisão de números naturais com resultado decimal, divisão de um número na fórma decimal por um número natural e divisão entre dois números na fórma decimal. Para isso, você pode propor que efetuem os seguintes cálculos:
1 dividido por 8 15,4 dividido por 5 3,125 dividido por 2,5
Forneça cédulas e moedas de real fictícias para que utilizem como apôio, caso julgue necessário.
Os estudantes podem calcular 1 dividido por 8 usando frações ou o algoritmo usual. O cálculo de 15,4 dividido por 5 pode ser feito com o uso de cédulas e moedas de real fictícias ou o algoritmo usual. Por fim, para calcular 3,125 dividido por 2,5, os estudantes podem se lembrar da seguinte propriedade: se o dividendo e o divisor de uma divisão forem multiplicados ou divididos por um mesmo número diferente de zero, a divisão realizada com os valores resultantes terá o mesmo resultado da divisão com os números iniciais.
Por meio dessa propriedade, podem aplicar o algoritmo usual.
Para as aulas iniciais
Na seção Revisão dos conteúdos de anos anteriores, recorda-se como dividir um número na fórma decimal por um número natural. Peça aos estudantes que leiam essa revisão e façam as atividades 60 e 61.
Você também pode apresentar alguns problemas que envolvam o cálculo de divisões entre números naturais com resultado decimal e cálculo de divisões entre dois números na fórma decimal. Depois, peça que, em grupos, discutam e resolvam esses problemas. Incentive os estudantes com mais facilidade a ajudar aqueles com dificuldade.
Divisão por um número natural diferente de zero
Antes de apresentar o cálculo de 135 : 6 utilizando o algoritmo usual, mostre como esse cálculo pode ser feito utilizando frações:
(ê éfe zero seis ême ah um um) Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e a potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem uso de calculadora.
Outros exemplos:
a) 1 dividido por 4
A divisão de 1 por 4 resulta em zero unidade e resta 1, que transformamos em 10 décimos. Dividimos 10 décimos por 4 e obtemos 2 décimos no quociente e sobram 2 décimos.
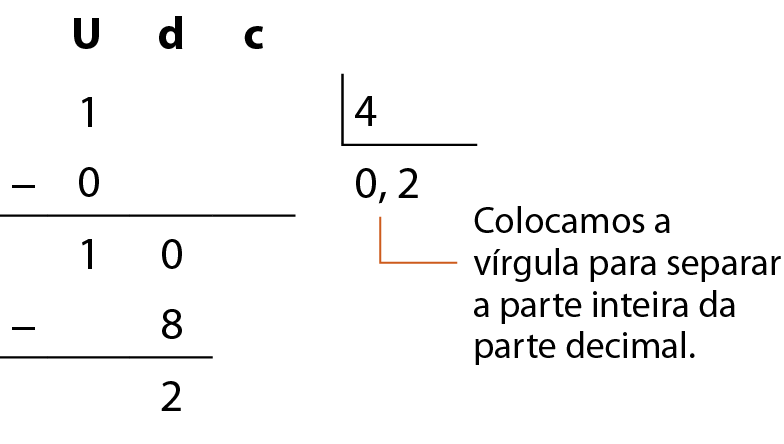
Transformamos 2 décimos em 20 centésimos e dividimos por 4 e obtemos 5 centésimos e resta zero.
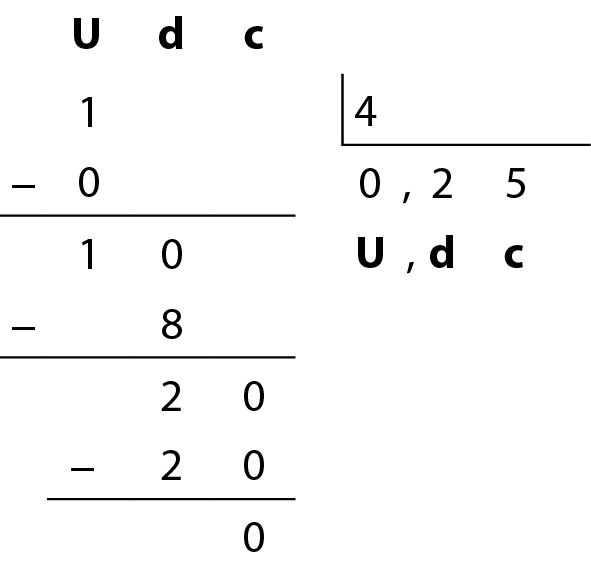
Logo, 1 dividido por 4 = 0,25.
b) 20,3 dividido por 5
Dividimos 20 unidades por 5 e obtemos 4 unidades, restando 0 unidade.
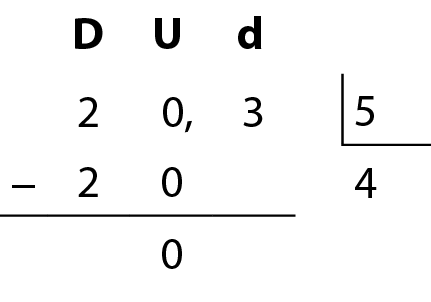
Dividimos 3 décimos por 5. O resultado é 0 décimo e sobram 3 décimos.
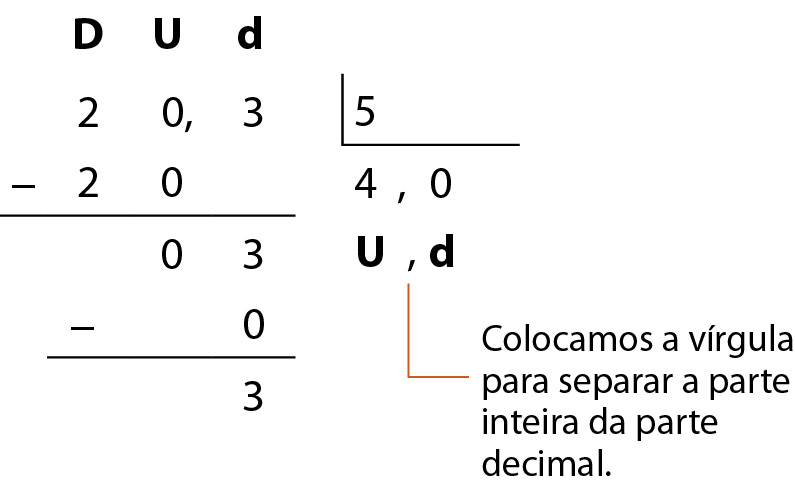
Agora, transformamos 3 décimos em 30 centésimos e continuamos a divisão.
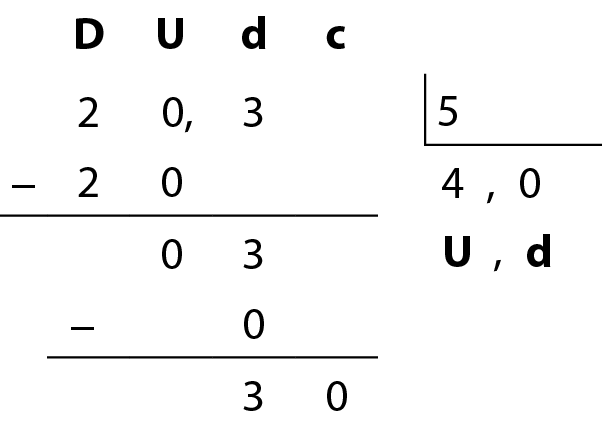
Dividimos 30 centésimos por 5 e obtemos 6 centésimos. Escrevemos 6 no quociente, na casa dos centésimos, restando zero centésimo.
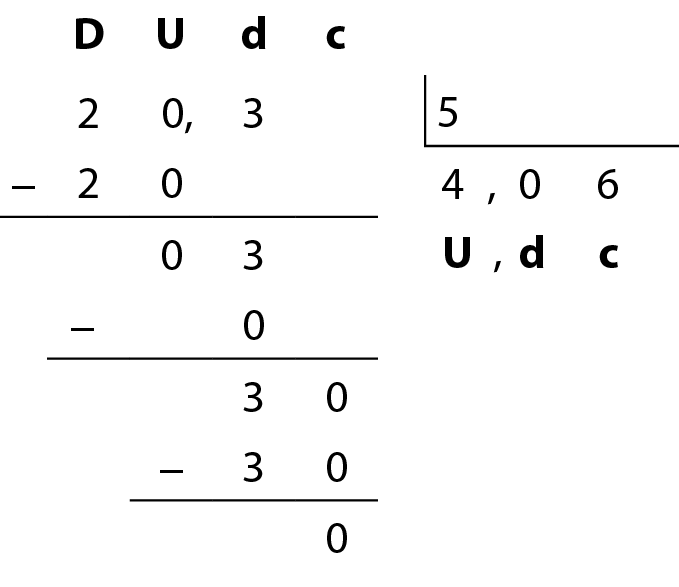
Logo, 20,3 dividido por 5 = 4,06.
Respostas e comentários
• Comente com os estudantes que a divisão 20,3 dividido por 5 poderia ter sido feita de fórma direta, ou seja, sem indicar as subtrações:
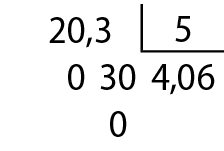
Divisão por um número decimal
Estudantes do 6º ano e do 7º ano fizeram um passeio a uma fazenda de maçãs. O fazendeiro separou maçãs para os estudantes, como mostra a imagem.

Sabendo que há 14 estudantes no 6º ano e 28 estudantes no 7º ano, quem receberá mais maçãs: um estudante do 6º ano ou um estudante do 7º ano?
Para responder a essa questão, observe que o barril do 7º ano contém o dôbro de maçãs do barril do 6º ano e que, no 7º ano, há o dôbro de estudantes do 6º ano.
Assim, podemos perceber que um estudante do 6º ano receberá a mesma quantidade de maçãs que um estudante do 7º ano, ou seja, 5 maçãs.
Podemos verificar se esse cálculo está correto efetuando as divisões 70 dividido por 14 = 5 e 140 dividido por 28 = 5. Como você pôde observar, 140 é o dôbro de 70 e 28 é o dôbro de 14, por isso, os quocientes são iguais.
Nas divisões entre números naturais, podemos observar o seguinte fato:
Quando se multiplicam abre parêntesesou se dividemfecha parênteses o dividendo e o divisor por um mesmo número diferente de zero, o quociente não se altera, mas o resto fica multiplicado abre parêntesesou divididofecha parênteses por esse número. Por exemplo:
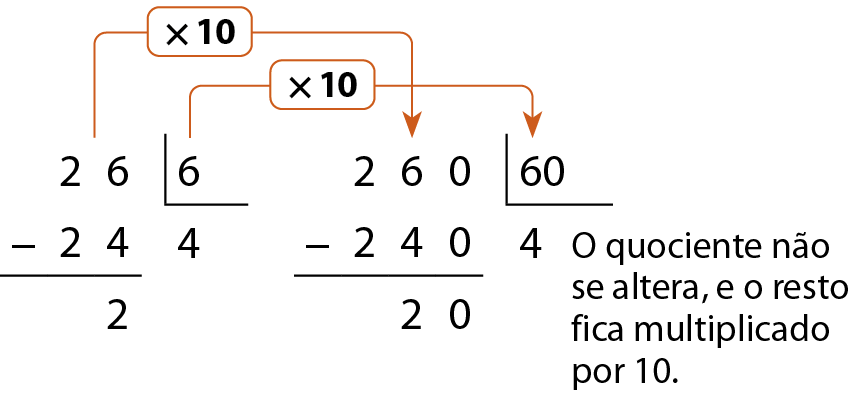
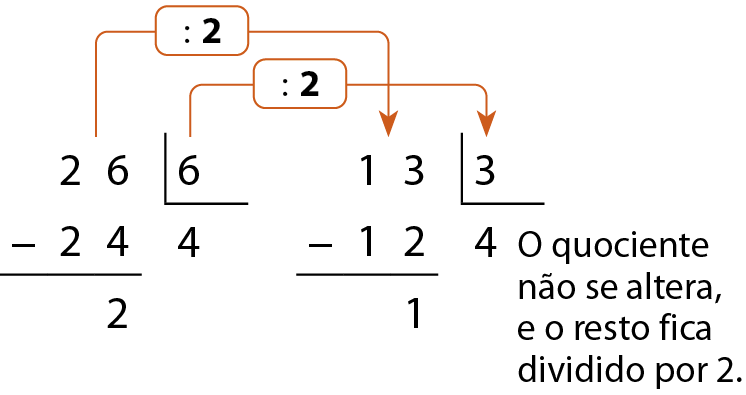
Analise outros exemplos:
a)
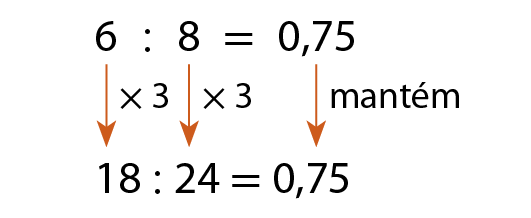
b)
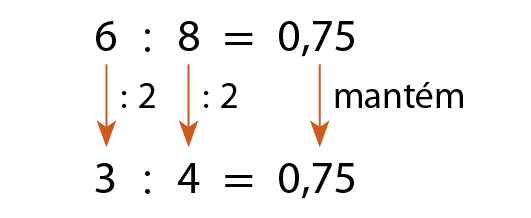
Nas divisões envolvendo números decimais, usamos essa propriedade para transformar o divisor e/ou o dividendo em números naturais. Observe os exemplos:
a) 6 dividido por 0,12
Multiplicando o dividendo e o divisor por 100, obtemos um número natural no divisor. Como é mais fácil multiplicar um número decimal por 10, 100, .1000 etcétera, escolhemos uma das potências de 10 para obter um divisor natural.

Logo, 6 dividido por 0,12 = 50.
Respostas e comentários
Divisão por um número decimal
A divisão por um número decimal é explorada por meio da seguinte propriedade: se o dividendo e o divisor de uma divisão forem multiplicados ou divididos por um mesmo número diferente de zero, a divisão realizada com os valores resultantes terá o mesmo resultado da divisão com os números iniciais. É importante que os estudantes compreendam que essa propriedade é usada para transformar o divisor em um número natural.
b) 4,096 dividido por 1,6
Multiplicando o dividendo e o divisor por .1000, obtemos números naturais no dividendo e no divisor. A escolha de uma das potências de 10, no caso .1000, facilita a multiplicação na busca de números naturais no dividendo e no divisor.
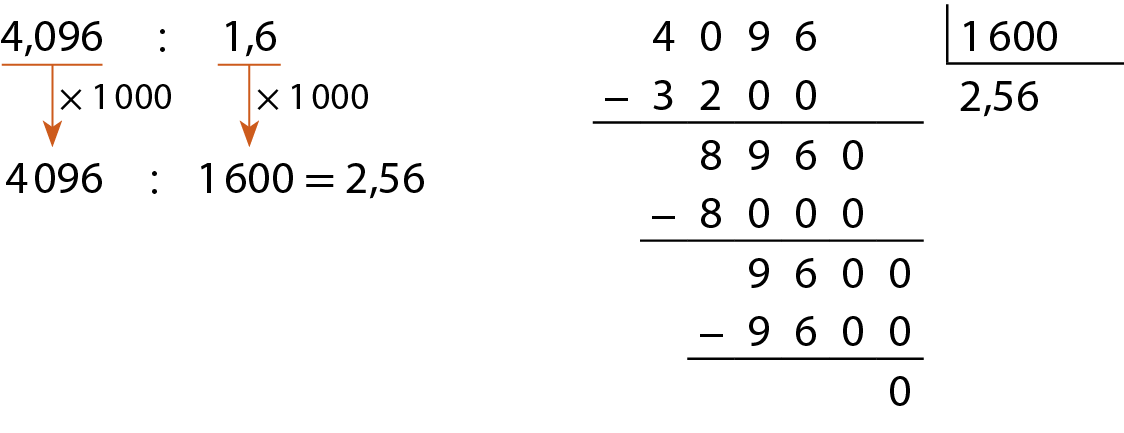
Logo, 4,096 dividido por 1,6 = 2,56.
Atividades
Faça as atividades no caderno.
39. Efetue as divisões.
a) 9,68 dividido por 4
b) 13,2 dividido por 12
c) 3 dividido por 60
d) 2,25 dividido por 1,5
e) 0,09 dividido por 0,008
f) 0,9 dividido por 0,6
g) 0,08 dividido por 0,002
h) 2,7 dividido por 0,54
i) 15,475 dividido por 1,25
j) 90,1 dividido por 2,5
• Responda: o quociente de dois números decimais pode ser um número natural?
40.

Investigue com a calculadora o que ocorre com os quocientes da divisão de um número decimal por 10, 100, .1000reticências
Agora, responda no caderno:
a) O que você observou nos resultados obtidos?
b) Você saberia calcular mentalmente 56,74 dividido por 100? Justifique sua resposta.
41.

Calcule mentalmente as divisões e depois registre o resultado no caderno.
a) 3,76 dividido por 10
b) 0,6 dividido por 100
c) 2 dividido por .1000
d) 152,4 dividido por 100
e) 5,6 dividido por 10
f ) 38,2 dividido por .1000
g) 90,6 dividido por .1000
h) 576,4 dividido por 100
42. Uma fábrica de laticínios produz diariamente 220 quilogramas de manteiga. Essa quantidade de manteiga permite formar quantas embalagens de 0,25 quilograma por dia?
43. Calcule as divisões e responda à pergunta.
a) 8 dividido por 0,1
b) 8 dividido por 0,01
c) 8 dividido por 0,001
• O que você observou?
44.

Usando uma calculadora, determine o resultado das divisões e registre-o no caderno.
a) 1,024 dividido por 0,032
b) 8 dividido por 0,004
45. Para fazer esta atividade, pesquise os valores atuais do euro e do dólar em relação ao real. No caderno, copie o quadro a seguir substituindo os

pelos dados coletados.

|
1 € (1 euro) |
R$ |
|---|---|
|
1 US$ (1 dólar) |
R$ |
Com base na sua pesquisa, responda:
a) Qual é o valor aproximado, em euro, de R$ 2.000,00dois mil reais?
b) Qual é o valor de quinhentos e cinquenta dólares em reais?
Respostas e comentários
39. a) 2,42
39. b) 1,1
39. c) 0,05
39. d) 1,5
39. e) 11,25
39. f) 1,5
39. g) 40
39. h) 5
39. i) 12,38
39. j) 36,04
39. sim
40. a) Espera-se que os estudantes observem que o quociente tem os mesmos algarismos do dividendo e a vírgula é deslocada para a esquerda tantas casas quantos forem os zeros do divisor.
40. b) 0,5674. Ao dividir por 100, a vírgula é deslocada duas casas para a esquerda.
41. a) 0,376
41. b) 0,006
41. c) 0,002
41. d) 1,524
41. e) 0,56
41. f) 0,0382
41. g) 0,0906
41. h) 5,764
42. oitocentas e oitenta embalagens
43. a) 80
43. b) 800
43. c) .8000
43. Resposta pessoal.
44. a) 32
44. b) .2000
45. Respostas de acôrdo com o valor atual do euro e do dólar.
• O objetivo da atividade 40 é mostrar o deslocamento da vírgula de acôrdo com a divisão de um número decimal por uma potência de 10.
• No item a, espera-se que os estudantes observem que o quociente tem os mesmos algarismos do dividendo e a vírgula é deslocada para a esquerda tantas casas quantos forem os zeros do divisor.
• No item b, a vírgula é deslocada duas casas para a esquerda. Como a vírgula não ficaria entre nenhum número, foi necessário colocar um zero do lado esquerdo dela. Questione os estudantes: “Se, em vez de o valor ser dividido por 100, fosse por .1000 ou .10000, como ele ficaria?”.
• Na atividade 45, oriente os estudantes a consultar o valor do dólar e do euro no câmbio turismo, e não no câmbio comercial.
• Caso questionem a diferença entre os dois câmbios, diga, de maneira simples, que o câmbio turismo é usado para viagens, por exemplo, e o câmbio comercial é usado em transações financeiras feitas pelo govêrno fóra do país ou na realização de importação e exportação de mercadorias, e que cotação é o preço pelo qual se negociam mercadorias e moedas estrangeiras.
• No item a, explique aos estudantes que o euro é a moeda oficial adotada em 19 dos 27 países-membros da União Europeia: Bélgica, Alemanha, Irlanda, Espanha, França, Itália, Luxemburgo, Países Baixos, Áustria, Portugal, Finlândia, Grécia, Eslovênia, Chipre, Malta, Eslováquia, Letônia, Lituânia e Estônia.
46. Roberta comprou um carro bicombustível. Inicialmente, ele rodou .1000 quilômetros utilizando apenas gasolina, que custava R$ 6,50seis reais e cinquenta centavos o litro. Depois, rodou mais .1000 quilômetros utilizando apenas etanol, que custava R$ 4,60quatro reais e sessenta centavos o litro. No total, Roberta gastou R$ 1.176,50mil cento e setenta e seis reais e cinquenta centavos em gasolina e R$ 975,20novecentos e setenta e cinco reais e vinte centavos em etanol.
Agora, responda:
a) Quantos litros ela utilizou de cada combustível?
b) Quantos quilômetros, aproximadamente, ela rodou com um litro de gasolina? E com um litro de etanol?
c) Quanto Roberta gastou, aproximadamente, para rodar 1 quilômetro com gasolina? E com etanol?
47. Uma lancha tem 15,656 metros de medida de comprimento. Uma miniatura dessa lancha tem medida de comprimento 15,2 vezes menor que a da lancha real. Qual é a medida do comprimento da miniatura?
48. Na primeira etapa do ano, Paulinho tirou as seguintes notas em Matemática: 3,0; 7,0; 6,0 e 5,0. Para calcular a média de Paulinho, o professor adicionou as 4 notas e dividiu a soma por 4. Qual é a média de Paulinho nessa etapa?
49. Lena vendeu 15 canetas por R$ 3,80três reais e oitenta centavos cada uma e mais 12 cadernetas, recebendo um total de R$ 109,80cento e nove reais e oitenta centavos. Qual é o preço de cada caderneta?
50.


Mônica utilizou uma calculadora e fez o seguinte cálculo:

Elabore um problema que possa ser resolvido utilizando a operação inversa da multiplicação que Mônica efetuou.
51.

Pense em dois números decimais e solicite a um colega que adicione, multiplique e divida o maior pelo menor. Verifique se seu colega fez os cálculos corretamente.

7 Decimais exatos e dízimas periódicas
Considere as seguintes divisões:
• 25 dividido por 4
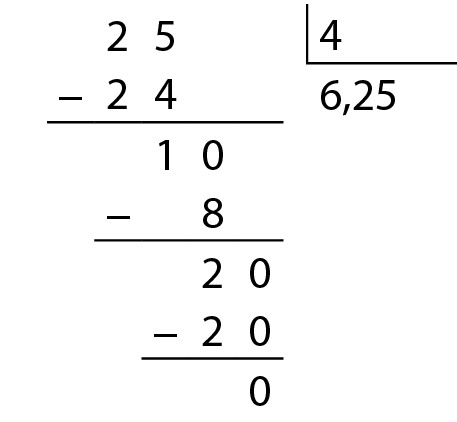
• 3,42 dividido por 0,5

As duas divisões têm quociente decimal e resto zero.
Os números 6,25 e 6,84 são exemplos de decimais exatos.
Mas há divisões com quociente decimal em que, por mais que continuemos a dividir, sempre sobrará resto diferente de zero. Analise, por exemplo, a divisão de 50 por 27:
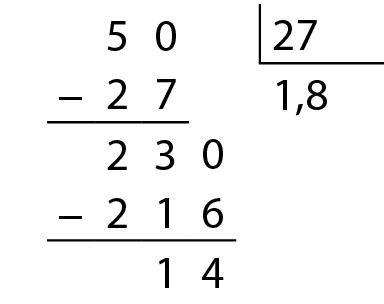
Respostas e comentários
46. a) gasolina: 181 litros; etanol: 212 litros
46. b) gasolina: 5,52 quilômetros por litro; etanol: 4,72 quilômetros por litro
46. c) gasolina: R$ 1,18um reais e dezoito centavos; etanol: R$ 0,97zero reais e noventa e sete centavos
47. 1,03 metro
48. 5,25
49. R$ 4,40quatro reais e quarenta centavos
50. Resposta pessoal.
51. Resposta pessoal. Exemplo de resposta: 3,5 e 0,7. A soma é 4,2; o produto é 2,45; o quociente é 5.
Decimais exatos e dízimas periódicas
Objetivo:
Classificar os números na fórma decimal em decimal exato ou dízima periódica.
Justificativa
Nos anos seguintes, ao estudar os números racionais, os estudantes terão a oportunidade de verificar que a representação decimal desses números é um decimal exato ou uma dízima periódica. Nesse âmbito, saber distinguir essas duas representações pode contribuir para a compreensão desse conjunto numérico.
Mapeando conhecimentos
Proponha aos estudantes que calculem 2 dividido por 5 e 2 dividido por 6. Depois, peça que comparem o quociente obtido nas duas divisões e verbalizem o que sabem. Espera-se que alguns estudantes reconheçam que o quociente de 2 dividido por 5 é um decimal exato e que o quociente de 2 dividido por 6 é uma dízima periódica.
Para as aulas iniciais
Escreva alguns decimais exatos e dízimas periódicas na lousa e desafie os estudantes a encontrar e determinar a divisão que tem como quociente esses números. Se houver oportunidade, distribua calculadoras para que façam algumas tentativas, incentivando-os, após o experimento, a estabelecer conjecturas.
Como não encontramos o resto zero, dizemos que 1,8 é um quociente aproximado até a casa dos décimos.
Continuando a divisão:
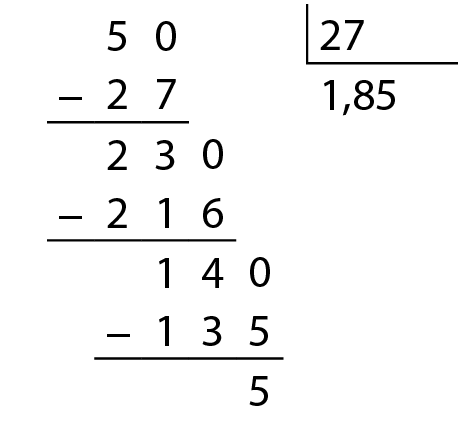
Como não encontramos o resto zero, dizemos que 1,85 é um quociente aproximado até a casa dos centésimos.
Continuando a divisão:
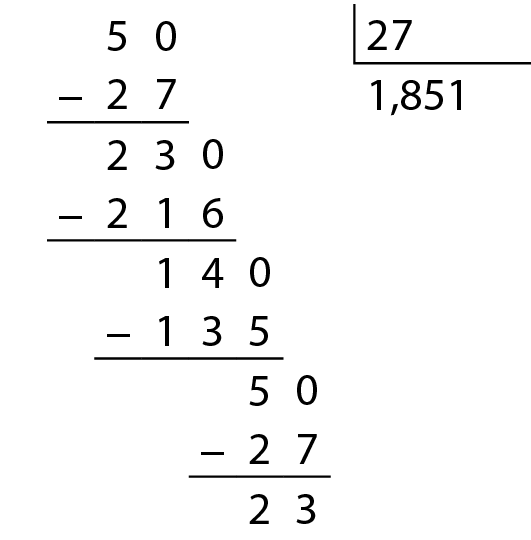
Como não encontramos o resto zero, dizemos que 1,851 é um quociente aproximado até a casa dos milésimos.
Se necessário, podemos continuar a divisão de 50 por 27, obtendo um quociente com maior número de casas decimais.
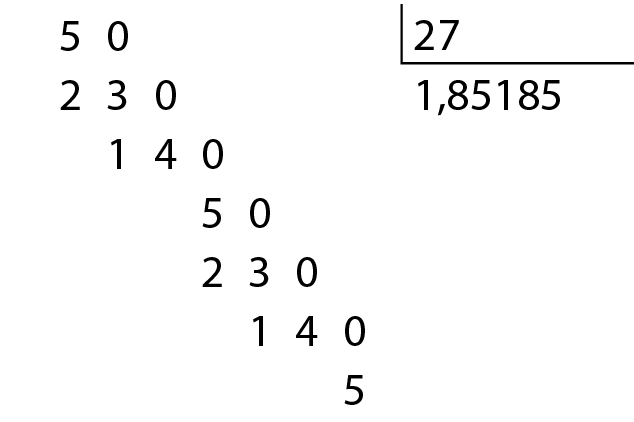
Considere, agora, as seguintes divisões:
• 2 dividido por 3
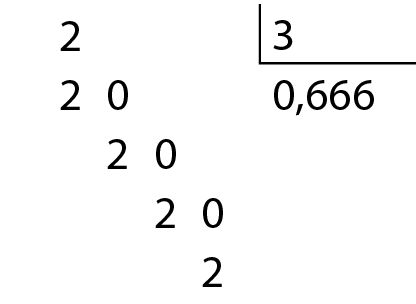
• 64 dividido por 99
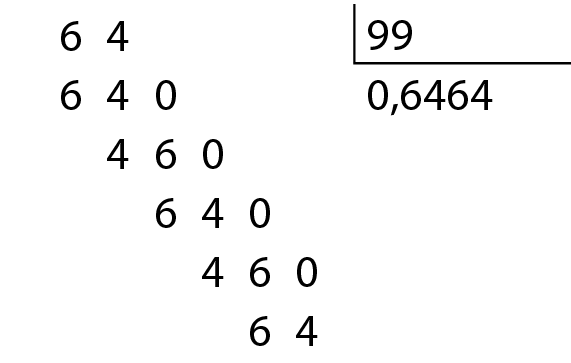
Mesmo que continuássemos indefinidamente, não chegaríamos ao resto zero.
Indicamos esse fato escrevendo 2 dividido por 3 = 0,666reticências e 64 dividido por 99 = 0,646464reticências
As reticências indicam que os números têm infinitas casas decimais.
Os números 0,666reticências e 0,646464reticências são exemplos de dízimas periódicas. Elas podem ser indicadas por
0,6 de período 6e
0,64 de período 64.
Chamamos o algarismo que se repete, ou o grupo de algarismos que se repete, de período.
O período da dízima periódica 0,666reticências é 6, o da 0,646464reticências é 64 e o da 1,851851851reticências é 851.
Respostas e comentários
Para melhor compreensão das representações de uma dízima periódica, escreva algumas na lousa (com o uso das reticências) e peça aos estudantes que escrevam no caderno outra maneira de representá-las. Espera-se que eles utilizem a representação com o traço acima dos algarismos que se repetem.
Atividades
Faça as atividades no caderno.
52. Efetue as divisões a seguir e responda à pergunta.
a) 2 dividido por 5
b) 3 dividido por 8
c) 5 dividido por 20
d) 9 dividido por 25
e) 5,6 dividido por 0,8
f) 64 dividido por 0,08
• Podemos afirmar que os quocientes encontrados são decimais exatos? Justifique sua resposta.
53. Calcule o quociente aproximado até a casa dos milésimos.
a) 19 dividido por 23
b) 40 dividido por 17
c) 50 dividido por 21
54.

Calcule e escreva no caderno o período de cada dízima periódica obtida.
a) 1 dividido por 3
b) 2 dividido por 11
c) 232 dividido por 45
d) .1540 dividido por 9
55. Faça tentativas para descobrir três novas divisões que tenham como quocientes dízimas periódicas com períodos de 1, 2 e 3 algarismos.
56. Faça o que se pede:
a)

Com o auxílio de uma calculadora, calcule 49 dividido por 13.
b)

O resultado obtido por você no item anterior é um decimal exato ou um quociente aproximado? Por quê? Converse com os colegas. O resultado obtido por você no item anterior é um decimal exato ou um quociente aproximado? Por quê? Converse com os colegas.
c)

Com o auxílio de uma calculadora, multiplique o resultado obtido no item a por 13. O que você pode concluir?

8 Expressões numéricas com números decimais
O cálculo de expressões numéricas envolvendo números decimais segue esta ordem:
1º) potenciações, na ordem em que aparecem;
2º) multiplicações e divisões, na ordem em que aparecem;
3º) adições e subtrações, na ordem em que aparecem.
Quando, nas expressões, aparecem sinais de associação, as operações que eles contêm devem ser resolvidas na ordem a seguir.
1º) parênteses ( ); 2º) colchetes [ ]; 3º) chaves { }.
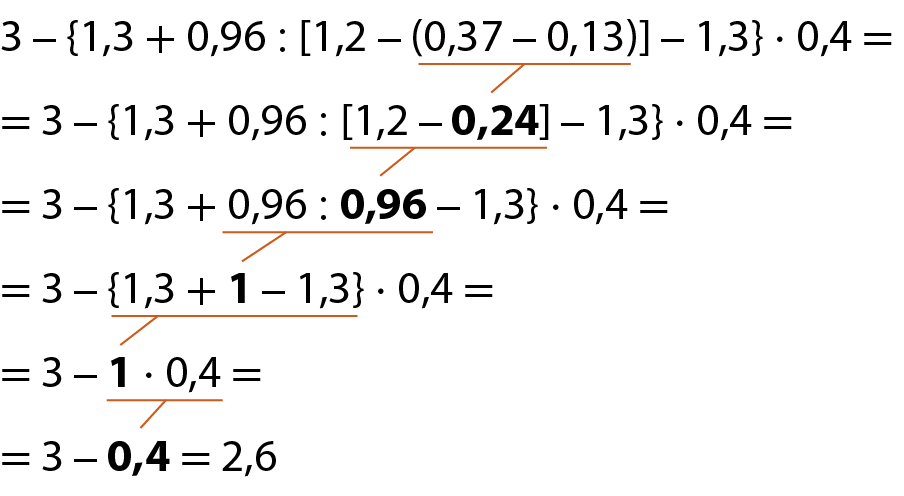
a)
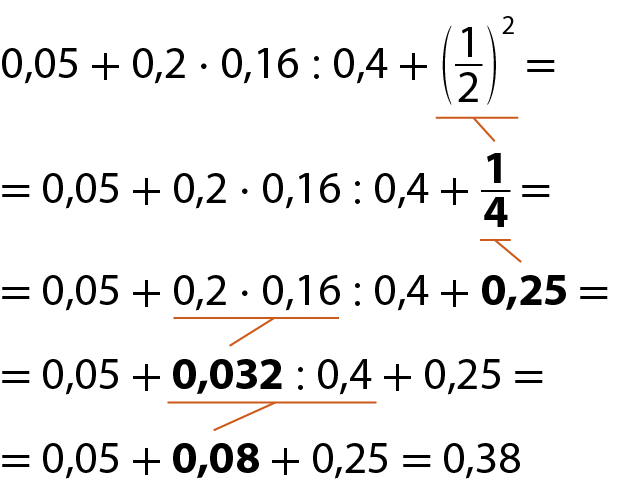
b)
Sugestão de leitura
RAMOS, Luzia Faraco. Aventura decimal. São Paulo: Ática, 2008. (Coleção A descoberta da Matemática).
Paulo, um craque de futebol, vai parar na Terra do Povo Pequeno e precisará de seus conhecimentos em números decimais. Nesse livro, você vai conhecer essa história e outras curiosidades matemáticas.
Respostas e comentários
52. a) 0,4
52. b) 0,375
52. c) 0,25
52. d) 0,36
52. e) 7
52. f) 800
52. Sim, pois as divisões têm resto zero.
53. a) 0,826
53. b) 2,352
53. c) 2,380
54. a) 0,333reticências ; período: 3
54. b) 0,1818reticências ; período: 18
54. c) 5,1555reticências ; período: 5
54. d) 171,111reticências ; período: 1
55. Resposta pessoal.
56. a) 3,7692307
56. b) Resposta pessoal.
56. c) Espera-se que os estudantes concluam que o número obtido no item a é um quociente aproximado, pois o resultado não é igual a 49.
Expressões numéricas com números decimais
BNCC:
Habilidade ê éfe zero seis ême ah um um.
Objetivo:
Calcular o valor de expressões numéricas envolvendo números decimais.
Justificativa
Inúmeros problemas podem ser traduzidos por meio de expressões numéricas. Nesse sentido, saber calcular o valor dessas expressões contribui para a resolução desses problemas e, consequentemente, favorece o desenvolvimento da habilidade ê éfe zero seis ême ah um um.
Mapeando conhecimentos
Organize a turma em grupos e, para cada grupo, proponha a resolução de um problema cuja solução demanda o cálculo do valor de uma expressão numérica envolvendo números na fórma decimal. Deixe os grupos à vontade para finalizar a tarefa. Depois, peça a cada grupo que eleja um representante para explicar aos demais como fizeram para resolver o problema proposto. Aproveite a oportunidade para observar se levaram em consideração os sinais de associação e se resolveram as expressões respeitando a ordem das operações.
Para as aulas iniciais
Recorde o cálculo de expressões numéricas envolvendo números naturais e números na fórma de fração. Depois, avance um pouco mais e explore o cálculo de algumas expressões numéricas simples, envolvendo números na fórma decimal.
(ê éfe zero seis ême ah um um) Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e a potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem uso de calculadora.
Atividades
Faça as atividades no caderno.
57. Calcule o valor das expressões numéricas.
a) 12,7 menos 3,88 ⋅ 0,5
b) 0,2 ⋅ 0,05 + 0,048
c) 2 menos 0,6 dividido por 4
d) 4,4 dividido por 0,01 menos 400
e) abre parênteses6,4 menos 1,25 ⋅ 4fecha parênteses dividido por 0,5
f) abre parênteses4 menos 1,6 ⋅ 0,2fecha parênteses dividido por 0,8
g) abre colchete0,35 menos abre parênteses0,18 ⋅ 0,2fecha parêntesesfecha colchete menos 0,03
h) abre parênteses2 menos 1,6fecha parênteseselevado a 2 + abre parênteses0,3 + 0,5fecha parênteseselevado a 2
i) abre parênteses5 menos 4,4fecha parênteseselevado a 3 dividido por abre parênteses0,1fecha parênteseselevado a 2
58.

Gabriela pensou e escreveu um número em seu caderno. Na linha seguinte, escreveu uma adição de dois números cuja soma era o número da linha anterior. Na linha seguinte, substituiu esses dois números, respectivamente, por uma multiplicação de outros três números e por uma divisão do quadrado de um número pelo dôbro de outro. Na linha seguinte, substituiu o primeiro número da linha anterior por uma subtração e o segundo por uma adição. Assim, ela obteve uma expressão numérica, sabendo antecipadamente seu valor.

Analise o que ela fez:
18,6 =
= 4,2 + 14,4 =
= 2 ⋅ 3 ⋅ 0,7 + 12elevado a 2 dividido por abre parênteses2 ⋅ 5fecha parênteses =
= abre parênteses10,31 menos 8,31fecha parênteses ⋅ abre parênteses2,6 + 0,4fecha parênteses ⋅ 0,7 + 12elevado a 2 dividido por abre parênteses2 ⋅ 5fecha parênteses
Agora, invente duas expressões com cinco operações diferentes e troque-as com as de um colega, sem que ele saiba o número em que você pensou inicialmente. Cada um deve resolver as expressões inventadas pelo outro. Depois, destroquem as expressões para corrigi-las.
59. Analise as ofertas do mercado onde Sandra vai comprar 3 litros de leite, 4 pacotes de biscoito, 3 copos de iogurte e
Um quarto.de quilograma de azeitona.

a) Se Sandra comprar 3 litros de leite, 3 pacotes de biscoito, 3 copos de iogurte e
Um quarto.de quilograma de azeitona, o valor da compra diminuirá?
b) Com R$ 25,00vinte e cinco reais, Sandra conseguirá fazer a compra?
c) Se o dinheiro não for suficiente, elimine uma unidade do produto mais barato e calcule o troco.
60. Dados a = abre parênteses1,2 dividido por 0,5fecha parênteseselevado a 2 e b = abre parênteses1,2 ⋅ 0,5fecha parênteseselevado a 2, calcule o valor de a + b.
61. Em uma distribuidora de bolas de pingue‑pongue há este quadro de preços:
|
Quantidade de bolas |
Preço |
|---|---|
|
Cinco dúzias |
R$ 237,00 |
|
Uma centena |
R$ 370,00 |
Ao optar pela compra de uma centena de bolas, quanto o consumidor economizaria, por unidade, em relação à compra de cinco dúzias do produto?
62.


Crie uma expressão numérica em que apareçam adições, subtrações, multiplicações e divisões e peça a um colega que a resolva. Verifique se o resultado está correto.
Respostas e comentários
57. a) 10,76
57. b) 0,058
57. c) 1,85
57. d) 40
57. e) 2,8
57. f) 4,6
57. g) 0,284
57. h) 0,8
57. i) 21,6
58. Resposta pessoal.
59. a) Sim, diminuirá o valor de 1 pacote de biscoito.
59. b) Não, o total é R$ 25,34vinte e cinco reais e trinta e quatro centavos.
59. c) Tirando um iogurte, o total fica R$ 23,50vinte e três reais e cinquenta centavos e o troco é R$ 1,50um reais e cinquenta centavos.
60. 6,12
61. R$ 0,25zero reais e vinte e cinco centavos
62. Resposta pessoal. Exemplo de resposta: 3,5 + abre parênteses3,2 ⋅ 0,5fecha parênteses + 2 ⋅ abre parênteses5,6 dividido por 2fecha parênteses menos 1,5 = 9,2
• Na atividade 58, caso considere conveniente, promova uma gincana com os estudantes utilizando a situação apresentada no enunciado da atividade.
• Na atividade 59, peça aos estudantes que, antes de responderem aos itens do exercício, montem uma expressão numérica com os dados apresentados no enunciado. Em seguida, peça que calculem o valor dos 4 pacotes de biscoito, substituindo o valor encontrado referente à compra dos pacotes de biscoito na expressão inicial para, então, resolvê-la.

Lendo e aprendendo

Brasil, planeta fome
Qualquer brasileiro que vá ao mercado com frequência percebe que está cada vez mais difícil fechar as compras do mês. Para os mais vulneráveis, porém, é impossível. Nos últimos meses, cenas de pessoas garimpando restos em um caminhão de lixo em Fortaleza, procurando ossos descartados no Rio de Janeiro e de um homem implorando por comida em Brasília chocaram o país. Segundo uma pesquisa da Rede Brasileira de Pesquisa em Soberania e Segurança Alimentar e Nutricional (Rede Penssan), 19 milhões de brasileiros passam fome e 55% da população apresenta algum nível de insegurança alimentar. A principal causa é a carestiaglossário dos alimentos: em outubro, a cesta básica aumentou em todas as localidades em comparação ao mesmo período do ano passado. Os dados são da Pesquisa Nacional da Cesta Básica de Alimentos, realizada mensalmente pelo Dieése (Departamento Intersindical de Estatística e Estudos Socioeconômicos) em dezessete capitais. Da cesta mais cara para a mais barata, são elas: Florianópolis, São Paulo, Porto Alegre, Rio de Janeiro, Vitória, Campo Grande, Brasília, Curitiba, Belo Horizonte, Goiânia, Fortaleza, Belém, Natal, João Pessoa, Salvador, Recife e Aracaju. Em outubro, os preços variaram de R$ 464,17quatrocentos e sessenta e quatro reais e dezessete centavos a R$ 700,69setecentos reais e sessenta e nove centavos nessas cidades. [reticências]
Em 2020, 19,1 milhões de pessoas passavam fome no Brasil ‒ isso representa 9% dos brasileiros. Além disso, o número é equivalente à população do Chile, que tem 19,6 milhões de habitantes. Mais de 43 milhões não tinham alimentos suficientes no mesmo período (ou seja, insegurança alimentarglossário moderada/grave).
A insegurança alimentar moderada/grave atingiu em maior proporção os domicílios que receberam o auxílio emergencialglossário em 20201nota de rodapé . De cada 10 casas que solicitaram e receberam o benefício, 3 estavam sob essa condição. Já entre os que não solicitaram, apenas 1.
Nos domicílios em que há moradores que perderam o emprêgo durante a pandemia, a fome foi maior. Em 2020, 34% desses domicílios estavam em situação de insegurança alimentar moderada/grave. Já entre os que continuaram com a jornada de trabalho normal, a fome atingiu parcela menor: 10%.
A parcela média do Auxílio Brasil, programa do govêrno que substituirá o Bolsa Família em 2022, não compra uma cesta básica em nenhuma das capitais listadas pelo estudo. A mais barata da lista, a de Aracaju, custa R$ 464,17quatrocentos e sessenta e quatro reais e dezessete centavos, o dôbro do benefício médio, que é de R$ 224,41duzentos e vinte e quatro reais e quarenta e um centavos. A mais cara, de Florianópolis, custa o triplo (R$ 700,69setecentos reais e sessenta e nove centavos). Em comparação a outubro de 2020, o preço da cesta básica subiu em todas as dezessete capitais que fazem parte do levantamento.


Respostas e comentários
Lendo e aprendendo
BNCC:
• Competência geral 7 (a descrição está na página seis).
• Competência específica 3 (a descrição está na página sete).
Objetivos:
• Desenvolver a competência leitora.
• Aplicar a ideia de parte de um todo das frações.
• Relacionar frações e porcentagens.
• Identificar e obter frações equivalentes.
• Calcular multiplicações com números decimais.
• Promover a reflexão sobre a importância do combate à fome e sobre o enfrentamento da alta dos preços dos alimentos.
Temas contemporâneos transversais:

O problema da fome no Brasil é o tema central do texto da seção. Comente com os estudantes que a fome sempre foi um problema grave no país, mas, com a Covid-19, a situação piorou muito em 2021. Faça a leitura coletiva do texto com a turma e a cada parágrafo discuta com eles os dados trazidos. Se possível, faça um paralelo com a situação vivida atualmente.
É importante enfatizar com a turma que a alimentação em quantidade e qualidade inadequada traz impactos na saúde, como enfraquecimento do corpo, prejuízos no desenvolvimento físico e mental e deixa as pessoas mais vulneráveis a doenças.
Caso seja possível, reproduza para a turma os infográficos disponíveis no site https://oeds.link/Pz3JYm (acesso em: 3 julho 2022). Dê um tempo para que analisem e compartilhem o que mais lhes chamou a atenção. Esses infográficos complementam o texto trabalhado na seção e mobilizam o que os estudantes viram sobre pictogramas. Como eles são convidados a argumentar com base em dados e informações confiáveis, a competência geral 7 tem o seu desenvolvimento favorecido. Além disso, eles precisam mobilizar conhecimentos dos campos da Aritmética e da Estatística para interpretar os dados, o que favorece o desenvolvimento da competência específica 3 da Bê êne cê cê.
No texto são mencionados, em diversos momentos, os diferentes graus de insegurança alimentar e, por esse motivo, convém esclarecê-los aos estudantes. Apresente a eles as seguintes definições, segundo o Instituto Brasileiro de Geografia e Estatística (í bê gê É):
• Insegurança alimentar leve: quando há preocupação ou incerteza quanto ao acesso aos alimentos no futuro ou quando a qualidade dos alimentos é comprometida para manter a quantidade de alimentos necessária para a família.
• Insegurança alimentar moderada: quando há redução quantitativa de alimentos entre os adultos e ou ou ruptura nos padrões de alimentação resultante da falta de alimentos.
Continua
Lendo e aprendendo
Em média, os moradores das 17 capitais listadas pelo estudo que ganham um salário mínimo gastaram 58,35% do valor líquido com a alimentação. O piso nacional é de R$ 1.100mil cem reais, e sobram R$ 1.017mil dezessete reais após os descontos da Previdência Social. Para garantir condições de sobrevivência básica em Florianópolis, onde a cesta é mais cara, o valor deveria ser [reticências]: R$ 5.886cinco mil oitocentos e oitenta e seis reais. O cálculo considera uma família de dois adultos e duas crianças.
Atualmente, R$ 100cem reais cobrem a compra de onze dos itens que formam uma cesta básica: 1 litro leite + 1 quilograma feijão + 1 quilograma arroz + 1 quilograma farinha + 1 quilograma batata + 1 quilograma tomate + 1 quilograma pão + 1 quilograma açúcar + 1 quilograma café + uma dúzia banana + 1 óleo. Em 2016, com o mesmo valor, era possível comprar tudo isso e + 1 quilograma carne.
O valor médio de 1 quilograma de carne quase triplicou nos últimos dez anos. Em 2011, o brasileiro precisava desembolsar R$ 15quinze reais para levar o produto para casa. Em outubro de 2021, a mesma quantidade do alimento custou, em média, R$ 40quarenta reais. O valor é 2,7 vezes maior que o de outubro de 2011.
Fontes: Dieése; Rede Penssan; Instituto Nacional de Estadísticas (Chile); govêrno Federal.

GORZIZA, A.; GUIMARÃES, H.; BUONO, R. Brasil, planeta fome. Piauí, 6 dezembro 2021.Disponível em: https://oeds.link/Pz3JYm. Acesso em: 28 abril 2022.
Atividades
1. Responda às questões no caderno.
a) Quando a matéria anterior foi publicada?
b) Segundo a Rede Penssan, quantos brasileiros aproximadamente passavam fome em dezembro de 2021?
c) Em qual capital a cesta básica era mais cara? E mais barata?
d) A cesta básica em Goiânia (Goiás) era mais cara ou mais barata do que em Campo Grande (Mato Grosso do Sul)?
2. Identifique o tema que não foi abordado no texto.
a) Alta do preço dos alimentos.
b) Insegurança alimentar.
c) Relação entre o valor do salário mínimo e o valor da cesta básica.
d) Relação entre desemprego e fome.
3. Leia o seguinte trecho extraído do texto.
[reticências] A mais barata da lista, a de Aracaju, custa R$ 464,17quatrocentos e sessenta e quatro reais e dezessete centavos, o dôbro do benefício médio, que é de R$ 224,41duzentos e vinte e quatro reais e quarenta e um centavos. A mais cara, de Florianópolis, custa o triplo (R$ 700,69setecentos reais e sessenta e nove centavos). [reticências]
Agora, responda no caderno:
a) Nesse trecho, há algumas imprecisões do ponto de vista matemático. Quais são elas?
b) Na sua opinião, essas imprecisões prejudicam o entendimento do texto? Por quê?
4.

Responda às questões no caderno. Depois, compartilhe as respostas com os colegas. Responda às questões no caderno. Depois, compartilhe as respostas com os colegas.
a) Você conhece alguma ação voltada para o combate à fome? Se sim, conte um pouco sobre ela.
b) Na sua opinião, o que é possível fazer para enfrentar a alta dos preços dos alimentos.
Respostas e comentários
1. a) No dia 6 de dezembro de 2021.
1. b) 19 milhões de brasileiros.
1. c) Florianópolis; Aracaju.
1. d) Mais barata.
2. alternativa c
3. a) Espera-se que os estudantes percebam que R$ 464,17quatrocentos e sessenta e quatro reais e dezessete centavos não é o dôbro de R$ 224,41duzentos e vinte e quatro reais e quarenta e um centavos e que R$ 700,69setecentos reais e sessenta e nove centavos não é o triplo de R$ 224,41duzentos e vinte e quatro reais e quarenta e um centavos.
3. b) Respostas pessoais.
4. a) Resposta pessoal.
4. b) Resposta pessoal.
Continuação
• Insegurança alimentar grave: quando há redução quantitativa de alimentos também entre as crianças, ou seja, ruptura nos padrões de alimentação resultante da falta de alimentos entre todos os moradores, incluindo as crianças. Nessa situação, a fome passa a ser uma experiência vivida no domicílio.
• Na atividade 1, os estudantes vão responder a algumas questões sobre o texto. Após terminarem, faça a correção coletiva. É possível ampliar a proposta da atividade e propor outras perguntas, como: “Quais são as fontes dos dados presentes no texto?”, “Qual era o valor do salário mínimo em dezembro de 2021?”, “A situação de insegurança alimentar moderada/grave era maior ou menor nas famílias em que moradores perderam o emprêgo?”, “Todas as capitais brasileiras fizeram parte do estudo descrito no texto?”. É possível também pedir aos estudantes que elaborem questões.
• A atividade 2 explora o reconhecimento dos assuntos tratados no texto. Ao fazer a correção, avalie cada uma das alternativas com os estudantes e incentive-os a identificar no texto os trechos em que os assuntos foram abordados.
• A atividade 3 leva os estudantes a perceber que nem sempre as informações publicadas na mídia são precisas do ponto de vista matemático, porém essa imprecisão nem sempre prejudica o entendimento do que está sendo publicado. Após fazerem os cálculos e constatarem que R$ 464,17quatrocentos e sessenta e quatro reais e dezessete centavos e R$ 700,69setecentos reais e sessenta e nove centavos não são o dôbro e o triplo, respectivamente, de R$ 224,41duzentos e vinte e quatro reais e quarenta e um centavos, peça que reescrevam o trecho para tornar a informação mais precisa. É possível ampliar a proposta desta atividade pedindo aos estudantes que identifiquem outras imprecisões do ponto de vista matemático no texto.
• A atividade 4 propõe duas questões aos estudantes. A primeira foca em ações de cidadania voltadas ao combate à fome. Os estudantes podem citar campanhas de doação de alimentos, ações como a de distribuições de marmitas ou cestas básicas, plantio de hortas comunitárias etcétera. A segunda está direcionada ao enfrentamento da alta dos preços dos alimentos. Espera-se que os estudantes apontem medidas como evitar o desperdício, realizar pesquisa de preços, planejar bem as compras da semana ou do mês etcétera. É importante reservar um momento para que todos tenham a oportunidade de compartilhar suas respostas.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Décimos, centésimos e milésimos
|
Parte inteira |
Parte decimal |
|||||
|---|---|---|---|---|---|---|
|
Centena |
Dezena |
Unidade |
Décimo |
Centésimo |
Milésimo |
|
|
1 |
, |
2 |
||||
|
1 |
8 |
, |
0 |
1 |
6 |
|
|
0 |
, |
1 |
5 |
7 |
||
Podemos ler esses números da seguinte maneira:
• 1,2

um inteiro e dois décimos.
• 18,016

dezoito inteiros e dezesseis milésimos.
• 0,157

cento e cinquenta e sete milésimos.
1. No caderno, escreva por extenso os números decimais.
a) 0,8
b) 1,510
c) 4,36
d) 2,95
e) 9,056
f) 0,007
2. Utilize algarismos para escrever cada um dos números decimais.
a) Dez inteiros e nove décimos.
b) Duzentos e trinta e dois milésimos.
c) Um inteiro e trinta e sete milésimos.
Comparação de números decimais
• Quando as partes inteiras são diferentes, o maior número é o que tem a maior parte inteira.
• Quando as partes inteiras são iguais, o maior número é o que tem a maior parte decimal.
• Na reta numérica, o maior número fica à direita.
3. Copie os itens no caderno substituindo os

pelos sinais < ou >.
a) 4,3

4,05
b) 5,04

5,14
c) 12,05

10,99
d) 25,09

25,10
e) 9,2

0,92
f) 12,19

12,20
4. Escreva os números decimais de cada item em ordem crescente.
a) 0,95; 0,48; 0,71; 0,19
b) 4,12; 4,5; 4,07; 4,29
c) 27,13; 15,06; 27,09; 18,15
d) 6,99; 0,198; 7,08; 1,9
5. Observe a reta numérica a seguir.

Relacione os pontos a, B, C e D aos números decimais a seguir.
um ‒ 1,78 dois ‒ 0,98 três ‒ 1,29 quatro ‒ 0,35
Adição e subtração com números decimais
Adição: 18,2 + 11,94
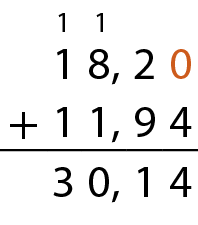
Subtração: 15,2 ‒ 12,01
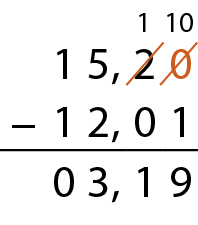
6. Calcule o resultado das operações.
a) 1,2 + 5,7
b) 25,43 + 2,08
c) 0,92 + 11,7
d) 0,12 + 11,08
e) 53,2 ‒ 18,1
f) 2,003 ‒ 1,12
g) 8,47 ‒ 4,03
h) 9,95 ‒ 9,07
7. Em uma loja de artigos esportivos, Marcos comprou uma mochila por R$ 178,90cento e setenta e oito reais e noventa centavos e um tênis por R$ 253,50duzentos e cinquenta e três reais e cinquenta centavos. Quanto Marcos gastou no total?
8. Joana gastou R$ 47,50quarenta e sete reais e cinquenta centavos no mercado. Ela entregou ao caixa três cédulas de R$ 20,00vinte reais. Qual foi o troco recebido por Joana?
Multiplicação com números decimais
Multiplicação: 5,14 ⋅ 2,5
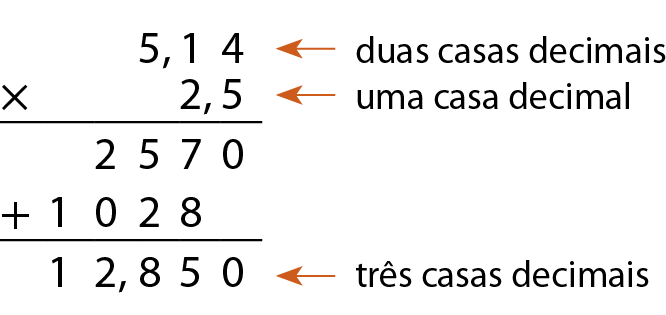
Respostas e comentários
1. a) exemplo de resposta: oito décimos
1. b) exemplo de resposta: um inteiro e quinhentos e dez milésimos
1. c) exemplo de resposta: quatro inteiros e trinta e seis centésimos
1. d) exemplo de resposta: dois inteiros e noventa e cinco centésimos
1. e) exemplo de resposta: nove inteiros e cinquenta e seis milésimos
1. f) exemplo de resposta: sete milésimos
2. a) 10,9
2. b) 0,232
2. c) 1,037
3. a) >
3. b) <
3. c) >
3. d) <
3. e) >
3. f) <
4. a) 0,19; 0,48 ; 0,71; 0,95
4. b) 4,07; 4,12; 4,29; 4,5
4. c) 15,06; 18,15; 27,09; 27,13
4. d) 0,198; 1,9; 6,99; 7,08
5. A ‒ quatro; B ‒ dois; C ‒ três e D ‒ um
6. a) 6,9
6. b) 27,51
6. c) 12,62
6. d) 11,2
6. e) 35,1
6. f) 0,883
6. g) 4,44
6. h) 0,88
7. R$ 432,40quatrocentos e trinta e dois reais e quarenta centavos
8. R$ 12,50doze reais e cinquenta centavos
Revisão dos conteúdos deste capítulo
Décimos, centésimos e milésimos
• Na atividade 1, oriente os estudantes a representar os números de cada item em um quadro de ordens antes que escrevam cada um por extenso.
• Caso os estudantes tenham dificuldades para fazer a atividade 2, incentive-os a utilizar o quadro de ordens como apôio.
Comparação de número decimais
• A atividade 3 propõe aos estudantes que comparem números decimais. Oriente-os a representar os números em um quadro de ordens ou a utilizar a reta numérica para que possam compará-los com mais facilidade.
• Se achar conveniente, faça a atividade 4 coletivamente. Pergunte aos estudantes como eles ordenariam os números de cada item. Na lousa, mostre como utilizar a reta numérica para realizar esta atividade.
• Na atividade 5, caso os estudantes apresentem dificuldade, oriente-os a escrever os números (um, dois, três e quatro) em ordem crescente, para depois relacioná-los aos pontos indicados na reta.
Adição e subtração com números decimais
• Na atividade 6, os estudantes vão adicionar e subtrair números decimais. Incentive-os a aplicar a ideia de que a adição e a subtração são operações inversas para conferirem os resultados obtidos.
• Para resolver o problema proposto na atividade 7, espera-se que os estudantes percebam que devem calcular R$ 178,90cento e setenta e oito reais e noventa centavos + R$ 253, 50duzentos e cinquenta e três reais e cinquenta centavos. Caso apresentem dificuldades, incentive o uso de cédulas e moedas de real fictícias.
• Para resolver o problema proposto na atividade 8, espera-se que os estudantes percebam que devem calcular R$ 60,00sessenta reais ‒ R$ 47, 50quarenta e sete reais e cinquenta centavos. Incentive-os a fazer esse cálculo mentalmente.
9. Efetue as multiplicações.
a) 5,4 ⋅ 3
b) 4,18 ⋅ 5
c) 0,5 ⋅ 2,36
d) 1,4 ⋅ 0,02
10. Calcule mentalmente o resultado de cada multiplicação.
a) 8,2 ⋅ 10
b) 6,19 ⋅ 10
c) 0,9 ⋅ 100
d) 18,1 ⋅ .1000
11. Luan vai trocar o piso do quintal da casa onde mora. Ele vai pagar R$ 78,50setenta e oito reais e cinquenta centavos em cada caixa de porcelanato. Se Luan vai precisar comprar no mínimo 15 caixas, quantos reais ele vai gastar somente com o porcelanato?
12. Rose vai fazer uma festa de aniversário para a filha dela. Ela vai comprar duas dúzias de garrafas de suco de laranja e uma dúzia de garrafas de suco de uva. Se cada garrafa de suco de laranja custa R$ 2,80dois reais e oitenta centavos e cada garrafa de suco de uva custa R$ 3,10três reais e dez centavos, quantos reais Rose vai gastar com suco?
Divisão com números decimais
Divisão: 12,6 : 0,12
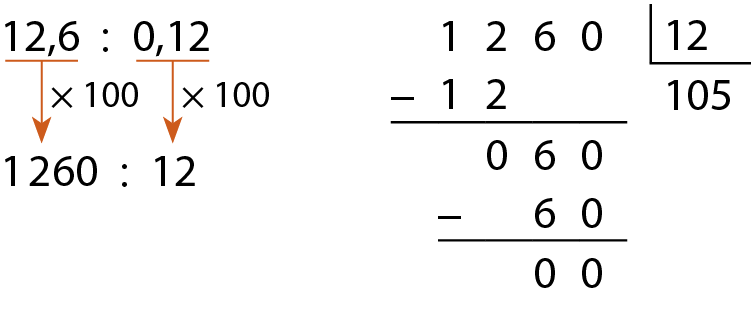
Logo, 12,6 : 0,12 = 105.
13. Efetue as divisões.
a) 9,1 : 2
b) 15,2 : 8
c) 0,85 : 0,5
d) 4,42 : 0,02
14. Calcule mentalmente o resultado de cada divisão.
a) 3,58 : 10
b) 26,8 : 10
c) 10,9 : 100
d) 507,1 : .1000
15. Ana comprou 5 metros de fita para fazer laços. Se cada laço usa 0,40 métro de comprimento de fita, quantos laços Ana conseguirá fazer?
16. Mariana comprou uma dúzia de laranjas e pagou R$ 4,80quatro reais e oitenta centavos. Quanto custou cada laranja?
17. Roberto usa ladrilhos coloridos com 0,0005 métro quadrado de medida de área para fazer mosaicos. Sabendo que o próximo mosaico dele medirá 2,5 métros quadrados de área, quantos ladrilhos coloridos serão utilizados?
Decimais exatos e dízimas periódicas
Quando a divisão tem quociente decimal e resto zero, os quocientes são chamados decimais exatos.
Quando a divisão tem quociente decimal e não encontramos resto zero, os quocientes são chamados dízimas periódicas. Podemos escrevê-los como um quociente aproximado para determinada ordem ou acompanhados de reticências (reticências) para indicar que têm infinitas casas decimais.
Nas dízimas periódicas, um algarismo, ou um grupo de algarismos, se repete; essa repetição é chamada de período.
18. Quais divisões têm como quociente um decimal exato?
a) 18 : 5
b) 95 : 12
c) 99 : 8
d) 120 : 15
19. Calcule o quociente aproximado até a casa dos milésimos.
a) 40 : 13
b) 50 : 12
c) 98 : 15
d) 110 : 19
20. Calcule e escreva no caderno o período de cada dízima periódica obtida.
a) 1 : 9
b) 37 : 30
c) 4 : 33
d) 400 : 9
Expressões numéricas com números decimais
O cálculo de expressões numéricas envolvendo números decimais segue esta ordem:
1º) potenciações, na ordem em que aparecem;
2º) multiplicações e divisões, na ordem em que aparecem;
3º) adições e subtrações, na ordem em que aparecem.
Quando aparecem sinais de associação, as operações que eles contêm devem ser resolvidas na seguinte ordem:
1º) parênteses ( ); 2º) colchetes [ ]; 3º) chaves { }.
21. Calcule o valor das expressões.
a) 45,2 ‒ 5,8 ⋅ 5 + 0,18
b) 18,2 + 25,09 ‒ 1,2 ⋅ 4,2
c) (1,32 : 4) ⋅ 1,5 + (3,2)2 ‒ 0,078
d) {5,25 + 10,5 : 2} + 25,5 ‒ [4,5 ⋅ (2)3]
Respostas e comentários
9. a) 16,2
9. b) 20,9
9. c) 1,18
9. d) 0,028
10. a) 82
10. b) 61,9
10. c) 90
10. d) .18100
11. R$ 1.177,50mil cento e setenta e sete reais e cinquenta centavos
12. R$ 104,40cento e quatro reais e quarenta centavos
13. a) 4,55
13. b) 1,9
13. c) 1,7
13. d) 221
14. a) 0,358
14. b) 2,68
14. c) 0,109
14. d) 0,5071
15. 12 laços
16. R$ 0,40zero reais e quarenta centavos
17. .5000 ladrilhos coloridos
18. itens: a, c e d
19. a) 3,076
19. b) 4,166
19. c) 6,533
19. d) 5,789
20. a) 0,111reticências; período: 1
20. b) 1,2333reticências; período: 3
20. c) 0,1212reticências; período: 12
20. d) 44,444reticências; período: 4
21. a) 16,38
21. b) 38,25
21. c) 10,657
21. d) 0
Multiplicação com números decimais
• Para efetuar as multiplicações propostas na atividade 9, os estudantes podem transformar os números decimais em frações ou aplicar o algoritmo usual. Incentive-os a utilizar as duas estratégias.
• Para resolver o problema proposta na atividade 11, espera-se que os estudantes reconheçam que devem calcular 15 ⋅ R$ 78,50setenta e oito reais e cinquenta centavos.
• Na atividade 12, os estudantes devem realizar o seguinte cálculo para resolver o problema proposto:
24 ⋅ R$ 2,80dois reais e oitenta centavos + 12 ⋅ R$ 3,10três reais e dez centavos
Divisão com números decimais
• Nas atividades 13 e 14, oriente-os a utilizar a multiplicação para conferirem os resultados obtidos nas divisões.
Decimais exatos e dízimas periódicas
A título de curiosidade, comente com os estudantes que, além dos números decimais exatos e das dízimas periódicas, também existem os números irracionais, que eles aprenderão mais adiante, e que apresentam infinitas casas decimais sem a repetição de um período.
Expressões numéricas com números decimais
Comente com os estudantes que, embora estejam operando com números decimais, a hierarquia das operações e a prioridade dos cálculos são as mesmas que eles já aplicavam ao calcular expressões numéricas com números inteiros.
• Faça a correção coletiva da atividade 21 na lousa. Se achar necessário, convide alguns estudantes para que mostrem como calcularam o valor das expressões numéricas de alguns itens.
É hora de extrapolar

Faça as atividades no caderno.
Você conhece a agenda 2030 para o desenvolvimento sustentável?
Os cartazes são bastante utilizados em campanhas de conscientização para informar à população diferentes assuntos, como vacinação para combater epidemias, uso consciente de água e energia elétrica para evitar desperdício e preservação dos recursos naturais.
Em 2015, a Organização das Nações Unidas (ônu) estabeleceu um plano de ação, chamado Agenda 2030, para o desenvolvimento sustentável em suas três dimensões: econômica, social e ambiental. O documento propõe 17 Objetivos de Desenvolvimento Sustentável (ó dê ésse), que devem ser alcançados até 2030.

Objetivos: Pesquisar os 17 ó dê ésse da Agenda 2030 estabelecida pela ônu e construir cartazes com informações relevantes, tratadas na Agenda 2030, que serão expostos na escola para os estudantes e também para toda a comunidade escolar.

Etapa 1: Análise do cartaz que apresenta os 17 ó dê ésse da Agenda 2030 da ônu.
1. Reúna-se em grupo com os colegas, leiam o cartaz anterior e respondam às questões.
a) Quais são os elementos que se repetem em cada quadrado colorido?
b) Que ícone é usado para representar a mensagem “vida terrestre”?
c) O ícone que apresenta um caderno e um lápis está associado a qual frase?
d) Em qual objetivo aparece a palavra “desigualdades”? Qual símbolo matemático foi usado no ícone?
e) Vocês acham que os ícones representam bem as frases de cada quadrado?
f) Qual dos objetivos apresentados no cartaz vocês acham mais importante? Por quê?
g) Vocês modificariam a informação apresentada em algum quadrado? Por quê?
2. Pesquisem o significado da expressão “desenvolvimento sustentável”.
3. Escolham um dos objetivos apresentados no cartaz e criem outro ícone para substituir o que já existe. Lembrem que o ícone deve ser legível e estar relacionado à frase do objetivo escolhido.
4. Agora, escolham outro objetivo e criem uma nova frase para substituir a existente.
5. Na abertura desta Unidade, foi dito que a cidade de Morungaba, no interior de São Paulo, atingiu cêrca de
três quartosda medida da distância para o desempenho ótimo nos ó dê ésse. O que isso quer dizer?
Respostas e comentários
1. a) número, frase e ícone
1. b) uma árvore e três pássaros
1. c) educação de qualidade
1.d) redução das desigualdades; sinal de igual
1. e) Resposta pessoal.
1. f) Respostas pessoais.
1. g) Respostas pessoais.
2. Segundo o dicionário Uáis, desenvolvimento sustentável é: “desenvolvimento econômico planejado com base na utilização de recursos e na implantação de atividades industriais, de fórma a não esgotar ou degradar os recursos naturais; ecodesenvolvimento”.
3. Resposta pessoal.
4. Resposta pessoal.
5. Espera-se que os estudantes respondam que isso quer dizer que a cidade atingiu 3 das 4 partes da medida da distância para alcançar o desempenho ótimo.
É hora de extrapolar
BNCC:
• Competências gerais 2, 4, 7, 9 e 10 (as descrições estão na página seis).
• Competências específicas 2, 4, 5, 6, 7 e 8 (as descrições estão na página sete).
Tema contemporâneo transversal:

Essa seção retoma as questões propostas na abertura da Unidade, propondo o seu fechamento por meio de um trabalho colaborativo que explora a pesquisa, a comunicação e a elaboração de um produto final (um cartaz, nesse caso), que será compartilhado com a turma e com a comunidade escolar.
Com a finalidade de organizar o trabalho, a seção é dividida em etapas que promovem:
• Entendimento do contexto e dos objetivos do trabalho a ser realizado.
• Pesquisa individual ou coletiva.
• Elaboração, em grupo, do produto proposto.
• Apresentação e exposição do produto.
• Reflexão e síntese do trabalho.
As etapas de pesquisa e elaboração do produto podem ser realizadas extraclasse. Verifique o perfil dos estudantes e oriente-os com relação ao prazo, aos materiais e a outros aspectos necessários à realização do trabalho.
A seção também favorece o desenvolvimento das competências gerais 2, 4, 7, 9 e 10 e das competências específicas de Matemática 2, 4, 5, 6, 7 e 8, procurando mobilizar conteúdos estudados nos capítulos que integram a Unidade. Portanto, é recomendável trabalhar a seção depois de estudar os capítulos, mas, se preferir trabalhar as etapas da seção à medida que os capítulos forem estudados, atente para os conhecimentos prévios necessários.
Antes de iniciar o trabalho com a seção, faça um levantamento das opiniões dos estudantes sobre temas como direitos humanos, exploração da natureza, desigualdade social, aquecimento global, animais em extinção, racionamento de água, entre outros. Peça que digam o que eles entendem de cada tema e como esses temas influenciam nossas vidas, se positiva ou negativamente; caso seja negativamente, pergunte-lhes o que podemos fazer para reverter a situação. Poderá haver divergências de opiniões; caso isso ocorra, promova o respeito à opinião do outro.
• A atividade 5 da etapa 1 retoma um dos questionamentos feitos na abertura desta Unidade. Espera-se que os estudantes respondam que a cidade de Morungaba (São Paulo) atingiu 3 das 4 partes da medida da distância para alcançar o desempenho ótimo. Caso tenham demonstrado alguma dificuldade, represente na lousa, por meio de uma figura, o desempenho alcançado pela cidade.

Etapa 2: Pesquisa e análise de alguns ó dê ésse.
6. Naveguem pelo site da ônu e encontrem os 17 ó dê ésse.
7. No item 3.1 do objetivo 3, está escrito: “reduzir a taxa de mortalidade materna global para menos de 70 mortes por .100000 nascidos vivos”.
a) Representem com uma fração a expressão “70 mortes por .100000 nascidos vivos”.
b) Representem a mesma expressão com um número decimal.
8. No item 3.2 do objetivo 3, está escrito: “acabar com as mortes evitáveis de recém-nascidos e crianças menores de 5 anos, com todos os países objetivando reduzir a mortalidade neonatal para pelo menos 12 por .1000 nascidos vivos e a mortalidade de crianças menores de 5 anos para pelo menos 25 por .1000 nascidos vivos”.
a) No trecho, qual expressão representa uma ideia de desigualdade?
b) Quais expressões podem ser representadas por frações?
9. No item 10.1 do objetivo 10, está escrito: “alcançar e sustentar o crescimento da renda dos 40% da população mais pobre a uma taxa maior que a média nacional”. Reescrevam a frase substituindo a porcentagem apresentada por uma fração correspondente.
10. O item 14.5 do objetivo 14 diz “conservar pelo menos 10% das zonas costeiras e marinhas, de acôrdo com a legislação nacional e internacional, e com base na melhor informação científica disponível”. Expliquem o significado da expressão “pelo menos 10%”.


Etapa 3: Escolha de um ó dê ésse e elaboração de cartazes.
11. Leiam o texto do item 6.3 do objetivo 6 e respondam às questões.
“melhorar a qualidade da água, reduzindo a poluição, eliminando despejo e minimizando a liberação de produtos químicos e materiais perigosos, reduzindo à metade a proporção de águas residuais não tratadas e aumentando substancialmente a reciclagem e reutilização segura globalmente”.
a) O que vocês, em conjunto, podem fazer para contribuir com esse objetivo? E o que podem fazer, individualmente, como cidadãos conscientes?
b) Que tipo de ação vocês podem executar em casa? E na escola em que estudam? E no bairro em que moram ou onde a escola está inserida?
12. Escolham um ó dê ésse para estudar mais a fundo e reflitam sobre as questões da atividade anterior.
13. Agora, elaborem cartazes com informações de alguns itens do ó dê ésse escolhido e com propostas de ações para serem realizadas individualmente ou em conjunto. Representem os dados com frações, porcentagens e números decimais quando for conveniente. Vocês podem complementar os cartazes com notícias de jornais e revistas relacionadas ao tema do ó dê ésse. Não se esqueçam de buscar fontes confiáveis e citá-las nos cartazes.


Etapa 4: Apresentação e análise dos cartazes.
14. Disponibilizem os cartazes criados pelo grupo para que os outros analisem e opinem sobre a clareza das informações e as ações propostas.
15. Anotem as dúvidas, as opiniões e as sugestões dos colegas.
16. Depois dos ajustes necessários, façam uma exposição na escola distribuindo os cartazes pelas paredes.


Etapa 5: Síntese do trabalho realizado.
17. Algumas questões que devem ser discutidas:
a) Os cartazes atenderam os objetivos propostos?
b) É possível atingir mais pessoas da escola ou da comunidade? Como?
18. Com base na reflexão sobre as questões anteriores, tentem atingir mais pessoas com os cartazes.
19. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.
Respostas e comentários
7. a)
Setenta sobre cem mil, ou sete sobre dez mil.7. b) 0,0007
8. a) “crianças menores de 5 anos”
8. b) “12 por .1000” e “25 por .1000”
9. “alcançar e sustentar o crescimento da renda dos
40 centésimosda população mais pobre a uma taxa maior que a média nacional”
10. Espera-se que os estudantes percebam que “pelo menos 10%” significa que pode ser exatamente 10% ou mais que 10%; portanto, a conservação deve ser “maior ou igual a 10%”.
11. Respostas pessoais.
12. Resposta pessoal.
13. Comentários em Orientações.
Etapa 4: Comentários em Orientações.
17. Respostas pessoais.
18. Comentários em Orientações.
19. Resposta pessoal.
Essa atividade poderá ser realizada com o auxílio dos professores de Geografia, Língua Portuguesa e Arte.
Se possível, divida a turma de fórma que todos os 17 objetivos de desenvolvimento sustentável sejam analisados na etapa 2.
Na etapa 3, para a elaboração do cartaz, peça aos estudantes que utilizem materiais recicláveis, reutilizando-os o máximo que conseguirem, para promover a ideia de sustentabilidade.
• Na atividade 13, se os estudantes optarem por incluir notícias de jornais ou revistas, oriente-os sobre a importância de checar a veracidade das informações e da confiabilidade da fonte.
Na etapa 4, peça a cada grupo que exponha seu cartaz para a turma. Após a exposição, oriente os demais estudantes a questionar o grupo sobre os materiais utilizados, o ícone, entre outros aspectos.
• Na atividade 18, promova uma roda de conversa para que os estudantes discutam e definam quais estratégias serão empregadas para a maior divulgação do trabalho realizado.
Glossário
- Carestia
- : preço elevado.
- Voltar para o texto
- Insegurança alimentar
- : quando há preocupação ou incerteza quanto ao acesso aos alimentos no futuro ou quando a qualidade dos alimentos é comprometida para manter a quantidade de alimentos necessária para a família.
- Voltar para o texto
- Auxílio emergencial
- : benefício financeiro concedido pelo Governo Federal às pessoas mais vulneráveis durante a pandemia de côvid dezenóve.
- Voltar para o texto
- 1
- Nota metodológica: a pesquisa foi realizada quando o auxílio emergencial estava no seu quarto mês de redução à metade do valor inicial, ou seja, com a parcela de R$ 300trezentos reais para a maioria.
- Voltar para o texto