Página 141

Capítulo 6 Linguagem algébrica e regularidades

Trocando ideias

A sequência de fibonáti tem origem em um problema proposto pelo matemático Leonardo de Pisa, conhecido como fibonáti, no livro Liber abaci, de 1202, sobre o crescimento de uma população de coelhos. Observe esta sequência:

(1, 1, 2, 3, 5, 8, 13, reticências)

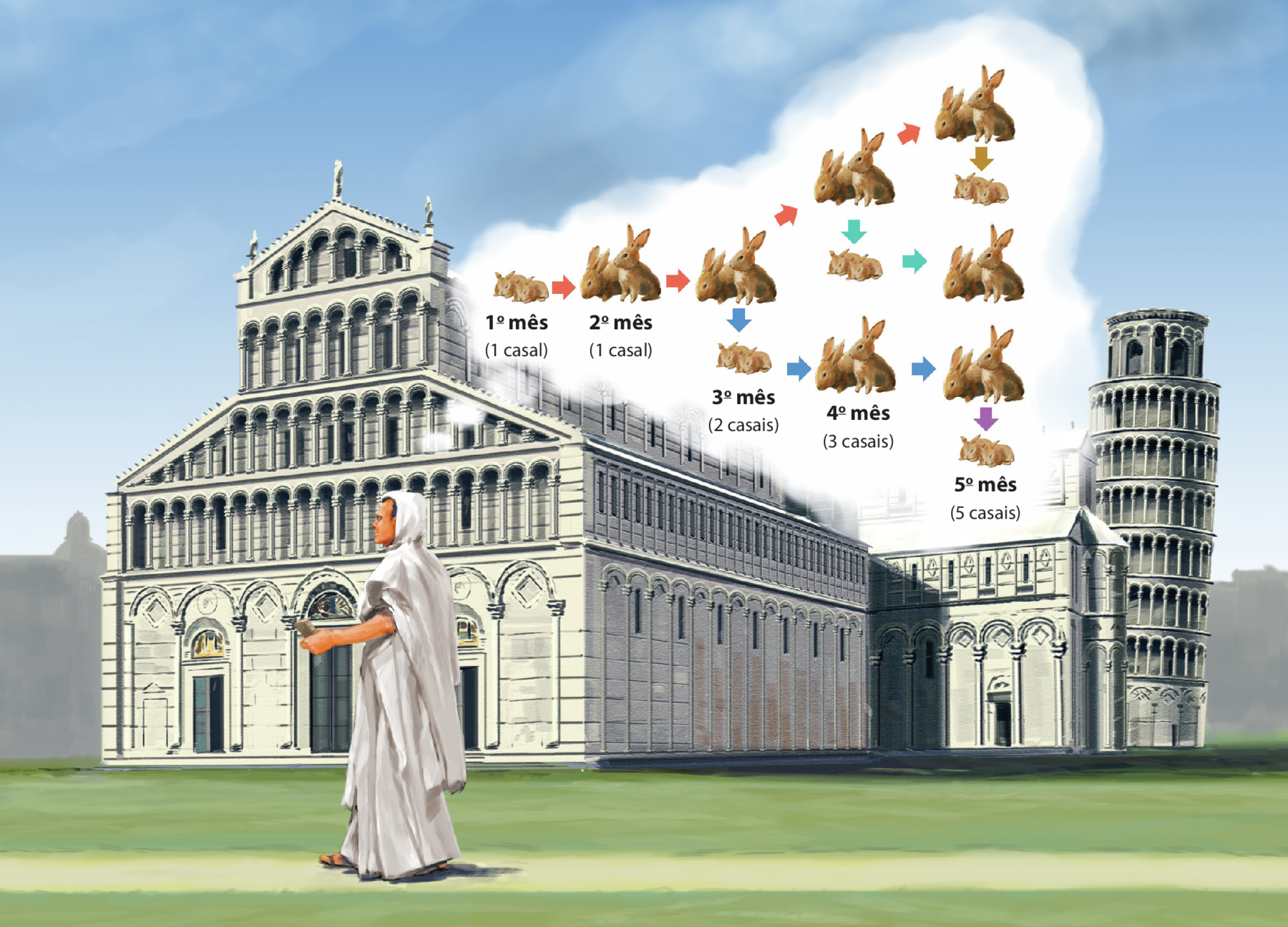
Ilustração. Homem vestido com uma túnica branca caminhando em um gramado próximo a uma catedral, enquanto pensa em um esquema com coelhos. O esquema é composto por coelhos marrons e está organizado da esquerda para a direita.

No início do esquema, é representado o primeiro mês com apenas um casal de coelhos.
No segundo mês, há uma seta vermelha apontando para o mesmo casal de coelhos, indicando que não houve aumento no número de coelhos.
No terceiro mês, há uma seta vermelha apontando para o mesmo casal de coelhos e uma seta azul para baixo apontando para outro casal de coelhos, indicando agora dois casais de coelhos.
No quarto mês, há uma seta vermelha apontando para um casal de coelhos, há uma seta verde apontando para um novo casal e uma seta azul apontando para o mesmo casal, indicando agora três casais de coelhos.
No quinto mês, na parte superior do esquema há uma seta vermelha apontando para o mesmo casal de coelhos e uma seta amarela para baixo apontando para um novo casal de coelhos. No meio do esquema, há uma seta verde apontando para o mesmo casal de coelhos. Na parte inferior do esquema, há uma seta azul apontando para o mesmo casal de coelhos e abaixo uma seta roxa apontando para outro casal de coelhos. No total, aparecem cinco casais de coelhos. — Ilustração artística, em cores-fantasia, que representa fibonáti caminhando próximo à catedral de Pisa, na Itália, pensando a respeito do problema dos coelhos.

O problema que originou a sequência foi o seguinte: “Supondo que um casal de coelhos só se reproduzirá pela primeira vez depois de 2 meses do seu nascimento e gerará um casal de filhotes por mês, quantos casais vão existir ao final de 12 meses?”.

▸ Qual é o próximo número dessa sequência? E o número depois dele? Escreva em seu caderno.

▸

Explique para os colegas como você descobriu os números anteriores.

Neste capítulo, vamos estudar a linguagem algébrica e as sequências numéricas.

Página 142

1 Expressões algébricas

Neste polígono, as medidas de comprimento dos lados foram indicadas por x, y, z e m. Podemos representar a medida do perímetro desse polígono pela expressão:

x + x + y + z + m

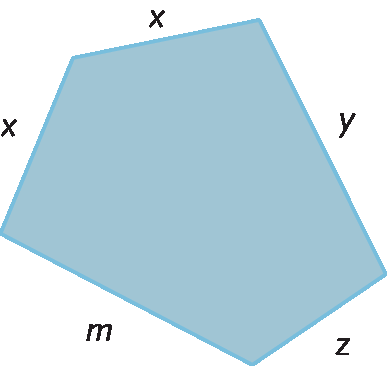
Figura geométrica. Polígono azul de seis lados diferentes. À esquerda da figura, há dois lados com comprimento X cada um, enquanto do lado direito há um lado com comprimento Z. Na parte superior, há um lado com comprimento Y, enquanto na parte inferior há um lado com comprimento M.

Uma expressão matemática formada por números e letras ou somente por letras é chamada de expressão algébrica.

Veja como podemos representar algumas situações utilizando expressões algébricas.

Situação 1

O tabuleiro de xadrez tem o formato de um quadrado, dividido em 64 quadradinhos menores. Nesta figura, a medida de comprimento dos lados do tabuleiro está indicada pela letra a.

Esquema. Tabuleiro de xadrez, à esquerda peças brancas e à direita, peças pretas. Há uma cota na parte inferior indicando que seu comprimento mede a e outra na parte lateral esquerda indicando que sua altura mede a. — O xadrez é um jogo de tabuleiro para duas pessoas. Pode ser jogado tanto por lazer quanto em competições.

A medida da área desse tabuleiro pode ser representada pela seguinte expressão algébrica:

a ⋅ a ou aelevado a 2

Situação 2

Um quintal de formato retangular tem lados de medidas b e c de comprimento. Em seu interior, há uma região gramada de formato quadrado com lados cujo comprimento mede a, conforme mostra a figura a seguir.

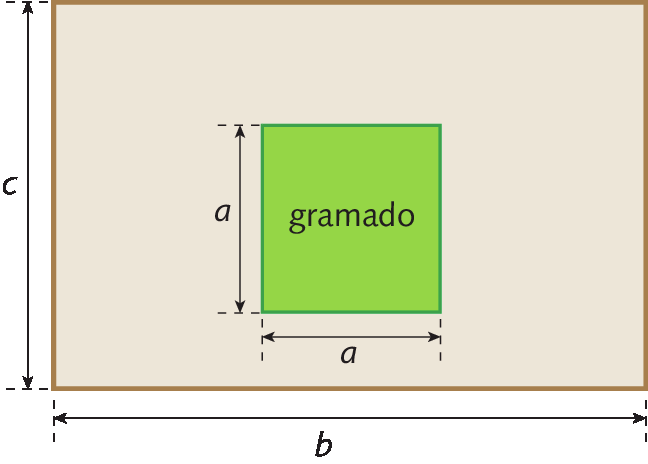
Esquema. Um retângulo na horizontal representa o quintal, com uma cota na parte inferior indicando que seu comprimento mede B e outra na parte lateral esquerda indicando que sua altura mede C. No centro do retângulo há um quadrado verde, representando a área gramada, com uma cota na parte inferior indicando que seu comprimento mede A e outra na parte lateral esquerda indicando que sua altura mede A.

Para determinar a medida da área do piso desse quintal abre parêntesesem begefecha parênteses, podemos subtrair da medida da área total do quintal a medida da área do gramado. Observe:

• A medida da área total do quintal é representada por:

b ⋅ c ou bc

• A medida da área do gramado é representada por:

a ⋅ a ou aelevado a 2

Assim, podemos representar a medida da área desse piso pela seguinte expressão algébrica:

b ⋅ c menos a ⋅ a ou bc menos aelevado a 2

Página 143

Atividades

Faça as atividades no caderno.

1. Em seu caderno, escreva a expressão algébrica correspondente a cada item.

a) O triplo de um número.

b) O quíntuplo de um número.

c) A metade de um número.

d) A quarta parte de um número.

e) Dois quintos de um número.

f) A diferença entre um número e sua terça parte.

g) A soma do dobro de um número com sua metade.

h) A soma de três números consecutivos.

2. Na figura a seguir, a medida de comprimento m é equivalente a 3x.

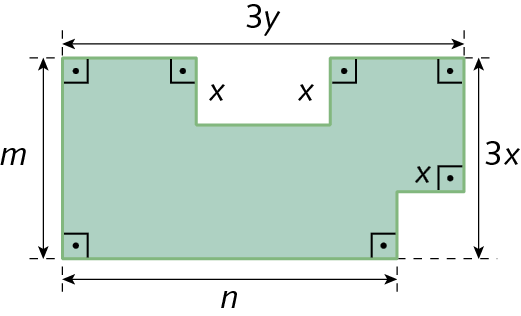
Esquema. Figura geométrica horizontal com ângulos internos retos de 90 graus identificados. À direita, há uma cota indicando que o comprimento mede 3X e à mesma altura, à esquerda, outra cota indicando que o comprimento mede M. Na parte superior, há uma cota indicando que o comprimento total mede 3Y e outra cota indicando que o comprimento mede N, há uma linha tracejada de comprimento x até o comprimento total.

A medida de comprimento n pode ser escrita com base em x e y. Usando essas medidas, escreva uma expressão algébrica que represente n.

3. Um prédio tem nove andares com três janelas em cada andar. Todas as janelas têm um único vidro com medida de comprimento a e medida de largura b. Escreva a expressão algébrica que representa a medida da área total envidraçada de cada andar.

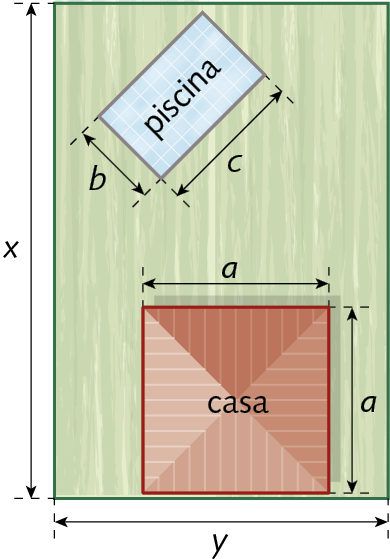
4. Observe a representação de um terreno retangular com casa, piscina e gramado.

Represente no caderno, usando expressões algébricas, a medida da área total do terreno, da casa, da piscina e do gramado.

Ilustração. Um retângulo na vertical representa o terreno de uma casa com gramado e piscina. No retângulo gramado, há uma cota na parte inferior indicando que seu comprimento mede Y e outra na parte lateral direita indicando que sua altura mede X.

Na parte inferior há um telhado no formato de quadrado, com uma cota na parte superior indicando que seu comprimento mede A e outra na parte lateral direita indicando que sua altura mede A.

Na parte superior há uma piscina no formato de um retângulo, com uma cota na parte inferior indicando que seu comprimento mede B e outra na parte lateral direita indicando que sua altura mede C.

Valor numérico de uma expressão algébrica

Em expressões algébricas, as letras são chamadas de variáveis. Isso significa que o valor de cada letra pode ser substituído por um valor numérico.

Por exemplo, vamos considerar a expressão algébrica 3x + 2y + a.

• Se considerarmos que x = 5, y = 3 e a = 2, poderemos determinar o valor da expressão algébrica substituindo as variáveis x, y e a por 5, 3 e 2, respectivamente. Assim:

3x + 2y + a = 3 ⋅ 5 + 2 ⋅ 3 + 2 = 23

Para esses números, o valor numérico da expressão algébrica 3x + 2y + a é igual a 23.

• Se considerarmos que x = 1, y = 2 e a = 0, qual será o valor dessa expressão algébrica?

3x + 2y + a = 3 ⋅ 1 + 2 ⋅ 2 + 0 = 7

Neste caso, o valor numérico da expressão algébrica 3x + 2y + a é igual a 7. Observe que o valor numérico não foi o mesmo, pois mudamos os valores atribuídos às variáveis.

Valor numérico é o resultado das operações efetuadas em uma expressão algébrica após a substituição das variáveis por números.

Vamos determinar o valor numérico da expressão

\frac{b \cdot h}{2} - a^{2}

, para a = 10, b = 50 e h = 70:

\frac{b \cdot h}{2} - a^{2} = \frac{50 \cdot 70}{2} - 10^{2} = \frac{3 500}{2} - 100 = 1 750 - 100 = 1 650

Página 144

O cálculo do valor numérico de expressões algébricas pode nos ajudar na resolução de problemas. Acompanhe as situações a seguir.

Situação 1

Uma fábrica de parafusos tem um custo fixo mensal de R$ 12.000,00doze mil reais, além de R$ 0,20zero reais e vinte centavos por peça produzida.

Fotografia. Diversos parafusos prateados.

Vamos representar o custo mensal por meio de uma expressão algébrica com base na quantidade de peças produzidas. A quantidade de peças será indicada por x.

.12000 + 0,20x

Com essa expressão, podemos determinar, por exemplo, o custo para um mês em que a fábrica produzir .10000 parafusos.

.12000 + 0,20x =

= .12000 + 0,20 ⋅ .10000 =

= .12000 + .2000 =

= .14000

Nesse mês, o custo foi de R$ 14.000,00quatorze mil reais e foi obtido com base no número de parafusos produzidos.

Situação 2

A locadora de carros Alfa cobra de seus clientes uma taxa de uso diário mais um valor por quilômetro percorrido com o veículo.

lustração: Uma locadora de carros em uma rua. Na locadora, há uma porta na entrada e uma placa com o nome 'Alfa'. Na rua, há um carro azul e um vermelho passando

A taxa cobrada pela locadora é de R$ 110,00cento e dez reais por dia de utilização do automóvel, e o valor cobrado por quilômetro percorrido é de R$ 2,00dois reais. Vamos indicar um valor desconhecido de quilômetros rodados pela letra n.

A expressão algébrica que permite calcular o valor a ser pago pelo uso do carro por 1 dia é:

110 + 2n

Se em um dia de utilização uma pessoa percorrer 60 quilômetros, o valor a ser pago à locadora Alfa poderá ser calculado da seguinte fórma:

110 + 2n =

= 110 + 2 ⋅ 60 =

= 110 + 120 =

= 230

Em um dia de utilização, percorrendo 60 quilômetros, uma pessoa deverá pagar R$ 230,00duzentos e trinta reais à locadora.

Página 145

Atividades

Faça as atividades no caderno.

5. Copie no caderno o quadro de valores numéricos a seguir substituindo cada

pelo número correspondente.

x	−3	−4	0	+ 8	−1	+4	+3	−7
3x		−12				12	9
− xelevado a 2				−64				−49
xelevado a 3	−27
$divisão de x sobre 2$			0		$menos divisão de 1 sobre 2$
‒ x						−4
2x

6. Determine o valor numérico da expressão algébrica de cada item.

a) x elevado a 2 + 2xy + y elevado a 2, para x = menos1 e y = menos3

b) x elevado a 2y menos xy elevado a 2, para x = 0,2 e y = 0,5

c) x elevado a 2 menos y elevado a 2, para x = 3 e y = menos5

7. Paulo comprou 8 metros de fio elétrico por R$ 27,20vinte e sete reais e vinte centavos.

a) Quanto custou cada metro desse fio?

b) Escreva uma expressão algébrica para representar quanto Paulo gastaria para comprar x metro desse fio.

c) Quanto Paulo gastaria se comprasse 15 metros desse fio?

8. Em um circo, na apresentação das vinte e duas horas, foi vendida uma quantidade a de ingressos para adultos e uma quantidade c de ingressos para crianças.

Ilustração: Circo com crianças e adultos entrando. O circo tem uma tenda amarela e uma bandeira vermelha no alto. Na entrada, há uma cortina vermelha, ao redor árvores e grama. À esquerda, há uma placa com as informações: Circo. Criança 12 reais e adulto 24 reais

a) Que expressão algébrica representa o total arrecadado para a apresentação?

b) Quantos reais foram arrecadados na apresentação das vinte e duas horas, sabendo que a = 150 e c = 240?

9. Uma escola promoveu uma campanha de arrecadação de alimentos para serem doados a uma instituição de caridade. Para isso, os estudantes foram divididos em 3 equipes: verde, vermelha e azul. A equipe azul arrecadou 20 quilogramas de alimentos a mais que a equipe vermelha. A equipe verde arrecadou 10 quilogramas a menos que a equipe vermelha.

a) Representando o total de alimentos arrecadados pela equipe vermelha por x, determine as expressões algébricas que indicam as quantidades arrecadadas pelas outras equipes.

b) Que expressão algébrica representa o total de alimentos arrecadados pelas equipes?

c) Se a equipe vermelha arrecadou 80 quilogramas de alimentos, quanto cada uma das outras equipes arrecadou? Qual foi o total arrecadado nesse caso?

d) Se o total arrecadado tivesse sido de 310 quilogramas, a equipe vermelha poderia ter arrecadado 120 quilogramas de alimentos? Converse com o professor e os colegas sobre como você pensou para responder a essa questão.

Página 146

Termos algébricos

Observe as figuras a seguir.

Figura geométrica. Polígono amarelo com quatro lados de comprimentos diferentes. Na parte superior do polígono, há um lado com comprimento Z. À esquerda, há um lado com comprimento X, no lado direito há dois lados com comprimentos diferentes: o lado superior tem comprimento 2, enquanto o lado inferior tem comprimento 3Y.

A medida do perímetro desta figura é igual a:

x + 3y + z + 2

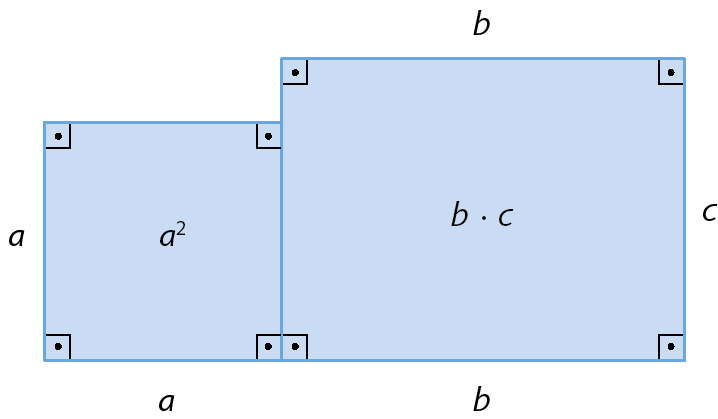
Figura geométrica. um retângulo e um quadrado lado a lado, destacando seus ângulos retos com 90 graus.

À esquerda, há um quadrado com indicações na lateral que mostram que a altura mede A, e na parte inferior a indicação que o comprimento também mede A. No interior do quadrado, indicação que a medida de área é A ao quadrado.

À direita, há um retângulo, com uma marcação na parte superior indicando que seu comprimento mede B. Na parte lateral direita, há uma marcação indicando que a altura mede C. No interior do quadrado, indicação que a medida de área é igual a B vezes C

A medida da área desta figura é igual a:

a elevado a 2 + b ⋅ c

Cada parcela de uma expressão algébrica é denominada termo algébrico. Assim:

• a expressão x + 3y + z + 2 apresenta quatro termos: x, 3y, z e 2;

• a expressão a elevado a 2 + b ⋅ c possui dois termos: a elevado a 2 e b ⋅ c.

Um termo algébrico é formado por duas partes: a parte numérica, denominada coeficiente, e a parte com letras, denominada parte literal.

Considere alguns exemplos.

Esquema. Termo algébrico. 17A. Há um fio na horizontal indicando que o número 17 corresponde ao coeficiente e a variável A corresponde à parte literal

Esquema. Termo algébrico de uma fração. menos 3 meios vezes X ao quadrado vezes Y. Há um fio na horizontal indicando que a fração menos 3 meios corresponde ao coeficiente e as variáveis X ao quadrado e Y correspondem à parte literal.

Esquema. Termo algébrico. A ao quadrado B ao cubo e C elevado a quarta potência. Há um fio na horizontal indicando que 1 corresponde ao coeficiente e as variáveis A ao quadrado B ao cubo e C correspondem à parte literal.

Observação

Um número racional em uma expressão é considerado um termo algébrico sem parte literal. Analise os exemplos.

Esquema. Expressão algébrica 5M menos 3. Há um fio abaixo do número menos 3 indicando que corresponde ao coeficiente e que não há parte literal.

Esquema. Expressão algébrica, 3 vírgula 36 AB mais fração 7 meios. Há um fio abaixo da fração 7 meios indicando que corresponde ao coeficiente e que não há parte literal.

Adição e multiplicação de termos algébricos

Adição algébrica

Vamos considerar esta figura, que representa uma quadra de tênis, na qual se tomam como base as dimensões que medem 4 métros e 8 métros e as variáveis x e y, que representam medidas de comprimento em metro.

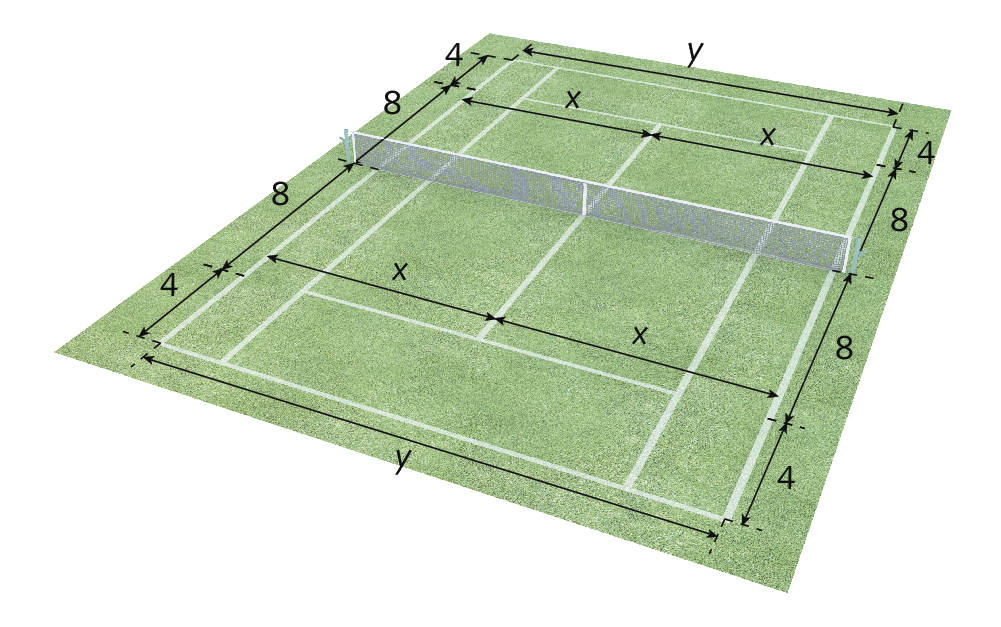
Esquema. Quadra de tênis retangular gramada, os limites são marcados de branco e há uma rede no meio.

À esquerda da quadra, há duas cotas paralelas à rede: uma cota partindo da rede e indo até a linha marcada da quadra de X metros na parte inferior e outra de X metros na parte superior, e outra cota no final da quadra indicando que a largura total da quadra mede Y metros.
Na parte superior da quadra, há mais duas cotas: uma cota da rede até a linha marcada, indicando um comprimento de 8 metros, e outra cota que vai até o final da quadra, indicando mais um comprimento de 4 metros.

À direita da quadra, há duas cotas paralelas à rede: uma cota partindo da rede e indo até a linha marcada da quadra de X metros na parte inferior e outra de X metros na parte superior, e outra cota no final da quadra indicando que a largura total da quadra mede Y metros.
Na parte superior da quadra, há mais duas cotas: uma cota da rede até a linha marcada, indicando um comprimento de 8 metros, e outra cota que vai até o final da quadra, indicando mais um comprimento de 4 metros.

Página 147

Para determinar a expressão algébrica que representa a medida da área total da quadra, vamos primeiro encontrar a expressão algébrica da medida da área de cada uma das partes da quadra.

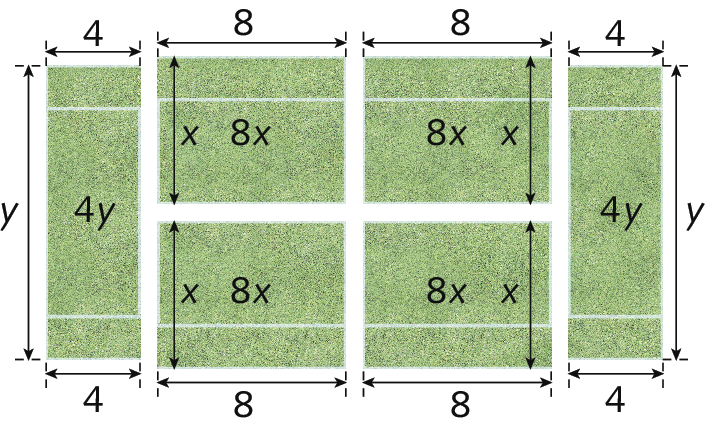
a em 6 partes: 2 retângulos nas extremidades e 4 outros retângulos no centro da quadra. À esquerda, há um retângulo vertical com uma cota na parte inferior indicando que seu comprimento mede 4 metros, e outra cota na parte lateral esquerda indicando que sua altura mede Y metros. No centro, há 4 retângulos horizontais de tamanhos iguais, sendo dois na parte superior e dois na parte inferior. Na parte superior, há uma cota indicando que seu comprimento mede 8 metros, e outra cota na parte lateral esquerda indicando que sua altura mede X metros. Na parte inferior, há uma cota na parte inferior indicando que seu comprimento mede 8 metros, e outra cota na parte lateral direita indicando que sua altura mede X metros. À direita, encontra-se um retângulo vertical com uma cota na parte inferior indicando que seu comprimento mede 4 metros, e outra cota na parte lateral esquerda indicando que sua altura mede Y metros.

Adicionando os termos algébricos que representam as medidas de área de todas as partes da quadra de tênis, obtemos a expressão algébrica que representa a medida da área total. Observe:

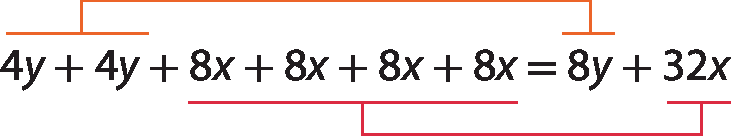
Esquema. Expressão algébrica na horizontal da medida da área total

4Y mais 4Y mais 8X mais 8X mais 8X mais 8X é igual a 8Y mais 32X

Na parte superior, há um fio vermelho entre os termos 4Y mais 4Y para 8Y após o sinal de igual, indicando a soma dos termos
Na parte inferior, há um fio vermelho entre todos os termos 8X para 32X indicando a soma dos termos

Para adicionar termos algébricos que têm a mesma parte literal, devemos adicionar os coeficientes e conservar a parte literal.

Considere os exemplos.

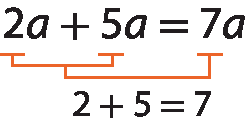
Esquema. Expressão algébrica. 2A mais 5A igual a 7A.
Na parte inferior, há um fio vermelho nos números 2 e 5 indicando o número 7, abaixo a sentença matemática de 2 mais 5 é igual a 7.

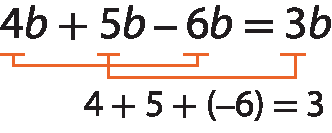
Esquema. Expressão algébrica. 4B mais 5B menos 6B é igual a 3B.
Na parte inferior, há um fio vermelho nos números 4, 5 e 6 indicando para o número 3, abaixo a sentença matemática de 4 mais 5 mais, abre parênteses menos 6, fecha parênteses é igual a 3.

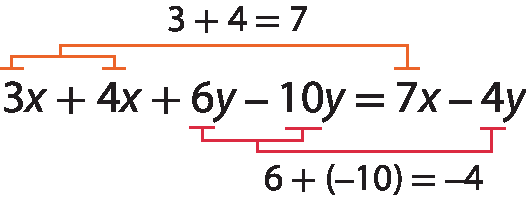
Esquema. Expressão algébrica. 3X mais 4X mais 6Y menos 10Y é igual a 7X menos 4Y

Na parte superior, há um fio vermelho nos números 3 e 4 indicando o número 7, acima a sentença matemática 3 mais 4 é igual a 7.

Na parte inferior, há um fio vermelho nos números 6 e menos 10 indicando o número 4, abaixo a sentença matemática 6 mais, abre parênteses menos 10, fecha parênteses é igual a menos 4

Multiplicação algébrica

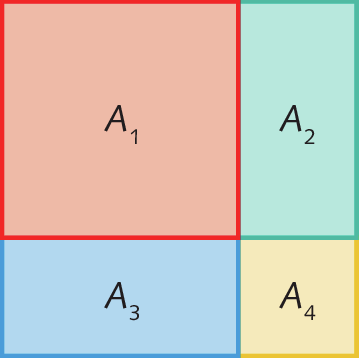
Vamos considerar um quadrado cujo comprimento de cada um dos lados mede 2a + 3b.

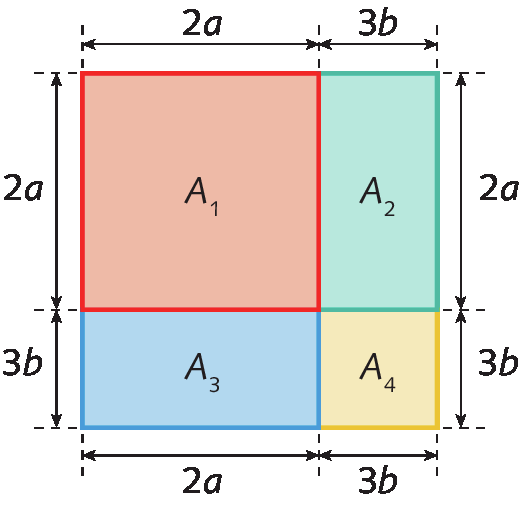
Esquema. Quadrado dividido em 4 partes.

Na parte superior, à esquerda, há um quadrado vermelho com a indicação da medida de área A com índice 1. À direita, há um retângulo verde na vertical com a indicação da medida de área A com índice 2. Na parte inferior, à esquerda, há um retângulo azul na horizontal com a indicação da medida de área A com índice 3. À direita, há um quadrado com a indicação da medida de área A com índice 4.

Ao lado esquerdo do quadrado total, há duas cotas: uma entre o quadrado vermelho, indicando que o comprimento mede 2A, e o retângulo azul indicando que a altura mede 3B. No lado direito, há duas cotas: uma entre o retângulo verde, indicando que o comprimento mede 2A, e o quadrado amarelo, indicando que o comprimento mede 3B.

Na parte inferior do esquema, há uma cota entre o retângulo azul, indicando que o comprimento mede 2A, e o quadrado amarelo, indicando que a altura mede 3B. Na parte superior, há uma cota entre o quadrado vermelho, indicando que o comprimento mede 2A, e o retângulo verde, indicando que a altura mede 3B.

Podemos calcular as medidas das áreas á₁, á₂, á₃ e á₄ da seguinte forma:

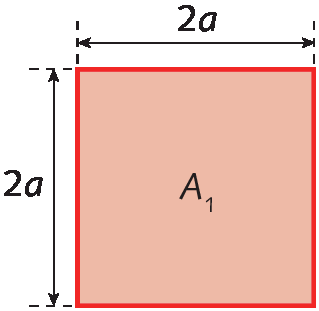
Esquema. Quadrado vermelho. Cota à direita e na parte inferior, indicando 2A. No interior do quadrado há indicação de medida de área, A com índice 1

á₁ = 2a ⋅ 2a = 2 ⋅ 2 ⋅ a ⋅ a = 4aelevado a 2

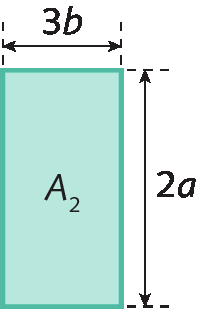
Esquema. Retângulo verde disposto na vertical. Cota na parte inferior indicando que seu comprimento mede 3B. Cota na parte lateral esquerda, indicando que sua altura mede 2A. No interior do quadrado, há indicação de medida de área, A com índice 2

á₂ = 2a ⋅ 3b = 2 ⋅ 3 ⋅ a ⋅ b = 6ab

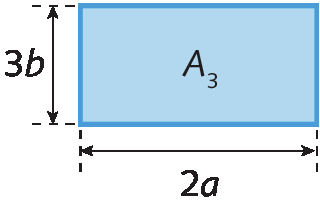
Esquema. Retângulo azul disposto na horizontal. Cota na parte inferior indicando que seu comprimento mede 2A. Cota na parte lateral esquerda, indicando que sua altura mede 3B. No interior do quadrado, há indicação de medida de área, A com índice 3

á₃ = 2a ⋅ 3b = 2 ⋅ 3 ⋅ a ⋅ b = 6ab

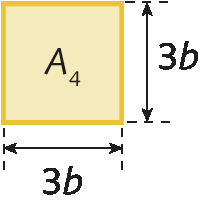
Esquema. Quadrado amarelo. Cota à direita e na parte inferior indicando 3B. No interior do quadrado, há indicação de medida de área, A com índice 4

á₄ = 3b ⋅ 3b = 3 ⋅ 3 ⋅ b ⋅ b = 9belevado a 2

Página 148

Para multiplicar dois termos algébricos, devemos:

• multiplicar os coeficientes numéricos entre si;

• multiplicar as partes literais entre si.

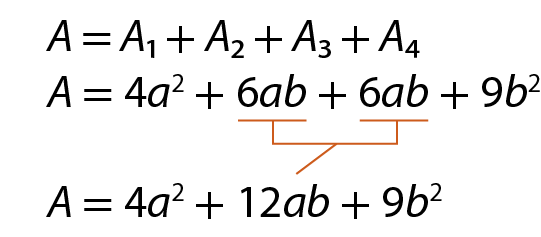
Agora, para representar a medida da área total (a) da figura, basta adicionarmos as medidas de área á₁, á₂, á₃ e á₄. Assim:

Sentença matemática. Na primeira linha: A é igual a A com índice 1 mais A com índice 2 mais A com índice 3 mais A com índice 4. Abaixo há substituição dos termos algébricos pelas medidas de áreas. Na segunda linha: A é igual a 4 A elevado ao quadrado mais 6 A B mais 6 A B mais 9 B elevado ao quadrado. Na terceira linha: A é igual a 4 A elevado ao quadrado mais 12 A B mais 9 B elevado ao quadrado Dos termos algébricos 6 A B mais 6 A B da segunda linha partem dois fios vermelhos para a terceira linha indicando que a soma é 12 A B

Clique no play e acompanhe as informações do vídeo.

Atividades

Faça as atividades no caderno.

10. Calcule as adições algébricas.

a) 5x menos abre parênteses2x menos 6x menos 8xfecha parênteses

b) 6y menos

(5 x ‒ y ‒ \frac{x}{2})

c) 10ab menos 5 + ab menos 7ab

11. Determine o resultado das adições algébricas.

a) 5a menos 3b menos abre parênteses6a + a menos 5bfecha parênteses

b) 0,8y menos 2,4y + y menos

\frac{y}{4}

c) 2x menos 3x + 5x menos 8x

12. Calcule as adições algébricas.

a) 10k menos 9k menos (12k + 3k menos 10k)

b) 12y + 23y menos 13y menos y

c) 8x menos 12x + 20x menos 32x

d) 7y menos 3z + abre parênteses5w menos w + zfecha parênteses

e) 23a + 32b menos 9a + abre parênteses4c menos 3c + afecha parênteses

f) x + y menos 3z menos abre parênteses4x menos 9y + 6zfecha parênteses

13. Determine os produtos algébricos.

a) menos2 ⋅ abre parêntesesmenos5xfecha parênteses

b) abre parêntesesmenosxyfecha parênteses ⋅ abre parêntesesmenos4x elevado a 2fecha parênteses

c) menos5 ⋅ abre parêntesesmenos2afecha parênteses ⋅ abre parênteses2bfecha parênteses

d) abre parêntesesmenos5yfecha parênteses ⋅ abre parêntesesmenos6yfecha parênteses ⋅ abre parêntesesmenos2fecha parênteses

e) 7x ⋅ abre parêntesesmenos2xyfecha parênteses ⋅ abre parêntesesmenos3yfecha parênteses

\frac{x y}{2}

⋅

(‒ \frac{3 y}{4})

(\frac{a}{2})

⋅

(‒ \frac{3 b}{4})

h) abre parêntesesmenos6xfecha parênteses ⋅ abre parêntesesmenosxfecha parênteses

14. Leia e faça o que se pede.

De acordo com a Agência Nacional de Aviação Civil (anáqui), nos aeroportos do Brasil, as medidas permitidas para uma bagagem de mão devem ser definidas pela companhia aérea, desde que a medida de massa não seja superior a 10 quilogramas.

Fotografia. Mala vermelha com cota na parte inferior indicando que o comprimento mede X, cota na lateral esquerda indicando que a altura mede Y e cota paralela à mala indicando que a largura mede Z.

a) Qual é a expressão algébrica que representa a medida do volume da mala?

b) Se as dimensões de uma bagagem medem 23 centímetros por 40 centímetros por 55 centímetros, determine a medida de seu volume máximo, em centímetro cúbico.

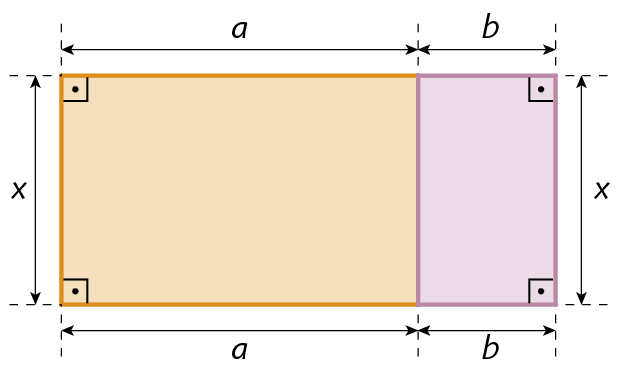
15. Escreva as expressões algébricas que representam a medida do perímetro e a medida da área da figura a seguir.

Esquema. Retângulo dividido em 2 partes.
À esquerda, há um retângulo amarelo na horizontal, enquanto à direita, há um retângulo roxo na vertical. Na parte superior e inferior do retângulo, há duas cotas: uma cota entre o retângulo amarelo indicando que o comprimento mede A, e outra cota entre o retângulo roxo indicando que o comprimento mede B. À direita e à esquerda, há uma cota indicando que a altura mede X

Página 149

2 Equações

Acompanhe as situações a seguir.

Situação 1

As balanças de dois pratos a seguir estão equilibradas.

ilustração. Duas balanças de dois pratos que estão equilibradas. Na primeira balança, o prato da esquerda tem 2 cubos marrons e 4 cilindros roxos, e o prato da direita tem 10 cilindros roxos. Na segunda balança, o prato da esquerda tem 2 cubos marrons e o prato da direita tem 6 cilindros roxos.

Por meio do equilíbrio das balanças, podemos verificar que:

e 4

equilibram 10

e que 2

equilibram 6

Considerando que a medida da massa de cada

equivale a y quilogramas e a medida da massa de cada

equivale a x quilogramas, podemos escrever:

2x + 4y = 10y e 2x = 6y

Assim, escrevemos duas sentenças matemáticas expressas por igualdades. Em cada uma delas, há dois elementos desconhecidos: x e y.

Situação 2

Luana percorreu

\frac{2}{3}

da medida da distância total de uma pista em uma hora. Faltam 10 quilômetros para ela concluir o percurso. Observe no esquema a seguir a representação da situação, em que w, em quilômetro, corresponde à medida da distância total.

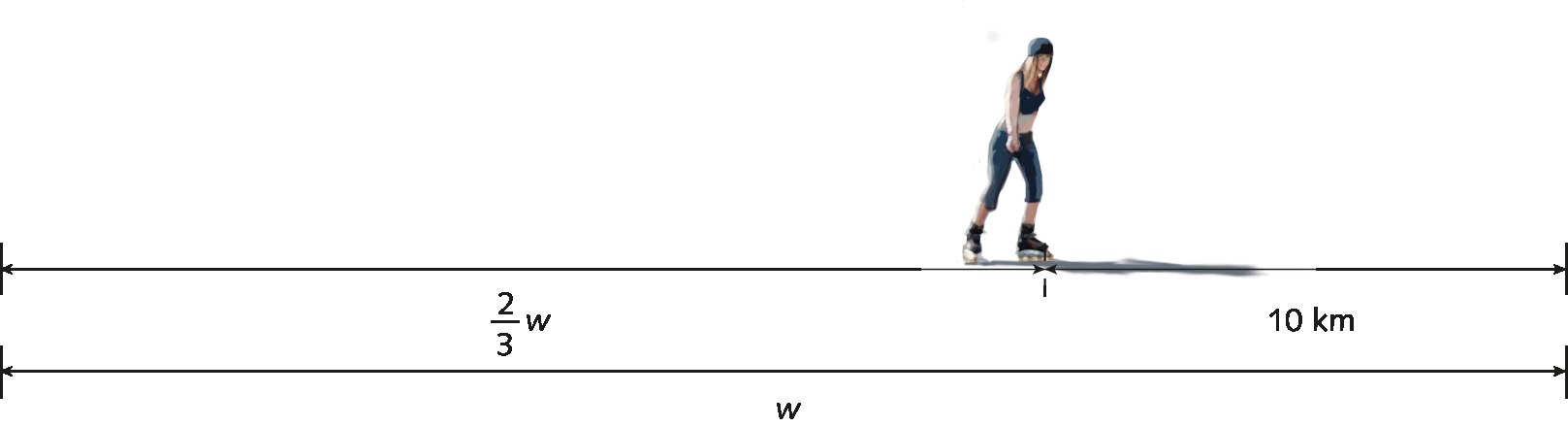
Ilustração. Duas Retas horizontais com medida total W
Na primeira reta, à esquerda, há uma indicação na fração de 2 terços de W e em 10 quilômetros. Acima, na outra reta horizontal, uma mulher está patinando e em sua posição há um tracinho, próximo à marca de 10 quilômetros

A sentença matemática

\frac{2 w}{3} + 10 = w

representa a situação. Essa sentença é expressa por uma igualdade e apresenta um elemento desconhecido: w.

As sentenças matemáticas 2x + 4y = 10, 2x = 6y e

\frac{2 w}{3} + 10 = w

são exemplos de equações.

Equação é uma sentença matemática expressa por uma igualdade que apresenta pelo menos um valor desconhecido representado por uma letra denominada incógnita.

Página 150

Considere alguns exemplos de equações.

a) 2x + 8 = 0 é uma equação cuja incógnita é x.

b) 5y menos 4 = 6y + 8 é uma equação cuja incógnita é y.

c) 3a menos b menos c = 0 é uma equação em que as incógnitas são a, b e c.

Observação

As sentenças matemáticas a seguir não são consideradas equações:

a) 4 + 8 = 7 + 5, pois não apresenta incógnita.

b) x menos 5 < 3, pois não é uma igualdade.

c) 5 ≠ menos2, pois não é uma igualdade e não apresenta incógnita.

Agora, vamos considerar a equação 2z menos 8 = 3z menos 10, cuja incógnita é z.

A expressão que está à esquerda do sinal de igualdade denomina-se 1º membro, e a expressão que está à direita denomina-se 2º membro.

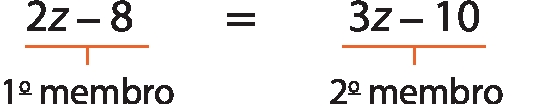
Esquema. Sentença matemática. 2Z menos 8 é igual a 3Z menos 10
No lado esquerdo, há um fio vermelho indicando primeiro membro
No lado direito, há um fio vermelho indicando segundo membro

Quando o maior expoente de uma incógnita em uma equação é 1, a denominamos equação do 1º grau.

Analise alguns exemplos.

a) 2z + 1 = 0 é uma equação de 1º grau, pois o expoente da incógnita z é 1.

b) 3x 2 menos 5 = 16x não é uma equação de 1º grau, pois o maior expoente da incógnita x é 2 e, portanto, diferente de 1.

\frac{1}{y}

+ 3 = 0 não é uma equação do 1º grau, pois o expoente da incógnita y é menos1 e, portanto, diferente de 1.

d) 5a + 11 = 6a é uma equação de 1º grau, pois o maior expoente da incógnita a é 1.

Raiz de uma equação

A incógnita de uma equação pode assumir diversos valores, mas apenas alguns deles tornam a sentença verdadeira. Um valor que torna a sentença verdadeira é chamado de raiz da equação.

Podemos verificar se um número é ou não raiz de uma equação substituindo a incógnita por esse número. Se a sentença for verdadeira, o número considerado é raiz da equação; se a sentença for falsa, o número não é raiz da equação.

Vamos verificar se 2 é raiz das equações 2x menos 3 = 1 e 2x + 1 = 6.

2x menos 3 = 1

2 ⋅ 2 menos 3 = 1

4 menos 3 = 1

1 = 1

sentença verdadeira

2x + 1 = 6

2 ⋅ 2 + 1 = 6

4 + 1 = 6

5 = 6

sentença falsa

Logo, 2 é raiz da equação 2x menos 3 = 1 , mas não é raiz da equação 2x + 1 = 6.

Página 151

Conjunto universo e conjunto solução de uma equação

O conjunto universo é formado por todos os números que uma incógnita pode assumir e é indicado por U. Acompanhe a situação a seguir.

Ilustração. História em quadrinhos. Há 3 diálogos em quadros com uma menina branca de cabelo loiro usando uma camiseta azul e um menino branco de cabelo castanho usando uma camiseta vermelha.

Na primeiro quadro, a menina está com a mão levantada e pergunta: Marcos, quantos irmãos você tem? e Marcos está pensativo.
No segundo quadro, Marcos responde: Considere que eu tenho x irmãos. Se subtrairmos 3 do dobro de x, obteremos 5. enquanto a menina está pensando.
No terceiro quadro, a menina diz: Já sei!

Podemos traduzir o que Marcos disse pela seguinte equação: 2x ‒ 3 = 5

Como x indica a quantidade de irmãos que Marcos tem, a incógnita dessa equação só pode assumir valores naturais. Por isso, nesse caso, U =

Simbolo, letra N maiúscula com tracinho paralelo, de indicação dos números naturais

Observe que, substituindo x por 4 na equação 2x ‒ 3 = 5, obtemos uma sentença verdadeira. Como 4 é um número natural e 4 é raiz da equação, dizemos que 4 é solução dessa equação e que o conjunto solução dessa equação é S = {4}.

As raízes da equação que pertencem ao conjunto universo são as soluções dessa equação e formam seu conjunto solução, que é indicado por S.

Atividades

Faça as atividades no caderno.

16. Observe a equação 2y ‒ 6 = 4 + y e, depois, responda às questões.

a) Qual é o 1º membro?

b) Qual é o 2º membro?

c) Qual é a incógnita dessa equação?

17. Identifique, no caderno, as sentenças que representam equações do 1º grau.

a) 2x + 5 < 3

b) 7 ‒ 3 = 2 + 2

c) 8 = 6y ‒ 4

d) x ‒ 1 ≠ 0

3 x + 7 = \frac{1}{2}

f) 2x 3 = ‒16

18. Verifique se o número 2 é raiz das seguintes equações:

a) 3x + 10 = 4x + 8

\frac{x}{2} + 5 = \frac{5 x}{3} ‒ 2

19.

Determine mentalmente a solução da equação x + 7 = 12, considerando o conjunto universo indicado em cada item.

a) U = {0, 2, 4, 6, reticências}

b) U =

símbolo representado pela letra Z maiúscula, indicando o conjunto dos números inteiros

20.

Determine mentalmente o conjunto solução de cada equação sendo U =

símbolo representado pela letra Q maiúscula que indica o conjunto dos números racionais

a) x ‒ 8 = 0

\frac{x}{4} = 3

c) 6x = ‒18

x + \frac{3}{4} = 0

x ‒ \frac{1}{4} = \frac{3}{4}

f) x + 8 = 0

Página 152

Resolução de equações do 1º grau com uma incógnita

Equações equivalentes

A balança a seguir está em equilíbrio.

ilustração. Balança de dois pratos que está equilibrada. No prato da esquerda, há 3 cubos vermelhos e 4 cilindros amarelos. e no prato da direita, há 2 cubos laranjas e 6 cilindros amarelos

Sabendo que a medida da massa de 1

é igual a 1 quilograma e se considerarmos a medida da massa de 1

igual a x quilogramas, podemos representar a situação com a seguinte equação:

3x + 4 = 2x + 6, com U =

Ao tirar 2

de cada prato, a balança ainda permanecerá em equilíbrio:

ilustração. Balança de dois pratos que está equilibrada. No prato da esquerda, há 1 cubo vermelho e 4 cilindros amarelos. e no prato da direita, há 6 cilindros amarelos

Observe que, para esse caso, podemos escrever a seguinte equação:

x + 4 = 6, com U =

Agora, se tirarmos 4

de cada prato, a balança ainda continuará em equilíbrio:

ilustração. Balança de dois pratos que está equilibrada. No prato da esquerda, há 1 cubo vermelho, e no prato da direita, há 2 cilindros amarelos

Nesse caso, a equação será x = 2 , com U =

, o que permite concluir que a medida da massa do

é de 2 quilogramas.

Observe que 2 é raiz das três equações:

3x + 4 = 2x + 6

3 ⋅ 2 + 4 = 2 ⋅ 2 + 6

6 + 4 = 4 + 6

10 = 10

x + 4 = 6

2 + 4 = 6

6 = 6

x = 2

2 = 2

Como as equações têm a mesma raiz e o mesmo conjunto universo, U =

, dizemos que essas equações são equivalentes.

Quando duas equações têm o mesmo conjunto universo e as mesmas raízes, elas são chamadas de equações equivalentes.

Em alguns casos, é necessário obter equações equivalentes para encontrar as raízes de uma equação.

Princípio aditivo e princípio multiplicativo das igualdades

A balança representada a seguir está em equilíbrio. No prato da esquerda, foram colocados 4

de 1 quilograma cada um e 1

de medida de massa desconhecida. No prato da direita, foram colocados 7

de 1 quilograma cada um. Qual é a medida da massa de

ilustração. Balança de dois pratos que está equilibrada. No prato da esquerda, há 1 cubo verde e 4 cilindros laranjas, e no prato da direita, há 7 cilindros laranjas

Indicando por x a medida da massa do

, em quilogramas, a situação pode ser representada pela equação:

x + 4 = 7

Observe que, se retirarmos 4

de cada prato, a balança continuará equilibrada.

ilustração. Balança de dois pratos que está equilibrada. No prato da esquerda, há 1 cubo verde, e no prato da direita, há 3 cilindros laranjas

Nesse caso, podemos representar a situação pela equação:

x + 4 ‒ 4 = 7 ‒ 4

x = 3

Portanto, cada

tem medida de massa igual a 3 quilogramas.

Página 153

Quando adicionamos ou subtraímos uma mesma quantidade nos dois membros de uma equação, obtemos uma equação equivalente à primeira. Esse é o princípio aditivo das igualdades. Resolvemos a equação x + 4 = 7 aplicando esse princípio. Agora, acompanhe outra situação.

A balança de pratos a seguir está em equilíbrio. No prato da esquerda, foram colocados 3

de y quilograma cada um. No prato da direita, foram colocados 15

de 1 quilograma cada um.

Esquema. Balança de dois pratos que está equilibrada. No prato da esquerda, há 3 cubos azuis representando Y quilogramas, e no prato da direita, há 15 cilindros laranjas, representando 15 quilogramas. Abaixo há a equação 3 Y é igual a 15.

3y = 15

Quando multiplicamos ou dividimos por um mesmo número não nulo os dois membros de uma equação, obtemos uma equação equivalente à primeira. Esse é o princípio multiplicativo das igualdades.

Para resolver a equação 3y = 15, vamos utilizar o princípio multiplicativo das igualdades, acompanhe:

3y = 15

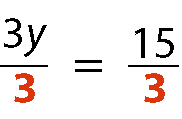
3y sobre 3 destacado em vermelho igual a 15 sobre 3 destacado em vermelho

Dividimos cada membro por 3.

y = 5

Portanto, cada

tem medida de massa igual a 5 quilogramas.

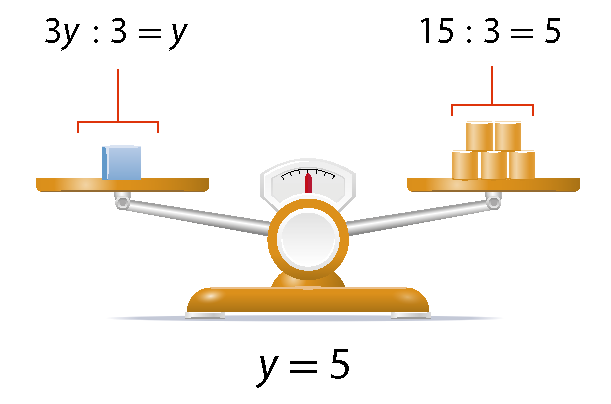
Esquema. Balança de dois pratos que está equilibrada. No prato da esquerda, há 1 cubo azul representando Y quilogramas, e no prato da direita, há 5 cilindros laranjas, representando 5 quilogramas.

Acima há um fio vermelho do lado esquerdo com a equação: 3 Y dividido por 3 é igual a Y. No lado direito, há outro fio indicando 15 dividido por 3 é igual a 5

Abaixo, há a equação Y é igual a 5.

Para resolver uma equação, aplicamos os princípios aditivo e multiplicativo das igualdades, de modo a obter equações equivalentes mais simples do que as iniciais, determinando, assim, as soluções da equação. Veja outros exemplos.

a) Vamos resolver a equação

\frac{2 x}{5} ‒ 4 = x

, sendo U =

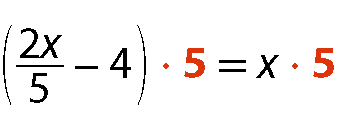
abre parênteses fração 2x sobre 5 menos 4 fecha parênteses vezes 5 destacado em vermelho igual x vezes 5 destacado em vermelho

Multiplicamos os dois membros da equação por 5 (princípio multiplicativo das igualdades).

2x menos 20 = 5x

2x menos 20 menos 2x = 5x menos 2x

Subtraímos 2x de cada membro da equação (princípio aditivo das igualdades).

‒20 = 3x

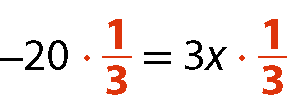
menos 20 vezes 1 terço destacado em vermelho igual a 3x vezes 1 terço destacado em vermelho

Multiplicamos os dois membros da equação por

\frac{1}{3}

(princípio multiplicativo das igualdades).

‒ \frac{20}{3} = x

x = ‒ \frac{20}{3}

Temos que

‒ \frac{20}{3}

é raiz da equação, porém, não pertence ao conjunto universo. Nesse caso, dizemos que a equação não tem solução em

. Portanto, o conjunto solução da equação é conjunto vazio, isto é, S = ∅.

Sugestão de leitura

GUELLI, Oscar. Equação: o idioma da Álgebra. São Paulo: Ática, 1999. (Coleção Contando a história da Matemática).

Esse livro traz um pouco da história da Álgebra, muitas atividades desafiadoras e curiosidades sobre equações.

Observação

Se resolvermos a equação

\frac{2 x}{5} ‒ 4 = x

, sendo U =

‒ \frac{20}{3}

será solução, pois

‒ \frac{20}{3}

é um número racional. Nesse caso, o conjunto solução da equação é

S = \{‒ \frac{20}{3}\}

Página 154

b) Vamos resolver a equação

\frac{3 x}{5} ‒ 1 = \frac{x}{2}

, sendo U =

\frac{6 x}{10} ‒ \frac{10}{10} = x \cdot \frac{5}{10}

Usando frações equivalentes, escrevemos os termos da equação com o mesmo denominador.

(\frac{6 x}{10} ‒ \frac{10}{10}) \cdot 10 = (x \cdot \frac{5}{10}) \cdot 10

Multiplicamos os dois membros da equação por 10 (princípio multiplicativo das igualdades).

6x menos 10 = 5x

6x menos 10 menos 5x = 5x menos 5x

Subtraímos 5x de cada membro da equação (princípio aditivo das igualdades).

x menos 10 = 0

x menos 10 + 10 = 0 + 10

Adicionamos 10 unidades a cada membro da equação (princípio aditivo das igualdades).

x = 10

Como 10 é um número inteiro, 10 é a solução dessa equação. Portanto, seu conjunto solução é S = {10}.

Atividades

Faça as atividades no caderno.

21. Determine o conjunto solução de cada equação. Considere U =

a) x + 5 = 21

b) y menos 3 = 100

c) x + 17 = 10

d) x menos 3 = 10

22. A balança a seguir está em equilíbrio. Determine a medida da massa, em quilograma, de cada

, sabendo que cada

tem medida de massa igual a 200 gramas.

Esquema. Balança de dois pratos que está equilibrada. No prato da esquerda, há 6 pesos laranjas e, no prato da direita, há um peso verde e dois pesos laranjas

23. Obtenha o conjunto solução de cada equação, sabendo que U =

a) 3x menos 9 = 9

b) x menos 5 = menos7

c) y menos 6 = 5y + 8

d) 10x = 20 + 9x

24. Sabendo que U =

, resolva as equações.

a) 3x = menos 45 menos 2x

b) 6abre parêntesesx + 3fecha parênteses menos 2abre parêntesesx menos 5fecha parênteses = 20

c) menos18 = 2x + 15

d) 2abre parêntesesx menos 1fecha parênteses menos 1 = 8

25. Sabendo que U =

, obtenha o conjunto solução de cada equação.

\frac{2 x}{5} ‒ \frac{1}{4} = x ‒ \frac{1}{10}

2 m ‒ \frac{7}{5} ‒ \frac{m}{10} = \frac{1}{2}

\frac{y}{2} + \frac{y}{3} = \frac{3 y}{4} ‒ 6

\frac{3 y}{2} ‒ \frac{3}{4} = 1 ‒ 2 y

26. Sabendo que U =

, resolva as equações.

a) 2abre parêntesesx + 3fecha parênteses = 30

b) 8 menos 2abre parêntesesx + 5fecha parênteses = 5

c) 3abre parênteses y menos 1fecha parênteses menos 4abre parênteses y menos 2fecha parênteses = 6

d) 2abre parênteses5y + 1fecha parênteses = 27

27. Sabendo que U =

, resolva as equações e responda: x é maior ou menor que y ?

\frac{5 x}{2} ‒ \frac{1}{4} = 8

\frac{y}{3} + \frac{y + 1}{2} = \frac{5}{6} + y

Ilustração. Menina branca de cabelo castanho usando rabo de cavalo, uma camiseta verde e calças compridas. Ela está deitada de bruços com um livro aberto e olha para cima.

Página 155

3 Resolução de problemas

Alguns problemas podem ser resolvidos por meio de equações do 1º grau com uma incógnita.

Confira a seguir.

Situação 1

Um terreno retangular tem 144 métros de medida de perímetro. A medida do comprimento do terreno tem o triplo da medida da largura. Qual é a medida da área do terreno?

Observe a representação desse terreno. Considerando que o terreno tem largura de medida x, o comprimento mede 3x.

Ilustração. Terreno retangular na horizontal, com uma cota na parte inferior indicando que seu comprimento mede 3X e outra na parte lateral esquerda indicando que sua altura mede X.

Como a medida do perímetro de um polígono é igual à soma das medidas de comprimento dos lados, podemos escrever:

x + 3x + x + 3x = 144

8x = 144

x =

\frac{144}{8}

x = 18

Então:

• medida da largura: x = 18 abre parênteses18 métrosfecha parênteses

• medida do comprimento: 3x = 3 ⋅ 18 = 54 abre parênteses54 métrosfecha parênteses

• medida da área: abre parênteses54 ⋅ 18fecha parênteses métros quadrados = 972 métros quadrados

Portanto, a medida da área do terreno é 972 métros quadrados.

Situação 2

Pedro e Ernesto colheram, juntos, 55 laranjas. Pedro colheu

\frac{4}{7}

da quantidade colhida por Ernesto. Quantas laranjas Pedro colheu?

Ilustração. 2 meninos com sacos de laranjas.

À esquerda, há um menino negro de cabelo preto, usando camiseta vermelha e bermuda. Ele está com as mãos na cintura e o saco à frente dele está cheio de laranjas.

À direita, há um menino branco de cabelo castanho, usando camiseta verde e calça. Ele está segurando uma laranja com uma mão e o saco à frente dele tem algumas laranjas.

Indicando por x a quantidade de laranjas colhidas por Ernesto, a quantidade de laranjas colhidas por Pedro é igual a

\frac{4 x}{7}

Assim:

x +

\frac{4 x}{7}

= 55

(x + \frac{4 x}{7})

⋅ 7 = 55 ⋅ 7

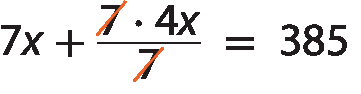
Esquema. Equação.
Na terceira linha: 7X mais fração com numerador 7 vezes 4X e denominador 7 é igual a 385. Nessa linha há dois tracinhos cortando os números 7 do numerador e do denominar.

7x + 4x = 385

11x = 385

x =

\frac{385}{11}

x = 35

Então:

• quantidade colhida por Ernesto: x = 35

• quantidade colhida por Pedro:

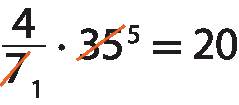
Esquema. Equação. fração numerador 4 e dominador 7 vezes 35 é igual a 20. Há um tracinho no denominador 7 e um índice 1 indicando o valor e outro tracinho no número 35 e um índice 5 indicando o valor

Portanto, Pedro colheu 20 laranjas.

Página 156

Situação 3

Alberto verificou que a terça parte do número de livros que possui mais 5 é igual a

\frac{4}{9}

do total desses livros. Quantos livros Alberto possui?

Considerando:

• número de livros que Alberto possui: y

• terça parte do número de livros:

\frac{y}{3}

•

\frac{4}{9}

do número de livros:

\frac{4 y}{9}

Vamos escrever a equação que representa o problema, resolvendo-a:

\frac{y}{3} + 5 = \frac{4 y}{9}

(\frac{y}{3} + 5) \cdot 9 = \frac{4 y}{9} \cdot 9

9 \cdot \frac{y}{3} + 45 = 4 y

3y + 45 = 4y

3y menos 4y = menos45

menosy = menos45

y = 45

Logo, Alberto possui 45 livros.

Sugestão de leitura

NETO, Egidio Trambaiolli. O aprendiz. São Paulo: éfe tê dê, 1997. (Coleção O contador de histórias e outras histórias da Matemática).

Para garantir o curso natural da história, Cronos, o Senhor do Tempo, e Felipe, um menino de 13 anos, resolverão problemas utilizando conhecimentos de História, Geografia e Matemática, como equações do 1º grau, múltiplos e divisores e operações com números racionais na forma decimal.

Atividades

Faça as atividades no caderno.

28. Qual é o número inteiro que, adicionado a seu dobro, é igual a 72?

29. O triplo de um número natural, aumentado de 15, é igual a 39. Qual é esse número?

30. Qual é o número inteiro que, adicionado a sua quarta parte, é igual a 60?

31. A diferença entre os

\frac{2}{3}

de um número racional e sua metade é igual a 10. Qual é esse número?

32. Ana tem cinco anos a mais que Paula. A soma da idade das duas é 35 anos. Qual é a idade de Ana?

33. Lúcio e Cândido têm, juntos, medida de massa igual a 124 quilogramas. Lúcio tem 16 quilogramas a mais que Cândido. Qual é a medida de massa de cada um deles?

34. Quais são os dois números pares consecutivos cuja soma é 138?

35. Qual é o número inteiro cuja soma com seu sucessor é 73?

36. A soma de quatro números naturais consecutivos é 150. Determine-os.

37. A soma de dois números inteiros é 103, e a diferença entre o maior e o menor é 23. Quais são esses números?

38. A soma de três números pares consecutivos é 90. Calcule o maior deles.

39. Luísa repartiu quatrocentas e sessenta figurinhas entre André, Breno e Caio, de modo que Breno recebesse o dobro de Caio e André ficasse com 60 figurinhas a mais que Breno. Quantas figurinhas André recebeu?

40. Telma comprou uma calça e pagou-a em três prestações. Na primeira prestação, ela pagou a metade do valor da calça; na segunda, a terça parte; na última, R$ 10,00dez reais. Qual foi o valor da calça?

Página 157

41. Em um campeonato de kitesurf são oferecidos R$ 30.000,00trinta mil reais aos três primeiros colocados. O primeiro colocado recebe R$ 10.000,00dez mil reais a mais que o terceiro. O segundo colocado recebe o dobro da quantia do terceiro. Qual é o prêmio de cada um?

Fotografia. Vista frontal de um homem no mar segurando no ar uma pipa grande em formato de arco. — O kitesurf é praticado com uma prancha e uma pipa, presa ao condutor por meio de cordas.

42. Em uma loja, foi vendido um lote de tênis brancos e pretos em apenas uma semana. Dois terços deles eram pretos, e 72, brancos. Quantos pares de tênis foram vendidos nessa loja ao final da semana?

43. Daqui a quatro anos, Aníbal terá o triplo da idade que tinha há 26 anos. Qual é a idade de Aníbal?

44. Pensei em um número natural, multipliquei por 5, dividi por 4 e subtraí 8, obtendo 12. Em que número pensei?

45. A medida do comprimento de um retângulo é 6 centímetros maior que a medida da largura. A medida do seu perímetro é igual à medida do perímetro de um quadrado cujos lados medem 30 centímetros de comprimento. Qual é a medida do comprimento do retângulo?

46. Um pai tem 40 anos, e seu filho, 10 anos. Quantos anos passarão até que o pai tenha o dobro da idade do filho?

47. Um terreno retangular mede 150 métros de comprimento. Se o terreno fosse 30 métros mais comprido e 20 métros mais largo, sua medida de área seria .6600 métros quadrados maior. Qual é a medida da largura do terreno?

Ilustração. Terreno retangular na horizontal.

Na parte superior, há uma cota indicando que o comprimento do retângulo mede 150 metros e outra cota ao lado indicando uma parte que mede 30 metros.

Na parte lateral esquerda, há uma cota indicando a largura que mede X metros e outra cota abaixo que mede 20 metros

48. Em um quadrado mágico, a soma dos números de cada linha, coluna ou diagonal é sempre a mesma. Descubra o valor de x no quadrado mágico a seguir e copie-o no caderno, substituindo os

por números.

x		x ‒ 2
	x + 1
13		x + 2

49.

Com o auxílio de uma calculadora, descubra o resultado de cada item após digitar as teclas indicadas.

a) Ilustração. Sequência de teclas da calculadora na horizontal. Da esquerda para direita: tecla 5, tecla de mais, tecla de igual, tecla de igual.

b) Ilustração. Sequência de teclas da calculadora na horizontal. Da esquerda para direita: tecla 5, tecla de mais, tecla de igual, tecla de igual, tecla de igual.

c) Ilustração. Sequência de teclas da calculadora na horizontal. Da esquerda para direita: tecla 5, tecla de mais, tecla de igual, tecla de igual, tecla de igual, tecla de igual.

d) Ilustração. Sequência de teclas da calculadora na horizontal. Da esquerda para direita: tecla 5, tecla de mais, tecla de igual, tecla de igual, tecla de igual, tecla de igual, tecla de igual.

Agora, responda:

Qual será o resultado se você digitar

Teclas da calculadora: 5 e sinal de mais

• a tecla

10 vezes?

• a tecla

n vezes?

50.

Elabore em seu caderno uma atividade sobre um evento ao qual uma quantidade desconhecida de pessoas deverá comparecer. O evento deve ter um custo para ser realizado e as pessoas devem pagar por um ingresso na entrada. Troque a atividade com um colega e resolva a que ele propôs. Ao receber a resolução do colega, dê um retorno a respeito da resposta dele, indicando os equívocos, se existirem.

51.

Elabore uma questão que envolva a quantidade de patas de uma aranha (oito patas) e a quantidade de patas de uma formiga (seis patas). Ela deve ser resolvida por meio de uma equação do primeiro grau. Troque sua atividade com um colega, resolva a atividade que ele criou e peça a ele que resolva a que você criou.

Página 158

4 Sequências

Nas Olimpíadas Escolares, houve uma prova de corrida de 1 quilômetro. Veja a sequência dos seis primeiros colocados.

Ilustração. Pista de corrida com 3 meninas e 3 meninos usando regatas brancas e bermudas azuis. A pista tem 6 faixas na horizontal e uma faixa quadriculada em preto e branco na vertical, indicando a linha de chegada. A ordem das posições das crianças é da esquerda para a direita.

Classificação dos alunos na prova de 1 km
Posição	Corredor
1ª	Adriana
2ª	Ana
3ª	Cláudio
4ª	Márcia
5ª	Daniel
6ª	Pedro

Essa sequência traz a lista de corredores com posições bem definidas. Em qualquer sequência, a posição de um elemento a define. Isto é, caso Adriana tivesse cruzado a linha de chegada atrás de Ana, ou seja, se Adriana ocupasse a 2ª posição em vez da 1ª, a sequência dos corredores seria outra.

A ideia de sequência aparece em muitas situações do dia a dia, como: a sequência de músicas que tocam em uma rádio, a sequência dos números das casas em um dos lados de uma rua, a sequência dos nomes dos estudantes na lista de chamada, entre outras.

Neste momento, vamos estudar algumas sequências com padrões numéricos.

Sequências numéricas

Uma sequência numérica é um conjunto de números escritos em uma certa ordem. Ela pode ser finita ou infinita. Se a sequência for infinita, usamos reticências para indicar que ela continua indefinidamente. No caso de ser finita, podemos listar todos os elementos.

Considere alguns exemplos de sequências numéricas.

(‒ 2, 7, 4, \frac{1}{2}, 0, 0, ‒ 5)

sequência finita

b) abre parênteses0, 1, 0, 1, 0, 1, reticênciasfecha parênteses

sequência infinita

c) abre parênteses1, 3, 5, 7, reticênciasfecha parênteses

sequência infinita

d) abre parênteses1, 2, 4, 8, 16fecha parênteses

sequência finita

Cada um dos elementos da sequência é chamado de termo da sequência.

Em uma sequência, o termo que ocupa a posição de número n é indicado pelo símbolo an.

Página 159

Ilustração. Homem negro de cabelo preto, usa óculos e veste avental branco, apontando para o quadro de giz e dizendo: Por exemplo, na sequência infinita, abre parênteses, 0, 1, 0, 1, 0, reticências, fecha parênteses, o segundo termo é A com índice 2 é igual a 1

No quadro de giz, está escrito:
Na primeira linha: Dada a sequência, abre parênteses , A com índice 1, A com índice 2, A com índice 3, reticências, A com índice n, reticências, fecha parênteses. temos:
Na segunda linha: A com índice 1 é o primeiro termo da sequência
Na terceira linha: A com índice 2 é o segundo termo da sequência
Na quarta linha: A com índice 3 é o terceiro termo da sequência
Na quinta linha: reticências
Na sexta linha: A com índice N é o enésimo termo da sequência

Lei de formação de uma sequência numérica

Observe as sequências numéricas.

•

(‒ 1, 0, ‒ 5, \sqrt{2}, \frac{1}{2}, ‒ \sqrt{7}, ...)

sequência criada aleatoriamente

• (0, 3, 6, 9, 12, 15, 18, reticências)

sequência dos múltiplos de 3

Qual é o próximo termo de cada sequência?

Para a sequência que foi criada aleatoriamente, não é possível dizer qual é o próximo termo. Já a sequência que é dada pelos múltiplos de 3, conseguimos dizer que o próximo termo é 21.

Algumas sequências têm uma lei de formação, ou seja, uma regra que mostra como a sequência progride ou é formada. A lei de formação de uma sequência numérica pode ser dada por extenso ou por meio de uma sentença algébrica. Analise os exemplos.

a) Lei de formação: sequência infinita dada pelos números primos em ordem crescente.

Sequência: abre parênteses2, 3, 5, 7, 11, reticênciasfecha parênteses

b) Lei de formação: án = 4n

Sequência: abre parênteses4, 8, 12, 16, reticênciasfecha parênteses

n = 1

á_₁ = 4 ⋅ 1 = 4

n = 2

á_₂ = 4 ⋅ 2 = 8

n = 3

á_₃ = 4 ⋅ 3 = 12

n = 4

á_₄ = 4 ⋅ 4 = 16

⋮

c) Lei de formação: án = 2n + 1

Sequência: abre parênteses3, 5, 7, 9, reticênciasfecha parênteses

n = 1

á₁ = 2 ⋅ 1 + 1 = 2 + 1 = 3

n = 2

á₂ = 2 ⋅ 2 + 1 = 4 + 1 = 5

n = 3

á_₃ = 2 ⋅ 3 + 1 = 6 + 1 = 7

n = 4

á_₃ = 2 ⋅ 4 + 1 = 8 + 1 = 9

⋮

Note que as expressões algébricas 4n e 2n + 1 trazem a variável n, que indica a posição dos termos na sequência. Portanto, o termo está sendo calculado a partir de sua posição. Como exemplo, observe que o 4º termo da sequência dada por án = 2n + 1 foi assim calculado:

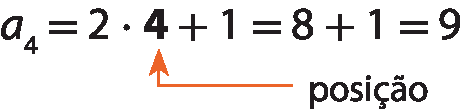
Sequência numérica. Quarto termo é igual a 2 vezes 4 mais 1 é igual a 8 mais 1 é igual a 9.

Abaixo seta no número 4 indicando posição.

Página 160

Observação

Dada uma sequência numérica infinita, não podemos dizer qual é o próximo termo sem saber exatamente qual é a lei de formação dessa sequência. Por exemplo, a sequência infinita (1, 3, 5, reticências) pode parecer a sequência dos números ímpares, e o próximo termo poderia ser 7. No entanto, a lei de formação dessa sequência também poderia ser

a_{n} = ‒ \frac{n^{3}}{6} + n^{2} + \frac{n}{6}

a ₁ = ‒ \frac{1^{3}}{6} + 1^{2} + \frac{1}{6} = 1

a ₂ = ‒ \frac{2^{3}}{6} + 2^{2} + \frac{2}{6} = 3

a ₃ = ‒ \frac{3^{3}}{6} + 3^{2} + \frac{3}{6} = 5

a ₄ = ‒ \frac{4^{3}}{6} + 4^{2} + \frac{4}{6} = 6

Nesse caso, o valor de á₄ seria 6.

Atividades

Faça as atividades no caderno.

52. Em seu caderno, escreva as sequências dadas por meio de suas leis de formação. Se a sequência for infinita, escreva apenas os seis primeiros termos.

a) Sequência dos números inteiros positivos, pares e menores que 20.

b) Sequência dos números inteiros positivos múltiplos de 3.

c) Sequência dos números inteiros positivos, múltiplos de 5, maiores que 20 e menores que 45.

d) Sequência dos números inteiros positivos cujo nome começa com a letra “d”.

53. Invente uma lei de formação para uma sequência numérica e registre a lei e a sequência no caderno.

54. Escreva em seu caderno os cinco primeiros termos das sequências dadas pelas leis de formação. Considere n um inteiro positivo.

a) an = 3n menos 2

b) an = abre parêntesesmenos1fecha parênteseselevado a n

a_{n} = \frac{1}{2 n}

d) an = (n + 1)(n menos 1)

55.

Encontre uma lei de formação para cada uma das sequências a seguir. Depois, explique ao professor e aos colegas como você pensou para determinar cada lei.

a) (6, 12, 18, 24, 30, 36, reticências)

b) (7, 8, 9, 10, 11, 12, reticências)

c) (10, 8, 6, 4, 2, 0, reticências)

(\frac{1}{3}, \frac{2}{3}, 1, \frac{4}{3}, \frac{5}{3}, 2, ...)

Página 161

Sequências recursivas

Em algumas sequências, é possível identificar uma recursividade entre os termos.

Vamos determinar os primeiros termos de uma sequência infinita na qual á₁ = 1, á₂ = 1 e án = án ‒ 1 + án ‒ 2, para todo n inteiro e maior que 2.

n = 3

á₃ = á₂ + á₁ = 1 + 1 = 2

n = 4

á₄ = á₃ + á₂ = 2 + 1 = 3

n = 5

á₅ = á₄ + á₃ = 3 + 2 = 5

n = 6

á₆ = á₅ + á₄ = 5 + 3 = 8

Essa lei de formação gera a sequência da abertura do capítulo, a sequência de fibonáti:

abre parênteses1, 1, 2, 3, 5, 8, reticênciasfecha parênteses

Como cada termo dessa sequência é definido em relação ao termo anterior, dizemos que ela é uma sequência recursiva. Acompanhe outro exemplo de sequência recursiva.

Vamos determinar o 5º termo de uma sequência infinita que é dada pela seguinte lei de formação: á₁ = 0 e án + 1 = án + 2, para todo n inteiro positivo.

Antes de determinar á₅, devemos encontrar os termos anteriores.

Sabemos que á₁ é igual a 0.

Vamos determinar á₂; para isso, substituímos n por 1 em an + 1 para obter á₂:

n = 1

á_n+ 1 = á₁ + 2 á_n+ 1 = á₁ + 2

á₂ = 0 + 2 = 2

Agora, determinamos os próximos termos:

n = 2

á2 + 1 = á₂ + 2

á₃ = 2 + 2 = 4

n = 3

á3 + 1 = á₃ + 2

á₄ = 4 + 2 = 6

n = 4

á4 + 1 = á₄ + 2

á₅ = 6 + 2 = 8

Assim, concluímos que á₅ = 8.

Essa lei de formação gera a sequência (0, 2, 4, 6, 8, reticências), que é a sequência de números naturais pares.

Observações

1. Para calcular o n-ésimo termo de uma sequência recursiva, precisamos calcular todos os termos anteriores a ele. Por exemplo, para calcular o 5º termo por meio da lei á_n₊ícone de altura₁ = a_n₊ícone de altura₂, adotamos n = 4. Assim:

a4 + 1 = a4 + 2, isto é, a5 = a4 + 2

Porém, a4 = a3 + 2 e a3 = a2 + 2.

E assim sucessivamente até chegarmos ao 1º termo, que foi definido como 0.

2. Podem existir diferentes leis de formação que geram a mesma sequência. A sequência dos números pares, por exemplo, pode ser gerada tanto pela lei do exemplo dado quanto pela lei de formação que depende da posição do termo na sequência: an = 2n menos 2, para todo n inteiro positivo. Verifique!

3. Quando não é possível estabelecer regras que definam cada termo em relação ao anterior, dizemos que a sequência é não recursiva. É o caso, por exemplo, da sequência dos números primos.

Página 162

Veja que interessante

Recursão na arte e na literatura

As Matrioskas são bonecas russas feitas de madeira que ficam guardadas umas dentro das outras. A ideia de recorrência (recursão) se dá pelo fato de que, quando abrimos uma boneca, há outra menor e parecida em seu interior. Existem Matrioskas com números impressionantes de camadas de bonecas.

Ilustração. 6 matrioskas vermelhas com imagem de uma mulher de cabelo loiro e flores na frente. Elas têm tamanhos diferentes e estão dispostas em ordem crescente de tamanho, da esquerda para a direita. Estão sobre uma bancada marrom

Além da arte, a ideia de recursão também aparece na literatura. Veja, por exemplo, o poema visual a seguir, no qual a estrutura recursiva de um labirinto serve de suporte para o texto.

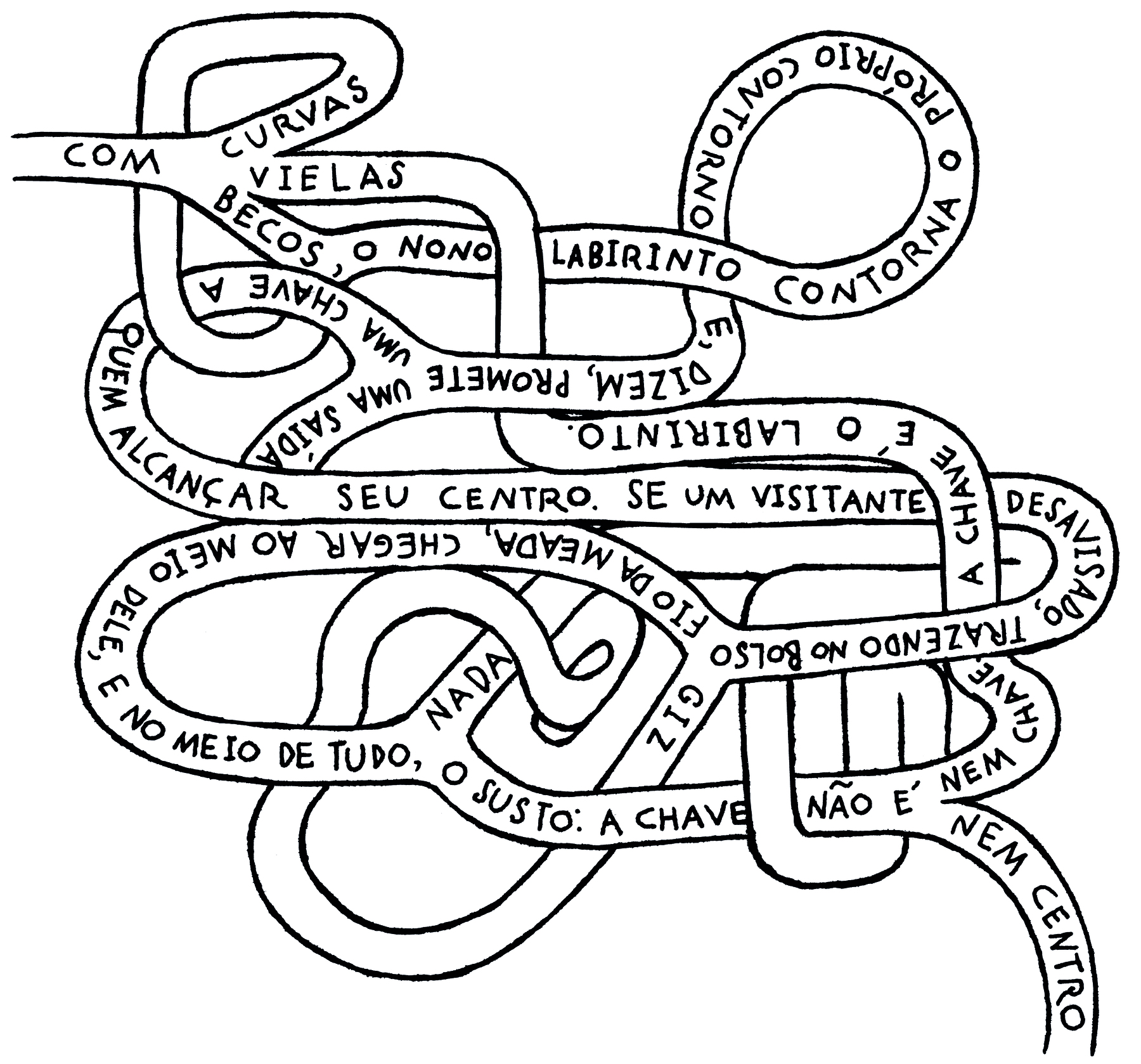
Ilustração em preto e branco. Fundo branco com poema em formato de labirinto com curvas entrelaçadas e informações. — MELLO, Roger. Zubair e os labirintos. São Paulo: Companhia das Letrinhas, 2007.

Atividade

Reúna-se com um colega e pesquisem outros exemplos da presença de recursão na arte ou na literatura. Depois, compartilhem os resultados da pesquisa com a turma.

Página 163

Atividades

Faça as atividades no caderno.

56. Em seu caderno, anote os cinco primeiros termos gerados pelas leis de formação a seguir.

a) á_n = á_n_{‒ 1} + 2, em que á₁ = 0, com n inteiro positivo maior que 1.

b) á_n = á_n_{‒ 1} + 2, em que á₁ = 1, com n inteiro positivo maior que 1.

c) á_n = menos2 ⋅ á_n_{‒ 1}, em que á₁ = menos1, com n inteiro positivo maior que 1.

57. Descreva, em seu caderno, usando uma lei de formação recursiva, cada uma das sequências a seguir.

a) abre parênteses3, 6, 9, 12, 15, reticênciasfecha parênteses

b) abre parênteses0, 1, 2, 3, 4, 5, reticênciasfecha parênteses

c) abre parênteses1, menos1, 1, menos1, 1, reticênciasfecha parênteses

d) abre parênteses1, 2, 4, 8, 16, 32, reticênciasfecha parênteses

58. Com azulejos quadrados brancos e azuis, todos com as medidas de comprimento de lado, construímos os seguintes mosaicos:

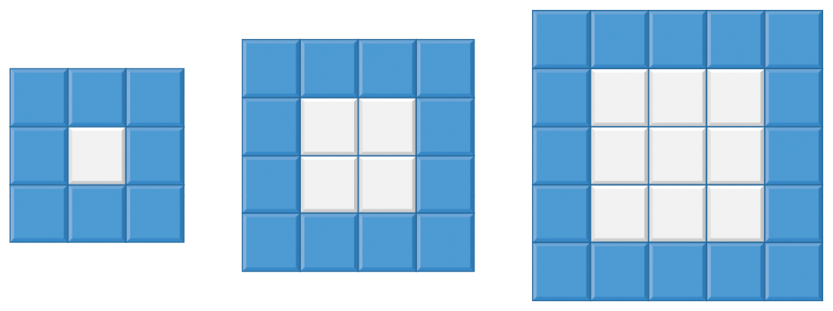
Ilustração: Mosaicos de azulejos quadrados brancos e azuis, com 3 tamanhos diferentes de azulejos.

À esquerda, o azulejo tem 3 linhas e 3 colunas, sendo 12 quadrados azuis nas laterais e 1 quadrado azul no centro.

No meio, o azulejo tem 4 linhas e 4 colunas, com 16 quadrados azuis nas laterais e 4 quadrados brancos no centro.

À direita, o azulejo tem 5 linhas e 5 colunas, com 20 quadrados azuis nas laterais e 9 quadrados brancos no centro.

A regra para construir esses mosaicos é a seguinte: inicialmente, formamos um quadrado com 1 azulejo branco cercado por azulejos azuis; em seguida, outro quadrado, este com 4 azulejos brancos cercado de azulejos azuis; e assim sucessivamente. Considerando a sequência de mosaicos com número crescente de azulejos, responda em seu caderno.

a) Quantos azulejos brancos terá o 15º mosaico dessa sequência?

b) Quantos azulejos brancos terá o n-ésimo mosaico dessa sequência?

c) Quantos azulejos azuis terá o 20º mosaico dessa sequência?

d) Quantos azulejos azuis terá o n-ésimo mosaico dessa sequência?

59.

Crie uma atividade envolvendo sequências numéricas recursivas. A atividade deve conter duas partes.

a) Elabore uma sequência dando os cinco primeiros termos, sem mostrar sua lei de formação. Peça a um colega que encontre a lei de formação na qual pensou.

b) Elabore uma sequência recursiva e entregue a atividade a um colega, pedindo a ele que liste os seis primeiros termos da sequência. Verifique se ele encontrou corretamente os termos, apontando eventuais equívocos.

Sequências numéricas em planilhas eletrônicas

Com um software de planilha eletrônica, é possível construir sequências numéricas inserindo a lei de formação em suas células.

Existem diferentes softwares de planilha eletrônica, mas a maioria tem funcionalidades muito parecidas em termos de manipulação das células e inserção de fórmulas.

Ilustração. Homem de pele morena e cabelo castanho, usando uma camisa verde, ele está sentado à mesa com notebook aberto. Na tela há uma planilha

Confira algumas funcionalidades de uma planilha eletrônica.

Página 164

Esquema. Planilha eletrônica. Na parte superior há três quadros, dispostos horizontalmente da esquerda para a direita. O primeiro quadro é indicado como A1 e exibe uma seta indicando 'campo que mostra a célula selecionada, A célula A1 está localizada na coluna A e linha 1'. O segundo quadro tem X V e fx. O terceiro está em branco, há seta que indica 'campo responsável por mostrar a fórmula associada à célula'.

Na primeira linha da planilha, as colunas são identificadas pelas letras, da esquerda para a direita: A, B, C, D, E, F e G, há uma seta indicando 'Letras que indicam as colunas da planilha". À esquerda, na vertical, a primeira coluna está numerada de 0 a 6, e uma seta indicando 'Números que indicam as linhas da planilha'.

Podemos gerar, em uma planilha eletrônica, os termos da sequência numérica de Fibonacci. Essa sequência pode ser dada por meio da seguinte lei de formação:

á₁ = á₂ = 1 e á_n = á_n_{‒ 1} + á_n_{‒ 2} , para todo n inteiro positivo maior que 2

Inserimos o 1º termo na célula a um (coluna a e linha 1). Em seguida, inserimos o 2º termo na célula a dois (coluna A e linha 2).

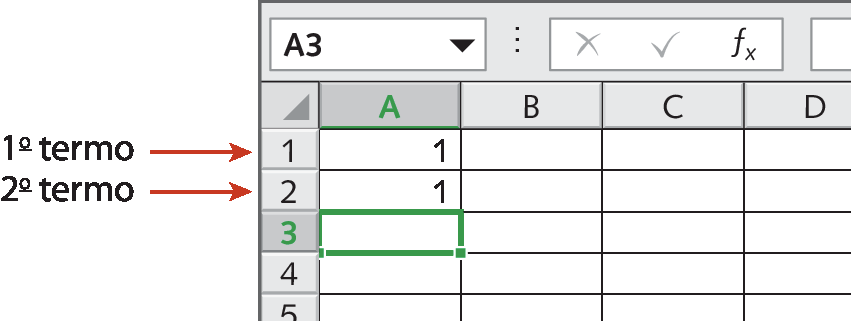
Esquema. Planilha eletrônica do esquema anterior, foram adicionados dois termos. Na parte superior, o primeiro quadro agora é indicado como A3.
Na primeira linha da planilha, a coluna A está destacada pela cor verde, e nela está presente o número 1. Há uma seta que aponta para esse campo indicando que o primeiro termo é 1.
Na segunda linha e na coluna A, novamente há o número 1 e outra seta indicando que esse é o segundo termo.
Na terceira linha, há apenas um destaque em verde sobre um campo em branco, indicando que não há um termo definido nessa célula.

Agora, vamos indicar na planilha eletrônica o 3º termo, que é dado pela soma dos dois primeiros. Primeiro, selecionamos a célula A três (coluna a e linha 3). Depois, no campo de fórmula, colocamos um sinal de igual e indicamos as células que contêm os valores que devem ser adicionados. Neste caso, a um e a dois.

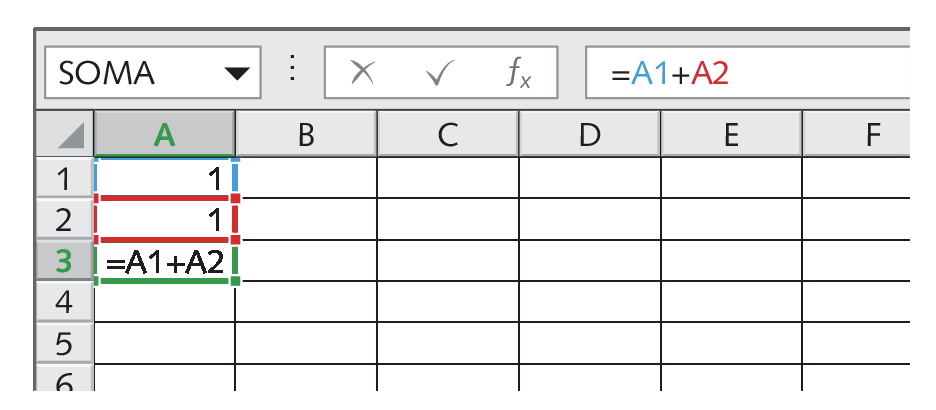
Esquema. Planilha eletrônica do esquema anterior foi atualizada com a adição do terceiro termo. Na primeira e segunda linha da coluna A, os números 1 continuam sendo identificados.
Na terceira linha, a célula apresenta uma fórmula de soma, indicada: igual A1 mais A2
Na parte superior da planilha, o primeiro campo que mostra a célula está identificado como 'Soma'. No terceiro campo, que exibe a fórmula, está escrito igual a A1 mais A2.

Após a indicação das células, devemos apertar a tecla Enter para que a soma seja calculada.

Esquema. Planilha eletrônica do esquema anterior com o terceiro termo. Na primeira e segunda linha da coluna A, os números 1 continuam sendo identificados, e na terceira linha, apresenta o número 2.
Na quarta linha há um destaque de verde para o campo

Página 165

A vantagem de usar uma planilha eletrônica está na praticidade de determinar os próximos termos, pois agora podemos apenas clicar no quadradinho que fica no canto inferior direito da célula A três e arrastar para baixo, copiando a fórmula para as células a quatro, A5, a seis e assim por diante.

Quando fazemos isso, definimos que o conteúdo da célula a quatro corresponde à soma dos valores das células a dois e A três; o mesmo ocorre para a célula A5, que corresponde à soma das células A três e a quatro; e assim sucessivamente.

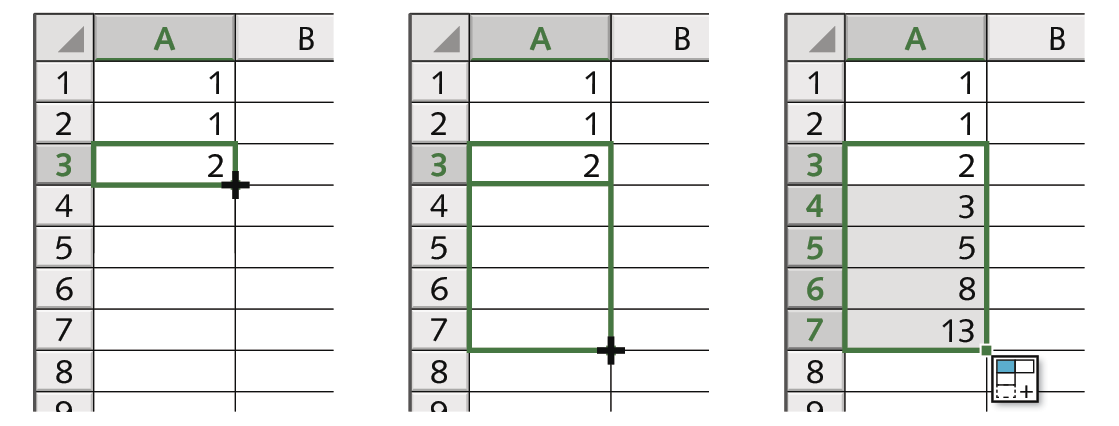
Esquema. Planilha eletrônica do esquema anterior com o terceiro termo.
Apresenta 3 planilhas. Da esquerda para a direita.

A primeira planilha, à esquerda, foi adicionada o terceiro termo. na primeira e segunda linha da coluna A, os números 1 continuam sendo identificados, e na terceira linha, apresenta o número 2.

Na segunda planilha, há um destaque em verde da terceira linha até a sétima linha da coluna A, e os campos sem identificação.

Na terceira planilha, à direita, continua o destaque em verde da terceira linha até a sétima linha da coluna A, e a identificação dos números nos campos. Na quarta linha, está o número 3, na quinta linha, o número 5, na sexta linha, o número 8, na sétima linha o número 13.

Veja que na coluna A apareceu até o 7º termo da sequência. Podemos estender essa técnica indefinidamente na planilha, descobrindo mais termos dessa sequência.

Por exemplo, se quiséssemos o 20º termo da sequência, precisaríamos clicar no quadradinho do canto inferior direito da célula A7 e arrastar para baixo até a célula A20, em que apareceria o 20º termo da sequência.

Atividades

Faça as atividades no caderno.

60.

Em uma planilha eletrônica, gere os termos da sequência de Fibonacci e responda:

a) Qual é o 15º termo da sequência?

b) O número .17711 é um termo dessa sequência? Justifique sua resposta.

c) O número .5213 é um termo dessa sequência? Justifique sua resposta.

61.

Elabore uma questão inspirada na atividade 60 e troque com um colega para que um resolva a questão criada pelo outro.

62.

Usando um software de planilha eletrônica, gere os termos das sequências a seguir e, em seu caderno, liste os 10 primeiros termos.

a) á_n = á_n_{‒ 1} + 7, em que á₁ = 4, com n inteiro positivo maior que 1.

b) á_n = á_n_{‒ 1} menos 10, em que á₁ = 50, com n inteiro positivo maior que 1.

c) á_n = (á_n_{‒ 1}) ⋅ (á_n_{‒ 2}), em que á₁ = 1 e á₂ = 2, com n inteiro positivo maior que 2.

d) á_n = (á_n_{‒ 1}) ⋅ 11, em que á₁ = 1, com n inteiro positivo maior que 1.

63.

Responda no caderno.

a) A célula de uma planilha eletrônica tem qual papel quando criamos a sequência numérica: variável ou incógnita? Justifique.

b) As fórmulas da atividade 62, inseridas nas células da planilha eletrônica, eram de sequências recursivas. É possível criar sequências definidas por fórmulas que dependem da posição do termo usando uma planilha eletrônica? Justifique.

Página 166

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Expressões algébricas

Uma sentença matemática formada por números e letras ou somente por letras é chamada de expressão algébrica. Por exemplo:

x + 4y + z + 2m

Valor numérico de uma expressão algébrica

Valor numérico é o resultado das operações efetuadas em uma expressão algébrica após a substituição das variáveis por números.

Adição e multiplicação de termos algébricos

Adição algébrica

Para adicionar termos algébricos que têm a mesma parte literal, devemos adicionar os coeficientes e conservar a parte literal.

Multiplicação algébrica

Para multiplicar dois termos algébricos, devemos:

• multiplicar os coeficientes numéricos entre si;

• multiplicar as partes literais entre si.

1. Indique o número desconhecido por x e represente cada frase por meio de uma expressão algébrica.

a) a soma de sete com o dobro de um número;

b) a sexta parte de um número;

c) o produto de um número pela sua sétima parte.

2. Teresa tem 32 anos. Escreva no caderno uma expressão algébrica que represente a idade que ela teve há x anos, sendo x um número natural.

3. Calcule o valor numérico da expressão algébrica em cada item.

a) xelevado a 2 menos 2x + y elevado a 2, para x = –1 e y = –2

b) x elevado a 2y menos 2xy, para x = –2 e y = 3

c) 4xy menos 3y elevado a 2, para x = 2 e y = menos1

4. Calcule estas adições algébricas.

a) 15x ‒ 8x + (12x + 3x ‒ 9x)

b) 11y menos 15y menos 9y + 25y

c) 25x + 12y + abre parênteses9x menos 6y menos zfecha parênteses

d) 2x + 4y menos z menos abre parênteses3x menos 5y + 5zfecha parênteses

5. Determine estes produtos algébricos.

a) menos 3 ⋅ abre parêntesesmenos 12xfecha parênteses

b) abre parêntesesmenos xyfecha parênteses ⋅ abre parênteses3y elevado a 2fecha parênteses

c) menos 3x ⋅ abre parêntesesmenos 2xy elevado a 2fecha parênteses ⋅ x elevado a 2 ⋅ abre parênteses4fecha parênteses

6. Escreva as expressões algébricas que representam a medida do perímetro e a medida da área da figura a seguir.

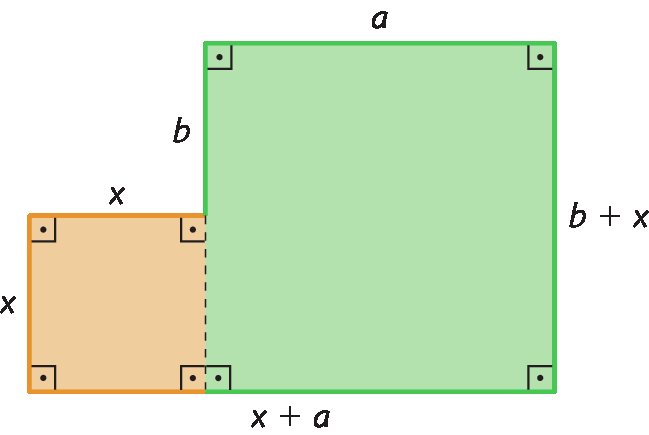
Ilustração: um retângulo e um quadrado lado a lado e destacando os ângulos retos com 90 graus. À esquerda, há um quadrado laranja com uma marcação na lateral indicando que a altura mede X e outra marcação na parte superior indicando que o comprimento também mede X. À direita, há um retângulo verde na vertical, com uma marcação na parte superior indicando que seu comprimento mede A e uma marcação abaixo indicando que a diferença entre o quadrado e o retângulo é B. Na parte lateral direita, há uma marcação indicando que a altura total mede B mais X, e na parte inferior há outra marcação indicando que o comprimento total é X mais A.

Equações

Equação é uma sentença matemática expressa por uma igualdade que apresenta pelo menos um valor desconhecido representado por uma letra denominada incógnita.

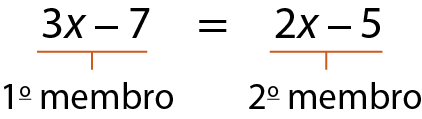
Esquema. Sentença matemática. 3X menos 7 é igual a 2X menos 5
No lado esquerdo, há um fio vermelho indicando primeiro membro
No lado direito, há um fio vermelho indicando segundo membro

Quando o maior expoente de uma incógnita em uma equação é 1, a denominamos equação do 1º grau.

Raiz de uma equação

Um valor que, substituindo a incógnita, torna a sentença verdadeira é chamado de raiz da equação.

O conjunto universo de uma equação é formado por todos os valores que uma incógnita pode assumir e é indicado por U.

As raízes da equação que pertencem ao conjunto universo são as soluções dessa equação e formam seu conjunto solução, que é indicado por S.

7. Identifique, no caderno, as sentenças que representam equações do 1º grau.

a) 3x menos 1 > 12

b) 5 + 12 = 20 menos 3

c) 15 = 6y menos 9

d) 2x + 15 = 18 menos 2

e) 5a + 4b ≠ 12

f) x2 + 12 = 25

Página 167

8. Verifique se o número 3 é raiz das seguintes equações:

a) 3x menos 3 = 9 menos x

\frac{x}{3} + 12 = \frac{4 x}{2} ‒ 1

c) 4x menos 14 = 7 menos 3x

9. Determine mentalmente o conjunto solução de cada equação, sendo U =

a) x menos 15 = 0

\frac{x}{5} = 5

x + \frac{1}{2} = 0

x ‒ \frac{4}{9} = \frac{3}{9}

Resolução de equações do 1º grau com uma incógnita

Quando duas equações têm o mesmo conjunto universo e as mesmas raízes, elas são chamadas de equações equivalentes.

Princípio aditivo e princípio multiplicativo das igualdades

• princípio aditivo das igualdades: quando adicionamos ou subtraímos uma mesma quantidade nos dois membros de uma equação, obtemos uma equação equivalente à primeira.

• princípio multiplicativo das igualdades: quando multiplicamos ou dividimos por um mesmo número não nulo os dois membros de uma equação, obtemos uma equação equivalente à primeira.

10. Sabendo que U =

, resolva as equações.

a) 2x + abre parênteses9 menos xfecha parênteses = 8 menos abre parênteses3x menos 6fecha parênteses

b) 8 ⋅ abre parênteses2x menos 1fecha parênteses = 6 ⋅ abre parênteses5x menos 2fecha parênteses menos 10

c) y menos abre colchetey menos abre parênteses2 menos 4fecha parênteses menos 1fecha colchete + 4 = menos abre parêntesesmenos 3 menos yfecha parênteses

\frac{2 x}{5} ‒ \frac{3}{4} = \frac{3 x}{20}

\frac{x}{4} + \frac{x + 3}{2} = 2

\frac{2 x}{5} + \frac{15 x ‒ 1}{20} = \frac{1}{3}

11. Determine o conjunto solução da equação

‒ \frac{1}{4} (x ‒ 2) = 2 x ‒ \frac{1}{3}

para:

a) U =

b) U =

12. Calcule o valor de m, considerando a equação (m menos 2) ⋅ x + 2x + 4 ⋅ (m menos 5) = 0, em que x é igual a 2.

13. Uma empresa de transporte aéreo está oferecendo um desconto de

\frac{3}{10}

do valor da passagem. Mário pagou R$ 210,00duzentos e dez reais pela passagem, já com desconto. Qual é o valor da passagem sem desconto?

14. Em uma indústria, o número de homens é igual a

\frac{3}{5}

do número de mulheres. Se fossem admitidos mais 20 homens, o número de funcionários ficaria igual ao número de funcionárias. Quantas mulheres e quantos homens trabalham nessa fábrica?

15. Em um cesto, há peras, laranjas e bananas. Ao todo, são 96 frutas. O número de peras é o triplo do de laranjas, e o número de bananas é igual ao de laranjas e peras reunidas. Quantas frutas há de cada tipo?

Sequências

Uma sequência numérica é um conjunto de números escritos em uma certa ordem. Ela pode ser finita ou infinita.

A lei de formação de uma sequência é uma regra que mostra como a sequência progride ou é formada.

Uma sequência recursiva é uma sequência em que cada termo é definido em relação ao termo anterior.

16. Escreva em seu caderno os seis primeiros termos das sequências a seguir.

a_{n} = 2 n + 5

a_{n} = n^{2} + n

a_{n} = \frac{n}{n + 1}

17. Em seu caderno, relacione as leis de formação que dão origem à mesma sequência numérica.

a_{n} = 2^{n}

, com n inteiro positivo

a_{n} = 3 n

, com n inteiro positivo

a_{n} = 3 n + 1

, com n inteiro positivo

a_{n} = 2 n

, com n inteiro positivo

a_{n} = a_{n ‒ 1} + 3

a_{1} = 4

, com n inteiro maior que 1

dois

a_{n} = a_{n ‒ 1} + 2

a_{1} = 2

, com n inteiro maior que 1

três

a_{n} = 2 \cdot a_{n ‒ 1}

a_{1} = 2

, com n inteiro maior que 1

quatro

a_{n} = a_{n ‒ 1} + 3

a_{1} = 3

, com n inteiro maior que 1

Página 168

É hora de extrapolar

Faça as atividades no caderno.

Você já ouviu falar do í dê agá? Sabe o que significa?

Índice de Desenvolvimento Humano (í dê agá) é uma medida usada para avaliar as condições de vida de uma população. Conhecer os parâmetros e o cálculo usados para a obtenção desse índice ajuda a compreender como e o que um valor numérico indica sobre o desenvolvimento humano de uma sociedade.

Objetivos: Pesquisar sobre o í dê agá, analisar os cálculos utilizados para determinar o í dê agá, produzir uma reportagem sobre o assunto e elaborar e apresentar um jornal.

Etapa 1: Pesquisa sobre o í dê agá.

Reúna-se em grupo. Pesquisem em sites ou livros especializados sobre í dê agá, buscando informações a respeito da origem desse índice, dos objetivos, dos significados, dos parâmetros utilizados em seu cálculo, das escalas usadas para a classificação dos países e dos resultados mais recentes.

2. A partir dos resultados obtidos, respondam:

a) O í dê agá é calculado a partir de indicadores em três áreas. Quais são elas?

b) Vocês acham que existem outros indicadores que poderiam ou deveriam ser considerados no cálculo para medir o desenvolvimento humano de uma sociedade? Se sim, quais?

3. O Relatório de Desenvolvimento Humano de 2020, publicado pelo Programa das Nações Unidas para o Desenvolvimento (penúdi), apresenta os valores de í dê agá de 189 países para o ano de 2019. Veja a tabela a seguir com alguns desses dados.

Índice de Desenvolvimento Humano de alguns países e classificação – 2019
Classificação	País	IDH
1º	Noruega	0,957
2º	Irlanda	0,955
2º	Suíça	0,955
4º	Hong Kong, China	0,949
185º	Sudão do Sul	0,433
187º	Chade	0,398
188º	República Centro-Africana	0,397
189º	Níger	0,394

Dados obtidos em: https://oeds.link/J95YLG. Acesso em: 20 junho 2022.

a) Qual é a diferença entre o í dê agá da Noruega e o í dê agá de Níger?

b) Qual é a diferença entre 1 e o índice obtido pela Noruega?

c) De acordo com o valor obtido no item a, podemos afirmar que o í dê agá da Noruega é próximo ao í dê agá de Níger? Por quê?

d) Escreva os valores do í dê agá de Róng Kóng e Sudão do Sul na fórma fracionária.

e) Ao escrever o valor do í dê agá de um país na fórma fracionária, o denominador será maior, igual ou menor que o numerador? Por quê?

Etapa 2: Análise do cálculo utilizado para determinar o í dê agá de uma localidade.

4. O índice relacionado à educação, um dos aspectos considerados na determinação do í dê agá (2019), pode ser obtido por meio do seguinte cálculo:

I_{educação} = \frac{\frac{M E}{15} + \frac{E E}{18}}{2},

sendo ME o número médio de anos que os indivíduos frequentam a escola e EE o número esperado de anos que os indivíduos passem na escola.

Determine o Ieducação do Brasil em 2019, sabendo que o ME foi de 8 e o EE de 15,4.

Página 169

5. O índice relacionado à saúde (expectativa de vida), no í dê agá de 2019, pode ser obtido por meio do seguinte cálculo:

I_{saúde} = \frac{EV ‒ 20}{85 ‒ 20},

sendo EV a expectativa de vida do país.

Sabendo que o Isaúde do Brasil em 2019 foi de 0,86, determine a EV do país nesse ano (use uma aproximação com uma casa decimal).

Etapa 3: Elaboração de reportagem sobre o Índice de Desenvolvimento Humano Municipal (i dê agá ême).

6. Além do í dê agá dos países, também é possível analisar os índices para os municípios brasileiros. O Atlas do Desenvolvimento Humano no Brasil é um site que abriga diversas informações sobre o desenvolvimento humano no país.

Um dos conteúdos explorados pelo Atlas é o rãnquin do Índice de Desenvolvimento Humano Municipal (i dê agá ême) por estados brasileiros. Veja as informações sobre os estados que obtiveram os maiores índices, em 2017:

IDHM – 2017
Posição	Estado	IDHM	IDHM renda	IDHM longevidade	IDHM educação
1ª	Distrito Federal	0,850	0,890	0,859	0,804
2ª	São Paulo	0,826	0,854	0,796	0,828

Dados obtidos em: https://oeds.link/Wrdbpb. Acesso em: 18 maio 2022.

Comparem os índices apresentados para Distrito Federal e São Paulo. É correto afirmar que o estado que ocupa o 1º lugar obteve índices superiores em todos os quesitos em relação ao estado que ocupa o 2º lugar?

7. Explorem o ranking de i dê agá ême disponível no site Atlas do Desenvolvimento Humano no Brasil, comparando municípios e explorando também o ranking dos estados. Selecionem dois municípios, ou dois estados, e elaborem uma reportagem comparando o i dê agá ême das localidades escolhidas. A reportagem deverá conter:

• uma manchete (título);

• explicação sobre o í dê agá (significado, objetivos, indicadores considerados etcétera);

• estado em que os municípios se localizam ou região em que os estados selecionados se localizam e número de habitantes;

• tabela com os valores de i dê agá ême das localidades selecionadas;

• comparação e análise dos índices;

• imagens do locais selecionados e outras informações que julgarem importantes.

Etapa 4: Elaboração e apresentação de um jornal.

Disponibilizem a reportagem elaborada para que os demais colegas comentem sobre a pertinência da manchete, a clareza das informações e a comparação e a análise dos índices das localidades escolhidas.

9. Anotem as dúvidas, as opiniões e as sugestões dos colegas.

10. Depois dos ajustes necessários, organizem um jornal, digital ou impresso, composto das reportagens elaboradas pela turma. Divulguem o jornal para que todos da comunidade escolar tenham acesso às informações.

Etapa 5: Síntese do trabalho realizado.

11.

Algumas questões que devem ser discutidas:

a) Como a pesquisa realizada na etapa 1 ajudou na elaboração da reportagem?

b) Quais ações devem ser tomadas para que um país, estado ou município eleve seu í dê agá?

12. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.