Página 184

Capítulo 8 Proporcionalidade

Trocando ideias

De acordo com o Instituto Brasileiro de Geografia e Estatística (í bê gê É), em 2060, uma em cada 3 pessoas no Brasil terá idade superior a 60 anos. Uma das maiores conquistas dessa parcela da população foi o Estatuto do Idoso (Lei número 10.741/2003), que trata dos principais direitos dos idosos e dos deveres da sociedade, da família e do Poder Público para com eles.

Fotografia: Um idoso branco, de camisa branca e bermuda jeans e uma idosa branca, de camiseta cinza e calça preta, caminham em um parque. O homem está um pouco à frente da mulher. A mulher passeia com um cachorro amarrado na guia. À direita da pista de caminhada tem um gramado, com árvores e bancos de concreto. À esquerda, um lago. O dia está ensolarado com algumas nuvens no céu. — Casal de idosos passeando com cachorro no Parque das Águas, em Cambuquira (Minas Gerais). Foto de 2021.

▸

Você conhece algum direito dos idosos? Se sim, qual? Converse com os colegas a respeito disso.

Sabendo que a razão entre dois números, aêbê, com b ≠ 0, nessa ordem, é dada por

\frac{a}{b}

, em seu caderno, escreva:

▸ na fórma de fração a razão entre o número de idosos e o número total de habitantes no Brasil em 2060.

▸ na fórma de porcentagem a razão entre o número de idosos e o número total de habitantes no Brasil em 2060.

Neste capítulo, vamos estudar razão, proporção e grandezas diretamente e inversamente proporcionais.

Página 185

1 Razão

A palavra “razão” tem origem no latim ratio, que significa “divisão”. Podemos expressar a razão na fórma de fração, de porcentagem ou de número decimal.

Analise os exemplos a seguir:

a) Leia a orientação de uso no rótulo desta garrafa de suco concentrado.

Ilustração: Uma embalagem roxa de suco de uva. No rótulo está escrito "Suco de Uva" e tem um desenho de um cacho de uva roxa. À direita da embalagem, um círculo destaca uma parte do rótulo, com a indicação "1 porção de suco para 5 porções iguais de água".

De acordo com a orientação do rótulo, podemos dizer que para cada litro de suco concentrado devem ser colocados 5 litros de água na mistura.

• A razão entre a quantidade de suco concentrado e a quantidade de água é:

\frac{1}{5}

= 0,20 =

\frac{20}{100}

= 20%

• A razão entre a quantidade de água e a quantidade de suco concentrado é:

\frac{5}{1} = \frac{500}{100}

= 500%

b) De 100 pessoas convidadas para determinada cerimônia, 75 eram mulheres.

A razão entre o número de mulheres e o número de convidados é:

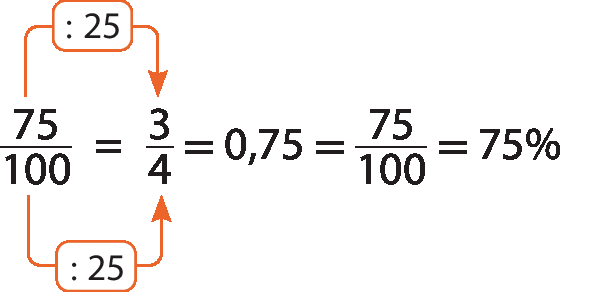
Esquema: Da esquerda para a direita, setenta e cinco sobre cem, igual a três sobre quatro.
Acima da fração setenta e cinco sobre cem uma seta alaranjada vai até a fração três sobre quatro. No meio dessa seta a indicação divisão por 25.
Abaixo da fração setenta e cinco sobre cem uma seta alaranjada vai até a fração três sobre quatro. No meio dessa seta a indicação divisão por 25.
À direita, zero, vírgula setenta e cinco, igual a setenta e cinco sobre cem, igual a setenta e cinco por cento.

A razão indica que, em cada grupo de 4 convidados, 3 eram mulheres.

Essa razão também pode ser expressa em porcentagem. Se havia 75 mulheres entre 100 convidados, 75% dos convidados eram mulheres.

A razão entre dois números, aêbê, com b ≠ 0, nessa ordem, é dada por

\frac{a}{b}

Atividades

Faça as atividades no caderno.

1. Escreva, no caderno, uma razão entre os números ou medidas presentes em cada uma das frases.

a) Um corretor de imóveis recebe R$ 5,00cinco reais de comissão para cada R$ 100,00cem reais em imóveis vendidos.

b) Um time de futebol feminino venceu 15 dos 22 jogos que disputou.

c) Melissa acertou 17 das 20 questões de uma prova de Matemática.

d) No Brasil, o combustível usado nos carros movidos a gasolina tem sido, na verdade, um composto em que para 4 litros do combustível há 1 litros de álcool anidro.

Página 186

2. Carlos e Antônio brincaram de cobrar pênaltis. Carlos cobrou 8 pênaltis e fez 5 gols. Antônio cobrou 10 pênaltis e fez 7 gols.

a) Escreva, na fórma de fração irredutível, a razão entre o número de pênaltis cobrados por Carlos e o número de pênaltis cobrados por Antônio.

b) Escreva, na fórma de porcentagem, a razão entre o número de gols feitos e o número de pênaltis cobrados por Antônio.

c) Escreva, na fórma decimal, a razão entre o número de gols feitos e o número de pênaltis cobrados por Carlos.

3. Em uma classe com 30 estudantes, 24 foram aprovados nas provas finais.

Ilustração: uma professora branca, de camiseta rosa, saia azul e jaleco branco está em pé em uma sala de aula, segurando um livro. À sua direita tem uma mesa e uma cadeira, sobre a mesa um livro aberto. À sua esquerda, a porta da sala. Atrás da professora, uma lousa verde. À frente da professora, 30 alunos estão sentados, em 5 fileiras com 6 alunos cada. Sobre as mesas dos alunos está uma folha de papel.

Determine a razão entre o número de estudantes:

a) aprovados e o total de estudantes;

b) reprovados e o total de estudantes;

c) aprovados e reprovados.

4. Escreva na fórma de fração irredutível a razão entre cada par de medidas, na ordem apresentada.

a) 5 centímetros e 10 centímetros

b) 200 gramas e 40 gramas

c) 7 quilogramas e 10,5 quilogramas

d) 14 litros e 35 litros

5. Em uma prova com 80 testes, a razão entre o número de testes que Daniele acertou e o número total de testes foi de 2 para 5.

a) Represente essa razão na fórma de fração irredutível, de número decimal e de porcentagem.

b) Calcule o número de testes que Daniele acertou.

Ilustração: Menina negra, de cabelos encaracolados pretos, óculos de grau, camiseta branca e calça rosa, ela está sentada em uma cadeira escrevendo em um papel branco, que está sobre uma mesa. Sobre a mesa, além do papel, há uma borracha.

6. Ivan e Sílvio caminham no parque todos os dias. Ontem, Ivan caminhou .2000 métros e Sílvio, .3500 métros. Determine a razão entre as medidas das distâncias percorridas por Ivan e Sílvio.

7. Um terreno tem 750 métros quadrados de medida de área total e 500 métros quadrados de medida de área construída. Qual é a razão entre a medida da área construída e a medida da área livre?

2 Proporção

Em carros com motor bicombustível (flex), é possível utilizar como combustível uma mistura de etanol e gasolina.

Vamos supor que, no tanque de 50 litros de um carro, tenham sido colocados 10 litros de etanol e 40 litros de gasolina. Já o tanque de 60 litros de outro carro foi preenchido com 12 litros de etanol e 48 litros de gasolina.

Observe as razões entre a quantidade de etanol e a de gasolina nos dois tanques:

• tanque de 50 litros

\frac{10}{40} = \frac{1}{4}

• tanque de 60 litros

\frac{12}{48} = \frac{1}{4}

Verificamos que as duas razões são iguais; nesse caso, dizemos que as duas razões formam uma proporção. Essa proporção é assim indicada:

\frac{10}{40} = \frac{12}{48}

Proporção é uma igualdade entre duas razões.

Página 187

A proporção

\frac{10}{40} = \frac{12}{48}

também pode ser indicada assim: 10 : 40 = 12 : 48

Dados quatro números não nulos, a, b, c e d, nessa ordem, dizemos que eles formam uma proporção quando

\frac{a}{b} = \frac{c}{d}

(lemos: “a está para b, assim como c está para d ” ).

Os termos de uma proporção são assim denominados:

Esquema: a sobre b igual a c sobre d. Uma seta alaranjada parte da letra a e da letra d com a indicação: extremo. Uma seta verde parte da letra b e da letra c, com a indicação: meio.

Esquema: Na horizontal, a dividido por b, igual a c dividido por d. Uma seta alaranjada parte da letra a e da letra d com a indicação: extremos. Uma seta verde parte da letra b e da letra c com a indicação: meios.

Por exemplo, na proporção

\frac{3}{4} = \frac{27}{36}

, os extremos são 3 e 36, e os meios, 4 e 27.

Um pouco de história

A ideia de proporção na história da Matemática

A ideia de proporção é atribuída a Pitágoras (cêrca de 580 antes de Cristo-500 antes de Cristo), embora haja dúvida sobre isso. Na Antiguidade, o estudo das proporções presumivelmente fazia parte da Aritmética ou da teoria pitagórica dos números.

Eudoxo de Cnido, discípulo de Platão, matemático e filósofo grego que viveu entre 408 antes de Cristo e 355 antes de Cristo, deu nova definição para os teoremas relacionados a proporções. Essa definição foi exposta no Livro cinco de Os elementos, de Euclides (330 a.C.-?), e é a que conhecemos e usamos hoje em dia.

Fonte: BOYER, Carl Benjamin. História da Matemática. São Paulo: Edgard Blücher/êduspi, 1974. página 34, 61, 66.

Ilustração: caricatura de Eudoxo de Cnido, representado como um homem de barba, usando uma touca na cabeça e vestindo uma túnica. — Caricatura de Eudoxo de Cnido.

Atividade

Reúna-se com três colegas e pesquisem um pouco mais sobre como a ideia de proporção se desenvolveu ao longo da história da Matemática. Vocês podem consultar livros, revistas ou páginas da internet.

Atividades

Faça as atividades no caderno.

8. Por que podemos afirmar que

\frac{2}{7}

\frac{8}{28}

formam uma proporção?

9. Escreva, no caderno, como se leem as proporções, identificando os meios e os extremos de cada uma delas

\frac{3}{5} = \frac{9}{15}

\frac{7}{8} = \frac{14}{16}

10. Observe estas razões:

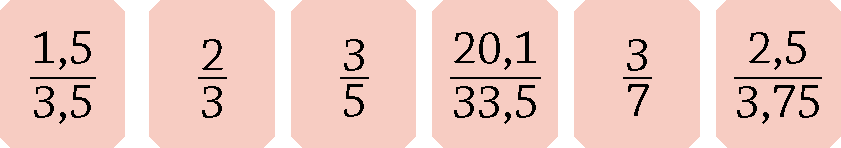
Esquema: da esquerda para a direita, razões em quadros laranjas. Um vírgula cinco sobre três vírgula cinco; dois sobre três; três sobre cinco; vinte vírgula um sobre trinta e três vírgula cinco; três sobre sete; dois vírgula cinco sobre três vírgula setenta e cinco.

Indique os pares de razões que formam proporções.

Página 188

11. Observe os retângulos a seguir e responda às questões.

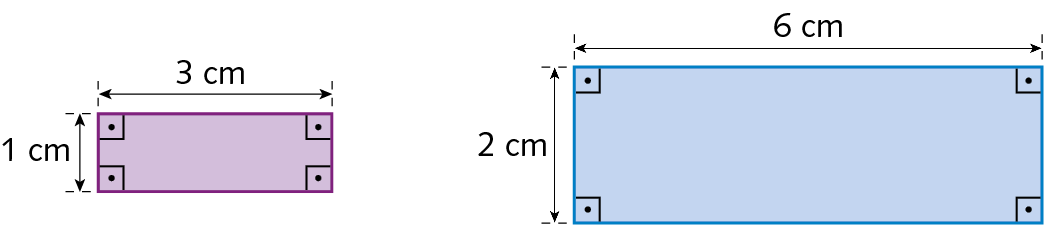
Ilustrações. À esquerda, retângulo que mede 3 centímetros de comprimento e 1 centímetro de altura e à direita um retângulo que mede 6 centímetros de comprimento e 2 centímetros de altura

a) Qual é a razão entre as medidas do comprimento da largura dos dois retângulos?

b) Qual é a razão entre as medidas do comprimento dos dois retângulos?

c) Podemos afirmar que as medidas de comprimento correspondentes das figuras são proporcionais? Justifique sua resposta.

Propriedade fundamental das proporções

A nau Santa Maria era uma das embarcações da esquadra comandada por Cristóvão Colombo (1451-1506) na viagem em que os europeus chegaram ao continente americano, em 1492. Em um museu, há uma miniatura dessa nau que mede 56 centímetros de comprimento. Sabendo que cada 1 centímetro de comprimento na miniatura corresponde a 65 centímetros de comprimento na embarcação real, qual era a medida do comprimento real da embarcação?

Ilustração: Um barco a velas. O casco do barco é marrom, e as velas são bege com um símbolo vermelho que se assemelha a uma cruz. — Miniatura da nau Santa Maria.

Para responder a essa questão, vamos indicar por x a medida, em centímetro, do comprimento real da embarcação; portanto, x é diferente de 0. Assim, podemos escrever a seguinte proporção:

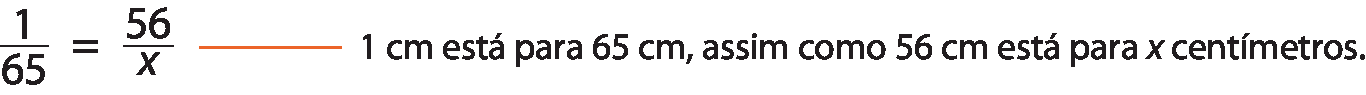
Esquema: um sobre sessenta e cinco igual a cinquenta e seis sobre x. À direita, traço alaranjado. À direita do traço, a indicação: 1 centímetro está para sessenta e cinco centímetros assim como cinquenta e seis centímetros está para x centímetros.

Para determinar o valor de x, podemos multiplicar ambos os membros dessa igualdade por x e, em seguida, por 65. Assim, temos:

\frac{1}{65} = \frac{56}{x}

Sentença matemática. um sobre sessenta e cinco vezes x igual a cinquenta e seis sobre x (há um traço alaranjado sobre o x) vezes x (há um traço alaranjado sobre o x). À direita, traço horizontal alaranjado. À direita do traço, a indicação 'ao multiplicar os dois membros de uma igualdade por um mesmo número, diferente de zero, obtemos outra igualdade'.

\frac{1 \cdot x}{65} = 56

Sentença matemática. um vezes x sobre sessenta e cinco (há um traço alaranjado sobre o 65) vezes sessenta e cinco (há um traço alaranjado sobre o 65) igual a cinquenta e seis vezes sessenta e cinco.

1 ⋅ x = 56 ⋅ 65

x = .3640

Portanto, a medida do comprimento real da embarcação era .3640 centímetros ou 36,40 métros.

Ao desenvolver os cálculos para obter o valor de x nessa proporção, podemos observar uma igualdade entre o produto dos meios e o produto dos extremos:

\frac{1}{65} = \frac{56}{x}

⇒ 1 ⋅ x = 56 ⋅ 65

Página 189

Essa propriedade é válida para todas as proporções. Acompanhe a demonstração a seguir.

Demonstração

Considere

\frac{a}{b} = \frac{c}{d}

, em que a, b, c e d representam números racionais não nulos.

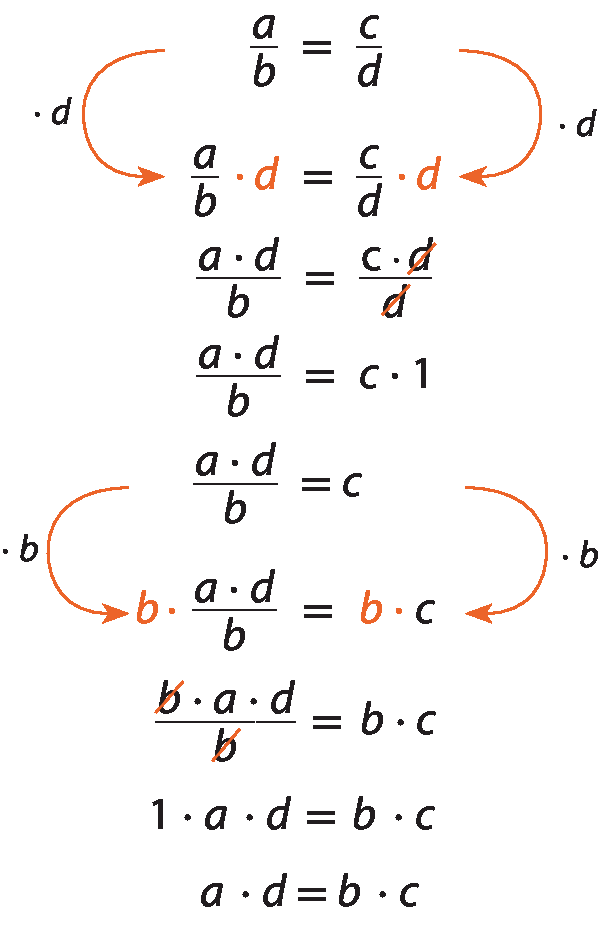
Esquema: de cima para baixo, a sobre b igual a c sobre d.
Abaixo, a sobre b vezes d (alaranjado) igual a c sobre d vezes d (alaranjado). Há uma seta alaranjada que liga a sobre b da primeira linha com a sentença a sobre b vezes d da segunda linha. No meio dessa seta, a indicação de multiplicação por d. Há uma seta alaranjada que liga a fração c sobre d da primeira linha com a sentença c sobre d vezes d da segunda linha. No meio dessa seta, a indicação de multiplicação por d.
Abaixo, a vezes d sobre b igual a c vezes d (com um traço alaranjado sobre o d) sobre d (com um traço alaranjado sobre o d).
Abaixo, a vezes d sobre b igual a c vezes um.
Abaixo, a vezes d sobre b igual a c.
Abaixo, b (alaranjado) vezes a vezes d sobre b igual a b (alaranjado) vezes c.
Há uma seta alaranjada que liga a linha acima com a linha abaixo, com a indicação multiplicado por b.
Abaixo, b (com um traço alaranjado sobre o b) vezes a vezes d sobre b (com um traço alaranjado sobre o b) igual a b vezes c.
Abaixo, um vezes a vezes d igual b vezes c.
Abaixo, a vezes d igual b vezes c.

Ilustração: Um menino negro, de cabelos castanhos, camiseta branca e calça azul está sentado em uma cadeira escrevendo. Sobre a mesa que está a sua frente, um caderno e um estojo azul. O menino diz: "como a, b, c e d representam números racionais quaisquer, diferentes de zero, essa propriedade é válida para toda proporção".

Em toda proporção, o produto dos extremos é igual ao produto dos meios, ou seja, dados a, b, c e d racionais não nulos, com

\frac{a}{b} = \frac{c}{d}

, temos: a ⋅ d = b ⋅ c

Denominamos essa propriedade de propriedade fundamental das proporções.

Podemos empregar a propriedade fundamental das proporções para resolver diversos problemas, sejam puramente matemáticos ou contextualizados. Acompanhe os exemplos a seguir.

a) Sabendo que 5 está para 8, assim como 15 está para x, qual é o valor de x?

Para determinar o valor de x, inicialmente escrevemos a proporção:

\frac{5}{8} = \frac{15}{x}

Em seguida, aplicamos a propriedade fundamental das proporções e resolvemos a equação encontrada:

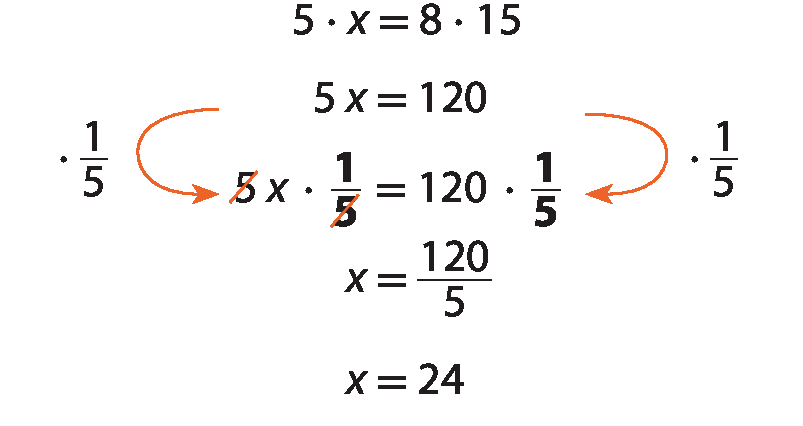
Esquema: De cima para baixo, cinco vezes x igual a oito vezes quinze.
Abaixo, cinco x igual a cento e vinte.
Abaixo, cinco x (com um traço alaranjado sobre o 5) vezes um quinto (com um traço alaranjado sobre o 5) igual a cento e vinte vezes um quinto. Há uma seta alaranjada ligando a linha de cima com a de baixo. No meio da seta, a indicação multiplicado por um quinto.
Abaixo, x igual a cento e vinte quintos.
Abaixo, x igual a vinte e quatro.

Portanto, o valor de x é 24.

Página 190

b) Em uma salina, de cada .1000 decímetros cúbicos de água salgada são retirados 40 decímetros cúbicos de sal. Para obter 800 decímetros cúbicos de sal, quantos decímetros cúbicos de água salgada são necessários?

(A quantidade de sal retirada é proporcional à medida do volume de água salgada.)

Indicando por x a quantidade, em decímetros cúbicos, de água salgada a ser determinada, podemos escrever a seguinte proporção:

\frac{1 000}{40} = \frac{x}{800}

Fotografia: Ao fundo de um terreno, montes de sal. Há uma passagem para que o sal chegue até esse monte. O dia está ensolarado. — Extração de sal em Macau (Rio Grande do Norte). Foto de 2019.

Em seguida, aplicamos a propriedade fundamental das proporções e resolvemos a equação encontrada:

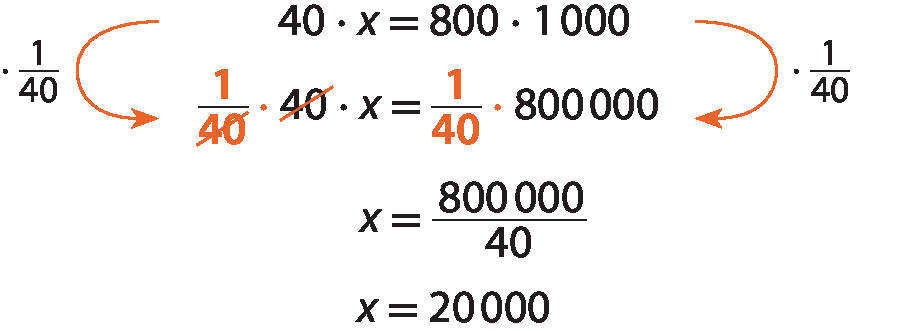
Esquema: De cima para baixo, quarenta vezes x igual a oitocentos vezes mil.
Abaixo, um sobre quarenta (alaranjado) vezes quarenta (com um traço alaranjado sobre o 40) vezes x igual a um sobre quarenta (alaranjado) vezes oitocentos mil. Há uma seta laranja ligando a linha de cima com a de baixo. No meio da seta, a indicação multiplicado por um sobre quarenta.
Abaixo, x igual a oitocentos mil sobre quarenta.
Abaixo, x igual a vinte mil.

Portanto, são necessários .20000 decímetros cúbicos de água salgada para obter 800 decímetros cúbicos de sal.

Observações

1. Nos problemas que acabamos de resolver, a letra x representa um valor desconhecido em uma igualdade obtida por meio da propriedade fundamental das proporções. Nesse contexto, a letra x assume o papel de incógnita da equação obtida.

2. Quando não estiver explícito, vamos assumir que o conjunto universo das equações encontradas por meio das proporções é o conjunto dos números racionais.

Atividades

Faça as atividades no caderno.

12. Copie no caderno apenas as razões que formam proporções.

\frac{3}{11}

\frac{15}{44}

\frac{4}{0, 2}

\frac{2}{40}

\frac{\frac{1}{2}}{5}

\frac{3}{30}

\frac{10}{500}

\frac{4}{200}

13. No caderno, determine o valor de x nas proporções.

\frac{x}{5} = \frac{21}{35}

\frac{\frac{3}{4}}{\frac{1}{5}} = \frac{90}{x}

\frac{9}{13} = \frac{x}{26}

\frac{1}{7} = \frac{x ‒ 6}{49}

\frac{2 x + 1}{10} = ‒ \frac{21}{30}

\frac{3 x + 2}{x + 3} = ‒ \frac{40}{25}

14. No caderno, determine o valor de w na proporção

w : 2, 5 = \frac{3}{4} : 0, 25

15. No caderno, determine o valor de k, sabendo que os números 4k ‒ 1, 50, k + 5 e 20 formam uma proporção nessa ordem.

16. Em um restaurante, de cada dez sucos vendidos seis são de maracujá. Em um domingo, foram vendidos 500 sucos. Quantos sucos de maracujá foram vendidos?

17. Um relógio atrasa 5 minutos a cada 8 horas. Quanto tempo ele atrasará em 4 dias?

Página 191

Sequências de números diretamente proporcionais

Fotografia: Impressora 3D está imprimindo um boneco laranja, estilo super-herói. — Impressão de brinquedo em 3-D utilizando resíduos de plástico reciclado. Almaty, Cazaquistão. Foto de 2017.

Uma impressora 3-D produz, em duas horas, 40 bonecos. Em 3 horas, essa mesma impressora produz 60 bonecos, em 4 horas, 80 bonecos, e, em 5 horas, 100 bonecos.

Calculando a razão entre o número de bonecos produzidos e a medida do tempo de produção, observamos uma igualdade.

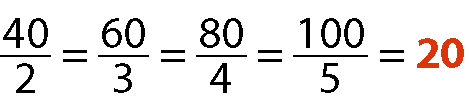
Sentença matemática: quarenta sobre dois igual a sessenta sobre três igual a oitenta sobre quatro igual a cem sobre cinco, igual a vinte (alaranjado).

O quociente de cada número da sequência (40, 60, 80, 100) (número de bonecos produzidos) pelo número correspondente da sequência (2, 3, 4, 5) (número de horas de produção da impressora) é sempre o mesmo que denominamos constante de proporcionalidade.

Portanto, dizemos que os números 40, 60, 80 e 100 são diretamente proporcionais aos números 2, 3, 4 e 5, nessa ordem. Dizemos ainda que o número de bonecos produzidos é diretamente proporcional à medida do tempo de produção, pois, conforme aumenta a medida do tempo, aumenta, na mesma proporção, a produção de bonecos.

Quando duas sequências de números são diretamente proporcionais, ao dobrar o número de uma delas, o correspondente da outra também dobra; ao reduzir pela metade o número de uma, o correspondente da outra também se reduz pela metade; e assim por diante.

Agora, acompanhe outra situação.

Simone dividiu 30 pitangas entre seus sobrinhos de 2, 3 e 5 anos de idade. Qual foi a quantidade de pitangas que cada um deles recebeu, sabendo que a divisão foi diretamente proporcional à idade de cada sobrinho?

Vamos indicar por a, b e c, respectivamente, as quantidades de pitangas recebidas pelos sobrinhos de 2, 3 e 5 anos. Assim:

Esquema: Na horizontal, a mais b mais c igual a trinta. Abaixo do a, temos um traço alaranjado com a indicação: quantidade de pitangas recebidas pelo sobrinho de 2 anos. Acima do b, seta alaranjada com a indicação: quantidade de pitangas recebidas pelo sobrinho de 3 anos. Abaixo do c, traço alaranjado com a indicação: quantidade de pitangas recebidas pelo sobrinho de 5 anos.

Página 192

As quantidades de pitangas a, b e c são diretamente proporcionais aos números 2, 3 e 5. Então:

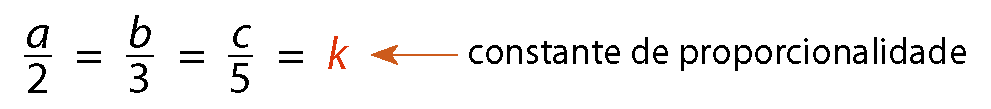
Esquema: a sobre dois igual a b sobre três igual a c sobre cinco igual a k (alaranjado). À direita, uma seta alaranjada. À direita da seta, a indicação 'constante de proporcionalidade'.

Agora, observe as igualdades:

\frac{a}{2} = k

a = 2k (um)

\frac{b}{3} = k

b = 3k (dois)

\frac{c}{5} = k

c = 5k (três)

Substituindo a por 2k, b por 3k e c por 5k na equação a + b + c = 30, temos:

a + b + c = 30

2k + 3k + 5k = 30

10k = 30

k = 3

Então, substituindo k por 3 em um, dois e três, obtemos:

a = 2k

a = 2 ⋅ 3

a = 6

b = 3k

b = 3 ⋅ 3

b = 9

c = 5k

c = 5 ⋅ 3

c = 15

Assim, dividimos o número 30 em partes diretamente proporcionais a 2, 3 e 5.

Portanto, os sobrinhos de 2, 3 e 5 anos receberam 6, 9 e 15 pitangas, respectivamente.

Atividades

Faça as atividades no caderno.

18. Verifique se os números 15, 20 e 30 são diretamente proporcionais aos números 24, 32 e 48.

19. Divida o número 600 em partes diretamente proporcionais a 2, 3 e 5.

20. Divida o número 23,8 em partes diretamente proporcionais a 5 e 9.

21. Os números a, b e c são diretamente proporcionais a 3, 5 e 9, e o fator de proporcionalidade é 16. Determine a, b e c.

22. Mário dividiu R$ 60.000,00sessenta mil reais entre sua irmã Ana, de 56 anos, e seus sobrinhos Paula, de 24 anos, e Carlos, de 16 anos. Essa divisão foi diretamente proporcional à idade de cada um deles. Quanto cada um recebeu?

23. Um sítio de 120 hectares foi repartido entre Karine (24 anos), Kátia (26 anos) e Cristina (30 anos) em partes diretamente proporcionais à idade de cada uma. Que parte, em hectare, coube a Karine?

24. Uma mistura com 300 mililitros é formada por duas substâncias, A e B, tomadas em quantidades proporcionais a 3 e 7, respectivamente. Quantos mililitros de cada substância são utilizados para formar a mistura?

25. Um prêmio de R$ 16.200,00dezesseis mil duzentos reais foi dividido em partes proporcionais à quantidade de pontos obtidos pelos dois primeiros colocados em uma competição. O primeiro colocado obteve 220 pontos, e o segundo, 140 pontos. Quanto recebeu cada um?

Página 193

Sequências de números inversamente proporcionais

Um pedreiro constrói um muro em 12 dias; dois pedreiros poderiam construir o mesmo muro em 6 dias; três pedreiros precisariam de 4 dias, e assim por diante.

Podemos escrever esses dados como igualdades de razões:

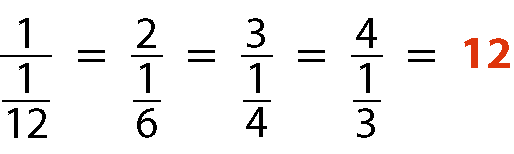
Sentença matemática: um sobre a fração um doze avos igual a dois sobre a fração um sexto igual a três sobre a fração um quarto igual a quatro sobre a fração um terço igual a doze (alaranjado).

O quociente de cada número da sequência (1, 2, 3, 4) (número de pedreiros) pelo inverso do número correspondente da sequência (12, 6, 4, 3) (número de dias necessários para a construção do muro) é sempre o mesmo, que chamamos de constante de proporcionalidade.

Portanto, dizemos que os números 1, 2, 3 e 4 são inversamente proporcionais aos números 12, 6, 4 e 3, nessa ordem.

Note que 1, 2, 3 e 4 são diretamente proporcionais aos inversos de 12, 6, 4 e 3, nessa ordem.

Agora, acompanhe outro exemplo.

Vamos dividir o número 310 em partes inversamente proporcionais a 2, 3 e 5.

Indicando por a, b e c os números procurados, temos:

a + b + c = 310

Sabendo que a, b e c são inversamente proporcionais aos números 2, 3 e 5 respectivamente, então:

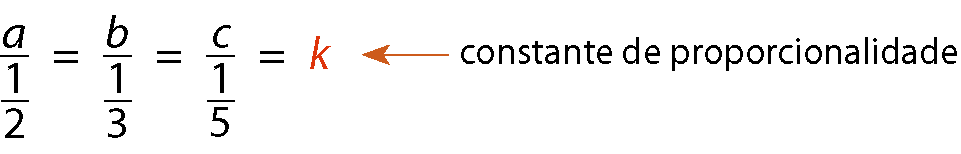
Esquema: a sobre fração um meio igual b sobre fração um terço igual c sobre fração um quinto igual a k alaranjado. À direita, uma seta alaranjada. À direita da seta, a indicação 'constante de proporcionalidade'.

Agora, observe que:

\frac{a}{\frac{1}{2}} = k \Rightarrow a = \frac{1}{2} \cdot k = \frac{k}{2}

\frac{b}{\frac{1}{3}} = k \Rightarrow b = \frac{1}{3} \cdot k = \frac{k}{3}

\frac{c}{\frac{1}{5}} = k \Rightarrow c = \frac{1}{5} \cdot k = \frac{k}{5}

Substituindo a por

\frac{k}{2}

, b por

\frac{k}{3}

e c por

\frac{k}{5}

na equação a + b + c = 310, obtemos:

a + b + c = 310

\frac{k}{2} + \frac{k}{3} + \frac{k}{5} = 310

(\frac{1}{2} + \frac{1}{3} + \frac{1}{5}) \cdot k = 310

(\frac{15}{30} + \frac{10}{30} + \frac{6}{30}) \cdot k = 310

\frac{31}{30} \cdot k = 310

Abaixo, trinta sobre trinta e um vezes trinta e um sobre trinta, vezes k. Há traços alaranjados sobre os números trinta e trinta e um. Acima dos números, à esquerda, o número um. Igual a trinta sobre trinta e um vezes trezentos e dez. Há traços alaranjados sobre o trinta e um e sobre o trezentos e dez. Abaixo do número trinta e um, à esquerda, o número um. Acima do número trezentos e dez, à direita o número dez.

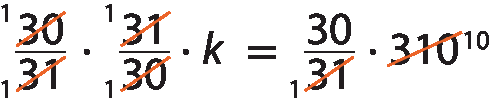
1 · k = 30 · 10

k = 300

Sabendo que k é igual a 300, obtemos os valores de a, b e c:

a = \frac{1}{2} \cdot k = \frac{1}{2} \cdot 300 = 150

b = \frac{1}{3} \cdot k = \frac{1}{3} \cdot 300 = 100

c = \frac{1}{5} \cdot k = \frac{1}{5} \cdot 300 = 60

Portanto, 150, 100 e 60 são inversamente proporcionais a 2, 3 e 5, respectivamente.

Página 194

Atividades

Faça as atividades no caderno.

26. Verifique se os números 3, 4 e 5 são inversamente proporcionais aos números 60, 45 e 36.

27. Verifique se os números 10, 8 e 6 são inversamente proporcionais aos números 30, 38 e 50.

28. Os números a, b e c são inversamente proporcionais a 2, 5 e 7, e a constante de proporcionalidade é 70. Determine a, b e c.

29. Divida o número 340 em partes inversamente proporcionais a 2, 4 e 10.

30. Divida 182 em partes inversamente proporcionais a

\frac{1}{3}

\frac{1}{4}

\frac{1}{6}

31. Uma herança no valor de R$ 60.000,00sessenta mil reais deverá ser dividida em valores inversamente proporcionais às idades de três herdeiros. Sendo 20, 30 e 60 anos a idade de cada um deles, qual será o valor recebido por cada um?

32. Lúcio dividiu duzentas e sessenta laranjas em três caixas, em quantidades inversamente proporcionais a 2, 3 e 4. Quantas laranjas foram colocadas em cada caixa?

Ilustração: um homem branco, de camisa quadriculada de azul e branco, calça azul e chapéu de palha, está com um balde com laranjas na mão. No chão ,há três caixas. Da esquerda para a direita, a primeira caixa está cheia de laranjas, na segunda caixa, o homem despeja as laranjas do balde. A terceira caixa está vazia.

33. Rosa resolveu dividir 33 livros entre Beto, Ana e Vera em partes inversamente proporcionais às suas faltas à escola durante o mês. Quantos livros recebeu cada um deles, sabendo que Beto, Ana e Vera tiveram uma, duas e três faltas, respectivamente?

3 Grandezas e proporcionalidade

No dia a dia são comuns situações em que relacionamos duas ou mais grandezas.

Considere os exemplos a seguir.

a) Na produção de metais fundidos, como o alumínio, utilizam‑se fornos para gerar o calor necessário à fusãoglossário . Quanto maior for a medida do tempo de uso do forno, maior a medida da massa de alumínio produzida. As grandezas, nesse caso, são tempo e massa.

Fotografia: Um homem com uma roupa especial cinza está de costas olhando para uma máquina de fundição de alumínio. — Fundição de alumínio em indústria de reciclagem, em Pindamonhangaba (São Paulo). Foto de 2018.

b) Já em uma corrida de quilômetro contra o relógioglossário , quanto maior a medida da velocidade, menor a medida do tempo gasto na prova. As grandezas, nesse caso, são velocidade e tempo.

Fotografia: Atleta mulher está pedalando bicicleta em uma pista profissional azul e verde. A atleta veste um macacão azul, um capacete cinza e óculos escuros. — A francesa Mathilde Gors, competindo na final dos 500 métros contra o relógio feminino durante a Copa das Nações de Ciclismo em Pista realizada em 2021, em Cali, na Colômbia.

Página 195

Entendemos por grandeza tudo o que pode ser medido ou contado. O comprimento, a área, o volume, a massa, a capacidade, a velocidade, o tempo, a temperatura, a produção ou o custo são alguns exemplos de grandeza.

Em algumas situações, duas ou mais grandezas podem estar relacionadas. Essa relação pode ser direta ou inversamente proporcional. Há casos também em que não há proporcionalidade entre as grandezas.

Grandezas diretamente proporcionais

Vamos, agora, explorar a situação da produção de metais fundidos. Observe no quadro a seguir as medidas das grandezas referentes à produção de alumínio fornecidas por uma metalúrgica.

Medida do tempo (min)	Medida da massa de alumínio produzido (kg)
5	100
10	200
15	300
20	400
25	500

De acordo com os dados, podemos observar que:

• quando duplicamos a medida do tempo, a medida da massa de alumínio produzido também duplica.

Esquema: De cima para baixo, cinco minutos. À direita, seta alaranjada. À direita da seta, cem quilos.
Na linha de baixo, dez minutos. À direita, seta alaranjada. À direita da seta, duzentos quilos.
Há uma seta alaranjada que liga cinco minutos a dez minutos. No meio da seta, a indicação multiplicado por dois.
Há uma seta alaranjada que liga cem quilos com duzentos quilos. No meio da seta, a indicação multiplicado por dois.

• quando triplicamos a medida do tempo, a medida da massa de alumínio produzido também triplica.

Esquema: De cima para baixo, cinco minutos. À direita, seta alaranjada. À direita da seta, cem quilos.
Na linha de baixo, quinze minutos. À direita, seta alaranjada. À direita da seta, trezentos quilos.
Há uma seta alaranjada que liga cinco minutos a quinze minutos. No meio da seta, a indicação multiplicado por três.
Há uma seta alaranjada que liga cem quilos a trezentos quilos. No meio da seta, a indicação multiplicado por três.

Nesse exemplo, verifique que a razão entre duas medidas de uma grandeza (tempo) é igual à razão entre as duas medidas correspondentes da outra grandeza (massa de alumínio produzido). Dizemos, então, que essas grandezas são diretamente proporcionais.

Duas grandezas são diretamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual à razão entre os valores correspondentes da segunda.

Tomando, ao acaso, 5 e 15 na coluna referente à medida da grandeza tempo e seus correspondentes na coluna referente à medida da grandeza massa de alumínio produzido, temos:

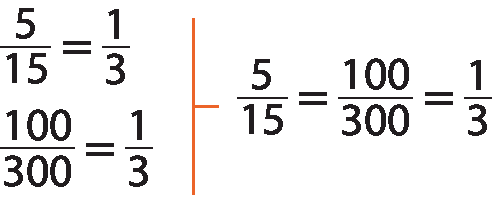
Esquema: do lado esquerdo: cinco sobre quinze igual a um terço; abaixo, cem sobre trezentos igual a um terço; que correspondem a cinco sobre quinze igual a cem sobre trezentos igual a um terço, que estão do lado direito do esquema

Como as grandezas são diretamente proporcionais, podemos escrever proporções com suas medidas e determinar a constante de proporcionalidade.

Por exemplo, no caso da metalúrgica, podemos obter a seguinte igualdade de razões:

\frac{5}{100} = \frac{10}{200} = \frac{15}{300} = \frac{20}{400} = \frac{25}{500} = \frac{1}{20}

Página 196

Essas proporções nos permitem encontrar uma sentença algébrica que relaciona as medidas das duas grandezas. Como exemplo, podemos relacionar a constante de proporcionalidade com a razão

\frac{t}{p}

, em que t representa a medida do tempo (em minuto) e p, a medida da massa de alumínio produzido (em quilograma), supondo que ambas sejam, sempre, diferentes de zero:

\frac{1}{20} = \frac{t}{p}

Pela propriedade fundamental das proporções, temos:

p = 20 ⋅ t

Essa sentença algébrica nos permite calcular a medida p da massa de alumínio produzido para qualquer medida t do tempo e vice-versa. Observe no quadro como podemos obter p para um t conhecido.

t (min)	p (kg)
3	20 ⋅ t = 20 ⋅ 3 = 60
7	20 ⋅ t = 20 ⋅ 7 = 140
9	20 ⋅ t = 20 ⋅ 9 = 180
50	20 ⋅ t = 20 ⋅ 50 = 1.000

Observação

Note que as letras t e p, na sentença algébrica p = 20 ⋅ t, têm o papel de variáveis, pois podem assumir qualquer medida possível para as grandezas tempo e massa de alumínio produzido. Se quisermos calcular a medida da massa de alumínio produzido a partir da medida do tempo, poderemos fazê-lo para qualquer medida de tempo possível. O mesmo vale se quisermos calcular a medida do tempo a partir da medida da massa de alumínio produzido.

Grandezas inversamente proporcionais

Considere a situação a seguir.

Uma ciclista faz um treino para uma prova de .1000 metros contra o relógio. Mantendo em cada volta uma medida da velocidade constante, ela obtém uma medida do tempo correspondente, conforme o quadro a seguir.

Medida da velocidade (m/s)	Medida do tempo (s)
5	200
8	125
10	100
16	62,5
20	50

Observe que:

• quando duplicamos a medida da velocidade, a medida do tempo fica reduzida à metade.

Esquema: De cima para baixo, cinco metros por segundo. À direita, seta alaranjada. À direita da seta, duzentos segundos.
Na linha de baixo, dez metros por segundo. À direita, seta alaranjada. À direita da seta, cem segundos.
Há uma seta alaranjada que liga cinco metros por segundo a dez metros por segundo. No meio da seta, a indicação multiplicado por dois.
Há uma seta alaranjada que liga duzentos segundos a cem segundos. No meio da seta, a indicação dividido por dois.

• quando quadruplicamos a medida da velocidade, a medida do tempo fica reduzida à quarta parte.

Esquema: De cima para baixo, cinco metros por segundo. À direita, seta alaranjada. À direita da seta, duzentos segundos.
Na linha de baixo, vinte metros por segundo. À direita, seta alaranjada. À direita da seta, cinquenta segundos.
Há uma seta alaranjada que liga cinco metros por segundo a vinte metros por segundo. No meio da seta a indicação multiplicado por quatro.
Há uma seta alaranjada que liga duzentos segundos com cinquenta segundos. No meio da seta a indicação dividido por quatro.

Página 197

Nesse exemplo, podemos verificar que a razão entre duas medidas de uma grandeza (velocidade) é igual ao inverso da razão entre as duas medidas correspondentes da outra grandeza (tempo). Dizemos, então, que essas grandezas são inversamente proporcionais.

Observe.

Esquema: da esquerda para a direita. dez sobre dezesseis igual a cinco oitavos. À direita, cem sobre sessenta e dois vírgula cinco igual a oito quintos. Há uma seta alaranjada que parte da fração cinco oitavos e chega à fração oito quintos. No meio da seta, há a indicação:razão inversa.

Esquema: À direita, um traço preto na vertical.
À direita do traço, oito sobre vinte igual a dois quintos. À direita, cento e vinte e cinco sobre cinquenta igual a cinco sobre dois. Há uma seta alaranjada que parte da fração dois quintos e chega à fração cinco sobre dois. No meio da seta, há a indicação: razão inversa.

Duas grandezas são inversamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual ao inverso da razão entre os valores correspondentes da segunda.

Da mesma fórma que fizemos com as grandezas diretamente proporcionais, podemos escrever proporções com as medidas das grandezas inversamente proporcionais, determinando a constante de proporcionalidade. Assim, no exemplo da ciclista, temos:

\frac{5}{\frac{1}{200}} = \frac{8}{\frac{1}{125}} = \frac{10}{\frac{1}{100}} = \frac{16}{\frac{1}{62, 5}} = \frac{20}{\frac{1}{50}} = 1 000

Agora, vamos determinar a sentença algébrica que relaciona as medidas dessas grandezas. Para isso, vamos escrever uma proporção com a constante de proporcionalidade representando a medida do tempo pela letra t (em segundo) e a medida da velocidade pela letra v (em metro por segundo), supondo que ambas sejam, sempre, diferentes de zero:

\frac{t}{\frac{1}{v}} = 1 000

Pela propriedade fundamental das proporções, temos

t = \frac{1 000}{v}

Essa sentença algébrica nos permite, por exemplo, calcular a medida t do tempo para qualquer medida v da velocidade conhecida, como podemos observar no quadro.

v (m/s)	t (s)
2	$divisão de 1000 sobre V igual a divisão de 1000 sobre 2 igual a 500$
4	$divisão de 1000 sobre V igual a divisão de 1000 sobre 4 igual a 250$
25	$divisão de 1000 sobre V igual a divisão de 1000 sobre 25 igual a 40$
2.000	$divisão de 1000 sobre V igual a divisão de 1000 sobre 2000 igual a 0,5$

Ilustração: Um menino branco, de cabelo loiro e camiseta vermelha diz: há algo estranho na última linha do quadro. O que você acha? Converse com um colega sobre as medidas encontradas.

Observação

Há situações em que não há proporcionalidade direta e nem inversa entre as grandezas. Por exemplo:

a) Um aluno com 10 anos mede 1,50 métro de altura. É lógico que, com 20 anos, ele não medirá 3,00 métros de altura.

b) Um jogador fez 10 cestas de três pontos em dois jogos. Não podemos garantir que ele fará 20 cestas de três pontos em quatro jogos.

Página 198

Atividades

Faça as atividades no caderno.

34. Em cada item, classifique as grandezas envolvidas em diretamente ou inversamente proporcionais.

a) Medida da distância entre duas cidades e medida do tempo gasto no deslocamento entre elas.

b) Número de operários para a construção de um muro e medida do tempo para construí-lo.

c) Medida do comprimento do lado de um quadrado e a medida de seu perímetro.

d) Medida do tempo para realizar uma terraplenagem (conjunto de operações que preparam um terreno para uma construção) e número de tratores utilizados.

e) Medida da área de um retângulo e medida do seu comprimento, sendo a medida da largura constante.

f) Número de máquinas e medida do tempo necessário para asfaltar um trecho de uma avenida.

Fotografia: Um homem, com roupa laranja, está utilizando uma máquina para asfaltar o trecho de uma rua. O dia está ensolarado, ao fundo da imagem, prédios e árvores. — Recapeamento do asfalto da avenida Ayrton Senna, em Londrina (Paraná). Foto de 2020.

35. Leia estas afirmações.

• Cinco canetas custam R$ 35,00trinta e cinco reais.

• Dez canetas custam R$ 70,00setenta reais.

a) O número de canetas e o respectivo custo são grandezas diretamente ou inversamente proporcionais? Justifique.

b) Encontre uma sentença algébrica que relacione a quantidade (q) e o custo (c) das canetas.

c) No caderno, crie um quadro relacionando a quantidade de canetas e o custo delas com as informações fornecidas anteriormente, acrescentando mais duas linhas. Em uma delas, calcule o custo de 11 canetas. Na outra, calcule quantas canetas se pode comprar com R$ 98,00noventa e oito reais.

36. Um prêmio de R$ 60.000,00sessenta mil reais vai ser dividido entre os funcionários de uma empresa. Leia as afirmações a seguir.

• Se houver 24 funcionários, cada um receberá R$ 2.500,00dois mil quinhentos reais.

• Se houver 32 funcionários, cada um receberá R$ 1.875,00mil oitocentos e setenta e cinco reais.

Agora, responda:

a) Qual é a razão entre as quantidades de funcionários?

b) Qual é a razão entre os valores recebidos?

c) A quantidade de funcionários e o valor recebido são grandezas diretamente ou inversamente proporcionais?

37. O quadro a seguir mostra a relação entre a medida do tempo de funcionamento de uma máquina e a quantidade de parafusos produzidos por ela. Observe.

Medida do tempo	Quantidade de parafusos produzidos
5 horas	1.000 parafusos
8 horas	1.600 parafusos

a) Qual é a razão entre as medidas de tempo?

b) Qual é a razão entre as quantidades de parafusos produzidos?

c) A quantidade de parafusos produzidos e a medida do tempo de funcionamento da máquina são grandezas diretamente ou inversamente proporcionais?

d) Obtenha uma sentença algébrica que relacione a medida do tempo de funcionamento (t ) e a quantidade de parafusos produzidos (p) por essa máquina.

e) Quantos parafusos serão produzidos se a máquina funcionar por 36 horas?

38. Choveu em cinco dos dez primeiros dias de março. Com base nesse fato, é possível afirmar que nos próximos 20 dias de março choverá por 10 dias? Justifique sua resposta.

Página 199

Regra de três simples

Quando um problema tem duas grandezas, direta ou inversamente proporcionais, podemos resolvê-lo utilizando um procedimento chamado regra de três simples.

Acompanhe os exemplos a seguir.

a) Ana comprou 3 cadernos de um mesmo modelo por R$ 36,00trinta e seis reais. Quanto ela gastaria para comprar 9 cadernos desse modelo?

Perceba como Ana resolveu essa questão usando a Aritmética.

Ilustração: Um senhor branco calvo, de bigode e camisa azul, está atrás de um balcão. Sobre o balcão há um computador. Atrás do senhor, uma estante com cadernos e porta-canetas. Uma mulher branca, de camiseta rosa, está em frente ao balcão entregando três cadernos para o senhor. A mulher diz: 'Como 36 dividido por 3 é igual a 12, cada caderno custa 12 reais. Se eu levar 9 cadernos, então: 12 vezes 9 é igual a 108. Gastaria 108 reais'.

Agora, vamos resolver usando a Álgebra. Para isso, representamos o valor desconhecido (preço total de 9 cadernos) por uma letra, por exemplo, c. E, assim, organizamos as informações no quadro a seguir.

Quantidade de cadernos	Preço (em R$)
3	36
9	c

Verificando que a quantidade de cadernos e o preço sejam diretamente proporcionais, temos a seguinte proporção:

\frac{3}{9} = \frac{36}{c}

Agora, aplicamos a propriedade fundamental das proporções e resolvemos a equação.

3 ⋅ c = 9 ⋅ 36

3c = 324

c =

\frac{324}{3}

= 108

Portanto, Ana gastaria R$ 108,00cento e oito reais para comprar 9 cadernos.

b) O Maglev (Magnetic levitation transport), trem de levitação magnética, ao se deslocar a uma medida de velocidade média de 400 quilômetros por hora, faz determinado percurso em 3 horas. Em quanto tempo esse trem faria o mesmo percurso se a medida de velocidade fosse de 480 quilômetros por hora?

Construímos inicialmente um quadro em que x representa a medida do tempo, em hora, gasto pelo trem para cumprir o percurso a uma medida de velocidade de 480 quilômetros por hora.

Medida de velocidade média (km/h)	Medida do tempo (h)
400	3
480	x

Fotografia: Trem de alta velocidade sobre trilho. Às margens do trilho, um rio. O dia está ensolarado, sem nuvens no céu. Na paisagem há árvores e uma construção ao fundo. — Maglev em Xangai, China. Foto de 2021.

Página 200

Verifique que, ao dobrar a medida da velocidade média do trem, a medida do tempo utilizado no percurso fica reduzida à metade; ao triplicar a medida de velocidade média do trem, a medida do tempo utilizado fica reduzida à terça parte, e assim por diante. Dessa fórma, as grandezas velocidade média e tempo são inversamente proporcionais. Então, podemos escrever a proporção:

\frac{400}{480} = \frac{x}{3}

Invertemos a razão.

Em seguida, aplicamos a propriedade fundamental das proporções e resolvemos a equação:

480 ⋅ x = 400 ⋅ 3

480x = .1200

x = \frac{1200}{480} = 2, 5

Portanto, o trem faria o mesmo percurso em 2,5 horas (2 horas e 30 minutos) se a medida da velocidade fosse 480 quilômetros por hora.

Atividades

Faça as atividades no caderno.

39. Três escavadeiras transportam 200 métros cúbicos de areia. Para transportar .1600 métros cúbicos de areia, quantas escavadeiras iguais a essas seriam necessárias?

40. Um aparelho em alta medida de velocidade irriga 2 hectares em 40 minutos. Quantos hectares seriam irrigados por esse aparelho em duas horas, mantendo a mesma medida de velocidade?

41. Usando 10 litros de óleo de copaíba, árvore nativa da Amazônia, um caminhão que trafega a uma medida de velocidade média de 60 quilômetros por hora percorre 80 quilômetros. Quantos litros seriam utilizados em um percurso de 200 quilômetros na mesma medida de velocidade?

42. De uma amostra de 100 gramas de um minério, foi extraído 0,2 grama de ouro. Quantos gramas de ouro podem ser extraídos de 1 quilograma desse minério?

43. O supertrem que liga Londres a Paris, através do Eurotúnel, tem medida de velocidade média de 160 quilômetros por hora e leva 40 minutos para atravessar o Canal da Mancha. Se a medida de velocidade média fosse aumentada para 200 quilômetros por hora, em quanto tempo o trem atravessaria o túnel?

44. Uma equipe de operários, trabalhando 8 horas por dia, realizou uma obra em 20 dias. Se o número de horas de serviço fosse reduzido para 5 horas por dia, em que prazo essa equipe faria o mesmo trabalho?

45. Em uma empresa trabalham 3 telefonistas; cada uma atende, em média, 125 ligações diárias. Aumentando para 5 o número de telefonistas, quantas ligações, em média, cada uma atenderá por dia?

46.

Em uma folha, crie uma lista com 10 pares de grandezas diretamente proporcionais, inversamente proporcionais e não proporcionais. Deixe uma linha entre cada par para que um colega possa anotar se as grandezas são diretamente, inversamente ou não proporcionais.

47.

Elabore um problema para cada item a seguir.

a) Envolvendo duas grandezas diretamente proporcionais.

b) Envolvendo duas grandezas inversamente proporcionais.

• Agora, troque um problema de cada vez com um colega para que ele o resolva enquanto você resolve o dele. Por fim, analisem as resoluções em conjunto e discutam as estratégias que adotaram para solucionar os problemas.

Página 201

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Razão

A razão entre dois números, aêbê, com b ≠ 0, nessa ordem, é dada por

\frac{a}{b}

1. Escreva na fórma de fração irredutível a razão entre cada par de medidas apresentadas, na ordem dada.

a) .64000 quilogramas de .2000 quilogramas

b) 5 litros e 25 litros

c) 4 centímetros e 100 centímetros

d) 2 métros cúbicos e 8 métros cúbicos

2. Em um jogo de basquete, Marcelo acertou 20 dos 28 arremessos que fez. Qual foi a razão entre os números de arremessos e de cestas?

3. A razão entre o número de médicos e o número de habitantes de uma cidade é

\frac{1}{3000}

. Determine a população dessa cidade sabendo que há 42 médicos.

Proporção

Proporção é uma igualdade entre duas razões.

Os termos de uma proporção são:

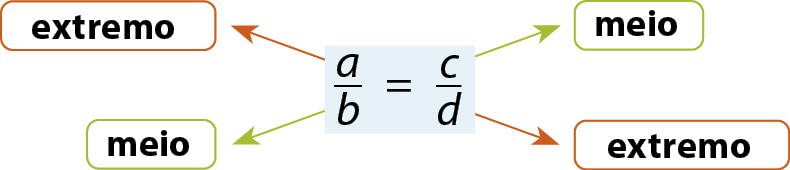
Propriedade fundamental das proporções

Em toda proporção, o produto dos extremos é igual ao produto dos meios, ou seja, dados a, b, c e d racionais não nulos, com

\frac{a}{b} = \frac{c}{d}

, temos: a ⋅ d = b ⋅ c

4. Determine o valor de x em cada proporção.

\frac{x}{10} = \frac{14, 4}{12}

\frac{7}{14} = \frac{3, 5}{x}

, com x ≠ 0

5. Copie no caderno apenas as razões que formam proporções.

\frac{10}{5}

\frac{20}{10}

\frac{0, 5}{25}

\frac{\frac{1}{4}}{12}

\frac{25}{1, 5}

\frac{50}{3}

\frac{\frac{1}{2}}{40}

\frac{0, 5}{20}

6. Um reservatório contém .12000 litros de água. Um produto químico deve ser misturado à água na razão de 40 gramas para cada 320 litros de água. Quantos pacotes de 100 gramas desse produto químico deverão ser adicionados ao reservatório?

7. Em um canal de televisão, são intercalados 25 minutos de programação com 7 minutos de anúncios comerciais. Em um filme de 70 minutos, quantos minutos, aproximadamente, deveriam ser reservados para os anúncios?

Grandezas e proporcionalidade

Duas grandezas são diretamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual à razão entre os valores correspondentes da segunda.

Duas grandezas são inversamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual ao inverso da razão entre os valores correspondentes da segunda.

8. Três sócios investiram os valores indicados neste quadro para montar uma empresa.

Sócio	Investimento
A	R$ 20.000,00
B	R$ 35.000,00
C	R$ 45.000,00

A empresa, porém, foi à falência, causando um prejuízo de R$ 42.000,00quarenta e dois mil reais. Sabendo que o prejuízo foi diretamente proporcional ao investimento, calcule a parcela de prejuízo de cada sócio.

9. Se 15 homens podem fazer um serviço em 40 dias, em quanto tempo o mesmo serviço será feito empregando-se mais 10 homens com o mesmo rendimento dos outros?

10. Doze marujos pintaram o casco de um navio em 4 dias e 4 horas. Quantos marujos, com o mesmo rendimento de trabalho, serão necessários para pintar o mesmo casco em 6 dias e 6 horas?

Glossário

Fusão: : transformação da matéria do estado sólido para o estado líquido.; Voltar para o texto

Quilômetro contra o relógio: : modalidade em que cada ciclista larga sozinho na pista, em intervalos de 90 segundos de diferença em relação aos demais competidores.; Voltar para o texto