Página 202

Capítulo 9 Transformações geométricas

Trocando ideias

Alguns artistas brasileiros foram influenciados pela cultura e pelas tradições dos povos africanos, compondo uma produção artística afro-brasileira. Um dos brasileiros que receberam essa influência foi Rubem Valentim (1922-1991). Observe a seguir a reprodução de uma de suas obras.

Fotografia. Reprodução de um quadro. Na parte superior há um retângulo amarelo com um círculo azul. No interior deste círculo azul há um círculo vermelho e uma figura simétrica preta.
Na lateral esquerda e na lateral direita do quadro há uma faixa vertical preta. Em cada faixa, há um semicírculo preto com uma ponta de seta que aponta para o círculo azul que está dentro do retângulo amarelo.
Na parte inferior do retângulo amarelo há 3 figuras simétricas idênticas dispostas lado a lado. Cada uma destas figuras tem uma ponta de seta na parte superior.
Na parte inferior do quadro há uma faixa marrom. — VALENTIM, Rubem. Sem título, serigrafia, 70 centímetros por 100 centímetros, 1989.

Conheça mais

No site do Instituto Rubem Valentim, é possível conhecer mais sobre o artista, suas exposições e suas obras.

▸

Alguns elementos dessa obra apresentam simetria em relação a uma reta. Você consegue identificá-los? Converse com os colegas.

▸

Reúna-se com 3 colegas e pesquisem a influência da cultura africana na formação do povo brasileiro. Depois, compartilhe com a turma suas descobertas.

Neste capítulo, vamos estudar as isometrias (translação, rotação e reflexão) e a representação de polígonos no plano cartesiano.

Página 203

1 Isometrias

Observe a faixa decorativa formada por figuras geométricas que se repetem seguindo uma regularidade.

Ilustração. Sequência de figuras que lembram losangos na horizontal, cada um composto por quatro partes. Na primeira e segunda linha, há 12 figuras intercalados pelas cores marrom e preto. A sequência começa com um figura marrom e termina com as últimas figuras sendo pretas.

As figuras a seguir se repetem ao longo de toda a faixa.

Ilustração. Continuação da ilustração anterior, agora com 2 figuras na horizontal, à esquerda, uma marrom e à direita, uma preta.

Essa repetição foi obtida por meio de transformações geométricas.

As transformações geométricas podem ou não preservar o formato e as medidas das figuras. Quando o formato e as medidas são preservados, essas transformações geométricas são chamadas de isometriasglossário .

As figuras obtidas por meio de isometrias são chamadas de congruentes às figuras que as originaram.

São exemplos de isometrias no plano: translação, rotação e reflexão. Neste capítulo vamos estudar cada uma dessas isometrias.

Translação

Translação é a isometria pela qual a figura é deslocada em determinada direção e sentido, mantendo uma mesma medida da distância entre cada um dos pontos da figura original e o correspondente da figura obtida.

Observe a seguir onde podemos identificar a translação na sequência de figuras da faixa decorativa.

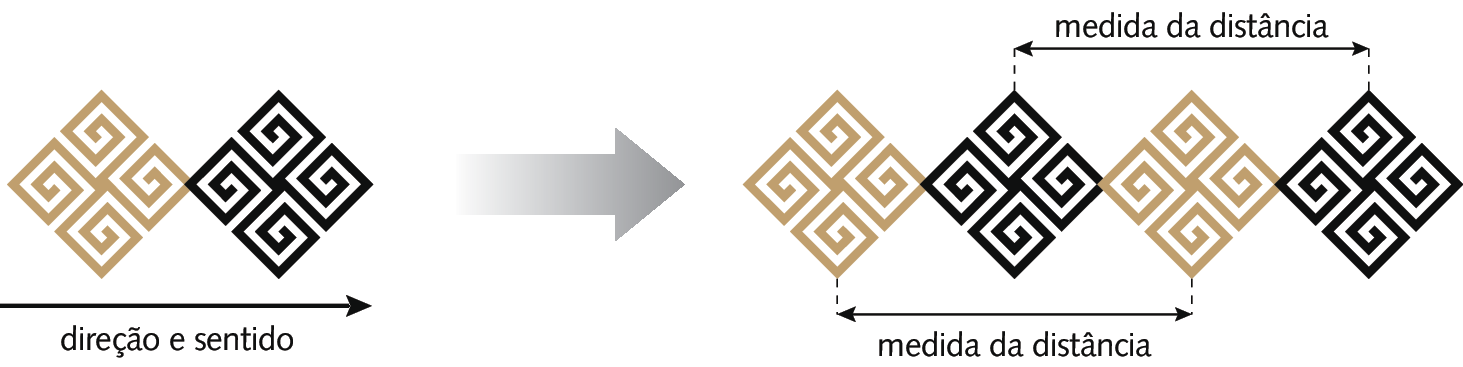
Esquema. Continuando a representação dos losangos, agora há 2 figuras à direita. Abaixo deles, há uma seta indicando a direção e sentido para a direita. No centro, há uma seta apontando para 4 figuras, intercalados pelas cores marrom e preto, seguindo a sequência: marrom, preto, marrom e preto. Abaixo das figuras marrons, há uma seta indicando a medida da distância. Acima das figuras pretas, há uma seta indicando a medida da distância.

Observe que a medida da distância é a mesma para todos os pontos correspondentes das figuras.

Para transladar qualquer figura, é preciso saber a direção, o sentido e a medida da distância em que ela será deslocada. Em geral, essas informações são representadas por uma seta que chamamos de vetor da translação.

Página 204

Analise outros exemplos:

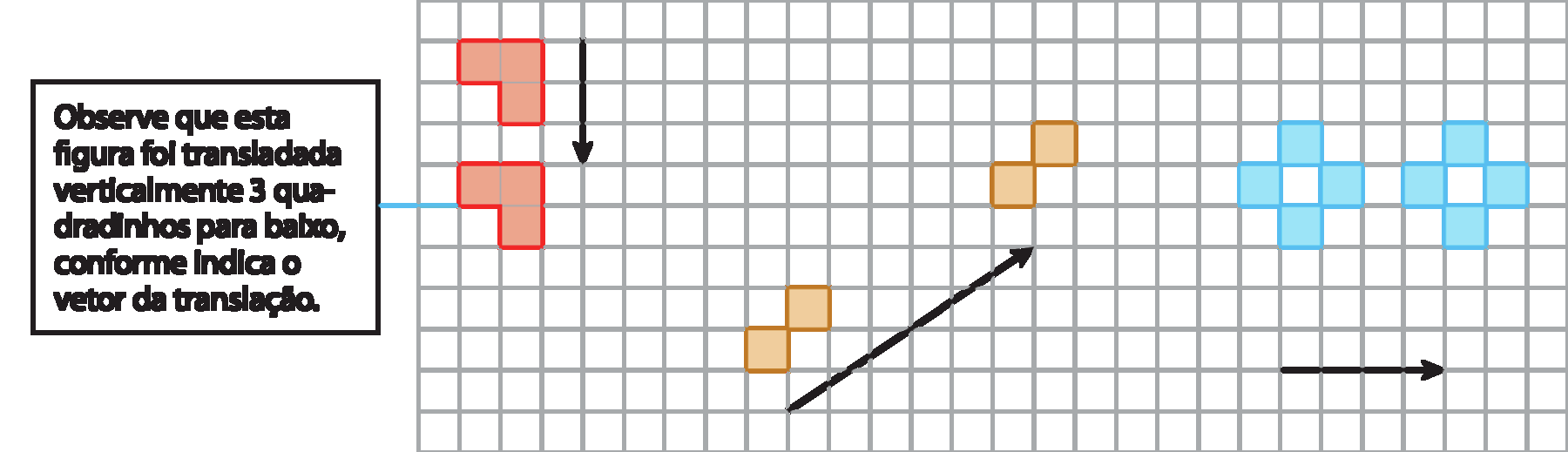
Ilustração. Malha quadriculada com exemplos de translação de figuras. No canto superior esquerdo, estão representadas duas figuras idênticas, uma embaixo da outra. Estas figura são compostas por 2 quadradinhos na horizontal e um quadradinho abaixo do segundo. À direita destas duas figuras está representado o vetor de translação que é vertical, aponta para baixo e tem medida de comprimento igual a de 3 lados de quadradinhos da malha.
No centro da malha estão representadas das figuras idênticas em diagonal. Estas figura são compostas por 2 quadradinhos da malha em diagonal. Alinhado com estas duas figuras está representado o vetor de translação que está sobre a diagonal de um retângulo composto por 4 fileiras com 6 quadradinhos cada.
No canto superior direito, estão representadas duas figuras idênticas, lado a lado. Estas figura são compostas por 4 quadradinhos que forma uma figura que se parece com um cruz. Embaixo destas duas figuras está representado o vetor de translação que é horizontal, aponta para a direita e tem medida de comprimento igual a de 4 lados de quadradinhos da malha.
À esquerda da malha, há o texto: Observe que esta figura foi transladada
verticalmente 3 quadradinhos para baixo,
conforme indica o vetor da translação.

Rotação

Rotação é a isometria pela qual uma nova figura é obtida a partir de um giro da figura original ao redor de um único ponto fixo. Esse ponto é chamado de centro de rotação.

Em uma rotação, o giro pode ser feito no sentido horário ou no sentido anti-horário, segundo certa medida da abertura de um ângulo.

Considere o recorte a seguir. Observe que, se rotacionarmos esse recorte no sentido horário, em torno do ponto A, segundo ângulos de medidas de abertura de 90graus, 180graus e 270graus, formaremos uma das figuras da faixa decorativa.

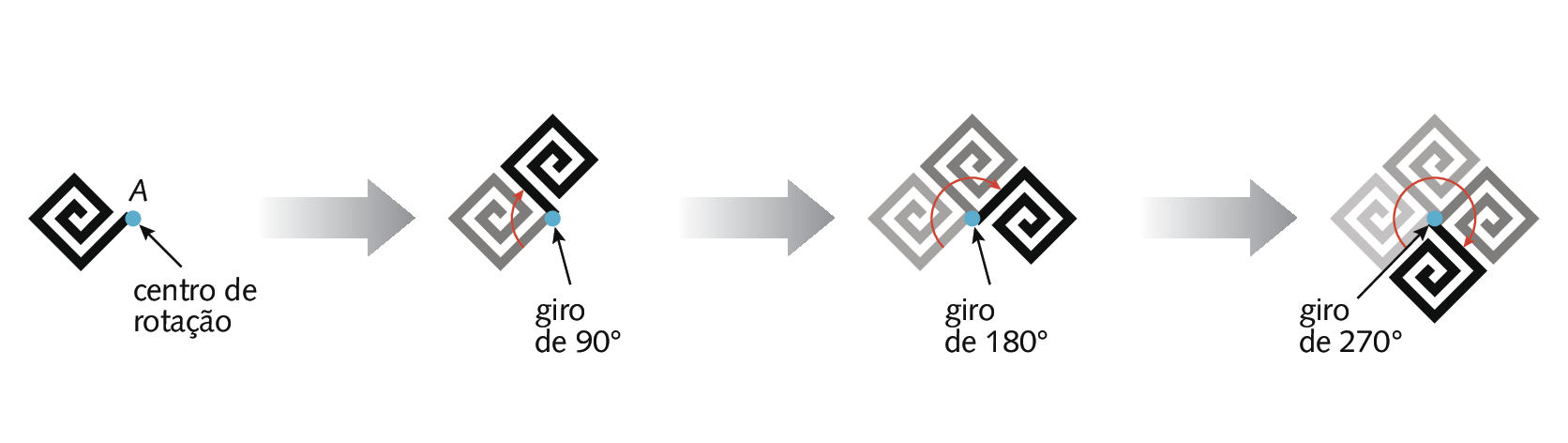
Esquema. Figura geométrica quadrada em espiral, com um ponto A azul localizado na parte final, e uma seta para o ponto indicando o centro de rotação.

Há três sequências de rotação:
O primeiro conjunto é composto por duas figuras quadradas em espiral, com uma seta indicando uma rotação de 90 graus no ponto de encontro.

O segundo conjunto é composto por duas figuras quadradas em espiral, uma invertida em relação à outra, com uma seta indicando uma rotação de 180 graus no ponto de encontro.

O terceiro conjunto é composto por três figuras quadradas em espiral que formam um quadrilátero, com uma seta indicando uma rotação de 270 graus no ponto de encontro.

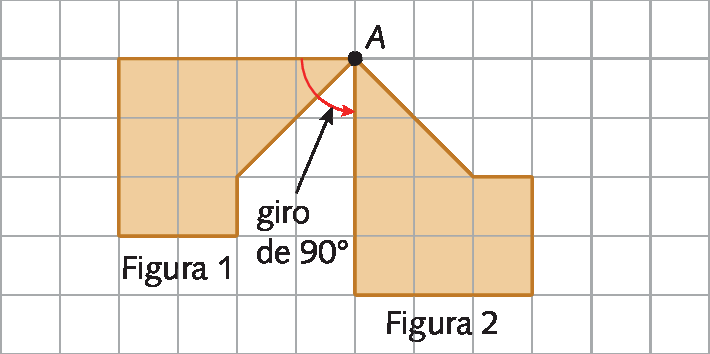
No exemplo a seguir, a figura 2 foi obtida a partir de um giro de 90graus da figura 1, no sentido anti-horário. Observe que o centro de rotação (ponto a) é comum às duas figuras.

Ilustração. À esquerda, pentágono sendo um dos vértices um ponto indicada pela letra A. À direita o mesmo pentágono em outra posição que corresponde ao giro e 90 graus no sentido anti horário em torno do ponto A do pentágono da esquerda. O pentágono da esquerda está indicado como Figura 1 e o da direita como Figura 2.

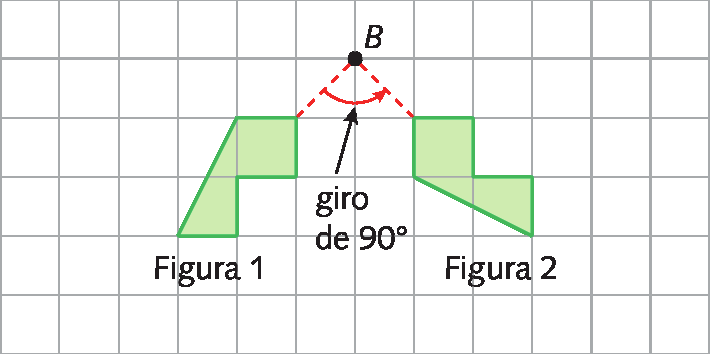
Agora, neste outro exemplo, observe que o centro de rotação (ponto B) é externo às duas figuras.

Ilustração. À esquerda, hexágono. À direita o mesmo hexágono em outra posição que corresponde ao giro e 90 graus no sentido anti horário em torno do ponto B que é externo às figuras. O hexágono da esquerda está indicado como Figura 1 e o da direita como Figura 2.

Para rotacionar figuras, precisamos conhecer o centro da rotação, a medida da abertura do ângulo de giro e o sentido da rotação (horário ou anti-horário).

Página 205

Reflexão

Reflexão é a isometria pela qual uma figura pode ser refletida, em um plano, de dois modos: em relação a uma reta e em relação a um ponto. Vamos estudar os dois casos.

Reflexão em relação a uma reta

Reflexão em relação a uma reta é a isometria que associa cada ponto P a um ponto pê linha, no mesmo plano, de modo que P e pê linha estejam a uma mesma medida da distância de uma reta. Chamamos essa reta de eixo de simetria.

Considere um detalhe da faixa decorativa (figura 1) e a reta r. A figura 2 é obtida após uma reflexão da figura 1 em relação à reta r.

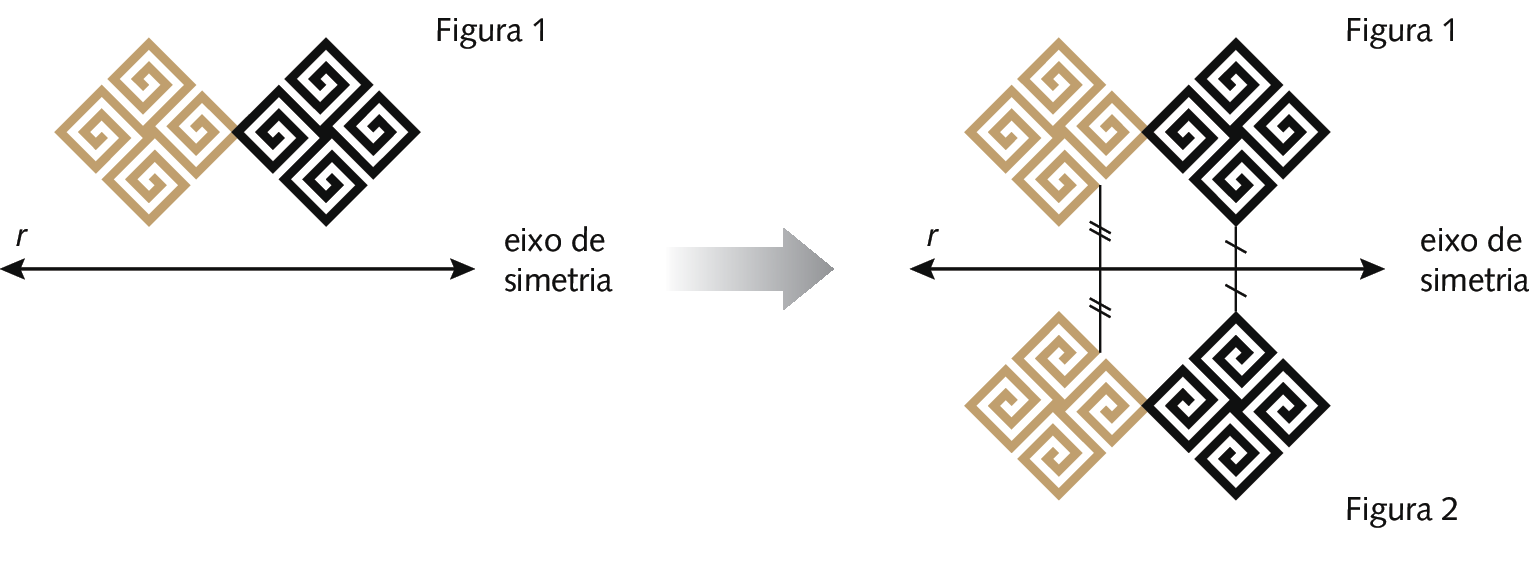
O esquema representa uma sequência de figuras que se parecem com losangos, dividida em duas figuras numeradas como 1 e 2. Na figura 1, há duas figuras, um marrom e outra preta, abaixo de uma reta identificada como eixo de simetria.

À direita, há uma seta para direita, na parte superior mantém a figura 1, com um par de figuras marrom e preta, abaixo do eixo de simetria é adicionado a figura 2 enquanto, com mais duas figuras na mesma sequência de cor, marrom e preta. Na vertical, há um fio preto que conecta as figuras marrons da parte superior e inferior, e ao lado há outro fio preto conectando as figuras pretas.

Observe que, se as figuras fossem dobradas na linha do eixo de simetria, as partes correspondentes ficariam sobrepostas.

Considere outros exemplos.

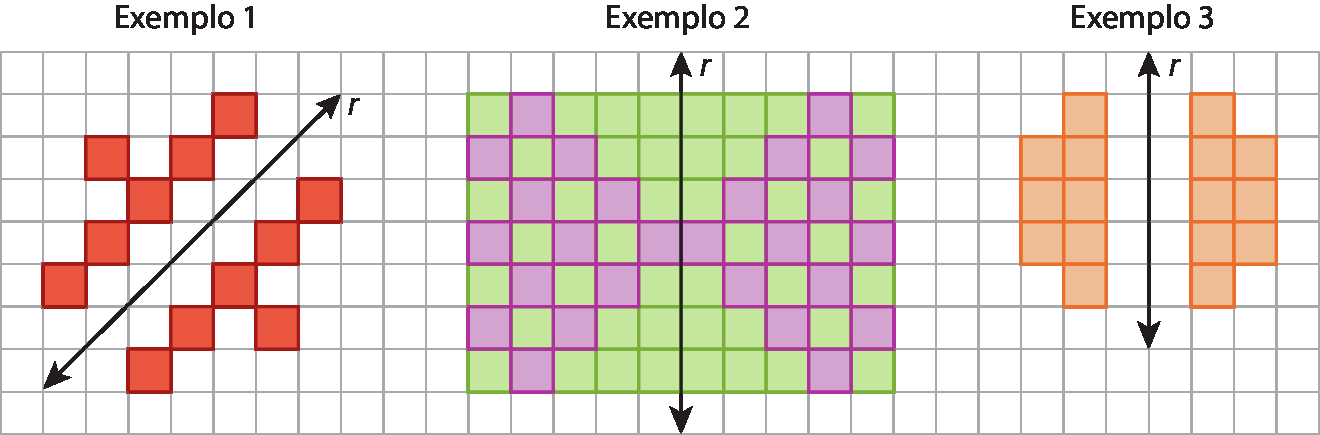
Esquema. Malha quadriculada com 3 figuras dobradas na linha do eixo de simetria.

À esquerda, no exemplo 1, há 5 quadradinhos vermelhos na diagonal e 1 ao meio do lado esquerdo, há uma reta diagonal e r ao meio e ao lado, 5 quadradinhos vermelhos na diagonal e 1 ao meio do lado direito.

No meio da malha, exemplo 2, há um retângulo verde formadas por quadradinhos, na primeira coluna na vertical é intercalados, sendo 4 quadradinhos verdes e 3 rosas. Na segunda coluna na vertical é intercalados, sendo 3 quadradinhos verdes e 4 rosas. Na terceira coluna na vertical é intercalados, sendo 4 quadradinhos verdes e 3 rosas. Na quarta coluna na vertical é intercalados, sendo 4 quadradinhos verdes e 2 rosas. Na quinta coluna na vertical há 6 quadradinhos verdes e 1 rosas. Há uma reta vertical r, e à direita, na primeira coluna na vertical há 6 quadradinhos verdes e 1 rosas. Na segunda coluna na vertical é intercalados, sendo 4 quadradinhos verdes e 2 rosas. Na terceira coluna na vertical é intercalados, sendo 4 quadradinhos verdes e 3 rosas. Na quarta coluna na vertical é intercalados, sendo 3 quadradinhos verdes e 4 rosas. Na quinta coluna na vertical é intercalados, sendo 4 quadradinhos verdes e 3 rosas.

À esquerda, exemplo 3, há 5 quadradinhos laranjas na vertical e 3 quadradinhos laranjas ao lado à esquerda. No meio reta r e a direita, 5 quadradinhos laranjas na vertical e 3 quadradinhos laranja ao lado à direita.

Perceba que nos exemplos 1 e 3 há duas figuras. Essas figuras não possuem pontos em comum com o eixo de simetria. Dizemos, nesse caso, que as figuras são simétricas em relação à reta r.

Já no exemplo 2, há uma única figura que foi dividida em duas partes simétricas pela reta r. Nesse caso, dizemos que a figura apresenta simetria de reflexão.

Reflexão em relação a um ponto

Reflexão em relação a um ponto é a isometria que associa cada ponto P a um ponto pê linha no mesmo plano, de modo que P e pê linha estejam a uma mesma medida da distância de um ponto.

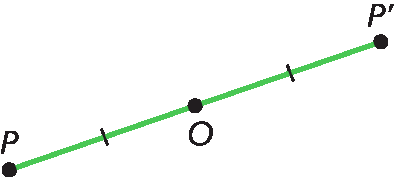
Ilustração. Segmento de reta com extremidades nos pontos P e P linha. Neste segmento de reta, está representado o ponto O de modo que os pontos P e P linha estão à mesma medida da distância do ponto O.

Nessa figura, estão representados o ponto óh e o segmento de reta

\overline{P P ’}

. Os pontos P e pê linha estão à mesma medida da distância do ponto óh.

Página 206

Dizemos que pê linha é simétrico a P em relação ao ponto óh. Chamamos esse ponto óh de centro de reflexão. Confira outro exemplo.

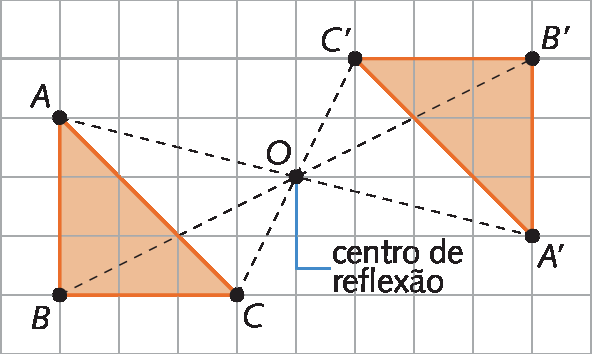
Ilustração. Triângulos ABC e A linha, B linha e C linha representados em uma malha quadriculada. O triângulo linha, B linha e C linha é simétrico do triângulo ABC em relação ao ponto O representado no centro da malha. Há um fio para o ponto O, indicando: centro de reflexão.

Observe que a reflexão em relação a um ponto óh é equivalente a uma rotação de centro óh e ângulo de medida de abertura igual a 180graus.

Veja que interessante

Faça a atividade no caderno.

A simetria na arte da cerâmica

A cerâmica é uma arte e uma técnica de fabricação de utensílios que tem a argila como principal matéria-prima. A palavra “cerâmica” vem do grego keramikós, que significa “de argila”.

Em seu processo de fabricação, a cerâmica é submetida a altas medidas de temperatura, o que a torna muito resistente e faz com que seu uso seja abrangente. Podemos encontrá-la em louças, tijolos, esculturas, revestimentos e até em componentes de foguetes espaciais. A utilização varia do artístico ao industrial, incluindo tecnologias de ponta.

Praticada há séculos, com registros de peças encontradas em sítios arqueológicos localizados em uma área ocupada pela cultura Jomon (Japão), datando de 5000 antes de Cristo, a cerâmica evoluiu em quase todos os povos ao mesmo tempo e se diversificou de maneira a refletir a cultura local pelas formas, cores e desenhos.

Na imagem a seguir, temos um exemplo de objeto de cerâmica. Nele, podemos identificar a aplicação de propriedades matemáticas, como a simetria.

Fotografia. Vaso de cerâmica. Na superfície do vaso há desenhos na parte inferior e na parte superior há linhas que que se parecem com uma espiral. — Cerâmica marajoara, produzida na Ilha de Marajó (Pará).

Atividade

Na pintura da cerâmica marajoara anterior, é possível reconhecer alguma das isometrias estudadas? Qual?

Página 207

Atividades

Faça as atividades no caderno.

Observe a imagem e responda.

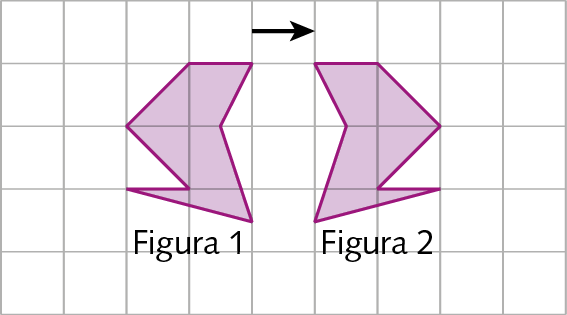
Ilustração. Heptágono e seu simétrico representados em uma malha quadriculada. Acima um vetor horizontal, apontando para a direita e que tem medida da distância equivalente a de um lado de quadradinho. O heptágono da esquerda está identificado como figura 1 e o da direita como figura 2.

A figura 2 foi obtida por meio de uma translação da figura 1? Converse com o professor e os colegas para justificar sua resposta.

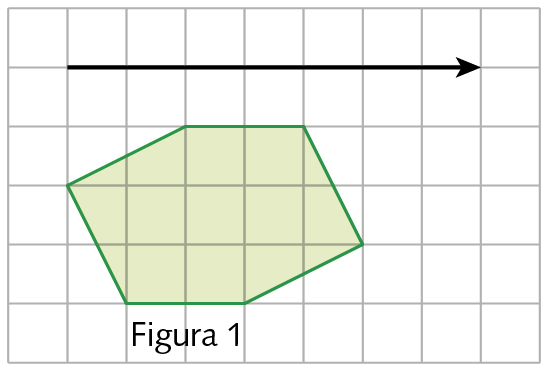
2. Copie o polígono a seguir em uma folha de papel quadriculado. Depois, translade-o de acordo com o vetor da translação.

Ilustração. Hexágono não regular representado em uma malha quadriculada. Acima, um vetor na horizontal, apontando para a direita e que tem medida de comprimento equivalente a de 7 lados de quadradinho.

3. Observe a reprodução da obra do artista brasileiro Luiz Sacilotto (1924-2003) e responda à questão.

Fotografia. Reprodução de uma obra de arte. A obra tem o formato de um quadrado. No canto superior esquerdo há uma figura amarela que se parece com a letra L. No canto inferior direito, se encontra uma figura idêntica em posição diferente, com abertura para o lado esquerdo. — SACILOTTO, Luiz. C0254, têmpera acrílica sobre tela, 70 centímetros por 70 centímetros, 2002.

Podemos dizer que as figuras amarelas que compõem essa obra são simétricas? Justifique sua resposta.

4. Represente a figura 1 em uma malha quadriculada. Depois, desenhe a figura obtida por meio da rotação da figura 1 em um ângulo de medida da abertura de 90graus, no sentido anti-horário, com centro de rotação a.

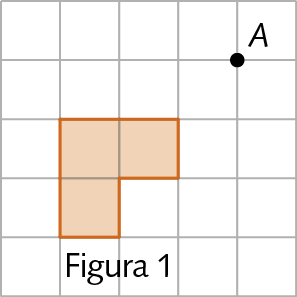
Ilustração. Figura 1 e ponto A representados em uma malha quadriculada. A figura 1 é composta por 3 quadradinhos da malha: 2 na horizontal e um abaixo do segundo. O ponto A está externo à figura. Abaixo da figura, há a indicação: Figura 1.

5. Observe as figuras a seguir.

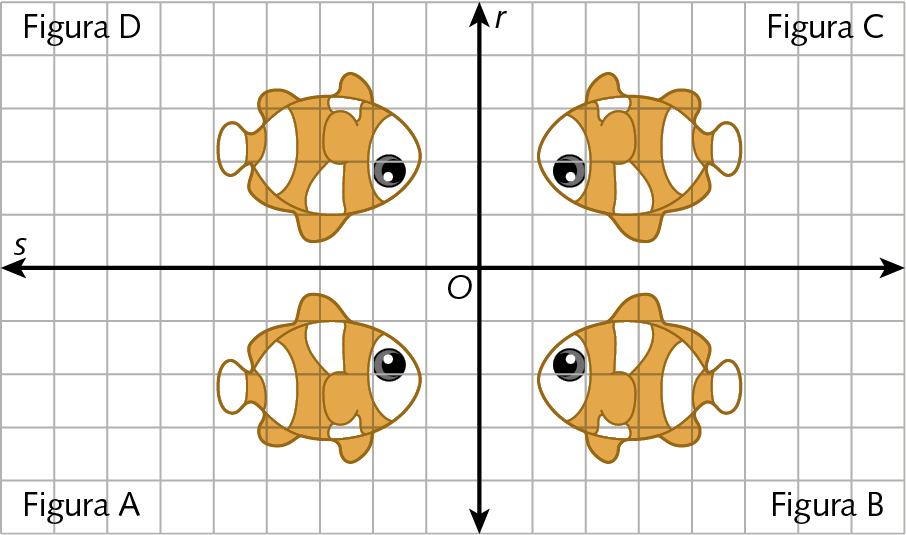
Ilustração. Duas retas r e s perpendiculares entre si que se interceptam em um ponto O e que estão representadas em uma malha quadriculada.
No canto inferior esquerdo, a representação de um peixe que está identificado como Figura A. No canto inferior direito a simétrica da Figura A em relação à reta r e que está identificada como Figura B. No canto superior direito, a simétrica da Figura B em relação à reta s e que está identificada como Figura C. No canto superior esquerdo, a simétrica da Figura C em relação à reta r e que está identificada como Figura D.

Qual dessas figuras representa a simétrica da figura A em relação:

a) à reta r.

b) à reta s.

c) ao ponto óh.

6. Em quais das imagens a seguir podemos identificar simetria de reflexão? Justifique sua resposta.

Fotografia. Figura quadrada composta por um círculo com ondas na cor amarela nas extremidades. No centro, hastes amarelas e círculo azul. Ao redor, losango branco com borda amarela e dois pontos azuis em cada lado. — Figura 1

fotografia. Quadro com outros 4 quadros, sendo 2 na parte superior e 2 na parte inferior. Os quadros são marrom e tem as bordas arredondadas e é dividida em 4 partes. Cada parte é composta por uma textura. — Figura 2

7. Represente um triângulo retângulo á bê cê em uma malha quadriculada e uma reta r distante 2 quadradinhos do vértice A. Depois, construa o triângulo a linha bê linha cê linha simétrico ao á bê cê em relação à reta r.

Página 208

Construções de figuras simétricas

Utilizando régua e compasso, vamos construir a figura obtida por meio de uma reflexão em relação a um ponto.

Considere o triângulo á bê cê e o ponto óh representados.

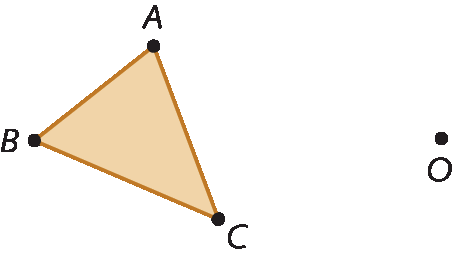
Esquema. À direita figura geométrica de um Triângulo ABC, à direita ao um ponto O identificado

Para construir a figura simétrica ao triângulo á bê cê pela reflexão de centro óh, devemos seguir os passos a seguir.

1º) Com o auxílio de uma régua, trace a semirreta

\vec{A O}

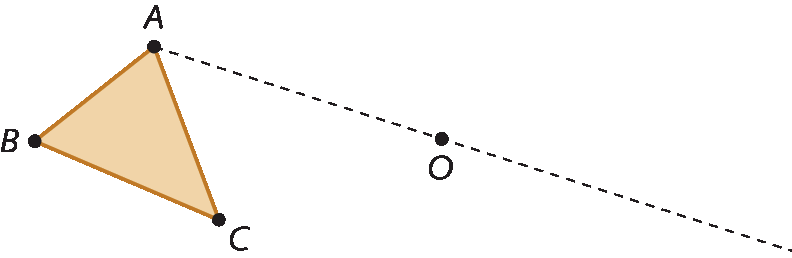
Esquema. Continuando o esquema anterior, agora no triângulo ABC temos uma semirreta que parte do ponto A e é dividida em duas partes, contendo também o ponto O.

2º) Coloque a ponta-seca do compasso em óh e abra-o até o ponto a.

3º) Mantendo a abertura, gire o compasso e trace um arco que intercepte a semirreta em um ponto distinto de a.

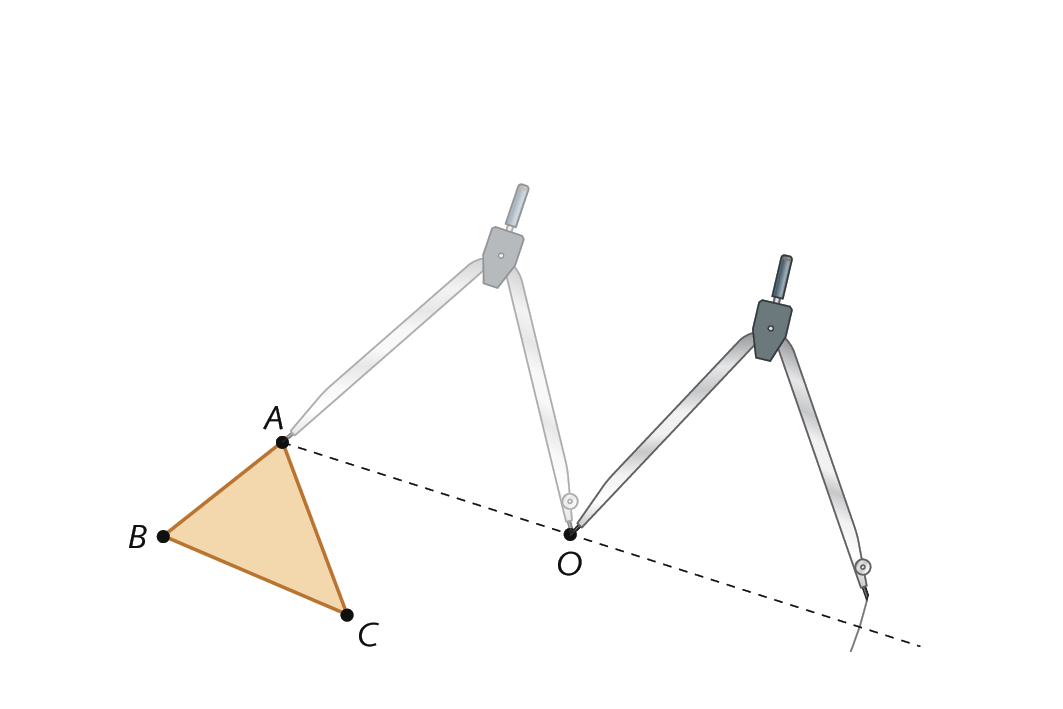
Esquema. Continuando com o esquema anterior, agora na semirreta são utilizados dois compassos. Um dos compassos tem uma das suas pontas no ponto O e é aberto até o ponto A, enquanto o outro compasso demostra que foi girado do ponto A até o final da semirreta.

4º) Nomeie o ponto obtido como á linha. O ponto á linha é o simétrico de a pela reflexão de centro em óh.

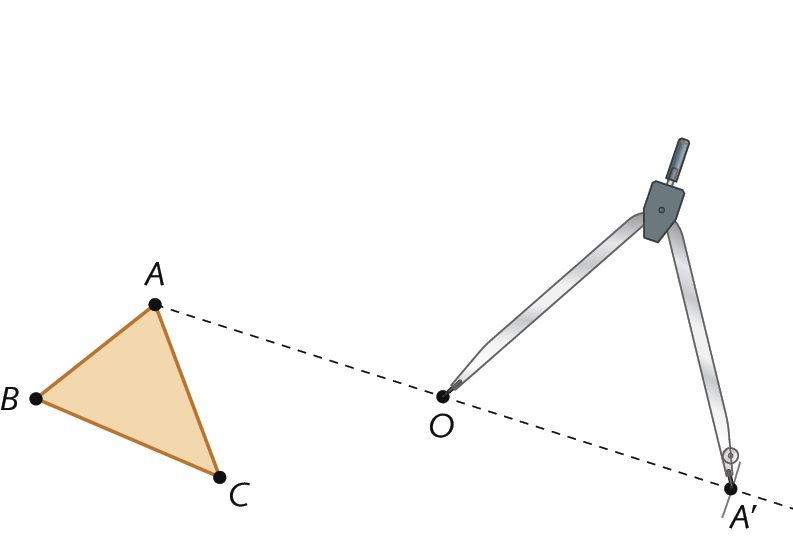
Esquema. Continuando com o esquema anterior, agora na semirreta é utilizado apenas um compasso para marcar o ponto A linha na semirreta tal que a distância de A até O e de O até A linha são iguais.

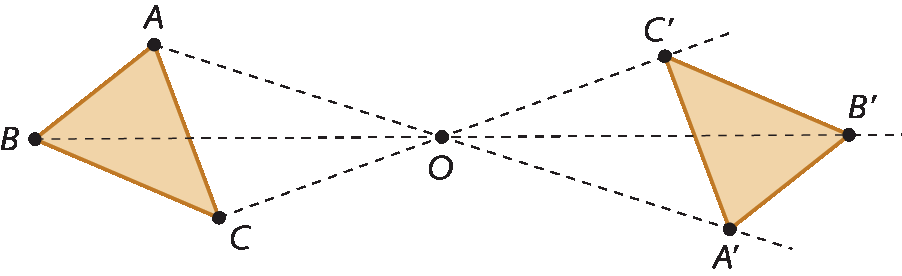
5º) Repita os passos anteriores para a construção dos pontos bê linha e cê linha. Una os pontos á linha, bê linha e cê linha para obter o triângulo a linha bê linha cê linha, que é simétrico ao triângulo á bê cê pela reflexão de centro em óh.

Esquema. Continuando com o esquema anterior, agora há dois triângulos um à esquerda e outro à direita, e estão unidos por segmento de retas que estão entre as vértices.
Vértice A do triângulo à esquerda ligado por segmento de reta passando pelo ponto O a vértice A linha do triângulo à direita
Vértice B do triângulo à esquerda ligado por segmento de reta passando pelo ponto O a vértice B linha do triângulo à direita
Vértice C do triângulo à esquerda ligado por segmento de reta passando pelo ponto O a vértice C linha do triângulo à direita

Página 209

Tecnologias digitais em foco

Figuras obtidas por meio de transformações geométricas

Nesta seção, vamos refletir, transladar e rotacionar polígonos com o auxílio do GeoGebra (ou outro software de geometria dinâmica que seu professor pode indicar). Além disso, vamos investigar uma propriedade dessas transformações geométricas.

Construa

Translação

Siga os passos para transladar um polígono qualquer.

1º) Construa um polígono qualquer.

2º) Use a ferramenta

Ilustração. Botão no formato de um quadro com pontos azuis e uma seta diagonal

e construa um vetor qualquer. Esse será o vetor da translação.

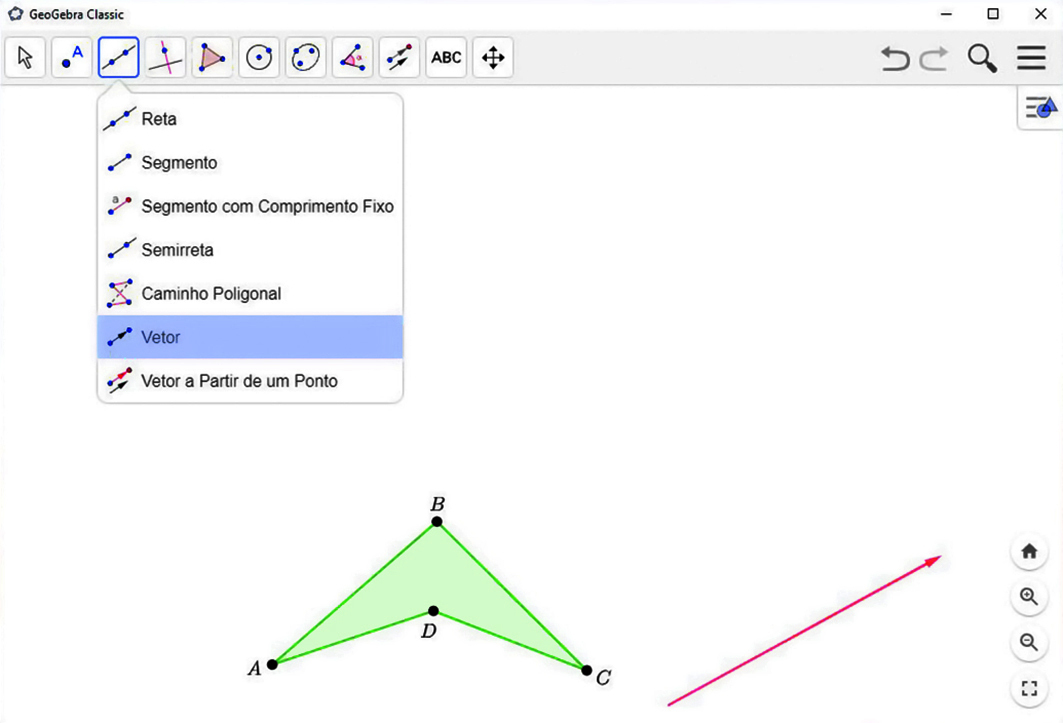
Captura de tela. Tela do software de geometria dinâmica GeoGebra.

Na parte superior há uma barra com ícones com botões de comandos. Destaque para botão com dois bolinhas azuis e uma seta diagonal. ferramenta para construção de um vetor.

Há uma uma aba com várias opções e um destaque para a opção vetor.

Abaixo, na tela, há uma figura geométrica verde com as vértices ABCD. À uma seta obliqua para cima.

3º) Clique na ferramenta

Ilustração. Botão no formato de um quadro com uma pontos azul e uma vermelha com seta diagonal. Ao lado, outra seta diagonal.

. Depois, clique sobre o polígono e o vetor. O polígono que aparecerá na tela é a figura transladada.

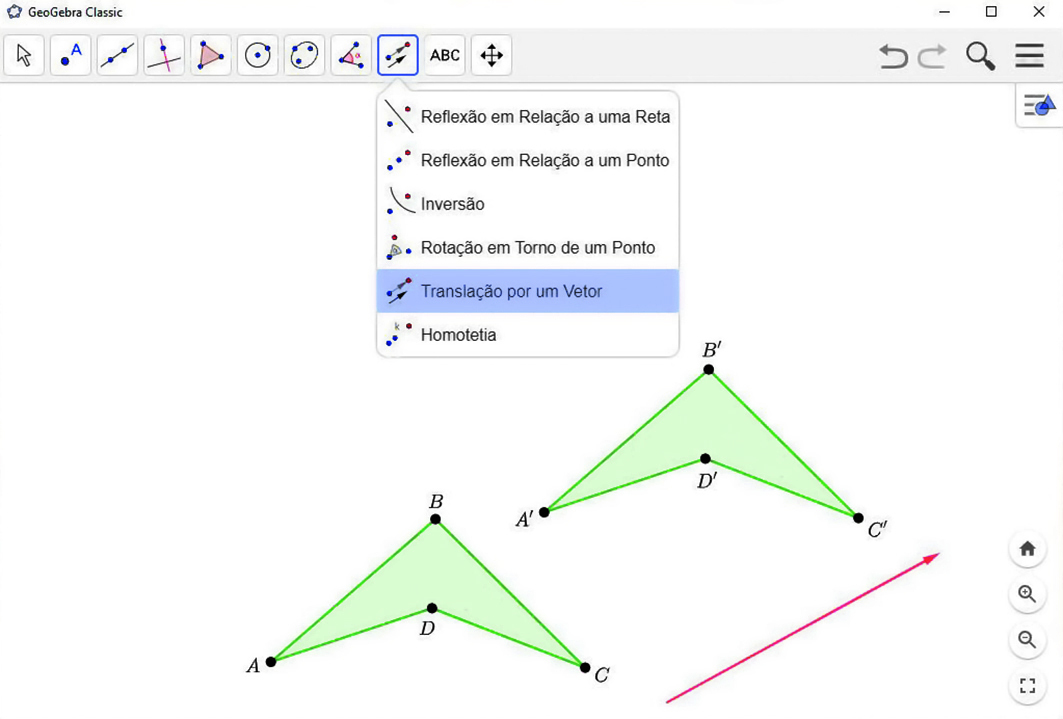
Captura de tela. Continuação da construção mostrada na fotografia anterior, agora na parte superior está destacado a botão de comando no formato de um quadro com uma pontos azul e uma vermelha com seta diagonal e ao lado, outra seta diagonal.

Há uma uma aba com várias opções e um destaque para a opção: translação por um vetor

Abaixo, na tela, há duas figuras geométrica verde, continua a figura do esquema anterior, e é adicionado na direção da seta outra figura geométrica com as vértices A linha B linha C linha D linha

Rotação

Siga os passos para rotacionar um polígono qualquer em torno de um ponto por um ângulo.

1º) Construa um polígono qualquer.

2º) Marque um ponto P qualquer. Esse ponto será o centro da rotação.

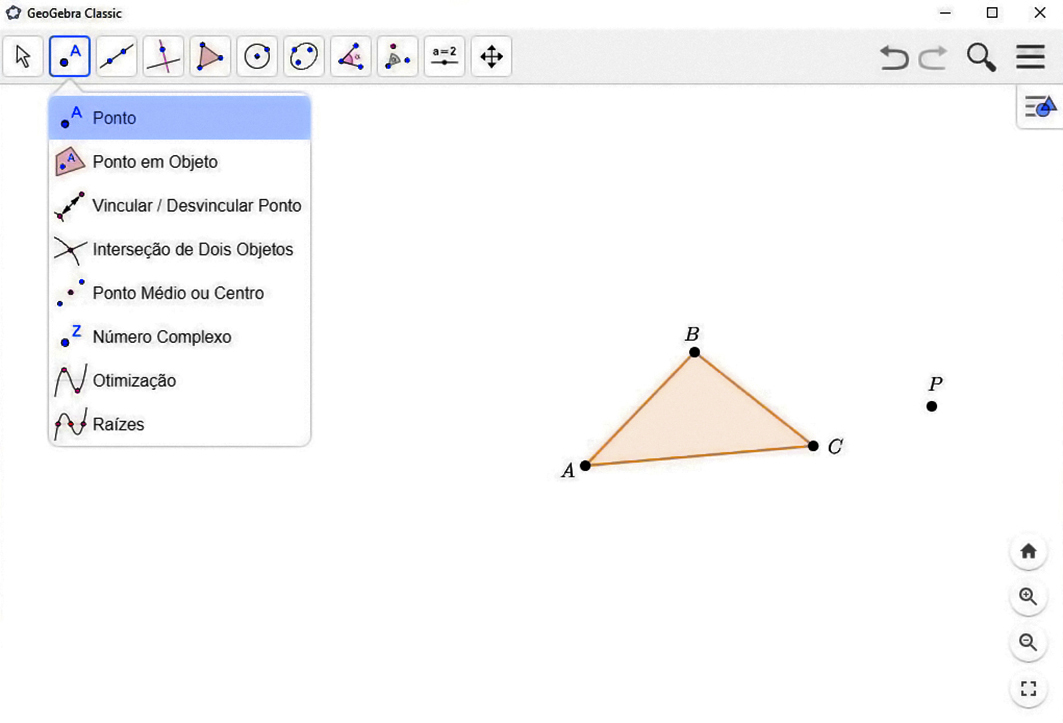
Captura de tela. Tela do software de geometria dinâmica GeoGebra.
Na parte superior está destacado a botão de comando no formato de um quadro com a letra A e um ponto abaixo.

Há uma uma aba com várias opções e um destaque para a opção: Ponto

Abaixo, na tela, há um triângulo laranja com as vértices ABC e à direita do triângulo há um ponto P.

Página 210

Tecnologias digitais em foco

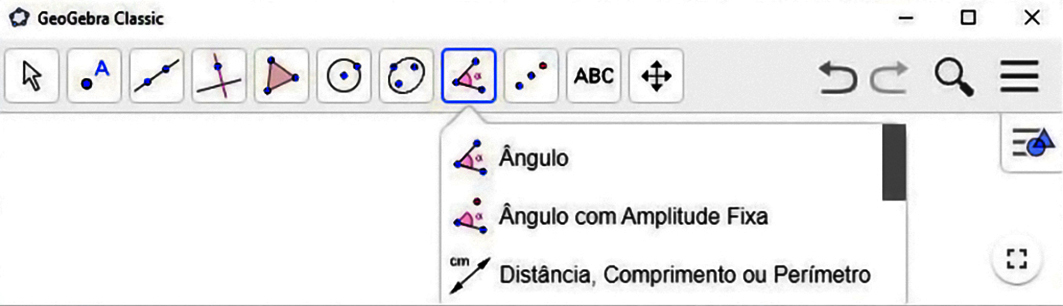
3º) Clique na ferramenta

Ilustração. Botão no formato de um quadro com duas pontos azuis e uma vermelha. Ângulo alfa entre as pontos

. Depois, clique sobre o polígono e o ponto P. Por fim, escolha a medida da abertura do ângulo de giro e o sentido da rotação. O polígono que aparecerá na tela é a figura rotacionada.

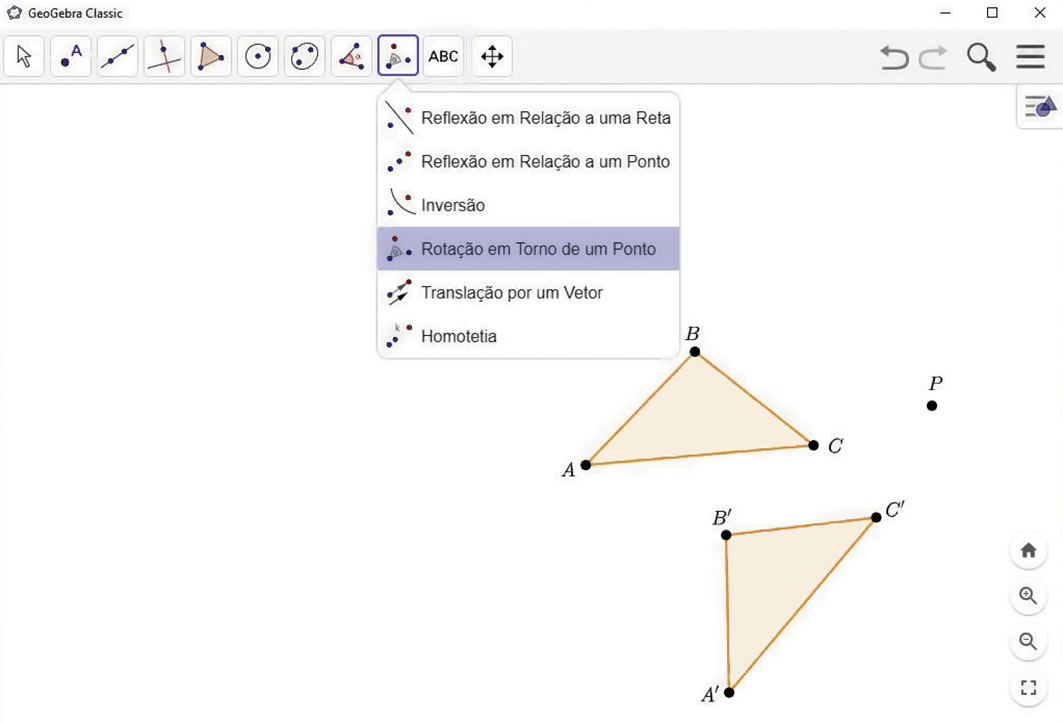
Captura de tela. Continuação da construção mostrada na fotografia anterior, agora na parte superior está destacado a botão de comando formato de um quadro com duas pontos azuis e uma vermelha. Ângulo alfa entre as pontos

Há uma uma aba com várias opções e um destaque para a opção: Rotação em torno de um ponto

Abaixo, na tela, há dois triângulo, continua o triangulo anterior, agora é adicionado outro triângulo laranja na vertical A linha B linha C linha e há uma seta azul indicando O triângulo A linha B linha C linha foi obtido do triângulo ABC por meio de uma rotação de um ângulo de medida da abertura de 45 graus no sentido anti-horário — O triângulo a linha bê linha cê linha foi obtido do triângulo á bê cê por meio de uma rotação de um ângulo de medida da abertura de 45graus no sentido anti-horário.

Reflexão em relação a uma reta

Siga os passos para construir o simétrico de um polígono qualquer em relação a uma reta.

1º) Construa um polígono qualquer.

2º) Trace uma reta r qualquer. Essa reta será o eixo de simetria.

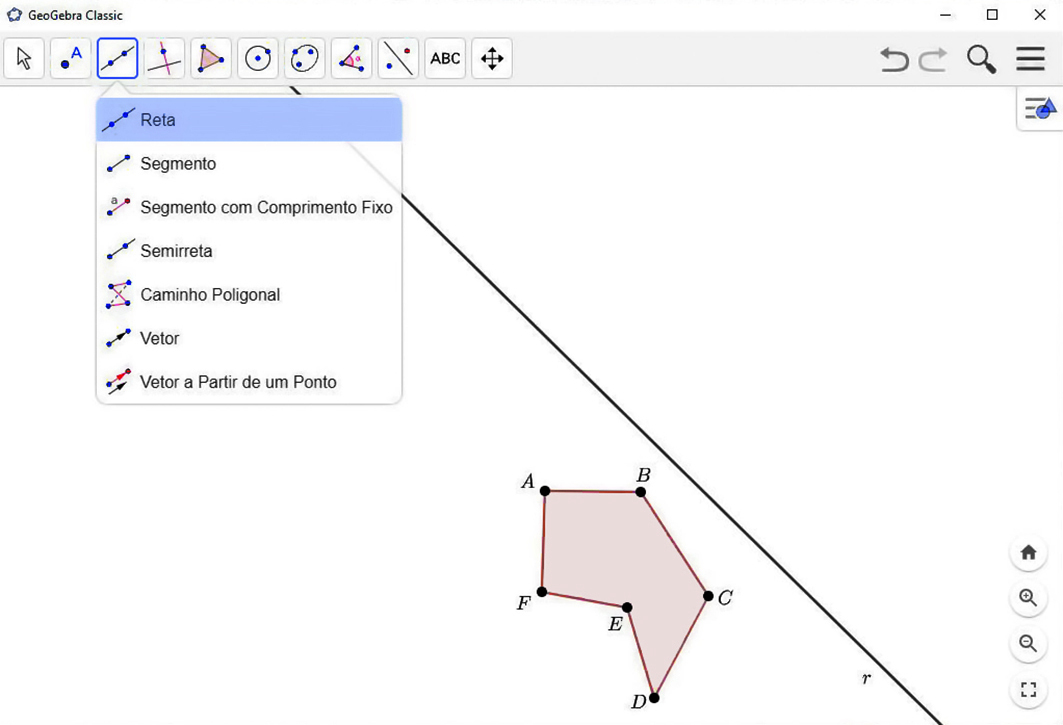
Captura de tela. Tela do software de geometria GeoGebra.
Na parte superior está destacado a botão de comando formato de um quadro com uma reta com dois pontos.

Há uma uma aba com várias opções e um destaque para a opção: Reta

Abaixo, na tela, há um polígono à esquerda com as vértices ABCDEF e à direita uma reta obliqua r.

3º) Clique na ferramenta

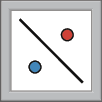
Ilustração. Botão no formato de um quadro com uma diagonal no centro e um poto azul de um lado e ponto vermelha do outro lado.

. Depois, clique sobre o polígono e a reta r. O polígono que aparecerá na tela é o simétrico do polígono inicial em relação à reta r.

Página 211

Tecnologias digitais em foco

Reflexão em relação a um ponto

Siga os passos para construir o simétrico de um polígono qualquer em relação a um ponto.

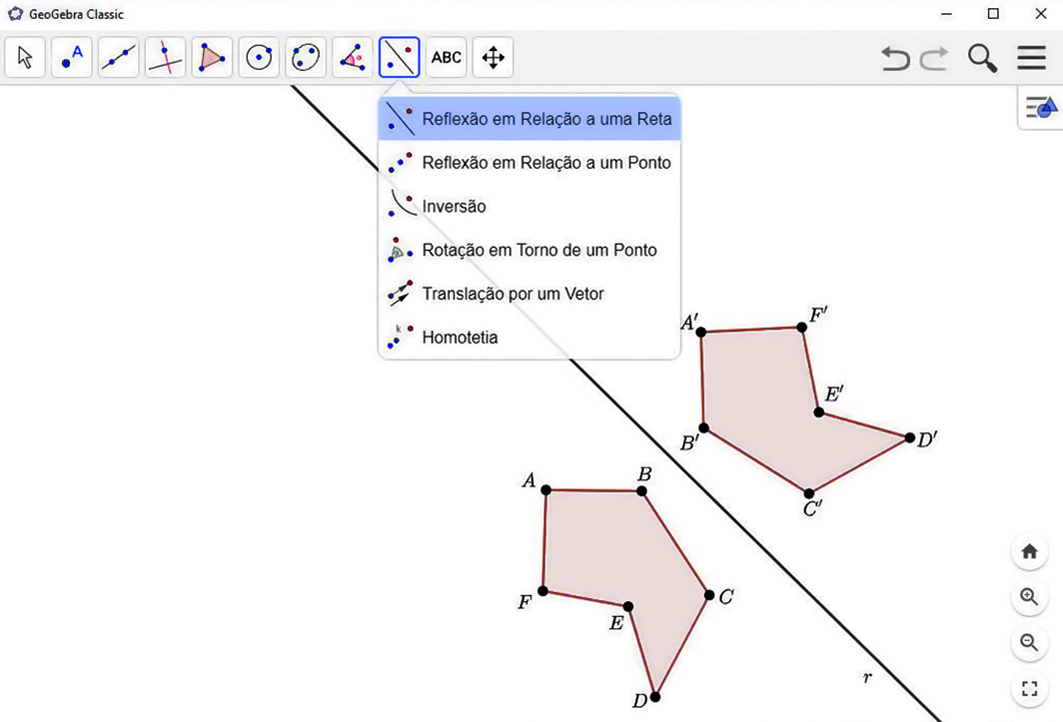
1º) Construa um polígono qualquer.

2º) Marque um ponto óh qualquer. Esse ponto será o centro de reflexão.

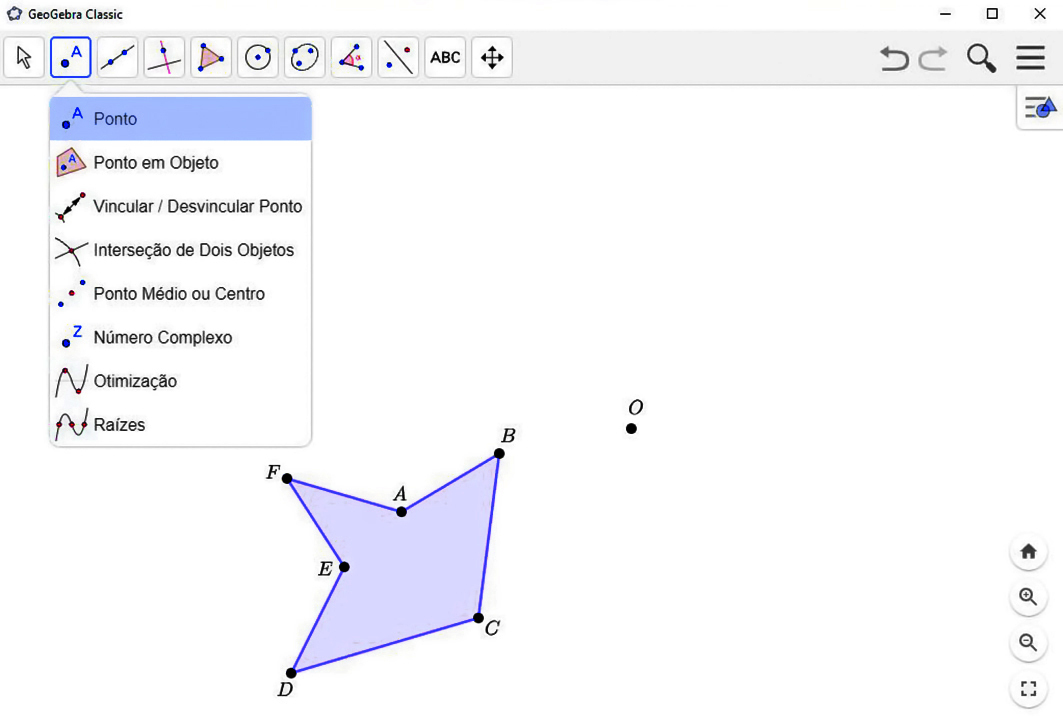
3º) Clique na ferramenta

Ilustração. Botão no formato de um quadro com dois pontos azuis e um ponto vermelha na diagonal.

. Depois, clique sobre o polígono e o ponto óh. O polígono que aparecerá na tela é o simétrico do polígono inicial em relação ao ponto óh.

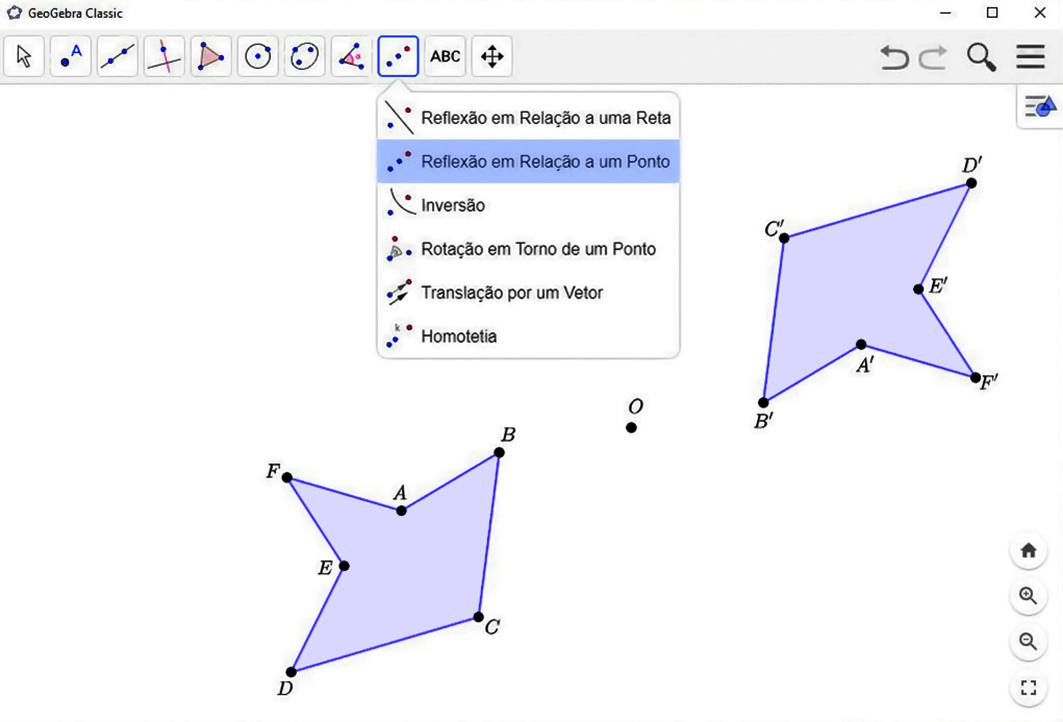
Captura de tela. Continuação da construção mostrada na fotografia anterior, agora na parte superior está destacado a botão no formato de um quadro com dois pontos azuis e um ponto vermelha na diagonal

Há uma uma aba com várias opções e um destaque para a opção: reflexão em relação a um ponto.

Abaixo, na tela, há dois polígono, continua o polígono roxo anterior com as vértices A B C D E e F, agora é adicionado outro polígono igual com as vértices A linha B linha C linha D linha e E linha à direita, do O.

Explore

Em cada construção que você realizou, meça o comprimento dos lados e a abertura dos ângulos correspondentes dos polígonos. Para isso, utilize as ferramentas

Ilustração. Botão no formato de um quadro com reta e centímetros ao lado.

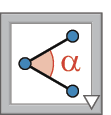
Ilustração. Botão no formato de um quadro com duas retas formando ângulo alfa

Captura de tela. Tela do software de geometria dinâmica GeoGebra.
Na parte superior está destacado a Botão no formato de um quadro com duas retas formando ângulo alfa.

Há uma uma aba com várias opções e um destaque para as opções: ângulo, ângulo com amplitude fixa, distância e comprimento ou perímetro.

Depois, movimente os vértices dos polígonos iniciais. O que você pode observar?

Página 212

Atividades

Faça as atividades no caderno.

Cuidado! Evite acidentes ao usar o compasso na atividade 9.

8. Em seu caderno, construa um quadrado a bê cê dê e um ponto O externo a ele.

Depois, construa o quadrado á linha bê linha cê linha dê linha obtido pela reflexão do quadrado a bê cê dê em relação ao ponto óh.

Usando régua e compasso é possível construir uma figura transladada em relação a uma figura inicial.

Para construir a figura transladada, você deve determinar a direção, o sentido e a medida da distância em que a figura será deslocada.

Reúna-se com dois colegas e, usando régua e compasso, construam no caderno um triângulo á bê cê e o triângulo a linha bê linha cê linha obtido por meio da translação.

Depois, ainda no caderno, escrevam um texto ou façam um fluxograma indicando os procedimentos utilizados nessa construção.

10.

Na seção Tecnologias digitais em foco das páginas anteriores, vimos que podemos construir figuras rotacionadas utilizando o GeoGebra. Analise o desafio proposto pela professora de Mariana:

Esquema. Quadro de giz, à esquerda com a informação: Na primeira linha com desafio, abaixo está escrito 'Usando as ferramentas do GeoGebra, obtenha a figura ao lado a partir da aplicação de diferentes rotações em um losango, com centro de rotação em C'.

Abaixo, há um losango amarelo com ponto C na parte inferior.

À direita, figura composta por 8 losangos em formato circular, sendo F1, F2, F3, F4, F5, F6, F7 e F8. No Losango F1 há uma seta indicando que é o losango original.

Confira algumas das ferramentas do GeoGebra que Mariana utilizou:

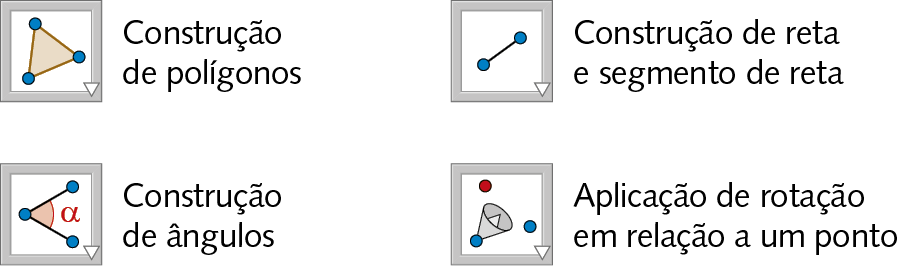
Esquema. Ferramentas do GeoGebra.
Na primeira linha, à esquerda há um quadro com triângulo no interior, ao lado há indicação de construção de polígonos. À direita há um quadro com uma reta e pois pontos na extremidade, ao lado há indicação de Construção de reta e segmento de reta.

Na segunda linha, à esquerda há um quadro com duas retas medindo ângulo de abertura de 30 alfa, ao lado há indicação de construção de ângulos. À direita há um quadro com megafone entre uma bolinha vermelha e uma bolinha azul, ao lado há indicação Aplicação de rotação em relação a um ponto

a) Quais dessas ferramentas Mariana pode utilizar para construir o losango inicial?

b) Se ela optar por construir o losango usando as ferramentas “Segmento” e “Ângulo”, que cuidados ela deve tomar para obter um losango?

c) A figura final é formada por quantos losangos?

d) Quais devem ser as medidas de abertura dos ângulos de rotação e o sentido aplicados em éfe 1 para se obter a éfe₅? E para se obter a éfe₃?

e) Ao usar a ferramenta “Rotação em Torno de um Ponto”, Mariana deverá selecionar o losango inicial, o ponto C, digitar a medida de abertura do ângulo de rotação e indicar o sentido (horário ou anti-horário). No caderno, escreva a medida de abertura do ângulo de rotação e o sentido que Mariana deverá indicar ao usar essa ferramenta para obter todos os losangos.

Página 213

11.

Com o auxílio do GeoGebra (ou outro software de geometria dinâmica que seu professor pode indicar), siga as instruções para construir uma figura como esta representada.

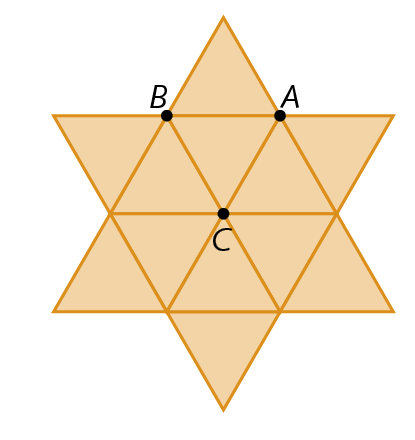
Figura geométrica. A partir de um triângulo equilátero ABC, utilizando rotações foi construída uma estrela de seis pontas formada por 12 triângulos equiláteros.

1. Construa um triângulo equilátero á bê cê.

2. Rotacione o triângulo á bê cê, com centro de rotação em a, no sentido horário e ângulo de medida da abertura de 60graus. A composição desses dois triângulos fórma um losango.

3. Rotacione o losango formado, com centro de rotação em C, no sentido horário e ângulo de medida da abertura de 60graus. Obteremos um novo losango.

4. Rotacione esse novo losango, com centro em C, no sentido horário e ângulo de medida da abertura de 60graus.

5. Continue o processo até representar a figura.

Na construção anterior, utilizamos somente rotação, mas é possível construir a mesma figura utilizando somente reflexão. Junte-se a um colega e, no caderno, escrevam um roteiro ou façam um fluxograma descrevendo os passos que devem ser seguidos para a construção, no GeoGebra, usando somente reflexão.

2 Representação de um polígono no plano cartesiano

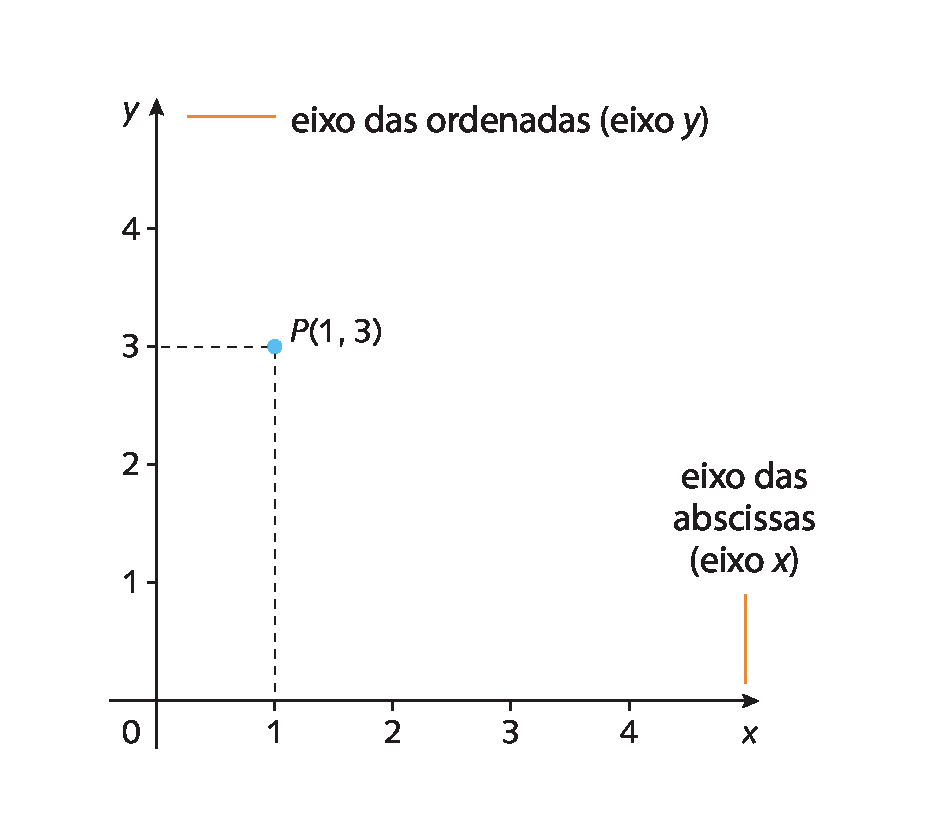
O plano cartesiano é composto de dois eixos, um horizontal e um vertical, chamados de eixo das abscissas (eixo x) e eixo das ordenadas (eixo y), respectivamente. Para representar um ponto no plano cartesiano, utilizamos dois números que são expressos por meio de um par ordenado.

Esse par de números é assim chamado porque existe uma ordem predeterminada para escrevê-lo. Considere, por exemplo, o ponto P(1,3) representado nesse plano cartesiano. Esse ponto tem abscissa x = 1 e ordenada y = 3.

Plano cartesiano. Retas numéricas perpendiculares que se intersectam no ponto O que corresponde ao número zero. Na reta numérica horizontal estão representados os números 0, 1, 2, 3, e 4 e ela está identificada com a letra x. Há uma seta para ela com a indicação: Eixo das abscissas.
Na reta numérica vertical estão representados os números 0, 1, 2, 3 e 4 e ela está identificada com a letra y. Há uma seta para ela com a identificação: Eixo das ordenadas.
No plano cartesiano, está representado o ponto P que corresponde ao par ordenado (1, 3). Do número 1 representado no eixo das abscissas, parte uma linha vertical tracejada. Do número 3 representado no eixo das ordenadas parte uma linha horizontal tracejada. As duas linhas tracejadas se encontram no ponto P.

Os quadrantes do plano cartesiano

Podemos ampliar os eixos x e y, representando também os números negativos. Assim, os eixos dividem o plano cartesiano em quatro partes que chamamos de quadrantes.

• No 1º quadrante, representamos os pontos de coordenadas positivas.

• No 2º quadrante, representamos os pontos com abscissa negativa e ordenada positiva.

• No 3º quadrante, representamos os pontos de coordenadas negativas.

• No 4º quadrante, representamos os pontos com abscissa positiva e ordenada negativa.

Página 214

Analise alguns exemplos.

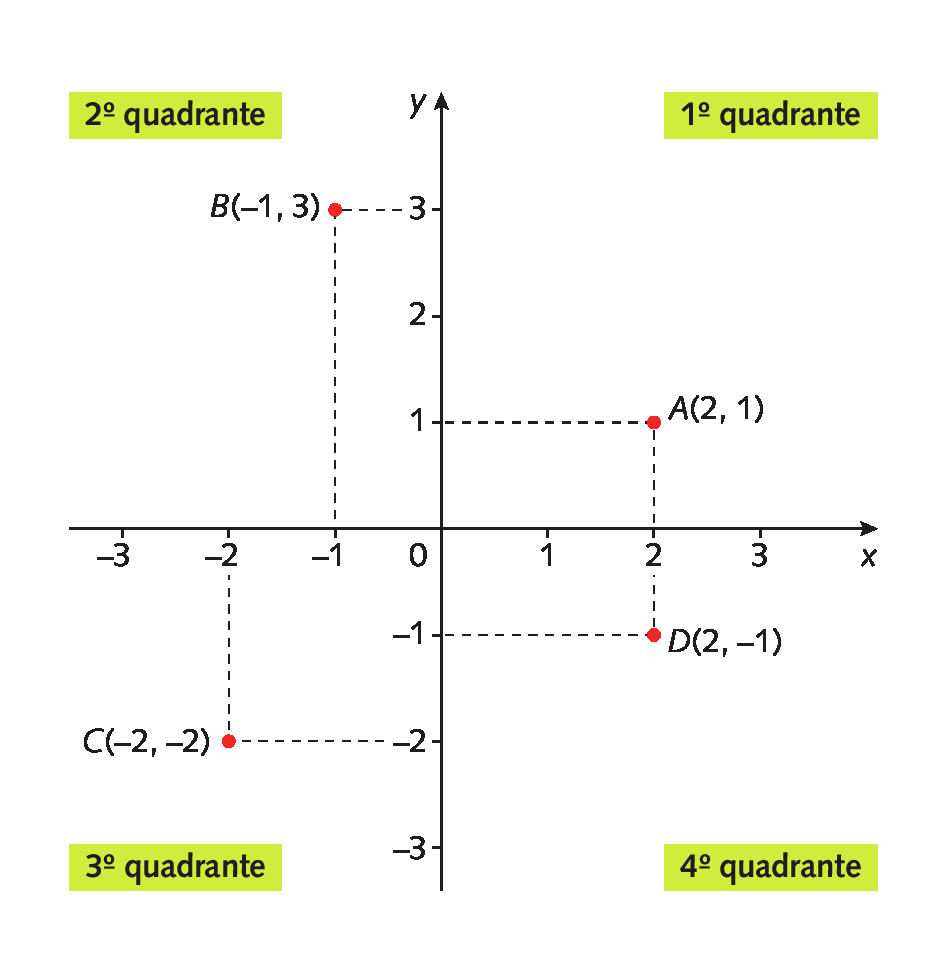
a) O ponto a(2, 1) está representado no 1º quadrante, pois tem coordenadas positivas (x = 2 > 0 e y = 1 > 0).

b) O ponto B(menos1, 3) está representado no 2º quadrante, pois tem abscissa negativa (x = menos1 < 0) e ordenada positiva (y = 3 > 0).

c) O ponto C(‒2, ‒2) está representado no 3º quadrante, pois tem coordenadas negativas (x = y = menos2 < 0).

d) O ponto D(2, menos1) está representado no 4º quadrante, pois tem abscissa positiva (x = 2 > 0) e ordenada negativa (y = menos1 < 0).

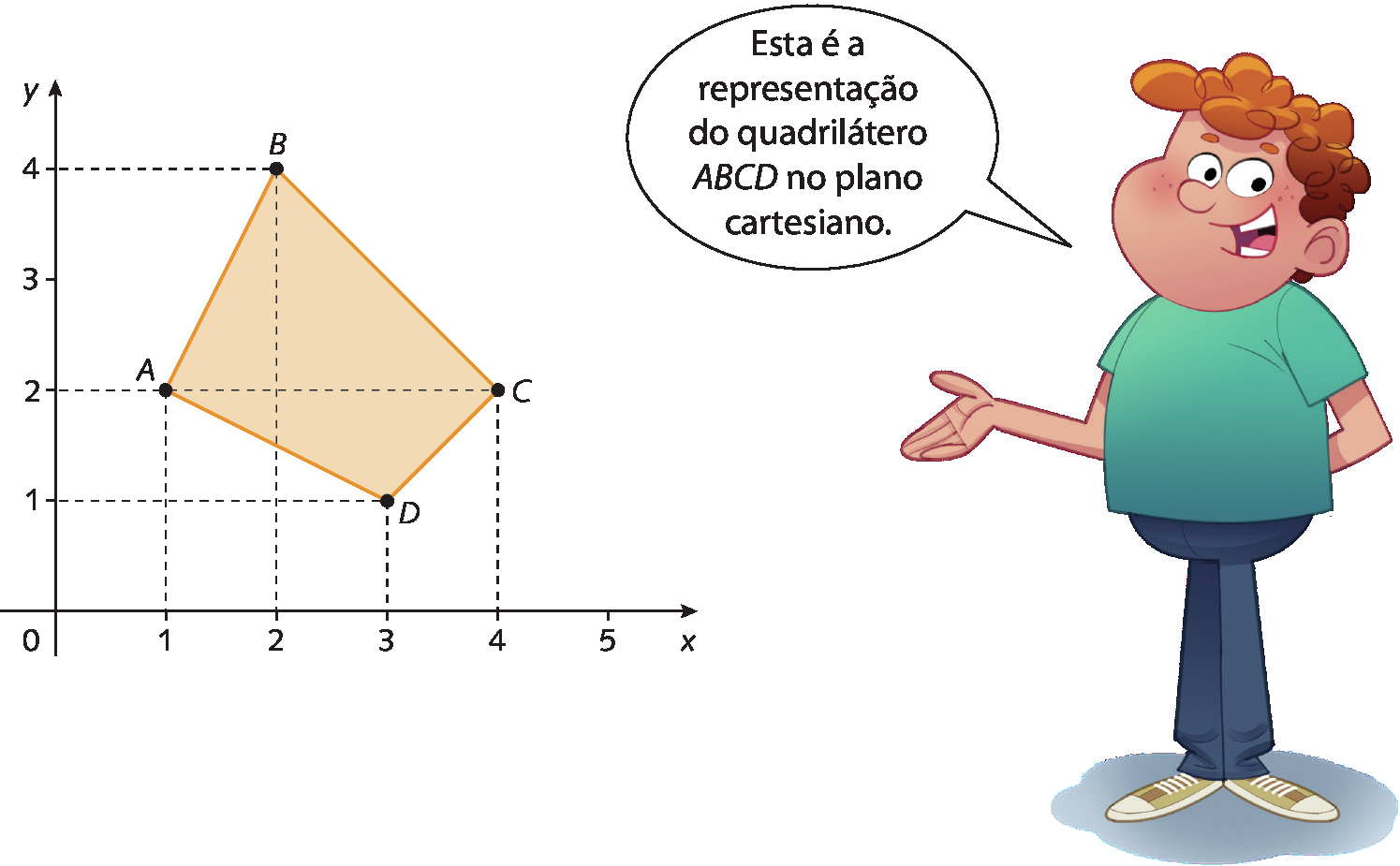
O polígono no plano cartesiano

Podemos representar um polígono, no plano cartesiano, associando seus vértices a pares ordenados. Observe, a seguir, a representação do polígono de vértices a(1, 2), B(2, 4), C(4, 2) e D(3, 1).

Esquema. No lado direito, há um Plano cartesiano. Eixo x com as representações dos números 0, 1, 2, 3, 4 e 5 e eixo y com as representações dos números 0, 1, 2, 3, e 4. No plano está representado um quadrilátero laranja com vértices nos pontos A de abscissa 1 e ordenada 2, B de abscissa 2 e ordenada 4, C de abscissa 4 e ordenada 2 e D de abscissa 3 e ordenada 1.
No lado esquerdo, há um menino pardo de cabelo castanho, usando uma camisa verde e uma calça. Ele está em pé e dizendo: Esta é a representação do quadrilátero ABCD no plano cartesiano.

Página 215

Atividades

Faça as atividades no caderno.

12. Construa, em seu caderno, um plano cartesiano e marque os seguintes pontos: A(3, 2), B (menos1, 0), C (0, menos3), D (menos2, menos2), ê (3, menos4), F (0, 0), G (menos4, 3) e H (3, menos2).

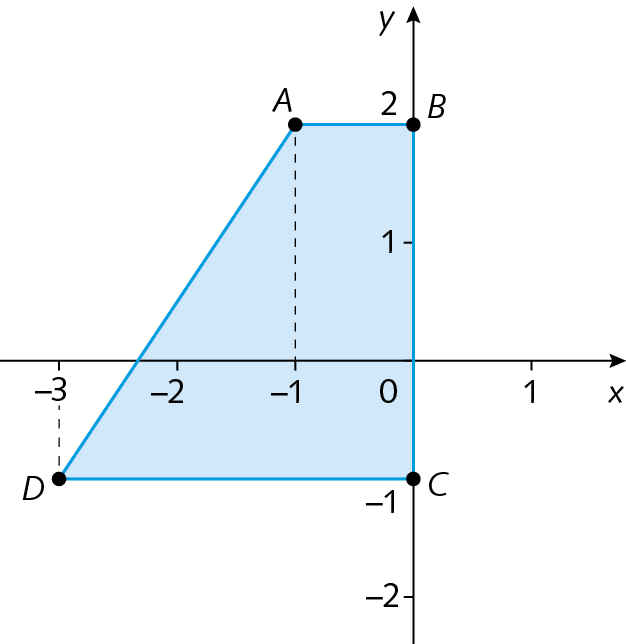
13. Quais são os pares ordenados correspondentes aos vértices do trapézio?

Plano cartesiano. Eixo x com as representações dos números menos 3, menos 2, menos 1, 0, 1 e eixo y com as representações dos números menos 2, menos 1. 0, 1 e 2. No plano está representado um trapézio azul com vértices nos pontos A de abscissa menos 1 e ordenada 2, B de abscissa 0 e ordenada 2, C de abscissa 0 e ordenada menos 1 e D de abscissa menos 3 e ordenada menos 1.

14.

Um pentágono de vértices R (menos1, menos1), S (menos2, menos1), T (menos3, menos2), U (menos2, menos3) e V (menos1, menos2) está localizado em qual quadrante? É possível justificar sua resposta sem representar esse polígono? Converse com o professor e os colegas.

15. Um triângulo á bê cê de vértices a (2, 2), B (menos3, menos1) e C (1, menos1) tem pontos em quais quadrantes?

16. Os pontos a (1, menos1) e B (4, menos1) são vértices de um quadrado a bê cê dê construído no 4º quadrante. Quais são os pares ordenados correspondentes aos outros vértices desse quadrado?

17. Em seu caderno, construa um plano cartesiano e represente um hexágono que tenha pontos em todos os quadrantes.

3 Transformações geométricas no plano cartesiano

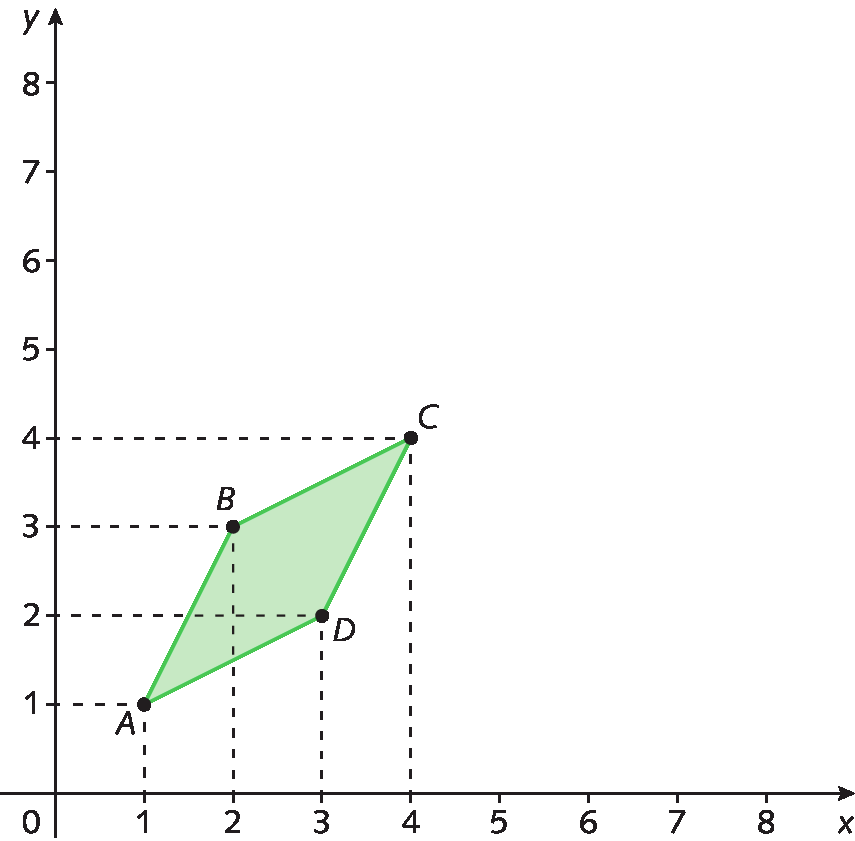
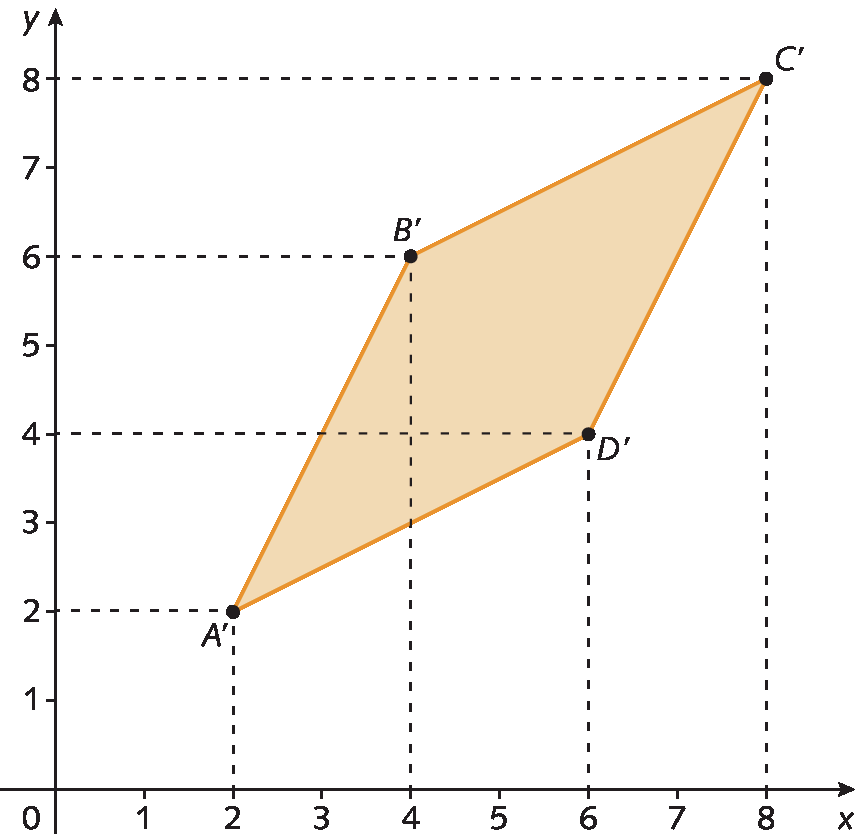
Considere o losango verde, de vértices a(1, 1), B(2, 3), C(4, 4) e D(3, 2). Observe que, se multiplicarmos as coordenadas dos vértices desse losango por 2, obteremos os pontos á linha(2, 2), bê linha(4, 6), cê linha(8, 8) e dê linha(6, 4), que correspondem aos vértices do losango laranja.

▸ Qual é a relação entre os dois losangos?

Ilustração. Losango ABCD, representado em um plano cartesiano, O ponto A tem abcissa 1 e ordenada 1, o ponto B tem abscissa 2 e ordenada 3, o ponto C tem abcissa 4 e ordenada 4 e o ponto D tem abscissa 3 e ordenada 2.

Ilustração. Losango A linha, B linha, C linha e D linha representado em um plano cartesiano. O ponto A linha tem abcissa 2 e ordenada 2, o ponto B linha tem abscissa 4 e ordenada 6, o ponto C linha tem abcissa 8 e ordenada 8 e o ponto D linha tem abscissa 6 e ordenada 4.

Página 216

Agora, considere o quadrilátero FGHI de vértices F(1, 1), G(3, 4), H(4, 4) e ih(4, 3). Se multiplicarmos essas coordenadas por menos1, obteremos os vértices do quadrilátero F’G’H’I’.

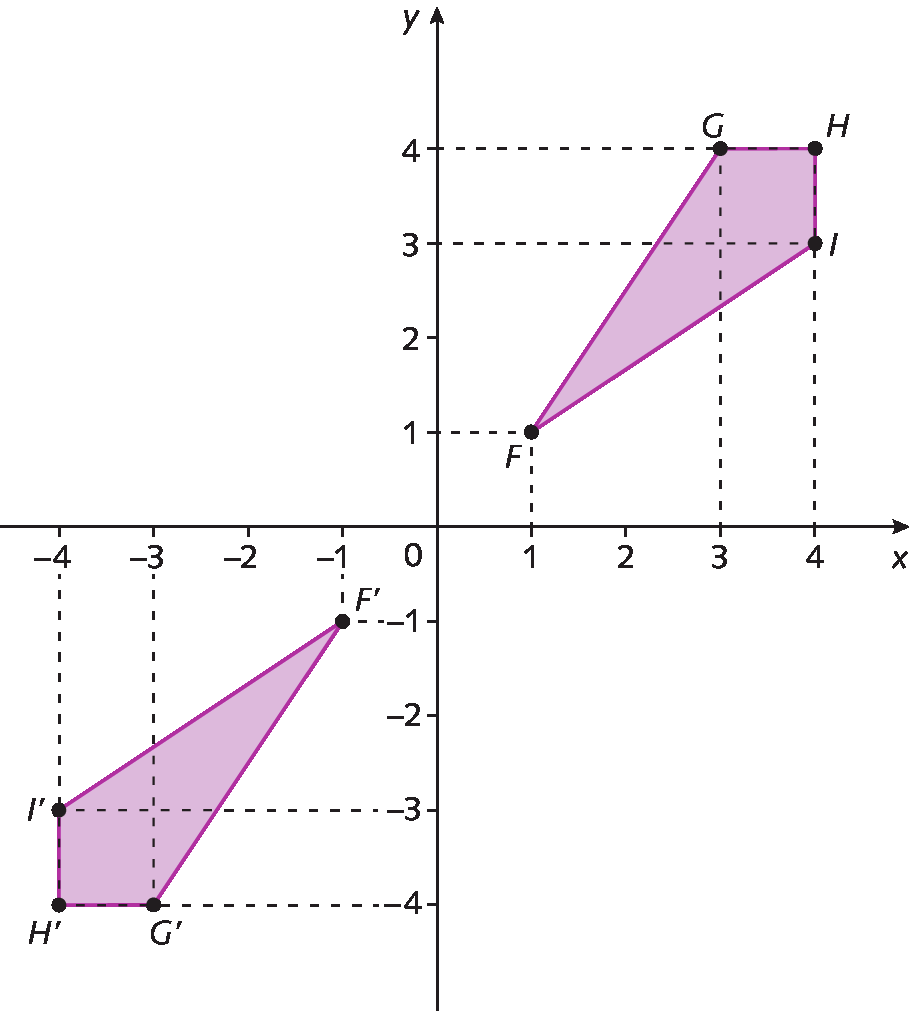
Ilustração. Quadriláteros representados em um plano cartesiano. No primeiro quadrante, quadrilátero FGHI. O ponto F tem abcissa 1 e ordenada 1, o ponto G tem abscissa 3 e ordenada 4, o ponto H tem abcissa 4 e ordenada 4 e o ponto I tem abscissa 4 e ordenada 3. No terceiro quadrante, quadrilátero F linha G linha H linha I linha . O ponto F linha tem abcissa menos 1 e ordenada menos 1, o ponto G linha tem abscissa menos 3 e ordenada menos 4, o ponto H linha tem abcissa menos 4 e ordenada menos 4 e o ponto I linha tem abscissa menos 4 e ordenada menos 3.

▸ Qual é a relação entre os dois quadriláteros?

Vimos nessas situações que, quando multiplicamos as coordenadas dos vértices de um polígono por números inteiros, obtemos um outro polígono, que pode ser simétrico ou não ao polígono inicial. Vamos estudar esses casos.

Ampliação

Considere os losangos a bê cê dê e á linha bê linha cê linha dê linha representados anteriormente. Se medirmos o comprimento de todos os lados e a abertura dos ângulos das duas figuras, vamos verificar que as medidas de comprimento dos lados do losango á linha bê linha cê linha dê linha dobraram em relação às medidas de comprimento dos lados correspondentes do losango a bê cê dê, e as medidas de abertura dos ângulos internos das duas figuras permaneceram iguais. Assim, concluímos que o losango á linha bê linha cê linha dê linha é uma ampliação do losango a bê cê dê.

Agora, observe os trapézios a seguir. O trapézio érre linha ésse linha tê linha ú linha é uma ampliação do trapézio érre ésse tê ú, resultado da multiplicação das coordenadas dos vértices R(menos3, 1), S(menos2, 2), T(menos1,2) e U(menos1,1) por 3. Note que o trapézio érre linha ésse linha tê linha ú linha também é uma ampliação do trapézio érre ésse tê ú, resultado da multiplicação das coordenadas dos vértices desse trapézio por menos2, porém também há uma mudança de quadrante e de sua posição em relação aos eixos x e y.

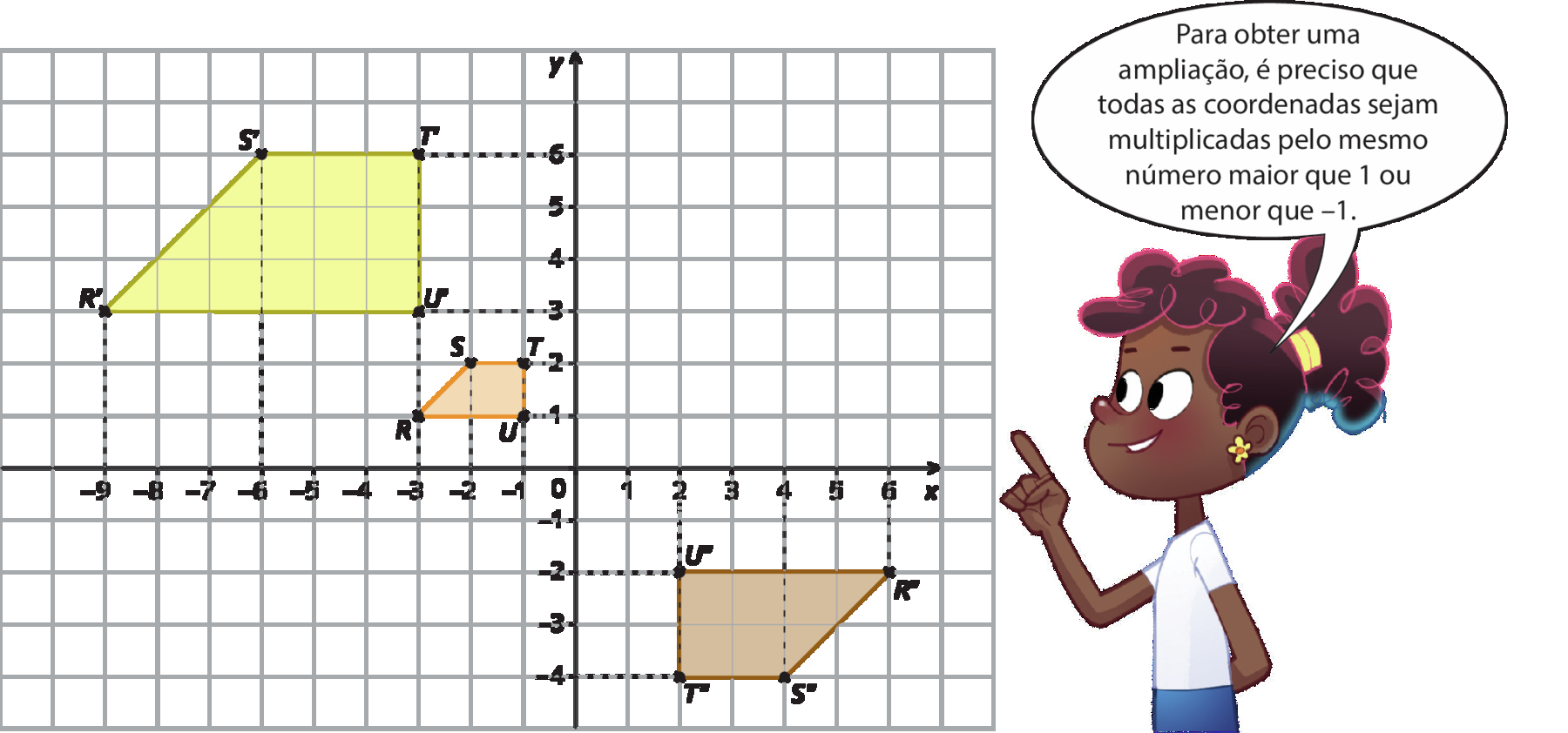
Plano cartesiano. Retas numéricas perpendiculares que se intersectam no ponto O que corresponde ao número zero. Eixo x com as representações dos números, menos 9, menos 8, menos 7, menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5 e 6. O eixo y com as representações dos números, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5 e 6. No plano há representação de 3 trapézios

No segundo quadrante, há dois trapézios, o primeiro com as vértices:
Ponto R: abscissa menos 3 e ordena 1
Ponto S: abscissa menos 2 e ordena 2
Ponto T: abscissa menos 1 e ordena 2
Ponto U: abscissa menos 1 e ordena 1

O segundo trapézios, é a ampliação do primeiro trapézios, as vértices:
Ponto R linha: abscissa menos 9 e ordena 3
Ponto S linha: abscissa menos 6 e ordena 6
Ponto T linha: abscissa menos 3 e ordena 6
Ponto U linha: abscissa menos 3 e ordena 3

No quarto quadrante, também há outro trapézios ampliado, as vértices são:
Ponto R duas linhas: abscissa 6 e ordena menos 2
Ponto S duas linhas: abscissa 4 e ordena menos 4
Ponto T duas linhas: abscissa 2 e ordena menos 4
Ponto U duas linhas: abscissa 2 e ordena menos 2

No lado esquerdo, há um menina negra de cabelo preto, usando uma camisa branca. Ele está em pé e dizendo: Para obter uma ampliação, é preciso que todas as coordenadas sejam multiplicadas pelo mesmo número maior que 1 ou menor que menos 1.

Para ampliar um polígono no plano cartesiano, multiplicamos todas as coordenadas dos vértices desse polígono por um mesmo número maior que 1 ou menor que ‒1.

Página 217

Simetria em relação à origem do plano cartesiano

Observe, a seguir, os pentágonos representados no plano cartesiano.

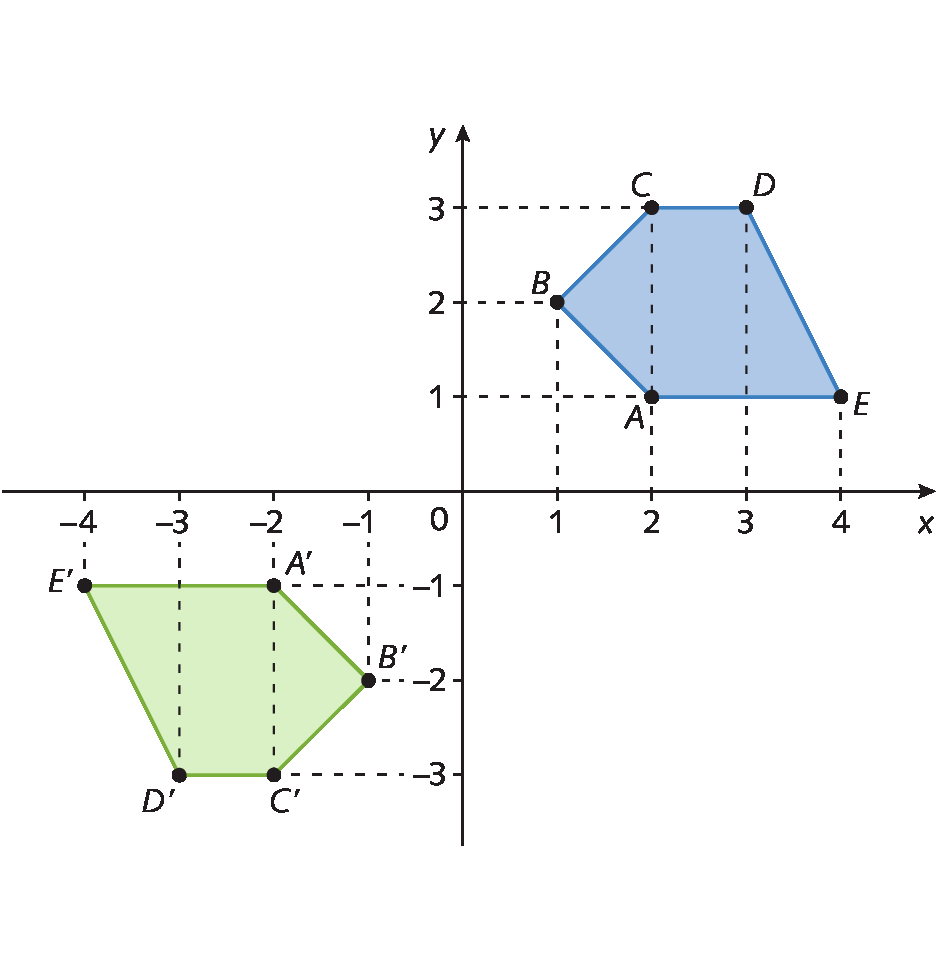
Ilustração. Pentágonos representados em um plano cartesiano. No primeiro quadrante, pentágono ABCDE. O ponto A tem abcissa 2 e ordenada 1, o ponto B tem abscissa 1 e ordenada 2, o ponto C tem abcissa 2 e ordenada 3, o ponto D tem abscissa 3 e ordenada 3 e o ponto E tem abscissa 4 e ordenada 1. No terceiro quadrante, pentágono A linha B linha C linha D linha E linha. O ponto A linha tem abcissa menos 2 e ordenada menos 1, o ponto B linha tem abscissa menos 1 e ordenada menos 2, o ponto C linha tem abcissa menos 2 e ordenada menos 3, o ponto D linha tem abcissa menos 3 e ordenada menos 3 e o ponto E linha tem abscissa menos 4 e ordenada menos 1.

O pentágono azul tem vértices a(2, 1), B(1, 2), C(2, 3), D(3, 3) e ê(4, 1). Se multiplicarmos todas as coordenadas dos vértices desse pentágono por ‒1, obteremos as coordenadas dos vértices do pentágono verde: á linha(menos2, menos1), bê linha(menos1, menos2), cê linha(menos2, menos3), dê linha(menos3, menos3) e é linha(menos4, menos1).

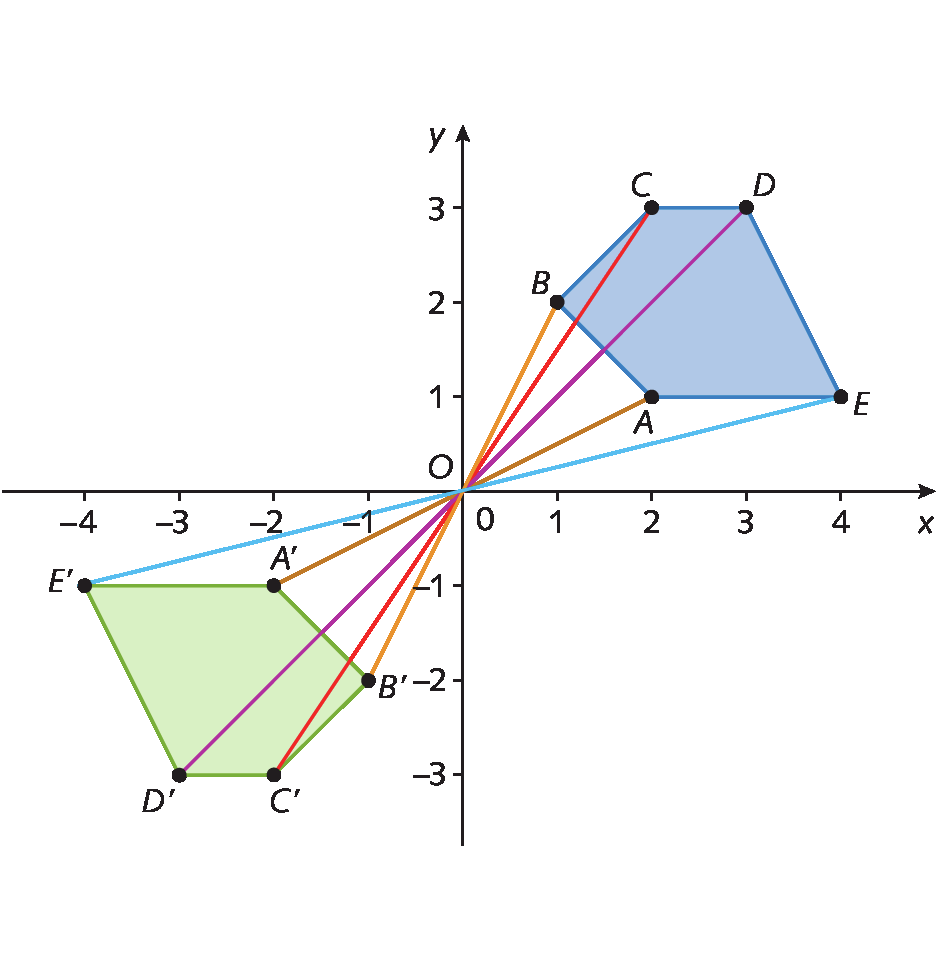
Usando segmentos de reta, vamos unir os vértices correspondentes desses polígonos.

Observe que todos os segmentos de reta passam pela origem do plano cartesiano – ponto óh(0, 0). Além disso, a medida da distância da origem do plano cartesiano a cada vértice do pentágono á bê cê dê é é igual à medida da distância da origem do plano cartesiano ao vértice correspondente do outro pentágono á linha bê linha cê linha dê linha é linha.

\overline{O A} ≅ \overline{O A ’}

\overline{O B} ≅ \overline{O B ’}

\overline{O C} ≅ \overline{O C ’}

\overline{O D} ≅ \overline{O D ’}

\overline{O E} ≅ \overline{O E ’}

Concluímos, então, que os pentágonos á bê cê dê é e á linha bê linha cê linha dê linha é linha são simétricos em relação à origem do plano cartesiano.

Para encontrar as coordenadas dos vértices de um polígono simétrico a outro, em relação à origem do plano cartesiano, multiplicamos todas as coordenadas dos vértices desse polígono por menos1, ou seja, consideramos os opostos das ordenadas e das abscissas. Assim, o simétrico do ponto P(x, y) em relação à origem é o ponto pê linha(menosx, menosy).

Página 218

Observação

Podemos associar o pentágono á linha bê linha cê linha dê linha é linha (verde) à:

• reflexão do pentágono á bê cê dê é (azul) em relação à origem do plano cartesiano;

• rotação do pentágono á bê cê dê é (azul) em um ângulo de medida da abertura de 180graus com a origem do plano cartesiano como centro de rotação.

Simetria em relação aos eixos do plano cartesiano

Simetria em relação ao eixo x

Observe o triângulo xis ípsilon zê de vértices X(1, 1), Y(3, 4) e Z(4, 2). Se refletirmos esse triângulo em relação ao eixo x, obteremos o triângulo décimo‘Y‘Z‘.

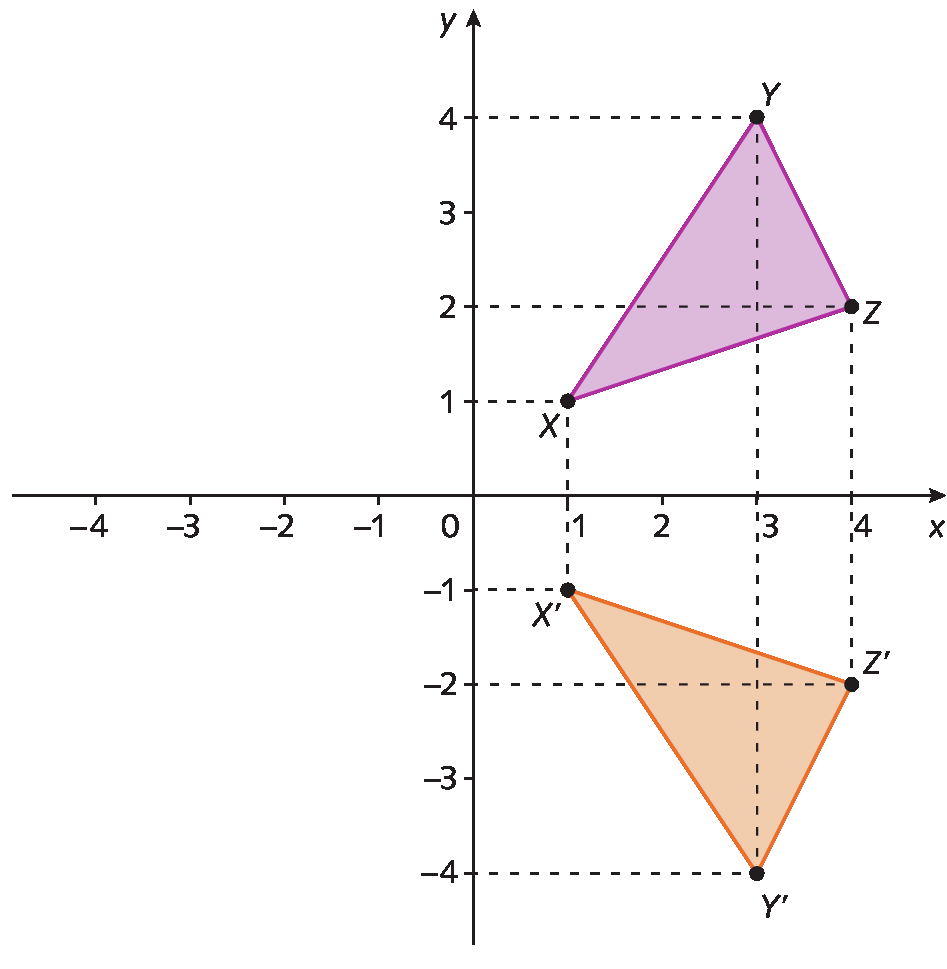
Ilustração. Triângulos representados em um plano cartesiano. No primeiro quadrante triângulo XYZ.. O ponto X tem abcissa 1 e ordenada 1, o ponto Y tem abscissa 3 e ordenada 4 e o ponto Z tem abcissa 4 e ordenada 2.
No segundo quadrante triângulo X linha Y linha Z linha .. O ponto X linha tem abcissa 1 e ordenada menos 1, o ponto Y linha tem abscissa 3 e ordenada menos 4 e o ponto Z tem abcissa 4 e ordenada menos. 2.

Os vértices do triângulo xis linha y linha zê linha são X‘(1, ‒1), Y‘(3, ‒4) e Z‘(4, ‒2). Note que as abscissas dos pontos X, Y e Z são iguais às abscissas dos pontos xis linha, Y’ e Z’ e as ordenadas desses pontos são opostas ou simétricas.

No plano cartesiano, para encontrar as coordenadas dos vértices de um polígono simétrico em relação ao eixo x, repetimos as abscissas e consideramos os opostos das ordenadas. Assim, o simétrico do ponto P(x, y) em relação ao eixo x é o ponto P‘(x, ‒y).

Simetria em relação ao eixo y

De maneira análoga, podemos refletir o triângulo xis ípsilon zê em relação ao eixo y, obtendo o triângulo X”Y”Z” de vértices décimopolegadas(‒1, 1), Ypolegadas(‒3, 4) e Zpolegadas(‒4, 2). Nesse caso, as abscissas dos pontos xis duas linhas, y duas linhas e zê duas linhas são simétricas às abscissas dos pontos X, Y e Z e as ordenadas são iguais.

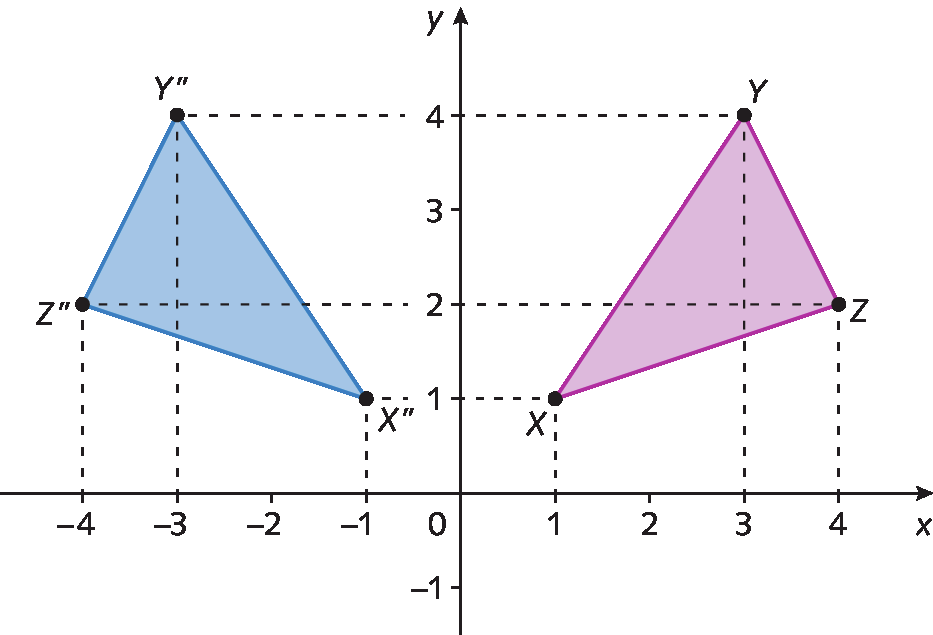
No plano cartesiano, para encontrar as coordenadas dos vértices de um polígono simétrico em relação ao eixo y, consideramos os opostos das abscissas e repetimos as ordenadas. Assim, o simétrico do ponto P(x, y) em relação ao eixo y é o ponto P‘(‒x, y).

Página 219

Atividades

Faça as atividades no caderno.

18. Considere o hexágono representado a seguir.

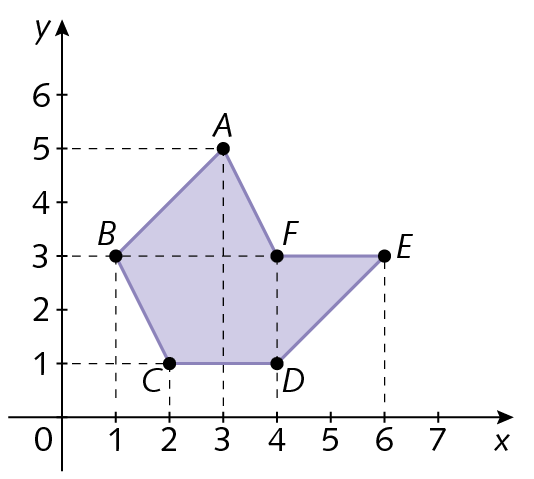
Plano cartesiano. Retas numéricas perpendiculares que se intersectam no ponto O que corresponde ao número zeroNo eixo x, com as representações dos números 0, 1, 2, 3, 4, 5, 6 e 7 e eixo y com as representações dos números 0, 1, 2, 3, 4, 5 e 6. No plano está representado um hexágono roxo com vértices nos pontos A de abscissa 3 e ordenada 5, B de abscissa 1 e ordenada 3, C de abscissa 2 e ordenada 1, D de abscissa 4 e ordenada 1, E de abscissa 6 e ordenada 3 e F de abscissa 4 e ordenada 3

a) Quais são os pares ordenados correspondentes aos vértices desse hexágono?

b) Ao multiplicar as coordenadas dos vértices desse hexágono por 2, a figura obtida corresponderá a uma ampliação ou será simétrica em relação à origem do plano cartesiano?

c) Quais são os pares ordenados correspondentes aos vértices da figura obtida no item b?

d) Represente a figura inicial e a obtida no item b em um plano cartesiano.

19. O triângulo a seguir representa a ampliação do triângulo á bê cê. Quais são os possíveis pares ordenados que correspondem aos vértices do triângulo á bê cê?

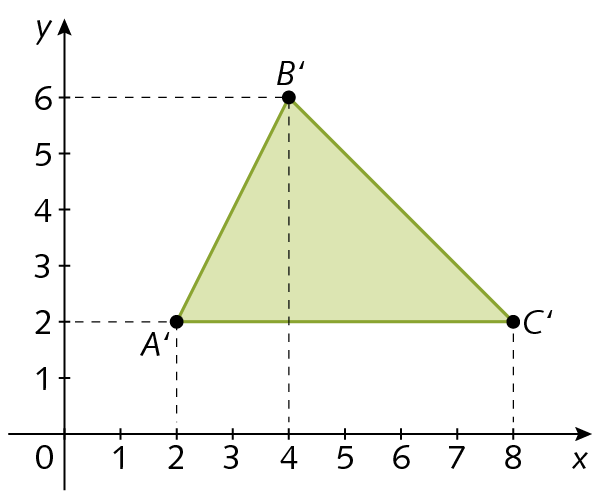
20. Em um plano cartesiano, faça o que se pede.

a) Represente um segmento

\overline{A B}

em que a(2, 3) e B(2, 0).

b) Considerando

\overline{C D}

simétrico de

\overline{A B}

em relação ao eixo y, de modo que o ponto C seja simétrico ao ponto a e o ponto D seja simétrico ao ponto B, quais são os pares ordenados correspondentes aos pontos C e D?

c) Traçando os segmentos

\overline{A C}

\overline{B D}

, obtemos o contorno de um polígono. Que polígono é esse?

d) Usando essa mesma estratégia, quais poderiam ser os pares ordenados correspondentes aos pontos aêbê para se obter o contorno de um quadrado?

21. Observe a representação do polígono no plano cartesiano a seguir.

a) Quais são os pares ordenados correspondentes aos vértices do seu simétrico em relação ao eixo y?

b) Construa um plano cartesiano em seu caderno para representar o polígono FGHIJKLMNOPQ e seu simétrico em relação ao eixo y.

22. Em seu caderno, construa o triângulo BCD e seu simétrico em relação à origem do plano cartesiano.

Quais são os pares ordenados correspondentes aos vértices do triângulo B’C’D’, simétrico ao triângulo bê cê dê?

Página 220

23. Qual das figuras a seguir representa uma simetria, em relação à origem do plano cartesiano, de um quadrado de vértices a(‒3, 1), B(‒2, 3), C(0, 2) e D(‒1, 0)?

24. Se um triângulo tem dois vértices no eixo y e um vértice no 1º quadrante, o que acontece ao multiplicarmos as coordenadas desses vértices por ‒1? Onde ficará o vértice que estava no 1º quadrante?

25. Considere um polígono inteiramente contido no 2º quadrante. Em quais quadrantes estarão, respectivamente, os simétricos em relação à origem do plano cartesiano, em relação ao eixo das abscissas e em relação ao eixo das ordenadas?

26. No plano cartesiano a seguir, os triângulos B, C e D são simétricos ao triângulo a, respectivamente, em relação:

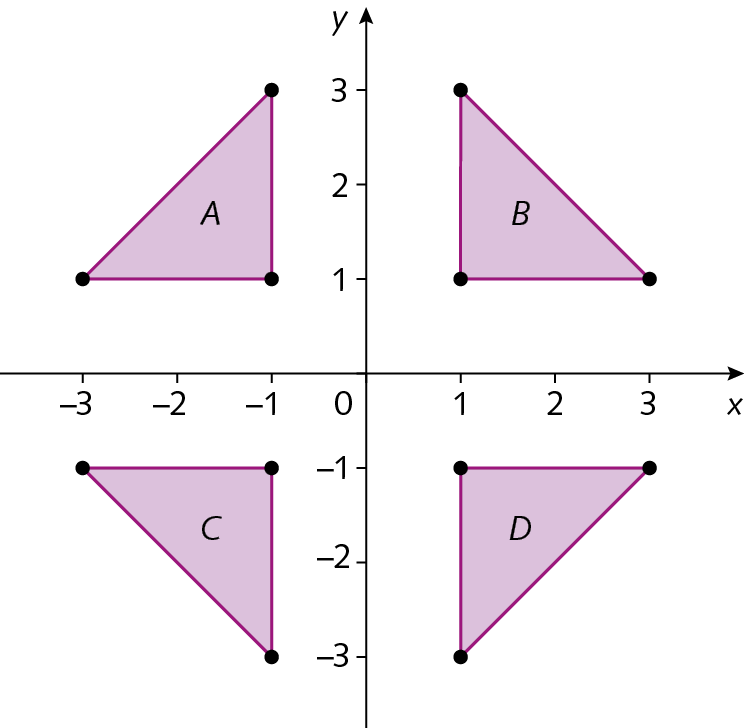
a) ao eixo x, ao eixo y e à origem.

b) ao eixo x, à origem e ao eixo y.

c) ao eixo y, ao eixo x e à origem.

d) ao eixo y, à origem e ao eixo x.

27. Com relação ao triângulo de coordenadas dos vértices a(‒3, 1), B(‒1, 3) e C (2, 1), classifique as sentenças a seguir em verdadeiras ou falsas, corrigindo as sentenças falsas em seu caderno.

a) O triângulo á bê cê está inteiramente localizado no 2º quadrante do plano cartesiano.

b) O triângulo simétrico ao triângulo á bê cê, em relação ao eixo x, está localizado no 3º e no 4º quadrante.

c) O triângulo simétrico ao triângulo á bê cê, em relação ao eixo y, tem coordenadas dos vértices á linha(‒3, ‒1), bê linha(‒1, ‒3) e cê linha(2, ‒1).

d) O triângulo simétrico ao triângulo á bê cê, em relação à origem do plano cartesiano, tem coordenadas dos vértices á linha (3, ‒1), bê linha (1, ‒3) e cê linha (‒2, ‒1).

Página 221

Veja que interessante

Faça a atividade no caderno.

Oscar Niemeyer, o gênio das formas

Oscar Ribeiro de Almeida de Niemáier Soares nasceu no Rio de Janeiro, em 15 de dezembro de 1907, e faleceu na mesma cidade, em 5 de dezembro de 2012. Ele é considerado um dos arquitetos mais influentes do mundo contemporâneo.

Fotografia. Homem branco com cabelos grisalhos. Ele está vestindo uma camisa branca a e casaco escuro. — Oscar Niemáier, Rio de Janeiro (Rio de Janeiro). Foto de 15 de dezembro de 2007.

O “gênio das formas” é reconhecido pela beleza, ousadia e leveza de seus projetos. O Museu de Arte Contemporânea, no Rio de Janeiro (Rio de Janeiro), o Palácio do Itamaraty, em Brasília (Distrito Federal), o Museu Oscar Niemáier, em Curitiba (Paraná), e o Auditório Ibirapuera, em São Paulo (São Paulo), são marcas de sua genialidade.

Em suas obras, é possível notar a presença de diferentes tipos de simetria.

Fotografia. Construção de um Palácio composta por arcos em suas laterais. Ao lado, um lago há um lago, gramado e plantas. — O Palácio do Itamaraty, também conhecido como Palácio dos Arcos, é a séde do Ministério das Relações Exteriores do Brasil, situado em Brasília (Distrito Federal). Foto de 2021.

Fotografia. Catedral, construção redondas, composta por estruturas brancas arqueadas na vertical. — Catedral de Brasília, Brasília (Distrito Federal). Foto de 2020.

Atividade

Em quais objetos cotidianos você consegue reconhecer a presença de translações, rotações ou reflexões? Converse com os colegas.

Página 222

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Isometrias

Isometrias são transformações geométricas que preservam o formato e as medidas da figura original. São exemplos de isometria a translação, a rotação e a reflexão (em relação a uma reta ou a um ponto).

Translação

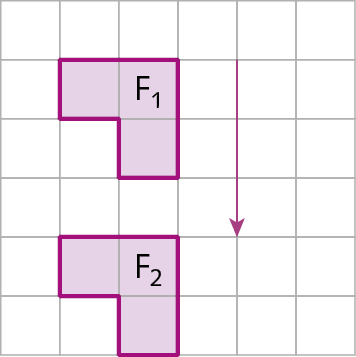
Esquema. Malha quadriculada de 6 linhas com 6 quadradinhos cada. Na malha há duas figuras, iguais com 2 quadradinhos rosa na horizontal e um quadradinho abaixo. Na centro da figura da parte superior está identificado F1 e na figura inferior há identificação de F2. À direita das figuras, seta vertical de cima para baixo.

Rotação

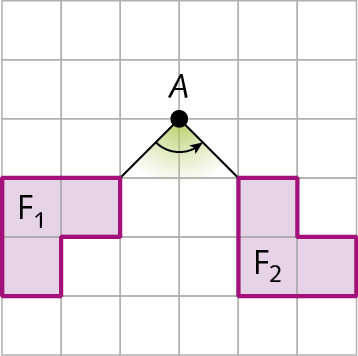
Esquema. Malha quadriculada de 6 linhas com 6 quadradinhos cada. Na malha há duas figuras, à esquerda há 2 quadradinhos na vertical e 1 quadradinho na horizontal na parte superior, no interior da figura está identificado F1. À esquerda há 2 quadradinhos na vertical e 1 quadradinho na horizontal na parte inferior, no interior da figura está identificado F2. Entre as figuras geométricas na parte superior, há uma reta na diagonal entre as figuras F1 e F2, com o ponto A formando um ângulo.

Reflexão

Reflexão em relação a uma reta

Ilustração. Figuras simétricas em relação a uma reta r. As figuras são congruentes e estão a uma mesma medida de distância da reta r.

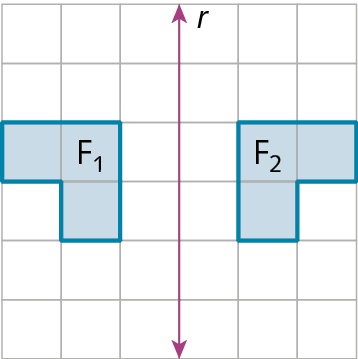
Reflexão em relação a um ponto

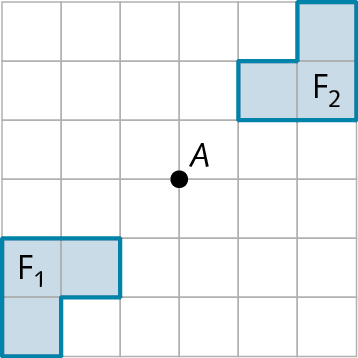
Ilustração. Figuras simétricas em relação a a um ponto A, As figuras são congruentes e os pontos correspondentes das duas estão a uma mesma medida de distância do ponto A.

1. Observe a imagem e responda no caderno.

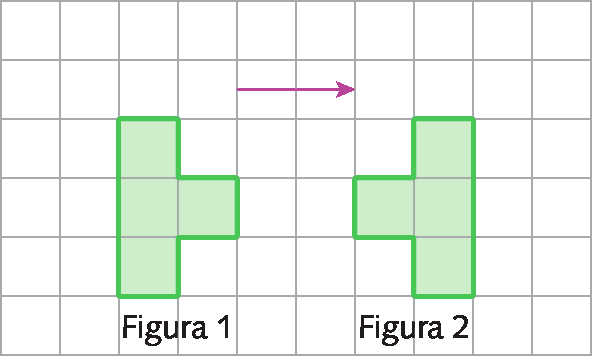
Esquema. Malha quadriculada, de 6 linhas com 10 quadradinhos. Ha duas figuras geométricas, uma à esquerda composta por 3 quadradinhos na cor verde na vertical e um quadradinho ao meio à direita. A outra a esquerda composta por 3 quadradinhos na cor verde na vertical e um quadradinho ao meio à esquerda. Acima, entre as figuras geométricas há uma seta horizontal da esquerda para direita.

A figura 2 foi obtida por meio de uma translação da figura 1? Justifique sua resposta.

2. Em uma malha quadriculada, represente um quadrilátero a bê cê dê e uma reta r distante 3 quadradinhos do vértice D. Depois, construa o quadrilátero á linha bê linha cê linha dê linha simétrico a a bê cê dê em relação à reta r.

3. Em uma malha quadriculada, desenhe a figura a seguir e translade-a de acordo com este vetor da translação.

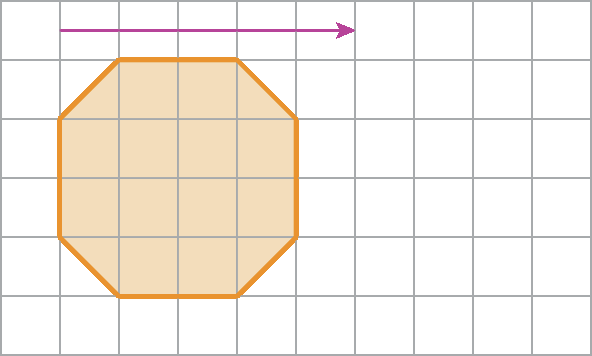
Esquema. Malha quadriculada, com 6 linhas e 10 quadradinhos cada. À esquerda há representação de uma figura geométrica de laranja com oito lados. Acima, seta horizontal para direita.

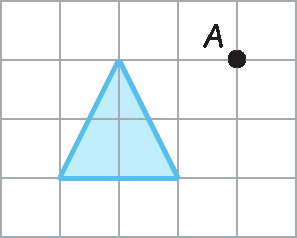
4. Represente a figura a seguir em uma malha quadriculada. Depois, desenhe a figura obtida por meio da rotação dessa figura em um ângulo de medida de abertura de 180graus, no sentido horário, com centro de rotação a.

Esquema. Malha quadriculada, de 4 linhas com 5 quadradinhos cada. Há um triângulo azul, á esquerda e no canto superior à direito, há um ponto A.

Representação de um polígono no plano cartesiano

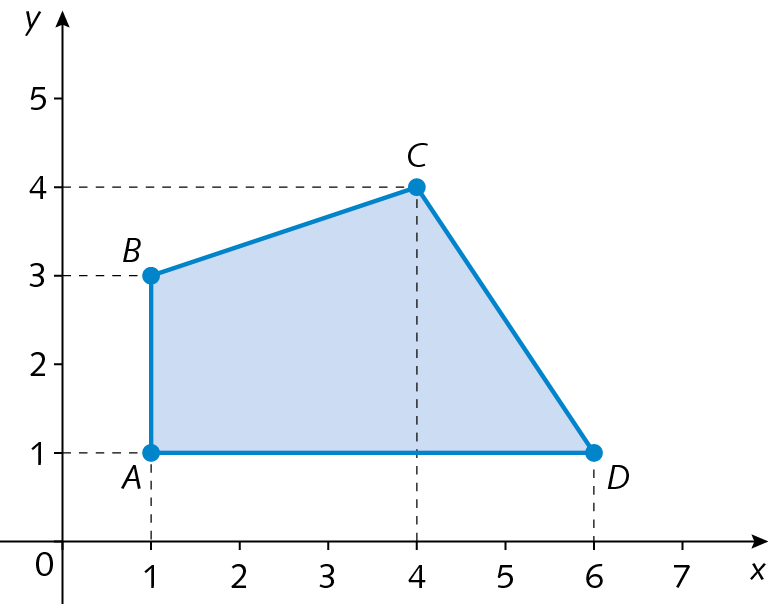
Observe a seguir a representação do polígono a bê cê dê com vértices a(1, 1), B(1, 3), C(4, 4) e D(6, 1) no plano cartesiano.

5. Construa, em seu caderno, um plano cartesiano e marque os seguintes pontos: a(1, 4), B(–1, 2), C(–2, –3), D(–2, 2), ê(3, –4), F(3, 3) e G(–4, 3).

6. Em seu caderno, construa um plano cartesiano e represente um pentágono que passe por todos os quadrantes.

Página 223

Transformações geométricas no plano cartesiano

Ampliação

Para ampliar um polígono no plano cartesiano, multiplicamos todas as coordenadas dos vértices desse polígono por um mesmo número maior que 1 ou menor que ‒1.

Simetria em relação à origem do plano cartesiano

Para encontrar as coordenadas dos vértices de um polígono simétrico a outro em relação à origem do plano cartesiano, multiplicamos todas as coordenadas dos vértices desse polígono por ‒1, ou seja, consideramos os opostos das ordenadas e das abscissas.

Simetria em relação aos eixos do plano cartesiano

No plano cartesiano, para encontrar as coordenadas dos vértices de um polígono simétrico em relação ao eixo x, repetimos as abscissas e consideramos os opostos das ordenadas. Para encontrar as coordenadas dos vértices de um polígono simétrico em relação ao eixo y, consideramos os opostos das abscissas e repetimos as ordenadas.

7. Em seu caderno, construa um quadrilátero de vértices a(‒3, 4), B(‒1, 2), C(‒5, 1) e D(‒6, 3). Depois, faça uma ampliação dessa figura, de modo que as medidas de comprimento dos lados tenham o dobro das medidas de comprimento dos lados originais.

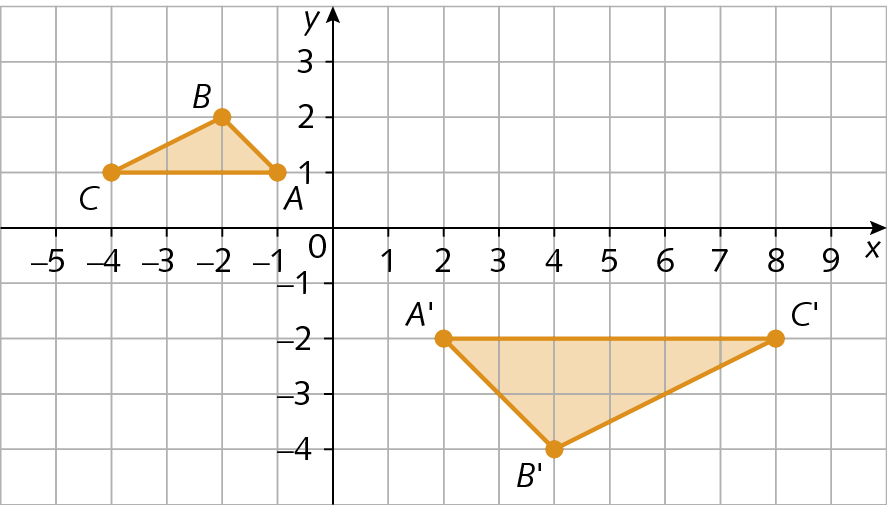
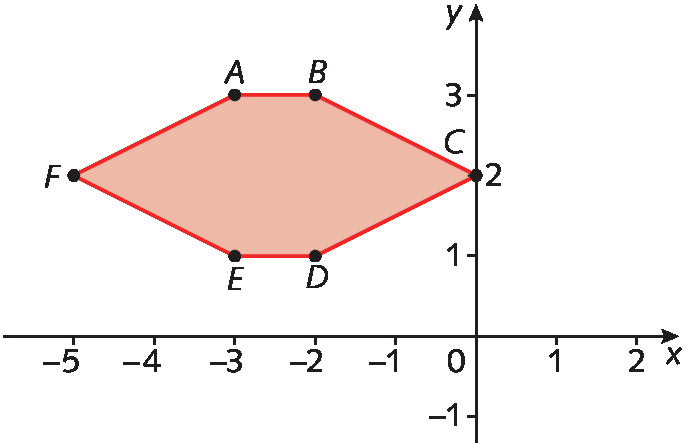
8. Quais são as coordenadas dos vértices do polígono simétrico ao polígono á bê cê dê é éfe em relação ao eixo das abscissas?

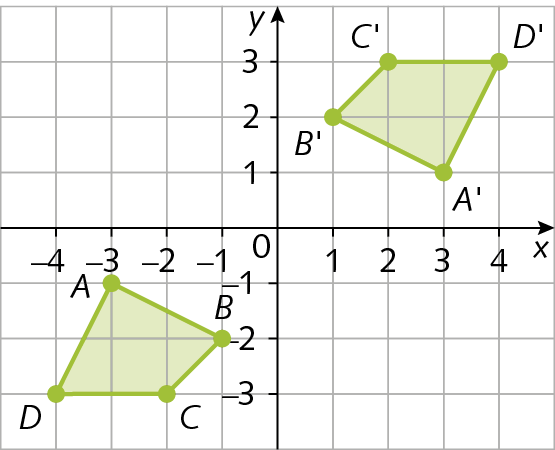
9. Quais são as coordenadas dos vértices do polígono simétrico ao quadrilátero a bê cê dê em relação à origem do plano cartesiano?

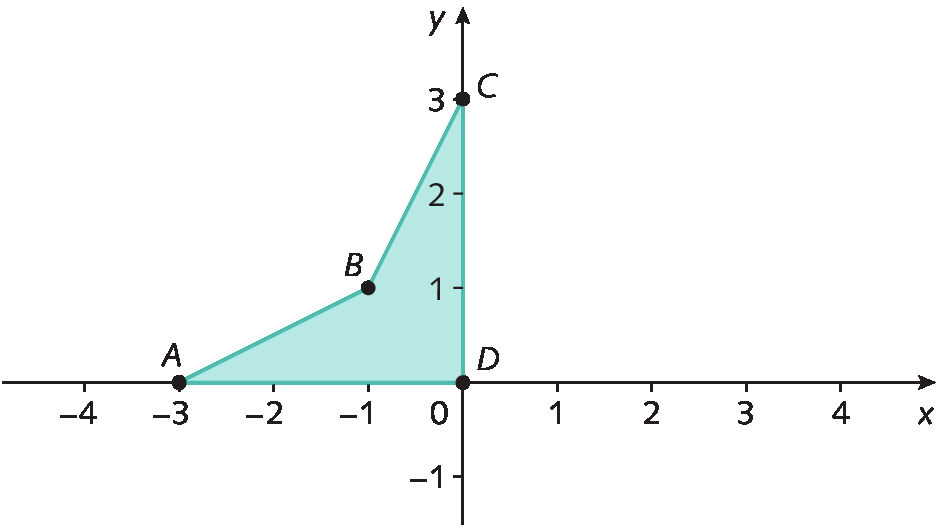
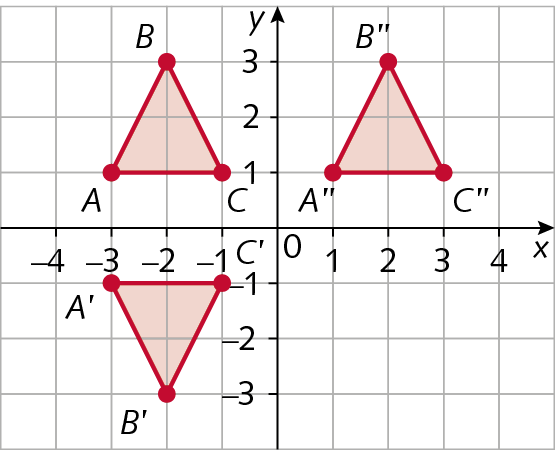
10. Observe a representação do polígono no plano cartesiano a seguir.

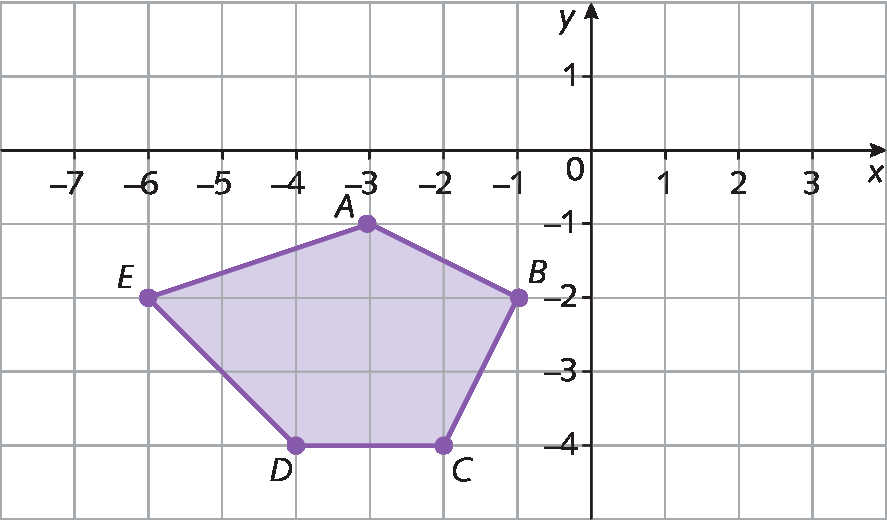
No caderno, construa um plano cartesiano e represente o polígono á bê cê dê é e os seus simétricos em relação ao eixo x e em relação ao eixo y.

Página 224

É hora de extrapolar

Faça as atividades no caderno.

O que você sabe sobre as Paralimpíadas?

Os Jogos Paralímpicos são o maior evento esportivo do mundo envolvendo atletas com deficiências. A primeira edição das Paralimpíadas ocorreu em Roma, em 1960, com cêrca de 400 atletas. Em 2021, os jogos foram realizados em Tóquio, no Japão. Aproximadamente .4400 atletas participaram do evento, celebrando o esporte, a superação e a diversidade.

Fotografia. Imagem em preto e branco. Pessoas carregando uma bandeira. Ao fundo, mais pessoas caminham. — Atletas carregam a bandeira oficial dos Jogos Paralímpicos durante a cerimônia de abertura em Roma (Itália). Foto de 1960.

Fotografia. Imagem em preto e branco. Mulher de camisa branca, calça e luvas sentada em uma cadeira de rodas. Ela está segurando um arco e fecha apontado para o lado. Atrás dela, uma pessoa sentada em cadeira de rodas. — Kathleen Comley, da Grã-Bretanha, concorre na categoria de tiro com arco nos Jogos Paralímpicos, em 1960. cêrca de 400 atletas de vinte e duas nações participaram dos jogos.

Fotografia. Imagem em preto e branco. Pessoas sentadas em cadeiras de rodas, uma ao lado da outra. Atrás, árvores e bandeiras. — Equipe italiana na vila olímpica antes do início dos primeiros Jogos Paralímpicos, em Roma (Itália). Foto de 1960.

Objetivos: Analisar o conceito envolvido nos emblemas dos Jogos Olímpicos e Paralímpicos de Tóquio, analisar dados sobre a Paralímpiada de Tóquio ocorrida em 2021, pesquisar esportes paralímpicos e produzir vídeos que serão apresentados para a comunidade escolar.

Etapa 1: Pesquisa e análise dos emblemas das Olimpíadas e das Paralimpíadas de Tóquio.

1. Reúnam-se em grupos. Observem os emblemas dos Jogos Olímpicos e Paralímpicos de Tóquio, no Japão.

Fotografia. 2 símbolos dos jogos olímpicos e paralímpicos. À direita, na parte superior, há uma figura de um símbolo, composta por vários retângulos em preto que um globo. Abaixo do globo está escrito TOKYO 2020. Na parte inferior, há seis argolas coloridas entrelaçadas.

À esquerda, na parte superior, há uma figura de um símbolo, composta por vários retângulos em preto que se unem para formar um globo, sendo a parte superior é aberta acima, abaixo escrito TOKYO 2020 paralympic games. Na parte inferior, há três linhas curvas nas cores vermelha, azul e verde.

Agora, pesquisem na internet o conceito envolvido na criação dos emblemas e analisem a estrutura deles, respondendo às questões:

a) Que relação existe entre as composições de retângulos nos dois emblemas e que mensagem essa composição tem intenção de passar?

b) Existe algum tipo de simetria nesses símbolos? Se sim, qual?

c) Vocês concordam com a afirmação “Diversidade torna o mundo um lugar vibrante”, que faz parte das explicações sobre as concepções dos emblemas? Justifiquem a resposta.

Página 225

Etapa 2: Análise de dados das Paralimpíadas de Tóquio.

2. A tabela a seguir mostra o número de medalhas conquistadas pelo Brasil nas Paralimpíadas de Tóquio.

Distribuição das medalhas conquistadas pelo Brasil nas Paralimpíadas de Tóquio
Medalha	Atletas
Medalha	Homens	Mulheres	Misto	Total
Ouro	15	7	0	22
Prata	12	7	1	20
Bronze	16	12	2	30
Total	43	26	3	72

Dados obtidos em: https://oeds.link/p6ZsZw. Acesso em: 30 maio 2022.

Com base na tabela, respondam às questões.

É correto afirmar que as medalhas de prata correspondem a menos de 33% do total de medalhas conquistadas pelos atletas brasileiros nas Paralimpíadas? Como verificar sem realizar contas armadas ou utilizar calculadora?

Com o auxílio de uma calculadora, responda: Nas Paralimpíadas de Tóquio, qual foi a porcentagem de medalhas de ouro conquistadas pelo Brasil em relação ao total?

Elaborem problemas com base nos dados da tabela anterior. Depois, troquem-nos com outro grupo e resolvam os problemas elaborados por ele.

3. Maria Carolina Santiago foi o grande destaque no centro aquático de Tóquio, em 2021, ganhando cinco medalhas – 4 individuais (3 de ouro e uma de bronze) e uma de prata no revezamento. A atleta levou 26,82 segundos para completar a prova de 50 metros nado livre, e 59,01 segundos para completar a de 100 metros nado livre. Ela ganhou medalhas de ouro pelo desempenho em ambas as provas.

Fotografia. Mulher branca de cabelos escuros, usa casaco verde e amarelo. Ela usa um casaco amarelo e verde. Ela está sorrindo enquanto segura uma medalha de ouro com a mão direita, pendurada em seu pescoço. Na mão esquerda, um buquê de flores coloridas. — Maria Carolina Santiago com a medalha de ouro dos 100 metros nado livre. Foto de 2021.

a) Se Maria Carolina nadasse os 100 metros nado livre com a mesma medida de velocidade média da prova de 50 metros nado livre, quanto tempo ela levaria para completar os 100 metros? E 200 metros?

b) A medida de tempo obtida no item a corresponde à medida de tempo de prova que a atleta obteve nos 100 metros nado livre nas Paralimpíadas de Tóquio? Por que vocês acham que isso ocorreu?

Página 226

Etapa 3: Pesquisa sobre esportes paralímpicos e planejamento para a produção do vídeo.

4. O quadro a seguir mostra as modalidades esportivas que foram disputadas nos Jogos Paralímpicos de Tóquio.

Atletismo	Badminton	Basquetebol (CR )	Bocha	Canoagem	Ciclismo (estrada e pista)
Esgrima (CR)	Futebol de 5	Goalball	Hipismo	Judô	Levantamento de peso
Natação	Remo	Rugby (CR)	Taekwondo	Tênis (CR)	Tênis de mesa
Tiro com arco	Tiro esportivo	Triatlo	Vôlei sentado

Dados obtidos em: https://oeds.link/724uDf. Acesso em: 20 maio 2022.

Escolham uma modalidade esportiva e busquem, em sites, revistas ou livros especializados, informações sobre a história dela nos Jogos Paralímpicos, as categorias, as regras, como esse esporte é disputado, curiosidades e a participação brasileira nos jogos de Tóquio.

5. Com base nas informações obtidas na pesquisa, vocês produzirão um vídeo que apresente informações sobre a modalidade esportiva escolhida.

Visando a uma boa etapa de produção do vídeo, é interessante fazer um planejamento. Para isso, confiram as dicas a seguir.

• Elaboração do roteiro: produzam um documento com todas as ideias e informações, definindo o que será exposto e orientando a gravação, com a descrição de falas e cenas e prevendo a inserção de imagens. O roteiro determina a hierarquia para as informações.

• Distribuição das tarefas: definam os responsáveis pelas etapas da produção do vídeo — pesquisa de imagens, apresentadores (distribuição das falas), escolha dos cenários, gravação (câmera, diretor), edição do vídeo etcétera

• Duração do vídeo: vídeos com conteúdo extenso (uma ou duas horas de duração) tendem a dispersar a atenção do espectador. O consumo de conteúdo na internet, por exemplo, é feito, em geral, de maneira rápida e simples.

• Local de gravação: escolham um local sem muitos ruídos para realizar a gravação e cuidem para que o áudio das falas seja captado com clareza.

Etapa 4: Análise do material de planejamento, produção e exibição dos vídeos.

6. Compartilhem o material elaborado no planejamento da produção do vídeo com a turma para que todos analisem e façam comentários em relação à clareza das informações e das imagens escolhidas.

7. Anotem as dúvidas, as opiniões e as sugestões dos colegas.

8. Depois dos ajustes necessários, realizem a gravação e edição do vídeo.

9. Com os vídeos finalizados, organizem uma exibição sobre os esportes paralímpicos para os colegas e a comunidade escolar.

Etapa 5: Síntese do trabalho realizado.

10. Algumas questões que devem ser discutidas:

a) Quais informações sobre as modalidades esportivas das Paralimpíadas vocês acharam mais interessantes?

b) Qual é a importância dos Jogos Paralímpicos?

c) Vocês conhecem situações em que as pessoas com deficiência não são incluídas de maneira adequada? Se sim, o que pode ser feito para que isso não ocorra?

11. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.

Glossário

Isometria: : Do grego isos (igual) + metria (medida), mesma medida.; Voltar para o texto