Página 251

Capítulo 11 Figuras geométricas planas

Trocando ideias

Entre 2021 e 2022, ocorreu em São Paulo a exposição “Sombras Milenares – O Mundo de HYBYCOZO”. Conhecido por aliar tecnologia ao estudo da Geometria e pela materialização das sombras como manifestação artística, o duo HYBYCOZO, formado pela artista visual ucraniana Yelena Filipchuk e pelo designer industrial canadense Serge Beaulieu, trouxe para a exposição nove obras e instalações: Trocto, Rhombi, Ivov, Icozo, Dodi, Illuminati, Cylinder, Sunscope e a obra em larga escala Star.

Fotografia: Dentro de uma sala, há uma escultura semelhante a uma figura geométrica espacial. As faces aparentes são um losango no meio, e dois quadrados de cada lado. A escultura é vazada, com várias formas padronizadas em suas faces. Dentro da escultura há uma iluminação. Essa iluminação dá o efeito de sombras nas paredes da sala. — As esculturas da exposição “Sombras Milenares – O Mundo de HYBYCOZO” são iluminadas por dentro e seus padrões são projetados nas paredes e no chão da sala.

▸

Com quais figuras geométricas planas se parecem algumas partes das esculturas da foto anterior?

▸

As sombras projetadas no chão e nas paredes se parecem com quais figuras geométricas planas?

Neste capítulo, vamos estudar as figuras geométricas planas e suas propriedades.

Página 252

1 Circunferência e círculo

Circunferência

Na tela a seguir, o artista russo vaciíli candinsqui (1866 - 1944) faz uma composição com figuras que se parecem com circunferências, círculos e retas.

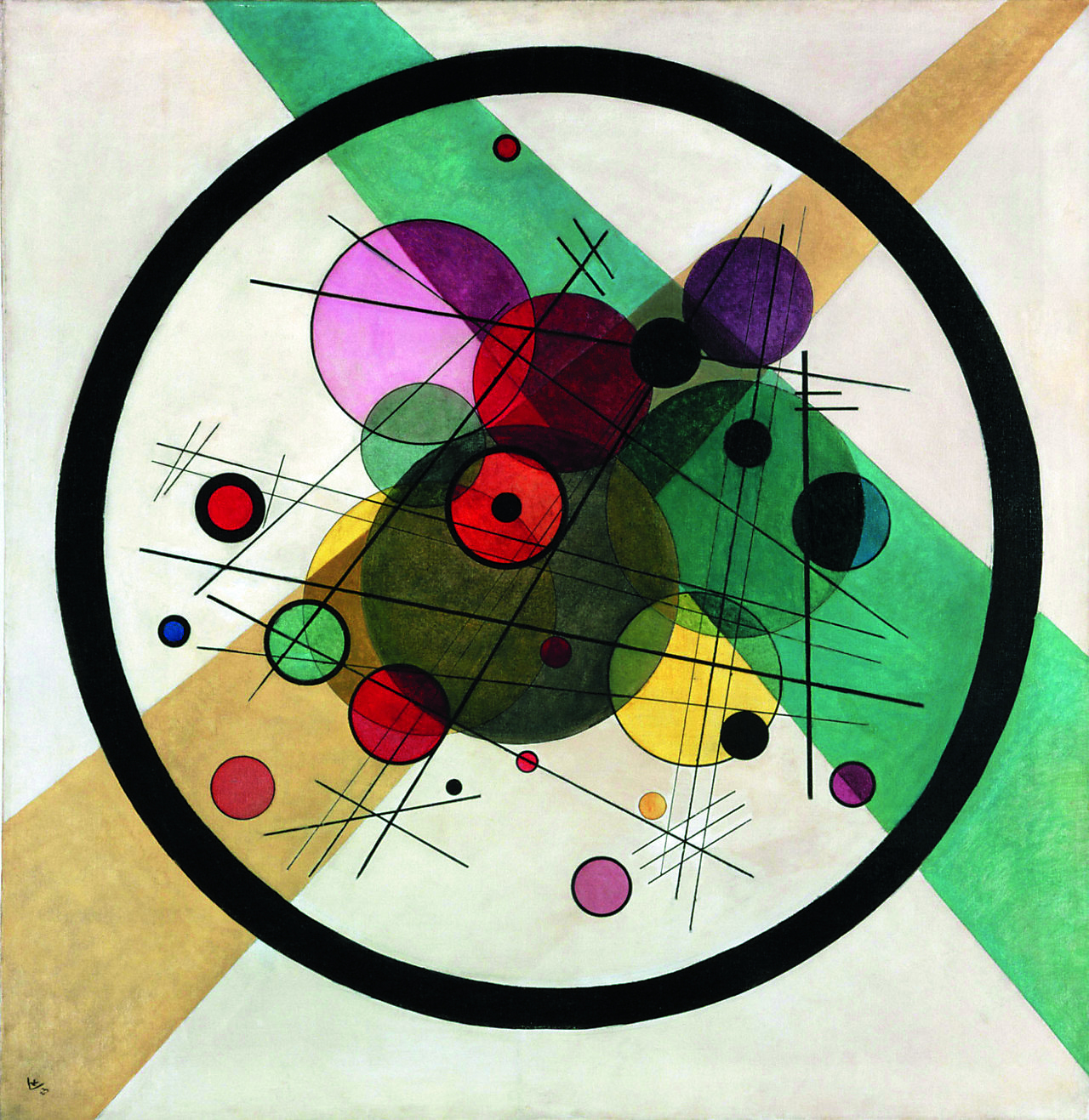
Conheça mais

No site do Museu Guggenheim de Nova York (Estados Unidos da América), é possível conhecer mais obras de vaciíli candinsqui.

Circunferência é a figura formada por todos os pontos de um plano que estão à mesma medida da distância de um ponto fixo desse plano. O ponto fixo é chamado centro da circunferência.

Na representação, o ponto óh é o centro da circunferência.

a, B, C e D são alguns pontos da circunferência.

Figura geométrica: circunferência azul. O centro da circunferência é O, Há a indicação do diâmetro da circunferência, que é a reta que liga os pontos A e B, passando pelo centro O. Há também a indicação de um raio da circunferência, representado pela reta que liga o centro O ao ponto C. Há uma marcação de um ponto D na circunferência.

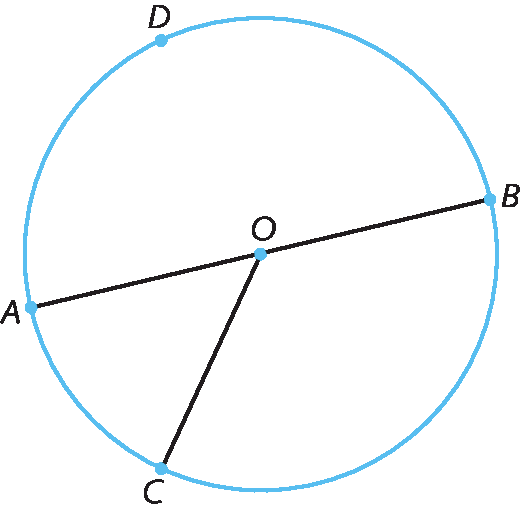
Todo segmento de reta que une o centro óh a um ponto qualquer da circunferência é chamado raio. Os segmentos de reta

\overline{O A}, \overline{O B} e \overline{O C}

, por exemplo, são raios da circunferência.

O segmento de reta que tem duas extremidades na circunferência e que passa pelo centro dela é chamado diâmetro. O segmento

\overline{A B}

é um diâmetro da circunferência.

Construção de uma circunferência com compasso

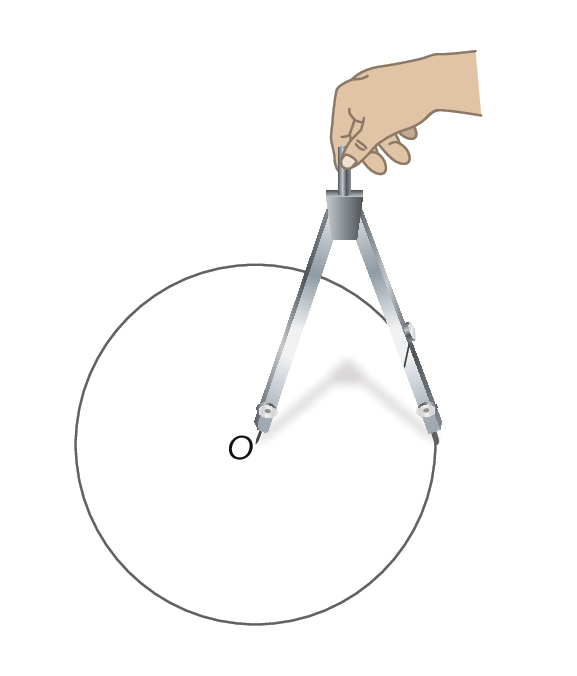
Observe, a seguir, a construção da circunferência de centro óh e raio medindo 1,5 centímetro de comprimento.

1º) Usando uma régua, abrimos o compasso em 1,5 centímetro.

Ilustração: Uma régua milimetrada de 5 centímetros. Uma mão branca segura um compasso. A ponta seca do compasso está sobre o número 0 na régua. A ponta com grafite está sobre o 1,5 centímetros da régua.

2º) Marcamos o centro óh e, em seguida, com a ponta-seca no centro óh e abertura de 1,5 centímetro, seguramos a parte superior do compasso e giramos até completar uma volta inteira.

Ilustração: Circunferência de centro O. Uma mão branca segura um compasso. A ponta seca do compasso está sobre o centro O e a ponta com grafite está sobre um ponto na circunferência.

Página 253

Circunferência como lugar geométrico

Lucas fixou um lápis em uma das extremidades de um barbante que estava preso a um alfinete fixado em uma mesa, como mostra a figura. Maíra, usando um software de geometria dinâmica, construiu um segmento de reta

\overline{O A}

de medida de comprimento fixa.

Ilustração: Um menino negro, de cabelos cacheados, camiseta verde e calça azul está em pé. O menino está com a mão esquerda sobre uma folha de papel branco, e a mão direita está segurando um lápis, amarrado a um barbante, que está amarrado em um ponto fixo sobre o centro da folha. À direita do menino, uma menina branca, de cabelos pretos e camiseta rosa está sentada, em frente a um computador que está sobre a mesa. Na tela do computador, de cima para baixo, a indicação "Geometria dinâmica", e as representações das ferramentas ponto, segmento de reta, polígono e circunferência. À direita, a indicação da construção de segmento de reta com extremidades O e A.

Girando o lápis em torno do alfinete, Lucas traçou o caminho percorrido pelo lápis. Maíra utilizou o software, habilitando a opção de rastrear, e movimentou o ponto a, extremidade móvel do segmento de reta, traçando o caminho percorrido por esse ponto.

Note que, nas duas situações, o caminho traçado é o conjunto dos pontos do plano que têm uma propriedade em comum: estão todos a uma mesma medida da distância de um ponto fixo. Em Geometria, costumamos chamar conjuntos de pontos que têm uma ou mais propriedades em comum de lugar geométrico.

Circunferência é o lugar geométrico dos pontos do plano que estão à mesma medida da distância de um ponto fixo desse plano.

Página 254

Medida do perímetro ou do comprimento de uma circunferência

A medida do perímetro corresponde à medida de comprimento do contorno de uma figura geométrica. Para calcular a medida do perímetro de um quadri látero, podemos medir o comprimento dos quatro lados com uma régua e adicionar as medidas obtidas.

Ilustração: menina negra, de cabelo cacheado amarrado, com camiseta rosa, está sentada em frente a uma mesa. Sobre a mesa há uma folha de papel branca, um estojo com lápis, uma borracha e um lápis verde. Na folha há a indicação do algoritmo usual da adição, 5 mais 4 mais 2 mais 3 igual a 14. A menina segura uma régua e mede um dos lados de um quadrilátero.

Para medir o perímetro de uma circunferência, ou seja, medir o comprimento dela, podemos, por exemplo, utilizar uma fita métrica ou contorná-la com um fio de barbante e medir seu comprimento.

Observe as medidas do comprimento, representadas por C, de três pratos que Lara e João obtiveram.

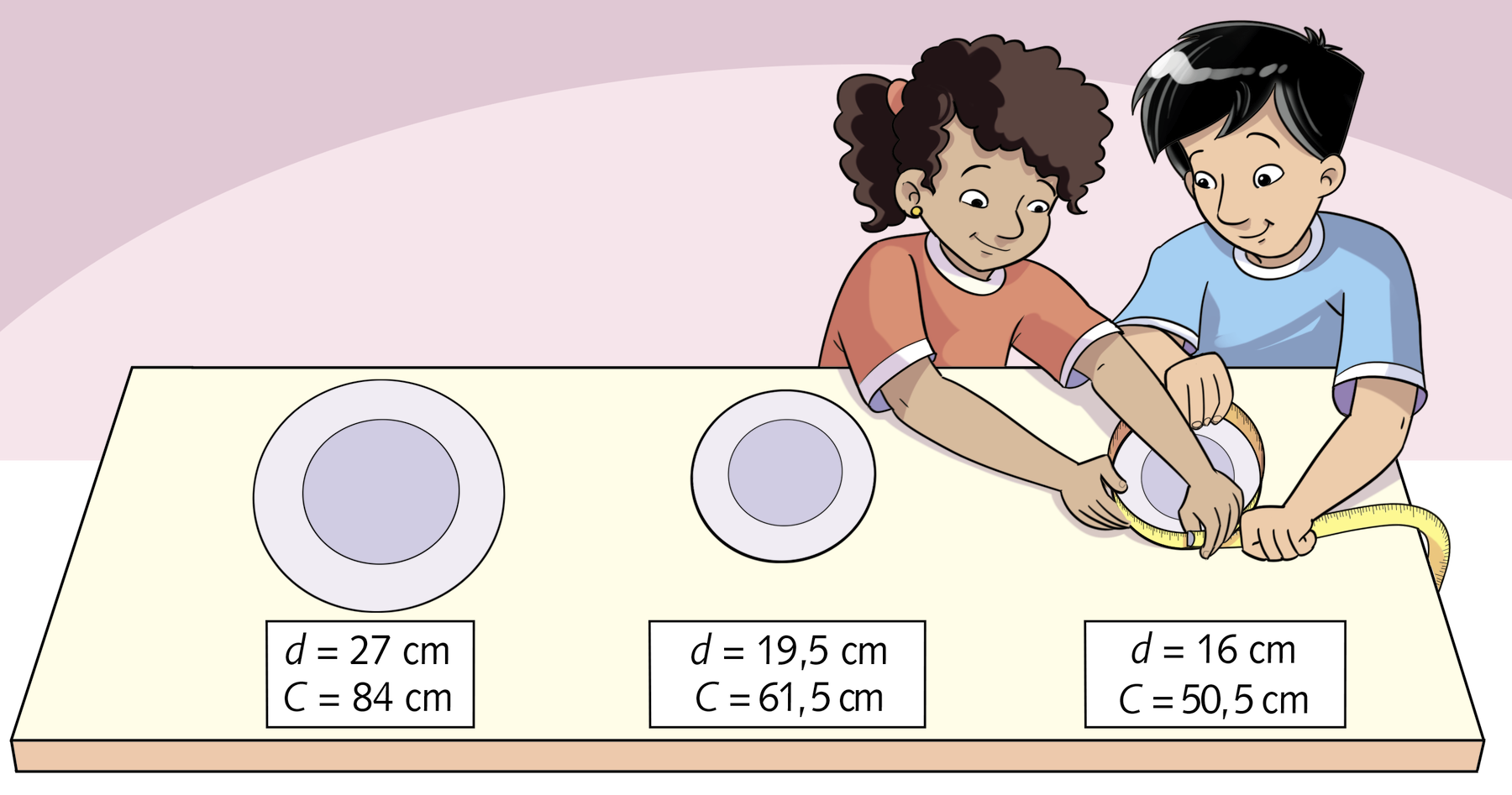
Ilustração: Sobre uma mesa, da esquerda para a direita. Um prato, com a indicação de diâmetro igual a 27 centímetros e comprimento da circunferência igual a 84 centímetros. À direita, um prato, com a indicação de diâmetro igual a 19,5 centímetros e comprimento da circunferência igual a 61,5 centímetros. À direita, Um prato, com a indicação de diâmetro igual a 16 centímetros e comprimento da circunferência igual a 50,5 centímetros. Uma menina negra, de cabelo cacheado amarrado, de camiseta laranja e um menino branco, de cabelo preto e camiseta azul, estão em pé com uma fita amarela passando em volta do terceiro prato, o menor.

Se dividirmos cada medida do comprimento dos pratos pelas medidas do comprimento dos diâmetros, representadas por d, obteremos os valores aproximados 3,11; 3,15 e 3,16, respectivamente.

Na verdade, a razão entre a medida C do comprimento de qualquer circunferência e a medida d do comprimento do diâmetro é uma constante indicada pela letra grega π (pi), ou seja,

\frac{C}{d} = π

. Usualmente, utilizamos π = 3,14, mas esse é um valor aproximado.

Um pouco de história

Faça as atividades no caderno.

O número π

É provável que os primeiros valores para π tenham sido obtidos por meio de medidas. O papiro de Rhind (documento egípcio escrito por volta de 1650 antes de Cristo) apresenta a razão entre a medida do comprimento de uma circunferência e a medida de comprimento do diâmetro dela como 3,1604, uma aproximação para o número π.

Mais tarde, o matemático grego Arquimedes (287 antes de Cristo - 212 antes de Cristo) apresentou um cálculo para essa razão que resultou em um número entre

\frac{223}{71}

\frac{22}{7}

Conta-se que, somente no início do século quinze, o matemático britânico Willian Jones adotou a letra grega π para o que hoje chamamos de número pi, por corresponder à letra P, que se refere ao perímetro da circunferência. O uso dessa letra grega foi popularizado por Leonhard Euler.

Ilustração: Caricatura de Leonhard Euler. — Caricatura de Leonhard Euler.

Atividades

1. Meça o comprimento de um objeto circular (prato, copo, bacia etc.) e o comprimento do diâmetro desse objeto e determine a razão entre essas medidas. Por que a razão obtida não éexatamente igual a π?

2. O número π teve diversas aproximações ao longo da história. Pesquise aproximações que não estão indicadas no texto.

Página 255

Círculo

Círculo é uma figura geométrica plana formada por uma circunferência e toda sua região interna.

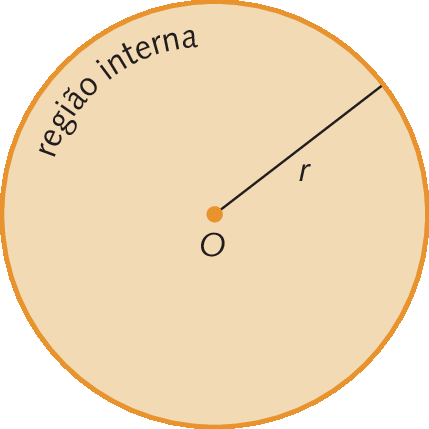
A partir da definição de círculo, podemos dizer que uma circunferência corresponde ao contorno de um círculo.

Atividades

Faça as atividades no caderno.

Cuidado! Evite acidentes ao usar o compasso na atividade 2.

1. Com uma régua, determine, em centímetro, as medidas de comprimento do raio e do diâmetro de cada uma das circunferências a seguir e registre.

Figura geométrica. Duas circunferências. Circunferência verde de centro O e diâmetro AB. Ao lado direito, circunferência roxa com centro O e diâmetro CD. A circunferência roxa tem o dobro da medida de comprimento do diâmetro da circunferência verde.

2. Com um compasso, trace uma circunferência de centro óh e medida de comprimento do diâmetro de 5 centímetros.

3. Descreva a diferença entre círculo e circunferência.

4. Copie as frases no caderno, completando‑as.

a) O comprimento do raio de uma circunferência mede 5 centímetros; então, o comprimento do diâmetro mede

b) Uma circunferência cujo comprimento do diâmetro mede 16 centímetros tem

de medida de comprimento do raio.

Organizem-se em duplas e façam, em uma folha de papel sulfite ou cartolina, uma releitura da obra Circles in a circle, de candinsqui, que aparece no tópico Circunferência. A releitura é uma obra nova, inspirada na anterior; nela, podemos dar o nosso toque pessoal.

6. Na circunferência de centro óh a seguir, destacamos 3 pontos, a, B e C, pertencentes a ela. É correto afirmar que:

Figura geométrica: circunferência de centro O, com marcação dos pontos A, B e C sobre a circunferência.

a) A medida da distância entre os pontos aêcê é igual à medida da distância entre os pontos B e C.

b) As medidas da distância do centro óh aos pontos a, B e C são iguais.

c) Não podemos afirmar nada sobre as medidas das distâncias entre os pontos porque não foram fornecidas essas medidas.

d) A medida da distância entre os pontos aêbê é a mesma medida da distância entre os pontos óh e C.

7. Se o comprimento do raio de uma circunferência mede 5 centímetros, o comprimento dessa circunferência mede:

a) 15,7 centímetros.

b) 10 centímetros.

c) 31,4 centímetros.

8. Em qual das figuras geométricas a seguir todos os pontos estão à mesma medida da distância do ponto a?

Figura geométrica: circunferência de centro A.

Figura geométrica: Contorno de um quadrado com um ponto A marcado no seu centro.

Figura geométrica: Contorno de um triângulo com um ponto A marcado no seu centro.

Versão adaptada acessível

1. Com um compasso, represente uma circunferência em um papel. Depois, meça a medida do comprimento do seu diâmetro e de seu raio.

Qual é a relação entre essas duas medidas?

Página 256

2 Polígonos

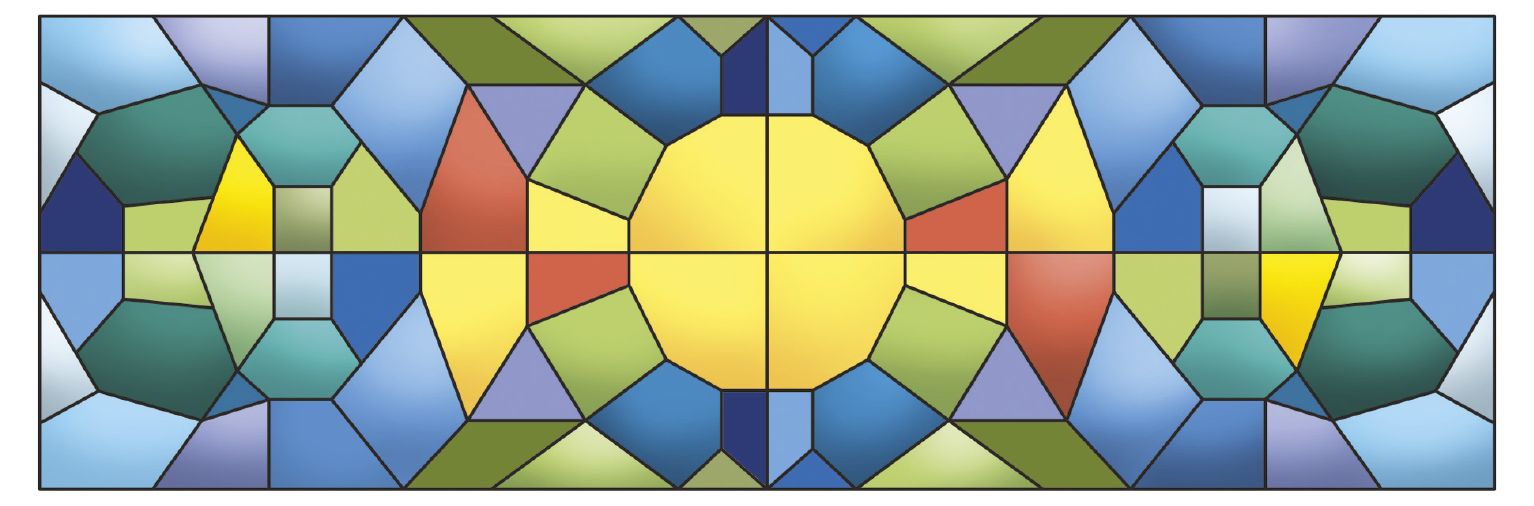
O mosaico ilustrado a seguir é composto de diversos polígonos convexos que se encaixam perfeitamente, cobrindo toda a área.

Ilustração: um mosaico formado por vários polígonos coloridos. Há uma simetria entre o lado direito e esquerdo do mosaico.

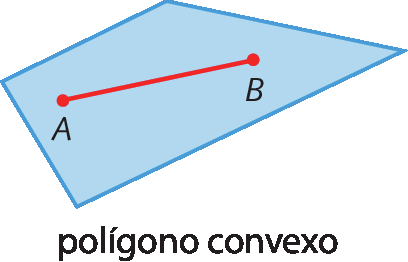
Polígono é uma linha poligonal fechada simples com sua região interna. Um polígono é convexo quando, ao se unir dois pontos quaisquer de sua região interna, obtém-se um segmento de reta integralmente contido nessa região. Caso contrário, o polígono será não convexo. Considere os exemplos a seguir.

Figura geométrica: polígono azul de quatro lados. Dentro do polígono, um segmento de reta vermelho, com os pontos A e B em suas extremidades.

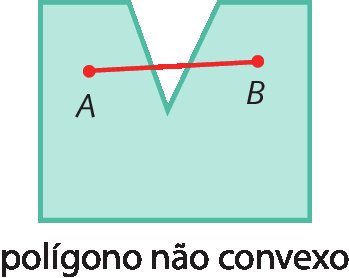
Ilustração. Polígono verde de 7 lados, que se parece com uma bandeira típica de festa junina virada para cima. Há um segmento de reta vermelho, com os pontos A e B em suas extremidades. Esse segmento de reta tem os pontos A e B dentro do polígono e uma de suas partes é fora do polígono.

Observação

Quando não há especificação sobre o tipo, o polígono considerado é convexo.

Elementos de um polígono

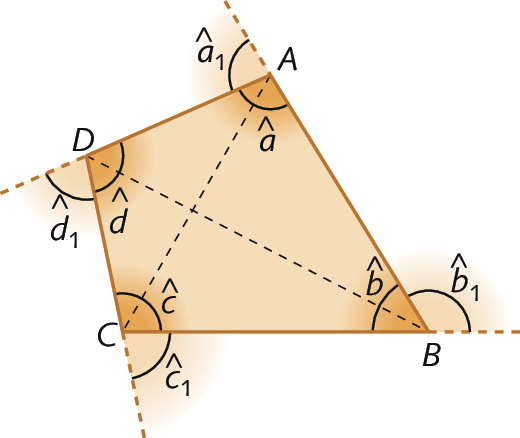
Podemos identificar os seguintes elementos no polígono á bê cê dê é a seguir:

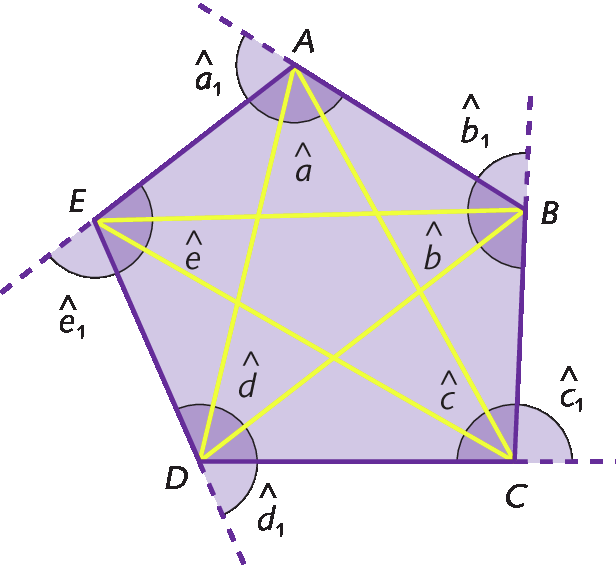
Figura geométrica: um polígono lilás com 5 lados. Dentro do polígono há um pentagrama amarelo. Os vértices do pentagrama encostam nos vértices do polígono. Nos vértices do polígono há a indicação A, B, C, D e E, letras maiúsculas e sobre elas o símbolo que se parece com o acento circunflexo. Nos ângulos internos do polígono há a indicação a, b, c, d e e, letras minúsculas e sobre elas o símbolo que se parece com o acento circunflexo. Em cada um dos lados, há um prolongamento, com a indicação dos ângulos externos do polígono.

• lados: segmentos de reta que formam o contorno do polígono;

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{E A}

• vértices: pontos de encontro de dois lados consecutivos;

a, B, C, D, ê

• diagonais: segmentos de reta que unem dois vértices não consecutivos;

\overline{A C}, \overline{A D}, \overline{B D}, \overline{B E}, \overline{C E}

• ângulos internos: ângulos formados por dois lados consecutivos;

\hat{a}, \hat{b}, \hat{c}, \hat{d}, \hat{e}

• ângulos externos: ângulos formados por um lado do polígono e pelo prolongamento do lado consecutivo a ele.

\hat{a_{1}}

\hat{b_{1}}

\hat{c_{1}}

\hat{d_{1}}

\hat{e_{1}}

Página 257

Soma das medidas de abertura dos ângulos internos de um polígono

Para obter a soma das medidas de abertura dos ângulos internos de um polígono, vamos começar pela soma das medidas de abertura dos ângulos internos de um triângulo qualquer.

Considere o triângulo á bê cê, cujas aberturas dos ângulos internos medem a, b e c. Traçamos uma reta s, paralela à reta suporte do lado

\overline{A B}

, passando pelo vértice C.

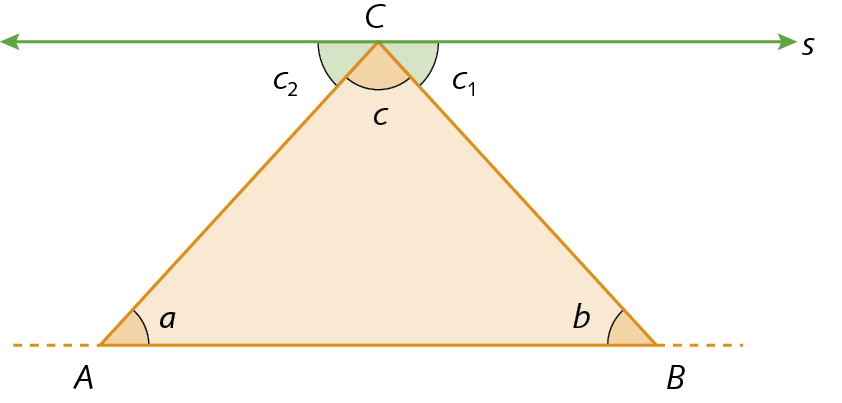
Figura geométrica: polígono alaranjado de 3 lados, com seus vértices marcados com pontos A, B e C. Há a indicação dos ângulos internos, a, b e c. Sobre o vértice C do polígono, há uma reta s verde traçada. Essa reta formam dois ângulos externos C1 e C2 com o polígono.

Nessa figura, podemos notar que:

centésimo₂ + centésimo₁ + c = 180graus

Como:

• centésimo₁ = b (ângulos alternos internos)

• centésimo₂ = a (ângulos alternos internos)

temos que:

a + b + c = 180graus

Então:

A soma das medidas de abertura dos ângulos internos de qualquer triângulo é sempre 180graus.

Agora, confira que o quadrilátero representado a seguir foi decomposto em triângulos a partir de uma das diagonais que partem de um vértice.

Observe que a diagonal

\overline{A C}

divide o quadrilátero a bê cê dê em 2 triângulos. Como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus, a soma das medidas de abertura dos ângulos internos de um quadrilátero é 2 ⋅ 180graus, ou seja, 360graus.

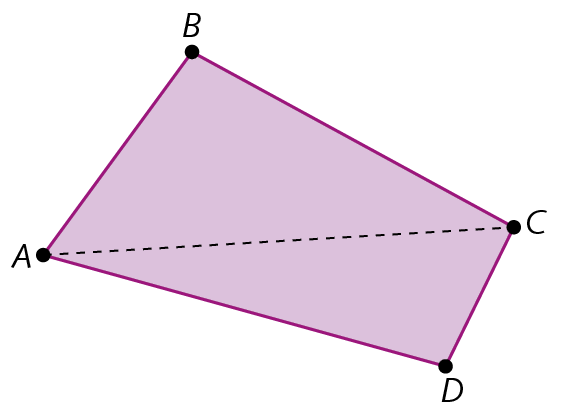
Figura geométrica: polígono roxo de 4 lados, com seus vértices marcados com pontos A, B, C e D. Há um segmento de reta pontilhada, ligando os vértices A e C do polígono. — Quadrilátero decomposto em 2 triângulos.

Então:

A soma das medidas de abertura dos ângulos internos de qualquer quadrilátero é sempre 360graus.

Observação

Ao traçarmos todas as diagonais que partem de um único vértice, decompomos um polígono na quantidade mínima de triângulos.

Página 258

Agora, analise este pentágono.

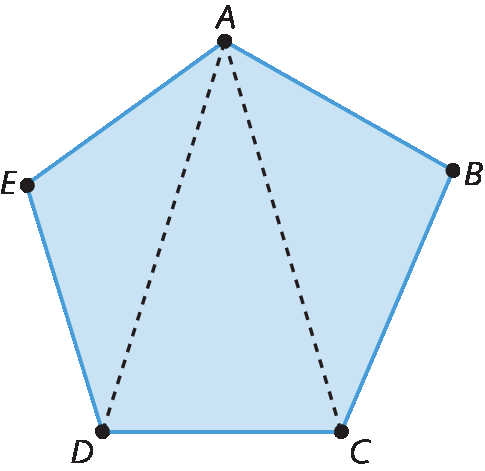
Figura geométrica: polígono azul de 5 lados, com seus vértices marcados com os pontos A, B, C, D e E. Há um segmento de reta tracejado ligando os vértices A e D e um segmento de reta tracejado ligando os vértices A e C. — Pentágono decomposto em 3 triângulos.

As diagonais traçadas,

\overline{A C}

\overline{A D}

, dividem o pentágono á bê cê dê é em 3 triângulos, então a soma das medidas de abertura dos ângulos internos do pentágono é 3 ⋅ 180graus, ou seja, 540graus.

Seguindo esse método, podemos determinar a soma das medidas de abertura dos ângulos internos de qualquer polígono: traçamos todas as diagonais que partem de um único vértice, decompondo o polígono em triângulos, e multiplicamos a quantidade de triângulos por 180graus (soma das medidas de abertura dos ângulos internos de um triângulo).

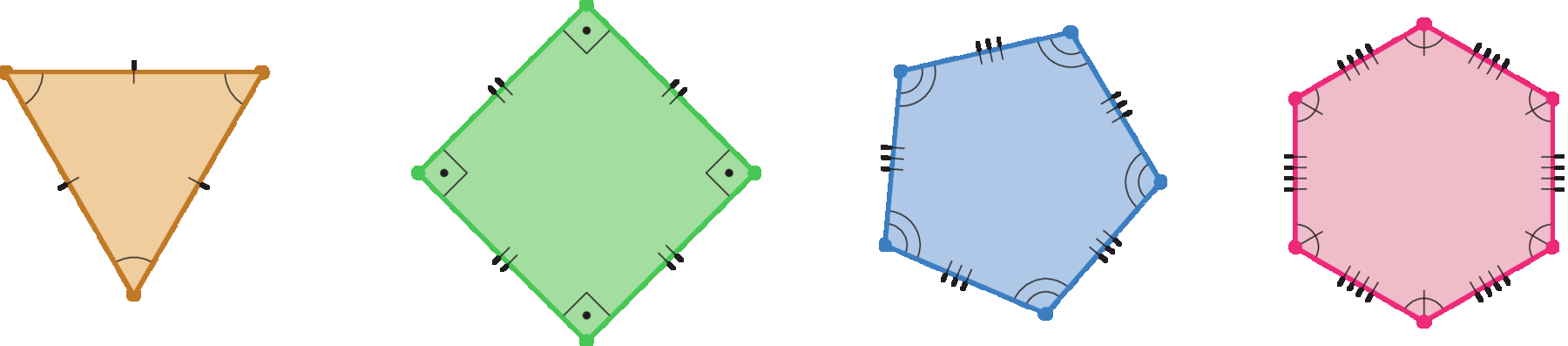
Polígono regular

Um polígono é regular quando todos os ângulos internos têm mesma medida de abertura e todos os lados têm mesma medida de comprimento. Dessa fórma, o triângulo equilátero é um polígono regular, assim como o quadrado, o pentágono regular, o hexágono regular, entre outros.

Figura geométrica: polígono alaranjado de 3 lados. Há a indicação de que os 3 lados possuem a mesma medida. Figura geométrica: polígono verde de 4 lados. Há a indicação de que os 4 lados possuem a mesma medida e que os 4 ângulos internos são retos. Figura geométrica: polígono azul de 5 lados. Há a indicação de que os 5 lados possuem a mesma medida. Figura geométrica: polígono vermelho de 6 lados. Há a indicação de que os 6 lados possuem a mesma medida.

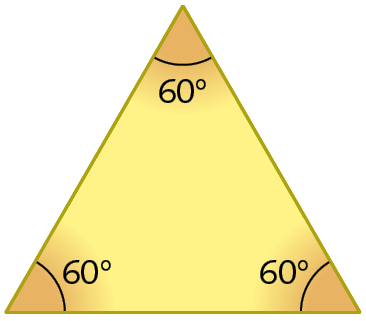
Ângulos internos de um polígono regular

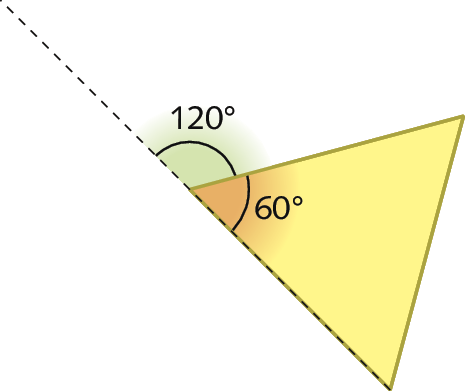
A soma das medidas de abertura dos ângulos internos de qualquer triângulo é 180graus. Como os ângulos internos de um polígono regular têm a mesma medida de abertura, para descobrir a medida de abertura de cada ângulo interno de um triângulo equilátero, dividimos 180graus por 3, que resulta em 60graus.

Figura geométrica: um polígono alaranjado de 3 lados. Há a indicação de que cada ângulo interno mede 60°.

Ilustração: uma menino branco de cabelo ruivo e camiseta verde está com um lápis escrevendo num quadro na parede. No quadro, há desenhado um polígono de 4 lados, indicando que cada ângulo interno mede 90 graus. O menino diz: "Ah! No quadrado é só dividir 360° por 4!".

Página 259

Ângulos externos de um polígono regular

Os ângulos internos e externos dos polígonos são suplementares, ou seja, a soma das medidas de abertura de um ângulo interno e de um ângulo externo é 180graus.

Por isso, conhecendo a medida de abertura de um ângulo interno de qualquer polígono regular, podemos calcular a medida de abertura de um ângulo externo dele.

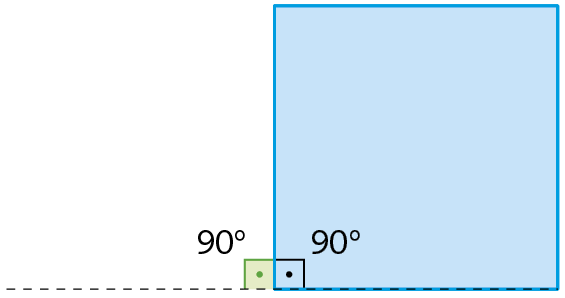
Analise as medidas de abertura dos ângulos indicados nesse triângulo equilátero e nesse quadrado.

Figura geométrica. Triângulo amarelo, com prolongamento em um dos lados da sua base. No ângulo externo desse prolongamento a indicação de 120° e no ângulo interno a indicação de 60°.

Figura geométrica. Quadrado azul, com prolongamento em um dos lados da sua base. Há a indicação de ângulo de 90° no prolongamento e no ângulo interno a ele.

Construindo mosaicos

Um mosaico é uma composição de peças ou figuras que preenche totalmente uma superfície sem haver buracos ou sobreposições.

Para construir um mosaico de quadrados congruentes, no lugar do ângulo externo de um quadrado, podemos encaixar outro quadrado, e depois outro e mais outro, de fórma que, ao redor de um mesmo vértice, a soma das medidas de abertura dos ângulos internos dos quadrados encaixados seja 360graus.

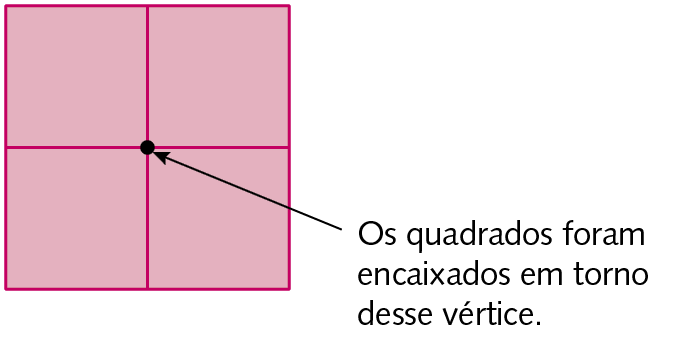
Esquema: Um quadrado rosa dividido em 4 quadrados menores e iguais. No centro do quadrado há um ponto preto. Há uma seta preta chegando ao ponto central, com a indicação: os quadrados foram encaixados em torno desse vértice.

Para construir um mosaico, a soma das medidas de abertura dos ângulos em torno de um mesmo vértice deve ser 360graus.

Atividades

Faça as atividades no caderno.

9. Entre estas figuras, quais são polígonos?

Figura geométrica: figura plana azul, que se assemelha a planificação de um cone.

Ilustração. Linha poligonal aberta formada por 4 segmentos de reta.

Figura geométrica: uma figura azul com formato de elipse.

Figura geométrica: figura plana azul com 8 lados.

Ilustração. Linha poligonal aberta formada por 5 segmentos de reta.

10. No caderno, identifique os lados, os vértices e as diagonais destes polígonos.

Figura geométrica: polígono azul de 4 lados, com seus vértices marcados com as letras, A, B, C e D. As duas diagonais do polígono estão traçadas.

Figura geométrica: polígono alaranjado de 6 lados, com seus vértices marcados com as letras, A, B, C, D, E e F e todas as suas diagonais traçadas.

11. Este polígono é um eneágono (polígono com 9 lados).

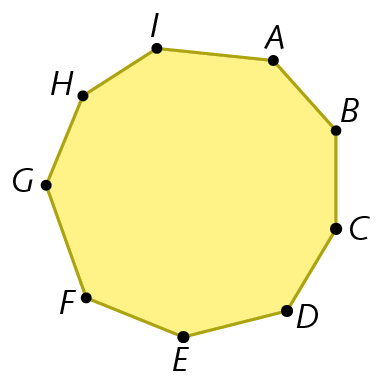
Figura geométrica: polígono amarelo de 9 lados, com seus vértices marcados com os pontos A, B, C, D, E, F, G, H e I.

a) Quantos são seus ângulos internos?

b) Quantos são seus vértices?

12. Luana quer construir um hexágono regular usando uma régua e um transferidor. Para isso, ela precisa saber a medida de abertura de um ângulo interno desse polígono. Como Luana pode descobrir essa medida?

13. É possível construir um mosaico usando somente triângulos equiláteros? Justifique sua resposta.

14. É possível construir um mosaico usando somente pentágonos regulares? Justifique sua resposta.

Página 260

Tecnologias digitais em foco

Mosaicos

Nesta seção, utilizaremos o software de geometria dinâmica GeoGebra (ou outro software de geometria dinâmica que seu professor pode indicar) para construir mosaicos de polígonos regulares. Para isso, os polígonos precisam ter pelo menos um vértice em comum e se encaixar perfeitamente, de modo que não se sobreponham nem haja espaços entre eles.

Construa

Siga os passos a seguir para construir mosaicos de polígonos regulares. Para a construção de cada polígono, use a ferramenta

Print da ferramenta Geogebra Classic: comando que tem formato de um polígono de 5 lados.

, selecione dois pontos quaisquer e escolha a quantidade de lados do polígono regular desejado.

Mosaico de quadrados

1º) A partir de dois pontos quaisquer, construa um quadrado.

2º) Selecione dois vértices consecutivos do quadrado construído e construa outro quadrado.

3º) Construa outros quadrados a partir de dois vértices consecutivos de um quadrado já existente até formar o mosaico desejado.

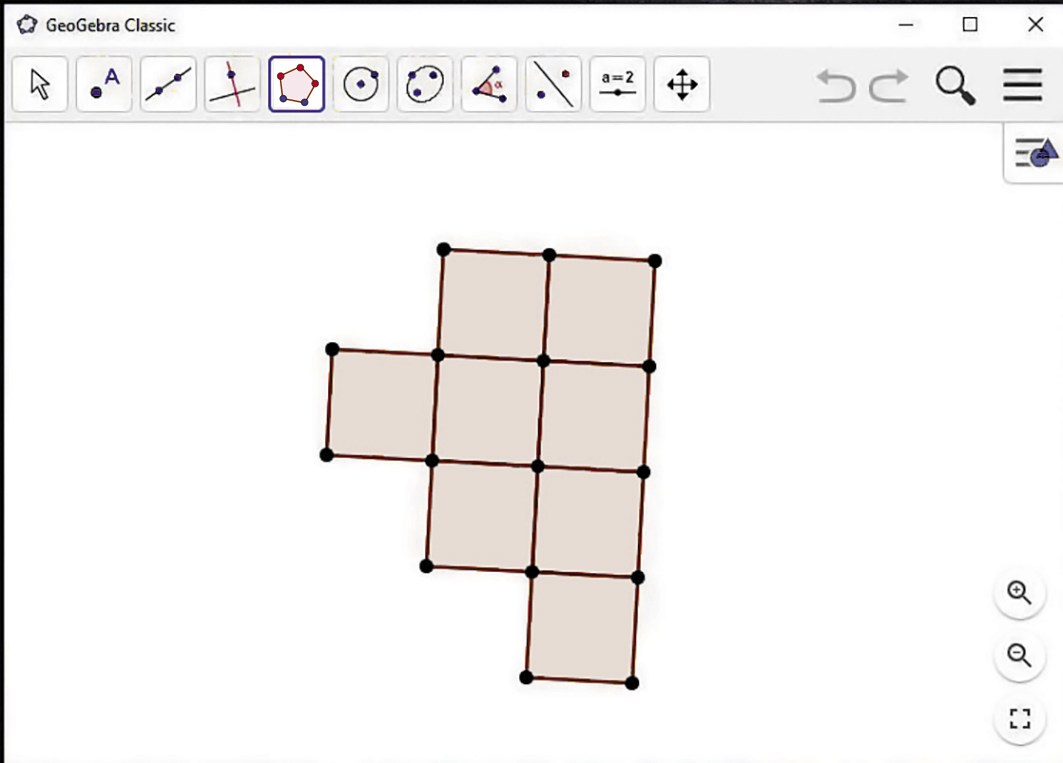
Print da ferramenta Geogebra Classic: na parte superior está o nome Geogebra Classic. Abaixo, há um menu, com as algumas ferramentas descritas. A ferramenta que tem o formato de um polígono de cinco lados está selecionada. Na tela está desenhada uma figura composta oito quadrados. De cima para baixo, dois quadrados, abaixo, três quadrados, abaixo, dois quadrados, e abaixo um quadrado.

Mosaico de triângulos equiláteros

1º) A partir de dois pontos quaisquer, construa um triângulo equilátero.

2º) Selecione dois vértices consecutivos do triângulo construído e construa outro triângulo equilátero.

3º) Construa outros triângulos equiláteros a partir de dois vértices consecutivos de um triângulo já existente até formar o mosaico desejado.

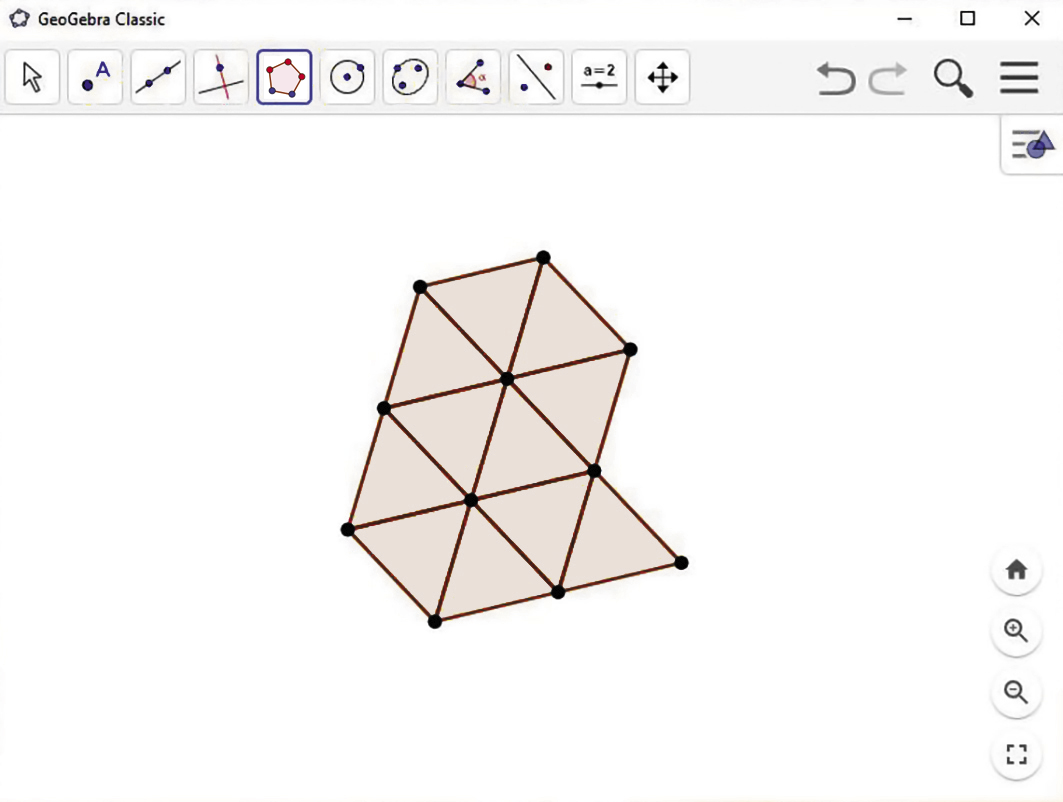
Mosaico de hexágonos regulares

1º) A partir de dois pontos quaisquer, construa um hexágono regular.

2º) Selecione dois vértices consecutivos do hexágono construído e construa outro hexágono regular.

3º) Construa outros hexágonos regulares a partir de dois vértices consecutivos de um hexágono já existente até formar o mosaico desejado.

Página 261

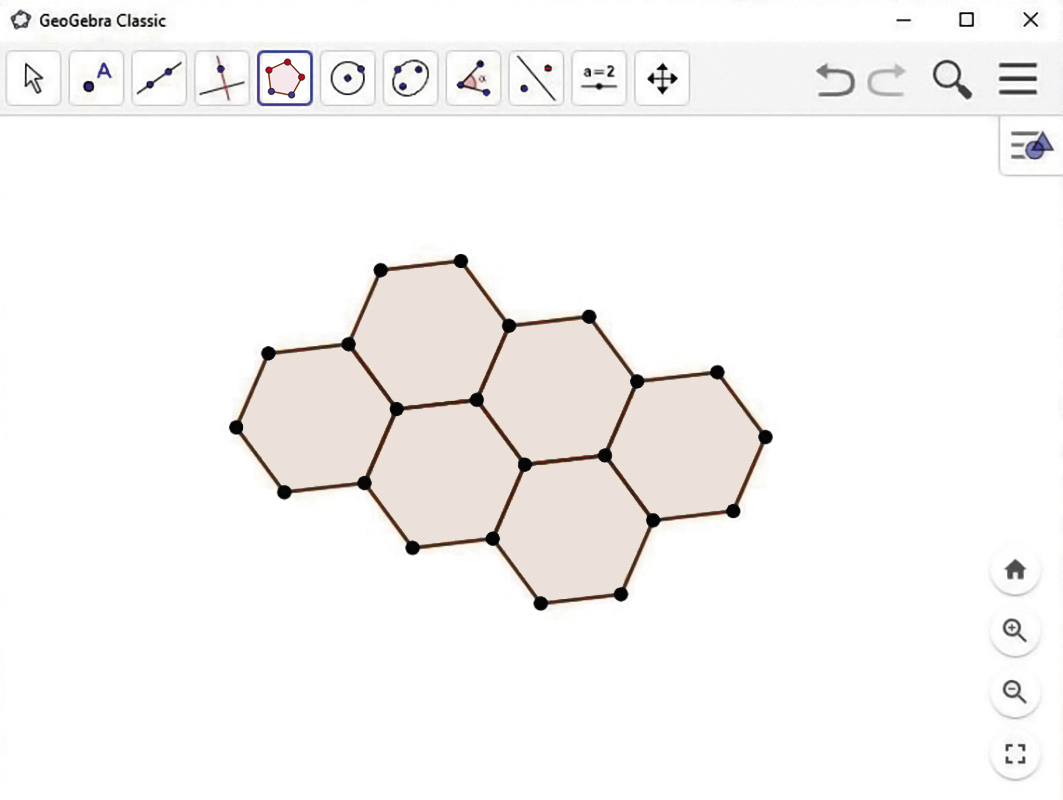
Tecnologias digitais em foco

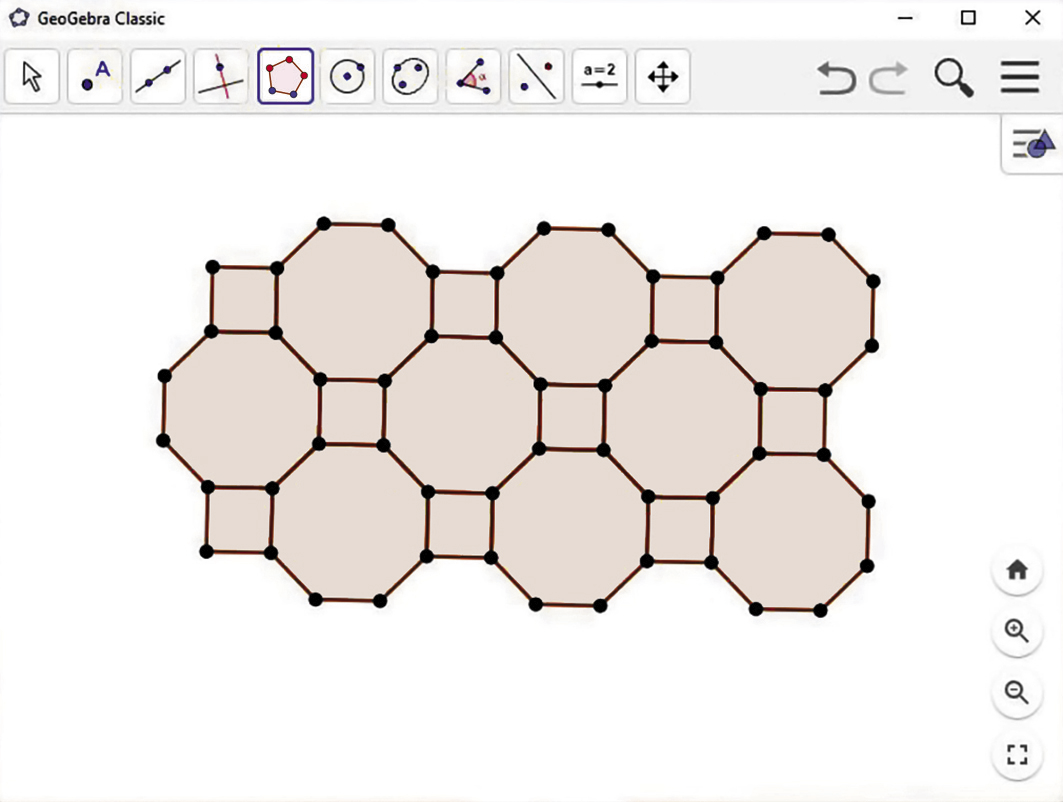
Mosaico composto de dois polígonos regulares diferentes

Para compor um mosaico, também podemos combinar dois ou mais polígonos regulares. Siga os passos a seguir e construa um mosaico formado por octógonos regulares e quadrados.

1º) A partir de dois pontos quaisquer, construa um quadrado.

2º) Selecione dois vértices consecutivos do quadrado construído e construa um octógono regular.

3º) Alterne a construção de octógonos e quadrados seguindo o padrão mostrado nesse mosaico até formar o mosaico desejado.

Explore

Faça o que se pede utilizando as ferramentas do software.

a) Movimente os pontos móveis dos mosaicos construídos, modificando a medida de comprimento dos lados. O que acontece com as medidas de abertura dos ângulos internos dos polígonos quando modificamos as medidas de comprimento dos lados dos polígonos?

b) Se em um dos três primeiros mosaicos construídos escolhermos um vértice de um polígono cercado por polígonos, a soma das medidas de abertura dos ângulos internos dos polígonos ao redor desse vértice será 360graus.

Print de recortes da tela da ferramenta Geogebra Classic, da esquerda para a direita, um mosaico com figuras que se assemelham com quadriláteros. À direita, um mosaico com figuras que se assemelham com triângulos. À direita, um mosaico com figuras que se assemelham com polígonos.

Considerando essa informação, calcule a medida da abertura do ângulo interno do triângulo equilátero e do hexágono regular.

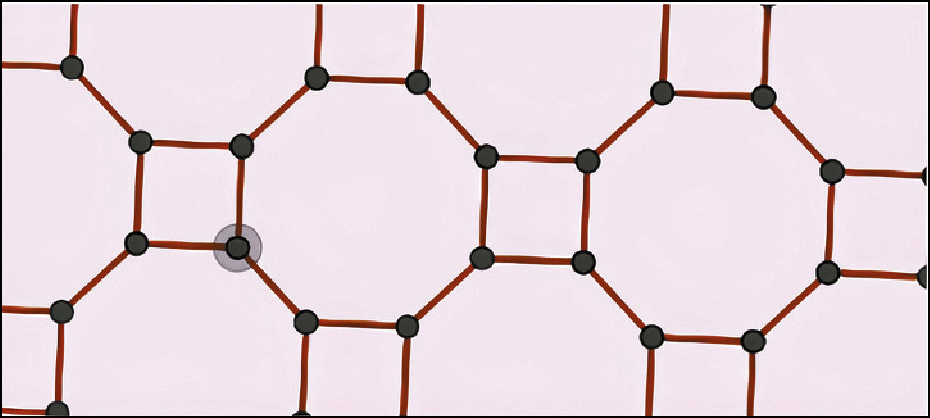
c) Observe o mosaico construído com octógonos regulares e quadrados e responda: Como podemos descobrir a medida da abertura do ângulo interno do octógono regular? Qual é essa medida?

Print de recortes da tela da ferramenta Geogebra Classic. Um mosaico rosa formado por polígonos de oito lados e quadrados. Os vértices dos polígonos de oito lados são comuns aos dos quadrados. Os vértices estão marcados com pontos pretos.

Página 262

3 Triângulo

Triângulo é o polígono de três lados.

Podemos usar a notação △á bê cê para identificar o triângulo com vértices a, B e C.

Figura geométrica: um triângulo azul, com as marcações dos vértices A, B e C.

Principais elementos de um triângulo

Nesta figura, destacamos alguns elementos do triângulo á bê cê.

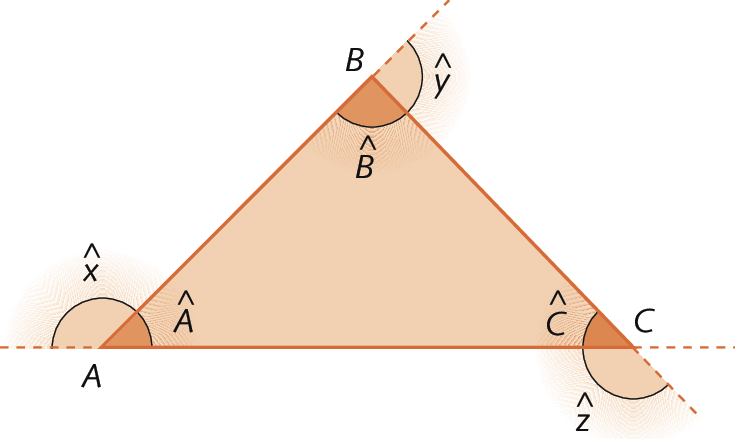
Figura geométrica: triângulo alaranjado, com os vértices identificados com as letras A, B e C. Os ângulos internos estão com as indicações de A, B e C. Há prolongamentos dos 3 lados do triângulo, com as indicações dos ângulos externos x, y e z.

• vértices: a, B e C

• lados:

\overline{A B}, \overline{A C} e \overline{B C}

• ângulos internos:

\hat{A}, \hat{B} e \hat{C}

• ângulos externos:

\hat{x}, \hat{y} e \hat{z}

Observações

1. Podemos representar os ângulos

\hat{A}, \hat{B} e \hat{C}

por

B \hat{A} C, A \hat{B} C e A \hat{C} B

, respectivamente.

2. Na figura anterior, os lados

\overline{A B}, \overline{A C} e \overline{B C}

são, respectivamente, opostos aos vértices C, B e a.

3. O triângulo não tem diagonais.

4. Cada ângulo externo é suplementar do ângulo interno adjacente, ou seja, a soma das medidas de abertura do ângulo externo e do ângulo interno adjacente é 180graus.

m e d (\hat{A}) + m e d (\hat{x}) = 180 °

m e d (\hat{B}) + m e d (\hat{y}) = 180 °

m e d (\hat{C}) + m e d (\hat{z}) = 180 °

5. Considerando o △pê quê érre a seguir, podemos indicar as medidas de abertura dos ângulos internos e as medidas de comprimento dos lados, da seguinte fórma:

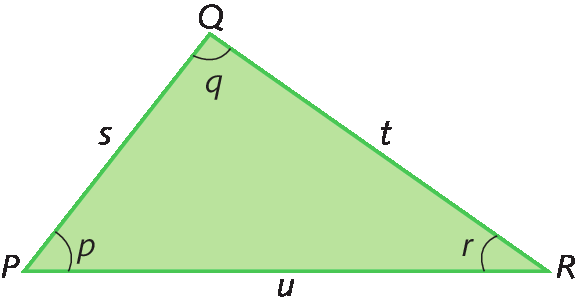
Figura geométrica: triângulo verde, com vértices identificados com as letras P, Q e R maiúsculas. Os ângulos internos estão com a marcação p, q e r minúsculas. O lado oposto ao vértice R está identificado com a letra s. O lado posto ao vértice P está identificado com a letra t. O lado oposto ao vértice Q, está identificado com a letra u.

m e d (\hat{P}) = p

m e d (\hat{Q}) = q

m e d (\hat{R}) = r

m e d (\overline{P Q}) = P Q = s

m e d (\overline{P R}) = P R = u

m e d (\overline{Q R}) = Q R = t

6. A medida do perímetro de um triângulo é a soma das medidas de comprimento dos lados.

No triângulo PQR anterior, temos:

PQ + PR + QR = s + t + u

Página 263

Veja que interessante

Faça as atividades no caderno.

Rigidez de um triângulo

As figuras a seguir representam estruturas de varetas fixadas com pinos.

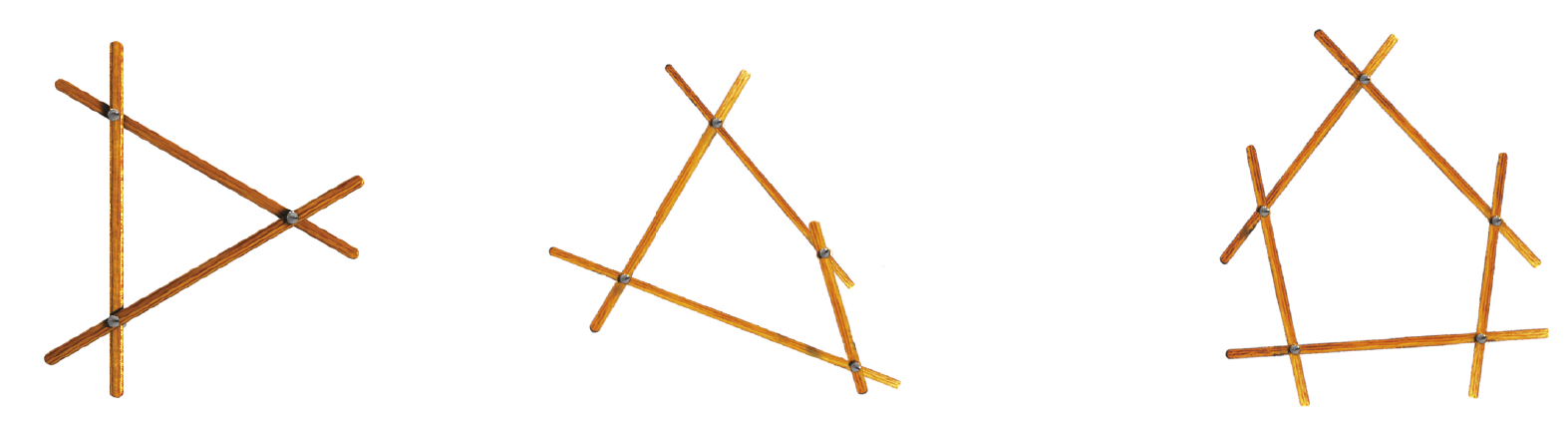
Ilustração: da esquerda para a direita, três varetas formando uma figura semelhante a um triângulo. À direita, quatro varetas formando uma figura semelhante a um quadrilátero. À direita, cinco varetas formando uma figura semelhante a um polígono de cinco lados.

Observe que, caso seja exercida certa pressão nessas estruturas, a que tem formato triangular não se deforma, mas as que se parecem quadriláteros ou pentágonos podem se deformar e adquirir outros formatos.

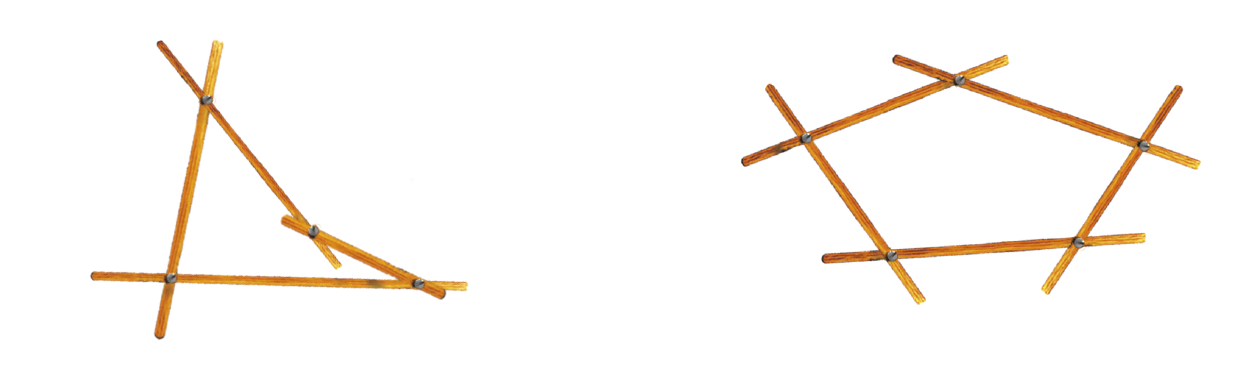
Ilustração: da esquerda para a direita, quatro varetas formando uma figura semelhante a um triângulo. À direita, cinco varetas formando uma figura semelhante a um polígono de cinco lados.

A “rigidez” dos triângulos é responsável por sua frequente utilização nas construções e em estruturas, como pontes e torres.

Fotografia: Uma ponte de ferro, sobre uma baía. Sobre a água, uma embarcação. Ao fundo, uma construção com telhados brancos. O dia está nublado. — A ponte da Baía de Sydney liga o centro financeiro da cidade à costa norte, residencial e comercial. Sydney, Austrália. Foto de 2020.

Atividades

1. Como poderíamos transformar as estruturas com fórma de quadrilátero ou de pentágono em estruturas rígidas?

2. Cite exemplos de estruturas ao seu redor em que você percebe a presença da "rigidez" dos triângulos.

Página 264

Construção de triângulos

Agora, vamos ver como construir triângulos utilizando régua e compasso. Acompanhe as três situações a seguir.

1ª situação: construir um triângulo conhecendo as medidas de comprimento dos três lados

Indicando as medidas de comprimento dos lados do triângulo á bê cê por x, y e z, temos:

Ilustração: uma reta com as extremidades identificadas com as letras B e C. No meio da reta tem a indicação da letra x. Ilustração: uma reta menor que a primeira com as extremidades identificadas com as letras A e C. No meio da reta tem a indicação da letra y. Ilustração: uma reta menor que as duas primeiras, com as extremidades identificadas com as letras A e B. No meio da reta tem a indicação da letra z.

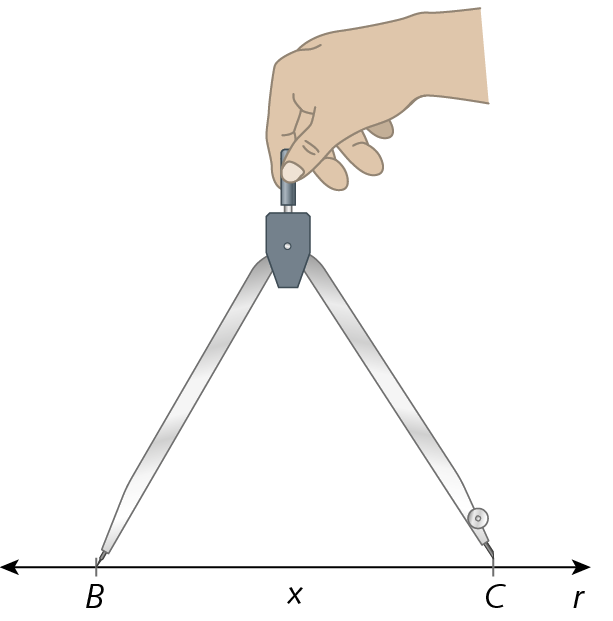
Para construir um triângulo com as medidas indicadas, realizamos os seguintes passos.

1º) Traçamos a reta suporte r, marcamos o ponto B em r e, com o auxílio de um compasso, transportamos a medida x de comprimento do segmento de reta

\overline{B C}

, a partir do ponto B, traçando um arco que corta a reta r. Então, marcamos o ponto C (intersecção da reta r com a marca feita com o compasso).

Ilustração. Uma mão branca segura um compasso, que está sobre uma reta r. A ponta-seca do compasso está sobre o ponto B da reta e a ponta com grafite está sobre o ponto C. A letra x entre os pontos B e C representa a medida do segmento de reta.

2º) Transportamos agora a medida y de comprimento do segmento de reta

\overline{A C}

, a partir do ponto C, traçando um arco com o compasso.

Ilustração. Uma mão branca segura um compasso. A ponta-seca está sobre o ponto C da reta r, que possui a marcação de dois pontos, B e C, e medida x. A ponta com grafite do compasso está construindo um arco fora da reta r.

3º) Transportamos a medida z de comprimento do segmento de reta

\overline{A B}

, a partir do ponto B, traçando um arco que cruze o arco traçado no passo anterior. Então, marcamos o ponto a, intersecção dos dois arcos.

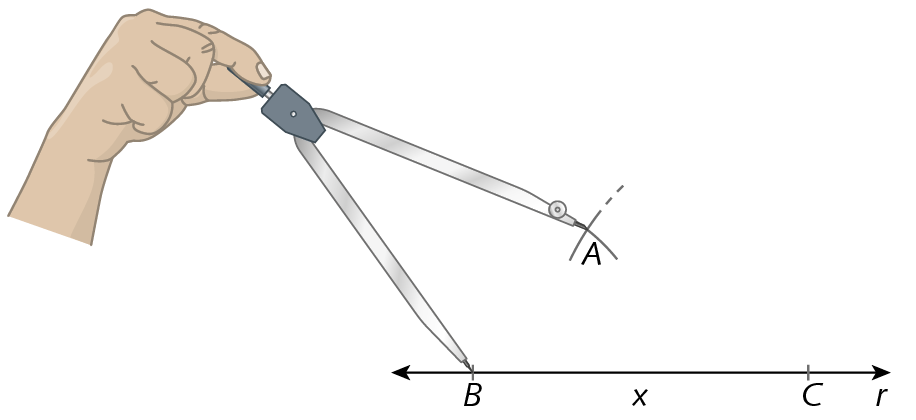
Ilustração. Uma mão branca segura um compasso. A ponta-seca do compasso está sobre o ponto B da reta r. A ponta com grafite está sobre o ponto A fora da reta r. A medida x está entre os pontos B e C.

4º) Com uma régua, unimos o ponto a ao ponto B e o ponto a ao ponto C. Em seguida, colorimos o interior da figura, formando um triângulo com as medidas fornecidas.

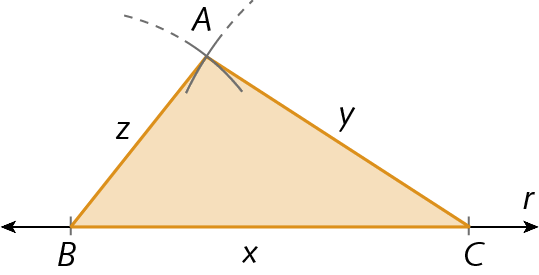
Ilustração. Um triângulo ABC alaranjado, com a base formada pelo segmento de reta BC que tem a reta r como suporte. Há a indicação dos lados x, y e z.

Página 265

2ª situação: construir um triângulo conhecendo as medidas de abertura de dois ângulos e a medida de comprimento do lado compreendido entre eles

Vamos construir o △á bê cê, sendo

\hat{B}

\hat{C}

os ângulos dados do triângulo, e x, a medida de comprimento do lado compreendido entre esses ângulos.

Ilustração. Segmento de reta, com extremidades identificadas com as letras B e C. No centro desse segmento de reta a letra x. Ao lado, ponto B que é origem de duas semirretas que formam um ângulo de medida de 30 graus. Ao lado, ponto C que é origem de duas semirretas que formam um ângulo de medida 60 graus.

Para construir um triângulo com as medidas indicadas, realizamos os seguintes passos.

1º) Traçamos a reta suporte r, marcamos o ponto B em r e transportamos, com o auxílio de um compasso, a medida x de comprimento do segmento de reta

\overline{B C}

, a partir do ponto B, marcando o ponto C em r.

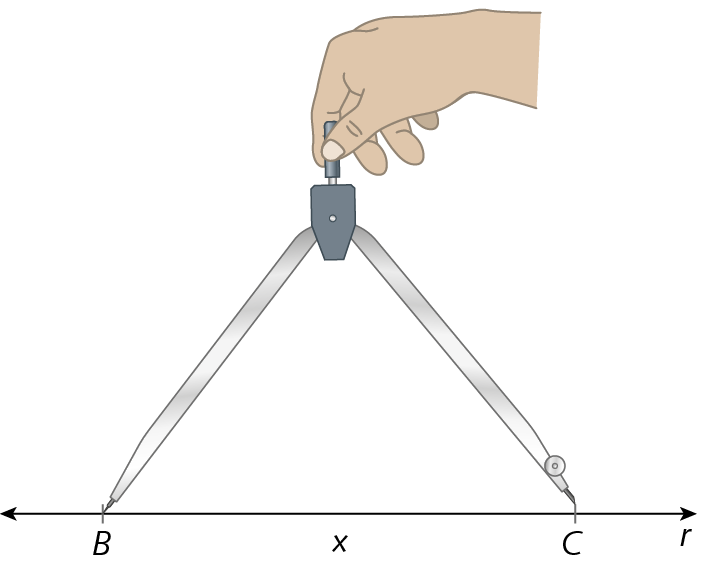
2º) Com qualquer abertura de compasso, apoiamos a ponta-seca sobre o ponto B do ângulo dado e traçamos um arco que passe por suas duas semirretas. Sem alterar a abertura do compasso, apoiamos a ponta-seca no ponto B da figura que estamos desenhando e também traçamos um arco.

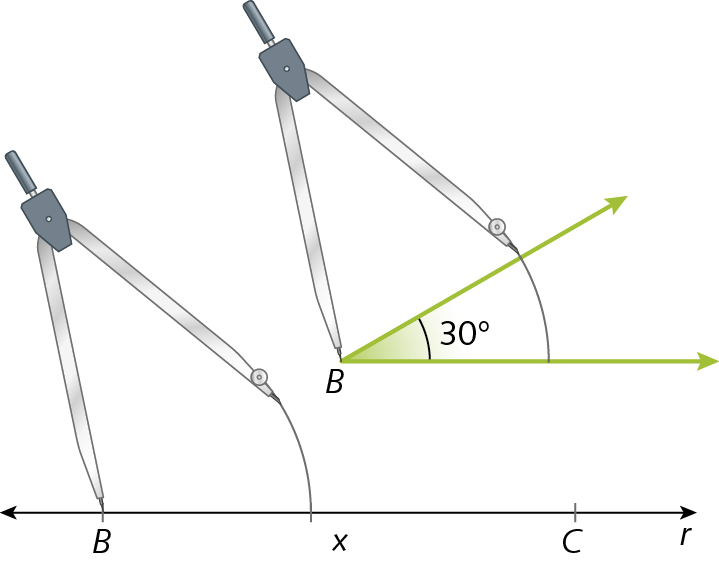
Ilustração: a ponta seca está sobre o ponto B da reta r, que possui a marcação dois pontos B e C e medida x. A ponta com grafite do compasso está construindo um arco. Ao lado há outro compasso, sobre a abertura de um ângulo de 30 graus.

3º) Usamos a abertura do compasso para medir a distância entre as intersecções do arco traçado com o ângulo dado e transportamos essa medida para o arco traçado na figura que estamos construindo e determinamos a reta s.

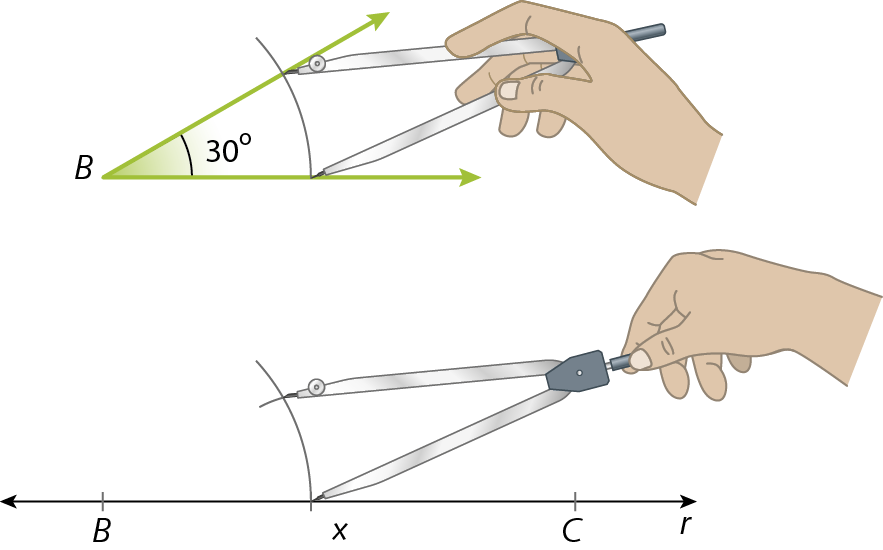
Ilustração: uma mão branca segura um compasso. A ponta seca do compasso está sobre a reta r. A ponta com grafite forma um arco com a reta r. Acima há outra mão branca com um compasso que forma um arco na abertura de um ângulo de 30 graus.

4º) Transportamos o ângulo

\hat{C}

, seguindo o 2º e o 3º passo, determinando a reta t.

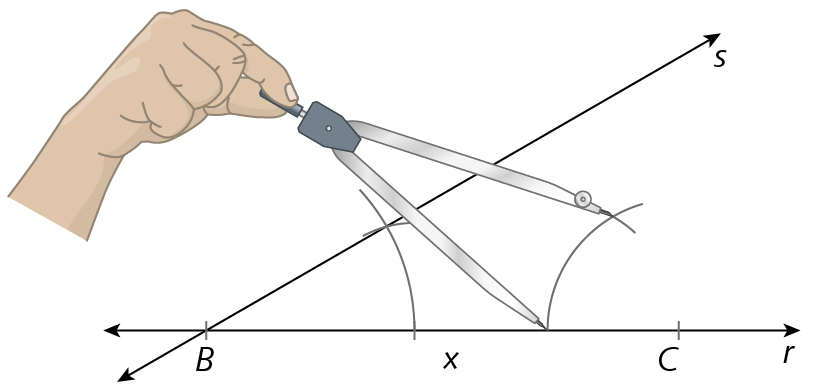
Ilustração: uma mão branca segura um compasso. A ponta seca do compasso está sobre a reta r e a ponta de grafite forma um arco com essa reta. Há uma reta s concorrente a reta r.

Página 266

5º) Marcamos o ponto a na intersecção das retas s e t. Em seguida, colorimos o interior da figura, formando um triângulo com as medidas fornecidas.

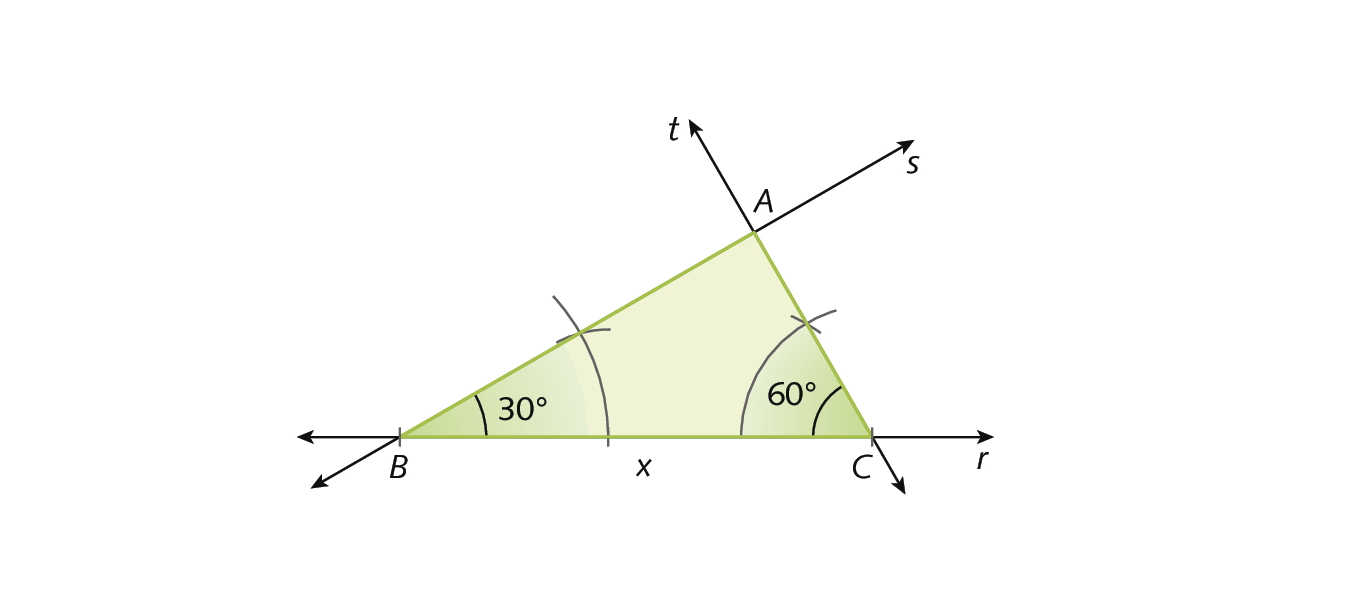
Figura geométrica: um triângulo verde, com vértices indicados pelas letras A, B e C. Os lados do triângulos são as retas r, s e t. No triângulo há a indicação dos ângulos de 30 graus e de 60 graus.

3ª situação: construir um triângulo conhecendo as medidas de comprimento de dois lados e a medida de abertura do ângulo formado por esses lados

As medidas de comprimento de dois lados conhecidos do triângulo ABC são x e y, e

\hat{B}

é o ângulo formado por esses lados.

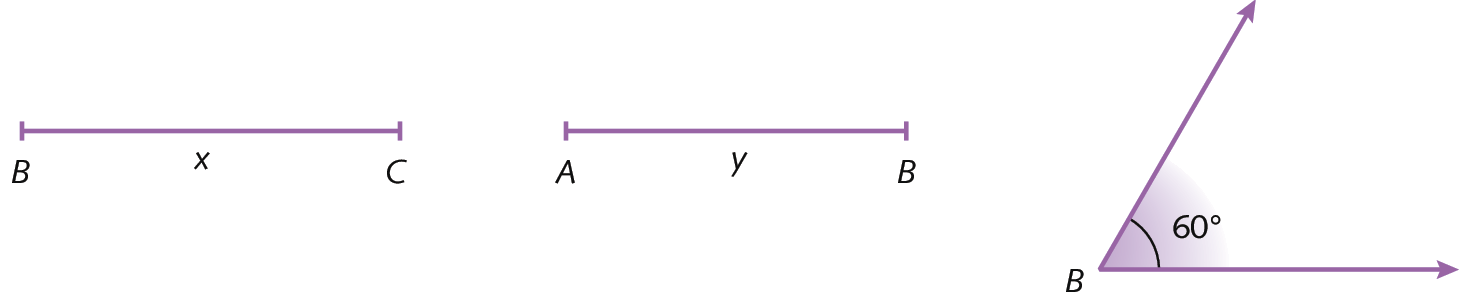
Ilustração. Segmento de reta, com extremidades identificadas com as letras B e C. No centro desse segmento de reta a letra x. Ao lado, segmento de reta, com extremidades identificadas com as letras A e B. No centro desse segmento de reta a letra y. Ao lado, ponto B que é origem de duas semirretas que formam um ângulo de medida 60 graus.

Para construir um triângulo com as medidas indicadas, realizamos os seguintes passos.

1º) Traçamos a reta suporte r, marcamos o ponto B em r e transportamos, com o auxílio de um compasso, a medida x de comprimento do segmento de reta

\overline{B C}

, a partir do ponto B, marcando o ponto C em r.

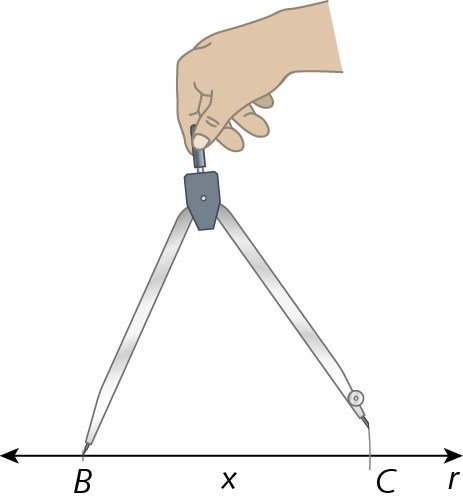
2º) Transportamos o ângulo

\hat{B}

, tomando como vértice o ponto B da reta r, determinando a reta s.

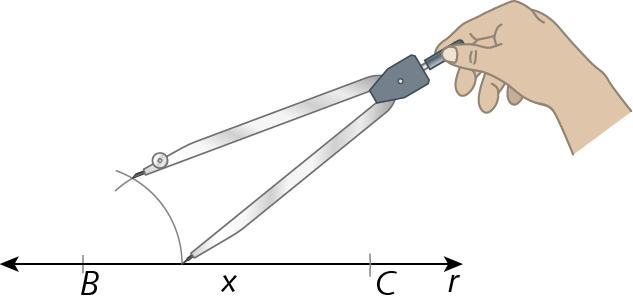
Ilustração. Uma mão branca segura um compasso. A ponta-seca está sobre a reta r, que possui a marcação de dois pontos, B e C, e letra x indica o lado formado pelos pontos A e B. A ponta com grafite do compasso está construindo um arco.

3º) Transportamos a medida y de comprimento do segmento

\overline{A B}

, a partir do ponto B, marcando o ponto a em s.

Ilustração: Uma mão branca segura um compasso. A ponta seca do compasso está sobre o ponto B da reta r. A ponta com grafite está sobre o ponto A da reta s, que forma um ângulo agudo com a reta r.

4º) Traçamos

\overline{A C}

e, em seguida, colorimos o interior da figura, formando um triângulo com as medidas fornecidas.

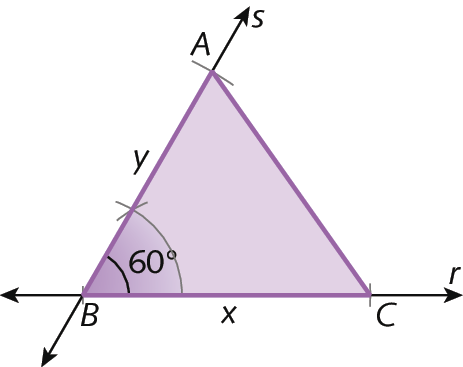
Ilustração. Um triângulo ABC roxo. Há a indicação do ângulo de medida igual a sessenta graus.

Página 267

Desigualdade triangular

Ilustração: um menino branco, de cabelo preto com traços orientais, de camiseta roxa, está conversando com um menino negro, de camiseta amarela. O menino branco diz: Se eu tiver três medidas de comprimento quaisquer, sempre conseguirei construir um triângulo?. O menino negro diz: Não, em alguns casos, não é possível formar um triângulo.

▸ No caderno, tente construir triângulos usando cada trio de medidas de comprimento a seguir.

a) 10 centímetros, 8 centímetros e 6 centímetros;

b) 10 centímetros, 6 centímetros e 4 centímetros;

c) 10 centímetros, 6 centímetros e 2 centímetros.

Para ser possível construir um triângulo, é necessário que a medida de comprimento do lado maior seja menor que a soma das medidas de comprimento dos outros dois lados. É o que chamamos de desigualdade triangular.

Em um triângulo, a medida de comprimento de qualquer um dos lados é menor que a soma das medidas de comprimento dos outros dois lados.

Atividades

Faça as atividades no caderno.

Cuidado! Evite acidentes ao usar o compasso nas atividades 19, 21 e 22.

15. Observe esta figura e, no caderno, escreva:

Figura geométrica: triângulo roxo, com marcações das letras F, G e H nos vértices. Há prolongamentos nos três lados do triângulo. No prolongamento do vértice F, tem a marcação do ângulo externo x. No prolongamento do vértice H, tem a marcação do ângulo externo y. No prolongamento do vértice G, tem a marcação do ângulo externo z.

a) os vértices do triângulo;

b) os lados do triângulo;

c) os ângulos internos do triângulo;

d) os ângulos externos do triângulo;

e) o lado oposto ao ângulo

\hat{F}

16. No caderno, determine a medida do perímetro dos triângulos com lados cujas medidas de comprimento são:

a) 5 centímetros, 6 centímetros e 7 centímetros

b) 6 centímetros, 8 centímetros, 10 centímetros

c) 8 milímetros, 15 milímetros, 17 milímetros

d) 20 decímetros, 21 decímetros, 29 decímetros

17. No caderno, desenhe um triângulo cujas medidas de comprimento dos lados sejam:

a) 6 centímetros, 9 centímetros e 12 centímetros;

b) 7 centímetros, 5 centímetros, 10 centímetros;

c) 4 centímetros, 2 centímetros, 5 centímetros;

d) 2 centímetros, 7 centímetros e 8 centímetros.

18.

Escolha as medidas de comprimento dos lados de um triângulo equilátero e troque com um colega para que um represente o triângulo do outro no caderno.

Página 268

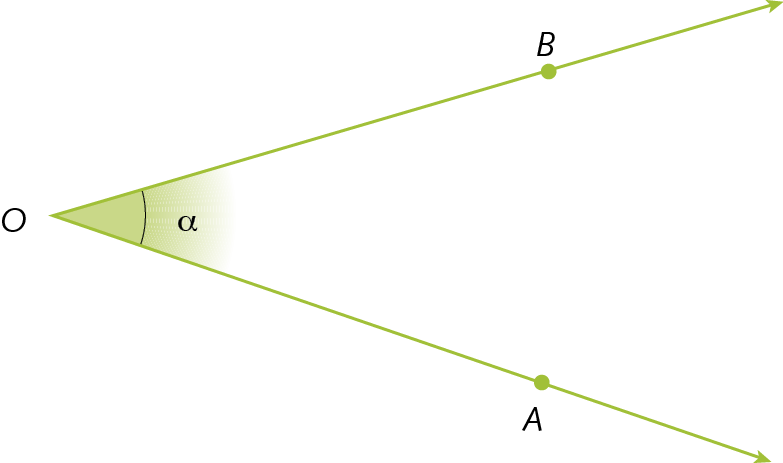
19. Com régua e compasso, reproduza, no caderno, o ângulo

A \hat{O} B

Ilustração: Ângulo com origem no ponto O, abertura de medida alfa. Há os pontos A e B marcados sobre as semirretas que formam o ângulo.

20. Em cada caso, analise se é possível construir um triângulo com lado

\overline{B C}

medindo 5 centímetros de comprimento e com as medidas de abertura dos ângulos indicadas.

m e d (\hat{B}) = 110 °

m e d (\hat{C}) = 50 °

m e d (\hat{B}) = 110 °

m e d (\hat{C}) = 70 °

m e d (\hat{B}) = 110 °

m e d (\hat{C}) = 90 °

21. Utilizando régua e compasso, construa no caderno os triângulos a seguir, sendo conhecidos dois lados e o ângulo formado por esses lados.

a) Dois lados:

Ilustração: Dois segmentos de reta vermelhos, paralelos. O segmento de reta de cima tem medida de comprimento menor que a medida do segmento de baixo.

Ângulo formado pelos lados dados:

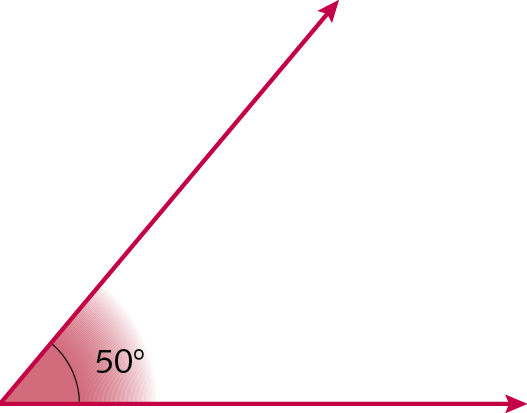
Ilustração: ângulo com abertura de 50 graus.

b) Dois lados:

Ilustração: Dois segmentos de reta verdes, paralelos. O segmento de reta de cima tem medida de comprimento menor que a medida do segmento de baixo.

Ângulo formado pelos lados dados:

Ilustração: ângulo com abertura de 30 graus.

22. Utilizando régua e compasso, construa os triângulos a seguir, sendo conhecidos dois ângulos e o lado compreendido entre eles.

a) Dois ângulos:

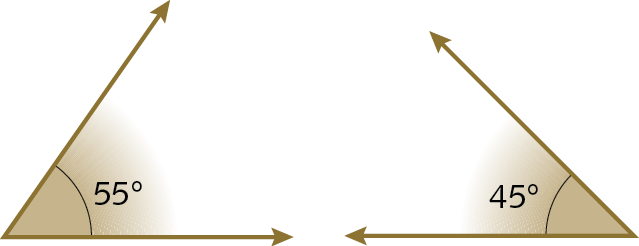
Ilustração: da esquerda para a direita, um ângulo de abertura 55 graus. À direita, um ângulo com abertura de 45 graus.

Lado compreendido entre os ângulos dados:

b) Dois ângulos:

Ilustração: da esquerda para a direita, um ângulo de abertura 60 graus. À direita, um ângulo com abertura de 60 graus.

Lado compreendido entre os ângulos dados:

23. Construa um quadrado a partir de dois triângulos retângulos. Descreva como fez a construção.

24. Em cada caso, analise se é possível construir um triângulo com as medidas de comprimento dos lados indicadas em centímetros.

a) 6, 10 e 18

b) 3, 10 e 7

c) 8, 4 e 6

d) 3, 4 e 5

25. Quais são as medidas de comprimento possíveis para o terceiro lado dos triângulos a seguir?

a) Um triângulo tem dois lados de medida de comprimento 11 centímetros e 6 centímetros.

b) Um triângulo tem dois lados de medida de comprimento 21 centímetros e 221 centímetros.

Página 269

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Circunferência e círculo

Circunferência é a figura formada por todos os pontos de um plano que estão à mesma medida da distância de um ponto fixo desse plano. O ponto fixo é chamado centro da circunferência.

A razão entre a medida do comprimento de qualquer circunferência e a medida de comprimento do diâmetro é indicada por π, ou seja,

\frac{C}{d}

= π.

Costumamos aproximar o valor de π para 3,14.

Círculo é uma figura geométrica plana formada por uma circunferência e toda sua região interna.

1. Identifique em cada item se a figura é uma circunferência ou um círculo.

2. Todos os pontos de uma circunferência estão à mesma medida da distância:

a) do centro da circunferência.

b) de um ponto externo à circunferência.

c) de qualquer outro ponto da circunferência.

d) de qualquer ponto interno à circunferência.

3. Uma pista circular tem diâmetro medindo 100 métros de comprimento. Quantas voltas completas um atleta precisa percorrer nessa pista para correr pelo menos .1000 métros?

Polígonos

Polígono é uma linha poligonal fechada simples com sua região interna. São elementos de um polígono:

• lados: segmentos de reta que formam o contorno do polígono;

• vértices: pontos de encontro de dois lados consecutivos;

• diagonais: segmentos de reta que unem dois vértices não consecutivos;

• ângulos internos: ângulos formados por dois lados consecutivos;

• ângulos externos: ângulos formados por um lado do polígono e pelo prolongamento do lado adjacente a ele.

4. Observe o polígono e, em seguida, identifique:

Figura geométrica: polígono alaranjado com 4 lados. Seus vértices estão marcados com as letras A, B, C e D. As duas diagonais estão tracejadas. Há um prolongamento dos lados, indicando o ângulo externo e o ângulo interno a esse ângulo.

a) os lados;

b) os vértices;

c) os ângulos internos;

d) os ângulos externos;

e) as diagonais.

5. Qual é o polígono que não tem diagonais?

Triângulo

Triângulo é o polígono de três lados.

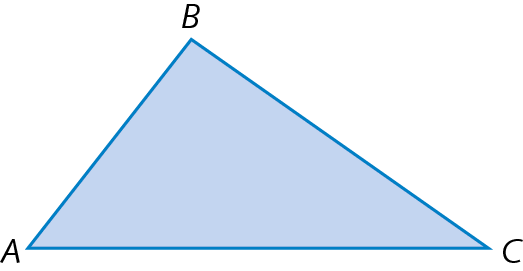
Desigualdade triangular

Em um triângulo, a medida de comprimento de qualquer um dos lados é menor que a soma das medidas de comprimento dos outros dois lados.

6. Podemos construir um triângulo de medidas de comprimento dos lados de 5,5 métros, 3 métros e 1,5 métro? Justifique sua resposta.

7. No caderno, desenhe um triângulo cujas medidas de comprimento dos lados sejam:

a) 6 centímetros, 5 centímetros e 7 centímetros;

b) 4 centímetros, 5 centímetros e 8 centímetros;

c) 9 centímetros, 12 centímetros e 8 centímetros;

d) 3 centímetros, 7 centímetros e 9 centímetros.