Resoluções e comentários das atividades
Parte 1
REVISÃO DOS CONTEÚDOS DE ANOS ANTERIORES
Para o capítulo 1: Números inteiros
Páginas 10 e 11
1. Compondo a reta com pontos espaçados com mesma distância e apontando a origem, temos:

2. a) A reta representada tem pontos espaçados a cada uma unidade; assim, associamos: a → 8 e B → 29.
b) A reta representada tem pontos espaçados a cada duas unidades; assim, associamos: C → 11 e D → 21.
c) A reta representada tem pontos espaçados a cada cinco unidades; assim, associamos: ê → 25, F → 30 e G → 35.
3. Representação b, já que é a única em que os pontos representados na reta estão igualmente espaçados e no sentido crescente para a direita.
4. Considerando que a reta representada tem pontos espaçados a cada 10 unidades, temos: M → 50 e N → 70.
5. a) Elemento neutro da adição, pois há a adição de zero.
b) Comutativa, já que a ordem das parcelas não interfere na soma.
c) Associativa, porque podemos fazer adições parciais com diferentes parcelas e obter a mesma soma.
d) Elemento neutro e comutativa, já que, comparando as igualdades, alteramos a ordem das parcelas da soma e adicionamos o zero.
6. Utilizando a propriedade comutativa, alteramos a ordem e obtemos os valores possíveis para os itens hachurados.
a) 26 + 52 = 52 + 26
b) 150 + 63 = 63 + 150
c) 100 + 98 = 98 + 10
d) 89 + 52 = 52 + 89
7. Sentença c: usamos parênteses para selecionar parcelas a serem adicionadas em cada caso.
8. a) “um”. O número 1 como fator de uma multiplicação não altera o valor do produto.
b) “comutativa”. A propriedade comutativa garante a troca dos fatores sem alteração do produto.
c) “associativa”. A propriedade associativa pode ser utilizada em multiplicações com mais de dois fatores.
9. Após aplicar a propriedade distributiva, temos:
a) 2 ⋅ 91 + 2 ⋅ 12 = 182 + 24 = 206
b) 15 ⋅ 9 + 15 ⋅ 10 = 135 + 150 = 285
c) 10 ⋅ 20 + 10 ⋅ 180 = 200 + .1800 = .2000
10. Utilizando a propriedade associativa, podemos obter:
a) 7 ⋅ (50 ⋅ 12) = (7 ⋅ 50) ⋅ 12
b) (14 ⋅ 10) ⋅ 5 = 14 ⋅ (10 ⋅ 5)
c) 120 ⋅ (3 ⋅ 5) = (120 ⋅ 3) ⋅ 5
11. Pela definição de potência de expoente natural, podemos dizer que:
a) 51 ⋅ 51 ⋅ 51 ⋅ 51 = 514
b) 10 ⋅ 10 ⋅ 10 = 10³
12. a) Em 29² o número 2 é chamado de expoente.
b) O número 6 é base de 65.
c) O resultado de 32 é chamado de potência.
13. 25 = 32; 5² = 25; 15¹ = 15; 115 = 1; 09 = 0; 12² = 144.
Assim, resulta a associação: a ‒ quatro; B ‒ cinco; C ‒ três; D ‒ dois; ê ‒ um; F ‒ seis.
Para o capítulo 2: Múltiplos e divisores
Páginas 12 e 13
14. a) 0, 6, 12, 18, 24
b) 0, 10, 20, 30, 40
c) 0, 9, 18, 27, 36
d) 0, 15, 30, 45, 60
15. Pela definição de múltiplo, podemos identificar as possibilidades a seguir.
a) 1, 10
b) 1, 2, 3, 6
c) 3, 12
d) 2, 4, 8
16. Justificando cada afirmação, temos:
a) Verdadeira; podemos representar todo natural como uma multiplicação com 1 como fator.
b) Falsa; zero é múltiplo de todos os números, mas com exceção do próprio zero, não há natural a tal que a x 0 = a.
c) Falsa; não há natural a tal que 6 ⋅ a = 3. Por consequência, se b < c, com b e c naturais e diferentes de zero, não há como b ser múltiplo de c. Use este item para introduzir ideias relacionadas a abstração, verificando com os estudantes que é impossível localizar um valor que satisfaça 6 ⋅ a = 3 nos naturais observando a lista dos múltiplos de 6.
d) Falsa; 5 é múltiplo de 1 e 1 é divisor de 5, mas 1 não é múltiplo de 5.
e) Verdadeiro; zero é múltiplo de todos os números.
f) Falsa; 100 é múltiplo de 25 e 25 é divisor de 100, mas 25 não é múltiplo de 100.
17. Considerando os possíveis números, temos as seguintes possibilidades para cada caso.
a) 1, 3 ou 5
b) 1, 2, 3 ou 4
c) 1 ou 3
d) 1 ou 3
18. a) 1, 2, 5 e 10
b) 1, 2, 4, 8 e 16
c) 1 e 17
d) 1, 3, 11 e 33
19. Considerando os números do quadro e os critérios de divisibilidade apresentados, temos as seguintes distribuições:
a) Temos todos os pares, assim, 12, 14, 16, 18 e 20.
b) Somando os algarismos, os divisíveis por 3 são 12, 15 e 18.
c) São os números 12, 16 e 20.
d) São os números terminados em 5 ou 0, ou seja, 15 e 20.
e) São os números divisíveis por 2 e 3, ou seja, 12 e 18.
f) É divisível por 9 somente 18 (1 + 8 = 9).
20. Dos números dispostos, os divisíveis por 3 são: 102, 204 e 312. É possível verificar adicionando os algarismos dos números e verificando se a soma é divisível por 3 (1 + 0 + 2 = 3; 2 + 0 + 4 = 6; 3 + 1 + 2 = 6).
21. Justificando cada uma das afirmações, temos:
a) Verdadeira; 100 é divisível por 2 (100 é par) e por 5 (é um número terminado em 0).
b) Falsa; 21 é divisível por 3 (a soma dos algarismos é 3) e não é divisível por 6 (não é par).
c) Verdadeira; 32 é divisível por 2 (par) e é divisível por 4 (ele é divisível por 2 duas vezes).
d) Falsa; 25 é divisível por 5 (terminado em 5) e não é divisível por 10 (não é terminado em 0).
e) Verdadeira; .2000 é divisível por 4 (é terminado em 00) e por 8 (terminado em 000).
22. Considerando os valores apresentados, temos que:
a) todos os números são divisíveis por 10, pois todos são terminados em 0;
b) somente 200, 300, .1500 e .2000 são divisíveis por 100 (terminados em 00);
c) somente .2000 é divisível por .1000, pois é o único terminado em 000.
23. Justificando cada afirmativa, temos:
a) Falsa; 2 é divisível por 2 e por 1 somente, ou seja, é primo.
b) Falsa; 33 tem como divisores 33, 11, 3 e 1, tendo mais de 2 divisores distintos.
c) Verdadeira; os divisores de 45 são 45, 15, 5, 3 e 1.
d) Verdadeira; os únicos divisores de 17 são 17 e 1.
24. a) Os divisores de 42 são 1, 2, 3, 6, 7,14, 21 e 42.
b) Os divisores de 41 são 1 e 41.
c) Os divisores de 36 são 1, 2, 3, 4, 6, 9, 12, 18 e 36.
d) Os divisores de 35 são 1, 5, 7 e 35.
e) Os divisores de 53 são 1 e 53.
25. a) Primos: 41 e 53, pois têm somente dois divisores.
b) Compostos: 42, 36 e 35. Esses números possuem mais de dois divisores.
Para o capítulo 3: Retas e ângulos
Páginas 13 a 15
26. Justificando cada afirmação, temos:
a) Falsa. Semirretas têm apenas uma extremidade.
b) Verdadeira. Segmentos de retas são limitados por duas extremidades.
c) Falsa. Segmentos de retas são definidos por dois pontos ou extremidades.
d) Verdadeira. A semirreta possui um ponto de origem e é ilimitada em uma direção e sentido.
27. Exemplos de respostas (há outras possibilidades):
a)
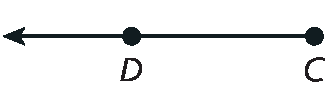
b)

c)

d)
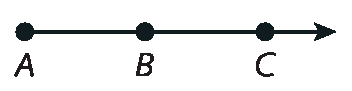
28. O ângulo
CAB.precisa ser representado com o ponto a como vértice do ângulo. Assim, a representação correta é a do item a.
29. Justificando cada afirmação, temos:
a) Falsa. Um ângulo obtuso mede mais de 90graus.
b) Verdadeira. Como 75graus < 90graus, temos então um ângulo agudo.
c) Verdadeira. Todo ângulo reto mede 90graus.
d) Falsa. A medida do ângulo obtuso está entre 90graus e 180graus. Um ângulo de 180graus é chamado raso.
e) Falsa. Todo ângulo agudo mede menos de 90graus.
30. Considerando as descrições dos itens, podemos sugerir como resposta:
a)

b)

c)
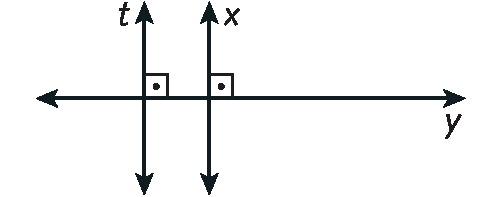
31. Por definição, retas concorrentes que formam ângulo reto são perpendiculares.
Para o capítulo 4: Frações
Página 16
32. a)
Fração: cinco oitavosb)
Fração: 10 milésimos.c)
Fração: um quintod)
Fração: 3 sobre 1233. Associando cada fração com a respectiva leitura, resulta: a ‒ dois; B ‒ cinco; C ‒ quatro; D ‒ três; ê ‒ um.
34. Representado cada fração mista, temos:
a)
Três meios igual a um mais um meio igual a número misto um inteiro e um meio.b)
Onze sobre cinco igual a dois mais um quinto igual a número misto dois inteiros mais um quinto.c)
Sete terços igual a dois mais um terço igual a dois inteiros mais um terço.d)
Dezessete terços igual a cinco mais dois terços igual a cinco inteiros e dois terços.35. Associando cada fração à respectiva equivalente, temos: a – dois; B – cinco; C – um; D – quatro; ê – três.
36. Simplificando as frações, temos:
a)
Dezesseis sobre quarenta igual a fração de numerador dezesseis dividido por oito e denominador quarenta dividido por oito, igual a dois quintos.b)
Nove sobre trinta e três igual a fração de numerador nove dividido por três e denominador trinta e três dividido por três, igual a três onze avos.c)
Cinquenta sobre quarenta e oito, igual a fração de numerador cinquenta dividido por dois sobre quarenta e oito dividido por dois, igual a vinte e cinco sobre vinte e quatro.d)
Quatro sobre vinte, igual a fração de numerador quatro dividido por quatro e denominador vinte dividido por quatro igual a um quinto.Para o capítulo 5: Números racionais
Páginas 16 a 18
37. Completando os espaços, temos:
a) >; como ambas têm o mesmo denominador, é maior a fração de maior numerador.
b) >; como ambas têm o mesmo numerador, é maior a fração de menor denominador.
c) <;
Fração: cinco sextosé maior que a metade.
d) <;
Fração: quatro nonosé mais próximo da metade que
Fração: três décimos.
e) >; comparando as partes decimais, 0,52 > 0,45.
f) <; comparando as partes inteiras, 10 < 11.
g) <; comparando as partes decimais, 0,004 < 0,010.
h) >; comparando as partes decimais, 0,45 > 0,40.
38. Ordenando as frações e decimais dos itens propostos, temos:
a)
Fração: seis sobre treze.,
Fração: seis décimos,
Fração: seis quintos(crescente à medida que o denominador diminui).
b)
Fração: um décimo.,
Fração: cinco décimos.,
Fração: sete décimos.(crescente à medida que o numerador aumenta).
c) 0,025; 0,205; 0,25 (crescente à medida que o número se aproxima de 1).
d) 0,168; 1,68; 16,8 (crescente à medida que a parte inteira aumenta).
39. a)
Cinco nonos mais dez sobre nove igual a fração de numerador cinco mais dez e denominador nove, igual a quinze nonos igual a fração de numerador quinze dividido por três e denominador nove dividido por três igual a cinco terços.b)
Três sobre treze menos um sobre treze igual a fração de numerador três menos um e denominador treze, igual a dois sobre treze.c)
Cinco sobre vinte e quatro mais cinco sobre doze, igual a cinco sobre vinte e quatro mais dez sobre vinte e quatro igual a fração de numerador cinco mais dez e denominador vinte e quatro igual a quinze sobre vinte e quatro igual a fração de numerador quinze dividido por três e denominador vinte e quatro dividido por três, igual a cinco oitavos.d)
Um terço menos quatro sobre trinta igual a dez sobre trinta menos quatro sobre trinta igual a fração de numerador dez menos quatro e denominador seis sobre trinta igual a fração de numerador seis dividido por seis e denominador trinta dividido por seis, igual a um quinto.40. Para cada soma de decimais, temos:
a)
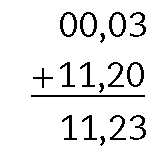
b)
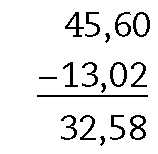
c)
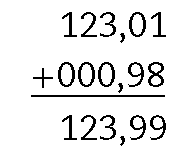
d)
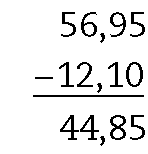
41. a)
Três sétimos vezes um quinto igual a fração de numerador três vezes um e denominador sete vezes cinco, igual a três sobre trinta e cinco.b)
Dois nonos vezes dois nonos igual a fração de numerador dois vezes dois e denominador nove vezes nove, igual a quatro sobre oitenta e um.c)
Um meio vezes dois sétimos igual a fração de numerador dois e denominador dois vezes sete igual a dois sobre catorze igual a um sétimo.d)
Três sobre dez vezes três igual a três sobre dez vezes três sobre um igual a fração de numerador três vezes três e denominador dez vezes um, igual a nove sobre dez.42. Realizando as operações, temos:
a. 9,5 ⋅ 0,3 = 2,85
B. 12,1 ⋅ 0,01 = 0,121
C. 3,004 ⋅ 2 = 6,008
D. 14,2 ⋅ 0,6 = 8,52
Associando as multiplicações aos respectivos produtos, temos: a – três; B – quatro; C – dois; D – um.
43. a)
Um sétimo dividido por dois quintos igual a um sétimo vezes cinco sobre dois igual a fração de numerador um vezes cinco e denominador sete vezes dois igual a cinco sobre catorze.b)
Cinco oitavos dividido por três oitavos igual a cinco oitavos vezes oito terços, igual a fração de numerador cinco vezes oito e denominador oito vezes três, igual a quarenta sobre vinte e quatro igual a cinco terços.c)
Um meio dividido por três sobre dez igual a um meio vezes dez terços igual a fração de numerador um vezes dez e denominador dois vezes três, igual a dez sextos, igual a cinco terços.d)
Cinco quartos dividido por quatro, igual a cinco quartos vezes um sexto igual a fração de numerador cinco e denominador quatro vezes seis igual a cinco sobre vinte e quatro.44. a) 15,6 : 5 = 3,12
b) 73,2 : 12 = 6,1
c) 10,24 : 1,25 = 8,192
d) 34,5 : 0,03 = .3450 : 3 = .1150
Para o capítulo 6: Linguagem algébrica e regularidades
Página 18
45. a) 2 ⋅ 3 ⋅ 4 = 24; 2 + 3 + 4 = 9. A sentença original é verdadeira.
b) 23 ⋅ 1 + 9 = 32 ≠ 230. A sentença original é falsa.
c) 15 ⋅ 3 = 45; 5 ⋅ 3 ⋅ 3 = 45. A sentença original é falsa.
d) 140 : 14 = 10; 140 : 10 = 14. A sentença original é verdadeira.
46. a) 57 ‒ 30 = 27; 5 ⋅ 10 = 50; 57 ‒ 30 < 5 ⋅ 10
b) 2 ⋅ 8 ⋅ 9 = 144; 2 + 8 + 9 = 19; 2 ⋅ 8 ⋅ 9 = 2 + 8 + 9
c) 100 + 20 + 5 = 125; 25 ⋅ 5 = 125; 100 + 20 + 5 = 25 ⋅ 5
47. Seguindo as orientações de cada item, temos os seguintes exemplos de respostas:
a) 23 + 9 = 4 ⋅ 8
b) 8 + 1 + 3 = 10 + 2
c) 2 ⋅ 30 = 80 ‒ 20
48. Seguindo as orientações em cada item, temos:
a) 33 ‒ 3 + 12 = 30 + 12
30 + 12 = 42
42 = 42
b) 33 ‒ 3 ‒ 5 = 30 ‒ 5
30 ‒ 5 = 25
25 = 25
c) (33 ‒ 3) ⋅ 3 = 30 ⋅ 3
30 ⋅ 3 = 30 ⋅ 3
90 = 90
d) (33 ‒ 3) : 3 = 30 : 3
30 : 3 = 30 : 3
10 = 10
Para o capítulo 7: Porcentagem e juro simples
Páginas 19 e 20
49. Utilizando a definição de porcentagem, temos:
A.
Doze sobre cem igual a doze por cento.B.
Cento e vinte sobre cem igual a cento e vinte por cento.C.
Quatro sobre cem igual a quatro por cento.D.
Quarenta sobre cem igual a quarenta por cento.Assim, associamos: a – dois; B – três; C – quatro; D – um.
50. Temos:
a)
Três sobre dez igual a trinta sobre cem igual a trinta por cento.b)
Vinte e sete sobre cem igual a vinte e sete por cento.
c)
Um quarto igual a vinte e cinco sobre cem igual a vinte e cinco por cento.d)
Sessenta sobre duzentos igual a trinta sobre cem igual a trinta por cento.51. Temos:
a)
Sessenta e seis por cento igual a sessenta e seis sobre cem, igual a zero vírgula sessenta e seis.b)
Cento e sessenta e seis por cento igual a cento e sessenta e seis sobre cem igual a um vírgula sessenta e seis.c)
Um vírgula vinte e cinco por cento igual a um vírgula vinte e cinco sobre cem igual a cento e vinte e cinco sobre dez mil, igual a zero vírgula zero, um, dois, cinco.d)
Cem sobre cem igual a um.52. a) 28% = 0,28 ≠ 2,8. Incorreto.
b) 32% = 0,32 ≠ 0,032. Incorreto.
c) 6,3% = 0,063. Correto.
d) 131% = 1,31 ≠ 13,1. Incorreto.
53. a)
Fração cinquenta e cinco sobre cem de 60 é igual a fração cinquenta e cinco sobre cem vezes 60 é igual a trinta e três.b)
Fração 28 sobre 100 de 10 é igual a fração 28 sobre 100 vezes 10 que é igual a dois vírgula 8c)
Fração 30 sobre 100 de 300 é igual a 30 sobre 100 vezes 300 que é igual a 90d)
Fração 90 sobre 100 de 15 é igual a 90 sobre 100 vezes 15 que é igual a 13 vírgula 554. a) Verdadeira;
Fração 10 sobre 100 de 66 é igual a fração 10 sobre 100 vezes 66 que é igual a 6 vírgula 6.
b) Verdadeira;
Fração 15 sobre 100 de 200 é igual a fração 15 sobre 100 vezes 200 que é igual a 30.
c) Falsa;
Fração 75 sobre 100 de 120 é igual a fração 75 sobre 100 vezes 120 que é igual a 90.
d) Falsa;
Fração 82 sobre 100 de 12 é igual a fração 82 sobre 100 vezes 12 que é igual a 9 vírgula 84.
55. a) uma parte de 4 está pintada, assim, temos:
Fração um quarto é igual a fração 25 sobre 100 que é igual a 25 por cento
b) 3 partes de 4 estão pintadas, assim, temos:
Fração três quartos é igual a fração 75 sobre 100 que é igual a 75 por cento
c) 5 de 10 partes estão pintadas, assim, temos:
Fração 5 sobre 10 é igual a fração 50 sobre 100 que é igual a 50 por cento
d) 1 parte de 4 está pintada, assim, temos:
Fração um quarto é igual a fração 25 sobre 100 que é igual a 25 por cento
56. a) Temos 5 de 10, ou seja, a metade está pintada (50%).
b) Temos 10 de 16, ou seja, mais da metade está pintada (> 50%).
c) Temos 2 de 6, ou seja, menos da metade está pintada (< 50%).
d) Temos 4 de 12, ou seja, menos da metade está pintada (< 50%).
Para o capítulo 8: Proporcionalidade
Página 20
57. Se em uma caixa temos 250 gramas, em 3 caixas temos o triplo da massa, ou seja, 750 gramas, já em 9 caixas, temos o triplo da massa de 3 caixas, ou seja, .2250 gramas.
58. Utilizando a proporcionalidade e completando o quadro, temos:
|
NÚMERO DE CADERNOS |
VALOR A PAGAR |
|---|---|
|
1 |
R$ 12,00 |
|
2 |
R$ 24,00 |
|
5 |
R$ 60,00 (× 5) |
|
10 |
R$ 120,00 (× 10) |
|
15 |
R$ 180,00 (× 15) |
|
100 |
R$ 1.200,00 |
Para o capítulo 9: Transformações geométricas
Página 21
59. a) Verificando as coordenadas, temos:
a(0,2); B(1,3) e C(4,3).
b) Os pontos com a mesma abscissa são êêéfe, na abscissa x = 3.
c) Temos aêê na ordenada y = 2 e B e C na ordenada y = 3.
d) Verificando as coordenadas encontramos o ponto F.
60. Um triângulo, pois é definido por 3 vértices (três pontos não alinhados).
61. Exemplo de resposta:
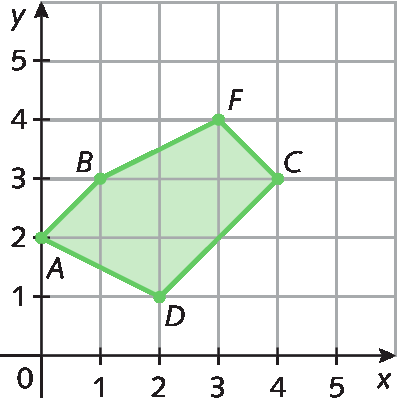
62. As coordenadas do triângulo original são: a(2, 7); B(8, 7) e C(5, 2). Assim:
a) Multiplicamos cada coordenada por 2, obtendo:
á linha(4, 14); bê linha(16, 14) e cê linha(10, 4).
b) Dividindo cada coordenada por 2, temos:
Par ordenado A duas linhas: 1 e 7 sobre 2
;
Par ordenado B duas linhas: 4 e 7 sobre 2e
Par ordenado C duas linhas: 5 sobre 2 e 1.
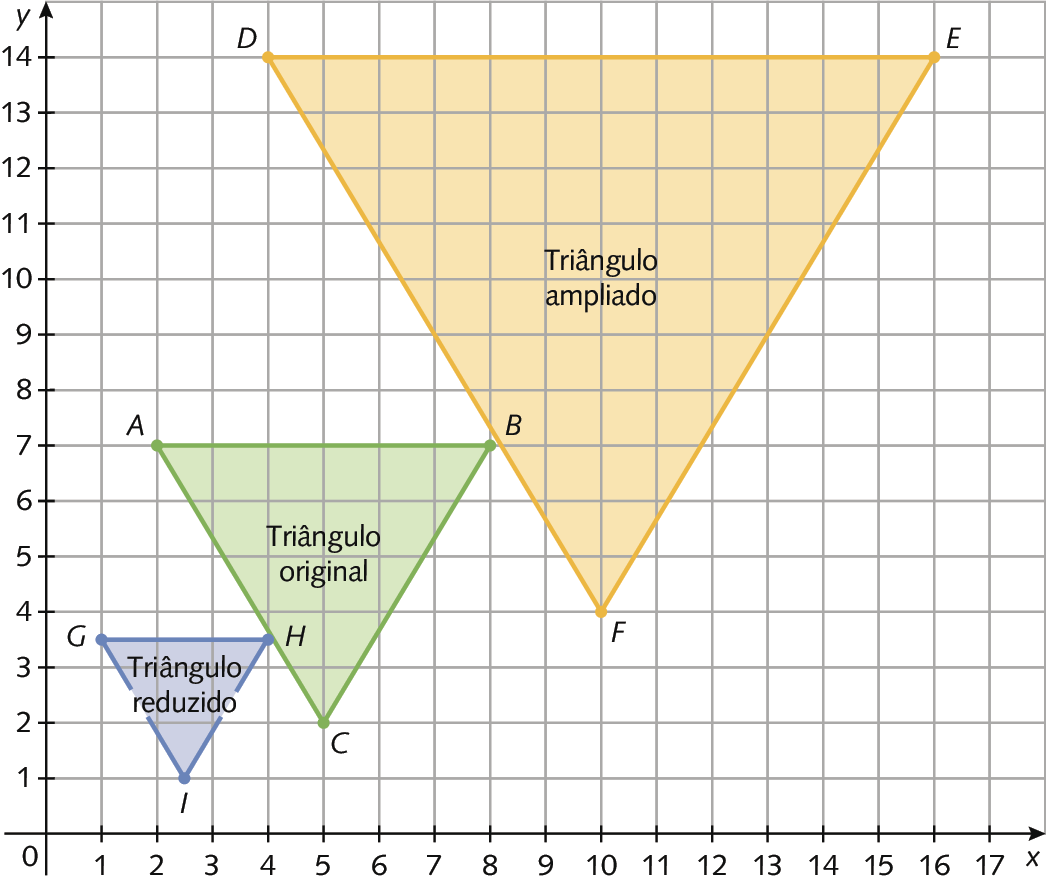
63. Representando os triângulos no mesmo plano, temos:
Para o capítulo 10: Grandezas e medidas
Páginas 21 a 23
64. a) Há 5

compondo a figura, assim, a medida da área será de 5

.
b) Como cada

pode ser decomposto em 2

, a medida da área será de 2 ⋅ 5 = 10

.
65. Utilizando as medidas da área de retângulos e triângulos, temos:
a) Aret = base ⋅ altura = 2,5 ⋅ 10 = 25 ⇒ Aret = 25 centímetros quadrados
b)
Altura do triângulo é igual a meio multiplicado pelo produto da base pela altura que é igual a fração de numerador 8 vezes 6 e denominador 2, que é igual a 48 sobre 2 que é igual a 24. Que implica que a altura do triângulo é de 24 centímetros quadrados66. Utilizando o

como padrão, temos:
a) 2 ⋅ 3 ⋅ 2 = 12

b) 4 ⋅ 2 ⋅ 2 = 16

67. Podemos calcular as medidas dos volumes pelo produto das suas dimensões (comprimento, altura e largura).
a. V = 5 ⋅ 7 ⋅ 4 = 140 ⇒ V = 140 métros cúbicos
b. V = 2,5 ⋅ 2,5 ⋅ 2,5 = 15,625 ⇒ V = 16,625 métros cúbicos
Para o capítulo 11: Figuras geométricas planas
Páginas 23 e 24
68. a) C e F são vértices.
b)
Lado ABe
Lado EDsão lados.
c)
Ângulo ABCé um ângulo interno.
d)
Lado FCe
Lado FB.são diagonais.
69. a) Polígono de 9 lados ‒ eneágono
b) Polígono de 10 lados ‒ dodecágono
c) Polígono de 5 lados ‒ pentágono
d) Polígono de 6 lados ‒ hexágono
70. a) Falso; nenhum dos triângulos é retângulo.
b) Falso; o triângulo da direita não é isósceles.
c) Verdadeiro; o triângulo de esquerda é equilátero e o da direita é escaleno.
d) Verdadeiro; o triângulo da esquerda é acutângulo e o da direita é obtusângulo.
71. Classificando cada triângulo, temos:
a) Acutângulo; há somente ângulos agudos no triângulo.
b) Escaleno; os três lados têm medidas diferentes.
c) Retângulo e isósceles; o triângulo apresenta um ângulo reto e dois lados de medidas iguais.
Para o capítulo 12: Probabilidade e estatística
Página 24
72. Para os eventos, temos:
a) 3 resultados desejados (2, 4 e 6) entre 6, assim, a probabilidade é
3 sobre 6 é igual a 1 sobre 2.
b) 3 resultados desejados (2, 3 e 5) entre 6, assim, a probabilidade é
Fração: um meio..
c) agora somente 2 resultados desejados (1 e 2) entre 6, assim, a probabilidade é
2 sobre 6 é igual a 1 sobre 3.
73. Espera-se que os estudantes, em sites, jornais ou revistas, busquem gráficos que representem dados diversos. É importante que eles identifiquem o tema que cada gráfico explora, visualizando as informações presentes nos seus eixos e no título. Verifique também, com os estudantes, as fontes das informações apresentadas no gráfico, garantindo a veracidade do que está sendo apresentado nas mídias pesquisadas. Por fim, espera-se que os estudantes consigam realizar conclusões ou inferências a respeito das informações apresentadas no gráfico.
UNIDADE 1
Abertura — página 25
Na abertura de unidade, espera-se recolher as concepções dos estudantes a respeito da presença dos números inteiros no cotidiano, verificando seu uso em temperaturas. Questione os estudantes a respeito do significado das temperaturas negativas (‒18 graus Célsius e ‒20 graus Célsius), podendo verificar o conhecimento prévio dos estudantes com questionamentos como: “O que é mais frio, ‒18 graus Célsius ou ‒20 graus Célsius?”.
CAPÍTULO 1 - NÚMEROS INTEIROS
Trocando ideias — página 26
• Para compreender os impactos das atividades humanas no aquecimento global, leia com os estudantes o artigo sobre mudanças climáticas do WWF, disponível em: https://oeds.link/c040vl. Acesso em: 12 maio 2022.
É importante trazer o impacto do uso de combustíveis fósseis para geração de energia e transporte no aumento da concentração de gases geradores de efeito estufa, aumentando a temperatura terrestre.
• Menor. Espera-se que os estudantes respondam que sabem que é menor por causa da presença do sinal de menos (‒) antes dos números.
Atividades — página 30
1. a) +7, +4, +18, +76, +25
b) ‒3, ‒9, ‒36
c) Não é positivo nem negativo.
2. a) Débitos são representados por valores negativos: ‒R$ 3.000,00três mil reais
b) Lucros são representados por valores positivos: +R$ 1.200,00mil duzentos reais
c) Elevações são representadas por valores positivos: +.2300 métros
d) Depressões são representadas por valores negativos: ‒500 métros
3. Podemos representar o 3º subsolo como ‒3 e o 10º andar como +10, assim, ela percorreu 13 andares.
4. Saldo de gols de cada país:
Brasil: 40 ‒ 5 = 35
Argentina: 27 ‒ 8 = 19
Uruguai: 22 ‒ 22 = 0
Equador: 27 ‒ 19 = 8
Peru: 19 ‒ 22 = ‒3
Colômbia: 20 ‒ 19 = 1
Chile: 19 ‒ 26 = ‒7
Paraguai: 12 ‒ 26 = ‒14
Bolívia: 23 ‒ 42 = ‒19
Venezuela: 14 ‒ 34 = ‒20
5. Considerando o saldo inicial (dia 20/1) de R$ 1.560,00mil quinhentos e sessenta reais, temos:
• em 21/1 → retirou metade do saldo, ou seja, R$ 780,00setecentos e oitenta reais, sobrando a outra metade como saldo;
• em 22/1 → depositou R$ 180,00cento e oitenta reais, aumentando seu saldo para R$ 960,00novecentos e sessenta reais;
• em 23/1 → retirou R$ 300,00trezentos reais, diminuindo seu saldo para R$ 660,00seiscentos e sessenta reais.
Completando o quadro, temos:
|
DIA |
SALDO ANTERIOR |
CRÉDITO |
DÉBITO |
SALDO |
|---|---|---|---|---|
|
21/1 |
R$ 1.580,00 |
– |
R$ 780,00 |
R$ 780,00 |
|
22/1 |
R$ 780,00 |
R$ 180,00 |
R$ 960,00 |
|
|
23/1 |
R$ 960,00 |
– |
R$ 300,00 |
R$ 660,00 |
6. Um exemplo de problema é dado a seguir:
“Pedro, ao verificar o seu extrato no banco, notou um saldo de +R$ 300,00trezentos reais na sua conta. Ao realizar a compra de um eletrodoméstico, verificou novamente seu extrato bancário e constatou saldo negativo de ‒R$ 150,00cento e cinquenta reais. Quanto custou o eletrodoméstico?”.
7. A temperatura variou de ‒1 graus Célsius para ‒6 graus Célsius; assim, a temperatura diminuiu em 5 graus Célsius. É importante notar que, neste caso, não podemos dizer que a temperatura diminuiu em ‒5 graus Célsius, pois isso implica aumento de temperatura de 5 graus Célsius.
8. A medida era menor em Berna, já que ‒8 graus Célsius é menor que ‒2 graus Célsius.
Balão de fala — página 31
Espera-se que os estudantes percebam que, repetindo o procedimento, representaríamos os pontos situados à esquerda da origem na reta r, aos quais corresponderiam os números inteiros negativos.
Atividades — página 32
9. a) O número ‒1 corresponde ao ponto B.
b) O ponto a é correspondente ao número ‒4.
c) O ponto D é correspondente ao número +5.
d) O ponto C corresponde ao número +2.
e) O ponto ê corresponde ao número +6.
10. Representando a reta, temos:
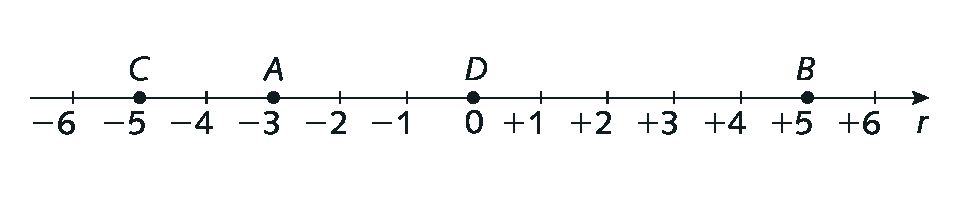
11. Traçando uma reta conforme orientado, temos:
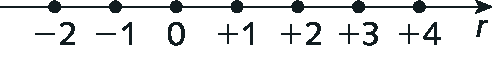
12. Podemos representar a situação da seguinte fórma:
Assim, o número inteiro correspondente é ‒4.
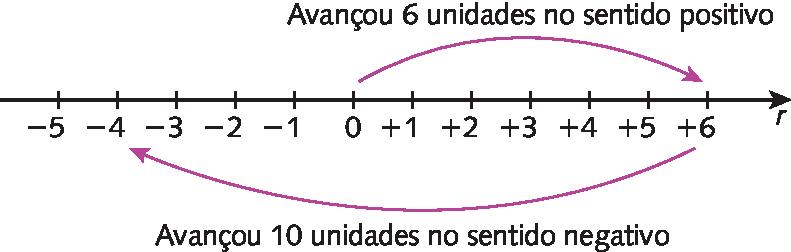
13. Pelas informações do gráfico, temos:
a) Fevereiro, pois foi o mês em que o saldo é dado por ‒40.
b) 35 mil reais ou +R$ 35.000,00trinta e cinco mil reais.
c) Somando todos os valores, temos:
25 ‒ 40 + 35 ‒ 25 + 40 + 10 = 45, resultando em um lucro de 45 mil reais.
Atividades — página 33
14. a) O oposto de ‒6 é ‒(‒6) = +6
b) O oposto de 100 é ‒(100) = ‒100
c) O posto de ‒7 é ‒(‒7) = +7
d) O oposto de 8 é ‒(8) = ‒8
15. Determinar o valor absoluto significa determinar o módulo do número:
a) |+13| = 13
b) |+50| = 50
c) |‒21| = ‒(‒21) = 21
d) |‒116| = ‒(‒116) = 116
16. a) |‒16| = ‒(‒16) = 16
b) |‒20| = ‒(‒20) = 20
c) |+35| = 35
d) |‒1| = ‒(‒1) = 1
e) |0| = 0
f) |‒14| = ‒(‒14) = 14
g) |+239| = 239
h) |‒524| = ‒(‒524) = 524
17. a) |‒13| = ‒ (‒13) = 13
b) ‒(‒318) = +318
c) +17 e ‒17
18. a) Nenhum, pois não há medidas de distância negativas.
b) Um único número, o zero, já que ele coincide com a origem.
c) Infinitos números, pois todo número com exceção do zero representa uma distância da origem maior que zero.
19. Espera-se que os estudantes percebam que qualquer número positivo pode ser usado para completar a frase.
Atividades — página 35
20. Verificando a representação a seguir, temos:

a) O maior dos números citados é o 7.
b) O menor dos números citados é o ‒6.
c) O número inteiro entre ‒4 e ‒2 é o ‒3.
21. Ordenando em ordem decrescente, temos:
7 > 6 > 3 > 0 > ‒1 > ‒4 > ‒8
22. a) +3 > +2. O natural de maior módulo é maior.
b) ‒5 > ‒6. O número negativo de maior módulo é menor.
c) ‒4 < +4. Números positivos são maiores que negativos.
d) 0 > ‒1. O zero é maior que todo negativo.
e) +2 > 0. O zero é menor que todo positivo.
f) ‒2 < ‒1. O número negativo de maior módulo é menor.
g) ‒3 > ‒4. O número negativo de maior módulo é menor.
h) 0 > ‒10. O zero é maior que todo negativo.
23. Achar o antecessor equivale a subtrair uma unidade, achando seu vizinho pela esquerda. Achar o sucessor equivale a somar uma unidade, localizando seu vizinho pela direita.
a) (‒9) ‒ (1) = ‒10, assim, ‒10 é o antecessor de ‒9.
b) ‒14 + 1 = ‒13, assim ‒13 é o sucessor de ‒14.
c) Pela reta numérica, temos: 0, ‒1 e ‒2.
d) ‒13 + 1 = ‒12, então, ‒12 é o sucessor de ‒13.
24. a) Tales de Mileto, pois nasceu em ano anterior ao nascimento de Pitágoras (624 antes de Cristo aconteceu antes de 580 antes de Cristo).
b) Entre 624 antes de Cristo e 580 antes de Cristo temos 44 anos
(‒580 ‒ (‒624) = 44).
25. a) Seu antecessor, ou seja, ‒51.
b) ‒999, pois é o sucessor de ‒.1000, maior número negativo de quatro algarismos.
Atividade em grupo — página 36
a) A adição de números positivos resulta em valores positivos.
b) A adição de números negativos resulta em valores negativos.
c) Espera-se que os estudantes percebam que o resultado de uma adição em que uma das parcelas é zero será:
• positivo se a outra parcela for positiva;
• negativo se a outra parcela for negativa;
• zero se a outra parcela for igual a zero.
d) Os resultados podem ser positivos, negativos ou iguais a zero. Espera-se que os estudantes percebam que o sinal do resultado é o mesmo do número de maior módulo ou que, se um número é o oposto do outro, o resultado é igual a zero.
Atividades — páginas 37 e 38
26. a) (+5) + (+3) = 5 + 3 = 8
b) (‒7) + (‒10) = ‒7 ‒ 10 = ‒17
c) 0 + (‒8) = 0 ‒ 8 = ‒8
d) (+5) + (‒20) = 5 ‒ 20 = ‒15
e) (‒40) + (+13) = ‒40 + 13 = ‒27
f) (‒8) + (‒17) = ‒ 8 ‒ 17 = ‒25
27. Como a pessoa retirou mais dinheiro do que havia de saldo, seu saldo se tornou negativo:
600 ‒ .1000 = ‒400: o saldo será de ‒R$ 400,00quatrocentos reais.
28. Consideramos cada subida uma adição, e cada descida uma subtração:
.8000 métros + .3000 métros ‒ .4500 métros = .11000 métros ‒ .4500 métros = .6500 métros
29. Considerando as informações do problema, temos:
a) Somando as parcelas das semanas, temos:
+R$ 5.680,00cinco mil seiscentos e oitenta reais ‒ R$ 1.329,00mil trezentos e vinte e nove reais + R$ 2.400,00dois mil quatrocentos reais ‒ R$ 4.260,00quatro mil duzentos e sessenta reais = +R$ 2.491,00dois mil quatrocentos e noventa e um reais
b) O número é positivo, representando lucro.
30. Exemplo de resposta: “No último campeonato, meu time marcou 3 gols e sofreu 28. Qual foi o saldo de gols do meu time?”.
31. Pelas definições, temos:
a) Elemento neutro (soma com o 0) e comutativa (ordem das parcelas).
b) Comutativa (ordem das parcelas).
c) Elemento oposto (soma de elementos opostos resultando em zero).
d) Associativa (realizando a soma por meio de diferentes associações de parcelas).
32. a) Não, eles foram realizados de maneiras diferentes.
b) Espera-se que os estudantes respondam que foi Ilda, porque ela identificou na soma parcelas com valores opostos, e aplicou a propriedade do elemento oposto.
c) O método de Rita consiste em realizar, em cada passagem, a operação com os dois primeiros números da expressão, repetindo os demais:
(‒18) + 101 + 9 + (‒101) + (‒38) + 22 + 18 + 38 =
= 83 + 9+ (‒101) + (‒38) + 22 + 18 + 38 =
= 92 + (‒101) + (‒38) + 22 + 18 + 38 =
= (‒9) + (‒38) + 22 + 18 + 38 =
= (‒47) + 22 + 18 + 38 =
= (‒25) + 18 + 38 =
= (‒7) + 38 = 31
Atividade em grupo — página 40
Justificando item a item, temos:
um Verdadeiro.
dois Falso. Um contraexemplo: (‒2) ‒ (‒4) = (‒2) + 4 = 2.
três Verdadeiro.
quatro Falso. Basta tomar 1 ‒ 1 = 0.
Atividades — páginas 41 e 42
33. a) (‒8) ‒ (+7) = ‒8 ‒ 7 = ‒15
b) (‒30) ‒ (+70) = ‒30 ‒ 70 = ‒100
c) (‒72) ‒ (+30) = ‒72 ‒30 = ‒102
d) (‒3) ‒ (+7) = ‒3 ‒ 7 = ‒10
e) (+10) ‒ (+30) = 10 ‒ 30 = ‒20
f) (+80) ‒ (‒15) = 80 + 15 = 95
34. a) (‒650) ‒ (+300) = ‒650 ‒ 300 = ‒950
b) (‒850) ‒ (‒850) = ‒850 + 850 = 0
c) (+.1300) ‒ (‒.1100) = .1300 + .1100 = .2400
35. a) O resultado na calculadora foi 5.
b) ‒10 ‒ (‒15) = ‒10 + 15 = 5
36. a) (+8) + (‒7) + (‒3) = 8 ‒ 7 ‒ 3 = ‒2
b) (+2) ‒ (+5) ‒ (+3) = 2 ‒ 5 ‒ 3 = ‒ 3 ‒ 3 = ‒ 6
c) (+10) ‒ (‒20) ‒ (+30) = 10 + 20 ‒ 30 = 30 ‒ 30 = 0
37. a) ‒76 ‒ (7 ‒ 18) + [70 ‒ (49 ‒ 81)] =
= ‒76 ‒ (‒11) + [70 ‒ (‒32)] =
= ‒76 + 11 + 70 + 32 = 37
b) {[(73 ‒ 64) + 20] ‒ (40 ‒ 31)} + (‒3) =
= {[9 + 20] ‒ (9)} + (‒3) = {29 ‒ 9} ‒3 = 17
38. Vamos utilizar as propriedades que conhecemos para resolver cada caso, somando e subtraindo elementos opostos.
a)

+ (‒8) ‒ (‒3) = +7; somando o oposto de ‒8:

‒8 + (+8) ‒ (‒3) = 7 + (+8)

‒ (‒3) = 15; somando o oposto de ‒3

+ 3 + (‒3) = 15 + (‒3)

= +12
b) (+8) + (

) + (‒3) = ‒5; somando o oposto de +8 e o oposto de ‒3:
(+8) + (‒8) + (

) + (‒3) + (+3) = ‒5 + (‒8) + (+3)
+ (

) = ‒10, ou seja,

= ‒10
c) (+48) ‒ (‒36) + (‒40) ‒ (

) = ‒75; somando o oposto de (+48), subtraindo o oposto de (‒36) e somando o oposto de (‒40):
(+48) + (‒48) ‒ (‒36) ‒ (+36) + (‒40) + (+40) ‒ (

) =
= ‒75 + (‒48) ‒ (+36) (+40)
‒ (

) = ‒119

= +119
39. Podemos expressar a situação por meio da seguinte operação: 18 ‒ (‒5) = 23
40. Podemos expressar a situação por meio da seguinte operação: 160 ‒ 120 = 40 bilhões de dólares (saldo positivo).
Atividades — páginas 44 e 45
41. Calculando as expressões, temos:
a) (+11) ⋅ (+3) = +33
b) (‒1) ⋅ (‒5) = +5
c) (+9) ⋅ (‒7) = ‒63
d) (‒7) ⋅ (‒7) = 49
e) 0 ⋅ (‒10) = 0
f) (‒11) ⋅ (+7) = ‒77
g) (‒12) ⋅ (+23) = ‒276
h) (‒16) ⋅ (‒6) = +96
i) (‒12) ⋅ (12) = ‒144
j) (‒20) ⋅ (+15) = ‒300
42. a) (‒7) ⋅ (‒8) ⋅ (+3) = +168
b) (‒4) ⋅ (+2) ⋅ (‒11) = +88
c) (+7) ⋅ (+2) ⋅ (+3) ⋅ (‒1) = ‒42
d) (+4) ⋅ (‒7) ⋅ (+9) ⋅ (‒11) = +.2772
e) (+8) ⋅ (‒6) ⋅ (‒5) ⋅ (+3) ⋅ (+2) = +.1440
f) (‒5) ⋅ (‒6) ⋅ (‒3) ⋅ (‒2) ⋅ (‒1) = ‒180
43. Os quatro maiores números inteiros negativos são ‒4, ‒3, ‒2 e ‒1, então, temos:
(‒4) ⋅ (‒3) ⋅ (‒2) ⋅ (‒1) = (+12) ⋅ (+2) = +24
44. Não. Ao multiplicar (‒1) por qualquer número inteiro não nulo, o produto será o oposto desse número.
45. * Produto da soma dos números ‒9, +6, ‒2, +8 e ‒15:
(‒9) + (+6) + (‒2) + (+8) + (‒15) = ‒12
* Simétrico da diferença entre ‒6 e ‒3:
‒ [(‒6) ‒ (‒3)] = ‒[‒3] = +3
Calculando o produto, temos então: (‒12) ⋅ (+3) = ‒36.
46. a) Como alteramos os fatores na operação, usamos a propriedade associativa.
b) Como trocamos a ordem dos fatores, utilizamos a propriedade comutativa.
c) Ao realizar a multiplicação por (+1), fazemos uso do elemento neutro.
d) Ao distribuir a multiplicação sobre as parcelas da soma, utilizamos a propriedade distributiva.
47. a) (‒3) ⋅ (‒20 + 7) = (‒3) ⋅ (‒20) + (‒3) ⋅ (+7) = +60 ‒ 21 = 39
b) (25 ‒ 18) ⋅ (‒5) = (+25) ⋅ (‒5) + (‒18) ⋅ (‒5) = ‒125 + 90 = ‒35
c) 2 ⋅ (‒7 + 5) = 2 ⋅ (‒7) + 2 ⋅ (+5) = ‒14 + 10 = ‒4
d) (8 ‒ 3) ⋅ (‒4) = (+8) ⋅ (‒4) + (‒3) ⋅ (‒4) = ‒32 + 12 = 20
48. São as seguintes:
1 ⋅ 12; 12 ⋅ 1; 2 ⋅ 6; 6 ⋅ 2; ‒1 ⋅ (‒12); ‒12 ⋅ (‒1); ‒2 ⋅ (‒6);
‒6 ⋅ (‒2); ‒3 ⋅ (‒4); ‒4 ⋅ (‒3)
49. Temos como resultado:
(‒7) ⋅ (400 + 20 + 1) = (‒7) ⋅ 400 + (‒7) ⋅ 20 + (‒7) ⋅ 1 = ‒ .2800 ‒ 140 ‒ 7 = ‒.2947
50. Realizando os cálculos dos delimitadores mais internos para os mais externos, fazendo as multiplicações antes das adições e subtrações, temos:
a) ‒30 ‒ 5 ⋅ [(‒1) ⋅ (15 ‒ 3 ⋅ 6) + 9 ‒ 3 ⋅ 4] =
= ‒30 ‒ 5 ⋅ [(‒1) ⋅ (15 ‒ 18) + 9 ‒ 12] =
= ‒30 ‒ 5 ⋅ [‒ 15 + 18 ‒ 3] = ‒30 ‒ 5 ⋅ [0] = ‒30
b) ‒5 + [(‒20) ⋅ (‒15 + 30) ⋅ (‒1)] = ‒5 + [(‒20) ⋅ (15) ⋅ (‒1)] =
= ‒5 + [(‒20) ⋅ (‒15)] = ‒5 + (300) = +295
c) 18 + 4 ⋅ [‒6 ‒ 4 ⋅ (‒5 + 6)] = 18 + 4 ⋅ [‒6 ‒ 4 ⋅ (+1)] =
= 18 + 4 ⋅ [‒6 ‒ 4] = 18 + 4 ⋅ [‒10] = 18 ‒ 40 = ‒22
51. Exemplo de resposta: “Para comprar material de desenho, João precisou retirar dinheiro do seu cofrinho. Ele retirou duas notas de R$ 50,00cinquenta reais para comprar o que precisava. Após algum tempo, conseguiu repor R$ 60,00sessenta reais do que gastou. Qual é o saldo do cofrinho de João?”.
Discussões — página 45
• Os estudantes devem perceber que os resultados obtidos sugerem que em uma divisão de números inteiros, se o dividendo e o divisor tiverem os mesmos sinais, o quociente será um número positivo. Enfatize que essa afirmação é verdadeira, mas não será demonstrada.
• Os estudantes devem perceber que os resultados obtidos sugerem que em uma divisão de números inteiros, se o dividendo e o divisor tiverem os mesmos sinais, o quociente será um número positivo. Enfatize que essa afirmação é verdadeira, mas não será demonstrada nesse momento.
Atividades — página 46
52. a) (+6) : (+3) = (+2)
b) (+10) : (‒5) = (‒2)
c) (‒32) : (‒4) = (+8)
d) (‒1) : (+1) = (‒1)
e) 0 : (‒1) = 0
f) (‒63) : (‒21) = +3
g) (+.1296) : (‒48) = ‒27
53. a) 2 ⋅ 12 = 24
b) (‒38) : (+2) = ‒19, porque (‒19) ⋅ (+2) = ‒38
c) O dobro de 15 é 30 (15 ⋅ 2 = 30), e seu oposto é ‒30 (30 ⋅ (‒1) = ‒30)
d) Calculamos primeiro o oposto, depois, a metade. Assim, temos: (‒60) ⋅ (‒1) = 60, e sua metade é 60 : 2 = 30.
e) a terça parte de ‒36 é igual a (‒36) : (3) = (‒12), já que (‒12) ⋅ (+3) = (‒36)
54. a) (16 ‒ 30 + 48) : (‒2) = (+34) : (‒2) = ‒17
b) (‒15 + 20 + 40) : (+5) = (+45) : (+5) = +9
c) (‒5 + 7 ‒ 35) : (‒11) = (‒33) : (‒11) = +3
55. Vamos realizar os cálculos com base na operação inversa.
a) Se

: (‒5) = 8, então (‒5) ⋅ (+8) = (‒40); logo,

= (‒40)
b) Se (‒30) :

= ‒6, então (‒6) ⋅

= (‒30); logo,

= +5
c) Se

: (‒7) = 0, então (‒7) ⋅ 0 = 0; logo,

= 0
d) Se (‒20) :

= ‒1, então (‒1) ⋅

= (‒20); logo,

= (+20)
56. a) ‒2 + {‒1 + [5 ‒ 3 ⋅ (10 + 1) : 3] ‒5 ⋅ 7} =
= ‒2 + {‒1 + [5 ‒ 3 ⋅ (11) : 3] ‒5 ⋅ 7} =
= ‒2 ‒ 1 + [5 ‒ 33 : 3] ‒35 = ‒2 ‒ 1 + (‒6) ‒ 35 = ‒44
b) ‒5 ‒ [3 ⋅ (7 ‒ 5 ‒ 3) ‒ 22 : 11] = ‒5 ‒ [3 ⋅ (‒1) ‒ 22 : 11] =
= ‒5 ‒ [3 ⋅ (‒1) ‒ 2] = ‒5 ‒ [‒3 ‒ 2] = ‒5 ‒ [‒5] =
= ‒5 + 5 = 0
c) 2 ‒ (5 ⋅ 10 + 6) ‒ 5 ⋅ 20 : (‒17 + 13) =
= 2 ‒ (50 + 6) ‒ 5 ⋅ 20 : (‒4) =
= 2 ‒ (56) ‒ 100 : (‒4) = 2 ‒ 56 + 25 = ‒54 + 25 = ‒29
d) 3 ‒ {30 : 5 ‒ [‒7 ⋅ (5 ‒ 2) + 3] : 6} =
= 3 ‒ {6 ‒ [‒7 ⋅ 3 + 3] : 6} =
= 3 ‒ {6 ‒ [‒21 + 3] : 6} = 3 ‒ {6 ‒ [‒18] : 6} =
= 3 ‒ {6 + 3} = ‒ 6
57. a) 1, já que é o resultado de uma divisão de um número por ele mesmo.
b) ‒1, já que é o oposto da divisão entre um número por ele mesmo.
Balão de fala — página 47
Espera-se que, de acordo com a primeira observação, os estudantes cheguem à conclusão de que 01 é igual a 0 e que a segunda potência é impossível de calcular, já que, de acordo com a segunda observação, toda potência de expoente zero tem que ter base diferente de zero.
Atividades — página 48
58. a) (+2)3 = (+2) ⋅ (+2) ⋅ (+2) = +8
b) (‒7)4 = (‒7) ⋅ (‒7) ⋅ (‒7) ⋅ (‒7) = +.2401
c) (‒9)3 = (‒9) ⋅ (‒9) ⋅ (‒9) = ‒729
d) (+3)2 = (+3) ⋅ (+3) = +9
e) (‒17)0 = +1
f) (‒11)2 = (‒11) ⋅ (‒11) = +121
g) (‒35)1 = (‒35) = ‒35
h) (‒1)3 = (‒1) ⋅ (‒1) ⋅ (‒1) = ‒1
i) (+.1992)0 = 1 (por definição)
59. a) Positivo, independentemente de o expoente ser par ou ímpar, já que o produto sempre é positivo.
b) Positivo, se o expoente for par, e negativo, se o expoente for ímpar, já que a multiplicação pode ter resultado com sinais diferentes dependendo da quantidade de números negativos como fatores.
60. Como temos uma quantidade par de fatores, o sinal resultante é positivo, assim, (‒1)30 = +1.
61. Cada geração pode ser representada como uma potência de base 2, sendo a pessoa relacionada ao expoente 0, pais ao expoente 1, avós ao 2, e assim sucessivamente. Dessa fórma, temos: bisavós: 23 = 8; trisavós: 24 = 16.
62. a) (‒4) ‒ [(‒8) : (+2)]2 ‒ 6 = (‒4) ‒ [‒4]2 ‒ 6 = (‒4) ‒ [16] ‒ 6 =
= ‒26
b) (+20) : (‒1)4 ‒ 22 + (‒2)5 : (+2)4 ‒ 50 =
= (+20) : (+1) ‒ 4 + (‒32) : (+16) ‒ 1 =
= (+20) ‒ 4 ‒ (2) ‒ 1 = 13
c) (‒576) : (‒12)2 ‒ (‒125) : (‒5)2 =
= (‒576) : (+144) ‒ (‒125) : (25) = (‒4) ‒ (‒5) =
= ‒4 +5 = 1
63. a) (5 + 3)² = (+8)² = 64
b) 5² + 3² = 25 + 9 = 34
c) (2 ‒ 4)³ = (‒2)³ = ‒8
d) 2³ ‒ 4³ = 8 ‒ 64 = ‒ 56
• As respostas dos itens a) e d) sugerem que a igualdade proposta não se verifica.
64. a. 15
b) Espera-se que os estudantes resolvam previamente as expressões elaboradas, certificando-se de que têm solução. Um exemplo pode ser dado a seguir:
480 : {20 ⋅ [86 ‒ 12 ⋅ (5 + 2)]2} , cuja solução é 6.
Atividades — página 50
65. a)
Sentença matemática: Raiz quadrada de trinta e seis igual a seis.pois (+6)² = 36
b)
Sentença matemática: raiz quadrada de zero igual a zero., pois 0² = 0
c)
Sentença matemática: menos raiz quadrada de cento e noventa e seis igual a menos catorze., pois ‒[(14)²] = ‒(196)
d)
Sentença matemática: menos raiz quadrada de cem igual a menos dez., pois ‒[(10)²] = ‒(100)
66. a)
Sentença matemática: raiz quadrada de oitenta e um menos raiz quadrada de cem mais raiz quadrada de sessenta e quatro, igual a nove menos dez mais oito, igual a sete.b)
Sentença matemática: menos raiz quadrada de trinta e seis menos raiz quadrada de cento e vinte e um mais raiz quadrada de sessenta e quatro, igual a menos seis menos onze mais oito igual a menos nove.c)
Sentenças matemáticas: raiz quadrada de um mais raiz quadrada de quatro mais raiz quadrada de nove mais raiz quadrada de dezesseis mais raiz quadrada de quarenta e nove mais raiz quadrada de sessenta e quatro, igual. Abaixo, igual a um mais dois mais três mais quatro mais sete mais oito igual a vinte e cinco.67.
Sentenças matemáticas: abre chaves, abre colchetes, raiz quadrada de quarenta e nove mais, abre parênteses, dois elevado a quatro menos um, fecha parênteses, fecha colchetes, vezes raiz quadrada de sessenta e quatro, fecha chaves, mais raiz quadrada de mil e vinte e quatro, igual.=
= {[7 + ( 16 − 1 )] ⋅ 8} + 32 = {[7 + ( 15 )] ⋅ 8} + 32 = 208
68.
Sentença matemática: raiz quadrada de quatrocentos igual a, início da raiz, vinte vezes vinte, final da raiz, igual a vinte.A medida do lado do quadrado é 20 métros.
69.
Sentenças matemáticas: Início da raiz quadrada, abre parênteses, menos dois, fecha parênteses, vezes, abre parênteses, mais quatro, fecha parênteses, elevado a dois, vezes, abre parênteses, menos oito, fecha parênteses, final da raiz quadrada, igual a, início da raiz quadrada, abre parênteses, menos dois, fecha parênteses, vezes, abre parênteses, mais dezesseis, fecha parênteses, vezes, abre parênteses, menos oito, fecha parênteses, final da raiz, igualAbaixo, igual, início da raiz, abre parênteses, mais dezesseis, fecha parênteses, vezes, abre parênteses, mais dezesseis, fecha parênteses, final da raiz, igual a dezesseis.
70. Dentre os números apresentados, temos que os quadrados perfeitos são:
4 = 2², 9 = 3², 36 = 4² e 121 = 11².
Assim, as raízes que não resultam em números inteiros são:
Raiz quadrada de cinco.
,
Raiz quadrada de dez.,
Raiz quadrada de duzentos..
71. a)
Sentença matemática: início da raiz quadrada, dezesseis mais nove, fim da raiz quadrada, igual a raiz quadrada de vinte e cinco igual a cinco.b)
Raiz quadrada de dezesseis mais raiz quadrada de nove igual a quatro mais três igual a sete.c)
Sentença matemática: início da raiz quadrada, cem menos trinta e seis, final da raiz quadrada, igual a, raiz quadrada de sessenta e quatro, igual a oito.d)
Sentença matemática: raiz quadrada de cem menos raiz quadrada de trinta e seis, igual a dez menos seis, igual a quatro.• As respostas dos itens a) e d) sugerem que a igualdade proposta não se verifica.
72.
|
‒10 |
‒8 |
100 |
|
‒200 |
20 |
‒2 |
|
4 |
‒50 |
‒40 |
73. Exemplo de resposta: “A medida do lado de um terreno quadrado é igual a raiz quadrada da sua área. Uma plantação de vegetais foi feita em um terreno quadrado de área igual a 25 métros quadrados. Qual é a medida do seu lado?
Resposta: “Como
Sentença matemática: raiz quadrada de vinte e cinco igual a cinco., o lado do quadrado mede 5 métros.”
Resolvendo em equipe — página 51
Resolução da questão: Como a viagem entre as cidades demora 6 horas, no início da viagem, o horário na cidade B era de 18 ‒ 6 = 12 horas. Assim, há uma diferença de 3 horas de fuso entre as cidades A e B (15 ‒ 12 = 3 horas). Portanto, se é necessário chegar às 13 horas na cidade a (o que equivale a 10 horas na cidade B), o executivo precisaria sair às 4 horas (10 horas ‒ 6 horas do voo). Alternativa d.
Interpretação e identificação dos dados
O horário da cidade B está com 3 horas de atraso em relação ao da cidade a.
a) São 18 horas + 3 horas = vinte e uma horas.
b) 3 horas.
Plano de resolução
Na elaboração dos esquemas, é importante que os estudantes evidenciem os fusos horários das cidades e as diferenças em relação ao voo.
Um exemplo é dado a seguir:
|
VIAGEM |
CIDADE A |
FUSO |
CIDADE B |
VIAGEM |
|---|---|---|---|---|
|
+6 h |
Partida de A (horário de A): 15 h |
‒3 h |
Partida de A (horário de B): 12 h |
+6 h |
|
+6 h |
Partida de B (horário de A):? |
‒3 h |
Partida de B (horário de B):? |
+6 h |
Resolução
Nas respostas, espera-se que os estudantes determinem que, se o executivo precisa estar às 13 horas na cidade a, os relógios em B marcarão 10 horas (3 horas a menos). Como o voo dura 6 horas, é preciso, então, sair às 4 horas.
Apresentação
O estudo dos fusos horários pode ser feito em parceria com o professor de Geografia.
Revisão dos conteúdos deste capítulo — páginas 52 a 54
1. a) São números positivos: +27, +91, +15
b) São números negativos: ‒12, ‒4, ‒8, ‒59, ‒18
2. a) O número ‒4 corresponde ao ponto a.
b) O ponto B é correspondente ao número ‒3.
c) O ponto C corresponde ao número 1.
d) O ponto correspondente ao número +3 é o D.
e) O número correspondente ao ponto ê é o 5.
3.

4. a) O oposto de ‒8 é +8.
b) O oposto de 85 é ‒85.
c) O módulo de ‒2 é 2.
d) O módulo de ‒1 é 1.
e) O oposto de 15 é ‒15.
f) O oposto de ‒75 é +75.
5. a) |‒19| = 19
b) |+36| = 36
c) |+16| = 16
d) |‒120| = 120
e) |0| = 0
f) |‒212| = 212
6. ‒5 < ‒3 < ‒2 < 0 < 2 < 3 < 4

7. a) (+4) < (+6) (Quanto maior o valor absoluto do número positivo, maior ele é.)
b) (‒6) < (‒5) (Quanto maior o valor absoluto do número negativo, menor ele é.)
c) (+5) > (‒5) (Um número positivo é maior que um número negativo.)
d) (+10) > 0 (Todo número positivo é maior que zero.)
e) (‒14) < (+1) (Um número positivo é maior que um número negativo.)
f) (+35) > (+25) (35 está à direita de 25 na reta numérica)
8. a) ‒15 ‒ 1 = ‒16
b) +9 ‒ 1 = +8
c) ‒99 + 1 = ‒98
d) ‒36 + 1 = ‒35
9. a) (+12) + (+11) = 12 + 11 = +23
b) (‒15) + (‒20) = ‒15 ‒ 20 = ‒35
c) 0 + (+18) = 0 + 18 = 18
d) (+9) + (‒12) = 9 ‒ 12 = ‒3
e) (‒21) + (+21) = ‒21 + 21 = 0
f) (‒7) + (‒17) = ‒7 ‒ 17 = ‒24
10. a) Elemento neutro e propriedade comutativa.
b) Elemento oposto.
c) Propriedade associativa.
d) Propriedade comutativa.
11. ‒(238) + (250) = +12
Após o depósito, o saldo de João é de R$ 12,00doze reais.
12. 25 ‒ 18 + 11 ‒ 22 = 36 ‒ 40 = ‒4
Saldo de pontos: ‒4 pontos.
13. a) (‒15) ‒ (‒12) = ‒15 + 12 = ‒3
b) (+82) ‒ (+31) = +82 ‒ 31 = +51
c) (‒74) ‒ (+44) = ‒74 ‒ 44 = ‒118
d) (‒19) ‒ (‒12) = ‒19 + 12 = ‒7
e) (‒12) ‒ (+45) = ‒12 ‒ 45 = ‒57
f) (+77) ‒ (‒25) = +77 + 25 = +102
14. a) (‒18) ‒ (15 ‒ 19) + [94 ‒ (75 ‒ 86)] =
= (‒18) ‒ (‒4) + [94 ‒ (‒11)] = ‒18 + 4 + 105 = 91
b) {[(25 ‒ 67) + 12] ‒ (40 ‒ 16)} + (‒27) =
= {[(‒42) + 12] ‒ (24)} + (‒27) =
= ‒42 + 12 ‒ 24 ‒ 27 = ‒81
15. ‒2 ‒ (‒ 8) = ‒2 + 8 = 6
A diferença entre as temperaturas é de 6 graus Célsius.
16. a) (+11) ⋅ (+4) = +44
b) (‒5) ⋅ (‒12) = +60
c) (‒14) ⋅ (+20) = ‒280
d) (‒10) ⋅ (+15) = ‒150
e) (‒9) ⋅ (+25) = ‒225
f) (+12) ⋅ (‒6) = ‒72
17. a) Propriedade comutativa, já que há a alteração na ordem dos fatores.
b) Uso do elemento neutro, onde há uma multiplicação por (+1).
c) Uso da propriedade distributiva, onde a multiplicação por uma soma se torna uma soma de multiplicações.
d) Propriedade associativa, onde a organização das multiplicações a serem efetuadas não altera o resultado final.
18. a) (‒4) ⋅ (‒10 + 8) = (‒4) ⋅ (‒10) + (‒4) ⋅ (+8) =
= (+40) + (‒32) = +8
b) (15 ‒ 9) ⋅ (‒10) = (+15) ⋅ (‒10) + (‒9) ⋅ (‒10) =
= (‒150) + (+90) = ‒60
c) 7 ⋅ (‒11 + 7) = 7 ⋅ (‒11) + 7 ⋅ (+7) = (‒77) + (+49) = ‒28
d) (15 ‒ 7) ⋅ (+6) = (+15) ⋅ (+6) + (‒7) ⋅ (+6) =
= (+90) + (‒42) = +48
19. a) 22 + 9 ⋅ [‒15 ‒ 2 ⋅ (‒9 + 11)] = 22 + 9 ⋅ [‒15 ‒ 2 ⋅ (+2)] =
= 22 + 9 ⋅ [‒15 ‒ 4] = 22 + 9 ⋅ [‒19] = 22 ‒ 171 = ‒149
b) [(‒25) ⋅ (‒11 + 45) ⋅ (‒9)] = [(‒25) ⋅ (+34) ⋅ (‒9)] =
= [(‒25) ⋅ (+34) ⋅ (‒9)] = +.7650
c) ‒8 ⋅ [(‒12) ⋅ (28 ‒ 4 ⋅ 10) + 15 ‒ 7 ⋅ 8] =
= ‒8 ⋅ [(‒12) ⋅ (28 ‒ 40) + 15 ‒ 56] =
= ‒8 ⋅ [(‒12) ⋅ (‒12) ‒ 41] = ‒8 ⋅ [(+144) ‒ 41] =
= ‒8 ⋅ [+103] = ‒824
20. (‒8) ⋅ 342 = (‒8) ⋅ 300 + (‒8) ⋅ 40 + (‒8) ⋅ 2 =
= ‒2400 ‒ 320 ‒ 16 = ‒.2736
21. a) (+12) : (+2) = (+6), pois (+6) ⋅ (+2) = (+12)
b) (‒36) : (‒9) = (+4), pois (+4) ⋅ (‒9) = (‒36)
c) (‒15) : (+15) = (‒1), pois (‒1) ⋅ (+15) = (‒15)
d) 0 : (+11) = (0), pois (0) ⋅ (+11) = (0)
e) (‒66) : (+33) = (‒2), pois (‒2) ⋅ (+33) = (‒66)
f) (‒369) : (‒3) = (+123), pois (+123) ⋅ (‒3) = (‒369)
22. a)

: (‒6) = +9; assim,

= ‒54, pois (‒6) ⋅ (+9) = ‒54
b) (+225) :

= ‒15; assim,

= ‒15, pois (+255) : (‒15) = ‒15
c)

: (‒12) = ‒16; assim,

= +192, pois (‒12) ⋅ (‒16) = +192
d) (+120) :

= ‒1; assim,

= ‒120, pois (+120) : (‒120) = ‒1
23. a) (+8)² = (+8) ⋅ (+8) = +64
b) (‒7)³ = (‒7) ⋅ (‒7) ⋅ (‒7) = ‒ 343
c) (‒5)4 = (‒5) ⋅ (‒5) ⋅ (‒5) ⋅ (‒5) = +625
d) (‒12)¹ = ‒12
e) (+.1000)0 = 1 (por definição)
f) (‒12)² = (‒12) ⋅ (‒12) = +144
24. a)
Sentença matemática: raiz quadrada de dezesseis igual a, início da raiz quadrada, quatro vezes quatro, final da raiz quadrada, igual a raiz quadrada de quatro ao quadrado igual a quatro.b) –
Sentença matemática: menos raiz quadrada de cento e quarenta e quatro igual a menos, raiz quadrada, abre parênteses, doze, fecha parênteses, elevado a dois, igual a menos doze.c)
Sentença matemática: raiz quadrada de quatrocentos, igual a raiz quadrada, abre parênteses, vinte, fecha parênteses, elevado a dois, igual a vinte.d) –
Sentença matemática: menos raiz quadrada de cento e vinte e um, igual a menos, raiz quadrada, abre parênteses, onze, fecha parênteses, elevado a dois, igual a menos onze.e) –
Sentença matemática: menos raiz quadrada de oitenta e um igual a menos raiz quadrada, abre parênteses, nove, fecha parênteses, elevado a dois, igual a menos nove.f)
Sentença matemática: raiz quadrada de quatrocentos e oitenta e quatro igual a raiz quadrada, abre parênteses, vinte e dois, fecha parênteses, elevado a dois igual a vinte e dois.25.
Sentenças matemáticas: abre chaves, abre colchetes, raiz quadrada de sessenta e quatro, mais, abre parênteses, três elevado a três menos dez, fecha parênteses, fecha colchetes, vezes raiz quadrada de cem, fecha chaves, menos raiz quadrada de novecentos igual, abre chaves, abre colchetes, oito mais, abre parênteses, vinte e sete menos dez, fecha parênteses, fecha colchetes, vezes dez, fecha chaves, menos trinta igual. Abaixo, igual a, abre chaves, abre colchetes, oito mais dezessete, fecha colchetes, vezes dez, fecha chaves, menos trinta igual a duzentos e vinte.
= {[8 + 17]⋅ 10} ‒30 = 220
26. A medida do comprimento será igual a raiz quadrada da medida da área, assim, temos:
Sentença matemática: raiz quadrada de cento e quarenta e quatro, igual a raiz quadrada, abre parênteses, doze, fecha parênteses, elevado a dois, igual a doze.Portanto, a medida do comprimento do lado será de 12 métros.
CAPÍTULO 2 – MÚLTIPLOS E DIVISORES
Trocando Ideias — página 55
Para que um ano seja bissexto, ele precisa ser múltiplo de 4 (ou seja, ser divisível por 4). Caso ele termine em 00, ele precisa ser divisível por 400. Vamos verificar caso a caso:
2000 termina em 00 e é divisível por 400, então é bissexto.
2021 não é divisível por 4.
2024 é divisível por 4 e não é terminado em 00, então é bissexto.
Semelhante ao ano citado anteriormente, 2028 é bissexto pelos mesmos motivos.
2033 não é bissexto por não ser divisível por 4.
2100 não é bissexto, pois, embora seja divisível por 4, termina em 00, mas não é divisível por 400, então, não é bissexto.
Assim, os anos bissextos são 2000, 2024 e 2028.
Atividades — página 57
1. a) Utilizando a sequência dos inteiros negativos, temos como exemplos:
3 × (‒1) = ‒3
3 × (‒2) = ‒6
3 × (‒3) = ‒9
3 × (‒4) = ‒12
3 × (‒5) = ‒15
b) Utilizando a sequência dos múltiplos de 3, temos como exemplos: ‒24; ‒18; 6; 12; 15; 18.
2. Semelhante ao que fizemos na seção “Trocando Ideias”, podemos verificar se os números atendem aos critérios necessários. Assim, temos:
a) 1822 não é múltiplo de 4, então, não é bissexto.
b) 1900 termina em 00, mas não é divisível por 400, então, não é bissexto.
c) 2000 é terminado em 00 e é divisível por 400; então, é bissexto.
d) 2118 não é bissexto, pois não é divisível por 4.
3. a) Verdadeira. ‒6, ‒3, ‒2, ‒1, 1, 2, 3 e 6, totalizando 8 divisores.
b) Verdadeira. Não é possível dividir nenhum número por zero.
c) Falsa.
d) Verdadeira. 1 é o menor valor possível dentre os naturais para realizar divisões, porque 0 não é divisor de nenhum número.
e) Falsa. ‒3 também pode ser dividido pelo próprio ‒3. Exemplo de correção: “‒3 é o menor divisor inteiro de ‒3”.
Observação — página 59
Para realizar a verificação, pode-se realizar a decomposição em fatores primos de 36 e 24, comparando com as decomposições de 18 e 12. Ao multiplicar por 2, adiciona-se um fator comum de 2 a cada número, assim, ao calcular o ême dê cê, multiplica-se por 2 devido à presença do novo fator. Pode-se sugerir aos estudantes que verifiquem também se o resultado é válido para multiplicação por 3 ou por 5, generalizando resultados.
Atividades — páginas 59 e 60
4. a) Divisores de 24: 1, 2, 3, 4, 6, 8, 12 e 24.
b) Divisores de 40: 1, 2, 4, 5, 8, 10, 20 e 40.
c) Observando ambas as listas, temos como divisores comuns 1, 2, 4 e 8.
d) Dos divisores do item c, o maior é o 8.
5. Espera-se que os estudantes concluam que o ême dê cê de dois números tais que um é divisor do outro é o próprio divisor.
6. Em cada par de números, o primeiro número é divisor do segundo, sendo assim, podemos tomá-lo como divisor comum.
a) ême dê cê(50, 100) = 50
b) ême dê cê(16, 80) = 16
c) ême dê cê(72, 216) = 72
d) ême dê cê(20, 100) = 20
7. Os fatores em comum são 2 e 3, assim, o ême dê cê será 2 ⋅ 3 = 6.
8. a) ême dê cê(64, 40)
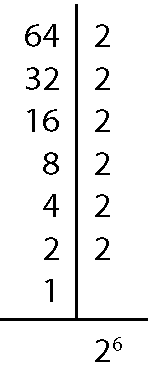
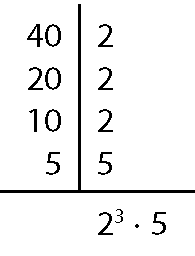
Assim, ême dê cê(64, 40) = 23 = 8
b) ême dê cê(80, 100, 120)
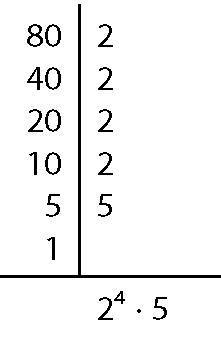
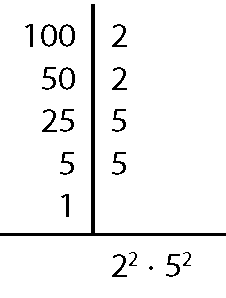
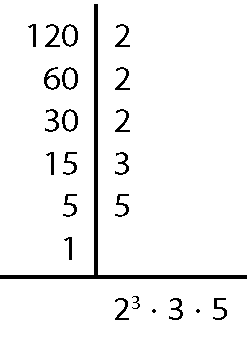
Assim, ême dê cê(80, 100, 120) = 22 ⋅ 5 = 20
c) ême dê cê(40, 70, 90)
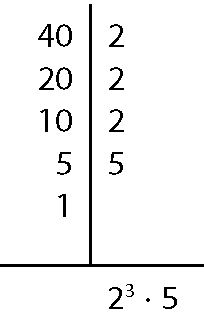
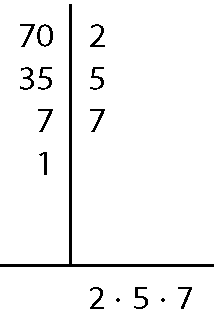
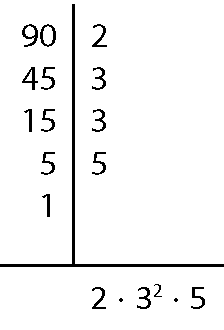
Assim, ême dê cê(40, 70, 90) = 2 ⋅ 5 = 10
d) ême dê cê(576, 96)
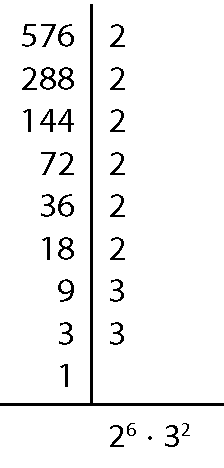
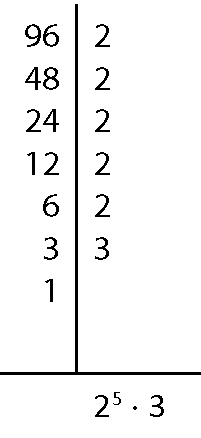
Assim, ême dê cê(576, 96) = 25 ⋅ 3 = 96.
9. a) 4 e 5 são primos entre si, pois ême dê cê(4, 5) = 1.
b) 16 e 25 são primos entre si, pois ême dê cê(16, 25) = 1.
c) 15 e 21 não são primos entre si, pois ême dê cê(15, 21) = 3.
d) 18 e 42 não são primos entre si, pois ême dê cê(18, 42) = 6.
10. a) Será 1, já que dois números consecutivos não possuem fatores em comum, exceto o 1.
b) Será 1, já que os quadrados perfeitos consecutivos não têm fatores em comum, exceto o 1.
11. O único fator comum entre os dois será o próprio 28, então, o ême dê cê será 28.
12. Se multiplicarmos dois números por um fator, o ême dê cê também se multiplica por esse fator; o mesmo ocorre na divisão: se dividirmos os valores por 3, o ême dê cê também será dividido, assim 18 : 3 = 6.
Atividades – páginas 62 e 63
13. Seguindo a sequência dos múltiplos por meio da multiplicação pelos naturais, temos:
a) Múltiplos de 15: (0, 15, 30, 45, 60, reticências)
b) Múltiplos de 20: (0, 20, 40, 60, 80, reticências)
c) Múltiplos comuns de 15 e 20: (0, 60, 120, 180, 240, reticências)
d) Mínimo múltiplo comum de 15 e 20: 60.
14. Espera-se que os estudantes concluam que o ême ême cê de dois números tais que um é múltiplo do outro é o próprio múltiplo.
15. Em cada par de números, o segundo número é múltiplo do primeiro, assim, podemos tomá-lo como múltiplo comum.
a) 6
b) 20
c) 45
d) 100
16. O ême ême cê será o produto de todos os fatores que aparecem, com o maior expoente. Temos então: ême ême cê = 23 ⋅ 3 ⋅ 5 ⋅ 7 = 840
17. Aplicando a decomposição simultânea dos trios:
a) ême ême cê(18, 27, 45)

ême ême cê(18, 27, 45) = 270
b) ême ême cê(18, 30, 48)

ême ême cê(18, 30, 48) = 720
c) ême ême cê(120, 132, 20)

ême ême cê(150, 300, 375) = .1320
d) ême ême cê(150, 300, 375)

ême ême cê(150, 300, 375) = .1500
18. Como temos números primos, a decomposição simultânea deles não exibirá fatores comuns; sendo assim, o ême ême cê será o seu produto.
19. Utilizando a decomposição simultânea, temos:
a)
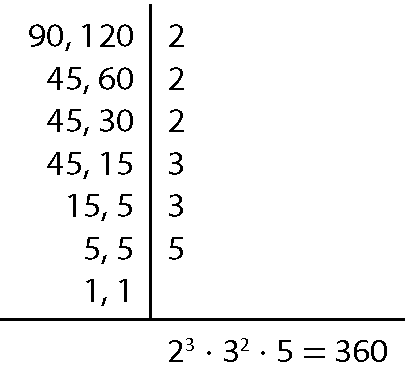
ême ême cê(90, 120) = 360
b)

ême ême cê(45, 54, 72) = .1080
c)

ême ême cê(120, 300, 450) = .1800
d)
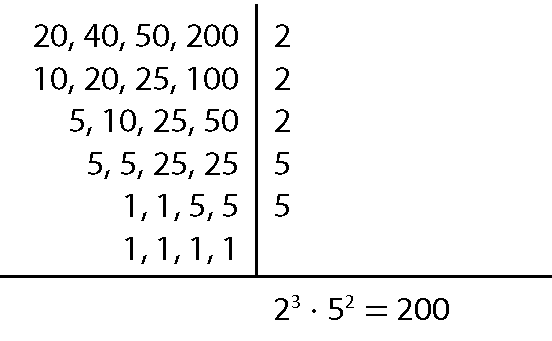
ême ême cê(20, 40, 50, 200) = 200
20. Espera-se que os estudantes concluam que o produto dos números e o produto do ême dê cê com o mmc desses números são iguais.
21. a) Para 12 e 15:
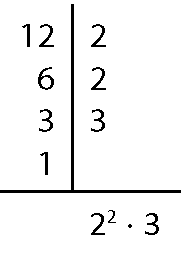
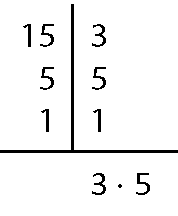
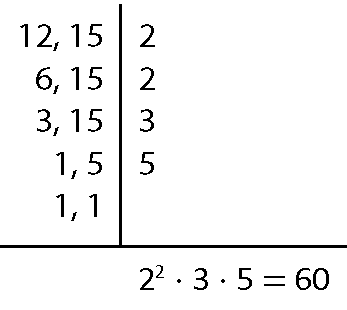
12 ⋅ 15 = 180; ême dê cê(12, 15) = 3; ême ême cê(12, 15) = 60; produto entre o ême ême cê e o ême dê cê = 3 ⋅ 60 = 180.
b) Para 48 e 16:
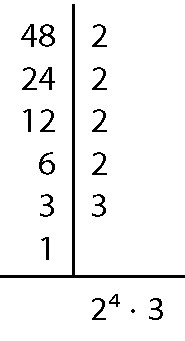
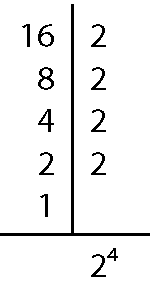
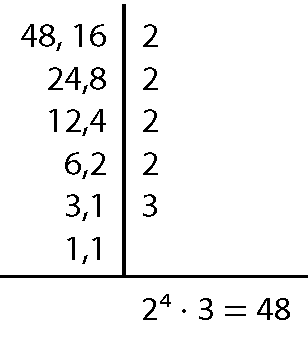
48 ⋅ 16 = 768; ême dê cê(48, 16) = 16, ême ême cê(48, 16) = 48; produto entre o ême ême cê e o ême dê cê = 16 ⋅ 48 = 768.
c) Para 11 e 121:
11 é primo, e 121 = 112; assim:
11 ⋅ 121 = .1331; ême dê cê(11, 121) = 11; ême ême cê(11, 121) = 121; produto entre o ême ême cê e o ême dê cê = 11 ⋅ 121 = .1331.
d) Para 36 e 49:
36 = 62 = (2 ⋅ 3)2 = 22 ⋅ 32 e 49 = 72, portanto:
36 ⋅ 49 = .1764; ême dê cê(36, 49) = 1; ême ême cê(36, 49) = .1764; produto entre o ême ême cê e o ême dê cê = 1 ⋅ .1764 = .1764.
22. Sabemos que o produto entre dois números naturais é igual ao produto entre o ême ême cê e o ême dê cê dos mesmos números. Assim, ême ême cê ⋅ ême dê cê = 24 ⋅ 504 = .12096; para determinar o número desconhecido, basta dividir esse valor por 168; sabendo que .12096 : 168 = 72, então, o outro número é o 72.
23. Calculando o mínimo múltiplo comum entre os tempos dos semáforos, temos:

Dessa fórma, os semáforos ficam verdes ao mesmo tempo a cada 600 segundos, ou a cada 10 minutos (600 segundos : 60). Assim, o próximo horário em que os semáforos ficarão verdes simultaneamente será às 18 horas 10.
24. Exemplo de resposta: “Cláudia, ao perceber que comprou um pacote no dia em que as três embarcações estão ancoradas no porto, pediu para realizar a troca para um dia diferente. Em quantos dias as embarcações estarão novamente juntas, ancoradas no porto?”.
25. Os navios vão sair juntos nos dias que são múltiplos comuns de 8, 12 e 18. O próximo dia que eles partirão juntos será o mmc entre eles:
ême ême cê(8, 12, 18) = 72, portanto, os navios partirão juntos novamente daqui a 72 dias.
26. Júlia precisará visitar as três cidades novamente em uma quantidade de dias que será um múltiplo das três frequências (10, 30 e 50). Assim, se ême ême cê(10, 30, 50) = 150, ela visitará as três cidades após 150 dias, ou seja, 5 meses após março, em agosto.
Resolvendo em equipe — página 64
Espera-se que os estudantes determinem que o número de ingressos que cada escola receberá representa o ême dê cê entre 320 e 400: ême dê cê(320, 400) = 80, ou seja, 80 ingressos. Os 400 ingressos para assistir à sessão vespertina serão distribuídos entre 5 escolas, e os 320 ingressos para assistir à sessão noturna serão distribuídos entre 4 escolas, totalizando 9 escolas escolhidas.
Revisão dos conteúdos deste capítulo — página 65
1. a) Exemplo de resposta: ‒30; ‒25; ‒20; ‒15; ‒10.
b) Exemplo de resposta: ‒15, ‒10, ‒5, 5, 10.
2. a) ‒12, ‒9, ‒6, ‒3, 0, 3, 6 e 9.
b) ‒14, ‒7, 0, 7, 14, 21 e 28.
3. a) 1, 2, 3, 4, 6 e 12
b) 1, 2, 3, 6, 9 e 18
c) 1, 2, 3 e 6
d) 6
4. a) 0, 25, 50, 75, 100, reticências
b) 0, 50, 100, 150, 200, reticências
c) 0, 50, 100, reticências
d) 50
5. a)
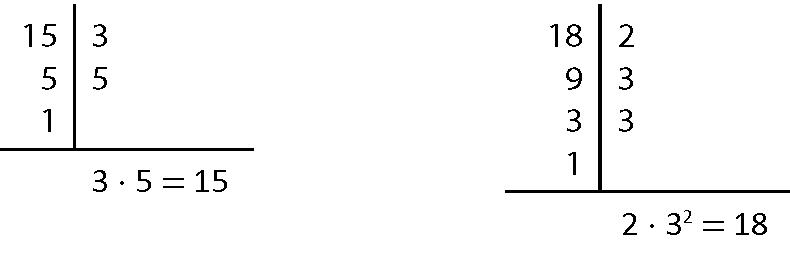
ême dê cê(18, 15) = 3
b)
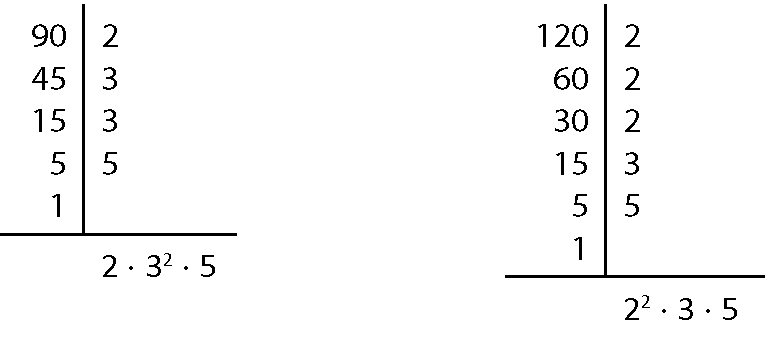
ême dê cê(90, 120) = 2 ⋅ 3 ⋅ 5 = 30
c)
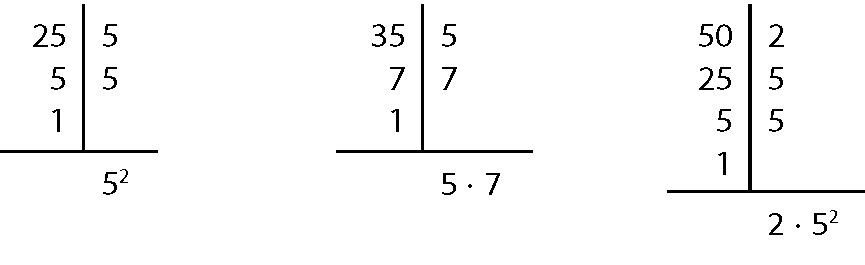
ême dê cê(25, 35, 50) = 5
d)
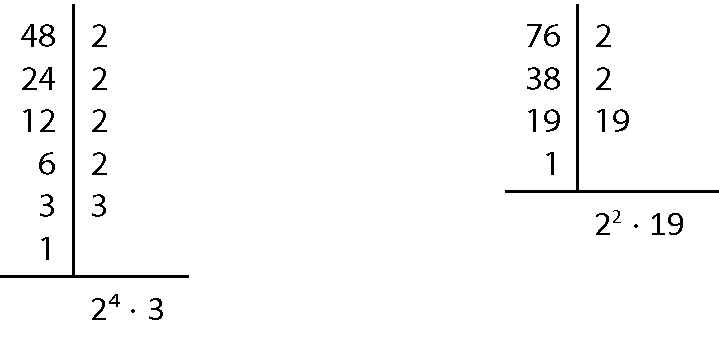
ême dê cê(48, 76) = 22 = 4
e)
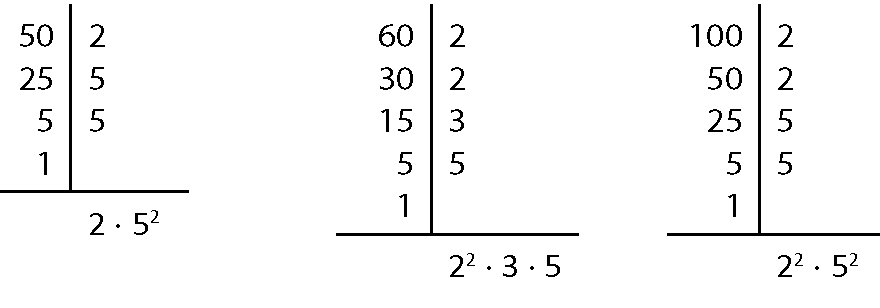
ême dê cê(50, 60, 100) = 2 ⋅ 5 = 10
f)
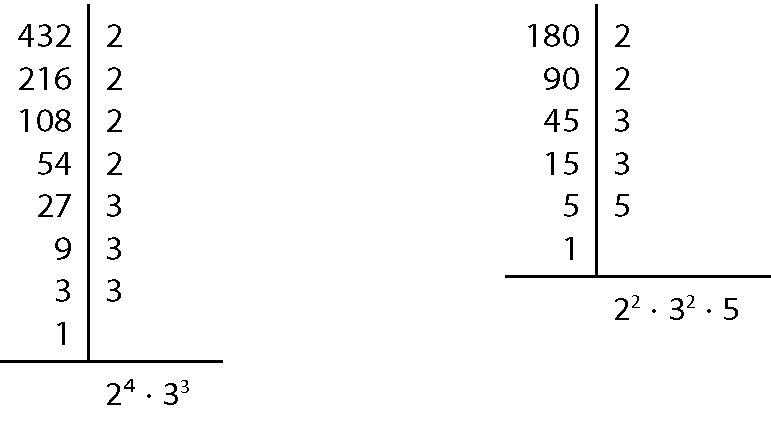
ême dê cê(432, 180) = 22 ⋅ 32 = 36
6. a)

ême ême cê(25, 40) = 200
b)

ême ême cê(38, 24) = 456
c)

ême ême cê(18, 30, 56) = 2 520
d)

ême ême cê(36, 124) = 1 116
e)
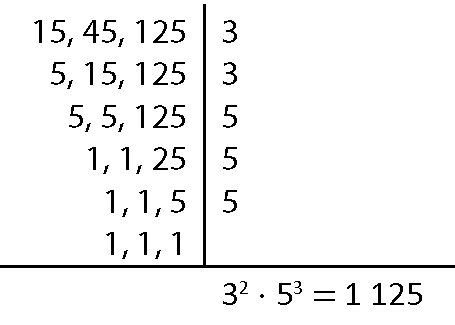
ême ême cê(15, 45, 125) = 1 125
f)
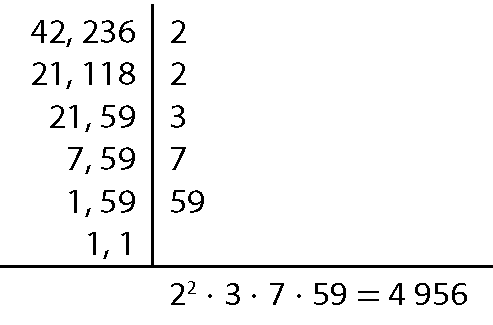
ême ême cê(42, 236) = 4 956
7. É possível que 3 pessoas joguem, pois 21 e 18 são divisíveis por 3, mas 6 pessoas não, pois 21 não é divisível por 6.
8. Como o máximo divisor comum entre 15 e 21 é 3, cada pedaço de tecido terá 3 métros.
9. Observando os múltiplos de 3 e 5 entre 25 e 50, temos:
27, 30, 33, 35, 36, 39, 40, 42, 45, 48.
Se contarmos de 5 em 5 sobram 3, os resultados podem ser: 28, 33, 38, 43, 48. Eliminando os múltiplos de 3, temos como possibilidades 28, 38 e 43. Se contarmos de 3 em 3 sobram 2, a única possibilidade das listadas é 38. Assim sendo, há 38 pessoas na fila.
CAPÍTULO 3 – RETAS E ÂNGULOS
Trocando ideias — página 66
• As linhas de divisão contínua e dupla contínua lembram partes de retas paralelas.
• As linhas seccionadas lembram segmentos de reta.
Página 68
1. Espera-se que os estudantes consigam identificar na imagem ruas que estejam lado a lado e não se cruzem em nenhum ponto, bem como ruas que acabem se cruzando de alguma fórma e nomeiem corretamente o que observam usando os termos “paralela” e “concorrente”.
Atividades — página 69
1. a) Os pares de retas paralelas são: aêbê; c e d.
b) Os pares de retas concorrentes encontradas na imagem são: aêcê; aêdê; aêê; b e c; b e d; bêêê; d êê (apesar de que, neste caso específico, a intersecção não seja representada).
2. Os pares de retas perpendiculares são: vê e r; u e s; u e t.
3. Espera-se que os estudantes utilizem o algoritmo proposto para construção de retas paralelas, elaborando uma reta, um ponto e a paralela que passa por esse ponto. Um exemplo de resposta é dado a seguir:
4.
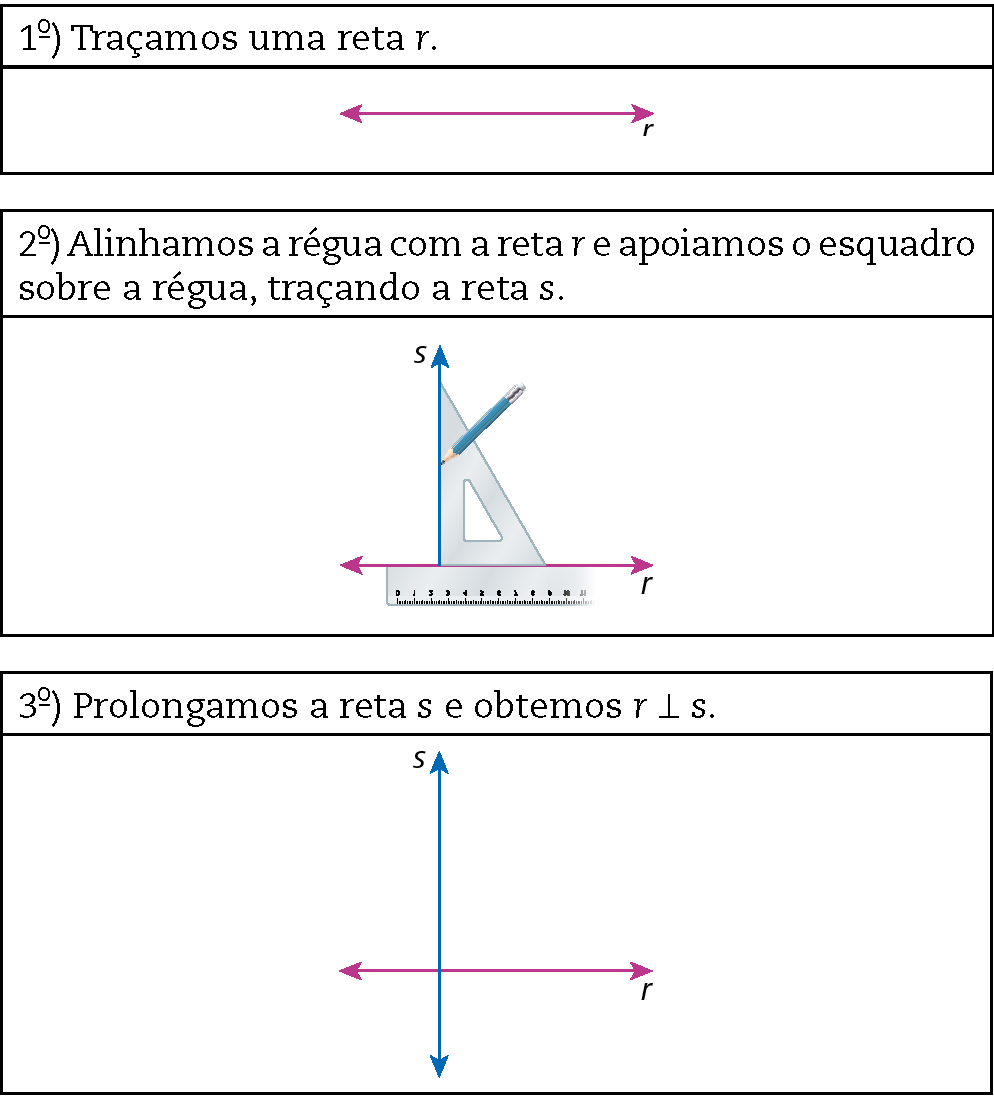
Lendo e aprendendo — Atividades — página 71
1. a) Além de traços geométricos, pode ser representada por figuras simbólicas de animais como pássaros, peixes ou répteis.
b) Expressar seus valores culturais e podem ser relacionadas com fórça, autenticidade e valores de suas nações.
c) Frutos de cores fortes, como o urucum e o jenipapo, além de carvão.
2. A alternativa a é a correta, pois duas linhas que se encontram e não formam ângulos retos são retas concorrentes.
3. Espera-se que os estudantes criem padrões artísticos como os exemplos das imagens a partir do padrão de repetição.
4. Espera-se que os estudantes vejam como a cultura que temos hoje em nosso dia a dia foi fundamentalmente formada, entre outras culturas, pelos povos originários brasileiros. Isso é visto na culinária com base na mandioca, em muitas palavras usadas em nosso cotidiano (formação de nossa língua), grande parte das rotas das estradas que temos que eram essencialmente os caminhos que os indígenas faziam em épocas de migração, influências em nossa agricultura etcétera.
Atividades — página 73
5. a) ângulo:
Ângulo AOBou
Ângulo BOA; vértice: óh; lados:
Letras OA maiúsculas com seta para a direita acima.e
Letras OB maiúsculas com seta para a direita acima.b) ângulo:
Ângulo RSTou
Ângulo TSR; vértice: S; lados:
Letras SR maiúsculas com seta para a direita acima.e
Letras ST maiúsculas com seta para a direita acima.c) ângulo:
Ângulo ABCou
Ângulo CBA; vértice: B; lados:
Letras BA maiúsculas com seta para a direita acima.e
Letras BC maiúsculas com seta para a direita acima.d) ângulo:
Ângulo PQRou
Ângulo RQP; vértice: Q; lados:
Letras QP maiúsculas com seta para a direita acima.e
Letras QR maiúsculas com seta para a direita acima.6. Um exemplo de desenho que pode ser realizado é dado a seguir:
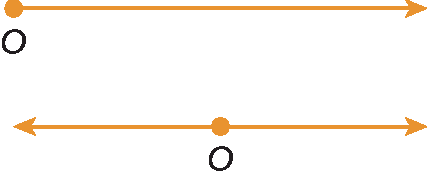
a) Sim. Ambas são compostas por semirretas. No caso do ângulo raso, a união das semirretas fórma uma reta.
b) Os lados do ângulo raso e do ângulo nulo têm a mesma reta suporte.
c) Os lados do ângulo raso não são coincidentes; já os lados do ângulo nulo são.
Atividades — página 78
7. Utilizando as notações indicadas, temos:
a) 60graus
b) 90graus
c) 102graus 35minutos
d) 110graus 32minutos 48segundos
8. Conforme as medições, temos:
a)
medida do ângulo GOF é igual a 30 grausb)
medida do ângulo GOE é igual a 50 grausc)
medida do ângulo DOC é igual a 20 grausd)
medida do ângulo GOD é igual a 70 grause)
medida do ângulo AOD é igual a 90 grausf)
medida do ângulo AOB é igual a 110 grausg)
medida do ângulo COF é igual a 60 graush)
medida do ângulo AOG é igual a 160 graus9. Conforme as medições, temos:
a) 45graus
b) 40graus
c) 100graus
d) 110graus
e) 135graus
f) 170graus
10. a)
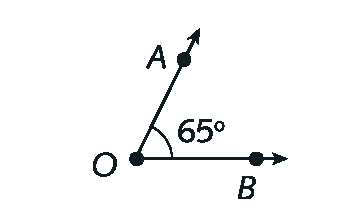
Agudo, já que mede menos de 90graus.
b)
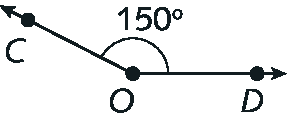
Obtuso, já que mede mais de 90graus.
c)
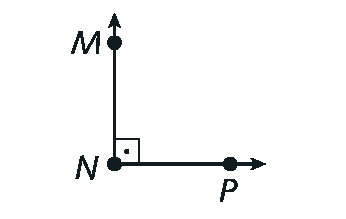
Reto, já que mede 90graus.
d)
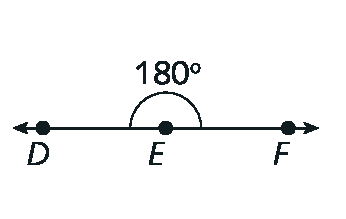
Raso, já que mede 180graus.
11. Para construção dos ângulos, é interessante usar o que foi explanado na seção “Construção de alguns ângulos com um par de esquadros”. Em cada item está indicada a soma dos ângulos notáveis que podem ser utilizados para a construção:
a)
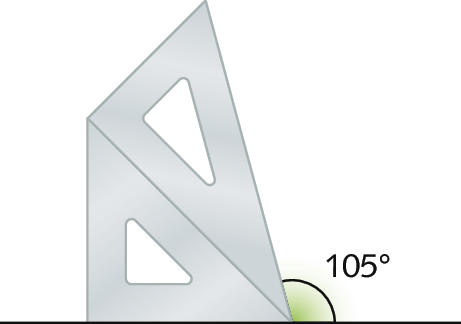
b) Um exemplo: 30graus + 30graus + 90graus = 150graus; outro exemplo: 180graus ‒ 30graus = 150graus (ver figura)

c) Um exemplo: 60graus + 60graus = 120graus; outro exemplo: 180graus ‒ 60graus = 120graus (ver figura)
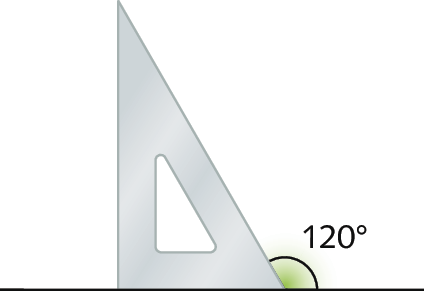
d) Um exemplo: 90graus + 45graus = 135graus; outro exemplo: 180graus ‒ 45graus = 135graus (ver figura)
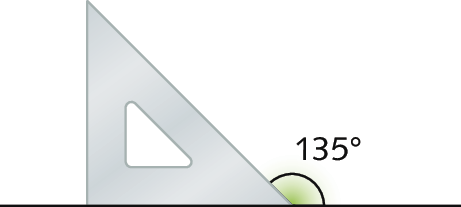
e) Um exemplo: 90graus+ 45graus + 30graus = 165graus (ver figura)
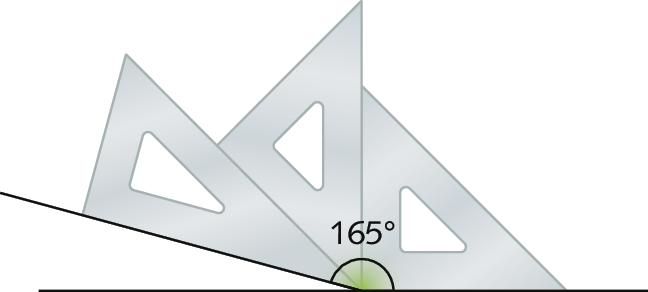
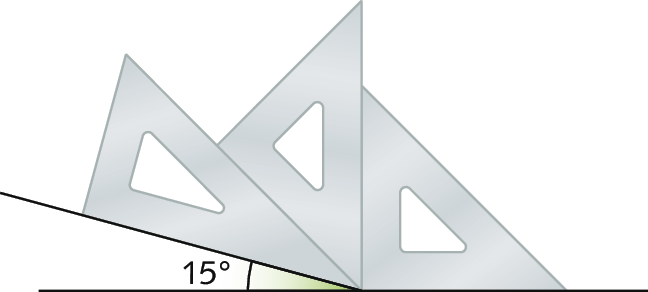
f) 45graus ‒ 30graus = 15graus, conforme o Livro do estudante; outro exemplo: 180graus ‒ 165graus (ver figura)