Página 104

Unidade 2

Capítulo 4 Frações

Capítulo 5 Números racionais

Capítulo 6 Linguagem algébrica e regularidades

Fotografia. Imagem de prédios e casas à beira de um cais. No centro da fotografia, há três prédios de madeira com 4 andares e telhados pontiagudos similares ao de casas. O prédio à esquerda é marrom com telhado marrom avermelhado, janelas brancas e um letreiro escrito "jebsens". O prédio do meio é amarelo com telhado marrom avermelhado e janelas brancas. O prédio à direita é vermelho com telhado marrom escuro e janelas cinza. Em frente aos prédios há um ponto de transporte público. Os prédios e o ponto estão acima do nível da água, sendo possível ver na lateral do cais pneus de carros fixados na parede. A água reflete as cores dos prédios. Ao fundo, há vários telhados pontiagudos de casas e prédios, indicando uma inclinação do terreno. — Cidade de Bergen, na Noruega. Foto de 2020. A Noruega ocupava a 1ª colocação no ranking do Índice de Desenvolvimento Humano (í dê agá) de países em 2019, com nota 0,957. As notas variam de 0 a 1. O que esse índice avalia? Qual é a diferença entre 1 e o índice obtido pela Noruega? Ao final desta Unidade, você responderá essas e outras questões.

Respostas e comentários

Abertura da Unidade

Bê êne cê cê:

• Competência geral 9 (a descrição está na página seis).

• Competência específica 8 (a descrição está na página sete).

Objetivos:

• Motivar os estudantes a estudar os conteúdos da Unidade 2.

• Levantar os conhecimentos prévios dos estudantes sobre a representação decimal de números racionais.

• Verificar as estratégias empregadas pelos estudantes na subtração com números racionais.

• Verificar se os estudantes conhecem o Índice de Desenvolvimento Humano (í dê agá).

Pergunte aos estudantes se já ouviram falar sobre o í dê agá (Índice de Desenvolvimento Humano). Reserve um tempo para escutá-los. Promova uma discussão, perguntando o que eles acham que seria interessante considerar para medir o desenvolvimento humano. Depois, explique que o í dê agá avalia indicadores da saúde (expectativa de vida), da educação (anos de escolaridade de adultos e expectativa de anos de escolaridade para crianças) e de renda (Renda Nacional Bruta). Momentos como esse, em que o diálogo e a interação entre os estudantes são incentivados, favorecem o desenvolvimento da competência geral 9 e da competência específica 8 da Bê êne cê cê.

Explore com os estudantes a leitura e o valor dos algarismos do número 0,957. Espera-se que alguns deles percebam que o algarismo 7, que ocupa a terceira casa à direita da vírgula, representa 7 milésimos; que o algarismo 5 representa 5 centésimos; e que o algarismo 9, que ocupa a primeira casa à direita da vírgula, representa 9 décimos. Caso alguns tenham dificuldades, recorde as representações de números na fórma decimal em um quadro de ordens. Amplie a discussão para outros números, caso julgue pertinente.

Uma das questões propostas exige o cálculo de 1 ‒ 0,957. Neste primeiro momento, deixe os estudantes à vontade para empregar a estratégia que preferirem. Você não precisa esgotar o trabalho com esse cálculo agora, pois esta mesma pergunta será retomada na seção É hora de extrapolar ao final desta Unidade.

No capítulo 4, será aprofundado o estudo sobre frações e, no capítulo 5, o foco será estudar os números racionais e suas operações. No capítulo 6, os estudantes vão ampliar seus conhecimentos sobre a linguagem algébrica, que utiliza letras para representar valores desconhecidos na resolução de problemas e na representação de regularidades.

Ao final desta Unidade, na seção É hora de extrapolar, os estudantes vão pesquisar sobre o í dê agá, confeccionar uma reportagem sobre Índice de Desenvolvimento Humano Municipal (i dê agá ême) e apresentá-la no formato de um jornal.

Página 105

Capítulo 4 Frações

Trocando ideias

Para que a tarefa de lavar roupas seja rápida e efetiva, é preciso planejar bem cada etapa. Observe o infográfico a seguir.

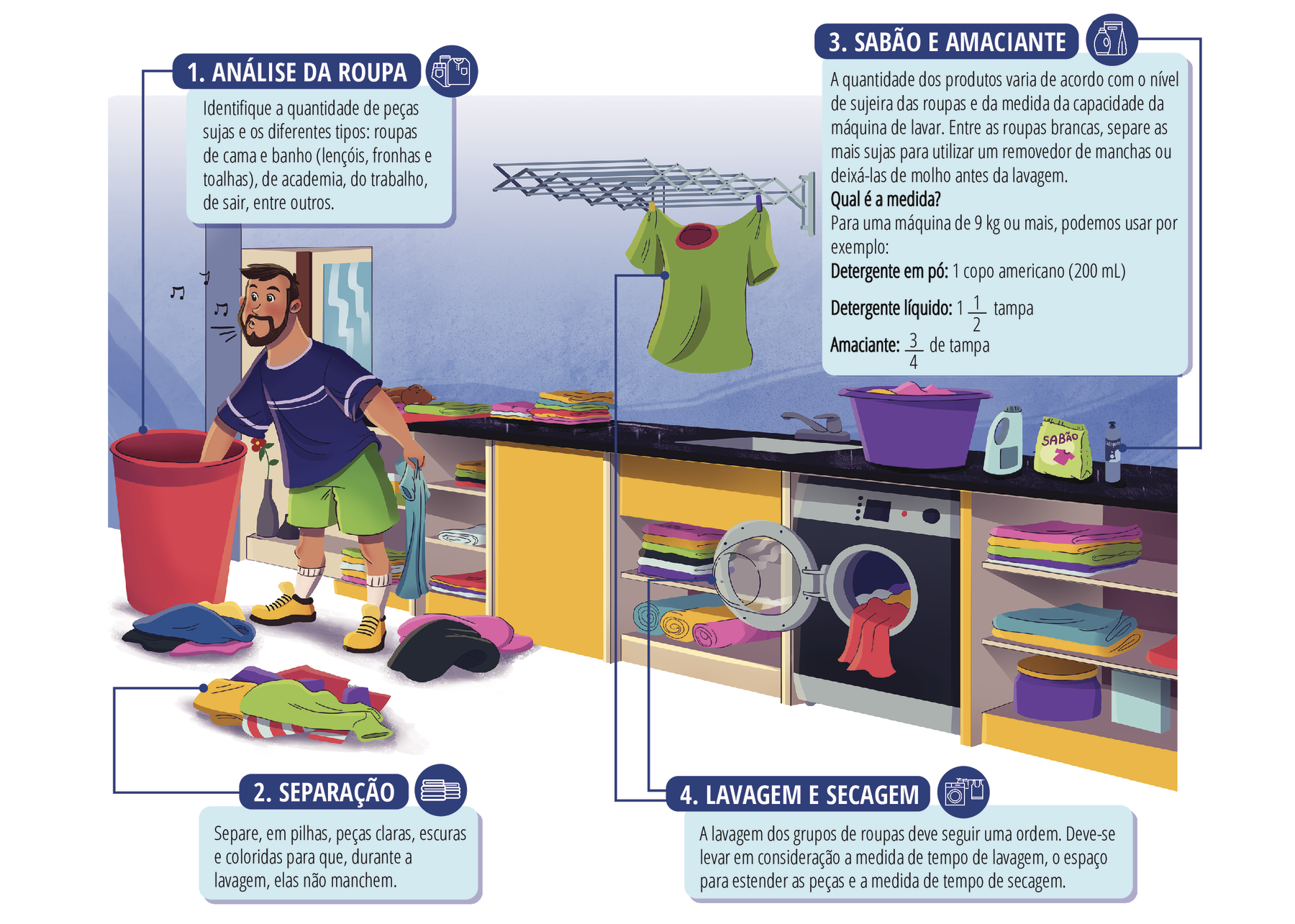
Infográfico. À esquerda, homem branco de cabelo castanho, barba castanha, camiseta roxa e bermuda verde está segurando uma peça de roupa com uma mão e a outra mão está dentro de um cesto vermelho. Ele está em uma lavanderia. No chão à sua frente, há três pilhas de roupas. Atrás do homem há um varal de parede com uma camiseta verde pendurada e uma bancada com roupas dobradas, produtos de limpeza de roupas e uma máquina de lavar com porta aberta. Há quatro quadros indicando as etapas das ações. Primeiro quadro associado à pilha de roupas no chão: ANÁLISE DA ROUPA. Identifique a quantidade de peças sujas e os diferentes tipos: roupas de cama e banho (lençóis, fronhas e toalhas), de academia, do trabalho, de sair, entre outros. Segundo quadro associado ao cesto vermelho: SEPARAÇÃO. Separe, em pilhas, peças claras, escuras e coloridas para que, durante a lavagem, elas não manchem. Terceiro quadro associado aos produtos de limpeza de roupas: SABÃO E AMACIANTE. A quantidade dos produtos varia de acordo com o nível de sujeira das roupas e da medida da capacidade da máquina de lavar. Entre as roupas brancas, separe as mais sujas para utilizar um removedor de manchas ou deixá-las de molho antes da lavagem. Qual é a medida? Para uma máquina de 9 quilogramas ou mais, podemos usar por exemplo: Detergente em pó: 1 copo americano entre parênteses (200 mililitros) Detergente líquido: fração mista uma e meia tampa. Amaciante: fração 3 sobre 4 de tampa. Quarto quadro associado ao varal e à máquina de lavar: LAVAGEM E SECAGEM. A lavagem dos grupos de roupas deve seguir uma ordem. Deve-se levar em consideração a medida de tempo de lavagem, o espaço para estender as peças e a medida de tempo de secagem.

▸

Você consegue fazer a ordenação de alguma outra situação cotidiana? Explique para os colegas.

▸

A quantidade de amaciante utilizada para lavar as roupas em uma máquina de 9 quilogramas ou mais é maior ou menor do que a quantidade de detergente líquido?

Neste capítulo, aprofundaremos as ideias relacionadas ao conceito de fração e veremos como ordenar frações.

Respostas e comentários

Trocando ideias: primeiro item: resposta pessoal; segundo item: menor.

CAPÍTULO 4 – FRAÇÕES

Trocando ideias

Bê êne cê cê:

• Competências gerais 4 e 9 (as descrições estão na página seis).

• Competências específicas 6 e 8 (as descrições estão na página sete).

• Habilidades ê éfe zero sete ême ah zero cinco e ê éfe zero sete ême ah zero sete.

Objetivos:

• Verificar se os estudantes recordam a ideia de fração como parte de um todo.

• Verificar se os estudantes recordam a ideia de número misto.

• Explorar a noção intuitiva de pensamento computacional.

A proposta deste Trocando ideias é trabalhar intuitivamente com o pensamento computacional. Nele, é apresentado um infográfico que mostra a sequência de etapas a serem cumpridas para lavar roupas. Se achar conveniente, proponha aos estudantes que elaborem o fluxograma correspondente ao processo apresentado. Considere o exemplo a seguir:

[Fluxograma] 6 quadros em sequência, separados por setas. Primeiro quadro: início. Segundo quadro: análise da roupa. Terceiro quadro: separação da roupa. Quarto quadro: sabão e amaciante. Quinto quadro: lavagem e secagem. Sexto quadro: fim.

Depois, reserve um momento para que os estudantes conversem sobre a questão proposta no primeiro item. Amplie a discussão e peça a alguns deles que representem na lousa o fluxograma correspondente ao processo que mencionaram.

Para explorar a primeira questão, deixe que troquem ideias e que exponham opiniões e vivências.

A segunda questão mobiliza a ideia de fração como parte de um todo, conceito de número misto e a comparação de frações. Após responderem, peça que justifiquem suas respostas.

A mobilização da linguagem verbal e de fluxogramas contribui para o desenvolvimento da competência geral 4 e a competência específica 6. A competência geral 9 e a competência específica 8 também têm os seus desenvolvimentos favorecidos, uma vez que o diálogo e a interação entre os estudantes são incentivados.

(EF07MA05) Resolver um mesmo problema utilizando diferentes algoritmos.

(EF07MA07) Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas.

Página 106

1 Ideias associadas às frações

Neste capítulo, vamos retomar e estudar algumas ideias associadas às frações.

A ideia de parte de um inteiro

Uma fração pode representar a ideia de parte de um inteiro. Observando a situação a seguir, temos que a medida do comprimento de três lápis equivale à medida do comprimento do caderno. Assim:

Ilustração. Imagem representada de cima para baixo de um menino de cabelo castanho claro sentado de frente para uma mesa com um caderno e lápis azul ao lado do caderno, com seu final alinhado com o canto inferior direito do caderno. Ao longo da lateral do caderno, a imagem do lápis se repete três vezes, uma após a outra, sendo as duas de cima com cor mais opaca. A ponta do terceiro lápis coincide com o canto superior direito do caderno. O menino fala: A medida do comprimento do lápis é a fração 1 sobre 3 da medida do comprimento do caderno.
Esquema. À esquerda, a fração um sobre três, com uma seta amarela amarela apontando para a expressão, lemos: um terço.

Agora, em um novo exemplo, vamos analisar a fração

\frac{2}{5}

(lemos: “dois quintos”).

Essa fração indica que o inteiro foi dividido em 5 partes iguais e que consideramos duas dessas 5 partes.

O denominador indica em quantas partes iguais o inteiro foi dividido, e o numerador indica quantas partes do inteiro nos interessam, ou seja, na fração

\frac{2}{5}

, o 5 é o denominador e o 2 é o numerador.

Podemos representar a fração

\frac{2}{5}

de várias formas. Analise duas delas.

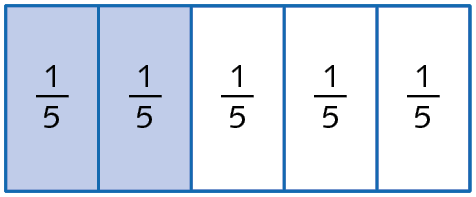
Figura geométrica. Retângulo dividido em cinco retângulos iguais. Em cada parte tem-se a fração 1 quinto. As duas partes da esquerda estão pintadas de azul, e as três da direita têm fundo branco.

O inteiro foi representado pelo retângulo, que foi dividido em 5 partes iguais. As partes do inteiro que interessavam foram coloridas de azul (duas das 5 partes).

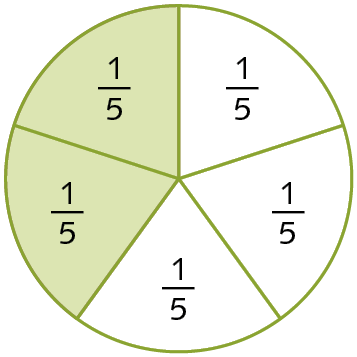
Figura geométrica. Círculo dividido em cinco fatias iguais, semelhante a uma pizza. Em cada parte tem-se a fração 1 quinto. Duas partes estão pintadas de verde, e as três restantes têm fundo branco.

O inteiro foi representado pelo círculo, que foi dividido em 5 partes iguais. Assim, 2 das 5 partes foram coloridas de verde.

Podemos usar as frações para representar partes de inteiros de diferentes tipos. Acompanhe as situações a seguir.

Respostas e comentários

Ideias associadas às frações

Bê êne cê cê:

• Competência geral 3 (a descrição está na página seis).

• Competências específicas 2, 6 e 8 (as descrições estão na página sete).

• Habilidades ê éfe zero sete ême ah zero oito e ê éfe zero sete ême ah zero nove.

Objetivo:

Compreender as diferentes ideias de fração: parte de um inteiro, quociente, razão e operador.

Justificativa

As frações são utilizadas em diferentes situações do cotidiano. Explorar essa representação possibilita aos estudantes lidarem com maior flexibilidade e segurança com números inteiros e não inteiros. Além disso, a compreensão dessas ideias favorece o desenvolvimento das habilidades ê éfe zero sete ême ah zero oito e ê éfe zero sete ême ah zero nove.

Mapeando conhecimentos

Para mapear os conhecimentos prévios dos estudantes sobre as diferentes ideias de fração, proponha os seguintes questionamentos para eles:

• Uma torta foi dividida em 5 partes iguais e alguém comeu 2 pedaços. Que fração da torta essa pessoa comeu? (Resposta:

\frac{2}{5}

• Em uma confraternização foram distribuídos 3 rocamboles para 9 crianças. Quanto de rocambole cada pessoa recebeu aproximadamente? (Resposta:

\frac{3}{9}

do rocambole ou

\frac{1}{3}

do rocambole).

• Quanto é um terço de 6 ovos? (Resposta: 2 ovos).

• Em uma árvore há 4 pássaros azuis e 9 pássaros amarelos. Qual é a razão entre o número de pássaros azuis e amarelos? (Resposta:

\frac{4}{9}

Para as aulas iniciais

Retome as situações da dinâmica inicial e discuta com a turma a diferença entre cada uma. Incentive os estudantes a darem outros exemplos de situações em que as frações são utilizadas com as ideias de parte de um inteiro, quociente, razão e operador.

Considere também pedir que recordem o conteúdo de frações presente na seção Revisão dos conteúdos de anos anteriores. Realize com eles as atividades de 32 a 36 e tire as eventuais dúvidas.

A ideia de parte de um inteiro

Antes de iniciar a explicação do conteúdo, relembre o nome das partes de uma fração (numerador e denominador). Se julgar interessante, relembre também a leitura das frações de acordo com os denominadores.

Comente com os estudantes que as partes do todo devem ser sempre equivalentes, ou seja, devem ser do mesmo tamanho.

(EF07MA08) Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.

(EF07MA09) Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração

\frac{2}{3}

para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.

Página 107

Situação 1

Gabriela tem que escolher

\frac{2}{5}

de 15 maçãs. Quantas maçãs Gabriela vai escolher?

Ilustração. Menina branca de cabelo castanho, liso, com franja, sua blusa é roxa e ela olha para 15 maçãs dispostas em 3 fileiras e cinco colunas.

Em vez de uma única maçã, nessa situação o inteiro é representado pelo total de maçãs. Para considerar

\frac{2}{5}

dessas maçãs, podemos, por exemplo, selecionar duas das cinco colunas de maçãs, como indicado a seguir.

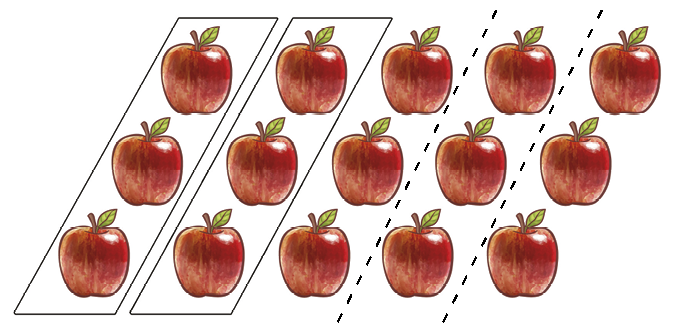
Ilustração. 15 maçãs dispostas em 5 colunas com três maçãs cada. Duas colunas da esquerda com 3 maçãs cada estão destacadas com um retângulo em volta de cada coluna. As colunas restantes estão separadas por linhas tracejadas.

Poderíamos selecionar

\frac{2}{5}

das maçãs mesmo se não estivessem organizadas em colunas.

Ilustração. 15 maçãs divididas em cinco grupos de 3 maçãs cada, com linhas tracejadas ao redor de cada grupo. As maçãs estão dispostas de forma desordenada e os grupos de três maçãs não forma colunas. Os dois grupos mais à esquerda têm fundo tracejado, enquanto os três restantes têm fundo branco.

Portanto, Gabriela vai escolher 6 maçãs

(\frac{2}{5} d e 15 m a ç ã s)

Situação 2

Vamos considerar que uma pizza foi dividida em 8 pedaços iguais e que

\frac{1}{4}

foi consumido. Essa situação pode ser representada pela seguinte figura.

Ilustração. Pizza dividida em 8 pedaços iguais. Dois pedaços estão faltando na pizza, um à direita, na parte de cima, e outro à esquerda, na parte de baixo da imagem.

Parte consumida da pizza:

\frac{1}{4} = \frac{2}{8}

Nesse caso, uma pizza é considerada como o inteiro.

Respostas e comentários

Comente que, quando a fração está relacionada à parte de um todo, esse todo pode ser uma grandeza discreta (situação 1), por exemplo, uma quantidade de objetos, de pessoas, de dinheiro etcétera ou uma grandeza contínua (situação 2), como a medida de massa de um produto, a medida de comprimento de uma barra etcétera

Página 108

Lembre-se: Escreva no caderno.

Agora, vamos considerar duas pizzas como o inteiro, mas novamente

\frac{1}{4}

foi consumido. Assim, temos a seguinte possibilidade de representação.

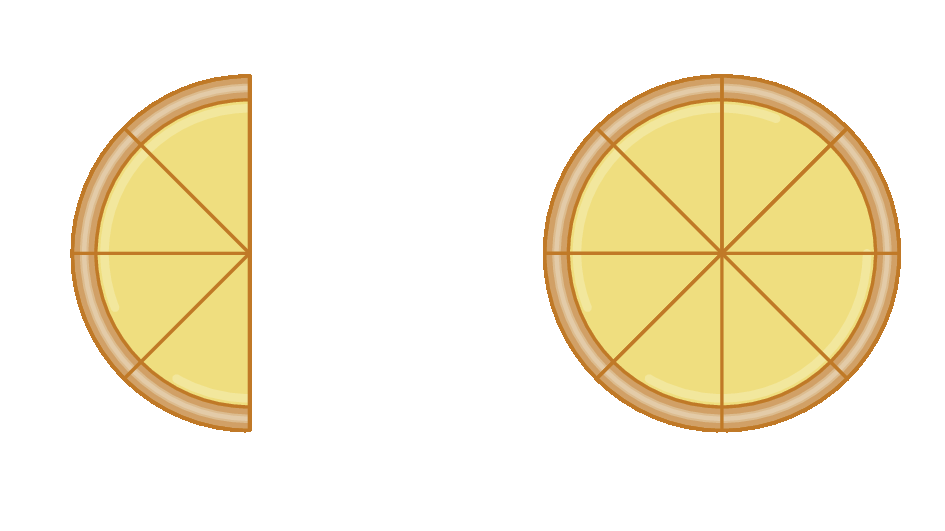
Ilustração. Metade de uma pizza, à esquerda, dividida em 4 pedaços iguais e, à direita, a pizza inteira dividida em 8 pedaços iguais.

Parte consumida das pizzas:

\frac{1}{4} = \frac{4}{16}

Observe que, dependendo do inteiro escolhido, a quantidade de pedaços de pizza consumidos indicada por

\frac{1}{4}

pode variar:

• no caso em que o inteiro é uma pizza,

\frac{1}{4}

desse inteiro equivale a 2 pedaços;

• no caso em que o inteiro são duas pizzas,

\frac{1}{4}

desse inteiro equivale a 4 pedaços.

Situação 3

Leia as adivinhas a seguir e tente descobrir a que se referem.

Um palácio tem doze damas,

Cada dama tem quatro quartos,

Todas elas usam meias

E nenhuma usa sapato.

Tem folhas e não é planta,

Tem lombo e anda de capa

O estudante que o abandona

Da nota má não escapa.

Responda depressa

Não seja bocó,

Está no pomar

E no seu paletó.

Essas adivinhas vão compor uma página de um livro de brincadeiras; por isso, vamos considerá-las como o inteiro.

Temos 12 frases distribuídas em 3 adivinhas. Podemos dizer que cada adivinha corresponde a

\frac{1}{3}

do total de frases, pois cada uma delas tem 4 frases.

Com base nas situações apresentadas, podemos concluir que é necessário conhecer o inteiro para encontrar uma fórma adequada de dividi-lo. Assim, podemos representar a quantidade de partes do inteiro que nos interessam usando uma fração.

Respostas e comentários

Resposta: o relógio analógico

Resposta: o livro

Resposta: a manga

Se adotarmos duas pizzas como inteiro, a fração

\frac{1}{4}

que representa a quantidade de pedaços de pizza consumidos equivale a 4 pedaços, pois o inteiro, nesse caso, é representado por 16 pedaços. Porém, se adotarmos o inteiro como três pizzas, essa fração equivale a 6 pedaços, pois, nesse caso, o inteiro é representado por 24 pedaços. Chame a atenção dos estudantes para o seguinte: a representação da quantidade de pedaços de pizza consumidos, na fórma fracionária, decorre da escolha do inteiro e do número de partes em que esse inteiro foi dividido.

Sugestão de atividade extra

Faça um levantamento de lendas, mitos, canções infantis, quadrinhas e adivinhas lembrados ao longo de uma aula. Com a ajuda dos estudantes, selecione alguns textos e faça uma atividade similar à proposta na situação 3, contar frases ou versos e representá-los na fórma de fração.

Oriente os estudantes a montar um painel com as adivinhas para que fique exposto à comunidade escolar.

Esse tipo de atividade favorece o desenvolvimento da competência geral 3.

Página 109

A ideia de quociente

Além da ideia de parte de um inteiro, as frações podem representar um quociente, ou seja, o resultado de uma divisão. Acompanhe as situações a seguir.

Situação 1

Carolina e seus amigos estão começando um jogo de aventura.

Ilustração. Mesa circular com cinco crianças ao redor. Sobre a mesa, tabuleiro e pinos. Da esquerda para a direita da imagem, tem-se uma menina branca com cabelo cacheado castanho escuro, usando camiseta laranja, um menino branco com cabelo loiro e camiseta listrada vermelha e amarela, um menino branco com cabelo castanho e camiseta azul, uma menina asiática com cabelo liso e preto, usando óculos e camiseta verde, e uma menina negra de cabelo castanho em tranças e camiseta amarela. Ela segura parte de um conjunto de cartas e fala: São 40 cartas para distribuir entre a gente.

Carolina tem 40 cartas para distribuir igualmente entre ela e seus amigos. Como são 5 pessoas, podemos representar a quantidade que cada um vai receber por 40 : 5 ou

\frac{40}{5}

Nesse caso, o número fracionário

\frac{40}{5}

indica que cada amigo vai receber 8 cartas para iniciar esse jogo.

Situação 2

Fabrício foi passar o fim de semana com os amigos no sítio de sua avó Vera. Ela estava mostrando o pomar para as crianças e colheu 3 laranjas maduras para dividir igualmente entre Fabrício e seus 3 amigos.

Ilustração. ao centro da imagem há uma mulher branca de cabelo vermelho e curto, camisa branca, calça azul e botas. Ela está à frente de uma mesa com laranjas. Ao redor, quatro crianças: um menino branco com camiseta vermelha, uma menina branca com cabelo preto e óculos, uma menina branca e loira, e um menino negro com camiseta verde. Ao fundo, árvores com laranjas, algumas à esquerda e uma à direita.

Nessa situação, a ideia de quociente ocorre devido à divisão das 3 laranjas entre as 4 crianças. Podemos representar essa divisão por 3 : 4 ou

\frac{3}{4}

Isso significa que, se Vera dividir cada uma das laranjas em 4 pedaços, cada criança receberá 3 pedaços.

Nas duas situações, podemos associar a fração com a operação de divisão, pois estão relacionadas à distribuição de cartas ou de laranjas.

Na primeira situação, a divisão resultou em um número natural e cada jogador recebeu a mesma quantidade de cartas. Na segunda situação, a divisão das laranjas resultou em um número fracionário, então cada criança recebeu parte de cada uma das laranjas, mas todas as crianças receberam a mesma quantidade de laranja.

Respostas e comentários

A ideia de quociente

Pergunte aos estudantes o que aconteceria se houvesse quarenta e duas cartas para serem distribuídas entre 5 crianças. Faria sentido dizer que cada criança receberia

\frac{42}{5}

de cartas? Nesse caso, seria necessário tirar duas cartas do monte para distribuí-las igualmente, pois 42 dividido por 5 tem resto 2 e não é possível distribuir duas cartas para 5 pessoas, já que, nesse caso, é impossível recortar as cartas.

Na situação 2 (divisão das laranjas), admite-se a divisão fracionária, o que sugere a diferença no tratamento de grandezas discretas e contínuas. Na situação 1 (divisão das quarenta e duas cartas), o resto 2 é separado para garantir quociente inteiro, o que não se considera na divisão das laranjas.

Página 110

A ideia de razão

Até aqui vimos as ideias de frações para representar a parte de um inteiro ou indicar um quociente. Além dessas ideias, as frações também podem indicar uma razão. Acompanhe as situações a seguir.

Situação 1

A professora de Ana Paula dividiu a turma em grupos de 5 estudantes e propôs que fizessem uma maquete da cidade. O grupo de Ana Paula é composto de duas meninas e 3 meninos.

A razão entre as quantidades de meninas e meninos é de duas meninas para 3 meninos. Podemos representar essa razão por

\frac{2}{3}

(lemos: “dois para três ou dois em três”).

Situação 2

É comum, em jogos de tabuleiro, encontrar dados com mais de seis faces. Carolina tem um jogo de aventura em que há um “dado honesto” com oito faces numeradas de 1 a 8, que se parece com um octaedro.

Ilustração. criança negra de cabelo castanho na altura do pescoço, em tranças e com camiseta azul. Ela segura um dado na mão direita, com a palma para cima.

Ao jogar um “dado honesto” de seis faces, a chance de sair o número 2 na face de cima, por exemplo, é de 1 em 6; no “dado honesto” de Carolina, a chance de sair o número 2 é de 1 em 8. Podemos representar essas razões por

\frac{1}{6}

(lemos: “uma em seis”) e

\frac{1}{8}

(lemos: “uma em oito”).

Situação 3

A razão entre a medida da distância percorrida por um carro e a medida de tempo que ele levou para percorrer essa medida da distância fornece a medida de velocidade média.

Por exemplo, se um automóvel percorreu 60 quilômetros em duas horas, a razão entre as medidas da distância e do tempo pode ser dada por

\frac{60 k m}{2 h} .

Podemos simplificar a fração

\frac{60}{2}

dividindo o numerador e o denominador por 2, obtendo a fração

\frac{30}{1}

Assim, um carro que desenvolve uma medida de velocidade de 30 quilômetros por hora percorre uma medida de distância de 30 quilômetros em uma hora. Dessa fórma, utilizando essa razão, podemos descobrir a medida da distância percorrida pelo carro. Por exemplo, em 4 horas, serão percorridos 120 quilômetros.

Uma propriedade interessante das razões é a possibilidade de obter, por meio da equivalência de frações, valores desconhecidos.

A ideia de operador

Vamos relembrar o cálculo da fração de uma quantidade.

Para isso, vamos determinar

\frac{3}{4}

de 80:

• primeiro, podemos calcular

\frac{1}{4}

de 80, dividindo 80 por 4, ou seja, 80 : 4 = 20

• multiplicamos a quarta parte de 80 por 3, ou seja, 3 ⋅ 20 = 60

Assim, temos que

\frac{3}{4}

de 80 é 60.

Respostas e comentários

A ideia de razão

Comente que a ideia de fração como comparação é o que chamamos de razão, ou seja, uma relação expressa na fórma de fração. Na situação 1, o número de meninos e meninas foi comparado por meio de uma razão; na situação 2, as razões foram empregadas para expressar probabilidades; e, na situação 3, a medida da velocidade do automóvel foi expressa pela razão entre a medida da distância percorrida e a medida do tempo. Outro uso bastante comum é no trabalho com escalas, conteúdo que será formalizado no 9º ano.

Aproveite a situação e pergunte aos estudantes: “Se em uma hora o veículo percorre 30 quilômetros e mantiver a mesma medida de velocidade, em 5 horas quanto ele percorrerá?”. Espera-se que os estudantes percebam que o veículo deverá percorrer o quíntuplo de 30 quilômetros, ou seja, 150 quilômetros.

A ideia de operador

A intenção é mostrar que

\frac{3}{4}

de 80 é o mesmo que 3 vezes

\frac{1}{4}

de 80.

Página 111

Também podemos representar essa operação por

\frac{3}{4} \cdot 80 = 60

(lemos: “três quartos de oitenta é igual a sessenta”).

Agora, analise a ideia de fração como operador em outras situações.

Situação 1

Sabendo que um bolo de laranja custa R$ 60,00sessenta reais, quanto Lucinda vai pagar por

\frac{2}{3}

do bolo?

Para determinar o valor que Lucinda pagará, temos de calcular

\frac{2}{3}

de R$ 60,00sessenta reais. Para isso, podemos calcular

\frac{1}{3}

de R$ 60,00sessenta reais e tomar o dobro desse valor. No entanto, podemos representar a fração por um operador, assim:

\frac{2}{3} \cdot 60 = 2 \cdot \frac{60}{3} = 2 \cdot 20 = 40

Portanto, Lucinda pagará R$ 40,00quarenta reais por

\frac{2}{3}

do bolo.

Situação 2

O jornal da escola em que João estuda publicou uma pesquisa que apontou que 40% dos estudantes preferem maçã a outras frutas. Se a escola de João tem 500 estudantes, quantos são os que preferem maçã?

Ilustração. Menino negro de cabelo curto, preto e camiseta azul. Ele lê um jornal com a imagem de uma maçã vermelha. O título do jornal é "jornal da escola" e a manchete diz "40 por cento dos alunos preferem maçã a outras frutas".

Nessa situação, a fração como operador aparece como uma porcentagem da quantidade de estudantes. Precisamos calcular quanto é 40% de 500, assim:

\frac{40}{100} \cdot 500 = 40 \cdot \frac{500}{100} = 40 \cdot 5 = 200

Portanto, 200 estudantes da escola de João preferem maçã a outras frutas.

Nas duas situações apresentadas, as frações foram utilizadas como um fator multiplicativo. No caso do preço a ser pago pelo bolo, o uso das frações permitiu calcular o valor do pedaço comprado por Lucinda. No caso da fruta predileta dos estudantes, o uso das frações permitiu calcular quantos estudantes preferem maçã a outras frutas.

Em ambos os casos, partimos de uma situação inicial, efetuamos uma operação com fração e chegamos a uma resposta para uma situação final.

Atividades

Faça as atividades no caderno.

1. Com base na representação a seguir, responda às questões no caderno.

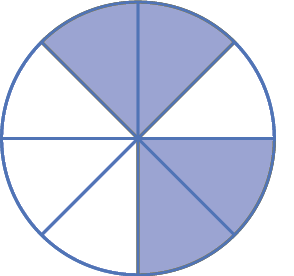
Figura geométrica. Círculo dividido em oito partes iguais. Quatro partes estão pintadas de azul, sendo duas na parte de cima da imagem e duas na parte inferior direita. as outras partes tem fundo branco.

a) Qual seria o inteiro se a parte azul correspondesse a

\frac{1}{2}

do inteiro?

b) Qual seria o inteiro se a parte azul correspondesse a

\frac{1}{8}

dele?

2. Joana tem jabuticabeiras em seu sítio. Para o lanche da tarde, ela colheu 28 jabuticabas para distribuir entre 4 crianças. Que fração representa a quantidade de jabuticabas que cada criança vai receber? Quantas jabuticabas cada criança vai receber?

Respostas e comentários

1. a) O inteiro seria um círculo.

1. b) O inteiro seriam 4 círculos.

\frac{28}{4}

(ou fração equivalente); 7 jabuticabas

Na situação 1, comente que

\frac{2}{3}

de 60 corresponde ao dobro de

\frac{1}{3}

de 60 e que, na situação 2,

\frac{40}{100}

de 500 é o mesmo que 40 vezes a centésima parte de 500.

Conversar sobre as diversas fórmas de se referir a esses enunciados pode enriquecer o vocabulário matemático dos estudantes e fornecer excelentes estratégias para o desenvolvimento do cálculo mental.

• Na atividade 1, item b, 4 partes correspondem a

\frac{1}{8}

; logo,

\frac{8}{8}

ou 1 inteiro seria representado por 8 ⋅ 4 partes, ou seja, trínta e duas partes. Como cada círculo é composto de 8 partes, precisamos de 4 círculos, ou seja, o inteiro será representado por 4 círculos.

• Na atividade 2, se julgar interessante, comente que a fração resultante representa um número natural; nesse caso, o 7.

Página 112

3. A mãe de Jorge encontrou uma coleção de bolinhas de gude que ela juntou quando era criança e com a qual brincava com seus amigos. Ela resolveu distribuir as 25 bolinhas entre Jorge e duas amigas dele.

a) Que fração representa a quantidade de bolinhas de gude que cada criança vai receber?

b) Sobraram bolinhas? Como você faria a distribuição?

4. Observe as imagens e as duas indicações de inteiro em cada item. A seguir, responda às perguntas no caderno.

a) Cada barra de chocolate é formada por 9 pedaços retangulares iguais.

Ilustração. Duas barras de chocolate em formato retangular. A barra da esquerda tem 3 colunas com 3 pedaços iguais cada. A barra da direita tem duas colunas com 3 pedaços iguais cada. A terceira coluna está desenhada com linhas tracejadas.

• Considerando duas barras de chocolate como o inteiro, qual fração representa a quantidade de chocolate da ilustração?

• Considerando quatro barras de chocolate como o inteiro, qual fração representa a quantidade de chocolate da ilustração?

b) Cada copo representado a seguir foi marcado e dividido em 4 partes iguais, que tem a mesma medida de capacidade.

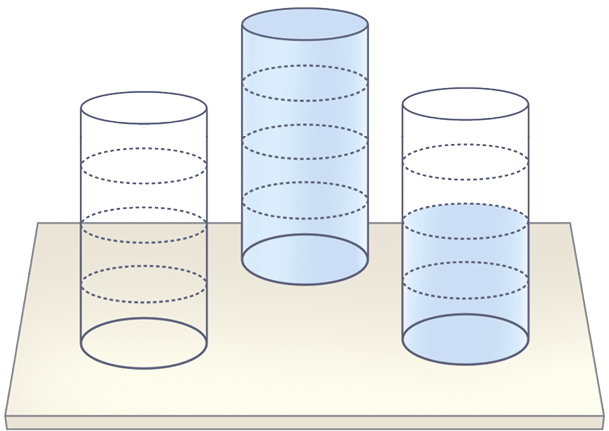
Ilustração. Três copos iguais sobre uma mesa, cada um dividido em 4 partes iguais, como fatias horizontais. À esquerda, um copo vazio. No centro, um copo tem as quatro partes preenchidas com a cor azul. À direita, copo com duas partes de baixo preenchidas com a cor azul.

• Considerando dois copos como o inteiro, qual fração representa a quantidade de água da ilustração?

• Considerando três copos como o inteiro, qual fração representa a quantidade de água da ilustração?

5. A lista de ingredientes a seguir faz parte da receita de bolo de fubá cremoso de Joaquim.

Fotografia. Bolo de fubá redondo com furo no meio. Texto: 3 ovos; 4 xícaras (chá) de leite; 3 xícaras (chá) de açúcar; fração mista: uma e meia xícara (chá) de farinha de trigo; fração mista: uma e meia xícara (chá) de fubá; 2 colheres (sopa) de margarina; 100 gramas de queijo ralado; 1 colher de fermento em pó.

Responda no caderno.

a) Qual é a razão de xícaras de açúcar para xícaras de leite?

b) Se a receita fosse para fazer mais de um bolo e 9 ovos fossem utilizados, qual seria a quantidade de queijo para o preparo dos bolos?

6. Cláudia adora jogos de corrida e jogos de aventura. Ela tem, no celular, 14 jogos, dos quais 9 são de corrida e os demais, de aventura.

Ilustração. Menina branca de cabelo castanho preso com um elástico azul, com franja e blusa amarela, segura um celular virado para a frente com a imagem de um carro em uma pista de corrida.

Qual é a razão do número de jogos de aventura para o número de jogos de corrida?

7. Luís ganhou um novo videogame de sua tia. Como ele tinha muitos jogos do videogame antigo, resolveu presentear alguns amigos que tinham o mesmo videogame. Luís tinha 21 jogos e queria dar 4 jogos para cada amigo. Responda no caderno.

a) Que fração representa a quantidade de jogos que cada amigo vai receber?

b) Quantos amigos Luís pode presentear?

Respostas e comentários

3. a)

\frac{25}{3}

3. b) Sobrou uma bolinha; 8 bolinhas para cada criança.

4. a) Primeiro item:

\frac{5}{6}

(ou fração equivalente); segundo item:

\frac{5}{12}

(ou fração equivalente).

4. b) Primeiro item:

\frac{6}{8}

(ou fração equivalente); segundo item:

\frac{6}{12}

(ou fração equivalente).

5. a)

\frac{3}{4}

5. b) 300 gramas

\frac{5}{9}

7. a)

\frac{21}{4}

7. b) 5

• No item b da atividade 3, comente que, para ser possível fazer a divisão sem sobrar bolinhas, o numerador deve ser múltiplo do denominador, e isso seria possível retirando-se uma bolinha, ou seja, com 24 bolinhas.

• No item a da atividade 4, para resolver o primeiro item, pode-se pensar em quantas partes iguais à retirada correspondem as duas barras, obtendo, então, o valor 6. Como 5 dessas partes estão representadas, temos a fração

\frac{5}{6}

• A atividade 5 utiliza a fração para expressar duas partes de uma mesma grandeza ou duas partes de grandezas diferentes, como nos itens a e b, expressando 3 xícaras de açúcar para 4 xícaras de leite e 3 ovos para cada 100 gramas de queijo, respectivamente.

Página 113

8. Ana Lúcia tem dois irmãos e duas irmãs. Nos fins de semana, eles podem comer um pouco de chocolate. Seus pais compram, geralmente, três barras para dividir entre os cinco irmãos. Qual fração representa a quantidade de chocolate que cada irmão vai receber? Faça um esquema para representar que parte das barras de chocolate cada irmão vai receber.

9. No final do ano, no prédio em que Carlos mora, haverá um sorteio entre 44 apartamentos para a utilização do salão de festas. Se Carlos e sua prima moram no mesmo prédio, mas em apartamentos diferentes, escreva, no caderno, a razão que representa a chance de a família de Carlos ter acesso ao salão de festas no final do ano.

10. Pedro tem 144 figurinhas para colar em um álbum de futebol. Se

\frac{1}{3}

delas é repetido, quantas são inéditas?

11. Um pacote de arroz tem 5 quilogramas. Para um churrasco serão preparados

\frac{3}{5}

desse pacote. Quantos quilogramas de arroz serão utilizados?

12. A medida de velocidade média de um corredor de elite de maratonas é de 20 quilômetros por hora. Se uma prova de maratona tem aproximadamente 40 quilômetros, quantas horas um corredor levará, em média, para concluí-la?

13. Em uma receita de bolo, são necessários 4 ovos. No entanto, na geladeira de José há apenas 3. Por quanto ele deve multiplicar as quantidades de outros ingredientes da receita para que consiga fazer um bolo menor?

14.

\frac{2}{7}

de 21 vale 6, por quanto se deve multiplicar 6 para obter 21?

2 Problemas

Vamos agora resolver alguns problemas envolvendo as ideias de fração estudadas.

Atividades

Faça as atividades no caderno.

15. Luísa fez um esboço da bandeira do Brasil no caderno.

Ilustração. Bandeira do Brasil, como se fosse pintada com lápis de cor. Retângulo verde. Dentro, losango amarelo com círculo azul no centro.

Ao observar o desenho, afirmou que

\frac{1}{3}

é amarelo. Você concorda com a avaliação de Luísa? Explique no caderno.

16. Um estacionamento pode acomodar 200 automóveis em 8 fileiras. Sabendo que cada fileira acomoda a mesma quantidade de automóveis, que fração representa a quantidade de automóveis por fileiras? Quantos automóveis cabem por fileira?

17. Se 3 tortas redondas forem divididas em 5 partes iguais cada uma, quantas pessoas poderão receber 1 pedaço de torta?

18. Escreva no caderno a razão entre as maçãs que não têm folha no caule e aquelas que têm folha.

19. Uma mala custa R$ 280,00duzentos e oitenta reais. Paulo pediu um desconto e o dono da loja ofereceu 15% de desconto no valor da mala.

a) Escreva no caderno a expressão que permite calcular o valor do desconto.

b) De quanto será o desconto?

Respostas e comentários

\frac{3}{5}

; cada irmão vai receber o equivalente a 3 pedaços, cujo tamanho é

\frac{1}{5}

da barra de chocolate.

\frac{2}{44}

\frac{1}{22}

10. 96 figurinhas

11. 3 quilogramas

12. duas horas

13.

\frac{3}{4}

14.

\frac{7}{2}

15. Não, pois bastaria comparar a parte pintada de amarelo com a pintada de verde para perceber que a medida da área em amarelo é menor do que

\frac{1}{3}

da medida da área do total.

16.

\frac{200}{8}

; 25 automóveis por fileira.

17. 15 pessoas

18.

\frac{6}{9}

19. a)

\frac{15}{100} \cdot 280

19. b) R$ 42,00quarenta e dois reais

• Peça aos estudantes que representem, no caderno, as divisões das três barras de chocolate da atividade 8.

• Na atividade 11, comente que queremos obter

\frac{3}{5}

de 5 quilogramas, o que corresponde ao triplo de

\frac{1}{5}

de 5 quilogramas.

• Na atividade 14, leve os estudantes a perceber que

\frac{7}{2}

é inversa de

\frac{2}{7}

Problemas

Bê êne cê cê:

• Competências gerais 2 e 9 (as descrições estão na página seis).

• Competência específica 5 (a descrição está na página sete).

• Habilidades ê éfe zero sete ême ah zero cinco, ê éfe zero sete ême ah zero seis, ê éfe zero sete ême ah zero sete, ê éfe zero sete ême ah zero oito e ê éfe zero sete ême ah zero nove.

Objetivos:

• Resolver problemas que envolvem diferentes ideias de fração.

• Resolver problemas utilizando diferentes algoritmos.

Justificativa

Resolver problemas que envolvem as diferentes ideias de fração desenvolve o raciocínio lógico e amplia o repertório de estratégias de resolução de problemas dos estudantes. Além disso, contribui para que habilidades como ê éfe zero sete ême ah zero oito e ê éfe zero sete ême ah zero nove sejam desenvolvidas.

Mapeando conhecimentos

Peça aos estudantes que resolvam alguns problemas que envolvam diferentes ideias de fração. Você pode antecipar algumas atividades propostas no próprio livro.

Para as aulas iniciais

Resolva com a turma os problemas propostos na dinâmica inicial. Mostre a eles como é possível estabelecer uma sequência de passos para resolver determinados problemas.

Na atividade 15, mesmo sem realizar cálculos, podemos constatar visualmente que a parte pintada de amarelo é menor que

\frac{1}{3}

da bandeira.

• Na atividade 19, 15% de 280 é equivalente a 15 vezes a centésima parte de 280. Peça aos estudantes que calculem mentalmente essa divisão.

(EF07MA05) Resolver um mesmo problema utilizando diferentes algoritmos.

(EF07MA06) Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmos procedimentos.

(EF07MA07) Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas.

(EF07MA08) Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.

(EF07MA09) Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração

\frac{2}{3}

para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.

Página 114

20. Em uma turma de 7º ano, 24 estudantes são destros e

\frac{1}{7}

dos estudantes é canhoto. Quantos estudantes há na turma?

21.

No cotidiano, muitas vezes temos que fazer uma ordenação, tarefa que envolve comparar e decidir se um elemento vem antes ou depois de outro. A ideia de ordem aparece, por exemplo, na classificação de vencedores de uma prova de atletismo, na agenda de contatos do celular, entre outras situações. Existem muitas estratégias de ordenação, e uma delas é a ordenação por seleção.

Considere que você tenha que ordenar várias cartas numeradas. Um dos montes, formado por cartas que não estão ordenadas, será chamado de Y e o outro, que será formado por meio da transferência sucessiva das cartas de Y, será chamado de X. Veja o fluxograma a seguir.

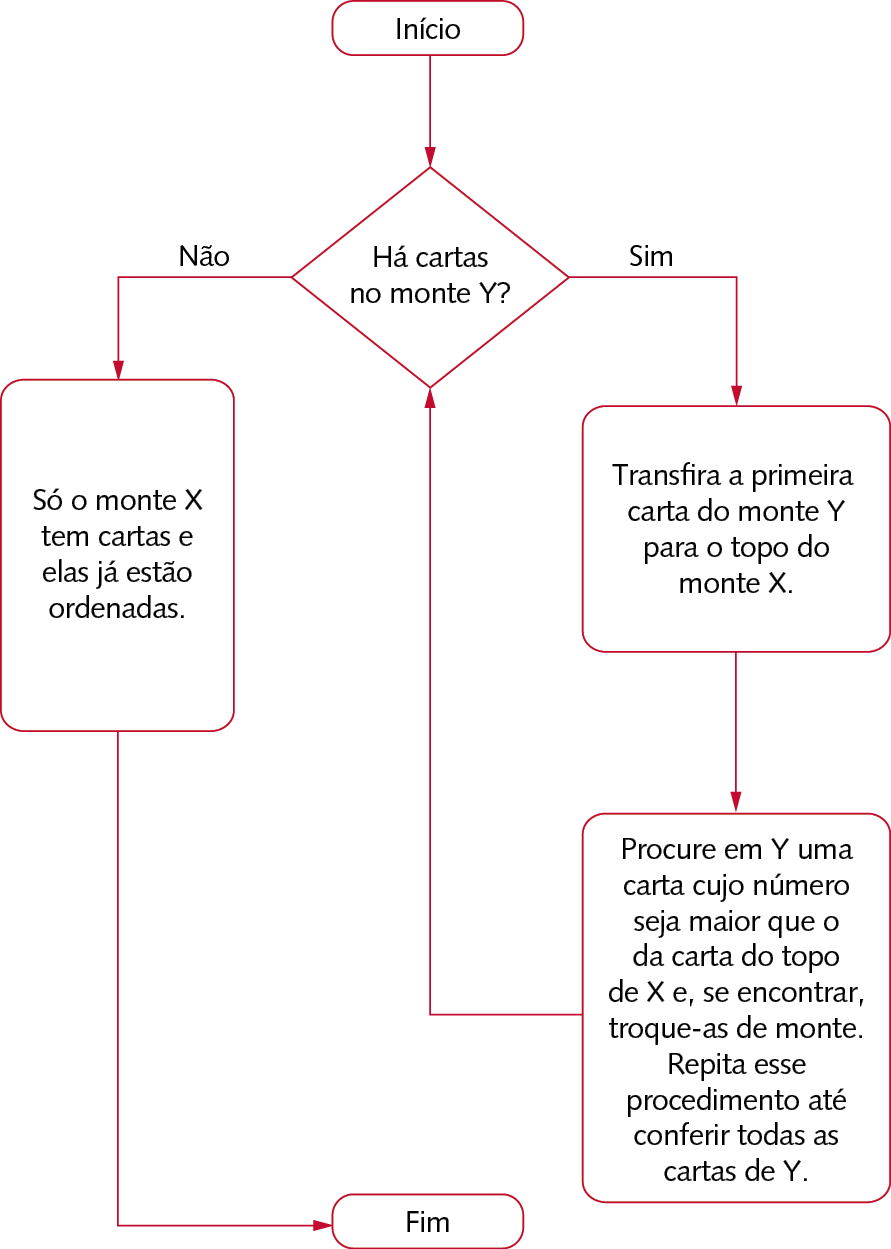
Fluxograma. Quadro na parte de cima: Início. Seta apontando para losango: Há cartas no monte Y? Seta para a esquerda, partindo do losango com texto sobre a seta: Não. A seta aponta para o retângulo escrito: Só o monte X tem cartas e elas já estão ordenadas. Do retângulo sai uma seta para o quadro: Fim. Seta para a direita, partindo do losango com texto sobre a seta: Sim. a seta aponta para o retângulo escrito: Transfira a primeira carta do monte Y para o topo do monte X. Do retângulo sai uma seta para o quadro: Procure em Y uma carta cujo número seja maior que o da carta do topo de X e, se encontrar, troque-as de monte. Repita esse procedimento até conferir todas as cartas de Y. Do retângulo sai uma seta retornando para o losango.

É possível usar esse método para ordenar frações de denominadores iguais ou diferentes?

22. Fernanda levou os filhos para visitar a avó em outra cidade. Eles foram de carro e percorreram dois trechos com medidas de velocidade diferentes. No primeiro trecho, a medida da velocidade máxima permitida era 80 quilômetros por hora e a medida da distância percorrida foi 80 quilômetros. No segundo trecho, a medida da velocidade máxima permitida era 120 quilômetros por hora e a medida da distância percorrida foi 60 quilômetros.

Se Fernanda manteve sempre a medida da velocidade máxima permitida para cada trecho, qual foi a medida de tempo necessária para percorrê-los?

\frac{7}{10}

hora

\frac{14}{10}

hora

\frac{3}{2}

hora

\frac{4}{2}

horas

\frac{5}{2}

horas

23. (ó bê mépi) A capacidade do tanque de gasolina do carro de João é de 50 litros. As figuras mostram o medidor de gasolina do carro no momento da partida e no momento da chegada de uma viagem feita por João.

Ilustração. Dois velocímetros, com visor com as marcações: vazio, fração 1 quarto, fração 1 meio, fração 3 quartos, cheio. À esquerda, o velocímetro tem a indicação partida e uma seta vermelha apontando para a fração 3 quartos. À direita, o velocímetro tem a indicação chegada e uma seta vermelha apontando para a fração 1 quarto.

Quantos litros de gasolina João gastou nessa viagem?

a) 10

b) 15

c) 18

d) 25

e) 30

24.

Crie uma situação-problema sobre um veículo que precisa percorrer uma estrada de alguns quilômetros. A pergunta pode ser a respeito da medida da velocidade desenvolvida pelo veículo ou da medida de tempo necessária para percorrer a medida da distância a uma dada medida de velocidade. Lembre-se de que é preciso respeitar as leis de trânsito. Se necessário, peça ajuda ao professor para verificar se a medida da velocidade está muito alta. Entregue seu problema a um colega para que ele resolva.

25.

Crie uma situação-problema sobre um produto que seja comprado com desconto sobre o preço de venda. Peça a um colega que resolva a questão.

Respostas e comentários

20. 28 estudantes

21. Sim, mas, se os denominadores forem diferentes, precisaremos obter frações equivalentes às iniciais que tenham o mesmo denominador.

22. alternativa c

23. alternativa d

24. Resposta pessoal.

25. Resposta pessoal.

• Na atividade 24, os estudantes poderão criar uma situação como: “No planejamento das férias da família Souza, Luiz calculou que, a uma medida de velocidade constante, a viagem de 270 quilômetros levaria 3 horas. Qual foi a medida da velocidade desenvolvida pelo veículo?” (Resposta: 90 quilômetros em cada hora.)

• Na atividade 25, os estudantes poderão criar uma situação como: “Um comerciante resolveu fazer uma grande liquidação de inverno vendendo cada blusa de lã por R$ 30,00trinta reais, porém, se o cliente levasse 5 blusas, teria um desconto de 20% no valor da compra. Para aproveitar os preços, Marília resolveu presentear a família inteira comprando uma blusa para cada familiar. Quanto ela pagou por 15 blusas de lã?” (Resposta: R$ 360,00trezentos e sessenta reais.)

Página 115

Resolvendo em equipe

Faça a atividade no caderno.

Partindo do algoritmo de ordenação visto na atividade 21, ordenem 10 cartas numeradas. Mas há um detalhe: quem ordenar não pode ver as cartas!

Para a confecção das cartas, dividam uma folha de papel em branco em 10 retângulos. Em cada carta, escrevam uma fração equivalente, com denominador 12, às frações a seguir.

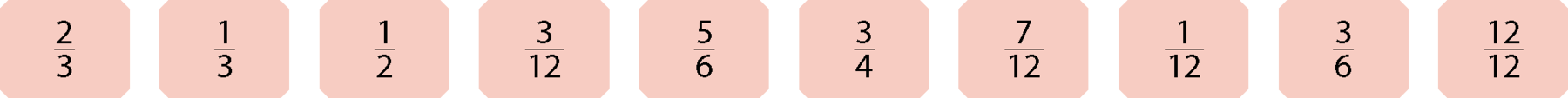
Esquema. 10 retângulos, cada um com uma fração: 2 terços; 1 terço; 1 meio; 3, 12 avos; 5 sextos; 3 quartos; 7, 12 avos; 1, 12 avos; 3 sextos; 12, 12 avos

O integrante responsável por ordenar as cartas não poderá ver a carta, mas poderá mostrá-la para a equipe e fazer a pergunta: “O número desta carta é menor, maior ou igual ao número da que está no topo das cartas ordenadas?”. O restante da equipe deve responder à pergunta, sem dizer o valor da carta.

Ilustração. Duas crianças de frente para uma mesa com cartas. A criança à esquerda é uma menina negra com cabelos pretos e camiseta amarela. Ela segura uma carta com a fração 3, 12 avos, com o número voltado para o colega, e fala: O número é maior, menor ou igual ao do topo? O menino branco, com cabelo castanho e camiseta azul olha para a carta.

Interpretação e identificação dos dados	• Leia novamente a atividade 21 e anote o que considerar relevante para ajudá-lo na ordenação das cartas.
Plano de resolução	• Forme grupo com a quantidade de integrantes indicada pelo professor. • Embaralhe as cartas e coloque-as na mesa com os números voltados para baixo. • Converse com os colegas como organizar os montes de cartas.
Resolução	• Todos os integrantes devem ordenar as cartas pelo menos uma vez, aplicando o algoritmo de ordenação. Um integrante do grupo deve anotar as frações ordenadas dos demais colegas.
Verificação	• Cada integrante do grupo conseguiu a mesma ordem de cartas? • A ordem que conseguiram está correta? Por quê?
Apresentação	• Discuta com os colegas se existem outras maneiras de ordenar as cartas. Se descobrirem mais alguma, apresentem para a turma.

Respostas e comentários

Resolvendo em equipe:

\frac{8}{12}

;

\frac{4}{12}

;

\frac{6}{12}

;

\frac{3}{12}

;

\frac{10}{12}

;

\frac{9}{12}

;

\frac{7}{12}

;

\frac{1}{12}

;

\frac{6}{12}

;

\frac{12}{12}

Interpretação e identificação dos dados: Ter o fluxograma pode ajudar os estudantes a relembrar os passos para ordenar as cartas.

Plano de resolução: Na atividade 21, há a sugestão de nomear os montes de cartas para que lembrem qual está ordenado e qual não está.

Verificação: primeiro item: resposta pessoal; segundo item: Se todos seguiram corretamente o algoritmo, as frações devem estar nesta ordem:

\frac{1}{12}; \frac{3}{12}; \frac{4}{12}; \frac{6}{12}; \frac{6}{12}; \frac{7}{12}; \frac{8}{12}; \frac{9}{12}; \frac{10}{12}; \frac{12}{12}

Apresentação: Resposta pessoal.

Resolvendo em equipe

Bê êne cê cê:

• Competências gerais 4 e 9 (as descrições estão na página seis).

• Competências específicas 2, 5 e 6 (as descrições estão na página sete).

A seção destaca as etapas selecionadas para encaminhar a resolução de problemas. Elas devem ser analisadas e discutidas com os estudantes. Além de favorecer o desenvolvimento das competências gerais 4 e 9 e das competências específicas 2, 5 e 6, a seção permite a transferência de estratégias de resolução para outros contextos e situações.

Se necessário, relembre como obter frações equivalentes já sendo conhecidos os denominadores.

Uma opção para a atividade é enfileirar as cartas com a frente voltada para baixo. O ordenador mostra a primeira carta ao grupo e, em seguida, vai mostrando as outras uma a uma. Se as cartas mostradas forem menores que a primeira, ele as trocará de lugar.

Comente com os estudantes que o ordenador não precisa saber os valores das cartas para ordená-las, mas deve saber compará-las. Comente também que esse tipo de algoritmo é usado em linguagem de programação.

Se julgar conveniente, escolha alguns grupos para discutirem as dificuldades encontradas e as experiências na tarefa de ordenação.

Comente com os estudantes que esse algoritmo é capaz de resolver uma classe de problemas com a mesma estrutura (por exemplo, com algumas adaptações, pode ser usado para colocar uma lista de letras ou mesmo de palavras em ordem alfabética), e não apenas um problema específico. Entretanto, um mesmo problema pode ser resolvido por meio de diferentes algoritmos. Se julgar oportuno, peça aos estudantes que pesquisem sobre algoritmos de ordenação.

Página 116

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Ideias associadas às frações

A ideia de parte de um inteiro

Frações podem representar a parte de um inteiro. Por exemplo, a fração

\frac{3}{5}

indica que o inteiro foi dividido em 5 partes iguais e que consideramos 3 dessas 5 partes.

A ideia de quociente

Frações podem representar um quociente, ou seja, o resultado de uma divisão. Por exemplo:

30 : 6 ou

\frac{30}{6}

A ideia de razão

Frações podem indicar uma razão. Por exemplo: Um automóvel percorreu 100 quilômetros em duas horas; a razão entre a medida da distância e a medida de tempo pode ser dada por

\frac{100 km}{2 h}

A ideia de operador

Frações podem ser usadas como operador. Por exemplo:

Uma torta de morango custa R$ 36,00trinta e seis reais. João vai comprar

\frac{3}{4}

dessa torta, quanto ele vai pagar?

\frac{3}{4} \cdot 36 = 27

Logo, João vai pagar R$ 27,00vinte e sete reais por

\frac{3}{4}

da torta de morango.

1. Com base na figura dividida em partes iguais a seguir, responda às questões.

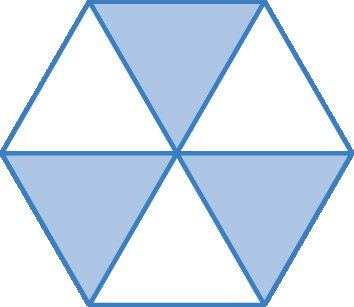
Figura geométrica. Hexágono dividido em 6 partes iguais. Três partes estão pintadas de azul e três têm fundo branco, que se alternam.

a) Qual seria o inteiro se a parte azul correspondesse a

\frac{1}{2}

do inteiro?

b) Qual seria o inteiro se a parte azul correspondesse a

\frac{1}{4}

do inteiro?

2. Se duas pizzas forem dividas em 8 partes iguais cada uma, quantas pessoas poderão receber 1 pedaço de pizza?

3. Uma sala de cinema tem capacidade de acomodar duzentas e oitenta e oito pessoas em 16 fileiras. Que fração representa a quantidade de pessoas por fileira? Quantas pessoas cabem por fileira?

4. Evandro vai distribuir sua coleção de figurinhas entre 4 colegas. Sabendo que Evandro tem quatrocentas e dezesseis figurinhas, responda às questões.

a) Que fração representa a distribuição das figurinhas?

b) Quantas figurinhas cada colega vai receber?

5. Um automóvel percorre a medida da distância de 198 quilômetros em 3 horas. Qual é a medida da velocidade média desse veículo?

6. Marcos e Anderson foram correr no parque no sábado. Marcos correu .10000 métros e Anderson correu .12500 métros. Indique a razão entre as medidas das distâncias percorridas por Marcos e Anderson.

7. Juliano vai comprar uma mochila que custa R$ 190,00cento e noventa reais. Para pagamento à vista, obteve 12% de desconto no preço da mochila.

a) Escreva no caderno a expressão que permite calcular o valor do desconto.

b) De quanto será o desconto?

8. Maria fez uma pesquisa para saber se os colegas dela gostam de ir ao teatro e descobriu que 20 colegas gostam e

\frac{1}{6}

deles não gosta. Quantos colegas de Maria participaram da pesquisa?

9. Se

\frac{4}{5}

de 90 resultam em 72, por qual fração devemos multiplicar 72 para obter 90?

10. Nair recebeu R$ 4.600,00quatro mil seiscentos reais de salário. Para pagar as despesas mensais dela, foi necessário usar

\frac{2}{5}

desse valor. Quantos reais Nair já utilizou do salário dela?

11. Um avião de pequeno porte viaja com medida de velocidade constante de 250 quilômetros por hora. Em quantas horas ele percorrerá 750 quilômetros?

Respostas e comentários

1. a) O inteiro seria um hexágono.

1. a) O inteiro seriam 2 hexágonos.

2. 16 pessoas

\frac{288}{16}

; 18 pessoas por fileira.

4. a)

\frac{416}{4}

4. b) 104 figurinhas

5. 66 quilômetros por hora

\frac{4}{5}

7. a)

\frac{12}{100} \cdot 190

7. b) R$ 22,80 vinte e dois reais e oitenta centavos

8. 24 colegas

\frac{5}{4}

10. R$ 1.840,00mil oitocentos e quarenta reais

11. 3 horas

Revisão dos conteúdos deste capítulo

Ideias associadas às frações

• A atividade 1 explora a ideia de parte de um inteiro. Amplie a proposta e peça aos estudantes que elaborem questões inspiradas nas questões dos itens a e b. Depois, solicite que troquem as questões com um colega e as respondam.

• Na atividade 2, peça aos estudantes que contem quantas fatias existem em duas pizzas com 8 pedaços cada uma e verifiquem quantas pessoas podem comer apenas 1 pedaço.

• A atividade 3 trabalha a ideia de quociente, uma vez que os estudantes devem calcular o número de pessoas que cabem em cada fileira de uma sala de cinema. Se achar conveniente, oriente-os a estimar o resultado de 288 : 16 antes de realizarem os cálculos.

• A atividade 4 explora duas ideias associadas às frações: a ideia de razão (item a) e a ideia de quociente (item b). Ao fazerem o item a, é possível que alguns estudantes percebam que a razão obtida representa um número natural. Ao calcularem 416 : 4, no item b, incentive o cálculo mental.

• A ideia de razão é trabalhada na atividade 5. Após determinarem a medida da velocidade média do automóvel, considere fazer na lousa um quadro relacionando a medida da distância percorrida pelo automóvel e a medida do tempo. Dessa maneira, o conceito pode ficar mais claro para alguns estudantes.

• Na atividade 6, retome o termo “razão” e esclareça a importância de obedecer à ordem proposta na atividade; a medida da distância percorrida por Marcos deve aparecer no numerador da fração e a percorrida por Anderson, no denominador.

• A atividade 7 envolve a ideia de operador. Retome com a turma o conceito de porcentagem e o significado do termo “desconto” se achar conveniente.

• Na atividade 8, caso perceba que os estudantes precisam de uma dica, comente com eles que 20 colegas representam

\frac{5}{6}

do total de colegas de Maria.

• Na atividade 9, se necessário, leve os estudantes a perceber que a fração

\frac{5}{4}

é inversa de

\frac{4}{5}

• A atividade 10 explora a ideia de operador. Após concluírem a atividade, você pode ampliar a proposta pedindo aos estudantes que determinem a fração do salário de Nair que sobrou. Eles podem determinar essa fração fazendo 1 ‒

\frac{2}{5}

ou determinando a razão entre o valor que sobrou e o valor total do salário:

\frac{2 760}{4 600}

• A atividade 11 pode ser realizada por meio de cálculo mental. Caso os estudantes apresentem dificuldades, oriente-os a fazer um quadro relacionando as medidas de distância percorrida a cada hora.