Revisão dos conteúdos de anos anteriores
Para o capítulo 1: Conjuntos numéricos
Números naturais
O conjunto dos números naturais é representado por:

= {0, 1, 2, 3, 4, 5, reticências}
As reticências indicam que o conjunto é infinito.
Números inteiros
O conjunto dos números inteiros é representado por:

= {reticências, ‒3, ‒2, ‒1, 0, +1, +2, +3, reticências}
Para representar os números inteiros em uma reta numérica, traçamos uma reta r e sobre ela marcamos o ponto O, chamado origem, que corresponde ao número zero.
Usando a mesma unidade de medida de comprimento, assinalamos pontos consecutivos à direita da origem e, para cada ponto, fazemos corresponder um número inteiro positivo. O mesmo deve ser feito para representar pontos situados à esquerda da origem, que correspondem aos números inteiros negativos.
Teremos, então:

1. No caderno, escreva os números naturais de cada item. Em seguida, escreva os números inteiros.
a)
5; um quinto; menos 5; menos um quintob) ‒0,20; ‒2,0; ‒2,3; ‒1,2
c) ‒5; ‒3,0; 10; 12
d)
5 meios; 5,1; 6,3; oito nonos2. Copie as retas em seu caderno e substitua por números os pontos indicados por letras:
a)

b)

c)
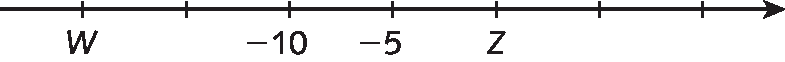
d)

3. Em seu caderno, indique se a afirmação é verdadeira (V) ou falsa (F).
a) ‒12 > 5
b) 12 > ‒5
c) ‒12 > ‒5
d) 12 > 5
Números racionais
O conjunto dos números racionais é representado por:

Podemos estabelecer uma correspondência entre os números racionais e os pontos na reta numérica. Vamos analisar alguns exemplos:
O ponto que corresponde ao número
Fração. Menos 7 sobre 4., que equivale a
Número misto. Menos 1 inteiro e 3 quartos., está localizado entre os pontos correspondentes aos números ‒2 e ‒1. Podemos dividir o segmento entre ‒2 e ‒1 em quatro partes iguais e marcar o ponto B, conforme mostramos a seguir.
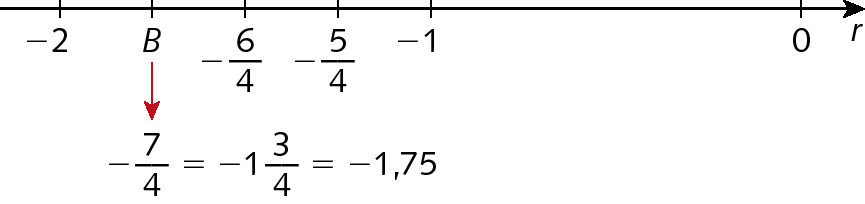
4. Em seu caderno, indique quais afirmações são verdadeiras.
a) O número
Fração. Menos 5 sobre 7.é racional, mas não é natural.
b) O número ‒7 é inteiro, mas não é racional.
c) O número 8,8 não é inteiro nem racional.
d) Os números ‒9 e 6,5 são racionais.
5. Em seu caderno, copie as sentenças e complete com os sinais >, < ou = para que elas sejam verdadeiras.
a) ‒12

7
b) 2,7

‒5
c) ‒2,2

‒2,1
d) ‒
1 quinto
Fração. Menos meio
6. Estes números do quadro foram indicados por letras na reta numérica a seguir.
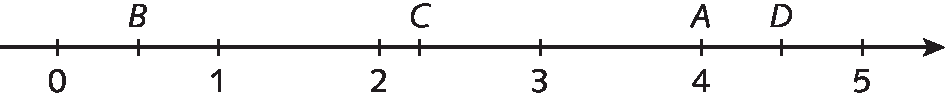
Associe cada letra a um número do quadro.
Para o capítulo 2: Potenciação e radiciação
Potenciação de números racionais
Para um número racional a com expoente natural n maior que 1, definimos:
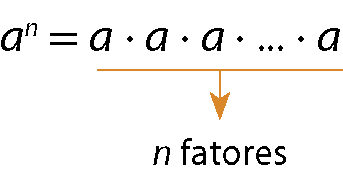
Para todo número racional a com expoente 1, temos: a1 = a
Considere os exemplos:
a) (‒2)1 = ‒2
b) (+0,5)1 = +0,5
c)
Sentença matemática. Abre parênteses, a fração 7 sobre 2, fecha parênteses, elevado a 1 é igual a fração 7 sobre 2.=
Sentença matemática. Abre parênteses, a fração 7 sobre 2, fecha parênteses, elevado a 1 é igual a fração 7 sobre 2.Para todo número racional a não nulo, com expoente igual a zero, temos: a0 = 1
Analise os exemplos:
a) (+18)0 = 1
b)
Sentença matemática. Abre parênteses, a fração menos 2 sobre 5, fecha parênteses, elevado a 0 é igual a 1.= 1
c) (‒6,4)0 = 1
Se o expoente for um número par, a potência será um número positivo.
Analise os exemplos:
a) (+3)4 = (+3) ⋅ (+3) ⋅ (+3) ⋅ (+3) = +81
b) (‒5)2 = (‒5) ⋅ (‒5) = +25
c)
Sentença matemática. Abre parênteses, a fração menos 1 sobre 3, fecha parênteses, elevado a 2 é igual a abre parênteses, a fração menos 1 sobre 3, fecha parênteses, vezes abre parênteses, a fração menos 1 sobre 3, fecha parênteses, é igual a fração 1 sobre 9.Se o expoente for um número ímpar, a potência terá o mesmo sinal da base.
Confira os exemplos:
a) (‒3)3 = (‒3) ⋅ (‒3) ⋅ (‒3) = ‒27
b) (+5)3 = (+5) ⋅ (+5) ⋅ (+5) = +125
c) (‒0,6)3 = (‒0,6) ⋅ (‒0,6) ⋅ (‒0,6) = ‒0,216
7. Sem realizar cálculos, responda em seu caderno: Quais destas potências têm resultado positivo?
a) (‒25)10
b) (+15)1
c) (300)12
d) (‒29)63
e) (‒0,25)9
f)
Sentença matemática. Abre parênteses, a fração 15 sobre 8, fecha parênteses, elevado a 15.g) (‒0,36)0
h) (‒200,1)55
8. Em seu caderno, calcule as potências a seguir.
a) (‒6)4
b) (+6)3
c) (‒3)6
d) 26
e) (‒1,1)3
f)
Sentença matemática. Abre parênteses, menos a fração 1 sobre 2, fecha parênteses, elevado a 3.g) 0,34
h)
Sentença matemática. Abre parênteses, fração 1 sobre 2, fecha parênteses, elevado a 5.Raiz quadrada de números racionais
• Quando o índice da raiz é 2, podemos omiti-lo. Assim:
Sentença matemática. Raiz quadrada de 100 com índice 2 aparente é igual a raiz quadrada de 100 com índice 2 omisso.• Os quadrados perfeitos são números racionais que podem ser escritos como potência de base racional e expoente 2. Os números 0; 0,01; 0,04; 0,09; 0,16; 0,25; 1; 4; 9; 16 e 25 são exemplos de quadrados perfeitos.
• A raiz quadrada de um quadrado perfeito é o número racional não negativo cujo quadrado é igual ao número dado.
Então:
Raiz quadrada de 0 vírgula 09= 0,3, pois (0,3)2 = 0,9.
• A raiz quadrada de zero é zero:
Sentença matemática. Raiz quadrada de 0 é igual a 0., pois 02 = 0
• A raiz quadrada de números racionais negativos não é um número racional, pois o quadrado de um número racional nunca é negativo. Por exemplo:
Raiz quadrada da fração menos 1 sobre 9.
não é um número racional, pois não existe número racional que multiplicado por ele mesmo resulte em
Fração. menos 1 sobre 9. Fração. menos 1 sobre 9..
• A raiz quadrada de um número que não é um quadrado perfeito não é um número racional. Por exemplo:
Raiz quadrada de 0 vírgula 1.
não é um número racional, pois 0,1 não é um quadrado perfeito.
9. Calcule a raiz quadrada dos números a seguir.
a)
Raiz quadrada de 64,b)
Sentença matemática. Menos raiz quadrada de 81.c)
Sentença matemática. Raiz quadrada de 100.d)
Sentença matemática. Menos raiz quadrada de 16.e)
Raiz quadrada de 49f)
Sentença matemática. Menos raiz quadrada de 4.10. Associe cada item ao seu resultado:
A.
Sentença matemática. Raiz quadrada de 0 vírgula 0001.B.
Sentença matemática. Raiz quadrada de 1 vírgula 44.C.
Sentença matemática. Raiz quadrada de 0 vírgula 81.D.
Sentença matemática. Raiz quadrada de 0 vírgula 25.I. 1,2
II. 0,01
III. 0,5
IV. 0,9
11. Determine o valor das seguintes raízes.
a)
Sentença matemática. Raiz quadrada de 4 sobre 25.b)
Sentença matemática. Raiz quadrado de 9 sobre 64.c)
Sentença matemática. Menos raiz quadrada de 100 sobre 4.d)
Sentença matemática. Raiz quadrada de 1 sobre 16.12. Copie em seu caderno apenas as afirmações verdadeiras.
a) 100 é quadrado perfeito.
b) 0 não é um quadrado perfeito.
c) A raiz quadrada de
Fração. 35 sobre 10.é um número racional.
d) A raiz quadrada de 0,4 não é um número racional.
13. Determine os valores de W, X, Y e Z.
a)
Sentença matemática. Raiz quadrada de W é igual a 4.b)
Sentença matemática. Raiz quadrada de X é igual a 9c)
Sentença matemática. Raiz quadrada de Y é igual a 8.d)
Sentença matemática. Raiz quadrada de Z é igual a 0 vírgula 2.Para o capítulo 3: Sistemas de equações do 1º grau
O plano cartesiano
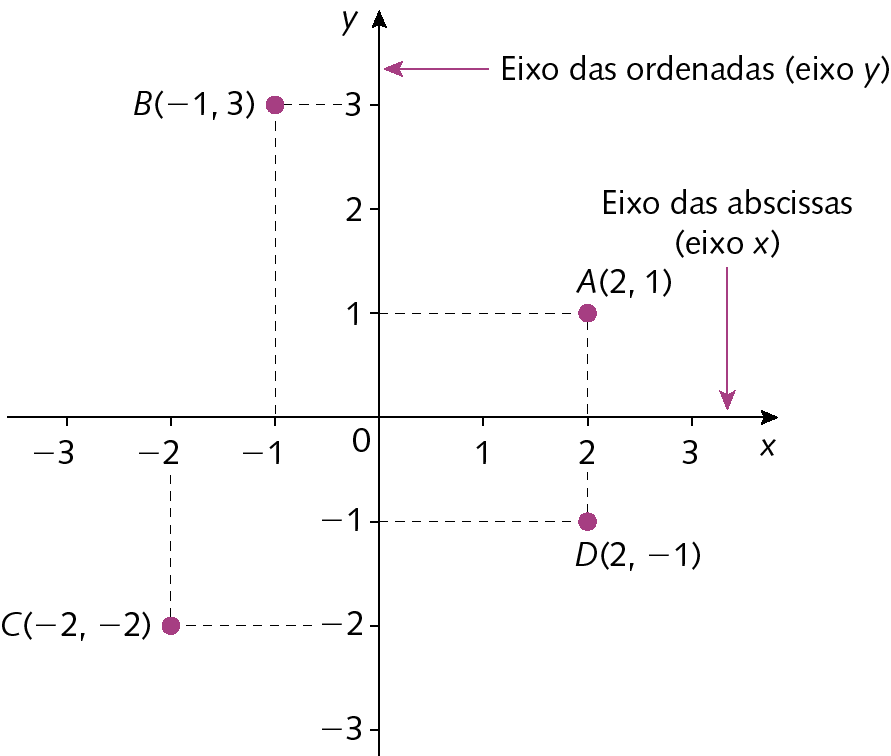
O plano cartesiano é composto de dois eixos, um horizontal e um vertical, chamados de eixo das abscissas (eixo x) e eixo das ordenadas (eixo y), respectivamente. Para representar um ponto no plano cartesiano, utilizamos um par ordenado.
• O ponto a(2, 1) tem abscissa x = 2 e ordenada y = 1.
• O ponto B(‒1, 3) tem abscissa x = ‒1 e ordenada y = 3.
• O ponto C(‒2, ‒2) tem abscissa x = ‒2 e ordenada y = ‒2.
• O ponto D(2, ‒1) tem abscissa x = 2 e ordenada y = ‒1.
14. Observe os pontos representados no plano cartesiano.
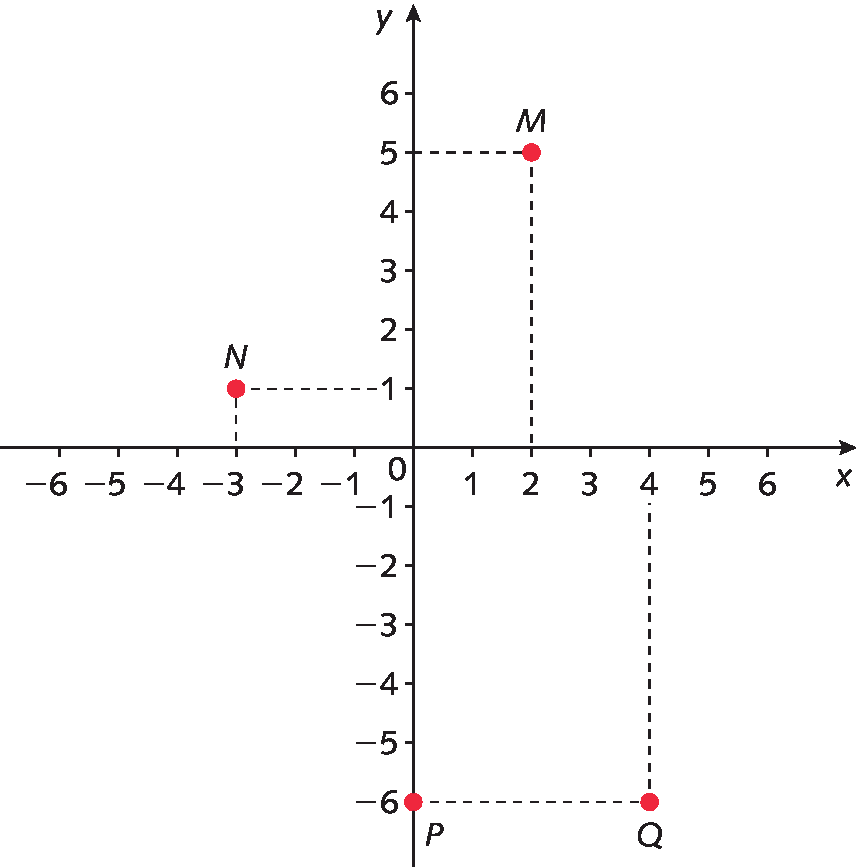
Em seu caderno, escreva as coordenadas de cada um deles.
15. Faça em seu caderno um plano cartesiano e nele represente estes pontos.
a) A(‒5, 2)
b) B(‒1, ‒3)
c) C(0, ‒2)
d) D(4, 0)
Para o capítulo 4: Ângulos e transformações geométricas
Ângulos
Ângulo é a união de duas semirretas de mesma origem, com uma das regiões do plano limitada por elas.
Os lados de um ângulo são as semirretas que o determinam, e o vértice é a origem comum dessas semirretas.
Medida da abertura de um ângulo
Ao medir um ângulo, consideramos a abertura entre seus lados. Podemos utilizar como unidade de medida de ângulo o grau (grau).
Ângulo reto, ângulo agudo e ângulo obtuso
Ângulo reto: ângulo que tem medida de abertura igual a 90graus.
Ângulo agudo: ângulo que tem medida de abertura maior que 0grau e menor que 90graus.
Ângulo obtuso: ângulo que tem medida de abertura maior que 90graus e menor que 180graus.
é reto,
Símbolo. Ângulo COD.é agudo e
Símbolo. Ângulo EOF.é obtuso:

Ângulos congruentes
Ângulos congruentes são ângulos que têm a mesma medida de abertura.
16. Em seu caderno, escreva se a afirmação é verdadeira (V) ou falsa (F).
a) A abertura de um ângulo reto mede 70graus.
b) Dois ângulos retos são sempre congruentes.
c) A medida de abertura de um ângulo obtuso é maior que 90graus.
d) A medida de abertura de um ângulo agudo é maior que 90graus.
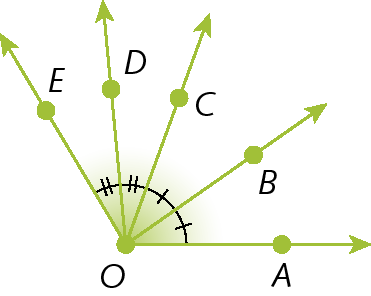
17. Identifique os pares de ângulos congruentes e registre-os em seu caderno.
Transformações geométricas
Isometrias são transformações geométricas que preservam o formato e as medidas da figura original.
Translação é a isometria pela qual a figura é deslocada em determinada direção e sentido, mantendo uma mesma medida da distância entre cada um dos pontos da figura original e o correspondente da figura obtida.

Rotação é a isometria pela qual uma nova figura é obtida a partir de um giro da figura original ao redor de um único ponto fixo. Esse ponto é chamado de centro de rotação.
Em uma rotação, o giro pode ser feito no sentido horário ou no sentido anti-horário, segundo certa medida da abertura de um ângulo.

Reflexão é a isometria pela qual uma figura pode ser refletida, em um plano, de dois modos:
em relação a uma reta

em relação a um ponto
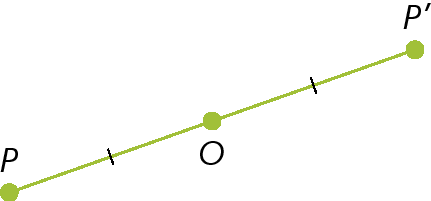
18. Observe as figuras a seguir.
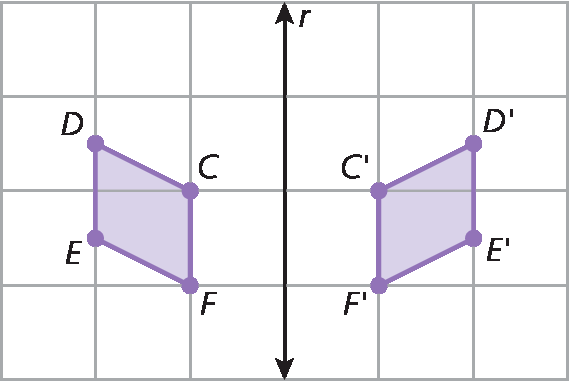
A figura a bê cê dê passou por uma transformação geométrica, originando a figura á′bit′centésimo′divisores de ′. Em seu caderno, responda:
a) Qual transformação foi feita?
b) O que é a reta r?
19. Usando uma folha quadriculada, copie as figuras e faça o que se pede em cada item.
a) A figura á bê cê dê é sofreu uma translação e o ponto E′ é o correspondente ao ponto ê. Represente a figura á′bit′centésimo′divisores de ′E′.
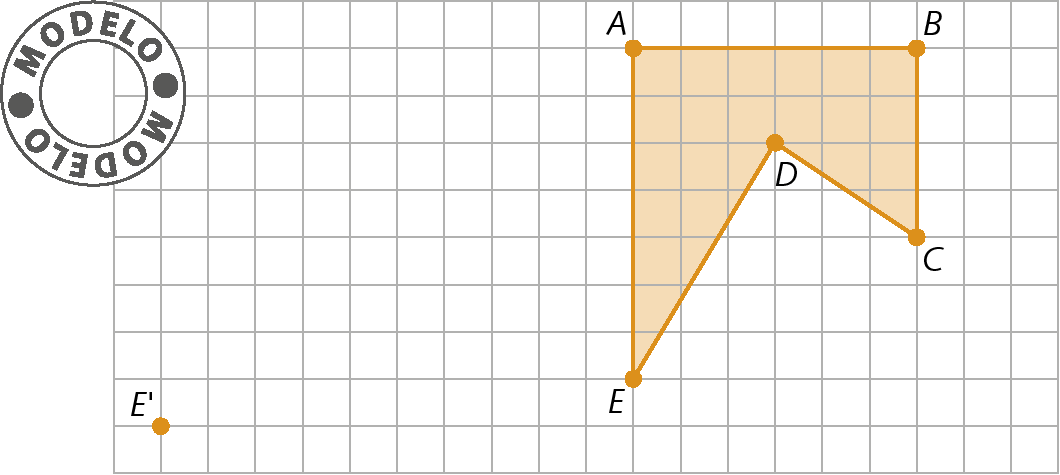
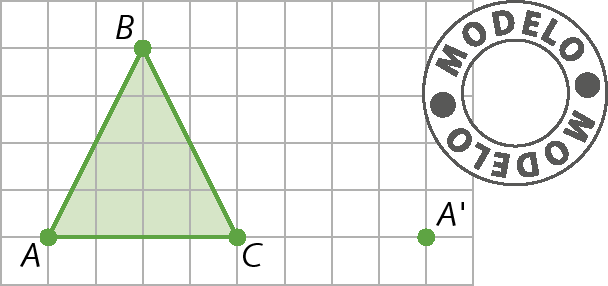
b) A figura á bê cê sofreu uma rotação e o ponto á′ é o correspondente ao ponto a. Represente a figura á′bit′centésimo′.
Para o capítulo 5: Polígonos
Elementos e medidas de um polígono
Podemos identificar os seguintes elementos no polígono á bê cê dê é:
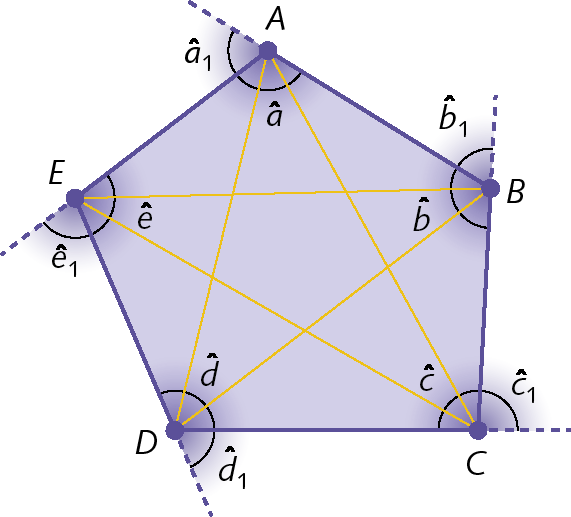
• lados: segmentos de reta que formam o contorno do polígono (
Símbolo. Segmento de reta AB. Símbolo. Segmento de reta BC. Símbolo. Segmento de reta CD. Símbolo. Segmento de reta DE .Símbolo. Segmento de reta EA.);
• vértices: pontos de encontro de dois lados consecutivos (a, B, C, D, ê );
• diagonais: segmentos de reta que unem dois vértices não consecutivos (
Símbolo. Segmento de reta AC. Símbolo. Segmento de reta AD. Símbolo. Segmento de reta BD. Símbolo. Segmento de reta BE. Símbolo. Segmento de reta CE.);
• ângulos internos: ângulos formados por dois lados consecutivos (
Símbolo. Ângulo a. Símbolo. Ângulo b. Símbolo. Ângulo c. Símbolo. Ângulo d. Símbolo. Ângulo e.);
• ângulos externos: ângulos formados por um lado do polígono e pelo prolongamento do lado consecutivo a ele (
Símbolo. Ângulo a1. Símbolo. Ângulo b1. Símbolo. Ângulo c1. Símbolo. Ângulo d1. Símbolo. Ângulo e1.).
Soma das medidas de abertura dos ângulos internos de um polígono
A soma das medidas de abertura dos ângulos internos de qualquer triângulo é sempre 180graus.
Para determinar a soma das medidas de abertura dos ângulos internos de qualquer polígono, traçamos todas as diagonais que partem de um único vértice, decompondo o polígono em triângulos, e multiplicamos a quantidade de triângulos por 180graus.
20. Em seu caderno:
• trace o polígono á bê cê dê é;
• trace uma diagonal;
• marque dois ângulos internos;
• marque um ângulo externo.
21. Para cada um dos polígonos a seguir, encontre o valor de x. Registre a resposta em seu caderno.
a)
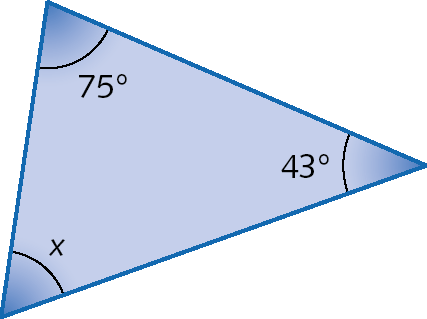
b)
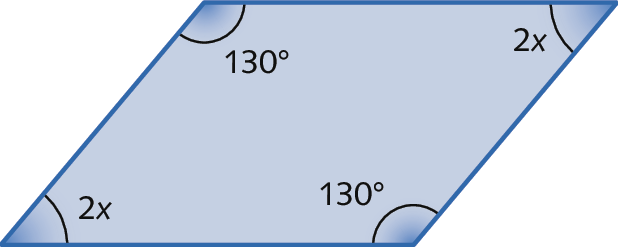
c)
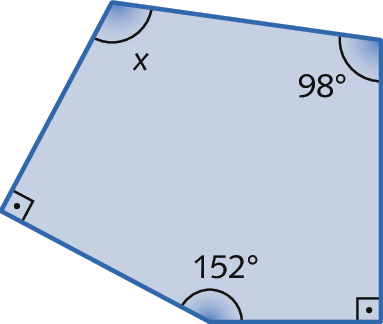
Polígono regular
Um polígono é regular quando todos os ângulos internos têm mesma medida de abertura e todos os lados têm mesma medida de comprimento.
Ângulos internos de um polígono regular
Como os ângulos internos de um polígono regular têm a mesma medida de abertura, para descobrir a medida de abertura de cada ângulo interno de um triângulo equilátero, por exemplo, dividimos 180graus por 3, que resulta em 60graus.
Ângulos externos de um polígono regular
Os ângulos internos e externos dos polígonos são suplementares, ou seja, a soma das medidas de abertura de um ângulo interno e de um ângulo externo é 180graus.
Por isso, conhecendo a medida de abertura de um ângulo interno de qualquer polígono regular, podemos calcular a medida de abertura de um ângulo externo dele.
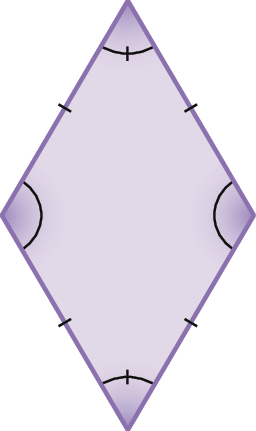
22. Qual dos polígonos seguintes é regular? Por quê?
a)
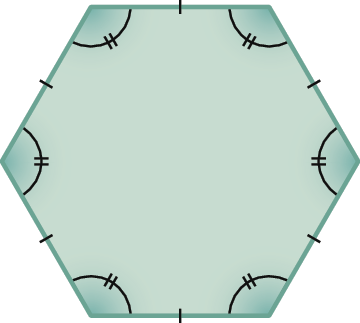
b)
23. Escreva no caderno, qual é o polígono regular cuja abertura de:
a) cada ângulo interno mede 90graus?
b) cada ângulo externo mede 120graus?
Para o capítulo 6: Probabilidade
Probabilidade
Um experimento aleatório é um acontecimento que conhecemos os resultados possíveis, mas não podemos assegurar qual será o resultado. Por não ser possível prever o resultado com exatidão, procuramos medir as chances, ou seja, determinar a probabilidade de certo resultado ocorrer.
A probabilidade de determinado resultado em um experimento aleatório é a razão entre o número de possibilidades favoráveis e o número total de possibilidades.
24. Em seu caderno, registre apenas as afirmações verdadeiras.
a) Quando lançamos uma "moeda honesta", há sempre mais chance de sair cara do que coroa.
b) No lançamento de um "dado honesto" de 6 faces, há a mesma chance de sair um número par e um número ímpar.
c) A probabilidade de sair um número maior que 6 em um "dado honesto" de 6 faces é igual a zero.
25. Em uma urna, há 12 fichas nas seguintes cores:

Ao retirar uma ficha dessa urna, sem olhar, qual é a probabilidade de ela ser da cor:
a) amarela?
b) vermelha?
c) azul?
d) branca?
Para o capítulo 7: Triângulos e quadriláteros
Triângulos
Triângulo é um polígono com três lados.
Principais elementos de um triângulo
• Vértices: a, B e C
• Lados:
Símbolo. Segmento de reta AB. Símbolo. Segmento de reta AC. Símbolo. Segmento de reta BC.• Ângulos internos:
Símbolo. Ângulo A. Símbolo. Ângulo B. Símbolo. Ângulo C.• Ângulos externos:
Símbolo. Ângulo x. Símbolo. Ângulo y. Símbolo. Ângulo z.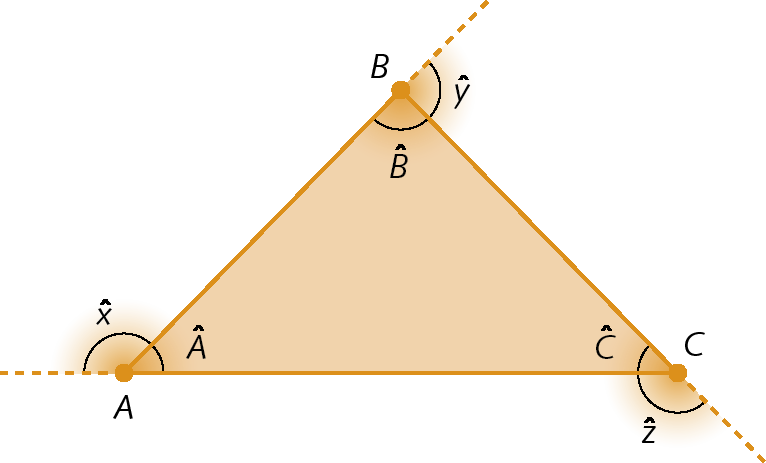
26. Em seu caderno, desenhe um triângulo PQR e indique todos seus ângulos internos.
27. Analise este triângulo.
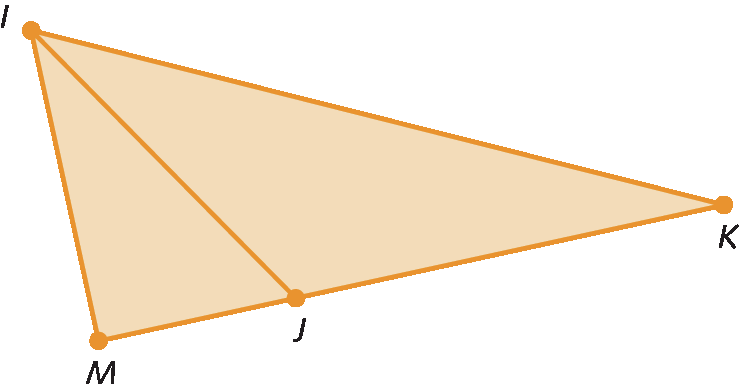
Em seu caderno, indique as afirmações falsas (F) e as verdadeiras (V).
a)
ângulo Mé um ângulo interno do triângulo IMK.
b)
Símbolo. Segmento de reta MJ.é um lado do triângulo IMK.
c)
Símbolo. Ângulo J.é um ângulo externo do triângulo IJK.
d) J é um vértice do triângulo IMK.
Quadriláteros
Quadrilátero é um polígono com quatro lados.
Paralelogramo é um quadrilátero que tem dois pares de lados paralelos.
Trapézio é um quadrilátero que tem apenas um par de lados paralelos.
28. Com o auxílio de régua e esquadro, classifique cada quadrilátero como paralelogramo, trapézio ou outro quadrilátero.
a)

b)

c)

d)

Versão adaptada acessível
28. Desenhe em seu caderno três quadriláteros: um trapézio, um paralelogramo e um outro que não seja quadrilátero nem paralelogramo.
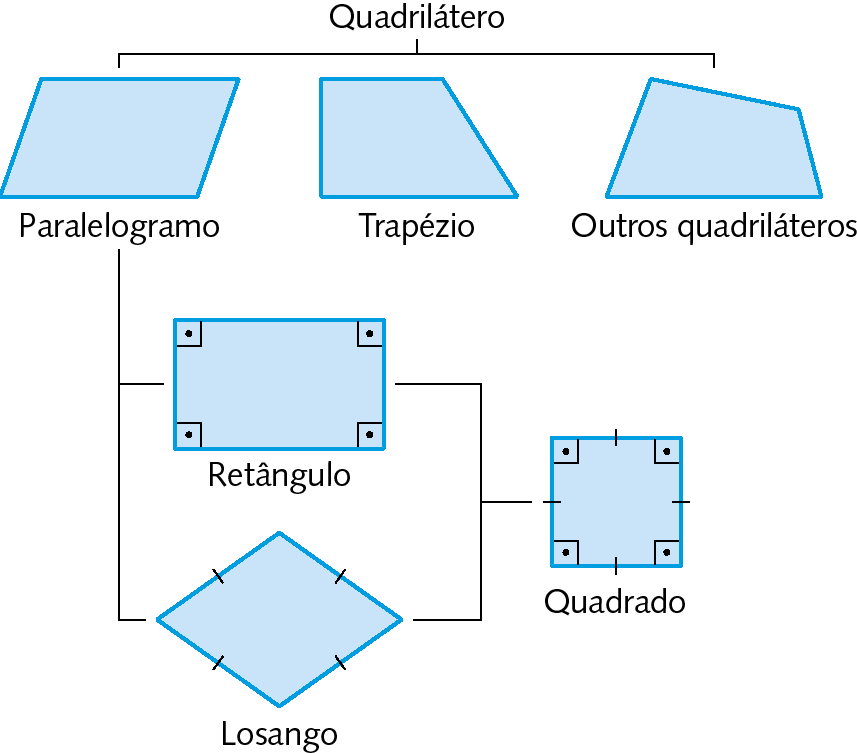
29. Quais afirmações a seguir são verdadeiras?
a) Todo quadrado é um retângulo.
b) Todo retângulo é um losango.
c) Todo retângulo tem quatro ângulos com medida de abertura de 90graus.
d) Todo quadrado tem os quatro lados congruentes.
e) Alguns losangos têm lados com medidas diferentes.
f) Todo retângulo é um quadrado.
Para o capítulo 8: Área, volume e capacidade
Medida da área
Ao calcular a medida da área de polígonos, as medidas de comprimento consideradas devem estar na mesma unidade de medida.
Retângulo
b

medida do comprimento ou medida de comprimento da base
h

medida da largura ou medida de comprimento da altura

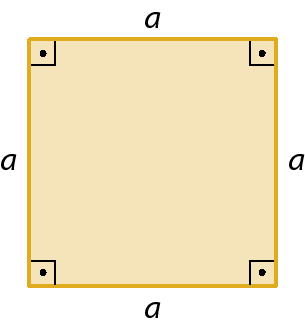
Quadrado
a

medida de comprimento do lado
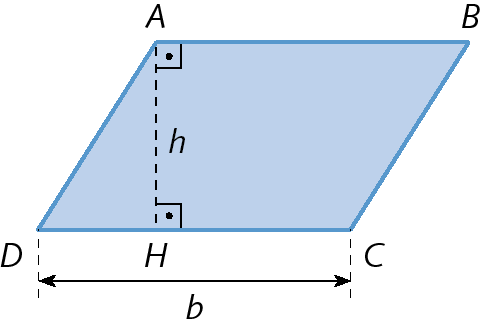
Paralelogramo
b

medida de comprimento da base
h

medida de comprimento da altura relativa à base
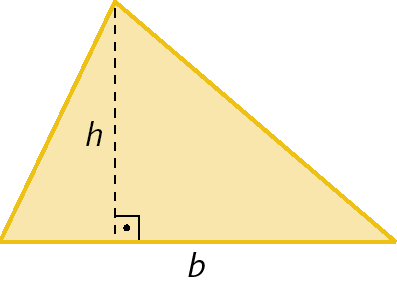
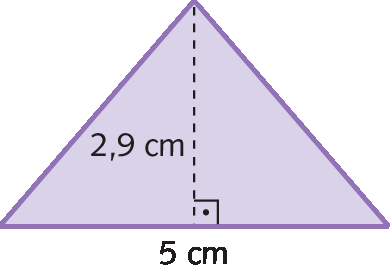
Triângulo
b

medida do comprimento da base
h

medida do comprimento da base
Atriângulo =
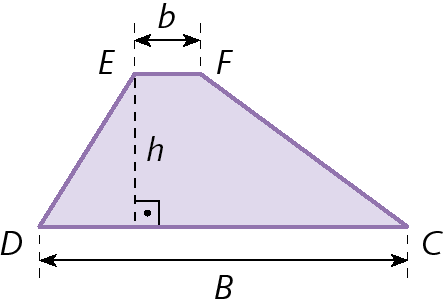
Sentença matemática. Medida da área do triângulo é igual a medida do comprimento da base vezes a medida do comprimento da altura, tudo dividido por 2.Trapézio
a

medida de comprimento da base maior
b

medida de comprimento da base menor
h

medida de comprimento da altura
Atrapézio =
Sentença matemática. Medida da área do trapézio é igual a fração de numerador: Abre parênteses, Medida do comprimento da base maior mais medida do comprimento da base menor, fecha parênteses, vezes, medida da altura e denominador 2.Losango
D

medida de comprimento da diagonal maior
d

medida de comprimento da diagonal menor
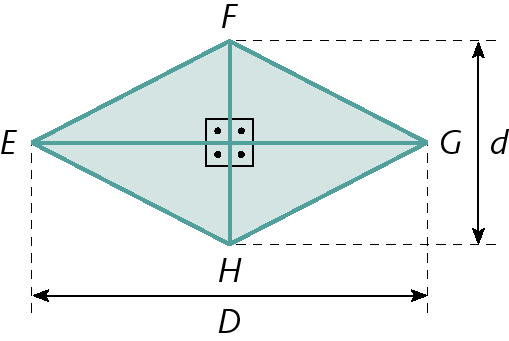
Alosango =
Sentença matemática. Medida da área do losango é igual a medida do comprimento da diagonal maior vezes a medida do comprimento da diagonal menor, tudo dividido por 2.30. Determine a medida da área dos seguintes polígonos:
a)
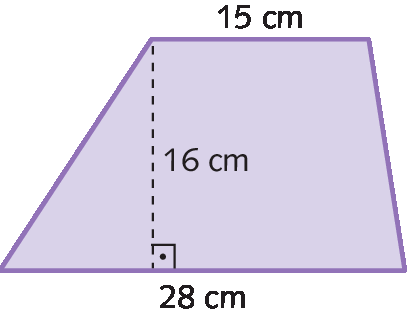
b)
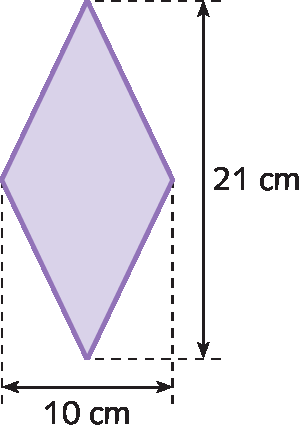
c)
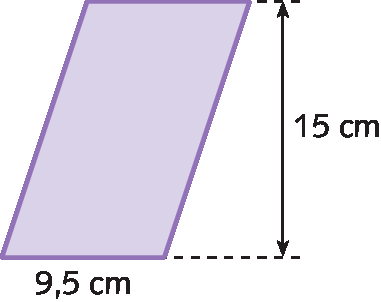
d)
Medida de volume
Ao calcular a medida de volume de sólidos geométricos, as medidas de comprimento consideradas devem estar na mesma unidade de medida.
Paralelepípedo reto-retângulo
A medida de volume de um paralelepípedo reto-retângulo é igual ao produto das medidas do comprimento (c), da largura (a) e da altura (h).
Vparalelepípedo = c ⋅ a ⋅ h
Cubo
O cubo é um caso particular de paralelepípedo, pois tem todas as arestas com a mesma medida de comprimento. Assim, para um cubo cuja medida de comprimento da aresta é a, temos:
Vcubo = a ⋅ a ⋅ a = a3
31. Qual é a medida de volume deste paralelepípedo?
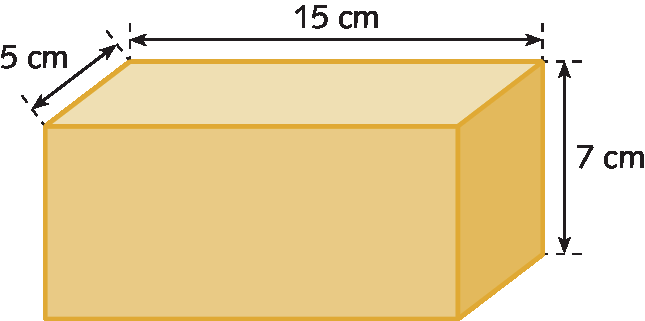
32. Calcule a medida de volume do cubo de cada item, conhecendo a medida de comprimento da aresta (a):
a) a = 12 centímetros
b) a = 0,4 métro
c) a = 9 centímetros
Para o capítulo 9: Equações do 2º grau
Equações do 1º grau
Equação é uma sentença matemática expressa por uma igualdade que apresenta pelo menos um valor desconhecido representado por uma letra denominada incógnita.
• 3x + 5 = 2 é uma equação cuja incógnita é x.
• 5m ‒ 2 = 7n é uma equação cujas incógnitas são m e n.
• 4b ‒ 9 < 6 não é uma equação, pois não é uma igualdade.
• 5 + 13 = 2 ⋅ 9 não é uma equação, pois não tem incógnita.
Quando o maior expoente de uma incógnita em uma equação é 1, a denominamos equação do 1º grau.
• ‒1 ‒ 0,4x = 7 é uma equação de 1º grau.
• x2 + 1 = 0 não é uma equação de 1º grau.
33. Em seu caderno, indique quais sentenças a seguir são equações:
a) 3x + 5 = ‒0,4 + 2x
b) (‒1) ⋅ 32 = 10 ‒ 42
c) a + b + c =
fração 10 sobre 7d) 2x 2 ⩽ 52
34. Escreva, em seu caderno, quais são as afirmações verdadeiras.
a) 2m + 1 ≠ m é uma equação.
b) 35 = 2t ‒ 0,5 é uma equação de 1º grau.
c) 2m ‒ 9 + j = 4 é uma equação cujas incógnitas são m, j e 4.
d) As incógnitas da equação x 2 + y = a são x, y e a.
e) k 3 =
Sentença matemática. k elevado a 3 é igual a 9 oitavos.é uma equação, mas não de 1º grau.
Raiz de uma equação
Quando a incógnita de uma equação assume um valor que torna a sentença verdadeira, esse valor é chamado de raiz da equação.
Vamos considerar as equações 3x + 12 = 42 e 5x = ‒10. Para saber se o número 10 é raiz de uma delas, fazemos a substituição:
3x + 12 = 42
3 ⋅ 10 + 12 = 42
30 + 12 = 42
42 = 42

sentença verdadeira
Logo, 10 é raiz dessa equação.
5x = ‒10
5 ⋅ 10 = ‒10
50 = ‒10

sentença falsa
Logo, 10 não é raiz dessa equação.
O conjunto universo é formado por todos os números que uma incógnita pode assumir e é indicado por conjunto universo.
As raízes da equação que pertencem ao conjunto universo são as soluções dessa equação e formam seu conjunto solução, que é indicado por S.
No exemplo anterior, se considerarmos que a incógnita da equação 3x + 12 = 42 só assume valores naturais, temos conjunto universo =

. Como 10 é número natural e é raiz da equação, dizemos que ele é solução dessa equação e que o conjunto solução dessa equação é S = {10}.
35. Sendo conjunto universo =

, anote no caderno as equações cujo conjunto solução é S = {‒1}.
a) ‒3 = 5x ‒ 2x
b) 8x ‒ 10 = ‒2
c) 5x ‒ 14 = 12x
d)
Sentença matemática. x sobre 2, fim da fração, menos 2, igual a menos 5 meios.36. Considere conjunto universo =

e a equação ‒8x + 23 = 23 + x. Qual dos conjuntos a seguir é o conjunto solução dessa equação?
a) S = {0}
b) S = {1}
c) S = {‒2}
d) S = {‒4}
Resolução de equações de 1º grau com uma incógnita
Quando duas equações têm o mesmo conjunto universo e as mesmas raízes, elas são chamadas de equações equivalentes.
Princípio aditivo das igualdades: quando adicionamos ou subtraímos uma mesma quantidade nos dois membros de uma equação, obtemos uma equação equivalente à primeira.
Princípio multiplicativo das igualdades: quando multiplicamos ou dividimos por um mesmo número não nulo os dois membros de uma equação, obtemos uma equação equivalente à primeira.
Para resolver uma equação, aplicamos os princípios aditivo e multiplicativo das igualdades, de modo a obter equações equivalentes mais simples que as iniciais, determinando, assim, as soluções da equação. Por exemplo:
6x ‒ 10 = 50, sendo conjunto universo =

6 x ‒ 10 + 10 = 50 + 10
6x = 60
=
Sentença matemática. A fração 6x sobre 6 é igual a fração 60 sobre 6.x = 10
S = {10}
37. Sabendo que conjunto universo =

, resolva estas equações no caderno.
a) 5x + 10 = ‒10
b) x ‒ 12 = 29
c) 2x = ‒2 + 6x
38. Para conjunto universo =

, identifique quais afirmações são verdadeiras.
a) O conjunto solução da equação 2x + 3 = ‒8 + x é S = ∅.
b) S = {10} é o conjunto solução da equação 9 + 5x = 5,9.
c) S = {12} é o conjunto solução da equação ‒48 = 3x ‒ 7x.
Para o capítulo 10: Grandezas e proporcionalidade
Razão e proporção
A razão entre dois números, a e bê, com b ≠ 0, nessa ordem, é dada por
Fração. a sobre b..
Podemos expressar a razão na fórma de fração, de porcentagem ou de número decimal.
Exemplo:
Se uma pessoa gastou R$ 10,00dez reais com bebidas e R$ 50,00cinquenta reais com alimentos, podemos dizer que a razão entre o gasto com bebidas e comidas foi
Fração.10 sobre 50., que equivale a
Sentença matemática. 20 sobre 100.= 20% = 0,2.
Proporção é uma igualdade entre duas razões.
Exemplos:
e
Sentença matemática. 6 sobre 15 é igual a 4 sobre 10.Propriedade fundamental das proporções
Em toda proporção, o produto dos extremos é igual ao produto dos meios, ou seja, dados a, b, c e d racionais não nulos, com
Sentença matemática. a sobre b é igual a c sobre d., temos a ⋅ d = b ⋅ c.
Por exemplo, usando as proporções citadas anteriormente, temos que:
3 ⋅ 30 = 9 ⋅ 10
6 ⋅ 10 = 4 ⋅ 15
39. Observe este quadro com os valores das 3 peças que compõem um produto.
|
Peça |
Valor |
|---|---|
|
Peça 1 |
R$ 30,00 |
|
Peça 2 |
R$ 3,00 |
|
Peça 3 |
R$ 90,00 |
|
Total |
R$ 123,00 |
Escreva em seu caderno:
a) a razão entre o valor da peça 1 e o da peça 2.
b) a razão entre o valor da peça 2 e o da peça 1.
c) a razão entre o valor da peça 3 e o total.
40. Quais pares de razões são proporções?
a)
Fração. 11 sobre 9 e Fração. 22 sobre 18.b)
Fração. 1 sobre 3 e Fração. 3 sobre 8.c)
Fração. 216 sobre 600. Fração. 36 sobre 100.d)
Fração. 4 sobre 7 e Fração. 10 sobre 11.41. Determine o valor de x nas proporções sabendo que x é um número real diferente de zero.
a)
Sentença matemática. 2 sobre 3 é igual a 10 sobre x.b)
Sentença matemática. 8 sobre x é igual a 4 sobre 15.c)
Sentença matemática. x sobre cem é igual a 13 sobre 26.Grandezas e proporcionalidade
Grandezas diretamente proporcionais
Duas grandezas são diretamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual à razão entre os valores correspondentes da segunda.
Grandezas inversamente proporcionais
Duas grandezas são inversamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual ao inverso da razão entre os valores correspondentes da segunda.
42. Copie estes quadros no caderno e complete-os, considerando que as grandezas X e Y são diretamente proporcionais.
a)
|
X |
Y |
|---|---|
|
5 |
12 |
|
10 |
24 |
|
2,5 |
6 |
|
15 |
b)

|
X |
Y |
|---|---|
|
0,2 |
16 |
|
1 |
|
|
10 |
800 |
|
0,1 |
8 |
43. As grandezas M e N são inversamente proporcionais, conforme indicado neste quadro.
|
M |
N |
|---|---|
|
4 |
24 |
|
8 |
12 |
|
12 |
8 |
|
6 |
16 |
Qual será o valor de N quando M for 1?
Para o capítulo 11: Medidas de tendência central e pesquisa estatística
Médias
Muitas vezes, em uma pesquisa, podemos sintetizar as informações calculando a média aritmética ou a média aritmética ponderada e utilizar essas medidas para representar o conjunto de dados da pesquisa.
Acompanhe a situação.
Vamos analisar o quadro dos pontos obtidos por um estudante no vestibular:
|
Disciplina |
Nota |
|---|---|
|
Matemática |
8 |
|
Redação |
7 |
|
Inglês |
5 |
|
História |
9 |
Se a pontuação final for a média aritmética (em que todas as pontuações têm o mesmo peso), calculamos assim:
=
Sentença matemática. Fração de numerador 8 mais 7 mais 8 mais 9 e denominador 4 igual a fração 29 quartos que é igual a 7 vírgula 25.= 7,25
Se a pontuação final for a média ponderada considerando que Matemática tem peso 2, Redação tem peso 3 e as demais disciplinas, peso 1, calculamos assim:
44. Analise este quadro com preços de um mesmo produto encontrado em diferentes mercados.
|
Mercado |
Preço (em reais) |
|---|---|
|
Mercado 1 |
36,80 |
|
Mercado 2 |
42,90 |
|
Mercado 3 |
39,90 |
|
Mercado 4 |
31,80 |
|
Mercado 5 |
40,00 |
Calcule, em seu caderno, o preço médio desse produto.
45. Confira a pontuação que duas marcas de chocolate receberam de um cliente, considerando alguns critérios.
|
Critério |
Marca A |
Marca B |
|---|---|---|
|
Preço (peso 2) |
7 |
8 |
|
Sabor (peso 3) |
8 |
7 |
|
Aroma (peso 1) |
7 |
7 |
Em seu caderno, calcule a média ponderada para cada uma dessas marcas.
Para o capítulo 12: Gráficos estatísticos
Gráficos
Gráfico de barras
Esse tipo de gráfico é utilizado principalmente para comparar informações. Podemos ter gráficos de barras verticais (exemplo a seguir) ou barras horizontais.
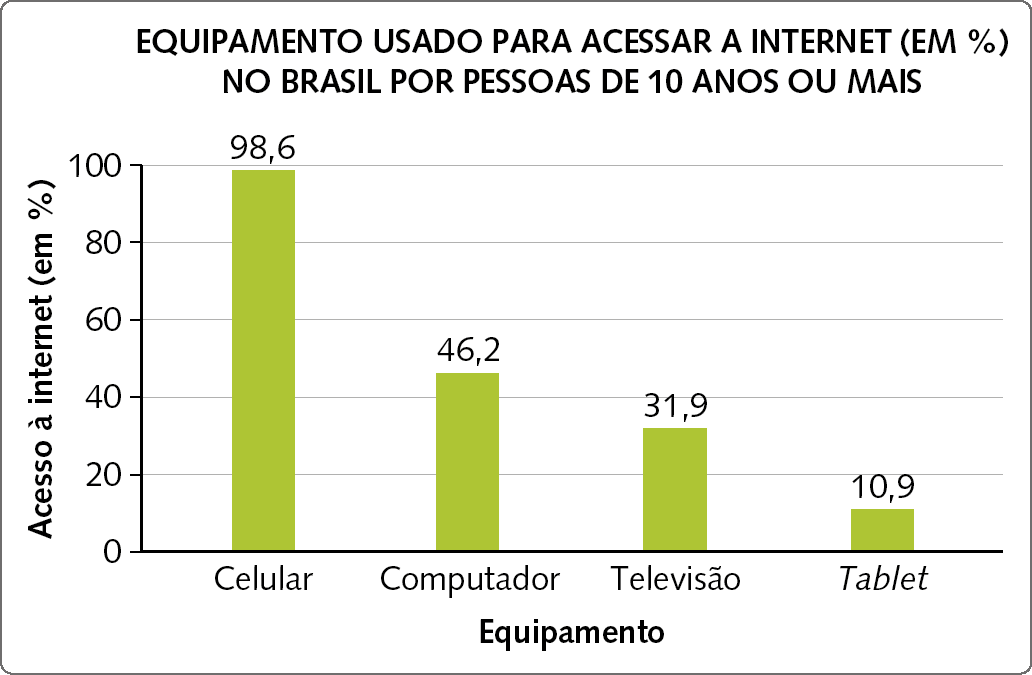
Dados obtidos em: https://oeds.link/0A3tBp. Acesso em: 4 julho 2022.
Gráfico de segmentos
Esse tipo de gráfico é usado quando queremos observar a variação de algum fato ao longo do tempo.

Dados obtidos em: https://oeds.link/LDPePJ. Acesso em: 4 julho 2022.
Gráficos de setores
Esse tipo de gráfico é usado quando queremos representar partes de um total.
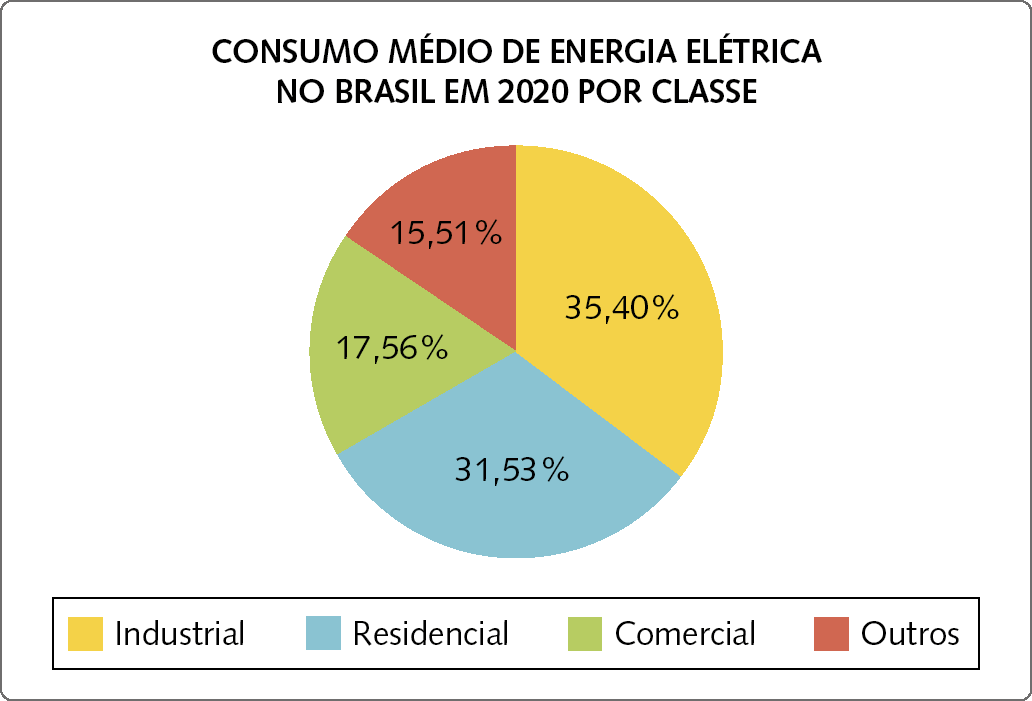
Dados obtidos em: https://oeds.link/1ZvWpg. Acesso em: 4 julho 2022.
46. O que é possível interpretar de cada gráfico dado como exemplo?