Página 42

Capítulo 2 Potenciação e radiciação

Trocando ideias

Armazenamento em nuvem é a tecnologia que permite a usuários e empresas armazenar, manter e acessar dados via internet. A “nuvem” é um ambiente virtual em que podem ser armazenados os arquivos (textos, fotos, vídeos, músicas, planilhas etcétera) de modo que não ocupem o celular, o computador, o tablet ou qualquer outro dispositivo pessoal. Além disso, a nuvem possibilita ao usuário acessar esses arquivos a qualquer momento de qualquer lugar por meio da internet.

Ilustração. Ao centro duas nuvens. Da esquerda para a direita, estão conectados a essas nuvens por meio de fios: um notebook touchscreen, um desktop com CPU, um notebook convencional, um celular, um tablet, um desktop sem CPU e uma câmera fotográfica. Ao redor das nuvens estão presentes símbolos de sinais de wifi e de globos de internet.

Alguns serviços de armazenamento na nuvem disponibilizam 15 GBglossário de espaço gratuito para os usuários.

▸

Você já armazenou algum arquivo na nuvem? O que você pensa a respeito dessa tecnologia? Converse com os colegas.

▸

Aproximadamente, quantos bytes alguns serviços de armazenamento na nuvem disponibilizam para os usuários?

Neste capítulo, vamos ampliar os conhecimentos sobre operações nos diversos conjuntos numéricos, fazendo uso da potenciação e da radiciação.

Página 43

1 Potenciação

Quando um objeto é abandonado no vácuoglossário ou quando desconsideramos a ação do ar sobre esse objeto, ele cai em direção vertical, caracterizando um movimento chamado queda livre.

Um objeto em queda livre, a partir do repouso e durante uma medida de tempo (t ), em segundo, percorre uma medida de distância (d ), em metro. Para representar esse movimento, utiliza-se a seguinte fórmula:

d = \frac{g \cdot t^{2}}{2}

, em que g é a medida da aceleração da gravidade a que um objeto está submetido; considerando que esse objeto esteja próximo à superfície terrestre, essa medida é da ordem de 10 metros por segundo ao quadrado.

Considere a situação a seguir.

Se soltássemos uma esfera metálica de uma altura de medida igual a 320 métros (a mesma medida da altura da Torre Eiffel), a medida da distância aproximada percorrida pela esfera após 2 segundos de queda seria:

d = \frac{10 {m/s}^{2} \cdot t^{2}}{2} = \frac{10 {m/s}^{2} \cdot {(2 s)}^{2}}{2} = \frac{10 {m/s}^{2} \cdot 4 s^{2}}{2} = 20 m

Portanto, a esfera teria percorrido, aproximadamente, 20 métros após 2 segundos.

Esquema. Fotografia de uma torre treliça de ferro de base larga e topo estreito, Na base há arcos. Na parte central há vãos que se parecem com trapézios. Do lado esquerdo da torre há uma cota vertical, indicando torre tem 320 metros de altura. Também está representado um esfera em queda livre. — Torre Eiffel, Paris, França. Foto de 2022.

No cálculo realizado, para encontrar a medida da distância percorrida, utilizamos as operações de multiplicação, potenciação e divisão.

Vamos retomar o estudo da potenciação considerando os casos a seguir, em que a base da potência é um número real e o expoente é um número inteiro.

Observe esta sequência de figuras.

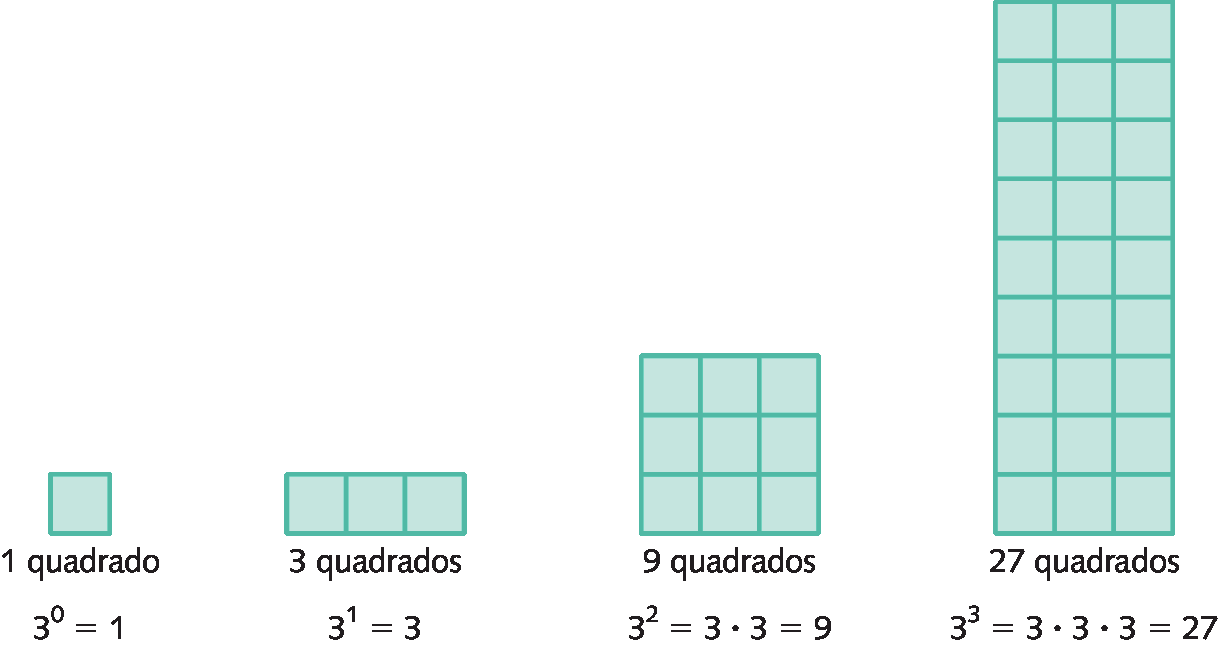
Esquema: Quadradinho verde. Abaixo, está indicado: 1 quadrado. Abaixo, está indicada a sentença matemática: 3 elevado a zero igual a 1. Esquema: 3 quadradinhos verdes dispostos na horizontal. Abaixo, está indicado: 3 quadrados. Abaixo, está indicada a sentença matemática: 3 elevado a um igual a 3. Esquema: 9 quadradinhos verdes dispostos 3 linhas com 3 quadradinhos cada. Abaixo, está indicado: 9 quadrados. Abaixo, está indicada a sentença matemática: 3 ao quadrado igual a 3 vezes 3 igual a 9. Esquema: 27 quadradinhos verdes dispostos 9 linhas com 3 quadradinhos cada. Abaixo, está indicado: 27 quadrados. Abaixo, está indicada a sentença matemática: 3 ao cubo igual a 3 vezes 3 vezes 3 igual a 27.

Qualquer potência de base real e expoente inteiro maior que 1 é produto dessa base por ela mesma tantas vezes quantas indica o expoente. Assim, sendo a um número real e n um número inteiro maior que 1, temos:

Esquema.
a elevado a n igual, a vezes a vezes a vezes reticências virgula n maior que 1.
Um fio laranja sai dos fatores dessa multiplicação e indica n fatores.

Página 44

• Qualquer potência de base real e expoente 1 é igual à própria base. Assim, sendo a um número real, temos:

a elevado a 1 = a

• Qualquer potência de base real não nula e expoente zero é igual a 1. Assim, sendo a um número real, temos:

a elevado a 0 = 1, a ≠ 0

Confira estes exemplos.

a) 2elevado a 3 = 2 ⋅ 2 ⋅ 2 = 8

b) (menos7)elevado a 2 = (menos7) ⋅ (menos7) = 49

{(- \frac{1}{5})}^{4} = (- \frac{1}{5}) \cdot (- \frac{1}{5}) \cdot (- \frac{1}{5}) \cdot (- \frac{1}{5}) = \frac{1}{625}

d) (0,1)elevado a 3 = (0,1) ⋅ (0,1) ⋅ (0,1) = 0,001

{(- \frac{5}{8})}^{1} = - \frac{5}{8}

f) (0,666...)elevado a 1 = 0,666...

g) (0,232323...)elevado a 0 = 1

{(\frac{3}{4})}^{0} = 1

Considere, agora, esta sequência.

Esquema. Quadro com 7 colunas e 1 linha. Números que aparecem em cada coluna da esquerda para a direita: 125, 25, 5, 1, 1 quinto, um 25 avos. um 125 avos. Da primeira para a segunda coluna seta para a direita dividido por 5. Da segunda para a terceira coluna seta para a direita dividido por 5. Da terceira para quarta coluna seta para a direita dividido por 5 e assim sucessivamente até da sexta para a sétima coluna.

Podemos escrever esses números na fórma de potências de base 5. Como cada termo é o termo anterior dividido por 5, os expoentes das potências de base 5 diminuirão uma unidade a cada termo.

Esquema. Quadro com 7 colunas e 2 linhas. Na primeira linha, os números que aparecem em cada coluna da esquerda para a direita: 125, 25, 5, 1, 1 quinto, um 25 avos. um 125 avos. Na segunda linha, as sentenças matemáticas que aparecem em cada coluna da esquerda para a direita: 5 elevado a 3, 5 elevado a 2, 5 elevado a 1, 5 elevado a zero, 5 elevado a menos 1, 5 elevado a -2, 5 elevado a -3. Abaixo da segunda linha, da primeira para a segunda coluna seta para a direita dividido por 5. Da segunda para a terceira coluna seta para a direita dividido por 5. Da terceira para quarta coluna seta para a direita dividido por 5 e assim sucessivamente até da sexta para a sétima coluna.

Analise as potências com expoentes negativos que obtivemos no quadro anterior.

5^{- 1} = 1 : 5 = 1 \cdot \frac{1}{5} = \frac{1}{5}

5^{- 2} = \frac{1}{5} : 5 = \frac{1}{5} \cdot \frac{1}{5} = {(\frac{1}{5})}^{2}

5^{- 3} = {(\frac{1}{5})}^{2} : 5 = \frac{1}{5} \cdot \frac{1}{5} \cdot \frac{1}{5} = {(\frac{1}{5})}^{3}

Qualquer potência de base real não nula e expoente inteiro negativo é igual à potência do inverso da base dada e expoente igual ao oposto do expoente dado. Assim, sendo a um número real não nulo e menosn um expoente inteiro negativo, temos:

a^{- n} = \frac{1}{a^{n}} = {(\frac{1}{a})}^{n}, a \neq 0

Verifique mais alguns exemplos.

2^{‒ 2} = \frac{1}{2^{2}} = \frac{1}{4}

(‒ 3)^{‒ 4} = \frac{1}{{(- 3)}^{4}} = \frac{1}{81}

{(\frac{2}{3})}^{- 2} = \frac{1}{{(\frac{2}{3})}^{2}} = \frac{1}{\frac{4}{9}} = \frac{9}{4}

Página 45

Notação científica

Considere as potências de 10 a seguir.

Esquema. 10 ao quadrado igual a 100. Uma chave para baixo indica 2 zeros do 100.Esquema. 10 elevado a 3 igual a mil. Uma chave para baixo indica 3 zeros do mil. Esquema. 10 elevado a 4 igual a 10 mil. Uma chave para baixo indica 4 zeros do 10 mil. Esquema. 10 elevado a 5 igual a 100 mil. Uma chave para baixo indica 5 zeros do 100 mil.

Note que cada potência de 10, com expoente natural, é igual a um número representado por 1 seguido de zeros. Assim:

Esquema. 10 elevado a n igual a 1 zero zero zero zero zero reticências zero. Uma chave para baixo indica os n zeros.

As potências de 10 são utilizadas para expressar números excessivamente grandes ou extremamente pequenos, como nos exemplos a seguir.

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.

Fotografia. Fundo escuro com planeta Terra. — A medida da massa da Terra é de aproximadamente 5,972 ⋅ 10elevado a 24 quilogramas.

Fotografia. Fundo escuro com esferas alaranjadas e interior vermelho. À esquerda, manchas na cor verde. — Partículas do vírus sárs cóv dois, causador da côvid dezenóve, em microfotografia em cores realçadas produzida por microscópio eletrônico. Foto ampliada em 191.200 vezes. Segundo estudos, o comprimento do diâmetro desse vírus mede entre 5 ⋅ 10elevado a menos 8 métros e 2 ⋅ 10elevado a menos 7 métros.

Os números 5,972 ⋅ 10elevado a 24, 5 ⋅ 10elevado a menos 8 e 2 ⋅ 10elevado a menos 7 estão representados em notação científica. Nesse tipo de representação, o número que multiplica a potência de base dez deve estar entre o número 1 e o 10.

Um número escrito em notação científica apresenta o formato a ⋅ 10elevado a bê, em que b é um expoente inteiro e a pertence ao intervalo 1 < a < 10.

Confira mais alguns exemplos.

a) ...3000000000 = 3 ⋅ ...1000000000 = 3 ⋅ 10elevado a 9 (a = 3 e b = 9)

b) .....476000000000000000 = 4,76 ⋅ .....100000000000000000 = 4,76 ⋅ 10elevado a 17 (a = 4,76 e b = 17)

c) 0,00000008 = 8 ⋅ 0,00000001 = 8 ⋅ 10elevado a menos 8 (a = 8 e b = −8)

d) 0,0000032 = 3,2 ⋅ 10elevado a menos 6 (a = 3,2 e b = −6)

Página 46

Atividades

Faça as atividades no caderno.

1. Calcule as potências a seguir.

a) 2elevado a 4

{(\frac{1}{2})}^{- 3}

c) 2elevado a menos 3

{(\frac{1}{5})}^{3}

e) abre parêntesesmenos4fecha parênteseselevado a 3

f) 10elevado a 3

g) abre parênteses0,1fecha parênteseselevado a menos 2

{(- \frac{3}{7})}^{- 2}

i) 10elevado a menos 3

{(\frac{2}{3})}^{2}

k) 0 elevado a 10

l) abre parênteses0,181818...)elevado a 2

2. Calcule o valor de:

a) 3x elevado a 3 menos 2x elevado a 2 menos x + 5, para x = menos1

b) abre parêntesesmenos1fecha parênteseselevado a 8 menos 3 ⋅ abre parêntesesmenos1fecha parênteseselevado a 5 + abre parêntesesmenos1fecha parênteseselevado a 16

c) 2elevado a 6 menos 2elevado a 5 + 2elevado a 4 menos 2elevado a 3 + 2elevado a 2 menos 2elevado a 1 + 2elevado a 0

3. Os resultados de menos 9 entre parênteses elevado a 2 e menos9elevado a 2 são iguais? Justifique sua resposta.

4. Escreva os números a seguir em notação científica.

a) .5400

b) 0,0025

c) ..300000000

d) 0,00000637

5. Qual expressão tem maior valor: a ou B ?

ei =

{(\frac{1}{1})}^{- 2} + {(\frac{1}{2})}^{2} + {(\frac{1}{3})}^{- 2} + {(\frac{1}{4})}^{2} + {(\frac{1}{5})}^{- 2}

B =

{(\frac{1}{1})}^{2} + {(\frac{1}{2})}^{- 2} + {(\frac{1}{3})}^{2} + {(\frac{1}{4})}^{- 2} + {(\frac{1}{5})}^{2}

6. A partir do repouso, um corpo em queda livre percorre, no vácuo, uma medida de distância d (em metro) que corresponde a

\frac{g \cdot t^{2}}{2}

, em que g é a medida da aceleração da gravidade (considere g = 10 metros por segundo ao quadrado).

Fotografia. Um homem em queda livre no ar com os braços para frente e pernas para cima. Eles está com capacete, óculos e a uma espécie de mochila nas costas em que fica o paraquedas dobrado. Abaixo, está o solo. mostrando como o homem está bem alto.

Desprezando a resistência do ar, que medida de distância percorre um paraquedista em queda livre durante os 12 primeiros segundos?

7. Copie o quadro no caderno e complete com as medidas expressas em notação científica.

Medidas das distâncias médias de alguns planetas até o Sol
Planeta	Medida da distância média ao Sol (km)	Medida expressa em notação científica (km)
Saturno	1.429.400.000
Vênus	108.200.000
Urano	2.870.990.000
Mercúrio	57.910.000

Dados obtidos em: https://oeds.link/rWdxPJ. Acesso em: 4 julho 2022.

Página 47

Propriedades da potenciação para potências de base real e expoente inteiro

Todas as propriedades da potenciação são válidas para as potências de base real e expoente inteiro, desde que as condições para a existência das potências sejam obedecidas.

Produto de potências de mesma base

Em uma multiplicação de potências de mesma base, conservamos a base e adicionamos os expoentes.

Esquema. Início da potência, 2 elevado a 2, fim da potência, vezes, início da potência, 2 elevado a 3, fim da potência, igual, abre parênteses, 2 vezes 2, fecha parênteses, vezes, abre parênteses, 2 vezes 2 vezes 2, fecha parênteses, igual a 2 vezes 2 vezes 2 vezes 2 vezes 2 igual a 2 elevado a 5 igual a 2 elevado ao expoente 2 mais 3. Uma chave para baixo a partir do 2 vezes 2, indicando 2 elevado a 2. Uma chave para baixo a partir do 2 vezes 2 vezes 2, indicando 2 elevado a 3.

Considere mais alguns exemplos.

a) (0,15)elevado a 2 ⋅ (0,15)elevado a 3 = (0,15)elevado a 2 mais 3 = (0,15)elevado a 5

b) (0,777reticências)elevado a menos 1 ⋅ (0,777reticências)elevado a 5 = (0,777reticências)elevado a menos 1 mais 5 = (0,777reticências)elevado a 4

De modo geral: a elevado a m ⋅ a elevado a n = a elevado a m mais n, em que ei é um número real não nulo e m e n são números inteiros.

Quociente de potências de mesma base

Em uma divisão de potências de mesma base não nula, conservamos a base e subtraímos os expoentes.

Sentença matemática. Fração de numerador 3 elevado a 5 e denominador 3 elevado a 3. Essa fração é igual a fração de numerador 3 vezes 3 vezes 3 vezes 3 vezes 3 e denominador 3 vezes 3 vezes 3 que é igual a 3 vezes 3 que é igual a 3 ao quadrado que é igual a 3 elevado ao expoente 5 menos 3.

Analise mais alguns exemplos.

a) (0,19)elevado a 6 : (0,19)elevado a 2 = (0,19) elevado a 6 menos 2 = (0,19)elevado a 4

\frac{5^{7}}{5^{- 3}} = 5^{7 - (- 3)} = 5^{10}

De modo geral: a elevado a m : a elevado a n = a elevado a m menos n, em que ei é um número real não nulo e m e n são números inteiros.

Potência de uma potência

Uma potência elevada a um expoente pode ser escrita mantendo-se a base e multiplicando-se os expoentes.

abre parênteses4elevado a 2fecha parênteseselevado a 4 = 4elevado a 2 ⋅ 4elevado a 2 ⋅ 4elevado a 2 ⋅ 4elevado a 2 = 4elevado a 2 mais 2 mais 2 mais 2 = 4elevado a 8 = 4elevado a duas vezes 4

Verifique mais alguns exemplos.

a) abre colcheteabre parênteses0,32fecha parênteseselevado a 3fecha colcheteelevado a 2 = abre parênteses0,32fecha parênteseselevado a 3 vezes 2 = abre parênteses0,32fecha parênteseselevado a 6

{[{(- \frac{1}{5})}^{3}]}^{5} = {(- \frac{1}{5})}^{3 \cdot 5} = {(- \frac{1}{5})}^{15}

De modo geral: (a elevado a m)elevado a n = aelevado a m vezes n, em que a é um número real não nulo e m e n são números inteiros.

Página 48

Potência de um produto

Em uma multiplicação de dois ou mais fatores elevados a um mesmo expoente, podemos elevar cada um desses fatores a esse mesmo expoente.

(2 ⋅ 5)elevado a 3 = (2 ⋅ 5) ⋅ (2 ⋅ 5) ⋅ (2 ⋅ 5) = 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5 ⋅ 5 = 2elevado a 3 ⋅ 5elevado a 3

Verifique mais alguns exemplos.

a) (2 ⋅ 5)⁻elevado a 3 = 2⁻elevado a 3 ⋅ 5⁻elevado a 3

{(\frac{3}{5} \cdot \frac{1}{2})}^{- 2} = {(\frac{3}{5})}^{- 2} \cdot {(\frac{1}{2})}^{- 2}

De modo geral: (a ⋅ b)^m = a^m ⋅ b^m, em que a ê b são números reais não nulos e m é um número inteiro.

Potência de um quociente

Em uma divisão elevada a um expoente, podemos elevar o dividendo e o divisor a esse mesmo expoente.

{(7 : 6)}^{2} = {(\frac{7}{6})}^{2} = (\frac{7}{6}) \cdot (\frac{7}{6}) = \frac{7^{2}}{6^{2}}

Verifique mais alguns exemplos.

a) (8 : 3)elevado a 2 = 8elevado a 2 : 3elevado a 2

{(\frac{4}{3} : \frac{3}{16})}^{- 3} = {(\frac{4}{3})}^{- 3} : {(\frac{3}{16})}^{- 3}

De modo geral: (a : b)^m = a^m : b^m, em que a ê b são números reais não nulos e m é um número inteiro.

Observação

Confira atentamente estas desigualdades.

• 2elevado a 3 + 2⁴ ≠ 2elevado a 3 ⁺ elevado a 4, pois: 24 ≠ 128

• 2elevado a 3 menos 2⁴ ≠ 2elevado a 3 ⁻ ⁴, pois:

‒ 8 \neq \frac{1}{2}

•

(5^{2})^{3} \neq 5^{2^{3}}

, pois: 5elevado a 6 ≠ 5elevado a 8

• (5 + 3)elevado a 2 ≠ 5elevado a 2 + 3elevado a 2, pois: 64 ≠ 34

• (5 menos 3)elevado a 2 ≠ 5elevado a 2 menos 3elevado a 2, pois: 4 ≠ 16

Atividades

Faça as atividades no caderno.

8. Indique sob a fórma de uma só potência.

a) 2elevado a 3 ⋅ 2elevado a 4 ⋅ 25 ⋅ 26

b) (2elevado a 3)elevado a 2

c) (6 : 3)elevado a 3

d) 10elevado a 3 ⋅ 10 ⋅ 10

e) (3elevado a 4)elevado a menos 3

f) 6elevado a 4 : 6elevado a 2

g) (2 ⋅ 3)elevado a 3

h) 7 elevado a 15 : 7 elevado a 10

i) 10elevado a menos 1 ⋅ 10elevado a 2 ⋅ 10elevado a menos 1

9. Calcule o valor de cada potência usando as propriedades da potenciação.

\frac{2^{4} \cdot 2^{10} \cdot 2^{3}}{2^{5} \cdot 2^{6}}

b) (7 ⋅ 4)2

{(\frac{1}{4})}^{3}

{[{(- \frac{1}{2})}^{3}]}^{2}

10. Determine o valor da expressão numérica:

(1, 666. ..)^{‒ 1} + \frac{{(3^{10} \cdot 3^{- 5})}^{3}}{9^{8}}

11. Calcule o valor das expressões numéricas.

a) 3elevado a 2 ⋅ 4elevado a 1 menos 2elevado a 0 + 3elevado a 1 ⋅ 3elevado a 2 ⋅ 3elevado a 3

b) (menos2)elevado a menos 6 ⋅ 8elevado a 2 + 30

c) 6elevado a 1 ⋅ 3elevado a menos 2 + 4elevado a menos 1 menos 4 ⋅ 7 elevado a 0

d) 8elevado a 4 ⋅ 8elevado a 3 ⋅ 8elevado a 4 : 8elevado a 8

12. Em seu caderno, avalie cada sentença como verdadeira ou falsa.

a) (2 ⋅ 5)elevado a 3 = 2elevado a 3 ⋅ 5elevado a 3

b) (2 + 5)elevado a 3 = 2elevado a 3 + 5elevado a 3

c) (17 ‒ 1)elevado a 2 = 17elevado a 2 menos 1elevado a 2

Página 49

2 Radiciação

No movimento de queda livre de um objeto a partir do repouso apresentado no início do tópico Potenciação, indicamos que esse objeto percorre, durante uma medida de tempo (t ), em segundo, uma medida de distância (d ), em metro, que corresponde aproximadamente a:

d = \frac{g \cdot t^{2}}{2}

, em que g é a medida da aceleração da gravidade a que um objeto está submetido, correspondendo a 10 metros por segundo ao quadrado para um objeto próximo à superfície terrestre.

Se soltássemos uma esfera metálica de uma altura medindo, por exemplo, 320 métros (a mesma medida da altura da Torre Eiffel), desprezando a resistência do ar, após 2 segundos, a esfera teria percorrido aproximadamente 20 métros.

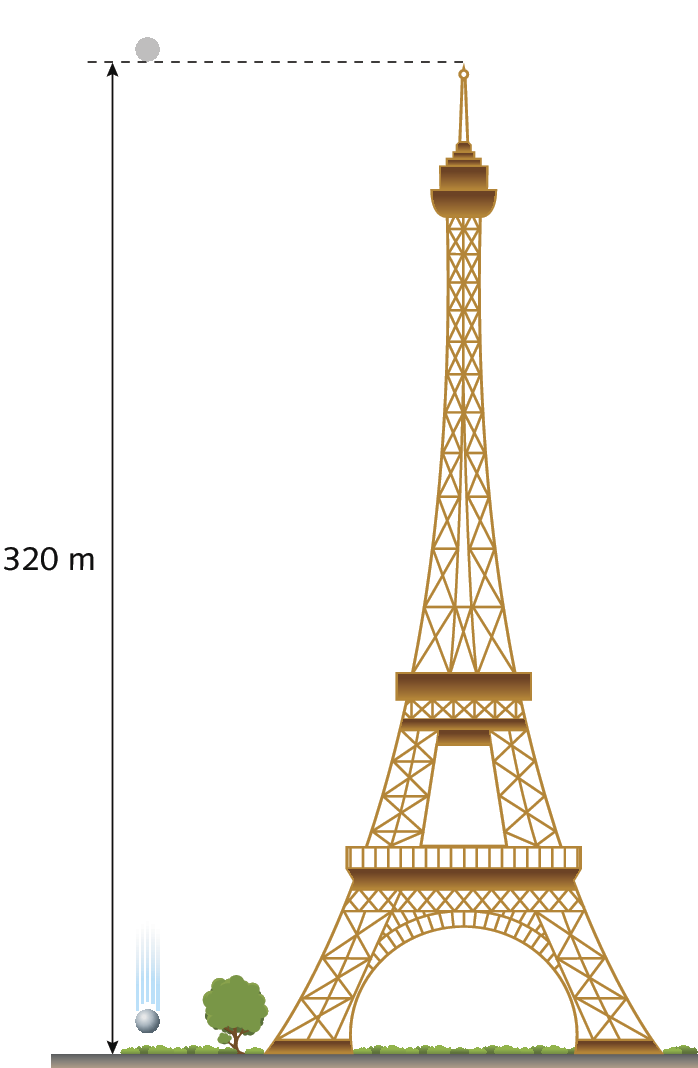
Esquema. Representação de uma torre treliça de base larga e topo estreito, Na base há um arco e na parte central uma abertura com formato similar a de um trapézio.
Do lado esquerdo da representação da torre há uma cota vertical, indicando que a torre tem 320 metros de altura. Também está representado um esfera em queda livre.

Agora, vamos determinar a medida aproximada do tempo que essa esfera demoraria para chegar ao solo.

d = \frac{g \cdot t^{2}}{2}

320 = \frac{10 \cdot t^{2}}{2}

10 ⋅ t2 = 640

t^{2} = \frac{640}{10}

t 2 = 64

Sabemos que t representa a medida do tempo da queda e, por isso, t > 0. Para obter o número positivo que elevado ao quadrado resulta em 64, fazemos:

\sqrt{64} = 8

Logo:

t = \sqrt{64}

t = 8

Portanto, a esfera metálica levaria aproximadamente 8 segundos para chegar ao solo.

Nesses cálculos realizados para encontrar a medida aproximada do tempo de queda da esfera metálica, utilizamos as operações de multiplicação, divisão e radiciação.

Nesse exemplo, vimos que

\sqrt{64} = 8

, pois 8elevado a 2 = 64.

Além da raiz quadrada

(\sqrt{...} ou \sqrt[2]{...})

, temos também as raízes cúbicas

(\sqrt[3]{...})

, quartas

(\sqrt[4]{...})

, quintas

(\sqrt[5]{...})

, entre outras. Os números 2, 3, 4 e 5 nesses símbolos são chamados índices.

Raiz quadrada

A raiz quadrada de um número real positivo x é um número não negativo que, elevado ao quadrado, resulta em x.

Confira alguns exemplos.

\sqrt{36} = 6

, pois: 62 = 36 b)

\sqrt{0,16} = 0,4

, pois: (0,4)elevado a 2 = 0,16 c)

\sqrt{\frac{49}{81}} = \frac{7}{9}

, pois:

{(\frac{7}{9})}^{2} = \frac{49}{81}

Observação

Há dois números que, elevados ao quadrado, resultam em 64:

8elevado a 2 = 64 e (‒8)elevado a 2 = 64

Porém, pela definição, a raiz quadrada é um número não negativo. Logo,

\sqrt{64} = 8

Página 50

Raiz quadrada exata

Considere as operações:

• 1 ⋅ 1 = 1elevado a 2 = 1

• 2 ⋅ 2 = 2elevado a 2 = 4

• 3 ⋅ 3 = 3elevado a 2 = 9

• 4 ⋅ 4 = 4elevado a 2 = 16

• 5 ⋅ 5 = 5elevado a 2 = 25

• 6 ⋅ 6 = 6elevado a 2 = 36

• 7 ⋅ 7 = 7elevado a 2 = 49

• 8 ⋅ 8 = 8elevado a 2 = 64

• 9 ⋅ 9 = 9elevado a 2 = 81

• 10 ⋅ 10 = 10elevado a 2 = 100

• 11 ⋅ 11 = 11elevado a 2 = 121

• 12 ⋅ 12 = 12elevado a 2 = 144

Os números 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121 e 144 são exemplos de quadrados perfeitos, pois podem ser escritos como uma potência de base racional e expoente 2.

Se x for um número racional e for quadrado perfeito,

\sqrt{x}

será um número racional. Em casos assim, podemos obter a raiz quadrada exata desses números.

Assim:

•

\sqrt{1} = 1

•

\sqrt{4} = 2

•

\sqrt{9} = 3

•

\sqrt{16} = 4

•

\sqrt{25} = 5

•

\sqrt{36} = 6

•

\sqrt{49} = 7

•

\sqrt{64} = 8

•

\sqrt{81} = 9

•

\sqrt{100} = 10

•

\sqrt{121} = 11

•

\sqrt{144} = 12

Para determinar a raiz quadrada de números quadrados perfeitos, podemos utilizar a decomposição em fatores primos.

Analise os exemplos.

a) Vamos determinar a raiz quadrada de .1296.

Inicialmente, decompomos .1296 em fatores primos.

Esquema. Decomposição na vertical do número mil 296. Entre os números da esquerda e da direita há um traço vertical. À esquerda o número mil 296 e à direita, o número 2. Abaixo, à esquerda o 648, à direita o 2. Abaixo, à esquerda o 324 e à direita o 2. Abaixo, à esquerda o 162 e à direita o 2. Abaixo, à esquerda o 81 e à direita o 3. Abaixo, à esquerda o 27 e à direita o 3. Abaixo, à esquerda o 9 e à direita o 3. Abaixo, à esquerda o 3 e à direita outro 3. Abaixo apenas à esquerda o 1.

.1296 = 24 ⋅ 34

.1296 = (22 ⋅ 32)2 = 362

Portanto,

\sqrt{1 296} = 36

, pois 362 = .1296.

b) Vamos determinar a raiz quadrada de 10,89.

Inicialmente, transformamos o número decimal 10,89 na fração decimal

\frac{1 089}{100}

Em seguida, decompomos em fatores primos o numerador e o denominador. Confira:

\frac{1 089}{100} = \frac{3^{2} \cdot 11^{2}}{2^{2} \cdot 5^{2}} = \frac{{(3 \cdot 11)}^{2}}{{(2 \cdot 5)}^{2}} = \frac{33^{2}}{10^{2}} = {(\frac{33}{10})}^{2} = {(3,3)}^{2}

Portanto,

\sqrt{10,89} = \sqrt{{(\frac{33}{10})}^{2}} = \frac{33}{10} = 3, 3

, pois (3,3)2 = 10,89.

Página 51

Observação

Se x for um número não negativo e não for quadrado perfeito,

\sqrt{x}

será um número com infinitas casas decimais não periódicas, ou seja, será um número irracional.

Verifique os exemplos.

a) 3 não é um quadrado perfeito e

\sqrt{3}

é um número irracional.

\frac{1}{11}

não é um quadrado perfeito e

\sqrt{\frac{1}{11}}

é um número irracional.

Raiz quadrada aproximada

Podemos calcular a raiz quadrada de qualquer número real não negativo, mas, se ela for um número irracional, não será exata. Nesse caso, podemos obter um valor aproximado, ou seja, uma raiz quadrada aproximada.

Acompanhe a situação.

Jonas comprou um terreno quadrado que tem medida de área igual a 500 métros quadrados. Qual é a medida de comprimento do lado desse terreno?

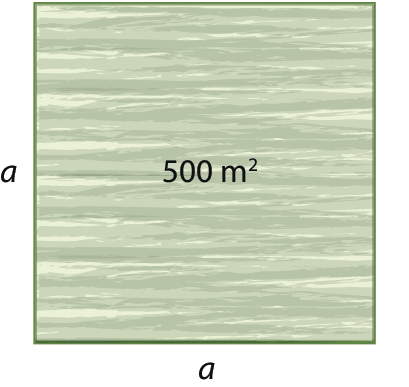
Figura geométrica. Quadrado verde. A medida do comprimento do lado do quadrado está indicada pela letra a. Dentro dele está escrito 500 metros quadrados,

Considerando a como a medida de comprimento do lado do quadrado que representa o terreno, temos:

a ⋅ a = 500 ⇒ a2 = 500 ⇒

a = \sqrt{500}

Portanto, a medida de comprimento do lado do terreno é

\sqrt{500}

metros. Mas qual é o valor de

\sqrt{500}

Com o auxílio de uma calculadora, poderíamos facilmente determinar o valor aproximado de

\sqrt{500}

. Porém, como nem sempre podemos contar com uma calculadora, vamos aprender a estimar esse valor por meio do uso de quadrados perfeitos.

Note que o número 500 situa-se entre os quadrados perfeitos 484 e 529.

Como

\sqrt{484} = 22

\sqrt{529} = 23

\sqrt{500}

é um número que está entre 22 e 23.

Calculamos os quadrados de alguns números situados entre 22 e 23, com uma casa decimal. Confira:

Sentenças matemáticas. Cálculo de quadrados de alguns números situados entre 22 e 23 com uma casa decimal. 22 vírgula 1 ao quadrado, igual, 488 vírgula 41. 22 vírgula 2 ao quadrado, igual, 492 vírgula 84. 22 vírgula 3 ao quadrado, igual, 497 vírgula 27. Abre parênteses, menor que 500, fecha parênteses. 22 vírgula 4 ao quadrado, igual, 500 vírgula 76. Abre parênteses, maior que 500, fecha parênteses. Todas essa sentença está em um caixa com borda laranja.

Assim, 22,4 corresponde a uma aproximação de

\sqrt{500}

com uma casa decimal.

Página 52

Para uma maior aproximação, podemos calcular os quadrados de números de duas casas decimais situados entre 22,3 e 22,4. Verifique:

Ilustração. Menino de cabelo preto, camiseta vermelha e calça azul. Ele está sentado segurando um livro aberto e fala: O número 499,9696 está mais próximo de 500 que o 500,4169. Ao lado dele, um cachorro sentado. Sentenças matemáticas. Cálculo de quadrados de alguns números situados entre 22 virgula 3 e 22 vírgula 4 com duas casas decimais. 22 vírgula 31 ao quadrado, igual, 497 vírgula 7361. 22 vírgula 32 ao quadrado, igual, 498 vírgula 1824. 22 vírgula 33 ao quadrado, igual, 498 vírgula 6289. 22 vírgula 34 ao quadrado, igual, 499 vírgula 0764. 22 vírgula 35 ao quadrado, igual, 499 vírgula 5225. 22 vírgula 36 ao quadrado, igual, 499 vírgula 9696. 99 vírgula 9696 está em destaque. Abre parênteses, menor que 500, fecha parênteses. 22 vírgula 37 ao quadrado, igual, 500 vírgula 4169. Abre parênteses, maior que 500, fecha parênteses. Todas essa sentença está em uma caixa com borda laranja.

Assim, 22,36 corresponde a uma aproximação de

\sqrt{500}

com duas casas decimais.

Logo, o comprimento do lado desse terreno mede aproximadamente 22,36 metros.

Atividades

Faça as atividades no caderno.

13. Determine o valor das raízes quadradas.

\sqrt{81}

\sqrt{0}

\sqrt{\frac{4}{25}}

\sqrt{144}

\sqrt{1}

\sqrt{\frac{64}{169}}

\sqrt{\frac{1}{16}}

\sqrt{225}

\sqrt{0,49}

14. Determine a raiz quadrada dos números com aproximação de uma casa decimal.

a) 40

b) 65

c) 85

d) 93

e) 122

f) 140

g) 800

h) 940

i) .1010

j) .1050

15. Sabendo que os números a seguir são quadrados perfeitos, determine a raiz quadrada de cada um deles.

a) .1225

b) .2401

c) .3136

d) .6561

e) .6400

f) .7744

16. Determine a raiz quadrada dos números a seguir.

a) 1,44

b) 12,96

c) 30,25

d) 72,25

e) 39,69

f) 94,09

17.

Utilizando uma calculadora, determine a raiz quadrada destes números, com aproximação de duas casas decimais.

a) 30

b) 8,6

c) 77

d) 110

e) 95

f) 50,8

g) 150

h) 86,25

i) 94

j) 125

18. Determine o valor das adições, com aproximação de uma casa decimal.

\sqrt{2} + \sqrt{3}

\sqrt{5} + \sqrt{7}

\sqrt{3} + \sqrt{5}

\sqrt{7} + \sqrt{11}

19. Determine o menor número inteiro não nulo pelo qual devemos multiplicar 360 para obter como resultado um quadrado perfeito.

20.

Faça os cálculos mentalmente, começando pela raiz quadrada de 1.

\sqrt{43 + \sqrt{31 + \sqrt{21 + \sqrt{13 + \sqrt{7 + \sqrt{3 + \sqrt{1}}}}}}}

21. Determine o valor de x, com uma casa decimal, que satisfaça

\sqrt{36} < x < \sqrt{38}

22. Coloque em ordem crescente os números

\sqrt{8}

\sqrt{4}

\frac{4}{5}

\frac{7}{2}

23. A raiz quadrada de um número natural compreendido entre 200 e 250 é um número inteiro. Que número é esse?

24. Um quadrado tem medida de área igual a 60 centímetros quadrados. Qual é a medida de comprimento do lado desse quadrado, com aproximação de duas casas decimais?

Página 53

Raiz enésima

O processo usado para obter o valor de outras raízes é similar ao utilizado para obter o valor das raízes quadradas.

A raiz enésima de um número real a, que tem como índice um número natural n ⩾ 2, é assim representada:

Esquema. raiz enésina de a, sai um fio laranja de n indicando índice e um fio laranja de a indicando radicando.

O cálculo da raiz enésima pode ser analisado considerando-se dois casos: o índice n par e o índice n ímpar.

• A raiz enésima de índice par de um número real a (a ⩾ 0) é o número real b (b ⩾ 0) tal que belevado a n = a. Assim, temos:

\sqrt[n]{a} = b

se, e somente se, belevado a n = a e b ⩾ 0

Analise os exemplos.

\sqrt[4]{0,0081} = 0,3

, pois 0,3elevado a 2 = 0,0081 e 0,3 > 0.

\sqrt[6]{64} = 2

, pois 2elevado a 6 = 64 e 2 > 0.

Observação

Se a for um número real negativo, a raiz enésima de a, com n par, não será um número real. Dessa forma,

\sqrt{- 0, 25}

\sqrt[6]{- 1}

não são números reais. Isso ocorre porque não existe um número real que, elevado a um expoente par, resulte em um número negativo.

• A raiz enésima de índice ímpar de um número real a é o número real b tal que belevado a n = a. Assim, temos:

\sqrt[n]{a} = b

se, e somente se, belevado a n = a

Analise os exemplos.

\sqrt[3]{- 125} = - 5

, pois: (‒5)elevado a 3 = ‒125

\sqrt[5]{1.024} = 4

, pois: (4)elevado a 5 = .1024

Atividades

Faça as atividades no caderno.

25. A raiz cúbica de um número natural compreendido entre 200 e 400 é um número ímpar. Que número é esse?

26. A medida V de volume de um cubo é 200 decímetros cúbicos. Qual é a medida a de comprimento da aresta desse cubo com aproximação de uma casa decimal sabendo que V = aelevado a 3?

27. Determine as raízes dos números a seguir.

\sqrt[3]{64}

\sqrt[3]{- 27}

\sqrt[6]{64}

\sqrt[3]{0,343}

\sqrt[5]{243}

\sqrt[4]{\frac{16}{625}}

Página 54

Veja que interessante

Faça as atividades no caderno.

Potência com expoente fracionário

Estudamos potências de base real e expoente inteiro, mas o expoente de uma potência também pode ser um número na fórma de fração. Por exemplo:

3^{\frac{1}{2}}

5^{\frac{2}{3}}

{0, 25}^{\frac{3}{5}}

{1, 3}^{\frac{1}{7}}

As propriedades de potências com expoentes inteiros continuam válidas quando o expoente é um número racional e a base é um número real positivo.

Assim, aplicando a propriedade da potência de uma potência e a definição de raiz enésima, temos:

{(3^{\frac{1}{2}})}^{2} = 3^{\frac{1}{2} \cdot 2} = 3^{1}

Como

{(3^{\frac{1}{2}})}^{2} = 3^{1}

3^{\frac{1}{2}} > 0

, então:

\sqrt[2]{3^{1}} = 3^{\frac{1}{2}}

{(5^{\frac{2}{3}})}^{3} = 5^{\frac{2}{3} \cdot 3} = 5^{2}

Como

{(5^{\frac{2}{3}})}^{3} = 5^{2}

, então:

\sqrt[3]{5^{2}} = 5^{\frac{2}{3}}

{({0, 25}^{\frac{3}{5}})}^{5} = {0,25}^{\frac{3}{5} \cdot 5} = {0,2 5}^{3}

Como

{({0,25}^{\frac{3}{5}})}^{5} = {0,25}^{3}

, então:

\sqrt[5]{{0,2 5}^{3}} = {0,25}^{\frac{3}{5}}

{({1, 3}^{\frac{1}{7}})}^{7} = {1,3}^{\frac{1}{7} \cdot 7} = + 1,3

Como

{({1,3}^{\frac{1}{7}})}^{7} = {1,3}^{1}

, então:

\sqrt[7]{{1,3}^{1}} = {1,3}^{\frac{1}{7}}

Da mesma maneira, podemos escrever outras potências de expoente fracionário como raiz.

De modo geral, para todo número real positivo a, número inteiro m e número natural n e n ⩾ 2, temos:

a^{\frac{m}{n}} = \sqrt[n]{a^{m}}

Atividades

a) Calcule

{0,16}^{\frac{1}{2}} - {0,027}^{\frac{1}{3}}

Escreva uma raiz em uma folha avulsa. Em seguida, troque de folha com um colega e escreva a raiz indicada por ele como potência de expoente fracionário. Confira se a representação do seu colega está correta.

Junte-se a um colega e escreva três raízes quadradas exatas. Em seguida, peça a ele que calcule os valores dessas três raízes, escrevendo-as como potências de expoente fracionário e utilizando a decomposição em fatores primos e as propriedades de potenciação. Por fim, verifique se as representações e os cálculos que seu colega fez estão corretos.

Página 55

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Potenciação

• Qualquer potência de base real e expoente inteiro maior que 1 é produto dessa base por ela mesma tantas vezes quantas indica o expoente. Assim, sendo a um número real e n um número inteiro maior que 1, temos:

• Qualquer potência de base real e expoente 1 é igual à própria base. Assim, sendo a um número real, temos:

aelevado a 1 = a

• Qualquer potência de base real não nula e expoente zero é igual a 1. Assim, sendo a um número real, temos:

aelevado a 0 = 1, a ≠ 0

• Qualquer potência de base real não nula e expoente inteiro negativo é igual à potência do inverso da base dada e expoente igual ao oposto do expoente dado. Assim, sendo a um número real não nulo e ‒n um expoente inteiro negativo, temos:

a^{- n} = \frac{1}{a^{n}} = {(\frac{1}{a})}^{n}, a \neq 0

Notação científica

Um número escrito em notação científica apresenta o formato a ⋅ 10elevado a bê, em que b é um expoente inteiro e a é um número racional que pertence ao intervalo 1 < a < 10.

1. Calcule as potências a seguir.

a) 3elevado a 3

b) ‒2elevado a 2

c) (‒2)elevado a 2

{(\frac{2}{3})}^{2}

{(- \frac{4}{5})}^{- 2}

f) 5elevado a 0

g) (‒1)elevado a 3

h) 2elevado a 1

2. Calcule o valor das expressões.

a) 3xelevado a 2 ‒ xelevado a menos 1 + 2, para x = ‒1

(‒ 1)^{2} - 3 \cdot {(- \frac{1}{2})}^{- 2}

2^{0} + 4^{2} \cdot 3 : (\frac{1}{2})

3. Escreva os números a seguir em notação científica.

a) 0,27

b) 895

c) .3600

d) 0,0012

e) ..50000000

f) 0,000000044

Propriedades da potenciação para potências de base real e expoente inteiro

Produto de potências de mesma base

a elevado a m ⋅ a elevado a n = a elevado a m mais n, em que a é um número real não nulo e m e n são números inteiros.

Quociente de potências de mesma base

a elevado a m : a elevado a n = a elevado a m menos n, em que a é um número real não nulo e m e n são números inteiros.

Potência de uma potência

abre parêntesesa elevado a mfecha parênteseselevado a n = a elevado a m vezes n, em que a é um número real não nulo e m e n são números inteiros.

Potência de um produto

abre parêntesesa ⋅ bfecha parênteseselevado a m = a elevado a m ⋅ b elevado a m, em que a ê b são números reais não nulos e m é um número inteiro.

Potência de um quociente

abre parêntesesa dividido por bfecha parênteseselevado a m = a elevado a m dividido por b elevado a m, em que a ê b são números reais não nulos e m é um número inteiro.

4. Indique cada item como uma só potência.

a) 3elevado a 2 ⋅ 3elevado a 4 ⋅ 3elevado a 3 ⋅ 3elevado a 9

b) abre parênteses5elevado a 2fecha parênteseselevado a 3

c) abre parênteses2elevado a 3fecha parênteseselevado a menos 2

d) 8elevado a 3 : 8elevado a 5

e) 2elevado a 1 ⋅ 4elevado a 1 ⋅ 4elevado a 2 ⋅ 4elevado a 0

Página 56

5. Calcule o valor das expressões numéricas.

a) 4elevado a 4 : 4elevado a 3 + 3 ⋅ 3elevado a 2

b) abre parênteses2elevado a 3fecha parênteseselevado a 2 ‒ abre parênteses2elevado a 3fecha parênteseselevado a 2

c) abre parênteses‒1fecha parênteseselevado a 3 + 3elevado a 4 : 3elevado a 4

d) 3elevado a 0 + 5elevado a 3 : 5elevado a 2

e) abre parênteses2elevado a 4fecha parênteseselevado a 2 : 4elevado a 1 + 3elevado a 0 ‒ 3elevado a 2

Radiciação

Raiz quadrada

A raiz quadrada de um número real positivo x é um número não negativo que, elevado ao quadrado, resulta em x.

Raiz quadrada exata

Os números 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121 e 144 são exemplos de quadrados perfeitos, pois podem ser escritos como uma potência de base racional e expoente 2.

Se x for um número racional e for quadrado perfeito,

\sqrt{x}

será um número racional. Em casos assim, podemos obter a raiz quadrada exata desses números.

Raiz quadrada aproximada

Se x for um número não negativo e não for quadrado perfeito,

\sqrt{x}

será um número com infinitas casas decimais não periódicas, ou seja, será um número irracional.

Nos casos em que a raiz é um número irracional, podemos obter um valor aproximado, ou seja, uma raiz quadrada aproximada.

6. Determine os valores das raízes quadradas.

\sqrt{49}

\sqrt{25}

\sqrt{169}

\sqrt{225}

\sqrt{\frac{4}{9}}

\sqrt{\frac{16}{49}}

\sqrt{\frac{121}{100}}

\sqrt{\frac{4}{169}}

\sqrt{\frac{25}{225}}

Utilizando uma calculadora, determine a raiz quadrada dos números, com aproximação de duas casas decimais.

\sqrt{27}

\sqrt{300}

\sqrt{6}

\sqrt{2,5}

8. Calcule as raízes a seguir com aproximação de uma casa decimal.

\sqrt{75}

\sqrt{7}

\sqrt{3,57}

\sqrt{500}

9. Calcule o valor das expressões.

\sqrt{13^{2} - 12^{2}}

\sqrt{1,21} + \sqrt{1,44} + \sqrt{0,49} + \sqrt{0,16} + \sqrt{0,36}

\sqrt{16} + \sqrt{\frac{1}{9}} + \sqrt{\frac{1}{4}} + 7^{1} - 12^{0}

10. Responda às questões.

a) Qual é o maior número inteiro quadrado perfeito de quatro algarismos?

b) Qual é a raiz quadrada do número .11236?

c) A terça parte da raiz quadrada de um número x é igual a 12. Qual é o valor de x ?

Raiz enésima

A raiz enésima de um número real a, que tem como índice um número natural n ⩾ 2, é assim representada:

O cálculo da raiz enésima pode ser analisado considerando-se dois casos: o índice n par e o índice n ímpar.

• A raiz enésima de índice par de um número real a (a ⩾ 0) é o número real b (b ⩾ 0) tal que belevado a n = a. Assim, temos:

\sqrt[n]{a} = b

se, e somente se, belevado a n = a e b ⩾ 0

• A raiz enésima de índice ímpar de um número real a é o número real b tal que belevado a n = a. Assim, temos:

\sqrt[n]{a} = b

se, e somente se, belevado a n = a.

11. Determine as raízes dos números a seguir.

\sqrt[3]{- 729}

\sqrt[5]{32}

\sqrt[4]{81}

\sqrt[6]{\frac{729}{4 096}}

12. Simplifique a expressão a seguir.

\frac{\sqrt[2]{\sqrt[]{16} + 5 \sqrt[3]{1 000} + 10^{1}}}{\sqrt[3]{- 343}}

Glossário

GB: : símbolo utilizado para representar a unidade de medida de armazenamento gigabyte; 1 gigabyte (GB) é aproximadamente igual a ...1000000000 bytes ou 109 bê; Voltar para o texto

vácuo: : na prática, utilizamos esse termo para nos referir a um espaço no qual a maior parte do ar ou de outro gás foi retirada e no qual a pressão é extremamente pequena.; Voltar para o texto