Capítulo 3 Sistemas de equações do 1º grau
Trocando ideias

O Artigo 25 do Decreto Federal nº 5.296/04 que regulamenta a Lei Federal nº 10.098/00, também consolidada na Resolução 304/08, estabelece a obrigatoriedade de reservar 2% do total de vagas regulamentadas de estacionamento para veículos que transportem pessoas com alguma deficiência física ou visual.

▸


Em sua opinião, por que é importante que os estacionamentos tenham vagas reservadas para veículos que transportam pessoas com alguma deficiência física ou visual? Converse com os colegas.
▸

Considere que um estacionamento tem quinhentas vagas, que x indica a quantidade de vagas que não são reservadas para veículos que transportam pessoas com alguma deficiência física ou visual e que y indica a quantidade de vagas reservadas a esse público. Então, faça o que se pede.
a) Escreva, em seu caderno, uma equação que relacione x e y.
b) Que valores x e y podem assumir?
c) Calculem a quantidade de vagas reservadas e não reservadas para veículos que transportam pessoas com alguma deficiência física ou visual nesse estacionamento.
Neste capítulo, vamos estudar a resolução de problemas envolvendo sistemas de equações do 1º grau com duas incógnitas.

1 Pares ordenados e plano cartesiano
Em Matemática, a localização de pontos em um plano é feita com o auxílio de duas retas numéricas perpendiculares, chamadas de eixos. Esses eixos determinam o plano cartesiano. Observe a figura a seguir.
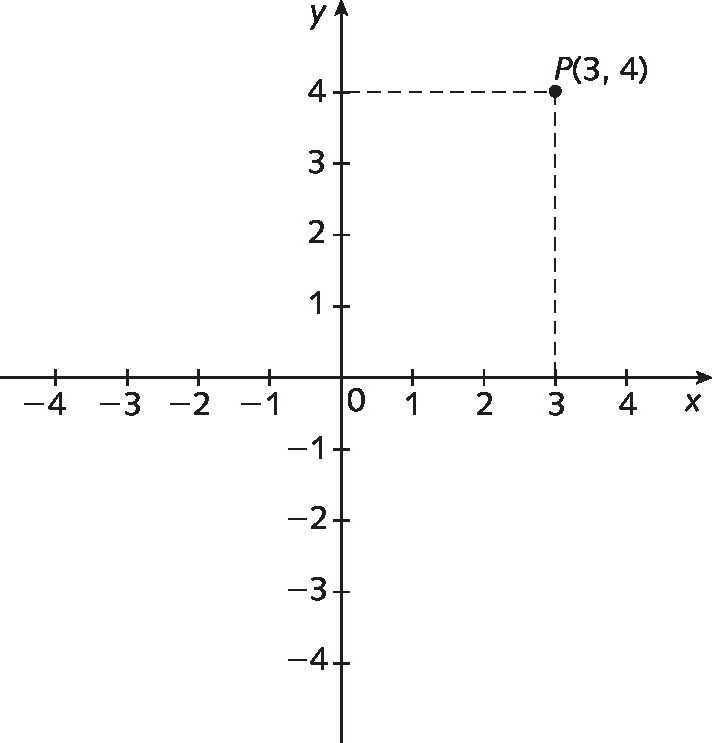
• A reta horizontal é o eixo x ou eixo das abscissas.
• A reta vertical é o eixo y ou eixo das ordenadas.
• O ponto de intersecção entre as retas que representam esses eixos é denominado origem e corresponde ao ponto cujo par ordenado é (0, 0).
Para localizar um ponto no plano cartesiano, usamos dois números. Esses números são expressos na fórma de um par ordenado. Esse par de números é assim chamado porque existe uma ordem predeterminada para escrevê-lo.
Os elementos desses pares são chamados de coordenadas cartesianas dos pontos. Em cada par ordenado, a primeira coordenada é a abscissa do ponto, e a segunda é a ordenada do ponto. Então, para o ponto P representado, temos:

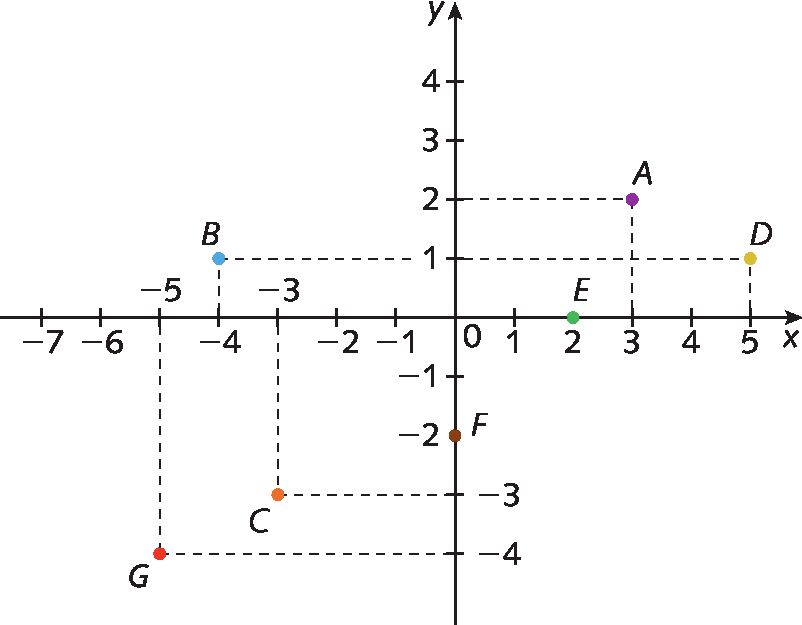
Agora, analise a representação no plano cartesiano dos pontos a(3, 2), B(menos 4, 1), C(menos3, menos3), D(5, 1), ê(2, 0), F(0, menos2) e G(menos5, menos4).
Atividades
Faça as atividades no caderno.
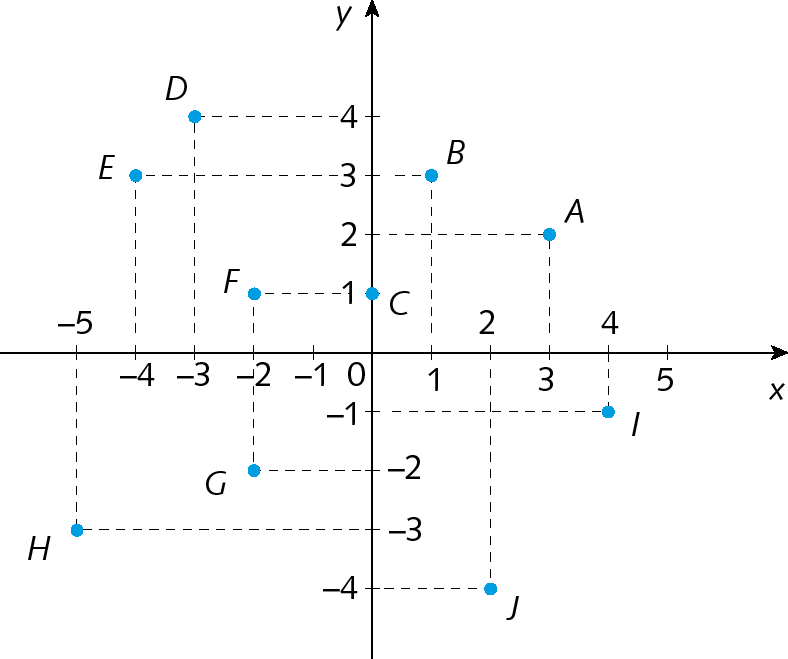
1. Determine as coordenadas de cada um dos pontos indicados no plano cartesiano a seguir.
2. Trace um plano cartesiano no caderno. Em seguida, represente os pontos a, B, C, D, ê, F, G, H, ih e J, cujas coordenadas são:
a(0, menos2)
B (menos3, 4)
C (0, 0)
D (2, 0)
ê (menos2, 3)
F (1, 3)
G (3, 3)
H (menos1, 2)
ih (menos1, 0)
J (menos1, 1)
3.

Reúna-se com um colega e, no caderno, tracem duas retas numéricas perpendiculares entre si, determinando o plano cartesiano. Em seguida, representem cinco pontos cujos pares ordenados tenham:
a) coordenadas iguais;
b) coordenadas opostas;
c) abscissa igual a 3;
d) abscissa igual a menos3;
e) ordenada igual a 2;
f) ordenada igual a menos1.
4.

Considerando as respostas dadas na atividade anterior, respondam às questões.
a) Em cada item, se unirmos os pontos, a linha formada se parecerá com uma reta?
b) Em relação ao eixo x, qual é a posição da reta que contém os pontos do item c? E da reta que contém os pontos do item d?
c) Em relação ao eixo x, qual é a posição da reta que contém os pontos do item ê? E da reta que contém os pontos do item f?

2 Equação do 1º grau com duas incógnitas
Considere a situação a seguir.
Emília comprou uma caneta e dois lápis por R$ 10,00dez reais.

Indicando por x o preço de uma caneta e por y o preço de um lápis, podemos representar a situação da seguinte maneira:
x + 2y = 10
Esse é um exemplo de equação do 1º grau com duas incógnitas.
Denominamos equação do 1º grau com duas incógnitas (x e y) aquela que pode ser reduzida a uma equação do tipo ax + by = c, em que a, b e c são números reais, chamados coeficientes, com a ≠ 0 e b ≠ 0.
Observe alguns exemplos de equações do 1º grau com duas incógnitas.
a)
Sentença matemática. 0 vírgula 5 x menos raiz quadrada de 2 vezes y é igual a 10.b)
Sentença matemática. fração x sobre 7 mais 1 vírgula 3 é igual a 5 yc)
Sentença matemática. Menos x mais a fração y sobre 5 é igual à raiz quadrada de 21d) 500 + 33y = x
Podemos verificar se um par ordenado (x, y) é solução de uma equação do 1º grau com duas incógnitas substituindo as incógnitas pelos valores numéricos correspondentes. Se a sentença obtida for verdadeira, o par ordenado é solução da equação. Caso contrário, não é solução.
Por exemplo, o par ordenado (1; 4,5) é solução da equação x + 2y = 10, pois:
x + 2y = 10
1 + 2 ⋅ 4,5 = 10
1 + 9 = 10
10 = 10 (sentença verdadeira)
▸ A equação x + 2y = 10 tem infinitas soluções, mas a situação descrita no início do tópico impõe algumas condições para os valores de x e de y. Quais são essas condições?
Atividades
Faça as atividades no caderno.
5. No quadro a seguir indicamos os Valores Diários de Referência (VDR) de um café da manhã que contenha um pão com margarina e um suco de laranja.
|
Porção de pão com margarina(50 g+ 14 g) |
Porção de suco(200 mL) |
VDR |
|
|---|---|---|---|
|
Carboidratos (g) |
28 |
30 |
300 |
|
Proteínas (g) |
4 |
1 |
75 |
Indicando por x a quantidade de porções em grama de pão com margarina e por y a quantidade de porções de suco em mililitro, responda:
a) Que equação relaciona as quantidade de porções em grama de pão e em mililitro de suco que poderiam ser consumidas em um dia, tendo em vista o VDR de carboidratos?
b) Qual é a equação que relaciona as quantidades x e y com o valor de proteínas?
6. Escreva uma equação para representar cada uma das situações a seguir.
a) A medida do perímetro de um retângulo com lados de medidas x e y é 48 centímetros.
b) A medida x do comprimento de um retângulo excede a medida de sua largura y em 9 centímetros.
c) De um total de 20 lançamentos de dardos, Julinho acertou no alvo x lançamentos e errou y lançamentos.
d) No tiro ao alvo, Julinho ganhou 5 pontos em cada um dos x tiros acertados e perdeu 3 pontos em cada um dos y tiros errados.
7. No sítio de Pedro, há x galinhas e y porcos, em um total de 140 pés. Escreva uma equação que represente essa situação.
Representação gráfica das soluções de uma equação do 1º grau com duas incógnitas
Considere a equação do 1º grau com duas incógnitas x + 2y = 16.
É possível representar no plano cartesiano as soluções (pares ordenados) dessa equação. Para isso, primeiro atribuímos alguns valores a x, calculamos os valores correspondentes de y e organizamos os dados em um quadro. Depois, localizamos no plano cartesiano os pontos que representam os pares e traçamos a reta que passa por eles.
|
Valor atribuído a x |
Equação em y |
Valor de y |
Par ordenado (x, y) |
|---|---|---|---|
|
−4 |
−4 + 2y = 16 |
10 |
(−4, 10) |
|
−2 |
−2 + 2y = 16 |
9 |
(−2, 9) |
|
0 |
0 + 2y = 16 |
8 |
(0, 8) |
|
2 |
2 + 2y = 16 |
7 |
(2, 7) |
|
4 |
4 + 2y = 16 |
6 |
(4, 6) |
|
10 |
10 + 2y = 16 |
3 |
(10, 3) |
|
16 |
16 + 2y = 16 |
0 |
(16, 0) |
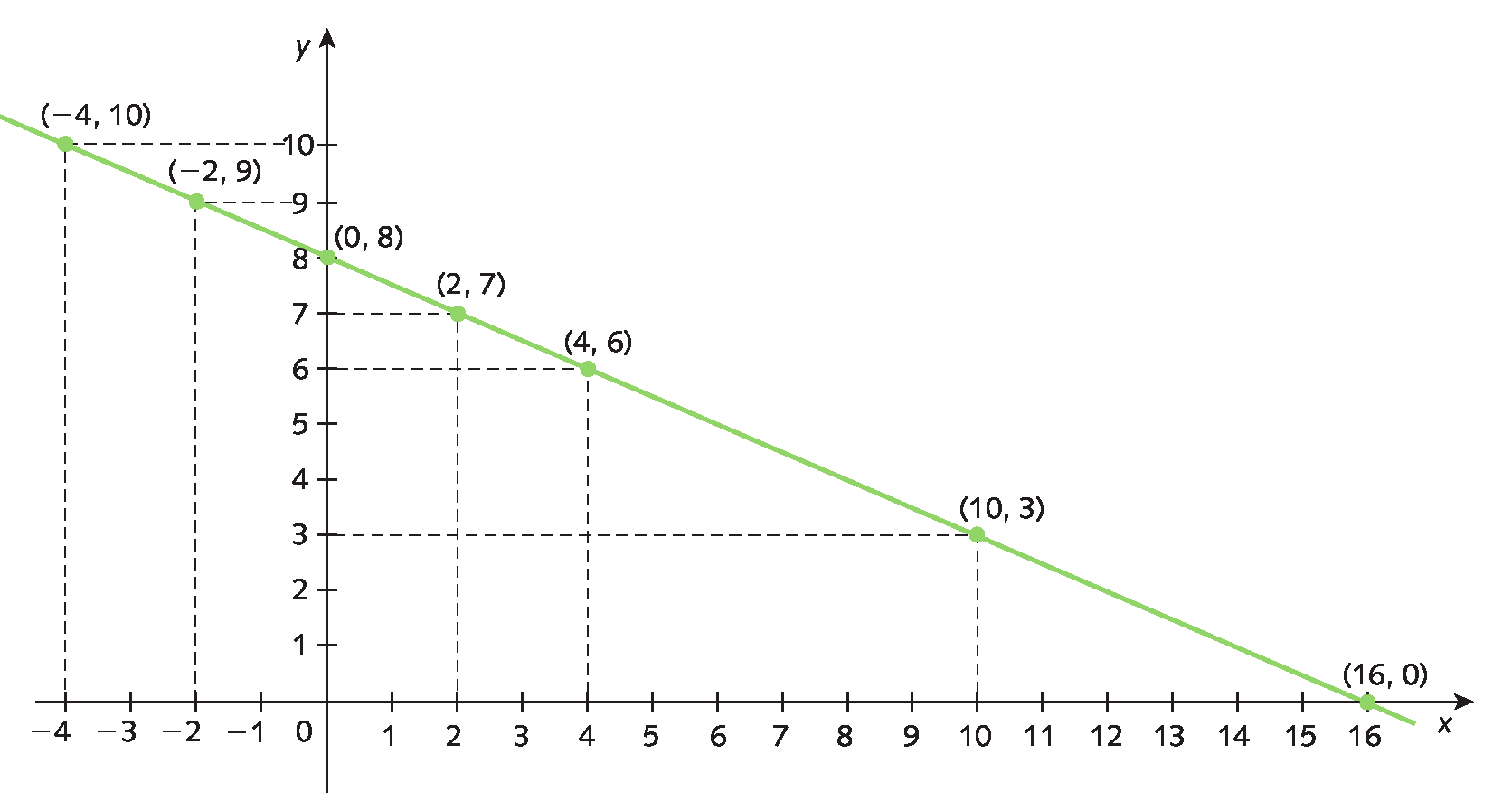
Observe que os pontos que representam os pares do quadro estão alinhados. Podemos demonstrar que o conjunto de todas as soluções de x + 2y = 16, em que x e y são números reais, é representado por uma reta.
O conjunto de soluções de qualquer equação do 1º grau com duas incógnitas, sendo estas números reais, é representado no plano cartesiano por uma reta.
O conjunto das soluções de uma equação do 1º grau com duas incógnitas pode ter nenhum elemento, finitos ou infinitos elementos, dependendo da equação e dos números que as incógnitas podem assumir.
Sugestão de leitura
RAMOS, Luzia Faraco. Encontros de primeiro grau. São Paulo: Ática, 2008. (Coleção A descoberta da Matemática).
Contextualizado pelo sumiço da filha do protagonista, o livro é uma aventura que busca apresentar equações de maneira interessante por meio das situações que Wang precisa passar para encontrar sua filha.
Atividades
Faça as atividades no caderno.
8. Copie a representação no plano cartesiano das soluções da equação x + 2y = 16. Depois, na equação, substitua x por cinco outros números e calcule os valores correspondentes de y. Localize no plano os pontos que representam os pares (x, y) obtidos. Os novos pontos estão alinhados com os pontos anteriores?
9. Represente graficamente as soluções das equações:
a) x + y = 3
b) y = x
c) x + 4y = 4
d) x ‒ y = 6
e) 2x ‒ y = 4
f) x + y = menos5
g) x + y = 0
h) x + y = 6

3 Sistema de equações do 1º grau com duas incógnitas
Considere a situação a seguir.

Um grupo de amigos foi a uma mercearia e gastou R$ 44,00quarenta e quatro reais na compra de mangas e abacaxis para uma sobremesa.
Vamos indicar por x a quantidade de mangas e por y a quantidade de abacaxis. Assim, podemos representar essa situação em linguagem algébrica da seguinte fórma:
x + y = 12

O grupo comprou 12 frutas.
3x + 5y = 44

O grupo gastou R$ 44,00quarenta e quatro reais.
Temos, portanto, duas equações do 1º grau com as mesmas duas incógnitas, x e y, que formam um sistema de equações do 1º grau com duas incógnitas.
Indicamos o sistema de equações assim:
Sistema de duas equações com uma equação abaixo da outra. Abre chave, primeira linha: x mais y é igual a 12. Segunda linha: 3 x mais 5 y é igual a 44.
Assim como as equações do 1º grau com duas incógnitas, o sistema de equações do 1º grau com duas incógnitas pode ter nenhuma, uma ou infinitas soluções. Se tiver solução, cada uma das soluções será um par ordenado (x, y).
A seguir, vamos estudar métodos de resolução de sistemas de equações do 1º grau com duas incógnitas.
Resolução de sistemas de equações do 1º grau com duas incógnitas
Acompanhe a situação a seguir.
Jonas possui R$ 130,00cento e trinta reais em cédulas de R$ 10,00dez reais e R$ 20,00vinte reais, em um total de 9 cédulas. Quantas cédulas de cada espécie Jonas possui?
Indicando por x o número de cédulas de R$ 10,00dez reais e por y o número de cédulas de R$ 20,00vinte reais, podemos representar essa situação por meio de um sistema de duas equações do 1º grau com duas incógnitas em que x e y representam números naturais.
Sistema de duas equações com uma equação abaixo da outra. Abre chave, primeira linha: x mais y é igual a 9. Segunda linha: 10 x mais 20 y é igual a 130.
A solução do sistema deve satisfazer as duas equações.
Na busca dessa solução, podemos testar alguns valores para x e para y e verificar se as soluções encontradas estão de acordo com os dados do problema. Assim:
|
Soma x + y |
Valor atribuído a x |
Valor de y |
Valor de 10x + 20y |
|---|---|---|---|
|
9 |
2 |
7 |
10 ⋅ 2 + 20 ⋅ 7 = 160 |
|
9 |
3 |
6 |
10 ⋅ 3 + 20 ⋅ 6 = 150 |
|
9 |
4 |
5 |
10 ⋅ 4 + 20 ⋅ 5 = 140 |
|
9 |
5 |
4 |
10 ⋅ 5 + 20 ⋅ 4 = 130 |
Observe que x = 5 e y = 4, ou seja, o par ordenado (5, 4) é uma solução do sistema, pois satisfaz as duas equações.
Resolvemos esse sistema pelo método da tentativa e erro. A desvantagem desse método é que ele não nos garante que vamos achar uma solução, nem que essa solução, se encontrada, seja única. Assim, precisamos de métodos mais sistemáticos que possam nos garantir a existência ou não de soluções e a quantidade de soluções (quando existir). Nesse sentido, vamos estudar agora os métodos da substituição e da adição para resolver um sistema de equações do 1º grau com duas incógnitas.
Método da substituição
Considere o sistema:
Sistema de duas equações com uma equação abaixo da outra. Abre chave, primeira linha: x menos y é igual a menos 5. Segunda linha: 2 x mais 3 y é igual a 10.Para resolver esse sistema pelo método da substituição, inicialmente escolhemos uma das equações e isolamos uma das incógnitas. Isolando x na equação x menos y = menos5, temos:
x = menos5 + y
Em seguida, substituímos x por menos5 + y na equação 2x + 3y = 10 para obter uma equação com apenas a incógnita y.
2x + 3y = 10
2(menos5 + y) + 3y = 10
menos10 + 2y + 3y = 10
5y = 20
y = 4
Depois, substituímos y por 4 em uma das equações, determinando x :
x = menos5 + y
x = menos5 + 4
x = menos1
Portanto, a solução do sistema é o par ordenado (menos1, 4).
Método da adição
Considere o sistema:
Sistema de duas equações com uma equação abaixo da outra. Abre chave, primeira linha: x mais y é igual a 16. Segunda linha: x menos y é igual a 2.Adicionando essas equações membro a membro, obtemos uma equação com apenas a incógnita x. Resolvendo-a, obtemos o valor de x.

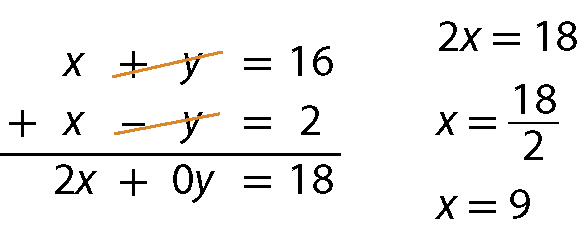
Substituindo x por 9 em uma das equações, determinamos o valor de y :
x + y = 16
9 + y = 16
y = 16 ‒ 9
y = 7
Portanto, a solução do sistema é o par ordenado (9, 7).
Agora, observe como podemos determinar a solução do sistema:
Sistema de duas equações com uma equação abaixo da outra. Abre chave, primeira linha: x mais 5 y é igual a menos 28. Segunda linha: 2 x mais 3 y é igual a menos 7.Observe que nenhuma das incógnitas tem os coeficientes opostos.
Para aplicar o método da adição, é preciso preparar uma das equações, multiplicando-a por um número, de modo que as equações fiquem com coeficientes opostos para uma das incógnitas.
Multiplicando a equação x + 5y = ‒28 por (‒2), obtemos coeficientes opostos para x.
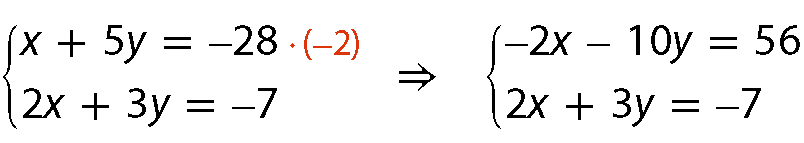
Adicionando membro a membro as duas equações, temos:

Substituindo y por ‒7 na equação x + 5y = ‒28, determinamos o valor de x :
x + 5 ⋅ (‒7) = ‒28
x ‒ 35 = ‒28
x = 7
Portanto, a solução do sistema é o par ordenado (7, ‒7).
Atividades
Faça as atividades no caderno.
10. Observe a situação a seguir em que Cássio e Leonardo conversam sobre os jogos de basquete na escola em que estudam.

Indicando por x o número de vitórias do time de Cássio e por y o número de vitórias do time de Leonardo, podemos montar o seguinte sistema de equações:

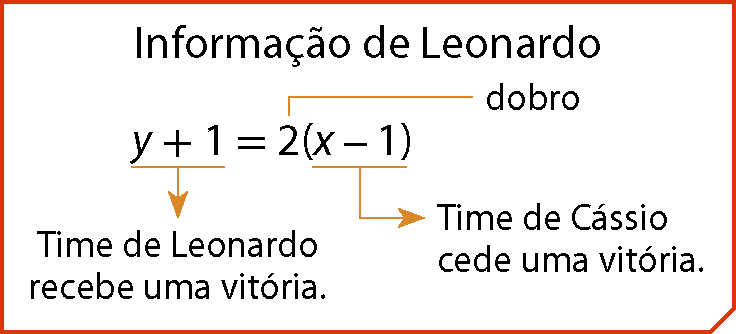

Agora, reúnam-se em duplas para discutir e respondam:
a) Que valores x e y podem assumir? Por quê?
b) Por tentativas, atribuindo valores a x e a y, determine a quantidade de vitórias de cada time.
11. Resolva novamente o sistema apresentado ao estudar o método da substituição, mas agora isolando a incógnita y na equação x ‒ y = 5. A solução também é o par ordenado (‒1, 4)?
12. Determine a solução dos sistemas aplicando os métodos da substituição e da adição. Considere que x e y podem ser qualquer número real.
a)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais y igual a menos 2 e a segunda equação é 2x menos y igual a 26.b)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 3x menos y igual a menos 11 e a segunda equação é x mais 2y igual a 8.c)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x mais 2y igual a 4 e a segunda equação é 3x menos 2y igual a 1.d)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x mais 3y igual a 9 e a segunda equação é 4x menos 5y igual a 7..13. Hoje, Ronaldo tem o dobro menos quatro anos da idade de Pedro. Há dez anos, a idade de Ronaldo era o triplo da idade de Pedro. Quantos anos eles têm hoje?
14. Julinho está brincando de tiro ao alvo. A cada tiro que acerta no alvo, ele ganha cinco pontos, e a cada tiro que erra, perde três pontos. Ele já deu 20 tiros e ganhou 68 pontos. Quantos tiros Julinho acertou até agora?
15. Em um estacionamento há automóveis e bicicletas, totalizando 32 veículos e 88 pneus. Determine o número de veículos de cada tipo.
16. Os times de basquete Boa Esperança e Camisa Verde estão disputando a final de um campeonato. Até o momento, o time Boa Esperança só tem uma vitória a menos do que o time Camisa Verde. Porém, se o vencedor da partida final for o Camisa Verde, eles terão, ao todo, o dobro de vitórias do time adversário.
Com base nas informações do texto, faça o que se pede.
a) Determine um sistema de equações que represente a situação.
b) Quantas vitórias cada time teve até o momento?
17. Em um circo eram cobrados valores de ingresso: um para os adultos e outro para as crianças. Um grupo, de seis crianças e um adulto, pagou R$ 71,00setenta e um reais pelos ingressos. Outro grupo, de sete crianças e quatro adultos, pagou R$ 131,00cento e trinta e um reais. Qual era o preço de cada ingresso?
18. Tenho avestruzes e coelhos, totalizando 35 cabeças e 110 pés. Calcule o número de avestruzes e o de coelhos.

19.


Elabore um problema no qual uma pessoa precisa sacar determinada quantia em dinheiro em um caixa eletrônico. Entretanto, o caixa eletrônico só possui notas de R$ 20,00vinte reais e R$ 50,00cinquenta reais. Informe no problema a quantidade total de notas que saíram do caixa eletrônico. A resolução deve envolver um sistema de equações do 1º grau com duas incógnitas. Sente-se em dupla, troque seu problema com o do colega e resolva o que ele propôs. Em seguida, corrijam as resoluções um do outro e conversem caso discordem de algum passo da resolução.
20.


Elabore um problema sobre a idade de dois primos, um mais novo e um mais velho, cuja solução envolva um sistema de equações do 1º grau com duas incógnitas. Sente-se em dupla, troque seu problema com o do colega e resolva o que ele propôs. Em seguida, corrijam as resoluções um do outro e conversem caso discordem de algum passo da resolução.
Análise da solução por meio da representação gráfica
Vamos analisar graficamente a solução de alguns sistemas em que x e y são números reais.
a) Considere o sistema:
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais y igual a 5 e a segunda equação é 2y menos x igual a 4.Inicialmente vamos determinar a reta que representa as soluções de cada uma das equações.
Para traçar uma reta, basta conhecer dois pontos distintos dela. Assim, atribuímos dois valores a uma das incógnitas e calculamos os valores correspondentes da outra, obtendo, assim, pares ordenados que são coordenadas de dois dos pontos de cada reta.
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
5 |
(0, 5) |
|
5 |
0 |
(5, 0) |
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
2 |
(0, 2) |
|
−4 |
0 |
(−4, 0) |
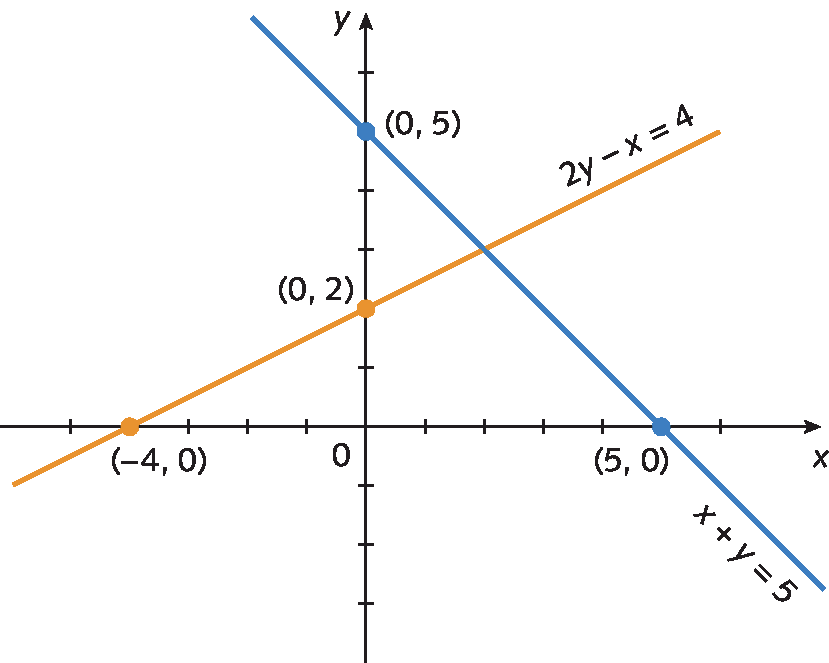
As coordenadas do ponto de intersecção das retas formam o par ordenado que é a solução do sistema. Resolvendo esse sistema por qualquer um dos métodos estudados, obtemos como solução o par ordenado (2, 3).
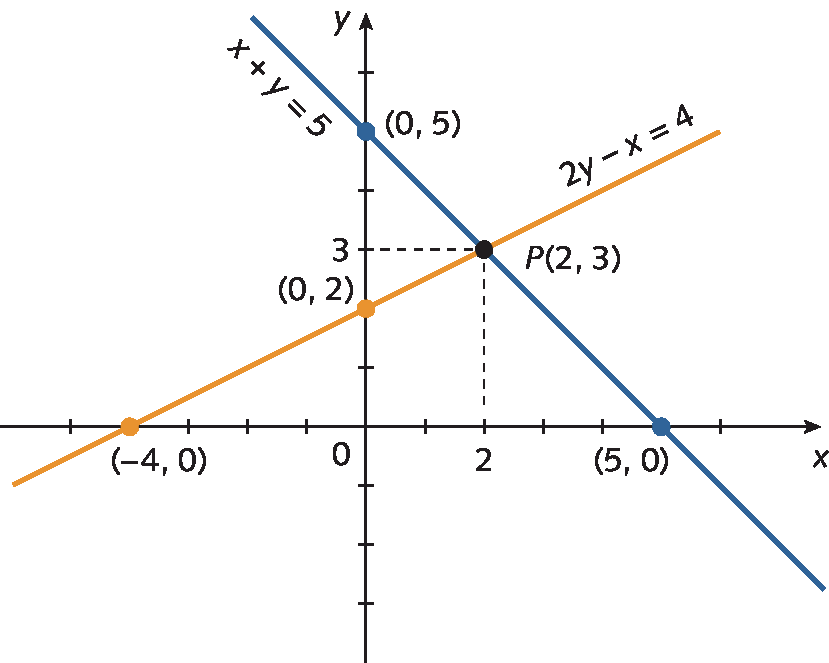
Nesse caso, as retas são concorrentes e o par ordenado (2, 3) é a única solução do sistema. Assim, dizemos que o sistema é possível e determinado, pois tem uma única solução.
b) Vamos analisar graficamente o sistema:
Sistema de duas equações com uma equação abaixo da outra. Abre chave, primeira linha: x mais 2 y é igual a 4. Segunda linha: 2 x mais 4 y é igual a menos 8.Inicialmente, traçamos em um mesmo plano cartesiano as retas que representam as soluções das equações.
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
2 |
(0, 2) |
|
4 |
0 |
(4, 0) |
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
−2 |
(0, −2) |
|
−4 |
0 |
(−4, 0) |
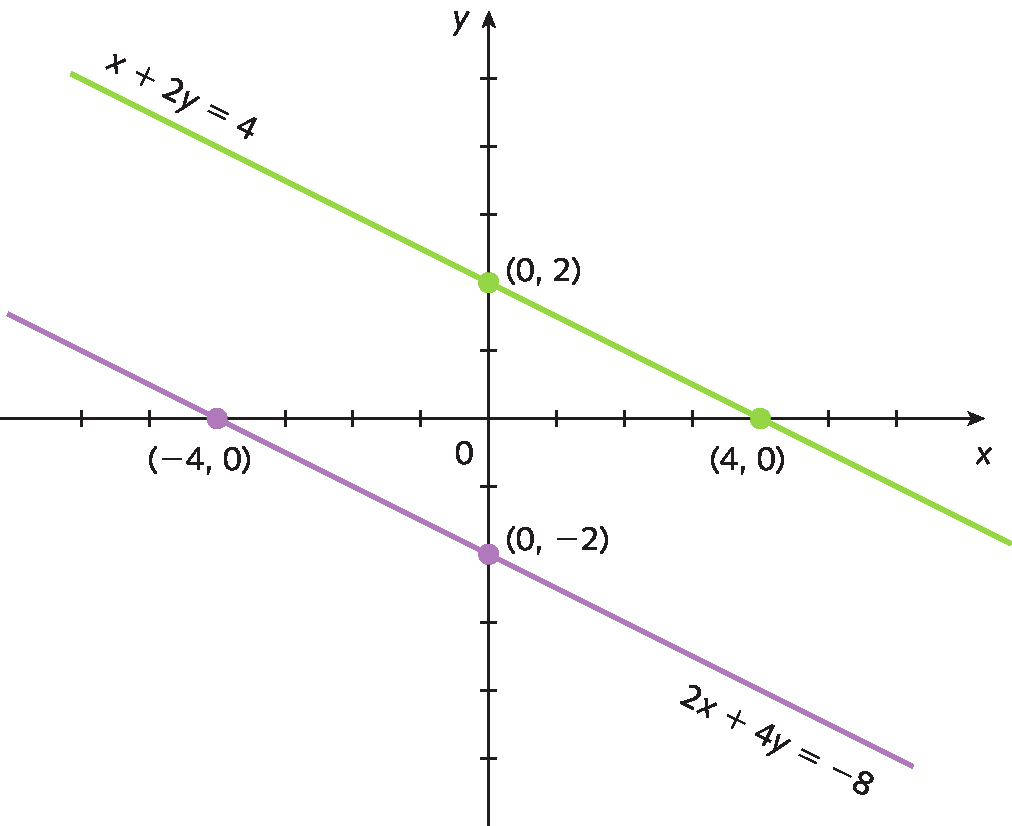
Como as retas são paralelas, não há ponto cujas coordenadas satisfaçam as duas equações. Logo, o sistema não tem solução. Esse é um exemplo de sistema impossível.
Analise a resolução do sistema pelo método da adição:

Na igualdade 0x + 0y = ‒16 obtida, temos uma sentença falsa, pois 0x e 0y serão iguais a zero para quaisquer valores de xis e y. Logo, 0x + 0y é igual a zero, e não a ‒16.
Portanto, o sistema é impossível, como já tínhamos visto na solução gráfica.
c) Vamos analisar graficamente o sistema:
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais mais y igual a 3 e a segunda equação é 8x mais 8y igual a 24.Inicialmente, traçamos em um mesmo plano cartesiano as retas que representam as soluções das equações.
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
3 |
(0, 3) |
|
3 |
0 |
(3, 0) |
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
3 |
(0, 3) |
|
3 |
0 |
(3, 0) |

Como as retas são coincidentes, têm infinitos pontos comuns. Logo, o sistema tem infinitas soluções. Esse é um exemplo de sistema possível e indeterminado. Para obter qualquer uma dessas infinitas soluções, basta, em uma das equações, atribuir um valor para uma das incógnitas e calcular o valor correspondente da outra.
Observando as equações, percebemos que, ao multiplicar cada termo da primeira equação por 8, obtemos a segunda equação. Assim, as equações são equivalentes, isto é, têm as mesmas soluções.

Tecnologias digitais em foco
Análise da solução de sistemas de equações do 1º grau com duas incógnitas por meio da representação gráfica
Nesta seção, você vai utilizar um software de construção de gráficos para representar graficamente as soluções de uma equação do tipo ax + by = c. Além disso, você vai utilizar esse software para analisar quando um sistema possui uma, infinitas ou nenhuma solução.
Tecnologias digitais em foco
CONSTRUA
Para obter a representação gráfica das soluções de uma equação do tipo ax + by = c, basta digitarmos a equação no campo apropriado.
1º) Construa a representação gráfica das soluções da equação x + 2y = 2.
2º) Construa a representação gráfica das soluções da equação 2x ‒ y = 4.
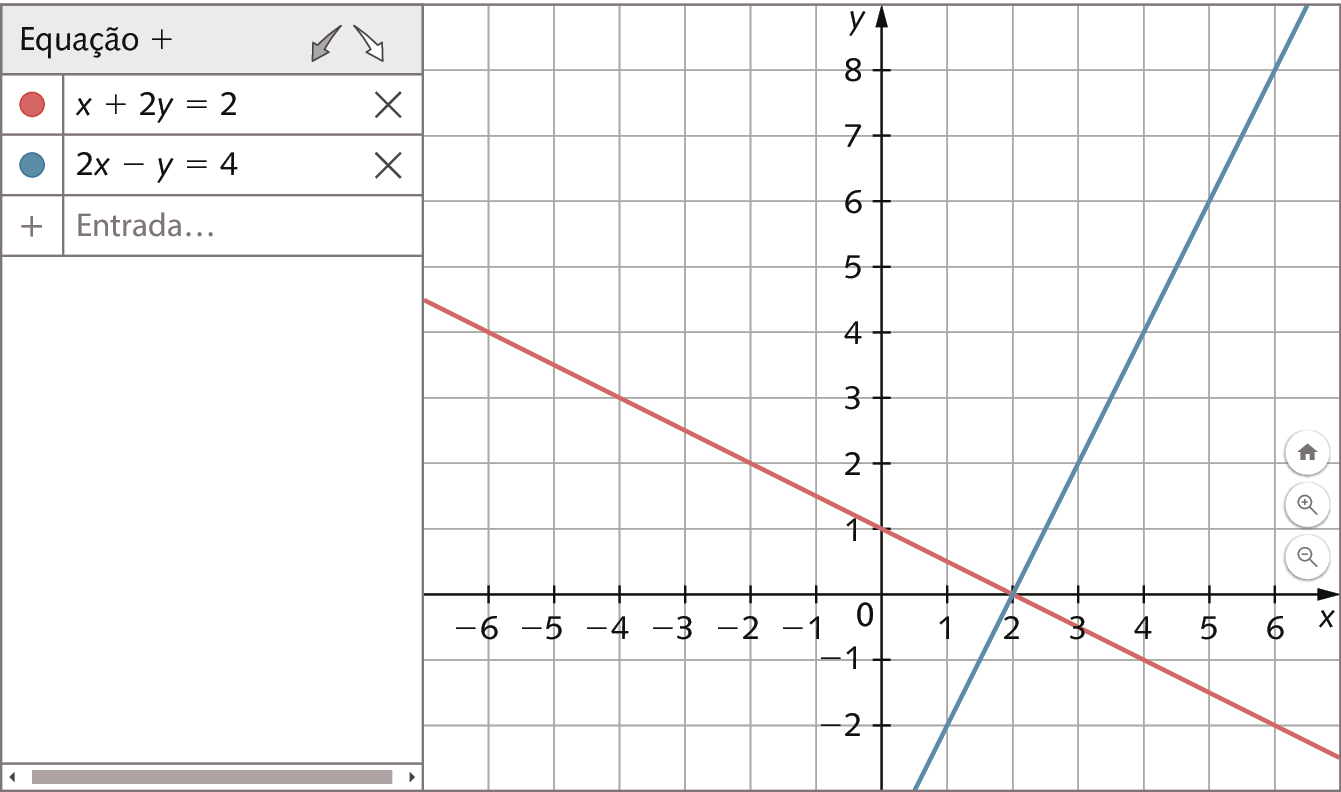
• O sistema
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais 2y igual a 2 e a segunda equação é 2x menos y igual a 4.é possível e determinado, possível e indeterminado ou impossível?
3º) Construa a representação gráfica das soluções da equação x + y = 3.
4º) Construa a representação gráfica das soluções da equação x + y = 0.

• O sistema
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais y igual a 3 e a segunda equação é x mais y igual a zero.é possível e determinado, possível e indeterminado ou impossível?
EXPLORE
Construa a representação gráfica das soluções de cada uma das equações de um sistema possível e indeterminado qualquer. Como ficaram as retas que você construiu?
Atividades
Faça as atividades no caderno.
21. Represente graficamente cada sistema, em que x e y são números reais. Em seguida, classifique cada um dos sistemas em possível e determinado, possível e indeterminado ou impossível.
a)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x menos 5y igual a 10 e a segunda equação é 2x menos 10y igual a 20.b)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x menos 3y igual a 12 e a segunda equação é 4x menos 6y igual a 14.c)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x menos 4y igual a 10 e a segunda equação é x menos 2y igual a 5d)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x mais y igual a 8 e a segunda equação é x menos 2y igual a menos 6.e)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x menos y igual a 7 e a segunda equação é 6x menos 3y igual a 15.f)
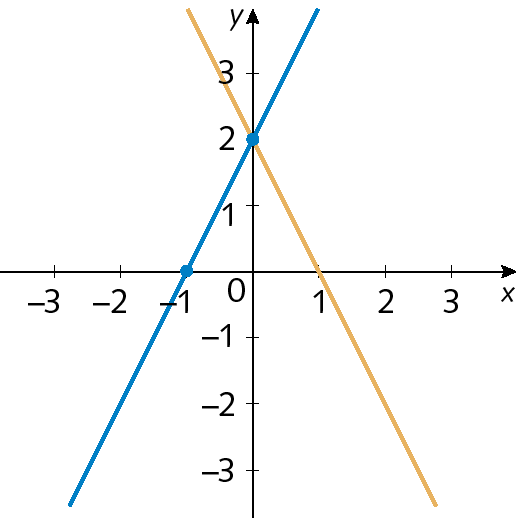
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais y igual a 6 e a segunda equação é x menos y igual a 2.22. Observe o gráfico.
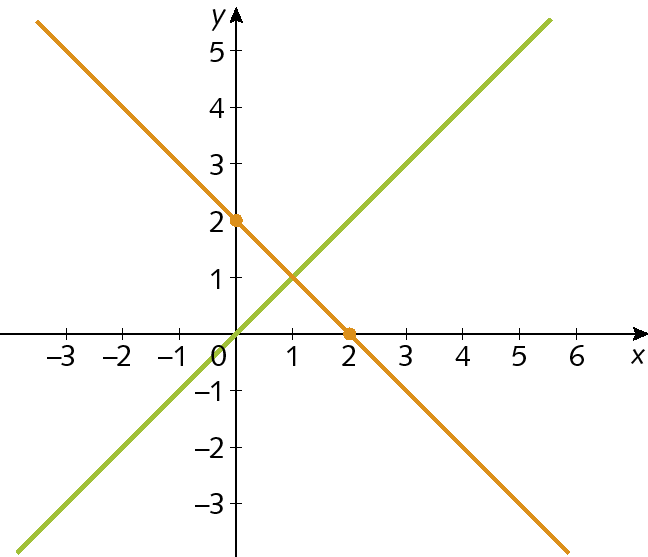
Agora, verifique qual dos sistemas de equação a seguir está de acordo com o gráfico.
Sistema um:
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x mais 2y igual a 4 e a segunda equação é x menos y igual a zero.Sistema dois:
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é 2x mais 2y igual a 4 e a segunda equação é menos 3x mais 6y igual a 12.23. Observe o sistema de equações a seguir.
Sistema de duas equações com uma equação abaixo da outra. Abre chave, primeira linha: 4 x menos 2 y é igual a menos 4. Segunda linha: menos 4 x menos 2 y é igual a menos 4.
Agora, verifique qual dos gráficos a seguir pode ser uma representação do sistema de equações anteriores.
Gráfico um

Gráfico dois
24. Joana tem uma oficina mecânica e, no final de um dia de trabalho, observou que arrecadou R$ 640,00seiscentos e quarenta reais em cédulas de R$ 10,00dez reais e R$ 50,00cinquenta reais. Sabendo que, no total, ela recebeu 24 cédulas, faça o que se pede.
a) Determine um sistema de equações para representar a situação.
b) Construa um plano cartesiano no caderno e represente as equações do sistema indicado como resposta no item anterior. Esse sistema é possível e determinado, possível e indeterminado ou impossível?
c) Quantas cédulas de R$ 10,00dez reais Joana recebeu? E de R$ 50,00?cinquenta reais

Resolvendo em equipe
Faça a atividade no caderno.
(ó bê ême) Numa loja de ferragens, vários produtos são vendidos pelo peso [massa]. Um prego, três parafusos e dois ganchos pesam 24 gramas. Dois pregos, cinco parafusos e quatro ganchos pesam 44 gramas. Juquinha comprou 12 pregos, 32 parafusos e 24 ganchos. Quanto pesou sua compra?
a) 200 gramas
b) 208 gramas
c) 256 gramas
d) 272 gramas
e) 280 gramas
|
Interpretação e identificação dos dados |
• Analise as informações do enunciado e anote aquelas que julgar relevantes para a resolução do problema. • Se um prego, três parafusos e dois ganchos tem medida de massa igual a 24 g, quanto mede a massa de dois pregos, seis parafusos e quatro ganchos? • Com a informação obtida no item anterior, associada à informação dada no enunciado de que dois pregos, cinco parafusos e quatro ganchos têm medida de massa igual a 44 g, é possível encontrar a medida da massa de um parafuso. Determine-a. |
|---|---|
|
Plano de resolução |
• Escreva três equações com as informações do respectivo enunciado. • Monte um sistema com as três equações. • Multiplique a primeira equação por 12 e relacione-a com a terceira equação. Que conclusões você obteve? |
|
Resolução |
• Reúna-se com mais dois colegas. • Mostre a eles seu plano de resolução e verifique se há ideias em comum entre vocês. • Discutam quais são as diferenças e as semelhanças de cada plano e escolham um dos planos para a execução do processo de resolução. • Verifique, com seus colegas, qual é o plano de resolução que alcança o objetivo de maneira mais eficiente e adequada. Observação Resolvam o problema de forma coletiva, mas façam o registro individual no caderno. |
|
Verificação |
• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas. |
|
Apresentação |
• Cada grupo deverá criar duas novas situações de compra na loja de ferragens, buscando sempre quantidades de pregos, parafusos e ganchos que sejam múltiplas das quantidades originais. Em seguida, deverão escrever as equações que permitem responder às questões formuladas. Essas novas situações devem ser apresentadas na forma de cartazes e explicadas para toda a turma. |
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Pares ordenados e plano cartesiano
Em um plano, traçamos duas retas com orientação crescente, x e y, perpendiculares entre si, para fazer a representação geométrica de pares ordenados. Analise a figura a seguir.

1. Construa um plano cartesiano em seu caderno e, depois, marque os pontos indicados a seguir.
a(‒2, 3); B(1, 1); C(3, 5); D(‒2; ‒3); ê(3, ‒3)
Equação do 1º grau com duas incógnitas
Denominamos equação do 1º grau com duas incógnitas (x e y) aquela que pode ser reduzida a uma equação do tipo ax + by = c, em que a, b e c são números reais, chamados coeficientes, com a ≠ 0 e b ≠ 0.
Representação gráfica das soluções de uma equação do 1º grau com duas incógnitas
O conjunto de soluções de qualquer equação do 1º grau com duas incógnitas, sendo estas números reais, é representado no plano cartesiano por uma reta.
2. Lana possui cédulas de R$ 5,00cinco reais e R$ 10,00dez reais. São 20 cédulas que totalizam R$ 140,00cento e quarenta reais. Há quantas cédulas de cada valor?
Sistema de equações do 1º grau com duas incógnitas
Duas equações do 1º grau com as mesmas duas incógnitas, x e y, formam um sistema de equações do 1º grau com duas incógnitas. Indicamos esse sistema organizando as equações em uma chave. Observe um exemplo:
Análise da solução por meio da representação gráfica
• Um sistema é possível e determinado quando tem apenas uma solução. As retas que representam as soluções das equações de um sistema possível e determinado são concorrentes, ou seja, interceptam-se em um único ponto.
• Um sistema é impossível quando não tem solução. As retas que representam as soluções das equações de um sistema impossível são distintas e paralelas, não têm ponto comum.
• Um sistema é possível e indeterminado quando tem infinitas soluções. As retas que representam as soluções das equações de um sistema possível e indeterminado são coincidentes.
3. Determine a solução dos sistemas aplicando os métodos da substituição e da adição. Considere que x e y podem ser qualquer número real.
a)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais y igual a 5 e a segunda equação é x menos y igual a 1b)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais y igual a 3 e a segunda equação é 2x menos y igual a menos 6.c)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x mais y igual a 9 e a segunda equação é x menos y igual a 3.d)
Sistema de duas equações do primeiro grau com duas incógnitas. A primeira equação é x igual a 2 mais y e a segunda equação é y igual a 6 menos x.
É hora de extrapolar
Faça as atividades no caderno.
As condições de vida e de trabalho são iguais para homens e mulheres?
Nos últimos séculos, as mulheres conseguiram conquistar vários direitos e espaços, especialmente no Ocidente, mas, ainda hoje, as perspectivas das mulheres em relação ao trabalho, à autonomia e à representação política não atingiram a igualdade desejada. Um dos objetivos da Agenda 2030 da ONU é a igualdade de gênero, que, para ser atingida, depende dos esforços de toda a sociedade.

Objetivos: Analisar dados sobre a desigualdade de gênero; pesquisar a biografia de mulheres de destaque; produzir e divulgar um póde kést com a biografia da personalidade escolhida.

Etapa 1: Análise de dados sobre a desigualdade de gênero no país.
1. A turma deverá se organizar em cinco grupos e ler o trecho a seguir sobre o Índice de Desigualdade de Gênero.
O Relatório de Desenvolvimento Humano de 2020, publicado pelo Programa das Nações Unidas para o Desenvolvimento (penúdi), traz a classificação de 189 países em relação ao Índice de Desenvolvimento Humano (í dê agá) para o ano de 2019, com o Brasil ocupando a 84a posição. Além dos valores de í dê agá, há valores que se referem ao Índice de Desigualdade de Gênero (í dê gê), cuja definição é:
O Índice de Desigualdade de Gênero (í dê gê) reflete desigualdades com base no gênero em três dimensões – saúde reprodutiva, autonomia e atividade econômica. A saúde reprodutiva é medida pelas taxas de mortalidade materna e de fertilidade entre as adolescentes; a autonomia é medida pela proporção de assentos parlamentares ocupados por cada gênero e a obtenção de educação secundária ou superior por cada gênero; e a atividade econômica é medida pela taxa de participação no mercado de trabalho para cada gênero. O í dê gê reticências mostra a perda no desenvolvimento humano devido à desigualdade entre as conquistas femininas e masculinas nas três dimensões do IDG. penúdi Brasil. O que é í dê agá.
Disponível em: https://oeds.link/J95YLG. Acesso em: 4 julho 2022.
Quando o í dê gê é analisado, constata-se uma piora na classificação do Brasil no ranking publicado pelo penúdi em 2018, pois o país passou a ocupar a 95a posição. As altas taxas de mortalidade materna, as desigualdades salariais entre homens e mulheres e a baixa representação feminina na política são fatores que contribuem para que o valor do í dê gê brasileiro seja baixo.
a) Leiam o relatório Estatísticas de gênero: indicadores sociais das mulheres no Brasil, produzido pelo í bê gê É, que traz dados estatísticos sobre alguns indicadores que tratam das diversidades sociais entre o sexo feminino ou o masculino. Para ler o relatório, consulte: https://oeds.link/rf7LPR (acesso em: 5 julho 2022).
b) Cada grupo deverá escolher um dos cinco domínios do relatório em que os indicadores foram organizados:
• estruturas econômicas, participação em atividades produtivas e acessos e recursos;
• educação;
• saúde e serviços relacionados;
• vida pública e tomada de decisões;
• direitos humanos das mulheres e meninas.
Elaborem um resumo sobre os dados do domínio escolhido, identificando aqueles que se referem às dimensões consideradas para o cálculo do í dê gê.
c) Compartilhem o resumo elaborado com os colegas e montem um único documento que englobe todas as informações coletadas sobre os domínios abordados no relatório. Inclua no resumo afirmações sobre o infográfico da abertura desta Unidade.
2. Em novembro de 2021, o Brasil ficou na 142a posição no ranking da União Interparlamentar (UIP) que avalia 193 países e informa a quantidade de homens e mulheres atuantes na política. Um dos fatores relevantes para que o Brasil ocupasse essa colocação, a última posição entre os países da América do Sul, é que apenas 15,2% dos deputados federais são mulheres.
Sabendo que, em 2021, havia 513 deputados federais no Brasil, respondam às questões.
a) Qual é o cálculo que precisamos realizar para determinar a quantidade de deputadas federais na Câmara dos Deputados? Qual foi o resultado obtido?
b) É conveniente utilizar o número obtido para representar o número de deputadas federais mulheres? Por quê?
c) Em 2021, o número de deputados do sexo masculino correspondia a 45 mais o quíntuplo do número de deputados do sexo feminino. Representem a relação entre o número de deputados do sexo feminino e o número de deputados do sexo masculino e determinem o número de cadeiras da Câmara de Deputados que foi ocupado por mulheres.
3. Agora, vocês vão se organizar em novos grupos.
Cada novo grupo será composto de, no mínimo, um integrante de cada grupo que elaborou o resumo para um dos domínios do relatório Estatísticas de gênero: indicadores sociais das mulheres no Brasil.
a) Elaborem uma lista com ações que consideram importantes para combater a desigualdade de gênero nos diversos aspectos sociais apresentados.
b) Apresentem a lista para os demais colegas e promovam uma discussão coletiva, a fim de criar uma lista única para a turma.

Etapa 2: Pesquisa e análise de informações sobre a participação feminina na sociedade.
4.
As projeções da ó í tê reunidas no relatório intitulado “Perspectivas Sociais e do Emprego no Mundo: Tendências 2021” (“World Employment and Social Outlook: Trends 2021 ”– WESO Trends) indicam que o déficit de empregos resultante da crise global chegará a 75 milhões em 2021, antes de cair para 23 milhões em 2022. [reticências]
A crise também atingiu as mulheres de fórma desproporcional. Em 2020, a [não] contração do emprego feminino foi de 5%, em comparação com 3,9% do emprego masculino. O percentual de mulheres que ficaram de fóra do mercado de trabalho e passaram para a inatividade também foi maior. Por outro lado, o aumento das responsabilidades domésticas resultante do confinamento devido à crise aumentou o risco de um “retorno à tradicionalização” no que diz respeito aos papéis de gênero.
[reticências]
Disponível em: https://oeds.link/LvSpZw. Acesso em: 4 julho 2022.
Agora, respondam às questões.
a) Na opinião de vocês quais são os impactos das desigualdades de gênero no mercado de trabalho?
b) Vocês acham importante que homens e mulheres sejam contratados na mesma proporção? Por quê?
5. Observem os nomes e as fotos das mulheres mostradas a seguir e respondam: quais delas vocês conhecem? Por que são consideradas mulheres de destaque?







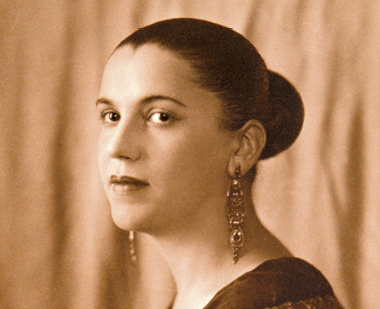
6. Escolham uma das mulheres apresentadas e pesquisem sua biografia e os desafios enfrentados por ela em seu campo de atuação. Façam também uma pesquisa sobre as conquistas ou os desafios enfrentados pela população feminina na sociedade da época em que essa mulher viveu.

Etapa 3: Pesquisa e planejamento para a produção de um podcast.
7. Façam uma pesquisa que tenha como objetivo responder às seguintes questões:
a) O que são podcasts?
b) Como os podcasts são produzidos e reproduzidos?
c) Indiquem uma vantagem de se consumir podcasts.
8. Organizem e elaborem um roteiro para a produção de um podcast sobre a personalidade feminina pesquisada.
O objetivo do podcast é divulgar a história dessas mulheres de destaque para a comunidade escolar, trazendo dados biográficos e desafios vividos, e informar uma conquista ou um desafio enfrentado pela população feminina na época em que essas mulheres viveram.
Analisem as dicas a seguir.
• Estudem bem o assunto, pois é importante que se tenha domínio sobre o que se vai falar.
• Criem uma lista com o planejamento de todo o conteúdo que vai entrar no episódio com a divisão das tarefas para a produção.
• Usem a criatividade. Mesmo que o podcast não seja visível, criem cenários com a voz, sempre priorizando o entendimento do público.
• Elaborem um roteiro visando à organização do conteúdo que será apresentado. O roteiro pode conter: vinheta de início, apresentação dos locutores, rápida introdução do tema, abordagem do tema, preparação para o fechamento e encerramento.
• Guardem uma cópia da gravação original, evitando possíveis problemas com erros de edição do áudio.
9. Com a turma, escolham um único nome para os podcasts, como se fizessem parte de um programa. Todos os podcasts devem iniciar com a mesma vinheta.

Etapa 4: Análise dos roteiros e gravação do podcast.
10. Disponibilizem o roteiro elaborado para que os demais colegas comentem a clareza das informações e os recursos sonoros que o grupo pretende utilizar.
11. Anotem as dúvidas, as opiniões e as sugestões dos colegas.
12. Depois dos ajustes necessários, ensaiem algumas vezes antes do momento da gravação.
13. Gravem o podcast. Lembrem-se de escolher um local sem ruídos e cuidem para que os áudios sejam captados de fórma clara.
14. Divulguem o produto para a comunidade escolar. Vocês podem organizar um momento para executar o áudio na própria escola, por exemplo, durante o intervalo.

Etapa 5: Síntese do trabalho realizado.
15. Algumas questões devem ser discutidas.
a) Vocês acham importante que as pessoas conheçam as histórias dessas mulheres? Por quê?
b) O que pode ser feito pela sociedade para garantir uma maior igualdade de gênero no mercado de trabalho?
16. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 2 e 3.