Unidade 2
Capítulo 4 Ângulos e transformações geométricas
Capítulo 5 Polígonos
Capítulo 6 Probabilidade


Segundo o Instituto Brasileiro de Geografia e Estatísca (í bê gê É), em 2019 os idosos brasileiros representavam 16,2% da população do país, e projeções indicavam que esse percentual dobrará em 2045.
Você conhece os direitos dos idosos? Na sua opinião, as pessoas viverem mais tempo significa que estão vivendo saudavelmente e tendo suas necessidades atendidas? Ao final desta Unidade, você responderá essas e outras questões.
Capítulo 4 Ângulos e transformações geométricas
Trocando ideias

Considerada a mais antiga arte em cerâmica do Brasil e uma das mais antigas das Américas, a arte marajoara é o conjunto de artefatos, sobretudo em cerâmica, dos habitantes da Ilha de Marajó, no Pará.

▸


Reúna-se com três colegas e pesquisem sobre a arte marajoara. Depois, compartilhem com a turma o que tiverem encontrado.
▸

Que transformações geométricas você reconhece nos grafismos presentes nas peças de cerâmica marajoara anteriores?
Neste capítulo, vamos retomar e nos aprofundar em assuntos como ângulos e transformações geométricas.
Conheça mais
No site do Museu Paraense Emílio Goeldi, há um catálogo com diversos exemplares da cerâmica marajoara no livro digital Cerâmica marajoara: a comunicação do silêncio, de Lilian Bayma de Amorim.

1 Ângulos
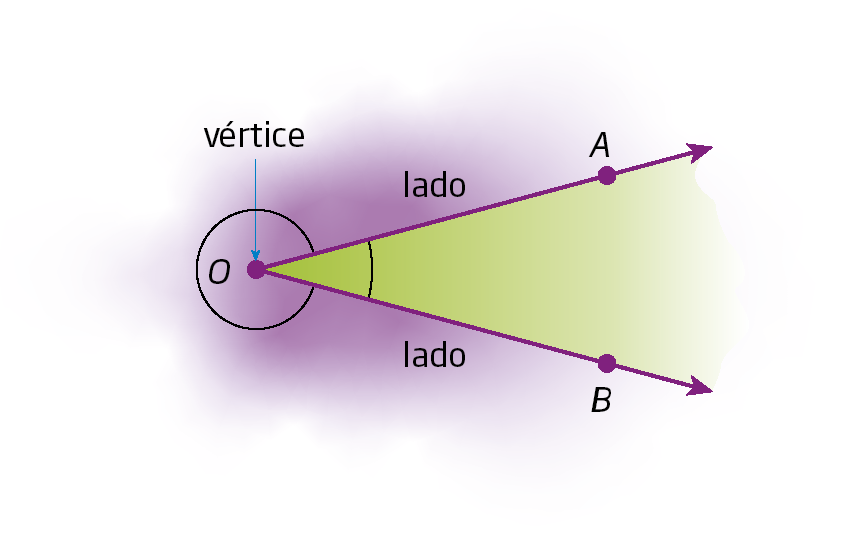
Duas semirretas de mesma origem determinam no plano duas regiões, que, nesta figura, estão destacadas com cores diferentes.
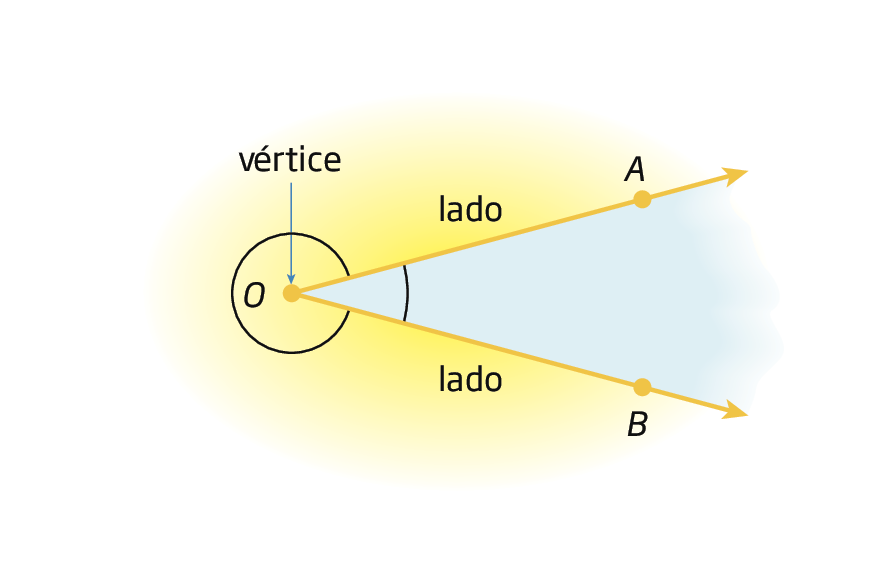
As semirretas
Semirreta OA.e
Semirreta OB.determinam dois ângulos que podem ser indicados por
Ângulo AOB..
Ângulo é a união de duas semirretas de mesma origem, com uma das regiões do plano limitada por elas.
Classificação de ângulos
De acordo com a medida da abertura, um ângulo pode ser classificado em:
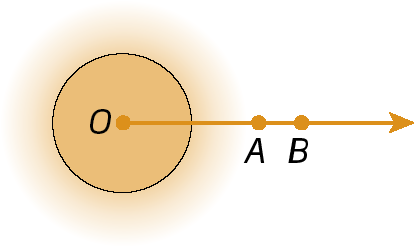
• Ângulo nulo

Sentença matemática. Medida do ângulo AOB igual à 0 graus.
• Ângulo de uma volta
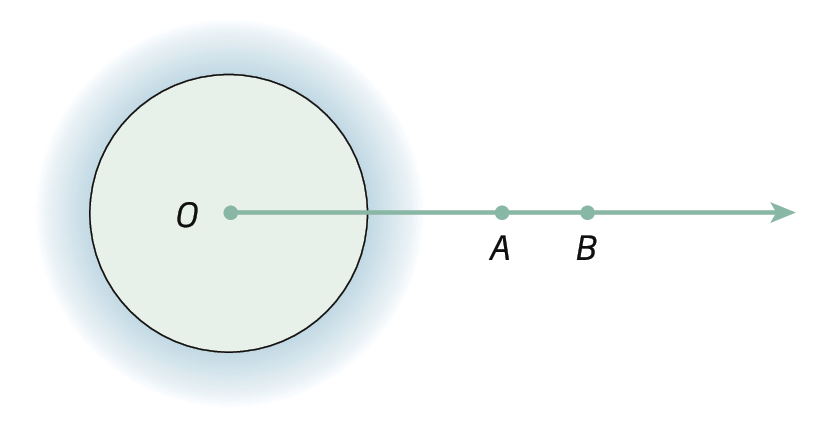
Sentença matemática. Medida do ângulo AOB igual à 360 graus.
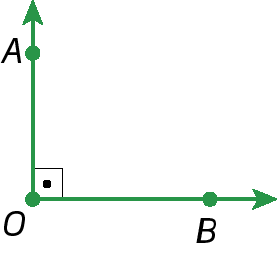
• Ângulo reto
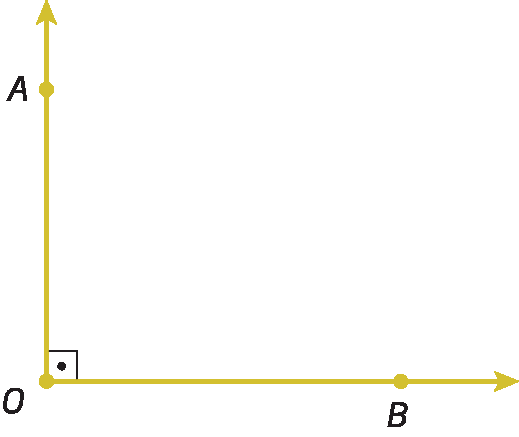
Sentença matemática. Medida do ângulo AOB igual à 90 graus.
• Ângulo raso ou de meia-volta
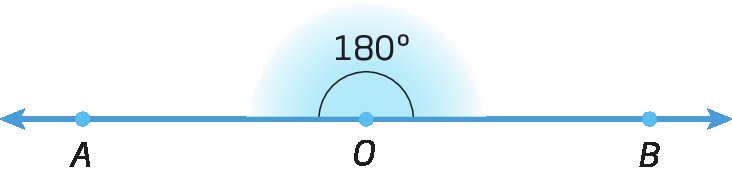
Sentença matemática. Medida do ângulo AOB igual à 180 graus.
• Ângulo agudo
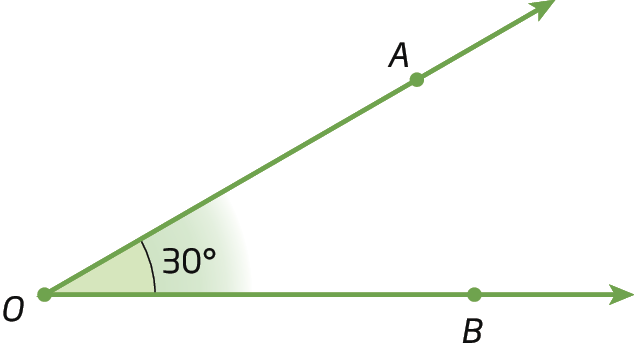
Sentença matemática. 0 grau menor que medida do ângulo AOB menor que 90 graus.
• Ângulo obtuso
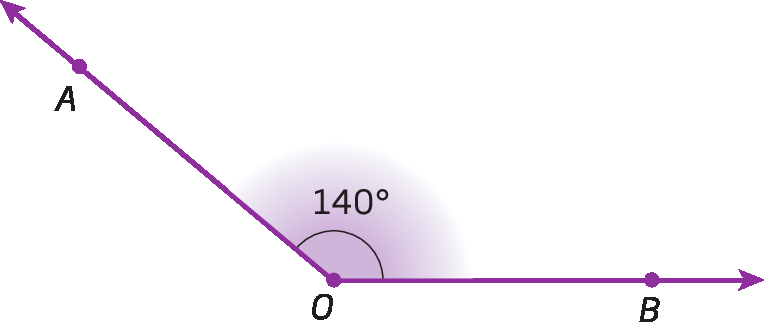
Sentença matemática. 90 graus menor que medida do ângulo AOB menor que 180 graus.
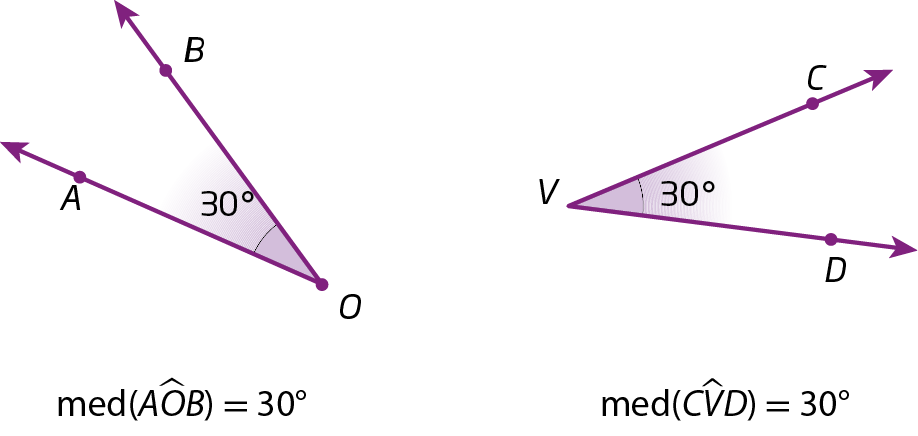
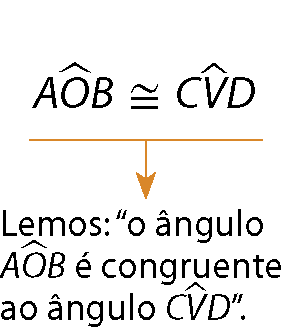
Ângulos congruentes
Dois ângulos são congruentes quando têm a mesma medida de abertura.
Atividades
Faça as atividades no caderno.
1. Classifique os ângulos a seguir em nulo, raso, de uma volta, reto, agudo ou obtuso.
a)

b)

c)

d)

e)
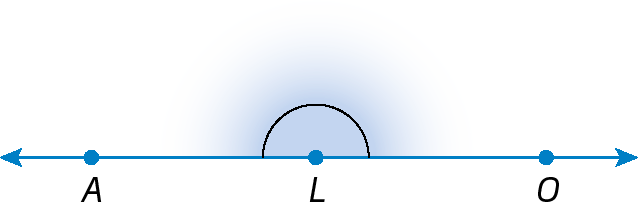
f)
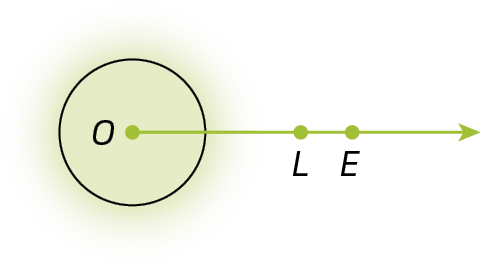
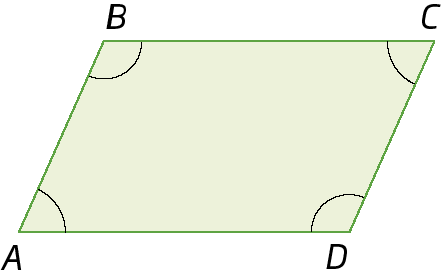
2. Classifique cada ângulo destacado nos quadriláteros a seguir em agudo, reto ou obtuso.
a)
b)
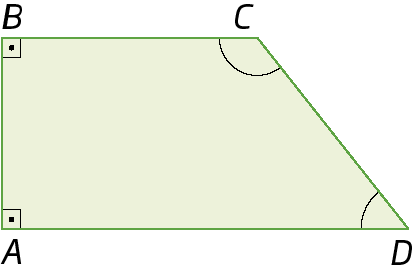
3. Determine o valor de a, sabendo que
Ângulo AOB.e
Ângulo MNP.são congruentes.

Bissetriz de um ângulo
Na figura a seguir, a semirreta
Semirreta OC, interna ao ângulo
Ângulo AOB., divide
Ângulo AOB.em dois ângulos congruentes. Assim, a semirreta
Semirreta OCé a bissetriz do ângulo
Ângulo AOB..
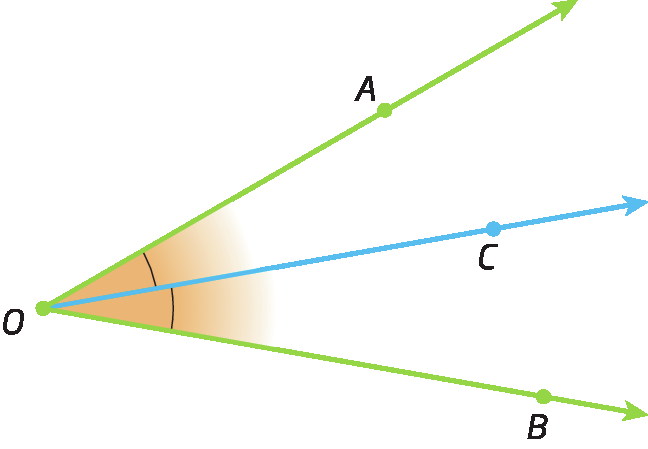
Bissetriz de um ângulo é a semirreta interna a esse ângulo com origem no vértice do ângulo que o divide em dois ângulos congruentes.
Construção geométrica da bissetriz de um ângulo
Para construir a bissetriz do ângulo
AOB, podemos realizar os seguintes passos.
Cuidado! Evite acidentes ao usar o compasso.
1º) Dado um ângulo
Ângulo AOB, centramos o compasso em O e, com uma abertura qualquer, determinamos os pontos C e D sobre as semirretas
Semirreta OA.e
Semirreta OB., respectivamente.
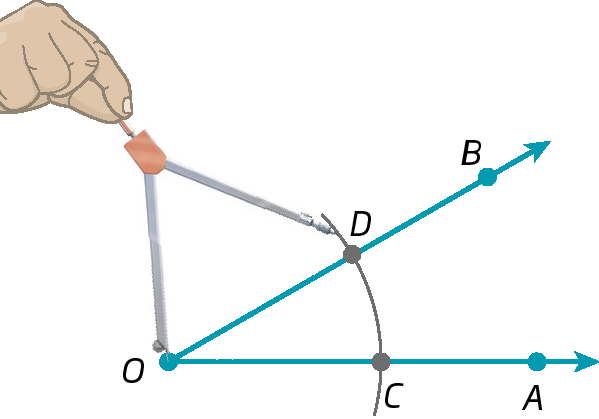
2º) Centramos o compasso em C e em D e traçamos arcos que se cruzam na região interna do ângulo, obtendo um ponto ê.
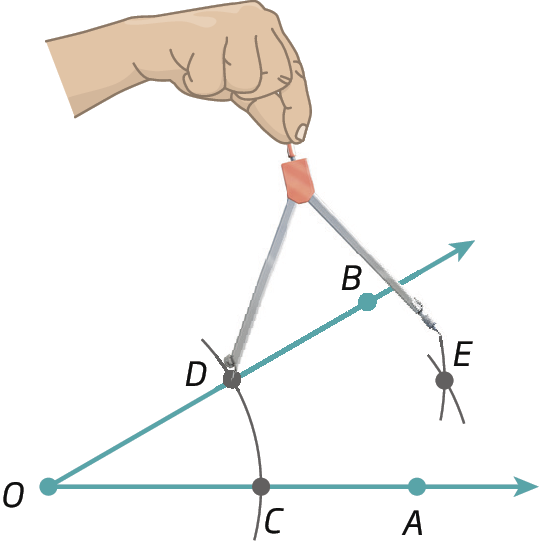
3º) Traçamos
Semirreta OE.determinando, assim, a bissetriz de
Ângulo AOB.
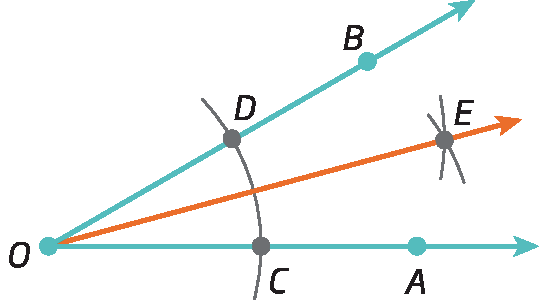

Tecnologias digitais em foco
Bissetriz
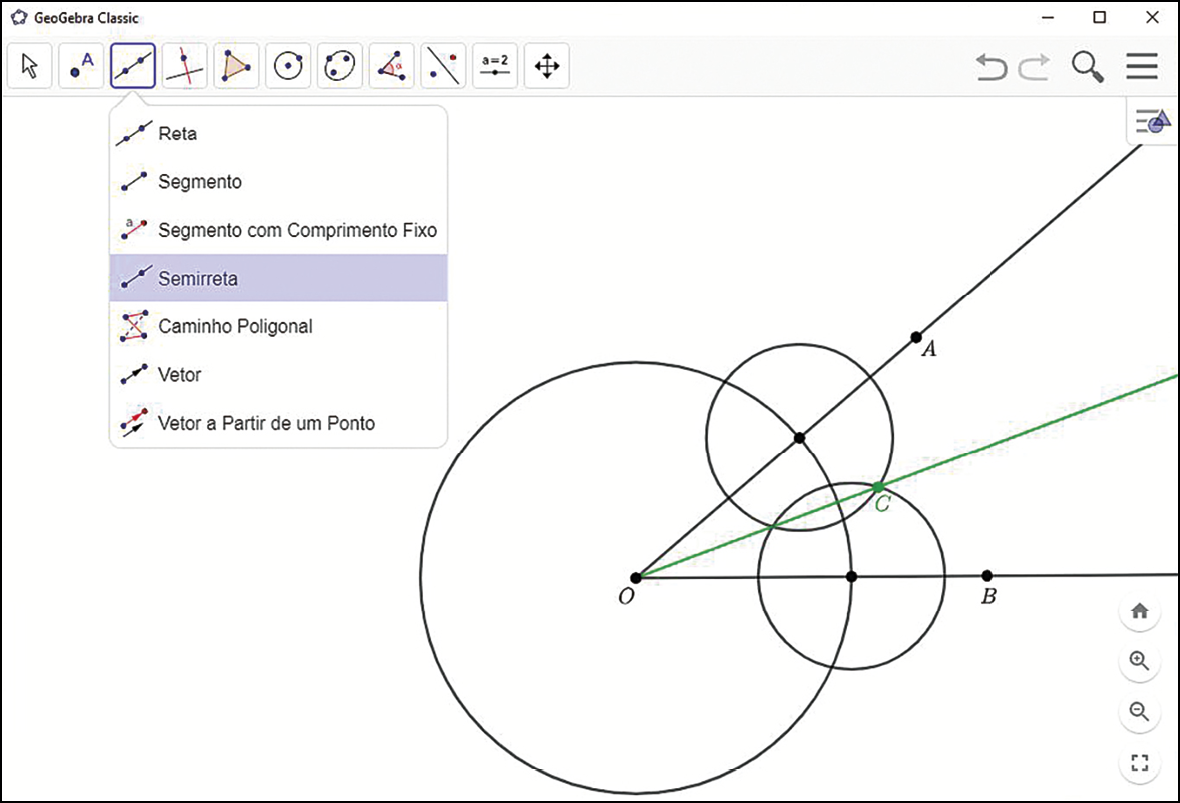
Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para construir a bissetriz de um ângulo e realizar algumas investigações.
Construa
Siga os passos a seguir para construir a bissetriz de um ângulo.
1º) Construa um ângulo
AOBqualquer. Para isso, utilize a ferramenta
e trace duas semirretas de mesma origem óh:
Semirreta OA.e
Semirreta OB.Tecnologias digitais em foco
2º) Siga o passo a passo da construção geométrica da bissetriz de um ângulo da página anterior e construa a bissetriz
Semirreta OCdo ângulo
AOB.
Utilize a ferramenta

para construir circunferências que podem ter qualquer medida de comprimento do raio.
Utilize a ferramenta

para construir circunferências que têm uma medida de comprimento do raio definida.
Explore
Faça o que se pede usando as ferramentas do GeoGebra.
a) Meça a abertura dos ângulos
Ângulo COA.e
BOC. Em seguida, movimente os pontos móveis da construção. Que relação podemos identificar entre as medidas realizadas?
b) Marque um ponto D qualquer na semirreta
Semirreta OC. Utilize a ferramenta
e trace uma reta r, perpendicular a
Semirreta OA.passando por D, e uma reta s, perpendicular a
Semirreta OB.passando por D. Depois, marque ê e F, intersecções das perpendiculares com os lados do ângulo.
• O que as medidas de comprimento dos segmentos
Segmento de reta DE.e
Segmento de reta DF.representam?
c) Meça o comprimento desses segmentos. Em seguida, movimente o ponto D sobre a semirreta
Semirreta OC. Que relação podemos identificar entre as medidas realizadas?

Observação
Note que nessa imagem “escondemos” algumas construções. Você pode fazer o mesmo clicando com o botão direito do mouse sobre a construção e desabilitando a opção “Exibir Objeto”. É interessante utilizar esse recurso e esconder alguns traçados, permitindo melhor visualização nas investigações.
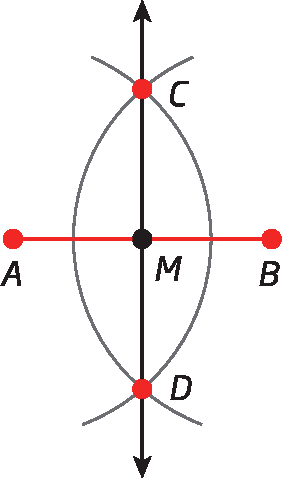
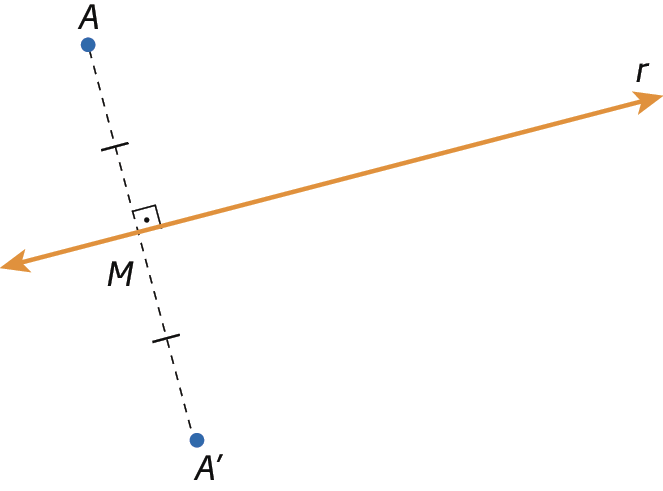
Mediatriz de um segmento de reta
Na figura a seguir, a reta m é perpendicular ao segmento de reta
Segmento de reta AB.e passa pelo ponto M, ponto médio de
Segmento de reta AB.. O ponto médio de um segmento de reta é aquele que o divide em dois segmentos congruentes. Assim, m é mediatriz do segmento de reta
Segmento de reta AB..
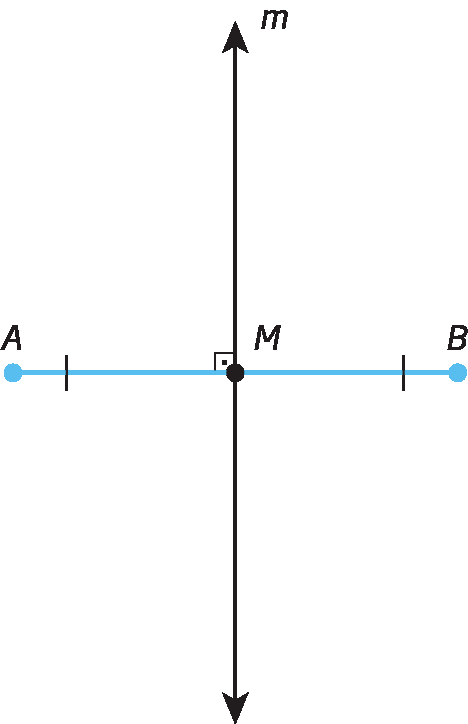
Mediatriz é a reta perpendicular a um segmento de reta que passa pelo ponto médio desse segmento.
Observação
Podemos indicar a medida de comprimento de um segmento de reta
Segmento de reta AB.por
Medida do segmento reta AB.ou, simplesmente, por AB.
Construção geométrica da mediatriz de um segmento de reta
Para construir a mediatriz do segmento de reta
Segmento de reta AB., podemos realizar os seguintes passos.
Cuidado! Evite acidentes ao usar o compasso.
1º) Dado um segmento de reta
Segmento de reta AB., centramos o compasso em a e, com uma abertura maior que a metade do segmento de reta, traçamos um arco de circunferência.

2º) Centramos o compasso em B e, com a mesma abertura, traçamos outro arco que cruze o primeiro. Com isso, obtemos os pontos C e D.
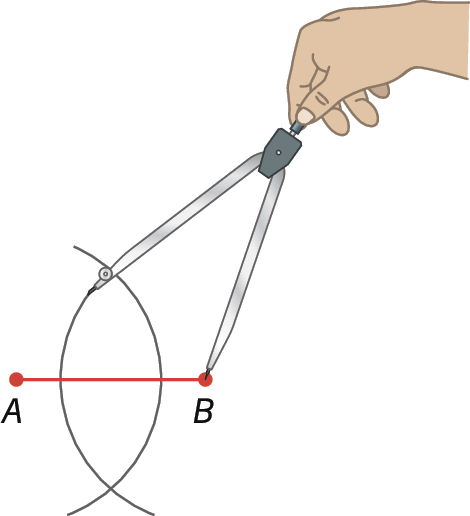
3º) Traçamos
Reta CD.determinando, assim, a mediatriz de
Segmento de reta AB.. Confira que M, intersecção de
Segmento de reta AB.com
Reta CD., é o ponto médio do segmento de reta.

Tecnologias digitais em foco
Mediatriz e ponto médio
Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para construir a mediatriz e o ponto médio de um segmento de reta e realizar algumas investigações.
Construa
Siga os passos seguintes para construir a mediatriz e o ponto médio de um segmento de reta.
1º) Utilize a ferramenta

e construa um segmento de reta
Segmento de reta AB..
2º) Siga o passo a passo do tópico Construção geométrica da mediatriz de um segmento de reta e construa a mediatriz m e o ponto médio M do segmento de reta
Segmento de reta AB..

Explore
Faça o que se pede usando as ferramentas do GeoGebra.
a) Utilize a ferramenta

e meça o comprimento dos segmentos de reta
Segmento de reta AM.e
Segmento de reta MB.. Depois, utilize a ferramenta

e meça a abertura dos ângulos formados entre m e o segmento de reta
Segmento de reta AB.. Por fim, movimente a construção por meio dos pontos móveis (a ê B). Que relação podemos identificar em relação às medidas obtidas?
b) Marque um ponto P qualquer sobre a reta m e, utilizando a ferramenta

, meça o comprimento dos segmentos de reta
Segmento de reta AP.e
Segmento de reta PB.. Depois, movimente o ponto P ao longo da reta m. Que relação podemos identificar?

Atividades
Faça as atividades no caderno.
Cuidado! Evite acidentes ao usar o compasso nas atividades 6, 7, 11 e 12.
4. Nesta ilustração,
Semirreta OB.é a bissetriz de
Ângulo AOC., e
Semirreta OD.é a bissetriz de
Ângulo COE..

a) Qual é a medida da abertura de
Ângulo AOB.se
Medida do ângulo BOC igual à35graus?
b) Qual é a medida da abertura de
Ângulo COD.se
Medida do ângulo DOE igual à25graus?
c) Qual é a medida da abertura de
Ângulo DOA.?
5. Na figura seguinte,
Semirreta OC.é a bissetriz de
Ângulo AOB.e
Sentença matemática. Medida do ângulo AOB igual à 25 graus.. Determine as medidas da abertura de
Ângulo AOB.e de
BOC.

6. Construa no caderno, com o auxílio de um transferidor, um ângulo cuja abertura meça 80graus. Em seguida, utilizando régua e compasso, determine a bissetriz desse ângulo e escreva a medida da abertura de cada ângulo obtido.
7. No caderno, utilizando régua e compasso:
a) construa um ângulo qualquer;
b) divida o ângulo em quatro ângulos congruentes.
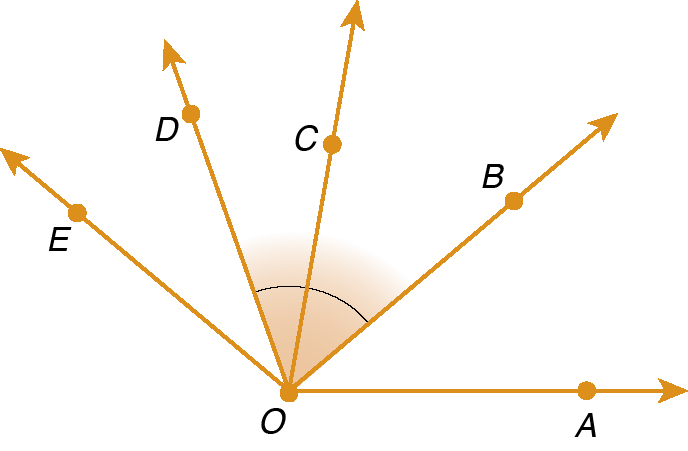
8. Na figura seguinte,
Semirreta OB.é bissetriz de
Ângulo AOC.,
Semirreta OD.é bissetriz de
Ângulo COE.,
Sentença matemática. Medida do ângulo AOB igual à 80 graus.e
Sentença matemática. Medida do ângulo COE igual à 60 graus.. Determine
Medida do ângulo BOD..
9. Na figura a seguir, M é o ponto médio de
Segmento de reta AB.e N é o ponto médio de
Segmento de reta BC..
Se
Sentença matemática. Medida do segmento de reta AB igual à 10 centímetros.e
Sentença matemática. Medida do segmento de reta BC igual à 8 centímetros., determine
Medida do segmento de reta MN.
10. Na figura seguinte, R, S e T são os pontos médios dos segmentos de reta
Segmento de reta AB.,
Segmento de reta BC.e
Segmento de reta CD., respectivamente.

Determine:
a) a medida de comprimento de
Segmento de reta RS.;
b) a medida de comprimento de
Segmento de reta ST.;
c) a medida de comprimento de
Segmento de reta SD.;
d) a medida de comprimento de
Segmento de reta RD..
11. Copie o segmento de reta
Segmento de reta AB.no caderno e, com o auxílio de um compasso, determine sua mediatriz.

12. Copie o △ á bê cê no caderno e, com o auxílio de um compasso, trace as mediatrizes dos segmentos
Segmento de reta AB.,
Segmento de reta BC.e
Segmento de reta AC..

Construção de ângulos com régua e compasso
A seguir, vamos verificar como podemos construir alguns ângulos com o auxílio de régua e compasso. Esses ângulos podem ser utilizados, por exemplo, na construção de figuras planas ou em transformações geométricas.
Cuidado! Evite acidentes ao usar o compasso.
Ângulo de medida da abertura de 60graus
Confira o passo a passo para a construção de um ângulo cuja medida de abertura é 60graus.
1º) Traçamos uma semirreta
Semirreta OA.. Centramos o compasso em óh e, com uma abertura qualquer, traçamos um arco, determinando em
Semirreta OA.o ponto B.
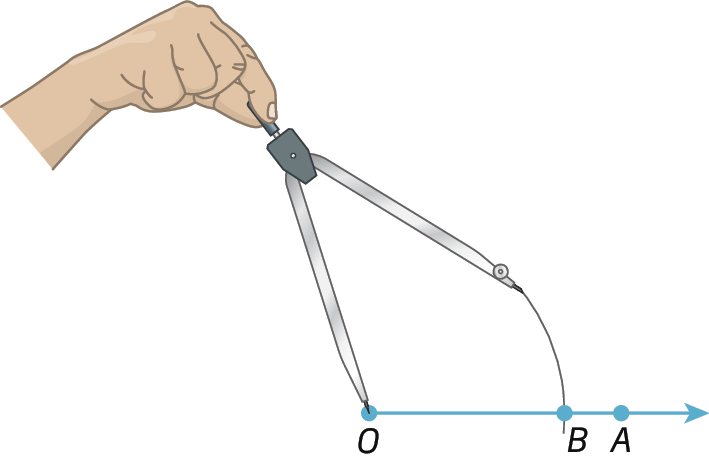
2º) Centramos o compasso em B e, com a mesma abertura, traçamos um arco cruzando o arco anterior, determinando o ponto C.
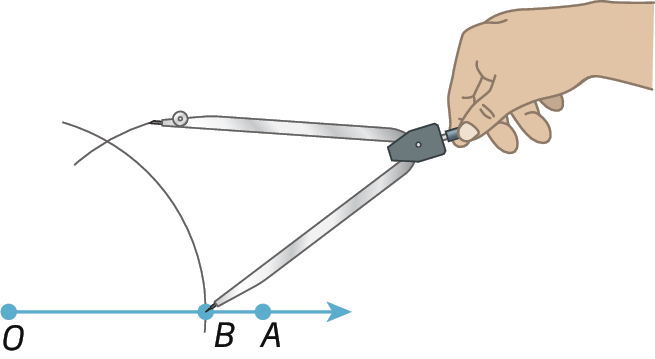
3º) Traçamos
Semirreta OC.determinando, assim, o ângulo
Ângulo BOC.cuja abertura mede 60graus.
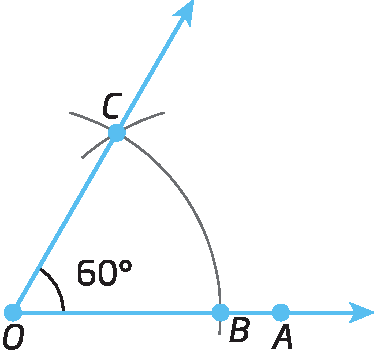
Um ângulo cuja medida de abertura é 30graus pode ser construído traçando-se a bissetriz de um ângulo cuja abertura mede 60graus.

Tecnologias digitais em foco
Ângulo de medida da abertura de 60graus
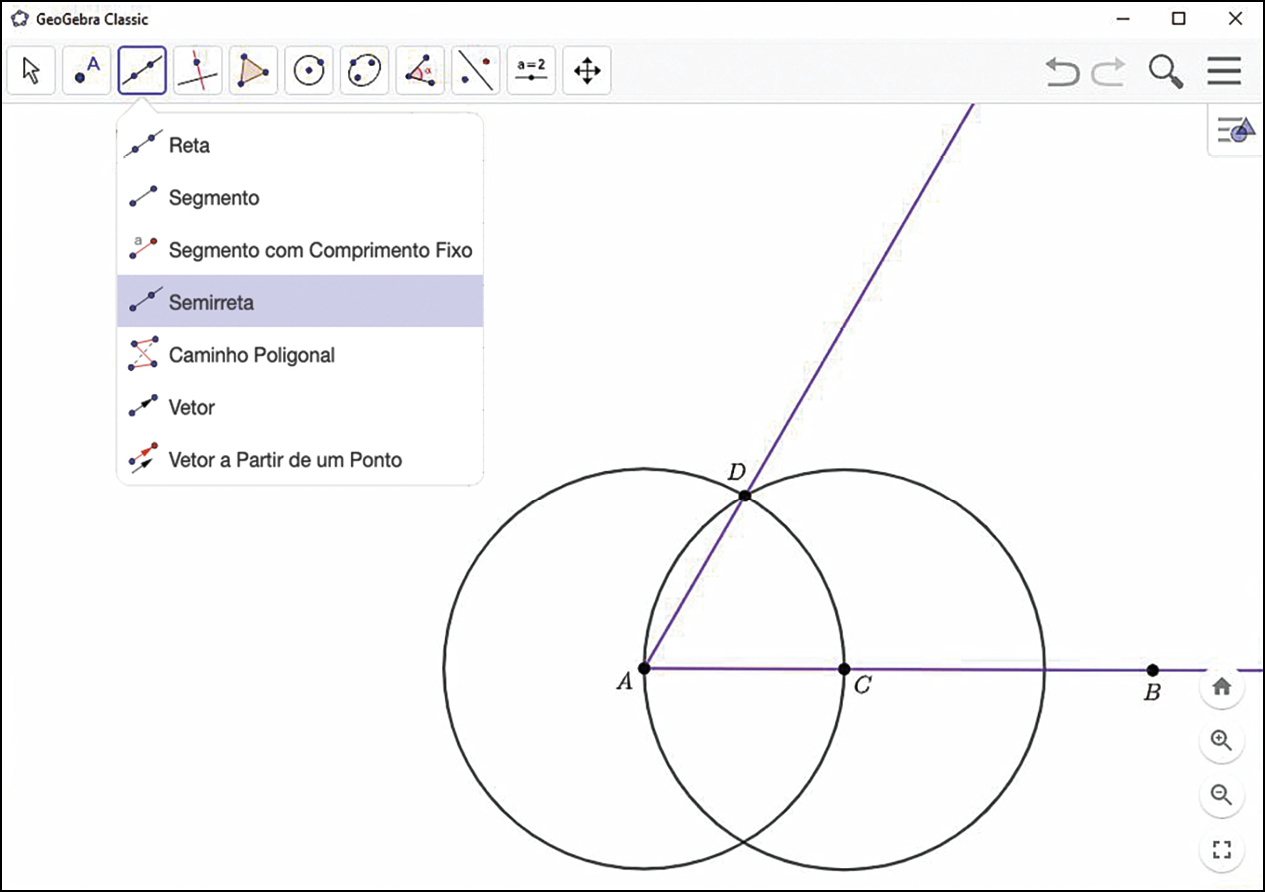
Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para construir um ângulo cuja abertura mede 60graus e realizar algumas investigações.
Construa
Siga os passos a seguir para construir um ângulo de medida da abertura de 60graus.
1º) Utilize a ferramenta

e construa uma semirreta
semirreta AB.
2º) Siga o passo a passo do início deste tópico e construa um ângulo
ângulo BADcuja abertura mede 60graus.
Tecnologias digitais em foco
Explore
a) Utilize a ferramenta

e meça a abertura do ângulo
Ângulo BAD.. Depois, movimente os pontos móveis. O que você pode concluir?
b) Utilize a ferramenta
e construa o triângulo cujos vértices sejam os pontos a, C e D .
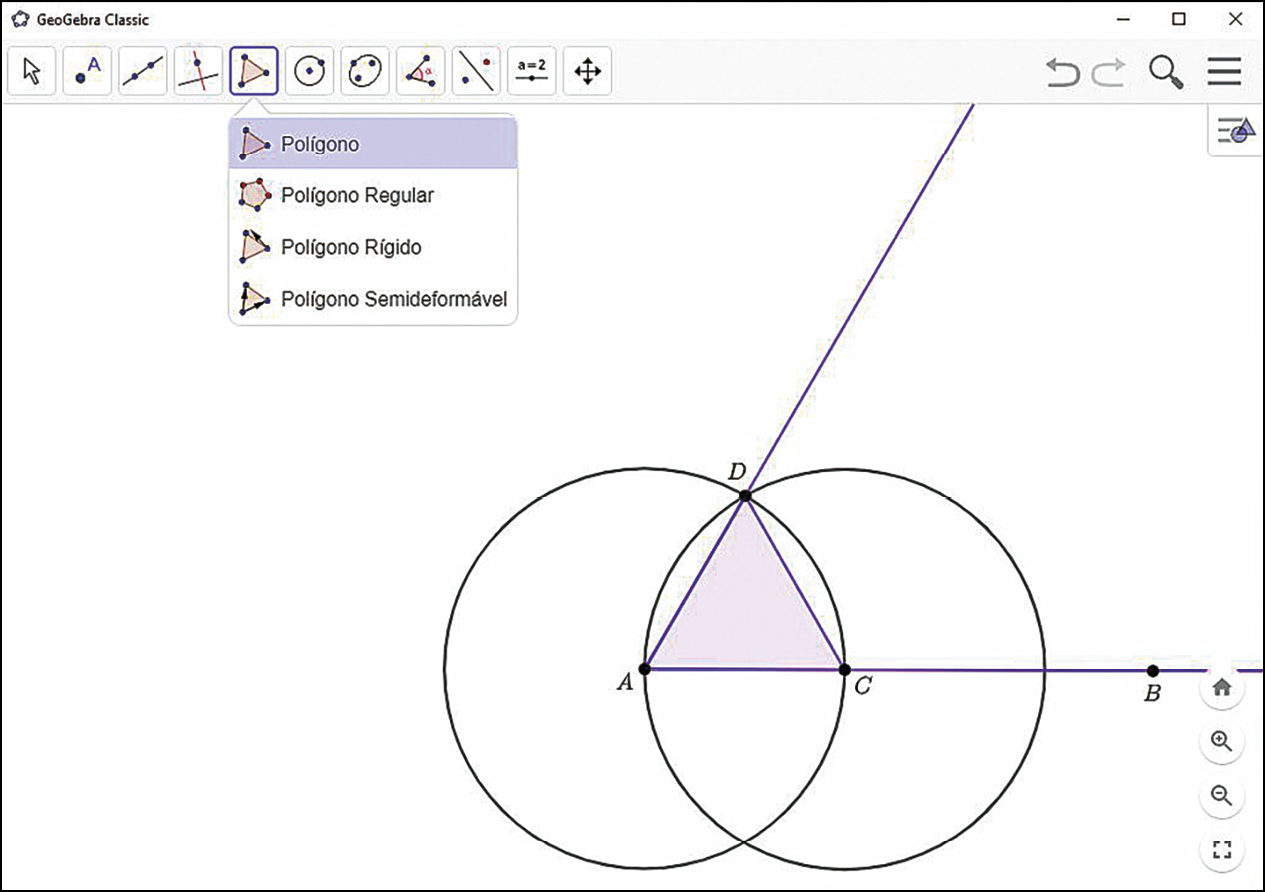
Agora, utilize a ferramenta

e meça o comprimento dos lados desse triângulo. O que você pode concluir?
c) Por que podemos garantir que a abertura do ângulo construído mede 60graus?
Ângulo de medida da abertura de 90graus
Analise o passo a passo para a construção de um ângulo cuja medida de abertura é 90graus.
Cuidado! Evite acidentes ao usar o compasso.
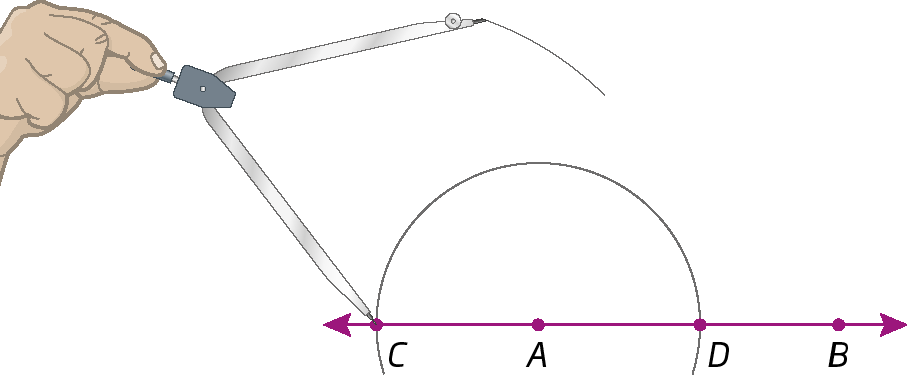
1º) Traçamos a reta
Reta AB.. Centramos o compasso em a e, com uma abertura qualquer, traçamos um arco cruzando a reta
Reta AB.em dois pontos, determinando os pontos C e D.

2º) Centramos o compasso em C e, com uma abertura maior que
Segmento de reta CA., traçamos um arco.
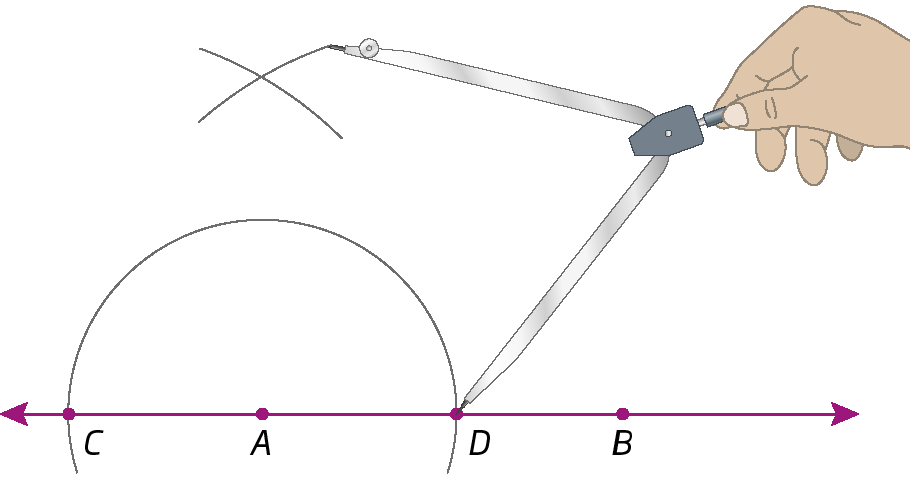
3º) Centramos o compasso em D e, com a mesma abertura do passo anterior, traçamos um arco, cruzando o arco anterior e determinando o ponto ê.
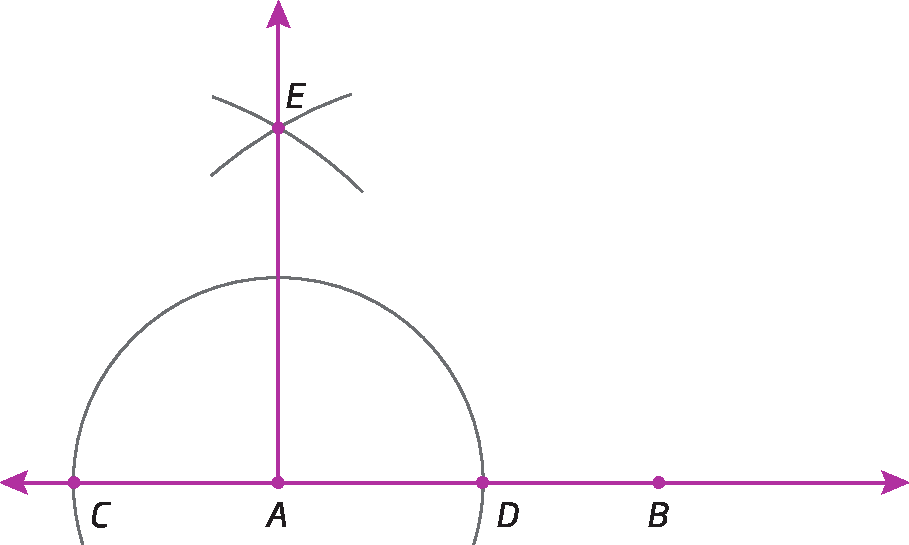
4º) Traçamos
Semirreta AE.determinando, assim, o ângulo
Ângulo BAE.,que mede 90graus.
Observação
Na construção do ângulo de medida da abertura de 90graus, determinamos dois pontos (C e D) equidistantesglossário do vértice do ângulo (a) e, com isso, repetimos os mesmos passos da construção da mediatriz.
Um ângulo cuja medida de abertura é 45graus pode ser construído traçando-se a bissetriz de um ângulo reto.
Cuidado! Evite acidentes ao usar o compasso.
Retas paralelas
No 7º ano, construímos retas paralelas com o uso de esquadros. Agora, vamos estudar como construir retas paralelas usando régua e compasso.
1º) Traçamos a reta s e marcamos um ponto óh qualquer em s. Centramos o compasso em óh e traçamos um arco que intercepta s em a e em B.

2º) Com centros em a e em B e uma abertura menor que
Segmento de reta AB., traçamos arcos que interceptam o arco do passo anterior e determinamos os pontos M e N.
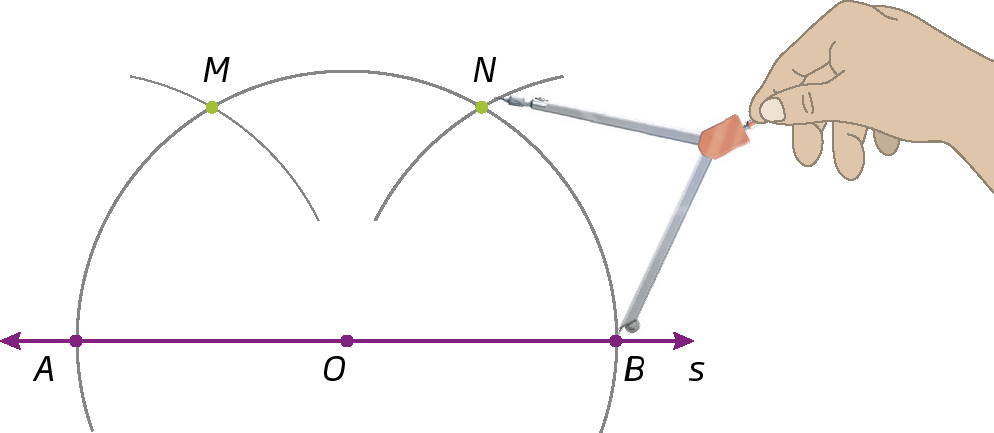
3º) Traçamos t ⫽ s passando por M e por N.

Atividades
Cuidado! Evite acidentes ao usar o compasso nas atividades.
Faça as atividades no caderno.
13. No caderno, trace a semirreta
Semirreta AC.e construa o ângulo
Ângulo BAC.de medida da abertura de 15graus.
14. No caderno, construa um ângulo reto utilizando as construções passo a passo do ângulo de medida da abertura de 60graus e da bissetriz.
15. Dos ângulos de medida de abertura de 30graus, 45graus, 100graus, 125graus e 150graus, quais podem ser construídos com régua e compasso usando as construções que aprendemos até aqui? Construa, no caderno, aqueles que forem possíveis.
16. Desenhe, em seu caderno, uma reta r e um ponto P externo a essa reta. Em seguida, construa, com régua e compasso, uma reta s paralela à r, passando pelo ponto P.

2 Lugares geométricos
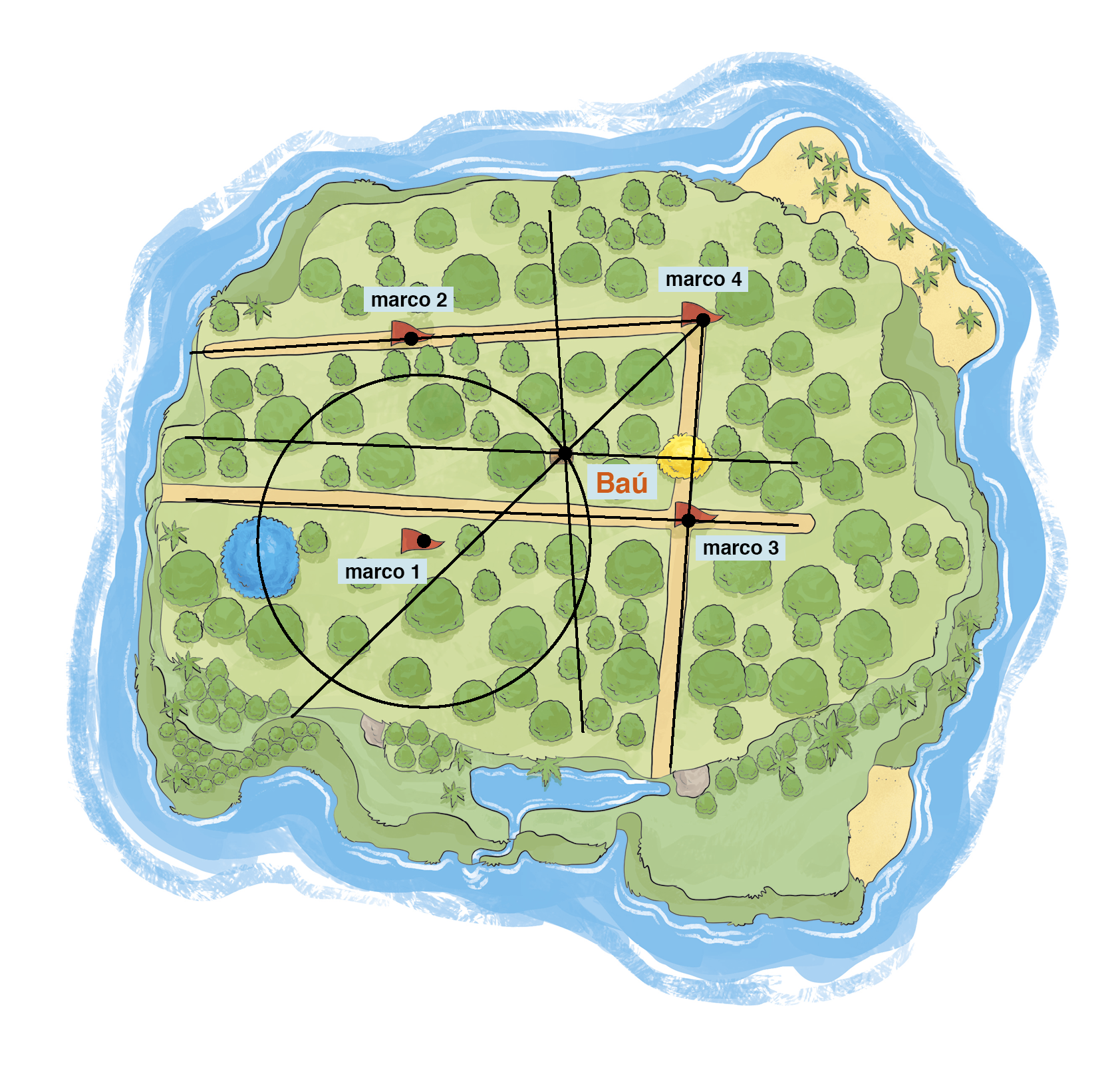
Você já brincou de caça ao tesouro? Analise a ilha e as pistas que levam ao local em que está localizado um baú camuflado.

Com base nessas pistas, é possível determinar as regiões onde o baú está localizado. Para saber a localização exata do baú, é necessário decifrar as pistas.
Cada pista sugere uma propriedade das seguintes construções: circunferência, mediatriz, retas paralelas e bissetriz. A essas pistas damos o nome de lugar geométrico.
Lugar geométrico é a figura formada por todos os pontos do plano que têm em comum uma determinada propriedade.
Circunferência
Verifique este recorte da ilustração da ilha.
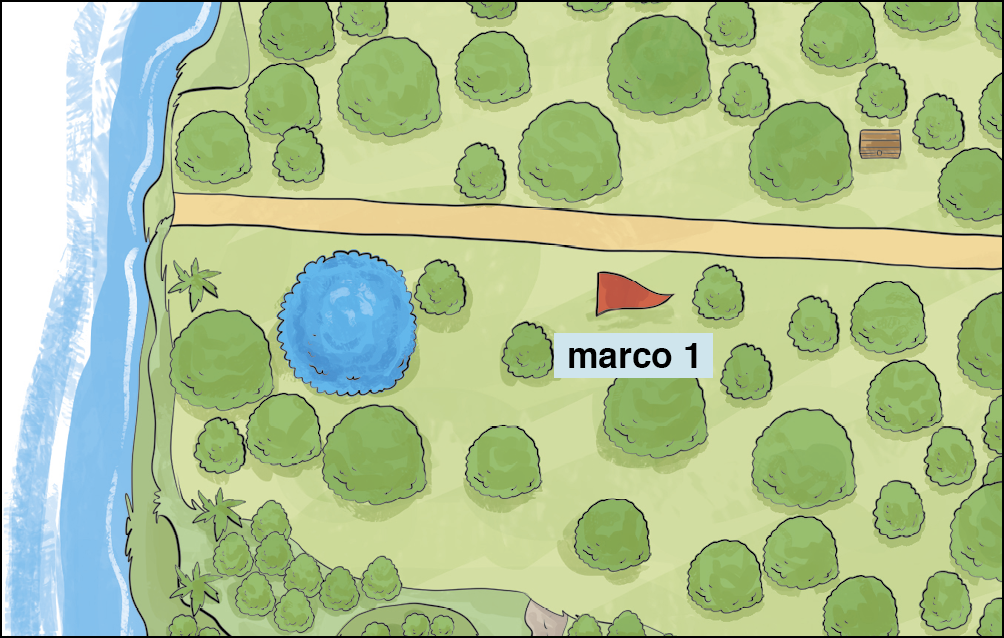
A pista que será utilizada é a seguinte:

Como sabemos a medida da distância do marco 1 à árvore, é possível delimitar uma linha em que seja possível encontrar o baú. Sabemos que na circunferência encontram-se todos os pontos do plano que mantêm a mesma medida da distância a partir do seu centro. Isso significa que o baú do tesouro está em algum lugar da circunferência.
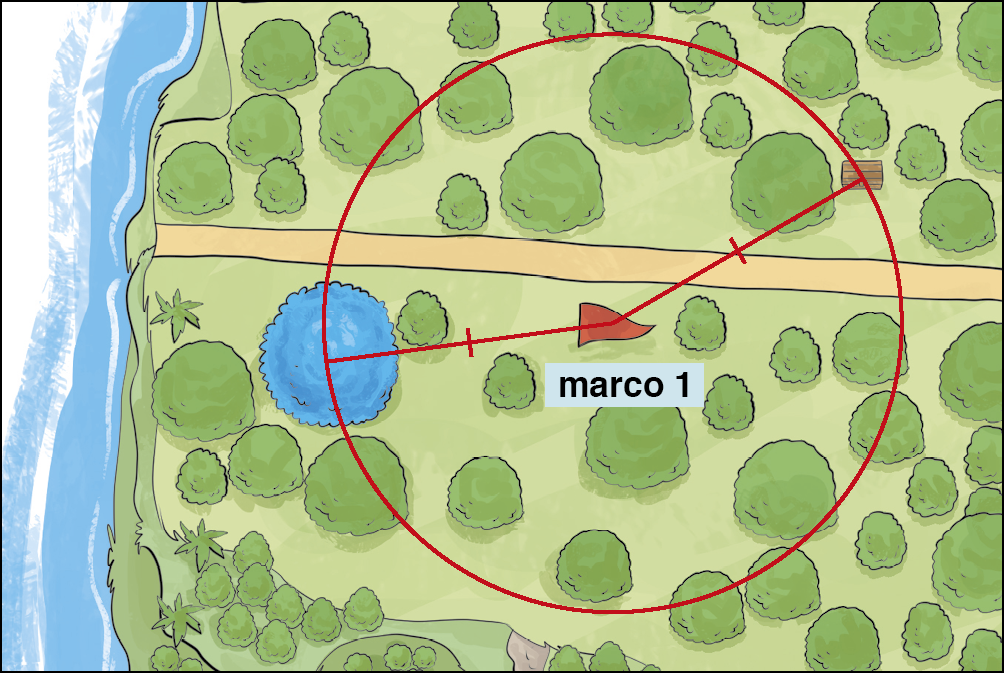
Circunferência é o lugar geométrico dos pontos do plano que equidistam de um ponto fixo.
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Círculos nas plantações
Duração: 3:26min. Página: 89.
>> [LOCUTORA] Círculos nas plantações
Música de fundo.
>> [Pena]: Felipe, você sabe o que são agroglifos?
>> [Felipe] Agroglifos?! São aqueles círculos e símbolos nas plantações?
>> [Pena] Sim, exatamente isso! E você sabe como são feitos os agroglifos?
>> [Felipe] Ah! Certamente são feitos por aliens, né?
Som de nave espacial.
>> [Pena] Então, será que não tem outro jeito de fazer isso? Será que os alienígenas vão atravessar todo o Universo para vir aqui e ficar amassando trigo?
>> [Felipe] É, acho que não, né? Mas como é possível então fazer uma coisa dessas? A gente precisaria estar em uma nave espacial, porque os desenhos são enormes!
>> [Pena] Será? Você sabe traçar esses símbolos em um papel?
>> [Felipe] Sei, Pena. Basta usar um compasso. Com ele, dá para fazer essas curvas, bissetrizes. Existe toda uma gama de desenhos que podemos fazer com uma régua e um compasso. Mas, Pena, a gente não tem compassos gigantes para fazer círculos em plantações. Aonde você está querendo chegar?
>> [Pena] De fato, não temos compassos gigantes, mas, com um pouco de imaginação e técnicas matemáticas, nós podemos fazer a mesma coisa. Por exemplo, imagine que uma pessoa fique parada no meio de uma plantação, segurando a ponta de uma corda. Aí, uma segunda pessoa, a certa distância, segurando a outra ponta da corda e mantendo-a sempre esticada, caminhe ao redor da que está no centro. Ao andar em volta da outra, essa pessoa forma um círculo.
Efeito sonoro de ideia.
>> [Felipe] É verdade, Pena! Afinal, os passos da pessoa ao redor vão estar sempre a uma mesma distância da pessoa que estiver no centro, né?
>> [Pena] Exatamente! E, se ela vai amassando o trigo por onde ela passa, depois de completar uma volta terá formado um círculo ali!
>> [Felipe] E como ela amassa o trigo? Com os pés?
>> [Pena] Na verdade, ela pode usar uma tábua de madeira ou qualquer outro material um pouco maior. E, conforme o trigo vai sendo amassado, ele se prende no que já está no chão e não levanta mais.
>> [Felipe] Tá, Pena. O círculo eu até entendi, mas os agroglifos não são só círculos, são desenhos complexos, formas geométricas…
>> [Pena] Ora! Mas tudo o que você pode fazer no papel com compasso você pode fazer numa plantação, só dá um pouco mais de trabalho. Você tem de fato um compasso gigante, que é basicamente o uso de uma corda esticada na medida do raio que você quer desenhar. Inclusive, você sabia que em 1992 foi criada uma competição de agroglifos? Foi o primeiro e último “Concurso Internacional de Círculos na Plantação”, que aconteceu na Inglaterra. E, adivinha, foram os humanos que ganharam! Nenhum alienígena veio competir. Três engenheiros fizeram desenhos incríveis. Olha como eles foram espertos: usaram canos para amassar o trigo e escadas para fazer pontes na plantação e não deixar marcas erradas no chão, estragando o desenho. Então, Felipe, é bem possível que por trás desses desenhos todos exista um pessoal na verdade muito criativo e muito bom de matemática e geometria! E aí, você ainda acha que são os aliens que fazem os agroglifos?
>> [Felipe] Poxa, Pena, você me convenceu! É incrível o que dá para fazer com a geometria, né?
>> [Pena] Pois é, com geometria e criatividade!
Vinheta.
Créditos Os áudios inseridos neste conteúdo são da Free Sound e da Sonys. A trilha sonora “Royale” executada por George Lipe and Overtimes está disponível no YouTube.
Mediatriz
Analise outro recorte feito a partir da ilustração da ilha.
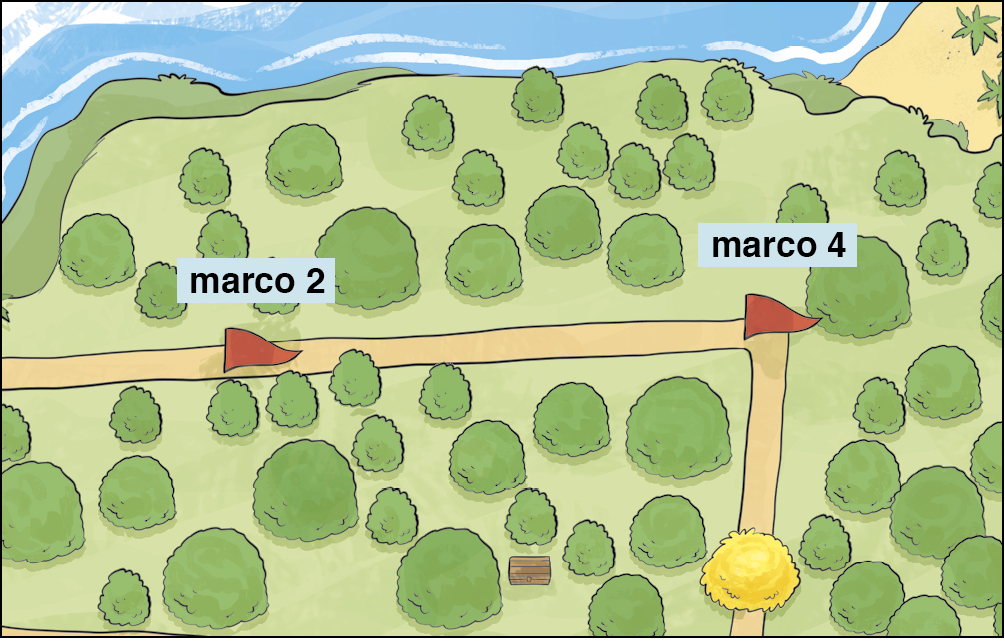
Vamos utilizar a seguinte pista:

Não sabemos a posição do baú, mas conhecemos a localização dos marcos 2 e 4; então, a partir do ponto médio do segmento de reta que une os marcos 2 e 4, as medidas de distância d são iguais.
A mediatriz é a reta perpendicular que passa pelo ponto médio, e é possível demostrar que, dado um ponto qualquer da mediatriz, a medida da distância entre esse ponto e uma das extremidades do segmento de reta (nesse caso, por exemplo, ponto que localiza o marco 2) é igual à medida da distância entre esse mesmo ponto e a outra extremidade do segmento de reta (ponto que localiza o marco 4).
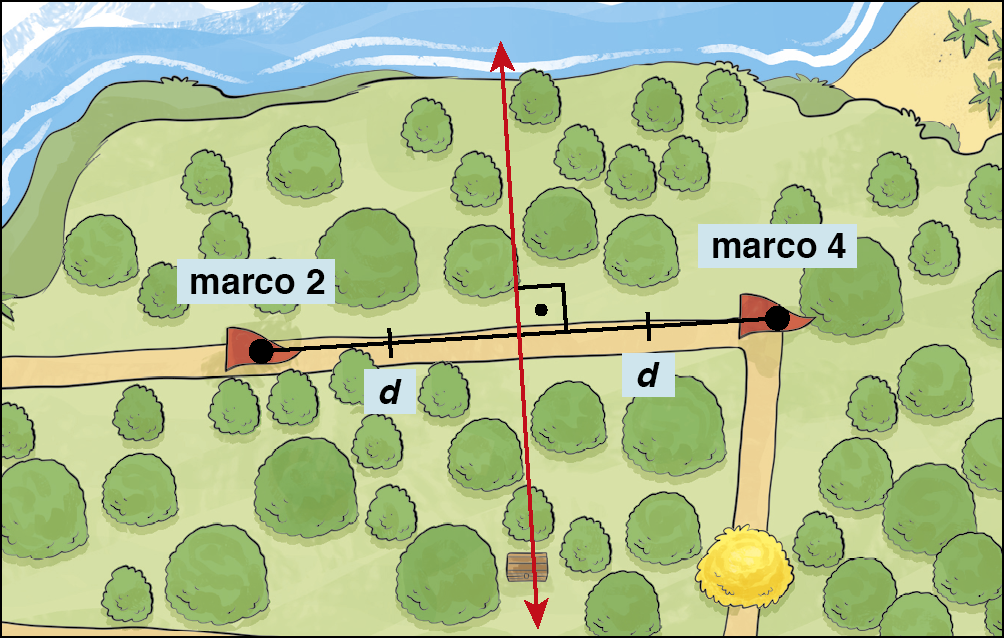
Mediatriz é o lugar geométrico dos pontos do plano que são equidistantes de dois pontos fixos dados (extremidades de um segmento de reta).
Assim, o tesouro está em algum lugar da mediatriz, o que reduz as possibilidades de localização do baú aos pontos de intersecção entre a mediatriz e a circunferência.
Retas paralelas
Confira outro recorte da ilustração da ilha.
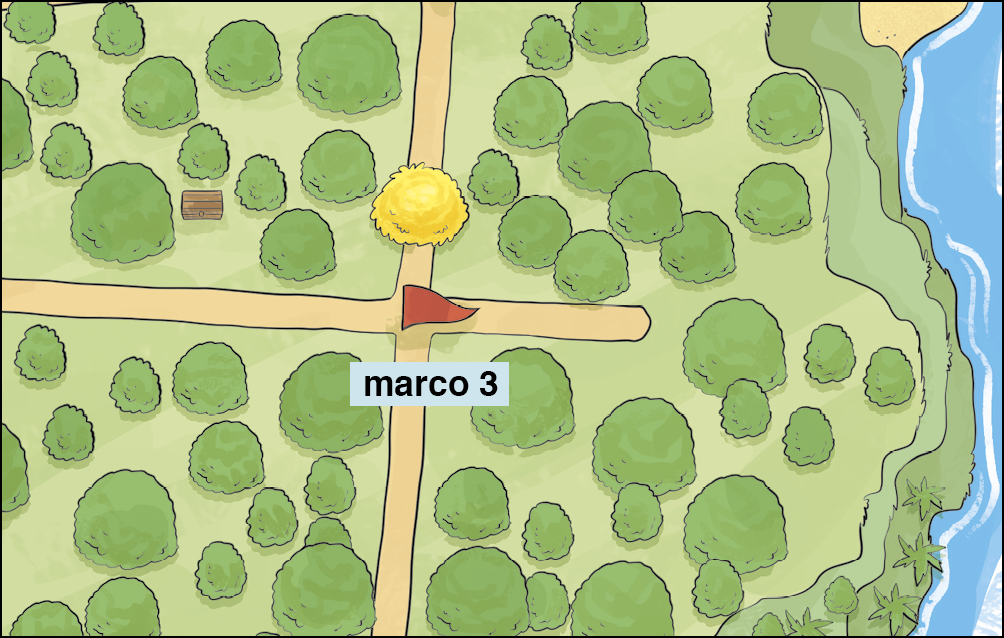
A pista que vamos utilizar diz:

Como conhecemos a medida da distância h entre o marco 3 e a árvore de copa amarela, e o baú está à mesma medida da distância da trilha que contém apenas esse marco, podemos concluir que o baú está em uma reta paralela a essa trilha, passando pela árvore de copa amarela.
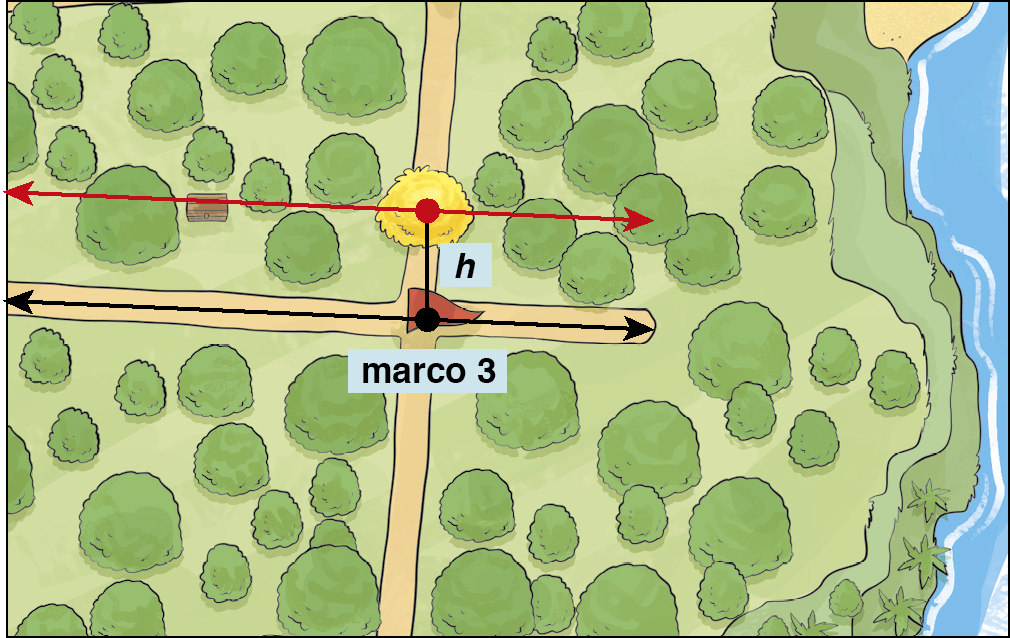
Reta paralela é o lugar geométrico dos pontos do plano que equidistam de uma reta dada.
Com essa pista, podemos garantir a localização exata do baú.
Observação
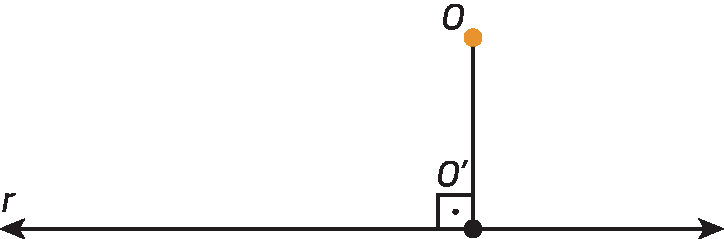
A medida da distância entre um ponto óh e uma reta r é dada pela medida de comprimento do segmento de reta perpendicular a r, com uma extremidade no ponto óh e a outra extremidade no ponto ó linha, na intersecção do segmento com a reta r.
Bissetriz
Verifique este último recorte da ilustração da ilha.
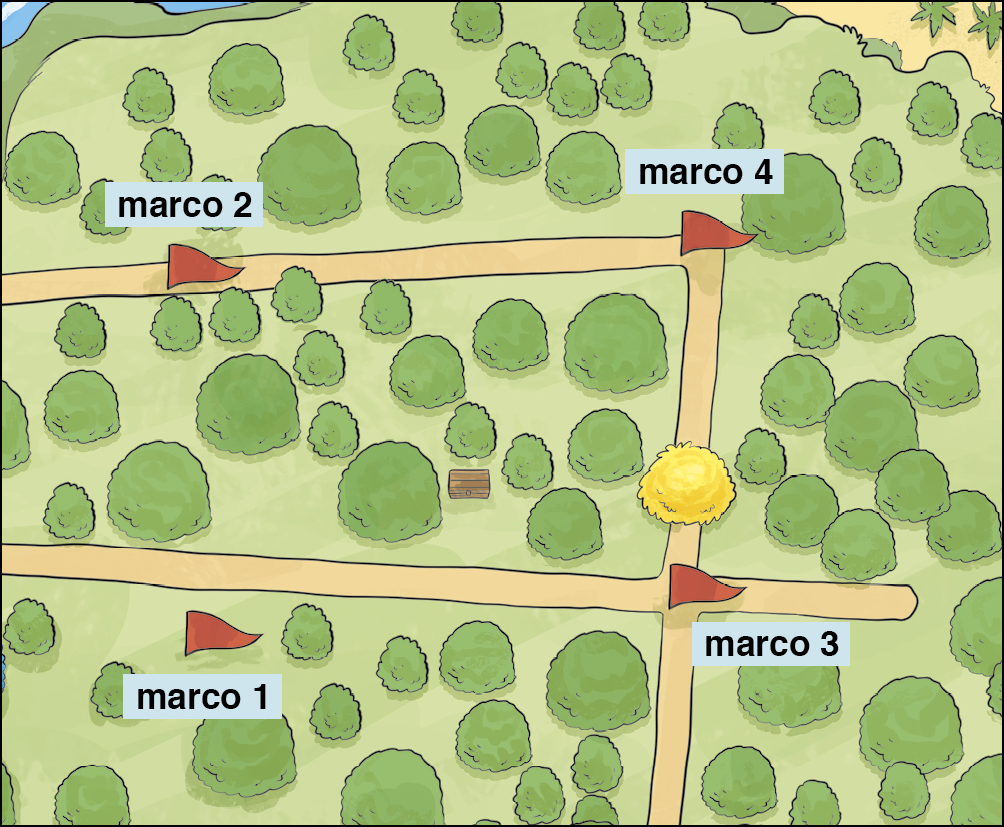
A última pista traz a seguinte informação:

Poderíamos ter utilizado essa pista antes de outras. Verifica-se que as semirretas (trilhas) que saem do marco 4 e passam pelos marcos 2 e 3 formam um ângulo e que um ponto qualquer da bissetriz desse ângulo tem a mesma medida de distância a cada lado do ângulo. Essa informação confirma a localização do baú.
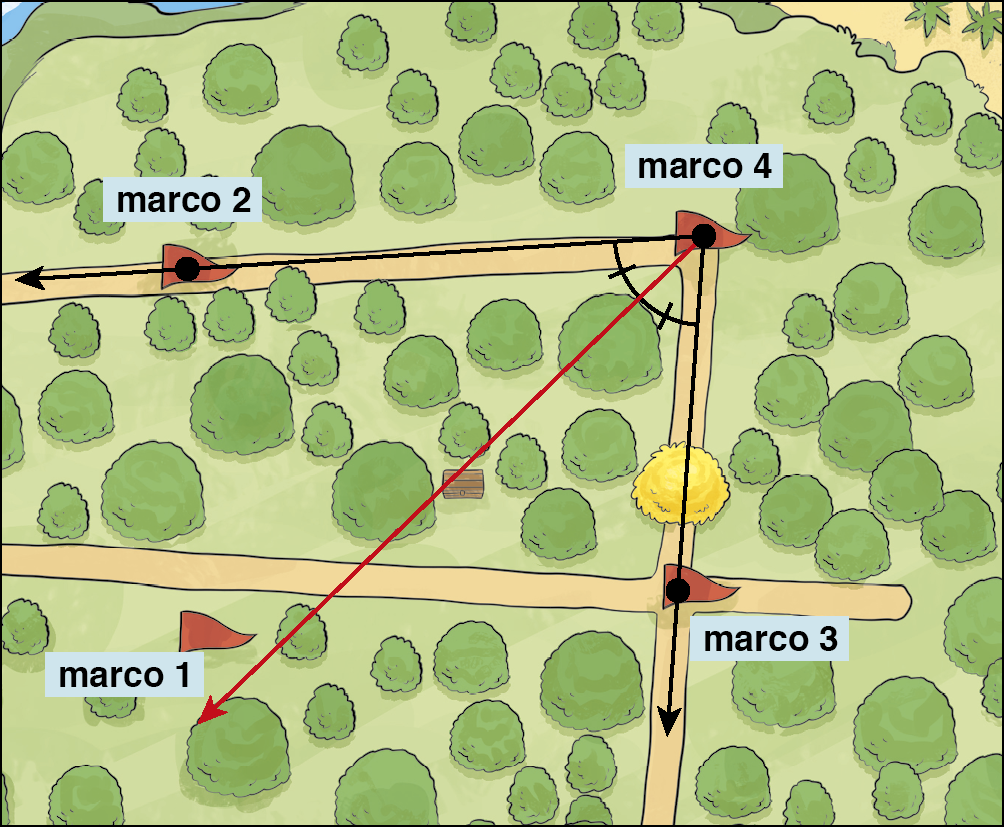
Bissetriz de um ângulo é o lugar geométrico dos pontos do plano que equidistam dos lados desse ângulo.
Note na ilustração a seguir a localização exata do baú.
Atividades
Faça as atividades no caderno.
17. O lugar geométrico dos pontos do plano que equidistam de dois pontos fixos é denominado:
a) semirreta.
b) ponto médio.
c) mediatriz.
d) bissetriz.
18. A afirmação a seguir é verdadeira? Justifique.
A medida da distância entre a rua das Américas e a dos Eucaliptos é a mesma em qualquer ponto, pois elas são paralelas.

19. Na figura a seguir, as mesas de madeira no centro são denominadas tribunas. Qual delas o palestrante deve ocupar para que esteja à mesma medida de distância de cada poltrona de uma mesma fileira da plateia?

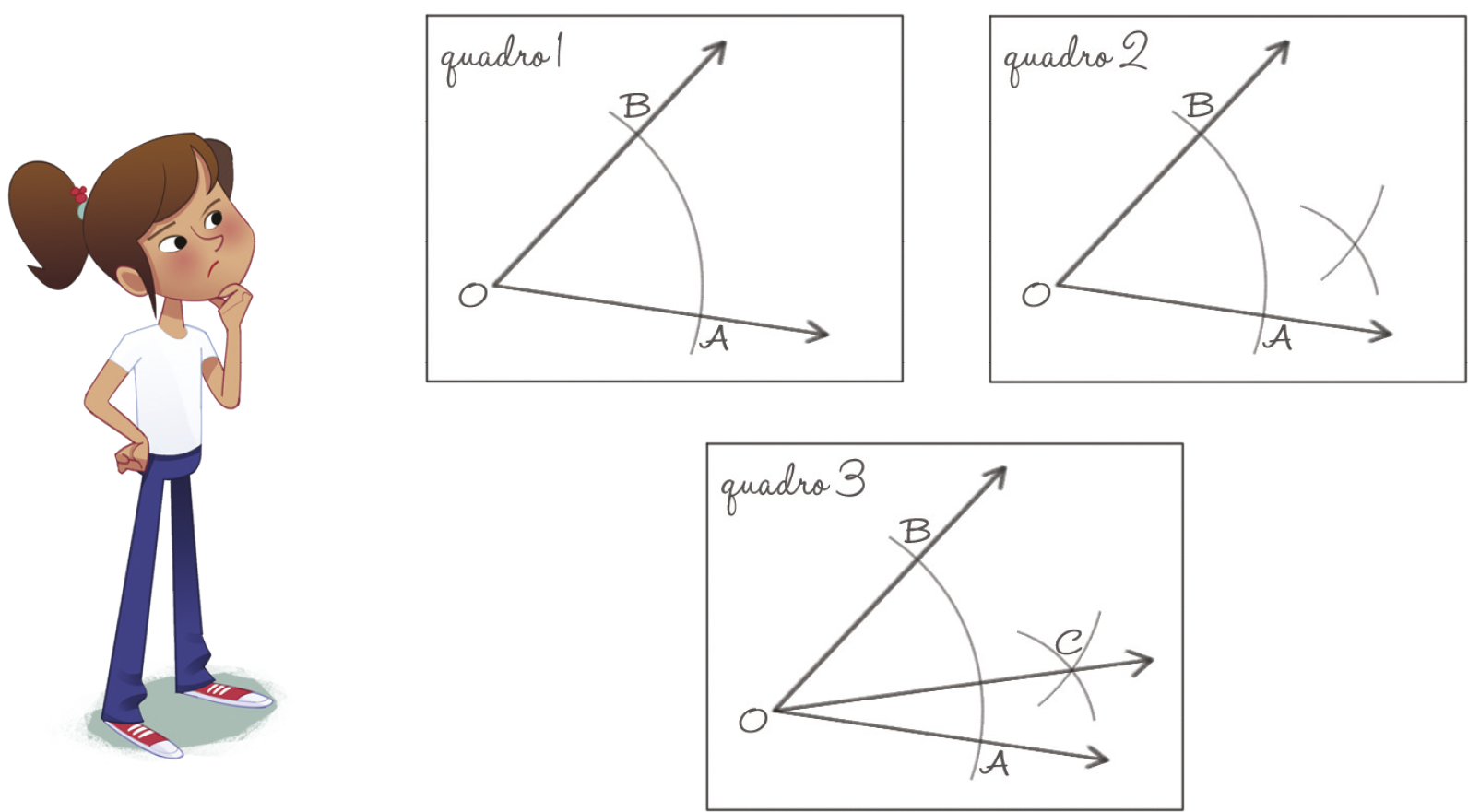
20. Mariana tentou construir a bissetriz do ângulo
Ângulo AOB.conforme os passos seguintes e percebeu, na última etapa, que a construção tinha um erro. Em qual quadro ocorreu o erro? Como Mariana deve corrigi-lo?

3 Transformações geométricas
Isometrias são transformações geométricas que preservam o formato e as medidas da figura inicial, como translação, rotação e reflexão, que podemos encontrar na ilustração a seguir.

A figura obtida a partir de uma transformação geométrica é chamada de imagem dessa transformação.
Translação
Translação é o deslocamento de uma figura dado por um vetor.
Um vetor (

) pode ser representado por um segmento orientado que indica a direção, o sentido e a medida da distância do deslocamento.
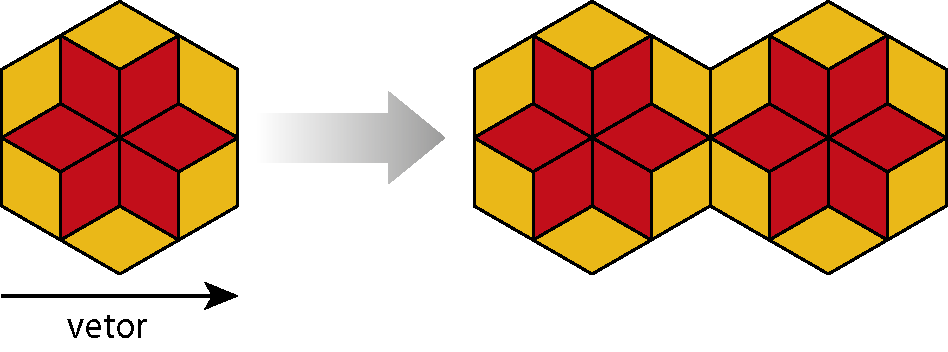
Confira a seguir algumas translações de polígonos na malha quadriculada.
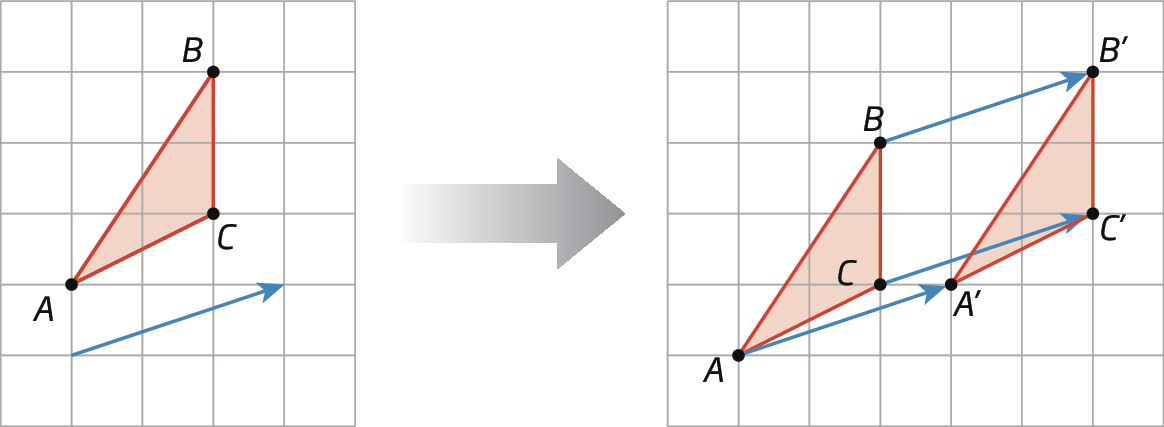
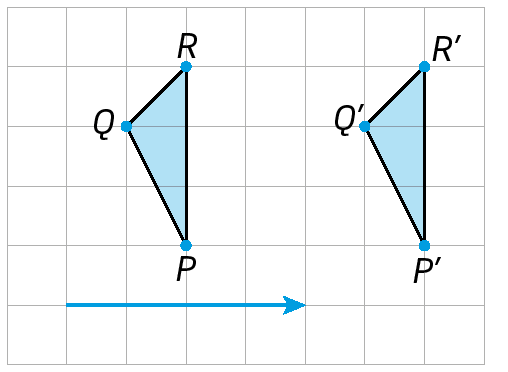
O vetor (em azul) indica a direção, o sentido e a medida da distância do deslocamento. Note que cada ponto do triângulo foi transladado de acordo com o vetor. Assim, o triângulo á linha bê linha cê linha é a translação do triângulo á bê cê.
Verifique mais um exemplo de translação.
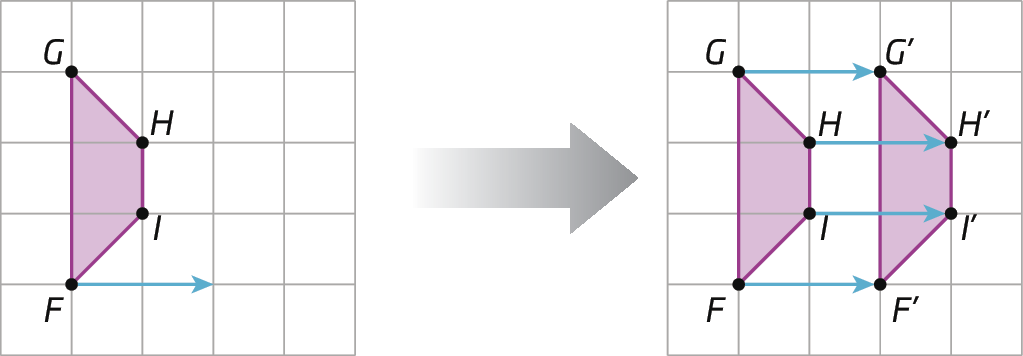
Atividades
Faça as atividades no caderno.
21. Em uma malha quadriculada, copie estas figuras e as translade de acordo com o vetor.
a)
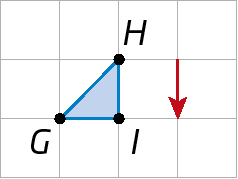
b)

Rotação
Rotação é o giro de uma figura em torno de um centro de rotação, em determinado sentido (horário ou anti-horário), segundo um ângulo de rotação.
A figura seguinte foi rotacionada a partir de um giro de 60graus no sentido horário. Sucessivas rotações de giro de 60graus nesse sentido produzem a figura em vermelho a seguir.

Na figura, o centro de rotação é um vértice do polígono, mas podemos escolher o centro de rotação em qualquer posição, inclusive externo ou interno à figura a ser rotacionada.
Cuidado! Evite acidentes ao usar o compasso.
Construção de uma rotação com transferidor e compasso
Podemos rotacionar uma figura utilizando um transferidor e um compasso.
Acompanhe os passos a seguir para obter a rotação de uma figura, dados o centro, a medida de abertura do ângulo e o sentido da rotação.
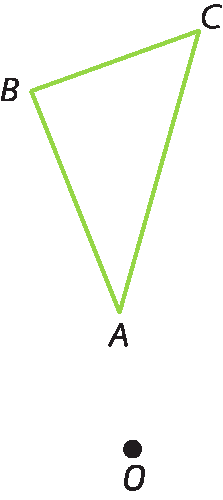
• centro de rotação: óh
• medida da abertura do ângulo de rotação: 40graus
• sentido da rotação: anti-horário
1º) Centramos o compasso no ponto óh e traçamos um arco passando pelo ponto a, outro passando por B e um terceiro passando por C.
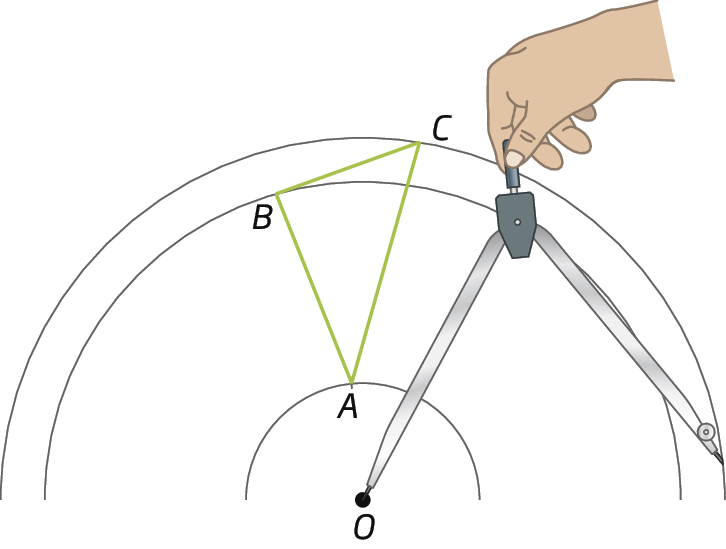
2º) Colocamos o centro do transferidor em óh e, alinhando o transferidor com
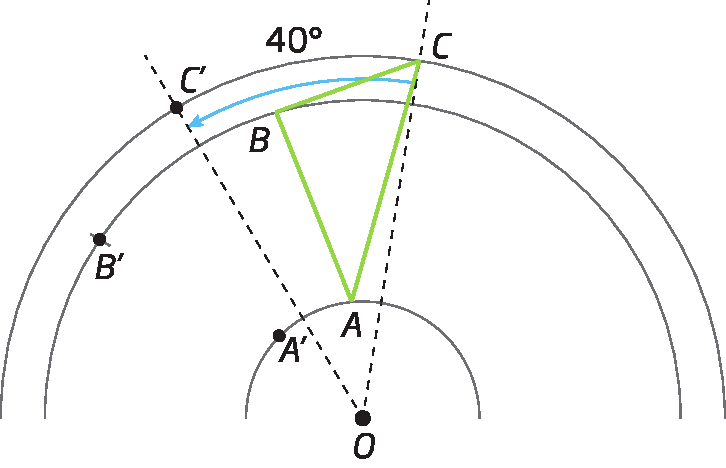
Segmento de reta AO., marcamos 40graus; onde a medida de abertura do ângulo cruzar com o arco que passa pelo ponto a, marcamos o ponto á linha. Fazemos o mesmo com os pontos B e C, marcando os pontos bê linha e cê linha , atentando para o sentido do giro.
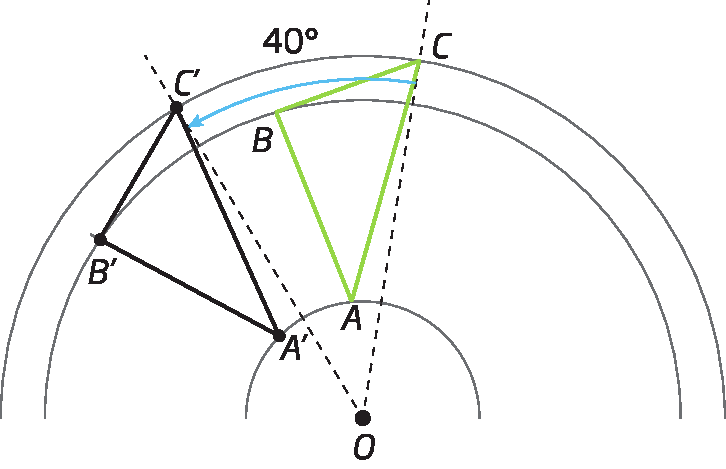
3º) Unimos os pontos á linha, bê linha e C ', obtendo a rotação do triângulo á bê cê de um ângulo de medida da abertura de 40graus no sentido anti-horário em torno do ponto óh.
Atividades
Faça as atividades no caderno.
22. Em uma malha quadriculada, copie as figuras a seguir e obtenha as rotações de centro óh :
a) do ponto a, com um giro de 90graus, no sentido horário;

b) do ponto D, com um giro de 45graus, no sentido horário;

c) do segmento de reta
Segmento de reta AB., com um giro de 60graus, no sentido horário.
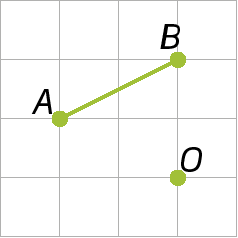
23. Copie as figuras seguintes em uma malha quadriculada e obtenha as rotações:
a) de centro P, no sentido horário, com uma rotação de um giro de 90graus;
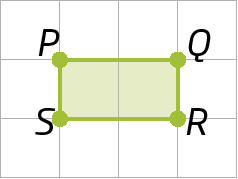
b) de centro óh, no sentido anti-horário, com uma rotação de um giro de 180graus;
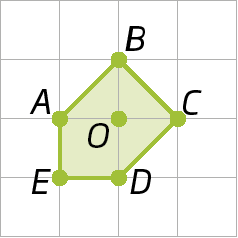
c) de centro P, no sentido anti-horário, com uma rotação de um giro de 45graus.

Reflexão
Reflexão é a transformação geométrica que reflete todos os pontos de uma figura em relação a uma reta (simetria axial) ou a um ponto (simetria central), mantendo cada ponto da figura à mesma medida da distância do eixo de simetria ou do centro de reflexão, respectivamente.
Simetria axial
Reconhecemos a simetria axialglossário pela presença de um eixo de simetria. Uma figura pode ter mais de um eixo de simetria.
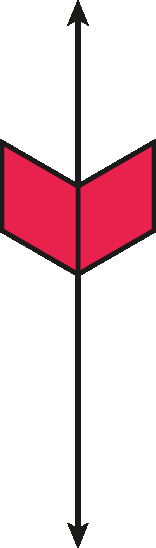
um eixo de simetria

dois eixos de simetria
vários eixos de simetria
Vamos representar o eixo de simetria pela reta r. Podemos determinar, em relação a esse eixo, a figura simétrica de um ponto, de um segmento de reta, de uma reta ou de uma figura plana qualquer.
Simetria de um ponto
Dois pontos distintos a e á linha são simétricos em relação a uma reta r se esta divide o segmento de reta
Segmento de reta A, A linhaperpendicularmente no seu ponto médio.
A‘ é simétrico de a em relação à reta r.
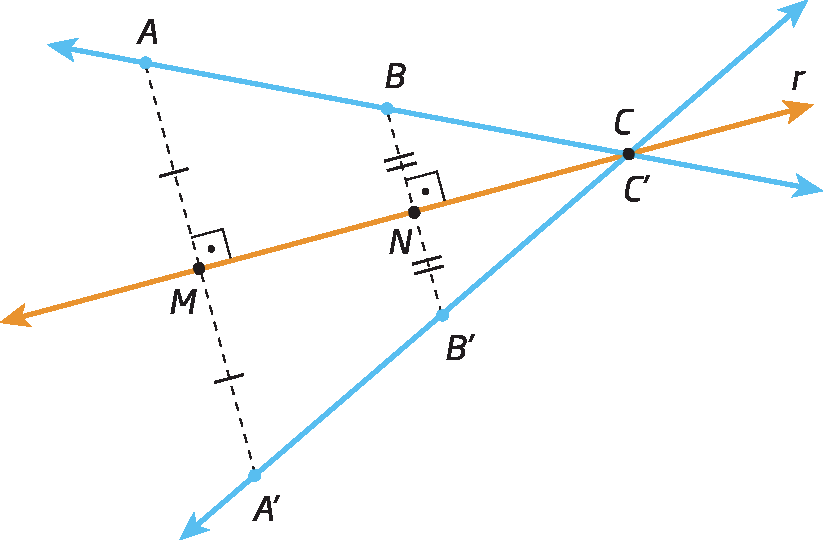
Simetria de um segmento de reta
Na figura a seguir, os pontos á linha e bê linha são, respectivamente, simétricos de a ê B em relação à reta r. Dizemos, então, que os segmentos
Segmento de reta AB.e
Segmento de reta A linha, B linha.são simétricos em relação à reta r.

é simétrico de
Segmento de reta AB.em relação à reta r.
Simetria de uma reta
Os pontos a, B e C estão alinhados, assim como seus simétricos á linha, bê linha e cê linha . As retas
Reta ABe
Segmento de reta A linha, B linha.são simétricas em relação à reta r.
é simétrica de
Reta ABem relação à reta r.
Simetria de um círculo
Os centros óh e ó linha são simétricos em relação à reta r, e os círculos têm raios com a mesma medida de comprimento.

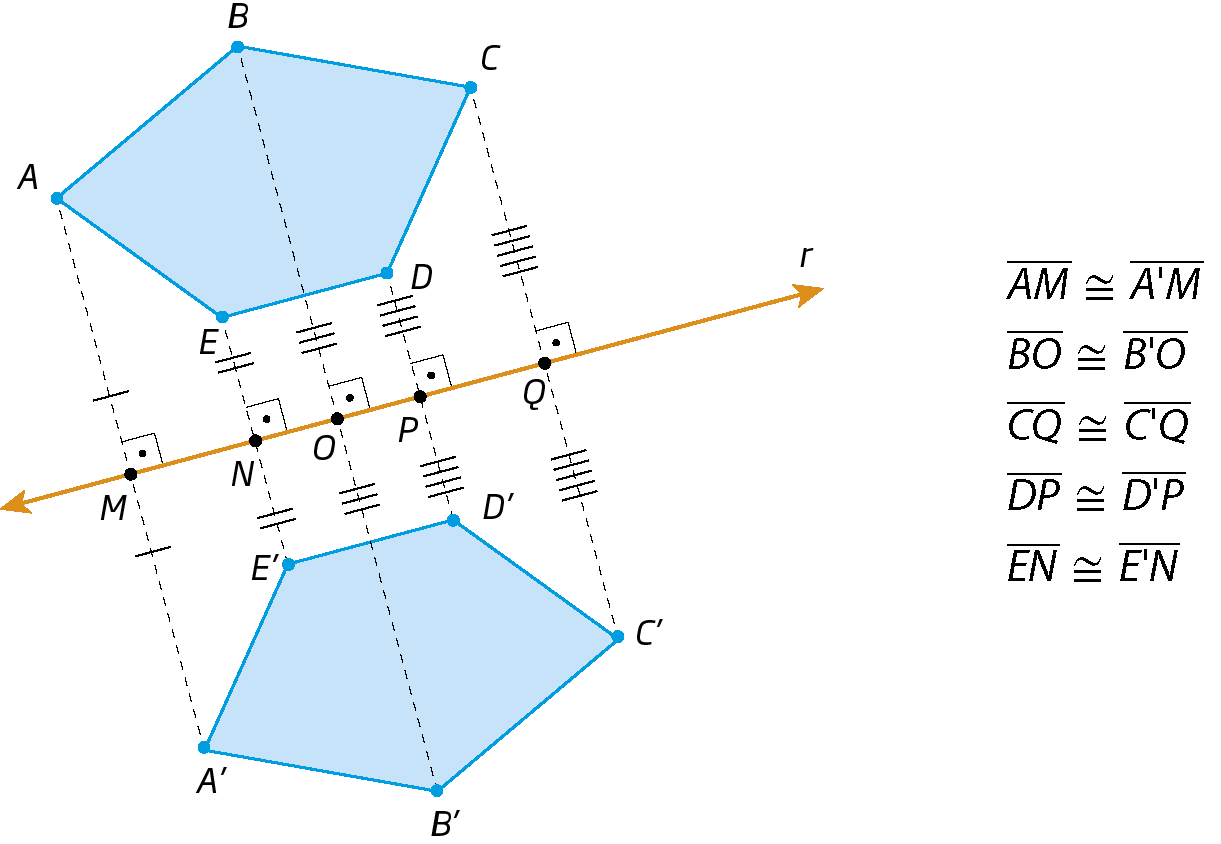
Simetria de um polígono
Na figura, note que os pontos á linha, bê linha, cê linha, dê linha e E ' são, respectivamente, simétricos de a, B, C, D e ê em relação à reta r. Dizemos que os polígonos á bê cê dê é e á linha bê linha cê linha dê linha é linha são simétricos em relação à reta r.
Simetria central
A simetria central é determinada em relação a um ponto denominado centro de simetria.
Essa transformação é equivalente a uma rotação de um giro de 180graus em qualquer sentido (horário ou anti-horário).
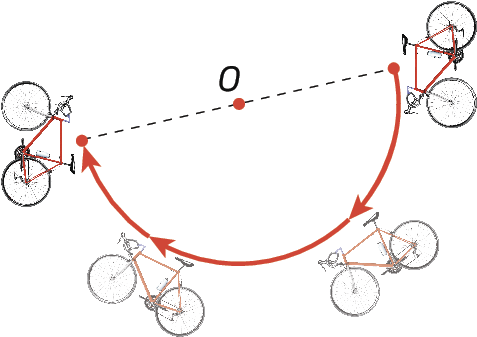
Simetria de um ponto
O simétrico de um ponto M em relação a um ponto óh é o ponto M' tal que óh é o ponto médio do segmento
Segmento de reta M, M linha..

M' é simétrico de M em relação ao ponto óh.
Simetria de um segmento de reta
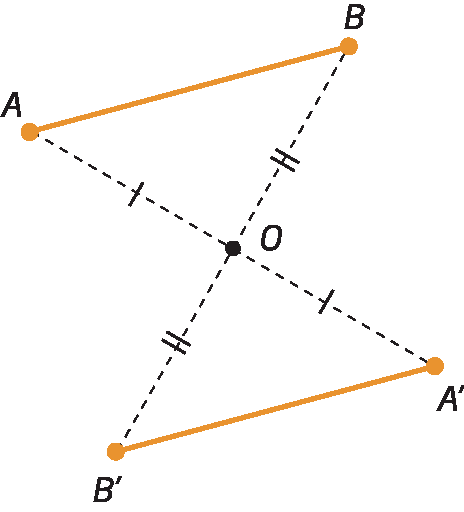
é simétrico de
Segmento de reta AB.em relação ao ponto óh.
Simetria de uma reta
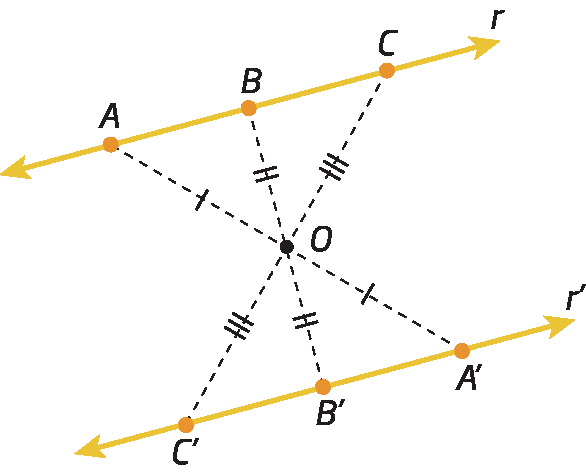
érre linha é simétrica de r em relação ao ponto óh.
Simetria de um círculo

C e cê linha são simétricos em relação ao ponto óh, e os círculos têm raios com a mesma medida de comprimento, ou seja, os círculos são simétricos em relação ao ponto óh.
Simetria de um polígono

O polígono á'bit'centésimo'divisores de 'E' é simétrico ao polígono á bê cê dê é em relação ao ponto óh.

Lendo e aprendendo

Máscaras
As máscaras africanas tradicionais são um dos elementos da grande arte africana que mais evidentemente influenciou a Europa e a arte ocidental em geral no século vinte.
São representações ou manifestações de forças normalmente invisíveis, usadas em ritos agrários, funerários ou de iniciaçãoglossário , rememorando mitos e outras tradições, através de suas fórmas, movimentos, cores e materiais. Às vezes, as máscaras têm pouca semelhança com a aparência humana, para deixar claro que um indivíduo ao usá-las, introjeta um personagem do mundo sobrenatural, tornando visível a presença desse personagem no mundo natural e humano. Habitualmente, são consideradas máscaras apenas objetos faciais e os adornos de cabeça esculpidos, sem levar em conta o traje que os acompanha. Do ponto de vista africano, porém, a máscara é todo um conjunto: a máscara é o próprio mascarado quando se põe em movimento.
Museu Afro Brasileiro (MAFRO). Disponível em: https://oeds.link/mDJmis. Acesso em: 4 julho 2022.


Atividades
1. Responda às questões no caderno.
a) Em que ocasiões as máscaras africanas são utilizadas?
b) As máscaras africanas sempre têm aparência humana? Por quê?
c) O que é a máscara para os africanos?
2. Estas imagens foram criadas tomando como inspiração algumas máscaras africanas.

a) Que tipo de simetria está presente nestas imagens? Justifique.
b) Em uma folha de papel sulfite, desenhe uma máscara inspirada em uma máscara africana, aplicando o que você aprendeu sobre as transformações geométricas no plano.
3.

Reúna-se com os colegas e façam uma pesquisa sobre a influência da cultura africana na formação do povo brasileiro.
Atividades
Faça as atividades no caderno.
Cuidado! Evite acidentes ao usar o compasso na atividade 25.
24. Em uma malha quadriculada, copie a figura seguinte. Depois, obtenha os pontos á linha, bê linha e cê linha simétricos aos pontos a, B e C em relação à reta r.
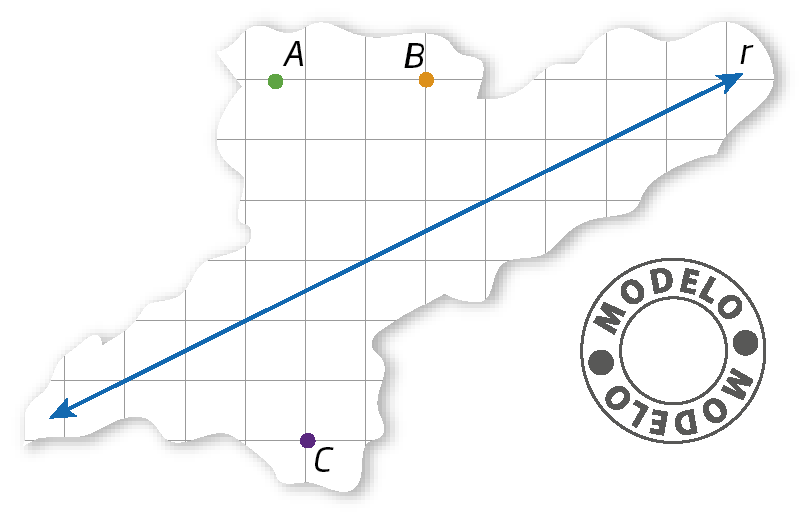
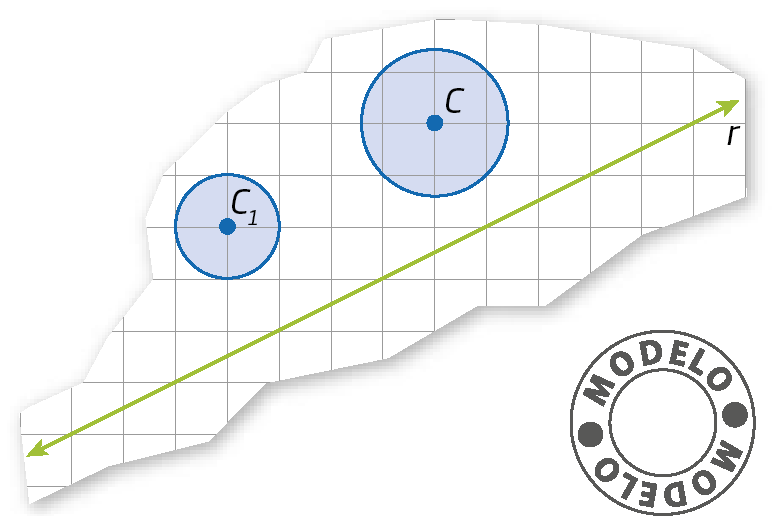
25. Em uma malha quadriculada, utilize o compasso para copiar os círculos seguintes. Depois, construa o simétrico de cada círculo em relação à reta r.
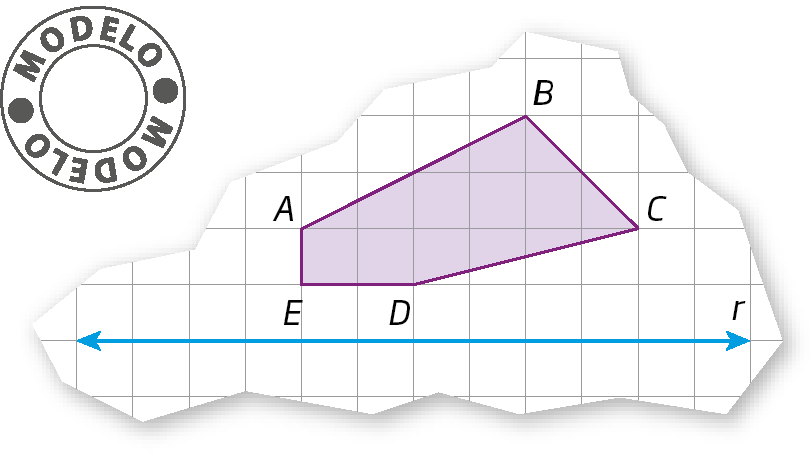
26. Em uma malha quadriculada, copie o polígono seguinte. Depois, construa o simétrico desse polígono em relação à reta r.
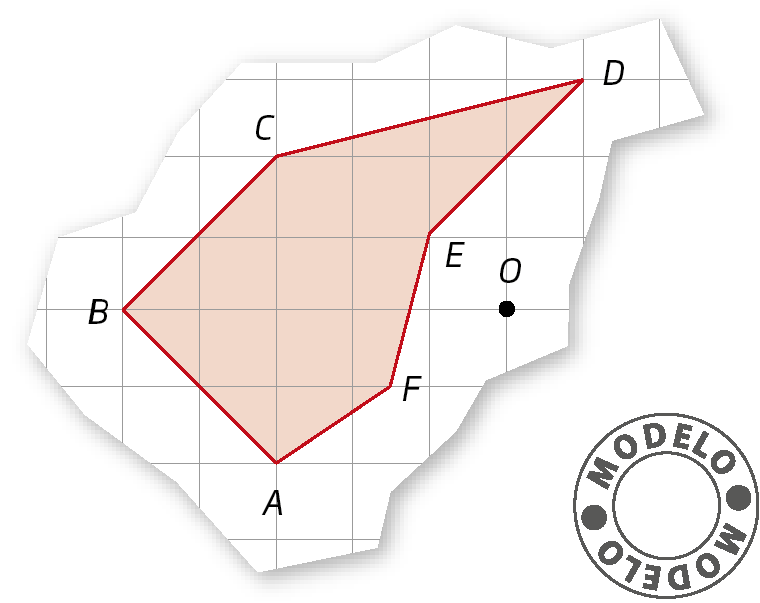
27. Em uma malha quadriculada, copie a figura seguinte. Depois, construa o polígono á linha bê linha cê linha dê linha é linha éfe linha simétrico do polígono á bê cê dê é éfe em relação ao ponto óh.
Composição de transformações
Podemos compor transformações realizando as mesmas transformações geométricas sucessivas vezes, ou combinar transformações diferentes.
Composição de translações
Esta figura mostra translações sucessivas. Transladamos o triângulo pê quê érre utilizando o vetor verde e sua imagem (triângulo P'Q'R'), utilizando o vetor vermelho.
A primeira translação leva o triângulo pê quê érre ao triângulo P'Q'R' e está representada pelo vetor verde. A segunda translação leva o triângulo P'Q'R' ao triângulo P"Q"R" e está representada pelo vetor vermelho.
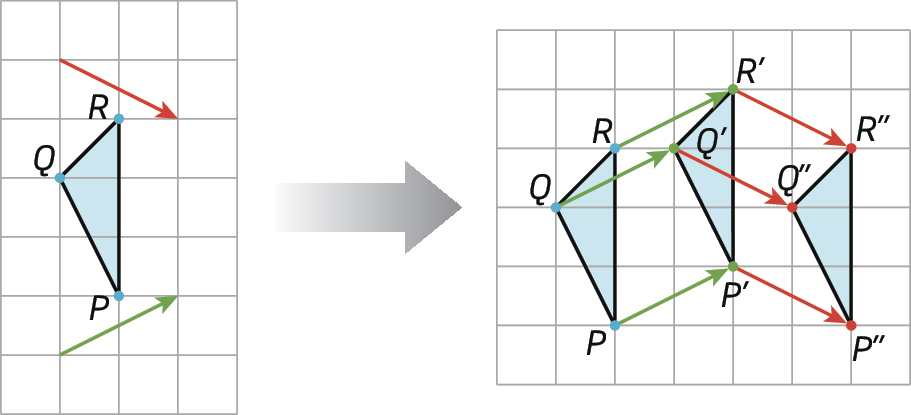
Ao transladar o mesmo triângulo por outro vetor, como mostra o exemplo a seguir, podemos obter, diretamente, o resultado final da translação sucessiva feita anteriormente.

Tecnologias digitais em foco
Composição de translações
Nesta seção, vamos verificar experimentalmente, por meio do GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, uma propriedade da composição de translações.
Construa
Siga os passos seguintes para transladar sucessivamente um polígono qualquer.
1º) Utilize a ferramenta
e construa um polígono qualquer. Pode ser, por exemplo, um triângulo á bê cê.
2º) Use a ferramenta
e construa dois vetores quaisquer.
3º) Clique na ferramenta

. Depois, clique sobre o triângulo á bê cê e sobre o vetor vermelho. O polígono que aparecerá na tela (triângulo á linha bê linha cê linha ) é a imagem da translação pelo vetor vermelho.
4º) Clique na ferramenta

. Depois, clique sobre o triângulo á linha bê linha cê linha e sobre o vetor azul. O polígono que aparecerá na tela (triângulo á duas linhas bê duas linhas cê duas linhas ) é a imagem da translação pelo vetor azul.
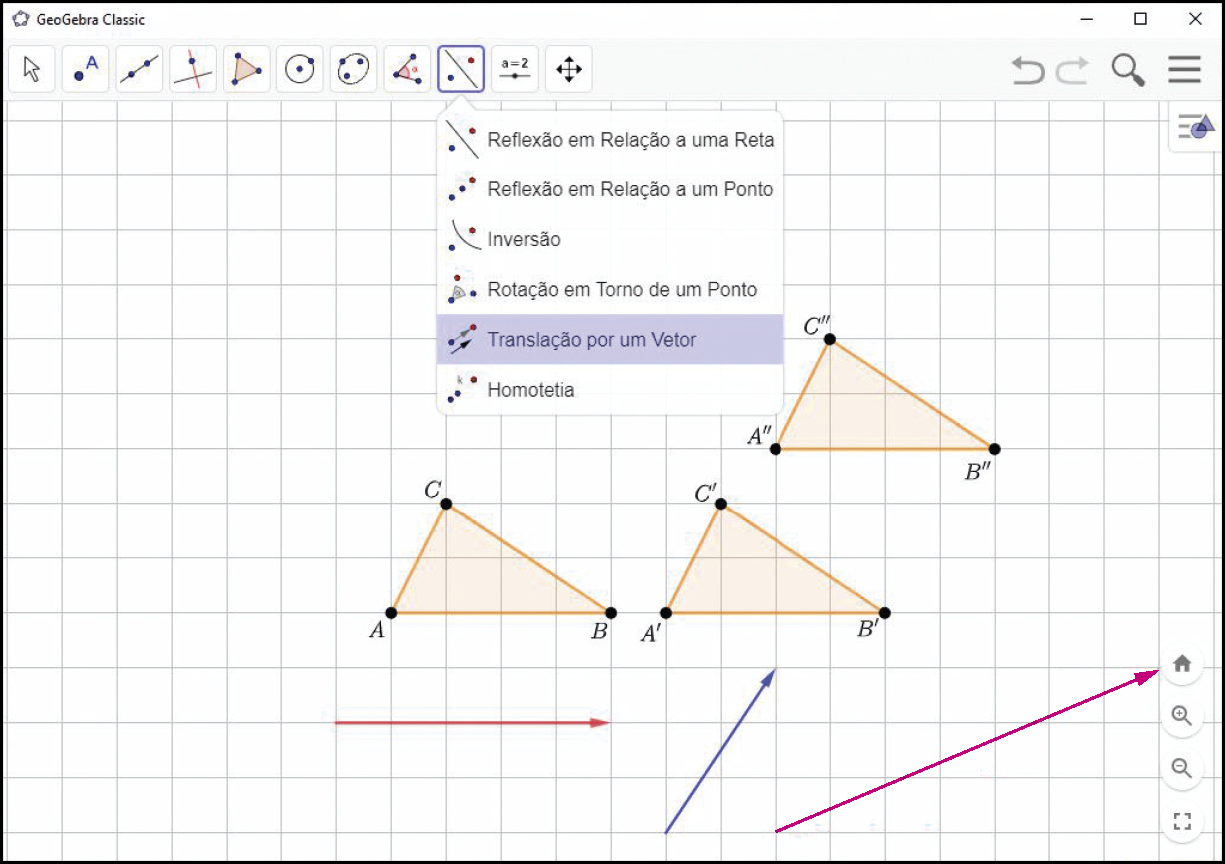
Explore
É possível obter o triângulo á duas linhas bê duas linhas cê duas linhas por meio de uma única translação do triângulo á bê cê. Descubra o vetor dessa translação e represente-o no GeoGebra.
Composição de reflexões
Na figura a seguir, foram feitas duas reflexões em sequência do quadrilátero a bê cê dê: uma em relação à reta r e outra em relação à reta s.
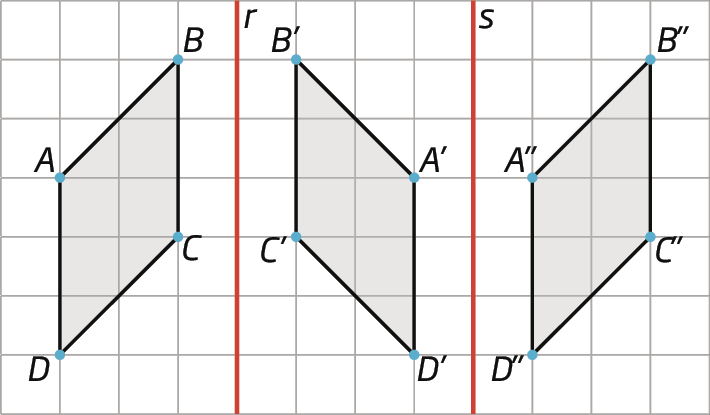
Note que o quadrilátero á linha bê linha cê linha dê linha foi obtido do quadrilátero a bê cê dê a partir da reflexão em relação à reta r. Já o quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas foi obtido do quadrilátero á linha bê linha cê linha dê linha por meio da reflexão em relação à reta s.
A reflexão da figura á linha bê linha cê linha dê linha equivale uma translação da figura a bê cê dê.

Tecnologias digitais em foco
Composição de reflexões em relação a retas
Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para explorar propriedades da composição de reflexões em relação a retas.
Construa
Siga os passos seguintes para refletir um polígono qualquer.
1º) Utilize a ferramenta
e construa um polígono qualquer. Pode ser, por exemplo, um quadrilátero a bê cê dê.
2º) Use a ferramenta
e construa uma reta r.
3º) Use a ferramenta

e construa uma reta s paralela à reta r.
4º) Clique na ferramenta
. Depois, clique sobre o polígono e sobre a reta r. O polígono que aparecerá na tela (quadrilátero á linha bê linha cê linha dê linha ) é a imagem da reflexão pela reta r.
5º) Clique na ferramenta

. Depois, clique sobre o quadrilátero á linha bê linha cê linha dê linha e sobre a reta s. O polígono que aparecerá na tela (quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas ) é a imagem da reflexão pela reta s.
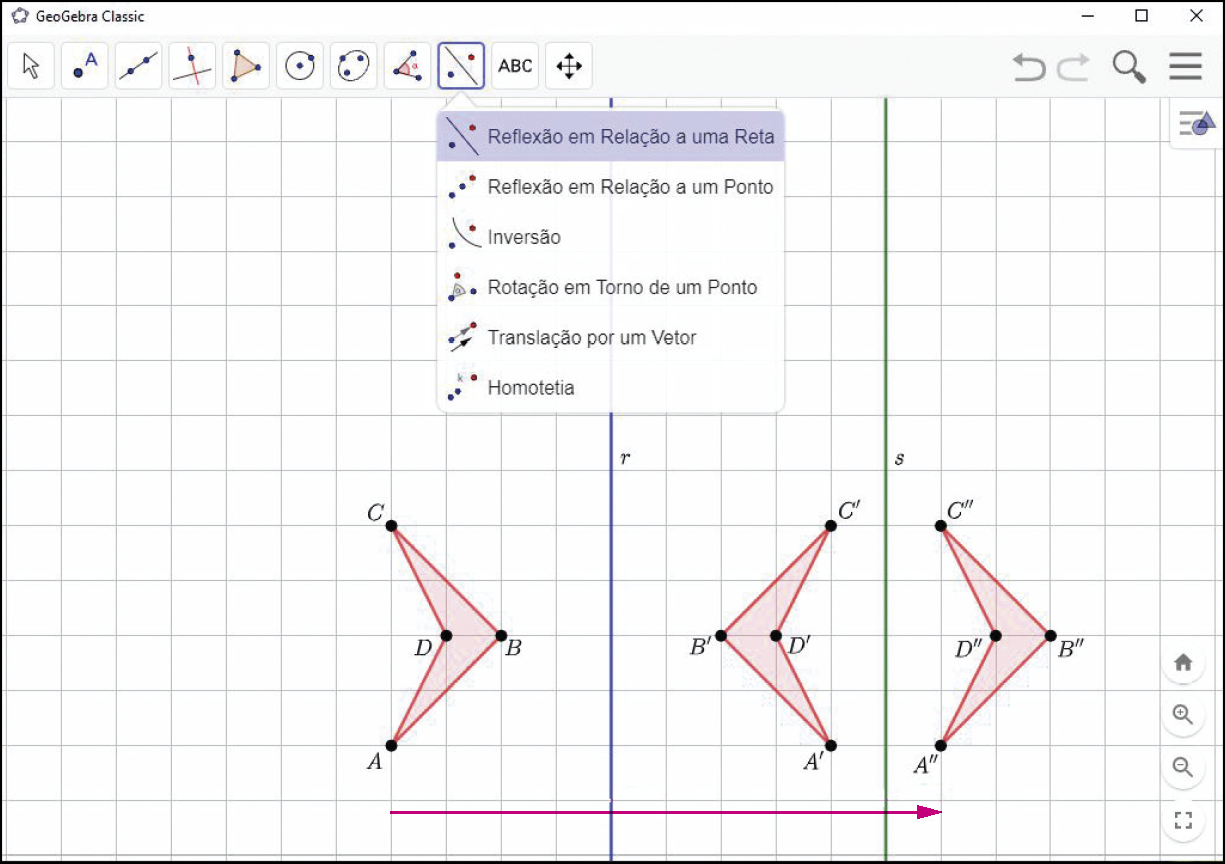
Tecnologias digitais em foco
Explore
a) É possível obter o quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas por meio de uma translação do quadrilátero a bê cê dê. Represente o vetor dessa translação no GeoGebra.
b) Faça o que se pede.
1º) Utilize a ferramenta
e trace uma reta que seja perpendicular às retas r e s e que intercepte r no ponto P e s no ponto Q.
2º) Utilize a ferramenta

e meça a distância entre as retas r e s.
3º) Utilize a ferramenta

e meça a distância entre os pontos a e A". Ao que corresponde essa medida? Movimente o quadrilátero a bê cê dê e verifique o que ocorre.
c) O que podemos afirmar em relação à medida de comprimento do vetor da translação que leva a bê cê dê a á duas linhas bê duas linhas cê duas linhas dê duas linhas?
d) E se as retas r e s não fossem paralelas? Seria possível obter o quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas por meio de uma única transformação geométrica do quadrilátero a bê cê dê? Investigue e escreva sua conclusão no caderno. Dica: Meça a abertura do ângulo formado pelas retas r e s.
Composição de rotações
Podemos rotacionar figuras sucessivamente em torno de um mesmo ponto ou em torno de pontos diferentes. Analise os exemplos a seguir.
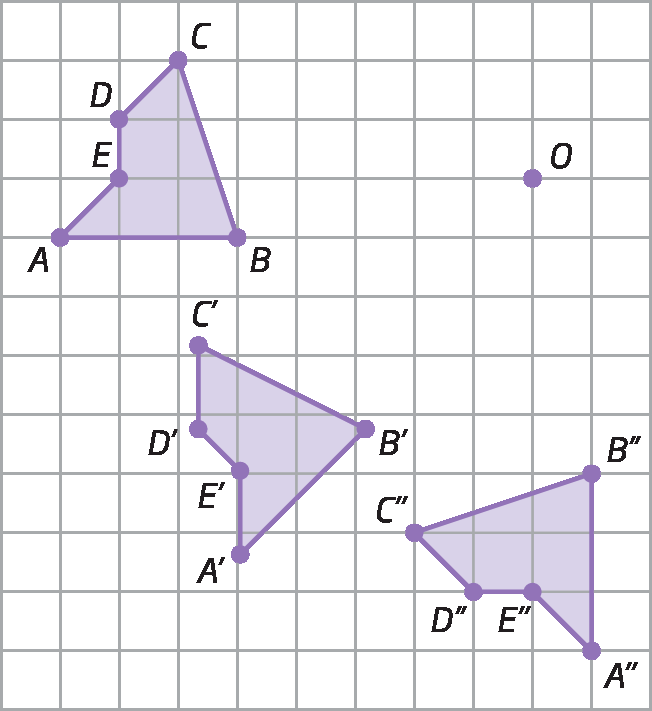


Tecnologias digitais em foco
Composição de rotações em torno de um mesmo ponto
Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para explorar propriedades da composição de rotações em torno de um mesmo ponto.
Construa
Siga os passos seguintes para realizar rotações sucessivas de um polígono qualquer em torno de um mesmo ponto.
1º) Construa um polígono qualquer, utilizando a ferramenta

. Pode ser, por exemplo, um pentágono á bê cê dê é.
2º) Marque um ponto óh qualquer utilizando a ferramenta

. Esse ponto será o centro da rotação.
3º) Clique na ferramenta

. Depois, clique sobre o polígono e sobre o ponto óh. Por fim, escolha a medida da abertura do ângulo e o sentido da rotação. O polígono que aparecerá na tela (pentágono á linha bê linha cê linha dê linha é linha ) é a imagem da rotação.
4º) Clique na ferramenta

. Depois, clique sobre o pentágono á linha bê linha cê linha dê linha é linha e sobre o ponto óh. Por fim, escolha a medida da abertura do ângulo. O sentido da rotação deve ser o mesmo do 3º passo. O polígono que aparecerá na tela (pentágono á duas linhas bê duas linhas cê duas linhas dê duas linhas é duas linhas ) é a imagem da rotação.
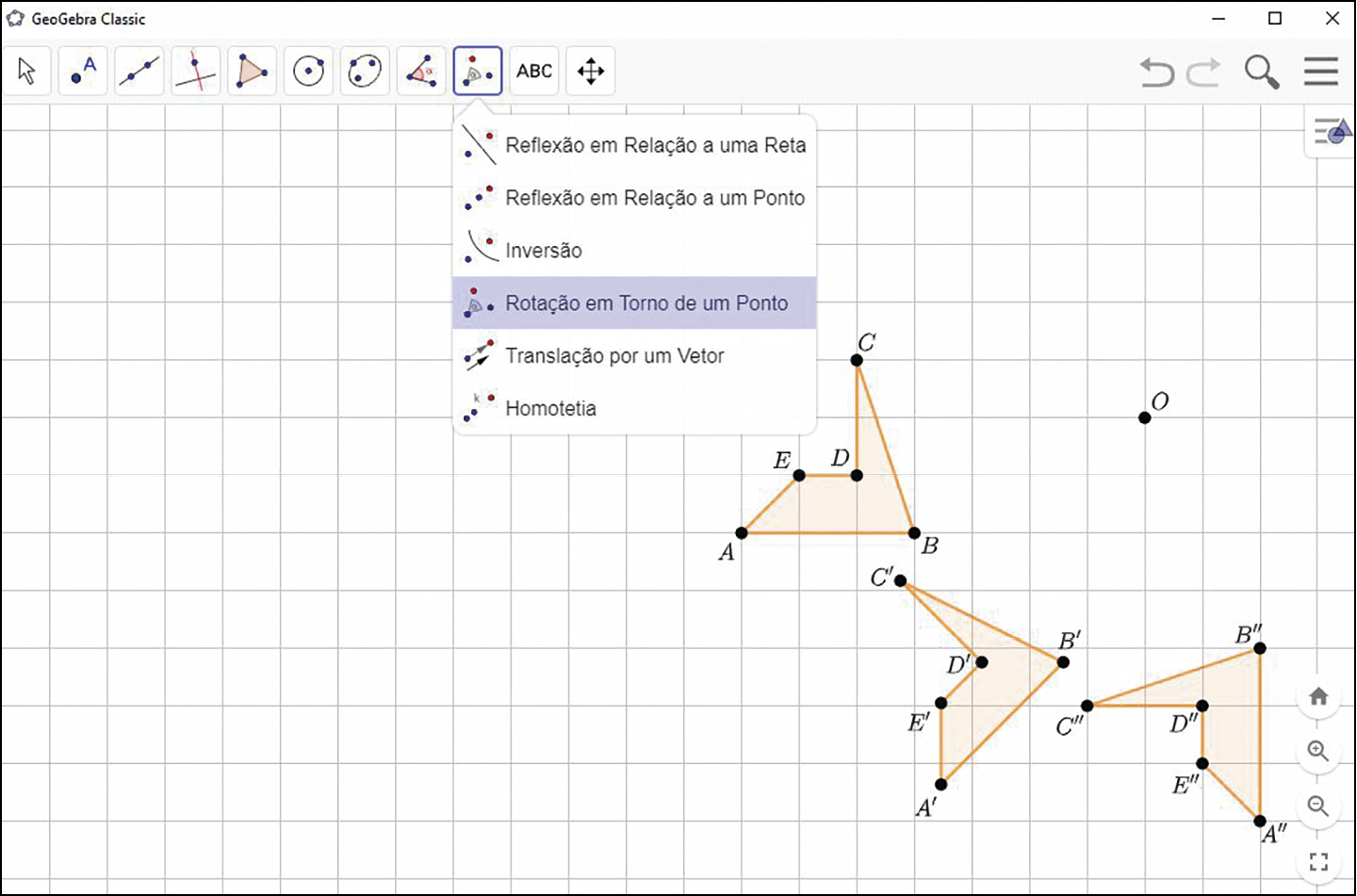
Explore
a) É possível obter o pentágono á duas linhas bê duas linhas cê duas linhas dê duas linhas é duas linhas por meio de uma única transformação geométrica do pentágono á bê cê dê é? Se sim, descreva essa transformação.
b) O que a investigação feita por você, no item anterior, sugere?
Atividades
Faça as atividades no caderno.
28. Em uma malha quadriculada, copie a figura seguinte e a translade utilizando primeiro o vetor azul e, depois, o vetor verde.
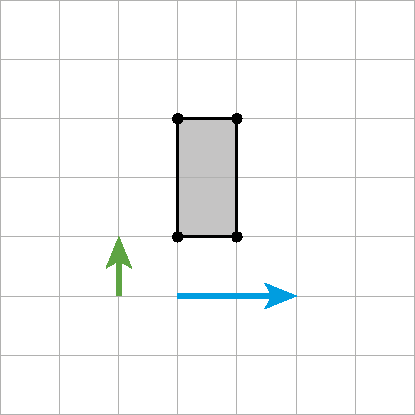
29. Em uma malha quadriculada, copie novamente a figura da atividade 28 e a translade primeiro utilizando o vetor verde e, depois, o vetor azul.
30. Copie a figura a seguir em uma malha quadriculada e faça 3 rotações sucessivas em torno do ponto C, no sentido horário, com um giro de 90graus.

31.

Analise a figura a seguir.

a) No caderno, elabore duas questões que possam ser respondidas observando as transformações geométricas.
b) Troque de caderno com um colega e responda às questões criadas por ele.
c) Analise as respostas do colega e dê um retorno a ele, dizendo o que ele respondeu corretamente e onde ele se equivocou.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Ângulo
Ângulo é a união de duas semirretas de mesma origem, com uma das regiões do plano limitada por elas.
Classificação de ângulos
De acordo com a medida da abertura, um ângulo pode ser classificado em:
Ângulo nulo

Ângulo de uma volta
Ângulo reto
Ângulo raso ou de meia-volta

Ângulo agudo
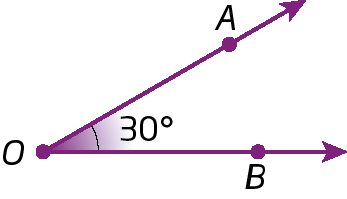
Ângulo obtuso

1. Analise os ângulos seguintes e indique:

a) os ângulos agudos;
b) os ângulos obtusos;
c) o ângulo raso;
d) os ângulos retos.
Ângulos congruentes
Dois ângulos são congruentes quando têm a mesma medida de abertura.
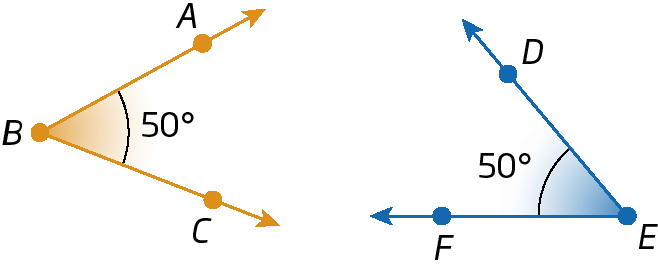
Os ângulos
Ângulo ABC.e
Ângulo DEF.são congruentes. Indicamos:
À esquerda o ângulo ABC, à direita símbolo similar ao sinal de igual com símbolo similar ao til acima e à direita o ângulo DEF.Bissetriz de um ângulo
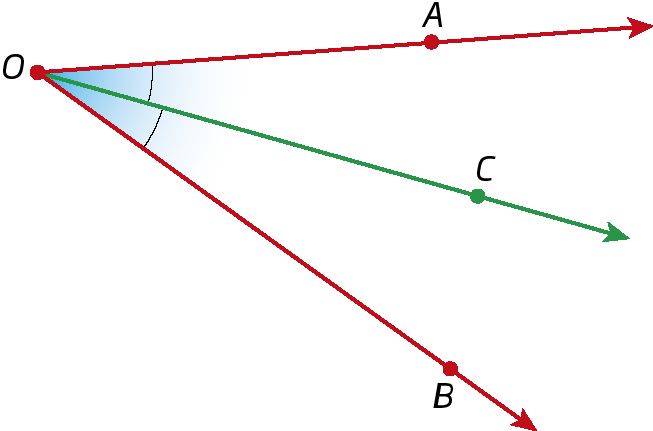
Bissetriz de um ângulo é a semirreta interna a esse ângulo com origem no vértice do ângulo que o divide em dois ângulos congruentes.
Mediatriz de um segmento
Mediatriz é a reta perpendicular a um segmento de reta que passa pelo ponto médio desse segmento.

2. Nesta figura, a semirreta
Semirreta OC.é a bissetriz de
Ângulo AOB.e
Medida de ângulo AOC igual à 10 graus. Determine a medida da abertura do ângulo
Ângulo AOB..
3. Em uma reta, tomamos os pontos a, B e C, nessa ordem, com A bê = 8 centímetros e BC = 10 centímetros. Sendo P o ponto médio de
Segmento de reta AC., quanto mede o comprimento de
Segmento de reta BP.?
Lugares geométricos
Lugar geométrico é a figura formada por todos os pontos do plano que têm em comum uma determinada propriedade.
Circunferência
Circunferência é o lugar geométrico dos pontos do plano que equidistam de um ponto fixo.
Mediatriz
Mediatriz é o lugar geométrico dos pontos do plano que são equidistantes de dois pontos fixos dados (extremidades de um segmento de reta).
Retas paralelas
Reta paralela é o lugar geométrico dos pontos do plano que equidistam de uma reta dada.
Bissetriz
Bissetriz de um ângulo é o lugar geométrico dos pontos do plano que equidistam dos lados desse ângulo.
4. Para manter a horta, um jardineiro sugeriu a instalação de uma torneira de irrigação em um lugar que tenha a mesma medida da distância dos muros. Descreva, em seu caderno, os possíveis lugares em que a torneira pode ser instalada.

Transformações geométricas
Translação é o deslocamento de uma figura dado por um vetor.
Rotação é o giro de uma figura em torno de um centro de rotação, em determinado sentido (horário ou anti-horário), segundo um ângulo de rotação.
Reflexão é a transformação geométrica que reflete todos os pontos de uma figura em relação a uma reta (simetria axial) ou a um ponto (simetria central), mantendo cada ponto da figura à mesma medida da distância do eixo de simetria ou do centro de reflexão, respectivamente.
Composição de transformações
Podemos compor transformações realizando as mesmas transformações geométricas sucessivas vezes, ou combinar transformações diferentes.
5. As transformações realizadas a seguir podem ser, na ordem apresentada:
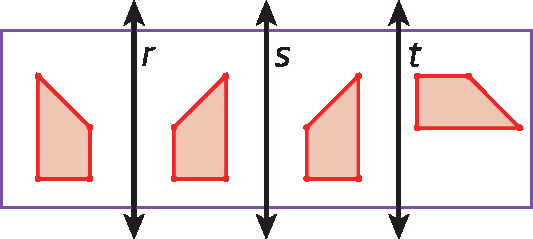
a) translação, reflexão e rotação.
b) reflexão, translação e rotação.
c) rotação, reflexão e translação.
d) reflexão, reflexão e translação.
Glossário
- equidistante
- :tem a mesma medida de distância entre dois ou mais objetos (pontos, por exemplo).
- Voltar para o texto
- axial
- : palavra derivada de axis, termo latino que significa “eixo”.
- Voltar para o texto
- rito de iniciação
- : cerimônia (realização de uma tarefa ou ritual particular), que ocorre em muitas sociedades, para introduzir um novo membro.
- Voltar para o texto