Página 110

Capítulo 5 Polígonos

Trocando ideias

origâmi é uma técnica japonesa de dobradura com a qual se constroem representações de determinados objetos ou seres sem cortar ou colar o papel.

Ilustração. Figuras feitas de origamis. Figura redonda vermelha e amarela com tiras, parecida com um catavento. Um sapo verde, um pássaro azul, um elefante marrom, figura redonda verde e azul com tiras, parecida com catavento, um avião vermelho e um barco azul. — Representações utilizando a técnica do origâmi.

▸

As partes de algumas das representações na foto anterior se parecem com polígonos. Que polígonos são esses?

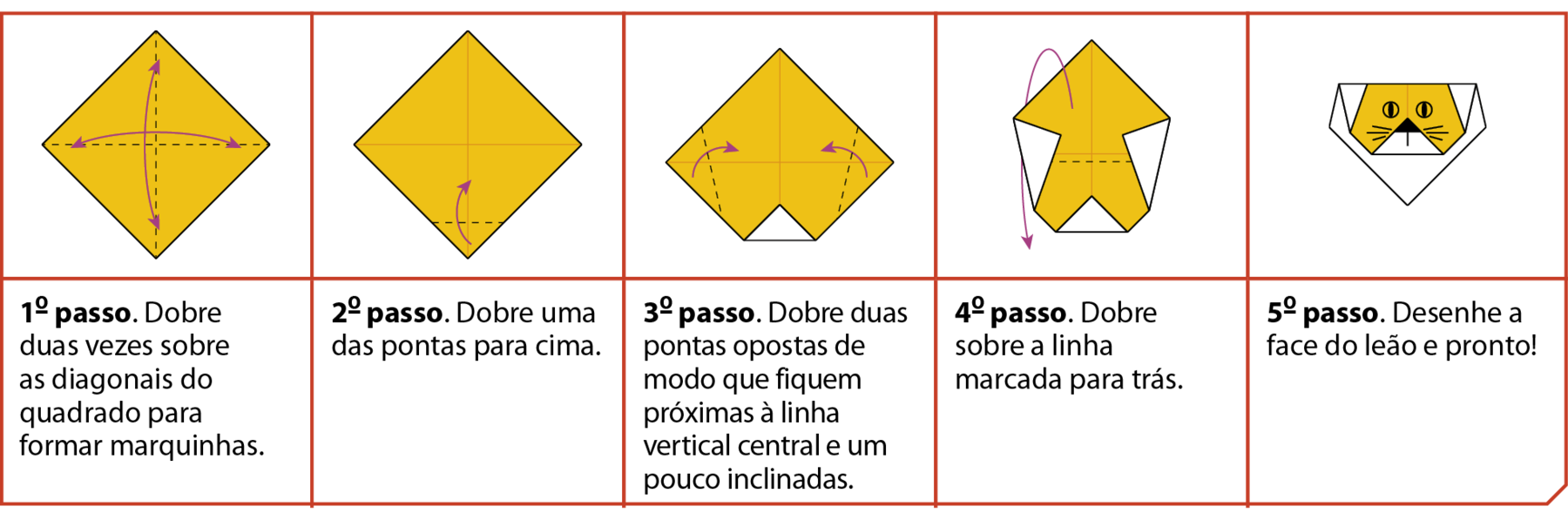
▸ Siga os passos seguintes e construa a representação da cabeça de um leão.

Quadro. Losango laranja com seta vertical e diagonal. 1º passo. Dobre duas vezes sobre as diagonais do quadrado para formar marquinhas. Losango com seta de baixo para cima na ponta inferior direita. 2º passo. Dobre uma das pontas para cima. Losango com a parte inferior dobrada e setas nas laterais de fora para dentro. 3º passo. Dobre duas pontas opostas de modo que fiquem próximas à linha vertical central e um
pouco inclinadas. Losango com a ponta inferior e laterais dobradas para dentro. Linha vertical e horizontal dentro. Seta de baixo para cima passando por trás da figura. 4º passo. Dobre sobre a linha marcada para trás. Rosto de um leão formado. 5º passo. Desenhe a face do leão e pronto

Neste capítulo, vamos ampliar o estudo dos polígonos, dando atenção às diagonais, aos ângulos internos e ângulos externos e aos polígonos regulares.

Página 111

1 Polígonos

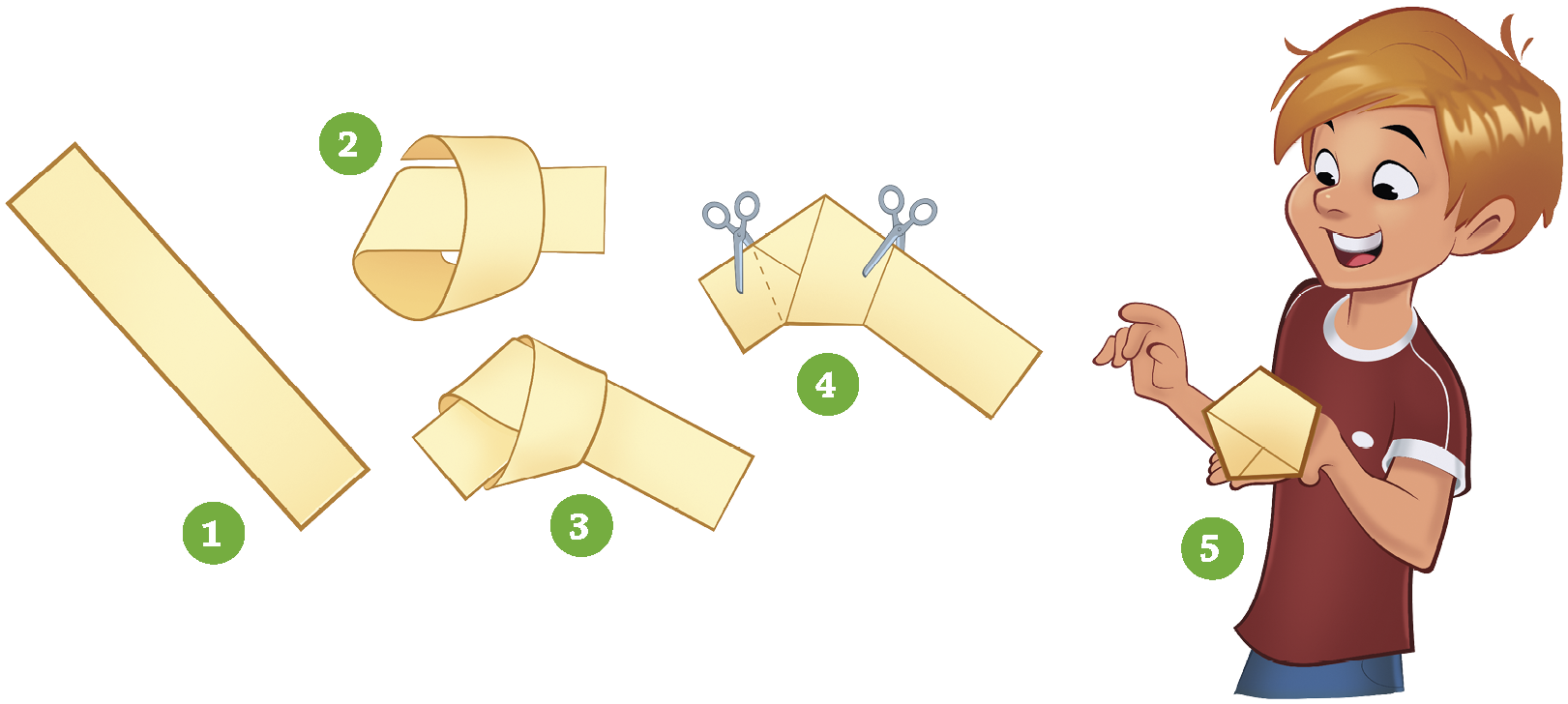
Observe o passo a passo que Lucas realizou utilizando um pedaço de papel retangular e uma tesoura de pontas arredondadas. A figura formada por Lucas após finalizada a dobradura se parece com um polígono.

Ilustração. 1. Tira de papel retangular. 2. Papel com uma extremidade voltada para cima. 3. Papel com uma volta semelhante a um nó. 4. Destaque para tesoura dos dois lados recortando a sobra do papel. 5. Menino de cabelo castanho, camisa vermelha segura um modelo de polígono feito com dobraduras,

Um polígono pode ser convexo ou não convexo. Para ser convexo, é necessário que todos os segmentos de reta, com extremidades no interior do polígono, tenham todos os seus pontos situados no interior desse polígono.

Continuaremos a estudar somente os polígonos convexos e, para simplificar, vamos tratá-los simplesmente por polígonos.

Elementos de um polígono

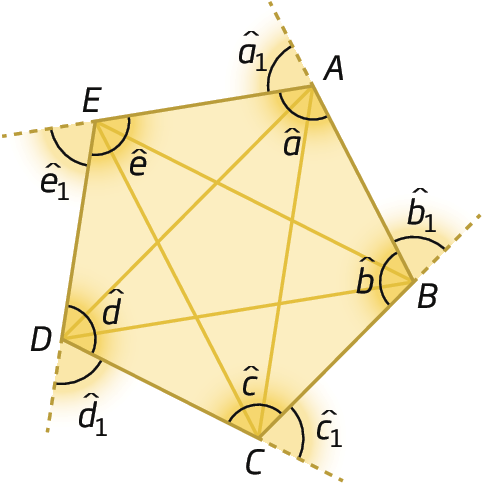
Observe o polígono á bê cê dê é a seguir:

Figura geométrica. Pentágono amarelo ABCDE. Dentro, cinco diagonais: AC, AD, BE, BD e CE. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1 e e1. Ângulos internos: a, b, c, d, e.

Sugestão de leitura

GENOVA, Carlos. origâmi : dobras, contas e encantos. São Paulo: Escrituras, 2008.

Além de apresentar origamis a serem confeccionados, o livro explora a importância de figuras geométricas na composição das dobraduras.

Podemos destacar alguns de seus elementos.

• Lados são os segmentos de reta que formam o contorno do polígono:

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E} e \overline{E A}

• Vértices são os pontos que são extremidades dos lados do polígono: a, B, C, D e ê

• Diagonais são os segmentos de reta cujas extremidades são vértices que não pertencem a um mesmo lado do polígono:

\overline{A C}, \overline{A D}, \overline{B D}, \overline{B E} e \overline{C E}

• Ângulos internos são os ângulos formados por dois lados consecutivos que contêm a região interna do polígono:

\hat{a}, \hat{b}, \hat{c}, \hat{d} e \hat{e}

• Ângulos externos são os ângulos formados pelo prolongamento de um dos lados do polígono e por seu lado adjacente e que não contêm a região interna do polígono:

{\hat{a}}_{1}, {\hat{b}}_{1}, {\hat{c}}_{1}, {\hat{d}}_{1} e {\hat{e}}_{1}

Página 112

Nome dos polígonos

Um polígono é nomeado de acordo com o número de lados, que é igual ao número de ângulos internos. Observe o nome de alguns polígonos.

Número de lados	Nome do polígono
3	Triângulo
4	Quadrilátero
5	Pentágono
6	Hexágono
7	Heptágono
8	Octógono

Número de lados	Nome do polígono
9	Eneágono
10	Decágono
11	Undecágono
12	Dodecágono
15	Pentadecágono
20	Icoságono

Atividades

Faça as atividades no caderno.

1. Nas figuras a seguir, nomeie o polígono e identifique seus lados, vértices e diagonais.

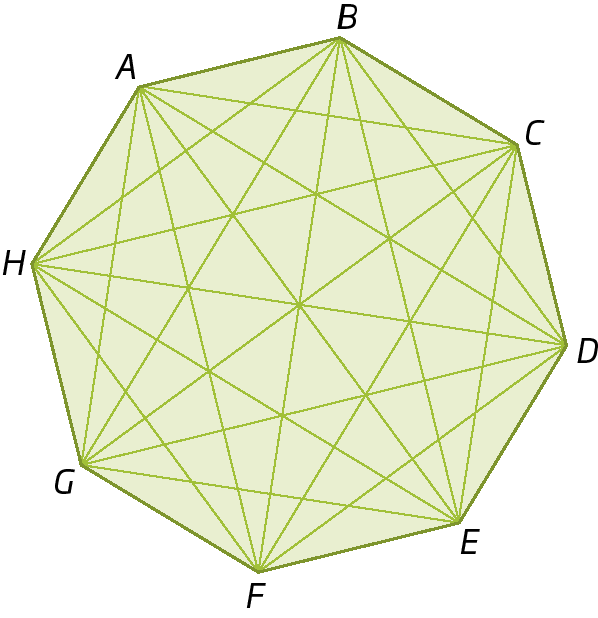
Octógono ABCDEFGH com as diagonais traçadas

2. Use uma régua e construa, em seu caderno, os polígonos seguintes.

a) pentágono á bê cê dê é;

b) octógono á bê cê dê é éfe gê agá;

c) quadrilátero a bê cê dê.

3. Responda às questões sobre um eneágono.

a) Quantos são seus ângulos internos?

b) Quantos são seus vértices?

4. Responda aos itens a seguir sobre um pentágono á bê cê dê é.

a) Quantos lados ele possui?

b) Quantas diagonais diferentes ele possui?

c) Identifique todas as suas diagonais.

5. A abertura do ângulo formado por dois lados consecutivos de um octógono mede 135graus. Qual é a soma das medidas das aberturas de todos os ângulos internos desse octógono, sendo todos eles congruentes?

Página 113

2 Diagonais de um polígono

O número de diagonais de um polígono varia de acordo com o número de lados que ele possui.

Analise o número de diagonais que partem do vértice a em cada polígono a seguir.

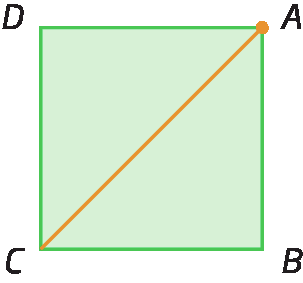
Figura geométrica. Quadrado verde ABCD com diagonal AC dentro. — 4 lados uma diagonal (4 menos 3 = 1)

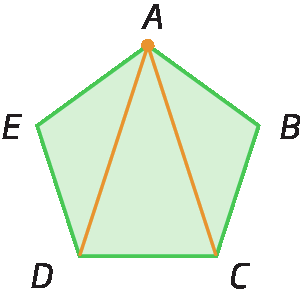
Figura geométrica. Pentágono verde ABCDE com diagonais de AC e AD — 5 lados duas diagonais (5 menos 3 = 2)

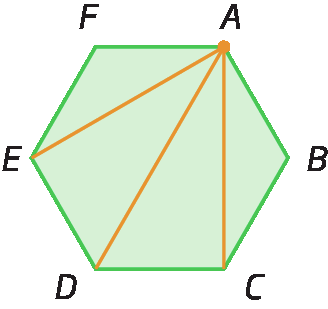
Figura geométrica. Hexágono verde ABCDEF com diagonais de AF, AD e AC — 6 lados 3 diagonais (6 menos 3 = 3)

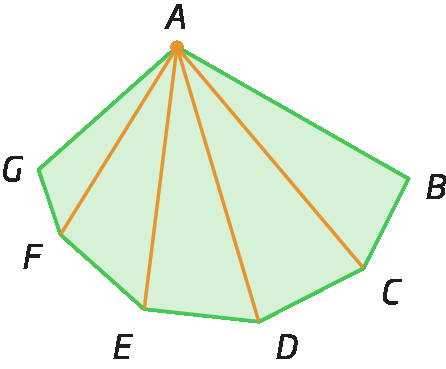
Figura geométrica. Heptágono verde ABCDEFG com diagonais de AF, AE, AD, AC, AB. — 7 lados 4 diagonais (7 menos 3 = 4)

Assim, se um polígono tem n lados, podemos traçar (n menos 3) diagonais a partir de cada vértice. E como esse polígono possui n vértices, então podemos traçar n ⋅ (n menos 3) diagonais. Porém, dessa fórma, estamos contando a mesma diagonal duas vezes. Por exemplo, no hexágono á bê cê dê é éfe anterior, partindo do vértice a, temos a diagonal

\overline{A C}

e, partindo do vértice C, temos a diagonal

\overline{C A}

, mas

\overline{A C}

\overline{C A}

determinam a mesma diagonal.

Logo, para determinar o número de diagonais (d ) de um polígono de n lados, fazemos:

d = \frac{n \cdot (n - 3)}{2}

Considere um outro exemplo.

O dodecágono tem 12 lados. Vamos calcular o número de diagonais desse polígono.

n = 12

d = \frac{12 \cdot (12 - 3)}{2} = 54

Logo, o dodecágono tem 54 diagonais.

Figura geométrica. Dodecágono laranja ABCDEFGHIJKL com as diagonais traçadas dentro. — Representação de todas as diagonais de um dodecágono.

Página 114

3 Ângulos internos e ângulos externos de um polígono

Soma das medidas das aberturas dos ângulos internos de um polígono

Analise o experimento feito por João para verificar que a soma das medidas das aberturas dos ângulos internos de um triângulo é 180graus.

Ilustração. Três quadros. 1. Triângulo ABC com ângulos a, b e c. 2. Destaque para uma tesoura recortando os ângulos do triângulo ABC. 3. Os ângulos a, b e c unidos. Ao lado, homem negro de cabelo preto e camisa vermelha diz: Primeiro, marquei, com cores diferentes, os ângulos internos do triângulo ABC. Na sequência, recortei o modelo de triângulo em 3 partes, em que cada parte continha um ângulo interno; e, por último,
coloquei os ângulos marcados lado a lado, de modo a torná-los adjacentes. Assim, obtive os 180 graus!

Traçando as diagonais que partem de um mesmo vértice, é possível decompor qualquer polígono em triângulos. Observe as figuras a seguir.

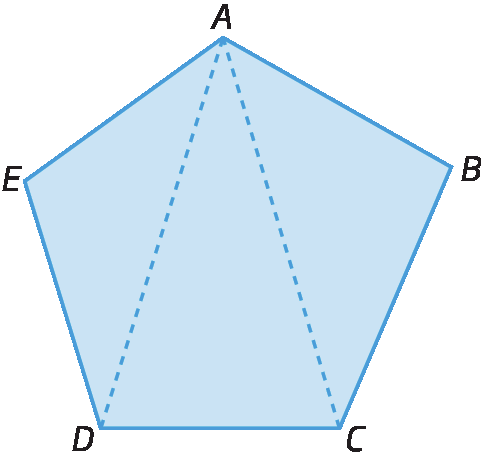
Figura geométrica. Pentágono azul ABCDE com diagonais de AC e AD. — O polígono de 5 lados foi decomposto em 3 triângulos.

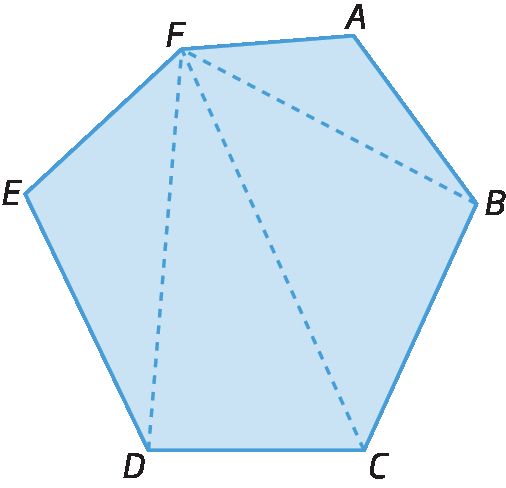
Figura geométrica. Hexágono azul ABCDEF com diagonais de FB, FC e FD. — O polígono de 6 lados foi decomposto em 4 triângulos.

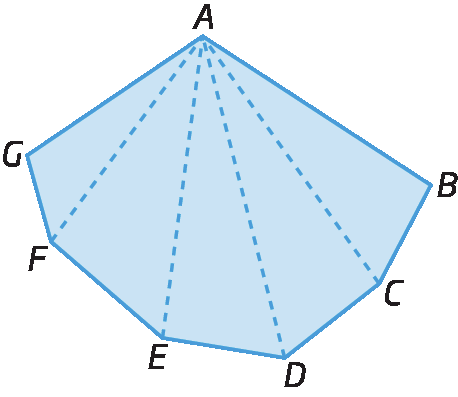
Figura geométrica. Heptágono azul ABCDEFG com diagonais de AC, AD, AE e AF. — O polígono de 7 lados foi decomposto em 5 triângulos.

Fixando um dos vértices de um polígono e traçando as diagonais que partem desse vértice, decompomos o polígono de n lados em (n – 2) triângulos.

Como a soma das medidas das aberturas dos ângulos internos de cada triângulo é 180graus, podemos afirmar que a soma das medidas das aberturas dos ângulos internos (Si ) de um polígono de n lados corresponde a:

Si = (n ‒ 2) ⋅ 180graus

Página 115

Considere mais alguns exemplos.

a) Qual é a soma das medidas das aberturas dos ângulos internos de um hexágono?

n = 6

Si = (n ‒ 2) ⋅ 180graus

Si = (6 ‒ 2) ⋅ 180graus

Si = 4 ⋅ 180graus

Si = 720graus

A soma das medidas das aberturas dos ângulos internos de um hexágono é 720graus.

b) A soma das medidas das aberturas dos ângulos internos de um polígono é 900graus. Qual é esse polígono?

Si = 900graus

Si = (n ‒ 2) ⋅ 180graus

900graus = (n ‒ 2) ⋅ 180graus

\frac{900 °}{180 °} = \frac{(n - 2) \cdot 180 °}{180 °}

5 = n ‒ 2 ⇒ n = 7

Logo, o polígono é um heptágono.

Soma das medidas das aberturas dos ângulos externos de um polígono

Considere o hexágono á bê cê dê é éfe. Cada ângulo interno com o ângulo externo correspondente são adjacentes suplementares. Assim:

a + a1 = 180°

b + b1 = 180°

c + c1 = 180°

d + d1 = 180°

e + e1 = 180°

f + f1 = 180°

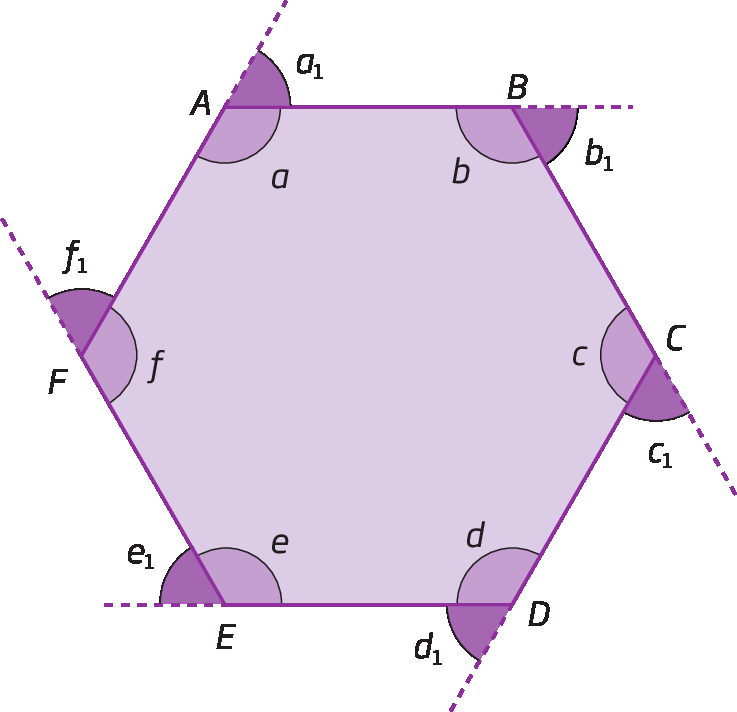
Figura geométrica. Hexágono roxo ABCDEF. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1, e1, f1. Ângulos internos: a, b, c, d, e, f.

Adicionando as medidas das aberturas de todos os ângulos, temos:

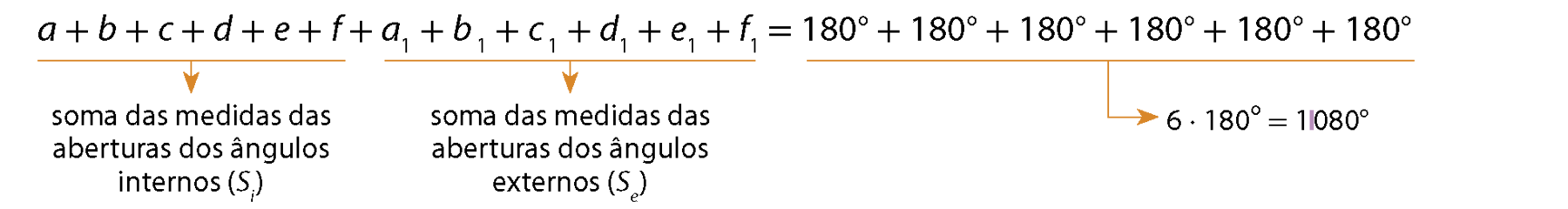
Sentença matemática com esquema. A mais b mais c mais d mais e mais f mais a1 mais b1 mais c1 mais d1 mais e1 mais f1 igual a 180 graus mais 180 graus 180 graus 180 graus 180 graus 180 graus. Seta para baixo saindo de a mais b mais c mais d mais e mais f: soma das medidas das aberturas dos ângulos internos abre parênteses, S i, fecha parênteses. Seta para baixo saindo de a1 mais b1 mais c1 mais d1 mais e1 mais f1: soma das medidas das aberturas dos ângulos externos, abre parênteses, S e, fecha parênteses. Seta para baixo saindo de 180 graus mais 180 graus 180 graus 180 graus 180 graus 180 graus: 6 vezes 180 graus igual a 1 080 graus.

Assim: Si + Se = .1080°. Como Si = (n ‒ 2) ⋅ 180° e n = 6, então:

(6 ‒ 2) ⋅ 180° + Se = .1080°

4 ⋅ 180° + Se = .1080°

720° + Se = .1080°

Se = 360°

Logo, a soma das medidas das aberturas dos ângulos externos do hexágono é 360graus.

Para qualquer polígono de n lados, temos:

Si + Se = n ⋅ 180°

(n ‒ 2) ⋅ 180° + Se = n ⋅ 180°

n ⋅ 180° ‒ 360° + Se = n ⋅ 180°

Se = 360°

Ilustração. Menino negro de camiseta azul e calça. Ele está deitado segurando um livro aberto e com a cabeça encostada na mochila, pensa: Realmente, quando adicionamos as medidas das aberturas de todos os ângulos do hexágono ABCDEF, obtivemos: Si + Se = 1080 graus. seta para baixo indicando 6 (número de lados do hexágono) vezes 180 graus.

Assim:

Em qualquer polígono, a soma das medidas das aberturas dos ângulos externos é 360graus.

Página 116

Veja que interessante

Faça as atividades no caderno.

Vamos fazer um experimento com os ângulos externos de um polígono?

Em uma folha de papel, desenhe um polígono qualquer e indique seus ângulos externos. Verifique o modelo.

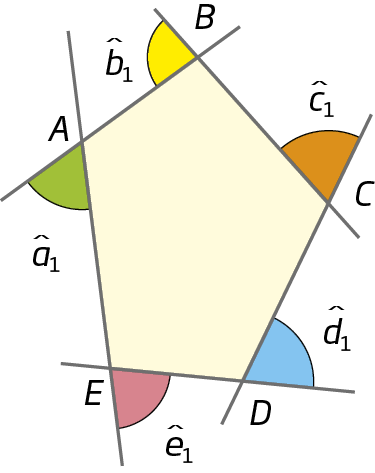
Figura geométrica. Pentágono ABCDE. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1, e1.

Em seguida, recorte, com uma tesoura de pontas arredondadas, cada um dos ângulos e una-os em torno de um dos vértices, de modo que se tornem adjacentes dois a dois.

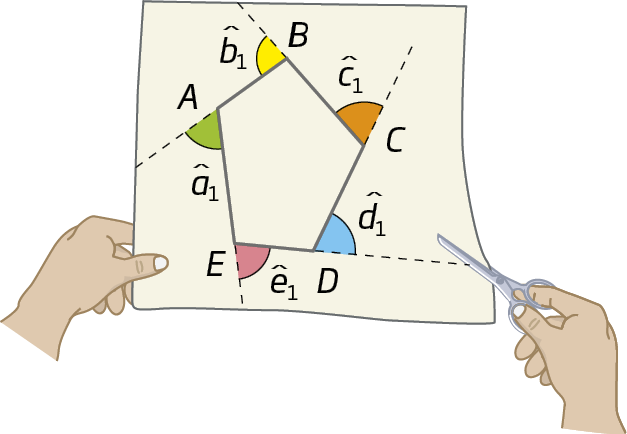
Ilustração. Folha de papel com pentágono ABCDE. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1, e1. Destaque para a mão de uma pessoa com uma tesoura no papel.

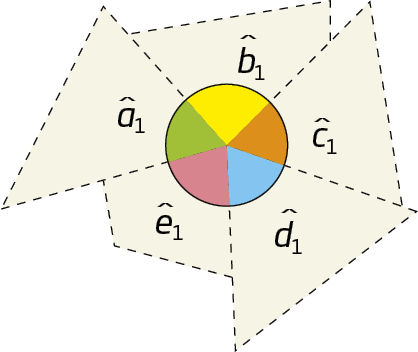
Ilustração. Formas triangulares com os ângulos recortados: a1, b1, c1, d1, e1 unidos no centro e formando um círculo.

Atividade

O que você pode verificar com esse experimento?

Atividades

Faça as atividades no caderno.

6. Determine o número de diagonais de um polígono de:

a) 5 lados;

b) 9 lados;

c) 15 lados;

d) 20 lados.

7. Determine a soma das medidas das aberturas dos ângulos internos dos polígonos a seguir.

a) Quadrilátero

b) Eneágono

c) Undecágono

d) Icoságono

8. Indique o nome dos polígonos cuja soma das medidas das aberturas dos ângulos internos é:

a) .1080graus

b) .1980graus

c) .2340graus

d) .1800graus

9. Em cada caso, calcule o valor de x, em grau.

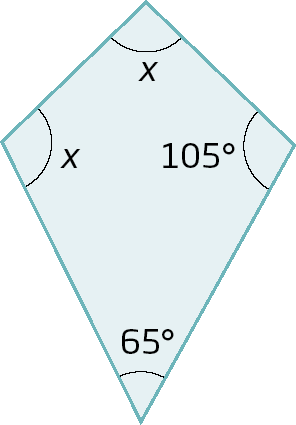
Figura geométrica. Quadrilátero com ângulos: x, x, 105 graus e 65 graus.

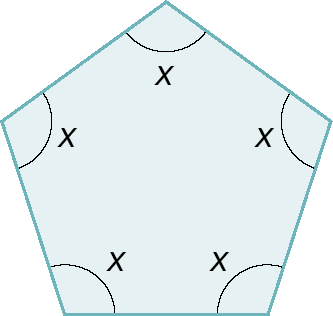
Figura geométrica. Pentágono com 5 ângulos x.

10. Determine o polígono que tem a soma das medidas das aberturas dos ângulos internos e a soma das medidas das aberturas dos ângulos externos iguais.

Página 117

4 Polígonos regulares

Um polígono que tem todos os lados com a mesma medida de comprimento e todos os ângulos com a mesma medida de abertura é denominado polígono regular. Os polígonos a seguir são exemplos de polígonos regulares.

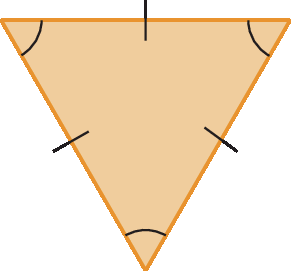
Figura geométrica. Triângulo com três lados e ângulos iguais. — triângulo equilátero

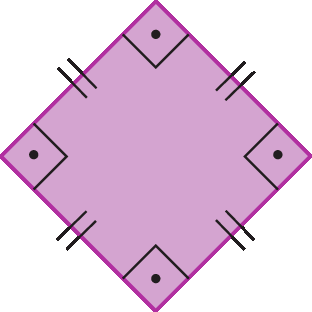
Figura geométrica. Quadrado com quatro lados e ângulos iguais. — quadrado

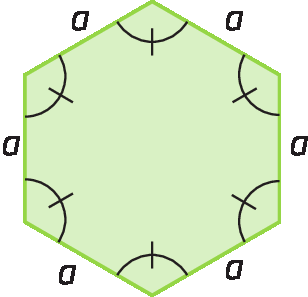
Figura geométrica. Hexágono com seis lados iguais, cada lado mede a. — hexágono regular

Medidas das aberturas do ângulo interno e do ângulo externo de um polígono regular

Em um polígono regular de n lados, indicando a medida da abertura do ângulo interno por ai e a medida da abertura do ângulo externo por ae , temos:

Sentença matemática. A i igual a s i dividido por n ou A i igual a, abre parênteses, n menos 2, fecha parênteses, vezes 180 graus, dividido por n.

Sentença matemática. A e igual a s e dividido por n ou A e igual a 360 graus dividido por n.

Agora, considere os exemplos a seguir.

a) Vamos determinar a medida da abertura do ângulo interno e a do ângulo externo de um decágono regular.

O decágono é o polígono que tem 10 lados.

Logo, n = 10. Assim:

a_{e} = \frac{S_{e}}{n} = \frac{360 °}{10} = 36 °

a_{i} = \frac{S_{i}}{n} = \frac{(n - 2) \cdot 180 °}{n} = \frac{(10 - 2) \cdot 180 °}{10} = 144 °

Logo, a medida da abertura do ângulo externo é 36graus e a medida da abertura do ângulo interno é 144graus.

Sugestão de leitura

SMOOTHEY, Marion. Atividades e jogos com quadriláteros. São Paulo: Scipione, 1998. (Coleção Investigação matemática).

Partindo de situações cotidianas, o livro traz desafios com fósforos, dobraduras e quebra-cabeças que ajudam a compreender conceitos como: quadriláteros, ângulos, diagonais, pontos e retas.

b) Vamos calcular o número de lados de um polígono regular cuja medida da abertura do ângulo interno é igual a 108graus.

Como

a_{i} = \frac{(n - 2) \cdot 180 °}{n}

, então:

108 ° = \frac{(n - 2) \cdot 180 °}{n}

108° ⋅ n = 180° ⋅ n ‒ 360°

72° ⋅ n = 360°

n = 5

Logo, o polígono tem 5 lados, ou seja, é um pentágono.

Página 118

Atividades

Faça as atividades no caderno.

11. Determine as medidas das aberturas dos ângulos internos e dos ângulos externos dos seguintes polígonos:

a) quadrilátero regular;

b) octógono regular;

c) eneágono regular;

d) icoságono regular.

12. Qual é o polígono regular cujas medidas das aberturas dos ângulos internos são iguais às medidas das aberturas dos ângulos externos?

13. Em um polígono regular, a medida da abertura do ângulo externo é 40graus. Quantos lados tem esse polígono?

14. Em um polígono regular, ai ‒ ae = 60graus. Qual é esse polígono?

Ângulo central de um polígono regular

Uma circunferência circunscrita a um polígono contém todos os vértices desse polígono. Nesse caso, podemos dizer também que o polígono está inscrito na circunferência.

Todo polígono regular pode ser inscrito em uma circunferência.

Denominamos ângulo central de um polígono regular aquele cujo vértice é o centro da circunferência e cujos lados passam por dois vértices consecutivos do polígono.

No pentágono regular á bê cê dê é a seguir, ac indica a medida da abertura do ângulo central.

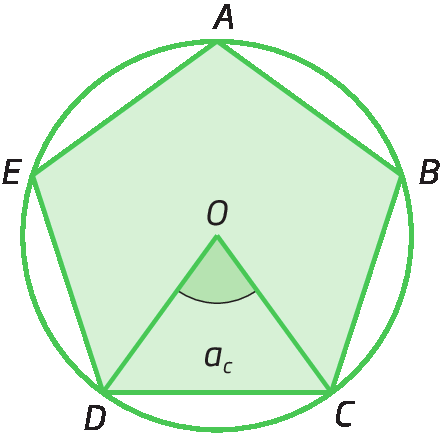
Figura geométrica. Circunferência com pentágono ABCDE inscrito, centro O, que é centro da circunferência. Está definido o triângulo OCD, o ângulo DOC está destacado e tem medida ac.

Sendo óh o centro de um polígono regular, a soma das medidas das aberturas de todos os ângulos centrais (ésse minúsculoc ) é 360graus (uma volta completa).

Sc = 360°

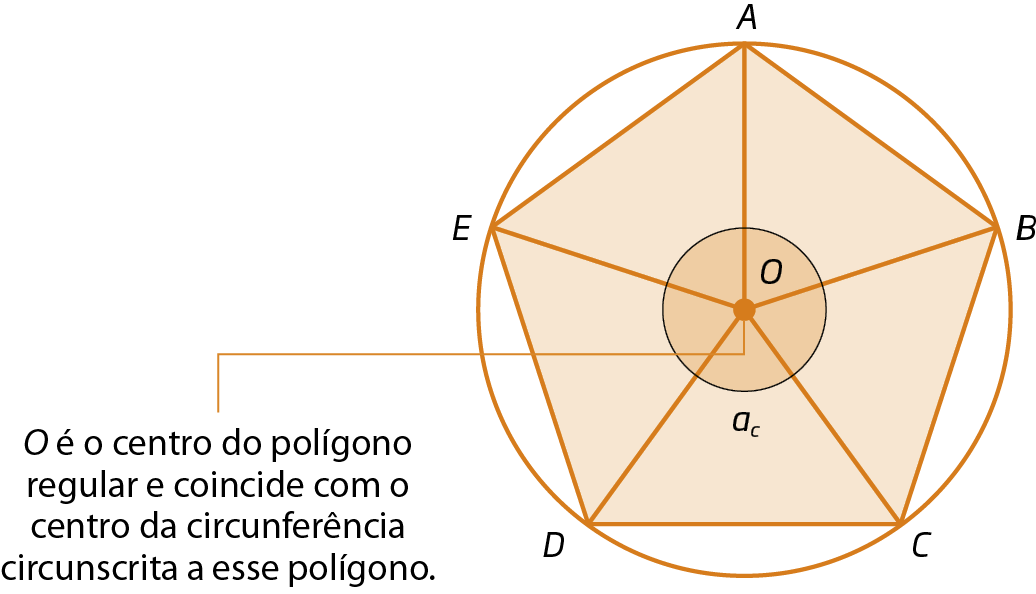
Figura geométrica. Circunferência circunscrita ao pentágono ABCDE laranja com centro em O. Há um outro círculo com centro em O, demarcando os ângulos centrais. Do centro O, tem-se uma reta diagonal para cada vértice do pentágono. De O sai uma seta para o texto: O é o centro do polígono regular e coincide com o centro da circunferência circunscrita a esse polígono

Logo, em um polígono de n lados, a medida da abertura do ângulo central é:

a_c =  

\frac{360 °}{n}

Página 119

Construção de polígonos regulares com régua e compasso

Podemos construir polígonos regulares a partir do seu ângulo central. Acompanhe a seguir a construção de um triângulo equilátero e a de um quadrado.

Cuidado! Evite acidentes ao usar o compasso.

Triângulo equilátero

A medida da abertura do ângulo central do triângulo equilátero é igual a 120graus. Observe a sequência de passos para construí-lo.

1º) Construímos uma circunferência de centro O com medida de comprimento de raio qualquer, e, com a mesma abertura do compasso, centrando-o em um ponto qualquer da circunferência, traçamos dois arcos, cruzando a circunferência em dois pontos, A e B. Construímos os segmentos de reta

\overline{A O} e \overline{O B}

, determinando o ângulo central

A \hat{O} B

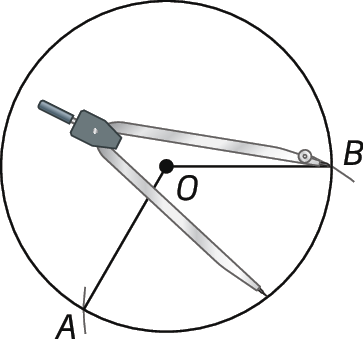
Ilustração. Circunferência com ponto O no centro. De O, tem-se uma reta horizontal com ponto B e reta diagonal para baixo com ponto A. Compasso aberto entre A e B traça linha em B.

2º) Centrando o compasso em B e mantendo a sua abertura inicial, traçamos mais dois arcos consecutivos na circunferência, marcando o ponto C. Traçamos

\overline{O C}

, determinando os ângulos centrais

B \hat{O} C e A \hat{O} C

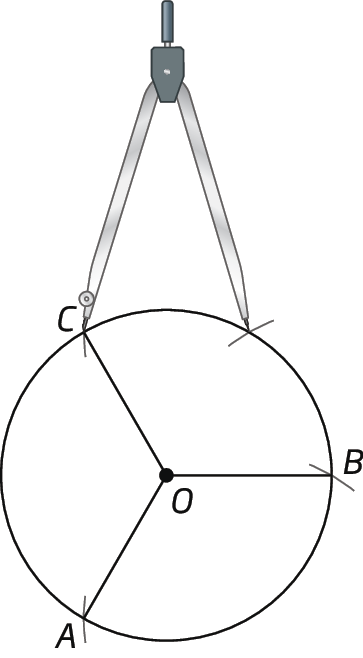
Ilustração. Circunferência com ponto O no centro. De O, tem-se reta horizontal com ponto B e reta diagonal para baixo com ponto A. Compasso aberto em C na reta de O e traça linha entre B e C.

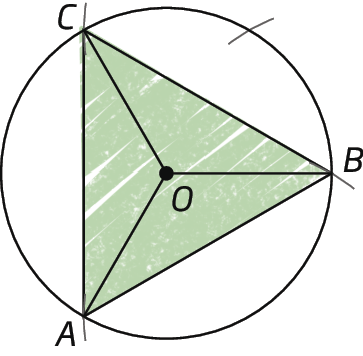
3º) Construímos os segmentos de reta

\overline{A B}, \overline{A C} e \overline{B C}

, formando, assim, o triângulo equilátero.

Ilustração. Circunferência com triângulo verde ABC e ponto O no centro.

Quadrado

A medida da abertura do ângulo central do quadrado é igual a 90graus. Observe a sequência de passos para construí-lo.

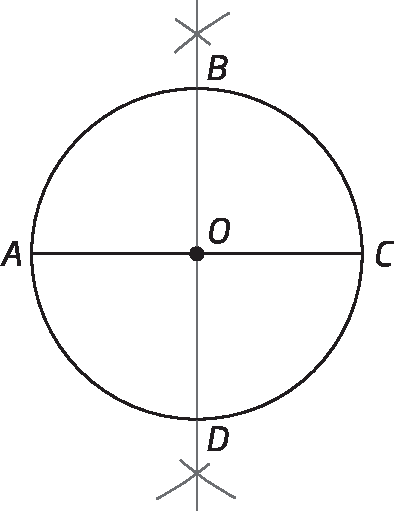
1º) Construímos uma circunferência de centro óh com medida de comprimento de raio qualquer. Traçamos um diâmetro, marcando os pontos a ê cê, intersecções do diâmetro com a circunferência.

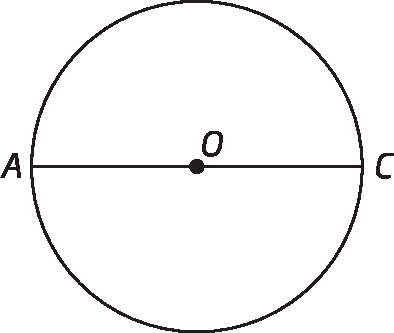
Ilustração. Circunferência com reta horizontal AC e ponto O no centro.

2º) Construímos uma reta perpendicular à

\overline{A C}

, passando por óh, marcando os pontos B e D, intersecção da reta perpendicular com a circunferência. Assim, determinamos 4 ângulos centrais com medida de abertura 90graus:

A \hat{O} B, B \hat{O} C, C \hat{O} D e D \hat{O} A

Ilustração. Circunferência com reta horizontal AC e ponto O no centro. Reta vertical BD passa em O.

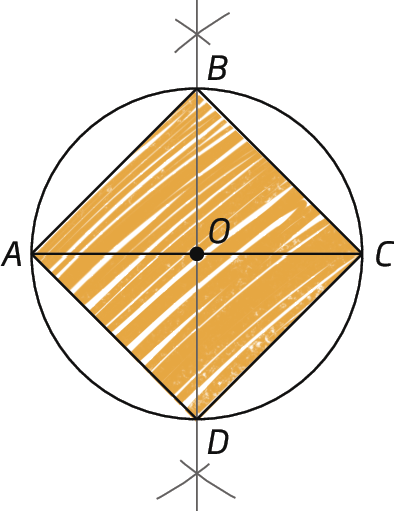
3º) Traçamos os segmentos de reta

\overline{A B}, \overline{B C}, \overline{C D} e \overline{D A}

, formando, assim, o quadrado.

Ilustração. Circunferência com reta horizontal AC e ponto O no centro. Reta vertical BD passa em O. As retas formam um losango laranja.

Observação

No capítulo 7, apresentaremos a justificativa para a validade das construções apresentadas nesta página.

Página 120

Atividades

Faça as atividades no caderno.

15. Calcule a medida da abertura do ângulo central de cada polígono regular.

a) hexágono;

b) decágono;

c) dodecágono;

d) icoságono.

16. Faça o que se pede.

a) Construa no caderno um triângulo equilátero inscrito em uma circunferência cujo raio mede 1,5 centímetro de comprimento.

b) Construa no caderno um quadrado inscrito em uma circunferência cujo raio mede 2 centímetros de comprimento.

17.

Observe as frases a seguir. Se as colocarmos na sequência correta, obteremos o passo a passo para construir um hexágono regular.

A. Construa um ângulo central cuja medida da abertura seja igual a 60graus.

B. Construa um ângulo central adjacente ao anterior.

C. Trace um segmento de reta consecutivo ao anterior, fechando o polígono.

D. Trace um segmento de reta unindo os pontos obtidos.

E. Marque a intersecção do último lado do ângulo construído com a circunferência.

F. Construa uma circunferência.

G. Trace o segmento de reta consecutivo ao anterior, unindo-o ao último ponto obtido.

H. Marque a intersecção dos lados do ângulo com a circunferência.

a) Reproduza o fluxograma a seguir em seu caderno e complete-o com as letras correspondentes a cada uma das frases anteriores. Note que, no fluxograma, há um grupo de passos que devem ser repetidos para obtermos o hexágono regular. Indique, no campo adequado, a quantidade de vezes que esse grupo deve ser repetido.

Fluxograma. Modelo. Início. Oito espaços para respostas. Fim. Do quinto ao oitavo espaço para resposta, (repita, espaço para resposta, vezes).

b) Utilizando a ideia anterior como referência, elabore, no caderno, um esquema com uma sequência de comandos para a construção de outro polígono regular.

c) Troque de caderno com um colega e tente construir o polígono conforme a orientação no esquema.

d) Discuta com o colega os fluxogramas elaborados, analisando se as instruções produziram o polígono desejado. Caso isso não tenha ocorrido, investiguem se houve falha no comando ou na sequência dos comandos inseridos no esquema.

Página 121

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Polígonos

Uma linha poligonal fechada simples com sua região interna fórma uma figura geométrica plana chamada polígono.

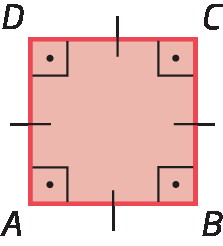
1. Dê o nome do polígono e identifique seus lados, vértices e diagonais.

Figura geométrica. Quadrilátero ABCD vermelho com os quatro lados iguais destacados e os quatro ângulos retos destacados.

2. Um heptágono possui:

a) quantos vértices?

b) quantos lados?

Diagonais de um polígono

O número de diagonais de um polígono varia de acordo com o número de lados que ele possui. Logo, para determinar o número de diagonais (d) de um polígono de n lados, fazemos:

d = \frac{n \cdot (n - 3)}{2}

3. Determine o número de diagonais de um polígono de:

a) 8 lados

b) 3 lados

Ângulos internos e ângulos externos de um polígono

Soma das medidas das aberturas dos ângulos internos de um polígono

A soma das medidas das aberturas dos ângulos internos (ésse minúsculoi) de um polígono de n lados corresponde a:

Si = (n ‒ 2) ⋅ 180°

Soma das medidas das aberturas dos ângulos externos de um polígono

Em qualquer polígono, a soma das medidas das aberturas dos ângulos externos é 360graus.

4. A soma das medidas das aberturas dos ângulos internos de um polígono é 720graus. Qual é esse polígono?

5. Determine a soma das medidas das aberturas dos ângulos internos de um pentágono.

Polígonos regulares

Um polígono que possui todos os lados com a mesma medida de comprimento e todos os ângulos com mesma medida de abertura é denominado polígono regular.

Medidas das aberturas do ângulo interno e do ângulo externo de um polígono regular

Em um polígono regular de n lados, indicando a medida da abertura do ângulo interno por ái e a medida da abertura do ângulo externo por áe , temos:

a_{i} = \frac{S_{i}}{n} ou a_{i} = \frac{(n - 2) \cdot 180 °}{n}

a_{e} = \frac{S_{e}}{n} ou a_{e} = \frac{360 °}{n}

Ângulo central de um polígono regular

Denominamos ângulo central de um polígono regular aquele cujo vértice é o centro da circunferência e cujos lados passam por dois vértices consecutivos do polígono.

Sendo óh o centro de um polígono regular, a soma das medidas das aberturas de todos os ângulos centrais (ésse minúsculoc ) é 360graus (uma volta completa).

S_c = 360°

Logo, em um polígono de n lados, a medida da abertura do ângulo central é:

a_{c} = \frac{360 °}{n}

6. A medida da abertura do ângulo interno de um polígono regular é o triplo da medida da abertura do seu ângulo externo. Qual é esse polígono?