Página 122

Capítulo 6 Probabilidade

Trocando ideias

Em muitas situações que vivenciamos nos jogos, conhecemos os resultados possíveis, mas não podemos prever o resultado final. É o que acontece, por exemplo, ao lançarmos um “dado honesto” ou retirarmos uma carta de um baralho.

Fotografia. Peças de jogos diversos, dados e algumas cartas de baralho. No canto superior esquerdo há algumas pelas de um jogo de damas e dois dados de cor preta. No canto inferior esquerdo, há 3 cartas de baralho: rei de copas, rei de espada e rei de paus. No canto superior direito, há algumas peças de xadrez e pinos nas cores vermelha azul, verde e amarela. No canto inferior direito estão presentes algumas varetas e 2 dados: de cor bege. Três faces de um deles tem os números 4, 16 e 32. O outro dado é convencional. No centro da imagem há algumas peças de dominó na cor preta. É possível ver também partes de alguns tabuleiros. — Algumas peças de diferentes tipos de jogos: damas, xadrez, dominó, cartas etcétera.

▸

Quais são as possibilidades de resultado que podem aparecer no lançamento de um “dado honesto” como um dos dados preto da imagem? Qual é a probabilidade de sair a face 2?

▸

Qual é a probabilidade de se retirar, ao acaso, a carta “ás de copas” de um baralho comum?

Neste capítulo, vamos aprofundar as ideias sobre cálculo de probabilidade com base na construção do espaço amostral.

Página 123

1 Possibilidades

Situações em que conhecemos os resultados possíveis mas nas quais não podemos assegurar o resultado final são chamadas de experimentos aleatórios.

Todas as possibilidades, ou seja, todos os resultados possíveis em um experimento aleatório, compõem o espaço amostral desse experimento.

Vamos estudar alguns modos de obter e organizar o espaço amostral. Acompanhe as situações a seguir.

Situação 1

Quais resultados podemos obter ao lançar duas “moedas honestas” diferentes?

Para obter o espaço amostral desse experimento, podemos construir uma árvore de possibilidades.

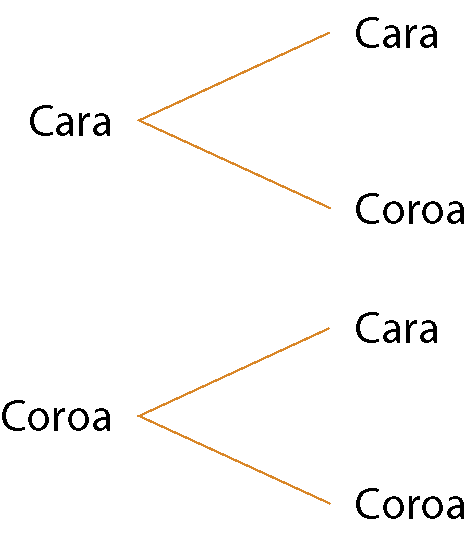
Esquema. Na parte superior, a palavra Cara. Desta palavra partem dois fios: um para a palavra Cara e outro para a palavra Coroa. Na parte inferior, a palavra Coroa. Desta palavra partem dois fios: um para a palavra Cara e outro para a palavra Coroa.

Observe que há 4 possibilidades de resultado ao lançar duas “moedas honestas”: pode “sair” cara nas duas moedas, cara na primeira moeda e coroa na segunda, coroa na primeira moeda e cara na segunda e coroa nas duas moedas.

Situação 2

Jéferson tem bolas com os números 1, 3, 5 e 7 em uma caixa verde, e bolas com os números 2, 4 e 8 em uma caixa roxa. Caso ele sorteie uma bola de cada caixa, quais são as possibilidades diferentes de sorteio?

Para responder à pergunta, vamos organizar as possibilidades do sorteio, ou espaço amostral, em um quadro.

		Bolas numeradas da caixa verde

Bolas numeradas da caixa roxa

Portanto, Jéferson tem 12 possibilidades diferentes de sortear uma bola de cada caixa.

Página 124

Princípio multiplicativo

Em cada uma das situações apresentadas anteriormente, calculamos o total de possibilidades de o experimento ocorrer, determinando todo o espaço amostral desse experimento, ou seja, todos os resultados possíveis.

No entanto, é possível calcular o total de possibilidades sem determinar o espaço amostral. Vamos ver como isso poder ser feito, retomando as situações anteriores.

Situação 1

Ao lançar duas “moedas honestas”, podemos obter cara ou coroa na primeira (duas possibilidades) e cara ou coroa na segunda (duas possibilidades). Dessa forma, o total de resultados possíveis ao lançar duas “moedas honestas” é:

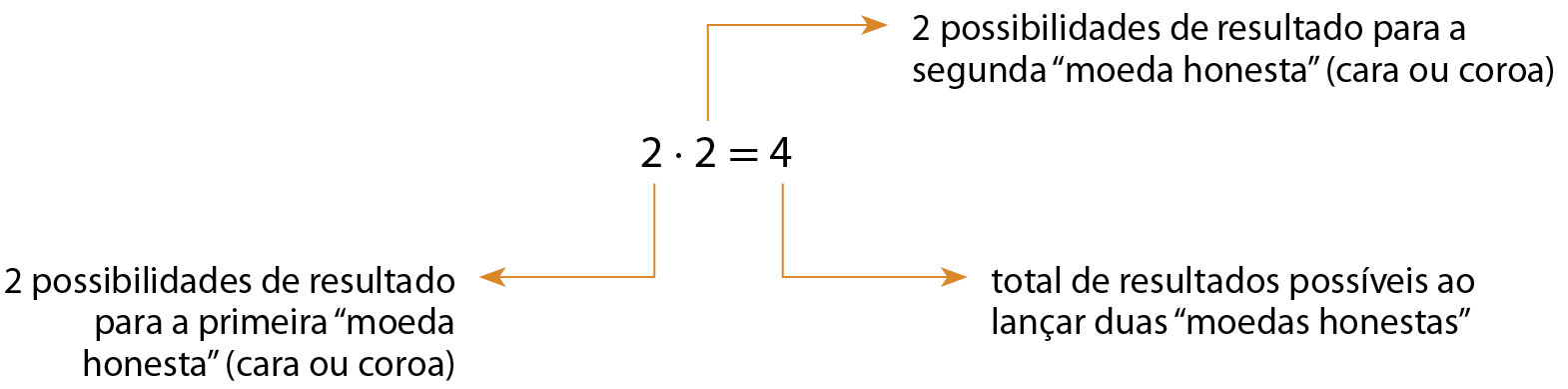
Esquema. 2 vezes 2 igual a 4. Do primeiro fator 2 parte uma seta laranja indicando: 2 possibilidades de resultado para a primeira moeda honesta, abre parênteses, cara ou coroa, fecha parênteses. Do segundo fator 2, parte uma seta laranja indicando: 2 possibilidades de resultado para a segunda moeda honesta, abre parênteses, cara ou coroa, fecha parênteses. Do número 4, parte uma seta laranja, indicando: total de resultados possíveis ao lançar duas moedas honestas.

O cálculo foi realizado com base no princípio multiplicativo.

Clique no play e acompanhe as informações do vídeo.

Considere que um acontecimento ocorra em duas etapas sucessivas, a ê B. Se a ocorrer de m maneiras, e se, para cada uma delas, B pode ocorrer de n maneiras, o número de maneiras que o acontecimento pode ocorrer é m · n.

Situação 2

Jéferson tinha 4 possibilidades (1, 3, 5 e 7) de sortear uma bola da caixa verde e 3 possibilidades (2, 4 e 8) de sortear uma bola da caixa roxa. O total de possibilidades de sortear uma bola de cada caixa pode ser dado pela seguinte multiplicação:

Ilustração. Quadro com 4 círculos verdes. No interior de cada círculo há um número:: 1, 3, 5 e 7. Abaixo, quadro com 3 círculos roxos. No interior de cada círculo há um número:: 2, 4 e 8.

Esquema. 4 vezes 3 igual a 12. Do número 4 parte uma seta laranja indicando: 4 possibilidades de bolas que podem ser sorteadas da caixa verde, Do número 3, parte uma seta laranja indicando: 3 possibilidades de bolas que podem ser sorteadas da caixa roxa. Do número 12, parte uma seta laranja, indicando: total de possibilidades de sortear uma bola de cada caixa.

O princípio multiplicativo pode ser estendido para três ou mais etapas. Considere a situação a seguir.

Três “dados honestos” com as faces numeradas de 1 a 6 serão lançados simultaneamente. Quantas são as possibilidades de resultado?

6 vezes 6 vezes 6 = 216

Portanto, há 216 resultados possíveis ao lançar, simultaneamente, três “dados honestos”.

Página 125

Atividades

Faça as atividades no caderno.

1. Dois estudantes serão eleitos monitores da turma por sorteio. Em uma urna estão os nomes de José, Joaquim e Marcela e na outra urna os nomes de Maria, Manoela, Marília e Aline.

a) Construa uma árvore de possibilidades com os possíveis resultados desse sorteio.

b) Quantas possibilidades de resultado esse sorteio pode ter?

2. Uma moeda será lançada duas vezes. Quais são os possíveis resultados que podem ocorrer?

3. Angélica é deficiente visual, e para uma viagem de negócios levou 3 camisetas, 4 calças e 2 pares de sapatos. Para uma reunião, solicitou que Arthur (seu assistente) separasse uma troca de roupas qualquer para ela.

Ilustração. Acima, camisa azul, camisa roxa e camisa verde. Abaixo, calça preta, calça laranja, calça azul e calça vermelha. Na parte inferior, sapato bege e sapato marrom.

a) Quais são as possibilidades de combinação que Artur pode separar para Angélica?

b) Quantas opções de combinação ela tem?

4. A senha de acesso a um sáite é composta de uma letra e 3 algarismos.

a) De quantas maneiras diferentes um usuário desse site poderá escolher uma letra para compor sua senha? Considere as letras de nosso alfabeto.

b) De quantas maneiras diferentes ele poderá escolher os algarismos para compor sua senha? Justifique.

c) Qual é o total de senhas diferentes que podem ser compostas para o acesso a esse site?

d) Júlio esqueceu os dois primeiros dígitos de sua senha e solicitou a seus dois filhos que fossem, um a um, tentando descobrir a senha que usava; aquele que ganhasse escolheria o que iriam jantar. Quantas possibilidades de combinação eles tinham como espaço amostral nesse caso?

Ilustração. Monitor de computador com a representação de uma senha de 4 dígitos, sendo que só os 2 últimos são conhecidos: Retângulo branco, retângulo branco, 5, 7.

Um computador fará um sorteio, com os algarismos 0, 4, 5, 8 e 9, para compor um número seguindo o esquema a seguir.

Milhar

Centena

Dezena

Unidade

Em duplas, verifiquem quantos números podem ser formados com a condição de que os algarismos não podem se repetir e a de que o número não pode começar em zero.

Elabore um problema que envolva um experimento aleatório e o princípio multiplicativo. Depois, troque de problema com um colega e resolva o problema que ele elaborou.

Página 126

2 Probabilidade

Neste momento, vamos relembrar como é feito o cálculo da probabilidade de ocorrência de um evento. Para isso, considere a situação a seguir.

Um experimento aleatório poderia ser, por exemplo, a retirada, sem ver, de uma bolinha de um saco que contém 6 bolinhas verdes e 4 bolinhas vermelhas. Não é possível afirmar que seria retirada necessariamente uma bolinha verde ou uma vermelha, poderia ser qualquer uma das duas.

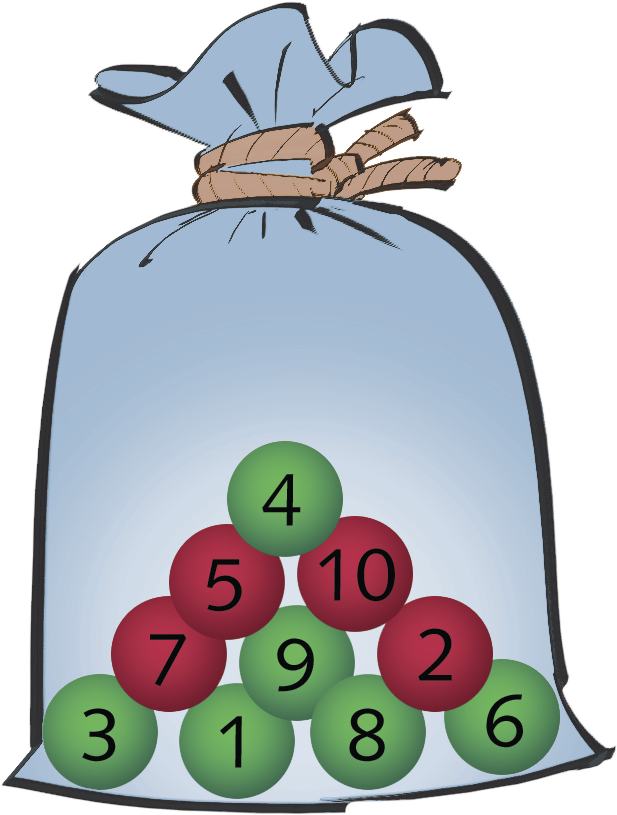
Ilustração. Saquinho transparente com bolinhas. As bolinhas verdes são: 1, 3, 4, 8, 9 e 6. As bolinhas vermelhas são: 2, 5, 7, 10.

• Mas qual seria a probabilidade de se retirar uma bolinha verde desse saco?

• E qual seria a probabilidade de se retirar uma bolinha vermelha?

O conjunto das 10 bolinhas (6 bolinhas verdes e 4 bolinhas vermelhas) fórma o espaço amostral.

Chamamos de evento qualquer subconjunto do espaço amostral; nesse caso, temos dois eventos:

• evento a: retirar uma bolinha verde;

• evento B: retirar uma bolinha vermelha.

Observe que 6 casos são favoráveis ao evento a (retirar uma bolinha verde) e 4 casos são favoráveis ao evento B (retirar uma bolinha vermelha).

A probabilidade P da ocorrência de um evento é uma medida que pode assumir um valor de 0 a 1 e é dada pela razão entre o número de casos favoráveis e o número de elementos do espaço amostral:

Esquema. Probabilidade de um evento é igual ao número de casos favoráveis do evento sobre o número de elementos do espaço amostral.

Desse modo, a probabilidade de ocorrência do evento a, retirar uma bolinha verde, é:

Sentença matemática. P, abre parênteses, A, fecha parênteses, igual a 6 décimos, igual a 3 quintos. De P, abre parênteses, A, fecha parênteses parte uma seta laranja indicando: probabilidade de ocorrer o evento A.

Como também podemos indicar a probabilidade por meio de um número na fórma decimal ou uma porcentagem, nesse caso, a probabilidade de se retirar uma bolinha verde é 0,6 ou 60%.

Já a probabilidade de ocorrência do evento B, retirar uma bolinha vermelha, é:

Sentença matemática. P, abre parênteses, B, fecha parênteses, igual a 4 décimos, igual a 2 quintos. De P, abre parênteses, B, fecha parênteses parte uma seta laranja indicando: probabilidade de ocorrer o evento B.

Logo, a probabilidade de se retirar uma bolinha vermelha é 0,4 ou 40%.

Observe, na situação apresentada que a soma das probabilidades dos dois eventos é igual a 1:

P (A) + P (B) = \frac{3}{5} + \frac{2}{5} = 1

Por esse motivo, dizemos que os eventos a ê B são complementares.

Página 127

Agora, considere um novo evento:

• evento C : retirar a bolinha de número 7.

A probalidade de o evento C ocorrer é:

Sentença matemática. P, abre parênteses, C, fecha parênteses, igual a 1 décimo, De P, abre parênteses, C, fecha parênteses parte uma seta laranja indicando: probabilidade de ocorrer o evento C.

Logo, para cada uma das bolinhas, a probabilidade de ser retirada é de 0,1 ou 10%.

Podemos determinar a probabilidade dos eventos a ê B de outra maneira. Observe:

• evento a: retirar uma bolinha verde.

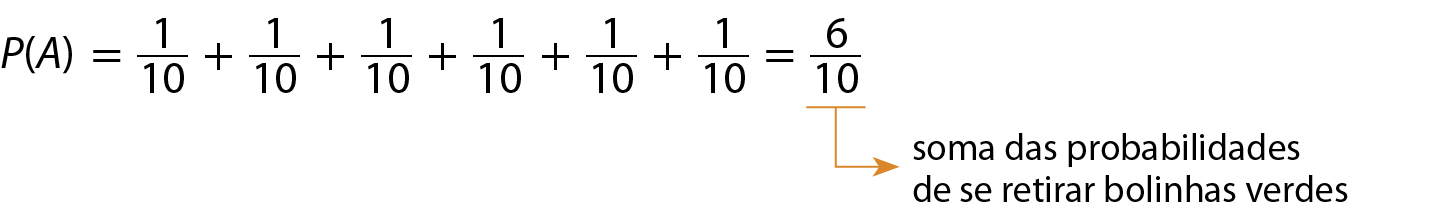
Esquema. Probabilidade de ocorrer o evento A é igual a 1 décimo mais 1 décimo mais 1 décimo mais 1 décimo mais 1 décimo mais 1 décimo que é igual a 6 décimos. De 6 décimos parte uma seta laranja indicando: soma das probabilidades de se retirar bolinhas verdes.

• evento B: retirar uma bolinha vermelha.

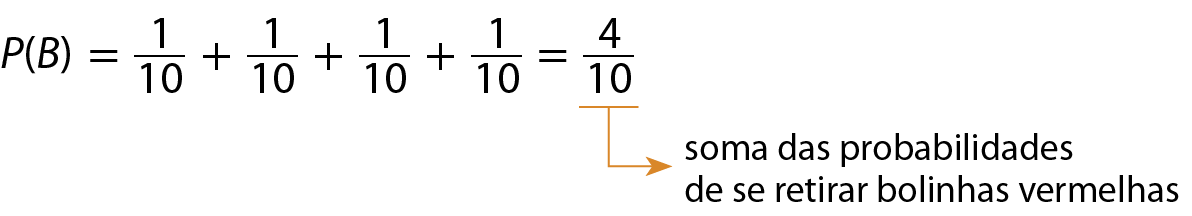
Esquema. Probabilidade de ocorrer o evento A é igual a 1 décimo mais 1 décimo mais 1 décimo mais 1 décimo é igual a 4 décimos. De 4 décimos parte uma seta laranja indicando: soma das probabilidades de se retirar bolinhas vermelhas.

Note que a soma de todas essas probabilidades é igual a 1:

\frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} + \frac{1}{10} = \frac{10}{10} = 1

Observações

1. A soma das probabilidades de todos os elementos do espaço amostral é igual a 1.

2. Quando a probabilidade de um evento ocorrer é 1, dizemos que esse evento é certo.

3. Quando a probabilidade de um evento ocorrer é 0, dizemos que esse evento é impossível.

Agora, observe a situação a seguir.

Na aula de Matemática, a professora Roberta organizou a turma em duplas e entregou um “dado honesto” a cada dupla. Ela solicitou que os estudantes construíssem o espaço amostral, listando as possibilidades da soma de pontos ao lançar o “dado honesto” duas vezes, e que, com base nos resultados, respondessem às seguintes perguntas:

Ilustração. quadro de giz com as informações: 1. Qual soma tem a maior probabilidade de aparecer após dois lançamentos? E qual é a probabilidade de essa soma aparecer? 2. Quais sãos os dois valores que têm a menor probabilidade de aparecer? E qual é a probabilidade de cada uma dessas somas aparecer? 3. Se adicionarmos a probabilidade de as três menores somas aparecerem, que valor obteremos? E se adicionarmos a probabilidade de todas as somas, que valor obteremos?

Página 128

Primeiramente, Janaína e Ricardo organizaram o espaço amostral da soma de pontos dos lançamentos do “dado honesto” em um quadro.

Espaço amostral da soma de pontos dos lançamentos do "dado honesto"
1 + 1 = 2	2 + 1 = 3	3 + 1 = 4	4 + 1 = 5	5 + 1 = 6	6 + 1 = 7
1 + 2 = 3	2 + 2 = 4	3 + 2 = 5	4 + 2 = 6	5 + 2 = 7	6 + 2 = 8
1 + 3 = 4	2 + 3 = 5	3 + 3 = 6	4 + 3 = 7	5 + 3 = 8	6 + 3 = 9
1 + 4 = 5	2 + 4 = 6	3 + 4 = 7	4 + 4 = 8	5 + 4 = 9	6 + 4 = 10
1 + 5 = 6	2 + 5 = 7	3 + 5 = 8	4 + 5 = 9	5 + 5 = 10	6 + 5 = 11
1 + 6 = 7	2 + 6 = 8	3 + 6 = 9	4 + 6 = 10	5 + 6 = 11	6 + 6 = 12

Após construírem o espaço amostral, para responder à primeira pergunta, verificaram que a soma 7 é a que aparece mais vezes. Como ela aparece 6 vezes de um total de 36, a probabilidade será de

\frac{6}{36}

, ou seja,

\frac{1}{6}

Para responder à segunda pergunta, notaram que a soma 2 e a soma 12 só apareceram uma vez cada uma. Portanto, a probabilidade de cada uma aparecer é

\frac{1}{36}

Para a terceira pergunta, verificaram que as três menores somas são: 2(1 + 1); 3(1 + 2); e 3(2 + 1). Como a probabilidade de obter cada soma é

\frac{1}{36}

, fizeram o seguinte cálculo:

\frac{1}{36} + \frac{1}{36} + \frac{1}{36} = \frac{3}{36} = \frac{1}{12}

Para completar a resposta a essa pergunta, consideraram que há 36 possibilidades, e que cada uma tem

\frac{1}{36}

de probabilidade de ocorrer. Desse modo, calcularam:

36 \cdot \frac{1}{36} = \frac{36}{36} = 1

Logo, constataram que a soma de todas as probabilidades é igual a 1.

Atividades

Faça as atividades no caderno.

7. Em um jogo de tabuleiro são usados um “dado honesto” de 6 faces, numerado de 1 a 6, e outro de 8 faces, numerado de 1 a 8. Em cada rodada, os jogadores lançam os dois “dados honestos” simultaneamente.

a) Determine o espaço amostral do lançamento simultâneo desses dois “dados honestos”.

b) Qual é a probabilidade de saírem os números 7 e 5 em um lançamento?

c) Qual é a probabilidade de saírem os números 6 e 5 em um lançamento?

d) Considerando a soma dos números nos dois “dados honestos” em um lançamento, qual é a probabilidade de a soma dos pontos resultar em um número par?

Página 129

8. Um sorteio será realizado entre os estudantes de quatro turmas diferentes da escola de Lúcio. Ele verificou a quantidade de estudantes de cada turma, calculou as probabilidades correspondentes e registrou:

• Probabilidade de o estudante sorteado ser da turma a:

\frac{1}{6}

• Probabilidade de o estudante sorteado ser da turma B:

\frac{1}{4}

• Probabilidade de o estudante sorteado ser da turma C:

\frac{1}{3}

• Probabilidade de o estudante sorteado ser da turma D:

Considerando que os cálculos de Lúcio estejam corretos, qual é a probabilidade de um estudante da turma D ser sorteado?

9. Fábio e Cecília fazem aula em uma escola de dança. A turma deles, com ambos incluídos, possui 14 alunos, sendo 6 homens e 8 mulheres. No fim do ano, um rapaz e uma moça serão escolhidos, de fórma aleatória, para fazer uma apresentação.

a) Quantas possibilidades de casais diferentes existem?

b) Qual é a probabilidade de Fábio ser escolhido?

c) Qual é a probabilidade de Cecília ser escolhida?

d) Qual é a probabilidade de Fábio e Cecília serem escolhidos?

10. Uma indústria de brinquedos fabrica a mesma boneca com algumas variações de roupas e tons de cabelo. Essas bonecas são comercializadas em “saquinhos surpresa”, em que não é possível verificar a combinação de roupas antes da compra. A seguir são apresentadas algumas variações.

Ilustração. Uma boneca em pé. À direita da boneca, um cabelo amarelo, um preto e um vermelho. Um vestido amarelo, uma camiseta verde com calça vermelha e uma regata rosa com saia azul. Abaixo, um sapato preto e um sapato marrom.

a) Conforme as opções anteriores, de quantas maneiras diferentes essa boneca pode ser vendida?

b) A mãe de Mariana comprou uma dessas bonecas. Qual é a probabilidade de ela ter comprado uma boneca de cabelo preto, vestido amarelo e sapato preto?

11. Ana, Renata e Daniel estão participando da gincana da escola, mas em equipes diferentes. A equipe de Ana tem 14 participantes, a de Renata tem 13 participantes e a de Daniel, 15 participantes. Será sorteado um integrante de cada equipe para a execução de uma das provas da gincana.

a) De quantas maneiras diferentes esse sorteio poderá ser realizado?

b) Qual é a probabilidade de os sorteados serem Ana, Renata e Daniel?

12.

Pense em um experimento aleatório e elabore duas perguntas em que um dos eventos tenha mais de 50% de probabilidade de ocorrer e em que o outro evento tenha 50% de probabilidade de ocorrência. Apresente seu problema a um colega para que ele possa confirmar as probabilidades previstas.

Página 130

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Possibilidades

Situações em que conhecemos os resultados possíveis mas nas quais não podemos assegurar o resultado final são chamadas de experimentos aleatórios.

Todas as possibilidades, ou seja, todos os resultados possíveis em um experimento aleatório compõem o espaço amostral desse experimento.

Princípio multiplicativo

Considere que um acontecimento ocorra em duas etapas sucessivas, a ê B. Se a ocorrer de m maneiras e se, para cada uma delas, B pode ocorrer de n maneiras, o número de maneiras que o acontecimento pode ocorrer é m · n.

Esse princípio pode ser estendido para três ou mais etapas.

1. Quantos resultados possíveis podemos obter, ao lançar simultaneamente dois “dados honestos” com 8 faces numeradas de 1 a 8?

2. Um restaurante realizou um trabalho comunitário e ofertou a moradores em situação de rua uma cestinha com alguns itens para o café da manhã. Para a montagem da cesta, o restaurante disponibilizou 3 opções de café, duas opções de pães e 4 opções de patês. Quantas possibilidades diferentes de café da manhã havia para os moradores em situação de rua?

Probabilidade

A probabilidade P da ocorrência de um evento é uma medida que pode assumir um valor de 0 a 1 e é dada pela razão entre o número de casos favoráveis e o número de elementos do espaço amostral.

3. Em uma urna há 6 bolas azuis e 5 bolas pretas. Qual é a probabilidade de uma pessoa sortear uma bola de cor preta?

4. Suponha que um “dado honesto” que tenha em cada uma de suas faces as letras a, B, C, D, ê e F será lançado.

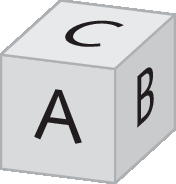
Ilustração. Dado com letra C na face superior, letra A na face frontal e letra B na face lateral direita.

a) Qual é o espaço amostral desse experimento?

b) Qual é a probabilidade de “sair” a letra D na face superior ao lançar esse “dado honesto”?

5. Em uma sala de aula há 50 estudantes matriculados, dos quais 20 usam óculos e 30 não usam. Um estudante será sorteado. Determine a probabilidade desse estudante:

a) não usar óculos;

b) usar óculos.

6. Considere uma sequência com os números: 2, 3, 4, 5, 8, 11, 12, 15, 16, 17, 19, 21. Ao escolher um desses números ao acaso, qual é a probabilidade de o número escolhido:

a) ser par?

b) ser ímpar?

7. Júlia separou de dois naipes de um baralho apenas cartas de Ás até 7 e sorteou uma carta de cada naipe. Em seguida, pediu a João que tentasse adivinhar quais cartas ela tinha sorteado.

a) Copie no caderno o quadro a seguir referente ao espaço amostral desse experimento e complete-o.

Espaço amostral
Ás, Ás	2, Ás	3, Ás	4, Ás	5, Ás	6, Ás
Ás, 2	2, 2		4, 2	5, 2
		3, 3
		3, 4	4, 4
Ás, 5
Ás, 6	2, 6	3, 6	4, 6	5, 6	6, 6
Ás, 7			4, 7	5, 7	6, 7

b) Qual é a probabilidade de João acertar as duas cartas?

c) Qual é a probabilidade de Júlia ter sorteado duas cartas de mesmo valor?

Que dica Júlia poderia dar a João para que a probabilidade de ele acertar fosse de

\frac{1}{7}

? Converse com o professor e os colegas.

Página 131

É hora de extrapolar

Faça as atividades no caderno.

Ícone do tema FORMAÇÃO CIDADÃ.
Ícone do tema SAÚDE.

Quais são os direitos dos idosos?

Segundo a Pesquisa Nacional por Amostra de Domicílios (pê nádi), realizada pelo í bê gê É, o número de idosos brasileiros atingiu a marca de 34 milhões no quarto trimestre de 2019, representando 16,2% da população do país. As projeções do í bê gê É para a população brasileira apontam que esse percentual dobrará até o ano de 2045. Por isso, é fundamental que busquemos fórmas de assegurar os direitos e atender às necessidades dessa parcela expressiva da população do nosso país e também nos preparar para essa longa fase da vida.

Dados obtidos em: https://oeds.link/X4l4fZ. Acesso em: 4 julho 2022.

Fotografia vista de trás de um casal de idosos caminhando de mãos dadas em um parque. À esquerda, grama e árvores. — Idosos caminhando no Parque das Águas em São Lourenço (Minas Gerais). Foto de 2021.

Objetivo: Pesquisar os direitos dos idosos; analisar informações do Relatório Mundial de Envelhecimento e Saúde, da Organização Mundial da Saúde; pesquisar os cuidados com a saúde do idoso, e produzir e divulgar uma cartilha sobre os direitos dos idosos e com dicas de prevenção de queda para a população.

Etapa 1: Pesquisa sobre os direitos dos idosos no Brasil.

1. Responda às questões a seguir.

a) A partir de que idade uma pessoa é considerada idosa pela legislação brasileira?

b) Qual(ais) direito(s) dos idosos você conhece?

Reúnam-se em grupo e pesquisem na internet o Estatuto do Idoso. A pesquisa deverá abranger o ano em que foi criado, os objetivos, a categoria de pessoas incluída no estatuto e os principais direitos assegurados aos idosos. Selecionem pelo menos oito direitos.

Comparem as respostas da atividade 1 aos resultados da pesquisa da atividade 2. Depois, respondam às questões a seguir.

a) A classificação de idoso que vocês consideravam inicialmente está de acordo com a encontrada no estatuto?

b) Vocês tinham conhecimento dos direitos dos idosos?

c) Vocês acham que a população idosa tem conhecimento desses direitos?

Elaborem uma lista única para a turma com todos os direitos dos idosos levantados na pesquisa.

Etapa 2: Análise de dados do Relatório Mundial de Envelhecimento e Saúde da ó ême ésse.

Em maio de 2020, a Assembleia Geral da ônu declarou que 2021-2030 será a Década para um Envelhecimento Saudável. De acordo com a Organização Pan-Americana da Saúde (ôpas), “embora as pessoas vivam mais tempo, isso não significa que elas estejam vivendo saudavelmente e tendo suas necessidades atendidas”, pois ainda ocorrem muitos erros e falta de atendimentos.

Dados obtidos em: https://oeds.link/pSZEdb. Acesso em: 12 julho 2022.

a) Vocês concordam com a afirmação feita no texto?

b) Vocês conseguem identificar características que indiquem a qualidade de vida dos idosos que conhecem?

Página 132

Também de acordo com o relatório: “o gasto com populações mais velhas é um investimento, não um custo”. Leiam o trecho a seguir e depois respondam à pergunta.

O gasto com populações mais velhas é um investimento, não um custo

Os gastos em sistemas de saúde, cuidados de longo prazo e ambientes propícios mais amplos são frequentemente retratados como custos. Este relatório assume uma abordagem diferente. Essa abordagem considera os gastos como investimentos que permitem a capacidade e, portanto, o bem-estar das pessoas maiores. Esses investimentos também ajudam as sociedades a atender suas obrigações relacionadas aos direitos fundamentais das pessoas mais velhas. Em alguns casos, o retorno sobre esses investimentos é direto (sistemas de saúde melhores conduzem a uma melhor saúde, que permite maior participação e bem-estar). Outros retornos podem ser menos óbvios, porém exigem o mesmo grau de consideração: por exemplo, investimento em cuidado de longo prazo ajudará pessoas com perda significativa de capacidade a manter vidas dignas e também pode permitir que as mulheres permaneçam no mercado de trabalho, além de promover a coesão social por meio do compartilhamento de riscos em uma comunidade.

reticências

Organização Mundial da Saúde. Relatório Mundial de Envelhecimento e Saúde, 2015. página 11.

• O que vocês diriam a uma pessoa que acredita que o gasto com idosos é um custo e que não se deveria reservar recursos para cuidar dessa parcela da população? Como vocês a convenceriam do contrário?

Etapa 3: Análise de dados sobre o risco de quedas entre os idosos.

7. Um dos direitos garantidos pelo Estatuto do Idoso é a determinação de assentos preferenciais identificados nos transportes públicos. A imagem a seguir mostra os grupos de pessoas que têm direito ao uso dos assentos preferenciais em transportes públicos.

Fotografia. Retângulo azul com ícones: pessoa com muletas, mulher grávida, mulher segurando uma criança no colo, pessoa com uma bengala e uma pessoa obesa. Acima, a informação: Acento preferencial. Abaixo, Priority Seat. À direita: Pessoas com deficiência, gestantes, com crianças de colo, idosos e obesos. Na ausência de pessoas nessas condições, o uso do acento é livre.

a) Quais são os grupos de pessoas que possuem esse direito?

b) Por que é importante que esses grupos tenham direito aos assentos preferenciais?

c) Se em um ônibus há 46 assentos, sendo 6 deles preferenciais, e um jovem ocupa, aleatoriamente, um dos assentos, qual é a probabilidade de ele ocupar um assento preferencial?

8. Segundo o Instituto Nacional de Traumatologia e Ortopedia do Ministério da Saúde, “a queda é um evento bastante comum e devastador em idosos. Embora não seja uma consequência inevitável do envelhecimento, pode sinalizar o início de fragilidade ou indicar doença aguda. Além dos problemas médicos, as quedas apresentam custo social, econômico e psicológico enormes, aumentando a dependência e a institucionalização. Estima-se que há uma queda para um em cada três indivíduos com mais de 65 anos, e que um em vinte daqueles que sofreram uma queda sofram uma fratura ou necessitem de internação. Dentre os mais idosos, com 80 anos ou mais, 40% caem a cada ano. Dos que moram em asilos e casas de repouso, a frequência de quedas é de 50%. A prevenção de quedas é tarefa difícil devido à variedade de fatores que as predispõem”.

As normas que tratam do funcionamento das instituições destinadas ao atendimento de idosos (Portaria nº 810, de 22 de setembro de 1989) dizem que “os acessos ao prédio deverão possuir rampa com inclinação máxima de 5%, largura mínima de 1,50 métro, dotada de guarda-corpo e corrimão, piso revestido com material não derrapante, que permita o livre rolamento de cadeiras de rodas, inclusive”.

Página 133

a) Por que as rampas são mais indicadas que as escadas?

b) A seguir, temos o projeto de uma rampa que não é adequada ao uso pelos idosos. Sabe-se que, para adequá-la, é preciso diminuir a medida da abertura do ângulo de inclinação pela metade.

Figura geométrica. Triângulo retângulo. A medida da abertura do ângulo que a hipotenusa forma com o lado horizontal do triângulo mede aproximadamente 45 graus.

Cuidado! Evite acidentes ao usar o compasso na atividade 8.

• Determinem a medida da abertura do ângulo de inclinação do projeto da nova rampa usando apenas régua e compasso.

• Descrevam o passo a passo.

9. Os temas a seguir se referem à prevenção de acidentes com idosos. Escolham um deles para pesquisar e, depois, listem dicas.

• TEMA 1: Dicas gerais para prevenir quedas.

• TEMA 2: Orientações e modificações para o quarto visando à prevenção de quedas.

• TEMA 3: Modificações na sala e no corredor para prevenir quedas.

• TEMA 4: O que mudar na cozinha para prevenir quedas.

• TEMA 5: Como evitar quedas em escadas.

Etapa 4: Confecção de uma cartilha coletiva.

10. Agora, vocês vão elaborar uma cartilha informativa. Cada página deve ter 16 centímetros × 10 centímetros.

Mas, antes, respondam: o que é uma cartilha informativa? Pesquisem essa fórma de transmitir informações e tragam exemplos.

11. A cartilha deverá conter explicações sobre os direitos dos idosos e fornecer dicas para a prevenção de quedas. Retomem a lista de direitos dos idosos feita na etapa 1 e escolham um dos direitos para ser explicado pelo grupo. Organizem-se para que não haja abordagens repetidas entre os grupos.

12. Cada página elaborada deverá conter uma imagem produzida por vocês. Não usem imagens prontas de revistas, livros ou da internet. A imagem deverá se relacionar ao tema abordado na página da cartilha.

Discutam quais, quantas e como serão as imagens do grupo, produzam-nas e depois montem as páginas da cartilha com a imagem e o texto sobre o direito ou a dica escolhida.

13. Todos os grupos deverão elaborar uma capa para a cartilha.

Etapa 5: Apresentação e análise das páginas elaboradas e divulgação da cartilha.

14. Mostrem aos colegas as páginas elaboradas pelo grupo para que eles as analisem e comentem se as informações estão claras e se a imagem é adequada.

15. Anotem as dúvidas, as opiniões e as sugestões dos colegas.

16.

Depois dos ajustes necessários, confeccionem a cartilha da turma.

Façam uma votação para escolher a capa da cartilha. Organizem a cartilha em duas partes: a primeira, com as páginas sobre os direitos dos idosos; a segunda, com dicas para prevenção de quedas.

17. Divulguem a cartilha da turma para a comunidade escolar.

Etapa 6: Síntese do trabalho realizado.

18. Algumas questões devem ser discutidas.

a) Por que é importante garantir com leis os direitos dos idosos?

b) Apenas os idosos devem conhecer seus direitos ou estes devem ser conhecidos por toda a população? Por quê?

c) É necessário se preparar física e financeiramente para a velhice? Como vocês fariam isso?

19. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 4 e 5.