Página 134

Unidade 3

Capítulo 7 Triângulos e quadriláteros

Capítulo 8 Área, volume e capacidade

Capítulo 9 Equações do 2º grau

Fotografia. Seis remos de madeira cada um pintado com um tipo de grafismo indígena. — Remos de madeira decorados da etnia Pataxó, em Porto Seguro (Bahia). Foto de 2019.

O artesanato indígena, com sua diversidade de cores e formatos, representa a preservação da cultura e a valorização da ancestralidade indígena.

O que você sabe sobre a diversidade cultural dos povos indígenas no Brasil? As figuras presentes no artesanato indígena se parecem com quais figuras geométricas planas? Ao final desta Unidade, você responderá a essas e outras questões.

Página 135

Capítulo 7 Triângulos e quadriláteros

Trocando ideias

Pieter Cornellis Mondrian (1872-1944), também conhecido como Piête Môndrian, foi um pintor holandês. Suas obras se caracterizam pela presença de linhas retas e de figuras retangulares, nas cores vermelha, azul, amarela, preta e branca, que ele considerava as cores elementares do Universo. Analise esta reprodução de uma de suas obras.

Fotografia. Reprodução de obra de arte composta por linhas retas e de figuras retangulares, nas cores vermelha, azul, amarela, preta e branca, — MONDRIAN, Piet. Composição com vermelho, amarelo, azul e preto, óleo sobre tela, 59,5 centímetros × 59,5 centímetros, 1921.

Conheça mais

No site do Museu de Arte Moderna de Nova York (Estados Unidos da América), é possível conhecer mais obras de Piet Mondrian.

▸

Cite duas características dos retângulos.

▸

Reúna-se com um colega e pesquisem obras de arte em que é possível identificar figuras que se parecem com triângulos e quadriláteros. Depois, compartilhem com a turma o que encontraram.

Neste capítulo, vamos estudar os triângulos e os quadriláteros.

Página 136

1 Triângulos

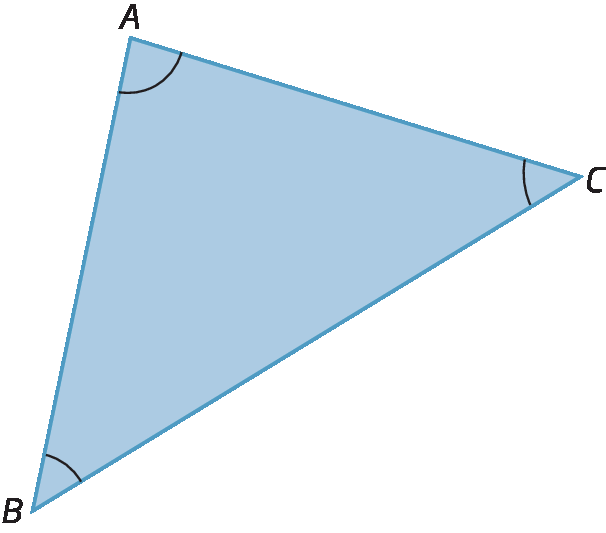
O triângulo é um polígono de três lados.

O formato triangular é muito utilizado na arquitetura e na engenharia pela rigidez que a estrutura triangular apresenta. Além disso, podemos observar o formato triangular em obras de arte, em revestimentos e em diferentes artigos de artesanato.

Vamos destacar alguns elementos deste triângulo á bê cê.

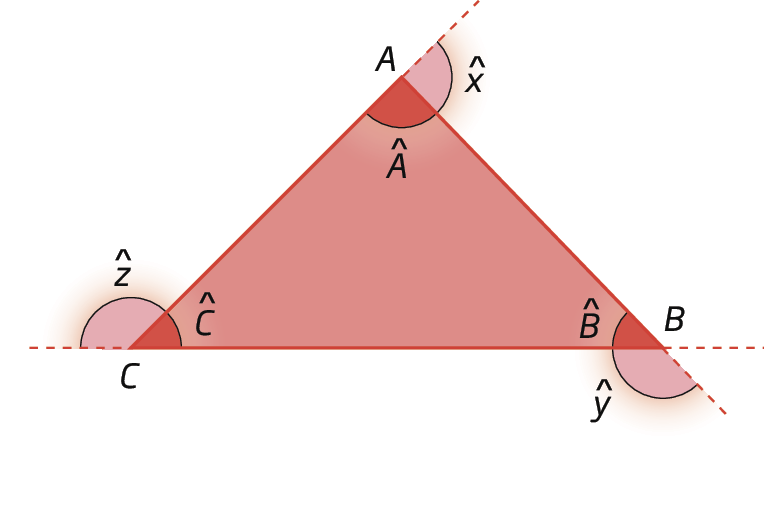
• Vértices: a, B e C.

• Lados:

\overline{A B}, \overline{A C} e \overline{B C}

• Ângulos internos:

\hat{A}, \hat{B} e \hat{C}

• Ângulos externos:

\hat{x}, \hat{y} e \hat{z}

Classificação de triângulos

Os triângulos podem ser classificados quanto às medidas de comprimento dos lados e quanto às medidas de abertura dos ângulos.

Quanto às medidas de comprimento dos lados

• Equilátero: os três lados são congruentes.

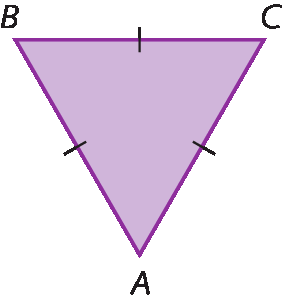
Figura geométrica. Triângulo ABC com os 3 lados com mesma medida de comprimento.

\overline{A B} ≅ \overline{B C} ≅ \overline{C A}

• Isósceles: dois lados são congruentes.

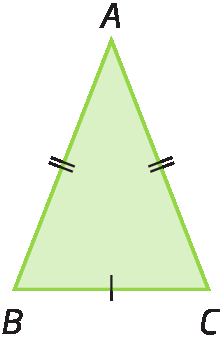
Figura geométrica. Triângulo ABC. Os lados AB e AC têm a mesma medida de comprimento.

\overline{A B} ≅ \overline{A C}

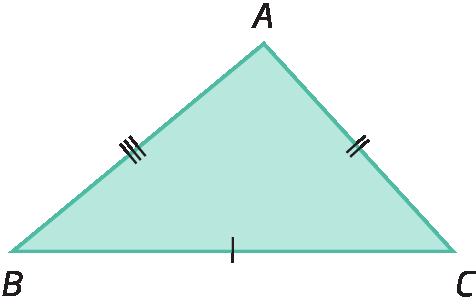
• Escaleno: não tem lados congruentes.

Figura geométrica. Triângulo ABC com os 3 lados com medidas de comprimento diferentes.

Ilustração. Menina amarela sentada à uma mesa desenhando um triângulo isósceles. Sobre a mesa estão também uma borracha e uma régua. A menina diz: 'Vamos combinar: em um triângulo, os lados (ou os ângulos) marcados com a mesma quantidade de tracinhos têm a mesma medida de comprimento, ou seja, os lados (ou os ângulos) são congruentes.'

Observações

1. No triângulo isósceles á bê cê anterior:

•

\overline{B C}

é a base;

•

\hat{B} e \hat{C}

são os ângulos da base e, para qualquer triângulo isósceles, os ângulos da base são congruentes

(\hat{B} ≅ \hat{C})

;

•

\hat{A}

é o ângulo do vértice oposto à base.

2. Em qualquer triângulo equilátero, todos os ângulos são congruentes.

Página 137

Quanto às medidas de abertura dos ângulos

• Acutângulo: os três ângulos internos são agudos.

Figura geométrica. Triângulo ABC com os 3 ângulos internos com aberturas medindo menos do que 90 graus.

m e d (\hat{A}) < 90 °, m e d (\hat{B}) < 90 ° e m e d (\hat{C}) < 90 °

• Retângulo: tem um ângulo interno reto.

Figura geométrica. Triângulo retângulo DEF, Os ângulos internos com vértices em D e F tem aberturas medindo menos do que 90 graus e o ângulo interno com vértice em E tem abertura medindo 90 graus.

m e d (\hat{E}) = 90 °

• Obtusângulo: tem um ângulo interno obtuso.

Figura geométrica. Triângulo MNO. Os ângulos internos com vértices em M e O têm aberturas medindo menos do que 90 graus e o ângulo interno com vértice em N tem abertura medindo mais do que 90 graus.

m e d (\hat{N}) > 90 °

Observação

A soma das medidas de abertura dos ângulos internos de um triângulo é 180graus. Assim, em um triângulo retângulo, há um ângulo reto e dois ângulos agudos, pois a soma das medidas de abertura dos outros dois ângulos deve ser 90graus. O mesmo acontece com um triângulo obtusângulo: há um ângulo de medida de abertura maior que 90graus; logo, os outros dois ângulos também são agudos, pois a soma de suas medidas de abertura é menor que 90graus.

Atividades

Faça as atividades no caderno.

1. Classifique cada um dos triângulos a seguir quanto às medidas de comprimento dos lados e às medidas de abertura dos ângulos.

Figura geométrica. Triângulo com os 3 lados medindo 5 centímetros de comprimento e com os 3 ângulos internos com abertura medindo 60 graus.

Figura geométrica. Triângulo com os 2 lados medindo 4 centímetros de comprimento e 1 lado medindo 4 vezes raiz quadrada de 3 centímetros de comprimento. As medidas das aberturas dos ângulos internos opostos aos lados que medem 4 centímetros, são de 30 graus. A medida da abertura do ângulo opostos ao lado que mede 4 vezes raiz quadrada de 3 centímetros de comprimento é de 120 graus.

Figura geométrica. Triângulo cuja medida do comprimento dos lados está indicada pelas letras a, b e c. A medida da abertura do ângulo oposto ao lado que mede c tem 30 graus. A medida da abertura do ângulo oposto ao lado que mede a tem 20 graus. A medida da abertura do ângulo oposto ao lado que mede b tem 120 graus.

2. É possível construir um triângulo que tenha dois ângulos obtusos? Justifique sua resposta.

Página 138

Cevianas notáveis: mediana, altura e bissetriz

Agora, vamos estudar a mediana, a altura e a bissetriz de um triângulo, que são chamadas de cevianas.

Ceviana é qualquer segmento de reta com uma extremidade em um vértice de um triângulo e a outra extremidade na reta suporte do lado oposto a esse vértice.

Reta suporte de um segmento de reta é a reta que contém esse segmento.

No triângulo á bê cê a seguir,

\overline{A D}

é uma ceviana relativa ao lado

\overline{B C}

Figura geométrica. Triângulo ABC. Sobre o lado BC está representada uma reta r. Há um ponto D representado entre os pontos B e C. Há também um segmento de reta com extremidades no ponto A e ponto D.

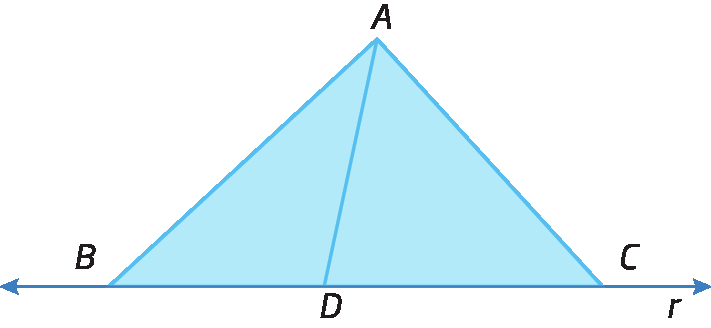
r (ou

\overset{\leftrightarrow}{B C}

) é a reta suporte do lado

\overline{B C}

Medianas de um triângulo

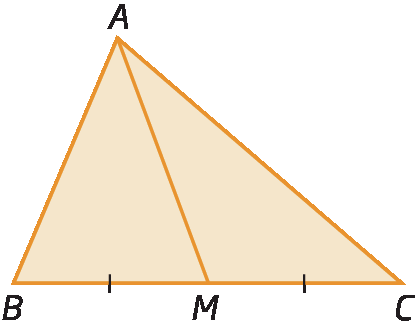
As medianas de um triângulo são as cevianas que têm uma extremidade em um dos vértices do triângulo e a outra extremidade no ponto médio do lado oposto a esse vértice.

No triângulo á bê cê a seguir,

\overline{A M}

é a mediana relativa ao lado

\overline{B C}

. Como M é ponto médio de

\overline{B C}

\overline{B M} e \overline{M C}

são congruentes.

Figura geométrica. Triângulo ABC. Sobre o lado BC está representado o ponto M, de modo que a medida do comprimento do segmento de reta BM é igual a medida do comprimento do segmento de reta MC. Está representado também um segmento de reta com extremidades no ponto A e M.

BM = MC

Em um triângulo, podemos traçar uma mediana relativa a cada lado.

A intersecção das medianas de um triângulo determina um ponto chamado baricentro (G).

A seguir, temos que o ponto G é o baricentro do triânguloá bê cê, e pode-se provar que ele divide a medida do comprimento das medianas na razão de 1 para 2, ou seja:

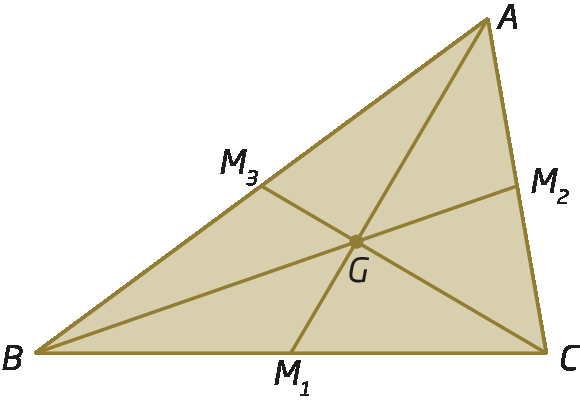
Figura geométrica. Triângulo ABC. Estão representados por M1, M2 e M3 os pontos médios dos lados BC, AC e AB, respectivamente. Também estão representadas as medianas AM1, BM2 e CM3. As medianas se intersectam no ponto G.

\frac{M_{1} G}{A G} = \frac{M_{2} G}{B G} = \frac{M_{3} G}{C G} = \frac{1}{2}

Observação

O baricentro de um objeto qualquer é considerado seu centro de gravidade (ou centro de massa). Isso quer dizer que, se apoiarmos um objeto em seu baricentro, ele ficará em equilíbrio.

Página 139

Alturas de um triângulo

As alturas de um triângulo são as cevianas que têm uma extremidade em um dos vértices do triângulo e a outra extremidade na reta suporte do lado oposto ao vértice, formando um ângulo cuja abertura mede 90graus com essa reta.

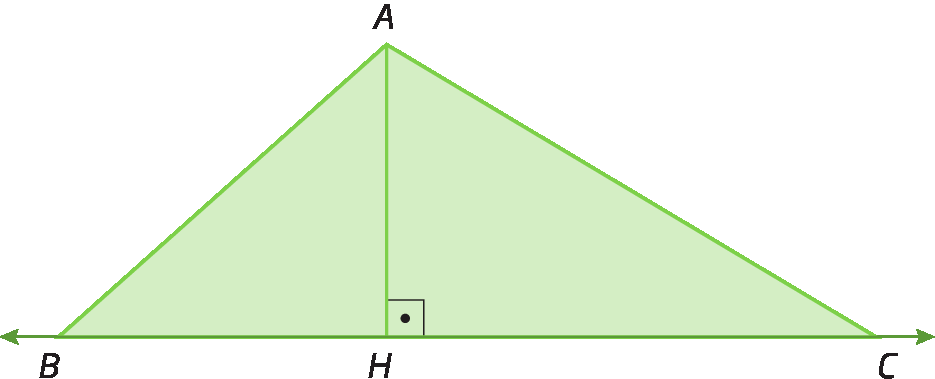
Figura geométrica. Triângulo ABC. Sobre o lado BC está representada uma reta. Há um ponto H representado entre os pontos B e C. Há também um segmento de reta com extremidades no ponto A e ponto H que forma um ângulo de 90 graus com o lado BC.

\overline{A H}

é a altura relativa ao lado

\overline{B C}

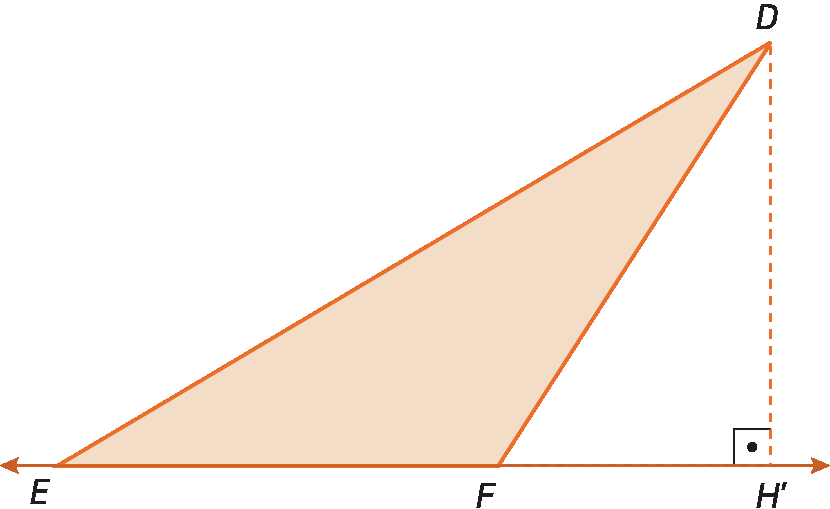
Figura geométrica. Triângulo DEF. Sobre o lado EF está representada uma reta. Há um ponto H linha representado à direita do ponto F, na reta. Há também um segmento de reta tracejado com extremidades no ponto D e ponto H linha que forma um ângulo de 90 graus com a reta.

\overline{D H'}

é a altura relativa ao lado

\overline{E F}

A intersecção das retas suporte das três alturas determina um ponto chamado ortocentro (H).

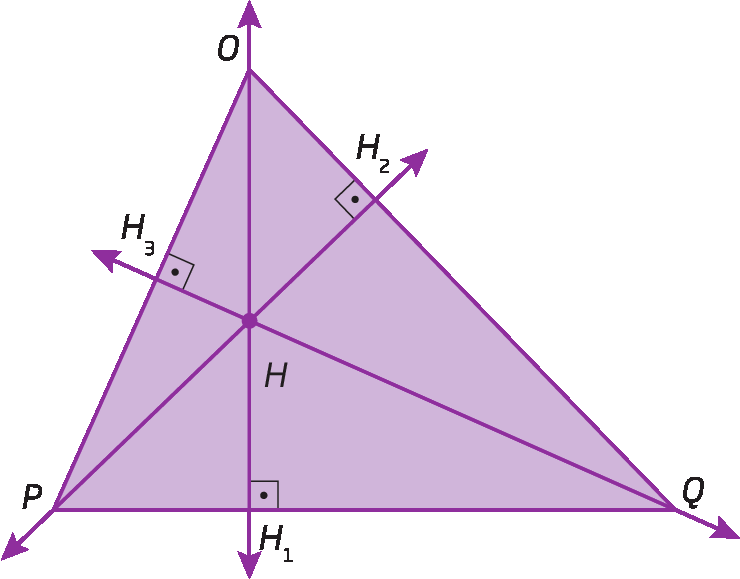
Figura geométrica. Triângulo OPQ acutângulo. Estão representados sobre o triângulo 3 retas. Uma reta passa pelo ponto O e pelo ponto H1 que está no lado PQ, formando com o lado PQ um ângulo de 90 graus. A outra reta. passa pelo ponto P e pelo ponto H2 que está no lado OQ, formando com o lado OQ um ângulo de 90 graus. Já a outra reta, passa pelo ponto Q e pelo ponto H3 que está no lado OP, formando com o lado OP um ângulo de 90 graus. As três retas se intersectam no interior do triângulo no ponto H.

H é o ortocentro do triânguloOPQ.

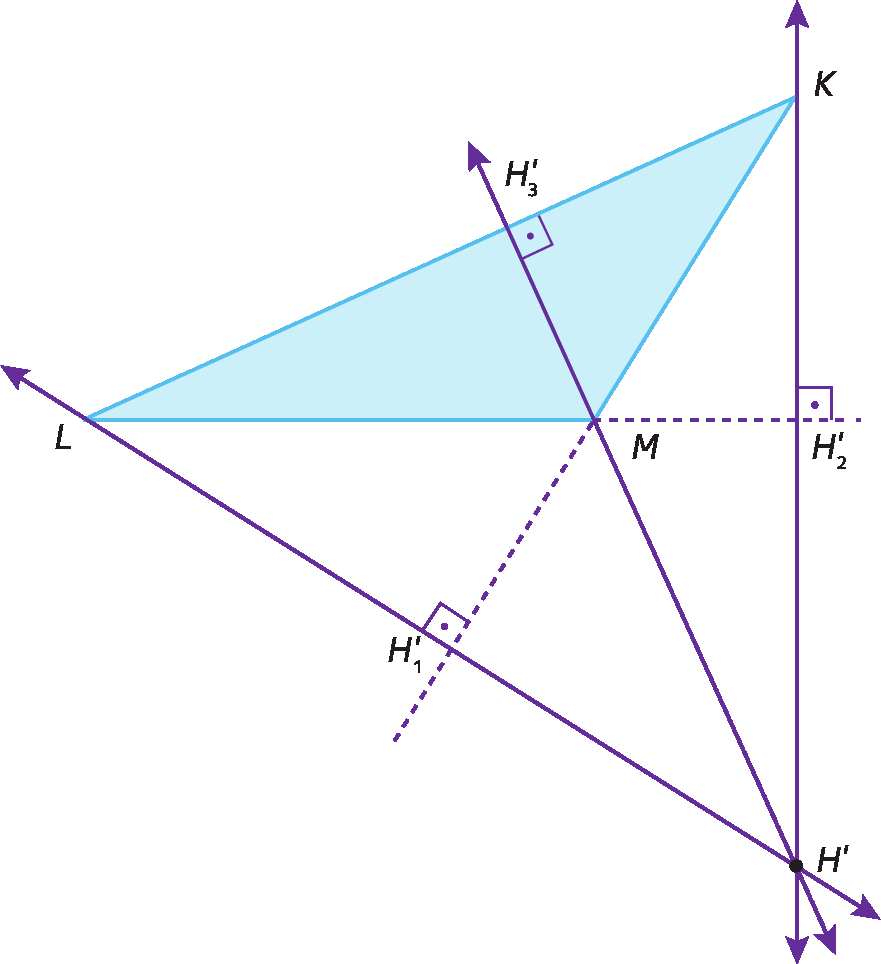
Figura geométrica. Triângulo KLM obtusângulo.. Estão representados sobre o triângulo 3 retas. Uma reta passa pelo ponto K e pelo ponto H2 linha que está no prolongamento do lado LM, formando com o prolongamento deste lado um ângulo de 90 graus. A outra reta. passa pelo ponto M e pelo ponto H3 linha que está no lado KL, formando com o lado KL um ângulo de 90 graus. Já a outra reta, passa pelo ponto L e pelo ponto H1 linha e forma 90 graus com o prolongamento do lado KM. As três retas se intersectam no ponto H linha, exterior ao triângulo.

H’ é ortocentro do triânguloKLM.

Observações

1. No triângulo acutângulo, o ortocentro é interno ao triângulo.

2. No triângulo retângulo, o ortocentro coincide com o vértice do ângulo reto.

3. No triângulo obtusângulo, o ortocentro é externo ao triângulo.

Bissetrizes de um triângulo

As bissetrizes internas de um triângulo são as cevianas que têm uma extremidade em um dos vértices do triângulo e a outra extremidade no lado oposto a esse vértice, dividindo cada ângulo interno em dois ângulos congruentes.

Neste triângulo á bê cê,

\overline{A D}

é a bissetriz interna relativa ao ângulo

B \hat{A} C

Figura geométrica. Triângulo ABC. Sobre o lado BC está representado o ponto D, Está representado também um segmento de reta com extremidades no ponto A e D, de modo que a medida da abertura do ângulo BAD é igual a medida da abertura do ângulo DAC.

m e d (B \hat{A} D) = m e d (D \hat{A} C)

Página 140

O ponto de intersecção das três bissetrizes de um triângulo é denominado incentro (I).

A bissetriz equidista dos lados que formam um ângulo; então, como o incentro é a intersecção das bissetrizes, esse ponto é equidistante dos três lados do triângulo, ou seja, a medida da distância entre o incentro e qualquer um dos lados do triângulo é sempre a mesma.

Essa propriedade permite traçar uma circunferência de centro I que intercepta cada lado do triângulo em um único ponto (dê linha em

\overline{B C}

, é linha em

\overline{A C}

e éfe linha em

\overline{A B}

). Essa circunferência é inscrita ao triângulo.

Figura geométrica. Triângulo ABC. Estão representadas as bissetrizes AD, BE e CF. As bissetrizes se intersectam no ponto I que é interior ao triângulo. Também está representada uma circunferência de centro I que tangencia o lado AB no ponto F linha, o lado AC no ponto E linha e o lado BC no ponto D linha.

ih é o incentro do triânguloá bê cê,

\overline{I D'} ≅ \overline{I E'} ≅ \overline{I F'}

Observações

1. As mediatrizes de um triângulo são as mediatrizes de seus lados, ou seja, são as retas perpendiculares às retas suporte dos lados que passam pelo ponto médio do lado correspondente.

2. As mediatrizes dos lados de um triângulo se interceptam em um ponto chamado circuncentro (O).

3. A mediatriz equidista dos extremos de um segmento de reta; então, como o circuncentro é a intersecção das mediatrizes, esse ponto é equidistante dos três vértices do triângulo, ou seja, a medida da distância entre o circuncentro e qualquer um dos vértices do triângulo é sempre a mesma. Essa propriedade permite traçar uma circunferência de centro O que passa pelos três vértices do triângulo. Essa circunferência é circunscrita ao triângulo.

4. Em alguns triângulos, assim como ocorre com o ortocentro, o circuncentro pode ser interno ou externo ao triângulo.

5. O baricentro, o ortocentro, o incentro e o circuncentro são chamados de pontos notáveis de um triângulo.

Figura geométrica. Triângulo ABC. Estão representadas as 3 mediatrizes. que intersectam no ponto O, interior ao triângulo. Também está representada uma circunferência de centro O e que passam pelos pontos A, B e C.

Atividades

Faça as atividades no caderno.

Cuidado! Evite acidentes ao usar o compasso nas atividades 3, 4 e 6.

3. Utilizando régua e compasso, copie este triângulo no caderno, trace suas medianas e determine seu baricentro.

4. Utilizando régua e compasso, construa, no caderno, um triângulo cujos lados tenham medidas de comprimento iguais a 6 centímetros, 5 centímetros e 8 centímetros. Em seguida, trace suas bissetrizes e determine seu incentro.

5. No caderno, desenhe um triângulo cujos lados tenham medidas de comprimento iguais a 7 centímetros, 4 centímetros e 6 centímetros. Em seguida, determine o encontro das alturas desse triângulo (ortocentro).

6. No caderno, desenhe um triângulo cujos lados tenham medidas de comprimento iguais a 6 centímetros, 7 centímetros e 8 centímetros. Depois, faça o que se pede.

a) Trace as mediatrizes dos lados, determinando o circuncentro do triângulo. Então, com o auxílio de um compasso, trace uma circunferência que circunscreva esse triângulo.

b) Trace as bissetrizes dos ângulos, determinando o incentro do triângulo. Então, com o auxílio de um compasso, trace uma circunferência inscrita nesse triângulo.

Página 141

Tecnologias digitais em foco

Pontos notáveis de triângulos isósceles e equiláteros

Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para explorar propriedades dos pontos notáveis de triângulos isósceles e equiláteros.

Construa

Siga os passos seguintes para construir um triângulo isósceles.

1º) Utilize a ferramenta

Ilustração. Botão da ferramenta Segmento do software GeoGebra.

e trace um segmento de reta

\overline{A B}

qualquer.

2º) Utilize a ferramenta

Ilustração. Botão da ferramenta Circunferência dado centro e um ponto do software GeoGebra.

e trace a circunferência com centro em a passando por B.

3º) Escolha um ponto C qualquer na circunferência e, com a ferramenta

Ilustração. Botão da ferramenta Polígono do software GeoGebra.

, construa o triângulo com vértices nos pontos a, B e C.

Print. Tela do software GeoGebra. Na parte superior, há uma barra com diversos botões. Da esquerda para a direita, os botões correspondem às ferramentas: mover, ponto, reta, reta perpendicular, polígono, circunferência, elipse, ângulo, reflexão, controle deslizante e mover janela.. O botão polígono aparece selecionado e abaixo deste botão aparecem, de cima para baixo, os botões que correspondem às seguintes ferramentas: Polígono; Polígono Regular; Polígono Rígido e Polígono semideformável.
No canto superior direito aparecem os botões minimizar, maximizar e fechar.
Na tela está representada uma circunferência de centro A e um triângulo ABC, sendo B e C, pontos da circunferência. — O triângulo á bê cê é isósceles, pois A bê = á cê (medidas de comprimento dos raios da circunferência).

4º) Utilize as ferramentas

Ilustração. Botão da ferramenta Ponto médio ou Centro do software GeoGebra.

e trace as medianas do triângulo. Depois, determine o baricentro (G).

5º) Esconda as construções, deixando visíveis apenas a mediana relativa à base e o baricentro.

6º) Utilize as ferramentas

Ilustração. Botão da ferramenta Reta perpendicular do software GeoGebra.

e trace as alturas do triângulo. Depois, determine o ortocentro (H).

7º) Esconda as construções, deixando visíveis apenas a altura relativa à base e o ortocentro.

8º) Utilize as ferramentas

Ilustração. Botão da ferramenta Bissetriz do software GeoGebra.

e trace as bissetrizes dos ângulos internos do triângulo. Depois, determine o incentro (ih ).

9º) Esconda as construções, deixando visíveis apenas a bissetriz relativa ao ângulo oposto à base e o incentro.

10º) Utilize a ferramenta

Ilustração. Botão da ferramenta Mediatriz do software GeoGebra.

e trace as mediatrizes dos lados do triângulo. Depois, determine o circuncentro (óh).

Página 142

11º) Esconda as construções, deixando visíveis apenas a mediatriz relativa à base e o circuncentro.

Explore

a) Movimente os vértices do triângulo isósceles construído a fim de modificar sua configuração. O que acontece com a mediatriz, a altura e a mediana relativas à base

\overline{B C}

e com a bissetriz relativa ao ângulo oposto a essa base?

b) Os pontos notáveis do triângulo isósceles construído estão alinhados? Isso acontece mesmo quando você movimenta os vértices do triângulo?

c) Construa um triângulo equilátero e determine seus pontos notáveis (baricentro, ortocentro, incentro e circuncentro). Depois, movimente os vértices do triângulo. O que você nota em relação aos pontos notáveis?

2 Congruência de triângulos

Analise estes triângulos.

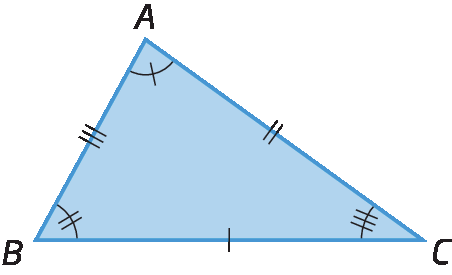
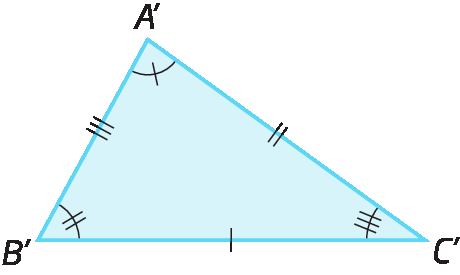
Figura geométrica. Triângulos ABC e A linha, B linha e C linha. Lado AB congruente ao lado A linha B linha. Lado AC congruente ao lado A linha C linha. Lado BC congruente ao lado B linha C linha. Ângulo A congruente ao ângulo A linha; ângulo B congruente ao ângulo B linha; ângulo C congruente ao ângulo C linha.

Note que esses triângulos têm três pares de lados congruentes e três pares de ângulos congruentes. Se os recortássemos, poderíamos sobrepor um ao outro sem sobras ou faltas. Nesse caso, dizemos que esses triângulos são congruentes entre si. Podemos escrever:

\overline{A B} ≅ \overline{A' B'}

\hat{A} ≅ \hat{A}'

\overline{A C} ≅ \overline{A' C'}

\hat{B} ≅ \hat{B}'

\overline{B C} ≅ \overline{B' C'}

\hat{C} ≅ \hat{C}'

Página 143

Logo, o triângulo á bê cê é congruente ao triângulo á linha bê linha cê linha. Indicamos essa congruência assim:

triânguloá bê cê ≅triânguloá linha bê linha cê linha

Dois triângulos são congruentes quando os lados correspondentes e os ângulos correspondentes são congruentes.

Podemos concluir que dois triângulos são congruentes mesmo sem conhecer todas as medidas de comprimento dos lados e as medidas de abertura dos ângulos. Verifique a seguir os casos de congruência de triângulos.

1º caso de congruência: éle á éle (Lado-Ângulo-Lado)

Dois triângulos são congruentes quando dois lados e o ângulo compreendido entre eles são, respectivamente, congruentes.

Confira os triângulos á bê cê e á linha bê linha cê linha.

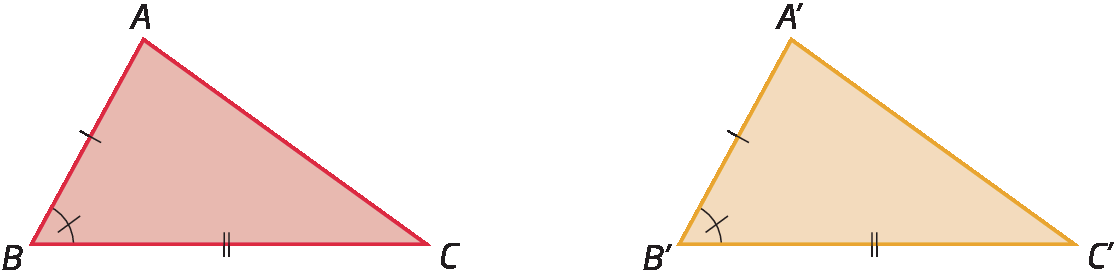
Figura geométrica. Triângulo ABC ao lado do triângulo A linha, B linha, C linha. Lado AB congruente ao lado A linha B linha. Ângulo B congruente ao ângulo B linha. Lado BC congruente ao lado B linha C linha. Implica que triângulo ABC é congruente ao triângulo A linha B linha C linha.

Temos:

Ilustração. Mulher amarela, cabelo preto, jaleco de professora, dizendo que O símbolo representado por uma seta significa que, se as afirmações à sua esquerda são verdadeiras, então as afirmações à sua direita também são verdadeiras.

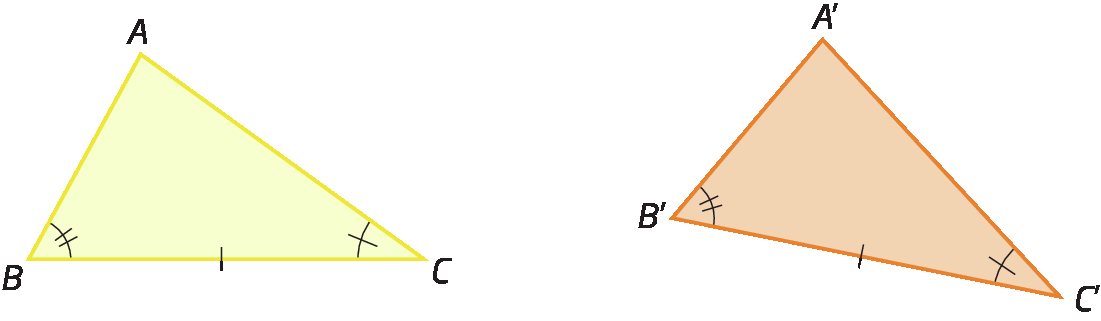
2º caso de congruência: á éle á (Ângulo-Lado-Ângulo)

Dois triângulos são congruentes quando um lado e dois ângulos adjacentes a esse lado são, respectivamente, congruentes.

Analise os triângulos á bê cê e á linha bê linha cê linha.

Figura geométrica. Triângulo ABC ao lado do triângulo A linha, B linha, C linha. Ângulo B congruente ao ângulo B linha. Lado BC congruente ao lado B linha C linha. Ângulo C congruente ao ângulo C linha. Implica que triângulo ABC é congruente ao triângulo A linha B linha C linha.

Temos:

Página 144

3º caso de congruência: éle éle éle (Lado-Lado-Lado)

Dois triângulos são congruentes quando os três lados são, respectivamente, congruentes.

Verifique os triângulos á bê cê e á linha bê linha cê linha.

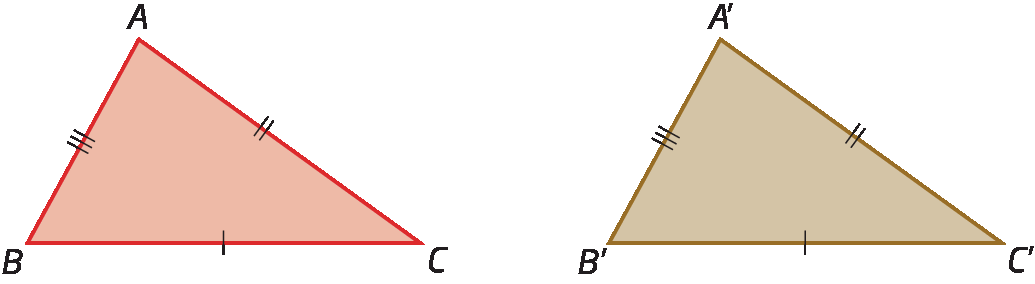
Figura geométrica. Triângulo ABC ao lado do triângulo A linha, B linha, C linha. Lado AB congruente ao lado A linha B linha. Lado AC congruente ao lado A linha C linha. Lado BC congruente ao lado B linha C linha. Implica que triângulo ABC é congruente ao triângulo A linha B linha C linha.

Temos:

4º caso de congruência: éleaAo (Lado-Ângulo-Ângulo oposto)

Dois triângulos são congruentes quando um lado, um ângulo adjacente e o ângulo oposto a esse lado são, respectivamente, congruentes.

Confira os triângulos á bê cê e á linha bê linha cê linha.

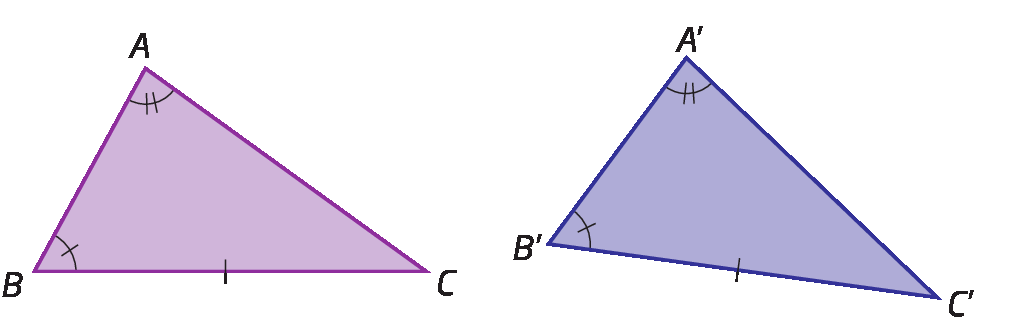
Figura geométrica. Triângulo ABC ao lado do triângulo A linha, B linha, C linha. Lado BC congruente ao lado B linha C linha. Ângulo B congruente ao ângulo B linha. Ângulo A congruente ao ângulo A linha. Implica que triângulo ABC é congruente ao triângulo A linha B linha C linha.

Temos:

Atividades

Faça as atividades no caderno.

7. Em cada item, verifique se os triângulos são congruentes e, em caso afirmativo, indique o caso correspondente.

Figura geométrica. Triângulo retângulo ABC ao lado de triângulo retângulo DEF. Comprimento do lado AB medindo 3 vírgula 2 centímetros; comprimento do lado AC medindo 3 vírgula 6 centímetros. Comprimento do lado DE medindo 3 virgula 2 centímetros; comprimento do lado EF medindo 3 vírgula 6 centímetros.

Figura geométrica. Triângulo ABC ao lado de triângulo DEF. Abertura do angulo A medindo 70 graus, abertura do angulo C medindo 30 graus e comprimento do lado AC medindo 3 centímetros. Abertura do ângulo D medindo 30 graus, abertura do ângulo F medindo 70 graus e comprimento do lado DF medindo 3 centímetros.

Figura geométrica. Triângulo retângulo ABC ao lado de triângulo retângulo DEF. Abertura do ângulo A medindo 60 graus, abertura do ângulo C medindo 30 graus. Abertura do ângulo D medindo 31 graus, ângulo F medindo 59 graus.

Figura geométrica. Triângulo ABC acima do triângulo DEF. Abertura do ângulo A medindo 30 graus, comprimento do lado AB medindo 5 centímetros e comprimento do lado AC medindo 5 centímetros. Abertura do ângulo D medindo 30 graus, comprimento do lado DE medindo 5 centímetros e comprimento do lado DF medindo 5 centímetros.

Página 145

Figura geométrica. Triângulo retângulo ABC ligado pelo vértice C ao triângulo retângulo CDE. Lado BC medindo 5 centímetros. Lado CD medindo 5 centímetros.

8. Os triângulos de cada item são congruentes. Indique qual caso garante a congruência e quais são os ângulos e lados correspondentes que justificam o caso de congruência.

a) triânguloá dê bê e triânguloCBD

Figura geométrica. Triângulo ABD unido ao triângulo CBD pelo lado BD. Lado BC congruente ao lado AD. Ângulo B congruente ao ângulo D.

b) triânguloCAD e triânguloCBD

Figura geométrica. Triângulo CAD retângulo em D unido ao triângulo CBD, retângulo em D, pelo lado CD. Ângulo C com mesma medida em ambos os triângulos.

9. Por que podemos afirmar que

\overline{A M} ≅ \overline{M B}

Figura geométrica. Triângulo ACM retângulo em A unido pelo vértice M ao triângulo BDM retângulo em B. Lado CM congruente ao lado DM.

10. No quadrado a bê cê dê, M é o ponto médio de

\overline{A B}

. Prove que

\overline{M C} ≅ \overline{M D}

Figura geométrica. Quadrado ABCD. No lado AB, ponto M do qual saem dois segmentos de reta, um até o vértice D, formando o triângulo ADM, e outro até o vértice C, formando o triângulo BCM. Também forma-se o triângulo CDM.

11. Justifique a congruência dos triângulos na figura a seguir.

Figura geométrica. Segmento AD e segmento BC concorrentes no ponto M. Formam-se os triângulos AMB e CMF na cor lilás. Os lados BM, do triângulo AMB, e DM, do triângulo CMD, são congruentes e os ângulos B, do triângulo AMB, e D do triângulo CMD, são congruentes.

3 Justificativas de algumas propriedades e construções com régua e compasso

Demonstração da propriedade dos ângulos internos de um triângulo equilátero

Vamos demonstrar que, em qualquer triângulo equilátero, os três ângulos internos são congruentes, com 60graus de medida de abertura cada um.

Considere o triângulo equilátero á bê cê a seguir e a mediana

\overline{C M}

relativa ao lado

\overline{A B} .

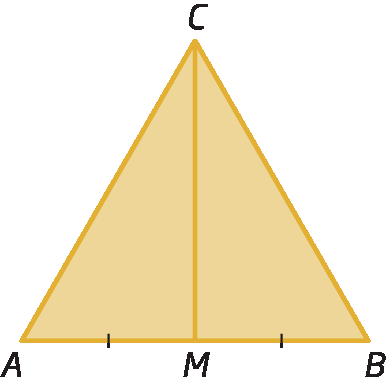
Figura geométrica. Triângulo ABC, sendo CM a mediana ao lado AB, de modo que AM é congruente ao lado MB.

Temos que:

•

\overline{C M}

é lado comum.

•

\overline{M A} ≅ \overline{M B}

, pois M é ponto médio de

\overline{A B}

•

\overline{C A} ≅ \overline{C B}

, pois triânguloá bê cê é um triângulo equilátero.

Logo, pelo caso éle éle éle: triângulocê ême á ≅ triânguloCMB.

Portanto,

\hat{A} ≅ \hat{B}

(um)

Página 146

Considere agora a mediana

\overline{B N}

relativa ao lado

\overline{C A} .

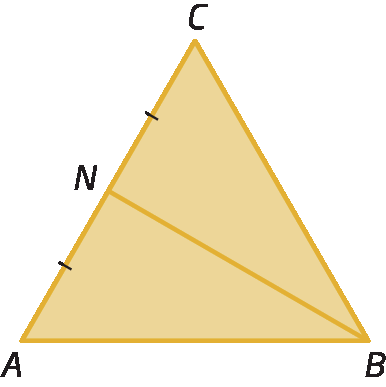
Figura geométrica. Triângulo ABC, mediana BN dividindo o lado AC em duas partes congruentes.

Temos que:

•

\overline{B N}

é lado comum.

•

\overline{N C} ≅ \overline{N A}

, pois N é ponto médio de

\overline{A C}

•

\overline{C B} ≅ \overline{A B}

, pois triânguloá bê cê é um triângulo equilátero.

Logo, pelo caso éle éle éle: triânguloBNC ≅ triânguloBNAponto

Portanto,

\hat{C} ≅ \hat{A}

(II)

De um e dois, temos:

\hat{A} ≅ \hat{B} ≅ \hat{C}

Como

m e d (\hat{A}) + m e d (\hat{B}) + m e d (\hat{C}) = 180 °

, temos que:

m e d (\hat{A}) = m e d (\hat{B}) = m e d (\hat{C}) = 60 °

Assim, demonstramos que os ângulos internos de um triângulo equilátero são congruentes e medem, cada um, 60graus de abertura.

Justificativa da construção da bissetriz

A bissetriz do ângulo

A \hat{O} B

foi construída seguindo o procedimento apresentado no capítulo 4.

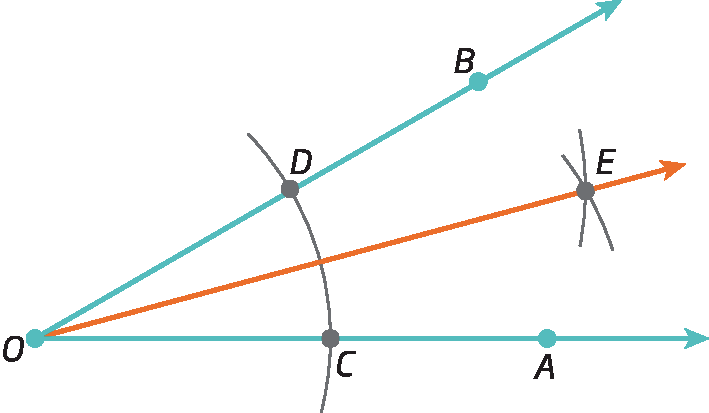
Figura geométrica. Semirreta OA forma ângulo com a semirreta OB. Semirreta OE é bissetriz do ângulo AOB. Na semirreta OA está o ponto C e na semirreta OB está o ponto D. Há um arco que passa por C e D. No ponto E há um cruzamento de dois pequenos arcos.

Vamos verificar que, de fato, com os passos realizados,

\vec{O E}

é a bissetriz do ângulo

A \hat{O} B

Considere o triânguloDOE e o triânguloCOE.

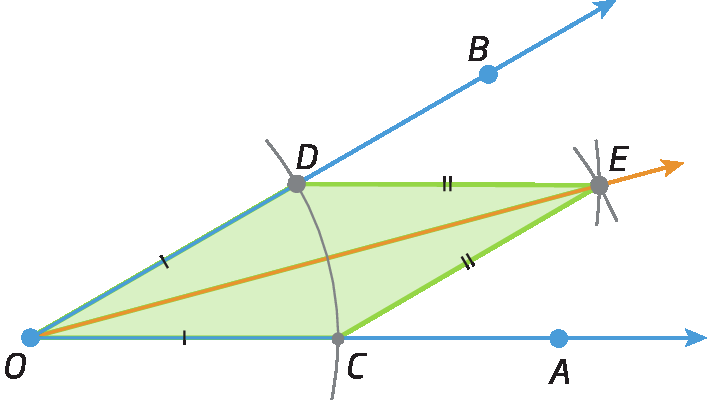
Com base na construção realizada, temos que

\overline{O D} ≅ \overline{O C}

\overline{D E} ≅ \overline{C E}

\overline{O E}

é lado comum aos triângulos.

Logo, pelo caso éle éleéle: triânguloDOE ≅ triânguloCOEponto

Então,

B \hat{O} E ≅ A \hat{O} E

e, portanto,

\vec{O E}

é a bissetriz do ângulo

A \hat{O} B

Página 147

Demonstração da propriedade dos ângulos da base de um triângulo isósceles

Vamos demonstrar que, em todo triângulo isósceles, os ângulos da base são congruentes.

Considere o triângulo isósceles á bê cê a seguir com

\overline{C A} ≅ \overline{C B}

, sendo

\overline{C I}

a bissetriz relativa ao ângulo

\hat{C}

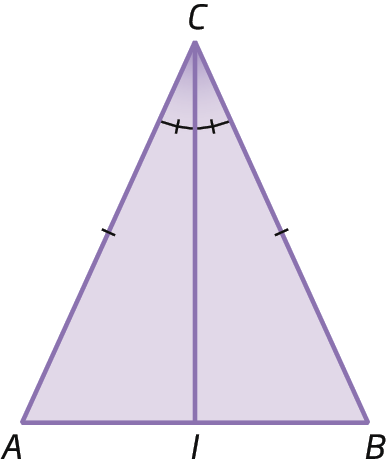
Figura geométrica. Triângulo ABC. Segmento de reta CI, dividindo o ângulo C em dois congruentes entre si. Ponto I no segmento de reta AB. Lado AC congruente ao lado BC.

Temos que:

•

\overline{C I}

é lado comum.

•

I \hat{C} A ≅ I \hat{C} B

, pois

\overline{C I}

é bissetriz.

•

\overline{C A} ≅ \overline{C B}

, pois triânguloá bê cê é um triângulo isósceles.

Logo, pelo caso éle á éle: triânguloCIA ≅ triângulocê í bêponto

Portanto,

\hat{A} ≅ \hat{B}

Assim, concluímos que os ângulos da base de um triângulo isósceles são congruentes.

Justificativa da construção do ângulo de medida da abertura de 60graus

O ângulo de medida da abertura de 60graus da figura a seguir foi construído seguindo o procedimento apresentado no capítulo 4.

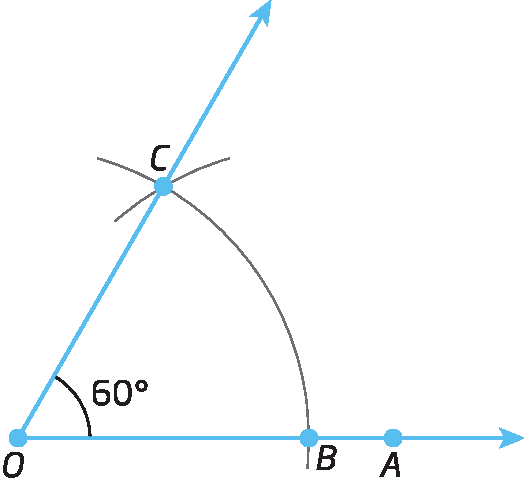
Figura geométrica. Abertura de ângulo medindo 60 graus. Os lados do ângulo são compostos pelas semirretas OA e OC. Há um ponto B sobre a semirreta OA. Há um arco que passa pelo pontos B e C.

Vamos verificar que, de fato, com os passos realizados, a abertura de

B \hat{O} C

mede 60graus.

Considere o triânguloó bê cê.

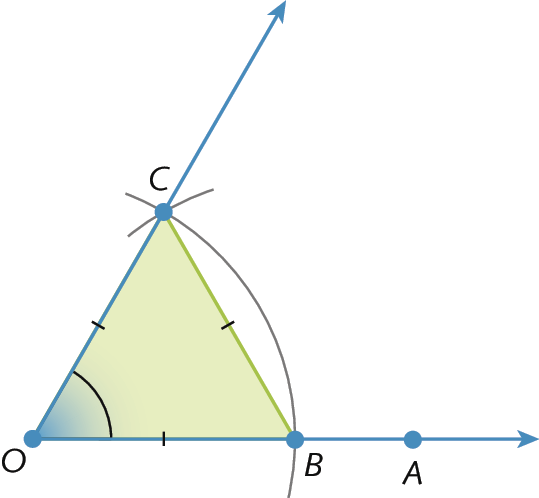
Figura geométrica. Abertura de ângulo feita com semirretas OA e OC, ângulo em O. Arco BC, sendo B em OA. Segmento de reta liga os pontos B e C, formando o triângulo OBC, de modo que todos os lados dele são congruentes entre si.

Com base na construção realizada, temos que

\overline{O C} ≅ \overline{O B} ≅ \overline{C B}

Logo, o triânguloó bê cê é equilátero e, portanto, seus ângulos internos medem 60graus de abertura.

Então,

m e d (B \hat{O} C) = 60 °

Página 148

Justificativa da construção do triângulo equilátero

O triângulo equilátero a seguir foi construído seguindo o procedimento apresentado no capítulo 5.

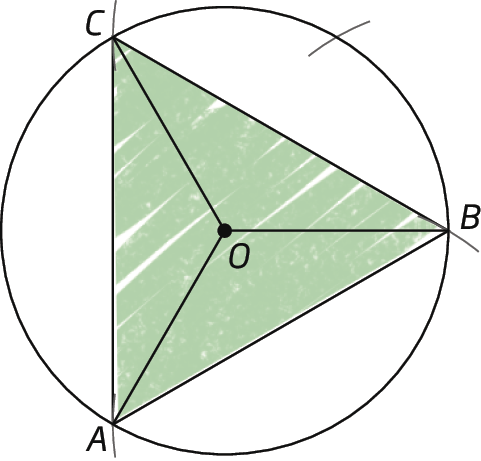
Figura geométrica. Triângulo ABC inscrito a uma circunferência. Dos vértices saem semirretas que se encontram no ponto O, centro da circunferência e interno ao triângulo.

Vamos verificar que, de fato, com os passos realizados, o triângulo construído é equilátero.

Com base na construção realizada, sabemos que a abertura de cada ângulo central mede 120graus (360graus : 3 = 120graus), ou seja,

m e d (A \hat{O} B) = m e d (B \hat{O} C) = m e d (C \hat{O} A) = 120 °

Além disso,

\overline{A O} ≅ \overline{B O} ≅ \overline{C O}

, pois esses segmentos de reta correspondem a raios da circunferência e, portanto, têm a mesma medida de comprimento.

Logo, pelo caso éle á éle: triânguloá ó bê ≅ triângulobê ó cê ≅ triânguloCOAponto

Assim:

\overline{A B} ≅ \overline{B C} ≅ \overline{C A}

e, portanto, o triânguloá bê cê é um triângulo equilátero.

Justificativa da construção do quadrado

O quadrado a seguir foi construído seguindo o procedimento apresentado no capítulo 5.

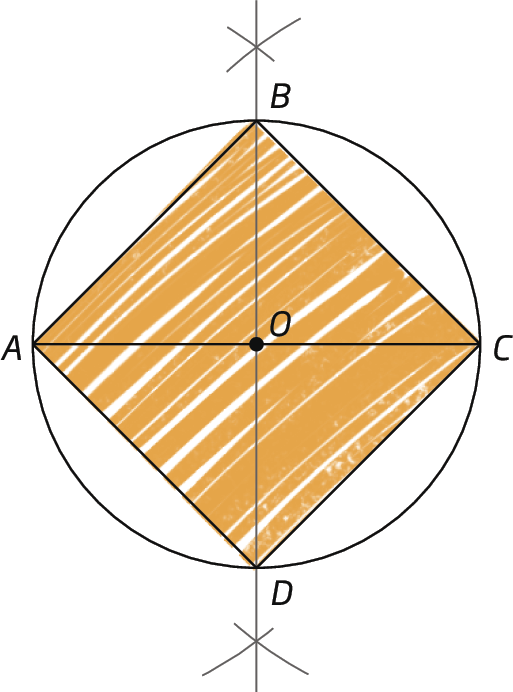
Figura geométrica. Quadrado ABCD inscrito a uma circunferência. Diagonal BD se encontra com diagonal AC no ponto O, centro da circunferência e interno ao quadrado. Internos ao quadrado, há 4 triângulos: AOD, DOC, COB e BOA

Vamos verificar que, de fato, com os passos realizados, o quadrilátero obtido é um quadrado.

Com base na construção realizada, sabemos que a abertura de cada ângulo central mede 90graus (360graus : 4 = 90graus), ou seja,

m e d (A \hat{O} D) = m e d (D \hat{O} C) = m e d (C \hat{O} B) = m e d (B \hat{O} A) = 90 °

Além disso,

\overline{A O} ≅ \overline{D O} ≅ \overline{C O} ≅ \overline{B O}

, pois esses segmentos de reta correspondem a raios da circunferência e, portanto, têm a mesma medida de comprimento.

Logo, pelo caso éle á éle: triânguloAOD ≅ triânguloDOC ≅ triângulocê ó bê ≅ triânguloBOA

Assim:

\overline{A D} ≅ \overline{D C} ≅ \overline{C B} ≅ \overline{B A}

e, portanto, o quadrilátero a bê cê dê é um quadrado.

Página 149

Demonstração da propriedade da mediana, altura e bissetriz de um triângulo isósceles

Vamos demonstrar que, em qualquer triângulo isósceles, a mediana e a altura relativas à base coincidem com a bissetriz relativa ao ângulo oposto à base.

Considere o triângulo isósceles á bê cê a seguir com

\overline{A B} ≅ \overline{A C}

e mediana

\overline{A M}

relativa à base

\overline{B C}

Figura geométrica. Triângulo ABC. Segmento de reta AM, sendo o ponto M no segmento de reta BC, dividindo o triângulo em outros dois: ABM e ACM, sendo o lado AM comum aos dois. Lado AB congruente ao lado AC. Lado BM congruente ao lado CM.

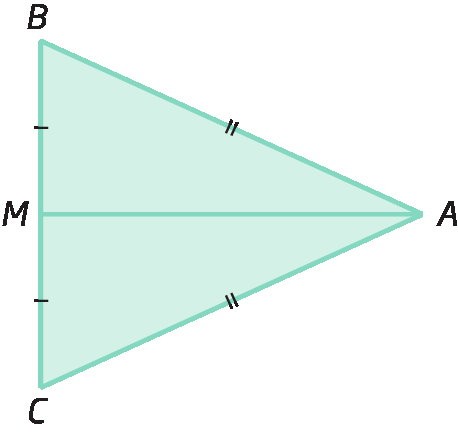
Primeiro, vamos demonstrar que

\overline{A M}

também é a bissetriz relativa ao ângulo

\hat{A}

Considerando os triângulos á ême bê e á ême cê, temos que:

•

\overline{A M}

é lado comum.

•

\overline{B M} ≅ \overline{C M}

, pois M é ponto médio de

\overline{B C}

•

\overline{A B} ≅ \overline{A C}

, pois △á bê cê é um triângulo isósceles.

Logo, pelo caso éle éle éle: △á ême bê ≅ △á ême cêponto

Assim:

M \hat{A} B ≅ M \hat{A} C

e, portanto,

\overline{A M}

é a bissetriz relativa ao ângulo

\hat{A}

Agora, vamos demonstrar que

\overline{A M}

também é a altura relativa à base

\overline{B C}

Como △á ême bê ≅ △á ême cê, temos:

A \hat{M} B ≅ A \hat{M} C

Além disso,

A \hat{M} B e A \hat{M} C

são ângulos suplementares, ou seja,

m e d (A \hat{M} B) + m e d (A \hat{M} C) = 180 °

Dessa forma, temos:

2 \cdot m e d (A \hat{M} B) = 180 °

, ou seja,

m e d (A \hat{M} B) = 90 °

Portanto,

\overline{A M}

é a altura relativa à base

\overline{B C}

Atividades

Faça a atividade no caderno.

12.

A mediatriz do segmento de reta

\overline{A B}

foi construída seguindo o procedimento apresentado no capítulo 4.

Figura geométrica. Segmento de reta AB com pontos C e D acima e abaixo dele, respectivamente. Pontos C e D ligados por uma reta, que corta perpendicularmente o segmento AB no ponto M

Reúna-se com um colega e verifiquem que, de fato, com os passos realizados,

\overset{\leftrightarrow}{C D}

é a mediatriz do segmento de reta

\overline{A B}

Dica: Considere os triângulos á cê dê e BCD e os triângulos A cê bê e á dê bê.

Página 150

4 Quadriláteros

O quadrilátero é um polígono de quatro lados. Verifique alguns elementos do quadrilátero a bê cê dê a seguir.

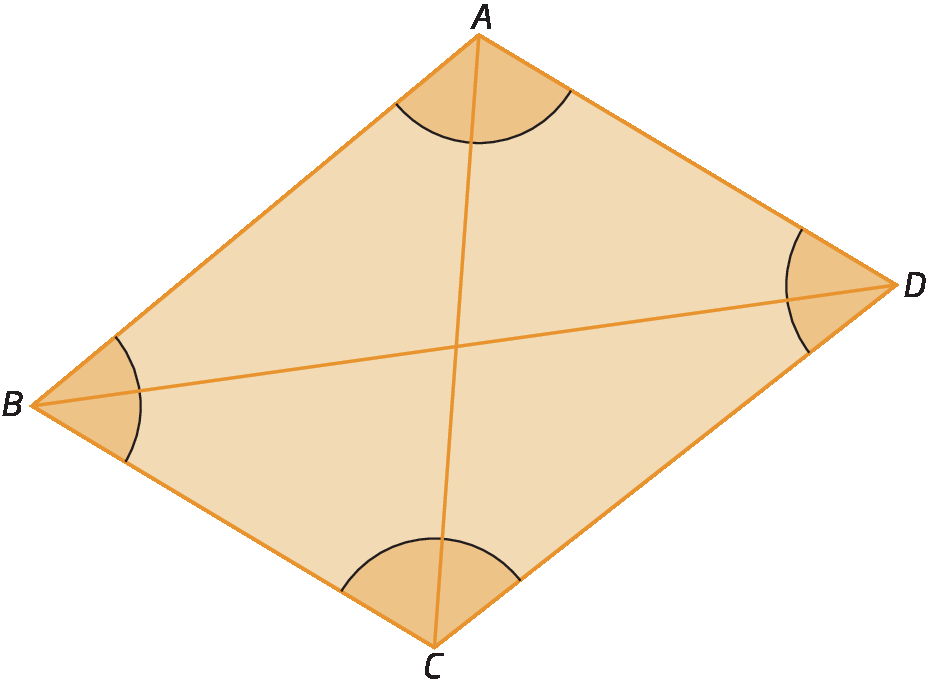
Figura geométrica. Quadrilátero ABCD com 4 ângulos demarcados e diagonais AC e BD traçadas.

• Vértices: a, B, C e D.

• Lados:

\overline{A B}, \overline{B C}, \overline{C D} e \overline{D A}

• Diagonais:

\overline{A C} e \overline{B D}

• Ângulos internos:

\hat{A}, \hat{B}, \hat{C} e \hat{D}

Ilustração. Mulher loira, branca, com jaleco de professora dizendo: Dois ângulos são adjacentes quando, ao contornarmos o polígono, um ângulo vem em seguida do outro. Por exemplo, no quadrilátero ABCD, ângulo A e ângulo B , ângulo B e ângulo C são pares de ângulos adjacentes.

Em um quadrilátero, dois lados ou dois ângulos não adjacentes são chamados opostos. Então, no quadrilátero a bê cê dê, temos:

•

\overline{A B} e \overline{C D}, \overline{B C} e \overline{D A}

são pares de lados opostos;

•

\hat{A} e \hat{C}, \hat{B} e \hat{D}

são pares de ângulos opostos.

Assim como qualquer outro polígono, um quadrilátero pode ser convexo ou não convexo. Para ser convexo, é necessário que todos os segmentos de reta, com extremidades no interior do quadrilátero, tenham todos os seus pontos situados no interior desse quadrilátero. Uma consequência disso é que a medida de abertura de qualquer ângulo interno de um quadrilátero convexo é menor que 180graus.

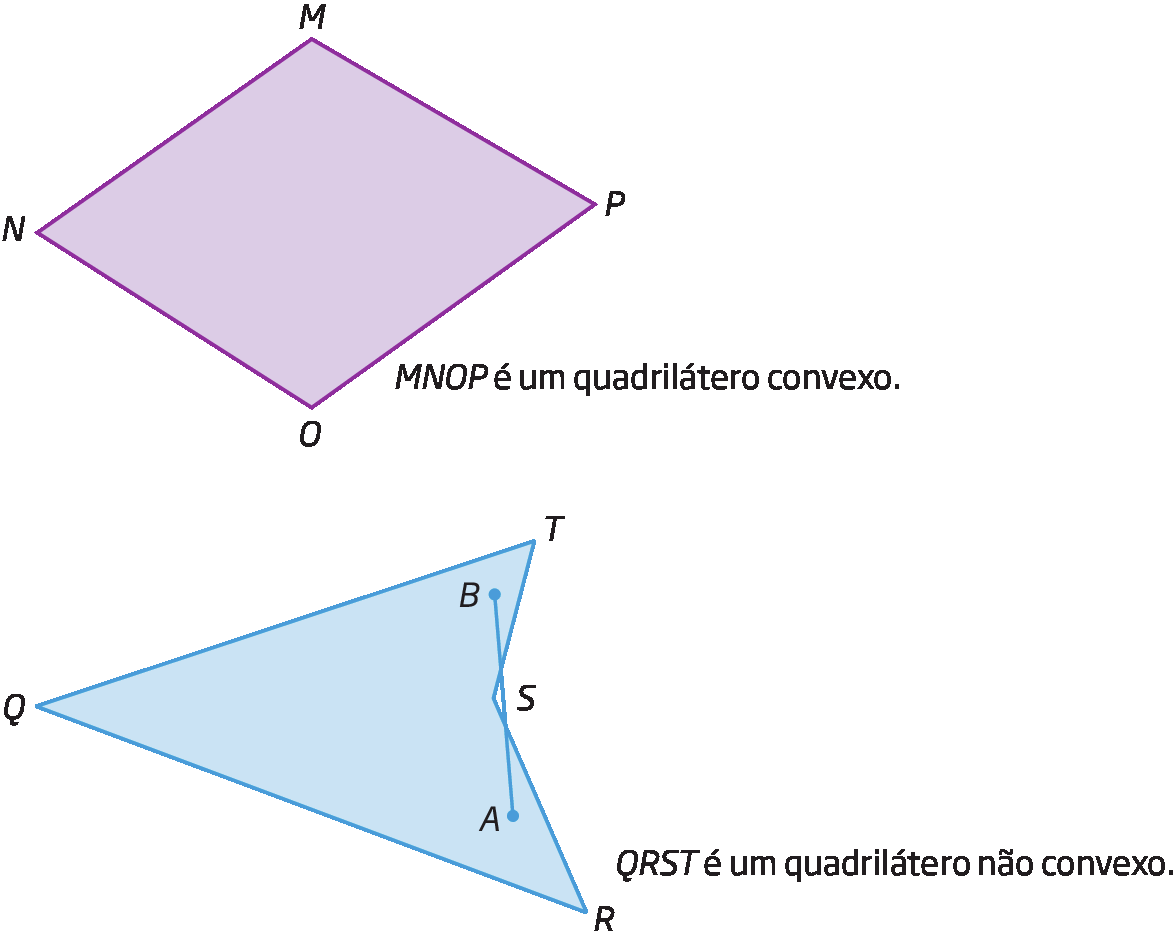
Figura geométrica. Quadrilátero MNOP convexo.

Figura geométrica. Quadrilátero QRST não convexo. Segmento de reta AB passando pelos lados TS e SR e tendo alguns de seus pontos externos ao quadrilátero.

Vamos estudar apenas os quadriláteros convexos.

Página 151

Atividades

Faça as atividades no caderno.

13. Analise este quadrilátero ême êne ó pê.

Figura geométrica. Quadrilátero convexo MNOP. Diagonais NP e MO.

Agora, no caderno, identifique:

a) os vértices;

b) os lados;

c) o lado oposto ao lado

\overline{M P}

;

d) as diagonais;

e) o ângulo oposto ao ângulo

\hat{P}

14.

Desenhe dois quadriláteros não convexos e dois quadriláteros convexos. Em seguida, troque os desenhos com um colega e verifique como ele fez os dele.

Soma das medidas de abertura dos ângulos internos de um quadrilátero convexo

A soma das medidas de abertura dos ângulos internos de um quadrilátero convexo é 360graus.

Podemos verificar essa relação desenhando um quadrilátero, marcando seus ângulos e recortando-o, como mostrado a seguir.

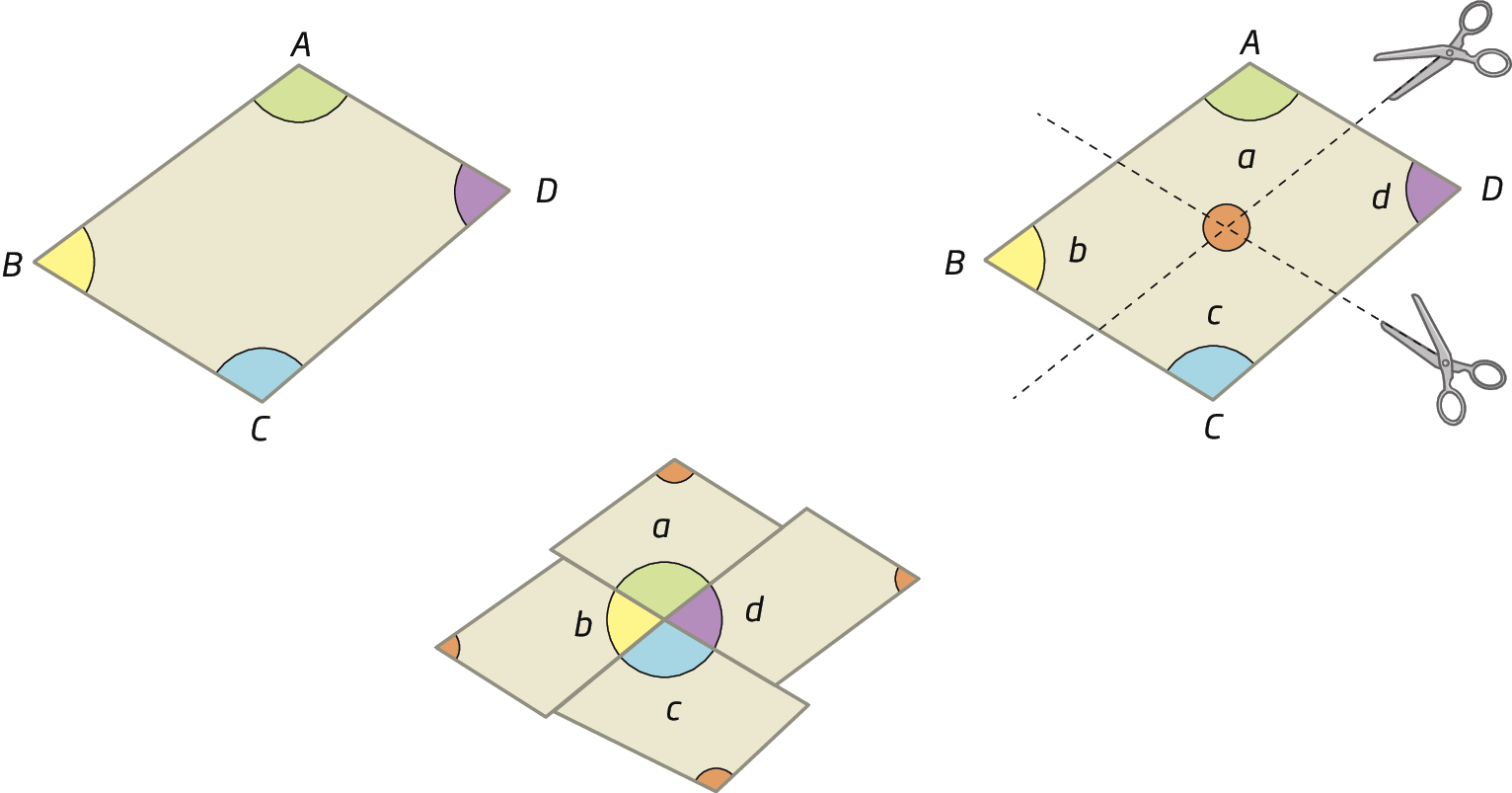
Ilustração. Mesmo quadrilátero ABCD em 3 situações diferentes. Na primeira, quadrilátero ABCD com 4 ângulos demarcados, cada um de uma cor: ângulo em A verde; ângulo em B amarelo; ângulo em C azul; ângulo em D roxo. Na segunda, quadrilátero ABCD com os mesmos ângulos coloridos, agora identificados como a (verde), b (amarelo), c (azul) e d (roxo) e tesouras demonstrando dois cortes no quadrilátero: um na horizontal e outro na vertical. Na região onde os cortes se encontram, há uma circunferência demonstrando os ângulos formados pelos cortes. Os cortes dividiram o quadrilátero ABCD em quatro outros menores. Na terceira situação, os quadriláteros menores recortados foram reorganizados, de modo que os ângulos a, b, c e d formassem uma circunferência.

a + b + c + d = 360graus

Observações

1. A fórmula geral para determinar a soma das medidas de abertura dos ângulos internos de qualquer polígono convexo é:

S_i = (n ‒ 2) · 180graus, em que n é o número de lados do polígono.

Como, no caso dos quadriláteros, n = 4, temos:

S_i = (4 ‒ 2) · 180graus = 2 · 180graus = 360graus

2. A soma das medidas de abertura dos ângulos externos de um polígono convexo qualquer é 360graus.

S_e = 360graus

Página 152

Atividades

Faça as atividades no caderno.

15. Em cada caso, determine o valor de x, em grau, indicado nos quadriláteros.

Figura geométrica. Quadrilátero ABCD. Ângulos: em A, x; em B 110 graus; em C 80 graus; em D 60 graus.

Figura geométrica. Quadrilátero ABCD. Ângulos: em A, x; em B, 4x; em C, 5x; em D, 2x.

Figura geométrica. Quadrilátero ABCD. Ângulos: em A, 90 graus; em B 80 graus; em C 120 graus; em D x.

16. Sabendo que as aberturas dos ângulos internos de um quadrilátero convexo medem, em grau, x, 2x, 3x e 4x, determine essas medidas.

17. Em um quadrilátero convexo, as aberturas dos ângulos internos medem, em grau, x + 20graus, x + 40graus, x + 50graus e x ‒ 10graus. Calcule as medidas de abertura dos ângulos desse quadrilátero.

18. Considere este quadrilátero não convexo a bê cê dê. Mostre que a soma das medidas de abertura dos ângulos internos, tal como nos quadriláteros convexos, também é igual a 360graus.

Figura geométrica. Quadrilátero não convexo ABCD.

Versão adaptada acessível

18. Seu professor vai lhe fornecer um modelo de quadrilátero não convexo para realizar esta atividade.

Mostre que a soma das medidas de abertura dos ângulos internos, tal como nos quadriláteros convexos, também é igual a 360 graus.

5 Classificação dos quadriláteros

Os quadriláteros podem ser classificados em paralelogramos, trapézios e trapezoides.

Observe o diagrama a seguir.

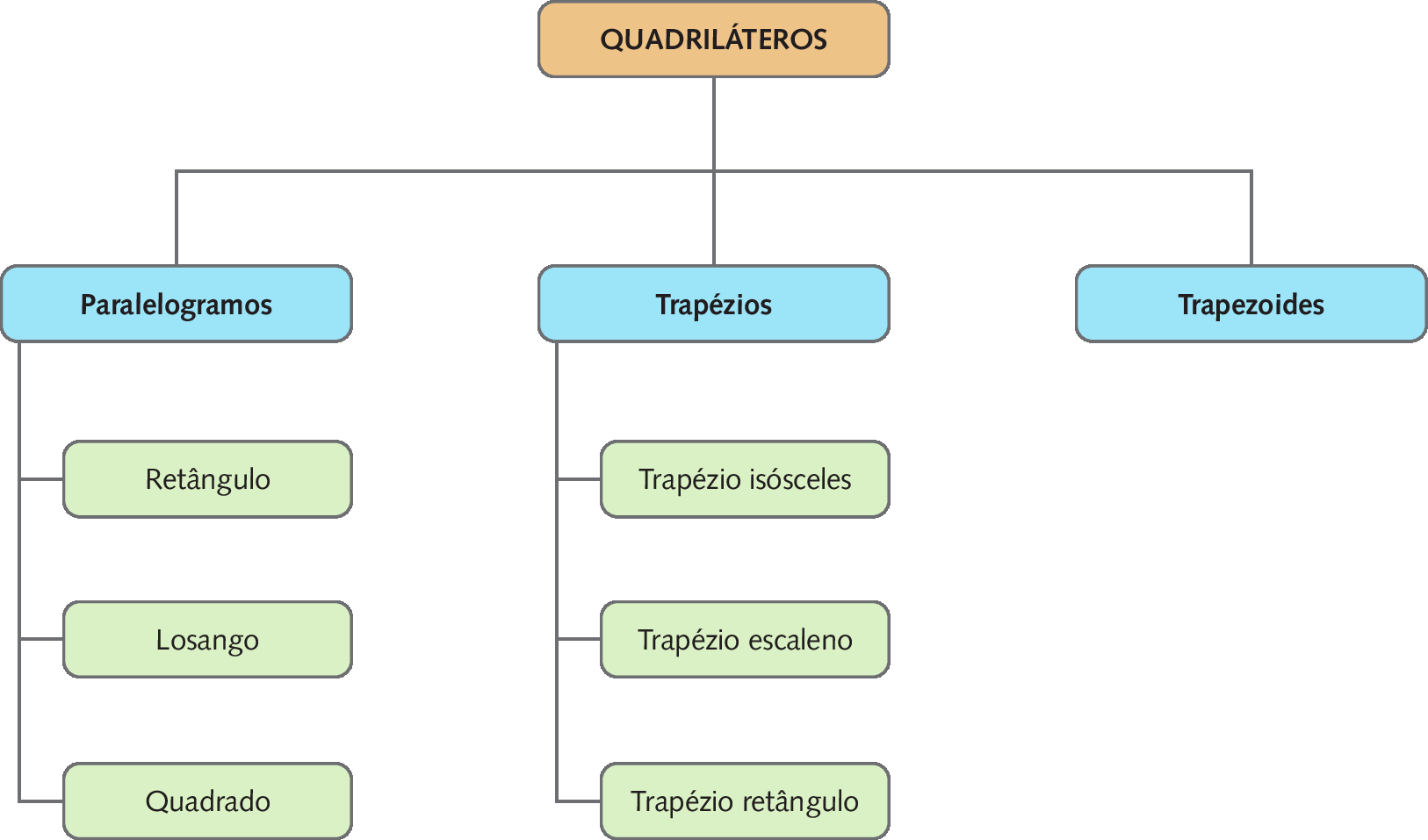
Esquema. No primeiro nível, aparece a palavra Quadriláteros. Dela, 3 outras aparecem no segundo nível: paralelogramos, trapézios e trapezoides. Em paralelogramos, estão as palavras retângulo, losango e quadrado. Em Trapézios, estão trapézio isósceles, trapézio escaleno e trapézio retângulo.

Essa classificação é feita de acordo com algumas características em comum. Vamos estudar essas características e algumas propriedades.

Página 153

Paralelogramos

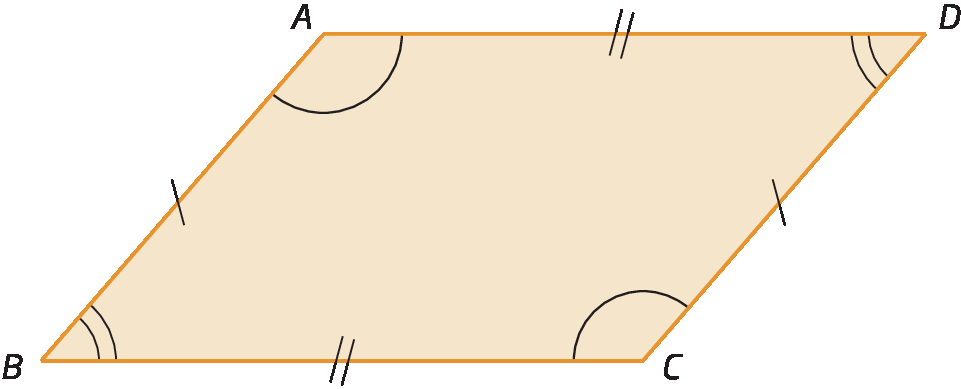
Paralelogramo é o quadrilátero convexo que tem os dois pares de lados opostos paralelos.

Confira o paralelogramo a bê cê dê a seguir.

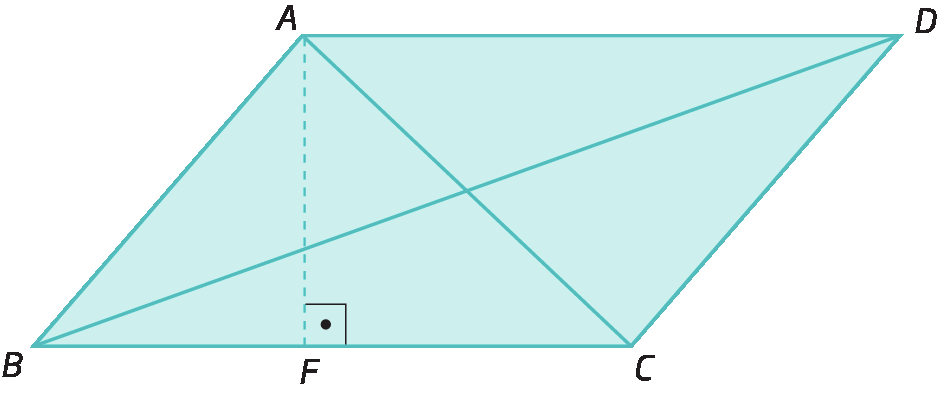
Figura geométrica. Paralelogramo ABCD. De A, linha tracejada perpendicularmente ao lado BC, encontrando-o em F. Diagonais BD e AC identificadas.

\overline{A B} / / \overline{C D}

\overline{A D} / / \overline{C B}

Temos que:

• Os lados opostos

\overline{A B}

\overline{C D}

são paralelos.

• Os lados opostos

\overline{A D}

\overline{C B}

são paralelos.

• Qualquer lado pode ser considerado base.

•

\overline{A F}

é uma altura relativa à base

\overline{B C}

• Os segmentos de reta

\overline{B D}

\overline{A C}

são as diagonais do quadrilátero.

• Os ângulos internos

A \hat{B} C

A \hat{D} C

são opostos.

• Os ângulos internos

B \hat{A} D

D \hat{C} B

são opostos.

• A soma das medidas de abertura dos ângulos internos é 360graus.

Tecnologias digitais em foco

Propriedades dos paralelogramos

Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para explorar algumas propriedades dos paralelogramos.

Construa

Siga os passos seguintes para construir um paralelogramo.

1º) Utilize a ferramenta

e trace um segmento de reta

\overline{A B}

qualquer.

2º) Com a ferramenta

Ilustração. Botão da ferramenta Ponto do software GeoGebra.

, marque um ponto C qualquer, tal que C não pertença a

\overline{A B}

3º) Utilize a ferramenta

Ilustração. Botão da ferramenta Reta paralela do software GeoGebra.

e trace a reta r, paralela ao segmento de reta

\overline{A B}

, passando por C.

4º) Utilize a ferramenta

e trace o segmento de reta

\overline{A C}

5º) Utilize a ferramenta

e trace a reta s, paralela ao segmento de reta

\overline{A C}

, passando por B.

6º) Com a ferramenta

Ilustração. Botão da ferramenta Intersecção de dois objetos do software GeoGebra.

, marque o ponto D, intersecção das retas r e s.

7º) Construa o paralelogramo á bê dê cê utilizando a ferramenta

Página 154

8º) Esconda todas as construções auxiliares e trace, com a ferramenta

, os segmentos de reta

\overline{A D}

\overline{B C}

, diagonais do paralelogramo.

9º) Com a ferramenta

, marque o ponto M, intersecção das diagonais.

Explore

a) Com a ferramenta

Ilustração. Botão da ferramenta Distância/Comprimento do software GeoGebra.

, meça o comprimento dos lados do paralelogramo e movimente-o. O que você pode verificar em relação a essas medidas?

b) Com a ferramenta

Ilustração. Botão da ferramenta Ângulo do software GeoGebra.

, meça a abertura dos ângulos internos do paralelogramo e movimente-o. O que você pode verificar em relação a essas medidas?

c) Meça agora o comprimento dos segmentos de reta

\overline{A M} e \overline{M D}

, faça o mesmo com os segmentos de reta

\overline{B M} e \overline{M C}

e movimente o paralelogramo. O que é possível verificar?

Página 155

Algumas propriedades do paralelogramo

Considere um paralelogramo a bê cê dê qualquer. Traçando a diagonal

\overline{A C}

, obtemos os triângulos á dê cê e cê bê á.

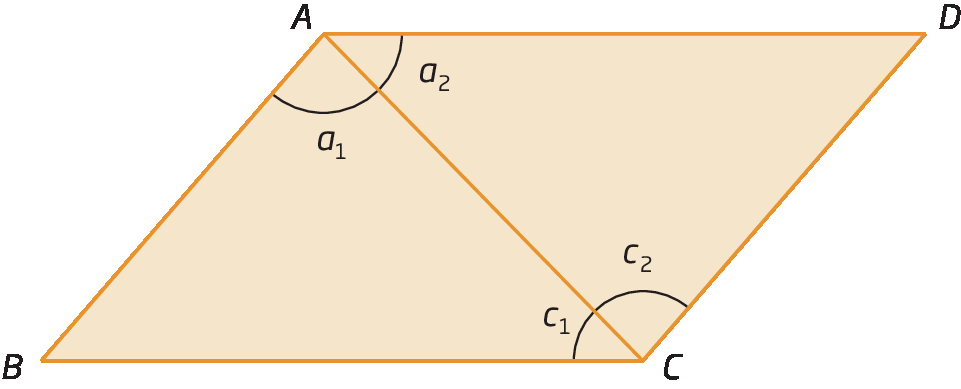
Figura geométrica. Paralelogramo ABCD. Diagonal AC dividindo o paralelogramo em dois triângulos, sendo triângulo ABC, com ângulos a1 em A e c1 em C; e triângulo ACD, com ângulo a2 em A e c2 em C.

Comparando esses triângulos, podemos observar que:

• a1 = c2 (ângulos alternos internos formados por paralelas têm a mesma medida de abertura).

•

\overline{A C}

é o lado comum aos triângulos á dê cê e cê bê á.

• a2 = c1(ângulos alternos internos).

Assim, pelo caso á éle á , temos que △á dê cê ≅ △cê bê á. De maneira análoga, traçando a diagonal

\overline{B D}

, concluímos que △bê á dê ≅ △dê cê bê.

Como os triângulos á dê cê e cê bê á são congruentes, assim como os triângulos BAD e DCB, podemos concluir que:

\overline{A B} ≅ \overline{C D}

\overline{D A} ≅ \overline{B C}

), e, portanto, os lados opostos de um paralelogramo são congruentes.

Figura geométrica. Paralelogramo ABCD. Ângulo A congruente ao ângulo C e ângulo B congruente ao ângulo D. Lado AB congruente ao lado CD e lado AD congruente ao lado BC.

Da congruência dos triângulos á dê cê e cê bê á, concluímos também que

m e d (\hat{D}) = m e d (\hat{B}

) e, da congruência dos triângulos BAD e DCB, concluímos que

m e d (\hat{A}) = m e d (\hat{C})

Portanto, os ângulos internos opostos de um paralelogramo são congruentes.

Ao traçar as diagonais

\overline{A C} e \overline{B D}

do paralelogramo a bê cê dê, verificamos que as diagonais se encontram no ponto M e obtemos os triângulos á ême dê e CMB. Confira.

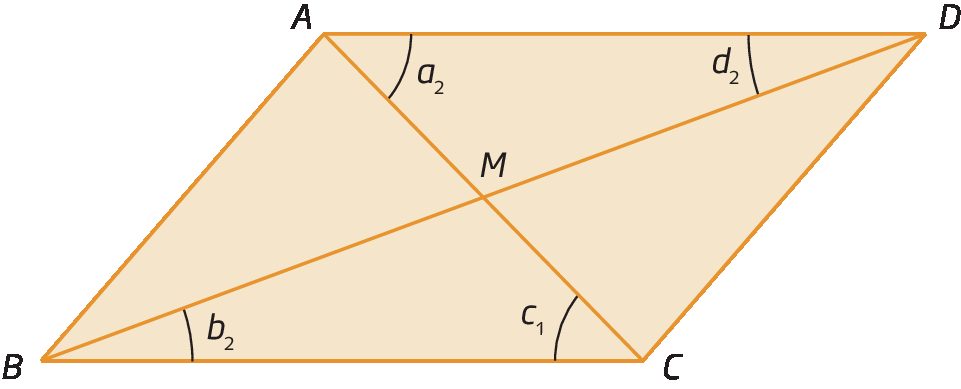
Figura geométrica. Paralelogramo ABCD. Diagonal AC e Diagonal BD se encontram no ponto M, formando 4 triângulos: triângulo ABM, triângulo CDM, triângulo AMD, com ângulos a2 em A e d2 em D; e triângulo BCM, com ângulo b2 em B e c1 em C.

Comparando esses triângulos, podemos notar que:

• a2 = c1 (ângulos alternos internos).

•

\overline{A D} ≅ \overline{C B}

(lados opostos de um paralelogramo).

• b2 = d2 (ângulos alternos internos).

Página 156

Assim, pelo caso á éle á , temos que △á ême dê ≅ △CMB e, portanto,

\overline{A M} ≅ \overline{C M}

\overline{B M} ≅ \overline{D M}

. Isso significa que M é o ponto médio de

\overline{A C}

e de

\overline{B D}

. Assim, concluímos que as diagonais de um paralelogramo se cruzam nos respectivos pontos médios.

Ilustração. Dois meninos, um negro de calça azul e camiseta laranja e outro ruivo, branco de camisa rosa e bermuda verde, carregando um quadro em que se lê: Em um paralelogramo, temos: cada diagonal o divide em dois triângulos congruentes; os lados opostos são congruentes; os ângulos internos opostos são congruentes; os ângulos consecutivos são suplementares; as diagonais interceptam-se em seus pontos médios. O menino ruivo diz: Agora, tenho um desafio para você: Por que os ângulos consecutivos de um paralelogramo são suplementares?

Atividades

Faça as atividades no caderno.

19. Analise os paralelogramos a seguir e, em cada caso, determine x e y.

Figura geométrica. Paralelogramo ABCD. Lado AB mede 4 centímetros, lado BC mede y, lado CD tem medida igual a x, lado AD mede 2 centímetros.

Figura geométrica. Quadrado ABCD. Diagonal BD dividindo-o em dois triângulos: ABD e BCD. No triângulo BCD, ângulo em C igual a 90 graus, em B igual a y e em D igual a x.

Figura geométrica. Paralelogramo ABCD. Lados AB, BC, CD e DA congruentes entre si. Diagonal BC e diagonal BD dividindo o paralelogramo em quatro triângulos. ângulo em D dividido em 30 graus e x. ângulo em A, formado pelo lado AB e a digonal AC igual a y.

20. Construa um paralelogramo a bê cê dê tal que: BC = 8 centímetros, AB = 4 centímetros e

m e d (A \hat{B} C) = 60 °

21. A medida de perímetro de um paralelogramo é igual a 66 centímetros. Calcule as medidas de comprimento dos lados, sabendo que a diferença entre elas é de 14 centímetros.

22. A abertura de um ângulo externo de um paralelogramo mede 64graus. Faça um esboço da figura e calcule as medidas de abertura dos ângulos internos.

23. No paralelogramo a bê cê dê, a diagonal

\overline{B D}

fórma com o lado

\overline{B C}

um ângulo cuja abertura mede 38graus e com o lado

\overline{C D}

, um ângulo cuja abertura mede 54graus. Calcule as medidas de abertura dos ângulos internos desse paralelogramo.

Figura geométrica. Quadrilátero ABCD. Diagonal BD dividindo-o em dois triângulos: ABD e BCD. No triângulo BCD, ângulo em B igual a 38 graus, em C igual a 54 graus.

Página 157

24. No paralelogramo a seguir, temos:

m e d (\hat{C}) = 70 °, \vec{C M}

é bissetriz do ângulo

D \hat{C} B

, e

\vec{B M}

é bissetriz do ângulo

A \hat{B} C

. Determine a medida de abertura do ângulo

B \hat{M} C

Figura geométrica. Quadrilátero ABCD. Semirretas saindo dos vértices B e C se cruzam no ponto M internamente ao quadrilátero.

25. A diferença entre as medidas de abertura de dois ângulos consecutivos de um paralelogramo é 80graus. Quais são as medidas de abertura, em grau, dos ângulos desse quadrilátero?

A seguir, estudaremos alguns paralelogramos que podem ser classificados em retângulos, losangos ou quadrados, por apresentarem propriedades particulares.

Retângulo

Retângulo é o paralelogramo que tem os quatro ângulos internos retos.

Dado um retângulo a bê cê dê qualquer, temos:

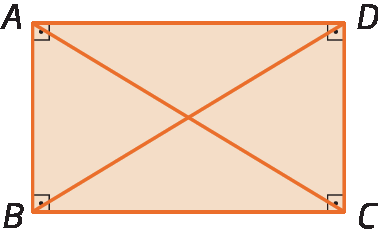
Figura geométrica. Retângulo ABCD. Diagonais AC e BD

m e d (\hat{A}) = m e d (\hat{B}) = m e d (\hat{C}) = m e d (\hat{D}) = 90 °

Como o retângulo é um paralelogramo, são válidas as propriedades do paralelogramo. Além disso, podemos afirmar que, em todo retângulo, as diagonais são congruentes (

\overline{A C} ≅ \overline{B D}

Vamos demonstrar que em todo retângulo as diagonais são congruentes.

Considerando os triângulos equiláteros á bê cê e DCB, temos que:

•

\overline{A B} ≅ \overline{D C}

, pois o retângulo é um paralelogramo e seus lados opostos são congruentes.

•

A \hat{B} C ≅ D \hat{C} B

, pois são ângulos retos.

•

\overline{B C}

é lado comum.

Logo, pelo caso éle á éle: △á bê cê ≅ △dê cê bê.

Portanto,

\overline{A C} ≅ \overline{D B}

, ou seja, as diagonais do retângulo são congruentes.

Observação

A recíproca da propriedade demonstrada anteriormente não é verdadeira. Isto significa que existem quadriláteros que têm as diagonais congruentes mas não são retângulos.

Página 158

Losango

Losango é o paralelogramo que tem os quatro lados congruentes.

Como o losango é um paralelogramo, são válidas as propriedades dos paralelogramos.

Também podemos afirmar que, em todo losango, as diagonais são perpendiculares entre si e estão contidas nas respectivas bissetrizes dos ângulos internos.

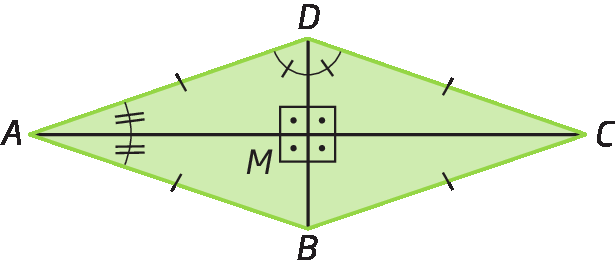
Figura geométrica. Losango ABCD. Estão representadas as diagonais AC e BD que são perpendiculares entre si. As diagonais se cruzam no ponto M. Os ângulos DAC e BAC são congruentes. Os ângulos ADB e CDB também são congruentes.

Então, dado um losango a bê cê dê qualquer, temos:

\overline{A B} ≅ \overline{B C} ≅ \overline{C D} ≅ \overline{A D}

Vamos demonstrar essas propriedades.

Considerando os triângulos á ême dê e CMD, temos que:

•

\overline{A D} ≅ \overline{C D}

, pois são lados do losango.

•

\overline{A M} ≅ \overline{C M}

, pois M é ponto médio de

\overline{A C}

•

\overline{M D}

é lado comum.

Logo, pelo caso éle éle éle: △á ême dê ≅ △cê ême dê.

Assim,

A \hat{D} M ≅ C \hat{D} M

e, portanto,

\overline{D B}

é bissetriz de

A \hat{D} C

De maneira análoga, pelo caso éle éle éle, △á ême bê ≅ △CMB, △á ême bê ≅ △á ême dê e △cê ême dê ≅ △CMB.

Assim,

A \hat{B} M ≅ C \hat{B} M

B \hat{A} M ≅ D \hat{A} M

D \hat{C} M ≅ B \hat{C} M

Portanto,

\overline{D B}

é bissetriz de

A \hat{B} C

\overline{A C}

é bissetriz de

B \hat{A} D

B \hat{C} D

Além disso,

\overline{A C}

\overline{B D}

são perpendiculares, pois

A \hat{M} D

C \hat{M} D

são congruentes e suplementares, ou seja, são ângulos retos.

Observação

Também podemos enunciar que todo quadrilátero cujas diagonais estão contidas nas respectivas bissetrizes dos ângulos internos e são perpendiculares entre si é um losango. Essa afirmação pode ser demonstrada, mas não o faremos aqui.

Quadrado

Quadrado é o paralelogramo que tem os quatro ângulos internos retos e os quatro lados congruentes.

O quadrado é um paralelogramo e um caso particular de retângulo e de losango; assim, valem, além das propriedades do paralelogramo, todas as propriedades dos retângulos e dos losangos:

• As diagonais são congruentes.

• As diagonais são perpendiculares entre si.

• As diagonais estão contidas nas respectivas bissetrizes dos ângulos internos.

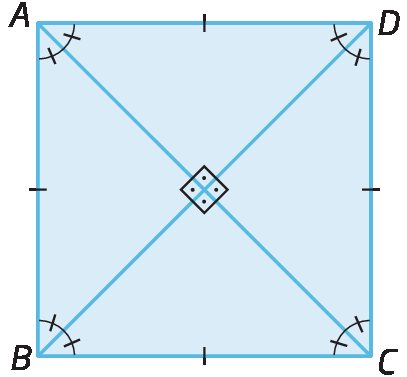
Figura geométrica. Quadrado ABCD. Estão representadas as diagonais AC e BD que são perpendiculares entre si. As diagonais são bissetrizes dos ângulos internos do quadrado.

Então, dado um quadrado a bê cê dê qualquer, temos:

m e d (\hat{A}) = m e d (\hat{B}) = m e d (\hat{C}) = m e d (\hat{D}) = 90 °

\overline{A B} ≅ \overline{B C} ≅ \overline{C D} ≅ \overline{D A}

\overline{A C} ≅ \overline{B D}

Página 159

Atividades

Faça as atividades no caderno.

26. Quais das sentenças a seguir são verdadeiras?

a) Todo quadrado é um losango.

b) Existem retângulos que são losangos.

c) Todo paralelogramo é um quadrilátero.

d) Todo quadrado é um retângulo.

e) Um losango pode não ser um paralelogramo.

f) Em um losango, os quatro lados são sempre congruentes.

g) Todo retângulo é um paralelogramo e todo paralelogramo é um retângulo.

27. Quais das sentenças a seguir são verdadeiras?

Figura geométrica. Quadrilátero ABCD. Todos os lados congruentes. Diagonais AC e BD tracejadas que se encontram no ponto O.

m e d (B \hat{O} C) = 90 °

m e d (D \hat{A} C) = m e d (B \hat{C} A)

c) AO = OC

d) BO = OD

e) AC = BD

f) △bê cê dê é isósceles

g) △á bê cê é equilátero

28. Sabendo que a abertura do ângulo

B \hat{A} D

mede 100graus, determine, em grau, as medidas de abertura indicadas pelas letras no losango a bê cê dê.

Figura geométrica. Quadrilátero ABCD. Diagonais AC e BD, que dividem os ângulos assim: em A, a e b; em B c e d; em C, e e f; em D, g e h.

29. Uma diagonal de um losango fórma com um lado um ângulo cuja abertura mede 36graus. Calcule, em grau, as medidas de abertura dos ângulos desse losango.

30. As diagonais de um retângulo formam um ângulo cuja abertura mede 114graus. Determine as medidas de abertura, em grau, dos ângulos que essas diagonais formam com os lados do retângulo.

Figura geométrica. Retângulo ABCD. Diagonais AC e BD. Um dos triângulos formados pelas diagonais têm ângulos de medidas x, no vértice A, x, no vértice D, 114 graus, no encontro das diagonais. No vértice D, a outra parte do ângulo mede y.

31. A abertura de um ângulo externo de um losango mede 140graus 30minutos. Qual é a medida de abertura, em grau, do maior de seus ângulos internos?

Figura geométrica. Losango ABCD. Prolongamento do lado BC forma um ângulo de 140 graus e 30 minutos

32. A bissetriz de um ângulo obtuso de um losango forma, com um dos lados, um ângulo cuja abertura mede 64graus. Determine a medida de abertura, em grau, de cada ângulo desse losango.

33. Na figura a seguir, temos um quadrado a bê cê dê e um triângulo equilátero á bê é. Sabendo que o triângulo BEC é isósceles, determine a medida de abertura do ângulo

B \hat{E} C

Figura geométrica. Quadrado ABCD. Internamente ao quadrado, triângulo ABE, cujo lado AB é o mesmo do quadrilátero. Do ponto E há um segmento de reta traçado até C, formando um ângulo x em E.

Página 160

Trapézios

Trapézio é todo quadrilátero convexo que tem apenas um par de lados paralelos.

A partir deste trapézio a bê cê dê, temos:

Figura geométrica. Trapézio ABCD. Diagonais AC e BD. Altura AE, perpendicular a BC.

\overline{A D} / / \overline{B C}

• Base maior:

\overline{B C}

• Base menor:

\overline{A D}

•

\overline{A E}

é uma altura do trapézio.

• Pares de ângulos suplementares:

A \hat{B} C e B \hat{A} D

;

A \hat{D} C e D \hat{C} B

• Diagonais:

\overline{A C}

\overline{B D}

Os trapézios são classificados em trapézio retângulo, trapézio isósceles e trapézio escaleno.

Trapézio retângulo

Trapézio retângulo é aquele que tem dois ângulos retos.

\overline{A D} / / \overline{B C}

m e d (\hat{A}) = m e d (\hat{B}) = 90 °

Trapézio isósceles

Trapézio isósceles é aquele em que os lados não paralelos são congruentes.

Considere um trapézio isósceles a bê cê dê qualquer.

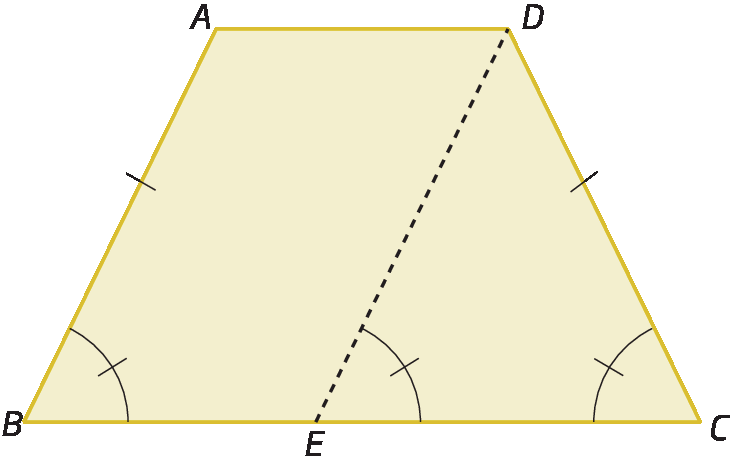
Figura geométrica. Trapézio ABCD. Segmento de reta AD paralelo ao segmento de reta BC. Segmento de reta AB congruente ao segmento de reta DC. Há um ponto E no segmento de reta BC. Segmento de reta DE tracejado, de modo que o ângulo DCE seja congruente ao ângulo DEC. Os ângulos ABE e DEC são congruentes e ângulo DCE congruente ao ângulo ABE.

Confira que, traçando pelo vértice D uma reta paralela a

\overline{A B}

, determinamos o ponto ê na base maior, obtendo o triângulo DEC e o paralelogramo ADEB.

Dessa forma, temos que:

•

\overline{A B} ≅ \overline{D E}

(lados opostos de um paralelogramo).

•

\overline{A B} ≅ \overline{D C}

(trapézio isósceles).

Como

\overline{A B} ≅ \overline{D E}

\overline{A B} ≅ \overline{D C}

, concluímos que

\overline{D E} ≅ \overline{D C}

e, assim, o triângulo é dê cê é isósceles.

Temos ainda que:

•

D \hat{C} E ≅ D \hat{E} C

(ângulos da base do triângulo isósceles).

•

A \hat{B} E ≅ D \hat{E} C

(ângulos correspondentes).

Como

D \hat{C} E ≅ D \hat{E} C

A \hat{B} E ≅ D \hat{E} C

, concluímos que

D \hat{C} E ≅ A \hat{B} E

, ou seja, os ângulos adjacentes à base maior são congruentes.

Página 161

B \hat{A} D

C \hat{D} A

são ângulos colaterais internos, respectivamente, a

A \hat{B} E

D \hat{C} E

. Como

A \hat{B} E ≅ D \hat{C} E,

seus suplementares são congruentes, ou seja,

B \hat{A} D ≅ C \hat{D} A

. Portanto, os ângulos adjacentes à base menor também são congruentes.

Assim, se um trapézio é isósceles, os ângulos adjacentes às mesmas bases são congruentes.

Traçando as diagonais

\overline{A C}

\overline{B D}

, obtemos os triângulos BAD e CDA, que são congruentes pelo caso éle á éle de congruência de triângulos. Podemos, assim, concluir que as diagonais do trapézio isósceles são congruentes.

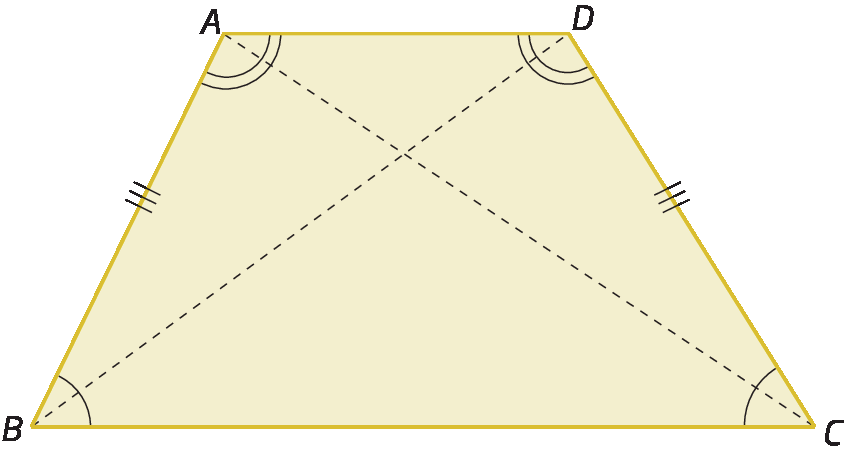
Figura geométrica. Trapézio ABCD. Diagonais AC e BD. AD paralelo a BC. AB congruente a EC. ângulo A congruente a ângulo D. ângulo B congruente a ângulo C.

\overline{A B} ≅ \overline{D C}

m e d (\hat{A}) = m e d (\hat{D})

m e d (\hat{B}) = m e d (\hat{C})

\overline{A C} ≅ \overline{D B}

Trapézio escaleno

Trapézio escaleno é aquele em que os lados não paralelos não são congruentes.

\overline{A B}

não é congruente a

\overline{D C}

Observação

Todo trapézio retângulo é escaleno.

Trapezoides

Trapezoide é todo quadrilátero convexo que não tem lados paralelos.

Figura geométrica. Quadrilátero ABCD.

Segmento de reta AB não paralelo a segmento de reta DC

Segmento de reta AD não paralelo a segmento de reta BC

Página 162

Atividades

Faça as atividades no caderno.

34. Em um trapézio isósceles, a abertura de um dos ângulos externos mede 100° 40’. Determine as medidas de abertura dos ângulos internos desse trapézio.

35. Em um trapézio isósceles, a soma das medidas de abertura dos ângulos obtusos é 250graus. Quanto medem as aberturas dos ângulos agudos?

36. A abertura de um dos ângulos obtusos de um trapézio isósceles mede 100graus. Determine, em grau, a medida x de abertura do ângulo

\hat{E}

formado pelas bissetrizes dos ângulos internos da base maior.

Figura geométrica. Trapézio ABCD. Segmentos de reta que saem dos vértices B e C se encontram no ponto E e formam o triângulo BCE. ângulo em E igual a x. ângulos em B divididos em dois congruentes entre si; ângulos em C divididos em dois congruentes entre si. ângulo em A igual a 100 graus e ângulo em D igual a 100 graus.

37.

Reúna-se com um colega e resolvam as questões a seguir.

a) O quadrilátero da figura a seguir é formado por losangos idênticos. O quadrilátero azul, no centro, é um retângulo. Justifiquem essa afirmação.

Figura geométrica. Quadrilátero verde formado por 16 losangos dispostos em 4 linhas e 4 colunas. 4 diagonais de 4 losangos formam um retângulo azul no meio do quadrilátero verde. O retângulo está dividido em 4 triângulos, em que cada um tem 2 ângulos internos congruentes entre si e esses ângulos dos triângulos 1 e 2 também são congruentes entre si, assim como os ângulos dos triângulos 3 e 4 também são congruentes entre si.

b) Em um trapézio retângulo, a bissetriz de um ângulo reto fórma com a bissetriz do ângulo agudo do trapézio um ângulo cuja abertura mede 110graus. Determinem a medida de abertura do suplemento do maior ângulo do trapézio.

38.

Identifique cada figura a seguir como trapézio retângulo, isósceles ou escaleno. Em seguida, junte-se a um colega e converse com ele sobre o porquê de sua resposta.

Figura geométrica. Trapézio com dois ângulos de 90 graus e lados com medidas diferentes entre si.

Figura geométrica. Trapézio ABCD. Segmento de reta AI, com I em DC, e segmento de reta BH, perpendicular a DC, com H em DC. Quadrilátero ABHI dentro do trapézio. Triângulo retângulo BHC, com ângulos de 90 graus em H, 45 graus em B e 45 graus em C. AB medindo 9, IH medindo 9, DI medindo 4 e HC medindo 4

Figura geométrica. Trapézio PQRS com lados de medidas diferentes entre si.

Figura geométrica. Trapézio com dois ângulos de 90 graus.

Figura geométrica. Trapézio com lados de medidas diferentes entre si.

Figura geométrica. Trapézio ABCD com lados não paralelos congruentes entre si e ângulos A e D congruentes entre si.

39. Qual é a diferença entre um trapézio e um trapezoide?

40. Desenhe, em seu caderno, um trapézio retângulo e um trapézio isósceles. Faça, quando necessário, as marcações para indicar congruência de lados e de ângulos.

Página 163

Resolvendo em equipe

Faça a atividade no caderno.

As quatro retas da figura a seguir formam alguns ângulos.

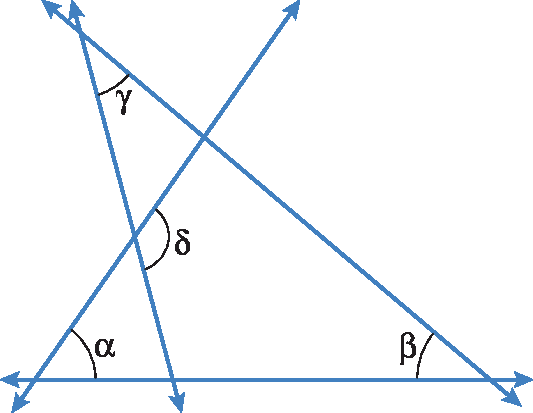
Figura geométrica. 4 retas que se cruzam entre si e formam ângulos. Duas retas à esquerda formam o ângulo alfa. Uma das retas que formou o ângulo alfa, em junção com outra reta forma o ângulo beta. A reta que formou beta forma gama com outra reta. a reta que formou gama e a reta que formou alfa formam o ângulo delta. O encontro dessas retas também formam triângulos. Um deles tem como ângulos alfa e beta. Outro tem como ângulos beta e gama.

Considerando que α = 54graus, β = 39graus e γ = 36graus, qual é a medida de abertura δ?

a) 99graus

b) 105graus

c) 121graus

d) 126graus

e) 129graus

Interpretação e identificação dos dados	• Analise as informações do enunciado e anote as que você julgar relevantes para a resolução do problema. • Na figura, há contornos de triângulos com duas medidas de abertura de ângulos internos dadas? Se sim, podemos determinar a medida de abertura do terceiro ângulo?
Plano de resolução	• Conhecidas as medidas de abertura dos três ângulos do enunciado e as medidas de abertura dos ângulos determinados anteriormente, qual é o procedimento para encontrar a medida de abertura δ? • Que conceito sobre triângulos e quadriláteros é fundamental para a resolução deste problema? • Determine a medida de abertura δ.
Resolução	• Reúna-se com dois colegas. • Mostre a eles seu plano de resolução e verifique se há ideias em comum entre vocês. • Discutam as diferenças e as semelhanças entre cada plano e escolham um deles para a execução do processo de resolução. Observação Resolvam o problema de forma coletiva, mas façam o registro individual no caderno.
Verificação	• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas.
Apresentação	• Elaborem uma síntese, por meio de cartazes, sobre triângulos e quadriláteros. Triângulos: classificação de triângulos quanto às medidas de comprimento dos lados e quanto às medidas de abertura dos ângulos; pontos notáveis; casos de congruência; soma das medidas de abertura dos ângulos internos. Quadriláteros: classificação e elementos de paralelogramos e trapézios; soma das medidas de abertura dos ângulos internos; propriedades dos paralelogramos, dos retângulos, dos losangos e dos quadrados; propriedades dos trapézios.

Página 164

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Triângulos

O triângulo é um polígono de três lados. Vamos destacar alguns elementos deste triângulo.

• Vértices: a, B e C.

• Lados:

\overline{A B}, \overline{A C} e \overline{B C}

• Ângulos internos:

\hat{A}, \hat{B} e \hat{C}

• Ângulos externos:

\hat{x}, \hat{y} e \hat{z}

A soma das medidas de abertura dos ângulos internos de um triângulo é 180graus.

Cevianas notáveis: mediana, altura e bissetriz

Ceviana é qualquer segmento de reta com uma extremidade em um vértice de um triângulo e a outra extremidade na reta suporte do lado oposto a esse vértice.

1. Em um quadrado a bê cê dê, traçamos a diagonal

\overline{D B}

e obtemos o triângulo BCD.

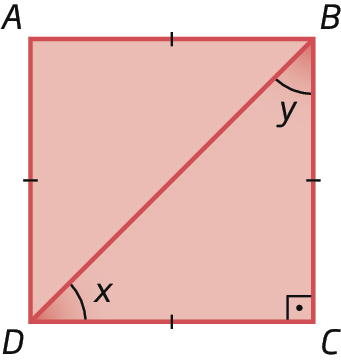
Figura geométrica. Quadrado ABCD. Diagonal BD dividindo o quadrado em 2 triângulos, de modo que os ângulos do triângulo BCD são 90 graus, x e y.

Sabendo que x = y, determine as medidas de abertura dos ângulos internos do triângulo BCD.

2. Associe cada ceviana à sua definição.

um. Medianas dois. Alturas três. Bissetrizes

A. Cevianas que têm uma extremidade em um dos vértices do triângulo e a outra extremidade no lado oposto a esse vértice, dividindo cada ângulo interno em dois ângulos congruentes.

B. Cevianas que têm uma extremidade em um dos vértices do triângulo e a outra extremidade no ponto médio do lado oposto a esse vértice.

C. Cevianas que têm uma extremidade em um dos vértices do triângulo e a outra extremidade na reta suporte do lado oposto ao vértice, formando um ângulo cuja abertura mede 90graus com essa reta.

Congruência de triângulos

Dois triângulos são congruentes quando os lados correspondentes e os ângulos correspondentes são congruentes. Há quatro casos de congruência de triângulos.

1º caso de congruência: éle á éle (Lado-Ângulo-Lado)

Dois triângulos são congruentes quando dois lados e o ângulo compreendido entre eles são, respectivamente, congruentes.

2º caso de congruência: á éle á (Ângulo-Lado-Ângulo)

Dois triângulos são congruentes quando um lado e dois ângulos adjacentes a esse lado são, respectivamente, congruentes.

3º caso de congruência: éle éle éle (Lado-Lado-Lado)

Dois triângulos são congruentes quando os três lados são, respectivamente, congruentes.

4º caso de congruência: éle á áo (Lado-Ângulo-Ângulo oposto)

Dois triângulos são congruentes quando um lado, um ângulo adjacente e o ângulo oposto a esse lado são, respectivamente, congruentes.

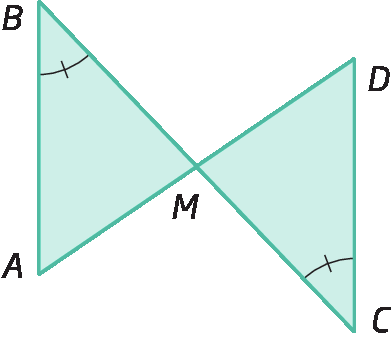
3. Sabendo que

α = β e \overline{A B} ≅ \overline{B C}

, prove que

\hat{A} ≅ \hat{C}

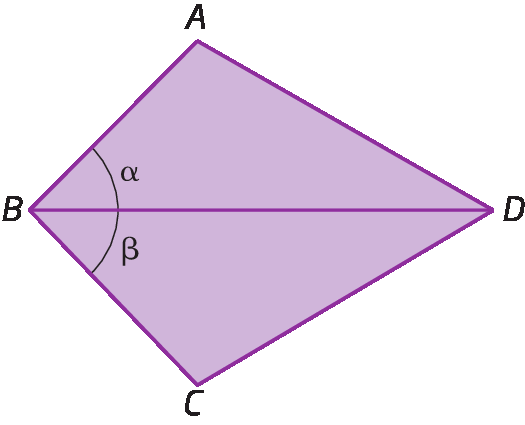
Figura geométrica. Triângulos ABD e BDC unidos pelo lado BD. Ângulo ABD igual a alfa e ângulo CBD igual a beta

4. Sabendo que

\overline{C M} ≅ \overline{M B}

\hat{B} ≅ \hat{C}

, prove que

\overline{A M} ≅ \overline{M D}

Figura geométrica. Triângulos ABM e DCM unidos pelo vértice M. Ângulo B congruente a ângulo C.

Página 165

Quadriláteros

O quadrilátero é um polígono de quatro lados. Verifique alguns elementos deste quadrilátero.

• Vértices: a, B, C e D.

• Lados:

\overline{A B}, \overline{B C}, \overline{C D} e \overline{D A}

• Diagonais:

\overline{A C} e \overline{B D}

• Ângulos internos:

\hat{A}, \hat{B}, \hat{C} e \hat{D}

Um quadrilátero pode ser convexo ou não convexo. Para ser convexo, é necessário que todos os segmentos de reta, com extremidades no interior do quadrilátero, tenham todos os seus pontos situados no interior desse quadrilátero.

A soma das medidas de abertura dos ângulos internos de um quadrilátero convexo é 360graus.

5. As medidas de abertura dos ângulos de um quadrilátero convexo são indicadas por a, b, c e d. Sabendo que b = 2a, c = 2b e d = a + c, determine as medidas de abertura a, b, c e d, em grau.

Classificação dos quadriláteros

Paralelogramos

Paralelogramo: quadrilátero convexo que tem os lados opostos paralelos; seus lados opostos e ângulos opostos são congruentes; seus ângulos consecutivos são suplementares; suas diagonais interceptam-se nos pontos médios.

Retângulo: paralelogramo que tem os quatro ângulos internos retos; todas as propriedades do paralelogramo são válidas para ele; suas diagonais são congruentes.

Losango: paralelogramo que tem os quatro lados congruentes; todas as propriedades do paralelogramo são válidas para ele; suas diagonais são perpendiculares entre si e estão contidas nas respectivas bissetrizes dos ângulos internos.

Quadrado: paralelogramo que é um caso particular de retângulo e de losango; todas as propriedades do paralelogramo, do retângulo e do losango são válidas para ele.

Trapézios

Trapézio: todo quadrilátero convexo que tem apenas um par de lados paralelos.

Trapézio retângulo: tem dois ângulos retos.

Trapézio isósceles: os lados paralelos são congruentes.

Trapézio escaleno: os lados não paralelos não são congruentes.

6. Copie as afirmações verdadeiras no caderno.

a) Retângulo é o paralelogramo que tem os quatro ângulos internos retos.

b) Losango é o paralelogramo que tem os quatro ângulos internos retos e os quatro lados congruentes.

c) Os lados opostos e os ângulos opostos de um paralelogramo são congruentes.

d) Todo retângulo é um quadrado.

e) As diagonais de um paralelogramo interceptam-se em seus pontos médios.

7. A diferença entre as medidas de abertura de dois ângulos consecutivos de um paralelogramo é 108graus. Calcule as medidas de abertura desses ângulos, em grau.

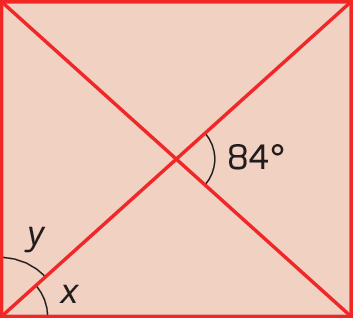
8. Neste retângulo, determine xis e y, em grau.

Figura geométrica. Retângulo com as duas diagonais traçadas. Um dos vértices do retângulo tem ângulos de medidas y e e x. A intersecção das diagonais forma um ângulo de 84 graus.

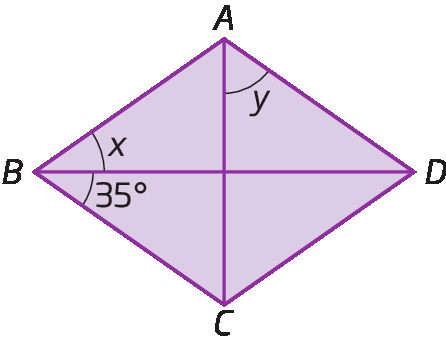
9. Nos losangos a seguir, determine x e y, em grau.

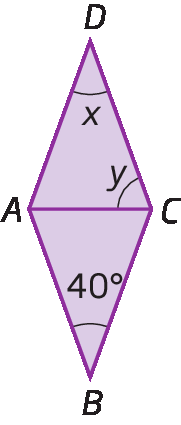
Figura geométrica. Losango ABCD. Diagonal AC. Ângulo ACD tem medida y, ângulo ADC mede x, ângulo ABC mede 40 graus.

Figura geométrica. Losango ABCD. Diagonais AC e BD. ângulo ABD igual a x; ângulo DBC igual a 35 graus; ângulo CAD igual a y.

10. Em um trapézio isósceles, as bases medem 25 centímetros e 5 centímetros de comprimento, respectivamente, e o perímetro mede 64 centímetros. Quanto mede o comprimento de cada um dos outros lados?