Capítulo 8 Área, volume e capacidade
Trocando ideias
O tangram é um quebra-cabeça chinês composto de 7 peças. Com ele é possível formar diferentes figuras sem sobrepor peças.

▸

As peças do tangram se parecem com quais figuras geométricas planas?
▸


As figuras ao redor do tangram central foram formadas com peças de um mesmo tangram. O que podemos afirmar sobre a medida da área de cada uma destas figuras? Por quê? Converse com os colegas.
Neste capítulo vamos estudar medidas de área, volume e capacidade.

1 Medida da área de figuras planas
Vamos retomar o cálculo da medida da área de alguns quadriláteros, como retângulos, quadrados, paralelogramos, trapézios e losangos, além do cálculo de área de triângulos.
Medidas das áreas do retângulo e do quadrado
Acompanhe as situações.
Situação 1
Joana foi encarregada de comprar um terreno para uma empresa, sabendo que poderia pagar até R$ 500,00quinhentos reais pelo metro quadrado do terreno.

Joana lembrou que para determinar a medida da área de um retângulo deve multiplicar a medida do comprimento da base pela medida do comprimento da altura.

Substituindo os valores correspondentes à medida da largura e à medida do comprimento do terreno na expressão, Joana determinou a medida da área do terreno.
Aterreno = 12 métros ⋅ 20 métros = 240 métros quadrados
Para determinar o valor máximo que poderia pagar pelo terreno, Joana multiplicou o valor correspondente à medida da área encontrada por 500.
240 ⋅ 500 = .120000
Portanto, Joana poderia pagar, no máximo, R$ 120.000,00cento e vinte mil reais por esse terreno.
Observações
1. Os matemáticos já provaram que a fórmula Aretângulo = b ⋅ h vale para quaisquer valores racionais positivos de b e h.
2. Não se esqueça de que, para obter a medida da área de qualquer figura, as medidas usadas no cálculo devem estar expressas na mesma unidade de medida de comprimento.
Situação 2
Após visitarem o primeiro terreno, o corretor convidou Joana para conhecer outro.

Joana sabia que um quadrado é um caso particular de retângulo; logo, para determinar a medida da área de um quadrado, ela deveria proceder como no cálculo da medida da área de um retângulo.

Substituindo a medida do lado do terreno nessa expressão, Joana determinou a medida da área do terreno.
Aíndice terreno = 9 métros ⋅ 9 métros = (9 métros)elevado a 2 = 81 métros quadrados
Para determinar o valor máximo a pagar por esse terreno, Joana calculou:
81 ⋅ 500 = .40500
Portanto, Joana poderia pagar, no máximo, R$ 40.500,00quarenta mil quinhentos reais por esse terreno.
Medidas das áreas do triângulo e do paralelogramo
O esquema a seguir indica as medidas de comprimento da horta que Vitória vai construir. Entre as regiões triangulares há um espaço que se parece com um paralelogramo; nesse espaço, ela colocará placas de granito, compondo um caminho.

Para comprar o material necessário, Vitória precisa calcular as respectivas medidas de áreas destinadas à horta e ao caminho.
A medida da área de um triângulo pode ser determinada pela metade do produto da medida de comprimento da base pela medida de comprimento da altura correspondente.

Substituindo as medidas correspondentes, a medida da área de uma região triangular é:
Sentença matemática. Área do triângulo é igual a 2 metros vezes 1 metro dividido por 2, igual, 1 metro quadrado.
Como a horta será construída em duas regiões triangulares com as mesmas medidas de altura e comprimento, a medida de suas áreas são iguais. Logo, 2 métros quadrados será a medida da área reservada para à construção da horta.
O caminho se parece com um paralelogramo cuja base mede 0,5 métro de comprimento e a altura mede 1 métro de comprimento. A medida da área de um paralelogramo é dada pela multiplicação entre a medida de comprimento de uma das bases pela medida de comprimento da altura correspondente a essa base.

Logo, a medida da área desse caminho é de:
Sentença matemática. A igual a 0 vírgula 5 metros vezes 1 metro igual a 0 vírgula cinco metros quadrados.
Medidas das áreas do trapézio e do losango
Juliano precisa calcular a medida da área aproximada de um terreno que se parece com um hexágono. A figura a seguir corresponde à planta desse terreno.
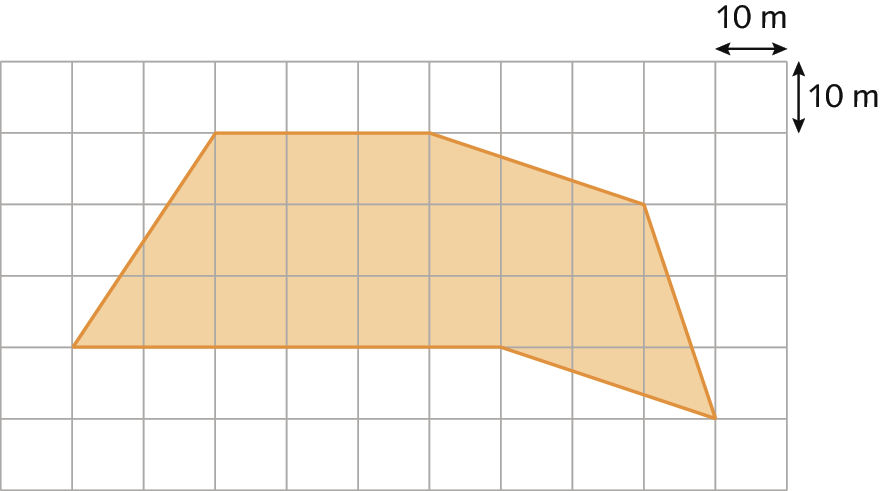
Nessa planta, cada centímetro equivale à medida de 10 métros de comprimento real.
Analisando a planta, Juliano percebeu que é possível decompor esse terreno em dois quadriláteros: um trapézio e um losango.
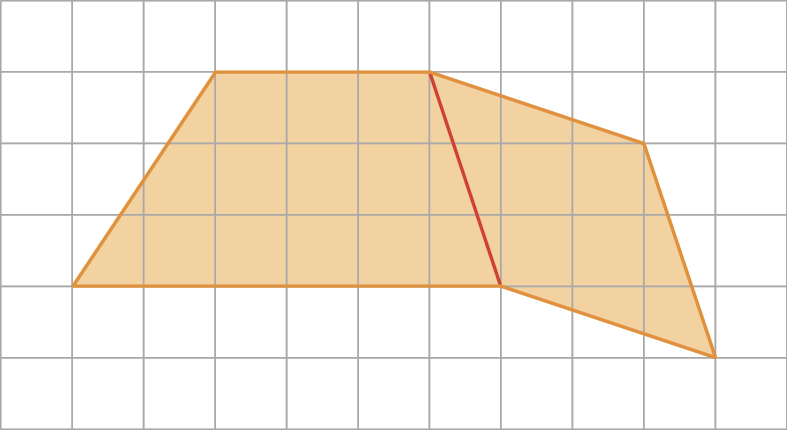
Juliano sabe que a medida da área de um trapézio é dada pela metade do produto da soma das medidas de comprimento das bases maior e menor pela medida de comprimento da altura.

Com base na planta, Juliano percebeu que no trapézio a medida do comprimento da base menor (b) é 30 métros, a medida do comprimento da base maior (B) é 60 métros e a medida do comprimento da altura (h) é 30 métros. Substituindo esses valores na expressão, ele determinou a medida da área do trapézio.
Sentença matemática. A, igual, abre parênteses, 30 metros mais 60 metros, fecha parênteses, vezes 30 metros dividido por 2, igual, 90 metros vezes 30 metros dividido por 2, igual, 2 mil e 700 dividido por 2, metros quadrados, igual a mil e 350 metros quadrados.
Com uma régua, Juliano mediu as diagonais do losango e obteve 2,8 centímetros como medida de comprimento aproximada para a diagonal menor e 5,7 centímetros para a diagonal maior. A medida da área de um losango é igual à metade do produto das medidas de comprimento das diagonais maior e menor.

Considerando que cada centímetro corresponde a 10 métros de comprimento real, Juliano determinou que a medida do comprimento da diagonal menor (d ) é aproximadamente 28 métros e a medida do comprimento da diagonal maior (D) é aproximadamente 57 métros. Logo, a medida da área aproximada será:
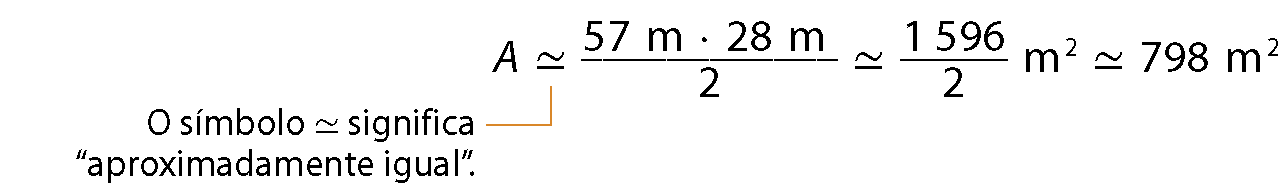
Desse modo, Juliano concluiu que a medida da área aproximada do terreno é de .2148 métros quadrados, pois:
.1350 métros quadrados + 798 métros quadrados = .2148 métros quadrados
Atividades
Faça as atividades no caderno.
1. A comunidade de um bairro resolveu restaurar o gramado de um antigo campo de futebol. Quantos metros quadrados de grama serão necessários para cobrir o campo, que tem medida de comprimento igual a 105 métros e medida de comprimento da largura igual a 68 métros?
2. Um quadrado tem diagonal medindo 5 centímetros de comprimento. Qual é a medida da área desse quadrado? Explique como você pensou para responder a essa questão.
3.

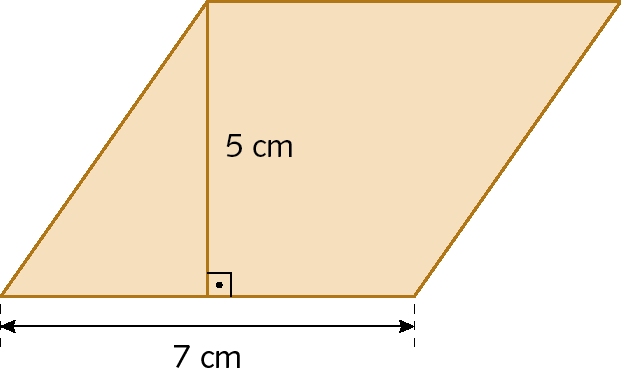
Determine a medida da área do paralelogramo e, depois, responda à questão a seguir.
Se dobrarmos a medida do comprimento da altura do paralelogramo e dividirmos a medida do comprimento da base por 2, o que poderemos afirmar sobre a medida da área dessa nova figura? Converse com o professor e com os colegas.
4. Heloísa vai pintar as paredes de três quartos de sua residência. Para saber a quantidade de tinta necessária, ela avaliou a planta de um desses quartos, sabendo que todos têm as mesmas medidas de comprimento.
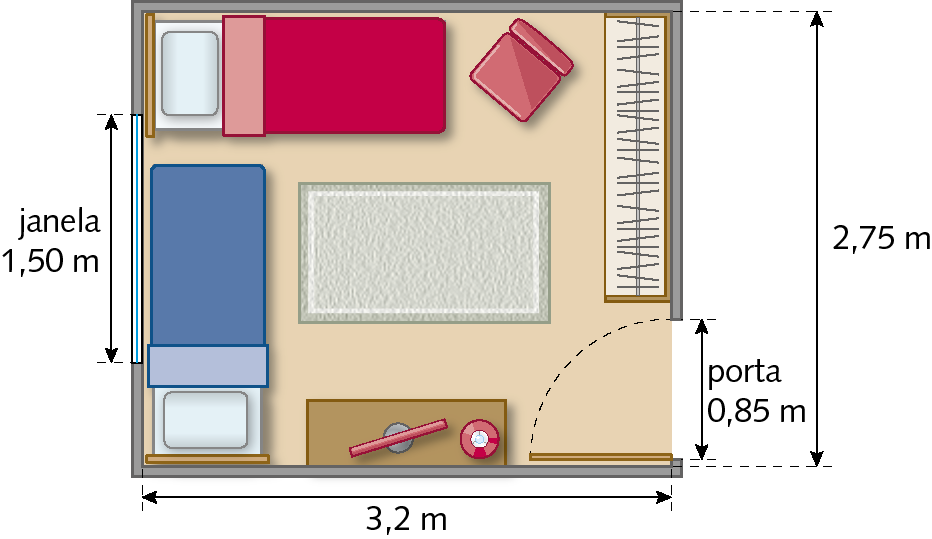
A medida da distância do chão ao teto do quarto de Heloísa é de 2 métros, a medida do comprimento da altura da porta é igual a 1,90 métro e a janela tem 1,50 métro de medida de comprimento de largura e 1,50 métro de medida de comprimento de altura. Com base nessas informações, determine a medida da área total das paredes que serão pintadas.
5. Observe os polígonos a seguir.
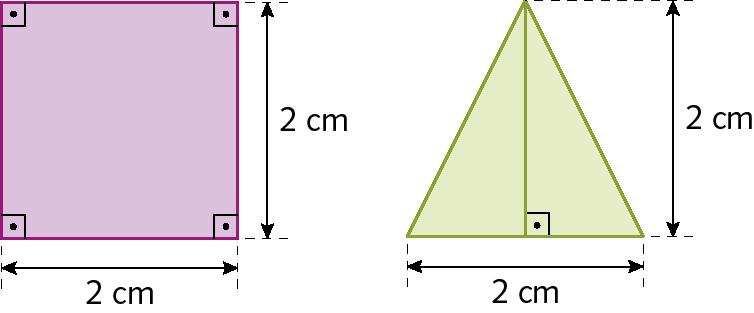
a) Qual é a relação entre a medida das áreas desses dois polígonos?
b)

Desenhe no caderno um triângulo que tenha a mesma medida de área desse quadrado. Há somente um modo de desenhar esse triângulo? Converse com o professor e com os colegas.
6. Determine a medida da área das figuras a seguir, sabendo que a medida do comprimento do lado de cada quadradinho é igual a 1 centímetro.
a)

b)
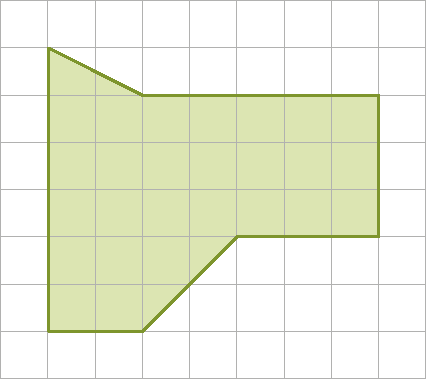
c)
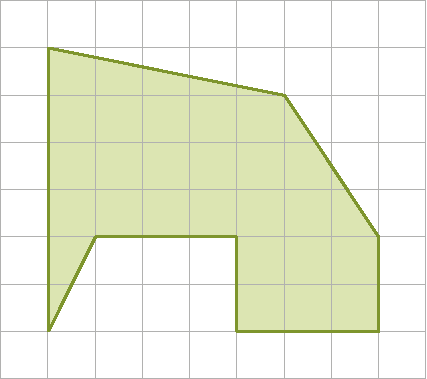
d)
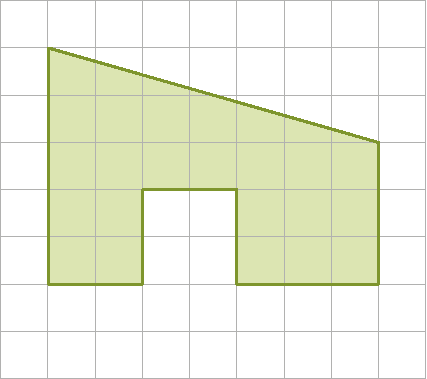
7. Calcule a medida da área da parte pintada de laranja de cada figura.
a)
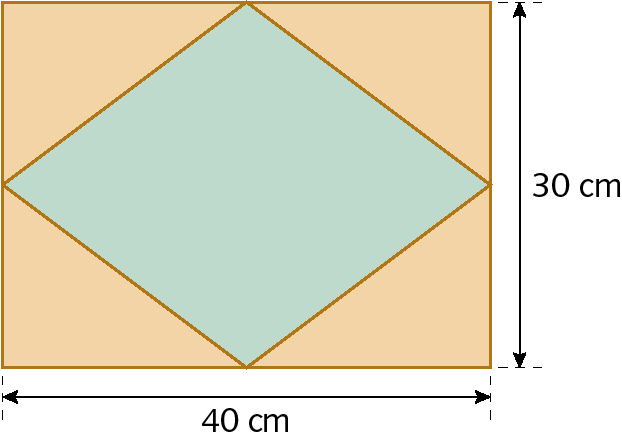
b)
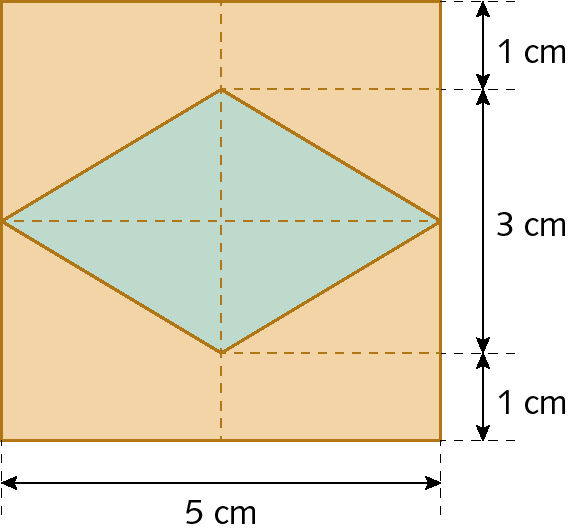
8.


Desenhe a planta de um cômodo de sua residência e indique as respectivas medidas. Elabore um problema envolvendo a planta desenhada por você e faça o cálculo de área. Troque seu problema com um colega e solicite a ele que o resolva. Depois, verifiquem se as resoluções estão corretas.

2 Medida da área do círculo
Considere o círculo de centro óh e raio de medida de comprimento r. Podemos decompor esse círculo em 18 setores circulares congruentes. Confira as figuras a seguir.
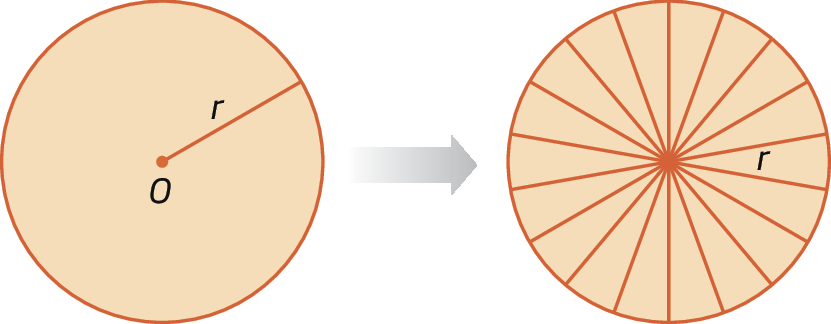
É possível reagrupar esses setores em uma figura que se parece com um paralelogramo. A medida do comprimento da altura h é aproximadamente igual a r, e a medida de comprimento da base b é aproximadamente igual a
Fração. C sobre 2., em que C é a medida do comprimento da circunferência.
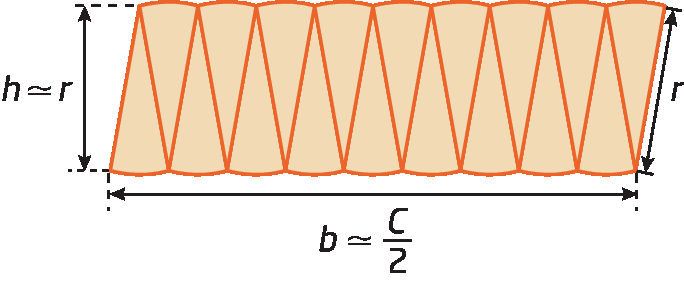
Ao decompor qualquer círculo em n setores circulares congruentes, sendo n um número muito grande, cada setor é tão pequeno que sua medida de área é próxima da medida da área de um triângulo. Quanto maior for a quantidade n de setores em que dividirmos o círculo, maior será essa aproximação. Nesse caso, verificamos que a medida da área do círculo corresponde aproximadamente à medida da área do paralelogramo formado pelos n triângulos.
Como a medida do comprimento da base do paralelogramo é aproximadamente igual à metade da medida do comprimento da circunferência e a medida do comprimento da altura é aproximadamente igual à medida do comprimento do raio, podemos escrever:
A é aproximadamente igual à 2 pi r sobre 2, vezes r
Tomando por base essa ideia, pode-se inferir que:
Acírculo = pirelevado a 2
Acompanhe a situação a seguir.
Andreia sabe que com 1 novelo de determinada linha, ela consegue confeccionar um tapete de tricô de .1500 centímetros quadrados de medida de área. Quantos novelos dessa linha Andreia usará para fazer um tapete circular cujo raio mede 100 centímetros de comprimento?

Inicialmente, vamos determinar a medida aproximada da área do tapete de formato circular. Para isso, vamos considerar pi = 3,14:
Atapete ≃ 3,14 · (100 centímetros)elevado a 2 ≃ 3,14 · .10000 centímetros quadrados ≃ .31400 centímetros quadrados
Para determinar a quantidade de novelos para a confecção do tapete, basta dividir a medida aproximada da área total do tapete pela medida da área confecionada a partir de 1 novelo:
.31400 : .1500 ≃ 20,93
Logo, Andreia precisará de 21 novelos para confeccionar o tapete.
Medida da área da coroa circular
Coroa circular é uma região limitada por duas circunferências concêntricas (os centros são coincidentes) situadas em um mesmo plano e com medidas de comprimento de raio diferentes.
Na ilustração, temos a circunferência Cíndice 1 de centro óh e raio com medida de comprimento R e a circunferência Cíndice 2, também de centro O e raio com medida de comprimento r.
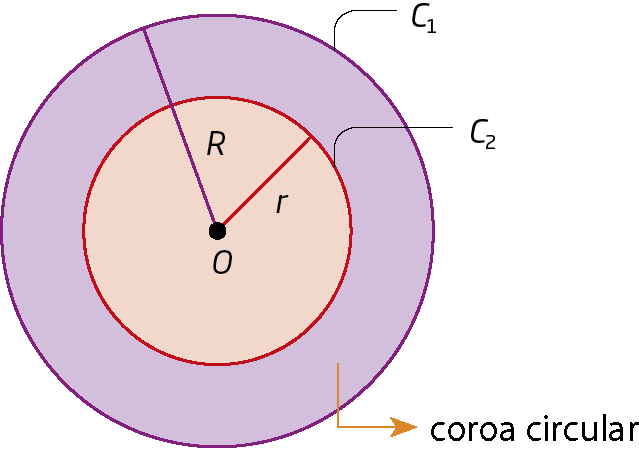
A medida da área (a) da coroa circular é obtida pela diferença entre a medida da área
do círculo Cíndice 1 e a medida da área
do círculo Cíndice 2.
A =
−
A = piRelevado a 2 − pir elevado a 2
A = pi(Relevado a 2 − r elevado a 2)
Acompanhe o exemplo a seguir.
Um clube esportivo construirá uma pista de corrida que se parece com uma coroa circular, como mostra a figura.

Qual é a medida aproximada da área da pista, considerando pi = 3,14?
A medida aproximada da área da pista é obtida pela diferença entre as medidas das áreas do círculo Cíndice 1 , cujo raio mede 4,5 métros de comprimento (3 métros + 1,5 métro), e do círculo Cíndice 2 , cujo raio mede 3 métros de comprimento:
Área do círculo C1 é aproximadamente igual a 3,14 vezes, abre parênteses, 4,5 metros, fecha parênteses, ao quadrado, que é aproximadamente igual a 3,14 vezes 20,25 metros quadrados, que é aproximadamente igual a 63,585 metros quadrados.
Área do círculo C2 é aproximadamente igual a 3,14 vezes, abre parênteses, 3 metros, fecha parênteses, ao quadrado, que é aproximadamente igual a 3,14 vezes 9 metros quadrados, que é aproximadamente igual a 28,26 metros quadrados.
Logo, para determinar a medida aproximada da área da pista, fazemos:
63,585 métros quadrados ‒ 28,26 métros quadrados = 35,325 métros quadrados
Poderíamos determinar a medida aproximada da área da pista utilizando a expressão da medida da área de uma coroa circular:
A = pi(Relevado a 2 ‒ r elevado a 2)
Substituindo os valores correspondentes a R (medida do comprimento do raio de Cíndice 1) e r (medida do comprimento do raio de Cíndice 2), temos:
ei ≃ 3,14 · [(4,5 métros)elevado a 2 – (3 métros)elevado a 2 ] ≃ 3,14 ⋅ [20,25 métros quadrados – 9 métros quadrados ] ≃ 3,14 ⋅ 11,25 métros quadrados ≃ 35,325 métros quadrados
Logo, a medida aproximada da área da pista é de 35,325 métros quadrados.
Sugestão de leitura
GUELLI, Oscar. A invenção dos números. São Paulo: Ática, 1996. (Coleção Contando a história da Matemática).
Este livro apresenta um pouco da história dos diversos sistemas de numeração, a descoberta do número pi e outros contextos que alteraram a história da humanidade.
Medida da área de um setor circular
Considere o setor circular da figura. A medida da abertura do seu ângulo central é α e a medida da sua área é diretamente proporcional à medida da abertura desse ângulo (em grau).
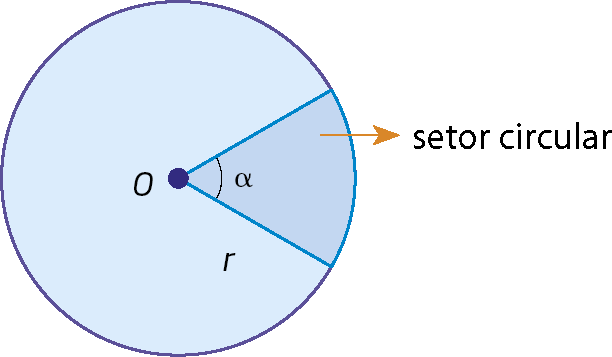
Assim, podemos escrever:

Logo, a medida da área de um setor circular de raio r e ângulo central de medida de abertura α, em grau, é dada por:
Área do setor é igual a alfa dividido por 360 graus, vezes pi r ao quadrado.
Acompanhe o exemplo.
Qual é a medida da área do setor circular de ângulo central com abertura medindo 40graus e raio de 20 centímetros de medida de comprimento?
Podemos calcular a medida da área do setor usando a expressão:
Área do setor é igual a alfa dividido por 360 graus, vezes pi r ao quadrado.
Substituindo os valores correspondentes, temos:
A, igual, 40 graus dividido por 360 graus, vezes pi vezes, abre parênteses, 20 centímetros, fecha parênteses, ao quadrado, igual, 1 nono, vezes pi vezes 400 centímetros quadrados, aproximadamente igual, 44 vírgula 44 pi centímetros quadrados.
Portanto, a medida da área desse setor é de aproximadamente 44,44pi centímetros quadrados.
Atividades
Faça as atividades no caderno.
9. Calcule a medida da área de um círculo cujo raio mede 9 métros de comprimento.
10. Calcule a medida da área de um setor circular de ângulo central com abertura medindo 108graus e raio de 8 centímetros de comprimento.
11. Calcule a medida da área da parte vermelha da figura.
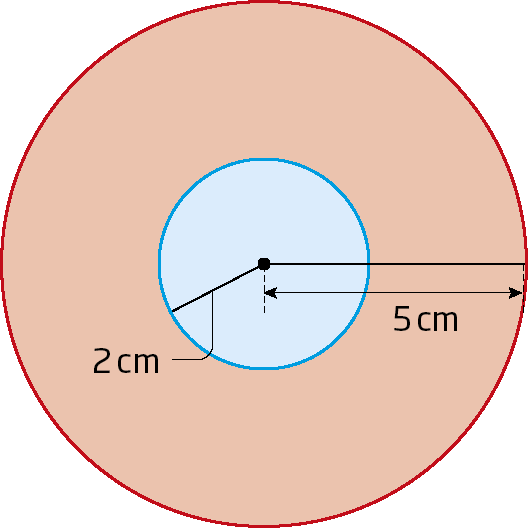
12. Calcule a medida da área da coroa circular determinada por duas circunferências concêntricas cujos raios medem 8 centímetros e 5 centímetros de comprimento.
13. Uma piscina de formato circular ocupará, aproximadamente, 28,26 métros quadrados de medida de área. Considerando π = 3,14, qual é a medida do comprimento do diâmetro dessa piscina?
14. Em um jardim, Fabiana fará um canteiro circular, onde plantará algumas árvores de médio porte. Ao redor desse canteiro, ela plantará algumas flores. Observe o esboço que ela fez com as respectivas medidas desse canteiro.
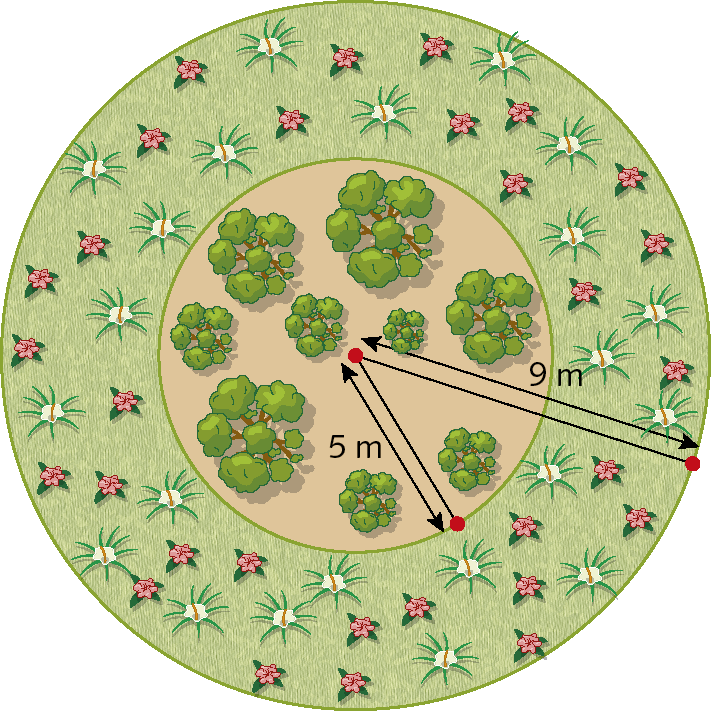
Para cada um dos canteiros, Fabiana utilizará um tipo de adubo. O adubo a, que será usado no canteiro das árvores, custa R$ 10,00dez reais o quilograma. Já o adubo B, que será usado nos canteiros das flores, custa R$ 7,00sete reais o quilograma. Cada quilograma será usado para adubar 1 métro quadrado de cada espaço. Considerando π = 3,14, responda:
a) Quantos quilogramas de cada adubo serão necessários?
b) Quanto Fabiana gastará em adubo?

3 Medidas de volume e capacidade
Anderson ganhou três latas de tinta que haviam sobrado da reforma da casa de um amigo. As latas não estavam cheias.

Anderson pretendia usar o que sobrou das latas de tinta para pintar as paredes de três cômodos de sua residência. Para saber a quantidade de tinta de cada lata, ele primeiro colocou um pedaço de madeira até encostar no fundo da lata e, depois, mediu o comprimento da madeira suja de tinta. As medidas obtidas por Anderson estão representadas a seguir.
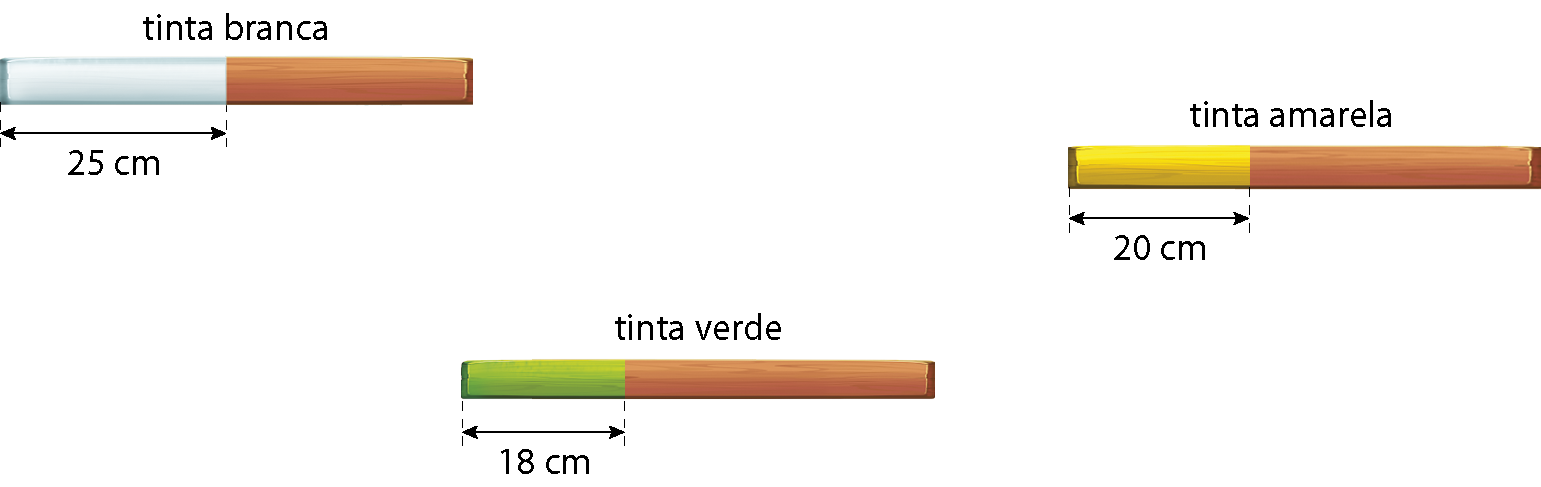
Sabendo que a medida do comprimento e a da largura das latas é 23 centímetros, qual é a medida do volume aproximado de tinta em cada lata?
Quando enchemos um recipiente com líquido, verificamos que ele ocupa o formato do recipiente. Logo, podemos imaginar que as tintas no interior das latas ocupam o espaço correspondente ao volume de um paralelepípedo.
A medida do volume de um paralelepípedo é obtida multiplicando-se as medidas de comprimento, largura e altura, conforme a expressão a seguir.

Então, como Anderson obteve as medidas aproximadas das alturas, temos:
• medida aproximada do volume de tinta branca:
vôlts = 23 centímetros · 23 centímetros · 25 centímetros = .13225 centímetros cúbicos
• medida aproximada do volume de tinta amarela:
vôlts = 23 centímetros · 23 centímetros · 20 centímetros = .10580 centímetros cúbicos
• medida aproximada do volume de tinta verde:
vôlts = 23 centímetros · 23 centímetros · 18 centímetros = .9522 centímetros cúbicos
Após medir a área das paredes de seus cômodos, Anderson verificou que seriam necessários 10 litros de tinta branca, 9 litros de tinta amarela e 8 litros de tinta verde. A quantidade de tinta disponível será suficiente?
Antes de responder a essa pergunta, vamos relembrar as unidades de medida de capacidade e de volume que fazem parte do Sistema Internacional de Unidades (ésse Í).
O litro (L) é a unidade-padrão de medida de capacidade e corresponde à medida da capacidade de um cubo com arestas medindo 1 decímetro de comprimento, ou seja, 1 litro corresponde à medida de volume igual a 1 decímetro cúbico.

1 litro = 1 decímetro cúbico
O decímetro cúbico (dê ême 3 sobrescrito) é uma das unidades de medida de volume, assim como o centímetro cúbico (cê ême 3 sobrescrito).
Observe, no quadro a seguir, os múltiplos e os submúltiplos do litro, que estão no ésse Í.
|
Múltiplos |
Unidade-padrão |
Submúltiplos |
|||||
|---|---|---|---|---|---|---|---|
|
Unidade |
quilolitro |
hectolitro |
decalitro |
litro |
decilitro |
centilitro |
mililitro |
|
Símbolo |
kL |
hL |
daL |
L |
dL |
cL |
mL |
|
Relação com o litro |
1.000 L |
100 L |
10 L |
1 L |
0,1 L |
0,01 L |
0,001 L |
Em relação às unidades de medida de volume, o metro cúbico (ême 3 sobrescrito), que corresponde à medida do volume de um cubo cujas arestas medem 1 métro, é a unidade-padrão de medida de volume. O quadro a seguir apresenta os múltiplos e os submúltiplos do metro cúbico.
|
Múltiplos |
Unidade-padrão |
Submúltiplos |
|||||
|---|---|---|---|---|---|---|---|
|
Unidade |
quilômetro cúbico |
hectômetro cúbico |
decâmetro cúbico |
metro cúbico |
decímetro cúbico |
centímetro cúbico |
milímetro cúbico |
|
Símbolo |
km3 |
hm3 |
dam3 |
m3 |
dm3 |
cm3 |
mm3 |
|
Relação com o metro cúbico |
109m3 |
1.000.000 m3 |
1.000 m3 |
1 m3 |
0,001 m3 |
10−6m3 |
10−9m3 |
Observe que cada unidade de medida de volume equivale a .1000 vezes a unidade de medida imediatamente inferior.

Voltando ao problema inicial, vamos verificar se a quantidade de tinta disponível é suficiente para Anderson.
• Ele precisa de 10 litros de tinta branca e tem .13225 centímetros cúbicos dessa tinta. Vamos expressar a medida do volume de tinta disponível em decímetros cúbicos; para isso, basta dividir .13225 centímetros cúbicos por .1000:
.13225 centímetros cúbicos : .1000 = 13,225 decímetros cúbicos
Como 1 decímetro cúbico corresponde a 1 litro, a quantidade de tinta disponível é aproximadamente 13,225 litros. Portanto, a quantidade de tinta branca disponível é suficiente para Anderson.
Usando o mesmo raciocínio, verificamos se as quantidades de tintas amarela e verde são suficientes:
• tinta amarela:
.10580 centímetros cúbicos : .1000 = 10,58 decímetros cúbicos
• tinta verde:
.9522 centímetros cúbicos : .1000 = 9,522 decímetros cúbicos
Logo, Anderson tem disponível aproximadamente 10,58 litros de tinta amarela e aproximadamente 9,522 litros de tinta verde. Respondendo à pergunta do problema, ele tem tinta suficiente, pois precisa de 9 litros de tinta amarela e 8 litros de tinta verde.
Agora, observe mais uma situação.
Antonela contratou a empresa de Enzo para construir em seu sítio uma piscina com medida de capacidade de .60000 litros.
Para o projeto, a única restrição era que a medida da profundidade da piscina não poderia ser maior do que 1,6 metro. Com isso, Enzo propôs a Antonela uma piscina com as seguintes medidas: 7,5 métros de largura, 5 métros de comprimento e 1,6 métro de altura.
Antonela, então, perguntou: “Com essas medidas, a piscina teria medida de capacidade suficiente para 60 mil litros?”.
Para responder, Enzo expôs os seguintes cálculos:

Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Oxigênio
Duração: 3:50min. Página: 178.
>> [LOCUTOR]: Oxigênio
>> [LOCUTOR] O oxigênio é um dos elementos essenciais para a vida humana. Como será que os astronautas fazem para respirar em suas missões espaciais? Conversamos com a astrofísica Carla Martinez Canelo para descobrir. Vamos ouvi-la?
>> [Carla Martinez Canelo] O meu nome é Carla. Eu sou formada em Física, tenho mestrado em Astronomia e estou no doutorado em Astronomia. Trabalho com Astrobiologia, que basicamente estuda a vida na Terra e no Universo. Minha pesquisa envolve procurar moléculas importantes para a origem da vida na Terra e em outros lugares do Universo, como outras galáxias.
>> [LOCUTOR] Qual é a importância do armazenamento de oxigênio em missões espaciais? Como ele é feito?
>> [Carla Martinez Canelo] Em missões espaciais tripuladas, ou seja, em que há pessoas no espaço, precisamos ter oxigênio armazenado para que elas possam respirar. Além disso, ele pode ser usado como combustível para que os ônibus espaciais possam decolar da Terra e se locomover no Espaço. O oxigênio fica armazenado dentro de tanques e é importante dizer que ele está pressurizado, ou está sob alta pressão, e por um bom motivo: em um gás, as moléculas estão mais afastadas umas das outras do que o mesmo material em estado líquido ou sólido. E, se aumentarmos a temperatura, faremos com que o gás se expanda. Então, se quisermos colocar gás oxigênio num recipiente, podemos diminuir sua temperatura e aumentar a pressão sobre ele para que as moléculas fiquem mais próximas umas das outras. Dessa forma, ele muda para o estado líquido e ocupa menos volume do que quando estava no estado gasoso. Embora a quantidade de oxigênio dentro de um tanque pressurizado possa variar, dependendo da pressão ou da temperatura, a capacidade do tanque permanece sempre a mesma. Ou seja, o tamanho do tanque não muda. Suponha que um desses tanques seja cúbico e tenha 50 centímetros de aresta ou 5 decímetros. Seu volume total será de 5 × 5 × 5, ou 125 decímetros cúbicos. Lembrando que, dentro de 1 decímetro cúbico, cabe 1 litro de qualquer líquido. Podemos dizer que esse tanque tem a capacidade volumétrica de 125 litros.
>> [LOCUTOR] Qual é a quantidade de oxigênio necessária para uma estação espacial?
>> [Carla Martinez Canelo] A quantidade de oxigênio necessária para uma estação espacial depende de quantos astronautas estão a bordo e por quanto tempo. Por exemplo, para uma tripulação de seis pessoas ficar doze dias na estação, numa temperatura de 25 graus Celsius e na mesma pressão que temos na Terra no nível do mar, precisaríamos de cerca de 49 000 litros de oxigênio. Isso equivale a 49 000 decímetros cúbicos ou simplesmente 49 metros cúbicos.
>> [LOCUTOR] Como é feito o reabastecimento de oxigênio?
>> [Carla Martinez Canelo] Na Estação Espacial Internacional, um dos processos para gerar oxigênio é a eletrólise. Nele, eletricidade quebra moléculas de água em oxigênio e hidrogênio. O oxigênio é então ventilado para a tripulação. Mas, antes da instalação desse sistema, tanques com oxigênio pressurizado foram o primeiro suprimento dos astronautas. Hoje, eles ainda funcionam como suporte para a eletrólise e são recarregados por missões espaciais não tripuladas de reabastecimento, que levam também água, comida e equipamentos para a estação espacial.
Vinheta.
Créditos Studio Núcleo de Criação
Sugestão de leitura
POSKIT, Kjartan. Medidas desesperadas: comprimento, área e volume. São Paulo: Melhoramentos, 2006. (Coleção Saber Horrível)
Utilizando um contexto irreverente, criativo e intrigante, o livro contempla situações que auxiliam na compreensão de conteúdos como: medidas antigas e atuais, área, perímetro, volume, ângulos e figuras geométricas.
Atividades
Faça as atividades no caderno.
15. Calcule a medida do volume dos sólidos a seguir.
a)

b)

16. Sara e André passaram em uma lojinha quando estavam voltando para casa de um passeio e compraram uma forminha de gelo diferente. O gelo, quando formado, se parecia com um bloco retangular. Na embalagem está escrito que o gelo formado tem as seguintes medidas: 12 milímetros de largura, 12 milímetros de altura e 96 milímetros de comprimento. Qual é a medida do volume do gelo feito nessa forma?

17. Um vaso se parece com um bloco retangular, como indica a figura a seguir. Se colocarmos água até um terço da sua medida de altura, quantos litros de água colocaremos nesse vaso?
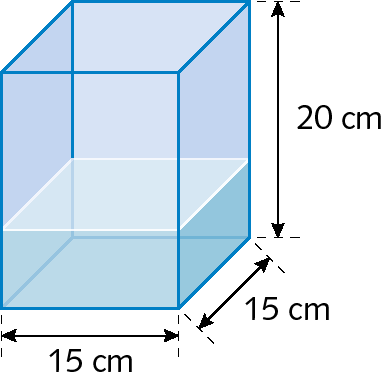
18. Camila vai construir uma piscina em seu quintal que ocupará uma região retangular cujos lados medem 3 métros e 5 métros de comprimento. Qual deverá ser a medida da profundidade dessa piscina de modo que a medida de capacidade total seja .22500 litros?
19.


Ivan pediu a um designer que criasse uma embalagem que se parecesse com um paralelepípedo reto-retângulo e que ocupasse uma medida de volume de 216 centímetros cúbicos.
a) Desenhe duas opções de embalagem com essas características.
b) Acrescente uma característica à encomenda de Ivan para que a embalagem possa ter um único formato.

Lendo e aprendendo

Só o dilúvioglossário salva
Cenário otimista para chuvas prevê reservatórios brasileiros em 2022 ainda mais abaixo do que já estão hoje
Foi em agosto deste ano, quando a conta de luz começou a subir, que a dona de casa Ana Paula Barbosa anunciou à família: não se liga mais o ventilador. Em Duque de Caxias, na Baixada Fluminense, ventilador em agosto não é luxo. Apesar do inverno, a temperatura na cidade chegou a 36 graus Célsius — e parece um pouco mais alta dentro da casa onde vivem cinco pessoas. Às vezes a sensação de calor é sufocante. Os dois filhos mais velhos, que agora trabalham e estudam em casa, tiveram que se adaptar. “A nossa qualidade de vida foi para o buraco”, resume a mãe. Ela inaugurou outras medidas para economizar na conta de luz. Passou a lavar a roupa na mão, cortou o ferro de passar e manteve as luzes do quintal desligadas. Para os dois filhos mais velhos, o aperto foi um pouco maior. “É muito ruim pedir para o seu filho, que está estudando o dia todo nesse calor, não ligar o ventilador de teto”, conta Barbosa. “Todo mundo começa a ficar irritado porque está desconfortável. É desconforto para trabalhar, desconforto para estudar e até para dormir. E todos os dias são assim.” O ventilador foi cortado até na hora de dormir. Mesmo com as restrições, a conta de luz do mês ficou em 400 reais, 10% da renda mensal da família, e 120 reais mais cara que a de julho. Parece pouco, mas é quase o preço do botijão de gás, lembra Barbosa.
O jeito foi tirar do orçamento destinado à alimentação. O leite do lanche teve que ser cortado. O queijo e o presunto do sanduíche também. A variedade de legumes foi substituída por anguglossário , e as frutas foram reduzidas. A preocupação é com o futuro. “Como vamos passar o verão no Rio de Janeiro sem ligar o ventilador? Fico pensando o que mais vou ter que cortar para pagar a luz. A única coisa que dá para tirar é a alimentação”, diz Barbosa. Ela vai ter que enxugar ainda mais o orçamento nos próximos meses, porque a crise energética só tende a piorar: as projeções sobre a capacidade dos reservatórios de hidrelétricas do Sudeste e Centro-Oeste indicam que o Brasil caminha para chegar ao ano que vem num cenário de escassez hídrica e energética ainda pior que o de 2021, afirmam especialistas reticências.
A estimativa é de que em fevereiro de 2022 os reservatórios dessas regiões — os mais importantes para a geração de energia elétrica no país — estejam num volume perto de 17% da capacidade total. Esses mesmos reservatórios fecharam o mês de fevereiro de 2021 com 29,7% da capacidade. As previsões são de meteorologistas da consultoria MegaWhat, especializada no setor energético, e levam em conta os mapas de chuva dos próximos seis meses, convertidos em vazão dos rios. No cenário mais pessimista, o nível desses reservatórios pode chegar a 11% em fevereiro do ano que vem — e no mais otimista de todos, a 22,9%, ainda muito abaixo do registrado em 2021. O racionamento está batendo à porta, e não só na casa de Caxias.
reticências
O cenário de escassez prolongada calculado pela MegaWhat é confirmado pelo Operador Nacional do Sistema Elétrico (ONS), responsável por despachar a energia elétrica no Brasil e regular o setor. O órgão estima que os reservatórios do Sudeste e Centro‑Oeste chegarão a novembro deste ano com apenas 11,3% do volume total (em 2020, estava em torno de 20%). Isso na melhor das hipóteses, caso o governo consiga gerar mais energia e retire a pressão sobre as hidrelétricas. Na pior das hipóteses, esses reservatórios podem chegar a 8%. Essa é uma média de toda a região, o que significa que algumas reservas poderão estar com volume ainda mais baixo do que esse.
Lendo e aprendendo
reticências
Na análise de Altino Ventura, ex-presidente da Eletrobras, um tipo de racionamento de energia elétrica já está em vigor agora, por meio dos preços. Um racionamento com “r” minúsculo, diz ele. É o que está acontecendo com a família de Ana Paula Barbosa, em Duque de Caxias. Todo dia, ela vai ao relógio da casa, que mede o consumo de energia elétrica, e verifica quantos quilowatts a família está gastando. Não dá para passar de 7, senão o orçamento estoura. “Quando passa um pouco eu tenho que pedir para alguém deixar de usar alguma coisa, algum aparelho, para não ultrapassar os quilowatts determinados”, explica a dona de casa. Mas se o preço continuar aumentando, não vai ter de onde tirar, diz ela. Além do ventilador, o micro-ondas já não é mais usado, nem a fritadeira elétrica. “Chegamos ao ponto de ter os aparelhos e não conseguirmos mais usá-los. Se eu cortar mais eu chego na pré-história. Mudar de hábito é legal quando se tem economia, não quando você precisa fazer isso para sobreviver.”
Para Ventura, o racionamento por aumento de preço é o pior que existe, porque penaliza mais quem tem menos condição de pagar e ainda dá um sinal inflacionário. Dados do Ipea mostram que, entre os mais pobres, o peso do aumento de energia elétrica na inflação é três vezes o observado entre os mais ricos. Agora em setembro, começa a valer a bandeira de escassez hídrica, com taxa extra de 14,20 reais para cada 100 kWhglossário consumidos, acima da bandeira vermelha patamar 2 — até então, o máximo de cobrança adicional feita por energia. A bandeira de escassez será aplicada até abril do ano que vem.
O aumento aconteceu porque as termelétricas começaram a ser acionadas para compensar o déficitglossário de energia diante da baixa dos reservatórios — o menor desde 2001. Hoje, todas as termelétricas do país estão em operação, e o custo dessa fonte energética — mais cara e poluente — foi progressivamente repassado aos consumidores. reticências
LICHOTTI, C. Só o dilúvio salva. Piauí, 9 setembro 2021. Disponível em: https://oeds.link/HrCu1B. Acesso em: 6 julho 2022.

Lendo e aprendendo
Faça as atividades no caderno.
Atividades
1. Responda às questões no caderno.
a) Quando a matéria foi publicada?
b) Qual era a renda mensal aproximada da família de Ana Paula Barbosa em 2021?
c) Qual foi o valor da conta de luz no mês de julho da família de Ana Paula Barbosa?
d) Por que foi cobrada uma taxa extra na conta de luz dos brasileiros em setembro de 2021?
2. Qual é o tema principal da matéria?
a) A história da dona de casa Ana Paula Barbosa.
b) O aumento das chuvas do Brasil em 2021.
c) O uso de fontes renováveis de energia.
d) A crise hídrica no Brasil em 2021.
3. Qual é a intenção por trás do título “Só o dilúvio salva”?
4. Segundo o ex-presidente da Eletrobras, Altino Ventura, o país estava vivendo, em setembro de 2021, um racionamento de energia com “r” minúsculo. O que ele quis dizer com isso?
5. Qual das imagens a seguir melhor retrata o nível dos reservatórios de hidrelétricas das regiões Sudeste e Centro-Oeste em fevereiro de 2021?
a)

b)

c)

d)

6. Em 2021, Ana Paula Barbosa tomou uma série de medidas para diminuir o consumo de energia de sua residência e, consequentemente, pagar um valor menor de conta de luz. Quais das medidas adotadas por ela são também adotadas na sua casa? Além dessas medidas, você e sua família adotam outras? Responda no caderno.
7.

Na sua opinião, como crises hídricas como a que ocorreu no Brasil em 2021 podem ser combatidas? Produza um pequeno texto com sua opinião e, depois, compartilhe-o com os colegas.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Medida da área de figuras planas
Medida da área de um retângulo
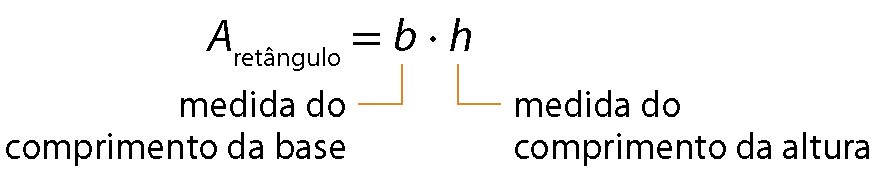
Medida da área do quadrado
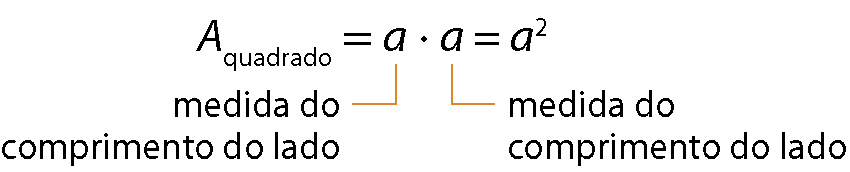
Medida da área do triângulo

Medida da área do paralelogramo
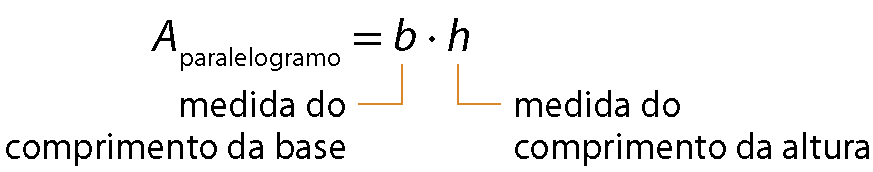
Medida da área do trapézio
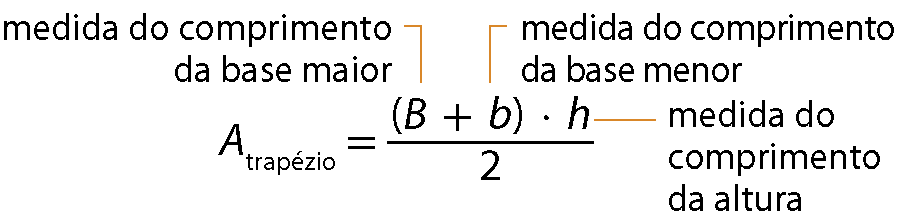
Medida da área do losango

1. Determine a medida da área do paralelogramo a seguir.
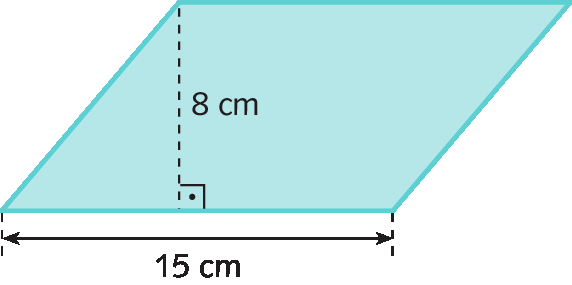
2. Determine a medida da área da figura plana de cada item.
a)
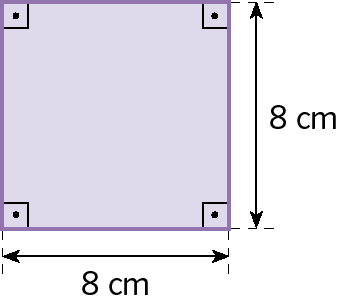
b)
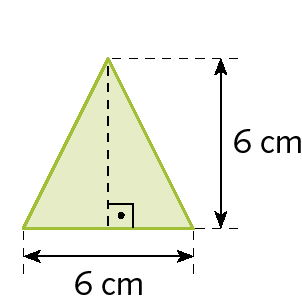
3. Calcule a medida da área da parte pintada de azul.

Medida da área do círculo
Medida da área do círculo

Medida da área da coroa circular
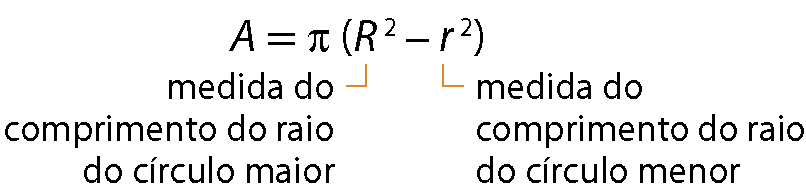
Medida da área de um setor circular
A medida da área de um setor circular de raio r e ângulo central de medida de abertura α, em grau, é dada por: Asetor =
alfa dividido por 360 graus⋅ πr 2
4. Calcule a medida da área da região determinada por duas circunferências concêntricas cujos raios medem 10 cm e 4 cm de comprimento.
5. Calcule a medida da área do setor circular cuja medida da abertura do ângulo central é 30graus e a medida do comprimento do raio é 5 centímetros.
Medidas de volume e capacidade

O litro (L) é a unidade-padrão de medida de capacidade e corresponde à medida de capacidade de um cubo com arestas medindo 1 decímetro de comprimento, ou seja, 1 litro = 1 decímetro cúbico
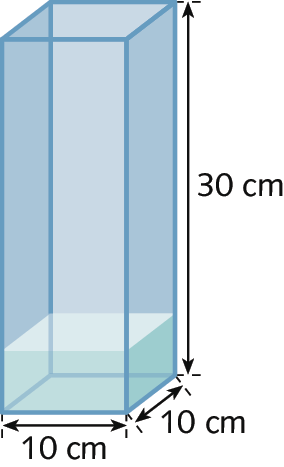
6. Uma caixa se parece com um bloco retangular. Colocando água em até um sexto de sua medida da altura, quantos litros de água serão inseridos nessa caixa?
Glossário
- Dilúvio
- : Chuva muito abundante.
- Voltar para o texto
- Angu
- : Massa espessa que se faz misturando, ao fogo, farinha de milho (fubá), de mandioca ou de arroz com água e, às vezes, sal.
- Voltar para o texto
- kWh
- : Símbolo de quilowatt-hora que corresponde à energia produzida ou consumida no intervalo de 1 h com potência de 1 quilouát ou 103 uáts, no contexto da Eletricidade.
- Voltar para o texto
- Déficit
- : Diferença entre o valor previsto e o valor realmente obtido.
- Voltar para o texto