Capítulo 9 Equações do 2º grau
Trocando ideias

A raiva transmitida por cães e gatos a humanos é uma doença que não tem cura, e sua transmissão pode acontecer por meio de mordida, lambida ou arranhão do animal infectado. Por ano, cêrca de 60 mil pessoas morrem pela doença, e a vacinação é uma fórma de erradicá-la.

▸


Você tem um cão ou gato de estimação? Se sim, ele já foi vacinado contra a raiva? Converse com os colegas.
▸

Sabendo que a medida da área do cartaz oficial é .2944 centímetros quadrados e que seus lados medem x e
23x sobre 32.de comprimento, determine a medida, em centímetro, do comprimento dos lados do cartaz oficial. Faça os cálculos no caderno.
Neste capítulo, vamos aprender a resolver algumas equações do 2º grau com uma incógnita e a resolver problemas como o do item anterior.

1 Equação do 2º grau com uma incógnita
Acompanhe a situação a seguir.
Um curral tem formato retangular e medida de área igual a 288 métros quadrados. Sabendo que uma das dimensões mede o dobro da outra, quanto mede cada uma das dimensões desse curral?

Indicando por x a medida do comprimento da menor dimensão, temos que 2x corresponde à medida do comprimento da maior dimensão e x ⋅ 2x corresponde à medida da área do curral. Assim:
x ⋅ 2x = 288
2x elevado a 2 = 288
Uma maneira de calcular a medida do comprimento de cada uma das dimensões desse curral é resolver essa equação.
A equação 2x elevado a 2 menos 288 = 0 é um exemplo de equação do 2º grau com uma incógnita, nesse caso, indicada pela letra x.
Denominamos equação do 2º grau na incógnita x aquela que pode ser reduzida a uma equação do tipo ax elevado a 2 + bx + c = 0, em que a, b e c são números reais, com a ≠ 0.
Os números a, b e c são chamados coeficientes da equação do 2º grau. Agora, observe alguns exemplos em que identificamos os valores dos coeficientes de equações do 2º grau.
a) x elevado a 2 menos 5x + 6 = 0 é uma equação do 2º grau, com a = 1, b = menos5 e c = 6.
b) 6x elevado a 2 menos x menos 1 = 0 é uma equação do 2º grau, com a = 6, b = menos1 e c = menos1.
c) 7x elevado a 2 menos x = 0 é uma equação do 2º grau, com a = 7, b = menos1 e c = 0.
d) x elevado a 2 menos 36 = 0 é uma equação do 2º grau, com a = 1, b = 0 e c = menos36.
Observação
As equações a seguir não são equações do 2º grau com uma incógnita:
a) x elevado a 2 + 2y elevado a 2 = 8, pois possui duas incógnitas: x e y.
b) x elevado a 3 + 4x elevado a 2 menos x = menos7, pois o maior expoente da incógnita x é 3.
c) (3y elevado a 2 menos 2)elevado a 2 = 0, pois o maior expoente da incógnita y é 4, já que (3y elevado a 2 menos 2)elevado a 2 é igual a 3y elevado a 4 menos 6y elevado a 2 + 4.
Equações completas e incompletas
Quando uma equação do 2º grau com uma incógnita, na fórma ax elevado a 2 + bx + c = 0, tem todos os coeficientes (a, b, c) diferentes de zero, dizemos que a equação é completa. Considere os exemplos.
a)
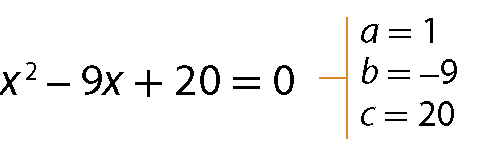
b)
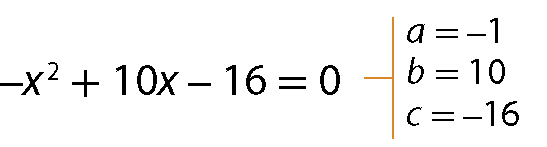
Quando b e/ou c são iguais a zero, dizemos que a equação é incompleta. Considere os exemplos.
a)
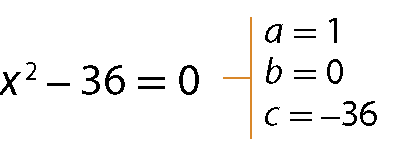
b)
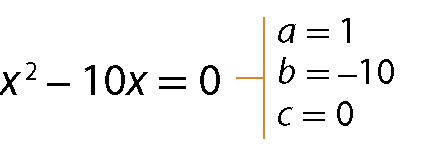
c)
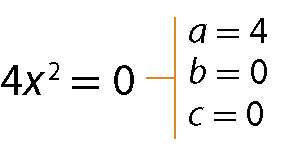
Neste capítulo, vamos estudar as equações do 2º grau incompletas; no próximo ano, será aprofundado o trabalho com as equações consideradas completas.
Atividades
Faça as atividades no caderno.
1. Uma quadra de basquete tem medida de área igual a 420 métros quadrados. Escreva a equação do 2º grau que pode ser utilizada para determinar a medida do comprimento e a medida da largura da quadra, de acordo com a figura representada a seguir.
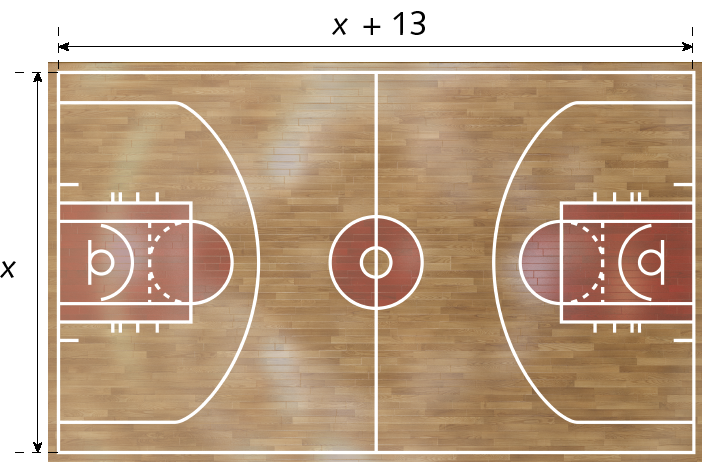
2. Identifique as equações do 2º grau.
a) 6x + 5 = 0
b) x elevado a 2 menos 6x + 9 = 0
c) y elevado a 2 menos 4y = 0
d) 0x elevado a 2 + 5x + 6 = 0
e) 9 menos y elevado a 2 = 0
f) (2z ‒ 3)elevado a 2 = 0
3. Considerando ax elevado a 2 + bx + c = 0, com a ≠ 0, determine os coeficientes das equações.
a) menos3x elevado a 2 + 6x = 0
b) 3x elevado a 2 menos 12 = 0
c) 25 menos 10x + x elevado a 2 = 0
d) (k + 1)x elevado a 2 menos 2kx = 0, com k + 1 ≠ 0
4. Escreva no caderno a equação ax elevado a 2 + bx + c = 0, em que:
a) a = 5, b = menos1 e c = 0
b) a = 4, b = 0 e c = menos9
c) a = 0,2, b = 1 e c = 0,5
5. Um quadrado cujo comprimento do lado mede x tem medida da área igual a 625 métros quadrados. Escreva uma equação do 2º grau para determinar o valor de x.
6. Classifique as equações do 2º grau em completas ou incompletas.
a) 3x elevado a 2 + 5x = 0
b) menos3x elevado a 2 + 9 = 0
c) x elevado a 2 + 7x + 12 = 0
d) 6x elevado a 2 = 0
e)
x ao quadrado menos 3 vezes raiz quadrada de 2, fim da raiz, vezes x mais 4 igual a zero.7. Determine os valores possíveis de m na equação (3m menos 2)x elevado a 2 + (2m + 1)x menos 4 = 0, de modo que ela seja do 2º grau.
8. Escreva a equação
Sentença matemática. 5 menos, numerador da fração, abre parênteses, x menos 3, fecha parênteses, denominador: 4, tudo igual a 2x menos, abre parênteses, x menos 2, fecha parênteses, ao quadrado.na fórma ax elevado a 2 + bx + c = 0, com a ≠ 0.
Raiz de uma equação do 2º grau
Raiz de uma equação é um número que, ao substituir a incógnita, torna a sentença verdadeira.
Podemos verificar se um número é ou não raiz de uma equação substituindo a incógnita por esse número. Se a sentença for verdadeira, o número considerado é raiz da equação; se a sentença for falsa, o número não é raiz da equação.
Vamos verificar se, por exemplo, os números menos3, 0, 1 e 3 são raízes da equação 3x elevado a 2 menos 27 = 0.
Para x = menos3:
3x elevado a 2 menos 27 = 0
3 ⋅ (menos3)elevado a 2 menos 27 = 0
3 ⋅ 9 menos 27 = 0
0 = 0

sentença verdadeira
Para x = 0:
3x elevado a 2 menos 27 = 0
3 ⋅ (0)elevado a 2 menos 27 = 0
3 ⋅ 0 menos 27 = 0
‒27 = 0

sentença falsa
Para x = 1:
3x elevado a 2 menos 27 = 0
3 ⋅ (1)elevado a 2 menos 27 = 0
3 ⋅ 1 menos 27 = 0
‒24 = 0

sentença falsa
Para x = 3:
3x elevado a 2 menos 27 = 0
3 ⋅ (3)elevado a 2 menos 27 = 0
3 ⋅ 9 menos 27 = 0
0 = 0

sentença verdadeira
Então, verificamos que menos3 e 3 são raízes da equação, enquanto 0 e 1 não são raízes de 3x elevado a 2 menos 27 = 0.
Agora, vamos verificar um novo exemplo em que precisamos determinar p na equação (2p menos 1)x elevado a 2 menos 2 = 0, sabendo que 2 é raiz.
Substituindo a incógnita x por 2, já que 2 é raiz da equação, podemos obter o valor de p.
(2p menos 1) ⋅ (2)elevado a 2 menos 2 = 0
(2p menos 1) ⋅ 4 menos 2 = 0
8p menos 4 menos 2 = 0
8p menos 6 = 0
8p = 6
Sentença matemática. p igual a 6 oitavos.
Sentença matemática. p igual a 3 quartos.
Portanto, o valor de p é
Fração três quartos, sabendo que a raiz da equação (2p menos 1)x elevado a 2 menos 2 = 0 é 2.
Atividades
Faça as atividades no caderno.
9. Dados os números menos4, menos2, menos1, 0, 1, 2 e 4, quais deles são raízes da equação menos2x elevado a 2 + 8 = 0?
10. Em
Sentença matemática. Abre parênteses, 3k sobre 2, fecha parênteses, vezes x ao quadrado menos 5 meios igual a zero. Sentença matemática. k diferente de zero., qual é o valor de k para que
Fração. menos meio.seja raiz dessa equação?
11. Verifique se ‒0,2 é raiz das equações a seguir.
a) x elevado a 2 + 9 = 0
b) 125x elevado a 2 menos 5 = 0
12. Dê um exemplo de equação do 2º grau com uma incógnita, de modo que:
a) 0 seja uma raiz;
b) não possua raízes reais.

2 Resolução de equações do 2º grau
Resolver uma equação do 2º grau consiste em encontrar as raízes dessa equação que pertencem ao conjunto universo dela. Essas raízes, que pertencem ao conjunto universo, são as soluções dessa equação e formam o seu conjunto solução, que é indicado por S.
Acompanhe nos exemplos a seguir como resolver algumas equações do 2º grau incompletas.
a) Vamos resolver a equação 2x elevado a 2 menos 72 = 0, sendo conjunto universo =

.
2x elevado a 2 menos 72 + 72 = 0 + 72

Adicionamos 72 a ambos os membros da equação.
2x elevado a 2 = 72
2 vezes x ao quadrado, tudo sobre 2 igual a 72 sobre 2. O denominador 2 dos dois membros da igualdade está destacado na cor laranja.

Dividimos os dois membros por 2.
x elevado a 2 = 36
x igual a raiz quadrada de 36 que é igual a 6.
= 6 ou
x igual a menos raiz quadrada de 36 que é igual a menos 6.Como ‒6 e 6 são raízes da equação e pertencem ao conjunto universo, então S = {menos6, 6}.
b) Vamos resolver a equação menos3x elevado a 2 = 0, em

.
Sentença matemática. Menos 3 vezes x ao quadrado, tudo sobre menos 3 igual a 0 sobre menos 3. O denominador menos 3 dos dois membros da igualdade está destacado na cor laranja.

Dividimos os dois membros por menos3.
x elevado a 2 = 0
x = menos0 = 0 ou x = +0 = 0
Como a equação tem duas raízes reais iguais a zero e 0 pertence ao conjunto universo, então S = {0}.
Observação
Quando a raiz da equação não pertence ao conjunto universo, podemos representar o conjunto solução como ∅ ou { }. Observe o exemplo a seguir.
• Vamos resolver a equação 3x elevado a 2 + 6 = 0, sendo conjunto universo =

.
3x elevado a 2 + 6 menos 6 = 0 menos 6

Subtraímos 6 de ambos os membros da equação.
3x elevado a 2 = menos6
Sentença matemática. 3 vezes x ao quadrado, tudo sobre 3 igual a menos 6 sobre 3. O denominador 3 dos dois membros da igualdade está destacado na cor laranja.

Dividimos os dois membros por 3.
x elevado a 2 = menos2
Como não existe um número real que, elevado ao quadrado, seja igual a menos2, dizemos que a equação não tem raízes reais ou não tem solução em

. Ou seja, S = ∅ ou S = { }.

Veja que interessante
Faça as atividades no caderno.

Você já ouviu falar em í ême cê?
O í ême cê (Índice de Massa Corpórea) é calculado a partir da razão entre a medida da massa (em quilograma) e o quadrado da medida do comprimento da altura (em metro) de uma pessoa adulta. Esse índice foi desenvolvido no século dezoito pelo cientista belga Adolphe Quételet, mas somente em 1980 passou a ser utilizado como um dos padrões internacionais de referência para medidas de obesidade pela Organização Mundial da Saúde (ó ême ésse).
O í ême cê pode ser utilizado como parâmetro para adultos de 20 a 59 anos de idade. Esse índice não se aplica a crianças e adolescentes nem a idosos; para essas faixas etárias, são aplicados métodos específicos. Em pessoas muito musculosas, também pode acontecer de o índice indicar sobrepeso indevidamente.

Tomando como exemplo um rapaz com 82 quilogramas e 1,85 métro, temos:
Sentença matemática. IMC igual a, fração com numerador 82 e denominador, abre parênteses, 1 vírgula 85, fecha parênteses, ao quadrado, igual a outra fração com numerador 82 e denominador 3 vírgula 4225, aproximadamente 23 vírgula 96.
De acordo com o resultado do í ême cê obtido, classificamos o indivíduo dentro de uma faixa, conforme o quadro.
|
IMC |
Classificação |
|---|---|
|
abaixo de 17 |
muito abaixo do ideal |
|
de 17 a 18,49 |
abaixo do ideal |
|
de 18,5 a 24,99 |
ideal |
|
de 25 a 29,99 |
acima do ideal |
|
de 30 a 34,99 |
obesidade de grau 1 |
|
de 35 a 39,99 |
obesidade de grau 2 |
|
a partir de 40 |
obesidade de grau 3 |
Algumas classificações podem trazer riscos à saúde, como a "obesidade", que pode gerar problemas como hipertensão, diabetes (tipo dois), doenças cardiovasculares etcétera, e o "abaixo do ideal", que pode causar queda de cabelo, infertilidade, estresse, entre outras complicações.
O í ême cê é considerado um parâmetro para avaliar se a massa de um adulto em relação à sua altura é adequada, mas, para verificar se uma pessoa é saudável, há outras ferramentas para essa verificação. Os profissionais de saúde, por exemplo, conseguem avaliar de fórma mais criteriosa se a medida de massa de um indivíduo está ou não adequada utilizando algumas técnicas e outros parâmetros, como:
• análise do percentual de gordura;
• medida do comprimento da circunferência da cintura;
• relação cintura × quadril.
Atividades
1. Observando como parâmetro somente o í ême cê de um homem adulto de 42 anos com 82 quilogramas de medida de massa e 1,85 métro de medida de comprimento de altura, o que podemos afirmar? E se a medida de sua massa aumentar para 105 quilogramas?
2. Calcule o í ême cê de algum adulto da sua casa e verifique em qual classificação ele se encontra. (Lembre-se de verificar se ele possui idade entre 20 e 59 anos.)
Atividades
Faça as atividades no caderno.
13. Calcule as raízes reais de cada equação.
a) abre parêntesesx − 2fecha parênteseselevado a 2 + 4x = 4
b)
2 vezes x ao quadrado menos 3 quartos igual a x ao quadrado mais 1 quarto.
c)
Fração de numerador x menos 3 e denominador 2 mais fração de numerador 2x menos 3 e denominador 4 é igual a x ao quadrado mais x menos 17 meios.d) 3m elevado a 2 + 2 = 4m elevado a 2 + 2
e)
Sentença matemática. Abre parênteses, fração x sobre 5, toda a fração menos 5, fecha parênteses, vezes, abre parênteses, fração x sobre 5, toda a fração mais 5, fecha parênteses, igual a zero.14. Determine o conjunto solução de cada equação, sendo conjunto universo =

.
a) x elevado a 2 − 64 = 0
b) 3x elevado a 2 + 7 = 0
c) 9x elevado a 2 − 16 = 0
d) 3x elevado a 2 = 0
15. Responda às questões, sabendo que o retângulo e o quadrado a seguir têm a mesma medida de área, 64.

a) Qual é a medida do comprimento do lado do quadrado?
b) Qual é a medida do perímetro do quadrado? E a do retângulo?
16. A diferença entre o quadrado de x e 4 é igual a 140. Qual é o valor de x?
Resolução de problemas
Na resolução de problemas com equações do 2º grau, podemos seguir as etapas do fluxograma a seguir:

Acompanhe a resolução de alguns problemas que envolvem equações do 2º grau.
Problema 1
Sebastião tem um terreno quadrado para o plantio de milho. Um vizinho vendeu um pedaço de terra para Sebastião, aumentando a medida da largura do terreno inicial em 20%. Sebastião pretende cercar todo o terreno para evitar que alguns animais estraguem a plantação. Se a medida da área do terreno com a parte vendida pelo vizinho é de 750 métros quadrados, qual será a medida do comprimento total da cêrca?
Vamos indicar por x a medida do comprimento da lateral do terreno de Sebastião.
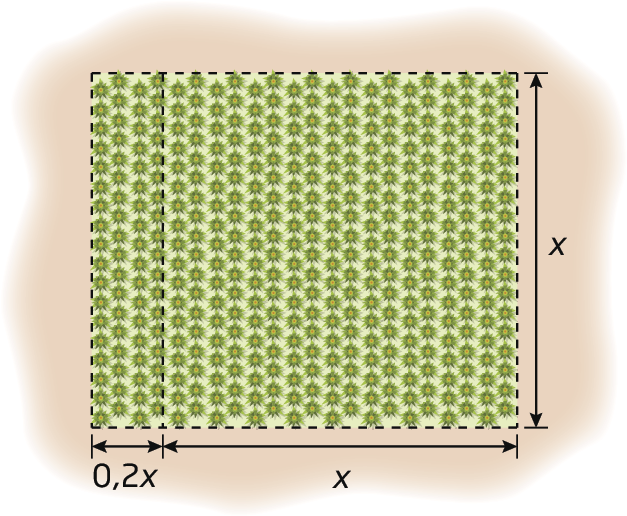
Precisamos encontrar o valor de x para determinar a medida do perímetro do terreno. Podemos traduzir o problema pela seguinte equação:
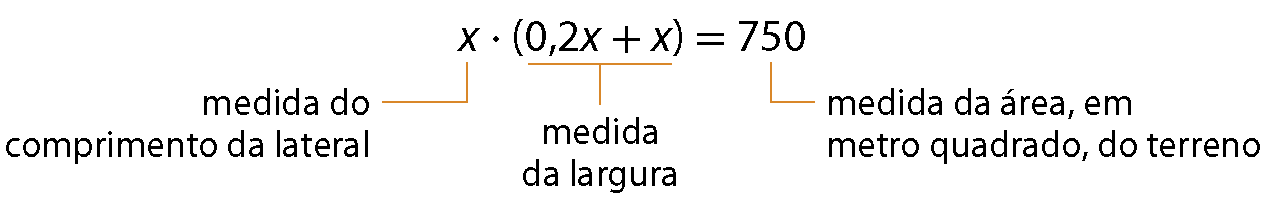
Calculando as raízes da equação, temos:
Sentença matemática. x vezes 1vírgula 2x igual a 750 implica em 1 vírgula 2x ao quadrado igual a 750, implica em, x ao quadrado, igual a, fração 750 sobre 1 vírgula 2, implica em, x ao quadrado igual a 625, implica em, x igual a 25 ou x igual a menos 25.
Como x é uma medida de comprimento, não pode ser um número negativo; portanto: x = 25.
Assim, as dimensões do terreno medem 30 métros e 25 métros; então, a medida do comprimento total da cêrca será de 110 métros.
Problema 2
Luiz tem dois irmãos.

O produto da idade do irmão mais novo pela idade do irmão mais velho é igual a 144. Se o irmão mais novo tem 5 anos a menos que Luiz e o mais velho, 5 anos a mais que Luiz, qual é a idade de Luiz?
Indicando a idade de Luiz por x, a idade do irmão mais novo pode ser representada pela expressão x menos 5 e a idade do irmão mais velho, por x + 5. Podemos, então, traduzir o problema pela seguinte equação:
(x menos 5) ⋅ (x + 5) = 144
Calculando as raízes da equação, temos:
x elevado a 2 menos 25 = 144 ⇒ x elevado a 2 = 169 ⇒ x = 13 ou x = menos13
Como o valor de x representa a idade de Luiz, não faz sentido considerar a raiz menos13. Portanto, Luiz tem 13 anos.
Atividades
Faça as atividades no caderno.
17. O produto de um número positivo por sua quarta parte é igual a 100. Calcule esse número.
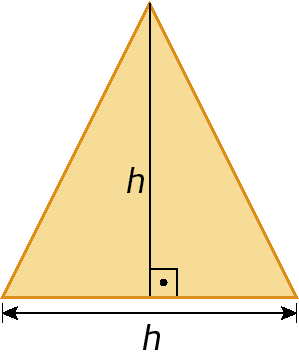
18. Em determinado triângulo, a medida do comprimento da base é numericamente igual à medida do comprimento da altura. Se a medida da área do triângulo é 72 centímetros quadrados, qual é a medida do comprimento da altura desse triângulo?
19. A soma da medida do comprimento da base maior com a medida do comprimento da base menor é numericamente igual à medida do comprimento da altura de um trapézio de medida de área 18 centímetros quadrados. Qual é a medida do comprimento da altura desse trapézio?

20. Se x é um número par positivo e o produto do número par anterior a ele com o número par posterior a ele resulta em 60, qual é o valor de x?
21. Ricardo vai construir um chiqueiro retangular cuja medida da área é 32 métros quadrados.

Quais serão as dimensões desse chiqueiro se a medida do comprimento de um dos lados for o dobro da medida do comprimento do outro?
Resolução de equações incompletas do 2º grau com calculadora ou planilha eletrônica
As equações que resolvemos até agora são da fórma ax elevado a 2 + c = 0, com incógnita x, a ≠ 0 e a e c como números reais. Vamos isolar a incógnita x, realizando a mesma operação em ambos os membros da igualdade.
ax elevado a 2 + c = 0
ax elevado a 2 + c menos c = menosc

Adicionamos menosc nos dois membros.
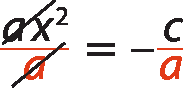

Dividimos os dois membros por a.
x igual a raiz quadrada de menos c sobre a
ou
x igual a menos raiz quadrada de menos c sobre a

Extraímos a raiz quadrada dos dois membros da igualdade.
Assim, podemos calcular as raízes de equações da fórma ax elevado a 2 + c = 0 realizando as operações com o auxílio de uma calculadora ou, até mesmo, utilizando uma planilha eletrônica.
Acompanhe as situações a seguir.
Situação 1
Roberta revestiu com lajotas quadradas o chão de um salão, que se parece com um retângulo cuja medida do comprimento é o quádruplo da medida da largura. Ela precisa comprar material para fazer o rodapé do salão, que estará presente em três paredes, sendo duas delas as mais longas. Se a medida da área do salão é 36 métros quadrados, ela precisará comprar material para quantos metros de rodapé?

Primeiro, Roberta precisa calcular a medida do comprimento dos lados do retângulo que representa o salão. Ela indicou a medida da largura do salão por x e traduziu o problema pela seguinte equação:
4x ⋅ x = 36 ou 4x elevado a 2 = 36
Após testar alguns valores, Roberta percebeu que x podia ser igual a 3 ou menos3, pois 4 ⋅ (menos3)elevado a 2 = 4 ⋅ 9 = 36 e 4 ⋅ (3)elevado a 2 = 4 ⋅ 9 = 36. Assim, ela descobriu duas raízes para a equação 4x elevado a 2 = 36, uma positiva e outra negativa. No entanto, como x indica uma medida, então x = 3, ou seja, a medida da largura do salão é igual a 3 métros.
A raiz positiva da equação 4xelevado a 2 = 36 também poderia ser encontrada usando uma calculadora. Analise a sequência de teclas que Roberta pressionou:

Ao fazer isso, no visor de sua calculadora apareceu o número 3.

Portanto, Roberta deve comprar material suficiente para duas paredes de 12 métros de medida de comprimento e uma de 3 métros de medida de largura, ou seja, 27 métros de rodapé.
Situação 2
Para calcular, por exemplo, a medida do tempo de queda de um objeto que foi abandonado de uma altura medindo 80 métros, usaremos uma planilha eletrônica. A equação que pode nos dar a medida do tempo aproximado é a seguinte:
5x elevado a 2 menos 80 = 0
Em um software de planilha eletrônica, preparamos a planilha assim:


Em seguida, inserimos os valores de a e de menosc nas células B7 e C7, respectivamente.

Por fim, em D7, digitamos = RAIZ (C7/B7), indicando que o resultado desta célula corresponde a
x igual raiz de menos c sobre a. Como precisamos determinar a medida de tempo, apenas a raiz positiva da equação nos interessa.

Assim, teremos a raiz positiva da equação.

Portanto, x = 4, ou seja, a medida do tempo de queda do objeto é 4 s.
Atividades
Faça as atividades no caderno.
22.

Usando uma calculadora ou planilha eletrônica, determine a raiz positiva de cada equação.
a) 5x elevado a 2 menos 20 = 0
b) 7x elevado a 2 = 252
c) 2x elevado a 2 = 162
d) 4x elevado a 2 = .3844
e) 4x elevado a 2 = 49
f) 5x elevado a 2 = .534645
23.



Crie uma equação incompleta da fórma axelevado a 2 + c = 0 e proponha a um colega que utilize uma planilha eletrônica para resolvê-la. Você deve resolver a que ele propuser. Se discordarem da resolução, conversem a respeito e procurem entender qual foi o equívoco.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Equação do 2º grau com uma incógnita
Denominamos equação do 2º grau na incógnita x aquela que pode ser reduzida a uma equação do tipo ax elevado a 2 + bx + c = 0, em que a, b e c são números reais, com a ≠ 0.
1. Identifique as equações do 2º grau com uma incógnita.
a) 2x ‒ 5 = 0
b) melevado a 2 ‒ 2m ‒ 5 = 0
c) 9 ‒ zelevado a 2 = 0
d) 0televado a 2 + 3x ‒ 5 = 0
e) (2x ‒ 1)elevado a 2 = 0
f) xelevado a 2 + 2y ‒ 3 = 0
2. Escreva no caderno a equação ax elevado a 2 + bx + c = 0, em que:
a) a = 2, b = ‒3 e c = 7
b) a = ‒3, b = 1 e c = 5
c) a = 3, b = 3 e c = 3
d) a = ‒2, b = 0 e c = 4
e) a = 1, b = 6 e c = 0
f) a = 3, b = 0, c = 0
3. Um quadrado cuja medida do comprimento de cada lado é igual a x tem medida de área igual a 144 métros quadrados. Escreva uma equação do 2º grau que torne possível encontrar o valor de x.
Equações completas e incompletas
Quando uma equação do 2º grau com uma incógnita, na fórma ax elevado a 2 + bx + c = 0, tem todos os coeficientes (a, b e c) diferentes de zero, dizemos que a equação é completa.
Exemplo: x elevado a 2 ‒ 8x + 10 = 0.
Quando b e/ou c são iguais a zero, dizemos que a equação é incompleta.
Exemplos:
a) x elevado a 2 ‒ 3x = 0;
b) x elevado a 2 ‒ 9 = 0
c) x elevado a 2 = 0
4. Classifique as equações do 2º grau em completas ou incompletas.
a) 2x elevado a 2 + 4x = 0
b) ‒x elevado a 2 + 7x + 2 = 0
c) ‒x elevado a 2 ‒ 9 = 0
d) 8 + 3x ‒ x elevado a 2 = 0
Raiz de uma equação do 2º grau
Raiz de uma equação é um número que, ao substituir a incógnita, torna a sentença verdadeira.
5. Verifique quais dos números a seguir são raízes da equação 4x elevado a 2 ‒ 16 = 0.
a) 3
b) 4
c) 2
d) ‒2
e) 0
6. Dados os números ‒3, ‒2, ‒1, 0, 1, 2 e 3, quais deles são raízes da equação x elevado a 2 ‒ 5x + 6 = 0?
7. O número 1 é raiz de qual(is) equação(ões) a seguir?
a) x elevado a 2 ‒ 4x ‒ 4 = 0
b) x elevado a 2 ‒ 1 = 0
c) x elevado a 2 + x ‒ 2 = 0
d) ‒2x elevado a 2 + 16x = 0
Resolução de equações do 2º grau
Resolver uma equação do 2º grau consiste em encontrar as raízes dessa equação que pertencem ao conjunto universo dela.
8. Determine o conjunto solução das equações, sendo conjunto universo =

.
a) x elevado a 2 ‒ 49 = 0
b) ‒x elevado a 2 = 0
c) 4 ‒ x elevado a 2 = 0
d) 5x elevado a 2 + 8 = 0
9. Determine os valores de x em cada caso.
a) A diferença entre o quadrado de x e 8 é igual a 41.
b) A soma entre o quadrado de x e 10 é igual a 74.
10. O produto de um número positivo por sua sexta parte é igual a 24. Calcule esse número.
11. Determine a medida de perímetro de um retângulo cuja área mede 243 centímetros quadrados e a medida do comprimento é o triplo da medida da largura.
É hora de extrapolar
Faça as atividades no caderno.

O que você sabe sobre a diversidade cultural dos povos indígenas no Brasil?
Segundo o Censo demográfico de 2010, feito pelo í bê gê É, aproximadamente 897 mil pessoas se declararam ou se consideraram indígenas, o que representou um aumento em relação ao número obtido na pesquisa censitária realizada no ano 2000, que foi de 734 mil pessoas. O Censo 2010 também revelou a existência de 274 línguas indígenas faladas entre as 305 etnias diferentes. Os modos de cultura desses importantes povos brasileiros apresentam semelhanças e diversidades que vale a pena conhecer.

Objetivos: Analisar dados sobre a população indígena, pesquisar e analisar informações sobre os tipos de habitação dos povos indígenas e a arte da cerâmica e da cestaria indígenas e realizar uma exposição de painéis para a comunidade escolar.
Etapa 1: Análise de dados do fôlder O Brasil Indígena produzido pelo í bê gê É.
1.

Reúnam-se em grupos. Antes de realizar a pesquisa sobre os povos indígenas, respondam às perguntas a seguir no caderno.
a) Vocês conhecem alguns povos indígenas? Se sim, citem os nomes.
b) O que vocês sabem sobre os modos de viver dos índios brasileiros?
2. Pesquisem e leiam o fôlder O Brasil Indígena, que traz os principais resultados sobre a população indígena brasileira apurados pelo Censo demográfico 2010 realizado pelo í bê gê É, e respondam às questões a seguir:
a) Foram realizadas pesquisas censitárias nos anos de 1991 e 2000 para contabilizar a população indígena brasileira. Os números obtidos nessas pesquisas foram 294 mil e 734 mil, respectivamente. O relatório aponta que esse crescimento expressivo não poderia ser explicado apenas pelos efeitos demográficos comuns (natalidade, mortalidade e migração). Que outro fator é apontado para explicar esse aumento dos valores populacionais?
b) “Não existem terras indígenas em áreas urbanas.” Segundo dados sobre a distribuição espacial dos indígenas, essa afirmação é verdadeira ou falsa?
Etapa 2: Analisar informações sobre os tipos de habitação indígena e sobre a arte da cerâmica e da cestaria.
3. Leia o trecho a seguir e, depois, faça o que se pede.
A aldeia Yanomami é uma casa de fórma circular ou poligonal de diâmetro entre 20 e 40 metros. A parte superior é aberta para permitir a penetração de luz solar e a saída da fumaça. Essa abertura coincide internamente com a “praça central” da aldeia, onde se realizam cerimônias e pajelanças. reticências A aldeia-casa dura apenas um ou dois anos; após esse período é reconstruída em outro lugar.
Habitação indígena: a aldeia. Terra Brasileira, sem data Disponível em: https://oeds.link/TY4gmF. Acesso em: 6 julho 2022.

a) Qual é a medida de área aproximada de uma casa yanomami de formato circular cujo raio mede 30 metros de comprimento? Considere π = 3,14.
b) Se uma aldeia A circular tem raio medindo 20 metros de comprimento e outra, B, tem raio medindo 40 metros de comprimento, podemos afirmar que a medida da área da aldeia B corresponde ao dobro da medida da área da a? Justifique.
4. Escavações arqueológicas revelaram que a confecção de artefatos de cerâmica fazia parte dos costumes de diversos povos indígenas que habitaram ou ainda habitam o Brasil. Foram encontrados objetos que visavam ao armazenamento ou ao uso culinário, além de vasos e outros objetos ornamentais que provavelmente eram utilizados em cerimoniais. Atualmente, as mulheres cadiuéu produzem vasos, enfeites de parede e outros ornamentos. Tais peças são preenchidas por padrões compostos de figuras de várias cores, como mostrado nas imagens.


Muitos dos padrões e desenhos utilizados pelos indígenas se parecem com figuras geométricas. Analisem as imagens dos vasos e identifiquem essas figuras.
5. Outras manifestações artísticas ocorrem na cestaria e na pintura corporal. Pesquisem na internet imagens desses tipos de arte com padrões que contenham figuras geométricas. Selecionem duas delas e identifiquem as figuras geométricas. Então, apresentem as imagens, que poderão ser utilizadas na etapa de produção do painel para os colegas de turma. Caso elas não sejam referentes ao povo indígena selecionado, disponibilize-as para os demais colegas.
Etapa 3: Produção dos painéis sobre as características de povos indígenas brasileiros.
6. Leia o texto a seguir e responda à questão.
Muitos povos [indígenas] reúnem, em seu cotidiano, modos de viver herdados de seus antepassados, além de produtos, instituições e relações sociais adquiridas após a intensificação do contato com os “brancos”.
Quem são? Povos Indígenas no Brasil, 25 janeiro 2021. Disponível em: https://oeds.link/P159wf. Acesso em: 6 julho 2022.
Podemos afirmar que, atualmente, os modos de viver dos brasileiros “não índios” também são influenciados e modificados por outras tradições culturais, inclusive as tradições indígenas? Se sim, citem alguns exemplos. Se não, expliquem por quê.
7. Escolham uma das populações indígenas do país e realizem uma pesquisa sobre: local, número populacional, língua falada, organização da sociedade, história e aspectos culturais. Além dessas informações, selecionem imagens e não se esqueçam de anotar as referências de todos os materiais utilizados.
8. Com base nas informações obtidas, elaborem um painel informativo, digital ou impresso, sobre o povo indígena escolhido.
Etapa 4: Apresentação e análise dos painéis.
9. Disponibilizem o painel elaborado pelo grupo para que os colegas analisem e façam comentários em relação à clareza das informações, à escolha das imagens e ao tamanho e à disposição de textos e imagens.
10. Anotem as dúvidas, as opiniões e as sugestões dos colegas.
11. Depois dos ajustes necessários, organizem uma exposição dos painéis para a comunidade escolar.
Etapa 5: Síntese do trabalho realizado.
12. Algumas questões que devem ser discutidas:
a) As informações que vocês conheciam sobre os povos indígenas no início do trabalho correspondem às informações obtidas nas pesquisas?
b) É importante que a população brasileira conheça mais sobre os povos indígenas? Por quê?
13. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.
Glossário
- ℝ*﹢
- : Conjunto dos números reais positivos.
- Voltar para o texto