125_197_208_mcp8_c10_f2

Capítulo 10 Grandezas e proporcionalidade

Trocando ideias

A leitura dos rótulos dos alimentos é uma importante fonte de informação sobre o que estamos consumindo. Nos rótulos, encontramos os ingredientes, a tabela nutricional, a data de validade, o modo de preparo, entre outras informações.

Ilustração. Mulher branca de cabelo castanho preso para trás e regata vermelha em um supermercado. Levemente encurvada segura em uma das mãos uma cesta de compras e na outra mão um pacote de leite em pó. Olha a parte de trás do pacote de leite em pó. À frente dela, prateleiras com produtos. Destaque para as informações contidas na parte de trás do pacote de leite em pó: à esquerda, três ilustrações a respeito do modo de preparo: primeira etapa: ilustração azul de um copo de vidro com uma colher acima despejando leite em pó em seu interior, com a seguinte informação dentro de uma tarja laranja: 1. Coloque 78 gramas de leite em pó em um copo. Segunda etapa: ilustração azul de um copo de vidro com uma jara acima despejando aguá em seu interior, com a seguinte informação dentro de uma tarja laranja: 2. Adicione 200 mililitros de água filtrada ou fervida, quente ou fria. Terceira etapa: ilustração azul de um copo de vidro com uma colher em seu interior sugerindo um movimento de rotação da colher, com a seguinte informação dentro de uma tarja laranja: 3. Misture até dissolver. Ao lado direito, tabela com informações nutricionais: Porção de 26 gramas (duas colheres de sopa). Quantidade por porção: valor energético: 129 quilocalorias, igual a, 542 quilojoules. Porcentagem, valores diários: 6. Quantidade por porção: carboidratos: 9,6 gramas. Porcentagem, valores diários: 3. Quantidade por porção: proteínas: 6,7 gramas. Porcentagem, valores diários: 9. Quantidade por porção: gorduras totais: 7,1 gramas. Porcentagem, valores diários: 13. Quantidade por porção: gorduras saturadas: 4,4 gramas. Porcentagem, valores diários: 20. Quantidade por porção: gorduras trans: 0. Porcentagem, valores diários: dois asteriscos. Quantidade por porção: fibra alimentar: 0. Porcentagem, valores diários: 0. Quantidade por porção: sódio: 75 miligramas. Porcentagem, valores diários: 3. Quantidade por porção: cálcio: 239 miligramas. Porcentagem, valores diários: 24. Abaixo da tabela: asteriscos e simbolo de porcentagem: valores diários com base em uma dieta de 2 mil quilocalorias ou 8 mil e 400 quilojoules. Seus valores diários podem ser maiores ou menores dependendo de suas necessidades energéticas.

▸

Se foram colocados 156 gramas de leite em pó em um recipiente, quantos mililitros de água fervida ou filtrada deverão ser adicionados?

▸

Em 500 mililitros de água fervida ou filtrada, quantos gramas de leite em pó devem ser usados no preparo?

▸

Nos rótulos das embalagens há uma tabela nutricional. Você sabe para que ela serve? Converse com os colegas.

Neste capítulo, vamos relembrar as ideias de grandezas diretamente proporcionais e inversamente proporcionais. Além disso, vamos analisar a variação dessas grandezas construindo gráficos no plano cartesiano que as relacionam.

Página 199

1 Grandezas e proporcionalidade

Grandeza é tudo aquilo que pode ser medido ou contado. São exemplos de grandeza: comprimento, massa, tempo, temperatura, área, volume, capacidade, velocidade, população, valor monetário etcétera.

Vamos estudar o que são grandezas diretamente proporcionais e grandezas inversamente proporcionais.

Grandezas diretamente proporcionais

Um engenheiro de produção fez um levantamento sobre a produtividade de uma máquina de envasar leite e organizou os dados no quadro a seguir.

Quantidade de leite envasado (litro)	Medida do tempo de produção (hora)
900	0,5
1.800	1
2.700	1,5
7.200	4
14.400	8

Duas grandezas são diretamente proporcionais quando a razão entre os valores da primeira grandeza é igual à razão entre os valores correspondentes da segunda grandeza.

Essa propriedade pode ser identificada entre os valores presentes no quadro: quantidade de leite envasado e medida do tempo de produção. Analise:

•

\frac{1800}{900} = \frac{1}{0,5} = 2

•

\frac{7200}{1800} = \frac{4}{1} = 4

•

\frac{2700}{1800} = \frac{1,5}{1} = \frac{3}{2}

•

\frac{14400}{7200} = \frac{8}{4} = 2

A razão entre os valores correspondentes das duas grandezas é sempre a mesma. Essa razão é chamada de constante de proporcionalidade. Confira:

Esquema. 900 sobre 0,5, igual a 1 mil e 800 sobre 1, igual a 2 mil e 700 sobre 1,5, igual a 7 mil e 200 sobre 4, igual a, símbolo de reticências, igual a, 1 mil e 800. Seta laranja para mil e 800 indicando constante de proporcionalidade.

A partir da constante de proporcionalidade e da propriedade fundamental das proporções, podemos determinar uma sentença algébrica que relacione as medidas dessas grandezas.

Vamos indicar a quantidade de leite envasado, em litro, pela letra p e a medida do tempo de produção, em hora, por t. Temos que p e t representam números reais positivos. A razão entre p e t resulta na constante de proporcionalidade, ou seja,

\frac{p}{t} = 1 800

. Assim, temos:

p = .1800 · t

Com essa sentença, podemos encontrar a quantidade de leite envasado, em litro, para qualquer medida de tempo de produção, em hora, e vice-versa. Acompanhe os exemplos.

a) Vamos calcular quantos litros de leite são envasados em 12 horas de produção da máquina.

p = .1800 · t

p = .1800 · 12

p = .21600

São envasados .21600 litros de leite em 12 horas de produção da máquina.

Página 200

b) Quantas horas de produção da máquina são necessárias para envasar .12600 litros de leite?

.12600 = .1800 · t

\frac{12600}{1800} = t

t = 7

São necessárias 7 horas de produção da máquina para envasar .12600 litros de leite.

Observações

1. Nos problemas que acabamos de resolver, as letras p e t assumem o papel de incógnitas das equações obtidas.

2. Quando não estiver explícito, vamos assumir que o conjunto universo das equações encontradas a partir das proporções é o conjunto dos números reais.

Grandezas inversamente proporcionais

Um professor de Física fez um experimento com os estudantes para mostrar a relação entre as medidas da corrente elétrica e da resistência de um resistor.

Usando um amperímetro, ele obteve algumas medidas, disponibilizando-as para a turma no quadro a seguir.

Fotografia. Amperímetro, instrumento com formato retangular. Lateral amarela e parte superior preta com botão circular no centro e um visor. Ao lado, dois cabos conectores, um preto outro vermelho. — Amperímetro é um instrumento usado para medir a corrente elétrica.

Medida da corrente elétrica (ampère)	Medida da resistência (ohm)
5	44
10	22
20	11
44	5

Duas grandezas são inversamente proporcionais quando a razão entre os valores da primeira grandeza é igual ao inverso da razão entre os valores correspondentes da segunda grandeza.

Isso pode ser observado para as medidas da corrente elétrica e da resistência. Confira:

•

Esquema 10 sobre 5 igual a 2 sobre 1. E 22 sobre 44 igual a 1 sobre 2. Fio amarelo ligando as razões 2 sobre 1 e 1 sobre 2 indicando razões inversas.

•

Esquema. 20 sobre 5 igual a 4 sobre 1. E 11 sobre 44 igual a 1 sobre 4. Fio amarelo ligando as razões 4 sobre 1 e 1 sobre 4 indicando razões inversas.

•

Esquema. 44 sobre 10 igual a 22 sobre 5 e 5 sobre 22. Fio amarelo ligando as razões 22 sobre 5 e 5 sobre 22 indicando razões inversas.

A razão entre os valores de uma grandeza pelo inverso dos valores correspondentes da outra grandeza é sempre a mesma.

Esquema. 5 sobre um quarenta e quatro avos, igual a 10 sobre um vinte e dois avos, igual a 20 sobre um onze avos, igual a 44 sobre um quinto, igual a, reticências, igual a, 220. Abaixo de 220, sai uma seta laranja apontando para a direita indicando constante de proporcionalidade.

Com a constante de proporcionalidade e a propriedade fundamental das proporções, podemos encontrar uma sentença algébrica que relacione as medidas dessas grandezas.

Página 201

Lembre-se: Escreva no caderno.

Vamos indicar a medida da corrente elétrica, em ampère, pela letra ih e a medida da resistência de um resistor, em ohm, por r, sendo que ih e r representam números reais positivos. A razão entre ih e o inverso de r resulta na constante de proporcionalidade

\frac{i}{\frac{1}{r}} = 220

. Assim, temos:

i = \frac{220}{r}

Com isso, podemos determinar a medida da corrente elétrica, em ampère, para qualquer medida de resistência, em ohm, e vice-versa. Vamos analisar alguns exemplos dessa aplicação.

a) Se a medida da corrente elétrica é 0,5 ampère, qual é a medida da resistência?

i = \frac{220}{r}

ou

r = \frac{220}{i}

r = \frac{220}{0,5}

r = 440

A medida da resistência é 440 ohms.

b) Para uma medida de resistência de .1000 ohms, qual é a medida da corrente elétrica?

i = \frac{220}{r}

i = \frac{220}{1 000}

i = 0,22

A medida da corrente elétrica é 0,22 ampère.

c) Se a medida da corrente elétrica é 0,8 ampère, é possível que a medida da resistência seja igual a 300 ohms?

i = \frac{220}{r} ou r = \frac{220}{i}

r = \frac{220}{0,8}

r = 275

Não é possível, pois a medida da resistência é 275 ohms.

Transcrição do áudio

Velocidade do avião Duração: 3:52min. Página: 201. >> [LOCUTORA] Velocidade do avião

>> [Locutora] Um voo direto entre Rio de Janeiro e Paris, a bordo de um avião comercial de grande porte, demora mais de onze horas. Agora, imagine-se fazendo o mesmo trajeto a bordo de um avião supersônico, viajando a uma velocidade acima de 2 mil quilômetros por hora e chegando ao destino praticamente na metade do tempo!

>> [Locutora] Isso não é ficção científica e, sim, uma realidade que começou em 21 de janeiro de 1976 e durou até 31 de março de 1982. Nesse período, realizaram-se vários voos comerciais em velocidade supersônica de Paris ao Rio de Janeiro, com escala em Dakar, capital do Senegal, na África.

>> [Locutora] O avião capaz de realizar esse feito era o Concorde, um avião cofabricado por França e Reino Unido, voltado à aviação comercial. Era um avião supersônico, ou seja, podia voar mais rápido que a velocidade do som.

Som de alerta sonoro.

>> [Locutora] A distância e o tempo são grandezas, pois podem ser medidas. Se a velocidade for constante, dizemos que a distância percorrida é diretamente proporcional ao tempo, ou seja, ambos variam sempre na mesma razão. Isso quer dizer que, se o valor de uma grandeza dobra, o valor da outra também dobra; se é reduzido pela metade o valor de uma, o valor da outra também se reduz pela metade; e assim por diante.

Som de alerta sonoro.

>> [Locutora] Supondo que o Concorde mantivesse uma velocidade máxima constante de 2 100 quilômetros por hora, ele percorria 2 100 quilômetros em uma hora, 4 200 quilômetros em duas horas. Já um avião comercial de grande porte, que se desloca a uma velocidade máxima constante de 900 quilômetros por hora, percorre 900 quilômetros em uma hora, 1 800 quilômetros em duas horas, e assim por diante. Comparando a um avião comercial de grande porte, o Concorde percorria uma distância maior no mesmo intervalo de tempo.

Som de alerta sonoro.

>> [Locutora] Agora, vamos comparar as grandezas velocidade e tempo.

>> [Locutora] Se a distância percorrida for a mesma, podemos dizer que o valor da velocidade média é o inverso do valor correspondente ao tempo gasto, ou seja, a velocidade média e o tempo são grandezas inversamente proporcionais. Assim, se o valor de uma dobra, o valor da outra se reduz pela metade; se o valor de uma é dividido por 3, o valor da outra é multiplicado por 3; e assim por diante.

Som de alerta sonoro.

>> [Locutora] Após vinte aviões supersônicos terem sido construídos e operados por duas companhias aéreas, suas atividades encerraram-se em 2003. Isso se deveu a algumas razões: o alto gasto de combustível, o que gerava passagens muito caras, e o excesso de ruído, que gerava restrições para os voos supersônicos, que só podiam acontecer sobre o oceano. O temor era de que a energia gerada pelo excesso de pressão do ar durante a quebra da barreira do som pudesse quebrar vidros e gerar acidentes em solo.

>> [Locutora] Você consegue imaginar que um avião no céu a uma velocidade maior que a do som poderia causar estragos aqui no chão onde estamos?

>> [Locutora] Antes de terminar, vamos escutar o som gerado por um avião quebrando a barreira do som.

Som de um avião quebrando a barreira do som.

>> [Locutora] Incrível, não é? Até a próxima!

Vinheta.

Créditos Os áudios inseridos neste conteúdo são da Free Sound e da Sound Bible.

Atividades

Faça as atividades no caderno.

1. Entre estes pares de grandezas, identifique os de grandezas diretamente proporcionais.

a) Número de trabalhadores e quantidade de morangos coletados em uma plantação.

b) Medida do tempo de crescimento de um animal e a idade dele.

c) Medidas de perímetro e de comprimento do lado de um quadrado.

d) Medida de comprimento de uma corda e o preço pago por ela.

e) Medida do tempo decorrido em uma partida de basquete e número de cestas.

2. Se a constante de proporcionalidade entre os valores de um par de grandezas diretamente proporcionais (x e y) vale 10, escreva em seu caderno uma sentença algébrica que os relacione.

Página 202

3. Um professor de Ciências fez uma experiência e obteve as seguintes medidas de duas grandezas em laboratório.

A	2	4	5	8	10
B	5	2,5	2	1,25	1

Sobre os valores de A e B, podemos afirmar que:

a) os valores de a são diretamente proporcionais aos valores de B.

b) a razão entre os valores de A e B é constante.

c) os valores de a podem ser obtidos multiplicando-se os valores de B por 2,5.

d) os valores de a são inversamente proporcionais aos valores de B.

4. Um motorista levará um passageiro de uma cidade a para uma cidade B. Se ele dirigir um trecho da estrada a 80 quilômetros por hora constantes, percorrerá esse trecho em duas horas. Em quanto tempo ele percorrerá esse mesmo trecho se dirigir a 100 quilômetros por hora constantes?

5. Carla tem uma caminhonete e trabalha como entregadora de mercadorias para uma loja. Ela está viajando por uma estrada até outra cidade a uma medida de velocidade constante. Neste quadro, analise a medida da distância percorrida e a medida do tempo de viagem em dois momentos.

Medida da distância(km)	Medida do tempo(h)
105	$1 divisão de 1 sobre 2$
122,5	$1 divisão de 3 sobre 4$

a) Qual é a constante de proporcionalidade entre essas medidas de grandezas?

b) Escreva uma sentença algébrica que as relacione.

c) Se Carla permaneceu a uma medida de velocidade constante durante 4 horas 15 minutos, qual foi a medida da distância percorrida?

6. Neste quadro, os valores de x são inversamente proporcionais aos valores de y.

x	y
2	10
5	4

Escreva em seu caderno:

a) a constante de proporcionalidade;

b) uma sentença algébrica que relacione os valores de x e y;

c) os valores de y para x = 2,5 e para x = 40, usando a sentença algébrica.

7. Uma gráfica imprime cartões de visita usando uma impressora nova. Confira, neste quadro, a relação entre o número de cartões impressos e a medida do tempo de funcionamento da impressora.

Número de cartões impressos	Medida do tempo de funcionamento da impressora
8.000	2 h
14.000	3 h 30 min

a) Quantos cartões a impressora produz em uma hora 30 minutos de funcionamento?

b) Escreva, em seu caderno, uma sentença algébrica que relacione o número de cartões impressos e a medida do tempo, em hora, que a impressora funcionou.

c) Em 37 horas 30 minutos de funcionamento da impressora, quantos cartões foram impressos?

8.

Elabore, em seu caderno, uma atividade na qual haja duas grandezas diretamente proporcionais ou inversamente proporcionais e seja necessário encontrar uma sentença algébrica que relacione os valores dessas grandezas. O objetivo de encontrar a sentença algébrica nesta atividade é calcular alguns valores que não estão entre aqueles fornecidos na situação elaborada por você. Troque sua atividade com um colega e resolva a atividade proposta por ele. Se houver divergências entre as sentenças algébricas encontradas e as esperadas, conversem e tentem chegar a uma conclusão. Se tiverem dificuldades, peçam ajuda para o professor.

Página 203

2 Representação da relação entre grandezas no plano cartesiano

Já analisamos como os valores de duas grandezas variam por meio de quadros e sentenças algébricas. Agora, vamos estudar que é possível relacionar os valores de uma grandeza aos valores de outra por meio de um gráfico no plano cartesiano.

Gráficos de grandezas diretamente proporcionais

Acompanhe as situações a seguir, em que vamos representar graficamente a variação dos valores de grandezas diretamente proporcionais.

Situação 1

Gabriel fará aniversário no final de semana. Seus pais pretendem comprar alguns lanches e convidar os amigos da escola para comemorar em casa. Para isso, estão fazendo os cálculos de quanto vão gastar na comemoração.

Ilustração. Homem negro conversando com mulher branca e loira no interior de um supermercado. Ao fundo é possível ver prateleiras com mercadorias. O homem diz: Vamos comprar lanches e sucos para as crianças, certo? A mulher diz: Certo! E vamos gastar, em média, 12 reais por criança.

Analise o quadro com estimativas de gasto a seguir.

Número de crianças (n)	3	4	5	6
Custo da comemoração em reais (c)	36	48	60	72

Cada um desses pares de valores (número de crianças e custo) pode ser associado a um ponto do plano cartesiano. Podemos representar o número de crianças pela letra n e o custo, em reais, por c, em que n é um número natural, e c, um número real positivo. Assim, temos pares ordenados na fórma (n, c).

Como o número de crianças só pode ser um número natural, o gráfico que representa a relação entre o número de crianças e o custo da comemoração não é uma linha contínua, mas pontos alinhados, como você pode notar a seguir.

Ilustração. Do lado esquerdo, mulher branca de cabelo preto curto. Ela está utilizando um jaleco branco e diz: No eixo das abscissas, indicamos o número de crianças, abre parênteses n, fecha parênteses; no eixo das ordenadas, o custo da comemoração em reais, abre parênteses, c, fecha parênteses.
Do lado direito, um quadro de giz com um plano cartesiano representado nele. No eixo horizontal estão representados os números 3, 4, 5 e 6. Abaixo, está a letra n. No eixo vertical, estão representados os números 36, 48, 60 e 72. À esquerdam está indicada a letra c.
No plano estão representados 4 pontos: o ponto de abscissa 3 e ordenada 36, o ponto de abscissa 4 e ordenada 48, o ponto de abscissa 5 e ordenada 60 e o ponto de abscissa 6 e ordenada 72.

Página 204

Situação 2

Em um posto de gasolina, em 2022, cada litro de etanol custava R$ 5,00cinco reais. Neste quadro, confira como o preço a ser pago se relaciona com a quantidade de litros de etanol abastecidos.

Litros de etanol (l)	5,0	10,0	15,0	20,0
Preço em R$ (p)	25,00	50,00	75,00	100,00

O gráfico a seguir ilustra a situação.

Ilustração. Do lado esquerdo, mulher branca de cabelo preto curto. Ela está utilizando um jaleco branco e diz: Podemos considerar que a quantidade de litros de etanol abastecidos e o preço correspondente formam um par ordenado. Nesse caso, o primeiro número do par ordenado indica a quantidade de litros de etanol e o segundo, o preço correspondente. Assim, temos pares ordenados na forma abre parênteses l vírgula p, fecha parênteses. Neste plano cartesiano, os pares ordenados do quadro estão representados por pontos.
Do lado direito, um quadro de giz com um plano cartesiano representado nele. No eixo horizontal estão representados os números 5, 10, 15 e 20. Abaixo, está a letra l. No eixo vertical, estão representados os números 25, 50, 75 e 100. À esquerdam está indicada a letra p.
No plano estão representados 4 pontos: o ponto de abscissa 5 e ordenada 25, o ponto de abscissa 10 e ordenada 50, o ponto de abscissa 15 e ordenada 75 e o ponto de abscissa 20 e ordenada 100. Na origem do plano, há uma pequena circunferência representada. Da origem parte uma linha reta que passa pelos 4 pontos que foram representados.

Note que os pontos representados no plano cartesiano estão alinhados. Como o preço a ser pago pode assumir qualquer valor real maior que 0, o gráfico que representa a relação entre essas grandezas será uma linha contínua que parte do par ordenado (0, 0), passa pelo par ordenado (5, 25) e continua infinitamente.

Observação

O par ordenado (0, 0) não faz parte do gráfico, pois

\frac{p}{l} = 5

e éle ≠ 0.

Atividades

Faça as atividades no caderno.

9. Em cada item, determine a sentença algébrica que expressa a relação entre os valores das grandezas.

a)

k	1	3	6
j	3	9	18

b)

m	4	5	6
n	16	20	24

c)

p	8	16	24
q	10	20	30

10. Os valores de duas grandezas estão relacionados pela sentença algébrica y = 1,2 · x. Construa, em seu caderno, o gráfico dessa relação, sabendo que tanto x quanto y podem assumir qualquer valor real positivo.

11. Considere que o preço de 10 folhas de sulfite é R$ 0,70zero reais e setenta centavos. Em seu caderno, expresse a relação, entre o número de folhas e o preço a ser pago por elas por meio de:

a) uma sentença algébrica;

b) um gráfico no plano cartesiano.

12. Em seu caderno, para cada item da atividade 9, desenhe um gráfico supondo que as duas grandezas têm seus valores representados no conjunto dos números reais positivos.

Página 205

Gráficos de grandezas inversamente proporcionais

O gráfico que representa a relação entre os valores de duas grandezas inversamente proporcionais não é uma linha reta. Acompanhe as situações a seguir.

Situação 1

Um prêmio será dividido igualmente entre mais de um ganhador. Neste quadro, confira o valor estimado, em milhões de reais, do prêmio com base no número de ganhadores.

Número de ganhadores (g)	2	3	5	8	10
Prêmio em milhões de reais (p)	10,5	7	4,2	2,625	2,1

O gráfico a seguir relaciona o número de ganhadores e o valor estimado do prêmio, em milhões de reais.

Ilustração. Menino asiático de cabelo preto e camisa vermelha ao lado direito de um gráfico. Ele fala: Qual é a sentença algébrica que expressa a relação entre o prêmio, abre parênteses p, fecha parênteses, em milhões de reais, e o número de ganhadores, abre parênteses g, fecha parênteses? Gráfico. Eixo horizontal com os números de 0 a 14 representados. Abaixo, está indicada a letra g. Eixo vertical com os números de 0 a 11 representados. À esquerda a letra p. No plano estão representados 5 pontos: ponto de abscissa 2 e ordenada 10 vírgula 5; ponto de abscissa 3 e ordenada 7; ponto de abscissa 5 e ordenada 4 vírgula 2; ponto de abscissa 8 e ordenada 2 vírgula 625 e ponto de abscissa 10 e ordenada 2 vírgula 1.

Como o número de ganhadores só pode ser um número natural, o gráfico que representa a relação entre o número de ganhadores e o prêmio não é uma linha contínua, mas pontos que pertencem a uma curva.

Situação 2

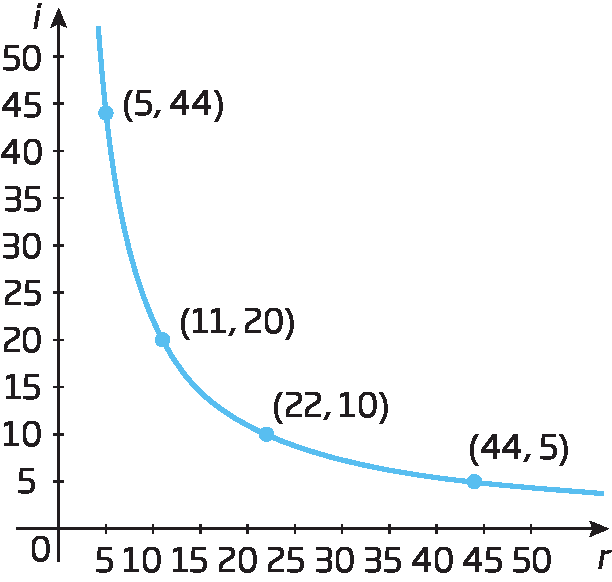
Vamos representar graficamente a relação entre a medida da corrente elétrica e a medida da resistência estudada no tópico Grandezas inversamente proporcionais.

Medida da resistência (ohm)	Medida da corrente elétrica (ampère)
44	5
22	10
11	20
5	44

Podemos dizer que a corrente elétrica e a resistência são grandezas inversamente proporcionais. Podemos representar por pontos no plano cartesiano os pares ordenados formados pela medida de resistência r e pela medida de corrente elétrica ih correspondente. Como a resistência pode assumir qualquer valor real positivo, o gráfico que representa a relação entre essas grandezas é uma linha curva contínua.

Gráfico. Eixo horizontal com os números 0, 5, 10, 15, 20, 25, 30, 35, 40, 45 e 50 representados. Abaixo, está indicada a letra r. Eixo vertical com os números 0, 5, 10, 15, 20, 25, 30, 35, 40, 45 e 50 representados. À esquerda a letra i. No plano estão representados 4 pontos: ponto de abscissa 5 e ordenada 44; ponto de abscissa 11 e ordenada 20; ponto de abscissa 22 e ordenada 10; ponto de abscissa 44 e ordenada 5. Há uma curva com concavidade para cima que passa pelos 4 pontos representados e que não toca nenhum dos 2 eixos.

Ilustração. Menino asiático de cabelo preto e camisa vermelha ao lado direito de um gráfico. Ele diz: Lembre-se de que a relação entre i e r pode ser expressa pela seguinte sentença algébrica: i igual a fração 220 sobre r, em que r é um número real positivo.

Página 206

Atividades

Faça as atividades no caderno.

13. Uma palestrante, ao ser convidada para um evento sobre a escassez de alimento no mundo, levou um pacote de maçãs contendo 80 unidades para dividir entre a plateia. O evento não possuía um número limitado de participantes e a palestrante dividiria as maçãs igualmente entre eles, cortando-as em partes iguais se necessário. No caderno, represente graficamente a relação entre a quantidade de maçãs e o número de participantes do evento.

14. A medida da área de um retângulo é igual a 30 centímetros quadrados. Indicando a medida do comprimento por c e a medida da largura por éle e considerando que c e éle são números reais positivos, construa um gráfico em seu caderno relacionando os possíveis valores para c e éle. Marque pelo menos 4 pontos no gráfico.

15. Duas grandezas inversamente proporcionais têm valores no conjunto dos números reais, que estão relacionados por meio da sentença algébrica x · y = 2. No caderno, represente graficamente a relação entre os valores dessas grandezas, marcando pelo menos 4 pontos pertencentes à curva.

16. Analise este gráfico e responda às perguntas no caderno.

Gráfico. Eixo horizontal com os números 0, 5, 10, 15, 20, 25, 30, 35, 40 e 45 representados. Abaixo, está indicada a letra r. Eixo vertical com os números 0, 5, 10, 15, 20, 25, 30 e 35 representados. À esquerda a letra s. No plano estão representados 3 pontos: ponto de abscissa 2 e ordenada 30; ponto de abscissa 6 e ordenada 10; ponto de abscissa 30 e ordenada 2. Há uma curva com concavidade para cima que passa pelos 3 pontos representados e que não toca nenhum dos 2 eixos.

a) Qual é a constante de proporcionalidade da relação entre os valores r e s das grandezas?

b) Escreva uma sentença algébrica que relacione os valores dessas grandezas.

17.

Confira o gráfico a seguir e crie uma atividade conforme a orientação.

Gráfico. Gráfico representados em um plano cartesiano. Eixo horizontal x com os números de 0 a 10 representados e eixo vertical y com os números de 0 a 9 representados. O gráfico é uma curva descendente com concavidade para cima. A curva não toca nenhum dos eixos.

Elabore um contexto no qual o gráfico anterior represente a relação entre os valores das duas grandezas. Troque sua atividade com um colega, solicitando que ele encontre uma sentença algébrica que relacione os valores dessas grandezas, indicando a constante de proporcionalidade.

Página 207

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Grandezas e proporcionalidade

Grandeza é tudo aquilo que pode ser medido ou contado. Duas ou mais grandezas podem estar relacionadas e variar seus valores de acordo com determinada proporção.

Grandezas diretamente proporcionais

Duas grandezas são diretamente proporcionais quando a razão entre os valores da primeira grandeza é igual à razão entre os valores correspondentes da segunda grandeza.

Grandezas inversamente proporcionais

Duas grandezas são inversamente proporcionais quando a razão entre os valores da primeira grandeza é igual ao inverso da razão entre os valores correspondentes da segunda grandeza.

1. Em cada item, indique se a relação descrita entre as medidas é diretamente proporcional.

a) A medida de temperatura de um corpo e a hora em que foi medida.

b) A medida de comprimento dos lados de um polígono regular e sua medida de perímetro.

c) A medida do tempo de produção de uma impressora e o número de páginas impressas.

d) A medida de tempo de uma partida de futebol e o número de gols.

2. Sabendo que a constante de proporcionalidade entre os valores de um par de grandezas diretamente proporcionais, indicadas por aêbê, vale 8, escreva em seu caderno uma sentença algébrica que relacione aêbê.

3. A máquina de uma gráfica produz 120 livros em uma hora. Em quanto tempo 4 máquinas iguais produziriam a mesma quantidade de livros?

4. Uma mulher vai de uma cidade a outra dirigindo seu carro em um trecho de estrada a 60 quilômetros por hora constantes. Ela percorre esse trecho em 3 horas. Qual seria a medida de tempo necessária para ela fazer esse mesmo trajeto a 90 quilômetros por hora constantes?

5. Um caminhoneiro entrega mercadorias para uma empresa de cosméticos. Ele viaja pela estrada de uma cidade a outra com uma medida de velocidade constante. Este quadro mostra a medida da distância percorrida e a medida de tempo gasto na viagem.

Medida da distância (km)	Medida de tempo (h)
125	2,5
150	3,0

a) Determine a constante de proporcionalidade entre as medidas das grandezas.

b) Escreva uma sentença algébrica relacionando as medidas das grandezas.

c) Se a medida de tempo em uma terceira viagem feita por esse caminhoneiro foi 1,75 hora, qual foi a medida da distância percorrida por ele?

6. Neste quadro, os valores de a são inversamente proporcionais aos valores de B.

A	B
3	15
5	9

Escreva no caderno:

a) a constante de proporcionalidade;

b) uma sentença algébrica que relaciona os valores de aêbê;

c) o valor de B para a = 2.

7. Usando os valores de P e Q apresentados neste quadro, escreva no caderno uma sentença algébrica que os relacione.

P	2	4	6
Q	6	12	18

Representação da relação entre grandezas no plano cartesiano

É possível relacionar os valores de uma grandeza aos valores de outra por meio de um gráfico no plano cartesiano.

Página 208

Gráficos de grandezas diretamente proporcionais

Se os valores da grandeza do eixo das abscissas são números naturais, o gráfico da relação entre os valores não é uma linha contínua, mas pontos alinhados; se os valores dessa grandeza são números reais, o gráfico é uma linha reta contínua.

Gráficos de grandezas inversamente proporcionais

O gráfico da relação entre os valores de duas grandezas inversamente proporcionais não é uma linha reta.

Se os valores da grandeza do eixo das abscissas são números naturais, o gráfico da relação entre os valores não é uma linha contínua, mas pontos que pertencem a uma curva; se os valores dessa grandeza são números reais, o gráfico é uma linha curva contínua.

8. Os valores das grandezas x e y estão relacionados por meio da sentença algébrica y = 3,4 · x. No caderno, represente graficamente esta relação, sendo que x e y podem assumir qualquer valor real positivo.

9. Este gráfico relaciona o preço pago, em reais, p (eixo y), com a quantidade de litros abastecida éle (eixo x). Com base neste gráfico, determine o preço do litro do etanol.

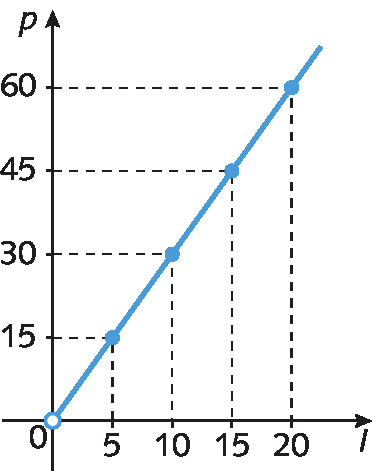
Gráfico. Eixo horizontal com os números 0, 5, 10, 15 e 20 representados. Abaixo, está indicada a letra l. Eixo vertical com os números 0, 15, 30, 45 e 60 representados. À esquerda a letra p. No plano estão representados 4 pontos: ponto de abscissa 5 e ordenada 15; ponto de abscissa 10 e ordenada 30; ponto de abscissa 15 e ordenada 45 e ponto de abscissa 20 e ordenada 60. Há uma pequena circunferência representada na origem. Da origem parte uma linha reta que passa pelos pontos representados.

10. Duas grandezas, s e r, são inversamente proporcionais.

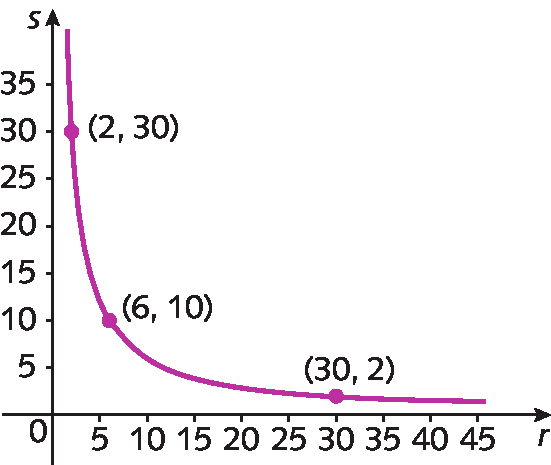
Analisando o gráfico referente a elas, determine:

a) uma sentença algébrica que relaciona s e r.

b) o valor de s quando r = 10;

c) o valor de r quando s = 5.

11. Analise estes gráficos e classifique a relação entre as grandezas que eles representam como diretamente, inversamente ou não proporcional.

a)

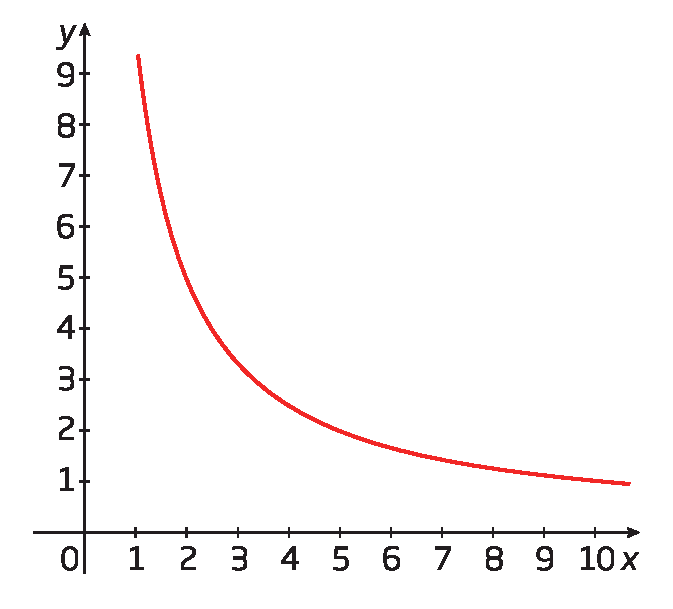
b)

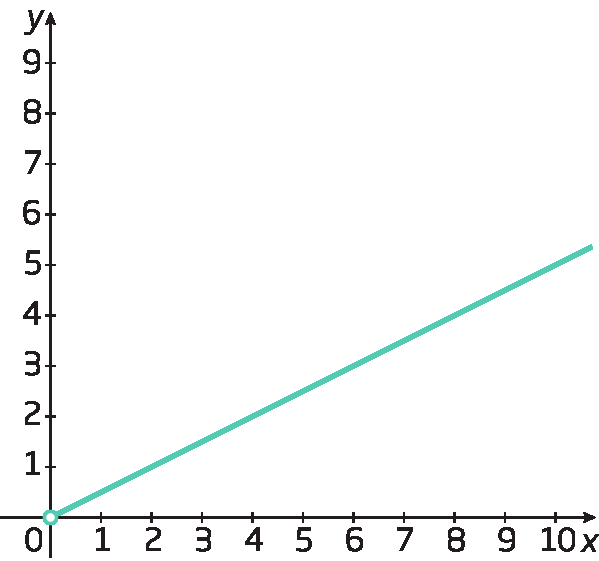
Gráfico. Eixo horizontal com os números de 0 a 10 representados. Abaixo, está indicada a letra x. Eixo vertical com os números de 0 a 9 representados. À esquerda a letra y. Há uma pequena circunferência representada na origem. Da origem parte uma linha reta. Os pontos dessa linha têm coordenadas positiva. A linha está mais próxima do eixo horizontal do que do eixo vertical.

c)

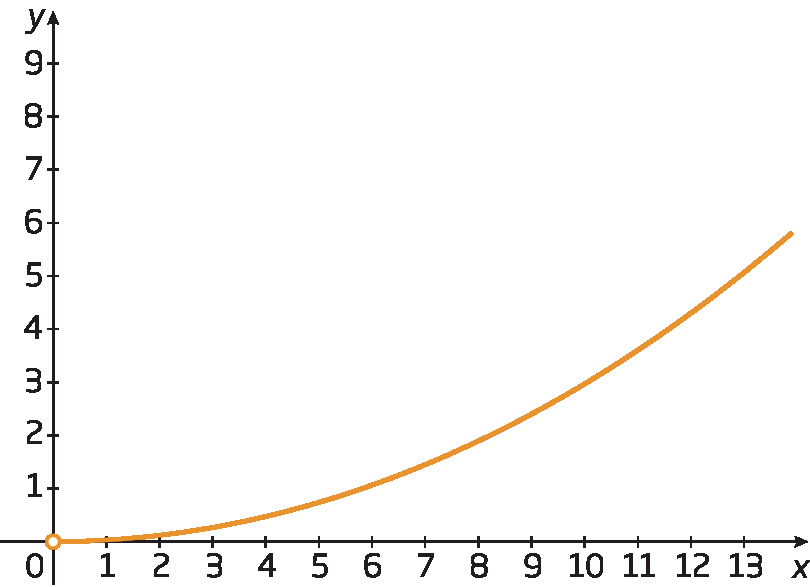
Gráfico. Gráfico representados em um plano cartesiano. Eixo horizontal x com os números de 0 a 13 representados e eixo vertical y com os números de 0 a 9 representados. O gráfico é uma curva crescente com concavidade para cima. A curva toca o eixo x apenas no ponto de par ordenado 0, 0.

d)