Capítulo 11 Medidas de tendência central e pesquisa estatística
Trocando ideias

Em 2021 e 2022, o Brasil sofreu com a alta no preço dos alimentos. Fatores climáticos, a pandemia de coronavírus e a alta no preço dos combustíveis estiveram entre os principais fatores que levaram o país a conviver com esse problema.
Analise, a seguir, o preço médio de alguns alimentos na capital de São Paulo no dia 4 de fevereiro de 2022.

Dados disponíveis em: https://oeds.link/guWdym. Acesso em: 9 fevereiro 2022.
▸


Em sua opinião, o que podemos fazer para lidar com a alta dos preços dos alimentos? Converse com os colegas.
▸

O preço do quilograma da melancia era R$ 3,10três reais e dez centavos em qualquer lugar da capital de São Paulo em 4 de fevereiro de 2022? Por quê?
▸


Como você acha que foi calculado o preço médio da caixa de 25 quilogramas de batata na capital de São Paulo em 4 de fevereiro de 2022? Converse com os colegas.
Neste capítulo retomaremos alguns conceitos que podem nos ajudar com pesquisas estatísticas e aprenderemos novas medidas que vão nos auxiliar na compreensão do comportamento dos dados de uma pesquisa.

1 Pesquisa estatística
Leia a seguinte informação.

Dados disponíveis em: Associação Brasileira da Indústria de Produtos para Animais de Estimação. Mercado PET Brasil 2021. São Paulo: Abinpet, 2021.
Estatísticas como essa motivam os pesquisadores a buscar mais informações a respeito do assunto. Por exemplo: “Por qual motivo as pessoas estão gastando mais com seus animais de estimação?”.
A seguir, vamos retomar alguns conceitos e apresentar outros que podem contribuir para realizar e analisar pesquisas estatísticas.
População, amostra e pesquisa censitária ou amostral
A diretora de uma escola quer saber a opinião dos estudantes a respeito da qualidade do lanche servido no intervalo.
Para isso, ela vai realizar uma pesquisa e coletar informações dos estudantes. Portanto, todos os estudantes da escola compõem a população (ou universo estatístico) de interesse.

Ao planejar a pesquisa, a diretora percebeu que demoraria muito tempo para entrevistar todos os estudantes. Então, para viabilizar a pesquisa, decidiu escolher aleatoriamente 10 estudantes de cada sala.
O grupo de estudantes selecionados compõe uma amostra. Toda amostra deve ser escolhida de fórma conveniente e estratégica, para que os dados coletados por meio dela retratem a população como um todo.

Um pouco de história
Faça as atividades no caderno.
Estatística: origem e finalidade
Os primeiros dados estatísticos foram encontrados no Egito antigo e datam de aproximadamente 5000 antes de Cristo, e estão relacionados a prisioneiros de guerra. A palavra "estatística" vem do latim státus, que significa estado; essa palavra passou a ser utilizada porque os recenseamentos eram feitos por ordem dos governantes, que queriam obter dados da população para taxar impostos; daí vem também a palavra censo, derivada de cesere, que em latim significa taxar.
Outras contagens populacionais foram realizadas no Egito e em outras regiões. Há registros de que, por volta de 2300 antes de Cristo, na China, por ordem do imperador Yao, foi realizado um censo da população e das lavouras cultivadas. Posteriormente, por volta dos séculos oitavo ao quarto antes de Cristo, os gregos e romanos também realizaram censos da população para recrutar soldados para o exército.

A palavra "estatística", no sentido de obtenção, estudo e interpretação de dados, foi utilizada pela primeira vez na Alemanha, por volta do século décimo oitavo. No Brasil, o primeiro censo foi realizado em 1872.
Atividade
Os questionários dos censos no Brasil eram realizados em papel. Pesquise: em que ano foi realizado o primeiro censo digital?
Pesquisa censitária
A pesquisa censitária é aquela em que são obtidos os dados de toda a população, garantindo maior precisão na análise e na interpretação das informações. Um exemplo de pesquisa censitária é o Censo Demográfico, realizado pelo Instituto Brasileiro de Geografia e Estatística (í bê gê É).
A pesquisa censitária pode ser inviável em algumas situações. Por exemplo, no período que antecede as eleições são realizadas diversas pesquisas de intenção de voto. Se toda a população brasileira fosse entrevistada, haveria muitos dados para serem processados e cada pesquisa seria equivalente ao próprio processo eleitoral.
Pesquisa amostral
A pesquisa amostral é aquela em que são obtidos os dados de parte de uma população, ou seja, de uma amostra. Esse tipo de pesquisa é bastante comum em nosso cotidiano, principalmente de maneira informal. Por exemplo, em feiras de rua, é comum os vendedores oferecerem aos clientes um pedaço ou uma unidade de determinada fruta para convencê-lo de que as frutas são de boa qualidade. Em situações como essa, a pesquisa amostral é a mais adequada, pois não faria sentido o cliente provar todas as frutas à venda antes de comprá-las.

Feira livre em Londrina (Paraná). Foto de 2020.
Percebeu que nem sempre a pesquisa censitária se mostra viável? Assim, uma pesquisa amostral pode ser mais vantajosa ou a única possível, dependendo do objeto de estudo e das características que pretendemos investigar.
Imagine que a intenção seja analisar a medida do tempo que um lote de lâmpadas leva para queimar. Para chegar a um resultado, não é possível testar todas elas e tomar a média dessa medida de tempo, pois esse seria um processo destrutivo. Nesse caso, como podemos escolher a amostra?

Vamos conhecer algumas técnicas de amostragem.
a) Em uma linha de produção, as peças costumam sair com qualidade muito parecida e apresentam-se ordenadas. Por esse motivo e por produzirem uma enorme quantidade de peças por hora, o contrôle de qualidade é feito por amostragem. Nesse caso, a seleção da amostra é feita por meio da retirada periódica de um elemento da população, ou seja, a cada determinada quantidade de elementos, um é retirado para análise.

Chamamos esse tipo de amostragem de sistemática.
b) O professor de Educação Física quer descobrir o esporte preferido de seus estudantes. Como não teria tempo suficiente para consultar todos eles, resolveu selecionar uma amostra de seis estudantes de cada turma escolhidos aleatoriamente. Para isso, escreveu em um papel o número de chamada dos estudantes, sorteando seis deles por turma. Essa técnica de amostragem se chama casual simples.

Nesse tipo de seleção de amostra, os elementos da população são rotulados e, por meio de sorteio, os integrantes da amostra são selecionados para participar da pesquisa.
c) Uma livraria realizou uma pesquisa para saber quais gêneros literários eram os preferidos dos seus leitores. Para isso, entrevistou 90 pessoas, sendo 30 crianças, 30 adolescentes e 30 adultos. A divisão da amostra em 3 segmentos (ou estratos) caracteriza uma amostragem estratificada.

Atividades
Faça as atividades no caderno.
1. A cidade de Pouso Alegre, em Minas Gerais, tem aproximadamente .154000 habitantes. Uma empresa de tecnologia da cidade realizou uma pesquisa com .3080 pessoas para saber quantas delas têm acesso à internet no celular.

No caderno, responda às perguntas.
a) Qual é a população dessa pesquisa?
b) Quantas pessoas compõem a amostra da pesquisa?
c) Que porcentagem do universo estatístico a amostra representa?
2. Em seu caderno, indique o tipo de pesquisa mais adequada para cada situação. Se a pesquisa for amostral, informe a técnica de amostragem (estratificada, casual simples ou sistemática). Justifique suas escolhas.
a) Em uma escola com 3 mil estudantes, conhecer a profissão dos pais deles. A escola fica na fronteira entre a zona urbana e a zona rural.
b) Conhecer a opinião de estudantes sobre a lista de exercícios aplicada em uma turma do 8º ano.
c) Determinar a resistência da borracha de bexigas de festas de aniversário.
d) Determinar o representante de classe de uma turma do 8º ano.
e) Determinar a altura média dos estudantes do 8º ano de uma escola.
Variáveis estatísticas
A medida do tempo de duração de uma lâmpada e a porcentagem de lares brasileiros que possuem animais de estimação são características (ou atributos) chamadas, em Estatística, de variáveis. Observe que essas variáveis têm valores com significados diferentes e que podemos classificá-las conforme veremos a seguir.
Variável qualitativa
Quando o valor de uma variável representa uma característica ou atributo, dizemos que ela é uma variável qualitativa. Por exemplo, no caso de uma amostra de determinada fruta como a cereja, poderíamos dizer que as frutas são muito doces, pouco doces, sem sabor, ácidas ou muito ácidas. Outro exemplo de variável qualitativa seria a preferência por um determinado time de futebol, podendo ser qualquer time.
Observe outros exemplos.
a) Estado civil: casado(a), solteiro(a), divorciado(a);
b) Cidade em que nasceu: Manaus, Amapá, Rio de Janeiro ou qualquer outra cidade;
c) Cor dos olhos: verdes, castanhos, azuis, entre outros.
Uma variável qualitativa pode ser de dois tipos: ordinal ou nominal.
Variável qualitativa ordinal: é uma variável cujos valores podem ser ordenados. São exemplos: o grau de dificuldade das questões de uma prova (fácil, médio ou difícil), o nível de escolaridade, a satisfação quanto a um serviço prestado por alguma empresa (pouco satisfeito, satisfeito ou muito satisfeito), entre outros.

Variável qualitativa nominal: os valores desse tipo de variável não podem ser ordenados. São exemplos: a cidade de nascimento, a cor favorita, o sexo, a cor do cabelo, entre outros.

Variável quantitativa
Os valores de uma variável quantitativa são expressos por números indicando geralmente contagem ou medida de alguma grandeza. Acompanhe os exemplos a seguir.
a) Medida de comprimento
b) Número de animais de estimação
c) Número de irmãos
d) Medida de massa
e) Medida de volume
f) Medida de tempo
Uma variável quantitativa também pode ser de dois tipos: discreta ou contínua.
Variável quantitativa discreta: é aquela que indica, geralmente, contagem de algo, como o número de vezes que se toma o transporte público por semana, o número de filhos, a quantidade de sapatos que se tem, a quantidade de pontos feitos em uma partida de basquete, entre outras.

Variável quantitativa contínua: indica, geralmente, uma medida. Essa variável pertence ao conjunto dos números reais. Pode indicar, por exemplo, a medida da distância percorrida de casa até a escola, a medida da altura dos estudantes de uma turma, a medida do tempo para completar a prova de 100 metros rasos etcétera.

O esquema a seguir sintetiza as variáveis e seus tipos.

Conhecer a categoria da variável pode ajudar na escolha do tipo de gráfico mais adequado para representar os dados.
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Tipos de gráficos
Duração: 5 min 41 s. Página: 215.
>> [LOCUTOR] Tipos de gráficos
>> [Locutor] Gráficos são importantes para sintetizar e apresentar informações. Mas como saber qual o tipo de gráfico usar em cada situação? Cileda de Queiroz, matemática e especialista em Educação Estatística, conversou conosco sobre esse tema. Vamos ouvi-la?
>> [Locutor] Que critérios podemos usar para escolher qual gráfico devemos utilizar para representar um conjunto de dados de uma pesquisa?
>> [Cileda de Queiroz] Bom, se eu quero representar o conjunto de dados que eu coletei [pequena pausa] pra tentar responder a uma pergunta de pesquisa, um questionamento de pesquisa, algumas coisas eu tenho que observar. Por exemplo, como são esses dados? Eles vêm de variável [tom enfático] quantitativa, ou seja, [que] podem ser [tom enfático] medidas por meio de números? Ou variáveis [tom enfático] qualitativas, que não podem ser medidas, se referem a [tom enfático] qualidades: cor dos olhos, cor do cabelo e coisas do gênero. Uma vez sabendo isso, eu já tenho um primeiro olhar pra saber o tipo de gráfico... né? Eu preciso entender qual é o objetivo que eu quero atingir.
>> [Cileda de Queiroz] Se o meu gráfico, os meus dados querem me levar a uma análise ao longo, por exemplo, de um período de tempo, como são as pesquisas eleitorais, um gráfico de linha é muito... ele fala muito pra gente, ele dá uma informação mais natural. Se eu quero comparar as proporções que existem dentro de um conjunto, aquele momento então é uma relação [tom pausado] parte-todo, eu vou usar o gráfico de setores, que é o nosso conhecido gráfico de pizza. Se eu quero comparar parte com parte, então, por exemplo, eu quero comparar o voto de determinado candidato antes e depois, a proporção de eleitores nele, o gráfico de colunas permite melhor essa comparação parte e parte.
>> [Cileda de Queiroz] Existem outros gráficos também muito interessantes que infelizmente não tão no nosso currículo. Por exemplo, o gráfico de pontos é superfa... é o mais simples de todos, porque simplesmente você colocar um pontinho lá no valor daquele dado e ele te dá a “cara” da distribuição como um todo. Então, aí você vai poder estudar o todo, não só pedaços do gráfico.
>> [Locutor] É possível manipular informações escolhendo um tipo de gráfico em vez de outro?
>> [Cileda de Queiroz] Primeiro, bom, vamos lá, hã... se eu quero garantir que essas informações não sejam manipuladas, é fundamental mostrar a escala nos eixos desses gráficos. Escolher o gráfico adequado, lógico!, né? Então, eu vou escolher um gráfico de linha para uma variável quantitativa; se for qualitativa, a linha não vai representar nada, e aí eu posso dar a interpretação que eu quiser, com margens de manipulação.
>> [Cileda de Queiroz] Se eu tiver um gráfico de colunas, eu preciso da escala. Da linha também, lógico! Eu preciso de uma escala pra saber qual é o ritmo de crescimento desses gráficos. Vou te dar um exemplo: se nós olharmos os gráficos que hoje em dia se divulgam das campanhas eleitorais e, mesmo assim, gráficos da economia, taxa Selic..., né? Hoje em dia, não importa o nível de escolaridade, nós temos acesso a várias informações e quase todas em forma de gráfico. Então, ele vem ao longo do tempo. Vamos supor, ele tem um centímetro [que] representa o primeiro mês, um centímetro [que] representa o segundo mês. De repente, um centímetro representa uma semana. Então, no primeiro mês o candidato “X” tinha tantos por cento de voto, no segundo mês ele tinha... cresceu; então, ele tinha mais votos. Aí vem que, em uma semana, ele cresceu mais um pouquinho, vão dizer que esse crescimento está [tom enfático] muito forte, e isso é uma forma de manipular dado, de manipular o eleitor, porque aquele espaço não é de uma semana, é de um mês — e ele tá sendo representado erroneamente, tá?, numa medida errada. Mesma coisa, a inflação! A inflação no Brasil desceu. Ok! Mostra o ano de 2015, 2016, 2017 e, de repente, em 2018, ela passa a mostrar o valor da inflação mês a mês, mostrando um decréscimo absurdamente rápido. [Tom enfático] Não! Porque a escala está errada! Eu não posso induzir, hã, que as pessoas pensem alguma coisa, que as pessoas concluam alguma coisa, a partir de uma representação gráfica errada.
Vinheta.
Créditos Studio Núcleo de Criação
Atividades
Faça as atividades no caderno.
3. Uma pequena empresa está expandindo seus serviços e organizou na seguinte planilha alguns dados de todos os funcionários contratados.
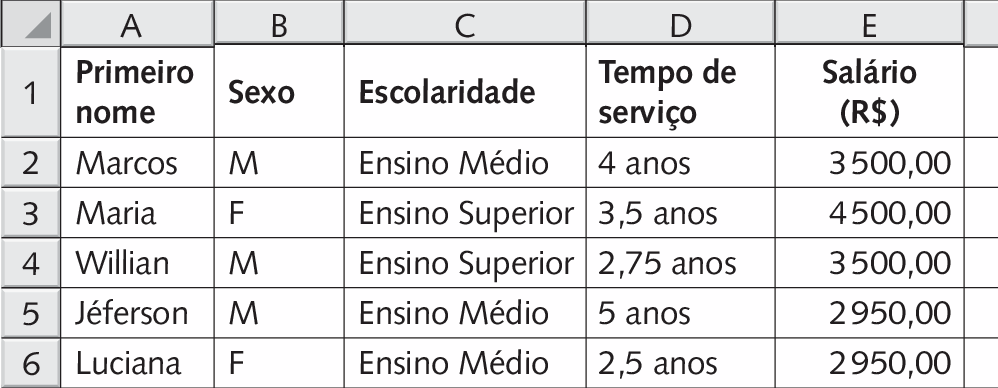
• Em seu caderno, identifique as variáveis e seus tipos.
4. Em seu caderno, classifique as variáveis em qualitativas (ordinal ou nominal) ou quantitativas (contínuas ou discretas):
a) cor da água coletada em um rio;
b) número de peças produzidas por uma máquina por hora;
c) precipitação pluviométrica durante um ano na cidade de Nova Serrana (Minas Gerais);
d) nível de escolaridade;
e) salários dos funcionários de uma empresa;
f) medida do tempo que leva para ir ao trabalho;
g) número de livros de uma biblioteca;
h) número de ações negociadas na bolsa de valores de Nova York;
i) grau de proficiência em um idioma.
5. Em uma pesquisa realizada com os participantes de um workshop sobre empreendedorismo, coletou-se dados relacionados aos seguintes indicadores: idade, sexo, quantidade de filhos, grau de instrução, renda, área de formação e fonte de renda.
a) Dessas variáveis, quais são as quantitativas e quais são as qualitativas?
b) Das variáveis quantitativas, quais são as discretas?
6.


No caderno, elabore um pequeno questionário para que um colega o responda. No questionário deve haver perguntas que permitam coletar dados de 5 variáveis quantitativas diferentes, discretas ou contínuas.
Troque de questionário com seu colega e peça a ele que responda às suas perguntas, e você responderá às perguntas elaboradas por ele. Próximo de cada resposta, anotem se a variável é quantitativa discreta ou contínua. Verifiquem se a classificação das variáveis e as respostas dadas estão de acordo com o esperado. Caso haja divergência na resposta, conversem e tentem resolver as dúvidas. Se as dúvidas permanecerem, consultem o professor.

2 Medidas de tendência central
Vamos estudar as medidas de tendência central (ou de posição) média, mediana e moda, que são obtidas a partir dos dados coletados da população ou de uma amostra, e que nos ajudam a compreender a distribuição dos valores das variáveis quantitativas e analisar a amplitude de um conjunto de dados. Para isso, considere a seguinte situação.
Clara anotou no calendário as medidas de temperatura máxima dos últimos 15 dias do mês de janeiro de 2023 em sua cidade.
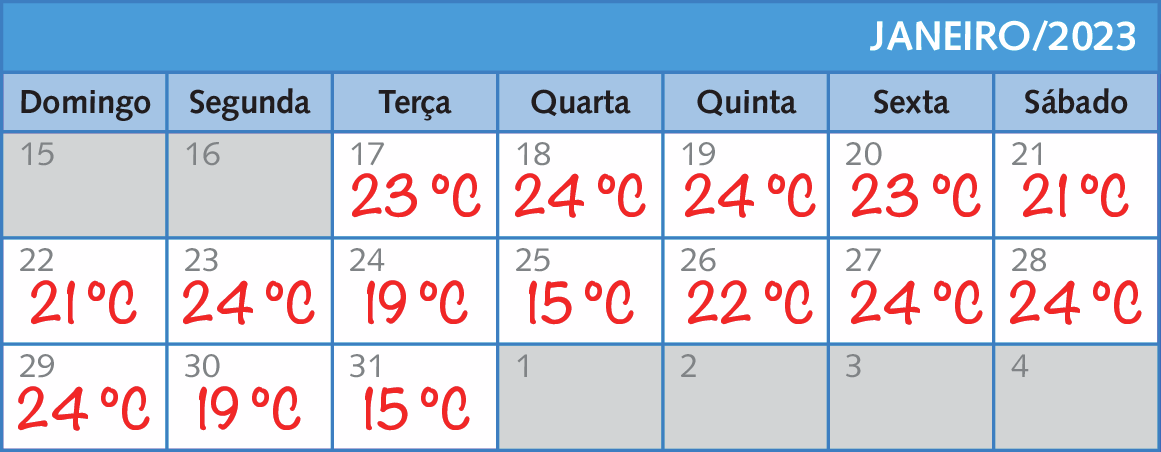
Médias
A média aritmética simples dos números décimo₁, décimo₂, décimo₃, reticências, décimon, que podemos indicar por
Letra x minúscula com uma barra horizontal acima., é dada por:

Considerando as medidas de temperatura máxima dos últimos 15 dias do mês de janeiro anotadas por Clara, o cálculo da média aritmética simples é obtido por:

A média das medidas de temperatura máxima na última quinzena de janeiro de 2023 foi de, aproximadamente, 21,47 graus Célsius.
A média aritmética ponderada pode facilitar o cálculo da média quando temos valores repetidos ou quando os valores possuem graus de importância diferentes. Para obter a média ponderada, multiplicamos cada valor por seu respectivo peso (frequência com que o valor ocorre ou grau de importância dado) e adicionamos os produtos. Depois, dividimos o resultado obtido pela soma dos pesos.
A média aritmética ponderada dos números décimo₁, décimo₂, décimo₃, reticências, décimon , em que décimo₁ tem peso pê₁, décimo₂ tem peso pê₂, décimo₃ tem peso pê₃ etcétera, é dada por:

Para facilitar, organizamos no quadro as medidas de temperatura máxima anotadas por Clara e indicamos a frequência com que cada uma delas ocorreu nos últimos 15 dias do mês de janeiro.
|
Medidas da temperatura máxima (°C) |
Frequência |
|---|---|
|
15 |
2 |
|
19 |
2 |
|
21 |
2 |
|
22 |
1 |
|
23 |
2 |
|
24 |
6 |
Portanto, a média ponderada das medidas de temperatura máxima é dada por:
Assim como a média aritmética simples, a média aritmética ponderada das medidas de temperatura máxima da última quinzena de janeiro na cidade de Clara é de, aproximadamente, 21,47 graus Célsius.
Mediana
A mediana (emi dê ) é o valor que ocupa a posição central de um conjunto de dados colocados em ordem crescente ou decrescente. A essa ordenação, damos o nome de rol.
Se a distribuição tiver um número ímpar de dados, haverá um valor que ocupa a posição central, e este será a mediana.
Se a distribuição tiver um número par de dados, haverá dois valores que ocupam as posições centrais. Assim, a mediana será a média aritmética desses dois valores centrais.
Clara registrou 15 medidas de temperatura em seu calendário; portanto, uma dessas medidas ocupa a posição central. Vamos dispor as medidas em ordem crescente.

Se, por algum motivo, não houver informação para o dia 17 de janeiro, em que a medida da temperatura máxima registrada foi de 23 graus Célsius, a mediana é calculada assim:

Nesse caso, a mediana é 22,5 graus Célsius.
Moda
Moda é o valor ou os valores que apresentam a maior frequência em um conjunto de dados, ou seja, que ocorrem mais vezes. Para as medidas de temperatura máxima anotadas por Clara, sabemos que:
• a frequência da medida 15 graus Célsius é 2;
• a frequência da medida 19 graus Célsius é 2;
• a frequência da medida 21 graus Célsius é 2;
• a frequência da medida 22 graus Célsius é 1;
• a frequência da medida 23 graus Célsius é 2;
• a frequência da medida 24 graus Célsius é 6.
Assim, podemos concluir que a moda é 24 graus Célsius pois é a medida que apresenta a maior frequência. Portanto, a medida de temperatura máxima que mais ocorreu nos últimos 15 dias de janeiro de 2023 na cidade de Clara foi 24 graus Célsius.
Observação
Ao contrário da média ou da mediana, a moda não é necessariamente única. Podemos ter um conjunto de dados com duas modas (bimodal), sem nenhuma moda (amodal) ou com mais de dois valores modais (multimodal).
Amplitude
A amplitude de um conjunto de dados é a diferença entre o menor e o maior valor que aparecem nesse conjunto. Considerando as medidas de temperaturas anotadas por Clara, podemos notar que a menor medida é 15 graus Célsius e a maior é 24 graus Célsius. Nesse caso, a amplitude é calculada assim:
24 graus Célsius ‒ 15 graus Célsius = 9 graus Célsius
Logo, a amplitude desse conjunto de dados é 9 graus Célsius.

A partir dos valores da média (21,47 graus Célsius), da mediana (23 graus Célsius) e da moda (24 graus Célsius), mesmo sem observar todos os dados diretamente, podemos concluir que as medidas obtidas estão mais próximas de 24 graus Célsius do que de 15 graus Célsius.
Atividades
Faça as atividades no caderno.
7. A tela do computador a seguir mostra o número de visitantes em um parque nos 31 dias do mês de julho de 2023.

a) Calcule a média aritmética, a mediana e a moda desse conjunto de dados.
b) Na sua opinião, qual dessas medidas de tendência central é mais significativa para a avaliação do número de visitantes no mês de julho? Justifique.
c) Em quantos dias o público presente no parque foi acima da média?
d) Calcule a amplitude desse conjunto de dados. Escreva uma frase relacionando-a às medidas de tendência central calculadas.
8. Uma instituição que atende crianças carentes cadastrou, em janeiro de 2024, 50 crianças para receber roupas como doação. Na tabela a seguir , observe o tamanho das roupas e a quantidade de crianças.
|
Tamanho da roupa |
Quantidade de crianças |
|---|---|
|
8 |
9 |
|
10 |
14 |
|
12 |
12 |
|
14 |
7 |
|
16 |
8 |
Dados obtidos pela instituição de caridade em janeiro de 2024.
a) Calcule a moda, a mediana e a amplitude desses dados.
b) O que cada uma dessas medidas representa nessa situação? Converse com o professor e os colegas.
9. A distribuição dos salários de uma empresa está representada na tabela a seguir.
|
Salário |
Número de funcionários |
|---|---|
|
R$ 800,00 |
22 |
|
R$ 900,00 |
9 |
|
R$ 1.000,00 |
8 |
|
R$ 1.050,00 |
8 |
|
R$ 1.100,00 |
7 |
|
R$ 1.300,00 |
6 |
|
R$ 2.300,00 |
4 |
|
R$ 5.220,00 |
1 |
Dados obtidos pelo departamento pessoal da empresa em dezembro de 2023.
Calcule o salário médio dos funcionários dessa empresa, a moda desses salários e a amplitude do conjunto de dados. Depois, escreva um parágrafo relacionando essas medidas.
10.


Reúna-se com um colega e, juntos, escolham um dos seguintes temas:
• Alimentação saudável
• Transporte urbano
• Atividade física
A partir do tema escolhido, planejem uma pesquisa amostral. A população deve ser formada por estudantes da sua escola. Pensem em uma amostra que represente a população em pelo menos 4 variáveis (duas qualitativas e duas quantitativas). Elaborem questões adequadas para coletar esses dados. Entrevistem a amostra definida por vocês. Organizem os dados e calculem a média, a mediana, a moda e a amplitude das variáveis quantitativas.

Veja que interessante

A Estatística na área de Saúde
Assim como em outras áreas (Educação, Economia etcétera), estudos mostram que a Estatística tem papel relevante nos avanços na área da Saúde obtidos nos últimos séculos, podendo utilizar a análise de dados para testar hipóteses e assim verificar determinada evidência.

Pensando em um tratamento inovador, por exemplo, é possível fazer diversos testes em laboratório e verificar que, em determinadas condições, algumas reações químicas sempre ocorrem, mas, devido à diversidade entre os seres humanos, as reações a determinado tratamento podem ocorrer de fórma diferente entre as pessoas. Nesse contexto, a Estatística pode não garantir que uma pessoa será curada de uma doença utilizando certo tratamento, mas é possível inferir que, se em um estudo de determinado grupo com .1000 pacientes com a mesma patologia 990 obtiverem resultado favorável após esse tratamento, há grandes chances de ele ser eficaz.

Em contrapartida, o uso inadequado da Estatística também pode ser responsável por erros de interpretação, mostrando resultados falsos ou suposições sem justificativas.
Atividade
Realize uma pesquisa sobre “Gráficos que induzem ao erro” e como os dados estatísticos podem ser manipulados para produzir notícias falsas. Leve para a sala de aula o conteúdo encontrado e converse com seus colegas e com seu professor.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Pesquisa estatística
Pesquisa censitária: todos os elementos da população são consultados.
Pesquisa amostral: uma parte da população é consultada. Uma pesquisa amostral pode ser sistemática, casual simples ou estratificada.
• Amostra sistemática: nos casos em que os elementos da população se apresentam ordenados, a cada determinada quantidade de elementos, um é retirado para análise.
• Amostra casual simples: Nesse tipo de seleção da amostra, os elementos da população são rotulados e, por meio de alguma espécie de sorteio, os integrantes da amostra são selecionados para participar da pesquisa.
• Amostra estratificada: Muitas vezes, a população estudada se divide em subpopulações, chamadas estratos. A amostra é obtida por meio da seleção de indivíduos de cada estrato.
1. Uma empresa multinacional possui .15000 funcionários. O RH da empresa selecionou .4500 funcionários para saber quantas pessoas querem aderir ao novo plano de saúde proposto por eles. Em seu caderno, responda:
a) qual é a população da pesquisa?
b) quantos funcionários compõem a amostra da pesquisa?
c) que porcentagem do universo estatístico a amostra representa?
2. Uma universidade realizou uma pesquisa para saber em quais cursos os estudantes entrevistados estavam matriculados. Para isso, entrevistou 120 estudantes, sendo 40 de humanas, 40 de exatas e 40 de biológicas. Que tipo de pesquisa amostral foi realizada?
a) sistemática
b) casual simples
c) estratificada
d) probabilística
3. Uma fábrica mantém seu contrôle de qualidade por meio de amostragem. A cada 100 peças, é selecionada uma para a inspeção do contrôle de qualidade. Que tipo de pesquisa amostral essa fábrica realiza?
a) sistemática
b) casual simples
c) estratificada
d) probabilística
Variáveis estatísticas
O tempo de duração de uma lâmpada e a porcentagem de lares brasileiros que possuem animais de estimação são características (ou atributos) chamadas, em Estatística, de variáveis.
O esquema a seguir sintetiza as variáveis e seus tipos.

4. Em seu caderno, classifique as variáveis em qualitativas (ordinal ou nominal) ou quantitativas (contínuas ou discretas):
a) cor dos olhos;
b) salários dos professores de uma escola;
c) quantidade de semáforos em São Paulo;
d) quantidade de palavras em um texto;
e) altura dos estudantes do 8º ano;
f) nome dos pacientes de um hospital;
g) gêneros masculino e feminino.
Medidas de tendência central
São medidas de tendência central a média aritmética, a mediana e a moda.
A média aritmética simples dos números décimo1, décimo2, décimo3, …, décimon, que podemos indicar por
Letra x minúscula com uma barra horizontal acima.é dada por:
A média aritmética ponderada dos números décimo₁, décimo₂, décimo₃, …, décimon, em que décimo₁ tem peso pê₁, décimo₂ tem peso pê₂, décimo₃ tem peso pê₃ etcétera, é dada por:
Mediana é o valor que ocupa a posição central de um conjunto de dados colocados em ordem crescente ou decrescente.
• Se a distribuição tiver um número ímpar de dados, haverá um valor que ocupa a posição central, e este será a mediana.
• Se a distribuição tiver um número par de dados, haverá dois valores que ocupam as posições centrais. Assim, a mediana será a média aritmética desses dois valores centrais.
Moda é o valor ou os valores que apresentam a maior frequência em um conjunto de dados, ou seja, que ocorrem mais vezes.
5. Em uma semana de funcionamento, uma doceria registrou o número de brigadeiros vendidos a cada dia da semana.
|
Seg |
Ter |
Qua |
Qui |
Sex |
|---|---|---|---|---|
|
60 |
58 |
55 |
62 |
68 |
Determine a média aritmética do número de brigadeiros vendidos nesses dias.
6. Uma confeitaria tem 4 funcionários cujos salários são:
R$ 2.300,00dois mil trezentos reais ; R$ 1.570,00mil quinhentos e setenta reais ; R$ 1.370,00mil trezentos e setenta reais ; R$ 1.440,00mil quatrocentos e quarenta reais
a) Calcule a média de salários dos funcionários dessa confeitaria.
b) Será necessário contratar um cozinheiro especializado em doces, visando o crescimento da confeitaria. Qual será a nova média dos salários, sabendo que esta nova mão de obra custará R$ 3.200,00três mil duzentos reais?
7. Na tabela a seguir está o número de filhos dos 50 funcionários de uma empresa.
|
Número de filhos |
Frequência absoluta |
|---|---|
|
0 |
10 |
|
1 |
5 |
|
2 |
25 |
|
3 |
10 |
Dados obtidos pelo RH da empresa em janeiro de 2024.
Com base nos dados da tabela, determine:
a) a moda;
b) a quantidade média de filhos;
c) a mediana.
8. Determine a média das notas de Matemática de cada um dos estudantes a seguir.
|
Renata |
6,5 |
7,8 |
6,0 |
6,8 |
|---|---|---|---|---|
|
Cátia |
8,0 |
8,5 |
6,5 |
7,5 |
|
Marcos |
5,0 |
5,5 |
4,5 |
6,0 |
|
Mateus |
4,5 |
7,5 |
8,5 |
9,0 |
9. Na tabela a seguir está descrita a quantidade de proteína, em gramas, que alguns atletas de uma academia consomem por mês.
|
Quantidade de proteína |
Frequência |
|---|---|
|
2.510 g |
8 |
|
2.620 g |
11 |
|
2.700 g |
10 |
|
2.860 g |
12 |
|
2.950 g |
18 |
|
3.200 g |
11 |
Dados obtidos pelos atletas da academia em 2023.
Com base na tabela, determine:
a) a quantidade de atletas que participaram da pesquisa;
b) a média de proteína consumida mensalmente;
c) a moda da quantidade de proteína;
d) a mediana da quantidade de proteína.