Página 243

Teste seus conhecimentos

1. Qual dos números racionais a seguir tem dízima periódica como representação decimal?

\frac{12}{15}

\frac{8}{16}

\frac{9}{13}

\frac{99}{8}

2. O 4º termo da sequência dada por a1 = 0 e

a_{n + 1} = \frac{1}{2} a_{n} ‒ 5

é:

a) ‒ 8,75

b) ‒7,5

c) ‒3

d) ‒3,75

3. Um cientista obteve as seguintes medidas de massa de 4 elementos que está estudando:

A: 0,2 ⋅ 105 gramas

B: 2,7 ⋅ 10‒5 gramas

C: 8,3 ⋅ 10‒6 gramas

D: 0,1 ⋅ 102 gramas

Qual dos elementos tem menor medida de massa?

a) a

b) B

c) C

d) D

4. O valor de

18^{\frac{1}{2}} \cdot 27^{\frac{1}{3}}

é um número entre:

a) 4 e 5

b) 12 e 13

c) 22 e 23

d) 80 e 82

5. Uma loja vende apenas triciclos e bicicletas para o transporte de adultos, totalizando 150 rodas no estoque. Quantas bicicletas estão disponíveis nessa loja, se há 22 triciclos?

a) vinte e duas

b) 28

c) quarenta e duas

d) 53

6. Fernando foi à feira comprar algumas frutas. Em uma barraca, ele reparou que, se levasse 12 unidades de laranja e 7 unidades de limão, pagaria R$ 7,75sete reais e setenta e cinco centavos. Caso levasse 6 unidades de laranja e 4 unidades de limão, pagaria R$ 4,00quatro reais. O preço da unidade de limão nessa barraca é:

a) R$ 0,25zero reais e vinte e cinco centavos

b) R$ 0,50zero reais e cinquenta centavos

c) R$ 1,00um reais

d) R$ 1,25um reais e vinte e cinco centavos

7. A prefeitura de certa cidade deseja construir uma estrada que seja equidistante de dois prédios, a e B, da cidade. No rascunho do projeto elaborado pelo engenheiro, esses dois prédios foram marcados como dois pontos. Com isso, a estrada pode ser representada pela:

a) circunferência que passa por a e B.

b) semirreta

\vec{A B}

c) bissetriz de

\overline{A B}

d) mediatriz de

\overline{A B}

8. Observe a seguinte imagem.

Fotografia. Retângulo preto na horizontal com quatro fileiras de paralelogramos na cor laranja na parte superior e quatro fileiras na parte inferior.

As 4 camadas horizontais inferiores podem ser obtidas a partir de uma transformação geométrica das 4 camadas horizontais superiores. Que transformação é essa?

a) Rotação com um giro de 360graus, no sentido horário, em relação ao centro da imagem.

b) Rotação com um giro de 90graus, no sentido horário, em relação ao centro da imagem.

c) Reflexão em relação a uma reta horizontal que passa no centro da imagem.

d) Translação vertical de 4 camadas para baixo.

9. Bruno construiu um polígono regular com 30 lados em um sófitiuér de geometria dinâmica. Ao medir a abertura de um ângulo interno do polígono, qual medida deve aparecer?

a) 12graus

b) 162graus

c) 168graus

d) 192graus

10. Para criar a senha de acesso a um sáite, o usuário precisa escolher três elementos nesta ordem: um símbolo entre quadrado, círculo e triângulo, uma vogal e um número de 1 a 5. Suelen decidiu que vai utilizar o triângulo ou o círculo como símbolo. Quantas senhas são possíveis criar com essa escolha?

a) 25

b) 45

c) 50

d) 75

11. Em um evento escolar estão 24 professores, 46 estudantes e 56 pais. No evento, será sorteado um livro. Se cada pessoa tem a mesma chance de ser sorteada, qual é a probabilidade de o ganhador não ser um professor?

\frac{4}{21}

\frac{51}{63}

\frac{40}{63}

\frac{13}{21}

12. Laís desenhou um losango e traçou suas diagonais. Sabendo que a abertura do ângulo formado entre a maior diagonal e um dos lados do losango mede 15graus, qual é a medida de abertura do maior ângulo interno desse losango?

a) 15graus

b) 30graus

c) 75graus

d) 150graus

Página 244

Teste seus conhecimentos

13. Mateus está em dúvida entre qual tecido deve comprar. Na loja, há os seguintes formatos:

• quadrado, cuja medida de comprimento do lado é 85 centímetros;

• triângulo, cujas medidas de comprimento da base e da altura são, respectivamente, 90 centímetros e 1,5 métro;

• losango, cujas medidas de comprimento das diagonais são 1,2 métro e 1,8 métro;

• círculo, cuja medida de comprimento do raio é 50 centímetros.

Se ele deseja comprar o tecido com maior medida da área, deve escolher o formato de:

a) quadrado.

b) triângulo.

c) losango.

d) círculo.

14. Thaís tem um recipiente em formato que lembra um paralelepípedo com medida de comprimento de altura de 15 centímetros e base quadrada com lado medindo 9 centímetros de comprimento. É possível despejar 1 litro de água nesse recipiente sem derramar?

a) Não, pois seriam derramados 215 mililitros.

b) Não, pois seriam derramados 35 mililitros.

c) Sim e ainda caberiam mais 215 mililitros.

d) Sim e ainda caberiam mais 35 mililitros.

15. Marisa tem uma plantação em formato de quadrado e vai ampliar sua medida de comprimento do lado em 15%, mantendo o formato quadrado. Sabendo que a nova área da plantação medirá 529 métros quadrados, qual é a medida de comprimento do lado da plantação atual?

a) 20 métros

b) 23 métros

c) 27 métros

d) 30 métros

16. Da casa de Estefani até a casa de Lucas são 40 quilômetros de viagem. Ela realizou esse percurso em 48 minutos com medida de velocidade média de 50 quilômetros por hora. Se a medida de velocidade média fosse 60 quilômetros por hora, quantos minutos ela economizaria de viagem?

a) 8 minutos.

b) 10 minutos.

c) 24 minutos.

d) 40 minutos.

17. Em uma pesquisa estatística foi registrada a quantidade de viagens de avião feitas pelos entrevistados:

0 4 6 0 5 3

4 duas 4 4 uma duas

A menor medida estatística desse conjunto de dados é:

a) a amplitude.

b) a média.

c) a moda.

d) a mediana.

18. Em uma pesquisa amostral sobre os pacientes de seu consultório, Ronaldo utilizou a amostragem casual simples, selecionando 3 pacientes em sequência a cada 10 pacientes, para verificar a variável qualitativa ordinal “nível de satisfação da consulta” e a variável quantitativa contínua “medida do tempo de espera”.

Sobre os termos estatísticos apresentados nessa situação, o que está errado é o tipo:

a) de pesquisa.

b) de amostragem.

c) da variável qualitativa.

d) da variável quantitativa.

19. Em uma pesquisa sobre a medida de massa, em quilograma, dos frequentadores de um clube, foram obtidos estes dados em 2023.

Distribuição de frequência das medidas de massa dos frequentadores do clube
Medida de massa (em kg)	Frequência (F)
30 ⊢ 45	142
45 ⊢ 60	148
60 ⊢ 75	108
75 ⊢ 90	80
90 ⊢ 105	70
105 ⊢ 120	12

Dados obtidos pelo clube em 2023.

Qual era a frequência relativa dos frequentadores desse clube que estavam na classe 90 ⊢ 105?

a) 11,6%

b) 12,5%

c) 14,3%

d) 70%

20. Cássia é dona de algumas lojas de calçados. Em junho de 2023, ela elaborou este gráfico para verificar a quantidade de pares de sapatos vendidos em cada loja.

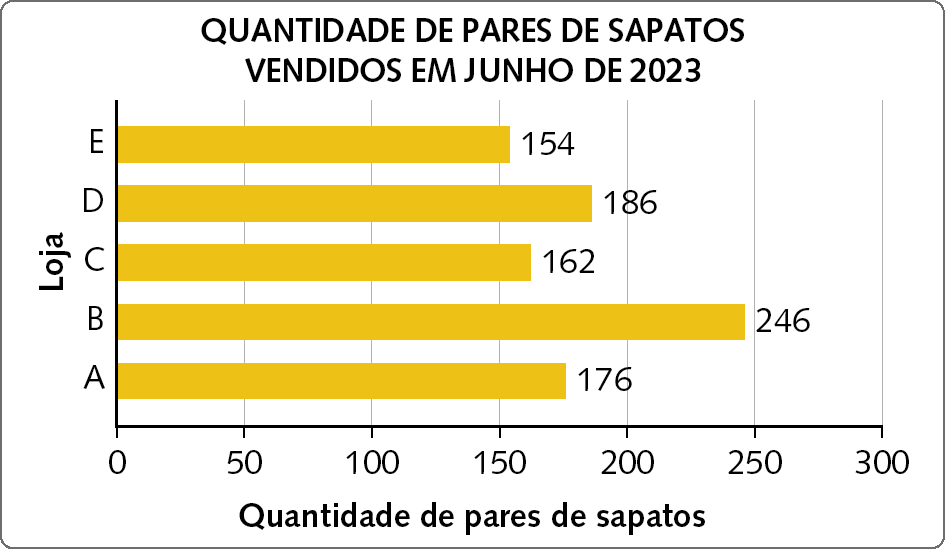
Gráfico em barras horizontais. QUANTIDADE DE PARES DE SAPATOS VENDIDOS EM JUNHO DE 2023. Eixo horizontal x, Quantidade de pares de sapatos. Eixo vertical y, loja. Os dados são: Loja A: 176. Loja B: 246. Loja C: 162. Loja D: 186. Loja E: 154.

Dados obtidos por Cássia em junho de 2023.

Nesse mês, quantas lojas ficaram abaixo da média mensal de vendas?

a) 0

b) uma

c) duas

d) 3

Página 245

Respostas

Revisão dos conteúdos de anos anteriores

Para o capítulo 1: Conjuntos numéricos

Página 10

1. a) número natural: 5; números inteiros: 5 e ‒5

b) nenhum número natural; número inteiro: ‒2,0

c) números naturais: 10 e 12; números inteiros: todos os números

d) nenhum número natural; nenhum número inteiro

2. a) a → 5; C → ‒3

b) X → ‒34; Y → ‒33

c) Z → 0; W → ‒20

d) M → ‒ 60; N → 0

3. a. F

b. V

c. F

d. V

4. itens a, d

5. a) <

b) >

c) <

d) >

6. A: 4; B:

\frac{1}{2}

; C:

\frac{9}{4}

; D:

\frac{9}{2}

Para o capítulo 2: Potenciação e radiciação

Páginas 11 e 12

7. itens a, b, c, f, g

8. a) +.1296

b) +216

c) +729

d) 64

e) ‒1,331

‒ \frac{1}{8}

g) 0,0081

\frac{1}{32}

9. a) 8

b) ‒9

c) 10

d) ‒4

e) 7

f) ‒2

10. A – dois; B – um; C – quatro; D – três

11. a)

\frac{2}{5}

\frac{3}{8}

c) ‒5

\frac{1}{4}

12. itens a, d

13. a) 16

b) 81

c) 64

d) 0,04

Para o capítulo 3: Sistemas de equações do 1º grau

Página 12

14. M(2, 5); N(‒3, 1); P(0, ‒6); Q(4, ‒6)

15. Construção de figuras.

Para o capítulo 4: Ângulos e transformações geométricas

Páginas 12 a 14

16. a. F

b. V

c. V

d. F

17.

E \hat{O} B

D \hat{O} C

;

C \hat{O} B

B \hat{O} A

18. a) reflexão

b) eixo de simetria

19. Construção de figuras.

Para o capítulo 5: Polígonos

Páginas 15 e 16

20. Construção de figura.

21. a) x = 62graus

b) x = 25graus

c) x = 110graus

22. Polígono do item a, pois todos os ângulos internos têm a mesma medida de abertura e todos os lados têm a mesma medida de comprimento.

23. a) quadrado

b) triângulo equilátero

Para o capítulo 6: Probabilidade

Página 16

24. itens b, c

25. a)

\frac{1}{6}

\frac{1}{4}

\frac{1}{2}

\frac{1}{12}

Para o capítulo 7: Triângulos e quadriláteros

Páginas 16 e 17

26. Construção de figura.

27. a) V

b. F

c. V

d. F

28. a) trapézio

b) outro quadrilátero

c) paralelogramo

d) trapézio

29. itens a, c, d

Para o capítulo 8: Área, volume e capacidade

Páginas 18

30. a) 344 centímetros quadrados

b) 105 centímetros quadrados

c) 142,5 centímetros quadrados

d) 7,25 centímetros quadrados

31. 525 centímetros cúbicos

32. a) .1728 centímetros cúbicos

b) 0,064 métro cúbico

c) 729 centímetros cúbicos

Para o capítulo 9: Equações do 2º grau

Páginas 19 e 20

33. itens a, c

34. itens b, d, e

35. itens a, d

36. alternativa a

37. a) S = {‒ 4}

b) S = {41}

S = \{\frac{1}{2}\}

38. itens a, c

Para o capítulo 10: Grandezas e proporcionalidade

Páginas 20 e 21

39. a)

\frac{30}{3} = 10

\frac{3}{30} = \frac{1}{10}

\frac{90}{123}

40. itens a, c

41. a) x = 15

b) x = 30

c) x = 50

42. a) 36

b) 80

43. 96

Para o capítulo 11: Medidas de tendência central e pesquisa estatística

Página 21

44. R$ 38,28trinta e oito reais e vinte e oito centavos

45. marca A: 7,5; marca B: 7,3

Para o capítulo 12: Gráficos estatísticos

Página 22

46. Resposta pessoal.

Capítulo 1

Revisão dos conteúdos deste capítulo

Página 41

1. a) V

b) F

c) F

2. a) antecessor: 210; sucessor: 212

b) antecessor: 198; sucessor: 200

c) antecessor: 299; sucessor: 301

3. 2, 5, 7, 12, 19, 31

4. a) 8, 9, 10, 11

b) ‒10, ‒9

5. R$ 2.590,00dois mil quinhentos e noventa reais

6. itens a, b, d

7. a) 0, 5

b) 0,6

c) 1,23

d) ‒1,111reticências

8. a)

\frac{5}{9}

\frac{12}{90}

\frac{122}{99}

\frac{22}{900}

9. a) V

b) F

c) F

d. V

10. ‒12 pertence aos conjuntos dos inteiros, racionais e reais;

\sqrt{7}

pertence aos conjuntos dos irracionais e reais;

\frac{15}{3}

pertence ao conjunto dos naturais, inteiros, racionais e reais; 1,88 pertence ao conjunto dos racionais e reais; π pertence ao conjunto dos irracionais e reais;

\frac{3}{7}

pertence ao conjunto dos racionais e reais.

Capítulo 2

Revisão dos conteúdos deste capítulo

Páginas 55 e 56

1. a) 27

b) ‒4

c) 4

\frac{4}{9}

\frac{25}{16}

f) 1

g) ‒1

h) 2

2. a) 6

b) ‒11

c) 97

3. a) 2,7 ⋅ 10‒1

b) 8,95 ⋅ 102

c) 3,6 ⋅ 103

d) 1,2 ⋅ 10‒3

e) 5 ⋅ 107

f) 4,4 ⋅ 10‒8

4. a) 318

b) 56

c) 2‒6

d) 8‒2

e) 27

5. a) 31

b) 0

c) 0

d) 6

e) 56

6. a) 7

b) 5

c) 13

d) 15

\frac{2}{3}

\frac{4}{7}

\frac{11}{10}

\frac{2}{13}

\frac{1}{5}

7. a) 5,20

b) 17,32

c) 2,45

d) 1,58

8. a) 8,7

b) 2,6

c) 1,9

d) 22,4

9. a) 5

b) 4

\frac{65}{6}

10. a) .9801

b) 106

c) .1296

11. a) ‒9

b) 2

c) 3

\frac{3}{4}

12. ‒

\frac{8}{7}

Página 246

Respostas

Capítulo 3

Revisão dos conteúdos deste capítulo

Página 72

1. Construção de figura.

2. 12 cédulas de R$ 5,00cinco reais e 8 de R$ 10,00dez reais.

3. a) (3, 2)

b) (‒1, 4)

c) (6, 3)

d) (4, 2)

Capítulo 4

Revisão dos conteúdos deste capítulo

Páginas 108 e 109

1. a)

A \hat{O} B

B \hat{O} C

C \hat{O} D

C \hat{O} E

D \hat{O} E

D \hat{O} F

E \hat{O} F

A \hat{O} D

A \hat{O} E

B \hat{O} E

B \hat{O} F

A \hat{O} F

A \hat{O} C

B \hat{O} D

C \hat{O} F

m e d (A \hat{O} B) = 20 °

3. 1 centímetro

4. A torneira deve ser instalada em qualquer ponto da bissetriz do ângulo formado pelos muros do terreno.

5. alternativa b

Capítulo 5

Revisão dos conteúdos deste capítulo

Página 121

1. quadrado a bê cê dê; lados:

\overline{A B}

\overline{B C}

\overline{C D}

\overline{D A}

vértices: A, B, C, D; diagonais:

\overline{A C}

\overline{B D}

2. a) 7

b) 7

3. a) 20

b) 0

4. hexágono

5. 540graus

6. octógono

Capítulo 6

Revisão dos conteúdos deste capítulo

Página 130

1. 64 resultados possíveis.

2. 24 possibilidades diferentes.

\frac{5}{11}

4. a) {a, B, C, D, ê, F}

\frac{1}{6}

5. a)

\frac{3}{5}

\frac{2}{5}

6. a)

\frac{5}{12}

\frac{7}{12}

7. a)

Espaço amostral
Ás, Ás	2, Ás	3, Ás	4, Ás	5, Ás	6, Ás	7s, Ás
Ás, 2	2, 2	3, 2	4, 2	5, 2	6, 2	7, 2
Ás, 3	2, 3	3, 3	4, 3	5, 3	6, 3	7, 3
Ás, 4	2, 4	3, 4	4, 4	5, 4	6, 4	7, 4
Ás, 5	2, 5	3, 5	4, 5	5, 5	6, 5	7, 5
Ás, 6	2, 6	3, 6	4, 6	5, 6	6, 6	7, 6
Ás, 7	2, 7	3, 7	4, 7	5, 7	6, 7	7, 7

\frac{1}{49}

\frac{7}{49}

d) Exemplo de resposta: Júlia poderia informar o valor de uma das cartas.

Capítulo 7

Revisão dos conteúdos deste capítulo

Páginas 164 e 165

1. 45graus, 45graus, 90graus

2. três-a, um-B e dois-C

3. △á bê dê ≅ △cê bê dê (caso LAL); logo:

\hat{A} ≅ \hat{C}

4. △á bê ême ≅ △DCM (caso ALA); logo:

\overline{A M} ≅ \overline{M D}

5. a = 30graus, b = 60graus, c = 120graus e d = 150graus

6. afirmações a, c, e

7. 144graus e 36graus

8. x = 42graus, y = 48graus

9. a) x = 40graus, y = 70graus

b) x = 35graus, y = 55graus

10. 17 centímetros

Capítulo 8

Revisão dos conteúdos deste capítulo

Página 182

1. 120 centímetros quadrados

2. a) 64 centímetros quadrados

b) 18 centímetros quadrados

3. .2000 centímetros quadrados

5. 2,08π centímetros quadrados

4. A = 84π centímetros quadrados

6. 0,5 litro

Capítulo 9

Revisão dos conteúdos deste capítulo

Página 194

1. alternativas b, c, e

2. a) 2x2 ‒ 3x + 7 = 0

b) ‒3x2 + x + 5 = 0

c) 3x2 + 3x + 3 = 0

d) ‒2x2 + 4 = 0

e) x2 + 6x = 0

f) 3x2 = 0

3. Exemplo de resposta: x2 ‒ 144 = 0, com conjunto universo =

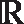
conjunto dos números reais positivos não nulos.

4. a) incompleta

b) completa

c) incompleta

d) completa

5. a) não

b) não

c) sim

d) sim

e) não

6. 2 e 3

7. b, c

8. a) S = {‒7, 7}

b) S = {0}

c) S = {‒2, 2}

d) S = { } ou S = ∅

9. a) x = ‒7 ou x = 7

b) x = ‒8 ou x = 8

10. 12

11. 72 centímetros

Capítulo 10

Revisão dos conteúdos deste capítulo

Páginas 207 e 208

1. a) não

b) sim

c) sim

d) não

2. Exemplo de resposta: a = 8 ⋅ b

3. 15 minutos

4. duas horas

5. a) 50

b) Exemplo de resposta: d = 50 ⋅ t, em que t é um número real positivo.

c) 87,5 quilômetros

6. a) 45

b) Exemplo de resposta: A ⋅ B = 45

c) B = 22,5

7. Exemplos de resposta:

P = \frac{Q}{3}

ou Q = 3 ⋅ P

8. Construção de gráfico.

9. R$ 3,00três reais

10. a) Exemplo de resposta: s ⋅ r = 60

b) s = 6

c) r = 12

11. a) inversamente proporcional

b) diretamente proporcional

c) e d) não proporcional

Capítulo 11

Revisão dos conteúdos deste capítulo

Páginas 221 e 222

1. a) os .15000 funcionários

b) .4500 funcionários

c) 30%

2. alternativa c

3. alternativa a

4. a), f. e g. qualitativa nominal

b) e e. quantitativa contínua

c) e d. quantitativa discreta

5. 60,6

6. a) R$ 1.670,00mil seiscentos e setenta reais

b) R$ 1.976,00mil novecentos e setenta e seis reais

7. a) 2

b) 1,7

c) 2

8. Renata: 6,75; Cátia: 7,62; Marcos: 5,25; Mateus: 7,37

9. a) 70

b) .2836 gramas

c) .2950 gramas

d) .2860 gramas

Capítulo 12

Revisão dos conteúdos deste capítulo

Página 239

1. a) 2 quilogramas

b) 20 estudantes

c) 44 ⊢ 46: 0,1; 46 ⊢ 48: 0,3; 48 ⊢ 50: 0,35; 50 ⊢ 52: 0,25

2. a) Sudeste; Norte

b) Centro-Oeste

3. a) das 8 horas às 12 horas

b) 108 alunos

c) 504 alunos

Teste seus conhecimentos

1. alternativa c

2. alternativa a

3. alternativa c

4. alternativa b

5. alternativa c

6. alternativa a

7. alternativa d

8. alternativa c

9. alternativa c

10. alternativa c

11. alternativa b

12. alternativa d

13. alternativa c

14. alternativa c

15. alternativa a

16. alternativa a

17. alternativa b

18. alternativa b

19. alternativa b

20. alternativa d

Página 247

Referências bibliográficas comentadas

AABOE, Asger. Episódios da história antiga da Matemática. Rio de Janeiro: Sociedade Brasileira de Matemática, 1984.

Este livro, organizado em quatro capítulos, permite que o leitor tenha contato com os primórdios da Matemática por meio de episódios históricos.

BERLONQUIN, Pierre. 100 jogos geométricos. Lisboa: Gradiva, 2005.

Este livro apresenta 100 jogos geométricos ordenados criteriosamente pelo autor, do mais fácil para o mais difícil, para que, enquanto o leitor se diverte, adquira maior rapidez de raciocínio e uma notável flexibilidade intelectual.

BOLT, Brian. Actividades matemáticas. Lisboa: Gradiva, 1991.

Este livro contém atividades matemáticas destinadas a estimular o pensamento criativo e incentivar o leitor a desenvolver a compressão de números, conceitos espaciais e pensamento matemático em geral.

BOYER, Carl Benjamin. História da Matemática. tradução Elza F. Gomide. São Paulo: Edgard Blücher; êduspi, 2010.

Este livro apresenta um estudo aprofundado da história da Matemática desde o Egito antigo até as tendências mais recentes. Mostra também a fascinante relação entre o desenvolvimento dos conhecimentos sobre números, fórmas e padrões e a evolução da humanidade.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília: Méqui; sébi, 2018.

Documento de caráter normativo que define o conjunto orgânico e progressivo de aprendizagens essenciais que todos os estudantes devem desenvolver ao longo das etapas e modalidades da Educação Básica.

BROCARD, Joana; SERRAZINA, Lurdes; ROCHA, Isabel. O sentido do número: reflexões que entrecruzam teoria e prática. Lisboa: Escolar, 2008.

Neste livro reúne-se um conjunto de textos produzidos no âmbito do projeto “Desenvolvendo o sentido do número: perspectivas e exigências curriculares”, cujo trabalho se centrou em torno do desenvolvimento do sentido do número para as crianças, concebeu materiais para aulas e refletiu sobre características do currículo que favorecem o sentido do número.

CARVALHO, Dione Lucchesi de. Metodologia do ensino da Matemática. São Paulo: Cortez, 2009.

Este livro subsidia o futuro professor no domínio dos conteúdos básicos e da metodologia da Matemática e sugere uma transformação no modo de perceber e compreender o papel dessa disciplina no currículo escolar.

CENTURIÓN, Marília. Conteúdo e metodologia da Matemática: números e operações. São Paulo: Scipione, 2001.

Este livro baseia-se na ideia de que o estudante constrói seu próprio conhecimento com base em suas ações e problematizações. Aborda as principais dúvidas tanto do estudante de Pedagogia quanto do professor dos anos iniciais do Ensino Fundamental.

DANTE, Luiz Roberto. Didática da resolução de problemas de Matemática. São Paulo: Ática, 2002.

Este livro propõe a discussão dos fatores que atuam negativamente no aprendizado de Matemática, classifica os vários tipos de problema que se apresentam e mostra as etapas envolvidas na sua resolução.

EVES, Howard. Introdução à história da Matemática. Campinas: unicâmpi, 2011.

Este livro busca introduzir a história da Matemática aos estudantes de graduação dos cursos superiores dessa disciplina. Assim sendo, além da narrativa histórica, há muitos expedientes pedagógicos visando assistir, motivar e envolver o estudante.

GRANDO, Regina Célia. O jogo e a Matemática no contexto da sala de aula. São Paulo: Paulus, 2004.

Este livro mostra a riqueza pedagógica que existe na utilização correta de jogos, para ensinar Matemática, para desenvolver o pensamento criativo e até mesmo para transformar o erro em aprendizado.

IFRAH, Georges. História universal dos algarismos. Rio de Janeiro: Nova Fronteira, 1997.

Este livro oferece, em linguagem acessível, uma visão completa e inovadora da epopeia do cálculo entre as civilizações. Um convite para uma viagem impressionante às origens da representação simbólica dos números.

IFRAH, Georges. Os números: a história de uma grande invenção. Rio de Janeiro: Globo, 1998.

Este livro traça uma resumida, mas completa, história da Matemática, acompanhando a evolução do raciocínio de nossos ancestrais desde a Pré-História, passando por civilizações como a dos egípcios, babilônios, fenícios, gregos, romanos, hebreus, maias, chineses, hindus e árabes.

Página 248

Referências bibliográficas comentadas

IMENES, Luiz Márcio. A numeração indo-arábica. São Paulo: Scipione, 1990. (Vivendo a Matemática).

Este livro discorre sobre os sistemas de numeração, em uma proposta integrada com História, explorando a Matemática de uma maneira divertida, mas comprometida com o conteúdo.

KAMII, Constance. Reinventando a Aritmética: implicações da teoria de Piaget. Campinas: Papirus, 1995.

Este livro faz uma análise crítica do ensino da Aritmética para as crianças dos primeiros anos do Ensino Fundamental. Com toda sua sensibilidade e seu conhecimento da teoria piagetiana, a autora aborda temas como importância da interação social, autonomia como finalidade da educação, numerais, adição e subtração.

KARLSON, Paul. A magia dos números. Rio de Janeiro: Globo, 1961.

Este livro usa a história da Matemática como bússola em uma jornada desde a Aritmética até o cálculo diferencial e integral. O que destaca essa obra não é apenas a linguagem informal e muitas vezes mordaz do autor, mas principalmente o grau de detalhismo que ele concedeu aos inúmeros assuntos que compõem o livro.

LIMA, Elon lages. Meu professor de Matemática e outras histórias. Rio de Janeiro: Sociedade Brasileira de Matemática, 2004.

Este livro é composto de pequenos ensaios sobre Matemática elementar. Em uma coleção de capítulos independentes, aborda tópicos de Matemática que constam dos programas escolares dos diferentes níveis de ensino.

MARANHÃO, Maria Cristina S. Matemática. São Paulo: Cortez, 1994. (Magistério).

Este livro reflete sobre a problemática do ensino da Matemática com base na experiência da autora, bem como nos estudos e nas pesquisas na área. Dessa maneira, a autora sugere o desenvolvimento de alguns temas que considera indispensáveis para preparar um estudante para o Ensino Médio.

PÓLYA, George. A arte de resolver problemas. traduçãoHeitor Lisboa de Araújo. Rio de Janeiro: Interciência, 2006.

Este livro aborda a resolução de problemas como um recurso para desafiar a curiosidade dos leitores. O autor destaca a importância de situações que apresentam indagações aos estudantes e contribuem para que desenvolvam o interesse pelo raciocínio independente.

ROSA Neto, Ernesto. Didática da Matemática. São Paulo: Ática, 2010.

Este livro é destinado a educadores interessados em educação matemática. Levando em consideração o interacionismo e a psicogenética, discute os principais tópicos da Matemática de Pré-escola e Ensino Fundamental, viabilizando sua aplicação em sala de aula.

SMOLE, Kátia Stocco; DINIZ, Maria Ignez. Ler, escrever e resolver problemas: habilidades básicas para aprender Matemática. Porto Alegre: artimédi, 2001.

Este livro contribui para a discussão sobre o lugar e o significado das competências e das habilidades no Ensino Fundamental, enfatizando as habilidades de ler, escrever e resolver problemas de Matemática.

TAHAN, Malba. Matemática divertida e curiosa. Rio de Janeiro: Record, 2012.

Este livro traz recreações e curiosidades da Matemática que transformam a aridez dos números e a exigência de raciocínio em brincadeira, ao mesmo tempo útil e prazerosa. O autor consegue fazer a união da ciência com o lúdico, transformando a leitura em um agradável passatempo.

TAHAN, Malba. O homem que calculava. Rio de Janeiro: Record, 2001.

O livro narra a história de Beremiz Samir, um viajante com o dom intuitivo da Matemática, manejando os números com a facilidade de um ilusionista. Problemas aparentemente sem solução tornam-se de uma transparente simplicidade quando expostos a ele.

TOLEDO, Marília; TOLEDO, Mauro. Teoria e prática de Matemática. São Paulo: FTD, 2009.

O livro constitui uma valiosa ferramenta para os professores dos anos iniciais do Ensino Fundamental. A obra trabalha o desenvolvimento das habilidades matemáticas básicas fundamentado em problemas ligados à experiência prática do estudante, em jogos e em situações que estimulam sua participação na construção de conceitos e o ajudam a compreender a relevância da Matemática como instrumento de transformação da realidade.

ZABALA, Antoni (organizador). Como trabalhar os conteúdos procedimentais em aula. tradução Ernani Rosa. segunda ediçãoPorto Alegre: Artmed, 1999.

Este livro, por meio de uma abordagem prática, mostra como trabalhar 42 conteúdos procedimentais que pertencem a diferentes áreas do Ensino Fundamental.

ZARO, Milton. Matemática experimental. São Paulo: Ática, 1996.

O objetivo deste livro é estimular a criatividade do professor no desenvolvimento de atividades com os estudantes, aplicando o método científico na Matemática por meio da técnica da redescoberta, exercitando a redação de textos e experimentos.