Página sessenta e quatro

Parte 4

Se T é ponto médio de

\overline{C D}

, para calcular

med (\overline{C T})

, podemos fazer:

med (\overline{C T}) = \frac{med (\overline{C D})}{2} = \frac{6 cm}{2} = 3 cm

Assim, temos:

med (\overline{S T}) = med (\overline{S C}) + med (\overline{C T}) = 1 cm + 3 cm = 4 cm

Portanto,

m e d (\overline{S T}) = 4 c m

c) Observe que

med (\overline{S D}) = med (\overline{S C}) + med (\overline{C D})

. De acôrdo com o item b:

med (\overline{S C}) = 1 cm

Assim, temos:

med (\overline{S D}) = med (\overline{S C}) + med (\overline{C D}) = 1 cm + 6 cm = 7 cm

Portanto,

m e d (\overline{S D}) = 7 c m

d) Observe que:

med (\overline{R D}) = med (\overline{R B}) + med (\overline{B C}) + med (\overline{C D})

De acôrdo com o item a:

med (\overline{R B}) = 2 cm

Assim, temos:

med (\overline{R D}) = med (\overline{R B}) + med (\overline{B C}) + med (\overline{C D}) =

= 2 centímetros + 2 centímetros + 6 centímetros = 10 centímetros

Portanto,

med (\overline{R D}) = 10 cm .

11. Exemplo de construção.

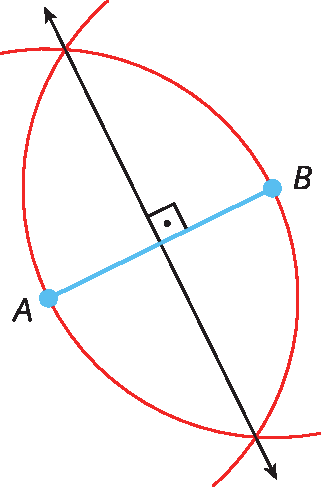
Figura geométrica. Segmento AB. Arco com centro em A que passa por B, arco com centro em B que passa por A. pela interseção dos arcos passa uma reta que é perpendicular ao segmento AB.

12. Traçando as mediatrizes dos segmentos

\overline{A B}

\overline{B C}

\overline{A C}

no triângulo ABC, obtemos a seguinte figura:

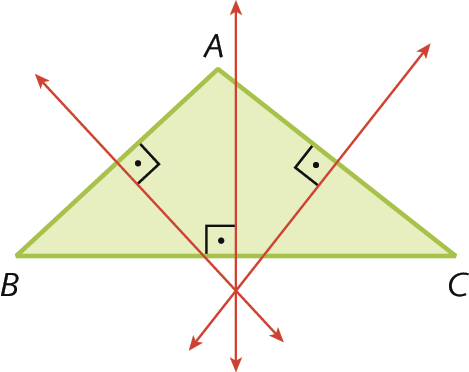
Figura geométrica. Triângulo ABC com três mediatrizes, que são perpendiculares a cada um dos lados. O encontro das mediatrizes está fora do triângulo.

Tecnologias digitais em foco – Páginas 85 e 86

a) Espera-se que os estudantes concluam que a abertura do ângulo

B \hat{A} D

mede 60graus independentemente da medida de comprimento do raio das circunferências que foram traçadas na construção de

B \hat{A} D

b) Espera-se que os estudantes concluam que o triângulo ACD é um triângulo equilátero.

c) Porque o ângulo construído é um dos ângulos internos de um triângulo equilátero e, portanto, sua abertura mede 60graus.

Atividades – Página 88

13. Os estudantes devem construir um ângulo de 60graus e sua bissetriz

\overline{A D}

. Em seguida, devem construir uma nova bissetriz

\overline{A B}

, localizando o ângulo de medida de abertura 15graus. Exemplo de construção:

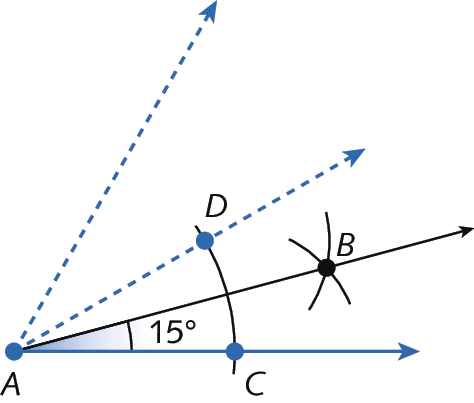
Figura geométrica. Ângulo CAD. A semirreta AB é bissetriz do ângulo CAD e define o ângulo CAB, cuja abertura mede 15 graus.

14. Os estudantes devem construir um ângulo

B \hat{A} D

de medida de abertura de 120graus, formado por dois ângulos adjacentes (

B \hat{A} C

C \hat{A} D

) de medida de abertura de 60graus, e traçar a bissetriz

\vec{A E}

C \hat{A} D

. O ângulo

B \hat{A} E

será reto.

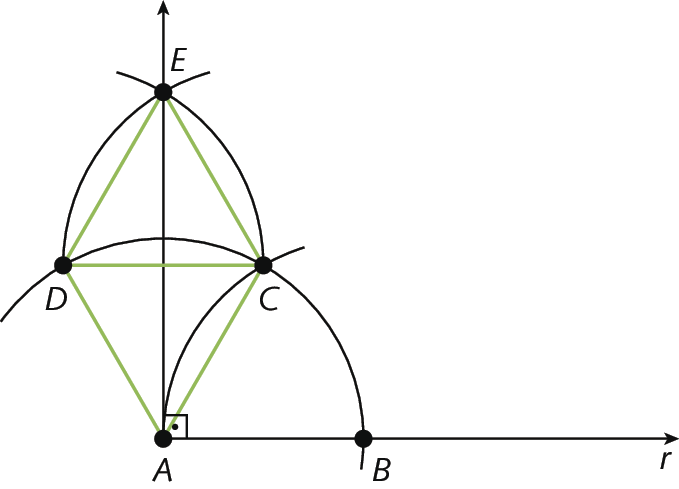
Figura geométrica. Semirreta horizontal r com que inicia em A e passa por B. Arco com centro em A e abertura AB. Arco com centro em B e raio AB. O encontro desses arcos definem o ponto C. Com centro em C e raio AB traça um arco. O encontro desse arco, com o arco de centro em A e raio AB define o ponto D. Os pontos ACD definem um triângulo equilátero. Com centro em D e raio AB traça um arco, que encontra o arco de centro em C e define um ponto E. Os pontos CDE definem um triângulo equilátero congruente ao outro triângulo anteriormente definido.

15. É possível construir os ângulos de medida de abertura de:

• 30graus, traçando a bissetriz de um ângulo de 60graus de medida de abertura:

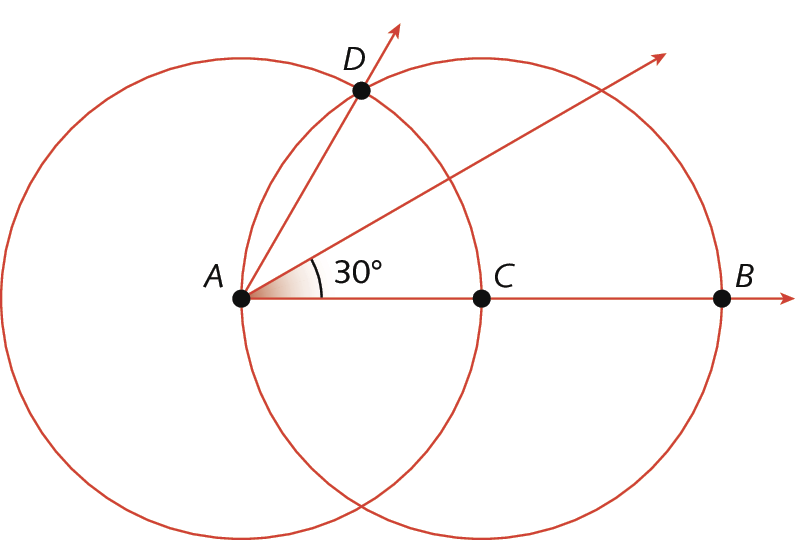
Figura geométrica. Ângulo CAD, o lado AC tem semirreta suporte AB. Circunferência de centro em A e raio AC. Circunferência de centro em C e raio AC. Definem o ponto D. A medida da abertura do ângulo CAD é igual 60 graus e sua bissetriz está representada.

• 45graus, traçando a bissetriz de um ângulo reto:

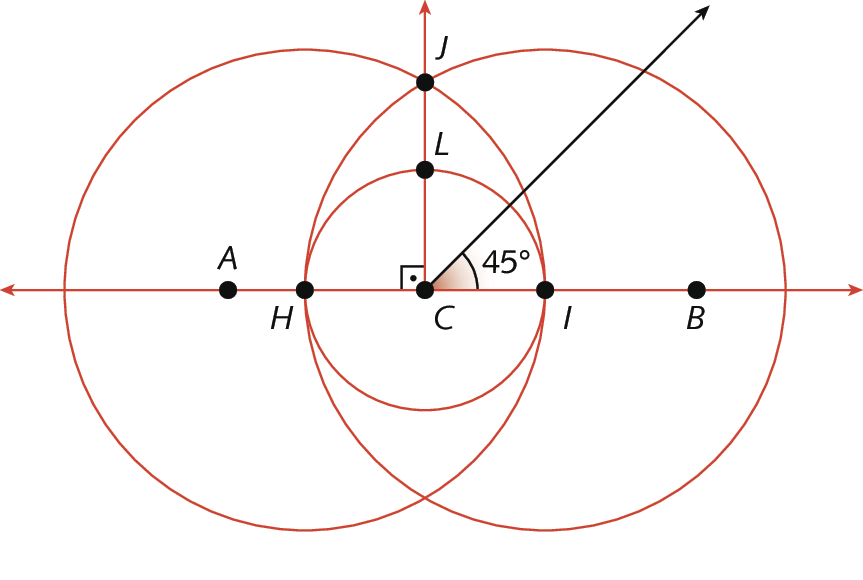
Figura geométrica. Reta horizontal com ponto A à esquerda e ponto B à direita. Sobre a reta, duas circunferências, de centro H e I respectivamente, que ficam entre os pontos A e B. Na intersecção das circunferências, circunferência com ponto C, que é ponto médio entre A e B. Por C traça uma semirreta perpendicular a reta definida por AB. E definido um ângulo de abertura medindo 45 graus pela reta definida por AB.

Página sessenta e cinco

• 150graus, traçando um ângulo reto e um adjacente a ele com medida de abertura de 60graus:

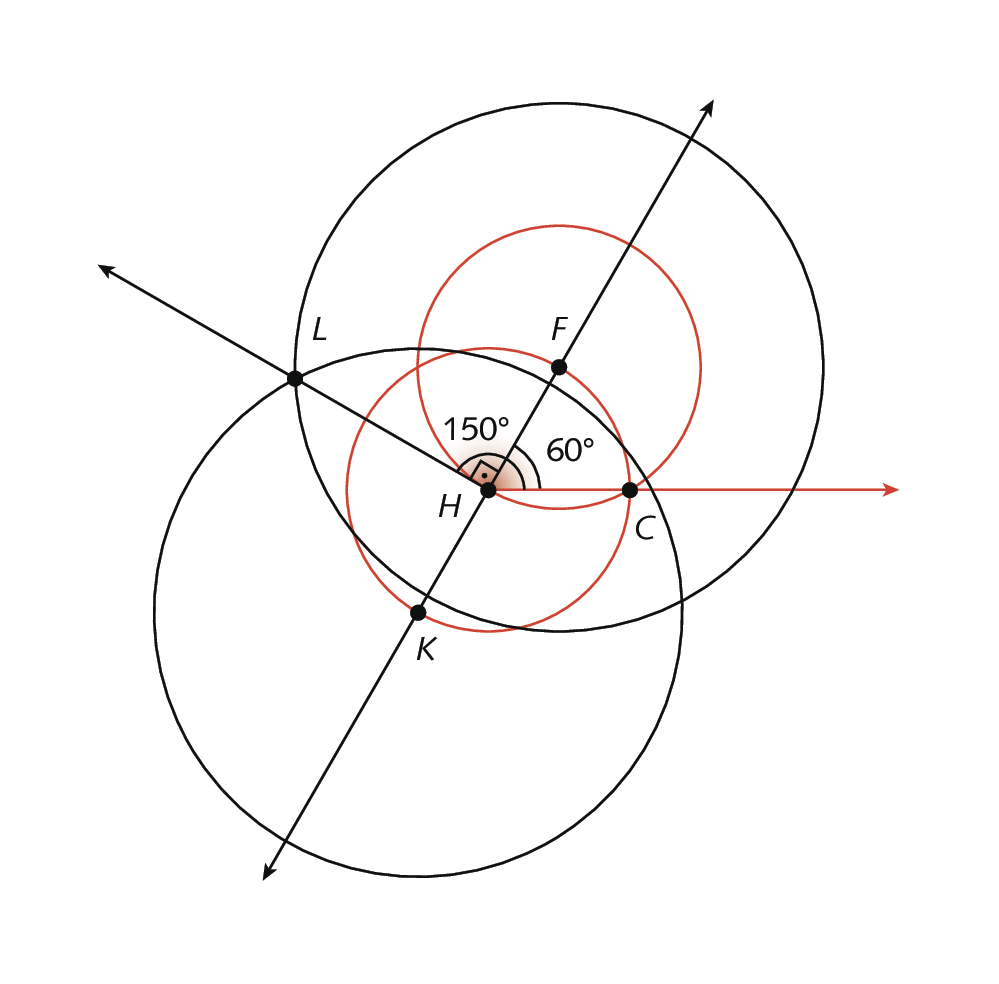
Figura geométrica. Construção geométrica. Por meio de duas circunferências de mesmo raio define-se a reta perpendicular para definir um ângulo de 90 graus. A partir desse ângulo traçam-se duas circunferências menores afim de definir o ângulo de 60 graus adjacente ao ângulo de 90 graus para obter o ângulo de 150 graus.

16. Exemplo de construção:

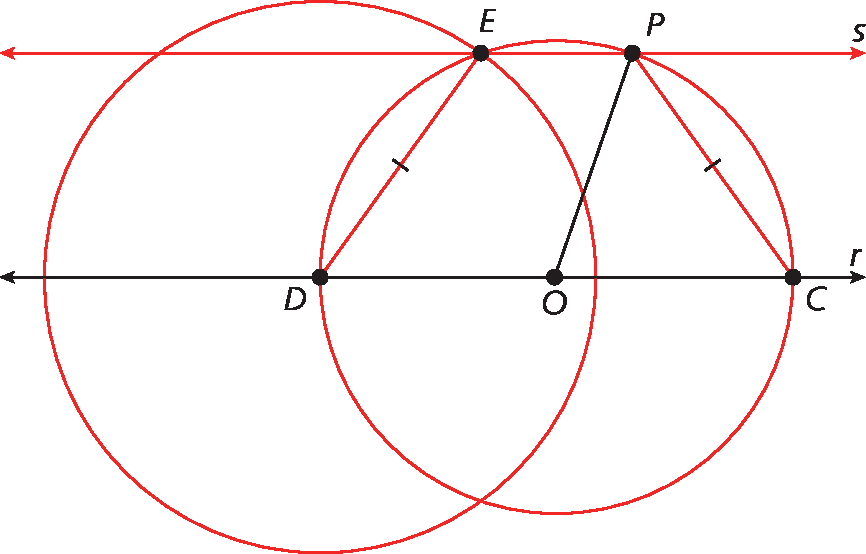
Figura geométrica. Duas circunferências secantes e com medidas de comprimento de raios diferentes. Uma tem centro no ponto D e a outra tem centro no ponto O. Está representada uma reta r que passa por D e O e corta a circunferência de centro em O no ponto C. Também está representada uma reta s paralela a r, que passa por um dos pontos de intersecção das duas circunferências, ponto E e intersecta a circunferência de centro em O no ponto P. Estão, representados os segmentos de reta DE, OP e CP. DE e CP são congruentes.

Atividades – Páginas 93 e 94

17. A mediatriz é o lugar geométrico dos pontos do plano que são equidistantes de dois pontos fixos. Alternativa c.

18. Sim, pois as ruas são paralelas, e retas paralelas são o lugar geométrico do plano que mantém a mesma medida da distância de uma reta.

19. A tribuna deve estar no centro; portanto, a de número 2.

20. O erro aconteceu no quadro 2. Para traçar os arcos que determinam o ponto C, a abertura do compasso deve ser a mesma.

Atividade – Página 95

21. a. Fazendo a translação da figura na direção, sentido e com a medida de distância de deslocamento do vetor vermelho, temos a seguinte figura:

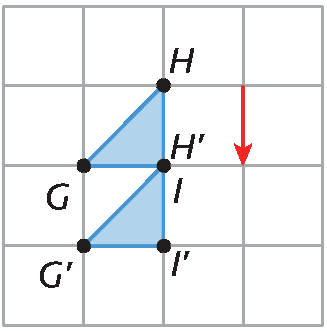
Figura geométrica, Malha quadriculada com a representação do triângulo GHI e do triângulo G linha, H linha e I linha. H linha coincide com o ponto I. Os dois triângulos são congruentes e G linha, H linha e I linha foi obtido de GHI por meio de uma translação, na vertical, de cima para baixo, com uma distância equivalente ao lado de um quadradinho. A direção , o sentido e a medida de distância do deslocamento estão representados por um vetor representado na malha.

b) Fazendo a translação da figura na direção, sentido e com a medida de distância de deslocamento do vetor azul, temos a seguinte figura:

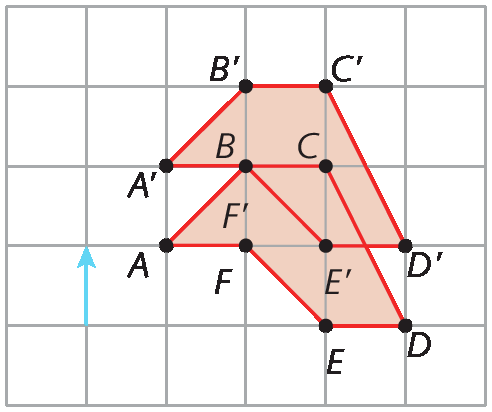
Figura geométrica, Malha quadriculada com a representação do polígono ABCDEF e do polígono A linha, B linha, C linha, D linha, E linha e F linha. Os dois polígonos são congruentes e A linha, B linha, C linha, D linha, E linha e F linha foi obtido de ABCDEF por meio de uma translação, na vertical, de baixo para cima, com uma distância equivalente ao lado de um quadradinho. A direção , o sentido e a medida de distância do deslocamento estão representados por um vetor representado na malha.

Atividades – Página 97

22. a) Fazendo uma rotação do ponto a, com centro O, no sentido horário, com um giro de 90graus, obtemos a seguinte figura:

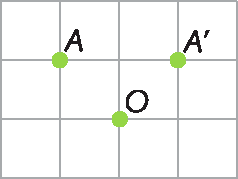
Figura geométrica. Malha quadriculada com pontos O, A e A linha representados. Os pontos A e O são vértices opostos de um quadradinho da malha. Os pontos A linha e O também são vértices opostos de um quadradinho da malha. Os pontos A linha está à direita do ponto A, na mesma linha horizontal.

b) Fazendo uma rotação do ponto D, com centro óh, no sentido horário, com um giro de 45graus, obtemos a seguinte figura:

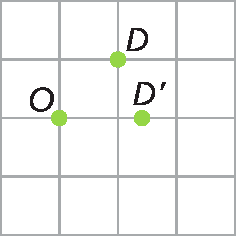
Figura geométrica. Malha quadriculada com pontos O, D e D linha representados. Os pontos O e D são vértices opostos de um quadradinho da malha. O ponto D linha está na mesma linha horizontal do ponto O e aproximadamente abaixo do ponto D.

c) Fazendo uma rotação do segmento

\overline{A B}

, com centro O, no sentido horário, com um giro de 60graus, obtemos a seguinte figura:

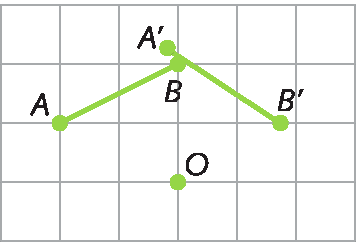
Figura geométrica. Malha quadriculada com o ponto O e os segmentos de reta AB e A linha B linha representados. O segmento de reta AB corresponde a diagonal de um retângulo composto por 2 quadradinhos da malha dispostos na horizontal. O ponto A está à esquerda do ponto B. Na mesma linha vertical do ponto B está o ponto O, dois lados de quadradinho para baixo. O segmento de reta A linha, B linha corresponde a uma rotação de centro O, no sentido horário, de 60 graus do segmento de reta AB.

23. a) Fazendo uma rotação da figura PQRS, com centro P, no sentido horário, com um giro de 90graus, obtemos a seguinte figura:

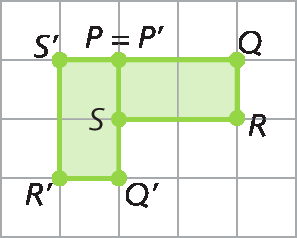
Figura geométrica. Malha quadriculada com os retângulos PQRS e P linha, Q linha, R linha e S linha representados. O retângulo PQRS corresponde a dois quadradinhos da malha na horizontal. O retângulo P linha, Q linha, R linha e S linha corresponde a dois quadradinhos da malha na vertical. Os pontos P e P linha coincidem e o ponto S é o ponto médio do lado P linha Q linha. P linha, Q linha, R linha e S linha está representado à esquerda de PQRS.

b) Fazendo uma rotação da figura á bê cê dê é, com centro óh, no sentido anti-horário, com um giro de 180graus, obtemos a seguinte figura:

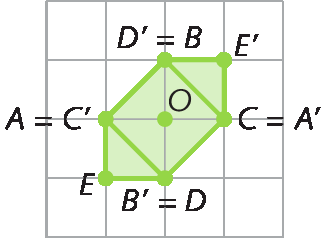
Figura geométrica. Malha quadriculada com centro em O. A figura ABCDE tem centro em O. Quando rotacionada em 180 graus, A coincide com C linha, B coincide com D linha, E linha está entre B e C, C coincide com A linha, D coincide com B linha e E está entre D e A

c) Fazendo uma rotação da figura a bê cê dê, com centro P, no sentido anti-horário, com um giro de 45graus, obtemos a seguinte figura:

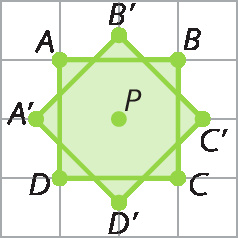
Figura geométrica. Malha quadriculada com quadrado verde composta pelos pontos: ABCD. Com centro em P. Sobre ela, quadrado rotacionado composto pelos pontos A linha, B linha, C linha, D linha.

Página sessenta e seis

Lendo e aprendendo – Página 101

1. a) Em ritos agrários, funerários ou de iniciação.

b) Não, porque em alguns casos, ao utilizá-la, o indivíduo introjeta uma personagem do mundo sobrenatural.

c) É o próprio mascarado, quando se põe em movimento.

2. a) Simetria axial, em todas as máscaras, o lado esquerdo é o simétrico do lado direito.

b) Os estudantes deverão construir uma máscara africana utilizando transformações geométricas.

3. Os estudantes deverão realizar uma pesquisa sôbre a influência da cultura africana na formação do povo brasileiro. O objetivo dessa atividade é mostrar que a cultura africana vai muito além das máscaras. É importante que eles reconheçam que essa cultura tem influência na culinária, no aspecto religioso, na música, entre outros.

Atividades – Página 102

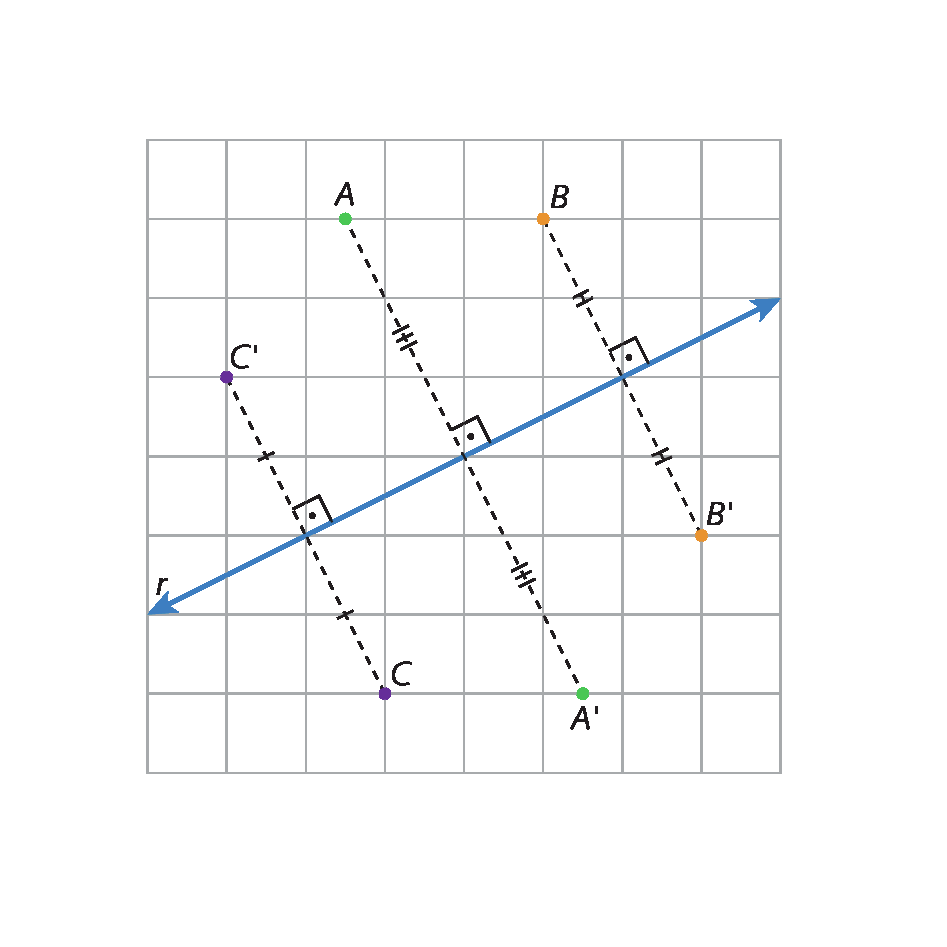
24. Na figura a seguir, os pontos á linha, bê linha e cê linha são simétricos aos pontos A, B e C, respectivamente, em relação à reta r.

Figura geométrica. Malha quadriculada com reta r na diagonal. Os pontos A e A linha estão de lados opostos da reta r e equidistantes a ela. Os pontos B e B linha estão de lados opostos da reta r e equidistantes a ela. Os pontos C e C linha estão de lados opostos da reta r e equidistantes a ela.

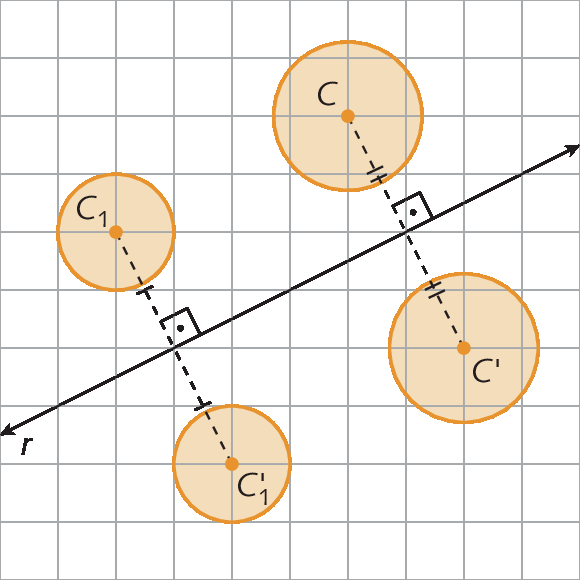
25. Na figura a seguir, os círculos de centro cê linha e cê linha₁ são simétricos aos círculos de centro centésimo e cê linha₁, respectivamente, em relação à reta r.

Figura geométrica. Malha quadriculada com a representação de uma reta r. Estão representadas na malha os círculos com centos nos pontos C e C linha, que têm a mesma medida de comprimento do raio. Estes círculos estão em lados opostos da reta r e os centros estão equidistantes dela. Também estão representadas na malha os círculos com centos nos pontos C1 e C1 linha, que têm a mesma medida de comprimento do raio. Estes círculos estão em lados opostos da reta r e os centros estão equidistantes dela.

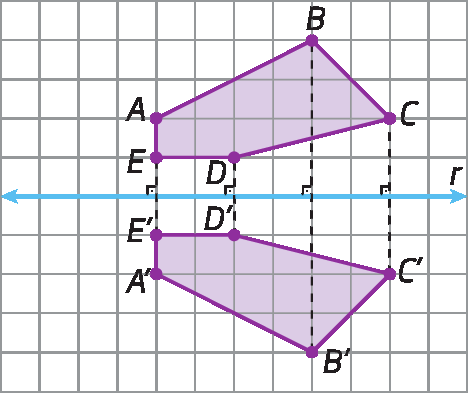
26. Na figura a seguir, o polígono á linha bê linha cê linha dê linha é linha é simétrico ao polígono á bê cê dê é em relação à reta r.

Figura geométrica. Malha quadriculada com a representação de uma reta r na horizontal. Acima um pentágono ABCDE. Abaixo, um pentágono A linha, B linha, C linha, D linha e E linha, Os pentágonos são congruentes. Os vértices correspondentes dos dois pentágonos estão equidistantes da reta r.

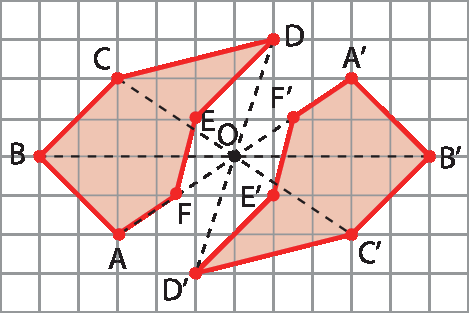
27. Na figura a seguir, o polígono á linha bê linha cê linha dê linha é linha éfe linha é simétrico ao polígono ABCDEF em relação ao ponto óh.

Figura geométrica. Malha quadriculada com a representação dos polígonos ABCDEF, A linha, B linha, C linha, D linha, E linha e F linha e de um ponto O. Os polígonos são congruentes e os vértices correspondentes dos dois polígonos são equidistantes do ponto O.

Tecnologias digitais em foco – Página 103

Observando os triângulos á bê cê e á duas linhas bê duas linhas cê duas linhas, identificamos que uma única translação pode ser feita por este vetor:

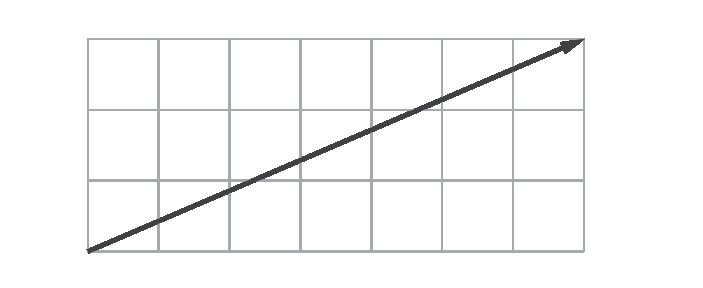
Figura geométrica. Vetor representado na diagonal de um retângulo composto por 3 fileiras com 7 quadradinhos cada. A origem do vetor está no vértice inferior esquerdo e a outra extremidade no vértice superior direito.

Tecnologias digitais em foco – Páginas 104 e 105

a) Observando os quadriláteros a bê cê dê e á duas linhas bê duas linhas cê duas linhas dê duas linhas, identificamos que uma translação pode ser feita por este vetor:

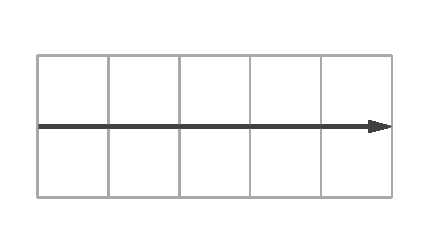
Figura geométrica. Vetor representado na horizontal em uma malha composta por 2 fileiras com 5 quadradinhos cada. A medida do comprimento do vetor é igual à 5 vezes a medida do comprimento do lado de um quadradinho. A origem do vetor está à esquerda e a outra extremidade está à direita.

b) Espera-se que os estudantes respondam que essa medida é igual ao dôbro da medida da distância entre as retas r e s e que essa igualdade se mantém verdadeira com as movimentações.

c) Espera-se que os estudantes percebam que a medida do comprimento do vetor é igual ao dôbro da medida da distância entre as retas r e s.

d) Espera-se que os estudantes percebam que, nesse caso, a reflexão sucessiva pelas retas r e s é equivalente a uma rotação no sentido anti-horário com centro no ponto de intersecção das retas e ângulo de medida da abertura igual ao dôbro da medida do ângulo formado por r e s.

Tecnologias digitais em foco – Página 106

a) Sim; espera-se que os estudantes, após algumas investigações, percebam que o pentágono á duas linhas bê duas linhas cê duas linhas dê duas linhas é duas linhas pode ser obtido do pentágono á bê cê dê é por meio de uma rotação, no sentido anti-horário, de um giro de 90graus ao redor do ponto óh.

b) Espera-se que os estudantes respondam que a investigação feita sugere que realizar duas rotações sucessivas, no mesmo sentido, uma com um giro de xgraus e outra com um giro de ygraus, em torno de um ponto óh qualquer, corresponde a realizar uma única rotação, no mesmo sentido das rotações anteriores, de um giro de (x + y)grausao redor de óh.

Atividades – Página 107

28. Transladando a figura primeiro utilizando o vetor azul e depois o vetor verde, obtemos a figura mostrada a seguir.

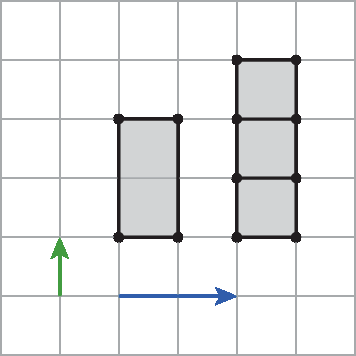
Figura geométrica. Figuras representadas em uma malha quadriculada. Retângulo composto por 2 quadradinhos na vertical. Vetor vertical que aponta para cima e tem medida de comprimento igual a de um lado de quadradinho. Vetor horizontal que aponta para a direita e tem medida de comprimento igual a de dois lados de quadradinho. Representação da translação do retângulo inicial pelo vetor horizontal. Representação da translação do retângulo anterior pelo vetor vertical. Os dois últimos retângulos ficaram parcialmente sobrepostos.

Página sessenta e sete

29. Transladando a figura primeiro utilizando o vetor verde e depois o vetor azul, obtemos a figura mostrada a seguir.

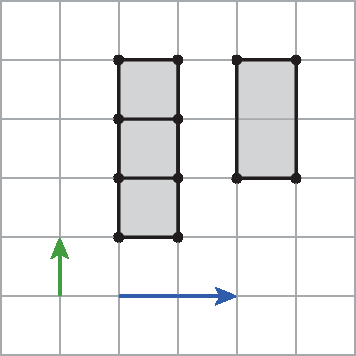
30. Fazendo 3 rotações sucessivas da figura á bê cê, em torno do ponto C, no sentido horário, com um giro de 90graus, obtemos a figura mostrada a seguir.

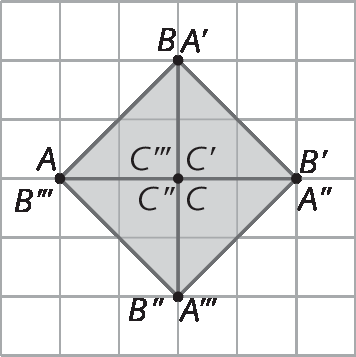
Figura geométrica. Malha quadriculada com a representação de 4 triângulos retângulos congruentes. Triângulo ABC. Triângulo A linha, B linha e C linha. Triângulo A duas linhas, B duas linhas e C duas linhas. Triângulo A três linhas, B três linhas e C três linhas. Os pontos A e B três linhas são coincidentes. Os pontos B e A uma linhas são coincidentes. Os pontos B linha e A duas linhas são coincidentes. Os pontos A três linhas e B duas linhas são coincidentes. Os pontos C, C linha, C duas linhas e C três linhas são coincidentes.

31. a) Resposta pessoal. Exemplo de questões que podem ser elaboradas:

Qual transformação geométrica foi realizada da primeira figura para a segunda? E da primeira para a terceira?

(Respostas: Simetria de reflexão; simetria de translação.)

b) Os estudantes realizarão os exercícios dos colegas.

c) Os estudantes analisarão as respostas dos colegas.

Revisão dos conteúdos deste capítulo – Páginas 108 e 109

1. Pelas definições de ângulo, temos:

A \hat{O} B

B \hat{O} C

C \hat{O} D

C \hat{O} E

D \hat{O} E

D \hat{O} F

E \hat{O} F

A \hat{O} D

A \hat{O} E

B \hat{O} E

B \hat{O} F

A \hat{O} F

A \hat{O} C

B \hat{O} D

C \hat{O} F

2. Como

\vec{O C}

é bissetriz, temos:

m e d (A \hat{O} B) = 2 \cdot 10 ° = 20 °

3. Representando a situação, temos:

Esquema. Linha reta horizontal com a representação dos pontos A, B, P e C, dispostos nesta ordem. A medida do comprimento entre A e B é igual a 8 centímetros e a medida do comprimento entre P e C é igual a 10 centímetros.

m e d (\overline{B P}) = m e d (\overline{B C}) - m e d (\overline{P C}) = 10 c m - (\frac{18}{2}) c m =

= (10 - 9) c m = 1 c m

4. A torneira deve ser instalada em qualquer ponto da bissetriz do ângulo formado pelos muros do terreno, que será o lugar geométrico dos pontos equidistantes dos muros.

5. A primeira transformação foi reflexão, a segunda, translação, e a última, rotação. Alternativa b.

Capítulo 5 – Polígonos

Trocando ideias – Página 110

• Exemplo de resposta: triângulos, quadriláteros e pentágonos.

• Os estudantes construirão o origami cabeça de leão.

Atividades – Página 112

1. a) Triângulo á bê cê

Lados:

\overline{A B}

\overline{B C}

\overline{A C}

Vértices: a, B e C.

Diagonais: não há.

b) Octógono á bê cê dê é éfe gê agá

Lados:

\overline{A B}

\overline{B C}

\overline{C D}

\overline{D E}

\overline{E F}

\overline{F G}

\overline{G H}

\overline{A H}

Vértices: a, B, C, D, E, F, G e H.

Diagonais:

\overline{A C}

\overline{A D}

\overline{A E}

\overline{A F}

\overline{A G}

\overline{B D}

\overline{B E}

\overline{B F}

\overline{B G}

\overline{B H}

\overline{C E}

\overline{C F}

\overline{C G}

\overline{C H}

\overline{D F}

\overline{D G}

\overline{D H}

\overline{E G}

\overline{E H}

\overline{F H}

2. a) Exemplo de resposta:

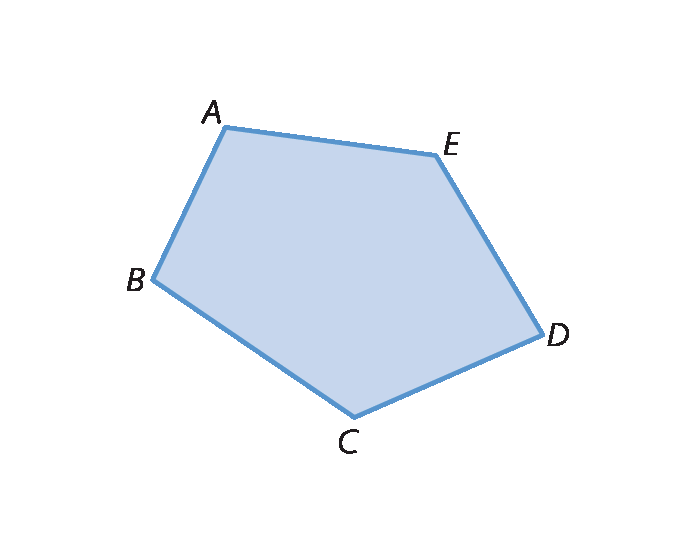
b) Exemplo de resposta:

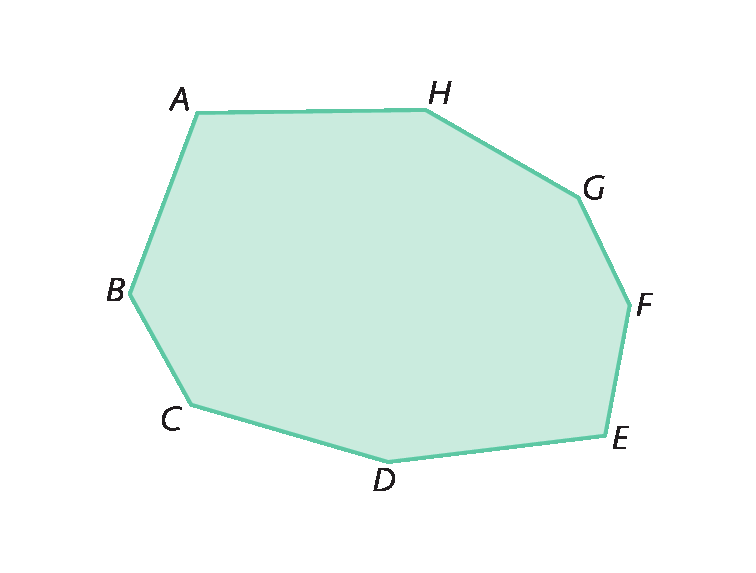
Figura geométrica. Polígono ABCDEFGH verde.

c) Exemplo de resposta:

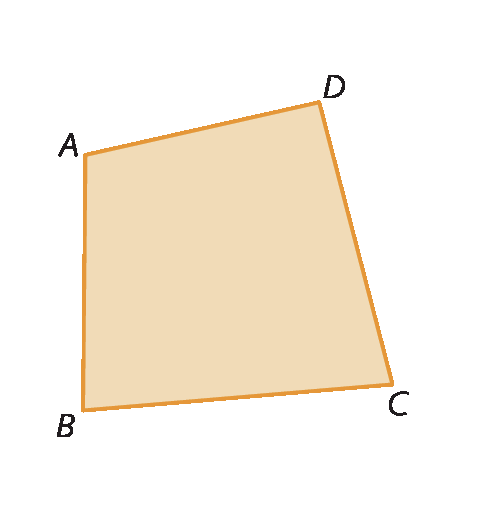
3. a) O eneágono tem 9 ângulos internos.

b) O eneágono tem 9 vértices.

4. a) O pentágono possui 5 lados.

b) O pentágono possui 5 diagonais.

c) São elas:

\overline{A C}

\overline{A D}

\overline{B D}

\overline{B E}

\overline{C E}

5. Como cada ângulo interno do octógono tem medida de abertura igual a 135graus e há 8 ângulos internos, temos: 135graus ⋅ 8 = .1080graus

Portanto, a soma das medidas das aberturas de todos os ângulos internos desse octógono é .1080graus.

Veja que interessante – Página 116

Espera-se que os estudantes percebam que, com o experimento, verificamos que a soma das medidas das aberturas dos ângulos externos de um polígono é 360graus.

Página sessenta e oito

Atividades – Página 116

6. a)

d = \frac{n \cdot (n - 3)}{2} = \frac{5 \cdot (5 - 3)}{2} = \frac{5 \cdot 2}{2} = 5

Portanto, um polígono de 5 lados tem 5 diagonais.

d = \frac{n \cdot (n - 3)}{2} = \frac{9 \cdot (9 - 3)}{2} = \frac{9 \cdot 6}{2} = 27

Portanto, um polígono de 9 lados tem 27 diagonais.

d = \frac{n \cdot (n - 3)}{2} = \frac{15 \cdot (15 - 3)}{2} = \frac{15 \cdot 12}{2} = 90

Portanto, um polígono de 15 lados tem 90 diagonais.

d = \frac{n \cdot (n - 3)}{2} = \frac{20 \cdot (20 - 3)}{2} = \frac{20 \cdot 17}{2} = 170

Portanto, um polígono de 20 lados tem 170 diagonais.

7. a) S = (n – 2) ⋅ 180graus = (4 – 2) ⋅ 180graus = 2 ⋅ 180graus = 360graus

b) S = (n – 2) ⋅ 180graus = (9 – 2) ⋅ 180graus = 7 ⋅ 180graus = 1 260graus

c) S = (n – 2) ⋅ 180graus = (11 – 2) ⋅ 180graus = 9 ⋅ 180graus = 1 620graus

d) S = (n – 2) ⋅ 180graus = (20 – 2) ⋅ 180graus = 18 ⋅ 180graus = 3 240graus

8. a) Temos, pela soma das medidas de abertura dos ângulos internos, que:

S = (n – 2) ⋅ 180graus

.1080graus = (n – 2) ⋅ 180graus

\frac{1 080}{180} = n - 2

6 = n – 2

6 + 2 = n

n = 8

É um octógono.

b) Temos, pela soma das medidas de abertura dos ângulos internos, que:

S = (n – 2) ⋅ 180graus

.1980graus = (n – 2) ⋅ 180graus

\frac{1 980}{180} = n - 2

11 = n – 2

11 + 2 = n

n = 13

É um polígono de 13 lados.

c) Temos, pela soma das medidas de abertura dos ângulos internos, que:

S = (n – 2) ⋅ 180graus

.2340graus = (n – 2) ⋅ 180graus

\frac{2 340}{180} = n - 2

13 = n – 2

13 + 2 = n

n = 15

É um pentadecágono.

d) Temos, pela soma das medidas de abertura dos ângulos internos, que:

S = (n – 2) ⋅ 180graus

.1800graus = (n – 2) ⋅ 180graus

\frac{1 800}{180} = n - 2

10 = n – 2

10 + 2 = n

n = 12

É um dodecágono.

9. a) 2x + 105graus + 65graus = 360graus

2x + 170graus = 360graus

2x = 360graus – 170graus

2x = 190graus

x = \frac{190 °}{2}

x = 95 °

b) 5x = 540graus

x = \frac{540 °}{5}

x = 108graus

10. Como a soma das aberturas dos ângulos externos sempre é 360graus, podemos assumir S = 360graus. Assim:

S = (n – 2) ⋅ 180graus

360graus = (n – 2) ⋅ 180graus

\frac{360 °}{180 °} = n - 2

2 = n – 2

2 + 2 = n

n = 4

É um quadrilátero.

Atividades – Página 118

11. a.

a_{i} = \frac{(n - 2) \cdot 180 °}{n}

a_{e} = \frac{360 °}{n}

a_{i} = \frac{(4 - 2) \cdot 180 °}{4}

a_{e} = \frac{360 °}{4}

a_{i} = \frac{2 \cdot 180 °}{4}

a_{e} = 90 °

a_{i} = 90 °

a_{i} = \frac{(n - 2) \cdot 180 °}{n}

a_{e} = \frac{360 °}{n}

a_{i} = \frac{(8 - 2) \cdot 180 °}{8}

a_{e} = \frac{360 °}{8}

a_{i} = \frac{6 \cdot 180 °}{8}

a_{e} = 45 °

a_{i} = 135 °

a_{i} = \frac{(n - 2) \cdot 180 °}{n}

a_{e} = \frac{360 °}{n}

a_{i} = \frac{(9 - 2) \cdot 180 °}{9}

a_{e} = \frac{360 °}{9}

a_{i} = \frac{7 \cdot 180 °}{9}

a_{e} = 40 °

a_{i} = 140 °

a_{i} = \frac{(n - 2) \cdot 180 °}{n}

a_{e} = \frac{360 °}{n}

a_{i} = \frac{(20 - 2) \cdot 180 °}{20}

a_{e} = \frac{360 °}{20}

a_{i} = \frac{18 \cdot 180 °}{20}

a_{e} = 18 °

a_{i} = 162 °

12.

a_{i} = a_{e}

a_{i} + a_{e} = 180 °

a_{i} + a_{i} = 180 °

2 a_{i} = 180 °

a_{i} = \frac{180 °}{2}

a_{i} = a_{e} = 90 °

Logo, é um quadrado.

13.

a_{e} = \frac{360 °}{n}

40 ° = \frac{360 °}{n}

n = \frac{360 °}{40 °}

n = 9

O polígono tem 9 lados.

14. Como ái + áe = 180graus e com a informação do enunciado, podemos montar o seguinte sistema de equações:

\{\begin{array}{c} a_{i} + a_{e} = 180 ° \\ a_{i} - a_{e} = 60 ° \end{array}

Página sessenta e nove

Adicionando membro a membro as equações, temos:

2 a_{i} = 240 °

a_{i} = \frac{240 °}{2}

a_{i} = 120 °

Substituindo ai por 120graus na equação ái + áe = 180graus, temos:

ái + áe = 180graus

a_{e} = 180 ° - 120 °

a_{e} = 60 °

Calculando o número de lados n do polígono:

a_{e} = \frac{360 °}{n} \Rightarrow 60 ° = \frac{360 °}{n} \Rightarrow n = \frac{360 °}{60 °} \Rightarrow n = 6

Logo, o polígono é um hexágono.

Atividades – Página 120

15. a)

a_{c} = \frac{360 °}{n} \Rightarrow a_{c} = \frac{360 °}{6} \Rightarrow a_{c} = 60 °

a_{c} = \frac{360 °}{n} \Rightarrow a_{c} = \frac{360 °}{10} \Rightarrow a_{c} = 36 °

a_{c} = \frac{360 °}{n} \Rightarrow a_{c} = \frac{360 °}{12} \Rightarrow a_{c} = 30 °

a_{c} = \frac{360 °}{n} \Rightarrow a_{c} = \frac{360 °}{20} \Rightarrow a_{c} = 18 °

16. a) Exemplo de construção:

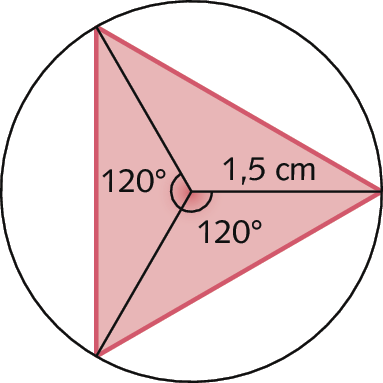
Figura geométrica. Triângulo equilátero inscrito em uma circunferência cuja medida do comprimento do raio é de 1 vírgula 5 centímetro. No triângulo, estão indicados dois ângulos centrais, cada um, com abertura medindo 120 graus.

b) Exemplo de construção:

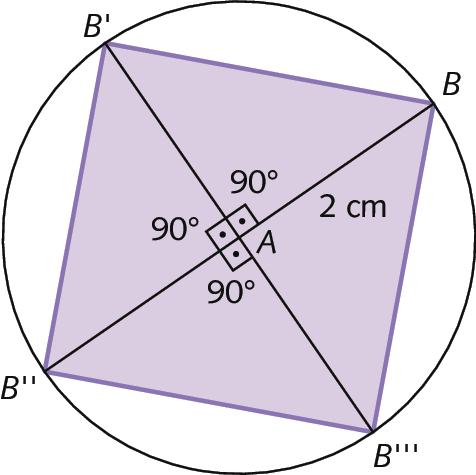
Figura geométrica. Quadrado B, B linha, B duas linhas e B três linhas, inscrito em uma circunferência cuja medida do comprimento do raio é de 2 centímetros. Estão representadas as diagonais do quadrado e os ângulos centrais com vértice no ponto A. Cada ângulo central tem abertura medindo 90 graus.

17. a)

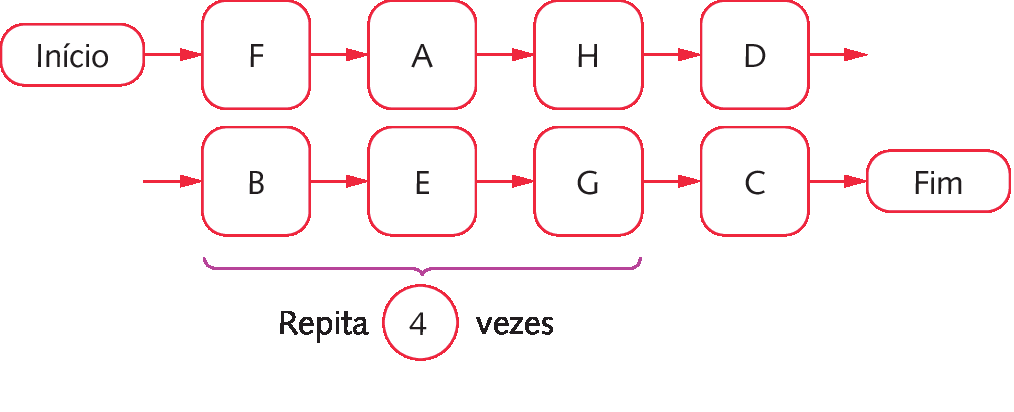
Fluxograma. Início. F, A, H, D, B, E, G, (repita 4 vezes as etapas BEF) etapa C, fim.

b) Resposta pessoal. Exemplo de resposta:

Construção de um triângulo equilátero.

c) Os estudantes construirão o polígono seguindo o fluxograma elaborado pelo colega.

d) Os estudantes discutirão se as instruções foram adequadas.

Revisão dos conteúdos deste capítulo – Página 121

1. Quadrado a bê cê dê

Lados:

\overline{A B}

\overline{B C}

\overline{C D}

\overline{D A}

Vértices: a, B, C e D.

Diagonais:

\overline{A C}

\overline{B D}

2. a) 7 vértices.

b) 7 lados

3. a)

d = \frac{n \cdot (n - 3)}{2} = \frac{8 \cdot (8 - 3)}{2} = \frac{8 \cdot 5}{2} = 20

d = \frac{n \cdot (n - 3)}{2} = \frac{3 \cdot (3 - 3)}{2} = \frac{3 \cdot 0}{2} = 0

4. S = (n – 2) · 180graus

720 = (n – 2) · 180graus

\frac{720}{180}

= n – 2

4 = n – 2

4 + 2 = n

n = 6

É um hexágono.

5. S = (n – 2) ⋅ 180graus = (5 – 2) ⋅ 180graus = 3 ⋅ 180graus = 540graus

a_{i} = 3 a_{e}

a_{i} + a_{e} = 180 °

3 a_{e} + a_{e} = 180 °

4 a_{e} = 180 °

a_{e} = \frac{180 °}{4}

a_{e} = 45 °

\frac{360 °}{n} = 45 ° \Rightarrow \frac{360 °}{45} = n \Rightarrow n = 8

Logo, é um octógono.

Capítulo 6 – Probabilidade

Trocando ideias – Página 122

• No lançamento de um dado, podem aparecer as faces: 1, 2, 3, 4, 5 e 6. A probabilidade de sair a face 2 é uma chance em 6 possibilidades. Logo, a probabilidade é

\frac{1}{6} .

• Como o baralho tem 52 cartas e a carta “ás de copas” aparece uma única vez, temos

\frac{1}{52} .

Atividades – Página 125

1. a)

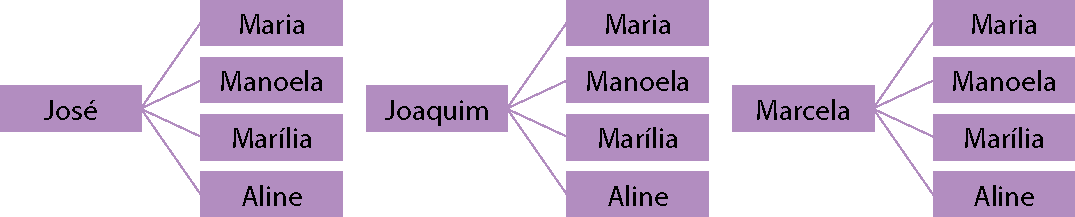
Esquema. Da caixinha José, partem os nomes: Maria, Manoela, Marília e Aline. Da caixinha Joaquim, partem os nomes: : Maria, Manoela, Marília e Aline. Da caixinha Marcela, partem os nomes: : Maria, Manoela, Marília e Aline.

b) O sorteio pode ter 12 resultados possíveis.

2. Os possíveis resultados são: (cara, cara), (cara, coroa), (coroa, coroa) e (coroa, cara).

Página setenta

3. a) Construindo uma árvore de possibilidades, temos as seguintes combinações:

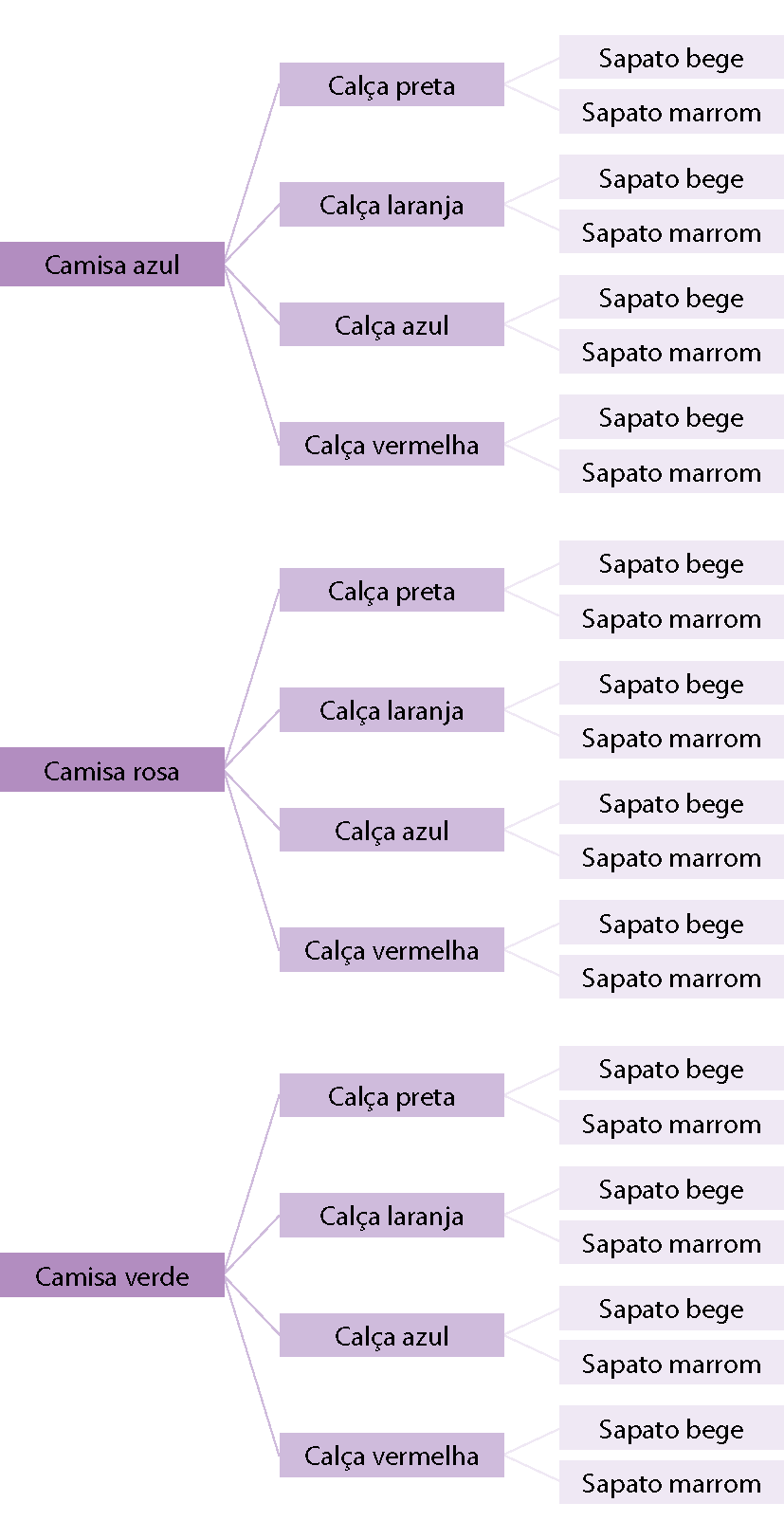
Esquema. Árvore de possibilidades. Camisa azul. Calça preta. Sapato bege. Camisa azul. Calça preta. Sapato marrom. Camisa azul. Calça laranja. Sapato bege. Camisa azul. Calça laranja. Sapato marrom. Camisa azul. Calça azul. Sapato bege. Camisa azul. Calça azul. Sapato marrom. Camisa azul. Calça vermelha. Sapato bege. Camisa azul. Calça vermelha. Sapato marrom. Camisa rosa. Calça preta. Sapato bege. Camisa rosa. Calça preta. Sapato marrom. Camisa rosa. Calça laranja. Sapato bege. Camisa rosa. Calça laranja. Sapato marrom. Camisa rosa. Calça azul. Sapato bege. Camisa rosa. Calça azul. Sapato marrom. Camisa rosa. Calça vermelha. Sapato bege. Camisa rosa. Calça vermelha. Sapato marrom. Camisa verde. Calça preta. Sapato bege. Camisa verde. Calça preta. Sapato marrom. Camisa verde. Calça laranja. Sapato bege. Camisa verde. Calça laranja. Sapato marrom. Camisa verde. Calça azul. Sapato bege. Camisa verde. Calça azul. Sapato marrom. Camisa verde. Calça vermelha. Sapato bege. Camisa verde. Calça vermelha. Sapato marrom.

b) São 24 possibilidades.

4. a) Como nosso alfabeto tem 26 letras, o usuário terá 26 possibilidades de escolha para a letra.

b) O usuário terá .1000 possibilidades de escolha, pois 10 · 10 · 10 = .1000. As opções vão de 000 a 999.

c) 26 · .1000 = .26000

O usuário terá .26000 senhas diferentes.

d) 26 · 10 = 260

Terão 260 possibilidades de combinação.

4	4	3	2
Milhar	Centena	Dezena	Unidade

A ordem de milhar tem 4 possibilidades (4, 5, 8 e 9), não podendo assumir o 0.

A ordem da centena tem 4 possibilidades, as cinco apresentadas, menos o algarismo utilizado na unidade de milhar.

A ordem da dezena tem 3 possibilidades, as cinco apresentadas, menos os dois algarismos utilizados na unidade de milhar e na centena.

A ordem da unidade tem 2 possibilidades, as cinco apresentadas, menos os três algarismos utilizados na unidade de milhar, na centena e na dezena.

Então, 4 · 4 · 3 · 2 = 96 ou seja, 96 números.

6. Resposta pessoal. Exemplo de problema que pode ser elaborado: Quantos números de três algarismos distintos existem?

Exemplo de resolução: 9 ⋅ 9 ⋅ 8 = 648, ou seja, 648 números.

Atividades – Páginas 128 e 129

7. a)

	1	2	3	4	5	6
1	(1, 1)	(2, 1)	(3, 1)	(4, 1)	(5, 1)	(6, 1)
2	(1, 2)	(2, 2)	(3, 2)	(4, 2)	(5, 2)	(6, 2)
3	(1, 3)	(2, 3)	(3, 3)	(4, 3)	(5, 3)	(6, 3)
4	(1, 4)	(2, 4)	(3, 4)	(4, 4)	(5, 4)	(6, 4)
5	(1, 5)	(2, 5)	(3, 5)	(4, 5)	(5, 5)	(6, 5)
6	(1, 6)	(2, 6)	(3, 6)	(4, 6)	(5, 6)	(6, 6)
7	(1, 7)	(2, 7)	(3, 7)	(4, 7)	(5, 7)	(6, 7)
8	(1, 8)	(2, 8)	(3, 8)	(4, 8)	(5, 8)	(6, 8)

b) O evento “saírem números 7 e 5” aparece apenas uma vez; logo, a probabilidade será

\frac{1}{48}

c) O evento “saírem números 6 e 5” aparece duas vezes; logo, a probabilidade será

\frac{2}{48} = \frac{1}{24}

d) Metade das somas são pares, e a outra metade, ímpares; logo, a probabilidade será

\frac{24}{48} = \frac{1}{2}

8. Para que os cálculos estejam corretos, a soma das probabilidades deve resultar em 1 ou 100%.

\frac{1}{6} + \frac{1}{4} + \frac{1}{3} + x = 1

\frac{2}{12} + \frac{3}{12} + \frac{4}{12} + \frac{12 x}{12} = \frac{12}{12}

9 + 12x = 12

12x = 12 – 9

12x = 3

x = \frac{3}{12} = \frac{1}{4}

A probabilidade de o estudante sorteado ser da turma D é

\frac{1}{4}

9. a) 6 · 8 = 48, ou seja, existem 48 possibilidades de casais diferentes.

b) Na turma há 6 homens, então a probabilidade de Fábio ser escolhido é

\frac{1}{6}

c) Na turma há 8 mulheres, então a probabilidade de Cecília ser escolhida é

\frac{1}{8}

d) Como calculado no item a, na turma há 48 possibilidades de casais diferentes. Só há uma possibilidade de Fábio e Cecília serem escolhidos juntos, então:

\frac{1}{48}

Logo, a probabilidade de Fábio e Cecília serem escolhidos é

\frac{1}{48}

10. a) 3 · 3 · 2 = 18, ou seja, 18 maneiras diferentes.

\frac{1}{18}

Página setenta e um

11. a) 14 ⋅ 13 ⋅ 15 = 2 730, ou seja, 2 730 maneiras diferentes.

b) Só há uma possibilidade de eles serem sorteados juntos, então:

\frac{1}{2 730}

12. Resposta pessoal. Exemplo de perguntas que podem ser elaboradas: Uma urna contém 50 bolinhas amarelas, 25 azuis e 25 vermelhas. Qual é a probabilidade de sair uma bolinha amarela ou azul? E a probabilidade de sair uma bolinha amarela?

Exemplo de resolução:

\frac{50}{100} + \frac{25}{100} = \frac{75}{100} = 75 %

, ou seja, 75% de chance de sair uma bolinha amarela ou azul.

\frac{50}{100} = 50 %

, ou seja, 50% de chance de sair uma bolinha amarela.

Revisão dos conteúdos deste capítulo – Página 130

1. 64 resultados possíveis, pois 8 ⋅ 8 = 64.

2. 24 possibilidades diferentes, pois 3 ⋅ 2 ⋅ 4 = 24.

3. Serão 11 bolas no total (5 + 6 = 11); assim, a probabilidade de retirar uma bola preta (5 das bolas totais) será

\frac{5}{11} .

4. a) Será composto pelas faces do dado, ou seja, {a, bê, cê, dê, ê, éfe}.

b) A probabilidade será:

\frac{1}{6}

5. a) A probabilidade será:

\frac{30}{50} = \frac{3}{5}

b) A probabilidade será:

\frac{20}{50} = \frac{2}{5}

6. a) Temos 5 pares, do total de 12 números. Logo, a probabilidade será

\frac{5}{12} .

b) Temos 7 pares, do total de 12 números. Logo, a probabilidade será

\frac{7}{12} .

7. a)

ESPAÇO AMOSTRAL
Ás, Ás	2, Ás	3, Ás	4, Ás	5, Ás	6, Ás	7, Ás
Ás, 2	2, 2	3, 2	4, 2	5, 2	6, 2	7, 2
Ás, 3	2, 3	3, 3	4, 3	5, 3	6, 3	7, 3
Ás, 4	2, 4	3, 4	4, 4	5, 4	6, 4	7, 4
Ás, 5	2, 5	3, 5	4, 5	5, 5	6, 5	7, 5
Ás, 6	2, 6	3, 6	4, 6	5, 6	6, 6	7, 6
Ás, 7	2, 7	3, 7	4, 7	5, 7	6, 7	7, 7

b) Apenas uma chance de um total de 49 possibilidades. Logo, a probabilidade será de

\frac{1}{49}

c) Aparecem 7 pares iguais de um total de 49 possibilidades. Logo, a probabilidade será de

\frac{7}{49}

d) Os estudantes devem perceber que se Júlia contar qual é o valor de uma das cartas, a probabilidade de João acertar é de

\frac{1}{7}

É hora de extrapolar – Páginas 131 a 135

1. a) A partir de 60 anos.

b) Resposta pessoal. Os estudantes poderão citar: Atendimento preferencial, medicamento gratuito, transporte público gratuito, isenção de pagamento de Imposto predial e territorial urbano, entre outros.

2. Os estudantes deverão fazer uma pesquisa sôbre o Estatuto do Idoso, abrangendo o ano em que foi criado, os objetivos, a categoria de pessoas incluídas e os principais direitos assegurados. Uma referência de pesquisa pode ser encontrada a seguir:

https://oeds.link/1Xvk35 (acesso em: 2 agosto 2022).

3. a) Resposta pessoal. Os estudantes devem comparar a resposta do item a da atividade 1 com a idade encontrada no estatuto para indicar que uma pessoa é idosa (idade igual ou superior a 60 anos).

b) Resposta pessoal. Os estudantes responderão se já conheciam o estatuto.

c) Resposta pessoal. Os estudantes colocarão suas opiniões sôbre o conhecimento da população idosa quanto ao estatuto.

4. Resposta pessoal. Os estudantes construirão uma lista única para a turma com todos os direitos dos idosos pesquisados.

5. a) Resposta pessoal. Os estudantes responderão de acôrdo com sua opinião.

b) Resposta pessoal. Espera-se que os estudantes percebam que os idosos que se preocupam mais com a qualidade de vida praticam atividade física, têm uma boa alimentação etcétera

6. Respostas pessoais. Espera-se que os estudantes construam um texto defendendo a ideia de que o gasto com o idoso é um investimento, tendo em vista o bem-estar do idoso, aumentando a longevidade e a qualidade de vida.

7. a) Os grupos que possuem o direito ao assento preferencial em transportes públicos são: pessoas com deficiência ou mobilidade reduzida, gestantes, lactantes, pessoas acompanhadas de crianças de colo, autistas, idosos e obesos.

b) Resposta pessoal. Espera-se que os estudantes respondam que é importante porque esses grupos têm mobilidade reduzida e os assentos preferenciais são uma garantia de que vão conseguir se acomodar nos transportes públicos.

c) A probabilidade será de

\frac{6}{46} = \frac{3}{23} ≃ 13 %

8. a) Resposta pessoal. Espera-se que os estudantes respondam que as rampas são mais indicadas que as escadas porque exigem menos esforço de quem as utiliza, principalmente das pessoas que utilizam cadeiras de roda para se locomover.

b) Os estudantes deverão construir a bissetriz do ângulo de inclinação seguindo estes passos:

• Traçar um arco com a ponta-seca do compasso no vértice do ângulo, abertura qualquer, de fórma a cruzar os dois lados do ângulo nos pontos a e B.

• Com a ponta-seca do compasso em a, traçar um arco.

• Com a ponta-seca do compasso em B, traçar outro arco com mesma abertura do passo anterior, até interceptar o arco anterior.

• A bissetriz será a semirreta com origem no vértice que passa pelo cruzamento dos dois arcos.

9. Resposta pessoal. Os estudantes optarão por um dos temas disponibilizados.

Página setenta e dois

10. Os estudantes construirão uma cartilha informativa. Para isso, farão uma pesquisa para descobrir o que é uma cartilha informativa. Espera-se que na pesquisa descubram que uma cartilha informativa é um material que procura educar e informar. É importante que tenha adequação ao público-alvo; linguagem clara e objetiva; visual leve e atraente e informações confiáveis.

11. Os estudantes escolherão um dos direitos da etapa 1 para ser explicado pelo grupo.

12. Os estudantes devem discutir e construir as imagens e os textos da cartilha.

13. Os grupos deverão elaborar uma capa para a cartilha.

14. Os grupos compartilharão as páginas elaboradas para análises e sugestões dos colegas.

15. Os estudantes deverão anotar dúvidas, opiniões e sugestões dos colegas.

16. Os estudantes farão uma votação para escolher a capa da cartilha, que deve estar organizada em duas partes: a primeira, com as páginas sôbre os direitos dos idosos; a segunda, com dicas para prevenção de quedas.

17. Divulgação da cartilha.

18. Os estudantes farão uma síntese do trabalho com base na discussão sôbre a importância de garantir com leis os direitos dos idosos por toda a população e sôbre como os estudantes fariam para se preparar para a velhice.

19. Os estudantes construirão um texto descrevendo o processo de confecção de uma cartilha coletiva e a apresentação e análise das páginas elaboradas e divulgação da cartilha.

Capítulo 7 – Triângulos e quadriláteros

Trocando ideias – Página 135

• Exemplos de resposta: todos seus ângulos internos têm a mesma medidade abertura, têm dois pares de lados paralelos, têm todos os ângulos internos retos.

• Resposta pessoal.

Atividades – Página 137

1. a) Como todas as medidas de comprimento dos lados do triângulo são iguais, podemos classificá-lo como equilátero; em relação aos ângulos, é classificado como acutângulo, pois todas as medidas das aberturas dos ângulos internos são menores que 90graus e maiores que 0grau.

b) Esse triângulo tem dois lados com a mesma medida de comprimento, então pode ser classificado como isósceles; em relação aos ângulos, é classificado como obtusângulo, pois um ângulo tem a medida de abertura maior que 90graus e menor que 180graus.

c) Esse triângulo tem todos os lados com medidas de comprimento diferentes, sendo classificado como escaleno; em relação aos ângulos, é classificado como obtusângulo, pois um ângulo tem a medida de abertura maior que 90graus e menor que 180graus.

2. Não, pois a soma das medidas de abertura de dois ângulos obtusos é maior que 180graus. Então é impossível ter um triângulo com dois ângulos obtusos, uma vez que a soma das medidas de abertura dos ângulos internos de qualquer triângulo é 180graus.

Atividades – Página 140

3. Os estudantes deverão copiar o triângulo no caderno e traçar as medianas relativas a cada lado do triângulo; o encontro dessas cevianas determinará o baricentro do triângulo.

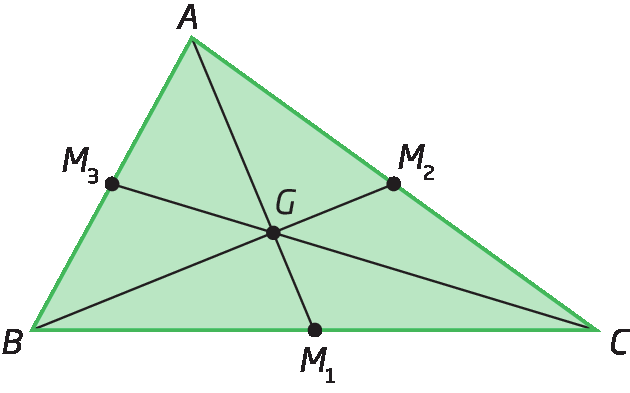
Figura geométrica. Triângulo ABC. Mediana AM1 com M1 no lado BC, Mediana BM2 com M2 no lado AC, Mediana CM3 com M3 no lado AB
As medianas se cruzam em G.

4. Traçando a bissetriz de cada ângulo interno do triângulo, o ponto I encontrado na intersecção das cevianas é o incentro.

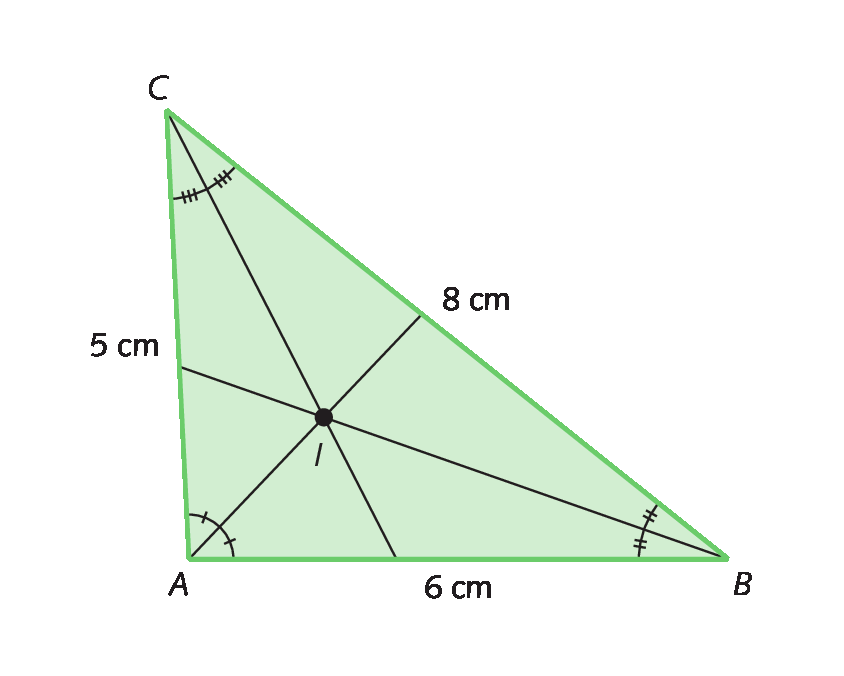
Figura geométrica. Triângulo escaleno ABC com lados medindo 6 centímetros, 8 centímetros e 5 centímetros de comprimento. De cada ângulo interno do triângulo se traça uma bissetriz. As três bissetrizes se encontram no ponto I.

5. Traçando a altura relativa a cada lado do triângulo, o ponto H encontrado na intersecção das cevianas é o ortocentro.

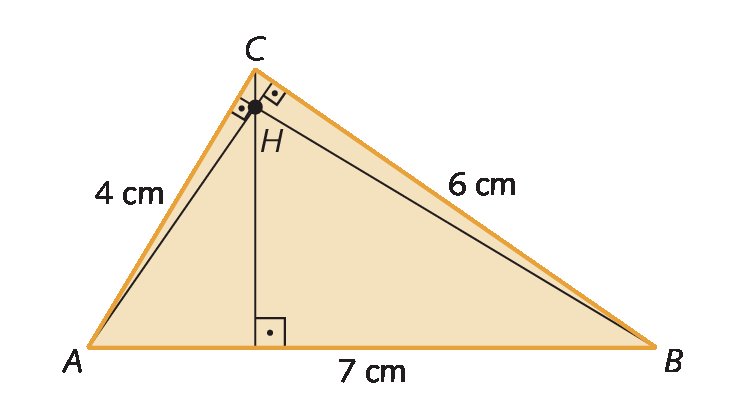
Figura geométrica. Triângulo escaleno ABC. Com lados medindo 4 centímetros, 6 centímetros e 7 centímetros de comprimento. Estão representadas as 3 alturas do triângulo que se encontram no ponto H interno a ele.

6. • Os estudantes devem traçar as mediatrizes do triângulo e encontrar o circuncentro; o raio da circunferência circunscrita corresponde à distância do circuncentro a qualquer vértice do triângulo.

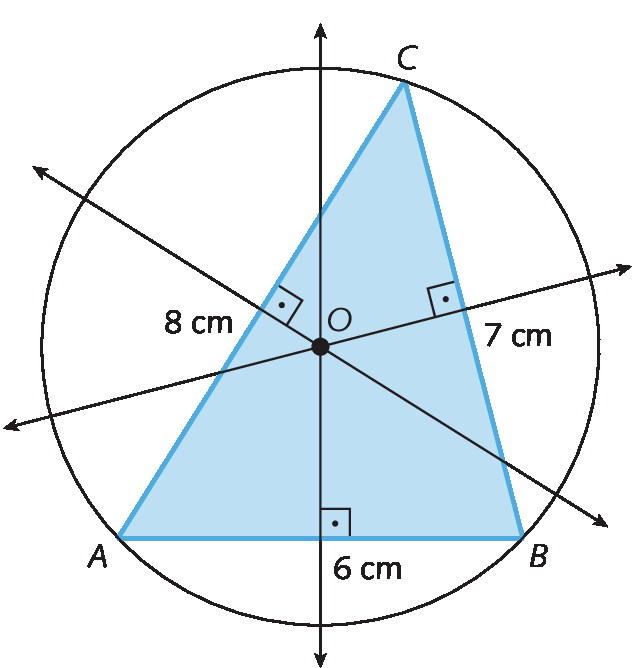
Figura geométrica. Triângulo escaleno ABC de lados medindo 8 centímetros, 7 centímetros e 6 centímetros de comprimento. Estão representadas as 3 mediatrizes do triângulo que se encontram no ponto O interno a ele. Além disso, representada a circunferência circunscrita ao triângulo que tem centro em O e passa pelos vértices A, B e C.

Página setenta e três

• Os estudantes devem traçar as bissetrizes do triângulo e encontrar o incentro; o raio da circunferência inscrita corresponde à distância do incentro a qualquer lado do triângulo.

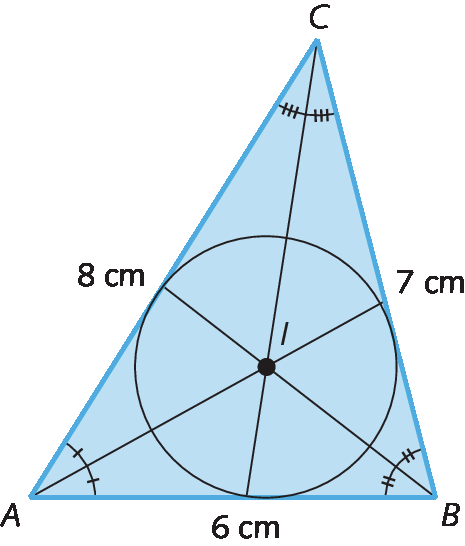
Figura geométrica. Triângulo escaleno ABC de lados 8 centímetros, 7 centímetros e 6 centímetros de comprimento..
De cada vértice do triângulo são traçadas as bissetrizes que se encontram no ponto I. Está representada a circunferência inscrita ao triângulo que tem centro no ponto I e tangencia cada um dos lados.

Tecnologias digitais em foco – Páginas 141 e 142

a) Nesse caso, espera-se que os estudantes concluam que a mediatriz, a altura e a mediana coincidem e estão contidas na reta, que é a mediatriz relativa à base.

b) Espera-se que os estudantes observem que os pontos notáveis em um triângulo isósceles estão sempre alinhados.

c) Espera-se que os estudantes verifiquem que os pontos notáveis em um triângulo equilátero coincidem.

Atividades – Páginas 144 e 145

7. a) Sendo

\overline{A B} ≅ \overline{E D}

\hat{A} ≅ \hat{E}

\overline{A C} ≅ \overline{E F}

, podemos afirmar que os triângulos á bê cê e EDF são congruentes pelo caso éle á éle.

b) Sendo

\hat{A} ≅ \hat{F}

\overline{C A} ≅ \overline{F D}

\hat{C} ≅ \hat{D}

, podemos afirmar que os triângulos á bê cê e FED são congruentes pelo caso á éle á .

c) Como as medidas das aberturas dos ângulos internos desses triângulos não são congruentes, eles não são congruentes.

d) Sendo

\overline{A B} ≅ \overline{D E}

\hat{A} ≅ \hat{D}

\overline{A C} ≅ \overline{D F}

, podemos afirmar que os triângulos á bê cê e DEF são congruentes pelo caso éle á éle.

e) Sendo

\hat{B} ≅ \hat{D}

\overline{B C} ≅ \overline{C D}

B \hat{C} A ≅ D \hat{C} E

(opostos pelo vértice), podemos afirmar que os triângulos á bê cê e EDC são congruentes pelo caso á éle á .

8. a) Como

\overline{A D} ≅ \overline{C B}

A \hat{D} B ≅ C \hat{B} D

\overline{B D}

é lado comum, podemos afirmar que os triângulos á dê bê e CBD são congruentes pelo caso éle á éle.

b) Como

A \hat{C} D ≅ B \hat{C} D

\overline{C D}

é lado comum e

A \hat{D} C ≅ B \hat{D} C

, podemos afirmar que os triângulos CAD e CBD são congruentes pelo caso á éle á .

9. Como

\overline{C M} ≅ \overline{M D}

C \hat{M} A ≅ D \hat{M} B

(o postos pelo vértice) e

M \hat{A} C ≅ M \hat{B} D

que são ângulos retos e opostos aos lados

\overline{C M}

\overline{M D}

, podemos afirmar que os triângulos á cê ême e BDM são congruentes pelo caso LAA_o

. Dessa maneira, concluímos que existe uma correspondência em relação aos lados e ângulos, sendo

\overline{A M} ≅ \overline{M B}

10. Como

\overline{D A} ≅ \overline{C B}, m e d (D \hat{A} M) = m e d (C \hat{B} M) = 90 ° e \overline{A M} ≅ \overline{B M}

podemos afirmar que os triângulos á ême dê e BMC são congruentes pelo caso éle á éle. Dessa maneira, concluímos que existe uma correspondência em relação aos ângulos e lados, sendo

\overline{M D} ≅ \overline{M C}

11. Como

A \hat{B} M ≅ C \hat{D} M

\overline{B M} ≅ \overline{D M}

B \hat{M} A ≅ D \hat{M} C

(oposto pelo vértice), então ∆á bê ême ≅ ∆cê dê ême pelo caso á éle á .

Atividade – Página 149

12. Precisamos provar que o ponto M é o ponto médio de

\overline{A B}

e que

\overset{\leftrightarrow}{C D}

\overline{A B}

são perpendiculares.

Como

\overline{A C} ≅ \overline{A D} ≅ \overline{B C} ≅ \overline{B D}

(raios da circunferência criados com a abertura do compasso) e

\overline{C D}

é lado comum aos dois triângulos, então ∆á cê dê ≅ ∆bê cê dê pelo caso éle éle éle. Temos que:

A \hat{C} D ≅ B \hat{C} D

A \hat{D} C ≅ B \hat{D} C

Analogamente, ∆ACB ≅ ∆ADB, então:

C \hat{A} B ≅ D \hat{A} B

D \hat{B} A ≅ A \hat{B} C

Por essas congruências, temos que á ême dê ≅ ∆AMC pelo caso á éle á , então:

A \hat{M} D ≅ A \hat{M} C

Analogamente, ∆BMD ≅ ∆BMC, então:

B \hat{M} D ≅ B \hat{M} C

Como

m e d (B \hat{M} D) + m e d (B \hat{M} C) = 180 °

, então

m e d (B \hat{M} D) = m e d (B \hat{M} C) = 90 ° .

Como

m e d (A \hat{M} D) + m e d (A \hat{M} C) = 180 °, e n t ã o m e d (A \hat{M} D) = m e d (A \hat{M} C) = 90 °

Como

A \hat{M} D ≅ B \hat{M} D

\overline{M D}

lado comum e

A \hat{D} C ≅ B \hat{D} C

, temos que

∆

á ême dê ≅

∆

BMD pelo caso á éle á , então:

\overline{A M}

≅

\overline{B M}

Assim, concluímos que

\overset{\leftrightarrow}{C D}

é a mediatriz de

\overline{A B}

Atividades – Página 151

13. a) M, N, O e P

\overline{M N}, \overline{N O}, \overline{O P} e \overline{M P}

\overline{N O}

\overline{M O} e \overline{N P}

\hat{N} o u M \hat{N} O

14. Resposta pessoal. Exemplo de resposta:

Quadriláteros convexos:

Ilustrações. À esquerda, losango. À direita, trapézio.

Quadriláteros não convexos:

Atividades – Página 152

15. Considerando que, em um quadrilátero convexo, a soma das medidas de abertura dos ângulos internos é igual a 360graus, temos:

a) x + 110graus + 60graus + 80graus = 360graus

x = 110graus